研究 - 麻省理工学院人工智能研究专业

研究

A mathematical model of ephaptic interactions in
neuronal ﬁber pathways: Could there be more
than transmission along the tracts?

Hiba Sheheitli

1 and Viktor K. Jirsa1

1Aix-Marseille University, Inserm, INS UMR_S 1106, Marseille, 法国

关键词: Ephaptic interaction modeling, Axonal cable theory, Fiber pathways, Neuronal commu-
nication, White matter, Spatiotemporal patterns

开放访问

杂志

抽象的

While numerous studies of ephaptic interactions have focused on either axons of peripheral
nerves or on cortical structures, no attention has been given to the possibility of ephaptic
interactions in white matter tracts. Inspired by the highly organized, tightly packed geometry
of axons in ﬁber pathways, we aim to investigate the potential effects of ephaptic interactions
along these structures that are resilient to experimental probing. We use axonal cable theory
to derive a minimal model of a sheet of N ephaptically coupled axons. Numerical solutions
of the proposed model are explored as ephaptic coupling is varied. We demonstrate that
ephaptic interactions can lead to local phase locking between adjacent traveling impulses
然后, as coupling is increased, traveling impulses trigger new impulses along adjacent
axons, resulting in ﬁnite size traveling fronts. For strong enough coupling, impulses
propagate laterally and backwards, resulting in complex spatiotemporal patterns. 尽管
common large-scale brain network models often model ﬁber pathways as simple relays of
signals between different brain regions, our work calls for a closer reexamination of the
validity of such a view. The results suggest that in the presence of signiﬁcant ephaptic
互动, the brain ﬁber tracts can act as a dynamic active medium.

作者总结

Starting from the FitzHugh-Nagumo cable model, we derive a system of nonlinear coupled
partial differential equations (偏微分方程) to model a sheet of N ephaptically coupled axons. 我们
also present a continuous limit approximation transforming the model into a two-dimensional
ﬁeld equation. We numerically solve the equations exploring the dynamics as coupling
strength is varied. We observe phase locking of adjacent impulses and coordination of
subthreshold dynamics. Strong enough coupling generates complex spatiotemporal patterns
as new impulses form traveling fronts propagating laterally and backwards. The transition
between different dynamic regimes happens abruptly at critical values of parameter. 这
results put into question the validity of assuming the role of ﬁber pathways to be that of mere
interneuronal transmission and call for further investigation of the matter.

介绍

It has long been thought that signals exchanged between different brain regions are faithfully
transmitted along the white matter tracts through axons that can be modeled as passive electric
cables (Hodgkin & Huxley, 1952). This has led many large-scale network models to assume

引文: Sheheitli, H。, & Jirsa, V. K.
(2020). A mathematical model of
ephaptic interactions in neuronal ﬁber
pathways: Could there be more than
transmission along the tracts?
网络神经科学, 4(3), 595–610.
https://doi.org/10.1162/netn_a_00134

DOI:
https://doi.org/10.1162/netn_a_00134

支持信息:
https://doi.org/10.1162/netn_a_00134

已收到: 8 九月 2019
公认: 26 二月 2020

通讯作者:
Hiba Sheheitli
hs497@cornell.edu

处理编辑器:
Mason Porter

版权: © 2020
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照

麻省理工学院出版社

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

Ephaptic interaction:
A form of indirect communication
between cells through the exchange
of ions via the shared extracellular
空间.

that signals communicated between different brain regions are relayed along the axons of ﬁber
pathways with a ﬁnite speed without any interaction occurring between the traveling signals
along the way (Bassett, Zurn, & 金子, 2018; Breakspear, 2017; Sanz-Leon, Knock, Spiegler, &
Jirsa, 2015). The aim of this work is to motivate a reexamination of this latter highly consequen-
tial assumption. 在 1940, Katz and Schmitt investigated the nonsynaptic electrical interaction
between adjacent nerve ﬁbers (Katz & 施密特, 1940). In their work, two large parallel non-
myelinated axons were isolated from the crab limb nerve. They succeeded in demonstrating
那 (A) the passage of an action potential (impulse) in one ﬁber causes subthreshold excitabil-
ity changes in the adjacent ﬁber and (乙) when impulses are set up simultaneously along both
ﬁbers, a mutual interaction occurs that can lead to speeding up or slowing down of the impulses
and also possibly to synchronization between the two impulses, depending on the initial phase
relationship. The effect was observed to be ampliﬁed when the resistance of the extracellular
space surrounding the axons was increased. In the next year, a similar study was presented by
Arvanitaki (1942) on giant axons of Sepia ofﬁcinalis (common cuttleﬁsh). In that study, Arvanitaki
coined the term “ephapse” to denote “the locus of contact or close vicinity of two active func-
tional surfaces” (p. 90). The term is derived from the Greek term signifying the act of touching,
as opposed to “synapse” which is derived from the Greek term signifying the act of joining or
linking. 自那以后, the term ephaptic interaction has been used to refer to communication be-
tween neuronal cells via electrical conduction through the surrounding extracellular space, 作为
opposed to communication mediated by chemical synapses or gap-junctions. 在 1980, ephap-
tic transmission was observed between spontaneously active single nerve ﬁbers in the spinal
nerve roots of dystrophic mice (Rasminsky, 1980). Shortly after, ephaptic interactions were ob-
served to contribute to neuronal synchrony in rat hippocampal slices (泰勒 & Dudek, 1982).
然后在 1984, experiments suggested a role for ephaptic transmission in hemifacial spasm
pathophysiology by causing “cross-talk” between facial nerve ﬁbers (Nielsen, 1984). 更多的
最近, hallmarks of ephaptic interaction were observed in rat cortical pyramidal neurons in
slices, and supported the idea that this interaction facilitates the coordination and possibly the
synchrony of neighboring neurons in the gray matter (Anastassiou, Perin, Markram, & 科赫,
2011).
此外, there have been numerous other experimental and modeling investiga-
tions of ephaptic interaction (Anastassiou & 科赫, 2015; Barr & Plonsey, 1992; 钟, 1981;
Bokil, Laaris, Blinder, Ennis, & 凯勒, 2001; Goldwyn & Rinzel, 2016; Grindrod & Sleeman,
1984; 霍尔特 & 科赫, 1999; Ramón & 摩尔, 1978; Stacey, Hilbert, & Quail, 2015). 然而,
it can be seen that all these previous studies focused on one of two contexts: (A) cortical ar-
EAS, particularly interactions between neighboring neurons through the resulting local ﬁeld
潜在的 (Anastassiou & 科赫, 2015; Anastassiou et al., 2011; Blot & Barbour, 2014; Fröhlich
& McCormick, 2010; Goldwyn & Rinzel, 2016; 霍尔特 & 科赫, 1999; 泰勒 & Dudek, 1982)
或者 (乙) peripheral nerves, particularly interactions between myelinated axons in a nerve bun-
dle and inquiries into effects of demyelination (Binczak, Eilbeck, & 斯科特, 2001; J. 瓦. 克拉克 &
Plonsey, 1970; Marrazzi & Lorente, 1944; Nielsen, 1984; Ramón & 摩尔, 1978; Rasminsky,
1980; Reutskiy, Rossoni, & Tirozzi, 2003). To our knowledge, there has been no discussion on
ephaptic interaction between axons of the white matter tracts. While the predominant myelina-
tion in white matter axons might be presumed to be preventing ephaptic interference, 学习
of myelinated axons in nerves suggest otherwise (Binczak et al., 2001; Marrazzi & Lorente,
1944; Rosenblueth, 1941). 而且, some ﬁber pathways can have a considerably high pro-
portion of unmyelinated axons, 例如 30% (in regions of the corpus callosum of the adult
rhesus monkey; Lamantia & Rakic, 1990) 和 45% (in the splenium of the corpus callosum
of the adult rabbit; Waxman & Swadlow, 1977). It is known that ﬁber pathways in the brain
are constituted of densely packed long axons running in parallel.
In Wedeen et al. (2012),
diffusion magnetic resonance imaging results were presented to illustrate that “cerebral path

网络神经科学

596

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

crossings formed well-deﬁned 2D sheets” (p. 1631) and that “this sheet structure was found
throughout cerebral white matter and in all species, orientations, and curvatures. 而且,
no brain pathways were observed without sheet structure” (Wedeen et al., 2012, p. 1632).
此外, electron micrograph images show that neighboring axons in ﬁber pathways are
often separated by distances as small as 20 nm (Waxman & Swadlow, 1977), which would sug-
gest a relatively high extracellular space resistance. These latter geometric characteristics set
favorable conditions for ephaptic exchanges to be at play in white matter ﬁber pathways. Ide-
盟友, direct experimental examination of the activity of axons in the white matter would serve
to accurately quantify ephaptic interactions there. 然而, probing into the inner workings
of the white matter remains a challenging endeavor, mainly because of technical limitations
on the temporal and spatial resolution of current noninvasive imaging techniques (他, 哪个,
威尔克, & Yuan, 2011). Inspired by these facts, we wish to investigate the matter by putting
forward a simple but realistic mathematical model of excitable axons arranged in a sheetlike
geometry and coupled through a resistive extracellular space.

In the Materials and Methods, we start from local circuit theory and the cable model of an
axon to derive a model for a sheet of N ephaptically coupled axons. We then make a contin-
uous limit approximation to transform the resulting model of N coupled 1D partial differential
方程 (偏微分方程) into a 2D PDE that can be seen as a ﬁeld equation governing the dynamics
of a sheet of coupled axons. In the Results section, we numerically solve the equations and
explore the different possible dynamical regimes along with examining the equivalence of the
two proposed models. In the Discussion section, we discuss the potential ramiﬁcations of the
results along with future work directions that this work motivates.

材料和方法

The Mathematical Model

Our goal here is to put forward a minimal model that possesses the key elements that allow
the study of the effects of ephaptic interactions on action potential transmission along ﬁber
pathways. Given the densely packed parallel geometric arrangement of axons in the white
事情, we assume that currents generated during action potential propagation are mainly
axial in direction, both inside the axons and in the surrounding extracellular space ( J. 克拉克
& Plonsey, 1968; Plonsey, 1977). Then the axons can be represented by what is known as
the cable equation, while the extracellular space between axons can be represented by an
effective longitudinal resistance per unit length (Rall, 1962; 斯科特, 2002). Such a model for two
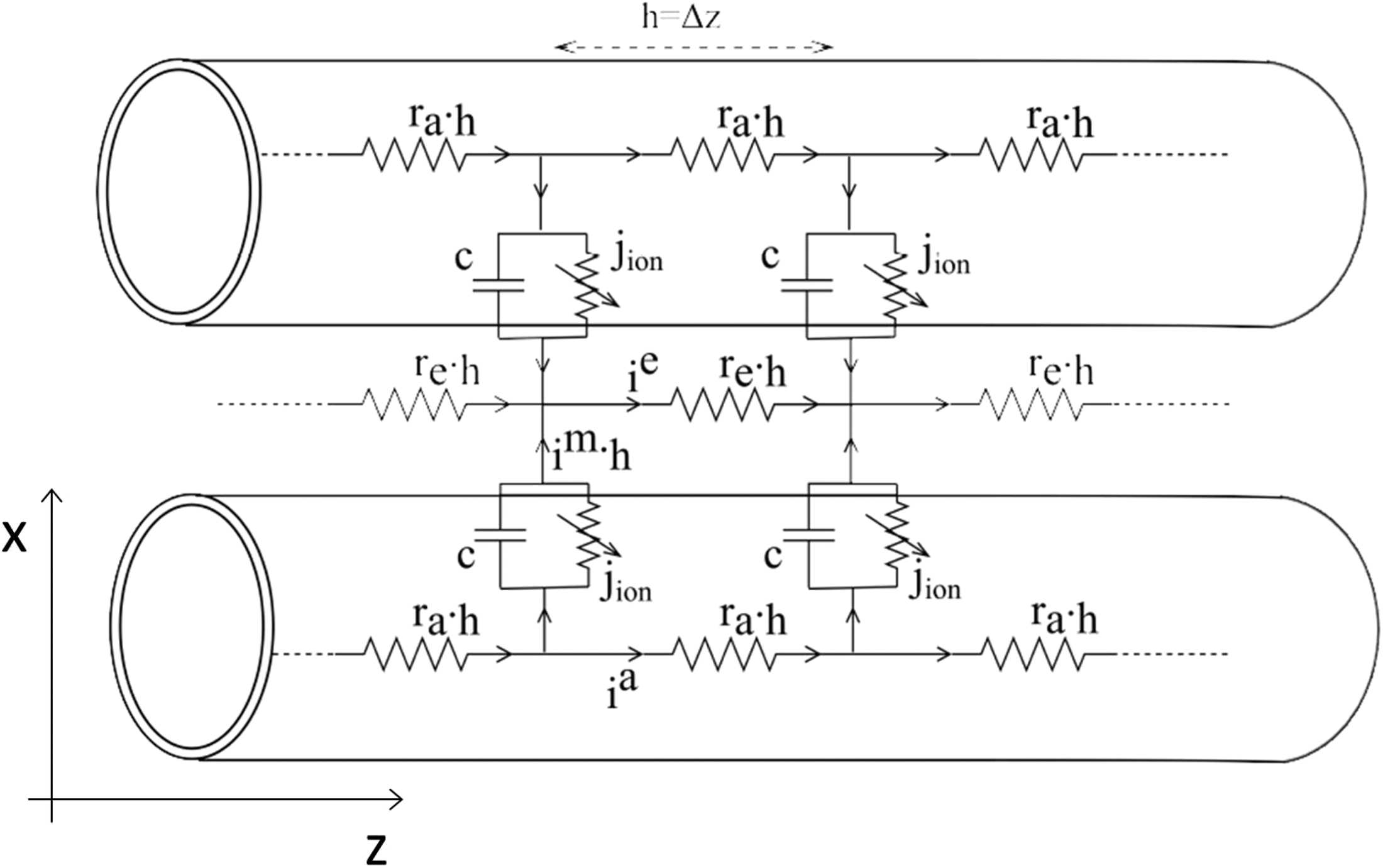
ephaptically coupled axons is derived in Bell (1981). 数字 1 depicts the equivalent circuit
model used to derive the cable equations for two ephaptically coupled axons. 下列
notation is used here:

ia: axial (axoplasmic) current inside the axon per unit length
ie: axial current in the extracellular space surrounding the axons per unit length
im: axonal transmembrane current per unit area
拉: axoplasmic resistance per unit length
关于: extracellular space resistance per unit length
C: axonal membrane capacitance per unit length
jion: active ionic current ﬂowing across the axonal membrane per unit length
G: membrane conductance per unit length
z: distance along the axon
vm: transmembrane potential of an axon

Cable equation:
A partial differential equation
describing the evolution of cell
membrane voltage and currents as
functions of distance and time.

网络神经科学

597

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

数字 1. Schematic of the equivalent circuit model for two ephaptically coupled axons.

va: axoplasmic potential inside an axon
ve: electric potential in the extracellular space
我: external applied current per unit length
A, 乙: parameters of the FitzHugh-Nagumo model

这里, all currents and potential variables are varying functions of time and axial location z.

Kirchoff’s law:
The law of conservation of electric
收费.

In the limit of ∆z

0, Kirchoff’s current law gives the following relationships between the
transmembrane, axial, and extracellular currents; 下标 1 和 2 each refer to one of the
two identical axons:

→

im
1 =

im
2 =

∂ia
2
∂z

;

= im

1 + im
2 .

∂ia
1
∂z
∂ie
∂z

Ohm’s law:
The law of proportionality between
the electric current and voltage
across a conductor.

此外, Ohm’s law relates the currents to the electric potentials as follows:

∂va
1
∂z

raia

1 ,

∂va
2
∂z

raia
2

∂ve
∂z

reie.

此外, the transmembrane current for each axon can be expressed as

im = c

∂vm
∂t

+ jion −

我, where vm = va

ve.

(1)

(2)

(3)

(4)

The term jion represents the active transmembrane currents due to ion channel activity that is
nonlinearly dependent on the transmembrane voltage. Detailed mathematical representation
of the dependence of jion on vm was described in the seminal work by Hodgkin and Huxley
(1952), which utilized three variables to represent the kinetics of ion channel activation. 在
1961, FitzHugh proposed a simpliﬁcation of that model that utilizes only one recovery variable
(FitzHugh, 1961):

jion = gf (vm, w) , where f(v, w) =

- (西德:18)

v3
3 -

(西德:19)

(5)

和

∂w
∂t

= ε (v + A

bw) .

这里, w is a slow recovery variable. To arrive at the cable equation model, we need to combine
all the above relationships to eliminate the current variables. We start by differentiating the

网络神经科学

598

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

expression for vm with respect to z and substituting Equation 3 in it:

∂vm
1
∂z

raia

1 + reie

∂vm
2
∂z

raia

2 + reie.

Differentiating again and substituting Equation 1, we obtain the following:

∂2vm
1
∂z2 = (拉 + 关于) im
∂2vm
2
∂z2 = (拉 + 关于) im

1 + reim
2 ,

2 + reim
1 .

(6)

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

Solving the above system of two equations for an expression for im
2 , then combining the
result with Equation 4, we arrive at the cable equations for two ephaptically coupled axons:

1 and im

∂2vm
1
∂z2 −
∂2vm
2
∂z2 −

∂2vm
2
∂z2 = c
∂2vm
1
∂z2 = c

∂vm
1
∂t

∂vm
2
∂t

+ jion,1

+ jion,2

I1,

I2,

where γ =

拉 + 关于
2稀有的 + r2

A (西德:19)

(西德:18)

, α =

关于
2稀有的 + r2

A (西德:19)

(西德:18)

(7)

We can see that for zero extracellular resistance, the two cable equations are uncoupled such
that any current exiting one axon will immediately dissipate in the extracellular space and no
exchange between the axons can occur. The resulting single FitzHugh-Nagumo cable was ﬁrst
put forward by Nagumo in Nagumo, Arimoto, and Yoshizawa (1962). It can be seen that the
cable equation is the classical 1D diffusion equation with an added term, jion. The presence of
the nonlinear active currents renders the cable excitable, 这样, if the membrane potential
is perturbed from its resting value, it will return to that value unless the perturbation is strong
enough to elicit the large action potential response that will then be propagated along the
axon, away from the location of perturbation, with the signal’s shape preserved.

We wish to extend the model to a sheet of ephaptically coupled axons, 那是, an N number
of axons coupled through the extracellular space. 数字 2 shows a schematic of a cross-
sectional view of such an arrangement where we represent the cross sections of axonal cables
as nodes on a line, interspaced with nodes representing extracellular space.

A model of such a conﬁguration of N number of coupled axons was presented in Grindrod
and Sleeman (1984). The main assumption made in this latter work is that each axon is only
coupled to the two axons that are positioned directly next to it. While this later assumption
is common in network models, the authors offered no physiological justiﬁcation for it in the
context of ephaptically coupled axons. 反而, we will start from the more physical assump-
tion that transmembrane currents are radially uniform, such that we can reasonably consider
im for each cable to be equally partitioned into two parts feeding into the extracellular space
(represented as nodes) adjacent to it. 最后, while the previously presented model

数字 2. Schematic of a cross-sectional view of the sheet of N axons model.

网络神经科学

599

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

restricts ephaptic interactions to nearest neighbor axons (Grindrod & Sleeman, 1984), 我们的
model allows each axon to interact with all other axons through the shared extracellular space
with the coupling strength decaying with distance between interacting axons. To arrive at that,
we take the potential in the extracellular space for an axon positioned at a node q to be the
average of the potential at its adjacent extracellular nodes such that

q = va
vm

q −

1
2 (西德:16)

ve
q

1 + ve

q+1

(西德:17)

(8)

Note that the index q refers to the node number on the line, so for N axons, q takes values
之间 1 and 2N + 1, such that va
q on nodes
q = 1, 3, . . . , 氮 + 1. Differentiating Equation 8 with respect to z, and making use of Ohm’s
法律, we obtain

q is deﬁned on nodes q = 2, 4, . . . , N and ve

∂vm
q
∂z

raia

q +

1
2

关于

ie
q

(西德:16)

1 + ie

q+1

(西德:17)

(9)

From Kirchoff’s ﬁrst law of current, we have the following:

∂ia
q
∂z

im
q ,

∂ie
q
-
∂z
∂ie

q+1
∂z

1
2 (西德:16)
1
2 (西德:16)

2 + im
q

im
q
-

im
q+2 + im
q

(西德:17)

These latter equations are a generalization of Equations 1 和 2. Differentiating Equation 9

again and plugging in the above current relationships, we arrive at

∂2vm
q
∂z2 =

拉 +

(西德:18)

1
2

关于(西德:19)

im
q +

1
4

关于

im
q
-

(西德:16)

2 + im

q+2

(西德:17)

(10)

For the cables that are at the two ends of the line, the corresponding relationship would be

下列:

∂2vm
2
∂z2 =

拉 +

(西德:18)

∂2vm
氮
∂z2 =

拉 +

(西德:18)

1
2

im
2 +

关于(西德:19)

1
4

关于 (im

4 ) ,

im
氮 +

关于(西德:19)

1
4

关于

im
氮

(西德:1)

(西德:0)

We have obtained a system of N equations relating im and vm of all the axons. This is the
equivalent of Equation 6 for the two-axon system. The linear system of N equations can be
解决了, such that we can express each im explicitly in terms of vm of all the axons. The solution
takes the form

im
p =

4
关于

氮
∑
s=1

αps

∂2vm
s
∂z2

;

(11)

p = 1, 2, . . . , N referring to the N axons. The α’s represent coupling strength between each
, where A is

pair of axons and are obtained as the elements of the inverse matrix A−
the tridiagonal matrix:

1 =

αij

(西德:2)

(西德:3)

600

网络神经科学

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

D 1
1 D 1
1 D
. . .

A =




















1
. . .
. . .

. . .
. . .
1




















. . .
D 1
1 D 1
1 D

with D = 4

右 +

(西德:18)

1
2 (西德:19)

and R =

拉
关于

Explicit algebraic expressions for the elements of the inverse of such a tridiagonal matrix are
presented in Usmani (1987) and indicate that the ephaptic effect increases as the ratio R de-
creases and that α for two axons on the line decreases as the distance between them increases.
然而, for the numerical solutions presented in the sections to follow, we found it simpler
to numerically compute the inverse of A instead of the individual α′s.

Combining Equations 11, 5, 和 4, we obtain the model for a sheet of N ephaptically

coupled FitzHugh-Nagumo cables:

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

4
关于

氮
∑
s=1

αps

∂2vm
s
∂z2 = c

∂vm
p
∂t

+ gf

vm
p , wp

Ip,

(西德:17) -

(西德:16)

(12)

∂wp
∂t

vm
p + A

= ε

(西德:16)

bwp

(西德:17)

We nondimensionalize the space and time variables as follows:

˜z =

G (拉 + 关于)

(西德:19)

(西德:18)q

z ,

˜t =

G
C

The system becomes

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

4 (右 + 1)

氮
∑
s=1

αps

∂2vm
s
∂ ˜z2 =

∂vm
p
∂˜t

+ F

vm
p

(西德:16)

(西德:17) -

ˆIp,

∂wp
∂˜t

vm
p + A

= ˆε

(西德:16)

bwp

(西德:17)

where ˆIp =

我
G

ˆε = ε

C
G

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

From now on, we drop the superscript of the transmembrane voltage along with the tilde and
hat. The ﬁnal equations take the following form:

4 (右 + 1)

氮
∑
s=1

αps

∂2vs
∂z2 =

∂vp
∂t

+ F

vp, wp

(西德:0)

Ip,

(西德:1)

(13)

∂wp
∂t

= ε

vp + A

(西德:0)

bwp

(西德:1)

For the results that will follow, we choose the following values for the FitzHugh-Nagumo re-
covery variable: a = 0.7, b = 0.5, and ǫ = 0.1. 然后, we are left with one free parameter R
that reﬂects the strength of the ephaptic interaction. The goal is to investigate the dynamics
of the system as this parameter is varied. We note here that the resulting emergent network

网络神经科学

601

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

behavior is robust against variations of the FitzHugh-Nagumo parameters within a reasonable
range that preserves the relevant dynamic features of the neuron model (planar, 班级 1 in terms
of excitability, existence of refractory period, and slow manifold). Multiple parameters were
尝试过, and only one example is presented here for brevity.

Estimation of the Coupling Strength Parameter

To estimate the physically plausible range of values for parameter R, we start from the deﬁnition

R =

拉
关于

1
ρ

Ae
氨基酸

where Ae and Aa are the cross-sectional areas of the extracellular space and the axon, 重新指定-
主动地. ρ is the ratio of extracellular to intracellular resistivity, and is typically assumed to be in
the range of 1 到 4 (Goldwyn & Rinzel, 2016). Given that axons of the ﬁber pathways are very
tightly packed, we consider that the cross-sectional area of the space between adjacent axons
can range from a tenth to several multiples of the cross-sectional area of the axon. Based on
那, we consider R to vary between 0 和 1.

Continuous Limit Approximation

Our model is a system of N coupled nonlinear PDEs, each representing one distinct cable
and accompanied by an ordinary differential equation for the corresponding slow recovery
variable. 然而, neighboring axons in ﬁber pathways are often very densely packed, 这样的
as the distances separating two adjacent axons are considerably small relative to the axonal
diameter (Waxman & Swadlow, 1977). 为此原因, we will make the approximation that
the variables vm and im, while being only physically deﬁned for the axonal space, 可
abstractly represented by continuous ﬁeld variables v and i. If we go back to Equation 10, 我们
notice that the last two terms can be rewritten by using the following discrete approximation
of a second partial derivative (Abramowitz & Stegun, 2012):

∂2im
∂x2 ≈

im
q
-

2 -

然后

q + im

q+2

2im
4δ2

im
q
-

2 + im
q
-

2 ≈

4δ2 ∂2im

∂x2 + 2im
q ,

where δ is the small separation between adjacent axons. Using this latter ﬁnite difference

stencil, 方程 10 is transformed to

∂2vm
∂z2 = (拉 + 关于) im + δ2re

∂2im
∂x2 .

(14)

This equation relates the transmembrane voltage and current approximate ﬁeld variables.
The second relationship between the two is given by the balance of currents Equation 4. 这
approximate continuous system then takes the following form:

∂2v
∂z2 = (拉 + 关于) 我 + δ2re

∂2i
∂x2

i = c

∂v
∂t

+ gf (v, w)

我,

和

∂w
∂t

= ε (v + A

bw) ,

网络神经科学

602

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

where the superscripts were dropped for brevity. 下一个, we nondimensionalize the equations
using the following rescaling:

˜z =

G (拉 + 关于)

(西德:19)

(西德:18)q

z ,

˜t =

G
C

˜x =

X
λ

这里, λ is a characteristic lateral length scale of the same order of magnitude as the average
axonal diameter (µm). The resulting system becomes

∂2v
∂ ˜z2 = i + K
∂w
∂˜t

= ˆε (v + A

∂2i
∂ ˜x2

i =

∂v
∂˜t

+ F (v, w)

ˆI;

bw)

, with K =

δ2
λ2

1
右 + 1

Dropping the tilde and hat for brevity, we obtain the ﬁnal form of the approximate continuous
ﬁeld equations for a sheet of ephaptically coupled axons:

∂2i
∂x2

i =

∂v
∂t

+ F (v, w)

我;

(15)

∂2v
∂z2 = i + K
∂w
∂t

= ε (v + A

bw) .

Green’s function:
An integral transform that aids
in reformulating and solving
differential equations.

We note here that the latter equations governing v and i can be transformed into a more
compact form of one partial integro-differential equation using Green’s function and contour
一体化, such that the system becomes the following:

∂v (X, z, t)
∂t

F (v, w) + 我 +

X, x′

(西德:0)

(西德:1)

∂2v (x′, z, t)
∂z2

dx′,

∂w (X, z, t)
∂t

= ε (v + A

bw) ,

where g

X, x′

= g

(西德:0)
In the results that follow, we take δ2

(西德:0)

(西德:1)

x′

(西德:1)

1
√K

罪

(西德:18)

1
√K (西德:0)

x′

(西德:19)

(西德:1)

0.01, to be consistent with the assumption that the
interaxonal spacing is very small compared with the characteristic length. 因此, we consider
values of K in the range of 0 到 0.1 to be in line with the above choice of R being between 0
和 1.

λ2 ≈

We also note that the model can be extended to the 3D case by considering axons on a
two-dimensional grid (X, y) instead of a 1D line (X). While deriving the N coupled PDE system
will be more tedious in this case, the continuous limit approximation leads to Equation 15 和
one added term on the right-hand side of the ﬁrst equation:

∂2v
∂z2 = i + K

∂2i
∂x2 +

∂2i
∂y2 (西德:19)

(西德:18)

i =

∂v
∂t

+ F (v, w)

我;

(16)

∂w
∂t

= ε (v + A

bw) .

Numerical Implementation

Numerical solutions of the two model systems were obtained using the Crank-Nicolson ﬁ-
nite difference method. After numerical experiments were performed with smaller values and

网络神经科学

603

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

conﬁdence in the stability of the solution was established, we chose a time step of 0.05 and a
spatial step of 0.5 和 1 for the z and x directions, 分别. Zero ﬂux boundary conditions
were enforced, such that the ﬁrst spatial derivative of v remains 0 at the boundaries for all time.
To investigate the response of the system, impulses were initiated at the inlet of axons using
a brief and localized input current I = 2 applied to the axon for t
[0, 4]. 全部
numerical computation was implemented using Python.

[0, 2] and z

∈

结果

Numerical simulations were performed to investigate the dynamics of the system as the ephap-
tic interaction strength was varied. 此外, we compared the dynamics of the continuous
limit system (方程 15) to that of the original discrete model (方程 13).

Phase Interactions

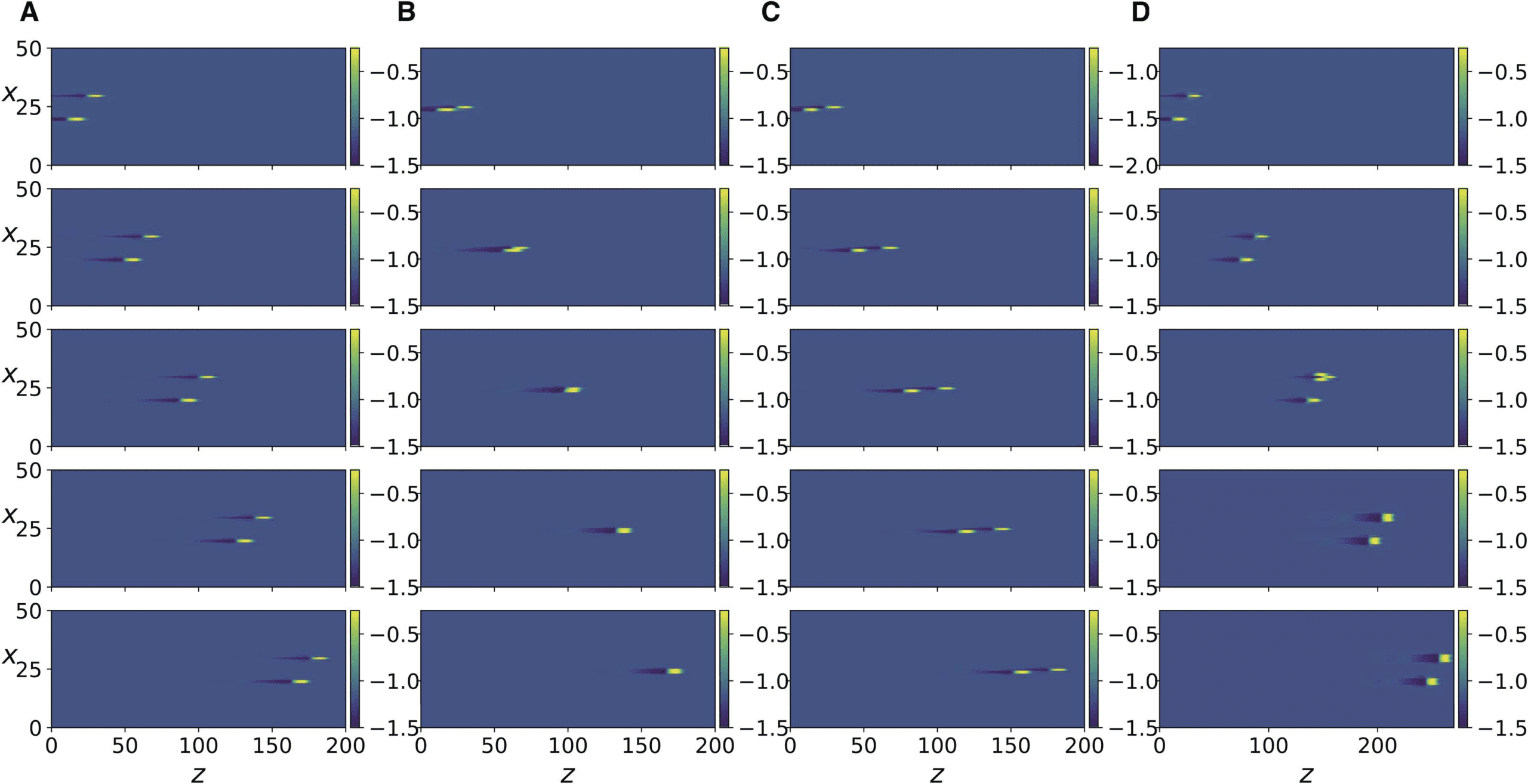
图中 3, two adjacent axons are stimulated such that an action potential is initiated along
each of them and travels from left to right. The timing of the stimulation is such that one
impulse lags behind the other. The shape of the action potentials and their propagation along
the z-direction can be seen in the Supporting Information (是的数字 1). In Figure 3A, where we
set R = 0.8 corresponding to weak ephaptic coupling, the two impulses travel independently
without inﬂuencing each other.
In Figure 3B and C, for the same value of R but with the
stimulated axons directly adjacent to each other, ephaptic interaction causes the two impulses
to attract/repel each other such that the lag between them decreases/increases, 之后
they remain locked together, depending on the initial time lag between them. This type of
interaction has been experimentally observed in Katz and Schmitt (1940).

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

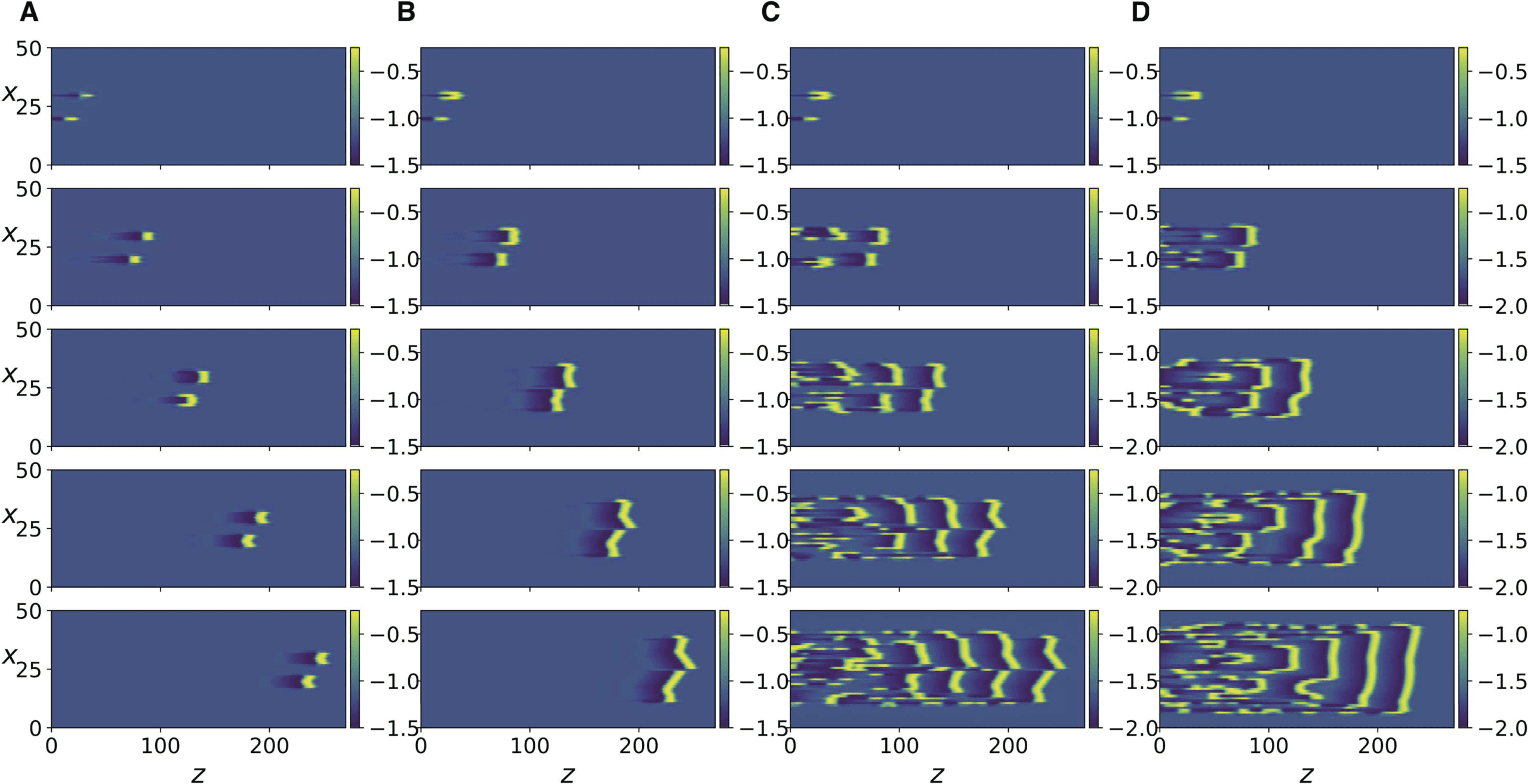
数字 3. Numerical simulation of Equation 13. The color bar indicates the value of v, the x
variable indicates the axon number. Each column corresponds to a simulation with a speciﬁc value
of the parameter; snapshots show progress of time from top to bottom. (A) R = 0.8, axons number
30 和 20 are stimulated at t = 0 and t = 10, 分别, and the panel rows from top to bottom
correspond to t = 500, 1100, 1700, 2300, 2900. (乙) Same as in A but with axons number 25 和
24 stimulated. (C) Same as in B but with stimulation at t = 0 and t = 11. (D) same as in A but with
R = 0.4, and panels show t = 500, 1400, 2300, 3200, 4100.

网络神经科学

604

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

Spatial Patterns Generation

下一个, we increase the coupling strength by decreasing R, and observe that a transition occurs
where each traveling impulse triggers new action potentials in its two immediately adjacent
axons and the three neighboring impulses move together as a ﬁnite size traveling front, 作为
shown in Figure 3D. Further increase in coupling strength leads to the next two adjacent axons
being activated (Figure 4A). Because of the presence of the scaling factor δ2
λ2 in the expression
for K, we do not expect Equation 15 to be equivalent to Equation 13 for the same values
of R. 尽管如此, it can be seen in Supporting Information Figure 2 that the same behavior
described so far also occurs in Equation 15 as the coupling strength K is increased. 此外,
as coupling strength is further increased, more and more impulses are triggered as the traveling
front of impulses diffuses laterally and widens (Figure 5A and B). Even further increase in

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 4.
as in Figure 3D but with R = 0.19 and R = 0.15, 分别.

(A, 乙) same as in Figure 3A but with R = 0.33 and R = 0.191, 分别. (C, D) 相同的

数字 5. Same as in Figure 3 but for Equation 15, with different values of K and for t = 500,
1300, 2200, 3100, 3999. (A) K = 0.0255. (乙) K = 0.026. (C) K = 0.038. (D) K = 0.04.

网络神经科学

605

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

K (Figure 5C and D) leads to new fronts of impulses being induced in the forward but also
backward direction, resulting in dynamic spatiotemporal patterns.

Cosine similarity:
The cosine of the angle between two
vectors; computed as the dot product
between the two vectors divided by
the product of their magnitudes.

Poisson process:
A series of independent stochastically
occurring events with a constant
average time interval between events.

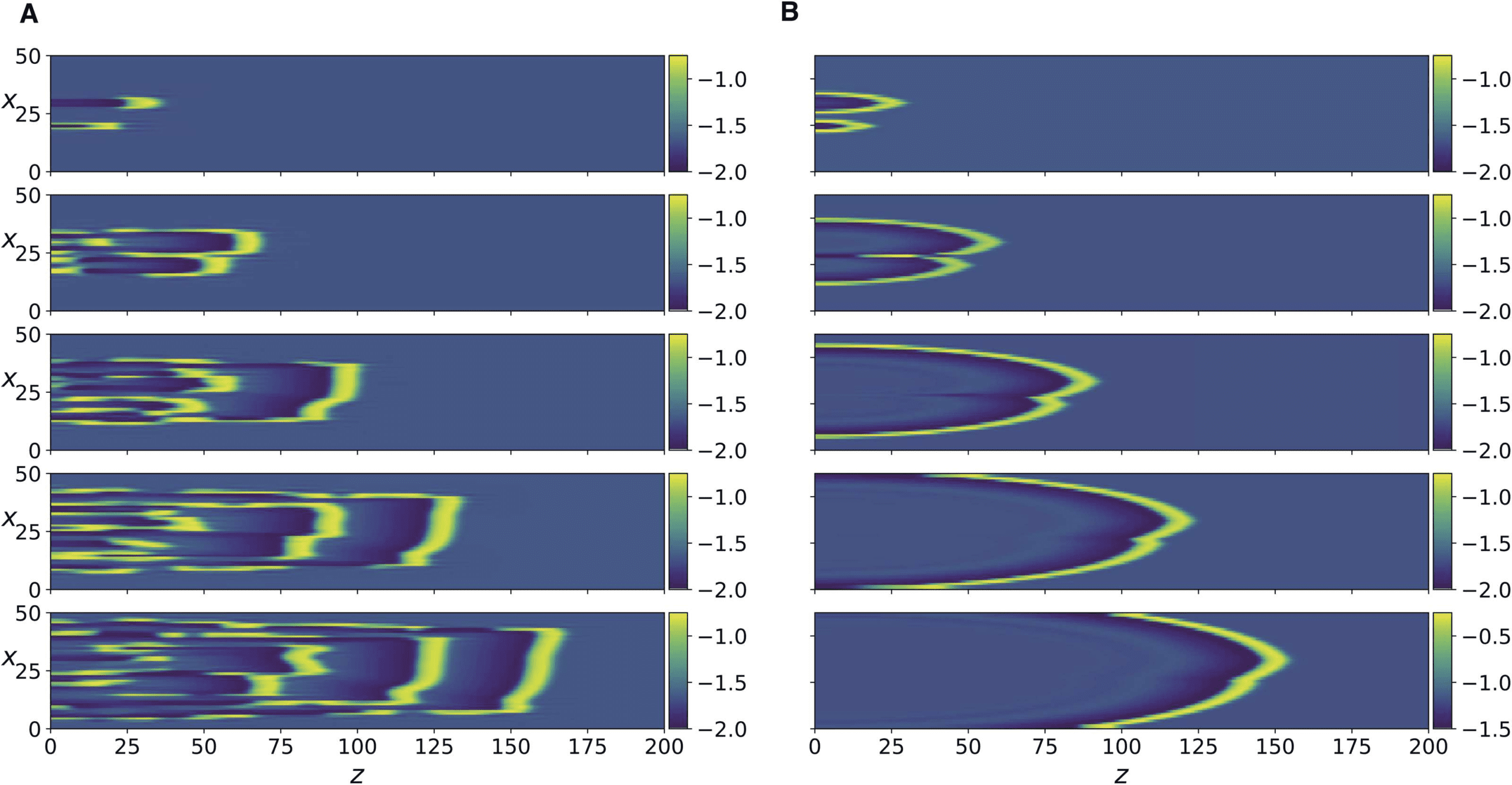
Figure 4B, C, and D show that the same transitions also occur in Equation 13 as R is de-
有折痕的, albeit the resulting patterns are more discrete and irregular. To better compare the
responses of the two systems in this regime, we compare the discrete Fourier transform of the
spatial patterns of the two systems at several time instants (Supporting Information Figure 3).
It can be seen that the spatial modal decomposition of the two is rather close, as quantiﬁed
by the cosine similarity between the discrete Fourier transforms at every time step (配套
0.006, which indicates close
Information Figure 4). The mean value over time was
相似. 然而, for Equation 15, these spatiotemporal patterns persist only for a small
range of the parameter, as a further increase in K causes the system to revert back to the later-
ally diffusing traveling front (数字 6, right column). This is unlike Equation 13 其中
complex spatio-temporal patterns persist as R is further decreased (数字 6, left column).

0.96

≈

Spike Trains Interactions

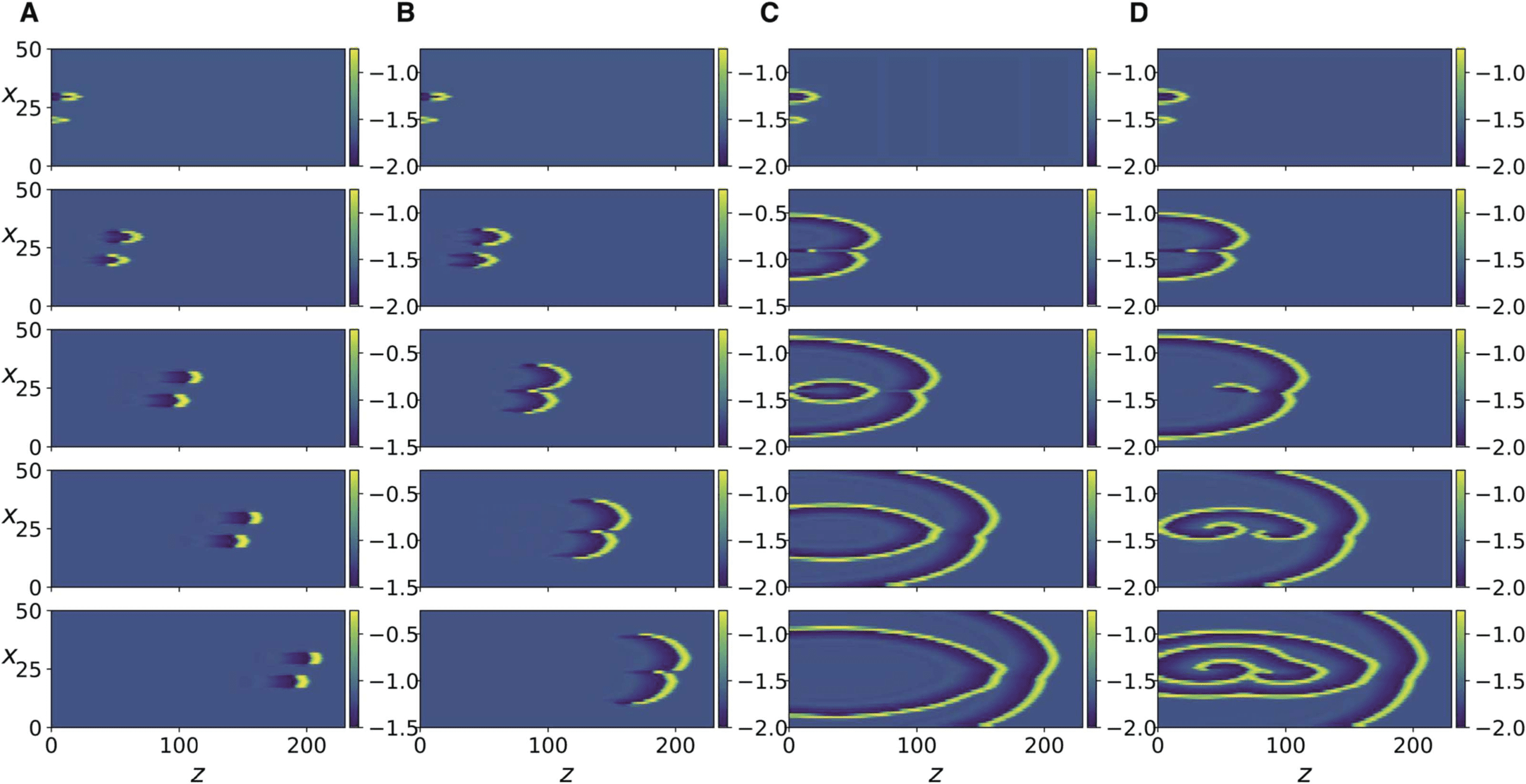
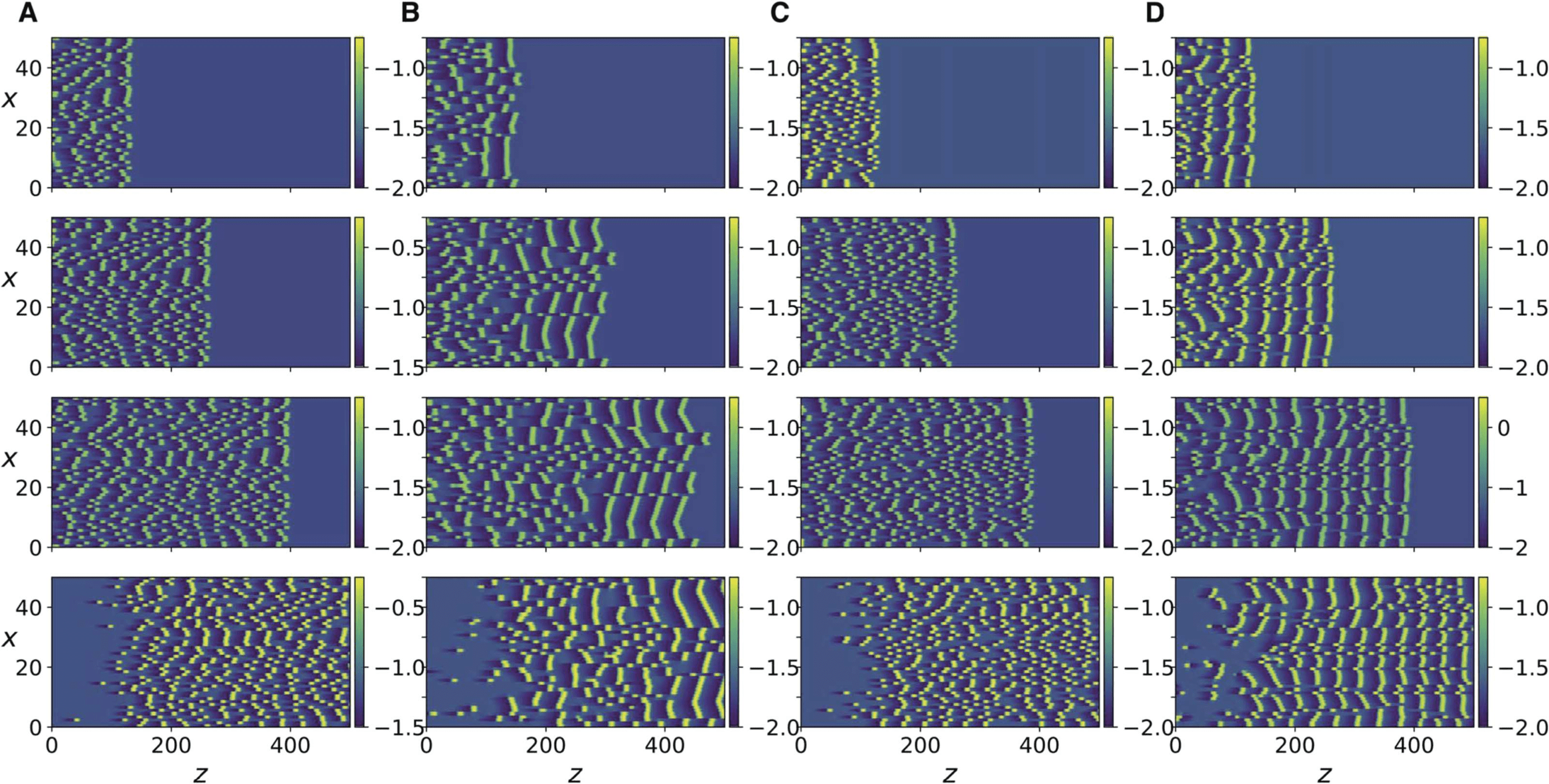
下一个, we stimulate all of the 50 axons and observe the collective dynamics. Each axon is
stimulated by a ﬁnite train of 10 impulses. The intervals between impulses are generated by
(The mean interval is the mean value of
a Poisson process with a speciﬁed mean interval.
the intervals between consecutive impulses.) The evolution of the resulting action potentials
for the case of negligible ephaptic coupling is shown in Figure 7A. When ephaptic coupling
becomes signiﬁcant, as in Figure 7B, the impulses self-organize into phase-locked traveling
fronts. A similar effect also occurs for Equation 15 (compare Figure 7C and D).

It has been stated that “in theory, whereas the pattern of Poisson-like impulse codes was
modiﬁed during long-distance propagation, their mean rate was conserved” (Moradmand &
Goldﬁnger, 1995, p. 2415). 相反, here in the presence of ephaptic interactions, 这
mean interspike interval (mISI), which is the inverse of the mean rate, decreases with increasing
z location (Supporting Information Figure 5 and Supporting Information Figure 6). The effect is
clearly seen when the mISI is averaged over the 50 axons at downstream z locations (数字 8).

数字 6. Numerical simulation of Equation 13 for R = 0.05 (左边) and of Equation 15 for K = 0.05
(正确的). The panels from top to bottom correspond to t = 500, 1100, 1700, 2300, 2900.

网络神经科学

606

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

数字 7. Numerical simulation of Equation 13 (A, 乙) and Equation 15 (C, D). spike trains of an
平均数 10 impulses are triggered along each axon, with a mean interimpulse interval of 10. 这
panels from top to bottom correspond to t = 2499, 4999, 7499, 9999.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

数字 8. Mean interspike interval (mISI) averaged over the 50 axons for downstream z locations
for the simulations in Figure 7A (红色的), 7乙 (light red), 7C (蓝色的), and 7D (light blue) (low coupling
in dark colors and high coupling in light colors).

Note that Figure 7 shows only a portion of the simulation; in order to compute the mISI values
shown in Supporting Information Figure 5 and Supporting Information Figure 6, we let the
simulation run long enough until all the impulses that were initiated at one end of the axon
reach the other end, such that the total simulation time was 18,000.

讨论

We presented a minimal model for a sheet or volume of ephaptically coupled axons and
explored its dynamics for a physically plausible range of parameters. We found that the
model captures the experimentally observed attraction/repulsion effect between neighboring

网络神经科学

607

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

impulses. For strong enough coupling, the model predicts that action potentials traveling down
an axon can trigger new action potentials in adjacent axons to be initiated and carried along
with it, forming a ﬁnite size traveling front. These fronts increase in size as more axons are
recruited at higher coupling strength. Simulations with even higher coupling strength result
in recurrence of impulses and backward propagation such that a pair of individual impulses
initiated on two nonadjacent axons evolve into trains of impulses that diffuse laterally in the x
direction as well as in both +ve and -ve z directions along the axons. We have also observed
that ephaptic coupling can lead to self-organization among trains of impulses and signiﬁcant
alteration in the timing of action potentials, which is known to be a key element in neuronal
编码 (Debanne, 2004). This suggests that ephaptic interactions along ﬁber pathways can
theoretically play an active role in neuronal signal processing in the brain. The numerical
simulations showed that the continuous limit approximation system mimics the qualitative be-
havior of the original model for a speciﬁc range of parameters. This continuous limit model
offers the advantage of being mathematically more compact, more analytically tractable, 和
less numerically expensive to solve, and it allows for easy extension of the model to full 3D
几何学.
It furthermore allows for a more intuitive interpretation of the ephaptic coupling
terms and, in its integro-differential form, makes it intuitive that the ephaptic coupling creates
a modulation of the diffusion in the axial direction with an alternating positive and negative
diffusion term on a spatial length scale favoring structures on the scale of √K.

综上所述, we propose that the various nontrivial responses observed in our numeri-
cal exploration of ephaptic interaction might play an important and complex active role in
interarea neuronal signal transmission and processing in the brain. We hope these results will
motivate a critical examination of the validity of the common assumption that neuronal ﬁber
pathways merely act as transmission cables relaying signals between different brain regions.
In contrast to that latter viewpoint, this theoretical investigation suggests that ephaptic inter-
actions enhanced by the orientations and bundling of neuronal tracts in three-dimensional
space can render the ﬁber pathways an active axonal medium that can give rise to complex
spatiotemporal dynamics.
If this emergent dynamics occurs under physiologically realistic
状况, then it would be a major so far unknown contributor to information processing
in neural systems. We see various directions that this work can take in the future, 包括
further exploration of the rich repertoire of responses for different types of stimuli, 帐户-
ing for variability in axonal diameters that will add spatial heterogeneity in the parameters.
此外, a natural extension to a more biophysically detailed treatment of the matter is
possible through incorporating the effect of myelination into the cable equation used in the
模型. 最后, we hope that our work will inspire experimental work that can provide precise
quantiﬁcation and characterization of the elusive effects of ephaptic interactions in the axonal
tracts of the brain.

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00134.

作者贡献

Hiba Sheheitli: 概念化; 数据管理; 形式分析; 调查; Methodol-
奥吉; 验证; 可视化; Writing – Original Draft; Writing – 审查 & Editing. Viktor K.
Jirsa: 概念化; 形式分析; 资金获取; 调查; 方法;
项目管理; 资源; 监督; Writing – 审查 & Editing.

网络神经科学

608

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

资金信息

Viktor K. Jirsa, 欧盟委员会 (http://dx.doi.org/10.13039/501100000780), 奖项ID:
H2020-720270.

参考

Abramowitz, M。, & Stegun, 我.

(2012). Handbook of mathemati-
cal functions: With formulas, 图表, and mathematical tables.
纽约, 纽约: Dover Publications.

Anastassiou, C. A。, & 科赫, C.

(2015). Ephaptic coupling to en-
dogenous electric ﬁeld activity: Why bother? Curent Opinion in
Neurobiology, 31, 95–103.

Anastassiou, C. A。, Perin, R。, Markram, H。, & 科赫, C.

(2011).
Ephaptic coupling of cortical neurons. 自然神经科学, 14,
217–223.

Arvanitaki, A. (1942). Effects evoked in an axon by the activity of a
contiguous one. 神经生理学杂志, 5(2), 89–108.

Barr, 右. C。, & Plonsey, 右.

(1992). Electrophysiological interac-
tion through the interstitial space between adjacent unmyeli-
nated parallel ﬁbers. Biophysical Journal, 61(5), 1164–1175.
Bassett, D. S。, Zurn, P。, & 金子, J. 我. (2018). On the nature and use of
models in network neuroscience. 自然评论神经科学,
19, 566–578.

钟, J. (1981). Modeling parallel, unmyelinated axons: Pulse trap-
ping and ephaptic transmission. SIAM Journal on Applied Math-
信息学, 41(1), 168–180.

Binczak, S。, Eilbeck, J. C。, & 斯科特, A. C. (2001). Ephaptic coupling
of myelinated nerve ﬁbers. Physica D: Nonlinear Phenomena,
148(1–2), 159–174.
Blot, A。, & Barbour, 乙.

(2014). Ultra-rapid axon-axon ephaptic
inhibition of cerebellar Purkinje cells by the pinceau. 自然
神经科学, 17, 289–295.

Bokil, H。, Laaris, N。, Blinder, K., Ennis, M。, & 凯勒, A.

(2001).
Ephaptic interactions in the mammalian olfactory system. 杂志
of Neuroscience, 21(20), RC173.

他, B., 哪个, L。, 威尔克, C。, & Yuan, H. (2011). Electrophysiological
imaging of brain activity and connectivity—Challenges and op-
portunities. IEEE Transaction on Biomedical Engineering, 58(7),
1918–1931.

Hodgkin, A. L。, & Huxley, A. F.

(1952). A quantitative descrip-
tion of membrane current and its application to conduction and
excitation in nerve. 生理学杂志, 117(4), 500–544.

霍尔特, G. R。, & 科赫, C.

(1999). Electrical interactions via the ex-
tracellular potential near cell bodies. Journal of Computational
神经科学, 6(2), 169–184.

Katz, B., & 施密特, 氧. H. (1940). Electric interaction between two
adjacent nerve ﬁbres. 生理学杂志, 97(4), 471–488.

Lamantia, A. S。, & Rakic, 磷.

(1990). Cytological and quantitative
characteristics of four cerebral commissures in the rhesus mon-
钥匙. Journal of Comparative Neurology, 291(4), 520–537.

Marrazzi, A. S。, & Lorente, 右. (1944). Interaction of neighboring ﬁbres
in myelinated nerve. 神经生理学杂志, 7(2), 83–101.
Moradmand, K., & Goldﬁnger, 中号. (1995). Computation of long dis-
tance propagation of impulses elicited by Poisson-process stim-
计算. Journal Neurophysiology, 74(6), 2415–2426.

Nagumo, J。, Arimoto, S。, & Yoshizawa, S. (1962). An active pulse
transmission line simulating nerve axon. Proceedings of the IRE,
50(10), 2061–2070.

Nielsen, V. K. (1984). Pathophysiology of hemifacial spasm: 我. Ephaptic
transmission and ectopic excitation. Neurology, 34(4), 418–426.
Plonsey, 右. (1977). Action potential sources and their volume con-

ductor ﬁelds. Proceedings of the IEEE, 65(5), 601–611.

Rall, 瓦.

(1962). Electrophysiology of a nendritic neuron model.

Breakspear, 中号. (2017). Dynamic models of large-scale brain activity.

Biophysical Journal, 2(2), 145–167.

自然神经科学, 20, 340–352.

克拉克, J。, & Plonsey, 右. (1968). The extracellular potential ﬁeld of
the single active nerve ﬁber in a volume conductor. Biophysical
杂志, 8(7), 842–864.

克拉克, J. W., & Plonsey, 右. (1970). A mathematical study of nerve

ﬁber interaction. Biophysical Journal, 10(10), 937–957.

Debanne, D. (2004). Information processing in the axon. 自然

评论神经科学, 5, 304–316.

FitzHugh, 右. (1961). Impulses and physiological states in theoretical
models of nerve membrane. Biophysical Journal, 1(6), 445–466.
Fröhlich, F。, & McCormick, D. A. (2010). Endogenous electric ﬁelds
may guide neocortical network activity. 神经元, 67(1), 129–143.
(2016). Neuronal coupling by en-
dogenous electric ﬁelds: Cable theory and applications to coin-
cidence detector neurons in the auditory brain stem. 杂志
Neurophysiology, 115(4), 2033–2051.

Goldwyn, J. H。, & Rinzel, J.

Grindrod, P。, & Sleeman, 乙. D.

(1984). Qualitative analysis of
reaction-diffusion systems modelling coupled unmyelinated
nerve axons. Mathematical Medicine and Biology, 1(3), 289–307.

Ramón, F。, & 摩尔, J. 瓦. (1978). Ephaptic transmission in squid
giant axons. American Journal Physiology, 234(5), C162–C169.
Rasminsky, 中号. (1980). Ephaptic transmission between single nerve
fibres in the spinal roots of dystrophic mice. 生理学杂志
350, 151–169.

Reutskiy, S。, Rossoni, E., & Tirozzi, 乙. (2003). Conduction in bun-
dles of demyelinated nerve ﬁbers: Computer simulation. Biolog-
ical Cybernetics, 89(6), 439–448.

Rosenblueth, A.

(1941). The stimulation of myelinated axons by
nerve impulses in adjacent myelinated axons. American Journal
of Physiology, 132(1), 119–128.

Sanz-Leon, P。, Knock, S. A。, Spiegler, A。, & Jirsa, V. K. (2015). 数学-
ematical framework for large-scale brain network modeling in
The Virtual Brain. 神经影像, 111, 385–430.

斯科特, A. (2002). 神经科学: A mathematical primer. 纽约,

纽约: Springer US.

Stacey, 右. G。, Hilbert, L。, & Quail, 时间. (2015). Computational study
of synchrony in ﬁelds and microclusters of ephaptically coupled
神经元. 神经生理学杂志, 113(9), 3229–3241.

网络神经科学

609

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d

乙
y
G
你
e
s
t

哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3

A mathematical model of ephaptic interactions in neuronal ﬁber pathways

泰勒, C。, & Dudek, F. (1982). Synchronous neural afterdischarges
in rat hippocampal slices without active chemical synapses. Sci-
恩斯, 218(4574), 810–812.

Usmani, 右. A. (1987). Applied linear algebra. 纽约, 纽约: Marcel

Dekker.

Waxman, S. G。, & Swadlow, H. A. (1977). The conduction proper-
ties of axons in central white matter. Progress in Neurobiology,
8, 297–324.

威登, V. J。, Rosene, D. L。, 王, R。, Dai, G。, Mortazavi, F。,
哈格曼, P。, . . . Tseng, 瓦. 是. 我. (2012). The geometric structure
of the brain ﬁber pathways. 科学, 335(6076), 1628–1634.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
n
e
n
A
r
t
我
C
e
–
p
d

我

F
/

4
3
5
9
5
1
8
6
7
3
2
8
n
e
n
_
A
_
0
0
1
3
4
p
d