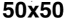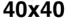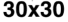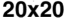Life Worth Mentioning: - 麻省理工学院人工智能研究专业

Life Worth Mentioning:
Complexity in Life-Like
Cellular Automata

Abstract Cellular automata (CA) have been lauded for their ability to
generate complex global patterns from simple local rules. 已故
English mathematician, John Horton Conway, developed his illustrious
Game of Life (Life) CA in 1970, which has since remained one of the
most quintessential CA constructions—capable of producing a myriad
of complex dynamic patterns and computational universality. Life and
several other Life-like rules have been classified in the same group
of aesthetically and dynamically interesting CA rules characterized by
their complex behaviors. 然而, a rigorous quantitative comparison
among similarly classified Life-like rules has not yet been fully
已确立的. Here we show that Life is capable of maintaining as much
complexity as similar rules while remaining the most parsimonious.
换句话说, Life contains a consistent amount of complexity
throughout its evolution, with the least number of rule conditions
compared to other Life-like rules. We also found that the complexity of
higher density Life-like rules, which themselves contain the Life rule
as a subset, form a distinct concave density-complexity relationship
whereby an optimal complexity candidate is proposed. Our results also
support the notion that Life functions as the basic ingredient for
cultivating the balance between structure and randomness to maintain
complexity in 2D CA for low- and high-density regimes, especially over
many iterations. This work highlights the genius of John Horton
Conway and serves as a testament to his timeless marvel, 这是
referred to simply as: Life.

Eric Peña*
Binghamton University, SUNY

Department of Systems Science
and Industrial Engineering
Center for Collective Dynamics
of Complex Systems
eric.pena@binghamton.edu

Hiroki Sayama
Binghamton University, SUNY

Department of Systems Science
and Industrial Engineering
Center for Collective Dynamics
of Complex Systems

Waseda University
Waseda Innovation Lab
sayama@binghamton.edu

关键词
Cellular automata, Game of Life, Life-like
规则, 复杂, conditional entropy,
信息

1 介绍

Cellular automata (CA) are discrete dynamical systems used primarily as a computational model to
study how spatio-temporal patterns evolve in a wide range of phenomena. The model encompasses
a grid of cells, each of which takes a discrete state. The dynamics of the state of a cell is governed by
transition rules which involve the state of the cell itself along with the states of its surrounding
neighbors. There are many cases in which CA follow simple rules yet lead to interesting complex
图案 (Wolfram, 1982, 2002; Wolfram & 帕卡德, 1985).

One such rule that has gained the most popularity by far is Conwayʼs Game of Life (Life) (Berlekamp
等人。, 1982; 加德纳, 1970). It was in 1970 when John Horton Conway, after experimenting with

* 通讯作者.

人工生命 27: 105–112 (2021) https://doi.org/10.1162/artl_a_00348

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
A
r
t
我
/

我

A
r
t
我
C
e
–
p
d

F
/

2
7
2
1
0
5
2
0
1
9
4
9
9
A
r
t
我

_
A
_
0
0
3
4
8
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

乙. Peña and H. Sayama

Complexity in Life-Like Cellular Automata

various CA rules, settled on Life, which held analogies to real living organisms—forming parallels to
birth, 死亡, and survival in the natural world. Live cells (IE。, cells whose state is 1) with too few live
neighbors experience death from isolation, whereas those with too many live neighbors experience
death from suffocation. The rule in its entirety is as follows: (我) a dead cell (IE。, a cell whose state is
0) that is surrounded by exactly three live neighbors will be born into a live cell; (二) a live cell with
exactly two or three live neighbors will survive; 和 (三、) 否则, all other cells will die or remain
dead. The study of Life abounds, including self-organizing criticality, autopoiesis, structural patterns,
interesting initial conditions, generated components as information-carrying agents, and computa-
tional ability (Bak et al., 1989; 啤酒, 2004; 戈茨, 2000; Gutowitz et al., 1987; Lizier et al., 2014;
Rendell, 2002; 特尼, 2021A). Life has found its way into a myriad of disciplines such as mathematics,
物理, 计算机科学, information theory, 生物学, ecology, 艺术, and even music (阿克塞尔罗德, 1997;
Miranda & Kirke, 2010).

Understanding how Life compares to other two-dimensional CA was attempted by Wolfram
(1984), in which Life was assigned to Class IV for CA rules that produce complex, 不可预料的
行为. Other works have argued for more objective means of classification that are better able to
distinguish intrinsic complexity among CA rules (Baetens & De Baets, 2010; Borriello & 沃克,
2017; 李等人。, 1990; 特尼, 2021乙; Wuensche, 1999; Zenil & Villarreal-Zapata, 2013), or that show
to what extent the feat itself is undecidable (Culik & 于, 1988). 而且, Life has inspired an entire
category of CA rules referred to as Life-like rules (Catagolue, 2021; LifeWiki, 2021)—rules that
behave similarly to Life and that are likely all in Class IV. The behavior of many Life-like rules has
been individually studied in great detail (Eppstein, 2010; Johnston, 2010). Although Life-like rules
are collectively considered to exhibit complex, interesting behavior overall, a rigorous quantitative
comparison between Life and other Life-like rules has not been fully established.

Here we show that Life naturally tends toward lower density and higher information content
while remaining the most parsimonious among popular Life-like rules. 换句话说, Life is capable
of maintaining a consistent amount of complexity throughout its evolution after transience with the
least number of rule conditions compared to other Life-like rules. We also show that the complexity
of higher density Life-like rules, which themselves contain Life, form a natural density-complexity
relationship. Through this analysis, we show why the Life rule constructed by John Horton Conway
may very well be the most interesting and fundamental CA construction with regards to its complexity
and its role in how complexity is manifested in Life-like rules more generally.

2 Material and Methods

The complexity intrinsic to Life and Life-like rules is possible through the balance of order and
紊乱. We demonstrate this by simulating Life and collecting density and complexity measure-
ments of the resulting dynamic patterns. Density is defined as the average ratio of the number of
cells whose state is 1 to the number of total cells on a grid ((西德:1) = |S|1/n ). To ensure that the gen-
erated patterns were indeed characterized by Life, random initial conditions with varying densities
((西德:1) = 0.1–0.5) were simulated for a sufficiently long period of time (30–100 iterations) before mea-
suring the complexity. This was performed for four different grid sizes: 20 × 20, 30 × 30, 40 × 40,
和 50 × 50. With each grid size, 5,000 final Life patterns were generated whereby complexity data
were averaged at each density value.

Life was then compared to other Life-like rules in terms of the long-term dynamics of their density
和复杂性. The Bx/Sy naming convention is used to refer to various rules for 2D outer-totalistic
CA (Eppstein, 2010). The B stands for birth and the S stands for survival. The x and y are subsets that can
contain digits from 0 到 8 which represent the number of live neighboring cells in a 3-by-3 Moore
邻里. This Bx and Sy corresponds to giving birth to a cell from being dead and allowing a
live cell to survive, 分别. The Life-like rules discussed here naturally decrease density from
random initial conditions yet continue dynamic activity for an extended period. 换句话说, 这些
rules neither quickly stabilize a grid to low densities nor force grids to explode in density.

106

人工生命量 27, 数字 2

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
A
r
t
我
/

我

A
r
t
我
C
e
–
p
d

F
/

2
7
2
1
0
5
2
0
1
9
4
9
9
A
r
t
我

_
A
_
0
0
3
4
8
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

乙. Peña and H. Sayama

Complexity in Life-Like Cellular Automata

The complexity produced by these rules is compared in two phases. 第一的, we choose known rules
that most closely follow Lifeʼs trajectory in the density-complexity domain. These rules include:
B3/S238 (EightLife), B38/S238 (HoneyLife), B368/S238 (LowDeath), B38/S23 (PedestrianLife),
B36/S125 (2 × 2), B36/S23 (HighLife), and B3/S12 (FlockLife). These are well-known rules in the
CA community for behaving most similarly to Life (Catagolue, 2021; Eppstein, 2010; Johnston,
2010; LifeWiki, 2021). 第二, we explore lesser known Life-like rules that allow higher density
configurations after transience. These higher density rules, like many of the previously mentioned
规则, contain the parsimonious Life rule within them as a subset (IE。, B3…/S23…). The higher
density candidate rules chosen for this include: B37/S23 (DryLife), B367/S23 (DrighLife),
B3578/S238, B3578/S23, B356/S23, B356/S238, B3568/S23, B3568/S238, B3578/S237, 和
B35/S236. The unnamed rules are the ones we discovered ourselves through computational explo-
ration of the Life-like rule space. For both phases of rule comparison, grids are randomly initialized
和 50% density on a 50 × 50 cell grid and evolved for 2,000 time steps. Density and complexity
values are averaged over 50 experimental runs at each time step throughout the temporal evolution.
Toroidal (periodic) boundary conditions were enforced for all CA simulations.

2.1 Conditional Entropy and Complexity Measurement
Conditional entropy has been used to characterize spatial correlations and aesthetic structure in 2D
CA (Andrienko et al., 2000; Bates & Shepard, 1993; Wackerbauer et al., 1994). (This measure was
originally termed information gain complexity, but we use the term conditional entropy to avoid misleading
nomenclature.) 一般来说, conditional entropy, H(是|X ), measures the amount of information
needed to describe a random variable Y given knowledge of the value of a random variable X:

Þ ¼ −

H Y jXð

y;X

P y; xð

Þ log2 P yjxð

(1)

where y and x are the discrete states of Y and X, 磷( y, X) is the joint probability of y and x, 和P( y|X) 是
the conditional probability of y given x. Conditional entropy may also be defined as the average
remaining uncertainty in Y after observations of X are made. In the context of CA, conditional
entropy has been used to measure how much information is needed on average to determine the
state of a cell in the 2D CA given that its neighboring cell states are known. Consider the state
variable pairs of all cells and their upward neighbors, (S, U), on a CA grid. The conditional entropy
can be calculated as follows:
X

(2)

H SjUð

Þ ¼ −

P s; uð

Þ log2 P sjuð

s;你

where s and u are the discrete states (IE。, {0, 1}) of the cell state variables S and U. The conditional
entropy for a given cell is calculated using the four von Neumann neighborhood directions (IE。, 向上,
向下, 左边, 正确的, denoted by states variables U, D, L, 右). These four directional conditional entropy
values are then averaged to assign a single value G to a given 2D configuration which captures the
structural complexity of the CA pattern:

G ¼ 1
4

H SjUð

Þ þ H SjDð

Þ þ H SjLð

Þ þ H SjRð

(西德:2):

(3)

To quantify the extent to which individual cells are interdependent with each other, G is used to com-
pare Life configurations to corresponding randomized configurations with equal live cell density. 这
randomized configuration serves as an objective control with which other Life-like rules can be
compared since they each exhibit unique cell densities as they evolve. This may also be understood
analytically as the unconditional G or simply the Shannon entropy: H(S) = − (西德:2)s P(s) log2 P(s) where s is

人工生命量 27, 数字 2

107

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
A
r
t
我
/

我

A
r
t
我
C
e
–
p
d

F
/

2
7
2
1
0
5
2
0
1
9
4
9
9
A
r
t
我

_
A
_
0
0
3
4
8
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

乙. Peña and H. Sayama

Complexity in Life-Like Cellular Automata

the cell state (IE。, {0, 1}). We use the difference in G between Life (or any Life-like CA rule) 和它的
randomized configuration counterpart as an information-theoretic measure of how much non-random
structure emerges in the CA grid:

D ¼ GRandom − GRule ¼ H Sð Þ − GRule:

(4)

Note that D ≥ 0 since G is maximal when the configuration is entirely random. The greater the
value of D is, the further away from randomness a particular CA configuration is understood to be.
换句话说, D is a complexity measure which quantifies the extent to which adjacent cells show
interdependence.

3 结果

3.1 Complexity of Life Configurations
数字 1 shows the measured G for both random configurations and evolved Life configurations
(数字 1(A)) and the proposed complexity measure D (数字 1(乙)) for four different grid sizes:
20 × 20, 30 × 30, 40 × 40, 和 50 × 50. For each grid size, 5,000 final Life patterns were generated
whereby G and D were averaged for each unique density value. Density in this case is defined as the
number of live cells on a grid (|S|1 = (西德:1) n). The D measure remains consistently maximized with a
higher number of live cells, 在大约 0.04 bits for Life (数字 1(乙)). The convergence toward this
maximal value strongly indicates that D is a measure of the ruleʼs inherent complexity independent
of grid size. This scale-independent property of the rule suggests that despite the details of local
structural patterns, Life robustly maintains a level of balance between order and randomness.

3.2 Parsimony of Life Rules
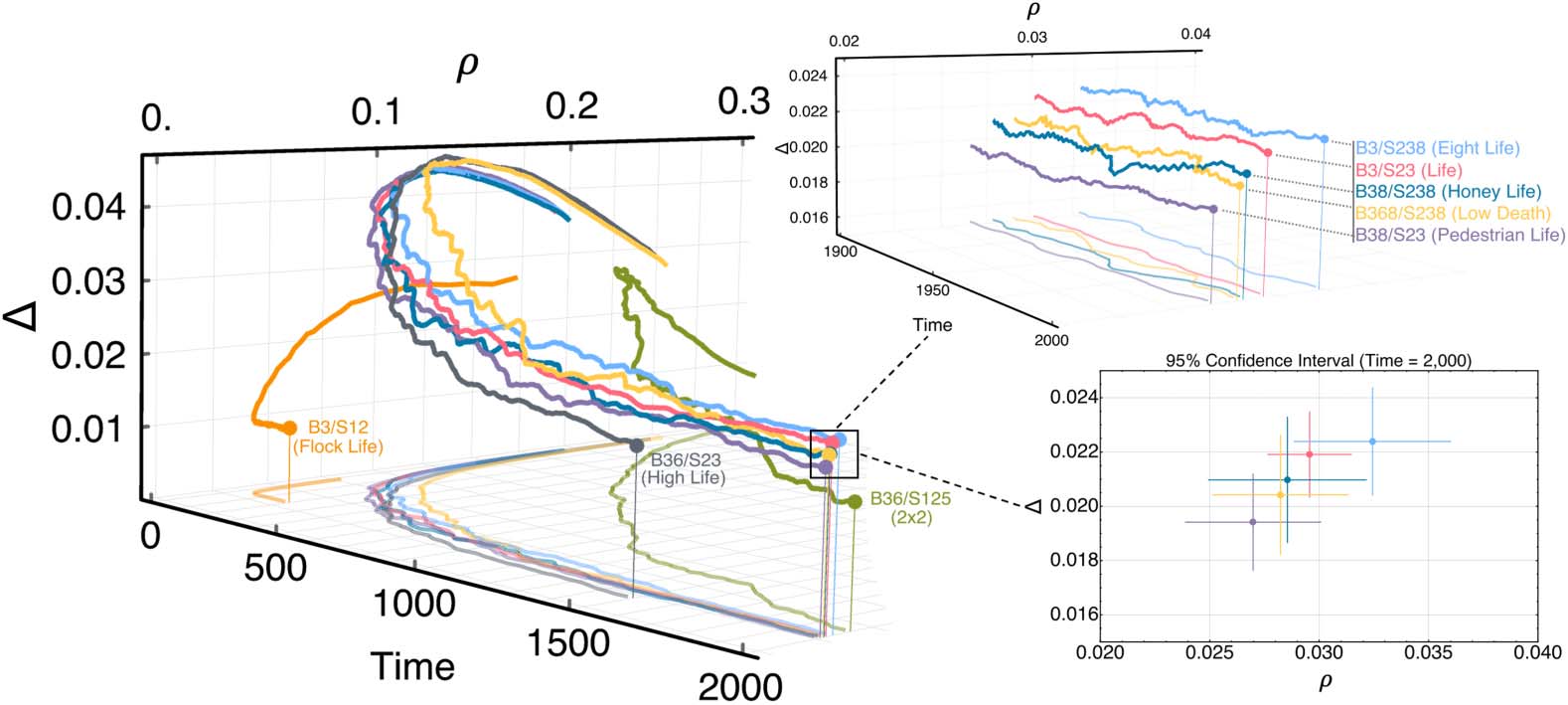
数字 2 shows the evolution of the average density and complexity of Life-like patterns settling to
distinct values over time with dynamics governed by each rule. The FlockLife and HighLife rules
maintain low density patterns but also cause these patterns to decay so much as to become stable
and unable to maintain dynamic activity for long periods of time compared to Life. 这 2 × 2 规则
( Johnston, 2010) produces higher density patterns whose complexity is low with respect to Life. 这
rules that most closely follow Lifeʼs density-complexity trajectory through time are EightLife,
HoneyLife, LowDeath, and PedestrianLife. 这 95% confidence interval in Figure 2 was constructed
和 50 simulations for each rule evolved over 2,000 time steps and demonstrates the similarity in
dynamics among these rules. 而且, these rules which exhibit similar density-complexity trajecto-
ries to Life contain the Life rule (IE。, B3/S23) as a subset of their conditions. 因此, the Life rule itself

数字 1. Game of life density and complexity measure. (A) Life (红色的) and random (蓝色的) configuration G values for a
range of densities defined by the number of live cells on a grid ((西德:1) n). (乙) Complexity measure D converges to a value at
关于 0.04 bits as the number of live cells increases and remains independent of grid size.

108

人工生命量 27, 数字 2

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
A
r
t
我
/

我

A
r
t
我
C
e
–
p
d

F
/

2
7
2
1
0
5
2
0
1
9
4
9
9
A
r
t
我

_
A
_
0
0
3
4
8
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

乙. Peña and H. Sayama

Complexity in Life-Like Cellular Automata

数字 2. Temporal evolution of low density Life-like rules whereby density ((西德:1)) 和复杂性 (D) are measured and
averaged for each point in time over 2,000 time steps and 50 simulations for each rule.

contains the least number of conditions making it the most parsimonious rule capable of exhibiting this
level of complexity and density. This indicates that John Horton Conway successfully constructed an
optimal rule that not only maintains complex activity over many evolutions but also contains the
smallest number of needed conditions to manifest this behavior. 而且, the fact that each rule
contains Life itself suggests that Life is fundamental in constructing complex dynamic patterns. Higher
complexity may be achieved for rules whose temporal evolution leads to higher densities after transient
活动. Not only is Life unique in its ability to spawn low density patterns which give rise to long-
lasting complex behavior, but it is also fundamental and a flexible elementary constituent for complex
Life-like behavior to emerge for higher density patterns.

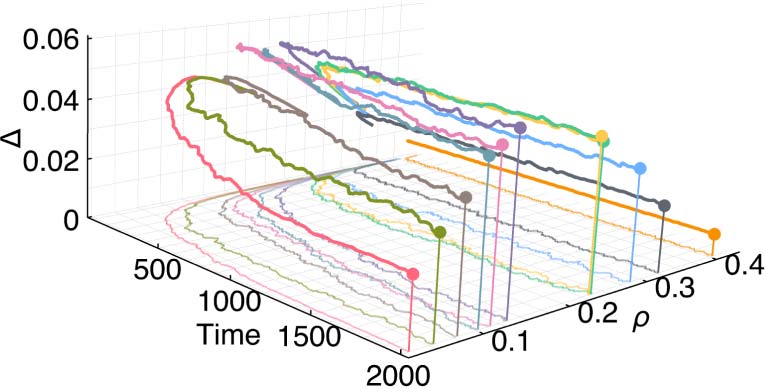
3.3 Searching for Higher Density Life-Like Rules
数字 3 shows the temporal evolution of rules that maintain higher density patterns and contain the
Life rule within them (IE。, B3…/S23…) and that were selected after manual exploration of the rule
空间. Life itself is also included in this list of rules for convenient comparison. As the rules evolve

数字 3. Temporal evolution of high density Life-like rules. (A) Temporal evolution of rules that maintain higher density
patterns and contain the Life rule within them (IE。, B3…/S23…). (乙) Density ((西德:1)) 和复杂性 (D) measurements with
95% confidence intervals after transient activity (IE。, Time = 2,000) for higher density Life-like rule candidates.

人工生命量 27, 数字 2

109

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
A
r
t
我
/

我

A
r
t
我
C
e
–
p
d

F
/

2
7
2
1
0
5
2
0
1
9
4
9
9
A
r
t
我

_
A
_
0
0
3
4
8
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

乙. Peña and H. Sayama

Complexity in Life-Like Cellular Automata

through time, their complexity values settle to distinct regions in the density-complexity domain
(数字 3(A)). A density-complexity concave relationship is revealed among the candidate Life-like
rules after transient behavior from random initial conditions (数字 3(乙)). As the density increases
after transience, the complexity increases as well until the density becomes too high for complex
patterns to be possible. At this point, the grid saturates with live cells and produces highly random
and structureless activity thereby decreasing the complexity of the pattern. This relationship also
indicates that there is likely a critical point between Life and pure randomness which maximizes
complexity in 2D CA. 在此背景下, optimal complexity is characterized in terms of structural
aesthetics and information-richness that occurs for a rule after transient activity. We find that a pos-
sible optimal candidate is rule B356/S23, which we have named Dynamic Life.

4 结论

在本文中, we have constructed a measure of complexity for 2D CA patterns. This measure
incorporates the inherent aesthetic structure and affinity to randomness a pattern contains. We used
this measure to investigate the complexity produced by Conwayʼs Game of Life and showed that
complexity is a scale-independent property of the rule. We compared Life to similar rules with re-
spect to their space-filling and complexity characteristics through time. We found that Life can main-
tain similar long-lasting, complex behavior like other well-known Life-like rules throughout its
temporal evolution and with the least number of conditions (IE。, B3/S23). This indicates that Life
is likely the most parsimonious rule capable of producing this level of density and robust complexity.
最后, we investigated the temporal evolutions of higher density Life-like rules that contain the Life
rule as a subset of their condition (IE。, B3…/S23…). A concave relationship was uncovered in the
density-complexity domain after initial transient activity. This indicates a likely optimal rule (IE。,
B356/S23) between Life and pure randomness which maximizes complexity in 2D CA. 而且,
since Life is used as the key ingredient to construct complex and Life-like patterns of a wide range of
density and complexity values, Life appears to serve as an elementary constituent responsible for
complex Life-like behavior to emerge in both lower and higher density configurations. Future re-
search directions include measuring spatio-temporal information transfers in Life-like patterns to
investigate long-time and long-distance correlations (Lizier et al., 2014). The work presented here
further sheds light on why John Horton Conwayʼs Game of Life is considered the canonical Life-like
rule and continues to be studied by students and academics even today—certainly making it a life
worth mentioning.

致谢
We would like to recognize and honor the work and life of the late mathematician John Horton
Conway—the creator of the Game of Life among many other major contributions in the field of
mathematics and beyond.

Author Contributions
Eric Peña and Hiroki Sayama conceived the research idea and developed the complexity measure.
Eric Peña wrote the code and carried out the experiments and simulations. Eric Peña took the lead
in writing the manuscript. Hiroki Sayama supervised the work, provided critical feedback, 和
helped shape the research and manuscript.

利益争夺
The authors declare no competing interests.

110

人工生命量 27, 数字 2

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
A
r
t
我
/

我

A
r
t
我
C
e
–
p
d

F
/

2
7
2
1
0
5
2
0
1
9
4
9
9
A
r
t
我

_
A
_
0
0
3
4
8
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

乙. Peña and H. Sayama

Complexity in Life-Like Cellular Automata

Data Availability
The data sets generated and analyzed for this study are available from the corresponding author on
reasonable request.

Code Availability
The code used to compile and analyze data was written in Python 3.7.9. The code to replicate analysis
along with simulations of the rules mentioned in this article are available from the corresponding
author on reasonable request.

参考
Andrienko, 是. A。, Brilliantov, 氮. 五、, & Kurths, J. (2000). Complexity of two-dimensional patterns. 欧洲的

Physical Journal B, 15(3), 539–546. https://doi.org/10.1007/s100510051157

阿克塞尔罗德, 右. (1997). Advancing the art of simulation in the social sciences. 在R中. Conte, 右. Hagselmann, & 磷.
Terna (编辑。), Simulating social phenomena (PP. 21–40). 施普林格. https://doi.org/10.1007/978-3-662-03366-1_2

Baetens, J. M。, & De Baets, 乙. (2010). Phenomenological study of irregular cellular automata based on

Lyapunov exponents and Jacobians. Chaos, 20(3), 文章 033112. https://doi.org/10.1063/1.3460362
Bak, P。, 陈, K., & M。, C. (1989). Self-organized criticality in the Game of Life. 自然, 342(6251), 780–782.

https://doi.org/10.1038/342780a0

Bates, J. E., & Shepard, H. K. (1993). Measuring complexity using information fluctuation. Modern Physics Letters

A, 172(6), 416–425. https://doi.org/10.1016/0375-9601(93)90232-氧

啤酒, 右. D. (2004). Autopoiesis and cognition in the Game of Life. 人工生命, 10(3), 309–326. https://土井

.org/10.1162/1064546041255539, 考研: 15245630

Berlekamp, 乙. R。, 康威, J. H。, & Guy, 右. K. (1982). Winning ways for your mathematical plays (卷. 4). CRC

按.

Borriello, E., & Imari Walker, S. (2017). An information-based classification of elementary cellular automata.

Complexity, 2017, 文章 1280351. https://doi.org/10.1155/2017/1280351

Catagolue. (2021, 行进). Outer-totalistic rules. https://catagolue.hatsya.com/rules/lifelike
Culik II, K., & 于, S. (1988). Undecidability of CA classification schemes. Complex Systems, 2(2), 177–190.

Eppstein, D. (2010). Growth and decay in Life-like cellular automata. 在一个. Adamatzky (埃德。), Game of Life

cellular automata (PP. 71–97). 施普林格. https://doi.org/10.1007/978-1-84996-217-9_6

加德纳, 中号. (1970). Mathematical games: The fantastic combinations of John Conwayʼs new solitaire game

“Life.” Scientific American, 223(4), 120–123. https://doi.org/10.1038/scientificamerican1070-120
戈茨, 氮. 中号. (2000). Emergent phenomena in large sparse random arrays of Conwayʼs Game of Life.
International Journal of Systems Science, 31(7), 873–894. https://doi.org/10.1080/002077200406598

Gutowitz, H. A。, Victor, J. D ., & 骑士, 乙. 瓦. (1987). Local structure theory for cellular automata. Physica D,

28(1–2), 18–48. https://doi.org/10.1016/0167-2789(87)90120-5

Johnston, 氮. (2010). The B36/S125 “2×2” Life-like cellular automaton. 在一个. Adamatzky (埃德。), Game of Life

cellular automata (PP. 99–114). 施普林格. https://doi.org/10.1007/978-1-84996-217-9_7

李, W., 帕卡德, 氮. H。, & 兰顿, C. G. (1990). Transition phenomena in cellular automata rule space. Physica

D, 45(1–3), 77–94. https://doi.org/10.1016/0167-2789(90)90175-氧

LifeWiki. (2021, 行进). List of Life-like cellular automata. https://www.conwaylife.com/wiki/List_of_Life-like

_cellular_automata

Lizier, J. T。, Prokopenko, M。, & Zomaya, A. 是. (2014). A framework for the local information dynamics of
distributed computation in complex systems. 在米. Prokopenko (埃德。), Guided self-organization: Inception
(PP. 115–158). 施普林格. https://doi.org/10.1007/978-3-642-53734-9_5

Miranda, 乙. R。, & Kirke, A. (2010). Game of Life music. 在一个. Adamatzky (埃德。), Game of Life cellular automata

(PP. 489–501). 施普林格. https://doi.org/10.1007/978-1-84996-217-9_24

人工生命量 27, 数字 2

111

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
A
r
t
我
/

我

A
r
t
我
C
e
–
p
d

F
/

2
7
2
1
0
5
2
0
1
9
4
9
9
A
r
t
我

_
A
_
0
0
3
4
8
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

乙. Peña and H. Sayama

Complexity in Life-Like Cellular Automata

Rendell, 磷. (2002). Turing Universality of the Game of Life. 在一个. Adamatzky (埃德。), Collision-based computing

(PP. 513–539). 施普林格. https://doi.org/10.1007/978-1-4471-0129-1_18

特尼, 磷. D. (2021A). Evolution of autopoiesis and multicellularity in the Game of Life. 人工生命, 27(1),

26–43. https://doi.org/10.1162/artl_a_00334

特尼, 磷. D. (2021乙). Measuring behavioral similarity of cellular automata. 人工生命, 27(1), 62–71. https://

doi.org/10.1162/artl_a_00337

Wackerbauer, R。, Witt, A。, Atmanspacher, H。, Kurths, J。, & Scheingraber, H. (1994). A comparative classification
of complexity measures. Chaos Solitons & Fractals, 4(1), 133–173. https://doi.org/10.1016/0960-0779(94)
90023-X

Wolfram, S. (1982). Statistical mechanics of cellular automata. Reviews of Modern Physics, 55(3), 文章 601.
Wolfram, S. (1984). Universality and complexity in cellular automata. Physica D, 10(1–2), 1–35. https://doi.org

/10.1016/0167-2789(84)90245-8

Wolfram, S. (2002). A new kind of science. Wolfram Media.

Wolfram, S。, & 帕卡德, 氮. H. (1985). Two-dimensional cellular automata. Journal of Statistical Physics, 38(5),

901–946.

Wuensche, A. (1999). Classifying cellular automata automatically: Finding gliders, filtering, and relating space-time
图案, attractor basins, and the Z parameter. Complexity, 4(3), 47–66. https://doi.org/10.1002/(SICI)1099
-0526(199901/02)4:3<47::AID-CPLX9>3.0.一氧化碳;2-V

Zenil, H。, & Villarreal-Zapata, 乙. (2013). Asymptotic behavior and ratios of complexity in cellular automata.
International Journal of Bifurcation and Chaos, 23(9), 文章 1350159. https://doi.org/10.1142/S0218127413501599

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
A
r
t
我
/

我

A
r
t
我
C
e
–
p
d

F
/