Isomorphic Controllers and
Dynamic Tuning: Invariant
Fingering over a Tuning
Continuum
Andrew Milne,* William Sethares,** and James
Plamondon†
*音乐系
于韦斯屈莱大学
芬兰
andymilne@tonalcentre.org
**Department of Electrical and
Computer Engineering
威斯康星大学麦迪逊分校
麦迪逊, WI 53706 美国
sethares@ece.wisc.edu
†Thumtronics Inc.
6911 Thistle Hill Way
Austin, TX 78754 美国
jim@thumtronics.com
In the Western musical tradition, two pitches are
generally considered the “same” if they have nearly
equal fundamental frequencies. 同样地, 二
pitches are in the “same” pitch class if the frequency
of one is a power-of-two multiple of the other. 二
intervals are the “same” (in one sense, 至少) 如果
they are an equal number of cents wide, 即使
their constituent pitches are different. Two melodies
are the “same” if their sequences of intervals, 在
rhythm, are identical, even if they are in different
keys. Many other examples of this kind of “same-
ness” exist.
It can be useful to “gloss over” obvious differ-
ences if meaningful similarities can be found. 这
article introduces the idea of tuning invariance, 经过
which relationships among the intervals of a given
scale remain the “same” over a range of tunings.
This requires that the frequency differences be-
tween intervals that are considered the “same” are
“glossed over” to expose underlying similarities.
This article shows how tuning invariance can be a
musically useful property by enabling (除其他外
事物) dynamic tuning, 那是, real-time changes
to the tuning of all sounded notes as a tuning vari-
able changes along a smooth continuum. On a key-
board that is (1) tuning invariant and (2) equipped
with a device capable of controlling one or more
continuous parameters (such as a slider or joystick),
one can perform novel real-time polyphonic musi-
cal effects such as tuning bends and temperament
modulations—and even new chord progressions—
电脑音乐杂志, 31:4, PP. 15–32, 冬天 2007
© 2007 麻省理工学院.
all within the time-honored framework of tonality.
Such novel musical effects are discussed briefly in
the section on dynamic tuning, but the bulk of this
article deals with the mathematical and perceptual
abstractions that are their prerequisite.
How can one identify those note layouts that are
tuning invariant? What does it mean for a given in-
terval to be the “same” across a range of tunings?
How is such a “range of tunings” to be defined for a
given temperament? The following sections answer
these questions in a concrete way by examining two
ways of organizing the perception of intervals (这
rational and the ordinal), by defining useful meth-
ods of mapping an underlying just intonation (JI)
template to a simple tuning system and scalic struc-
真实, and by describing the isomorphic mapping of
that tuning system to a keyboard layout so that the
resulting system is capable of both transpositional
and tuning invariance.
Background
On the standard piano-style keyboard, intervals and
chords often have different shapes in different keys.
例如, the geometric pattern of the major
third C–E is different from the geometric pattern of
the major third D–F-sharp. 相似地, the major
scale is fingered differently in each of the twelve
keys. (在本文中, the term “fingering” is used to
denote the geometric pattern, without regard to
which digits of the hand press which keys.) 其他
playing surfaces, such as the keyboards of Bosan-
quet (1877) and Wicki (1896) have the property that
Milne et al.
15
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
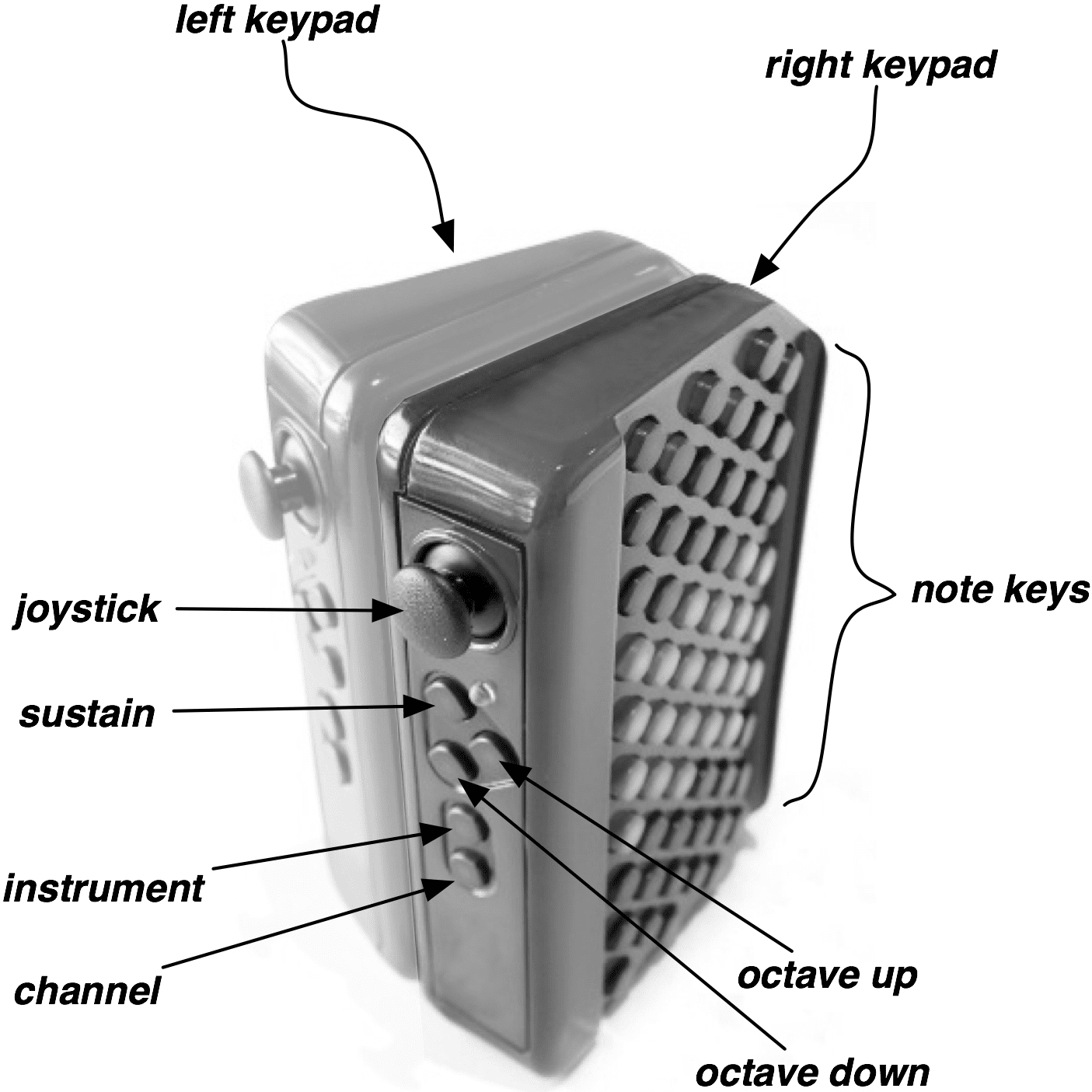
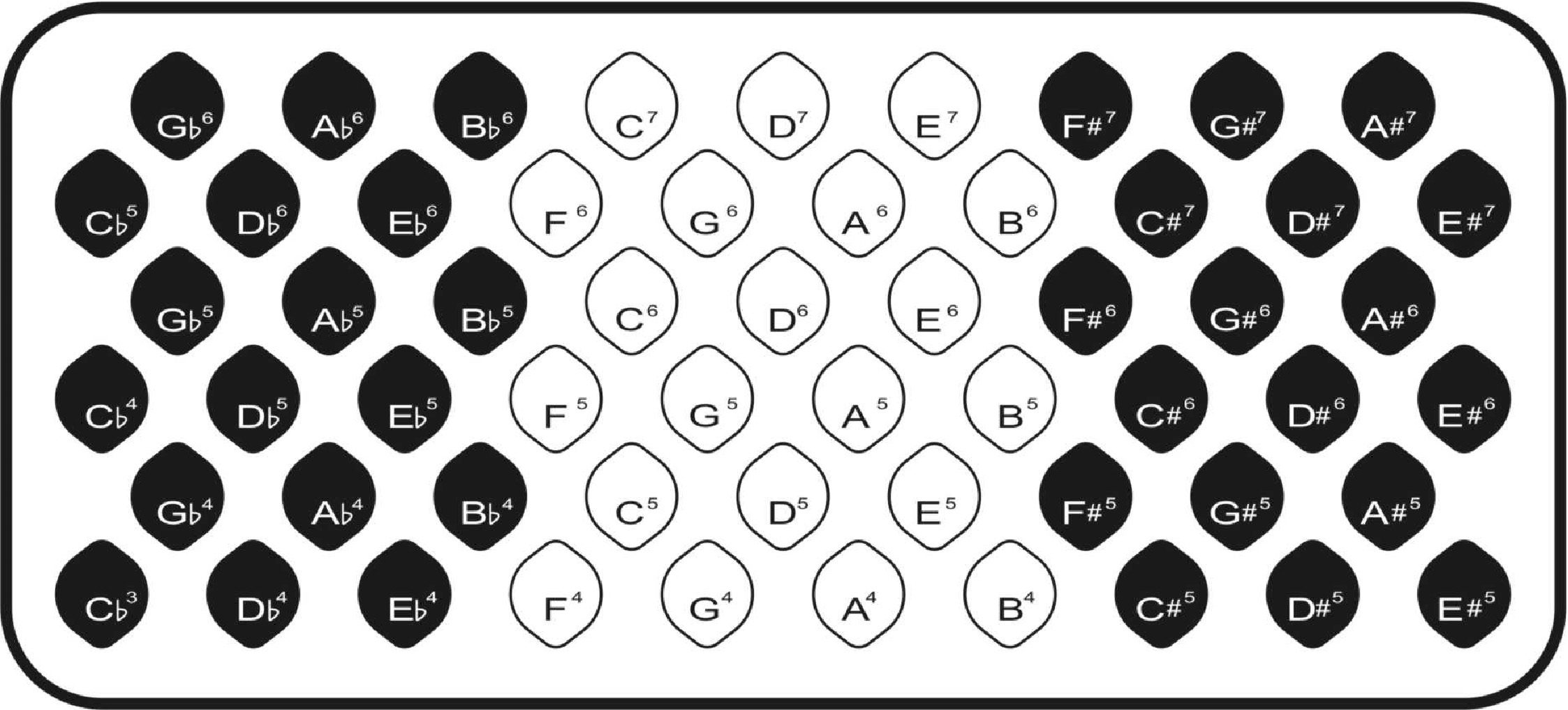
数字 1. Thumtronics’
forthcoming USB-MIDI
controller, the Thummer,
contains two Wicki-layout
keyboards, 每个都有 57
note-controlling buttons.
A variety of controllers in-
clude two thumb-operated
joysticks and optional in-
ternal motion sensors.
The Thummer can be held
like a concertina (A) 或者
laid flat, like most key-
board instruments (乙).
(A)
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
other keyboard layouts such as those of Fokker
(1955) or Bosanquet could have been used instead.
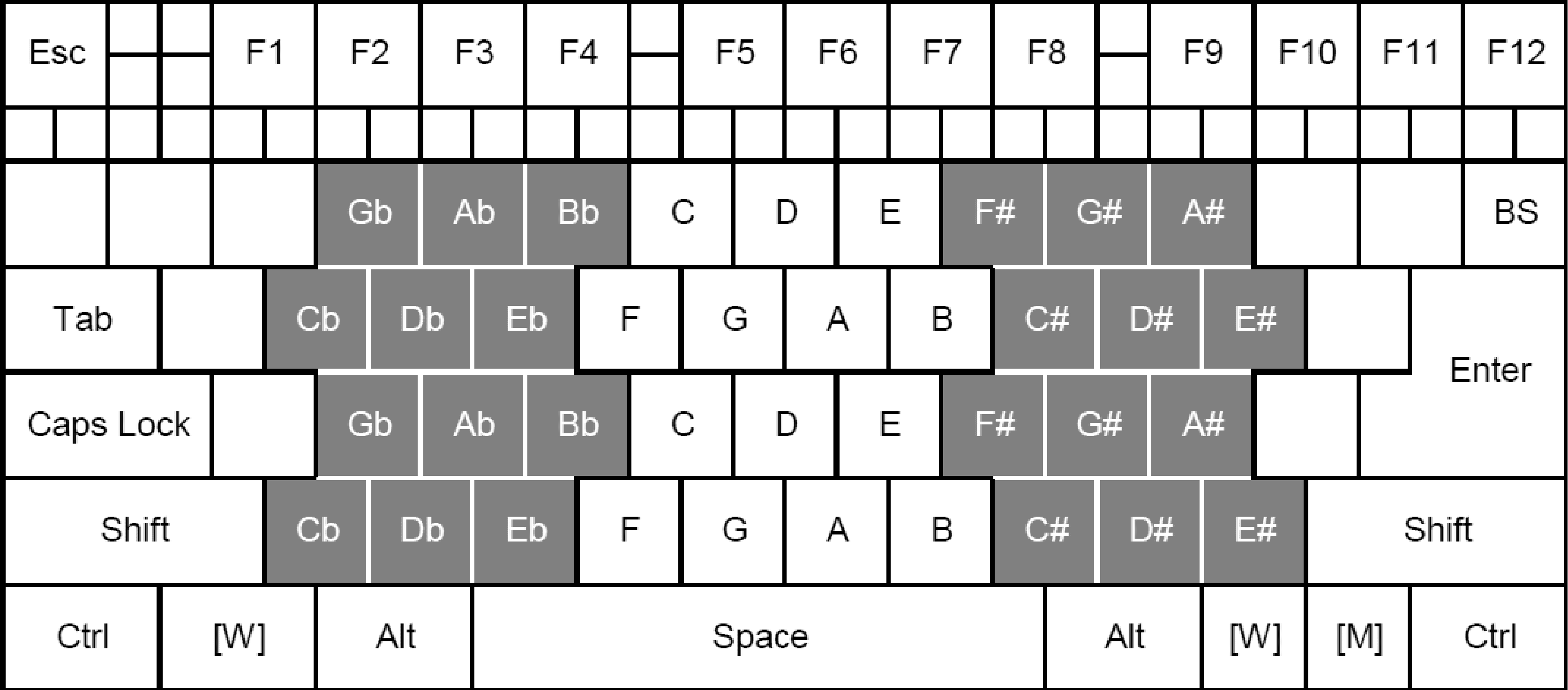
The Wicki layout can be conveniently mapped to a
standard computer keyboard, facilitating the explo-
ration of the ideas presented in this article.
Thumtronics’ forthcoming Thummer music con-
troller (see www.thummer.com), shown in Figure 1,
uses the Wicki note layout by default.
There are several technical, musical, and percep-
tual questions that must be addressed to realize a
keyboard that is both transpositionally and tuning
invariant. 第一的, there must be a range of tunings
over which pitch intervals—and therefore their fin-
gerings—remain in some sense the “same.” This re-
quires that differently tuned intervals be identified
as serving the same role; 例如, the 12-TET
fifth must be identified with the just fifth and the
19-TET fifth. Said differently, tuning invariance re-
quires that there be a number of distinguishable in-
tervals by which the invariance can be measured,
because to say that two numerically different inter-
vals are both “perfect fifths,” it is necessary to iden-
tify a perfect fifth as an interval distinguishable
from a major third, or a perfect fourth, or a dimin-
ished fifth, 等等. This issue of the identity of
each interval, 弦, and scale type have the same
geometric shape in every key. Such keyboards are
said to be transpositionally invariant (Keislar 1987).
There are many possible ways to tune musical in-
tervals and scales, and the introduction of computer
and software synthesizers makes it possible to real-
ize any sound in any tuning (Carlos 1987). 典型-
卡莉, 然而, keyboard controllers are designed
primarily for the familiar 12-tone equal tempera-
蒙特 (12-TET), which divides the octave into twelve
logarithmically equal pieces. Is it possible to create
a keyboard surface that is capable of supporting
many possible tunings? Is it possible to do so in a
way that analogous musical intervals are fingered
the same throughout the various tunings, so that
(例如) the 12-TET fifth is fingered the same
as the just fifth and the 17-TET fifth? (Just intervals
are those consisting of notes whose constituent fre-
quencies are related by ratios of small integers; 为了
例子, the just fifth is given by the ratio 3:2, 和
the just major third is 5:4.)
This article answers this question by presenting
examples of two related tuning continua (parameter-
ized families of tunings where each specific tuning
corresponds to a particular value of the parameter)
that exhibit tuning invariance (在哪里, on an appro-
priate instrument, all intervals and chords within a
specified set have the same geometric shape in all of
the tunings of the continuum). A keyboard that is
transpositionally invariant, tuning-invariant, 和
has a continuous controller has three advantages.
第一的, having a single set of fingerings within and
across all keys of any given tuning makes it easier
to visualize the underlying structure of the music.
第二, having this same single set of interval
shapes across the tuning continuum makes it easier
for musicians to explore the use of alternative tun-
ings such as the various meantones, Pythagorean,
17-TET, and beyond. 第三, assigning the continu-
ous parameter to a control interface enables a
unique form of expression, 例如, dynami-
cally tuning (or retuning) all sounded notes in real
时间, where the scalic function of the notes remains
相同, even as the tuning changes.
在本文中, the Wicki layout is used to con-
cretely demonstrate the formation of the pitches
and notes on a practical keyboard surface, 尽管
16
电脑音乐杂志
Figure 1—continued
(乙)
musical intervals is discussed in detail in the next
部分 (“Intervals”) by contrasting rational and or-
dinal modes of interval identification. The rational
mode is determined by the correspondence of an in-
terval to a low-ratio JI interval, and the ordinal
mode is determined by the number of scale notes an
interval spans.
第二, there must be a tuning system that is itself
transpositionally invariant with regard to both forms
of identification. This requires that each and every
note in the system has identical intervals above and
以下, and that the presumed temperament-mapping
of JI to this tuning system is consistent. Such a tun-
ing system is called a regular tuning system, 和
the embodiment of a such a temperament-mapping
in a regular tuning system is called a regular tem-
perament. These are defined more fully in the sec-
tion “Tuning Systems and Temperaments.”
第三, given such a tuning system, it is necessary
to define useful sets of scales. The section entitled
“Scales” focuses on those scales known as MOS or
well-formed, which have a number of musically
advantageous properties.
that are not) invariant in both transposition and
tuning. The tuning continuum pictured in Figure 2
provides the primary example of this article. It be-
gins at 7-TET, and by varying the size of the perfect
fifth, it moves continuously through various mean-
tone tunings, 12-TET, Pythagorean, and many other
tunings, ending at 5-TET, while retaining fingering
invariance throughout. 最后, a musical example
illustrates static snapshots of the dynamic retuning
过程.
Intervals
This section investigates how intervals are identi-
fied and distinguished, and it discusses criteria by
which two numerically different intervals may be
said to play analogous roles in different tuning sys-
特姆斯. Intervals may be identified—and therefore
discriminated—in at least two ways, here defined as
the rational and the ordinal.
第四, it is necessary to layout-map the regular
Rational Identification
temperament to a keyboard or button-field in a
manner that maintains transpositional and tuning
invariance. The layout-mappings described in the
section “Button-Lattices and Layouts” translate
the generating intervals of the tuning to the key-
board surface. It is shown that transpositional
invariance is identical to linearity of the layout-
映射. Successive sections then provide ex-
amples of keyboard layouts that are (和别的
The rational mode of identification is presumed to
occur primarily for harmonic intervals,即, 那些
formed from simultaneously sounded notes. It pre-
sumes that just intervals that are perceived as con-
sonant act as perceptual and cognitive landmarks (A
template) against which sounded intervals can be
mentally compared and identified. This is reason-
ably uncontroversial for orchestral instruments
Milne et al.
17
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
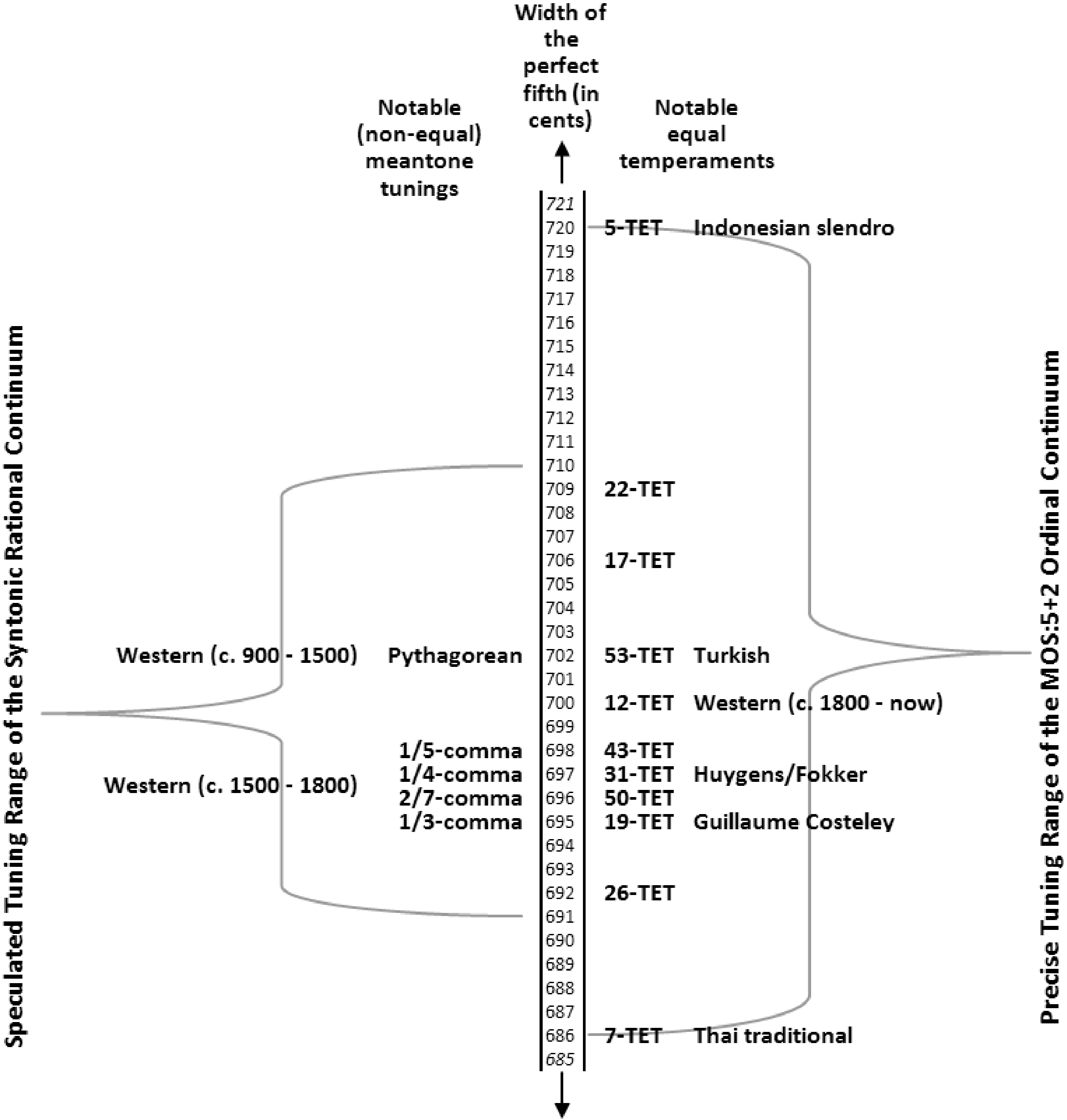
数字 2. The syntonic ra-
tional continuum and
MOS:5+2 ordinal contin-
uum (both defined later).
The figure also shows the
historical and ethnic us-
ages of many notable tun-
ings found within these
continua (compiled from
information in Barbour
1951, Lorentz 2001,
塞塔雷斯 2004, 和
Huygens-Fokker Founda-
tion Web site at
www.xs4all.nl/huygensf).
with harmonic spectra. For inharmonic, 电脑-
generated sounds, inharmonic bells, 和非-
Western instruments such as the metallophones of
the Indonesian gamelan, these sensory consonances
may occur at different intervals (塞塔雷斯 2004), 和
so other templates may be more appropriate.
For sounds with harmonic spectra, when a sounded
interval is tuned close to a small-integer-ratio JI in-
terval (例如 3:2 或者 5:4), it may be heard as a repre-
sentation of that ratio. Using semiotic terminology,
the sounded interval is an indexical signifier of the
just ratio it approximates. 例如, when an in-
terval is tuned to 702 cents (the closest integer
value to 3:2), it is likely to be heard as a representa-
tion of the 3:2 just fifth. As the interval’s tuning is
moved away from 702 cents, it gradually moves to a
state where it is likely to be heard as an imperfect
representation of 3:2. (It will sound more or less
“out of tune.”) As the tuning is moved still further
从 702 cents, the perceived interval will eventu-
ally no longer represent 3:2 (and not even an out-of-
tune 3:2). At this point, the just interval is no longer
signified by the sounded interval. When an interval
is not just, but is within its range of rational identi-
fication, it is called a tempered interval.
Ordinal Identification
The ordinal mode of identification is presumed to
occur primarily for melodic intervals (formed from
successively sounded notes). It presumes that when
an interval is played as part of an aesthetically con-
sistent or conventionalized scale, it is identified by
the number of scale notes (or steps) it spans. 对于前-
充足, Wilson (1975) writes that “our perception of
Fourth-ness is not just acoustic, IE。, 4/3-determined,
it is melodic and/or rhythmic-influenced to a high
degree” (p. 1). Like rational identification, this is an
indexical signification but one that requires the
presence of a scalic background (IE。, 语境) 给予
meaning to “second-ness,” “third-ness,” “fourth-
内斯,” etc. For a scale to serve as a background, 它
must have intrinsic aesthetic consistency (IE。, 是
perceived as somehow complete and “correct”)
and/or be conventionalized (IE。, made familiar
through repetitive use).
The diatonic scale can serve as a scalic back-
ground for common-practice music. 例如,
against the background of a C-major (diatonic) 规模,
the intervals C–D, D–E, E–F, F–G, 等等, 是
heard as “seconds” because they each span two ad-
jacent scale notes; the intervals C–E, D–F, E–G, F–A,
等等, are heard as “thirds” because they each
span three successive scale notes.
Dual Identification
The two modes of identification overlap: the ra-
tional mode plays a part in the identification of
melodic intervals, the ordinal in the identification
of harmonic intervals. 例如, a melodic inter-
val of approximately 3:2 will usually be heard as “in
tune” or “out of tune” according to its proximity to
this just interval; similarly, a harmonic interval ap-
proximating 3:2 将要, in a traditional diatonic con-
文本, be heard as spanning five notes of the scale.
此外, in real-world music it is not always
18
电脑音乐杂志
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
possible to make a strict distinction between har-
monic intervals and melodic intervals. An arpeggio
is at least partially a harmonic structure. The bass
note of a “stride bass” pattern, which is sounded
only for the first and third beats of a bar, cognitively
grounds the rest of the bar. Counterpoint, 这是
the interweaving of many melodies into a coherent
harmonic structure, blurs the distinction between
melody and harmony.
Thus the rational and ordinal modes of identifica-
tion are intertwined. 的确, in Western tonal mu-
原文如此, there is a consistent linkage between the number
of steps an interval contains and its harmonic ratio.
例如, the interval that spans three scale
笔记 (IE。, the third) is commonly an interval that is
close to 5:4 或者 6:5 (hence the names major third and
minor third). 相似地, the interval that spans four
scale notes (IE。, the fourth) is typically an interval
that is close to 4:3. 此外, where these links
differ, the interval often has a tonally dissonant
function that requires resolution to a more stable
间隔. (例如, an augmented second com-
monly resolves to a perfect fourth; a diminished
fifth commonly resolves to a major third.)
In conventionalized musical systems such as
Western tonal music, where particular step sizes
and harmonic ratios are consistently associated,
ordinality can (by association) symbolically signify
比率, and ratio can (by association) symbolically
signify ordinality. 这意味着, within such a
conventionalized context, the tuning ratio over
which an interval can still signify a given just ratio
may be wider than expected if it were judged by
analyzing harmonies isolated from the musical con-
文本. In common practice, 例如, the conven-
tional association of “5:4-ness” and “third-ness”
means that a melodic third can be tuned very wide
but still signify 5:4. 例如, the ultra-sharp
supra-Pythagorean major thirds (greater than 408
cents) that are sometimes used by string players for
expressive intonation (Sundberg et al. 1989) may be
harmonically uncomfortable, but they still signify
the same musical interval as the just quarter-
comma meantone thirds of 386 cents. (他们是,
毕竟, different expressions of the same notated
interval.) Thus the tuning range over which a given
interval can be identified and therefore discrimi-
nated from other intervals has “fuzzy” boundaries
that are context-dependent.
Tuning Ranges of Invariant Identification
The previous discussion suggests that it may be ad-
vantageous to define the tuning range over which an
interval preserves both its rational and ordinal iden-
tity as that interval’s tuning range of invariant
识别. Because there are two modes by
which an interval can be identified, there are two
relevant tuning ranges to be considered that them-
selves depend on a listener’s innate abilities, expe-
riences, and training. Musical context is also
重要的; the tuning range of invariant rational
identity may also change based on the spectrum
and/or timbre of the sounds (塞塔雷斯 2004). 为了
these reasons, the final judgment as to the specific
tuning boundaries may best lie in the hands of the
artist and not the theorist.
尽管如此, in the presence of a scalic back-
地面, invariant ordinal identification can be pre-
cisely bounded; furthermore, given a scale in a
regular tuning system (as defined subsequently), 这
size of every interval in the scale is determined by
the values of the generating intervals. This implies
that the range of generator tunings over which all of
that scale’s intervals can be retuned but still main-
tain their ordinal identity—that scale’s ordinal con-
tinuum—is limited by the points at which one or
more of that scale’s steps shrink in size to zero (或者
equivalently, the points at which two of the scale
steps “cross”).
In a regular temperament (as defined in the next
部分), the sizes of all the intervals that are ca-
pable of being rationally identified are controlled by
the values of its generating intervals. This implies
that the range over which all of that temperament’s
identifiable intervals can be retuned but still main-
tain their rational identity—that temperament’s
rational continuum—is delimited by context and
subject-dependent “fuzzy” boundaries.
数字 2 shows the precisely bounded continuum
for the twelve-note chromatic scale generated by
Milne et al.
19
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
fifths and octaves. Also shown on this chart is a
conjectured “fuzzy” boundary for the rational con-
tinuum of the regular temperament defined by the
syntonic comma (which is explained in the next
部分). This conjectured range has been estimated
by assuming that only the common practice conso-
nances are rationally identifiable, and that their ra-
tional identification switches from one common
practice consonance to another at the tuning that is
midway between their just tunings. In common-
练习音乐, these two continua are convention-
ally associated, though the ordinal continuum is
wider than the rational.
Tuning Systems and Temperaments
A tuning system is defined here to be a collection of
precisely tuned musical intervals. There are many
ways in which the intervals may be chosen: A “bou-
tique” tuning system might have all of its intervals
chosen arbitrarily, and another tuning system might
be generated by a predefined mathematical proce-
dure (McLaren 1991). The regular tunings form one
class of tuning systems in which all of the intervals
are generated multiplicatively from a finite number
of generating intervals (or generators). Such tuning
systems ensure that every given note has the same
set of intervals above and below it as every other
note in the system; this means that regular tuning
systems are inherently transpositionally invariant.
An example regular tuning system is 3-limit JI (还
known as Pythagorean tuning), which has two gen-
erators G1 = 2 and G2 = 3, and consists of all prod-
j = 2i × 3j, where i and j are
ucts of the form G1
整数. Thus the intervals of 3-limit JI can all be
found in a series of stacked just perfect fifths, allow-
ing for octave equivalence. 一般来说, a regular tun-
ing is characterized by n generators G1 to Gn and
consists of all intervals G1
i2, . . . , in are integer-valued exponents.
在, where the i1,
i2 . . . Gn
i1 G2
i G2
Altering the tuning of a generator affects the tun-
ing of the system in a predictable way. 例如,
–1 G2 (IE。, 2–1 × 3). 如果
the perfect fifth in 3-limit JI is G1
A (non-JI) regular tuning is created by changing the
value of G2, the value of the fifth, and all other in-
tervals, changes in a patterned way. Assigning the
magnitude of one or more of the generating inter-
vals to a control interface provides a convenient
means to “navigate” the tuning continuum. Partic-
ular values within this continuum may produce
some intervals that approximate JI intervals and so
are rationally identifiable; we might consider, 那里-
fore, that there has been a mapping of JI intervals to
that tuning system.
For such a temperament-mapping to be transposi-
tionally invariant, it must be linear, though it need
not be invertible (IE。, it need not be one-to-one).
The embodiment of such a temperament-mapping
in a suitable tuning system is called a regular tem-
perament, and it can be characterized by the small
JI intervals called commas that are tempered to
unison (史密斯 2006). This means that a regular
temperament is characterized by its temperament-
映射, not its tuning, so any given temperament
has a range of suitable tunings. To be concrete, 二
or more intervals a1, a2, . . . , an are said to be multi-
plicatively dependent if there are integers z1,
z2, . . . , zn, not all zero, such that a1
z2 . . . 一个
zn = 1.
If there are no such zi, then the ai are said to be mul-
tiplicatively independent. The rank of a tuning sys-
tem is the number of multiplicatively independent
intervals needed to generate it. A regular tempera-
ment typically has lower rank than the JI system
that is temperament-mapped to it (IE。, the mapping
is non-invertible). When the temperament-mapping
loses rank, all intervals can no longer be just. 如何-
曾经, as long as there is a range of generator values
over which the intervals are correctly rationally
identified, the regular temperament can be consid-
ered to be valid.
z1 a2
This is analogous to the way a projection of the
three-dimensional surface of a globe to a two-
dimensional map inevitably distorts distance, 区域,
and angle. 然而, so long as the countries have
identifiable shapes, the projection can be considered
valid. Different map projections result in different
distortions, and some map projections are more or
less suitable to specific purposes. Some projections
(such as the Mercator Projection) have the virtue of
wide familiarity; so it is also with temperament-
mappings (such as those that lead to 12-TET).
例如, 3-limit JI can be temperament-
mapped to a one-dimensional system using an ap-
20
电脑音乐杂志
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
a G2
b = 1, where a and b are
propriate comma G1
整数. One notable tempering retains the octave
G1 = 2 and tempers G2 to 219/12 ≈ 3, which requires
that a = 19 and b = –12, resulting in the familiar 12-
TET. This comma can be interpreted musically by
saying that in this temperament, 19 octaves minus
twelve equal-tempered perfect twelfths equals a
unison. A second example is in 5-limit JI, 哪个
consists of all intervals of the form 2i 3j 5k, where i,
j, and k are integers. This can be reduced to a two-
dimensional regular temperament by choosing G1
(typically near 2), G2 (near 3), and G3 (near 5) so that
G G Ga
C
3
乙
2
1
1=
(1)
where a, 乙, and c are specified integers. 方程 1
defines a comma that is tempered to unison. 这
well known syntonic comma (which has an untem-
pered tuning of 81/80) is the special case where a =
–4, b = 4, and c = –1; tempering the generators so
that Equation 1 holds, produces various tunings of
the syntonic temperament (as illustrated in Figure 2).
The comma can be solved for one of its terms as
G3 = G1
–b/c, and a typical interval of the regular
temperament can be written in terms of two gener-
ating intervals α = G1
where GCD(n, 米) is the greatest common divisor of
n and m. Thus G1 = α|C|/GCD(A,C), G2 = β|C|/GCD(乙,C), G3 =
α–aSIGN(C)/|GCD(A,C)| β–b/SIGN(C)|GCD(乙,C)|, and a typical inter-
val G1
A(ci–ak)/|GCD(A,C)| β(cj–bk)/|GCD(乙,C)|. In matrix notation, 这
向量 (我, j, k)T is temperament-mapped by
k of the JI is temperament-mapped to
GCD(A,C)/|C| and β = G2
–a/c G2
GCD(乙,C)/|C|
jG3
iG2
C
R =
GCD
a c
( , )
0
C
0
GCD
b c
( , )
− ⋅
A
GCD
− ⋅
乙
GCD
C
( )
SIGN
a c
( , )
C
( )
SIGN
b c
( , )
到
i c
-
ak
SIGN
C
( )
j c
-
bk
SIGN
C
( )
时间
a c
GCD( , )
b c
GCD( , )
where T is the transpose operator. 因此, 这
temperament-mapping is linear and (typically)
loses rank. For the syntonic comma,
R =
1
0
0
1
-
4
4
(3)
and any note (我, j, k)T is mapped to (i – 4k, j + 4k)时间.
例如, a just major third 5/4 = 2–2 30 51 是
represented by the vector (–2, 0, 1)时间. 这是
temperament-mapped by G to (–6, 4)时间, which repre-
sents the tempered interval α–6β4. If α were tem-
pered to 2 (no change in the octave) and β were
tempered to 230/19 (the 19-TET twelfth), then α–6β4 =
2–62120/19 ≈ 1.24469 ≈ 5/4 is the 19-TET approxima-
tion to the just major third. 相似地, if α were tem-
pered to 2 and β were tempered to 3 × (81/80)–1/4 (这
quarter-comma meantone fifth), then α–6β4 = 5/4 是
the justly tuned major third found in the quarter-
comma meantone tuning.
Syntonic Rational Continuum
The rational continuum of a rank-r regular tem-
perament is here defined as that (r-dimensional)
range of generator tunings within which the ra-
tional identity of all rationally identifiable intervals
is maintained. The rational continuum of the syn-
tonic temperament is therefore called the syntonic
rational continuum. As described previously, 这
tuning range of this continuum is context-
dependent and not easily specified a priori.
The syntonic rational continuum extends beyond
the narrower range implied by “meantone,” which
usually refers to the range of syntonic tunings pro-
viding reasonably pure-sounding tunings (for sounds
with harmonic spectra) and/or which have an estab-
lished historical use—a range of approximately 19-
TET to 12-TET. (见图 2.)
A scale is here defined to be a subset of a tuning sys-
tem used for a specific musical purpose. When using
a rank-2 tuning system with generators α and β, A
scale can be simply constructed by stacking integer
powers of β and then reducing (dividing or multiply-
ing by integer powers of α) so that every term lies
之间 1 and α. This is called an α-reduced β-chain,
and it produces a scale that repeats at intervals of α;
α = 2, representing repetition at the octave, 是个
most common value. Any arbitrary segment of an
Milne et al.
21
(2)
Scales
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
⎡
⎣
⎢
⎤
⎦
⎥
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
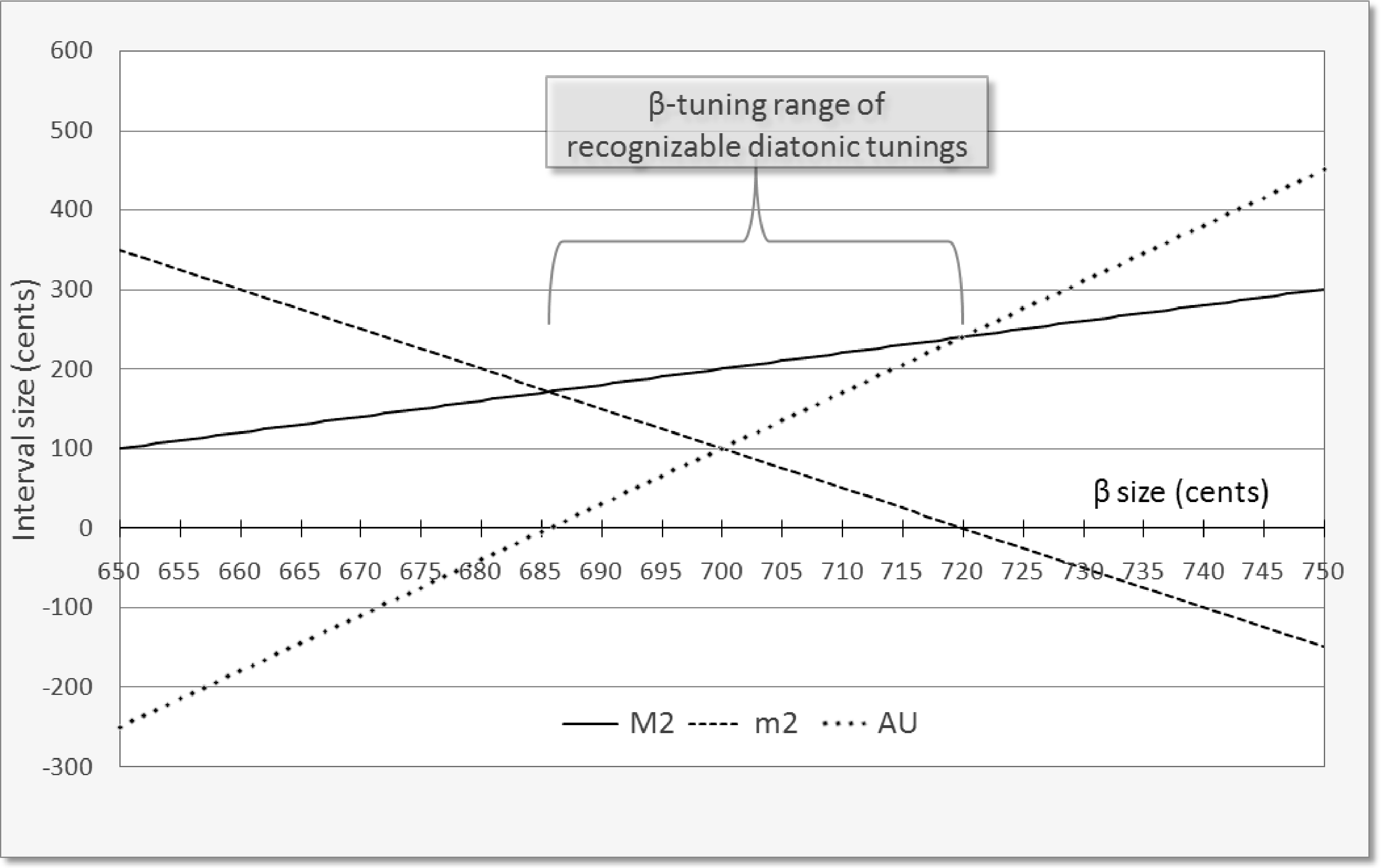
数字 3. Sizes of the major
第二 (M2), minor second
(平方米), and augmented uni-
儿子 (AU), over a range of
β generator tunings.
α-reduced β-chain can be used to form a scale, 和
the number of notes it contains is called its cardi-
nality. For a given tuning of α and β, α-reduced β-
chains with certain cardinalities are called moment
of symmetry (MOS) scales (Wilson 1975; also known
as well-formed scales after Carey and Clampitt
1989). Such scales have a number of musically ad-
vantageous properties: they are distributionally
甚至, which means that the scale has two step sizes
that are distributed as evenly as possible (Clough et
阿尔. 1999); they have constant structure, 哪个
means that every given interval always spans the
same number of notes (Grady 1999). Two familiar
MOS scales generated by α = 2 and β ≈ 3/2 are the
five-note pentatonic scale (例如, D, 乙, G, A, C) 和
the seven-note diatonic scale (例如, C, D, 乙, F, G, A,
乙); other β-values generate MOS scales with quite
different intervallic structures. These provide fertile
resources for non-standard microtonal scales.
Every MOS scale with specified generators and
cardinality has a valid tuning range over which it
can exist; beyond this range, notes must be added to
or removed from the scale to regain distributional
evenness and constant structure. The boundaries of
this tuning range mark the tuning points at which
some of the scale’s steps shrink to unison, 和
therefore the tuning points at which the ordinal
identity of intervals in that scale changes. An MOS
scale generated by α and β with cardinality c has a
two-dimensional valid tuning range of αp/q < β < αr/s,
where p/q and r/s are adjacent members of a Farey
sequence of order c–1. (A Farey sequence of order n
is the set of irreducible fractions between 0 and 1
with denominators less than n, arranged in increas-
ing order.)
For example, the 12-note MOS scale generated by
α = 2 and β ≈ 3/2, which is the chromatic scale that
provides the background for common practice mu-
sic, has a valid tuning range of 24/7 < β < 23/5 (4/7 and
3/5 being adjacent members of the Farey sequence
of order 11). Expressing this range in simpler terms,
the “perfect fifth” is between 1200 × 4/7 = 685.7 and
1200 × 3/5 = 720 cents in size. Consider the familiar
seven-note diatonic scale as the tuning traverses
this range: starting with a generating interval β
tuned to the 12-TET fifth 27/12, the scale consists of
five large steps (whole tones) and two small steps
(half tones). As β is increased, the whole tones grow
larger and the half tones grow smaller. When β
reaches 23/5, the semitones disappear completely;
above 23/5, there is no seven-note MOS scale avail-
able, because the seven-note scale contains three
different step sizes. On the other hand, as β is de-
creased below 27/12, the tones get smaller and the
semitones get larger. When β reaches 24/7, the tones
and semitones become the same size; below 24/7, the
MOS scale’s internal structure changes so that it
has five small intervals and two large intervals, a
scale structure that is the inverse of the familiar di-
atonic scale. These changing step sizes are illus-
trated in Figure 3. This tuning range is equivalent to
Blackwood’s “range of recognizable diatonic tun-
ings” (1985). The valid tuning ranges for MOS scales
are, therefore, a generalization of the concept of
range of recognizability beyond the familiar dia-
tonic/chromatic context.
The MOS scale that is recognizably diatonic is
called MOS:5+2 (i.e., it contains five large steps and
two small steps). The valid tuning range of this
MOS scale is 24/7 < β < 23/5 (see Figure 2) and it pre-
serves, therefore, the ordinal identity of the diatonic
and chromatic intervals used in common practice.
When intervals are played as a part of a conven-
tionalized or aesthetically consistent scale, they can
be ordinally identified by the number of notes or in-
tervals they span. Owing to their distributional
evenness and constant structure, MOS scales are
likely to be heard as intrinsically aesthetically con-
sistent, so the valid tuning range of any given MOS
scale is equivalent to the range within which all of
22
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
c
o
m
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
its intervals are ordinally invariant. Furthermore,
these ranges hold for many musically useful alter-
ations of MOS scales such as the harmonic minor
scale (A, B, C, D, E, F, G-sharp).
generating intervals (1, 0) and (0, 1), and the layout-
mapping L is the 2 × 2 matrix
L =
ψ
ψ
x
y
ω
ω
x
y
(4)
MOS:5+2 Ordinal Continuum
The ordinal continuum of an MOS:a+b scale,
which has a large steps and b small steps, is here
defined as the (two-dimensional) range of generator
tunings that gives this scale form. It is equivalent
to αp/q < β < αr/s, where p/q and r/s are adjacent
members of a Farey sequence of order 2a + b – 1.
The ordinal continuum of MOS:5+2 is, therefore,
called the MOS:5+2 ordinal continuum.
Button Lattices and Layouts
Instruments capable of playing a number of discrete
pitches may use many buttons (or keys). For an in-
strument to have transpositional invariance, it is
necessary that the buttons are arranged in a regular
and spatially repeating pattern; such a structure is
called a lattice (Insall, Rowland, and Weisstein
2007). If the lattice has one dimension, it may be
called a button row; if it has two dimensions, it may
be called a button field. A layout is here defined as
the physical embodiment of an invertible, but not
necessarily linear, layout-mapping from a regular
temperament to an integer-valued button lattice. In
the same way that a regular temperament has a fi-
nite number of generating intervals (e.g., α and β)
that generate all its intervals, a lattice can be repre-
sented with a finite number of basis vectors that
generate all its vectors. The logical means to layout-
map from a temperament to a button lattice is to
map the temperament’s generating intervals to the
lattice’s basis vectors.
Let L : Zn → Zn map from the n generating inter-
vals of the temperament to the n-dimensional but-
ton lattice. For example, with n = 2, the temperament
contains two generating intervals α and β. Any in-
terval of the temperament can be expressed as a
two-vector (j, k) representing the interval αjβk. The
standard basis for the temperament consists of the
x, ω
x, ψ
y)
which transforms the temperament’s generating in-
tervals into the lattice’s basis vectors ψ = (ψ
and ω = (ω
y). The elements of L must be integers
(or else some intervals will be layout-mapped to lo-
cations without buttons), L must be invertible (that
is, the determinant of L is nonzero, or else either
some buttons would have no assigned note or some
notes would have no corresponding button), and the
determinant of L must be ±1 (or else the inverse
will not be integer-valued). This mapping provides
the mathematical setting for two results. First, if
the layout-mapping L is linear, the layout is trans-
positionally invariant (Theorem 1). Second, the
converse holds as well: if the keyboard layout is
transpositionally invariant, the layout-mapping L
must be linear (Theorem 2).
Theorem 2 justifies the use of linear (matrix) no-
tation for the layout-mapping. Proof of the theo-
rems is given in Appendices A and B. The theorems
presume an infinitely sized button-lattice; physical
keyboards will necessarily have finite size, and the
linearity will be violated at the edges. The finite
size also limits the number of octaves that can be
realized. There are many possible layout matrices L,
and several concrete examples are given in the next
section. The choice of L impacts the ease with which
particular scales and chords can be fingered, as well
as the balance between the number of octave-
reduced intervals and overall octave range that can
fit on a keyboard of a given geometry. For some lay-
outs, such as that of Fokker, the playability-related
metrics vary greatly as the tuning is changed,
whereas these metrics are more stable across a wide
range of tunings on some other layouts, such as the
Wicki. Identifying and quantifying such metrics is
an important area for future investigation.
Because a layout-mapping is invertible, by defini-
tion, it can be linear only if it does not lose rank.
Linear and invertible mappings are called isomor-
phic, and henceforth all layouts with this type of
layout-mapping will be referred to as isomorphic
layouts. The theorems show that given a regular
Milne et al.
23
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
c
o
m
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
⎡
⎣
⎢
⎤
⎦
⎥
temperament, transpositional invariance requires
an isomorphic layout; and given a regular tempera-
ment and an MOS-scalic background, tuning invari-
ance requires that the tunings of the generating
intervals (as embodied in the layout) remain within
that temperament’s and MOS scale’s tuning range
for invariant identification. This means that trans-
positional invariance on a button-row is only pos-
sible for a rank-one (i.e., equal) temperament. To get
transpositional invariance across the tuning range
of rank-two temperaments (like the non-equal
meantone tunings), a button field of at least two di-
mensions is required. Because it is difficult to con-
ceive of a button lattice operating effectively in
more than two dimensions, only rank-one and rank-
two temperaments are considered in this article.
The following examples illustrate these points by
demonstrating concrete isomorphic layouts that are
invariant in both transposition and tuning.
Examples of Layout-Mappings
The examples in this section use the syntonic tem-
perament tuned to quarter-comma meantone, 12-
TET, and 19-TET, and assume an MOS:5+2 scalic
background—design choices that are compatible
with common-practice tonal music. Two types of
layouts are shown. One-dimensional button rows
provide the simplest setting; drawings such as Fig-
ures 4–6 should be interpreted as consisting of a
single row of identical buttons. For two-dimensional
button fields, there are several ways in which the
buttons can be arranged: in a rectangular grid, in off-
set rows (like brickwork), in a hexagonal grid, or as a
tiling of parallelograms. The Wicki layout provides
our primary two-dimensional example, though ob-
viously other layouts could be used.
Layout-Mapping from a Rank-One Temperament to
a Button Row
The familiar 12-TET has a single generating interval
α of 21/12 (100 cents) and tempers out the syntonic
comma (among other commas). An octave consists
of twelve of these generating intervals, a perfect
fifth contains seven, and a major third contains four.
The layout-mapping can be either L = 1 or L = –1. If
the 12-TET generating interval is layout-mapped to
+1, the notes progress sequentially higher in pitch
from left to right, which corresponds to a linear key-
board as shown in Figure 4.
The tuning range of rational invariance for this
temperament is small. Increasing the size of the
generator by just two cents increases the size of the
octave by 24 cents. Though the piano is frequently
tuned with stretched octaves, this stretching is typi-
cally less than about half a cent on the generating
interval (about six cents per octave). The tuning
range of ordinal invariance is unbounded, because
no amount of retuning of the generator changes the
order of the notes. For this case, the ordinal range is
not a useful measure.
Owing to the isomorphic layout-mapping, this
layout has the property that any rationally identifi-
able interval or chord (such as the major triad) is fin-
gered the same for any position on the button-row.
Starting on any note (for instance C), a major triad is
played using the buttons four and seven steps to the
right. The geometric shape of a major triad is, there-
fore, always 0–4–7 for all transpositions. Similarly,
a melody is fingered the same wherever it is located
on the button-row. Starting on any note (for in-
stance C), the melody Re–Mi–Fa–Fi–Sol is played
using a button, then a button two steps to the right,
then one more step to the right, then one more step
to the right, then one more step to the right. The
geometric shape of this melody is, therefore, always
0–2–3–4–5 for all transpositions.
A different rank-one temperament that also tem-
pers out the syntonic comma (among others) is 19-
TET, as shown in Figure 5. This temperament has a
single generating interval α = 21/19 (approximately
63.2 cents), and the octave consists of 19 of these
generating intervals. The perfect fifth is eleven gen-
erating intervals wide, and the major third is six
generating intervals wide. Any isomorphic layout-
mapping of 19-TET (e.g., L = 1) has, like the above
12-TET example, a small range of rational tuning
invariance and a similar transpositional invariance.
However, the fingering of both the major triad 0–6–
11 and the Re–Mi–Fa–Fi–Sol melody 0–3–5–6–8 are
24
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
c
o
m
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. The one-
dimensional keyboard lay-
out L = 1 in 12-TET.
Figure 5. Note positions of
19-TET using L = 1.
Figure 6. Nonlinear piano-
style layout for a rank-2
temperament, such as
quarter-comma meantone.
Figure 4
Figure 5
Figure 6
different from the 12-TET design in Figure 4. This
shows concretely how the linear one-dimensional
design fails to be tuning invariant.
Layout-Mapping from a Rank-Two Temperament to
a Button Row
A layout-mapping is invertible by definition, so a
layout-mapping from a rank-two regular tempera-
ment to a one-dimensional button-row must be
nonlinear. As established previously, a nonlinear
(non-isomorphic) layout-mapping “breaks” transpo-
sitional invariance. A common example of a nonlin-
ear layout-mapping is a piano-style layout, which
takes a finite subset of the notes produced by a
rank-two meantone (such as quarter-comma), and
layout-maps them in pitch order to a twelve-note-
per-octave keyboard, as illustrated in Figure 6. The
physical/geometrical irregularity of the piano key-
board, interpreted as a row of black keys inter-
spersed with a row of white keys, is collapsed here
to a single row for the sake of simplicity.
Such layout-mappings (as applied to standard,
geometrically irregular keyboards) were used in the
17th century (Barbour 1951), though sometimes A-
flat was used in place of G-sharp. In quarter-comma
(or any other meantone tuning requiring two gener-
ating intervals), major thirds (e.g., C–E) are tuned
differently than diminished fourths (e.g., C-sharp–
F). In the nonlinear layout of Figure 6, ascending
four steps sometimes produces a major third and
sometimes produces a diminished fourth, thus
breaking transpositional invariance. For example,
starting from C and proceeding four steps to E pro-
duces a just major third of size 386 cents, which is
clearly identifiable as 5:4. On the other hand, start-
ing at C-sharp and ascending four steps to F pro-
duces a diminished fourth of 427 cents. This is a
so-called “wolf” interval that is unlikely, in this
context (where there exist more closely tuned major
thirds), to be rationally identified as 5:4.
The only way to gain transpositional invariance
for this layout is to tune the fifths to 27/12, which is
the only (octave-reduced) tuning that does not dif-
ferentiate between major thirds and diminished
fourths. This is consistent with the theorem be-
cause when the fifth is tuned to 27/12 and the octave
is tuned to 2, the two generating intervals are no
longer multiplicatively independent. In this case,
the rank of the temperament has collapsed to one
and the tuning has become 12-TET. A similar argu-
ment shows that for a button-row with N notes per
octave, any tuning that produces an n-TET where n
= N will have transpositional invariance, but for
this tuning only.
To summarize: On a button-row with keys of
fixed size, the physical size of any given interval is
different in 12-TET, 17-TET, 19-TET, quarter-
Milne et al.
25
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
c
o
m
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. The position of
notes using the Wicki
layout on a Thummer
keyboard.
Figure 8. The position of
notes using the Wicki
layout on a QWERTY
keyboard.
comma, or any alternative tuning. In each tuning,
the performer’s fingers have to press different keys
to produce intervals that are the same (within the
definition of a given temperament). A keyboard that
is tuning-invariant is preferable, so that the per-
former’s fingers press the same keys to produce the
same intervals (within a given temperament), inde-
pendent of the current tuning.
Layout-Mapping from a Rank-Two Temperament to
a Button Field
One solution to these problems is to use a two-
dimensional button-field so that the layout-
mapping from the rank-two syntonic temperament
to the button-field is isomorphic. The simplicity af-
forded by the invariant fingering of an isomorphic
layout is illustrated in the following examples using
the Wicki layout.
To be concrete, Wicki is a layout-mapping to a
hexagonal button-field (which can be approximated
by rotating an integer valued button-field by 45°),
such that the two generating intervals α and β are
layout-mapped to the basis vectors ψ = (1, 1)T and
ω = (1, 0)T, i.e.,
L =
1
1
1
0
as illustrated in Figure 7.
This layout provides a good balance of octave-
reduced intervals versus overall octave range for rel-
atively small button fields (such as the QWERTY
computer keyboard as illustrated in Figure 8) when
using syntonic tunings (α ≈ 3/2), and it also func-
tions well over many non-syntonic tuning continua
(where β may take any value). Additionally, the
Wicki layout allows a wide range of pitches to be
played with a single hand, and all notes of any MOS
scale are always clustered in a simple vertical band.
(Proof of the latter property is beyond the scope of
this article.) However, it has a less obvious relation-
ship between pitch and button position than is
found, for instance, in the design of Bosanquet. (For
syntonic tunings, Bosanquet has an “easterly” pitch
axis, like the standard keyboard, while the Wicki
layout has a less obvious “north-northeasterly”
pitch axis.) The basic principles illustrated in the
following examples may also be applied to other
regular temperaments, MOS scales, and layouts.
Tuning Ranges of Invariance
Assuming that the generating intervals are α = 2 (an
octave), and β = F (an alterable tempered perfect
fifth), the pitch order of buttons on a Wicki layout
that is ten buttons wide has seven different configu-
rations as the tuning of F moves across the MOS:5+2
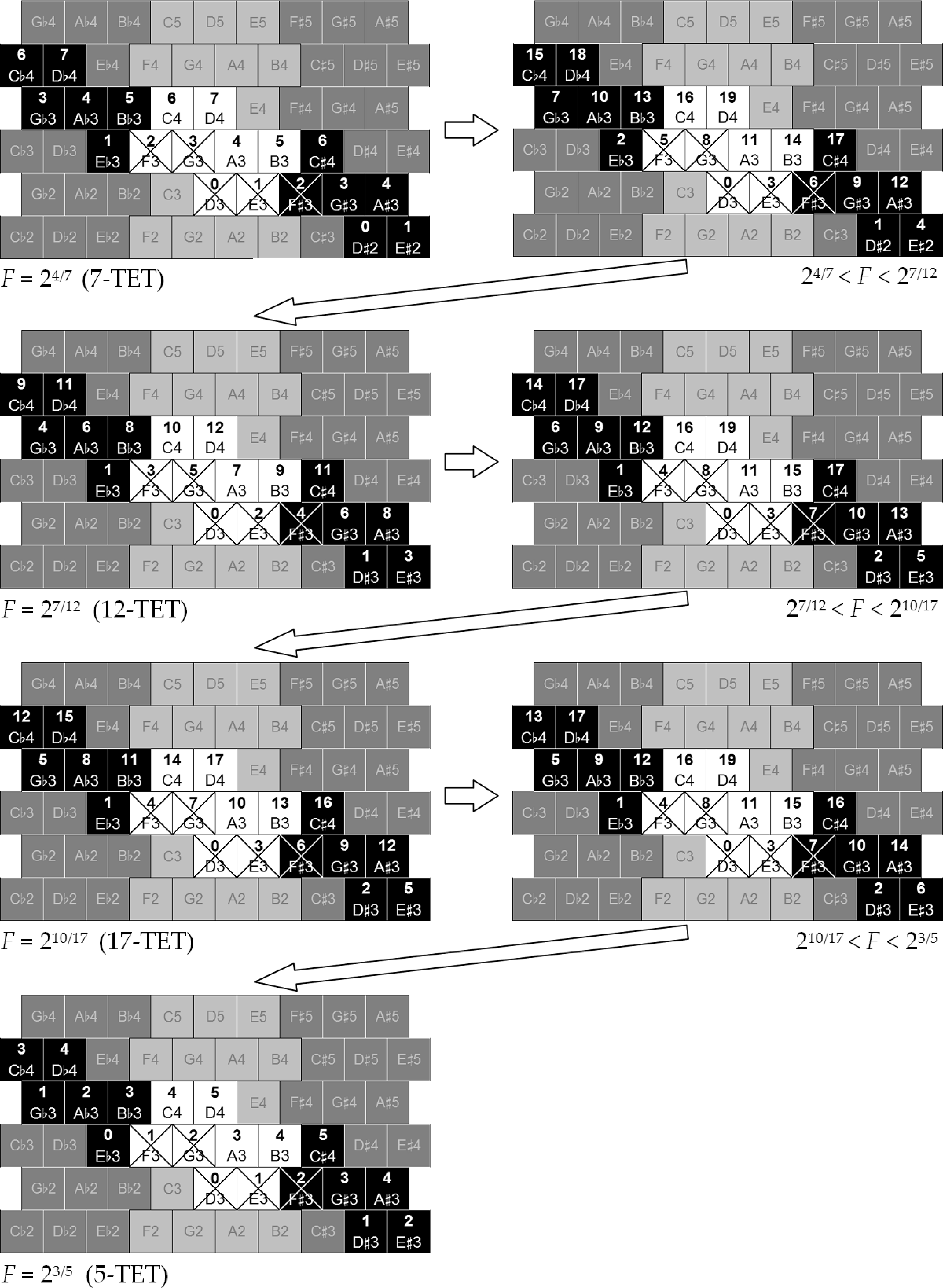
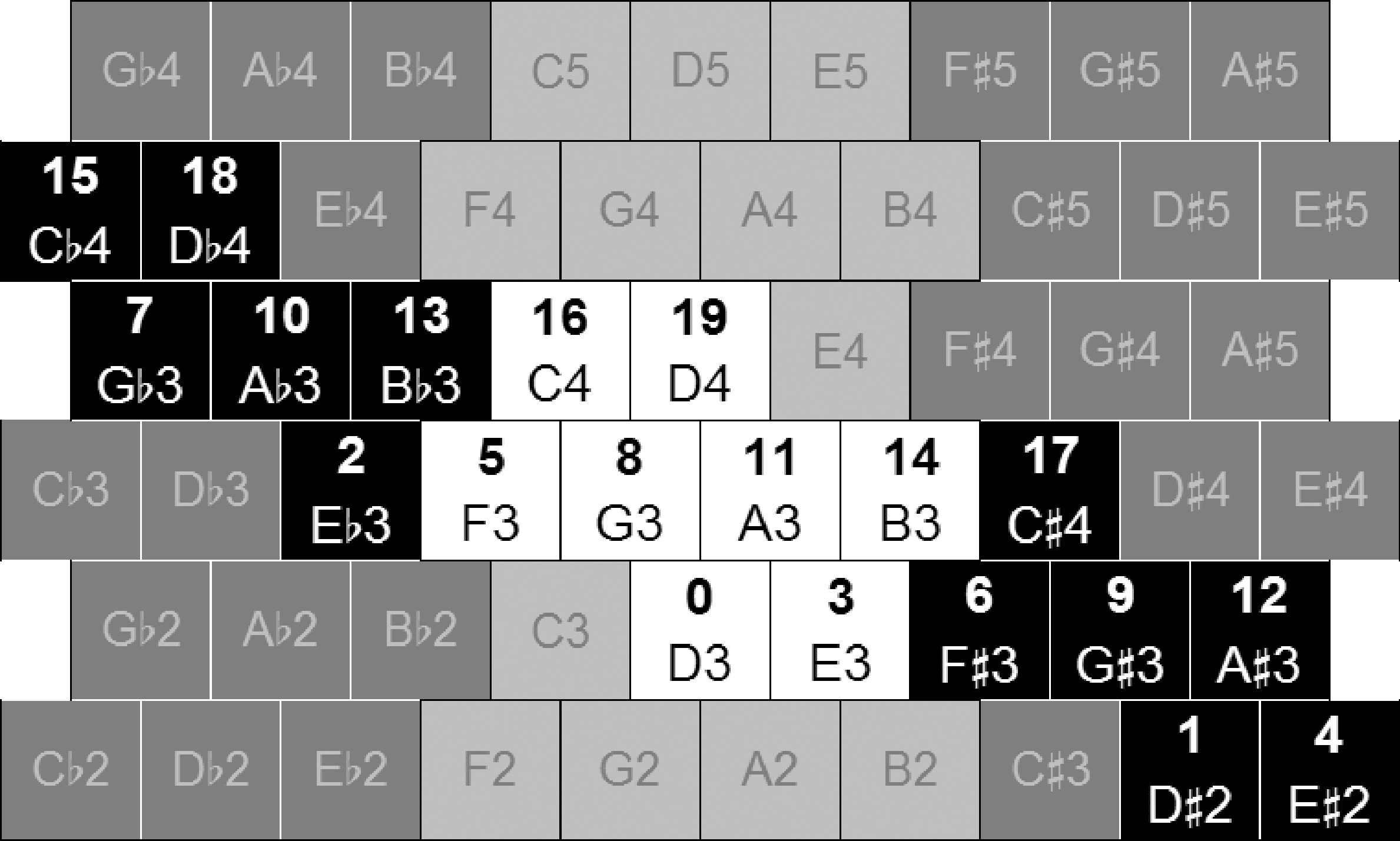
ordinal continuum of 24/7 < F < 23/5. Figure 9 shows
the pitch order of the buttons, starting from D3 (num-
bered 0) up to D4 (an octave above), as F traverses
this range. Despite these different configurations,
every melodic interval that is “legal” to common
practice has its order preserved. (Intervals such as
G-sharp–A-flat, F-flat–E-sharp, or C-flat–B-sharp
typically have no melodic function in common-
practice music.) For example, observe that although
the pitch order changes as the tuning is raised from
24/7 to 23/5, the diatonic notes (colored white in this
figure) remain in the same order, and so do the “le-
gal” chromatic intervals. The shape of the chromatic
melody Re–Mi–Fa–Fi–Sol is indicated by crosses,
26
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
c
o
m
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
⎡
⎣
⎢
⎤
⎦
⎥
Figure 9. Pitch order of
notes across the MOS:5+2
ordinal continuum’s tun-
ing range. The notes within
the D3 to D4 octave have
been highlighted. (a) F =
24/7 (7-TET); (b) 24/7 < F <
27/12; (c) F = 27/12 (12-TET);
(d) 27/12 < F < 210/17; (e) F =
210/17 (17-TET); (f) 210/17 < F
< 23/5; (g) F = 23/5 (5-TET).
(a)
(c)
(e)
(g)
(b)
(d)
(f)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
c
o
m
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Milne et al.
27
Figure 10. The step posi-
tions for a selection of
meantone n-TETs. The
notes within the D3 to D4
octave have been high-
lighted. For n-TETs where
n > 19, some of the notes
fall beyond the edges of
this button-field. (A) 意思是-
tone n-TET (19-TET); (乙)
meantone n-TET (50-TET);
(C) meantone n-TET (31-
TET); (d) meantone n-TET
(43-TET); (e) meantone
n-TET (12-TET).
(A)
(C)
(e)
(乙)
(d)
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
not easily specified a priori. 数字 2 shows the
MOS:5+2 ordinal tuning range, which corresponds
roughly with a reasonable (though inexact) syntonic
rational tuning range.
Using an isomorphic keyboard, a performer can
maintain the same fingerings of chords and melodies
throughout the relevant range of this tuning contin-
uum. Note that Figure 2 indicates only the syntonic
temperament, but a given tuning can belong to
more than one regular temperament. 例如,
it is likely that 53-TET tuning falls within the tun-
ing ranges of invariant rational identity for both the
syntonic and the schismatic temperament (哪个
tempers the 5-limit generators of Equation 1 和
a = –15, b = 8, and c = 1).
Dynamic Tuning
Keyboard designs that are invariant in both transpo-
sition and tuning offer several performance possibil-
ities to the computer-based musician and composer.
All the tunings of the syntonic (or MOS:5+2) 骗局-
tinuum can be characterized by the width of their
tempered fifth. The exact value of this fifth can be
and the pitch order within this shape remains the
相同的, only breaking down when F ≤ 24/7 or F ≥ 23/5.
Another natural consequence of invariant finger-
ing is that the steps of the various n-TETs falling
within any given continuum automatically line up
to the correct button position. This is illustrated by
数字 10, which shows a selection of meantone
n-TETs.
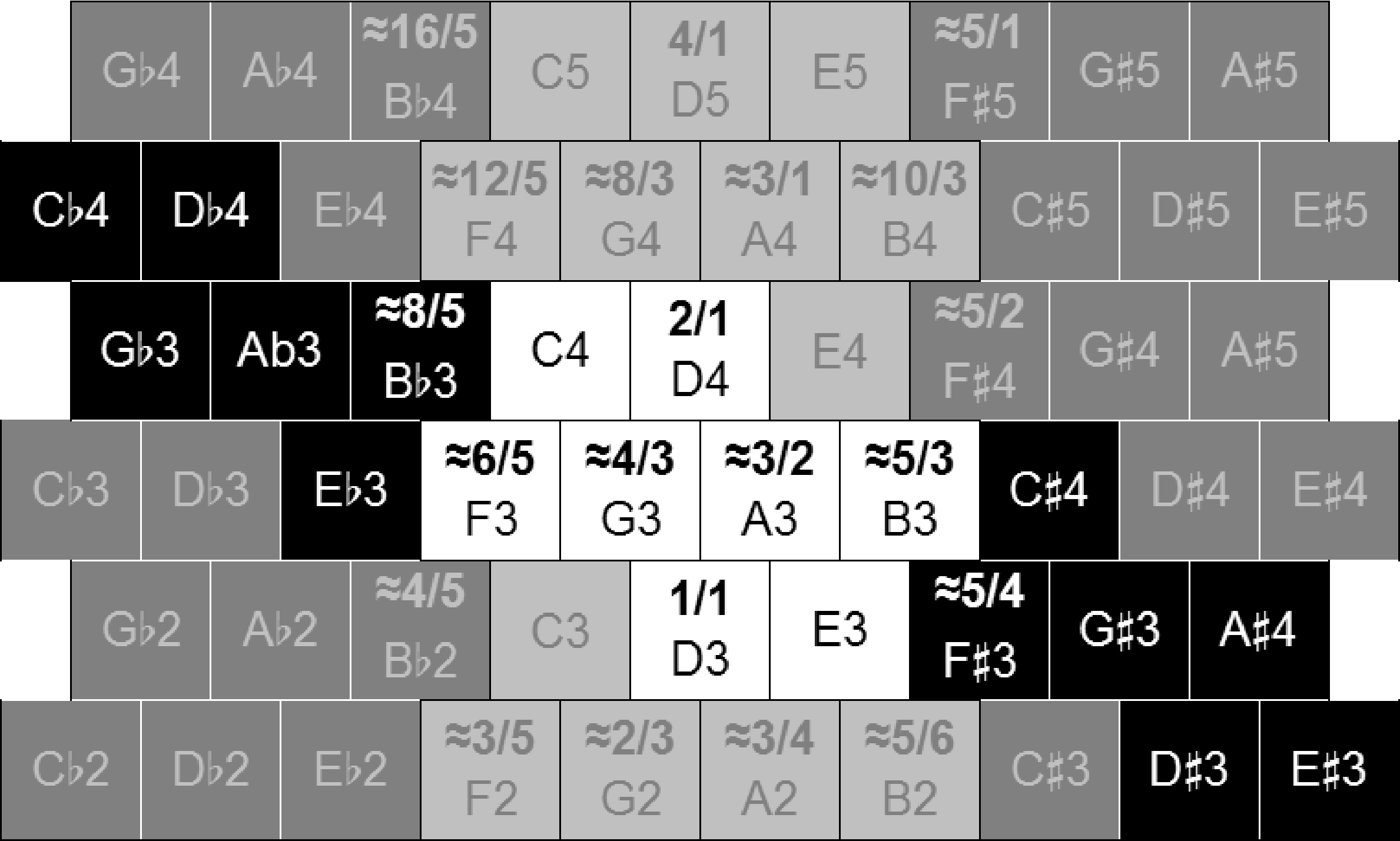
数字 11 shows the positions on the Wicki layout
of the common practice harmonic consonances that
can be signified over a range of values of the fifth F.
This example is again centered on the note D3 (一个
arbitrary choice).
As discussed previously, the limits for invariant
rational identification are context-dependent and
28
电脑音乐杂志
数字 11. Position of the
signified common practice
harmonic consonances us-
ing the Wicki layout and
the syntonic temperament.
数字 12. A simple chord
progression annotated
with the scale-step num-
bers in 31-TET, 12-TET,
and 17-TET. On an isomor-
phic keyboard, this chord
progression can be played
with identical fingerings
in all keys and all tunings
of the syntonic rational
continuum.
linked to a single slider, modulation wheel, joystick
轴, or other control device. As the performer
moves this control, thereby changing the width of
the tempered perfect fifth, the pitches of all sounded
notes will change correspondingly to match the cur-
rent tuning. If the extremes of the control’s range
correspond to the extremes of the MOS:5+2 ordinal
continuum, then sliding that control from one end
to the other will result in the continuum of tunings
shown in Figures 2 和 9.
例如, one might choose to perform a
simple I–IV–V–I pattern such as shown in Figure 12.
The three staves show the score as it would be writ-
ten in conventional notation; the numerical annota-
tions show the scale steps in each of three tunings
(31-TET, 12-TET, and 17-TET) as the parameter β
moves from 218/31 到 27/12 到 210/17. As shown in Fig-
乌尔 9, the fingering remains the same throughout
the continuum. 因此, players of a tuning-invariant
keyboard may be able to transfer competence in one
tuning (such as 12-TET) to others; hard-won manual
dexterity can be transferred directly to other tun-
ings within the continuum. This is not possible on
the piano keyboard, guitar fretboard, or other com-
mon musical interfaces.
The tuning can also be changed dynamically dur-
ing performance. By analogy with pitch bend, 这
might be called “tuning bend,” where the exact tun-
ing of each note in each interval is changed in re-
sponse to the physical motion of the controller. 为了
例子, the performer might push up into a supra-
Pythagorean tuning (like 17-TET) to give melodies
more expressive power, drop down to 12-TET to
perform a smooth enharmonic modulation, 和
then drop down to a quasi-meantone tuning (喜欢
31-TET) for more pleasing triads. This may give
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
keyboard players greater flexibility in mimicking
the kinds of expressive pitch deviations that string
(and aerophone) players reveal when altering their
intonation phrase by phrase (Sundberg et al. 1989).
而且, tuning bends are not limited to mono-
phonic implementations. Rocking the controller
back-and-forth describes a kind of (polyphonic) 六-
brato where each note might have a different
amount and direction of pitch deviation.
讨论
Music education, 表现, and composition
can benefit from the transpositional and tuning in-
variance provided by isomorphic button fields. 这
piano-style keyboard is incapable of achieving the
advantages of an isomorphic keyboard for three rea-
儿子们. 第一的, it is essentially one-dimensional, 和
Milne et al.
29
one-dimensional layouts can only have transposi-
tional invariance for equal temperaments. 第二,
its offset pattern of twelve keys per octave is only
well suited to tunings that use twelve (or fewer)
notes per octave. 第三, the piano keyboard’s offset
white and black keys hide the consistent patterns of
12-TET—let alone any other tunings—forcing stu-
dents to learn each key’s scales, chords, 和别的
properties by rote.
相比之下, with an isomorphic button-field, A
student need only learn the geometric shape of a
given interval once (within a given temperament),
and thereafter apply that knowledge to all occur-
rences of that interval, independent of its location
within a key, across keys, or across tunings. This re-
duces rote memorization considerably and engages
the student’s visual and tactile senses in discerning
the consistency of music’s patterns.
此外, the MOS:5+2 ordinal continuum
includes the tunings of many cultures and eras.
At one of the continuum’s extremes, 例如,
7-TET provides a close approximation to tradi-
tional Thai music (Morton 1980) and to tradition-
ally tuned African balafon music (Jessup 1983),
and at the other extreme, 5-TET is close to Indone-
sian slendro (Surjodiningrat, Sudarjana, and Susanto
1993). Between these two extremes can be found
many tunings that have been explored in European
历史, such as quarter-comma meantone,
Pythagorean tuning, and today’s ubiquitous 12-TET.
A student, having mastered the use of an isomor-
phic button field in any one of these tunings, 能
apply the same motor skills and music theory to all
其余的部分, making multi-cultural music education
considerably easier.
Although this article has focused on the syntonic
temperament and diatonic and chromatic scales,
the benefits of tuning invariance are gained by all
rank-two regular temperaments, such as schis-
matic, porcupine, magic, and hanson (Tonalsoft
2007), and their respective MOS scales. The differ-
ent geometries of different temperaments and MOS
scales on the same keyboard make it easier for stu-
dents to compare, 对比, and understand them,
experiencing those differences through sight and
touch in addition to hearing.
boards. Consider that accompanists are often asked
to transpose a piece at sight to accompany the range
of a particular vocalist. Being able to transpose on
the fly may be the mark of a master musician today,
but with an isomorphic keyboard, the task becomes
significantly easier. With an isomorphic keyboard
and dynamic tuning, performers can also execute
real-time polyphonic tuning bends, temperament
modulations, and other effects that are simply im-
possible on a piano keyboard or guitar fretboard.
Composers can also benefit from the transposi-
tional and tuning invariance of isomorphic key-
boards. Just as Beethoven was the first to exploit the
novel technology of the metronome to specify pre-
cise tempi (Stadlen 1967), composers writing for iso-
morphic keyboards can indicate appropriate tunings
for pieces that are meant to imply a baroque (quarter-
comma), medieval Ars Nova (Pythagorean), or mod-
ern atonal (12-TET) feel.
当然, there are also disadvantages to such
isomorphic keyboards compared to that of the pi-
ano. The playing of diatonic intervals connected by
parallel motion is more complex than on the white
keys of the piano, and with some layouts, 有一个
less obvious linear relationship between pitch
height and location on the keyboard. Although iso-
morphic keyboards have been proposed and built in
the past, they do not have a large installed user base
or a deep repertoire. This paper has shown that iso-
morphic keyboards can be coupled with appropriate
computer technology to provide the deeper benefits
of tuning invariance and dynamic tuning.
参考
Barbour, J. 中号. 1951. Tuning and Temperament: A Histori-
cal Survey. East Lansing, Michigan: Michigan State
College Press. Reprint, 纽约: 达卡波出版社, 1973.
Reprint, 纽约, Dover, 2004.
Blackwood, 乙. 1985. The Structure of Recognizable Dia-
tonic Tunings. 普林斯顿大学, New Jersey: 普林斯顿大学-
大学出版社.
Bosanquet, 右. H. 中号. 1877. Elementary Treatise on Musi-
cal Intervals and Temperament. 伦敦: Macmillan.
Cited in Helmholtz (1877).
凯里, N。, 和D. Clampitt. 1989. “Aspects of Well-
Performers can also benefit from isomorphic key-
Formed Scales.” Music Theory Spectrum 11:187–206.
30
电脑音乐杂志
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Carlos, 瓦. 1987. “Tuning: At the Crossroads.” Computer
Tonalsoft. 2007. “Equal Temperament.” Encyclopedia of
音乐杂志 11(1):29–43.
Clough, J。, 氮. Engebretsen, 和 J. Kochavi. 1999. “Scales,
Sets, and Interval Cycles.” Music Theory Spectrum
10:19–42.
Fokker, A. D. 1955. “Equal Temperament and the Thirty-
One-Keyed Organ.” The Scientific Monthly 81(4):161–
166. Available online at www.xs4all.nl/~huygensf/doc/
fokkerorg.html. (Accessed 26 行进 2007.)
Grady, K. 1999. “CS.” Message posted to Alternate Tun-
ings Mailing List. Available online at launch.groups
.yahoo.com/group/tuning/message/5244. (Accessed 11
十月 2006.)
Helmholtz, H. L. F. 1877. On the Sensations of Tone.
反式. A.J. Ellis. Reprint, 纽约: Dover, 1954.
Insall, M。, 时间. Rowland, and E. Weisstein. 2007. “Point
Lattice.” MathWorld—A Wolfram Web Resource.
Available online at mathworld.wolfram.com/
PointLattice.html. (Accessed 4 六月 2007.)
Jessup, L. 1983. The Mandinka Balafon: 一个介绍
with Notation for Teaching. La Mesa, 加利福尼亚州: Xylo
Publications.
Keislar, D. 1987. “History and Principles of Microtonal
Keyboards.” Computer Music Journal, 11(1):18–28.
Published with corrections in 1988 as “History and
Principles of Microtonal Keyboard Design,” Report
STAN-M-45, 斯坦福大学. 在线提供:
ccrma.stanford.edu/STANM/stanms/stanm45. (乙酰胆碱-
cessed 13 六月 2007.)
Lorentz, 右. 2001. “19-TET in a Renaissance Chanson by
Guillaume Costeley.” Paper presented at Microfest,
Claremont, 加利福尼亚州, 四月 6.
McLaren, 乙. 1991. “General Methods for Generating Mu-
sical Scales.” Xenharmonikon 13:20–44.
Morton, D. 1980. “The Music of Thailand.” In E. 可能, 编辑.
Music of Many Cultures. 伯克利, 加利福尼亚州: 大学-
sity of California Press, pp.63–82.
塞塔雷斯, 瓦. A. 2004. Tuning, 音色, Spectrum, Scale,
2ND版. 伦敦: Springer-Verlag.
史密斯, G.W. 2006. “Xenharmony.” Available online at
bahamas.eshockhost.com/xenharmo. (Accessed Octo-
误码率 2006.)
Stadlen, 磷. 1967. “Beethoven and the Metronome.” Music
and Letters 48:330–349.
Sundberg, J。, F. Anders, 和L. Frydén. 1989. “Rules for
Automated Performance of Ensemble Music.” Con-
temporary Music Review 3(1):89–109.
Surjodiningrat, W., 磷. J. Sudarjana, 和一个. Susanto. 1993.
Tone Measurements of Outstanding Javanese Gamelan
in Yogyakarta and Surakarta. Yogyakarta, 印度尼西亚:
Gadjah Mada University Press.
Microtonal Music Theory. 在线提供:
tonalsoft.com/enc/e/equal-temperament.aspx.
(Accessed 26 行进 2007.)
Wicki, K. 1896. “Tastatur für Musikinstrumente.” Swiss
patent 13329.
Wilson, 乙. 1975. “Letter to Chalmers Pertaining to Mo-
ments Of Symmetry/Tanabe Cycle.” Available online
at www.anaphoria.com/mos.PDF. (Accessed 26 行进
2007.)
附录A: Proof of Theorem 1
Let f : Z2 → Z2 be an invertible mapping from the
two-dimensional generators of a rank-2 tempera-
ment to the two-dimensional button-lattice. 任何
note N in the temperament can be represented in
terms of its generators α and β as N = αn βm, 哪个
can be written as the vector (n, 米) for n, m ∈ Z. 这
note is located on the button-lattice at f(氮) = f(n, 米).
An interval I is a ratio of two notes
=
氮
1
氮
2
n m
1
(西德:2) (西德:3)
1
(西德:2) (西德:3)
2
n m
2
(A.1)
which can be written (j, k), where j = n1–n2 and k =
m1–m2. A layout is transpositionally invariant if
every fixed interval I is fingered in the same man-
ner, IE。, 如果
f N
)
(
1
-
f N
(
)
2
=
f N
(
)
3
-
f N
(
)
4
(A2)
每当
氮
1
氮
2
=
氮
氮
3
4
=
我
(A.3)
因此, transpositional invariance requires that the
difference in locations between notes on the key-
board depends only on the interval (the j and k) 和
not on the particular notes (the n1 and m1). Expand-
ing Equation A.2 yields
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
F
⎟ −
n
1
米
1
F
+
n
j
1
+
m k
1
⎟ =
F
⎟ −
n
3
米
3
F
+
n
j
3
+
m k
3
(A.4)
where we used the equality of the intervals from
Equation A.3, IE。, that n2 = n1 + j, m2 = m1 + k, n4 =
n3 + j, and m4 = m3 + k. If the mapping f is linear,
then this can be rewritten
Milne et al.
31
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎟
F
⎟ −
n
1
米
1
F
⎟ +
n
1
米
1
F
j
⎟ =
k
F
⎟ −
n
3
米
3
F
⎟ +
n
3
米
3
F
j
k
(A.5)
which collapses to an identity for any ni and mi.
This demonstrates that linear layout mappings are
transpositionally invariant. An analogous argument
works for any invertible rank-r mapping f : Zr → Zr.
Additivity
Because Equation B.1 holds for all x and y, 它必须
hold for x = j and y = 0. Substituting into Equation
B.1 shows f(j + 我) – f(j) = f(0 + 我) – f(0). Because f(0) = 0,
this can be rearranged to show f(我 + j) = f(我) + F(j).
附录B: Proof of Theorem 2
Homogeneity
The converse of Theorem 1 is demonstrated by
showing that transpositional invariance implies lin-
earity of f. This will first be shown in the scalar
案件, where the defining Equation (A.1) for transpo-
sitional invariance is that for all fixed intervals i,
+
-
=
+
-
我
)
f x
(
f x
( )
(B.1)
for every x, y ∈ Z. We also assume that f(0) = 0. 林-
earity of f is shown by demonstrating additivity and
homogeneity.
f y
( )
f y
(
我
)
Since Equation B.1 holds for all x and y, 它必须
hold for x = i and y = 0. Substituting into Equation
B.1 shows f(我 + 我) – f(我) = f(0 + 我) – f(0). Because f(0) = 0,
this can be rearranged to show f(2我) = 2f(我). Induction
can be used to show the general case. Suppose that
F((k – 1)我) = (k – 1)F(我). Let x = (k – 1)i and y = 0. Substi-
tuting into Equation B.1 shows f((k – 1)我 + 我) – f((k –
1)我) = f(我). Using the inductive hypothesis, this can
be rearranged to show f(ki) = (k – 1)F(我) + F(我) = kf(我).
The generalization to two (or n) dimensions is
直截了当.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
C
哦
米
j
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
3
1
4
1
5
1
8
5
4
9
5
6
/
C
哦
米
j
.
.
2
0
0
7
3
1
4
1
5
p
d
.
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
32
电脑音乐杂志
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎟