Arbabyazd, L。, Petkoski, S。, Breakspear, M。, 索洛德金, A。, Battaglia, D ., & Jirsa, V. (2023). State switching and high-order
spatiotemporal organization of dynamic Functional Connectivity are disrupted by Alzheimer’s Disease. 网络神经科学, Advance
出版物. https://doi.org/10.1162/netn_a_00332.
State switching and high-order spatiotemporal
organization of dynamic Functional Connectivity are
disrupted by Alzheimer’s Disease
Lucas Arbabyazd1,* , Spase Petkoski1, Michael Breakspear2, Ana Solodkin3, Demian
Battaglia1,4+,@, Viktor Jirsa1,+,@
1
Université Aix-Marseille, INSERM UMR 1106, Institut de Neurosciences des Systèmes,
Marseille, 法国
2 University of Newcastle, Callaghan, NSW, 澳大利亚
3 神经科学, School of Behavioral and Brain Sciences. UT Dallas. 理查森, TX, 美国
4 University of Strasbourg Institute for Advanced Studies, 斯特拉斯堡, 法国.
*first author; +shared last authors; @corresponding authors
Contacts: demian.battaglia@univ-amu.fr; viktor.jirsa@univ-amu.fr
Short title (< 70 characters) Spatiotemporal dFC organization in AD Keywords (up to six) Dynamic Functional Connectivity | High-Order Interactions | Resting State | fMRI | Alzheimer’s Disease | Mild Cognitive Impairment 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / t . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 Abstract (< 200 words) Spontaneous activity during the resting state, tracked by BOLD fMRI imaging, or shortly rsfMRI, gives rise to brain-wide dynamic patterns of inter-regional correlations, whose structured flexibility relates to cognitive performance. Here we analyze resting state dynamic Functional Connectivity (dFC) in a cohort of older adults, including amnesic Mild Cognitive Impairment (aMCI, N = 34) and Alzheimer’s Disease (AD, N = 13) patients, as well as normal control (NC, N = 16) and cognitively “super-normal” (SN, N = 10) subjects. Using complementary state-based and state-free approaches, we find that resting state fluctuations of different functional links are not independent but are constrained by high-order correlations between triplets or quadruplets of functionally connected regions. When contrasting patients with healthy subjects, we find that dFC between cingulate and other limbic regions is increasingly bursty and intermittent when ranking the four groups from SNC to NC, aMCI and AD. Furthermore, regions affected at early stages of AD pathology are less involved in higher- order interactions in patient than in control groups, while pairwise interactions are not significantly reduced. Our analyses thus suggest that the spatiotemporal complexity of dFC organization is precociously degraded in AD and provides a richer window into the underlying neurobiology than time-averaged FC connections. (199 words) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / t / . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t Author Summary (< 125 words) Brain functions emerge from the coordinated dynamics of many brain regions. Dynamic Functional Connectivity (dFC) analyses are a key tool to describe such dynamic complexity and have been shown to be good predictors of cognitive performance. This is particularly true in the case of Alzheimer’s Disease (AD) in which an impoverished dFC could indicate compromised functional reserve due to the detrimental effects of neurodegeneration. Here we observe that in healthy ageing dFC is indeed spatiotemporally organized, as reflected by high- order correlations between multiple regions. However, in people with aMCI or AD, dFC becomes less “entangled”, more random-like, and intermittently bursty. We speculate that this degraded spatiotemporal coordination may reflect dysfunctional information processing, thus ultimately leading to worsening of cognitive deficits. (120 words) f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 Introduction Alzheimer’s Disease (AD) is the most common neurodegenerative illness with an estimated prevalence of 10-30% in people older than 65 years (Hou et al., 2019; Masters et al., 2015). Yet, despite substantial research, we are far from fully understanding the mechanisms that link pathophysiology to cognitive impairments. Neurodegeneration in AD has been traditionally associated with the extracellular accumulation of insoluble amyloid-β42 (Aβ) neuritic plaques (Glenner and Wong, 1984; Lemere et al., 1996) along with the intracellular accumulation of abnormally phosphorylated tau (pTau), that constitute the neurofibrillary tangles (Spires-Jones and Hyman, 2014). These processes yield to widespread neuronal death, synaptic loss, and atrophy (Bateman et al., 2012), with a progression of structural damages not occurring uniformly throughout the brain (Braak and Braak, 1991). However, the progression of neurodegenerative processes does not correlate linearly with the severity of cognitive impairment possibly due to a “cognitive reserve” accrued through education, cognitive training and a healthy lifestyle (Rentz et al., 2010; Snowdon, 2003). Furthermore, the severity of cognitive impairment symptoms in a patient can fluctuate substantially within the same day, faster than the time scales of neurodegeneration (Palop et al., 2006). Together, these findings suggest that AD involve alterations of neural dynamics and that these dynamical changes may be the mechanistic substrate leading to functional impairment or preservation. As molecular and structural changes alone do not fully account for cognitive impairment, alternative studies based on Functional Connectivity (FC) analyses have sought to fill the gap. In particular, resting state FC (Fox and Raichle, 2007) quantifies brain-wide correlations of BOLD signals, capturing interactions between regions. In this context it has been suggested that structural alterations in AD lead to FC changes (Dennis and Thompson, 2014), and that the early manifestation of Aβ toxicity preceding overt atrophy can be detected using resting state functional Magnetic Resonance Imaging (rsfMRI) (Hedden et al., 2009; Sheline et al., 2010a; Sheline et al., 2010b; Mormino et al., 2011). Changes in FC in AD include reduced connectivity within the default mode network (DMN, Greicius et al., 2004; Rombouts et al., 2005; Wang et al., 2006, 2007; Sorg et al., 2007; Fleisher et al., 2009; Zhang et al., 2009, 2010; Jones et al., 2011; Petrella et al., 2011), in a spatially non-uniform fashion (Damoiseaux et al., 2012). Besides Aβ, the deposition of pTau affects FC as well (Franzmeier et al., 2022). Furthermore, additional FC alterations have been reported, leading to functional disconnection between hemispheres (Shi et al., 2020; Wang et al., 2015) and a reduction of small-world l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 88 89 90 91 92 93 94 95 96 97 98 99 topology (Brier et al., 2014; Sanz-Arigita et al., 2010; Stam et al., 2009, 2007; Supekar et al., 2008). More recently, investigations of FC in AD have been extended to encompass time-varying, rather than time-averaged FC. Indeed, rsfMRI networks undergo a continuous reconfiguration of their weighed topology, and the statistical structure of spontaneous network reconfiguration carries information potentially useful to discriminate cohorts (Calhoun et al., 2014; Hutchison et al., 2013; Preti et al., 2017). The flexibility of dynamic Functional Connectivity (dFC) has been shown to correlate with cognitive performance (Bassett et al., 2011; Battaglia et al., 2020; Braun et al., 2015; Jia et al., 2014; Lombardo et al., 2020; Shine et al., 2016). In this view, ongoing variability of FC networks is not noise but rather, an actual resource subserving computation. The capacity to actively maintain a spatiotemporally organized yet variable dFC would confer the system resilience to cope with variable cognitive and environmental 100 conditions (Lombardo et al., 2020). Hence, the preservation of a “healthy” structured dFC 101 variability may provide a form of functional compensation and a likely neural substrate for 102 103 “cognitive reserve” (cf. also other studies linking mental training with enhanced dFC variability, e.g. Premi et al., 2020). Conversely, dynamic FC-based metrics thus promise to 104 better characterize the impact of AD pathology. 105 106 107 A number of studies have quantified dFC changes in healthy aging (Battaglia et al., 2020; Davison et al., 2016; Hutchison and Morton, 2015; Lavanga et al., 2022; Petkoski et al., 2023; Qin et al., 2015; Viviano et al., 2017) and in conditions such as schizophrenia (Damaraju et al., 108 2014; Sakoğlu et al., 2010), epilepsy (Liao et al., 2014; Liu et al., 2017) and Parkinson’s disease 109 (Fiorenzato et al., 2019; Kim et al., 2017). In AD, probabilities of temporal transitions between 110 alternative FC states have been shown to be altered (Jones et al., 2011; Fu et al., 2019; Gu et 111 112 al., 2020; Schumacher et al., 2019). Moreover, machine learning applications have achieved greater accuracy in differentiating between healthy control and aMCI or AD subjects when 113 trained with dFC-based rather than static FC metrics (Chen et al., 2017, 2016; de Vos et al., 114 2018; Wee et al., 2016). Although the contributions of these studies are promising, they are 115 largely descriptive and do not propose an explicit theory of why dFC changes lead to functional 116 117 consequences. Furthermore, the plethora of methods for dFC quantification (Hutchison et al., 2013; Preti et al., 2017) – from extracting discrete FC states (Allen et al., 2014; Thompson and 118 Fransson, 2016) to continuously time-resolved approaches (Battaglia et al., 2020; Lindquist et 119 al., 2014)– hinder the convergence of results. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / . / t / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 120 Here, we start from a theoretical tenet: efficient cognition requires spatiotemporally 121 organized FC variability, which is neither trivial, nor random, but complex. This assumption is 122 based on empirical evidence. Fluctuations in dFC are not a mere unstructured “Drunkard’s 123 walk”: More highly structured dFC trajectories are observed in individuals with higher 124 125 performance on general cognition domains (Battaglia et al., 2020; Lavanga et al., 2022). Further, individual FC links do not fluctuate independently but with network reconfigurations 126 governed by higher order coordination patterns, manifest by: non-trivial inter-link covariance 127 patterns (Davison et al., 2015; Faskowitz et al., 2020; Petkoski et al., 2023); “back-bones” 128 partially scaffolding dFC (Braun et al., 2015); and dFC flowing under the influence of 129 130 competing “meta-hubs (Lombardo et al., 2020). Reiterating, our hypothesis suggests that spatiotemporal structure of dFC between order and randomness allows for rich computation to 131 emerge from the systems’ collective activity (cf. Crutchfield, 2012). Correspondingly, we 132 predict that individuals with higher cognitive performance should display an enhanced 133 organization of dFC compared to those with impaired cognition (aMCI or AD) in which, 134 conversely, a loss of dFC spatiotemporal organization should be evident. 135 Here we analyze resting-state fMRI data acquired from individuals with better-than-normal 136 or normal cognitive performance –“supernormal” (SNC) and “normal controls (NC)– and those 137 clinically diagnosed with amnestic Mild Cognitive Impairment (aMCI) or Alzheimer’s Disease 138 139 (AD). We first characterized dFC across groups using two complementary methods. First, we use a state-based dFC analysis paradigm, in which we assume the existence of a small set of 140 possible discrete FC configurations and quantify dwell times in different states and the temporal 141 stability of different FC network links along state switching transitions (Thompson and 142 Fransson (2016)). Second, we use a state-free dFC analysis paradigm, where FC networks are 143 144 described as continually morphing in time. Through these complementary but convergent approaches, as described in the following, we find that the fluctuations of different links show 145 different degrees of mutual inter-dependence across the considered groups, shifting from a 146 “liquid-like” dFC (flexible but constrained) for SNC and NC toward a “gas-like” dFC 147 (uncorrelated and disordered) for patient groups. We also show that these changes in dFC 148 149 coordination cannot be fully accounted by changes occurring at the level of ordinary pairwise FC, but stem from the weakening of genuine higher-order interactions observed especially for 150 regions which are among the first to be physio-pathologically affected by AD. 151 152 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 153 Results 154 FC and dFC across a spectrum of cognitive performance 155 156 We considered an fMRI dataset including resting state sessions from subjects with varying degrees of cognitive skills. As our interest focusses not only on disease but also in healthy 157 cognition, healthy controls were subclassified in two groups (SNC and NC) based primarily on 158 composite memory Z scores to define the SNC and NC groups. That is, SNC had a higher 159 performance in the composite memory scores (Z > 1.5) and at least a Z > 0.7 in all other
160
161
cognitive domains (注意力, 语言, visuo-spatial and executive; see Materials and Methods
for more details). Healthy control subjects between NC and SNC or below NC were not
162
considered in the study. As shown in Fig. 1A, 从 73 subjects, 10 were classified as
163
supernormal controls (SNC), 16 as normal controls (NC), 34 as amnesic mild cognitive
164
impairment (aMCI), 和 13 as Alzheimer’s disease (广告). Across the four clinical groups, 那里
165
were no significant differences in age and sex.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
166
Based on rsfMRI time-series from these cohorts, we then computed (and compared across
F
/
d
哦
我
/
.
t
/
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
167
团体) a variety of static and dynamic Functional Connectivity (FC and dFC) 指标,
168
extracted with complementary approaches, assuming or not the existence of discrete FC states
169
170
in time (如图. 1乙). 重要的, as detailed below, we did not uniquely consider pairwise
interactions between two brain regions at a time, but also considered more complex
171
coordination patterns between larger groups of regions. Classic FC links express the existence
172
of a correlation between the BOLD fluctuations of two brain regions and are represented as a
173
link between two regional nodes: we refer hence to them as dimers, since they are computed
174
175
out of two parts. In classical FC analyses, dimers are static, as their strength is averaged over
the duration of complete resting state sessions. In dFC analyses, however dimer strengths
176
fluctuate in time. We can thus also compute correlations between different dimers. Estimating
177
these “correlations between correlations” requires jointly monitoring the BOLD fluctuations of
178
三 (如图. 1C, 顶部) or four (如图. 1C, 底部) 地区, hence the names of trimers and tetramers
179
–collections of three or four parts, respectively– used in the following.
180
We chose to focus in this study on dFC within a network of limbic brain regions of particular
181
兴趣 (如图. 1D). The rationale was twofold: 第一的, the regions included in the chosen limbic
182
subnetwork are highly interconnected brain regions that degenerate early in the disease process
183
(Arnold et al., 1991; Braak and Braak, 1991); 第二, previous modelling work confirmed their
184
185
central role in shaping the evolution of FC alterations comparing healthy controls to aMCI or
AD stages (J. Zimmermann et al., 2018).
我
D
哦
w
n
哦
A
d
e
d
F
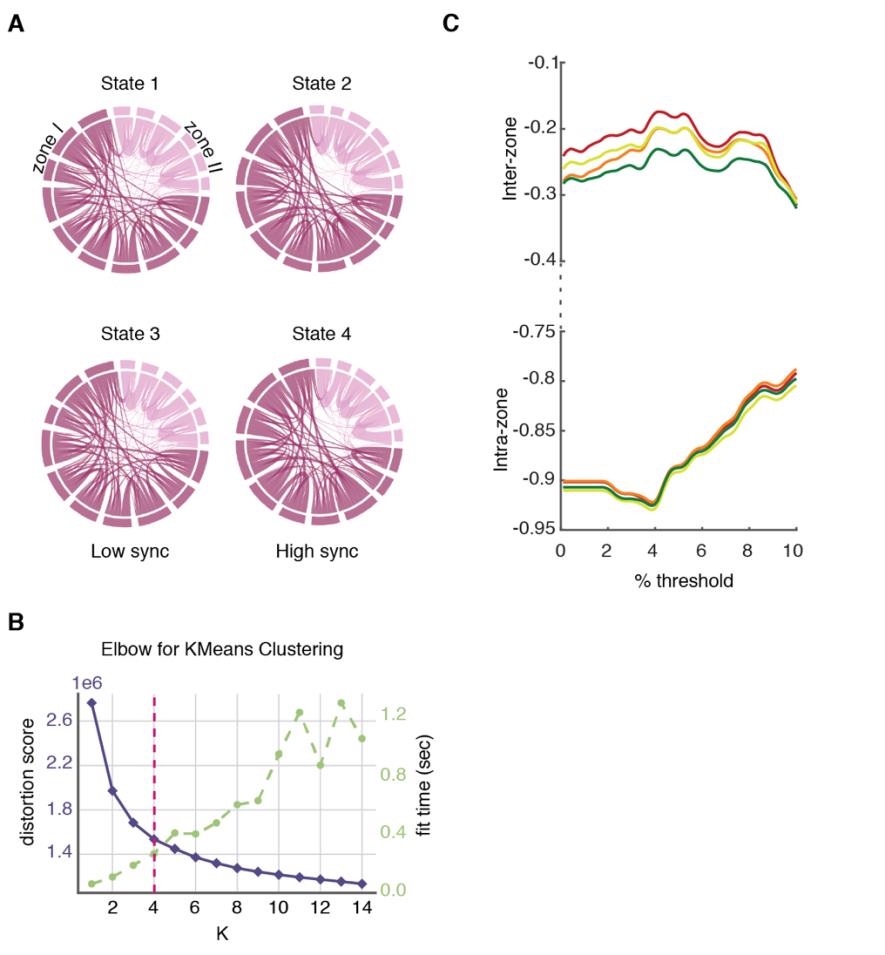
r
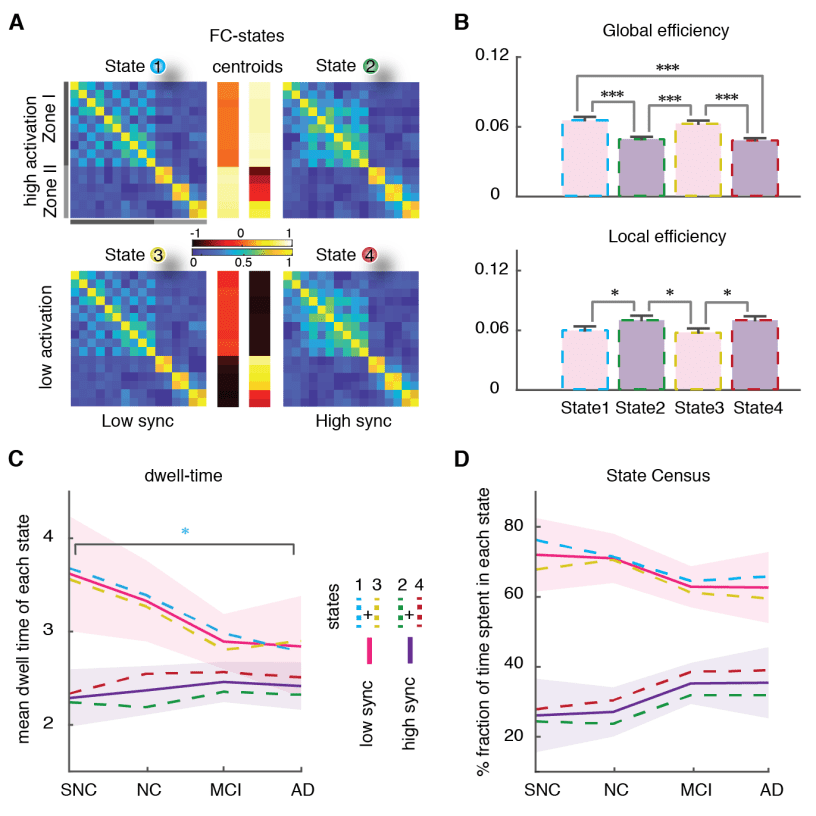
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
186
187
188
189
190
191
192
193
194
195
196
197
198
199
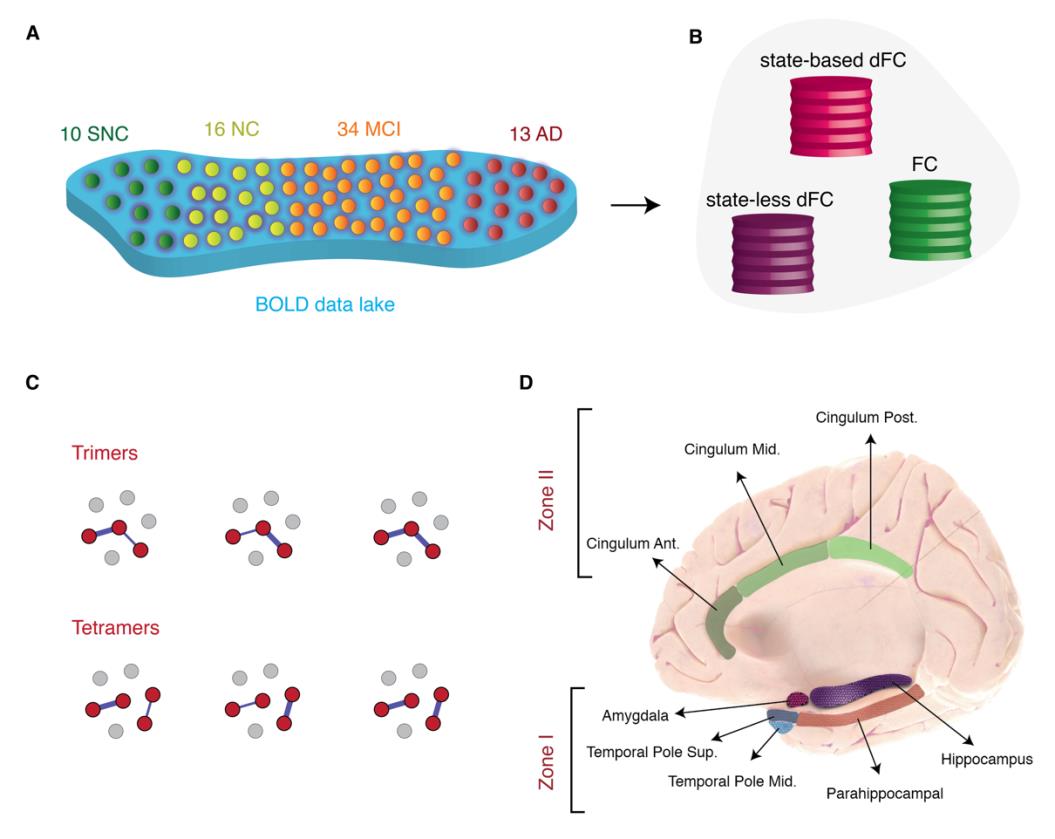
如图. 1. Overview of approaches. (A) Subjects were stratified in 4 different clinical groups: Supernormal
controls (SNC), Normal controls (NC), amnesic MCI (aMCI) and Alzheimer’s disease (广告) (乙) 我们
used two dynamic functional connectivity (dFC) methods to study the spatiotemporal properties of
resting-state fMRI signals: A state-based dFC called point-based method (PBM) and a state-free dFC
method called meta-connectivity (MC) 方法. Both approaches address the dynamics of pairwise
links of interactions, which we call here “dimers”. (C) The study of coordinated fluctuations of dimers
is at the core of the MC approach. Coordination can occur between dimers converging on a common
root (“trimers”) or between non-incident dimers (“tetramers”). (D) We focused on a limbic subnetwork
based on the AAL parcellation that was divided into two zones: a ventrally located “Zone I” that
included the temporal pole (superior and medial), parahippocampal gyrus, hippocampus proper and
amygdala; and a dorsally located Zone II included the anterior, medial and posterior cingulate cortices.
200
State-based dFC: two zones and four dFC states
201
In order to assess FC changes along time, we started with a state-based dFC approach, 被称为
202
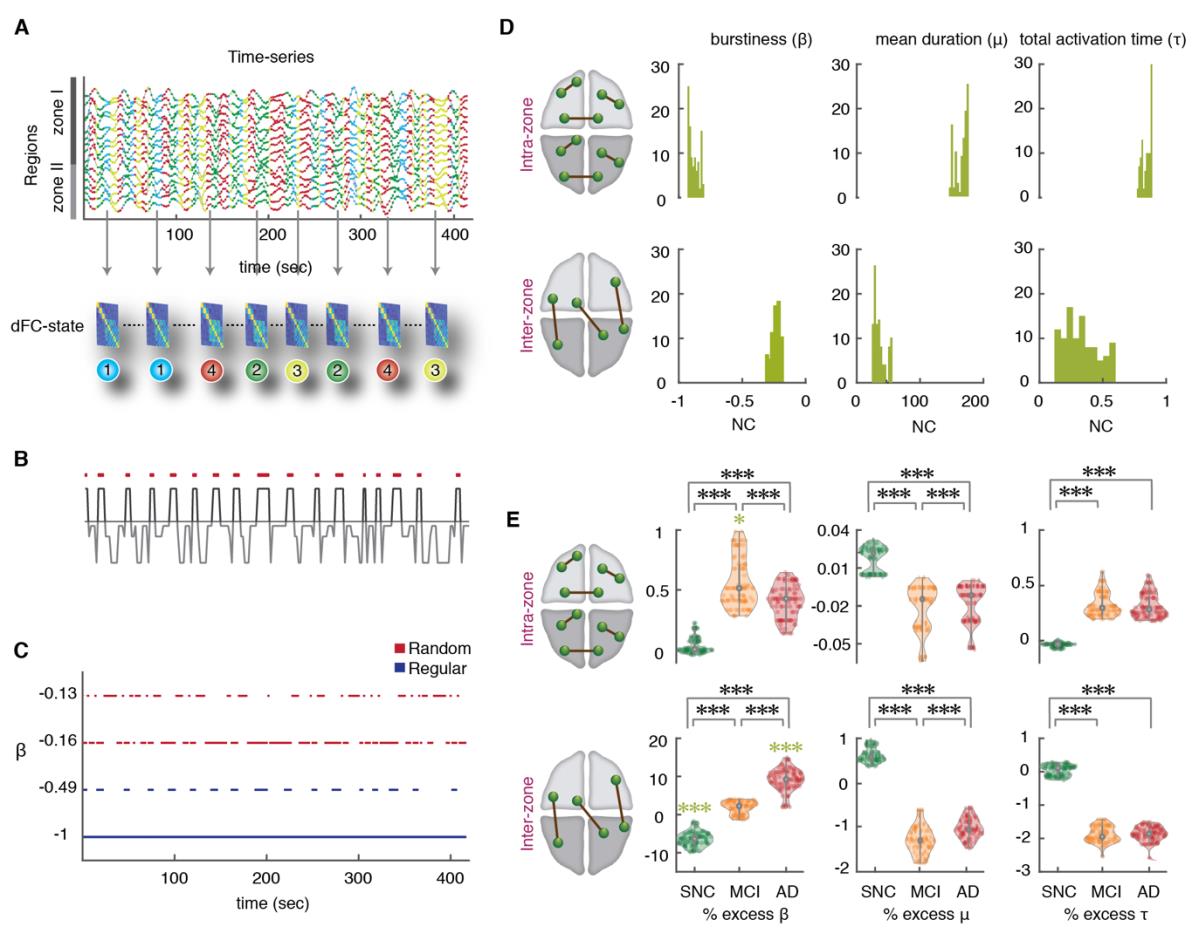
the point-based method (PBM) and first introduced by Thompson and Fransson (2016). 在这个
203
204
框架, different instantaneous images of brain-wide BOLD activation are first clustered
via an unsupervised procedure into K states, and state-specific FC matrices FC(λ) are constructed
F
/
d
哦
我
/
/
.
/
t
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
205
by evaluating BOLD correlations limited to timeframes assigned to a given state cluster
206
(λ = 1…K, see Materials and Methods for details). 如图. 2A show the weighed adjacency
207
matrices FC(λ) (obtained as centroids of their respective cluster) for each of four different states
208
of dFC, called S-graphlets by Thompson and Fransson (2016). An alternative graph
209
210
representation of these templates is shown in Fig. S1A. The optimal number of K = 4 曾是
determined based on a statistical elbow criterion (如图. S1B) and confirmed post-hoc by the
211
consistency of our results.
212
Based on these four dFC states, we obtained the spatial profile of neural activation across
213
地区 (如图. 2A). The spatial organization of the observed neural activation profiles naturally
214
215
suggests, in this study, to group the regions in two subsets, characterized by having an activity
level transiently higher or lower than their average level. We defined “zone I” as the subset of
216
ventral limbic regions including amygdala, temporal pole (superior and medial), hippocampus,
217
and parahippocampal gyrus. “Zone II”, included the cingulate gyrus (前部, medial, 和
218
后部). In states 1 和 2, zone II (dorsal regions) and zone I (ventral regions) 是
219
220
221
respectively active above average level (high activation states). 相比之下, in states 3 和 4,
zone II and zone I regions were respectively active below average levels (low activation states).
此外, these four states were noted based on the topology of their FC(λ) networks and
222
the level of internal synchronization within zone I. Quantitatively, connection weights between
223
224
regions within zone I tended to be stronger for states 2 和 4 than for states 1 和 3 (average
within zone I FC weights = 0.23 ± 0.16 for states 1 和 3 vs = 0.29 ± 0.18 for states 2 和 4).
225
因此, 状态 2 和 4 displayed higher internal synchrony, in contrast to states 1 和 3. 然后
226
we computed local and global efficiency metrics (Achard and Bullmore, 2007; Latora and
227
228
229
Marchiori, 2001) for the four FC(λ) 网络. Global efficiency quantifies how well
communication pathways can be established between any two nodes in a weighed network.
Local efficiency quantifies the robustness of communication and the possibility to find
230
alternative routes if local connectivity is disrupted. We found that the high sync states 2 和 4
231
have a lower global efficiency (如图. 2乙; Mann-Whitney U test, p < 0.001) but a greater local 232 efficiency (Fig. 2B, Mann-Whitney U test, p ~ 0.023), reflecting a denser within-zone but a 233 234 235 weakened between-zone connectivity (average between zone I and zone II FC weights = 0.026 ± 0.069 for states 1 and 3 vs = -0.013 ± 0.071 for states 2 and 4). Thus, in short, the overall four states that we find are obtained as combinations of two 236 qualitatively different network topologies an two possible levels of activation, so that each 237 topology can exist in a low and high activity versions. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / . t / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / / / t . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 Fig. 2. State-based dynamic Functional Connectivity (dFC) analyses: four dFC states. (A) BOLD time-series of all subjects were concatenated temporally and then z-scored and clustered based on BOLD activation to extract four states. The associated FC-state matrices (FC(λ), λ = 1…4) were constructed by evaluation BOLD fluctuation correlations limited to time-points within a given state (cf. also Fig. S1A). The centroids of activation of four states (middle) distinguished two subsets of regions (Zone I and Zone II) where their activity was transiently higher or lower than average. States 1 and 2 (or 3 and 4) showed above (or below) average level activation for zones II and I, respectively, therefore were labelled as high (or low) activation states. We referred to states 2 and 4 as high synchronization states because the FC connection weights within zone I tended to be stronger than states 1 and 3 (low synchronization; average within zone I FC weights = 0.23 ± 0.16 for states 1 and 3 vs = 0.29 ± 0.18 for states 2 and 4). (B) Global and Local efficiency as measure of robustness in the communication pathways can be established between regions and was applied on the FC-states. States 1 and 3 with low synchronization showed higher global and lower local efficiency compared to high synchronization states 2 and 4. (C) States with low synchronization showed decrease in mean dwell-time across clinical groups (~3.6 TR = 7.4 s, for SNC; ~2.8 TR = 5.7 s, for AD), where the decrease of state 1 was significant (blue; p-value ~ 0.032; Mann-Whitney U test). States 2 and 4 showed a slight increase from the control groups to the patient groups. A decrease in average dwell-time of states with relatively higher global efficiency indicates that they are less stable. (D) Analogously, the relative fraction of time spent in states with low synchronization was decreased in aMCI and AD compared to NC. Note the increase from SNC to AD groups for states with high synchronization. 260 261 Stability of globally efficient dFC states decreases along the clinical spectrum 262 We quantified the stability of dFC both by the longer or shorter duration of transient epochs 263 within a given state (average dwell time, Fig. 2C) and by the overall time fraction spent within 264 265 a state (average state census, Fig. 2D). As shown in Fig. 2C, group differences were identified in the mean dwell-time of low sync states, with longer dwell-time for the two control groups 266 (~3.6 TR = 7.4 s, for SNC at one extreme) and shorter for the MCI and AD groups 267 (~2.8 TR = 5.7 s, for AD at the other extreme). However, the mean dwell-time of high sync 268 states were not different. 269 270 Analogously, Fig. 2D shows that the relative fraction of time spent in low sync states decreased in aMCI and AD compared to healthy controls (ranging from 62% for AD to 72% 271 for SNC). 272 In summary, low-sync and globally efficient dFC states were less frequent and more 273 transient in aMCI and AD, suggesting a reduction of their overall stability. 274 275 Inter-zone dFC dimers are more intermittent in patient than in control groups 276 The next step, also following Thompson and Fransson (2016), was to map a state-based dFC 277 temporal network to each subject’s resting-state acquisition. To do so, we constructed a 278 279 sequence of network time-frames FC(t) set to be equal to the FC(λ) graph specific for the state λ visited at time t (Fig. 3A; see Materials and Methods for details). Thompson and Fransson 280 (2016) called such a temporal network a T-graphlet. 281 In this approach, each link can assume up to four possible strength values, corresponding to its 282 283 284 strengths in the FC(λ) associated to each of the four states. Hence, any variability of dFC dimers reflects exclusively state-switching dynamics. Figure 3B shows the time-course for a representative fluctuating dFC dimer. The temporal organization of link fluctuations (periodic 285 or bursty) can be highlighted by a binarization procedure, where a link is set to 1 if its 286 instantaneous strength is above the threshold θ, or to 0 otherwise (see Materials and Methods). 287 The result of this procedure is shown in Fig. 3C, for a few representative links and a specific 288 289 choice of threshold. A link whose strength remains steadily above (below) threshold will result as constantly –or tonically– “active” (“inactive”). In contrast, a link whose fluctuating strength 290 crosses the threshold through the different dFC-state frames will undergo several activation and 291 inactivation events at specific threshold crossing times. Yet, there can be various types of l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / t / . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 292 intermittency, with different temporal statistical properties. The durations of different link 293 activation and inactivation epochs could all be roughly similar, resulting in a more periodic 294 type of intermittency (blue color link activation rasters in Fig. 3C). Alternatively, they could be 295 more variable, stochastically alternating between shorter and longer activation epochs (red 296 297 color rasters in Fig. 3C). The degree of temporal regularity in link activation and deactivation dynamics can be evaluated, link-by-link, by the quantification of a burstiness coefficient (β). 298 We also define the mean duration of a link’s transient activation events as mean activation (μ) 299 and the total fraction of time in which a link is active relative to imaging session duration, total 300 active time fraction (τ). The burstiness coefficient is bounded in the range -1 ≤ β ≤ 1, with: 301 302 β < 0, corresponding to near-tonic or periodic link activation dynamics; β = 0, corresponding to Poisson (random-like) link activation dynamics; and β > 0, corresponding to time-clustered
303
(bursty) events of link activation. Mean activation times μ are bounded to the length of time-
304
系列. Total active time fraction is also bounded, 0 ≤ τ ≤ 1.
305
306
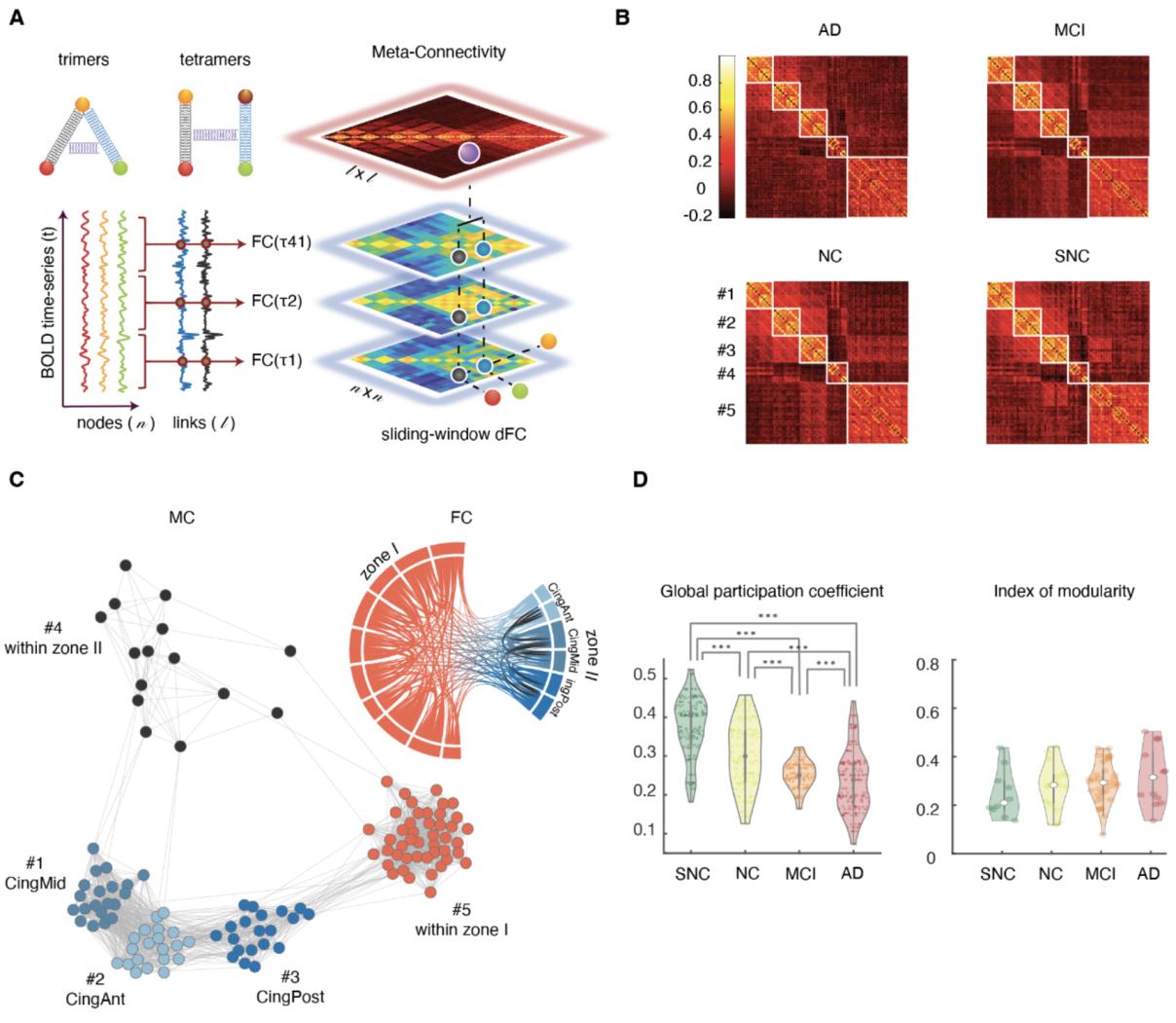
307
In this approach, three numbers β (burstiness coefficient), μ (mean activation) and τ (全部的
active fraction) fully characterize the binarized dynamics of a link (for a given choice of the
308
strength threshold θ). These metrics were evaluated for the two categories of dFC dimers: intra-
309
zone (between two regions within either zone I or II) and inter-zone (between one region in
310
311
zone I and one region in zone II). Our results show that these two categories have distinct
distributions of β, μ and τ, first exemplified in NC subjects (如图. 3D). Whereas Inter-zone dFC
312
dimers are closer to a Poisson-like intermittency (β = -0.229 ± 0.020, median ± m.a.d), intra-
313
zone dimers, present a tonic activation time-course (β = -0.890 ± 0.027, median ± m.a.d). 在
314
添加, inter-zone dimers are also less active (τ = 0.312 ± 0.099 for inter-zone vs.
315
316
τ = 0.855 ± 0.027
为了
intra-zone dimers) and activate
for shorter
transient
次
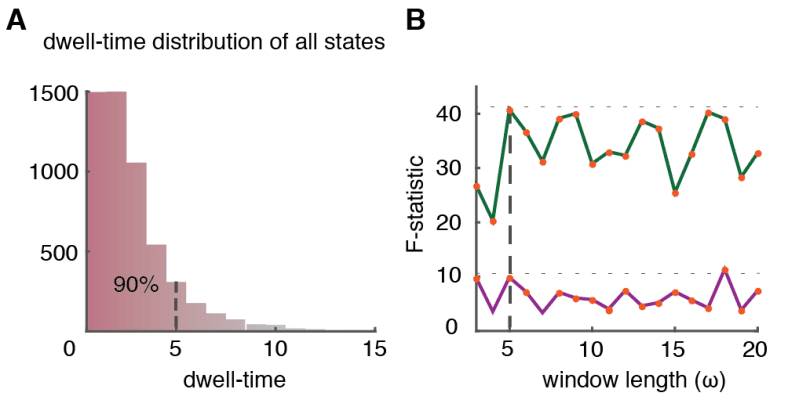
(μ = 34.926 ± 4.439 for inter-zone vs. μ = 178.995 ± 7.378 for intra-zone dimers). These results
317
suggest a smaller average strength of inter-zone time-averaged FC than for intra-zone FC.
318
Using NC subjects as reference group, we measure indeed an average FC(t) strength = 0.083 ±
319
0.135 for inter-zone and of 0.564 ± 0.155 for intra-zone dimers (average ± s.d.). 相似的
320
321
differences were found for all groups (Table S1). The relative differences in β, μ and τ between
intra- and inter-zone dimers are maintained over the entire range of possible thresholds θ (如图.
322
S1C for bustiness coefficient). Inter-zone dimers also displayed more burstiness, were more
323
transient and less active than intra-zone dimers in all groups.
324
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
.
/
t
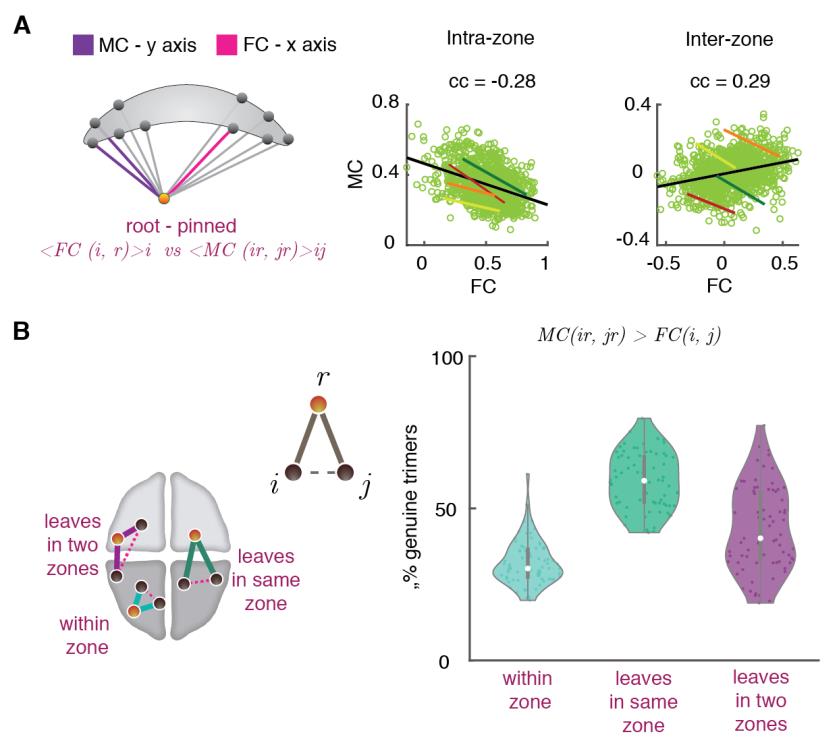
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
/
.
F
乙
y
G
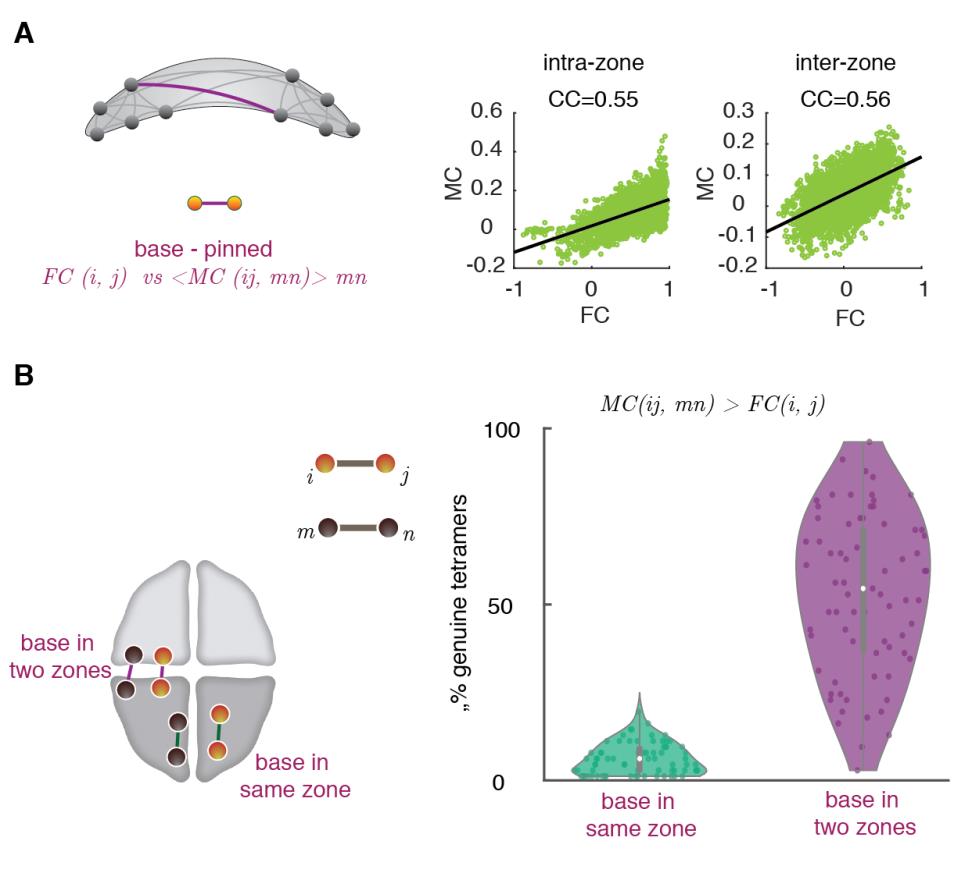
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
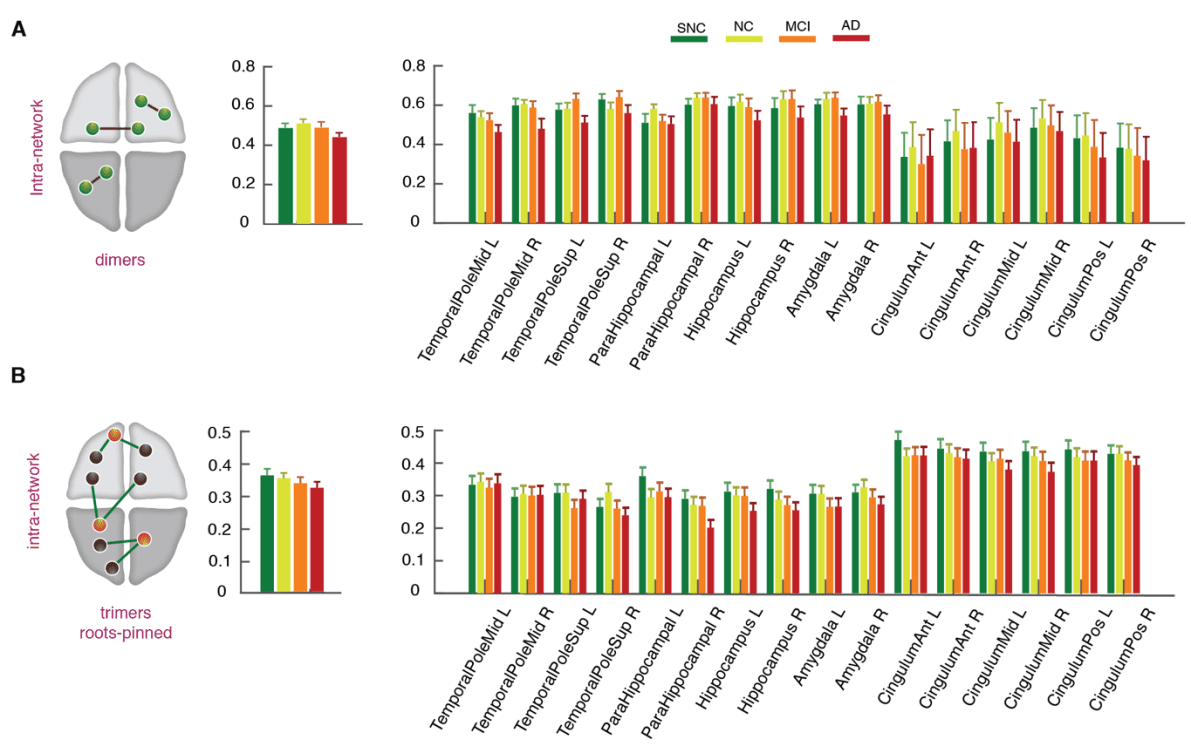
r
2
0
2
3
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
t
/
.
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
t
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
如图. 3. State-based dFC analyses: increase of intermittency in inter-zone links. (A) To construct the
state-based dFC temporal network, a specific FC(λ) graph was assigned to each BOLD signal intensity
time-point (we show here 416 time-points = 20 minutes of rsfMRI acquisition, for two concatenated
subjects). 最后, there is a time-course for every FC links where they can assume up to four
possible different strength values (link dynamics due to state switching). (乙) The temporal organization
of link fluctuations can be assessed by determining intervals of link activation and inactivation (via a
thresholding of dynamic strengths with a global threshold θ on all the links). The threshold θ ranges
从 1 到 10 % of the maximum strength over the dataset. The figure shows binarization for a
representative dFC dimer. (C) The degree of temporal regularity in link activation/deactivation was
assessed by quantifying the burstiness coefficient β, the mean activation time μ and the total activation
time τ for every link and subject. The burstiness coefficient is bounded in the range -1 ≤ β ≤ 1 where it
approaches to -1 if the link is tonic/periodic (blue lines), or it can approach to 0 if it has Poissonian
(random-like) patterns of activation (red lines); β = +1 corresponds to links with bursty-like events of
activation. (D) Distributions of β, μ and τ for the NC group, later used as reference. Upper and lower
rows represent distributions over, 分别, intra zone and inter zone links (for an intermediate
临界点, 0.0087 < θ < 0.0870). Left: Distribution of burstiness coefficients across different thresholds averaged over two subsets of intra- and inter-zone links. The β of intra-zone dimers approach to -1 and have more tonic/periodic patterns of activation (β = -0.890 ± 0.027, median ± m.a.d), while the β inter- 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 zone are closer to 0 and show more Poisson-like intermittency (β = -0.229 ± 0.020, median ± m.a.d). Middle: The mean duration μ which is bounded to the length of time-series for one subject (208 time- points), for the intra-zone links was longer than inter-zone links. Right: Analogously, the normalized total activation time (τ) of intra-zone links were longer than inter-zone links. (E) Mean values for the NC group were used as reference and percent relative variations were computed for the other SNC, aMCI and AD groups, combining relative values for different thresholds (see Materials and Methods). Upper and lower rows refer to intra- and inter-zone links. Left: Notice the large burstiness increase across groups for the inter-zone links (~1.8% for aMCI and ~9% for AD; green stars, p-value < 0.001; Mann-Whitney U-test) compared to a slight increase in the burstiness values of intra-zone links (~0.5%). In contrast, SNCs showed a significant decrease of ~ -6.5% relative to NC group in the inter-zone links. Comparisons between SNC, aMCI and AD for both intra- and inter-zone links were all significant (black stars). Middle: The mean activation durations of inter-zone links showed a relative negative decrease of roughly -1% for aMCI and AD subjects. Right: Total activation time τ was reduced to roughly -2% in aMCI and AD compared to NCs. Thus, temporal dynamics of dFC dimers are more tonic/periodic in SNCs than NCs and more intermittent in aMCI and AD subjects, particularly for inter-zone dimers. To achieve a robust and more precise comparison of β, μ and τ distributions between the cohorts (Fig. 3E), we computed percent changes of the three indicators in SNC, aMCI and AD 363 groups relatively to normal controls. The advantage of relative comparisons is that they can be 364 collated for different threshold values θ, resulting in a threshold-independent analysis. We 365 found that, moving from NC to aMCI and AD subjects, many dFC dimer links tended to have 366 367 larger burstiness values. In contrast, moving from NC to SNC subjects, dFC dimers tended to be more tonic. These trends of β were smaller yet significant for intra-zone FC dimers (Fig. 368 3E), compared to inter-zone dimers, reaching +1.869 ± 1.663 % for aMCI patients, +9.071 ± 369 3.001 % for AD patients and -6.404 ± 1.938 % for SNC subjects (Fig. 3E) that had larger values. 370 371 372 These results reinforce the notion of a significant reduction of inter-zone time-averaged FC along the clinical spectrum (cf. Table. S1). More importantly and beyond this reduction of average strength, our results point to a degradation of the temporal regularity of FC fluctuations. 373 While the total active time fraction τ of inter-zone dFC dimers decreased by less than -2% from 374 NC subjects to aMCI and AD patients (Fig. 3E; and even increased for intra-zone dimers), the 375 376 burstiness of inter-zone links increased over 10%, showing a real alteration in the temporal statistics of link activation, well beyond the trivial decrease necessarily induced by the observed 377 reduction of average strength. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / . / / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 378 We also observed a significant decrease of the mean activation time μ (Fig. 3E), for both 379 intra-zone and inter-zone dFC dimers (-1.275 ± 0.227 % for aMCI and AD subjects compared 380 to NCs). For SNC relative to NC, however inter-zone link burstiness decreased and their 381 activation time increased (+0.613 ± 0.161 % for SNCs). 382 383 Goh and Barabasi (2008) also defined another metric related to burstiness, the memory coefficient. This coefficient λ (see Methods for exact definition) becomes significantly positive 384 when autocorrelation exists in the duration of consecutive link activation events, i.e. when long- 385 (short-) lasting activation events tend to be followed by activation events which also are long 386 (short). Computing λ, we found a weak median autocorrelation in all four groups, for both intra- 387 388 and inter-zone links. Values (see Supplementary Table S2) were small but still significant given the large number of activation events. Furthermore, memory was decreasing across the four 389 groups from SNC to AD, providing yet another indication of increased disorder. 390 In summary, the temporal dynamics of dFC dimers between regions in different zones is 391 altered along the SNC-AD spectrum from tonic and periodic in SNC to more intermittent in 392 393 aMCI and AD subjects. Together with the finding of altered dwell times and transition dynamics between dFC states (Figs. 2C, D), our state-based dFC analyses based on the PBM 394 approach suggest that changes towards AD involve a degradation of global integration and an 395 increased disorderliness of dynamic functional interactions between zones. 396 397 State-free dFC: entangled dFC flows in continuous time 398 The PBM approach to dFC analyses reduces the description of FC network reconfiguration 399 to the tracking of discrete state switching events. Alternatively, sliding-window approaches 400 evaluate the evolution of FC links as a continuous reconfiguration along time. As shown in Fig. 401 402 4A, all dFC dimers FC(t1) can be evaluated in a time-resolved manner restricting their estimation to BOLD signal time-series within a window centered at time t1. The window is then 403 shifted at a slightly increased time t1 + δt, providing an updated set of values FC(t1 + δt). The 404 result is a collection of smoothly varying continuous time-series FC(t) for each possible dFC 405 dimer (Allen et al., 2014; Battaglia et al., 2020). 406 407 As in the case of node activity time-series, it is possible to study covariance between the temporal evolutions of different dimers. The case in which their fluctuations are not 408 independent –or, in other words, that the dimers are “entangled”– will be signaled by 409 significantly positive or negative correlations between dimers. These correlations can be l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 410 represented graphically by trimer and tetramer diagrams in which the two entangled dimers are 411 linked by a spring (Fig. 4A, top left; we will omit in the following to draw this spring, for the 412 sake of a clearer visualization). The stronger the correlation between the fluctuations of 413 different dFC dimers in a trimer or tetramer, the stronger will be their “entanglement” (i.e., 414 metaphorically, the stiffness of the spring). 415 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / / t . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 416 417 418 419 420 421 422 423 424 425 Fig. 4. State-free dFC: Meta-Connectivity. (A) We slid a window of length 𝜔 = 5 TRs (10 s) with no overlap on the BOLD signals from the n considered regions. We then computed n x n FC matrices for each window using Pearson’s correlation between pair of regions. In this way each of the l possible pairwise links of FC becomes associated to a continuous time-series of varying FC strength. Correlations between these link time-series can be compiled in a l x l Meta-Connectivity (MC) matrix. We represent here trimer and tetramers with a spring between the involved dimers, as, in presence of meta- connectivity, pairwise links are not free to fluctuate independently. (B) Group average MC matrices for the four clinical groups. Louvain algorithm was applied on the MC matrices resulting in five modules. (C) A graph representation of the MC for the NC group, together with a chord-diagram of FC for the 426 427 428 429 430 431 432 433 434 same group. Each node in the MC graph corresponds to a link in the FC graph. The different MC graph modules correspond thus to different types of links: MC modules #1, #2 and #3 include inter-zone links incident, respectively, to medial, anterior and posterior cingulate cortices (edges within these modules are thus inter-zone trimers rooted in Zone II); MC module #4 and #5 include links, respectively, within zones II and I. (D) Modules are also connected between them. The relative amount of inter-module meta-links is captured by the global participation coefficient (averaged over the five modules) which showed a significant decrease across the clinical groups (Mann-Whitney U-test, p < 0.001). These strengths of entanglement between FC dimers can be compiled into a meta- connectivity matrix (MC; Fig. 4A). The notion of MC (Lombardo et al., 2020) is strongly related 435 to the edge-centric FC discussed by Faskowitz et al. (2020). The key difference is that MC is 436 obtained by using a short smoothing window in the estimation of the stream of FC(t) matrices, 437 while edge-centric connectivity captures coincidences between instantaneous fluctuations. The 438 439 denoising brought by the smoothing window allows an easier extraction of the modular structure of MC, with respect to edge-centric FC (cf. Lombardo et al., 2020), but the two 440 concepts are otherwise equivalent. The choice of window size (here 5 TRs, Materials and 441 Methods) was motivated by the fact that the state-based PBM method suggested that ~90% of 442 epochs within a coherent state lasted less than 5 TRs (Fig. S2A), indicating a fast intrinsic 443 444 timescale of link fluctuation. Furthermore, we can observe post-hoc that the use of larger (or smaller) windows would not improve the capability to separate our groups based on MC values 445 (Fig. S2B). 446 Group-averaged MC matrices are shown in Fig. 4B for the four groups. Their modular 447 structure is evident at simple visual inspection. A module in the MC matrix –also called dFC 448 449 module or meta-module (Lombardo et al. (2020))– corresponds to a set of co-fluctuating dynamic FC links, i.e. to FC subnetworks whose overall strength waxes and wanes transiently 450 along the resting state in an internally synchronous manner. The existence of non-uniform MC 451 matrices indicates that the flow of dFC reconfiguration is not mere noise but rather, it is 452 organized by specific arrangements of “springs between the links”. In other words, fluctuations of FC dimers are entangled in complex patterns reflecting higher-order correlations (non- vanishing trimers and tetramers) between the coordinated activation of multiple regions. 453 454 455 456 dFC flow in patients is less globally entangled 457 458 MC matrices can also be represented as graphs, in which MC-nodes correspond to different FC-links and MC-links appear due to the entanglement between the FC-links. An example l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / . / / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 459 graph embedding is shown in Fig. 4C for the MC matrix of the NC group. Graph vertices are 460 color-coded depending on the type of associated FC link (i.e. start and end zones of the links, 461 cf. FC diagram with matching colors at the top right of Fig. 4C). Notably, the different dFC 462 modules, visible as blocks in the MC matrices of Fig. 4B and as uniform-color node 463 464 communities in the graph of Fig. 4C, are composed of FC dimers with internally homogeneous start and ending zones. 465 A standard graph-theoretical notion useful when commenting about dimer arrangements into 466 trimers and tetramers is the one of incidence: a link is incident to a node (or a node incident to 467 a link), if the link is attached to the node (the notion of incidence complements the more familiar 468 469 one of adjacency, where two nodes are said to be adjacent if connected by a link). Equipped with this terminology, we call root the common region incident to both the dimers within a 470 trimer, while the other two regions form the leaves of the trimer. We can then describe the first 471 three dFC modules (#1, #2 and #3) of the MC matrix as including mutually entangled FC dimers 472 originating in either one of the Zone II cingulate regions and terminating in Zone I. The 473 474 entanglement of FC dimers gives thus rise to strong inter-zone trimers with “roots” in Zone II and “leaves” reaching out to Zone I regions. The two other dFC modules #4 and #5 include 475 dimers within Zone I and Zone II, respectively, forming strong within-zone trimers or tetramers. 476 Entanglement is thus particularly strong between dimers within a same zone and between inter- 477 zone dimers incident on a common root region (in Zone II). 478 Although the MC graph is highly modular, it is not split into disconnected components and 479 some entanglement exists also between dimers located in different dFC modules. Inter-module 480 connections in the MC graph can arise e.g. due to the existence of trimers with a root in zone I 481 (entangling dimers across dFC modules #1, #2 and #3) or inter-zone tetramers (entangling 482 483 dimers across dFC modules #4 and #5). In other words, MC reveals some degree of global, widespread entanglement between FC dimers, beyond modular entanglement. The strength of 484 such global entanglement is quantified by the so-called average participation coefficient of the 485 MC matrix, a graph-theoretical quantity measuring inter-module coupling (Guimerà & Amaral, 486 2005; see Materials and Methods). 487 488 The distribution of MC participation coefficients for each group are shown in Fig. 4D. We found that the participation coefficients decreased significantly (Fig. 4D, left; Mann-Whitney 489 U-test, p <0.001) from SNC to AD, while overall modularity did not vary significantly (Fig. 490 4D, right). These results suggest that, in patients, coordination structure between fluctuations l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / t . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 491 of FC dimers is impoverished: global entanglement is disrupted, making dimer fluctuations in 492 different modules more random and mutually independent. 493 494 Interlude: trimers and tetramers are genuine or “dimers are not enough”! 495 496 Before entering a more detailed and regional specific account of changes to dFC organization observed at the regional level along the SNC-to-AD spectrum, it is important to stress that 497 trimer and tetramer analyses are not redundant with the dimer-based analyses. Indeed, some 498 studies have suggested that correlation between edges (captured by higher-order trimer and 499 tetramer in a MC matrix) could just be an automatic byproduct of existing lower-order dimer 500 501 interactions (Novelli and Razi, 2022). This can be easily understood through some examples. Let consider for instance two strong dimers FCri and FCrj sharing a common root region r. If a 502 third strong dimer FCij also exists –closing the triangle of edges (ri), (rj), (ij), then it is not 503 surprising that a strong trimer MCri, rj is also detected: indeed, the fluctuations of the two leaf 504 regions i and j are coordinated through a transverse dimer interaction, i.e. the strength of the 505 506 trimer would be the byproduct of a triangular motif of dimers and would thus be a redundant consequence of them. Analogously, we may consider the case of a square motif of dimers FCij, 507 FCjk , FCkl and FCli which could also give rise to strong tetramers because of the presence of 508 one or more pairs of strong dimers. In other words, the detection of strong trimer and tetramer 509 510 entries within the MC (or other forms of edge-centric FC) is not a sufficient condition for the existence of genuine high-order interactions (Battiston et al., 2020) that cannot be explained as 511 stemming from motif arrangements of lower-order pairwise interactions. On the contrary, the 512 existence of genuinely high-order interactions could be established by detecting trimer or 513 tetramer couplings between the dimers in a motif, stronger than the dimers themselves involved 514 515 516 in the motif. The question that then arises is, what is the structure of MC that we observe in our data? To investigate the genuine or spurious nature of trimer and tetramer interactions, we 517 systematically studied the inter-relations between MC and FC entries. First, we define the dimer 518 strength FCr = Σi FCri of a region r as the sum of the strengths of all the dimers incident to it. 519 520 Analogously, we introduced the (root-pinned) trimer strength MCr = Σij MCri, rj of a region r as the sum of the strengths of all the trimers of which r is the root. Conceptually, whereas FCr 521 measures the average coordinating influence that the region r exerts on its adjacent nodes, MCr 522 can be understood as quantifying the coordinating influence that r exerts on its incident links. 523 As shown by Fig. 5A, the correlations between dimer and trimer strengths of a region are weak l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / t / . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 524 and not significant, both at the global (black lines) and within each group (bundles of colored 525 lines) levels, and for both within-zone and inter-zone trimers and dimers strengths. Of note, the 526 average strength of between-zone trimers and dimers strengths had a larger variance across 527 groups, hence the positively slanted shape of the global point cloud when confounding all 528 529 groups, despite negative trends within each group. Although weak, within-subject correlations between FCr and MCr were negative, suggesting that some regions can be “meta-hubs” 530 (Lombardo et al., 2020) but not “hubs”, i.e. they can be the center of an entangled star subgraph 531 of incident dimers, even if these dimers are individually weak and unable to systematically 532 synchronize the fluctuations of adjacent nodes. Such meta-hubs could not have been identified through ordinary pairwise FC analyses only and manifest thus the existence of a real high-order multi-regional coordination. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Fig. 5. State-free dFC: Inter-relations between dFC trimers and FC dimers. We studied whether regions with a large FC strength (“FC hubs”, i.e. they are the center of a star of links strong on average) also have a large trimer strength (MC “meta-hubs”, i.e. they are the center of a star of links whose fluctuations are temporally correlated). (A) To do so we computed the correlation between dimer and FC strengths, for both within and between zones trimers and dimers. As shown by the scatter plots, these correlations were low, both at the global (light green cloud) and at the single clinical group (colored solid lines; green: SNC, yellow: NC, orange: aMCI, red: AD) levels. Within each group, they were furthermore moderately negative. Therefore, FC hubness and MC meta-hubness tend to be slightly anti- correlated. (B) Trimers were divided into three groups dependent on the location of their roots and 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 leaves. We considered genuine a trimer such that the MC between the two dimers composing the trimer is stronger than the FC between the trimer leaves. The violin plots at the right show fractions of genuine trimers (for all trimers and subjects) as a function of the trimer type. For all types, there were substantial fractions of genuine trimers (i.e. higher-order interactions not fully explained by the underlying dimer interactions arrangement). See Figure S3 for analogous analyses on tetramers. We then moved to consider how many trimers cannot be considered as a manifestation of underlying triangular motifs of dimers. We defined a trimer rooted in a region r to be genuine if MCri,rj > FCij , i.e. if the observed trimer strength cannot be fully explained by a strong
555
synchronization between the leaves. We then measured the observed fractions of genuine
556
trimers. As shown by Fig. 5乙, substantial fractions of genuine trimers could be found for all
557
trimer types: genuine fractions amounted to 32 ± 7 % for within zone trimers (root and both
558
559
leaves in a same zone) and increased to 43 ± 13 % for inter-zone trimers with leaves in two
different zones, 或者 58 ± 9 % for inter-zone trimers with the root in a different zone than the
560
树叶. Especially for inter-zone trimers, many trimers could not be trivially explained by the
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
561
existence of triangles of dimers.
F
/
d
哦
我
/
562
563
Considering tetramers, we found larger redundancy with dimers. We defined the tetramer
strength MCij = Σkl MCij, kl of a link (ij) as its total entanglement with other links. Figure S3A
564
shows that a significant positive correlation existed between the dimer strength FCij of a link
565
(ij) and its tetramer strength. That is, the stronger links were also the most entangled.
566
有趣的是, several tetramers could still be considered genuine. We defined a tetramer
567
568
genuine when MCij,kl > FCij , i.e. when the two composing dimers were strongly correlated,
尽管 (at least one of) the dimers being individually weak. Under this definition, Figure S3B
569
shows that up to 55 ± 10 % of tetramers composed of interzone dimers were genuine.
570
We conclude that in general, the information conveyed by trimer and tetramer analyses is
571
not completely redundant with the one conveyed by dimers, as many trimer and tetramer
572
573
metrics cannot be explained solely in terms of dimers and thus express actual higher-order
correlations.
574
dFC trimers and tetramers are more impacted in aMCI and AD than FC dimers
575
After defining various metrics to quantify the involvement of specific regions and links into
576
pairwise and higher-order interactions, as previously described, we then studied how dimer,
577
trimer and tetramer strengths varied across the four cohorts in our study.
/
/
.
t
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
t
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
578
第一的, we found that for both dimer and trimer interactions, the stronger effects were found
579
considering inter-zone interactions. Figure 6A reports group differences for inter-zone dimers
580
and Figure 6B for inter-zone trimers (mixed-zone or same-zone leaves are not treated
581
separately). Results for within-zone dimers and trimers are shown in Figures S4A and S4B,
582
583
584
585
分别. In contrast to within-zone interactions, group-level comparisons for within-zone
dimer and trimer interactions were not significant.
一般来说, when averaging over all brain regions (Figs. 6A and 6B, 左边), general averages
586
of dimer and trimer strengths progressively decreased from SNC, to NC, aMCI and AD groups.
587
588
This decrease, 尤其, was significant when comparing the two extreme SNC and AD groups.
The effect was particularly strong for inter-zone trimer strengths (p = 0.005, Mann-Whitney U-
589
测试, Bonferroni correction, for trimers), whose average value for the AD group not only
590
decreased but changed its sign as it became negative. 相比之下, within-zone trimer strengths
591
remained strongly positive (如图. S4B). 这意味着, in the AD group, several regions are
592
593
involved in a mixture of negative and positive trimer interactions. Positive interactions tend to
synchronize the fluctuations of FC links, unlike negative interactions that tend to push them in
594
an anti-phase interaction. 此外, the mixture of positive and negative couplings results
595
in a dynamic conflict scenario, known in the statistical mechanics as “frustration”
596
597
(Vannimenus and Toulouse, 1977) and has been associated to disordered organization and a
slowed-down relaxation to equilibrium (Mezard et al., 1988). The emergence of frustrated inter-
598
zone trimer interactions is a strong qualitative discriminative marker of the AD group (看
599
Discussion for possible interpretations of this finding).
600
601
602
The decrease of inter-zone trimer-strengths and their switch to negativity in the AD group is
confirmed also when focusing on individual brain regions, rather than the average (Figure 6B,
正确的). 值得注意的是, strong decrease in trimer strengths were observed in regional subdivisions
603
of the Temporal Pole and of the Parahippocampal gyrus, along the Hippocampus proper and
604
Amygdala. Some of these regions (Entorhinal cortex in the Parahimpocampal gyrus and the
605
Hippocampus), are among the first to be affected by neurofibrillary accumulation in AD
606
607
pathology (Braak stages 1 和 2). In these same regions, we found a similar trend at the level
of dimer strengths even when differences were not significant (Figure 6A, 正确的). Of interest,
608
the stronger effects at the level of dimer strengths were found in the Cingulate gyrus which are
609
affected by early beta amyloid depositions and later on with neurofibrillary accumulation.
610
有趣的是, the regions exhibiting the strongest effects at the level of trimers were not the
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
/
t
.
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
611
ones with the strongest effects at the level of dimers (and vice versa; 如图. 6A right vs Fig. 6乙
612
正确的). The two analyses reveal thus complementary aspects of how pathology affects the
613
spatiotemporal organization of functional interactions.
614
615
616
617
618
619
620
621
622
623
624
625
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
t
/
/
.
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
如图. 6. State-free dFC: strengths of inter-zone FC dimers, trimers and tetramers across clinical
团体. (A) Average strength of inter-zone FC dimers decreased from SNC-to-AD both globally (左边)
and locally at the level of individual regions (正确的). At the global level, significant differences were
found between the SNC and AD groups (p-value = 0.005, Mann-Whitney U-test, Bonferroni correction).
Locally the decrease was significant in anterior and posterior cingulate gyrus, bilaterally (Mann-
Whitney U-test, Bonferroni correction). (乙) Inter-zone trimer strengths, similarly to FC dimers, 显示
a reduction trend across the groups, both globally (左边) and locally (正确的). At the regional-level the
reductions in dFC trimers were widespread among regions, including early-affected regions without
noticeable FC strength variations across clinical groups, with an interesting tendency toward negative
trimer strengths in the AD group, associated to developing “frustration” of higher-order interactions in
626
627
628
629
630
a statistical mechanics sense (和, correspondingly, increased dynamical disorder and conflict; 看
讨论). 最后, (C-D) tetramers strength showed a significant drop from SNC to AD groups in
both brain-wide averaged intra-zone (C) and inter-zone (D) subsets. See Figure S4 for intra-zone dimer
and trimer strengths, not showing significant variations across groups.
最后, we assessed differences on tetramer strengths across groups. 图中 6 we show the
631
average tetramer strengths for intra-zone (如图. 6C) and inter-zone (如图. 6D) tetramers. 同时
632
633
案例, we observed a significant reduction of tetramer interactions from the SNC, to the NC,
MCI and AD groups. In the case of inter-zone tetramers, the drop in strength was large in the
634
MCI group, with levels close to those in the AD group.
635
总之, AD was associated with extensive reductions of not only dimer strengths, 但
636
more importantly, trimer and tetramer strengths. 此外, inter-group differences were
salient when considering higher-order trimer and tetramer compared to dimer interactions.
637
638
639
640
讨论
641
We have shown a large variety of changes associated with dFC across the cognitive spectrum
642
from cognitively over-performing SNC subjects to AD. The rich set of complementary analysis
643
approaches we deployed consistently converge toward a common message: AD is associated
644
with a disordering of the rich spatiotemporal fluctuations that characterize healthy dFC.
645
646
It is worth noting that while BOLD activity misses many fast neuronal processes due to its
slow sampling rate, what Functional Connectivity dynamics track are not neural level processes
647
but variations of global brain state that can occur on much slower time-scales. So dFC with a
648
long TR accounts for variations of the way in which the repertoire of internal states is sampled,
649
more than for variations of neural signals themselves. As a side note, these slow fluctuations
650
651
are also what mean-field connectome-based whole-brain models are fit to reproduce via the
stochastic sampling of their emergent repertoire of dynamic modes (Hansen et al., 2015, Fousek
652
等人。, 2022).
653
Our results showed that a pertinent description of dFC organization and its changes across
654
groups can be formulated in terms of two anatomical zones segregating ventral from dorsal
655
656
地区 (如图. 6D). We found that the system spends less time in states with fluid Zone I dynamics
and high global integration, visiting them more transiently, while it gets stuck on the contrary
657
in less integrated states exhibiting Zone I hypersynchronisation (如图. 2). At the dimer level,
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
.
/
t
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
658
pairwise interactions between regions in different zones get more irregularly bursty (如图. 3). 在
659
the level of higher order trimers and tetramers, meta-connectivity analysis revealed a loss of
660
coordination between the fluctuations of different sets of links, as quantified by dropping
661
participation coefficients (如图. 4D). Trimer interactions between Zone I and Zone II, 也
662
663
tetramers, were weakened more distinctively than the inter-zone dimer interactions.
值得注意的是, regions in our limbic subnetwork for which conventional dimer analyses were not
664
different between groups, showed a remarkably reduced involvement in trimer interactions
665
between zones (如图. 6). 全面的, these findings point together toward a “loss of structure” in
666
dFC in parallel to the cognitive gradient across groups. This is in agreement with previous
667
668
669
studies that showed a reduction of the complexity of spontaneous fluctuations of coordinated
活动 (Tait et al., 2020).
尽管如此, even though being quite encouraging, a conclusive validation of our findings
670
would require using larger cohorts, which preferably contains information on cortical thinning
671
and PET scans of tau and Aβ depositions, to test whether their distributions correlate with the
672
673
local network dynamics alterations we observe (thus establishing them as potential
physiopathological causes of these changes) 或不 (advocating for alternative explanations, 看
674
later discussion). 相似地, our choice of regions and parcellations was arbitrary, 一般来说
675
based on the successful use of the same parcellation in previous modelling-based analyses of
676
677
the same cohort (Zimmermann et al., 2018乙). A better resolution fMRI from further cohorts
would allow validating our results with finer and more extended parcelations, especially for the
678
subcortical regions (Tian et al., 2020) that constitute the core of the limbic network on which
679
we have focused.
680
681
682
有趣的是, our qualitative description emerges from radically different approaches to dFC
parameterization: a state-based approach (the PBM method by Thompson and Fransson,
(2016)); and a state-less approach (the random walk descriptions of dFC by Battaglia et al.
683
(2020) and Lombardo et al. (2020)). The PBM method is firmly rooted in the developing field
684
of temporal network theory (Holme and Saramäki, 2012). Temporal networks allow describing
685
inter-regional communication as it unfolds in time, similarly to a call-center, where operators
686
687
can handle a multitude of brief first-contact calls at certain moments and dedicate extensive
time to select customers at other times (Kovanen et al., 2013). Or to a primary school, 在哪里
688
students interact in small groups during lectures and play in mixed larger groups in the
689
playground during school-breaks (Gemmetto et al., 2014). 最终, even fluctuations
690
between segregated or integrated states in brain systems at different scales (Shine et al., 2016;
691
Pedreschi et al., 2020) give rise to network dynamics not dissimilar to these social systems.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
.
t
/
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
/
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
692
Note that our use of terms such as “burstiness” or “activation” (比照. 如图. 3D and E) is also
693
mediated from the jargon of temporal networks theory and should not be mistaken with the
694
usual meaning of these terms in neuroscience, as they refer to FC link dynamics rather than to
695
neuronal firing rates (exactly as we use the adjective “temporal” in the sense of “time-
696
dependent” and not in association with “temporal lobe”).
697
The dFC random walk approach (Arbabyazd et al., 2020; Battaglia et al., 2020; Lombardo
698
等人。, 2020; Petkoski et al., 2023) models rs dFC as a temporal network as well, but focuses on
699
the variation from one network frame to the next, more than on the geometry of individual
700
network frames. dFC is seen as a flow in network space and the non-randomness of network
701
702
reconfiguration was investigated via a time-to-time correlation approach known as Meta-
Connectivity (Lombardo et al., 2020). In a dFC context in which the mode of coordination
703
between regions is not frozen in time but changes smoothly, meta-connectivity reveals how the
704
fluctuations of one or more regions modulate the degree of coordination between the
705
fluctuations of other regions. 换句话说, meta-connectivity is an indicator of “many-body
706
707
coordination”. 的确, the terminology of dFC “dimers, trimers, tetramers” is reminiscent of
perturbative diagrammatic expansions in Statistical Physics, such as the virial expansion
708
(Landau and Lifshitz, 1980), in which clusters of increasingly large size account for
709
progressively more elaborate and nonlinear patterns of many-body interactions. MC can thus
710
711
be considered yet another form of high-order functional connectivity, adding up to a list of other
approaches to track higher-order coupling (Torres et al., 2021; Santoro et al., 2023) 作为
712
hypergraph or homological methods (Battiston et al., 2020; Petri and Barrat, 2018; Sizemore et
713
等人。, 2018), which have already identified synergistic aspects of human brain functioning (Luppi
714
等人。, 2022; Varley et al., 2023).
715
716
很遗憾, both of the dFC methods implemented in this study provide results depending
on specific parameter choices. 例如, concerning the state-less random walk approach,
717
the selection of a window-size remains ultimately arbitrary. The window-size selected was short
718
in contrast to other studies. 然而, our statistical analyses suggest that this window size
719
results in similar discriminatory power as longer windows (如图. S2A). 此外, 这是
720
721
necessary to use short windows because the PBM method suggests that dwell-times in
consistent FC state epochs are often short and thus dFC is intrinsically fast (如图. S2B). The need
722
to track the covariance of fast FC fluctuations has inspired additional approaches analogous to
723
MC, as edge-centric Functional Connectivity (eFC; Faskowitz et al., 2020). In this approach,
724
covariance is estimated between individual events of instantaneous co-fluctuation, 没有
725
arbitrary windowing. 然而, we showed in Lombardo et al. (2020) 那, despite the
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
t
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
726
significant relation between MC and eFC, the use of a sliding-window in the MC approach
727
produces a smoothing effect that partially denoises the graph structure of inter-link meta-
728
连接, allowing a cleaner determination of modules and “meta-hub” nodes with large
729
trimer strengths.
730
731
An additional aspect of the state-based PBM approach, is that it involves partially arbitrary
steps as the choice of a number of states. The retrieved FC states depend on the extracting
732
algorithm that depends on the brain parcellation and choice of regions of interest utilized. 我们
733
found four states and increased dwell-times in states with hyper-connectivity within Zone I.
734
This finding of increased probability in AD of visiting hyper-connected states is in agreement
735
736
with some state-based dFC studies (Gu et al., 2020), but in contrast with others (Fu et al., 2019;
Schumacher et al., 2019), which instead find higher dwell-times in disconnected states. 这样的
737
discrepancies may arise because in the PBM method clustering of states is performed on
738
activation patterns rather than on time-resolved functional networks. Our procedure has the
739
advantage of showing that network dynamics is partially dissociated from node dynamics, 和
740
741
the possibility of hyper-connected FC modules arising both in presence of higher or lower
activity of the nodes composing this module (如图. 2A). It may reduce the chance, 然而, 的
742
detecting extreme events along dFC or transient atypical network configurations that would be
743
naturally assigned to separate clusters when directly clustering networks. 最后, the mentioned
744
745
studies used reference parcellations with a larger number of regions or focusing on more
distributed network components, while here we particularly emphasize selected regions of
746
兴趣, such as temporal and paralimbic cortices, known to develop epileptiform activity
747
(Bakker et al., 2012; Cretin et al., 2016; Vossel et al., 2013). 因此, within the probed sub-
748
system of interest, hypersynchrony may become particularly prominent and over-expressed
749
750
751
(因此, the enhanced dwell-time in hyper-connected FC states), a fact that has direct
pathophysiological relevance.
Despite the arbitrary steps involved, both approaches independently provide sets of results
752
with a high mutual consistency, making unlikely that our analyses reflect exclusively methods
753
artefacts. Both methods confirm indeed that a dFC description in terms of two zones is
754
755
pertinent, as the distinction between Zones I and II organizes the modular structure of both FC
states in the state-based PBM approach (如图. 2A) and of the MC matrices in the state-free dFC
756
random walk approach (如图. 5B and C). 此外, both methods confirm that the increased
757
severity of cognitive decline across the four groups correlates with a reduced inter-zone
758
协调: more time spent in states with weaker integration (Figs. 2B-C) and reduced inter-
759
zone trimer strengths (如图. 6乙). Such semantic agreement is remarkable especially given the
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
t
.
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
760
limitations of our approaches. Meta-connectivity analyses could be improved by seeking,
761
beyond plain module detection, for a hierarchical community structure, that is often present in
762
large networks (Jeub et al., 2018; Peixoto, 2014). State-based analyses could profit of better
763
clustering approaches, as used by Rasero et al. (2018). 然而, while acknowledging these
764
765
766
局限性, we found our four states and MC communities to be already highly interpretable,
in term of the anatomical nature of the entangled links.
Particularly interesting is the fact that the weakening of inter-zone trimer interactions across
767
the four groups decreases to such extent that some of these trimer switch from a positive to a
768
negative value. As previously mentioned, the coexistence of negative and positive couplings in
769
770
a graph or a hypergraph of interacting units is referred to in statistical physics as “frustration”
(Toulouse, 1986), since it is associated with the emergence of conflicts preventing smooth
771
relaxation to an equilibrium. To put these results in context, let us imagine that a dynamic FC
772
link (a dimer FCij) is positively coupled to a second dimer FCkl and negatively coupled to a
773
third dimer FCmn, and that the second and the third dimer simultaneously increase in strength
774
775
(i.e. FCkl and FCmn get larger). Then the dynamics of FCij will “freeze” under the contrasting
influence of the positive bias applied by FCkl (pushing it to assumer stronger values), 和
776
negative bias applied by FCmn (pushing it to assume smaller values). 因此, the change of
777
positive to a negative inter-zone influence –as the one signaled by the negative inter-zone trimer
778
779
strengths of many limbic region within Zone I– gives rise to conflicts between the flows of
Zone I and Zone II regions in AD patients, in contrast to control subjects where the fluctuations
780
of the same regions are naturally synchronized.
781
In particular in the context of cognition, Zone II regions such as the posterior Cingulate
782
Cortex (pCC) have been postulated to play a regulatory role on the level of brain meta-stability,
783
784
balancing “free-wheeling” internal cognition and focused outward attention (Leech et al., 2012;
Leech and Sharp, 2014). In control groups, pCC has strong positive dimer coupling and
785
moderately negative trimer coupling with regions in Zone I (如图. 6). This could allow the pCC
786
to quickly coordinate with individual Zone I regions (and share information with them via direct
787
positive FC dimers), while simultaneously “lowering the volume” of
intra-zone I
788
789
沟通 (via pCC-rooted negative trimers with Zone I leaves). In AD subjects, 这
subtle equilibrium is lost, resulting potentially in perturbed integration of information within
790
and between Zone I regions. 值得注意的是, pCC is also a key hub of the Default Mode Network
791
(Raichle et al., 2001), a system whose dFC had already been suggested as a biomarker in the
792
conversion to AD (Jones et al., 2012; Puttaert et al., 2020).
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
t
.
/
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
793
有趣的是, our analyses on trimer strengths could detect inter-group differences within
794
Zone I regions, for which the dimer analyses did not found significant differences. A possible
795
explanation for the better sensitivity of trimer-based analyses could trivially be due to a larger
796
sample-size, as there were more possible trimers than dimers, resulting in similar average
797
798
strengths but with a lower variance. 然而, another possibility could be that higher-order
interactions are readily affected by the pathology process earlier or at a higher degree than
799
pairwise interactions. This fact is difficult to assess from our dataset, which is not longitudinal.
800
然而, this possibility is supported by our results showing that higher-order trimers and tetramers
801
terms convey in many cases genuinely new information, not redundant with dimer analyses.
802
803
的确, even if we agree with other reports (Novelli and Razi, 2022) that dimer terms can
sometimes explain trimer and tetramer term, we found in addition important trimer
804
entanglement among otherwise individually weak dimers (如图. 5A) that lacked strong pairwise
805
interactions between their dangling leaves (如图. 5乙). Such genuine trimers cannot be explained
806
by dimer motifs and describe thus a qualitatively different phenomenology, invisible to
807
808
conventional FC analyses. Similar considerations apply to tetramers (如图. S3), which although
generally weaker in strength than dimers and trimers, form an additional and pervasive
809
background “medium” which also actively steer coordinated FC dimer fluctuations, with an
810
overall influence degraded by the pathological process (如图. 5C and D). 将来, for an
811
812
even better appreciation of pathology effects on higher-order interactions, one may use methods
that facilitates the generalization to arbitrarily high orders, even higher than the third or the
813
fourth one, such as maximum entropy fitting (Ezaki et al., 2018; Savin and Tkačik, 2017) 或者
814
other information-theory approaches (Rosas et al., 2019).
815
816
817
Another question is what the mechanistic origin could be of the observed spatio-temporal
complexity of dFC (and of its alterations). Previous studies have shown that structured dFC
may emerge as an effect of global brain network dynamics to be tuned at a slightly subcritical
818
working point (Arbabyazd et al., 2020; Glomb et al., 2017; Hansen et al., 2015), or as a
819
consequence of cascades of neuronal activations (Rabuffo et al., 2021) that occur due to the
820
flow on the manifold created by the symmetry breaking of the connectome (Fousek et al., 2022).
821
822
然而, these studies did not use very precise criteria when referring to their capacity to
render dFC. 将来, the statistical descriptors of dFC alterations that we introduce here,
823
such as regional spectra of trimer and tetramer strengths, may be used as more detailed fitting
824
targets for the tuning of mean-field models aiming at explaining the circuit mechanisms for the
825
emergence of higher-order interactions. Such models, once fitted, may also allow reverse-
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
t
/
.
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
826
engineering the physiological changes that are responsible for the degradation of spatiotemporal
827
dFC complexity along the SNC-to-AD spectrum.
828
It is likely that the dFC alterations we observe between groups are caused at least in part by
829
underlying biological causes of AD, as the aggregation of misfolded proteins that cause cell
830
831
death and atrophy (Soto & Pritzkow, 2018). 然而, not all the symptoms can be explained
by these mechanisms. Among them, the existence of symptom severity fluctuating across hours
832
in a way not accountable for sudden variations of amyloid load (Palop et al., 2006) 或者, 然而, 这
833
phenomenon of cognitive reserve where subjects with virtually identical or even higher amount
834
of amyloid load than others can maintain a very efficient cognition, (比照. Snowdon (2005) 为了
835
836
the famous “Nun Study” or Rentz et al., (2010) for a review of other studies with similar
结论). These findings suggest that neurodegeneration may coexist with compensations
837
of unspecified nature that allow “cognitive software” to operate properly despite “hardware
838
damage” (see e.g. Petkoski et al. (2023) for examples of dynamic compensation in healthy
839
老化, or Courtiol et al. (2020) for a similar phenomenon in epilepsy). 这里, we propose the
840
841
hypothesis that preserved dFC complexity may act as a possible form of cognitive reserve. 我们
stress once again that, to check the soundness of this hypothesis, future analysis should rely on
842
richer datasets that contain PET scans of tau and Aβ depositions, and possibly even a
843
mechanistic model (Stefanovski et al., 2019; 2021) for their impact to the neuronal activity.
844
845
最终, the degradation of dFC organizational complexity that we here described may
not only correlate with cognitive decline but also, 最终, contribute to cause it. 的确, A
846
dFC with a complex organization could be the hallmark of brain dynamics implementing
847
“healthy” cognitive processing. Computation can emerge from collective dynamics as long as
848
this dynamics is sufficiently complex, i.e. neither too ordered nor too random (Crutchfield,
849
850
2012; Crutchfield and Mitchell, 1995). More fundamentally, the existence of alternative
information processing states –transient FC networks?– and of non-random transitions between
851
these states –structured and complex dFC switching?– are two necessary conditions for
852
whatever information processing system to perform computation (图灵, 1937). A speculative
853
hypothesis is thus that the complexity of neural dynamics –and, more specifically the
854
855
complexity of ongoing dFC which is a measurable shadow of hidden neural processes– is an
instrumental resource for cognitive information processing. Cognitive deficits in pathology
856
could arise just in virtue of this resource becoming scarcer, because of less structured and more
857
random dynamics. This phenomenon has been speculatively observed in hippocampal neuronal
858
assembly dynamics in epilepsy (Clawson et al, 2021). In this line of thinking, preserved dFC
859
complexity would act as a “dynamic reserve” allowing the implementation of elaborate neural
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
.
/
t
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
860
computations (or “software patches”) to compensate for progressing neurodegeneration.
861
Analogously, enhanced dynamic complexity could be the substrate for the superior cognitive
862
performance achieved by subjects in the SNC group with respect to NC subjects. A more direct
863
exploration of the link between dFC complexity and cognitive processing in the healthy and
864
pathological brain will be needed to inquire into this suggestive hypothesis.
865
866
867
Materials and methods
868
参加者
869
870
871
The study included 73 subjects between 70 和 90 years of age from the fourth wave of the
Sydney Memory and Ageing study (Sachdev et al., 2010; Tsang et al., 2013). The use of the
database was approved by the Human Research Ethics Committee of the University Texas at
872
达拉斯. For detailed descriptive summaries on neuropsychological assessments for AD and
873
amnesic aMCI, we refer the reader to Zimmermann et al. (2018).
874
875
A specificity of our approach is the stratification of healthy controls with an additional
“super normal” category putting our focus not only on mechanisms of disease but also on
876
mechanisms of “health” based on cognitive performance. 结果
从
twelve
877
neuropsychological
tests were combined
在
这
following
cognitive domains:
878
attention/processing speed, 记忆, 语言, visuospatial ability, and executive function. 在
879
880
简短的 (Mapstone et al., 2017) we classified cognitive membership for each subject based on the
composite Z-scores as supernormal controls (SNC) or normal controls (NC). For this, 这
881
supernormal (SNC) group was defined as Zmem > 1.35 标清 (~90th percentile) and Zcog > 0.7 标清.
882
The normal control participants are conservatively defined with Zmem ± 0.7 标清 (~15th %ile–
883
85th %ile) of the cohort median. The classification of subjects as AD and aMCI described in
884
885
Zimmermann et al was done by consensus included the following: The amnesic MCI group
was described by a cognitive decline at least in the memory domain (Zmem and/or Zcog < 1.5 SD 886 below normative values), paired to subjective complaint of cognitive deficit and without deficits 887 in activities of daily living (ADL). The AD group in presence of a diagnosis of Alzheimer's 888 Disease according to DSM-IV criteria (American Psychiatric Association, 2000) assessed by a 889 890 clinical expert panel that included significant cognitive decline in several cognitive domains in addition to significant decrease in ADLs (American Psychiatric Association, 2000; J. 891 Zimmermann et al., 2018). 892 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / / . t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 893 fMRI acquisition and preprocessing 894 Details about resting state functional MRI acquisition and preprocessing can be found in 895 Zimmermann et al. (2018). We briefly mention, as relevant here that during the fMRI 896 acquisition, participants were instructed to lie quietly in the scanner with their eyes closed. The 897 898 TR used for the T2* weighted EPI sequence of time-resolved BOLD imaging was 2000 ms. The acquisition time was of ~7 minutes. Data from all MRI modalities was preprocessed using 899 FSL and QA followed Smith et al. (Smith et al., 2004). Subjects were removed if any of their 900 scan acquisitions contained excessive artifacts including slice dropouts on the diffusion-images 901 (defined by zebra-like blurring or complete dropout; Pannek et al., 2012), the presence of 902 903 orbitofrontal EPI signal dropout (Weiskopf et al., 2007), excessive motion on T1-images (i.e., ringing), or severe geometric warping. For details of additional fMRI preprocessing details 904 (slice-timing correction, realignment and co-registration, linear detrending, head motion 905 regression, probabilistic segmentation, spatial smoothing, etc.) please refer to Perry et al. 906 (2017). 907 908 Network parcellation 909 For structural and functional parcellation the AAL atlas was used focused on 16 limbic 910 regions (see Fig. 6D) associated with early degeneration in AD according to Braak and Braak 911 912 staging as we did before (Joelle Zimmermann et al., 2018). The regions of interest included: Cingulate cortices (anterior, medial and posterior), Parahippocampal gyrus (including 913 Entorhinal cortex), Hippocampus proper, amygdala, and temporal pole (superior and middle). 914 In this study, as pertinent given the spatial organization retrieved in many of the analysis results, 915 we categorize regions as belonging: either to “Zone I”, including ventral regions (superior and 916 917 medial portion of the temporal pole, parahippocampal gyrus, hippocampus proper and amygdala in both hemispheres); or to “Zone II”, which included the six cingulate cortical 918 regions (posterior, medial, and anterior) in both hemispheres; Fig. 6D). This subdivision in two 919 separate zones allowed us the categorization of network links from dimers to higher-order 920 arrangements (trimers, tetramers) determining “within zone” or “between zone” interactions 921 922 based on the relative zone membership of the different nodes involved. We remark that the delimitations of Zone I and Zone II are inspired from data-driven considerations (the spatial 923 organization of FC state centroids in Figs 2 and MC modules in Fig. 4) rather than from a-priori 924 subdivisions. 925 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / / / . t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 926 State-based dynamic Functional Connectivity 927 In this study, we applied two complementary dynamic functional connectivity (dFC) 928 approaches to investigate non-stationarity of BOLD signals and capture the recurring, time- 929 varying, functional patterns. The first one was the so called point-based method (PBM) 930 931 932 introduced by Thompson and Fransson (2016), referred here as state-based dFC. This method assumes the existence of a small set of possible discrete FC configurations. In this approach, BOLD signals of each subject were concatenated along the temporal 933 dimension and transformed to z-scores using Fisher’s z-transformation to stabilize variance 934 prior to further analysis. Following Thompson and Fransson (2016), we applied a k-means 935 936 clustering algorithm on the concatenated time-series (Lloyd, 1982), to determine states based on global activity patterns (best partition out of 100 repetitions, max iterations 100). The 937 optimal number of 4 clusters (k = 4) was validated based on detecting an elbow in the variation 938 of the distortion score as a function of changing number of clusters k (Fig. S1B). Based on the 939 collections of activity patterns at times assigned to each of the states, we computed Pearson 940 941 correlation matrices, yielding k state-specific FC matrix FC(λ) (λ =1…4). A state was hence characterized by the centroid activation pattern of time-frames within the state cluster and by 942 its state-specific FC matrix (see Fig. 2A and Fig. S1A). To characterize the spatial properties 943 of state-specific FC, we then used a graph-theoretical approach and measured global and local 944 945 946 efficiencies (Achard and Bullmore, 2007; Latora and Marchiori, 2001) of the four FC(λ) networks (Fig. 2B) using the Brain Connectivity Toolbox (Rubinov and Sporns, 2010). To study the properties of the sequence of the dynamical states and the resulting temporal 947 network dynamics, we followed Thompson and Fransson (2016) to construct a temporal 948 network by using as network frame at a time t the graph FC(λ) of the state λ observed at time t. 949 This procedure transformed each fMRI session with T timestamps into a temporal network with 950 T frames, each including 𝑙 = 𝑛(𝑛 − 1)/2 links between each undirected pair of nodes. These 951 temporal networks were binarized thresholding links as a function of an arbitrary common 952 953 threshold θ. We then computed various temporal metrics describing network dynamics. First, we calculated the mean dwell-time for each subject by averaging the number of consecutive 954 time-points belonging to a given state before changing to a different state (Fig. 2C). Second, 955 we computed the proportion of time spent in each state as measured by percentage relative time 956 (state census) (Fig. 2D). Third (for this step, binarization was necessary), we measured inter- 957 958 contact times (ICT) of different links. ICTs for each link was defined as the temporal distance between events of link activation (i.e. link strength going above threshold) and offset (link l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 959 strength going below threshold). For each link and each value of threshold θ, we computed the 960 mean activation μ as a measure of mean duration of a link’s active intervals; the total active 961 time fraction τ which is the total fraction of time in which a link was active relative to the 962 duration of the imaging acquisition; and the burstiness coefficient (Goh and Barabási, 2008) 963 assessed by: 964 θ = 𝛽𝑙 𝜎𝜏 − 𝜇𝜏 𝜎𝜏 + 𝜇𝜏 965 where 𝜎𝜏 and 𝜇𝜏 are, respectively, standard deviation and the mean of the ICTs along the 966 considered temporal network instance. The burstiness coefficient is bounded in the range 967 −1 ≤ 𝛽 ≤ 1, such that 𝛽 = −1 indicates a periodic/tonic link activation time-course, 𝛽 = 0 a 968 sequence with Poisson-like activation, and 𝛽 = 1 corresponds to bursty (time-clustered) events 969 of link activation (Fig. 3C). We finally evaluated also the memory coefficient (see always Goh 970 and Barabási, 2008), which is the autocorrelation of the sequence of link activation times; i.e., 971 972 973 974 975 if E(l) s is the duration of the s-th individual activation of link l, then memory coefficient for link l is λ(l) = CC(E(l) s , E(l) s+1), where CC denotes normalized Pearson correlation. Analogously, the burstiness and memory coefficients were averaged across links (or link classes, such as between-zone or within-zone links). Unlike the mean dwell-time or state census, mean ICTs and the quantifications computed 976 from them, depend on the specific choice of threshold θ. In absence of clear criteria to choose 977 an optimum threshold value, we varied systematically θ in the range 1% 𝑀𝐴𝑋 < 𝜃 < 978 10% 𝑀𝐴𝑋 and MAX is the global maximum FC entry across the retained FC(λ) state. The 979 maximum value was equal to MAX = 0.87, therefore the range was 0.0087 < 𝜃 < 0.087. 980 Absolute values of μ, τ and 𝛽 varied with θ, however we pooled them together across different 981 threshold values by computing relative variations (at each fixed θ) with respect to reference 982 values (threshold-dependent), based on the NC group. For instance, for burstiness, we 983 computed the relative excess burstiness for SNC, aMCI, and AD groups with respect to NCs 984 (Fig. 2E) as: 985 %𝛽𝜑,𝑧 θ = θ θ − 𝛽𝑁𝐶,𝑧 𝛽𝜑,𝑧 θ abs(𝛽𝜑,𝑧 θ + 𝛽𝑁𝐶,𝑧 ) 986 where 𝜑 = SNC, aMCI, AD and 𝑧 refer to intra-zone, and subsets of inter-zone links. 987 Analogously, we evaluated excess deviations for the SNC, aMCI, and AD relative to the NCs, 988 across all possible thresholds, for μ and τ. 989 990 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / . t / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 991 State-free dynamic Functional Connectivity 992 In a second approach, we assumed that FC networks are continually morphing in time, 993 without priors on the existence of discrete state switching events, following Battaglia et al. 994 (2020), that conceptualized the evolution of FC as a stochastic walk in the high-dimensional 995 996 space of possible network configurations. This stochastic walk however is not trivial, as different inter-regional links covary according to a specific higher-order correlation structure 997 called meta-connectivity (Lombardo et al., 2020). State-free and smoothly varying dFC 998 temporal networks were extracted using a sliding window approach, adopting the random- 999 walks and meta-connectivity approaches (Battaglia et al., 2020; Lombardo et al., 2020; Petkoski 1000 et al., 2023) released within the dFCwalk toolbox (Arbabyazd et al., 2020). 1001 A short window of size 𝜔 = 5 TRs (10 s) was stepped without overlap over the BOLD time- 1002 series acquired in each fMRI session and then functional connectivity matrices (FC) were 1003 computed as window-restricted Pearson’s correlation matrices between BOLD time-series 1004 segments. Each temporal frame provides hence 𝑙 = 𝑛(𝑛 − 1)/2 undirected time-resolved link 1005 estimates, which can be collected into a 𝑙 × 𝑇 dFC stream, where T is the total number of 1006 windows. Each row of this stream provides the time-series of smoothed “instantaneous” 1007 variation of each FC link and the covariance between these variations can be described by a 1008 l x l matrix called the meta-connectivity (MC, Fig. 3B, (Lombardo et al., 2020)). The general 1009 entry of MC is given by: 1010 MC𝑙𝑖𝑗𝑙𝑚𝑛 = 𝑐𝑜𝑟𝑟 [dFC𝑙𝑖𝑗, dFC𝑙𝑚𝑛] 1011 for every pair of links (𝑙𝑖𝑗 and 𝑙𝑚𝑛) formed respectively between the regions (ij) and (mn). Our 1012 choice of window length 𝜔 = 5 TRs was guided by: first, the observation from state-based dFC 1013 analyses that ~90% of epochs within a state lasted less than 5 TRs (Fig. S2A), so that fast dFC 1014 dynamics may be lost using much longer windows; second, one-way ANOVA analysis on MC 1015 for a range of windows (from 3 to 20 TRs) showed that the best discrimination between SNC, 1016 NC, MCI and AD groups was achieved for 𝜔 = 5 TRs, with high between-group standard 1017 deviation and low within-group standard deviation (Fig. S2B). These analyses together suggest 1018 a small window of size 𝜔 = 5 TRs is both needed and sufficient to describe ongoing fast dFC 1019 fluctuations. 1020 Following and based on the correlation matrix between “dimers” (dynamic FC links between 1021 two regions i and j), the entries MCij, kl of the MC matrix are either computed based on the 1022 dynamics of four regions involved in the links (ij) and (kl), or at least three regions, when the l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / / t . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 1023 two considered dimers share a common vertex (e.g. i = k). MC can thus be seen as a collation 1024 of higher-order interactions within the system, involving more than “two parts” (tetramers or 1025 trimers). In the case of a trimer, the region on which the two dimers converge to a “root” region, 1026 and the other two regions are the “leaves” of the trimer. In the case of a tetramer, each of the 1027 two non-incident dimers are called a “base”. 1028 MC modularity 1029 We used a graph-theory approach to quantify the communities of MC matrices. MC for all 1030 subjects were constructed and then averaged for each of the four subject’s groups (Fig. 3B). To 1031 detect the modular structures of MC, we used the community Louvain algorithm (Rubinov and 1032 Sporns, 2011). We used a parameter Γ = 1.4, determined heuristically to yield a modular 1033 partition naturally interpretable in anatomical terms. To quantify the modularity changes across 1034 the groups, we computed the index of modularity (Q*) as measure of degree of intra-module 1035 connectivity. Since MC is a signed matrix, we applied disproportionate scaling to the positive 1036 and negative values of modularity indices to consider a lower contribution of negative meta- 1037 link weights to the index of modularity (Rubinov and Sporns, 2011). To quantify the degree of 1038 inter-modular connectivity of group averaged MCs, we computed the Participation coefficient 1039 of each dFC dimer node following (Guimera, Roger; Amaral et al., 2005). This metric can be 1040 computed exactly as for an ordinary graph keeping in mind that FC links and meta-links among 1041 them are, respectively nodes and links in the MC graph. The Participation coefficient is close 1042 to one when meta-links of a link are distributed uniformly, therefore, integrated across MC 1043 modules and it is zero when all the meta-links of a link are segregated within its own MC 1044 module. 1045 Meta-strengths 1046 MC describes largely delocalized interactions but, for enhanced interpretability, it is 1047 important to describe the overall contribution of individual regions to the different higher-order 1048 interactions. Hence, we defined various indices of meta-strength. 1049 Concerning trimer interaction, a natural definition of the trimer strength of a region j is given 1050 by: 1051 MC𝑗 3 = ∑ ∑ MC𝑖𝑗,𝑗𝑛 𝑛 𝑖 ; 𝑖, 𝑛 ≠ 𝑗 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 1052 Here j is the root of the summed trimers, hence the name of “root-pinned” trimer strength (to 1053 contrast it with alternative definitions, not used in this study, where the pinned region may lie 1054 at a leaf). Analogously, we can define tetramer strengths of a link (ij): 1055 MC𝑖𝑗 4 = ∑ ∑ MC𝑖𝑗,𝑚𝑛 ; 𝑖𝑗 ≠ 𝑚𝑛 𝑛𝑚 1056 denoted as “base-pinned” as the frozen link is a dimer base of the tetramer. 1057 A trimer is defined between zones or within zones depending on the zones to which its leaves 1058 belong. If all leaves are in the same zone (independently from where the root is) then the trimer 1059 is considered within zone, otherwise it is considered between zones. For tetramers we 1060 distinguished tetramers with base within a zone (if both bases are within zone dimers) or base 1061 between zones (if both bases are between zones). There are more combinatorial cases for 1062 tetramers that were ignored in this study for simplicity. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . 1063 1064 Comparing MC and FC 1065 1066 We also computed more conventional FC strengths (dimer strengths) for each node as: FC𝑟 𝜆 = ∑ FC𝑖𝑟 𝑖 1067 where 𝜆 is an index referring to intra-zone if 𝑖 and 𝑟 are in the same zones (Fig. S4A), or inter- 1068 zone if they belong to different zones (Fig. 5A). To evaluate MC-FC redundancy on the single 1069 subject-level, we computed the Pearson’s correlation between roots-pinned trimers and FC 1070 node-degrees for all nodes and subject (Fig. 4A)., by the following formula: 1071 ∆𝑛𝑜𝑑𝑒−𝑙𝑒𝑣𝑒𝑙 = 𝑐𝑜𝑟𝑟[FC𝑟 𝜆, MC𝑟 3𝜆 ] 1072 For the tetramers case, the same MC-FC comparison was done for edges computing: 1073 ∆𝑒𝑑𝑔𝑒−𝑙𝑒𝑣𝑒𝑙 = 𝑐𝑜𝑟𝑟[FC𝑖𝑗 𝜆 , MC𝑖𝑗 4𝜆 ] 1074 on the subject-level and for two intra- and inter-zone subsets (Fig. S3A). 1075 We also introduced notions of genuine trimer and tetramers, to identify higher-order 1076 interactions that were not completely explained by existing motifs of dimer interactions. We 1077 separated trimers into three groups: 1) within zone, 2) leaves in same zone, and 3) leaves in two 1078 zones. For a given trimer with 𝑟 as root and 𝑖, 𝑗 as leave regions, we defined the following 1079 condition: 1080 𝑀𝐶𝑖𝑟,𝑗𝑟 > 𝐹𝐶𝑖𝑗
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
.
/
t
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1081
for a trimer to be considered “genuine”, meaning that the trimer interaction coupling 𝑖 and 𝑗 via
1082
𝑟 is not a mere byproduct of the dimer between 𝑖 and 𝑗 but it is actually stronger (其他
1083
interpretation is that the interaction path between i and j is “shorter” when the interaction is
1084
mediated by r than when it is direct). Analogously, we separated tetramers into two groups: 1)
1085
base in two zones, 和 2) base in same zone. For a give tetramer with (𝑖, 𝑗) 和 (𝑚, 𝑛) dimers,
1086
we the defined the following genuinity condition:
1087
1088
1089
参考
𝑀𝐶𝑖𝑗,𝑚𝑛 > 𝐹𝐶𝑖𝑗
1090
1091
1092
1093
1094
1095
1096
1097
1098
1099
1100
1101
1102
1103
1104
1105
1106
1107
1108
1109
1110
1111
1112
Achard, S。, 布莫尔, E., 2007. Efficiency and cost of economical brain functional networks. 公共科学图书馆
电脑. Biol. https://doi.org/10.1371/journal.pcbi.0030017
艾伦, E.A., Damaraju, E., Plis, S.M., Erhardt, E.B., Eichele, T。, Calhoun, V.D., 2014. Tracking
whole-brain connectivity dynamics in the resting state. Cereb. Cortex 24, 663–676.
https://doi.org/10.1093/cercor/bhs352
American Psychiatric Association, 2000. Diagnostic and statistical manual of mental disorders (4th
Ed. text revised). Diagnostic Stat. 男人. Ment. Disord. 4th Ed. TR.
Arbabyazd, L.M., Lombardo, D ., Blin, 奥。, Didic, M。, Battaglia, D ., Jirsa, 五、, 2020. 动态的
Functional Connectivity as a complex random walk: Definitions and the dFCwalk toolbox.
MethodsX 7, 101168. https://doi.org/10.1016/j.mex.2020.101168
Arnold, S.E., 海曼, B.T., Flory, J。, Damasio, A.R., Van Hoesen, G.W., 1991. The topographical and
neuroanatomical distribution of neurofibrillary tangles and neuritic plaques in the cerebral cortex
of patients with alzheimer’s disease. Cereb. Cortex 1. https://doi.org/10.1093/cercor/1.1.103
Bakker, A。, Krauss, G.L., 阿尔伯特, M.S., Speck, C.L., 琼斯, L.R., Stark, C.E., Yassa, M.A., Bassett,
S.S., Shelton, A.L., 加拉格尔, M。, 2012. Reduction of Hippocampal Hyperactivity Improves
Cognition in Amnestic Mild Cognitive Impairment. 神经元.
https://doi.org/10.1016/j.neuron.2012.03.023
Bassett, D.S., Wymbs, N.F., Porter, M.A., Mucha, P.J., 卡尔森, J.M., Grafton, S.T., 2011. 动态的
reconfiguration of human brain networks during learning. PNAS.
https://doi.org/10.1073/pnas.1018985108
Bateman, R.J., Xiong, C。, Benzinger, T.L.S., 费根, A.M., Goate, A。, 狐狸, 北卡罗来纳州, 马库斯, D.S., Cairns,
新泽西州, Xie, X。, Blazey, T.M., Holtzman, D.M., Santacruz, A。, Buckles, 五、, Oliver, A。, Moulder,
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
t
.
/
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
t
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1113
1114
1115
1116
1117
1118
1119
1120
1121
1122
1123
1124
1125
1126
1127
1128
1129
1130
1131
1132
1133
1134
1135
1136
1137
1138
1139
1140
1141
1142
1143
1144
1145
1146
K., Aisen, P.S., Ghetti, B., Klunk, W.E., McDade, E., 马丁斯, R.N., Masters, C.L., Mayeux, R。,
Ringman, J.M., Rossor, M.N., Schofield, P.R., Sperling, R.A., Salloway, S。, 莫里斯, J.C., 2012.
Clinical and biomarker changes in dominantly inherited Alzheimer’s disease. 氮. Engl. J. Med.
https://doi.org/10.1056/NEJMoa1202753
Battaglia, D ., Boudou, T。, 汉森, E.C.A., Lombardo, D ., Chettouf, S。, Daffertshofer, A。, McIntosh,
A.R., Zimmermann, J。, 里特尔, P。, Jirsa, 五、, 2020. Dynamic Functional Connectivity between
order and randomness and its evolution across the human adult lifespan. Neuroimage 222,
117156. https://doi.org/10.1016/j.neuroimage.2020.117156
Battiston, F。, Cencetti, G。, Iacopini, 我。, Latora, 五、, Lucas, M。, Patania, A。, Young, J.G., Petri, G。, 2020.
Networks beyond pairwise interactions: Structure and dynamics. Phys. Rep. 874, 1–92.
https://doi.org/10.1016/j.physrep.2020.05.004
Braak, H。, Braak, E., 1991. Neuropathological stageing of Alzheimer-related changes. Acta
Neuropathol. https://doi.org/10.1007/BF00308809
布劳恩, U。, Schäfer, A。, Walter, H。, Erk, S。, Romanczuk-Seiferth, N。, Haddad, L。, Schweiger, J.I.,
Grimm, 奥。, Heinz, A。, Tost, H。, Meyer-Lindenberg, A。, Bassett, D.S., 2015. 动态的
reconfiguration of frontal brain networks during executive cognition in humans. PNAS.
https://doi.org/10.1073/pnas.1422487112
Brier, M.R., 托马斯, J.B., 费根, A.M., Hassenstab, J。, Holtzman, D.M., Benzinger, T.L., 莫里斯,
J.C., Ances, B.M., 2014. Functional connectivity and graph theory in preclinical Alzheimer’s
疾病. Neurobiol. 老化. https://doi.org/10.1016/j.neurobiolaging.2013.10.081
Calhoun, V.D., 磨坊主, R。, Pearlson, G。, Adali, T。, 2014. The Chronnectome: Time-Varying
Connectivity Networks as the Next Frontier in fMRI Data Discovery. 神经元 84, 262–274.
https://doi.org/10.1016/j.neuron.2014.10.015
陈, X。, 张, H。, 高, Y。, Wee, C.Y., 李, G。, 沉, D ., 2016. High-order resting-state functional
connectivity network for MCI classification. Hum. Brain Mapp.
https://doi.org/10.1002/hbm.23240
陈, X。, 张, H。, 张, L。, 沉, C。, 李, S.W., 沉, D ., 2017. Extraction of dynamic functional
connectivity from brain grey matter and white matter for MCI classification. Hum. Brain Mapp.
https://doi.org/10.1002/hbm.23711
Courtiol, J。, Guye, M。, Bartolomei, F。, Petkoski, S。, Jirsa, V.K., 2020. Dynamical mechanisms of
interictal resting-state functional connectivity in epilepsy. J. Neurosci. 40, 5572–5588.
土井:10.1523/JNEUROSCI.0905-19.2020
Cretin, B., Sellal, F。, Philippi, N。, Bousiges, 奥。, Di Bitonto, L。, Martin-Hunyadi, C。, Blanc, F。, 2016.
Epileptic Prodromal Alzheimer’s Disease, a Retrospective Study of 13 New Cases: Expanding
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
/
t
.
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1147
1148
1149
1150
1151
1152
1153
1154
1155
1156
1157
1158
1159
1160
1161
1162
1163
1164
1165
1166
1167
1168
1169
1170
1171
1172
1173
1174
1175
1176
1177
1178
1179
1180
the Spectrum of Alzheimer’s Disease to an Epileptic Variant? J. Alzheimer’s Dis.
https://doi.org/10.3233/JAD-150096
Crutchfield, J.P., 2012. Between order and chaos. Nat. Phys. https://doi.org/10.1038/nphys2190
Crutchfield, J.P., 米切尔, M。, 1995. The evolution of emergent computation. PNAS.
https://doi.org/10.1073/pnas.92.23.10742
Damaraju, E., 艾伦, E.A., Belger, A。, Ford, J.M., McEwen, S。, Mathalon, D.H., Mueller, B.A.,
Pearlson, G.D., Potkin, S.G., Preda, A。, 车工, J.A., Vaidya, J.G., Van Erp, T.G., Calhoun,
V.D., 2014. Dynamic functional connectivity analysis reveals transient states of dysconnectivity
in schizophrenia. NeuroImage Clin. https://doi.org/10.1016/j.nicl.2014.07.003
Damoiseaux, J.S., Prater, K.E., 磨坊主, B.L., Greicius, M.D., 2012. Functional connectivity tracks
clinical deterioration in Alzheimer’s disease. Neurobiol. 老化.
https://doi.org/10.1016/j.neurobiolaging.2011.06.024
Davison, E.N., Schlesinger, K.J., Bassett, D.S., Lynall, M.E., 磨坊主, M.B., Grafton, S.T., 卡尔森,
J.M., 2015. Brain Network Adaptability across Task States. PLoS Comput. Biol.
https://doi.org/10.1371/journal.pcbi.1004029
Davison, E.N., 车工, B.O., Schlesinger, K.J., 磨坊主, M.B., Grafton, S.T., Bassett, D.S., 卡尔森,
J.M., 2016. Individual Differences in Dynamic Functional Brain Connectivity across the Human
Lifespan. PLoS Comput. Biol. https://doi.org/10.1371/journal.pcbi.1005178
de Vos, F。, Koini, M。, 舒腾, T.M., Seiler, S。, van der Grond, J。, Lechner, A。, 施密特, R。, 的
Rooij, M。, Rombouts, S.A.R.B., 2018. A comprehensive analysis of resting state fMRI measures
to classify individual patients with Alzheimer’s disease. Neuroimage.
https://doi.org/10.1016/j.neuroimage.2017.11.025
丹尼斯, E.L., 汤普森, P.M., 2014. Functional brain connectivity using fMRI in aging and
阿尔茨海默氏病. Neuropsychol. 牧师. https://doi.org/10.1007/s11065-014-9249-6
Ezaki, T。, 离婚, M。, Watanabe, T。, Masuda, N。, 2018. Age-related changes in the ease of dynamical
transitions in human brain activity. Hum. Brain Mapp. https://doi.org/10.1002/hbm.24033
Faskowitz, J。, Esfahlani, F.Z., Jo, Y。, 斯波恩斯, 奥。, 贝策尔, R.F., 2020. Edge-centric functional network
representations of human cerebral cortex reveal overlapping system-level architecture. Nat.
Neurosci. 23, 1644–1654. https://doi.org/10.1038/s41593-020-00719-y
Fiorenzato, E., Strafella, A.P., Kim, J。, Schifano, R。, Weis, L。, Antonini, A。, Biundo, R。, 2019.
Dynamic functional connectivity changes associated with dementia in Parkinson’s disease.
Brain. https://doi.org/10.1093/brain/awz192
Fleisher, A.S., Sherzai, A。, 泰勒, C。, Langbaum, J.B.S., 陈, K., Buxton, R.B., 2009. Resting-state
BOLD networks versus task-associated functional MRI for distinguishing Alzheimer’s disease
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
t
/
/
.
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1181
1182
1183
1184
1185
1186
1187
1188
1189
1190
1191
1192
1193
1194
1195
1196
1197
1198
1199
1200
1201
1202
1203
1204
1205
1206
1207
1208
1209
1210
1211
1212
1213
risk groups. Neuroimage. https://doi.org/10.1016/j.neuroimage.2009.06.021
Fousek, J。, Rabuffo, Gi., Gudibanda, K., Sheheitli, H。, Jirsa, 五、, Petkoski, S。, 2022. The structured
flow on the brain’s resting state manifold. eNeuro 8. 土井:10.1523/ENEURO.0283-21.2021.
狐狸, M.D., Raichle, M.E., 2007. Spontaneous fluctuations in brain activity observed with functional
magnetic resonance imaging. Nat Rev Neurosci 8, 700–711. https://doi.org/10.1038/nrn2201
福, Z。, Caprihan, A。, 陈, J。, Du, Y。, Adair, J.C., Sui, J。, Rosenberg, G.A., Calhoun, V.D., 2019.
Altered static and dynamic functional network connectivity in Alzheimer’s disease and
subcortical ischemic vascular disease: shared and specific brain connectivity abnormalities.
Hum. Brain Mapp. https://doi.org/10.1002/hbm.24591
Gemmetto, 五、, Barrat, A。, Cattuto, C。, 2014. Mitigation of infectious disease at school: Targeted class
closure vs school closure. BMC Infect. 迪斯. https://doi.org/10.1186/s12879-014-0695-9
Glenner, G.G., 黄, C.W., 1984. 阿尔茨海默氏病: Initial report of the purification and
characterization of a novel cerebrovascular amyloid protein. Biochem. Biophys. Res. Commun.
https://doi.org/10.1016/S0006-291X(84)80190-4
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
Glomb, K., Ponce-Alvarez, A。, Gilson, M。, 里特尔, P。, 德科, G。, 2017. Resting state networks in
F
/
d
哦
我
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
empirical and simulated dynamic functional connectivity. Neuroimage.
https://doi.org/10.1016/j.neuroimage.2017.07.065
Goh, K.I., 巴拉巴斯, A.L., 2008. Burstiness and memory in complex systems. EPL.
https://doi.org/10.1209/0295-5075/81/48002
Greicius, M.D., Srivastava, G。, Reiss, A.L., Menon, 五、, 2004. Default-mode network activity
distinguishes Alzheimer’s disease from healthy aging: Evidence from functional MRI. PNAS.
https://doi.org/10.1073/pnas.0308627101
Gu, Y。, 林, Y。, 黄, L。, Ma, J。, 张, J。, Xiao, Y。, Dai, Z。, 2020. Abnormal dynamic functional
connectivity in Alzheimer’s disease. CNS Neurosci. Ther. https://doi.org/10.1111/cns.13387
Guimera, 罗杰; Amaral, L.N., NICO, Guimerà, R。, Amaral, L.A.N., 2005. Functional cartography of
complex metabolic networks. 自然 433, 895–900. https://doi.org/10.1038/nature03286.1.
Guimerà, R。, Amaral, L.A.N., 2005. Functional cartography of complex metabolic networks. 自然.
https://doi.org/10.1038/nature03288
汉森, E.C.A., Battaglia, D ., Spiegler, A。, 德科, G。, Jirsa, V.K., 2015. Functional connectivity
dynamics: Modeling the switching behavior of the resting state. Neuroimage 105, 525–535.
https://doi.org/10.1016/j.neuroimage.2014.11.001
Hedden, T。, Van Dijk, K.R.A., Becker, J.A., Mehta, A。, Sperling, R.A., 约翰逊, K.A., 巴克纳, R.L.,
2009. Disruption of functional connectivity in clinically normal older adults harboring amyloid
1214
1215
1216
1217
1218
1219
1220
1221
1222
1223
1224
1225
1226
1227
1228
1229
1230
1231
1232
1233
1234
1235
1236
1237
1238
1239
1240
1241
1242
1243
1244
1245
1246
1247
burden. J. Neurosci. https://doi.org/10.1523/JNEUROSCI.3189-09.2009
Holme, P。, Saramäki, J。, 2012. Temporal networks. Phys. Rep.
https://doi.org/10.1016/j.physrep.2012.03.001
Hou, Y。, Dan, X。, Babbar, M。, Wei, Y。, Hasselbalch, S.G., Croteau, D.L., Bohr, V.A., 2019. Ageing as
a risk factor for neurodegenerative disease. Nat. 牧师. Neurol. https://doi.org/10.1038/s41582-
019-0244-7
和记黄埔, R.M., Morton, J.B., 2015. Tracking the brain’s functional coupling dynamics over
发展. J. Neurosci. https://doi.org/10.1523/JNEUROSCI.4638-14.2015
和记黄埔, R.M., Womelsdorf, T。, 艾伦, E.A., Bandettini, P.A., Calhoun, V.D., 科尔贝塔, M。, Della
Penna, S。, Duyn, J.H., Glover, G.H., Gonzalez-Castillo, J。, Handwerker, D.A., Keilholz, S。,
Kiviniemi, 五、, Leopold, D.A., 帕斯卡莱, F。, 斯波恩斯, 奥。, Walter, M。, 张, C。, 2013.
Dynamic functional connectivity: Promise, 问题, and interpretations. Neuroimage.
https://doi.org/10.1016/j.neuroimage.2013.05.079
Jeub, L.G.S., 斯波恩斯, 奥。, Fortunato, S。, 2018. Multiresolution Consensus Clustering in Networks. Sci.
Rep. 8. 土井:10.1038/s41598-018-21352-7
Jia, H。, 胡, X。, 德什潘德, G。, 2014. Behavioral relevance of the dynamics of the functional brain
connectome. Brain Connect. https://doi.org/10.1089/brain.2014.0300
琼斯, D.T., MacHulda, M.M., Vemuri, P。, McDade, E.M., 曾, G。, Senjem, M.L., Gunter, J.L.,
Przybelski, S.A., Avula, R.T., Knopman, D.S., Boeve, B.F., 彼得森, R.C., 杰克, C.R., 2011.
Age-related changes in the default mode network are more advanced in Alzheimer disease.
Neurology. https://doi.org/10.1212/WNL.0b013e318233b33d
琼斯, D.T., Vemuri, P。, 墨菲, M.C., Gunter, J.L., Senjem, M.L., Machulda, M.M., Przybelski,
S.A., Gregg, B.E., Kantarci, K., Knopman, D.S., Boeve, B.F., 彼得森, R.C., 杰克, C.R., 2012.
Non-stationarity in the “resting brain’s” modular architecture. 公共图书馆一号.
https://doi.org/10.1371/journal.pone.0039731
Kim, J。, Criaud, M。, 给, S.S., Díez-Cirarda, M。, Mihaescu, A。, Coakeley, S。, Ghadery, C。, Valli, M。,
Jacobs, M.F., Houle, S。, Strafella, A.P., 2017. Abnormal intrinsic brain functional network
dynamics in Parkinson’s disease. Brain. https://doi.org/10.1093/brain/awx233
Kovanen, L。, Kaski, K., Kertész, J。, Saramäki, J。, 2013. Temporal motifs reveal homophily, 性别-
specific patterns, and group talk in call sequences. PNAS.
https://doi.org/10.1073/pnas.1307941110
LANDAU, L.D., LIFSHITZ, E.M., 1980. COURSE OF THEORETICAL PHYSICS Volume 5,
STATISTICAL PHYSICS Part 1. Stat. Phys.
Latora, 五、, Marchiori, M。, 2001. Efficient behavior of small-world networks. Phys. 牧师. Lett.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
t
/
.
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
/
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1248
1249
1250
1251
1252
1253
1254
1255
1256
1257
1258
1259
1260
1261
1262
1263
1264
1265
1266
1267
1268
1269
1270
1271
1272
1273
1274
1275
1276
1277
1278
1279
1280
1281
https://doi.org/10.1103/PhysRevLett.87.198701
Lavanga, M。, Stumme, J。, Yalcinkaya, B.H., Jockwitz, C。, Sheheitli, H。, Bittner, N。, Hashemi, M。,
Petkoski, S。, Caspers, S。, Jirsa, V.K., 2022. The virtual aging brain : a model-driven explanation
for cognitive decline in older subjects. bioRxiv (preprint) 1–57.
水蛭, R。, 布拉加, R。, 锋利的, D.J., 2012. Echoes of the brain within the posterior cingulate cortex. J.
Neurosci. https://doi.org/10.1523/JNEUROSCI.3689-11.2012
水蛭, R。, 锋利的, D.J., 2014. The role of the posterior cingulate cortex in cognition and disease. Brain.
https://doi.org/10.1093/brain/awt162
Lemere, C.A., Blusztajn, J.K., Yamaguchi, H。, Wisniewski, T。, Saido, T.C., Selkoe, D.J., 1996.
Sequence of deposition of heterogeneous amyloid β-peptides and APO E in down syndrome:
Implications for initial events in amyloid plaque formation. Neurobiol. 迪斯.
https://doi.org/10.1006/nbdi.1996.0003
Liao, W., 张, Z。, Mantini, D ., 徐, Q., 吉, G.J., 张, H。, 王, J。, 王, Z。, 陈, G。, Tian, L。,
Jiao, Q., Zang, Y.F., 鲁, G。, 2014. Dynamical intrinsic functional architecture of the brain during
absence seizures. Brain Struct. Funct. https://doi.org/10.1007/s00429-013-0619-2
Lindquist, M.A., 徐, Y。, Nebel, M.B., Caffo, B.S., 2014. Evaluating dynamic bivariate correlations in
resting-state fMRI: A comparison study and a new approach. Neuroimage.
https://doi.org/10.1016/j.neuroimage.2014.06.052
刘, F。, 王, Y。, 李, M。, 王, W., 李, R。, 张, Z。, 鲁, G。, 陈, H。, 2017. Dynamic functional
network connectivity in idiopathic generalized epilepsy with generalized tonic–clonic seizure.
Hum. Brain Mapp. https://doi.org/10.1002/hbm.23430
Lloyd, S.P., 1982. Least Squares Quantization in PCM. IEEE Trans. Inf. 理论.
https://doi.org/10.1109/TIT.1982.1056489
Lombardo, D ., Cassé-Perrot, C。, Ranjeva, J.P., Le Troter, A。, Guye, M。, Wirsich, J。, Payoux, P。,
Bartrés-Faz, D ., Bordet, R。, 理查森, J.C., Felician, 奥。, Jirsa, 五、, Blin, 奥。, Didic, M。,
Battaglia, D ., 2020. Modular slowing of resting-state dynamic functional connectivity as a
marker of cognitive dysfunction induced by sleep deprivation. Neuroimage 222.
https://doi.org/10.1016/j.neuroimage.2020.117155
Luppi, A.I., Mediano, P.A.M., Rosas, F.E., Holland, N。, Fryer, T.D., O’Brien, J.T., 罗维, J.B.,
Menon, D.K., Bor, D ., Stamatakis, E.A., 2022. A synergistic core for human brain evolution and
认识. Nat. Neurosci. 25. 土井:10.1038/s41593-022-01070-0
Mapstone, M。, Cheema, A.K., Zhong, X。, Fiandaca, M.S., Federoff, H.J., 2017. Biomarker validation:
Methods and matrix matter. Alzheimer’s Dement. https://doi.org/10.1016/j.jalz.2016.11.004
Masters, C.L., Bateman, R。, Blennow, K., 罗维, C.C., Sperling, R.A., Cummings, J.L., 2015.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
t
/
/
.
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1282
1283
1284
1285
1286
1287
1288
1289
1290
1291
1292
1293
1294
1295
1296
1297
1298
1299
1300
1301
1302
1303
1304
1305
1306
1307
1308
1309
1310
1311
1312
1313
1314
阿尔茨海默氏病. Nat. 牧师. 迪斯. Prim. https://doi.org/10.1038/nrdp.2015.56
Mezard, M。, 帕里西, G。, Virasoro, M.A., Thouless, D.J., 1988. Spin Glass Theory and Beyond. Phys.
今天 41. https://doi.org/10.1063/1.2811676
Mormino, E.C., Smiljic, A。, Hayenga, A.O., H. Onami, S。, Greicius, M.D., Rabinovici, G.D., Janabi,
M。, 贝克, S.L., V. Yen, 我。, 麦迪逊, C.M., 磨坊主, B.L., Jagust, W.J., 2011. Relationships
between beta-amyloid and functional connectivity in different components of the default mode
network in aging. Cereb. Cortex. https://doi.org/10.1093/cercor/bhr025
Novelli, L。, Razi, A。, 2022. A mathematical perspective on edge-centric brain functional connectivity.
Nat. Commun. 13, 2693. https://doi.org/10.1038/s41467-022-29775-7
Palop, J.J., Chin, J。, Mucke, L。, 2006. A network dysfunction perspective on neurodegenerative
疾病. 自然 443, 768–773. https://doi.org/10.1038/nature05289
Pannek, K., Guzzetta, A。, Colditz, P.B., Rose, S.E., 2012. Diffusion MRI of the neonate brain:
Acquisition, processing and analysis techniques. Pediatr. Radiol. https://doi.org/10.1007/s00247-
012-2427-X
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
Pedreschi, N。, Bernard, C。, Clawson, W., Quilichini, P。, Barrat, A。, Battaglia, D ., 2020. Dynamic core-
F
/
d
哦
我
/
periphery structure of information sharing networks in entorhinal cortex and hippocampus. Netw
Neurosci 4, 946–975. https://doi.org/10.1162/netn_a_00142
Peixoto, T.P., 2014. Hierarchical block structures and high-resolution model selection in large
网络. Phys. 牧师. X 4. 土井:10.1103/PhysRevX.4.011047
Petkoski, S。, 里特尔, P。, Jirsa, V.K., 2023. White-matter degradation and dynamical compensation
support age-related functional alterations in human brain. Cereb. Cortex bhac500, 1–16.
https://doi.org/doi.org/10.1093/cercor/bhac500
Petrella, J.R., Sheldon, F.C., 王子, S.E., Calhoun, V.D., Doraiswamy, P.M., 2011. Default mode
network connectivity in stable vs progressive mild cognitive impairment. Neurology.
https://doi.org/10.1212/WNL.0b013e31820af94e
Petri, G。, Barrat, A。, 2018. Simplicial Activity Driven Model. Phys. 牧师. Lett.
https://doi.org/10.1103/PhysRevLett.121.228301
Premi, E., Gazzina, S。, Diano, M。, Girelli, A。, Calhoun, V.D., Iraji, A。, 锣, Q., 李, K., Cauda, F。,
Gasparotti, R。, Padovani, A。, Borroni, B., Magoni, M。, 2020. Enhanced dynamic functional
连接性 (whole-brain chronnectome) in chess experts. Sci. Rep.
https://doi.org/10.1038/s41598-020-63984-8
Preti, M.G., Bolton, T.A., Van De Ville, D ., 2017. The dynamic functional connectome: State-of-the-
art and perspectives. Neuroimage. https://doi.org/10.1016/j.neuroimage.2016.12.061
/
t
.
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
t
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1315
1316
1317
1318
1319
1320
1321
1322
1323
1324
1325
1326
1327
1328
1329
1330
1331
1332
1333
1334
1335
1336
1337
1338
1339
1340
1341
1342
1343
1344
1345
1346
1347
1348
Puttaert, D ., Coquelet, N。, Wens, 五、, Peigneux, P。, Fery, P。, Rovai, A。, Trotta, N。, Sadeghi, N。, Coolen,
T。, Bier, J.C., 高盛, S。, De Tiège, X。, 2020. Alterations in resting-state network dynamics
along the Alzheimer’s disease continuum. Sci. Rep. https://doi.org/10.1038/s41598-020-76201-3
Qin, J。, 陈, S.G., 胡, D ., 曾, L.L., Fan, Y.M., 陈, X.P., 沉, H。, 2015. Predicting individual
brain maturity using dynamic functional connectivity. Front. Hum. Neurosci.
https://doi.org/10.3389/fnhum.2015.00418
Rabuffo, G。, Fousek, J。, Bernard, C。, Jirsa, 五、, 2021. Neuronal cascades shape whole-brain functional
dynamics at rest. eNeuro 8. https://doi.org/10.1523/ENEURO.0283-21.2021
Raichle, M.E., MacLeod, A.M., 斯奈德, A.Z., 权力, W.J., Gusnard, D.A., 舒尔曼, G.L., 2001. A
default mode of brain function. PNAS. https://doi.org/10.1073/pnas.98.2.676
Rasero, J。, Aerts, H。, 科尔特斯, J.M., Stramaglia, S。, Marinazzo, D ., Fisica, D ., Aldo, S。, Bari, M。,
Nazionale, 我。, Bari, S。, 2018. Predicting functional networks from region connectivity profiles in
task-based versus resting-state fMRI data 1–15. 土井:10.1101/259077
Rentz, D.M., Locascio, J.J., Becker, J.A., Moran, E.K., Eng, E., 巴克纳, R.L., Sperling, R.A.,
约翰逊, K.A., 2010. 认识, reserve, and amyloid deposition in normal aging. 安. Neurol.
https://doi.org/10.1002/ana.21904
Rombouts, S.A.R.B., Barkhof, F。, Goekoop, R。, 斯塔姆, C.J., Scheltens, P。, 2005. Altered resting state
networks in mild cognitive impairment and mild Alzheimer’s disease: An fMRI study. Hum.
Brain Mapp. https://doi.org/10.1002/hbm.20160
Rosas, F.E., Mediano, P.A.M., Gastpar, M。, 詹森, H.J., 2019. Quantifying high-order
interdependencies via multivariate extensions of the mutual information. Phys. 牧师. 乙 100,
32305. https://doi.org/10.1103/PhysRevE.100.032305
Rousseeuw, P.J., 1987. Silhouettes: A graphical aid to the interpretation and validation of cluster
分析. J. 电脑. Appl. 数学. https://doi.org/10.1016/0377-0427(87)90125-7
鲁比诺夫, M。, 斯波恩斯, 奥。, 2011. Weight-conserving characterization of complex functional brain
网络. Neuroimage 56, 2068–2079. https://doi.org/10.1016/j.neuroimage.2011.03.069
鲁比诺夫, M。, 斯波恩斯, 奥。, 2010. Complex network measures of brain connectivity: Uses and
解释. Neuroimage 52, 1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003
Sachdev, P.S., Brodaty, H。, Reppermund, S。, Kochan, N.A., Trollor, J.N., Draper, B., Slavin, M.J.,
克劳福德, J。, Kang, K., Broe, G.A., Mather, K.A., Lux, 奥。, 2010. The Sydney Memory and
Ageing Study (MAS): Methodology and baseline medical and neuropsychiatric characteristics of
an elderly epidemiological non-demented cohort of Australians aged 70-90 年. Int.
Psychogeriatrics. https://doi.org/10.1017/S1041610210001067
Sakoğlu, Ü., Pearlson, G.D., Kiehl, K.A., 王, Y.M., 迈克尔, A.M., Calhoun, V.D., 2010. A
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
t
/
.
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1349
1350
1351
1352
1353
1354
1355
1356
1357
1358
1359
1360
1361
1362
1363
1364
1365
1366
1367
1368
1369
1370
1371
1372
1373
1374
1375
1376
1377
1378
1379
1380
1381
1382
method for evaluating dynamic functional network connectivity and task-modulation:
Application to schizophrenia. Magn. Reson. Mater. Physics, Biol. Med.
https://doi.org/10.1007/s10334-010-0197-8
Santoro, A。, Battiston, F。, Petri, G。, & Amico, 乙. (2023). Higher-order organization of multivariate
time series. Nature Physics, 1-9.
Sanz-Arigita, E.J., Schoonheim, M.M., Damoiseaux, J.S., Rombouts, S.A.R.B., 马里斯, E., Barkhof, F。,
Scheltens, P。, 斯塔姆, C.J., 2010. Loss of “Small-World” Networks in Alzheimer’s Disease: 图形
Analysis of fMRI Resting-State Functional Connectivity. 公共图书馆一号.
https://doi.org/10.1371/journal.pone.0013788
Savin, C。, Tkačik, G。, 2017. Maximum entropy models as a tool for building precise neural controls.
Curr. Opin. Neurobiol. https://doi.org/10.1016/j.conb.2017.08.001
Schumacher, J。, Peraza, L.R., Firbank, M。, 托马斯, A.J., Kaiser, M。, 加拉格尔, P。, O’Brien, J.T.,
Blamire, A.M., 泰勒, J.P., 2019. Dynamic functional connectivity changes in dementia with
Lewy bodies and Alzheimer’s disease. NeuroImage Clin.
https://doi.org/10.1016/j.nicl.2019.101812
Sheline, Y.I., 莫里斯, J.C., 斯奈德, A.Z., Price, J.L., 严, Z。, D’Angelo, G。, 刘, C。, Dixit, S。,
Benzinger, T。, 费根, A。, Goate, A。, Mintun, M.A., 2010A. APOE4 allele disrupts resting state
fMRI connectivity in the absence of amyloid plaques or decreased CSF Aβ42. J. Neurosci.
https://doi.org/10.1523/JNEUROSCI.3987-10.2010
Sheline, Y.I., Raichle, M.E., 斯奈德, A.Z., 莫里斯, J.C., Head, D ., 王, S。, Mintun, M.A., 2010乙.
Amyloid Plaques Disrupt Resting State Default Mode Network Connectivity in Cognitively
Normal Elderly. Biol. Psychiatry. https://doi.org/10.1016/j.biopsych.2009.08.024
Shi, J.Y., 王, P。, 王, B.H., 徐, Y。, 陈, X。, 李, H.J., 2020. Brain Homotopic Connectivity in
Mild Cognitive Impairment APOE-ε4 Carriers. 神经科学.
https://doi.org/10.1016/j.neuroscience.2020.04.011
Shine, J.M., Bissett, PG, 钟, P.T., Koyejo, 奥。, Balsters, J.H., Gorgolewski, K.J., Moodie, C.A.,
Poldrack, R.A., 2016. The Dynamics of Functional Brain Networks: Integrated Network States
during Cognitive Task Performance. 神经元. https://doi.org/10.1016/j.neuron.2016.09.018
Sizemore, A.E., Giusti, C。, Kahn, A。, Vettel, J.M., 贝策尔, R.F., Bassett, D.S., 2018. Cliques and
cavities in the human connectome. J. 电脑. Neurosci. https://doi.org/10.1007/s10827-017-
0672-6
史密斯, S.M., 詹金森, M。, 伍尔里奇, M.W., 贝克曼, C.F., 贝伦斯, T.E.J., Johansen-Berg, H。,
栏干, P.R., De Luca, M。, Drobnjak, 我。, Flitney, D.E., Niazy, R.K., Saunders, J。, Vickers, J。,
张, Y。, De Stefano, N。, 布雷迪, J.M., Matthews, P.M., 2004. Advances in functional and
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
t
.
/
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1383
1384
1385
1386
1387
1388
1389
1390
1391
1392
1393
1394
1395
1396
1397
1398
1399
1400
1401
1402
1403
1404
1405
1406
1407
1408
1409
1410
1411
1412
1413
1414
1415
1416
structural MR image analysis and implementation as FSL, 在: 神经影像.
https://doi.org/10.1016/j.neuroimage.2004.07.051
Snowdon, D.A., 2003. Healthy Aging and Dementia: Findings from the Nun Study, 在: Annals of
Internal Medicine. https://doi.org/10.7326/0003-4819-139-5_part_2-200309021-00014
Sorg, C。, Riedl, 五、, Mühlau, M。, Calhoun, V.D., Eichele, T。, Läer, L。, Drzezga, A。, Förstl, H。, Kurz,
A。, Zimmer, C。, Wohlschläger, A.M., 2007. Selective changes of resting-state networks in
individuals at risk for Alzheimer’s disease. PNAS. https://doi.org/10.1073/pnas.0708803104
Soto, C。, Pritzkow, S。, 2018. Protein misfolding, aggregation, and conformational strains in
neurodegenerative diseases. Nat. Neurosci. 土井:10.1038/s41593-018-0235-9
Spires-Jones, T.L., 海曼, B.T., 2014. The Intersection of Amyloid Beta and Tau at Synapses in
Alzheimer’s Disease. 神经元. https://doi.org/10.1016/j.neuron.2014.05.004
斯塔姆, C.J., De Haan, W., Daffertshofer, A。, 琼斯, B.F., Manshanden, 我。, Van Cappellen Van Walsum,
A.M., Montez, T。, Verbunt, J.P.A., De Munck, J.C., Van Dijk, B.W., 贝伦德塞, H.W., Scheltens,
P。, 2009. Graph theoretical analysis of magnetoencephalographic functional connectivity in
阿尔茨海默氏病. Brain. https://doi.org/10.1093/brain/awn262
斯塔姆, C.J., 琼斯, B.F., 诺尔特, G。, Breakspear, M。, Scheltens, P。, 2007. Small-world networks and
functional connectivity in Alzheimer’s disease. Cereb. Cortex.
https://doi.org/10.1093/cercor/bhj127
Stefanovski, L。, Triebkorn, P。, Spiegler, A。, Diaz-Cortes, M.-A., 索洛德金, A。, Jirsa, 五、, McIntosh,
A.R., 里特尔, P。, 倡议, A.D.N., 2019. Linking Molecular Pathways and Large-Scale
Computational Modeling to Assess Candidate Disease Mechanisms and Pharmacodynamics in
Alzheimer’s Disease. Front Comput Neurosc 13, 54. https://doi.org/10.3389/fncom.2019.00054
Stefanovski, L。, Meier, J.M., Pai, R.K., Triebkorn, P。, Lett, T。, 马丁, L。, Bülau, K., Hofmann-
Apitius, M。, 索洛德金, A。, McIntosh, A.R., 里特尔, P。, 2021. Bridging Scales in Alzheimer’s
Disease: Biological Framework for Brain Simulation With The Virtual Brain. Frontiers
神经信息学 15, 630172. https://doi.org/10.3389/fninf.2021.630172
Supekar, K., Menon, 五、, 鲁宾, D ., Musen, M。, Greicius, M.D., 2008. Network analysis of intrinsic
functional brain connectivity in Alzheimer’s disease. PLoS Comput. Biol.
https://doi.org/10.1371/journal.pcbi.1000100
Tait, L。, Tamagnini, F。, Stothart, G。, Barvas, E., Monaldini, C。, Frusciante, R。, Volpini, M。, Guttmann,
S。, Coulthard, E., 棕色的, J.T., Kazanina, N。, 好人, M。, 2020. EEG microstate complexity
for aiding early diagnosis of Alzheimer’s disease. Sci. Rep. https://doi.org/10.1038/s41598-020-
74790-7
汤普森, W.H., Fransson, P。, 2016. Bursty properties revealed in large-scale brain networks with a
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
.
/
t
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
t
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1417
1418
1419
1420
1421
1422
1423
1424
1425
1426
1427
1428
1429
1430
1431
1432
1433
1434
1435
1436
1437
1438
1439
1440
1441
1442
1443
1444
1445
1446
1447
1448
1449
1450
point-based method for dynamic functional connectivity. Sci. Rep.
https://doi.org/10.1038/srep39156
Tian, Y。, 马古利斯, D.S., Breakspear, M。, 扎莱斯基, A。, 2020. Topographic organization of the human
subcortex unveiled with functional connectivity gradients. Nat. Neurosci. 23.
土井:10.1038/s41593-020-00711-6
Torres, L。, Blevins, A. S。, Bassett, D ., & Eliassi-Rad, 时间. (2021). The why, 如何, and when of
representations for complex systems. SIAM Review, 63(3), 435-485.
Toulouse, G。, 1986. Theory of the frustration effect in spin glasses: 我.
https://doi.org/10.1142/9789812799371_0009
Tsang, R.S.M., Sachdev, P.S., Reppermund, S。, Kochan, N.A., Kang, K., 克劳福德, J。, Wen, W.,
Draper, B., Trollor, J.N., Slavin, M.J., Mather, K.A., Assareh, A。, Seeher, K.M., Brodaty, H。,
2013. Sydney Memory and Ageing Study: An epidemiological cohort study of brain ageing and
失智. Int. 牧师. Psychiatry. https://doi.org/10.3109/09540261.2013.860890
图灵, A.M., 1937. On computable numbers, with an application to the entscheidungsproblem. Proc.
London Math. Soc. https://doi.org/10.1112/plms/s2-42.1.230
Vannimenus, J。, Toulouse, G。, 1977. Theory of the frustration effect. 二. Ising spins on a square lattice.
J. Phys. C Solid State Phys. 10. https://doi.org/10.1088/0022-3719/10/18/008
Varley, T.F., Pope, M。, Faskowitz, J。, 斯波恩斯, 奥。, 2023. Multivariate Information Theory Uncovers
Synergistic Subsystems of the Human Cerebral Cortex. Commun. Biol. 6, 1–12.
土井:10.1038/s42003-023-04843-w
Viviano, R.P., Raz, N。, Yuan, P。, Damoiseaux, J.S., 2017. Associations between dynamic functional
connectivity and age, metabolic risk, and cognitive performance. Neurobiol. 老化.
https://doi.org/10.1016/j.neurobiolaging.2017.08.003
Vossel, K.A., Beagle, A.J., Rabinovici, G.D., Shu, H。, 李, S.E., Naasan, G。, Hegde, M。, Cornes, S.B.,
亨利, M.L., 纳尔逊, A.B., Seeley, W.W., Geschwind, M.D., Gorno-Tempini, M.L., Shih, T。,
Kirsch, H.E., 加西亚, P.A., 磨坊主, B.L., Mucke, L。, 2013. Seizures and epileptiform activity in
the early stages of Alzheimer disease. JAMA Neurol.
https://doi.org/10.1001/jamaneurol.2013.136
王, K., 梁, M。, 王, L。, Tian, L。, 张, X。, 李, K., Jiang, T。, 2007. Altered functional
connectivity in early Alzheimer’s disease: A resting-state fMRI study. Hum. Brain Mapp.
https://doi.org/10.1002/hbm.20324
王, L。, Zang, Y。, 他, Y。, 梁, M。, 张, X。, Tian, L。, 吴, T。, Jiang, T。, 李, K., 2006. 变化
in hippocampal connectivity in the early stages of Alzheimer’s disease: Evidence from resting
state fMRI. Neuroimage. https://doi.org/10.1016/j.neuroimage.2005.12.033
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
/
.
t
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
t
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
王, Z。, 王, J。, 张, H。, Mchugh, R。, Sun, X。, 李, K., 哪个, Q.X., 2015. Interhemispheric
functional and structural disconnection in Alzheimer’s disease: A combined resting-state fMRI
and DTI study. 公共图书馆一号. https://doi.org/10.1371/journal.pone.0126310
Wee, C.Y., 哪个, S。, Yap, P.T., 沉, D ., 2016. Sparse temporally dynamic resting-state functional
connectivity networks for early MCI identification. Brain Imaging Behav.
https://doi.org/10.1007/s11682-015-9408-2
Weiskopf, N。, Hutton, C。, Josephs, 奥。, 车工, R。, Deichmann, R。, 2007. Optimized EPI for fMRI
studies of the orbitofrontal cortex: Compensation of susceptibility-induced gradients in the
readout direction. Magn. Reson. Mater. Physics, Biol. Med. https://doi.org/10.1007/s10334-006-
0067-6
张, H.Y., 王, S.J., 刘, B., Ma, Z.L., 哪个, M。, 张, Z.J., Teng, G.J., 2010. Resting brain
连接性: Changes during the progress of Alzheimer disease. Radiology.
https://doi.org/10.1148/radiol.10091701
张, H.Y., 王, S.J., Xing, J。, 刘, B., Ma, Z.L., 哪个, M。, 张, Z.J., Teng, G.J., 2009.
Detection of PCC functional connectivity characteristics in resting-state fMRI in mild
阿尔茨海默氏病. Behav. Brain Res. https://doi.org/10.1016/j.bbr.2008.08.012
Zimmermann, Joelle, Griffiths, J.D., McIntosh, A.R., 2018. Unique mapping of structural and
functional connectivity on cognition. J. Neurosci. 38, 9658–9667.
https://doi.org/10.1523/JNEUROSCI.0900-18.2018
Zimmermann, J。, Perry, A。, Breakspear, M。, Schirner, M。, Sachdev, P。, Wen, W., Kochan, N.A.,
Mapstone, M。, 里特尔, P。, McIntosh, A.R., 索洛德金, A。, 2018. Differentiation of Alzheimer’s
disease based on local and global parameters in personalized Virtual Brain models. 神经影像
Clin. 19, 240–251. https://doi.org/10.1016/j.nicl.2018.04.017
1451
1452
1453
1454
1455
1456
1457
1458
1459
1460
1461
1462
1463
1464
1465
1466
1467
1468
1469
1470
1471
1472
1473
1474
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
.
t
/
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1475
Supplementary tables
1476
1477
1478
1479
1480
1481
1482
1483
1484
1485
1486
1487
1488
1489
1490
1491
Table S1. Differential impact of pathology on FC dimers and MC trimers and tetramers.
Intra-zone
SNC
NC
aMCI
广告
FC
0.543±0.170
0.564±0.155
0.549±0.186
0.490±0.180
Trimers
0.359±0.139
0.348±0.126
0.333±0.146
0.318±0.144
Tetramers***
0.222±0.096
0.196±0.087
0.186±0.077
0.156±0.088
Inter-zone
FC**
0.101±0.114
0.083±0.135
0.054±0.126
0.021±0.088
Trimers**
0.039±0.078
0.019±0.083
0.013±0.072
-0.012±0.052
Tetramers***
0.183±0.134
0.187±0.117
0.138±0.137
0.139±0.120
Average strengths of dimer, trimer and tetramer interactions, by clinical group and relation to anatomical zones.
Values are means ± SD; * significantly inter-group variations with P < 0.05; ** with P < 0.01; *** with P < 0.001 (one-way ANOVA test). Table S2. Memory coefficients for dynamic links in the four groups 5% 50% 95% 5% 50% 95% SNC 0.1561 0.1653 0.1746 0.1407 0.1452 0.1498 Intra-zone Inter-zone aMCI 0.1168 0.1238 0.1307 0.1404 0.1443 0.1481 NC 0.1310 0.1383 0.1457 0.1391 0.1428 0.1465 AD 0.1037 0.1098 0.1158 0.0901 0.0928 0.0954 The memory coefficient, by clinical group and relation to anatomical zones. Values are means and the confidence intervals; Intra-zone: SNC >>> NC, aMCI >>> NC, AD >>> NC ; Inter-zone : aMCI >>> NC, AD >>> NC ;
在哪里, >>> means p-value smaller than 0.001.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
t
.
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
.
/
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Supplementary figures
1492
1493
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
/
t
.
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1494
1495
1496
1497
1498
1499
1500
1501
1502
1503
1504
1505
1506
1507
1508
如图. S1. Addition information on state-based dFC analyses. (A) Chord diagrams of FC(λ) states as an
alternative illustration of Fig. 1A. Dark pink regions correspond to Zone I and light pink regions to Zone
二. 状态 1 和 3 with low synchronization have stronger inter-zone connections than states 2 和 4 和
high synchronization. (乙) We used an elbow criterion based on the Silhouette score to guess the optimal
number of clusters. The distortion (linked to the distance between cluster centroids) slows down its
decrease with k while the time of clustering keeps growing, leadings to estimate a number of retained
clusters around four (C). We show here the dependence of the average burstiness coefficient β for all
groups on different choices of binarization thresholds θ. which were averaged over dFC dimers into two
intra- and inter-zone categories of links is shown (colored solid lines; 绿色的: SNC, 黄色的: NC, orange:
aMCI, 红色的: 广告). The fact that the gap and the relative ranking between curves for the different groups
remain consistent over different thresholds justifies the use of relative excess values for the analyses of
Figure 3E.
1509
1510
1511
1512
1513
1514
1515
1516
1517
1518
1519
如图. S2. Length of window in MC approach. (A) Distribution of the duration of mean dwell-times in
a consistent state (from the state-based PBM method), pooled over subjects and states (see Fig 2C). 我们
see that ~90% of epochs last less than 5 TRs. (乙) We applied one-way ANOVA on average MC strengths
to determine the existence of inter-group differences. Shown here is the value of the F-statistic for
existence of inter-group differences, as a function of changing window size, from 3TRs to 20TRs. 我们
performed the analysis separately for intra-zone (green line) and inter-zone (violet line) subsets of
trimers. Using larger windows would not improve the statistical detection of inter-group differences. A
short window of length ω = 5TRs is thus already sufficient to capture between-group differences,
maintaining at the same time the capability to track the very fast dFC fluctuations revealed by Fig. S2A.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
t
.
/
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
.
/
/
t
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
t
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
如图. S3. State-free dFC: Inter-relations between dFC tetramers and FC dimers. (A) Similarly to
the MC-FC comparison at the trimer level (见图. 5A), we compared dimer and tetramer strengths now
for edges. The scatter plots show values of FC dimers paired with the corresponding base-pinned
tetramer strength of that dimer (i.e. the overall meta-coupling of that dimer to other remote and non-
incident dimers). 再次, values are separated for intra- and inter-zone dimers and tetramers. Unlike for
trimers, strong dimers are also the ones with the strongest tetramer strengths, as revealed by significant
positive correlations. (乙) Generalizing Fig. 5B for trimers, we also computed the fraction of genuine
tetramers. The base in same zone subset of tetramers contained a low fraction of genuine tetramers,
while this fraction raised for tetramers with an inter-zone base.
1520
1521
1522
1523
1524
1525
1526
1527
1528
1529
1530
1531
1532
1533
1534
1535
1536
1537
1538
1539
1540
如图. S4. State-free dFC: intra-zone FC dimers and dFC trimers strengths. (A) 和 (乙) The FC
dimers and dFC trimers for the intra-zone subset did not show any significant reduction of strength from
SNC-to-AD group, despite moderately decreasing average values, both globally (左边) and locally at the
single region level (正确的).
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
d
哦
我
/
t
.
/
/
1
0
1
1
6
2
n
e
n
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
n
e
n
_
A
_
0
0
3
3
2
p
d
/
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3