The Physics of Forgetting:
Thermodynamics of
Information at
IBM 1959–1982
Aaron Sidney Wright
Universidad de Harvard
The origin and history of Landauer’s principle is traced through the develop-
ment of the thermodynamics of computation at IBM from 1959 a 1982.
This development was characterized by multiple conceptual shifts: memory
came to be seen not as information storage, but as delayed information trans-
mission; information itself was seen not as a disembodied logical entity, but as
participating in the physical world; and logical irreversibility was connected
with physical, thermodynamic, irreversibility. These conceptual shifts were
characterized by an ambivalence opposing strong metaphysical claims to prac-
tical considerations. Three sorts of practical considerations are discussed. Primero,
these conceptual shifts engaged materials central to IBM’s business practice.
Segundo, arguments for metaphysical certainties were made with reference to the
practical functioning of typical computers. Tercero, arguments for metaphysical
certainties were made in the context of establishing the thermodynamics of
information as a sub-discipline of physics.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
Introducción
1.
This paper charts conceptual shifts in the development of the thermo-
dynamics of information as practiced at IBM from 1959 a 1982 (ver tabla 1).
It begins with a careful examination of how disembodied formal concepts like
information were merged with physical concepts like volume and entropy in
1959 at IBM in a discourse about the fundamental limits of computing. A
logical operation called “RESTORE TO ONE” became “erasure” and was equiva-
lent to the erasing of logical histories; these logical entities were taken to re-
side in physical objects or to be physical objects. Metaphorically twinned
logical/physical systems moved toward forgetting information. This paper
traces the genealogical origins of how computers came to forget. It elucidates
a moment in the history of physics and computing when a disembodied,
Perspectives on Science 2016, volumen. 24, No. 1
©2016 by The Massachusetts Institute of Technology
doi:10.1162/POSC_a_00194
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
112
Perspectives on Science
113
theoretical concept became physical. And it displays a fundamental tension
between the practical exigencies of computing and metaphysical claims. Este
began in the institutional context of IBM’s research division from the late
1950s and 1960s. John Swanson made the transition from writing about
the information stored per symbol in information theory to writing about
information per volume of a computer memory device. He also shifted the
concept of memory from a way of storing information to a delayed transmission
of information. These two shifts allowed him to use the tools and concepts
of Claude Shannon’s information theory in his study of physical computer
memory. Swanson’s work prompted Rolf Landauer to formulate what became
known as “Landauer’s principle” that connected the erasure of information—
a logical operation—to a thermodynamic process, dissipating heat.
These conceptual shifts were characterized by a pronounced ambi-
valence between strong metaphysical shifts and practical concerns. Three
sorts of practical concerns can be seen to be operating in three phases
throughout this conceptual development. In the first phase in 1959, allá
was Swanson’s metaphysical assertion that information can be defined
per unit volume rather than per symbol as in Shannon’s information theory.
This step is not singled out for special attention in his paper, Pero nunca-
theless marks a bold claim that disrupts the traditional division between
abstracto, logical entities and physical entities. This took place in the prac-
tical context of an analysis of ferrite core memory systems, a critical aspect
of IBM’s business practice. In the second phase in 1961, Landauer devel-
oped the equivalence of logical irreversibility with thermodynamic physi-
cal irreversibility. Crossing the same boundary Swanson trespassed,
Landauer asserted that logical, informational “bits” could be in thermal
equilibrium, and that their manipulation inevitably resulted in an increase
in entropy of the computer system. The practical concern at work here
lies in the fact that Landauer’s discussion centered on the functioning of
practical, standard computers. In the third phase from 1970 a 1982,
the claimed philosophical implications of Landauer’s principle were
Table1. Three phases of the development of the thermodynamics of
information at IBM.
Fase
Date
Metaphysical Claim
Practical Concern
I
II
III
1959
Información / volumen
IBM’s business
1961
1970–1982
Logical / physical irreversibility
Practical computation
Fundamental limits
Discipline building
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
114
Physics of Forgetting
strengthened and extended to all information handling in any physical
sistema. The practical context during this phase was discipline building.
Through rhetorical assertions of fundamentality and engagement with ques-
tions at the foundations of thermodynamic theory, Landauer and coworkers
tried to carve out a space for their work as a sub-discipline of physics.
Landauer’s principle’s origin and context falls in the interstices of many
areas of scholarship. It has a place in the history of information theory, el
history of computing, and the history of physics. Sin embargo, “interstices” is
more appropriate than “intersection:” little attention has been paid to it.
This is despite its central role in modern (cuántico) information theory and
an exponential growth of interest among physicists. A standard graduate
text in quantum computing asks: What is the connection between energy
consumption and irreversibility in computation? Landauer’s principle provides
the connection stating that, in order to erase information, it is necessary to
dissipate energy (Nielsen and Chuang 2010, 153).
Citation analysis to Landauer’s first paper on the subject shows an
exponential curve, picking up speed in the 1990s (Higo. 1). This assertion
of the physicality of information has been used to make grand meta-
physical claims about the role of information processing in physics and
even cosmology. Landauer claimed in 1967 that his work required limiting
the laws of physics to quantities that computers could handle, even chal-
lenging the use of π (Landauer 1967). Charles Bennett claimed that
Landauer’s principle could save the Second Law of Thermodynamics from
the challenge of Maxwell’s demon (vea abajo) (bennett 1982). Tommaso
Toffoli went so far as to use the physicality of information to imagine the
universe as a computer. “In a sense, nature has been continually computing
the ‘next state’ of the universe for billions of years; all we have to do—and,
actually, all we can do—is ‘hitch a ride’ on this huge ongoing computation,
and try to discover which parts of it happen to go near to where we want”
(Toffoli 1982, p.165, Landauer citation, pag. 171).
In the history of physics, this subject would fall under the history of
solid-state physics.1 However, the chronological range of recent work in
this history has stopped just short of Landauer’s work (Hoddeson 1992).
In the history of computing, the foci of recent work have been on cor-
porate, institutional, engineering, and military aspects of computing.
The standard economic history of IBM mentions research little, en todo caso
(Fisher et al. 1983). Kenneth Flamm briefly notes the turn toward research
and development in the late 1950s and its importance from a business
1. This categorization fits the intellectual content of Landauer’s work—it was the field
of his PhD and concerned the behavior of materials such as ferroelectrics—as well as its
institutional context: Landauer was head of IBM’s Solid-State Science Department.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
115
Cifra 1. Citation statistics to Landauer (1961) from ISI Web of Knowledge
(does not include books). Google Scholar finds 1053 total records. Análisis
performed 26 Abril 2011.
perspectiva, but does not detail actual research work at the corporation
(Flamm 1988, cap. 4). Where the focus has been on research it has been
concentrated on the years up to the commercialization of computers in the
1950s (Ceruzzi 2003, Introducción, páginas. 1–12). The history and philosophy
of information theory offers more direct contact with the thermodynamics
of computation. There is a literature on the history of cybernetics, anuncio-
dressing early military origins, its impact on twentieth-century social theory,
and its practice as a science (Galison 1994; Recolección 2010; Geoghegan
2011). Perhaps most relevant to the current discussion is the work of
Geoffrey Bowker, who has studied the concept of the archive in cybernetics
(Bowker 1993). In Landauer and Swanson’s work discussed below, el
physicalization of information seems of a kind for these physicists and
the cyberneticians: “something quintessentially abstract, of the mind (el
ability to make hypotheses) became for the cyberneticians a physical fact of
naturaleza. Our modes of scientific practice were projected directly onto nature”
(Bowker 2005, pag. 82). The analogy is:
ability to make decisions : cyberneticians :: información : Landauer et al.
Though Bowker’s assertion is strong, the analogy is supported by the brute
manner in which Landauer et al. often simply asserted—or left implicit—
the physicality of information. Eso es, it was more of a direct projection
than the result of explicit argument (vea abajo).
The most sustained historical and philosophical attention to Landauer et al.
has been motivated by an inquiry into the Second Law of thermodynamics
and Maxwell’s demon. The concern is whether and how “Landauer’s principle”
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
116
Physics of Forgetting
might be used to save the Second Law from Maxwell’s demon. Briefly, el
Second Law states that there is a quantity called entropy that can be cal-
culated for physical systems; if this system is closed—i.e., does not inter-
act with its surroundings—entropy must either stay constant or increase
(Uffink 2001). What exactly Maxwell’s demon is or was is rather compli-
cated. The idea is that it is a hypothetical microscopic creature capable of
manipulating thermodynamic systems such that the Second Law would
be broken: the demon lowers the entropy of closed systems. Economy does
not allow the introduction of the historical or technical apparatus necessary
to give more detail; see the excellent introduction by Leff and Rex (en un
volume dedicated to Landauer) (Leff and Rex 2003). The historical question
es: How has Landauer’s principle been used to save the Second Law from the
demon? The philosophical question is: Have any of these attempts worked,
or is it even possible? Though the purpose of this paper is not to adjudicate
the philosophical debate, sustained high-quality work by John Earman
and John Norton seems to have settled on two negative answers. Incluso
champions of Landauer’s work have been (parcialmente) convinced (Earman
and Norton 1999; norton 2005; norton 2011). It is obvious from reading
Landauer’s original work that he did not intend his analysis to be used
in this way, so Earman and Norton’s work does not invalidate the work
outside discussions of Maxwell’s demon. Eso es, if one is willing to accept
the Second Law (in some context) one may happily apply Landauer’s
principle. En este sentido, the history of the thermodynamics of information
is distinct from the history of cybernetics. Cybernetics has essentially died in
the physical sciences, but the thermodynamics of information is growing
rapidly.2
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
2. The Physics of “Forgetting”
En esta sección, I will trace a discourse on the fundamental limits of com-
putation in research and polemical articles from 1959 a 1982. At its early
etapas, the conceptual progression joined physical limits in machines, de
Brownian motion or “noise,” with information theory through Brillouin
and Shannon. This connection of the physical with the informational
was developed and extended to the pair: irreversible logic and irreversible
thermodynamic processes, and hence to entropy. This process established what
would eventually be called Landauer’s principle: erasing a bit of information
2. This paper connects to the others in this special issue by showing how concepts of
noise in one context (teoría de la información) were brought into another (física), y cómo
other related concepts (información) changed in the process. Swanson’s engagement with
Shannon’s noisy channel theorems set the course for a change in our fundamental concepts
and for the development of a sub-discipline.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
117
creates kT ln2 of entropy.3 Through this process the concepts “information,"
“erasure,” “memory,” and “forgetting” were intertwined and pushed between
the disembodied and the physical.
En 1961, Rolf Landauer (1927–1999) shifted between researcher in, y
manager of, the Physics Division of the Solid-State Science Department at
IBM’s Thomas J. Watson Research Center under construction in Yorktown
Heights, Nueva York (ver figura. 8). He was trained as a theoretical solid-state phys-
icist (Doctor. Cosecha, 1950). Since the appointment of E. R. Piore as IBM’s
director of research in 1955—promoted to vice president in 1960—the
culture of the corporation had been changing. “Under Piore, the corpora-
tion moved away from a strict emphasis upon product development toward
support for basic research …. The scientists under Piore’s direction were
given unusual latitude to pursue basic research” (McCuen 2003, Back-
ground Note). Landauer characterized the late-1950s at IBM as “explor-
atory days.”4 In this atmosphere, a small group of theorists—including
Landauer, John Swanson, Robert Keyes, James Woo and later Charles
Bennett—began exploring the fundamental limits of computation. El
practical motivation, alongside intellectual exploration, for their work
was the rapid development of miniaturization of computing circuits
(Swanson 1960; Landauer [1961] 2000). Though I will not speak of an
absolute beginning, the beginning of this research at IBM was a posthu-
mous paper by Swanson, who prepared a “preliminary and relatively com-
plete version” of a manuscript, which was then “brought into its present
form by R. Landauer” in 1960 (Swanson 1960, pag. 305).
2.1 Phase I: Swanson and the Context of IBM’s Business
Swanson sought “what ultimate limitations the laws of physics impose on
the progress” of miniaturization. These laws are manifested as “the increas-
ingly important effects of quantum-mechanical tunneling and thermal
agitation on the reliability of a memory, as the physical system storing
an individual bit becomes very small” (Swanson 1960, pag. 305; emphasis
agregado). It is worth pausing here to note the conceptual state of play. El
laws of physics of thermodynamics and quantum mechanics are settled,
and they impose on technological progress. Bits are not physical systems,
they are stored in physical systems. Before a decade passed, workers at IBM
asserted fundamental changes to both of these conceptual arrangements.
3. Where k is Boltzmann’s constant, T is temperature, and ln is the natural logarithm.
4. Interview of Dr. Rolf Landauer by Dr. Joan Bromberg on October 17, 1984. Niels
Bohr Library & Archivo, American Institute of Physics, parque universitario, Maryland, EE.UU. http://
www.aip.org/history/ohilist/4726.html (Accedido 28 Septiembre 2013)
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
118
Physics of Forgetting
Swanson considered miniaturized “binary symmetric storage elements”—
he used the example of a ferromagnetic block of metal that was clearly meant
to stand in for the magnetic core memory IBM used, Por ejemplo, en el 705
Electronic Data Processing Machine introduced in 1955. We can get a sense
of the material culture and business context underlying Swanson’s analysis in
a 1955 advertising photograph of the cores alongside a pencil and a circuit-
element (Higo. 2).
According to Swanson, quantum-mechanical and thermal effects may
cause such an element to undergo a “spurious transition from one of its
states to the other.” These “may lead to error in the interpretation of what
information has been stored in memory” (Swanson 1960, pag. 305). At some
punto, the likelihood of a fluctuation is so high that it would not be stable
suficiente, de término medio, to hold information. Though Swanson’s research into
the “ultimate limits” of computation may seem detached from the business
practices of IBM, the behavior of magnetic cores was of central concern.
The importance of the new arrays of cores can be seen in their placement
in the center of the 705 manual’s wonderful mid-century cover, clearly the
focus of attention (Higo. 3). It floats in its own section above other memory
storage technologies: punch cards and magnetic tape. The claims in the
705 manual were somewhat divergent from Swanson’s analysis. Bajo
the heading “Magnetic core memory” the manual effused that:
Magnetic cores are tiny, doughnut-shaped objects that can
“remember” information indefinitely …. A network of ferrite
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 2. Magnetic core memory elements, 1955 IBM archives (VV2116) http://
www-03.ibm.com/ibm/history/exhibits/vintage/images/4506VV2116.jpg
Perspectives on Science
119
magnetic cores is strung on screens of wire. When current is passed
through a pair of wires it causes the core affected to store the data
involucrado. Information is called out of memory by reversing the
process … (IBM 1955, pag. 6)
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 3. IBM 705 Manual (1955), cubrir. Magnetic core array in center.
120
Physics of Forgetting
Cifra 4. The cores are at the intersections of the wires in the center of the image
(Image courtesy of Computer History Museum, Accession 102627814).
Unsurprisingly for marketing material,
the manual hyperbolically
represented magnetic core memory as capable of “indefinite” retention of
información, a perfect artificial memory.
A ten-bit magnetic core memory plane from the IBM 702 is preserved in
the collection of the Computer History Museum and is shown in Fig. 4. El
grid-wiring allows information to be stored and read out of the cores in the
center of the image. The looping wires allow the computer to identify which
core in the array is which. Here is a simplified picture of how one bit of a
ferrite-core memory functioned. Inicialmente, the core is not magnetized. Entonces,
a current is directed to a wire running through the center of the core causing
it to be magnetized according to direction of the current. The core then has
two magnetization states, up and down, according to whether the current
came from the top or the bottom of the wire. By convention, one magnetiza-
tion state is called 1 or ONE, the other 0 or ZERO. As long as the core retains its
magnetization, the information is stored. To “read out” the information in the
core, another current is passed through the wire. According to which magne-
tization state the core is in, the current will either be attenuated or amplified.
This change in the current is interpreted by the computer as the information
in the core. It is important to note that this “read out” current demagnetizes
the core, erasing the information. The first thing the computer does after
receiving the “read out” current with a ONE or ZERO signal is re-write the orig-
inal memory core. De este modo, it should be understood that information erasure was
a necessary physical process in the functioning of magnetic core memory.
We move now from the material context of Swanson’s work to the con-
tent of his paper “Physical versus Logical Coupling in Memory Systems”
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
121
(1960). Swanson first established the meaning of the term “physical cou-
pling” between memory elements. Physical couplings were understood as,
Por ejemplo, chemical bonds between elements of the storage material.
One could imagine trying to use a fleck of iron filing in place of the
more-robust doughnut-shaped cores of the 705. Or the existing cores
could be strung together so that they touched each other, creating a mem-
ory element twice as large. For each additional physical piece of storage
unit there is a probability less than one that it will spontaneously transi-
tion from one memory state to another. As more memory states are added,
por lo tanto, the overall probability of the entire coupled system going
through a transition decreases. Próximo, Swanson introduced a programma-
bolle, “logical coupling” between storage elements that would be mediated
by computer coding. Por ejemplo, a logical coupling could introduce a
redundancy in the memory system such that for each memory element
assigned to ZERO, decir, three more surrounding elements were assigned to
the same state. De nuevo, for each additional redundant memory element, el
chance of unwanted transitions decreases. A memory element and simple
examples of physical and logical couplings are depicted in Fig. 5. Here a
representation of a memory element “doughnut” is shown next to a string of
physically connected elements along a wire which is next to a graphic in-
dicating that the binary value of the topmost element is to be copied to
three redundant elements in some way.
The connection between the physical and the logical began with
Swanson’s thesis that errors would be reduced by a “suitable coupling be-
tween the storage elements” and emerged when he defined both physical
and logical coupling (Swanson 1960, pag. 305). By defining these couplings,
Swanson set the stage to connect the disembodied world of logic to the
physical world of ferromagnets through information theory. A “[pag]hysical
coupling between n storage elements” was understood as “a connection such
that a transition may occur if and only if all n elements make the same
Cifra 5. Depiction of storage elements and physical and logical couplings.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
122
Physics of Forgetting
transition simultaneously” (Swanson 1960, pag. 305). This created new,
more stable, storage elements. Entonces, for an amount of ferromagnets to count
as a storage element it must have only one domain—when some of the
element switches spin orientation the rest follows.
Mathematically, Swanson’s analysis of the switching of a single element
proceeded by describing the transition probability as a Poisson process. A
Poisson process has the characteristic that the probability P of a number of
events k=0,1,2,…, occurring in a time t is given by
P k½ (cid:2) ¼ γtð
Þ ke−γt
k!
where γ is a constant. In the situation Swanson imagined, all the elements
begin in one state.
P k½ (cid:2) ¼ γtð
Þ 0e−γt
0!
¼ e−γt
The transition probability for a physical element to move from one state to
otro (if they are equally probable) such that for a number of elements all
in one state n0 the number of transitions to the other state is in a time, t, es:
n ¼ n0
2
d
1 − e−2γt
Þ
where Swanson has inserted an extra factor of two in the exponent. Entonces
the probability q of finding an element that started in one state to have
transitioned to the other is
q ¼ 1
2
d
1 − e−2γt
Þ
Because there are only two possible states, a double transition takes the par-
ticle back to its original position. Swanson takes the limit where γt is small
to find q=γt and calls γ “the transition probability per unit time” (Swanson
1960, pag. 306).
Swanson analyzed the “behavior of transition probabilities under physical
coupling,” from an “intuitive” and a “physical” viewpoint (Swanson 1960,
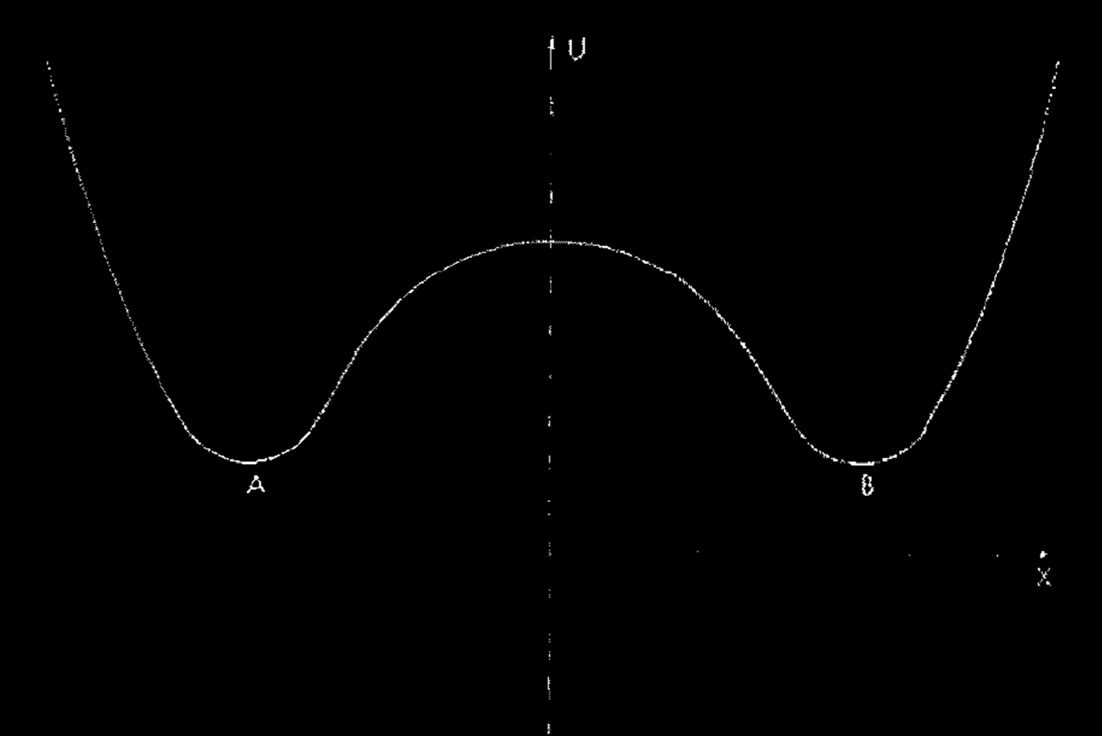
páginas. 306, 310). Here the physical viewpoint—an appendix to Swanson’s
paper—will be discussed, in which “one assumes a memory element to
be equivalent to a particle in a potential with two minima” depicted in
Higo. 6. The figure “shows the energy (or perhaps free energy) of the switching
system as a function of the coordinate x being switched. A and B are the two
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
123
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 6. Swanson’s figure of a double potential well (Swanson 1960, pag. 310).
possible stable states denoting ‘0’ and ‘1’ respectively” (Swanson 1960,
pag. 310). Under these assumptions, Swanson argued that “the transition
probability due to thermal agitation or quantum-mechanical tunneling of
n physically coupled elements is proportional to the exponential of a nega-
tive constant times n” (Swanson 1960, pag. 306). Eso es, if each memory
element depicted in Fig. 5 has a characteristic constant determining the
probability of random switching U, than the probability of n elements
switching will have characteristic nU. His first example is of transfer by
thermal agitation. “The probability for transfer from A to B by thermal
agitation is then of the form v exp(−U/kT),” where v is a frequency factor
(typical of the well A), U is the height of the potential barrier, and kT is
Boltzmann’s constant multiplied by the temperature (Swanson 1960, pag. 310).5
Swanson’s more intuitive argument does not rely on the assumption of a
system characterized by a one-dimensional potential graph, Higo. 6, pero
picks up the assumptions of the Poisson process analyzed earlier of a system
characterized by a transition probability per unit time, do. Swanson sought
to find γn, the probability per unit time of a physically coupled system on
n identical elements. Acting under the assumption that there is some
5. Swanson also wrote down the probability for quantum mechanical tunneling, pero
argued that if there is enough thermal scattering in the transfer that quantum coherence
would be destroyed.“That is, the system after arriving in B [quería] go through a consid-
erable history before it arrive[d] once more at the portion of the barrier which permits
maximum tunneling. In this period it [quería] have an opportunity to interact sufficiently with
other systems to lose its quantum-mechanical phase memory” (Swanson 1960, pag. 310).
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
2
4
1
1
1
2
1
7
9
0
1
2
8
pag
oh
s
C
_
a
_
0
0
1
9
4
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
124
Physics of Forgetting
characteristic time τ governed the switching, Swanson asserted that the
probability for switching to occur was (γτ)norte, making the probability per
time τ
By performing the common trick of writing a quantity as its logarithm
raised to an exponential,
¼ τ−1 γτð
Þn
do
norte
Swanson re-arranged this into
do
norte
¼ veμn
where v=τ−1 and μ≡−logeγτ. This is the same form as the expression for
thermal tunneling above. Though Swanson leaves this obscure, in order to
proceed to a general expression for the probability for switching in some
general time t, one must begin again with the Poisson analysis. Swanson
μn, γnt≪1 and wrote, skipping the
simply notes that he assumed qn = vte
assertion that the physically coupled elements must also behave as a Poisson
proceso, just as the individual elements do.
Swanson’s connection to information theory came in his discussion of
logical couplings. A logical coupling among n elements was
the introduction of a redundancy such that only k(k