TRABAJO DE INVESTIGACIÓN

Comparative Evaluation and Comprehensive Analysis of
Machine Learning Models for Regression Problems

Boran Sekeroglu1,5†, Yoney Kirsal Ever2,5, Kamil Dimililer3,5, Fadi Al-Turjman4,5

1Information Systems Engineering Department, Near East University, Nicosia, Cyprus, Mersin 10, Pavo

2Software Engineering Department, Near East University, Nicosia, Cyprus, Mersin 10, Pavo

3Electrical and Electronic Engineering Department, Near East University, Nicosia, Cyprus, Mersin 10, Pavo

4Artificial Intelligence Engineering Department, Near East University, Nicosia, Cyprus, Mersin 10, Pavo

5Research Centre for AI and IoT, Near East University, Nicosia, Cyprus, Mersin 10, Pavo

Palabras clave: Machine learning; Regression; Comparative evaluation; Análisis; Validación

Citación: Sekeroglu, B., et al.: Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression

Problems. Data Intelligence 4(3), 620-652 (2022). doi: 10.1162/dint_a_00155

Recibió: Ene. 10, 2022; Revised: Mar. 15, 2022; Aceptado: Apr. 11, 2022

ABSTRACTO

Artificial intelligence and machine learning applications are of significant importance almost in every field
of human life to solve problems or support human experts. Sin embargo, the determination of the machine
learning model to achieve a superior result for a particular problem within the wide real-life application areas
is still a challenging task for researchers. The success of a model could be affected by several factors such as
dataset characteristics, training strategy and model responses. Por lo tanto, a comprehensive analysis is required
to determine model ability and the efficiency of the considered strategies. This study implemented ten
benchmark machine learning models on seventeen varied datasets. Experiments are performed using four
different training strategies 60:40, 70:30, y 80:20 hold-out and five-fold cross-validation techniques.
We used three evaluation metrics to evaluate the experimental results: mean squared error, mean absolute
error, and coefficient of determination (R2 score). The considered models are analyzed, and each model’s
advantages, disadvantages, and data dependencies are indicated. As a result of performed excess number of
experimentos, the deep Long-Short Term Memory (LSTM) neural network outperformed other considered
modelos, a saber, decision tree, linear regression, support vector regression with a linear and radial basis
function kernels, random forest, gradient boosting, extreme gradient boosting, shallow neural network, y
deep neural network. It has also been shown that cross-validation has a tremendous impact on the results of
the experiments and should be considered for the model evaluation in regression studies where data mining
or selection is not performed.

† Corresponding Author: Boran Sekeroglu (Correo electrónico: boran.sekeroglu@neu.edu.tr; ORCID: 0000-0001-7284-1173).

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

/

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

© 2022 Academia China de Ciencias. Publicado bajo una atribución Creative Commons 4.0 Internacional (CC POR 4.0) licencia.

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

1. INTRODUCCIÓN

Artificial intelligence (AI) and machine learning (ML) models have overachievement in the ability to
create relations between the variables (atributos) and the observations (instancias) for different kinds of tasks
such as classification and regression. Unlike classification applications, in which samples are assigned to
certain labels, regression applications aim to draw a regression line or plane on all samples with the least
error. In several studies, researchers considered the real-valued outputs as bucketed outputs and converted
regression problems into the classification domain if possible [1]. This led more implementations of ML
models on classification than regression tasks that aimed to predict real-valued infinite outputs. Sin embargo,
the deployments of regression studies also affected multidisciplin ary fields such as the healthcare sector [2, 3],
education [4], price predictions [5], Deportes [6], and finance [7].

The primary concern of the ML applications is determining the model suitable for the dataset used for
the particular application. This has vital importance since determining the optimal ML model for all kinds
of applications in both problem domains is almost impossible because of the different characteristics of
datasets and the ability of the models [1]. Además, the characteristics of the considered datasets can
increase the complexity of the studies in both domains. Based on the attribute properties, datasets can be
structured-unstructured datasets, numeric-categorical, and combined datasets. Sin embargo, they can most
importantly be defined as linear/nonlinear or high/low correlated when the relations between attributes and
outputs are considered—these cause ML models to produce different results in applications on datasets
with different characteristics. Por lo tanto, the analysis of the success of an ML model should be performed
on datasets containing different and varied conditions.

Besides the characteristics of the datasets, training of the ML models (validation techniques) and evaluation
techniques differ in most of the studies. The hold-out method, which splits the train and test data using
different ratios (60:40, 70:30, 75:25, 80:20, etc.), is common in AI and ML implementations [2, 4, 6]. El
other commonly used training and validation method for ML models is k-fold cross-validation, which is
used for hyperparameter tuning and evaluating final results [6]. The main drawback of the hold-out method
is that the samples are only used in training or testing, and the actual prediction abilities of the models
differ according to the training and testing samples. En cambio, k-fold cross-validation, which finds the average
result by dividing the data into k equal parts and training models k times, produces more accurate results [8]
because of the consideration of all data both in testing and training. Sin embargo, obtaining results using all
data samples could affect the obtained results, negatively or positively, slightly or significantly. El número
of training data and the validation of methods significantly affect the model trained with random data
selection and do not determined by data mining. The recent regression studies differ in how they were
implemented in terms of model selection, evaluación, y entrenamiento. Sin embargo, the implementation of multiple
models and the consideration of several evaluation metrics are common in these studies, even though the
training strategies are different [2, 6, 9, 10, 11].

The use of hold-out ratios or cross-validation method does not have a standard implementation even in
recent research. The reasons for this are the number of instances in the dataset, the researchers’ preferences,
and the responses of the models. Sin embargo, in ML, it is known that even a small change in the trained data

Data Intelligence

621

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

t

/

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

can significantly affect the results in a positive or negative direction, especially in datasets with different
characteristics or in big data. Por lo tanto, it is crucial to investigate the effect of cross-validation as well as
the hold-out ratios on models and results using varied datasets [8].

Although most machine learning studies included the comparative analysis in determining the optimal
modelo, a few direct comparison studies were also performed. Huang et al. [12] compared the three ML
modelos (backpropagation neural network, support vector regression, and extreme learning machine) para el
regression problems using a total of four datasets. The evaluation was performed using mean squared error
(MSE), mean absolute percentage error (MAPE), and coefficient of determination (R2 score). Además,
20-fold cross-validation was considered to estimate the prediction errors and the authors concluded that
the use of integrated models produced superior scores than single models. Bratsas et al. [13] comparado
four models, namely multilayer perceptron, linear regression, random forest, and support vector regression,
to predict the traffic status of Thessaloniki, Greece. The comparison was performed using three scenarios
created from a single dataset. The evaluation of the models was performed using Root Mean Square Error
(RMSE). It was concluded that the performances of Neural Networks (NN) and Supoort Vector Regression
(RVS) models outperformed both Random Forest (RF) and Linear Regression (LR). Recent comparative
research showed that considering multiple and varied datasets, modelos, and validation techniques were of
crucial importance to analyzing the models’ abilities and the effect of training strategies.

Automated Machine Learning (AutoML) has been started to be implemented recently, and besides finding
the model that produces superior results among different ML models, it aims to achieve the best result with
the ensemble method. Sin embargo, although AutoML provides great advantages to users in terms of ease of
implementación, its’ computational costs and computer crashes, even in relatively small datasets, son los
major disadvantages of the AutoML.

This study aims to compare ML models for regression tasks with different scenarios that have not been
studied together in recent studies. An excessive number of multi-character datasets such as time-series,
multivariate, high instance, and high attribute, are considered with varied validation strategies to analyze
the response of the models to the different numbers of training data, conjuntos de datos, and the effect of hold-out
and cross-validation on the regression tasks. Finalmente, it aims to achieve the primary goal of the study, cual
is to determine starting points for future regression studies to minimize model and validation strategy
selection procedure.

For this purpose, in this paper, ten benchmark ML models were selected to be included in the comparisons

due to their frequency of use and the formation of the basis for other models.

Linear Regression is still one of the most frequently used statistical models in regression tasks, particularly
for the data with a linear relationship. Decision Tree (DT) is another common ML model for regression
problems and also forms the basis for other tree-ensemble models such as Random Forest (RF), Degradado
Boosting (GradBoost), and Extreme Gradient Boosting (XGBoost). RF, GradBoost, and XGBoost minimize
the error obtained by the DT either with bagging or boosting strategies and have increasing popularity in

622

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

.

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

regression tasks. Even though the XGBoost and GradBoost do not have higher popularity as much as RF,
their implementation in regression tasks is becoming common. The superior results of the support vector
machine in classification problems lead the implementation of Support Vector Regression (RVS) for the
regression problems, and the use of SVR also spreads. Sin embargo, the different kernel functions make it
difficult to implement all of them, and in this study, Support Vector Regression with Radial Basis Function
(FBR) kernel (SVRBF), Support Vector Regression with the linear kernel (SVRL) are considered. el neural
redes, which are the primary tools for obtaining reasonable results, particularly in nonlinear data, are of
significant importance to regression studies. Por esta razón, two artificial neural networks with shallow and
deep versions (NN and DNN) and a special type of recurrent neural network which is significant importance
to regression tasks, deep Long-Short Term Memory Neural Network (deep LSTM), are implemented.

A total of 680 experiments were performed on 17 considered datasets to perform a comprehensive
evaluation and comparison. The obtained results were analyzed using three common evaluation metrics
for regression problems: MSE, MAE, and R2 Scores. The analysis of considering the hold-out method with
different ratios was performed. The effect of increment or decrement in training data was analyzed for each
modelo. The data dependency of the models was determined. The obtained hold-out results were compared
to the five-fold cross-validation method, and the effect of cross-validation was demonstrated. Además,
the fold analysis in cross-validation was performed to present the changes for each model in each fold with
statistical descriptions. The model-based evaluation was performed, and the advantages and disadvantages
of the models were presented. Finalmente, the recommendations for models and validation strategies are presented.

2. MATERIALES Y MÉTODOS

2.1 Datasets

Un total de 17 regression datasets from different real-life application areas such as environmental sciences,
Ciencias Sociales, civil engineering, finance and sales sector, and energy consumption were selected in our
study to compare machine learning models for different application fields and obtain more generalizable
resultados. The datasets consisted of a varied number of attributes and instances to analyze the ability of the
models on different data. Además, the datasets are selected to analyze the performances of the models
with different data, such as time-series and multivariate.

Air Quality [14], Wine Quality [15], Combined Cycle Power Plant (CCPP) [16], Behavior of the urban
traffic of the city of Sao Paulo in Brazil Dataset (SPB) [17], Real Estate (RE) Valuation [18], Concrete
Compressive Strength (CON) Data Set [19], Daily Demand Forecasting Orders Data (DDFO) Set [20], two
Student Performance (SP) conjuntos de datos [21] and three Power consumption of Tetouan city (TCPC) conjuntos de datos [22]
each of which is for a single zone, were used to analyze and evaluate the considered machine learning
modelos. Mesa 1 shows the number of instances and attributes included in the datasets used in this study.

Data Intelligence

623

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

.

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

Mesa 1. The number of instances and attributes included in the datasets for this study.

No.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

Dataset

RE
AQ
SPB
WQW
WQR
CCPP-1
CCPP-2
CCPP-3
CCPP-4
CCPP-5
STM
STP
DDFO
CON
TCPC Z1
TCPC Z2
TCPC Z3

No. of instances

No. of attributes

Tipo

414
9358
135
4898
1599
9568
9568
9568
9568
9568
395
649
60
1030
52,417
52,417
52,417

7
14
18
11
11
4
4
4
4
4
32
30
12
8
7
7
7

Multivariate
Multivariate, Time Series
Multivariate, Time Series
Multivariate
Multivariate
Multivariate
Multivariate
Multivariate
Multivariate
Multivariate
Multivariate
Multivariate
Time Series
Multivariate
Multivariate, Time Series
Multivariate, Time Series
Multivariate, Time Series

Numerical representation of the attributes makes it difficult for humans to observe the relationships of
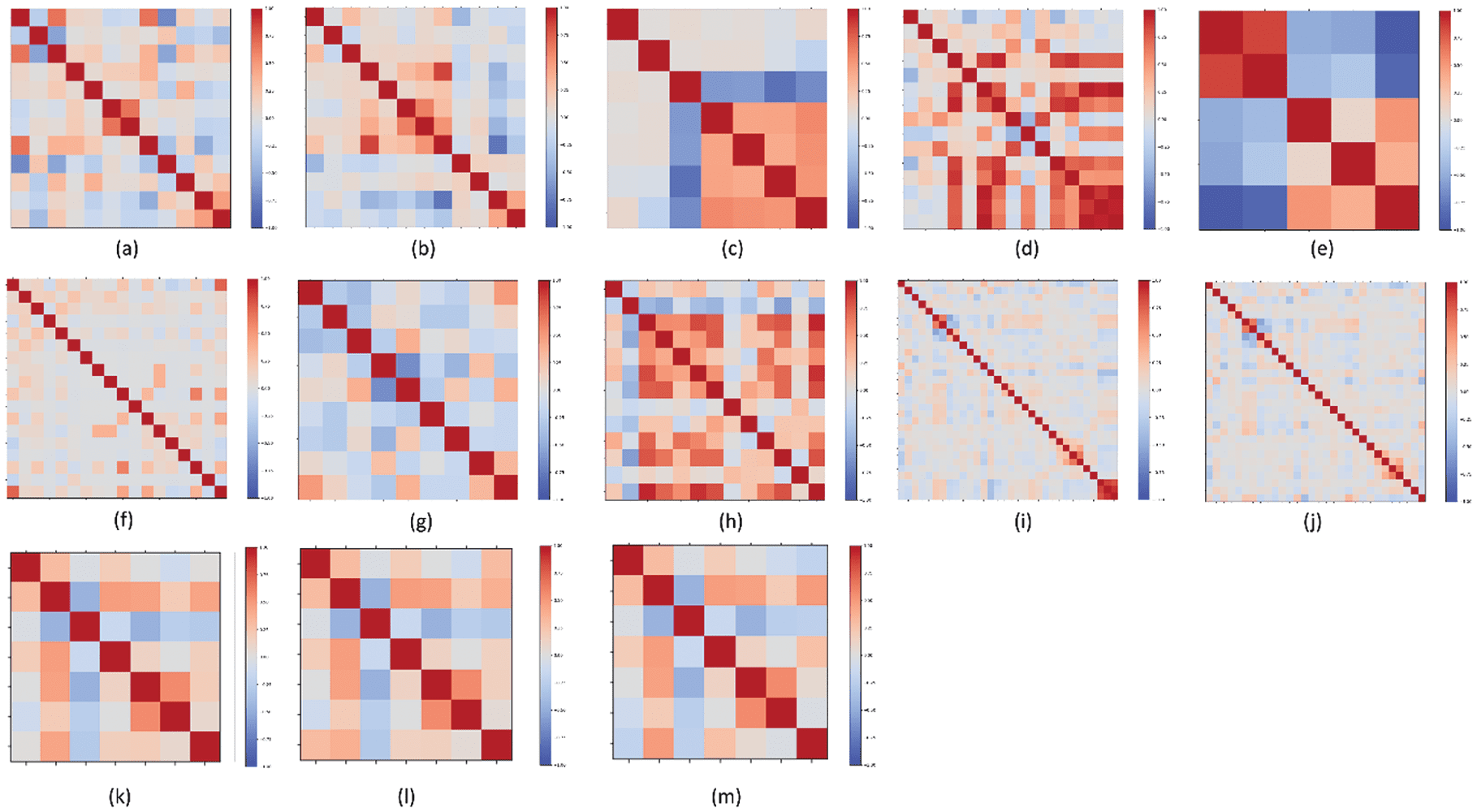
data and the characteristics of the dataset. Cifra 1 shows the correlation analysis of the datasets. El
highest correlation between the attributes was observed in AQ and DDFO datasets (Cifra 1 (d) y (h)),
and the lowest can be listed in WQR, WQW, RE, and STP datasets (Cifra 1 (a-c) y (j)). The correlation
provided by the last three attributes of the STM dataset has been eliminated by removing the two attributes
from the STM dataset, and a more challenging dataset has been obtained in STP, as mentioned above.

2.2 Brief Review of Machine Learning Algorithms

The following section summarizes the basic principles of the mentioned ML models.

2.2.1 Artificial Neural Networks

Backpropagation is the most frequently considered neural network for optimization, regression, y
classification problems. Interconnections of neurons which are the weights, are updated by considering the
actual response of the neural network and expected or observed data. Gradient-descent is the algorithm to
calculate the weight change and update each interconnection. It is still one of the most implemented
algorithms for comparative studies of neural networks and machine learning models [23]. en este estudio, el
shallow version was used with a single hidden layer, and the deep version was implemented using four
hidden layers.

624

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

t

.

/

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

.

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 1. Correlation heatmaps of dataset attributes (a) WQ – Red, (a) WQ – White, (C) RE, (d) AQ, I CC–P – for
all sub-datasets, (F) SPB, (gramo) CON, (h) DDFO, (i) STM, (j) STP, (k) TCPC Z1, (yo) TCPC Z2, y (metro) TCPC Z3.

2.2.2 Linear Regression

Linear Regression is a statistical method that draws the best-fitting regression through the real points.
It is frequently and successfully used in regression problems, especially on datasets whose attributes have
a linear correlation [24].

2.2.3 Support Vector Regression

Support Vector Regression (RVS) was improved to get real-valued outputs instead of binary numbers for
regression problems [25]. Error is minimized while the hyperplane margin is maximized, which provides
an efficient distinguishment of data from each other [26, 27]. Different kernel functions can be used to
project data into higher dimensions, and in this study, Linear and Radial-Basis Function kernels were
considered in the comparisons.

2.2.4 Long-Short Term Memory Neural Network

LSTM is an effective special version of recurrent networks and can be used for both classification and
regression problems [28]. Cell, input gate, output gate, and forget gate are the four major components of
its architecture. It uses gradients to update weights; sin embargo, it remembers previous errors, which improves
the netw’rk’s error minimization in minimized iterations [29].

Data Intelligence

625

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

2.2.5 Decision Tree

Decision Trees are tree-structured algorithms with an initial root node, decision nodes, and leaf nodes.
They are using the divide-and-conquer strategy, which brings several advantages and disadvantages for
a ellos [8]. The simplicity and speed are the main advantages of decision trees; sin embargo, the determination
of the initial root or the sequence of nodes is the main drawback.

2.2.6 Random Forests

Random forests are a kind of tree-based ensemble learning and can be used for both classification and
regression [30, 31]. It constructs several decision trees during the training and optimizes the mean regression
of the individual trees.

2.2.7 Gradient Boosting Algorithm

Gradient Boosting is another tree-based ensemble machine learning algorithm [32]. It aims to optimize
the outputs by minimizing the loss obtained by the constructed weak learners, which are decision trees.
The loss is calculated, and then a new or modified tree is added to reduce the total loss using a gradient
descent algorithm. The mo’el’s output is modified after adding each tree to the model, and different stopping
criteria such as no decrement in loss, adding a fixed number of trees, etc., can be applied to obtain the
final output of the model.

2.2.8 Extreme Gradient Boosting

Similar to Gradient Boosting, Extreme Gradient Boosting [33] is also an ensemble tree method and
applies the principle of boosting weak learners using the gradient descent algorithm. Sin embargo, XGBoost
includes some enhancements to minimize the used resources and to improve the obtained results. Different
regularization models (es decir., LASSO) are used to overcome overfitting problems during the learning.
The built-in cross-validation is applied in each iteration to determine the exact number of iterations on a
single run.

2.3 Evaluation and Comparison Criteria

Three commonly used evaluation metrics were considered to compare the obtained results: Significar

Squared Error (MSE), Mean Absolute Error (MAE), and coefficient of determination (R2 score).

MSE takes the square of error before averaging them, and this provides a relatively higher weight to
significant errors (outliers). This supports researchers in observing the errors of the datasets with larger
valores. Sin embargo, the frequency of the errors has a significant effect on MSE results, and the repetition of
the error causes the increment of MSE.

626

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

t

/

.

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

Sin embargo, reaching minimum error does not always show that the predictions will be more accurate than
other models. Particularly, some significant errors within the dataset may increase the error. Por lo tanto, él
causes overestimating mod’ls’ errors due to the higher value of MSE. This is because the nature of MSE that
considers outliers more than other evaluation metrics. Por otro lado, small errors between predicted
and actual data may cause underestimating the error. De este modo, it is required to consider other evaluation criteria
and consider all of these during the evaluation of the models.

The other metric that is used to evaluate the ability of regression models is the MAE, which is the mean
of absolute errors. MAE focuses on the magnitude of the errors between predicted and actual outputs and
does not consider the direction of the error. It is assumed that more stable results could be obtained using
the MAE.

The R2 score, which is strongly related to MSE, is used to measure the correlation level of predicted and
observed values within the considered dataset. This provides scaled evaluation results for the models and
allows researchers to perform a more robust evaluation between them.

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

2.4 The Design of Relevant Experiments

The design of experiments was based on four varied training of the considered ML models to obtain

results with different training ratios and k-fold cross-validation.

Models were trained by three hold-out ratios, 60:40, 70:30, y 80:20 of the considered datasets, y
scores were obtained from the untrained (prueba) data separately. Además, the ML models were trained
using five-fold cross-validation to provide a more accurate and robust evaluation and analysis of the ML
modelos. The results of five-fold cross-validation experiments were obtained by taking the mean of the fold
resultados.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

.

t

i

The results obtained by the five-fold cross-validation also provided the analysis of how the hold-out
and k-fold cross-validation strategies positively or negatively affect the obtained scores. This analysis was
performed using the results obtained by all hold-out ratios and five-fold cross-validation and individual fold
results obtained in five-fold cross-validation. During the training, the architectures of neural network models,
NN, DNN, and deep LSTM, were fixed; sin embargo, parameters were tuned depending on the dataset
performances of the related model.

The experiments used fixed training and testing data for each hold-out ratio. Por lo tanto, the effect of
change in the training data in the results has been eliminated. In cross-validation experiments, each fold
was fixed, and it was ensured that each model performed training with the same data in each fold.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Deep Neural Network (DNN) was implemented with four hidden layers, 500 neurons within each hidden
capa, and the Sigmoid function was used as an activation function for each layer. ‘Adam’ and MSE were
used as optimizers and loss functions, respectivamente. A shallow Neural Network (NN) was used with a single
hidden layer and 500 neuronas. The other parameters were set as the same as DNN.

Data Intelligence

627

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

Deep Long-Short Term Memory Neural Network was used as four-layered, and the maximum iteration
number was determined based on the highest scores obtained. The experiments were repeated in DNN,
NN, and LSTM experiments with different iterations for each dataset to obtain superior results.

The grid search was applied to obtain optimized scores in Support Vector Regression, Random Forest,
GradBoost, and XGBoost. The best parameters are used to train each fold in five-fold cross-validation
experiments and all ratios of hold-out experiments. Mean Squared Error was used to build a decision tree
regressor structure.

3. RESULTS AND COMPARISONS

This section summarizes the results obtained in the experiments and compares the models at different
training ratios by presenting quantitative results. All models produced fluctuating results at different learning
rates and datasets. The results are compared and discussed in the following sections in detail. S1 Table, S2
Mesa, and S3 Table present the obtained MSE, MAE, and R2 score results for all datasets in all experiments.
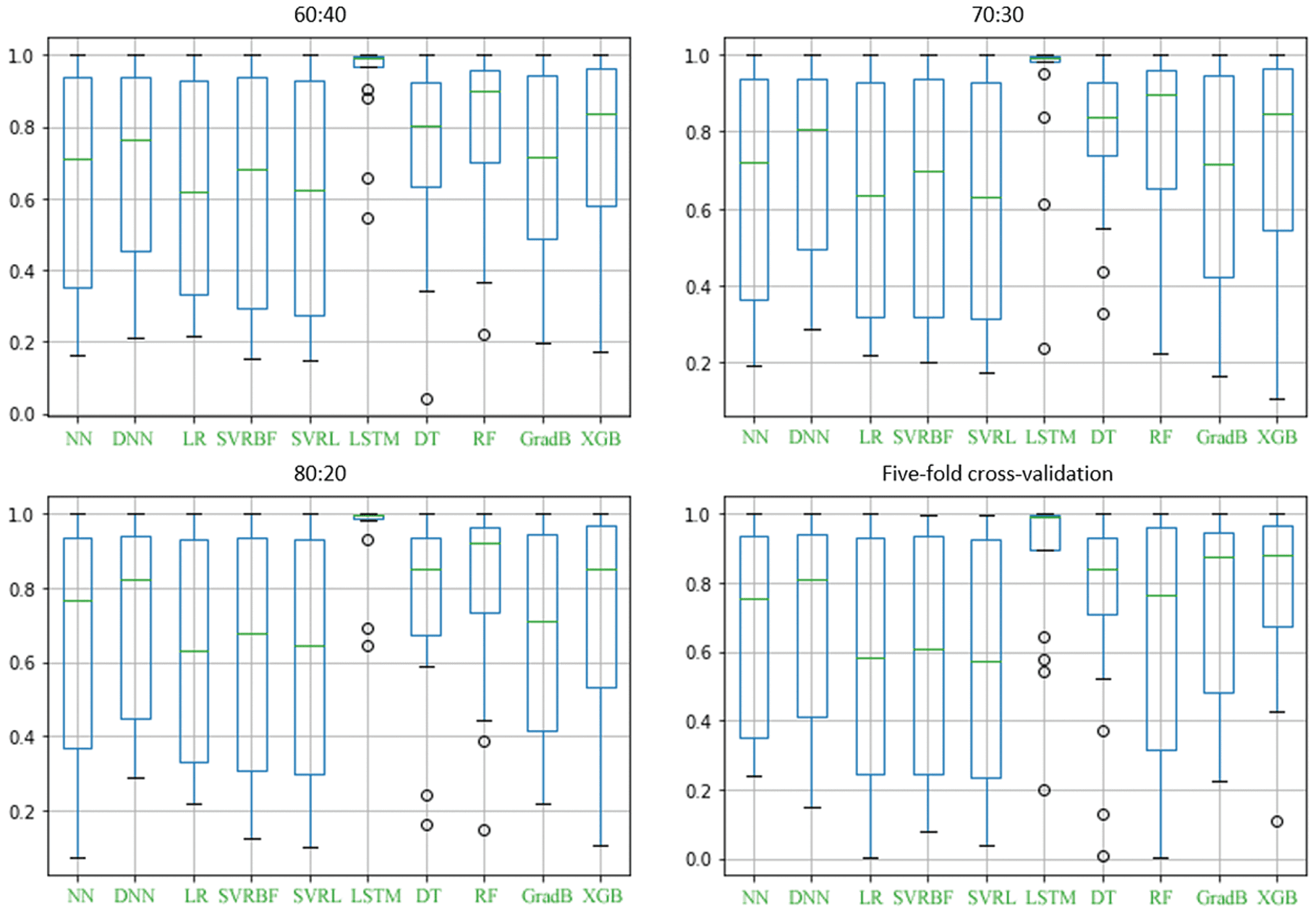
Cifra 2 demonstrates the visualization of the obtained R2 scores of the datasets for each hold-out ratio and
five-fold cross-validation experiments. Bold values within the tables indicate superior results.

3.1 Comparisons for Hold-Out Ratios and Cross-Validation

The analysis of the effect of hold-out ratios on the prediction performance of the models should be

performed in two stages.

The first stage analyseszes the increment or decrement in the number of training data for the models.
The second stage is to determine the impact of different training ratios and cross-validation on the
performance of a particular model. This would yield to determine the data dependency and the sensitivity
of the models for the change in the number of training data.

In this stage, the R2 scores were used to analyze the obtained results since the R2 score is scaled results
and provides a more effective evaluation. Por lo tanto, the analysis was performed using the number of highest
R2 scores obtained in the experiments and the statistical descriptions obtained using the R2 scores for each
dataset and model individually.

NN, DT, and RF produced fluctuated and similar results when the hold-out results were considered. Su

lowest and highest R2 scores were obtained in the 70:30 y 80:20 hold-out ratios.

Por otro lado, GradBoost and XGBoost produced fluctuated results. Although their lowest R2 scores

were obtained in the 70:30 hold-out ratio, they achieved their highest scores in 60:40 experimentos.

Models in which the increment of training data linearly affected the performances negatively were LSTM,
SVRL, SVRBF, and LR. While the highest R2 scores of these models were obtained at 60:40 ratios, el
produced results decreased as the training data increased, and the lowest results were obtained in 80:20
experimentos.

628

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

t

.

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

t

/

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 2. Visualization of R2 scores for all experiments.

The most positively affected model by the increase in the number of training data was DNN. DNN,
which could not produce the highest R2 scores for any dataset with the lowest training ratio (60:40),
achieved higher results at 70:30 y 80:20 ratios. The experiments in which DNN was most successful
were the 80:20 hold-out experiments.

Sin embargo, considering the five-fold cross-validation experiments, the obtained results significantly changed
for NN, DNN, LR, DT, GradBoost, and XGBoost. Performing experiments using five-fold cross-validation

Data Intelligence

629

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

provided these models to improve their performances and achieve the highest number of superior results
in experiments. Sin embargo, it should be noticed that the training of SVRL, SVRBF, and RF using five-fold
cross-validation did not positively impact these models.

Determining the highest scores obtained in different hold-out ratios is valuable for analyzing models.
Sin embargo, the statistical descriptions, such as mean, median, minimum, and maximum R2 scores, standard
deviation between the obtained results, 25%, y 75% quartiles, are also effectively used in analyzing the
order and the change in results. Además, they provide information to determine the models’ sensitivity
for the number of training data and adaptation of training data. Por lo tanto, we provided the maximum and
minimum standard deviation of the results obtained for each model using a dataset with different training
ratios.

The obtained mean, median, quartile, and standard deviation results demonstrated that different models
could achieve superior, fluctuated, or decreased prediction levels based on the number of training data.
Sin embargo, the deep LSTM achieved superior results in all descriptions for all experiment scenarios. El
SVRL and LR produced the highest standard deviation and lowest mean and median results for different
hold-out and cross-validation experiments which are the worst results in this study. Mesa 2 presenta el
statistical descriptions for the hold-out and cross-validation experiments, Cifra 3 shows the model-based
distribution of the results for all experiments, y figura 4 presents the hold-out and cross-validation results
per model independently.

Además, we provided the maximum and minimum standard deviation of the results obtained for
each model using a dataset with different training ratios. The close minimum and maximum standard
deviations were calculated in the obtained R2 scores of NN and DNN. While’NN’s minimum and maximum
standard deviations were 0.0006 y 0.0612, it was calculated as 0.0003 y 0.0641 for DNN. Estos
obtained maximum standard deviation results were the lowest maximum standard deviations among all
experimentos.

The model that followed the NN and DNN models was LR with a 0.0797 maximum standard deviation.
LR produced more stable R2 scores for all datasets, and the lowest average standard deviation was calculated
(0.0215), even though it could not produce superior results in most of the experiments.

There were no significant differences in the maximum standard deviations of the R2 scores of SVRBF,
SVRLR, and DT. Por lo tanto, the average standard deviations of these models were calculated as 0.0154,
0.0173, y 0.0275. Results showed that the SVR models had the lowest average standard deviation.

Tree ensemble models achieved more fluctuated results than other models except for deep LSTM.
The maximum standard deviations calculated for RF, GradBoost, and XGBoost were 0.1384, 0.1569, y
0.1461. The average standard deviations of these models were 0.0305, 0.0322, y 0.0331, respectivamente.

630

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

t

.

/

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

Mesa 2. Statistical descriptions of experimental results.

60:40 Statistical Descriptions

NN

0.665
0.299
0.165
0.352
0.708
0.937

NN

0.668
0.291
0.194
0.366
0.720
0.938
1.000

NN

0.672
0.303
0.074
0.368
0.766
0.937

NN

0.679
0.280
0.242
0.353
0.757
0.936

Significar
estándar
mín.
25%
Median
75%

Significar
estándar
mín.
25%
Median
75%
Significar

Significar
estándar
mín.
25%
Median
75%

Significar
estándar
mín.
25%
Median
75%

DNN

0.700
0.273
0.213
0.454
0.764
0.936

DNN

0.713
0.264
0.285
0.495
0.805
0.940
1.000

DNN

0.719
0.267
0.289
0.448
0.825
0.940

DNN

0.693
0.282
0.148
0.409
0.810
0.939

LR

SVRBF

SVRL

Deep LSTM

DT

RF GradBoost XGBoost

0.630
0.309
0.216
0.333
0.617
0.930

0.644
0.315
0.155
0.292
0.680
0.937

0.622
0.328
0.148
0.276
0.624
0.930

0.935
0.132
0.547
0.966
0.994
0.997

0.729
0.265
0.042
0.633
0.804
0.925

0.789
0.243
0.221
0.703
0.898
0.958

0.693
0.264
0.199
0.486
0.713
0.945

0.746
0.261
0.173
0.580
0.835
0.963

70:30 Statistical Descriptions

LR

SVRBF

SVRL

Deep LSTM

DT

RF GradBoost XGBoost

0.632
0.309
0.218
0.316
0.635
0.930
1.000

0.645
0.310
0.199
0.318
0.700
0.938
0.999

0.624
0.321
0.172
0.314
0.630
0.930
0.999

0.915
0.200
0.238
0.983
0.992
0.997
1.000

0.778
0.206
0.327
0.737
0.838
0.930
1.000

0.790
0.244
0.224
0.651
0.896
0.961
1.000

0.676
0.289
0.164
0.422
0.714
0.945
1.000

0.730
0.297
0.106
0.544
0.847
0.965
1.000

80:20 Statistical Descriptions

LR

SVRBF

SVRL

Deep LSTM

DT

RF GradBoost XGBoost

0.631
0.308
0.219
0.331
0.633
0.930

0.644
0.317
0.125
0.306
0.680
0.937

0.620
0.331
0.102
0.301
0.647
0.929

0.950
0.111
0.645
0.985
0.995
0.998

0.760
0.257
0.164
0.673
0.850
0.935

0.794
0.262
0.148
0.735
0.922
0.964

0.673
0.284
0.217
0.414
0.711
0.946

0.730
0.292
0.106
0.535
0.851
0.967

Five-fold cross-validation Statistical Descriptions

LR

SVRBF

SVRL

Deep LSTM

DT

RF GradBoost XGBoost

0.570
0.381
0.003
0.246
0.585
0.929

0.580
0.368
0.076
0.245
0.606
0.936

0.562
0.381
0.038
0.234
0.570
0.928

0.867
0.233
0.199
0.895
0.992
0.996

0.725
0.304
0.008
0.708
0.838
0.930

0.637
0.350
0.004
0.317
0.762
0.962

0.727
0.254
0.227
0.481
0.874
0.948

0.780
0.253
0.110
0.676
0.883
0.966

The largest and most significant changes in standard deviations of R2 scores obtained in different hold-
out and five-fold cross-validation experiments were calculated in deep LSTM. The maximum and average
standard deviations for deep LSTM were calculated as 0.3467 y 0.0629. These results were the highest
standard deviation values calculated within the considered models. Mesa 3 shows the minimum, maximum,
and average standard deviations for all models calculated using the R2 scores obtained in the hold-out and
five-fold cross-validation experiments.

Data Intelligence

631

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

t

/

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

t

/

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

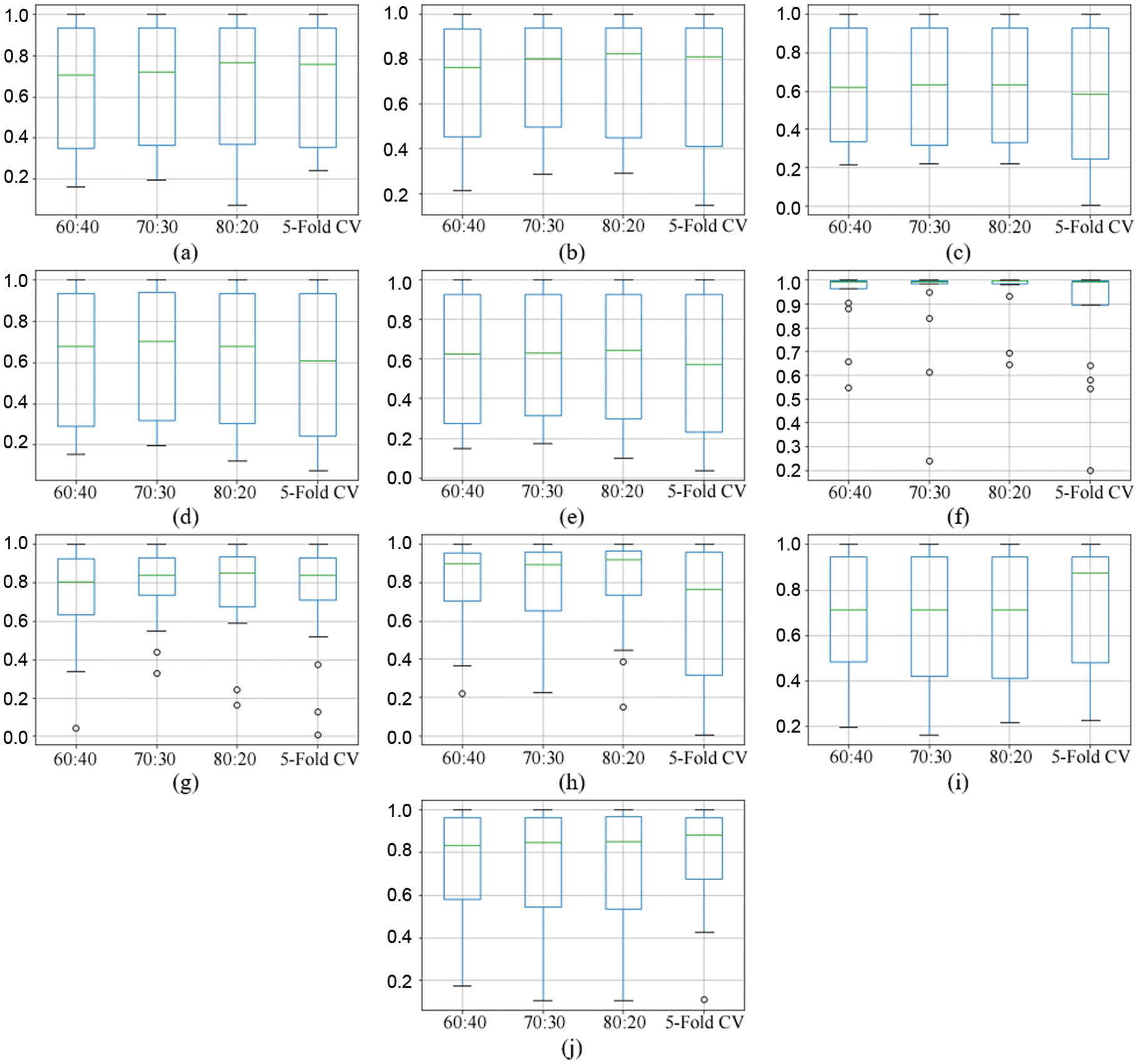
Cifra 3. Distribution of obtained R2 scores of the models for each experiment (model comparison).

3.2 Fold Comparisons of Five-Fold Cross-Validation Experiments

Five-fold cross-validation experiments were performed to analyze the effect of changing training data on
the learning and performance rates of the models. Por lo tanto, it was tried to show how much the changing
data will affect the results produced by the models in the experiments performed with hold-out ratios. Nosotros
used the Average θ value, where θ is the difference between the highest and the lowest R2 scores obtained
in the folds, to indicate the general change value produced by the models.

While presenting the results in this section, AQ and CCPP were not considered because the R2 scores
produced in each fold by each model were at the highest level. Además, the changes between folds
were tolerable since the obtained values were less than 0.001 on average.

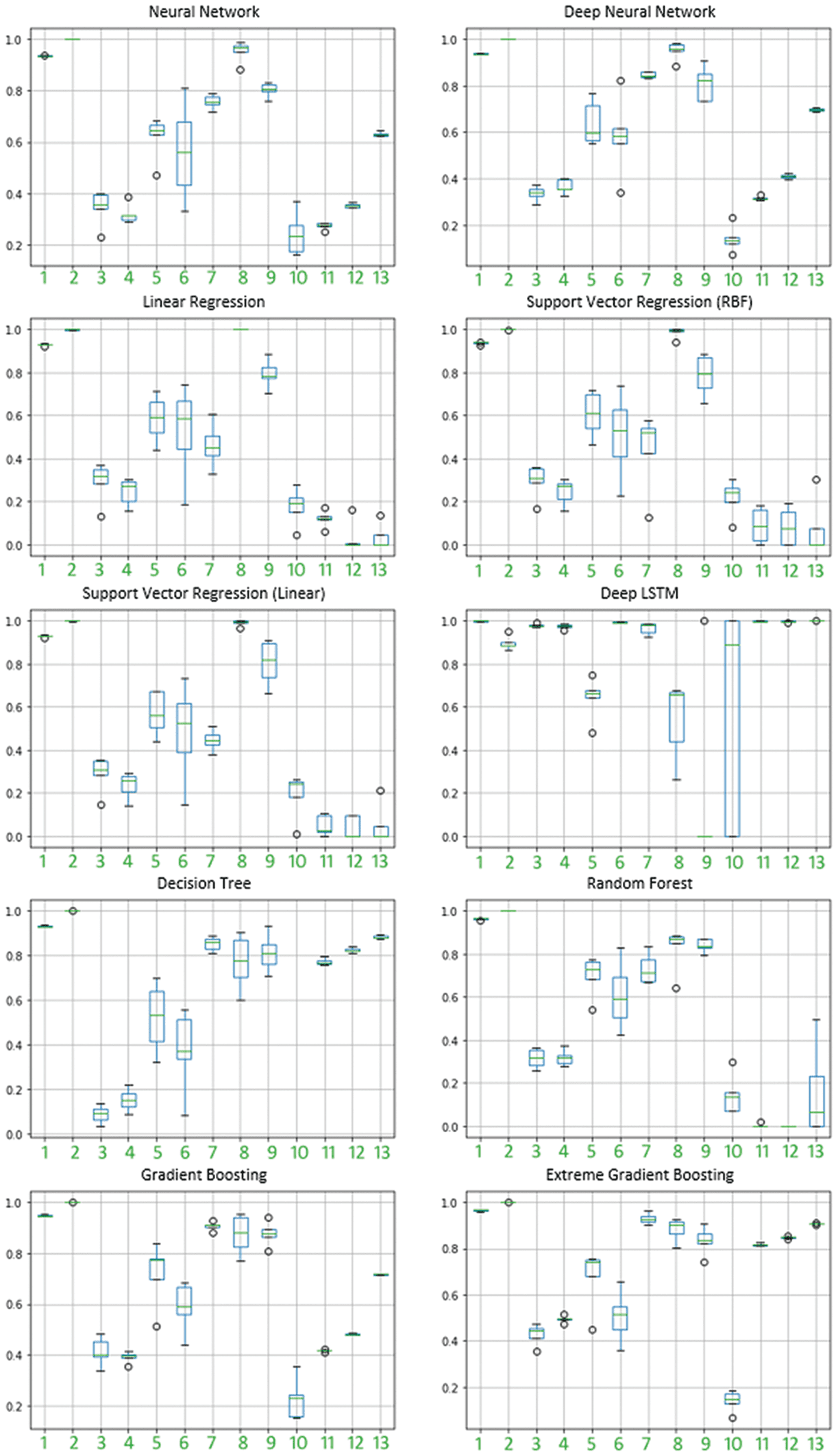
NN obtained the highest change (i) between folds in the SPB dataset with 0.48. In this dataset, el
highest R2 score reached in a fold was 0.81, while the lowest was 0.32. NN produced a minor change
between fold results in WQW, CON, DDFO, and STM datasets, giving more stable results. For these three
experimentos, θ was calculated between 0.07 y 0.10. More fluctuations occurred between folds in WQR,
RE, and STP datasets, and θ values were calculated as 0.17, 0.21, y 0.20.

632

Data Intelligence

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

t

/

i

Cifra 4. Model-based distribution of obtained R2 scores of the models for validation strategies—validation
strategy comparison: (a) NN, (b) DNN, (C) LR, (d) SVRBF, (mi) SVRL, (F) deep LSTM, (gramo) DT, (h) RF, (i) GradBoost, y
(j) XGBoost.

Mesa 3. Mínimo, maximum, and average standard deviations between hold-out ratios for all models.

NN

DNN

LR

SVRBF

SVRL

deep LSTM DT

RF

GradBoost

XGBoost

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Average STD 0.019 0.020
Min STD
Max STD

0.021
0.000 0.0003 0.000
0.079
0.061 0.064

0.017

0.015
0.0004 0.0003
0.106

0.112

0.062
0.001
0.346

0.027 0.030
0.000 0.00
0.118 0.138

0.032
0.00
0.156

0.031
0.00
0.141

Data Intelligence

633

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

In the DNN model, close results were obtained with NN. The differences observed between these two
models were that DNN produced more stable results in WQR, CON, STM, and STP datasets. The most
remarkable change among the fold results occurred in the SPB dataset (θ = 0.47) as in NN. The average θ
value of the DNN model was calculated as 0.16.

Since the LR model achieved total success with each fold in the DDFO dataset, no change was calculated
between the folds. Sin embargo, LR could not establish any correlation between attributes and instances in a
fold in the SPB dataset and could not produce results. This caused the θ value to be 0.74. The most stable
results obtained by the LR model, except for DDFO data, was the WQW dataset (θ = 0.15). The average θ
value of LR, which produces fluctuating results in other experiments, era 0.26.

SVRL and SVRBF models produced close θ values for WQR, WQW, RE, SPB, DDFO, and STM datasets.
The highest θ between the two models occurred in the CON (SVRL = 0.51 and SVRBF = 0.44) and STP
(SVRL = 0.26 and SVRBF = 0.30) conjuntos de datos. Sin embargo, both SVRL and SVRBF produced rather variable and
different results in SPB data in terms of θ as observed in other models (SVRL = 0.73 and SVRBF = 0.73).
The average θ value for both models was calculated as 0.29.

Although deep LSTM produced superior results in most experiments, the model produced the most
fluctuated and data-dependent results in five-fold cross-validation experiments considering DDFO, STM,
and STP data. While deep LSTM showed the most negligible variation between folds in other datasets, él
produced more stable results in the SPB dataset than in other models. Sin embargo, in STM and STP datasets,
it caused the θ to increase to 0.99 by making inaccurate and most successful predictions in different folds.
A more significant fluctuation was observed in the DDFO dataset compared to other models. While the
average θ value of deep LSTM was calculated as 0.36, it was marked as the most sensitive model in this study.

Since DT could not produce any results in any fold of the five-fold cross-validation experiments of the
STP dataset, the θ for STP was 0. Por lo tanto, the average θ value was calculated by ignoring the STP data.
Similarmente, WQR and WQW data failed to produce results in a fold. This caused an increase in θ values in
these experiments (0.13 y 0.21, respectivamente). In the SPB dataset, where other models (NN, DNN, SVRL,
SVRBF) produced fluctuating results, DT could produce a more stable result, although it could not produce
a superior result (θ = 0.23). Sin embargo, in the RE dataset, the highest and lowest R2 scores produced at
different folds were calculated as 0.69 y 0.32, resulting in the highest θ value for DT (0.37). el promedio
θ value is calculated as 0.22.

Although RF produced more reasonable and stable results than DT, it could not produce results in one
fold of CON and SPB datasets experiments. High R2 scores obtained in other folds caused the θ value to
increase significantly. Como resultado, θ values for both CON and SPB datasets were calculated as 0.83. Este,
Sucesivamente, affected the overall stability of the model, and the average θ was calculated as 0.33.

Although the general results of the GradBoost model were similar to RF, GradBoost produced more stable
results in CON and SPB datasets resulting in the average θ value being calculated as 0.17 and observed as
one of the most stable models.

634

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

.

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

XGBoost produced the lowest θ value for the WQW and STP experiments (0.01 y 0.11, respectivamente).
The experiments in which XGBoost produced the highest θ value were RE and SPB datasets (0.30 y 0.29,
respectivamente). Although it could not produce superior results in other datasets, it generally produced the
most stable results. This produced the lowest average θ value (0.15). The dataset-based plot of change
in R2 scores that show the minimum, maximum, and average R2 scores obtained in the folds is shown in
Cifra 5. Mesa 4 presents the θ values obtained by each model for each dataset and the average θ obtained
for a particular model.

Mesa 4. h values obtained for each model and dataset in fold analysis.

MODEL WQR WQW RE

SPB CON DDFO STM STP TCPC Z1 TCPC Z2 TCPC Z3 AVE. i

NN
DNN
LR
SVRBF
SVRL
DT
LSTM
RF
GradBoost
XGBoost

0.17
0.09
0.24
0.19
0.21
0.14
0.09
0.11
0.15
0.12

0.09
0.08
0.15
0.15
0.15
0.22
0.02
0.10
0.06
0.02

0.21
0.22
0.27
0.25
0.23
0.38
0.03
0.23
0.33
0.31

0.48
0.48
0.74
0.74
0.73
0.22
0.27
0.83
0.24
0.30

0.07
0.03
0.28
0.45
0.51
0.08
0.06
0.84
0.05
0.06

0.11
0.10
0.00
0.06
0.03
0.31
0.42
0.23
0.18
0.12

0.07
0.18
0.18
0.23
0.25
0.23
1.00
0.07
0.13
0.17

0.21
0.16
0.28
0.30
0.26
NA
1.00
0.23
0.20
0.12

0.03
0.02
0.11
0.18
0.10
0.03
0.004
0.02
0.01
0.01

0.02
0.02
0.15
0.19
0.09
0.02
0.009
NA
0.01
0.01

0.02
0.01
0.13
0.30
0.21
0.02
0.0009
0.49
0.004
0.01

0.134
0.126
0.230
0.276
0.251
0.150
0.263
0.286
0.127
0.113

4. DISCUSSIONS

Several points should be discussed by considering the obtained results. We separately analyzed the
performances of the models in terms of R2 scores and error minimization for different kinds of datasets, el
effects of training ratios of the hold-out strategy, and the impact of cross-validation on the models learning
to deduce general opinions. Además, the data dependency of the models was analyzed by combining
all the obtained results and performing a fold analysis. This also provided us to analyze the consistency
and the stability of the models.

4.1 Effect of Training Ratios on the Model Performances

When the results of varied hold-out ratios are compared without considering five-fold cross-validation
resultados, it is challenging to make a consistent analysis due to the responses to the new data added at
increasing training ratios, even if the same samples were considered. When we analyzed the results for all
experimentos, fluctuations were observed regardless of the training ratios. Sin embargo, it is debatable whether
there were very significant changes in the results produced by the models on a ratio basis.

The SVRBF and SVRL were the least affected models by the number of training data, indicating that the
projection of the data to another plane reduces the effect of the number of training data. SVRBF was the
most successful model at the point, as the model with the lowest average standard deviation value, seguido
by the SVRL. Sin embargo, the increase in the number of training data in both models affected the success

Data Intelligence

635

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

/

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

/

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 5. Dataset-based change in R2 scores of the folds for each model (1: Average of CCPP results, 2: AQ,
3: WQR, 4: WQW, 5: RE, 6: Bra, 7: Concrete, 8: DDFO, 9: STM, 10: STP, 11: TCPC Z1, 12: TCPC Z2, y 13:
TCPC Z3).

636

Data Intelligence

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

rates negatively. It has been once shown by the obtained results that SVR models could produce better
results with less training data.

NN and DNN showed that the neural-based models also minimized the changes due to the number of
datos. Although SVRBF, SVRL, NN, and DNN are less interpretable than other models, which complicates
the analysis of results, neural-based models could achieve more stable results since they are capable of
effective convergence because of hidden layers and neurons in these layers. Sin embargo, fewer hidden layers
and neurons might result in more inconsistent results, making it difficult to determine the proper training
data ratio.

On the other hand, in DNN with more hidden layers and neurons, the success rate increased as the
number of training data increased. Although the changes were not at significant levels, it was observed that
the number of data needed increases as the neural network architecture gets deeper. The results showed
the disadvantages of using a large number of processing elements with a minimized number of training
datos.

Determining the node sequences and decision leaf by DT is the most crucial factor in this’model’s
success. The results showed that DT produced fluctuating results depending on the training ratios. Sin embargo,
the need for DT to achieve better results using more training data has been reduced in the RF model and
eliminated in the GradBoost and XGBoost models.

The standard deviations of the RF, GradBoost and XGBoost models were higher than the other models.
It has been observed that these models produced more sensitive responses to the changing number of
training data. Still, the applied processes provided better results by minimizing the errors obtained in DT
and reducing their dependence on the training data number. Respectivamente, GradBoost and XGBoost achieved
higher results with fewer training data.

Deep LSTM was the model with the highest sensitivity to the number of training data. In terms of
produced R2 scores and the standard deviation between these scores, the most fluctuated results of this
study were provided by the deep LSTM. Although the fixed number of LSTM layers might lead to these
resultados, the states of input sequences as forgotten and remembered in the LSTM layers could be considered
one of the most significant factors both in the success and fluctuated results of this model. En el otro
mano, the deep LSTM model produced the highest results with the lowest training ratio, even though it was
used with a large amount of LSTM layers. The increment in training ratios did not positively affect the
models’ performance.

When we consider all the results obtained for all models, the ratio of 70:30 was found as a training ratio
that causes the minimum success of the models. Por otro lado, although higher results were obtained
en el 80:20 experimentos, el 60:40 ratio was observed as the training ratio with the highest results.

If cross-validation was not considered in regression studies, the consideration of 60:40 y 80:20 para
specific models based on the above-mentioned information would help researchers decrease experimental
costs and achieve superior results.

Data Intelligence

637

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

.

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

4.2 Effect of Cross-Validation and Data Dependency of the Models

Cross-validation was considered in many studies for hyper-parameter tuning or final performance
evaluation of the models. The results obtained in our study showed that cross-validation is vital to determining
the general abilities of the models. en este estudio, the consideration of the five-fold cross-validation provided
the training of the models with an 80:20 ratio using five different datasets in five folds. Por lo tanto, el
analyses of he models could be performed using all data.

The obtained average fold results showed that NN, DNN, LR, DT, GradBoost, and XGBoost achieved
their highest R2 scores in experiments using five-fold cross-validation (S3 Table). These results showed that
the use of cross-validation in studies where these models will be considered would be more consistent,
more reliable, and more successful. Sin embargo, SVRBF, SVRL, and LSTM did not make a remarkable difference
in experiments with five-fold cross-validation compared to training with other ratios.

On the other hand, when the R2 score differences (i) obtained between the folds were considered, a
more complex relationship was observed (Mesa 4). The obtained θ values showed the response of the
models to the training data in the learning process and the data dependency of the models, and the achieved
results demonstrated that the most successful model in this regard was XGBoost (min θ=0.01, max θ=0.31,
average θ=0.113).

XGBoost successfully minimized the error while adding new trees to the created ones and reduced the
dependency on new and different data. This caused the model to produce more stable results between
folds.

The models that followed XGBoost based on the θ values were GradBoost, DNN, and NN. A pesar de
GradBoost and DNN are completely different classifiers in structure, their average θ was calculated as equal
(0.17).

GradBoost, which has similar features to XGBoost, creates an ensemble model by adding new trees by
minimizing the error between the gradient descent algorithm and weak trees. This caused the model to
produce similar results with XGBoost and low data dependency.

Por otro lado, the DNN used in this study showed that higher numbers of hidden layers and neurons
could produce more stable results, although not superior. This property increased the impact of DNN on
learning the changing data in cross-validation.

Sin embargo, although NN with a single hidden layer produced more fluctuating results than DNN when
cross-validation was used, the change in R2 scores between the folds was minimal. This showed that
increasing the number of hidden layers could produce more stable results and reduce the number of
experiments to be performed but would not significantly change the overall results.

DT and LR produced close results considering θ values. These two models are successful on datasets
with more linear relationships than other models, and that increased the importance of the data they fed

638

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

.

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

in the training process and the test data. Sin embargo, LR produced more stable results in highly correlated
datos, but DT produced more significant differences in terms of the R2 scores it produced between the folds
in these datasets. The creation of a single tree and the node sequences were the most significant factors at
this point.

The SVRBF and SVRL produced reasonably similar results in this analysis. θ was calculated as 0.276 y
0.251, respectivamente. High variation between the folds was caused by the data projection, which reduces
the dependence on the number of data and is unpredictable when applied to the data containing different
información. While the data in one fold can be projected to draw the regression line with a minimum error,
the data in the other fold might not be appropriately projected to provide a best-fitted regression line. Este
created highly variable results for the two models.

The most unexpected results in this analysis of the study were produced by the RF and LSTM models.
As an ensemble model, RF was expected to produce more stable results between the folds, but it was
observed that the effect of the created trees and the number of trees used in the experiments on the model
was very high. Although it produced successful results, RF has become one of the most data-dependent
modelos.

In the deep LSTM model, although generally stable results were produced, the extreme results obtained
in the STP and STM dataset experiments determined the average θ as the highest. The data dependency of
the LSTM appeared to be in the upper level; sin embargo, it is also analyzed along with the analysis of the
characteristic features of the dataset in the next section.

4.3 Effect of Datasets on Model Performances

The dataset-based analysis was performed to evaluate the general responses of the models under different
condiciones. It is common knowledge that providing a large number of instances to a model with a high
number of attributes facilitates learning (es decir., the AQ Dataset). Sin embargo, the relevancy of these instances
and the information they feed the model have a vital role in the learning process of the models (es decir., el
WQW Dataset).

Neural network models, which were expected to be more accurate in solving nonlinear problems with
fewer relationships between their attributes, outperform or lag behind other models with a slight difference
in these datasets.

If the results for NN and DNN have been interpreted on the STM and STP dataset, removing two highly
correlated attributes from the training data severely reduced the success of NN and DNN, similar to other
modelos. Además, although these two models produced high results for highly correlated datasets (es decir.,
DDFO), they did not achieve the prediction rate of LR. En este punto, the achievement of better results than
LR in the highly correlated AQ dataset by these two models showed that the minimized number of instances
used during the training process had a significant and negative effect on the performances of NN and DNN.

Data Intelligence

639

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

t

/

.

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

Although SVRBF and SVRL models achieved results close to NN and DNN, it was observed that they
could achieve superior results in the highly correlated datasets with a minimal number of attributes and
instancias (es decir., DDFO). Sin embargo, SVR models produced lower results than the NN and DNN models in
other datasets with higher numbers of attributes and instances, even though the correlation between
attributes was high. This showed once again that the use of a more informative and limited number of
attributes and instances for data projection would increase the success of SVR models.

The DT model produced fluctuating results depending on the dataset characters, and it could not achieve
successful results in general. Even it was unable to make any predictions in the high attribute, low instance,
and low correlation STP dataset, DT succeeded in outperforming the RF, XGBoost, and GradBoost models
in the highly correlated DDFO dataset. It was observed that the success rate of DT decreased significantly
at low-instance high-attribute datasets. As with all other analyses, the success of DT in identifying the
starting nodes and the sequences of subsequent nodes proved to be vital to the model.

The obtained results showed that the tree-based ensemble models achieved more successful results in
datasets with a high number of instances. In AQ, CCPP, and WQW datasets, RF, GradBoost, and XGBoost
models generally achieved superior results than other models except for LSTM. The use of a high number
of instances provided successful results in these models since the creation or addition of different trees
allows them to perform more meaningful information connections systematically.

LSTM achieved results that outperformed all other models regardless of the correlation between attributes
when trained with many instances. LSTM, which produces highly fluctuating and variable results in STM,
STP, and DDFO datasets, was the model most affected by the dataset’s number of instances and attributes.
Training the deep LSTM with a low number of data makes it challenging to achieve high prediction rates.

4.4 Discussions on the General Results

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

t

/

i

En 57 out of a total of 68 experimentos, deep LSTM produced the highest R2 scores and superior error
minimization results, achieving a very high success rate compared to other models. The model that followed
the deep LSTM was GradBoost, which produced two times the superior and three times the second-highest
resultados. XGBoost, which achieved the superior result once and the second-highest result ten times, era
another model that produced stable results. Besides, LR produced superior results in an experiment and
the DT and RF models. Por otro lado, NN, DNN, and SVR models could not achieve optimal results
in any of the experiments.

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Although the increase in the number of hidden layers and neurons produced more stable results than
NN, DNN could not have the superior or even the second-superior score in any experiment. This caused
neural-based models not to outperform other models (es decir., deep LSTM, GradBoost, XGBoost) in this study.
The obtained results limit the success rate of the neural-based models in general; sin embargo, considering the
fixed architecture and parameters in this study could be one of the reasons for this. In NN, although the
use of a lower number of hidden layers and neurons did not significantly reduce the success rate to DNN,
it had a negative effect on the stability of the model. This instability also reduced the reliability of the model.

640

Data Intelligence

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

SVR models also produced similar results to neural-based models but slightly lower overall. As mentioned
arriba, although higher and more stable results were obtained compared to NN and DNN in datasets with
low instances and attributes, they lagged behind LSTM and tree-ensemble models in general.

DT could not achieve high results as tree-based ensemble models. It was seen as an inevitable improvement
that optimizing many trees to be created could yield superior results than a single tree, which was the main
aim of proposing tree-based ensemble models. Although the DT can be easily implemented and more
responsive model, the development of models such as RF, GradBoost, and XGBoost has overshadowed the
success of DT. The main limitation of DT, which is the sequence of the attributes, proved once again that
ensembling multiple trees achieve superior results.

LR, the most basic regression model, proved its success in linear problems once again and showed that
it could correlate between correctly selected data and nonlinear test data. Sin embargo, since the ability to
establish nonlinear correlations between all datasets is very limited, further experiments are required to
conclude this. LR attracted attention again as a model that must be considered among datasets containing
linearly related attributes.

RF lagged slightly behind the other two models (GradBoost and XGBoost) among tree-based models. Por
optimizing the regression results of the constructed trees, RF produced slightly more fluctuating and
inconsistent results than the performance of GradBoost and XGBoost, which considers the losses of weak
modelos. This is caused by randomly sampling (bagging) the instances while creating individual trees in RF;
since GradBoost and XGBoost consider weak samples in the re-creation of trees (boosting). While bagging
made RF more sensitive to overfitting, the boosting models are more advantageous in tree-based ensemble
methods.

GradBoost and XGBoost models have proven to be models that should be considered in terms of stability,
data dependency, and their results in regression problems. Considering that the optimization of the fixed
parameters could further increase the performance of these models, they stand out as the models that should
be preferred in the first place.

Sin embargo, the deep LSTM model, which achieved the highest results in almost all experiments and
produced high results even in datasets where other models failed to make predictions, showed that it is
one of the top ML models that should be considered for regression problems. Sin embargo, the most significant
disadvantage of deep LSTM is the data dependency, unstable response to changing training data, y
inconsistent results in some conditions. Even between folds, it was observed that while it could predict all
the data with high scores in one fold, it could not properly predict any data in the other fold. In LSTM cells,
the dependence of forgetting states on previous data and the effect on data from later sequences significantly
affected the consistency of the LSTM. Sin embargo, the fixed structure of LSTM might cause fluctuations and
require further experiments for this model to generalize its’ characteristics.

Considering that the data in all experiments in this study were randomly selected and then fixed, it can
be considered that the fluctuations and instability in many models were acceptable. The most significant

Data Intelligence

641

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

.

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

limitation of the LSTM model was not completing the learning process in datasets with a low number of
instances and the high number of attributes (STM and STP datasets). Por lo tanto, it could be concluded that
the deep LSTM would continue to achieve high-level results among regression models with appropriate
and sufficient data selection.

4.5 Outcomes and Recommendations for Further Studies

The outcomes and recommendations of the study are listed below:

•

•

•

•

•

•

•

•

•

•

•

Long-Short Term Memory Neural Network, Extreme Gradient Boosting, and Gradient Boosting were
the superior models in the overall experiments. It is recommended that these models be used more
widely in regression problems.
Random Forest, Support Vector Regression Models, and LSTM were the most data-dependent models.
Por lo tanto, cross-validation in studies involving these models is required to evaluate the prediction
abilities of the models.
Since which superior hold-out ratio in ML training varies depending on the data and the model, el
characteristics of the models should be considered in the experiments where hold-out will be used.
Sin embargo, el 60:40 hold-out was the ratio with the highest results.
The XGBoost was the model with the least dependence on the number of training and changing data.
GradBoost followed this model. Por lo tanto, any hold-out or cross-validation would not significantly
change the results of these models.
DNN and NN were not affected much by data changes, but cross-validation should be continued to
be implemented for these models’ parameter and structure determination.
Una vez más, it has been shown that as the number of data (instances and/or attributes) aumenta, el
deeper neural network produces higher results than the shallow neural network.
LSTM achieved superior results than other models in datasets of different types and sizes. Sin embargo,
the determination of its’ structure could lead to inconsistent results.
Even though the XGBoost and GradBoost could not achieve results as high as LSTM, they produced
more stable and data-independent results with low computational cost.
It has been determined that cross-validation could affect the results of all models on average 0.01-
0.20 R2 score, even though the XGBoost and GradBoost are data-independent. Por lo tanto, cross-
validation is essential for the models to obtain more consistent and comparable results.
It was observed that the data feed without selection to SVR models caused not produce higher results
than other considered models. Data minimization might increase the ability of SVR.
LR is still one of the superior methods for data with a linear relationship. Sin embargo, the success of the
model decreases drastically in complicated datasets.

AutoML approaches, which would become more widespread in parallel with the use of ML in every field
de la vida, would be able to offer more effective uses considering the characteristics of the models in parallel
with the results obtained in this study and to reduce the computational cost.

642

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

t

/

.

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

4.6 Limitations of the Study

This study has limitations. Using two kernels for the Support Vector Regression, implementing fixed
structures for deep LSTM, NN, and DNN, and optimizing the mentioned points could increase the obtained
results by the models. Además, considering the various k numbers in k-fold cross-validation technique
might provide additional information for the analysis of the models’ behaviours.

5. CONCLUSIÓN

Comparing machine learning models is a challenging and complicated task due to a large number of

modelos, excessively varied datasets, and different kinds of training strategies.

In this study, we performed a total of 680 experiments using 15 different datasets. Ten benchmark
machine learning models were trained with varied training strategies using three different train/test ratios
of the hold-out method and five-fold cross-validation.

The results obtained in this study have shown that each model has its unique weaknesses and strengths
that could be considered in the regression implementations in order to determine the optimal model for a
particular application.

Although it has a significant data dependency to produce consistent and optimal results, the recurrent
neural network, deep LSTM, significantly outperformed other considered models almost in all experiments
even though it is high-sensitive to the change of training data.

Linear Regression is still an essential model for regression implementations, especially with highly
correlated data. Tree-based ensemble models, particularly Gradient Boosting and Extreme Gradient Boosting,
are the models that could achieve reliable and consistent results which are low-sensitive to the change of
training data. Por otro lado, neural-based models produced stable results but were not superior, y
more training data is required for the deeper architectures. The support vector regression models achieved
their superior results in the minimized number of attributes and instances; sin embargo, the data-dependency
of the models complicated the implementation of the models.

It was observed that the different hold-out ratios do not significantly affect the model performances, y
using a 60:40 hold-out is more beneficial to the models. Sin embargo, training of the models with cross-
validation has a considerable impact on the prediction abilities, and the analysis should be performed not
by considering fixed and randomized training ratios.

DISPONIBILIDAD DE DATOS

The data that support the findings of this study are openly available in UCI Machine Learning Repository

at https://archive.ics.uci.edu/ [14–22].

Data Intelligence

643

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

t

/

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

CONTRIBUCIONES DE AUTOR

Boran Sekeroglu (boran.sekeroglu@neu.edu.tr): Conceptualización, Metodología, Software, Writing—

original draft preparation, Writing—review and editing.

Yoney Kirsal Ever (yoneykirsal.ever@neu.edu.tr): Conceptualización, Administración de proyecto, Metodología,

Writing—original draft preparation, Writing—review and editing.

Kamil Dimililer (kamil.dimililer@neu.edu.tr): Conceptualización, Metodología, Software, Escritura—original

draft preparation, Writing—review and editing.

Fadi Alturjman (fadi.alturjman@neu.edu.tr): Conceptualización, Metodología, Escritura: revisión, y

edición.

REFERENCIAS

[1]

[2]

Ever, Y.K., Dimililer, K., Sekeroglu, B.: Comparison of Machine Learning Techniques for Prediction Problems.
In Advances in Intelligent Systems and Computing 927, 713–723 (2019)
Sekeroglu, B., Tuncal, K.: Prediction of cancer incidence rates for the European continent using machine
learning models. Health Informatics Journal 27(1), 1460458220983878 (2021)

[3] Waheed, A., goyal, METRO., Gupta, D., Khanna, A., Al-Turjman, F., Pinheiro, P.R.: CovidGAN: Data Augmentation
Using Auxiliary Classifier GAN for Improved Covid-19 Detection. IEEE Access 8, 91916–91923 (2020)
[4] Mesaric, J., Sebalj, D.: Decision trees for predicting the academic success of students. Croatian Operational

Research Review 7, 367–388 (2016)

[5] Utomo, D., Pujiono, SM, et al.: Stock price prediction using back propagation neural network based on
gradient descent with momentum and adaptive learning rate. Journal of Internet Banking and Commerce 22,
1-dieciséis (2017)

[6] Oytun, METRO., Tinazci, C., Sekeroglu, B., Acikada, C., Yavuz, H.U.: Performance prediction and evaluation in

female handball players using machine learning models. IEEE Access 8, 116321–116335 (2020)

[7] Taboga, METRO.: Cross-country differences in the size of venture capital financing rounds: a machine learning

acercarse. Empirical Economics 5 (2021)

[8] Dougherty, GRAMO.: Pattern Recognition and Classification. Saltador (2013)
[9] Pekel, MI.: Estimation of soil moisture using decision tree regression. Theoretical and Applied Climatology 139

(2020)

[10] Pandey, S., Kumar, v., Kumar, PAG.: Application and analysis of machine learning algorithms for design of
concrete mix with plasticizer and without plasticizer. Journal of Soft Computing in Civil Engineering 5(1),
19–37 (2021)

[11] Kaveh, A., Eslamlou, A.D., Javadi, SM, Malek, N.G.: Machine learning regression approaches for predicting

the ultimate buckling load of variable-stiffness composite cylinders. Acta Mechanica 1–11 (2021)

[12] Huang J.C., Ko K.M., Shu M.H., Hsu B.M.: Application and comparison of several machine learning
algorithms and their integration models in regression problems. Neural Computing and Applications 32,
5461–5469 (2020)

[13] Bratsas, C., Koupidis, K., Salanova, J.M., Giannakopoulos, K., Kaloudis, A., Aifadopoulou, GRAMO.: A comparison
of machine learning methods for the prediction of traffic speed in Urban Places. Sustainability 12(1) (2020)

644

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

t

/

.

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

[14] DeVito, S., Massera, MI., Francia, GRAMO. Di, Piga, METRO., Martinotto, l:. On field calibration of an electronic nose for
benzene estimation in an urban pollution monitoring scenario: Sensors and Actuators B. Chemical 129(2),
750–757 (2008)

[15] Zhong, PAG., Fukushima, METRO.: Regularized non-smooth newton method for multi-class support vector machines.

Methods and Software 22(1), 225–236 (2007)

[16] Tufekci, PAG.: Prediction of full load electrical power output of a base load operated combined cycle power
plant using machine learning methods. International Journal of Electrical Power and Energy Systems 60,
126–140 (2014)

[17] Ferreira, R.P., Affonso, C., Sassi, R.J.: Combination of artificial intelligence techniques for prediction the
behavior of urban vehicular traffic in the city of Sao Paulo. In 10th Brazilian Congress on Computational
Inteligencia (CBIC), páginas. 1–7 (2011)

[18] Yeh, I.C., hsu, T.K.: Building real estate valuation models with comparative approach through case-based

reasoning. Computación blanda aplicada 65, 260–271 (2018)

[19] Yeh, I.-C.: Modeling of strength of high-performance concrete using artificial neural networks. Cement and

Concrete Research 28(12), 1797–1808 (1998)

[20] Ferreira, R.P., Martiniano, A., Ferreira, A., Ferreira, A., Sassi, R.J.: Study on daily demand forecasting orders

using artificial neural network. IEEE Latin America Transactions 14(3), 1519–1525 (2016)

[21] Cortez, PAG., silva, A.: Using data mining to predict secondary school student performance. In EUROSIS (2008)
[22] Salam, A.R., Hibaoui, A.E.: Comparison of machine learning algorithms for the power consumption
predicción: case study of Tetouan city. En 2018 6th International Renewable and Sustainable Energy
Conferencia (IRSEC), páginas. 1–5, (2018)

[23] Amirjanov, A., Dimililer, K.: Image compression system with an optimisation of compression ratio. IET Image

Procesando 13(11), 1960–1969 (2019)

[24] Eyvazian, METRO., Noorossana, r., Amiri, A.S.A., et al.: Phase II monitoring of multivariate multiple linear

regression profiles. Quality and Reliability Engineering International 27(3), 281–296 (2011)

[25] Smola, A.J., Scholkopf, B.: A tutorial on support vector regression. Statistics and Computing 14(3), 199–222

(2004)

[26] Henrique, B.M., Sobreiro, V.A., Kimura, h., et al.: Stock price prediction using support vector regression on

daily and up to the minute prices. The Journal of Finance and Data Science 4(3), 183–201 (2018)

[27] Azeez, O.S, Pradhan, B., Shafri, H.Z.M., et al.: Vehicular CO emission prediction using support vector

regression model and GIS. Sustainability 10(10) (2018)

[28] Ping, l., Jin, w., Sangaiah, A.K., Xie, y., Yin, X., et al.: Analysis and prediction of water quality using LSTM

deep neural networks in IoT environment. Sustainability 11, 2058 (2019)

[29] Wang, y.: A new concept using LSTM Neural Networks for dynamic system identification. In American

Control Conference (CAC), (2017)

[30] Cual, l., Wu, h., Jin, X., et al.: Study of cardiovascular disease prediction model based on random forest in

eastern China. Informes Científicos 10, 5245 (2020)

[31] Pahlavan-Rad, M.R., Dahmardeh, K., Hadizadeh, METRO., et al.: Prediction of soil water infiltration using multiple

linear regression and random forest in a dry flood plain, eastern Iran. CATENA 194, 104715 (2020)

[32] Friedman, J.: Greedy function approximation: A gradient boosting machine. Annals of Statistics 29, 1189–

1232 (2001)

[33] Chen, T., Guestrin, C.: XGBoost: A Scalable Tree Boosting System. arXiv preimpresión arXiv:1603.02754 (2016)

Data Intelligence

645

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

t

.

/

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

SUPPORTING INFORMATION

S1 Table – All MSE results obtained in this study.

Results of 60%-40% Hold-Out

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

AQ
WQR
WQW
RE
SPB
CCPP1
CCPP2
CCPP3
CCPP4
CCPP5
CON
DDFO
STM
STP
TCPC Z1
TCPC Z2
TCPC Z3

2×10-6
0.0187
0.0174
0.0046
0.0253
0.0033
0.0031
0.0032
0.0032
0.0035
0.0117
0.0011
0.0117
0.0264
0.0242
0.0208
0.0095

3.1×10-6
0.0187
0.0153
0.0042
0.0250
0.0033
0.0030
0.0031
0.0031
0.0033
0.0079
0.0029
0.0171
0.0329
0.0240
0.0194
0.0085

1.7×10-5
0.0165
0.0153
0.0060
0.0373
0.0035
0.0035
0.0035
0.0038
0.0035
0.0161
0
0.0112
0.0198
0.0266
0.0253
0.0137

2.5×10-5
0.0170
0.0160
0.0050
0.0270
0.0032
0.0031
0.0031
0.0032
0.0034
0.0128
0.0001
0.0134
0.0266
0.0268
0.0237
0.0115

2.4×10-5
0.0173
0.0169
0.0055
0.0277
0.0037
0.0036
0.0036
0.0036
0.0004
0.0150
4.4×10-5
0.0125
0.0269
0.0282
0.0260
0.0141

2.4×10-4
0.0030
0.0002
0.0003
0.0088
0.0003
0.0002
0.0003
0.0003
0.0004
0.0006
0.0354
4.3×10-5
0.0825
1.0×10-6
6.0×10-6
0.0001

1.8×10-5
0.0240
0.0201
0.0091
0.0230
0.0040
0.0038
0.0039
0.0037
0.0038
0.0081
0.0134
0.0135
0.0417
0.0095
0.0074
0.0038

Results of 70%-30% Hold-Out

0.2×10-7
0.0151
0.0120
0.0041
0.0235
0.0021
0.0020
0.0020
0.0021
0.0023
0.0041
0.0048
0.0076
0.0246
0.0045
0.0031
0.0017

1.1×10-7
0.0151
0.0136
0.0067
0.0220
0.0026
0.0026
0.0024
0.0028
0.0028
0.0043
0.0185
0.0072
0.0251
0.0201
0.0166
0.0072

5×10-8
0.0162
0.0122
0.0075
0.0217
0.0018
0.0018
0.0017
0.0020
0.0019
0.0032
0.0197
0.0097
0.0259
0.0070
0.0053
0.0024

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

AQ
WQR
WQW
RE
SPB
CCPP1
CCPP2
CCPP3
CCPP4
CCPP5
CON
DDFO
STM
STP
TCPC Z1
TCPC Z2
TCPC Z3

2.7×10-6
0.0162
0.0160
0.0050
0.0221
0.0033
0.0031
0.0032
0.0032
0.0034
0.0112
0.0009
0.0138
0.0219
0.0243
0.0204
0.0092

2.2×10-6
0.0169
0.0150
0.0050
0.0191
0.0032
0.0030
0.0031
0.0031
0.0034
0.0084
0.0014
0.0126
0.0279
0.0244
0.0191
0.0081

1.7×10-5
0.0160
0.0150
0.0064
0.044
0.0034
0.0037
0.0035
0.0036
0.0036
0.0154
0
0.0116
0.0201
0.0267
0.0254
0.0137

2.3×10-5
0.0160
0.0160
0.0053
0.0230
0.0031
0.0031
0.0031
0.0034
0.0032
0.0123
0.0001
0.0169
0.0218
0.0270
0.0239
0.0115

2.3×10-5
0.0162
0.0169
0.0059
0.0238
0.0036
0.0036
0.0035
0.0036
0.0039
0.0147
4.1×10-5
0.0164
0.0214
0.0286
0.0263
0.0143

0.0007
0.0003
0.0001
0.0008
0.0139
0.0001
0.0007
0.0001
0.0001
0.0003
0.0028
0.033
9×10-6
0.2384
7.0×10-6
0.0001
0.0001

1.7×10-7
0.0258
0.0218
0.0086
0.0230
0.0036
0.0038
0.0038
0.0033
0.0034
0.0091
0.0211
0.0104
0.0496
0.0090
0.0064
0.0032

1.0×10-8
0.014
0.0119
0.0049
0.0210
0.0020
0.0019
0.0019
0.0020
0.0022
0.0041
0.0026
0.0093
0.0211
0.0040
0.0020
0.0015

1.2×10-7
0.0163
0.0135
0.0073
0.0192
0.0026
0.0025
0.0024
0.0028
0.0027
0.0043
0.0260
0.0041
0.0268
0.0198
0.0166
0.0072

5×10-8
0.0165
0.0123
0.0083
0.0206
0.0017
0.0016
0.0016
0.0019
0.0018
0.0034
0.0233
0.0070
0.0287
0.0062
0.0049
0.0023

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

Results of 80%-20% Hold-Out

AQ
WQR
WQW
RE
SPB

646

0.2×10-5
0.0151
0.0174
0.0041
0.0228

0.2×10-5
0.0163
0.0165
0.0039
0.0225

1.7×10-5
0.0163
0.0159
0.0064
0.0441

0.2×10-5
0.0159
0.018
0.0046
0.0247

0.2×10-5
0.016
0.0183
0.0051
0.0247

0.0001
0.0017
0.0001
0.0006
0.0276

0.1×10-6
NA
0.0177
0.0052
0.023

0.2×10-7
0.0127
0.0131
0.0038
0.0256

0.1×10-6
0.0159
0.0134
0.0079
0.0159

0.4×10-7
0.015
0.0119
0.0085
0.0196

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

/

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

Results of 80%-20% Hold-Out

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

CCPP1
CCPP2
CCPP3
CCPP4
CCPP5
CON
DDFO
STM
STP
TCPC Z1
TCPC Z2
TCPC Z3

0.0032
0.003
0.0031
0.0034
0.0033
0.0096
0.0010
0.0131
0.0182
0.0241
0.0204
0.0093

0.0032
0.0028
0.0029
0.0031
0.0032
0.0074
0.0019
0.0116
0.0226
0.0240
0.0191
0.0079

0.0035
0.0038
0.0035
0.0036
0.0036
0.0144
0
0.0135
0.0209
0.0266
0.0254
0.0138

0.0032
0.0031
0.003
0.0033
0.0034
0.0132
0.0001
0.0162
0.0172
0.0270
0.0237
0.0115

0.0036
0.0035
0.0034
0.0036
0.0037
0.0169
4.5×10-5
0.0149
0.0177
0.0286
0.0262
0.0143

0.0005
0.0002
0.0002
0.0001
0.0001
0.0008
0.0332
4.7×10-5
0.2352
0.0001
5.3×10-6
0.0032

0.0032
0.0034
0.0035
0.0037
0.003
0.0061
0.0132
0.0089
0.0482
0.0069
0.0054
0.0025

0.0018
0.0018
0.0018
0.002
0.002
0.0032
0.0028
0.0086
0.0168
0.0034
0.0023
0.0013

0.0025
0.0025
0.0024
0.0027
0.0027
0.0052
0.0322
0.0051
0.0251
0.0202
0.0167
0.0073

0.0017
0.0017
0.0015
0.0016
0.0016
0.0041
0.0322
0.0079
0.0298
0.0062
0.0048
0.0023

Results of fi ve-fold cross-validation

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

AQ
WQR
WQW
RE
SPB
CCPP1
CCPP2
CCPP3
CCPP4
CCPP5
CON
DDFO
STM
STP
TCPC Z1
TCPC Z2
TCPC Z3

2.04×10-6
0.0172
0.0149
0.0060
0.0187
0.0033
0.0033
0.0033
0.0032
0.0033
0.0106
0.0015
0.0101
0.0218
0.0260
0.0201
0.0122

3.3×10-6
0.0174
0.0139
0.0057
0.0183
0.0031
0.0033
0.0032
0.0031
0.0031
0.0067
0.0018
0.0100
0.0247
0.0237
0.0156
0.0069

3.2×10-5
0.0177
0.0164
0.0066
0.0276
0.0036
0.0036
0.0036
0.0036
0.0036
0.0201
0
0.0105
0.0235
0.1662
0.2067
0.1353

4.4×10-5
0.0176
0.0164
0.0063
0.0270
0.0033
0.0033
0.0033
0.0033
0.0033
0.0215
0.0002
0.0112
0.0226
0.0289
0.0398
0.0202

4.1×10-5
0.0177
0.0166
0.0068
0.0279
0.0037
0.0037
0.0037
0.0037
0.0037
0.0263
0.0002
0.0104
0.0233
0.0305
0.0449
0.0212

2×10-4
0.0024
0.0001
0.0024
0.0316
0.0003
0.0002
0.0004
0.0003
0.0003
0.0021
0.0436
0.2429
0.1017
7.9×10-5
9.0×10-5
1.0×10-6

8.9×10-8
0.0262
0.0193
0.0075
0.0285
0.0035
0.0034
0.0036
0.0036
0.0035
0.0064
0.0064
0.0100
0.0401
0.0079
0.0057
0.0029

5.3×10-7
0.0171
0.0148
0.0048
0.0254
0.0019
0.0019
0.0020
0.0020
0.0019
0.0195
0.0047
0.0081
0.0229
0.0364
0.0392
0.0908

1.09×10-7 4.6×10-9
0.0150
0.0154
0.0111
0.0134
0.0052
0.0047
0.0231
0.0197
0.0017
0.0027
0.0017
0.0026
0.0017
0.0027
0.0017
0.0026
0.0017
0.0026
0.0029
0.0040
0.0038
0.0041
0.0085
0.0064
0.0247
0.0223
0.0063
0.0201
0.0049
0.0168
0.0023
0.0071

S2 Table – All MAE results obtained in this study.

Results of 60%-40% Hold-Out

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

AQ
WQR
WQW
RE
SPB
CCPP1
CCPP2
CCPP3
CCPP4
CCPP5
CON

0.0011
0.1064
0.1032
0.0467
0.1253
0.0442
0.0438
0.0442
0.0432
0.0450
0.0844

0.0015
0.1067
0.0967
0.0443
0.1200
0.0442
0.0436
0.0447
0.0433
0.0438
0.0683

0.0031
0.0999
0.0966
0.0557
0.1345
0.0477
0.0485
0.0482
0.0473
0.0479
0.1000

0.0042
0.0983
0.1005
0.0501
0.1315
0.0451
0.0447
0.0448
0.0446
0.0456
0.0880

0.0039
0.0988
0.1008
0.0536
0.1319
0.0478
0.0474
0.0474
0.0472
0.0482
0.0954

0.0149
0.0449
0.0121
0.0003
0.0784
0.0141
0.0126
0.0150
0.0137
0.0176
0.0196

0.0002
0.0979
0.0902
0.0568
0.1145
0.0421
0.0419
0.0435
0.0426
0.0434
0.0606

0.0001
0.0884
0.0801
0.0424
0.1181
0.0329
0.0330
0.0325
0.0327
0.0331
0.0459

0.0002
0.0978
0.0911
0.0444
0.1221
0.0388
0.0396
0.0385
0.0402
0.0399
0.0475

0.0002
0.0905
0.0800
0.0504
0.1205
0.0299
0.0308
0.0306
0.0315
0.0308
0.0373

Data Intelligence

647

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

/

.

t

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

Results of 60%-40% Hold-Out

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

DDFO
STM
STP
TCPC Z1
TCPC Z2
TCPC Z3

0.0204
0.0756
0.1127
0.1220
0.1152
0.0756

0.0403
0.0734
0.1272
0.1231
0.1111
0.0690

0
0.0727
0.1028
0.1340
0.1304
0.0931

0.0074
0.0657
0.1148
0.1254
0.1203
0.0822

0.0051
0.0592
0.1153
0.1316
0.1287
0.0926

0.1540
0.0050
0.1635
0.0025
0.0068
0.0115

0.0852
0.0618
0.1479
0.0483
0.0417
0.0300

0.0418
0.0554
0.1103
0.0428
0.0364
0.0257

0.0789
0.0501
0.1132
0.1111
0.1019
0.0639

0.0791
0.0540
0.1163
0.0599
0.0540
0.0342

Results of 70%-30% Hold-Out

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

AQ
WQR
WQW
RE
SPB
CCPP1
CCPP2
CCPP3
CCPP4
CCPP5
CON
DDFO
STM
STP
TCPC Z1
TCPC Z2
TCPC Z3

0.0014
0.0983
0.0995
0.0468
0.1170
0.0446
0.0438
0.0440
0.0444
0.0447
0.0820
0.0197
0.0751
0.1069
0.1210
0.1139
0.0737

0.0012
0.1024
0.0960
0.0458
0.1034
0.0448
0.0438
0.0437
0.0439
0.0447
0.0693
0.0261
0.0641
0.1177
0.1217
0.1087
0.0674

0.0031
0.0986
0.0979
0.0566
0.1369
0.0474
0.0480
0.0483
0.0475
0.0480
0.0961
0
0.0737
0.1005
0.1340
0.1308
0.0934

0.0041
0.0962
0.1008
0.0496
0.1217
0.0451
0.0447
0.0448
0.0445
0.0454
0.0856
0.0085
0.0731
0.1084
0.1256
0.1205
0.0820

0.0039
0.0965
0.1010
0.0531
0.1219
0.0478
0.0475
0.0472
0.0473
0.0482
0.0946
0.0054
0.0667
0.1062
0.1321
0.1292
0.0927

0.0215
0.0132
0.0080
0.0230
0.0959
0.0093
0.0220
0.0083
0.0084
0.0143
0.0480
0.1502
0.0030
0.2384
0.0077
0.0094
0.0095

0.0002
0.0930
0.0875
0.0541
0.1281
0.0406
0.0410
0.0424
0.0432
0.0398
0.0635
0.0925
0.0580
0.1576
0.0455
0.0380
0.0260

0.0001
0.0869
0.0790
0.0442
0.1111
0.0320
0.0323
0.0316
0.0319
0.0320
0.0446
0.0366
0.0577
0.1057
0.0398
0.0330
0.0235

0.0003
0.1011
0.0915
0.0471
0.1140
0.0388
0.0390
0.0380
0.0406
0.0394
0.0477
0.0965
0.0439
0.1153
0.1101
0.1016
0.0635

0.0002
0.0908
0.0796
0.0516
0.1180
0.0293
0.0300
0.0293
0.0306
0.0300
0.0362
0.0987
0.0518
0.1232
0.0569
0.0517
0.0338

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

Results of 80%-20% Hold-Out

AQ
WQR
WQW
RE
SPB
CCPP1
CCPP2
CCPP3
CCPP4
CCPP5
CON
DDFO
STM
STP
TCPC Z1
TCPC Z2
TCPC Z3

648

0.0012
0.0929
0.1030
0.0453
0.1186
0.0452
0.0431
0.0436
0.0449
0.0447
0.0748
0.0264
0.0751
0.0981
0.1217
0.1129
0.0731

0.0014
0.0986
0.1014
0.0442
0.1076
0.0444
0.0418
0.0425
0.0426
0.0433
0.0657
0.0300
0.0620
0.1104
0.1193
0.1090
0.0664

0.0031
0.0984
0.0988
0.0553
0.1409
0.0469
0.0477
0.0486
0.0476
0.0480
0.0929
0
0.0785
0.1031
0.1340
0.1308
0.0938

0.0040
0.0941
0.1043
0.0482
0.1218
0.0453
0.0442
0.0444
0.0447
0.0452
0.0870
0.0090
0.0722
0.0969
0.1254
0.1204
0.0816

0.0039
0.0946
0.1045
0.0512
0.1221
0.0480
0.0471
0.0469
0.0475
0.0478
0.0984
0.0058
0.0656
0.0949
0.1321
0.1291
0.0927

0.0070
0.0326
0.0079
0.0195
0.1077
0.0175
0.0102
0.0123
0.0081
0.0055
0.0226
0.1601
0.0064
0.2354
0.0085
0.0050
0.0032

0.0002
0.0939
0.0768
0.0487
0.1223
0.0390
0.0415
0.0409
0.0422
0.0385
0.0498
0.0839
0.0576
0.1593
0.0391
0.0340
0.0233

0.0001
0.0809
0.0816
0.0423
0.1219
0.0309
0.0309
0.0306
0.0313
0.0311
0.0397
0.0352
0.0549
0.0954
0.0363
0.0303
0.0218

0.0003
0.0997
0.0914
0.0429
0.1014
0.0381
0.0391
0.0382
0.0407
0.0394
0.0504
0.1225
0.0490
0.1124
0.1112
0.1025
0.0640

0.0002
0.0841
0.0784
0.0439
0.1015
0.0289
0.0304
0.0279
0.0294
0.0285
0.0393
0.1145
0.0513
0.1184
0.0569
0.0512
0.0335

Data Intelligence

yo

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
d
norte

/

i

t
/

yo

a
r
t
i
C
mi
–
pag
d

F
/

/

/

/

4
3
6
2
0
2
0
3
9
7
6
7
d
norte
_
a
_
0
0
1
5
5
pag
d

.

t

/

i

F

b
y
gramo
tu
mi
s
t

t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression
Problems

Results of fi ve-fold cross-validation

Dataset

NN

DNN

LR

SVRBF

SVRL

deep LSTM

DT

RF

GradBoost XGBoost

AQ
WQR
WQW
RE
SPB
CCPP1
CCPP2
CCPP3
CCPP4
CCPP5
CON
DDFO
STM
STP
TCPC Z1
TCPC Z2
TCPC Z3

0.0012
0.1018
0.0946
0.0513
0.1036
0.0449
0.0444
0.0443
0.0441
0.0444
0.0797
0.0254
0.0701
0.1076
0.1250
0.1124
0.0850

0.0015
0.1015
0.0921
0.0491
0.1052
0.0435
0.0445
0.0437
0.0433
0.0430
0.0617
0.0233
0.0573
0.1121
0.1212
0.1001
0.0614