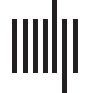ARTÍCULO DE INVESTIGACIÓN
A Linear Superposition Model of Envelope and
Frequency Following Responses May Help
Identify Generators Based on Latency
Tobias Teichert1,2,3
, GRAMO. Nike Gnanateja4
and Bharath Chandrasekaran4,5
, Srivatsun Sadagopan2,3,5
,
1Department of Psychiatry, University of Pittsburgh, pittsburgh, Pensilvania, EE.UU
2Department of Bioengineering, University of Pittsburgh, pittsburgh, Pensilvania, EE.UU
3Center for Neuroscience, University of Pittsburgh, pittsburgh, Pensilvania, EE.UU
4Department of Communication Sciences and Disorders, University of Pittsburgh, pittsburgh, Pensilvania, EE.UU
5Departamento de Neurobiología, University of Pittsburgh, pittsburgh, Pensilvania, EE.UU
Palabras clave: envelope following responses, frequency following responses, temporal fine structure,
macaque monkey, EEG, deconvolution
ABSTRACTO
Envelope and frequency-following responses (FFRENV and FFRTFS) are scalp-recorded
electrophysiological potentials that closely follow the periodicity of complex sounds such as
discurso. These signals have been established as important biomarkers in speech and learning
trastornos. Sin embargo, despite important advances, it has remained challenging to map altered
FFRENV and FFRTFS to altered processing in specific brain regions. Here we explore the utility of
a deconvolution approach based on the assumption that FFRENV and FFRTFS reflect the linear
superposition of responses that are triggered by the glottal pulse in each cycle of the
fundamental frequency (F0 responses). We tested the deconvolution method by applying it to
FFRENV and FFRTFS of rhesus monkeys to human speech and click trains with time-varying
pitch patterns. Our analyses show that F0ENV responses could be measured with high signal-to-
noise ratio and featured several spectro-temporally and topographically distinct components
that likely reflect the activation of brainstem (<5 ms; 200–1000 Hz), midbrain (5–15 ms;
100–250 and cortex (15–35 ∼90 Hz). In contrast, F0TFS responses contained only
one spectro-temporal component that likely reflected activity in the midbrain. summary,
our results support notion latency of F0 components map meaningfully onto
successive processing stages. This opens possibility pathologically altered FFRENV
or FFRTFS may be linked to F0ENV or from there specific stages
and ultimately spatially targeted interventions.
BACKGROUND
Envelope frequency-following (FFRENV FFRTFS) are scalp-recorded
electrophysiological potentials closely follow periodicity complex sounds such as
speech (Aiken & Picton, 2008; Chandrasekaran Kraus, 2010; Skoe 2010). Initially
thought reflect arising mostly cochlear nucleus inferior colliculus
(Chandrasekaran 2010), current thinking assumes multiple sources distributed across
brainstem, midbrain, (Coffey et al., 2019). Over past two decades, altered
FFRENV have been established as an important biomarker speech learning
a n o p e a c s s
j u r l
Citation: Teichert, T., Gnanateja, G. N.,
Sadagopan, S., Chandrasekaran, B.
(2022). A linear superposition model
of envelope frequency following
responses help identify
generators based on latency.
Neurobiology Language, 3(3),
441–468. https:>50 EM) (Alaín & Guastrico, 2012). Topography, es decir., the spatial distribution of electric
or magnetic fields across the scalp, can then be analyzed using source modeling approaches
to further narrow down the exact spatial location of the underlying neural generators. Reciente
work has shown that source modeling can also be leveraged to better understand the neural
generators of the FFR (Bidelman, 2015; Coffey et al., 2016; Gerken et al., 1975; Gorina-Careta
et al., 2021). Sin embargo, because of its dependence on high channel-count electroencephalo-
graph (EEG) and/or magnetoencephalograph (MEG) grabaciones, source modeling is often not
feasible for clinical FFRENV and FFRTFS data which is typically recorded with a 3-electrode
montage.
An alternative approach can be derived from the hypothesis that FFRENV and/or FFRTFS
reflect the linear superposition of responses to each glottal pulse (F0 response) that sequen-
tially activates processing stages in brainstem, midbrain, and cortex (Cifra 1) (Bidelman,
2015; Dau, 2003; Gerken et al., 1975; Janssen et al., 1991). Despite its theoretical relevance,
the superposition hypothesis has not been subject to much empirical scrutiny (Bidelman,
2015). If the superposition hypothesis is accurate, FFRENV and/or FFRTFS would arise as the
convolution of the F0 response with a series of impulses, mathematically described as Dirac
pulses, whose time and amplitude reflect the onset and intensity of each glottal pulse, or more
generalmente, each F0 cycle. Además, it should be possible to compute the underlying F0
responses by deconvolution. Deconvolution approaches have successfully been used in a
wide range of neuroscientific applications (Aquino et al., 2014; Teichert & Ferrera, 2015),
including the closely related 40 Hz auditory steady state response (Bohórquez & Özdamar,
2008) and continuous speech (Maddox & Sotavento, 2018; Polonenko & Maddox, 2021). Hasta la fecha,
sin embargo, deconvolution has never been used to recover the F0 response underlying FFRENV
or FFRTFS to stimuli with time-varying pitch. De este modo, it is unknown how well a linear superpo-
sition model can account for the considerable spectro-temporal complexity of FFRENV and
FFRTFS, and how much of their variance it can capture. If the F0 responses indeed account
for a substantial portion of FFRENV and/or FFRTFS, they may provide useful information about
the functional integrity of the different generators underlying FFRENV and/or FFRTFS.
Based on results from the 40 Hz steady state response and continuous speech (Bohórquez &
Özdamar, 2008; Maddox & Sotavento, 2018; Polonenko & Maddox, 2021), Presumimos que
the F0ENV responses can explain a large portion of the FFRENV. It is less clear if the same would
be true for the FFRTFS. If successful at explaining much of the variance, the F0ENV and F0TFS
may help link altered FFRENV and FFRTFS to altered function in specific auditory processing
etapas. As a first step in that direction, we addressed three main questions: (i) What percentage
of the variance of FFRENV and FFRTFS can be explained by the linear superposition of F0
Neurobiología del lenguaje
442
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
/
.
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Linear superposition model of envelope & frequency following responses
Cifra 1. Linear superposition hypothesis of the FFR. (A) Schematic of a hypothetical feedforward
model with nodes in brainstem, midbrain, and cortex (UN: auditory nerve, CN: cochlear nucleus,
SOC: superior olivary complex, NLL: nucleus of lateral lemniscus, IC1,2 inferior colliculus, Thal:
thalamus, L3/4, L5/6: capa 3/4 y 5/6 of primary auditory cortex). (B) Response of each node to
a single click-like event (F0 response). Hypothetical EEG response arises as the sum of activity over
all nodes. (C) Because the model is linear, the response to several click-like events in close temporal
proximity (FFR-like response) is identical to the sum of the same events presented in isolation
(convolution). En teoría, the F0 response can be recovered from the FFR-like response using
deconvolution.
respuestas? (II) How reliably can F0 responses be estimated? (III) Is there any evidence that the
latencies of F0 responses can be linked to anatomically distinct processing stages?
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
/
.
yo
We decided to perform our experiments in macaque monkeys for three reasons: Primero, el
monkey is a well-established model for the human auditory system in general because
their auditory system shares important functional (Bigelow & Poremba, 2014; Fishman &
Steinschneider, 2012; Gil-da-Costa et al., 2013; Javitt et al., 2000; Steinschneider et al.,
1992) and structural (Chaplin et al., 2013; Sweet et al., 2005) similarities with humans.
Segundo, macaques are known to exhibit human-like FFRENV (Ayala et al., 2017; Brugge
et al., 2009; Fishman et al., 2013; Gnanateja et al., 2021; Steinschneider et al., 1998,
2003). Tercero, this species will ultimately allow us to use invasive recordings to confirm the
predictions of the deconvolution method by directly measuring FFRENV and FFRTFS along
different stages of the auditory pathway.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
MÉTODOS
Sujetos
Data reported here was collected from two adult male macaque monkeys (Mota de macaa).
All experiments were performed in accordance with the guidelines set by the U.S. Departamento
of Health and Human Services (Institutos Nacionales de Salud) for the care and use of laboratory
animales. All methods were approved by the Institutional Animal Care and Use Committee at
the University of Pittsburgh. The animals had previously been exposed to pure tone and click-
stimuli in passive and active listening paradigms.
Neurobiología del lenguaje
443
Linear superposition model of envelope & frequency following responses
Cifra 2. Estímulos. (A) The four synthetic Mandarin tones in the time domain. (B) The corresponding click train stimuli. (C) A snippet containing
two F0 cycles of a Mandarin tone stimulus in the time (línea negra) and time-frequency domain (color). Timing of the clicks in the click train
stimuli matched the time of the highest pressure peak (second F0 cycle). We subsequently defined the onset of an F0 cycle as the first positive
pressure peak that coincides with the first of several peaks of power in the third formant that follows the opening of the glottis (first F0 cycle).
Temporal fine structure of the FFR,
or spectral FFR (FFRTFS):
Reflects the entrainment of neural
responses to individual cycles of
carrier frequencies below a certain
physiological limit.
Estímulos
Two types of stimuli were used: (a) synthesized Mandarin tones (Figura 2A) y (b) click train
versions thereof (Figura 2B). Mandarin tones: The synthesized Mandarin tones used the vowel
/yi/ in the context of four distinct F0 patterns: T1 (high-level, F0 = 129 Hz), T2 (low-rising, F0
que van desde 109 a 133 Hz), T3 (low-dipping, F0 ranging from 89 a 111 Hz), and T4 (alto-
falling, F0 ranging from 140 a 92 Hz). Mandarin tones were synthesized based on the F0
patterns derived from natural male speech production (Xie et al., 2017). All stimuli had a
sampling rate 96000 Hz and were 250 ms in duration and were presented at 78 dB SPL.
The stimuli were presented in both condensation and rarefaction polarities. By computing
either the sum or the difference of the two polarities, it was possible to highlight the neural
responses to either the temporal periodicity envelope (FFRENV) or the temporal fine structure
(FFRTFS) (Krizman & Kraus, 2019).
The stimuli were presented in a randomized manner, with randomly selected inter-stimulus
intervals between 300 y 500 EM. In each 40 min long recording session, we presented 500
repetitions of each tone and polarity for a total of 4,000 sweeps. Click train stimuli: From each
of the four synthesized Mandarin tone stimuli, we prepared a click train version that consisted
of trains of 0.1 ms long monophasic impulses. Timing and amplitude of the clicks in the click
trains matched the timing and amplitude of the F0 cycles of the Mandarin tone stimuli. El
timing of the F0 cycles was operationalized as the time of the peak pressure (Figura 2C, segundo
F0 cycle); the intensity was operationalized as twice the absolute amplitude of the peak activ-
ity to account for the fact that speech sounds are modulated bi-directionally.
The rationale for using the Mandarin tone sets was twofold. Primero, we were interested in
using a stimulus set that had already been used to study FFRENV and FFRTFS in numerous basic
and clinical studies (Chandrasekaran et al., 2014; Lau et al., 2021; Xie et al., 2018). If success-
lleno, the deconvolution technique may be able to extract further information from these existing
data sets. Segundo, we were interested in a stimulus set with a wide range of fundamental fre-
cicaciones, because otherwise the solution to the deconvolution is not unique. We introduced
the click-train stimuli to create a scenario that would be particularly amenable to the super-
position hypothesis and thus to our deconvolution-based analytic approach.
Configuración experimental
All experiments were performed in a small (40 × 40 × 80) sound-attenuating and electrically
insulated recording booth (Eckel Noise Control Technology). The animal was positioned and
Neurobiología del lenguaje
444
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
.
/
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Linear superposition model of envelope & frequency following responses
head-fixed in a custom-made primate chair (Scientific Design). Neural signals were recorded at a
sampling rate of 30 kHz with a 256-channel digital amplifier system (RHD2000, Intan).
Experimental control was handled by a Windows PC running an in-house modified version
of the Matlab (https://www.mathworks.com/) software package monkeylogic. Sound files were
generated prior to the experiments and presented by a subroutine of the Matlab package
Psychtoolbox. The sound files were presented using the right audio channel of a high-
definition stereo PCI sound card (M-192 from M-Audiophile) operating at a sampling rate of
96 kHz and 24-bit resolution. The analog audio signal was then amplified by a 300-watt ampli-
fier (QSC GX3). The amplified electric signals were converted to sound waves using a single
element 4-inch full-range driver (Tang Band W4-1879) situado 20 cm in front of the animals.
Over the relevant range of presented frequencies the sound pressure level of the speaker varied
±7.5 dB SPL.
To determine sound onset with high accuracy, a trigger signal was routed through the
unused left audio channel of the sound card directly to one of the analog inputs of the record-
ing system. De este modo, sound onset could be determined at a level of accuracy that was limited only
by the sampling frequency of the recording device (30 khz: correspondiente a 33 μs).
Cranial EEG
EEG activity was recorded from 33 EEG electrodes that were chronically implanted in 1 mm
deep non-penetrating holes in the cranium (Purcell et al., 2013; Teichert, 2016; Woodman
et al., 2007). Electrodes were positioned across the entire accessible part of the cranium at
positions approximately homolog to the international 10-20 system in the human (li &
Teichert, 2020). More details of the EEG recording setup have been provided in earlier work
(Teichert, 2016; Teichert et al., 2016). Data were recorded with an Intan RHD 2000 digital
amplificador. The midline electrode immediately anterior to Oz served as the recording reference
and ground electrode. Data were referenced offline to the Oz electrode. In one animal, todo
electrodes were functional, allowing us to perform the deconvolution for all electrodes and
thus visualize topographies of the F0 responses. In the second animal only a subset of the
electrodes was functional, thus preventing topographical analyses.
Pre-Processing
The raw data were band-pass filtered using a second-order zero-phase shift Butterworth filter
with cutoff frequencies of 60 y 2000 Hz. Time-locked epochs were extracted and down-
sampled to a rate of 10 khz. Epochs that exceeded an artifact-rejection criterion based on
the distribution of peak-to-peak amplitudes for each individual channel were excluded from
further analyses for that channel. If an epoch exceeded the relative amplitude criterion in two
or more channels, it was rejected for all channels. This relative amplitude criterion allowed us
to process a range of channels with different noise levels simultaneously, es decir., using the same
(relativo) criterion. The valid epochs were averaged separately for the four tones to obtain a
total of four waveforms. Además, the valid epochs were also averaged separately for all
tones and polarity to obtain eight waveforms.
Deconvolution Approach
Click trains
The starting points for the click train deconvolution approach were click onset times and their
amplitudes. The amplitudes were further normalized to an average value of 1 across all 4 click
Neurobiología del lenguaje
445
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
/
.
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Linear superposition model of envelope & frequency following responses
trains. The onset times were then shifted in steps of 0.1 EM (es decir., the sampling rate of the data)
entre 0 y 79.0 EM, for a total of 800 regressors. We then fit a linear model to the FFRENV
and FFRTFS using all 800 regressors. To that aim, FFRENV or FFRTFS, respectivamente, from all stimuli
and the corresponding regressors were concatenated into a single time series padded with
NaN (Not a Number) values between them to avoid cross talk between the end of one stimulus
and the beginning of the next. The FFRENV or FFRTFS kernel was then defined as the weights of
el 800 regressors. The deconvolution approach thus identified the kernel that best explained
the observed FFRENV or FFRTFS as the linear sum of overlapping responses to each individual
click in the click train. The time axis of the kernel thus corresponded to time after click onset.
Similarmente, the latency of specific components of the kernel were measured in time after click
onset. Note that the FFRENV or FFRTFS to all four stimuli were explained by a single 80 ms long
kernel. The deconvolution approach was implemented in the statistical software R, using an
in-house written deconvolution package (deconvolvR).
Mandarin tones
An almost identical procedure was used to create the predictors for the tone FFRENV and
FFRTFS. Sin embargo, to create the click trains, we placed individual clicks at the time of the peak
pressure of each F0 cycle (Figura 1C, second F0 cycle). This choice may have been subopti-
mal, as peak pressure does not coincide with the timing of the actual glottal pulse. We thus
identified an approach and operationalized the onset of each F0 cycle as the first positive pres-
sure peak that coincided with a peak of power in the third harmonic (Figura 1C, first F0 cycle).
The two different approaches yielded highly similar timing, but the estimated F0 onsets pre-
ceded the time of peak pressure very reliably by 1.01 EM. Tone FFRENV kernels were estimated
from both types of predictors based on the timing of the peak pressure and glottal pulse. Ambos
yielded almost identical results. Sin embargo, the FFRENV kernels from the peak pressure were
delayed by approximately 1 EM, and they explained a somewhat lower amount of variance.
Además, the timing of the tone kernel based on the glottal pulse matched the timing of the
click kernel much better than the tone kernel based on peak pressure. Following the theoret-
ical arguments and the empirical support, we report the tone FFRENV and FFRTFS kernels using
the glottal onset time rather than the time of peak pressure.
Nonlinear–Linear Model
We also developed a nonlinear–linear model to account for a very specific limitation of the
linear deconvolution model. The first nonlinear stage of the model accounts for short-term
adaptation in the early auditory system. The short-term adaptation stage uses two parameters,
tau and U, to estimate how quickly and how strongly early stages of the auditory system adapt
to the repeated F0 onsets (Teichert et al., 2016). The parameters U and tau were estimated
using a gradient descent approach. The output of the nonlinear stage corresponds to a series
of Dirac pulses whose amplitude reflects both the amplitude of the F0 cycle, and the degree of
adaptation accrued by responses to previous F0 cycles.
In addition to the nonlinear stage, we also modified the linear stage to include a stimulus
onset regressor. This allows for the possibility that the very first F0 onset triggers a stimulus
onset response that is qualitatively distinct from the remaining F0 responses. To keep the
number of regressors similar, we reduced the lag from 80 EM (800 regressors) a 45 ms for both
types of response (2 × 450 = 900 regressors). Como antes, the model was fit to the training set,
and model fit was evaluated in the testing set.
Neurobiología del lenguaje
446
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
.
/
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Linear superposition model of envelope & frequency following responses
Quantification of Model Fit
The primary variable used to quantify the quality of the model fit was percentage variance
explicado. Percentage variance explained is typically calculated as 100 * (TMS − RMS)/
TMS. Here RMS stands for the mean of the squares of the residuals, and TMS for the mean
of the squares of the total signal, es decir., including variance pertaining to the actual FFR as well
as measurement noise. Since no model can be expected to account for measurement noise,
this traditional metric cannot reach 100% unless there is no measurement noise. The limit of
percentage variance a model can explain is given by 100 − 100/signal-to-noise ratio. Como un
resultado, the metric is only comparable for data sets with similar signal-to-noise ratio. Porque
some of our recording sessions have a range of different signal-to-noise ratios, we decided to
use an alternative metric that adjusts for different signal-to-noise ratios. This metric sets out to
quantify how much of the “explainable” variance, es decir., the portion of the variance that exceeds
the variance of the baseline, can be explained by the model: 100 * (TMS − RMS)/(TMS − BMS).
In this context, BMS stands for the mean of the squares of the signal on the baseline, definido como
el 50 ms period before stimulus onset, and the period from 320 a 390 ms after stimulus
onset, es decir., 70 a 140 ms after stimulus offset. We had found the variance on the post-stimulus
baseline to be systematically smaller than on the pre-stimulus baseline. Hence the decision to
use the average of both periods.
Unless mentioned otherwise, we will refer to this signal-to-noise ratio-corrected measure of
percentage variance explained throughout the article. Percentage variance explained was cal-
culated across the entire simulation period (0 a 280 ms after stimulus onset), así como el
sustained period which excluded both on- and offset responses (50 a 250 EM). Note that in all
casos, the kernel was estimated by fitting it to the entire temporal duration of the data. Estafa-
sequently, any difference in percentage variance explained is not caused by requiring the
model to fit a simpler subset of the data, but rather depends on how well the same underlying
model accounts for the data in different epochs.
Además, we performed a wavelet decomposition of the signal as well as the residuals
and evaluated percentage variance explained in three different frequency bands, the fre-
quency range of the fundamental frequency F0 (70–170 Hz), the frequency range of the first
formant F1 (180–300 Hz), and the frequency range of harmonics beyond the first formant Fx
(400–1200 Hz). To account for the temporal smearing of the wavelet decomposition, el tiempo
ranges of all periods were shrunk by 20 ms on each side.
Data split control
To prevent overfitting caused by determining the kernel and the percentage variance explained
from the same data set, we randomly split the data of each recording session into two equally
sized subsets. The first subset of data (training set) was used to estimate the kernel. This kernel
was then used to determine percentage variance explained of the second subset (testing set). En
the context of the work presented here, the approach was only used for the data averaged
across all sessions.
Cross-day control
At the single session level, we used a different approach to prevent overfitting. Específicamente, a
explain FFRENV from one recording session we only used kernels extracted from different
recording sessions. The data fit metric for the session in question, p.ej., percentage variance
explicado, was then defined as the average of that metric using kernels from all other sessions.
Neurobiología del lenguaje
447
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
.
/
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Linear superposition model of envelope & frequency following responses
Shuffle control
To control for the large number of predictors in the linear model (80 [EM] × 10 [samples per
EM] = 800) we included a shuffle-control. The shuffle control used the same averaged data and
the same predictors. Sin embargo, the timing of the Dirac pulses was shuffled such that the timing
and amplitude designed to match the F0 onsets for tone 2 were used to predict data for tone 1,
the timing and amplitude designed for tone 3 were used for tone 2, etcétera. Este enfoque
was used for data averaged across all recording sessions as well as for data of individual
recording sessions.
Data Quality and Rejection of Recording Sessions
For the click train stimuli we recorded a total of 31 EEG sessions (animal B: 17, animal J: 14).
For the Mandarin tone stimuli we recorded a total of 20 EEG sessions (animal B: 2, animal J:
18). Sessions were included in the analyses if the noise of the averaged FFRs on the baseline
was below 0.008 uV2. Data quality for animal J was variable between sessions, and approx-
imately half of the sessions did not meet the criterion (animal J, click train stimuli: 8/14 ses-
siones; tono: 9/18 sesiones). Data quality for animal B was consistently high. Only one of the
click train sessions needed to be excluded because of noise. Además, we excluded one of
the click train sessions because the signal amplitude was less than half of the other sessions, a
clear outlier given the tight distribution of values for the other sessions. En resumen, we used
2/2 tone sessions and 15/17 click train sessions for animal B.
Noise amplitude on the excluded sessions were distributed bimodally: a small fraction of
recording sessions with an increase of well over tenfold, and a larger fraction with an increase
below twofold. Including the sessions with less than a twofold increase did not change the
main conclusions. Sin embargo, it did increase variability of the results between sessions and
decrease the percentage variance explained by a relatively modest amount. The key takeaway
from including the noisier sessions is not very unexpected: If data quality is lower, menos
variance can be explained.
RESULTADOS
Electrophysiological responses were recorded in response to two types of stimuli: (i) four syn-
thetic Mandarin tones using the syllable /yi/ and (II) click train versions of these Mandarin tone
estímulos. Click train stimuli were created by converting the four Mandarin tone stimuli into series
of monophasic clicks whose timing and amplitude matched the estimated time of onset of each
F0 cycle (Figura 2A, see Methods for details). We report data from a total of 23 EEG recording
sessions using the click train stimuli (15 sessions animal B; 8 sessions animal J) y 11 sesiones
using the Mandarin tone stimuli (2 sessions animal B; 9 sessions animal J). Each session lasted
40 min and contained a total of 4,000 estímulos, 500 from each type and polarity.
By computing either the sum or the difference of responses to the two polarities, the data can
highlight either the neural responses to individual cycles of carrier frequencies below a physi-
ological threshold (FFRTFS), or neural responses to periodic envelope modulations (FFRENV). Nuestro
results will initially focus on data averaged across both polarities, and thus FFRENV. El segundo
half of the Results section will focus on difference between polarities, and thus the FFRTFS.
Tone and Click Train FFRENV
Como se esperaba, both types of stimuli elicited periodic FFRENV-like responses in both animals.
Cifra 3 depicts the Mandarin tone stimuli as well as the grand average FFRENV in the time
Neurobiología del lenguaje
448
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
.
/
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Linear superposition model of envelope & frequency following responses
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
.
/
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 3. Mandarin Tone FFRENV. Representation of Mandarin tone stimuli and the corresponding FFRENV in the time and time-frequency
dominio. (A–D) Estímulos. (E–F) Monkey B FFRENV. (I–L) Monkey J FFRENV.
and time-frequency domains for both subjects. In the time domain, we observed a wide diver-
sity of shapes of the FFRENV as F0 changed both within and between different Mandarin tone
estímulos. In the time-frequency domain, we observed modulation of the fundamental frequency
(F0) and the first harmonic (H1) in concert with the dynamically changing fundamental
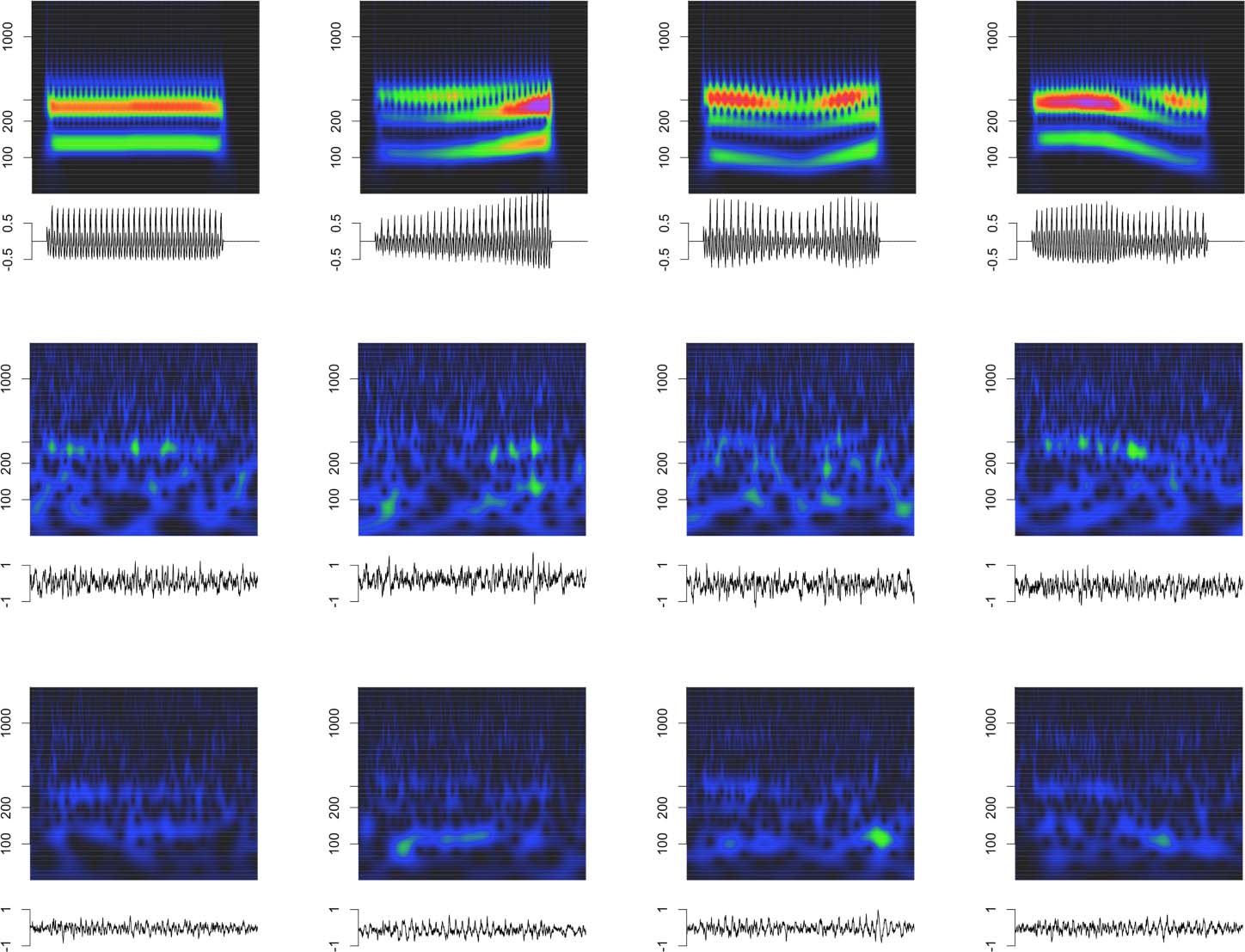
frequency of the Mandarin tone stimuli. Cifra 4 depicts the click train FFRENV in the time
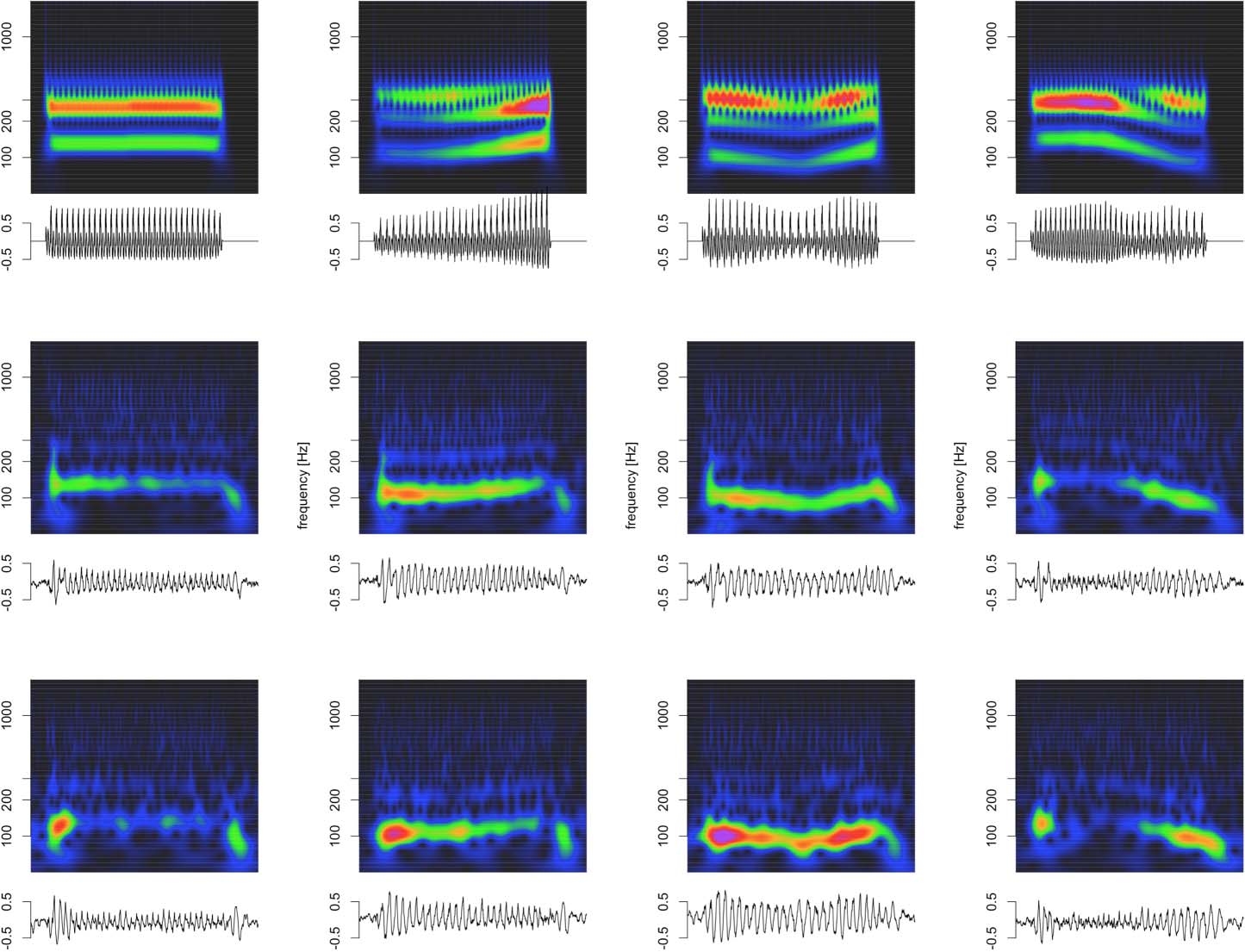
Cifra 4. Click train FFRENV. Representation of click train FFRENV in the time and time-frequency domains. (A–D) Monkey B click train
FFRENV. (E–H) Monkey J click train FFRENV.
Neurobiología del lenguaje
449
Linear superposition model of envelope & frequency following responses
and time-frequency domains. The click train FFRs were qualitatively similar, but of larger
amplitude than the Mandarin tone FFRENV. In the time-frequency domain, we observed power
above the first harmonic. Especially for animal B, there was evidence of a second harmonic
(F2) in cases when F0 was low, such as for click train #3 or toward the end of click train #4.
Además, we often observed power beyond the second harmonic in even higher frequency
bands >400 Hz. In contrast to the first and second harmonic, the frequency of these higher-
frequency components did not change in line with the fundamental frequency of the stimulus.
These higher frequencies were also present for the tone FFRENV, but harder to distinguish due
to their lower amplitude. Based on the time-frequency decomposition of the FFRENV, Lo haremos
focus on three different frequency bands: the frequency range of the fundamental frequency F0
(70–170 Hz), the frequency range of the first harmonic H1 (180–300 Hz), and the frequency
range beyond the second harmonic Hx (400–1200 Hz).
Deconvolution of Click Train FFRENV
We next set out to test if FFRENV with such a complex phenomenology both in the time and time-
frequency domains can be explained by a simple linear superposition model. Given their larger
amplitude and thus higher signal-to-noise ratio, we first focused on the click train FFRENV. A
further improve signal-to-noise ratio, we initially focused on data averaged across all recording
sesiones. To that aim, data from each session was randomly split into two equally sized sets,
subsequently referred to as the training set and test set, respectivamente. Within each set, trials were
averaged across the four different click train stimuli. The deconvolution was performed on the
four click train FFRENV averaged across all training sets. The model fit was then evaluated by
comparing the model predictions derived from the training set with the data from the testing set.
Cifra 5 visualizes the deconvolution process, the F0ENV response, also referred to as the
FFRENV kernel, and the model fits in the time domain for animal B. All key features of the click
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
.
/
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
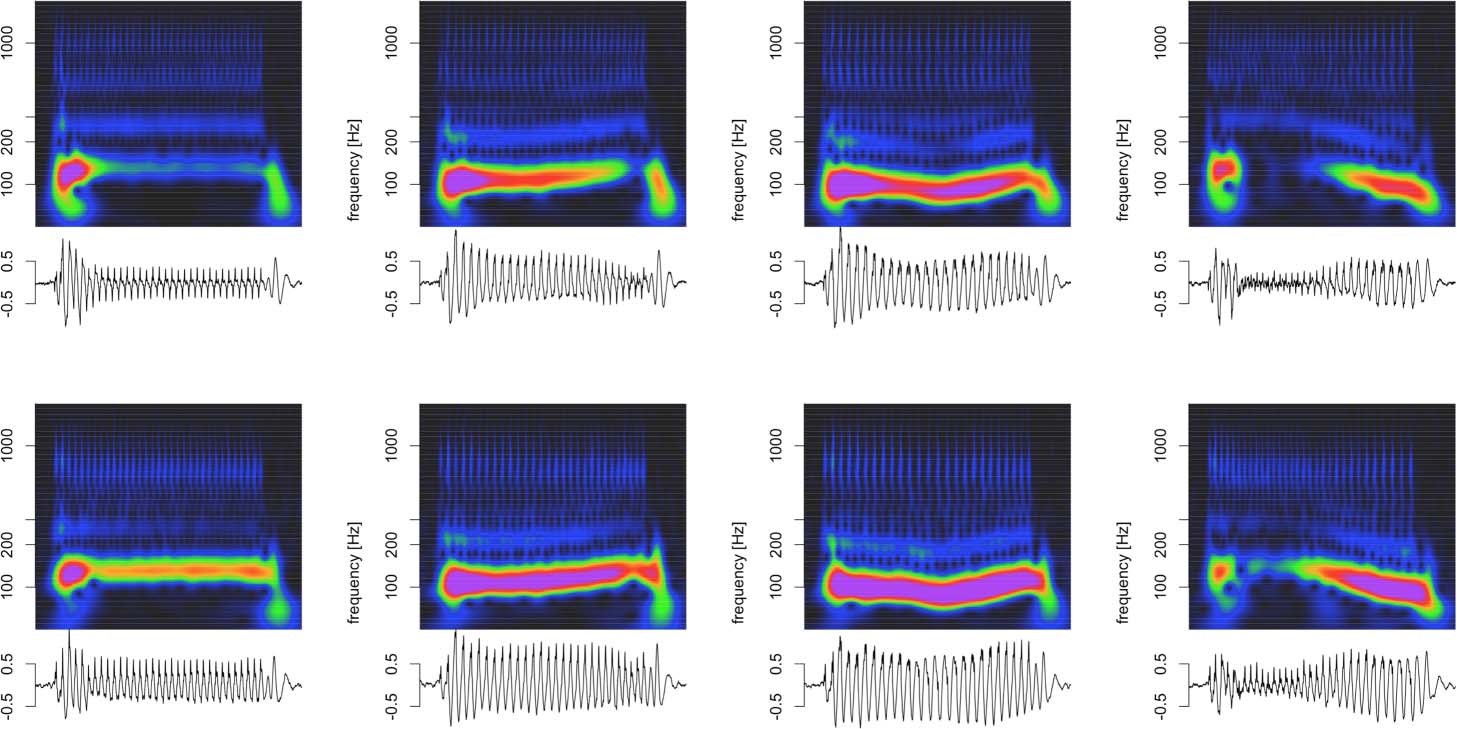
Cifra 5. Deconvolution of grand average click train FFRENV for animal B. (A) Click train regressor for the four click train stimuli. The F0
contour of click train #1 matches the high tone, #2 the rising tone, #3 the dipping tone, y #4 the falling tone. (B) Recovered kernel which can
be viewed as the impulse response to one click. (C) Observed click train FFRENV (color) and model fit (negro). (D) Enlargement of the steady
state period of the FFRENV response.
Neurobiología del lenguaje
450
Linear superposition model of envelope & frequency following responses
train FFRENV were well-captured by the convolution model (black lines in Figure 5C, D). Es
noteworthy that the wide range of shapes of the click train FFRENV could be accounted for with
just one underlying kernel. The different shapes of the click train FFRENV were created exclu-
sively by slight variations of constructive and destructive interference driven by subtle timing
and amplitude differences from otherwise identical F0ENV responses to individual clicks. En
both animals, the extracted kernels contained two key spectro-temporal features: una serie de
brisk peaks and troughs with short latencies and high-frequency, as well as wavelet-like
responses at longer latencies and a lower frequency (Figura 5B).
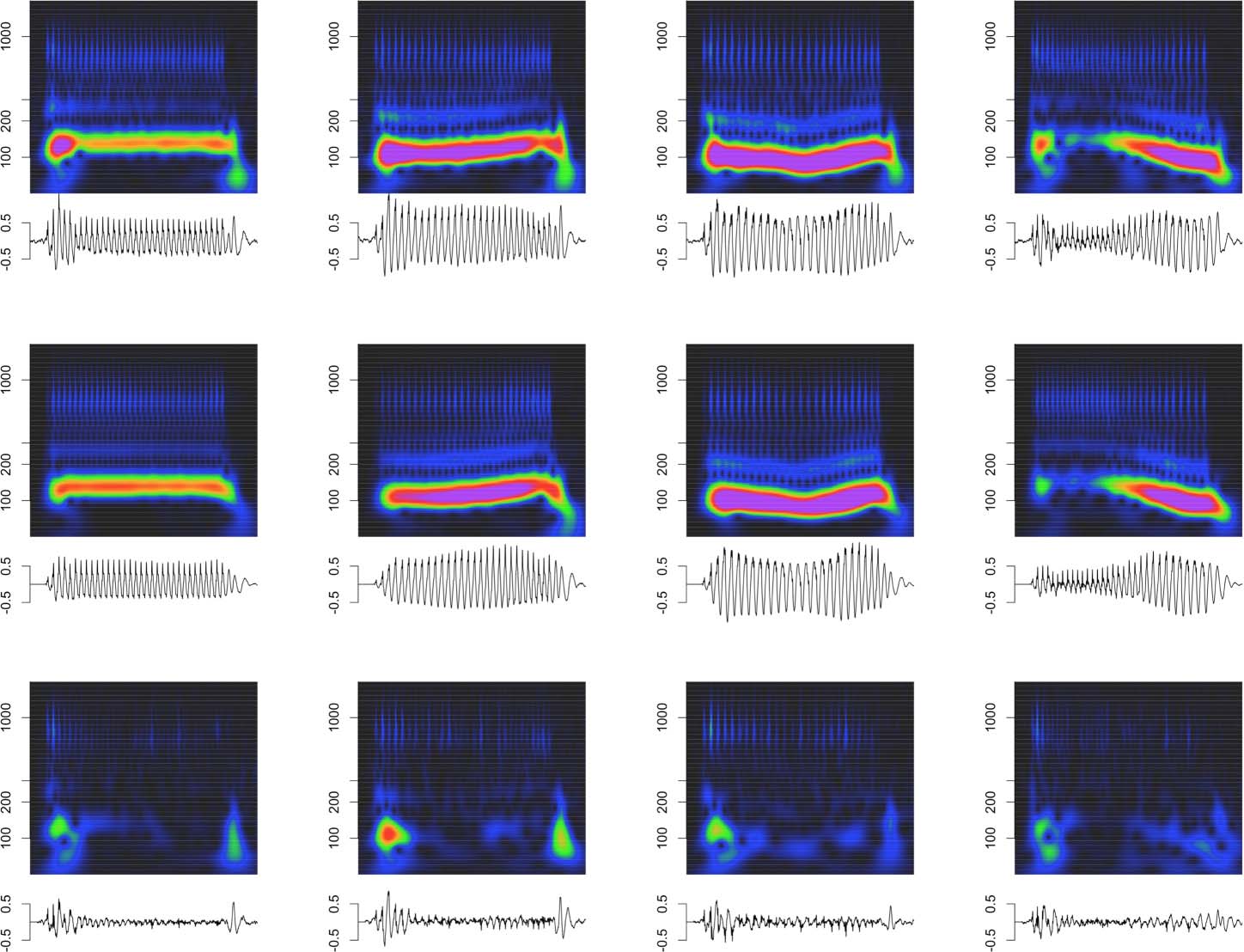
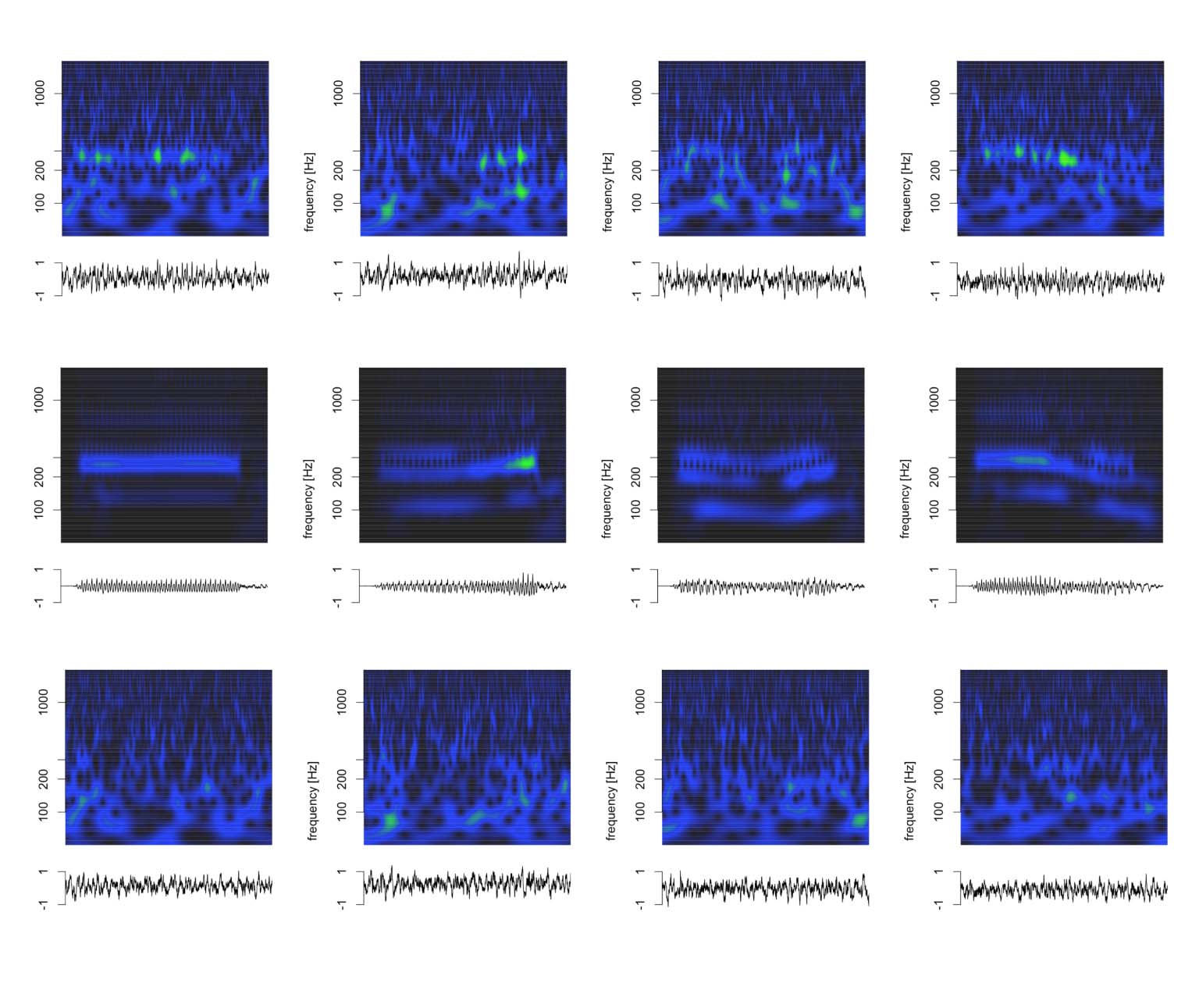
Cifra 6 visualizes the deconvolution process for animal J in the time and time-frequency
dominios. This visualization confirmed that the model captured key aspects in all relevant fre-
quency bands and not just the fundamental frequency. Note that the model captured the com-
ponents whose frequency changed dynamically with F0 (fundamental and first harmonic), como
well as the higher frequency components above F2 whose frequency is unaffected by dynamic
F0 of the stimulus (or the ensuing FFRENV).
Cifra 7 visualizes the deconvolution process for the Mandarin tone stimuli in the time
dominio. Other than using FFRENV recorded in response to Mandarin tone, the procedure for
obtaining the F0 kernels was identical, and the results closely resembled the ones obtained for
the click train stimuli.
While the convolution model captured all key aspects of the data, we also observed regions
of systematic deviations. En particular, the model underestimated the response amplitudes
during the first ∼50 ms of the stimulus. In part to compensate for this, the model tended to
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
/
.
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 6. Deconvolution of grand average click train FFRENV for animal J in the time and time-frequency domains. (A–D) Click train FFRENV.
(E–H) Fit of the deconvolution model. (I–J) Residuals of the model fit.
Neurobiología del lenguaje
451
Linear superposition model of envelope & frequency following responses
Cifra 7. Deconvolution of grand average tone FFRENV for animal J. Conventions as in Figure 4. Note that the click trains in panel A refer to
the predictors used in the deconvolution, not the Mandarin tone stimulus used to drive the FFRENV.
over-estimate the amplitudes for the remainder of the stimulus. This effect may likely be
caused by short-term adaptation, a nonlinear effect that cannot be accounted for by a strictly
linear model. We will briefly touch on this issue later in the article by introducing a nonlinear–
linear convolution approach that resolves most of the remaining systematic misfit during the
onset period.
Percentage Variance Explained: Click Train FFRENV
We next quantified the performance of the model as the percentage variance explained, cualquiera
calculated across the entire stimulation period (0 a 280 ms after stimulus onset), or the sus-
tained period which excluded both on- and offset responses (50 a 250 EM). Además, nosotros
evaluated percentage variance explained in three different frequency bands, the frequency
range of the fundamental frequency F0 (70–170 Hz), the frequency range of the first formant
F1 (180–300 Hz), and the frequency range beyond the first formant Fx (400–1200 Hz). Ver
Methods for details.
Because no model can be expected to account for measurement noise, percentage variance
explained cannot exceed a threshold of 100 − 100/signal-to-noise ratio. Como resultado, the tradi-
tional metric of percentage variance explained is only comparable for data sets with similar
signal-to-noise ratio. De este modo, we decided to quantify how much of the “explainable” variance,
es decir., the portion of the variance that exceeds the variance of the baseline, can be explained by
el modelo. See Methods for details.
In both animals, the convolution model explained the vast majority of the explainable var-
iance (monkey B: 79%; monkey J: 90%, solid circles in Figure 8A). This value was even higher
in the sustained period that excluded on- and offset responses (monkey B: 95%; monkey J:
97%; solid circles in Figure 8B). Within the sustained period, there was a gradient of percent-
age variance explained by frequency range. The largest fraction of variance could be
explained in the F0 range, followed by the H1 and Hx ranges (F0 range: 95% y 98%, para
Neurobiología del lenguaje
452
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
.
/
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Linear superposition model of envelope & frequency following responses
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
.
/
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 8. Percentage variance explained. (A) Percentage variance explained across the entire FFRENV as a function of baseline noise. Solid
points indicate fits to the grand averages across all sessions. Solid diamonds indicate fits to individual sessions. Unfilled symbols indicate
fits using shuffled predictors. (B) Same as (A) but percentage variance explained is only evaluated for steady state portion of the FFRENV
(50–250 ms). (C) Percentage variance explained by frequency band. (D-F) same as (C.A) but for Mandarin tone stimuli.
monkey B and J, respectivamente; F1 range: 96% y 95%; Fx range: 92% y 92%, solid circles
and lines in Figure 8C).
We next tested if the high percentage of explained variance was caused by overfitting. A
that aim, we used a shuffle control in which the number of predictors remained constant but
no longer matched the timing and amplitude of the actual F0 onsets (see Methods for details).
This shuffling dramatically attenuated the percentage variance explained (animal B: 7%,
animal J: 5%, open circles in Figure 8A). The percentage variance explained was even smaller
in the sustained period (animal B: 1%, animal J: 2%, open circles in Figure 8B). The lower values
for the sustained period likely occurred because the shuffled model tended to capture variance
at stimulus onset (which is identical for all stimuli) at the expense of the sustained period.
We next set out to quantify how much of the click train FFRENV can be explained by the
linear kernel in more common experimental settings, es decir., from data collected in individual
recording sessions. To that aim, we calculated the kernel from data averaged across one
recording session and evaluated the fit by comparing the predictions to the FFRENV of all
other recording sessions. The results largely replicated the findings at the level of the grand
averages and confirmed that a substantial amount of the explainable variance could be
Neurobiología del lenguaje
453
Linear superposition model of envelope & frequency following responses
captured by the linear model even at the level of individual recording sessions (animal B: 75 ±
2.7%, animal J: 85 ± 2.7%, mean standard deviation, solid diamonds in Figure 8A). An even
higher percentage of the variance was captured during the sustained period (animal B: 90 ±
4.0%, animal J: 92 ± 2.9%, solid diamonds in Figure 8B). Results from the shuffle control
predictor confirmed that overfitting was also not a major concern for the single session data
(animal B: 4 ± 0.9%, animal J: 2 ± 0.9%, open diamonds in Figure 8A). The percentage
variance explained by the shuffle predictor was even smaller in the sustained period (animal B:
−2 ± 1.3%, animal J: 0 ± 0.9%, open diamonds in Figure 8B). The negative values for animal B
indicate that the shuffle predictor inflated the variance in the sustained period.
Además, the single-session analysis confirmed that the model captured the most
variance in the frequency range of the F0 (animal B: 91 ± 4.4%, animal J: 94 ± 3.3%, solid dia-
monds in Figure 8C), followed by the frequency range of the F1 (animal B: 92 ± 2.7%, animal J:
82 ± 4.8%), and the highest frequency range Fx (animal B: 86 ± 2.9%, animal J: 82 ± 4.8%).
Percentage Variance Explained: Mandarin Tone FFRENV
The results so far suggest that the deconvolution method works rather well on artificial click train
estímulos. Por sí mismo, this is an important finding. Sin embargo, given the substantial differences between
click trains and speech, we then tested if the method also explains much of the variance of the
FFRENV in response to the spectro-temporally complex and realistic Mandarin tones.
As for the click train stimuli, we first computed the deconvolution on data combined across
all recording sessions for each animal. Kernels were fit to a training set and the quality of the
fits were then evaluated by comparing the predictions to the FFRENV of the test set. In both
animales, the convolution model explained a large proportion of the explainable variance
(monkey B: 77%; monkey J: 72%, solid circles in Figure 8D). This value was even higher in
the sustained period that excluded on- and offset responses (monkey B: 89%; monkey J: 88%,
solid circles in Figure 8E). Within the sustained period, there was a clear gradient of percent-
age variance explained by frequency range. The largest fraction of variance could be
explained in the F0 range, followed by the H1 and Hx ranges (F0 range: 93% y 92%, para
monkey B and J, respectivamente; F1 range: 82% y 90%; Fx range: 69% y 77%, solid circles
and lines in Figure 8F).
As for the click train stimuli, using the shuffled predictor dramatically attenuated the
percentage variance explained (animal B: 6%, animal J: 4%, open circles in Figure 8D).
The percentage variance explained was even smaller in the sustained period (animal B: 1%,
animal J: −1%, open circles in Figure 8E).
Despite the overall lower signal amplitudes for the tone FFRENV, a large proportion of the
variance was captured by the linear convolution model even on a session-by-session basis
(animal B: 75 ± 3.5%, animal J: 63 ± 4.0%, mean ± standard deviation, solid diamonds in
Figure 8D). Excluding on- and offset responses, the percentage variance explained is even
más alto (animal B: 87 ± 3.9%, animal J: 77 ± 4.6%, filled diamonds in Figure 8E). As for the
grand averages, shuffling dramatically attenuated the percentage variance explained at the
single session level (animal B: 4.0 ± 1.8%, animal J: 3.0 ± 1.9%, open diamonds in
Figure 8D; sustained period: animal B: −1 ± 2.4%, animal J: −1 ± 2.9%, open diamonds in
Figure 8E), again confirming that overfitting was not a substantial contribution to the high
percentage of variance explained.
Además, the single-session analysis confirmed that the model captured the most vari-
ance in the frequency range of the F0 (animal B: 93 ± 1.1%, animal J: 84 ± 3.8%, sólido
Neurobiología del lenguaje
454
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
norte
oh
/
yo
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
3
4
4
1
2
0
3
5
7
7
3
norte
oh
_
a
_
0
0
0
7
2
pag
d
.
/
yo
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Linear superposition model of envelope & frequency following responses
diamonds in Figure 8F), followed by the frequency range of the F1 (animal B: 76 ± 2.5%,
animal J: 66 ± 11.1%), and the highest frequency range Fx (animal B: 73 ± 8.7%, animal J:
47 ± 19.5%).
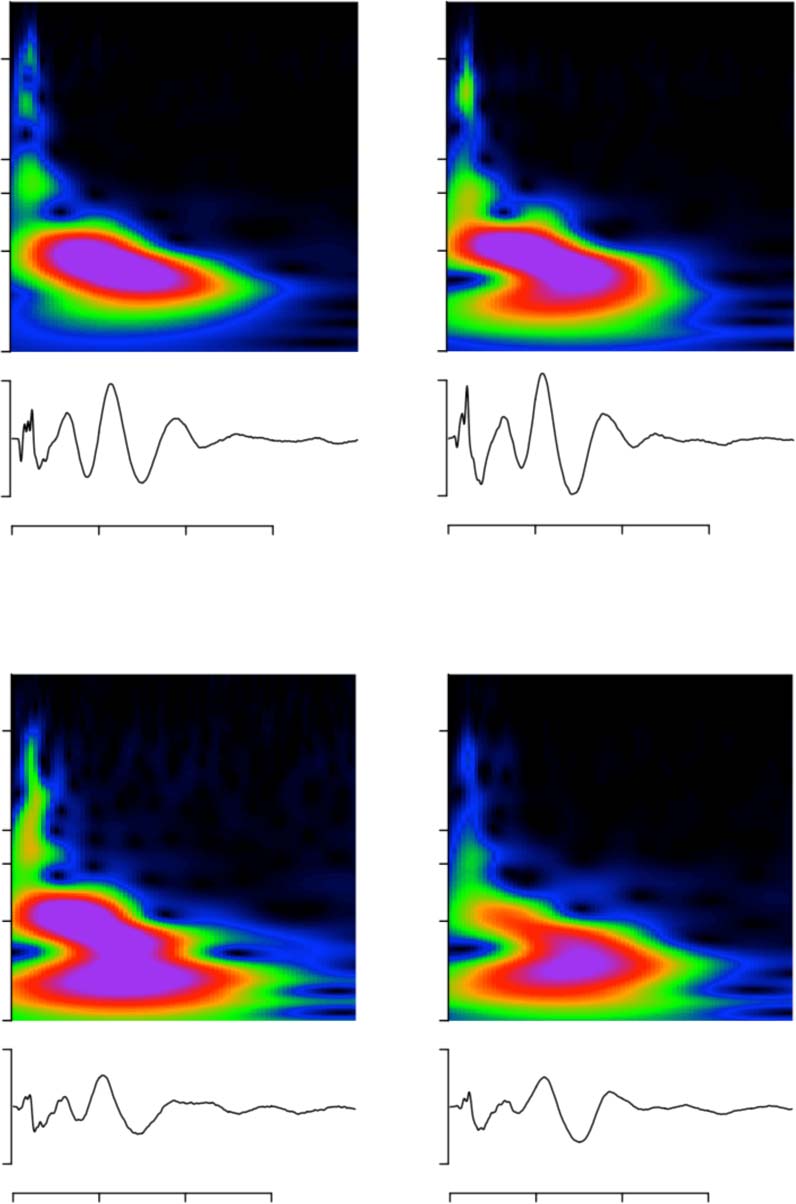
Consistency of Deconvolution Approach Across Recording Sessions
The ability to explain the FFRENV of one recording day using the kernel from a different session,
suggests that the kernels are remarkably similar between days. Figure 9A, B confirms the high
degree of similarity for the click train kernels. Especially early features of the kernel (<5 ms)
were highly preserved across sessions, to the point that it was hard even distinguish the
presence of more than one trace. Above 5 ms, differences between sessions became some-
what apparent. The largest between-session variability observed for late
wavelet-like response 15 and 35 ms. We quantified similarity kernels as
the Pearson correlation coefficient, which found be 0.97 ± 0.02 both animals (mean
plus minus standard deviation). Note while different were highly
similar, two quite distinct from each other. In particular, the
early features below ms are like a fingerprint uniquely identifies the
subject with high confidence on basis single session.
Cross correlations Mandarin tone stimuli (Figure 9C, D) similarly
high (animal B: 0.98 NA, animal J: 0.91 0.08; deviation not available for
animal B, since only recorded, resulting in cross-correlation value.
For monkey J, average attenuated mostly by session. As result
of leftward skew distribution, median coefficient good bit
higher probably robust estimate (median 0.95).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
>