On the Construction of Pareto-Compliant
Combined Indicators
j. GRAMO. Falcón-Cardona
Computer Science Department, CINVESTAV-IPN, Ciudad de México, 07360, México
jfalcon@computacion.cs.cinvestav.mx
METRO. t. METRO. Emmerich
LIACS, Universidad de Leiden, Leiden, 2333, Los países bajos
m.t.m.emmerich@liacs.leidenuniv.nl
C. A. Coello Coello
Computer Science Department, CINVESTAV-IPN, Ciudad de México, 07360, México
Basque Center for Applied Mathematics (BCAM) & Ikerbasque, España
ccoello@cs.cinvestav.mx
https://doi.org/10.1162/evco_a_00307
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Abstracto
The most relevant property that a quality indicator (QI) is expected to have is Pareto
compliance, which means that every time an approximation set strictly dominates an-
other in a Pareto sense, the indicator must reflect this. The hypervolume indicator
and its variants are the only unary QIs known to be Pareto-compliant but there are
many commonly used weakly Pareto-compliant indicators such as R2, IGD+, y (cid:2)+.
Actualmente, an open research area is related to finding new Pareto-compliant indicators
whose preferences are different from those of the hypervolume indicator. In this article,
we propose a theoretical basis to combine existing weakly Pareto-compliant indicators
with at least one being Pareto-compliant, such that the resulting combined indicator is
Pareto-compliant as well. Más importante, we show that the combination of Pareto-
compliant QIs with weakly Pareto-compliant indicators leads to indicators that inherit
properties of the weakly compliant indicators in terms of optimal point distributions.
The consequences of these new combined indicators are threefold: (1) to increase the
variety of available Pareto-compliant QIs by correcting weakly Pareto-compliant in-
dicators, (2) to introduce a general framework for the combination of QIs, y (3) a
generate new selection mechanisms for multiobjective evolutionary algorithms where
it is possible to achieve/adjust desired distributions on the Pareto front.
Palabras clave
Performance indicators, Pareto compliance, multiobjective optimization indicator-
based selection.
1
Introducción
The quality assessment of Pareto front approximations1 (also known as approxima-
tion sets) has been a critical factor to compare multi-objective evolutionary algorithms
(MOEAs) (Coello Coello et al., 2007). When assessing an approximation set, three qual-
ity aspects have been commonly considered: convergence towards the Pareto front,
spread, and diversity of solutions (Zitzler et al., 2000). The first evaluation method con-
sisted in qualitative comparisons by plotting the approximation sets (Horn et al., 1994).
Sin embargo, a visual comparison is insufficient when the number of objective functions,
1A Pareto front approximation is a finite set of objective vectors that aims to represent a Pareto front.
Manuscrito recibido: 19 December 2019; revisado: 7 Marzo 2021, 14 Enero 2022, 25 Enero 2022; aceptado:
11 Febrero 2022.
© 2022 Instituto de Tecnología de Massachusetts
Computación evolutiva 30(3): 381–408
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
Mesa 1: Relations on approximation sets based on Pareto dominance relations (Zitzler
et al., 2003; Guerreiro and Fonseca, 2020).
Relation
A (cid:2) B
A (cid:2) B
A ≺ B
A ≺≺ B
Descripción
Nombre
For every element (cid:2)b ∈ B, there is at least an element (cid:2)a ∈ A
Weak dominance
such that (cid:2)a (cid:2) (cid:2)b.
A (cid:2) B and B (cid:4)(cid:2) A.
A (cid:4)= ∅ and for every element (cid:2)b ∈ B, there is at least an
element (cid:2)a ∈ A such that (cid:2)a ≺ (cid:2)b.
A (cid:4)= ∅ and for every element (cid:2)b ∈ B, there is at least an
element (cid:2)a ∈ A such that (cid:2)a ≺≺ (cid:2)b.
Strict dominance
Strict elementwise
dominance
Strong dominance
MOEAs, and the cardinality of the approximation sets increases. To overcome this is-
sue, researchers extended the Pareto dominance relation and its variants (which give a
general notion of optimality) to be applied on approximation sets. A este respecto, given
two objective vectors (cid:2)tu, (cid:2)v ∈ Rm, (cid:2)u Pareto dominates (cid:2)v (denoted as (cid:2)u ≺ (cid:2)v) if and only if
ui ≤ vi for all i = 1, 2, . . . , m and there exists at least an index j ∈ {1, 2, . . . , metro} such that
uj < vj . In case that ui ≤ vi for all i, it is said that (cid:2)u weakly Pareto dominates (cid:2)v (denoted
as (cid:2)u (cid:2) (cid:2)v). If ui < vi for all i, (cid:2)u strongly Pareto dominates (cid:2)v (denoted as (cid:2)u ≺≺ (cid:2)v). The
extended Pareto dominance relations are shown in Table 1. An important drawback of
these set-based binary relations is their impossibility to take into account the spread and
diversity of solutions. To alleviate the issues of the two previous comparison methods,
quality indicators (QIs) were proposed as a quantitative methodology focused on mea-
suring the three main quality aspects previously indicated (Veldhuizen, 1999; Zitzler
et al., 2003; Jiang et al., 2014; Liefooghe and Derbel, 2016; Li and Yao, 2019).
1
Quality indicators are set functions that assign a real value to one or more approxi-
mation sets simultaneously, according to specific preference information (Zitzler et al.,
× · · · × Al → R,
2003; Li and Yao, 2019). Mathematically, an l-ary QI is a function I : A
where each Aj ⊂ Rm, j = 1, . . . , l is a non-empty approximation set. Due to its math-
ematical definition, they impose a total order on the set (cid:2) of all approximation sets
related to a multiobjective optimization problem. Hence, this property makes QIs a re-
markable option to compare the performance of MOEAs. In the specialized literature,
there are several QIs that aim to assess convergence, spread and uniformity of approxi-
mation sets (Li and Yao, 2019). QIs focused on measuring convergence have a notewor-
thy relevance since they have been used to assess the performance of MOEAs and also to
design their selection mechanisms (Falcón-Cardona and Coello Coello, 2020). Regard-
ing the assessment of MOEAs, Pareto compliance is a critical property of convergence
QIs2 that allows them to reflect the order imposed by the (cid:2)-relation (see Table 1). It is
worth noting that throughout the years, the term Pareto compliance has been commonly
used. However, Hansen and Jaszkiewicz (1998) firstly named this property as compati-
bility with an outperformance relation; Zitzler et al. (2003) denoted these indicators as
(cid:2)-complete; and, finally, Zitzler, Knowles, et al. (2008) refined the term as strict monotonic-
ity. In the following, we define the Pareto compliance and the weak Pareto compliance
2From this point onwards, convergence QIs will be denoted just as QIs.
382
Evolutionary Computation Volume 30, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
e
v
c
o
_
a
_
0
0
3
0
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combined Pareto-Compliant Indicators
properties, assuming, without loss of generality, that a lower indicator value implies a
better quality.
Property 1 (Pareto compliance): Given two approximation sets A and B, a unary indicator
I is (cid:2)-compliant (Pareto-compliant) if A (cid:2) B ⇒ I (A) < I (B).
Property 2 (Weak Pareto compliance): Given two approximation sets A and B, a unary
indicator I is weakly (cid:2)-compliant (weakly Pareto-compliant) if A (cid:2) B ⇒ I (A) ≤ I (B).
Pareto compliance implies that every time an approximation set A strictly dominates
another set B, the indicator I will reflect this situation by assigning a lower indicator
value to A. In contrast, weak Pareto compliance indicates that A and B at least have
the same quality. If the QI does not reflect the order imposed by the extended domi-
nance relations, then it is denoted as a non Pareto-compliant indicator. The importance
of Pareto-compliant indicators when assessing MOEAs lies in their impossibility of con-
tradicting the structure of order imposed by the (cid:2)-relation (Zitzler et al., 2003). Hence,
when comparing MOEAs, Pareto compliance avoids the generation of misleading con-
clusions regarding the use of Pareto dominance.
Among the plethora of convergence QIs currently available, the hypervolume indi-
cator (HV) is the only unary QI that is Pareto-compliant (Zitzler, 1999; Zitzler et al., 2003,
Zitzler, Knowles, et al., 2008). The HV measures the extent of the volume dominated by
an approximation set and bounded by a user-supplied reference point that should be
dominated by all points in the Pareto front approximation. For nonlinear Pareto front
shapes, the set of size μ that approximates the solution to the HV-based subset selec-
tion problem presents a non-uniform distribution of objective vectors (Shang, Ishibuchi,
He, et al., 2020). The consequences of these non-uniform optimal μ-distributions are
twofold: (1) HV penalizes uniform Pareto front approximations in comparison to certain
non-uniform approximation sets, and (2) MOEAs that use HV-based selection mech-
anisms, produce non-uniform approximation sets. To improve the uniformity of the
optimal μ-distributions of HV, the weighted HV (Zitzler et al., 2007), logarithmic HV
(Friedrich et al., 2011), free HV (Emmerich et al., 2014), and the transformation-based
HV (Shang, Ishibuchi, Nan, et al., 2020), which are all variants of HV, have been pro-
posed. Moreover, these variants preserve the Pareto compliance property of HV. Addi-
tionally, some other QIs have been proposed, having different preferences to those of
the HV but being weakly Pareto-compliant or non Pareto-compliant. For instance, the
most noteworthy weakly Pareto-compliant QIs are R2 (Brockhoff et al., 2012), the In-
) (Ishibuchi et al., 2015), and the unary additive
verted Generational Distance plus (IGD
(cid:2) indicator ((cid:2)+
) (Zitzler et al., 2003), while IGD (Coello Coello and Cruz Cortés, 2005)
and Generational Distance (Veldhuizen, 1999) are non-Pareto-compliant indicators.
+
Due to the imperative need to propose new Pareto-compliant QIs whose prefer-
ences are significantly different to those of the HV, we propose in this article a method-
ology to generate new Pareto-compliant QIs. It is worth noting that in this article we
provide both a theoretical and an experimental extension of the work introduced by
Falcón-Cardona et al. (2019). Under this methodology, we combine one or more weakly
Pareto-compliant indicators with at least one Pareto-compliant QI, using an order-
preserving combination function. Under these conditions, we demonstrate that the
combined indicators preserve the Pareto compliance property. Additionally, we show
through preference analysis and the approximate optimal μ-distributions, that our
framework allows to create Pareto-compliant QIs with different preferences to those
of the HV in two ways: (1) by exploiting the conflict that sometimes exists between
the preferences of indicators, such that the combined indicator shows intermediate
Evolutionary Computation Volume 30, Number 3
383
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
e
v
c
o
_
a
_
0
0
3
0
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. G. Falcón-Cardona, M. T. M. Emmerich, and C. A. Coello Coello
preferences, and (2) by keeping the original preferences of the weakly Pareto-compliant
QIs but using a correcting factor derived from the Pareto-compliant QI being used.
Overall, the contributions of this article are the following:
1. We provide guidelines for the construction of new Pareto-compliant QIs whose
preferences are essentially different from those of the HV.
2. Our proposed framework allows correcting weakly Pareto-compliant QIs, such
as R2, IGD
+
, and (cid:2)+
, so that they can become Pareto-compliant.
3. We provide an empirical study of the optimal μ-distribution of solutions gen-
erated by a steady-state MOEA based on some (selected) new Pareto-compliant
QIs.
The remainder of the article is organized as follows. Section 2 defines the quality
indicators that we use throughout the article. The previous related work is described in
Section 3. Our mathematical framework for the construction of new Pareto-compliant
QIs is introduced in Section 4. The experimental results using the combined indicators
is presented in Section 5. Finally, the main conclusions and future work are described
in Section 6.
2 Background
In this article, we consider, without loss of generality, multiobjective optimization prob-
lems (MOPs) for minimization which are defined as follows (Coello Coello et al., 2007):
f ((cid:2)x) = (f1((cid:2)x), f2((cid:2)x), . . . , fm((cid:2)x))T
(cid:3)
(cid:2)
,
min
(cid:2)x∈(cid:3)
where (cid:2)x = (x1, . . . , xn)T ∈ (cid:3) is a vector of n decision variables, and (cid:3) ⊆ Rn is the de-
cision space. f ((cid:2)x) is a vector of m ≥ 2 objective functions fi : (cid:3) → R, ∀i ∈ {1, 2, . . . , m}
where some or all of them are mutually in conflict. Since there is no single decision
vector (cid:2)x whose objective vector f ((cid:2)x) minimizes all objective functions simultaneously,
the goal is to find the so-called Pareto optimal solutions whose images in the objective
function space represent the best possible trade-offs among the objective functions. A
decision vector (cid:2)x ∈ (cid:3) is Pareto optimal if there is no other (cid:2)y ∈ (cid:3) such that f ((cid:2)x) ≺ f ((cid:2)y).
The set of all Pareto optimal solutions P ∗
is called Pareto set and its image, given by
P F ∗ = f (P ∗
), is known as the Pareto front.
In the following, we provide the mathematical definitions of HV, R2, IGD
, and (cid:2)+
,
which are extensively used throughout the article. In all cases, let A denote an approx-
imation set and Z be a reference set.
Definition 1 (Hypervolume indicator): Let (cid:4) denote the Lebesgue measure in Rm, the hy-
pervolume indicator (HV) is defined as follows:
+
HV(A, (cid:2)zref ) = (cid:4)
{(cid:2)x | (cid:2)a ≺ (cid:2)x ≺ (cid:2)zref }
,
(cid:6)
(cid:4)
(cid:5)
(cid:2)a∈A
where (cid:2)zref ∈ Rm is a reference point which should be dominated by all points in A.
HV measures the extent of volume jointly dominated by the points in A and
bounded by (cid:2)zref . Currently, HV and the closely related logarithmic HV (Friedrich et al.,
2011), the weighted HV (Auger et al., 2009), the free HV (Emmerich et al., 2014), and
the transformation-based HV (Shang, Ishibuchi, Nan, et al., 2020) are the only Pareto-
compliant QIs known so far. The two main drawbacks of the HV are the following. First,
384
Evolutionary Computation Volume 30, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
e
v
c
o
_
a
_
0
0
3
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combined Pareto-Compliant Indicators
under NP (cid:4)= P, its computational cost increases super-polynomially with the number of
objective functions (Bringmann and Friedrich, 2009, 2010). The other issue is related to
(cid:2)zref , since the preferences of HV strongly depend on it (Auger et al., 2009; Ishibuchi,
Imada, et al., 2017). In other words, the specification of the reference is dependent on
the Pareto front shape. It has been shown that the distribution of points is often concen-
trated on the boundary and in knee-point regions.
Definition 2 (Unary R2 indicator): The unary R2 indicator is defined as follows:
R2(A, W ) = 1
|W |
(cid:7)
(cid:2)w∈W
{u(cid:2)w(a)},
min
(cid:2)a∈A
where W is a set of m-dimensional weight vectors and u(cid:2)w : Rm → R is a utility function, pa-
rameterized by (cid:2)w ∈ W , that assigns a real value to each solution vector.
The R2 indicator is a convergence-diversity QI that measures the average minimum
utility values of the approximation set with respect to a set of weight vectors (Hansen
and Jaszkiewicz, 1998; Brockhoff et al., 2012). Its computational cost is in (cid:5)(m|W | · |A|).
Unlike the hypervolume indicator, the time complexity of R2 grows linearly with the
number of objectives. Its time complexity is, however, proportional to the number of
weight vectors,3 which has to grow exponentially in size, if the number of objectives
increases and the same resolution of sampling is desired. A major conceptual difference
with respect to the hypervolume indicator is that the R2 indicator does not require an
anti-optimal reference point. Instead, it works with an ideal or utopian reference point.
In many applications involving, for instance, error or cost minimization, there is a nat-
ural choice for an ideal point, but it is difficult to define an anti-optimal reference point.
So, in such cases, the R2 indicator could be a better choice than the hypervolume.
A problem, however, arises due to the fact that the R2 indicator is not Pareto-
compliant, and it is only weakly Pareto-compliant (Hansen and Jaszkiewicz, 1998;
Brockhoff et al., 2012). This makes it possible that a set might have equal R2 indicator
values than another set, although it is dominated in the set order, or that sets degen-
erate if this indicator is used as a guide in a Pareto optimization process. One might
argue that these are rare cases, as they always involve shared coordinate values among
points, and in most cases, the R2 indicator works well when comparing sets. In fact, in
continuous unconstrained optimization, such cases might occur with low probability,
but they are relatively likely to occur in continuous optimization and in cases in which
box constraints are introduced.
Definition 3 (Inverted Generational Distance plus): The IGD+, for minimization, is de-
fined as follows:
+
IGD
(A, Z ) = 1
|Z|
where d +
((cid:2)a, (cid:2)z) =
(cid:8)(cid:9)
m
k=1 (max{ak − zk, 0})2.
(cid:7)
min
(cid:2)a∈A
(cid:2)z∈Z
d +
((cid:2)a, (cid:2)z),
Ishibuchi et al. (2015) proposed IGD
as an improvement of the IGD indicator
(Coello Coello and Cruz Cortés, 2005). Both QIs measure convergence and diversity of
+
3The Simplex-Lattice-Design method is usually employed to construct the set of weight vectors (Das
and Dennis, 1998). Using this method, the number of weight vectors is the following combinatorial
number: N = CH +m−1
, where H ∈ N is a user-supplied parameter that determines the number of divi-
sions of the space, and m is the number of objectives.
m−1
Evolutionary Computation Volume 30, Number 3
385
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
e
v
c
o
_
a
_
0
0
3
0
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. G. Falcón-Cardona, M. T. M. Emmerich, and C. A. Coello Coello
solutions simultaneously. However, IGD+ is weakly Pareto-compliant while IGD is not
+
Pareto-compliant (Bezerra et al., 2017). IGD
measures the average distance from the
reference set to the dominated space of the approximation set. Its computational cost is
(cid:5)(m|Z| · |A|). A critical aspect is how to specify the reference set when no information
is available about P F ∗
Definition 4 (Unary (cid:2)+
(Ishibuchi et al., 2014).
indicator): Mathematically, it is defined as follows:
(cid:2)+
{zi − ai}.
(A, Z ) = max
(cid:2)z∈Z
min
(cid:2)a∈A
max
1≤i≤m
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
e
v
c
o
_
a
_
0
0
3
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The unary (cid:2)+
-indicator gives the minimum distance by which a Pareto front ap-
proximation needs to or can be translated in all dimensions at once in objective space
such that a reference set is weakly dominated. In consequence, this QI exclusively mea-
sures convergence to P F ∗
and it is weakly Pareto-compliant. A remarkable aspect is
that (cid:2)+ does not require any parameters but, as in the case of IGD+, a reference set has
to be supplied. Additionally, (cid:2)+
is not very sensitive to local changes in the solutions in
A (Bringmann et al., 2011).
+
+
Recently, the combination of the high interest in solving MOPs with more than
three objective functions and the expensive calculation of the HV have promoted the
utilization of weakly and non-Pareto-compliant QIs in spite of their clear drawbacks
when comparing MOEAs (Deb and Jain, 2014; Yuan et al., 2016; Tian et al., 2018; Li
et al., 2018). In the following, we analyze, using two examples, why weakly and non-
Pareto-compliant QIs are not good enough for comparing MOEAs (Zitzler, Knowles,
et al., 2008 also discussed these issues). First, Figure 1 shows two approximation sets
A and B, where A (cid:2) B, for which the HV, IGD
, and IGD4 values are calculated. It is
and IGD means higher quality in contrast to
worth noting that a lower value of IGD
the HV which aims to maximize the dominated volume. Due to its Pareto compliance,
the HV effectively shows that A strictly dominates B since HV(A, (cid:2)zref ) = 0.781875 and
HV(B, (cid:2)zref ) = 0.671250. On the other hand, IGD+ cannot reflect that A (cid:2) B since the
value (0.125) is assigned to both approximation sets. In contrast, IGD de-
same IGD
termines that B is better because IGD(B, Z ) = 0.125 and IGD(A, Z ) = 0.167705, even
though it is strictly dominated by A. Regarding the second example, let’s consider a
QI which we will call “Zero indicator”. It is defined as Z : (cid:2) → R with Z ≡ 0. Clearly,
for every A, B ∈ (cid:2) such that A (cid:2) B, it implies Z(A) = Z(B), i.e., Z is weakly Pareto-
compliant. Although indicators such as R2, IGD+ and (cid:2)+ are more complex than Z in a
mathematical sense, all of them are only weakly Pareto-compliant as the Zero indicator.
Based on the discussed examples, we can see that is not enough to construct weakly and
non Pareto-compliant QIs, since they can lead to misleading conclusions when compar-
ing approximation sets (Zitzler, Knowles, et al., 2008). Consequently, this is a motivation
to construct new Pareto-compliant QIs.
+
3
Previous Related Work
In this section, we briefly describe the previous work done in the direction of the em-
ployment of multiple QIs. Additionally, we first provide a discussion on the use of dif-
ferent terms to denote the Pareto compliance property.
4Given an approximation set A and a reference set Z, the IGD indicator is defined as follows:
, where d is the Euclidean distance and p > 0 is a user-
(cid:11)
1/pag
(cid:10)(cid:9)
IGD(A, z ) = 1
|z|
supplied parameter, usually set to 2.
(cid:2)z∈Z min(cid:2)a∈A d ((cid:2)a, (cid:2)z )pag
386
Volumen de cálculo evolutivo 30, Número 3
Combined Pareto-Compliant Indicators
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 1: Let A = {(0.125, 0.875),
(0.875,
(0.375, 0.625),
0.125)}, B = {(0.125, 1), (0.375, 0.75), (0.5, 0.625), (0.75, 0.375), (1, 0.125)}, and Z =
{(0, 1), (0.25, 0.75), (0.5, 0.5), (0.75, 0.25), (1, 0)}. Even though A (cid:2) B, IGD prefers B and
assigns the same quality to both sets, HV prefers A since it is Pareto-compliant.
IGD
(0.625, 0.375),
(0.575, 0.6),
+
3.1
Pareto Compliance
Pareto compliance (defined in Property 1) is a characteristic of convergence QIs which
allows them to reflect the order structure imposed by the (cid:2)-relation defined in Table 1.
A través de los años, this property has been named in different ways, a saber, compatibility,
completeness, and strict monotonicity. The origin of this property dates back to the work
of Hansen and Jaszkiewicz (1998). In that paper, the authors defined the general notion
of an outperformance relation5 R as a set-based binary order relation to compare approx-
imation sets. Based on the general outperformance relation, Hansen and Jaszkiewicz
defined the term compatibility, which is currently known as Pareto compliance, como
follows:
5Based on the general outperformance relation, Hansen and Jaszkiewicz defined four relations where
three of them were based on Pareto dominance and the remaining one was focused on utility functions
(Miettinen, 1999; Pescador-Rojas et al., 2017).
Volumen de cálculo evolutivo 30, Número 3
387
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
Definición 5: Compatibility with an outperformance relation (Hansen and Jaszkiewicz, 1998).
A comparison method R is compatible with an outperformance relation R if for each pair of
approximation sets A and B, such that ARB, R will evaluate A as being better than B.
Definición 6: Weak compatibility with an outperformance relation (Hansen and Jaszkiewicz,
1998). A comparison method R is weakly compatible with an outperformance relation R if for
each pair of approximation sets A and B, such that ARB, R will evaluate A as being not worse
than B.
The comparison method R in the above definitions can be replaced by a quality
indicator. Por eso, assuming that a lower indicator value implies better quality, entonces
ARB ⇒ I (A) < I (B) and ARB ⇒ I (A) ≤ I (B) imply that I is compatible and weakly
compatible, respectively. In case that R is replaced by (cid:2), we obtain Properties 1 and 2.
Following the definitions of Hansen and Jaszkiewicz, Zitzler et al. (2003) denoted
the compatibility as completeness with respect to an arbitrary binary relation R. How-
ever, the main diference was the consideration of an indicator vector (cid:2)I = (I1, . . . , Ik )
instead of a single QI. Moreover, the comparison method R was redefined as a func-
tion C(cid:2)I , E : A × B → {true, false}, where E : Rk × Rk → {true, false} is an interpretation
function. This newly defined comparison method aims to determine by a Boolean value
= E((cid:2)I (A), (cid:2)I (B)) is denoted as
if A is better than B. The comparison method C(cid:2)I , E
R-complete if either for any A, B ∈ (cid:2), it holds ARB ⇒ C(cid:2)I , E (A, B). This definition ex-
tended the compatibility of Hansen and Jaszkiewicz to consider multiple QIs when
comparing approximation sets. We can easily derive the compatibility definition from
the completeness one.
Finally, Zitzler, Knowles, et al. (2008) employed the term strict monotonicity to de-
note a QI for which the following holds: ∀A, B ∈ (cid:2) : A ≺ B ⇒ I (A) < I (B), where ≺
corresponds to the strict elementwise dominance in Table 1. According to Zitzler et al.
(2003), A ≺ B ⇒ A (cid:2) B, thus, for these subset of approximation sets for which ≺ holds,
we can employ the (cid:2)-relation as it is stated in the compatibility and completeness
definitions.
3.2 Combination of Multiple Indicators
Even though quality indicators have been widely employed by the evolutionary multi-
objective optimization community, the exploration of quantitative methods using mul-
tiple QIs has been scarce. In this section, we discuss some previous works in which the
combination of multiple indicators was discussed. Particularly, we focus on the works of
Zitzler et al. (2003), Knowles et al. (2006), Zitzler, Knowles, et al. (2008), and Zitzler et al.
(2010).
When assessing MOEAs, it is a common strategy to employ several QIs to charac-
terize different quality aspects of approximation sets. In this regard, Zitzler et al. (2003)
proposed to analyze such combinations or, more formally, quality indicator vectors
(cid:2)I = (I1, . . . , Ik ) to better interpret the results, based on multiple quality aspects, when
comparing two approximation sets. To this aim, the authors proposed to use compar-
ison methods based on interpretation functions E (defined in the previous section) to
analyze the indicator vectors. Depending on the several possibilities to define E, differ-
ent claims could be produced when comparing two approximation sets. However, no
theoretical properties about (cid:2)I or the interpretations functions were provided.
Knowles et al. (2006) briefly explained that the combination of indicators, ideally
using Pareto-compliant ones, could lead to powerful interpretations in contrast to em-
ploying a single QI. However, no mathematical definition was provided to support this
388
Evolutionary Computation Volume 30, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
e
v
c
o
_
a
_
0
0
3
0
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combined Pareto-Compliant Indicators
claim. In a subsequent work, Zitzler, Knowles, et al. (2008) explained that the combina-
tion of indicators could allow us to overcome the difficult situation of finding an ideal
indicator, that is, a QI being Pareto-compliant, scaling invariant, and cheap to compute.
To this aim, one has to look for a way to combine the resulting indicator values. Hence,
they were the first to suggest the use of a sequence of indicators to evaluate approxima-
tion sets.
Zitzler et al. (2010) mathematically defined a multi-indicator preference relation RS
that sequentially applies preference relations based on a single quality indicator. RS uti-
lizes a sequence S = ((cid:2)I1, (cid:2)I2, . . . , (cid:2)Ik ), where each (cid:2)Ij is a preference relation based on
the indicator Ij that compares the indicator values of two given approximation sets.
The backbone of this proposal is to create a chain of refinements of indicator prefer-
ences to compare two given approximation sets and, in this way, break ties (i.e., when
a QI cannot decide which approximation is better). Based on this idea, the authors pro-
posed an algorithm for the evaluation of A and B similar to the non-dominated sorting
algorithm (Deb et al., 2002). First, an index j is set to 1 to use (cid:2)I1, i.e., the value Ij =1
is calculated for both A and B. If Ij (A) = Ij (B), then j is increased to point to the next
indicator-based preference relation in the sequence if it exists. In case that (cid:2)Ij claims an
approximation set with better quality, the decision is returned. In consequence, the use
of these indicator-based preference relations could increase the sensitivity of an order
relation by solving cases of incomparability. Furthermore, Zitzler et al. proposed that
the first 1 ≤ t < k indicators are weakly Pareto-compliant and the remaining ones are
Pareto-compliant. This way, the Pareto-compliant QIs could be employed to refine the
preferences of the weakly Pareto-compliant indicators.
It is worth noting at this point what is the main focus of these multi-indicator-based
preference relations. Zitzler, Thiele, et al. (2008) and Zitzler et al. (2010) employed these
preference relations to construct the Set Preference Algorithm for Multiobjective Opti-
mization (SPAM) that uses populations as individuals instead of single decision vectors.
The reason to use populations as individuals is related to the utilization of the indicator-
based preference relations that require a population (a set of objective vectors) as an
input parameter. Internally, SPAM manages three populations: the main population P ,
the randomly mutated population P (cid:16)
. P is
compared with P (cid:16) and P (cid:16)(cid:16), using the indicator-based preference relations, to determine
the one that possibly replaces P . In case of using HV in the sequence of indicators, the
high computational cost of HV-based MOEAs such as the S-Metric Selection Evolution-
ary Multiobjective Algorithm (SMS-EMOA) (Beume et al., 2007) is avoided because it is
necessary to calculate only two HV values at each generation if necessary, that is, when
HV needs to refine the preferences. However, SPAM needs more function evaluations
than a usual MOEA due to the utilization of three populations.
, and the heuristically mutated population P (cid:16)(cid:16)
From the above discussion, it is clear that the indicator-based preference rela-
tions show remarkable advantages to derive set-based MOEAs such as SPAM. Fur-
thermore, another utilization of these binary relations could be the comparison of the
Pareto front approximations generated by different MOEAs. This is possible since the
indicator-based preference relations are basically a lexicographic order based on a se-
quence S = ((cid:2)I1, (cid:2)I2 , . . . , (cid:2)Ik ). Thus, they impose a preorder6 on the set of all approxi-
mation sets. In spite of the possibility of using the indicator-based preference relations to
6As long as we are concerned with how approximation sets are ordered, the indicator-based pref-
erence relations are not anti-symmestric since different approximation sets may have equal indicator
values.
Evolutionary Computation Volume 30, Number 3
389
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
e
v
c
o
_
a
_
0
0
3
0
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. G. Falcón-Cardona, M. T. M. Emmerich, and C. A. Coello Coello
compare MOEAs, there are some issues that should be pointed out. The preference
relation on its own, only determines what is the relationship between two given ap-
proximation sets but it does not numerically indicate the difference in quality between
them. Even though if we inspect the indicator values produced by the preference rela-
∈ S.
tion, there is a possibility that some of the comparisons do not employ the same (cid:2)Ij
Hence, we would have performance evaluations in a different scale of measure.
In the next section, we present a generalization of the multi-indicator-based prefer-
ence relations proposed by Zitzler et al. (2010). Our proposal is a framework to combine
multiple QIs in order to define new unary indicators. The resulting combined unary in-
dicator merges the preferences of all the baseline QIs, defining new preferences and
a common numerical field of comparisons to determine the difference in quality be-
tween Pareto front approximations. Another important aspect is that the user can spec-
ify the relative importance of all the baseline QIs in the combination. Furthermore, this
framework allows the construction of new Pareto-compliant indicators by combining as
many weakly Pareto-compliant indicators as needed, but including at least one Pareto-
compliant QI to retain the Pareto compliance property. Due to the use of at least one
Pareto-compliant QI, we refine the preferences of the weakly Pareto-compliant indica-
tors in a similar way as the one proposed by Zitzler et al.
4 New Pareto-Compliant Indicators
In this section, we propose a systematic framework for combining QIs, following the
basic idea introduced by Falcón-Cardona et al. (2019). Additionally, we provide the
mathematical argumentation to ensure that when combining QIs with specific prop-
erties, the resulting combined indicator will be Pareto-compliant. This leads not only
to new types of indicators but also proves to be a way to create new Pareto-compliant
indicators with very different properties than those of the HV in terms of the distribu-
tion of points that they favor, and in terms of the parameters provided by the user. In
the following, we present the mathematical framework for the combination of QIs. Let
A be an approximation set in (cid:2).
Definition 7 (Combination function): A combination function C : Rk → R assigns a real
value to a vector (cid:2)I (A) = (I1(A), I2(A), . . . , Ik (A)), where each Ij (A) is the value of the j th
unary indicator.
Definition 8 (Combined Indicator): Given an indicator vector (cid:2)I (A) = (I1(A), I2(A), . . . ,
Ik (A)) and a combination function C, a combined indicator I (A) is defined as follows: I (A) =
C((cid:2)I (A)).
Regarding Definition 8, a combined indicator I is a QI as well (since I : (cid:2) → R) but
it requires the combination function C to transform an indicator vector (cid:2)I (A) to a real
value. Figure 2 shows how to map Pareto front approximations (in objective space) to
the quality space Q ⊆ Rk, where each axis corresponds to a specific indicator. Then, the
indicator vectors in Q are assigned a real value, using the combination function C. Based
on the above definitions, nothing can be said about the properties of I at this point.
Hence, for getting more important theoretical results, we should say something about
the properties of each Ij , j = 1, . . . , k and the combination function C. We are interested
in analyzing the Pareto compliance of I. Based on Properties 1 and 2, we construct a
special vector of indicators that is necessary for the refinement of the combined indicator
model.
390
Evolutionary Computation Volume 30, Number 3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
e
v
c
o
_
a
_
0
0
3
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Combined Pareto-Compliant Indicators
Figure 2: The objective space contains the approximation sets X , Y, and Z that are
mapped to the quality space using an indicator vector. The points (cid:2)I (X ), (cid:2)I (Y ), and (cid:2)I (Z )
in quality space are then transformed each to a single real value by the combination
function C : R2 → R to generate the real values I (X ), I (Y ), and I (Z ).
Definition 9 (Compliant Indicator Vector): (cid:2)I (A) = (I1(A), I2(A), . . . , Ik (A)) ∈ Q is
called a compliant indicator vector (CIV) if ∀j = 1, . . . , k, Ij is weakly Pareto-compliant and
there exists at least one index t ∈ {1, . . . , k} such that It is Pareto-compliant. Q ⊆ Rk is denoted
as the quality space.
For the following theorem, let us assume, without loss of generality, that the unary
indicators I1, . . . , Ik are to be minimized.
Theorem 1 (Construction of Pareto-compliant combined indicators): Let I1, . . . , Ik be
unary indicators that form a compliant indicator vector (cid:2)I . A combined indicator I, based on the
combination function C((cid:2)I ), is (cid:2)-compliant (Pareto-compliant) if C has the order-preserving
property:
∀(cid:2)u, (cid:2)v ∈ Q, (cid:2)u ≺ (cid:2)v ⇒ C((cid:2)u) < C((cid:2)v).
Proof: Consider two approximation sets A and B such that A (cid:2) B and let (cid:2)I be a
CIV. Then, A (cid:2) B ⇒ (cid:2)I (A) ≺ (cid:2)I (B) because the Pareto-compliant indicators get better
and the weakly Pareto-compliant ones get better or stay equal. Moreover, by defini-
tion (cid:2)I (A) ≺ (cid:2)I (B) ⇒ C((cid:2)I (A)) < C((cid:2)I (B)). Hence, by transitivity of ⇒ and considering
that I (A) = C((cid:2)I (A)) and I (B) = C((cid:2)I (B)), it holds A (cid:2) B ⇒ I (A) < I (B), that is, I is
(cid:3)
Pareto-compliant.
Theorem 1 provides a sufficient condition for constructing Pareto-compliant
combined indicators on the basis of compliant indicator vectors. In other words, a com-
bined indicator preserves the Pareto compliance property because of the use of order-
preserving combination functions.
Remark 1: The condition of Theorem 1 is suffcient but not necessary. For instance, given
(cid:2)I (A) = (I1(A), I2(A), . . . , Ik (A)) where I1 is Pareto-compliant and the Ij , j = 2, . . . , k
are not Pareto-compliant, the “combined” indicator I (A) = C((cid:2)I (A)) = I1(A) is also
Pareto-compliant. Hence, there is a large number of possibilities to construct combined
and compliant indicators.
There exist many combination functions that have the property of Theorem 1. In
this article, we focus on order-preserving utility functions u : Rk → R (Miettinen, 1999;
Pescador-Rojas et al., 2017). A utility function (UF) is a model of the decision maker
Evolutionary Computation Volume 30, Number 3
391
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
e
d
u
e
v
c
o
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
e
v
c
o
_
a
_
0
0
3
0
7
p
d
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. G. Falcón-Cardona, M. T. M. Emmerich, and C. A. Coello Coello
preferences that assigns to each k-dimensional vector a utility value. Thus, a combi-
nation function C can be defined in terms of these functions. Generally, UFs employ a
(cid:9)
k
i=1 wi = 1, wi ≥ 0. However, for the combi-
convex weight vector (cid:2)w ∈ [0, 1]k such that
nation of QIs, we need wi > 0 for all i = 1, . . . , k such that all QIs contribute to the com-
bined indicator value. Based on the above, we denote u(cid:2)w((cid:2)I (A)) as a Pareto-compliant
utility indicator (PCUI) if u is order preserving and (cid:2)I is a CIV.
5
Experimental Results
Throughout this section, we analyze six newly created PCUIs, emphasizing the dis-
tribution of points in different Pareto fronts that they prefer. To define the PCUIs, nosotros
focused our attention on two well-known utility functions that are order-preserving,
a saber, the weighted sum function (WS) and a slightly modified augmented Tcheby-
cheff function (ATCH) (Pescador-Rojas et al., 2017). Dejar (cid:2)I ∈ Rk be an indicator vector
y (cid:2)w ∈ (0, 1)k be a convex weight vector. En el siguiente, we define WS and ATCH as
(cid:9)
k
WS(cid:2)w((cid:2)I ) =
i=1 Ii, respectivamente. Re-
garding ATCH, we modified its original definition by not considering the absolute value
of the term wixi such that the function is order-preserving in the whole Rk and α > 0 es
a user-supplied parameter. Since a PCUI requires all its baseline QIs to be minimized,
we exclusively consider −HV in their definition. The proposed PCUIs, defined in the
following, correspond to Pareto-compliant versions of the indicators R2, IGD+, y (cid:2)+:
i=1 wiIi and ATCH(cid:2)w((cid:2)I ) = maxi=1,…,k {wiIi} + a
(cid:9)
k
• WS(cid:2)w(−HV, R2) and ATCH(cid:2)w(−HV, R2);
• WS(cid:2)w(−HV, IGD
• WS(cid:2)w(−HV, (cid:2)+
) and ATCH(cid:2)w(−HV, (cid:2)+
) and ATCH(cid:2)w(−HV, IGD
).
+
+
);
In the following sections, we are interested in understanding the properties of the
adopted PCUIs as performance assessment functions to compare MOEAs’ performance.
To this aim, we proposed two main experiments. The first experiment aims to com-
pare how the PCUIs and their baseline QIs rank several state-of-the-art MOEAs that
produce Pareto front approximations with different specific distributions of objective
vectores (we employed the Lamé and Mirror superspheres problems proposed by Em-
merich and Deutz (2007)). The comparison is based on measuring the correlation of
preferences between all the adopted PCUIs and QIs, following the methodology of
Liefooghe and Derbel (2016). Por otro lado, the second experiment analyzes the
approximate optimal μ-distributions related to PCUIs to reinforce the preference in-
formación. To obtain the approximate optimal μ-distributions, we set up a steady-state
MOEA similar to the S-Metric Selection Evolutionary Multiobjective Algorithm (SMS-
EMOA) (Beume et al., 2007), that uses the PCUIs as part of its density estimator. El
proposed algorithm, denoted as PCUI-EMOA, is tested on MOPs from the Deb-Thiele-
Laumanns-Zitzler (DTLZ) (Deb et al., 2005), Walking-Fish-Group (WFG) (Huband et al.,
−1 (Ishibuchi, Setoguchi,
2006) test suites, and their minus versions, DTLZ
et al., 2017), respectivamente. It is worth noting that we turned off all the search difficulties
of these problems to avoid issues related to the PCUI-EMOA’s performance.
−1 and WFG
5.1 Weight Vector Effect
Before studying the properties of the newly created PCUIs, we need to punctualize the
relationship between the order-preserving functions and the PCUIs and we also need
392
Volumen de cálculo evolutivo 30, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Combined Pareto-Compliant Indicators
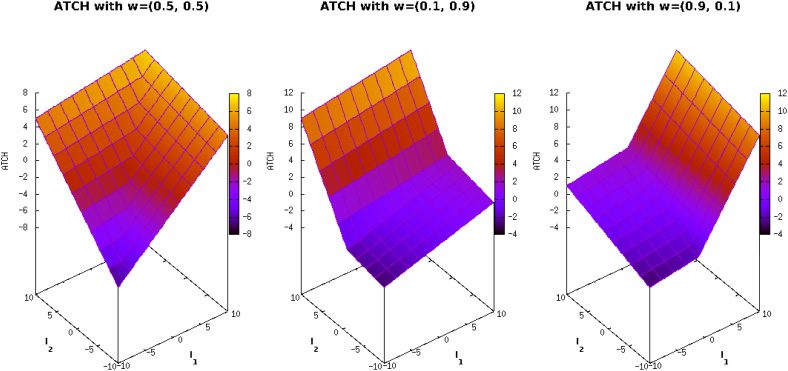
Cifra 3: Landscapes of ATCH function varying the weight vector (cid:2)w = (w1, w2).
to clarify what is the effect of the combination weight vector (cid:2)w that the PCUIs require.
Primero, PCUIs are invariant to the indicator scales because of the order-preserving com-
bination function u. Regardless of the order-preserving function being used, it ensures
that if (cid:2)x ≺ (cid:2)y, then u((cid:2)X) < u((cid:2)y). However, if (cid:2)x and (cid:2)y are mutually nondominated, we
cannot say what will be the relation between u((cid:2)x) and u((cid:2)y) unless we know the def-
inition of u. In consequence, each u expresses specific preferences when dealing with
non-dominated solutions and such preferences depend on the landscape of u (see Fig-
ure 3). On the other hand, PCUIs require a weight vector (cid:2)w = (w1, . . . , wk ) where wi > 0
for all i = 1, . . . , k. Each wj assigns a relative importance to its associated indicator Ij .
Por eso, this can control the impact of each indicator to the final preferences of the PCUI.
Cifra 3 shows the landscape of the ATCH function for three different settings of (cid:2)w.
This image shows that depending on the setting of (cid:2)w, the preferences of the PCUIs
may change, eso es, the total ordering induced by the order-preserving functions. En
specific cases where the preferences of the baseline QIs are in conflict, the weight vector
could lead to exploit the trade-off between them. En otras palabras, when all wi are equal,
the PCUI preferences are the intermediate point between the preferences of its baseline
QIs. For the other two cases in Figure 3, the preferences of the PCUI will be biased to the
indicator having the greatest wi. If we assume that a PCUI is integrated in the selection
mechanism of a MOEA, we could control the final distribution of points by defining (cid:2)w.
5.2 Analysis of Preferences
In this experiment, we are interested in analyzing how similarly the six adopted PCUIs
and their baseline QIs rank different Pareto front approximations corresponding to
the Lamé and Mirror superspheres problems with unimodal difficulty (Emmerich
and Deutz, 2007). The correlation analysis is based on the methodology proposed by
Liefooghe and Derbel (2016) where the main focus is the comparison of rankings of ap-
proximation sets obtained within each QI. The reason to use the Lamé superspheres
is their scalability in the objective space and the controlling of the Pareto front shapes.
Regarding the latter, a parameter γ controls the Pareto front geometry. For Lamé prob-
lemas, γ ∈ (0, 1), γ = 1, and γ > 1 correspond to convex, linear, and concave Pareto front
Volumen de cálculo evolutivo 30, Número 3
393
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
geometries. In case of the Mirror problems, γ ∈ (0, 1) corresponds to a concave geom-
etry while γ > 1 is related to convex shapes. For both Lamé and Mirror problems, nosotros
employed γ = 0.25, 0.50, 0.75, 1.00, 1.50, 2.00, 6.00 para 2, 3, y 4 objective functions.
Following the med-Q sampling methodology of Liefooghe and Derbel where a
black-box MOEA (they employed NSGA-II) produces Pareto front approximations, nosotros
selected MOEAs that exhibit particular distribution characteristics to have a represen-
tative sample of the set (cid:2). For each test instance, 30 independent executions were pro-
duced by each MOEA, where all the algorithms shared the same settings. For all the
objective functions, the size of all the produced approximation sets was 120. To avoid
performance issues of the selected MOEAs, all of them used Pareto optimal solutions
as their initial population.7 Hence, during the execution time, the MOEAs explore these
initial solutions to impose their own preferences. The adopted MOEAs are classified in
five classes as follows:
• Indicator-based MOEAs: SMS-EMOA (Beume et al., 2007), MOMBI2 (Hernán-
-MaOEA (Falcón-Cardona and
dez Gómez and Coello Coello, 2015), IGD
Coello Coello, 2018), y (cid:6)p-MaOEA8.
+
• Pareto-based MOEAs: NSGA-II (Deb et al., 2002) and SPEA2 (Zitzler et al.,
2001).
• Reference set-based MOEAs: NSGA-III (Deb and Jain, 2014).
• Decomposition-based MOEAs: MOEA/D (Zhang and Li, 2007).
• Image analysis-based MOEAs: MOVAP (Hernández Gómez et al., 2016).
Regarding the assessment of the Pareto front approximations generated by the
adopted MOEAs, we used the following settings on the QIs and PCUIs. Establecimos (cid:2)zref =
(1.12, . . . , 1.12) to calculate HV for all test instances. A set of convex weight vec-
tores (constructed by the Simplex-Lattice-Design method; Das and Dennis, 1998) era
employed as the set W for R2. The reference sets for IGD
are constructed by
collecting all the Pareto front approximations and, entonces, obtaining a set of 120 nondom-
inated solutions using a subset selection based on the Riesz s-energy as proposed by
Falcón-Cardona et al. (2020). For all the six adopted PCUIs, the weight vector was set as
(cid:2)w = (0.0001, 0.9999), dónde 0.0001 is the weight associated with the HV and 0.9999 is re-
lated to the weakly Pareto-compliant QI. This setting was employed to mostly preserve
the preferences of the weakly Pareto-compliant QIs while producing Pareto-compliant
results due to the use of the HV as a correction factor.
y (cid:2)+
+
We aim to correlate the rankings of MOEAs within each indicator, eso es, by how
much the PCUIs and QIs rank the MOEAs (es decir., the characteristic Pareto front approxi-
mations) similarmente. For each test instance and QI, the MOEAs are ranked by their mean
indicator value (as proposed by Liefooghe and Derbel (2016), using the med-Q sam-
pling). The ranks of MOEAs are then analyzed for correlation with the remaining QIs
7To generate the initial populations, we executed the algorithms several times to gather in and
archive the best-found solutions. Entonces, each time an algorithm runs, it randomly selects a subset of
the archive as its initial population.
+
8We proposed this algorithm based on the framework of IGD
Coello, 2018) but using the (cid:6)p indicator as the density estimator.
-MaOEA (Falcón-Cardona and Coello
394
Volumen de cálculo evolutivo 30, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Combined Pareto-Compliant Indicators
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
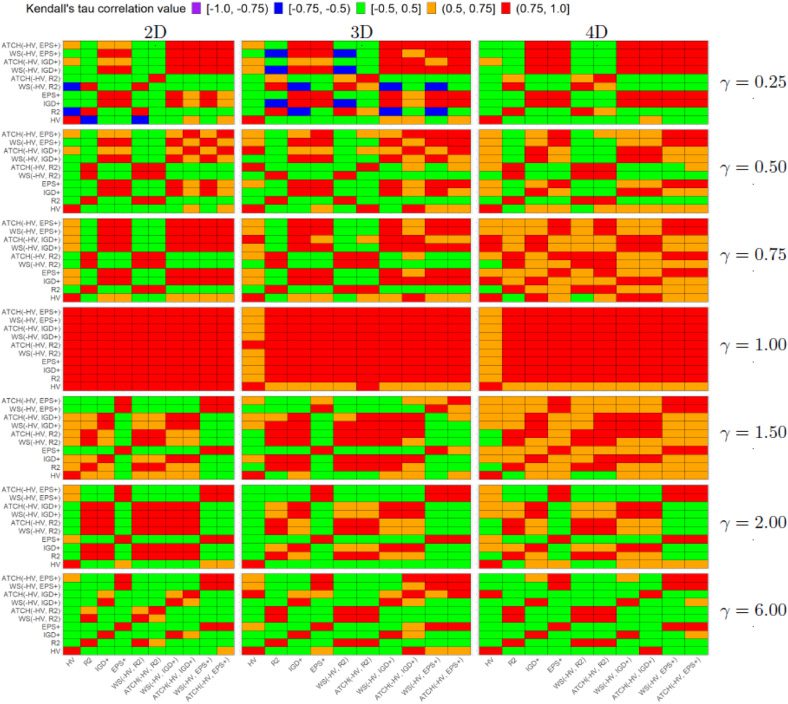
Cifra 4: Heatmap Kendall rank correlation τ for each pair of quality indicators and
each Lamé problem on different dimensions of the objective space.
using the Kendall’s τ correlation coefficient. It is worth emphasizing that Kendall’s τ
quantifies the difference between the proportion of concordant and discordant pairs
among all possible pairwise MOEAs. Since τ ∈ [−1, 1], where τ = −1 means perfect dis-
agreement and τ = 1 means perfect agreement of ranks, we decided to create intervals
of τ values in order to represent them using Heatmaps. Such intervals are the follow-
En g: [−1, −0.75), [−0.75, −0.5), [−0.5, 0.5], (0.5, 0.75], y (0.75, 1]. It is worth noting
that we consider τ ∈ [−0.5, 0.5] as a result of no correlation between two different rank-
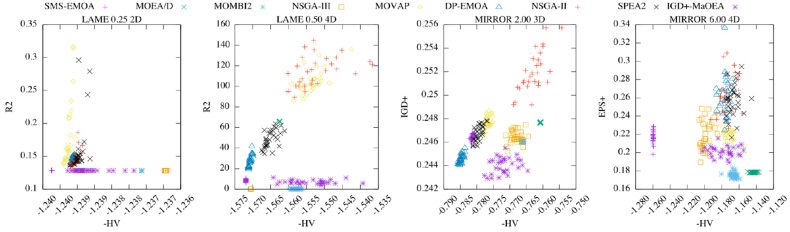
ings. Figures 4 y 5 show the τ values based on the intervals, using heatmaps for all
the adopted Lamé and Mirror test instances, respectivamente.
5.2.1 Correlation between PCUIs and Baseline QIs
Regarding the correlation analysis on Lamé problems in Figure 4, we have the fol-
lowing conclusions. For problems with γ = 0.75, 1.00, 1.50, the PCUIs are consistently
correlated with their baseline QIs (the correlation is stronger with the weakly Pareto-
compliant indicator), regardless of the dimension of the objective space. Regarding γ =
1.00, the Kendall’s τ is in (0.75, 1.0] in almost all comparisons although for three- y
Volumen de cálculo evolutivo 30, Número 3
395
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
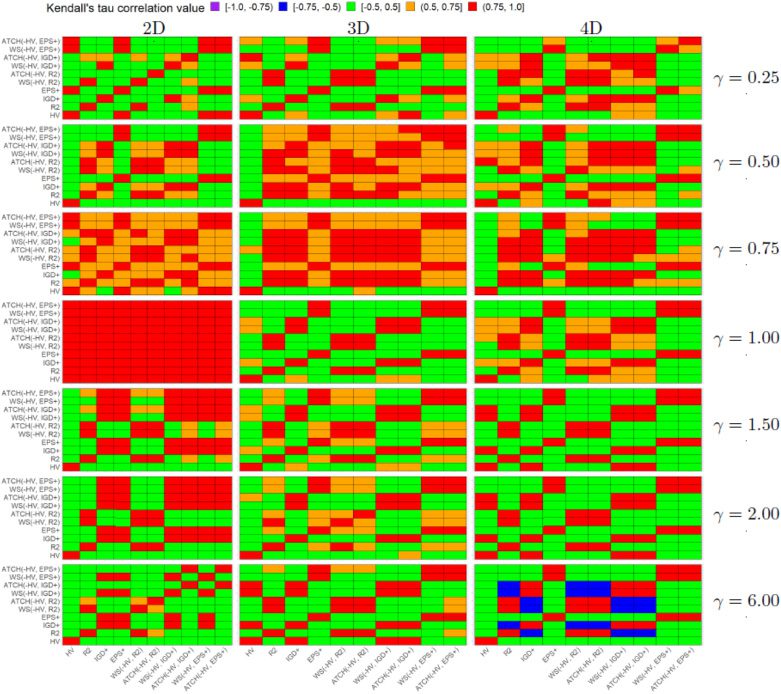
Cifra 5: Heatmap Kendall rank correlation τ for each pair of quality indicators and
each Mirror problem on different dimensions of the objective space.
+
, y (cid:2)+
four-objective MOPs, the correlation with all of the QIs with HV gets weaker (τ ∈
(0.5, 0.75]). This behavior can be explained from the studies where it is stated that in-
have strongly correlated preferences for MOPs
dicators such as HV, R2, IGD
with linear Pareto front shapes (Jiang et al., 2014; Liefooghe and Derbel, 2016; Falcón-
Cardona and Coello, 2019). For both highly convex and highly concave Pareto fronts,
+
,
the correlation is strongly positive with the weakly Pareto-compliant QI (es decir., R2, IGD
y (cid:2)+) y, en general, there is no significant correlation with HV (es decir., τ ∈ [−0.5, 0.5]).
For three- and four-objective MOPs, all the PCUIs present consistently a strong correla-
tion with their baseline weakly Pareto-compliant QIs. A diferencia de, they do not exhibit a
significant correlation with HV in most cases except for γ = 0.75, 1.00, 1.50. From the re-
sults, we have a preference bias towards the weakly Pareto-compliant indicators. Este
= 0.9999.
is an effect of giving more importance to these indicators, eso es, using w2
Por eso, the preferences of the PCUIs are very similar to those of their baseline weakly
Pareto-compliant indicators. En otras palabras, the PCUIs exhibit different preferences to
those of HV but they still are Pareto-compliant regardless of the Pareto front shape and
the dimensionality of the objective space.
396
Volumen de cálculo evolutivo 30, Número 3
Combined Pareto-Compliant Indicators
For the Mirror problems in Figure 5, we have some similar results. Sin embargo, en
these problems which represent inverted Pareto front shapes of the Lamé problems,
the PCUIs tend to be even more correlated to their baseline weakly Pareto-compliant
QIs. The only exception is the two-objective Mirror problem with γ = 1.00 where all the
PCUIs and QIs are positively correlated. This result is consistent with that of the two-
objective Lamé problem, using the same γ value due to the same Pareto front shape.
For all the other test instances, the preferences of the PCUIs are different to those of HV
because in almost all cases, the τ correlation value is in the interval [−0.5, 0.5]. A clear
example of the previous claim is the 4-objective Mirror problem with γ = 6.00 where no
PCUI is correlated with HV while they present a Kendall’s τ ∈ (0.75, 1.0] with respect
of their baseline weakly Pareto-compliant QIs.
En resumen, there are two important points to emphasize. The use of a setting of (cid:2)w
that gives more importance to the weakly Pareto-compliant QI in the combination, will
promote that the PCUIs inherit its preferences, leaving HV just as a correction factor to
make the PCUI Pareto-compliant. This is a remarkable result since we can create new
Pareto-compliant QIs but having preferences mostly different to those of HV. Por eso,
we can increase the number of Pareto-compliant indicators that researchers can employ
for different comparison situations (p.ej., when comparing MOEAs that can produce
evenly distributed solutions). The second point relates to the design of new selection
mechanisms where the distribution of solutions can be adjusted depending on the QIs
to combine. En otras palabras, PCUIs could be employed to manipulate the distribution
properties of MOEAs while maintaining the Pareto compliance property.
5.2.2 Correlation between PCUIs
We analyzed the correlation between the preferences of all PCUIs to ensure that the
combination does produce different indicators. Concerning both the Lamé and Mirror
problemas, the correlation analysis indicates that the PCUIs based on the same weakly
Pareto-compliant QI are strongly correlated between them. En consecuencia, the use of
WS or ATCH is basically producing the same PCUI although they have different land-
scapes. In the next section, we analyze that in some cases, the preferences of indicators
are in conflict which promotes the formation of a Pareto front in the Quality Space.
Por eso, the PCUI could exploit this trade-off to show preferences similar to those of its
baseline QIs or biased to one of them.
Another remarkable conclusion is that the preferences of PCUIs based on a different
weakly Pareto-compliant QI are, en general, independiente. Por eso, each class of PCUIs
are presenting distinct preferences. This is explained by the analysis of the correlation
that are mostly independent as shown in Fig-
between R2-IGD
ures 4 y 5. Además, due to the use of (cid:2)w = (0.0001, 0.9999), each PCUI inherits
the preferences of its weakly Pareto-compliant QI. Por eso, the PCUI will behave in a
similar way to its weakly Pareto-compliant QI but maintaining the Pareto compliance
propiedad.
, and IGD
, R2-(cid:2)+
-(cid:2)+
+
+
Pareto Fronts in Quality Space
5.2.3
In objective space, we find Pareto fronts that represent the solution to a MOP. Estos
Pareto fronts are formed due to the conflict among objective functions. In Quality Space
(ver figura 2), it is also possible to find Pareto fronts when the preferences of an indicator
are in conflict with the preferences of other QI. Based on the correlation analysis previ-
ously explained, we found that when there is independence of preferences between two
QIs or when the preferences are negatively correlated (as in the case of −HV and R2 for
the Lamé problem with γ = 0.25 in 2D), a Pareto front in the Quality Space Q is formed.
Volumen de cálculo evolutivo 30, Número 3
397
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
Cifra 6: From left to right, it is shown the Quality Spaces: −HV vs R2 for Lamé γ = 0.25
for Mirror γ = 2.00 3D, and −HV
2D, −HV vs R2 for Lamé γ = 0.50 4D, −HV vs IGD
vs (cid:2)+
for Mirror γ = 6.00 4D. All cases tend to show a Pareto front in Quality Space. Nosotros
use −HV to show the QIs in each plot for minimization.
+
+
, y (cid:2)+
Cifra 6 shows four examples where it is possible to see the tendency to a Pareto front
in quality space. These plots present the indicator vectors associated with each execu-
tion of the adopted MOEAs in the correlation study for a specific test instance. Desde
to use the PCUIs, it is possible to see that all
we are minimizing HV, R2, IGD
plots introduce convex Pareto front shapes. Por eso, this fact supports the observation
that there is no critical difference when using WS or ATCH for constructing PCUIs. El
rest of the cases of independence on both heatmaps in Figures 4 y 5 present convex
Pareto fronts. In case a PCUI is employed in the selection mechanism of a MOEA, a
compromise between the indicators will be found, resulting in new distributions on the
Pareto fronts that represent the solution to a MOP. En conclusión, this result supports
the fact that PCUIs could be employed to better control the diversity of a MOEA but
maintaining the Pareto compliance.
5.3 Analysis of Optimal μ-Distributions
En esta sección, we investigate the optimal μ-distributions of the selected PCUIs. To this
aim, we considered the framework of SMS-EMOA that uses a density estimator (DE)
based on HV but, in our case, a PCUI is employed in the DE. Algoritmo 1 presenta el
general framework of our proposed PCUI-EMOA whose main loop is in lines 2 a 12. En
each generation, a new solution is created using genetic operators and, entonces, this newly
created solution is added to the population P to create the temporary population Q.
Entonces, en línea 5, a set of ranks R1, . . . , Rt are created using the nondominated sorting
algoritmo (Deb et al., 2002), where Rt has the worst solutions according to the Pareto
dominance relation. If Rt has more than one solution, the individual contributions to
the PCUI are computed to delete the worst-contributing solution in line 11. Finalmente, el
Pareto front approximation is returned when the stopping criterion is fulfilled.
+
-MaOEA. The latter is similar to IGD
We focused our attention on studying the approximate optimal μ-distributions pro-
duced by PCUI-EMOA in comparison with those of four steady-state MOEAs based on
-MaOEA,
the indicators HV, R2, IGD
y (cid:2)+
-MaOEA. Regarding PCUI-EMOA, nosotros
employed the six PCUIs of the previous section. Since all the adopted indicator-based
MOEAs (IB-MOEAs) share the same structure, the parameters settings are the follow-
En g. For all objective functions, the population size is 120. All MOEAs use simulated
binary crossover and polynomial-based mutation as their genetic operators (Deb et al.,
, eso es, SMS-EMOA, R2-EMOA, IGD
, y (cid:2)+
+
+
398
Volumen de cálculo evolutivo 30, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Combined Pareto-Compliant Indicators
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
2002), dónde, for all cases, the crossover probability is set to 0.9, the mutation proba-
bility is 1/n (n is the number of decision variables), and both the crossover and muta-
tion distribution indexes are set to 20. PCUI-EMOA employs the combination vector as
(cid:2)w = (0.5, 0.5) to look for the knee point on the Pareto front in quality space, eso es, a
generate distributions similar to both baseline QIs. We tested the adopted MOEAs on 14
−1 for 2, 3, y 4 objetivo
MOPs from the benchmarks DTLZ, WFG, DTLZ
funciones. We employed the problems DTLZ1, DTLZ2, DTLZ5, DTLZ7, WFG1, WFG2,
WFG3, and their minus versions. It is worth noting that we turned off all the difficulties
of these MOPs to avoid biasing the results such that we can observe the approximate
optimal μ-distributions of the selected MOEAs. We adopted these MOPs since they pos-
sess Pareto fronts with different geometries, a saber, linear, concave, convex, degener-
ate, mezclado, disconnected, correlated with the simplex shape, and not correlated with it
(Ishibuchi, Setoguchi, et al., 2017).
−1, and WFG
The study proposed here is focused on determining the similarity between the ap-
proximate optimal μ-distributions produced by the six PCUI-EMOAs and those of the
selected IB-MOEAs. For each test instance, the MOEAs were executed N = 30 indepen-
dent times. De este modo, each one produced N approximation sets for each MOP. We investi-
gate the similarity between two sets of approximation sets produced by two MOEAs,
using a similarity measure based on the Hausdorff distance that we propose in the fol-
mugiendo:
Definición 10 (One-sided Hausdorff-based similarity measure): Given two sets A =
{A1, . . . , UN } and B = {B1, . . . , BN }, each one consisting of N Pareto front approximations,
the one-sided Hausdorff-based similarity measure S is given as follows:
S(A, B) = 1
norte
norte(cid:7)
yo=1
median(Ai, B),
Volumen de cálculo evolutivo 30, Número 3
399
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
where median(Ai, B) computes all the Hausdorff–Pompeiu distances from Ai to every element
in B and returns the median value. The median is used here to prevent outliers.
S(A, B) calculates the similarity of A to (mayoría) elements in B. It is worth noting that
S is a similarity measure, not a metric (distance function), as it is not symmetrical. Él
attains small values if every set in A is similar to at least half of the sets in B. It can,
sin embargo, be the case that B contains a number of sets that by no means resemble sets
in A. In that sense it is not symmetrical. To make it symmetrical, one would have to
compute also S(B, A) and take the maximum of these two values, as it is done in the
Hausdorff–Pompeiu Distance (on the level of points sets). En consecuencia, we propose
the two-sided Hausdorff-based similarity measure which is symmetric.
Definición 11 (Two-sided Hausdorff-based similarity measure): Given two sets A =
{A1, . . . , UN } and B = {B1, . . . , BN }, each one consisting of N Pareto front approximations,
the two-sided Hausdorff-based similarity measure H is given as follows:
h(A, B) = max(S(A, B), S(B, A)).
In the case that we are given three sets of approximation sets A, B, and C and we
would like to know if A is similar to B, to C, to both, or to none of them, a classification
function is required. Such classifier is given as follows.
Definición 12 (Classifier): Given three sets of approximation sets A, B, and C and a threshold
(cid:2) > 0, the classifier function is given as follows:
C(cid:2) (h(A, B), h(A, C)) =
⎧
⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
−1, h(A, B) ≤ (cid:2) ∧ H(A, C) > (cid:2)
h(A, B) ≤ (cid:2) ∧ H(A, C) ≤ (cid:2)
0,
h(A, B) > (cid:2) ∧ H(A, C) > (cid:2)
1,
h(A, C) ≤ (cid:2) ∧ H(A, B) > (cid:2)
2,
where −1 means that A is exclusively similar to B; 0 means that A is similar to both B and C;
1 means that A is not similar to B nor C; y, 2 means that A is exclusively similar to C.
√
Based on the classification function, we analyzed the similarities between the ap-
proximation sets produced by the PCUI-EMOAs and their corresponding IB-MOEAs
that use the baseline indicators for the construction of the PCUI. Mesa 2 shows the re-
sults for all the considered test instances using (cid:2) =
m/10. Since all PCUI-EMOAs use
(cid:2)w = (0.5, 0.5) as the combination weight vector for the order-preserving utility func-
ciones, our hypothesis is that the Pareto front approximations should be similar to both
IB-MOEAs that employ the baseline indicators. This hypothesis is true for several cases
related to the DTLZ and DTLZ−1 problems. Sin embargo, for most of the WFG and
−1 problems, the PCUI-EMOA tends to produce approximation sets with particular
WFG
distributions that are not similar to the baseline IB-MOEAs. This fact could be explained
by the independence of preferences between HV and the weakly Pareto-compliant in-
−1, es
dicators on these MOPs. Considering the linear problems DTLZ1 and DTLZ1
clear that in most cases the PCUI-EMOAs produce approximation sets similar to the
IB-MOEAs using their baseline indicators. This result is explained by the correlation
are strongly
analysis of Section 5.2 where in almost all cases HV, R2, IGD
correlacionado. The most important observation is related to the PCUI-EMOAs based on
WS(cid:2)w(−HV, R2) and ATCH(cid:2)w(−HV, R2). Por un lado, SMS-EMOA produces uni-
formly distributed solutions in convex and linear Pareto fronts and there is a bias to-
wards the knee and boundaries of concave Pareto fronts. Además, SMS-EMOA
presents good results in degenerate problems such as DTLZ5 and WFG3. En el otro
, y (cid:2)+
+
400
Volumen de cálculo evolutivo 30, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Combined Pareto-Compliant Indicators
Mesa 2: Distribution similarities between each PCUI-EMOA and the IB-MOEAs based
. For each test instance, it is shown if the distri-
on the indicators HV, R2, IGD
bution of the PCUI-EMOA is similar to one or other baseline indicator, to both or none
de ellos.
, y (cid:2)+
+
)
2
R
,
V
h
−
(
(cid:2)w
h
C
t
A
Ambos
Ambos
Ambos
Ambos
Ambos
HV
Ambos
R2
R2
)
2
R
,
V
h
−
(
(cid:2)w
S
W.
Ambos
Ambos
Ambos
Ambos
Ambos
HV
Ambos
R2
R2
)
+
D
GRAMO
I
,
V
h
−
(
(cid:2)w
h
C
t
A
Ambos
Ambos
Ambos
Ambos
Ambos
Ambos
)
+
D
GRAMO
I
,
V
h
−
(
(cid:2)w
S
W.
Ambos
Ambos
Ambos
Ambos
Ambos
Ambos
)
+
(cid:2)
,
V
h
−
(
(cid:2)w
h
C
t
A
Ambos
Ambos
Ambos
Ambos
Ambos
None
)
+
(cid:2)
,
V
h
−
(
(cid:2)w
S
W.
Ambos
Ambos
Ambos
Ambos
Ambos
HV
Ambos
Ambos
Ambos
Ambos
None None None None
Ambos
Ambos
Ambos
Ambos
HV
Ambos
Ambos
None None None None
HV
None None None None None None
HV
HV
Ambos
Ambos
Ambos
Ambos
HV
Ambos
Ambos
HV
Ambos
Ambos
IGD+
Ambos
Ambos
IGD+
Ambos
Ambos
(cid:2)+
Ambos
Ambos
(cid:2)+
Ambos
Ambos
HV
IGD+ None None None
HV
None None None None None None
HV
HV
Ambos
Ambos
Ambos
Ambos
Ambos
Ambos
IGD+ None None None
None None
None None None None None None
Ambos
Ambos
Ambos
R2
Ambos
Ambos
Ambos
R2
None None None
Ambos
Ambos
(cid:2)+
Ambos
Ambos
(cid:2)+
Ambos
Ambos
None
None None None None None None
None None None None None None
None
None None
IGD+
IGD+
(cid:2)+
R2
R2
None None None None
None None None None None None
None None None None None None
None None None None None None
None None None None None None
None None None None None None
MOP
Dim.
DTLZ1
DTLZ1−1
DTLZ2
DTLZ2−1
DTLZ5
DTLZ5−1
DTLZ7
DTLZ7−1
WFG1
WFG1−1
WFG2
2
3
4
2
3
4
2
3
4
2
3
4
2
3
4
2
3
4
2
3
4
2
3
4
2
3
4
2
3
4
2
3
4
Volumen de cálculo evolutivo 30, Número 3
401
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
Mesa 2: Continuado.
)
2
R
,
V
h
−
(
(cid:2)w
h
C
t
A
)
+
D
GRAMO
I
,
V
h
−
(
(cid:2)w
S
W.
)
2
R
,
V
h
−
(
(cid:2)w
S
W.
)
+
D
GRAMO
I
,
V
h
−
(
(cid:2)w
h
C
t
A
)
+
(cid:2)
,
V
h
−
(
(cid:2)w
h
C
t
A
)
+
(cid:2)
,
V
h
−
(
(cid:2)w
S
W.
None None None None None None
None None None None
None None None None None None
R2
R2
None None None None None None
Ambos
Ambos
Ambos
(cid:2)+
None None
Ambos
IGD+
Ambos
IGD+
Ambos
(cid:2)+
R2
Ambos
HV
R2
Ambos
HV
None None None None
Ambos
Ambos
HV
Ambos
Ambos
Ambos
Ambos
HV
MOP
Dim.
WFG2−1
WFG3
WFG3−1
2
3
4
2
3
4
2
3
4
mano, R2-EMOA (Brockhoff et al., 2015) does not produce uniformly distributed solu-
tions in convex Pareto fronts, but it does in linear and concave ones. Regarding degen-
erate MOPs, R2-EMOA does not produce good results since its weight vectors do not
completely intersect the Pareto front shape. Por eso, SMS-EMOA and R2-EMOA have
specific strengths and weaknesses depending on the MOP being tackled. We refer to
strengths and weaknesses of an IB-MOEA (y, more specifically, to the underlying QI)
as its capacity to generate (or failure to generate) Pareto front approximations with good
diversity. Por ejemplo, SMS-EMOA does not produce a uniform distribution in DTLZ2
(which has a concave Pareto front) because of the inner preferences of the HV while
R2-EMOA can produce uniformly distributed solutions in this problem.
Regarding DTLZ2 having three and four objective functions and concave Pareto
fronts, it is possible to see that the distribution of the PCUI-EMOAs based on
WS(cid:2)w(−HV, R2) and ATCH(cid:2)w(−HV, R2) are similar to the preferences of R2, eso es, R2-
−1 for the same objective functions,
EMOA. When we analyze the minus version DTLZ2
−1 3D
the distributions are similar to those of SMS-EMOA. This also happens for DTLZ5
which is inverted convex where the distributions are similar to those of SMS-EMOA as
Bueno. Por eso, we have empirical evidence on the compensation of weaknesses of one in-
dicator with the strengths of the other baseline indicator when employing PCUI-EMOA.
Cifra 7 shows some examples of this remarkable compensation.
5.4 Computational Complexity
Teorema 1 proposes the combination of as many weakly Pareto-compliant QIs as
required with at least one Pareto-compliant indicator. Actualmente, the only Pareto-
compliant QI available is the hypervolume indicator whose computational cost in-
creases super-polynomially with the number of objective functions (Bringmann and
Friedrich, 2009, 2010). In terms of computational cost, it is clear that the runtime com-
+
, which implies that a PCUI and,
plexity of HV dominates those of R2, IGD
, y (cid:2)+
402
Volumen de cálculo evolutivo 30, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Combined Pareto-Compliant Indicators
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 7: Pareto fronts that show the compensation of weaknesses of one indicator with
the strengths of other when coupled to PCUI-EMOA.
en general, all the QIs constructed by Theorem 1 inherit the cost of HV. Por eso, uno
may argue that this a clear disadvantage of the proposed method. Sin embargo, nosotros necesitamos
to emphasize that even though we showed that a PCUI can be utilized to guide the
evolutionary process of a MOEA (En realidad, we used PCUI-EMOA to study the approxi-
mate optimal μ-distributions of PCUIs), the primary focus of PCUIs is to increase the
number of available Pareto-compliant indicators for performance assessment. en contra-
secuencia, when using a PCUI to compare MOEAs, one may use fast HV calculation
methods such as the Walking-Fish-Group (WFG) algoritmo (While et al., 2012) that sig-
nificantly reduces the computational time to get exact HV values. Although following
Teorema 1 allows the construction of new Pareto-compliant QIs, this does not overcome
the runtime complexity of the HV, and it does not theoretically increase the overall com-
putational cost.9 Additionally, these combined indicators provide different preferences
to those of the HV and they are controlled by the user when setting the weight vec-
colina (cid:2)w. Por eso, we argue that we obtain more advantages than drawbacks by using our
proposed framework.
En este punto, it is worth comparing the PCUIs and the multi-indicator-based pref-
erence relations proposed by Zitzler et al. (2010) in terms of computational cost. Due to
the sequential application of the indicator-based preference relations ((cid:2)Ij ), it is likely
that a multi-indicator-based preference relation avoids the computational cost of cal-
culating HV whenever a cheaper QI could solve the comparison. A diferencia de, PCUIs
do always require the calculation of HV in furtherance of obtaining extra flexibility to
9Even in practice, the calculation of as many weakly Pareto-compliant QIs as required does not ag-
gregate a considerable overhead when computing a PCUI value.
Volumen de cálculo evolutivo 30, Número 3
403
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
control how the preferences are combined. Además, from the discussion throughout
this article, it is possible to visualize two distinct application paths. Por un lado,
PCUIs are useful for performance assessment of MOEAs, considering the Pareto com-
pliance property and offering different preferences to those of HV. Por otro lado,
the multi-indicator-based preference relations are a promising direction to construct
set-based MOEAs as in the case of SPAM (Zitzler et al., 2010). En consecuencia, cada
approach is specialized in different areas of evolutionary multiobjective optimization.
Sin embargo, it is worth noting that PCUIs and, en general, our proposed framework for
the combination of multiple QIs represent a generalization of the multi-indicator-based
preferences relations proposed by Zitzler et al. (2010).
6 Conclusions and Future Work
+
, y (cid:2)+
In this article, we proposed to construct new Pareto-compliant indicators by combin-
ing existing QIs, under specific conditions. In order to ensure the Pareto compliance
propiedad, it is mandatory to combine at least one Pareto-compliant indicator (como
the hypervolume indicator) with as many weakly Pareto-compliant QIs as required, por
using an order-preserving function. Following this framework, we proposed six new
, usando
Pareto-compliant QIs based on the combination of HV with R2, IGD
the weighted sum and augmented Tchebycheff utility functions as order-preserving
combination functions. We studied the properties of these six PCUIs from a prefer-
ences and approximate optimal μ-distributions perspective. Our experimental results
showed that the proposed PCUIs do exhibit different preferences to those of the HV
which implies that they can be used as an alternative to the HV to assess performance
of MOEAs while ensuring the Pareto compliance property. These results were sup-
ported by an analysis of approximate optimal μ-distributions. Además, when using
a steady-state MOEA based on a PCUI, we observed that the non-uniform distributions
produced by one of the baseline QIs of the PCUI could be compensated by the uni-
form distribution strengths of another baseline QI. It is worth emphasizing that the
main focus of PCUIs is the performance assessment of MOEAs. In this direction, nosotros
discussed that even though a PCUI requires the calculation of the HV, the main ad-
vantage of PCUIs lies on their different preferences with respect to those of the HV.
Además, PCUIs have the same theoretical runtime complexity as the HV while al-
lowing to draw conclusions supported by the Pareto compliance property. As part of
our future work, we aim to provide a mechanism that adapts the combination vector
depending on the geometrical features of the MOP. Además, we aim to theoretically
analyze the properties of PCUIs in order to define in which cases they can be used to
provide better information. Finalmente, an analysis considering MOPs with more than four
objective functions is also a task that we would like to undertake as part of our future
trabajar.
Expresiones de gratitud
The first author acknowledges support from CINVESTAV-IPN to pursue graduate stud-
ies in computer science and the 2018 IEEE CIS Graduate Student Research Grant. El
third author gratefully acknowledges support from CONACyT grant no. 2016-01-1920
(Investigación en Fronteras de la Ciencia 2016) and from a SEP-Cinvestav grant (pro-
posal no. 4). He was also partially supported by the Basque Government through the
BERC 2022–2025 program and by Spanish Ministry of Economy and Competitiveness
MINECO: BCAM Severo Ochoa excellence accreditation SEV-2017-0718.
404
Volumen de cálculo evolutivo 30, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Combined Pareto-Compliant Indicators
Referencias
Auger, A., Bader, J., Brockhoff, D., and Zitzler, mi. (2009). Theory of the hypervolume indicator:
Optimal {μ}-distributions and the choice of the reference point. In Proceedings of the Tenth
ACM SIGEVO Workshop on Foundations of Genetic Algorithms, páginas. 87–102.
Beume, NORTE., Naujoks, B., and Emmerich, METRO. (2007). SMS-EMOA: Multiobjective selection based
on dominated hypervolume. European Journal of Operational Research, 181(3):1653–1669.
10.1016/j.ejor.2006.08.008
Bezerra, l. C. T., López-Ibáñez, METRO., and Stützle, t. (2017). An empirical assessment of the proper-
ties of inverted generational distance on multi- and many-objective optimization. En curso-
ings of the 9th International Conference on Evolutionary Multi-Criterion Optimization, páginas. 31–45.
Bringmann, K., and Friedrich, t. (2009). Approximating the least hypervolume contributor: notario público-
hard in general, but fast in practice. In Fifth International Conference on Evolutionary Multi-
Criterion Optimization, páginas. 6–20. Lecture Notes in Computer Science, volumen. 5467. 10.1007/
978-3-642-01020-0_6
Bringmann, K., and Friedrich, t. (2010). Approximating the volume of unions and intersections of
high-dimensional geometric objects. Computational Geometry—Theory and Applications, 43(6–
7):601–610. 10.1016/j.comgeo.2010.03.004
Bringmann, K., Friedrich, T., Neumann, F., and Wagner, METRO. (2011). Approximation-guided evo-
lutionary multi-objective optimization. In Proceedings of the 21st International Joint Conference
sobre Inteligencia Artificial, páginas. 1198–1203.
Brockhoff, D., Wagner, T., and Trautmann, h. (2012). On the properties of the R2 indicator. En
Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), páginas. 465–472.
Brockhoff, D., Wagner, T., and Trautmann, h. (2015). R2 indicator-based multiobjective search.
Computación evolutiva, 23(3):369–395. 10.1162/EVCO_a_00135, PubMed: 24983593
Coello Coello, C. A., and Cruz Cortés, norte. (2005). Solving multiobjective optimization problems
using an artificial immune system. Genetic Programming and Evolvable Machines, 6(2):163–190.
10.1007/s10710-005-6164-x
Coello Coello, C. A., Lamont, GRAMO. B., and Van Veldhuizen, D. A. (2007). Evolutionary algorithms for
solving multi-objective problems. 2y ed.. Nueva York: Saltador.
El, I., and Dennis, j. mi. (1998). Normal-boundary intersection: A new method for generating the
Pareto surface in nonlinear multicriteria optimization problems. SIAM Journal on Optimiza-
ción, 8(3):631–657. 10.1137/S1052623496307510
Deb, K., and Jain, h. (2014). An evolutionary many-objective optimization algorithm us-
ing reference-point-based-nondominated sorting approach, part I: Solving problems with
box constraints. IEEE Transactions on Evolutionary Computation, 18(4):577–601. 10.1109/
TEVC.2013.2281535
Deb, K., Pratap, A., agarwal, S., and Meyarivan, t. (2002). A fast and elitist multiobjective genetic
algoritmo: NSGA–II. IEEE Transactions on Evolutionary Computation, 6(2):182–197. 10.1109/
4235.996017
Deb, K., Thiele, l., Laumanns, METRO., and Zitzler, mi. (2005). Scalable test problems for evolution-
ary multiobjective optimization. In A. Abrahán, l. jainista, y r. Goldberg (Editores.), Evolución-
ary multiobjective optimization. Theoretical advances and applications, páginas. 105–145. Nueva York:
Saltador.
Emmerich, METRO. T., and Deutz, A. h. (2007). Test problems based on lamé superspheres. In Fourth In-
ternational Conference on Evolutionary Multi-Criterion Optimization, páginas. 922–936. Lecture Notes
in Computer Science, volumen. 4403. 10.1007/978-3-540-70928-2_68
Volumen de cálculo evolutivo 30, Número 3
405
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
Emmerich, METRO. T., Deutz, A. h., and Yevseyeva, I. (2014). On reference point free weighted hy-
pervolume indicators based on desirability functions and their probabilistic interpretation.
Procedia Technology, 16:532–541. CENTERIS 2014 – Conference on ENTERprise Information
Systems/ProjMAN 2014 – International Conference on Project MANagement/HCIST 2014 –
International Conference on Health and Social Care Information Systems and Technologies.
10.1016/j.protcy.2014.10.001
Falcón-Cardona, j. GRAMO., and Coello, C. A. C. (2019). Convergence and diversity analysis of
indicator-based multi-objective evolutionary algorithms. In Proceedings of the Genetic and Evo-
lutionary Computation Conference (GECCO), páginas. 524–531.
Falcón-Cardona, j. GRAMO., and Coello Coello, C. A. (2018). Towards a more general many-objective
evolutionary optimizer. En 2018 Parallel Problem Solving from Nature.
Falcón-Cardona, j. GRAMO., and Coello Coello, C. A. (2020). Indicator-based multi-objective evolution-
ary algorithms: A comprehensive survey. ACM Computing Surveys, 53(2):1–35.
Falcón-Cardona, j. GRAMO., Emmerich, METRO. t. METRO., and Coello Coello, C. A. (2019). On the construction of
Pareto-compliant quality indicators. In Proceedings of the Genetic and Evolutionary Computation
Conference Companion (GECCO), páginas. 2024–2027.
Falcón-Cardona, j. GRAMO., Ishibuchi, h., and Coello Coello, C. A. (2020). Riesz s-energy-based ref-
erence sets for multi-objective optimization. In IEEE Congress on Evolutionary Computation,
páginas. 1–8.
Friedrich, T., Bringmann, K., Voß, T., and Igel, C. (2011). The logarithmic hypervolume indicator.
En Actas de la 2011 ACM/SIGEVO Foundations of Genetic Algorithms, páginas. 81–92.
Guerreiro, A. PAG., and Fonseca, C. METRO. (2020). An analysis of the hypervolume Sharpe-ratio indicator.
European Journal of Operational Research, 283(2):614–629. 10.1016/j.ejor.2019.11.023
Hansen, METRO. PAG., and Jaszkiewicz, A. (1998). Evaluating the quality of approximations to the non-
dominated set. Technical Report IMM-REP-1998-7. Technical University of Denmark.
Hernández Gómez, r., and Coello Coello, C. A. (2015). Improved metaheuristic based on the
R2 indicator for many-objective optimization. In Proceedings of the Genetic and Evolutionary
Computation Conference (GECCO), páginas. 679–686.
Hernández Gómez, r., Coello Coello, C. A., and Alba Torres, mi. (2016). A multi-objective evolu-
tionary algorithm based on parallel coordinates. In Proceedings of the Genetic and Evolutionary
Computation Conference (GECCO), páginas. 565–572.
Horn, J., Nafpliotis, NORTE., and Goldberg, D. mi. (1994). A niched Pareto genetic algorithm for mul-
tiobjective optimization. In Proceedings of the First IEEE Conference on Evolutionary Com-
putation, IEEE World Congress on Computational Intelligence, volumen. 1, páginas. 82–87. 10.1109/
ICEC.1994.350037
Huband, S., Hingston, PAG., Barone, l., and While, l. (2006). A review of multiobjective test problems
and a scalable test problem toolkit. IEEE Transactions on Evolutionary Computation, 10(5):477–
506. 10.1109/TEVC.2005.861417
Ishibuchi, h., Imada, r., Setoguchi, y., and Nojima, Y. (2017). Reference point specification in
hypervolume calculation for fair comparison and efficient search. In Proceedings of the Genetic
and Evolutionary Computation Conference (GECCO), páginas. 585–592.
Ishibuchi, h., Masuda, h., Tanigaki, y., and Nojima, Y. (2014). Difficulties in specifying reference
points to calculate the inverted generational distance for many-objective optimization prob-
lemas. En 2014 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making,
páginas. 170–177.
Ishibuchi, h., Masuda, h., Tanigaki, y., and Nojima, Y. (2015). Modified distance calcula-
tion in generational distance and inverted generational distance. In Proceedings of the 8th
406
Volumen de cálculo evolutivo 30, Número 3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Combined Pareto-Compliant Indicators
International Conference on Evolutionary Multi-Criterion Optimization, páginas. 110–125. Lecture
Notes in Computer Science, volumen. 9019. 10.1007/978-3-319-15892-1_8
Ishibuchi, h., Setoguchi, y., Masuda, h., and Nojima, Y. (2017). Performance of decomposition-
based many-objective algorithms strongly depends on Pareto front shapes. IEEE Transactions
on Evolutionary Computation, 21(2):169–190. 10.1109/TEVC.2016.2587749
Jiang, S., Ong, Y.-S., zhang, J., and Feng, l. (2014). Consistencies and contradictions of perfor-
mance metrics in multiobjective optimization. IEEE Transactions on Cybernetics, 44(12):2391–
2404. 10.1109/TCYB.2014.2307319, PubMed: 25415945
Knowles, J., Thiele, l., and Zitzler, mi. (2006). A tutorial on the performance assessment of stochas-
tic multiobjective optimizers. Informe 214, Computer Engineering and Networks Laboratory
(TIK), ETH Zurich, Suiza. Revised version.
li, F., cheng, r., Liu, J., and Jin, Y. (2018). A two-stage R2 indicator based evolutionary al-
gorithm for many-objective optimization. Computación blanda aplicada, 67:245–260. 10.1016/
j.asoc.2018.02.048
li, METRO., and Yao, X. (2019). Quality evaluation of solution sets in multiobjective optimisation: A
survey. ACM Computing Surveys, 52(2):26:1–26:38.
Liefooghe, A., and Derbel, B. (2016). A correlation analysis of set quality indicator values in mul-
tiobjective optimization. In Proceedings of the Genetic and Evolutionary Computation Conference
(GECCO), páginas. 581–588.
Miettinen, k. (1999). Nonlinear multiobjective optimization. Bostón: Kluwer Academic Publishers.
Pescador-Rojas, METRO., Hernández Gómez, r., montero, MI., Rojas-Morales, NORTE., Riff, M.-C., and Coello
Coello, C. A. (2017). An overview of weighted and unconstrained scalarizing functions. En
Proceedings of the 9th International Conference on Evolutionary Multi-Criterion Optimization, páginas.
499–513. Lecture Notes in Computer Science, volumen. 10173. 10.1007/978-3-319-54157-0_34
shang, K., Ishibuchi, h., Él, l., and Pang, l. METRO. (2020). A survey on the hypervolume indicator
in evolutionary multi-objective optimization. IEEE Transactions on Evolutionary Computation,
páginas. 1–20.
shang, K., Ishibuchi, h., Nan, y., and Chen, W.. (2020). Transformation-based hypervolume indi-
cator: A framework for designing hypervolume variants. En 2020 IEEE Symposium Series on
Computational Intelligence, páginas. 157–164.
tian, y., cheng, r., zhang, X., cheng, F., and Jin, Y. (2018). An indicator-based multiobjective evo-
lutionary algorithm with reference point adaptation for better versatility. IEEE Transactions
on Evolutionary Computation, 22(4):609–622. 10.1109/TEVC.2017.2749619
Veldhuizen, D. A. V. (1999). Multiobjective evolutionary algorithms: Classifications, analiza, y
new innovations. PhD thesis, Department of Electrical and Computer Engineering. Gradu-
ate School of Engineering. Air Force Institute of Technology, Wright-Patterson AFB, Ohio.
Mientras, l., Bradstreet, l., and Barone, l. (2012). A fast way of calculating exact hypervolumes.
IEEE Transactions on Evolutionary Computation, 16(1):86–95. 10.1109/TEVC.2010.2077298
Yuan, y., Xu, h., Wang, B., and Yao, X. (2016). A new dominance relation-based evolutionary
algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation,
20(1):16–37. 10.1109/TEVC.2015.2420112
zhang, P., and Li, h. (2007). MOEA/D: A multiobjective evolutionary algorithm based on
decomposition. IEEE Transactions on Evolutionary Computation, 11(6):712–731. 10.1109/
TEVC.2007.892759
Zitzler, mi. (1999). Evolutionary algorithms for multiobjective optimization: Methods and appli-
cations. PhD thesis, Swiss Federal Institute of Technology (ETH), Zurich, Suiza.
Volumen de cálculo evolutivo 30, Número 3
407
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
/
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
j. GRAMO. Falcón-Cardona, METRO. t. METRO. Emmerich, and C. A. Coello Coello
Zitzler, MI., Brockhoff, D., and Thiele, l. (2007). The hypervolume indicator revisited: On the de-
sign of Pareto-compliant indicator via weighted integration. In Proceedings of the 4th Interna-
tional Conference on Evolutionary Multi-Criterion Optimization, páginas. 862–876. Lecture Notes in
Computer Science, volumen. 4403. 10.1007/978-3-540-70928-2_64
Zitzler, MI., Deb, K., and Thiele, l. (2000). Comparison of multiobjective evolutionary algo-
rithms: Resultados empíricos. Computación evolutiva, 8(2):173–195. 10.1162/106365600568202,
PubMed: 10843520
Zitzler, MI., Knowles, J., and Thiele, l. (2008). Quality assessment of Pareto set approximations. En
j. Branke, k. Deb, k. Miettinen, y r. Slowinski (Editores.), Multiobjective optimization. Interac-
tive and evolutionary approaches, páginas. 373–404. Lecture Notes in Computer Science, volumen. 5252.
Berlina: Saltador. 10.1007/978-3-540-88908-3_14
Zitzler, MI., Laumanns, METRO., and Thiele, l. (2001). SPEA2: Improving the strength Pareto evolution-
ary algorithm. In EUROGEN 2001. Evolutionary Methods for Design, Optimization and Control
with Applications to Industrial Problems, páginas. 95–100.
Zitzler, MI., Thiele, l., and Bader, j. (2008). SPAM: Set Preference Algorithm for Multiobjective Op-
timization. In Parallel Problem Solving from Nature, páginas. 847–858. Lecture Notes in Computer
Ciencia, volumen. 5199.
Zitzler, MI., Thiele, l., and Bader, j. (2010). On set-based multiobjective optimization. IEEE Trans-
actions on Evolutionary Computation, 14(1):58–79. 10.1109/TEVC.2009.2016569
Zitzler, MI., Thiele, l., Laumanns, METRO., Fonseca, C. METRO., and da Fonseca, V. GRAMO. (2003). Actuación
assessment of multiobjective optimizers: An analysis and review. IEEE Transactions on Evo-
lutionary Computation, 7(2):117–132. 10.1109/TEVC.2003.810758
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
mi
d
tu
mi
v
C
oh
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
3
0
3
3
8
1
2
0
4
0
8
9
0
mi
v
C
oh
_
a
_
0
0
3
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
408
Volumen de cálculo evolutivo 30, Número 3