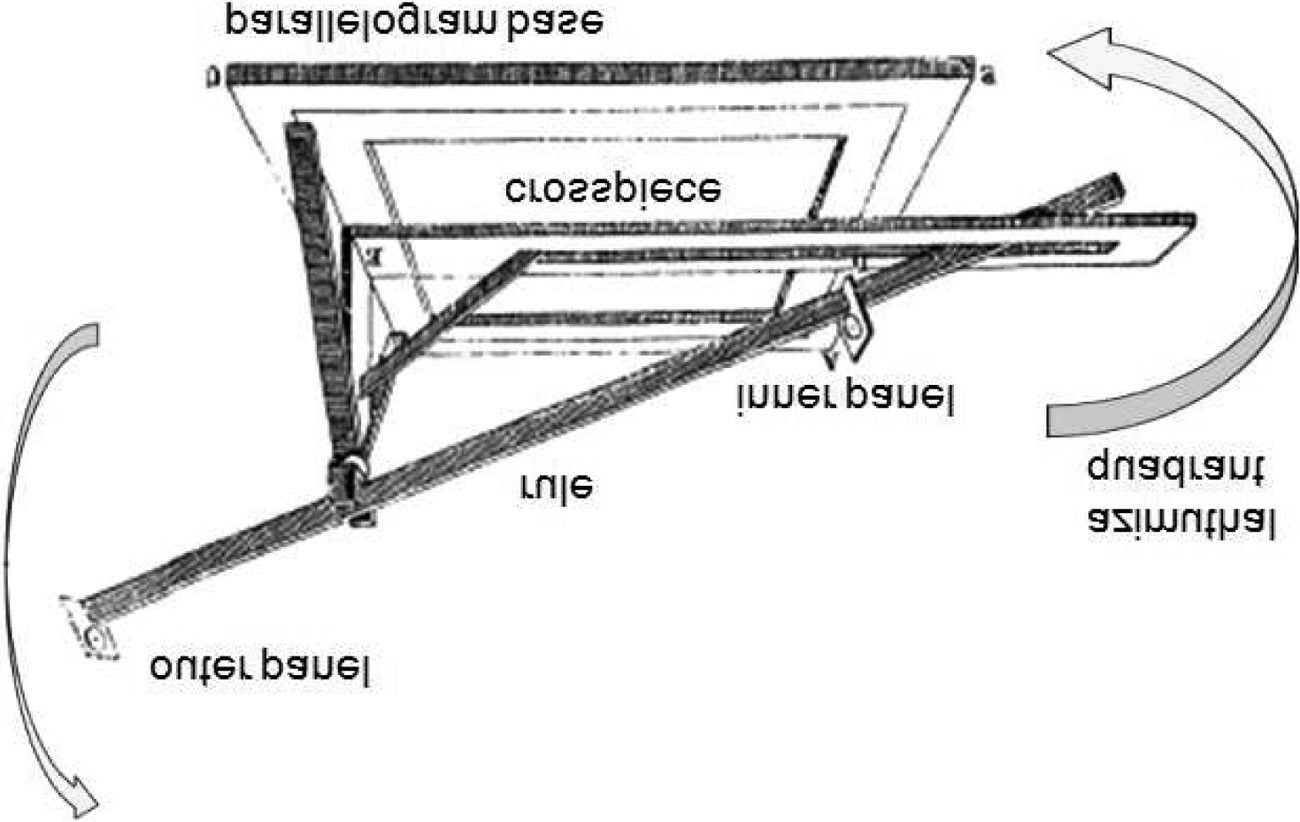
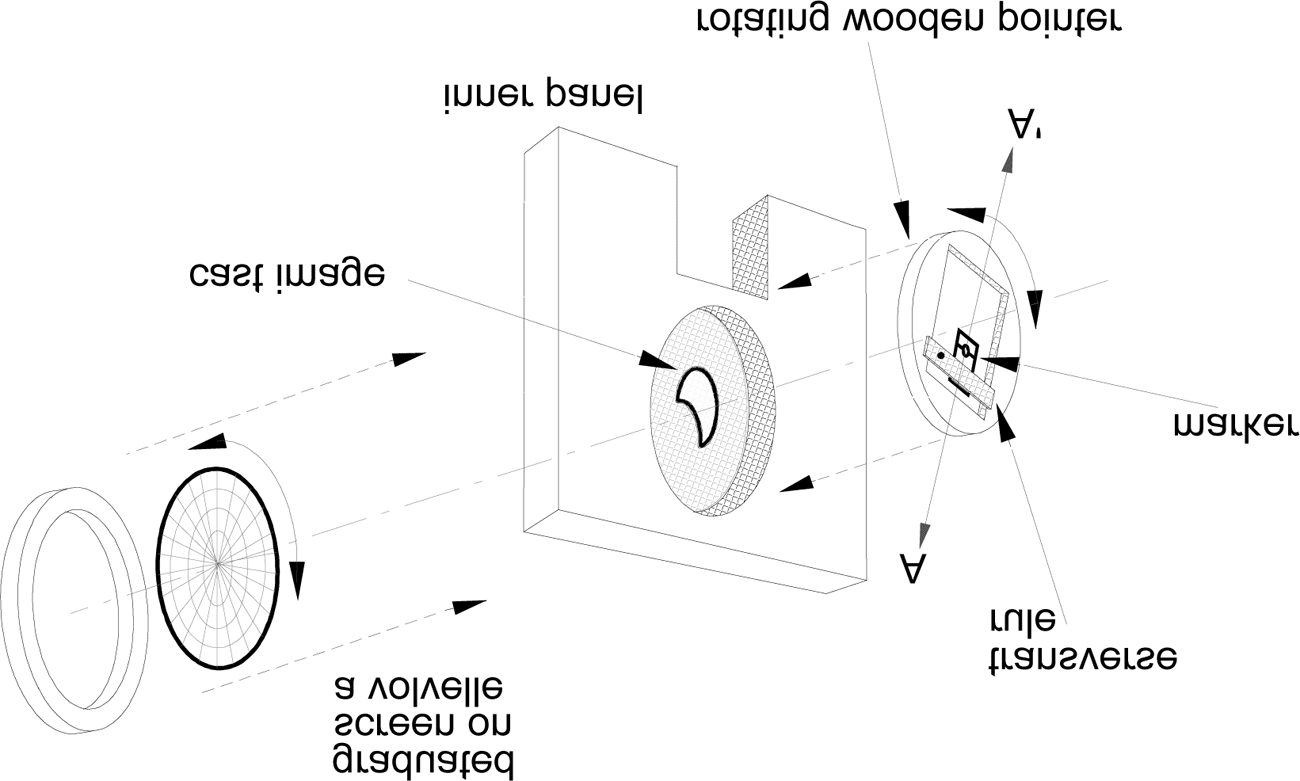
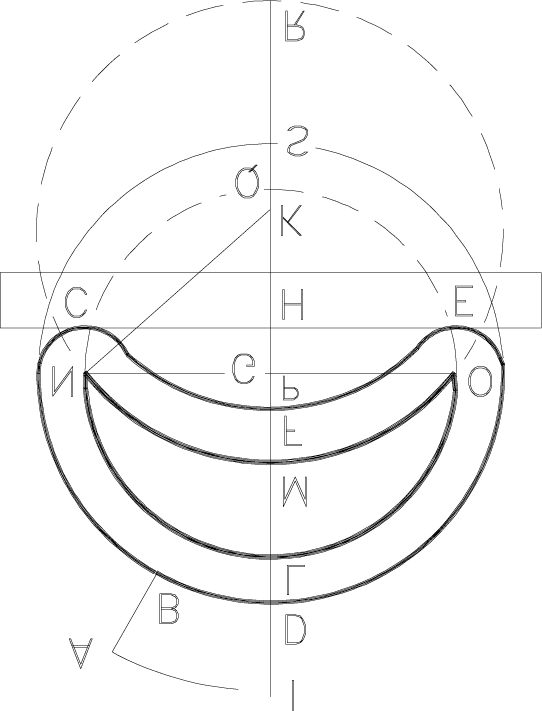
Kepler’s Optical Part of
Astronomy (1604):
Introducing the Ecliptic
Instrument
Giora Hon
University of Haifa
Yaakov Zik
University of Haifa
For William H. Donahue
The year 2009 marks the 400th anniversary of the publication of one of the
most revolutionary scientiªc texts ever written. In this book, appropriately en-
titled, Astronomia nova, Johannes Kepler (1571–1630) developed an as-
tronomical theory which departs fundamentally from the systems of Ptolemy
and Copernicus. One of the great innovations of this theory is its dependence
on the science of optics. The declared goal of Kepler in his earlier publication,
Paralipomena to Witelo whereby The Optical Part of Astronomy is
Treated (Ad Vitellionem Paralipomena, quibus astronomiae pars
optica traditvr, 1604), was to solve difªculties and expose illusions astron-
omers face when conducting astronomical observations with optical instru-
mentos. To avoid observational errors that had plagued the antiquated mea-
Early versions of this paper were presented in XXV Scientiªc Instruments Commission Sympo-
sium, “East and West: The Common European Heritage,” held in Krakow, Poland, 10–14
Septiembre, 2006; and in the meeting of the History of Science Society held in Vancouver, No-
vember 2–5, 2006. We are indebted to the participants of these meetings for their com-
mentos. En particular, we thank Wilbur Applebaum for his valuable remarks. We thank
Ron Alter of the University of Haifa Library for his help in acquiring material for our re-
buscar. We are grateful to Dov Freiman and Avishi Marson of Elbit Systems, Electro-
Optics ELOP, Limitado., for instructive discussions and optical simulations. We thank Ilan
Manulis, director of The Harry Kay Observatory at the Technoda, Hadera, Israel, for using
the Observatory infrastructure in September 2007. We gratefully acknowledge the helpful
correspondence and ensuing discussions with Noha Brosh, Dov Freiman, Richard Kremer,
Ilan Manulis, and Avishi Marson, on Kepler’s application of the pinhole camera. Finalmente,
we thank two anonymous referees of this journal for their helpful suggestions. This study
is supported by the Israel Science Foundation (grant no. 136/04). One of us [GH] is grate-
ful to the Netherlands Institute for Advanced Study (NIAS) at Wassenaar for facilitating
the completion of this research.
Perspectives on Science 2009, volumen. 17, No. 3
©2009 by The Massachusetts Institute of Technology
307
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
308
Kepler’s Optical Part of Astronomy
suring techniques for calculating the apparent diameter and angular position
of the luminaries, Kepler designed a novel device: the ecliptic instrument. En
this paper we seek to shed light on the role optical instruments play in Kep-
ler’s scheme: they impose constraints on theory, but at the same time render as-
tronomical knowledge secure. To get a comprehensive grasp of Kepler’s aston-
ishing achievements it is required to widen the approach to his writings and
study Kepler not only as a mathematico-physical astronomer, but also as a
designer of instruments and a practicing observer.
1. Introducción
It is well known that Johannes Kepler (1571–1630) announced in his New
Astronomy (1609) the discovery that the course of a planet is “an oval path,
perfectly elliptical” (Donahue 1992, pag. 68; KGW 3: pag. 35). Kepler re-
ported that he obtained this result by carrying out “most laborious proofs
y . . . computations on a very large number of observations” (Donahue
1992, pag. 68; KGW 3: pag. 35). He made it explicit that his success was
based on discarding the approach of Ptolemy (º. 150) who had considered
the mean motion of the Sun, rather than its apparent motion. According
to Kepler, Ptolemy was under the impression that there would be no per-
ceived difference between the two motions, so he chose the former method
for ease of calculation (Donahue 1992, páginas. 47–51; KGW 3: páginas. 19–22).
Nicolaus Copernicus (1473–1543) and Tycho Brahe (1546–1601) fol-
lowed Ptolemy, but for Kepler this was not the way to proceed. Already in
his early study, Mysterium cosmographicum (1596), Kepler indicated that the
apparent motion should be taken into consideration, eso es, the reference
point should be the true body of the Sun (Donahue 1992, pag. 121; KGW 3:
pag. 65; Duncan 1999, páginas. 159–163; KGW 1: páginas. 50–54).
But this was not enough. For Kepler a successful matching of calcula-
tions with observations is not sufªcient; the pattern hidden in the observa-
tions has to be accessible to physical explanation. Such a pattern should
correspond to the three distinct domains which together constitute for
Kepler the framework for the execution of the needed reformation of as-
tronomy: geometría, física, and observations (Donahue 1992, pag. 162;
KGW 3: pag. 93). For a method of inquiry to be successful in this framework
it must be in agreement with physical causes (Donahue 1992, pag. 49; KGW
3: pag. 21).
Recent scholarship has been principally engaged with Kepler’s attempt
at turning astronomy into a physical science (p.ej., Goldstein and Hon
2005; Barker and Goldstein 2001; Voelkel 2001; Martens 2000; Aiton et
Alabama. 1997, páginas. xi–xxxviii; Applebaum 1996; Donahue 1996; Barker and
Goldstein 1994; Kozhamthadam 1994; Field 1988; Stephenson 1987;
Lindberg 1986; and Rosen 1986). These studies highlight conceptual,
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
309
theological, metafísico, epistemological, metodológico, and rhetori-
cal aspects of Kepler’s New Astronomy. Against this rich background we of-
fer a study based on a detailed analysis of what Kepler called the ecliptic
instrument, in the hope to raise new fundamental questions concerning
the relation between observation and theory in the astronomical context.
We contend that understanding Kepler’s astronomical achievements takes
more than his archetypal principles, and concerns for Aristotelian philoso-
phy, Neo-Platonism, matemáticas, mecánica, as well as his own insights
concerning a new synthesis of natural philosophy and mathematics. Kep-
ler’s engagement with astronomical observations is complex and we seek
to contribute towards its clariªcation.
Kepler noted that astronomers measure with instruments the distances
between the ªxed stars, planets, and even the edges of the Sun and Moon,
and express these measurements in arcs of visual angles (anguli visorii).
These arcs are based on geometrical divisions of angles and arithmetical
calculations—they are in effect constructs of the mind. To put it bluntly,
arcs and their divisions do not exist in the physical world. The astronomi-
cal enterprise, por lo tanto, has to rest upon optical reasoning, the only way
to guarantee a reliable link between a mental construct and the physical
reality of heavenly bodies (Donahue 2000, pag. 321; KGW 2: páginas. 267–268).
Optics and astronomy are interwoven. Kepler writes,
Because of the eccentric, the planets appear either slow or fast. El
cause is partly physical, partly optical. The physical part of the
cause does not give the sense of vision a reason for error, pero también
represents to the vision that which in fact occurs, [an account] de
which is in the Commentaries on the motions of Mars. (Donahue 2000,
pag. 339; KGW 2: pag. 282)
En efecto, Kepler presented in the New Astronomy the physical causes of the
motions of the heavenly bodies. Pero, according to Kepler, of no less im-
portance is the study of the optical causes related to astronomical observa-
ciones. Kepler presented the study of these causes in his Paralipomena. Vi-
sual illusions and poor optical reasoning plagued the observations taken
by Kepler’s predecessors. According to Kepler these astronomers believed
“in the theorem without restrictions”1 and thus “fell into a large error”
(Donahue 2000, pag. 57; KGW 2: pag. 48) in estimating the motions of the
planets in relation to their courses and distances from Earth. But for
Kepler
1. By “the theorem” Kepler meant the method then used to measure with a compass
“the magnitudes [apparent diameters] of solar eclipse, the ratios of the [apparent] diame-
ters of the sun and moon, and the inclinations to the vertical of the circle drawn through
the centers of the luminaries” (Donahue 2000, pag. 57; KGW 2: pag. 48).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
310
Kepler’s Optical Part of Astronomy
the error was immediately obvious from the apparent magnitude
[of the sun], for the epicycles increased less at perigee than accords
with such a close approach, for which reason another cause for the
slowing down was seized upon, cual, as I have just said, Ptolemy
ascribed to the circle of the equant. In the sun, no epicycle was
needed, and as a consequence this error has remained to this day. Él
era, sin embargo, ªrst discovered by me, through an exact observation
of the visible diameter, as I shall say below [in the Paralipomena],
and then by Tycho’s most precise observations taken of the star
Mars, as I shall make plain at the proper time and place [in the New
Astronomy]. (Donahue 2000, pag. 341; KGW 2: páginas. 283–284)
As early as 1600, while considering the relation between theory and
observación, Kepler remarked that “for these speculations a priori must
not conºict with clear experimental evidence, indeed they must be in con-
formity with it.”2 The need to match the calculations of each planet’s path
with the observed positions of the planet at different places on its course
led Kepler to examine the optical part of astronomy. En 1602 Kepler ex-
pressed his opinion about the relation between optics and the study of the
motion of the planets:
I have committed myself to accomplish two goals: The ªrst, ser
completed by Passover is the commentary (or whatever its name
will be) on the theory of Mars, or the key to a universal astronomy,
dealing with the problems of second motions, as a result of Tycho
Brahe observations. El segundo, the optical part of astronomy, is to
be completed within 8 semanas, and will be of great importance, para
what you [Herwart] encouraged me [the investigation of the mo-
tion of the planets]. En este trabajo, from my observations which are
the foundation of computations and hypotheses and from many
pieces of information, I collect something general for the consider-
ation of one who wishes to contemplate a theory of luminous bod-
es. (Kepler To Herwart, Noviembre 12, 1602; KGW 14: páginas. 299–
300)
In the event it took seven more arduous years to accomplish the ªrst goal,
a saber, the theory of Mars, and two years to complete the second objec-
tivo: the optical part of astronomy. It is noteworthy that as early as 1602
Kepler had known that he would be able to conceive a new astronomical
theory, and it is equally striking that he ªrst opted to complete his optical
studies—a fundamental aspect of his new astronomy.
2. Kepler to Herwart, Julio 12, 1600; KGW 14: pag. 130: “non debent enim hae a priori
speculations in manifestam impingere experientiam: sed cum hac conciliarj.”
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
311
Kepler realized that “supposing the place of the celestial body to be
known with complete precision, throws the demonstrations into dif-
ªculty: the nature of light, beset by the inconstancy of optical causes, does
not always allow such precision of instruments” (Donahue 2000, pag. 6;
KGW 2: pag. 8). Observations have their limits and what is required is to
bring the calculations within a valid margin of accuracy. In Kepler’s
palabras: “by the best reasoning at our disposal, we have brought the calcu-
lation within the limits of observable error” (Donahue 1992, pag. 559;
KGW 3: pag. 355; see also Hon 2004, páginas. 72–79 and Hon 1987). It is evi-
dent that in Kepler’s view no idea concerning astronomy was of any use
unless it was supported by observations (Kepler To Fabricius, Julio 4,
1603; KGW 14: pag. 412), which in turn could be carried out only with in-
struments. Kepler emphasized time and again the need to study how as-
tronomical instruments function so that one could control the way obser-
vations and measurements are made, and determine how reliable they are
(Donahue 2000, páginas. 13, 15-dieciséis, 56–57, 157–158, 171, 227, 231–232,
350–351; KGW 2: páginas. 14, 15-dieciséis, 47–48, 134–135, 143–144, 190, 193,
290–291). This demand is most prominent in Kepler’s analysis of the pin-
hole camera.
In this paper we revisit Kepler’s study of the pinhole camera. We dis-
cuss his theoretical insights and their application in turning the pinhole
camera into an astronomical instrument, as presented in chapter 11 de
Kepler’s Paralipomena. This optical study is, among other things, a tour de
force of geometrical analysis of working instruments. Esto es, por así decirlo,
an applied geometry that takes into consideration the material limitations
of instruments. We seek to bring together historical and technical per-
spectives on some of Kepler’s optical procedures and to examine the re-
sults he obtained from the application of an ingenious arrangement of two
different instruments. In his ecliptic instrument Kepler combined the
pinhole camera (for aiming purposes and measuring the apparent diame-
ters of the luminaries) with the quadrant (for executing positional astron-
omy). We follow Kepler identifying problems, seeking solutions, develop-
ing an experimental setup to test his argument, and ªnally putting
forward an optical theory. This close study of Kepler’s theoretical insights
into a novel optical apparatus, the ecliptic instrument, sheds light on the
role instruments play in imposing constraints on epistemology, but at the
same time making knowledge claims secure.
2. El problema
In the 16th century the pinhole camera was at the center of interest of
scholars from different disciplines. The application of this device as an op-
tical imaging instrument for astronomical measurements posed an in-
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
312
Kepler’s Optical Part of Astronomy
triguing problem for astronomers, mathematicians, and opticians (magis
opticus).3 One such scholar was Tycho who in the latter part of the century
modiªed the pinhole sights of his astronomical instruments. He found
that the most suitable arrangement of pinholes is that in which the lower
sight, the one closest to the eye, has slits on all four sides.4 Tycho ªtted
this sight with a graduated disk which he then used as a screen on which
the upper pinhole cast a circular image when pointed toward the Sun
(Thoren 1973, pag. 29). This improvement allowed aiming the instrument
accurately and the observer could also measure the Sun’s apparent diame-
ter by the comparison of the projected image with the disk.
In March 1578, Tycho tried a different method: to calculate the appar-
ent solar diameter from measurements of the width of the Sun’s image cast
on the ºoor through a slit (rima) in the wall (Donahue 2000, páginas. 353–
354; KGW 2: páginas. 293–294; Straker 1981, páginas. 272–274; Straker 1970,
páginas. 332–334). In his solar observation of 1591 Tycho used yet another
method to calculate the apparent diameter of the Sun. He furnished a
wooden quadrilateral tube (canalis) with a square pinhole through which
the Sun’s image was projected onto a screen placed relatively close to the
pinhole. Tycho’s measurements of the cast images of the Sun and the
Moon involved large errors (Donahue 2000, páginas. 352–353; KGW 2:
pag. 292; Straker 1970, páginas. 336–345, 354–356, 399–406). Following his
observations of solar eclipses in the year 1598, Tycho reported in a letter
to Michael Mästlin (1550–1631) at Tübingen,
The moon during a solar eclipse does not appear to be the same size
as it appears at other times during full moons when it is equally far
away; but it appears as if it were constricted by about 1/5th. . . . Como
a result, it appears that the moon can never obscure the sun com-
pletely, and even if the moon interposes itself centrally, the remain-
ing light of the sun encircles it. . . . Although the diameter of the
moon . . . by our calculations ought to have been 34®(cid:2), it could
not have appeared in front of the sun to be more than 28(cid:2), cual
constriction I recognized and was noticed by no one before me.
(quoted by Straker 1981, pag. 278; see also Donahue 2000, pag. 57;
KGW 2: pag. 48)
3. For historical accounts and discussions on light and theories of pinhole images in the
Latin West, see Hon and Zik 2007; Ilardi 2007, páginas. 219–224; Lefèvre 2007; Thro 1996;
Thro 1994; Mancha 1989; Goldstein 1985; Lindberg and Cantor 1985; Lindberg 1984;
Straker 1981; Lindberg 1976, páginas. 185–188; Beer and Beer 1975, páginas. 789–861; Lindberg
1970; Straker 1970; Lindberg 1968.
4. See the appendix, Supplementum de subdivisione et dioptris instrumentorum: Brahe 1598,
appendix [82]. For an account of Tycho’s astronomical instruments and the operational
limits of his new sighting arrangement, see Thoren 1973 and Wesley 1979, pag. 99.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
313
Tycho appealed to a purely observational reasoning. His empirically based
method of observation was developed without an adequate theory of im-
age formation behind small pinholes (Straker 1981, páginas. 267, 276;
Donahue 2000, páginas. 57, 352–354; KGW 2: páginas. 48, 292–294). He noticed
a lunar diminution during solar eclipses and, por lo tanto, entered in his
lunar tables smaller values for the apparent diameter of the Moon than
he had actually measured (Straker 1981, pag. 278). Astronomers at the time
were familiar with Tycho’s data which were inconsistent with the ob-
servations they had made (Straker 1981, páginas. 280, 283; Donahue 2000,
páginas. 297–298; KGW 2: pag. 249). Kepler, Por ejemplo, considered the results
Tycho had obtained an indication that the Moon may be actually farther
away than lunar theory predicts. Something must have been wrong either
in astronomy or with Tycho’s observations (Starker 1981, pag. 278).
The traditional view maintained that the Sun’s apparent diameter does
not vary perceptibly from apogee to perigee, and is seen under the same
angle. Mathematicians and astronomers of the time thought that the
Moon’s apparent diameter is only seen to be equal to the Sun’s diameter
when the full Moon is situated at the apogee of its epicycle, while at peri-
gee the Moon appears to be greater than the Sun (Donahue 2000, páginas. 57,
309–310; KGW 2: páginas. 48, 257–258). Ellos, sin embargo, were confused by
the variety of methods and differences in the results of measurements of
the apparent diameters of the Sun and Moon (Donahue 2000, páginas. 310–
311; KGW 2: páginas. 257–258). Kepler too was intrigued by the observa-
tional fact “whether the ray be allowed in through a notch or received by
the eyes, always show the moon’s diameter to be much less than it ap-
peared at oppositions” (Donahue 2000, pag. 297; KGW 2: pag. 248). In chap-
ter 5 of his Paralipomena, Kepler had already explained “the causes, de
the actual structure of the sense of sight, why the edges of luminous ob-
jects are [seen] enlarged, particularly in darkness” (Donahue 2000, pag. 298;
KGW 2: pag. 248). This aspect of the functioning of the eye affects the way
the apparent diameter of the Moon is perceived in the dim light of the
eclipsed Sun and Kepler, por lo tanto, proceeded to study phenomena related
to the cast shadow of the Moon and daytime darkness during solar eclipse
(Donahue 2000, pag. 298; KGW 2: pag. 248). A similar phenomenon of this
nature occurs when a pillar obstructs the view of the whole Moon, while a
bright white halo is still distinguished from the Moon’s body. Kepler
sought to simulate this phenomenon; he writes,
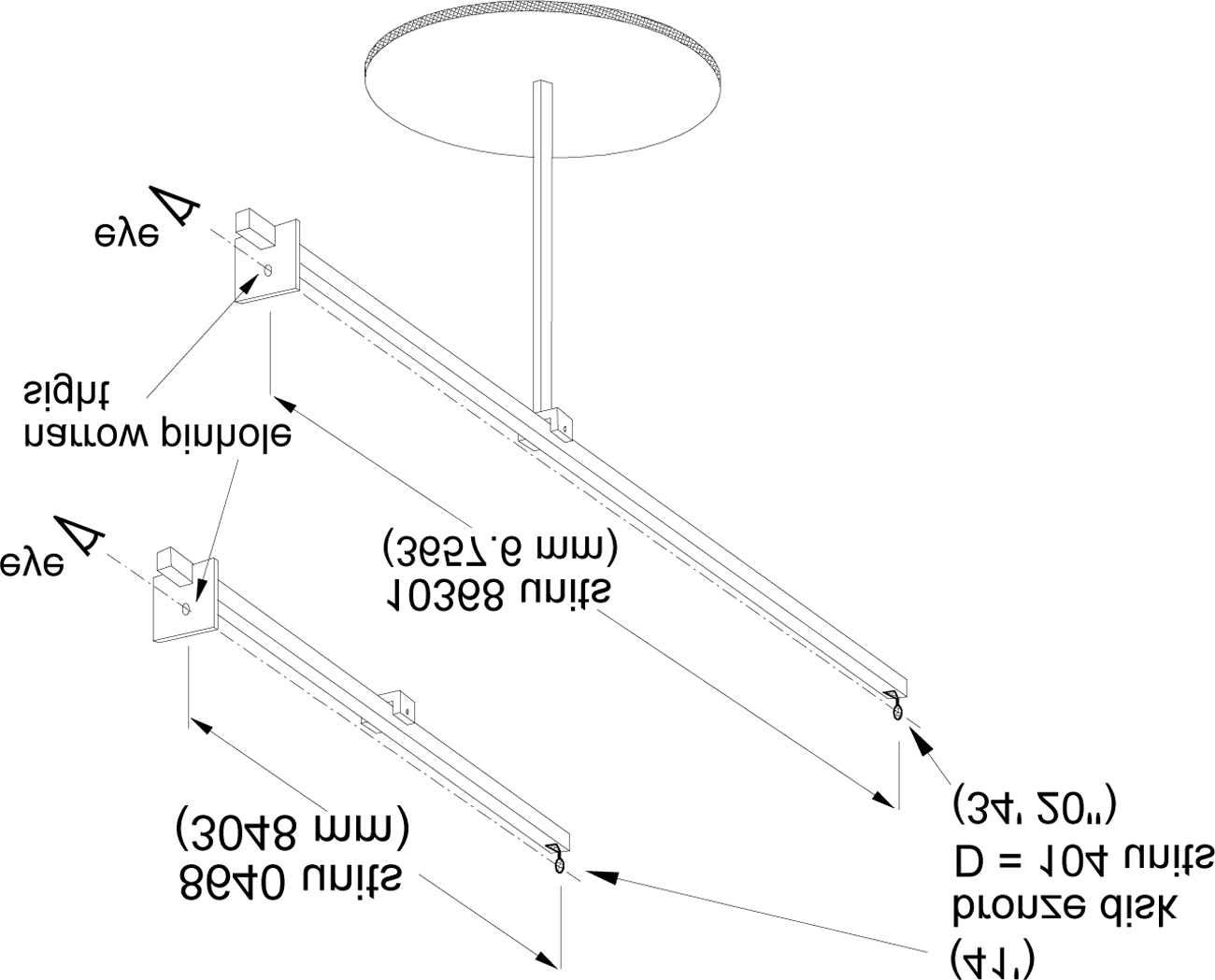
In the evening, the moon being near perigee, . . . I set up a bronze
rueda [ªgure 1], precisely circular, clasped with a spike to one end
of a pole twelve feet long [3657.6 mm], applied the eye at the
other end, and before the eye a very narrow opening in another
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
314
Kepler’s Optical Part of Astronomy
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
Cifra 1. Observing the Moon obstructed by a bronze wheel
bronze sheet, so that the eye would have a perpendicular view to
the wheel through the opening. . . . And since, where the distance
between the eye and the wheel was 10368 [units], the width of the
wheel would be 104, covering an arc of 34 1
3 minutos, I was hope-
ful that the moon was going to be completely covered by this
rueda, because of other ways of observing, which I was applying at
al mismo tiempo. And in fact, the moon was seen to protrude all
alrededor. Here I was troubled by anxiety that perhaps other ways of
observing, in which I had the greatest trust, might be false. Pero
that there was a fallacy became immediately plain when the eye was
brought nearer the wheel. For all that brightness still did not be-
take itself behind the wheel even when the eye came to a distance
de 10 pies. In this way the moon would have had to represent more
than 41 minutos, which every one knows is false. I was also unable
to recognize a determinate distance from which the moon would be
covered, for I always saw something bright on the circumference.
(Donahue 2000, páginas. 311–312; KGW 2: páginas. 259–260)
Kepler noticed the considerable difªculties in the prediction of eclipses
and in the reconstruction of the Moon’s motion (Donahue 2000, pag. 57;
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
315
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
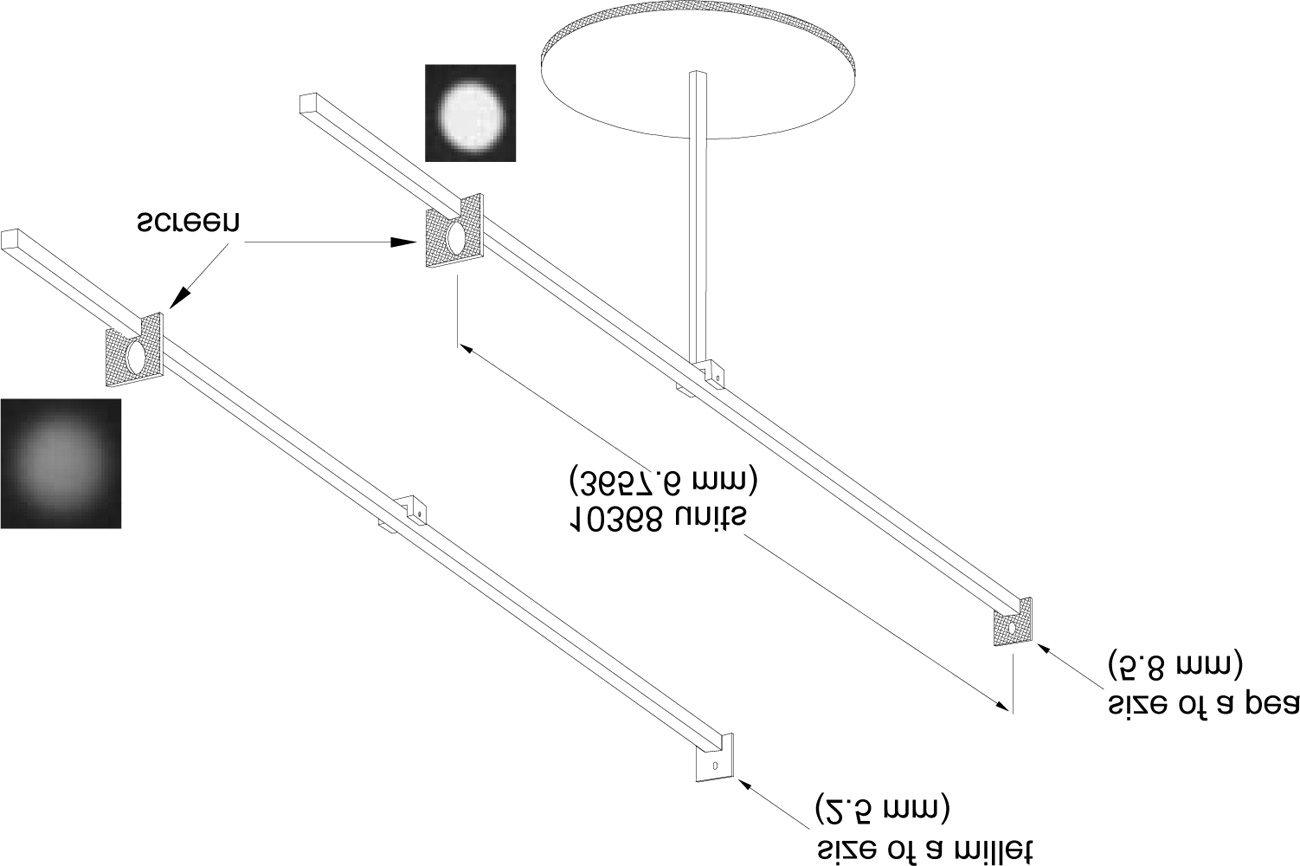
Cifra 2. Projection of the sun through pinholes of different diameters
KGW 2: pag. 48). As indicated, he attributed the problems to the methods
then used to measure the apparent diameters of solar eclipse and the ratios
of the apparent diameters of the Sun and Moon. Since the measurements of
the apparent diameters of the luminaries had been taken through small
holes, Kepler explored how the image of the Sun is cast behind holes of
different diameters,
When two holes were opened [ªgure 2], one the size of millet, el
other the size of a pea, and a pair of circles were painted on the op-
posite wall [pantalla], one of which exceeded the other by an interval
that was as great as the difference between the larger and smaller
holes, the ray of the sun admitted through the larger hole was in-
deed equal to the greater circle, but when the larger hole was
blocked, the ray that came through the smaller did not maintain an
evident boundary, and had the edge gradually passing over into a
dusky color, and ªnally, far exceeded the smaller circle. For the ray
of the sun, greatly weakened through such a small hole, was unable
to illuminate the paper much more brightly than the rays from the
air standing about the sun whose continuation with the solar rays
portrayed a breadth greater than the truth, and a brilliant color
(Donahue 2000, pag. 312; KGW 2: pag. 260).
316
Kepler’s Optical Part of Astronomy
Kepler pondered whether the experiments with the bronze wheel and the
two different pinholes could simulate the astronomical conjunction when
the Sun is obscured by the full Moon. His ªrst experiment conªrmed that
the full Moon indeed appears to the observer larger than its real size, pero
then the second experiment resulted in more questions than answers.
Though Kepler described his experiments of the projection of the Sun’s
images through two circular pinholes of different diameters, his account
suggests that he had actually experimented with a variety of pinhole set-
ups. Kepler, sin embargo, concluded that, since the sense of sight varies by in-
dividual cases, the projected images of the Sun and Moon are seen differ-
ently by different people (Donahue 2000, páginas. 297–298; KGW 2: pag. 248).
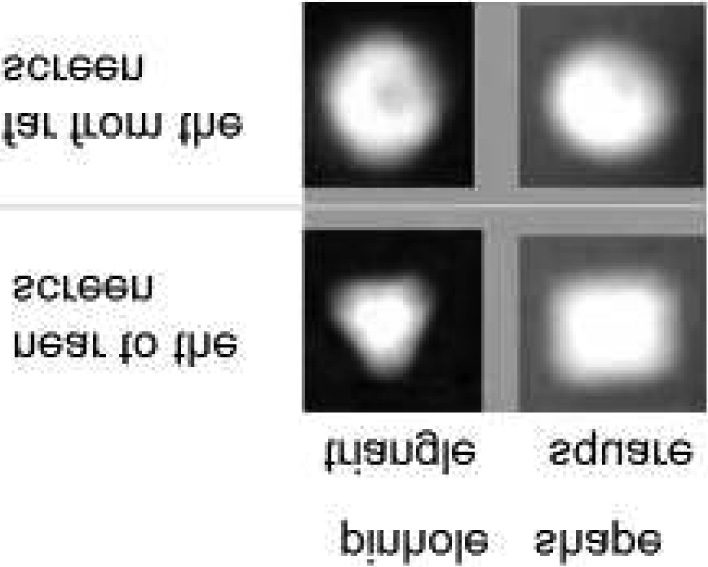
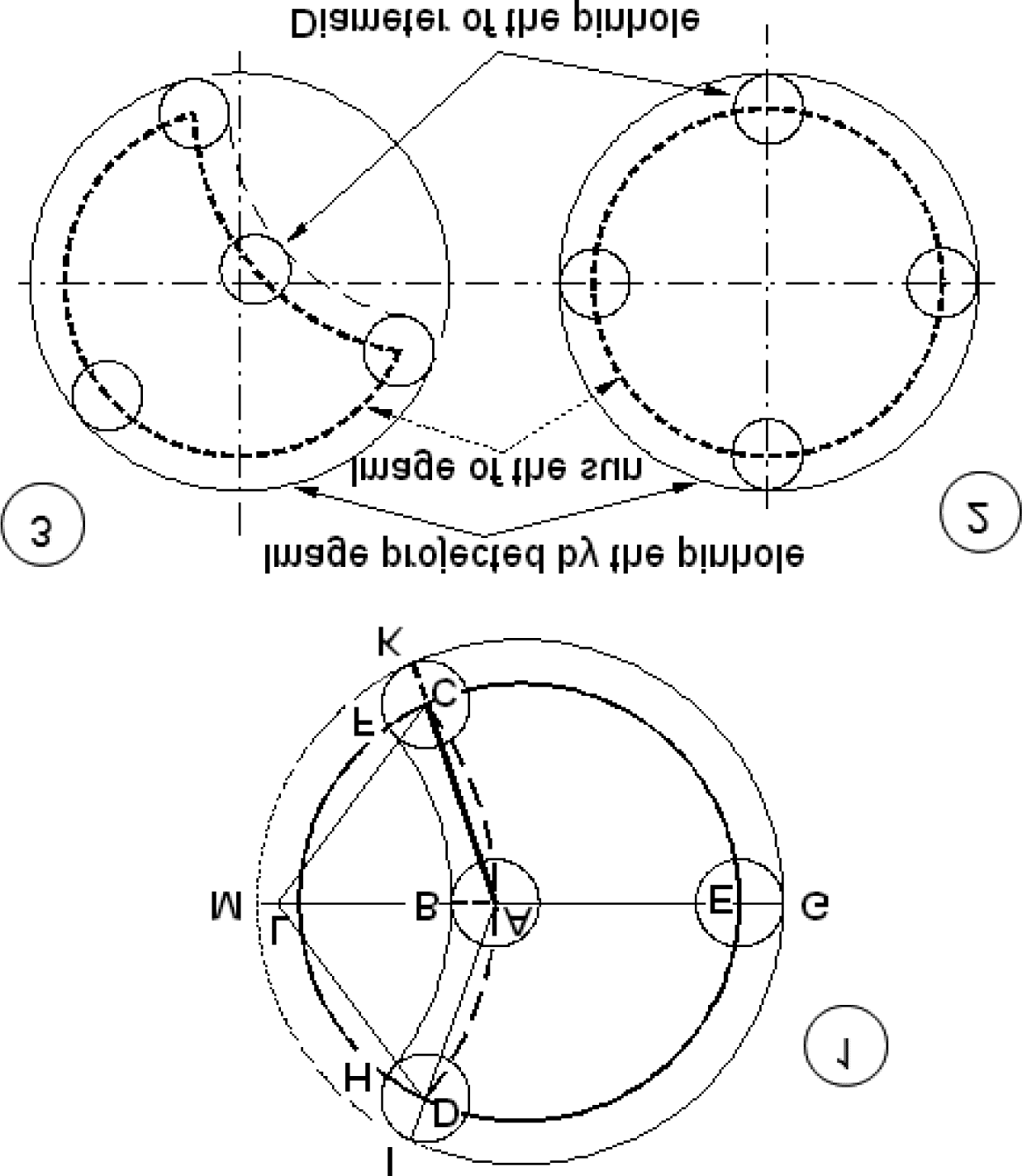
These differences are illustrated in ªgure 3 where projections and multi-
plication of the Sun’s image by different shapes and diameters of pinholes
as well as their distances from the screen are presented.
Kepler warned astronomers that they must not trust the sense of sight
when they measure the apparent diameter of the full Moon and that of the
Sol (Donahue 2000, pag. 298; KGW 2: pag. 249). In contrast to Tycho, Kep-
ler was convinced that the wide variations in the power of sight of individ-
ual observers make it impossible to establish correction tables. He re-
marked,
it cannot . . . be argued from this accident of the sense of sight to
what happens outside of consideration of the sense of sight, nor can
tables be established for the sake of the sense of sight, which repre-
sent neither the object itself nor the defects of all senses of sight.
For the astronomer should not present anything other than those
things that in actual fact occur. The sense of vision, sin embargo, nosotros
leave to the physicians to remedy (Donahue 2000, pag. 298; KGW 2:
pag. 249).
Kepler concluded that the luminous boundaries of the eclipsed Sun’s im-
edad, projected through a slit or a pinhole, spread out considerably. Por eso,
the problem: the projected image simply does not show the true diameter
of the luminaries and the observer is easily deceived. Kepler, por lo tanto, en-
deavored ªrst to gain a better understanding of the optical causes of this
phenomenon and then to “teach how to enter into a most certain proce-
dure for measuring the quantities of eclipses” (Donahue 2000, pag. 298;
KGW 2: pag. 249).
3. Image formation behind a pinhole: some modern optical considerations
Kepler worked within the tradition of geometrical optics. This tradition
was restricted to situations where—in current optical terminology—
the size of the pinhole is large compared to the wavelength of the light
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
norte
mi
mi
r
C
s
a
metro
oh
r
F
s
mi
C
norte
a
t
s
i
d
t
norte
mi
r
mi
F
F
i
d
s
a
yo
yo
mi
w
s
a
s
mi
yo
oh
h
norte
i
pag
F
oh
s
r
mi
t
mi
metro
a
i
d
d
norte
a
s
mi
pag
a
h
s
t
norte
mi
r
mi
F
F
i
d
metro
oh
r
F
s
mi
gramo
a
metro
i
d
mi
t
C
mi
j
oh
r
PAG
.
3
mi
r
tu
gramo
i
F
318
Kepler’s Optical Part of Astronomy
transmitted through it or the distance from the pinhole to the screen is
short compared to the width of the pinhole.
To have a better understanding of the argument which Kepler devel-
oped, it is instructive to recall in modern terms how an image is formed
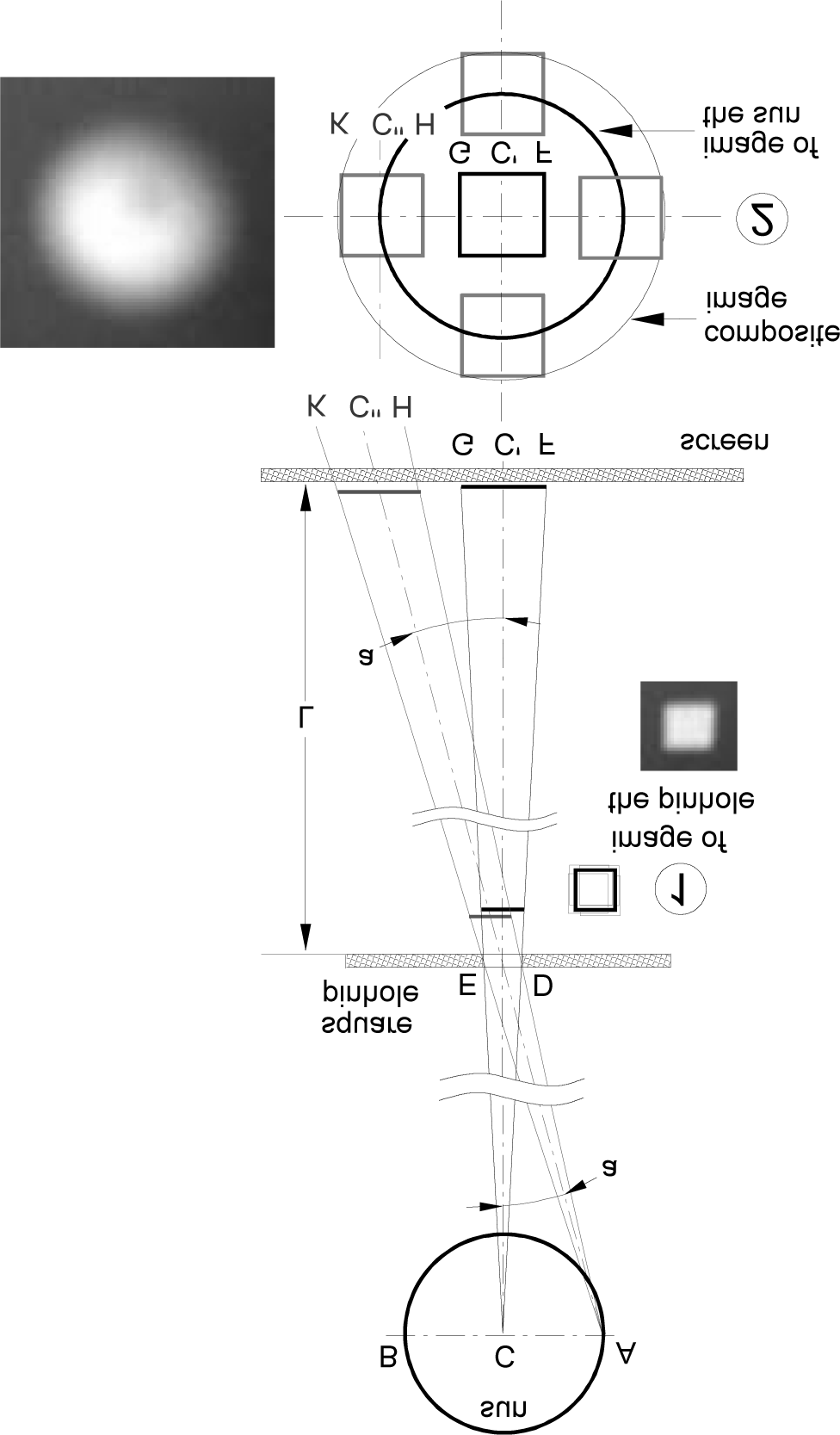
behind a pinhole. Let the rays issued from the center of the Sun, C, (ªgure
4) and a peripheral point, A, be projected through a square pinhole ED
onto a screen, where the centers of the cast images, GF and KH, are de-
noted by, C(cid:2) and C(cid:3), respectivamente. The shift between the images (C(cid:2)C(cid:3)) de-
pends on the radius of the apparent-mean Sun (a (cid:4) (cid:5)16 arc minutes) y
the distance, l, between the pinhole and the screen which is calculated
trigonometrically as, C(cid:2)C(cid:3)(cid:4)L tan a. Each point source of the Sun creates a
rectangular image of the pinhole on the screen and the overlapping partial
images produce a different composite image when the screen is placed
near to or far from the pinhole. In the latter case the radius of the compos-
ite image is the sum of C(cid:2)C(cid:3)(cid:6)C(cid:3)k; eso es, the radius of the Sun’s image
plus the half size of the square pinhole side (in the case of a circular pin-
agujero, C(cid:3)K would be its radius).
Por ejemplo, the shift between the images projected on a screen placed
at a distance of 200 mm from the pinhole would be 0.93 mm. De este modo, for a
square pinhole of 5.8 mm (ªgure 4.1), the shift is much smaller than the
partial images created by different point sources on the Sun which practi-
cally coincide and produce an image of the square pinhole whose edges are
therefore slightly blurred. In a different situation (ªgure 4.2), the shift be-
tween the partial images, projected through the same square pinhole on a
screen placed at 3657 mm from the pinhole, would be 17 mm. Desde el
shift of 17 mm is larger than the size of the partial images, the composite
imagen, whose radius is 19.9 mm, takes the shape of the Sun whose circum-
ference is slightly blurred.
Image formation behind a pinhole is part of the complex optical phe-
nomenon of diffraction which occurs when obstructions (such as pinholes)
modify the amplitude, or phase, of a portion of a wave front that encoun-
ters these opaque obstacles. Light does not travel in straight lines; it be-
haves like wave, bending around corners and obstructions, albeit to a
ªnite small degree. Diffraction phenomena are the result of interaction of
a large number of light waves whose mathematical analysis is extremely
intricate. Some of the phenomena Kepler referred to are caused by what
we call today near-ªeld diffraction (Huygens-Fresnel diffraction) and far-
ªeld diffraction (Fraunhofer diffraction).5
5. For an account of interference and diffraction, see Hecht 1990, páginas. 333–339, 392–
471. On the diffraction effects of apertures, vignetting, and resolution of optical systems,
see Smith 1990, páginas. 135–139, 148–155.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
319
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 4. Geometrical analysis of image formation behind a squared pinhole.
Geometrically, rays issued onto a screen through a point pinhole that
are perfectly free from any aberration would converge from an axial object-
point onto one and the same image-point. De este modo, for whatever size of the
pinhole and for any distance from the screen, the projected image invari-
ably would be sharp and take the shape of the pinhole. But these consider-
ations are idealized; in reality, a faithful depiction occurs only when the
screen is placed very close to the pinhole. No matter what pinhole system
320
Kepler’s Optical Part of Astronomy
Cifra 5. Indistinct edges of the image due to the appearance of light and dark
fringes.
Cifra 6. The diffraction fringes bordering a peg clasping a coin.
we use, we will always ªnd that when the size of the pinhole is gradually
reduced, or the screen is moved away, the edges of the image become in-
distinct due to the appearance of light and dark fringes (ªgure 5).
The effect is illustrated in ªgure 6: a bright pattern caused by the en-
ergy-density distribution borders the edge of the shadow cast by a peg
clasping a coin. The same happens when light passes through a large pin-
agujero; the bright bordering region diffuses the light in the image.
Circular pinholes produce patterns similar to those shown in ªgure 6,
except that the energy-density distribution exhibits radial symmetry.
When the pinhole is reduced, or the screen moved beyond a critical dis-
tance, the shape of the pinhole is no longer discernible and the image be-
comes larger instead of smaller. Por lo tanto, an extended light source pro-
jects the exact geometrical shape of the pinhole itself only when the
pinhole is placed very close to the screen. Even when the edge is smooth to
a very high degree, one observes near-ªeld diffraction patterns, no matter
how large the pinhole is. When the distance between the screen and the
pinhole grows (ªgure 7) the pattern of the projection becomes more struc-
tured and the multiplications of the image are more prominent.
When the screen is moved farther away, far-ªeld diffraction (Fraunhofer
diffraction) effects arise. The projected shape of the pinhole becomes
blurred and, as the distance increases, the blurred image bears increasingly
a resemblance to the shape of the light source (ªgure 8). Farther away, el
shape of the light source will have spread out considerably, changing only
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
321
Cifra 7. The multiplication of the image.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 8. As the distance between the pinhole and the screen grows, the shape
of the image increasingly resembles the shape of the light source.
the size of the pattern and not its shape. The boundary between near-ªeld
and far-ªeld diffraction depends upon the relative sizes of the pinhole and
its distance from the screen. Since far-ªeld domain may be calculated only
aproximadamente, the exact location of this boundary is problematic. Como un
rule of thumb the boundary between near-ªeld and far-ªeld diffraction can
be expressed in terms of Fresnel number which is deªned:
F(Fresnel number) (cid:4) r2 / (l (cid:7)),
where r is the radius of the pinhole, L is the distance of the pinhole from
the screen, y (cid:7) the wavelength involved. Depending on the Fresnel
number F, diffraction theory may be associated with two distinct domains:
(1) near-ªeld diffraction in which the Fresnel number is F ≥ 1, y (2) far-
ªeld diffraction in which the Fresnel number is F (cid:8) 1. De este modo, the Fresnel
number, which is an expression of the initial conditions, determines the
322
Kepler’s Optical Part of Astronomy
domain of validity of diffraction theory. The intermediary boundary be-
tween the two domains marks the distance L that produces the best reso-
lution of pinhole imaging system (Joven 1989). Por ejemplo, for a circu-
lar pinhole of 5.8 mm in diameter at wavelength of 5500Å, the boundary
between near-ªeld and far-ªeld diffraction would be at a screen distance of
acerca de 15.3 meter from the pinhole.
The pinhole camera had to be constructed and operated with care.
When the hole is not evenly bored, or not perfectly round (es decir., with rag-
ged edges), or when the thickness of the material in which the pinhole is
drilled is relatively large with respect to the diameter of the hole, the cast
diffused patterns will blur the image considerably (ªgures 9.1). Otro
set of problems may arise due to skew positioning or when the pinhole
and the screen are not parallel (ªgure 9.2 y 9.3).
These forms of stray light, spread out through the pinhole system, transmisión exterior-
scure faint signals, decrease the signal to noise ratio, reduce contrast and,
en general, disturb accurate projection of the image, resulting in poor op-
tical performance.
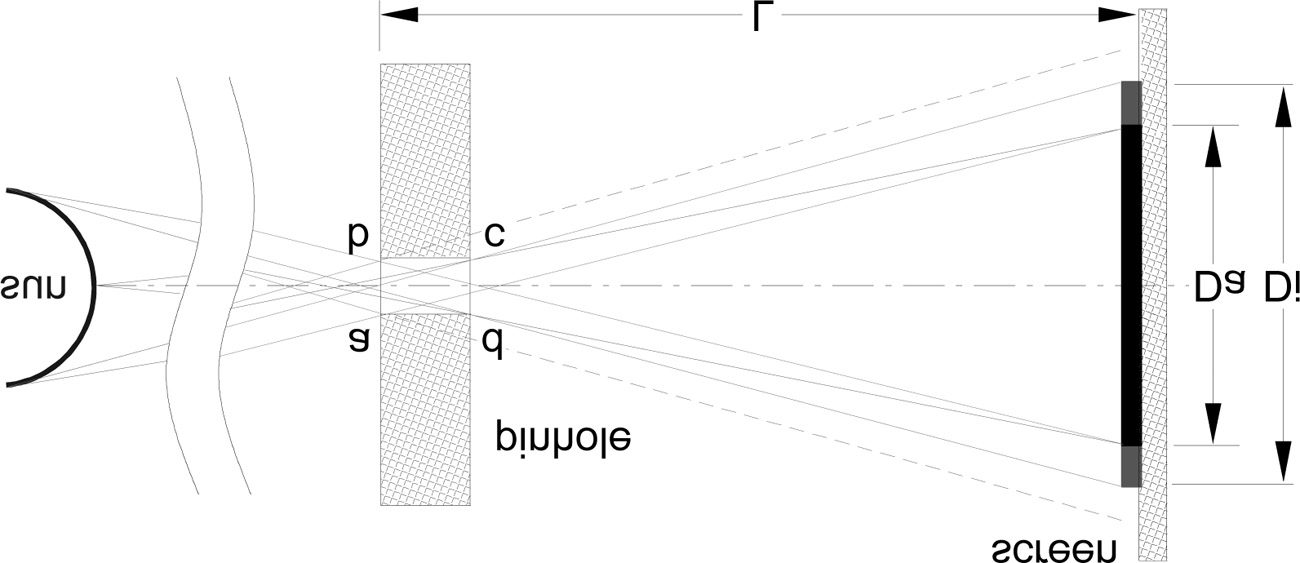
We position now a pinhole system, pointing directly to the Sun (ªgure
10). The light passes through the pinhole, bored in a plate, projects an im-
age of the Sun onto a screen placed at distance L. Geometrically, only part
Da of the image is exposed directly to the light of the Sun across the
whole width of the pinhole.6 Cut off by the sides of the pinhole (at points
a, b, C, d), image Di is partially illuminated by the light of the Sun in ad-
dition to illumination resulted from edge diffraction and light scattering
from the inner sides of the pinhole. Though the illumination at the mar-
gins of Di decreases, the faint edges of the image are still visible. The di-
ameter of the image Di, for a given width of the pinhole, is reduced due to
the thickness of the pinhole. When projected through a thin pinhole,
sin embargo, the margins towards the periphery of the image (the circumfer-
ence between Di and Da), will be smaller in comparison to the margins
projected through a thicker pinhole.
Optical processes can be recast as superposition of light waves.7 Phe-
nomena like polarization, interference, and diffraction share a common
conceptual basis since they deal with various aspects of superposition. El
image formed behind the pinhole is considered—in modern terms—a
6. Our analysis concerns the working of pinholes in the domain of near-ªeld diffraction
(Huygens-Fresnel diffraction).
7. Superposition occurs when two or more light waves overlap in some region. The re-
sultant form of the composite disturbance is determined by the speciªc properties of each
constituent wave, eso es, by its amplitude, phase, frequency and other physical parameters
(Hecht 1990, pag. 242).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
323
Cifra 9.1. Diffused patterns cast by light rays due to thickness and ragged
edges of the pinhole.
Cifra 9.2. Diffused patterns cast by light rays due to skew positioning.
Cifra 9.3. Pattern cast by light rays when the pinhole and screen are not paral-
lel.
superposition of an inªnite number of images which are slightly offset
against each other. De este modo, the projected image is the integral of all the
irradiance (es decir., the ºow of energy per unit of area per unit of time) del
object and the distribution function of illumination caused by impulse re-
sponse of the optical system (Hecht 1990, páginas. 242–269, 472–515). Su-
perposition is a process which results in blurring the input image and, en
the case of pinhole projection, also affects the magnitude of the image.
De este modo, the diameter of an image projected by a pinhole system working at
the domain of near-ªeld diffraction will be smaller than it should be in
comparison to the true apparent diameter of the Sun.
An analysis of the total irradiance map for absorbed ºux of the Sun,
projected through a pinhole onto a screen, demonstrates the amount by
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
324
Kepler’s Optical Part of Astronomy
Cifra 10. Geometrical analysis of the rays passing through the pinhole
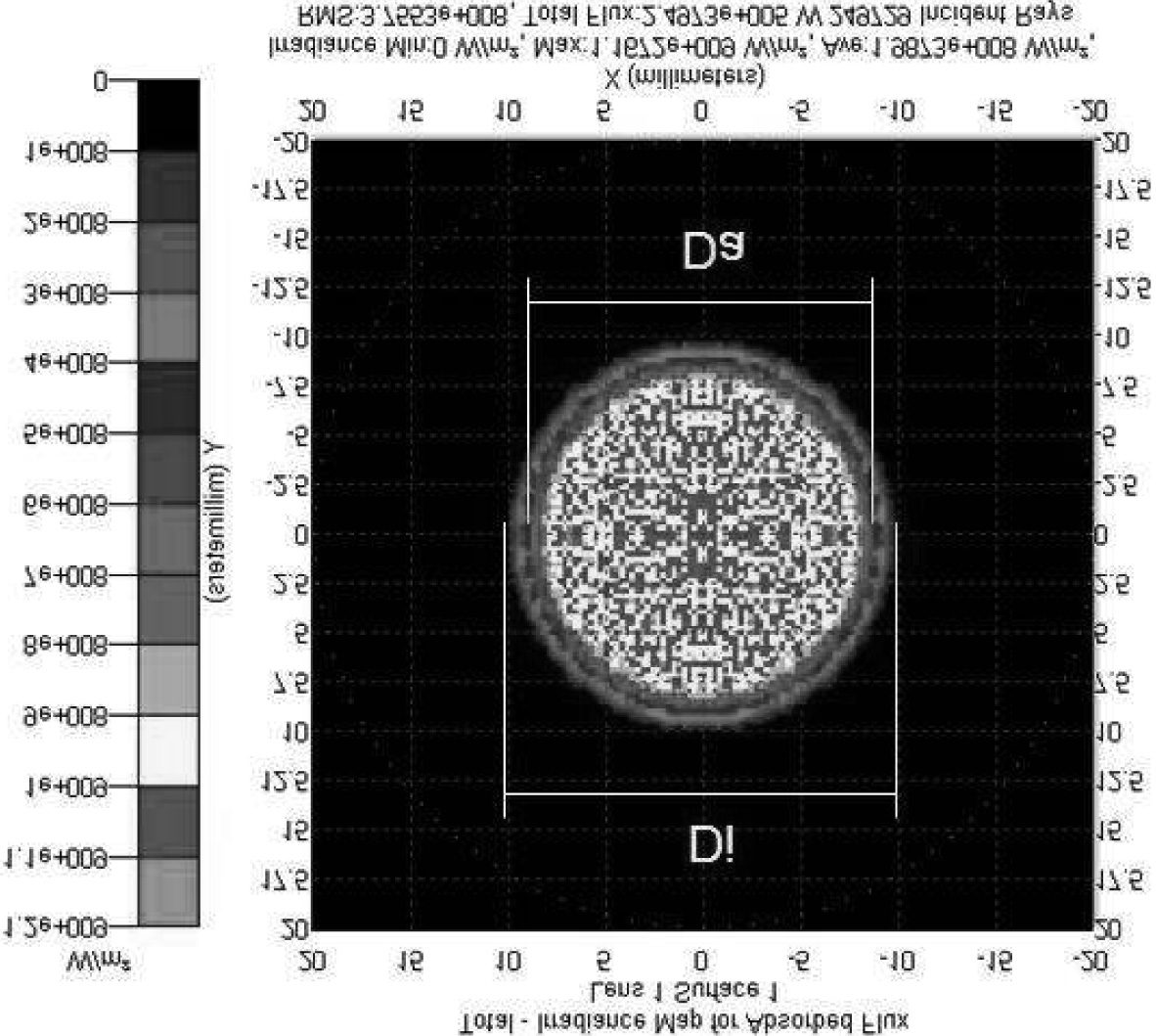
which the image is diminished.8 As shown in ªgure 11, the diameter of
the image, Di, presenting the total irradiance map of the Sun, is composed
of different levels of intensity. The irradiance at the center is substantially
higher than the irradiance distribution towards the margins of the image.
There is a considerable drop-off in the intensity of irradiance at a distance
denoted by the diameter, Da. The fuzzy demarcation line between diame-
ter, Di, and diameter, Da, measured on the irradiance map is a good ap-
proximation for the diameter of the pinhole. We simulate projection
through a pinhole system when the Sun presents an apparent angle of 31(cid:2)
50(cid:3).9 In this case the expected apparent diameter of the total irradiance
map should be the sum of the apparent diameter of the Sun (17.88 mm)
plus the diameter of the pinhole (3 mm); eso es, 20.88 mm. Sin embargo, como
shown in the irradiance map, the diameter of the projected image is 20.04
mm. The map suggests a diminution of about 4% in the diameter of the
Sun’s image. The same analysis is made when the Sun presents an apparent
angle of 32(cid:2) 30(cid:3).10 In this case the expected apparent diameter of the total
8. Flux density, measured in Watts/m2, is the quantity of light ºow. The irradiance
map was made by ELOP using TracePro. This is a powerful modeling software for analyz-
ing and simulating various system-performance criteria and constraints, including spatial
and angular light-output distribution, uniformity, intensidad, and spectral characteristics.
TracePro offers scientists and engineers the conªdence that the performance of the ªnished
product will agree with the simulated design without costly prototype iterations.
9. The properties of the pinhole in these simulations are: diameter, 3 mm; thickness,
0.1 mm y 1.5 mm; and the distance of the screen from the pinhole, 1931 mm.
10. The properties of the pinhole are in these simulations: diameter, 5.8 mm; thick-
ness, 0.1 mm y 1.5 mm; and the distance of the screen from the pinhole, 3658 mm.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
325
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
Cifra 11. Di denotes the diameter of the Sun’s total irradiance map depicted
en la pantalla. The demarcation line between diameter, Di, and diameter, Da, es un
good approximation for the diameter of the pinhole.
irradiance map should be the sum of the apparent diameter of the Sun
(34.58 mm) plus the diameter of the pinhole (5.8 mm), eso es, 40.38
mm. Sin embargo, as measured in the irradiance map the diameter of the pro-
jected image is 38.8 mm. The map suggests, once again, a diminution of
acerca de 4% in the diameter of the Sun’s image.
Considerándolo todo, cut-off effects caused by the sides of the pinhole camera, stray
luz, and the complex process of superposition, contribute to the diminu-
tion of an image projected by a pinhole system working at the domain of
near-ªeld diffraction. Our calculation shows that it is about 4% of the ap-
parent diameter of the Sun. Por ejemplo, taking the apparent diameter of
the Sun at perigee as 32(cid:2) 30(cid:3), the projected image will be a diameter of
acerca de 31(cid:2) 12(cid:3). For another example, the apparent diameter at apogee is
31(cid:2) 30(cid:3), while the image will be a diameter of about 30(cid:2) 14(cid:3). With this
optical analysis in mind, we now follow Kepler’s path in which he ªrst de-
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
326
Kepler’s Optical Part of Astronomy
veloped a theory of the projection of light through pinholes and then ap-
plied it in the design and construction of an accurate astronomical instru-
mento, by far better than the instruments employed by Tycho.
4. Kepler and the pinhole camera
To analyze the problem of image formation behind a pinhole, Kepler
adopted the thread model that Leon Battista Alberti (1404–1459) y
Albrecht Dürer (1471–1528) had used in their perspective instruments
(instrumento).11 Kepler reached a geometrical solution by appealing to an
experiment which helped him elucidate the highly obscure descriptions
provided by his predecessors:
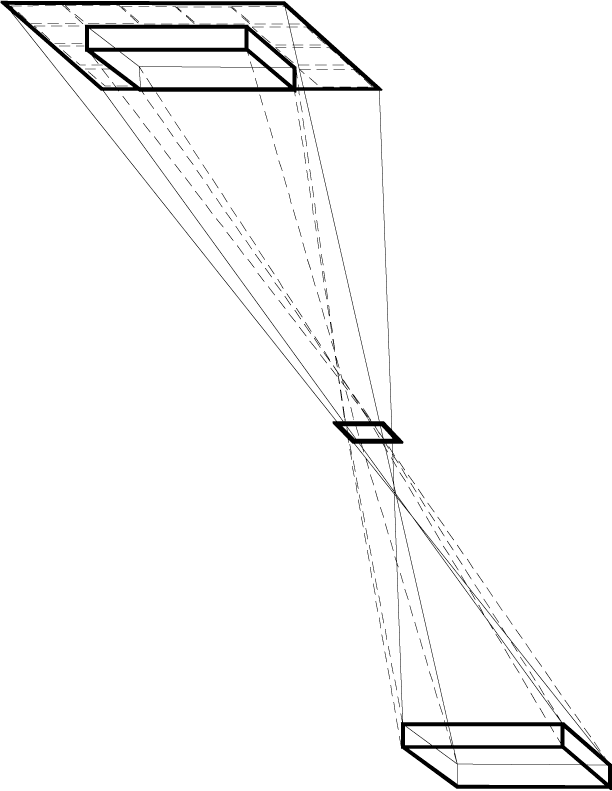
I [Kepler] set a book in a high place, which was to stand for a lu-
minous body. Between this and the pavement a tablet with a polyg-
onal hole was set up. Próximo [ªgure 12], a thread was sent down from
one corner of the book through the hole to the pavement, falling
upon the pavement in such a way as to graze the edges of the hole,
the image of which I traced with chalk. In this way a ªgure was
created upon the pavement similar to the hole.
The same thing occurred when an additional thread was added
from the second [ªgure 13], tercero, and fourth corners of the book,
as well as from the inªnite points of the edges. In this way, a nar-
row row of inªnite ªgures of the hole outlined the large quadrangu-
lar ªgure of the book on the pavement. It was thus obvious that
this was in agreement with the demonstration of the problem, eso
the round shape is not that of the visual ray but of the sun itself,
not because this is the most perfect shape, but because this is gen-
erally the shape of a luminous body. (Donahue 2000, pag. 56; KGW
2: pag. 47)
Kepler established the geometrical relations between the object and its
image by physically following with a thread the path of a ray. He realized
that there were more variables to account for. Kepler writes (ªgure 14),
If an window [oh] could be a mathematical point [punctum
mathematicum], the illumination of the squarely interposed wall
[FGH] would precisely assume the shape of the illuminating sur-
rostro [NPQ], but inverted; and the ratio of the diameters of the lu-
minous surface and the illuminated wall would come out the same
11. For Alberti, see Spencer 1966, páginas. 68–69; Dürer 1532, páginas. 183–185; Lindberg
1976, pag. 186; Straker 1970, pag. 391. Daniello Barbaro (1514–1570) describes an instru-
ment used by Dürer as an aid for drawing perspective (1569, pag. 191).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
327
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 12. A ªgure, similar to the
shape of the hole, is created on the
pavement
Cifra 13. Inªnite
de
ªgures of the hole outlining the ªgure
of the book on the pavement
numbers
as that of the distance of each from the point of the window.
(Donahue 2000, pag. 60; KGW 2: pag. 51)
Whereas ancient and medieval natural philosophers had explained the
formation of pinhole image in terms of a double visual pyramid and a
point pinhole, Kepler dealt with the phenomenon in terms of pencils of
rays emanating from point sources on the object. He considered the ªnite
pinhole a collection of point-holes, which together projected inverted im-
ages of the shape of the luminous source. The pinhole diameter and the
distance at which the screen was to be placed were of great signiªcance for
Kepler’s argument (Donahue 2000, páginas. 68–69; KGW 2: páginas. 58–59). Él
ªrst established the geometrical basis for this analysis.
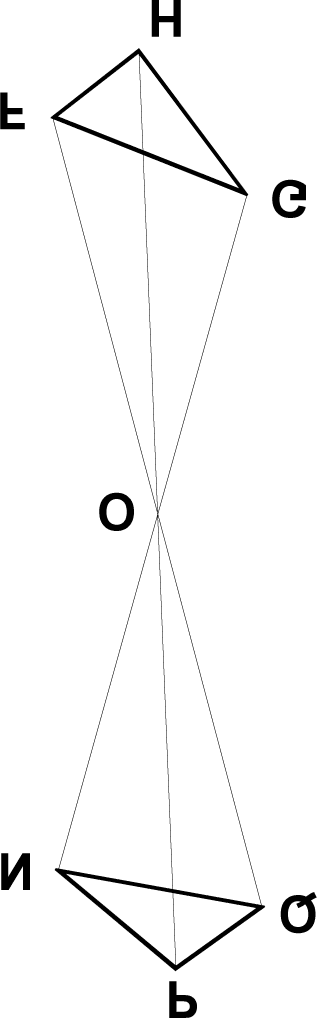
Let there be the straight line NEP [ªgure 15.1], divided into equal
parts at E, and let FOG be equidistant12 from it, likewise divided
into equal parts at O. Let the straight lines PO, EF be drawn until
they meet at K. In the same way, let EO and NF or PG be drawn
until they meet at I, and let K and I be joined. I say that KI is equi-
12. Donahue translates the Latin term, aequidistare (and its cognates), as “equidistant.”
In scholastic mathematics aequidistare connotes “being parallel.” Hence, in this passage, todo
four instances of “equidistant” stand for “parallel.”
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
328
Kepler’s Optical Part of Astronomy
Cifra 14. The geometrical relations between the object and its image
distant from the bases NEP and FOG. For in the triangles NEI,
FOI, the angles NEI, FOI are equal, by Euclid I 29. The same is
true of ENI, OFI, and the angle at I is common. Por lo tanto, the tri-
angles have equal angles, and by Euclid VI 4 the sides are propor-
tional. Por lo tanto, as NE is to FO so is EI to OI. In the same way it
is proved in EPK and FOK that as EP is to FO, so is PK to OK. Pero
EP, EN are equal. Por lo tanto, as NE is to FO, so is PK to OK. Pero
previously EI was also to OI in the same ratio. Como resultado, as PK is
to OK so is EI to OI. And by Euclid V 5 as PO is to OK, so is EO to
OI, and alternately, as PO is to OE so is KO to OI. Más, EOP is
equal to its vertical angle IOK. Por lo tanto, by Euclid VI 6, the trian-
gle EOP, IOK have equal angles, and OKI or PKI is equal to OPE or
KPE. Como resultado, by Euclid I 28, EP and KI are equidistant. El
same is also true of EPK and EPI, which in contrast have a common
base but cut off equal equidistant portions of FG. The proposition
is therefore evident. (Donahue 2000, páginas. 63–64; KGW 2: pag. 54)
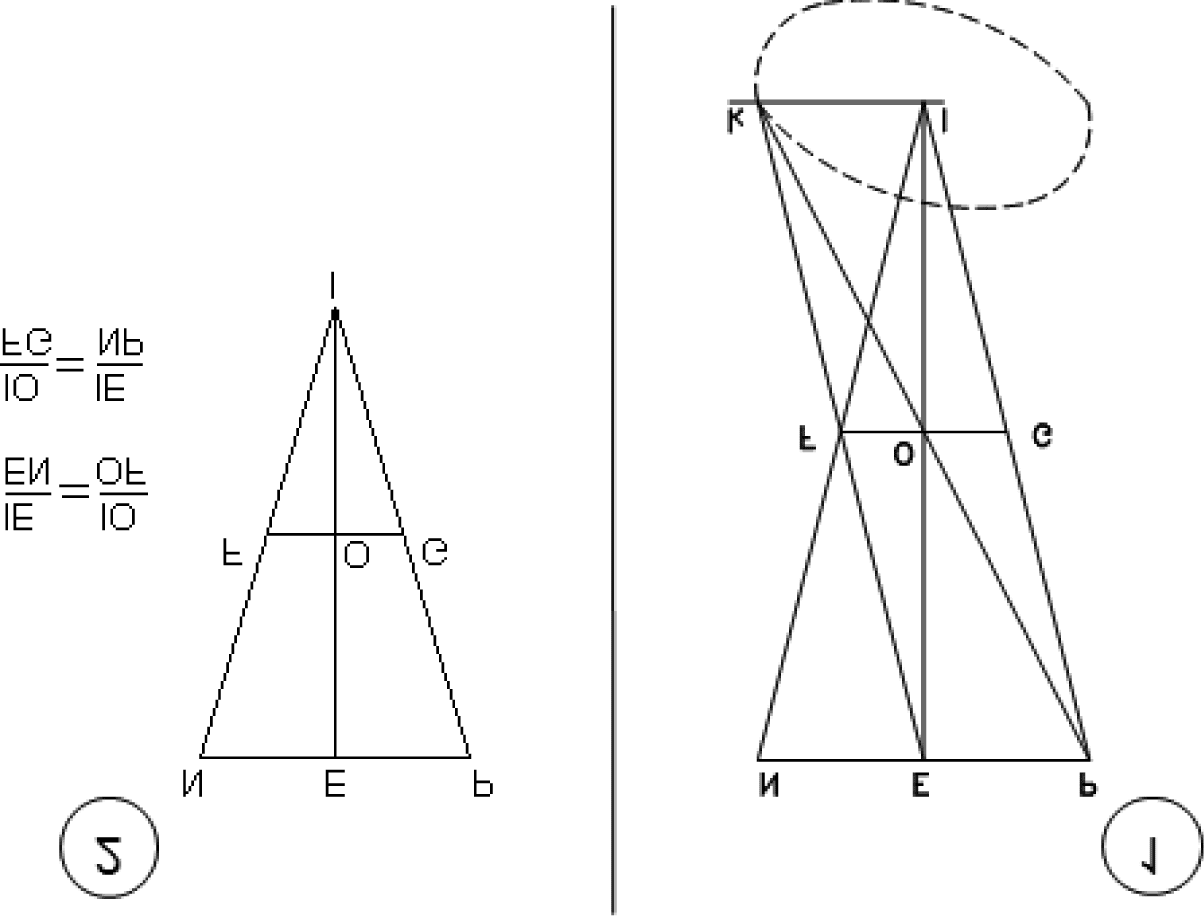
Kepler then proceeded to determine the point where the window should
be placed with respect to the luminous surface and the screen,
Let NEP be diameter of the luminous surface [ªgure 15.2], y
FOG be the diameter of the window [pinhole], equidistant from it
and lying perpendicularly below it, and let EO be the perpendicular
to the two. From N and P let straight lines be drawn through the
ends F and G, until they meet. Let the point of meeting be I. I say
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
329
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
Cifra 15. Image formation as a function of the distance between the pinhole
and the screen
that this is the required point. For since in triangle NIE, FO is
equidistant from the side NE, IE will be to EN as IO is to OF, con
the result that as IO (the distance of I from O) is to FG (twice OF,
which is the diameter of the window), so is IE (the distance of I
from the luminous surface E) to NP (twice NE and the diameter of
the luminous surface), which was to be accomplished. (Donahue
2000, pag. 64; KGW 2: páginas. 54–55)
The ratios EI/EN (cid:4) OI/OF, and OI/FG (cid:4) EI/NP (ªgure 15.2) facilitate
Kepler’s insight that the diameter of the pinhole must be less than the ap-
parent diameter of the luminous surface.
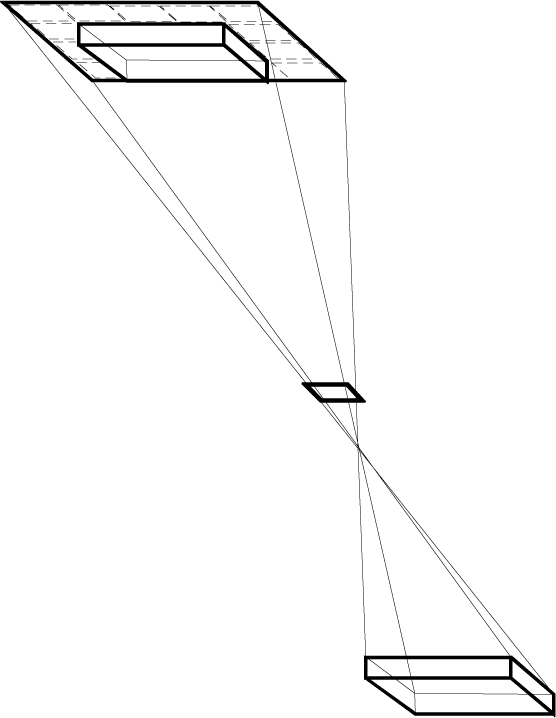
Kepler concluded that since the rays intersect at points K, L of surface I
(ªgure 16.2), KL is the common measure of both images, a saber, el en-
verted luminous object and the pinhole. As the screen is brought closer to
the pinhole, to point X (ªgure 16.1), the part MT represents the diameter
of the inverted image of the luminous object, and HV is the diameter of
the image of the pinhole. HV is greater than MT; it is the image of the
shape of the pinhole O. Entonces (ªgure 16.3), when the screen is moved far-
ther away from the pinhole, to point Y, the rays will intersect at points A,
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
330
Kepler’s Optical Part of Astronomy
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
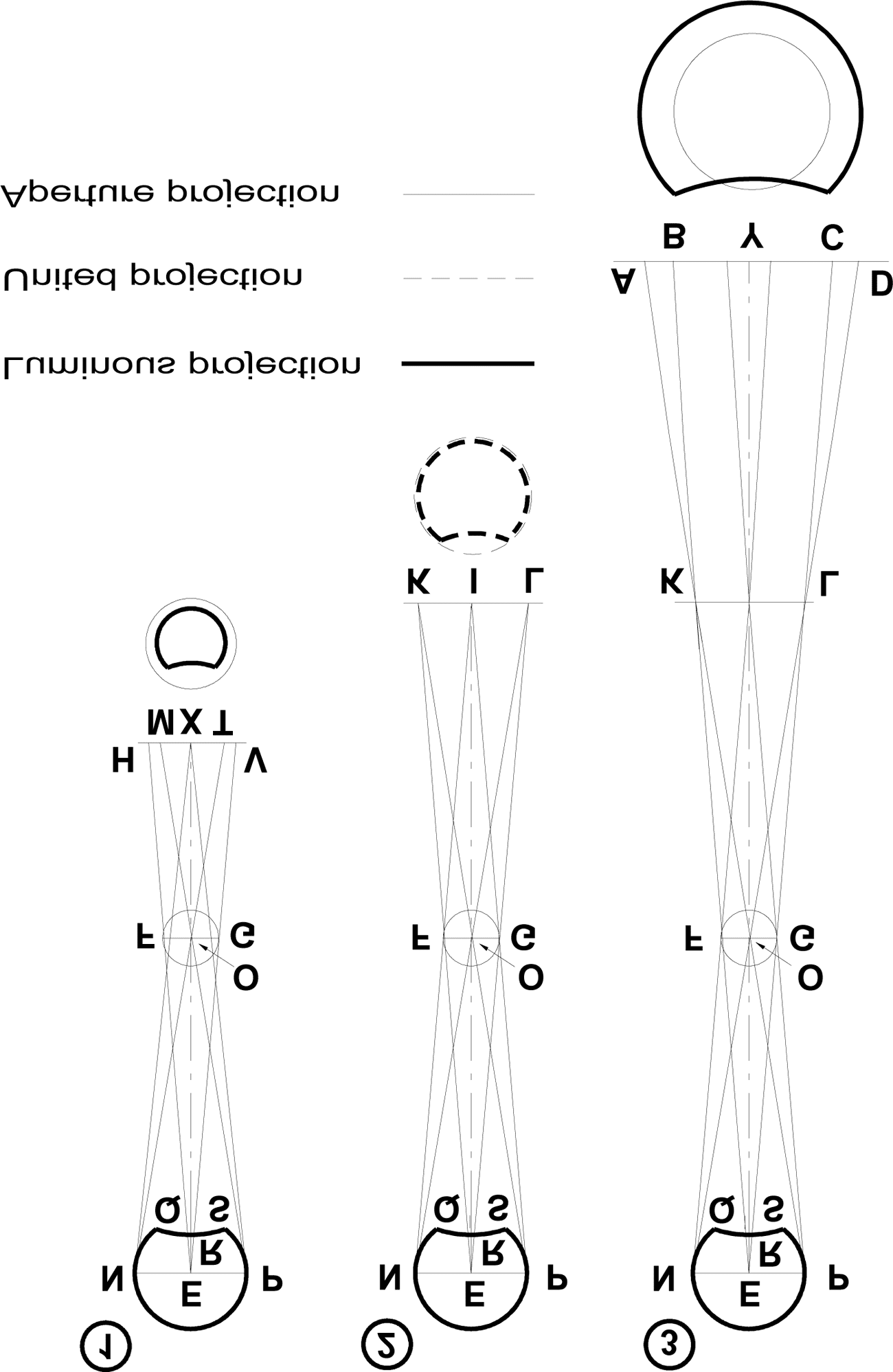
Cifra 16. The three domains of diffraction: (1) near-ªeld, (2) intermediary, y
(3) far-ªeld. The domain is determined by the distance of the screen from the pin-
agujero
B, C, D. Since the intersection of the rays already occurred at K and L
(ªgure 16.2), the rays that were on the inside are now on the outside at
points A, D. The image AD is the inverted image of the luminous object
and is greater than the diameter of the image BC that the pinhole projects
en la pantalla. AD takes the shape of the luminous object (Donahue 2000,
páginas. 65–67; KGW 2: páginas. 55–57).
It is instructive to recast Kepler’s analysis in current optical terminol-
ogia. We identify three domains, depending on the distance between the
pinhole and the screen. Cifra 16.2 presents a plane, KL, on which the
cast images of the Sun and that of the pinhole coincide. As shown earlier,
this plane for a given pinhole diameter (5.8 mm) and wavelength
(5500Å), would be at a distance corresponding to the Fresnel number 1;
Perspectives on Science
331
eso es, KL should be placed about 15.3 meter from the pinhole. This dis-
tance results in the best resolution for a pinhole imaging system, pero el
arrangement yields a dim, almost imperceptible image. Además, el
large distance is not practical and therefore not conducive to astronomical
usage. Cifra 16.3 shows a projection under the conditions of far-ªeld dif-
fraction. This arrangement is also impracticable because the image is faint
and the distance of the pinhole from the screen is too large for manipula-
ción. Cifra 16.1 presents an image under the conditions of near-ªeld dif-
fraction. The radius of the composite image HV is the sum of the radius of
the Sun’s image XM, plus the radius of the pinhole MH. The trade-off be-
tween the relatively short distance of the screen from the pinhole and a
large diameter of the pinhole yields discernable bright contrast of the cast
images so that accurate measurements could be taken.
How is the apparent diameter of the Sun calculated from the measured
imagen? Let AK (ªgure 17.1) be the radius of the projected image on the
pantalla, AB the radius of the pinhole, and KC, ID, EG, are equal to radius
AB. As shown in ªgure 17.1, the radius of the projected image AK in-
cludes both the image of the pinhole as well as the image of the Sun. El
radius of the combined image, AK, and the radius of the image of the Sun
sí mismo, AC, is shown in ªgure 17.1 y 17.2 respectivamente. Kepler then ex-
plains how to calculate the apparent diameter of the Sun: When the ra-
dius, AB, or CK, is subtracted from the radius of the image, AK, the re-
mainder will be, AC. The radius of the apparent Sun, AC, measured on
the screen, is then divided by the distance of the pinhole from the screen.
Kepler calculates the tangent of half the apparent angle of the Sun from
which he obtains the apparent diameter of the Sun (Donahue 2000,
pag. 351; KGW 2: pag. 291).
During an eclipse (ªgure 17.3), the image of the Sun is covered, fully or
parcialmente, by the image of the Moon. In order to measure the apparent di-
ameter of the eclipsed Sun one needs, according to Kepler, to draw a circle
from the center of the image of the Moon (ªgure 17.1), l, through points
h, B, and F. Entonces, add the radius of the pinhole, BA, to the radius of the
Moon, libra. Draw from the center of the Moon a circle D, A, C, con el
radius LA, representing the true body of the Moon. In the same way, sub-
tract from AG the radius of the pinhole, GE. Draw from the center A cir-
cle D, mi, C, with the radius, AE, representing the body of the Sun. Kepler
claimed that DECA is the image of the eclipsed Sun (Donahue 2000,
pag. 364; KGW 2: pag. 302).
Kepler put forward a reliable and accurate measurement procedure for
the investigation of the apparent sizes and distances of the Sun and Moon.
He established a geometrical framework within which he could analyze
the formation of pinhole images and execute two crucial calculations:
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
332
Kepler’s Optical Part of Astronomy
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 17. Kepler’s method for calculating the apparent diameter of the Sun
and Moon
(1) the apparent diameter of the Sun, y (2) the apparent diameter of the
Sun when eclipsed. Kepler sought a way to apply his new insights to im-
prove the accuracy of his novel instrument—the ecliptic instrument.
5. Kepler’s ecliptic instrument
As part of his reexamination of past claims, Kepler analyzed the astronom-
ical instruments of his predecessors and determined their limitations.13 It
was not enough for Kepler just to know how a projected image is cast be-
13. Among the scholars Kepler mentioned are: Hipparchus (190–120 BC), Ptolemy,
Proclus (410–485), Gemma Frisius (1508–1555), Federico Commandino (1509–1575),
Erasmus Reinhold (1511–1553), Giambattista Della Porta (1535–1615), Mästlin, y
Tycho. Kepler was familiar with Tycho’s book (1598): Astronomiae Instauratae Mechanica
(Donahue 2000, pag. 232; KGW 2: pag. 194). According to Kepler, Ptolemy’s observations
were never taken with accuracy better than 10 arc minutes, compared to the much more
accurate measurements of Tycho, accurate up to 3 arc minutes (Donahue 1992, páginas. 201
y 286; KGW 3: páginas. 120 y 177).
Perspectives on Science
333
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 18. Kepler’s ecliptic instrument (notice the horizontal positioning of the
crosspiece and the vertical possible orientation of the rule, as well as the panels on
the rule)
hind a pinhole; he realized the need to comprehend processes of deception
of sight, the working of the eye, and methods of observation. In his Parali-
pomena, capítulo 5, Kepler analyzed the deception of sight associated with
instruments and methods of observation. He further examined the opti-
cal structure of the eye and the geometrical principles of sight. He re-
marked, Por ejemplo, that without exception observers report that bright
images appear greater in proportion than those that are less bright; este
and other perceptual considerations had to be accounted for (Donahue
2000, páginas. 171–236; KGW 2: páginas. 143–197). He noted the importance of
technique and skill: proper aiming and alignment, ªrm support, clear
marking of the edges of the image, as well as accurately dividing the grad-
uation scale (Donahue 2000, páginas. 16, 56–57, 67–69, 157–158, 224–226,
229–236, 310–311, 319, 341, 352–353, 358–359, 362–363).
To avoid observational errors involved in old techniques, Kepler de-
signed an instrument for measuring the Sun’s angular position and appar-
ent diameter. In chapter 11 of his Paralipomena Kepler introduces an eclip-
tic instrument that consists of a solid wooden base (ªgure 18), cual
formed a right angled parallelogram in the place of the azimuthal circle.
The parallelogram supports a long rotating crosspiece beam with a slit in
the middle. The crosspiece holds in its slit an adjustable rule in the verti-
cal plane. The rule is set in such a way that it can be rotated as well as
raised towards the zenith or lowered towards the horizon, as much as the
altitude of the Sun at the beginning and the end of an eclipse requires.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
334
Kepler’s Optical Part of Astronomy
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 19. Application of the volvelle and the rotating pointer
This construction is in effect a quadrant for positional astronomy. Kep-
ler, sin embargo, did not furnish his ecliptic instrument with transverse grad-
uated scales. Instead of measuring degrees, he rather preferred to measure
length on three different linear scales: the azimutal quadrant, the cross-
piece, and the rule. On the basis of these measurements Kepler carried out
a series of trigonometric calculations in order to determine the position of
the luminary in question (Donahue 2000, páginas. 348, 381–382, 424–429;
KGW 2: páginas. 290, 319, 357–363; see also KGW 21, 1: pag. 244).
The rule carries two perpendicular panels parallel to each other. El
outer panel has a pinhole while the inner panel is a movable screen on
whose upward facing surface a graduated circle, as great as the width of
the panel allows, is inscribed (ªgure 19). The center of the panel is
equipped with a volvelle mounted with a rotating disk where the outline
of the image is drawn and measured.14 The space between the panels must
be covered with a tube which is black on the inside, so that no light may
enter except through the pinhole in the front panel. Kepler gives an ac-
count of the physical properties of the instrument he used in the context
of discussing the observations made in June and July 1600 and December
1601. The distance between the panels was 12 pies, divided into 10368
14. A volvelle is a medieval device consisting of concentric rotating graduated disks,
used to compute the phases of the Moon and its position in relation to the Sun (Donahue
2000, páginas. 347–350; KGW 2: páginas. 288–289).
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
335
units, and the diameter of the pinhole, perforated in a very thin sheet of
bronze, era 16.5 units (Donahue 2000, páginas. 350, 352, 367, 369; KGW 2:
páginas. 290, 292, 304–305, 306–307).15 For every screen distance there is
then an optimal pinhole diameter, which produces the sharpest possible
imagen.
Because of the difªculty in marking points and drawing the cast image
on the graduated screen (ªgure 19), Kepler attached to the volvelle a spe-
cial pointer made of solid wooden parts in such a way that it did not cover
the diameter of its graduated circle divided into digits. Above the solid
pointer he placed a transverse rule which could rotate perpendicularly to
the pointer and to the marked diameter. Kepler made a groove in the
transverse rule equal in its depth to the thickness of the wood of the
pointer, and attached the transverse rule to the wooden piece so that one
could move it back and forth along the groove. When the instrument is
oriented to the Sun, the pointer with the volvelle could be rotated on its
axle, and the transverse rule moved along the pointer, until the sharp edge
of a marker, placed on the transverse rule, comes into contact with both
marginal edges of the image. Kepler marks points where the sharp edge of
the transverse rule, placed on the pointer, cuts the diameter of the image.
The locations where the interior circumference of the image, or the Moon’s
shadow, cuts the same diameter are also marked, so Kepler could draw ac-
curately the circumference of the image of the eclipsed Sun (Donahue
2000, páginas. 364–365; KGW 2: páginas. 302–303).
The points inscribed on a paper attached to the screen, sometimes
marked with a grid, facilitate the drawing of the circumference of the cast
images and to calculate the apparent diameters for both the Sun or the
Moon. Kepler describes how to obtain the true image of the eclipsed Sun:
Let CDEF [ªgure 20] be the image of eclipsed ray, whose center is
GRAMO, the marked diameter DF, and with it, the line of pointer IDH
[line AA(cid:2) in ªgure 19]. And let there be the line CHE [as shown in
ªgure 20, CHE corresponds to the transverse rule on which the
marker is placed] touching the obtuse horns C, mi, and cutting the
marked diameter at H; and let the segment CFE cut the same di-
ameter at F. Próximo, let the radius of the opening be extended on the
diameter DH, and let this be DL, from D to L, as well as from F to
M and from H to P, and through P let the straight line NPO be
perpendicular to the diameter and equidistant from the rule. Entonces,
with center G and radius GL let the circle NLO be drawn, cual
will represent the true image of the sun, as in 9 of this chapter.
15. The length of the rule equals to 3658 mm and the diameter of the pinhole is about
5.8 mm.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
336
Kepler’s Optical Part of Astronomy
Cifra 20. Drawing the circumference of the eclipsed Sun
This will cut the line NPO: let it cut at N, oh. Próximo, through the
three points N, METRO, oh, let a circle be described, and let its center be
k. (Donahue 2000, páginas. 365–366; KGW 2: páginas. 303–304)
Kepler concludes that the circumference, NLOM, delineates the true im-
age of the eclipsed Sun. He writes,
Let the perpendicular NC, OE be drawn [ªgure 20]. So, since NC,
OE are perpendicular to the same CE, they will be equidistant.
And because DK, eso es, PH, is also perpendicular to the same CE,
from the structure of the instrument, por lo tanto, CAROLINA DEL NORTE, PH, OE will
be equal. But PH is the radius of the opening. Por lo tanto, NC and
OE are also. But since, por 10 of Chapter 2, the small circle of the
opening is also drawn around the points of the ends of the horns,
and since CHE is tangent to those small circles (for they are the ob-
tuse horns of the ray), it is necessary that NO be those points of the
end of the horns. For from any point of the circumference NLO
above N or O, a longer line would be dropped, and from others be-
low N, oh, a shorter line, than NC, OE, the radius of the hole in the
opening. Por lo tanto, if N, oh, are the points of the horns, the circle
of the moon cuts the solar circle there. But M is also on the moon’s
circle, as in 9. Por lo tanto, NMO is the moon’s circle. And NLO is
the sun’s. Por lo tanto, the true image is NLOM. (Donahue 2000,
pag. 366; KGW 2: pag. 304)
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
337
Kepler’s method for measuring the apparent diameter of both the Sun
and the Moon is formulated in the following argument (ªgure 20). El
image of the eclipsed Sun, projected onto a screen through a point-hole
(punctum mathematicum), casts a ªgure, NLOM; since the shape of the pin-
hole is also cast onto the screen, the image of the Sun is increased by the
radius of the pinhole, DL, to form the composite ªgure, CDEF. Mientras
the projected image of the Sun is increased, the image of the Moon, sobre el
pantalla (NMO), is decreased by the same amount: the radius of the pinhole,
eso es, MF. There arises, por lo tanto, the need to take account of the size of
the pinhole and to make the appropriate correction when calculating the
apparent diameters of the Sun and the Moon during a solar eclipse.
To maximize the performance of the ecliptic instrument, in terms of
contrast and brightness of the cast image, the diameter of the pinhole
needs to be adjusted. Por un lado, if the pinhole were to be too small,
the eyes dazzled by the brightness of daylight would have to be held in
place for a long time before they may see the faint image projected in an
abundance of light. Por otro lado, if the pinhole were to be enlarged
the image would be much brighter and more distinct than with a smaller
pinhole, but at the same time it would be proportionally coarser and
blurred. Kepler opted for an optimal solution: the pinhole should be of an
intermediate size. He instructed further that it is helpful to place a cover,
like a brow, on the outside, above the upper pinhole to keep “the sky or
the air” (eso es, stray light) from falling on the screen (where the image is
depicted) with bright light (Donahue 2000, páginas. 68–69; KGW 2: páginas. 58–
59). In order to minimize observational errors, Kepler also emphasized the
need to repeat the measurements of the diameter of the image carefully,
because unsteadiness will hinder you, with half of what you took
with the compass [circino], from the center of the panel (which takes
the place of the wall), draw a circle, and one slightly smaller than
eso, and again one slightly larger, as many times as you think nec-
essary. Then investigate again which of the described circles the ray
[imagen] es igual. (Donahue 2000, pag. 351; KGW 2: pag. 291)
The radiation of a luminous object is a right cone whose vertex is at the
pinhole. The screen must be positioned perpendicular to the source of ra-
diation, so that the projected image would be of a circular shape and not
skewed (Donahue 2000, páginas. 67–69, 362; KGW 2: páginas. 57–59, 300–301).
De este modo, by drawing a circle on the screen and adjusting the instrument in
such a way that the edge of the image should coincide everywhere with
the circumference of the drawn circle, one could ascertain that the screen
is indeed perpendicular to the cone of radiation. It is reasonable to expect
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
338
Kepler’s Optical Part of Astronomy
Cifra 21. Photo of the image the Sun cast by a pinhole, 4.9 mm in diameter,
placed 3050 mm from the screen, and the set of calculation by which the apparent
diameter is determined.
that all the measured diameters of the Sun’s images should be of the same
tamaño, as they are cast by the same source, a saber, the Sun. But this consid-
eration is idealized; in reality the results differ from each other, albeit by a
small degree due to variations in marking the edges of the image.
Kepler sought to calculate the value of the apparent diameter of the
Sun resulting from as many measurements as possible. In the case of the
Moon, in addition to the measure taken on the screen, Kepler estimated
its apparent diameter by a comparison with disks of various sizes which
match the interior circumference of the Moon’s image. Kepler’s calcula-
tions of the apparent diameters of the Sun and the Moon yielded, sin embargo,
slightly different results from each other. He therefore considered the
mean of his calculations as the true apparent diameter of the Sun and
Moon. Kepler’s example of how the distance of the centers of the images at
the beginning and end of eclipse is calculated suggests that he applied a
procedure based on arithmetic mean to obtain the apparent diameter of
the Sun and Moon (Donahue 2000, páginas. 366–368, 426–428; KGW 2:
páginas. 304–306, 361–362).
What is the quality of Kepler’s results? In ªgure 21 we can see the im-
age of the Sun cast by a pinhole 4.9 mm in diameter placed 3050 mm
from the screen. The measured diameter of the image is 32.44 mm which
yields a solar apparent diameter of 36(cid:2) 33.83(cid:3). By Kepler’s method, sub-
tracting the diameter of the pinhole from the measured diameter of the
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
339
Cifra 22. Photo of the cast image of the Sun projected through a pinhole of 3
mm in diameter
image gives 27.54 mm. The apparent diameter of the Sun, en este caso,
would be 31(cid:2) 2.46(cid:3).16
We evaluated the performance of a pinhole camera, with a pinhole of 3
mm in diameter placed 1931 mm from the screen.17 Sequential measure-
ments of the Sun’s image (ªgure 22) were taken with a compass directly
on the camera’s screen and on printed photos as well. The mean apparent
diameter of the Sun, measured and calculated similarly to what Kepler
did, era 30(cid:2) 17.7(cid:3). We found that the difference between the extremes of
twenty measurements of the cast image varies less than 2%.
Kepler’s technique yielded a solar apparent diameter of 30(cid:2) at apogee
y 31(cid:2) at perigee (Donahue 2000, pag. 354; KGW 2: pag. 294). As shown
earlier, the diminution of the Sun’s image projected through a 5.8 mm
pinhole is about 4%. Consider the apparent diameter of the Sun at apogee,
31(cid:2) 30(cid:3), and at perigee, 32(cid:2) 30(cid:3), the results of Kepler’s measurements
should have been 30(cid:2) 14(cid:3) y 31(cid:2) 12(cid:3), respectivamente. The differences be-
tween Kepler’s report of the apparent diameter of the Sun and our calcula-
tions is less than 1%. By comparison, according to Kepler, the measure-
16. The photo of the projected image of the Sun was taken on December 24, 2005. En
el tiempo, the true apparent diameter of the Sun was 32(cid:2) 31(cid:3).
17. The pinhole camera was mounted on a telescope at the Harry Kay Observatory
(32° 26(cid:2) norte; 34° 13(cid:2) mi) on September 19, 2007. En el momento, the true apparent diameter of
the Sun was 31(cid:2) 50.52(cid:3). The measurements and photos were made when the Sun reached
the highest point in the sky; eso es, cerca de 60 degrees above the horizon.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
340
Kepler’s Optical Part of Astronomy
ments of the Sun’s apparent diameter made by Tycho, eran 29(cid:2) 36(cid:3) en
apogee and 31(cid:2) 45(cid:3) at perigee (Donahue 2000, pag. 354; KGW 2: pag. 293).
We conclude that for an experienced observer, the ecliptic instrument as
described and operated by Kepler can produce consistent, confiable, and ac-
curate results.18
Kepler was well aware of the discrepancies among the reports of his
predecessors of the apparent diameters of the Sun and Moon. According to
Kepler, these discrepancies were caused partly by different observer’s eyes,
partly by different light conditions, and partly by the difference in optical
sights, which made the traditional procedures of observation using instru-
ments untrustworthy (Donahue 2000, páginas. 231–232; KGW 2: páginas. 193–
194).19 To be sure, Kepler was aware of the limitations of his instrument.
Sin embargo, the technique of aiming the ecliptic instrument accurately and
measuring the diameter of the image on the screen, as well as the method
of taking readings on three different linear scales (on the azimutal quad-
rant, on the crosspiece, and on the rule), made Kepler’s ecliptic instrument
the most accurate astronomical device of its kind in the early years of the
17th century (Donahue 2000, páginas. 358–359, 381–382, 423–429; KGW 2:
páginas. 297–298, 319, 356–362).
18. Sigismondi and Fraschetti (2001) presented an analysis of ªve measurements of the
solar diameter made with a pinhole camera by Tycho (1591) and Kepler (1601–1602). El
authors reproduced the measurements with a pinhole diameter of 6 mm. They located a
plane mirror before the pinhole in order to orient the light horizontally, and to obtain a fo-
cal length, F(Focal length) ≥ 20 meter, which is well within the domain of far-ªeld diffraction.
The authors then surmised that, due to the diurnal motion of the Sun, Kepler’s method
could achieve no better accuracy than about 15 arc-seconds. They applied modern error
analysis to Tycho’s and Kepler’s data, and concluded that the seasonal variation of the ap-
parent solar diameter with a mean solar diameter of 1924(cid:3) (cid:9) 35(cid:3) en 95% conªdence level
is consistent with the actual mean solar diameter; eso es, the pinhole camera is trustwor-
thy. The authors claimed that Kepler’s report of the smaller apparent diameters of the Sun,
30(cid:2) at apogee and 31(cid:2) at perigee, “is consistent with all the measurements made with pin-
hole that . . . [Kepler] examined, and also with the actual values of 31.5(cid:2) y 32.5(cid:2) once
the systematic ‘geometrical correction’ is taken into account” (2001, 385). Principally,
Tycho’s and Kepler’s pinhole cameras worked within the domain of near-ªeld diffraction
which affects the results of the measurements differently than the way it was considered by
Sigismondi and Fraschetti. Based on far-ªeld considerations, the authors missed the fact
that a cast image, in near-ªeld conditions, is reduced by about 4%. De este modo, the small appar-
ent diameters of the Sun, 30(cid:2) at apogee and 31(cid:2) at perigee, as reported by Kepler, is due to
the diminution of the projected image, rather than to “systematic geometrical correction”
which the authors claimed that Kepler had introduced into his calculations.
19. On the operational limits and accuracy of astronomical instruments of the time, ver
Chapman 1983; Roche 1981; Wesley 1979; Wesley 1978; and Thoren 1973, páginas. 29–30,
40–42.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
341
6. Conclusión
We revisited Kepler’s study of the pinhole camera. Astronomical interest
motivated Kepler’s optical researches; his awareness of the problem of ob-
servational error informed the method and scope of these studies (Hon
1987). The measurements of the diameters of the Sun and the Moon when
the images of these heavenly bodies are cast on a screen involved large er-
rors. Kepler, por lo tanto, endeavored ªrst to gain a better understanding of
the optical causes of the phenomenon of casting image and then to design
a procedure for measuring the apparent diameter of what he called the lu-
minaries, the Sun and the Moon.
To have a better understanding of the argument which Kepler devel-
oped, we recalled how in modern terms an image is formed behind a pin-
agujero. We simulated and analyzed optical phenomena related to the work-
ing of the pinhole camera. With the knowledge of the operational limits
and optical performance of the instrument, we can now explain the dimi-
nution suffered by an image projected by a pinhole system working at the
domain of near-ªeld diffraction; we calculated that the diminution is
acerca de 4% of the true apparent diameter of the Sun.
Además, we discussed Kepler’s theoretical insights and their appli-
cations in turning the pinhole camera into an astronomical instrument, como
presented in chapter 11 of Kepler’s Paralipomena. We followed Kepler
identifying the sources of observational errors, seeking a solution, devel-
oping an experimental setup to test his argument, and ªnally putting for-
ward an optical theory. Kepler thus established a geometrical framework
within which he could manipulate and analyze the formation of pinhole
images and execute two crucial calculations: (1) the apparent diameter of
the Sun, y (2) the apparent diameter of the Sun when eclipsed.
To avoid the observational errors that had plagued the antiquated mea-
suring techniques for calculating the apparent diameter and angular posi-
tion of the luminaries, Kepler designed a novel device: an ecliptic instru-
mento. The rule in this instrument is equipped with a pinhole camera
which substitutes the traditional aiming device of slits-sight. The pro-
jected image on the screen of the camera has now two functions: (1) el
shape of the image is used as a sensitive indicator for accurately aligning
the rule with the Sun—the closer the shape of the image is to a circle, el
better is the alignment; y (2) the cast image can be measured for
the apparent diameter of the luminaries. He then carried out a series of
calculations—based on the theory that he had developed—to determine
the position and apparent diameter of the luminary in question. este profesional-
cedure improved signiªcantly the accuracy of the results.
We made astronomical observations with a modern replication of the
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
342
Kepler’s Optical Part of Astronomy
pinhole camera, following closely Kepler’s instructions, took measure-
ments and calculated the apparent diameter of the Sun according to the
method Kepler had developed. We conªrmed that Kepler’s observations
and calculations of the apparent diameter of the Sun, which were 30(cid:2) en
apogee and 31(cid:2) at perigee due to the diminution of the pinhole image, son
accurate within the operational limits of the pinhole camera he had used.
We conclude, entonces, that for an experienced observer a pinhole camera, como
described and operated by Kepler, could produce consistent, confiable, y
accurate results of the apparent diameters of the luminaries.
This close study of Kepler’s theoretical insights into an optical appar-
atus, a saber, the pinhole camera, and its combination with the quad-
rant to form the ecliptic instrument, sheds light on the role optical in-
struments play in Kepler’s scheme: they impose constraints on theory, pero
at the same time render astronomical knowledge secure. To get a com-
prehensive grasp of Kepler’s astonishing achievements it is required to
widen the approach to his writings and examine his practice not only as a
mathematico-physical astronomer, but also as an instrument maker and a
practicing observer.
Referencias
Aiton, Eric J., Alistair M. Duncan, and Judith V. Field. Trans. 1997. Kep-
ler: The Harmony of the World. Memoirs of the American Philosophical
Sociedad, 209. Filadelfia: American Philosophical Society.
Applebaum, Wilbur. 1996. “Keplerian Astronomy after Kepler: Re-
searches and Problems.” History of Science 34: 451–504.
Barbaro, Daniello. 1569. La Pratica Della Perspettiva. Venice: Appersso
Camillo.
Pregonero, Peter, and Bernard R. Goldstein. 1994. “Distance and Velocity in
Kepler’s Astronomy.” Annals of Science 51: 59–73.
———. 2001. “Theological Foundations of Kepler’s Astronomy.” Osiris
16: 88–113.
Beer, Arthur, and Peter Beer. Editors. 1975. Kepler, Four Hundred Years.
Proceedings of conferences held in honor of Johannes Kepler. Nuevo
york: Prensa de Pérgamo.
Brahe, Tycho. 1598. Astronomiae Instauratae Mechanica. Wandesburgi.
Caspar, Max et al. Editors. 1937–. Johannes Kepler Gesammelte Werke
[KGW], 21 vols. München: C. h. Beck’sche Verlagsbuchhandlung.
Chapman, Allan. 1983. “A Study of the Accuracy of Scale Graduations on
a Group of European Astrolabes.” Annals of Science 40: 473–488.
Donahue, William H. 1992. Trans. Johannes Kepler: New Astronomy. Nuevo
México: Green Lion Press.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
343
———. 1996. “Kepler’s Approach to the Oval of 1602, From the Mars
Notebook.” Journal for the History of Astronomy 27: 281–295.
———. 2000. Trans. Johannes Kepler: Paralipomena to Witelo whereby The
Optical Part of Astronomy is Treated. New Mexico: Green Lion Press.
Duncan, Alistair M.
1999. Trans.
Johannes Kepler: Mysterium
Cosmographicum. Nueva York: Abaris Books.
Dürer, Albrecht. 1532. Institutiones Geometricae. París: Apud Christianum
Wechelum.
Field, Judith V. 1988. Kepler’s Geometrical Cosmology. chicago: Universidad
of Chicago Press.
Goldstein, Bernard R. 1985. The Astronomy of Levi ben Gerson. Nueva York:
Saltador.
Goldstein, Bernard R., and Giora Hon. 2005. “Kepler’s move from orbs to
orbits: documenting a revolutionary scientiªc concept.” Perspectives on
Ciencia 13: 74–111.
Hecht, Eugene. 1990. Optics. Menlo Park, California: Addison-Wesley.
Hon, Giora. 1987. “On Kepler’s Awareness of the Problem of Experimen-
tal Error.” Annals of Science 44: 545–591.
———. 2004. “Putting Error To (Histórico) Work: Error as a Tell-tale in
the Studies of Kepler and Galileo.” Centaurus 46: 58–81.
Hon, Giora, and Yaakov Zik. 2007. “Geometry of Light and Shadow:
Francesco Maurolyco (1494–1575) and the Pinhole Camera.” Annals of
Ciencia 64: 549–578.
Ilardi, Vincent. 2007. Renaissance Vision from Spectacles to Telescope. Philadel-
phia: American Philosophical Society.
Kepler, Johannes. (1572–) 2002. Manuscripta Astronomica (III). See KGW
21.1: páginas. 11–345.
———. (1596) 1993–. Mysterium Cosmographicum. See KGW 1: páginas. 4–80;
Duncan 1999.
———. (1604) 1939–. Ad Vitellionem Paralipomena, Quibus Astronomiae
Pars Optica traditur. See KGW 2: páginas. 6–391; Donahue 2000.
———.
(1609) 1990–. Astronomia Nova. See KGW 3: páginas. 5–424;
Donahue 1992.
———. (1619) 1940. Harmonices Mundi. See KGW 6: páginas. 8–377; Aiton
et al. 1997.
KGW. See Caspar et al. 1937–.
Kozhamthadam, Job. 1994. The Discovery of Kepler’s Laws: The Interaction of
Ciencia, Philosophy, and Religion. Indiana: University of Notre Dame
Prensa.
Lefèvre, Wolfgang. Editor. 2007. Inside the Camera Obscura—Optics and Art
Under the Spell of the Projected Image. Berlina: Max Planck Institute for the
History of Science (Preprint 333).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
344
Kepler’s Optical Part of Astronomy
Lindberg, David C.. 1968. “The Theory of Pinhole Images from Antiquity
to the Thirteenth Century.” Archive for History of Exact Sciences 5: 154–
176.
———. 1970. “The Theory of Pinhole Images in the Fourteenth Cen-
tury.” Archive for History of Exact Sciences 6: 299–325.
———. 1976. Theories of Vision from Al-Kindi to Kepler. chicago: universidad-
sity of Chicago Press.
———. 1984. “Optics in Sixteenth Century Italy.” Pp. 131–148, in P.
Galluzzi et al. Editors. Novità celecti e crisi dels saper: Atti del convegno
internazionale di studi Galileiani. Florencia: Giunti Barbèra.
———. 1986. “The Genesis of Kepler’s Theory of Light: Light
Metaphysics from Plotinus to Kepler.” Osiris 2: 5–42.
Lindberg, David C., and Geoffrey Cantor. 1985. The Discourse of Light from
the Middle Ages to the Enlightenment. Los Angeles: University of Califor-
nia.
Mancha, José L. 1989. “Egidius of Baisiu’s Theory of Pinhole Images. Ar-
chive for History of Exact Sciences 40: 1–35.
Martens, Rhonda. 2000. Kepler’s Philosophy and the New Astronomy. Príncipe-
tonelada: Prensa de la Universidad de Princeton.
Roche, John. 1981. “The Radius Astronomicus in England.” Annals of Sci-
ence 38: 1–32.
rosa, Eduardo. 1986. Three Imperial Mathematicians: Kepler Trapped Between
Tycho Brahe and Ursus. Nueva York: Abaris.
Sigismondi, Costantino, and Federico Fraschetti. 2001. “Measurements of
the Solar Diameter in Kepler’s Time.” The Observatory 121: 380–385.
Herrero, Warren. j. 1990. Modern Optical Engineering. 2nd edition. Nuevo
york: McGraw-Hill.
Spencer, John R. 1966. Trans. Alberti: On Painting. nuevo refugio: Yale Uni-
versity Press.
Stephenson, bruce. 1987. Kepler’s Physical Astronomy. Nueva York: Saltador.
Straker, esteban. 1970. Kepler’s optics. Doctor. tesis. Indiana: Indiana Uni-
versity Press.
———. 1981. “Kepler, Tycho, and the Optical Part of Astronomy: el
Genesis of Kepler’s Theory of Pinhole Images.” Archive for History of Ex-
act Sciences 24: 267–293.
Thoren, Victor E. 1973. “New Light on Tycho’s Instruments.” Journal for
the History of Astronomy 4: 25–45.
Thro, Broydrick E. 1994. “Leonardo da Vinci’s Solution to the Problem of
the Pinhole Camera.” Archive for History of Exact Sciences 48: 343–371.
———. 1996. “Leonardo’s Early Works on the Pinhole Camera: The As-
tronomical Heritage of Levi Ben Gerson.” Achademia Leonardi Vinci 9:
20–54.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Perspectives on Science
345
Voelkel, James R. 2001. The Composition of Kepler’s Astronomia Nova.
Princeton: Prensa de la Universidad de Princeton.
Wesley, Walter G. 1978. “The Accuracy of Tycho Brahe’s Instruments.”
Journal for the History of Astronomy 9: 42–53.
———. 1979. “Tycho Brahe’s Solar Observations.” Journal for the History
of Astronomy 10: 96–101.
Joven, Mate. 1989. “The Pinhole Camera: Imaging Without Lenses or
Mirrors.” The Physics Teacher 27: 648–655.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
pag
oh
s
C
/
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
7
3
3
0
7
1
7
8
9
5
8
3
pag
oh
s
C
.
2
0
0
9
1
7
3
3
0
7
pag
d
.
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3