Self-Replication in
Neural Networks
Thomas Gabor∗
LMU Munich
thomas.gabor@ifi.lmu.de
Abstract A key element of biological structures is self-replication.
Neural networks are the prime structure used for the emergent
construction of complex behavior in computers. We analyze how
various network types lend themselves to self-replication.
Backpropagation turns out to be the natural way to navigate the
space of network weights and allows non-trivial self-replicators to
arise naturally. We perform an in-depth analysis to show the
self-replicators’ robustness to noise. We then introduce artificial
chemistry environments consisting of several neural networks and
examine their emergent behavior. In extension to this work’s
previous version (Gabor et al., 2019), we provide an extensive
analysis of the occurrence of fixpoint weight configurations within
the weight space and an approximation of their respective
attractor basins.
Steffen Illium
LMU Munich
Maximilian Zorn
LMU Munich
Cristian Lenta
LMU Munich
Andy Mattausch
LMU Munich
Lenz Belzner
Technische Hochschule Ingolstadt
Claudia Linnhoff-Popien
LMU Munich
Keywords
Neural network, self-replication, artificial
chemistry system, soup, weight space
1 introduzione
Dawkins (1976) stressed the importance of self-replication to the origin of life. He argued that
proto-RNA was able to copy its molecule structure within a soup of randomly interacting elements.
This allowed it to reach a stability in concentration that could not be maintained by any other kind
of structure. As the story goes, life evolved more or less as an elaborate means to maintain the
copying of structural information.
Since the early days of computing, the recreation of biological structures has been a target of
research, starting from the early formulation of an evolutionary process by Turing (1950) and in-
cluding famous examples like Box (1957), Gardner (1970), or Dorigo and Di Caro (1999). Also
see the overviews given by Koza (1994) or Bäck et al. (1997). Although also conceived very early,
(Minsky & Papert, 1972; Rosenblatt, 1958), neural networks have only rather recently found broad
practical application for advanced tasks like image recognition (Krizhevsky et al., 2012), speech
recognition (Hinton et al., 2012), or strategic game playing (Silver et al., 2017). The variety of uses
shows that neural networks are a powerful tool of abstraction for various domains. Tuttavia, In
* Corresponding author.
© 2022 Massachusetts Institute of Technology Artificial Life 28: 205–223 (2022) https://doi.org/10.1162/artl_a_00359
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
8
2
2
0
5
2
0
3
2
7
7
7
UN
R
T
l
/
_
UN
_
0
0
3
5
9
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
T. Gabor et al.
Self-Replication in Neural Networks
all these cases neural networks are used with a certain intent, cioè., equipped with an extrinsic goal
function. Through backpropagation, the distance of the network’s output to the goal function can
be systematically minimized, making the network match the goal to an increasing extent.
The wide variety of application domains shows the power of neural networks as a functional ab-
straction. For other functional abstractions, such as expressions in the λ-calculus (Church, 1932)
or a variety of assembler-like instruction sets and automata (Dittrich et al., 2001; Görnerup &
Crutchfield, 2008), it is known that, when a population of random instances of said functional
abstractions is set up and allowed to interact, self-replicators arise naturally (see Fontana & Buss,
1996, or Dittrich & Banzhaf, 1998, rispettivamente). For neural networks, Chang and Lipson (2018)
have shown that self-application (cioè., constructing new neural networks by applying neural networks
to other neural networks) may lead to the formation of a self-replicating structure, albeit a rather
trivial instance of one. In questo articolo, we (UN) repeat these results for a broader range of neural network
architectures and (B) extend the interaction model by the notion of self-training, which yields lots of
non-trivial fixpoints. We then (C) subject these fixpoints to various degrees of noise and analyze their
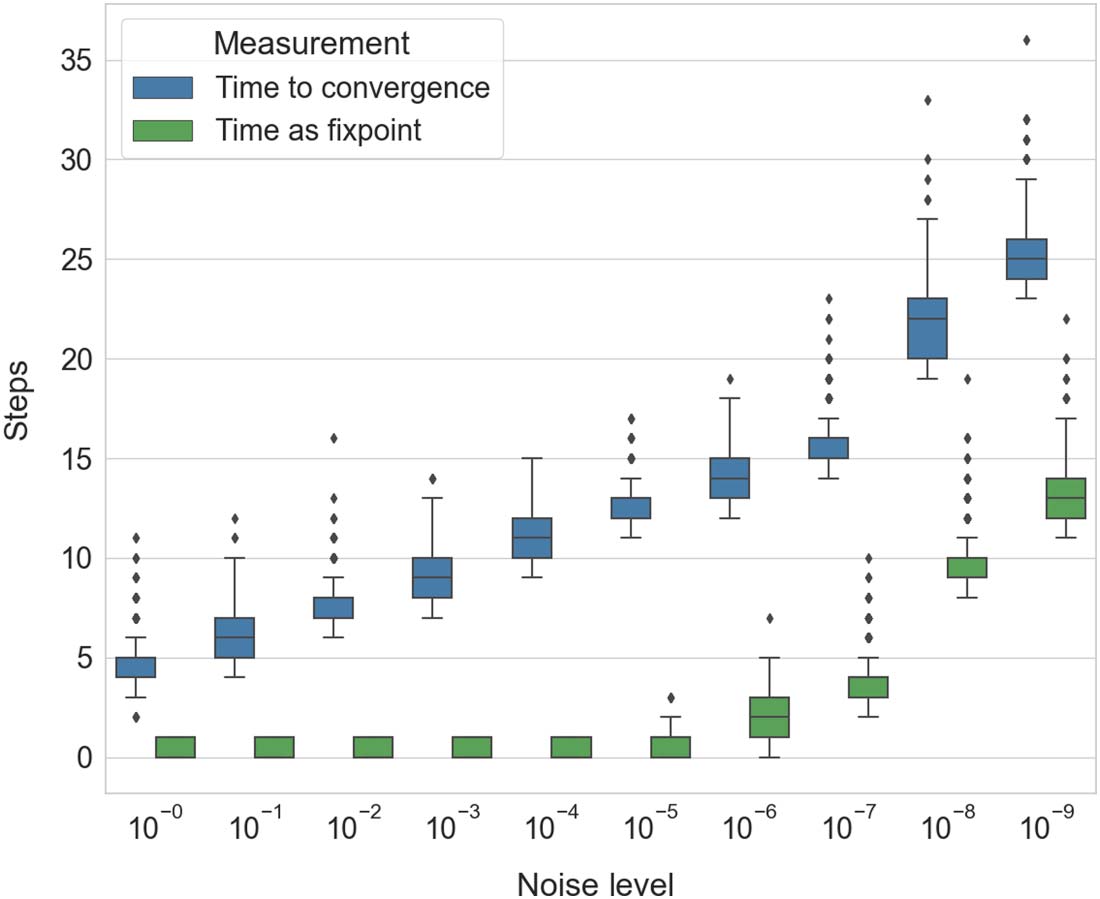
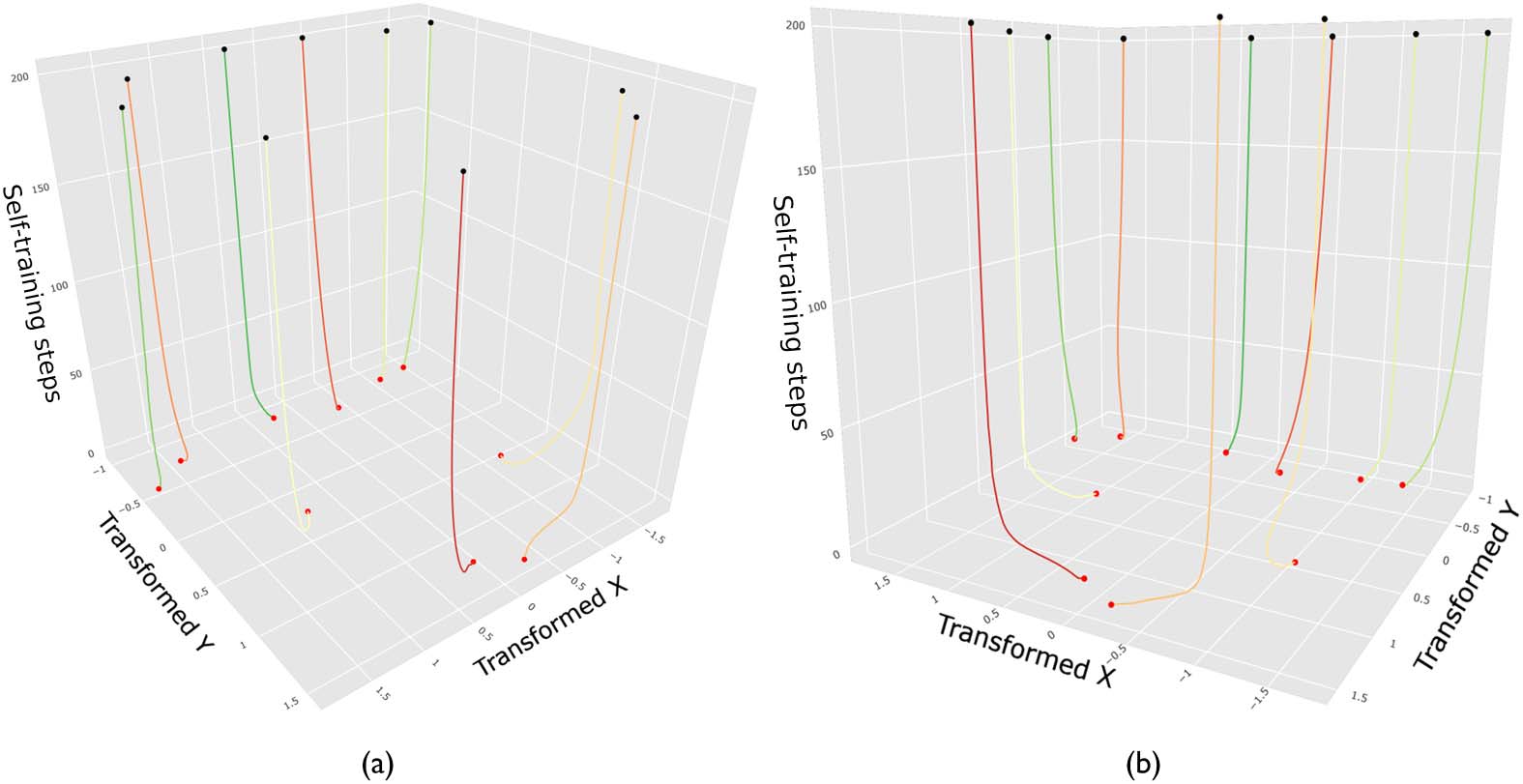
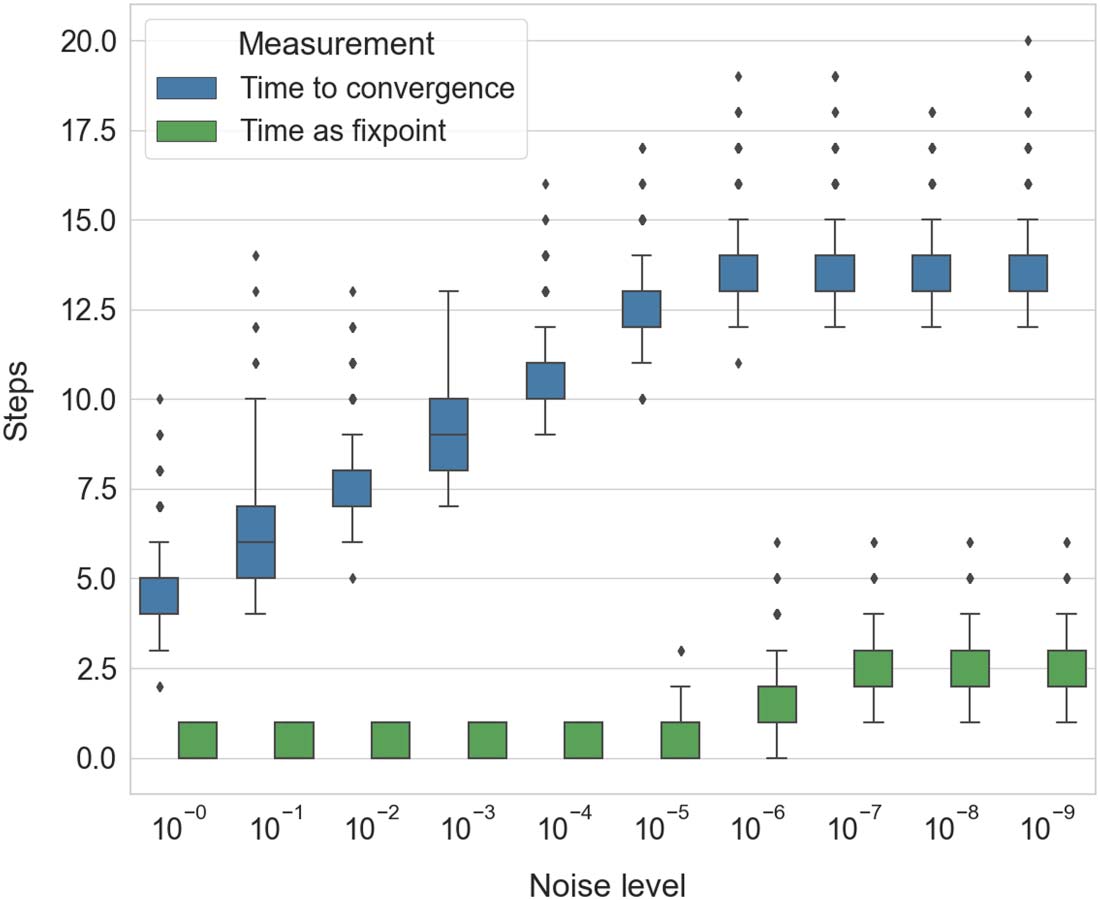
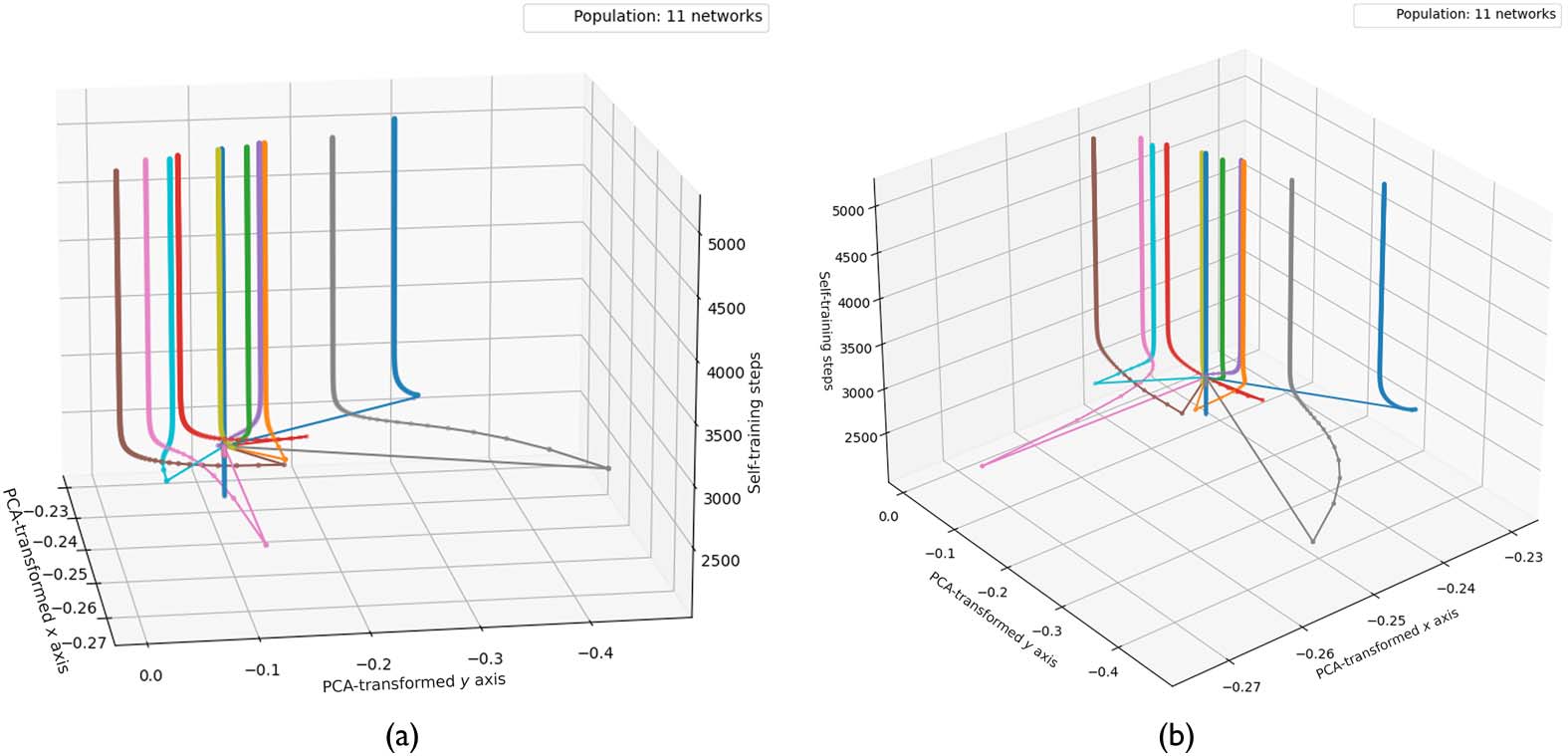
behavior, shedding light on how fixpoints occur within the network weight space. The examined
setup allows us to (D) construct an artificial chemistry setup using neural networks as individuals that
(under certain circumstances, Ovviamente) reliably produces a variety of non-trivial self-replicators.
This article is an extended version of the article originally published by Gabor et al. (2019) con
the substantial addition of contribution (C) as described above. The additional content can be found
mainly in the new section 3.3, Weight Space Analysis, including Figures 7–10, and the final exper-
iment described in section 3.5, including Figure 14. This article is structured as follows: We first
describe all formal definitions of our approach and then provide a series of experiments examining
the behavior of self-replicating networks; among the latter, we first discuss experiments on single
independent neural networks and then continue with experiments on soups consisting of multiple
interacting networks. After that, we briefly discuss related work and provide a conclusion.
2 Approach
We provide a brief introduction to how neural networks function, then we proceed to discuss how
to apply neural networks to other neural networks and how to train neural networks using other
neural networks.
2.1 Basics
Neural networks are most commonly made from layers of neurons that are connected to adjacent
layers of neurons. What all neurons have in common is the base functionality of receiving input
values (in the form of a matrix or vector), applying weights and biases (given as the network’s
parameters), and computing output values via a specific activation function (given as part of the
network’s architecture). Note that while neural networks originated as a model of biological neurons,
they cannot accurately fulfill that role with respect to modern knowledge about biological neurons
and instead serve as general function approximators in machine learning.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
2
8
2
2
0
5
2
0
3
2
7
7
7
UN
R
T
l
/
_
UN
_
0
0
3
5
9
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The most basic form of a feedforward network is a single-layer perceptron, consisting of many
fully connected cells that provide a transformation of the input based on their learned parameters.
Mathematically, each cell in such a network is described by a function
(cid:2)
y = f (
wixi + B)
io
where xi is the value produced by the i-th input cell, wi is the weight assigned to that connection,
b is a cell-specific bias, f is the activation function, and y is the cell’s output.
The recurrent neural network (RNN) structure allows cells to retain some information throughout
multiple executions: The result of the evaluation step t is passed to the evaluation at step t + 1 COME
vector ht+1. A recurrent cell’s activation at every timestep t is ht = f (Wxt + Wht−1) where W are
206
Artificial Life Volume 28, Numero 2
T. Gabor et al.
Self-Replication in Neural Networks
the network weights (Chung et al., 2014). This allows for more powerful models when processing
sequential inputs.
A neural network thus defines a function N : Rp → Rq for input length p and output length q.
For an input vector x ∈ Rp we write the computation of the corresponding output vector y ∈ Rq as
y = N (X). A neural network N is usually given by (UN) its architecture, cioè., the types of neurons used,
their activation function, and their topology and connections, as well as (B) its parameters, cioè., IL
weights assigned to the connections. Whenever the architecture of a neural network is fixed, we can
define a neural network by its parameters (cid:5)N ∈ Rr. Note that r =def | (cid:5)N | depends on the amount of
internal connection and hidden layers, but as all inputs and all outputs must be connected somehow
to other cells in the network it always holds that r > p and r > q.
2.2 Application
In the course of this work, we are interested in having neural networks that can be applied to
other neural networks (and can output other neural networks). It is evident that if we want neural
networks to self-replicate, we need to enable them to output an encoding of a neural network
containing at least as many weights as they contain themselves. We discuss multiple approaches to
do so but first introduce a general notation covering all the approaches: We write O = N (cid:2) M
to mean that O is the neural network that is generated as the output of the neural network N
when given the neural network M as input. When M and O are sufficiently smaller than N , cioè.,
if | (cid:5)M| (cid:6) | (cid:5)N | E | (cid:5)O| (cid:6) | (cid:5)N |, then we can simply define the output network O via its weights
(cid:5)O = N ( (cid:5)M). Tuttavia, these conditions obviously do not allow for self-replication. Così, we
introduce several reductions that allow us to define the application operator (cid:2) differently and open
it up for self-replication. Note that for these definitions, we assume that M and O have the same
architecture and that the application of N keeps the size of the input network, cioè., M : Rp → Rp
for some p and | (cid:5)M| = | (cid:5)O| = p.
Reduction 1 (Weightwise Application). We define N : R4 → R fixed. Let (cid:5)M = (cid:7)vi(cid:8)
then set
0≤i<| (cid:5)M|. We
(cid:5)O = (cid:7)wi(cid:8)
0≤i<| (cid:5)O|
where
wi = N (vi, l(i), c(i), p(i))
the number of
and l(i) is
the weight
i leads into, and p(i) is the positional number of weight i among the weights of its cell. We use (cid:5)O to define
O = N
the number of
the weight
c(i) is
layer of
that
cell
the
the
i,
M.
Note that l, c, p depend purely on the networks’ architectures and the index of the weight i, not
on the value of the weight vi. Theoretically, we could pass on i to the network directly, but it seemed
more reasonable to provide the network with the most semantically rich information we have. Also
note that we normalize l, c, p : N →[ 0; 1] ⊂ R, i.e., the positional values are encoded by real numbers
between 0 and 1 as is common for inputs to neural networks.
Intuitively, weightwise application calls N on every single weight of M and provides the
weight’s value and some information on where in the network the weight lives. N then outputs a
new value for that respective weight. After calling N for | (cid:5)M| = | (cid:5)O| times, we have a new output
net O. This approach is most similar to the one used by Chang and Lipson (2018).
Reduction 2 (Aggregating Application). Let agga : Ra → R be an aggregator function taking in an arbi-
trary number of parameters a. Let deagga : R → Ra be a de-aggregating function returning an arbitrary number
of outputs a. Let (cid:5)M = (cid:7)vi(cid:8)
0≤i<| (cid:5)M|. Let
M ↓agg
b
= (cid:7)aggai
(vi, . . . , vi+ai−1)(cid:8)0≤i