RESEARCH ARTICLE - Ricerca sull'intelligenza artificiale specializzata al MIT

RESEARCH ARTICLE

Total number of papers and in a single percentile
fully describes research impact—Revisiting
concepts and applications

Alonso Rodríguez-Navarro1,2

and Ricardo Brito2

1Departamento de Biotecnología-Biología Vegetal, Universidad Politécnica de Madrid,
Avenida Puerta de Hierro 2, 28040, Madrid, Spain
2Departamento de Estructura de la Materia, Física Térmica y Electrónica y GISC,
Universidad Complutense de Madrid, Plaza de las Ciencias 3, 28040, Madrid, Spain

Keywords: citation analysis, impact indicators, Leiden Ranking

ABSTRACT

This study uses the data provided by the Leiden Ranking 2020 to support the claim that
percentile-based indicators are linked by a power law function. A constant calculated from
this function, ep, and the total number of papers fully characterize the percentile distribution of
publications. According to this distribution, the probability that a publication from a country or
(2−lgx).
institution is in the global xth percentile can be calculated from a simple equation: P = ep
By taking the Leiden Ranking PPtop 10%/100 as an approximation of the ep constant, our results
demonstrate that other PPtop x% indicators can be calculated applying this equation.
Consequently, given a PPtop x% indicator, all the others are redundant. Even accepting that the
total number of papers and a single PPtop x% indicator are sufficient to fully characterize the
percentile distribution of papers, the results of comparisons between universities and research
institutions differ depending on the percentile selected for the comparison. We discuss which
Ptop x% and PPtop x% indicators are the most convenient for these comparisons to obtain reliable
information that can be used in research policy.

a n o p e n a c c e s s

j o u r n a l

Citation: Rodríguez-Navarro, A., &
Brito, R. (2021). Total number of papers
and in a single percentile fully describes
research impact—Revisiting concepts
e applicazioni. Quantitative Science
Studi, 2(2), 544–559. https://doi.org/10
.1162/qss_a_00130

DOI:
https://doi.org/10.1162/qss_a_00130

Received: 5 novembre 2020
Accepted: 11 Marzo 2021

Corresponding Author:
Alonso Rodríguez-Navarro
alonso.rodriguez@upm.es

Handling Editor:
Ludo Waltman

INTRODUCTION

The rapid progress in the availability of data on research output and faster methods for their anal-
ysis are “leading to a quantitative understanding of the genesis of scientific discovery, creativity,
and practice and developing tools and policies aimed at accelerating scientific progress”
(Fortunato, Bergstrom et al., 2018, P. 1). Among all the analyses that can be done on research
produzione, one of the most important is the efficiency analysis of the research carried out by insti-
tutions and countries; this importance is continually increasing in parallel with the increasing
importance that research plays in modern economies. Worldwide R&D (research and develop-
ment) expenditures amounted to $1,918 billion in 2015 (National Science Board, 2018), E
society needs to know the relevance of what research institutions produce with these expendi-
tures and their efficiency in producing it.

Describing this need, 28 years ago Garfield and Welljams-Dorof (1992) began a paper with
the following statement: “Government policy-makers, corporate research managers, E

Copyright: © 2021 Alonso Rodríguez-
Navarro and Ricardo Brito.
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza.

The MIT Press

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Total number of papers and in a single percentile fully describes research impact

university administrators need valid and reliable S&T indicators for a variety of purposes: for
esempio, to measure the effectiveness of research expenditures, identify areas of strength and
excellence, set priorities for strategic planning, monitor performance relative to peers and
competitors, and target emerging specialties and new technologies for accelerated develop-
ment.” Since then, and despite this obvious need, a method to measure the effectiveness of
research expenditures has not been indisputably established.

1.1. Citation-Based Indicators of Research Performance

Indicators of research performance have been sought for a long time (per esempio., Godin, 2003); since
Francis Narin (1976) used the term evaluative bibliometrics, many indicators have been pro-
posed and those based on citation counts are the most reliable (De Bellis, 2009; Moet, 2005).
Tuttavia, the use of citation counts for scientific assessments has triggered a long-standing
debate (Aksnes, Langfeldt, & Wouters, 2019). In the context of this debate, it should be strongly
emphasized that citation counts correlate with the scientific relevance or impact of a scientific
pubblicazione, but they do not always measure the relevance of a specific scientific publication.
There are several reasons why many papers receive more or fewer citations than they deserve
(MacRoberts & MacRoberts, 1989) O, more commonly, that they receive them belatedly
(Garfield, 1980). Even worse, recognition of novelty in science might be delayed and the re-
porting papers are ignored in short-term citation counting (Wang, Veugelers, & Stephan,
2017). In contrasto, when many papers are aggregated the numbers of papers with excessive
and scant number of citations are canceled out. In other words: “to a certain extent, the biased
are averaged out at aggregated levels” (Aksnes et al., 2019, P. 5). This canceling out cannot be
assured with a low number of papers, and this precludes the use of bibliometrics for the eval-
uation of small numbers of papers, as in the case of individual researchers. It is worth noting
that this does not prevent many papers from being correctly evaluated by bibliometric indices;
the impediment for their use is that not all papers are correctly evaluated. Unfortunately, Questo
issue is frequently ignored and bibliometric tools are used in the evaluation of researchers
(per esempio., Kaptay, 2020; Siudem, Zogala-Siudem et al., 2020). In contrasto, at the aggregation level
of institutions, citation indicators have been validated against peer review (Rodríguez-Navarro
& Brito, 2020UN; Traag & Waltman, 2019).

As mentioned above, many indicators have been proposed for the research evaluation of
institutions and countries, but those based on citation percentiles that refer to worldwide pro-
duction (Bornmann, 2010; Bornmann, Leydesdorff, & Wang, 2013; Mcallister, Narin, &
Corrigan, 1983) have demonstrated superiority and replaced others based on averages
(Opthof & Leydesdorff, 2010). Top percentile indicators have been used by the National
Science Board of the USA since 2010 (National Science Board, 2010) and by the Leiden
Ranking since 2011 (Waltman, Calero-Medina et al., 2012).

Several studies have addressed the need for research performance indicators to be validated
against peer review or other external criteria (Harnad, 2009). Many validation studies have
been performed, many of them against peer review. In an extensive study testing many indi-
cators, including percentile indicators (HEFCE, 2015), it has been concluded that “results at
output-by-author level (Supplementary Report II) [ha] shown that individual metrics give signif-
icantly different outcomes from the REF peer review process, and therefore cannot provide a
like-for-like replacement for REF peer review” (Wilsdon, Allen et al., 2015, P. 138). Tuttavia,
two further studies using the same data have proved that at the university level, which implies a
higher aggregation level, top percentile indicators show good correlations with peer review
(Rodríguez-Navarro & Brito, 2020UN; Traag & Waltman, 2019).

Quantitative Science Studies

545

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Total number of papers and in a single percentile fully describes research impact

In summary, there is strong evidence supporting the claim that citation-based percentile
indicators are excellent tools for the analysis of research outputs. The challenge is to convert
these bibliometric indicators into metrics that can be used by “government policy-makers, cor-
porate research managers, and university administrators” (Garfield & Welljams-Dorof, 1992)
to calculate the efficiency of research institutions.

1.2. Dichotomous and United Indicators

In a specific discipline and for certain years, a top percentile indicator records the number of
papers that an institution has among the set of global papers in that percentile, when they are
ranked from the most cited downwards. This evaluation implies the classification of papers
published by a research institution in two groups, depending on whether or not they belong
to a certain set of global papers. In terms of citations, the two groups are defined depending on
whether they are above or below a certain citation threshold—the issue of citation ties has
been discussed previously (Schreiber, 2013; Waltman & Schreiber, 2013). This dichotomous
classification of papers (Albarrán, Herrero et al., 2017; Bornmann, 2013) leads to the impor-
tant notion that “dichotomous procedures rely on the idea that only the upper part of the dis-
tribution matters” (Albarrán et al., 2017, P. 628). Consequently, in formal terms, dichotomous
indicators do not consider papers that are excluded by the criterion. Per esempio, the use of
the top 1% O 10% most highly cited papers as a frame of reference (Tijssen, Visser, & van
Leeuwen, 2002) implies that the 99% O 90% other papers are not counted. Così, it seems
that the numbers of such papers or of the citations that they received does not matter.

To integrate all papers in the indicators, after counting the papers in percentile ranks, different
weights can be assigned to each rank (higher for the ranks with higher citations), and the weighted
numbers of papers are added to obtain a united indicator (Bornmann & Mutz, 2011). Leydesdorff
and Bornmann (2011) called this type of percentile indicators integrated impact indicators
because they take into account the size and shape of the distribution, which is very skewed.
This approach has been extensively investigated and different percentile ranks and weights have
been proposed (Bornmann, 2013; Bornmann, Leydesdorff, & Mutz, 2013; Bornmann, Tekles, &
Leydesdorff, 2019; Leydesdorff & Bornmann, 2012; Leydesdorff, Bornmann, & Adams, 2019;
Leydesdorff, Bornmann et al., 2011). It is worth noting that weighted counts of publications in
ranks do not require that the ranks be based on percentiles (Vinkler, 2011).

The notion of dichotomy, according to which a single top percentile indicator does not take
into account the excluded papers, and that a united indicator is needed for research evalua-
zione, would be correct if the numbers of papers in percentiles were unpredictably distributed.
But if the numbers of papers in all percentiles obey a function, the number of papers in a single
top percentile could be sufficient to determine the numbers in all the other percentiles. Questo
implies that no paper is ignored if only one percentile is used for evaluation, because the num-
ber of papers in any percentile is dependent on the function that describes the citation-based
distribution of all papers. This type of function occurs frequently in natural sciences. For ex-
ample, physics textbooks tell us that the pressure (equivalent to percentile) and volume (equiv-
alent to number of papers in the percentile) of gases follow a strict law that depends on the
amount of gas (equivalent to the total number of papers) and the temperature (equivalent to the
efficiency of the research institution).

A law of this type also exists in bibliometrics. Citations are universally distributed (Radicchi,
Fortunato, & Castellano, 2008) and the numbers of papers in top percentiles obey a power
law. This power law is a consequence of another basic relationship in citation analysis: IL
double rank function. “By ranking publications by their number of citations from highest to

Quantitative Science Studies

546

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Total number of papers and in a single percentile fully describes research impact

lowest, publications from institutions or countries have two ranking numbers: one for the in-
ternal and other for world positions; the internal ranking number can be expressed as a func-
tion of the world ranking number”; this function is a power law (Rodríguez-Navarro & Brito,
2018UN, P. 31). Therefore, by knowing the total number of papers and the number of papers in a
single top percentile, the number of papers in any other percentile can be easily calculated.
The percentile law can be expressed in the following way:

The probability of publishing a paper in top percentile x ¼ ep

Þ
2– lg x
ð

(1)

) of the exponent ((cid:1)) of the power law that the num-
where ep is a mathematical derivative (10
bers of papers versus top percentiles obey (Brito & Rodríguez-Navarro, 2018; Rodríguez-
Navarro & Brito, 2019). For an institution with the same percentile distribution as the global
production, ep is equal to 0.1 E, in practice, the highest values of ep are around 0.3.

−(cid:1)

1.3. Discussion About Size-Independent Indicators

The present study is largely based on Eq. 1. This equation calculates a probability, che è
size independent. The usefulness of size-independent bibliometric indicators and of the appli-
cation of terms such as productivity, performance, and efficiency in research evaluation have
been debated (Abramo & D’Angelo, 2016UN, 2016B; Glänzel, Thijs, & Debackere, 2016; Ruiz-
Castillo, 2016; Waltman, van Eck et al., 2016). That discussion is out of the scope of this study.
Tuttavia, we think that the ideal for a research institution is size independent: that for a given
total number of papers, the number of highly cited papers should be as high as possible. Questo
conclusion emphasizes the importance of size-independent indicators for research evaluation
purposes, especially the convenience of the ep constant, because it allows calculation of the
probability of publishing a paper at any highly cited level.

Regarding the use of size-dependent and size-independent indicators, there are not many
differences. It is worth noting that if we know the cumulative probability function given by
Eq. 1, the cumulative frequency of papers in any top percentile is equal to the probability
multiplied by the total number of papers. Così, the most relevant size-dependent indicator of
a research system is the total number of publications, because the number of papers in top per-
centiles is a function of the total number of papers and the ep constant. Given the exponential
nature of Eq. 1 and the range of numerical values between which ep varies, to produce a signif-
icant number of highly cited papers institutions with a low ep constant must publish many more
papers than others that have high ep constants. In other words, the ep constant, mathematically
equivalent to PPtop 10%/100, measures the efficiency of a research system.

1.4. Aims of This Study

The above standpoint indicates that in the research assessment of the publications of institu-
tions or countries, only two parameters—the total number of papers and the ep constant—are
needed to characterize research performance at all citation levels. The former describes the
size and the latter describes the efficiency; if both are known, the number of papers in any
other top percentile can be calculated. As already described, this notion has theoretical and
empirical support (Brito & Rodríguez-Navarro, 2020; Rodríguez-Navarro & Brito, 2018UN,
2019), but it has not been tested against a large number of institutions. Therefore, the first
aim of this study was to test it at the university level, making use of the detailed information
provided by the Leiden Ranking.

The second aim was to investigate which top percentile should be used to compare the
research output of different institutions. It is worth noting that when comparing two institutions

Quantitative Science Studies

547

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Total number of papers and in a single percentile fully describes research impact

by their ratio of publications at different top percentiles, if their ep constants are different, IL
ratio will vary depending on which percentile is used for the comparison (per esempio., top 10% or top
1%). Even the question of which of the two institutions is ahead and which is lagging might
have opposite responses depending on the percentile used for the comparison and their total
numbers of publications (Guarda la figura 4 in Rodríguez-Navarro & Brito, 2019).

2. METHODS

For the aims of this study, we took advantage of the detailed data provided by the Leiden
Ranking 2020 (https://www.leidenranking.com/; Excel file downloaded on August 21, 2020;
these data have been deposited in Zenodo, DOI: 10.5281/zenodo.4603232), using in all cases
fractional counting. The Leiden Ranking includes five research fields: “Biomedical and health
sciences,” “Life and earth sciences,” “Mathematical and computer sciences,” Physical sci-
ences and engineering,” and “Social sciences and humanities.” Previous studies in different
research fields (Brito & Rodríguez-Navarro, 2020; Rodríguez-Navarro & Brito, 2018UN,
2018B, 2020UN, 2020B) demonstrate that the calculation of the ep constant is statistically robust
in three of the Leiden Ranking fields: “Biomedical and health sciences,” Life and earth sci-
enze,” and “Physical sciences and engineering.” There is no information in “Mathematical
and computer sciences,” and in “Social sciences and humanities” the ep constant has only
been studied economics and business (Rodríguez-Navarro & Brito, 2020UN).

Therefore, for the purpose of this study, any of the three aforementioned Leiden Ranking fields
could be studied. The field of “Biomedical and health sciences” was not the first choice because
“health sciences” might be weak in some universities. Between the other two fields, we selected
“Physical sciences and engineering” versus “Life and earth sciences.” Although the difference is
not large, the number of universities with at least four top 1% most cited papers in the Leiden
Ranking evaluation periods (4 years) was higher in “Physical sciences and engineering” than in
“Life and earth sciences”; this is a comparative advantage, come mostrato di seguito.

Henceforth, we will keep the notation of the Leiden Ranking: P is the total number of papers
and Ptop x% is the number of papers in the top x percentile; PPtop x% is the Ptop x%/P ratio multiplied
by 100.

The Leiden Ranking reports publications for four percentiles (50, 10, 5, E 1) and these are
the data that we compared with the calculated data. For the calculation of the number of pub-
lications in these percentiles we used Eq. 1, taking the value of the ep constant as PPtop 10%/
100. Because of the statistical variability of PPtop 10%, the best method for the calculation of the
ep constant is to count the number of papers in 5–10 top percentiles and fit them to a power
law (Rodríguez-Navarro & Brito, 2019). Tuttavia, for the purposes of this study, using the
PPtop 10%/100 as a substitute for the ep constant is sufficiently accurate. The same calculation
approach was used when we recorded more stringent percentiles, Per esempio 0.02.

Pearson and Spearman correlations were studied using the free statistics software calculators

of Wessa (2017UN, 2017B). Two-sided p-values are always recorded.

3. RESULTS

3.1. PPtop x% Indicators Are Qualitatively Redundant

The numbers of papers in the top percentiles of global publications follow a power law, before
and after dividing by the total number of papers (Rodríguez-Navarro & Brito, 2019). By defi-
nition, in all universities their PPtop x% plots have a common point when the top percentile is 100,
and according to Eq. 1, from this point the PPtop x% plots diverge if the universities do not have

Quantitative Science Studies

548

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Total number of papers and in a single percentile fully describes research impact

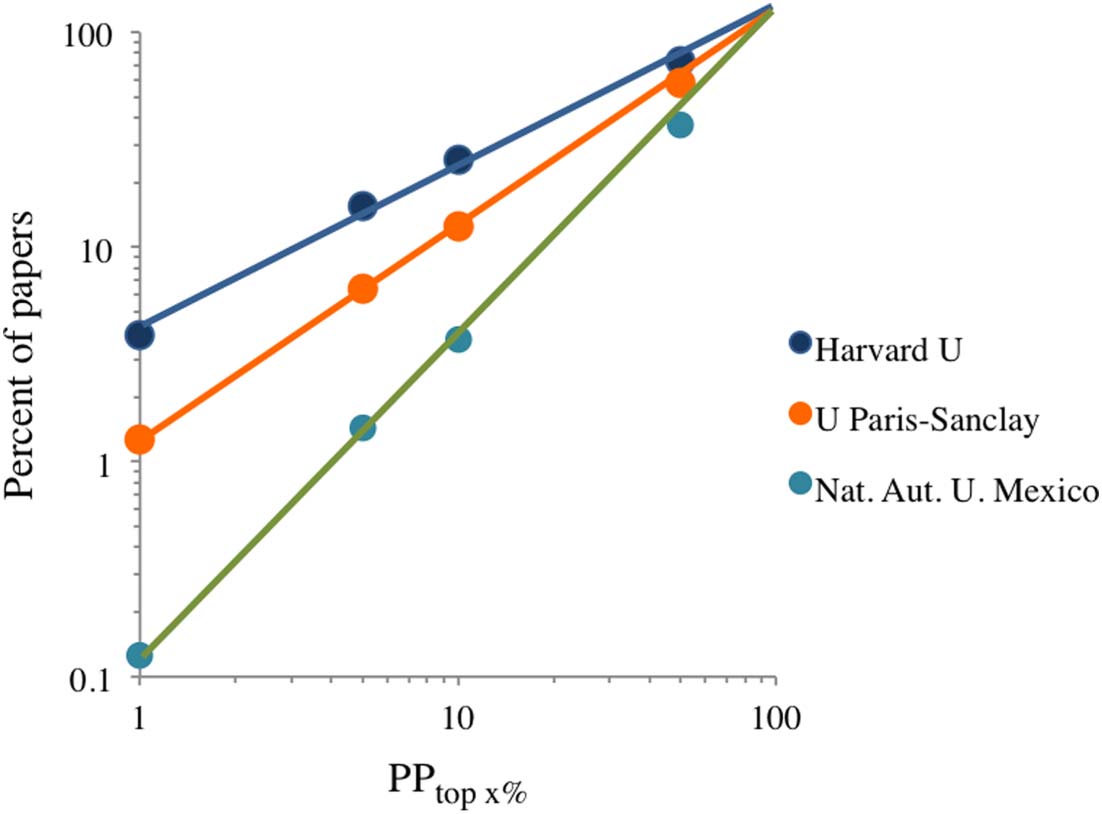
Figura 1. Double logarithmic plot of the four PPtop x% indicators reported in the Leiden Ranking,
PPtop 50%, PPtop 10%, PPtop 5%, and PPtop 1%, for three universities that are distant in the ranking. Field
of “Physical sciences and engineering,” time period 2009–2012.

identical ep constants. Therefore, if Eq. 1 is correct the order of universities in the Leiden Ranking
based on PPtop x% should be the same at any of the recorded percentiles: 1, 5, 10, E 50. In prac-
tice there will be some deviations, because the number of papers produced by universities is low
and the calculation of top percentile data is affected by statistical variability. Infatti, the data pro-
vided in the Leiden Ranking includes the lower and upper bounds of the stability interval for each
university’s PPtop x% indicator, and overlapping between these bounds in universities is frequent.
To avoid this problem, if we select a few universities that publish a high number of papers and that
are distant in the ranking, their relative positions will be maintained at all percentiles recorded in
the Leiden Ranking. Figura 1 shows that this in fact happens, but this is a small sample, which is not
sufficient to demonstrate that Eq. 1 is of general application.

Prossimo, we selected all the universities listed in the Leiden Ranking with more than 2,000 pa-
pers in the field of “Physical Sciences and Engineering.” This limitation in the number of papers
is intended to keep the variability of the PPtop x% data as low as possible. Then we calculated the
Spearman rank correlation coefficients between the PPtop x% data of different percentiles.
Tavolo 1 shows the correlation matrix between percentiles in the first (2006–2009) and last
(2015–2018) periods recorded in the Leiden Ranking (similar results are found for other periods).
The correlation coefficients are high (> 0.9 with a single exception) and the p values are very
–127. As might be expected, rank correlations are lower when the top 1%
low, from 10
and top 50% results are compared, but are still remarkable. Additionally, Figura 2 shows the
least and most dispersed scatter plots of ranks of the correlations studied (Tavolo 1).

–33 to 10

These results demonstrate that PPtop x% indicators are redundant, all showing the same rank-

ing information, although their values were obviously very different.

3.2. PPtop x% Indicators Can Be Easily Calculated from PPtop 10%

Before addressing the issue of whether empirical PPtop x% indicators follow Eq. 1, for guiding
purposes, we addressed a basic descriptive question about the distribution of universities ac-
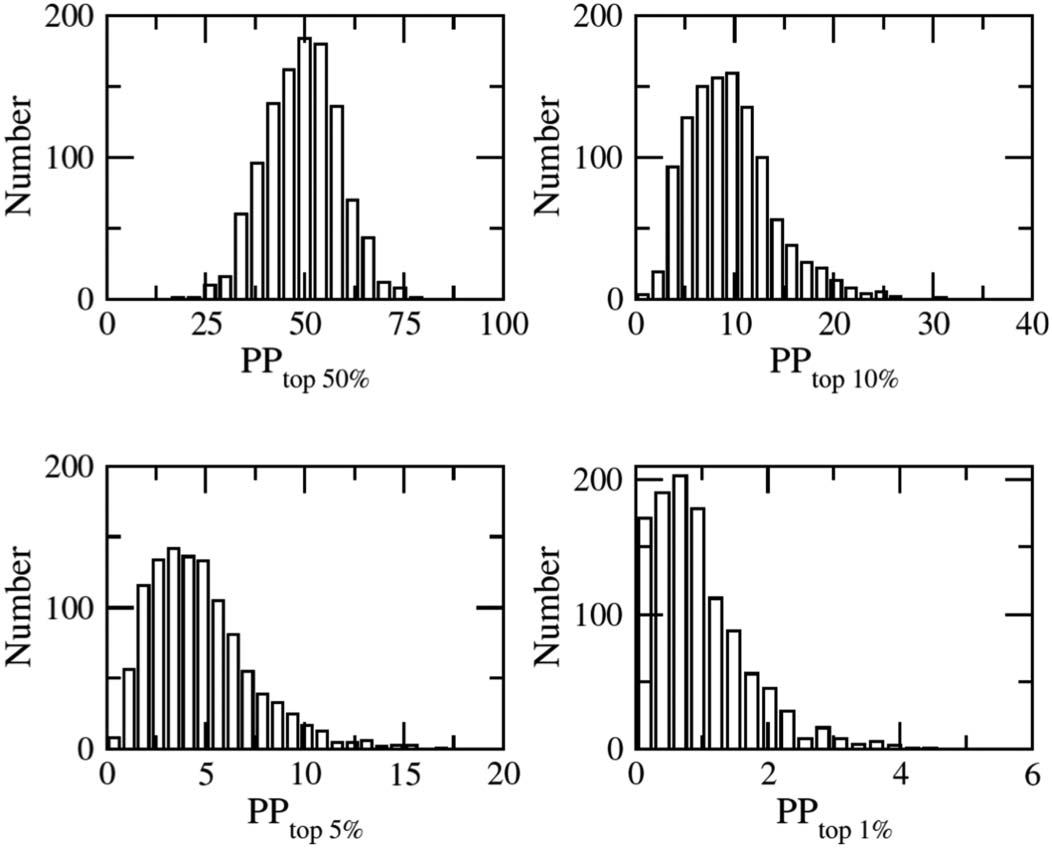
cording to these indicators. Figura 3 shows the distributions of universities based on the four

Quantitative Science Studies

549

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Total number of papers and in a single percentile fully describes research impact

Tavolo 1.
Leiden Ranking for universities with more than 2,000 publications

Spearman rank correlation matrix between the four PPtop x% indicators reported in the

2006–2009
PPtop 5%

PPtop 10%

PPtop 50%

2015–2018

PPtop 5%

PPtop 10%

PPtop 50%

PPtop 1%
0.98

0.97

0.94

PPtop 5%

PPtop 10%

0.99

0.97

0.98

PPtop 1%

PPtop 5%

PPtop 10%

0.96

0.95

0.89

0.99

0.94

0.96

Field of “Physical sciences and engineering.” Time periods 2006–2009, 71 università, and 2015–2018, 151
università. All 2-sided p-values are below 1 × 10

−32.

indicators PPtop 50%, PPtop 10%, PPtop 5%, and PPtop 1%, for the time period 2009–2012 (in other
time periods the distributions are similar). The PPtop 50% distribution resembles a normal dis-
tribution and meets normality criteria. The other three distributions show increasing kurtosis,
with a long right tail that resembles lognormal distributions. Tuttavia, although the distribu-
tions are heavy tailed, they do not meet the criteria for this type of distribution.

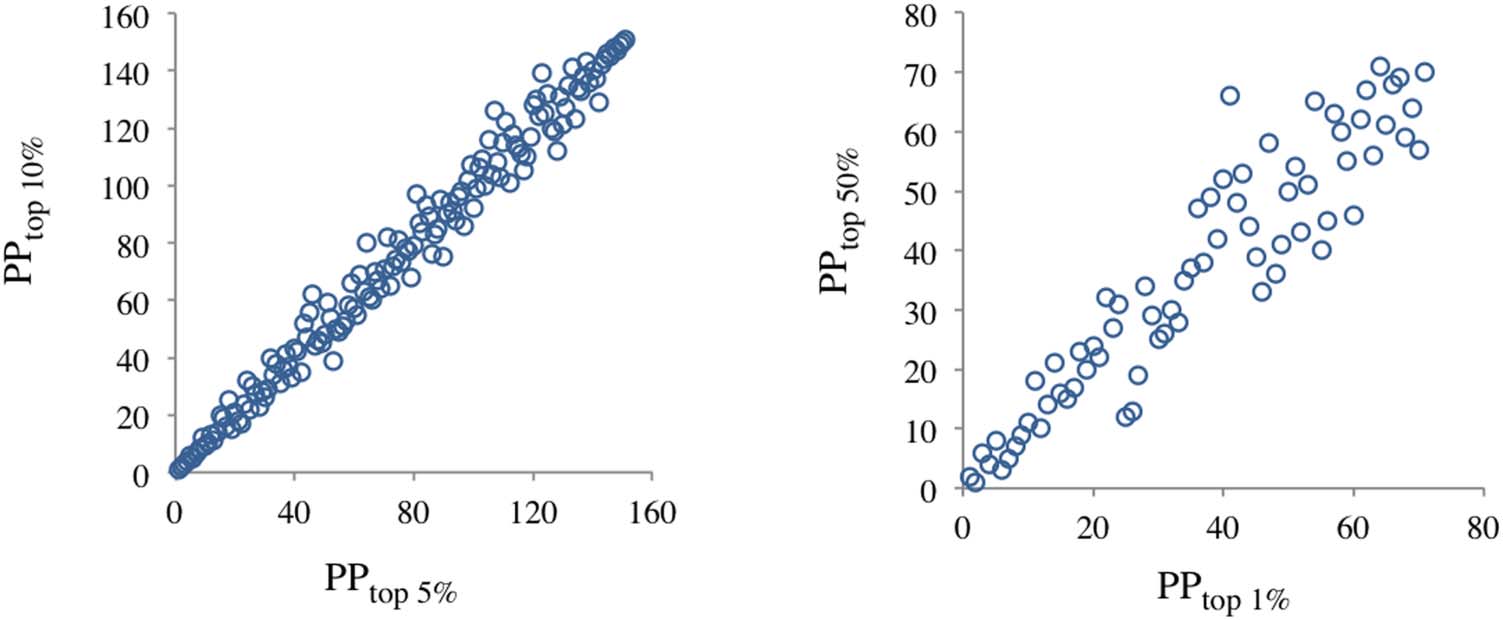
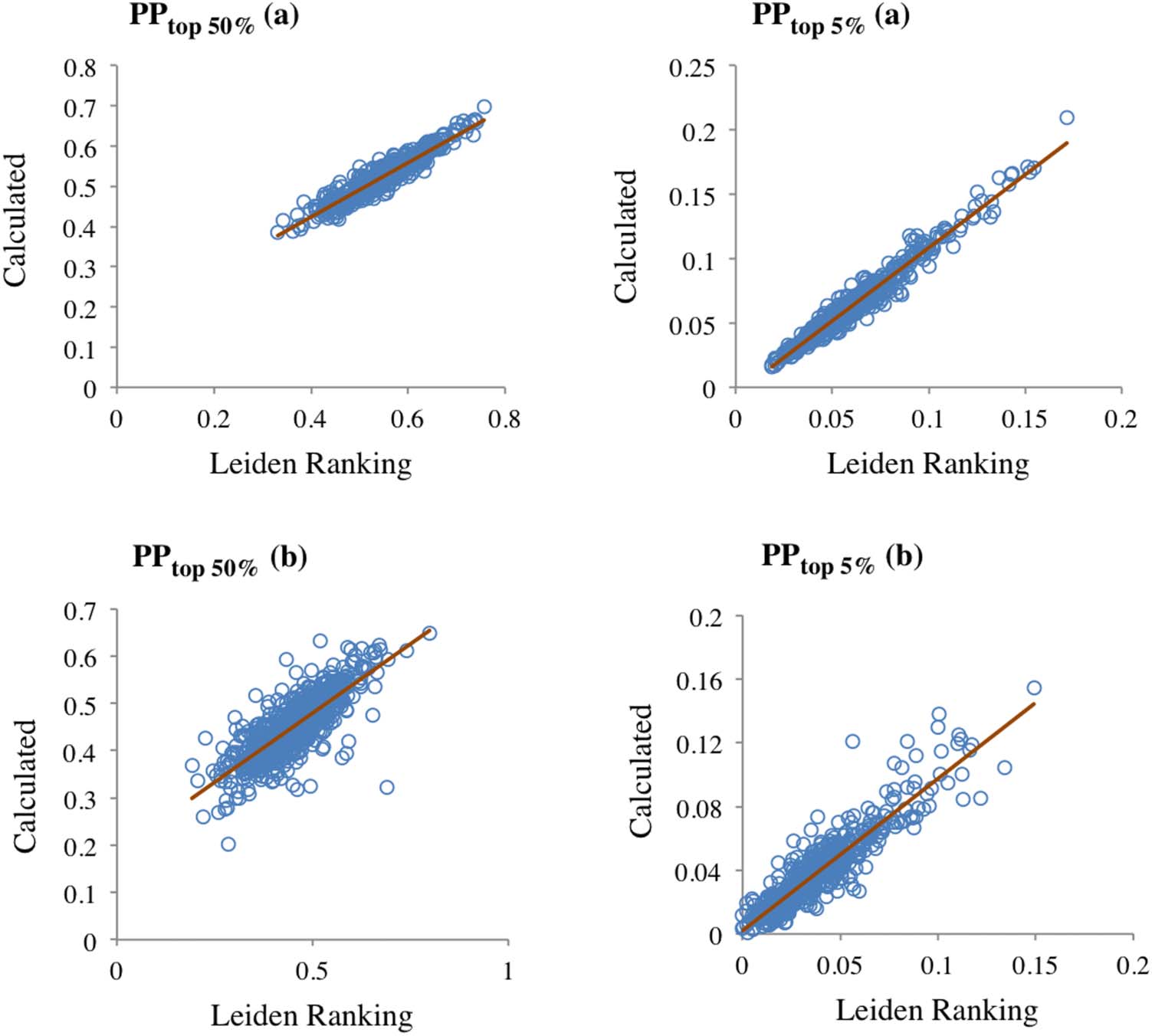
Prossimo, we tested the agreement between the PPtop x% indicators reported in the Leiden Ranking
and their calculated values from Eq. 1, taking PPtop 10%/100 as the value of ep. In a first attempt
we used the data of the 1,177 universities in the field of “Physical sciences and engineering” for
the time period 2009–2012. Visually, the scatter plots in Figure 4 show a strong linear relation-
ship between the two values for PPtop 50% and PPtop 5%. A linear relationship was also observed
for PPtop 1%, but in this case the data had too much noise. This high variability was due to the
large number of universities with a very low number of papers in Ptop 1%: The value was zero in
203 universities and 1 In 186; Infatti, low values of Ptop 1% are associated with large stability
intervals of PPtop 1% in the Leiden Ranking. The Pearson correlation coefficients for the

Figura 2.
Examples of scatter plots of ranks of the correlations reported in Table 1, the least and
most disperse plots. Left panel, PPtop 5% versus PPtop 10% in period 2015–2018, 151 università;
right panel, PPtop 1% versus PPtop 50% in period 2006–2009, 71 università.

Quantitative Science Studies

550

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Total number of papers and in a single percentile fully describes research impact

Figura 3. Histograms of the values PPtop 50%, PPtop 10%, PPtop 5%, and PPtop 1% reported in the
Leiden Ranking for the field of “Physical sciences and engineering” in the time period of 2009–
2012; 1,177 università.

calculated versus the empirical values of PPtop 50%, PPtop 5%, and PPtop 1% were high: 0.89, 0.96,
–242 for PPtop 1%.
E 0.78, rispettivamente. The p-values were very small; the largest was 3.9 × 10

Although these correlations were clear, the relationship between the Leiden Ranking and
calculated values of Ptop 1% was uncertain because the variability could conceal possible de-
viations of small groups of universities. To overcome this problem the obvious possibility was
to exclude from the analysis the universities with Ptop 1% values below a certain threshold. Questo
approach, Tuttavia, had to be carried out avoiding the introduction of biases, which were less
≥ 5, the total set of 1,177
likely if the threshold was low. By using the threshold of Ptop 1%
universities was divided into two sets, above and below the threshold, Di 474 E 703 univer-
sities. The corresponding scatter plots of the Leiden Ranking versus the calculated data of
PPtop 50% and PPtop 5% (Figura 5) show high similarity in the two sets and with the scatter plot
of the total set of universities (Figura 4). These results suggested that the set of 474 università
was reasonably representative of the total number of universities for the comparison of the
Leiden Ranking and calculated values, at least at the PPtop 50% and PPtop 5% levels.

Figura 4. Scatter plots of the two values of PPtop 50%, PPtop 5%, and PPtop 1%, one calculated from PPtop 10% and the other the reported in the
Leiden Ranking; research field of “Physical sciences and engineering” and time period 2009–2012; 1,177 università. The lines are meant
only to guide the eye.

Quantitative Science Studies

551

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Total number of papers and in a single percentile fully describes research impact

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 5.
two sets: Ptop 1%
only to guide the eye.

Scatter plot of the two values of PPtop 50% and PPtop 5% shown in Figure 4 divided into
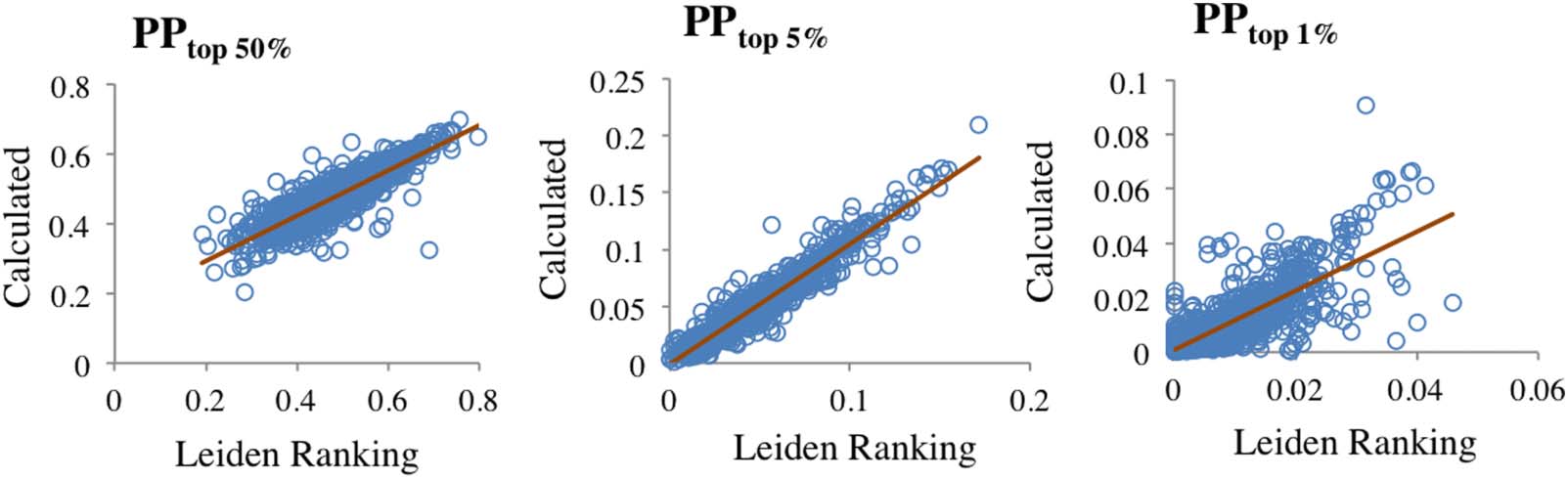
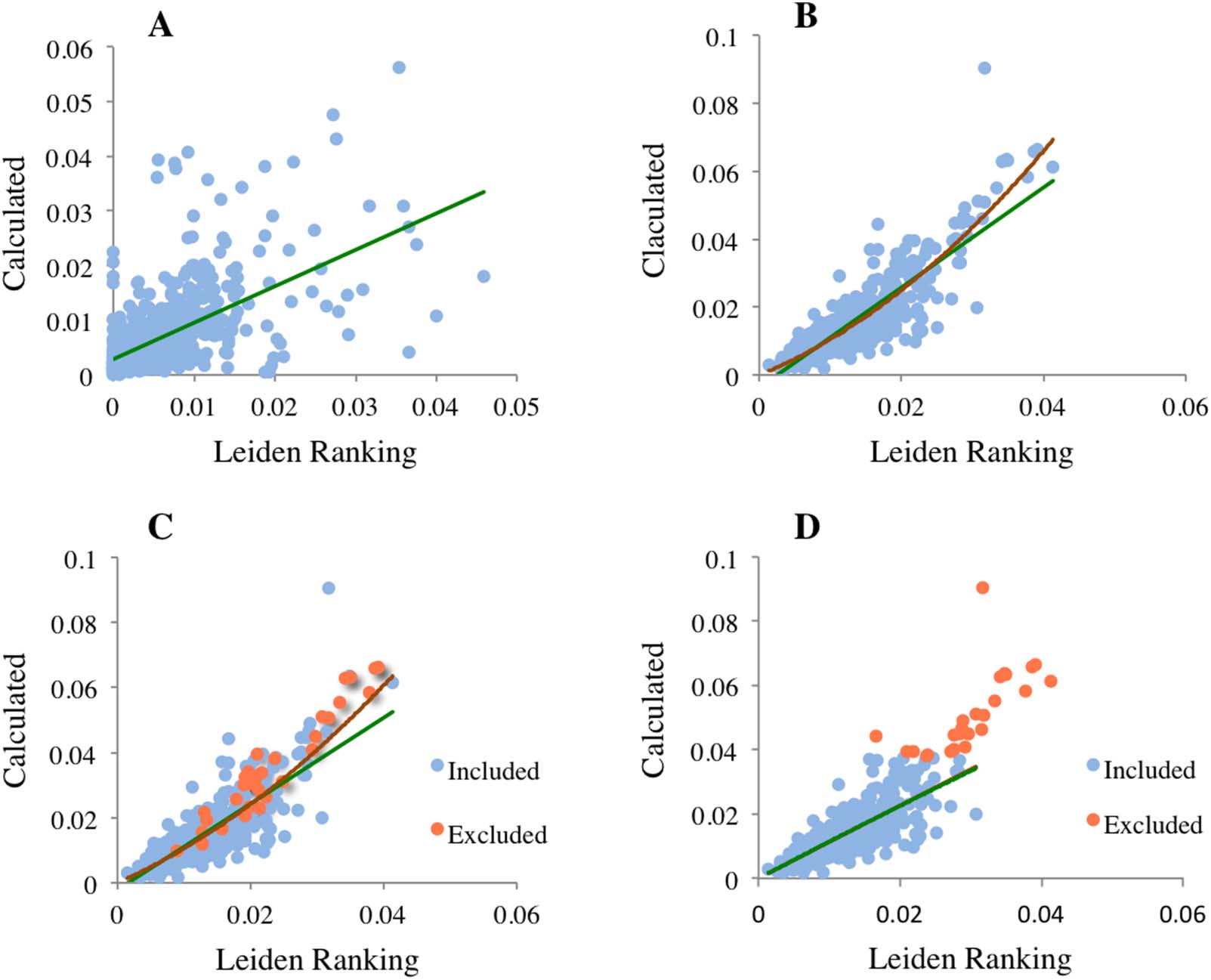
≥ 5 (UN; 474 università) and Ptop 1% < 5 (b; 703 universities). The lines are meant For PPtop 1%, the set of 703 universities (Figure 6A) shows high variability and the accuracy of fitting a regression line was very low. In the other set of 474 universities (Figure 6B) the variability was lower and the scatter plot reveals that some universities with high values of PPtop 1% deviate from the general trend of the other universities. Consequently, a second-order polynomial that passes through the origin fits the data better than a straight line; a higher order polynomial or eliminating the constraint of passing through the origin did not significantly im- prove the fitting. This finding suggested that a small set of universities could deviate from the relationship of the other universities. It is likely that this possible set of universities might have very large values of either Ptop 1% or PPtop 10%. The scatter plot in Figure 6C shows that the exclusion of 34 universities with Ptop 1% > 40 does not significantly affect the deviation from a
straight regression line observed in Figure 6B. In contrasto, the exclusion of 25 universities with
≥ 0.20 eliminates the deviation from a straight regression line. Figure 6D shows that
PPtop 10%
in this case the fittings of straight and polynomial lines overlap.

3.3. Research Efficiency and Contribution to the Progress of Knowledge

Although the total number of papers and their number in a single percentile are sufficient to
define the efficiency of research institutions, in the case of quantitative comparisons it is nec-
essary to select the percentile at which the comparison between institutions must be made.

Quantitative Science Studies

552

Total number of papers and in a single percentile fully describes research impact

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

Scatter plot of the two values of PPtop 1% shown in Figure 4 divided into two sets: Ptop 1%

Figura 6.
703 università). In panels C and D, the set of 474 was subdivided excluding the universities in which Ptop 1% > 40 (C) and PPtop 10%
(D). Green lines: straight linear regression. Brown lines: fitting to a second-order polynomial. In D, the green and brown lines overlap.

≥ 5 (UN; 474 università) and Ptop 1% < 5 (B; ≥ 0.20 / / / 2 2 5 4 4 1 9 3 0 7 1 7 q s s _ a _ 0 0 1 3 0 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 This is so because differences between institutions increase with the stringency of the percen- tile (Figure 1). However, we must distinguish two different cases, depending on whether we are interested in efficiency, which is size independent, or in the contribution to the progress of knowledge, which is size dependent. In the first case, if it is necessary to select a PPtop x% indicator, the selection might be simple. Considering the data reported in Figure 1 and the exponential form of Eq. 1, it is obvious that the differences increase following a known pattern, which indicates that the ratios between universities’ PPtop x% also increase or decrease following a known pattern. In these conditions, the convenient percentile cannot be established in general terms and will depend on the target that is pursued (Section 4.2). If we are interested in the contribution to the progress of knowledge, the relationships be- tween institutions become more complex because, as previously mentioned, the pertinent in- dicator is the size-dependent Ptop x%. If the institutions publish similar numbers of papers the case is not different from that described above for efficiency. For example, for Stanford University, Sorbonne University, and Kyushu University in Table 2, the differences increase when the percentile decreases, but the order of the universities does not change. In contrast, if the number of papers is different, even the order of the institutions could change when the stringency of the indicator increases. Table 2 shows this fact again with three universities: Quantitative Science Studies 553 Total number of papers and in a single percentile fully describes research impact Stanford University Sorbonne University Kyushu University Shanghai Jiao Tong University Sorbonne University Yale University Table 2. Variation of Ptop x% indicators in selected universities P 2,825 2,641 2,669 4,832 2,559 1,268 2006–2009 Ptop 50% 2,068 1,518 1,144 2009–2012 2,379 1,483 916 Ptop10% 741 Ptop 1% 109 321 188 437 314 298 31 13 37 29 42 Ptop 0.1% 50.97 4.72 0.93 3.57 4.73 16.46 Ptop 0.01% 13.37 0.57 0.07 0.32 0.58 3.87 The values of P, Ptop 50%, Ptop 10%, and Ptop 1% were taken from the Leiden Ranking, Ptop 0.1% and Ptop 0.01% were calculated from PPtop 10% as described in the text. Field of “Physical sciences and engineering.” Shanghai Jiao Tong University, Sorbonne University, and Yale University. This is the order (from higher to lower) when using P, Ptop 50%, and Ptop 10%, but for Ptop 1%, Yale University is now first, and the other two universities keep the same order as in the other percentiles. Interestingly, at this percentile the three universities are very similar. Finally, using Ptop 0.01%, the order changes again: Now, Yale University is first and Sorbonne University is ahead of Shanghai Jiao Tong University. At this percentile, the contribution of Yale University to the progress of knowledge is almost 10 and eight times higher than those of Shanghai Jiao Tong and Sorbonne Universities, respectively. With this complex behavior, the question of which university contributes the most to scientific progress is puzzling, unless we agree about the percentile that should be used to measure scientific progress. 4. DISCUSSION 4.1. All PPtop x% Indicators Can Be Calculated from Only One The purpose of our study was to demonstrate that Eq. 1 is correct by using the data reported by the Leiden Ranking for a large number of universities. This implies that a single PPtop x% indicator is sufficient to calculate all PPtop x% indicators and therefore to reveal the efficiency of a research institution. The size-independent PPtop x% indicators are 100 times the probabilities described by Eq. 1 and PPtop 10% is equal to the ep constant multiplied by 100 (Rodríguez-Navarro & Brito, 2019). This constant is normally calculated by statistical fitting from several percentile counts, but it can also be calculated with a lower precision from the value of a single PPtop x%. The high Spearman rank correlation coefficients found between the four Leiden Ranking PPtop x% indicators—PPtop 50% , PPtop 10%, PPtop 5%, and PPtop 1% —for universities with more than 2,000 papers (Table 1) imply that the four indicators reveal the same as predicted by Eq. 1. The same conclusion is reached when studying the correlation between the PPtop 50%, PPtop 5%, and PPtop 1% data recorded in the Leiden Ranking and the data calculated applying Eq. 1—substituting PPtop 10%/ 100 for the ep constant. A clear correlation is shown by the three scatter plots for PPtop 50%, PPtop 5%, and Ptop 1% in 1,177 universities (time period 2009–2012; Figure 4). However, the scatter plot for PPtop 1% is very noisy because in many universities Ptop 1% is very low and shows a large variability, which hinders the study of deviations that seem to occur. Eliminating the universities with fewer than five papers in Ptop 1%, there remain 474 universities. Comparison of the scatter plots of the two Quantitative Science Studies 554 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 2 2 5 4 4 1 9 3 0 7 1 7 q s s _ a _ 0 0 1 3 0 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Total number of papers and in a single percentile fully describes research impact sets, 474 and 703 universities, and the complete set of universities (Figures 5 and 6) strongly suggests that the set with 474 universities is a representative sample of the total number of universities and may be used to study possible deviations of PPtop 1%. In Figure 6, the PPtop 1% scatter plot shows higher variability than that observed for the PPtop 50% and PPtop 5% plots (Figure 5), and the best universities deviate from the trend followed by of the rest of the universities. Several factors contribute to these facts. In the first place, the exponent of Eq. 1 for PPtop 1% is higher than for PPtop 50% and PPtop 5%, which increases the error of substituting PPtop 10% for the ep constant—ep should be calculated by fitting the data of several percentiles. Furthermore, the number of Ptop 1% papers is low in many universities, which implies a higher variability in the counting of the papers in this percentile than in the counts of the other two percentiles. These general observations are not sufficient to explain the deviations that are observed in Figure 6 for the most efficient universities (panels B, C, and D); we found that by ≥ 0.20 from the set of 474 universities, the deviation excluding the 25 universities with PPtop 10% from a straight regression line disappears. This result indicates that Eq. 1 suffers slight deviations in highly competitive universities, which would not be surprising, because deviations of empirical data from a general law are common in many scientific fields. In the example of physics given in Section 1.2, the mentioned function applies to ideal gases but suffers devia- tions in real gases. However, for PPtop 1% the deviation is of minor importance for evaluation purposes because the number of these outstanding institutions is an insignificant portion of the total number of institutions: 25 out of 1,177. In summary, percentile indicators are dichotomous indicators only in appearance, because all of them can be calculated from the total number of papers and a mathematical constant that reveals the research efficiency of institutions and countries. The existence of slight devi- ations from Eq. 1 in some specific cases does not impede the use of this equation in general evaluations. 4.2. Which Top Percentile Should Be Used for Quantitative Evaluations? Our data demonstrate that if the purpose is to rank research institutions by the PPtop x% indicator, any percentile can be used. Conversely, for quantitative evaluations, such as comparison with research investments (de Marco, 2019), a certain percentile must be selected, because quantitative relationships between institutions change depending on the percentile (Figure 1). For example, let us imagine two research institutions, A and B, in which investments are similar, but the numbers of papers in the evaluation period are 1,000 and 500, and the PPtop 10% indicators are 14% and 20%, respectively. It is evident that if we are comparing the cost of a publication, institution A shows the better performance. The same occurs at the top 10% level (Ptop 10% = P · ep and ep = PPtop 10%), 140 versus 100 papers, but not at the top 1% level, where both institutions show the same Ptop 1%, 2). At a landmark level (percentile 0.02, Bornmann, Ye, & Ye, 2018) the equal to 20 (Ptop 1% = P · ep 3.7). Therefore, although advantage is for institution B: 0.69 for A versus 1.3 for B (Ptop 0.02% = P · ep A produces twice as many papers than B, the cost of a landmark level paper in A is almost twice the cost as in B. These bibliometric calculations show the importance of answering the question posed in the title of this section. From a scientific point of view, and if we are considering a size-dependent indicator, the top 0.01 percentile, close to the landmark level, might be a reasonable answer. For the contribution to the progress of knowledge, the same percentile should apply to sci- entifically advanced countries and to countries that are developing a research system. Because the target of scientific research is globally established, the research indicator should also be Quantitative Science Studies 555 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 2 2 5 4 4 1 9 3 0 7 1 7 q s s _ a _ 0 0 1 3 0 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Total number of papers and in a single percentile fully describes research impact globally established. The same reasoning does not apply to size-independent indicators, be- cause higher is not always better and high-level excellence is not always the right target. To our knowledge, many research policy makers do not address the evaluative puzzle aris- ing from the example given above, and they choose a certain percentile without much thought. Similarly, in many countries, especially in those with a generally low level of research performance (e.g., Spain), policy makers are preoccupied with the idea of having “excellent” research institutions, and they make important investments in a very few institutions with the purpose of making them “excellent.” Aside from the fact that in many cases in these countries research “excellence” is mismeasured by the journal impact factors (Brito & Rodríguez- Navarro, 2019), the results of these efforts are anything but excellent. This is because the con- tribution to the national research system of an excellent institution will most likely be of low relevance. This would be the case if, for example, in such an institution the PPtop 10% is 15% and the average in the rest of the country’s institutions is 9.0%, but the “excellent” institutions publish only less than one hundredth of the total number of publications. In this case a simple calculation demonstrates that more than 90% of the top 0.01 publications have been pub- lished in the underfunded institutions. Therefore, in countries with weak research systems, in- vesting to raise the average PPtop 10% of the country, for example to 0.12, would be more profitable than investing in the much desired “excellent” institutions. Another example illustrates why PPtop x% targets have to be adapted to circumstances. In Europe, in the field of technology there are no universities with the PPtop 10% (Leiden Ranking 2020, field of “Physical sciences and engineering”) as high as in some U.S. universities, such as Harvard University, Stanford University, and Massachusetts Institute of Technology (MIT). However, at the country level, several European countries have similar or even higher Ptop 0.01% per million inhabitants than the United States (Rodríguez-Navarro & Brito, 2018b). In these countries it might be a mistake to pursue universities with the high PPtop 10% of the aforementioned US universities. A country’s high PPtop 10% can be obtained from many types of institutions’ PPtop 10% distributions, and it seems that each country should pursue the highest possible Ptop 0.01% per million inhabitants rather than other targets. 5. CONCLUSIONS Making use of the data provided by the Leiden Ranking for many universities, we found further empirical evidence supporting the notion that the size-independent PPtop x% indicators are not dichotomous indicators: Any PPtop x% indicator is sufficient to define the research efficiency of a research institution and all PPtop x% indicators can be easily calculated from only one. Therefore, the information given by the Leiden Ranking and the National Science Board of the National Science Foundation, which report several PPtop x% indicators for the same institution or country, is obviously informative, but actually redundant. Similarly, in Ptop x% indicators, which are size dependent and measure the contribution of research institutions and countries to the advancement of science, by knowing the total number of papers all Ptop x% indicators can be easily calculated from only one, provided that the total number of papers is known. Both the Ptop x% and PPtop x% indicators vary depending on the top percentile selected, which raises the question of which percentile assessments should be made. Our results suggest that for the assessment of contribution to scientific progress, the top 0.01 percentile appears to be the most convenient. In the case of research efficiencies, any single percentile allows com- paring countries and research institutions, but for statistical reasons the top 10 percentile might be the best. Quantitative Science Studies 556 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 2 2 5 4 4 1 9 3 0 7 1 7 q s s _ a _ 0 0 1 3 0 p d / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Total number of papers and in a single percentile fully describes research impact The distributions of universities according to PPtop x% indicators (x ≤ 10) are heavy tailed, which implies that the highest probabilities of making important discoveries accumulate in a very low proportion of all universities. Research policy makers should study the PPtop x% in- dicators of their research institutions before launching research policies that are addressed to the scientific progress of the country. ACKNOWLEDGMENTS We thank two anonymous reviewers for their helpful suggestions on improving the original manuscript. AUTHOR CONTRIBUTIONS Alonso Rodríguez-Navarro: Conceptualization, Data curation, Formal analysis, Investigation, Supervision, Visualization, Writing—original draft, Writing—review & editing. Ricardo Brito: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Visualization, Writing—review & editing. COMPETING INTERESTS The authors declare that there are no competing interests. FUNDING INFORMATION This work was supported by the Spanish Ministerio de Economía y Competitividad, Grant Number FIS2017-83709-R. DATA AVAILABILITY The raw data were downloaded from the Leiden Ranking; these data are available at Zenodo (DOI 10.5281/zenodo.4603232). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u q s s / a r t i c e - p d l f / / / / 2 2 5 4 4 1 9 3 0 7 1 7 q s s _ a _ 0 0 1 3 0 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 REFERENCES Abramo, G., & D’Angelo, C. A. (2016a). A farewell to the MNCS and like size-independent indicators. Journal of Informetrics, 10, 646–651. DOI: https://doi.org/10.1016/j.joi.2016.04.006 Abramo, G., & D’Angelo, C. A. (2016b). A farewell to the MNCS and like size-independent indicators: Rejoinder. Journal of Informetrics, 10, 679–683. DOI: https://doi.org/10.1016/j.joi.2016.01.011 Aksnes, D. W., Langfeldt, L., & Wouters, P. (2019). Citations, citation indicators, and research quality: An overview of basic concepts and theories. SAGE Open, January. DOI: https://doi.org/10.1177 /2158244019829575 Albarrán, P., Herrero, C., Ruiz-Castillo, J., & Villar, A. (2017). The Herrero-Villar approach to citation impact. Journal of Informetrics, 11, 625–640. DOI: https://doi.org/10.1016/j.joi.2017.04.008 Bornmann, L. (2010). Towards an ideal method of measuring research performance: Some comments to the Opthof and Leydesdorff (2010) paper. Journal of Informetrics, 4, 441–443. DOI: https://doi .org/10.1016/j.joi.2010.04.004 Bornmann, L. (2013). How to analyze percentile citation impact data meaningfully in bibliometrics: The statistical analysis of dis- tributions, percentile rank classes, and top-cited papers. Journal of the American Society for Information Science and Technology, 64, 587–595. DOI: https://doi.org/10.1002/asi.22792 Bornmann, L., Leydesdorff, L., & Mutz, R. (2013). The use of percentile rank classes in the analysis of bibliometric data: Opportunities and limits. Journal of Informetrics, 7, 158–165. DOI: https://doi.org/10 .1016/j.joi.2012.10.001 Bornmann, L., Leydesdorff, L., & Wang, J. (2013). Which percentile- based appoach should be preferred for calculating normalized citation impact values? An empirical comparison of five approaches including a newly developed citation-rank approach (P100). Journal of Informetrics, 7, 933–944. DOI: https://doi.org/10.1016/j.joi.2013.09.003 Bornmann, L., & Mutz, R. (2011). Further steps towards an ideal method of measuring citation performance: The avoidance of citation (ratio) averages in field-normalization. Journal of Informetrics, 5, 228–230. DOI: https://doi.org/10.1016/j.joi.2010.10.009 Bornmann, L., Tekles, A., & Leydesdorff, L. (2019). How well does I3 perform for impact measurement compared to other bibliometric indicators? The convergent validity of several (field-normalized) indicators. Scientometrics, 119, 1187–1205. DOI: https://doi.org /10.1007/s11192-019-03071-6 Bornmann, L., Ye, A., & Ye, F. (2018). Identifying landmark publica- tions in the long run using field-normalized citation data. Journal of Documentation, 74, 278–288. DOI: https://doi.org/10.1108/JD -07-2017-0108 Quantitative Science Studies 557 Total number of papers and in a single percentile fully describes research impact Brito, R., & Rodríguez-Navarro, A. (2018). Research assessment by percentile-based double rank analysis. Journal of Informetrics, 12, 315–329. DOI: https://doi.org/10.1016/j.joi.2018.01.011 Brito, R., & Rodríguez-Navarro, A. (2019). Evaluating research and researchers by the journal impact factor: Is it better than coin flip- ping? Journal of Informetrics, 13, 314–324. DOI: https://doi.org/10 .1016/j.joi.2019.01.009 Brito, R., & Rodríguez-Navarro, A. (2020). The USA dominates world research in basic medicine and biotechnology. Journal of Scientometric Research, 9, 154–162. DOI: https://doi.org/10 .5530/jscires.9.2.19 De Bellis, N. (2009). Bibliometrics and Citation Analysis – From the Science Citation Index to Cybermetrics. Lanham, MD: The Scarecrop Press. De Marco, A. (2019). Metrics and evaluation of scientific productivity: Would it be useful to normalize the data taking in consideration the investments? Microbial Cell Factories, 18, 181. DOI: https:// doi.org/10.1186/s12934-019-1236-4, PMID: 31655596, PMCID: PMC6815394 Fortunato, S., Bergstrom, C. T., Börner, K., Evans, J. A., Helbing, D., … Barabási, A.-L. (2018). Science of science. Science, 359, eaao0185. DOI: https://doi.org/10.1126/science.aao0185, PMID: 29496846, PMCID: PMC5949209 Garfield, E. (1980). Premature discovery or delayed recognition – Why? Current Contents, 21, May 26, 5–10. Garfield, E., & Welljams-Dorof, A. (1992). Citation data: Their use as quantitative indicators for science and technology evaluation and policy-making. Science and Public Policy, 19, 321–327. Glänzel, W., Thijs, B., & Debackere, K. (2016). Productivity, per- formance, efficiency, impact – What do we measure anyway? Some comments on the paper “A farewell to the MNCS and like size-independent indicators” by Abramo and D’Angelo. Journal of Informetrics, 10, 658–660. DOI: https://doi.org/10.1016/j.joi .2016.04.008 Godin, B. (2003). The emergence of S&T indicators: Why did govern- ments supplement statistics with indicators? Research Policy, 32, 679–691. DOI: https://doi.org/10.1016/S0048-7333(02)00032-X Harnad, S. (2009). Open access scientometrics and the UK re- search assessment exercise. Scientometrics, 79, 147–156. DOI: https://doi.org/10.1007/s11192-009-0409-z HEFCE. (2015). The Metric Tide: Correlation analysis of REF2014 scores and metrics (Supplementary Report II to the independent Review of the Role of Metrics in Research Assessment and Management). DOI: https://doi.org/10.13140/RG.2.1.3362.4162 Kaptay, G. (2020). The k-index is introduced to replace the h-index to evaluate better the scientific excellence of individuals. Heliyon, 6(7), e04415. DOI: https://doi.org/10.1016/j.heliyon .2020.e04415, PMID: 32685733, PMCID: PMC7358733 Leydesdorff, L., & Bornmann, L. (2011). Integrated impact indica- tors compared with impact factors: An alternative research de- sign with policy implications. Journal of the American Society for Information Science and Technology, 62, 2133–2146. DOI: https://doi.org/10.1002/asi.21609 Leydesdorff, L., & Bornmann, L. (2012). Percentile ranks and the integrated impact indicator (I3). Journal of the American Society for Information Science and Technology, 63, 1901– 1902. DOI: https://doi.org/10.1002/asi.22641 Leydesdorff, L., Bornmann, L., & Adams, J. (2019). The integrated impact indicator revised (I3): A non-parametric alternative to the journal impact factor. Scientometrics, 119, 1669–1694. DOI: https://doi.org/10.1007/s11192-019-03099-8 Leydesdorff, L., Bornmann, L., Mutz, R., & Opthof, T. (2011). Turning the tables on citation analysis one more time: Principles for comparing sets of documents. Journal of the American Society for Information Science and Technology, 62, 1370–1381. DOI: https://doi.org/10.1002/asi.21534 MacRoberts, M. H., & MacRoberts, B. R. (1989). Problems of cita- tion analysis: A crtical review. Journal of the American Society for Information Science and Technology, 40, 342–349. DOI: https://doi.org/10.1002/(SICI)1097-4571(198909)40:5<342::AID -ASI7>3.0.CO;2-U

Mcallister, P. R., Narin, F., & Corrigan, J. G. (1983). Programmatic
evaluation and comparison based on standardized citation
scores. IEEE Transactions on Engineering Management, EM-30(4),
205–211. DOI: https://doi.org/10.1109/TEM.1983.6448622

Moet, H. F. (2005). Citation analysis in research evaluation. Berlin:

Springer Verlag.

Narin, F. (1976). Evaluative bibliometrics: The use of publication and
citation analysis in the evaluation of scientific activity. Computer
Horizon Inc.

National Science Board. (2010). Science and engineering indicators.

National Science Foundation.

National Science Board. (2018). Science and engineering indicators

2018. National Science Foundation

Opthof, T., & Leydesdorff, l. (2010). Caveats for the journal and
field normalizations in the CWTS (“Leiden”) evaluations of re-
search performance. Journal of Informetrics, 4, 423–430. DOI:
https://doi.org/10.1016/j.joi.2010.02.003

Radicchi, F., Fortunato, S., & Castellano, C. (2008). Universality of
citation distributions: Toward an objective measure of scientific
impact. Proceedings of the National Academy of Sciences of the
USA, 105, 17268–17272. DOI: https://doi.org/10.1073/pnas
.0806977105, PMID: 18978030, PMCID: PMC2582263

Rodríguez-Navarro, A., & Brito, R. (2018UN). Double rank analysis
for research assessment. Journal of Informetrics, 12, 31–41. DOI:
https://doi.org/10.1016/j.joi.2017.11.004

Rodríguez-Navarro, A., & Brito, R. (2018B). Technological research in
the EU is less efficient than the world average. EU research policy
risks Europeans’ future. Journal of Informetrics, 12, 718–731. DOI:
https://doi.org/10.1016/j.joi.2018.06.009

Rodríguez-Navarro, A., & Brito, R. (2019). Probability and expected
frequency of breakthroughs – basis and use of a robust method of
research assessment. Scientometrics, 119, 213–235. DOI: https://
doi.org/10.1007/s11192-019-03022-1

Rodríguez-Navarro, A., & Brito, R. (2020UN). Like-for-like biblio-
metric substitutes for peer review: Advantages and limits of indi-
cators calculated from the ep index. Research Evaluation, 29,
215–230. DOI: https://doi.org/10.1093/reseval/rvaa002

Rodríguez-Navarro, A., & Brito, R. (2020B). Might Europe one day
again be a global scientific powerhouse? Analysis of ERC publi-
cations suggests it will not be possible without changes in re-
search policy. Quantitative Science Studies, 1, 872–893. DOI:
https://doi.org/10.1162/qss_a_00039

Ruiz-Castillo, J. (2016). Research output indicators are not produc-
tivity indicators. Journal of Informetrics, 10, 661–663. DOI:
https://doi.org/10.1016/j.joi.2016.04.004

Schreiber, M. (2013). How much do different ways of calculating
percentiles influence the derived performance indicators?
Scientometrics, 97, 821–829. DOI: https://doi.org/10.1007
/s11192-013-0984-x

Siudem, G., Zogala-Siudem, B., Cena, A., & Gagolewski, M.
(2020). Three dimensions of scientific impact. Proceedings of
the National Academy of Sciences USA, 117, 13896–13900.
DOI: https://doi.org/10.1073/pnas.2001064117, PMID:
32513724, PMCID: PMC7322031

Tijssen, R. J. W., Visser, M. S., & van Leeuwen, T. N. (2002).
Benchmarking international scientific excellence: Are highly cited

Quantitative Science Studies

558

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

2
2
5
4
4
1
9
3
0
7
1
7
q
S
S
_
UN
_
0
0
1
3
0
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Total number of papers and in a single percentile fully describes research impact

research papers an appropriate frame of reference? Scientometrics,
54, 381–397. DOI: https://doi.org/10.1023/A:1016082432660
Traag, V. A., & Waltman, l. (2019). Systematic analysis of agreement
between metrics and peer review in the UK REF. Palgrave
Communications, 5, 29. DOI: https://doi.org/10.1057/s41599-019-0233-x
Vinkler, P. (2011). Application of the distribution of citations
among publications in scientometric evaluation. Journal of the
American Society for Information Science and Technology, 62,
1963–1928. DOI: https://doi.org/10.1002/asi.21600

Waltman, L., Calero-Medina, C., Kosten, J., Noyons, E. C. M.,
Tijssen, R. J. W., … Wouters, P. (2012). The Leiden ranking
2011/2012: Data collection, indicators, and interpretation. Journal
of the American Society for Information Science and Technology,
63, 2419–2432. DOI: https://doi.org/10.1002/asi.22708

Waltman, L., & Schreiber, M. (2013). On the calculation of percentile-
based bibliometric indicators. Journal of the American Society for
Information Science and Technology, 64, 372–379. DOI: https://
doi.org/10.1002/asi.22775

Waltman, L., van Eck, N. J., Visser, M., & Wouters, P. (2016). IL
elephant in the room: The problems of quantifying productivity in
evaluative scientometrics. Journal of Informetrics, 10, 671–674.
DOI: https://doi.org/10.1016/j.joi.2015.12.008

Wang, J., Veugelers, R., & Stephan, P. (2017). Bias against novelty
in science: A cautionary tale for users of bibliometric indicators.
Research Policy, 46, 1416–1436. DOI: https://doi.org/10.1016/j
.respol.2017.06.006

Wessa, P. (2017UN). Pearson Correlation (v1.0.13) in Free Statistics
Software (v1.2.1). Office for Research Development and
Education. https://www.wessa.net/rwasp_correlation.wasp/

Wessa, P. (2017B). Spearman Rank Correlation (v1.0.3) in Free
Statistics Software (v1.2.1). Office for Research Development
and Education. https://www.wessa.net/rwasp_spearman.wasp/
Wilsdon, J., Allen, L., Belfiore, E., Campbell, P., Curry, S., …
Johnson, B. (2015). The metric tide: Report of the independent
review of the role of metrics in research assessment and manage-
ment. DOI: https://doi.org/10.13140/RG.2.1.4929.1363