LETTER

Communicated by Razvan Pascanu

Effect of Depth and Width on Local Minima in Deep Learning

Kenji Kawaguchi
kawaguch@mit.edu
MIT, Cambridge, MA 02139, U.S.A.

Jiaoyang Huang
jiaoyang@math.harvard.edu
Harvard University, Cambridge, MA 02138, U.S.A.

Leslie Pack Kaelbling
lpk@csail.mit.edu
MIT, Cambridge, MA 02139, U.S.A.

in questo documento, we analyze the effects of depth and width on the quality
of local minima, without strong overparameterization and simplification
assumptions in the literature. Without any simplification assumption, for
deep nonlinear neural networks with the squared loss, we theoretically
show that the quality of local minima tends to improve toward the global
minimum value as depth and width increase. Inoltre, with a locally
induced structure on deep nonlinear neural networks, the values of local
minima of neural networks are theoretically proven to be no worse than
the globally optimal values of corresponding classical machine learning
models. We empirically support our theoretical observation with a syn-
thetic data set, as well as MNIST, CIFAR-10, and SVHN data sets. When
compared to previous studies with strong overparameterization assump-
zioni, the results in this letter do not require overparameterization and in-
stead show the gradual effects of overparameterization as consequences
of general results.

1 introduzione

Deep learning with neural networks has been a significant practical suc-
cess in many fields, including computer vision, machine learning, and arti-
ficial intelligence. Along with its practical success, deep learning has been
theoretically analyzed and shown to be attractive in terms of its expres-
sive power. Per esempio, neural networks with one hidden layer can ap-
proximate any continuous function (Leshno, Lin, Pinkus, & Schocken, 1993;
Barron, 1993), and deeper neural networks enable us to approximate func-
tions of certain classes with fewer parameters (Montufar, Pascanu, Cho,
& Bengio, 2014; Livni, Shalev-Shwartz, & Shamir, 2014; Telgarsky, 2016).

Calcolo neurale 31, 1462–1498 (2019) © 2019 Istituto di Tecnologia del Massachussetts.
doi:10.1162/neco_a_01195
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale (CC BY 4.0) licenza.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning

1463

Tuttavia, training deep learning models requires us to work with a seem-
ingly intractable problem: nonconvex and high-dimensional optimization.
Finding a global minimum of a general nonconvex function is NP-hard
(Murty & Kabadi, 1987), and nonconvex optimization to train certain types
of neural networks is also known to be NP-hard (Blum & Rivest, 1992).
These hardness results pose a serious concern only for high-dimensional
problems, because global optimization methods can efficiently approximate
global minima without convexity in relatively low-dimensional problems
(Kawaguchi, Kaelbling, & Lozano-Pérez, 2015).

A hope is that beyond the worst-case scenarios, practical deep learning
allows some additional structure or assumption to make nonconvex high-
dimensional optimization tractable. Recentemente, it has been shown with strong
simplification assumptions that there are novel loss landscape structures in
deep learning optimization that may play a role in making the optimization
tractable (Dauphin et al., 2014; Choromanska, Henaff, Mathieu, Ben Arous,
& LeCun, 2015; Kawaguchi, 2016). Another key observation is that if a neu-
ral network is strongly overparameterized so that it can memorize any data
set of a fixed size, then all stationary points (including all local minima and
saddle points) become global minima, with some nondegeneracy assump-
zioni. This observation was explained by Livni et al. (2014) and further re-
fined by Nguyen and Hein (2017, 2018). Tuttavia, these previous results
(Livni et al., 2014; Nguyen and Hein, 2017, 2018) require strong overparam-
eterization by assuming not only that a network’s width is larger than the
data set size but also that optimizing only a single layer (the last layer or
some hidden layer) can memorize any data set based on an assumed con-
dition on the rank or nondegeneracy of other layers.

In this letter, we analyze the effects of depth and width on the values
of local minima, without the strong overparameterization and simplifica-
tion assumptions in the literature. Di conseguenza, we prove quantitative upper
bounds on the quality of local minima, which shows that the values of local
minima of neural networks are guaranteed to be no worse than the globally
optimal values of corresponding classical machine learning models, and the
guarantee can improve as depth and width increase.

2 Preliminari

This section defines the optimization problem considered in this letter and
introduces the basic notation.

2.1 Problem Formulation. Let x ∈ Rdx and y ∈ Rdy be an input vector
i=1 be a training data set of
j=1 :=
j=1, define [M( j)]N
to be a block matrix of each column block being

and a target vector, rispettivamente. Let {(xi
size m. Given a set of n matrices or vectors {M( j)}N
(cid:2)
M(1) M(2)

· · · M(N)

, yi)}M

(cid:3)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1464

K. Kawaguchi, J. Huang, and L. Kaelbling

M(1), M(2), . . . , M(N). Define the training data matrices as X := ([xi]M
Rm×dx and Y := ([yi]M

(cid:3) ∈ Rm×dy .

i=1)

i=1)

This letter considers the squared loss function, with which the training
objective of the neural networks can be formulated as the following opti-
mization problem:

(cid:3) ∈

minimize
θ

l(θ ) := 1
2

(cid:4) ˆY(X, θ ) − Y(cid:4)2
F

,

(2.1)

Dove (cid:4) · (cid:4)F is the Frobenius norm, ˆY(X, θ ) ∈ Rm×dy is the output prediction
matrix of a neural network, and θ ∈ Rdθ is the vector consisting of all train-
m L(θ ) is the standard mean squared error, for which
able parameters. Here, 2
all of our results hold true as well, because multiplying L(θ ) by a constant
M (in θ ) changes only the entire scale of the optimization landscape.
2

The output prediction matrix ˆY(X, θ ) ∈ Rm×dy is specified for shallow
networks with rectified linear units (ReLUs) in section 3 and generalized
to deep nonlinear neural networks in section 4.

2.2 Additional Notation. Define P[M] to be the orthogonal projection
matrix onto the column space (or range space) of a matrix M. Let PN[M]
be the orthogonal projection matrix onto the null space (or kernel space)
of a matrix M(cid:3)
, we denote the standard vec-
torization of the matrix M as vec(M) = [M1,1
, . . . ,
, M1,2
M1,d(cid:5) , . . . , Md,D(cid:5) ]T.

. For a matrix M ∈ Rd×d(cid:5)

, . . . , Md,2

, . . . , Md,1

3 Shallow Nonlinear Neural Networks with Scalar-Valued Output

Before presenting our main results for deep nonlinear neural networks,
this section provides the results for shallow networks with a single hid-
den layer (or three-layer networks with the input and output layers) E
scalar-valued output (cioè., dy = 1) to illustrate some of the ideas behind the
discussed effects of the depth and width on local minima.

In this section, the vector θ ∈ Rdθ of all trainable parameters deter-
mines the entries of the weight matrices W (1) := W (1)(θ ) ∈ Rdx×d and W (2) :=
W (2)(θ ) ∈ Rd as vec([W (1)(θ ), W (2)(θ )]) = θ . Given an input matrix X and a
parameter vector θ , the output prediction matrix ˆY(X, θ ) ∈ Rm of a fully
connected feedforward network with a single hidden layer can be written
COME

ˆY(X, θ ) := σ (XW (1))W (2),

(3.1)

where σ : Rm×d → Rm×d is defined by coordinate-wise nonlinear activation
functions σ

io, j(Mi, j ) for each (io, j).

io, j as (P (M))io, j := σ

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning

1465

io, j is assumed to be ReLU as σ

3.1 Analysis with ReLU Activations. In this section, the nonlinear acti-
io, j(z) = max(0, z). Let (cid:4)1,k ∈
vation function σ
Rm×m represent a diagonal matrix with diagonal elements corresponding
to the activation pattern of the kth unit at the hidden layer over m different
samples as for all i ∈ {1, . . . , M} and all k ∈ {1, . . . , D},

(cid:4)

(cid:4)1,k
ii

=

1 if (XW (1))io,k
0 otherwise

> 0

.

Let (cid:5)(1) := (cid:5)(1)(X, θ ) := σ (XW (1)) ∈ Rm×d be the postactivation output of
the hidden layer.

Under this setting, proposition 1 provides an equation that holds at lo-
cal minima and illustrates the effect of width for shallow ReLU neural
networks.

Proposition 1. Every differentiable local minimum θ of L satisfies that

l(θ ) = 1
2

(cid:4)Y(cid:4)2
2

− 1
2

(cid:5)
(cid:5)
(cid:5)P

(cid:6)
N(2)
1

(cid:7)

(cid:5)(1)

Y

(cid:5)
(cid:5)
(cid:5)

2

2

−

(cid:5)
(cid:5)
(cid:5)P

1
2
(cid:9)

(cid:6)
N(1)
k D(1)
(cid:10)(cid:11)
≥0

k

D(cid:8)

k=1
(cid:9)

(cid:7)

2

(cid:5)
(cid:5)
(cid:5)
(cid:12)
2

Y

,

(cid:10)(cid:11)
further improvement as a network gets wider

(cid:12)

(3.2)

= W (2)
k

where D(1)
k
:= PN[ ¯Q(1)
{2, . . . , D}, and N(2)
1
for any k ∈ {1, . . . , D}.
k D(1)
N(1)

(cid:4)1,kX. Here, N(1)
1
D ], Dove

k

:= Im, N(1)
k
¯Q(1)
k

:= [Q(1)
1

:= PN[ ¯Q(1)

k−1]
, . . . , Q(1)

for any k ∈
:=

k ] and Q(l)

k

Proposition 1 is an immediate consequence of our general result (see the-
orem 1) in the next section (the proof is provided in section A.1). In the rest
of this section, we provide a proof sketch of proposition 1.

A geometric intuition behind proposition 1 is that a local minimum is
a global minimum within a local region in Rdθ (cioè., a neighborhood of the
local minimum), the dimension of which increases as a network gets wider
(or the number of parameters increases). Così, a local minimum is a global
minimum of a search space with a larger dimension for a wider network.
One can also see this geometric intuition in an analysis as follows. If θ is a
differentiable local minimum, then θ must be a critical point and thus,

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

∇θ L(θ ) =

(cid:13)
∇θ ˆY(X, θ )

(cid:14) (cid:13)

(cid:14)

ˆY(X, θ ) − Y

= 0.

1466

K. Kawaguchi, J. Huang, and L. Kaelbling

By rearranging this,

(cid:14)
(cid:13)
∇θ ˆY(X, θ )

ˆY(X, θ ) =

(cid:14)
(cid:13)
∇θ ˆY(X, θ )

Y,

(3.3)

where we can already see the power of strong overparameterization in that
if the matrix ∇θ ˆY(X, θ ) ∈ Rdθ ×m is left-invertible, ˆY(X, θ ) = Y, and hence ev-
ery differentiable local minimum is a global minimum. Here, ∇θ ˆY(X, θ ) is a
dθ by m matrix, so significantly increasing dθ (strong overparameterization)
can ensure the left invertibility.

Beyond the strong overparameterization, we proceed with the proof
sketch of proposition 1 by taking advantage of the special neural network
structures in ˆY(X, θ ) and ∇θ ˆY(X, θ ). We first observe that ˆY(X, θ ) = (cid:5)(1)W (1)
and ˆY(X, θ ) = D(1)vec(W (2)), where D(1) := [D(1)
k=1. Inoltre, at any dif-
ferentiable point, we have that ∇
ˆY(X, θ )
(cid:3)
= (D(1))

W (1) ˆY(X, θ ) = ((cid:5)(1))
. Combining these with equation 3.3 yields
(cid:17)(cid:18)

and ∇

k ]dθ

vec(W (2) )

(cid:15)

(cid:16)

(cid:3)

(cid:5)(1) D(1)

(cid:5)(1) D(1)

(cid:3)(cid:3)

(cid:2)

1
2

(cid:3)

W (1)
vec(W (2))

=

(cid:2)

(cid:5)(1) D(1)

(cid:3)(cid:3)

Y,

(cid:2)

Dove

(cid:2)

ˆY(X, θ ) = 1
2

(cid:5)(1) D(1)

(cid:16)

(cid:3)

W (1)
vec(W (2))

By solving for the vector

(cid:2)

W (1) vec(W (2))

(cid:17)

.

(cid:3)
,

ˆY(X, θ ) = P

(cid:2)(cid:2)

D(1) (cid:5)(1)

(cid:3)(cid:3)

Y.

Therefore,

l(θ ) = 1
2

(cid:5)
(cid:5)
Y − P

(cid:2)(cid:2)

D(1) (cid:5)(1)

(cid:3)(cid:3)

(cid:5)
(cid:5)2
2

Y

= (cid:4)Y(cid:4)2
2

−

(cid:2)(cid:2)

(cid:5)
(cid:5)

P

D(1) (cid:5)(1)

(cid:3)(cid:3)

(cid:5)
(cid:5)2
2

,

Y

where the second equality follows the idempotence of the projection. Fi-
nally, decomposing the second term (cid:4)P
2 by following the
Gram-Schmidt process on the set of column vectors of [D(1) (cid:5)(1)] yields the
desired statement of proposition 1, completing its proof sketch. In propo-
sition 1, the matrices N(l)
k ) are by-products of this Gram-Schmidt
k
processi.

(cid:3)
(cid:2)
[D(1) (cid:5)(1)]

(and Q(l)

Y(cid:4)2

3.2 Probabilistic Bound. From equation 2.2 in proposition 1, the loss
l(θ ) at differentiable local minima is expected to tend to get smaller as the

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning

1467

width of the hidden layer d gets larger. To further support this theoretical
observation, this section obtains a probabilistic upper bound on the loss L(θ )
for white noise data by fixing the activation patterns (cid:4)1,k for k ∈ {1, 2, . . . , D}
and assuming that the data matrix [ X Y ] is a random gaussian matrix,
with each entry having mean zero and variance one.

In this section, each nonlinear activation function σ
io, j(z) = max(0, z)) and leaky ReLU (P

io, j is assumed to be
io, j(z) = max(az, z) with any
ReLU (P
io, j(z) = |z|). Let (cid:4)1,k ∈ Rm×m rep-
fixed a ≤ 1) or absolute value activation (P
resent a diagonal matrix with diagonal elements corresponding to the acti-
vation pattern of the kth unit at the hidden layer over m different samples
COME

(cid:4)1,k
ii

:=

⎧
⎪⎨

⎪⎩

(cid:23)
(cid:23)
(cid:23)

∂σ (1)
io,k (z)
∂z

0

∂σ (1)
io,k (z)
∂z

(cid:23)
(cid:23)
(cid:23)
z=(XW (1) )io,k

if

exists

.

z=(XW (1) )io,k

otherwise

This definition of (cid:4)1,k
ii generalizes the corresponding definition in section
3.1. Proposition 1 holds for this generalized activation pattern by simply
replacing the previous definition of (cid:4)1,k
ii by this more general definition.
This can be seen from the proof sketch in section 3.1 and is later formalized
in the proof of theorem 1.

We denote the vector consisting of the diagonal entries of (cid:4)1,k by (cid:4)k ∈ Rm
∈
for k ∈ {1, 2, . . . , D}. Define the activation pattern matrix as (cid:4) := [(cid:4)k]D
Rm×d. For any index set I ⊆ {1, 2, . . . , M}, let (cid:4)I denote the submatrix of (cid:4)
that consists of its rows of indices in I. Let smin((cid:4)IO ) be the smallest singular
value of (cid:4)IO.

Proposition 2 proves that L(θ ) ≈ (1 − dxd/m)(cid:4)Y(cid:4)2
2

/2 in the regime dxd (cid:12)
M, and L(θ ) = 0 in the regime dxd (cid:13) M, under the corresponding condi-
tions on (cid:4); questo è, smin((cid:4)IO ) ≥ δ for any index set I ⊆ {1, 2, . . . , M} such that
|IO| ≥ m/2 in the regime dxd (cid:12) M, E |IO| ≤ d/2 in the regime dxd (cid:13) M. Questo
supports our theoretical observation that increasing width helps improve
the quality of local minima.
∈ Rm×d. Let
Proposition 2. Fix the activation pattern matrix (cid:4) = [(cid:4)k]D
(cid:2)
be a random m × (dx + 1) gaussian matrix, with each entry having mean
X Y
zero and variance one. Then the loss L(θ ) as in equation 3.2 satisfies both of the fol-
lowing statements:

k=1

k=1

(cid:3)

io. If m ≥ 64 ln2(dxdm/δ2)dxd and smin((cid:4)IO ) ≥ δ for any index set I ⊆

{1, 2, . . . , M} con |IO| ≥ m/2, Poi

(cid:15)

(cid:24)

(cid:18)

l(θ ) ≤

1 + 6

T
M

m − dxd
2M

(cid:4)Y(cid:4)2
2

,

with probability at least 1 − e−m/(64 ln(dxdm/δ2 )) − 2e−t.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1468

K. Kawaguchi, J. Huang, and L. Kaelbling

ii. If ddx ≥ 2m ln2(md/δ) with dx ≥ ln2(dm) and smin((cid:4)IO ) ≥ δ for any index

set I ⊆ {1, 2, . . . , M} con |IO| ≤ d/2, Poi

l(θ ) = 0

with probability at least 1 − 2e−dx/20.

The proof of proposition 2 is provided in appendix B. In that proof, we
first rewrite the loss L(θ ) as the projection of Y onto the null space of an
m × dd0 matrix ˜D, with an explicit expression in terms of the activation pat-
tern matrix (cid:4) and the data matrix X. By our assumption, the data matrix
X is a random gaussian matrix. The projection matrix ˜D is also a random
matrix. Proposition 2 then boils down to understanding the rank of the pro-
jection matrix ˜D, and we proceed to show that ˜D has the largest possible
rank, min{dd0
, M}, with high probability. Infatti, we derive quantitative es-
timates on the smallest singular value of ˜D. The main difficulties are that
the columns of the matrix ˜D are correlated and variances of different en-
tries vary. Our approach to obtain quantitative estimates on the smallest
singular value of ˜D combines the epsilon net argument with an iterative
argument.

In the regime dd0

(cid:13) M, results similar to proposition 2ii were obtained
under certain diversity assumptions on the entries of the weight matrices
in a previous study (Xie, Liang, & Song, 2017). When compared with the
previous study (Xie et al., 2017), proposition 2 specifies precise relations be-
tween the size dd0 of the neural network and the size m of the data set and
(cid:12) M. Inoltre, our proof arguments for
also holds true in the regime dd0
proposition 2ii are different. Xie et al. (2017), under the assumption that
(cid:13) M, show that ˜D ˜DT is close to its expectation in the sense of spec-
dd0
tral norm. As a consequence, the lower bound of the smallest eigenvalue
of E[ ˜D ˜DT ] gives the lower bound for the smallest singular value of ˜D.

Tuttavia, proposition 2 assumes a gaussian data matrix, which may be a
substantial limitation. The proof of proposition 2 relies on the concentration
properties of gaussian distribution. Whereas a similar proof would be able
to extend proposition 2 to a nongaussian distribution with these properties
(per esempio., distributions with subgaussian tails), it would be challenging to use
a similar proof for a general distribution without the properties similar to
quelli.

4 Deep Nonlinear Neural Networks

Let H be the number of hidden layers and dl be the width (O, equiva-
lently, the number of units) of the lth hidden layer. To theoretically ana-
lyze concrete phenomena, the rest of this letter focuses on fully connected
feedforward networks with various depths H ≥ 1 and widths dl
≥ 1, using
rectified linear units (ReLUs), leaky ReLUs, and absolute value activations,
evaluated with the squared loss function. In the rest of this letter, IL (finite)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning

1469

depth H can be arbitrarily large and the (finite) widths dl can arbitrarily dif-
fer among different layers.

4.1 Model and Notation. Let θ ∈ Rdθ be the vector consisting of all
trainable parameters, which determines the entries of the weight matrix
×dl at every lth hidden layer as vec([W (l)(θ )]H+1
l=1 ) = θ .
W (l) := W (l)(θ ) ∈ Rdl−1
H+1
Here, dθ :=
l=1 dl−1dl is the number of trainable parameters. Given an
input matrix X and a parameter vector θ , the output prediction matrix
ˆY(X, θ ) ∈ Rm×dH+1 of a fully connected feedforward network can be written
COME

(cid:25)

ˆY(X, θ ) := (cid:5)(H)W (H+1),

(4.1)

Dove (cid:5)(l) := (cid:5)(l)(X, θ ) ∈ Rm×dl is the postactivation output of lth hidden
layer,

(cid:5)(l)(X, θ ) := σ (l)((cid:5)(l−1)W (l)),

Dove (cid:5)(0)(X, θ ) := X, (cid:5)(H+1)(X, θ ) := ˆY(X, θ ), and σ (l) : Rm×dl → Rm×dl is
defined by coordinate-wise nonlinear activation functions σ (l)
io, j as (P (l)(M))io, j
:= σ (l)
io, j (Mi, j ) for each (l, io, j). Each nonlinear activation function σ (l)
io, j is al-
lowed to differ among different layers and different units within each
layer, but assumed to be ReLU (P (l)
io, j (z) =
max(az, z) with any fixed a ≤ 1) or absolute value activation (P (l)
io, j (z) = |z|).
= dx. Let (cid:4)l,k ∈ Rm×m represent a diagonal matrix
Here, dH+1
with diagonal elements corresponding to the activation pattern of the kth
unit at the lth layer over m different samples as

io, j (z) = max(0, z)), leaky ReLU (P (l)

= dy and d0

(cid:4)l,k
ii

:=

⎧
⎪⎪⎨

⎪⎪⎩

(cid:23)
(cid:23)
(cid:23)

∂σ (l)
io,k (z)
∂z

0

z=((cid:5)(l−1)W (l) )io,k

(cid:23)
(cid:23)
(cid:23)

∂σ (l)
io,k (z)
∂z

if

otherwise

z=((cid:5)(l−1)W (l) )io,k

exists

.

This definition of (cid:4)l,k

ii generalizes the corresponding definition in sec-
zione 3. Let Id be the identity matrix of size d by d. Define M ⊗ M(cid:5)
to be the
Kronecker product of matrices M and M(cid:5)
. Given a matrix M, M·, j and Mi,·
denote the jth column vector of M and the ith row vector of M, rispettivamente.

4.2 Theoretical Result. For the standard deep nonlinear neural net-
works, theorem 1 provides an equation that holds at local minima and il-
lustrates the effect of depth and width. Let d(cid:5)
l := dl for all l ∈ {1, . . . , H} E
D(cid:5)
H+1 := 1.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1470

K. Kawaguchi, J. Huang, and L. Kaelbling

Theorem 1. Every differentiable local minimum θ of L satisfies that

l(θ ) = 1
2

(cid:4)Y(cid:4)2
F

−

H+1(cid:8)

D(cid:5)
l(cid:8)

=1

kl

l=1
(cid:9)

(cid:6)

(cid:5)
(cid:5)
(cid:5)P

N(l)
kl

1
2
(cid:9)

(cid:7)

vec(Y)

2

(cid:5)
(cid:5)
(cid:5)
(cid:12)
2

,

(4.2)

D(l)
kl
(cid:10)(cid:11)
≥0

(cid:10)(cid:11)
further improvement as
a network gets wider and deeper

(cid:12)

where D(l)
kl
{1, . . . , H} and any kl

:= D(l)
kl

(θ ) and N(l)
kl

∈ {1, . . . , dl

:= N(l)
kl
},

(θ ) are defined as follows. For any l ∈

D(l)
kl

:=

dl+1(cid:8)

dH(cid:8)

· · ·

kl+1

=1

kH =1

(W (l+1)
,kl+1
kl

· · · W (H)
kH−1

,kH

W (H+1)
kH ,·

(cid:3) ⊗ (cid:4)l,kl · · · (cid:4)H,kH (cid:5)(l−1),
)

with D(H)
kl
{1, . . . , dl
Q(2)
1
D(H+1)

:= (W (H+1)
}, N(l)
kl
, . . . , Q(l)
1

(cid:3) ⊗ (cid:4)H,kH (cid:5)(H−1). For any l ∈ {1, . . . , H} and any kl
∈
)
kH ,·
:= PN[ ¯Q(l)
, . . . , Q(1)
:= Im where
−1] with N(1)
1
d1
kl
], Q(l)
:= N(l)
D(l)
. Here,
kl
kl
kl
(θ ) := PN[ ¯Q(H)
dH

, . . . , Q(l)
kl
⊗ (cid:5)(H) and N(H+1)

, and ¯Q(l)
0

:= ¯Q(l−1)
dl−1

:= [Q(1)
1

¯Q(l)
kl

, . . . , Q(2)
d2
(θ ) := IdH+1

].

,

1

1

The complete proof of theorem 1 is provided in section A.1. Theorem 1
is a generalization of proposition 1. Accordingly, its proof follows the proof
sketch presented in the previous section for proposition 1.

Unlike previous studies (Livni et al., 2014; Nguyen & Hein, 2017, 2018),
≥ m. Invece, it pro-
theorem 1 requires no overparameterization such as dl
vides quantitative gradual effects of depth and width on local minima,
from no overparameterization to overparameterization. Notably, theorem 1
shows the effect of overparameterization in terms of depth as well as width,
which also differs from the results of previous studies that consider overpa-
rameterization in terms of width (Livni et al., 2014; Nguyen & Hein, 2017,
2018).

≥ m and rank(D(1)) ≥ m, ∇

The proof idea behind these previous studies with strong overparam-
eterization is captured in the discussion after equation 3.3—with strong
vec(W ) ˆY(X, θ ) ∈
overparameterization such that dl
×m is left-invertible and hence every local minimum is a global minimum
Rdl
with zero training error. Here, rank(M) represents the rank of a matrix M.
The proof idea behind theorem 1 differs from those as shown in section 3.1.
What is still missing in theorem 1 is the ability to provide a prior guarantee
on L(θ ) without strong overparameterization, which is addressed in sec-
zioni 3.2 E 5 for some special cases but left as an open problem for other
cases.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning

1471

4.3 Experiments. In theorem 1, we have shown that at every differen-
tiable local minimum θ , the total training loss value L(θ ) has an analytical
formula L(θ ) = J(θ ), Dove

J(θ ) := 1
2

(cid:4)Y(cid:4)2
F

−

H+1(cid:8)

D(cid:5)
l(cid:8)

l=1

=1

kl

(cid:5)
(cid:5)
(cid:5)P

(cid:6)
N(l)
kl

1
2

(cid:7)
(θ )

(θ )D(l)
kl

(cid:5)
(cid:5)
(cid:5)

vec(Y)

2

2

, yi)}M

denotes the right-hand side of equation 4.1. In this section, we investigate
the actual numerical values of the formula J(θ ) with a synthetic data set and
standard benchmark data sets for neural networks with different degrees of
depth = H and hidden layers’ width = dl for l ∈ {1, 2, . . . , H}.

In the synthetic data set, the data points {(xi

i=1 were randomly
generated by a ground-truth, fully connected feedforward neural network
with H = 7, dl
= 50 for all l ∈ {1, 2, . . . , H}, tanh activation function, (X, sì) ∈
R10 × R and m = 5000. MNIST (LeCun, Bottou, Bengio, & Haffner, 1998), UN
popular data set for recognizing handwritten digits, contains 28 × 28 gray-
scale images. The CIFAR-10 (Krizhevsky & Hinton, 2009) data set consists
Di 32 × 32 color images that contain different types of objects such as “air-
plane,” “automobile,” and “cat.” The Street View House Numbers (SVHN)
insieme di dati (Netzer et al., 2011) contains house digits collected by Google Street
View, and we used the 32 × 32 color image version for the standard task of
predicting the digits in the middle of these images. In order to reduce the
computational cost, for the image data sets (MNIST, CIFAR-10, and SVHN),
we center-cropped the images (24 × 24 for MNIST and 28 × 28 for CIFAR-
10 and SVHN), then resized them to smaller gray-scale images (8 × 8 for
MNIST and 12 × 12 for CIFAR-10 and SVHN), and used randomly selected
subsets of the data sets with size m = 10,000 as the training data sets.

For all the data sets, the network architecture was fixed to be a fully con-
nected feedforward network with the ReLU activation function. For each
insieme di dati, the values of J(θ ) were computed with initial random weights
drawn from a normal distribution with zero mean and normalized stan-
dard deviation (1/
dl) and with trained weights at the end of 40 training
epochs. (Additional experimental details are presented in appendix C.)

√

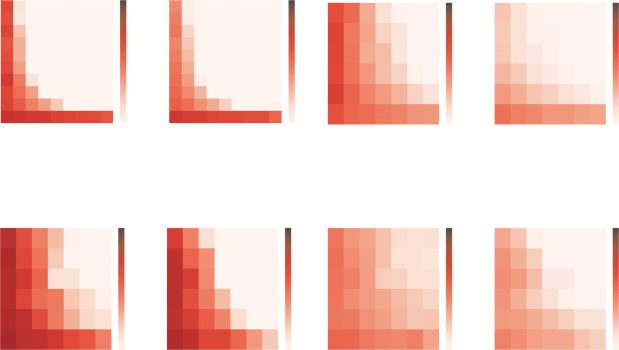
Figura 1 shows the results with the synthetic data set, as well as the
MNIST, CIFAR-10, and SVHN data sets. As it can be seen, the values of
J(θ ) tend to decrease toward zero (and hence the global minimum value),
as the width or depth of neural networks increases. In theory, the values of
J(θ ) may not improve as much as desired along depth and width if repre-
sentations corresponding to each unit and each layer are redundant in the
sense of linear dependence of the columns of D(l)
(θ ) (see theorem 1). Intu-
kl
itively, at initial random weights, one can mitigate this redundancy due to
the randomness of the weights, and hence a major concern is whether such
redundancy arises and J(θ ) degrades along with training. From Figure 1,

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1472

K. Kawaguchi, J. Huang, and L. Kaelbling

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

(cid:26)

J(θ ) for the training data sets (J(θ ) are on the right-
Figura 1: The values of
hand side of equation 4.1) with varying depth = H (y-axis) and width = dl for
J(θ ).
all l ∈ {1, 2, . . . , H} (x-axis). The heat map colors represent the values of
In all panels of this figure, the left heat map (initial) is computed with initial
random weights and the right heat map (trained) is calculated after training. It
can be seen that both depth and width helped improve the values of J(θ ).

(cid:26)

it can be also noticed that the values of J(θ ) tend to decrease along with
training. These empirical results partially support our theoretical observa-
tion that increasing the depth and width can improve the quality of local
minima.

5 Deep Nonlinear Neural Networks with Local Structure

Given the scarcity of theoretical understanding of the optimality of deep
neural networks, Goodfellow, Bengio, and Courville (2016) noted that it
is valuable to theoretically study simplified models: deep linear neural
networks. Per esempio, Saxe, McClelland, and Ganguli (2014) empirically
showed that in terms of optimization, deep linear networks exhibited sev-
eral properties similar to those of deep nonlinear networks. Following these
observations, the theoretical study of deep linear neural networks has be-
come an active area of research (Kawaguchi, 2016; Hardt & Mamma, 2017; Arora,
Cohen, Golowich, & Eh, 2018; Arora, Cohen, & Hazan, 2018), as a step to-
ward the goal of establishing the optimization theory of deep learning.

Effect of Depth and Width on Local Minima in Deep Learning

1473

As another step toward the goal, this section discards the strong linear-
ity assumption and considers a locally induced nonlinear-linear structure
in deep nonlinear networks with the piecewise linear activation functions
such as ReLUs, leaky ReLUs, and absolute value activations.

5.1 Locally Induced Nonlinear-Linear Structure. In this section, we de-
scribe how a standard deep nonlinear neural network can induce nonlinear-
linear structure. The nonlinear-linear structure considered in this letter is
defined in definition 1: condition i simply defines the index subsets S(l) Quello
pick out the relevant subset of units at each layer l, condition ii requires the
existence of n linearly acting units, and condition iii imposes weak separa-
bility of edges.

Definition 1. A parameter vector θ is said to induce (N, T) weakly separated
linear units on a training input data set X if there exist (H + 1 − t) sets
S(t+1), S(t+2), . . . , S(H+1) such that for all l ∈ {T + 1, T + 2, . . . , H + 1}, the follow-
ing three conditions hold:

io. S(l) ⊆ {1, . . . , dl
ii. (cid:5)(l)(X, θ )·,k
iii. W (l+1)(θ )k(cid:5),k

} con |S(l)| ≥ n.

= (cid:5)(l−1)(X, θ )W (l)(θ )·,k for all k ∈ S(l).
= 0 for all (k(cid:5), k) ∈ S(l) × ({1, . . . , dl+1

} \ S(l+1)) if l ≤ H −

1.

dH+1

Given a training input data set X, let (cid:8)N,t be the set of all parameter vec-
tors that induce (N, T) weakly separated linear units on the training input
data set X that defines the total loss L(θ ) in equation 2.1. For standard deep
nonlinear neural networks, all parameter vectors θ are in (cid:8)
,H, and some
parameter vectors θ are in (cid:8)N,t for different values of (N, T). Figura 2 a il-
lustrates locally induced structures for θ ∈ (cid:8)
1,0. For a parameter θ to be in
(cid:8)N,T, definition 1 requires only the existence of a portion n/dl of units to act
linearly on the particular training data set merely at the particular θ . Così,
all units can be nonlinear, act nonlinearly on the training data set outside of
some parameters θ , and operate nonlinearly always on other inputs x—for
esempio, in a test data set or a different training data set. The weak sep-
arability requires that the edges going from the n units to the rest of the
network are negligible. The weak separability does not require the n units
to be separated from the rest of the neural network.

Here, a neural network with θ ∈ (cid:8)N,t can be a standard deep nonlinear
neural network (without any linear units in its architecture), a deep linear
neural network (with all activation functions being linear), or a combination
of these cases. Whereas a standard deep nonlinear neural network can nat-
urally have parameters θ ∈ (cid:8)N,T, it is possible to guarantee all parameters
θ to be in (cid:8)N,t with desired (N, T) simply by using corresponding network
architectures. For standard deep nonlinear neural networks, one can also
restrict all relevant convergent solution parameters θ to be in (cid:8)N,t by using

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1474

K. Kawaguchi, J. Huang, and L. Kaelbling

Figura 2: Illustration of locally induced nonlinear-linear structures. (UN) Sim-
ple examples of the structure with weakly separated edges considered in this
section (see definition 1). (B) Examples of a simpler structure with strongly
separated edges (see definition 2). The red nodes represent the linearly acting
units on a training data set at a particular θ , and the white nodes are the re-
maining units. The black dashed edges represent standard edges without any
assumptions. The red nodes are allowed to depend on all nodes from the pre-
vious layer in panel a, whereas they are not allowed in panel b except for the
input layer. In both panels a and b, two examples of parameters θ are presented
with the exact same network architecture (including activation functions and
edges). Even if the network architecture (or parameterization) is identical, dif-
ferent parameters θ can induce different local structures. Con (cid:8)
1,4, this local
structure always holds in standard deep nonlinear networks with four hidden
layers.

some corresponding learning algorithms. Our theoretical results hold for
all of these cases.

1
2

(cid:4)M(X )R − Y(cid:4)2

5.2 Theoretical Result. We state our main theoretical result in theo-
rem 2 and corollary 1; a simplified statement is presented in remark 1.
Here, a classical machine learning method, basis function regression, È
used as a baseline to be compared with neural networks. The global min-
imum value of basis function regression with an arbitrary basis matrix
M(X ) is infR
F, where the basis matrix M(X ) does not de-
pend on R and can represent nonlinear maps, Per esempio, by setting M =
(cid:3) ∈ Rm×dφ with any nonlinear basis functions φ and any finite
([φ(xi)]M
(cid:3)
(cid:2)
Y represents the projection of Y
dφ. In theorem 2, the expression PN
(cid:3)
onto the null space of ((cid:5)(S))
, which is also (Y—the projection of Y onto
the column space of (cid:5)(S)). Given matrices (M( j)) j∈S with a sequence S =
· · · M(sn )
(s1
to be a block
matrix with columns being M(s1 ), M(s2 ), . . . , M(sn ). Let S ⊆ (s1
, . . . , sn) Di-
, s2
note a subsequence of (s1

, . . . , sn), define [M( j)] j∈S :=

M(s1 ) M(s2 )

, . . . , sn).

i=1)

(cid:5)(S)

, s2

, s2

(cid:2)

(cid:3)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning

1475

Theorem 2. For any t ∈ {0, 1, . . . , H}, every differentiable local minimum θ ∈
(cid:8)
,t of L satisfies that for any subsequence S ⊆ (T, T + 1, . . . , H) (including the
case of S being the empty sequence),

dH+1

l(θ ) ≤ 1
2
(cid:9)

(cid:7)

Y

(cid:5)
(cid:5)
(cid:5)PN

(cid:6)
(cid:5)(S)
(cid:10)(cid:11)
global minimum value of
basis function regression
with basis matrix (cid:5)(S)

(cid:5)
(cid:5)
(cid:5)

2

(cid:12)
F

−

H(cid:8)

dl(cid:8)

=1

kl

l=1
(cid:9)

(cid:5)
(cid:5)
(cid:5)P

(cid:6)
N(l)
kl

PN

1
2
(cid:9)

(cid:6)

(cid:7)

(cid:7)

D(l)
kl

¯(cid:5)(S)
(cid:10)(cid:11)
≥0

(cid:10)(cid:11)
further improvement as
a network gets wider and deeper

vec(Y)

2

(cid:5)
(cid:5)
,
(cid:5)
(cid:12)
2

(cid:12)

(5.1)

(cid:3)

(cid:2)
¯(cid:5)(S)

(cid:2)

(cid:3)

where PN
[IdH+1
trices D(l)
kl
PN[ ¯(cid:5)(S)]D(l)
N(l)
kl
kl

(cid:5)(S)

∈ Rm×m, PN

∈ RmdH+1
¯(cid:5)(S) =
⊗ (cid:5)(l)]l∈S. If S is empty, PN[(cid:5)(S)] = Im and PN[ ¯(cid:5)(S)] = ImdH+1 . The ma-
=

are defined in theorem 1 with the exception that Q(l)
kl

×mdH+1 , (cid:5)(S) = [(cid:5)(l)]l∈S,

and N(l)
kl
(instead of Q(l)
kl

:= N(l)
kl

D(l)
kl

).

Remark 1. From theorem 2 (or corollary 1), one can see the following prop-
erties of the loss landscape:

dH+1

io. Every differentiable local minimum, θ ∈ (cid:8)

,t has a loss value L(θ )
better than or equal to any global minimum value of basis func-
tion regression with any combination of the basis matrices in the set
{(cid:5)(l)}H
l=t of fixed deep hierarchical representation matrices. In partic-
ular with t = 0, every differentiable local minimum θ ∈ (cid:8)
,0 has a
loss value L(θ ) no worse than the global minimum values of standard
basis function regression with the handcrafted basis matrix (cid:5)(0) = X,
and of basis function regression with the larger basis matrix [(cid:5)(l)]H
l=0.
ii. As dl and H increase (O, equivalently, as a neural network gets wider
and deeper), the upper bound on the loss values of local minima can
further improve.

dH+1

The proof of theorem 2 is provided in section A.2. The proof is based on
the combination of the idea presented in section 3.1 and perturbations of a
local minimum candidate. Questo è, if a θ is a local minimum, then the θ is
a global minimum within a local region (cioè., a neighborhood of θ ). Così,
after perturbing θ as θ (cid:5) = θ + (cid:10)θ such that (cid:4)(cid:10)θ (cid:4) is sufficiently small (so
that θ (cid:5)
must be still a global
minimum within the local region and, hence, the θ (cid:5)
is also a local minimum.
The proof idea of theorem 2 is to apply the proof sketch in section 3.1 to not
only a local minimum candidate θ but also its perturbations θ (cid:5) = θ + (cid:10)θ .

stays in the local region) and L(θ (cid:5)

) = L(θ ), the θ (cid:5)

In terms of overparameterization, theorem 2 states that local minima of
deep neural networks are as good as global minima of the correspond-
ing basis function regression even without overparameterization, E

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1476

K. Kawaguchi, J. Huang, and L. Kaelbling

overparameterization helps to further improve the guarantee on local min-
ima. The effect of overparameterization is captured in both the first and
second terms on the right-hand side of equation 5.1. As depth and width in-
crease, the second term tends to increase, and hence the guarantee on local
minima can improve. Inoltre, as depth and width increase (for some of
T + 1, T + 2, . . . , Hth layers in theorem 2), the first term tends to decrease and
the guarantee on local minima can also improve. Per esempio, if [(cid:5)(l)]H
l=t
has rank at least m, then the first term is zero and, hence, every local min-
imum is a global minimum with zero loss value. As a special case of this
esempio, since every θ is automatically in (cid:8)
,H, if (cid:5)(H) is forced to have
rank at least m, every local minimum becomes a global minimum for stan-
dard deep nonlinear neural networks, which coincides with the observation
about overparameterization by Livni et al. (2014).

dH+1

Without overparameterization, theorem 2 also recovers one of the main
results in the literature of deep linear neural networks as a special case—
≤ min{dl : 1 ≤
questo è, every local minimum is a global minimum. If dH+1
l ≤ H}, every local minimum θ for deep linear networks is differentiable
and in (cid:8)
,0, and hence theorem 1 yields that L(θ ) ≤ 1
F. Because
dH+1
2
(cid:4)PN[X]Y(cid:4)2
1
F is the global minimum value, this implies that every local min-
2
imum is a global minimum for deep linear neural networks.

(cid:4)PN[X]Y(cid:4)2

Corollary 1 states that the same conclusion and discussions as in theorem
2 hold true even if we fix the edges in condition iii in definition 1 to be zero
(by removing them as an architectural design or by forcing it with a learning
algorithm) and consider optimization problems only with remaining edges.

Corollary 1. For any t ∈ {0, 1, . . . , H}, every differentiable local minimum θ ∈
(cid:8)
,t of L|I satisfies that for any subsequence S ⊆ (T, T + 1, . . . , H) (including
the case of S being the empty sequence),

dH+1

l(θ ) ≤ 1
2
(cid:9)

(cid:7)

Y

(cid:5)
(cid:5)
(cid:5)PN

(cid:6)
(cid:5)(S)
(cid:10)(cid:11)
global minimum value of
basis function regression
with basis matrix (cid:5)(S)

(cid:5)
(cid:5)
(cid:5)

2

(cid:12)
F

−

H(cid:8)

dl(cid:8)

=1

kl

l=1
(cid:9)

(cid:5)
(cid:5)
(cid:5)P

(cid:6)
ˆN(l)
kl

PN

1
2
(cid:9)

(cid:6)
¯(cid:5)(S)
(cid:10)(cid:11)
≥0

(cid:10)(cid:11)
further improvement as
a network gets wider and deeper

(cid:7)

(cid:7)

ˆD(l)
kl

vec(Y)

2

(cid:5)
(cid:5)
,
(cid:5)
(cid:12)
2

(cid:12)

(5.2)

where L|IO
1}, ∀(k(cid:5), k) ∈ S(l) × S(l+1), W (l+1)(θ (cid:5)
. . . , S(H+1) of the θ ∈ (cid:8)
(cid:5)(S) and ¯(cid:5)(S) are defined in theorem 2, and the matrices ˆD(l)
kl
come segue. For all l ∈ {1, . . . , T + 1}, ˆD(l)
kl
is defined in theorem 2). For all l ∈ {T + 2, . . . , H}, ˆD(l)
kl

is the restriction of L to I = {θ (cid:5) ∈ Rdθ : ∀l ∈ {T + 1, . . . , H −
= 0} with the index sets S(t+1), S(t+2),
} \ S(l). Here,
are defined
} (where D(l)
kl
∈ S(l), E

and ˆN(l)
kl
∈ {1, . . . , dl
for all kl

,t in definition 1 and S(l) := {1, . . . , dl

:= D(l)
kl

:= D(l)
kl

for all kl

)k(cid:5),k

dH+1

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning

1477

dl+1(cid:8)

dH(cid:8)

· · ·

ˆD(l)
kl

:=

(W (l+1)
,kl+1
kl

· · · W (H)
kH−1

W (H+1)
kH ,·

(cid:3)
)

,kH

=1

kH =1
kl+1
⊗(cid:4)l,kl · · · (cid:4)H,kH [(cid:5)(l−1)

·, j

] j∈S(l−1)

,

:= (W (H+1)

with ˆD(H)
kH ,·
kl
. . . , H} and any kl
, Q(2)
, . . . , Q(1)
[Q(1)
1
1
d1
:= ¯Q(l−1)
¯Q(l)
.
0
dl−1

(cid:3) ⊗ (cid:4)H,kH [(cid:5)(H−1)
)

∈ {1, . . . , dl
, . . . , Q(2)
d2

·, j
}, ˆN(l)
kl
, . . . , Q(l)
1

] j∈S(H−1) for all kl

:= PN[ ¯Q(l)
kl
, . . . , Q(l)
kl

−1] with N1
], Q(l)
kl

:= ˆN(l)
kl

∈ S(l). For any l ∈ {1,
1 := Im where ¯Q(l)
:=
kl
PN[ ¯(cid:5)(S)] ˆD(l)
, E
kl

The proof of corollary 1 is provided in section A.3 and follows the proof
of theorem 2. Here, (cid:5)(0) = X consists of training inputs xi in the arbi-
trary given feature space embedded in Rd0 ; Per esempio, given a raw in-
put xraw and any feature map φ : xraw (cid:17)→ φ(xraw) ∈ Rd0 (including identity
as φ(xraw) = xraw), we write x = φ(xraw). Therefore, theorem 2 and corol-
lary 1 state that every differentiable local minima of deep neural networks
can be guaranteed to be no worse than any given basis function regression
model with a handcrafted basis taking values in Rd with some finite d, come
as polynomial regression with a finite degree and radial basis function re-
gression with a finite number of centers.

to iii

To illustrate an advantage of the notion of weakly separated edges in def-
inition 1, one can consider the following alternative definition that requires
strongly separated edges.
Definition 2. A parameter vector θ is said to induce (N, T) strongly sep-
arated linear units on the training input data set X if there exist (H +
1 − t) sets S(t+1), S(t+2), . . . , S(H+1) such that for all l ∈ {T + 1, T + 2, . . . , H +
1}, conditions i
=
(cid:25)

in definition 1 hold and (cid:5)(l)(X, θ )W (l+1)(θ )·,k

k(cid:5)∈S(l) (cid:5)(l)(X, θ )·,k(cid:5)W (l+1)(θ )k(cid:5),k for all k ∈ S(l+1) if l (cid:18)= {H, H + 1}.
Let (cid:8)strong
N,T

be the set of all parameter vectors that induces (N, T) strongly-
separated linear units on the particular training input data set X that defines
the total loss L(θ ) in equation 2.1. Figura 2 shows a comparison of weekly
separated edges and strongly separated edges. Under this stronger restric-
tion on the local structure, we can obtain corollary 2.
Corollary 2. For any t ∈ {0, 1, . . . , H}, every differentiable local minimum θ ∈
(cid:8)strong
dH+1

,t of L satisfies that for any S ⊆ (T, H),

l(θ ) ≤ 1
2

(cid:5)
(cid:5)
(cid:5)PN

(cid:7)

(cid:6)
(cid:5)(S)

(cid:5)
(cid:5)
(cid:5)

2

F

Y

−

H(cid:8)

dl(cid:8)

l=1

=1

kl

(cid:6)

(cid:5)
(cid:5)
(cid:5)P

1
2

(cid:7)

(cid:6)
¯(cid:5)(S)

(cid:7)

D(l)
kl

N(l)
kl

PN

(cid:5)
(cid:5)
(cid:5)

vec(Y)

,

2

2

Dove (cid:5)(S), ¯(cid:5)(S), D(l)
kl

, and N(l)
kl

are defined in theorem 2.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1478

K. Kawaguchi, J. Huang, and L. Kaelbling

The proof of corollary 2 is provided in section A.4 and follows the proof
of theorem 2. As a special case, corollary 2 also recovers the statement that
every local minimum is a global minimum for deep linear neural networks
in the same way as in theorem 2. When compared with theorem 2, one can
see that the statement in corollary 2 is weaker, producing the upper bound
only in terms of S ⊆ (T, H). This is because the restriction of strongly sepa-
rated units forces neural networks to have less expressive power with fewer
effective edges. This illustrates an advantage of the notion of weakly sepa-
rated edges in definition 1.

A limitation in theorems 1 E 2 and corollary 1 is the lack of treatment of
nondifferentiable local minima. The Lebesgue measure of nondifferentiable
points is zero, but this does not imply that the appropriate measure of non-
differentiable points is small. Per esempio, if L(θ ) = |θ |, the Lebesgue mea-
sure of the nondifferentiable point (θ = 0) is zero, but the nondifferentiable
point is the only local and global minimum. Così, the treatment of nondif-
ferentiable points in this context is a nonnegligible problem. The proofs of
theorems 1 E 2 and corollary 1 are all based on the proof sketch in section
3.1, which heavily relies on the differentiability. Così, the current proofs do
not trivially extend to address this open problem.

6 Conclusione

In this letter, we have theoretically and empirically analyzed the effect of
depth and width on the loss values of local minima, with and without a
possible local nonlinear-linear structure. The local nonlinear-linear struc-
ture we have considered might naturally arise during training and also is
guaranteed to emerge by using specific learning algorithms or architecture
designs. With the local nonlinear-linear structure, we have proved that the
values of local minima of neural networks are no worse than the global min-
imum values of corresponding basis function regression and can improve
as depth and width increase. In the general case without the possible local
structure, we have theoretically shown that increasing the depth and width
can improve the quality of local minima, and we empirically supported this
theoretical observation. Inoltre, without the local structure but with
a shallow neural network and a gaussian data matrix, we have proven the
probabilistic bounds on the rates of the improvements on the local mini-
mum values with respect to width. Inoltre, we have discussed a major
limitation of this letter: all of its the results focus on the differentiable points
on the loss surfaces. Additional treatments of the nondifferentiable points
are left to future research.

Our results suggest that the values of local minima are not arbitrar-
ily poor (unless one crafts a pathological worst-case example) and can be
guaranteed to some desired degree in practice, depending on the degree of
overparameterization, as well as the local or global structural assumption.
Infatti, a structural assumption, namely the existence of an identity map,

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning

1479

was recently used to analyze the quality of local minima (Shamir, 2018;
Kawaguchi & Bengio, 2018). When compared with these previous stud-
ies (Shamir, 2018; Kawaguchi & Bengio, 2018), we have shown the effect of
depth and width, as well as considered a different type of neural network
without the explicit identity map.

In practice, we often “overparameterize” a hypothesis space in deep
learning in a certain sense (per esempio., in terms of expressive power). Theoreti-
cally, with strong overparameterization assumptions, we can show that ev-
ery stationary point (including all local minima) with respect to a single
layer is a global minimum with the zero training error and can memorize
any data set. Tuttavia, “overparameterization” in practice may not satisfy
such strong overparameterization assumptions in the theoretical literature.
In contrasto, our results in this letter do not require overparameterization
and show the gradual effects of overparameterization as consequences of
general results.

Appendix A: Proofs for Nonprobabilistic Statements

H

×

(cid:25)

l=1

be defined in theorem 2. Let D(l) := [D(l)
∈ RmdH+1

×dl dl−1 and D :=
k ]dl
k=1
l=1 dl−1dl . Given a matrix-valued function f (θ ) ∈ Rd(cid:5)×d, let
∈ Rd(cid:5)d×dl−1dl be the partial derivative of vec( F ) with re-
) =
. Let Null(M) be the null space of a matrix M. Let B(θ , (cid:11)) be an open

Let D(l)
kl
[D(l)]H
W (l) F (θ ) := ∂vec( F )
∂
∂vec(W (l) )
spect to vec(W (l)). Let { j, j + 1, . . . , j(cid:5)} := ∅ if j > j(cid:5)
I if l > l(cid:5)
ball of radius (cid:11) with the center at θ .

. Let M(l)M(l+1) · · · M(l(cid:5)

∈ RmdH+1

The following lemma decomposes the model output ˆY in terms of the
matrice dei pesi W (l) and D(l) that coincides with its derivatives at differen-
tiable points.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

Lemma 1. For all l ∈ {1, . . . , H},

vec( ˆY(X, θ )) = D(l)vec(W (l)(θ )),

and at any differentiable θ ,

∂
W (l) ˆY(X, θ ) = D(l).

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Proof. Define G(l) to be the preactivation output of the lth hidden layer
as G(l) := G(l)(X, θ ) := (cid:5)(l−1)(X, θ )W (l). By the linearity of the vec operation
and the definition of G(l), we have that

vec[G(l+1)(X, θ )] = vec

(cid:18)

(cid:4)l,kG(l)(X, θ )·,kW (l+1)

k,·

(cid:15)

dl(cid:8)

k=1

1480

K. Kawaguchi, J. Huang, and L. Kaelbling

dl(cid:8)

(cid:13)

=

(W (l+1)
k,·

(cid:3) ⊗ (cid:4)l,k
)

(cid:14)

(cid:13)
G(l)(X, θ )·,k

(cid:14)

vec

k=1
= F(l+1)vec

(cid:14)
(cid:13)
G(l)(X, θ )

,

where F(l+1) := [(W (l+1)

k,·

(cid:3) ⊗ (cid:4)l,k]dl
)

k=1. Therefore,

vec( ˆY) = F(H+1)F(H) · · · F(l+1)vec(G(l))
= F(H+1) · · · F(l+1)[Idl

⊗ (cid:5)(l−1)]vec(W (l)),

where F(H+1) · · · F(l+1)[Idl
] = D(l), Quale
proves the first statement that vec( ˆY) = D(l)vec(W (l)). The second statement
follows from the fact that the derivatives of D(l) with respect to vec(W (l)) are
(cid:2)
zeros at any differentiable point, and hence (∂

⊗ (cid:5)(l−1)] = [D(l)
1

· · · D(l)
dl

W (l) ˆY) = D(l) + 0.

D(l)
2

Lemma 2 generalizes part of theorem A.45 in Rao, Toutenburg, Shalabh,

and Heumann (2007) by discarding invertibility assumptions.

Lemma 2. For any block matrix [A B] with real submatrices A and B such that
UN(cid:3)B = 0,

P [[A B]] = P[UN] + P[B].

Proof. It follows a straightforward calculation as

P [[A B]] = [A B]

= [A B]

⎡

⎣

⎡

⎣

UN(cid:3)UN
0

⎤

†

⎦

0
B(cid:3)B

(cid:3)

[A B]

(UN(cid:3)UN)†
0

0
(B(cid:3)B)†

⎤

⎦

(cid:3)

[A B]

= P[UN] + P[B].

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

(cid:2)

Lemma 3 decomposes a norm of a projected target vector into a form that

clearly shows an effect of depth and width.
Lemma 3. For any t ∈ {0, 1, . . . , H} and any S ⊆ (T, T + 1, . . . , H),

(cid:6)

(cid:6)

(cid:5)
(cid:5)
(cid:5)P

PN

(cid:7)

(cid:7)
D

¯(cid:5)(S)

(cid:5)
(cid:5)
(cid:5)

vec(Y)

=

2

2

H(cid:8)

dl(cid:8)

l=1

=1

kl

(cid:5)
(cid:5)
(cid:5)P

(cid:6)
N(l)
kl

PN

(cid:7)

(cid:6)
¯(cid:5)(S)

D(l)
kl

(cid:7)

(cid:5)
(cid:5)
(cid:5)

vec(Y)

.

2

2

Effect of Depth and Width on Local Minima in Deep Learning

1481

Proof. Since the span of the columns of [A B] is the same as the span of the
columns of [A PN[UN]B] for submatrices A and B, the span of the columns
of PN[ ¯(cid:5)(S)]D = [[PN[ ¯(cid:5)(S)]D(l)
l=1 is the same as the span of the columns
kl
Di [[N(l)
PN[ ¯(cid:5)(S)]D(l)
]dl
=1]H
l=1. Then, by repeatedly applying lemma 2 to each
kl
kl
kl
PN[ ¯(cid:5)(S)]D(l)
block of [[N(l)
]dl
kl
kl
kl
(cid:16)(cid:31)(cid:6)

l=1, we have that

=1]H

=1]H

]dl
kl

(cid:17)

(cid:6)
(cid:7)
PN[ ¯(cid:5)(S)]D

P

= P

N(l)
kl

PN[ ¯(cid:5)(S)]D(l)
kl

(cid:7)
dl

H

=1

kl

l=1

H(cid:8)

dl(cid:8)

=

l=1

=1

kl

(cid:6)
N(l)
kl

P

PN[ ¯(cid:5)(S)]D(l)
kl

(cid:7)

.

From the construction of N(l)
kl

, we have that for all (l, k) (cid:18)= (l(cid:5), k(cid:5)),

P[N(l)

k PN[ ¯(cid:5)(S)]D(l)

k ]P[N(l(cid:5)

k(cid:5) PN[ ¯(cid:5)(S)]D(l(cid:5)

k(cid:5) ] = 0.

)

)

Therefore,

(cid:5)
(cid:5)

P

(cid:2)

(cid:2)
PN

(cid:3)

(cid:3)
D

¯(cid:5)S

vec(Y)

(cid:5)
(cid:5)2
2

=

=

(cid:5)
(cid:5)
(cid:5)
(cid:5)
(cid:5)
(cid:5)

H(cid:8)

dl(cid:8)

l=1

=1

kl

(cid:6)
N(l)
kl

P

PN[ ¯(cid:5)(S)]D(l)
kl

(cid:7)

2

(cid:5)
(cid:5)
(cid:5)
(cid:5)
(cid:5)
(cid:5)

vec(Y)

(cid:5)
(cid:5)
(cid:5)P

(cid:6)
N(l)
kl

(cid:6)

(cid:7)

(cid:7)

PN

¯(cid:5)(S)

D(l)
kl

H(cid:8)

dl(cid:8)

l=1

=1

kl

2
(cid:5)
(cid:5)
(cid:5)

vec(Y)

.

2

2

(cid:2)

The following lemma plays a major role in the proof of theorem 2.
Lemma 4. For any t ∈ {0, 1, . . . , H}, every differentiable local minimum θ ∈
(cid:8)

,t satisfies that for any l ∈ {T, T + 1, . . . , H},

dH+1

(cid:3)
((cid:5)(l))

( ˆY(X, θ ) − Y) = 0.

dH+1

1
for all θ (cid:5) ∈ ˜B(θ , (cid:11)

> 0 such that L(θ ) ≤ L(θ (cid:5)
1) ⊆ B(θ , (cid:11)

Proof. Fix t to be a number in {0, 1, . . . , H}. Let θ be a differentiable lo-
cal minimum in (cid:8)
,T. Then, from the definition of a local minimum,
there exists (cid:11)
1), and hence
l(θ ) ≤ L(θ (cid:5)
1) ∩
1) := B(θ , (cid:11)
)
{θ ∈ Rdθ : W (l+1)(θ )k(cid:5),k
= 0 for all l ∈ {T + 1, T + 2, · · · H − 1} and all (k(cid:5), k) ∈
} \ S(l+1))} with the index sets S(t+1), S(t+2), . . . , S(H+1) Di
S(l) × ({1, . . . , dl+1
the θ ∈ (cid:8)
,t in definition 1. Without loss of generality, we can permute
the indices of the units within each layer such that for all l ∈ {T + 1, t +
2, . . . , H + 1}, S(l) ⊇ {1, 2, . . . , dL} with some dL ≥ dH+1 in the definition of
(cid:8)
,T (see definition 1). Note that the considered activation functions

) for all θ (cid:5) ∈ B(θ , (cid:11)
1), where ˜B(θ , (cid:11)

dH+1

dH+1

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1482

K. Kawaguchi, J. Huang, and L. Kaelbling

P (l)
io, j (z) are continuous and act linearly on z ≥ 0 . Così, from the defini-
2) and all l ∈
tion of (cid:8)
{T, T + 1, . . . , H},

> 0 such that for all θ (cid:5) ∈ ˜B(θ , (cid:11)

,T, there exists (cid:11)

dH+1

2

ˆY(X, θ (cid:5)

) = (cid:5)(l)

(cid:17)

(cid:16)

UN(l+1)
C(l+1)

UN(l+2) · · · A(H+1)

+

H−1(cid:8)

l(cid:5)=l

Z(l(cid:5)+1)C(l(cid:5)+2)UN(l(cid:5)+3) · · · A(H+1),

(A.1)

where A(l), B(l) and C(l) are submatrices of W (l)(θ (cid:5)
Di (cid:5)(l)(X, θ (cid:5)
(cid:16)

) as defined below:

(cid:17)

ξ (l)

UN(l)
C(l) B(l)

:= W (l)(θ (cid:5)

),

), and Z(l) is a submatrix

E

(cid:15)

(cid:16)

Z(t+1) := σ (t+1)

(cid:5)(T)

(cid:17)(cid:18)

ξ (t+1)
B(t+1)

with Z(l) := σ (l)(Z(l−1)B(l)) for l ≥ t + 2.

Note that Z(l) depends only on (cid:5)(T), ξ (T), and B(k) for all k ≤ l. Here, (cid:5)(T)
does not depend on A(l) and C(l) for all l ≥ t + 1. Questo è, at each layer l ∈
{T + 2, T + 3, . . . , H}, UN(l) ∈ RdL×dL connects dL linearly acting units to next dL
−dL ) connects other units to next other
linearly acting units, B(l) ∈ R(dl−1
units (other units can include both nonlinear and linearly acting units), E
−dL )×dL connects other units to next linearly acting units, con
C(l) ∈ R(dl−1
dL ≥ dH+1. Here, UN(t+1), B(t+1), C(t+1), and ξ (t+1) connect the possibly unstruc-
tured layer (cid:5)(T) to the next structured layer, C(H+1) ∈ R(dH −dL )×dH+1 connects
other units in the last hidden layer to the output units, e A(H+1) ∈ RdL×dH+1
connects linearly acting units in the last hidden layer to the output units.

−dL )×(dl

Let (cid:11)

3

= min((cid:11)

, (cid:11)

2). Let l be an arbitrary fixed number in {T, T + 1, . . . , H}

1

in the following. Let r := ˆY(X, θ ) − Y. Define

R(l+1) :=

(cid:16)

(cid:17)

.

UN(l+1)
C(l+1)

From the condition of differentiable local minimum, we have that

0 = ∂

R(l+1) l(θ ) = vec(((cid:5)(l))

(cid:3)

(cid:3)
R(UN(l+2) · · · A(H+1))

),

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning

1483

since otherwise, R(l+1) can be moved to the direction of ∂
sufficiently small magnitude (cid:11)(cid:5)
3
implies that

R(l+1) l(θ ) con un
3) and decrease the loss value. Questo

∈ (0, (cid:11)

(cid:3)
((cid:5)(l))

R(UN(l+2) · · · A(H+1))

(cid:3) = 0.

If rank(UN(l+2) · · · A(H+1)) ≥ dH+1 or l = H, then this equation yields the de-
sired statement of this lemma as ((cid:5)(l))(cid:3)r = 0. Hence, the rest of this proof
considers the case of

(cid:3)
rank((UN(l+2) · · · A(H+1))

) < dH+1 and l ∈ {t, t + 1, . . . , H − 1}. Define an index l∗ as ∗ l := min{l (cid:5) ∈ Z+ : l + 3 ≤ l (cid:5) ≤ H + 2 ∧ rank(A(l(cid:5) ) · · · A(H+1)) ≥ dH+1 }, where A(H+2) · · · A(H+1) := IdH+1 . This minimum exists since the set contains at least H + 2 (nonempty) and is finite. Then we have that rank(A(l∗ l(cid:5) ∈ {l + 2, l + 3, . . . , l∗ − 1}, rank(M1M2) ≤ min(rank(M1), rank(M2)). Therefore, for all l(cid:5) ∈ {l + 1, l + 2, . . . , l∗ − 2}, we have that Null((A(l(cid:5)+1) (cid:3) · · · A(H+1)) ) (cid:18)= 0, and there exists a vector ul(cid:5) ∈ RdL such that ) · · · A(H+1)) ≥ dH+1 and rank(A(l(cid:5) ) · · · A(H+1)) < dH+1 for all since ul(cid:5) ∈ Null((A(l(cid:5)+1) · · · A(H+1)) (cid:3) ) and (cid:4)ul(cid:5) (cid:4) 2 = 1. Let ul(cid:5) denote such a vector for all l(cid:5) ∈ {l + 1, l + 2, . . . , l∗ − 2}. For all l(cid:5) ∈ {l + 2, l + 3, . . . , l∗ − 2}, define ˜A(l(cid:5) )(ν l(cid:5) ) := A(l(cid:5) ) + ν l(cid:5) u (cid:3) l(cid:5) and ˜R(l+1)(ν l+1) := R(l+1) + ν l+1u (cid:3) l+1 , where ν ∈ Rdl . Let ˜θ (ν l(cid:5) ∈ RdL and ν , ν l+1 and R(l+1) being replaced by ˜A(l(cid:5) l(cid:5) ) and ˜R(l+1)(ν )(ν 3, . . . , l∗ − 2}. Then for any (ν , . . . , ν , ν l+2 l+1 l∗−2), l+1 l+2 , . . . , ν l∗−2) be θ with A(l(cid:5) l+1) for all l(cid:5) ∈ {l + 2, l + ) ˆY(X, ˜θ (ν l+1 , . . . , ν l∗−2)) = ˆY(X, θ ) and L( ˜θ (ν l+1 , . . . , ν l∗−2)) = L(θ ), l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 1 7 1 4 6 2 1 0 5 3 1 9 6 n e c o _ a _ 0 1 1 9 5 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 since ˜A(l(cid:5) 3, . . . , l∗ − 2} and ˜R(l+1)(ν l(cid:5) )A(l(cid:5)+1) · · · A(H+1) = A(l(cid:5) )(ν For any sufficiently small vector (ν l+1)A(l+2) · · · A(H+1) = R(l+1)A(l+2) · · · A(H+1). , . . . , ν l∗−2) such that l+1 )A(l(cid:5)+1) · · · A(H+1) for all l(cid:5) ∈ {l + 2, l + l∗−2) ∈ ˜B(θ , (cid:11) . . . , ν a local minimum with respect to the entries of A(l(cid:5) because there exists (cid:11)(cid:5) = (cid:11) 3 /2), if θ is a local minimum, every ˜θ (ν ), B(l(cid:5) /2 > 0 such that

3

3

, . . . , ν
l+1
), and C(l(cid:5)

˜θ (ν
,
l+1
l∗−2) is also
) for all l(cid:5)

l( ˜θ (ν

l+1

, . . . , ν

l∗−2)) = L(θ ) ≤ L(θ (cid:5)

)

1484

K. Kawaguchi, J. Huang, and L. Kaelbling

for all θ (cid:5) ∈ ˜B( ˜θ (ν
3) ⊆ ˜B(θ , (cid:11)
1), Dove
the first inclusion follows the triangle inequality. Così, for any such
˜θ (ν
l∗−2) in the sufficiently small open ball, we have that

1) ⊆ B(θ , (cid:11)

3) ⊆ ˜B(θ , (cid:11)

l∗−2), (cid:11)(cid:5)

, . . . , ν

, . . . , ν

l+1

l+1

∂

UN(l

∗ −1) l( ˜θ (ν

l+1

, . . . , ν

l∗−2)) = 0,

UN(l

l+1

, . . . , ν

∗ −1) l( ˜θ (ν

where ∂
l∗−2)) exists within the sufficiently small open
ball from equation A.1 (composed with the squared loss). In particular, by
setting ν
l∗−2)) − Y = Y(X, θ ) −
Y = r,

= 0 and noticing that ˆY(X, ˜θ (ν

, . . . , ν

l+1

l+1

∗ −1) l( ˜θ (0, ν

l+2

, . . . , ν

l∗−2))

(cid:14)(cid:3)

∗ −1) ˆY(X, ˜θ (0, ν

l+2

, . . . , ν

l∗−2))

UN(l

vec(R),

0 = ∂
UN(l
(cid:13)
∂

=

0 = ∂
UN(l
(cid:13)
∂

=

and hence

∗ −1) l( ˜θ (ν

l+1

, . . . , ν

l∗−2))

∗ −1) (cid:5)(l)(ν

l+1u

UN(l

(cid:3)

l+1) ¯A(l+2) · · · ¯A(H+1)
(cid:14)(cid:3)

+ ∂

UN(l

∗ −1) ˆY(X, ˜θ (0, ν

l+2

, . . . , ν

l∗−2))

(cid:13)
∂

=

∗ −1) (cid:5)(l)(ν

l+1u

UN(l

(cid:3)

l+1) ¯A(l+2) · · · ¯A(H+1)

vec(R)
(cid:14)(cid:3)

vec(R),

Dove

(cid:4)

¯A(l(cid:5)

) =

˜A(l(cid:5)
UN(l

(cid:5)

l(cid:5) )

)(ν
)

if l(cid:5) ∈ {l + 2, . . . , l∗ − 2}
if l(cid:5) /∈ {l + 2, . . . , l∗ − 2}

.

Since

∂

UN(l

(cid:13)

∗ −1) (cid:5)(l)(ν
(UN(l∗

l+1ul+1) ¯A(l+2) · · · ¯A(H+1)
) · · · A(H+1))

(cid:3) ⊗ (cid:5)(l)(ν

=

l+1ul+1) ˜A(l+2)(ν

l+2) · · · ˜A(l∗−2)(ν

l∗−2)

this implies that

UN(l∗

) · · · A(H+1)R

(cid:3)(cid:5)(l)(ν

l+1ul+1) ˜A(l+2)(ν

l+2) · · · ˜A(l∗−2)(ν

l∗−2) = 0.

By the definition of l∗, this implies that

(cid:3)(cid:5)(l)(ν
R

l+1ul+1) ˜A(l+2)(ν

l+2) · · · ˜A(l

∗−2)(ν

l∗−2) = 0,

where ˜A(l+2)(ν

l+2) · · · ˜A(l+1)(ν

l+1) := IdL .

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

,

(cid:14)

Effect of Depth and Width on Local Minima in Deep Learning

1485

We now show that for any sufficiently small vector (ν
3

l∗−2) ∈ ˜B(θ , (cid:11)

, . . . , ν

/2),

that ˜θ (ν

l+1

l+1

, . . . , ν

l∗−2) come

(cid:3)(cid:5)(l)(ν
R

l+1ul+1) ˜A(l+2)(ν

l+2) · · · ˜A( j)(ν

j ) = 0,

by induction on the index j with the decreasing order j = l∗ − 2, l∗ −
3, . . . , l + 1. The base case with j = l∗ − 2 is proven above. Let
˜A(l) :=
˜A(l)(ν
l+2). For the inductive step, assuming that the statement holds for j,
we show that it holds for j − 1 COME

0 = r

= r

(cid:3)(cid:5)(l)(ν
(cid:3)(cid:5)(l)(ν

l+1u

l+1u

= r

(cid:3)(cid:5)(l)(ν

l+1u

(cid:3)

(cid:3)

l+1) ˜A(l+2) · · · ˜A( j)
l+1) ˜A(l+2) · · · A( j) + R
l+1) ˜A(l+2) · · · ˜A( j−1)ν

(cid:3)

,

(cid:3)
j

ju

(cid:3)(cid:5)(l)(ν

l+1u

(cid:3)

l+1) ˜A(l+2) · · · ˜A( j−1)ν

(cid:3)
j

ju

where the last line follows the fact that the first term in the second line is
zero because of the inductive hypothesis with ν
= 1, by
multiplying u j both sides from the right, we have that for any sufficiently
small ν

= 0. Since (cid:4)u j

∈ RdL ,

(cid:4)

2

j

j

(cid:3)(cid:5)(l)(ν
R

l+1u

(cid:3)

l+1) ˜A(l+2) · · · ˜A( j−1)ν

j

= 0,

which implies that

(cid:3)(cid:5)(l)(ν
R

l+1u

(cid:3)

l+1) ˜A(l+2) · · · ˜A( j−1) = 0.

This completes the inductive step and proves that

(cid:3)(cid:5)(l)(ν

l+1u

R

(cid:3)

l+1) = 0.

(cid:4)

Since (cid:4)ul+1
that for any sufficiently small ν
˜B(θ , (cid:11)

/2),

= 1, by multiplying ul+1 both sides from the right, we have
l∗−2) ∈

−dL such that ˜θ (ν

, . . . , ν

∈ Rdl

l+1

l+1

2

3

( ˆY(X, θ ) − Y)

(cid:3)(cid:5)(l)ν

= 0,

l+1

which implies that

(cid:3)
((cid:5)(l))

( ˆY(X, θ ) − Y) = 0.

(cid:2)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1486

K. Kawaguchi, J. Huang, and L. Kaelbling

A.1 Proof of Theorem 1. From the first-order necessary condition of

differentiable local minima,

0 = ∂

W (H+1) l(θ ) = (D(H+1)

1

(cid:3)
)

vec( ˆY(X, θ ) − Y),

and ˆY(X, θ ) = D(H+1)
1 W (H+1). From lemma 1 and the first-order neces-
sary condition of differentiable local minima, D(cid:3)vec( ˆY(X, θ ) − Y) = 0 E
vec( ˆY) = 1
l=1). Combining these, we have
Quello

1:H := vec([W (l)]H

1:H where θ

H Dθ

(cid:6)

D D(H+1)

1

!

(cid:7)(cid:3)

(cid:6)

1
H + 1

(cid:7)

D D(H+1)

1

”

θ − vec(Y)

= 0,

Dove 1
H+1

(cid:6)

D D(H+1)

1

(cid:7)

θ = vec( ˆY(X, θ )). This implies that

vec( ˆY(X, θ )) = P

(cid:6)(cid:6)

D D(H+1)

1

(cid:7)(cid:7)

vec(Y).

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

Therefore,

2l(θ ) = (cid:4)vec(Y) − P

(cid:6)(cid:6)

(cid:7)(cid:7)

D D(H+1)
(cid:6)(cid:6)

1

vec(Y)(cid:4)2
2
(cid:7)(cid:7)

= (cid:4)vec(Y)(cid:4)2
2

− (cid:4)P

D D(H+1)

1

vec(Y)(cid:4)2
2

,

(cid:2)

where the second line follows idempotence of the projection. Finalmente, Di-
composing the second term by directly following the proof of lemma 3 con
D D(H+1)
PN
this theorem.

yields the desired statement of
(cid:2)

D being replaced by

¯(cid:5)(S)

(cid:6)

(cid:7)

(cid:3)

1

A.2 Proof of Theorem 2. From lemma 4, we have that for any l ∈ {T, t +

1, . . . , H},

(IdH+1

(cid:3)
⊗ (cid:5)(l))

vec( ˆY(X, θ ) − Y) = 0.

From equation A.1, by noticing that Z(l+1)C(l+2) = (cid:5)(l+1)
also have that

(A.2)

(cid:2)

0

(cid:3)
(C(l+2))

(cid:3)(cid:3)

, we

vec( ˆY(X, θ )) =

H(cid:8)

l=t

(IdH+1

(cid:3)
⊗ (cid:5)(l))

vec( ¯R(l+1)UN(l+2) · · · A(H+1)),

(A.3)

/

/

/

3
1
7
1
4
6
2
1
0
5
3
1
9
6
N
e
C
o
_
UN
_
0
1
1
9
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Effect of Depth and Width on Local Minima in Deep Learning