ARTICLE

Communicated by Simon Shaolei Du

Every Local Minimum Value Is the Global Minimum Value
of Induced Model in Nonconvex Machine Learning

Kenji Kawaguchi
kawaguch@mit.edu
MIT, Cambridge, MA 02139, U.S.A.

Jiaoyang Huang
jiaoyang@math.harvard.edu
Harvard University, Cambridge, MA 02138, U.S.A.

Leslie Pack Kaelbling
lpk@csail.mit.edu
MIT, Cambridge, MA 02139, U.S.A.

For nonconvex optimization in machine learning, this article proves that
every local minimum achieves the globally optimal value of the per-
turbable gradient basis model at any differentiable point. Di conseguenza,
nonconvex machine learning is theoretically as supported as convex ma-
chine learning with a handcrafted basis in terms of the loss at differen-
tiable local minima, except in the case when a preference is given to the
handcrafted basis over the perturbable gradient basis. The proofs of these
results are derived under mild assumptions. Accordingly, the proven re-
sults are directly applicable to many machine learning models, includ-
ing practical deep neural networks, without any modification of practical
metodi. Inoltre, as special cases of our general results, Questo articolo
improves or complements several state-of-the-art theoretical results on
deep neural networks, deep residual networks, and overparameterized
deep neural networks with a unified proof technique and novel geomet-
ric insights. A special case of our results also contributes to the theoretical
foundation of representation learning.

1 introduzione

Deep learning has achieved considerable empirical success in machine
learning applications. Tuttavia, insufficient work has been done on the-
oretically understanding deep learning, partly because of the nonconvexity
and high-dimensionality of the objective functions used to train deep mod-
els. Generalmente, theoretical understanding of nonconvex, high-dimensional
optimization is challenging. Infatti, finding a global minimum of a gen-
eral nonconvex function (Murty & Kabadi, 1987) and training certain types

Calcolo neurale 31, 2293–2323 (2019) © 2019 Istituto di Tecnologia del Massachussetts.
https://doi.org/10.1162/neco_a_01234
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale (CC BY 4.0) licenza.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2294

K. Kawaguchi, J. Huang, and L. Kaelbling

of neural networks (Blum & Rivest, 1992) are both NP-hard. Considering
the NP-hardness for a general set of relevant problems, it is necessary to
use additional assumptions to guarantee efficient global optimality in deep
apprendimento. Accordingly, recent theoretical studies have proven global opti-
mality in deep learning by using additional strong assumptions such as
linear activation, random activation, semirandom activation, gaussian in-
puts, single hidden-layer network, and significant overparameterization
(Choromanska, Henaff, Mathieu, Ben Arous, & LeCun, 2015; Kawaguchi,
2016; Hardt & Mamma, 2017; Nguyen & Hein, 2017, 2018; Brutzkus & Glober-
figlio, 2017; Soltanolkotabi, 2017; Ge, Lee, & Mamma, 2017; Goel & Klivans, 2017;
Zhong, Song, Jain, Bartlett, & Dhillon, 2017; Li & Yuan, 2017; Kawaguchi,
Xie, & Song, 2018; Du & Lee, 2018).

A study proving efficient global optimality in deep learning is thus
closely related to the search for additional assumptions that might not hold
in many practical applications. Toward widely applicable practical theory,
we can also ask a different type of question: If standard global optimal-
ity requires additional assumptions, then what type of global optimality
does not? In other words, instead of searching for additional assumptions
to guarantee standard global optimality, we can also search for another type
of global optimality under mild assumptions. Inoltre, instead of an ar-
bitrary type of global optimality, it is preferable to develop a general theory
of global optimality that not only works under mild assumptions but also
produces the previous results with the previous additional assumptions,
while predicting new results with future additional assumptions. This type
of general theory may help not only to explain when and why an exist-
ing machine learning method works but also to predict the types of future
methods that will or will not work.

As a step toward this goal, this article proves a series of theoretical re-

sults. The major contributions are summarized as follows:

• For nonconvex optimization in machine learning with mild assump-
zioni, we prove that every differentiable local minimum achieves
global optimality of the perturbable gradient basis model class. Questo
result is directly applicable to many existing machine learning mod-
els, including practical deep learning models, and to new models to
be proposed in the future, nonconvex and convex.

• The proposed general theory with a simple and unified proof tech-
nique is shown to be able to prove several concrete guarantees that
improve or complement several state-of-the-art results.

• In general, the proposed theory allows us to see the effects of the
design of models, metodi, and assumptions on the optimization
landscape through the lens of the global optima of the perturbable
gradient basis model class.

Because a local minimum θ in Rdθ only requires the θ to be locally optimal
in Rdθ , it is nontrivial that the local minimum is guaranteed to achieve the

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Every Local Minimum Value Is the Global Minimum Value

2295

globally optimality in Rdθ of the induced perturbable gradient basis model
class. The reason we can possibly prove something more than many worst-
case results in general nonconvex optimization is that we explicitly take
advantage of mild assumptions that commonly hold in machine learning
and deep learning. In particular, we assume that an objective function to
be optimized is structured with a sum of weighted errors, where each error
is an output of composition of a loss function and a function of a hypothe-
sis class. Inoltre, we make mild assumptions on the loss function and a
hypothesis class, all of which typically hold in practice.

2 Preliminari

This section defines the problem setting and common notation.

2.1 Problem Description. Let x ∈ X and y ∈ Y be an input vector and
a target vector, rispettivamente. Define ((xi
i=1 as a training data set of size
M. Let θ ∈ Rdθ be a parameter vector to be optimized. Let f (X; θ ) ∈ Rdy be
the output of a model or a hypothesis, and let (cid:3) : Rdy × Y → R≥0 be a loss
function. Here, dθ , dy ∈ N>0. We consider the following standard objective
function L to train a model f (X; θ ):

, yi))M

l(θ ) =

M(cid:2)

i=1

λ
io

(cid:3)( F (xi

; θ ), yi).

This article allows the weights λ
1
λ
= · · · = λm = 1
1
L as a special case.

, . . . , λm > 0 to be arbitrarily fixed. Con
M , all of our results hold true for the standard average loss

2.2 Notation. Because the focus of this article is the optimization of the
vector θ , the following notation is convenient: (cid:3)sì(q) = (cid:3)(q, sì) and fx(q) =
F (X; q). Then we can write

l(θ ) =

M(cid:2)

i=1

λ
io

(cid:3)yi ( fxi (θ )) =

M(cid:2)

i=1

io((cid:3)yi
λ

◦ fxi )(θ ).

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

, . . . , ϕ

We use the following standard notation for differentiation. Given a
scalar-valued or vector-valued function ϕ : Rd → Rd(cid:6)
with components
(cid:6)× ¯d be the
ϕ = (ϕ
D(cid:6) ) and variables (v
1
matrix-valued function with each entry (∂v ϕ)io, j
. Note that if ϕ is a
scalar-valued function, ∂v ϕ outputs a row vector. Inoltre, ∂ϕ = ∂v ϕ if
(v
, let
∂
ϕ with respect to the kth variable of
k
ϕ. For the syntax of any differentiation map ∂, given functions ϕ and ζ , let

, . . . , v
1
ϕ : Rd → R be the partial derivative ∂

D ) are the input variables of ϕ. Given a function ϕ : Rd → Rd(cid:6)

, . . . , v ¯d ), let ∂v ϕ : Rd → Rd
= ∂ϕ
∂v

1

k

j

io

2296

K. Kawaguchi, J. Huang, and L. Kaelbling

∂ϕ(ζ (q)) = (∂ϕ)(ζ (q)) be the (partial) derivative ∂ϕ evaluated at an output
ζ (q) of a function ζ .

Given a matrix M ∈ Rd×d(cid:6)

, . . . ,
, vec(M) = [M1,1
M1,d(cid:6) , . . . , Md,D(cid:6) ]T represents the standard vectorization of the matrix M.
Given a set of n matrices or vectors {M( j)}N
= [M(1),
M(2), . . . , M(N)]
to be a block matrix of each column block being
M(1), M(2), . . . , M(N). Allo stesso modo, given a set I = {i1
, . . . , In) in-
creasing, define [M( j)] j∈I = [M(i1 )

j=1, define [M( j)]N

, . . . , In} con (i1

· · · M(In )].

, . . . , Md,2

, . . . , Md,1

, M1,2

j=1

3 Nonconvex Optimization Landscapes for Machine Learning

This section shows our first main result that under mild assumptions, ev-
ery differentiable local minimum achieves the global optimality of the per-
turbable gradient basis model class.

3.1 Assumptions. Given a hypothesis class f and data set, let (cid:8) be
a set of nondifferentiable points θ as (cid:8) = {θ ∈ Rdθ : (∃i ∈ {1, . . . , M})[ fxi
is not differentiable at θ ]}. Allo stesso modo, define ˜(cid:8) = {θ ∈ Rdθ : (∀(cid:9) > 0)(∃θ (cid:6) ∈
B(θ , (cid:9)))(∃i ∈ {1, . . . , M})[ fxi is not differentiable at θ (cid:6)
]}. Here, B(θ , (cid:9)) is the
open ball with the center θ and the radius (cid:9). In common nondifferentiable
models f such as neural networks with rectified linear units (ReLUs) E
pooling operations, we have that (cid:8) = ˜(cid:8), and the Lebesgue measure of
(cid:8)(= ˜(cid:8)) is zero.

This section uses the following mild assumptions.

i ∈ {1, . . . , M},
Assumption 1 (Use of Common Loss criteria). For all
the function (cid:3)yi : q (cid:9)→ (cid:3)(q, yi) ∈ R≥0 is differentiable and convex (per esempio., IL
squared loss, cross-entropy loss, or polynomial hinge loss satisfies this
assumption).

Assumption 2 (Use of Common Model Structures). There exists a function
G : Rdθ → Rdθ such that fxi (θ ) =
k fxi (θ ) for all i ∈ {1, . . . , M} E
k=1 g(θ )k
all θ ∈ Rdθ \ (cid:8).

(cid:3)

∂

dθ

k

dy

(cid:3)

(cid:3)

k=1 yk log exp(qk )
(cid:6) esp(qk

Assumption 1 is satisfied by simply using common loss criteria that
include the squared loss (cid:3)(q, sì) = (cid:10)q − y(cid:10)2
2, cross-entropy loss (cid:3)(q, sì) =
−
(cid:6) ) , and smoothed hinge loss (cid:3)(q, sì) = (max{0, 1 −
yq})p with p ≥ 2 (the hinge loss with dy = 1). Although the objective func-
tion L : θ (cid:9)→ L(θ ) used to train a complex machine learning model (per esempio., UN
neural network) is nonconvex in θ , the loss criterion (cid:3)yi : q (cid:9)→ (cid:3)(q, yi) is usu-
ally convex in q. In questo articolo, the cross-entropy loss includes the softmax
function, and thus fx(θ ) is the pre-softmax output of the last layer in related
deep learning models.

Assumption 2 is satisfied by simply using a common architecture in
deep learning or a classical machine learning model. Per esempio, consider
a deep neural network of the form fx(θ ) = Wh(X; tu) + B, where h(X; tu) È

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Every Local Minimum Value Is the Global Minimum Value

2297

dθ

∂

(cid:3)

an output of an arbitrary representation at the last hidden layer and θ =
vec([W, B, tu]). Then assumption 2 holds because fxi (θ ) =
k fxi (θ ),
where g(θ )k
k for all k corresponding to the parameters (W, B) in the last
= θ
layer and g(θ )k
= 0 for all other k corresponding to u. Generalmente, because g
is a function of θ , assumption 2 is easily satisfiable. Assumption 2 does not
require the model f (X; θ ) to be linear in θ or x.

k=1 g(θ )k

Note that we allow the nondifferentiable points to exist in L(θ ); for
esempio, the use of ReLU is allowed. For a nonconvex and nondifferen-
tiable function, we can still have first-order and second-order necessary
conditions of local minima (per esempio., Rockafellar & Wets, 2009, theorem 13.24).
Tuttavia, subdifferential calculus of a nonconvex function requires careful
treatment at nondifferentiable points (see Rockafellar & Wets, 2009; Kakade
& Lee, 2018; Davis, Drusvyatskiy, Kakade, & Lee, 2019), and deriving guar-
antees at nondifferentiable points is left to a future study.

3.2 Theory for Critical Points. Before presenting the first main result,
this section provides a simpler result for critical points to illustrate the ideas
behind the main result for local minima. We define the (theoretical) objec-
tive function Lθ of the gradient basis model class as

Lθ (α) =

M(cid:2)

i=1

λ
io

(cid:3) ( fθ (xi

; α), yi) ,

(cid:3)

∂

α
k

dθ
k=1

; α) =

Dove { fθ (xi
k fxi (θ ) : α ∈ Rdθ } is the induced gradient basis
model class. The following theorem shows that every differentiable crit-
ical point of our original objective L (including every differentiable local
minimum and saddle point) achieves the global minimum value of Lθ . IL
complete proofs of all the theoretical results are presented in appendix A.

Theorem 1. Let assumptions 1 E 2 hold. Then for any critical point θ ∈ (Rdθ \
(cid:8)) of L, the following holds:

l(θ ) = inf
α∈Rdθ

Lθ (α).

An important aspect in theorem 1 is that Lθ on the right-hand side is
convex, while L on the left-hand side can be nonconvex or convex. Here,
following convention, inf S is defined to be the infimum of a subset S of R
(the set of affinely extended real numbers); questo è, if S has no lower bound,
inf S = −∞ and inf ∅ = ∞. Note that theorem 1 vacuously holds true if
there is no critical point for L. To guarantee the existence of a minimizer
in un (nonempty) subspace S ⊆ Rdθ for L (or Lθ ), a classical proof requires
two conditions: a lower semicontinuity of L (or Lθ ) and the existence of a

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2298

K. Kawaguchi, J. Huang, and L. Kaelbling

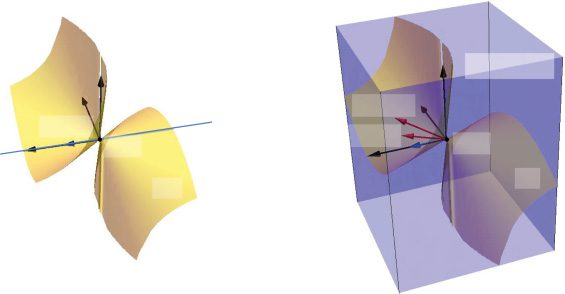
Figura 1: Illustration of gradient basis model class and theorem 1 with θ ∈ R2
and fX (θ ) ∈ R3 (dy
= 1). Theorem 1 translates the local condition of θ in the pa-
rameter space R2 (on the left) to the global optimality in the output space R3 (SU
the right). The subspace TfX (θ ) is the space of the outputs of the gradient basis
model class. Theorem 1 states that fX (θ ) is globally optimal in the subspace as
fX (θ ) ∈ argminf∈T fX (θ )

dist(F, sì) for any differentiable critical point θ of L.

q ∈ S for which the set {q(cid:6) ∈ S : l(q(cid:6)
compact (see Bertsekas, 1999, for different conditions).

) ≤ L(q)} (O {q(cid:6) ∈ S : Lθ (q(cid:6)

) ≤ Lθ (q)}) È

3.2.1 Geometric View. This section presents the geometric interpretation
of theorem 1 that provides an intuitive yet formal description of gradient
basis model class. Figura 1 illustrates the gradient basis model class and
theorem 1 with θ ∈ R2 and fX (θ ) ∈ R3. Here, we consider the following map
from the parameter space to the concatenation of the output of the model
at x1

, . . . , xm:

, x2

fX : θ ∈ Rdθ (cid:9)→ ( fx1 (θ )

(cid:15), fx2 (θ )

(cid:15), . . . , fxm (θ )

(cid:15)

(cid:15) ∈ Rmdy .
)

In the output space Rmdy of fX, the objective function L induces the notion
M)(cid:15) ∈ Rmdy to a vector f =

of distance from the target vector y = (sì(cid:15)
1
(F(cid:15)
1

M)(cid:15) ∈ Rmdy as

, . . . , sì(cid:15)

, . . . , F(cid:15)

dist(F, sì) =

M(cid:2)

i=1

λ
io

(cid:3)(fi

, yi).

We consider the affine subspace TfX (θ ) of Rmdy that passes through the point
fX (θ ) and is spanned by the set of vectors {∂

1 fX (θ ), . . . , ∂

dθ fX (θ )},

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Every Local Minimum Value Is the Global Minimum Value

2299

TfX (θ )

= span({∂

1 fX (θ ), . . . , ∂

dθ fX (θ )}) + { fX (θ )},

where the sum of the two sets represents the Minkowski sum of the
sets.

Then the subspace TfX (θ ) is the space of the outputs of the gradient ba-
sis model class in general beyond the low-dimensional illustration. This is
because by assumption 2, for any given θ ,

TfX (θ )

=

=

(cid:4)

dθ(cid:2)

(cid:4)

k=1

dθ(cid:2)

k=1

(cid:5)

(G(θ )k

+ α

k)∂

k fX (θ ) : α ∈ Rdθ

(cid:5)

α
k

∂

k fX (θ ) : α ∈ Rdθ

,

(3.1)

(cid:3)

dθ
E
k=1
= span({∂

∂

k fX (θ ) = ( fθ (x1

α
k
1 fX (θ ), . . . , ∂

; α)(cid:15), . . . , fθ (xm; α)(cid:15))(cid:15). In other words, TfX (θ )
; α)(cid:15), . . . , fθ (xm; α)(cid:15))(cid:15).

dθ fX (θ )}) (cid:16) ( fθ (x1

Therefore, in general, theorem 1 states that under assumptions 1 E 2,

fX (θ ) is globally optimal in the subspace TfX (θ ) COME

fX (θ ) ∈ argmin
f∈T fX (θ )

dist(F, sì),

for any differentiable critical point θ of L. Theorem 1 concludes this global
optimality in the affine subspace of the output space based on the local
condition in the parameter space (cioè., differentiable critical point). A key
idea behind theorem 1 is to consider the map between the parameter space
and the output space, which enables us to take advantage of assumptions 1
E 2.

Figura 2 illustrates the gradient basis model class and theorem 1 con un
union of manifolds and a tangent space. Under the constant rank condition,
the image of the map fX locally forms a single manifold. More precisely, if
there exists a small neighborhood U(θ ) of θ such that fX is differentiable in
U(θ ) and rank(∂ fX (θ (cid:6)
)) = r is constant with some r for all θ (cid:6) ∈ U(θ ) (the con-
stant rank condition), then the rank theorem states that the image fX (U(θ ))
is a manifold of dimension r (Lee, 2013, theorem 4.12). We note that the rank
map θ (cid:9)→ rank(∂ fX (θ )) is lower semicontinuous (cioè., if rank(∂ fX (θ )) = r,
then there exists a neighborhood U(θ ) of θ such that rank(∂ fX (θ (cid:6)
)) ≥ r for
any θ (cid:6) ∈ U(θ )). Therefore, if ∂ fX (θ ) at θ has the maximum rank in a small
neighborhood of θ , then the constant rank condition is satisfied.

For points θ where the constant rank condition is violated, the image of
the map fX is no longer a single manifold. Tuttavia, locally it decomposes
as a union of finitely many manifolds. More precisely, if there exists a small
neighborhood U(θ ) of θ such that fX is analytic over U(θ ) (this condition
is satisfied for commonly used activation functions such as ReLU, sigmoid,

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2300

K. Kawaguchi, J. Huang, and L. Kaelbling

1

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

Figura 2: Illustration of gradient basis model class and theorem 1 with man-
ifold and tangent space. The space R2 (cid:16) θ on the left is the parameter space,
and the space R3 (cid:16) fX (θ ) on the right is the output space. The surface M ⊂ R3
on the right is the image of fX, which is a union of finitely many manifolds.
The tangent space TfX (θ ) is the space of the outputs of the gradient basis model
class. Theorem 1 states that if θ is a differentiable critical point of L, then fX (θ )
is globally optimal in the tangent space TfX (θ ).

and hyperbolic tangent at any differentiable point), then the image fX (U(θ ))
admits a locally finite partition M into connected submanifolds such that
whenever M (cid:18)= M(cid:6) ∈ M with ¯M ∩ M(cid:6) (cid:18)= ∅ ( ¯M is the closure of M), we have

(cid:6) ⊂ ¯M, dim(M

(cid:6)

M

) < dim(M). See Hardt (1975) for the proof. If the point θ satisfies the constant rank condition, then TfX (θ ) is exactly the tangent space of the manifold formed by the image fX (U(θ )). Otherwise, locally the image decomposes into a finite union M of submanifolds. In this case, TfX (θ ) belongs to the span of the tangent space of those manifolds in M as TfX (θ ) ⊂ {TpM : p = fX (θ ), M ∈ M}, where TpM is the tangent space of the manifold M at the point p. 3.2.2 Examples. In this section, we show through examples that theorem 1 generalizes the previous results in special cases while providing new the- oretical insights based on the gradient basis model class and its geometric / e d u n e c o a r t i c e - p d / l f / / / / 3 1 1 2 2 2 9 3 1 8 6 5 1 6 5 n e c o _ a _ 0 1 2 3 4 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Every Local Minimum Value Is the Global Minimum Value 2301 view. In the following, whenever the form of f is specified, we require only assumption 1 because assumption 2 is automatically satisfied by a given f . For classical machine learning models, example 1 shows that the gradi- ent basis model class is indeed equivalent to a given model class. From the geometric view, this means that for any θ , the tangent space T fX (θ ) is equal to the whole image M of fX (i.e., TfX (θ ) does not depend on θ ). This reduces theorem 1 to the statement that every critical point of L is a global minimum of L. k θ (cid:3) dθ k=1 Example 1: Classical Machine Learning Models. For any basis func- tion model f (x; θ ) = φ(x)k in classical machine learning with any fixed feature map φ : X → Rdθ , we have that fθ (x; α) = f (x; α), and hence infθ ∈Rdθ L(θ ) = infα∈Rdθ Lθ (α), as well as (cid:8) = ∅. In other words, in this spe- cial case, theorem 1 states that every critical point of L is a global minimum of L. Here, we do not assume that a critical point or a global minimum exists or can be attainable. Instead, the statement logically means that if a point is a critical point, then the point is a global minimum. This type of statement vacuously holds true if there is no critical point. For overparameterized deep neural networks, example 2 shows that the induced gradient basis model class is highly expressive such that it must contain the globally optimal model of a given model class of deep neural networks. In this example, the tangent space TfX (θ ) is equal to the whole output space Rmdy . This reduces theorem 1 to the statement that every criti- cal point of L is a global minimum of L for overparameterized deep neural networks. Intuitively, in Figure 1 or 2, we can increase the number of parameters and raise the number of partial derivatives ∂ k fX (θ ) in order to increase the = Rmdy . This is in- dimensionality of the tangent space TfX (θ ) so that TfX (θ ) deed what happens in example 2, as well as in the previous studies of sig- nificantly overparameterized deep neural networks (Allen-Zhu, Li, & Song, 2018; Du, Lee, Li, Wang, & Zhai, 2018; Zou et al., 2018). In the previous studies, the significant overparameterization is required so that the tangent = Rmdy space TfX (θ ) does not change from the initial tangent space TfX (θ (0) ) during training. Thus, theorem 1, with its geometric view, provides the novel algebraic and geometric insights into the results of the previous stud- ies and the reason why overparameterized deep neural networks are easy to be optimized despite nonconvexity. Example 2: Overparameterized Deep Neural Networks. Theorem 1 im- plies that every critical point (and every local minimum) is a global mini- mum for sufficiently overparameterized deep neural networks. Let n be the number of units in each layer of a fully connected feedforward deep neu- ral network. Let us consider a significant overparameterization such that n ≥ m. Let us write a fully connected feedforward deep neural network with the trainable parameters (θ , u) by f (x; θ ) = Wφ(x; u), where W ∈ Rdy×n is l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 1 1 2 2 2 9 3 1 8 6 5 1 6 5 n e c o _ a _ 0 1 2 3 4 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 2302 K. Kawaguchi, J. Huang, and L. Kaelbling the weight matrix in the last layer, θ = vec(W ), u contains the rest of the parameters, and φ(x; u) is the output of the last hidden layer. Denote xi = )(cid:15), 1](cid:15) to contain the constant term to account for the bias term in the [(x(raw) i = 1 first layer. Assume that the input samples are normalized as (cid:10)x(raw) < 1 − δ with some δ > 0
for all i ∈ {1, . . . , M} and distinct as (X(raw)
io
for all i(cid:6) (cid:18)= i. Assume that the activation functions are ReLU activation func-
zioni. Then we can efficiently set u to guarantee rank([φ(xi
i=1) ≥ m (per esempio.,
by choosing u to make each unit of the last layer to be active only for each
sample xi).1 Theorem 1 implies that every critical point θ with this u is a
global minimum of the whole set of trainable parameters (θ , tu) because
infα Lθ (α) = inf f1

, yi) (with assumption 1).

(cid:15)X(raw)
)
io(cid:6)

; tu)]M

(cid:3)( fi

,…, fm

(cid:3)

λ
io

(cid:10)

2

io

M
i=1

For deep neural networks, esempio 3 shows that standard networks have
the global optimality guarantee with respect to the representation learned at
the last layer, and skip connections further ensure the global optimality with
respect to the representation learned at each hidden layer. This is because
adding the skip connections incurs new partial derivatives {∂
k that
span the tangent space containing the output of the best model with the
corresponding learned representation.

k fX (θ )}

Esempio 3: Deep Neural Networks and Learned Representations. Contro-
sider a feedforward deep neural network, and let I (skip) ⊆ {1, . . . , H} be the
set of indices such that there exists a skip connection from the (l − 1)th layer
to the last layer for all l ∈ I (skip) ; questo è, in this example,

F (X; θ ) =

(cid:2)

l∈I (skip)

W (l+1)H(l)(X; tu),

where θ = vec([[W (l+1)]l∈I (skip) , tu]) ∈ Rdθ with W (l+1) ∈ Rdy×dl and u ∈ Rdu .

The conclusion in this example holds for standard deep neural networks
without skip connections too, since we always have H ∈ I (skip) for standard
deep neural networks. Let assumption 1 hold. Then theorem 1 implies that
for any critical point θ ∈ (Rdθ \ (cid:8)) of L, the following holds:

l(θ ) = inf
α∈Rdθ

l(skip)
θ

(α),

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1

> 0 E (W (1)xi )io(cid:6) ≤ 0 for all i

Per esempio, choose the first layer’s weight matrix W (1) such that for all i ∈ {1, . . . , M},
(cid:6) (cid:18)= i. This can be achieved by choosing the ith row
(cid:15), (cid:9) − 1] con 0 < (cid:9) ≤ δ for i ≤ m. Then choose the weight matrices (cid:6) (cid:18)= j. This (W (1)xi )i of W (1) to be [(x(raw) for the lth layer for all l ≥ 2 such that for all j, W (l) j, j ; u)]m guarantees rank([φ(xi (cid:18)= 0 and W (l) j(cid:6), j = 0 for all j ) i i=1 ) ≥ m. Every Local Minimum Value Is the Global Minimum Value 2303 where L(skip) θ (α) = m(cid:2) i=1 λ i (cid:3)yi ⎛ ⎝ (cid:2) l∈I (skip) α(l+1) w h(l)(xi ; u) + ⎞ (αu)k ∂uk fxi (θ ) ⎠ , du(cid:2) k=1 with α = vec([[α(l+1)]l∈I (skip) , αu]) ∈ Rdθ with α(l+1) ∈ Rdy×dl and αu ∈ Rdu . vec(W (H+1) ) f (x; θ ))vec(W (H+1)), and thus assump- This is because f (x; θ ) = (∂ ; u) is the representation learned tion 2 is automatically satisfied. Here, h(l)(xi at the l-layer. Therefore, infα∈Rdθ L(skip) (α) is at most the global minimum value of the basis models with the learned representations of the last layer and all hidden layers with the skip connections. θ 3.3 Theory for Local Minima. We are now ready to present our first main result. We define the (theoretical) objective function ˜Lθ of the per- turbable gradient basis model class as ˜Lθ (α, (cid:9), S) = m(cid:2) i=1 λ i (cid:3)( ˜fθ (xi ; α, (cid:9), S), yi), where ˜fθ (xi ; α, (cid:9), S) is a perturbed gradient basis model defined as ˜fθ (xi ; α, (cid:9), S) = dθ(cid:2) |S|(cid:2) k=1 j=1 α k, j ∂ k fxi (θ + (cid:9)S j ). 2 , . . . , S|S| ∈ Rdθ and α ∈ Rdθ ×|S| Here, S is a finite set of vectors S1 be the set of all vectors v ∈ Rdθ such that (cid:10)v(cid:10) for any i ∈ {1, . . . , m}. Let S ⊆ S j (cid:9)S j ) (cid:18)= ∂ S ⊆ fin The following theorem shows that every differentiable local minimum denote a finite subset S of a set S(cid:6) ∈ V[θ , (cid:9)], we have fxi (θ + (cid:9)S j ) = fxi (θ ), but it is possible to have ∂ k fxi (θ ). This enables the greater expressivity of ˜fθ (xi . Let V[θ , (cid:9)] ≤ 1 and fxi (θ + (cid:9)v ) = fxi (θ ) . For an k fxi (θ + ; α, (cid:9), S) with a V[θ , (cid:9)] when compared with fθ (xi fin S(cid:6) ; α). of L achieves the global minimum value of ˜Lθ : Theorem 2. Let assumptions 1 and 2 hold. Then, for any local minimum θ ∈ (Rdθ \ ˜(cid:8)) of L, the following holds: there exists (cid:9) 0), > 0 such that for any (cid:9) ∈ [0, (cid:9)

0

l(θ ) = inf

˜Lθ (α, (cid:9), S).

f in

S⊆
V[θ,(cid:9)],
α∈Rdθ ×|S|

(3.2)

To understand the relationship between theorems 1 E 2, let us consider
the following general inequalities: for any θ ∈ (Rdθ \ ˜(cid:8)) con (cid:9) ≥ 0 being
sufficiently small,

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2304

K. Kawaguchi, J. Huang, and L. Kaelbling

l(θ ) ≥ inf
α∈Rdθ

Lθ (α) ≥ inf
S⊆
V[θ ,(cid:9) ],
α∈Rdθ ×|S|

f in

˜Lθ (α, (cid:9), S).

Here, whereas theorem 1 states that the first inequality becomes equality as
l(θ ) = infα∈Rdθ Lθ (α) at every differentiable critical point, theorem 2 stati
that both inequalities become equality as

l(θ ) = inf
α∈Rdθ

Lθ (α) = inf
S⊆
V[θ,(cid:9)],
α∈Rdθ ×|S|

f in

˜Lθ (α, (cid:9), S)

at every differentiable local minimum.

fin

k fxi (θ )}dθ

V[θ , (cid:9)] and α ∈ Rdθ ×|S|

From theorem 1 to theorem 2, the power of increasing the number of pa-
rameters (including overparameterization) is further improved. The right-
hand side in equation 3.2 is the global minimum value over the variables
S ⊆
. Here, as dθ increases, we may obtain the global
minimum value of a larger search space Rdθ ×|S|
, which is similar to theorem
1. A concern in theorem 1 is that as dθ increases, we may also significantly
increase the redundancy among the elements in {∂
k=1. Although this
remains a valid concern, theorem 2 allows us to break the redundancy by
the globally optimal S ⊆
V[θ , (cid:9)] to some degree.
Per esempio, consider f (X; θ ) = g(W (l)H(l)(X; tu); tu), which represents a
deep neural network, with some lth-layer output h(l)(X; tu) ∈ Rdl , a trainable
matrice dei pesi W (l), and an arbitrary function g to compute the rest of the for-
×m
ward pass. Here, θ = vec([W (l), tu]). Let h(l)(X; tu) = [H(l)(xi
E, allo stesso modo, F (X; θ ) = g(W (l)H(l)(X; tu); tu) ∈ Rdy×m. Then, all vectors v cor-
responding to any elements in the left null space of h(l)(X; tu) are in V[θ , (cid:9)]
(cioè., v
k is set to perturb
W (l) by an element in the left null space). Così, as the redundancy increases
such that the dimension of the left null space of h(l)(X; tu) increases, we have
a larger space of V[θ , (cid:9)], for which a global minimum value is guaranteed
at a local minimum.

= 0 for all k corresponding to u and the rest of v

; tu)]M
i=1

∈ Rdl

fin

k

3.3.1 Geometric View. This section presents the geometric interpretation
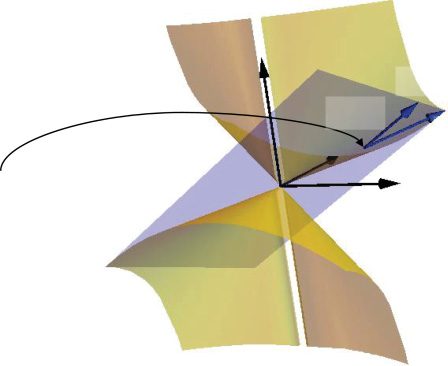
of the perturbable gradient basis model class and theorem 2. Figura 3 illus-
trates the perturbable gradient basis model class and theorem 2 with θ ∈ R2
and fX (θ ) ∈ R3. Figura 4 illustrates them with a union of manifolds and tan-
gent spaces at a singular point. Given a (cid:9) (≤ (cid:9)
0), define the affine subspace
˜TfX (θ ) of the output space Rmdy by

˜TfX (θ )

= span({f ∈ Rmdy : (∃v ∈ V[θ , (cid:9)])[f ∈ TfX (θ +(cid:9)v )]}).

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Every Local Minimum Value Is the Global Minimum Value

2305

Figura 3: Illustration of perturbable gradient basis model class and theorem 2
with θ ∈ R2 and fX (θ ) ∈ R3 (dy
= 1). Theorem 2 translates the local condition of
θ in the parameter space R2 (on the left) to the global optimality in the output
space R3 (on the right). The subspace ˜TfX (θ ) is the space of the outputs of the
perturbable gradient basis model class. Theorem 2 states that fX (θ ) is globally
optimal in the subspace as fX (θ ) ∈ argminf∈ ˜T fX (θ )
dist(F, sì) for any differentiable
local minima θ of L. In this example, ˜TfX (θ ) is the whole output space R3, while
TfX (θ ) is not, illustrating the advantage of the perturbable gradient basis over the
= R3, fX (θ ) must be globally optimal in the whole
gradient basis. Since ˜TfX (θ )
output space R3.

Then the subspace ˜TfX (θ ) is the space of the outputs of the perturbable gra-
dient basis model class in general beyond the low-dimensional illustration
(this follows equation 3.1 and the definition of the perturbable gradient ba-
sis model). Therefore, in general, theorem 2 states that under assumptions
1 E 2, fX (θ ) is globally optimal in the subspace ˜TfX (θ ) COME

fX (θ ) ∈ argmin
f∈ ˜T fX (θ )

dist(F, sì)

for any differentiable local minima θ of L. Theorem 2 concludes the global
optimality in the affine subspace of the output space based on the local con-
dition in the parameter space—that is, differentiable local minima. Here, UN
(differentiable) local minimum θ is required to be optimal only in an ar-
bitrarily small local neighborhood in the parameter space, and yet fX (θ ) È
guaranteed to be globally optimal in the affine subspace of the output space.
This illuminates the fact that nonconvex optimization in machine learning
has a particular structure beyond general nonconvex optimization.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2306

K. Kawaguchi, J. Huang, and L. Kaelbling

Figura 4: Illustration of perturbable gradient basis model class and theorem 2
with manifold and tangent space at a singular point. The surface M ⊂ R3 is
the image of fX, which is a union of finitely many manifolds. The line TfX (θ )
on the left panel is the space of the outputs of the gradient basis model class.
= R3 on the right panel is the space of the outputs of the
The whole space ˜TfX (θ )
perturbable gradient basis model class. The space ˜TfX (θ ) is the span of the set of
, TfX (θ (cid:6) ), and TfX (θ (cid:6)(cid:6) ). Theorem 2 states that
the vectors in the tangent spaces TfX (θ )
if θ is a differentiable local minimum of L, then fX (θ ) is globally optimal in the
space ˜TfX (θ ).

4 Applications to Deep Neural Networks

The previous section showed that all local minima achieve the global op-
timality of the perturbable gradient basis model class with several direct
consequences for special cases. In this section, as consequences of theorem
2, we complement or improve the state-of-the-art results in the literature.

4.1 Esempio: ResNets. As an example of theorem 2, we set f to be the
function of a certain type of residual networks (ResNets) that Shamir (2018)
studied. Questo è, both Shamir (2018) and this section set f as

F (X; θ ) = W (X + Rz(X; tu)),

(4.1)

where θ = vec([W, R, tu]) ∈ Rdθ with W ∈ Rdy×dx , R ∈ Rdx×dz , and u ∈ Rdu .
Here, z(X; tu) ∈ Rdz represents an output of deep residual functions with
a parameter vector u. No assumption is imposed on the form of z(X; tu),
and z(X; tu) can represent an output of possibly complicated deep resid-
ual functions that arise in ResNets. Per esempio, the function f can rep-
resent deep preactivation ResNets (Lui, Zhang, Ren, & Sun, 2016), Quale
are widely used in practice. To simplify theoretical study, Shamir (2018) COME-
sumed that every entry of the matrix R is unconstrained (per esempio., instead of R

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Every Local Minimum Value Is the Global Minimum Value

2307

representing convolutions). We adopt this assumption based on the previ-
ous study (Shamir, 2018).

4.1.1 Background. Along with an analysis of approximate critical points,
Shamir (2018) proved the following main result, proposition 1, under the
assumptions PA1, PA2, and PA3:

PA1: The output dimension dy = 1.
PA2: For any y, the function (cid:3)y is convex and twice differentiable.
PA3: On any bounded subset of the domain of L, the function Lu(W, R),
its gradient ∇Lu(W, R), and its Hessian ∇2Lu(W, R) are all Lipschitz
continuous in (W, R), where Lu(W, R) = L(θ ) with a fixed u.

Proposition 1 (Shamir, 2018). Let f be specified by equation 4.1, Let assumptions
PA1, PA2, and PA3 hold. Then for any local minimum θ of L,

M(cid:2)

l(θ ) ≤ inf

W∈Rdy ×dx

i=1

λ
io

(cid:3)yi (Wxi).

Shamir (2018) remarked that it is an open problem whether proposi-
zione 1 and another main result in the article can be extended to networks
with dy > 1 (multiple output units). Note that Shamir (2018) also provided
proposition 1 with an expected loss and an analysis for a simpler decou-
pled model, Wx + Vz(X; tu). For the simpler decoupled model, our theo-
rem 1 immediately concludes that given any u, every critical point with
respect to θ−u = (W, R) achieves a global minimum value with respect
; tu)) : W ∈ Rdy×dx , R ∈ Rdx×dz }
to θ−u as L(θ−u) = inf {
(≤ infW∈Rdy ×dx
(cid:3)yi (Wxi)). This holds for every critical point θ since any
critical point θ must be a critical point with respect to θ−u.

(cid:3)yi (Wxi

+ Rz(xi

M
i=1

M
i=1

(cid:3)

(cid:3)

λ
io

λ
io

4.2 Result. The following theorem shows that every differentiable local
minimum achieves the global minimum value of ˜L(ResNet)
(the right-hand
side in equation 4.2), which is no worse than the upper bound in propo-
, tu) O
sition 1 and is strictly better than the upper bound as long as z(xi
; α, (cid:9), S) is nonnegligible. Infatti, the global minimum value of ˜L(ResNet)
˜fθ (xi
(the right-hand side in equation 4.2) is no worse than the global minimum
value of all models parameterized by the coefficients of the basis x and
z(X; tu), and further improvement is guaranteed through a nonnegligible
˜fθ (xi

; α, (cid:9), S).

θ

θ

Theorem 3. Let
f be specified by equation 4.1. Let assumption 1 hold. As-
sume that dy ≤ min{dx, dz}. Then for any local minimum θ ∈ (Rdθ \ ˜(cid:8)) of L, IL

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2308

K. Kawaguchi, J. Huang, and L. Kaelbling

following holds: there exists (cid:9)

0

> 0 such that for any (cid:9) ∈ (0, (cid:9)

0),

˜L(ResNet)
θ

(α, αw, αr, (cid:9), S),

(4.2)

l(θ ) =

inf
S⊆
V[θ ,(cid:9)],
α∈Rdθ ×|S|,
αw∈Rdy ×dx ,αr∈Rdy ×dz

f in

Dove

˜L(ResNet)
θ

(α, αw, αr, (cid:9), S) =

M(cid:2)

i=1

λ
io

(cid:3)yi (αwxi

+ αrz(xi

; tu) + ˜fθ (xi

; α, (cid:9), S)).

Theorem 3 also successfully solved the first part of the open problem in
the literature (Shamir, 2018) by discarding the assumption of dy = 1. From
the geometric view, theorem 3 states that the span ˜TfX (θ ) of the set of the
vectors in the tangent spaces {TfX (θ +(cid:9)v ) : v ∈ V[θ , (cid:9)]} contains the output of
the best basis model with the linear feature x and the learned nonlinear
(cid:18)= Tf (θ ) E
; tu). Similar to the examples in Figures 3 E 4, ˜TfX (θ )
feature z(xi
the output of the best basis model with these features is contained in ˜TfX (θ )
but not in Tf (θ ).

Unlike the recent study on ResNets (Kawaguchi & Bengio, 2019), our the-
orem 3 predicts the value of L through the global minimum value of a large
search space (cioè., the domain of ˜L(ResNet)
) and is proven as a consequence of
our general theory (cioè., theorem 2) with a significantly different proof idea
(see section 4.3) and with the novel geometric insight.

θ

4.2.1 Esempio: Deep Nonlinear Networks with Locally Induced Partial Linear
Structures. We specify f to represent fully connected feedforward networks
with arbitrary nonlinearity σ and arbitrary depth H as follows:

F (X; θ ) = W (H+1)H(H)(X; θ ),

(4.3)

Dove

H(l)(X; θ ) = σ (l)(W (l)H(l−1)(X; θ )),

for all l ∈ {1, . . . , H} with h(0)(X; θ ) = x. Here, θ = vec([W (l)]H+1
l=1 ) ∈ Rdθ with
W (l) ∈ Rdl
= dx. Inoltre, P (l) : Rdl → Rdl repre-
sents an arbitrary nonlinear activation function per layer l and is allowed
to differ among different layers.

= dy, and d0

×dl−1 , dH+1

4.2.2 Background. Given the difficulty of theoretically understanding
deep neural networks, Goodfellow, Bengio, and Courville (2016) noted that
theoretically studying simplified networks (cioè., deep linear networks) È

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Every Local Minimum Value Is the Global Minimum Value

2309

worthwhile. Per esempio, Saxe, McClelland, and Ganguli (2014) empiri-
cally showed that deep linear networks may exhibit several properties anal-
ogous to those of deep nonlinear networks. Accordingly, the theoretical
study of deep linear neural networks has become an active area of research
(Kawaguchi, 2016; Hardt & Mamma, 2017; Arora, Cohen, Golowich, & Eh, 2018;
Arora, Cohen, & Hazan, 2018; Bartlett, Helmbold, & Lungo, 2019; Du & Eh,
2019).

Along this line, Laurent and Brecht (2018) recently proved the following

main result, proposition 2, under the assumptions PA4, PA5, and PA6:

PA4: Every activation function is identity as σ (l)(q) = q for every l ∈

{1, . . . , H} (cioè., deep linear networks).

PA5: For any y, the function (cid:3)y is convex and differentiable.
PA6: The thinnest layer is either the input layer or the output layer as

min{dx, dy} ≤ min{d1

, . . . , dH}.

Proposition 2 (Laurent & Brecht, 2018). Let f be specified by equation 4.3. Let
assumptions PA4, PA5, and PA6 hold. Then every local minimum θ of L is a global
minimum.

4.2.3 Result. Instead of studying deep linear networks, we now consider
a partial linear structure locally induced by a parameter vector with nonlin-
ear activation functions. This relaxes the linearity assumption and extends
our understanding of deep linear networks to deep nonlinear networks.

Intuitively, Jn,T[θ ] is a set of partial linear structures locally induced
by a vector θ , which is now formally defined as follows. Given a θ ∈ Rdθ ,
let Jn,T[θ ] be a set of all sets J = {J(t+1), . . . , J(H+1)} such that each set J =
{J(t+1), . . . , J(H+1)} ∈ Jn,T[θ ] satisfies the following conditions: there exists
(cid:9) > 0 such that for all l ∈ {T + 1, T + 2, . . . , H + 1},

for

Tutto

(k, θ (cid:6), io) ∈ J(l) × B(θ , (cid:9)) ×

1. J(l) ⊆ {1, . . . , dl
, θ (cid:6)
2. H(l)(xi

} con |J(l)| ≥ n.
))k

= (W (l)H(l−1)(xi

, θ (cid:6)

)k
{1, . . . , M}.

3. W (l+1)
io, j

= 0 for all (io, j) ∈ ({1, . . . , dl+1

} \ J(l+1)) × J(l) if l ≤ H − 1.

Let (cid:14)N,t be the set of all parameter vectors θ such that Jn,T[θ ] is nonempty.
As the definition reveals, a neural network with a θ ∈ (cid:14)
dy,t can be a standard
deep nonlinear neural network (with no linear units).

Theorem 4. Let f be specified by equation 4.3. Let assumption 1 hold. Then for
any t ∈ {1, . . . , H}, at every local minimum θ ∈ ((cid:14)
\ ˜(cid:8)) of L, the following
dy,T
holds. There exists (cid:9)
> 0 such that for any (cid:9) ∈ (0, (cid:9)
0),

0

l(θ ) =

inf
V[θ ,(cid:9)],

S⊆

f in
α∈Rdθ ×|S|,α
H

∈Rdt

˜L( f f )
θ ,T (α, α

H

, (cid:9), S),

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2310

Dove

K. Kawaguchi, J. Huang, and L. Kaelbling

˜L( f f )
θ ,T (α, α

H

, (cid:9), S) =

M(cid:2)

i=1

λ
io

(cid:3)yi

(cid:10)

H(cid:2)

l=t

α(l+1)
H

H(l)(xi

; tu) + ˜fθ (xi

; α, (cid:9), S)

,

(cid:11)

with α
H

= vec([α(l+1)

H

l=t ) ∈ Rdt , α(l+1)
]H

H

∈ Rdy×dl and dt = dy

(cid:3)

H
l=t dl.

Theorem 4 is a special case of theorem 2. A special case of theorem 4
then results in one of the main results in the literature regarding deep
linear neural networks, questo è, every local minimum is a global min-
imum. Consider any deep linear network with dy ≤ min{d1
, . . . , dH}.
Then every local minimum θ is in (cid:14)
dy,0. Hence, theorem
4 is reduced to the statement that for any local minimum, l(θ ) =
(cid:3)
(cid:3)yi (αxxi), Quale
infα
H
is the global minimum value. Così, every local minimum is a global
minimum for any deep linear neural network with dy ≤ min{d1
, . . . , dH}.
Therefore, theorem 4 successfully generalizes the recent previous result in
the literature (proposition 2) for a common scenario of dy ≤ dx.

; tu)) = infαx∈Rdx

\ ˜(cid:8) = (cid:14)

α(l+1)
H

H(l)(xi

(cid:3)yi (

H
l=0

M
i=1

M
i=1

dy,0

(cid:3)

(cid:3)

∈Rdt

λ
io

λ
io

Beyond deep linear networks, theorem 4 illustrates both the benefit of
the locally induced structure and the overparameterization for deep non-
(cid:3)
linear networks. In the first term,
θ ,T , we bene-
fit by decreasing t (a more locally induced structure) and increasing the
width of the lth layer for any l ≥ t (overparameterization). The second term,
˜fθ (xi
θ ,T , is the general term that is always present from theorem
2, where we benefit from increasing dθ because α ∈ Rdθ ×|S|

; α, (cid:9), S) in L(ff)

; tu), in L(ff)

α(l+1)
H

H(l)(xi

H
l=t

.

From the geometric view, theorem 4 captures the intuition that the span
˜TfX (θ ) of the set of the vectors in the tangent spaces {TfX (θ +(cid:9)v ) : v ∈ V[θ , (cid:9)]}
contains the best basis model with the linear feature for deep linear net-
works, as well as the best basis models with more nonlinear features as
more local structures arise. Similar to the examples in Figures 3 E 4,
(cid:18)= Tf (θ ) and the output of the best basis models with those features
˜TfX (θ )
are contained in ˜TfX (θ ) but not in Tf (θ ).

A similar local structure was recently considered in Kawaguchi, Huang,
and Kaelbling (2019). Tuttavia, both the problem settings and the obtained
results largely differ from those in Kawaguchi et al. (2019). Inoltre,
theorem 4 is proven as a consequence of our general theory (theorem 2),
and accordingly, the proofs largely differ from each other as well. Theo-
rem 4 also differs from recent results on the gradient decent algorithm for
deep linear networks (Arora, Cohen, Golowich, & Eh, 2018; Arora, Cohen,
& Hazan, 2018; Bartlett et al., 2019; Du & Eh, 2019), since we analyze the
loss surface instead of a specific algorithm and theorem 4 applies to deep
nonlinear networks as well.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Every Local Minimum Value Is the Global Minimum Value

2311

4.3 Proof Idea in Applications of Theorem 2. Theorems 3 E 4 are
simple consequences of theorem 2, and their proof is illustrative as a means
of using theorem 2 in future studies with different additional assumptions.
The high-level idea behind the proofs in the applications of theorem 2 È
captured in the geometric view of theorem 2 (see Figures 3 E 4). Questo è,
given a desired guarantee, we check whether the space ˜TfX (θ ) is expressive
enough to contain the output of the desired model corresponding to the
desired guarantee.

To simplify the use of theorem 2, we provide the following lemma. Questo
lemma states that the expressivity of the model ˜fθ (X; α, (cid:9), S) with respect
A (α, S) is the same as that of ˜fθ (X; α, (cid:9), S) + ˜fθ (X; α(cid:6), (cid:9), S(cid:6)
) with respect to
(α, α(cid:6), S, S(cid:6)
). As shown in its proof, this is essentially because ˜fθ is linear in
V[θ , (cid:9)] and S(cid:6) ⊆
α, and a union of two sets S ⊆
V[θ , (cid:9)] remains a finite
subset of V[θ , (cid:9)].
Lemma 1. For any θ , any (cid:9) ≥ 0, any S(cid:6) ⊆
{ ˜fθ (X; α, (cid:9), S) : α ∈ Rdθ ×|S|, S ⊆
α ∈ Rdθ ×|S|, α(cid:6) ∈ Rdθ ×|S(cid:6)|, S ⊆

V[θ , (cid:9)], and any x, it holds that
V[θ , (cid:9)]} = { ˜fθ (X; α, (cid:9), S) + ˜fθ (X; α(cid:6), (cid:9), S(cid:6)) :

f in
V[θ , (cid:9)]}.

f in

fin

fin

f in

(cid:3)

; α(cid:6), (cid:9), S(cid:6)
+ αrz(xi
α(l+1)
H
; α(cid:6), (cid:9), S(cid:6)

Based on theorem 2 and lemma 1, the proofs of theorems 3 E
4 are reduced to a simple search for finding S(cid:6) ⊆
V[θ , (cid:9)] such that
fin
) with respect to α(cid:6)
˜fθ (xi
the expressivity of
is no worse than
the expressivity of αwxi
; tu) with respect to (αw, αr) (see theo-
H
(see theorem
rem 3) and that of
l=t
H
4). In other words, { ˜fθ (xi
+ αrz(xi
; tu) : αw ∈
) : α(cid:6) ∈ Rdθ ×|S(cid:6)|} ⊇
Rdy×dx , αr ∈ Rdy×dz } (see theorem 3) E { ˜fθ (xi
(cid:3)
∈ Rdt } (see theorem 4). Only with this search for
{
S(cid:6)
, theorem 2 together with lemma 1 implies the desired statements for the-
orems 3 E 4 (see sections A.4 and A.5 in the appendix for further details).
Così, theorem 2 also enables simple proofs.

) : α(cid:6) ∈ Rdθ ×|S(cid:6)|} ⊇ {αwxi
; α(cid:6), (cid:9), S(cid:6)

; tu) with respect to α(l+1)

; tu) : α
H

α(l+1)
H

H(l)(xi

H(l)(xi

H
l=t

5 Conclusione

This study provided a general theory for nonconvex machine learning
and demonstrated its power by proving new competitive theoretical re-
sults with it. Generalmente, the proposed theory provides a mathematical tool
to study the effects of hypothesis classes f , metodi, and assumptions
through the lens of the global optima of the perturbable gradient basis
model class.

In convex machine learning with a model output f (X; θ ) = θ (cid:15)x with a
(nonlinear) feature output x = φ(X(raw)), achieving a critical point ensures
the global optimality in the span of the fixed basis x = φ(X(raw)). In noncon-
vex machine learning, we have shown that achieving a critical point en-
sures the global optimality in the span of the gradient basis ∂ fx(θ ), Quale
coincides with the fixed basis x = φ(X(raw)) in the case of the convex machine

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2312

K. Kawaguchi, J. Huang, and L. Kaelbling

apprendimento. Così, whether convex or nonconvex, achieving a critical point en-
sures the global optimality in the span of some basis, which might be ar-
bitrarily bad (or good) depending on the choice of the handcrafted basis
φ(X(raw)) = ∂ fx(θ ) (for the convex case) or the induced basis ∂ fx(θ ) (for the
nonconvex case). Therefore, in terms of the loss values at critical points,
nonconvex machine learning is theoretically as justified as the convex one,
except in the case when a preference is given to φ(X(raw)) over ∂ fx(θ ) (both
of which can be arbitrarily bad or good). The same statement holds for local
minima and perturbable gradient basis.

Appendix: Proofs of Theoretical Results

In this appendix, we provide complete proofs of the theoretical results.

A.1 Proof of Theorem 1. The proof of theorem 1 combines lemma 2 con
assumptions 1 E 2 by taking advantage of the structure of the objective
function L. Although lemma 2 is rather weak and assumptions 1 E 2 are
mild (in the sense that they usually hold in practice), a right combination of
these with the structure of L can prove the desired statement.

Lemma 2. Assume that for any i ∈ {1, . . . , M}, the function (cid:3)yi : q (cid:9)→ (cid:3)(q, yi) È
differentiable. Then for any critical point θ ∈ (Rdθ \ (cid:8)) of L, the following holds:
for any k ∈ {1, . . . , dθ },

M(cid:2)

i=1

λ
io

∂(cid:3)yi ( fxi (θ ))∂

k fxi (θ ) = 0.

Proof of Lemma 2. Let θ be an arbitrary critical point θ ∈ (Rdθ \ (cid:8)) Di
l. Since (cid:3)yi : Rdy → R is assumed to be differentiable and fxi
È
differentiable at the given θ , the composition ((cid:3)yi
◦ fxi ) is also differen-
tiable, and ∂
k fxi (θ ). Inoltre, L is differentiable
◦ fxi ) = ∂(cid:3)yi ( fxi (θ ))∂
because a sum of differentiable functions is differentiable. Therefore, for
any critical point θ of L, we have that ∂L(θ ) = 0, E, hence, ∂
kL(θ ) =
(cid:3)
k fxi (θ ) = 0, for any k ∈ {1, . . . , dθ }, from linearity of dif-
(cid:2)

∂(cid:3)yi ( fxi (θ ))∂

k((cid:3)yi

∈ Rdy

M
i=1

λ
io

ferentiation operation.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Proof of Theorem 1. Let θ ∈ (Rdθ \ (cid:8)) be an arbitrary critical point
fxi (θ ) =
of L. From assumption 2, there exists a function g such that
(cid:3)

dθ

k=1 g(θ )k

∂

k fxi (θ ) for all i ∈ {1, . . . , M}. Then, for any α ∈ Rdθ ,

Lθ (α) ≥

M(cid:2)

i=1

λ
io

(cid:3)yi ( fxi (θ )) + λ

io

∂(cid:3)yi ( fxi (θ ))( fθ (xi

; α) − f (xi

; θ ))

Every Local Minimum Value Is the Global Minimum Value

2313

=

M(cid:2)

i=1

λ
io

(cid:3)yi ( fxi (θ )) +

M(cid:2)

dθ(cid:2)

α
k

k=1

i=1
(cid:12)

λ
io

∂(cid:3)yi ( fxi (θ ))∂
(cid:13)(cid:14)
=0 from Lemma 2

k fxi (θ )
(cid:15)

−

M(cid:2)

i=1

λ
io

∂(cid:3)yi ( fxi (θ )) F (xi

; θ )

=

M(cid:2)

i=1

λ
io

(cid:3)yi ( fxi (θ )) −

dθ(cid:2)

k=1

G(θ )k

M(cid:2)

i=1
(cid:12)

= L(θ ),

λ
io

∂(cid:3)yi ( fxi (θ ))∂
(cid:13)(cid:14)
=0 from Lemma 2

,
k fxi (θ )
(cid:15)

where the first line follows from assumption 1 (differentiable and convex
(cid:3)yi ), the second line follows from linearity of summation, and the third line
follows from assumption 2. Così, on the one hand, we have that L(θ ) ≤
k fxi (θ ) ∈
infα∈Rdθ Lθ (α). D'altra parte, since f (xi
{ fθ (xi
k fxi (θ ) : α ∈ Rdθ }, we have that L(θ ) ≥ infα∈Rdθ Lθ (α).
Combining these yields the desired statement of L(θ ) = infα∈Rdθ Lθ (α). (cid:2)

k=1 g(θ )k

; α) =

; θ ) =

dθ
k=1

α
k

(cid:3)

(cid:3)

∂

∂

dθ

A.2 Proof of Theorem 2. The proof of theorem 2 uses lemma 3, IL

structure of the objective function L, and assumptions 1 E 2.
Lemma 3. Assume that for any i ∈ {1, . . . , M}, the function (cid:3)yi : q (cid:9)→ (cid:3)(q, yi)
is differentiable. Then for any local minimum θ ∈ (Rdθ \ ˜(cid:8)) of L, the following
holds: there exists (cid:9)
0), any v ∈ V[θ , (cid:9)], and any
k ∈ {1, . . . , dθ },

> 0 such that for any (cid:9) ∈ [0, (cid:9)

0

M(cid:2)

i=1

λ
io

∂(cid:3)yi ( fxi (θ ))∂

k fxi (θ + (cid:9)v ) = 0.

Proof of Lemma 3. Let θ ∈ (Rdθ \ ˜(cid:8)) be an arbitrary local minimum of L.
Since θ is a local minimum of L, by the definition of a local minimum,
there exists (cid:9)
1). Then for any
(cid:9) ∈ [0, (cid:9)
/2) and any ν ∈ V[θ , (cid:9)], the vector (θ + (cid:9)v ) is also a local minimum
1
because

> 0 such that L(θ ) ≤ L(θ (cid:6)

) for all θ (cid:6) ∈ B(θ , (cid:9)

1

l(θ + (cid:9)v ) = L(θ ) ≤ L(θ (cid:6)

)

for all θ (cid:6) ∈ B(θ + (cid:9)v, (cid:9)
1) (the inclusion follows from the tri-
angle inequality), which satisfies the definition of a local minimum for
(θ + (cid:9)v ).

/2) ⊆ B(θ , (cid:9)

1

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2314

K. Kawaguchi, J. Huang, and L. Kaelbling

2

Since θ ∈ (Rdθ \ ˜(cid:8)), there exists (cid:9)

, . . . , fxm are differen-
> 0 such that fx1
2). Since (cid:3)yi : Rdy → R is assumed to be differentiable and
2), the composition ((cid:3)yi
◦ fxi ) is also dif-
◦ fxi ) = ∂(cid:3)yi ( fxi (θ ))∂
k fxi (θ ) in B(θ , (cid:9)
2). Inoltre, L is
2) because a sum of differentiable functions is differ-

tiable in B(θ , (cid:9)
∈ Rdy is differentiable in B(θ , (cid:9)
fxi
ferentiable, and ∂
k((cid:3)yi
differentiable in B(θ , (cid:9)
entiable.

= min((cid:9)

Therefore, con (cid:9)

0) E
any ν ∈ V[θ , (cid:9)], the vector (θ + (cid:9)v ) is a differentiable local minimum, E
hence the first-order necessary condition of differentiable local minima im-
plies that

2), we have that for any (cid:9) ∈ [0, (cid:9)

/2, (cid:9)

1

0

∂

kL(θ + (cid:9)v ) =

M(cid:2)

i=1

λ
io

∂(cid:3)yi ( fxi (θ ))∂

k fxi (θ + (cid:9)v ) = 0,

for any k ∈ {1, . . . , dθ }, where we used the fact that fxi (θ ) = fxi (θ + (cid:9)v ) for
(cid:2)
any v ∈ V[θ , (cid:9)].

Proof of Theorem 2. Let θ ∈ (Rdθ \ ˜(cid:8)) be an arbitrary local minimum of
l. Since (Rdθ \ ˜(cid:8)) ⊆ (Rdθ \ (cid:8)), from assumption 2, there exists a function g
k fxi (θ ) for all i ∈ {1, . . . , M}. Then from lemma
such that fxi (θ ) =
3, there exists (cid:9)
V[θ , (cid:9)] and any
0), any S ⊆
α ∈ Rdθ ×|S|

> 0 such that for any (cid:9) ∈ [0, (cid:9)

k=1 g(θ )k

(cid:3)

fin

∂

dθ

0

,

˜Lθ (α, (cid:9), S) ≥

=

M(cid:2)

i=1

M(cid:2)

i=1

λ
io

(cid:3)yi ( fxi (θ )) + λ

io

∂(cid:3)yi ( fxi (θ ))( ˜fθ (xi

; α, (cid:9), S) − f (xi

; θ ))

λ
io

(cid:3)yi ( fxi (θ )) +

dθ(cid:2)

|S|(cid:2)

k=1

j=1

α

k, j

M(cid:2)

i=1
(cid:12)

λ
io

∂(cid:3)yi ( fxi (θ ))∂
(cid:13)(cid:14)
=0 from Lemma 3

k fxi (θ + (cid:9)S j )
(cid:15)

−

M(cid:2)

i=1

λ
io

∂(cid:3)yi ( fxi (θ )) F (xi

; θ )

=

M(cid:2)

i=1

λ
io

(cid:3)yi ( fxi (θ )) −

dθ(cid:2)

k=1

G(θ )k

M(cid:2)

i=1
(cid:12)

= L(θ ),

λ
io

∂(cid:3)yi ( fxi (θ ))∂
(cid:13)(cid:14)
=0 from Lemma 3

,
k fxi (θ )
(cid:15)

where the first line follows from assumption 1 (differentiable and con-
vex (cid:3)yi ), the second line follows from linearity of summation and the
; α, (cid:9), S), and the third line follows from assumption 2.
definition of ˜fθ (xi

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Every Local Minimum Value Is the Global Minimum Value

2315

(cid:3)

Così, on the one hand, there exists (cid:9)
l(θ ) ≤ inf{ ˜Lθ (α, (cid:9), S) : S ⊆
dθ
F (xi
l(θ ) ≤ inf{ ˜Lθ (α, (cid:9), S) : S ⊆
the desired statement.

0),
V[θ , (cid:9)], α ∈ Rdθ ×|S|}. D'altra parte, since
; α, (cid:9), S) : α ∈ Rdθ , S = 0}, we have that
V[θ , (cid:9)], α ∈ Rdθ ×|S|}. Combining these yields
(cid:2)

> 0 such that for any (cid:9) ∈ [0, (cid:9)

k fxi (θ ) ∈ { ˜fθ (xi

k=1 g(θ )k

; θ ) =

fin

fin

∂

0

A.3 Proof of Lemma 1. As shown in the proof of lemma 1, lemma 1 È
a simple consequence of the following facts: ˜fθ is linear in α and a union of
two sets S ⊆
fin
Proof of Lemma 1. Let S(cid:6) ⊆

fin
V[θ , (cid:9)] be fixed. Then,

V[θ , (cid:9)] is still a finite subset of V[θ , (cid:9)].

V[θ , (cid:9)] and S(cid:6) ⊆

fin

{ ˜fθ (X; α, (cid:9), S) : α ∈ Rdθ ×|S|, S ⊆

(cid:6)

fin

V[θ , (cid:9)]}
) : α ∈ Rdθ ×|S∪S(cid:6)|, S ⊆
) + ˜fθ (X; α(cid:6), (cid:9), S

(cid:6)

V[θ , (cid:9)]}
fin
) : α ∈ Rdθ ×|S\S

(cid:6)|, α(cid:6) ∈ Rdθ ×|S

(cid:6)|,

= { ˜fθ (X; α, (cid:9), S ∪ S
(cid:6)
= { ˜fθ (X; α, (cid:9), S \ S
V[θ , (cid:9)]}

S ⊆

fin

= { ˜fθ (X; α, (cid:9), S ∪ S

(cid:6)

) + fθ (X; α(cid:6), (cid:9), S

(cid:6)

) : α ∈ Rdθ ×|S∪S(cid:6)|, α(cid:6) ∈ Rdθ ×|S(cid:6)|,

S ⊆

fin

V[θ , (cid:9)]}

= { ˜fθ (X; α, (cid:9), S) + fθ (X; α(cid:6), (cid:9), S

(cid:6)

) : α ∈ Rdθ ×|S|, α(cid:6) ∈ Rdθ ×|S(cid:6)|,

S ⊆

fin

V[θ , (cid:9)]},

fin

where the second line follows from the facts that a finite union of finite sets
is finite and hence S ∪ S(cid:6) ⊆
V[θ , (cid:9)] (cioè., the set in the first line is a superset
of ⊇, the set in the second line), and that α ∈ Rdθ ×|S∪S(cid:6)|
can vanish the extra
terms due to S(cid:6)
) (cioè., the set in the first line is a subset
Di, ⊆, the set in the second line). The last line follows from the same facts.
The third line follows from the definition of ˜fθ (X; α, (cid:9), S). The fourth line
follows from the following equality due to the linearity of ˜fθ in α:

in ˜fθ (X; α, (cid:9), S ∪ S(cid:6)

(cid:6)

) : α(cid:6) ∈ Rdθ ×|S

(cid:6)|}

{ ˜fθ (X; α(cid:6), (cid:9), S
⎧
⎨

dθ(cid:2)

|S|(cid:2)

=

⎩

k=1

j=1

(α(cid:6)
k, j

+ ¯α(cid:6)

k, j )∂

k fx(θ + (cid:9)S

(cid:6)

j ) : α(cid:6) ∈ Rdθ ×|S

(cid:6)|
(cid:6)|, ¯α(cid:6) ∈ Rdθ ×|S

= { ˜fθ (X; α(cid:6), (cid:9), S

(cid:6)

) + ˜fθ (X; ¯α(cid:6), (cid:9), S

(cid:6)

) : α(cid:6) ∈ Rdθ ×|S

(cid:6)|, ¯α(cid:6) ∈ Rdθ ×|S

(cid:6)|}.

⎫
⎬

⎭

(cid:2)

A.4 Proof of Theorem 3. As shown in the proof of theorem 3, thanks to
theorem 2 and lemma 1, the remaining task to prove theorem 3 is to find a set

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2316

K. Kawaguchi, J. Huang, and L. Kaelbling

V[θ , (cid:9)] such that { ˜fθ (xi

S(cid:6) ⊆
+ αrz(xi
αw ∈ Rdy×dx , αr ∈ Rdy×dz }. Let Null(M) be the null space of a matrix M.

; α(cid:6), (cid:9), S(cid:6)) : α(cid:6) ∈ Rdθ ×|S

(cid:6)|} ⊇ {αwxi

fin

; tu) :

Proof of Theorem 3. Let θ ∈ (Rdθ \ ˜(cid:8)) be an arbitrary local mini-
is specified by equation 4.1, and hence f (X; θ ) =
mum of L. Since f
(∂
vec(W ) F (X; θ ))vec(W ), assumption 2 is satisfied. Così, from theorem 2,
there exists (cid:9)

> 0 such that for any (cid:9) ∈ [0, (cid:9)

0),

0

l(θ ) =

inf

V[θ ,(cid:9)],α∈Rdθ ×|S|

S⊆

fin

M(cid:2)

i=1

λ
io

(cid:3)( ˜fθ (xi

; α, (cid:9), S), yi),

Dove

|S|(cid:2)

˜fθ (xi

; α, (cid:9), S) =

αw, j(xi

+ (R + (cid:9)v

R, j )zi, j ) + (W + (cid:9)vw, j )α

R, jzi, j

j=1
+ (∂u fxi (θ + (cid:9)S j ))α

tu, j

,

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

with α = [α·1
, v
vec([vw, j
R, j
, vw, j
Here, αw, j
be fixed.

, . . . , α·|S|] ∈ Rdθ ×|S|, α· j
tu, j]) ∈ Rdθ , and zi, j
, v
∈ Rdy×dx , α
R, j

= vec([αw, j
, tu + (cid:9)v
tu, j

= z(xi
∈ Rdx×dz , and α

, v

R, j

R, j

, α

tu, j]) ∈ Rdθ , S j

, α
=
tu, j ) for all j ∈ {1, . . . , |S|}.
, v
0)

∈ Rdu . Let (cid:9) ∈ (0, (cid:9)

tu, j

Consider the case of rank(W ) ≥ dy. Define ¯S such that | ¯S| = 1 and ¯S1

0 ∈ Rdθ , which is in V[θ , (cid:9)]. Then by setting αu,1
that Wαr,1
sible since rank(W ) ≥ dy), we have that

− αw,1R with an arbitrary matrix αr,1

= α(1)
R,1

=
= 0 and rewriting αr,1 come
∈ Rdy×dz (this is pos-

{ ˜fθ (xi

; α, (cid:9), ¯S) : α ∈ Rdθ ×| ¯S|}
R,1 zi,1 : αw,1

+ α(1)

⊇ {αw,1xi

∈ Rdy×dx , α(1)
R,1

∈ Rdy×dz }.

2

= 0 ∈ Rdθ , and set ¯S(cid:6)

Consider the case of rank(W ) < dy. Since W ∈ Rdy×dx and rank(W ) < dy ≤ min(dx, dz) ≤ dx, we have that Null(W ) (cid:18)= {0}, and there exists a vector a ∈ = 1. Let a be such a vector. Define ¯S(cid:6) Rdx such that a ∈ Null(W ) and (cid:10)a(cid:10) as follows: | ¯S(cid:6)| = dydz + 1, ¯S(cid:6) j for all j ∈ {2, . . . , dydz + = ab(cid:15) 1} such that vw, j ∈ Rdz is an arbitrary = 0, v = 0, and v u, j r, j ≤ 1. Then ¯S(cid:6) column vector with (cid:10)b j ∈ V[θ , (cid:9)] for all j ∈ {1, . . . , dydz + 1}. (cid:10) j = 0 for all j ∈ {1, . . . , dydz + 1} and by rewriting = 0 and α By setting α r, j (cid:3) dydz+1 αw, j and αw, j (cid:9) q jaT for all j ∈ {2, . . . , dydz + 1} with − = α(1) αw,1 w,1 j=2 ∈ Rdy (this is possible since (cid:9) > 0 is fixed first and αw, j
an arbitrary vector q j
is arbitrary), we have that

j where b j

= 1

tu, j

1

2

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Every Local Minimum Value Is the Global Minimum Value

2317

(cid:6)

; α, (cid:9), ¯S
{ ˜fθ (xi
⎧
⎨

) : α ∈ Rdθ ×| ¯S(cid:6)|}
⎛

⊇

α(1)
w,1xi

⎩

+

⎝α(1)

w,1R +

dydz+1(cid:2)

j=2

⎞

(cid:15)
q jb
j

⎠ zi,1 : q j

∈ Rdy , b j

∈ Rdz

⎫
⎬

⎭

.

Since q j
α(2)
w,1

− α(1)

∈ Rdy and b j
w,1R with an arbitrary matrix α(2)
w,1

∈ Rdz are arbitrary, we can rewrite
∈ Rdy×dz , yielding

(cid:3)

dydz+1
j=2

q jb j

=

{ ˜fθ (xi

; α, (cid:9), ¯S

(cid:6)

⊇ {α(1)

w,1xi

) : α ∈ Rdθ ×| ¯S(cid:6)|}
w,1zi,1 : α(1)
w,1

+ α(2)

∈ Rdy×dx , α(2)
w,1

∈ Rdy×dz }.

By summarizing above, in both cases of rank(W ), there exists a set S(cid:6) ⊆

fin

V[θ , (cid:9)] such that

V[θ , (cid:9)]}
(cid:6)

{ ˜fθ (xi

= { ˜fθ (xi

; α, (cid:9), S) : α ∈ Rdθ ×|S|, S ⊆
; α, (cid:9), S) + ˜fθ (xi
: α ∈ Rdθ ×|S|, α(cid:6) ∈ Rdθ ×|S
; α, (cid:9), S) + αwxi

fin
; α(cid:6), (cid:9), S
(cid:6)|, S ⊆
+ αrz(xi
w ∈ Rdy×dx , α(2)
R

: α ∈ Rdθ ×|S|, α(1)

)

⊇ { ˜fθ (xi

V[θ , (cid:9)]}

fin
, tu)
∈ Rdy×dz , S ⊆

V[θ , (cid:9)]},

fin

where the second line follows from lemma 1. D'altra parte, since
the set in the first line is a subset of the set in the last line, { ˜fθ (xi
; α, (cid:9), S) :
α ∈ Rdθ ×|S|, S ⊆
, tu) : α ∈ Rdθ ×|S|,
+ αrz(xi
; α, (cid:9), S) + αwxi
fin
w ∈ Rdy×dx , α(2)
V[θ , (cid:9)]}. This immediately implies the
α(1)
(cid:2)
desired statement from theorem 2.

V[θ , (cid:9)]} = { ˜fθ (xi
∈ Rdy×dz , S ⊆

fin

R

A.5 Proof of Theorem 4. As shown in the proof of theorem 4, thanks
to theorem 2 and lemma 1, the remaining task to prove theorem 4
) : α(cid:6) ∈ Rdθ ×|S(cid:6)|} ⊇
is to find a set S(cid:6) ⊆
V[θ , (cid:9)] such that { ˜fθ (xi
(cid:3)
fin
∈ Rdt }. Let M(l(cid:6)
{
; tu) : α
.
H

; α(cid:6), (cid:9), S(cid:6)
) · · · M(l+1)M(l) = I if l > l(cid:6)

H(l)(xi

H
l=t

α(l+1)
H

Proof of Theorem 4. Since f is specified by equation 4.3 E, hence,

F (X; θ ) = (∂

vec(W (H+1) ) F (X; θ ))vec(W (H+1)),

\
assumption 2 is satisfied. Let t ∈ {0, . . . , H} be fixed. Let θ ∈ ((cid:14)
˜(cid:8)) be an arbitrary local minimum of L. Then from theorem 2, there
for any (cid:9) ∈ [0, (cid:9)
exists (cid:9)
V[θ ,(cid:9)],α∈Rdθ ×|S|
(cid:3)
fin
k fxi (θ +
α
M
i=1
(cid:9)S j ).

0), l(θ ) = infS⊆
(cid:3)
(cid:3)|S|
j=1

; α, (cid:9), S), yi), where ˜fθ (xi

> 0 such that

0
(cid:3)( ˜fθ (xi

; α, (cid:9), S) =

dθ
k=1

dy,T

λ
io

k, j

∂

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

2318

K. Kawaguchi, J. Huang, and L. Kaelbling

Let J = {J(t+1), . . . , J(H+1)} ∈ Jn,T[θ ] be fixed. Without loss of generality,
for simplicity of notation, we can permute the indices of the units of each
1) ∩ {θ (cid:6) ∈
layer such that J(t+1), . . . , J(H+1) ⊇ {1, . . . , dy}. Let ˜B(θ , (cid:9)
Rdθ : W (l+1)
} \
J(l+1)) × J(l)}. Because of the definition of the set J, in ˜B(θ , (cid:9)
> 0
being sufficiently small, we have that for any l ∈ {T, . . . , H},

= 0 for all l ∈ {T + 1, . . . , H − 1} and all (io, j) ∈ ({1, . . . , dl+1

1) = B(θ , (cid:9)

1) con (cid:9)

io, j

1

fxi (θ ) = A(H+1) · · · A(l+2)[UN(l+1) C(l+1)]H(l)(xi

; θ ) + ϕ(l)

xi (θ ),

Dove

xi (θ ) =
ϕ(l)

H−1(cid:2)

l(cid:6)=l

E

UN(H+1) · · · A(l

(cid:6)+3)C(l

(cid:6)+2) ˜h(l

(cid:6)+1)(xi

; θ )

˜h(l)(xi

; θ ) = σ (l)(B(l) ˜h(l−1)(xi

; θ )),

for all l ≥ t + 2 with ˜h(t+1)(xi

; θ ) = σ (t+1)([ξ (l) B(l)] H(T)(xi

; θ )). Here,

(cid:22)

(cid:23)

UN(l) C(l)
ξ (l)
B(l)

= W (l)

−dy )×dy . Let (cid:9)

−dy ), and ξ (l) ∈
with A(l) ∈ Rdy×dy , C(l) ∈ Rdy×(dl−1
R(dl
/2)) be
, (cid:9)
1
1
fixed so that both the equality from theorem 2 and the above form of fxi
hold in ˜B(θ , (cid:9)). Let R(l) = [UN(l) C(l)].

> 0 be a such number, and let (cid:9) ∈ (0, min((cid:9)

−dy ), B(l) ∈ R(dl

−dy )×(dl−1

0

We will now find sets S(T), . . . , S(H) ⊆

fin

V[θ , (cid:9)] such that

{ ˜fθ (xi

; α, (cid:9), S(l)) : α ∈ Rdθ } ⊇ {α(l+1)

H

H(l)(xi

; tu) : α(l+1)

H

∈ Rdy×dl }.

Find S(l) with l = H: Since

(∂

vec(R(H+1) ) fxi (θ ))vec(α(H+1)

H

) = α(H+1)

H

H(H)(xi

; θ ),

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
1
1
2
2
2
9
3
1
8
6
5
1
6
5
N
e
C
o
_
UN
_
0
1
2
3
4
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

S(H) = {0}⊆

fin

V[θ , (cid:9)] (Dove 0 ∈ Rdθ ) is the desired set.

Find S(l) with l ∈ {T, . . . , H − 1}: With α(l+1)

R

∈ Rdl+1

×dl , we have that

(∂

vec(R(l+1) ) fxi (θ ))vec(α(l+1)

R

) = A(H+1) · · · A(l+2)α(l+1)

R

H(l)(xi

; θ ).

Therefore,
α(l+1)
R

∈ Rdl+1

if
×dl } ⊇ {α(l+1)

H

rank(UN(H+1) · · · A(l+2)) ≥ dy,

∈ Rdy×dl }, S(l) = {0} ⊆

since {UN(H+1) · · · A(l+2)α(l+1)
:
V[θ , (cid:9)] (Dove 0 ∈ Rdθ )

R

fin

Every Local Minimum Value Is the Global Minimum Value

2319

is the desired set. Let us consider the remaining case: let rank(UN(H+1)
· · · A(l+2)) < dy and let l ∈ {t, . . . , H − 1} be fixed. Let l∗ = min{l(cid:6) ∈ Z+ : l + 3 ≤ l(cid:6) ≤ H + 2 ∧ rank(A(H+1) · · · A(l(cid:6) )) ≥ dy}, where A(H+1) · · · A(H+2) (cid:3) Idy and the minimum exists since the set is finite and contains at and rank(A(H+1) · · · A(l(cid:6) l(cid:6) ∈ {l + 2, l + 3, . . . , l∗ − 1}. Thus, for all l(cid:6) ∈ {l + 1, l + 2, . . . , l∗ − 2}, there exists a vector al(cid:6) ∈ Rdy such that least H + 2 (nonempty). Then rank(A(H+1) · · · A(l∗ )) < dH+1 )) ≥ dH+1 for all al(cid:6) ∈ Null(A(H+1) · · · A(l(cid:6)+1)) and (cid:10)al(cid:6) (cid:10) 2 = 1. Let al(cid:6) denote such a vector. Consider S(l) such that the weight matrices W are perturbed with ¯θ + (cid:9)S(l) j as l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . ) ˜A(l(cid:6) j = A(l(cid:6) (cid:15) ) + (cid:9)al(cid:6) b l(cid:6), j and ˜R(l+1) j = R(l+1) + (cid:9)al+1b (cid:15) l+1, j 2 (cid:10) (cid:10) for all l(cid:6) ∈ {l + 2, l + 3, . . . , l∗ − 2}, where (cid:10)bl(cid:6), j (cid:10)S(l) j responding to A(l(cid:6) V[θ , (cid:9)], since A(H+1) · · · A(l(cid:6)+1) ˜A(l 2, l + 3, . . . , l∗ − 2} and A(H+1) · · · A(l+2) ˜R(l+1) |S(l)| = 2N with some integer N to be chosen later. Define S(l) 1, . . . , N by setting S(l) not necessarily zero. By setting α Rdl 2 is bounded such that ≤ 1. That is, the entries of S j are all zeros except the entries cor- ) (for l(cid:6) ∈ {l + 2, l + 3, . . . , l∗ − 2}) and R(l+1). Then S(l) ∈ j = A(H+1) · · · A(l(cid:6)+1)A(l(cid:6) l(cid:6) ∈ {l + for all = A(H+1) · · · A(l+2)R(l+1). Let j+N for j = = 0 whereas bl+1, j is ∈ j except that bl+1, j+N = −α j for all j ∈ {1, . . . , N}, with α = S(l) ∗ ×dl j+N j+N ) ) j j j (cid:6) ∗ −1 , ˜fθ (xi = ; α, (cid:9), S(l)) N(cid:2) A(H+1) · · · A(l∗ )(α j + α j+N ) ˜A(l∗−2) · · · ˜A(l+2)R(l+1)h(l)(xi ; θ ) j=1 + N(cid:2) j=1 (∂ vec(A(l ∗ −1) ) xi (θ + (cid:9)S j ))vec(α ϕ(l) j + α j+N ) + (cid:9) N(cid:2) j=1 A(H+1) · · · A(l∗ )α j ˜A(l∗−2) · · · ˜A(l+2)al+1b (cid:15) l+1, jh(l)(xi ; θ ) = (cid:9) N(cid:2) j=1 A(H+1) · · · A(l ∗ )α j ˜A(l ∗−2) · · · ˜A(l+2)al+1b (cid:15) l+1, jh(l)(xi ; θ ), / e d u n e c o a r t i c e - p d / l f / / / / 3 1 1 2 2 2 9 3 1 8 6 5 1 6 5 n e c o _ a _ 0 1 2 3 4 p d . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 2320 K. Kawaguchi, J. Huang, and L. Kaelbling where we used the fact that ∂ Since rank(A(H+1) · · · A(l∗ ∈ Rdy×dl { 1 (cid:9) j : α(cid:6) α(cid:6) ∗ −1 }, we have that ∀α(cid:6) j j ϕ(l) xi (θ + (cid:9)S j ) does not contain bl+1, j. )) ≥ dy and {A(H+1) · · · A(l∗ ∗ −1 } = j : α ∈ Rdl vec(A(l ∗ −1) ) ∗ ×dl ∈ Rdy×dl )α ∗ −1 , ∃α ∈ Rdθ ×|S|, j ˜fθ (xi ; α, (cid:9), S(l)) = N(cid:2) j=1 α(cid:6) j ˜A(l∗−2) · · · ˜A(l+2)al+1b (cid:15) l+1, jh(l)(xi ; θ ). Let N = 2N1. Define S(l) that bl∗−2, j+N1 −α(cid:6) j for all j ∈ {1, . . . , N1 = S(l) = 0, whereas bl∗−2, j is not necessarily zero. By setting α(cid:6) for j = 1, . . . , N1 by setting S(l) j+N1 j+N1 j except = j+N1 ˜fθ (xi ; α, (cid:9), S(l)) = (cid:9) α(cid:6) (cid:15) jal∗−2b l∗−2, j ˜A(l∗−3) · · · ˜A(l+2)al+1b (cid:15) l+1, jh(l)(xi ; θ ). }, N1(cid:2) j=1 By induction, ˜fθ (xi ; α, (cid:9), S(l)) = (cid:9)t Nt(cid:2) j=1 α(cid:6) jal∗−2bl∗−2, jal∗−3bl∗−3, j (cid:15) · · · al+1b l+1, jh(l)(xi ; θ ), where t = (l∗ − 2) − (l + 2) + 1 is finite. By setting α(cid:6) j al−1 for all l = l∗ − 2, . . . , l ((cid:9) > 0),

˜fθ (xi

; α, (cid:9), S(l)) =

Nt(cid:2)

j=1

(cid:15)
l+1, jh(l)(xi
q jb

; θ ).

= 1

(cid:9)t q ja(cid:15)

l∗−2 and bl, j

=

Since q jbl+1, j are arbitrary, with sufficiently large Nt (Nt = dydl suffices), we
can set

∈ Rdθ ×dl , and hence

(cid:3)

= α(l)
H

for any α(l)
H

Nt
j=1 q jbl+1, j

{ ˜fθ (xi

; α, (cid:9), S(l)) : α ∈ Rdθ ×|S(l)|} ⊇ {α(l)

h h(l)(xi

; θ ) : α(l)
H

∈ Rdθ ×dl }.

Thus far, we have found the sets S(T), . . . , S(H) ⊆

; α, (cid:9), S(l)) : α ∈ Rdθ } ⊇ {α(l+1)
{ ˜fθ (xi
1, we can combine these, yielding

H

H(l)(xi

; tu) : α(l+1)

H

V[θ , (cid:9)] such that
∈ Rdy×dl }. From lemma

fin

{ ˜fθ (xi
; α, (cid:9), S) : α ∈ Rdθ , S ⊆
(cid:4)
H(cid:2)

V[θ , (cid:9)]}

fin

=

˜fθ (xi

; α(l), (cid:9), S(l)) + ˜fθ (xi

; α, (cid:9), S) : α(T), . . . , α(H) ∈ Rdθ ,

l=t

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H