ARTICLE

Communicated by Igor Goychuk

Fast and Accurate Langevin Simulations of Stochastic
Hodgkin-Huxley Dynamics

Shusen Pu
sxp600@case.edu
Department of Mathematics, Applied Mathematics, and Statistics, Case Western
Reserve University, Cleveland, OH 44106, U.S.A.

Peter J. Thomas
pjthomas@case.edu
Department of Mathematics, Applied Mathematics, and Statistics; Biology; Cognitive
Scienza; and Electrical, Computer, and Systems Engineering: Case Western Reserve
Università, Cleveland, OH 44106, U.S.A.

Fox and Lu introduced a Langevin framework for discrete-time stochas-
tic models of randomly gated ion channels such as the Hodgkin-
Huxley (HH) system. They derived a Fokker-Planck equation with
state-dependent diffusion tensor D and suggested a Langevin formula-
tion with noise coefficient matrix S such that SS(cid:2) = D. Subsequently,
several authors introduced a variety of Langevin equations for the HH
system. In questo articolo, we present a natural 14-dimensional dynamics for
the HH system in which each directed edge in the ion channel state tran-
sition graph acts as an independent noise source, leading to a 14 × 28
noise coefficient matrix S. We show that (1) the corresponding 14D sys-
tem of ordinary differential equations is consistent with the classical 4D
representation of the HH system; (2) the 14D representation leads to a
noise coefficient matrix S that can be obtained cheaply on each time step,
without requiring a matrix decomposition; (3) sample trajectories of the
14D representation are pathwise equivalent to trajectories of Fox and Lu’s
system, as well as trajectories of several existing Langevin models; (4) our
14D representation (and those equivalent to it) gives the most accurate in-
terspike interval distribution, not only with respect to moments but un-
der both the L1 and L∞ metric-space norms; E (5) the 14D representation
gives an approximation to exact Markov chain simulations that are as fast
and as efficient as all equivalent models. Our approach goes beyond ex-
isting models, in that it supports a stochastic shielding decomposition
that dramatically simplifies S with minimal loss of accuracy under both
voltage- and current-clamp conditions.

Calcolo neurale 32, 1775–1835 (2020) © 2020 Istituto di Tecnologia del Massachussetts
https://doi.org/10.1162/neco_a_01312

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1776

1 introduzione

S. Pu and P. Thomas

Many natural phenomena exhibit stochastic fluctuations arising at the
molecular scale, the effects of which impact macroscopic quantities. E-
derstanding when and how microscale fluctuations will significantly con-
tribute to macroscale behavior is a fundamental problem spanning the
sciences. The impact of random ion channel fluctuations on the timing of ac-
tion potentials in nerve cells provides an important example. Channel noise
can have a significant effect on spike generation (Mainen & Sejnowski, 1995;
Schneidman, Freedman, & Segev, 1998), propagation along axons (Faisal &
Laughlin, 2007), and spontaneous (ectopic) action potential generation in
the absence of stimulation (O’Donnell & van Rossum, 2015). At the network
level, channel noise can drive the endogenous variability of vital rhythms
such as respiratory activity (Yu, Dhingra, Dick, & Galán, 2017).

Hodgkin and Huxley’s quantitative model for active sodium and potas-
sium currents producing action potential generation in the giant axon of
Loligo suggested an underlying system of gating variables consistent with
a multistate Markov process description (Hill & Chen, 1972). The dis-
crete nature of individual ion channel conductances was confirmed ex-
perimentally (Neher & Sakmann, 1976). Subsequently, numerical studies
of high-dimensional discrete-state, continuous-time Markov chain models
produced insights into the effects of fluctuations in discrete ion channel
populations on action potentials (Skaugen & Walløe, 1979; Strassberg & De-
Felice, 1993), also known as channel noise (White, Klink, Alonso, & Kay, 1998;
White, Rubinstein, & Kay, 2000).

In the standard molecular-level HH model, which we adopt here, IL
K+
channel comprises four identical n gates that open and close indepen-
dently, giving a five-vertex channel-state diagram with eight directed edges;
the channel conducts a current only when in the rightmost state (see Fig-
channel comprises three identical m gates and a single
ure 1, top). The Na
h gate, all independent, giving an eight-vertex diagram with 20 directed
edges, of which one is conducting (Guarda la figura 1, bottom).

+

Discrete-state channel noise models are numerically intensive, whether
implemented using discrete-time binomial approximations to the underly-
ing continuous-time Markov process (Skaugen & Walløe, 1979; Schmandt
& Galán, 2012) or continuous-time hybrid Markov models with exponen-
tially distributed state transitions and continuously varying membrane po-
tential. The latter were introduced by Clay and DeFelice (1983) and are in
principle exact (Anderson, Ermentrout, & Thomas, 2015). Under voltage-
clamp conditions, the hybrid conductance-based model reduces to a
time-homogeneous Markov chain (Colquhoun & Hawkes, 1981) that can
be simulated using standard methods such as Gillespie’s exact algorithm
(Gillespie, 1977, 2007). Even with this simplification, such Markov chain
(MC) algorithms are numerically expensive to simulate with realistic

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1777

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

Figura 1: Molecular potassium (K+) and sodium (Na+) channel states for the
Hodgkin-Huxley model. Filled circles mark conducting states n4 and m31. Per
capita transition rates for each directed edge (α
H) are volt-
age dependent (cf. equations B.1 and B.6). Directed edges are numbered 1 A 8
(K+ channel) E 1 A 20 (Na+-channel), marked in small red numerals.

h and β

M, α

M, β

N, α

N, β

population sizes of thousands of channels or greater. Therefore, there is an
ongoing need for efficient and accurate approximation methods.

Following Clay and DeFelice’s exposition of continuous time Markov
chain implementations, Fox and Lu (1994) introduced a Fokker-Planck
equation (FPE) framework that captured the first- and second-order statis-
tics of HH ion channel populations in a 14-dimensional representation. Tak-
ing into account conservation of probability, one needs four variables to
represent the population of K
, and one for volt-
age, leading to a 12-dimensional state-space description. The resulting high-
dimensional partial differential equation is impractical to solve numerically.
Tuttavia, as Fox and Lu observed, “To every Fokker-Planck description,
there is associated a Langevin description” (Fox & Lu, 1994). They there-
fore introduced a Langevin stochastic differential equation:

channels, seven for Na

+

+

C

dV
dt

dM
dt
dN
dt

= Iapp(T) − ¯gNaM8 (V − VNa) − ¯gKN5 (V − VK) − gleak(V − Vleak),

= ANaM + S1

ξ

1

,

= AKN + S2

ξ

2

,

(1.1)

(1.2)

(1.3)

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1778

S. Pu and P. Thomas

+

+

and K

, and N5 the open channel fraction for K

where C is the capacitance, Iapp is the applied current, maximal conduc-
tances are denoted ¯gion, with Vion being the associated reversal potential,
and ohmic leak current gleak(V − Vleak). M ∈ R8 and N ∈ R5 are vectors for
channels in each state, with M8 representing the
the fractions of Na
+
open channel fraction for Na
(Vedere
Figura 1). Vectors ξ
2(T) ∈ R5 are independent gaussian white
1(T) ∈ R8 and ξ
1(T)ξ (cid:2)
δ(t − t(cid:6)
noise processes with zero mean and unit variances (cid:5)ξ
)
E (cid:5)ξ
). The state-dependent rate matrices ANa and
AK are given in equations 2.10 E 2.11. In Fox and Lu’s formulation, S must
satisfy S =
D, where D is a symmetric, positive semidefinite k × k “diffu-
sion matrix” (see appendix D for the D matrices for the standard HH K
E
Na
channels). We will refer to the 14-dimensional Langevin equations 1.1
A 1.3, with S =

D, as the Fox-Lu model.

2(T)ξ (cid:2)
2 (T(cid:6)
√

δ(t − t(cid:6)

)(cid:7) = I8

)(cid:7) = I5

1 (T(cid:6)

√

+

+

+

The original Fox-Lu model, later called the conductance noise model by
Goldwyn and Shea-Brown (2011), did not see widespread use until gains
in computing speed made the square root calculations more feasible. Seek-
ing a more efficient approximation, Fox and Lu (1994) also introduced a
four-dimensional Langevin version of the HH model. This model was sys-
tematically studied in Fox (1997), which can be written as

= Iapp(T) − ¯gNam3h (V − VNa) − ¯gKn4 (V − VK) − gleak(V − Vleak),

= αx(1 − x) − βxx + ξx(T), where x = m, H, O, N,

where ξx(T) are gaussian processes with covariance function

E[ξx(T), ξx(T

(cid:6)

)] =

αx(1 − x) + βxx
N

δ(t − t

(cid:6)

).

(1.4)

(1.5)

(1.6)

C

dV
dt

dx
dt

+

+

Here N represents the total number of Na
channels (rispettivamente, the total
channels), and δ(·) is the Dirac delta function. This model, Rif-
number of K
ferred to as the “subunit noise model” by Goldwyn and Shea-Brown (2011),
has been widely used as an approximation to MC ion channel models (Vedere
the references in Bruce, 2009; Goldwyn & Shea-Brown, 2011). Per esempio,
Schmid et al. (2001) used this approximation to investigate stochastic reso-
nance and coherence resonance in forced and unforced versions of the HH
modello (e.g. in the excitable regime). Tuttavia, the numerical accuracy of
this method was criticized in several studies (Mino, Rubinstein, & White,
2002; Bruce, 2009), which found that its accuracy does not improve even
with increasing numbers of channels.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1779

Although more accurate approximations based on Gillespie’s algorithm
(using a piecewise constant propensity approximation: Bruce, 2009; Mino
et al., 2002) and even based on exact simulations (Clay & DeFelice, 1983;
Newby, Bressloff, & Keener, 2013; Anderson et al., 2015) became avail-
able, they remained prohibitively expensive for large network simulations.
Nel frattempo, Goldwyn and Shea-Brown’s rediscovery of Fox and Lu’s ear-
lier conductance-based model (Goldwyn & Shea-Brown, 2011; Goldwyn,
Shea-Brown, & Rubinstein, 2010) launched a flurry of activity seeking the
best Langevin-type approximation. Goldwyn and Shea-Brown (2011) intro-
duced a faster decomposition algorithm to simulate equations 1.1 A 1.3 E
showed that Fox and Lu’s (1994) method accurately captured the fractions
of open channels and the interspike interval (ISI) statistics, in comparison
with Gillespie-type Monte Carlo (MC) simulations. Tuttavia, despite the
development of efficient singular value decomposition based algorithms
for solving S =
D, this step still causes a bottleneck in the algorithms
based on Fox and Lu (1994), Goldwyn and Shea-Brown (2011), and Gold-
wyn, Imennov, Famulare, and Shea-Brown (2011).

√

Many variations on Fox and Lu’s (1994) Langevin model have been pro-
posed in recent years (Dangerfield, Kay, & Burrage, 2010, 2012; Linaro,
Storace, & Giugliano, 2011; Orio & Soudry, 2012; Güler, 2013B; Huang, Rüdi-
ger, & Shuai, 2013, 2015; Pezo, Soudry, & Orio, 2014; Fox, 2018), including
Goldwyn et al.’s work (Goldwyn & Shea-Brown, 2011; Goldwyn et al., 2011),
each with its own strengths and weaknesses. One class of methods imposes
projected boundary conditions (Dangerfield et al., 2010, 2012); as we will
show in section 5, this approach leads to inaccurate interspike interval dis-
tribution and is inconsistent with a natural multinomial invariant manifold
structure for the ion channels. Several methods implement correlated noise
at the subunit level, as in equations 1.5 E 1.6 (Fox, 1997; Linaro et al.,
2011; Güler, 2013UN, 2013B). Tuttavia, if one recognizes that at the molec-
ular level, the individual directed edges represent the independent noise
sources in ion channel dynamics, then the approach incorporating noise at
the subunit level obscures the biophysical origin of ion channel fluctuations.
Some methods introduce the noisy dynamics at the level of edges rather
than nodes but lump reciprocal edges together into pairs (Orio & Soudry,
2012; Dangerfield et al., 2012; Huang et al., 2013; Pezo et al., 2014). This ap-
proach implicitly assumes, in effect, that the ion channel probability distri-
bution satisfies a detailed balance (or microscropic reversibility) condition.
Tuttavia, while detailed balance holds for the HH model under stationary
voltage clamp, this condition is violated during active spiking. Finalmente, IL
stochastic shielding approximation (Schmandt & Galán, 2012; Schmidt &
Thomas, 2014; Schmidt et al., 2018) does not have a natural formulation in
the representation associated with an n × n noise coefficient matrix S; in the
cases of rectangular S matrices used in Orio and Soudry (2012) and Danger-
field et al. (2012) stochastic shielding can only be applied to reciprocal pairs
of edges. We elaborate on these points in section 6.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1780

S. Pu and P. Thomas

In questo articolo, we introduce a new variation of Fox and Lu’s conductance-
noise model that avoids the limitations we have described. We show that
preserving each directed edge in the channel transition graph (Guarda la figura 1)
as an independent noise source leads to a natural, biophysically motivated
Langevin model that does not require any matrix decomposition step. Nostro
construction lends itself to direct application of stochastic shielding meth-
ods, leading to faster simulations that retain the accuracy of Fox and Lu’s
method.

As an additional benefit, our method answers an open question in the lit-
erature, arising from the fact that the decomposition D = SS(cid:2)
is not unique.
As Fox (2018) recently pointed out, subblock determinants of the D matrices
play a major role in the structure of the S matrix elements. Fox conjectured
that “a universal form for S may exist.” In this article, we obtain the uni-
versal form for the noise coefficient matrix S. Inoltre, we prove that our
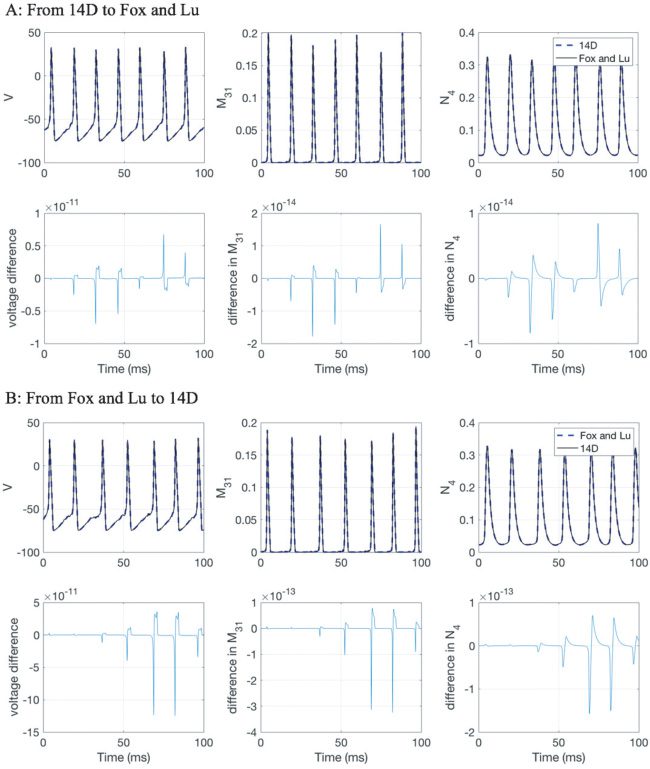
model is equivalent to Fox and Lu’s 1994 model in the strong sense of path-
wise equivalence.

The remainder of the article is organized as follows. In section 2, we re-
view the canonical deterministic 14D version of the HH model. We prove
a series of lemmas that show (1) the multinomial submanifold M is an
invariant manifold within the 14D space and (2) the velocity on the 14D
space and the pushforward of the velocity on the 4D space are identical.
Inoltre, we show (numerically) Quello (3) the submanifold M is globally
attracting, even under current clamp conditions. Figura 2 illustrates the
relationship between the 4D and 14D deterministic HH models. Sezione
3 lays out our 14 × 28 Langevin HH model. Like Orio and Soudry (2012),
Dangerfield et al. (2012), and Pezo et al. (2014), we avoid matrix decompo-
sition by computing S directly. The key difference between our approach
and its closest relative (Pezo et al., 2014) is to use a rectangular n × k matrix
S for which each directed edge is treated as an independent noise source
rather than lumping reciprocal edges together in pairs. In the new Langevin
modello, the form of our S matrix reflects the biophysical origins of the un-
derlying channel noise and allows us to apply the stochastic shielding ap-
proximation by neglecting the noise on selected individual directed edges.
As we prove in section 4, our model (without the stochastic shielding ap-
proximation) is pathwise equivalent to all those in a particular class of bio-
physically derived Langevin models, including those used in Fox and Lu
(1994), Goldwyn et al. (2011), Goldwyn and Shea-Brown (2011), Orio and
Soudry (2012), Pezo et al. (2014), and Fox (2018). In addition to 4D and 14D
deterministic trajectories, Figura 2 shows a stochastic trajectory generated
by our Langevin model. Finalmente, we compare our Langevin model to sev-
eral alternative stochastic neural models in terms of accuracy (of the full ISI
distribution) and numerical efficiency in section 5.

Matlab code to generate the figures throughout the article is available
on github from https://github.com/shusenpu/Stochastic_shielding and
on ModelDB at accession number 266551.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1781

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

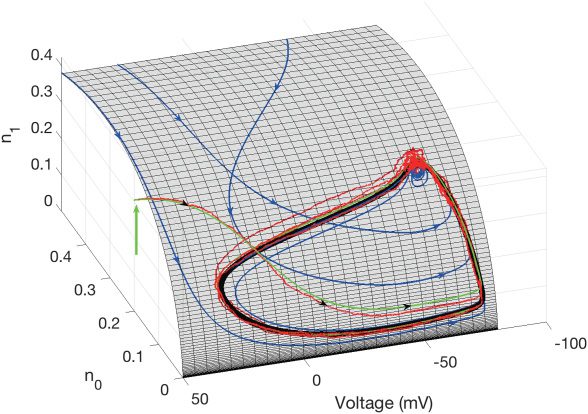
Figura 2: 4D and 14D HH models. The meshed surface is a three-dimensional
projection of the 14D state space onto three axes representing the voltage, v, IL
probability of all four potassium gates being in the closed state, n0, and the prob-
ability of exactly one potassium gate being in the open state, n1. Blue curves:
Trajectories of the deterministic 14D HH model with initial conditions located
on the 4D multinomial invariant submanifold, M. We prove that M is an in-
variant submanifold in section 2.3. Black curve: The deterministic limit cycle
solution for the 14D HH model, which forms a closed loop within M. Verde
curve: A trajectory of the deterministic 14D HH model with initial conditions
(vertical green arrow) off the multinomial submanifold. Red curve: A trajectory
of the stochastic 14D HH model (see section 3) with the same initial conditions
as the green trajectory. The blue and black arrows mark the directions of the
trajectories. Note that trajectories starting away from M converge to M, and all
deterministic trajectories converge to the deterministic limit cycle. Parameters
of the simulation are given in Table 5.

2 The Deterministic 4D and 14D HH Models

In this section, we review the classical four-dimensional model of Hodgkin
and Huxley (1952) HH), as well as its natural 14-dimensional version
(Dayan & Abbott, 2001, sec. 5.7), with variables comprising membrane
voltage and the occupancies of five potassium channel states and eight
sodium channel states. The deterministic 14D model is the mean field of
the channel-based Langevin model proposed by Fox and Lu (1994); this ar-
ticle describes both the Langevin and the mean field versions of the 14D
Hodgkin-Huxley system. For completeness of exposition, we briefly review

1782

S. Pu and P. Thomas

the 4D deterministic HH system and its 14D deterministic counterpart. In
section 4, we prove that the sample paths of a class of Langevin stochas-
tic HH models are equivalent; in section 2.3, we review analogous results
relating trajectories of the 4D and 14D deterministic ODE systems.

In particular, we show that the deterministic 14D model and the origi-
nal 4D HH model are dynamically equivalent, in the sense that every flow
(solution) of the 4D model corresponds to a flow of the 14D model. IL
consistency of trajectories between the 14D and 4D models is easy to ver-
ify for initial data on a 4D submanifold of the 14D space given by choos-
ing multinomial distributions for the gating variables (Dayan & Abbott,
2001; Goldwyn et al., 2011). Allo stesso modo, Keener established results on multi-
nomial distributions as invariant submanifolds of Markov models with ion
channel kinetics under several circumstances (Keener, 2009, 2010; Earnshaw
& Keener, 2010UN, 2010B), but without treating the general current-clamped
case. Consistent with these results, we show that the set of all 4D flows maps
to an invariant submanifold of the state space of the 14D model. Inoltre,
we show numerically that solutions of the 14D model with arbitrary ini-
tial conditions converge to this submanifold. Thus the original HH model
“lives inside” the 14D deterministic model in the sense that the former em-
beds naturally and consistently within the latter (Guarda la figura 2).

In the stochastic case, the 14D model has a natural interpretation as a hy-
brid stochastic system with independent noise forcing along each edge of
the potassium (8 directed edges) and sodium (20 directed edges) channel
state transition graphs. The hybrid model leads naturally to a biophysically
grounded Langevin model that we describe in section 3. In contrasto con il
ODE case, the stochastic versions of the 4D and 14D models are not equiv-
alent (Goldwyn & Shea-Brown, 2011).

2.1 The 4D Hodgkin-Huxley Model. The 4D voltage-gated ion channel

HH model is a set of four ordinary differential equations:

C

dv
dt
dm
dt
dh
dt
dn
dt

= − ¯gNam3h(v − VNa) − ¯gKn4(v − VK) − gL(v − VL) + Iapp

,

(2.1)

= αm(v )(1 − m) − βm(v )M,

= α

H(v )(1 − h) − β

H(v )H,

= αn(v )(1 − n) − βn(v )N,

(2.2)

(2.3)

(2.4)

where v is the membrane potential, Iapp is the applied current, E 0 ≤
+
M, N, h ≤ 1 are dimensionless gating variables associated with Na
E
channels. The constant ¯gion is the maximal value of the conductance
K
for the sodium and potassium channel, rispettivamente. Parameters Vion and C

+

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1783

are the ionic reversal potentials and capacitance, rispettivamente. The quanti-
ties αx and βx, x ∈ {M, N, H} are the voltage-dependent per capita transition
rates, defined in appendix B.
This system is a C∞

vector field on a four-dimensional manifold
(with boundary) contained in R4: X = {−∞ < v < ∞, 0 ≤ m, h, n ≤ 1} = R × [0, 1]3. The manifold is forward and backward invariant in time. If Iapp is constant then X has an invariant subset given by X ∩ {v }, max where v max are calculated in lemma 1. min and v ≤ v ≤ v min As pointed Keener and Sneyd (1998) and Keener (2009) pointed out, for voltage either fixed or given as a prescribed function of time, the equations for m, h, and n can be interpreted as the parameterization of an invariant manifold embedded in a higher-dimensional time-varying Markov system. Several papers developed this idea for a variety of ion channel models and related systems (Keener, 2009; Earnshaw & Keener, 2010b), but the theory developed is restricted to the voltage-clamped case. Under a fixed voltage clamp, the ion channels form a time-homogeneous Markov process with a unique (voltage-dependent) stationary probability distribution. Under a time-varying current clamp, the ion channels never- theless form a Markov process, albeit no longer time homogeneous. Under these conditions, the ion channel state converges rapidly to a multinomial distribution indexed by a low-dimensional set of time-varying parameters (m(t), h(t), n(t)) (Keener, 2010). In the current-clamped case, the ion chan- nel process, considered alone, is neither stationary nor Markovian, making the analysis of this case significantly more challenging from a mathematical point of view. 2.2 The Deterministic 14D Hodgkin-Huxley Model. For the HH kinet- ics given in Figure 1, we define the eight-component state vector M for the Na+ gates, respec- tively, as gates and the five-component state vector N for the K + M = [m00 , m10 N = [n0 , n2 , n1 (cid:2) (cid:2) , m20 , n3 , m30 , n4] , m11 , m01 (cid:2) ∈ [0, 1]5, (cid:2) = 1 and 4 i=0 ni = m31 and is N5 3 i=0 1 j=0 mi j where Na+ channel is M8 istic 14D HH equations may be written (compare equations 2.1 to 2.4) = 1. The open probability for the = n4 for the K+ channel. The determin- , m21 , m31] (cid:2) ∈ [0, 1]8. (2.5) (2.6) C dV dt dM dt dN dt = − ¯gNaM8(V − VNa) − ¯gKN5(V − VK) − gL(V − VL) + Iapp , (2.7) = ANa(V )M, = AK(V )N, (2.8) (2.9) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1784 S. Pu and P. Thomas where the voltage-dependent drift matrices ANa and AK are given by ANa(V ) = ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ 0 α h 0 0 0 ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ AK(V ) = 0 βm ANa(1) 0 3αm ANa(2) 2βm 0 0 2αm ANa(3) 3βm 0 β h 0 0 0 β h 0 αm ANa(4) 0 0 0 α h 0 0 0 α h 0 0 βm ANa(5) 0 3αm ANa(6) 2βm 0 0 2αm ANa(7) 3βm 0 αm ANa(8) 0 0 α h 0 0 0 0 β h 0 0 0 0 β h 0 AK(1) βn(V ) 4αn(V ) AK(2) 2βn(V ) 0 0 0 0 0 0 3αn(V ) AK(3) 3βn(V ) 0 0 2αn(V ) AK(4) 4βn(V ) αn(V ) AK(5) 0 0 0 0 ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ , ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ , (2.10) (2.11) and the diagonal elements Aion(i) = − (cid:9) j : j(cid:11)=i Aion( j, i), for ion ∈ {Na, K}. 2.3 Relation Between the 14D and 4D Deterministic HH Models. Earnshaw and Keener (2010b) suggest that it is reasonable to expect that the global flow of the 14D system should converge to the 4D submanifold but also that it is far from obvious that it must. Existing theory applies to the voltage-clamped case (Keener, 2009; Earnshaw & Keener, 2010b). Here, we consider instead the current-clamped case, in which the fluctuations of the ion channel state influences the voltage evolution, and vice versa. In the remainder of this section, we (1) define a multinomial submani- fold M and show that it is an invariant manifold within the 14D space, and (2) we show that the velocity on the 14D space and the pushforward of the velocity on the 4D space are identical. In section 2.4, we (3) provide numer- ical evidence that M is globally attracting within the higher-dimensional space. In order to compare the trajectories of the 14D HH equations with tra- jectories of the standard 4D equations, we define lower-dimensional and higher-dimensional domains X and Y, respectively, as X = {−∞ < v < ∞, 0 ≤ m ≤ 1, 0 ≤ h ≤ 1, 0 ≤ n ≤ 1} = R × [0, 1]3 ⊂ R4, l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Fast and Accurate Stochastic Hodgkin-Huxley Simulations 1785 Table 1: R: Map from the 14D HH Model (m00 Model (m, h, n). , . . . , m31 , n0 , . . . , n4) to the 4D HH 14D Model (v, m00 v 1 3 (m11 m01 n1 + m11 /4 + n2 , . . . , m31 , n0 , . . . , n4 ) + m20 ) + m31 + m10 ) + 2 + m21 /2 + 3n3 3 (m21 + m31 /4 + n4 4D Model (v, m, h, n) v m h n‘ + m30 Note: Note that both {m00 low multinomial distributions. , . . . , m31 } and {n0 , . . . , n4 } fol- Table 2: H: Map from the 4D HH Model (m, h, n) and the 14D HH Model (m00 , . . . , n4). , . . . , m31 , n0 4D Model (v, m, h, n) v (1 − n)4 4(1 − n)3n 6(1 − n)2n2 4(1 − n)n3 n4 (1 − m)3(1 − h) 3(1 − m)2m(1 − h) 3(1 − m)m2(1 − h) m3(1 − h) (1 − m)3h 3(1 − m)2mh 3(1 − m)m2h m3h (v, m00 , . . . , n4 ) 14D Model , n0 , . . . , m31 v n0 n1 n2 n3 n4 m00 m10 m20 m30 m01 m11 m21 m31 Y = {−∞ < v < ∞} ∩ ⎧ ⎨ ⎩0 ≤ mi j , 3(cid:9) 1(cid:9) i=0 j=0 mi j = 1 ⎫ ⎬ ⎭ (cid:16) ∩ 0 ≤ ni , (cid:17) ni = 1 4(cid:9) i=0 = R × (cid:6)7 × (cid:6)4 ⊂ R14, (2.12) where (cid:6)k is the k-dimensional simplex in Rk+1 given by y1 = 1, yi ≥ 0. The 4D HH model dx = F(x), equations 2.1 to 2.4, is defined for dt x ∈ X , and the 14D HH model dy = G(y), equations 2.7 and 2.9, is defined dt for y ∈ Y. We introduce a dimension-reducing mapping R : Y → X as in Table 1 and a mapping from lower to higher dimension, H : X → Y, as in Table 2. We construct R and H in such a way that R ◦ H acts as the identity on X , that is, for all x ∈ X , x = R(H(x)). The maps H and R are consistent with + . . . + yk+1 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1786 S. Pu and P. Thomas + a multinomial structure for the ion channel state distribution, in the follow- ing sense. The space Y covers all possible probability distributions on the eight sodium channel states and the five potassium channel states. Those distributions, which are products of one multinomial distribution on the -channel,2 K form a submanifold of (cid:6)7 × (cid:6)4. In this way we define a submanifold, de- noted M = H(X ), the image of X under H. + -channel1and a second multinomial distribution on the Na Before showing that the multinomial submanifold M is an invariant manifold within the 14D space, we first show that the deterministic 14D HH model is defined on a bounded domain. Having a bounded forward- invariant manifold is a general property of conductance-based models, which may be written in the form dV dt = f (V, N (cid:16) open) = 1 C Iapp − gleak(V − Vleak) − (cid:17) (cid:19) open(V − Vi) giNi (cid:9) (cid:18) i∈I dN dt = A(V )N and N open = O[N ]. (2.13) (2.14) (2.15) Here, C is the membrane capacitance, Iapp is an applied current with upper and lower bounds I±, respectively, and gi is the conductance for the ith ion channel. The index i runs over the set of distinct ion channel types in the model, I. The gating vector N represents the fractions of each ion chan- nel population in various ion channel states, and the operator O gives the fraction of each ion channel population in the open (or conducting) channel states. The following lemma establishes that any conductance-based model (including the 4D or 14D HH model) is defined on a bounded domain. Lemma 1. For a conductance-based model of the form 2.13 to 2.15 and for any ≤ I+, there exist upper and lower bounds Vmax bounded applied current I− ≤ Iapp and Vmin such that trajectories with initial voltage condition V ∈ [Vmin , Vmax] re- main within this interval for all times t > 0, regardless of the initial channel state.
} ∨ Vleak, where the index
Proof. Let V1
i runs over I, the set of distinct ion channel types. Note that for all i, 0 ≤

} ∧ Vleak, and V2

= max
i∈I

= min
i∈I

{Vi

{Vi

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Questo è, distributions indexed by a single open probability n, with the five states hav-

1

2

ing probabilities

(cid:20)

(cid:21)
4
io

ni(1 − n)4−i for 0 ≤ i ≤ 4.
(cid:20)

Questo è, distributions indexed by two open probabilities m and h, with the eight states

having probabilities

mi(1 − m)3−ih j (1 − h)1− j, for 0 ≤ i ≤ 3, E 0 ≤ j ≤ 1.

(cid:21)
3
io

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1787

(2.16)

(2.17)

(2.18)

(2.19)

(2.20)

(2.21)

(2.22)

(2.23)

Ni

open

≤ 1, and gi
(cid:16)

> 0, gleak

> 0. Therefore, when V ≤ V1,

dV
dt

= 1
C

Iapp

− gleak(V − Vleak) −

(cid:9)

(cid:18)
giNi

(cid:9)

i∈I
(cid:18)
giNi

(cid:17)
(cid:19)
open(V − Vi)
(cid:17)

(cid:19)
open(V − V1)

i∈I
(cid:9)

i∈I

(cid:17)

(cid:22)
gi

(cid:23)
× 0 × (V − V1)

(cid:16)

≥ 1
C

≥ 1
C

= 1
C

Iapp

− gleak(V − V1) −

(cid:16)

Iapp

− gleak(V − V1) −

(cid:24)
Iapp

(cid:25)
− gleak(V − V1)

.

= min
i∈I
> 0 and Ni

open

{Vi

} ∧ Vleak, and inequality 2.18

(cid:26)
≥ 0. Let Vmin := min

+

I−
gleak

> 0. Therefore, V will not decrease beyond Vmin.

Inequality 2.17 follows because V1

follows because V − V1

(cid:27)

≤ 0, gi

V1

. When V < Vmin, dV , V1 dt Similarly, when V ≥ V2, (cid:16) dV dt = 1 C Iapp − gleak(V − Vleak) − (cid:9) (cid:18) giNi (cid:9) i∈I (cid:18) giNi (cid:17) (cid:19) open(V − Vi) (cid:17) (cid:19) open(V − V2) i∈I (cid:9) i∈I (cid:17) (cid:22) gi (cid:23) × 0 × (V − V2) (cid:16) ≤ 1 C ≤ 1 C = 1 C Iapp − gleak(V − V2) − (cid:16) Iapp − gleak(V − V2) − (cid:24) Iapp (cid:25) − gleak(V − V2) . Inequality 2.21 holds because V2 = max i∈I {Vi } ∨ Vleak , and inequality 2.22 (cid:27) holds because V − V2 . When V > Vmax

, V2
We conclude that

V2

open

> 0 and Ni

≥ 0. Let Vmax

≥ 0, gi
, dV
dt

Iapp
gleak
< 0. Therefore, V will not go beyond Vmax. if V takes an initial condition in the interval (cid:2) + [Vmin , Vmax], then V (t) remains within this interval for all t ≥ 0. (cid:26) = max Given that y ∈ Y has a bounded domain, lemma 2 follows directly and establishes that the multinomial submanifold M is a forward-time– invariant manifold within the 14D space. The proof of lemma 2 is in appendix C. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1788 S. Pu and P. Thomas Lemma 2. Let X and Y be the lower-dimensional and higher-dimensional Hodgkin-Huxley manifolds given by equation 2.12, and let F and G be the vector fields on X and Y defined by equations 2.1 to 2.4 and 2.7 to 2.9, respectively. Let H : X → M ⊂ Y and R : Y → X be the mappings given in Tables 2 and 1, respec- tively, and define the multinomial submanifold M = H(X ). Then M is forward- time-invariant under the flow generated by G. Moreover, the vector field G, when restricted to M, coincides with the vector field induced by F and the map H. That is, for all y ∈ M, G(y) = DxH(R(y)) · F(R(y)). Lemma 2 establishes that the 14D HH model given by equations 2.7 to 2.9 is dynamically consistent with the original 4D HH model given by equa- tions 2.1 to 2.4. In section 2.4 we provide numerical evidence that the flow induced by G on Y converges to M exponentially fast. Thus, an initial probability dis- tribution over the ion channel states that is not multinomial quickly ap- proaches a multinomial distribution with dynamics induced by the 4D HH equations. Similar results, restricted to the voltage-clamp setting, were es- tablished by Keener and Earnshaw (Keener & Sneyd, 1998; Keener, 2009; Earnshaw & Keener, 2010b). 2.4 Local Convergence Rate. Keener and Earnshaw (Keener & Sneyd, 1998; Keener, 2009; Earnshaw & Keener, 2010b) showed that for Markov chains with constant (even time-varying) transition rates, (1) the multino- mial probability distributions corresponding to mean-field models (such as the HH sodium or potassium models) form invariant submanifolds within the space of probability distributions over the channel states, and (2) ar- bitrary initial probability distributions converged exponentially quickly to the invariant manifold. For systems with prescribed time-varying transi- tion rates, such as for an ion channel system under voltage clamp with a prescribed voltage V (t) as a function of time, the distribution of channel states had an invariant submanifold, again corresponding to the multino- mial distributions, and the flow on that manifold induced by the evolution equations was consistent with the flow of the full system. In the preceding section, we established the dynamical consistency of the 14D and 4D models with enough generality to cover both the voltage- clamp and current-clamp systems; the latter is distinguished by not hav- ing a prescribed voltage trace, but rather having the voltage coevolve along with the (randomly fluctuating) ion channel states. Here, we give numerical evidence for exponential convergence under current clamp similar to that established under voltage clamp by Keener and Earnshaw. Rather than providing a rigorous proof, we give numerical evidence for the standard deterministic HH model that y → M under current clamp (spontaneous firing conditions) in the following sense: if y(t) is a solution of ˙y = G(y) with arbitrary initial data y0 ∈ Y, then ||y(t) − H(R(y(t)))|| → 0 as t → ∞, exponentially quickly. Moreover, the convergence rate is bounded l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Fast and Accurate Stochastic Hodgkin-Huxley Simulations 1789 Na , λ , λ K), where λ by λ = max(λ ion is the least negative nontrivial eigen- v ≤ value of the channel state transition matrix (over the voltage range Vmin v ≤ Vmax) for a given ion, and −1/λ v is the largest value taken by the mem- ≤ v ≤ Vmax). In practice, we find that the brane time constant (for Vmin membrane time constant does not determine the slowest timescale for con- vergence to M. In fact it appears that the second-least-negative eigenvalues (not the least-negative eigenvalues) of the ion channel matrices set the con- vergence rate. gates, ∂M ∂m and gates, given by , i ∈ {0, 1, 2, . . . , 7} be the eight eigenvalues of ANa and v v i Note that y ∈ Y can be written as y = [V; M; N]. As shown in appendix ∂H C, the Jacobian matrix ∂x consists of three block matrices: one for the volt- ∂M ∂V ∂h ; and ∂v ; one associated with the Na age terms, ∂N ∂n . Fixing a particular voltage v, let one corresponding to the K λ i be the associ- i ated eigenvectors, that is, ANa i for the rate matrix in equations 2.8. Similarly, let η , i ∈ {0, 1, 2, . . . , 4} be the five eigenvalues and the asso- i i w ciated eigenvectors of AK, that is, AK i, for the rate matrix in equa- tions 2.9. If we rank the eigenvalues of either matrix in descending order, the leading eigenvalue is always zero (because the sum of each column for ANa and AK is zero for every V) and the remainder are real and negative. Let λ 1 denote the largest (least negative) nontrivial eigenvalues of ANa and AK, respectively, and let v ∈ R5 be the corresponding eigenvectors. ∈ R8 and w 1 and η = λ i = η , w w v + + 1 1 i i The eigenvectors of the full 14D Jacobian are not simply related to the eigenvectors of the component submatrices, because the first (voltage) row and column contain nonzero off-diagonal elements. However, the eigenvec- tors associated with the largest nonzero eigenvectors of ANa and AK (respec- tively, v 2) are parallel to ∂M/∂h and ∂N/∂n, regardless of voltage. In other words, the slowest decaying directions for each ion channel, v 1 and w 1, transport the flow along the multinominal submanifold of Y. Therefore, it is reasonable to make the hypothesis that if Y(t) is a solution of ˙y = G(y) with arbitrary initial data y ∈ Y, then 2 and w (cid:18)y(t) − H(R(y(t)))(cid:18) (cid:18)y(0) − H(R(y(0)))(cid:18) −λ 2t (cid:3) e (2.24) 2 being the second largest nonzero eigenvalue of AK and ANa over all v for λ in the range v max. The convergence behavior is plotted numeri- cally in Figure 3 and is consistent with the Ansatz equation 2.24. We calcu- late the distance from a point y to M as < v < v min ymax = argmax y∈Y (cid:28) (cid:28) (cid:28)2 . (cid:28) y − H(R(y)) (2.25) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1790 S. Pu and P. Thomas l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . 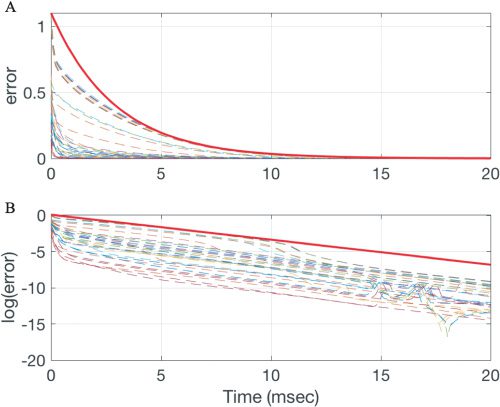/ f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 ∈ Y, Figure 3: Convergence of trajectories y(t), for arbitrary initial conditions y0 to the multinomial submanifold M, for an ensemble of random initial con- ditions. (A) Distance (see equation 2.25) between y(t) and M. (B) Logarithm of the distance in panel A. The red solid line shows dmaxe−λ 2t in panel A and log(dmax) − λ 2t in panel B. In order to obtain an upper bound on the distance as a function of time, we begin with the farthest point in the simplex from M by numerically finding the solution to the argument 2.25, which is ymax = [v, 0.5, 0, 0, 0.5, 0, 0, 0, 0, 0.5, 0, 0, 0, 0.5]. This vector represents the furthest possible departure from the multinomial distribution: all probability equally divided between the extreme states m00 and m03 for the sodium channel and the extremal states n0 and n4 for potas- sium. The maximum distance from the multinomial submanifold M, dmax, is calculated using this point. As shown in Figure 3, the function dmax e−λ 2t provides a tight upper bound for the convergence rate from arbitrary initial data y ∈ Y to the invariant submanifold M. 3 Stochastic 14D Hodgkin-Huxley Models Finite populations of ion channels generate stochastic fluctuations (“chan- nel noise”) in ionic currents that influence action potential initiation and timing (White et al., 1998; Schneidman et al., 1998). At the molecular level, fluctuations arise because transitions between individual ion channel states Fast and Accurate Stochastic Hodgkin-Huxley Simulations 1791 are stochastic (Hill & Chen, 1972; Neher & Sakmann, 1976; Skaugen & Walløe, 1979). Each directed edge in the ion channel state transition dia- grams (see Figure 1) introduces an independent noise source. It is of inter- est to be able to attribute variability of the interspike interval timing distri- bution to specific molecular noise sources, specifically individual directed edges in each channel state graph. In order to explore these contributions, we develop a system of Langevin equations for the Hodgkin-Huxley equa- tions, set in a 14-dimensional phase space. Working with a higher-dimensional stochastic model may appear incon- venient, but in fact has several advantages. First, any projection of an under- lying 14D model onto a lower (e.g., 4D) stochastic model generally entails loss of the Markov property. Second, the higher-dimensional representation allows us to assess the contribution of individual molecular transitions to the macroscopically observable variability of timing in the interspike inter- val distribution. Third, by using a rectangular noise coefficient matrix con- structed directly from the transitions in the ion channel graphs, we avoid a matrix decomposition step. This approach leads to a fast algorithm that is equivalent to the slower algorithm due to (Fox & Lu, 1994; Goldwyn & Shea-Brown, 2011) in a strong sense (pathwise equivalence) that we detail in section 4. 3.1 Exact Stochastic Simulation of HH Kinetics: The Random– Time-Change Representation. An “exact” representation of the Hodgkin- Huxley system with a population of Mtot sodium channels and Ntot potassium channels treats each of the 20 directed edges in the sodium chan- nel diagram, and each of the 8 directed edges in the potassium channel diagram, as independent Poisson processes, with voltage-dependent per capita intensities. As in the deterministic case, the sodium and potassium (cid:2) 4 i=0 Ni.3 channel population vectors M and N satisfy Thus, they are constrained, respectively, to a 7D simplex embedded in R8 and a 4D simplex embedded in R5. In the random-time-change rep- resentation (Anderson & Kurtz, 2015) the exact evolution equations are written in terms of sums over the directed edges E for each ion channel, E = {1, . . . , 8}, (see Figure 1), Na (cid:29) = {1, . . . , 20} and E 1 j=0 Mi j ≡ 1 ≡ 3 i=0 (cid:2) (cid:2) (cid:31) K (cid:30) M(t) = M(0) + 1 Mtot (cid:9) N(t) = N(0) + 1 Ntot t 0 ζ Na k YNa k Mtot αNa k (V (s))Mi(k)(s) ds , (3.1) k∈E (cid:9) Na (cid:29) ζ K k YK k Ntot k∈E K (cid:31) αK k (V (s))Ni(k)(s) ds . (3.2) (cid:30) t 0 3 We annotate the stochastic population vector M as either [M00 , . . . , M8], whichever is more convenient. In either notation M31 , M10 , . . . , M31] or as ≡ M8 is the conduct- channel. For the K channel, N4 denotes the conducting state. + [M1 ing state of the Na + l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1792 S. Pu and P. Thomas k k − eion = eion j(k) i(k).4 Each Yion Here ζ ion is the stoichiometry vector for the kth directed edge. If we write i(k) for the source node and j(k) for the destination node of edge k, then ζ ion (τ ) is an independent unit-rate Poisson pro- k cess, evaluated at “internal time” (or integrated intensity) τ , represent- ing the independent channel noise arising from transitions along the kth edge. The voltage-dependent per capita transition rate along the kth edge is αion (v ), and Mi(k)(s) (resp. Ni(k)(s)) is the fractional occupancy of the k source node for the kth transition at time s. Thus, for example, the quan- (V (s))Mi(k)(s) gives the net intensity along the kth directed edge tity Mtot channel graph at time s. in the Na αNa k + Remark 1. Under voltage-clamp conditions, with the voltage V held fixed, equations 3.1 and 3.2 reduce to a time-invariant first-order transition pro- cess on a directed graph (Schmidt & Thomas, 2014; Gadgil, Lee, & Othmer, 2005). Under current-clamp conditions, the voltage evolves according to a con- ditionally deterministic current balance equation of the form dV dt {Iapp(t) − ¯gNaM31 (V − VNa) − ¯gKN4 (V − VK) = 1 C − gleak(V − Vleak)}. (3.3) Here, C (μF/cm2) is the capacitance, Iapp (nA/cm2) is the applied current, the maximal conductance is ¯gchan (mS/cm2), Vchan (mV) is the associated reversal potential, and the ohmic leak current is gleak(V − Vleak). The random-time-change representation, equations 3.1 to 3.3, leads to an exact stochastic simulation algorithm, given in Anderson and Kurtz (2015); equivalent simulation algorithms have been used previously (Clay & DeFelice, 1983; Newby et al., 2013). Many authors substitute a simpli- fied Gillespie algorithm that imposes a piecewise-constant propensity ap- proximation, ignoring the voltage dependence of the transition rates αion between channel transition events (Goldwyn et al., 2011; Goldwyn & Shea- Brown, 2011; Orio & Soudry, 2012; Pezo et al., 2014). The two methods (cid:4) 40 (Anderson & Kurtz, give similar moment statistics, provided Ntot 2015); their similarity regarding path-dependent properties (including in- terspike interval distributions) has not been studied in detail. Moreover, both Markov chain algorithms are prohibitively slow for modest numbers (e.g., thousands) of channels; the exact algorithm may be even slower than the approximate Gillespie algorithm. For consistency with previous studies, in this article, we use the piecewise-constant propensity Gillespie algorithm = 1800 K+ channels as our gold standard with Mtot Markov chain (MC) model, as in Goldwyn and Shea-Brown (2011). = 6000 Na+ and Ntot , Mtot k 4 We write eNa i and eK i for the ith standard unit vector in R8 or R5, respectively. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Fast and Accurate Stochastic Hodgkin-Huxley Simulations 1793 In section 3.2 we develop a 14D conductance-based Langevin model with 28 independent noise sources – one for each directed edge – derived from the random-time-change representation equations 3.1 to 3.3. 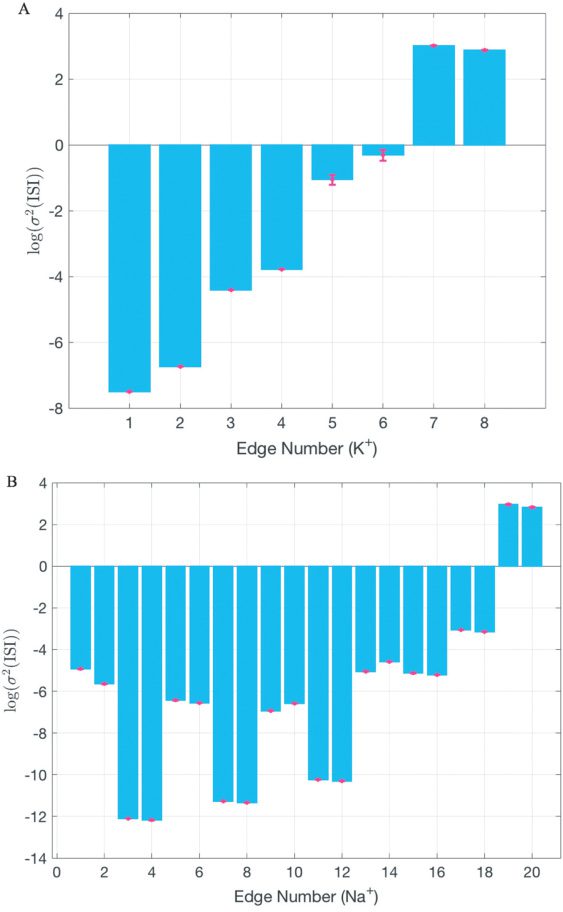In previous work (Schmidt & Thomas, 2014), we established a quantitative measure of edge importance, namely, the contribution of individual transitions (di- rected edges) to the variance of channel state occupancy under steady-state voltage-clamp conditions. Under voltage clamp, the edge importance was identical for each reciprocal pair of directed edges in the graph, a conse- quence of detailed balance. Some Langevin models lump the noise contri- butions of each pair of edges (Dangerfield et al., 2010, 2012; Orio & Soudry, 2012; Pezo et al., 2014). Under conditions of detailed balance, this simpli- fication is well justified. However, as we will show (see Figure 5), under current-clamp conditions (e.g., for an actively spiking neuron) detailed bal- ance is violated, the reciprocal edge symmetry is broken, and each pair of directed edges makes a distinct contribution to ISI variability. 3.2 Langevin Equations of the 14D HH Model. For sufficiently large number of channels, Schmidt and Thomas (2014) and Schmidt et al. (2018) showed that under voltage clamp, equations 3.1 and 3.2 can be ap- proximated by a multidimensional Ornstein-Uhlenbeck (OU) process (or Langevin equation) in the form5 dM = dN = 20(cid:9) k=1 8(cid:9) k=1 ζ Na k αNa k (V )Mi(k)dt + (cid:12)NaαNa k (V )Mi(k) dW Na k , ! " ! ζ K k k (V )Ni(k)dt + αK (cid:12)KαK k (V )Ni(k) dW K k " . (3.4) (3.5) k , and αion Here, M, N, ζ ion k have the same meaning as in equations 3.1 and 3.2. The channel state increments in a short time interval dt are dM and dN, respectively. The finite-time increment in the Poisson process Yion is now approximated by a gaussian process, namely, the increment dW ion in a Wiener (Brownian motion) process associated with each directed edge. These independent noise terms are scaled by (cid:12)Na = 1/Mtot and (cid:12)K = 1/Ntot, respectively. k k Equations 3.3 to 3.5 comprise a system of Langevin equations for the HH system (under current clamp) on a 14-dimensional phase space driven by 28 independent white noise sources, one for each directed edge. These equations may be written succinctly in the form dX = f(X) dt + √ (cid:12)G(X) dW(t) (3.6) 5 The convergence of the discrete channel system to a Langevin system under voltage clamp is a special case of Kurtz’s theorem (Kurtz, 1981). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1794 S. Pu and P. Thomas where we define the 14-component vector X = (V; M; N), and W(t) is a Wiener process with 28 independent components. The deterministic part of the evolution equation f(X) = dV is the same as the mean dt field, equations 2.7 to 2.9. The state-dependent noise coefficient matrix G is 14 × 28 and can be written as ; dM dt ; dN dt (cid:23) (cid:22) √ (cid:12)G = ⎞ ⎟ ⎟ ⎠ . ⎛ ⎜ ⎜ ⎝ 01×20 01×8 SNa 08×8 05×20 SK The coefficient matrix SK is ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ SK = 1√ Ntot √ − √ 4αnn0 √ βnn1 √ βnn1 − 4αnn0 0 0 0 · · · 0 0 0 0 0 2αnn2 2αnn2 √ − √ 0 3αnn1 √ − √ 3αnn1 0 0 ) 2βnn2 ) 2βnn2 0 − · · · 0 0 ) 0 3βnn3 ) − 3βnn3 0 0 0 0 0 0 ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ , 0 √ − √ αnn3 ) 4βnn4 ) 0 0 αnn3 − 4βnn4 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / and SNa is given in appendix D. Note that each of the 8 columns of SK cor- responds to the flux vector along a single directed edge in the K channel transition graph. Similarly, each of the 20 columns of SNa corresponds to the flux vector along a directed edge in the Na graph (see appendix D). + + Remark 2. Although the ion channel state trajectories generated by equa- tion 3.6 are not strictly bounded to remain within the nonnegative simplex, empirically, the voltage nevertheless remains within specified limits with overwhelming probability. To facilitate comparison of the model, equations 3.3 to 3.5, prior work (Fox & Lu, 1994; Fox, 1997; Goldwyn & Shea-Brown, 2011), we may rewrite the 14 × 28D Langevin description in the equivalent form: C dV dt = Iapp(t) − ¯gNaM8 (V − VNa) − ¯gKN5 (V − VK) − gleak(V − Vleak), (3.7) f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Fast and Accurate Stochastic Hodgkin-Huxley Simulations dM dt dN dt = ANaM + SNa ξ Na , = AKM + SK ξ K . 1795 (3.8) (3.9) The drift matrices ANa and AK remain the same as in Fox and Lu (1994), and are the same as in the 14D deterministic model, equations 2.10 and 2.11. SNa and SK are constructed from direct transitions of the underlying kinetics in Figure 1, and ξ ∈ R8 are vectors of independent gaussian white noise processes with zero mean and unit variance. ∈ R20 and ξ K Na Fox and Lu’s original approach (Fox & Lu, 1994) requires solving a ma- trix square root equation SS(cid:2) = D to obtain a square (8 × 8 for Na+ or 5 × 5 for K+) noise coefficient matrix consistent with the state-dependent diffu- sion matrix D. As an advantage, the ion channel representation equations 3.7 to 3.9, uses sparse, nonsquare noise coefficient matrices (8 × 20 for the Na+ channel and 5 × 8 for the K+ channel), which exposes the independent sources of noise for the system. The new Langevin model in equations 3.7 to 3.9 does not require detailed balance, which gives more insight into the underlying kinetics. Review pa- pers (e.g., Goldwyn & Shea-Brown, 2011; Pezo et al., 2014; Huang et al., 2015) did systematic comparison of various stochastic versions of the HH model. In sections 4 and 5, we quantitatively analyze the connection be- tween the new model and other existing models (Fox & Lu, 1994; Goldwyn et al., 2011; Goldwyn & Shea-Brown, 2011; Dangerfield et al., 2010, 2012; Orio & Soudry, 2012; Huang et al., 2013, 2015; Pezo et al., 2014; Fox, 2018). Problems such as the boundary constraints are beyond the scope of this ar- ticle; however, we would like to connect the new model to another type of approximation to the MC model; the stochastic shielding approximation. 3.3 Stochastic Shielding for the 14D HH Model. The stochastic shield- ing (SS) approximation was introduced by Schmandt and Galán (2012), in order to approximate the Markov process using fluctuations from only a subset of the transitions, namely, those corresponding to changes in the observable states. In Schmidt and Thomas (2014), we showed that under voltage clamp, each directed edge makes a distinct contribution to the steady-state variance of the ion channel conductance, with the total vari- ance being a sum of these contributions. We call the variance due to the kth directed edge the edge importance; assuming detailed balance, it is given by Rk = Jk n(cid:9) n(cid:9) (cid:29) i=2 j=2 (cid:31) −1 + λ j λ i (cid:2)v (c i) (cid:20) w(cid:2) i ζ k (cid:21) (cid:20) ζ (cid:2) k w j (cid:21) * v (cid:2) j c + . (3.10) Here, Jk is the steady-state probability flux along the kth directed edge; λn < λn−1 < 0 are the eigenvalues of the drift matrix (ANa or AK, ≤ . . . ≤ λ 2 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 1796 S. Pu and P. Thomas Figure 4: Stochastic shielding under voltage clamp. Redrawn (with permission) from Figures 10 and 13 of Schmidt and Thomas (2014). Each curve shows the edge importance Rk (see equation 3.10) as a function of voltage in the range [−100, 100] mV for a different edge pair. For the K+ kinetics, R7 = R8 are the largest Rk value in the voltage range above. For the Na+ kinetics, R11 = R12 have the largest Rk values in the subthreshold voltage range (c. [−100, −25] mV), = R20 have the largest Rk values in the suprathreshold voltage range and R19 (c. [−25, 100] mV). i (resp. w respectively), and v i) are the corresponding right (resp. left) eigen- vectors of the drift matrix. Each edge’s stoichiometry vector ζ k has compo- nents summing to zero; consequently, the columns of ANa and AK all sum to zero. Thus, each drift matrix has a leading trivial eigenvalue λ ≡ 0. The 1 vector c specifies the unitary conductance of each ion channel state; for the 8 or eK HH model, it is proportional to eNa 5 , respectively. and K Figure 4 shows the edge importance for each pair of edges in the HH + Na ion channel graph, as a function of voltage in the range [−100, 100] mV. Note that reciprocal edges have identical Rk due to detailed balance. Under voltage clamp, the largest value of Rk for the HH channels always corresponds to directly observable transitions, that is, edges k such that |c(cid:2)ζ | > 0, although this condition need not hold in general (Schmidt,
k
Galán, & Thomas, 2018).

+

To apply the stochastic shielding method under current clamp, we sim-
ulate the model with noise from only a selected subset E (cid:6) ⊂ E of directed
edges, replacing equations 3.8 A 3.9 con

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

,

ξ

Na

(cid:6)
Na

= AKM + S

= ANaM + S

dM
dt
dN
dt
where S(cid:6)
Na (resp. S(cid:6)
ficients from the most important edges E (cid:6)
edges with the largest edge-importance values Rk.

(cid:6)
K

ξ

K

,

K) is a reduced matrix containing only the noise coef-
. Questo è, E (cid:6)
contains a subset of

(3.11)

(3.12)

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1797

Schmandt and Galán (2012) assumed that the edges with the largest
contribution to current fluctuations under voltage clamp would also make
the largest contributions to variability in voltage and timing under current
= {7, 8}) and edges
clamp and included edges 7 E 8 of the K
= {11, 12, 19, 20}), yield-
11 E 12 E 19 E 20 of the Na
ing an 8 × 4 matrix S(cid:6)
K. They demonstrated numer-
ically that restricting stochastic forcing to these edges gave a significantly
faster simulation with little appreciable change in statistical behavior: un-
der voltage clamp, the mean current remained the same, with a small (Ma
noticeable) decrease in the current variance; meanwhile, similar interspike
interval (ISI) statistics were observed.

Na and a 5 × 2 matrix S(cid:6)

+
channel (E (cid:6)
Na

channel (E (cid:6)
K

+

Under current clamp, detailed balance is violated, and it is not clear from
mathematical principles whether the edges with the largest Rk under volt-
age clamp necessarily make the largest contribution under other circum-
stances. In order to evaluate the contribution of the fluctuations driven by
each directed edge on ISI variability, we test the stochastic shielding method
by removing all but one column of Sion at a time. Questo è, we restrict to a sin-
gle noise source and observe the resulting ISI variance empirically. For ex-
ample, to calculate the importance of the kth direct edge in the Na
channel,
we suppress the noise from all other edges by setting S(cid:6)
K

+
= 05×1 and

ξ

K

(cid:6)
Na

S

= [08×1

, · · · , SNa(:, k), · · · , 08×1] ,

questo è, we include only the kth column of SNa and set other columns to
be zeros. The ISI variance was calculated from an ensemble of 104 voltage
traces, each spanning about 500 ISIs.

Figure 5A plots the logarithm of the ISI variance for each edge in E
K.
Vertical bars (cyan) show the ensemble mean of the ISI variance, con un
95% confidence interval superimposed (magenta). Several observations are
in order. Primo, the ISI variance driven by the noise in each edge decreases
rapidly the farther the edge is from the observable transitions (edges 7,8),
reflecting the underlying “stochastic shielding” phenomenon. Secondo, IL
symmetry of the edge importance for reciprocal edge pairs—(1,2), (3,4),
(5,6), E (7,8)—that is observed under voltage clamp is broken under cur-
rent clamp. The contribution of individual directed edges to timing variabil-
ity under current clamp has another important difference compared with
the edge importance (current fluctuations) under voltage clamp. A simi-
lar breaking of symmetry for reciprocal edges is seen for the Na+
channel,
again reflecting the lack of detailed balance during active spiking.

Figure 5B shows the ISI variance when channel noise is included on in-
dividual edges of E
. Here, the difference between voltage and current
clamp is striking. Under voltage clamp, the four most important edges are
always those representing observable transitions, in the sense that the tran-
sition’s stoichiometry vector ζ is not orthogonal to the conductance vector c.

Na

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1798

S. Pu and P. Thomas

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figura 5: Logarithm of variance of ISI for stochastic shielding under current
clamp. The cyan bar is the mean of ISI, and the magenta plots the 95% con-
fidence interval of the mean ISI (see text for details). The applied current is
10 nA with other parameters specified in the appendixes. For the K+ kinetics,
the largest contribution edge is 7, E 8 is slightly smaller, ranking the second
largest. For the Na+ kinetics, the largest contribution pair is 19 E 20, con 20
slightly smaller than 19. Inoltre, edge 17 E 18 is the second largest pair.

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1799

Questo è, the four most important pairs are always 11 E 12 E 19 E
20, regardless of voltage (Guarda la figura 4). Under current clamp, the most im-
portant edges are 17, 18, 19, E 20. Although edges 11 E 12 are among
the four most important sources of channel population fluctuations under
voltage clamp, they are not even among the top 10 contributors to ISI vari-
ance when taken singly. Even though edges 17 E 18 are hidden, Senso
they do not directly change the instantaneous channel conductance, these
edges are nevertheless the second most important pair under current clamp.
Therefore, when we implement the stochastic-shielding based approxima-
zione, we include the pairs 17 E 18 E 19 E 20 in equation 3.11. We refer
to the approximate SS model driven by these six most important edges as
IL 14 × 6D HH model.

Given the other parameters we use for the HH model (Vedi la tabella 5 in ap-
= 10 nA is slightly beyond the region
pendix B), the input current of Iapp
of multistability associated with a subcritical Andronov-Hopf bifurcation.
In order to make sure the results are robust against increases in the applied
current, we tried current injections ranging from 20 A 100 nA. While inject-
ing larger currents decreased the ISI variance, it did not change the rank
order of the contributions from the most important edges.

4 Pathwise Equivalence for a Class of Langevin Models

Fox and Lu’s method has been widely used since its appearance (see ref-
erences in Bruce, 2009; Goldwyn & Shea-Brown, 2011; Huang et al., 2015),
and the “best” approximation for the underlying Markov chain (MC) modello
has been a subject of ongoing discussion for decades. Several studies (Mino
et al., 2002; Bruce, 2009; Sengupta, Laughlin, & Niven, 2010) attested to dis-
crepancies between Fox’s later approach (Fox, 1997) and the discrete-state
MC model, raising the question of whether Langevin approximations could
ever accurately represent the underlying fluctuations seen in the gold stan-
dard MC models. An influential review paper (Goldwyn & Shea-Brown,
2011) found that these discrepancies were due to the way in which noise
is added to the stochastic differential equations, 1.1 A 1.3. Recent studies,
including Dangerfield et al. (2010, 2012); Linaro et al. (2011); Goldwyn and
Shea-Brown (2011); Goldwyn et al. (2011); Orio and Soudry (2012); Güler
(2013B); Huang et al. (2013, 2015); Pezo et al. (2014); and Fox (2018), dis-
cussed various ways of incorporating channel noise into HH kinetics based
on the original work by Fox and Lu (Fox & Lu, 1994; Fox, 1997), some of
which have the same SDEs but with different boundary conditions. Differ-
ent boundary conditions (BCs) are not expected to have much impact on
computational efficiency. Infatti, if BCs are neglected, the main difference
between channel-based (or conductance-based) models is the diffusion ma-
trix S in the Langevin euqations 1.2 E 1.3. As the discussion about where
and how to incorporate noise into the HH model framework goes on, Fox

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1800

S. Pu and P. Thomas

(2018) recently asked whether there is a way of relating different models
with different S matrices. We give a positive answer to this question below.
In section 4.1 we demonstrate the equivalence (neglecting the bound-
ary conditions) of a broad class of previously proposed channel-based
Langevin models (Fox & Lu, 1994; Dangerfield et al., 2010, 2012; Goldwyn &
Shea-Brown, 2011; Orio & Soudry, 2012; Huang et al., 2013; Pezo et al., 2014;
Fox, 2018) and the 14D Langevin HH model with 28 independent noise
fonti (one for each directed edge in the channel state transition graph),
questo è, our 14 × 28D Langevin model.

4.1 When Are Two Langevin Equations Equivalent? Two Langevin
models are pathwise equivalent if the sample paths (trajectories) of one
model can be made to be identical to the sample paths of the other under an
appropriate choice of gaussian white noise samples for each. To make this
notion precise, consider two channel-based Langevin models of the form
dX = f(X) dt + G(X) dW with the same mean dynamics f ∈ Rd and two dif-
ferent d × n matrices (possibly with different values of n1 and n2), G1 and
G2. Denote

F : Rd → Rd,
G1 : Rd → Rd×n1 ,
G2 : Rd → Rd×n2 .

(4.1)

(4.2)

(4.3)

(cid:2)

and X∗

1 (T), X∗

trajectories produced by the

(T) = [X∗
two models,
1 (T), W ∗

(cid:2)
2 (T), . . . , X∗
(cid:2)
Let X(T) = [X1(T), X2(T), . . . , Xd(T)]
D (T)]
and let W(T) =
be
(cid:2)
2 (T), . . . , W ∗
and W∗
[W1(T), W2(T), . . . , Wn1 (T)]
n2 (T)]
be vec-
tors of Weiner processes. Questo è, Wi(T), i = 1, 2, . . . , n1 and W ∗
j (T), j = 1, 2,
δ(t − s)
. . . , n2 are independent Wiener processes with (cid:5)Wi(S)Wj(T)(cid:7) = δ
i j
E (cid:5)W ∗
δ(t − s). Note that n1 and n2 need not be equal. As
defined in (Allen, Allen, Arciniega, & Greenwood, 2008), the stochastic
differential equation (SDE) models

j (T)(cid:7) = δ

(T) = [W ∗

io (S)W ∗

i j

dX = f(T, X(T))dt + G1(T, X(T))dW(T)

E

dX

∗ = f(T, X

∗

∗
(T))dt + G2(T, X

∗
(T))dW

(T)

(4.4)

(4.5)

are pathwise equivalent if systems 4.4 E 4.5 possess the same probability
distribution and, Inoltre, a sample path solution of one equation is also a
sample solution to the other one. Allen et al. (2008) proved a theorem giving
general conditions under which the trajectories of two SDEs are equivalent.
We follow their construction closely below, adapting it to the case of two

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1801

different Langevin equations for the Hodgkin-Huxley system represented
in a 14-dimensional state space.

As in section 3, channel-based Langevin models for the stochastic dy-

namics of HH can be written as

dX = f(X) dt + S (X) dW(T),

(4.6)

(cid:23)

where the 14-component random vector X = (V; M; N) and f(X) =
(cid:22)
; dM
; dN
dV
is the same as the mean-field, equations 2.7 A 2.9. Recall that
dt
dt
dt
(cid:2)
x = [v, M, N]
. Here we write
⎛

⎞

S (X) =

⎝

01×m

01×n
SNa(M) 08×n
SK(N)

05×m

⎠ , con

SNa : R8 → R8×m,

for the Na

+

channel and

SK : R5 → R5×n

(4.7)

(4.8)

+

channel. Here, m is the number of independent white noise forc-
for the K
ing terms affecting the sodium channel variables, while n is the number
of independent noise sources affecting the potassium gating variables. Noi
write

(cid:2)
W(T) = [W1(T), W2(T), . . . , Wm+n(T)]

for a Wiener process incorporating both the sodium and potassium noise
forcing. Given two channel-based models with diffusion matrices,

SNa,1 : R8 → R8×m1 ,
SNa,2 : R8 → R8×m2 ,

for the Na+ channel, E

SK,1 : R5 → R5×n1 ,
SK,2 : R5 → R5×n2 ,

(4.9)

(4.10)

(4.11)

(4.12)

+

channel, we construct the diffusion matrix D = SS (cid:2)
for the K
. In order for
the two models to generate equivalent sample paths, it suffices that they
have the same diffusion matrix:

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1802

S. Pu and P. Thomas

D = S

S (cid:2)
1

1

=

⎛

⎞

⎝

01×1 01×8 01×5
08×1 DNa 08×5
05×1 05×8 DK

⎠ = S

S (cid:2)
2

.

2

The SDEs corresponding to the two channel-based Langevin models are

dX = f(T, X(T))dt + S
∗
(T))dt + S

∗ = f(T, X

1(T, X(T))dW(T),
∗
∗
2(T, X
(T))dW

dX

(T).

(4.13)

(4.14)

The probability density function p(T, X) for random variable X in equa-

zione 4.13 satisfies the Fokker-Planck equation:

∂ p(T, X)
∂t

= 1
2

−

= 1
2

8(cid:9)

8(cid:9)

i=1

j=1

8(cid:9)

i=1

∂
∂xi

8(cid:9)

8(cid:9)

i=1

j=1

(cid:18)

∂ 2
∂xix j

P(T, X)

+n1(cid:9)
m1

l=1

S (io,l)
1

(T, X)S ( j,l)

1

(cid:19)
(T, X)

(cid:18)
(cid:19)
fi(T, X)P(T, X)

(cid:18)

(cid:19)
D(io, j)(T, X)P(T, X)

−

∂ 2
∂xix j

(cid:18)
(cid:19)
,
fi(T, X)P(T, X)

8(cid:9)

i=1

∂
∂xi

where S (io, j)
zione 4.15 holds because

1

(T, X) is the (io, j)th entry of the diffusion matrix S

(4.15)

1(T, X). Equa-

D(io, j)(T, X) =

+n1(cid:9)
m1

l=1

S (io,l)
1

(T, X)S ( j,l)

1

(T, X).

If z1, z2

∈ R14 and z1

(cid:5) z2, Poi
(cid:30)

z2,14

P(z1

(cid:5) X(T) (cid:5) z2) =

(cid:30)

z2,13

(cid:30)

z2,1

· · ·

P(T, X)dx1dx2

· · · dx8

.

z1,14

z1,13

z1,1

Note that equations 4.13 E 4.14 have the same expression equation 4.15,
for the Fokker-Planck equation; Perciò, X and X∗
possess the same prob-
ability density function. In other words, the probability density function of
X in equation 4.6 is invariant for different choices of the diffusion matrix S.

4.2 Map Channel-based Langevin Models to Fox and Lu’s Model. Noi
now explicitly construct a mapping between Fox and Lu’s (1994) 14D model
and any channel-based model (given the same boundary conditions). Noi
begin with a channel-based Langevin description

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

dX = f(T, X(T))dt + S (T, X(T))dW(T),

and Fox and Lu’s (1994) modello,

dX

∗ = f(T, X

∗

(T))dt + S

∗
0(T, X

∗
(T))dW

(T),

1803

(4.16)

(4.17)

where S is a d by m matrix satisfying SS (cid:2) = D (note that S is not necessarily
a square matrix), and S

D.

√

=

0

Let T be the total simulation time of the random process in equations 4.16
E 4.17. For 0 (cid:5) T (cid:5) T, denote the singular value decomposition (SVD) Di
S as

S (T) = P(T)(cid:13)(T)Q(T),

where P(T) is a d × d orthogonal matrix (cioè., P(cid:2)P = PP(cid:2) = Id), Q(T) is an
m × m orthogonal matrix, E (cid:13)(T) is a d × m matrix with rank((cid:13)) = r (cid:5) D
positive diagonal entries and d − r zero diagonal entries.

Primo, we prove that given a Wiener trajectory, W(T), t ∈ [0, T] and the
(T) come
, is also a solution to equation 4.16. In
(T), such that

solution to equation 4.16 X(T), there exists a Wiener trajectory W∗
that the solution to equation 4.17, X∗
other words, for a Wiener process W(T), we can construct a W∗
X∗

(T) = X(T), for 0 ≤ t ≤ T.
Following Allen et al. (2008), we construct the vector W∗

(T) of d indepen-

dent Wiener processes as follows:

∗

(T) =

W

(cid:30)

T

0

(cid:18)(cid:20)

P(S)

(cid:13)(S)(cid:13)(cid:2)

(cid:19)+

(cid:21) 1

(S)

2

(cid:13)(S)Q(S)dW(S) +

(cid:30)

T

0

∗∗

P(S)dW

(S)

(4.18)

for 0 (cid:5) T (cid:5) T, where W∗∗(T) is a vector of length d with the first r entries
equal to 0 and the next d − r entries independent Wiener processes, E
(cid:18)(cid:20)

(cid:19)+

(cid:21) 1

(cid:21) 1

(S)

2

is the pseudoinverse of

(S)

2 . Consider that

(cid:20)
(cid:13)(S)(cid:13)(cid:2)

(cid:13)(S)(cid:13)(cid:2)

D(T) = S (T)S (cid:2)

(cid:18)
P(T)(cid:13)(T)Q(T)
(T) = P(T)(cid:13)(T)Q(T)

(cid:19)(cid:2)

= P(T)(cid:13)(T)(cid:13)(cid:2)
= [S
0(T)]2,

(T)P

(cid:2)

(T)

(4.19)

(4.20)

(4.21)

where S

*
(cid:13)(T)(cid:13)(cid:2)
0(T) = P(T)

+ 1

(T)

2

P(cid:2)

(T) is a square root of D, by construction.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

(4.22)

(4.23)

1804

S. Pu and P. Thomas

The diffusion term on the right side of equation 4.17 with X∗

(T) replaced

by X(T) satisfies

S

∗
0(T, X(T))dW

*

(T)
(cid:18)(cid:20)

= S

(T)

P(T)

0(T)
*
(cid:13)(T)(cid:13)(cid:2)
= P(T)
*
(cid:13)(T)(cid:13)(cid:2)
+ P(T)
(cid:25)
(cid:24)
P(T)(cid:13)(T)Q(T)

=

(cid:19)+

(cid:21) 1

(T)

2

(cid:13)(T)(cid:13)(cid:2)
+ 1

(cid:13)(T)Q(T)dW(T) + P(T)dW
(cid:18)(cid:20)

(cid:19)+

(cid:21) 1

∗∗

+

(T)

(cid:2)

2

P

(T)P(T)

(cid:13)(T)(cid:13)(cid:2)

(T)

2

(cid:13)(T)Q(T)dW(T)

(T)P(T)dW

∗∗

(T)

+ 1

2

(T)

(cid:2)

P

dW(T).

From the SVD of S = P(cid:13)Q, we conclude that

S

∗
0(T, X(T))dW

(T) = S (T, X(T))dW(T).

zione 4.17 X∗
processes as
(cid:30)

W(T) =

0

Hence, dX = f(T, X(T))dt + S
lution of equation 4.17.

0(T, X(T))dW

∗
T , questo è, X(T) is a sample path so-

Allo stesso modo, given a Wiener trajectory W∗

(T) and the solution to equa-
(T), we can construct a vector W(T) of m independent Winner

T

(cid:2)
Q

(S)(cid:13)+

(cid:22)
(S)

(cid:13)(S)(cid:13)(cid:2)

(cid:23)
(S)

1/2

(cid:2)

P

(S)dW

∗

(S) +

(cid:30)

T

0

(cid:2)
Q

(S)dW

∗∗∗

(S)

(4.24)

for 0 (cid:5) T (cid:5) T, where W∗∗∗
(T) is a vector of length m with the first r entries
equal to 0 and the next m − r entries independent Wiener processes, E
(cid:13)+
(S) is the pseudoinverse of (cid:13)(S). Then, by an argument parallel to equa-
zione 4.22, we conclude that

∗
S (T, X

(T))dW (T) = S

∗
0(T, X

∗
(T))dW

(T).

(4.25)

∗ = f(T, X∗

(T))dt + S (T, X∗

Hence, dX
(T) is also a solu-
tion to equation 4.16. Therefore, we can conclude that the channel-based
Langevin model in equation 4.16 is pathwise equivalent to Fox and Lu’s
modello.

(T))dW(T), questo è, X∗

To illustrate pathwise equivalence, Figura 6 plots trajectories of the
14 × 28D stochastic HH model and Fox and Lu’s model using noise traces
dictated by the preceding construction. In panel A, we generated a sam-
ple path for equation 4.16 and plot three variables in X: the voltage V,
channel open probability N4.
Na
The corresponding trajectory, X∗
, for Fox and Lu’s model was generated

channel open probability M31, and K

+

+

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1805

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

Figura 6: Pathwise equivalency of 14D HH model and Fox and Lu’s model.
(UN) Given a sample path of the 14 × 28D Langevin model in equation 4.16, we
construct the noise by equation 4.18 and generate the sample trajectory of Fox
and Lu’s model using equation 4.17. (B) Given a sample path of Fox and Lu’s
model in equation 4.17, we construct the noise by equation 4.24 and generate
the sample trajectory of the 14 × 28D Langevin model using equation 4.16. For
both cases, we plot the voltage V, the open probability of the Na+ channel (M31),
and the open probability of the K+ channel (N4). We obtain excellent agreement
in both directions.

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1806

S. Pu and P. Thomas

+

+
31 and K

, Na
4 in X∗

channel open probability M∗

from equation 4.17 and the corresponding Wiener trajectory was calculated
using equation 4.18. The top three subplots in panel A superposed the volt-
age V ∗
channel open proba-
bility N∗
against those in X. The bottom three subplots in panel A
plot the point-wise differences of each variable. Equations 4.16 E 4.17 are
numerically solved in Matlab using the Euler-Maruyama method with a
time step dt = 0.001 ms. The slight differences observed arise in part due
to numerical errors in calculating the singular value decomposition of S (In
equation 4.16); another source of error is the finite accuracy of the Euler-
Maruyama method.6 As shown in Figure 6, most differences occur near the
spiking region, where the system is numerically very stiff and the numerical
accuracy of the SDE solver accounts for most of the discrepancies (analysis
of which is beyond the scope of this article). To illustrate pathwise equiva-
lence, Figura 6 shows superposed voltage trajectories for each simulation,
as well as the point-wise voltage differences of each. We can conclude from
the comparison in Figure 6 that the 14 × 28D Langevin model is pathwise
equivalent with Fox and Lu’s model. Allo stesso modo, the same analogy applies
for other channel-based Langevin models such that with the same diffusion
matrix D(X).

We have shown that our 14 × 28D model, with a 14-dimensional state
space and 28 independent noise sources (one for each directed edge), È
pathwise equivalent to Fox and Lu’s original 1994 modello, as well as other
channel-based models (under corresponding boundary conditions) includ-
ing Goldwyn et al. (2011); Goldwyn and Shea-Brown (2011); Orio and
Soudry (2012); Pezo et al. (2014); Fox (2018). As we shall see in section 5, IL
pathwise equivalent models give statistically indistinguishable interspike
interval distributions under the same BCs. We emphasize the importance of
boundary conditions for pathwise equivalence. Two simulation algorithms
with the same Ai and Si matrices will generally have nonequivalent tra-
jectories if different boundary conditions are imposed. Per esempio, Dan-
gerfield et al. (2012) employ the same dynamics as Orio and Soudry (2012)
away from the boundary, where ion channel state occupancy approaches
zero or one. But where the latter allow trajectories to move freely across this
boundary (which leads only to small, short-lived excursions into “nonphys-
ical” values), Dangerfield imposes reflecting boundary conditions through
a projection step at the boundary. As we will see ln section 5, this difference
in boundary conditions leads to a statistically significant difference in the
ISI distribution, as well as a loss of accuracy when compared with the gold
standard Markov chain simulation.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

6

The forward Euler method is first-order accurate for ordinary differential equations,
dt) accurate for stochastic differen-

√

but the forward Euler-Maruyama method is only O(
tial equations (Kloeden & Platen, 1999).

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1807

5 Model Comparison

In section 3, we studied the contribution of every directed edge to the ISI
variability and proposed how stochastic shielding could be applied under
current clamp. Inoltre, in section 4, we proved that a family of Langevin
models is pathwise equivalent.

Here we compare the accuracy and computational efficiency of sev-
eral models,
including the “subunit model” (Fox, 1997; Goldwyn &
Shea-Brown, 2011), Langevin models with different S matrices or bound-
ary conditions (Fox & Lu, 1994; Goldwyn & Shea-Brown, 2011; Dangerfield
et al., 2012; Orio & Soudry, 2012; Pezo et al., 2014), the 14D HH model (pro-
posed in section 3.2), the 14D stochastic shielding model with six indepen-
dent noise sources (proposed in section 3.3), and the gold standard Markov
chain model (discussed in section 3.1). Where other studies have compared
moment statistics such as the mean firing frequency (under current clamp)
and stationary channel open probababilies (under voltage clamp), we base
our comparison on the entire interspike interval (ISI) distributions, under
current clamp with a common fixed driving current. We use two different
comparisons of ISI distributions, the first based on the L1 norm of the dif-
ference between two distributions (the Wasserstein distance; Wasserstein,
1969), in section 5.1 and the second based on the L∞ norm (the Kolmogorov-
Smirnov test; Kolmogorov, 1933; Smirnov, 1948), in section 5.2. We find
similar results using both measures: as expected, the models that produce
pathwise equivalent trajectories (Fox & Lu, 1994; Orio & Soudry; and our
14 × 28D model) have indistinguishable ISI statistics, while the nonequiv-
alent models (Fox, 1997; Dangerfield, 2010, 2012; Goldwyn & Shea-Brown,
2011; our 14 × 6D stochastic-shielding model) have significantly different
ISI distributions. Of these, IL 14 × 6D SS model is the closest to the models
in the 14 × 28D class and as fast as any other model considered.

5.1 L1 Norm Difference of ISIs. We first evaluate the accuracy of dif-
ferent stochastic simulation algorithms by comparing their ISI distributions
under current clamp to that produced by a reference algorithm, namely, IL
discrete-state Markov chain (MC) algorithm.

Let X1

, . . . , Xn be n independent samples of ISIs with a true cumu-
lative distribution function F. Let Fn(·) denote the corresponding empirical
cumulative distribution function (ECDF) defined by

, X2

Fn(X) = 1
N

N(cid:9)

i=1

1{Xi

≤x},

x ∈ R,

(5.1)

where we write 1A to denote the indicator function for the set A. Let Q and
QM be the quantile functions of F and FM, rispettivamente. The L1-Wasserstein

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1808

S. Pu and P. Thomas

Tavolo 3: Summary of the L1-Wasserstein Distances of ISI Distributions for
Langevin Type Hodgkin-Huxley Models Compared to the MC Model.

Model

MC
Fox94
Fox97
Dangerfield
Goldwyn
Orio
14 × 28D
SS

Variables
V+M+N S Matrix

Noise Dimensions
Na+K

L1 Norm (msec.)
(Wasserstein Dist.)

Run Time
(sec.)

1+8+5
1+7+4
1+2+1
1+8+5
1+8+5
1+8+5
1+8+5
1+8+5

n/a
√

S =

D

n/a
SEF
√

S =
D
Spaired
Ssingle
Sss

20+8
7+4
3
10+4
8+5
10+4
20+8
4+2

2.27 e-4 ± 7.15 e-5
4.74 e-2 ± 1.93 e-4
8.01 e-1 ± 9.48 e-4
2.18 e-1 ± 2.14 e-4
1.83 e-1 ± 1.93 e-4
4.52 e-2 ± 2.08 e-4
4.93 e-2 ± 1.94 e-4
7.62 e-2 ± 7.57 e-5

3790
2436
67
655
2363
577
605
73

Notes: Model (see text for details): MC: Markov chain. Fox94; From Fox and Lu (1994).
Fox97: Fox (1997). Goldwyn: Goldwyn and Shea-Brown (2011). Dangerfield: Dangerfield
et al. (2010, 2012). 14 × 28D: model proposed in section 3.2. SS: stochastic-shielding model
(see section 3.3). Variables: number of degrees of freedom in Langevin equation represent-
ing voltage, sodium gates, and potassium gates, rispettivamente. S Matrix: Form of the noise
coefficient matrix in equations 1.1 A 1.3. Noise dimensions: number of independent gaus-
sian white noise sources represented for sodium and potassium, rispettivamente. L1 Norm:
Empirically estimated L1-Wasserstein distance between the model’s ISI distribution and
the MC model’s ISI distribution. For MC versus MC, independent trials were compared.
a ± b: mean±standard deviation. Run time (in seconds): see text for details.

distance between two CDF’s FM and F can be written as (Shorack & Wellner,
2009)

ρ
1(F, FM) =

(cid:30) ∞

0

,
,

,
,
F(X) − FM(X)

dx =

(cid:30)

0

1

,
,

,
,
Q(X) − QM(X)

dx.

(5.2)

Note that ρ
Tavolo 3 have units of milliseconds.

1 has the same units as dx. Così, the L1 distances reported in

When two models have the same number of samples, N, equation 5.2 can

be estimated by

(cid:30)

0

1

,
,
,
,
Q(X) − QM(X)

dx ≈ 1
N

N(cid:9)

i=1

|Xi

− Yi

| := ρ

1(Fn, FM

N ),

(5.3)

, · · · , Xn and Y1

where X1
cending order with CDF F and FM, rispettivamente.

, · · · , Yn are n independent samples sorted in as-

We numerically calculate ρ

N ) to compare several Langevin mod-
els against the MC model. We consider the following models: “Fox94” de-
notes the original model proposed by Fox and Lu (1994), which requires

1(Fn, FM

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1809

√

+

+

gates and 8 Na

a square root decomposition (S =
D) for each step in the simulation (Vedere
equations 1.1 A 1.3). “Fox97” is the widely used “subunit model” of Fox
(1997); see equations 1.4 E 1.5). “Goldwyn” denotes the method taken
from Goldwyn and Shea-Brown (2011), where they restrict the 14D sys-
tem (V, 5 K
gates) to the 4D multinomial submanifold
(V, M, N, and h; see section 4.2), with gating variables truncated to [0,1].
We write “Orio” for the model proposed by Orio and Soudry (2012), Dove
they constructed a rectangular matrix S such that SS(cid:2) = D (referred to as
Spaired in Table 3) combining fluctuations driven by pairs of reciprocal edges,
thereby avoiding taking matrix square roots at each time step. The model
“Dangerfield” represents Dangerfield et al. (2012), which used the same S
matrix as in Orio and Soudry (2012) but added a reflecting (no-flux) bound-
ary condition via orthogonal projection (referred to as SEF in Table 3). Fi-
nally, we include the 14 × 28D model we proposed in section 3.2, or “14D”
(referred to as Ssingle in Table 3); “SS” is the stochastic shielding model spec-
ified in section 3.3.

For each model, we ran 10,000 independent samples of the simulation,
= 10 nA), and initial condi-
holding channel number, injected current (Iapp
tions fixed. Throughout the article, we presume a fixed channel density of
60 channels/μm2 for sodium and 18 channels/μm2 for potassium in a mem-
brane patch of area 100 μm2, consistent with prior work such as Goldwyn
and Shea-Brown (2011) and Orio and Soudry (2012). The initial condition
is taken to be the point on the deterministic limit cycle at which the volt-
age crosses upward through −60 mV. An initial transient corresponding to
10 A 15 ISIs is discarded, to remove the effects of the initial condition. (Vedere
Tavolo 5 in appendix B for a complete specification of simulation parame-
ters.) We compared the efficiency and accuracy of each model through the
following steps:

1. For each model, a single run simulates a total time of 84,000 millisec-

onds (ms) with time step 0.008 ms, recording at least 5000 ISIs.

2. For each model, repeat 10,000 runs in step 1.
3. Create a reference ISI distribution by aggregating all 10,000 runs of

the MC model, questo è, based on roughly 5 × 107 ISIs.

4. For each of 104 individual runs, align all ISI data into a single vector

and calculate the ECDF using equation 5.1.

5. Compare the ISI distribution of each model with the reference MC
distribution by calculating the L1-difference of the ECDFs using
equation 5.3.

6. To compare the computational efficiency, we take the average execu-
tion time of the MC model as the reference. The relative computa-
tional efficiency is the ratio of the average execution time of a model
with that of the MC model (Di 3790 sec).

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1810

S. Pu and P. Thomas

Tavolo 3 gives the empiricially measured L1 difference in ISI distribution
between several pairs of models.7 The first row (“MC”) gives the average
L1 distance between individual MC simulations and the reference distri-
bution generated by aggregating all MC simulations, in order to give an
estimate of the intrinsic variability of the measure. Figura 8 plots the L1-
Wasserstein differences versus the relative computational efficiency of sev-
eral models against the MC model. These results suggest that the Fox94,
Orio, E 14 × 28D models are statistically indistinguishable when com-
pared with the MC model using the L1-Wasserstein distance. This result
is expected in light of our results (see section 4) showing that these three
models are pathwise-equivalent. (We will make pairwise statistical com-
parisons between the ISI distributions of each model in see section 5.2.)
Among these equivalent models, Tuttavia, IL 14 × 28D and Orio mod-
els are significantly faster than the original Fox94 model (and the Gold-
wyn model) because they avoid the matrix square root computation. IL
Dangerfield model has speed similar to the 14 × 28D model, but the use
of reflecting boundary conditions introduces significant inaccuracy in the
ISI distribution. The imposition of truncating boundary conditions in the
Goldwyn model also appears to affect the ISI distribution. Of the models
considered, the Fox97 subunit model is the fastest; Tuttavia, it makes a par-
ticularly poor approximation to the ISI distribution of the MC model. Note
that the maximum L1-Wasserstein distance between two distributions is 2.
The ISI distribution of the Fox97 subunit model to that of the MC model is
more than 0.8, che è 10 times larger than the L1-Wasserstein distance of
the SS model, and almost half of the maximum distance. As shown in Fig-
ure 7, the Fox97 subunit model fails to achieve the spike firing threshold and
produces longer ISIs. Because of its inaccuracy, we do not include the sub-
unit model in our remaining comparisons. The stochastic shielding model,
on the other hand, has nearly the same speed as the Fox97 model, but it is
Sopra 100 times more accurate (in the L1 sense). The SS model is an order
of magnitude faster than the 14 × 28D model and has less than twice the
L1 discrepancy versus the MC model (L1 norm 76.2 versus 49.3 microsec-
onds). While this difference in accuracy is statistically significant, it may
not be practically significant, depending on the application (see section 6
for further discussion of this point).

5.2 Two-Sample Kolmogorov-Smirnov Test. In addition to using the
L1-Wasserstein distances to test the differences between two CDFs, we can
also make a pairwise comparison between each model by applying the
Dvoretzky-Kiefer-Wolfowitz inequality (Dvoretzky, Kiefer, & Wolfowitz,

7

Run times in Table 3, rounded to the nearest integer number of seconds, were ob-
tained by averaging the run times on a distribution of heterogeneous compute nodes from
Case Western Reserve University’s high-performance computing cluster.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1811

Figura 7: The probability density of interspike intervals (ISIs) for Fox97 (blue)
and the MC model (red). The probability densities were calculated over more
di 5.4 × 107 ISIs.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figura 8: The L1-Wasserstein distances and relative computational efficiency
versus the MC model. Fox94 (green circle), Goldwyn (black cross), Orio (cyan
square), 14D (blue star), SS (magenta downward-pointing triangle), Dangerfield
(red upward-pointing triangle), and the MC (brown diamond) modello. The L1 er-
ror for ISI distribution was computed using the L1-Wasserstein distance, equa-
zione 5.3, with discrete time Gillespie/Monte Carlo simulations as a reference.
The relative computational efficiency is the ratio of the recorded run time to
the mean recorded time of the MC mode (3790 seconds). The mean and 95%
confidence intervals were calculated using 100 repetitions of 10,000 runs each
(5 × 109 ISIs total).

1812

S. Pu and P. Thomas

1956) and the two-sample Kolmogorov-Smirnov (KS) test (Kolmogorov,
1933; Smirnov, 1948). While the Wasserstein distance is based on the L1
norm, the KS statistic is based on the L∞ (or supremum) norm.

The Dvoretzky-Kiefer-Wolfowitz inequality (Dvoretzky et al., 1956) es-
tablishes confidence bounds for the CDF. Specifically, the interval that con-
tains the true CDF, F(·), with probability 1 − α, is given by

|Fn(X) − F(X)| ≤ ε where ε =

–

ln 2
α
2N

.

(5.4)

When comparing samples XM
n obtained from an approximate
1
model M against the gold standard, in section 5.1 we computed the L1 dif-
ference of the empirical density functions as an approximation for the L1 dif-
ference of the true distributions. Invece, we work here with the L∞ norm:

, . . . , XM

, XM
2

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

ρ∞(Fn, FM

N ) = lim
p→∞

= sup
0≤x<∞ (cid:29)(cid:30) ∞ , , , ,p n (x) − Fn(x) FM (cid:31) 1/p dx 0 (cid:20), , , , n (x) − Fn(x) FM (cid:21) . (5.5) For each x ≥ 0, equation 5.4 bounds the discrepancy between the true and empirical distribution differences as follows. By the triangle inequality and independence of the Xi from the XM i , the inequality |FM − F| = |FM − FM n ≤ |FM − FM n ≤ 2ε + |FM n + Fn − F + FM n | + |Fn − F| + |FM n − Fn| − Fn| − Fn| holds with probability (1 − α)2. Similarly, |FM n − Fn| = |FM − FM n n ≤ |FM − FM n ≤ 2ε + |FM − F| + F − Fn + FM − F| | + |Fn − F| + |FM − F| (5.6) (5.7) holds with probability (1 − α)2. Together, equations 5.6 and 5.7 indicate that the discrepancy between the difference of empirical distributions and the difference of true distributions is bounded as , , ,|FM − F| − |FM n , , , ≤ 2ε − Fn| with probability (1 − α)2, for ε = ! ln 2 α 2n . (5.8) / e d u n e c o a r t i c e - p d / l f / / / / 3 2 1 0 1 7 7 5 1 8 6 5 2 8 5 n e c o _ a _ 0 1 3 1 2 p d . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Fast and Accurate Stochastic Hodgkin-Huxley Simulations 1813 We will use the pointwise difference of the ECDFs for a large sample as an estimate for the pointwise difference between two true CDFs. The two- sample Kolmogorov-Smirnov (KS) test (Kolmogorov, 1933; Smirnov, 1948) offers a statistics to test whether two samples are from the same distribution. The two-sample KS statistic is Dn,m = sup x |F1,n(x) − F2,m(x)|, (5.9) where F1,n and F2,m are two ECDFs for two samples defined in equation 5.1 and the sup is the supremum function. The reference statistic, Rn,m(α), depending on the significance level α, is defined as Rn,m(α) = . − log(α/2) 2 . n + m nm , (5.10) where n and m are the sample sizes. The null hypothesis that “the two sam- ples come from the same distribution” is rejected at the significance level α if Dn,m > Rn,M(α).

(5.11)

Figura 9 plots the logarithm of ratio of the two-sample KS statistics,
Dn,M
Rn,M (0.01) , for Fox94 (Fox & Lu, 1994), Goldwyn (Goldwyn & Shea-Brown,
2011), Dangerfiled (Dangerfield et al., 2012), Orio (Orio & Soudry, 2012), 14D
(IL 14 × 28D model we proposed in section 3.2). Data of “self-comparison”
(e.g. Fox94 versus Fox 94) was obtained by comparing two ISI ECDFs from
independent simulations. Come mostrato in figura 9, models that we previously
proved were pathwise equivalent in section 4, namely, the Fox94, Orio,
and 14D models, are not distinguishable at any confidence level justified
by our data. Note that those three models use the same boundary con-
ditions (free boundary condition as in Orio & Soudry, 2012) and the ra-
tio Dn,m/Rn,M(α) of pairwise comparison is on the same magnitude of that
for the self-comparisons. The models of Fox and Lu and Orio and Soudry,
and our 14D model generate indistinguishable ISI distributions but are dis-
tinguishable from Dangerfield’s model and Fox’s 97 modello. Così, as the
bottom panel of Figure 9 shows, Fox94, Orio, E 14 × 28D form a block
of statistically indistinguishable samples. Tuttavia, as pointed out above,
these statistically equivalent simulation algorithms have different computa-
tional efficiencies (Guarda la figura 8). Among these methods, Orio and Soundry’s
algorithm (14-dimensional state space with 14 undirected edges as noise
fonti) and our method (14-dimensional state space with 28 directed edges
as noise sources) have similar efficiencies, with Orio’s method being about
5% faster than our method. Nostro 14 × 28D method provides the additional

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1814

S. Pu and P. Thomas

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

the ratio of Kolmogorov-Smirnov test statistic
Figura 9: Logarithm of
/Rn,M(α), equations 5.9 E 5.10, for samples from the ISI distribution for
Dn,M
each pair of models. (Top) Box and whisker plots showing mean and 95% confi-
dence intervals based on 10,000 pairwise comparisons. The first five plots show
self-comparisons (green bars); the remainder compare distinct pairs (gray bars).
UN: Fox94 (Fox & Lu, 1994), B: Orio (Orio & Soudry, 2012), C: 14D (14 × 28D
modello, section 3.2), D: Dangerfield (Dangerfield et al., 2012), E: Goldwyn (Gold-
wyn & Shea-Brown, 2011). (Bottom) Mean logarithms (as in top panel) for all
pairwise comparisons.

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1815

advantage that it facilitates further acceleration under the stochastic shield-
ing approximation (see section 6).

In contrast to the statistically equivalent Orio, 14 × 28D, and Fox94
models, algorithms using different boundary conditions are not pathwise
equivalent, which is again verified in Figure 9. Algorithms with subunit ap-
proximation and truncated boundary condition (cioè., “Goldwyn”) and the
reflecting boundary condition (cioè., “Dangerfield”) are significantly differ-
ent in accuracy (E, in particular, they are less accurate) than models in the
14 × 28D class.

6 Discussion and Conclusions

6.1 Summary. The exact method for Markov chain (MC) simula-
tion for an electrotonically compact (single compartment) conductance-
based stochastic model under current clamp is a hybrid discrete (channel
state)/continuous (voltage) model of the sort used by Clay and DeFelice
(1983), Newby et al. (2013), and Anderson et al. (2015). While MC methods
are computationally expensive, simulations based on gaussian/Langevin
approximation can capture the effects of stochastic ion channel fluctua-
tions with reasonable accuracy and excellent computational efficiency. Since
Goldwyn and Shea Brown’s work focusing the attention of the computa-
tional neuroscience community on Fox and Lu’s Langevin algorithm for the
Hodgkin-Huxley system (Fox & Lu, 1994; Goldwyn & Shea-Brown, 2011),
several variants of this approach have appeared in the literature.

channel, and eight states of the Na

In questo articolo, we advocate for a class of models combining the best fea-
tures of conductance-based Langevin models with the recently developed
stochastic shielding approximation (Schmandt & Galán, 2012; Schmidt &
Thomas, 2014; Schmidt et al., 2018). We propose a Langevin model with
a 14-dimensional state space, representing the voltage, five states of the
K+
+
-channel; and a 28-dimensional rep-
resentation of the driving noise: one independent gaussian noise term for
each directed edge in the channel-state transition graph. We showed in sec-
zione 2 that the corresponding mean-field 14D ordinary differential equation
model is consistent with the classical HH equations in the sense that the
latter correspond to an invariant submanifold of the higher-dimensional
modello, to which all trajectories converge exponentially quickly. Figura 2
illustrated the relation between the deterministic 4D and 14D Hodgkin-
Huxley systems. Building on this framework, we introduced the 14 × 28D
modello, with independent noise sources corresponding to each ion channel
transition (see section 3). We proved in section 4 that given identical bound-
ary conditions, our 14 × 28D model is pathwise equivalent to Fox and Lu’s
original Langevin model and to a 14-state model with 14 independent noise
sources due to Orio and Soudry (2012).

The original 4D HH model, the 14D deterministic HH model, and the
family of equivalent 14D Langevin models we consider here form a nested

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1816

S. Pu and P. Thomas

family, each contained within the next. Specifically, the 14D ODE model is
the mean-field version of the 14D Langevin model, and the 4D ODE model
forms an attracting invariant submanifold within the 14D ODE model, COME
we establish in our lemma 2. So in a very specific sense, the original HH
equations “live inside” the 14D Langevin equations. Così, these three mod-
els enjoy a special relationship. In contrasto, the 4D Langevin equations stud-
ied in Fox (1997) do not bear an especially close relationship to the other
three.

In addition to rigorous mathematical analysis, we also performed nu-
merical comparisons (see section 5) showing that, as expected, the pathwise
equivalent models produced statistically indistinguishable interspike inter-
val (ISI) distributions. Inoltre, the ISI distributions for our model (E
its equivalents) were closer to the ISI distribution of the gold standard MC
model under two different metric space measures. Our method (along with
Orio and Soudry’s) proved computationally more efficient than Fox and
Lu’s original method and Dangerfield’s model (Dangerfield et al., 2012).
Inoltre, our method lends itself naturally to model reduction (via the
stochastic shielding approximation) to a significantly faster 14 × 6D simu-
lation that preserves a surprisingly high level of accuracy.

6.2 Discrete Gillespie Markov Chain Algorithms. The discrete-state
MC algorithm due to Gillespie is often taken to be the gold standard simu-
lation for a single-compartment stochastic conductance-based model. Most
former literature on Langevin HH models (Goldwyn & Shea-Brown, 2011;
Linaro et al., 2011; Orio & Soudry, 2012; Huang et al., 2013), when establish-
ing a reference MC model, consider a version of the discrete Gillespie algo-
rithm that assumes a piecewise-constant propensity approximation, questo è,
it does not take into account that the voltage changes between transitions,
which changes the transition rates. This approximation can lead to biophys-
ically unrealistic voltage traces for very small system sizes (Guarda la figura 2 Di
Kispersky & White, 2008; top trace with N = 1 ion channel) although the
differences appear to be mitigated for N (cid:4) 40 channels (Anderson et al.,
2015). In this article our MC simulations are based on 6000 Na+ and 1800
K+ channels (as in Goldwyn & Shea-Brown, 2011), and we too use the ISI
distribution generated by a piecewise-constant propensity MC algorithm
as our reference distribution. As shown in Table 3 and Figure 8, the com-
putation time for MC is one order of magnitude larger than efficient meth-
ods such as Orio and Soudry (2012) and Dangerfield et al. (2012) and the
14 × 28D model. The computational cost of the MC model increases dra-
matically as the number of ion channels grows; Perciò, even the approx-
imate MC algorithm is inapplicable for a large number of channels.

6.3 Langevin Models. It is worth pointing out that the accuracy of Fox
and Lu’s original Langevin equations has not been fully appreciated. Infatti,
Fox and Lu’s model (Fox & Lu, 1994) gives an approximation to the MC

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Fast and Accurate Stochastic Hodgkin-Huxley Simulations

1817

model that is just as accurate as that of Orio and Soudry (2012) both in the
gating variable statistics (Goldwyn & Shea-Brown, 2011) and the ISI dis-
tribution sense (see section 5), because, as we have established, these mod-
els are pathwise equivalent! Tuttavia, the original implementation requires
taking a matrix square root in every time step in the numerical simulation,
which significantly reduces its computational efficiency.

Models based on modifications of Fox and Lu’s (1994) work can be di-
vided into three classes: the subunit model (Fox, 1997), effective noise mod-
els (Linaro et al., 2011; Güler, 2013B), and channel-based Langevin models
(per esempio., Goldwyn & Shea-Brown, 2011; Dangerfield et al., 2012; Orio & Soudry,
2012; Pezo et al., 2014; Huang et al., 2013).

6.3.1 Subunit Model. The first modification of Fox and Lu’s model is the
subunit model (Fox, 1997), which keeps the original form of the HH model,
and adds noise to the gating variables (M, H, and n) (Fox, 1997; Goldwyn
& Shea-Brown, 2011). The subunit approximation model was widely used
because of its fast computational speed. Tuttavia, as Bruce (2009) and oth-
ers pointed out, the inaccuracy of this model remains significant even for
large number of channels. Inoltre, Goldwyn and Shea-Brown (2011) E
Huang et al. (2015) found that the subunit model fails to capture the statis-
tics of the HH Na+
gates. In questo articolo, we also observed that the
subunit model is more efficient than channel-based Langevin models but
tends to delay spike generation. Come mostrato in figura 7, the subunit model
generates significantly longer ISIs than the MC model.

and K

+

6.3.2 Effective Noise Models. Another modification to Fox and Lu’s algo-
rithm is to add colored noise to the channel open fractions. Though colored
noise models such as those of Linaro et al. (2011) and Güler (2013B) are not
included in our model comparison, Huang et al. (2015) found that both of
these effective noise models generate shorter ISIs than the MC model with
the same parameters. Though the comparison we provided in section 5 only
include the Fox and Lu 94, Fox97, Goldwyn, Dangerfield, Orio, SS, and the
14 × 28D models, combining the results from Goldwyn and Shea-Brown
(2011) and Huang et al. (2015), IL 14 × 28D model could be compared to a
variety of models (per esempio., Fox & Lu, 1994; Fox, 1997; Goldwyn & Shea-Brown,
2011; Linaro et al., 2011; Orio & Soudry, 2012; Dangerfield et al., 2012; Huang
et al., 2013; Güler, 2013B).

6.3.3 Channel-based Langevin Models. The main focus of this article is
the modification based on the original Fox and Lu’s matrix decomposi-
tion method, namely, the channel-based (or conductance-based) Langevin
models. We proved in section 4 that under the same boundary conditions,
Fox and Lu’s original model, Orio’s model, and our 14 × 28D model are
pathwise equivalent, which was also verified from our numerical simula-
tions in sections 4 E 5. In section 4 we discussed channel-based Langevin

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
N
e
C
o
_
UN
_
0
1
3
1
2
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

1818

S. Pu and P. Thomas

models (Fox & Lu, 1994; Goldwyn & Shea-Brown, 2011; Dangerfield et al.,
2012; Orio & Soudry, 2012; Fox, 2018). We excluded Fox’s more recent im-
plementation (Fox, 2018) in section 5 for two reasons. Primo, the algorithm is
pathwise equivalent to others considered there. Inoltre, the method is
vulnerable to numerical instability when the Cholesky decomposition is
performed. Specifically, some of the elements in the S matrix from the
Cholesky decomposition in Fox (2018) involve square roots of differences of
several quantities, with no guarantee that the differences will result in non-
negative terms—even with strictly positive value of the gating variables.
Nevertheless, this model would be in the equivalence class and in any case
would not be more efficient than the Orio model because of the noise dimen-
sion and complicated operations (involving taking multiple square roots) In
each step.

6.4 Model Comparisons. If two random variables have similar distri-
butions, then they will have similar moments, but not vice versa. Therefore,
comparison of the full interspike-interval distributions produced by dif-
ferent simulation algorithms gives a more rigorous test than comparison
of first and second moments of the ISI distribution. Most previous evalua-
tions of competing Langevin approximations were based on the accuracy
of low-order moments, Per esempio, the mean and variance of channel
state occupancy under voltage clamp, or the mean and variance of the
interspike interval distribution under current clamp (Goldwyn et al., 2011;
Goldwyn & Shea-Brown, 2011; Schmandt & Galán, 2012; Linaro et al., 2011;
Dangerfield et al., 2012; Orio & Soudry, 2012; Huang et al., 2013, 2015).
Here, we compare the accuracy of the different algorithms using the full ISI
distribution but using the L1 norm of the difference (Wasserstein metric)
and the L∞ norm (Kolmogorov-Smirnov test). Greenwood, McDonnell,
and Ward (2015) previously compared the ISI distributions generated by
the Markov chain (Gillespie algorithm) to the distribution generated by
different types of Langevin approximations (LA), including the original
Langevin models (Fox & Lu, 1994; Goldwyn & Shea-Brown, 2011), IL
channel-based LA with colored noise (Linaro et al., 2011; Güler, 2013B),
and LA with a 14 × 14 variant of the diffusion coefficient matrix S (Orio &
Soudry, 2012). They concluded that Orio and Soudry’s method provided
the best match to the Markov chain model, specifically, “Fox-Goldwyn, E
Orio-Kurtz8 methods both generate ISI histograms very close to those of
“Micro.”9 (Greenwood et al., 2015). We note that the comparison reported
in this article simply superimposed plots of the ISI distributions, allowing
a qualitative comparison, while our metric-space analysis is fully quan-
titative. In any case, their conclusions are consistent with our findings;
we showed in section 4 that the Fox-Goldwyn and the Orio-Kurtz model

8

9

We refer to this model as “Orio.”
This is the model we refer to as the Markov chain model.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H