ARTICLE
Communicated by Diego Pazò
A Mean-Field Description of Bursting Dynamics in Spiking
Neural Networks with Short-Term Adaptation
Richard Gast
rgast@cbs.mpg.de
Helmut Schmidt
hschmidt@cbs.mpg.de
Max Planck Institute for Human Cognitive and Brain Sciences,
04103 Leipzig, Germany
Thomas R. Knösche
knoesche@cbs.mpg.de
Max Planck Institute for Human Cognitive and Brain Sciences, 04103 Leipzig,
Germany, and Institute for Biomedical Engineering and Informatics, TU 98693
Ilmenau, Germany
Bursting plays an important role in neural communication. At the pop-
ulation level, macroscopic bursting has been identified in populations
of neurons that do not express intrinsic bursting mechanisms. For the
analysis of phase transitions between bursting and non-bursting states,
mean-field descriptions of macroscopic bursting behavior are a valuable
tool. In questo articolo, we derive mean-field descriptions of populations
of spiking neurons and examine whether states of collective bursting
behavior can arise from short-term adaptation mechanisms. Specifi-
cally, we consider synaptic depression and spike-frequency adaptation
in networks of quadratic integrate-and-fire neurons. Analyzing the
mean-field model via bifurcation analysis, we find that bursting be-
havior emerges for both types of short-term adaptation. This bursting
behavior can coexist with steady-state behavior, providing a bistable
regime that allows for transient switches between synchronized and
nonsynchronized states of population dynamics. For all of these find-
ing, we demonstrate a close correspondence between the spiking neural
network and the mean-field model. Although the mean-field model
has been derived under the assumptions of an infinite population
size and all-to-all coupling inside the population, we show that this
correspondence holds even for small, sparsely coupled networks. In
summary, we provide mechanistic descriptions of phase transitions
between bursting and steady-state population dynamics, which play
important roles in both healthy neural communication and neurological
disorders.
Calcolo neurale 32, 1615–1634 (2020) © 2020 Istituto di Tecnologia del Massachussetts
https://doi.org/10.1162/neco_a_01300
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
9
1
6
1
5
1
8
6
5
0
0
6
N
e
C
o
_
UN
_
0
1
3
0
0
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1616
R. Gast, H. Schmidt, and T. Knösche
1 introduzione
The brain, composed of billions of single cells, has been demonstrated
to possess a hierarchical, modular organization, indicative of a complex
dynamical system (Ballard, 2015). Within this hierarchy, populations of
neurons form functional entities, the states of which are defined by the
collective dynamics of the population rather than by the activities of each
single cell. Mean-field descriptions of the macroscopic dynamics of such
populations are a valuable tool for the mathematical analysis of collective
phenomena, as well as for computational models of multiple coupled pop-
ulations of neurons. Population bursting is a particular mode of collective
behavior that plays a major role in both healthy and pathological neural
dynamics. At the single neuron level, bursting is characterized by the neu-
ron firing a train of spikes, followed by a period of quiescence (Izhikevich,
2000). This behavior has been suggested to result from adaptive mecha-
nisms introducing a slow timescale that enables dynamic regimes of burst-
ing and controls the burst period (Izhikevich, 2000; Dhamala, Jirsa, & Ding,
2004). Mathematical descriptions of such adaptation mechanisms have been
developed accordingly at the level of single cells. Importantly, bursting has
also been reported in populations of cells without intrinsic bursting mecha-
nisms (Izhikevich, 2000; Marder & Thirumalai, 2002; Zeldenrust, Wadman,
& Englitz, 2018). In such cases, bursting can be conceived as a property of
the collective dynamic interactions within the population, henceforth re-
ferred to as emergent bursting.
In healthy neural communication, emergent bursting activity may allow
for a more reliable information transmission via chemical synapses (Lis-
Uomo, 1997). This can be explained by the synchronized activity of the pop-
ulation during the burst, which stabilizes neural information transmission
against different types of noise (Hahn, Ponce-Alvarez, Deco, Aertsen, & Ku-
mar, 2019). Increased bursting, Tuttavia, activity has been found in various
neurological diseases, such as epilepsy and Parkinson’s disease, and can
act disruptively on neural communication if it exceeds certain levels of oc-
currence (Connors, 1984; Lobb, 2014). The mechanisms behind emergent
bursting are not well understood, since most of the computational literature
on bursting focuses on single cells (Guckenheimer, Harris-Warrick, Peck, &
Willms, 1997; Izhikevich, 2000). Typical approaches to model bursting at
the population level either use coupled circuits of excitatory and inhibitory
populations (Kudela, Franaszczuk, & Bergey, 2003; Zeldenrust, Wadman, &
Englitz, 2018) or include an explicit bursting mechanism such as the action
of a neuromodulator (Marder & Thirumalai, 2002), feedforward inhibition
(Zeldenrust & Wadman, 2013), or spike-frequency adaptation (SFA) (van
Vreeswijk & Hansel, 2001). Per esempio, van Vreeswijk and Hansel (2001)
demonstrated in a network of coupled, excitatory leaky integrate-and-fire
neurons that SFA can lead to the emergence of network bursting.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
9
1
6
1
5
1
8
6
5
0
0
6
N
e
C
o
_
UN
_
0
1
3
0
0
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Bursting Dynamics in QIF Networks
1617
Importantly, these approaches investigate spiking neural networks,
where the macroscopic state variables have to be inferred from single cell
activities. Tuttavia, a direct mathematical description of the macroscopic
dynamics would be beneficial for both mathematical analyses of emergent
bursting and studies on multiple coupled bursting populations. This is ev-
ident from the number of neural mass models that have been applied to
study phase transitions between asynchronous and bursting states in cou-
pled neural populations ((Suffczynski, Kalitzin, & Lopes Da Silva, 2004);
(Breakspear et al., 2006; Spiegler et al., 2011; Chen et al., 2014); (Müller, van
Albada, Kim, & Robinson, 2017)). These models describe macroscopic state
variables such as average firing rates inside a population. Importantly, Essi
have not been derived from a spiking neural network but were designed to
resemble experimentally observed macroscopic features of neural behavior,
such as the input-output relationships of a population or spectral features
of population activity (Wilson & Cowan, 1972; Jansen & Rit, 1995; Robin-
figlio, Rennie, & Wright, 1997). Due to the continuous nature of such macro-
scopic state variables, neural mass models allow applying various methods
from dynamical systems theory that could not be applied to spiking neural
networks—for example, directly linking changes in the model structure to
phase transitions. Tuttavia, as the employed neural mass models are of a
phenomenological nature, the mechanistic link to the underlying spiking
neurons remains unclear in this type of work. While suited to investigate
the emergence of bursting behavior within circuits of coupled neural pop-
ulazioni, these models offer limited insight into the emergence of bursting
within a population based on its intrinsic dynamics.
The aim of this article is to provide and validate mean-field descriptions
of collective bursting emerging from the dynamic interaction of short-term
adaptation mechanisms and recurrent excitation in populations of coupled
spiking neurons. Hence, our work closes the gap between investigations
of population bursting in spiking neural networks and neural mass mod-
IL. First efforts into this direction were made for the special case of SFA
in a network of coupled linear integrate-and-fire neurons, employing the
Fokker-Planck formalism and an adiabatic approximation given long SFA
timescales (Gigante, Mattia, & Giudice, 2007). Analyzing this mean-field
description, Gigante et al. (2007) were able to identify different types of col-
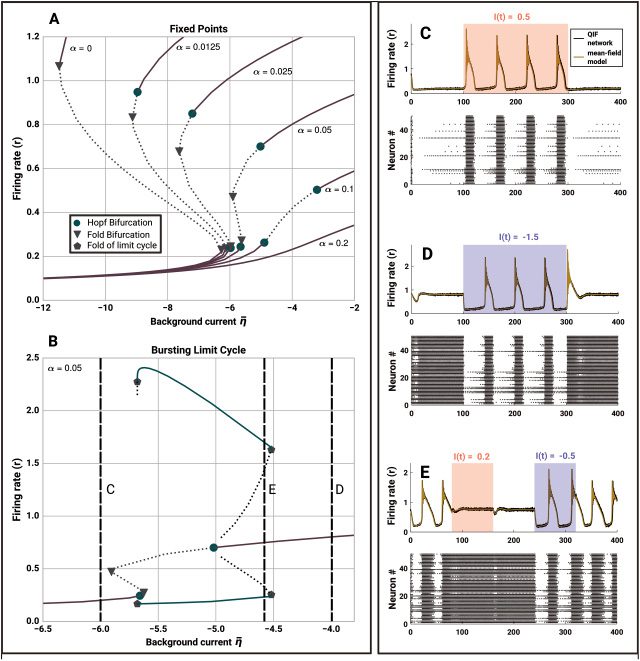
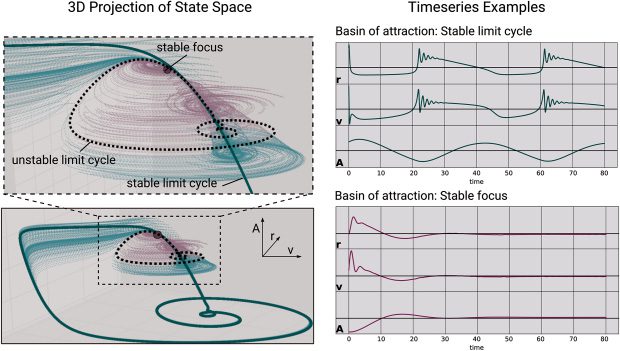
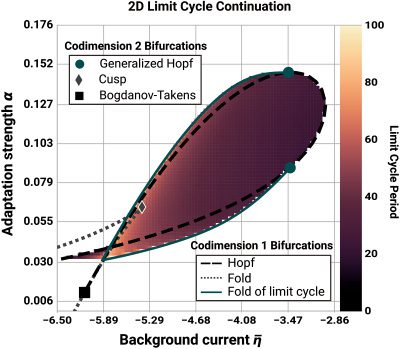
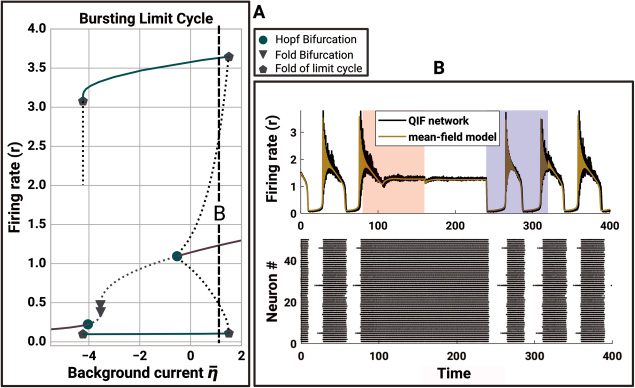
lective bursting. In questo articolo, we show under which conditions bursting
can emerge as a collective phenomenon from different short-term adapta-
zione (STA) mechanisms within a population of coupled spiking neurons.
A tal fine, we consider multiplicative and additive adaptation as general-
ized descriptions of the vast number of STA mechanisms that have been re-
ported to affect neural excitability. We incorporate these STA mechanisms in
a globally coupled population of quadratic integrate-and-fire (QIF) neurons
and derive mean-field descriptions of the macroscopic dynamics follow-
ing the approach by Montbrió, Pazó, and Roxin (2015). Using bifurcation
analysis, we identify states of collective bursting as well as the boundary
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
2
9
1
6
1
5
1
8
6
5
0
0
6
N
e
C
o
_
UN
_
0
1
3
0
0
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1618
R. Gast, H. Schmidt, and T. Knösche
conditions for such bursting to occur. Our results show how changes in ei-
ther the average input or the strength of short-term adaptation within a
neural population can drive the population into and out of collective burst-
ing. We find that short-term adaptation gives rise to bistable regimes of
concurrent bursting and nonbursting states, and we show how different
short-term adaptation mechanisms can have very similar effects on the pop-
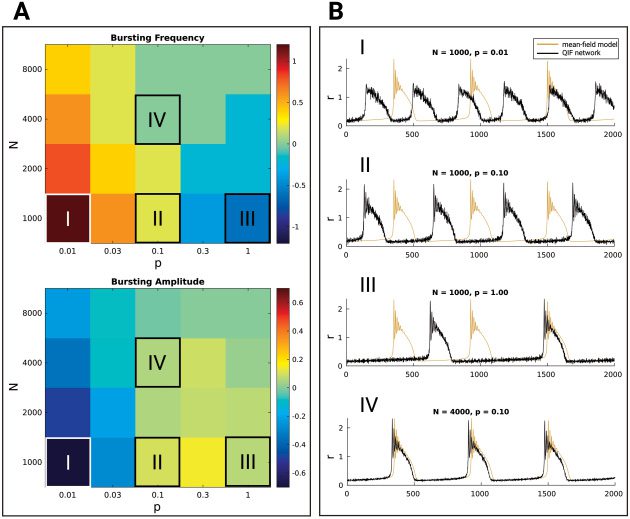
ulation dynamics. Finalmente, we perform a finite size analysis in which we ex-
amine the effects of network size and coupling probability of the spiking
neural network on the correspondence between this microscopic network
description and the mean-field model.
We find that emergent bursting can be found for all network sizes and
coupling probabilities we considered. Inoltre, we demonstrate that
the mean-field model generalizes well to networks of biologically plausible
size and coupling probability. This makes our work applicable to a broad
range of neurodynamic scenarios in which the impact of changes in pop-
ulation input or short-term adaptation strength on the behavior of spiking
neuron populations is of interest.
2 Model Definition
The QIF neuron is the canonical form of type 1 neurons and has previously
been used in combination with linear adaptation as a basis for models of
bursting cells (Izhikevich, 2000). The evolution equation of the membrane
potential Vi of a single QIF neuron i is given by
τ ˙Vi
= V 2
io
+ η
io
+ IO(T) + Jsτ,
(cid:2)
(cid:3)
T
N(cid:2)
s = 1
N
j=1
k\tk
J