A R T I S TS’ AR T Ic l e - Ricerca sull'intelligenza artificiale specializzata al MIT

A R T I S TS’ AR T Ic l e

From structure to atoms

From Compression/Tension Systems

to a Molecular Tensegrity

J . D avI D v a n ho r n An d D ay u W a n g

T
C
UN
R
T
S
B
UN

The authors reconsider macroscopic structures, including tensegrity
structures, as ensembles of compression and tension forces and fit
these structures to a triangular spectrum. They then present a derivative
structural analogy to the three classes of molecular bonding as a
bridge to microscopic structure. The construction of tensegrity sculptures
of particle interactions and covalent molecules using tension and
compression components follows. The authors derive and utilize two
properties in this analysis: (1) a “simplest tensegrity” subunit structure and
(2) interpenetrating, discontinuous compressive components—the tension
components may also be discontinuous in a structure. This approach
provides new artistic models for molecules and materials and may
inform future artistic, architectural, engineering and scientific endeavors.

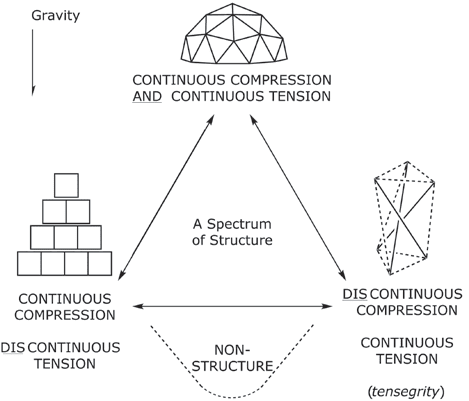
a spECtrum oF struCturE

For millennia, humans have been constructing all types of
utilitarian, artistic and architectural objects. These are formed
from natural or modified materials that possess the character
needed to adopt specific forms or functions [1,2]. Esempi
include a wheeled cart or an ax, a decorative serving bowl or
a pitcher, and a tent or a Greek temple. In all cases, the object’s
structure consists of compression (C) and tension (T) interac-
tions throughout and between the components making up the
object [3]. We use the terms compression and tension in their
usual physics sense, and we equate these terms to repulsion
and attraction forces, rispettivamente. Così, an object in com-
pression has internal repulsive forces acting against external
forces pushing inward, and an object in tension possesses
internal attractive forces to maintain its structural integrity.
Consider structure as existing on a spectrum composed
of compressive and tensile force networks, acting together
to form a three-dimensional object. This spectrum can be
thought of as having four extremes: (1) continuous com-

J. David Van Horn (scientist, educator), 5110 Rockhill Road, Department of
Chemistry, University of Missouri, Kansas City, MO 64110, U.S.A.
E-mail: vanhornj@umkc.edu.

Dayu Wang (scientist, educator), 5110 Rockhill Road, Department of
Chemistry, University of Missouri, Kansas City, MO 64110, U.S.A.
E-mail: dayuwang@mail.umkc.edu.

See https://direct.mit.edu/leon/issue/54/6 for supplemental files associated
with this issue.

pression/discontinuous tension networks; (2) continuous
compression and tension networks; (3) discontinuous com-
pression/continuous tension networks; E (4) both discon-
tinuous compression and tension networks (Fig. 1). Here,
“continuous” refers to a unified network of interactions with
paths between all elements; “discontinuous” denotes sepa-
rated or terminal elements and gaps in the networks of inter-
actions [4,5]. We include the case with discontinuous C and T
for completeness, but we set it aside because it does not lead
to structure. Gravity is pertinent here and is considered a ten-
sile, attractive force acting on objects and structures on earth.
A zero-gravity environment, and how structures perform
under this condition, is also relevant to the evaluation and
use of any type of structure in the spectrum. Other forces—
including torsion, shear and friction—are set aside to focus
on three-dimensional C/T structures in static equilibrium.
Examples of architecture exhibiting continuous compres-
sion but discontinuous tension include ancient monumen-
tal pyramids, certain arches and unmortared brick or stone
chimneys (Fig. 1). In these structures, gravity provides a sepa-
rate tensile force to each component but results in a con-
tinuous compression network throughout the structure. In a
zero-gravity environment, these structures would gradually
drift apart, having no internal tension elements.

Tensegrity is a discontinuous compression but continuous
tension system that resides at the other extreme of disconti-
nuity in our spectrum. This term was coined by R.B. Fuller
from “tensional integrity” [6]; others define it as an “endo-
skeletal floating-compression structure” [7] or a “minimal
self-tensile construction” [8]. Tensegrity encompasses the
discontinuous compression structural systems discovered
and described by Kenneth Snelson and others [9,10]. Tenseg-
rity structures are “comfortable” in zero gravity, retaining
their three-dimensional shapes without external influence.
Nevertheless, on Earth these structures must have enough
“tensional integrity” to overcome the added force of grav-
ity acting on the components. The key feature of the two
structural extremes above is the discontinuity of one of the
structural force networks.

https://doi.org/10.1162/leon_a_02051

LEONARDO, Vol. 54, No. 6, pag. 599–605, 2021 599

Scaricato da http://direct.mit.edu/leon/article-pdf/54/6/599/2028654/leon_a_02051.pdf by guest on 07 settembre 2023

of the discovery of discontinuous compression structures in
the mid-twentieth century and their development by Ken-
neth Snelson and others.

somE baCkgrounD on ChEmICal bonDIng

To relate architectural and artistic structures to molecules re-
quires some reference to the history and concept of chemical
bonding—i.e. the forces holding elements together in met-
COME, molecules and materials. The discovery of the electron
provided an entry into modern atomic structures of elements
and molecular combinations. Useful molecular theories of
the early twentieth century (Tavolo 1) described atomic ker-
nels held together by shared electrons for covalent structures
or composed of electrostatic interactions of ions for hold-
ing ionic structures together [11]. Metals and alloys may be
a more “elemental” aggregate, but the concept of metallic
bonding, notably free-electron theory [12], was also devel-
oped out of classical theory.

The observation of quantum behavior in molecules and
the proposal of wave-particle duality in the 1920s shifted the
particle theories of molecular structure toward wave-form
molecular orbital theory. This direction has led to our current
state-of-the-art, computational methods. Despite the success
of quantum mechanics, the rather “particle-based” molecular
structure theories of Gilbert Lewis [13], Irving Langmuir [14]
and others persist because of their conceptual utility in un-
derstanding basic molecular structure and reactivity. Lewis
dot structures are taught to students as a starting point for
understanding covalent and ionic molecular structures and
reactions. This conceptual thread of understanding mole-
cules as particle-based systems was supplemented by the de-
velopment of valence shell electron pair repulsion (VSEPR)
theory and other ideas and constructs [15–18], in parallel with
molecular orbital theory.

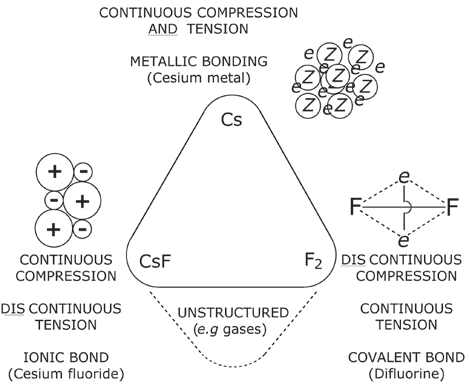
a ComprEssIon/tEnsIon molECular analogy

Considering macroscopic structure in terms of C/T forces,
and applying this to metallic, ionic and covalent bonding,
led us to make models of chemical interactions consisting
of a spectrum of continuous to discontinuous repulsive
(compressive, C) and attractive (tensile, T) forces (Tavolo 1;
Fig. 2). Primo, ionic bonding is analogous to a structure with

Fig. 1. Structures (under gravity) considered on a triangle with limiting
structures related to extremes in compression and tension (C/T) elements and
their continuity. (© J. David Van Horn)

Structures consisting of both continuous tension and
compression element networks are harder to visualize and
exemplify. Many objects—for instance, a sphere, a ring, UN
box, etc.—probably exhibit combined continuous tensile and
compressive forces, and derivative structures may have con-
tinuous parts but be constructed with discontinuities at the
interfaces of the parts. A geodesic hemisphere may serve as
an example (Fig. 1): This object may be engineered to retain
its shape in any placement, orientation or gravitational envi-
ronment via continuous C/T elements. On Earth, in normal
usage, this type of structure transmits a continuous compres-
sion force through the structure to the ground or base.

Compressive forces in structures and building methods
have predominated humanity’s historic approach to architec-
ture; large architectural tension elements are more recently
utilized. For instance, utilitarian structures that include ten-
sion elements such as prestressed concrete, large awnings,
cable- stayed construction, suspension bridges and so on
started to be notable features in the human landscape over the
last century. In contrasto, a zero-gravity environment would
seem to necessitate the use of tension elements foremost, A
keep structural components together. A more systematic
analysis of structure, examining varying degrees of C/T ele-
menti, should be fruitful and underscores the significance

tablE 1. Comparison of C/t structural types and molecular analogs

type

First Description

Compression

tension

Esempio

Ancient

Continuous

Discontinuous

Stone pyramid

Ancient

Continuous

Simple arch

ca. 1950
(Snelson;
Koleychuk)

Discontinuous

Continuous

A tensegrity
sculpture

Ancient or historic

Discontinuous

No structure

continuous: unified network of interactions. Discontinuous: separated elements or networks of interactions.

molecular
analog

Ionic
bonding

Metallic
bonding

Covalent
Bonding

bonding model

Berzelius to
Kossel (1800–1900)

Drude (ca. 1900)

Lewis (ca. 1916),
Linnett (1955)

Gases (cf. χάος
to “gas”)

Van Helmont
(ca. 1600)

600 Van Horn and Wang, From Structure to Atoms

Scaricato da http://direct.mit.edu/leon/article-pdf/54/6/599/2028654/leon_a_02051.pdf by guest on 07 settembre 2023

Fig. 2. A correlation of the three chemical bonding types (metallic, ionic
and covalent) to compression and tension elements and networks on a
van Arkel–Ketelaar triangle of bonding. (© J. David Van Horn)

continuous compression elements but discontinuous tensile
elements (e.g. salts; cesium fluoride). Prossimo, metallic bond-
ing corresponds to having both continuous compressive and
tensile elements (e.g. pure metals and alloys; cesium). Fi-
nally, covalent bonding is analogous to tensegrity as having
discontinuous compressive elements and continuous tension
elements (e.g. molecular materials; dihydrogen, difluorine).
Sculptures and models of idealized bonding types, here con-
ceptualized as C/T systems, may be constructed to represent
stable equilibrium structures for the three types of bond-
ing: ionic, metallic and covalent. Inoltre, we propose an
analogous van Arkel–Ketelaar bonding triangle [19] (Fig. 2),
describe structural units to make up molecular models, E
present noteworthy covalent molecules in terms of a “mo-
lecular tensegrity.”

thE C/t struCtural ConCEpt

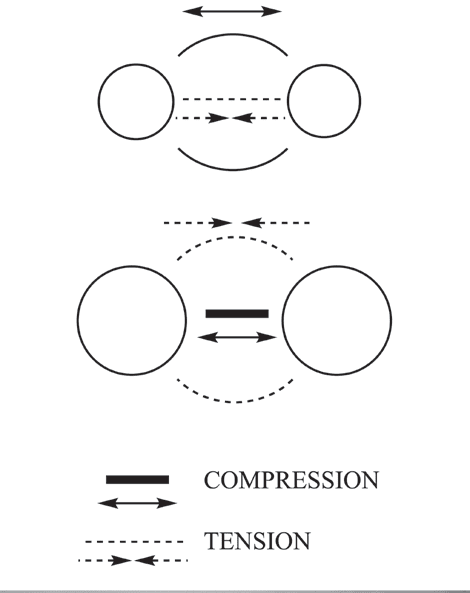
two particle interactions and a “Simplest t ensegrity”

To adapt tensegrity to these bonding interactions, consider a
new “simplest tensegrity” as a C/T structural unit [20]. Questo
unit is made up of two objects or particles with one (or more)
compression elements and one (or more) tension elements
interacting in a static equilibrium (Fig. 3). In questo articolo, UN
solid line (–) represents a compressive (repulsive) force, E
a dashed line (- – -) the tensile (attractive) force.

One can make or conceive of many two-body examples.
For example, a magnet constrained to float over another
identical magnet represents a two-body model, with gravity
acting as a tension element against a compressive element—
the repulsion between the magnets (Fig. 3, photo and middle
schematic). The strength of the magnetic field pushing the
magnets apart can be calculated from their mass and size
and using appropriate conversion factors (see the appendix
in the online supplemental materials). Also illustrated in
Fig. 3 (photo and top schematic) is an arrangement of coaxial
springs—one in compression, one in tension—making up a
“two-particle” simplest tensegrity.

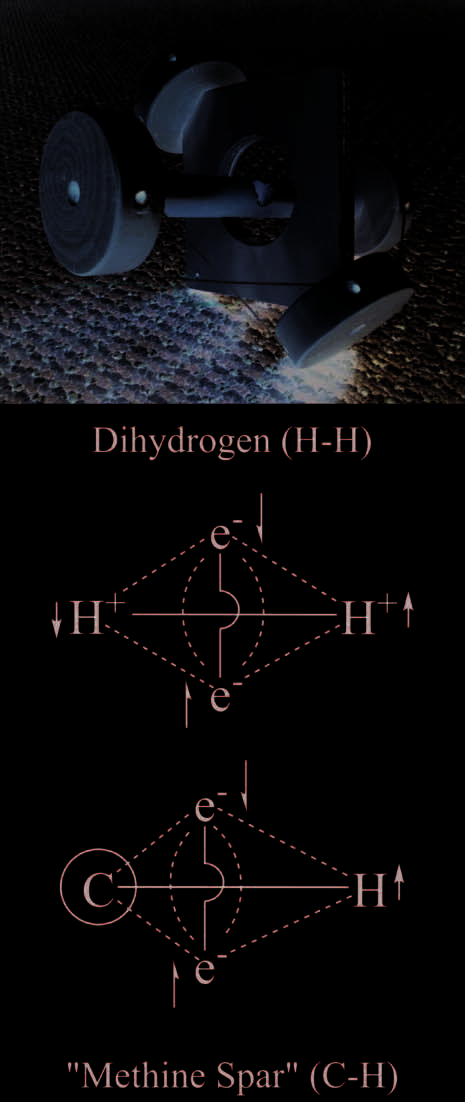
Dihydrogen and interpenetrating c/t elements

Covalently bonded molecules may be modeled as C/T
“tensegrity” systems using combinations of simpler units.
Two hydrogen atoms (see the supplemental appendix) are
paired to form dihydrogen as follows: The electrons and the
protons each separately exhibit repulsion elements while be-
ing held together by attractive elements that encompass all
four particles (Fig. 4). The attractive interactions in H–H
mainly arise from +/- electrostatic charge interactions, Ma
additional stability is attained via tension elements between
like particles—electrons in a spin-paired singlet form and
protons in a spin-paired arrangement. To follow the stipula-
tion of discontinuous compression elements in a tensegrity
structure (or here in a covalent bond), we utilize the property
of interpenetrating compression elements.

Fig. 3. Schematics and examples, rispettivamente, of objects made up of two
“particles” and C/T force components exhibiting a “simplest tensegrity”
(see notes 5 E 20). Compression as lines (–) and tension as dashes (- – -).
(© J. David Van Horn)

Methine Spar to Methane, Ammonia and Water

From the dihydrogen model, the replacement of hydrogen
with other atoms, while retaining the interpenetrating com-

Scaricato da http://direct.mit.edu/leon/article-pdf/54/6/599/2028654/leon_a_02051.pdf by guest on 07 settembre 2023

Van Horn and Wang, From Structure to Atoms 601

Fig. 4. A C/T model for dihydrogen (H–H): Its C/T diagram and that for a
C–H “methine spar,” including atomic spins, show the various compression
and tension elements in the constructs. The model demonstrates interpenetrating
compression elements (Property 2, Astratto). (©J. David Van Horn)

pressive elements, provides additional subunits for making up
covalent molecular structures. In this way, one can build a
C–H unit, here termed a “methine spar”; additionally, B–H,
N–H, O–H and other X–H units will have similar arrange-
menti. The merging of four methine spars provides for the
construction of methane (CH4, Fig. 5); likewise, three N–H
units plus a nonbonding electron pair lead to ammonia
(NH3) and a pair of O–H spars and two nonbonding electron
pairs are merged to form a C/T structure of water (H2O). Vedere
the online appendix for further elaboration.

Fig. 5. A three-dimensional Lewis structure of methane, and the molecule as
a C/T tensegrity; in the sculpture the methine spars have been simplified as
hexagonal paddles, but in turn are held to the sphere by a tension network.
(© J. David Van Horn)

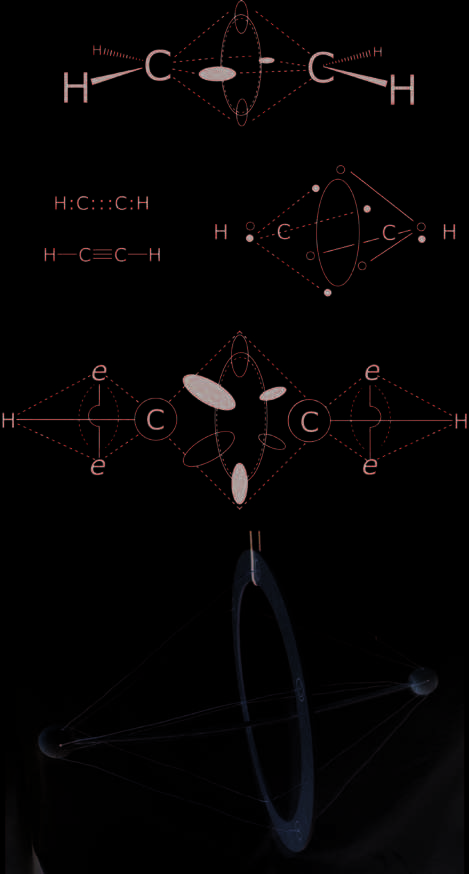
carbon-carbon Bonds

Singly and multiply bonded atoms can be addressed in the
C/T model as follows. For carbon atoms, a carbon-carbon
single bond (C–C) is made up of an arrangement like di-
hydrogen, but with carbon nuclei; a carbon-carbon double
legame (C=C) is made up of four electrons over the two atoms,
and a triple bond (C==C), six electrons over the two atoms.
We can retain the Lewis drawings of simple molecules, Ma
J.W. Linnett proposed a more detailed picture of the elec-
tron arrangements in multiply bonded atoms [21]; il suo lavoro
partially inspired the ideas of C/T systems presented in this
article. The C–C single bond and the C=C and C==C multiple
bonds can be built as valid “tensegrity” structures and can be
conceptualized as sets of two, four or six electrons providing
a tension framework for the stable combination of the carbon
atoms (Fig. 6). These constructs may represent a molecular

602 Van Horn and Wang, From Structure to Atoms

Scaricato da http://direct.mit.edu/leon/article-pdf/54/6/599/2028654/leon_a_02051.pdf by guest on 07 settembre 2023

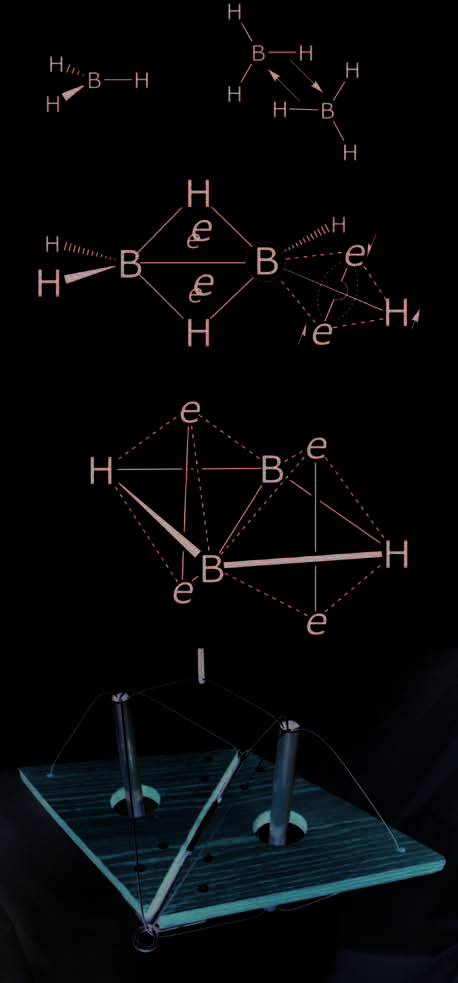
Diborane

Boron is an electron-deficient atom, and in borane, BH3, Questo
deficiency is accommodated by the dimerization of two BH3
units to form diborane (B2H6). Sharing of electrons from one
B–H bond to the adjacent boron atom provides stability in
the form of a two-electron, three-center bond. This bonding
arrangement is treated by many approaches, including the
present C/T concept.

The arrangement of particles in diborane as a C/T struc-
ture (Fig. 7) is described by considering the four external
B–H bonds to be B–H spars (see above)—a 2-e–/2-atom unit.
The two boron atoms and two central hydrogen atoms are

Fig. 6. Lewis dot and Linnett “double-quartet” depictions of acetylene
(HCCH) (top, adapted from R.J. Gillespie’s work [24]); C/T diagrams of C=C
and C==C bond structures; a tensegrity of Linnett acetylene (bottom) in which
the six electrons are considered as a single compression ring.
(© J. David Van Horn)

model of structures related to Linnett’s “double quartet” the-
ory [22]. Linnett proposed that Lewis’s electron “pair” shar-
ing concept was too limited, asserting that “double quartets”
or “diamagnetic sets” of electrons account for bonding in
C–C, C=C, O–O, F—F and other covalent systems.

Conceptually for basic C/T models, ideal molecular struc-
tures only consist of those particles interacting with their
nearest neighbors. In reality, particle interactions have a de-
pendence on distance and on the shielding effect of other
particles, and they have other dependencies that complicate
the exact description of molecular systems. Nevertheless, IL
idea of a tension network in the C/T molecular concept is
additionally useful for understanding possible longer-range
interactions within a molecule and allows for effects to be
transmitted over considerable distance in a molecule, e.g.
the nuclear spin coupling observed in magnetic resonance
esperimenti. In the C/T models as built here, and as known
in “tensegrity” sculptures, the individual parts of a structure
influence distant parts of a structure.

Fig. 7. Borane (BH3) and diborane (B2H6) chemical drawings with a partial
C/T diagram of diborane; detail of the [B2H2] C/T core; tensegrity sculpture
of the diborane core. (© J. David Van Horn)

Van Horn and Wang, From Structure to Atoms 603

Scaricato da http://direct.mit.edu/leon/article-pdf/54/6/599/2028654/leon_a_02051.pdf by guest on 07 settembre 2023

arranged as two triangular compression systems—each a
2-e–/3-atom unit. Placement of the four shared bonding elec-
trons above and below the plane of the boron atoms provides
tension elements holding the central hydrogen and boron
atoms together. In this fashion, all the hydrogen atoms are
satisfied with two electrons, and the boron atoms are stabi-
lized with eight electrons (an “octet” in Lewis’s terms, or a
“double quartet” in Linnett’s).

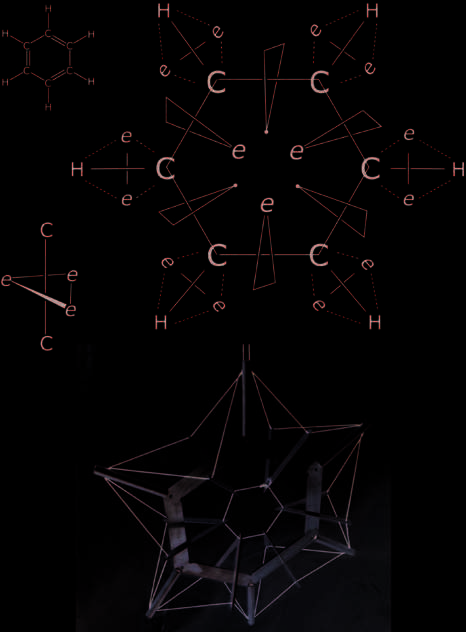
Benzene

A covalent molecule important to this discussion is benzene
(C6H6). The arrangement of atoms in benzene is uniform
and symmetric due to the distribution of six pi electrons
(their electron density) over the six carbon atoms rather
than “localized” as C=C double bonds. A C/T model of ben-
zene starts with six external methine spars (C–H, 2 e– over
2 atoms). The carbon–carbon bonding arrangement in the
ring consists of subunits with three electrons and two carbon
atoms (3 e– over 2 atoms), with interactions between these
units around the inside of the hexagonal ring. This arrange-
ment accounts for the uniform structure of benzene, E
its stability, by providing each carbon atom with a preferred
“octet” of electrons in suitably “spin-paired” configurations
(see Fig. 8). The electrons in the ring are spaced between
carbon atoms rather than colinear with the C–H spar, giving
an eight-electron arrangement for each carbon and a stable
ring of six electrons inside the ring, including an acceptable
spin pairing. A tensegrity model—employing trigonal com-
pression units for the ring electrons, spars for C–H compo-
nents, and a hexagonal compression unit for the carbon atom
ring—illustrates viable C/T properties applied to benzene
(Fig. 8). This benzene tensegrity is directly analogous to Lin-
nett’s theoretical structure for benzene [23].

ConClusIon

Here, we reevaluate structure in terms of compression (Rif-
pulsion) and tension (attraction) force elements. By analogy
and using Snelson’s descriptions, we model molecular bond-
ing as networks of differing continuous or discontinuous
C/T elements. We model covalent molecular structures (es-
pecially related to Linnett’s descriptions) as tensegrities and
approach a purely discontinuous compression/continuous
tension structure. Specifically, tensegrity structure provides

Fig. 8. Diagrams of the Lewis structure of benzene (C6H6), a 3-electron/
2-carbon C/T structural unit, and benzene as a tensegrity. In the benzene
tensegrity the carbon ring and electron triplet compression units have been
simplified as hexagon and open triangles, rispettivamente, and the methine spars
as rods. (© J. David Van Horn)

a molecular model for Linnett’s structural approach. The key
aspects of a molecular tensegrity and derivative artistic struc-
tures include (1) taking two particle interactions as a simplest
unit and (2) the use of interpenetrating, but not necessarily
interacting, compression units (or tension units). For artists,
architects and engineers, the classification of structure and
elements and the C/T models here may offer direction for
creating new works or for the study of old. For scientists,
the consideration of particle-based structures as C/T systems
offers new analogies of the microscopic universe.

Ringraziamenti

references and notes

This article is written in memory of Kenneth Snelson for his structural
discovery and for his production and description of tensegrity sculpture.
We thank Jami Wade for completing a history of bonding project and
Charles Smith for assisting in model building with a grant from the
University of Missouri, Kansas City undergraduate SEARCH program.
Architect Ted Seligson (Fellow, AIA; UMKC Architecture+Urban Plan-
ning and Design) greatly encouraged our investigations of tensegrity
structures.

1 C.S. Smith, “Metallurgy as a Human Experience,” Metallurgical

Transactions A 6A (1975) pag. 603–623.

2 C.S. Smith, From Art to Science: Seventy-Two Objects Illustrating the

Nature of Discovery (Cambridge, MA: CON Premere, 1980).

3 UN. Deplazes, ed., Constructing Architecture. Materials, Processes,

Structures, G.H. Söffker, trans. (Birkhäuser: Basel, 2008).

4 UN. Pugh, An Introduction to Tensegrity (Berkeley: University of Cali-

fornia Press, 1976).

604 Van Horn and Wang, From Structure to Atoms

Scaricato da http://direct.mit.edu/leon/article-pdf/54/6/599/2028654/leon_a_02051.pdf by guest on 07 settembre 2023

5 H. Kenner, Geodesic Math (Berkeley: Stampa dell'Università della California,

1976).

6 Pugh [4].

7 K. Snelson, “The Art of Tensegrity,” International Journal of Space

Structures 27 (2012) pag. 71–80.

8 V.F. Koleychuk, V. Polyakoff and V. Chudnovsky, “The Evolution of
My Kinetic Work,” Leonardo 27, No. 5, 395–398 (1994); V.F. Koley-
chuk, “The Dvizheniye Group: Toward a Synthetic Kinetic Art,"
Leonardo 27, No. 5, 433–436 (1994).

9 K. Snelson, X-Piece, sculpture, 1948; K. Snelson, “An Artist’s Atom,"
Leonardo 27, No. 3, 231–236 (1994); K. Snelson, “Art and Ideas” online
pubblicazione (2013): www.kennethsnelson.net/KennethSnelson_Art
_And_Ideas.pdf.

10 R. Motro, Tensegrity: Structural Systems for the Future (London:
Kogan Page Science, 2003); D.E. Ingber, “The Architecture of Life,"
Scientific American 278, No. 1, 48–57 (1998)

11 l. Pauling, The Nature of the Chemical Bond (Ithaca: Cornell Univ.

Press, 1967).

12 UN. Sommerfeld, “An Electron Theory of Metals from Fermi Statis-

tic,” Zeitschrift für Physik 47 (1928) pag. 1–3.

13 G.N. Lewis, “The Atom and the Molecule,” Journal of the American

Chemical Society 38 (1916) pag. 762–785.

14 IO. Langmuir, “The Arrangement of Electrons in Atoms and Mol-
ecules,” Journal of the American Chemical Society 41 (1919) pag. 868–
934.

15 R.J. Gillespie, “The Valence-Shell Electron-Pair Repulsion (VSEPR)
Theory of Directed Valency,” Journal of Chemical Education 40 (1963)
pag. 295–301.

16 R.J. Gillespie, “Fifty Years of the VSEPR Model,” Coordination Chem-

istry Reviews 252 (2008) pag. 1315–1327.

17 J.W. Linnett, The Electronic Structure of Molecules: A New Approach

(London: Methuen & Co, 1964).

18 J.W. Linnett, “A Modification of the Lewis-Langmuir Octet Rule,"
Journal of the American Chemical Society 83 (1961) pag. 2643–2653.

19 W.B. Jensen, “A Quantitative van Arkel Diagram,” Journal of Chemi-

cal Education 72 (1995) pag. 395–398.

20 Compare this “simplest” system with Kenner [5], who relates the
simplest tensegrity structure consisting of three compressive ele-
ments in a tension network—the classic tensegrity prism (Fig. 1).

21 Linnett [17].

22 Linnett [18].

23 Linnett [17].

24 Gillespie [15].

Manuscript received 13 Marzo 2020.

J. DAviD vAn Horn is associate professor of chemistry at the
University of Missouri, Kansas City. The ideas and structures
of a molecular tensegrity grew out of considering the question,
“What is a covalent bond?"; interacting with architecture stu-
dents; and teaching courses, including structure and bonding
concepts, from 2007 to present.

DAyu WAng joined the Department of Chemistry at the Uni-
versity of Missouri, Kansas City to pursue an interdisciplinary
doctoral degree in chemistry and physics. His dissertation re-
search work focused on bonding theory and mathematical and
computational analysis of microscopic interactions between
particles at molecular and atomic levels. He currently teaches
at St. Charles Community College, Cottleville, Missouri.