REVIEW

Communicated by Fernando Perez-Peña

Advancements in Algorithms and Neuromorphic
Hardware for Spiking Neural Networks

Amirhossein Javanshir
a.javanshir@deakin.edu.au
School of Engineering, Deakin University, Geelong, VIC 3216, Australia

Thanh Thi Nguyen
thanh.nguyen@deakin.edu.au
School of Information Technology, Deakin University (Burwood Campus)
Burwood, VIC 3125, Australia

M.. UN. Parvez Mahmud
m.a.mahmud@deakin.edu.au
Abbas Z. Kouzani
abbas.kouzani@deakin.edu.au
School of Engineering, Deakin University, Geelong, VIC 3216, Australia

Artificial neural networks (ANNs) have experienced a rapid advancement
for their success in various application domains, including autonomous
driving and drone vision. Researchers have been improving the perfor-
mance efficiency and computational requirement of ANNs inspired by
the mechanisms of the biological brain. Spiking neural networks (SNNs)
provide a power-efficient and brain-inspired computing paradigm for
machine learning applications. Cependant, evaluating large-scale SNNs on
classical von Neumann architectures (central processing units/graphics
processing units) demands a high amount of power and time. Donc,
hardware designers have developed neuromorphic platforms to execute
SNNs in and approach that combines fast processing and low power con-
sumption. Recently, field-programmable gate arrays (FPGAs) have been
considered promising candidates for implementing neuromorphic solu-
tions due to their varied advantages, such as higher flexibility, shorter de-
sign, and excellent stability. This review aims to describe recent advances
in SNNs and the neuromorphic hardware platforms (digital, analog, hy-
brid, and FPGA based) suitable for their implementation. We present
that biological background of SNN learning, such as neuron models and
information encoding techniques, followed by a categorization of SNN
entraînement. En outre, we describe state-of-the-art SNN simulators. Fur-
thermore, we review and present FPGA-based hardware implementation
of SNNs. Enfin, we discuss some future directions for research in this
field.

Neural Computation 34, 1289–1328 (2022) © 2022 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01499

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1290

UN. Javanshir, T. Nguyen, M.. Mahmud, et un. Kouzani

1 Introduction

Au cours des dernières années, artificial neural networks (ANNs) have become the best-
known approach in artificial intelligence (AI) and have achieved superb
performance in various domains, such as computer vision (Abiodun et al.,
2018), automotive control (Kuutti, Fallah, & Bowden, 2020), flight control
(Gu, Valavanis, Rutherford, & Rizzo, 2019), and medical systems (Shahid,
Rappon, & Berta, 2019). Taking inspiration from the brain, the third gener-
ation of neural networks, known as spiking neural networks (SNNs), a
been developed to bridge the gap between machine learning and neuro-
science (Maass, 1997). Unlike ANNs that process data values, SNNs use dis-
crete events (or spikes) to encode and process data, which makes them more
energy efficient and more computationally powerful than ANNs (Jang,
Simeone, Gardner, & Gruning, 2019).

SNNs and ANNs are different in terms of their neuron models. ANNs
typically use computation units, such as sigmoid, rectified linear unit
(ReLU), or tanh and have no memory, whereas SNNs use a nondifferen-
tiable neuron model and have memory, such as leaky integrate-and-fire
(LIF). Cependant, simulation of large-scale SNN models on classical von
Neumann architectures (central processing units (CPUs)/graphics process-
ing units (GPUs)) demands a large amount of time and power. Donc,
high-speed and low-power hardware implementation of SNNs is essential.
Neuromorphic platforms, which are based on event-driven computation,
provide an attractive solution to these problems. Thanks to neuromorphic
hardware benefits, SNNs have become applicable to emerging domains,
such as the Internet of Things and edge computing (Mead, 1990; Calimera,
Macii, & Poncino, 2013).

Neuromorphic hardware can be divided into analog, digital, and mixed-
mode (analog/digital) conception. Although analog implementation offers
small area and low power consumption, digital implementation is more
flexible and less costly for processing large-scale SNN models (Indiveri
et autres. 2011; Seo & Seok, 2015). Field-programmable gate arrays (FPGAs)
have been considered a suitable candidate for implementing digital neu-
romorphic platforms. Compared to ASICs, FPGAs offer shorter design and
implementation time and excellent stability (Perez-Peña, Cifredo-Chacon,
& Quiros-Olozabal, 2020). There have been several attempts to implement
SNNs on single FPGA devices, which demonstrate promising speed-up
compared to CPU implementation and lower power consumption com-
pared to GPU implementation (Ju, Fang, Yan, R., Xu, & Tang, 2020; Zhang
et autres. 2020).

Dans cette revue, we introduce recent progress in spiking neural net-
works and neuromorphic hardware platforms suitable for their implemen-
tation. Section 2 introduces the SNNs’ operation and typical spiking neuron
and encoding schemes. Section 3 discusses the learning algorithms for
SNNs, including unsupervised, supervised, and conversion approaches.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Advancements in Spiking Neural Networks

1291

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

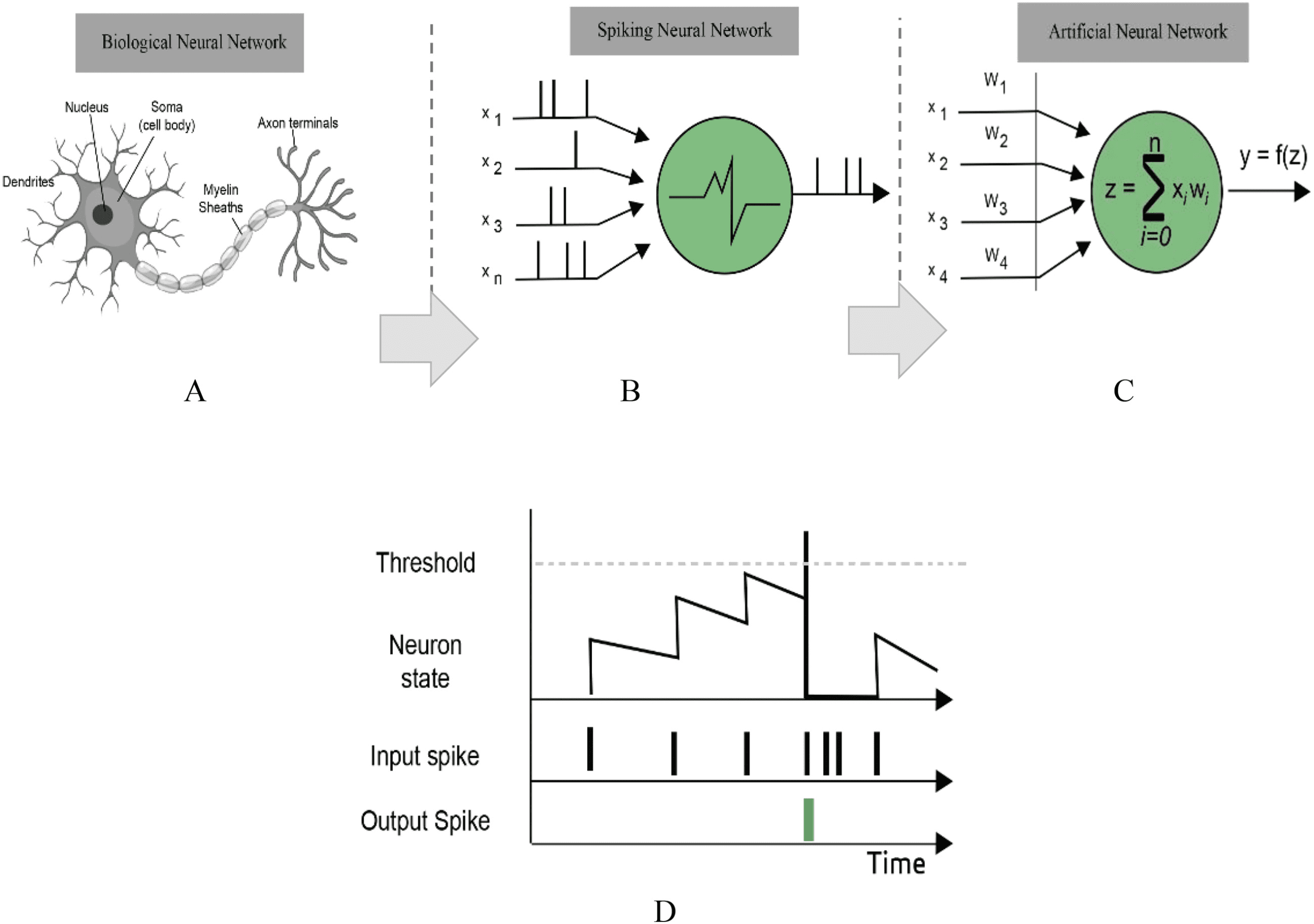
Chiffre 1: Schematic of a biological neural network, spiking neural network,
artificial neural network, and behavior of a leaky-integrate-and-fire spiking
neuron.

Performance comparison of the hardware and software implementations of
SNNs is given in section 5. In section 6, major challenges and future perspec-
tives of spiking neural networks and their neuromorphic implementations
are given. Section 7 concludes.

2 Spiking Neural Networks

Spiking neural networks, considered the third generation of neural net-
travaux (Maass, 1997), communicate by sequences of spikes, discrete events
that take place at points in time, as depicted in Figure 1. SNNs have been
widely used in numerous applications, including the brain-machine inter-
face (Mashford, Yepes, Kiral-Kornek, Tang, & Harrer, 2017), machine con-
trol and navigation systems (Tang & Michmizos, 2018), speech recognition
(Dominguez-Morales et al. 2018), event detection (Osswald, Ieng, Benos-
man, & Indiveri, 2017), forecasting (Lisitsa & Zhilenkov, 2017), fast signal
traitement (Simeone, 2018), decision making (Wei, Bu, & Dai, 2017), et
classification problems (Dora, Subramanien, Suresh, & Sundararajan, 2016).
They have increasingly received attention as powerful computational plat-
forms that can be implemented in software or hardware. Tableau 1 shows the
differences between SNNs and ANNs in terms of neuron, topology, et

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1292

UN. Javanshir, T. Nguyen, M.. Mahmud, et un. Kouzani

Tableau 1: Comparison between SNNs and ANNs.

Spiking Neural Network

Artificial Neural Network

Neurone

Spiking neuron (par exemple., integrate and

Artificial neuron (sigmoid,

fire, Hodgkin-Huxley, Izhikevich)

ReLU, tanh)

Information

Spike trains

representation

Scalars

Computation

Differential equations

Activation function

mode
Topology

LSM, Hopfield Network, RSNN,

RNN, CNN, LSTM, DBN,

SCNN

DNC

Features

Real-time, low power, online

Online learning,

learning, hardware friendly,
biological close, fast and
massively parallel data processing

computation intensive,
moderate parallelization
of computations

their features. A spiking neuron has a similar structure as an ANN neuron
but different behavior. There are various spiking neuron models.

2.1 Spiking Neuron Model. A spiking neuron has a similar structure
to that of an ANN neuron but shows different behavior. Over time, many
different neuron models have developed in the literature, such as Hodgkin-
Huxley (HH), Izhikevich, leaky integrate-and-fire (LIF), and spike response
models. These models differ not only on which biological characteristics of
real neurons they can reproduce but also based on their computational com-
plexity. Dans cette section, we review four popular and representative neuron
models that are widely used in the literature in terms of their biological
plausibility, the neuronal properties or behaviors that can be exhibited by
each model and computational efficiency, and the number of floating-point
operations needed to accomplish 1 millisecond (ms) of model simulation.

2.1.1 Hodgkin-Huxley Model. The HH model is the first biological model
of a spiking neuron that describes how action potentials in the neuron are
initiated and propagated (Hodgkin & Huxley, 1952). It shows the math-
ematical description of electric current through the membrane potential,
which can be calculated as

I = C

dv
dt

+ GNam3h(V − VNa) + Gkn4(V − Vk) + GL(V − VL),

(2.1)

where I is the external current, C is the capacitance of the circuit; VNa, Vk and
VL are called reverse potentials; and GNa, Gk, and GL are parameters model-
ing conductance of sodium, potassium, and leakage channels, respectivement.
Gating parameters n controls the potassium channel, while m and h control
the sodium channel. These parameters are determined by equations 2.2, 2.3,

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Advancements in Spiking Neural Networks

et 2.4, respectivement:

dm
dt
dn
dt
dh
dt

= αm(V )(1 − m) − βm(v )m

= αn(V )(1 − n) − βn(v )n

= α

h(V )(1 − h) − β

h(v )h.

1293

(2.2)

(2.3)

(2.4)

The HH model, the most biologically plausible spiking neuron model,
accurately capture the dynamics of many real neurons (Gerstner & Kistler
2002). Cependant, it is too computationally expensive due to the feedback
loop initiated and the differential equations for n, m, and h to be calcu-
lated continuously. De plus, the Hodgkin-Huxley model requires about
1200 floating-point computations (FLOPS) par 1 ms of simulation (Paugam-
Moisy & Bohte, 2012). Donc, this model is less suitable for com-
putational intelligence applications, such as large-scale neural network
simulations.

2.1.2 Izhikevich Model. This biologically plausible spiking neuron model
was proposed by Izhikevich (2003). This two-dimensional model can repro-
duce a large variety of spiking dynamics (Izhikevich, 2004). The model can
be described mathematically as

= 0.04υ2 + 5υ + 140 − u + je(t),

dv (t)
dt
du(t)
dt
ème) = c and u(υ > υ
υ(υ > υ

= a(bυ − u),

ème) = u + d.

(2.5)

(2.6)

(2.7)

Izhikevich is a 2D spiking neural model that offers a good trade-off be-
tween biological plausibility and computational efficiency. It can produce
various spiking dynamics and requires 13 FLOPS per 1 ms of simulation
(Paugam-Moisy & Bohte, 2012). Izhikevich is a suitable model for simula-
tion or implementation of spiking neural networks, such as hippocampus
simulation and engineering problems.

2.1.3 Integrate-and-Fire Model. Integrate-and-fire (IF), one of the simple
models, integrates input spikes to membrane potential; if it reaches the
defined threshold, an output spike is generated, and membrane potential
changes to a resting state. (Gerstner, Kistler, Naud, & Paninski, 2014; Gerst-
ner & Kistler, 2002). This model can be determined by

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1294

UN. Javanshir, T. Nguyen, M.. Mahmud, et un. Kouzani

Cm

dv
dt

= I(t), ν ← vrest when ν ≥ ν
ème

,

(2.8)

where Cm is the membrane capacitance, ν
th is the threshold, ν is the mem-
brane potential, and vrest is the resting potential. This model is the lowest one
in terms of computational power consumption. In a machine learning con-
text, spiking neurons are most often based on this simple model, which is
prevalent for digital hardware implementations (Nitzsche, Pachideh, Luhn,
& Becker, 2021). The leaky integrate-and-fire model, an important type of IF
neuron model, adds a leak to the membrane potential. This model is defined
by the following equation,

τ
leak

dv
dt

= [υ(t) − υrest] + rmI(t), υ ← υrest when υ ≥ υ
ème

,

(2.9)

leak

= rmcm is the membrane time constant and rm is the membrane
where τ
resistance. The LIF model is one of the widely used spiking neuron mod-
els because of its very low computational cost (it requires only five FLOPS;
Izhikevich, 2004), its accuracy in terms of replicating the spiking behavior
of biological neurons, and its speed in simulating (Brette et al., 2007; Maass,
1997). Donc, it is particularly attractive for large-scale network simu-
lation (Aamir et al., 2018; Benjamin et al., 2014; Merolla et al., 2014). Le
LIF model is very popular for analog hardware implementations since the
neuron’s integration and decay dynamics can easily be modeled by the be-
havior of subthreshold transistors and capacitors (Aamir et al., 2018).

There are also more complex types of IF model such as exponential
integrate-and-fire, quadratic integrate-and-fire, and adaptive exponential
integrate-and-fire (Borst & Theunissen, 1999).

2.1.4 Spike Response Model. The spike response model (SRM) is a bio-
inspired spiking neuron that describes more precisely the effect of input
spikes on the membrane potential. Similar to the LIF model, an SRM neu-
ron generates spikes whenever its internal membrane potential reaches the
threshold (Gerstner & Kistler, 2002). Cependant, in contrast to LIF, it includes
a function dependent on reset and refractory periods. De plus, unlike the
LIF model that uses differential equations for the voltage potential, the SRM
is formulated using response kernels (filters). The SRM model mathemati-
cal formulation is expressed as

υ(t) = η(t − ˆt) +

(cid:2) +∞

−∞

κ (t − ˆt, s) je(t − s)ds,

(2.10)

where υ(t) is the neuron’s internal potential, ˆt is the emission time of the
last neuron output spike, η describes the state of the action potential, κ is

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Advancements in Spiking Neural Networks

1295

a linear response to an input spike, et moi(t) represents the stimulating or
external current.

The 1D spike response model is simpler than other models on the level
of the spike generation mechanism. It offers low computational cost, as it
requires 50 computations (FLOPS) par 1 ms simulation. Cependant, it pro-
vides poor biological plausibility compared with the Hodgkin and Hux-
ley model (Paugam-Moisy, 2006). This model is computationally complex
when used in digital systems. Cependant, the equations that define it can be
modeled by analog circuits since the postsynaptic potential function can be
seen as charging and discharging RC circuits (Iakymchuk, Rosado-Muñoz,
Guerrero-Martínez, Bataller-Mompeán, & Francés-Víllora, 2015).

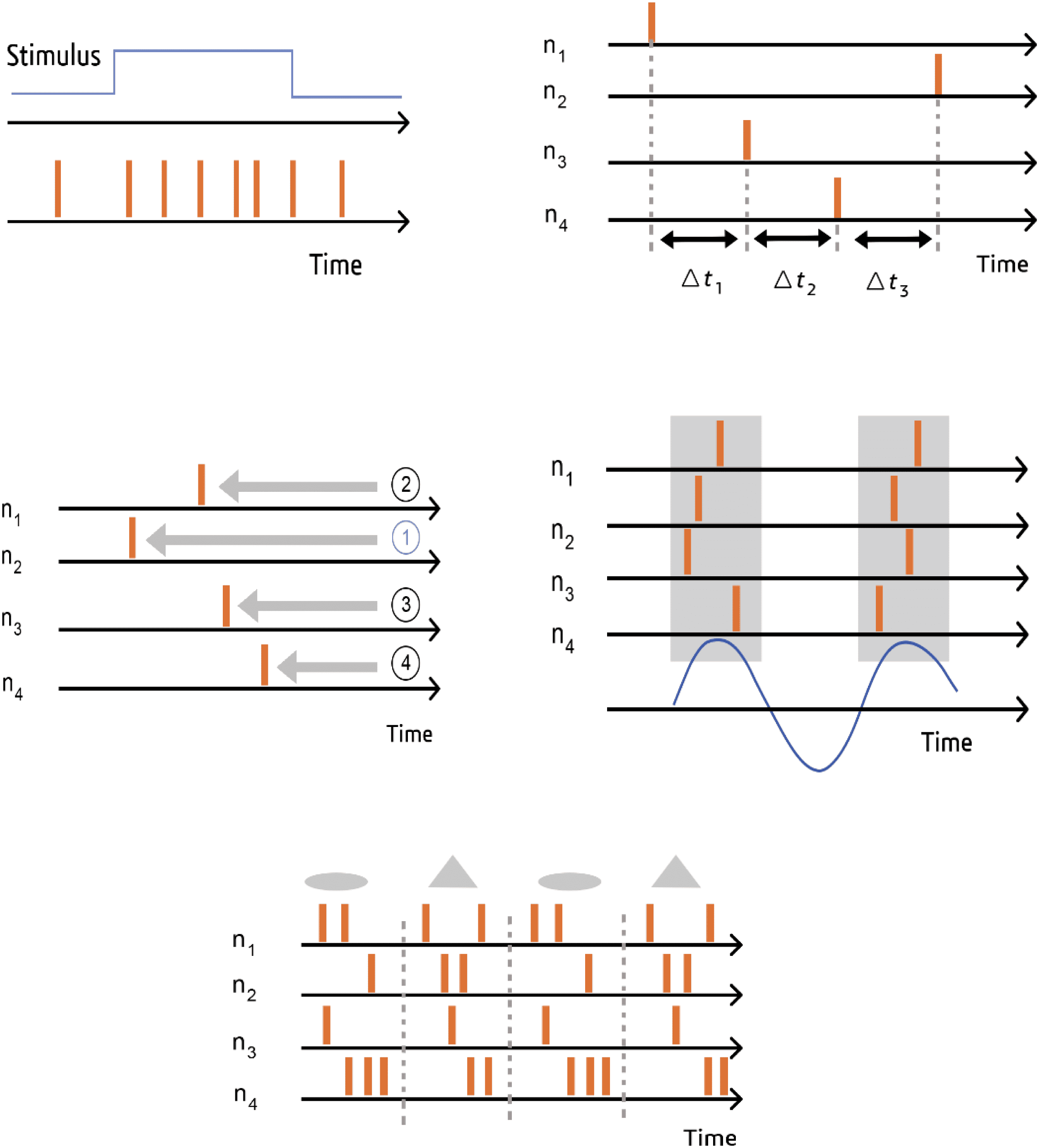
3 Information Coding

Neural coding is still a high-impact research domain for both neuroscien-
tists and computational artificial intelligence researchers (Borst & Theunis-
sen, 1999) Neurons use spikes to communicate with each other in SNN
architectures. Donc, frame-based images and feature vectors need to be
encoded to spike trains, a process called an encoding scheme. This scheme
has a significant influence on the performance of the network. Choosing
the optimal coding approaches is related to the choice of the neuron model,
application target, and hardware constraints (Thiele, 2019). Rate encod-
ing and temporal encoding are the two main encoding schemes (Kiselev,
2016).

Rate coding or frequency coding is one of the most used approaches
to encode information in SNNs where information is conveyed in the fir-
ing rate. Temporal coding is another efficient coding approach for SNNs,
where information is conveyed in the exact timing of spikes (Brette, 2015).
Temporal coding is normally used for time series processing. Various ap-
proaches are used to generate spikes based on temporal coding, tel que
latency code, rank-order coding (ROC), phase coding, and population cod-
ing. In latency coding, information is encoded in the timing of response
related to the encoding window (Fontaine & Peremans, 2009). Rank-order
coding strategies depend on the order of spike arrivals rather than on the
exact timing (Thorpe, Delorme, & Van Rullen, 2001). Compared to rate cod-
ing, ROC is able to bring more information with fewer spikes. Cependant,
it is sensitive to noise. The phase coding strategy encodes information in
the phase of a pulse according to the background oscillations. This method
has been used in robotic navigation and olfactory systems (Kayser, Mon-
temurro, Logothetis, & Panzeri, 2009). In the population coding method,
several neurons are used to encode one value. Sparse code is one of the ex-
amples of the population coding scheme (Wu, Amari, & Nakahara, 2002;
Tkaˇcik, Prentice, Balasubramanian, & Schneidman, 2010). An example of
spike-based information coding strategies is presented in Figure 2.

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1296

UN. Javanshir, T. Nguyen, M.. Mahmud, et un. Kouzani

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Chiffre 2: Spike-based information coding strategies, rate coding, latency cod-
, . . . , n4 are labels of
ing, rank coding, phase coding, and population coding. n1
neurons; (cid:9)t is the relative timing of spikes; and the numbers in the circles shows
the order of spike arrival.

4 Algorithms for SNNs

Learning in a spiking neural network is an arduous task. Backpropagation-
based gradient descent learning is a very successful method in traditional
artificial neural networks; cependant, training SNNs is difficult due to the
nondifferentiable nature of spike events. Par conséquent, considerable research
effort has been mobilized to develop suitable learning algorithms that can

Advancements in Spiking Neural Networks

1297

be applied to multilayer SNNs, which are thus interesting for deep learning.
There are four main strategies for training SNNs: unsupervised learning,
supervised learning, conversion from trained ANNs, and evolutionary al-
gorithm. These strategies are briefly reviewed in the following subsections.

4.1 Unsupervised Learning. Unsupervised learning is the process of
learning without preexisting labels. Unsupervised learning of SNNs is
based on the Hebbian rule that consists of adapting the network’s synaptic
connections to the data received by the neurons (Caporale & Dan, 2008). Le
spike-timing-dependent plasticity (STDP) algorithm is an implementation
of Hebb’s rule. STDP is a phenomenon observed in the brain and describes
how the efficacy of a synapse changes as a function of the relative timing
of presynaptic and postsynaptic spikes. A presynaptic spike in this context
is the spike arriving at the synapse of the neuron. The postsynaptic spike
is the spike emitted by the neuron itself (Markram, Gerstner, & Sjöström,
2011). The mechanism of STDP is based on the concept that the synapses
that are likely to have contributed to the firing of the neuron should be re-
inforced. De la même manière, the synapses that did not contribute or contributed in a
negative way should be weakened (Dan & Poo, 2006).

STDP is frequently used as part of the learning technique in unsuper-
vised learning in SNNs. According to STDP, a synaptic weight is strength-
ened if a presynaptic neuron fires shortly before the postsynaptic neuron.
Similar to that, the synaptic weight is weakened if the presynaptic spike
comes briefly after the postsynaptic neuron (Xu et al. 2020). The most ob-
served STDP rule is described by equation 4.1:
(cid:4)

(cid:5)

(cid:3)

+A+ exp

(cid:9)w =

−A− exp
(cid:9)t = tpost − tpre,

−(cid:9)t
τ

+(cid:9)t
τ

(cid:4)

(cid:5)

si (cid:9)t > 0

si (cid:9)t ≤ 0

(4.1)

(4.2)

where w is the synaptic weights, τ is the time constant, and A+ and A− are
constant parameters indicating the strength of potentiation and depression.
Au cours des dernières années, significant research efforts have been focused on train-
ing SNNs using STDP. Qu, Zhao, Wang, and Wang (2020) developed
two novel hardware-friendly methods, lateral inhibition and homeostasis,
which reduce the number of inhibitory connections that lead to lowering the
hardware overhead. An STDP rule was used to adapt the synapse weight
between input and the learning layer and achieved 92% reconnaissance
accuracy on the MNIST data set. Xu et al. (2020) proposed a hybrid learn-
ing framework, named deep CovDenseSNN, that combines the biological
plausibility of SNNs and feature extraction of CNNs. An unsupervised
STDP learning rule was used to update the parameters of their proposed
deep CovDenseSNN model, which is suitable for neuromorphic hard-
ware implementation. Supervised learning and reinforcement learning are

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1298

UN. Javanshir, T. Nguyen, M.. Mahmud, et un. Kouzani

other types of STDP methods for learning (Mozafari, Ganjtabesh, Nowzari-
Dalini, Thorpe, & Masquelier, 2018; Mozafari, Kheradpisheh, Masquelier,
Nowzari-Dalini, & Ganjtabesh, 2018).

Lee, Panda, Srinivasan, and Roy (2018) proposed a semisupervised
strategy to train a convolutional SNN with multiple hidden layers. Le
training scheme had two steps: initializing the weights of the network
by unsupervised learning (namely, SSTDP), and then employing the su-
pervised gradient descent backpropagation (BP) algorithm to fine-tune
the synaptic weight. Pretraining approaches led to better generalization,
faster training time, et 99.28% accuracy on the MNIST database. Tavanaei,
Kirby, and Maida (2018) developed a novel method to train multilayer spik-
ing convolutional neural networks (SCNNs). The training process includes
unsupervised (a novel STDP learning scheme for feature extraction) and su-
pervised (a supervised learning scheme to train spiking CNNs (ConvNets))
components.

4.2 Supervised Learning. One of the first algorithms to train SNNs
using backpropagation errors is SpikeProp, proposed by Bohte, Kok,
and La Poutre (2002). This model is applied successfully to classification
problems using a three-layer architecture. A later advanced version of
SpikeProp called spike train SpikeProp (ST-SpikeProp) used the weight up-
dating rule of the output layer to train the single-layer SNNs (Xu, Zeng,
Han, & Lequel, 2013). In order to solve the nondifferentiable problem of
SNNs, Wu et al. (2018). Proposed the spatiotemporal backpropagation
(STBP) algorithme, which combines the timing-dependent temporal domain
and the layer-by-layer spatial domain. Supervised learning using tempo-
ral coding has shown a significant decrease in the energy consumption of
SNNs. Mostafa (2017) developed a direct training approach via backpropa-
gation error with the temporal coding scheme. His network has no convolu-
tional layers, and the preprocessing method is not general. Zhou, Chen, Ye,
and Li (2019) improved on Mostafa’s work by incorporating convolutional
layers into the SNN, developing a new kernel operation, and proposing a
new way to preprocess the input data. Their SCNN achieved high recog-
nition accuracy with less trainable parameters. Stromatias, Soto, Serrano-
Gotarredona, and Linares-Barranco (2017) presented a supervised method
for training a classifier by using the stochastic gradient descent (SGD) al-
gorithm and then converting it to an SNN. In other work, Zheng and
Mazumder (2018un) proposed backpropagation-based learning for training
SNNs. Their proposed learning algorithm is suitable for implementation in
neuromorphic hardware.

4.3 Conversion from Trained ANN. In the third technique, an offline-
trained ANN is converted to an SNN so that the transformed network
can take advantage of a well-established, fully trained ANN model. Ce
approach is often called “spike transcoding” or “spike conversion.”

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Advancements in Spiking Neural Networks

1299

Converting an ANN to SNN offers several benefits. D'abord, a simulation of the
exact spike dynamics in a large network can be computationally expensive,
particularly if high firing rates and precise spike times are required. Là-
fore, this approach allows applying SNNs to complex benchmark tasks that
require large networks, such as ImageNet or CIFAR-10, and the accuracy
loss compared to their formal ANNs is small (Sengupta, Ye, Wang, Liu,
& Roy, 2018; Hu, Tang, & Pan, 2018). Deuxième, we can leverage highly ef-
ficient training techniques developed for ANNs and many state-of-the-art
deep networks for classification tasks for conversion to SNNs. De plus,
the optimization process can be performed on ANNs. This permits the use
of state-of-the-art optimization procedures and GPUs for training (Diehl
et coll., 2015). The main disadvantage is that the conversion technique fails
to provide on-chip learning capability. En outre, some particularities of
SNNs, which do not exist in the corresponding ANNs, cannot be considered
during training. For this reason, the inference performance of the SNNs is
typically lower than that of the original ANNs (Pfeiffer & Pfeil, 2018).

Significant research has been carried out to convert an ANN to an SNN
with successful performance on the MNIST data set. Diehl et al. (2015) pro-
posed a technique for converting an ANN into an SNN that has the min-
imum performance loss in the conversion process, and a recognition rate
de 98.64% was achieved on the MNIST database. In another work, Rueck-
auer, Lungu, Hu, Pfeiffer, and Liu (2017) converted continuous-valued deep
CNN to accurate spiking equivalent. This network, which includes com-
mon operations such as softmax, max-pooling, batch normalization, bi-
ases, and inception modules, demonstrates a recognition rate of 99.44% sur
the MNIST data set. Xu, Tang, Xing, and Li (2017) proposed a conversion
method that is suitable for mapping on neuromorphic hardware. They pre-
sented a threshold rescaling method to reduce the loss and achieved a maxi-
mum accuracy of 99.17% on the MNIST data set. Xu et al. (2020) established
an efficient and hardware-friendly conversion rule to convert CNNs into
spiking CNNs. They proposed an “n-scaling” weight mapping method that
achieves high accuracy and low-latency classification on the MNIST data
ensemble. Wang, Xu, Yan, and Tang (2020) proposed a weights-thresholds balance
conversion technique that needs fewer memory resources and achieves
high recognition accuracy on the MNIST data set. In contrast to the exist-
ing conversion techniques, which focus on the approximation between the
artificial neurons’ activation values and the spiking neurons’ firing rates,
they focused on the relationship between weights and thresholds of spik-
ing neurons during the conversion process.

4.4 Evolutionary Spiking Neural Networks. Evolutionary algorithms
(EAs) are population-based metaheuristics. Historically, their design was
motivated by observations about natural evolution in biological popula-
tion. Such algorithms can be used to directly optimize the network topol-
ogy and model hyperparameters or optimize synaptic weights and delays

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1300

UN. Javanshir, T. Nguyen, M.. Mahmud, et un. Kouzani

(Saleh, Hameed, Najib, & Salleh, 2014; Schaffer, 2015). Actuellement, evolution-
ary algorithms such as differential evolution (DE), grammatical evolution
(GE), harmony search algorithm (HSA), and particle swarm optimization
(PSO) are used to learn the synaptic weights of SNNs. Vazquez (2010),
López-Vázquez et al. (2019), and Yusuf et al. (2017) have shown how the
synaptic weights of a spiking neuron, including integrate-and-fire, Izhike-
vich, and spike response model (SRM) models can be trained by using al-
gorithms such as DE, GE, and HSA to perform classification tasks. Vazquez
and Garro (2011) applied the PSO algorithm to train the synaptic weights of
a spiking neuron in linear and nonlinear classification problems. They dis-
covered that input patterns of the same class produce equal firing rates.
The parallel differential evolution approach was introduced by Pavlidis,
Tasoulis, Plagianakos, Nikiforidis, and Vrahatis (2005) for training super-
vised feedforward SNNs. Their approach is tested on exclusive-OR, lequel
does not represent its benefits. Evolutionary algorithms can be an alter-
native to exhaustive search. Cependant, they are very time-consuming, Non-
tably because the fitness function is computationally expensive (Gavrilov
& Panchenko, 2016).

Tableau 2 shows the models for developing SNNs—their architectures and
learning type along with their accuracy rates on the MNIST data set. Ce
comparison provides an insight into different SNN architectures and learn-
ing mechanisms to choose the right tool for the right purpose in future
investigations.

The new concepts and architectures are still frequently tested on MNIST.
Cependant, we argue that the MNIST data set does not include temporal
information and does not provide spike events generated from sensors.
Compared to a static data set, a dynamic data set contains richer tem-
poral features and therefore is more suitable to exploit an SNN’s po-
tential ability. The event-based benchmark data sets include N-MNIST
(Orchard, Jayawant, Cohen, & Thakor, 2015), CIFAR10-DVS (Hongmin Li,
Liu, Ji, Li, & Shi, 2017), N-CARS (Sironi, Brambilla, Bourdis, Lagorce, &
Benosman, 2018), DVS-Gesture (Amir et al., 2017), and SHD (Cramer, Strad-
mann, Schemmel, & Zenke, 2020). Tableau 3 shows the models for developing
SNNs—their architectures and learning type along with their accuracy rates
on the neuromorphic data sets.

5 Available Hardware and Software/Frameworks

Different methods can be used for neural network implementation. Com-
putational cost, speed, and configurability are the main concerns for the
implementations. Although CPU-based simulations offer a relatively high-
speed execution, they are designed to be used for general-purpose and
everyday applications. They also offer a serial implementation that lim-
its the number of neurons that can be implemented at the same time.
Hardware implementations instead can provide a platform for parallel

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Advancements in Spiking Neural Networks

1301

)

%

(

t
s
e
T
/
g
n
je
n
je
un
r
T

UN
C

e
je
p
m
un
S

e
je
toi
R.
g
n

je

n
r
un
e
L

e
p
oui
T
g
n

je

n
r
un
e
L

e
p
oui
T
n
o
r
toi
e
N

n
o
je
t
un
r
toi
g
fi
n
o
C
e
r
toi
t
c
toi
r
t
S

d
o
h
t
e
M.
g
n
je
d
o
c
n
E

e
p
oui
T
–
k
r
o
w
t
e
N

e
c
n
e
r
e
F
e
R.

.
)
T
S
je
N

(

t
e
S
un
t
un
D
s
t
je
g
je
D
n
e
t
t
je
r

w
d
n
un
H
n
o
oui
c
un
r
toi
c
c
UN
r
je
e
h
T
d
n
un

s
je
e
d
o
M.
g
n
je
n
r
un
e
L
N
N
S
t
n
e
c
e
R.

F
o
oui
r
un
m
m
toi
S

:
2
e
je
b
un
T

7
2
.
9
9

0
0
0
,
0
1
/
0
0
0
,
0
6

+
d
je
o
h
s
e
r
h
t

e
je
b
un
je
r
un
V

d
e
s
je
v
r
e
p
toi
s
n
U

F
je
L

UN
N

g
n
je
d
o
c

r
e
d
r
o
k
n
un
R.

N
N
C
g
n
je
k
je
p
S

)
1
2
0
2
(
g
n
o
D
&
toi
F

)
1
2
0
2
(

4
.
7
9

0
0
0
,
0
1
/
0
0
0
,
0
6

P.
B
–
je

je

D
T
S

d
e
s
je
v
r
e
p
toi
S

M.
R.
S
r
un
e
n
L

je

0
1
–
0
0
5
–
4
8
7

g
n
je
d
o
c

je
un
r
o
p
m
e
T

N
N
S

.
je
un

t
e

je
h
g
e
d
un
s
r
je

M.

4
.
1
9

2
9

9
0
.
9
9

3
4
.
9
9

0
0
0
,
0
1
/
0
0
0
,
0
6

0
0
0
,
0
1
/
0
0
0
,
0
6

n
o
je
s
r
e
v
n
o
c

e
c
n
un
je
un
b

0
0
0
,
0
1
/
0
0
0
,
0
6

d
je
o
h
s
e
r
h
t
–
s
t
h
g
je
e

W

0
0
0
,
0
7

e
je
toi
r
n
o
je
s
r
e
v
n
o
C

d
e
s
je
v
r
e
p
toi
S

d
e
s
je
v
r
e
p
toi
S

P.
D
T
S

.

g
n

je

n
r
un
e
je

d
e
s
un
b
–
e
k
je
p
s
d
je
r
b
oui
H

d
e
s
je
v
r
e
p
toi
s
n
U

D
T
S

P.
D
T
S

d
e
s
je
v
r
e
p
toi
s
n
U

F
je
oui
k
un
e
je
n
o
N

F
je
L

F
je
L

F
je

0
1
–
C
F
8
2
1
–
P.
M.
2
–
3
C
4
6
–
2
P.
M.
–
3
C
4
6

C
F
0
1
–
P.
2
–
5
C
4
6
–
P.
2
–
5
C
5

g
n
je
d
o
c

e
t
un
R.

g
n
je
d
o
c

e
t
un
R.

N
N
C
g
n
je
k
je
p
S

)
0
2
0
2
(

.
je
un

t
e
toi
X

N
N
S
p
e
e
D

)
0
2
0
2
(

.
je
un
t
e
g
n
un
W

P.
–
5
C
4
2
–
5
C
2
1
–
8
2
×
8
2
@
6
C
6

g
n
je
d
o
c

e
t
un
R.

0
1
–
0
0
4
–
0
0
4
–
4
8
7

g
n
je
d
o
c

je
un
r
o
p
m
e
T

N
N
S
e
s
n
e
D
v
o
p C

e
e
D

N
N
S

)
0
2
0
2
(

.
je
un

t
e
toi
Q

)
0
2
0
2
(

.
je
un

t
e
toi
X

0
5
.
8
9

0
0
0
,
0
1
/
0
0
0
,
0
6

je
un
r
o
p
m
e
T

d
e
s
je
v
r
e
p
toi
S

F
je
oui
k
un
e
je
n
o
N

UN
N

g
n
je
d
o
c

je
un
r
o
p
m
e
T

N
N
C
g
n
je
k
je
p
S

)
9
1
0
2
(

.
je
un

t
e
toi
o
h
Z

e
t
un
m
je
X
o
r
p
p
un

t
n
e
c
s
e
d

8
.
7
9

0
0
0
,
0
1
/
0
0
0
,
0
6

g
n

je

n
r
un
e
je

e
n

je
je

n
Ô

d
e
s
je
v
r
e
p
toi
S

n
o
je
t
un
g
un
p
o
r
p
k
c
un
b

D
G
c
je
t
s
un
h
c
o
t
s

7
1
.
8
9

0
0
0
,
0
1
/
0
0
0
,
0
5

d
e
z
je
je
un
m
r
o
N

d
e
s
je
v
r
e
p
toi
S

F
je
L

F
je
L

0
1
–
2
1
1
8
–
4
8
7

UN
N

N
N
S

0
1
–
0
0
1
–
0
0
3
–
4
8
7

g
n
je
d
o
c

e
t
un
R.

N
N
S

d
n
un
g
n
e
h
Z

r
e
d
m
toi
z
un
M.

)
un
8
1
0
2
(

n
un
r
d
n
e
un
R.

j

d
n
un

je
n
r
un
k
je
toi
K

)
8
1
0
2
(

)
8
1
0
2
(

.
je
un

t
e

e
e
L

n
o
je
t
un
g
un
p
o
r
p
k
c
un
b

+
g
n

je

n

je
un
r
t
e
r
p

8
2
.
9
9

0
0
0
,
0
1
/
0
0
0
,
0
6

d
e
s
un
b
–
P.
D
T
S

d
e
s
je
v
r
e
p
toi
s
je

m
e
S

F
je
L

C
F
0
1
–
C
F
0
0
2
–
P.
2
–
5
C
0
5
–
P.
2
–
5
C
0
2
–
8
2
×
8
2

g
n
je
d
o
c

e
t
un
R.

N
N
S
e
s
n
e
D
v
o
p C

e
e
D

6
3
.
9
9

0
0
0
,
0
1
/
0
0
0
,
0
6

n
o
je
t
un
g
un
p
o
r
p
k
c
un
B

d
e
s
je
v
r
e
p
toi
S

0
6
.
8
9

0
0
0
,
0
1
/
0
0
0
,
0
6

g
n

je

n
r
un
e
je

.

p
e
r
P.
D
T
S

h
t
o
B

P.
D
T
S
–
P.
B
d
n
un

F
je
L

F
je
L

o
0
1
–
un
2
–
5
c
4
6
–
un
2
–
5
c
2
1
–
8
2
×
8
2

g
n
je
d
o
c

je
un
r
o
p
m
e
T

N
N
S
p
e
e
D

d
n
un
un
h
t
s
e
r
h
S

C
F
0
1
–
C
F
0
0
5
1
–
P.
2
–
5
C
4
6

g
n
je
d
o
c

je
un
r
o
p
m
e
T

N
N
C
g
n
je
k
je
p
S

.
je
un

t
e

je
e
un
n
un
v
un
T

)
8
1
0
2
(
d
r
un
h
c
r
Ô

)
8
1
0
2
(

4
1
.
7
9

0
0
0
,
0
1
/
0
0
0
,
0
6

je
un
r
o
p
m
e
T

d
e
s
je
v
r
e
p
toi
S

F
je
oui
k
un
e
je
n
o
N

0
1
–
0
0
4
–
0
0
4
–
4
8
7

g
n
je
d
o
c

je
un
r
o
p
m
e
T

N
N
S

)
7
1
0
2
(
un
F
un
t
s
o
M.

7
1
.
9
9

2
4
.
8
9

0
0
0
,
0
1
/
0
0
0
,
0
6

0
0
0
,
0
2

n
o
je
t
un
g
un
p
o
r
p
k
c
un
b

e
je
toi
r
n
o
je
s
r
e
v
n
o
C

D
G
c
je
t
s
un
h
c
o
t
S

d
e
s
je
v
r
e
p
toi
S

d
e
s
je
v
r
e
p
toi
S

F
je
L

F
je

o
0
1
–
F
4
2
0
1
–
s
2
–
5
c
4
6
–
s
2
–
5
c
2
3
–
8
2
×
8
2

g
n
je
d
o
c

e
t
un
R.

t
e
N
v
n
o
C
g
n
je
k
je
p
S

)
7
1
0
2
(

.
je
un

t
e
toi
X

UN
N

g
n
je
d
o
c

je
un
r
o
p
m
e
T

N
N
C
g
n
je
k
je
p
S

.
je
un

t
e

s
un
je
t
un
m
o
r
t
S

)
7
1
0
2
(

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1302

UN. Javanshir, T. Nguyen, M.. Mahmud, et un. Kouzani

Tableau 3: Summary of Recent SNN Learning Models and Their Accuracy on
Event-Based Data Set.

Réseau
Type

Learning Rule and Structure
Configuration

SNN

ANN-to-SNN conversion

Reference

Kugele et al.
(2020)

Wu et al.
(2018)
Wu et al.
(2019)

Spiking
MLP

SNN

Zheng et al.
(2020)

ResNet17
SNN

Spatiotemporal backpropagation
(STBP) 34 × 34 × 2-800-10

Spatiotemporal backpropagation (STBP)
128C3(Encoding)-128C3-AP2-384C3-
384C3-AP2-1024FC-512FC-Voting

Threshold-dependent batch

normalization method based on
spatiotemporal backpropagation
(STBP-tdBN)

Lee et al.
(2016)
Yao et al.
(2021)

SNN

Spiking
CNN

Supervised backpropagation

(34 × 34 × 2)-800-10

Temporal-wise attention SNN

(TA-SNN)

Data Set

Californie %

N-MNIST
CIFAR-DVS
DvsGesture
N-Cars
N_MNIST

95.54
66.61
96.97
94.07
98.78

N-MNIST
CIFAR-DVS

99.53
60.5

CIFAR-DVS
DvsGesture

67.80
96.87

N-MNIST

98.66

DvsGesture

98.61

(1) Input-MP4-64C3-128C3-AP2-128C3-

CIFAR-DVS

72

AP2-256FC-11

(2) Input-32C3-AP2-64C3-AP2-128C3-
AP2-256C3-AP2-512C3-AP4-256FC-
10

(3) Input-128FC-128FC-20
ANN-to-SNN conversion

SHD

91.08

N-MNIST

95.72

Neil and Liu
(2016)

Spiking
CNN

implementations. Although analog implementation is relatively efficient,
it suffers from an expensive and long design and implementation process.
FPGA instead offers a configurable platform that offers parallel processing,
which makes it a suitable candidate for SNN implementations.

5.1 Available Software. There are many different SNN simulators—for
exemple, BindsNET, Nengo, NeMo, Brian2GeNN, Nest, and CARLsim. Ex-
isting simulators have different levels of biological models, computational
speed, and support for hardware platforms. They are classified into three
main groups depending on how the neural model dynamic evaluation is
computed: event driven (asynchronous), where the membrane potential
is modified only when a spike arrives; clock-driven (synchronous), où
the neural state is updated at every tick of a clock; and hybrid strategies
(asynchronous and synchronous) (Rudolph-Lilith, Dubois, & Destexhe,
2012).

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Advancements in Spiking Neural Networks

1303

Event-driven simulators are not as widely used as clock-driven simula-
tors due to their implementation complexity. De plus, they are difficult
to parallelize due to their sequential nature. Their main advantage is their
higher operation speed because they do not calculate small update steps for
a neuron. Another benefit of event-driven simulators is that the timing of
spikes can be represented with high precision. These simulators are more
suitable for neural network layers with low and sparse activity (Naveros,
Garrido, Carrillo, Ros, & Luque, 2017).

The majority of SNN simulators are clock-driven. Because of high par-
allelism, clock-driven simulators take full advantage of parallel computing
resources in CPU and GPU platforms. Their platforms perform better for
small and medium-size groups of neurons with a low to medium math-
ematical complexity, whereas GPU clock-driven platforms perform better
for large-size groups of neurons with high mathematical complexity. Le
main advantage of clock-driven simulators is that they are suitable for sim-
ulating large networks when a large number of events is triggered. Many of
these simulators are built on top of the existing deep learning frameworks
because they are structurally similar to simulating an ANN. Their main
disadvantages are that spike timings are aligned to ticks of the clock and
threshold conditions are checked only at the ticks of the clock (Brette et al.,
2007). Selecting the most appropriate technique requires a trade-off among
three elements: (1) neural network architecture (par exemple., number of neurons,
neural model complexity, number of input and output synapses, mean fir-
ing rates), (2) hardware resources (number of CPU and GPU cores, RAM
size), et (3) simulation requirements and targets.

Among the SNN simulators that have been reported in the literature are
BindsNET (Hazan et al., 2018), Nengo (Bekolay et al., 2014), NeMo (Fid-
jeland, Roesch, Shanahan, & Luk, 2009), GeNN (Yavuz et al., 2016), Cerveau
2 (Stimberg, Brette, & Homme bon, 2019), Brian2GeNN (Stimberg, Good-
man, & Nowotny, 2020), NEST (Gewaltig & Diesmann, 2007), CARLsim
(Beyeler, Carlson, Chou, Dutt, & Krichmar, 2015; Chou et al., 2018), Neu-
Cube (Kasabov, 2014), PyNN (Davison, 2009), ANNarchy (Vitay, Dinkel-
bach, & Hamker, 2015), and NEURON (Hines & Carnevale 1997). Il y a
some major criteria for choosing an SNN simulator. It should be open ac-
cess; easy to debug and run; and support various hardware such as ASIC
and FPGA to execute the simulation and support the level of biological com-
plexity. We describe the main features of prominent existing SNNs simula-
tors in Table 3.

BindsNET is an open-source Python package for rapid building and sim-
ulation of SNNs, which developed on top of the PyTorch deep learning li-
brary for its matrix computation. BindsNET allows researchers to test the
software prototypes on CPUs or GPUs and then deploy the model to dedi-
cated hardware (Hazan et al., 2018).

Nengo is a neural simulator based on the neural engineering framework
for simulating both large-scale spiking and nonspiking neural models. Il

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1304

UN. Javanshir, T. Nguyen, M.. Mahmud, et un. Kouzani

is written in Python and supports the TensorFlow back end. This Python
library allows users to define neuron types, learning rules, and optimization
méthodes (Bekolay et al., 2014).

NeMo, a C++ class library for simulating SNNs, can simulate tens of
thousands of neurons on a single workstation. It has bindings for Matlab
and Python and one of the supported back ends for the PyNN simulator
interface (Fidjeland et al. 2009).

GeNN is an open-source library for accelerating SNN simulations on
CPUs or GPUs via code generation technology (Yavuz, Tourneur, & Nowotny,
2016).

Brain is a popular open-source simulator for SNNs written in Python. Il
is highly flexible, easily extensible, and commonly used in computational
neuroscience. Version 2 of Brain allows scientists to efficiently simulate
SNN models (Stimberg et al., 2019). In a newly developed software pack-
âge, Brian2GeNN, the GPU-enhanced neural network simulator (GeNN)
can be used to accelerate simulation in the Brain simulator (Stimberg et al.,
2020).

Another popular and open-source simulator for SNNs is NEST, focus-
ing on the dynamics, size, and structure of neural network. It is suitable
for large networks of spiking neurons (Gewaltig et al. 2007). CARLsim is a
user-friendly and GPU-accelerated SNN library written in C++ that sup-
ports CPU-GPU co-execution (Beyeler et al., 2015). Version 4 of CARLsim
has been improved to simulate large-scale SNN models in with real-time
constraints (Chou et al. 2018). Tableau 4 shows the features of the most SNNs
simulation software.

5.2 Available Hardware. Spiking neuromorphic hardware can be sub-
divided into analog and digital or mixed-mode (analog/digital) conception.
Analog hardware uses physical processes to model certain computational
functions of artificial neurons. The advantage of this approach is that
operations that might be costly to implement as an explicit mathematical
operation can be realized very efficiently by the natural dynamics of the sys-
thème (Neil & Liu, 2016). En plus, real-valued physical variables could
have almost infinite precision. Analog hardware implementations differ on
the degree to which analog elements are used. Many implementations per-
form only the computation in the neuron with analog elements, keeping
the communication of spike signals digital (Camuñas, Linares-Barranco, &
Serrano-Gotarredona, 2019).

Digital hardware represents all variables of the neurons by bits, juste
like a classical computer. This means that the precision of variables
depends on the number of bits used to represent the variables. This pre-
cision also strongly influences the energy consumption of the basic op-
erations and the memory requirements for variable storage. Le grand
advantage of digital designs compared to analog hardware is that the preci-
sion of variables is controllable and guaranteed. En plus, digital hard-
ware can be designed with established state-of-the-art techniques for chip

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Advancements in Spiking Neural Networks

1305

o
t

,
)

C
je
S
UN

,

UN
G
P.
F

,
.

g
.
e
(

e
r
un
w
d
r
un
h
t
n
e
r
e
F
F
je
d
o
t
d
e
t
c
e
n
n
o
c

e
b
n
un
c
T
E
N
s
d
n
je
B
•

n
o
s
N
N
S
g
n

je

n

je
un
r
t

r
o
F
oui
r
un
r
b
je
je

m
oui
g
je

UN
n
e
p
Ô
e
h
t
h
t
je

.
s
n
o
je
t
un
je
toi
m

je
s

e
h
t

e
t
toi
c
e
X
e

w
e
c
un
F
r
e
t
n
je
n
un
e
d
je
v
o
r
P.
•

r
e
t
toi
p
m
o
c

r
o
F
oui
r
un
r
b
je
je

e
h
t
o
t
n
je

d
e
t
un
r
g
e
t
n
je

s
un
h
t
e
s
un
t
un
d
n
o
je
s
je
v
h
c
r
o
T
UN

.

g
n

je

n
r
un
e
je

e
n
je
h
c
un
m

F
o
n
je
un
m
o
d
e
h
t
n
je
n
o
je
t
un
c
je
je

p
p
un
r
o
F

e
je
b
un
t
je
toi
S

.
t
n
e
m
n
o
r
je
v
n
e
g
n
je
n
r
un
e
je

t
n
e
m
e
c
r
o
F
n
je
e
r

.
s
k
s
un
t
n
o
je
s
je
v

o
g
n
e
N

,
je

h
je
o
L
o
g
n
e
N

,

UN
G
P.
F
o
g
n
e
N
s
un
h
c
toi
s

,
s
d
n
e
k
c
un
b
n
o
je
t
un
je
toi
m

je
s

s
un
H

.
s
k
r
o
w
t
e
n
je
un
r
toi
e
n
g
n
je
k
je
p
s

F
o
s
r
o
je
v
un
h
e
b
je
e
v
e
je
–
h
g
je
h
n
o
s
e
s
toi
c
o
F

.
s
U
P.
C
n
o
n
o
je
t
toi
c
e
X
e
d
e
d
un
e
r
h
t
je
t
je
toi
m

s
t
r
o
p
p
toi
S

e
v
je
t
p
un
d
un

,

g
n

je

n
r
un
e
je

p
e
e
d
h
t
je

w
p
je
e
h
o
t
d
e
n
g
je
s
e
d
e
r
un
s
e
je
r
un
r
b
je
je

s
'
o
g
n
e
N

.

L
C
n
e
p
Ô
o
g
n
e
N
d
n
un

,
r
e
k
un
N
N
p
S

je

U
P.
C
n
o
n
o
je
t
toi
c
e
X
e
d
e
d
un
e
r
h
t
je
t
je
toi
m

s
t
r
o
p
p
toi
S

.

g
n
je
je
e
d
o
m
e
v
je
t
je
n
g
o
c
d
n
un
,
je
o
r
t
n
o
c

.
s
n
o
je
t
un
r
toi
g
fi
n
o
c

e
r
un
w
d
r
un
h
d
n
un

s
je
e
d
o
m
n
o
r
toi
e
n
t
n
e
r
e
F
F
je
d
e
t
un
je
toi
m

je
s
o
t
n
un
C

.

g
n
je
n
r
un
e
je

e
n
je
h
c
un
m
n
je

s
n
o
je
t
un
c
je
je

p
p
un
r
o
F

je

e
t
un
d
d
n
un
c
d
o
o
G

.
s
U
P.
G
d
e
je
b
un
n
e
–
UN
D
U
C
n
o
n
toi
r
n
un
C

n
toi
r
o
t

s
r
e
s
toi
w
o
je
je
un
h
c
je
h
w

,
2
n
je
un
r
B
d
n
un
N
N
e
G
h
t
o
b
F
o
e
g
un
t
n
un
v
d
un

s
e
k
un
T
•

r
e
h
t
r
toi
F
oui
n
un
t
toi
o
h
t
je

je

je

w
s
r
o
t
un
r
e
je
e
c
c
un
U
P.
G
UN
D
V
N
n
o
s
t
p
je
r
c
s
2
n
un
je
r
B
r
je
e
h
t

o
t

s
n
e
t
oui
b
e
c
n
un
m
r
o
F
r
e
p
s
e
c
n
un
h
n
e
oui
r
un
r
b
je
je

N
N
e
G
2
n
un
je
r
B
e
h
t
g
n
je
s
U

.

g
n
je
m
m
un
r
g
o
r
p
oui
r
un
s
s
e
c
e
n

•

r
e
t
s
un
F

s
e
m

je
t

F
o
s
d
e
r
d
n
toi
h

.

m
e
t
s
oui
s
g
n
je
t
un
r
e
p
o
r
o
un
m

j

je
je
un

s
t
r
o
p
p
toi
S

•

•

•

•

•

•

•

•

•

•

•

+
+
C

n
o
h
t
oui
P.
(

)
e
g
un
k
c
un
p

+
+
C

n
o
h
t
oui
P.
(

)
e
g
un
k
c
un
p

n
e
v
je
r
d
–
k
c
o
je
C

s
e
Oui

s
e
Oui

T
E
N
s
d
n
B

je

n
e
v
je
r
d
–
k
c
o
je
C

s
e
Oui

s
e
Oui

o
g
n
e
N

+
+
C

n
e
v
je
r
d
–
k
c
o
je
C

s
e
Oui

s
e
Oui

o
M.
e
N

+
+
C

n
o
h
t
oui
P.
(

)
e
g
un
k
c
un
p

n
e
v
je
r
d
–
k
c
o
je
C

s
e
Oui

s
e
Oui

N
N
e
G
2
n
un
je
r
B

g
n
je
m
m
un
r
g
o
r
P.

s
e
r
toi
t
un
e
F

e
g
un
toi
g
n
un
L

n
o
je
t
un
je
toi
m
je
S

U
P.
G

n
e
p
Ô

e
c
r
toi
o
S

r
o
t
un
je
toi
m
je
S

.
e
r
un
w

t
F
o
S
N
N
S
n
w
o
n
K

–
t
s
e
B
e
h
t

F
o
s
e
r
toi
t
un
e
F

:
4
e
je
b
un
T

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

1306

UN. Javanshir, T. Nguyen, M.. Mahmud, et un. Kouzani

.
r
o
je
v
un
h
e
b
e
s
n
o
p
s
e
r
n
e
v
je
g
un
t
fi
t
s
e
b
t
un
h
t

N
N
S
n
un
F
o
s
r
e
t
e
m
un
r
un
p
n
e
p
o
s
d
n
je
F

.
t
r
o
F
F
e

je
un
m
je
n
je
m
h
t
je

w
e
r
toi
t
un
e
F

w
e
n
un
d
d
un
o
t

s
r
e
s
toi
s
w
o
je
je

UN

.
s
k
r
o
w
t
e
n
je
un
r
toi
e
n

•

•

je

D
o
w
n
o
un
d
e
d

F
r
o
m
h

t
t

p

:
/
/

d
je
r
e
c
t
.

m

je
t
.

/

e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d

/

je

F
/

/

/

/

3
4
6
1
2
8
9
2
0
2
3
3
1
8
n
e
c
o
_
un
_
0
1
4
9
9
p
d

.

/

F

b
oui
g
toi
e
s
t

t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

F
o
e
r
toi
t
c
toi
r
t
s
d
n
un

,
e
z
je
s

,
s
c
je
m
un
n
oui
d
e
h
t
n
o
s
toi
c
o
F

t
un
h
t

s
je
e
d
o
m

r
o
F
d
e
t
je
toi
s

e
s
un
e
r
c
n

je
o
t
k
r
o
w
t
e
n
je
un
c
o
je
un
n
je

r
e
t
toi
p
m
o
c
e
r
o
c
je
t
je
toi
m

F
o
e
g
un
t
n
un
v
d
un
e
k
un
t
n
un
C

.
s

m
e
t
s
oui
s

je
un
r
toi
e
n

•

d
e
z
je
m

je

je
t
p
o
g
n
d
je
v
o
r
p
oui
b
e
c
n
un
m
r
o
F
r
e
p
d
n
un
oui
t
je
je
je
b
je
X
e
fl
n
e
e
w
t
e
b
s
e
c
n
un
je
un
B
•

oui
je
je
un
c
je
g
o
je
o
je
b
F
o
r
e
b
m
toi
n
e
g
r
un
je
un
F
o
s
n
o
je
t
un
t
n
e
m
e
je
p
m

je

+
+
C
/
UN
D
U
C

.

n
o
je
t
un
je
toi
m

je
s

e
h
t
p
toi
d
e
e
p
s
o
t

r
o
oui
r
o
m
e
m
e
je
b
un
je
je
un
v
un

e
h
t

g
n

je
k
je
p
s

r
o
F

e
c
un
F
r
e
t
n
je
g
n
je
n
toi
t

e
c
un
F
r
e
t
n
je
g
n
je
m
m
un
r
g
o
r
p
e
s
toi
–
o
t
–
oui
s
un
e
n
un
s
e
d
je
v
o
r
P.
•

r
e
t
e
m
un
r
un
p
c
je
t
un
m
o
t
toi
un
d
e
t
un
r
g
e
t
n
je
n
un
s
e
d
je
v
o
r
P.
•

.
s
e
r
toi
t
un
e
F

je
e
d
o
m
e
je
b
je
s
toi
un
je
p

.
s
e
je
c
n
e
d
n
e
p
e
d

je
un
m
je
n
je
m
h
t
je

w

t
n
e
je
c
fi
F
e
oui
r
o
m
e
m
d
n
un
t
s
un
F

t
s
e
B
•

•

+
+
C

n
o
h
t
oui
P.
(

)
e
g
un
k
c
un
p

+
+
C

n
o
h
t
oui
P.
(

)
e
g
un
k
c
un
p

d
je
r
b
oui
H

o
N

s
e
Oui

T
S
E
N

n
e
v
je
r
d
–
k
c
o
je
C

s
e
Oui

s
e
Oui

m

je
s
L
R.
UN
C

g
n
je
m
m
un
r
g
o
r
P.

s
e
r
toi
t
un
e
F

e
g
un
toi
g
n
un
L

n
o
je
t
un
je
toi
m
je
S

U
P.
G

.

d
e
toi
n

je
t
n
o
C

:
4
e
je
b
un
T

n
e
p
Ô

e
c
r
toi
o
S

r
o
t
un
je
toi
m
je
S

Advancements in Spiking Neural Networks

1307

design and manufacturing. The digital solutions could be implemented on
either FPGAs or application-specific integrated circuits (ASICs) (Schuman
et coll., 2017). Alternativement, due to the high production costs of ASICs, other
research groups have focused on implementing SNNs on FPGAs.

5.2.1 Learning with Neuromorphic Hardware. Learning mechanisms are
crucial for the ability of neuromorphic systems to adapt to specific applica-
tion. Various types of learning can be performed depending on the number
of hyperparameters included in the learning, and the learning time can be
greatly varied. When such learning is performed in a neuromorphic chip,
the learning is referred to as on-chip training (Lee, Lee, Kim, Lee, & Seo,
2020). In order to perform on-chip training, the neuromorphic chip should
have almost all of the functions required for learning (Walter, Röhrbein,
& Knoll, 2015). Off-chip training is a method of implementing learning
outside a neuromorphic chip using, Par exemple, software. After external
learning is completed, the weights are postprocessed according to the neu-
romorphic system, or the neuromorphic system is fabricated using the post-
processed weights.