RECHERCHE
Frequency-based brain networks:
From a multiplex framework to a
full multilayer description
Javier M. Buldú1,2 and Mason A. Porter3,4,5
1Laboratory of Biological Networks, Center for Biomedical Technology (UPM), Pozuelo de Alarcón, Madrid, Espagne
2Complex Systems Group & G.I.S.C., Universidad Rey Juan Carlos, Móstoles, Madrid, Espagne
3Department of Mathematics, University of California Los Angeles, Les anges, Californie, Etats-Unis
4Oxford Centre for Industrial and Applied Mathematics, Mathematical Institute, University of Oxford, Oxford, ROYAUME-UNI
5CABDyN Complexity Centre, University of Oxford, Oxford, ROYAUME-UNI
un accès ouvert
journal
Mots clés: Functional brain networks, Magnetoencephalography, Multilayer networks, Multiplex
réseaux, Algebraic connectivity
ABSTRAIT
We explore how to study dynamical interactions between brain regions by using functional
multilayer networks whose layers represent different frequency bands at which a brain
operates. Specifically, we investigate the consequences of considering the brain as (je) un
multilayer network, in which all brain regions can interact with each other at different
frequency bands; and as (ii) a multiplex network, in which interactions between different
frequency bands are allowed only within each brain region and not between them. Nous
study the second-smallest eigenvalue λ
2 of the combinatorial supra-Laplacian matrix of
both the multiplex and multilayer networks, as λ
of network synchronizability and as a biomarker for several brain diseases. We show that
the heterogeneity of interlayer edge weights and, especially, the fraction of missing edges
crucially modify the value of λ
2, and we illustrate our results with both synthetic network
models and real data obtained from resting-state magnetoencephalography. Our work
highlights the differences between using a multiplex approach and a full multilayer approach
when studying frequency-based multilayer brain networks.
2 has been used previously as an indicator
RÉSUMÉ DE L'AUTEUR
For more than a decade, network analysis has been used to investigate the organization
and function of the human brain. Cependant, applications of multilayer network analysis to
neuronal networks are still at a preliminary stage, in part because of the difficulties of
adequately representing brain-imaging data in the form of multilayer networks. Dans ce
étude, we investigate the main differences in using multiplex networks versus more general
multilayer networks when constructing frequency-based brain networks. Specifically, nous
are concerned with the differences for estimating the algebraic connectivity λ
been related to structural, diffusion, and synchronization properties of networks. Using
synthetic network models and real data, we show how edge-weight heterogeneity and
missing interlayer edges crucially influence the value of λ
2, which has
2.
INTRODUCTION
During the last few years, network science has undergone a conceptual revolution with the
extension of well-established techniques of network analysis to multilayer brain networks
Citation: Buldú, J.. M., & Porter, M.. UN.
(2017). Frequency-based brain
réseaux: From a multiplex framework
to a full multilayer description. Réseau
Neurosciences, 2(4), 418–441. https://
doi.org/10.1162/netn_a_00033
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00033
Informations complémentaires:
https://doi.org/10.1162/netn_a_00033
Reçu: 17 Mars 2017
Accepté: 21 Octobre 2017
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Javier M. Buldú
javier.buldu@urjc.es
Éditeur de manipulation:
Olaf Sporns
droits d'auteur: © 2017
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
Multilayer brain network:
A brain network with more than
one layer. Layers are connected
to each other through interlayer
edges, which link node-layers from
different layers.
Node-layer:
Within each layer, a node-layer
represents the dynamics recorded
by a given magnetometer that is
filtered at a specific frequency
band. Ainsi, each magnetometer
has an associated node-layer on
each layer.
Layer:
A portion of a multilayer network
with a particular set of connections
(called “intralayer edges”) entre
nodes. In our paper, each layer
represents a specific frequency
band of a functional brain
réseau.
Multiplex brain network:
A particular kind of multilayer
brain network in which interlayer
edges occur only between
counterpart nodes (lequel, dans
this paper, represent the same
brain region) in different layers.
(Boccaletti et al., 2014; De Domenico et al., 2013; Kivelä et al., 2014), which provide a con-
venient way to simultaneously encode different types of interactions, subsystems, et autre
complications in networks. Par conséquent, it has been necessary to revisit our intuitive under-
standing of both structural and dynamical properties of networks—including structural phase
transitions (Radicchi & Arenas, 2013), diffusion and other spreading processes (De Domenico,
Granell, Porter, & Arenas, 2016; Gómez et al., 2013; Salehi et al., 2015), percolation and
robustness (Buldyrev, Parshani, Paul, Stanley, & Havlin, 2010; Gao, Buldyrev, Stanley, Xu, &
Havlin, 2013), synchronization (Aguirre, Sevilla-Escoboza, Gutiérrez, Papo, & Buldú, 2014),
and others—to the new possibilities in multilayer descriptions, leading in many cases to
counterintuitive results.
The study of brain networks is currently undergoing a process of adaptation of classical
single-layer (“monolayer”) concepts and analyses to a more general multilayer description.
(For reviews, see Betzel & Bassett, 2016; De Domenico, 2017; Vaiana & Muldon, 2018; aussi
voir la figure 1 of Betzel & Bassett, 2016 and Figures 1–2 of De Domenico, 2017 for relevant
schematics.) Some studies have considered integration of data from structural and functional
brain imaging into a multilayer network to account for both anatomical and dynamical infor-
mation. In an early study using monolayer networks, Honey, Koötter, Breakspear, and Sporns
(2007) showed that a dynamical model simulated on the anatomical network of a macaque
neocortex can successfully identify the positions of the anatomical hubs when signals are
averaged appropriately. Plus récemment, Stam et al. (2016) analyzed how anatomical networks
support activity, leading to specific functional networks (either undirected ones or directed
ones), demonstrating that a dynamical model close to a critical transition is able to unveil
interactions between structural and functional networks.
It is also possible to combine anatomical and functional interactions of just a few nodes
instead of an entire brain network. Par exemple, Battiston, Nicosia, Chavez, and Latora (2017)
examined network motifs (c'est à dire., overrepresented network substructures that consist of a few
nodes; Milo et al., 2002) that combine anatomical connections (in one layer) and functional
relations between cortical regions (in a second layer), linking data obtained, respectivement,
from diffusion-weighted magnetic resonance imaging (DW–MRI) and functional magnetic
resonance imaging (IRMf).
Efforts to combine anatomical and functional networks into a single multilayer network
face the challenge of how to normalize the weights of edges that arise from different origins.
To tackle this issue, Simas, Chavez, Rodriguez, and Díaz-Guilera (2015) proposed translat-
ing functional and anatomical networks into a common embedding space and then compar-
ing them in that space. They constructed functional networks (each with N nodes) from the
fMRIs of q healthy individuals. They then used the functional networks of the q = 20 dans-
dividuals to construct a single functional multiplex brain network, a special type of multi-
layer network in which corresponding entities (brain regions) in different layers (individuals)
can be connected to each other via interlayer edges, but other types of interlayer edges
cannot occur (Kivelä et al., 2014). They followed a similar procedure to construct an anatomi-
cal multiplex network using data obtained from DW–MRI. They then independently projected
each of the multiplex networks into a common embedding space using a series of algebraic
operations that allow one to calculate an “algebraic aggregation” of all layers into a single
layer (see Simas et al., 2015, for details). Using such a projection, it is possible to quantify
the differences between anatomical and functional networks. Simas et al. also calculated an
“averaged aggregation” for each of the functional and anatomical multiplex networks by aver-
aging the weights of the corresponding edges over all layers. They compared the two types of
Neurosciences en réseau
419
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
aggregation, and they were thereby able to identify certain brain regions (par exemple., ones related
to visual, auditory, and self-awareness processes) with significant differences between the
functional and anatomical networks for both types of aggregation. Cependant, only the alge-
braic aggregation was able to detect differences between the functional and anatomical net-
works in other regions (specifically, the thalamus, the amygdala, the postcentral gyrus, et
the posterior cingulate), suggesting that the averaged aggregation disregards significant infor-
mation (Simas et al., 2015).
One possible alternative for reducing the complexity of analysis of brain networks is to
concentrate only on “functional” (dynamical, in fact) interactions between brain regions and
to define multilayer functional networks as a concatenation of a series of layers, each of
which captures the interplay between brain regions during some time window. Cette approche,
in which a layer in a multilayer network represents connection similarities over some time
window, was taken in papers such as Bassett et al. (2011, 2013) and Braun et al. (2014) à
analyze the temporal evolution of network modules and examine dynamical reconfiguration
and “flexibility” of functional networks.
Another alternative is to construct functional multilayer networks whose layers correspond
to the well-known frequency bands at which a brain operates (Buzsáki, 2006). As demon-
strated by Brookes et al. (2016), it is possible to construct frequency-based multilayer net-
works from magnetoencephalographic (MEG) recordings by (je) band-pass filtering the raw
MEG signals, (ii) obtaining the envelope of the amplitude at each frequency band, et (iii)
measuring the pairwise correlations between each envelope (for whichever frequency it ac-
compte). Using such an approach, Brookes et al. (2016) constructed frequency-based multilayer
réseaux, in which each layer includes the interactions in a given frequency band, and showed
that the corresponding supra-adjacency matrices (which encode a linear-algebraic represen-
tation of connections in a multilayer network) convey statistically significant differences when
comparing a control group with a group of schizophrenia sufferers.
2, λ
1, λ
Recently, De Domenico, Sasai, and Arenas (2016) took the important step of analyzing
the spectral properties of matrices associated with frequency-based multiplex networks. Le
3, . . . , λ ˜N} of its eigenvalues, and it
spectrum of an ˜N × ˜N matrix consists of the set {λ
encodes valuable information about the structural properties of the corresponding network. Dans
turn, these eigenvalues (as we will explain later) are related to various dynamical properties,
such as network synchronizability, robustness, and diffusion (Newman, 2010). De Domenico,
Sasai, and Arenas (2016) compared a group of schizophrenic patients with a control group by
using fMRI data, and they found that the second-smallest eigenvalue (c'est à dire., the algebraic connec-
tivity or “Fiedler value”; Van Mieghem, 2011) λ
2 of the combinatorial supra-Laplacian matrix1
associated with a multiplex network is a better discriminator between the two groups than what
one can obtain by studying either unfiltered or single-band functional networks (c'est à dire., by using
monolayer networks). De Domenico et al. also calculated centrality measures (c'est à dire., measures
of the importance of network components; Newman, 2010) on the frequency-based multi-
plex networks to demonstrate the existence of hubs that had not been classified previously
as important brain regions for functional integration. Hubs of the control group were located
in anterior cingulate, superior frontal, insula, and superior temporal cortices; cependant, hubs
for schizophrenic patients were distributed over frontal, pariétal, and occipital cortices. These
results revealed that frequency-based multiplex networks include relevant information about
Magnetoencephalography (MEG):
Brain-imaging technique that
measures the magnetic field of the
brain using a set of magnetometers
placed on the head of an individual.
Algebraic connectivity:
The second-smallest eigenvalue
(λ
(or supra-Laplacian) matrice.
2) of the combinatorial Laplacian
Combinatorial supra-Laplacian
matrice:
The combinatorial Laplacian matrix
of a supra-adjacency matrix.
1 For such a matrix, λ
1
= 0. See the subsection Heterogeneity and Missing Interlayer Edges in Multiplex
Networks (in Results) for a detailed definition of the combinatorial supra-Laplacian matrix.
Neurosciences en réseau
420
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
the functional organization of brain networks that is not captured by using a classical mono-
layer approach.
Multiple recent papers have demonstrated the benefits of using a multiplex description for
analyzing the functional networks of patients suffering from Alzheimer’s disease (AD). For ex-
ample, Yu et al. (2017) constructed frequency-based multiplex networks from MEG data and
demonstrated that centrality measures calculated with layers analyzed independently are un-
able to detect significant differences between a control group and the AD group. Cependant,
when centralities are evaluated on a frequency-based multiplex network, one can find statisti-
cally significant differences in the hippocampus, posterior default-mode network, and occipital
domaines. Guillon et al. (2017) also used frequency-based multiplex networks to differentiate be-
tween controls and people with AD. Dans ce cas, the authors proposed the use of a multi-
participation coefficient (MPC) to enhance classification of which individuals are suffering from
AD. Their MPC consists of an adaptation of the classical (c'est à dire., monolayer) participation coef-
ficient (Guimerà & Amaral, 2005) to networks composed of several layers (see also Yu et al.,
2017). A potential benefit of using this MPC is that it does not depend on interlayer edge
weights, which thus do not need to be calculated. As shown in Guillon et al. (2017), using an
MPC yields better classification accuracy and sensitivity than using only monolayer network
diagnostics.
In this paper, we investigate how to translate the dynamics of different brain regions into
a frequency-based (c'est à dire., functional) multilayer network, in which individual layers account for
coordination within a given frequency band. We focus specifically on the consequences of an-
alyzing a multiplex network versus a more general multilayer one. The former allows interlayer
connections only between the same brain region (c'est à dire., node-layer) in different network layers,
so coupling between oscillations in different frequency bands occurs only between the same
brain region, whereas the latter allows one to model coordination between any brain region
at any frequency band. We use resting-state MEG recordings because of their high temporal
resolution (on the order of milliseconds), which makes it possible to analyze a broad spectrum
of frequency bands (de Pasquale et al., 2010; van Diessen et al., 2015). In our case, a set of
MEG signals consist of N time series, each of which comes from a sensor that captures the
activity above a different cortical region. We then filter signals at four frequency bands (theta,
alpha, beta, and gamma) and construct, pour chaque individu, a four-layer functional multilayer
network from the dynamical coordination within and between frequency bands. The existence
of interlayer edges in frequency-based functional networks relies on the phenomenon of cross-
frequency coupling (CFC), which is responsible for integrating brain activity at different spatial
and temporal scales (Canolty et al., 2006). The quantification of CFC is a hard task, because
the interplay between frequency bands is very intricate (Aru et al., 2015). To address this issue,
one can set the weights of the interlayer edges to a value p, which one can estimate by using
an optimization procedure. Par exemple, it is possible to construct multiplex networks of two
groups of individuals with different profiles and determine a value of p that best distinguishes
between the two groups (voir, par exemple., De Domenico, Sasai, & Arenas, 2016). Cependant, we adopt
a different strategy: We obtain the weights of the interlayer edges directly from time series by
calculating mutual information (MI; MacKay, 2003). We thereby capture heterogeneity (dans le
weights) of both intralayer edges and interlayer edges, and we investigate the influence of such
heterogeneity on the spectral properties of frequency-based functional networks.
Using both synthetic network models and data from laboratory experiments, we investi-
gate the effects that heterogeneity of interlayer edge weights have on the spectral properties of
both multiplex and more general multilayer networks. Specifically, we focus on the algebraic
Cross-frequency coupling (CFC):
In the brain, CFC is the mechanism
through which dynamics at a certain
frequency affect, or are affected by,
the dynamics at other frequencies.
Neurosciences en réseau
421
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
Combinatorial Laplacian matrix:
Given the adjacency matrix A of a
network and the degree matrix D,
which consists of the degree of the
nodes along the diagonal and 0s in
all other entries, the combinatorial
Laplacian matrix is defined as
L = D − A.
connectivity λ
2, which is closely related to both structural and dynamical properties of net-
travaux (Masuda, Porter, & Lambiotte, 2017; Newman, 2010; Van Mieghem, 2011). On one
main, algebraic connectivity is an indicator of modular structure in networks (Fortunato &
Hric, 2016). In the framework of multilayer networks, one can interpret the value of λ
2 et
how it changes as a function of interlayer coupling strength as a way to quantify structural
integration and segregation of different network layers (Radicchi & Arenas, 2013); also see the
discussions in DeFord and Pauls (2017). On the other hand, 1/λ
2 is proportional to the time
required to reach equilibrium in a linear diffusion process (Gómez et al., 2013). En plus,
the time tsync to reach synchronization of an ensemble of phase oscillators that are linearly
and diffusively coupled is also proportional to 1/λ
2 sont
positively correlated in some situations with nonlinear coupling (Almendral & Díaz-Guilera,
2007). A recent investigation of the consequences of modifying interlayer edge weights in mul-
tiplex networks has illustrated that enhancing interlayer coupling tends to shorten the time to
achieve interlayer synchronization in a Kuramoto model of coupled oscillators (Allen-Perkins,
Albuquerque de Assis, Pastor, & Andrade, 2017).
2, and it is known that tsync and 1/λ
In the framework of functional brain networks, algebraic connectivity has been used as an
indicator of AD, such as in de Haan et al. (2012), who obtained statistically significant differ-
ences for λ
2 of functional networks obtained from MEG in a comparison of a group of patients
suffering from AD with a control group. Phillips, McGlaughlin, Ruth, Jager, and Soldan (2015)
calculated the value of λ
2 in a group of individuals with mild cognitive impairment and AD,
although they did not report significant differences between them. Computing λ
2 is also nec-
essary for calculating the most standard type of synchronizability parameter, which is the
ratio λN/λ
2, where λN is the largest eigenvalue of the combinatorial Laplacian matrix
(Boccaletti, Latora, Moreno, Chavez, & Hwang, 2006).
In a series of studies, the synchro-
nizability of brain networks was calculated for different frequency bands (Bassett, Meyer-
Lindenberg, Achard, Duke, & Bullmore, 2006), during epileptic seizures (Schindler, Bialonski,
Horstmann, Élan, & Lehnertz, 2008), and for schizophrenic individuals (Siebenhühner, Blanc,
Coppola, Weinberger, & Bassett, 2013). We aim to improve the interpretation of algebraic
connectivity for functional brain networks, and we thus investigate (je) how the fact that a con-
siderable fraction of all possible interlayer edges are not present in multiplex networks leads
to a deviation from the theoretical values expected for λ
2 et (ii) how these deviations are
related to the mean weight of the interlayer edges. We thereby scrutinize the consequences
of using a multiplex formalism, in which only CFC inside the same brain region is allowed,
instead of employing a fully multilayer approach (c'est à dire., without any restrictions on the type of
coupling that one considers).
RÉSULTATS
Constructing Frequency-Based Multilayer Networks
In Figure 1, we illustrate the process of constructing frequency-based multiplex and multi-
layer brain networks. Our starting point is a data set of MEG recordings of a group of q = 89
individuals during resting state (see Materials and Methods for details), but one can use
other experimental paradigms—including different brain-imaging techniques, such as electro-
encephalography (EEG) or fMRI—to construct multilayer networks with the same procedure.
Specifically, we record MEG activity at N cortical regions, avec 235 ≤ N ≤ 246 (see the
Supplementary Information for details; Buldú & Porter, 2017), and we then clean the data to
remove artifacts and obtain corresponding unfiltered signals. We thereby analyze the signal
recorded by each sensor instead of carrying out a source reconstruction. We then band-pass
filter each signal to obtain four different filtered time series for each brain region. We use the
Neurosciences en réseau
422
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
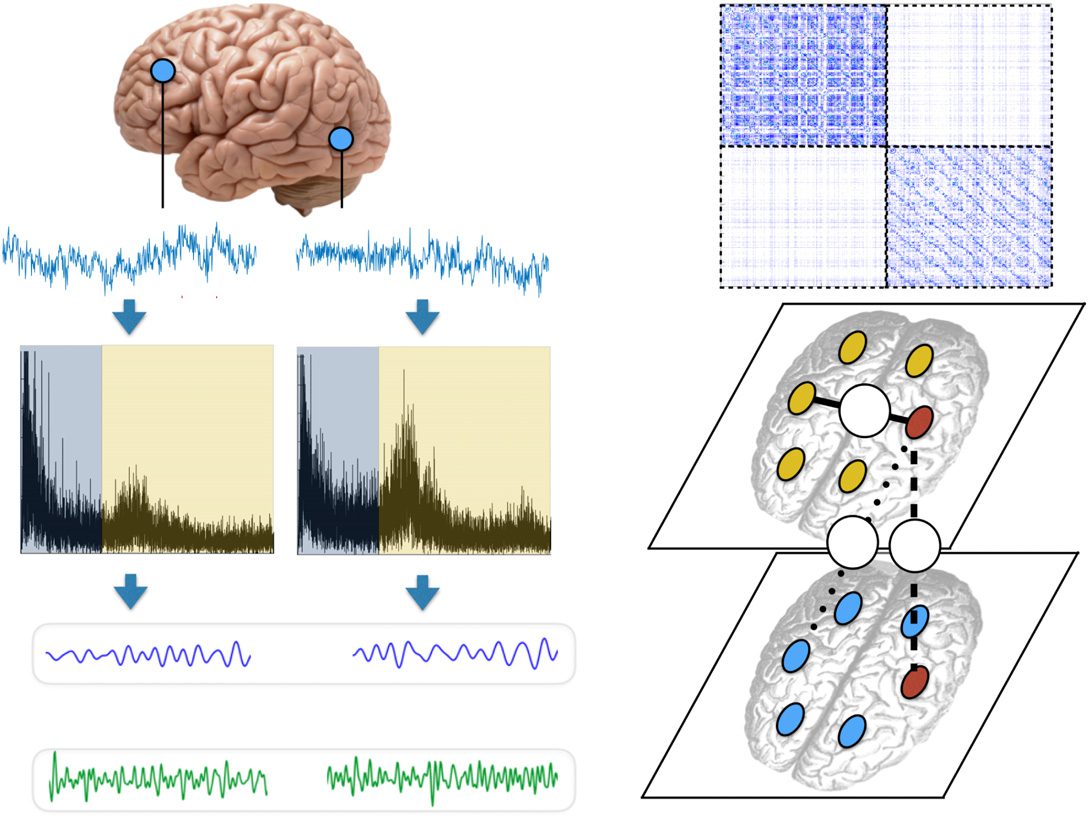
Chiffre 1. Encoding brain dynamics as a multilayer functional network. We show an illustrative
example with two frequency bands (alpha and beta). (UN) We band-pass filter the MEG signals at two
frequency bands: alpha [8–12] Hz and beta [12–30] Hz. We use mutual information (MI; MacKay,
2003) to quantify coordination between brain regions. This yields three different type of functional
edges: Edge type “1” quantifies coordination between different regions at the same frequency band;
edge type “2” corresponds to interlayer edges, which couple the activity of the same region at dif-
ferent frequency bands; and edge type “3” quantifies cross-frequency coupling (CFC) between two
brain regions. Multiplex networks include only edges of types 1 et 2, whereas more general multi-
layer networks include all three types of edges. (B) Schematic of the supra-adjacency matrix of a
two-layer network constructed from the data in panel A. (C) Schematic of the intralayer and interlayer
edges in the multilayer functional network.
four classical frequency bands: theta [3–8] Hz, alpha [8–12] Hz, beta [12–30] Hz, and gamma
[30–100] Hz. The number l of layers of the multilayer network is the number of different fre-
quencies that we examine (et 2 ≤ l ≤ 4 in our work), and the N nodes in each layer are
associated with the dynamics of the N sensors filtered at a given frequency band. We number
the nodes so that nodes n, n + N, n + 2N, …, n + l N (with n ∈ {1, . . . N}) correspond to the
signals of the same brain region n at the l different frequency bands (c'est à dire., layers).
Mutual information (MI):
A measure to evaluate statistical
interdependencies between a pair
variables, X and Y, based on
comparing a joint distribution
p(X, Oui) with the product p(X)p(Oui)
of marginal distributions.
Supra-adjacency matrix:
An adjacency matrix associated with
a multilayer network; it codifies how
much different node-layers interact
with each other.
We then quantify coordination between each pair of nodes of a multilayer network, concernant-
gardless of which layers they are in, using mutual information (see Materials and Methods).
Calculating mutual information (MI) between time series of the same frequency band yields
intralayer connections between brain regions (see edge type “1” in the bottom-left plot of Fig-
ure 1A for an example), so each layer corresponds to a specific frequency band. Edges between
the signals of the same sensor at different frequency bands result in interlayer connections be-
tween layers (see edge type “2”). Such “diagonal” interlayer edges are the only type of inter-
layer edges that are allowed in multiplex networks (Kivelä et al., 2014). Enfin, cross-frequency
coupling between different brain regions yields the other (“nondiagonal”) interlayer edges in
a full multilayer network (see edge type “3”). As we show in Figure 1B, we thereby obtain a
supra-adjacency matrix, where blocks along the diagonal account for intralayer connections
(layers alpha and beta in the two-layer example) and blocks off of the diagonal, marked as
P αβ
, encode the interlayer edges. Because MIij = MIji (see Equation 4 in Materials
and Methods) for time series of nodes i and j, the supra-adjacency matrix is symmetric, donc
Pαβ = [Pβα]T
and Pβα
.
Neurosciences en réseau
423
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
Surtout, although we have chosen to use MI, there are a diversity of similarity measures
for capturing amplitude–amplitude and phase–amplitude correlations between different
frequency bands (see Aru et al., 2015 for a review of cross-frequency coupling measures),
and each measure has its own advantages and drawbacks. Nevertheless, as we will see, le
same methodological implications exist no matter which specific measure one uses to evaluate
coordination between brain sites.
In our discussion, we focus on the analysis of a two-layer network with alpha and beta layers.
We will discuss the consequences of considering alternative frequency bands and numbers of
layers in the last section of the paper (see Conclusions and Discussion).
Our starting point is to compare the results from four different constructions of functional
réseaux:
1. Unfiltered functional networks. We obtain these networks from the original (unfiltered)
signals of each brain region—that is, without decomposing the signals into different fre-
quency bands—so these are monolayer networks.
2. Aggregated networks. We obtain these networks from componentwise addition of the
(Note that this is a
weights of the alpha and beta layers to form monolayer networks.
uniform aggregation.)
3. Multiplex networks. Each layer corresponds to a specific frequency band (as explained
au-dessus de), and interlayer edges are allowed only between node-layers that correspond to
the same brain region.
4. Full multilayer networks. These include the same layers as their multiplex counterparts,
but they allow all possible interlayer edges.
In Figure 2, we show the probability density functions (PDFs) for a group of q = 89 individ-
2, the standard deviation of the interlayer edge weights (to quantify their
uals of the values of λ
heterogeneity), and the percentage of missing interlayer edges (also see Table 1).
In column one of Figure 2, we observe that the (monolayer) unfiltered functional network
has a similar mean and standard deviation of λ
2 as the multilayer network (also see Table 1).
Cependant, the aggregated networks tend to have larger values of λ
2, which makes sense, as we
construct an aggregated network by adding the weights of the two layers (alpha and beta), et
the total “strength” of the network (c'est à dire., the sum of all of its edge weights) is close to double
the strength of each layer. Surtout, the mean λ
2 for the multiplex networks is two orders of
magnitude smaller than the mean λ
2 of the multilayer networks. We expect this discrepancy,
because we construct a multiplex network by deleting all interlayer edges of a full multilayer
réseau, except for edges (so-called “diagonal” edges) that link the same “physical” nodes (c'est à dire.,
the same brain regions). Ainsi, the total strength of the interlayer matrix Pαβ
is considerably
smaller in multiplex networks than in corresponding full multilayer networks. Because λ
2 est
an indicator of the amount of interconnections between communities in a network (Newman,
2010), one expects such drastic edge removals to yield a smaller value of λ
2, as one can
construe layers as communities with a small number of edges between them (only N of the
N2 possible interlayer edges of a full multilayer network).
In columns two and three of Figure 2, we quantify the heterogeneity and the number of miss-
ing interlayer edges of the four different functional networks. In column two, we plot the PDFs
of the standard deviation of all edges (for the unfiltered and aggregated networks) and inter-
layer edges (for the multiplex and multilayer networks). In all cases, we observe that the func-
tional networks that we construct from experimental data have non-negligible heterogeneity
Neurosciences en réseau
424
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
Chiffre 2. MEG data: from unfiltered data to a multilayer network. Probability density functions
(PDFs) of different network characteristics of a group of q = 89 individuals. (See Materials and
Methods for details.) We show the second-smallest eigenvalue λ
2 of the combinatorial Laplacian
matrice, the standard deviation σ of the matrix elements (to quantify their heterogeneity), et le
percentage of missing edges of four different networks: (je) the functional network obtained from
the unfiltered signals (first row), (ii) an aggregated network of the alpha and beta layers (second
row), (iii) a multiplex network (third row), and a (iv) full multilayer network (fourth row).
In all
cases, we only consider two layers (alpha and beta). For the multiplex and multilayer networks, note
that we do these computations with the combinatorial supra-Laplacian matrices. The percentage of
missing edges in the unfiltered and aggregated networks is equal to the percentage of 0 values in
the whole matrix, but it refers only to the interlayer edges for the multiplex and multilayer networks.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
t
.
(also see Table 1). Encore, aggregated networks have values that are roughly twice as large as
those of the other kinds of networks because of the (rough) doubling of the mean strength. Dans
column three, we show that there is a large percentage of missing edges. This arises from the
fact that we construe edges whose weights are smaller than those obtained with an appropri-
ate surrogate time series as not being statistically significant, so we set their values to 0 (voir
Materials and Methods for details). Le (monolayer) aggregated networks have the smallest
mean percentage, followed by the (monolayer) unfiltered networks, and then the two types of
multilayer networks. For the multiplex and full multilayer networks, the percentage of missing
edges, which is larger than 40% in both cases, refers to the number of all possible interlayer
edges. Note that missing edges are unavoidable in functional brain networks, because not all
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Tableau 1. For each kind of network (see the first column), we show the mean standard deviation
¯σ of the weights of the edges (unfiltered and aggregated) and interlayer edges (for both multiplex
networks and full multilayer networks) and the corresponding percentage of missing edges. (See the
Supplementary Information for more details; Buldú & Porter, 2017.)
Réseau
Unfiltered
Aggregated
Multiplex
(Full) Multilayer
¯σ
0.0823
0.1567
0.0618
0.0611
Missing Edges
22.75%
4.42%
52.17%
44.01%
Neurosciences en réseau
425
Multiplex/Multilayer Frequency-based Brain Networks
brain regions communicate with each other through direct connections2. De plus, the differ-
ent amounts of coordination between pairs of brain regions lead to functional networks with
heterogeneous weights.
Heterogeneity and Missing Interlayer Edges in Multiplex Networks
Given our prior observations, a crucial question arises: What are the consequences of hetero-
genous and missing interlayer edges, both of which are intrinsic features of brain-imaging data, sur
multiplex and full multilayer functional networks? More specifically, how do they affect the
value of λ
2, and what are the ensuing structural and dynamical implications of these differences?
With the aim of answering the above questions, we perform a series of numerical com-
putations in which we compare the theoretical values of λ
2 in multiplex and full multilayer
networks from homogeneous interlayer-edge distributions with ones from networks with het-
erogeneous and missing interlayer edges.
and Mβ
We start with a two-layer multiplex network, whose layers alpha and beta have Nα = Nβ
nodes and Lα = Lβ intralayer edges, respectivement. We number the nodes of the alpha layer
from k = 1 to k = Nα and the nodes of the beta layer from m = Nα + 1 to m = Nαβ = Nα + Nβ.
The matrices Mα
are the corresponding adjacency matrices for each layer. We then
introduce lc connector edges (c'est à dire., diagonal interlayer edges) between each node k of the alpha
layer to its corresponding node m = k + Nα of the beta layer to construct a multiplex network.
We suppose that intralayer edges have weight wintra
both belonging
either to the alpha layer or to the beta layer), and we set the weights of the interlayer edges
km = pkm (c'est à dire., for k ∈ α and m ∈ β), where pkm are the elements of a vector (cid:2)p of the
to winter
weights of the interlayer connections. Under these conditions, we obtain a supra-adjacency
matrix Mαβ
) and two off-diagonal blocks
and Pβα
(Pαβ
that consists of two diagonal blocks (Mα
, where Pαβ = [Pβα]T = (cid:2)p I, où (cid:2)p is a row vector). C'est,
(cid:2)
je(cid:4)j(cid:4) = 1 (c'est à dire., for i(cid:4)
and Mβ
and j(cid:4)
(cid:3)
Mαβ =
Mα
(cid:2)p I
(cid:2)p I Mβ
,
(1)
where I is an identity matrix. Following the same procedure, one can also extend the defi-
nition of a supra-adjacency matrix to include an arbitrary number of layers. Par exemple, si
one considers layers for each of the theta, alpha, beta, and gamma bands (see Materials and
Methods), one obtains a supra-adjacency matrix Mθαβγ
.
The combinatorial supra-Laplacian matrix Lαβ
of the multiplex network is
(cid:2)
Lαβ =
Lα + (cid:2)p I
−(cid:2)p I
−(cid:2)p I
Lβ + (cid:2)p I
(cid:3)
,
where the layer combinatorial Laplacians Lα,β
have coordinates
⎧
⎪⎨
⎪⎩
Lα,β
ij =
si ,
−1 ,
0 ,
if i = j
if i and j are adjacent
otherwise
,
(2)
(3)
and si = ∑i(cid:5)=j wij is the weighted degree (c'est à dire., total weight of incident edges) of node i.
2 En général, networks that are constructed from pairwise time-series similarities have nonzero edge weights in
tous (or almost all) intralayer adjacency entries (Bassett & Sporns, 2017). Cependant, in functional brain networks,
the deletion of entries that are not statistically significant can lead to a non-negligible number missing edges, comme
is the case with our data.
Neurosciences en réseau
426
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
Chiffre 3. Consequences of heterogenous and missing interlayer edges in a multiplex network.
2 of the combinatorial supra-Laplacian matrix Lαβ
Algebraic connectivity λ
. Each of the two layers
is a G(N, pcon) Erd ˝os–Rényi network with N = 250 nodes and a connection probability of pcon =
0.25. Each circle corresponds to a mean over 100 realizations. (UN) We quantify the heterogeneity
of the interlayer edges with the standard deviation σ of their weights: (je) σ = 0 (black circles),
(ii) σ ≈ 0.407 (red circles), (iii) σ ≈ 0.523 (green circles), et (iv) σ ≈ 0.581 (blue circles). Lines
correspond to analytical solutions for the case σ = 0 (c'est à dire., a homogenous multiplex network). Le
(Lα + Lβ) (Radicchi & Arenas, 2013;
= 2p, and the solid line is λ
λ
dashed line is λ
2,agg
2
2, the difference of λ
Sahneh et al., 2015). In the inset, we show Δλ
2 between the homogeneous
multiplex network and a multiplex network with heterogeneous interlayer edges. (In the inset, le
solid vertical line indicates the mean value (cid:7)p∗(cid:9) of the transition point.) (B) Algebraic connectivity
λ
2 of the multiplex networks as a function of the number of missing interlayer edges. In the inset,
2 between the homogeneous multiplex network (c'est à dire., σ = 0 et
we show Δλ
all possible interlayer edges) and the multiplex networks with missing interlayer edges. As before,
the solid vertical line indicates the mean value (cid:7)p∗(cid:9) of the transition point.
2, the difference of λ
= 1
2
2
In Figure 3, we show the consequences of heterogeneity in the distribution of the interlayer-
edge weights of the multiplex network Mαβ
. In this example, the multiplex network has an
interlayer connectivity matrix Pαβ = (cid:2)p I, where I is an Nα × Nα (equivalently, Nβ × Nβ, comme
Nα = Nβ in this example) identity matrix and (cid:2)p = p(cid:2)h is a row vector that controls the weights
(cid:2)h encodes the
of interlayer edges, where p modulates the vector’s magnitude and the vector
(cid:2)h to follow a uniform distribution
heterogeneity of the interlayer edges. We set the elements of
min, hmax]. These elements have a mean value of ¯h = 1 and a standard de-
over the interval [h
viation of σ. We set ¯h = 1 and construct networks with interlayer-edge-weight heterogeneities
that range from σ = 0 (blue circles) to σ ≈ 0.581 (green circles). We then examine the interplay
between the weights of the interlayer edges and the heterogeneity by increasing the value of
p. Note that σ = 0 corresponds to what we call a homogeneous multiplex network, lequel
has uniformly-weighted interlayer edges (c'est à dire., (cid:2)p = p for all interlayer edges). We obtain the
results in Figure 3 by calculating a mean over 100 realizations of two-layer networks with the
G(N, pcon) Erd ˝os–Rényi (ER) model (with pcon = 0.25) in each layer and N = Nα = Nβ = 250
nodes (Newman, 2010).
As explained in Radicchi and Arenas (2013), modifying the weight parameter p of the in-
terlayer edges has important consequences for the value of λ
2 for homogeneous multiplex
réseaux. The existence of two regimes of qualitatively distinct dynamics, separated at a tran-
sition point p∗
, was discussed in Radicchi and Arenas (2013) (and in various subsequent
papers): When p (cid:10) p∗
= 2p; pour
p (cid:11) p∗
2 approximates that of the (uniformly) aggregated network
2 follows the linear relation λ
, the algebraic connectivity λ
, cependant, the value of λ
2
Neurosciences en réseau
427
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
(Lα + Lβ)]. In Figure 3, the dashed and solid lines indicate the theoretical
= 1
λ
[c'est à dire., λ
2
2,agg
2
predictions of λ
2 in the homogeneous case for small (dashed) and large (solid) values of p. Nous
obtain a mean value of p∗ ≈ 2.870 by locating the intersection between the eigenvalues λ
2
and λ
3 of the supra-Laplacian matrix Lαβ
(Sahneh, Scoglio, & Van Mieghem, 2015).
2. En outre, values of p near p∗
In Figure 3A, we illustrate that the heterogeneity of the (weights of the) interlayer edges
leads to non-negligible differences in λ
have the maximum
discrepancy between heterogeneous cases (colored circles) and the homogeneous case (black
circles). In studies of multiplex networks, it is simplest to take interlayer edge weights to be
homogeneous (c'est à dire., given by a constant value p), especially when it is not clear how to estimate
their values Kivelä et al. (2014). When possible, cependant, it is desirable to be more sophisti-
cated, and it is possible to quantify the coupling strength between different frequency bands
in various ways when studying frequency-based functional brain networks (Aru et al., 2015).
The choice of incorporating versus ignoring heterogeneity of inter-frequency edge weights then
leads to unavoidable differences in the estimation of λ
2, especially near the transition point
p∗
. It is also important to think about the different interlayer edge weights that one obtains
from different measurements of coupling strength (see Materials and Methods).
Discrepancies in the values of λ
2 are typically even larger when some interlayer edges are
missing.
In Figure 3(B), we show the effects of removing some percentage of the interlayer
edges in a “holey” multiplex network (c'est à dire., a multiplex network with an interlayer connectivity
matrix Pαβ
whose elements are either 1 ou 0 along the diagonal and are 0 in all other entries).
We observe that increasing the number of missing interlayer edges causes the multiplex net-
works to have drastically reduced values of λ
2 always grows
with a slope that is smaller than 2p; for p (cid:11) p∗
2 never reaches the
value of λ
again have the largest
discrepancies with respect to the homogeneous case.
2 for the aggregated network. Enfin, values of p close to p∗
, cependant, the value of λ
2. When p (cid:10) p∗
, the value of λ
Mutilplex Networks Versus Full Multilayer Networks
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
We now identify the qualitative differences (and some of their consequences) between mul-
tiplex networks and full multilayer networks. The latter have an interlayer connectivity matrix
Pαβ = pC, where C has elements cij that account for the weight between each pair {je, j} de
nodes i ∈ α and j ∈ β, and the parameter p allows one to modulate the mean weight of the
interlayer edges. In Figure 4A, we connect the same layers as in our previous example, but now
we use a homogeneous interlayer connectivity matrix Pαβ
with weights pij = p (c'est à dire., cij = 1
for all i and j). Increasing p from 0 leads to the transition point p∗ ≈ 0.013, which we obtain
3 of the combinatorial supra-Laplacian Lαβ
from the intersection of the eigenvalues λ
2 and λ
.
We observe for p < p∗
= 2p(cid:7)c(cid:9) (see the
dashed line in Figure 4A), where (cid:7)c(cid:9) = 250 is the mean weighted degree of the matrix C, as
demonstrated in Radicchi and Arenas (2013). Interestingly, after the transition point p = p∗
,
one can describe the value of λ
2,min(α,β)
is the value of the smaller λ
2 of the two isolated layers. As we show in the inset of Figure 4A,
when we introduce a certain amount of heterogeneity into the interlayer connectivity matrix,
we observe slight differences from homogeneous case. Specifically, for heterogeneous cases,
these differences are larger for values of p above the mean (cid:7)p∗(cid:9) of the transition point.
2 follows the linear function λ
2 by the function λ
that the value of λ
2,min(α,β) + λ
(pC), where λ
= λ
2
2
2
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
As we saw in our analysis of multiplex networks, deleting interlayer edges from a full
multilayer network increases the discrepancy in λ
2 values between networks with homoge-
neous interlayer edges and networks with heterogeneous ones. As we show in Figure 4B, the
Network Neuroscience
428
Multiplex/Multilayer Frequency-based Brain Networks
2 for a homogeneous interlayer connectivity matrix Pαβ
Figure 4. Edge heterogeneity and missing interlayer edges in a full multilayer network. Alge-
2 of the combinatorial supra-Laplacian matrix Lαβ (black circles) as a function
braic connectivity λ
of the weight parameter p of the interlayer edges. Each of the two layers is a G(N, pcon) Erd ˝os–
Rényi network with N = 250 nodes and a connection probability of pcon = 0.25. Each circle
corresponds to a mean over 100 realizations of such multilayer networks. (A) Algebraic connec-
=pC, where each of the elements of
tivity λ
C is cij = 1. The dashed line, given by λ
= 2p(cid:7)c(cid:9), corresponds to the analytical solution for a homo-
geneous matrix Pαβ
, where C has a mean weighted degree of (cid:7)c(cid:9) = 250. The solid line is given
= λ
2,min(α,β) is the value of the smaller λ
by λ
2 of the two isolated
layers. The inset shows the differences Δλ
2 between a multilayer network with homogeneous inter-
layer connectivity matrix Pαβ
and a series of multilayer networks with increasing heterogeneity
(quantified by the standard deviation σ) in Pαβ
. Differences with the homogeneous case increase
after the mean (cid:7)p∗(cid:9) of the transition point (vertical solid line). (B) Algebraic connectivity λ
2 of the
full multilayer networks as a function of the percentage of missing interlayer edges. (See the values
of the percentages in the legend.) In the inset, we show the increment of λ
2 versus the number of
missing interlayer edges.
2,min(α,β) + λ
(pC), where λ
2
2
2
value of λ
2 decreases with the number of missing edges, which one should expect, because
having a smaller number of interlayer edges implies that one needs larger edge weights to
Interestingly, the deviation from the the-
maintain the same amount of interlayer coupling.
oretical predictions is significant even for p < (cid:7)p∗(cid:9). Additionally, for p > (cid:7)p∗(cid:9), we ob-
serve (as expected) a change in the slope of λ
2, but the theoretical predictions given by
(pC) (solid line) begin to fail, leading to a discrepancy that increases
λ
= λ
2,min(un,β) + λ
2
2
with the percentage of missing edges.
Because full multilayer networks have up to N2 interlayer edges, whereas multiplex net-
works can have only N of them, the former tend to have interlayer connectivity matrices with
larger strengths SP = ∑ij pij. In Figure 5, we show the algebraic connectivity λ
2 of the com-
binatorial supra-Laplacian matrices Lαβ
for a series of networks with identical layers and in-
terlayer strength SP, but with a different number of interlayer edges, ranging from a multiplex
réseau (with N interlayer edges) to a full multilayer network with no nonzero entries (c'est à dire.,
with N2 interlayer edges). The dashed lines correspond to the analytical solutions for the full
= 2p(cid:7)c(cid:9), avec (cid:7)c(cid:9) = 250) and the multiplex network
multilayer network (black dashed line; λ
2
= 2p) when p < p∗
(red dashed line; λ
. The solid curves are the corresponding theoretical
solutions when p > (cid:7)p∗(cid:9) for the full multilayer network (black line; λ
(pC))
(Lα + Lβ)). We observe the effect that
and the multiplex network (red curve; λ
adding interlayer edges to multiplex networks has on the value of λ
2 and the associated tran-
sition from a multiplex network to a full multilayer architecture.
Fait intéressant, the different
numbers of interlayer edges in the two types of networks leads to a difference in the position
2,min(un,β) + λ
= 1
2
= λ
2,agg
λ
2
2
2
2
Neurosciences en réseau
429
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
Chiffre 5. Transition from a multiplex network to a full multilayer network. Algebraic connectivity
2 of the combinatorial supra-Laplacian matrix Lαβ
λ
for different values of the percentage of edges in
the interlayer connectivity matrix Pαβ
. Departing from a multiplex network, we add interlayer edges
uniformly at random and calculate the percentage of existing edges in Pαβ
. Each circle corresponds
to a mean over 100 realizations. We set all active edges of the interlayer connectivity matrix Pαβ
to pij = p. The dashed lines correspond to the analytical solutions for the full multilayer network
(black dashed line; λ
= 2p(cid:7)c(cid:9), avec (cid:7)c(cid:9) = 250) and the multiplex network (red dashed line;
= 2p) for p < (cid:7)p∗(cid:9). The solid curves are the theoretical solutions when p > (cid:7)p∗(cid:9) for the full
λ
2
(pC)) and the multiplex network (red curve;
multilayer network (black line; λ
2 versus SP/(Sα + Sβ), where SP, Sα, and Sβ are,
λ
2,agg
respectivement, the strength of the interlayer connectivity matrix Pαβ
, the strength of the alpha layer,
and the strength of the beta layer. Note that differences between the values of λ
2 of the multilayer
structures increase significantly for SP/(Sα + Sβ) (cid:2) 0.1.
(Lα + Lβ)). In the inset, we show λ
2,min(un,β) + λ
= 1
2
= λ
λ
2
2
2
2
de (cid:7)p∗(cid:9) (which one can infer by looking at the change of slope of λ
orders of magnitude.
2) that can reach several
The inset of Figure 5 illustrates the same results normalized by the total strength of the inter-
layer connectivity matrices. C'est, we show SP/(Sα + Sβ), where Sα = ∑ Mα
ij and Sβ =
∑ Mβ
ij, respectivement, are the strengths of layers alpha and beta. This allows us to compare net-
works with the same value of SP, regardless of whether they are close to a multiplex archi-
tecture or to a fully multilayer architecture with no nonzero entries. For p < (cid:7)p∗(cid:9), we obtain
It is only for p > (cid:7)p∗(cid:9) that the particular
similar values of λ
structure of the interlayer connectivity matrix begins to play a role in the value of λ
2. Nous
observe that differences start to arise at SP/(Sα + Sβ) ≈ 0.1, which is a relatively small value.
2 for all network architectures.
Although we used ER intralayer networks in our above calculations, we obtain similar
results for other network models. En particulier, the results are qualitatively the same when we
construct the intralayer networks using a Barabási–Albert (BA) model (Barabási & Albert, 1999).
See the Supplementary Information for details (Buldú & Porter, 2017).
The Meaning of λ2 in Experimental Data
Now that we have analyzed the effects of edge-weight heterogeneity and the number of missing
interlayer edges, let’s revisit the multiplex and multilayer networks that we constructed from the
MEG recordings. As we saw in Figure 2, both edge-weight heterogeneity and missing interlayer
Neurosciences en réseau
430
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
2 of the combinatorial supra-Laplacian matrix Lαβ
Chiffre 6. Edge heterogeneity and missing interlayer edges in frequency-based functional brain
réseaux. Algebraic connectivity λ
as a function
of the mean strength of the interlayer connectivity matrix Pαβ= pC, where C encodes the weights
of the interlayer edges, for four different types of networks: (je) homogeneous multiplex networks
(black), (ii) heterogeneous multiplex networks (red), (iii) homogeneous full multilayer networks
(orange), et (iv) heterogeneous full multilayer networks (blue). Each circle is a mean over 89 indi-
viduals. The blue and black dashed lines, respectivement, are the values of λ
2 for the unfiltered and
= 2p(cid:7)c(cid:9), où (cid:7)c(cid:9) is the mean of the
aggregated networks. The red dashed line corresponds to λ
weighted degree. The red solid line is given by λ
2,min(un,β) is the
2
value of the smaller λ
2 of the two isolated layers.
2
2,min(un,β) + λ
(pC), where λ
= λ
2
edges occur in our experimental data, and it is thus desirable to investigate how close the
experimental networks that we are analyzing are to a transition point p∗
and how this proximity
(or lack thereof ) influences the expected value of λ
2.
In Figure 6, we show the values of λ
2 that we obtain for four different network reconstruc-
tions based on the MEG data: a homogeneous multiplex network (black circles), a hetero-
geneous multiplex network (red circles), a homogeneous full multilayer network (blue circles),
and a heterogeneous full multilayer network (cyan circles). Each network has two layers—one
for the alpha band and one for the beta band—and each point corresponds to the mean over
the group of 89 individuals. We obtain the heterogeneous versions of the multiplex and multi-
layer networks by calculating MI values between the brain regions in the frequency bands, comme
we described previously (also see Materials and Methods). Deuxième, we construct the homo-
geneous versions of both the multiplex and multilayer networks by assigning the same weight
(cid:7)c(cid:9) to all interlayer edges, où (cid:7)c(cid:9) is the mean of the weights of the interlayer edges in their
heterogeneous counterparts. Note that, in this case, the homogeneous multiplex and mul-
tilayer networks do not correspond to real functional networks; instead, they are reference
networks that we use to quantify the consequences on λ
2 of the intrinsic edge heterogeneity
and missing edges in real functional networks.
To assess how close the real networks are to the transition point p∗
, we multiply the values
of the interlayer edges by a parameter p, which we increase from p = 0 to a value above 1. Nous
then calculate the strength SP of the corresponding interlayer connectivity matrix Pαβ
to allow a
comparison between the multiplex network and the multilayer networks, and we plot the value
of λ
2 versus SP. The red dashed line in Figure 6 corresponds to the theoretical predictions for
p < p∗
= 2p(cid:7)c(cid:9), where (cid:7)c(cid:9) is the mean weighted degree of the nodes in the interlayer
(i.e., λ
connectivity matrix Pαβ
). The black and blue dashed lines are, respectively, the value of λ
2
2
Network Neuroscience
431
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
a
_
0
0
0
3
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
2
2
λ
2,agg
= 1
2
= 2p(cid:7)c(cid:9) to λ
(Lα + Lβ)) and the value of λ
for the aggregated network divided by 2 (i.e., λ
2
for the unfiltered (monolayer) functional network. The vertical solid line corresponds to the
case p = 1 for the mean of the heterogeneous full multilayers networks (i.e., the networks that
we obtain by taking into account all interlayer correlations without modifying their weights).
Interestingly, this network occupies the region in which the evolution of λ
2 with respect to
(pC), which suggests that the
p changes slope from λ
frequency-based multilayer networks that we are analyzing are close to the transition point
p∗
2 is most influenced by the
effects of edge heterogeneity and missing interlayer edges. It is also worth noting that the four
network representations have rather different values of algebraic connectivity (and hence, we
expect, have different spectral properties more generally), except when p (cid:10) p∗
(see the inset of
Figure 6). Although it looks from the plot that the algebraic connectivities of the heterogeneous
multilayer networks (cyan circles) and those of the homogeneous multiplex networks (black
circles) may converge to the same value for large SP, they eventually cross each other when
we further increase SP (not shown).
. As we have seen, it is near this point where the value of λ
2,min(α,β) + λ
= λ
2
2
In Figure 7, we show (top panel) the PDF of the values of p∗
for the multilayer networks of
each of the 89 individuals and (bottom panel) the percentage of deviation of λ
2 with respect
2,agg of the aggregated network. We observe that the peak of the PDF for p∗
to the value λ
is near p = 1. That is, the multilayer networks that we constructed from empirical data are
close to the transition point. Figure 7 also illustrates discrepancies in the values of λ
2 between
the aggregated and multilayer networks, indicating that it is necessary to differentiate between
the two cases when interpreting the value of λ
2, especially when comparing results from
different studies.
Finally, we investigate how the combination of layers from different frequency bands affects
the value of λ
2. In our analysis thus far, we have focused on a two-layer network that we
constructed using the alpha and beta frequency bands, because they are often associated with
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
a
_
0
0
0
3
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. MEG of full multilayer networks and the transition point p∗
point p∗
corresponds to p∗ = 1. (Bottom) Percentage of deviation of λ
= 100(λ
2,agg, where λ
gregated network: % Δλ
of the full multilayer network. Each circle represents one of the 89 individuals.
. (Top) PDF of the transition
for two-layer networks (of the alpha and beta layers) of the 89 individuals. The dashed line
2 with respect to the value of the ag-
2 denotes the algebraic connectivity
)/λ
− λ
2,agg
2
2
Network Neuroscience
432
Multiplex/Multilayer Frequency-based Brain Networks
2 of all possible combinations of two-layer networks versus λ
Figure 8. Combining different frequency bands into multilayer networks. We show the algebraic
connectivity λ
2,θαβγ of the four-layer
full multilayer networks. We construct the layers from the theta (θ), alpha (α), beta (β), and gamma
(γ) frequency bands. The labels at the top of each plot correspond to the associated frequency
bands. Each circle corresponds to one of the 89 individuals.
brain activity during the resting state. Nevertheless, because the signal has been filtered into
four different frequency bands, there are eight possible combinations of two layers. In Figure 8,
we show the relation between λ
2 for all possible combinations of two-layer networks versus
that for the full four-layer multilayer network. Observe the strong correlation of the two-layer
networks that include the gamma layer (especially the one that consists of the theta and gamma
layers) with the full multilayer network. One can explain such a correlation by inspecting the
In Table 2, we separate the intralayer and interlayer
total strength of each frequency band.
strengths to facilitate interpretation of the results. We observe that the gamma band is the
least-active layer, as it is the one with the smallest intralayer strength. Nevertheless, it has
the largest interlayer strength (i.e., the sum of the weights of its interlayer edges with all other
layers is the largest), so it is the layer that appears to interact most strongly with the other
layers. Because (as we have seen) the full multilayer functional networks are close to the mean
(cid:7)p∗(cid:9) of the transition point, the weight of the intralayer connections has a strong influence
on the value of λ
2. Therefore, the two-layer theta–gamma network, which includes the layers
with the largest interlayer strengths, is the one with the strongest correlation of λ
2 with the full
multilayer network (see Figure 8C).
CONCLUSIONS AND DISCUSSION
Using network analysis as a tool for analyzing brain-imaging data, and (more specifically) im-
plementing and studying a multilayer description of brain activity, has both advantages and
drawbacks that must be investigated carefully. As we have discussed, it is possible to en-
code such imaging data either as a multiplex network or as a more general type of multilayer
network, but different choices lead to different results, which one must then interpret from a
neuroscientific perspective. In our paper, we have analyzed the implications of such a choice
on spectral information—and specifically on the algebraic connectivity λ
2, which has been
Network Neuroscience
433
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
a
_
0
0
0
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
related to structural, diffusion, and synchronization properties of networks (Almendral & Díaz-
Guilera, 2007; Gómez et al., 2013; Masuda et al., 2017; Newman, 2010; Radicchi & Arenas,
2013; Van Mieghem, 2011). We have seen how heterogeneity (of the weights) of the interlayer
edges of multiplex networks leads to deviations of the theoretical predictions that one obtains
when all interlayer edges have an equal weight p, and we observed that the deviation is even
larger when interlayer edges are missing. The importance of these results, which entail large
differences in qualitative dynamics, is underscored by the fact that both edge heterogeneity
and missing interlayer edges are common features of brain-imaging data.
It is also important to understand that although a multiplex description of brain networks
is an important and useful approach to integrate multivariate information, and it is often an
extremely natural approach—such as for integrating anatomical and functional networks,
examining the temporal evolution of a functional network, and so on—it is just an initial step
towards developing increasingly complete models to better analyze the spatial and temporal
complexity of brain networks (Papo, Zanin, & Buldú, 2014).
In this quest, a natural step—
although certainly not the final step—is to use a full multilayer description for subsequent
analyses of frequency-based brain networks.3 In this type of network, it is more biologically
plausible to represent brain activity as a full multilayer network than as a multiplex network.
The reasons are twofold: (i) a brain region does not necessarily coordinate with itself at different
frequencies; and (ii) there may also exist CFCs between different brain regions. Consequently,
interlayer connections do not necessarily follow the multiplex paradigm, because some of the
interlayer edges probably should not be present, whereas others should be included to ac-
count for interlayer coupling between different nodes (i.e., different brain regions), thereby
necessitating a fully general multilayer approach.4 Nevertheless, the use of frequency-based
multiplex networks has been an effective strategy in previous work for successfully distin-
guishing between healthy individuals and individuals who are suffering from schizophrenia
(De Domenico, Sasai, and Arenas, 2016), so there are times when a multiplex approach
works well.
As we have illustrated with our computations, because the number of interlayer edges scales
with N in multiplex networks but with N2 in the multilayer networks that we examined, there
are important quantitative differences in the values of the algebraic connectivity in the two
types of networks. Nevertheless, the effects of edge-weight heterogeneity and missing inter-
layer edges on full multilayer networks are qualitatively similar to those in multiplex networks.
Specifically, the analytical predictions that we obtained with homogeneous multilayer net-
works deviate from those of heterogeneous cases, showing an important discrepancy for val-
ues of the coupling-strength parameter p that are larger than the transition point p∗
. The effect
of missing interlayer edges is particularly dramatic for p > p∗
.
Our analysis of experimental imaging data confirms our results with synthetic networks. Le
small number of interlayer edges in a multiplex network leaves the network in a region in which
layers behave as if they are structurally independent, and a deeper analysis reveals that it is
necessary to increase the weights of the interlayer edges from the experimental data by several
orders of magnitude to reach the transition point p∗
. Par conséquent, using a multiplex repre-
sentation leads to a network with structurally independent layers, unless one uses extremely
3 It is also desirable, Par exemple, to examine this type of network in a time-resolved manner (ideally using
continuous time), to incorporate spatial constraints, et ainsi de suite.
4 Analogous critiques are also relevant for research, including our own, on multilayer analysis of time-
dependent brain networks (voir, par exemple., Bassett et al., 2011), for which one can envision incorporating time delays
in coordination between brain regions.
Neurosciences en réseau
434
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
Tableau 2. Percentage of strength of each layer in a four-layer multilayer network from MEG data.
The first column indicates the layer. The second column indicates the percentage of strength of
all intralayer edges in the full four-layer multilayer network that come from that layer; c'est, pour
a layer l ∈ {je, un, β, c}, the percentage is given by 100 × (cid:12)Ml(cid:12)1
1 is the
(cid:12)Mθαβγ(cid:12)1
entrywise 1-norm of M, corresponding to the sum of all elements of the matrix. The third column
gives the percentage of the strength of the interlayer edges. C'est, for a layer l(cid:4)
, the percentage
est 100 × 2 ∑l(cid:5)=l(cid:4) (cid:12)Pl(cid:4) je (cid:12)1
, where l(cid:4) ∈ {je, un, β, c}. Each percentage in the table is a mean over the 89
(cid:12)Mθαβγ(cid:12)1
individuals.
Layer
theta (je)
alpha (un)
beta (β)
gamma (c)
Interlayer Strength
9.53%
7.49%
9.34%
10.47%
Intralayer Strength
12.69%
31.43%
12.18%
6.85%
, where the operator (cid:12)M.(cid:12)
large weights (c'est à dire., p (cid:11) 1) for the interlayer edges. Cependant, the weights of the interlayer edges
cannot be increased artificially without limits, because eventually they lose their biophysical
meaning in attempts to compare them to intralayer edge weights.
Fait intéressant, our results changed drastically when we used a full multilayer description, dans
which a brain region whose dynamics are in a given frequency band can now couple with
other brain regions in a different frequency band. When we considered all possible interlayer
edges, the majority of the 89 individuals in the experiment are close to the transition point p∗
,
even though the percentage of weight in the interlayer edges is always about 10% of that of
the intralayer ones (see Table 2). As we showed in our analysis of synthetic data, it is around
this point that edge-weight heterogeneity and missing interlayer edges begin to yield important
discrepancies from the theoretical results of homogeneous multilayer networks (see Figure 4A).
It is important to note that the percentage of total weight of interlayer edges (relative to the
total weight of all edges) depends strongly on how one measures coordination between brain
régions. When one uses diagnostics other than mutual information, one calculates different
values for the percentages, which can yield multilayer networks either above or below the
transition point p∗
. Ainsi, no matter what measure one uses, it is mandatory to first calculate
the percentage of total edge weight that arises from interlayer edges and to interpret the value
of λ
2 with respect to the value of p∗
.
The fact that, in frequency-based multilayer networks, the weights of interlayer edges
strongly influence the value of λ
2 despite being much smaller than the weights of intralayer
edges (see Table 2) highlights the importance of adequately evaluating CFCs, which tradition-
ally have been disregarded when representing brain activity in terms of functional networks.
As has been discussed prominently in neuroscience, including in critiques of connectomics
(Kopell, Gritton, Whittington, & Kramer, 2014), the dynamics matter, and investigations of
dynamics must include incorporation and analysis of coupling between different frequency
bands. The methodology that is used to quantify interactions between brain regions at differ-
ent frequencies leads to different values of λ
2; and there are also other important dynamical
issues, such as phase–amplitude correlations, that we have not investigated in this paper. (Voir
Bastos & Schoffelen, 2016 for a review of how common reference, volume conduction, field
spread, or common input affect the quantification of coordinated activity between brain re-
gions.) These caveats notwithstanding, our analysis illustrates a viable approach for examining
the effects of such phenomena on λ
2 (and hence on spectral structure) in multilayer functional
réseaux, and we expect that similar qualitative phenomena will arise in both multiplex and
Neurosciences en réseau
435
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
full multilayer networks that are constructed using other choices (par exemple., different measures than
MI) from the ones that we chose in order to provide a concrete illustration.
We initially studied two-layer networks of the alpha and beta frequency bands, because (je)
it is known that these bands incorporate a large portion of the power spectrum of brain activity
during resting state and (ii) these frequency bands typically exhibit stronger synchronization
between brain regions (par exemple., see Brookes et al., 2016) than the others. The alpha and beta
bands are thus the most commonly studied frequency bands in resting-state studies, and we
followed this tradition. Nevertheless, in our particular case, our comparison between two-
layer and four-layer networks illustrates that the gamma band is the one that most influences
the spectral properties of the full four-layer multilayer network (voir la figure 8). As we showed
in Table 2, the theta and gamma layers are the ones whose interlayer edges give the largest
contributions, thereby leading to the strongest correlation between a two-layer network (avec
theta and gamma layers) and the complete (four-layer) multilayer network. This fact high-
lights the importance of the well-known phase–amplitude correlations between the theta and
gamma frequency bands (Aru et al., 2015; Canolty et al., 2006), as the former acts as a carrier
of fast-amplitude fluctuations in the latter. Par conséquent, theta–gamma coupling may be of
fundamental importance for understanding the multilayer nature of functional brain networks.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
It also worth mentioning that the facts that we are constructing frequency-based multilayer
networks from (je) data at the sensor level and (ii) using MI as a measure to quantify mutual
interdependency between brain regions leads to unavoidable errors in the quantification of
edge weights, due to signal mixing and spurious correlations from common sources. Cependant,
to date, there does not exist an error-free methodology to construct functional brain networks,
and other alternatives (such as source reconstruction or using different measures to evaluate
interdependency between brain regions) have their own drawbacks. For a detailed discussion,
see the subsection Methodological Considerations (in Materials and Methods).
Enfin, although our calculations with experimental data used resting-state MEG record-
ings, we expect to observe similar behavior in frequency-based multilayer networks of different
origins—whether obtained from any of a large variety of different cognitive or motor tasks, avec
different brain-imaging techniques, or even if they come from a completely different system
(such as functional climate networks; Tsonis & Roebber, 2004). Cependant, despite the gener-
ality of our results, it is important to examine richer models of frequency-based brain network,
such as ones that include spatial constraints and temporal evolution.
MATERIALS AND METHODS
Data Acquisition
The data were made available by the Human Connectome Project (HCP); see http://www.
humanconnectome.org/ and Larson-Prior et al. (2013) for details. The experimental data con-
sist of magnetoencephalographic (MEG) recordings of a group of 89 individuals, during rest-
ing state, for a period of approximately 2 min. During the scan, subjects were supine and
maintained fixation on a projected red crosshair on a dark background. Brain activity was
scanned on a whole-head MAGNES 3600 (4D Neuroimaging, San Diego, Californie, Etats-Unis) système
housed in a magnetically-shielded room, and it included up to 248 magnetometer channels.
The root-mean-squared noise of the magnetometers is about 5 fT/sqrt (Hz) on average in the
white-noise range (au-dessus de 2 Hz). The data were recorded at a sampling rate of fs ≈ 508.63 Hz.
Five current coils attached to a subject, in combination with structural-imaging data and head-
surface tracings, were used to localize the brain in geometric relation to the magnetometers
Neurosciences en réseau
436
Multiplex/Multilayer Frequency-based Brain Networks
and to monitor and partially correct for head movement during MEG acquisition. Artifacts, bad
chaînes, and bad segments were identified and removed from the MEG recordings, lequel
were processed with a pipeline based on independent component analysis to identify and
clean environmental and subject artifacts (Larson-Prior et al., 2013). After this process, le
number N of channels considered for each individual was in the range 235 ≤ N ≤ 246
(with a mean of 243.42), because some channels were used as references and others were
disregarded.
Coordination Between Brain Regions
To estimate coordination between brain regions, we first apply a band-pass filter to the prepro-
cessed signals to obtain, for each of the N sensors, a set of four different time series, each of
which corresponds to a specific frequency band: theta [3–8] Hz, alpha [8–12] Hz, beta [12–30]
Hz, and gamma [30–100] Hz. We thereby obtain 4N time series of t = 149646 points for each
of the q = 89 individuals. We then order the filtered signals according to their corresponding
frequency band, so the time series Xs
with s ∈ {1, . . . , N} corresponds to the theta band,
Xs
with s ∈ {2N + 1, . . . , 3N}
corresponds to the beta band, and Xs
with s ∈ {3N + 1, . . . , 4N} corresponds to the gamma
band. Each of the 4N time series corresponds to a node-layer of a frequency-based network.
We calculate mutual information (MI) between the time series Xi
of a pair of nodes i
and j with the formula
with s ∈ {N + 1, . . . , 2N} corresponds to the alpha band, Xs
and X j
(cid:8)
(cid:9)
MIij = ∑
toi,v
puv ln
puv
pu pv
,
(4)
√
and X j
where pu is the probability that Xi = xu, the quantity pv is the probability that X j = xv, et
puv is the joint probability that Xi = xu and X j = xv at the same time point. We set the
number of bins of the PDFs to be u = v = 5 × (cid:13)(
t/10)(cid:15), where t the is the number of time
points and (cid:13)oui(cid:15) corresponds to the nearest integer function of the real number y (where we
round up for .5). When Xi
are independent variables, puv = pu pv, and the resulting
value of MIij is 0. When Xi = X j
for each time series, MIij achieves its maximum value. Note
that MIij = MIji, so we obtain an undirected edge between the two time series, and we are
disregarding causality. Calculating MIij allows one to detect coordinated activity even for time
series that include different frequency bands. See Bastos and Schoffelen (2016) and Pereda,
Quiroga, and Bhattacharya (2005) for a review of different measures for quantifying coordina-
tion between brain regions and a discussion of their advantages and pitfalls. Note that MIi(i+N)
measures the coordination between two different frequency bands in the same brain region i.
After calculating MIij using Equation 4, we generate surrogates (which we subsequently use
as a threshold for mutual information) by using a block-permutation procedure (Canolty et al.,
2006): We simultaneously cut each time series into blocks of 1018 points (à propos 2 s), et
we permute the resulting blocks uniformly at random. This procedure preserves lower fre-
quencies and time-series features (such as nonstationarity and nonlinearity) below the chosen
temporal scale. (See the Supplementary Information (Buldú & Porter, 2017) for further discus-
sion and a detailed investigation of the influence of block length on the surrogates.) We then
evaluate the mutual information between each surrogate time series to obtain MIrand.
Frequency-Based Multilayer Networks
We construct a frequency-based multilayer network for each individual from the matrix that
encodes the MI of each pair of sensors for the four different frequencies bands. Each layer
includes nodes with the same frequency band, yielding four different layers: theta (je), alpha
(un), beta (β), and gamma (c). We use MIrand from the surrogate times series as a threshold
Neurosciences en réseau
437
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
and construct a weighted supra-adjacency matrix W with elements Wij = MIij − MIrand
si
MIij > MIrand
and Wij = 0 otherwise. We thereby account only for edges with statistically-
significant edges. (In Figure 2, one can see what fractions of edges are 0 in each case.) Enfin,
we apply a linear normalization to W to obtain
ij
ij
Mij =
Wij − w
wmax − w
min
min
,
where w
min and wmax are, respectivement, the largest and smallest entries of W. This ensures that
Mij ∈ [0, 1] pour chaque individu, thereby facilitating comparisons between them. Le pondéré
supra-adjacency matrix M includes some number of 0 entries, which account for interac-
tions that we deem to not be statistically significant. It has four blocks along the diagonal that
encode interactions within each layer (c'est à dire., the same frequency band for different brain regions),
and it has off-diagonal blocks that quantify coordination between different frequencies. Voir
Figure 1B for a schematic.
Methodological Considerations
An important issue is the applicability of our results to functional brain networks that are con-
structed using different approaches, such as by using source reconstruction or with different
ways of evaluating coordination between brain regions.
Dans notre étude, we constructed func-
tional brain networks from magnetoencephalographic recordings, which are measured at the
sensor level, instead of using the actual magnetic field that is generated in each brain region
(c'est à dire., at a source). (One can infer such a field using source-reconstruction methods.) Working
with time series at the sensor level necessarily entails signal mixing (Schoffelen & Gross, 2009),
whereas the use of source reconstruction has what is known as the “inverse problem” (of in-
ferring the actual magnetic field that is created by the brain regions), and it thus requires the
introduction of a priori assumptions in the model that one uses for source reconstruction. Ce
issue has led to a diversity of algorithms to obtain source-reconstructed time series and, dans
many cases, different algorithms yield qualitatively different time series at the source level
(voir, par exemple., Schoffelen & Gross, 2009; Belardinelli, Ortiz, Barnes, Noppeney, & Preissl, 2012).
Par conséquent, there is an open debate about what constitutes the most appropriate method-
ology to construct functional networks using source reconstruction (Palva & Palva, 2012; van
Diessen et al., 2015).
Regardless of how one constructs a functional brain network (and whether one uses sensors
or sources), our analysis has the same qualitative implications. Specifically, estimating the
value of λ
2 from matrices associated with function brain networks is affected strongly by edge-
weight heterogeneity and missing interlayer edges. One also observes the same qualitative
differences between a multiplex construction and a full multilayer one, as this phenomenon
depends on the number of interlayer edges and not on specific details of the construction of
functional brain networks.
Similar reasoning applies to the construction of frequency-based brain networks using
different ways of quantifying coordination between brain regions. We used MI because it is
able to successfully capture both linear and nonlinear correlations, it is an adequate method
for quantifying interdependencies between signals that are split into frequency bands (David,
Cosmelli, & Friston, 2004), and it has been used widely in the past to construct functional
brain networks (voir, par exemple., Bassett et al., 2009; Becker et al., 2012; Chaï, Walther, Beck, &
Fei Fei, 2009; Deuker et al., 2009; Jin, Seol, Kim, & Chung, 2011). On the down side, MI
cannot avoid zero-lag correlations that originate from common sources. (This flaw also occurs
Neurosciences en réseau
438
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
in many other commonly-employed similarity measures, such as partial correlation, coher-
ence, and phase-locking value (Bastos & Schoffelen, 2016).) The systematic deletion of zero-
lag correlations entails a very strict assumption, but because not all zero-lag correlations are
due to common sources or volume conduction (Christodoulakis et al., 2013; Porz, Kiel, &
Lehnertz, 2014; Vicente, Gollo, Mirasso, Fischer, & Pipa, 2008), there does not exist a con-
sensus on how to eradicate them (voir, par exemple., Brookes, Woolrich, & Barnes, 2012; Stam, Nolte,
& Daffertshofer, 2007). It is thus important for future work to conduct a systematic comparison
between the most widespread coordination measures and their consequences on the spectral
properties of functional networks. As we stated previously, the effect that edge-weight hetero-
geneity and missing interlayer edges have on functional multiplex and multilayer networks is
a general phenomenon, as it does not rely on the specific similarity measure that one employs
to evaluate coordination between brain regions, as long as there is sufficient heterogeneity
in the weights of the interlayer edges. As shown in Brookes et al. (2016), such heterogeneity
is expected in frequency-based functional brain networks, given the complicated interactions
between different brain regions at different frequencies.
CONTRIBUTIONS DES AUTEURS
Javier M. Buldú: Conceptualisation; Conservation des données; Analyse formelle; Méthodologie; Writing —
brouillon original; Writing — revisions. Mason Alexander Porter: Conceptualisation; Methodol-
ogy; Writing — original draft; Writing — revisions.
REMERCIEMENTS
We thank John Allen for fruitful conversations. We also thank the referees for their helpful
suggestions.
J.M.B. acknowledges financial support from Spanish MINECO (project FIS2013-41057) et
from Salvador de Madariaga Program (PRX15/00107), which allowed him to visit University
of Oxford in summer 2016.
INFORMATIONS SUR LE FINANCEMENT
Javier M. Buldú, Ministerio de Economía y Competitividad (http://dx.doi.org/10.13039/
Javier M. Buldú,
501100003329), Award IDs:
Ministerio de Economía y Competitividad (http://dx.doi.org/10.13039/501100003329), Award
ID: PRX15/00107.
FIS2013-41057 and FIS2017-84151-P.
RÉFÉRENCES
Aguirre, J., Sevilla-Escoboza, R., Gutiérrez, R., Papo, D., & Buldú, J.. M..
(2014). Synchronization of interconnected networks: The role of
connector nodes. Physical Review Letters, 112, 248701.
Allen-Perkins, UN., Albuquerque de Assis, T., Pastor,
J.. M., &
Andrade, R.. F. S. (2017). Relaxation time of the global order
parameter on multiplex networks: The role of interlayer coupling
in Kuramoto oscillators. ArXiv:1708.01883v1.
J.. UN., & Díaz-Guilera, UN.
(2007). Dynamical and
spectral properties of complex networks. New Journal of Physics,
9, 187.
Almendral,
Aru, J., Aru, J., Priesemann, V., Wibral, M., Lana, L., Pipa, G., . . .
(2015). Untangling cross-frequency coupling in
Vicente, R..
neuroscience. Opinion actuelle en neurobiologie, 31, 51–61.
Barabási, A.-L., & Albert, R.. (1999). Emergence of scaling in ran-
dom networks. Science, 286, 509–512.
Bassett, D. S., Bullmore, E. T., Meyer-Lindenberg, UN., Apud, J.. UN.,
Weinberger, D. R., & Coppola, R.. (2009). Cognitive fitness
of cost-efficient brain functional networks. Actes du
National Academy of Sciences of the United States of America,
106, 11747–11752.
Neurosciences en réseau
439
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
Bassett, D. S., Meyer-Lindenberg, UN., Achard, S., Duke, T., &
Bullmore, E. T. (2006). Adaptive reconfiguration of fractal small-
world human brain functional networks. Actes du
National Academy of Sciences of the United States of America,
103, 19518–19523.
Bassett, D. S., & Sporns, Ô. (2017). Network neuroscience. Nature
Neurosciences, 20, 353–364.
Bassett, D. S., Wymbs, N. F., Porter, M.. UN., Mucha, P.. J., Carlson, J.. M.,
& Grafton, S. T. (2011). Dynamic reconfiguration of human brain
networks during learning. Proceedings of the National Academy
of Sciences of the United States of America, 118, 7641–7646.
Bassett, D. S., Wymbs, N. F., Rombach, M.. P., Porter, M.. UN., Mucha,
P.. J., & Grafton, S. T. (2013). Task-based core–periphery organ-
ization of human brain dynamics. Biologie computationnelle PLoS,
9, e1003171.
Bastos, UN. M., & Schoffelen, J.. M.. (2016). A tutorial review of func-
tional connectivity analysis methods and their interpretational
pitfalls. Frontiers in Systems Neuroscience, 9, 175.
Battiston, F., Nicosia, V., Chavez, M., & Latora, V. (2017). Multilayer
motif analysis of brain networks. Chaos, 27, 047404.
Becker, J.. T., Bajo, R., Fabrizio, M., Sudre, G., Cuesta, P., Aizenstein,
H. J., . . . Bagic, UN. (2012). Functional connectivity measured
with magnetoencephalography identifies persons with HIV dis-
ease. Brain Imaging and Behavior, 6, 366–373.
Belardinelli, P., Ortiz, E., Barnes, G., Noppeney, U., & Preissl, H.
(2012). Source reconstruction accuracy of MEG and EEG
Bayesian inversion approaches. PLoS ONE, 7, e51985.
Betzel, R.. F., & Bassett, D. (2016). Multi-scale brain networks.
NeuroImage, 160, 73–83.
Boccaletti, S., Bianconi, G., Criado, R., Del Genio, C. JE., Gómez-
Gardenes, J., Romance, M., . . . Zanin, M.. (2014). The structure
and dynamics of multilayer networks. Physics Reports, 544, 1–122.
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang,
D. (2006). Complex networks: Structure and dynamics. Physics
Reports, 424, 1–175.
Brun, U., Schäfer, UN., Walter, H., Erk, S., Romanczuk-Seiferth, N.,
Haddad, L., . . . Basset, D. S. (2014). Dynamic reconfiguration
of frontal brain networks during executive cognition in humans.
Proceedings of the National Academy of Sciences of the United
States of America, 112, 11678–11683.
Brookes, M.. J., Tewarie, P.. K., Hunt, B. UN., Robson, S. E., Gascoyne,
L. E., Liddle, E. B., . . . Morris, P.. G. (2016). A multi-layer
network approach to MEG connectivity analysis. NeuroImage,
132, 425–438.
Brookes, M.. J., Woolrich, M.. W., & Barnes, G. R.. (2012). Measuring
functional connectivity in MEG: A multivariate approach insen-
sitive to linear source leakage. NeuroImage, 63, 910–920.
Buldú, J.. M., & Porter, M.. UN.
(2017). Supplementary information
for “Frequency-based brain networks: From a multiplex frame-
work to a full multilayer description.” Network Neuroscience,
2(4), 418–441. https://doi.org/10.1162/netn_a_00033
Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E., & Havlin, S.
(2010). Catastrophic cascade of failures in interdependent net-
travaux. Nature, 464, 1025–1028.
Buzsáki, G.
(2006). Rhythms of the brain. Oxford, ROYAUME-UNI: Oxford
Presse universitaire.
Canolty, R.. T., Edwards, E., Dalal, S. S., Soltani, M., Nagarajan, S. S.,
kirsch, H. E., . . . Knight, R.. T. (2006). High gamma power is
phase-locked to theta oscillations in human neocortex. Science,
313, 1626–1628.
Chaï, B., Walther, D., Beck, D., & Fei Fei, L. (2009). Exploring
functional connectivities of the human brain using multivariate
information analysis. Dans: Advances in neural information process-
ing systems, 22, (éd.. Oui. Bengio, D. Schuurmans, J.. D. Lafferty,
C. K. je. Williams & UN. Culotta), 270–278.
Christodoulakis, M., Hadjipapas, UN., Papathanasiou, E. S.,
Anastasiadou, M., Papacostas, S. S., & Mitsis, G. D. (2013). Sur
the effect of volume conduction on graph theoretic measures of
brain networks in epilepsy. Neuromethods, 91, 103–130.
David, O., Cosmelli, D., & Friston, K. J.. (2004). Evaluation of dif-
ferent measures of functional connectivity using a neural mass
model. NeuroImage, 21, 659–673.
De Domenico, M.. (2017). Multilayer modeling and analysis of hu-
man brain networks. Gigascience, 6, 1–8.
De Domenico, M., Granell, C., Porter, M.. UN., & Arenas, UN. (2016).
The physics of spreading processes in multilayer networks.
Nature Physics, 12, 901–906.
De Domenico, M., Sasai, S., & Arenas, UN. (2016). Mapping multi-
plex hubs in human functional brain networks. Frontiers in
Neurosciences, 10, 326.
De Domenico, M., Solé-Ribalta, UN., Cozzo, E., Kivelä, M., Moreno,
Y., Porter, M.. UN., . . . Arenas, UN. (2013). The physics of spread-
ing processes in multilayer networks. Physical Review X, 3,
041022.
DeFord, D. R., & Pauls, S. D. (2018). A new framework for dynami-
cal models on multiplex networks. Journal of Complex Networks,
6(3), 353–381.
de Haan, W., van der Flier, W. M., Wang, H., Van Mieghem,
P.. F. UN., Scheltens, P., & Stam, C. J.. (2012). Disruption of func-
tional brain networks in Alzheimer’s disease: What can we learn
from graph spectral analysis of resting-state magnetoencephalog-
raphie? Brain Connectivity, 2, 45–55.
de Pasquale, F., Della Penna, S., Snyder, UN. Z., Lewis, C., Mantini,
D., Marzetti, L., . . . Corbetta, M.. (2010). Temporal dynamics of
spontaneous MEG activity in brain networks. Actes du
National Academy of Sciences of the United States of America,
107, 6040–6045.
Tremper, L., Bullmore, E. T., Forgeron, M., Christensen, S., Nathan, P.. J.,
Rockstroh, B., & Bassett, D. S. (2009). Reproducibility of graph
metrics of human brain functional networks. NeuroImage, 47,
1460–1468.
Fortunato, S., & Hric, D. (2016). Community detection in networks:
A user guide. Physics Reports, 659, 1–44.
Gao, J., Buldyrev, S. V., Stanley, H. E., Xu, X., & Havlin, S. (2013).
Percolation of a general network of networks. Physical Review E,
88, 062816.
Gómez, S., Díaz-Guilera, UN., Gómez-Gardeñes, J., Pérez-Vicente,
(2013). Diffusion dynamics on
C. J., Moreno, Y., & Arenas, UN.
multiplex networks. Physical Review Letters, 110, 028701.
Guillon, J., Attal, Y., Colliot, O., La Corte, V., Dubois, B., Schwartz,
D., . . . De Vico Fallani, F. (2017). Loss of brain inter-frequency
hubs in Alzheimer’s disease. Scientific Reports, 7, 10879.
Neurosciences en réseau
440
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Multiplex/Multilayer Frequency-based Brain Networks
Guimerà, R., & Amaral, L. UN. N. (2005). Functional cartography of
complex metabolic networks. Nature, 433, 895–900.
Honey, C. J., Kötter, R., Breakspear, M., & Sporns, Ô. (2007). Net-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. Proceedings of the National Academy of
Sciences of the United States of America, 104, 10240–10245.
Jin, S.-H., Seol, J., Kim, J.. S., & Chung, C. K. (2011). How reliable
are the functional connectivity networks of MEG in resting states?
Journal de neurophysiologie, 106, 2888–2895.
Kivelä, M., Arenas, UN., Barthelemy, M., Gleeson, J.. P., Moreno, Y.,
& Porter, M.. UN. (2014). Multilayer networks. Journal of Complex
Networks, 2, 203–271.
Kopell, N. J., Gritton, H. J., Whittington, M.. UN., & Kramer, M.. UN.
(2014). Beyond the connectome: The dynome. Neurone, 83,
1319–1328.
Larson-Prior, L. J., Oostenveld, R., Della Penna, S., Michalareas, G.,
Prior, F., Babajani-Feremi, J.-M., Schoffelen, . . . Snyder, UN. Z.
(2013). Adding dynamics to the Human Connectome Project
with MEG. NeuroImage, 80, 190–201.
MacKay, D. (2003). Information theory, inference, and learning
algorithms. Cambridge, ROYAUME-UNI: la presse de l'Universite de Cambridge.
Masuda, N., Porter, M.. UN., & Lambiotte, R.. (2017). Random walks
and diffusion on networks. Physics Reports, 716–717, 1–58.
Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D.,
(2002). Network motifs: Simple building blocks of
& Alon, U.
complex networks. Science, 298, 824–827.
Sahneh, F. D., Scoglio, C., & Van Mieghem, P.. (2015). Exact cou-
pling threshold for structural transition reveals diversified behav-
iors in interconnected networks. Physical Review E, 92, 040801.
Salehi, M., Sharma, R., Marzolla, M., Magnani, M., Siyari, P., &
Montesi, D. (2015). Spreading processes in multilayer networks.
IEEE Transactions on Network Science and Engineering, 2, 65–83.
Schindler, K., Bialonski, S., Horstmann, M.. T., Élan, C. E., & Lehnertz,
K. (2008). Evolving functional network properties and synchroniz-
ability during human epileptic seizures. Chaos, 18, 033119.
Schoffelen, J., & Gross, J.. (2009). Source connectivity analysis with
MEG and EEG. Human Brain Mapping, 30, 1857–1865.
(2013).
Siebenhühner, F., Blanc, S. UN., Coppola, R., Weinberger, D. R., &
Intra- and inter-frequency brain network
Bassett, D. S.
structure in health and schizophrenia. PLoS ONE, 8, e72351.
Simas, T., Chavez, M., Rodriguez, P.. R., & Díaz-Guilera, UN. (2015).
An algebraic topological method for multimodal brain networks
comparisons. Frontiers in Psychology, 6, 904.
Stam, C. J., Nolte, G., & Daffertshofer, UN. (2007). Phase lag index:
Assessment of functional connectivity from multi channel EEG
and MEG with diminished bias from common sources. Human
Brain Mapping, 28, 1178–1193.
Stam, C. J., van Straaten, E. C. W., Van Dellen, E., Tewarie, P., Gong,
G., Hillebrand, UN., . . . Van Mieghem, P.. (2016). The relation
between structural and functional connectivity patterns in com-
plex brain networks. International Journal of Psychophysiology,
103, 149–160.
Newman, M.. E. J.. (2010). Networks: An introduction. Oxford, ROYAUME-UNI:
Tsonis, UN. UN., & Roebber, P.. J.. (2004). The architecture of the
Presse universitaire d'Oxford.
Palva, S., & Palva, J.. M.. (2012). Discovering oscillatory interaction
networks with M/EEG: Challenges and breakthroughs. Trends in
Cognitive Sciences, 16, 219–230.
Papo, D., Zanin, M., & Buldú, J.. M.. (2014). Reconstructing func-
tional brain networks: Have we got the basics right? Frontiers in
Human Neuroscience, 8, 107.
Pereda, E., Quiroga, R.. Q., & Bhattacharya, J.. (2005). Nonlinear
multivariate analysis of neurophysiological signals. Progress in
Neurobiology, 77, 1–37.
Phillips, D. J., McGlaughlin, UN., Ruth, D., Jager, L. R., & Soldan, UN.
(2015). Disruption of functional brain networks in Alzheimer’s
maladie: What can we learn from graph spectral analysis of
resting-state magnetoencephalography? NeuroImage: Clinique,
7, 377–390.
Porz, S., Kiel, M., & Lehnertz, K. (2014). Can spurious indica-
tions for phase synchronization due to superimposed signals be
avoided? Chaos, 24, 033112.
Radicchi, F., & Arenas, UN. (2013). Abrupt transition in the struc-
tural formation of interconnected networks. Nature Physics, 9,
717–720.
climate network. Physica A, 333, 497–504.
Vaiana, M., & Muldon, S. (2018). Multilayer brain networks.
Journal of Nonlinear Science. https://doi.org/10.1007/s00332-
017-9436-8.
van Diessen, E., Numan, T., van Dellen, E., van der Kooi, UN. W.,
Boersma, M., Hofman, D., . . . Stam, C. J.. (2015). Opportu-
nities and methodological challenges in EEG and MEG resting
state functional brain network research. Clinical Neurophysiol-
ogy, 126, 1468–1481.
Van Mieghem, P.. (2011). Graph spectra for complex networks.
Cambridge, ROYAUME-UNI: la presse de l'Universite de Cambridge.
Vicente, R., Gollo, L. L., Mirasso, C. R., Fischer, JE., & Pipa, G.
(2008). Dynamical relaying can yield zero time lag neuronal
synchrony despite long conduction delays. Actes du
National Academy of Sciences of the United States of America,
105, 17157–17162.
Yu, M., Engels, M.. M., Hillebrand, UN., van Straaten, E. C., Gouw,
UN. UN., Teunissen, C., . . . Stam, C. J.. (2017). Selective impair-
ment of hippocampus and posterior hub areas in Alzheimer’s
maladie: An MEG-based multiplex network study. Cerveau, 140,
1466–1485.
Neurosciences en réseau
441
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
4
4
1
8
1
0
9
2
2
3
8
n
e
n
_
un
_
0
0
0
3
3
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3