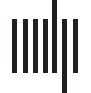RECHERCHE
Local connectome phenotypes predict social,
health, and cognitive factors
Michael A. Powell
1
, Javier O. Garcia
, Fang-Cheng Yeh
2,3
Jean M. Vettel
, and Timothy Verstynen
2,3,6
4,5
,
7
1Department of Mathematical Sciences, United States Military Academy, West Point, New York, Etats-Unis
2U.S. Army Research Laboratory, Aberdeen Proving Ground, MARYLAND, Etats-Unis
3Department of Bioengineering, University of Pennsylvania, Philadelphia, Pennsylvanie, Etats-Unis
4Department of Neurological Surgery, University of Pittsburgh Medical Center, Pittsburgh, Pennsylvanie, Etats-Unis
5Department of Bioengineering, University of Pittsburgh, Pittsburgh, Pennsylvanie, Etats-Unis
6Department of Psychological and Brain Sciences, Université de Californie, Santa Barbara, Californie, Etats-Unis
un accès ouvert
journal
7
Department of Psychology and Center for the Neural Basis of Cognition, Carnegie Mellon University, Pittsburgh, Pennsylvanie, Etats-Unis
Mots clés: Local connectome, White matter, Individual differences, Behavior prediction, Structural
connectivité
ABSTRAIT
The unique architecture of the human connectome is defined initially by genetics and
subsequently sculpted over time with experience. Ainsi, similarities in predisposition and
experience that lead to similarities in social, biological, and cognitive attributes should
also be reflected in the local architecture of white matter fascicles. Here we employ a
method known as local connectome fingerprinting that uses diffusion MRI to measure the
fiber-wise characteristics of macroscopic white matter pathways throughout the brain. Ce
fingerprinting approach was applied to a large sample (N = 841) of subjects from the
Human Connectome Project, revealing a reliable degree of between-subject correlation in
the local connectome fingerprints, with a relatively complex, low-dimensional substructure.
Using a cross-validated, high-dimensional regression analysis approach, we derived local
connectome phenotype (LCP) maps that could reliably predict a subset of subject attributes
measured, including demographic, health, and cognitive measures. These LCP maps were
highly specific to the attribute being predicted but also sensitive to correlations between
attributes. Collectively, these results indicate that the local architecture of white matter
fascicles reflects a meaningful portion of the variability shared between subjects along
several dimensions.
RÉSUMÉ DE L'AUTEUR
The local connectome is the pattern of fiber systems (c'est à dire., number of fibers, orientation, et
size) within a voxel, and it reflects the proximal characteristics of white matter fascicles
distributed throughout the brain. Here we show how variability in the local connectome is
correlated in a principled way across individuals. This intersubject correlation is reliable
enough that unique phenotype maps can be learned to predict between-subject variability in
a range of social, health, and cognitive attributes. This work shows, for the first time, how the
local connectome has both the sensitivity and the specificity to be used as a phenotypic
marker for subject-specific attributes.
Citation: Powell, M.. UN., Garcia, J.. O.,
Yeh, F.-C., Vettel, J.. M., & Verstynen, T.
(2017). Local connectome phenotypes
predict social, health, and cognitive
factors. Neurosciences en réseau. 2(1),
86–105. https://est ce que je.org/10.1162/
netn_a_00031
EST CE QUE JE:
https://doi.org/10.1162/netn_a_00031
Informations complémentaires:
https://doi.org/10.1162/netn_a_00031
Reçu: 29 Mars 2017
Accepté: 8 Octobre 2017
Intérêts concurrents: Les auteurs ont
a déclaré qu'aucun intérêt concurrent
exister.
Auteur correspondant:
Timothy Verstynen
timothyv@andrew.cmu.edu
droits d'auteur: © 2017
Massachusetts Institute of Technology
Publié sous Creative Commons
Attribution 4.0 International
(CC PAR 4.0) Licence
La presse du MIT
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
8
6
1
0
9
2
0
0
0
n
e
n
_
un
_
0
0
0
3
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Local connectome phenotypes
Connectome:
The complete set of connections
between neurons in the brain.
Diffusion MRI (dMRI):
An MRI technique that indirectly
measures voxel-wise white matter
architecture by quantifying the
diffusion patterns of water molecules
trapped within cells.
White matter:
The bundles of myelinated axons that
facilitate long-range communication
between distal brain regions.
Voxel:
Short for “volumetric pixel,” defines
the spatial resolution of MRI data.
Local connectome fingerprint:
The complete pattern of resolved
white matter fibers within all voxels
and between adjacent voxels.
INTRODUCTION
The unique pattern of connections among the billions of neurons in the brain is termed the con-
nectome (Sporns, Tononi, & Kotter, 2005), and this pattern encapsulates a fundamental con-
straint on neural computation and cognition (Gu et al., 2015; Thivierge & Marcus, 2007). Ce
connective architecture is initially structured by genetics and then sculpted by experience over
temps (Kochunov, Fu, et coll., 2016; Kochunov, Thompson, et coll., 2016; Yeh, Vettel, et coll., 2016).
Recent advancements in neuroimaging techniques, particularly diffusion MRI (dMRI), have
opened the door to mapping the macroscopic-level properties of the structural connectome in
vivo (Le Bihan & Johansen-Berg, 2012). Par conséquent, a growing body of research has focused on
quantifying how variability in structural connectivity associates with individual differences in
functional properties of brain networks (Muldoon et al., 2016; Passingham, Stephan, & Kötter,
2002), as well as associating with differences in social (Gianaros, Marsland, Sheu, Erickson,
& Verstynen, 2013; Molesworth, Sheu, Cohen, Gianaros, & Verstynen, 2015), biological
(Arfanakis et al., 2013; Miralbell et al., 2012; Verstynen et al., 2013), and cognitive (Muraskin
et coll., 2016; Muraskin et al., 2016; Verstynen, 2014; Ystad et al., 2011) attributes.
DMRI works by measuring the microscopic diffusion pattern of water trapped in cellular
tissues, allowing for a full characterization of white matter pathways, such as axonal fiber
direction and integrity (for a review see Jbabdi, Sotiropoulos, Haber, Van Essen, & Behrens,
2015; Le Bihan & Johansen-Berg, 2012). Previous studies have used dMRI to map the global
properties of the macroscopic connectome by determining end-to-end connectivity between
brain regions (Hagmann et al., 2010; Hagmann et al., 2008, 2010; Sporns, 2014). The re-
sulting connectivity estimates can then be summarized, often using graph theoretic tech-
niques that are then associated with variability across individuals (Bullmore & Sporns, 2009;
Rubinov & Sporns, 2010). While dMRI acquisition and reconstruction approaches have
the reli-
improved substantially in recent years (Fan et al., 2016; Van Essen et al., 2012),
ability and validity of many popular fiber tractography algorithms have come into question
(Daducci, Dal Palú, Descoteaux, & Thiran, 2016; Reveley et al., 2015; Thomas et al., 2014).
Par conséquent, the reliability of subsequent interregional connectivity estimates may be negatively
impacted.
Instead of mapping end-to-end connectivity between regions, we recently introduced the
concept of the local connectome as an alternative measure of structural connectivity that
does not rely on fiber tracking (Yeh, Badre, & Verstynen, 2016). The local connectome is
defined as the pattern of fiber systems (c'est à dire., number of fibers, orientation, and size) within
a voxel, as well as immediate connectivity between adjacent voxels, and can be quanti-
fied by measuring the fiber-wise density of microscopic water diffusion within a voxel. Ce
voxel-wise measure shares many similarities with the concept of a “fixel” proposed by others
(Raffelt et al., 2015). The complete collection of these multifiber diffusion density measure-
ments within all white matter voxels, termed the local connectome fingerprint, provides a
high-dimensional feature vector that can describe the unique configuration of the structural
connectome (Yeh, Vettel, et coll., 2016). In this way, the local connectome fingerprint provides
a diffusion-informed measure along the fascicles that supports interregional communication,
rather than determining the start and end positions of a particular fiber bundle.
We recently showed that the local connectome fingerprint is highly specific to an indi-
vidual, affording near-perfect accuracy on within- versus between-subject classification tests
among hundreds of participants (Yeh, Badre, et coll., 2016). Surtout, this demonstrated that
Neurosciences en réseau
87
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
8
6
1
0
9
2
0
0
0
n
e
n
_
un
_
0
0
0
3
1
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Local connectome phenotypes
Principal component
regression (PCR):
A regression approach that relies on
using principal component analysis
(APC) to reduce the dimensionality of
a model before analysis.
Local connectome phenotype:
A unique pattern of the local
connectome that reliably predicts
between-individual variability in a
particular feature.
a large portion of an individual’s local connectome is driven by experience. Whole-fingerprint
distance tests revealed only a 12.51% similarity between monozygotic twins, relative to almost
no similarity between genetically unrelated individuals. En outre, within-subject uniqueness
showed substantial plasticity, changing at a rate of approximately 12.79% every 100 jours
(Yeh, Vettel, et coll., 2016). Ainsi, the unique architecture of the local connectome appears to
be initially defined by genetics and then subsequently sculpted over time with experience.
The plasticity of the local white matter architecture suggests that it is important to consider
how whole-fingerprint uniqueness may mask more subtle similarities arising from common
experiences. If experience, including common social or environmental factors, is a major force
impacting the structural connectome, then common experiences between individuals may also
lead to increased similarity in their local connectomes.
En outre, since the white matter
is a fundamental constraint on cognition, similarities in local connectomes are expected to
associate with similarities in cognitive function. Ainsi, we hypothesized that shared variability
in certain social, biological, or cognitive attributes can be predicted from the local connectome
fingerprints.
To test this, we reconstructed multishell dMRI data from the Human Connectome Project
(HCP) to produce individual local connectome fingerprints from 841 sujets. A set of 32
subject-level attributes were used for predictive modeling, including many social, biological,
and cognitive factors. A model between each fiber in the local connectome fingerprint and
a target attribute was learned using a cross-validated, sparse version of principal component
regression. The predictive utility of each attribute map, termed a local connectome phenotype
(LCP), was evaluated by predicting a given attribute using cross validation. Our results show
that specific characteristics of the local connectome are sensitive to shared variability across
individuals, as well as being highly reliable within an individual (Yeh, Vettel, et coll., 2016),
confirming its utility for understanding how network organization reflects genetic and experi-
ential factors.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
8
6
1
0
9
2
0
0
0
n
e
n
_
un
_
0
0
0
3
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
MATERIALS AND METHODS
Participants
We used publicly available dMRI data from the S900 (2015) release of the Human Connectome
Project (HCP; Van Essen et al., 2013), acquired by Washington University in St. Louis and the
University of Minnesota. Out of the 900 participants released, 841 participants (370 male,
ages 22–37, mean age 28.76) had viable dMRI datasets. Our analysis was restricted to this
subsample. All data collection procedures were approved by the institutional review boards at
Washington University in St. Louis and the University of Minnesota. The post hoc data analysis
was approved as exempt by the institutional review board at Carnegie Mellon University, dans
accordance with 45 CFR 46.101(b)(4) (IRB Protocol Number: HS14-139).
Diffusion MRI Acquisition
The dMRI data were acquired on a Siemens 3T Skyra scanner using a two-dimensional spin-
echo single-shot multiband EPI sequence with a multiband factor of 3 and monopolar gradient
pulse. The spatial resolution was 1.25 mm isotropic (TR = 5,500 ms, LE = 89.50 ms). Le
2
b-values were 1,000, 2,000, et 3,000 s/mm
. The total number of diffusion sampling direc-
tions was 90 for each of the three shells in addition to six b0 images. The total scanning time
was approximately 55 min.
Neurosciences en réseau
88
Local connectome phenotypes
Local Connectome Fingerprint Reconstruction
An outline of the pipeline for generating local connectome fingerprints is shown in the top
panel of Figure 1. The dMRI data for each subject were reconstructed in a common stereotaxic
space using q-space diffeomorphic reconstruction (QSDR; Yeh & Tseng, 2011), a nonlinear
registration approach that directly reconstructs water diffusion density patterns into a common
stereotaxic space at 1 mm
resolution.
3
Using the HCP dataset, we derived an atlas of axonal direction in each voxel (publicly
available at http://dsi-studio.labsolver.org). A spin distribution function (SDF)
sampling framework was used to provide a consistent set of directions ˆu to sample the mag-
nitude of SDFs along axonal directions in the cerebral white matter. Since each voxel may
have more than one fiber direction, multiple measurements were extracted from the SDF for
voxels that contained crossing fibers, while a single measurement was extracted for voxels with
fibers in a single direction. The appropriate number of density measurements from each voxel
was sampled by the left-posterior-superior voxel order and compiled into a sequence of scalar
valeurs. Gray matter was excluded using the ICBM-152 white matter mask (MacConnell Brain
Imaging Centre, Université McGill, Canada). The cerebellum was also excluded because of
different slice coverage in the cerebellum across participants. Since the density measurement
has arbitrary units, the local connectome fingerprint was scaled to make the variance equal to 1
(Yeh, Vettel, et coll., 2016). The resulting local connectome fingerprint is thus a one-dimensional
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
8
6
1
0
9
2
0
0
0
n
e
n
_
un
_
0
0
0
3
1
p
d
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 1. Data analysis pipeline. dMRI from the HCP dataset were preprocessed consistent with
previous research investigating the local connectome fingerprint (top panel) and included registra-
tion via QSDR and estimation of SDF using an axonal directional atlas derived from the HCP dataset.
Once fingerprints were estimated for each individual, the pipeline for analysis of the continuous
response variables consisted of four major steps: (1) a PCA-based dimensionality reduction, (2) un
LASSO model based on the lower-dimensional components of the local connectome fingerprint,
(3) local connectome phenotype estimation from projection of the contributing components of the
LASSO model, et (4) prediction on the held-out dataset. A similar pipeline was used for categori-
cal response variables with the exception that a logistic LASSO model was used in the LASSO-PCR
step and prediction accuracy was assessed as percentage correct rather than as a predicted versus
observed correlation.
Neurosciences en réseau
89
Local connectome phenotypes
Least absolute shrinkage and
selection operator (LASSO):
A sparse regression approach for
dealing with high-dimensional
datasets.
Neurosciences en réseau
vector where each entry represents the density estimate of restricted water diffusion in a specific
direction along an average fiber. The magnitude of this value reflects the average signal across
a large number of coherently oriented axons, as well as support tissue like myelin and other
glia.
The local connectome fingerprint construction was conducted using DSI Studio (http://dsi-
studio.labsolver.org), an open-source diffusion MRI analysis tool for connectome analysis. Le
source code, documentation, and local connectome fingerprint data are publicly available on
the same website.
Response Variables
A total of 32 response variables across social, health, and cognitive factors were selected
from the public and restricted datasets released as part of
the HCP. Each variable is
summarized in Table 1, but additional details can be found in the HCP Data Dictionary
(https://wiki.humanconnectome.org/display/PublicData/HCP+Data+Dictionary+Public-+500
+Subject+Release). Tableau 1 provides a description of relevant distributional parameters of
all of the continuous variables tested. Descriptions of distributional properties of categori-
cal variables are provided in the descriptions below. Supplementary Table 1 Powell, Garcia,
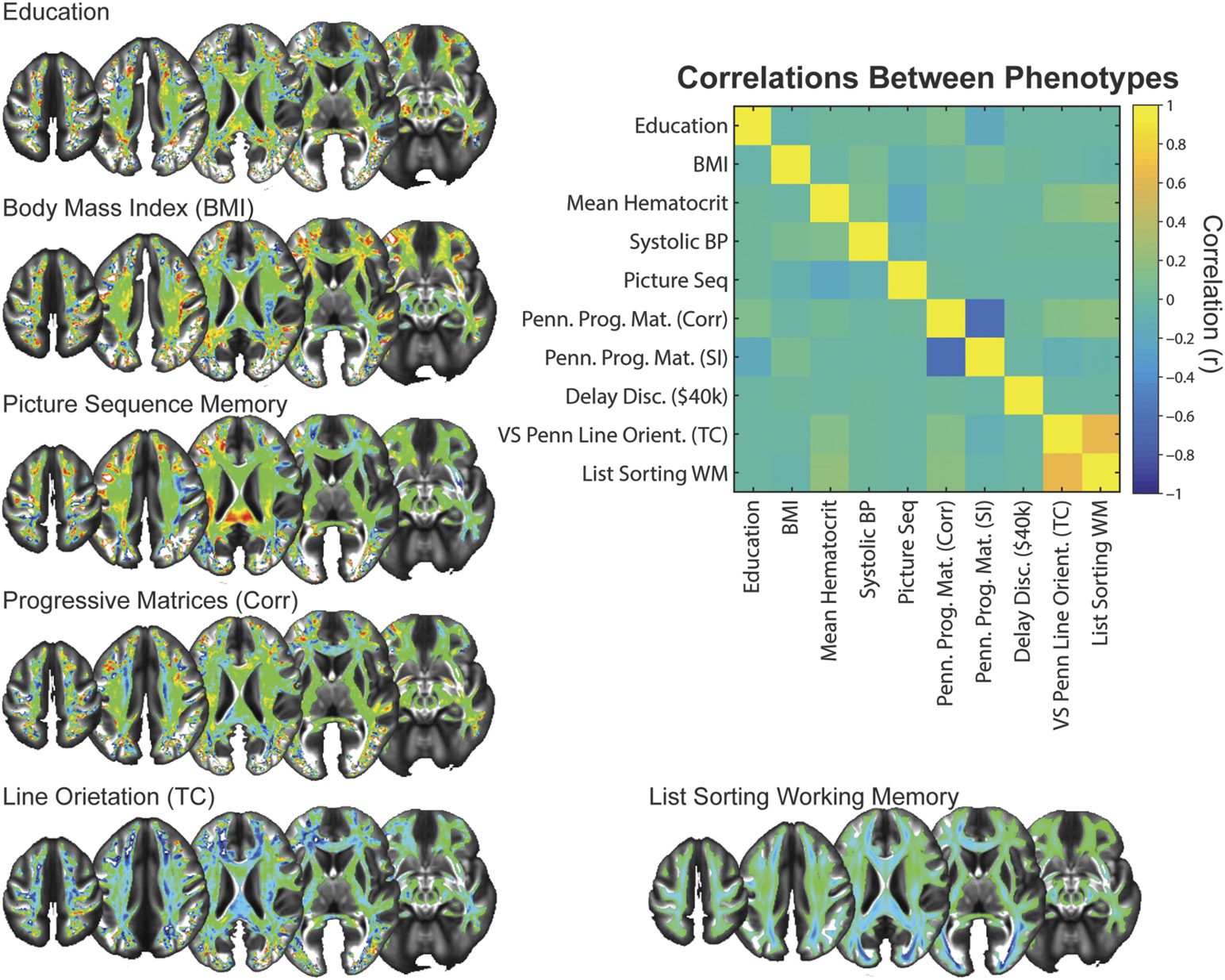
Yeh, Vettel, & Verstynen, 2017 shows the correlation between all continuous variables tested.
Demographic and social factors included age (années), genre (56% female, 44% male),
course (82% white and 18% black in a reduced subset of the total population), ethnicity (91.4%
Hispanic, 8.6% non-Hispanic), handedness, revenu (from the Semi-Structured Assessment
for the Genetics of Alcoholism, SSAGA, scale), éducation (SSAGA), and relationship status
(SSAGA, 44.3% in a “married or live-in relationship” and 55.7% not in such a relationship).
Health factors included body mass index, mean hematocrit, blood pressure (diastolic and
systolic), hemoglobin A1c, and sleep quality (Pittsburgh Sleep Quality Index).
Cognitive measures included 11 tests that sampled a broad spectrum of domains: (un) le
NIH Picture Sequence Memory Test assessed episodic memory performance; (b) NIH Dimen-
sional Change Card Sort tested executive function and cognitive flexibility; (c) NIH Flanker
Inhibitory Control and Attention Test evaluated executive function and inhibition control; (d)
Penn Progressive Matrices examined fluid intelligence and was measured using three perfor-
mance metrics (number of correct responses, total skipped items, and median reaction time
for correct responses); (e) NIH Oral Reading Recognition Test assessed language and reading
performance; (F) NIH Picture Vocabulary Test examined language skills indexed by vocabu-
lary comprehension; (g) NIH Pattern Comparison Processing Speed Test evaluated processing
speed; (h) Delay Discounting tested self-regulation and impulsivity control using two different
financial incentives (Area Under the Curve, AUC, for discounting of $200, AUC for discounting of $40,000); (je) Variable Short Penn Line Orientation assessed spatial orientation performance
and was measured using three metrics (total number correct, median reaction time divided
by expected number of clicks for correct, total positions off for all trials); (j) Penn Word
Memory Test evaluated verbal episodic memory using two performance metrics (total number
of correct responses, median reaction time for correct responses); et (k) NIH List Sorting Task
tested working memory performance.
LASSO Principal Components Regression (LASSO-PCR)
The primary goal of our analysis pipeline was to identify specific patterns of variability in the lo-
cal connectome that reliably predict individual differences in a specific attribute. These unique
90
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
8
6
1
0
9
2
0
0
0
n
e
n
_
un
_
0
0
0
3
1
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Local connectome phenotypes
Tableau 1. Summary statistics for 28 continuous HCP attributes used in the modeling analysis
Skewness
−0.08
−2.18
−0.28
1
% Mild
outliers
0.00
0.10
0.00
% Extreme
2
outliers
0.00
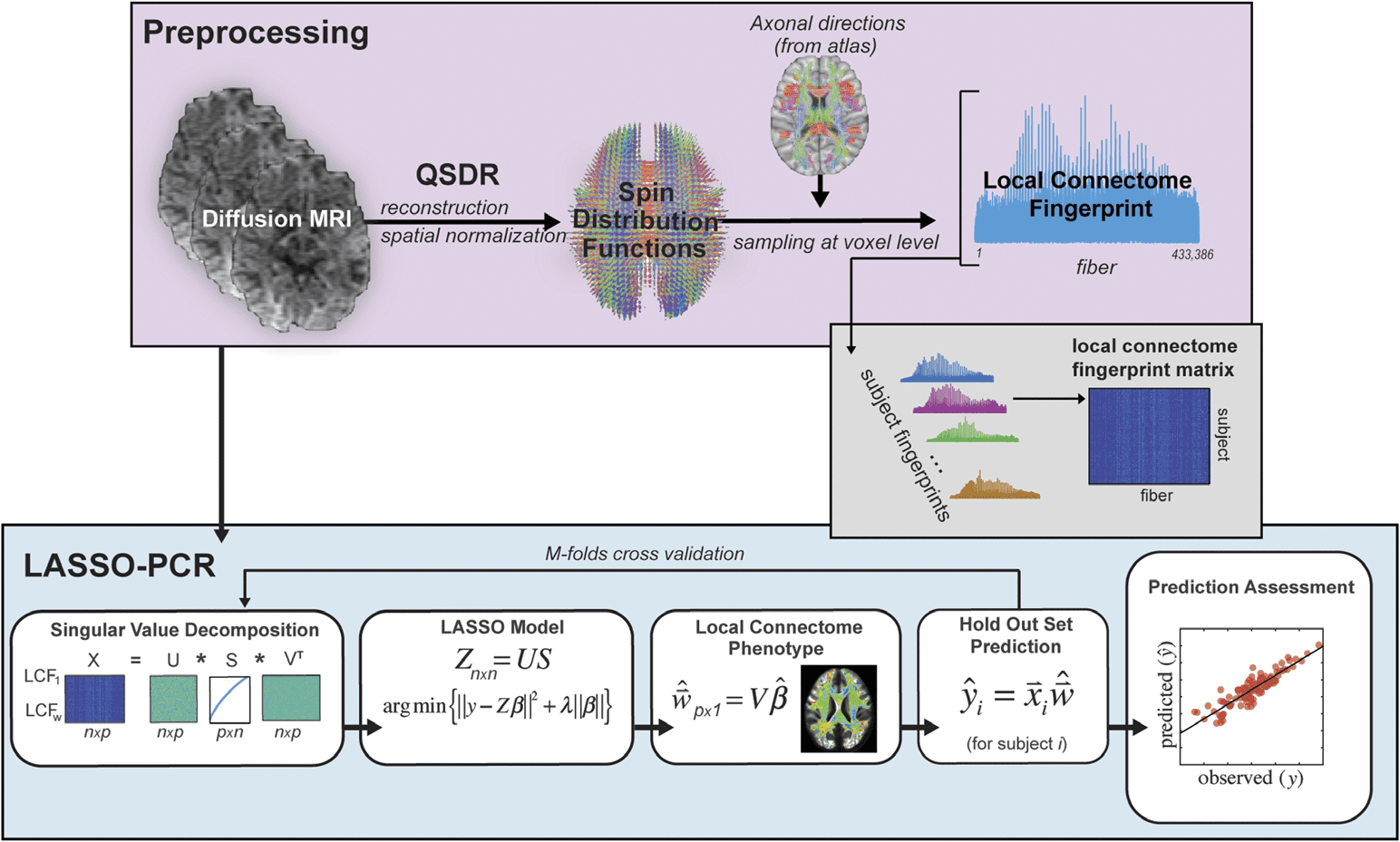
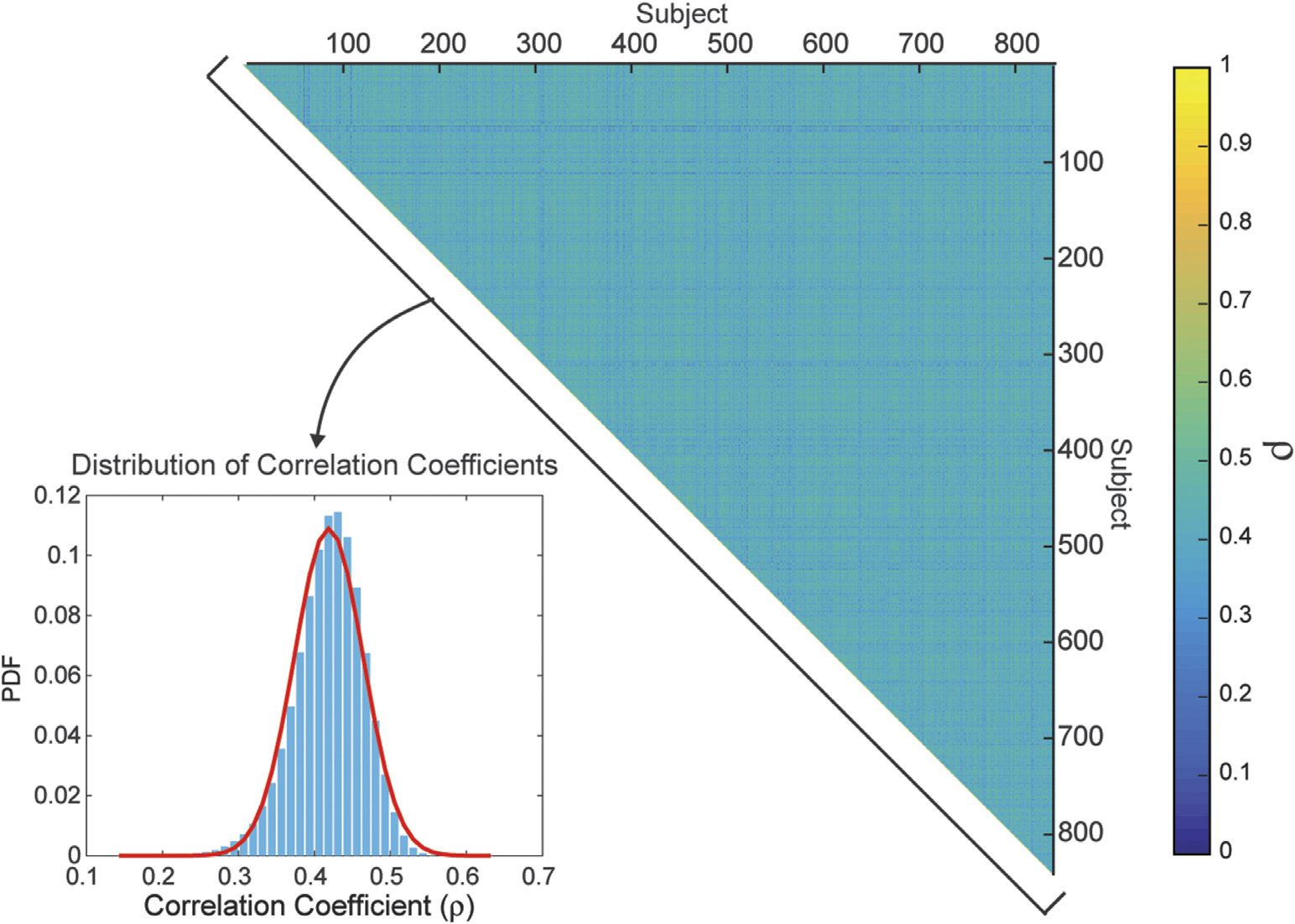
0.07
0.00
95% CI for mean
Upper
Lower
29.01
28.51
68.40
62.33
5.16
4.87
Measured quantity
Age (in years)
3
[−100,100]
Handedness
Total household income
(binned; 5 ∼ $40,000–49,999) Years of education completed Body mass index Mean hematocrit sample Diastolic blood pressure Systolic blood pressure Systolic-diastolic blood pressure ratio Hemoglobin A1C Pittsburgh Sleep Quality Index NIH Picture Sequence Memory Test NIH Dimensional Change Card Sort Test NIH Flanker Inhibitory Control and Attention Test Penn Progressive Matrices: Number of correct responses Penn Progressive Matrices: Total skipped items Penn Progressive Matrices: Median reaction time for correct responses (sec) NIH Oral Reading Recognition Test NIH Picture Vocabulary Test NIH Toolbox Pattern Comparison Processing Speed Test Delay Discounting: Area under the curve for discounting of $200
Delay Discounting: Area under the
curve for discounting of $40,000 Variable Short Penn Line Orientation: Total number correct Variable Short Penn Line Orientation: Median reaction time divided by expected number of clicks for correct (sec) Variable Short Penn Line Orientation: Total positions off for all trials Penn Word Memory Test: Total number of correct responses Penn Word Memory Test: Median reaction time for correct responses (sec) NIH List Sorting Working Memory Test Sample size 841 841 836 840 840 740 830 830 830 566 841 840 839 841 838 838 838 841 841 841 838 838 838 838 838 838 838 841 Mean 28.76 65.36 5.01 14.92 26.51 43.39 76.77 123.76 1.63 5.26 5.18 111.83 115.28 Median 29.00 80.00 5.00 16.00 25.42 43.50 76.00 123.00 1.61 5.30 5.00 110.70 115.07 112.52 112.21 −0.74 0.95 −0.68 0.33 0.51 0.97 0.12 0.91 0.11 0.18 0.25 16.76 18.00 −0.55 3.12 1.00 15.61 14.65 116.96 116.76 114.15 0.25 0.50 117.59 117.03 113.16 0.20 0.49 14.80 15.00 1.01 0.91 −0.14 0.09 0.22 1.39 0.05 −0.23 1.15 1.10 1.31 24.34 21.00 3.16 35.64 36.00 −0.82 1.56 1.51 111.21 108.06 1.85 0.16 0.00 0.03 0.02 0.02 0.01 0.03 0.05 0.01 0.00 0.02 0.01 0.00 0.00 0.01 0.01 0.01 0.03 0.05 0.00 0.00 0.03 0.05 0.01 0.03 0.02 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.02 0.00 0.01 0.00 14.80 26.15 43.05 76.06 122.80 1.61 5.22 4.98 110.92 114.59 15.04 26.86 43.73 77.49 124.71 1.64 5.29 5.39 112.73 115.97 111.84 113.20 16.44 17.09 2.86 3.39 14.99 16.23 116.24 116.12 113.14 117.67 117.40 115.16 0.24 0.48 0.27 0.52 14.51 15.10 1.13 1.17 23.33 25.35 35.44 35.84 1.54 1.58 110.45 111.97 l Téléchargé à partir du site Web : / / direct . m je t . t / / e d u n e n a r t i c e – pdlf / / / / / 2 1 8 6 1 0 9 2 0 0 0 n e n _ a _ 0 0 0 3 1 p d t . f par invité 0 7 Septembre 2 0 2 3 1 2 3 Using the interquartile range (IQR: 75th percentile minus 25th percentile), we define a mild outlier to be any point greater than the 75th percentile or less than the 25th percentile by an amount at least 1.5 times the IQR. Using the interquartile range (IQR: 75th percentile minus 25th percentile), we define an extreme outlier to be any point greater than the 75th percentile or less than the 25th percentile by an amount at least 3 times the IQR. Handedness is a bimodal distribution with a strong preference for right-handedness in the HCP cohort, thus labeling as extreme outliers a large number of individuals with strong left-hand dominance. patterns would reflect a local connectome phenotype for that attribute. The LASSO-PCR pipeline used to generate local connectome phenotype (LCP) maps is illustrated in the lower panel of Figure 1. This process relied on a fivefold cross-validation scheme in which a unique 20% of the participants were assigned to each of five subsamples. For each cross-validation Network Neuroscience 91 Local connectome phenotypes fold, we trained models using 80% of the participants in order to make predictions on the held- dehors 20% of participants. The large number of HCP participants and the infrequent occurrence of outliers in the continuous response variables (see Table 1) justified random fold assignments with little concern about a higher density of outliers existing in any one fold. The random assignment of subjects to folds could pose issues for any infrequent categories in the binary response variables, but the removal of insufficiently represented categories and a verification of near-even class distributions in each fold alleviated these concerns. The analysis pipeline consisted of four major steps. Step 1: Dimensionality reduction. The matrix of local connectome fingerprints (841 partic- ipants × 433,386 features) contains many more features than participants (p >> n), thereby posing a problem for fitting virtually any type of model. To efficiently develop and evaluate predictive models in a cross-validation framework, on each fold we first performed an econom- ical singular value decomposition (SVD) on the matrix of training subjects’ local connectome fingerprints (Wall, Rechtsteiner, & Rocha, 2003): X = USV T, (1) where X is an n × p matrix containing local connectome fingerprints for n participants in the cross-validation fold (∼673 subjects × 433,386 elements per fingerprint), V T is an n × p matrix with row vectors representing the orthogonal principal axes of X, and the matrix product US is an n × n matrix with rows corresponding to the principal components required to reproduce the original matrix X when multiplied by the principal axes matrix V T. Step 2: LASSO model. To reduce the chance of overfitting and improve the generalizability of the model for a novel test set, we employed LASSO regression, a technique that penalizes the multivariate linear model for excessive complexity (c'est à dire., number and magnitude of nonzero coefficients; Tibshirani, 2011). The penalty in this approach arises from the L1 sparsity con- straint in the fitting process, and this combined method, known as LASSO-PCR, has been used successfully in similar high-dimensional prediction models from neuroimaging datasets (Wager, Atlas, Leotti, & Rilling, 2011; Wager et al., 2013). In short, the LASSO-PCR approach identifies a sparse set of components that reliably associate individual response variables (voir la figure 1) and takes the following form: ˆβ = arg minβ{||y − Zβ||2 + λ||β||}, (2) where Z = US as defined above. Using a cross-validation approach, we estimated the optimal ˆβ coefficients using the “glmnet” package in R (Friedman, Hastie, & λ parameter and associated Tibshirani, 2010; see https://cran.r-project.org/web/packages/glmnet/glmnet.pdf for documen- tation). For each response-specific regression model, the model inputs included the principal components estimated from Equation 1, c'est, NOUS (voir la figure 2), and intracranial volume (ICV). For continuous variables (par exemple., reaction times), a linear regression LASSO was used. For binarized categorical variables (par exemple., genre), a logistic regression variant of LASSO was used. In order to assess the value of the local connectome fingerprint components in modeling continuous response variables, the LASSO-produced ) to exclude ICV and thereby restrict interpretation to the relationship between the response variables and the principal components. ˆβ vector was truncated ( ˆβ∗ The inclusion of ICV while building a model allows for the isolation of any predictive power present in the local connectome fingerprint and not to head size, which is a common adjust- ment used when attempting to understand structural differences between individuals or groups Network Neuroscience 92 l Téléchargé à partir du site Web : / / direct . m je t . / / t e d u n e n a r t i c e – pdlf / / / / / 2 1 8 6 1 0 9 2 0 0 0 n e n _ a _ 0 0 0 3 1 pd . t f b y g u e s t t o n 0 7 Septembre 2 0 2 3 Local connectome phenotypes to reduce the possibility of type-I errors (O’Brien et al., 2011). Our LASSO-PCR procedure considers ICV in every model, and in some cases, ICV is deemed a significant contributor to variance in the response variable. Dans d'autres cas, ICV is assigned a regression coefficient of zero. We observe empirically that the correlation of ICV to local connectome fingerprint principal component scores is quite small. This is to be expected considering the orthogo- nality of the principal components and small chance that ICV would align meaningfully with one or more components. Combining the observation that ICV has small, nonmeaningful cor- relations with the local connectome fingerprint principal components with the knowledge that the local connectome fingerprint components are themselves orthogonal, we mitigate a common result of regression modeling in which the inclusion of a highly correlated feature may drastically alter other features’ regression coefficients. Regardless of the coefficient as- signed to ICV, we ultimately want to make predictions for the continuous response variables without any knowledge of ICV by excluding the ICV coefficient and associated participant measurements from the model prediction step. While the quality of the resulting predictions (Step 4 below) may be negatively impacted by removing ICV as a potentially significant pre- dictor in a model, controlling for ICV in this manner ensures that any observed correlation is not related to intracranial volume. While truncating the LASSO-produced ˆβ vector allows for the calculation of ICV-ignorant predictions for the continuous response variables, the same procedure cannot be adopted for categorical response variables. Such an approach to our binary responses results in undesired artifacts due to the nonlinear nature of logistic regression. An alternate approach to assess the value of the local connectome fingerprint in a binary prediction is described in Step 4. Step 3: Local connectome phenotype map. For each response variable, we expect to contain nonzero weights on a subset of the orthogonal principal components (NOUS, or equiv- alently, XV), and these weights were used to construct a local connectome phenotype map, defined as the weighted influence of each fiber in the local connectome on the modeled re- sponse variable. To convert the regression coefficients into the dimensions of the local con- nectome, the sparse vector of regression coefficients was multiplied by the principal axes matrix V to produce a weighted linear combination of the principal axes deemed relevant to a particular subject attribute. ˆβ∗ ˆβ∗ ˆ(cid:2)w = V (3) ˆ(cid:2)w, represents a p × 1 vector reflecting the white This linear combination of principal axes, matter substructure of the local connectome fingerprint vector relevant to a particular observed ˆ(cid:2)w as the local connectome phenotype for the associated response. We refer to the vector response variable. ˆβ∗ Step 4: Prediction. Enfin, we use the reconstructed local connectome phenotype map to predict a variety of continuous social, biological, and cognitive responses for participants in the test set. Finalement, we sought a model that predicted a response variable ˆyi for subject i in the ˆ(cid:2)w is the response-related local connectome phenotype and test set such that (cid:2)yi (cid:2)xi is the individual participant’s local connectome fingerprint. A prediction was generated for all participants in the holdout set on each validation fold. Once predictions for all participants were generated for a given response variable, the performance of the model was evaluated using the correlation between predicted and observed values (continuous variables only). ˆ(cid:2)w where = (cid:2)xi While LCP maps were still constructed for categorical response variables, the utility of these LCP maps for prediction was estimated by comparing the classification accuracy of an ICV- only model with that of a model incorporating ICV and the local connectome fingerprint. In Network Neuroscience 93 l Téléchargé à partir du site Web : / / direct . m je t . / t / e d u n e n a r t i c e – pdlf / / / / / 2 1 8 6 1 0 9 2 0 0 0 n e n _ a _ 0 0 0 3 1 p d t . f par invité 0 7 Septembre 2 0 2 3 Local connectome phenotypes the case where the fingerprint-informed model outperforms the ICV-only model, the increase in classification accuracy can be attributed to information contained in the local connectome fingerprint map. The estimated significance of each continuous prediction model stems from a 10,000-trial nonparametric permutation test. In each trial, the response values were permuted prior to executing the LASSO model-fitting procedure while ensuring that the fingerprint PC-ICV mea- surements were still paired as same-subject inputs to the models. After permuting the response values, the LASSO model-fitting procedure was used to construct a response-specific model from the randomly permuted data. Correctly mapped fingerprint and ICV information was then used to predict subjects’ response values using the permutation test models. Correlation was computed for each set of model predictions and true observations to build a null distribution of the chance performance of a LASSO model for the given response. The proportion of trials in the permutation test in which the magnitude of the computed correlation met or exceeded the magnitude of the observed versus prediction correlation in Table 3 is reported as the cor- relation p value. In creating a LASSO model with permuted response values, we observed many cases in which no principal components (PCs) were retained as significant predictors of variance. A resulting intercept-only model yields a constant, thus having a standard deviation of 0. Correlation between the prediction and observation in this case is undefined and was not included in the calculation of the associated p value. RESULTS Covariance Structure and Dimensionality of Local Connectome Fingerprints Intervoxel white matter architecture, reflected in the local connectome fingerprint, has been shown to be unique to an individual and sculpted by both genetic predisposition and experi- ence (Yeh, Vettel, et coll., 2016); cependant, it is not yet clear whether the local connectome also exhibits reliable patterns of shared variability across individuals. To illustrate this, Figure 2A shows three exemplar fingerprints from separate subjects in the sample. These exemplars re- veal the sensitivity of the method to capture both common and unique patterns of variability. Par exemple, the highest peaks in the three fingerprints are similar in terms of their size and location. This pattern appears to exist across subjects and is generally expressed in the mean fingerprint (Figure 2C). Cependant, there are also clear differences between participants. Par exemple, consider the sharpness and location of the rightmost peaks in the three exemplar fingerprints in Figure 2A. This uniqueness supports our previous work highlighting single subject classification from the fingerprint across varying temporal intervals (Yeh, Vettel, et coll., 2016). In order to explicitly test for covariance across participants, we looked at the distribution of pairwise correlations between fingerprints. The histogram in Figure 3 shows the total distribu- tion of pairwise intersubject correlations, revealing a tight spread of correlations such that the middle 95% of the distribution lies between 0.32 et 0.50. This confirms that intersubject cor- relations are substantially lower, averaging a correlation of 0.42 across all pairs of 841 HCP participants, than intrasubject correlations, found to be well above 0.90 (Yeh, Vettel, et coll., 2016). Ainsi, the local connectome fingerprint exhibits a moderate but reliable covariance structure across participants, indicating its utility to examine shared structural variability across subjects that capture similarity in social, health, and cognitive factors. The dimensionality of the fingerprint itself (841 participants × 433,386 elements) poses a major challenge when examining the predictive value of the local connectome for group Network Neuroscience 94 l Téléchargé à partir du site Web : / / direct . m je t . / / t e d u n e n a r t i c e – pdlf / / / / / 2 1 8 6 1 0 9 2 0 0 0 n e n _ a _ 0 0 0 3 1 p d t . f par invité 0 7 Septembre 2 0 2 3 Local connectome phenotypes l D o w n o a d e d f r o m h t t p : / / direct . m je t . / / t e d u n e n a r t i c e – pdlf / / / / / 2 1 8 6 1 0 9 2 0 0 0 n e n _ a _ 0 0 0 3 1 p d t . Chiffre 2. Lower dimensional structure of the local connectome fingerprints. (UN) Three individual local connectome fingerprints, from three separate subjects, show coarse commonalities and unique patterns of variability. (B) Cumulative summation of variance explained from each component, sorted by the amount of variance explained by each component. Dotted lines indicate the number of components (697) needed to explain 90% of the variability in the fingerprint dataset. (C) Mean fingerprint across participants (blue, gauche) and linear summation of principal components that explain 90% of the variance (red, droite). f par invité 0 7 Septembre 2 0 2 3 similarité. The group fingerprint contains many more features than subjects (p >> n), leading to a strong risk of overfitting. We employed a dimensionality reduction routine that isolates independent principal components from the entire local connectome fingerprint matrix to de- compose the variance within the set of fingerprints. This analysis found that the dimensionality of the local connectome fingerprint matrix was still relatively high and complex, requiring 697 de 841 components to explain 90% of the variance (Figure 2B). While it appears that many components are required to meaningfully explain fingerprint variance, the pattern of the mean fingerprint could be successfully recovered by a linear combination of the principal compo- nents (Figure 2C), confirming that this lower dimensional projection is adequate to represent the much larger dimensional fingerprint. Neurosciences en réseau 95 Local connectome phenotypes l D o w n o a d e d f r o m h t t p : / / direct . m je t . / t / e d u n e n a r t i c e – pdlf / / / / / 2 1 8 6 1 0 9 2 0 0 0 n e n _ a _ 0 0 0 3 1 pd . t f b y g u e s t t o n 0 7 Septembre 2 0 2 3 Chiffre 3. Correlations between fingerprints. The matrix of between-subject correlations in local connectome fingerprints, sorted by participant index, is shown on the right. The distribution (inset) is the histogram of the upper triangle of the correlation matrix and the best fit kernel density estimate (red line). Predicting Intersubject Variability After identifying a covariance structure in the group fingerprint matrix, we fit regression models to test how well the fingerprints could predict participant attributes, including social, biologi- cal, and cognitive factors. Although we used the principal components as predictor variables, the underlying dimensionality of the local connectome fingerprint matrix (697 components for 90% variance) is still quite high relative to the sample size (841 participants). Donc, we applied an L1 sparsity constraint (c'est à dire., LASSO) in the fitting process of a principal components regression (LASSO-PCR), as this approach identifies a sparse set of components that reliably predict individual response variables (voir la figure 1). Tableau 2 shows the logistic LASSO-PCR results for the four binary categorical participant attributes: genre, course, ethnicity, and relationship status. An examination of the test accura- cies in Table 2 reveals that both gender and race predictions are significantly improved with the inclusion of local connectome fingerprint information in the associated logistic regression models. Le 95% confidence intervals for prediction accuracy (ICV and local connectome fingerprints) arise from bootstrapping prediction-observation pairs and reporting the appropri- ate percentiles from a distribution of 10,000 bootstrapped classification accuracy calculations (see Methods). The p values associated with the reported classification accuracy arise from a nonparametric permutation test performed for each response variable. The test began by permuting response values prior to the model-fitting step in order to establish a null distribu- tion for chance accuracy achievable by a LASSO logistic regression model (see Methods). The provided p values reflect the proportion of 10,000 trials in which the accuracy achieved in the permutation test met or exceeded the accuracy achieved in the cross-validation (CV) predic- tion of the indicated response. The models for ethnicity and relationship status revealed no relationships and perform at exactly the base rate for their respective categories. Neurosciences en réseau 96 Local connectome phenotypes Table 2. Logistic LASSO-PCR results for four categorical HCP attributes Model response (significant CV results italicized) Gender1∗ Race2∗ Ethnicity3 Relationship status4 Sample size 840 760 833 840 Significant correlation with intracranial intracranial volume Yes Yes No No Training accuracy (measure of model fit) 0.9405 0.9632 0.9136 0.6679 CV prediction accuracy (ICV only) 0.8071 0.8276 0.9136 0.5571 CV prediction accuracy (ICV and LCF PCs) 0.8691 0.9053 0.9136 0.5571 Confidence interval [lower, upper] (ICV and LCF PCs) 0.8905 0.9263 0.9316 0.5917 0.8452 0.8842 0.8944 0.5226 Accuracy ppp value 0 0 1.0000 0.7620 * The prediction accuracy was statistically significant after applying the false discovery rate (FDR) correction for multiple comparisons. 1 The female-male split in the 840 subjects was 56%-44%, respectivement. 2 The white and black subpopulations made up 82% et 18%, respectivement, of the 760 subjects reported here. 3 4 Relationship status included 44.3% of the population in a “married or live-in relationship” and 55.7% not in such a relationship. The Not Hispanic/Latino and Hispanic split in the 833 subjects was 91.4%-8.6%, respectivement. In addition to the binary participant attributes, we observed many reliable prediction models with the continuous variables. Tableau 3 (third column) shows the training results for the corresponding linear models. As expected, nearly all models were statistically significant in the training evaluation, even after adjusting for multiple comparisons. Only two variables, the Pittsburgh Sleep Quality Index and systolic blood pressure, were not significant when consid- ering this segment of the data, largely because the LASSO model did not contain any nonzero coefficients. The LASSO form of penalized regression can drive coefficients to be exactly zero when their effects are sufficiently weak. This results in an intercept-only model that produces a uniform set of predictions, and the observation-prediction correlation cannot be calculated when there is no variability in the set of predictions. To complement the model training results, we examined the predictive performance of the models using five-fold cross validation. This was done by projecting the regression weights in component space back into local connectome space in order to provide a weight map for each fiber in the local connectome to the target response variable. These maps reflect the local connectome phenotype for that attribute and were multiplied against a full local connectome fingerprint for each participant in the validation fold to generate a prediction for that participant (see bottom panel, Chiffre 1). We assessed the generalizability of 28 continuous response models in a cross-validation paradigm and, as shown in Table 3 (fourth column), 10 of these attributes were significant predictors after applying the false discovery rate (FDR) correction for multiple comparisons. These factors included years of education, measures of body type (body mass index), physiol- ogy (hematocrit sample, blood pressure measures), and several cognitive measures including episodic memory (NIH Picture Sequence Memory Test), fluid intelligence (Penn Progressive Matrices: number of correct responses and total skipped items), self-regulation (delay dis- counting: area under the curve for discounting of $40,000), spatial orientation (Variable Short
Penn Line Orientation: total number correct), and working memory (NIH List Sorting Working
Memory Test).
Specificity of Phenotypes to Response Variables
In our final analysis, we examined the specificity of a local connectome phenotype map by
considering whether the predictive maps were unique for each participant attribute being pre-
dicted. Autrement dit, we tested whether a single map could capture a generalized predictive
relationship for multiple response variables, indicating that the models themselves may lack
specificity. If so, any given model may perform suitably well at predicting any participant at-
tribute (par exemple., body mass index), even if derived from training on a different participant factor
(par exemple., years of education completed).
Neurosciences en réseau
97
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
/
/
/
/
2
1
8
6
1
0
9
2
0
0
0
n
e
n
_
un
_
0
0
0
3
1
p
d
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Local connectome phenotypes
Model response
(Significant CV
results italicized)
Age (in years)
Handedness
Total household income
Years of education completed
Body mass index
Mean hematocrit sample
Diastolic blood pressure
Systolic blood pressure
Systolic-diastolic blood
pressure ratio
Hemoglobin A1C
Pittsburgh Sleep Quality Index
NIH Picture Sequence
Memory Test
NIH Dimensional Change
Card Sort Test
NIH Flanker Inhibitory Control
and Attention Test
Penn Progressive Matrices:
Number of correct responses
Penn Progressive Matrices:
Total skipped items
Penn Progressive Matrices:
Median reaction time for
correct responses
NIH Oral Reading Recognition Test
NIH Picture Vocabulary Test
NIH Toolbox Pattern Comparison
Processing Speed Test
Delay Discounting:
Area under the curve for
discounting of $200 Delay Discounting: Area under the curve for discounting of $40,000
Variable Short Penn Line Orientation:
Total number correct
Variable Short Penn Line Orientation:
Median reaction time divided by
expected number of clicks for correct
Variable Short Penn Line Orientation:
Total positions off for all trials
Penn Word Memory Test:
Total number of correct responses
Penn Word Memory Test:
Median reaction time for correct responses
NIH List Sorting Working Memory Test
830
566
841
840
839
841
838
838
838
841
841
841
838
838
838
838
838
838
838
841
Oui
Non
Non
Non
Non
Oui
Oui
Oui
Oui
Oui
Oui
Non
Oui
Non
Oui
Oui
Oui
Non
Non
Oui
Tableau 3. Linear LASSO-PCR results for 28 continuous HCP attributes
Sample
size
841
841
836
840
840
740
830
830
Significant
correlation with
intracranial volume
Oui
Non
Oui
Non
Non
Oui
Non
Oui
Training correlation
(measure of model fit)
0.1430*
0.5581*
0.1604*
0.4377*
0.4976*
0.4348*
0.2058*
0.3596*
Observed vs.
CV prediction
correlation
0.0311
−0.0594
−0.0029
0.0729*
0.2736*
0.1324*
0.0615
0.1396*
−0.0240
0.0098
−0.0314
Confidence interval
[lower, upper]
−0.0378
−0.1208
−0.0753
0.0127
0.2067
0.0654
−0.0154
0.0745
−0.0926
−0.0794
−0.0966
0.1007
0.0017
0.0632
0.1343
0.3421
0.1939
0.1378
0.2076
0.0474
0.1071
0.0415
0.0977*
0.0290
0.1618
Correlation
ppp value
0.1776
0.9475
0.5181
<10E-4
<10E-4
<10E-4
0.0331
<10E-4
0.7457
0.4165
0.8277
<10E-4
−0.0299
−0.0945
0.0379
0.8071
−0.0001
−0.0706
0.0651
0.5161
0.0849*
0.0187
0.1502
0.0733*
0.0120
0.1383
0.0086
0.0008
0.0481
−0.0619
−0.0702
−0.0187
0.0754
0.0660
0.1142
<10E-4
<10E-4
0.4075
0.4748
0.0781
−0.0569
−0.1260
0.0061
0.9390
0.0275
−0.0311
0.0891
0.2202
<10E-4
<10E-4
0.0951*
0.0279
0.1589
−0.0572
−0.1302
0.0141
0.9520
0.0014
0.0474
−0.0391
0.0793*
−0.0621
−0.0228
−0.0965
0.0097
0.0735
0.4741
0.1189
0.0764
0.0191
0.1540
0.9034
<10E-4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
>