On Decoding Strategies for Neural Text Generators
Gian Wiher Clara Meister Ryan Cotterell
ETH Z¨urich, Suisse
{gian.wiher, clara.meister, ryan.cotterell}@inf.ethz.ch
Abstrait
When generating text from probabilistic mod-
le, the chosen decoding strategy has a pro-
found effect on the resulting text. Yet the
properties elicited by various decoding strate-
gies do not always transfer across natural lan-
guage generation tasks. Par exemple, alors que
mode-seeking methods like beam search per-
form remarkably well for machine translation,
they have been observed to lead to incoherent
and repetitive text in story generation. Malgré
such observations, the effectiveness of decod-
ing strategies is often assessed on only a sin-
gle task. This work—in contrast—provides a
comprehensive analysis of the interaction be-
tween language generation tasks and decoding
strategies. Spécifiquement, we measure changes
in attributes of generated text as a function of
both decoding strategy and task using human
and automatic evaluation. Our results reveal
both previously observed and novel findings.
Par exemple,
the nature of the diversity–
quality trade-off in language generation is very
task-specific; the length bias often attributed
to beam search is not constant across tasks.
https://github.com/gianwiher
/decoding-NLG
1
Introduction
Modern neural networks constitute an exciting
new approach for the generation of natural lan-
guage text. Much of the initial research into neural
text generators went into designing different ar-
chitectures (Sutskever et al., 2014; Rush et al.,
2015; Serban et al., 2017). Cependant, recent work
has hinted that which decoding strategy (c'est à dire., le
method used to generate strings from the model)
may be more important than the model architec-
ture itself. Par exemple, a well replicated recent
result is that, under a probabilistic neural text
generator trained with the maximum-likelihood
objective, the most probable string is often not
human-like or high quality (Stahlberg and Byrne,
2019; Eikema and Aziz, 2020). In light of this
finding, a plethora of decoding strategies have
997
been introduced in the literature, each claiming
to generate more desirable text than competing
approaches.
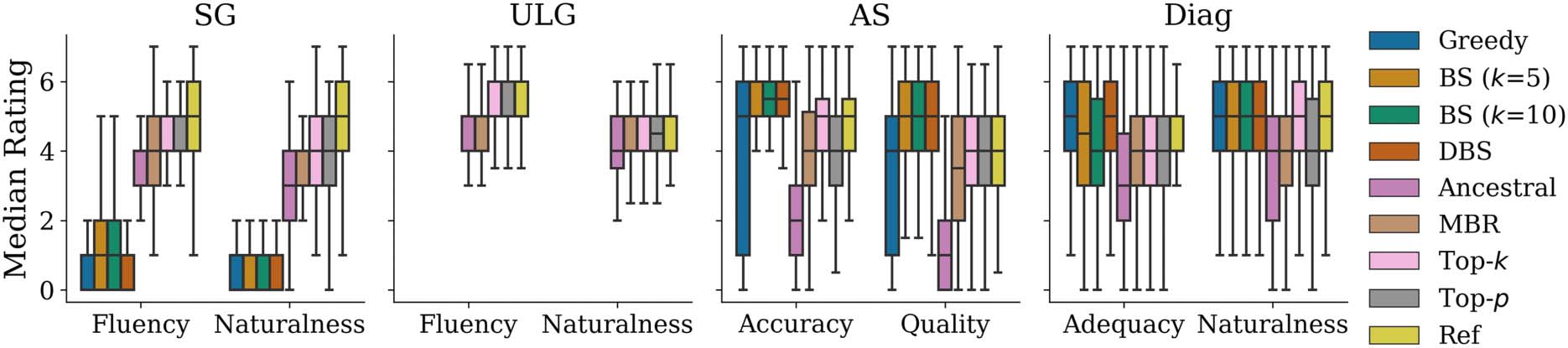
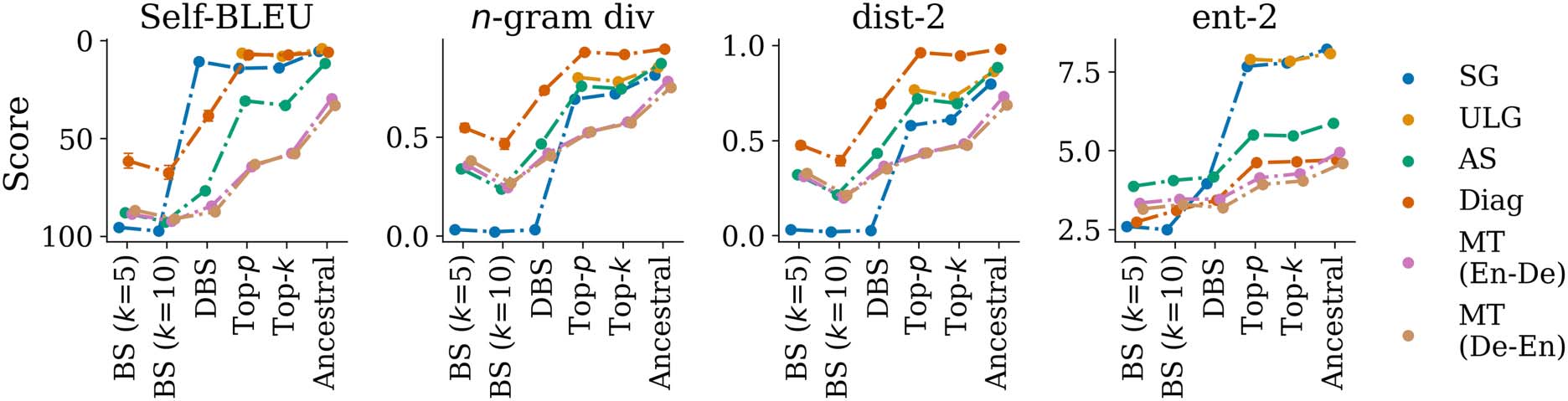
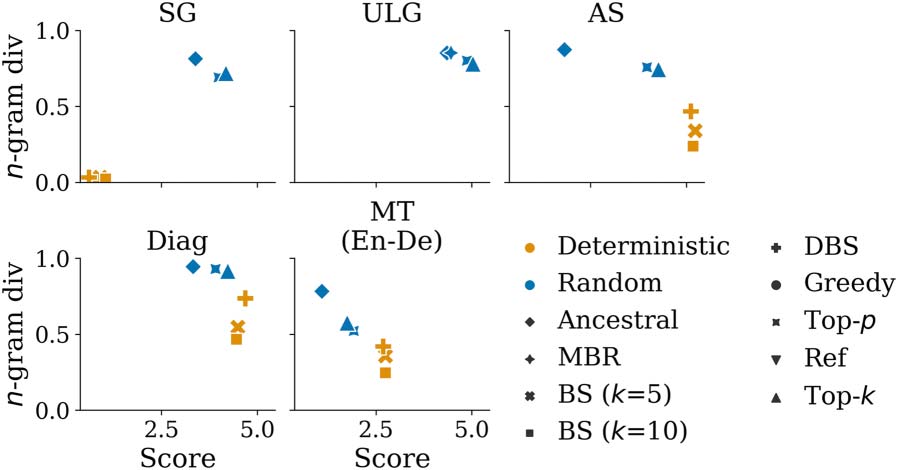
Lamentably, empirical studies of decoding stra-
tegies are typically evaluated on a single natural
language generation task—without investigation
into how performance may change across tasks—
despite the fact that these tasks differ qualitatively
across a large number of axes. These qualitative
differences manifest quantitatively as well: Pour
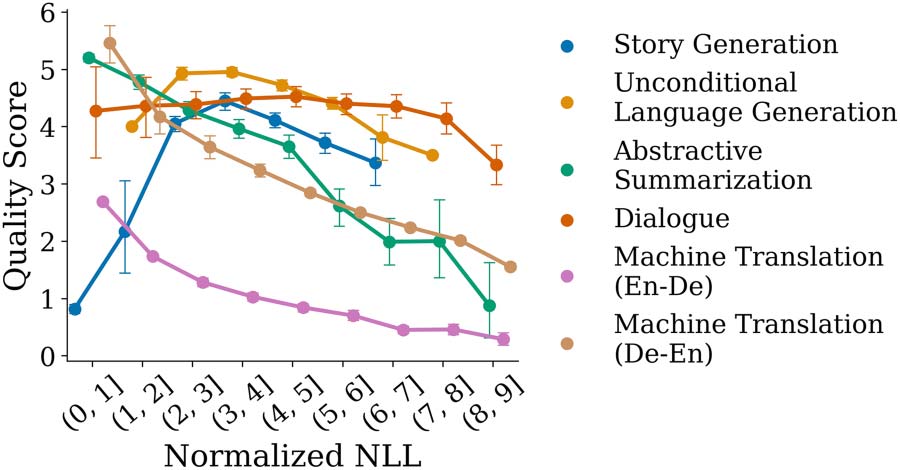
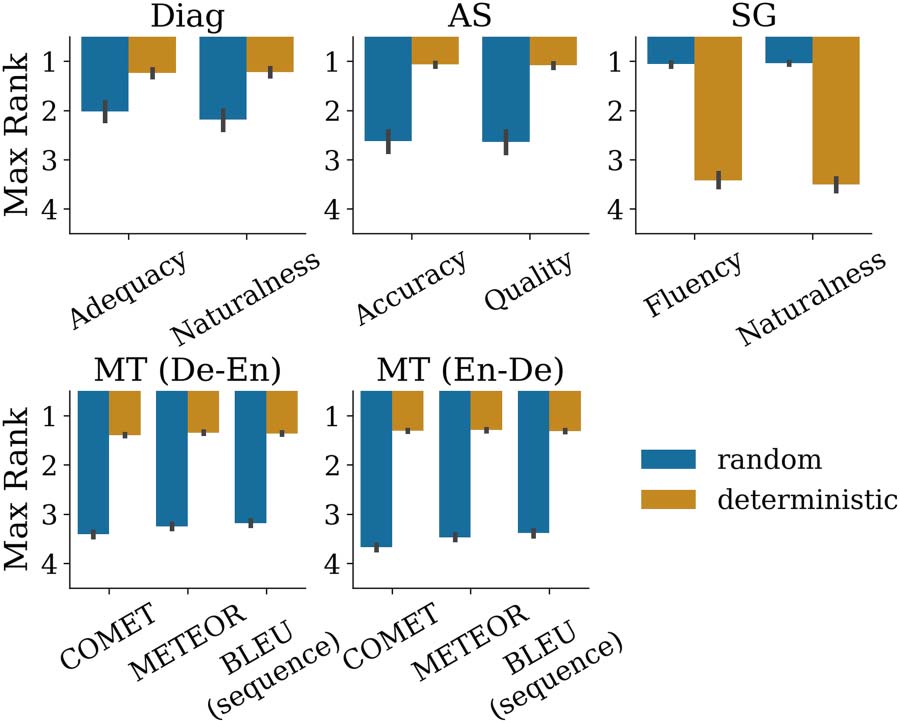
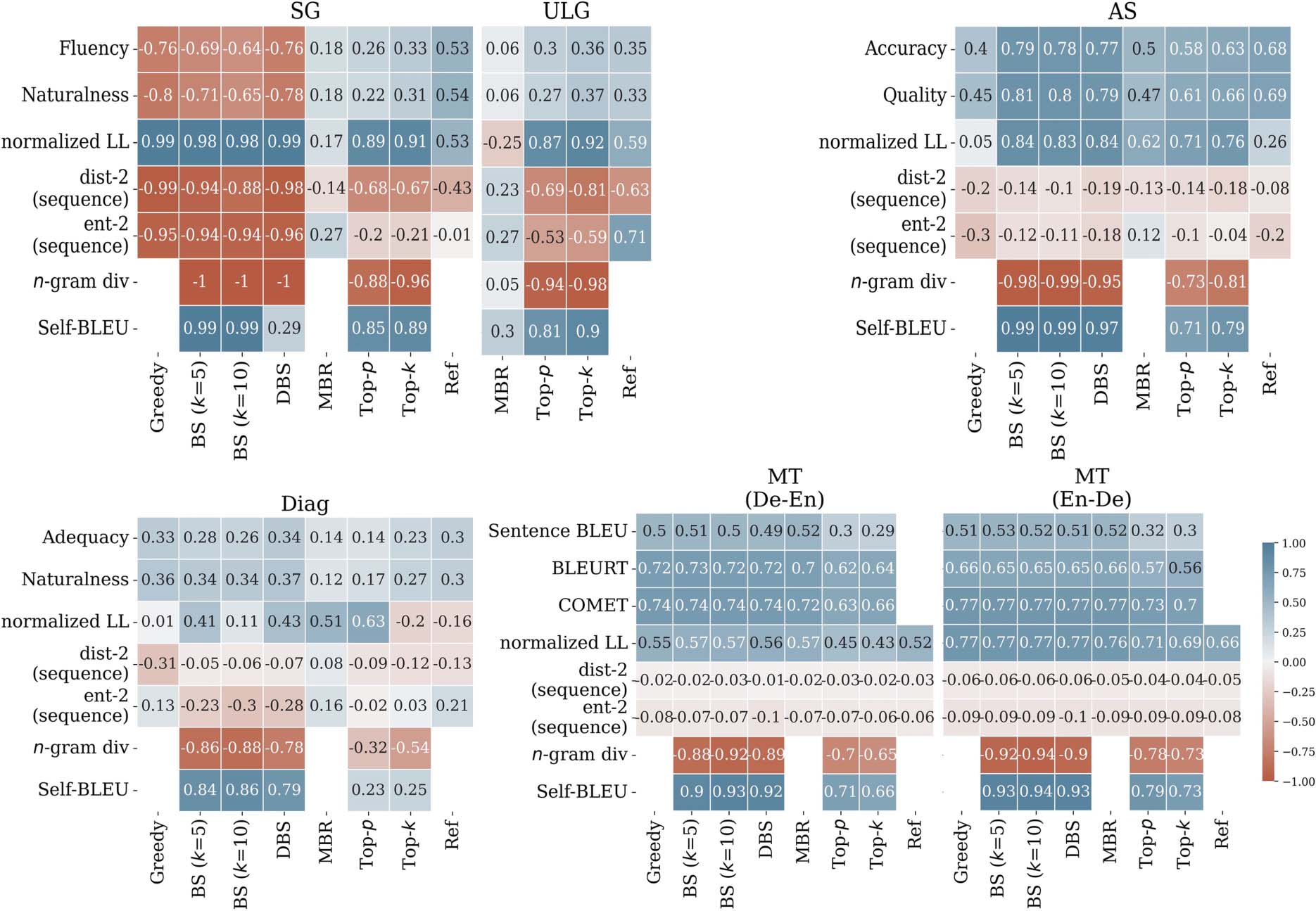
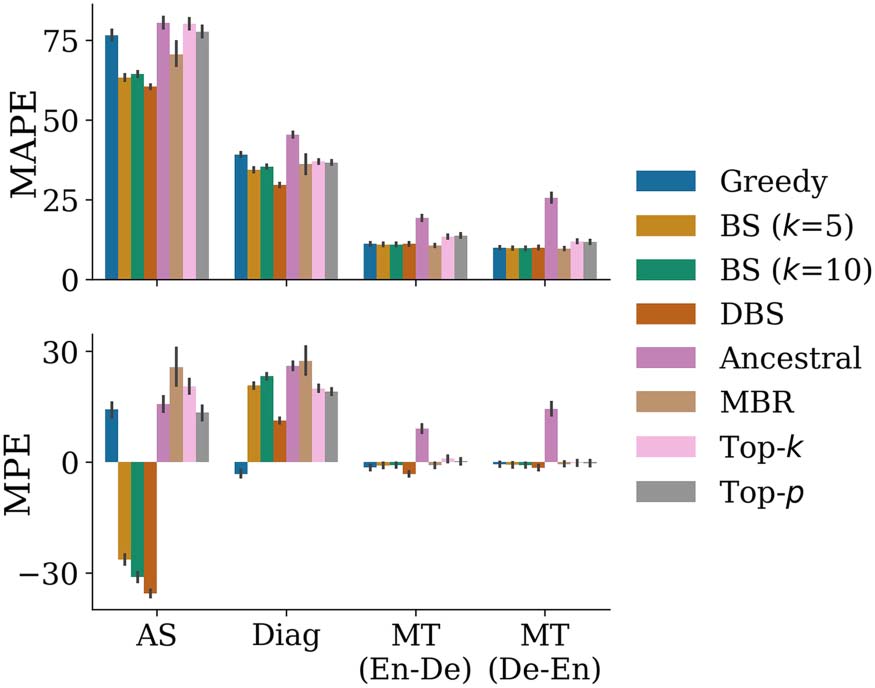
example, we can see in Figure 1 that high prob-
ability strings are favorable in some tasks, like
machine translation (MT), while heavily disfa-
vored in others, like story generation (SG). Conse-
quently, we should not a priori expect a strategy
that works well for one task to demonstrate the
same performance in another. En effet, several
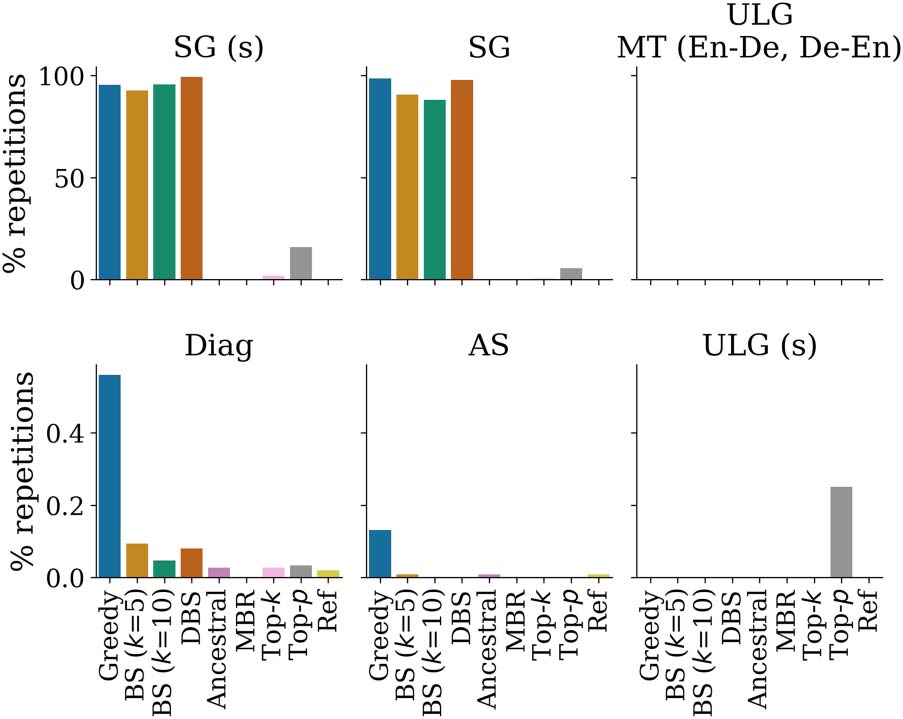
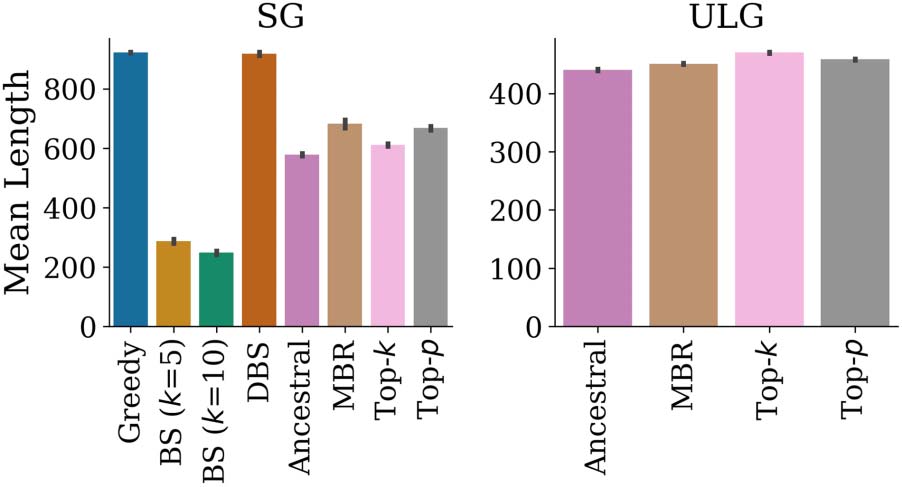
cases already show evidence of this: Beam search
works remarkably well for machine translation
mais, outside of this context, has been observed
to return dull text or degenerate text (Holtzman
et coll., 2020; DeLucia et al., 2021). This raises
a natural fear that decoding strategies have been
optimized for performance on a specific task, et
the task-agnostic claims about the effectiveness
of one decoding strategy over another are poten-
tially ill-founded. A broader analysis of decod-
ing strategies—both within and across tasks—is
needed in order to fully understand the extent of
such a problem.
Our work fills this gap, providing the first
comprehensive comparison of decoding strategies
across natural language generation tasks. Empiri-
cally, we compare strategy performance on several
axes, taxonomizing methods into groups such as
deterministic and stochastic, to understand the
importance of various strategy attributes for quan-
tifiable properties of text. En résumé, our main
findings include the following:
• Many previous
empirical observations,
among them the quality-diversity and quality-
probability trade-offs (Ippolito et al., 2019;
Transactions of the Association for Computational Linguistics, vol. 10, pp. 997–1012, 2022. https://doi.org/10.1162/tacl a 00502
Action Editor: Emily Pitler. Submission batch: 2/2022; Revision batch: 6/2022; Published 9/2022.
c(cid:2) 2022 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
5
0
2
2
0
4
3
9
3
6
/
/
t
je
un
c
_
un
_
0
0
5
0
2
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
probability distributions q over an output space
Y—(peut-être) conditioned on an input x—where
Y is the set consisting of all possible strings that
can be constructed from the vocabulary V:
Y def= {BOS ◦ v ◦ EOS | v ∈ V ∗}
(1)
where BOS and EOS stand for special reserved
beginning-of-sentence and end-of-sentence to-
kens, respectivement; V ∗
is the Kleene closure
of V.
Today’s language generators are typically
parameterized by encoder–decoder architectures
with attention mechanisms (Sutskever et al.,
2014), notably the transformer (Vaswani et al.,
2017), with trainable weights θ. These models
follow a local-normalization scheme, meaning
that for all t > 0, q( · | oui
(4)
Note that there is no formal guarantee that greedy
decoding will return the global optimum of the
decoding objective since decisions are only locally
optimal.
Beam Search. Beam search is a simple exten-
sion of greedy search. Rather than considering
only the highest probability continuation of our
string at each step, we keep the K ∈ Z+ highest
probability paths, where the hyperparameter K is
referred to as the beam:
Y0 = {BOS}
Yt = argmax
Oui (cid:9)
⊆Bt,
t
|Oui (cid:9)
|=K
t
(cid:3)
y∈Y (cid:9)
t
(5)
log q(oui | X)
(for t > 0)
2We define directed generation tasks as involving a strong
relationship between input and output (par exemple., as in MT); pour
open-ended tasks, input contexts only pose a soft constraint
on the output space, c'est à dire., there is a considerable degree of
freedom in what is a plausible output (par exemple., in dialogue or
story generation).
where for t > 0
(cid:4)
(cid:5)
Bt =
yt−1 ◦ y | y ∈ V and yt−1 ∈ Yt−1
(6)
is our beam, consisting of all possible extensions
of y ∈ Yt−1. As with greedy decoding, the recur-
sion is performed until all strings end in the EOS
symbol or some maximum time step T is reached.
The highest scoring string y∗ is then chosen from
this final set YT .
Beyond the log-probability, other scoring func-
tions have been proposed as modifications to
the vanilla beam search algorithm. Par exemple,
Vijayakumar et al. (2018) propose diverse beam
recherche (DBS) to address the issue of the lack of
diversity within the set of returned strings. Le
algorithm further splits the beam into several sub-
groups and adds an inner iteration at each time step
to maximize inter-group diversity. We refer the
reader to the original work for the full algorithm.
3.2 Stochastic Algorithms
Ancestral Sampling.
Instead of approximating
y∗, one can obtain generations by sampling y ∼
q(· | X). Due to the local normalization scheme of
the models that we consider, this can be achieved
simply by setting y0 = BOS and then drawing each
yt ∼ q(· | X, oui