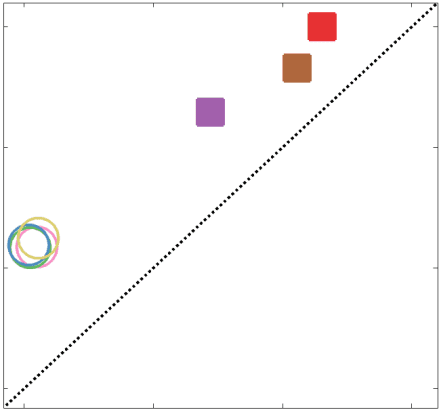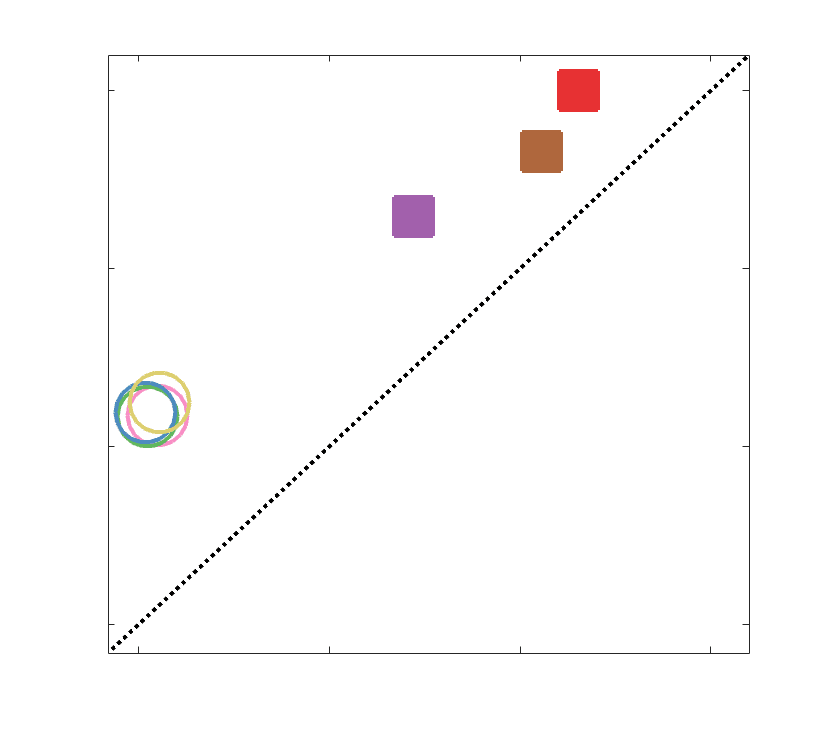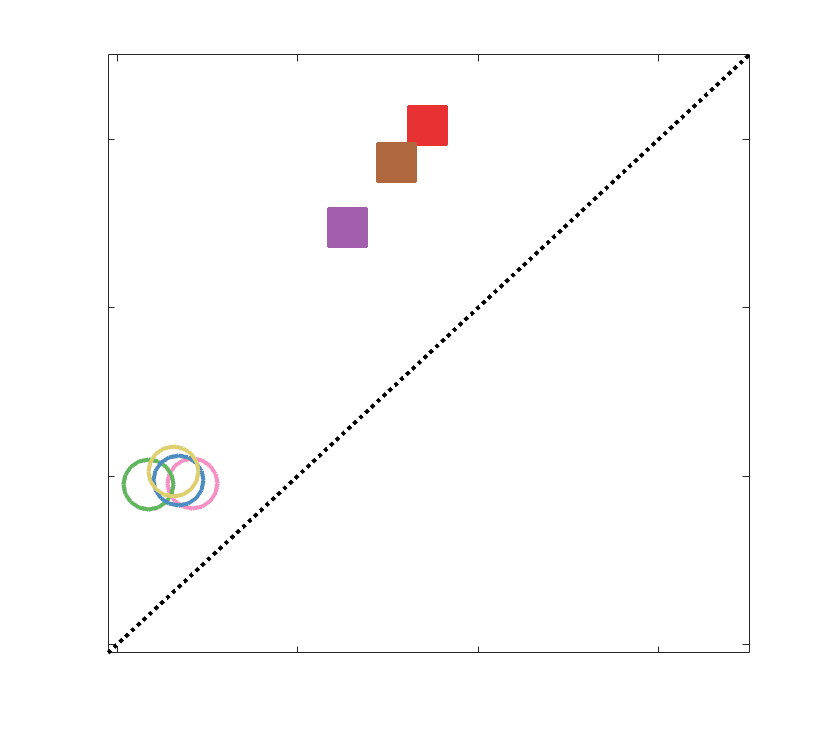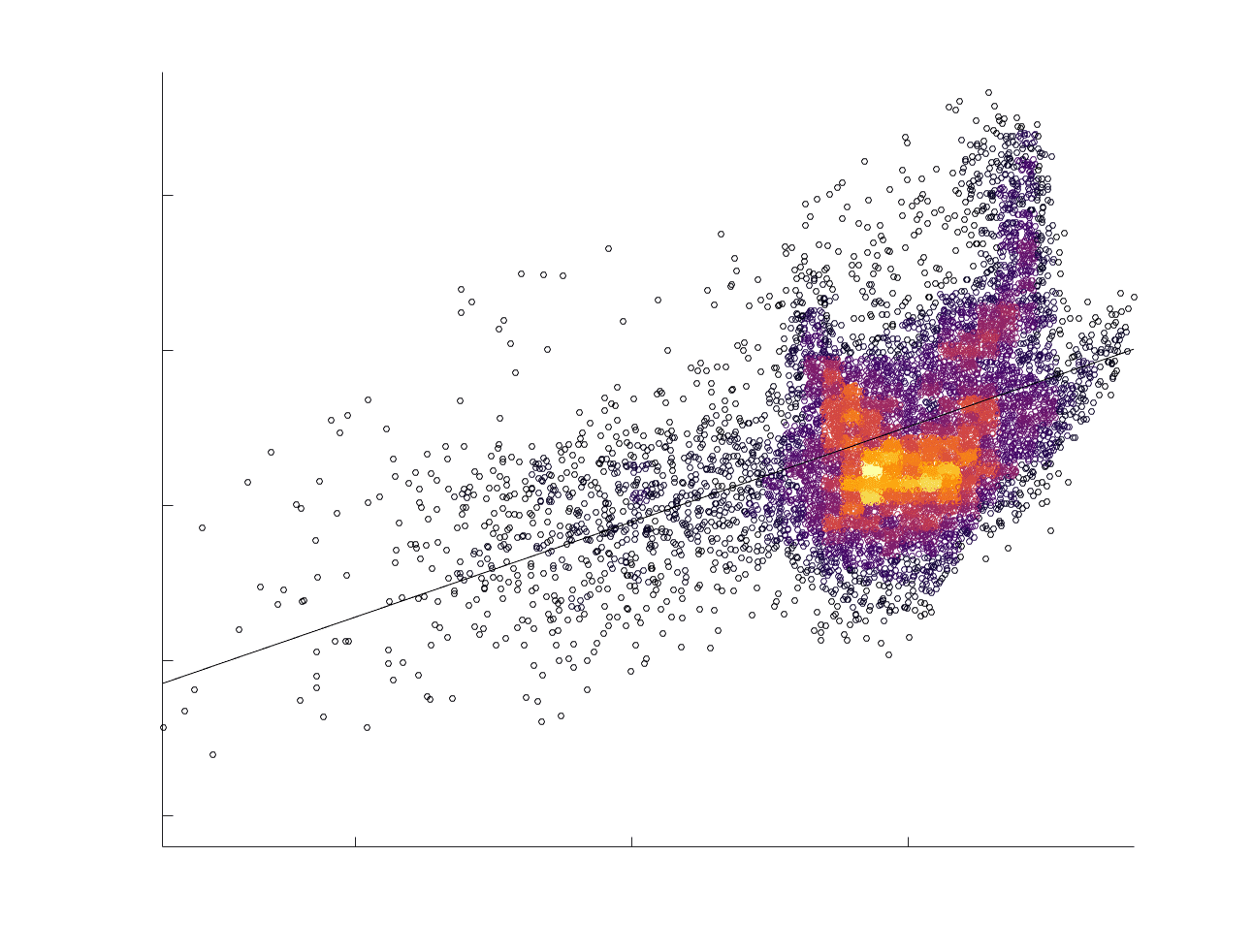Nelson, M.C., Royer, J., Lu, W.D., Leppert, I.R., Campbell, J., Schiavi, S., Jin, H., Tavakol, S., Vos de Wael, R., Cruces, R.R.,
Pike, G.B., Bernhardt, B., Daducci, UN., Misic, B., & Tardif, C. (2023). The Human Brain Connectome Weighted by the Myelin
Content and Total Intra-Axonal Cross-Sectional Area of White Matter Tracts. Neurosciences en réseau, Advance publication.
https://doi.org/10.1162/netn_a_00330.
The Human Brain Connectome Weighted by the Myelin Content
and Total Intra-Axonal Cross-Sectional Area of White Matter
Tracts
Short title:
Mark C. Nelson1,2, Jessica Royer1,2, Wen Da Lu2,3, Ilana R. Leppert2, Jennifer S.W. Campbell2,
Simona Schiavi4, Hyerang Jin1,2, Shahin Tavakol1,2, Reinder Vos de Wael1,2, Raul Rodriguez-
Cruces1,2, G. Bruce Pike5, Boris C. Bernhardt1,2, Alessandro Daducci4, Bratislav Misic1,2, et
Christine L. Tardif 1,2,3
1Department of Neurology and Neurosurgery, McGill university, Montréal, QC, Canada. 2McConnell Brain Imaging Centre, Montréal
Neurological Institute and Hospital, Montréal, QC, Canada. 3Department of Biomedical Engineering, Université McGill, Montréal, QC, Canada.
4Department of Computer Science, University of Verona, Verona, Italy. 5Hotchkiss Brain Institute and Departments of Radiology and Clinical
Neurosciences, University of Calgary, Calgary, Canada.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Auteur correspondant: Mark C Nelson, mark.nelson3@mail.mcgill.ca
17
18
Mots clés: connectomics; network neuroscience; structural connectivity; functional connectivity;
19
white matter; myelin; microstructure-weighted imaging
20
21
ABSTRAIT
22
A central goal in neuroscience is the development of a comprehensive mapping between
23
structural and functional brain features which facilitates mechanistic interpretation of brain
24
fonction. Cependant, the interpretability of structure-function brain models remains limited by a
1
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
/
/
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
25
lack of biological detail. Ici, we characterize human structural brain networks weighted by
26
multiple white matter microstructural features including total intra-axonal cross-sectional area
27
and myelin content. We report edge-weight-dependent spatial distributions, variance, petit-
28
worldness, rich club, hubs, as well as relationships with function, edge length and myelin.
29
Contrasting networks weighted by the total intra-axonal cross-sectional area and myelin content
30
of white matter tracts, we find opposite relationships with functional connectivity, an edge-
31
length-independent inverse relationship with each other, and the lack of a canonical rich club in
32
myelin-weighted networks. When controlling for edge length, networks weighted by either
33
fractional anisotropy, radial diffusivity or neurite density show no relationship with whole-brain
34
functional connectivity. We conclude that the co-utilization of structural networks weighted by
35
total intra-axonal cross-sectional area and myelin content could improve our understanding of the
36
mechanisms mediating the structure-function brain relationship.
37
38
RÉSUMÉ DE L'AUTEUR
39
For computational network models to provide mechanistic links between brain structure and
40
fonction, they must be informed by networks in which edge weights quantify structural features
41
relevant to brain function. Ici, we characterized several weighted structural networks capturing
42
multiscale features of white matter connectivity including total intra-axonal cross-sectional area
43
and myelin density. We describe these networks in terms of edge weight distribution, variance
44
and network topology, as well as their relationships with each other, edge length and function.
45
Dans l'ensemble, these findings support the joint use of structural networks weighted by the total intra-
46
axonal cross-sectional area and myelin content of white matter tracts in structure-function
2
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
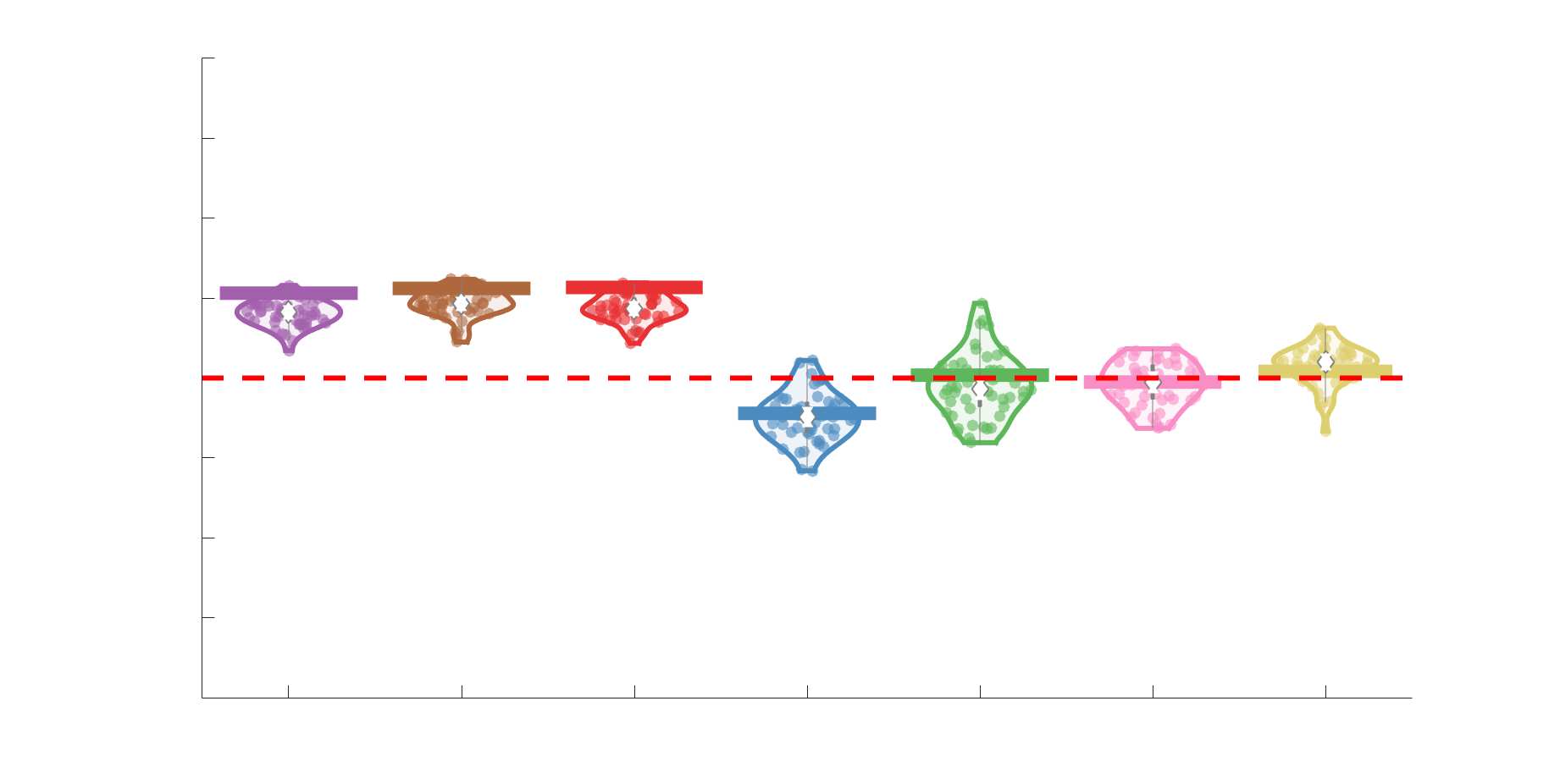
.
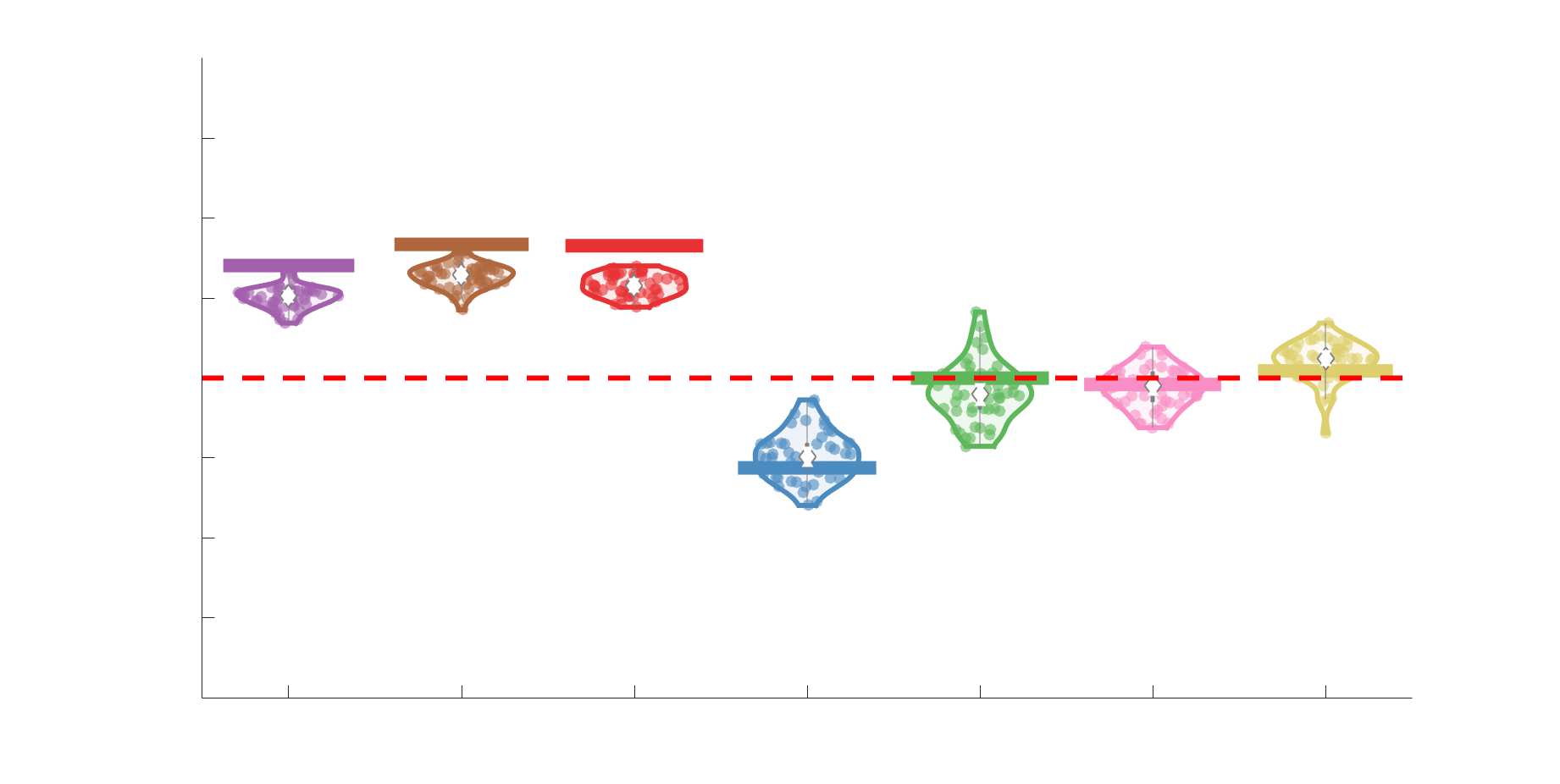
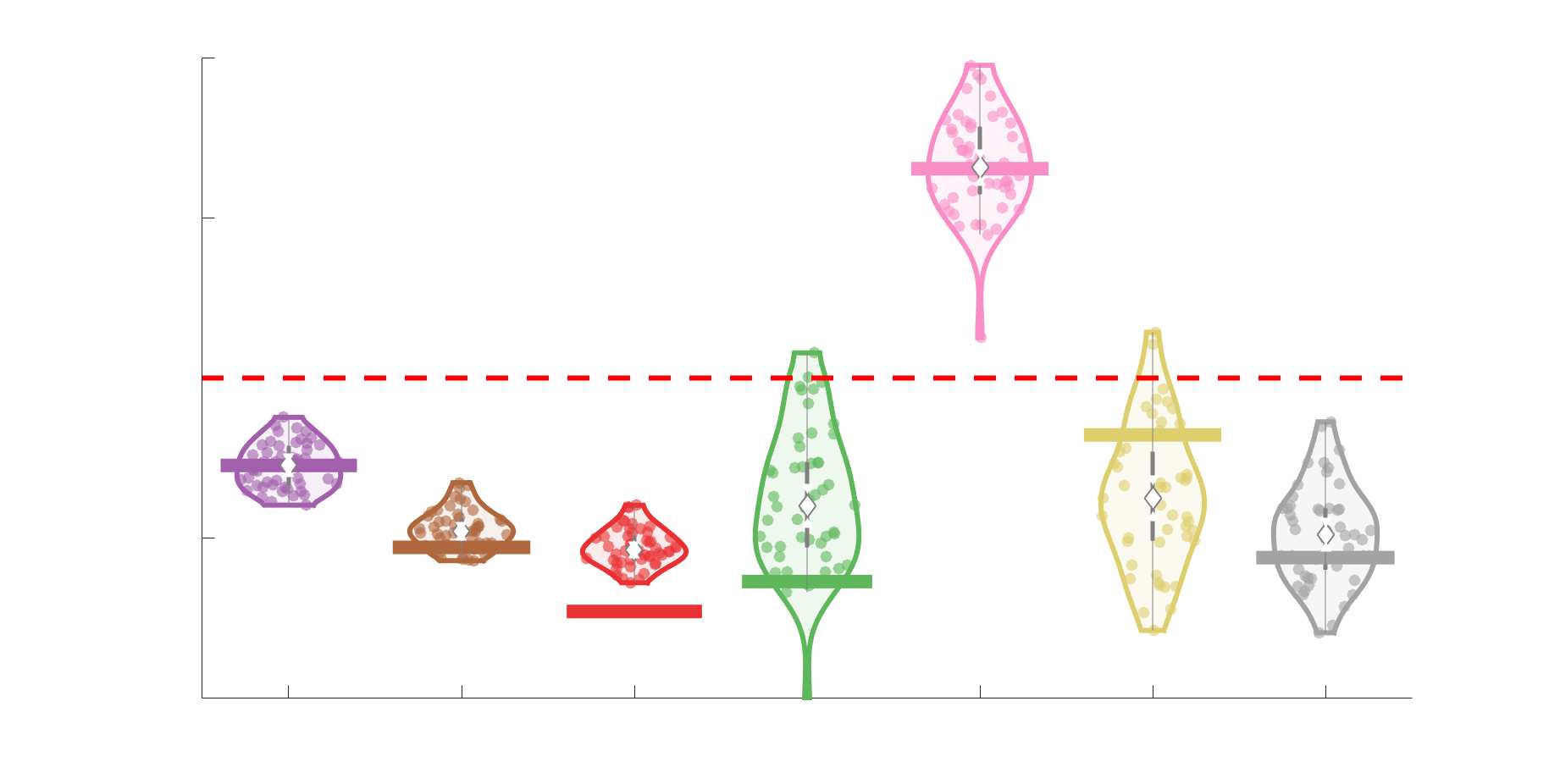
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
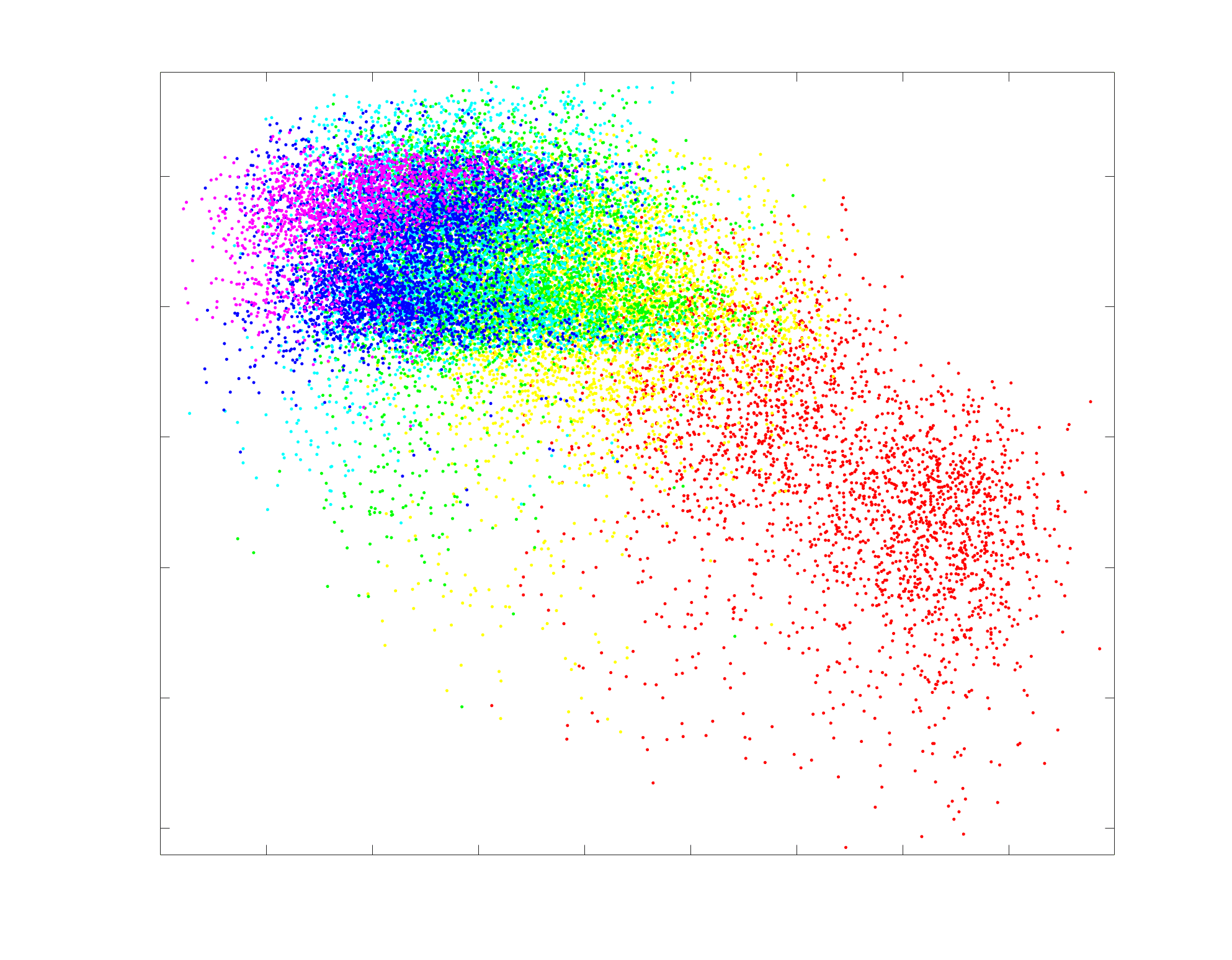
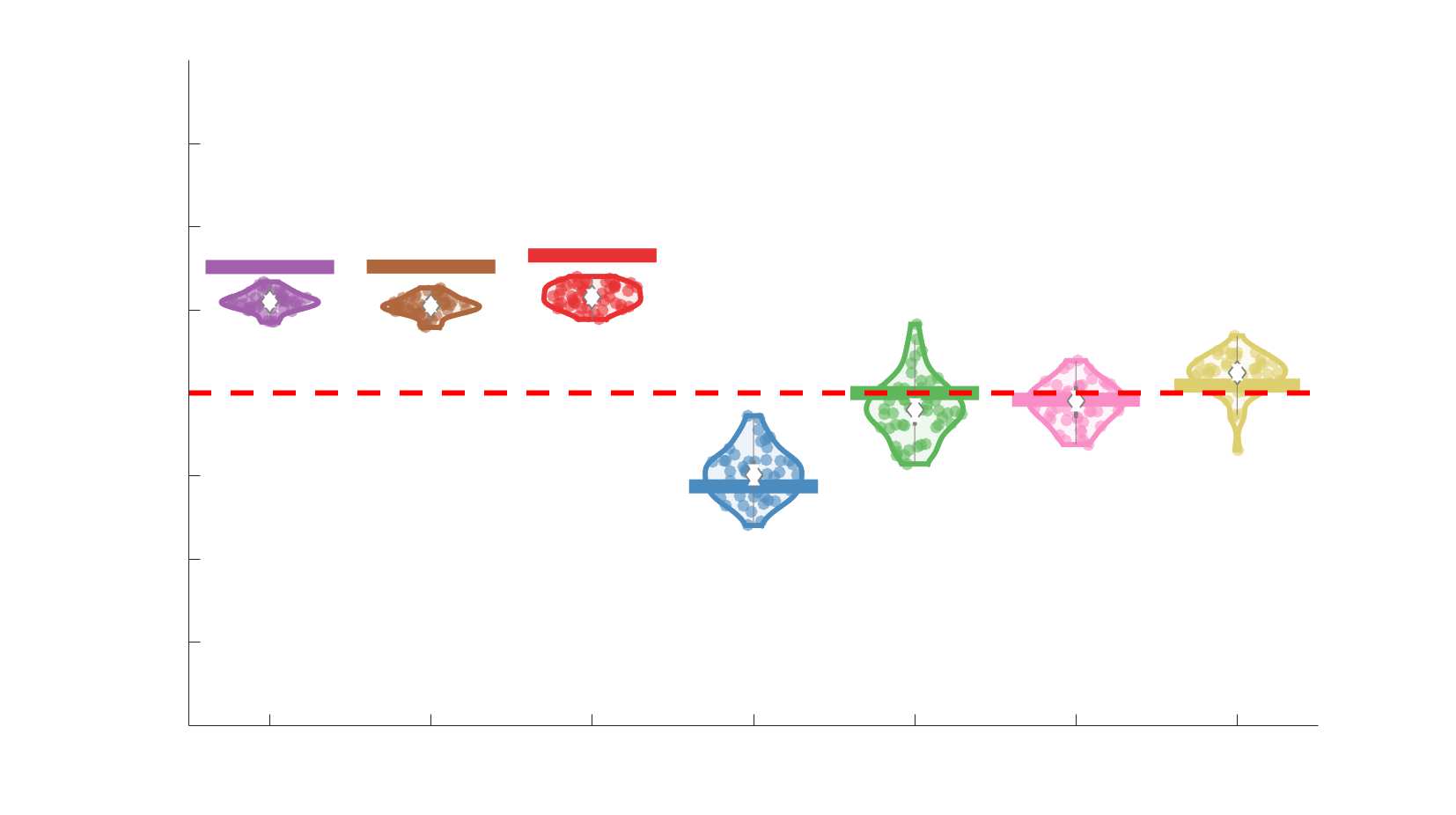
je
/
t
/
/
.
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
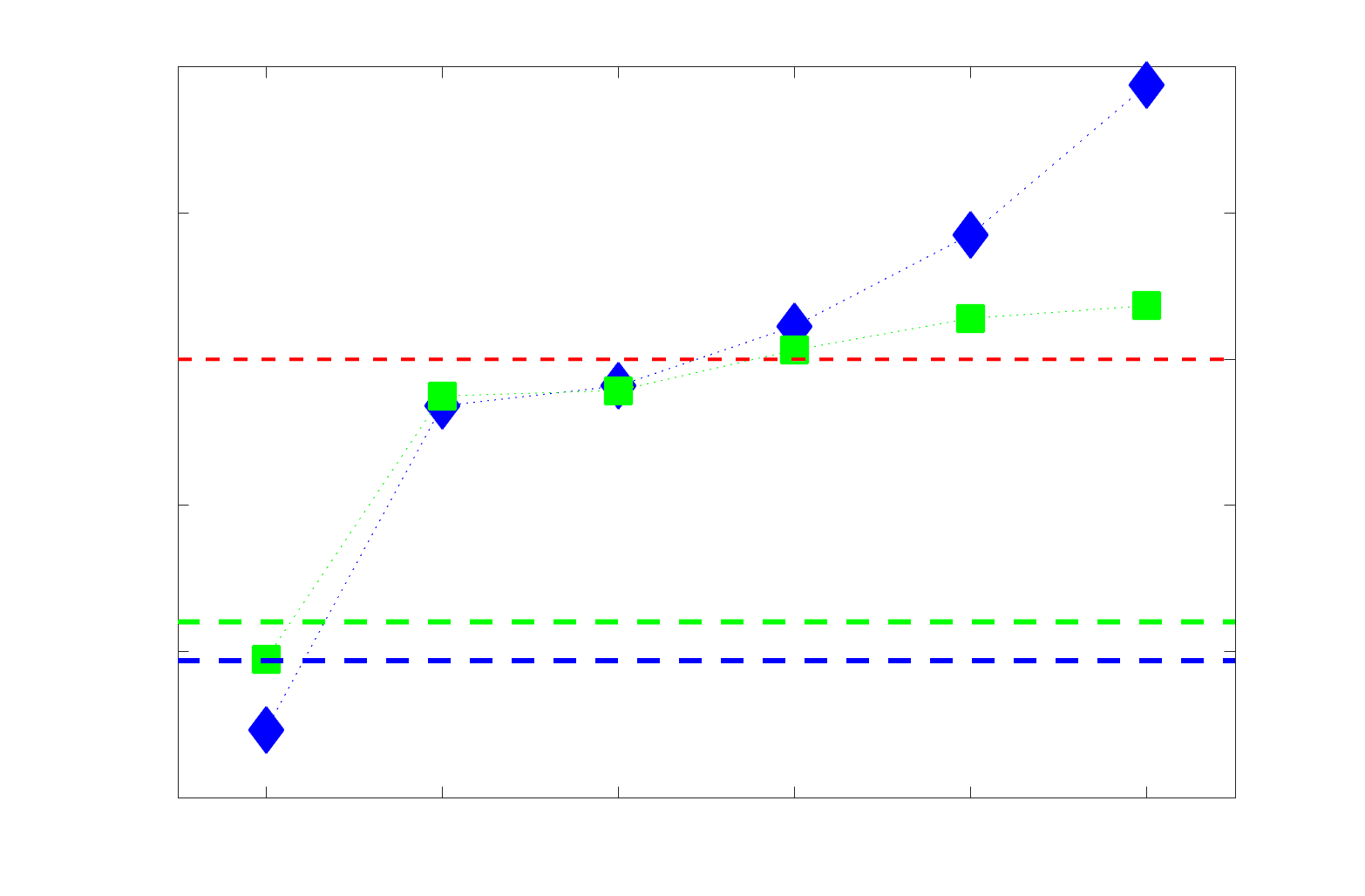
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
47
models. This thorough characterization serves as a benchmark for future investigations of
48
weighted structural brain networks.
49
50
51
INTRODUCTION
52
The quest to relate human structural and functional brain networks spans the spectrum of spatial
53
scale and repertoire of data modalities absolutely. At the macroscale, the human brain can be
54
modeled as an anatomical network of discrete neuronal populations (nodes) interconnected by
55
white matter fibers (edges) (Sporns, 2011). Coordinated spatiotemporal patterns of neuronal
56
activity unfolding upon this structural backbone are fine-tuned by white matter microstructure
57
(Hodgkin & Huxley, 1952; Huxley & Stämpfli, 1949; Moore et al., 2020; Pumphrey & Jeune,
58
1938) and form the basis of cognition and behavior (Biswal et al., 1995; Greicius et al., 2003;
59
Hampson et al., 2006; Liégeois et al., 2019; S. M.. Smith et al., 2009; Martijn P. Van Den Heuvel
60
et coll., 2009). Increasingly, MRI facilitates in vivo measurement of multi-scale properties of both
61
brain structure (par exemple., (Alexander et al., 2019; Drakesmith et al., 2019; Jeurissen et al., 2017;
62
Mancini et al., 2020)) and function (par exemple., (Finn et al., 2019; Friston, 2011; Gordon et al., 2017;
63
Liu et al., 2022)). Diffusion MRI streamline tractography and resting-state functional MRI are
64
often respectively used to estimate structural and functional connectivity (SC & FC) réseaux.
65
Network science provides a framework to bring these fundamentally different substrates into a
66
common space where their features can be quantified (Fornito et al., 2016; Sporns, 2010; Suárez
67
et coll., 2020) and used to probe the mechanisms mediating human brain function (par exemple., (Cabral et
68
al., 2017; Fornito et al., 2015)).
3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
t
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
69
70
SC network edges can be weighted by a range of MRI-derived metrics quantifying white matter
71
microstructural features relevant to brain function including: voxel-level estimates of tissue
72
diffusivity (par exemple., (Caeyenberghs et al., 2016)), neurite density (H. Zhang et al., 2012), axon
73
diameter distributions (Alexander et al., 2010; Assaf et al., 2008), myelin content (Heath et al.,
74
2018; Mancini et al., 2020), and the g-ratio (ratio of inner/outer diameters of myelinated axons)
75
(Stikov et al., 2011, 2015); as well as tract/bundle-level measures of axonal cross-sectional area
76
(Daducci, Dal Palù, et coll., 2015; R.. E. Smith et al., 2015). Subsets of these metrics have been
77
investigated using a microstructure-weighted connectomics approach (Boshkovski et al., 2021;
78
Caeyenberghs et al., 2016; Deligianni et al., 2016; Frigo et al., 2020; Mancini et al., 2018;
79
Messaritaki et al., 2021; Schiavi et al., 2020; M.. P.. van den Heuvel et al., 2010; Martijn P. van
80
den Heuvel & Sporns, 2011; F. C. Yeh et al., 2016). We aim to extend this work by providing a
81
comprehensive assessment of the fundamental characteristics of a range of standard and state-of-
82
the-art weighted structural brain networks including a network weighted by myelin.
83
84
The networks considered here can be grouped into two classes: those computed with tractometry
85
(S Bells et al., 2011) and those computed directly from the streamline weights in a tractogram
86
c'est à dire., streamline-specific. We consider three examples of the latter: (1) the number of streamlines
87
(NoS); and two methods which optimize the streamline weights in a tractogram to increase
88
specificity for white matter structural features (2) spherical-deconvolution informed filtering of
89
tractograms (SIFT2) (R.. E. Smith et al., 2015) et (3) convex optimization modeling for
90
microstructure informed tractography (COMMIT) (Daducci et al., 2013; Daducci, Dal Palù, et
91
al., 2015). SIFT2 and COMMIT were designed to overcome known limitations of streamline
4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
t
.
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
92
compte (Girard et al., 2014; Jones, 2010; Jones et al., 2013). While the edge weights in all three
93
networks generally capture white matter features relevant to connection strength, SIFT2 and
94
COMMIT more specifically quantify the total intra-axonal cross-sectional area of white matter
95
tracts (henceforth referred to as “edge caliber”). À ce jour, COMMIT and SIFT2 have not been
96
compared to NoS with uniform connection density (Frigo et al., 2020; Schiavi et al., 2020; C. H.
97
Yeh et al., 2016). Ainsi, it remains unclear how the edge weights themselves affect network
98
topology.
99
100
In contrast, tractometry allows network edge weights to be derived from any volumetric brain
101
image that is co-registered to the tractogram. This increase in methodological flexibility comes at
102
the expense of anatomical specificity. Tractometry is unable to resolve the separate contributions
103
of individual fiber populations to the aggregate value of a voxel. Given that an estimated ~90%
104
of white matter voxels at typical diffusion MRI resolutions (~2mm) contain multiple fiber
105
populations (Jeurissen et al., 2012), the quantitative link between white matter microstructure
106
and essentially all tractometry-derived edge weights is biased by partial volume effects.
107
108
In this work, tractometry is combined with a diffusion tensor model (Basser, 1995; Basser et al.,
109
1994) to derive networks weighted by FA (fractional anisotropy) and RD (radial diffusivity),
110
which respectively quantify the degree of diffusion anisotropy (c'est à dire., directional dependence) et
111
diffusion magnitude perpendicular to the major axis. The crossing fiber problem described above
112
is also known to limit the ability of diffusion tensor models to quantify white matter features (De
113
Santis et al., 2014; Jacques Donald Tournier et al., 2011). Additional tractometry networks
114
examined here include a network weighted by ICVF (intracellular volume fraction) computed
5
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
t
.
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
115
with NODDI (Neurite Orientation Dispersion and Density Imaging) (H. Zhang et al., 2012), comme
116
well as a network weighted by the longitudinal relaxation rate R1 (1/T1) derived from a
117
quantitative T1 map. The edge weights in this network are myelin-weighted as R1 has been
118
shown to correlate with histology-derived myelin content (Mancini et al., 2020; Mottershead et
119
al., 2003).
120
121
This characterization of weighted structural brain networks is carried out as follows: (1) within-
122
network features of edge weight distribution and variance; (2) edgewise relationships with FC,
123
edge length and myelin (R1); et (3) topological features of small-worldness, rich club and
124
network hubs. Surtout, uniform binary connectivity is enforced across all weighted network
125
variants i.e., the underlying binary connectivity map is identical. This allows the edge weights
126
themselves to drive the characterization.
127
128
129
RÉSULTATS
130
Dans 50 healthy adults (27 men; 29.54±5.62 years; 47 right-handed), structural brain networks were
131
estimated from multi-shell diffusion MRI data with probabilistic tractography. Each subject’s
132
structural network was used to compute 8 SC networks (Tableau 1) in which edges were weighted
133
par: NoS, SIFT2, COMMIT, FA, RD, ICVF, R1 and LoS (edge length computed as the mean
134
length of streamlines). NoS, SIFT2, COMMIT and LoS correspond to streamline-specific
135
metrics, whereas networks weighted by FA, RD, ICVF and R1 were computed using tractometry.
136
The edge weights in NoS, SIFT2 and COMMIT networks were normalized by node volume.
137
En plus, a static FC network was derived for each subject by zero-lag Pearson cross-
6
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
t
/
.
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
138
correlation of nodewise resting-state time series. Unless otherwise stated, all results shown
139
correspond to networks parcellated with the Schaefer-400 cortical atlas (Schaefer et al., 2018)
140
and include 14 subcortical nodes.
141
Short name
LoS
Long name
Length of Streamlines
NoS
Number of Streamlines
Method
streamline-
specific
streamline-
specific
streamline-
specific
streamline-
specific
Data source
diffusion
IRM
diffusion
IRM
diffusion
IRM
diffusion
IRM
tractometry multi-modal
Spherical-deconvolution
Informed Filtering of
Tractograms
Convex Optimization
Modeling for
Microstructure Informed
Tractography
longitudinal relaxation rate
Fractional Anisotropy
tractometry
Radial Diffusivity
tractometry
Intra-Cellular
Volume Fraction
tractometry
(diffusion +
relaxometry)
diffusion
IRM
diffusion
IRM
diffusion
IRM
Interpretation
Mean length of the streamlines
connecting two nodes
Number of streamlines
connecting two nodes; connection
strength
Fiber density from spherical
deconvolution summed across
streamlines; connection strength
Total intra-axonal cross-sectional
area summed across streamlines;
connection strength
R1=1/T1; index of tissue myelin
content
Diffusion directional dependence
Diffusion perpendicular to the
principal axis
Neurite density
SIFT2
COMMIT
R1
FA
RD
ICVF
142
Tableau 1. Summary of structural network weights.
143
144
145
Structural Brain Networks Vary in the Distribution of Their Edge Weights
146
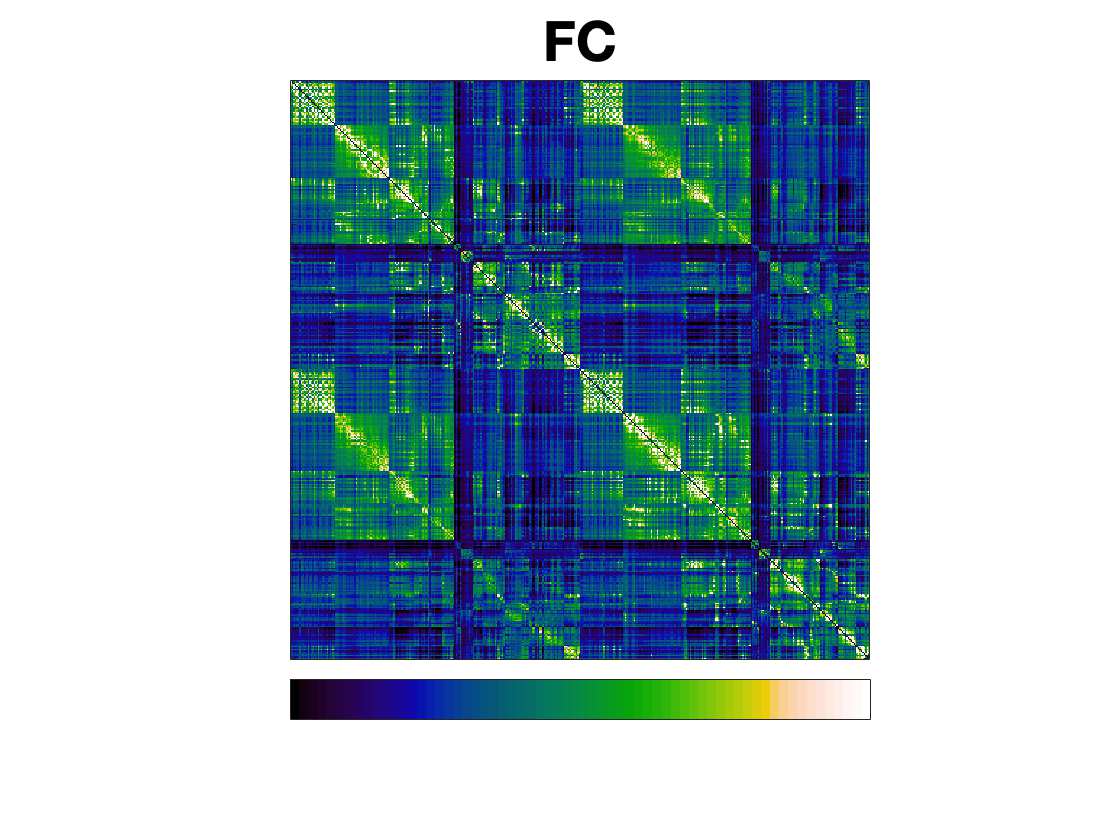
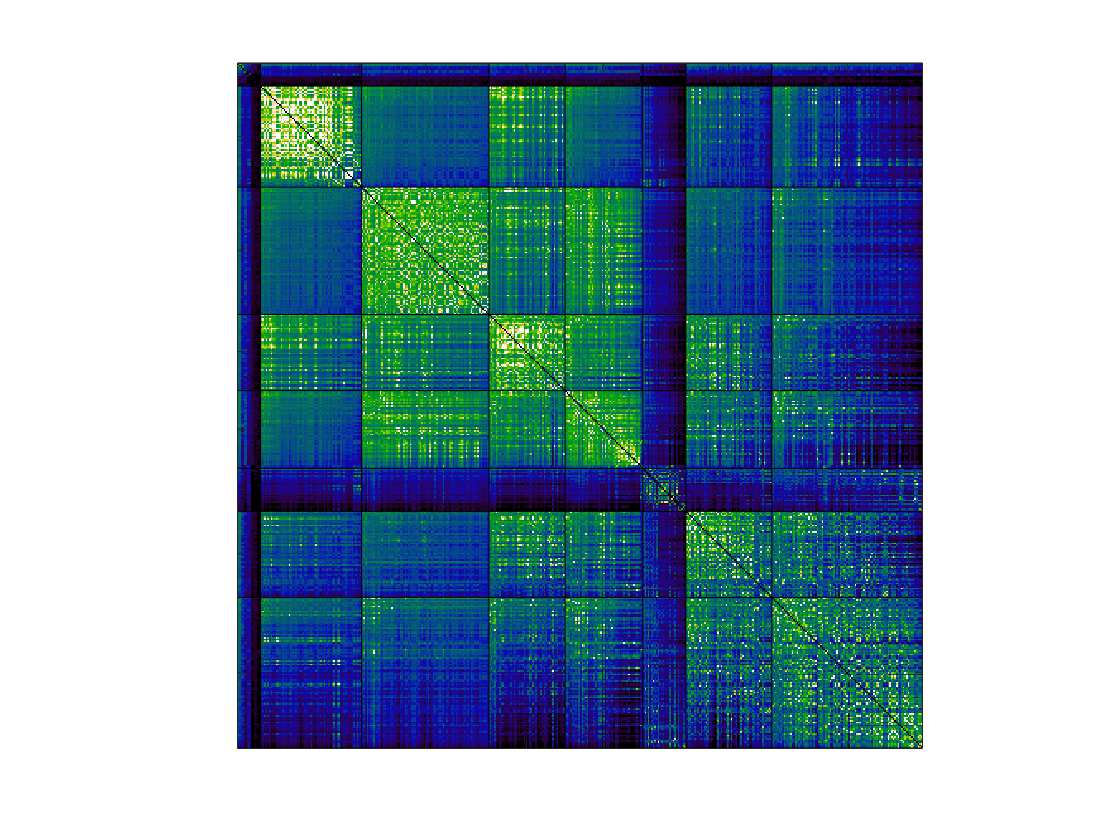
Group-level networks weighted by NoS, SIFT2 and COMMIT show spatially distributed patterns
147
of high magnitude edge weights and noticeably accentuate within-module connectivity (Chiffre
148
1). Modules correspond to the 7-canonical resting-state networks (Thomas Yeo et al., 2011) plus
149
the subcortex. These patterns are hallmarks of FC networks and are observed in the FC network
150
shown here. The contrast between high and low magnitude edge weights is most evident in
151
COMMIT. By comparison, the spatial variation of edge weight distribution in the tractometry
7
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
t
/
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
152
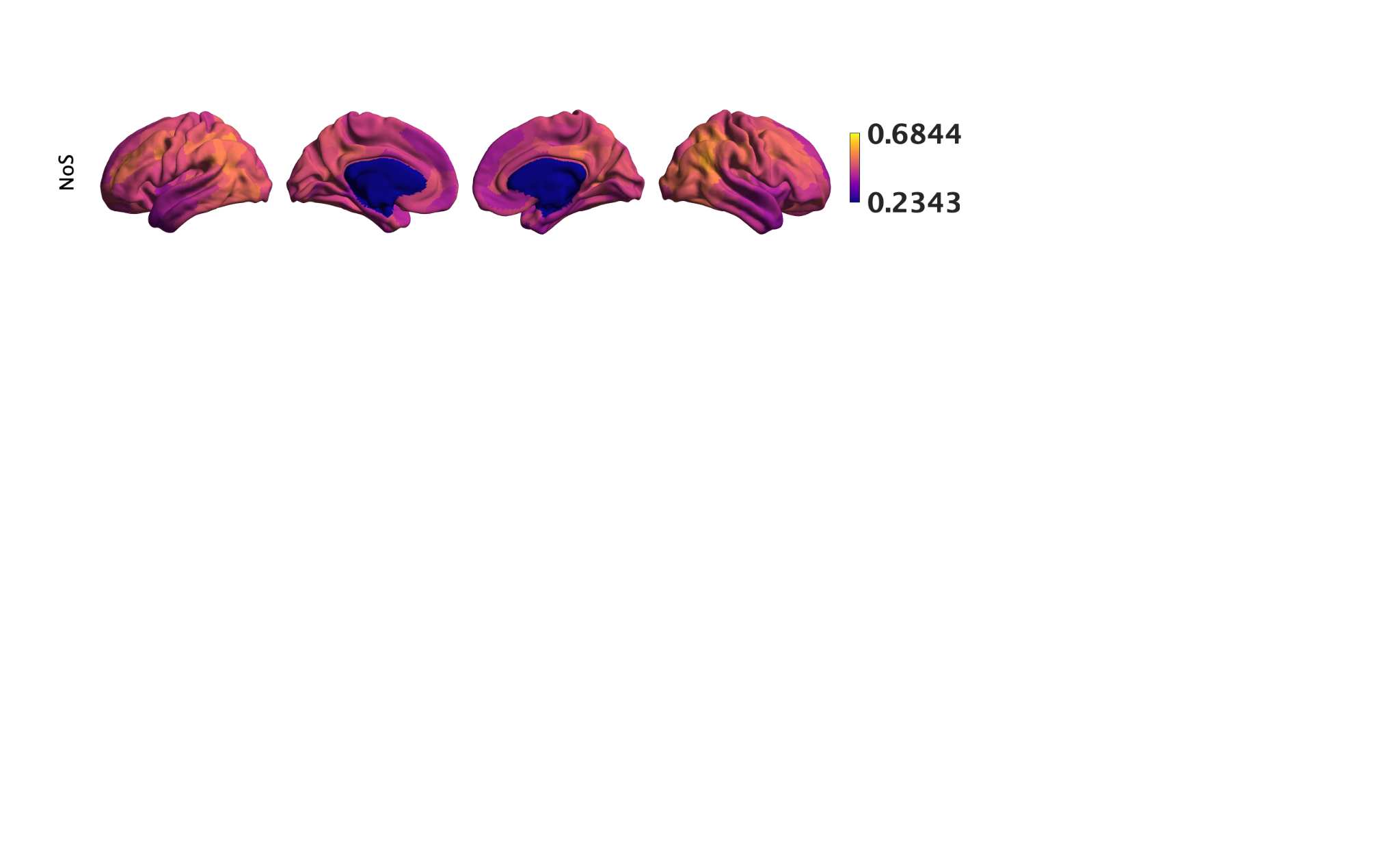
networks is smoother with more pronounced regional concentrations. R1 is highest in the edges
153
connecting the visual module to itself and to the rest of the brain; and lowest within the
154
subcortex and between the subcortical and limbic modules. The surface plot shows the highest
155
concentration of R1 in the white matter projections of posterior cortical regions.
156
157
158
159
160
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
t
.
/
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
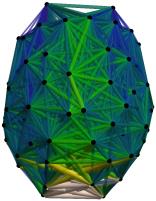
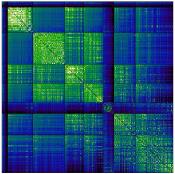
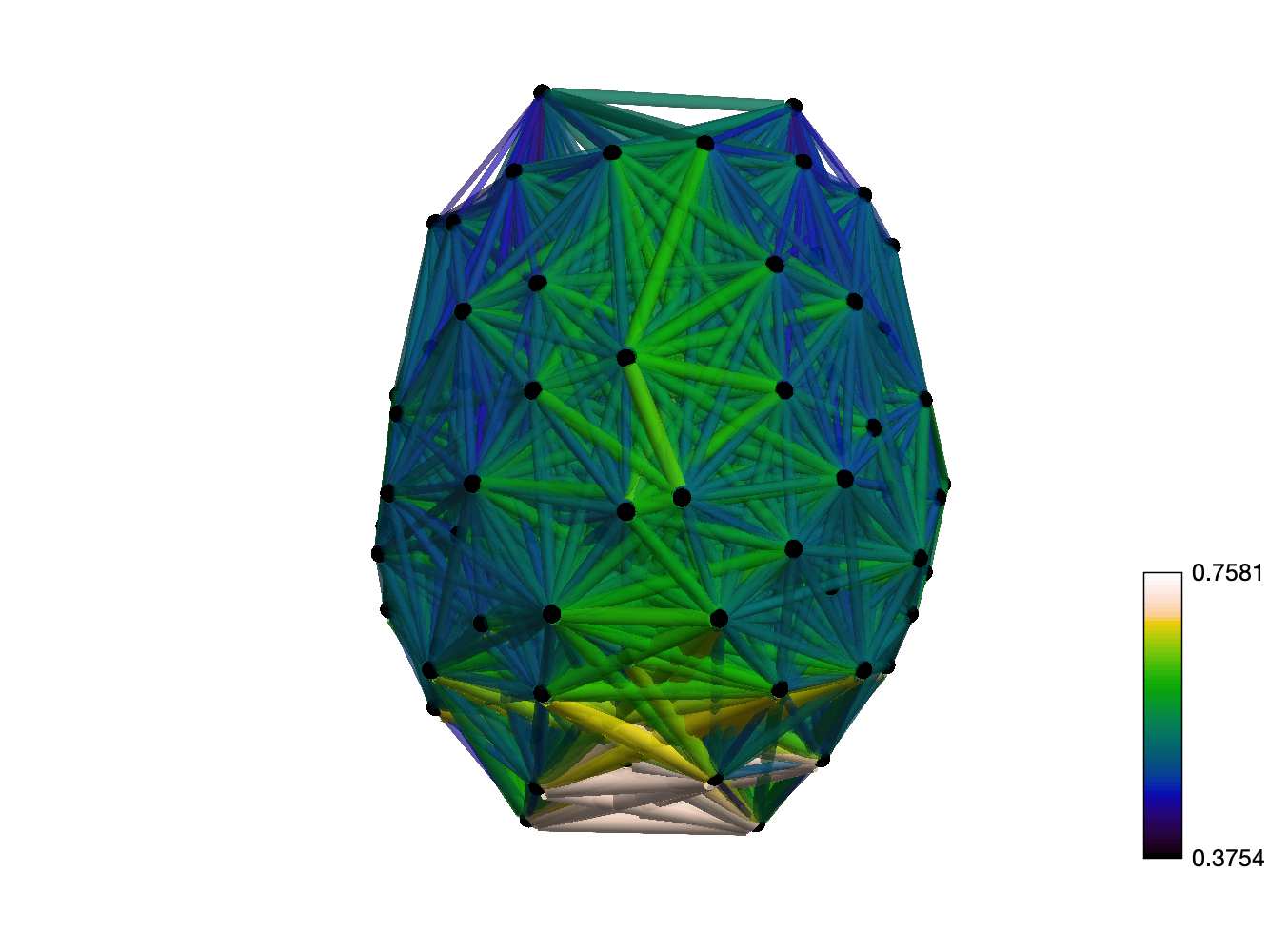
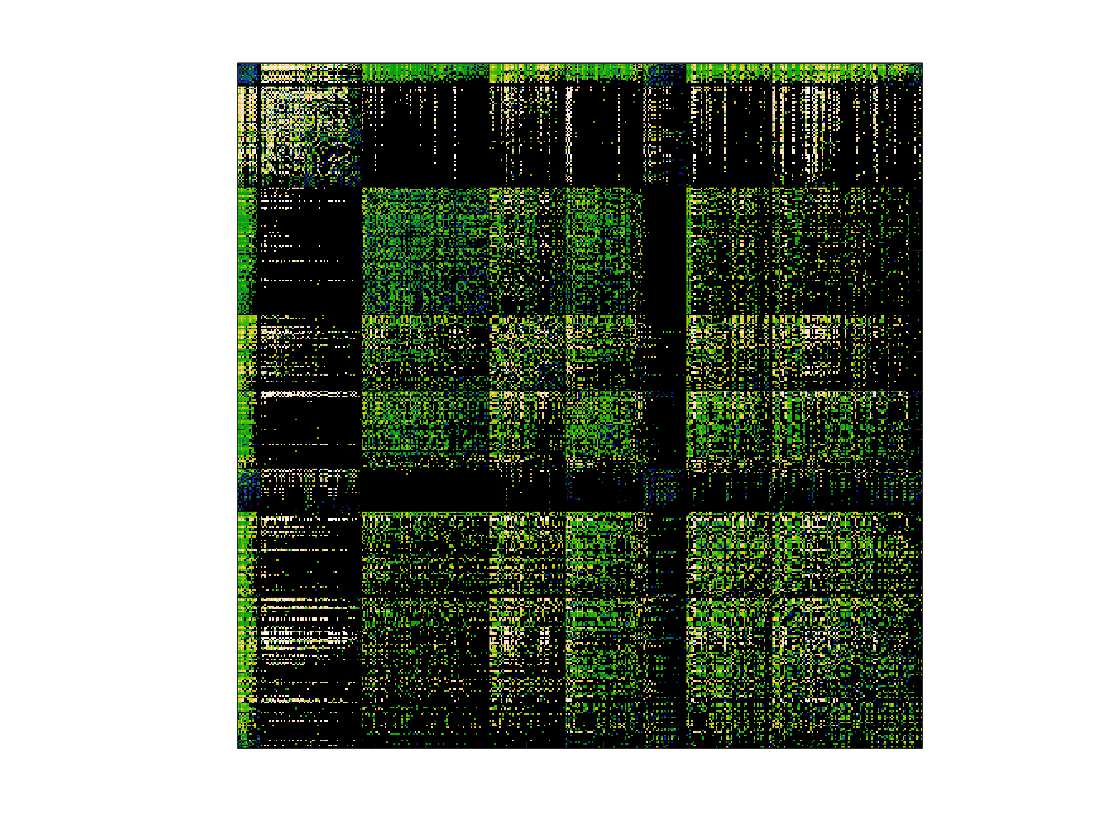
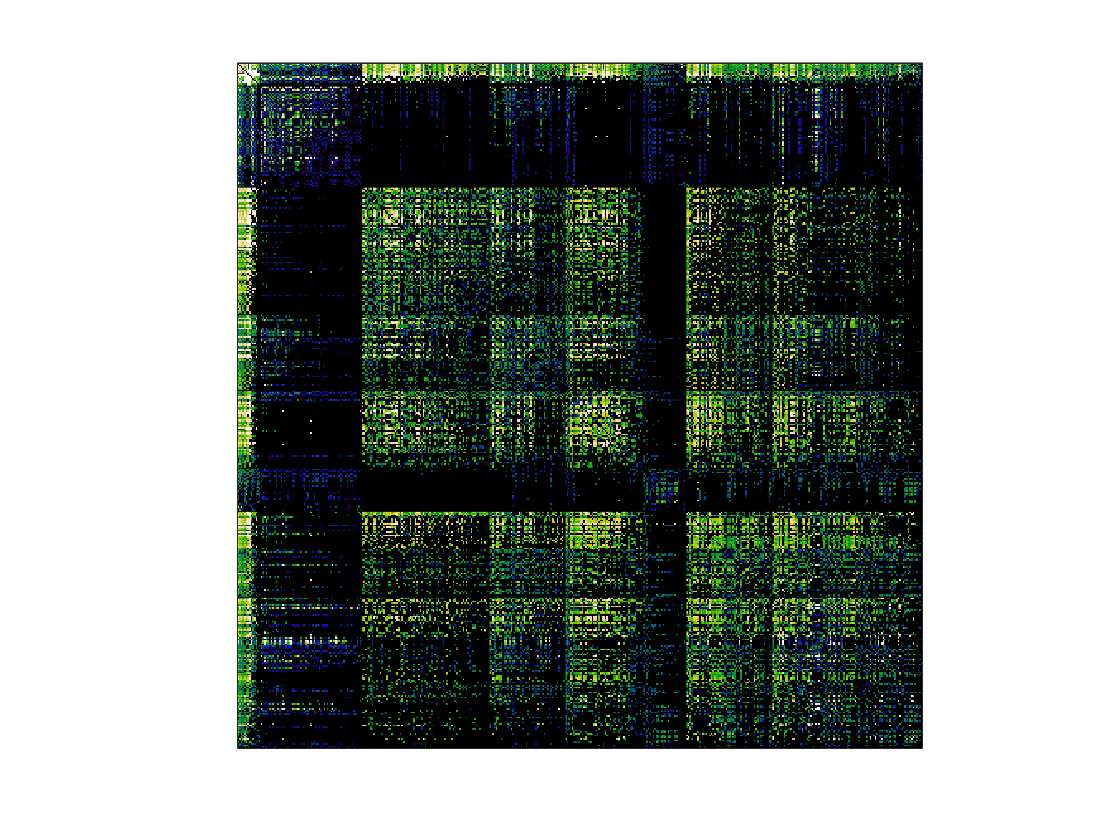
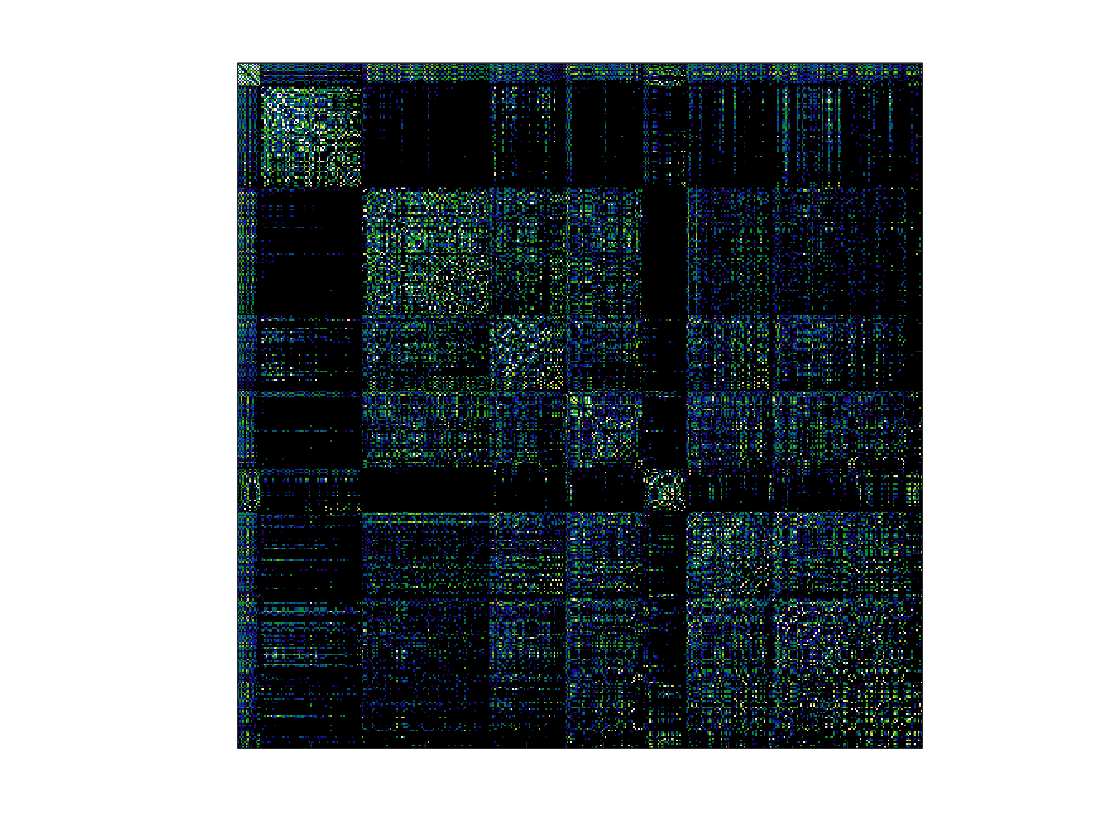
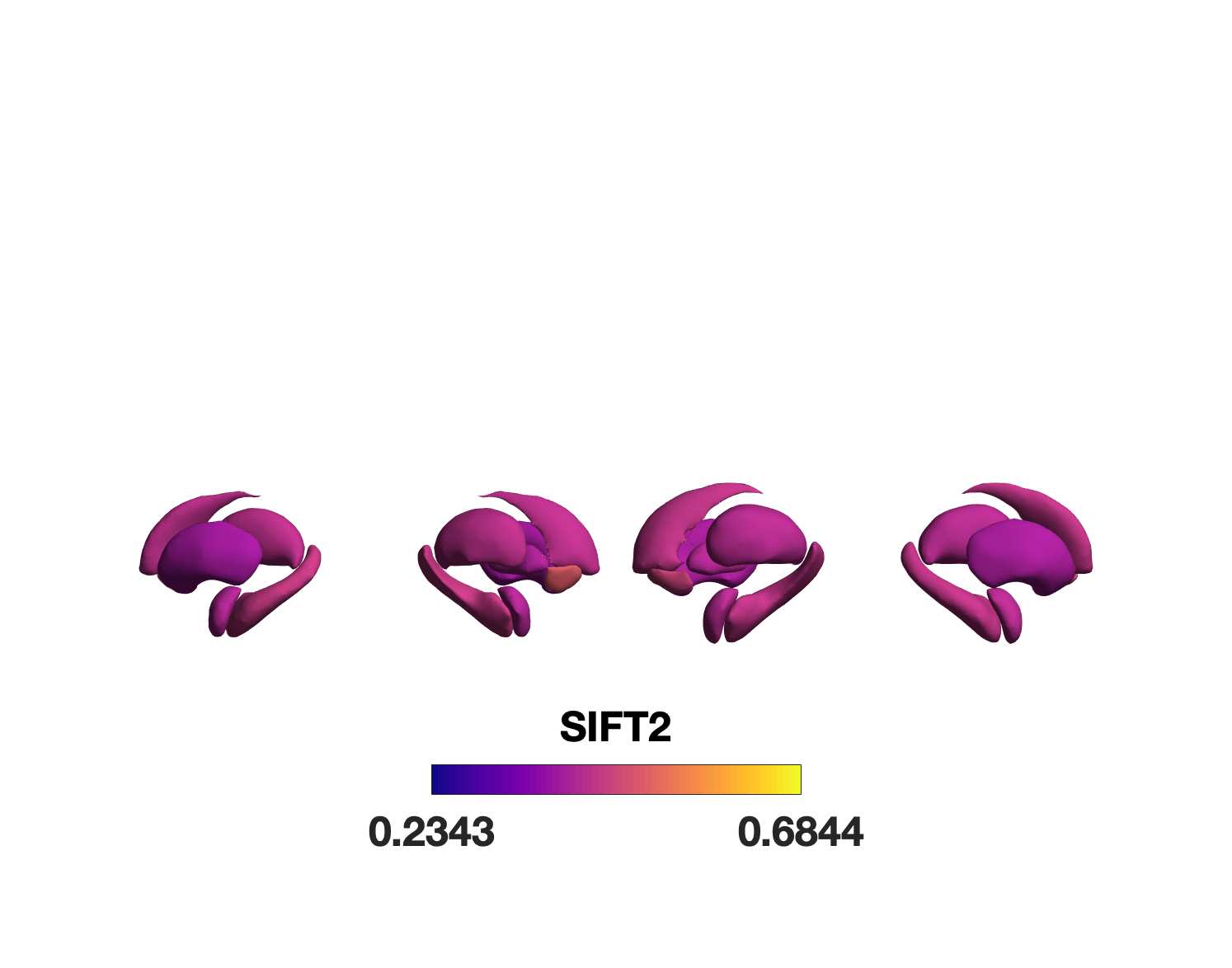
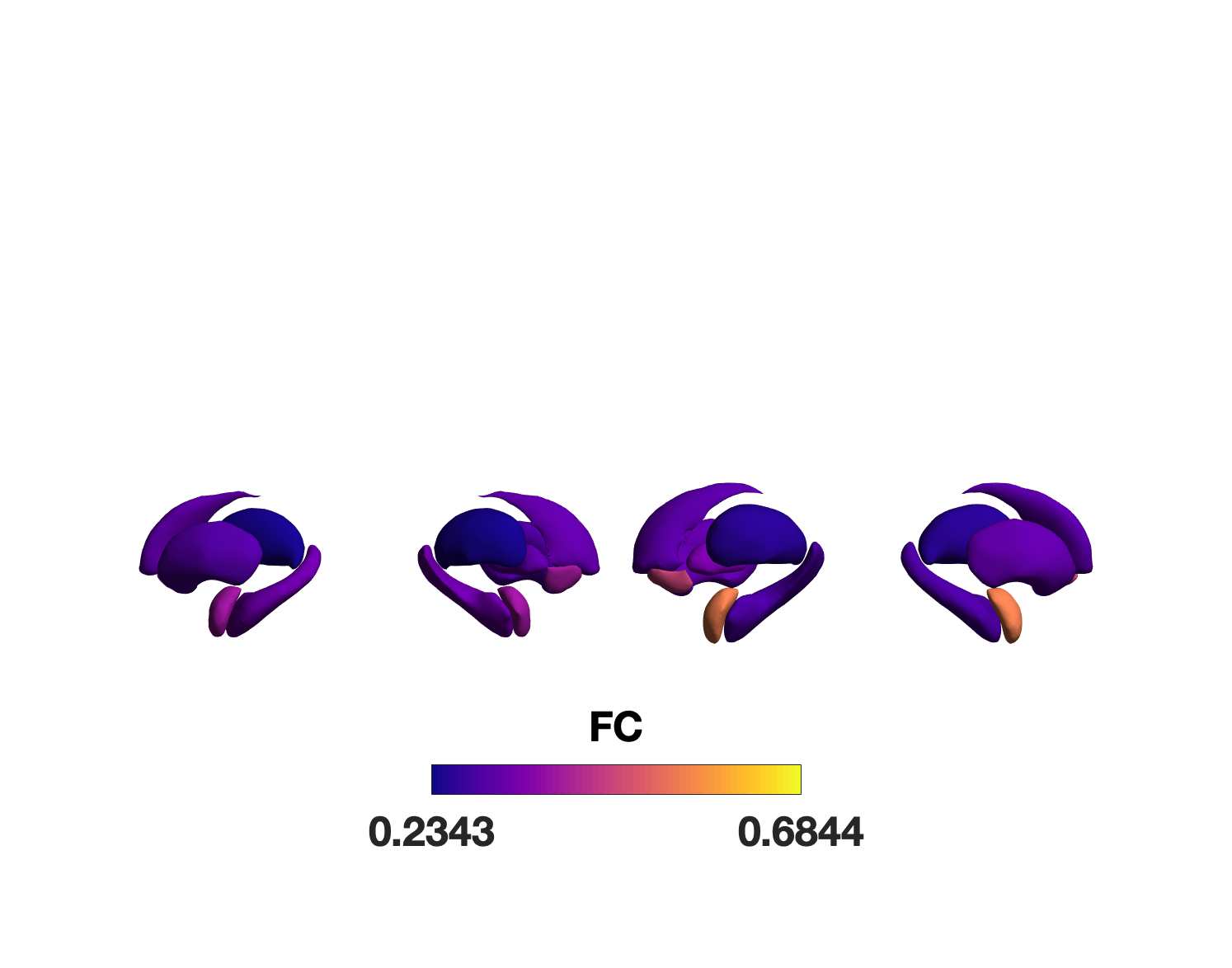
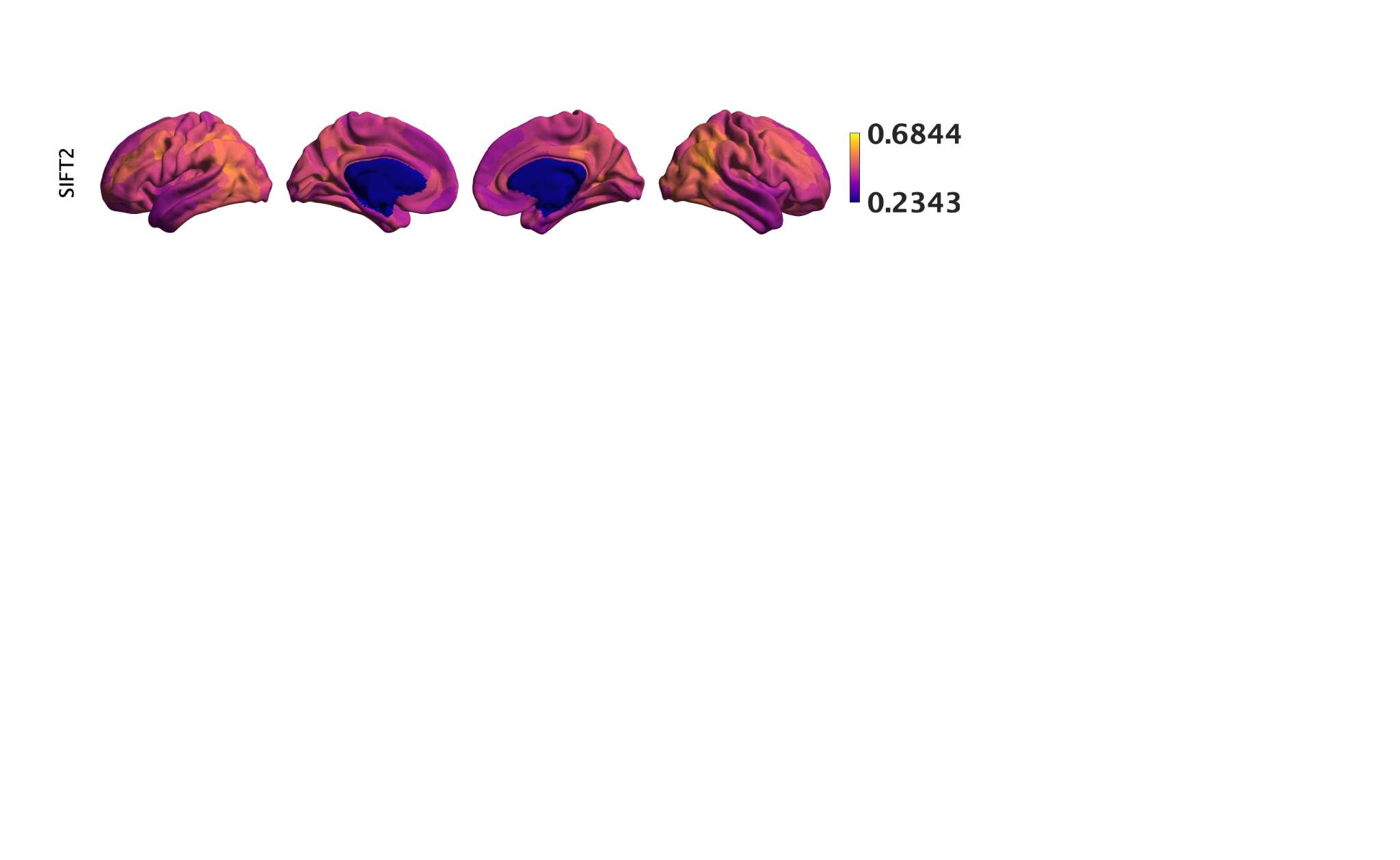
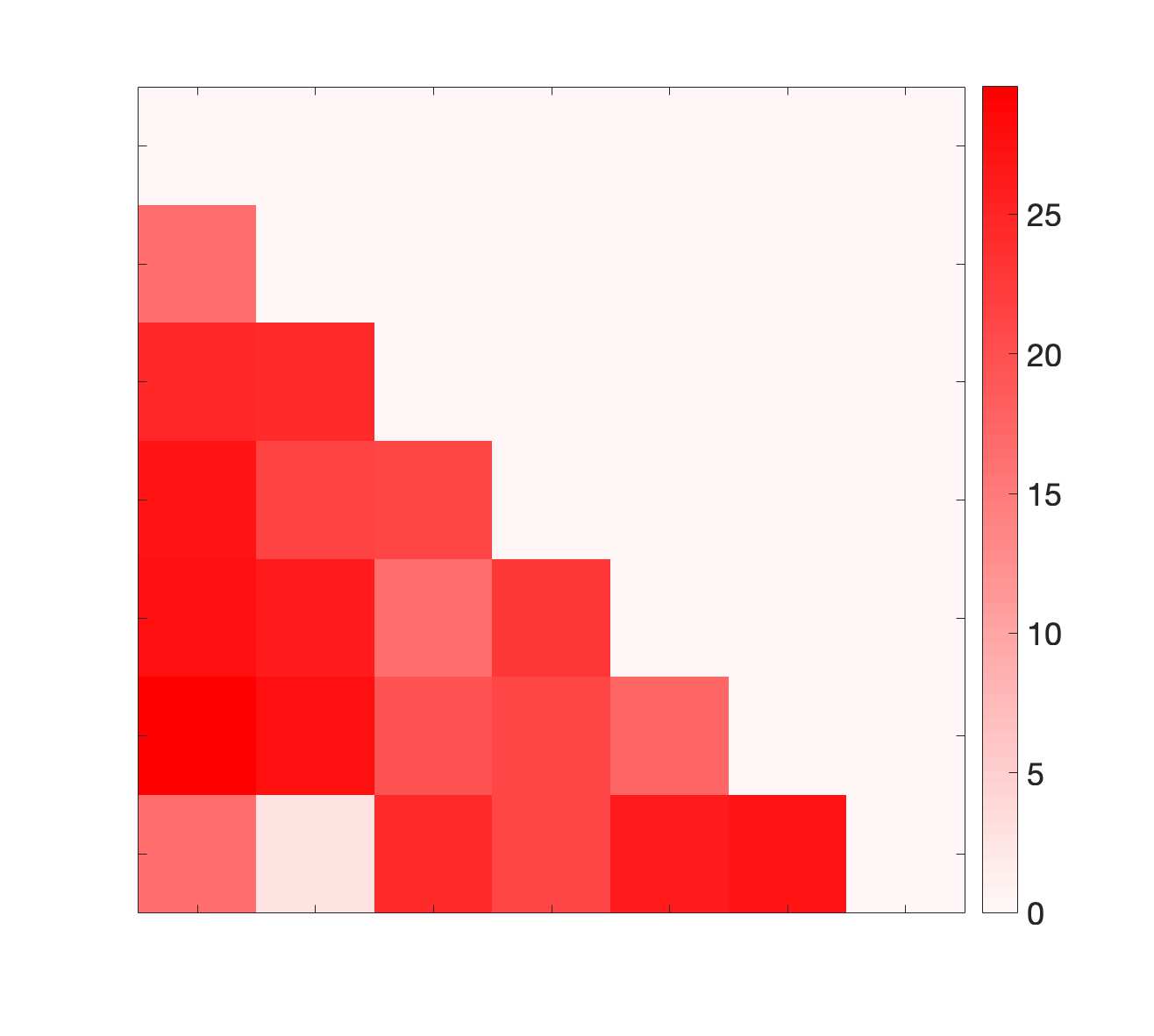
Chiffre 1. Edge Weight Spatial Distribution. Connectivity matrices of group-level edge weights for FC
(functional connectivity), NoS (number of streamlines), SIFT2 (spherical-deconvolution informed filtering
of tractograms), COMMIT (convex optimization modeling for microstructure informed tractography), R1
8
(longitudinal relaxation rate), ICVF (intra-cellular volume fraction), FA (fractional anisotropy), RD
(radial diffusivity) and LoS (mean length of streamlines). Each network is composed of 414 nodes as
defined by the Schaefer-400 cortical parcellation and 14 subcortical ROIs. Nodes are grouped into the
canonical resting state modules (Thomas Yeo et al., 2011) plus the subcortex: SUB (subcortex), VIS
(visuel), SMN (somatomotor), DAN (dorsal attention), SVAN (salience ventral attention), LIMB (limbic),
CONT (control), and DMN (default mode). 3D cortical surfaces (shown below) of group-level edge
weights in the Schaefer-100 parcellation generated with BrainNet Viewer (Xia et al., 2013). Edge
diameter and color indicate weight magnitude. The edge weights in NoS, SIFT2 and COMMIT networks
were log10 transformed for visualization.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
161
162
163
164
165
166
167
168
169
170
171
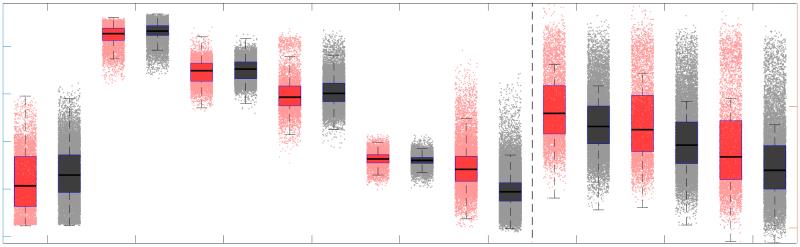
Group-level edge weight distributions are summarized with respect to two important
172
organizational patterns of brain function (Figure 2A): within and between resting state modules
173
(Thomas Yeo et al., 2011); and along the principal functional gradient (Margulies et al., 2016).
174
NoS, SIFT2 and COMMIT mirror FC in both plots with greater edge weight magnitude within
175
module, especially within unimodal modules. R1, ICVF, FA and RD generally mirror LoS with
176
the reverse trend: higher between module and lowest in unimodal modules. This suggests that
177
tractometry-derived networks may be influenced by edge length to a greater extent.
178
9
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
t
.
/
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
/
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
t
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
179
180
181
182
183
184
185
186
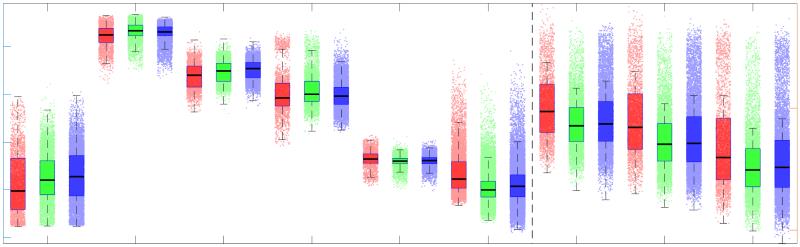
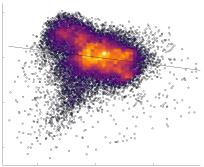
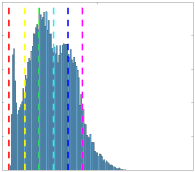
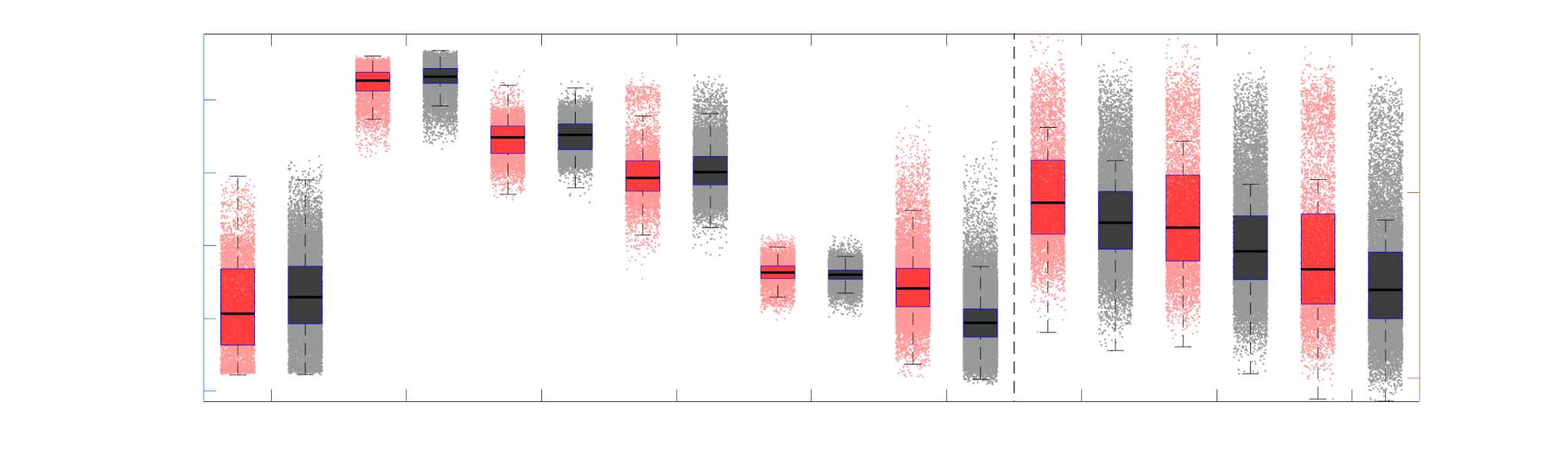
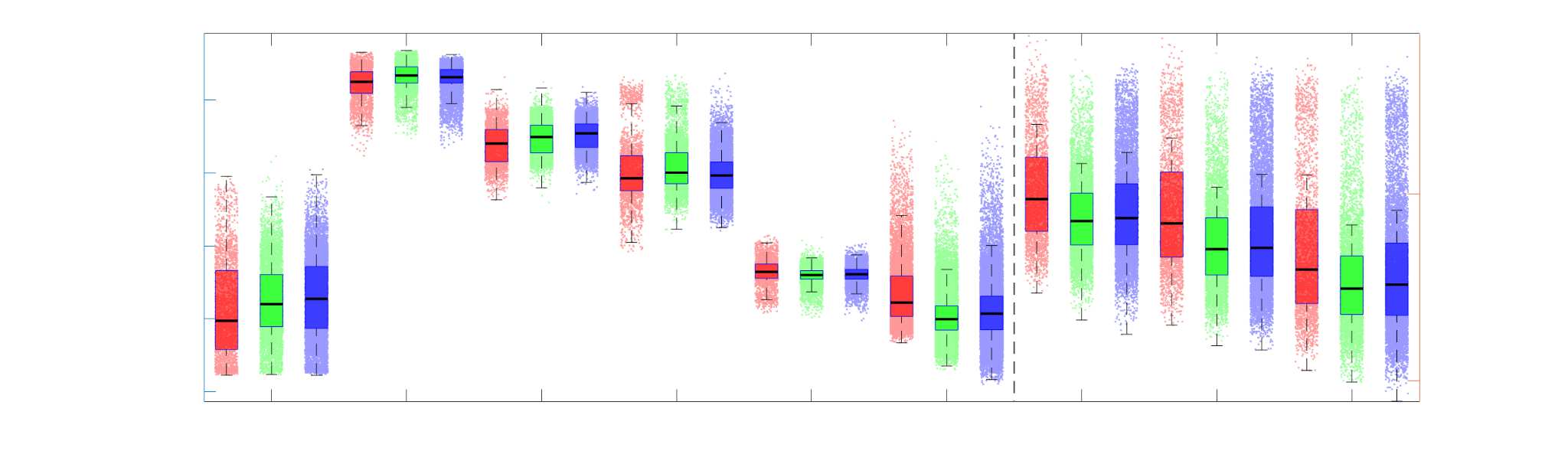
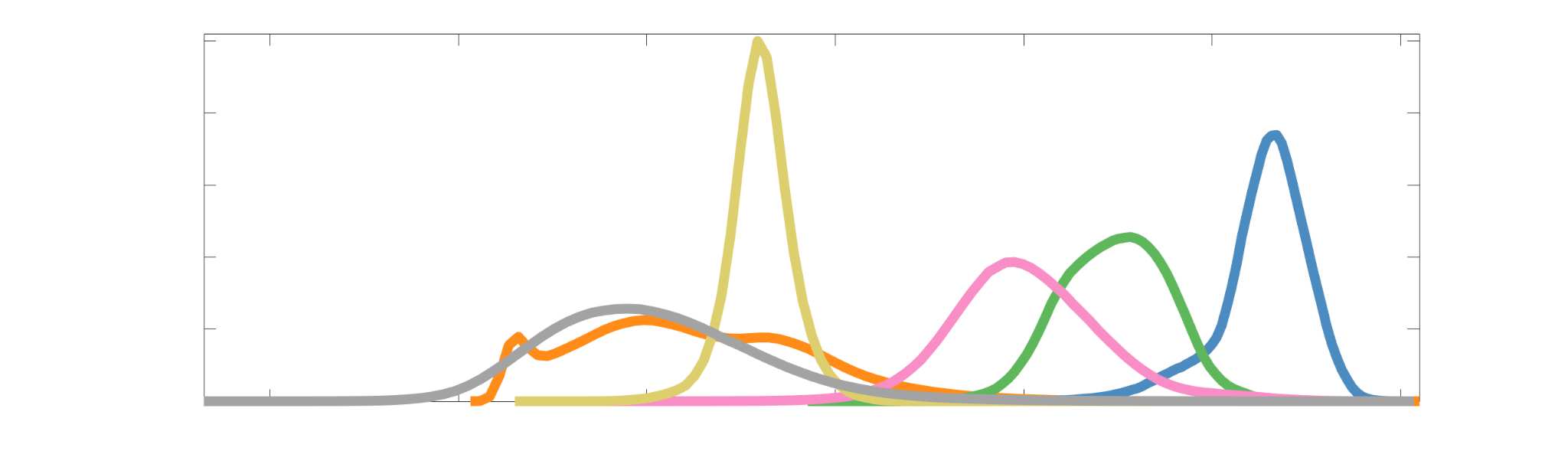
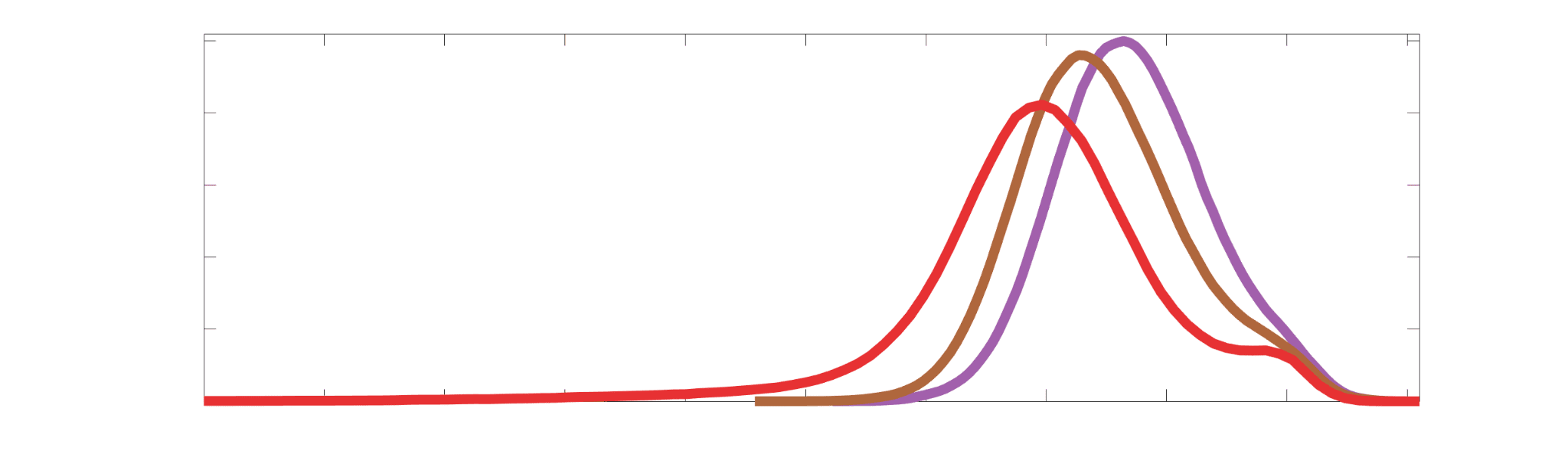
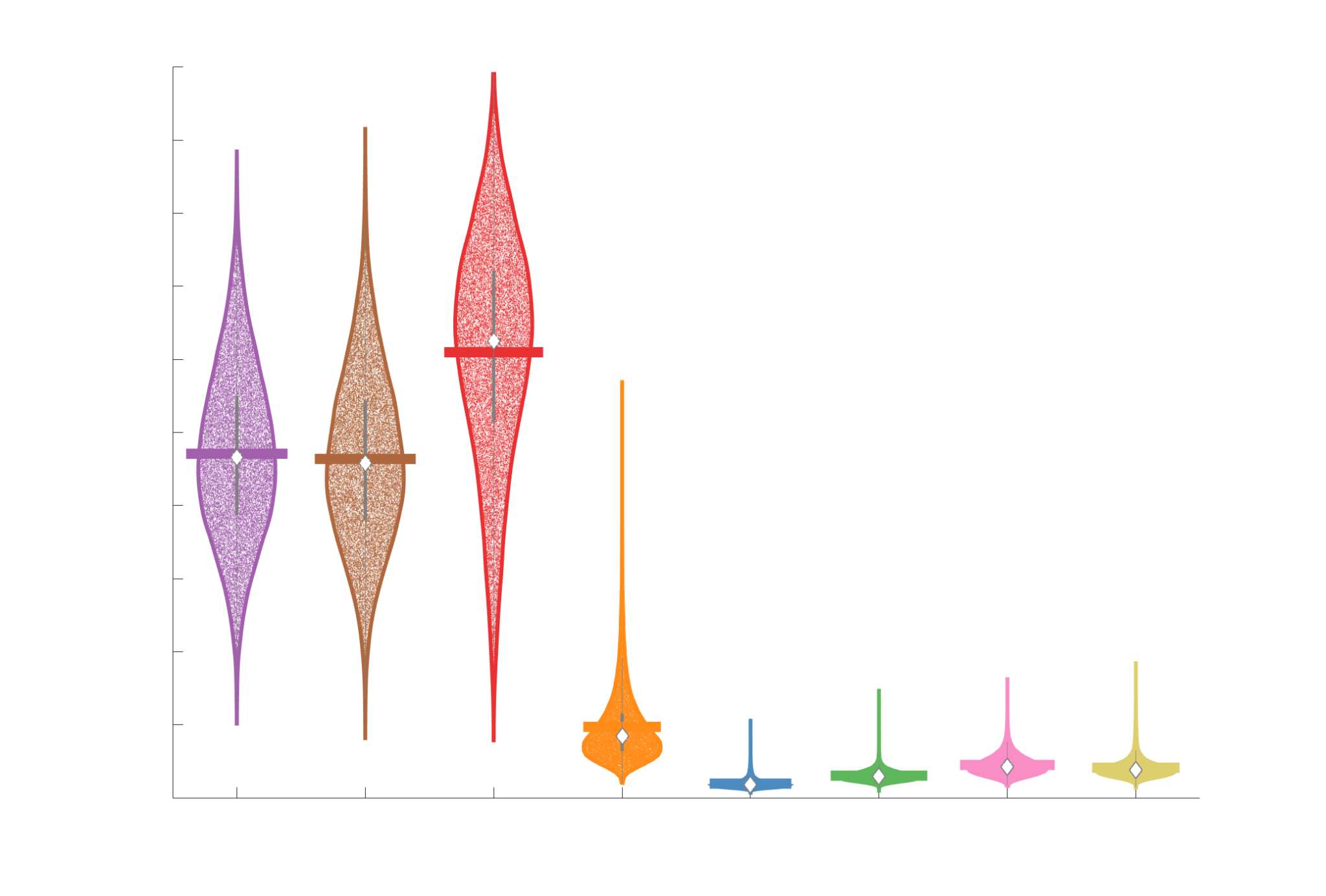
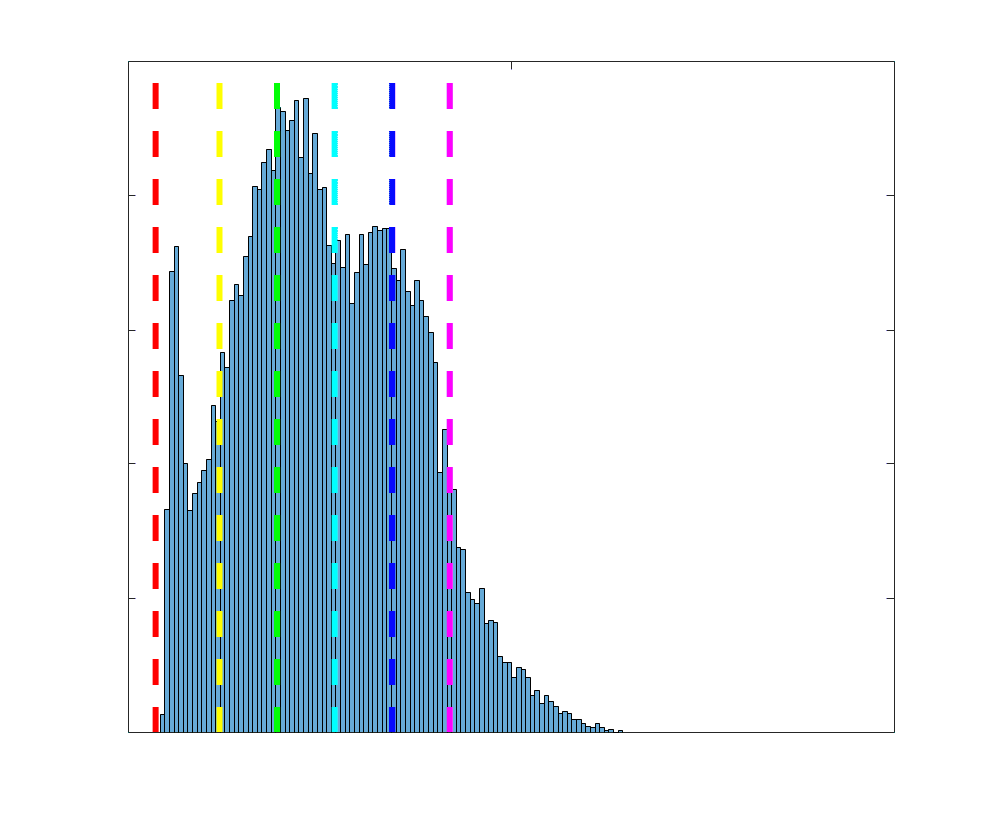
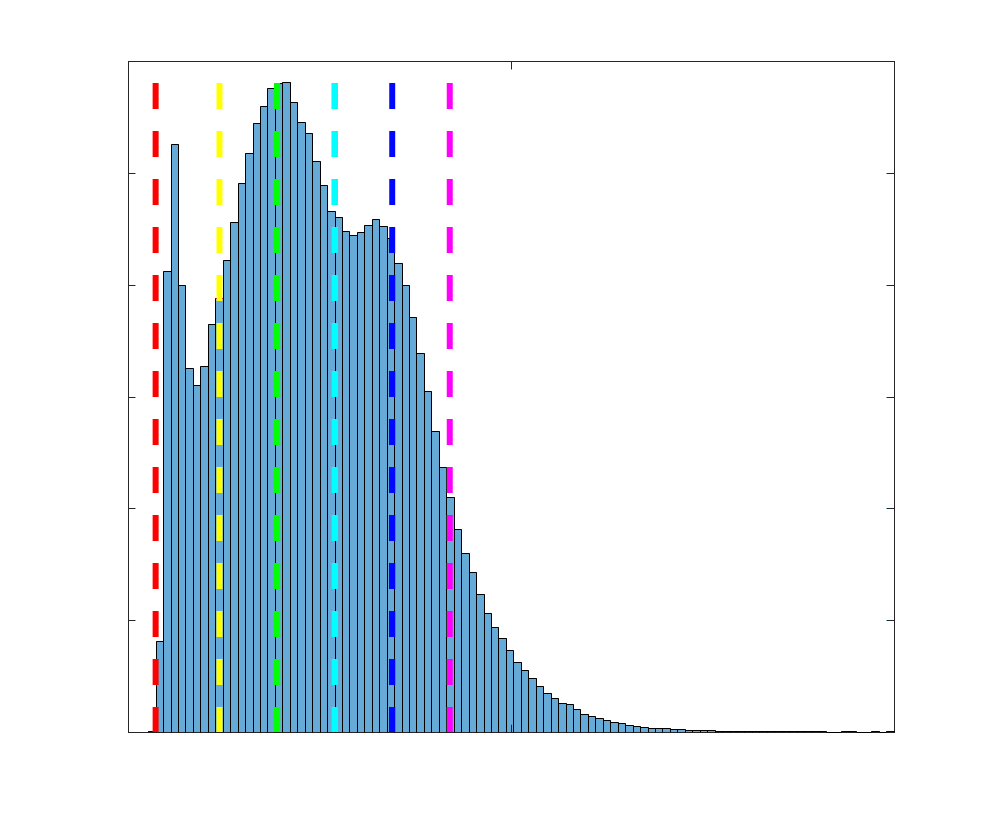
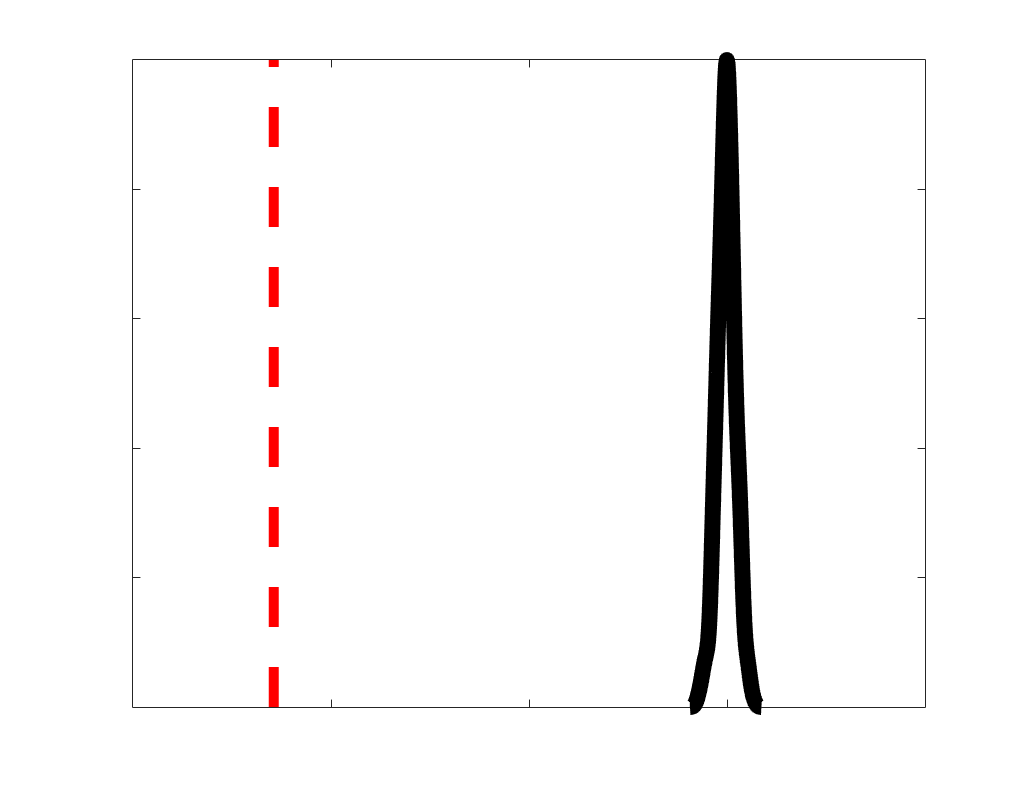
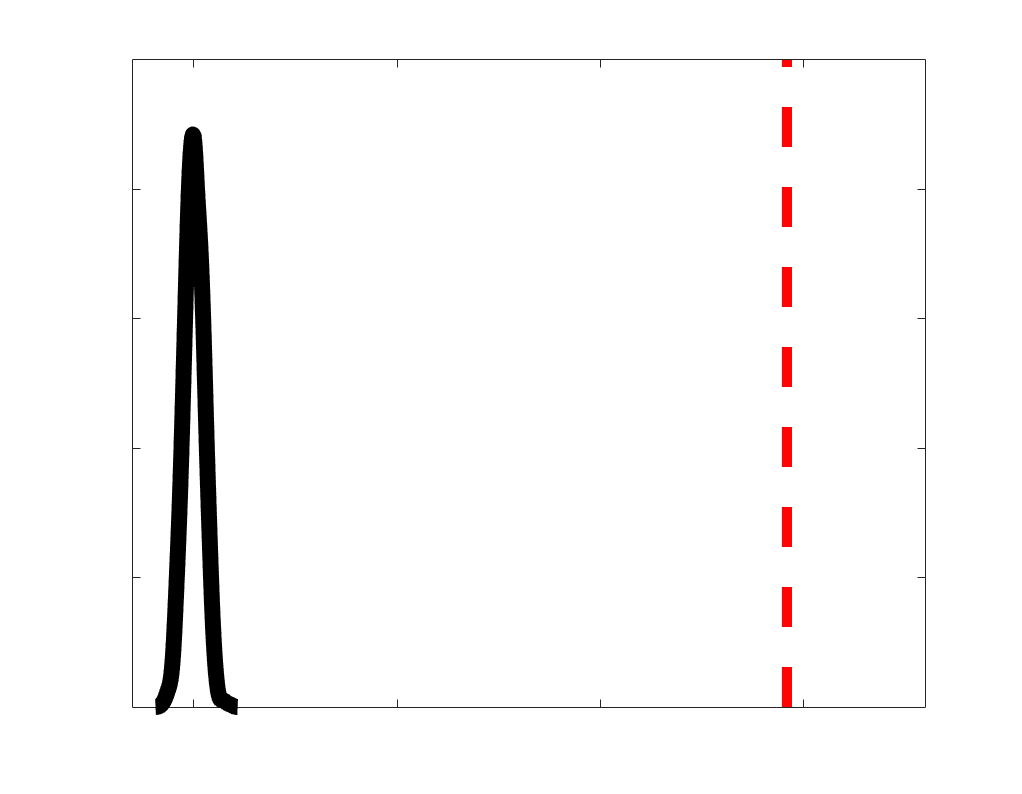
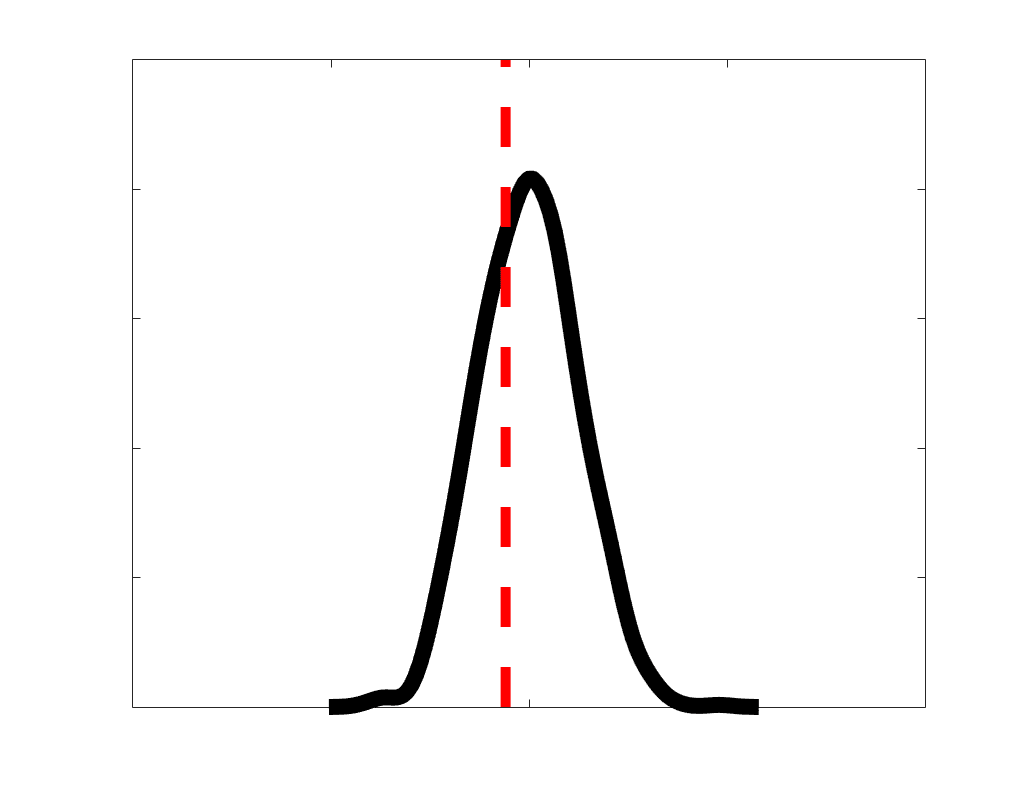
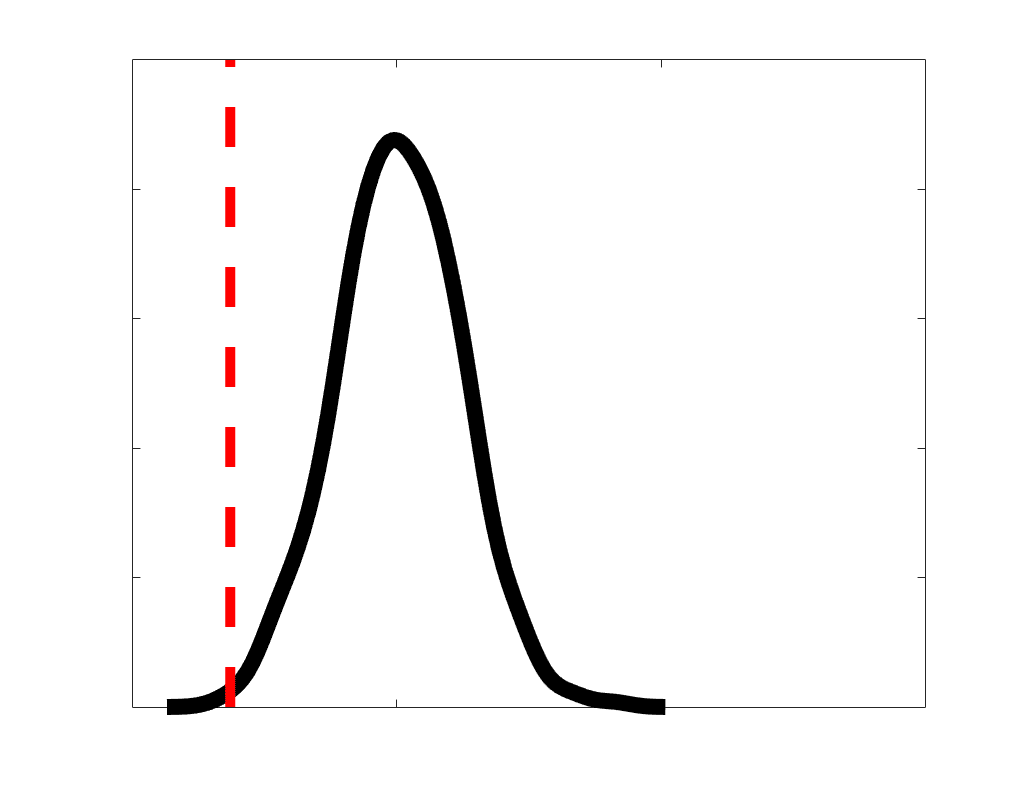
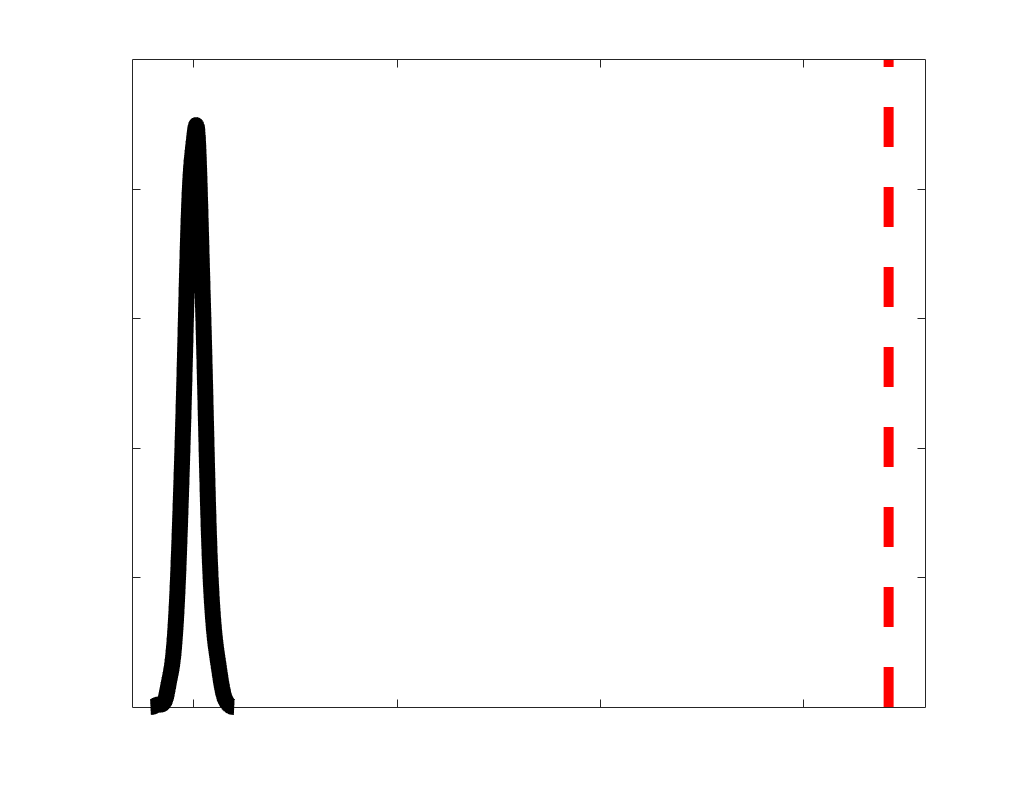
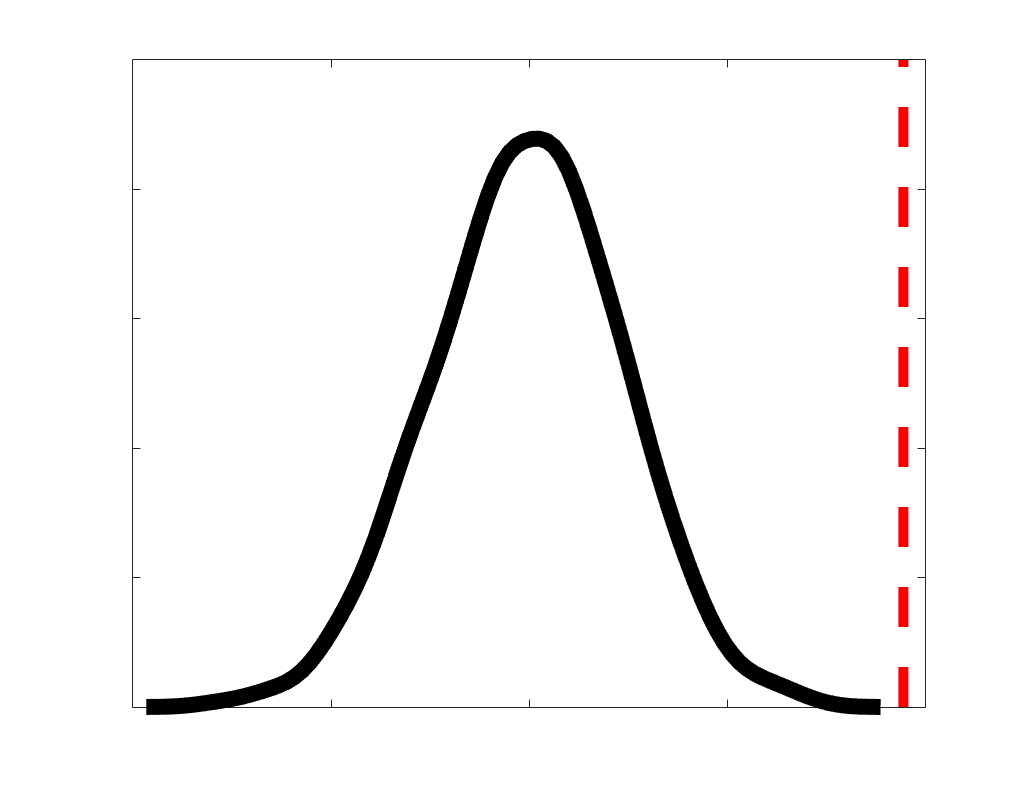
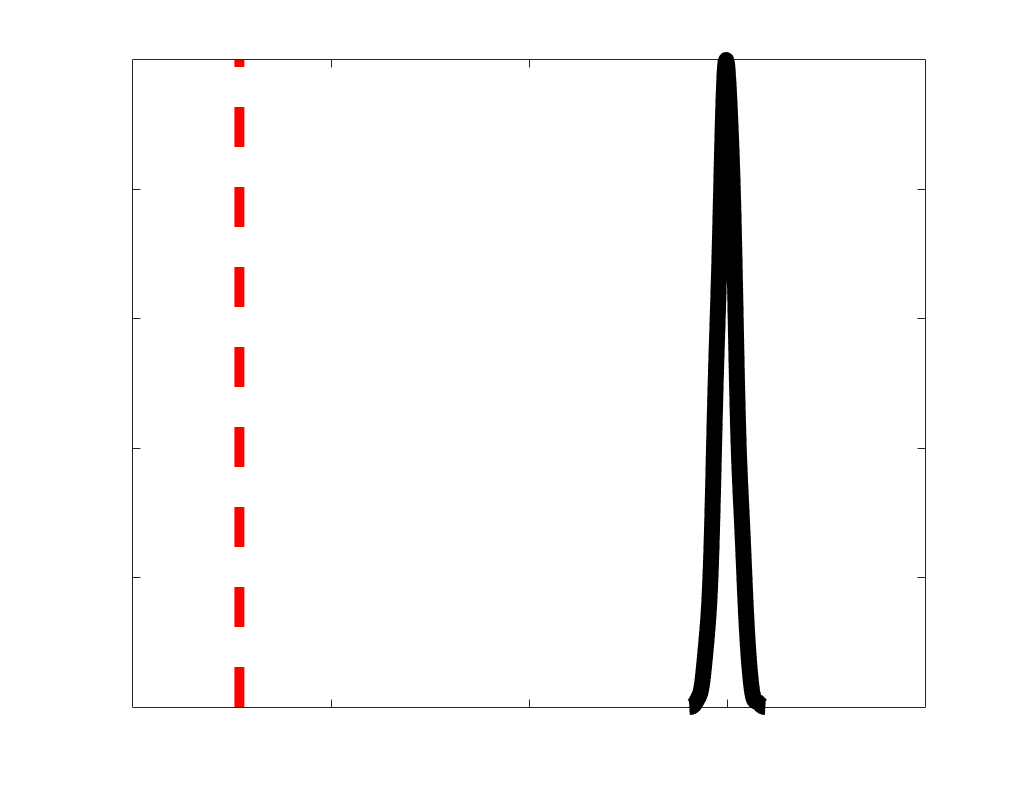
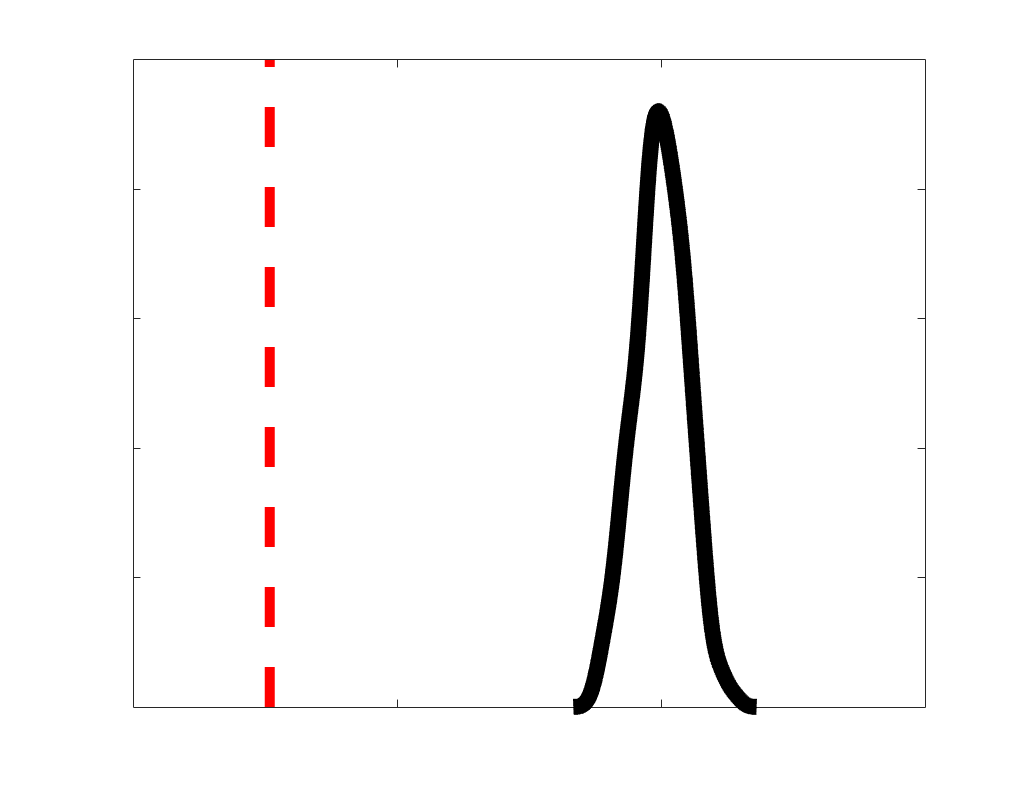
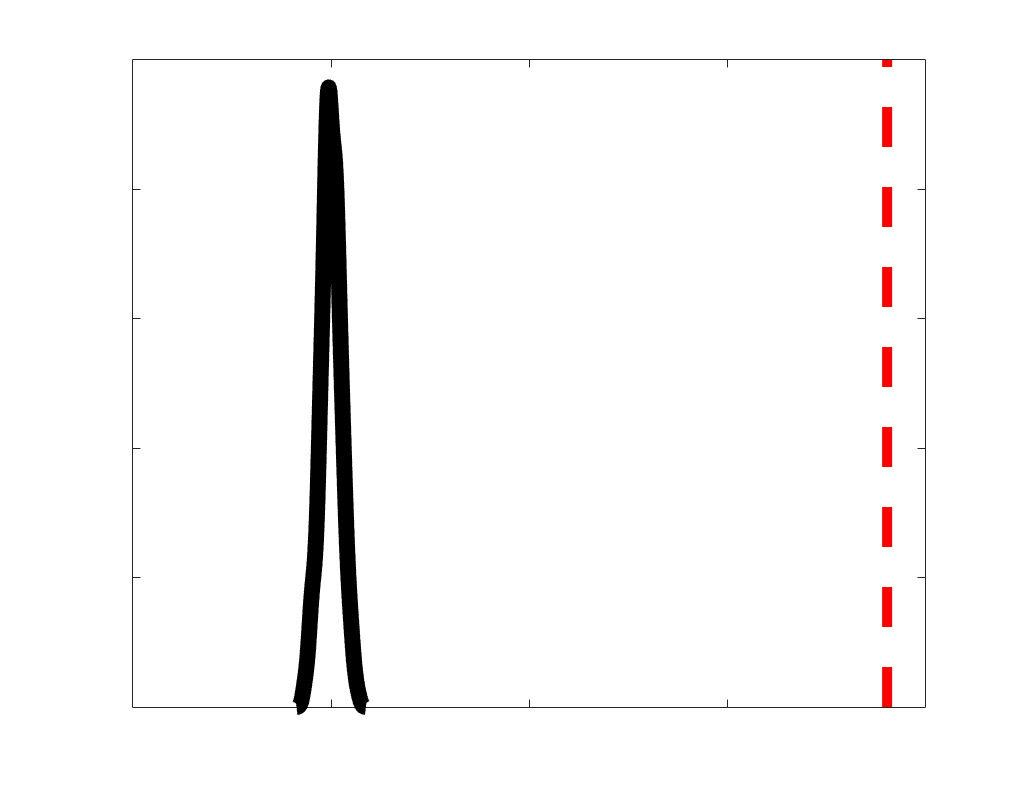
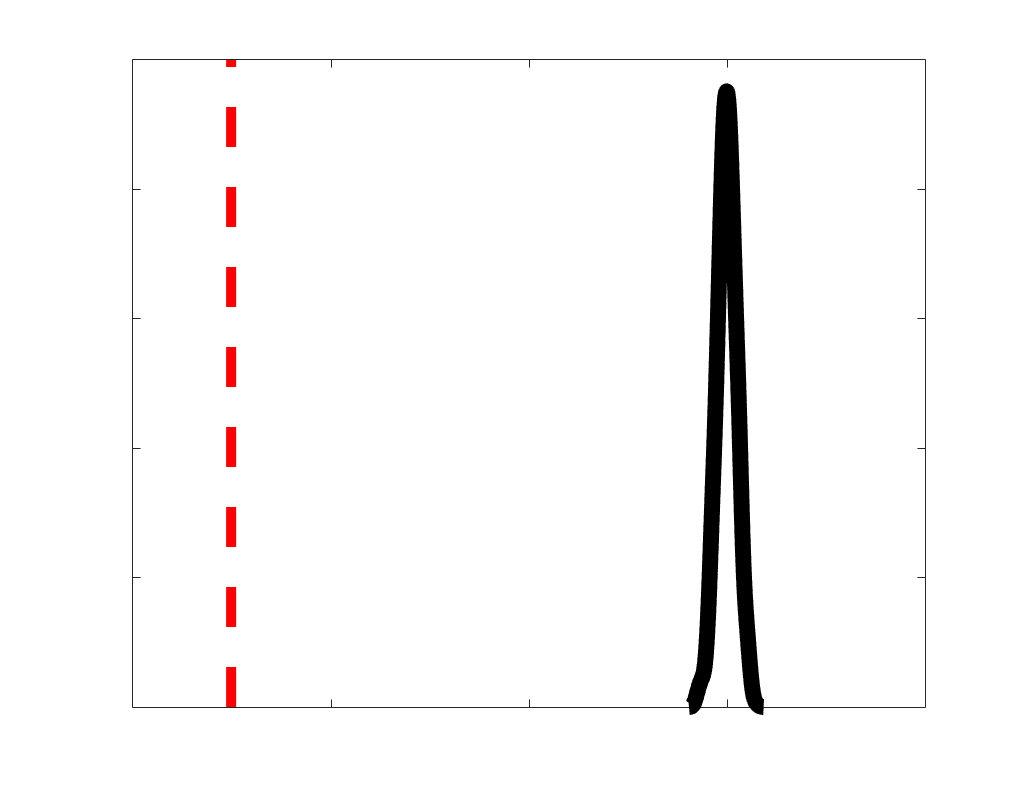
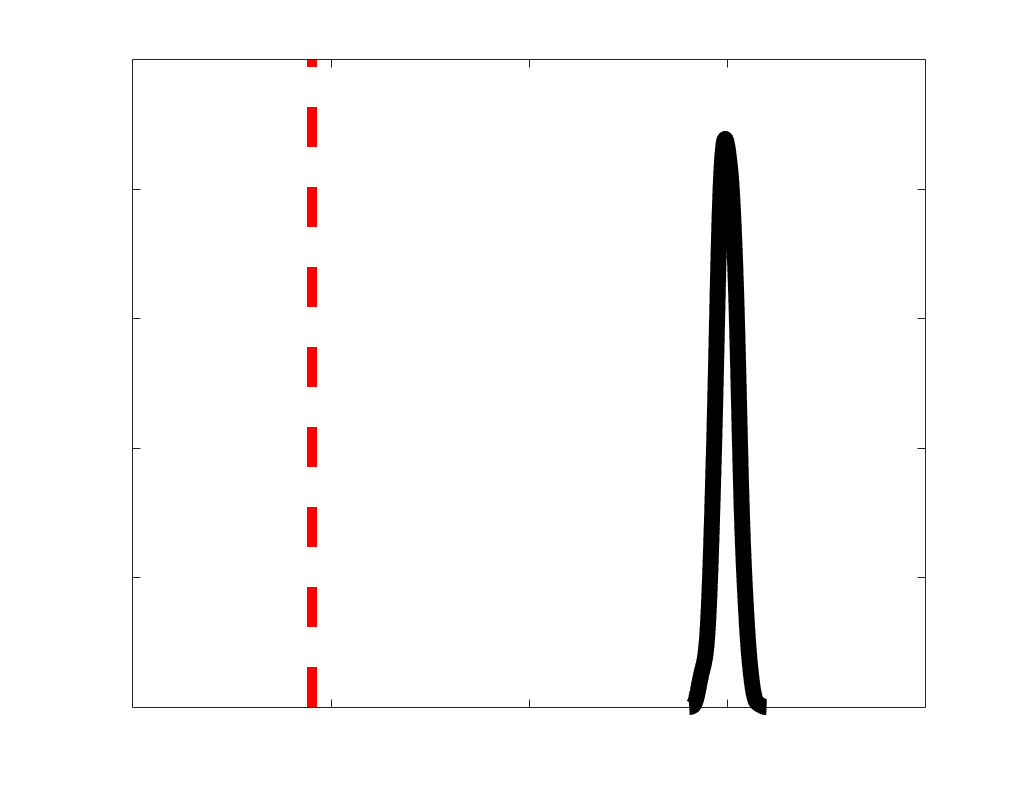
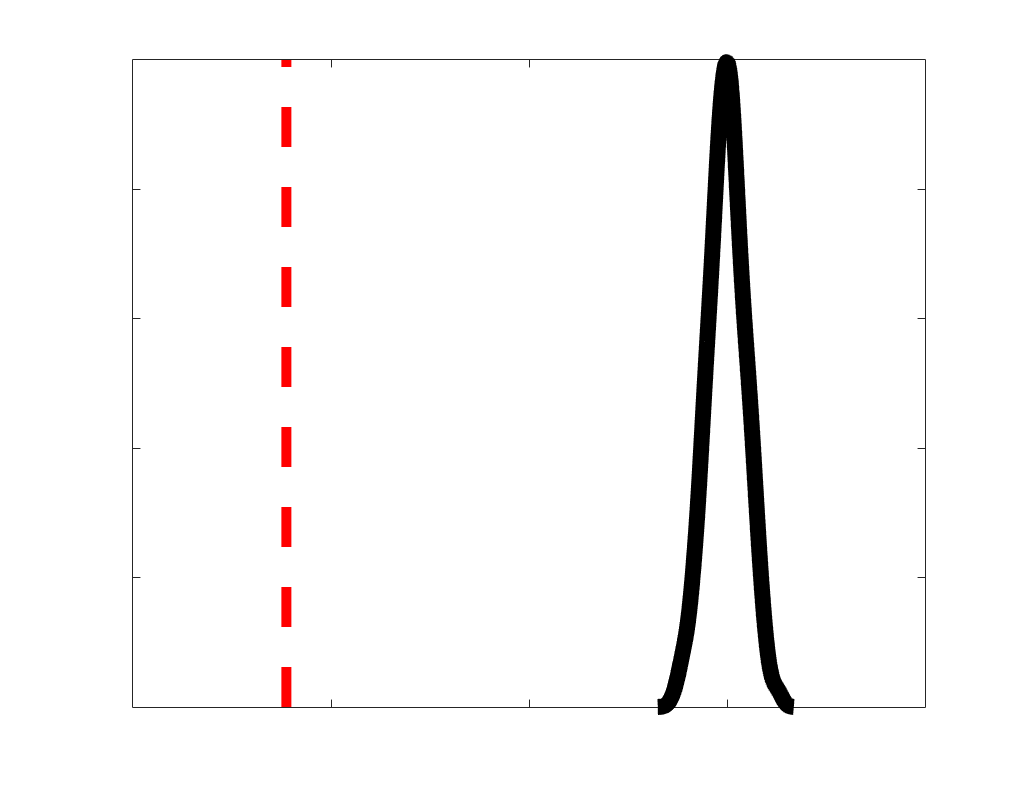
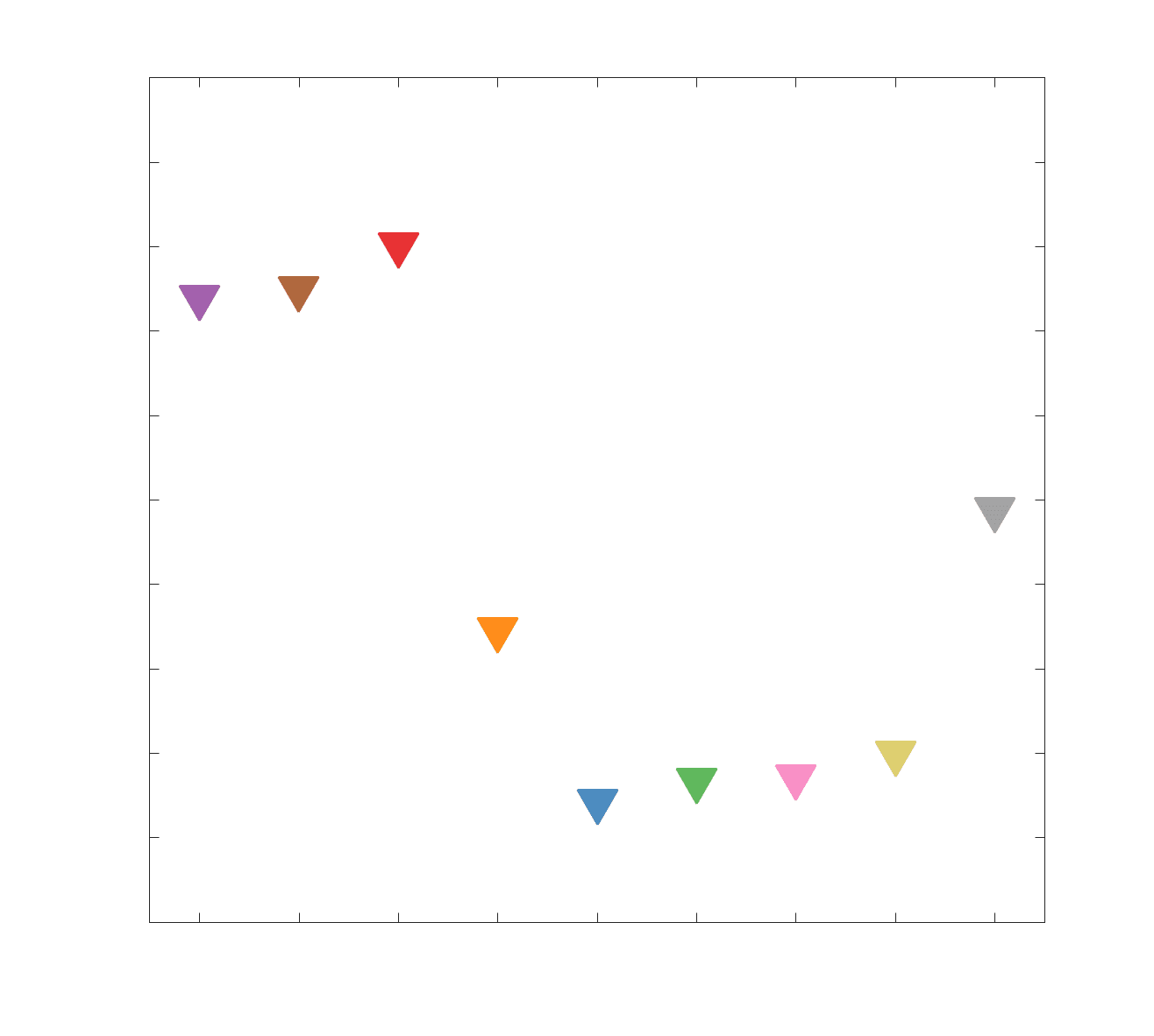
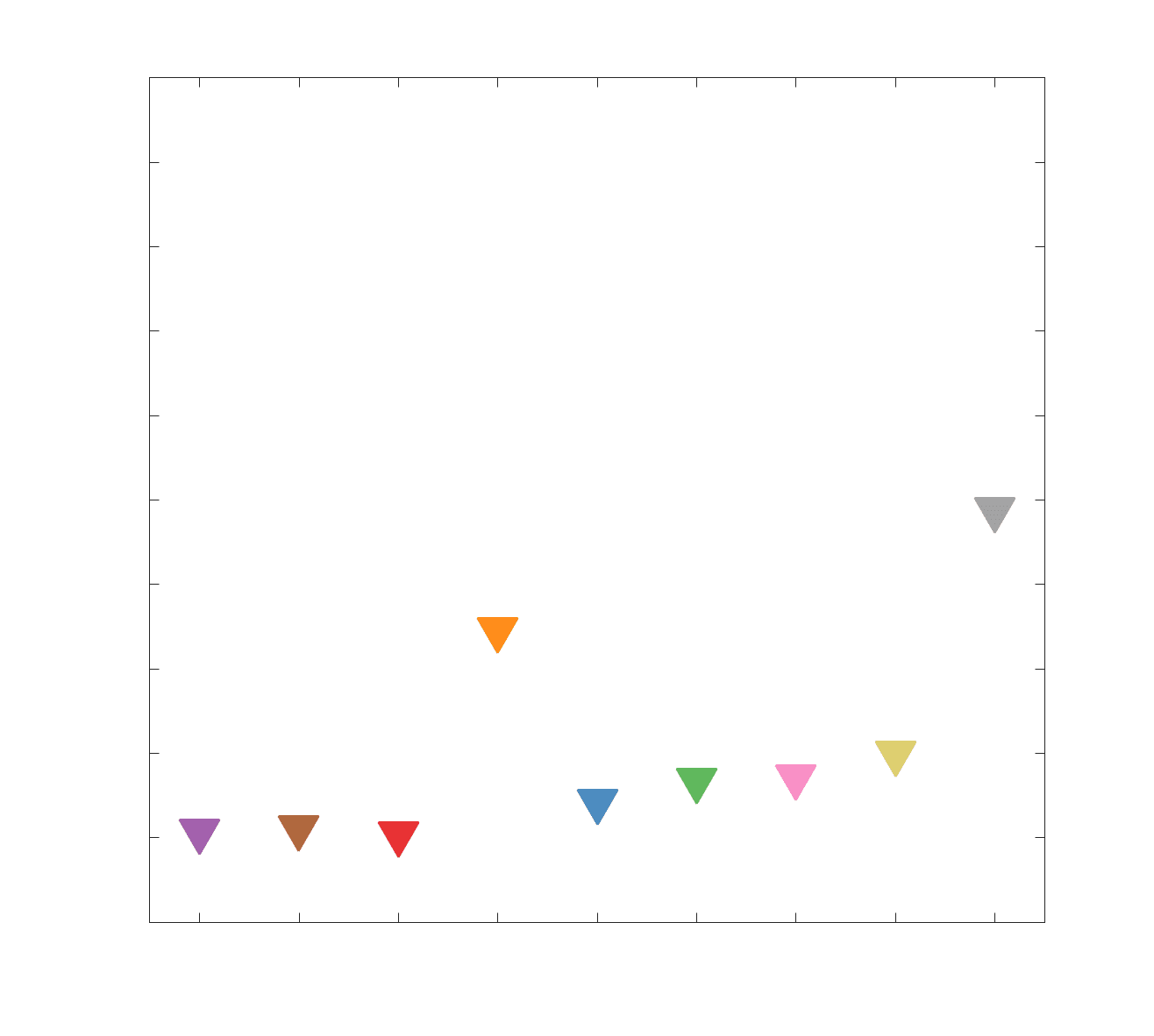
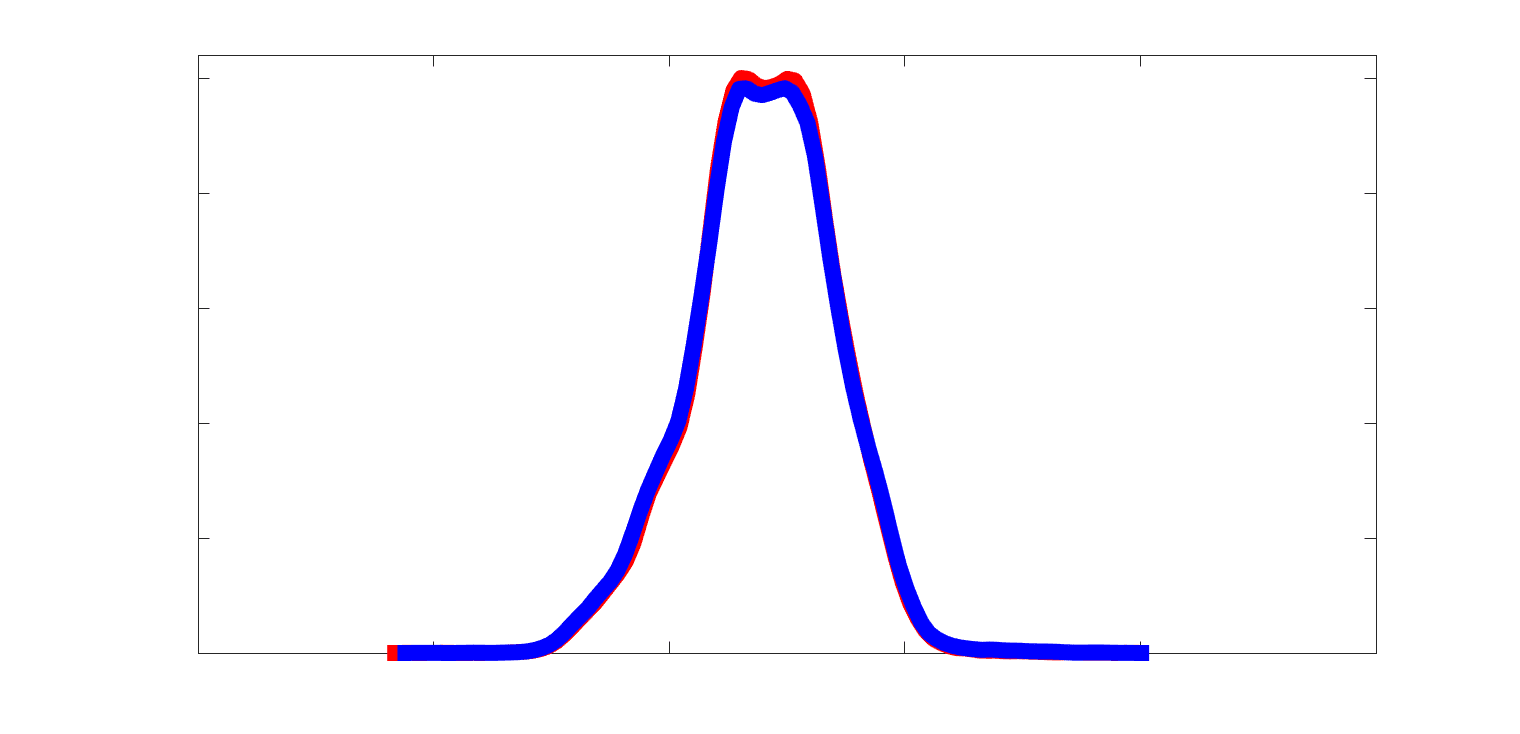
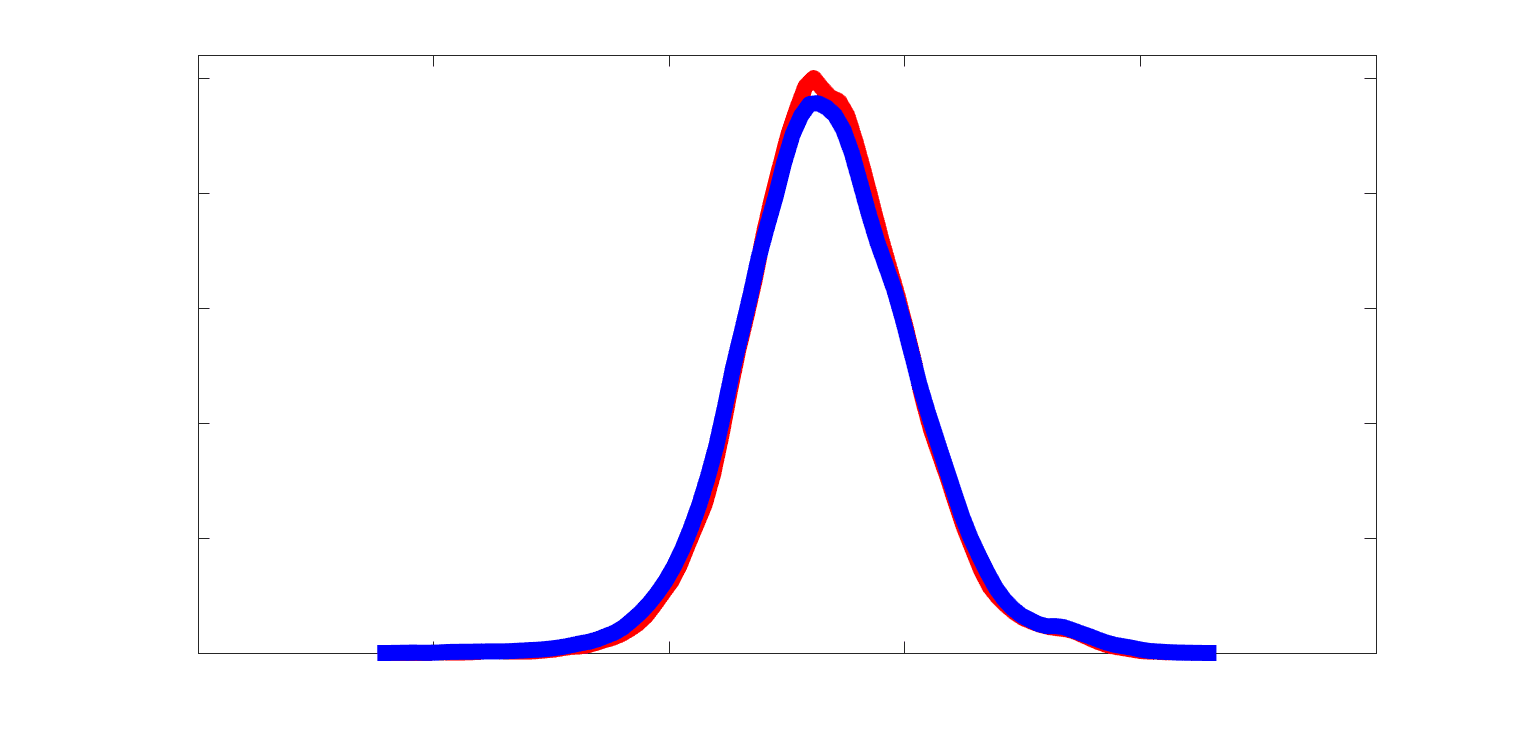
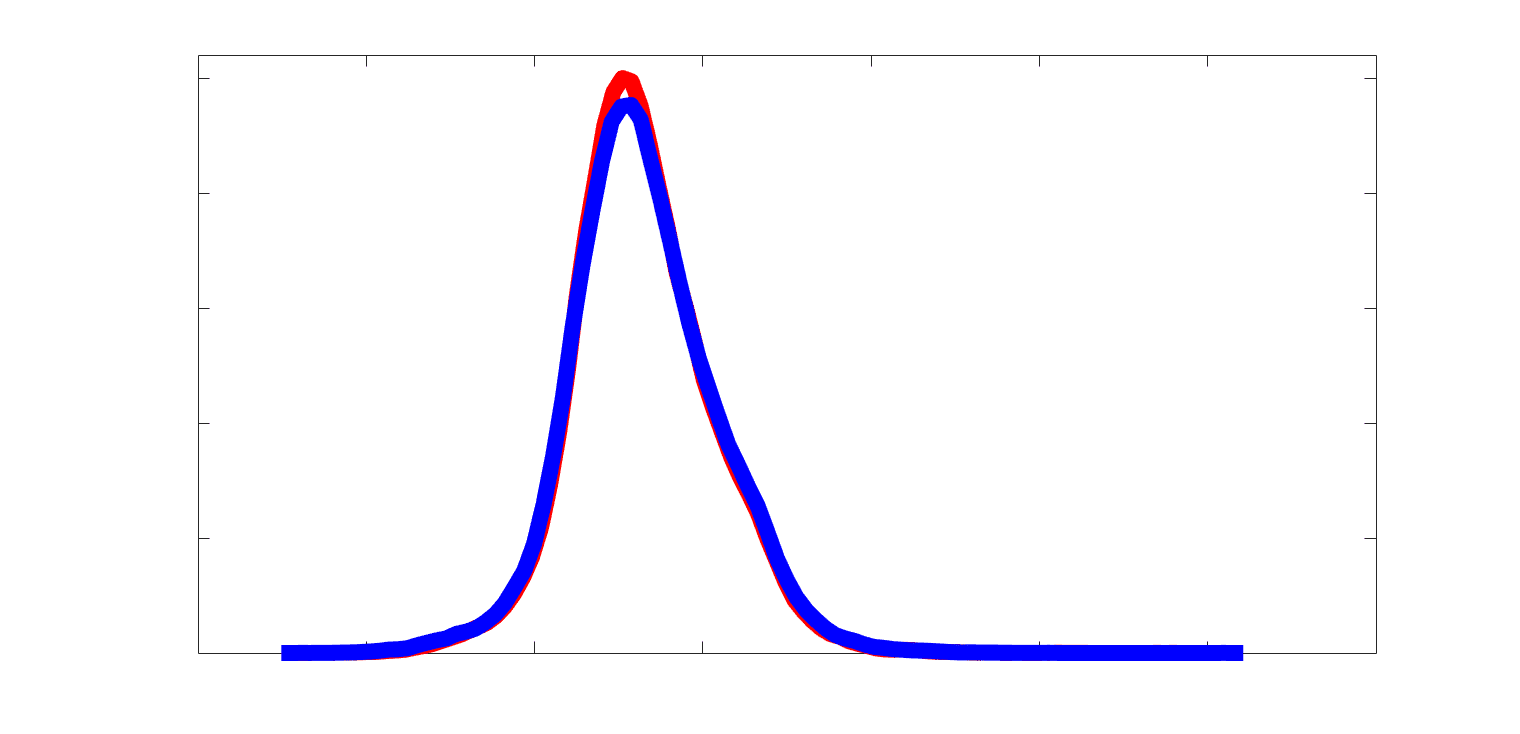
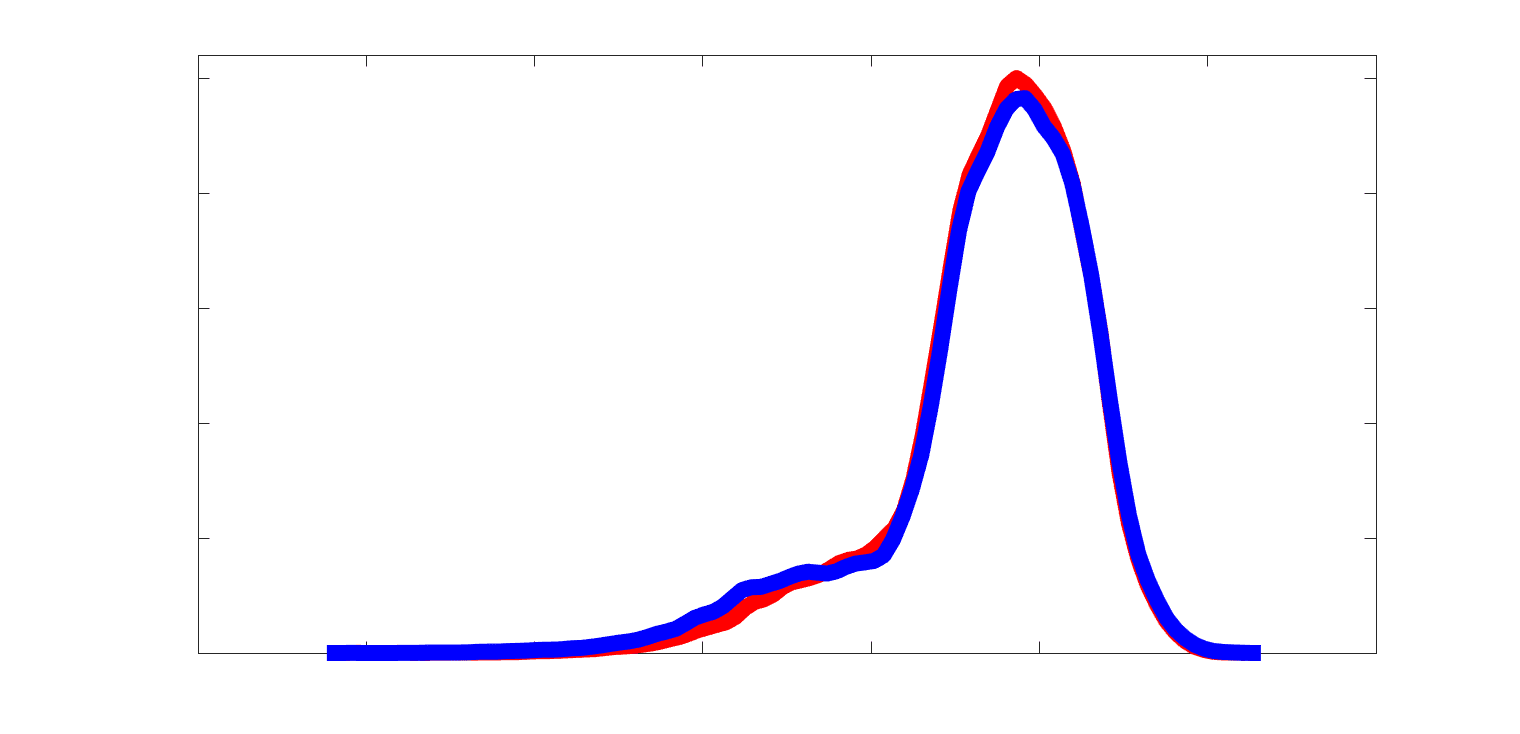
Chiffre 2. Edge Weight Distribution. (UN) Distribution of group-level edge weights binned by: (top) within
and between module; (bottom) unimodal, transmodal and between. Unimodal is defined as the VIS and
SMN modules. Transmodal is defined as the DMN, CONT, DAN and SVAN modules. (B) Probability
density of pooled subject-level edge weight distributions. R1, ICVF, FA, RD, LoS and FC are shown on a
linear x-axis (top), and NoS, SIFT2 and COMMIT are shown on a logarithmic x-axis (bottom). All
networks were normalized to the range [0 1] by dividing by the subject-level max for visualization.
187
Subject-level edge weight distributions in R1, ICVF, FA and RD are near-normal and network-
188
specific (Figure 2B). They differ in both the magnitude (R1 > ICVF > FA > RD) and dynamic
189
range (FA & ICVF > R1 & RD) of their edge weights. In contrast, NoS, SIFT2 and COMMIT
190
distributions are highly skewed and tend to be much lower in magnitude (dashed line). Ce
10
191
effect is greatest in COMMIT suggesting that the optimization performed by COMMIT exerts a
192
stronger scaling effect than SIFT2. These results support the conclusion that the structural
193
networks considered here quantify subsets of white matter features which are at least partially
194
non-overlapping.
195
196
197
Edge Weights in Streamline-Specific Networks Are More Variable
198
Edge weight variance was quantified using the Quartile Coefficient of Dispersion (CQD) due to
199
its robustness to outliers and skewed data. The CQD is computed from the 1st and 3rd quartiles as:
200
⁄
.
(𝑄3 + 𝑄1)
𝐶𝑄𝐷 = (𝑄3 − 𝑄1)
201
202
Intra-subject variance is roughly 2-fold greater in NoS, SIFT2 and COMMIT relative to LoS and
203
FC; and an order of magnitude greater than R1, ICVF, FA and RD in all subjects (Figure 3A).
204
COMMIT is the highest overall. Subjects are more tightly clustered in all weighted SC networks,
205
relative to FC: intra-subject CQD values span roughly a 4-fold greater range in FC. Ce
206
suggests that individual diversity of functional connectivity is not necessarily reflected in the
207
variability of their structural networks. These patterns are repeated for inter-subject variance.
208
Cependant, FC shows a small subset of highly variable edges with roughly 4-fold greater CQD
209
than the maximum values observed in COMMIT i.e., the most subject-specific connections are
210
functional. The very low edge weight variability in R1, ICVF, FA and RD is in part due to the
211
widespread blurring effect (partial voluming) resulting from the tractometry computation.
212
11
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
/
.
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
213
214
215
216
217
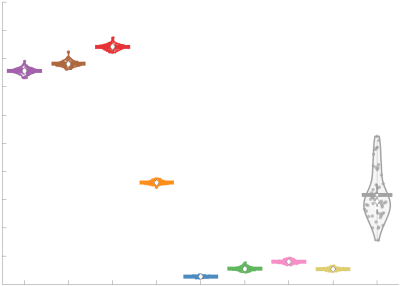
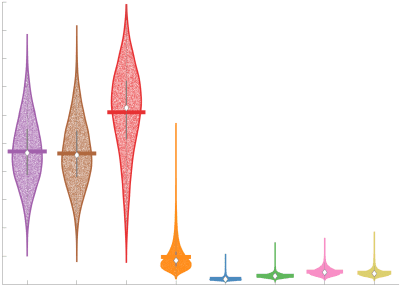
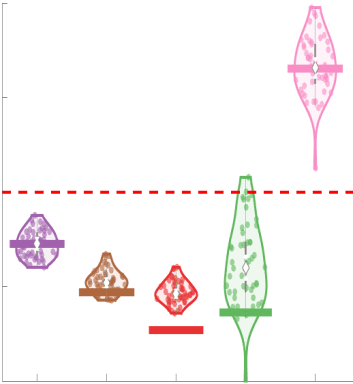
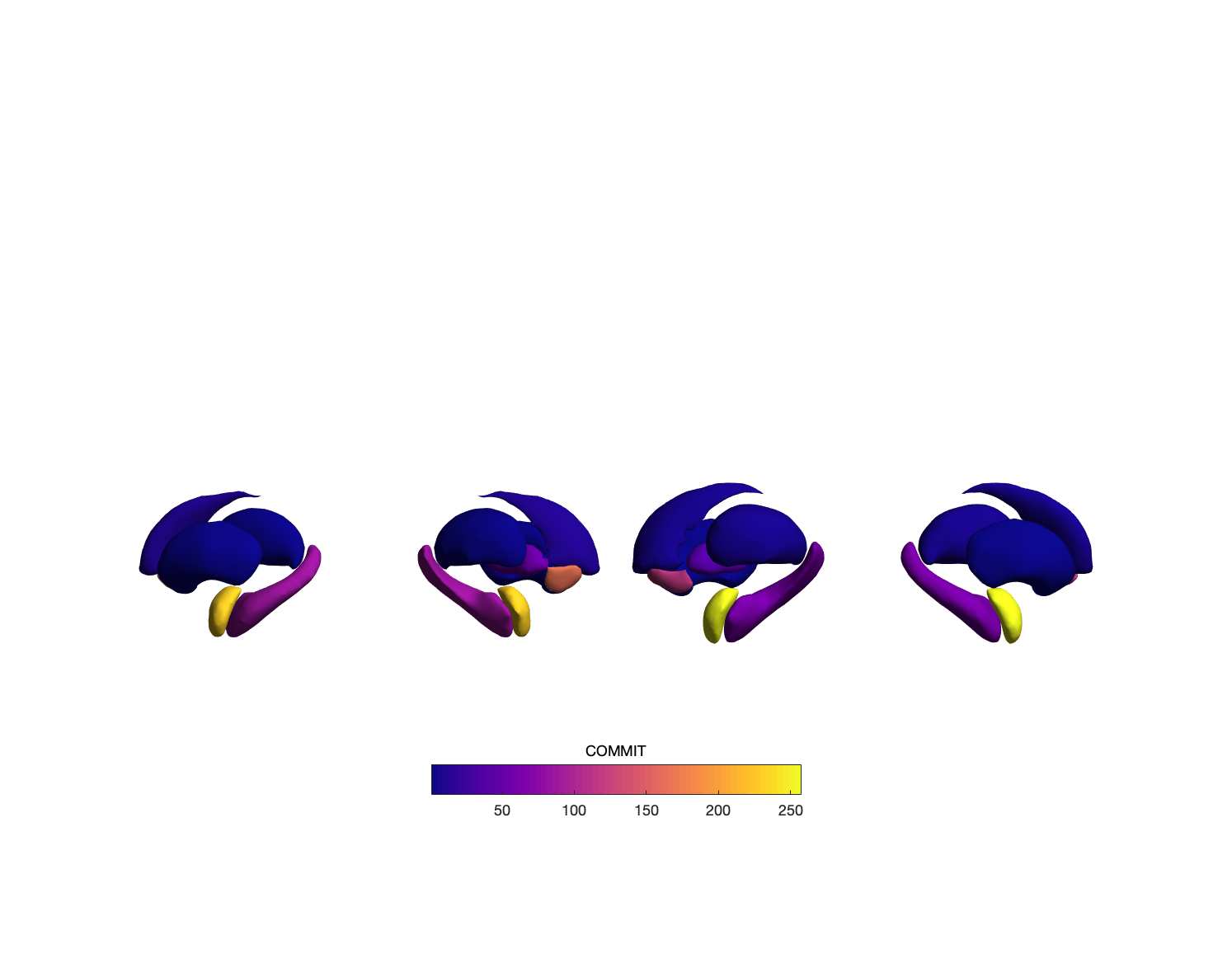
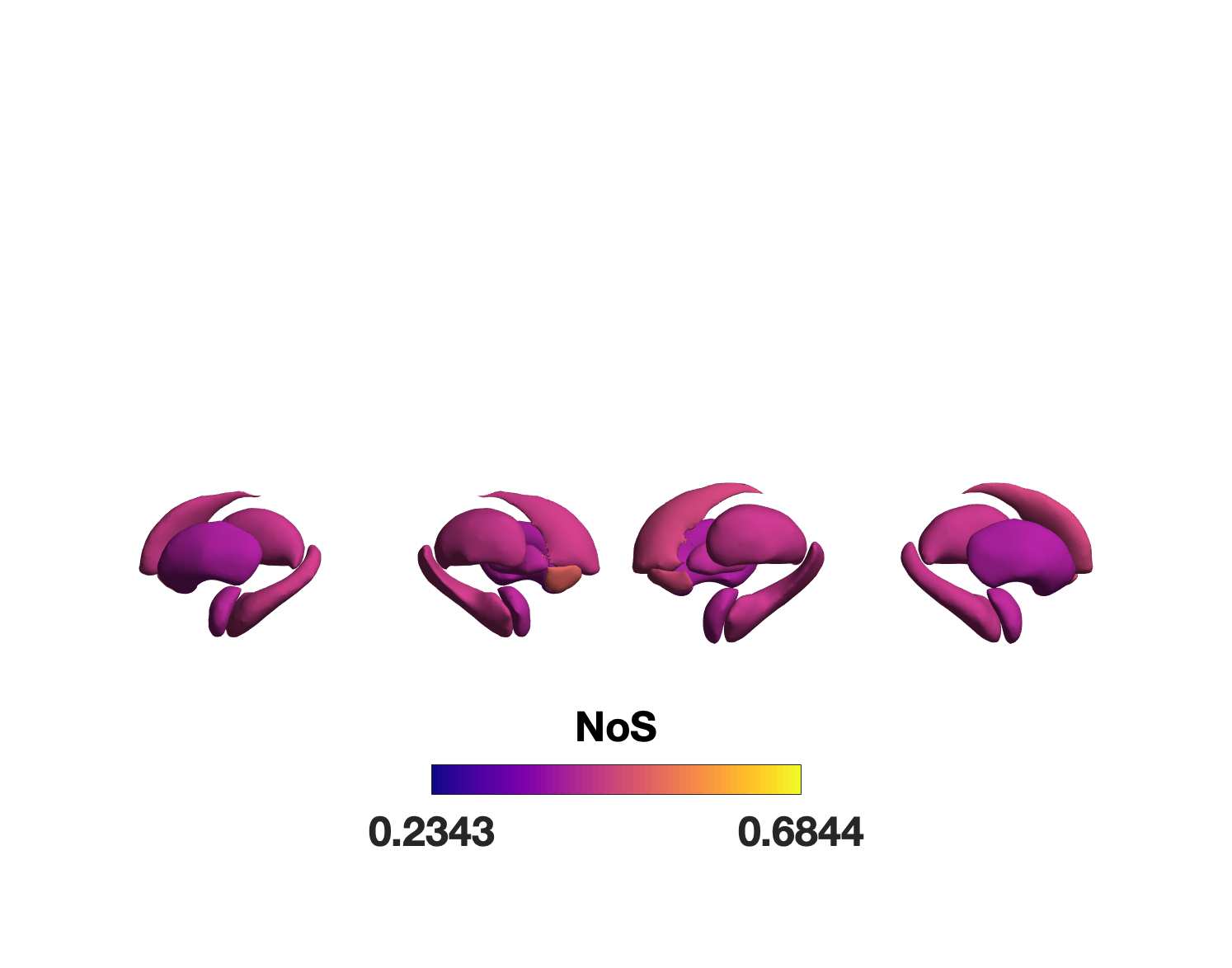
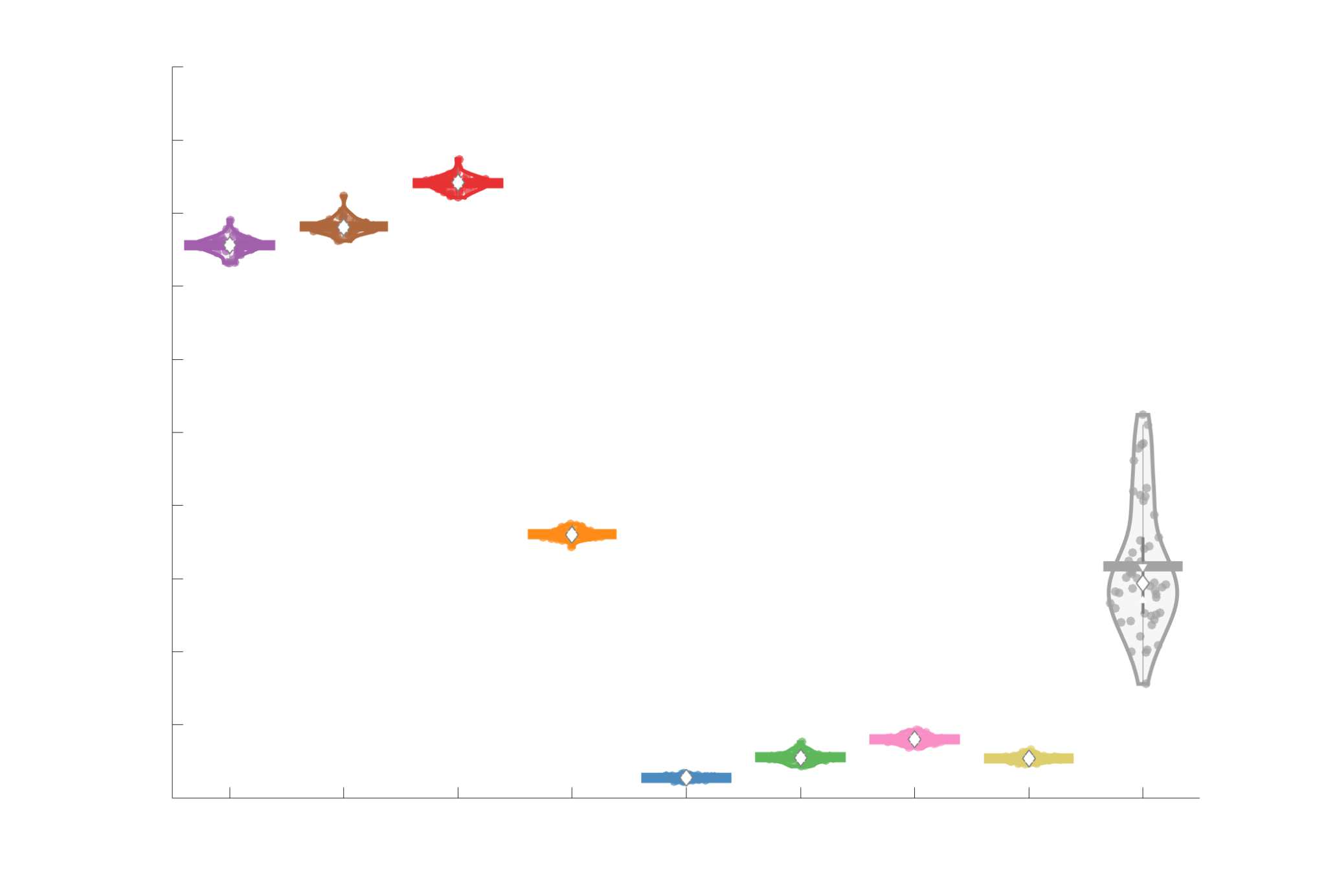
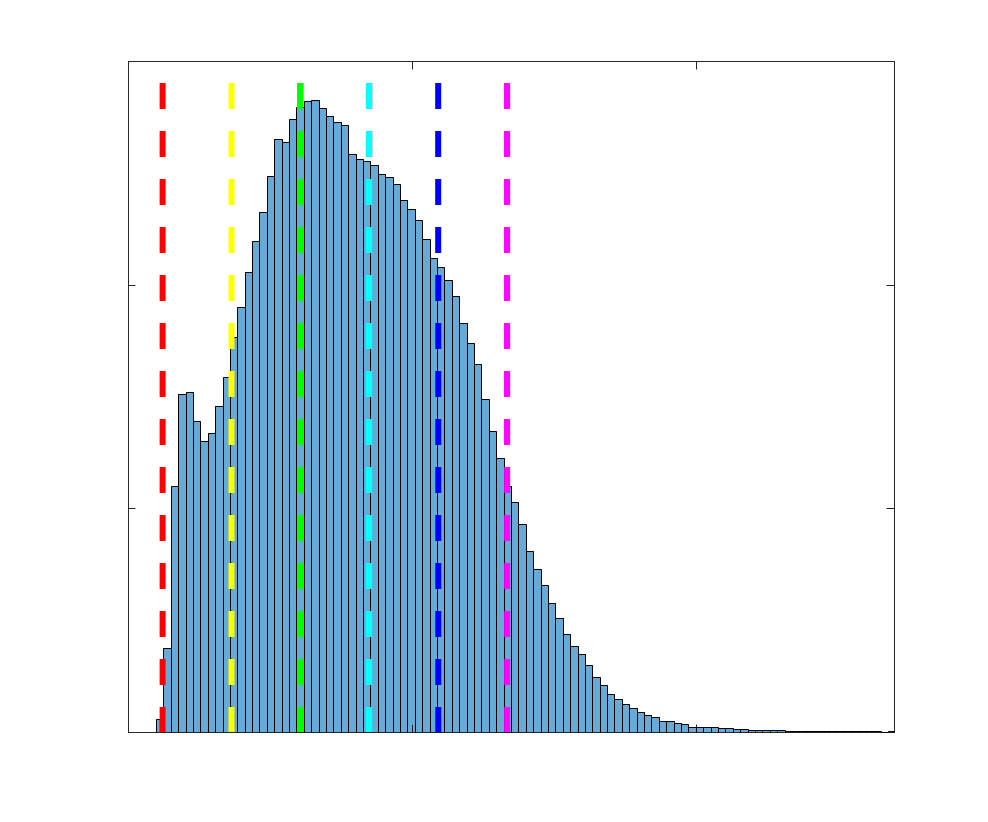
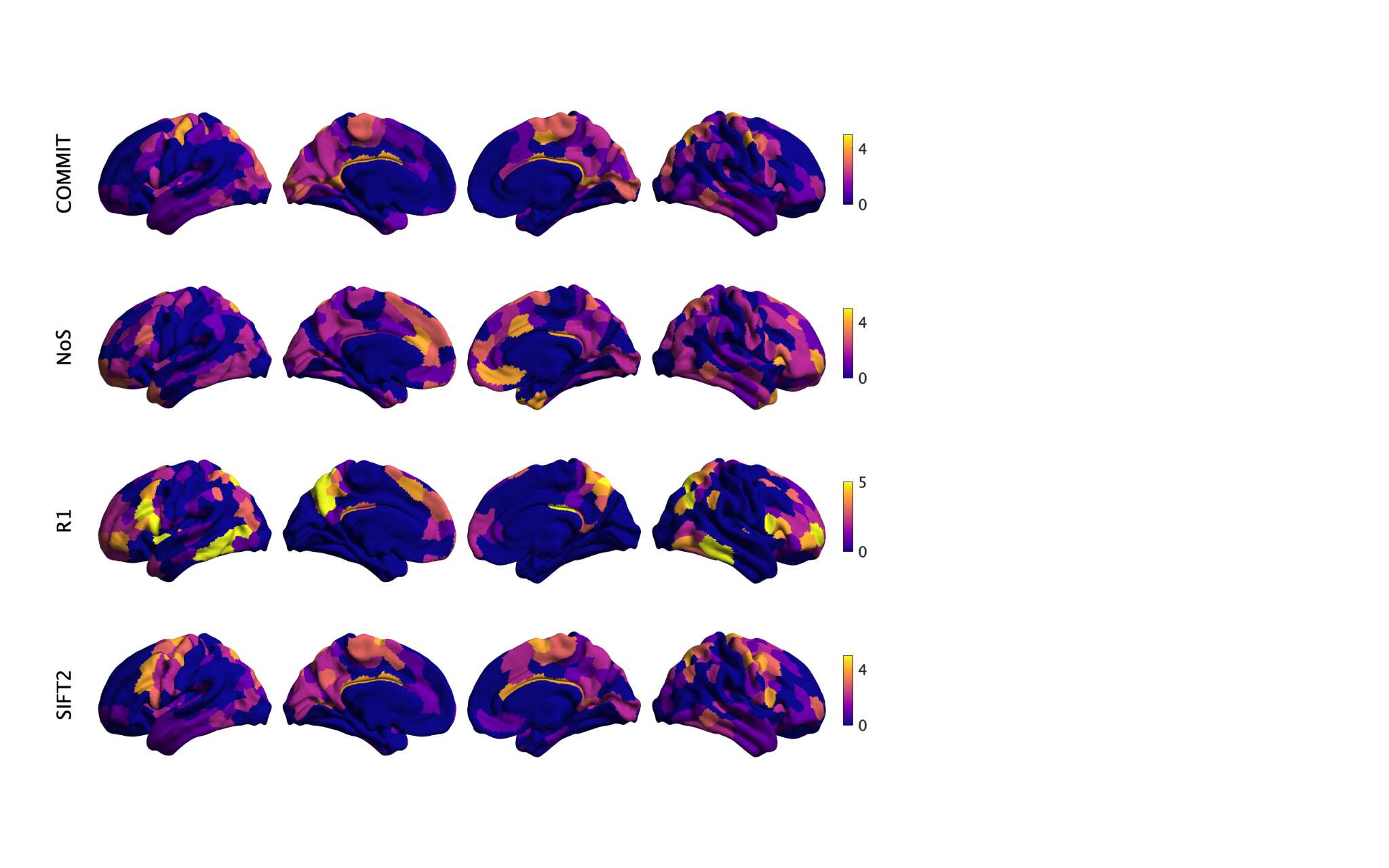
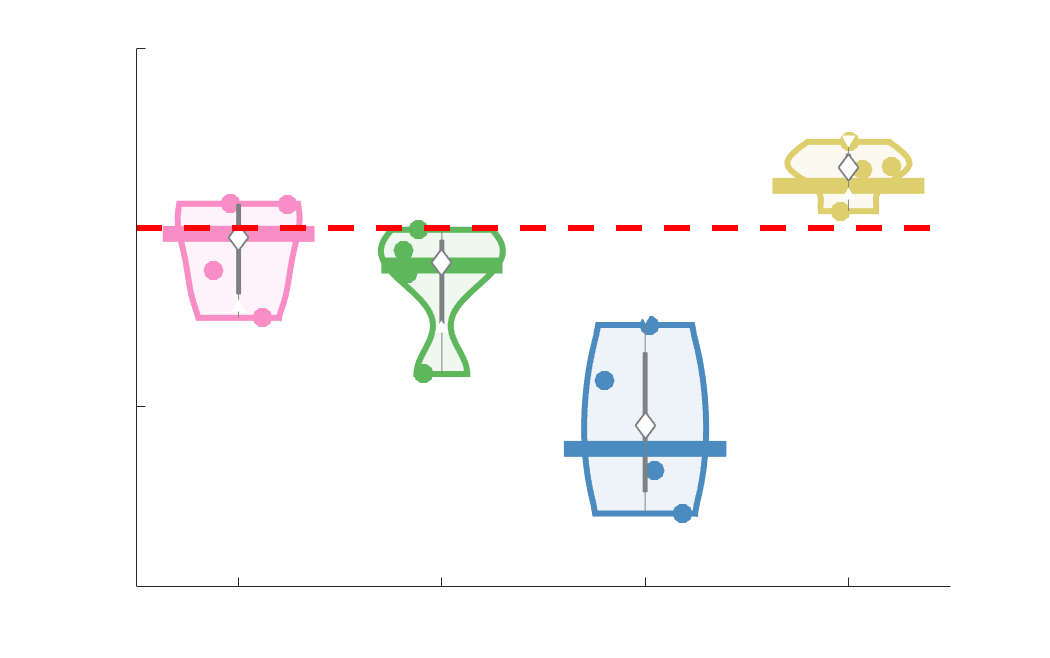
Chiffre 3. Edge Weight Variability. Variability is quantified using the coefficient of quartile dispersion
(CQD). (UN) Violin distributions of intra-subject (gauche) and inter-subject (droite) edge weight variance.
Colored data points respectively correspond to individual subjects (N=50) and edges (N=8549). (B)
Surface projections of edgewise mean inter-subject variance for cortical nodes in the Schaefer-400
12
parcellation (gauche) et 14 subcortical nodes (droite). Cortical and subcortical surfaces were respectively
generated with BrainSpace (Vos de Wael et al., 2020) and ENIGMA toolboxes (Larivière et al., 2021).
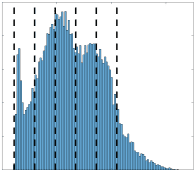
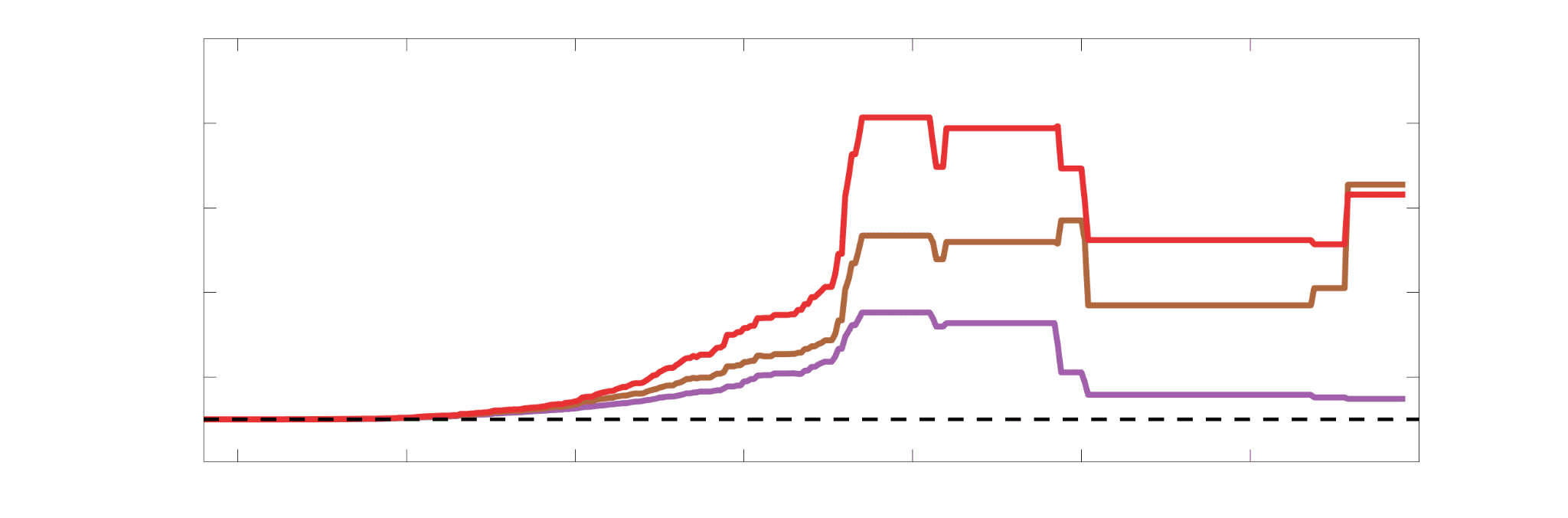
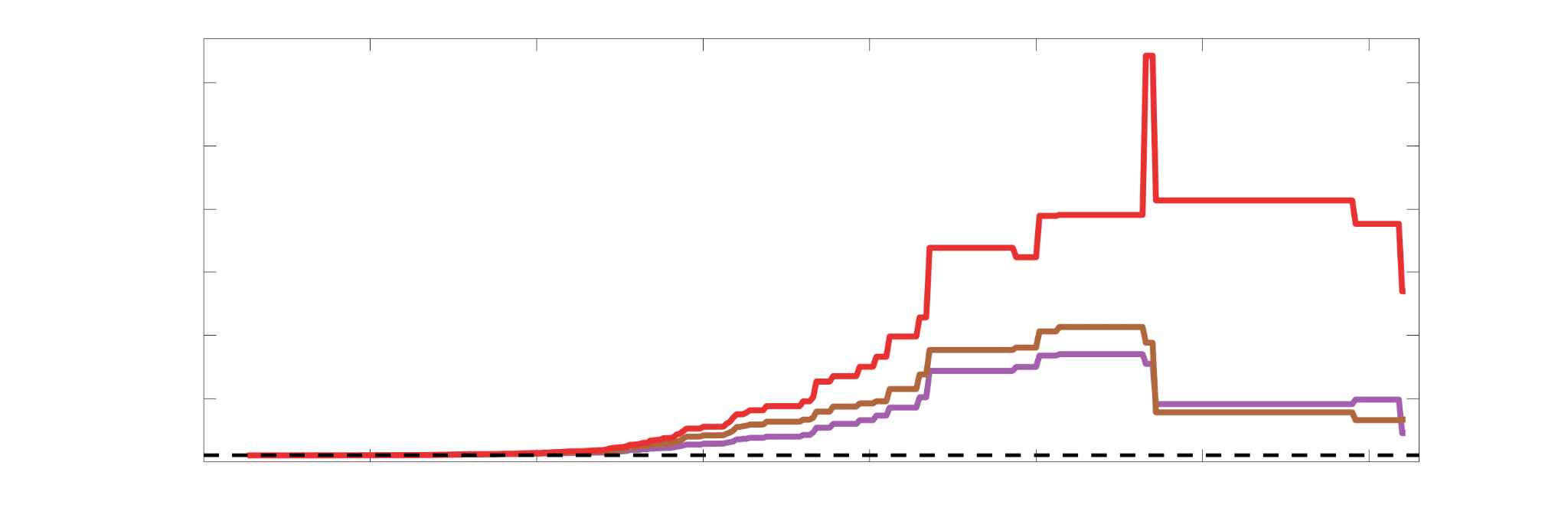
(C) The proportion of within-network max CQD is shown across edge length bins for FC, NoS, SIFT2,
COMMIT and R1 (gauche), as well as ICVF, FA and RD (middle). Edge weights are grouped into 6 bins
according to edge length, as illustrated by the histogram (droite). The edges of bins 1-5 were linearly
spaced of width, w. The edges of the final bin were of width 3w.
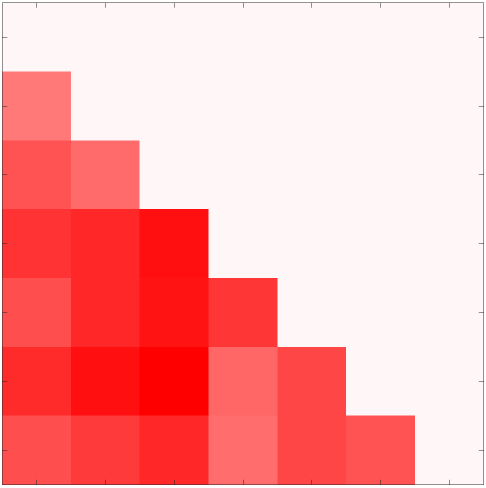
218
219
220
221
222
223
224
225
En général, inter-subject edge weight variance is more spatially distributed in SC networks
226
relative to FC (Figure 3B). COMMIT shows the highest mean CQD over the entire cortex and
227
subcortex. NoS, SIFT2 and COMMIT all show lateral-medial and posterior-anterior cortical
228
gradients. Mean CQD in FC shows the highest concentration in medial inferior frontal cortex and
229
to a lesser extent, the expected pattern of high variance in association cortex. The most variable
230
subcortical regions include the hippocampus, amygdala and accumbens.
231
232
Many features of brain networks (par exemple., connection probability, weight magnitude) are known to
233
vary with edge length. Ici, we examined the relationship between edge weight variability and
234
edge length by computing the CQD within subsets of group-level edge weights binned according
235
to their edge length (Figure 3C). Edge weight variance in NoS, SIFT2, COMMIT and R1 is
236
highest in the shortest edges and decreases with edge length. ICVF roughly follows the same
237
pattern. FA and RD instead show the highest variability in the longest edges. Dans l'ensemble, the edge
238
weights in streamline-specific SC networks (NoS, SIFT2 and COMMIT) show greater contrast
239
both within and across subjects. SC networks show network-dependent relationships between
240
edge weight variance and edge length. Shorter edges are more variable in myelin- et
13
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
/
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
241
connection strength-weighted networks, and longer edges are more variable in networks with
242
edge weights derived from a diffusion tensor model.
243
244
To complement the above results, a supplemental analysis was performed using intraclass
245
correlation to quantify edge weight variance within each edge weight (Figure S9).
246
247
248
Opposing Correlations with Function in Connection-Strength- & Myelin-Weighted Networks
249
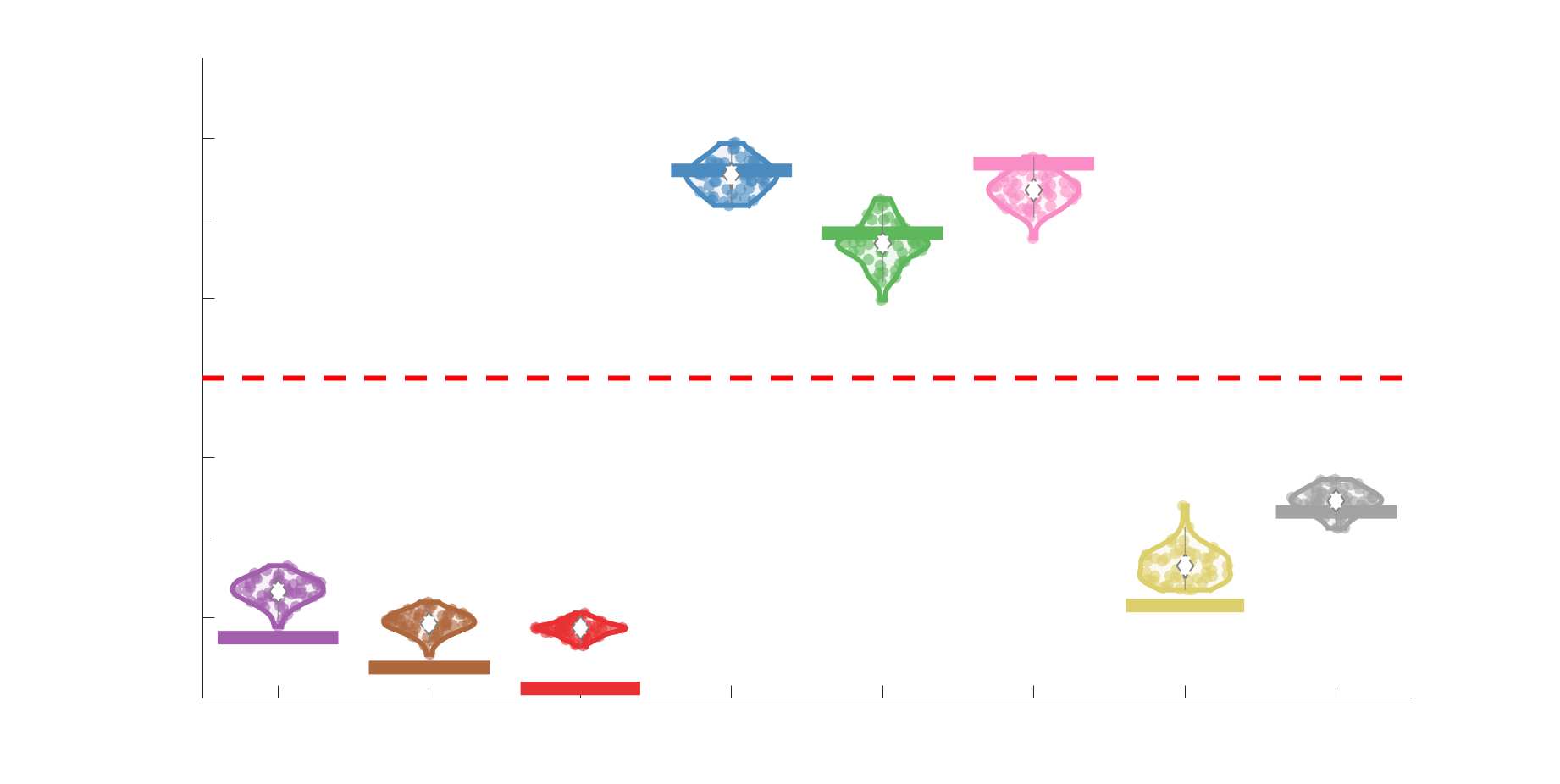
Shifting to inter-network edge weight relationships shows that SC networks are differentially
250
related to FC (Figure 4A). Surtout, we also see that all brain networks (SC and FC) sont
251
strongly and differentially related to edge length at the subject and group levels. Correlations
252
with edge length are negative for NoS, SIFT2, COMMIT, RD and FC; and positive for R1,
253
ICVF, and FA. Correlation magnitude is strongest in group-level COMMIT ( -0.8). À
254
account for this strong obscuring effect, we recomputed correlations using residual edge weights
255
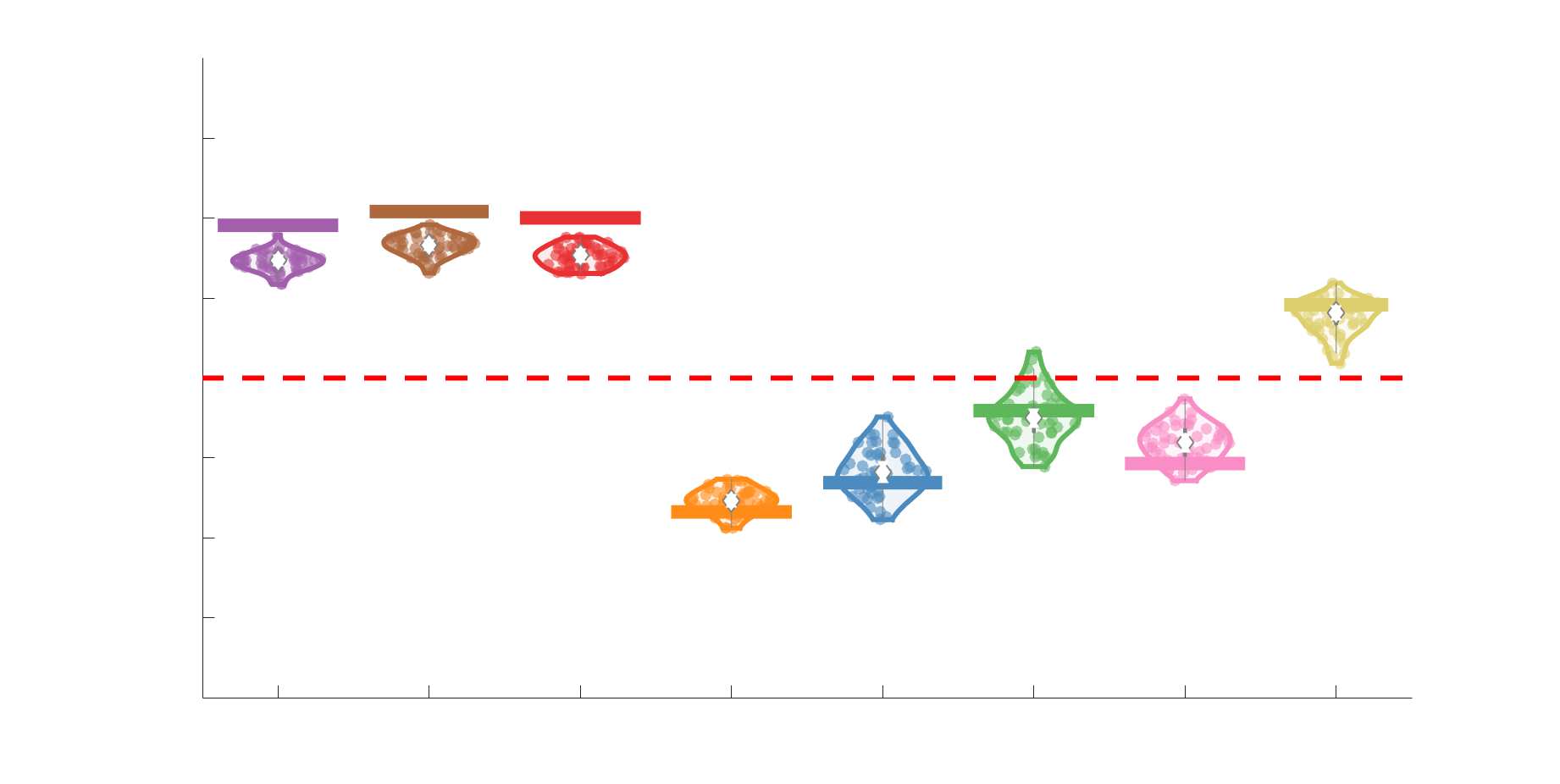
following linear regression of edge length (Figure 4B). NoS, SIFT2 and COMMIT remain
256
positively associated (group-level 0.35) and R1 remains negatively associated with FC
257
(group-level -0.22). Correlation magnitude was reduced following linear regression of edge
258
length in all cases. ICVF, FA and RD are reduced to 0 suggesting that they may not be useful in
259
modeling whole-brain FC. These results support the idea that R1-weighted SC networks provide
260
complementary information to NoS, SIFT2 and COMMIT about the brain structure-function
261
relationship.
262
14
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
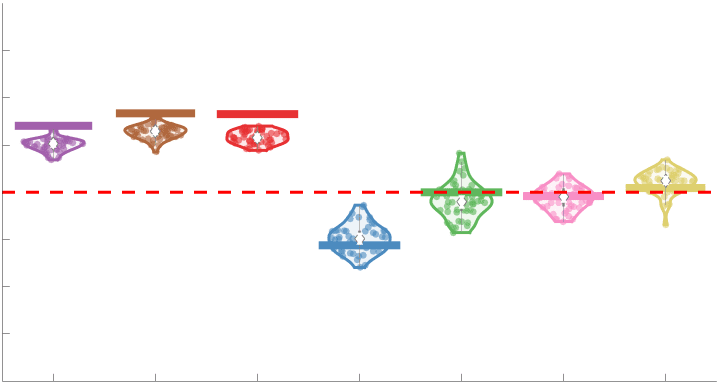
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
t
/
.
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
t
/
.
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
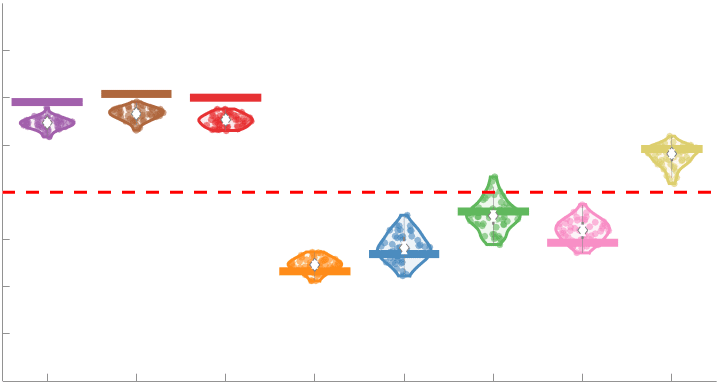
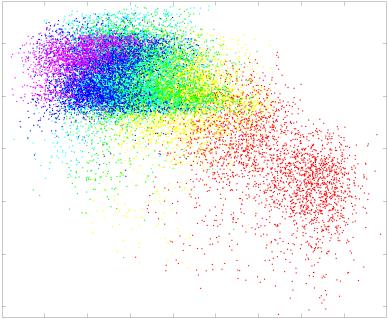
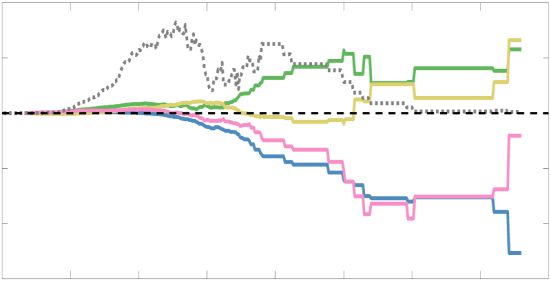
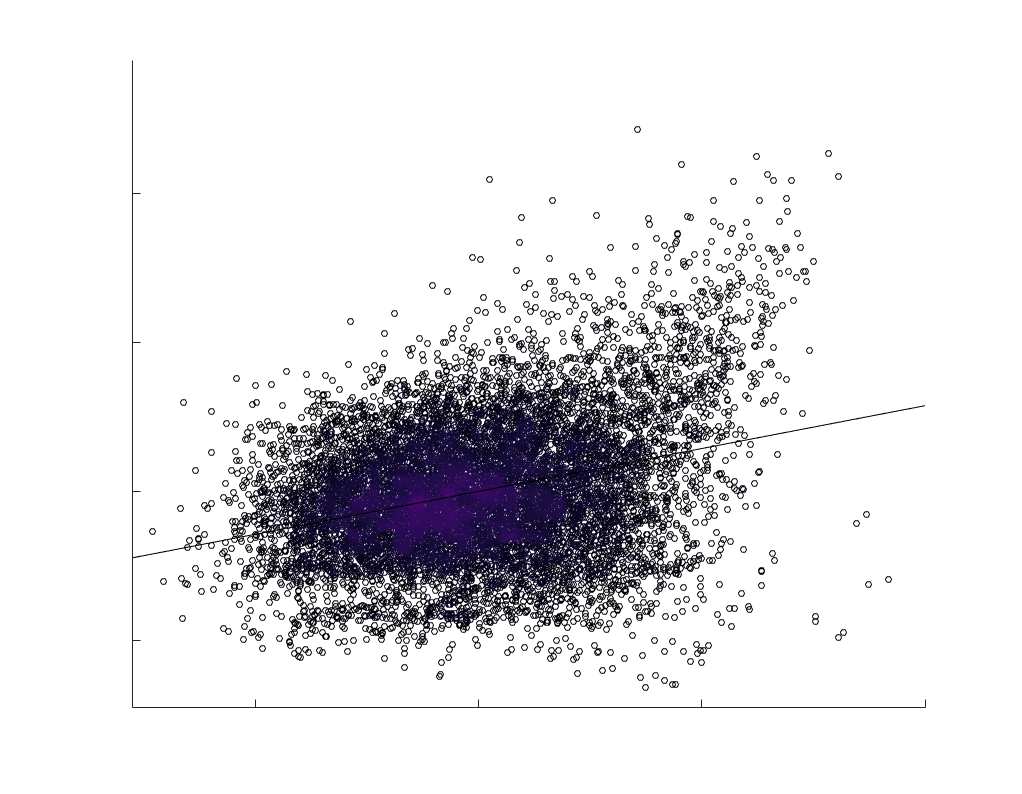
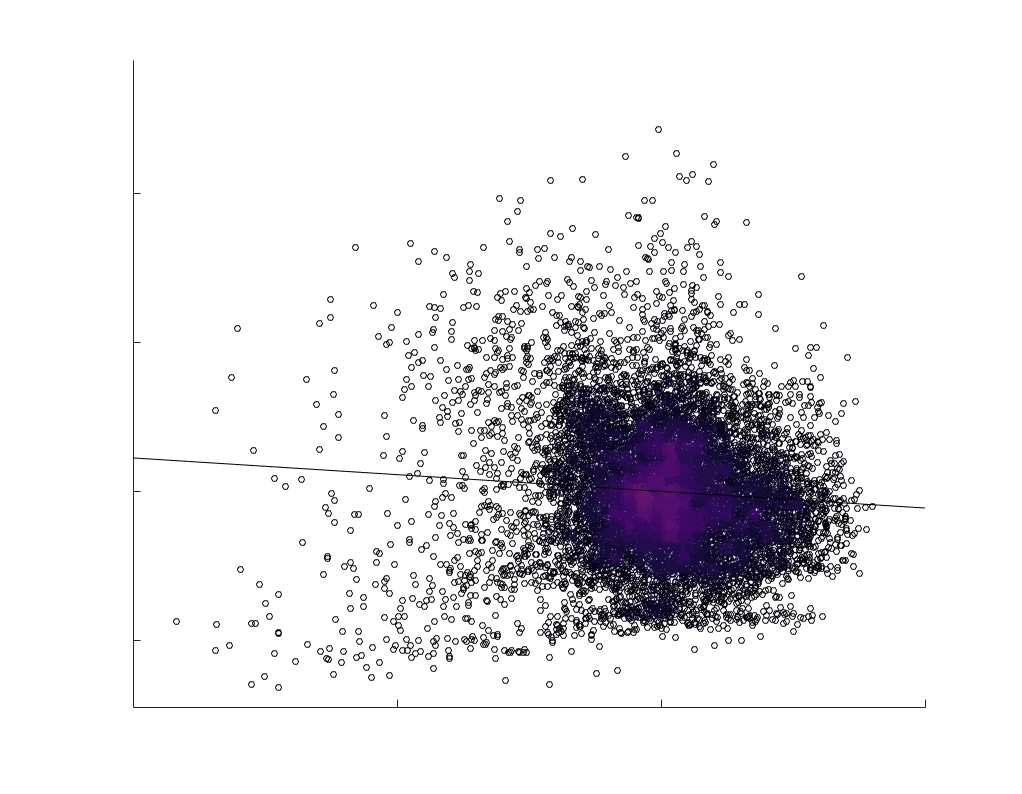
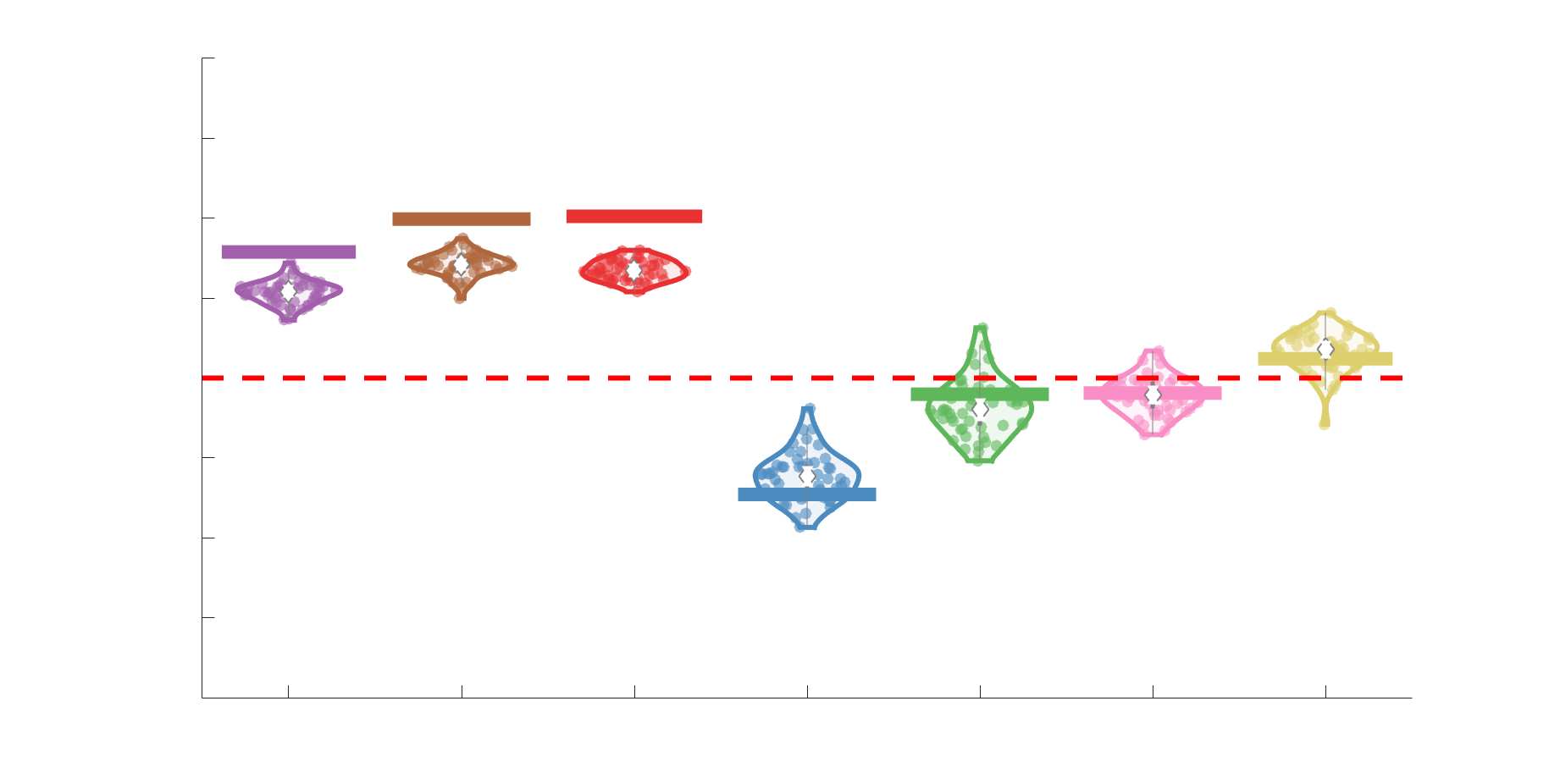
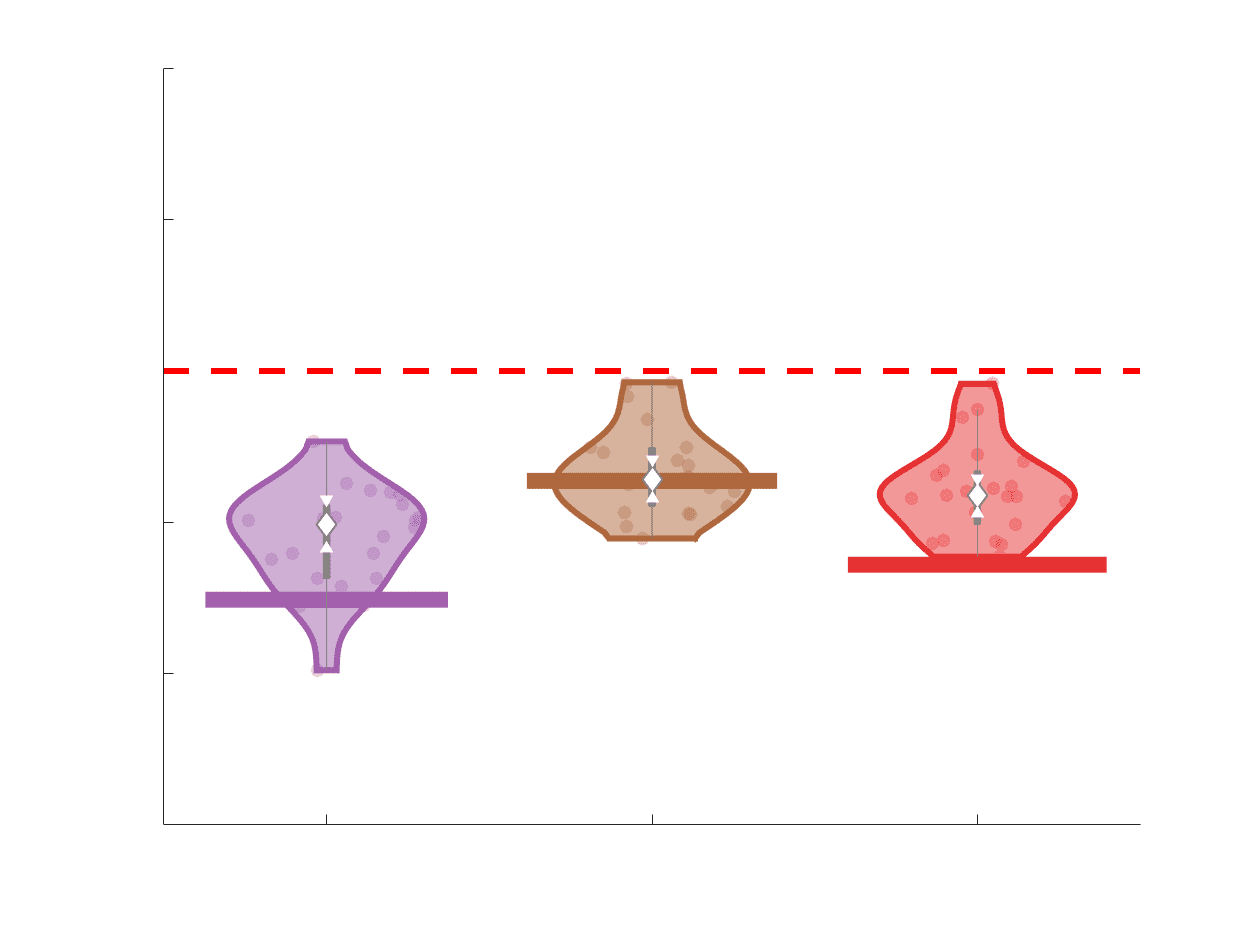
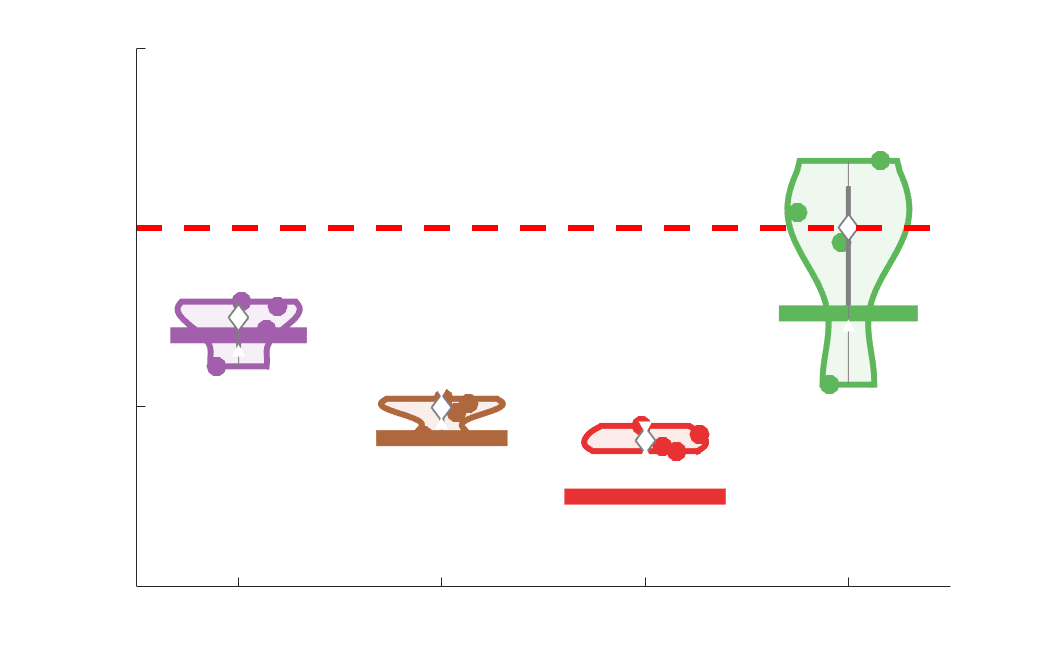
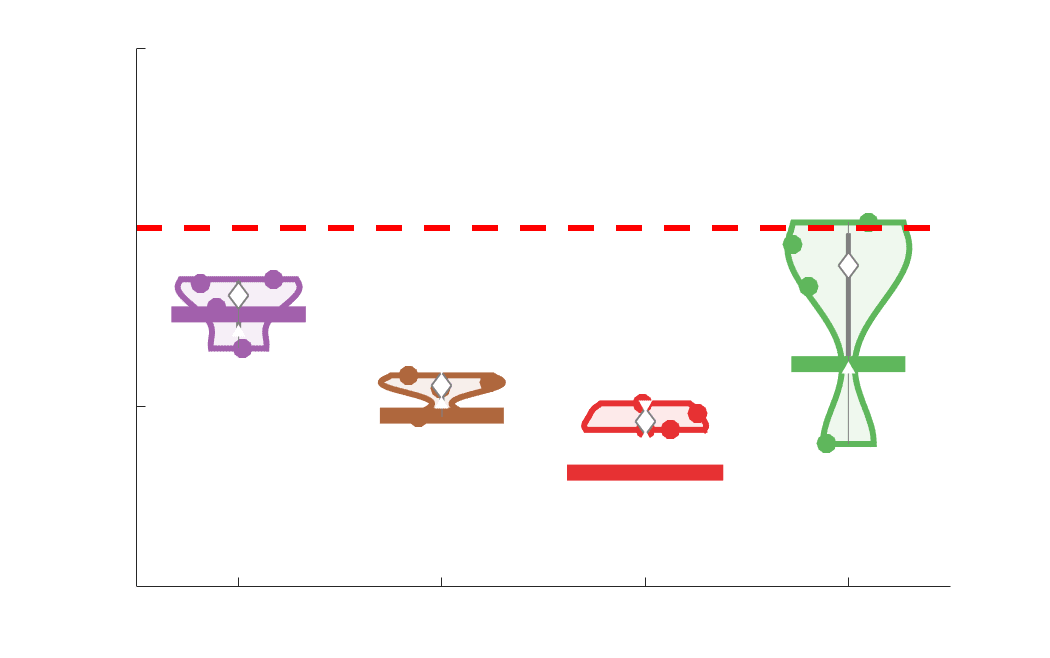
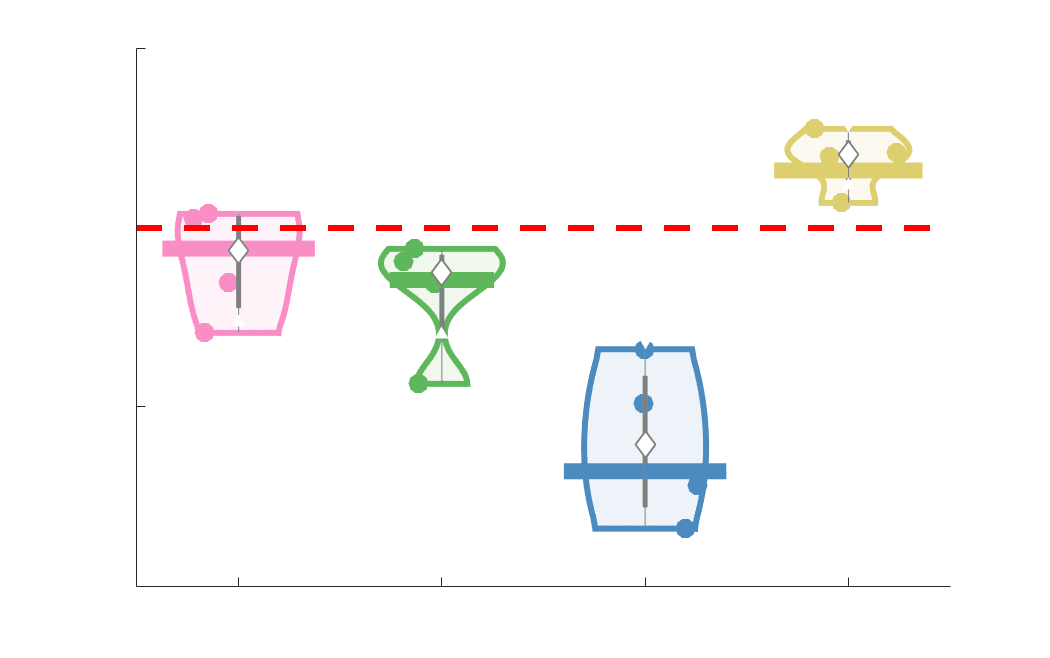
Chiffre 4. Edge Weight Correlations with FC and Edge Length. (UN) Violin distributions of edgewise
Spearman’s rank correlations of all networks with FC (gauche) and edge length (droite). (B) Violin
distributions of edgewise Spearman’s rank correlations of residual edge weights in all networks with
residual edge weights in FC. Residual edge weights were computed by linear regression of edge length.
Colored data points and bars respectively indicate subject-level and group-level correlations. Pperm gives
the one-sided p-value obtained from permutation testing (Figure S7).
263
264
265
266
267
268
269
270
271
272
Edge Caliber and Myelin Content are Inversely Related
15
273
Ici, we ask how R1, which we refer to as the myelin-weighted network, is related to the
274
connection-strength-weighted network COMMIT. Edge-length regressed residual edge weights
275
in NoS, SIFT2 and COMMIT show a negative association with R1 residuals for all subjects and
276
at the group level, which is strongest in COMMIT (group-level -0.29) (Figure 5A). Ce
277
suggests an edge-length independent inverse relationship between white matter structural
278
features related to connection strength and myelin content.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
t
.
/
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
.
/
279
280
281
282
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
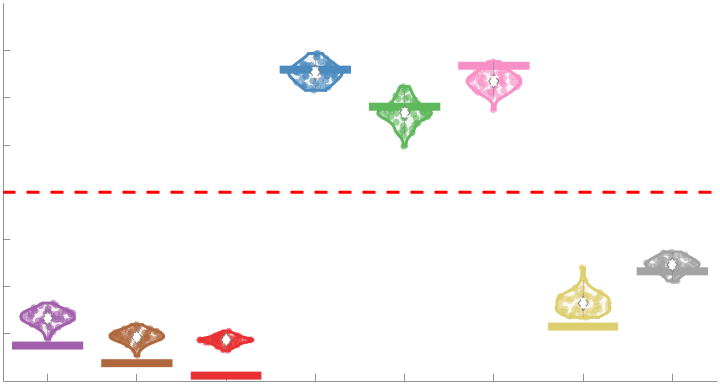
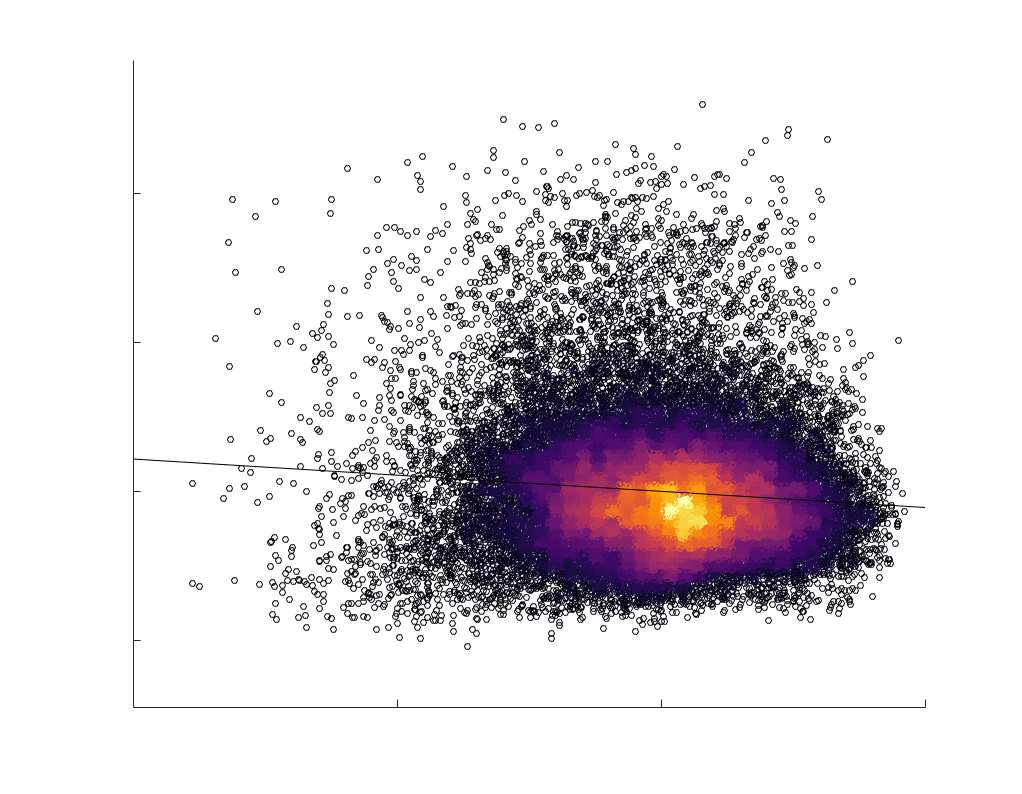
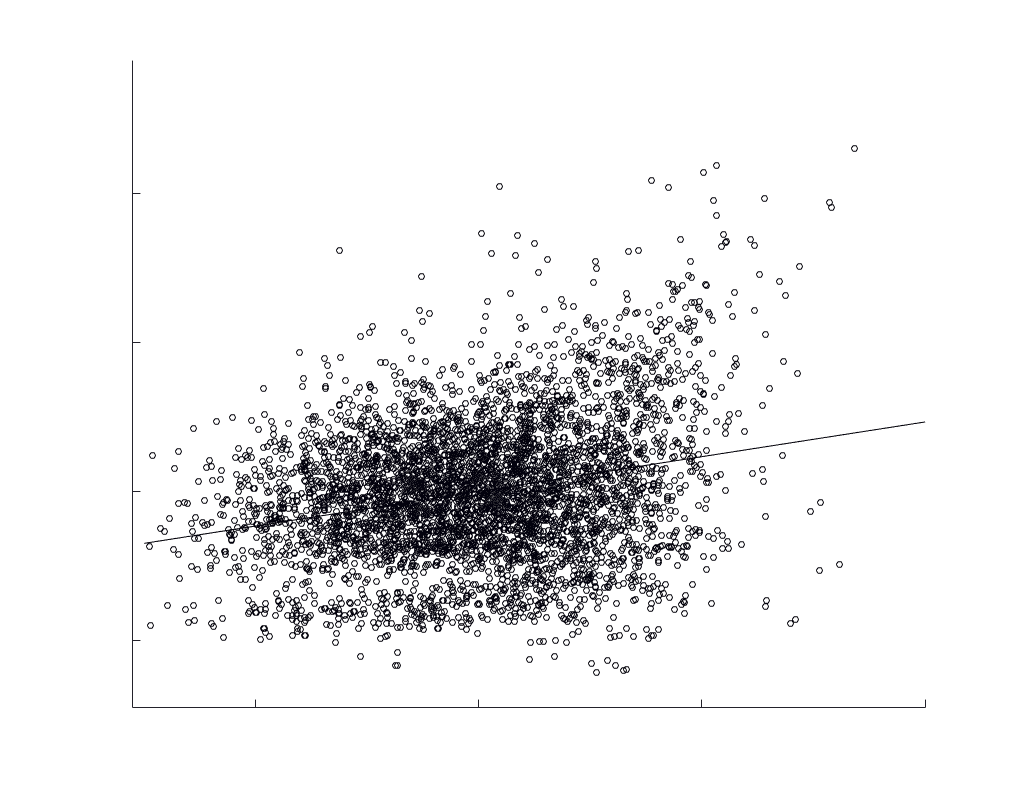
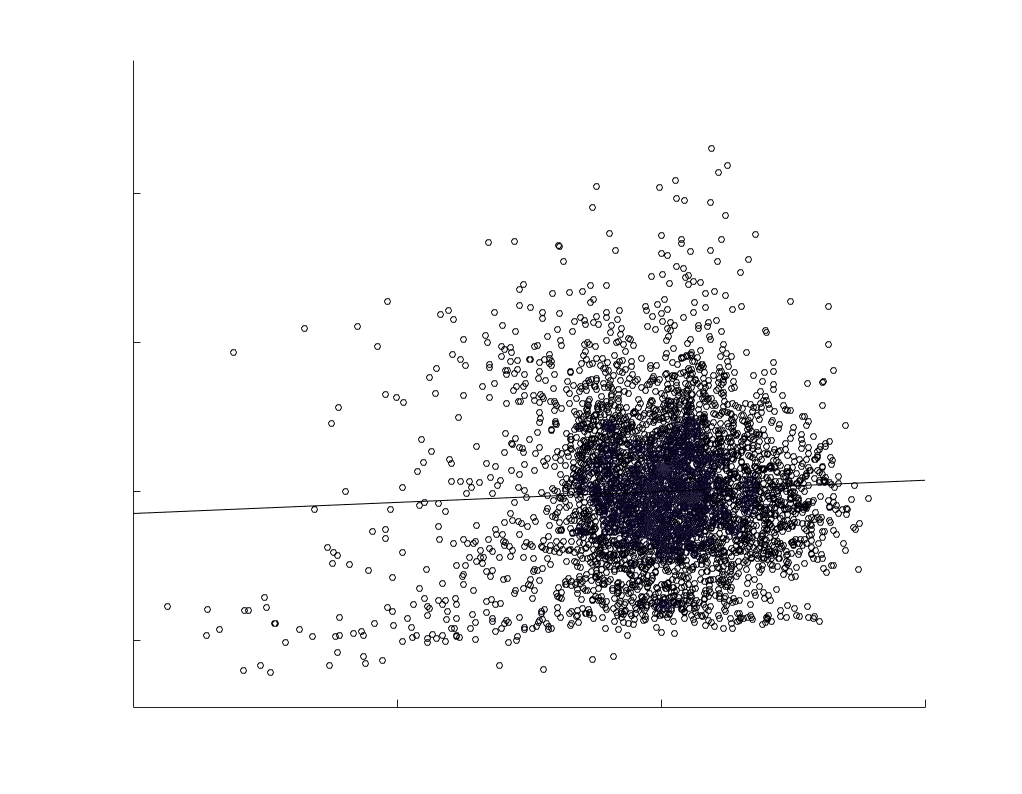
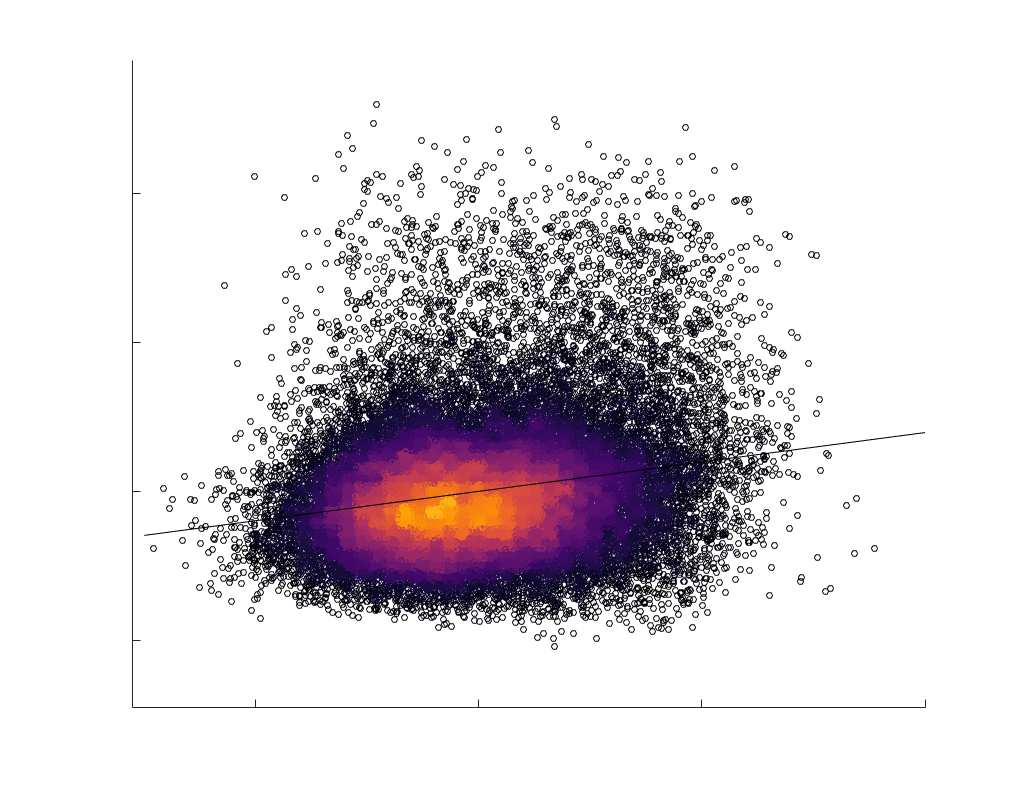
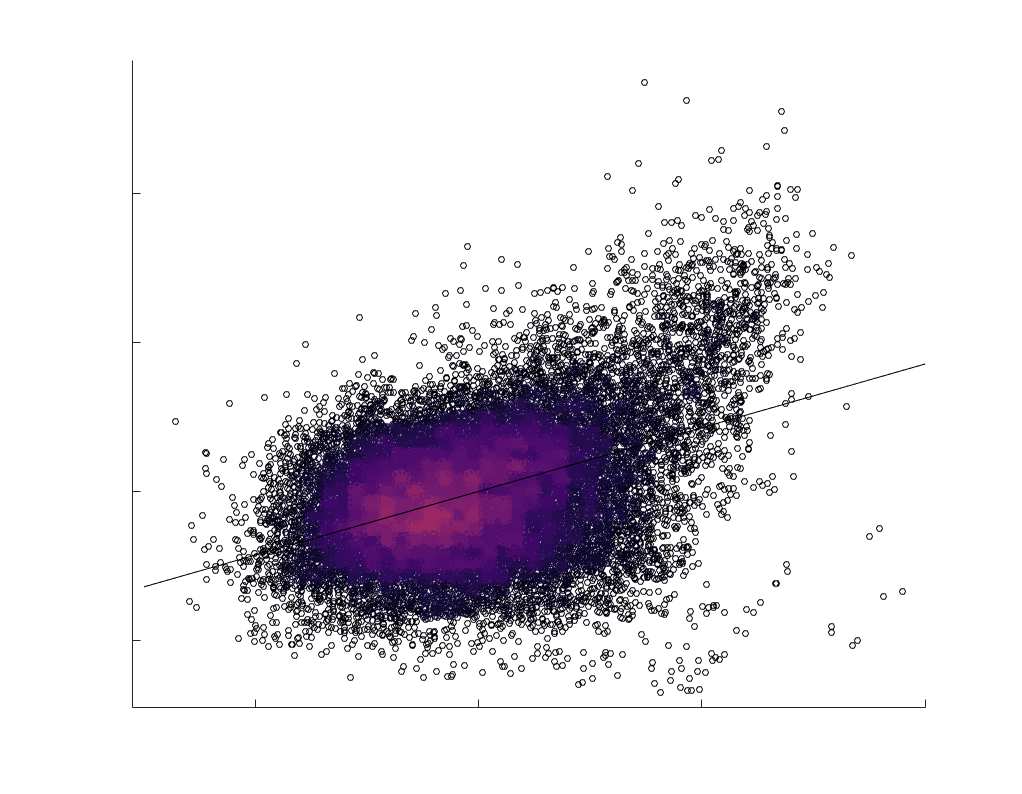
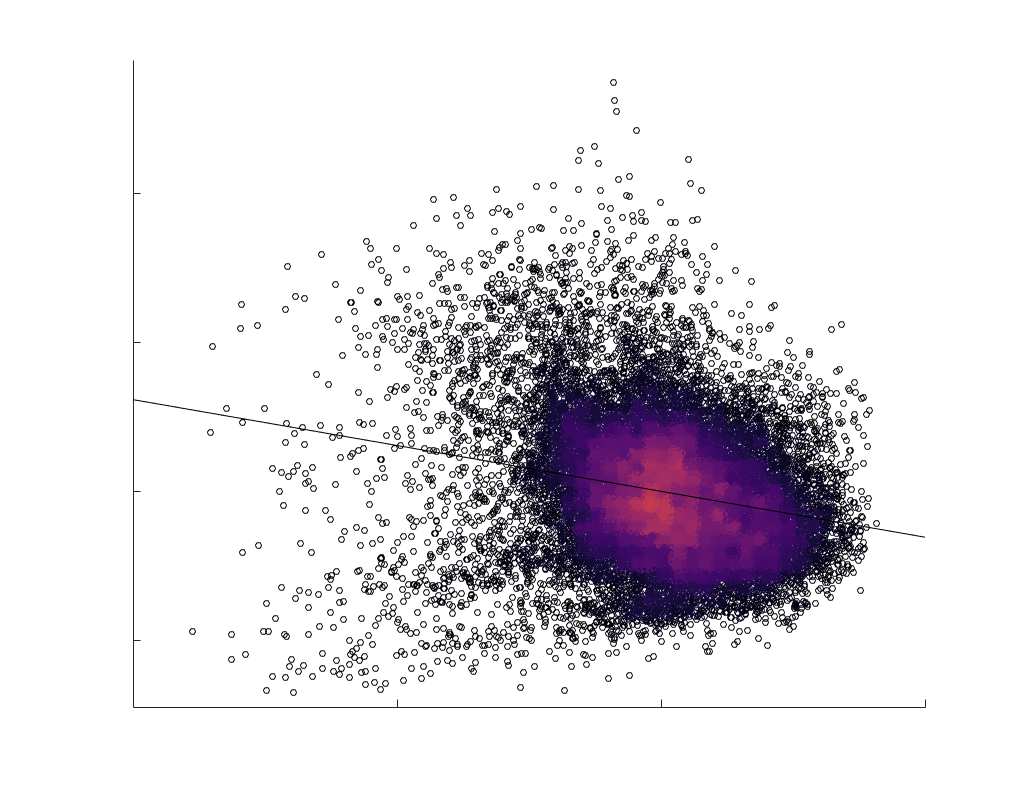
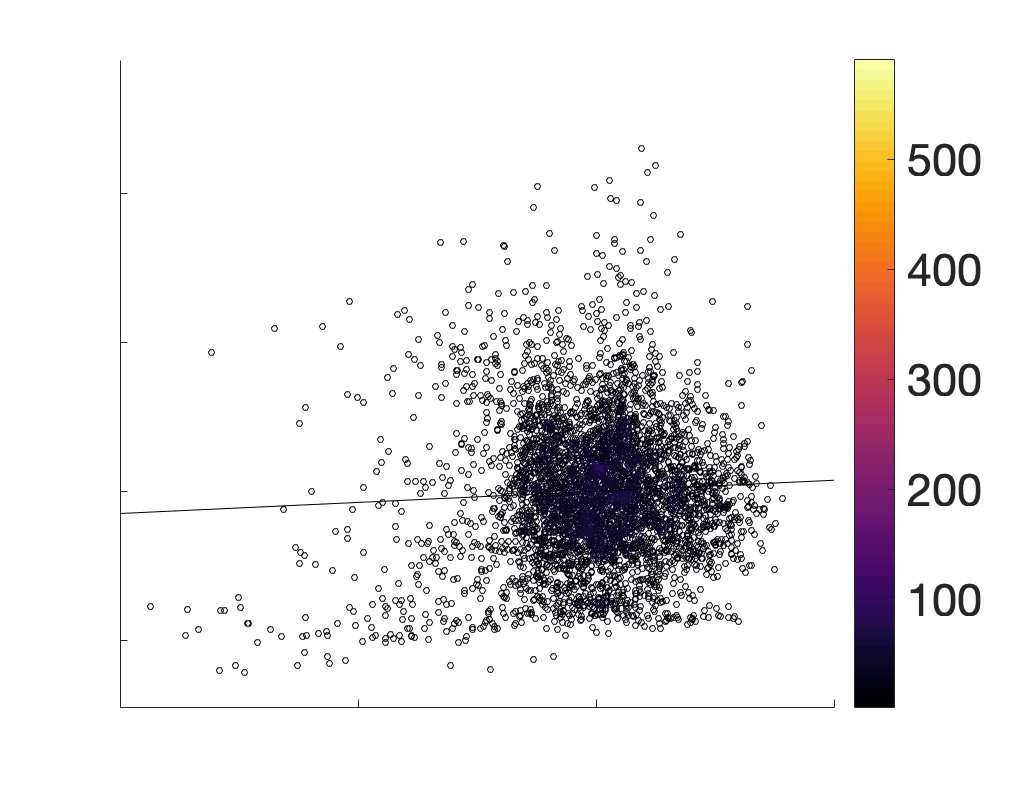
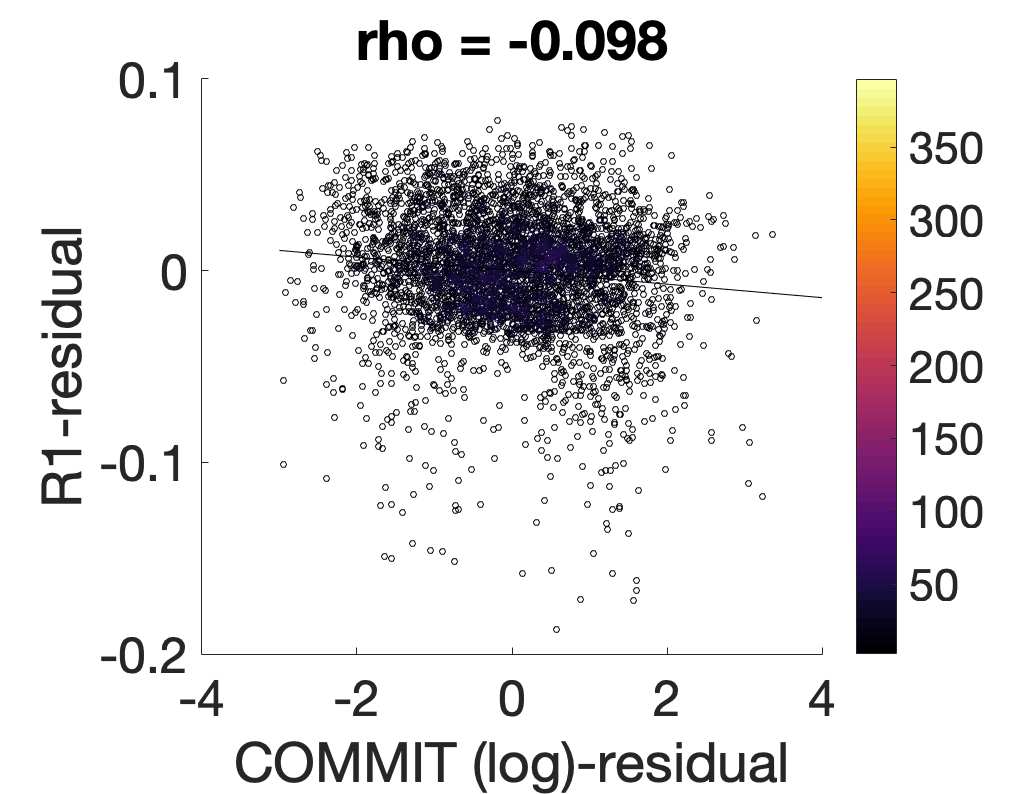
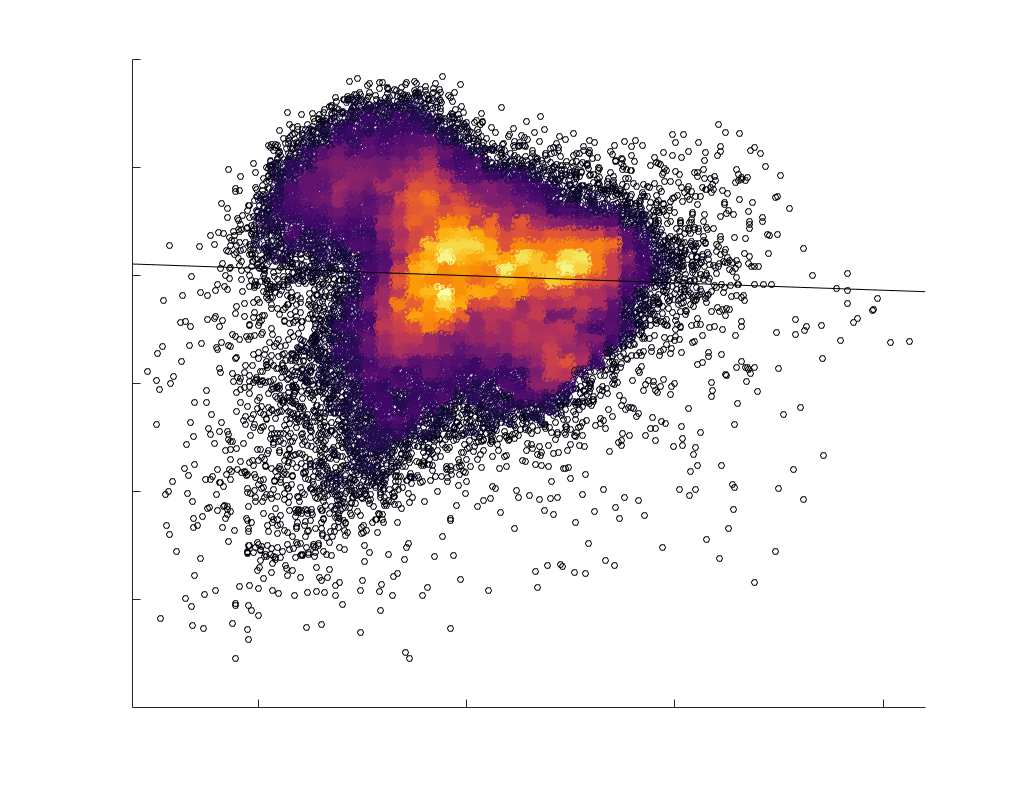
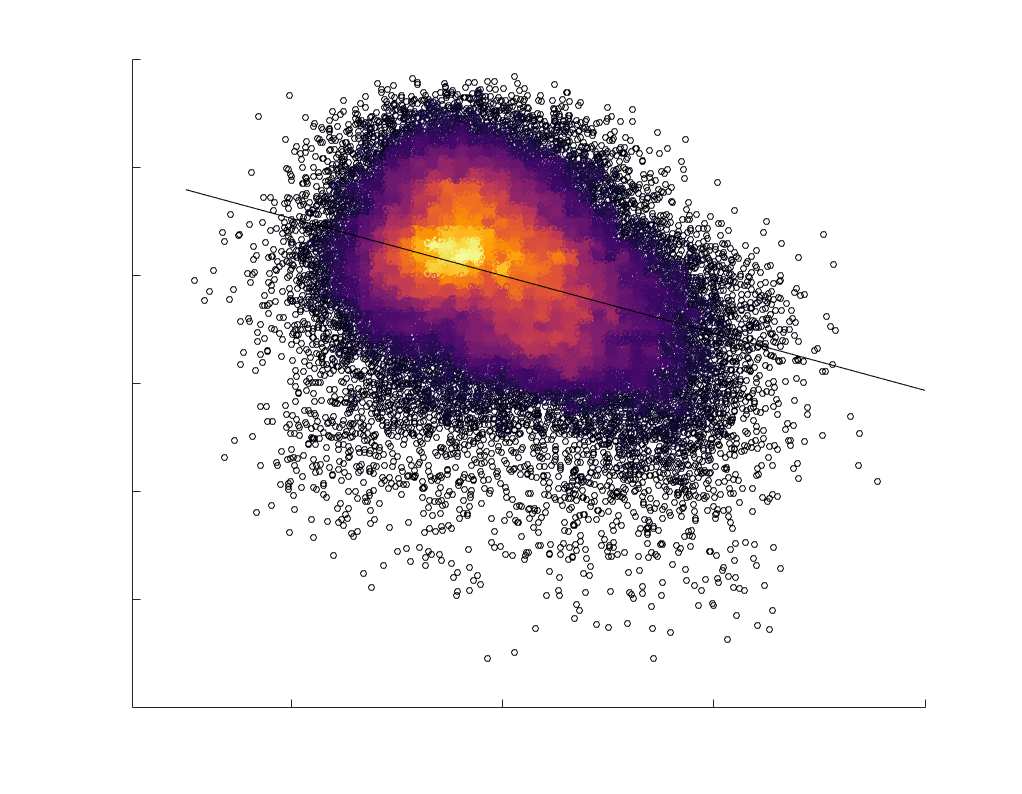
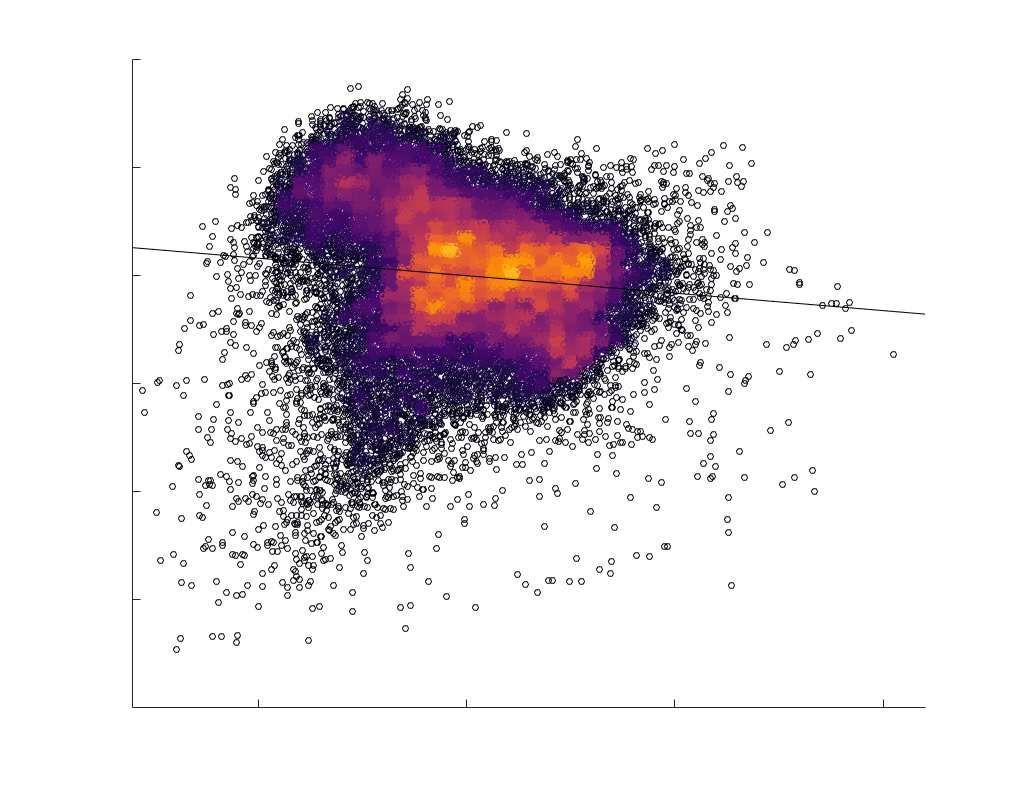
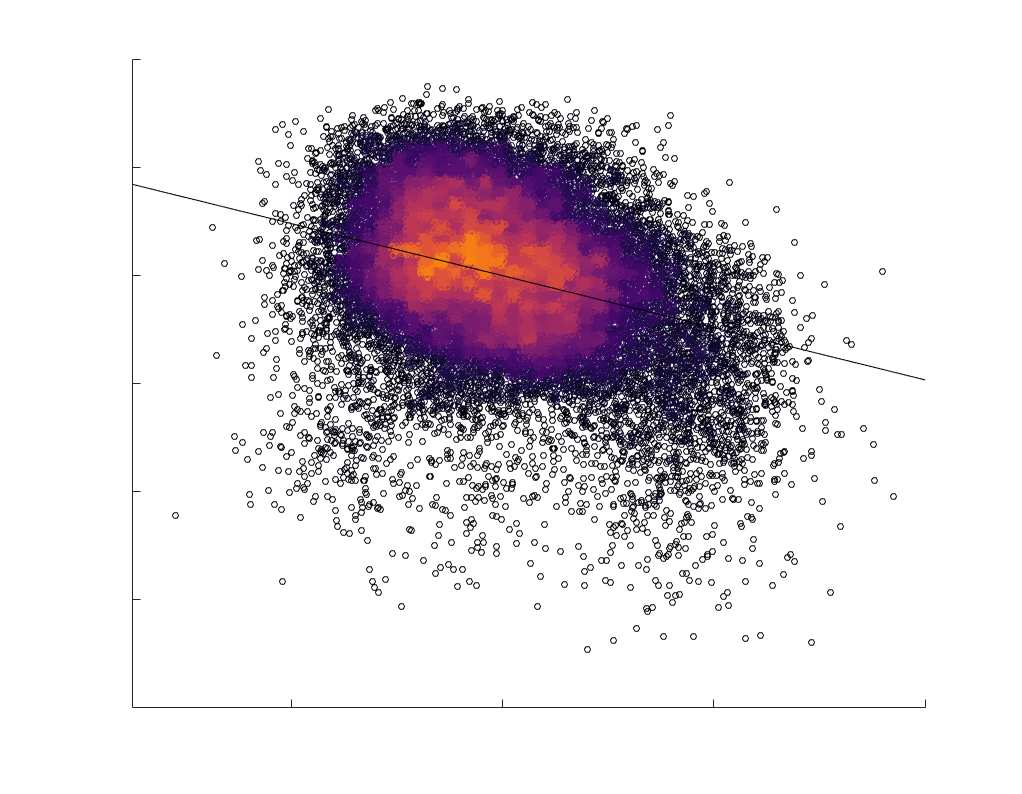
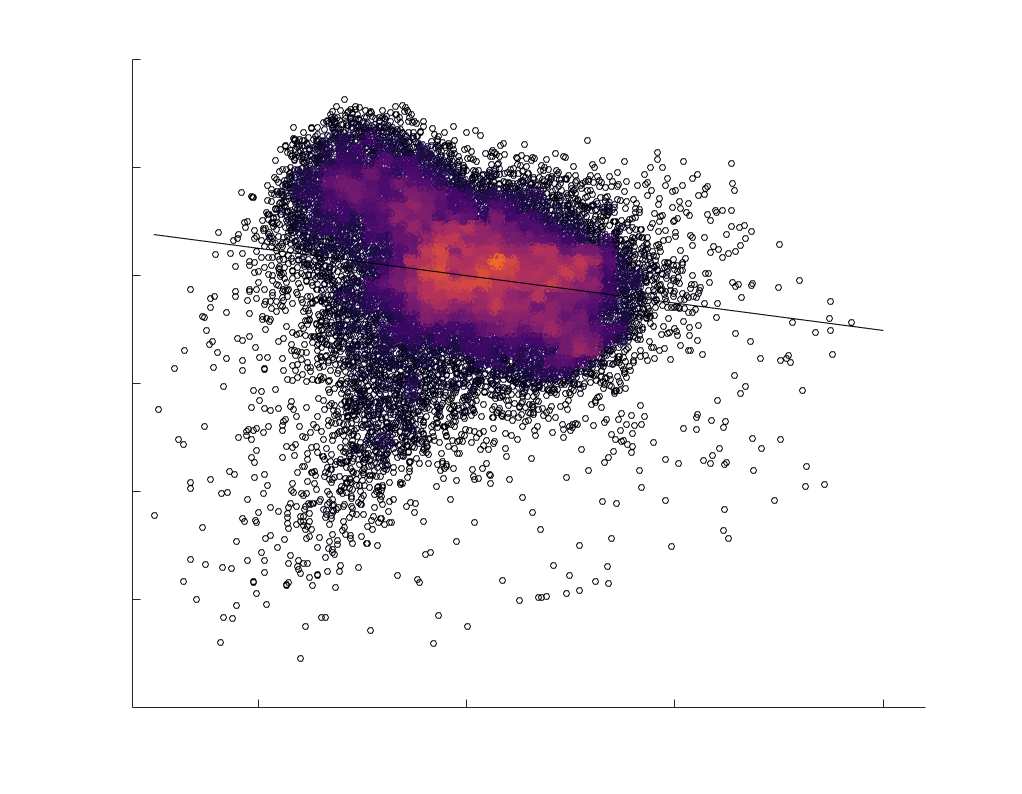
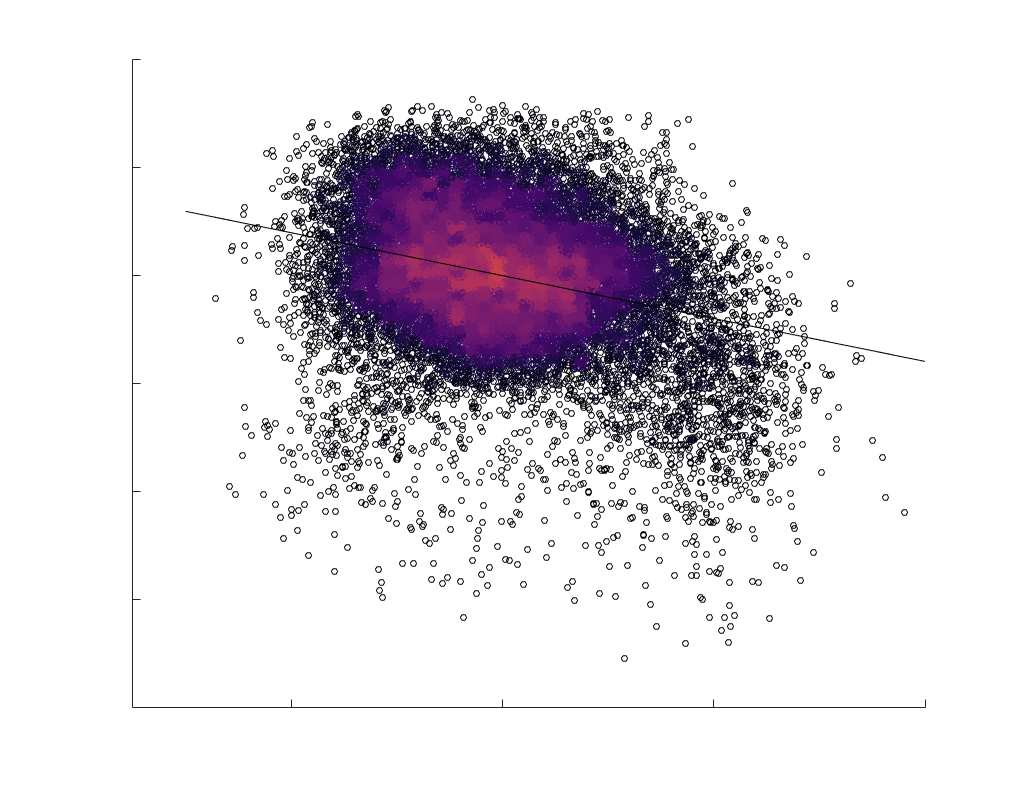
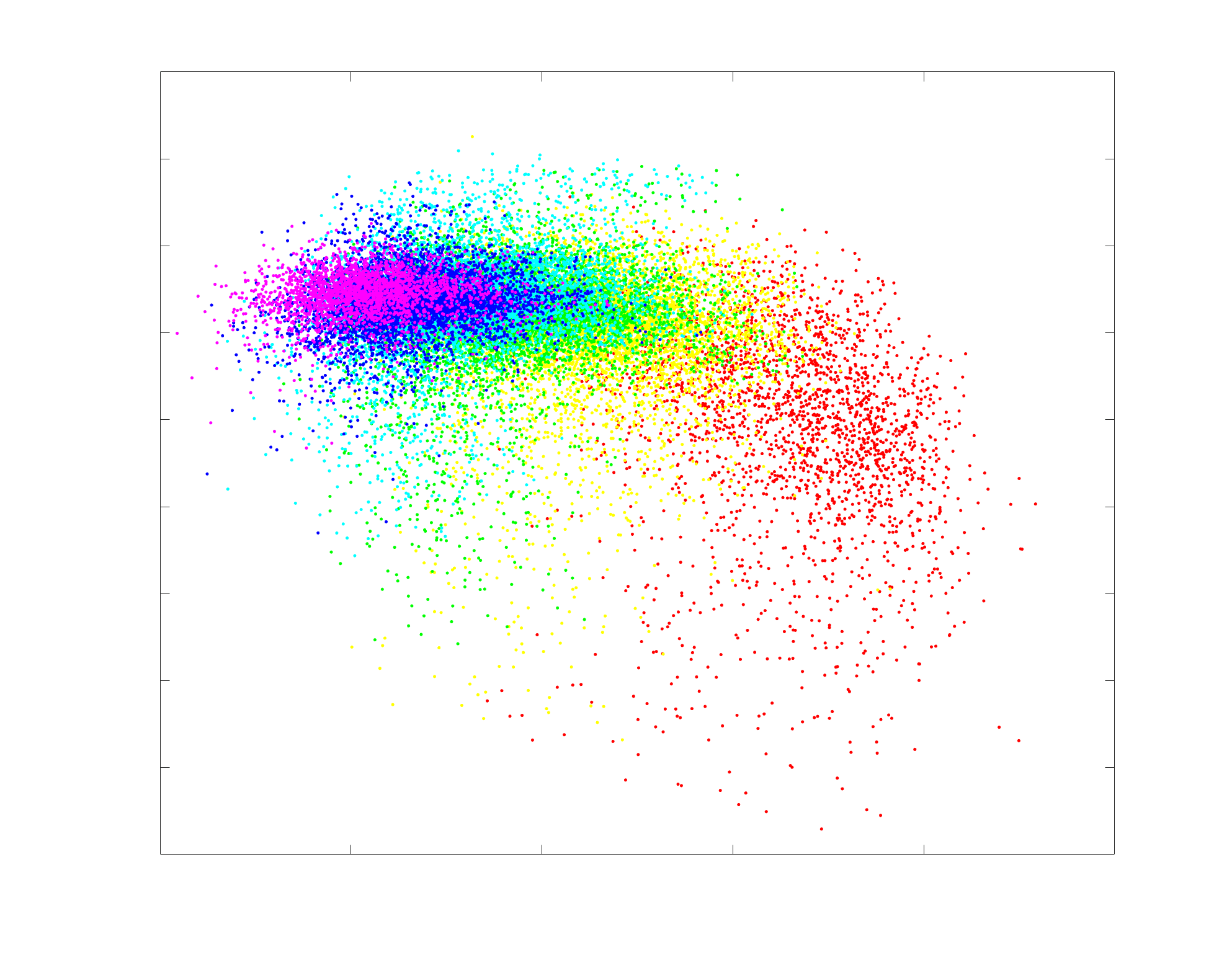
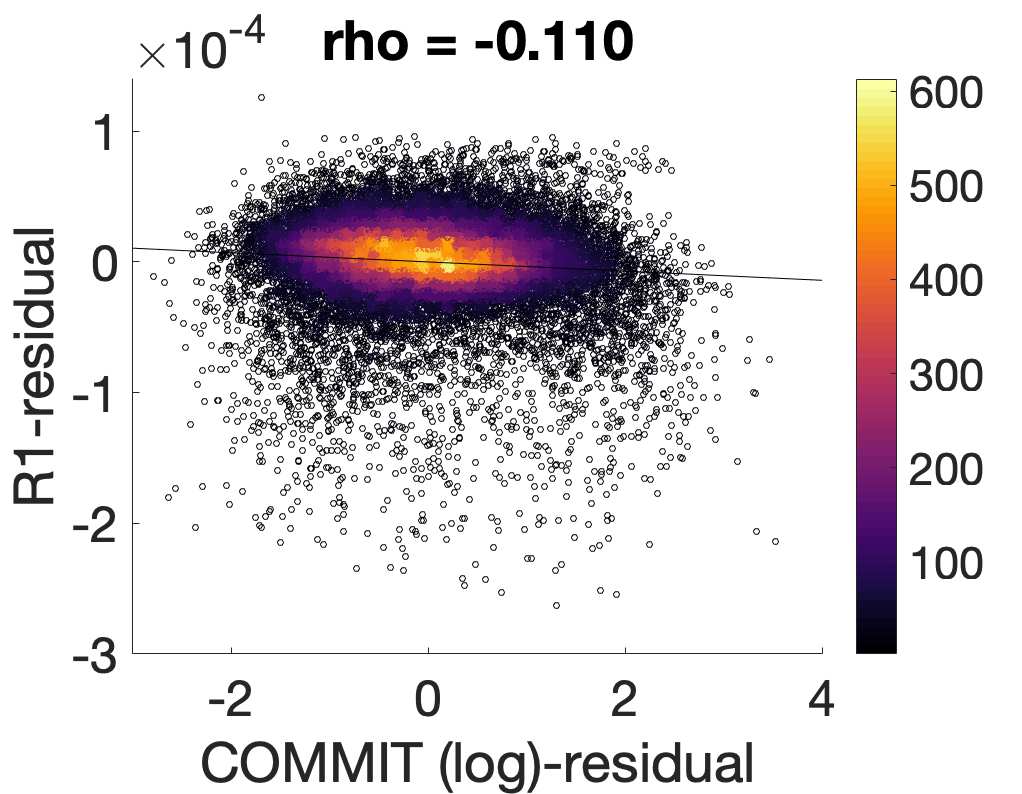
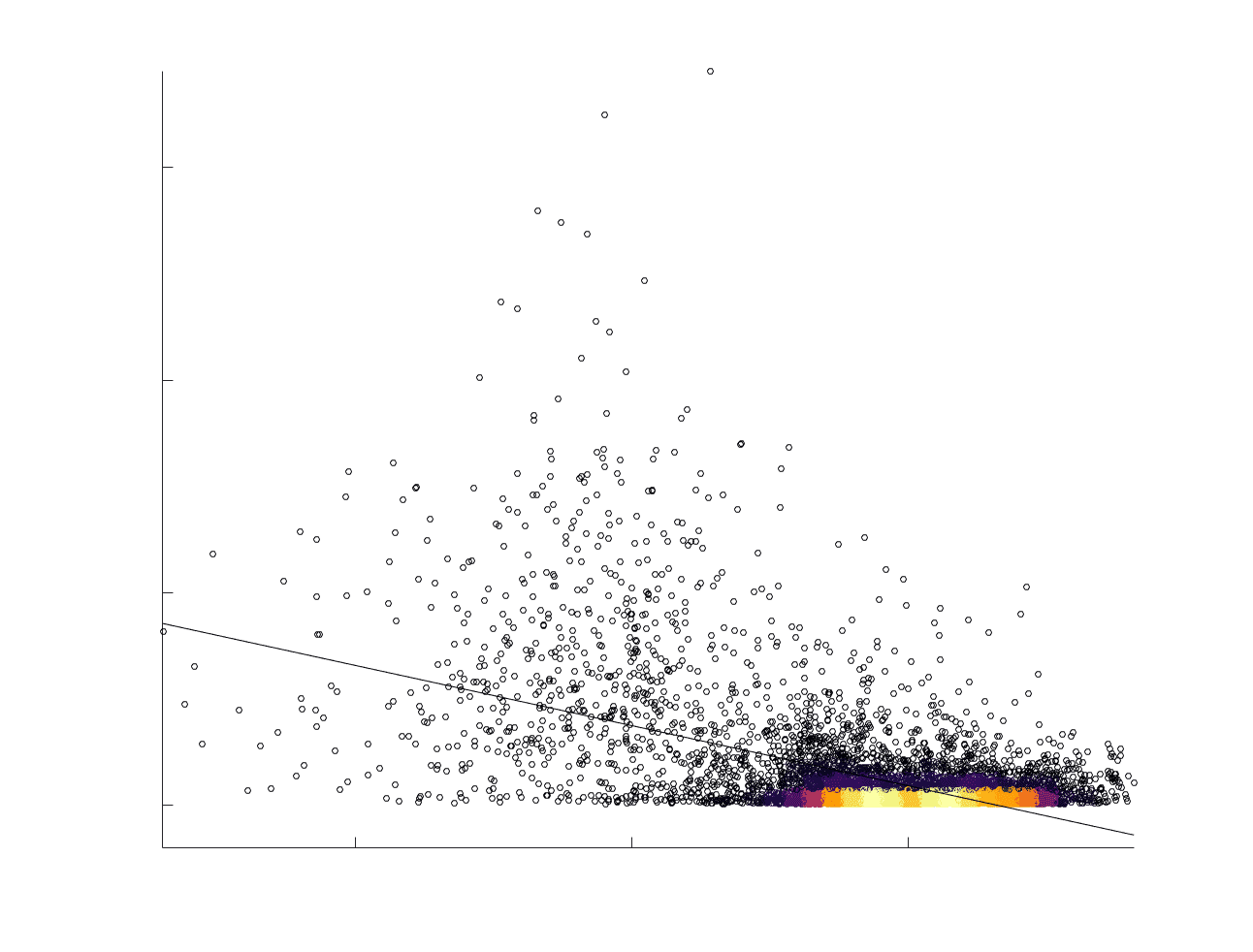
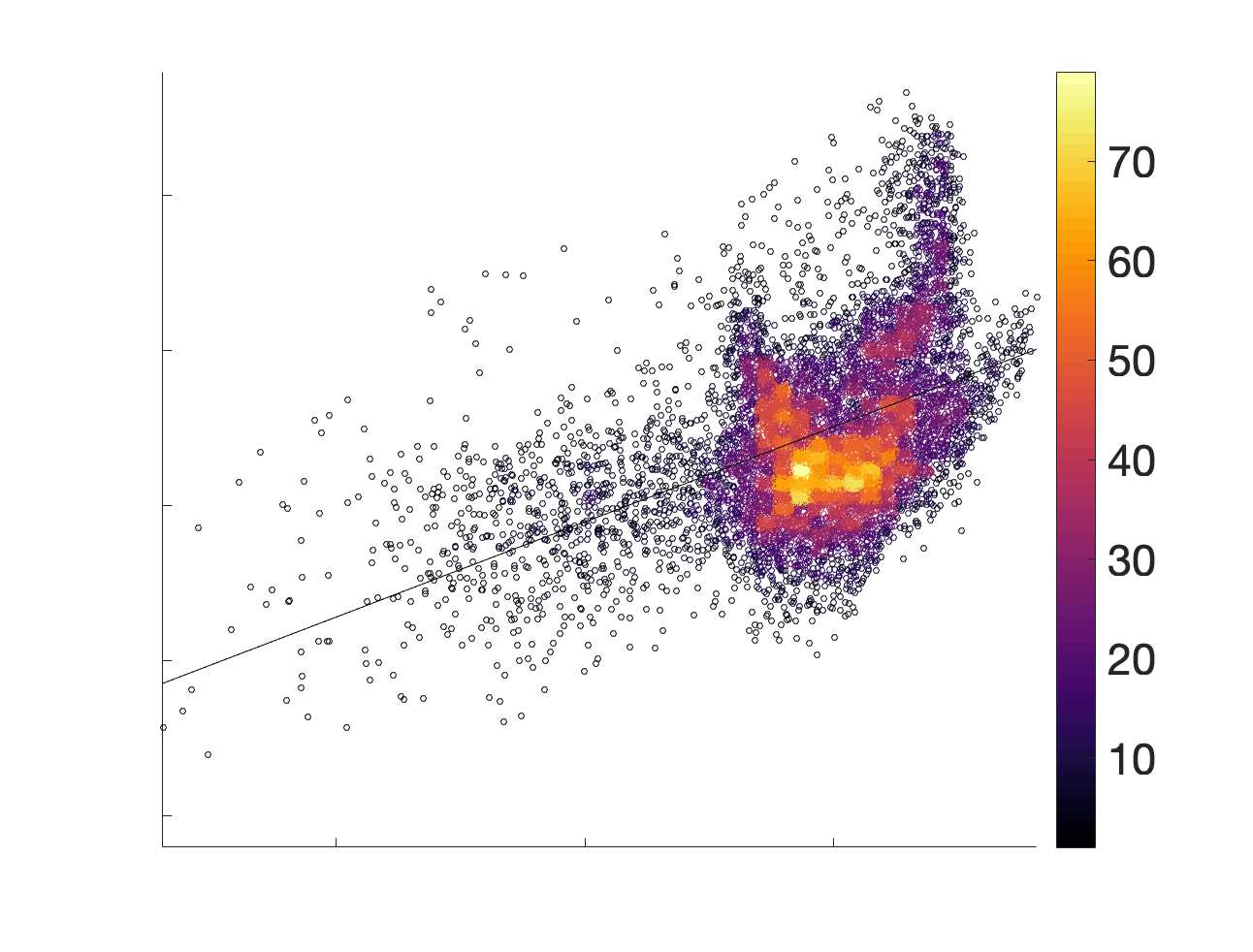
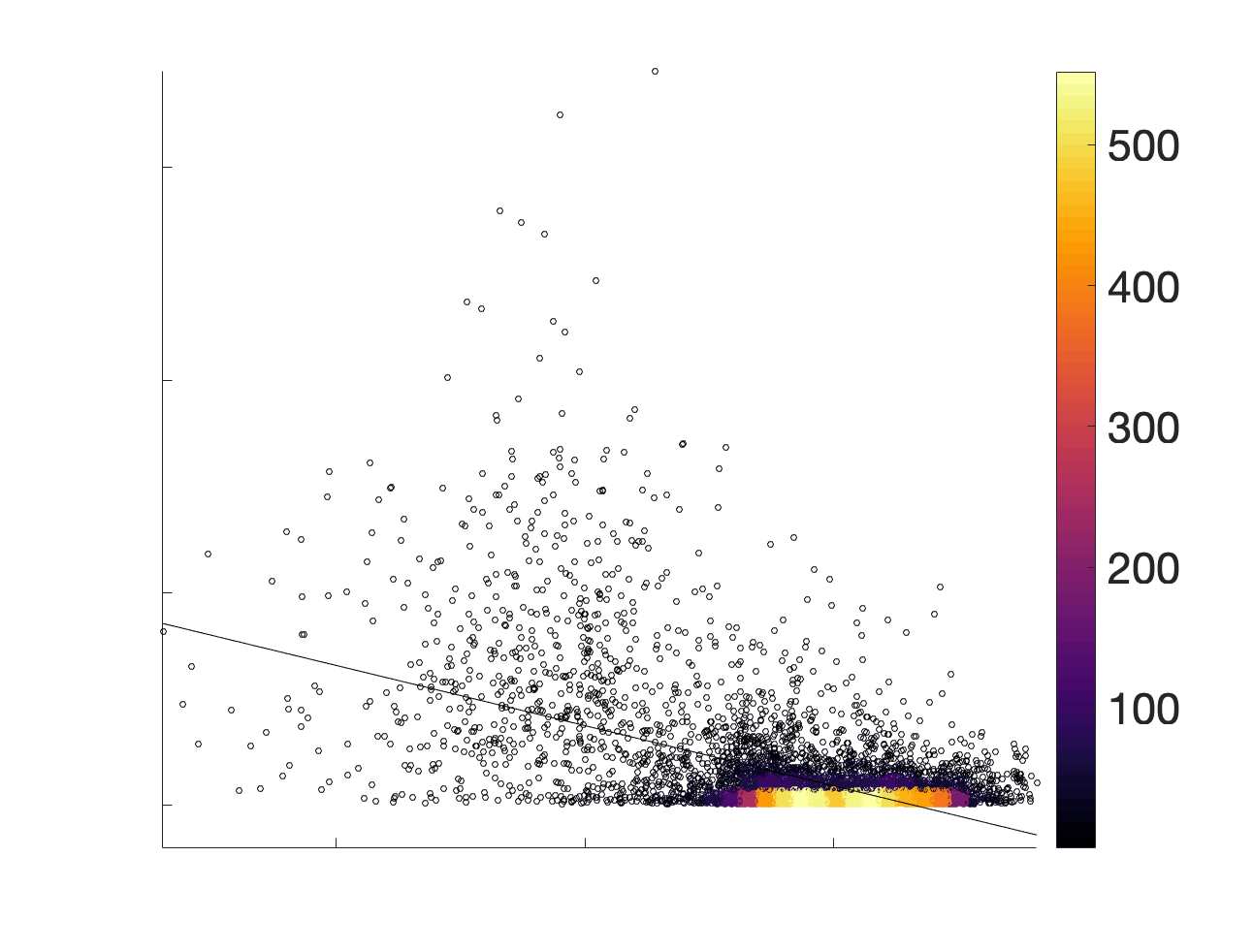
Chiffre 5. The Myelin-Dependence of Structural Brain Networks. (UN) Violin distributions (gauche) de
edgewise Spearman’s rank correlations with the myelin-weighted network R1. Residual edge weights are
16
compared following linear regression of edge length. Colored data points and bars respectively indicate
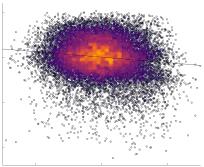
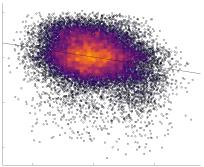
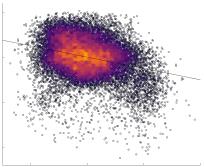
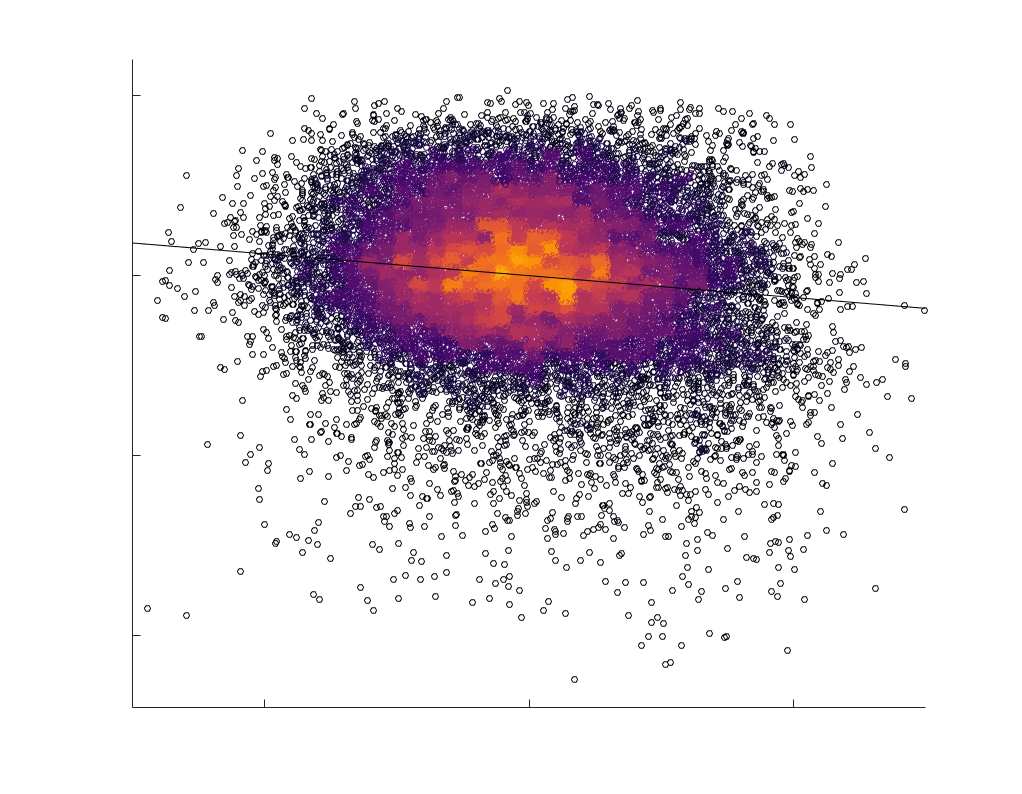
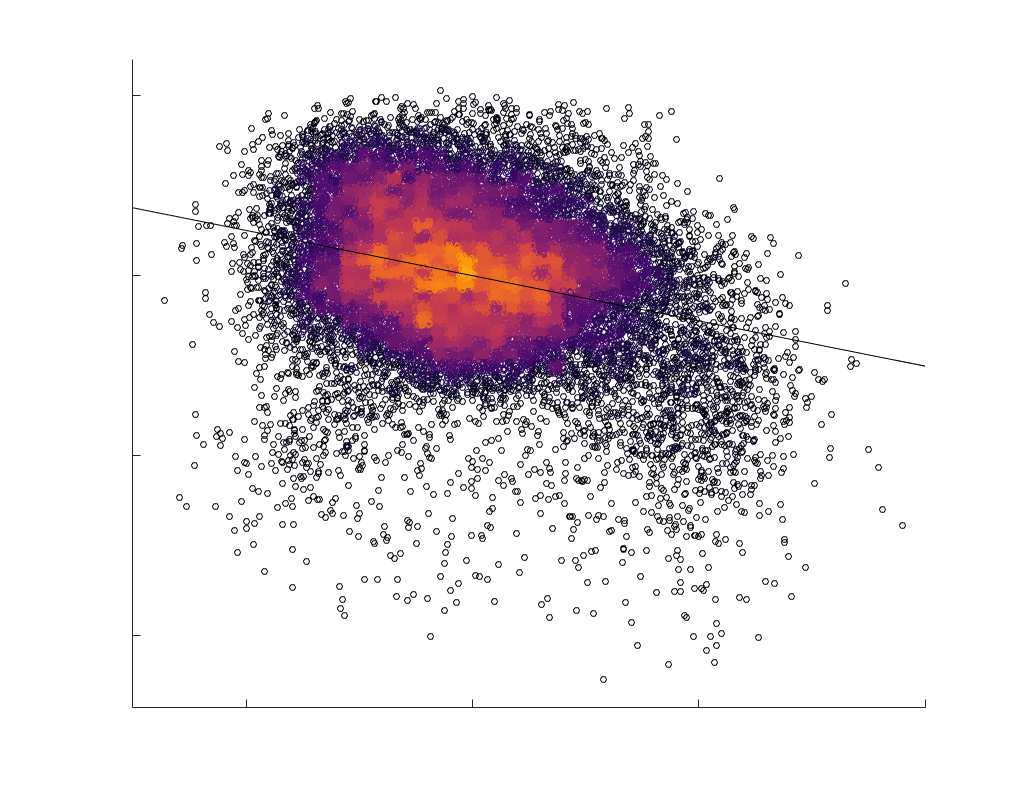
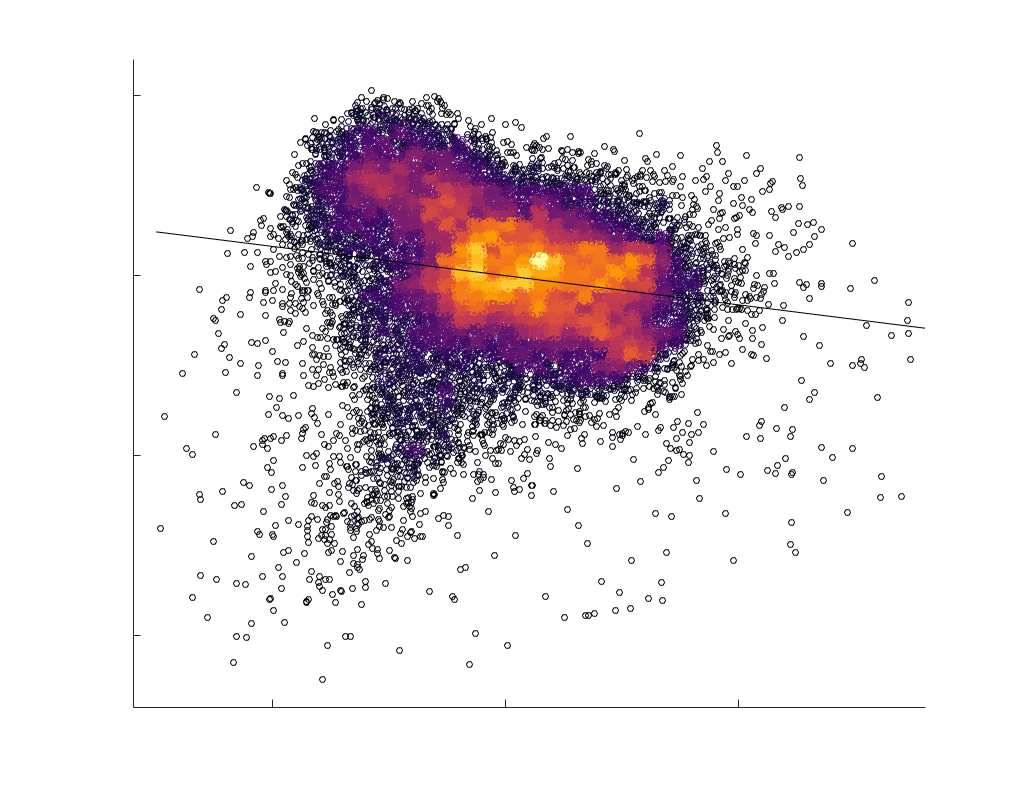
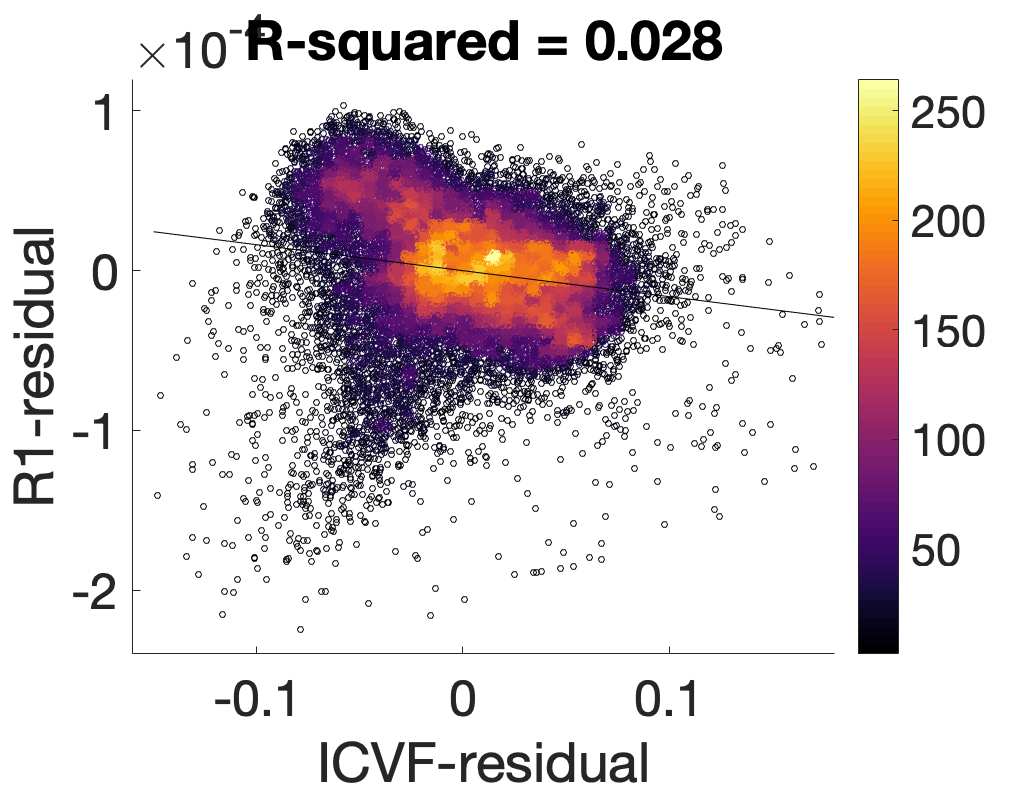
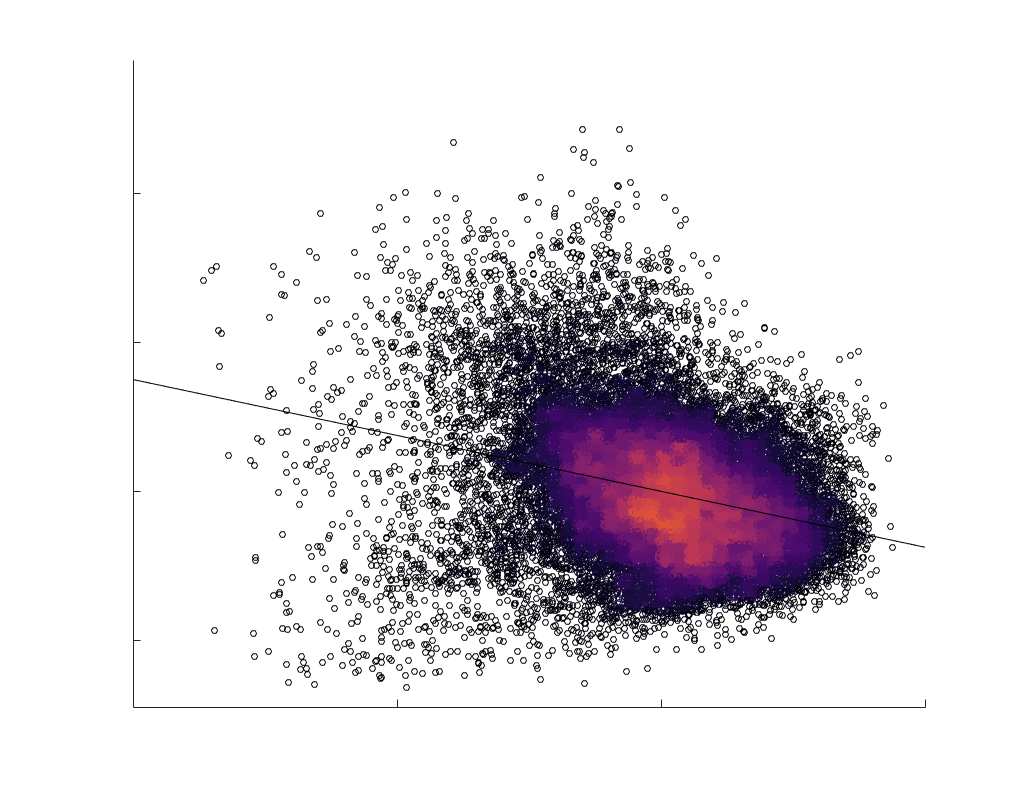
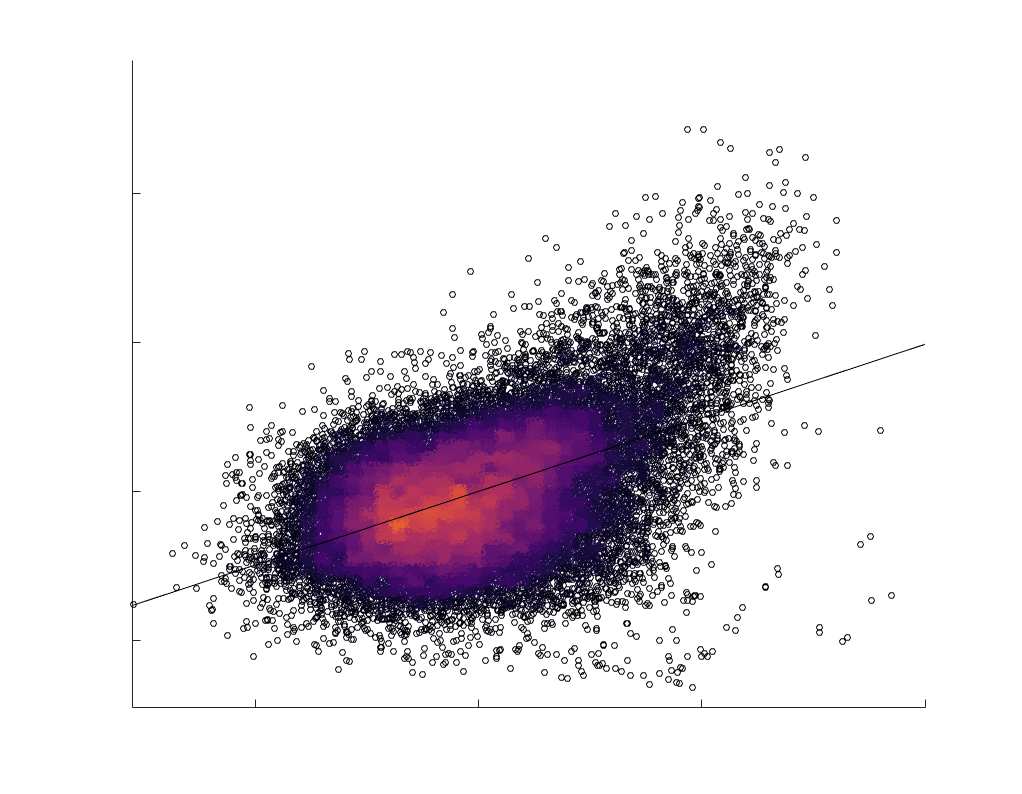
subject-level and group-level correlations. Heat scatter plots (droite) of group-level residual edge weights
in R1 as a function of NoS (gauche), SIFT2 (left middle), COMMIT (right middle) and ICVF (droite). The best
fit linear curve is shown in black, and R2 (coefficient of determination) is reported. Data color indicates
density. Permutation testing provided a one-sided p-value of Pperm = 0.000 for all edgewise correlations
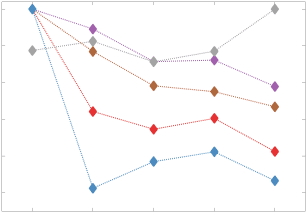
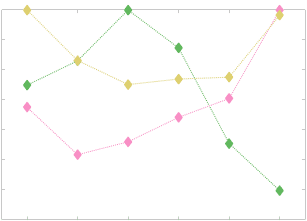
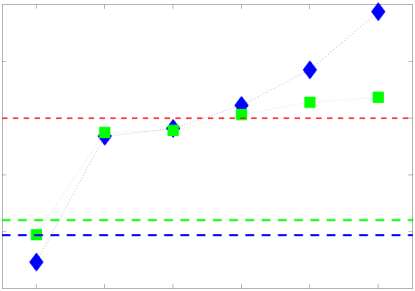
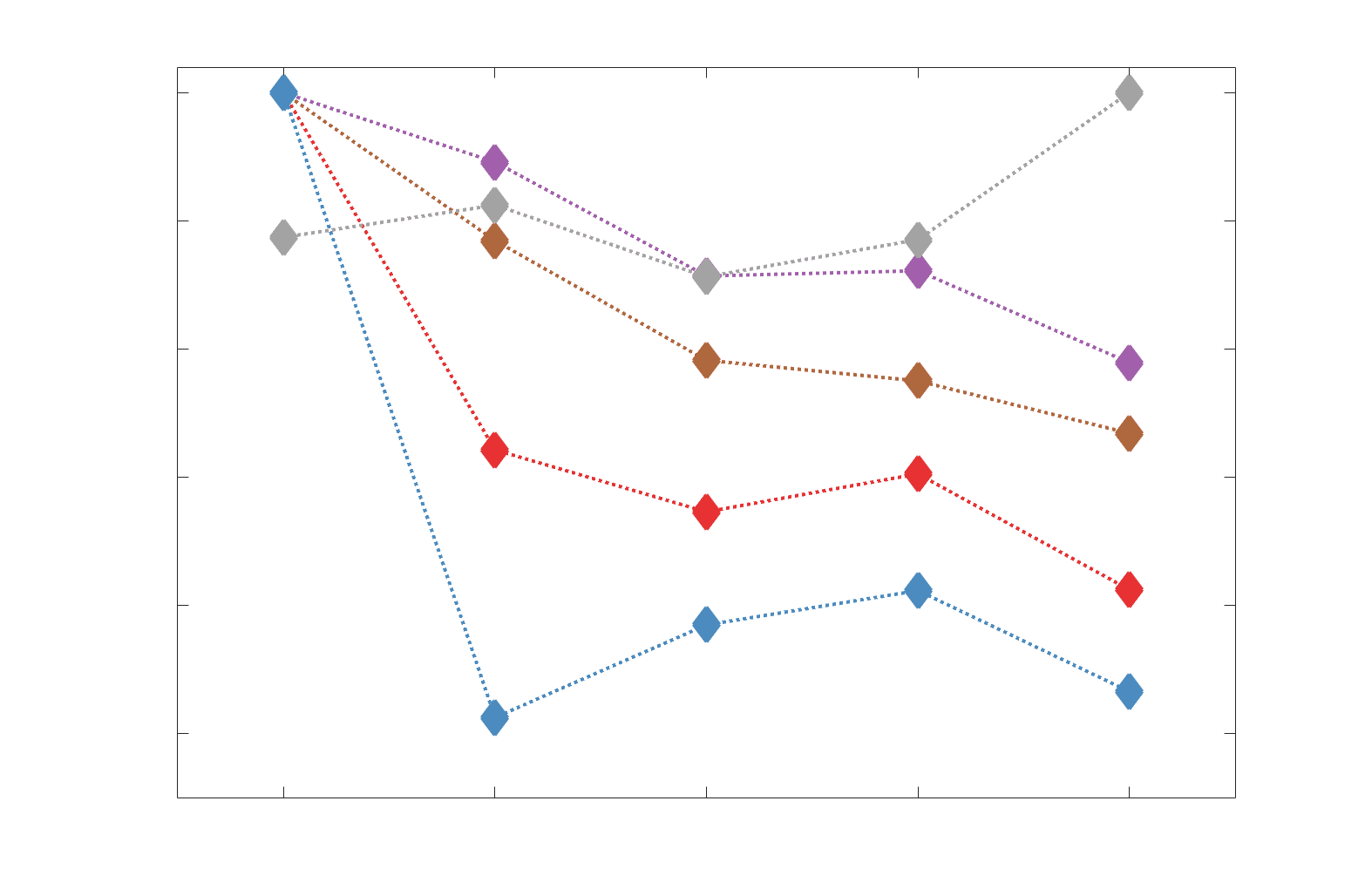
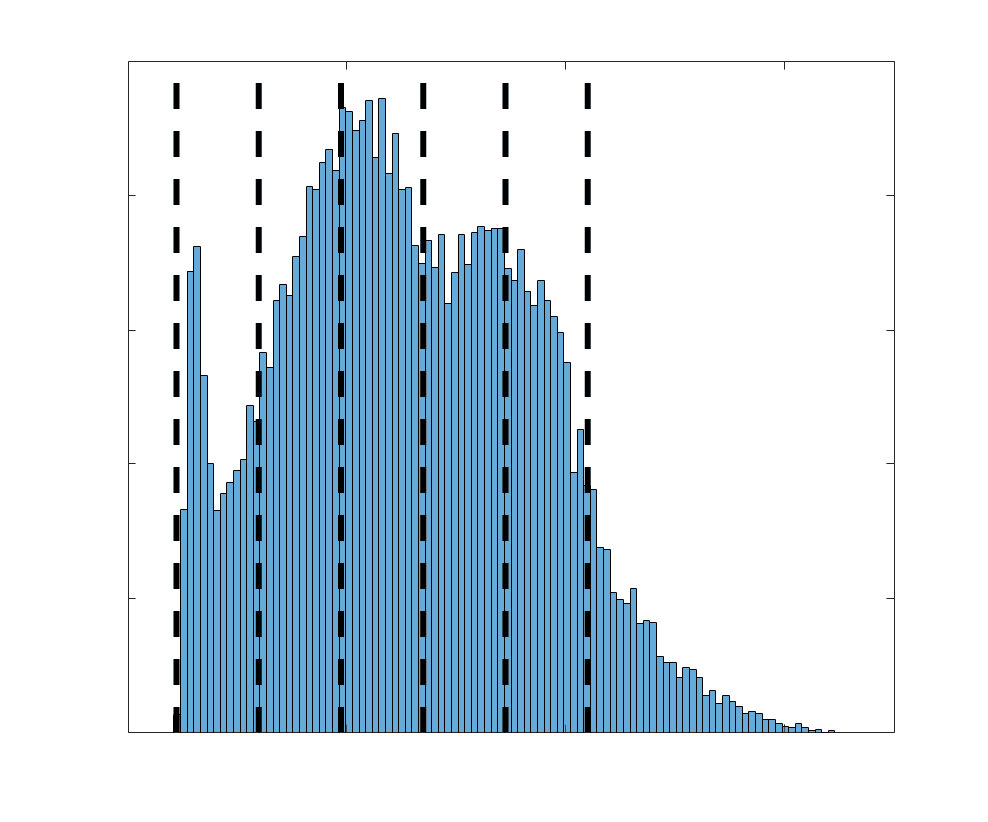
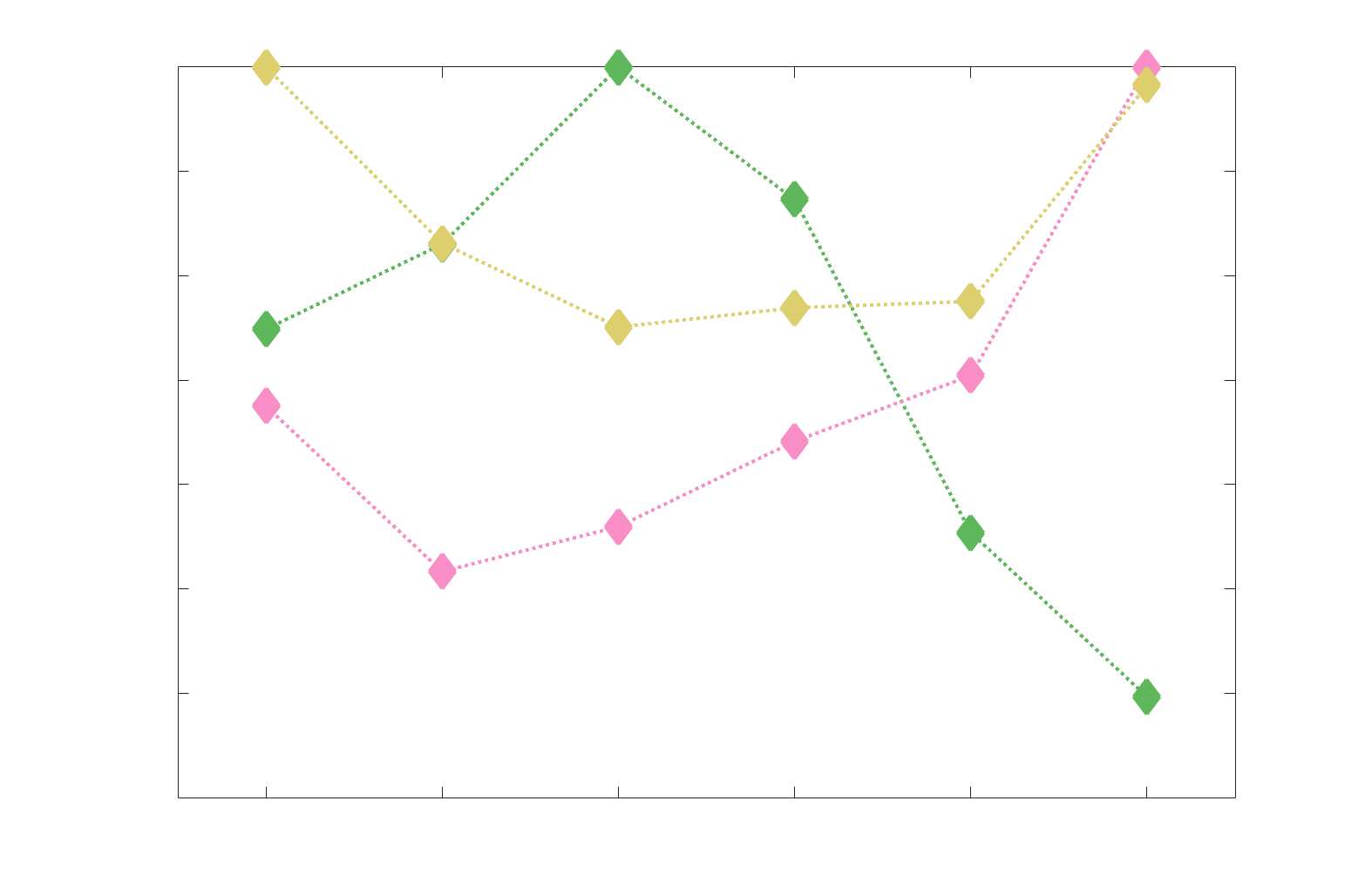
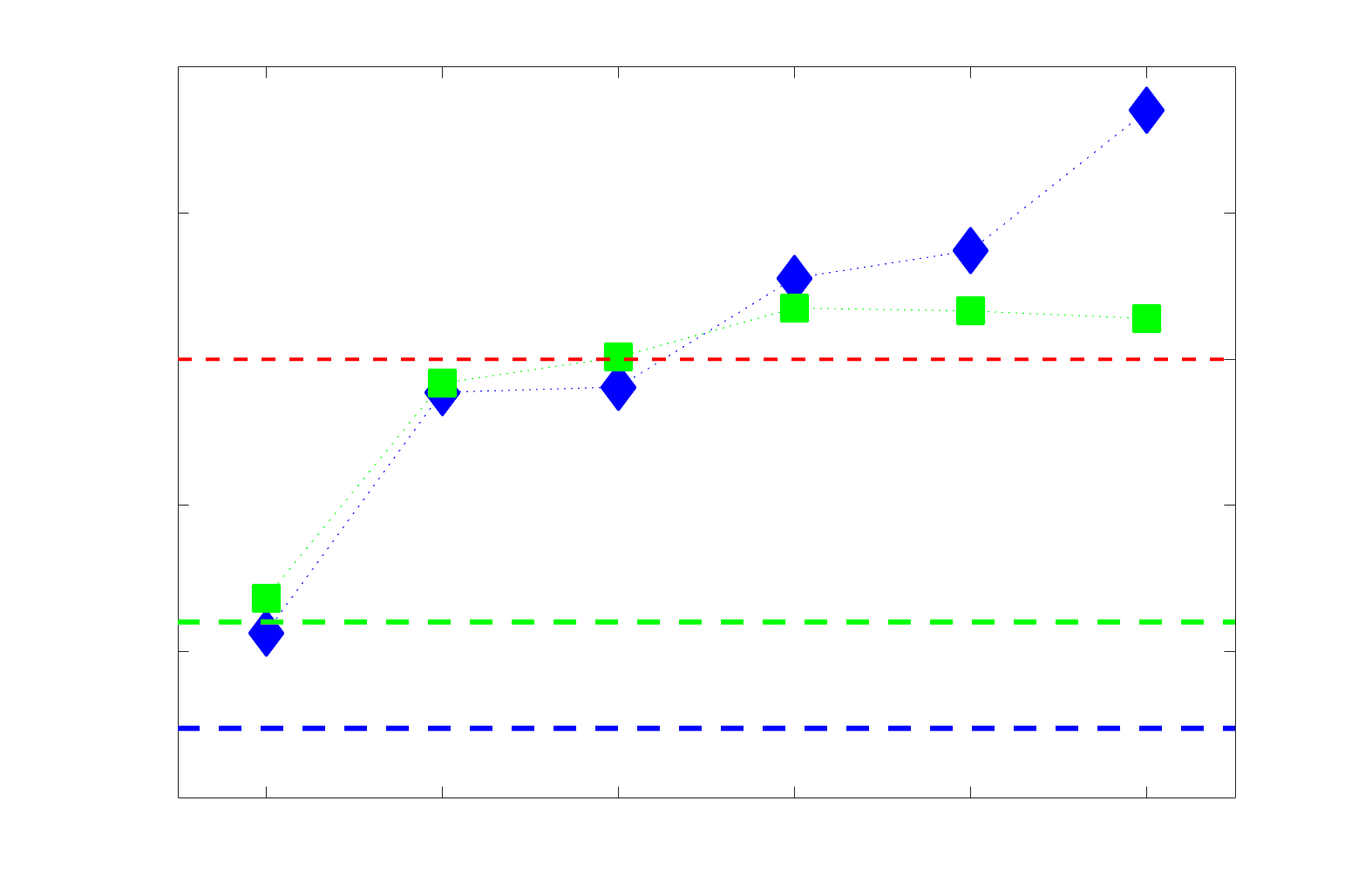
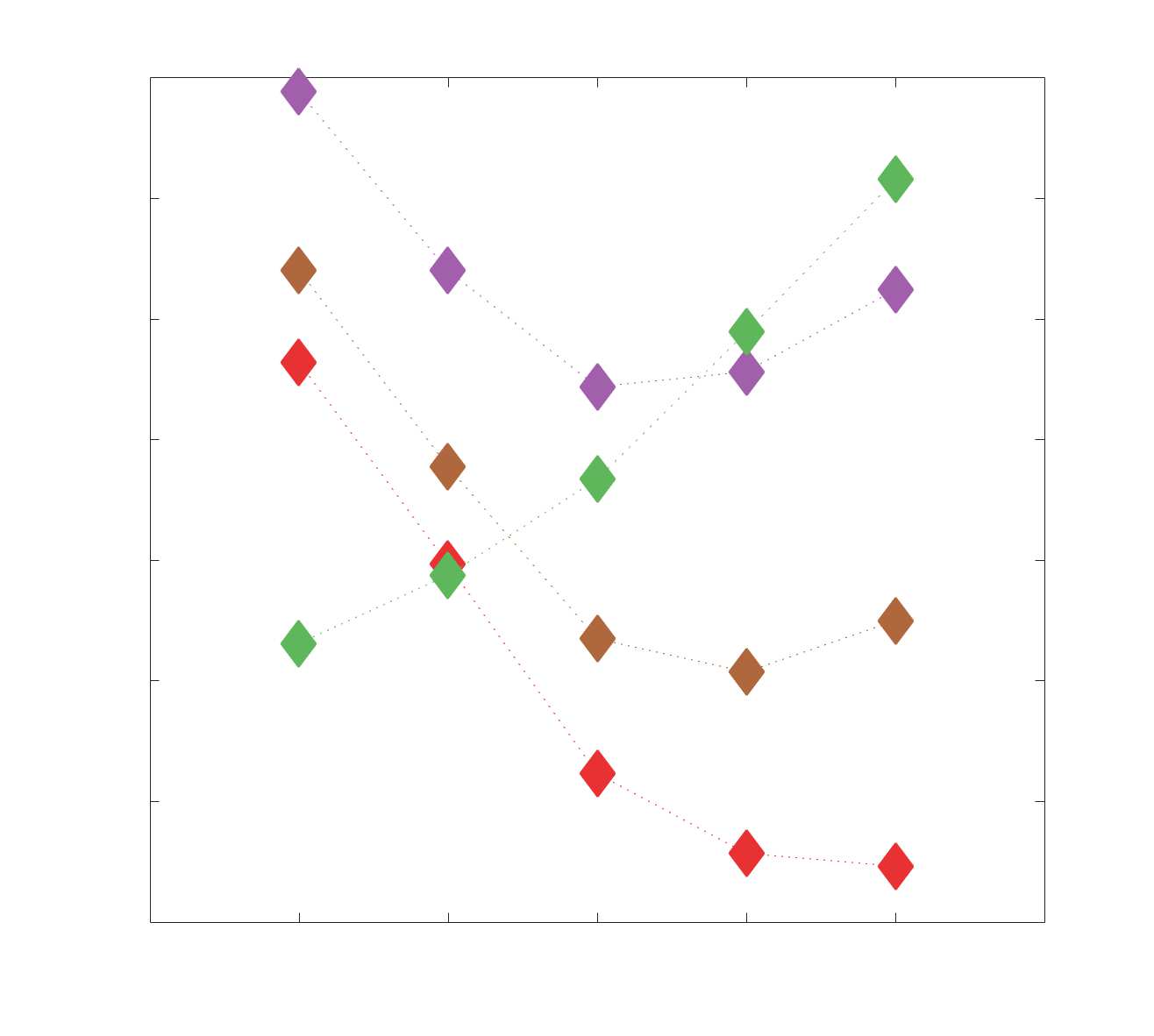
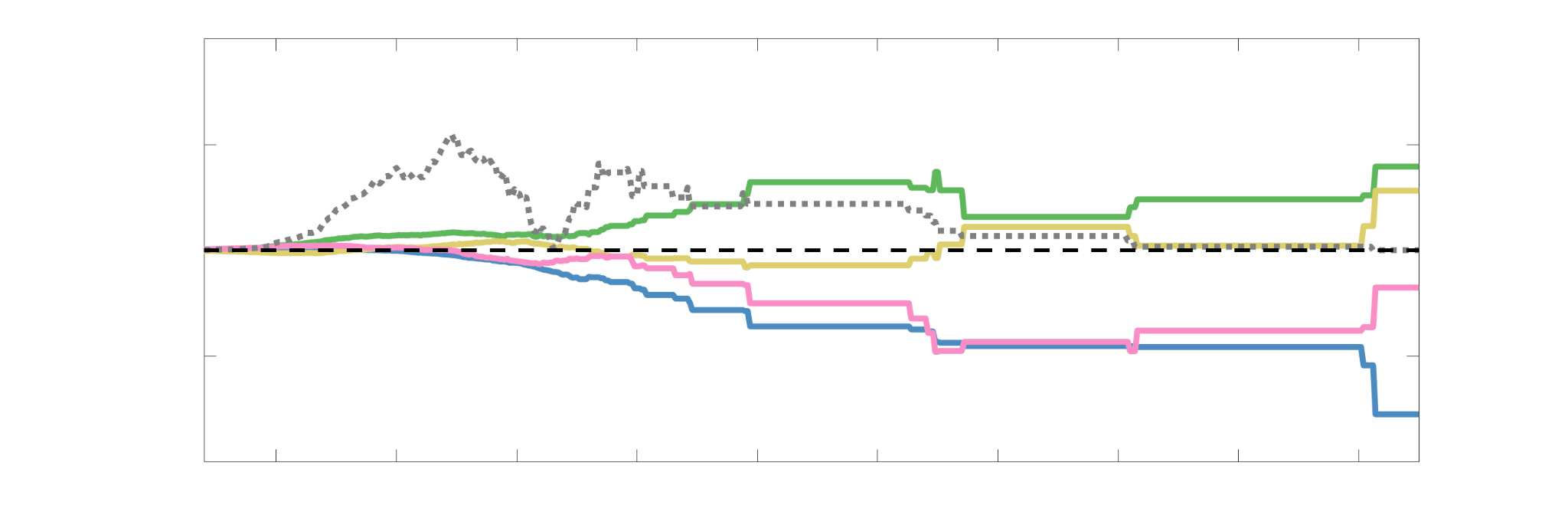
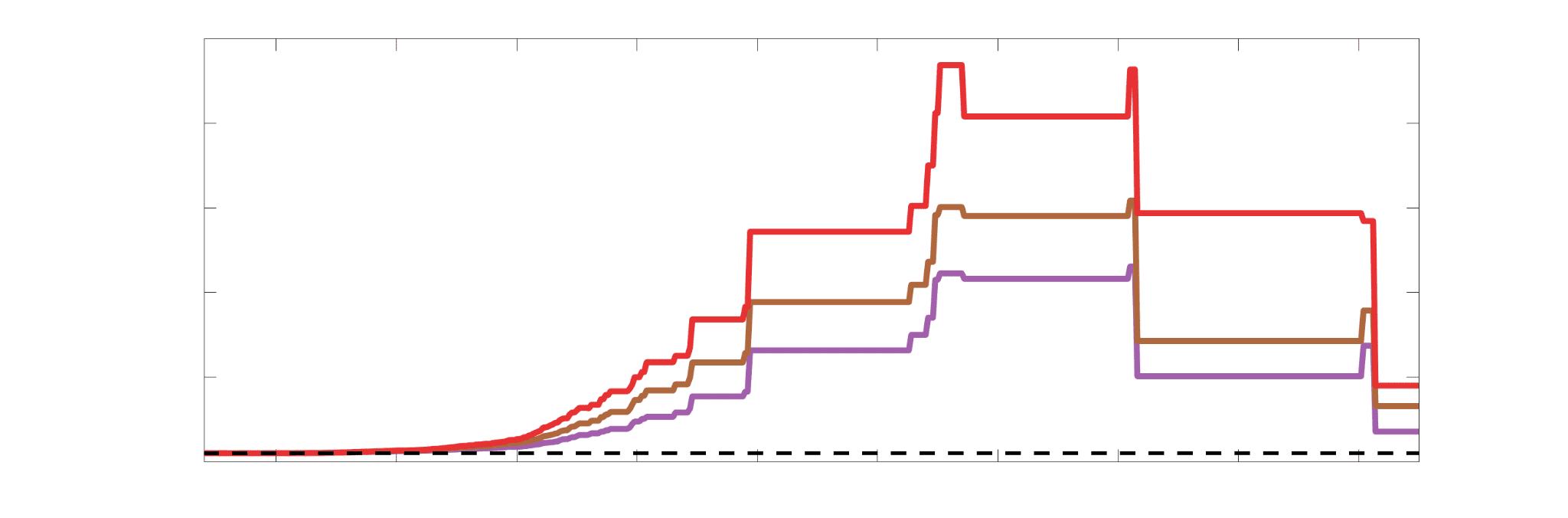
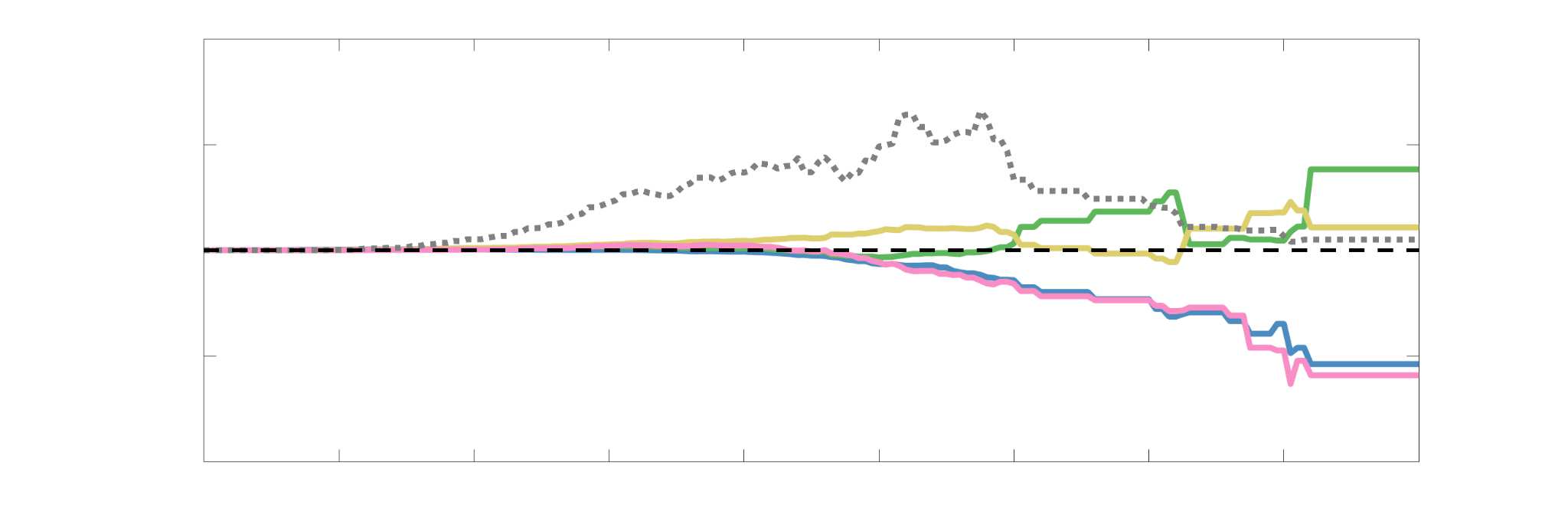
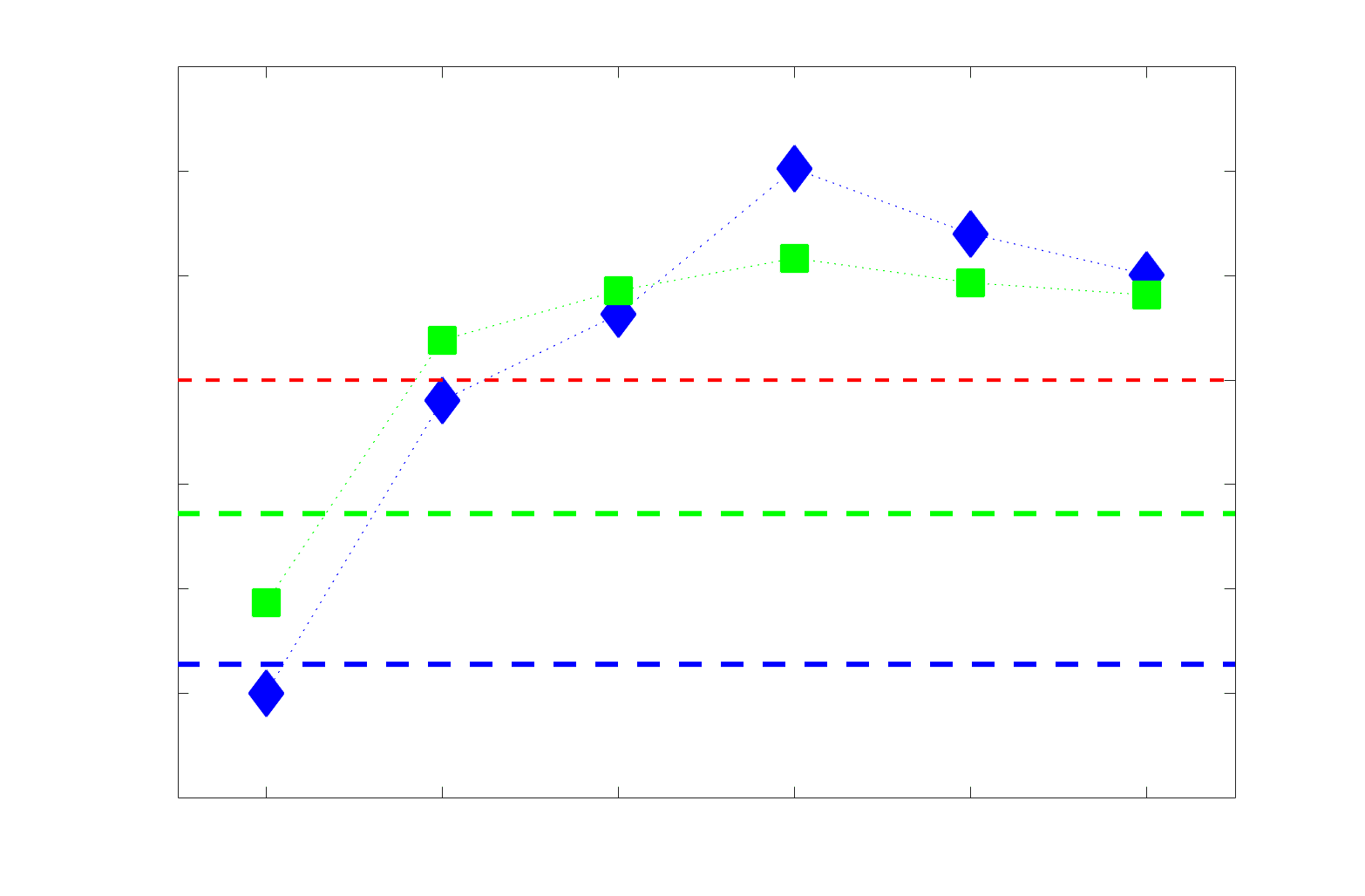
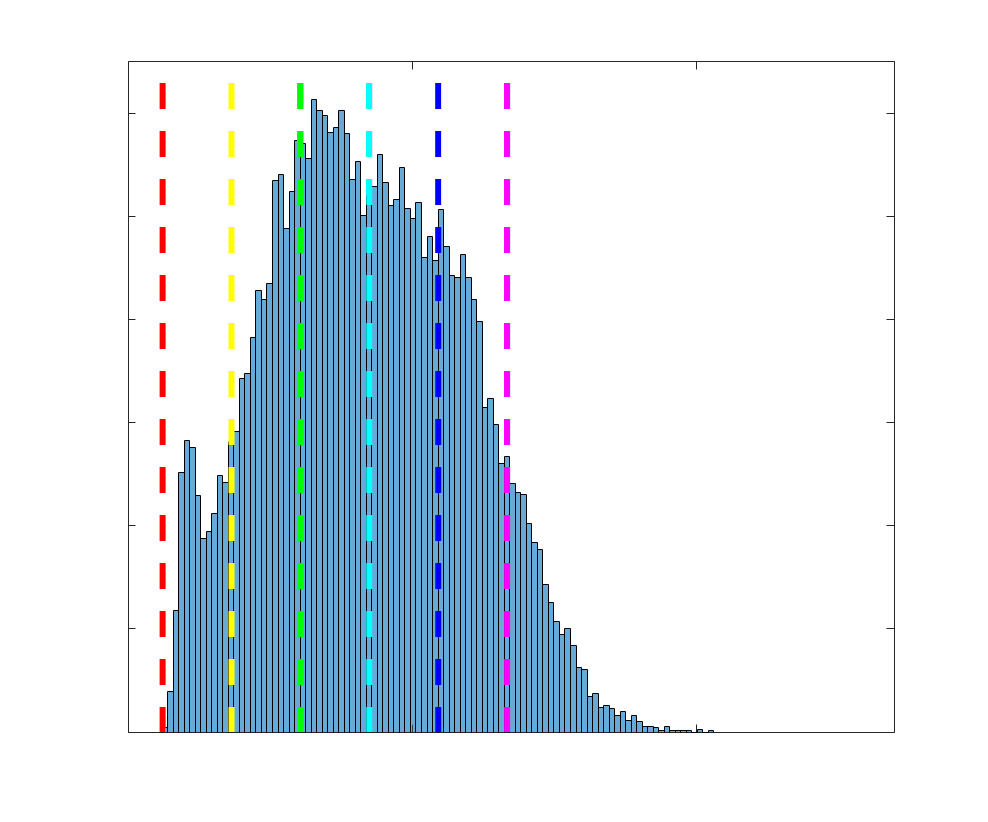
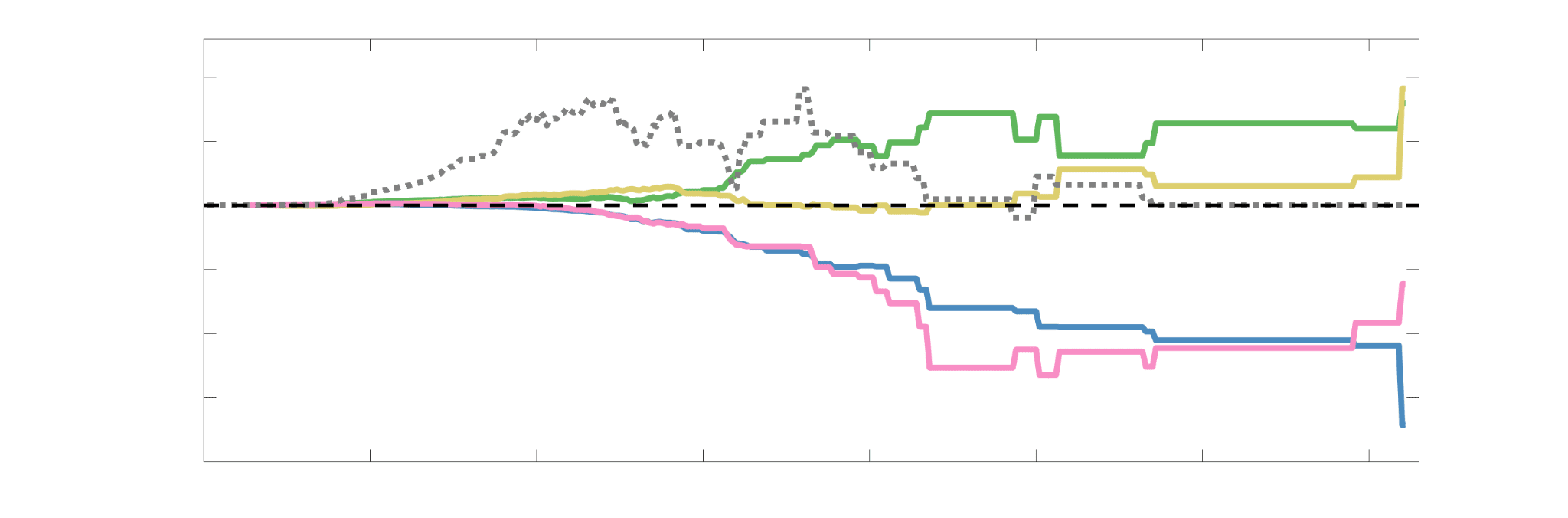
(Figure S8). (B) Line plot (gauche) of edgewise Spearman’s rank correlation of edge weights in R1 vs
COMMIT across edge length bins. Group-level and subject-level are respectively shown in green and
blue. The square and diamond markers connected by dotted lines show binned correlation values, et le
horizontal dashed green and blue lines mark the correlation values for all edges pooled together. Scatter
plot (middle) of group-level edge weights in R1 as a function of COMMIT with data points colored by bin
identité. Histograms (droite) illustrating subject- and group-level edge length bins.
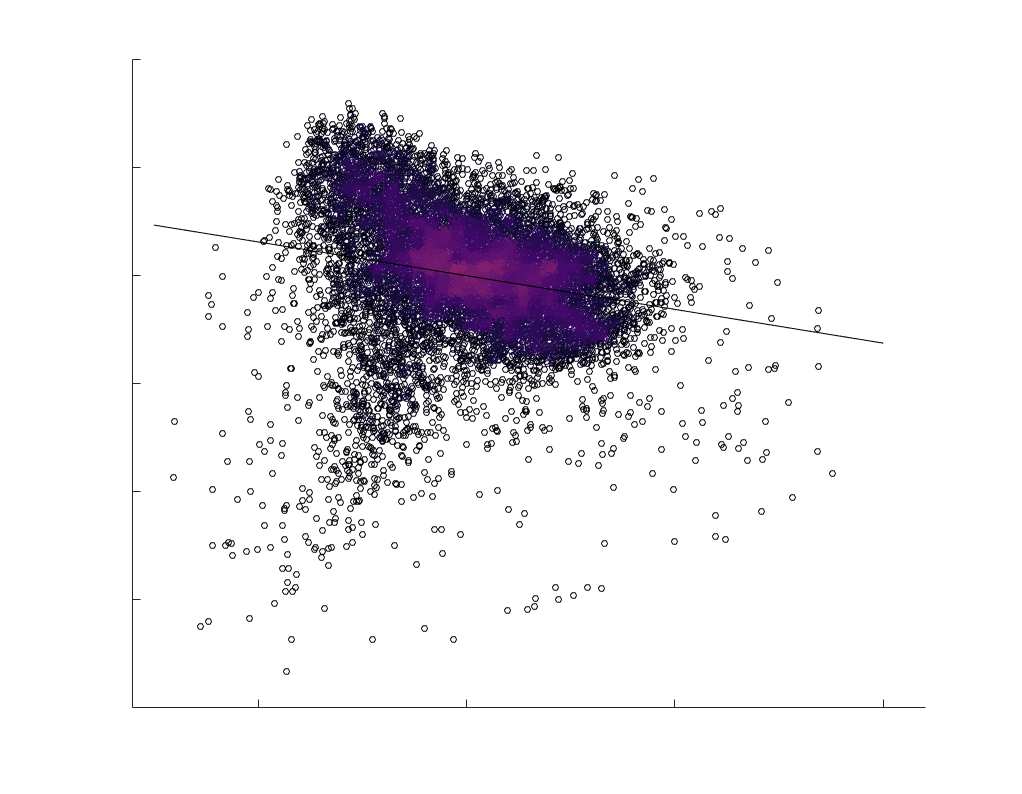
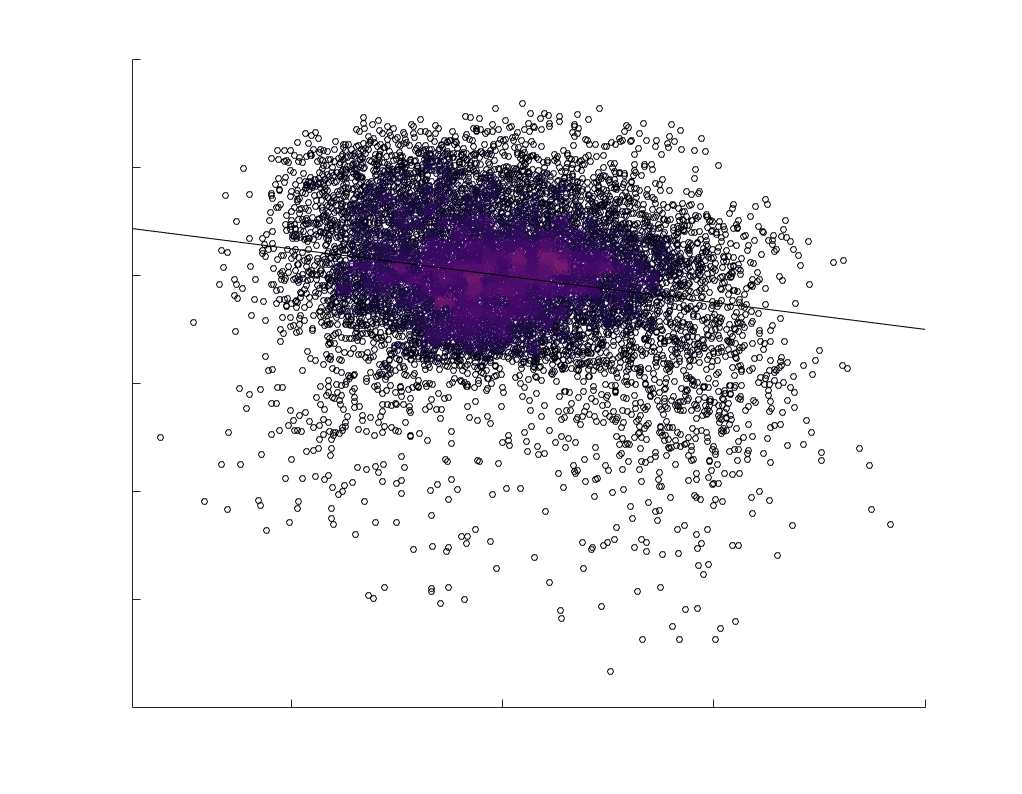
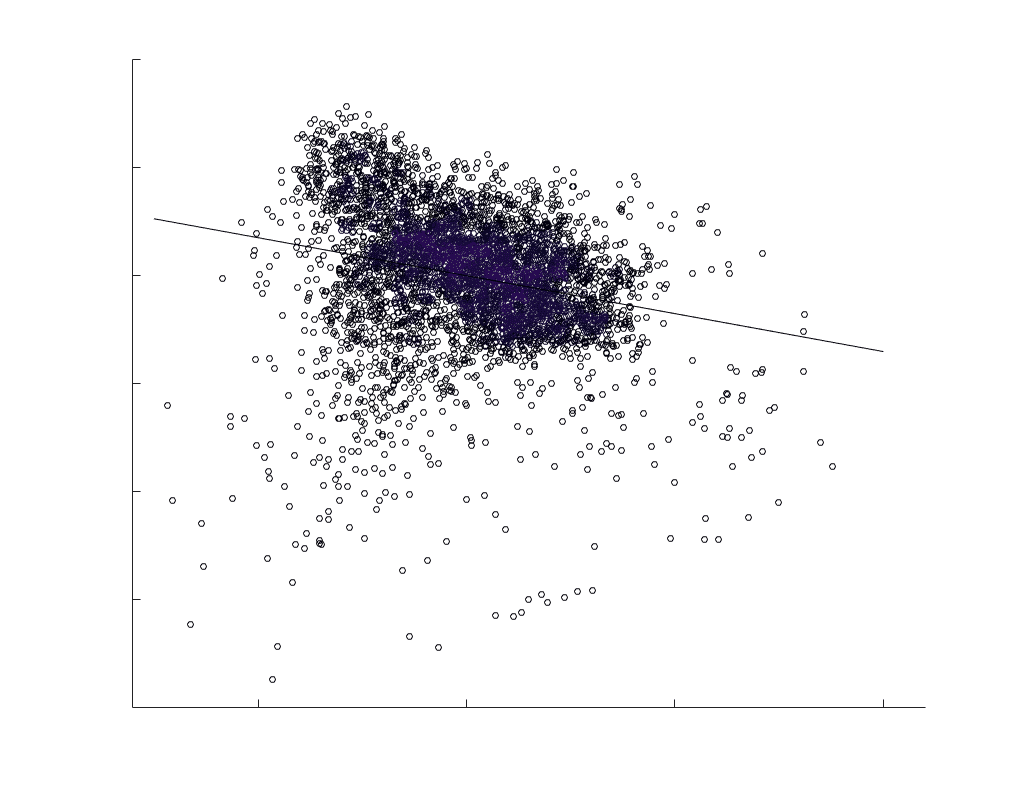
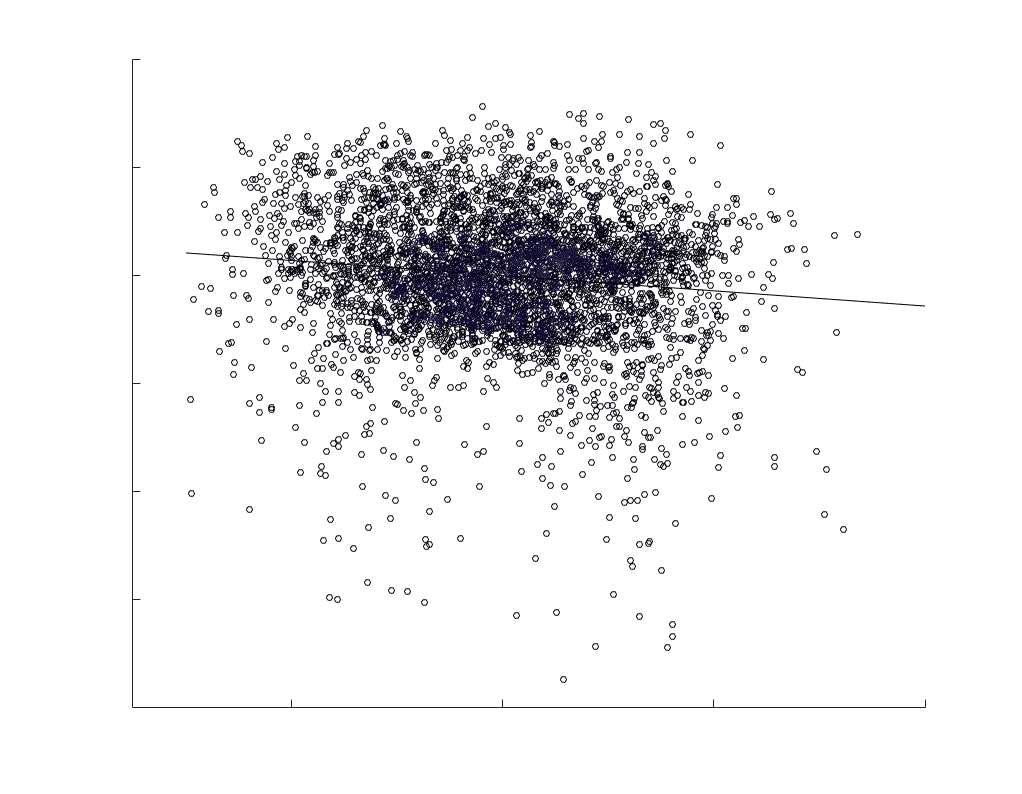
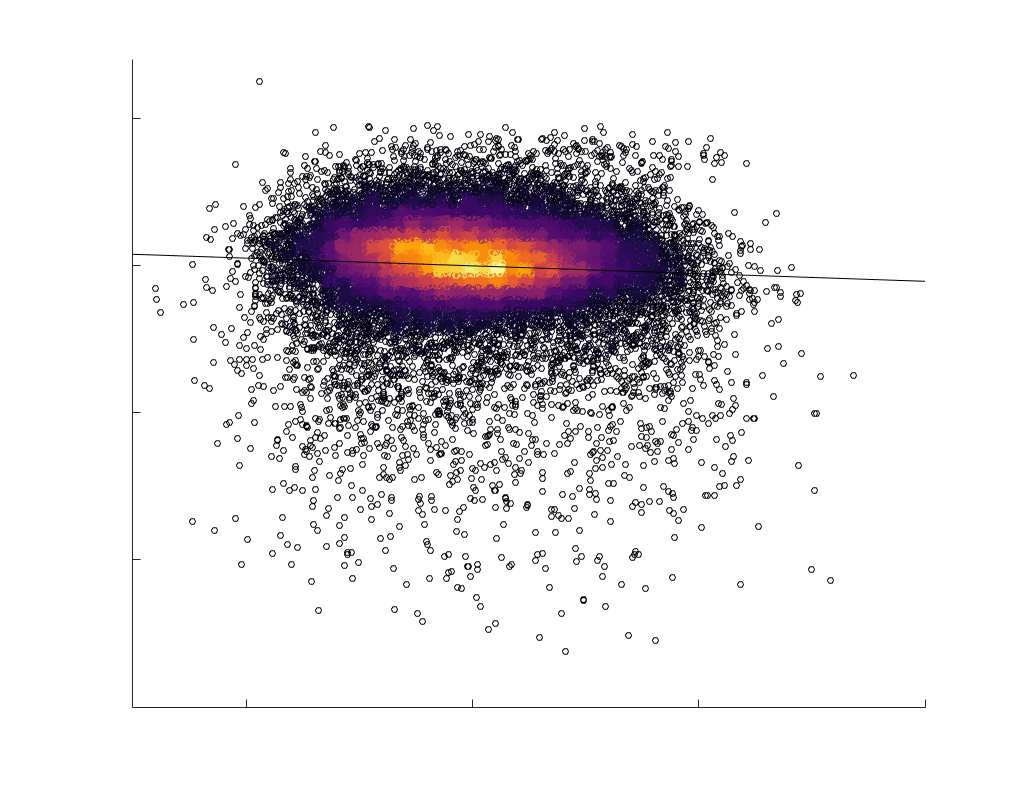
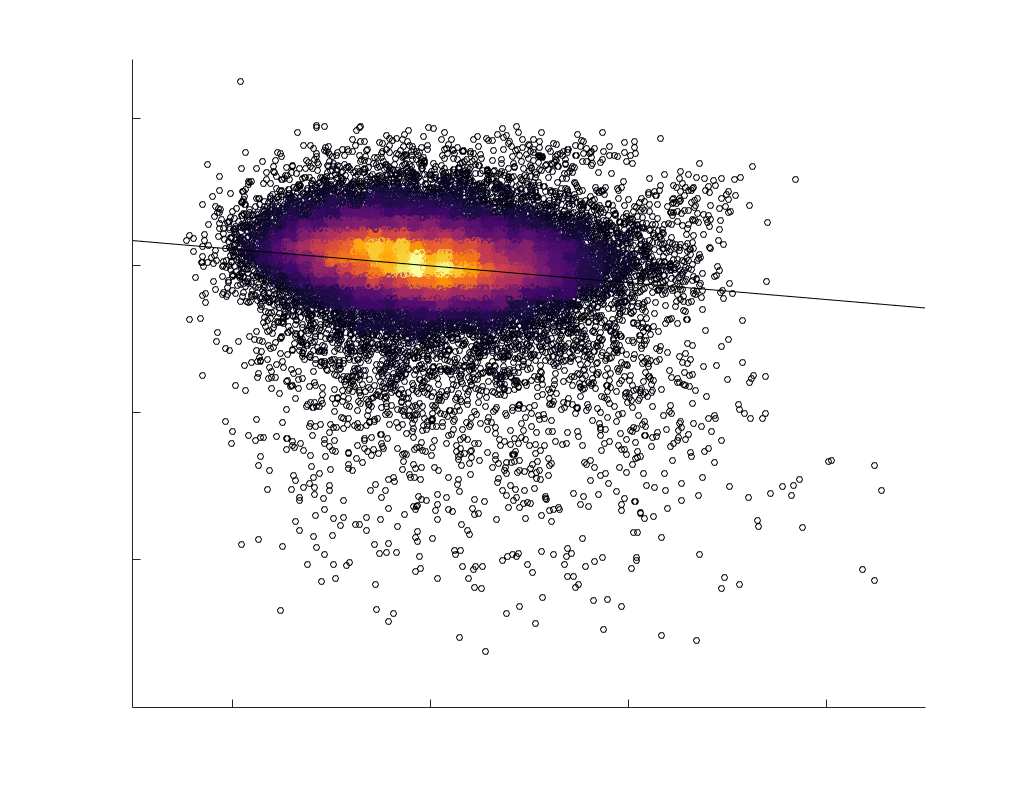
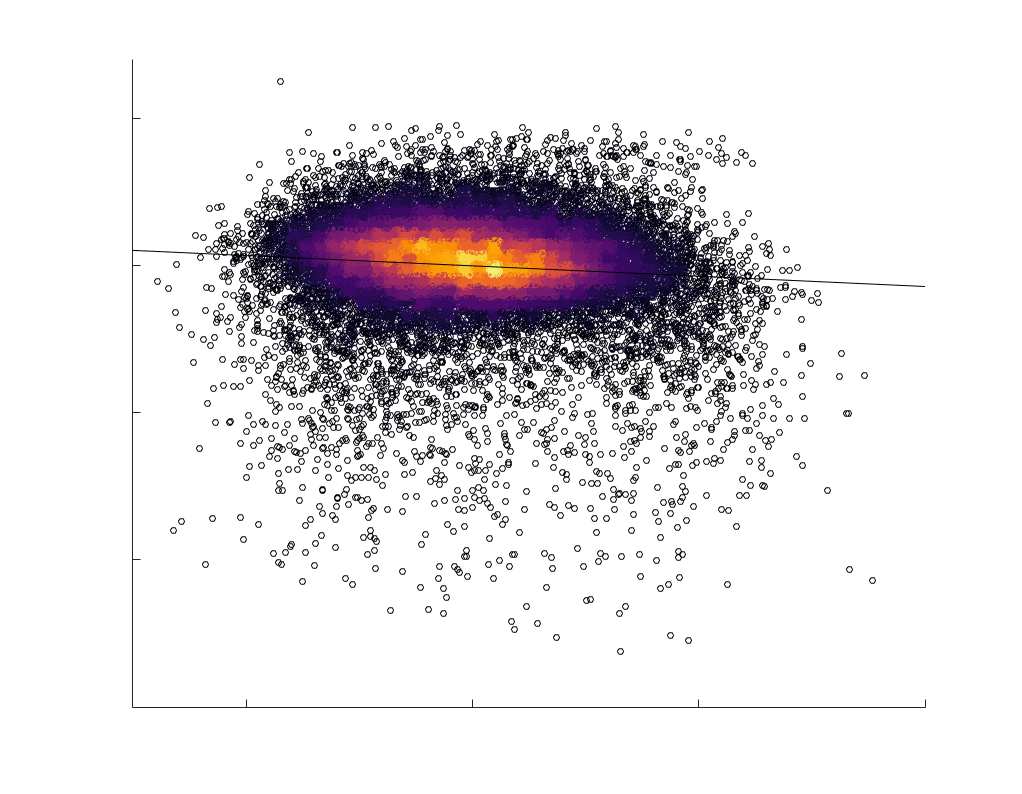
283
284
285
286
287
288
289
290
291
292
293
294
295
Computing correlations of edge weights (not residuals) within edge-length bins allows the
296
inverse relationship between R1 and COMMIT to be traced to the shortest edges of the network
297
(group -0.40, subject -0.50). As edge length increases, this relationship is reduced to 0,
298
then becomes strongly positive in the longest subject-level edges ( 0.39). The scatter plot of
299
group-level R1 vs COMMIT (middle) shows decreasing COMMIT and increasing R1 with
300
increasing edge length. All together, these results support an inverse relationship between the
301
edge caliber and myelin content of a given white matter tract. This can be partly explained by the
302
differential dependence of these structural features on edge length: longer tracts tend to be more
303
myelinated with lower total intra-axonal cross-sectional area. Cependant, this relationship is robust
304
to controlling for edge length supporting an intrinsic dependence between these white matter
305
features.
306
17
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
307
En outre, we show that our R1-weighted network corresponds well with a previously reported
308
(Boshkovski et al., 2021) R1-weighted structural connectome (Figure S13).
309
310
311
Divergent Small-Worldness, Hubness and Rich Club in Weighted Structural Networks
312
In this final section, we apply network analysis tools (Rubinov & Sporns, 2010) based on graph
313
théorie (Fornito et al., 2013; Sporns, 2018) to group-level weighted SC networks. This facilitates
314
high-level interpretation of general features of network communication such as integrative vs
315
segregative processing and the economy of network organization. Although the high material
316
and metabolic cost of brain tissue naturally tends to favor local connectivity (high clustering),
317
short overall network path length is achieved through a small number of relatively expensive
318
long-range connections (Bullmore & Sporns, 2012). These edges and the nodes they interlink
319
form a densely connected network core known as the rich club (Martijn P. van den Heuvel &
320
Sporns, 2011). While the general proclivity for high local clustering gives rise to segregated
321
functional modules, the rich-club nodes act as network communication hubs supporting inter-
322
modular integration (Collin et al., 2014; de Reus & van den Heuvel, 2014; Griffa & Van den
323
Heuvel, 2018; Kim & Min, 2020; Martijn P. van den Heuvel & Sporns, 2013). Ainsi, small-world
324
network topology (high clustering and low path length) (Bassett & Bullmore, 2006, 2017)
325
supports both integrative and segregative processing at a minimum of wiring cost, et le
326
underlying scaffold of hub brain regions tend to show high centrality, low path length (haut
327
closeness) and low clustering (M.. P.. van den Heuvel et al., 2010).
328
18
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
t
/
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
t
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
329
Ici, we report normalized small-worldness, normalized rich-club curves and nodal hubness
330
(Chiffre 6). Normalized small-worldness (S) is computed as the quotient of normalized measures
331
of clustering coefficient (C/Cnull) and path length (L/Lnull).
332
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
t
/
.
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
19
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
t
.
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
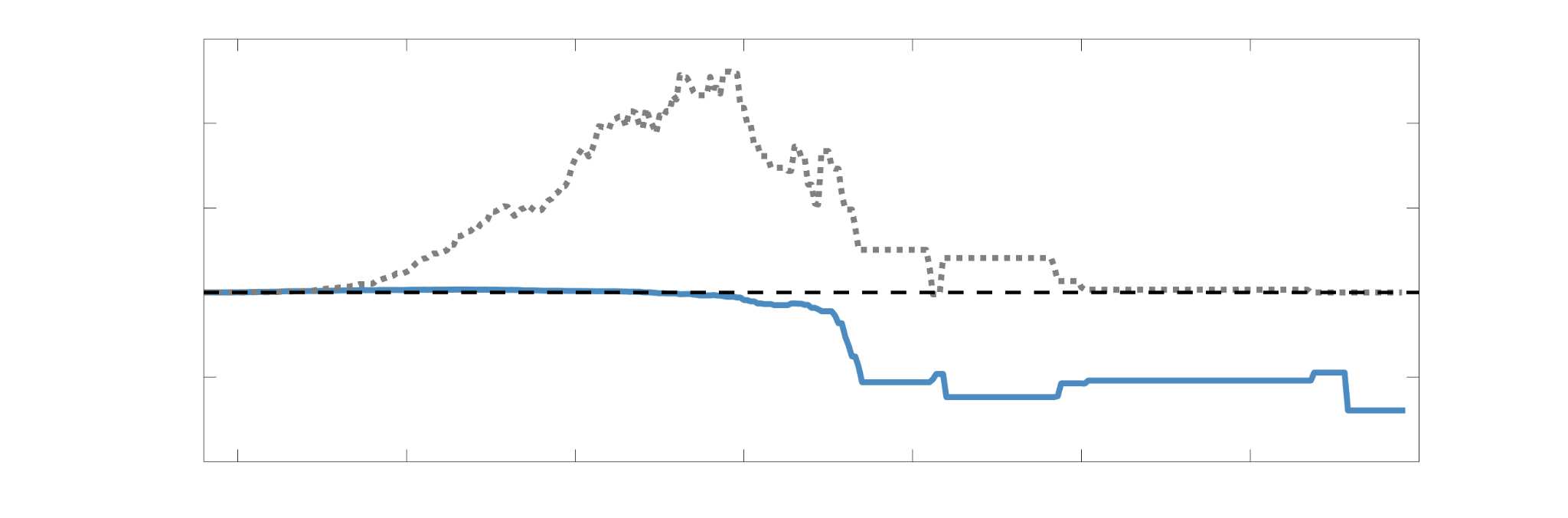
333
334
335
336
337
338
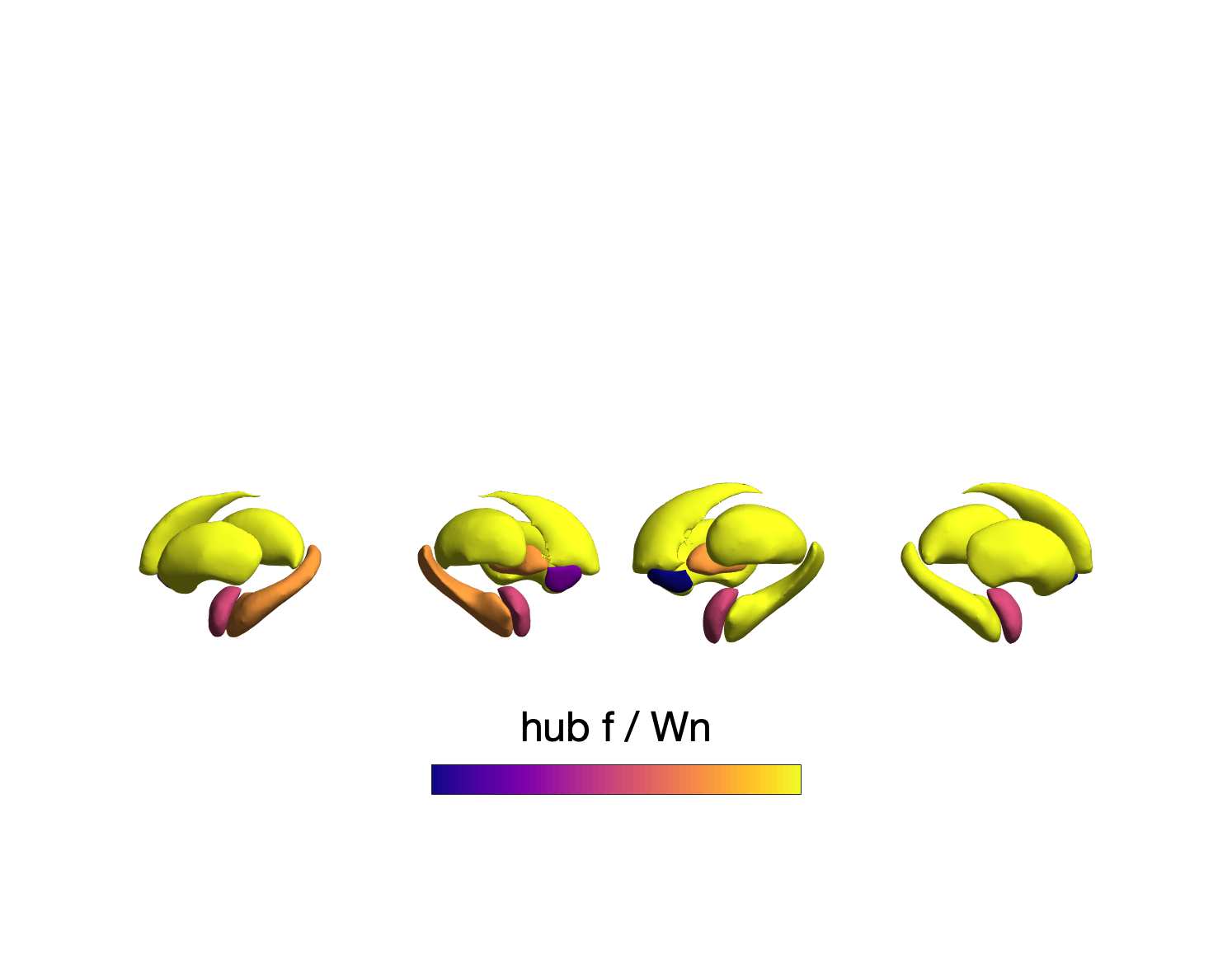
339
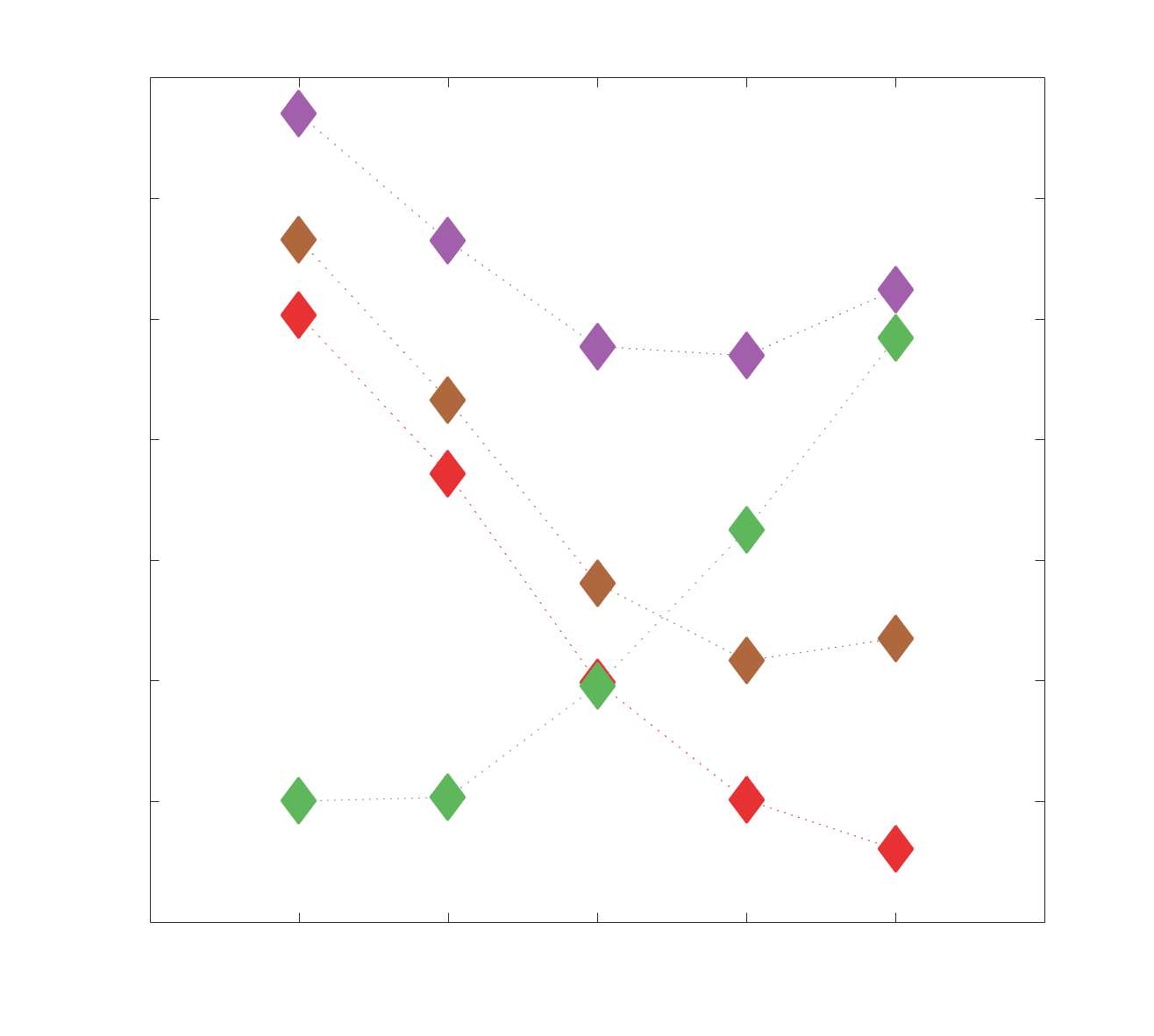
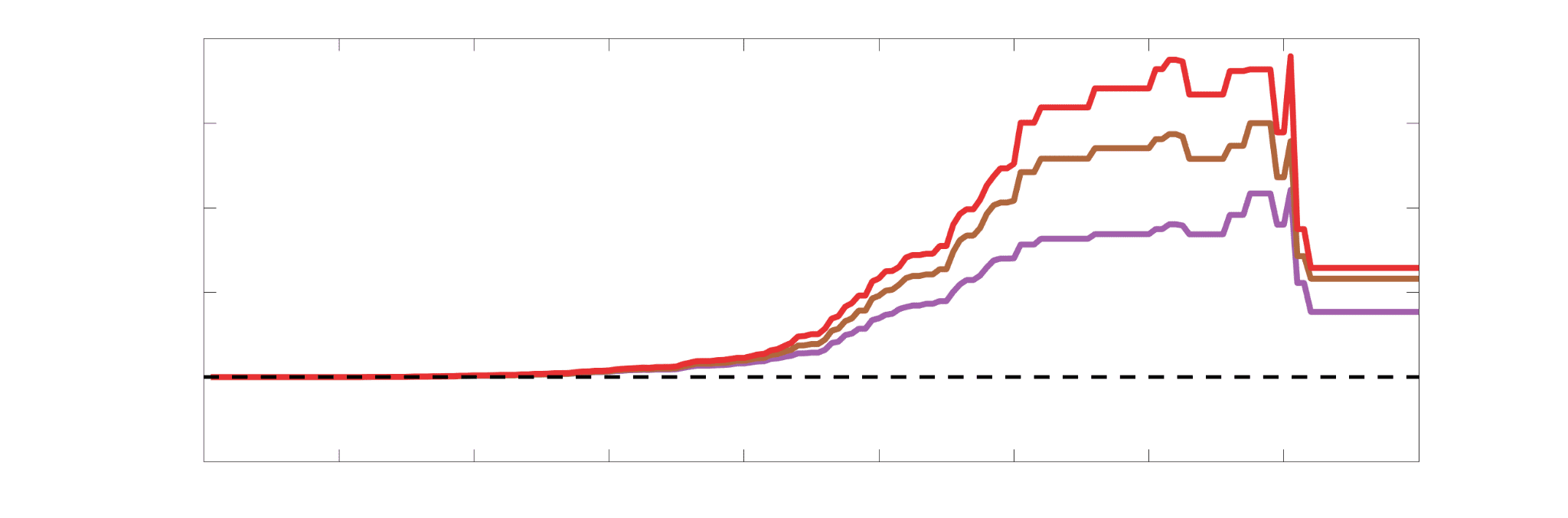
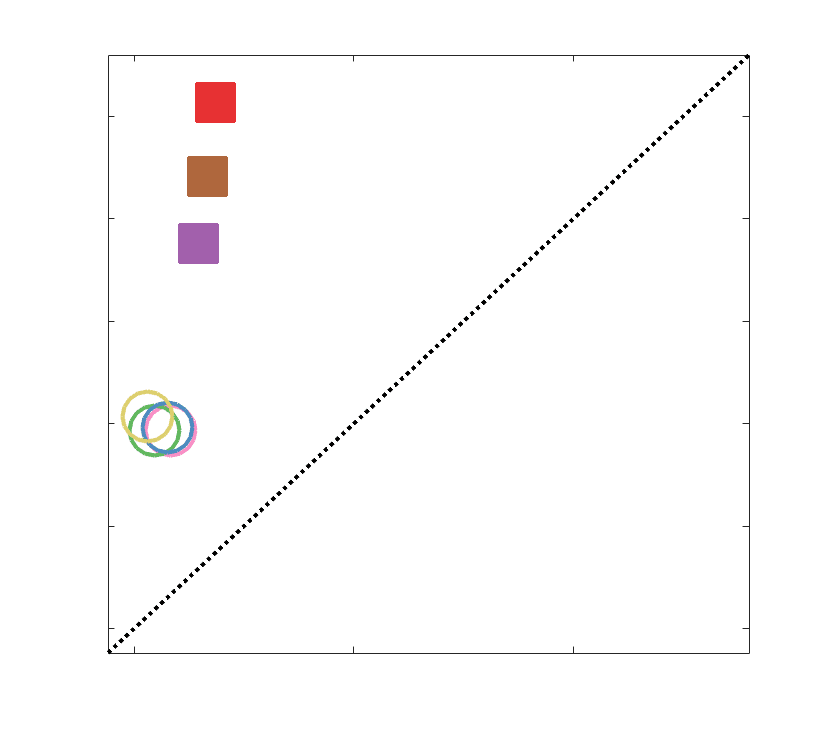
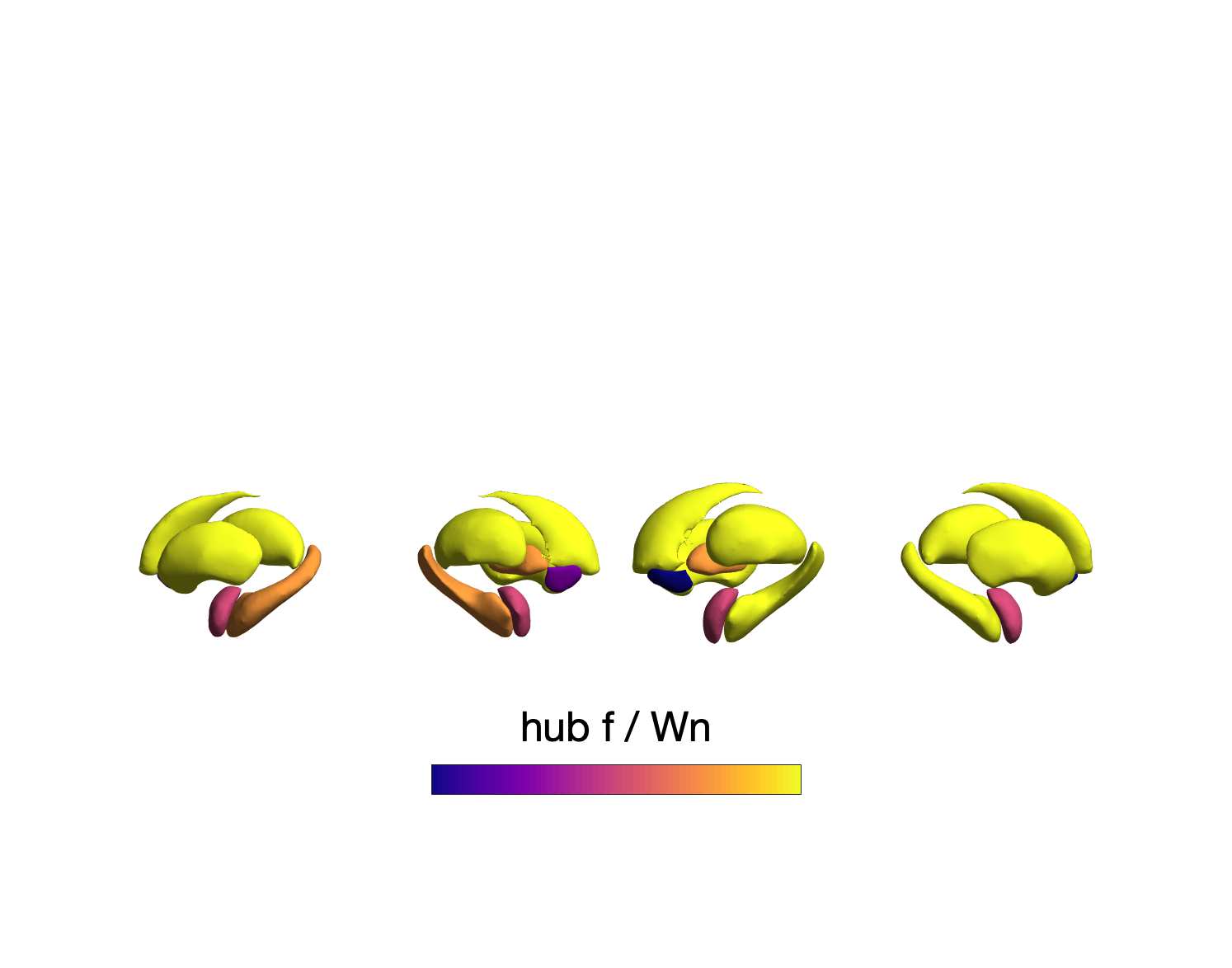
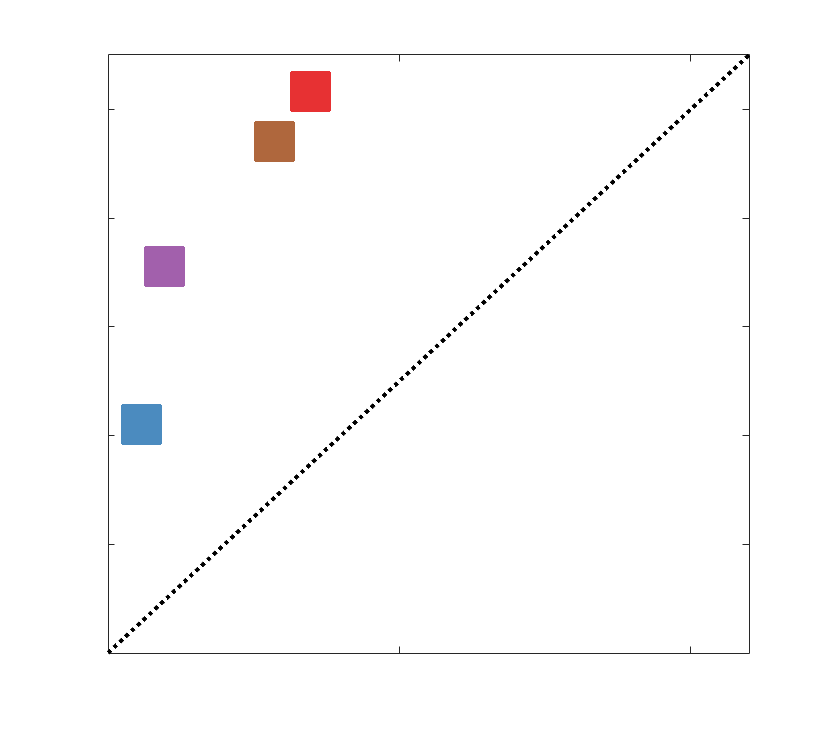
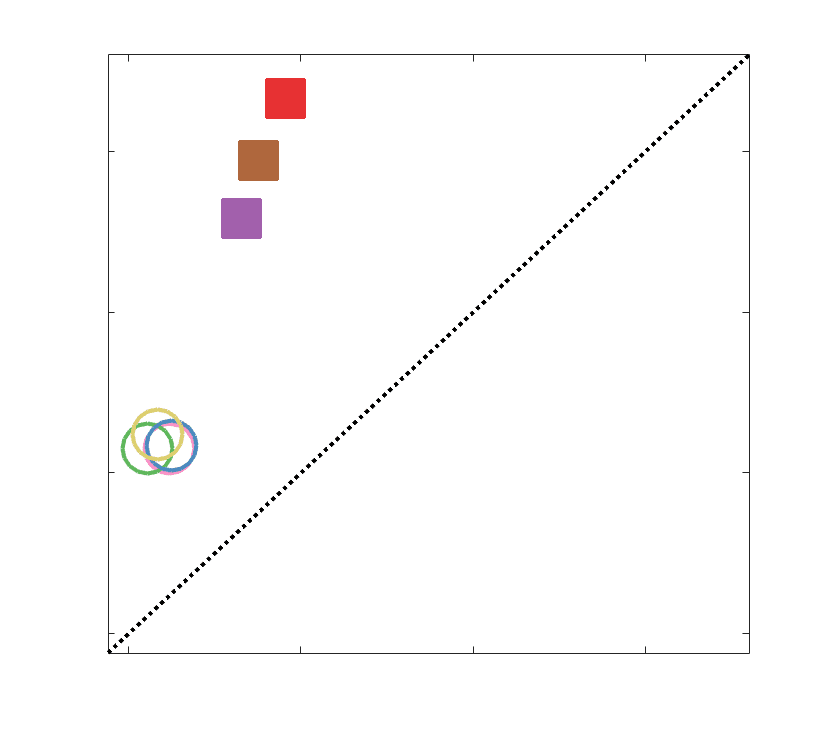
Chiffre 6. Group-Level Network Topology. (UN) Small-worldness was estimated in all structural networks:
clustering coefficient was normalized within each node, averaged across nodes (C/Cnull), then plot as a
function of normalized characteristic path length (L/Lnull). Topology measures averaged across 50 degree
and strength preserving null networks were used for normalization. Networks above the identity line
(dotted black) are characterized by the small world attribute. Tractometry networks are indicated by the
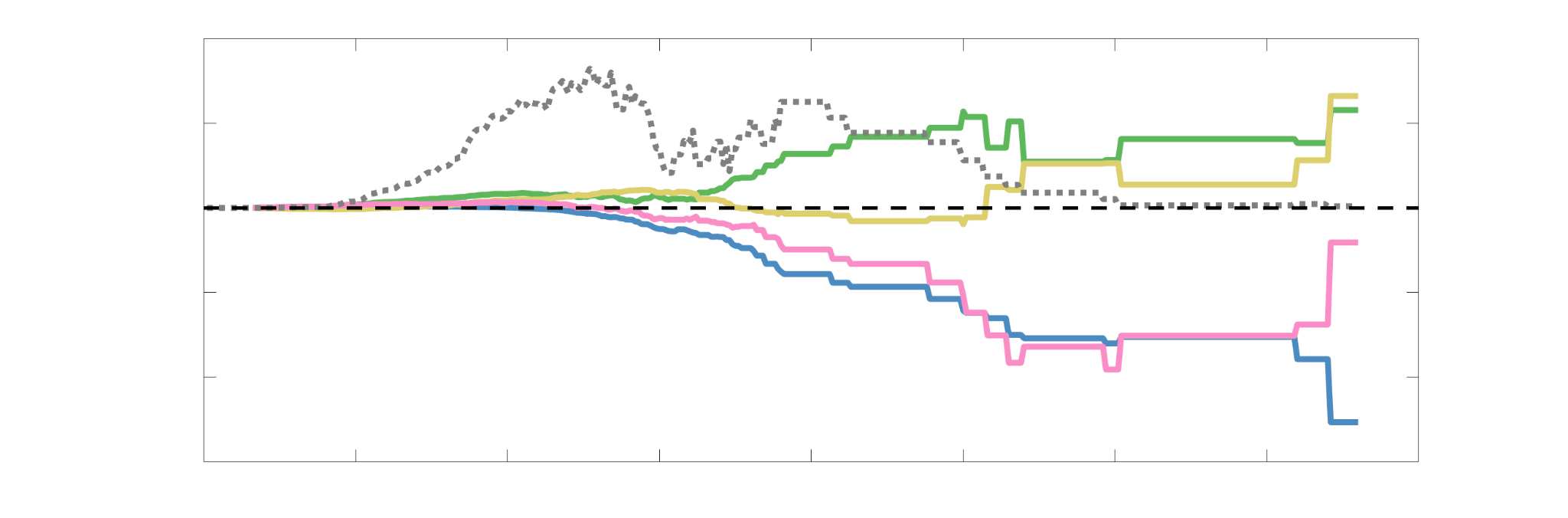
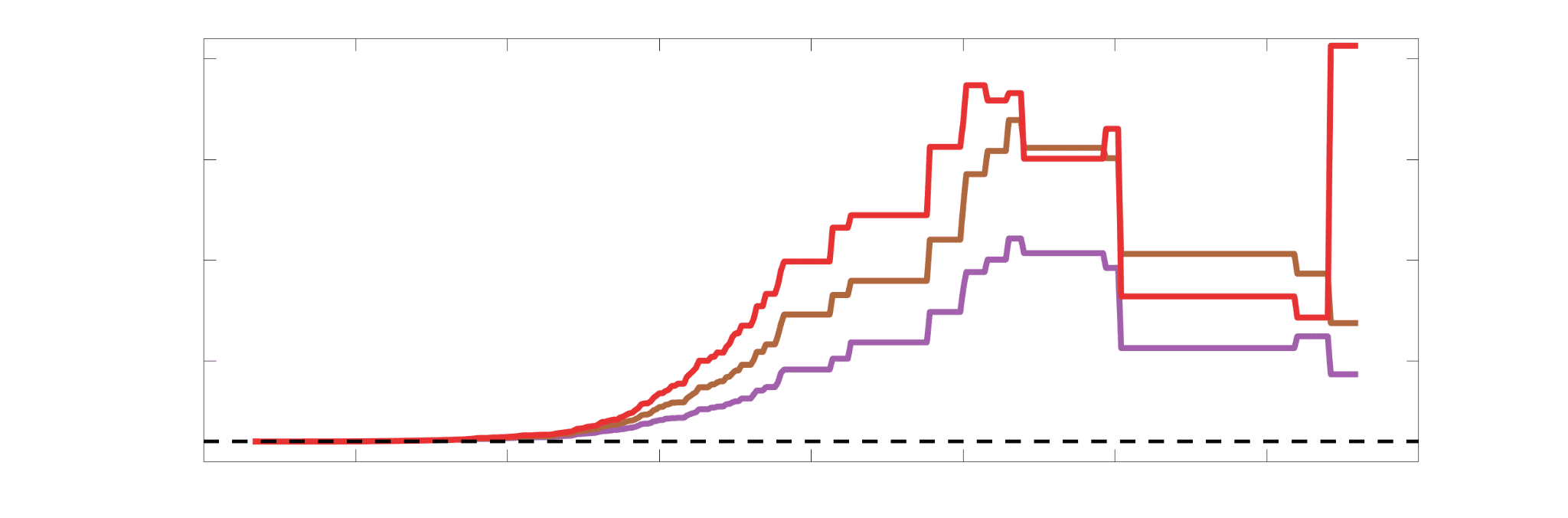
arrow. (B) Normalized rich-club curves are shown for COMMIT, NoS and SIFT2 (top), as well as ICVF,
20
RD, FA and R1 (bottom). A single binary network (dotted gray line) is also shown (bottom) as binary
connectivity was uniform across weighted networks. The normalized rich-club coefficient (norm) était
computed across the range of degree (k) and normalized against 1000 null networks (degree preserving
for binary and degree and strength preserving for weighted networks). A norm value > 1 (horizontal
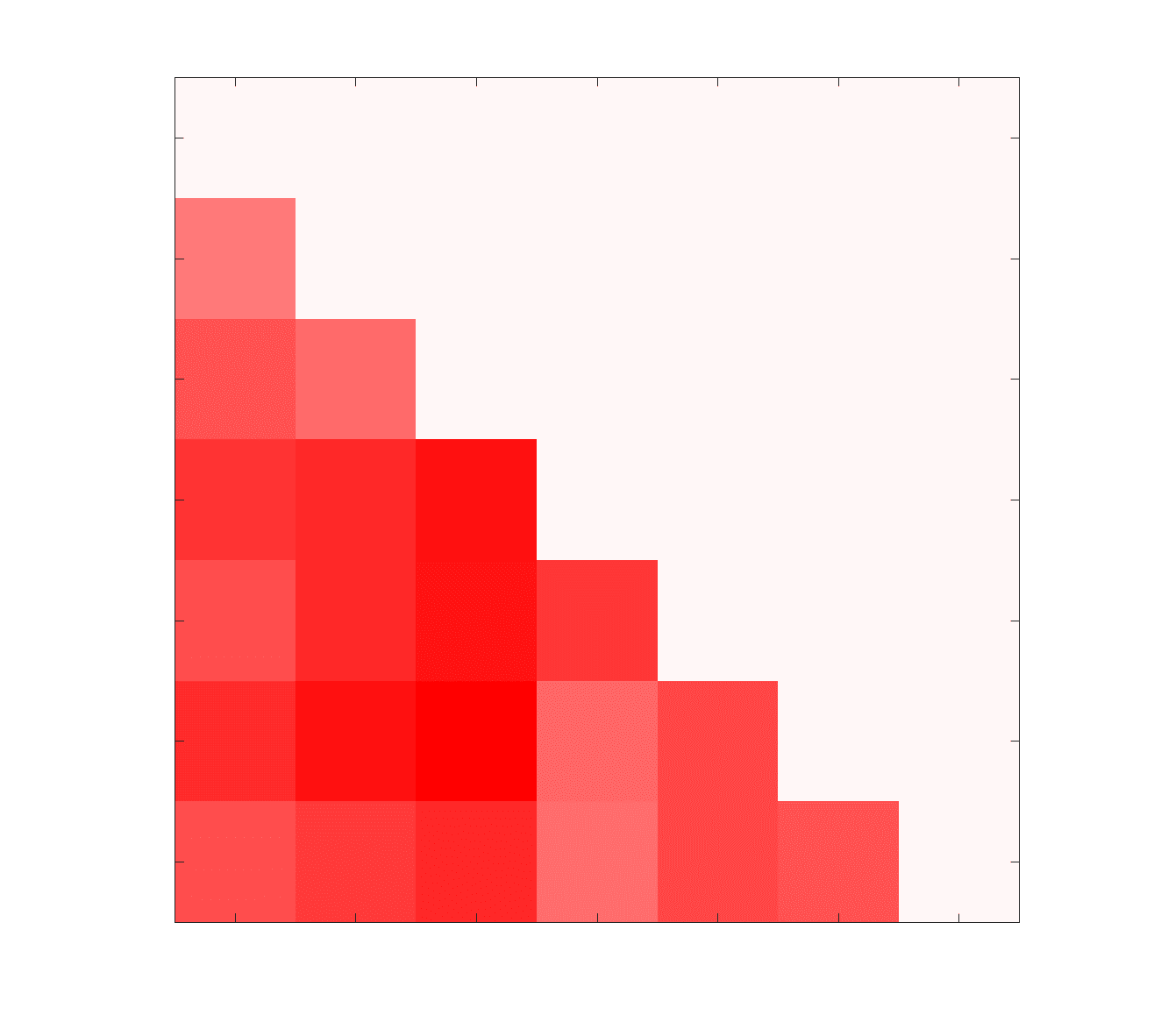
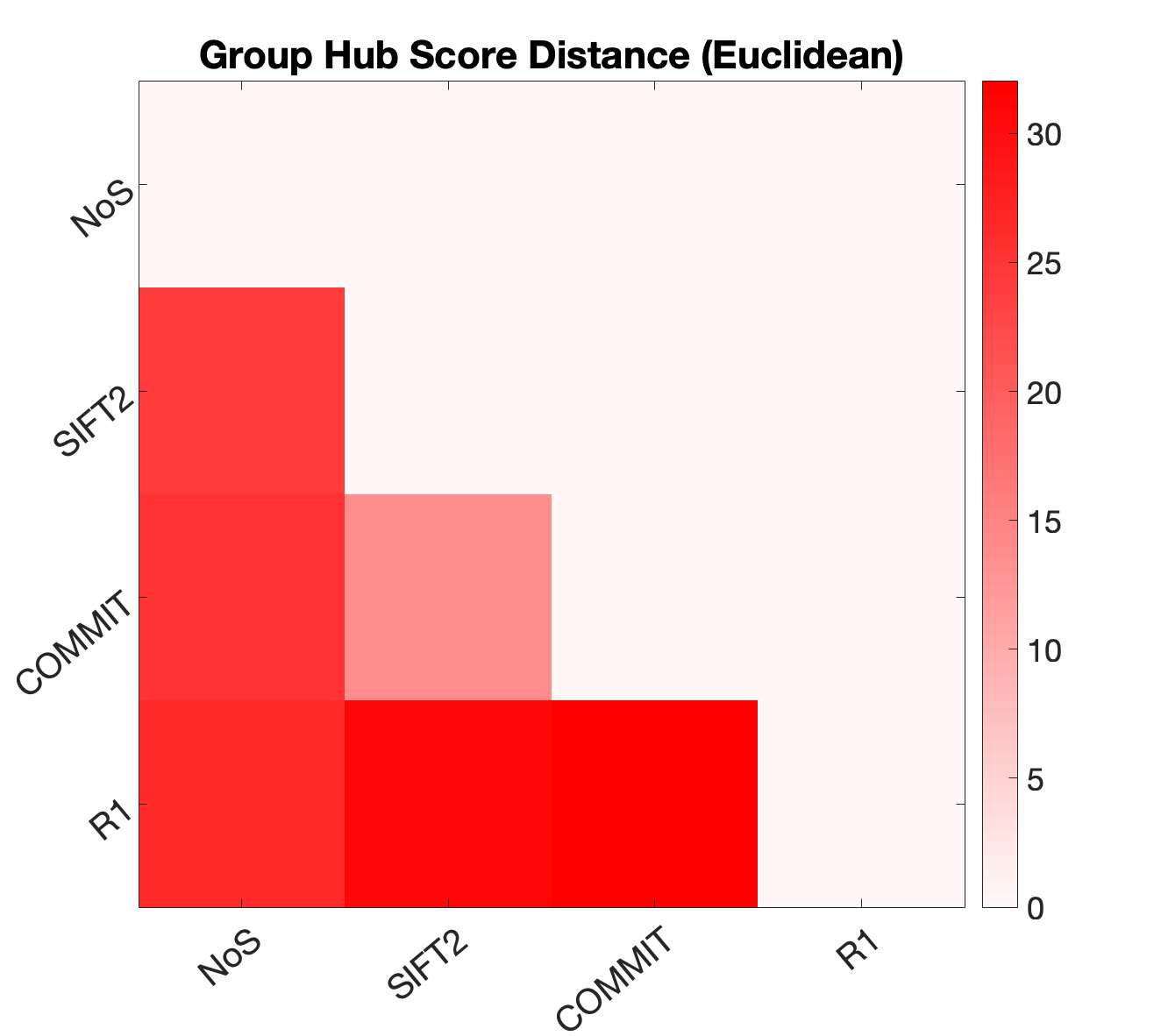
dashed black lines) over a range of k indicates the presence of a rich club. (C) Nodewise hubness scores
are projected onto Schaefer-400 cortical and 14-ROI subcortical surfaces. Scores (0-5) were computed
for each node as +1 point for all nodes in top 20% strength, betweenness, closeness and eigenvector
centrality, as well as bottom 20% clustering coefficient. The matrix (droite) shows the Euclidean distance
between all pairs of nodal hubness vectors.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
340
341
342
343
344
345
346
347
348
349
350
All group-level weighted SC networks show the normalized small-world property (S > 1) de
351
higher clustering and lower path length than would be expected by chance (Figure 6A). Petit-
352
worldness is highest in COMMIT (S 2.5) and lowest in R1, ICVF, FA and RD (S 1.6). Dans
353
contraste, all weighted SC networks did not show a canonical rich club (Figure 6B). Relative to
354
the tractometry and binary SC networks, the normalized rich-club coefficient (norm) was much
355
higher in magnitude in NoS, SIFT2 and COMMIT. A rich club was detected in these networks
356
across a large range of degree (k) levels (150 < k < 300). norm was maximal at k 265 in 357 COMMIT. A rich club was also detected across a similar range of k levels in ICVF and across k 358 in the range [250 300] for RD, albeit with much lower magnitude norm. However, no clear rich 359 club was observed in R1 or FA. In fact, the rich-club curves for these networks are roughly 360 symmetric about the norm = 1 line relative to COMMIT. A densely connected core was of course 361 recovered in all weighted SC networks (uniform binary connectivity), but these results suggest 362 that its interconnecting edges were consistently weaker than would be expected by chance in R1 21 / / t e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 363 and FA. By comparison, a rich club was observed in the binary SC network across the very large 364 range of k [50 300]. This supports two important concepts: (1) SC network edge weights can 365 provide an additional layer of information useful for refining the topology of binary SC; and (2) 366 different methods for computing SC network edge weights yield diverse network topology. 367 368 Weighted SC networks show network-dependent spatial topology of hubness scores (Figure 369 6C). The COMMIT and R1 averaged surface shows prominent hubs distributed throughout the 370 brain including the fronto-parietal network. Nearly all of the subcortex showed a hubness score 371 of 4 or greater in all networks. The Euclidean distance between hubness score vectors (right) was 372 lower for COMMIT and SIFT2 than for either network with NoS. Of the streamline-specific 373 networks, NoS was more similar to both R1 and IVCF. Overall, these results illustrate the 374 considerable impact that edge weighting can have on network topology. 375 376 377 DISCUSSION l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / t . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t / . 378 Structure-function brain models provide a flexible framework for investigating the mechanistic 379 relationship between human brain structure and function in vivo, yet the interpretability of these 380 models is currently limited by a lack of biological detail. Here, we assemble a thorough 381 characterization of structural brain networks weighted by a range of quantitative MRI metrics 382 capturing the macro- and microscopic features of white matter tracts. Notable trends included: 383 (1) greater edge weight contrast and skewed (heavy-tailed) distributions in the streamline- 384 specific networks NoS, SIFT2 and COMMIT; (2) whole-brain correlations with FC in networks 385 weighted by connection strength (positive) and myelin (negative) which were robust to f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 22 386 controlling for edge length; (3) whole-brain inverse relationships with myelin for networks 387 weighted by connection strength and neurite density independent of edge length; and (4) the 388 absence of a rich club in R1 and FA networks. All weighted SC networks showed a strong spatial 389 dependence and small-world architecture. Collectively, these results support the overall 390 conclusion that SC networks weighted by edge caliber (e.g., SIFT2 and COMMIT) and myelin 391 (e.g., R1) can be used to quantify non-overlapping subsets of white matter structural features 392 related to FC supporting their joint utilization in modeling function. 393 394 395 Interpretable Measures of Connection Strength Provided by COMMIT and SIFT2 396 A principal goal of this work is to identify what, if any, advantage over NoS is provided by the 397 global optimization methods SIFT2 and COMMIT. NoS has previously been used to inform the 398 strength of interregional coupling in computational models of function (e.g., (Honey et al., 399 2009)). However, important limitations restrict model interpretation. Besides suffering from a 400 range of biases related to the position, size, shape and length of white matter tracts (Girard et al., 401 2014), NoS varies as a function of tracking parameters limiting its specificity for white matter 402 structural features (Jones, 2010; Jones et al., 2013). 403 404 SIFT2 and COMMIT reportedly restore the quantitative link between connectome edge weights 405 and white matter structural features related to connection strength. COMMIT and SIFT2 solve 406 for the effective cross-sectional area (i.e., signal fraction) of each streamline using different 407 approaches. COMMIT uses the global diffusion signal to optimize these values, whereas SIFT2 408 seeks to fit the streamline density throughout the white matter to the fiber densities estimated 23 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 409 using spherical deconvolution. Thus, while both methods rely on the simplifying assumption that 410 streamline features are invariant along their length, SIFT2 additionally requires that the estimates 411 of fiber density derived from the fiber orientation distribution (FOD) are biologically accurate. 412 413 These networks also differ in the computation of their edge weights: SIFT2 is computed as the 414 simple sum of streamline weights, whereas COMMIT is computed as the length-weighted-sum 415 of streamline weights. Indeed, our analysis methods do not permit us to make strong claims as to 416 the relationship between these methodological differences and our observed results, however we 417 do show that both SIFT2 and COMMIT display comparable but not identical fundamental 418 characteristics to NoS. This supports the use of SIFT2 or COMMIT in place of NoS as a measure 419 of connection strength, which brings with it improved biological interpretability. 420 421 422 Myelin Complements Connection Strength in Predicting FC 423 Despite the differences between COMMIT, SIFT2 and NoS; our results indicate that their edge 424 weights show roughly equivalent positive correlations with FC over the whole brain. R1 was 425 negatively correlated with FC. Significant evidence indicates a link between cerebral myelin and 426 FC including: a relationship between intracortical myelin and FC (Huntenburg et al., 2017; 427 Wang et al., 2019); the prediction of cognition (Sonya Bells et al., 2017; Caeyenberghs et al., 428 2016) and FC-derived components (Messaritaki et al., 2021) using myelin-sensitive metrics; and 429 a relationship between damaged myelin sheaths and greater conduction delays in multiple 430 sclerosis (Sorrentino et al., 2022). At the cellular-level, myelin contributes to conduction velocity 431 (Huxley & Stämpfli, 1949), metabolic support (Nave & Werner, 2014) and plasticity (Gibson et 24 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / t / . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 432 al., 2018), all of which could be argued to support brain function. Myelin plasticity in particular 433 can be described in terms of “activity-dependence”, whereby an increase in the functional 434 activity of a given circuit stimulates cellular signaling cascades promoting greater myelination 435 (Douglas Fields, 2015; Mount & Monje, 2017). Coupled with our results, this complex mix of 436 functional roles supports the idea that structure-function models will be improved by integrating 437 measures of myelin and connection strength. 438 439 440 An Opposing Relationship with Edge Length for Edge Caliber and Myelin Content 441 When controlling for edge length, we found an inverse relationship between R1 and COMMIT 442 over the whole brain in all subjects and at the group level. This suggests that the aggregate g- 443 ratio (ratio of inner/outer diameters of myelinated axons) of a white matter tract may increase 444 with edge caliber. At the cellular-level, the diameter of an axon and the thickness of its myelin 445 sheath show nearly a linear relationship over a broad range of smaller diameter axons which 446 becomes increasingly nonlinear as axon diameter increases (Berthold et al., 1983; Hildebrand & 447 Hahn, 1978). In general, increasing axon diameter tends to outpace increasing myelin thickness 448 i.e., g-ratio tends to increase with increasing axon caliber (Hildebrand & Hahn, 1978). Our 449 findings suggest that this cellular-level principle may extend to the systems level: increases in 450 edge caliber tend to outpace changes in the myelin content resulting in a concomitant increase in 451 the g-ratio of white matter tracts. 452 453 We localized the inverse relationship between R1 and COMMIT to the shortest edges suggesting 454 that the g-ratio was the highest in the shortest connections. This result is supported by a previous 25 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / . / / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 455 imaging study showing the highest g-ratio in “local” connections (Mancini et al., 2018). In 456 general, we found that R1 increased and COMMIT decreased with increasing edge length, which 457 aligns with previously reported results of higher R1 and fewer streamlines for the white matter 458 connections between transmodal regions (Boshkovski et al., 2021). Both of these trends fit well 459 with theories of brain wiring economy in which the energetic cost of maintaining biological 460 material increases with connection length (Bullmore & Sporns, 2012). This natural pressure acts 461 to reduce the total axonal volume of longer white matter bundles. Increasing the myelin content 462 of longer tracts comes at a cost as well, but this may be at least partially offset as increasing 463 myelin content reduces the total membrane surface area along which expensive electrochemical 464 gradients must be maintained (Bullmore & Sporns, 2012). Although, a cost-benefit analysis of 465 the energetics of myelination concluded that the energetic cost of myelin maintenance outweighs 466 any savings on action potentials (Harris & Attwell, 2012). This suggests that higher myelination 467 of longer edges may be better explained as a mechanism to provide trophic support (Nave & 468 Werner, 2014) to vital inter-regional connections (Martijn P. Van Den Heuvel et al., 2012) or to 469 reduce conduction delays. 470 471 472 Edge Weight Variance Decreases with Edge Length in Most Weighted Structural Networks? 473 White matter features related to myelin content, connection strength and neurite density tend to 474 become more consistent across tracts as tract length increases. Greater variability in the weights 475 of the shortest connections could result from a higher proportion of false positive streamlines 476 influencing these edge weights. For SIFT2 and COMMIT, streamline weight computation 477 becomes increasingly unstable with decreasing length as fewer voxels contribute to the fit. 26 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / . / t / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 478 However, this result could also be explained more generally by contrasting the roles of shorter 479 and longer connections in the brain. Shorter white matter tracts connect brain regions near each 480 other in space e.g., within the same module. Just as we might expect the characteristics of 481 smaller roads and streets (e.g., width, building materials, markings, signs, sidewalks, etc.) to vary 482 by neighborhood and city, we might also expect the morphology of shorter white matter 483 connections to change as the functional specialization of any given region or module changes. 484 On the other hand, longer tracts (i.e., the freeways of the brain) may overlap more in both their 485 functional role and morphological features relative to shorter connections, hence lower edge 486 weight variability. Breaking with the above pattern, FA and RD showed the highest edge weight 487 variance in the longest connections. Given that structural measures derived using a voxel-wise 488 diffusion tensor model are particularly sensitive to the white matter “architectural paradigm” 489 (Jones et al., 2013), these results suggest that white matter features related to fiber orientation 490 and geometry actually diverge with increasing tract length. Note that we are unable to say 491 decisively whether the edge weight variance measured in these structural and functional brain 492 networks corresponds to true signal or noise. The inclusion of scan-rescan data (e.g., as in 493 (Amico & Goñi, 2018)) could support stronger conclusions as to the source of this variability. 494 495 496 The Absence of a Rich Club in Structural Networks Weighted by R1 and FA 497 Group-level R1 and FA did not show a normalized weighted rich club for any degree k. Higher 498 myelination in the white matter tracts connecting rich club nodes has previously been reported 499 (Collin et al., 2014); however, methodological differences limit comparability. A rich club has 500 previously been reported in FA-weighted networks using similar methods to ours (Martijn P. van 27 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 501 den Heuvel & Sporns, 2011). The source of this disagreement could potentially be attributed to 502 differences in our tractography algorithm, parcellation or null network computation. 503 504 In weighted rich-club detection, the identification of a densely connected core is independent of 505 edge weight (depends only on node degree), but the designation of this subnetwork as a rich club 506 requires that it contains a higher-than-chance proportion of the strongest edges from the full 507 network. Indeed, this is the case over a broad range of degree k for COMMIT. Over the same 508 range of k, the normalized rich-club curves for R1 and FA are inverted about the threshold value 509 of 1 with respect to COMMIT. This implies that the subnetwork found at a given k in this range 510 contains edges which tend to show higher COMMIT and lower R1 edge weights than expected 511 by chance. We previously showed edgewise inverse correlations between R1 and COMMIT 512 which were robust to controlling for edge length. We also showed that R1 and FA are positively 513 correlated under these same conditions. In this light, it is not surprising that the edges connecting 514 rich-club nodes tend to show opposite trends in R1- and FA-weighting with respect to COMMIT. 515 Nonetheless, it is possible that the lack of a rich club in our myelin-weighted network is an 516 artifact of tractometry. Future work will attempt to replicate this result using myelin-weighted 517 networks computed with a different methodology (Schiavi et al., 2022). 518 519 520 Replication Across Parcellation Resolution and in a Second Dataset 521 In this report, we have chosen to feature data in the Schaefer-400 cortical parcellation plus 14 522 subcortical nodes. However, there is little consensus on the best brain atlas, and the optimal 523 choice likely depends on the specifics of your data and the question being investigated. In a 28 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 524 supplementary analysis, we replicated our results across 100-900 node Schaefer cortical atlases. 525 We found that residual edgewise correlations with FC (Figure S1) and R1 (Figure S2), as well 526 as normalized rich club and normalized small worldness (Figure S3) were robust to parcellation 527 resolution. In contrast, the spatial topography of high-hubness brain regions appears qualitatively 528 dependent on parcellation granularity, although further analyses would be necessary to draw 529 stronger conclusions (Figure S4). 530 531 An independent multimodal dataset was also used to replicate the main SC results including the 532 residual edgewise correlations with R1 and the relationship between R1 and COMMIT across 533 edge length bins (Figure S5), as well as all network topology results (Figure S6). 534 535 536 Limitations 537 Streamline tractography is known to suffer from several important biases including both false 538 positive and negative streamlines, which can influence downstream analyses (Maier-Hein et al., 539 2017; Schilling et al., 2019; Sotiropoulos & Zalesky, 2019; Zalesky et al., 2016). Through 540 probabilistic tractography, we opted to minimize false negatives while maximizing false 541 positives. This allowed us to implement careful streamline- and edge-filtering strategies in post- 542 processing to address this known bias. Still, without a ground truth, we cannot quantify the 543 extent to which we were successful in mitigating this issue, nor can we guarantee that we did not 544 erroneously filter true positive streamlines or edges. All processing and filtering methods were 545 consistent and network density was uniform across weighted structural networks. Thus, any 546 major tractography bias should be as homogeneous as possible across networks. 29 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 547 548 Tractometry-derived brain networks suffer from widespread partial volume effects due to 549 crossing and kissing fibers in a majority of white matter voxels. The net effect of this bias is well 550 understood and is apparent in our results and previous work (De Santis et al., 2014; Schiavi et 551 al., 2022). Nonetheless, this method was included here as our goal was to characterize widely 552 used structural connectivity methods. New techniques for reducing this bias are currently being 553 developed which allow for the estimation of tract-specific microstructural features (e.g., 554 (Barakovic, Girard, et al., 2021; Barakovic, Tax, et al., 2021; De Santis et al., 2016; Leppert et 555 al., 2021, 2023; Schiavi et al., 2022)). 556 557 We were unable to assess repeatability in this work as we did not have scan-rescan data. 558 However, reproducibility has already been assessed for NODDI (Chung et al., 2016; Lehmann et 559 al., 2021), MP2RAGE-derived T1 maps (Marques et al., 2010), diffusion-tractography-based 560 structural connectivity (Bonilha et al., 2015), as well as COMMIT and SIFT2 tractogram 561 filtering (Koch et al., 2022). The reproducibility of the tractometry features (R1, FA, RD, ICVF) 562 will mainly depend on these previous steps and the accuracy of the spatial alignment of the 563 multi-modal data. 564 565 In this work, we have attempted to thoroughly examine the fundamental properties of a wide 566 range of standard and state-of-the-art metrics for quantifying white matter brain structure. 567 However, the scope of possible methods and their respective variants is too broad to treat 568 thoroughly in a single body of work. In particular, track-weighted imaging (Calamante, 2017; 569 Calamante et al., 2010, 2012) and fixel-based analysis (Dhollander et al., 2021; Raffelt et al., 30 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / t . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 570 2015, 2017) provide state-of-the-art solutions to the challenge of quantifying white matter 571 structural features in the presence of crossing fibers. 572 573 574 Conclusion 575 We presented a thorough characterization of weighted SC networks. Overall, our findings 576 support the joint use of SC networks weighted by connection strength and myelin in predicting 577 FC. In particular, using the COMMIT or SIFT2 algorithms to quantify connection strength 578 shows promise to improve model interpretability relative to NoS. Beyond R1, there is a wide 579 array of myelin sensitive metrics that could be used to compute useful myelin-weighted 580 networks. The integration of this microstructure-weighted connectivity approach into structure- 581 function models will advance the mechanistic interpretation of both the function and dysfunction 582 of the living human brain. 583 584 585 MATERIALS and METHODS 586 These data are available for download (https://portal.conp.ca/dataset?id=projects/mica-mics). See 587 Royer et al. (Royer et al., 2022), Cruces et al. (Cruces et al., 2022) for full details of data 588 acquisition and processing. All data processing and analysis code is openly available at 589 https://github.com/TardifLab/Weighted-SC-Networks. 590 591 592 Data Acquisition & Preprocessing 31 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / / t . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 593 Multimodal MRI data was collected in 50 healthy volunteers at 3 Tesla on a Siemens Magnetom 594 Prisma-Fit scanner equipped with a 64-channel head coil as follows: T1-weighted (T1w) anatomical: 3D magnetization-prepared rapid gradient-echo sequence (MP-RAGE; 0.8mm isotropic; TR = 2300ms; TE = 3.14ms; TI = 900ms; iPAT = 2; partial Fourier = 6/8) Multi-shell diffusion-weighted imaging (DWI): 2D pulsed gradient spin-echo echo-planar imaging sequence consisting of three shells with b-values 300, 700, and 2000s/mm2 and diffusion directions 10, 40, and 90, respectively (1.6mm isotropic; TR = 3500ms, TE = 64.40ms; multi-band factor = 3). b0 images were also acquired with reverse phase encoding direction to facilitate distortion correction of DWI data. 7 minutes of resting-state functional MRI: multi-band accelerated 2D-BOLD gradient echo echo-planar sequence (3mm isotropic; TR = 600ms, TE = 30ms; mb factor = 6; flip angle = 52°). Two spin-echo images with AP and PA phase encoding were additionally acquired (3mm isotropic; TR = 4029ms; TE = 48ms; flip angle=90°). Quantitative T1 relaxometry data was acquired with a 3D-MP2RAGE sequence (Marques et al., 2010) (0.8mm isotropic; TR = 5000ms, TE = 2.9ms, TI1 = 940ms, T12 = 2830ms; iPAT = 3; partial Fourier = 6/8). This was used to compute a T1 map which was sampled to estimate the edge weights in R1 (1/T1) networks (myelin-weighted). 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 The multi-modal processing pipeline micapipe (Cruces et al., 2022) 613 (https://micapipe.readthedocs.io/) was used to preprocess diffusion, anatomical, and functional 614 images. T1w images were deobliqued, reoriented to standard neuroscience orientation (LPI), 615 corrected for intensity non-uniformity (Tustison et al., 2010), intensity normalized and skull 32 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / / / . t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 616 stripped. Subcortical segmentations were performed with FSL FIRST (Jenkinson et al., 2012; 617 Patenaude et al., 2011) and tissue types were classified using FSL FAST (Y. Zhang et al., 2001). 618 A five-tissue-type image segmentation was generated for anatomically constrained tractography 619 (R. E. Smith et al., 2012). Cortical surface segmentations were generated with FreeSurfer 6.0 620 (Dale et al., 1999; Fischl, Sereno, & Dale, 1999; Fischl, Sereno, Tootell, et al., 1999). 621 622 Diffusion preprocessing was performed in native DWI space using tools from MRtrix3 (J. 623 Donald Tournier et al., 2012, 2019) and proceeded in the following sequence: (1) image 624 denoising (Cordero-Grande et al., 2019; Veraart, Fieremans, et al., 2016; Veraart, Novikov, et 625 al., 2016); (2) two b=0s/mm2 volumes with reverse phase encoding were used to correct for 626 susceptibility distortion, head motion, and eddy currents via FSL’s eddy and TOPUP tools 627 (Andersson et al., 2003; Andersson & Sotiropoulos, 2016; S. M. Smith et al., 2004); and (3) B1+ 628 bias-field correction (Tustison et al., 2010). This pre-processed data was used to estimate multi- 629 shell and multi-tissue response functions for constrained spherical-deconvolution (Christiaens et 630 al., 2015; Dhollander et al., 2016, 2019; Jeurissen et al., 2014) followed by intensity 631 normalization. Non-linear registration was performed with ANTs (Avants et al., 2008) to co- 632 register anatomical images to DWI space. 633 634 Resting-state fMRI pre-processing entailed discarding the first five TRs, reorientation (LPI), 635 motion correction by registering all volumes to the mean, and distortion correction using main 636 phase and reverse phase field maps. Nuisance signal was removed using an ICA-FIX (Salimi- 637 Khorshidi et al., 2014) classifier and by spike regression using motion outlier outputs from FSL 638 (Jenkinson et al., 2012). Volumetric timeseries were averaged for boundary-based registration 33 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / t . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 639 (Greve & Fischl, 2009) to native Freesurfer space and mapped to individual surfaces using 640 trilinear interpolation. Spatial smoothing (Gaussian, FWHM = 10mm) was applied to native- 641 surface and template-mapped cortical timeseries. 642 643 644 Tractography and Microstructural Metrics 645 To estimate structural connectomes, anatomically constrained tractography (R. E. Smith et al., 646 2012) was performed on the normalized white matter FOD image using the probabilistic 647 algorithm iFOD2 (J.-D. Tournier et al., 2010). Tractograms of 5 million streamlines were 648 generated by seeding the gray-white matter interface using the following parameters: 649 maxlength=400, minlength=10, angle=22.5, step=0.5, cutoff=0.06, backtrack, crop_at_gmwmi 650 (gray-matter-white-matter interface). These tractograms were filtered in a two-stage process. (1) 651 a temporary whole-brain connectome weighted by NoS was computed then decomposed into its 652 composite streamlines to derive a new tractogram in which any streamline which failed to 653 connect two gray matter ROIs in the temporary connectome was excluded. This “streamline- 654 filtering” step typically resulted in approximately a 5% decrease in the size of the tractogram 655 (~250k streamlines removed) and was undertaken to ensure that these erroneous streamlines did 656 not affect the COMMIT model. Streamline-filtered tractograms were used to compute NoS and 657 were used as inputs to both the SIFT2 and COMMIT models. COMMIT was run using a Stick- 658 Zeppelin-Ball forward model and default settings (see https://github.com/daducci/COMMIT). (2) 659 Any streamline with a COMMIT weight < 1e-12 (machine precision 0) was interpreted as a false 660 positive and filtered from the tractogram. This streamline-level COMMIT-filtering step typically 661 resulted in greater than a 90% decrease in the size of the tractogram with most containing 34 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / . / t / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 662 between ~300-600k streamlines. COMMIT-filtered tractograms were used not only in the 663 computation of COMMIT, but all tractometry networks as well. This additional filtering step was 664 performed on COMMIT streamline weights only (not SIFT2) to reduce the impact of false 665 positive streamlines in tractometry networks as much as possible. 666 667 In a supplemental analysis, the COMMIT streamline weights were additionally used in the 668 computation of edge weights in tractometry-derived networks by performing a COMMIT- 669 weighted average of a given tractometry metric (e.g., FA) over streamlines for each node pair 670 (Figure S10-S12). 671 672 673 Construction of Weighted Structural Networks 674 The streamline-specific SC networks were computed in the following manner: (1) NoS as the 675 summed streamline count; (2) LoS as the mean streamline length; (3) SIFT2 as the sum of SIFT2 676 streamline weights; and (4) COMMIT as the length-weighted sum of COMMIT streamline 677 weights as in (Schiavi et al., 2020). Explicitly, edgewise entries in COMMIT-weighted networks 678 were computed as: 679 𝛼𝑖𝑗 = 𝑁𝑖𝑗 𝑘 ∗ 𝑙𝑘) ∑ (𝑥𝑖𝑗 𝑘=1 𝐿̅𝑖𝑗 , 680 where 𝛼𝑖𝑗 is the edge weight between nodes i and j; 𝐿̅𝑖𝑗 is the mean streamline length; 𝑁𝑖𝑗 is the 681 number of streamlines; 𝑥𝑖𝑗 𝑘 is the COMMIT weight of streamline k; and 𝑙𝑘 is its length. Edge 682 weights in NoS, SIFT2 and COMMIT were normalized by node volume. 683 35 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / t / . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 684 SC networks weighted by FA, RD, ICVF (H. Zhang et al., 2012) and R1 were derived using 685 multi-modal tractometry (S Bells et al., 2011). Streamline weights were computed by: (1) co- 686 registering the tractogram and desired image; and (2) sampling the voxel-level aggregate value 687 along the length of each streamline. Edge weights were computed as the median along each 688 streamline and the mean across streamlines by node pair. Voxel-wise measures of FA and RD 689 were computed with a diffusion tensor model (Basser et al., 1994) and ICVF by applying the 690 NODDI multi-compartment model (H. Zhang et al., 2012) to preprocessed DWI data (Daducci, 691 Canales-Rodríguez, et al., 2015). 692 693 The 400-node Schaefer (Schaefer et al., 2018) cortical parcellation is used in all results. 694 Subcortical ROIs corresponded to 7 bilateral regions (14 nodes) including the amygdala, 695 thalamus, caudate, accumbens, putamen, hippocampus, and pallidum. A single static, zero-lag 696 FC network was derived by product-moment pairwise Pearson cross-correlation of node- 697 averaged time series. FC network edge weights were Fisher Z-transformed. 698 699 700 Connectome post-processing 701 COMMIT-weighted networks were used to filter all other weighted structural networks at the 702 edge level. This was chosen as COMMIT-weighted networks had the lowest connection density 703 to start, and all non-zero COMMIT edges were also non-zero in all other SC networks. All SC 704 networks were thresholded at the edge level within subject by: (1) setting edges = 0 in all 705 weighted SC networks if that edge had a COMMIT weight < 1e-12; and (2) applying a 50% 706 uniform threshold mask to facilitate group-consensus averaging. This minimized differences in 36 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 707 binary structural network density across subjects and enforced a uniform binary connectivity 708 map across weighted SC networks at the group level and within subject. Group-level networks 709 were computed as the subject-wise mean at each edge excluding zero-valued edges. 710 711 712 Network Analysis 713 Network analysis was performed using tools (Rubinov & Sporns, 2010) based on graph theory 714 (Fornito et al., 2013; Sporns, 2018). Measures of clustering coefficient and path length were 715 normalized against 50 degree and strength preserving null networks. Clustering coefficient was 716 normalized within node then averaged across nodes to obtain a scalar value per network. The 717 following weight (Wij) to length (Lij) transform was used in path length computation: Lij = - 718 log(Wij). Weighted rich-club curves were normalized against 1000 degree and strength 719 preserving null networks. The edges in all degree and strength preserving null networks were 720 rewired 1e6 times total, and the strength sequence was approximated using simulated annealing. 721 Rich-club curves were normalized in binary networks against 1000 degree preserving null 722 networks in which each edge was rewired 100 times. All edge rewiring followed the Maslov & 723 Sneppen rewiring model (Maslov & Sneppen, 2002). Similar to (M. P. van den Heuvel et al., 724 2010), hubness scores (0-5) were computed as 1 point for all nodes showing top 20% strength, 725 betweenness, closeness or eigenvector centrality; and lowest 20% clustering coefficient. 726 727 728 Permutation Testing 37 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / / t . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 729 Statistical significance for the edgewise correlation of residual edge weights in NoS, SIFT2, 730 COMMIT and R1 with FC (Figure S7); as well as all connection-strength-weighted networks 731 with R1 (Figure S8) was quantified using permutation testing as described in supplementary 732 material. One-sided p-values are reported in the main text figures as pperm. 733 734 735 ACKNOWLEDGMENTS 736 We acknowledge research support from the National Science and Engineering Research Council 737 of Canada (NSERC Discovery-1304413, DGECR-2018-00216 ), the CIHR (FDN-154298, PJT- 738 174995), SickKids Foundation (NI17-039), Azrieli Center for Autism Research (ACAR-TACC), 739 Brain Canada, Fonds de recherche du Québec – Santé (FRQ-S), Healthy Brains for Healthy 740 Lives, and the Tier-2 Canada Research Chairs program. 741 742 743 REFERENCES 744 745 746 747 748 749 750 751 752 753 754 755 Alexander, D. C., Dyrby, T. B., Nilsson, M., & Zhang, H. (2019). Imaging brain microstructure with diffusion MRI: practicality and applications. NMR in Biomedicine, 32(4), 1–26. https://doi.org/10.1002/nbm.3841 Alexander, D. C., Hubbard, P. L., Hall, M. G., Moore, E. A., Ptito, M., Parker, G. J. M., & Dyrby, T. B. (2010). Orientationally invariant indices of axon diameter and density from diffusion MRI. NeuroImage, 52(4), 1374–1389. https://doi.org/10.1016/j.neuroimage.2010.05.043 Amico, E., & Goñi, J. (2018). The quest for identifiability in human functional connectomes. Scientific Reports, 8(1), 1–14. https://doi.org/10.1038/s41598-018-25089-1 Andersson, J. L. R., Skare, S., & Ashburner, J. (2003). How to correct susceptibility distortions in spin-echo echo-planar images: Application to diffusion tensor imaging. NeuroImage, 20(2), 870–888. https://doi.org/10.1016/S1053-8119(03)00336-7 Andersson, J. L. R., & Sotiropoulos, S. N. (2016). An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage, 125, 1063–1078. https://doi.org/10.1016/j.neuroimage.2015.10.019 Assaf, Y., Blumenfeld-Katzir, T., Yovel, Y., & Basser, P. J. (2008). AxCaliber: A method for measuring axon diameter distribution from diffusion MRI. Magnetic Resonance in Medicine, 59(6), 1347–1354. https://doi.org/10.1002/mrm.21577 38 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 Avants, B. B., Epstein, C. L., Grossman, M., & Gee, J. C. (2008). Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis, 12(1), 26–41. https://doi.org/10.1016/j.media.2007.06.004 Barakovic, M., Girard, G., Schiavi, S., Romascano, D., Descoteaux, M., Granziera, C., Jones, D. K., Innocenti, G. M., Thiran, J.-P., & Daducci, A. (2021). Bundle-Specific Axon Diameter Index as a New Contrast to Differentiate White Matter Tracts. Frontiers in Neuroscience, 15(June), 1–13. https://doi.org/10.3389/fnins.2021.646034 Barakovic, M., Tax, C. M. W., Rudrapatna, U., Chamberland, M., Rafael-Patino, J., Granziera, C., Thiran, J. P., Daducci, A., Canales-Rodríguez, E. J., & Jones, D. K. (2021). Resolving bundle-specific intra-axonal T2 values within a voxel using diffusion-relaxation tract-based estimation. NeuroImage, 227(September 2020), 117617. https://doi.org/10.1016/j.neuroimage.2020.117617 Basser, P. J. (1995). Inferring microstructural features and the physiological state of tissues from diffusion‐ weighted images. NMR in Biomedicine, 8(7), 333–344. https://doi.org/10.1002/nbm.1940080707 Basser, P. J., Mattiello, J., & Lebihan, D. (1994). Estimation of the Effective Self-Diffusion Tensor from the NMR Spin Echo. In Journal of Magnetic Resonance, Series B (Vol. 103, Issue 3, pp. 247–254). https://doi.org/10.1006/jmrb.1994.1037 Bassett, D. S., & Bullmore, E. (2006). Small-world brain networks. Neuroscientist, 12(6), 512–523. https://doi.org/10.1177/1073858406293182 Bassett, D. S., & Bullmore, E. T. (2017). Small-World Brain Networks Revisited. Neuroscientist, 23(5), 499–516. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l https://doi.org/10.1177/1073858416667720 f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Bells, S, Cercignani, M., Deoni, S., & Assaf, Y. (2011). “Tractometry” – comprehensive multi-modal quantitative assessment of white matter along specific tracts. Proceedings of the International Society for Magnetic Resonance in Medicine, 19(2009), 678. http://cds.ismrm.org/protected/11MProceedings/files/678.pdf Bells, Sonya, Lefebvre, J., Prescott, S. A., Dockstader, C., Bouffet, E., Skocic, J., Laughlin, S., & Mabbott, D. J. (2017). Changes in white matter microstructure impact cognition by disrupting the ability of neural assemblies to synchronize. Journal of Neuroscience, 37(34), 8227– 8238. https://doi.org/10.1523/jneurosci.0560-17.2017 Berthold, C. H., Nilsson, I., & Rydmark, M. (1983). Axon diameter and myelin sheath thickness in nerve fibres of the ventral spinal root of the seventh lumbar nerve of the adult and developing cat. Journal of Anatomy, 136(Pt 3), 483–508. https://pubmed.ncbi.nlm.nih.gov/6885614/ Biswal, B., Zerrin Yetkin, F., Haughton, V. M., & Hyde, J. S. (1995). Functional connectivity in the motor cortex of resting human brain using echo-planar mri. Magnetic Resonance in Medicine, 34(4), 537–541. https://doi.org/10.1002/mrm.1910340409 Bonilha, L., Gleichgerrcht, E., Fridriksson, J., Breedlove, J. L., Rorden, C., Nesland, T., Paulus, W., Helms, G., & Focke, N. K. (2015). Reproducibility of the structural brain connectome derived from diffusion tensor imaging. PLoS ONE, 10(9), 1–17. https://doi.org/10.1371/journal.pone.0135247 Boshkovski, T., Kocarev, L., Cohen-Adad, J., Mišić, B., Lehéricy, S., Stikov, N., & Mancini, M. (2021). The R1-weighted connectome: complementing brain networks with a myelin-sensitive measure. Network Neuroscience, 5(2), 358–372. https://doi.org/10.1162/netn_a_00179 Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews Neuroscience, 13(5), 336–349. https://doi.org/10.1038/nrn3214 39 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 Cabral, J., Kringelbach, M. L., & Deco, G. (2017). Functional connectivity dynamically evolves on multiple time-scales over a static structural connectome: Models and mechanisms. NeuroImage, 160(March), 84–96. https://doi.org/10.1016/j.neuroimage.2017.03.045 Caeyenberghs, K., Metzler-Baddeley, C., Foley, S., & Jones, D. K. (2016). Dynamics of the human structural connectome underlying working memory training. Journal of Neuroscience, 36(14), 4056–4066. https://doi.org/10.1523/JNEUROSCI.1973-15.2016 Calamante, F. (2017). Track-weighted imaging methods: extracting information from a streamlines tractogram. Magnetic Resonance Materials in Physics, Biology and Medicine, 30(4), 317–335. https://doi.org/10.1007/s10334-017-0608-1 Calamante, F., Tournier, J. D., Jackson, G. D., & Connelly, A. (2010). Track-density imaging (TDI): Super-resolution white matter imaging using whole-brain track-density mapping. NeuroImage, 53(4), 1233–1243. https://doi.org/10.1016/j.neuroimage.2010.07.024 Calamante, F., Tournier, J. D., Smith, R. E., & Connelly, A. (2012). A generalised framework for super-resolution track-weighted imaging. NeuroImage, 59(3), 2494–2503. https://doi.org/10.1016/j.neuroimage.2011.08.099 Christiaens, D., Reisert, M., Dhollander, T., Sunaert, S., Suetens, P., & Maes, F. (2015). Global tractography of multi-shell diffusion-weighted imaging data using a multi-tissue model. NeuroImage, 123, 89–101. https://doi.org/10.1016/j.neuroimage.2015.08.008 Chung, A. W., Seunarine, K. K., & Clark, C. A. (2016). NODDI reproducibility and variability with magnetic field strength: A comparison between 1.5 T and 3 T. Human Brain Mapping, 37(12), 4550–4565. https://doi.org/10.1002/hbm.23328 Collin, G., Sporns, O., Mandl, R. C. W., & Van Den Heuvel, M. P. (2014). Structural and functional aspects relating to cost and benefit of rich l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l club organization in the human cerebral cortex. Cerebral Cortex, 24(9), 2258–2267. https://doi.org/10.1093/cercor/bht064 f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Cordero-Grande, L., Christiaens, D., Hutter, J., Price, A. N., & Hajnal, J. V. (2019). Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage, 200(March), 391–404. https://doi.org/10.1016/j.neuroimage.2019.06.039 Cruces, R. R., Royer, J., Herholz, P., Larivière, S., Vos de Wael, R., Paquola, C., Benkarim, O., Park, B., Degré-Pelletier, J., Nelson, M. C., DeKraker, J., Leppert, I. R., Tardif, C., Poline, J.-B., Concha, L., & Bernhardt, B. C. (2022). Micapipe: A pipeline for multimodal neuroimaging and connectome analysis. NeuroImage, 263(August), 119612. https://doi.org/10.1016/j.neuroimage.2022.119612 Daducci, A., Canales-Rodríguez, E. J., Zhang, H., Dyrby, T. B., Alexander, D. C., & Thiran, J. P. (2015). Accelerated Microstructure Imaging via Convex Optimization (AMICO) from diffusion MRI data. NeuroImage, 105, 32–44. https://doi.org/10.1016/j.neuroimage.2014.10.026 Daducci, A., Dal Palu, A., Lemkaddem, A., & Thiran, J. P. (2013). A convex optimization framework for global tractography. Proceedings - International Symposium on Biomedical Imaging, 524–527. https://doi.org/10.1109/ISBI.2013.6556527 Daducci, A., Dal Palù, A., Lemkaddem, A., & Thiran, J. P. (2015). COMMIT: Convex optimization modeling for microstructure informed tractography. IEEE Transactions on Medical Imaging, 34(1), 246–257. https://doi.org/10.1109/TMI.2014.2352414 Dale, A. M., Fischl, B., & Sereno, M. I. (1999). Cortical Surface-Based Analysis. NeuroImage, 9(2), 179–194. https://doi.org/10.1006/nimg.1998.0395 de Reus, M. A., & van den Heuvel, M. P. (2014). Simulated rich club lesioning in brain networks: A scaffold for communication and integration? Frontiers in Human Neuroscience, 8(AUG), 1–5. https://doi.org/10.3389/fnhum.2014.00647 De Santis, S., Assaf, Y., Jeurissen, B., Jones, D. K., & Roebroeck, A. (2016). T1 relaxometry of crossing fibres in the human brain. NeuroImage, 141, 133–142. https://doi.org/10.1016/j.neuroimage.2016.07.037 De Santis, S., Drakesmith, M., Bells, S., Assaf, Y., & Jones, D. K. (2014). Why diffusion tensor MRI does well only some of the time: Variance and covariance of white matter tissue microstructure attributes in the living human brain. NeuroImage, 89, 35–44. 40 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 https://doi.org/10.1016/j.neuroimage.2013.12.003 Deligianni, F., Carmichael, D. W., Zhang, G. H., Clark, C. A., & Clayden, J. D. (2016). NODDI and tensor-based microstructural indices as predictors of functional connectivity. PLoS ONE, 11(4), 1–17. https://doi.org/10.1371/journal.pone.0153404 Dhollander, T., Clemente, A., Singh, M., Boonstra, F., Civier, O., Duque, J. D., Egorova, N., Enticott, P., Fuelscher, I., Gajamange, S., Genc, S., Gottlieb, E., Hyde, C., Imms, P., Kelly, C., Kirkovski, M., Kolbe, S., Liang, X., Malhotra, A., … Caeyenberghs, K. (2021). Fixel-based Analysis of Diffusion MRI: Methods, Applications, Challenges and Opportunities. NeuroImage, 241(November 2020), 118417. https://doi.org/10.1016/j.neuroimage.2021.118417 Dhollander, T., Mito, R., Raffelt, D., & Connelly, A. (2019). Improved white matter response function estimation for 3-tissue constrained spherical deconvolution. Proc. Intl. Soc. Mag. Reson. Med, May 11-16, 555. https://www.researchgate.net/publication/331165168_Improved_white_matter_response_function_estimation_for_3- tissue_constrained_spherical_deconvolution Dhollander, T., Raffelt, D., & Connelly, A. (2016). Unsupervised 3-tissue response function estimation from single-shell or multi-shell diffusion MR data without a co-registered T1 image Predicting stroke impairment using machine learning techniques View project A novel sparse partial correlation method fo. ISMRM Workshop on Breaking the Barriers of Diffusion MRI, 35(September), 1–2. https://www.researchgate.net/publication/307863133 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l Douglas Fields, R. (2015). A new mechanism of nervous system plasticity: activity-dependent myelination. Nature Reviews Neuroscience, f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 0 2 1 5 2 2 7 7 n e n _ a _ 0 0 3 3 0 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 16(12), 756–767. https://doi.org/10.1007/s11065-015-9294-9.Functional Drakesmith, M., Harms, R., Rudrapatna, S. U., Parker, G. D., Evans, C. J., & Jones, D. K. (2019). Estimating axon conduction velocity in vivo from microstructural MRI. NeuroImage, 203(March), 116186. https://doi.org/10.1016/j.neuroimage.2019.116186 Finn, E. S., Huber, L., Jangraw, D. C., Molfese, P. J., & Bandettini, P. A. (2019). Layer-dependent activity in human prefrontal cortex during working memory. Nature Neuroscience, 22(10), 1687–1695. https://doi.org/10.1038/s41593-019-0487-z Fischl, B., Sereno, M. I., & Dale, A. M. (1999). Cortical surface-based analysis: II. Inflation, flattening, and a surface-based coordinate system. NeuroImage, 9(2), 195–207. https://doi.org/10.1006/nimg.1998.0396 Fischl, B., Sereno, M. I., Tootell, R. B. H., & Dale, A. M. (1999). High-resolution intersubject averaging and a coordinate system for the cortical surface. Human Brain Mapping, 8(4), 272–284. https://doi.org/10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4
Fornito, UN., Zalesky, UN., & Breakspear, M.. (2013). Graph analysis of the human connectome: Promise, progress, and pitfalls. NeuroImage, 80,
426–444. https://doi.org/10.1016/j.neuroimage.2013.04.087
Fornito, UN., Zalesky, UN., & Breakspear, M.. (2015). The connectomics of brain disorders. Nature Revues Neurosciences, 16(3), 159–172.
https://doi.org/10.1038/nrn3901
Fornito, UN., Zalesky, UN., & Bullmore, E. T. (2016). Fundamentals of Brain Network Analysis. In Fundamentals of Brain Network Analysis.
Elsevier. https://doi.org/10.1016/C2012-0-06036-X
Frigo, M., Deslauriers-Gauthier, S., Parker, D., Ismail, UN. UN. O., Kim, J.. J., Verma, R., & Deriche, R.. (2020). Diffusion MRI tractography
filtering techniques change the topology of structural connectomes. Journal of Neural Engineering, 17(6). https://doi.org/10.1088/1741-
2552/abc29b
Friston, K. J.. (2011). Functional and effective connectivity: a review. Brain Connectivity, 1(1), 13–36. https://doi.org/10.1089/brain.2011.0008
41
861
862
863
864
865
866
867
868
869
870
871
872
873
874
875
876
877
878
879
880
881
882
883
884
885
886
887
888
889
890
891
892
893
894
895
Gibson, E. M., Geraghty, UN. C., & Monje, M.. (2018). Bad wrap: Myelin and myelin plasticity in health and disease. In Developmental
Neurobiology (Vol. 78, Issue 2, pp. 123–135). John Wiley and Sons Inc. https://doi.org/10.1002/dneu.22541
Girard, G., Whittingstall, K., Deriche, R., & Descoteaux, M.. (2014). Towards quantitative connectivity analysis: Reducing tractography biases.
NeuroImage, 98, 266–278. https://doi.org/10.1016/j.neuroimage.2014.04.074
Gordon, E. M., Laumann, T. O., Gilmore, UN. W., Newbold, D. J., Vert, D. J., Berger, J.. J., Ortega, M., Hoyt-Drazen, C., Gratton, C., Sun, H.,
Hampton, J.. M., Coalson, R.. S., Nguyen, UN. L., McDermott, K. B., Shimony, J.. S., Snyder, UN. Z., Schlaggar, B. L., Petersen, S. E.,
Nelson, S. M., & Dosenbach, N. U. F. (2017). Precision Functional Mapping of Individual Human Brains. Neurone, 95(4), 791-807.e7.
https://doi.org/10.1016/j.neuron.2017.07.011
Greicius, M.. D., Krasnow, B., Reiss, UN. L., & Menon, V. (2003). Functional connectivity in the resting brain: A network analysis of the default
mode hypothesis. Proceedings of the National Academy of Sciences of the United States of America, 100(1), 253–258.
https://doi.org/10.1073/pnas.0135058100
Greve, D. N., & Fischl, B. (2009). Accurate and robust brain image alignment using boundary-based registration. NeuroImage, 48(1), 63–72.
https://doi.org/10.1016/j.neuroimage.2009.06.060
Griffa, UN., & Van den Heuvel, M.. P.. (2018). Rich-club neurocircuitry: fonction, evolution, and vulnerability. Dialogues in Clinical Neuroscience,
20(2), 121–132. https://doi.org/10.31887/DCNS.2018.20.2/agriffa
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
Hampson, M., Driesen, N. R., Skudlarski, P., Sang, J.. C., & Constable, R.. T. (2006). Brain connectivity related to working memory performance.
F
/
d
o
je
/
t
/
/
.
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Journal des neurosciences, 26(51), 13338–13343. https://doi.org/10.1523/JNEUROSCI.3408-06.2006
Harris, J.. J., & Attwell, D. (2012). The energetics of CNS white matter. Journal des neurosciences, 32(1), 356–371.
https://doi.org/10.1523/JNEUROSCI.3430-11.2012
Heath, F., Hurley, S. UN., Johansen-Berg, H., & Sampaio-Baptista, C. (2018). Advances in noninvasive myelin imaging. Developmental
Neurobiology, 78(2), 136–151. https://doi.org/10.1002/dneu.22552
Hildebrand, C., & Hahn, R.. (1978). Relation between myelin sheath thickness and axon size in spinal cord white matter of some vertebrate
species. Journal of the Neurological Sciences, 38(3), 421–434. https://doi.org/10.1016/0022-510X(78)90147-8
Hodgkin, UN. L., & Huxley, UN. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve.
The Journal of Physiology, 117(4), 500–544. https://doi.org/10.1113/jphysiol.1952.sp004764
Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.. P., Meuli, R., & Hagmann, P.. (2009). Predicting human resting-state functional
connectivity from structural connectivity. Proceedings of the National Academy of Sciences of the United States of America, 106(6),
2035–2040. https://doi.org/10.1073/pnas.0811168106
Huntenburg, J.. M., Bazin, P.. L., Goulas, UN., Tardif, C. L., Villringer, UN., & Margulies, D. S. (2017). A Systematic Relationship Between
Functional Connectivity and Intracortical Myelin in the Human Cerebral Cortex. Cortex cérébral, 27(2), 981–997.
https://doi.org/10.1093/cercor/bhx030
Huxley, UN. F., & Stämpfli, R.. (1949). Evidence for saltatory conduction in peripheral myelinated nerve fibres. The Journal of Physiology, 108(3),
315–339. http://www.ncbi.nlm.nih.gov/pubmed/16991863
Jenkinson, M., Beckmann, C. F., Behrens, T. E. J., Woolrich, M.. W., & Forgeron, S. M.. (2012). FSL. NeuroImage, 62(2), 782–790.
https://doi.org/10.1016/j.neuroimage.2011.09.015
42
896
897
898
899
900
901
902
903
904
905
906
907
908
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
927
928
929
930
Jeurissen, B., Descoteaux, M., Mori, S., & Leemans, UN. (2017). Diffusion MRI fiber tractography of the brain. NMR in Biomedicine, 32(4), 1–22.
https://doi.org/10.1002/nbm.3785
Jeurissen, B., Leemans, UN., Tournier, J.. D., Jones, D. K., & Sijbers, J.. (2012). Investigating the prevalence of complex fiber configurations in
white matter tissue with diffusion magnetic resonance imaging. Human Brain Mapping, 34(11), 2747–2766.
https://doi.org/10.1002/hbm.22099
Jeurissen, B., Tournier, J.. D., Dhollander, T., Connelly, UN., & Sijbers, J.. (2014). Multi-tissue constrained spherical deconvolution for improved
analysis of multi-shell diffusion MRI data. NeuroImage, 103, 411–426. https://doi.org/10.1016/j.neuroimage.2014.07.061
Jones, D. K. (2010). Challenges and limitations of quantifying brain connectivity in vivo with diffusion MRI. Imaging in Medicine, 2(3), 341–
355. https://doi.org/10.2217/iim.10.21
Jones, D. K., Knösche, T. R., & Tourneur, R.. (2013). White matter integrity, fiber count, and other fallacies: The do’s and don’ts of diffusion MRI.
NeuroImage, 73, 239–254. https://doi.org/10.1016/j.neuroimage.2012.06.081
Kim, D. J., & Min, B. K. (2020). Rich-club in the brain’s macrostructure: Insights from graph theoretical analysis. Computational and Structural
Biotechnology Journal, 18, 1761–1773. https://doi.org/10.1016/j.csbj.2020.06.039
Koch, P.. J., Girard, G., Brügger, J., Cadic-Melchior, UN. G., Beanato, E., Parc, C.-H., Morishita, T., Wessel, M.. J., Pizzolato, M., Canales-
Rodríguez, E. J., Fischi-Gomez, E., Schiavi, S., Daducci, UN., Piredda, G. F., Hilbert, T., Kober, T., Thiran, J.-P., & Hummel, F. C. (2022).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
Evaluating reproducibility and subject-specificity of microstructure-informed connectivity. NeuroImage, 258(Juin), 119356.
F
/
d
o
je
/
.
/
/
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
t
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
https://doi.org/10.1016/j.neuroimage.2022.119356
Larivière, S., Paquola, C., Parc, B. yong, Royer, J., Wang, Y., Benkarim, O., Vos de Wael, R., Valk, S. L., Thomopoulos, S. JE., Kirschner, M.,
Lewis, L. B., Evans, UN. C., Sisodiya, S. M., McDonald's, C. R., Thompson, P.. M., & Bernhardt, B. C. (2021). The ENIGMA Toolbox:
multiscale neural contextualization of multisite neuroimaging datasets. Nature Methods, 18(7), 698–700. https://doi.org/10.1038/s41592-
021-01186-4
Lehmann, N., Aye, N., Kaufmann, J., Heinze, H. J., Düzel, E., Ziegler, G., & Taubert, M.. (2021). Longitudinal Reproducibility of Neurite
Orientation Dispersion and Density Imaging (NODDI) Derived Metrics in the White Matter. Neurosciences, 457, 165–185.
https://doi.org/10.1016/j.neuroscience.2021.01.005
Leppert, je. R., Andrés, D. UN., Campbell, J.. S. W., Parc, D. J., Pike, G. B., Polimeni, J.. R., & Tardif, C. L. (2021). Efficient whole-brain tract-
specific T1 mapping at 3T with slice-shuffled inversion-recovery diffusion-weighted imaging. Magnetic Resonance in Medicine, 86(2),
738–753. https://doi.org/10.1002/mrm.28734
Leppert, je. R., Bontempi, P., Rowley, C. D., Campbell, J.. S., Nelson, M.. C., Schiavi, S., Pike, G. B., Daducci, UN., & Tardif, C. L. (2023). Dual-
encoded magnetization transfer and diffusion imaging and its application to tract-specific microstructure mapping. ArXiv, 1–26.
http://arxiv.org/abs/2303.03449
Liégeois, R., Li, J., Kong, R., Orban, C., Van De Ville, D., Ge, T., Sabuncu, M.. R., & Yeo, B. T. T. (2019). Resting brain dynamics at different
timescales capture distinct aspects of human behavior. Communications naturelles, 10(1). https://doi.org/10.1038/s41467-019-10317-7
Liu, Z. Q., Vázquez-Rodríguez, B., Spreng, R.. N., Bernhardt, B. C., Betzel, R.. F., & Misic, B. (2022). Time-resolved structure-function coupling
in brain networks. Communications Biology, 5(1), 1-dix. https://doi.org/10.1038/s42003-022-03466-x
Maier-Hein, K. H., Neher, P.. F., Houde, J.. C., Côté, M.. UN., Garyfallidis, E., Zhong, J., Chamberland, M., Yeh, F. C., Lin, Oui. C., Ji, Q., Reddick,
43
931
932
933
934
935
936
937
938
939
940
941
942
943
944
945
946
947
948
949
950
951
952
953
954
955
956
957
958
959
960
961
962
963
964
965
W. E., Verre, J.. O., Chen, D. Q., Feng, Y., Gao, C., Wu, Y., Ma, J., Renjie, H., Li, Q., … Descoteaux, M.. (2017). The challenge of
mapping the human connectome based on diffusion tractography. Communications naturelles, 8(1). https://doi.org/10.1038/s41467-017-
01285-X
Mancini, M., Giulietti, G., Dowell, N., Spanò, B., Harrison, N., Bozzali, M., & Cercignani, M.. (2018). Introducing axonal myelination in
connectomics: A preliminary analysis of g-ratio distribution in healthy subjects. NeuroImage, 182, 351–359.
https://doi.org/10.1016/j.neuroimage.2017.09.018
Mancini, M., Karakuzu, UN., Cohen-Adad, J., Cercignani, M., Nichols, T. E., & Stikov, N. (2020). An interactive meta-analysis of MRI
biomarkers of myelin. ELife, 9, 1–23. https://doi.org/10.7554/eLife.61523
Margulies, D. S., Ghosh, S. S., Goulas, UN., Falkiewicz, M., Huntenburg, J.. M., Langs, G., Bezgin, G., Eickhoff, S. B., Castellanos, F. X., Pétrides,
M., Jefferies, E., & Smallwood, J.. (2016). Situating the default-mode network along a principal gradient of macroscale cortical
organization. Proceedings of the National Academy of Sciences of the United States of America, 113(44), 12574–12579.
https://doi.org/10.1073/pnas.1608282113
Marques, J.. P., Kober, T., Krueger, G., van der Zwaag, W., Van de Moortele, P.. F., & Gruetter, R.. (2010). MP2RAGE, a self bias-field corrected
sequence for improved segmentation and T1-mapping at high field. NeuroImage, 49(2), 1271–1281.
https://doi.org/10.1016/j.neuroimage.2009.10.002
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
Maslov, S., & Sneppen, K. (2002). Specificity and stability in topology of protein networks. Science, 296(5569), 910–913.
F
/
d
o
je
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
https://doi.org/10.1126/science.1065103
Messaritaki, E., Foley, S., Schiavi, S., Magazzini, L., Routley, B., Jones, D. K., & Singh, K. D. (2021). Predicting meg resting-state functional
connectivity from microstructural information. Neurosciences en réseau, 5(2), 477–504. https://doi.org/10.1162/netn_a_00187
Moore, S., Meschkat, M., Ruhwedel, T., Trevisiol, UN., Tzvetanova, je. D., Battefeld, UN., Kusch, K., Kole, M.. H. P., Strenzke, N., Möbius, W., de
Hoz, L., & Nave, K. UN. (2020). A role of oligodendrocytes in information processing. Communications naturelles, 11(1), 1–15.
https://doi.org/10.1038/s41467-020-19152-7
Mottershead, J.. P., Schmierer, K., Clemence, M., Thornton, J.. S., Scaravilli, F., Barker, G. J., Tofts, P.. S., Newcombe, J., Cuzner, M.. L., Ordidge,
R.. J., McDonald's, W. JE., & Miller, D. H. (2003). High field MRI correlates of myelin content and axonal density in multiple sclerosis: UN
post-mortem study of the spinal cord. Journal of Neurology, 250(11), 1293–1301. https://doi.org/10.1007/s00415-003-0192-3
Mount, C. W., & Monje, M.. (2017). Wrapped to Adapt: Experience-Dependent Myelination. Neurone, 95(4), 743–756.
https://doi.org/10.1016/j.neuron.2017.07.009
Nave, K. UN., & Werner, H. B. (2014). Myelination of the nervous system: Mechanisms and functions. Annual Review of Cell and Developmental
Biology, 30, 503–533. https://doi.org/10.1146/annurev-cellbio-100913-013101
Patenaude, B., Forgeron, S. M., Kennedy, D. N., & Jenkinson, M.. (2011). A Bayesian model of shape and appearance for subcortical brain
segmentation. NeuroImage, 56(3), 907–922. https://doi.org/10.1016/j.neuroimage.2011.02.046
Pumphrey, R.. J., & Jeune, J.. Z. (1938). The Rates Of Conduction Of Nerve Fibres Of Various Diameters In Cephalopods. Journal de
Experimental Biology, 15(4), 453–466. https://doi.org/10.1242/jeb.15.4.453
Raffelt, D., Forgeron, R., Ridgway, G., Tournier, J.. D., Vaughan, D., Rose, S., Henderson, R., & Connelly, UN. (2015). Connectivity-based fixel
enhancement: Whole-brain statistical analysis of diffusion MRI measures in the presence of crossing fibres. NeuroImage, 117, 40–55.
44
966
967
968
969
970
971
972
973
974
975
976
977
978
979
980
981
982
983
984
985
986
987
988
989
990
991
992
993
994
995
996
997
998
999
https://doi.org/10.1016/j.neuroimage.2015.05.039
Raffelt, D., Tournier, J.. D., Forgeron, R., Vaughan, D., Jackson, G., Ridgway, G., & Connelly, UN. (2017). Investigating white matter fibre density
and morphology using fixel-based analysis. NeuroImage, 144, 58–73. https://doi.org/10.1016/j.neuroimage.2016.09.029
Royer, J., Rodríguez-Cruces, R., Tavakol, S., Larivière, S., Herholz, P., Li, Q., Vos de Wael, R., Paquola, C., Benkarim, O., Parc, B., Lowe, UN. J.,
Margulies, D., Smallwood, J., Bernasconi, UN., Bernasconi, N., Frauscher, B., & Bernhardt, B. C. (2022). An Open MRI Dataset For
Multiscale Neuroscience. Scientific Data, 9(1), 569. https://doi.org/10.1038/s41597-022-01682-y
Rubinov, M., & Sporns, Ô. (2010). Complex network measures of brain connectivity: Uses and interpretations. NeuroImage, 52(3), 1059–1069.
https://doi.org/10.1016/j.neuroimage.2009.10.003
Salimi-Khorshidi, G., Douaud, G., Beckmann, C. F., Glasser, M.. F., Griffanti, L., & Forgeron, S. M.. (2014). Automatic denoising of functional MRI
data: Combining independent component analysis and hierarchical fusion of classifiers. NeuroImage, 90, 449–468.
https://doi.org/10.1016/j.neuroimage.2013.11.046
Schaefer, UN., Kong, R., Gordon, E. M., Laumann, T. O., Zuo, X.-N., Holmes, UN. J., Eickhoff, S. B., & Yeo, B. T. T. (2018). Local-Global
Parcellation of the Human Cerebral Cortex from Intrinsic Functional Connectivity MRI. Cortex cérébral, 28(9), 3095–3114.
https://doi.org/10.1093/cercor/bhx179
Schiavi, S., Lu, P., Weigel, M., Lutti, UN., Jones, D. K., Kappos, L., Granziera, C., & Daducci, UN. (2022). Bundle Myelin Fraction ( BMF )
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
Mapping of Different White Matter Connections Using Microstructure Informed Tractography. NeuroImage, 118922.
F
/
d
o
je
/
https://doi.org/10.1016/j.neuroimage.2022.118922
Schiavi, S., Petracca, M., Battocchio, M., El Mendili, M.. M., Paduri, S., Fleysher, L., Inglese, M., & Daducci, UN. (2020). Sensory-motor network
topology in multiple sclerosis: Structural connectivity analysis accounting for intrinsic density discrepancy. Human Brain Mapping,
41(11), 2951–2963. https://doi.org/10.1002/hbm.24989
Schilling, K. G., Daducci, UN., Maier-Hein, K., Poupon, C., Houde, J.. C., Nath, V., Anderson, UN. W., Landman, B. UN., & Descoteaux, M.. (2019).
Challenges in diffusion MRI tractography – Lessons learned from international benchmark competitions. Magnetic Resonance Imaging,
57(Novembre 2018), 194–209. https://doi.org/10.1016/j.mri.2018.11.014
Forgeron, R.. E., Tournier, J.. D., Calamante, F., & Connelly, UN. (2012). Anatomically-constrained tractography: Improved diffusion MRI streamlines
tractography through effective use of anatomical information. NeuroImage, 62(3), 1924–1938.
https://doi.org/10.1016/j.neuroimage.2012.06.005
Forgeron, R.. E., Tournier, J.. D., Calamante, F., & Connelly, UN. (2015). SIFT2: Enabling dense quantitative assessment of brain white matter
connectivity using streamlines tractography. NeuroImage, 119, 338–351. https://doi.org/10.1016/j.neuroimage.2015.06.092
Forgeron, S. M., Fox, P.. T., Miller, K. L., Glahn, D. C., Fox, P.. M., Mackay, C. E., Filippini, N., Watkins, K. E., Toro, R., Laird, UN. R., &
Beckmann, C. F. (2009). Correspondence of the brain’s functional architecture during activation and rest. Actes de la Nationale
Academy of Sciences of the United States of America, 106(31), 13040–13045. https://doi.org/10.1073/pnas.0905267106
Forgeron, S. M., Jenkinson, M., Woolrich, M.. W., Beckmann, C. F., Behrens, T. E. J., Johansen-Berg, H., Bannister, P.. R., De Luca, M., Drobnjak,
JE., Flitney, D. E., Niazy, R.. K., Saunders, J., Vickers, J., Zhang, Y., De Stefano, N., Brady, J.. M., & Matthieu, P.. M.. (2004). Advances in
functional and structural MR image analysis and implementation as FSL. NeuroImage, 23(SUPPL. 1), 208–219.
t
.
/
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1000
https://doi.org/10.1016/j.neuroimage.2004.07.051
45
1001
1002
1003
1004
1005
1006
1007
1008
1009
1010
1011
1012
1013
1014
1015
1016
1017
1018
1019
1020
1021
1022
1023
1024
1025
1026
1027
1028
1029
1030
1031
1032
1033
1034
1035
Sorrentino, P., Petkoski, S., Sparaco, M., Troisi Lopez, E., Signoriello, E., Baselice, F., Bonavita, S., Pirozzi, M.. UN., Quarantelli, M., Sorrentino,
G., & Jirsa, V. (2022). Whole-Brain Propagation Delays in Multiple Sclerosis, a Combined Tractography-Magnetoencephalography
Étude. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience, 42(47), 8807–8816.
https://doi.org/10.1523/JNEUROSCI.0938-22.2022
Sotiropoulos, S. N., & Zalesky, UN. (2019). Building connectomes using diffusion MRI: why, how and but. In NMR in Biomedicine (Vol. 32, Issue
4). https://doi.org/10.1002/nbm.3752
Sporns, Ô. (2010). Networks of the Brain. In Networks of the Brain. La presse du MIT. https://doi.org/10.7551/mitpress/8476.001.0001
Sporns, Ô. (2011). The human connectome: A complex network. Annals of the New York Academy of Sciences, 1224(1), 109–125.
https://doi.org/10.1111/j.1749-6632.2010.05888.x
Sporns, Ô. (2018). Graph theory methods: applications in brain networks. Dialogues in Clinical Neuroscience, 20(2), 111–120.
https://doi.org/10.31887/DCNS.2018.20.2/osporns
Stikov, N., Campbell, J.. S. W., Stroh, T., Lavelée, M., Frey, S., Novek, J., Nuara, S., Ho, M.. K., Bedell, B. J., Dougherty, R.. F., Leppert, je. R.,
Boudreau, M., Narayanan, S., Duval, T., Cohen-Adad, J., Picard, P.. UN., Gasecka, UN., Côté, D., & Pike, G. B. (2015). In vivo histology of
the myelin g-ratio with magnetic resonance imaging. NeuroImage, 118, 397–405. https://doi.org/10.1016/j.neuroimage.2015.05.023
Stikov, N., Perry, L. M., Mezer, UN., Rykhlevskaia, E., Wandell, B. UN., Pauly, J.. M., & Dougherty, R.. F. (2011). Bound pool fractions complement
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
diffusion measures to describe white matter micro and macrostructure. NeuroImage, 54(2), 1112–1121.
F
/
d
o
je
/
/
.
/
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
https://doi.org/10.1016/j.neuroimage.2010.08.068
Suárez, L. E., Markello, R.. D., Betzel, R.. F., & Misic, B. (2020). Linking Structure and Function in Macroscale Brain Networks. Trends in
Cognitive Sciences. https://doi.org/10.1016/j.tics.2020.01.008
Thomas Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M.. R., Lashkari, D., Hollinshead, M., Roffman, J.. L., Smoller, J.. W., Zöllei, L.,
Polimeni, J.. R., Fisch, B., Liu, H., & Buckner, R.. L. (2011). The organization of the human cerebral cortex estimated by intrinsic
functional connectivity. Journal de neurophysiologie, 106(3), 1125–1165. https://est ce que je.org/10.1152/jn.00338.2011
Tournier, J.-D., Calamante, F., & Connelly, UN. (2010). Improved probabilistic streamlines tractography by 2 nd order integration over fibre
orientation distributions. Ismrm, 88(2003), 2010. https://cds.ismrm.org/protected/10MProceedings/PDFfiles/1670_4298.pdf
Tournier, J.. Donald, Calamante, F., & Connelly, UN. (2012). MRtrix: Diffusion tractography in crossing fiber regions. Revue internationale de
Imaging Systems and Technology, 22(1), 53–66. https://doi.org/10.1002/ima.22005
Tournier, J.. Donald, Forgeron, R., Raffelt, D., Tabbara, R., Dhollander, T., Pietsch, M., Christiaens, D., Jeurissen, B., Yeh, C. H., & Connelly, UN.
(2019). MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. NeuroImage, 202.
https://doi.org/10.1016/j.neuroimage.2019.116137
Tournier, Jacques Donald, Mori, S., & Leemans, UN. (2011). Diffusion tensor imaging and beyond. Magnetic Resonance in Medicine, 65(6),
1532–1556. https://doi.org/10.1002/mrm.22924
Tustison, N. J., Avants, B. B., Cook, P.. UN., Zheng, Y., Egan, UN., Yushkevich, P.. UN., & Gee, J.. C. (2010). N4ITK: Improved N3 bias correction.
IEEE Transactions on Medical Imaging, 29(6), 1310–1320. https://doi.org/10.1109/TMI.2010.2046908
van den Heuvel, M.. P., Mandl, R.. C. W., Stam, C. J., Kahn, R.. S., & Hulshoff Pol, H. E. (2010). Aberrant Frontal and Temporal Complex
Network Structure in Schizophrenia: A Graph Theoretical Analysis. Journal des neurosciences, 30(47), 15915–15926.
46
1036
1037
1038
1039
1040
1041
1042
1043
1044
1045
1046
1047
1048
1049
1050
1051
1052
1053
1054
1055
1056
1057
1058
1059
1060
1061
1062
1063
1064
1065
1066
1067
1068
https://doi.org/10.1523/JNEUROSCI.2874-10.2010
Van Den Heuvel, Martijn P., Kahn, R.. S., Goñi, J., & Sporns, Ô. (2012). High-cost, high-capacity backbone for global brain communication.
Proceedings of the National Academy of Sciences of the United States of America, 109(28), 11372–11377.
https://doi.org/10.1073/pnas.1203593109
van den Heuvel, Martijn P., & Sporns, Ô. (2011). Rich-club organization of the human connectome. Journal des neurosciences, 31(44), 15775–
15786. https://doi.org/https://doi.org/10.1523/JNEUROSCI.3539-11.2011
van den Heuvel, Martijn P., & Sporns, Ô. (2013). An anatomical substrate for integration among functional networks in human cortex. Journal de
Neurosciences, 33(36), 14489–14500. https://doi.org/10.1523/JNEUROSCI.2128-13.2013
Van Den Heuvel, Martijn P., Stam, C. J., Kahn, R.. S., & Hulshoff Pol, H. E. (2009). Efficiency of functional brain networks and intellectual
performance. Journal des neurosciences, 29(23), 7619–7624. https://doi.org/10.1523/JNEUROSCI.1443-09.2009
Veraart, J., Fieremans, E., & Novikov, D. S. (2016). Diffusion MRI noise mapping using random matrix theory. Magnetic Resonance in
Medicine, 76(5), 1582–1593. https://doi.org/10.1002/mrm.26059
Veraart, J., Novikov, D. S., Christiaens, D., Ades-aron, B., Sijbers, J., & Fieremans, E. (2016). Denoising of diffusion MRI using random matrix
théorie. NeuroImage, 142, 394–406. https://doi.org/10.1016/j.neuroimage.2016.08.016
Vos de Wael, R., Benkarim, O., Paquola, C., Lariviere, S., Royer, J., Tavakol, S., Xu, T., Hong, S. J., Langs, G., Valk, S., Misic, B., Milham, M.,
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
Margulies, D. S., Smallwood, J., & Bernhardt, B. C. (2020). BrainSpace: a toolbox for the analysis of macroscale gradients in
F
/
d
o
je
/
.
/
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
neuroimaging and connectomics datasets. Communications Biology, 3(1). https://doi.org/10.1038/s42003-020-0794-7
Wang, P., Kong, R., Kong, X., Liégeois, R., Orban, C., Deco, G., van den Heuvel, M.. P., & Thomas Yeo, B. T. (2019). Inversion of a large-scale
circuit model reveals a cortical hierarchy in the dynamic resting human brain. Science Advances, 5(1).
https://doi.org/10.1126/sciadv.aat7854
Xia, M., Wang, J., & Il, Oui. (2013). BrainNet Viewer: A Network Visualization Tool for Human Brain Connectomics. PLoS ONE, 8(7).
https://doi.org/10.1371/journal.pone.0068910
Yeh, C. H., Forgeron, R.. E., Liang, X., Calamante, F., & Connelly, UN. (2016). Correction for diffusion MRI fibre tracking biases: The consequences
for structural connectomic metrics. NeuroImage, 142, 150–162. https://doi.org/10.1016/j.neuroimage.2016.05.047
Yeh, F. C., Badre, D., & Verstynen, T. (2016). Connectometry: A statistical approach harnessing the analytical potential of the local connectome.
NeuroImage, 125, 162–171. https://doi.org/10.1016/j.neuroimage.2015.10.053
Zalesky, UN., Fornito, UN., Cocchi, L., Gollo, L. L., van den Heuvel, M.. P., & Breakspear, M.. (2016). Connectome sensitivity or specificity: lequel
is more important? NeuroImage, 142, 407–420. https://doi.org/10.1016/j.neuroimage.2016.06.035
Zhang, H., Schneider, T., Wheeler-Kingshott, C. UN., & Alexander, D. C. (2012). NODDI: Practical in vivo neurite orientation dispersion and
density imaging of the human brain. NeuroImage, 61(4), 1000–1016. https://doi.org/10.1016/j.neuroimage.2012.03.072
Zhang, Y., Brady, M., & Forgeron, S. (2001). Segmentation of brain MR images through a hidden Markov random field model and the expectation-
maximization algorithm. IEEE Transactions on Medical Imaging, 20(1), 45–57. https://doi.org/10.1109/42.906424
47
Chiffre 1
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
t
/
.
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
t
/
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
t
/
.
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
t
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
/
.
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 6
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
/
.
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 1
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
/
/
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 2
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
t
/
.
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 3
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
/
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
.
/
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 5
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
/
/
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 6
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
t
/
/
.
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 7
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
/
.
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 8
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
/
/
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
t
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 9
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
t
/
.
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 10
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
/
t
.
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
/
.
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 11
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
t
/
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
.
t
/
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 12
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
/
.
t
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Supplemental Figure 13
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
.
/
t
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Tableau
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
/
t
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Author Summary
RÉSUMÉ DE L'AUTEUR
For computational network models to provide mechanistic links between brain structure and
fonction, they must be informed by networks in which edge weights quantify structural features
relevant to brain function. Ici, we characterized several weighted structural networks capturing
multiscale features of white matter connectivity including total intra-axonal cross-sectional area
and myelin density. We describe these networks in terms of edge weight distribution, variance
and network topology, as well as their relationships with each other, edge length and function.
Dans l'ensemble, these findings support the joint use of structural networks weighted by the total intra-
axonal cross-sectional area and myelin content of white matter tracts in structure-function
models. This thorough characterization serves as a benchmark for future investigations of
weighted structural brain networks.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
t
/
e
d
toi
n
e
n
un
r
t
je
c
e
–
p
d
je
F
/
d
o
je
/
/
.
t
/
1
0
1
1
6
2
n
e
n
_
un
_
0
0
3
3
0
2
1
5
2
2
7
7
n
e
n
_
un
_
0
0
3
3
0
p
d
t
/
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3