LETTER
Communicated by Arindam Banerjee
Multilinear Common Component Analysis
via Kronecker Product Representation
Kohei Yoshikawa
yoshikawa.kohei615@gmail.com
Shuichi Kawano
skawano@ai.lab.uec.ac.jp
Graduate School of Informatics and Engineering, The University of
Electro-Communications, Chofu-shi, Tokyo 182-8585, Japan
We consider the problem of extracting a common structure from multi-
ple tensor data sets. For this purpose, we propose multilinear common
component analysis (MCCA) based on Kronecker products of mode-wise
covariance matrices. MCCA constructs a common basis represented by
linear combinations of the original variables that lose little information
of the multiple tensor data sets. We also develop an estimation algorithm
for MCCA that guarantees mode-wise global convergence. Numerical
studies are conducted to show the effectiveness of MCCA.
1 Introduction
Various statistical methodologies for extracting useful information from a
large amount of data have been studied over the decades since the appear-
ance of big data. In the present era, it is important to discover a common
structure of multiple data sets. In an early study, Flury (1984) focused on
the structure of the covariance matrices of multiple data sets and discussed
the heterogeneity of the structure. The author reported that population
covariance matrices differ among multiple data sets in practical applica-
tion. Many methodologies have been developed for treating the hetero-
geneity between covariance matrices of multiple data sets (voir, Flury, 1986,
1988; Flury & Gautschi, 1986; Pourahmadi, Daniels, & Parc, 2007; Wang,
Banerjee, & Boley, 2011; Parc & Konishi, 2020).
Among such methodologies, common component analysis (CCA; Wang
et coll., 2011) is an effective tool for statistics. The central idea of CCA is to
reduce the number of dimensions of data while losing as little information
of the multiple data sets as possible. To reduce the number of dimensions,
CCA reconstructs the data with a few new variables that are linear combi-
nations of the original variables. For considering the heterogeneity between
covariance matrices of multiple data sets, CCA assumes that there is a dif-
ferent covariance matrix for each data set. There have been many papers
on various statistical methodologies using multiple covariance matrices:
Neural Computation 33, 2853–2880 (2021) © 2021 Massachusetts Institute of Technology.
https://doi.org/10.1162/neco_a_01425
Publié sous Creative Commons
Attribution 4.0 International (CC PAR 4.0) Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2854
K. Yoshikawa and S. Kawano
discriminant analysis (Bensmail & Celeux, 1996), spectral decomposition
(Boik, 2002), and a likelihood ratio test for multiple covariance matrices
(Manly & Rayner, 1987). It should be noted that principal component anal-
ysis (APC) (Pearson, 1901; Jolliffe, 2002) is a technique similar to CCA. Dans
fact, CCA is a generalization of PCA; PCA can only be applied to one data
ensemble, whereas CCA can be applied to multiple data sets.
Entre-temps, in various fields of research, including machine learning and
computer vision, the main interest has been in tensor data, which has a mul-
tidimensional array structure. In order to apply the conventional statistical
méthodologies, such as PCA, to tensor data, a simple approach is to first
transform the tensor data into vector data and then apply the methodol-
ogie. Cependant, such an approach causes the following problems:
1. In losing the tensor structure of the data, the approach ignores the
higher-order inherent relationships of the original tensor data.
2. Transforming tensor data to vector data substantially increases the
number of features. It also has a high computational cost.
To overcome these problems, statistical methodologies for tensor data anal-
yses have been proposed that take the tensor structure of the data into
consideration. Such methods enable us to accurately extract higher-order
inherent relationships in a tensor data set. En particulier, many existing statis-
tical methodologies have been extended for tensor data, Par exemple, mul-
tilinear principal component analysis (MPCA) (Lu et al., 2008) and sparse
PCA for tensor data analysis (Allen, 2012; Wang, Sun, Chen, Pang, & Zhou,
2012; Lai, Xu, Chen, Lequel, & Zhang, 2014), as well as others (see Carroll &
Chang, 1970; Harshman, 1970; Kiers, 2000; Badeau & Boyer, 2008; Kolda &
Bader, 2009).
In this letter, we extend CCA to tensor data analysis, proposing multi-
linear common component analysis (MCCA). MCCA discovers the com-
mon structure of multiple data sets of tensor data while losing as little of
the information of the data sets as possible. To identify the common struc-
ture, we estimate a common basis constructed as linear combinations of
the original variables. For estimating the common basis, we develop a new
estimation algorithm based on the idea of CCA. In developing the estima-
tion algorithm, two issues must be addressed: the convergence properties
of the algorithm and its computational cost. To determine the convergence
propriétés, we investigate first the relationship between the initial values
of the parameters and global optimal solution and then the monotonic con-
vergence of the estimation algorithm. These analyses reveal that our pro-
posed algorithm guarantees convergence of the mode-wise global optimal
solution under some conditions. To analyze the computational efficacy, nous
calculate the computational cost of our proposed algorithm.
The rest of the letter is organized as follows. In section 2, we review
the formulation and the minimization problem of CCA. In section 3, nous
formulate the MCCA model by constructing the covariance matrices of
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2855
tensor data, based on a Kronecker product representation. Then we for-
mulate the estimation algorithm for MCCA in section 4. In section 5, nous
present the theoretical properties for our proposed algorithm and ana-
lyze the computational cost. The efficacy of the MCCA is demonstrated
through numerical experiments in section 6. Concluding remarks are pre-
sented in section 7. Technical proofs are provided in the appendixes. Notre
implementation of MCCA and supplementary materials are available at
https://github.com/yoshikawa-kohei/MCCA.
2 Common Component Analysis
, . . . X(g)Ng](cid:2) ∈ RNg×P with
Suppose that we obtain data matrices X(g)
Ng observations and P variables for g = 1, . . . , G, where x(g)i is the P-
dimensional vector corresponding to the ith row of X(g) and G is the number
of data sets. Then the sample covariance matrix in group g is
= [X(g)1
S(g)
= 1
Ng
Ng(cid:2)
je = 1
(cid:3)
X(g)je
− ¯x(g)
(cid:4) (cid:3)
X(g)je
− ¯x(g)
(cid:4)(cid:2) ,
g = 1, . . . , G,
(2.1)
∈ SP
where S(g)
ces of size P × P, and ¯x(g)
group g.
+, in which SP
= 1
Ng
(cid:5)
+ is a set of symmetric positive-definite matri-
Ng
i=1 x(g)i is a P-dimensional mean vector in
The main idea of the CCA model is to find the common structure of mul-
tiple data sets by projecting the data onto a common lower-dimensional
space with the same basis as the data sets. Wang et al. (2011) assumed that
the covariance matrices S(g) for g = 1, . . . , G can be decomposed to a prod-
uct of latent covariance matrices and an orthogonal matrix for the linear
transformation as
S(g)
= V(cid:2)
(g)V
(cid:2) + E(g)
,
(cid:2)
s.t. V
V = IR,
(2.2)
(cid:7)
(g)
∈ SP
∈ SR
(cid:6)
e(g)je
+ is the latent covariance matrix in group g, V ∈ RP×R is an
où (cid:2)
orthogonal matrix for the linear transformation, E(g)
+ is the error matrix
in group g, and IR is the identity matrix of size R × R. E(g) consists of the sum
of outer products for independent random vectors
(g)i with mean
(> O) (i = 1, 2, . . . , Ng). V de-
E
termines the R-dimensional common subspace of the multiple data sets. Dans
particular, by assuming R < P, the CCA can discover the latent structures
of the data sets. Wang et al. (2011) referred to the model, equation 2.2, as
common component analysis (CCA).
The parameters V and (cid:2)
(g) (g = 1, . . . , G) are estimated by solving the
= 0 and covariance matrix Cov
i=1 e(g)ie(cid:2)
(cid:6)
e(g)i
(cid:5)
Ng
(cid:7)
minimization problem,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
a
_
0
1
4
2
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2856
K. Yoshikawa and S. Kawano
G(cid:2)
g=1
min
V,(cid:2)
(g)
g=1,...,G
(cid:4)S(g)
− V(cid:2)
(g)V
(cid:2)(cid:4)2
F
,
(cid:2)
s.t. V
V = IR,
(2.3)
where (cid:4) · (cid:4)F denotes the Frobenius norm. The estimator of latent covari-
ance matrices (cid:2)
(g) for g = 1, . . . , G can be obtained by solving the mini-
= V(cid:2)S(g)V. By using the estimated value ˆ(cid:2)
mization problem as ˆ(cid:2)
(g), the
minimization problem can be reformulated as the following maximization
problem:
(g)
⎧
⎨
(cid:2)
⎩V
G(cid:2)
(cid:3)
g=1
max
V
tr
(cid:2)
S(g)VV
S(g)
(cid:4)
⎫
⎬
,
V
⎭
(cid:2)
s.t. V
V = IR,
(2.4)
where tr(·) denotes the trace of a matrix. A crucial issue for solving the
maximization problem 2.4 is the nonconvexity. Certainly the maximization
problem is nonconvex since the problem is defined on a set of orthogonal
matrices, which is a nonconvex set. Generally it is difficult to find the global
optimal solution in nonconvex optimization problems. To overcome this
drawback, Wang et al. (2011) proposed an estimation algorithm in which
the estimated parameters are guaranteed to constitute the global optimal
solution under some conditions.
3 Multilinear Common Component Analysis
In this section, we introduce a mathematical formulation of the MCCA, an
extension of the CCA in terms of tensor data analysis. Moreover, we for-
mulate an optimization problem of MCCA and investigate its convergence
properties.
Suppose that we independently obtain Mth order tensor data X
×...×PM for i = 1, . . . Ng. We set the data sets of the tensors X
×P2
, X
∈
RP1
=
×···×PM×Ng for g = 1, . . . , G, where G is the
[X
number of data sets. Then the sample covariance matrix in group g for the
tensor data set is defined by
(g)Ng] ∈ RP1
, . . . , X
×P2
(g)1
(g)2
(g)i
(g)
S
∗
(g) := S(1)
(g)
⊗ S(2)
(g)
⊗ · · · ⊗ S(M)
(g)
,
(3.1)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
a
_
0
1
4
2
5
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(cid:14)
+, in which P =
∈ SPk
k=1 Pk, ⊗ denotes the Kronecker product op-
+ is the sample covariance matrix for kth mode in group
M
∈ SP
where S∗
(g)
erator, and S(k)
(g)
g defined by
S(k)
(g) :=
1
(cid:14)
j(cid:7)=k Pj
Ng
(cid:15)
X(k)
(g)i
Ng(cid:2)
i=1
(cid:16) (cid:15)
− ¯X(k)
(g)
X(k)
(g)i
− ¯X(k)
(g)
(cid:16)(cid:2)
.
(3.2)
Multilinear Common Component Analysis
2857
(cid:14)
×(
(cid:14)
(g)
∈
×(
¯X
∈ RPk
= 1
Ng
j(cid:7)=k Pj ) is the mode-k unfolded matrix of X
(cid:5)
Here, X(k)
(g)i, and ¯X(k)
(g)i
(g)
(cid:14)
×(
Ng
RPk
j(cid:7)=k Pj ) is the mode-k unfolded matrix of
i=1
that the mode-k unfolding from an Mth order tensor X ∈ RP1
a matrix X(k) ∈ RPk
j(cid:7)=k Pj ) means that the tensor element (p1
maps to matrix element (pk
(cid:14)
t−1
, p2
m=1,m(cid:7)=k Pm, in which p1
(g)i. Note
×···×PM to
, . . . , pM)
t=1,t(cid:7)=k(pt − 1)Lt with Lt =
, l), where l = 1 +
, . . . , pM denote the indices of the Mth order
tensor X . For a more detailed description of tensor operations, see Kolda
and Bader (2009). A representation of the tensor covariance matrix by Kro-
necker products is often used (Kermoal, Schumacher, Pedersen, Mogensen,
& Frederiksen, 2002; Yu et al., 2004; Werner, Jansson, & Stoica, 2008).
X
×P2
, p2
(cid:5)
M
To formulate CCA in terms of tensor data analysis, we consider CCA for
the kth mode covariance matrix in group g as follows,
S(k)
(g)
= V(k)(cid:2)(k)
(g)V(k)
(cid:2)
+ E(k)
(g)
,
s.t. V(k)
(cid:2)
V(k) = IRk
,
(3.3)
∈ SRk
×Rk is an orthogonal matrix for the linear transformation, and E(k)
(g)
where (cid:2)(k)
+ is the latent kth mode covariance matrix in group g, V(k) ∈
(g)
RPk
∈ SPk
+
is the error matrix in group g. E(k)
(g) consists of the sum of outer products
(cid:5)
= 0 and
with mean E
for independent random vectors
Ng
(cid:18)
(cid:2)
i=1 e(k)
(> Ô) (i = 1, 2, . . . , Ng). Since S∗
(g)je
(g)ie(k)
(cid:17)
e(k)
(g)je
(g) can be de-
(g) for k = 1, . . . , M in formula 3.1, nous
covariance matrix Cov
composed to a Kronecker product of S(k)
obtain the following model,
(cid:17)
e(k)
(g)je
(cid:18)
S
∗
(g)
= V
∗(cid:2)∗
(g)V
∗(cid:2) + E
,
∗
(g)
s.t. V
∗(cid:2)
∗ = IR,
V
(3.4)
(cid:14)
where R =
⊗ (cid:2)(M.)
(g) , and E∗
M.
k=1 Rk, V∗ = V(1) ⊗ V(2) ⊗ · · · ⊗ V(M.), (cid:2)∗
(g) is the error matrix in group g. We refer to this model as
= (cid:2)(1)
(g)
⊗ (cid:2)(2)
(g)
⊗ · · ·
(g)
multilinear common component analysis (MCCA).
To find the R-dimensional common subspace between the multiple ten-
sor data sets, MCCA determines V(1), V(2), . . . , V(M.). As with CCA, we ob-
tain the estimate of (cid:2)∗
. With respect
to V∗
, we can obtain the estimate by solving the following maximization
problem, which is similar to equation 2.4:
(g) for g = 1, . . . , G as ˆ(cid:2)∗
(g)V∗
S∗
= V∗(cid:2)
(g)
⎧
⎨
⎩V
∗(cid:2)
G(cid:2)
(cid:15)
S
g=1
maximum
V∗
tr
∗
∗
(g)V
∗(cid:2)
V
S
∗
(g)
(cid:16)
∗
V
⎫
⎬
⎭
,
s.t. V
∗(cid:2)
∗ = IR.
V
(3.5)
Cependant, the number of parameters will be very large when we try to
solve this problem directly, and thus results in a high computational cost.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2858
K. Yoshikawa and S. Kawano
De plus, it may not be possible to discover the inherent relationships
among the variables in each mode simply by solving problem 3.5.
To solve the maximization problem efficiently and identify the inherent
relationships, the maximization problem 3.5 can be decomposed into the
mode-wise maximization problems represented in the following lemma.
Lemma 1. An estimate of the parameters V(k) for k = 1, 2, . . . , M in the maxi-
mization problem 3.5 can be obtained by solving the following maximization prob-
lem for each mode:
G(cid:2)
M.(cid:19)
maximum
V(k)
k=1,2,…,M.
g=1
k=1
(cid:20)
V(k)
(cid:2)
tr
S(k)
(g)V(k)V(k)
(cid:2)
S(k)
(g)V(k)
(cid:21)
,
s.t. V(k)
(cid:2)
V(k) = IRk
.
(3.6)
Cependant, we cannot simultaneously solve this problem for V(k), k =
1, 2, . . . , M.. Ainsi, by summarizing the terms unrelated to V(k) in maximiza-
tion problem 3.6, we can obtain the maximization problem for kth mode,
maximum
V(k)
fk(V(k)) = max
V(k)
tr
(cid:20)
V(k)
(cid:2)
M.(V(k))V(k)
(cid:21)
,
s.t. V(k)
(cid:2)
V(k) = IRk
,
(3.7)
where M(V(k)) =
(cid:5)
G
g=1
w(−k)
(g) S(k)
(g)V(k)V(k)
(cid:2)
(g), in which w(−k)
S(k)
(g)
is given by
w(−k)
(g)
=
(cid:20)
V( j)
(cid:2)
tr
(cid:19)
j(cid:7)=k
S( j)
(g)V( j)V( j)
(cid:2)
S( j)
(g)V( j)
(cid:21)
.
(3.8)
Although an estimate of V(k) can be obtained by solving maximization prob-
lem 3.7, this problem is nonconvex, since V(k) is assumed to be an orthog-
onal matrix. Ainsi, the maximization problem has several local maxima.
Cependant, by choosing the initial values of parameters in the estimation
near the global optimal solution, we can obtain the global optimal solu-
tion. In section 4, we develop not only an estimation algorithm but also an
initialization method for choosing the initial values of the parameters near
the global optimal solution. The initialization method helps guarantee the
convergence of our algorithm to the mode-wise global optimal solution.
4 Estimation
Our estimation algorithm consists of two steps: initializing the parameters
and iteratively updating the parameters. The initialization step gives us the
initial values of the parameters near the global optimal solution for each
mode. Suivant, by iteratively updating the parameters, we can monotonically
increase the value of the objective function 3.7 until convergence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2859
4.1 Initialization. The first step is to initialize the parameters V(k) pour
(cid:21)
(cid:4)
each mode. We define an objective function f (cid:8)
w(−k)
(g) S(k)
for k = 1, . . . , M., where M
(g). Suivant, we adopt a max-
imizer of f (cid:8)
k(V(k)) as initial values of the parameters V(k). To obtain the maxi-
(cid:18)
(cid:17)
w(−k)
mizer, we need an initial value of w(k) =
. The initial
(1)
value for w(k) is obtained by solving the quadratic programming problem,
k(V(k)) = tr
(g)S(k)
, . . . , w(−k)
(G)
, w(−k)
(2)
(cid:3)
je(k)
V(k)
G
g=1
je(k)
(cid:5)
M.
=
(cid:20)
V(k)
(cid:2)
(cid:3)
(cid:4)
(cid:2)
w(k)
λ(k)
0
λ(k)
0
(cid:2)
w(k),
min
w(k)
s.t. w(k) > 0, w(k)
(cid:2)
(cid:2)
λ(k)
1
λ(k)
1
w(k) = 1,
(4.1)
où
λ(k)
0
=
λ(k)
1
=
⎡
⎣
Pk(cid:2)
i=Rk
+1
,
λ(k)
(1)je
Pk(cid:2)
i=Rk
+1
, . . . ,
λ(k)
(2)je
(cid:26)
Pk(cid:2)
je = 1
,
λ(k)
(1)je
Pk(cid:2)
je = 1
, . . . ,
λ(k)
(2)je
Pk(cid:2)
je = 1
⎤
(cid:2)
⎦
λ(k)
(G)je
,
Pk(cid:2)
i=Rk
+1
(cid:27)(cid:2)
λ(k)
(G)je
,
(4.2)
in which λ( j)
(g)i is the ith largest eigenvalue of S( j)
(g)S( j)
(g).
0 by maximizing f (cid:8)
Using the initial value of w(k), we can obtain the initial value of the pa-
rameter V(k)
k(V(k)) for each mode. The maximizer consists
of Rk eigenvectors, corresponding to the Rk largest eigenvalues, obtained by
(cid:4)
je(k)
eigenvalue decomposition of M
. The theoretical justification for this
initialization is discussed in section 5.
(cid:3)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
4.2 Iterative Update of Parameters. The second step is to update pa-
rameters V(k) for each mode. We update parameters such that the objective
function fk(V(k)) is maximized. Let V(k)
s be the value of V(k) at step s. Alors
we solve the surrogate maximization problem,
(cid:20)
V(k)
s+1
(cid:2)
M.(V(k)
s )V(k)
s+1
(cid:21)
,
(cid:2)
s.t. V(k)
s+1
V(k)
s+1
= IRk
.
(4.3)
tr
maximum
V(k)
s+1
The solution of equation 4.3 consists of Rk eigenvectors, corresponding
to the Rk largest eigenvalues, obtained by eigenvalue decomposition of
M.(V(k)
s ). By iteratively updating the parameters, the objective function
fk(V(k)) is monotonically increased, which allows it to be maximized. Le
monotonically increasing property is discussed in section 5.
Our estimation procedure comprises the above estimation steps. Le
procedure is summarized as algorithm 1.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2860
K. Yoshikawa and S. Kawano
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
5 Theory
This section presents the theoretical and computational analyses for algo-
rithm 1. Theoretical analyses consist of two steps. D'abord, we prove that the
initial values of parameters obtained in section 4.1 are relatively close to
the global optimal solution. If the initial values are close to the global maxi-
mum, then we can obtain the global optimal solution even if the maximiza-
tion problem is nonconvex. Deuxième, we prove that the iterative updates of
the parameters in section 4.2 monotonically increase the value of objective
fonction 3.7 by solving the surrogate problem 4.3. From the monotonically
increasing property, the estimated parameters always converge at a sta-
tionary point. The combination of these two results enables us to obtain
the mode-wise global optimal solution. In the computational analysis, nous
calculate computational cost for MCCA and then compare the cost with
conventional methods. By comparing the costs, we investigate the compu-
tational efficacy of MCCA.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2861
5.1 Analysis of Upper and Lower Bounds. This section aims to pro-
vide the upper and lower bounds of the maximization problem 3.7. Depuis
the bounds, we find that the initial values in section 4.1 are relatively close
to the global optimal solution. Before providing the bounds, we define a
contraction ratio.
Definition 1. Let
je(k)
tr
be the global maximum of
. Then a contraction ratio of data for kth mode is defined by
(cid:28)
M.
(cid:4)(cid:29)
(cid:3)
F (cid:8) maximum
k
F (cid:8)
k(V(k)) and M(k) =
un(k) = f (cid:8) maximum
k
M.(k)
tr
=
(cid:3)
(cid:2)
(cid:20)
V(k)
0
(cid:28)
M.
tr
M.
(cid:3)
je(k)
je(k)
V(k)
0
(cid:4)
(cid:4)(cid:29)
(cid:21)
.
(5.1)
Note that a contraction ratio α(k) satisfies 0 ≤ α(k) ≤ 1 and α(k) = 1 if and
only if Rk
= Pk.
Using f (cid:8) maximum
and the contraction ratio α(k), we have the following theo-
rem that reveals the upper and lower bounds of the global maximum in
problem 3.7.
k
Theorem 1. Let f max
k
be the global maximum of fk(V(k)). Alors
un(k) F
(cid:8) maximum
k
≤ f max
k
≤ f
(cid:8) maximum
k
,
where α(k) is the contraction ratio defined in equation 5.1 and f (cid:8) maximum
maximum of f (cid:8)
k
k(V(k)).
(5.2)
is the global
k
→ f max
0 and w(k), V(k)
This theorem indicates that f (cid:8) maximum
k when α(k) → 1. Ainsi, it is im-
portant to obtain an α(k) that is as close as possible to one. Since α(k) depends
on V(k)
0 depends on w(k). From this dependency, if we could set
the initial value of w(k) such that α(k) is as large as possible, then we could
obtain an initial value of V(k)
. The following
0
theorem shows that we can compute the initial value of w(k) such that α(k)
is maximized.
Theorem 2. Let λ(k)
be the vectors consisting of eigenvalues defined
0
(k = 1, 2, . . . , M.), suppose
in equation 4.2. For w(k) =
that the estimate ˆw(k) is obtained by solving equation 4.1 for k = 1, 2, . . . , M.. Alors
ˆw(k) maximizes α(k).
that attains a value near f max
and λ(k)
(cid:17)
1
w(−k)
(1)
, . . . , w(−k)
(G)
, w(−k)
(2)
(cid:18)
k
En fait, un(k) is very close to one with the initial values given in theorem 2
even if Rk is small. This resembles the cumulative contribution ratio in PCA.
5.2 Convergence Analysis. We next verify that our proposed pro-
cedure for iteratively updating parameters maximizes the optimization
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2862
K. Yoshikawa and S. Kawano
problem 3.7. In algorithm 1, the parameter V(k)
s+1 can be obtained by solving
the surrogate maximization problem 4.3. Theorem 3 shows that we can
monotonically increase the value of the function fk(V(k)) in equation 3.7 par
algorithme 1.
Theorem 3. Let V(k)
valeurs, obtained by eigenvalue decomposition of M(V(k)
s+1 be Rk eigenvectors, corresponding to the Rk largest eigen-
s ). Alors
fk(V(k)
s ) ≤ fk(V(k)
s+1).
(5.3)
From theorem 1, we obtain initial values of the parameters that are near
the global optimal solution. By combining theorems 1 et 3, the solution
from algorithm 1 can be characterized by the following corollary.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
Corollary 1. Consider the maximization problem 3.7. Suppose that the initial
value of the parameter is obtained by V(k)
(V(k)), and the parameter
0
(cid:30)
fk
(cid:8)
= arg max
V(k)
V(k)
is repeatedly updated by algorithm 1. Then the mode-wise global maximum
s
for the maximization problem 3.7 is achieved when all the contraction ratios α(k)
for k = 1, 2, . . . , M go to one.
Algorithm 1 does not guarantee the global solution due to the fundamen-
tal problem of nonconvexity, but it is enough for pragmatic purposes. Nous
investigate the issue of convergence to global solution through numerical
studies in section 6.3.
5.3 Computational Analysis. D'abord, we analyze the computational cost.
Pj for j = 1, 2, . . . , M.. Ce
To simplify the analysis, we assume P = arg max
j
implies that P is the upper bound of R j for all j. We then calculate the upper
bound of the computational complexity.
The expensive computations of the each iteration in algorithm 1 con-
sist of three parts: the formulation of M(V(k)
s ), the eigenvalue decomposi-
tion of M(V(k)
s ), and updating latent covariance matrices (cid:2)(k)
g . These steps
are O(GM2P3), Ô(P3), and O(GMP3), respectivement. The total computational
complexity per iteration is then O(GM2P3).
Suivant, we analyze the memory requirement of algorithm 1. MCCA repre-
sents the original tensor data with fewer parameters by projecting the data
× Rk projection matri-
onto a lower-dimensional space. This requires the Pk
(cid:16)
ces V(k) for k = 1, 2, . . . , M.. MCCA projects the data with size of N
M.
k=1 Pk
(cid:5)
G
à N
g=1 Ng. Ainsi, the required size for the pa-
(cid:15)(cid:14)
M.
k=1 Rk
(cid:16)
, where N =
M.
k=1 PkRk
. MPCA requires the same amount of
(cid:15)(cid:14)
M.
k=1 Rk
(cid:5)
rameters is
+ N
(cid:15)(cid:14)
(cid:16)
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2863
Tableau 1: Comparisons of the Computational Complexity and the Memory
Requirement.
Method
Computational Complexity
APC
CCA
MPCA
MCCA
Ô(P3M )
Ô(GP3M )
Ô(NMPM+1 )
Ô(GM2P3 )
Memory Reqirement
(cid:15)(cid:14)
(cid:15)(cid:14)
R.
R.
(cid:16)
M.
k=1 Pk
M.
k=1 Pk
+ NR
(cid:16)
+ NR
(cid:15)(cid:14)
M.
k=1 PkRk
M.
k=1 PkRk
+ N
+ N
(cid:15)(cid:14)
M.
k=1 Rk
M.
k=1 Rk
(cid:5)
(cid:5)
(cid:16)
(cid:16)
memory as MCCA. Entre-temps, CCA and PCA need a projection matrix,
. The required size for the parameters is then
(cid:16)
(cid:15)(cid:14)
M.
k=1 Pk
which is size R
(cid:16)
(cid:15)(cid:14)
M.
k=1 Pk
R.
+ NR.
To compare the computational cost clearly, the upper bounds of compu-
tational complexity and the memory requirement are summarized in Table
1. Tableau 1 shows that the computational complexity of MCCA is superior
to that of the other algorithms and the complexity of MCCA is not limited
by sample size. In contrast, the MPCA algorithm is affected by the sample
size (Lu, Plataniotis, & Venetsanopoulos, 2008). En plus, MCCA and
MPCA require a large amount of memory when the number of modes in
a data set is large, but their memory requirements are much smaller than
those of PCA and CCA.
6 Experiment
To demonstrate the efficacy of MCCA, we applied MCCA, APC, CCA, et
MPCA to image compression tasks.
6.1 Experimental Setting. For the experiments, we prepared the follow-
ing three image data sets:
MNIST data set consists of data of handwritten digits 0, 1, . . . , 9 at im-
age sizes of 28 × 28 pixels. The data set includes a training data set
de 60,000 images and a test data set of 10,000 images. We used the
d'abord 10 training images of the data set for each group. The MNIST
data set (Lecun, Bottou, Bengio, & Haffner, 1998) is available at http:
//yann.lecun.com/exdb/mnist/.
AT&T (ORL) face data set contains gray-scale facial images of 40 people.
The data set has 10 images sized 92 × 112 pixels for each person. Nous
used images resized by a factor of 0.5 to improve the efficiency of the
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2864
K. Yoshikawa and S. Kawano
Tableau 2: Summary of the Data Sets.
Data Set
MNIST
AT&T(ORL)
Cropped AR
Groupe
Size
Sample Size
(/Groupe)
Number of
Dimensions
Nombre
of Groups
Petit
Petit
Medium
Large
Petit
Medium
Large
10
10
14
28 × 28 = 784
46 × 56 = 2576
30 × 41 × 3 = 7380
10
10
20
40
10
25
50
experiment. The AT&T face data set is available at https://git-disl.
github.io/GTDLBench/datasets/att_face_dataset/. All the credits of
this data set go to AT&T Laboratories Cambridge.
Cropped AR database has color facial images of 100 people. These im-
ages are cropped around the face. The size of images is 120 × 165 × 3
pixels. The data set contains 26 images in each group, 12 of which
are images of people wearing sunglasses or scarves. We used the
cropped facial images of 50 males who were not wearing sunglasses
or scarves. Due to memory limitations, we resized these images by
a factor of 0.25. The AR database (Martinez & Benavente, 1998; Mar-
tinez & Kak, 2001) is available at http://www2.ece.ohio-state.edu/∼
aleix/ARdatabase.html.
The data set characteristics are summarized in Table 2.
To compress these images, we performed dimensionality reductions by
MCCA, APC, CCA, and MPCA, as follows. We vectorized the tensor data
set before performing PCA and CCA. In MCCA, the images were com-
pressed and reconstructed according to the following steps:
1. Prepare the multiple image data sets X
∈ RP1
×P2
×···×PM×Ng for g =
(g)
1, 2, . . . , G.
(g) for g = 1, 2, . . . , G.
2. Compute the covariance matrix of X
3. From these covariance matrices, compute the linear transforma-
for i = 1, 2, . . . , M for mapping to the
×Ri
, . . . , RM)-dimensional latent space.
· · · ×M VM ∈
(g)je
is the i-mode product of
to X
×···×RM , where the operator ×
je
tion matrices Vi
(R1
, R2
4. Map the
ith sample X
∈ RPi
1 V1
2 V2
×R2
×
×
(g)je
RR1
tensor (Kolda & Bader, 2009).
5. Reconstruct ith sample ˜X
= X
×
1 V1V(cid:2)
1
(g)je
×
2 V2V(cid:2)
2
· · · ×M VMV(cid:2)
M..
(g)je
Entre-temps, PCA and MPCA each require a single data set. Ainsi, we ag-
gregated the data sets as X = [X
g=1 Ng and
performed PCA and MPCA for data set X .
(G)] ∈ RP1
, . . . , X
×···×PM×
, X
×P2
(2)
(1)
(cid:5)
G
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2865
6.2 Performance Assessment. For MCCA and MPCA, the reduced di-
mensions R1 and R2 were chosen as the same number, and then we fixed
R3 as two. All computations were performed by the software R (version 3.6)
(R Core Team, 2019). In the initialization of MCCA, solving the quadratic
programming problem was carried out using the function ipop in the pack-
age kernlab. MPCA was implemented as the function mpca in the package
rTensor. (The implementations of MCCA, APC, and CCA are available at
https://github.com/yoshikawa-kohei/MCCA.)
To assess their performances, we calculated the reconstruction error rate
(RER) under the same compression ratio (CR). RER is defined by
RER =
(cid:31)
(cid:31)
(cid:31)2
(cid:31)X − (cid:30)X
F
(cid:4)X (cid:4)2
F
,
(6.1)
, (cid:30)X
(cid:30)X = [
(cid:30)X
(g)
où
tensors
(g)2
norm of a tensor X ∈ RP1
(cid:30)X
(1)
= [ ˜X
, . . . , (cid:30)X
(2)
, ˜X
(g)1
, . . . , ˜X
×P2
(G)] is the aggregated data set of reconstructed
(g)Ng] for g = 1, 2, . . . , G and (cid:4)X (cid:4)F is the
×···×PM computed by
(cid:4)X (cid:4)F =
!
!
!
”
P1(cid:2)
P2(cid:2)
MP(cid:2)
· · ·
=1
p1
=1
p2
pM=1
x2
p1
,p2
,…,pM
,
(6.2)
in which xp1
fined CR as
,p2
,…,pM is an element (p1
, p2
, . . . , pM) of X . En outre, we de-
CR =
{The number of required parameters}
(cid:14)
M.
k=1 Pk
N ·
.
(6.3)
(cid:5)
M.
k=1 PkRk
+
(cid:16)
(cid:15)(cid:14)
M.
k=1 Pk
+ NR.
The number of required parameters for MCCA and MPCA is
(cid:16)
(cid:15)(cid:14)
M.
k=1 Rk
N
, whereas that for CCA and PCA is R
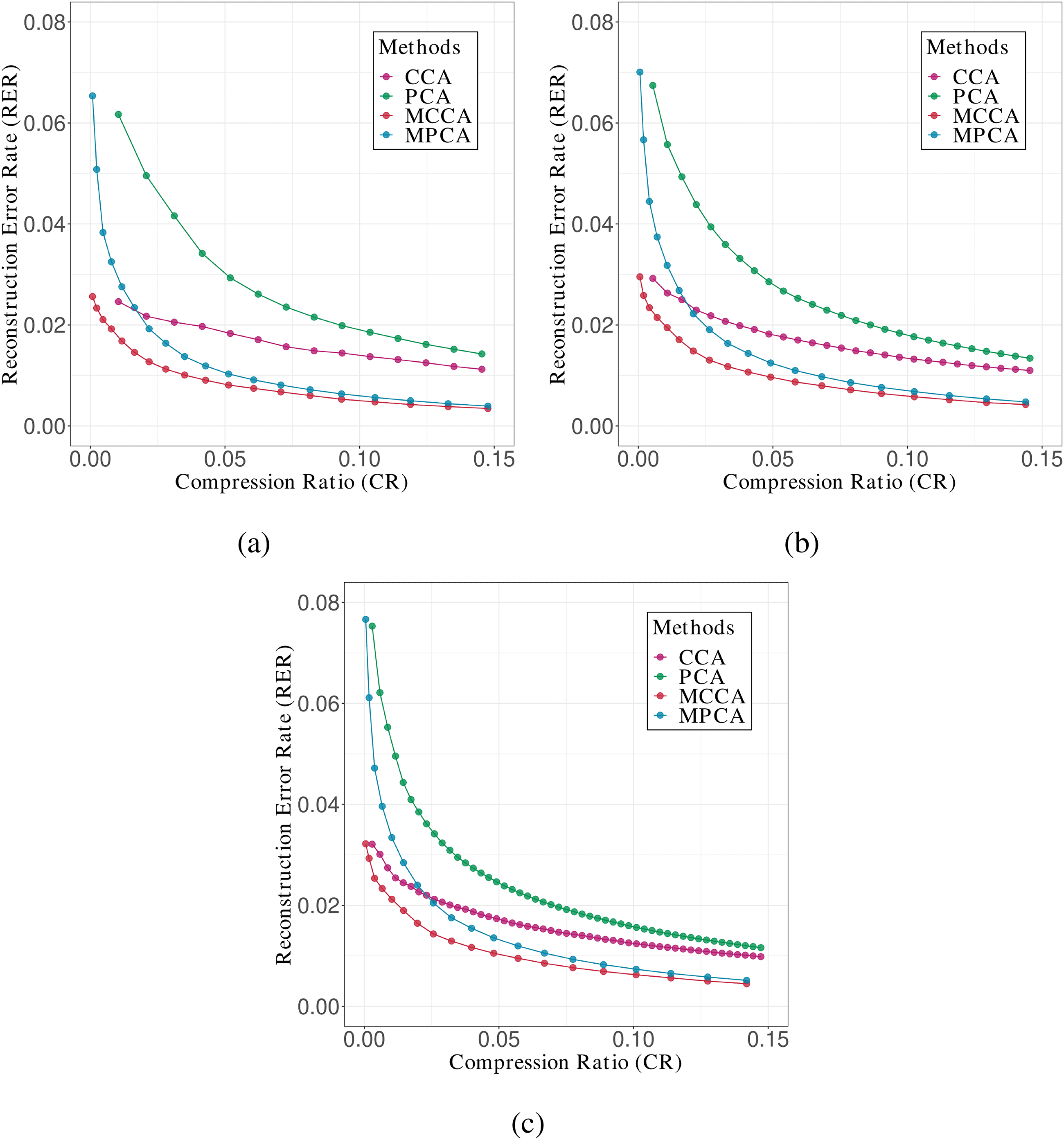
Chiffre 1 plots the RER obtained by estimating various reduced dimen-
sions for the AT&T(ORL) data set with group sizes of small, moyen, et
grand. As the figures for the results of the other data sets were similar to
Chiffre 1, we show them in the supplementary materials S1.
From Figure 1, we observe that the RER material MCCA is the smallest
for any value of CR. This indicates that MCCA performs better than the
other methods. En outre, note that CCA performs better than MPCA only
for fairly small values of CR, even though it is a method for vector data,
whereas MPCA performs better for larger values of CR. This implies the
limitations of CCA for vector data.
Next we consider group size by comparing panels a, b, and c in Figure 1.
The value of CR at the intersection of CCA and MPCA increases with
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2866
K. Yoshikawa and S. Kawano
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
Chiffre 1: Plots of RER versus CR for the AT&T(ORL) data set of various group
sizes: (un) petit, (b) moyen, et (c) grand.
increasing the group size. This indicates that MPCA has more trouble ex-
tracting an appropriate latent space as the group size increases. Since MPCA
does not consider the group structure, it is not possible to properly estimate
the covariance structure when the group size is large.
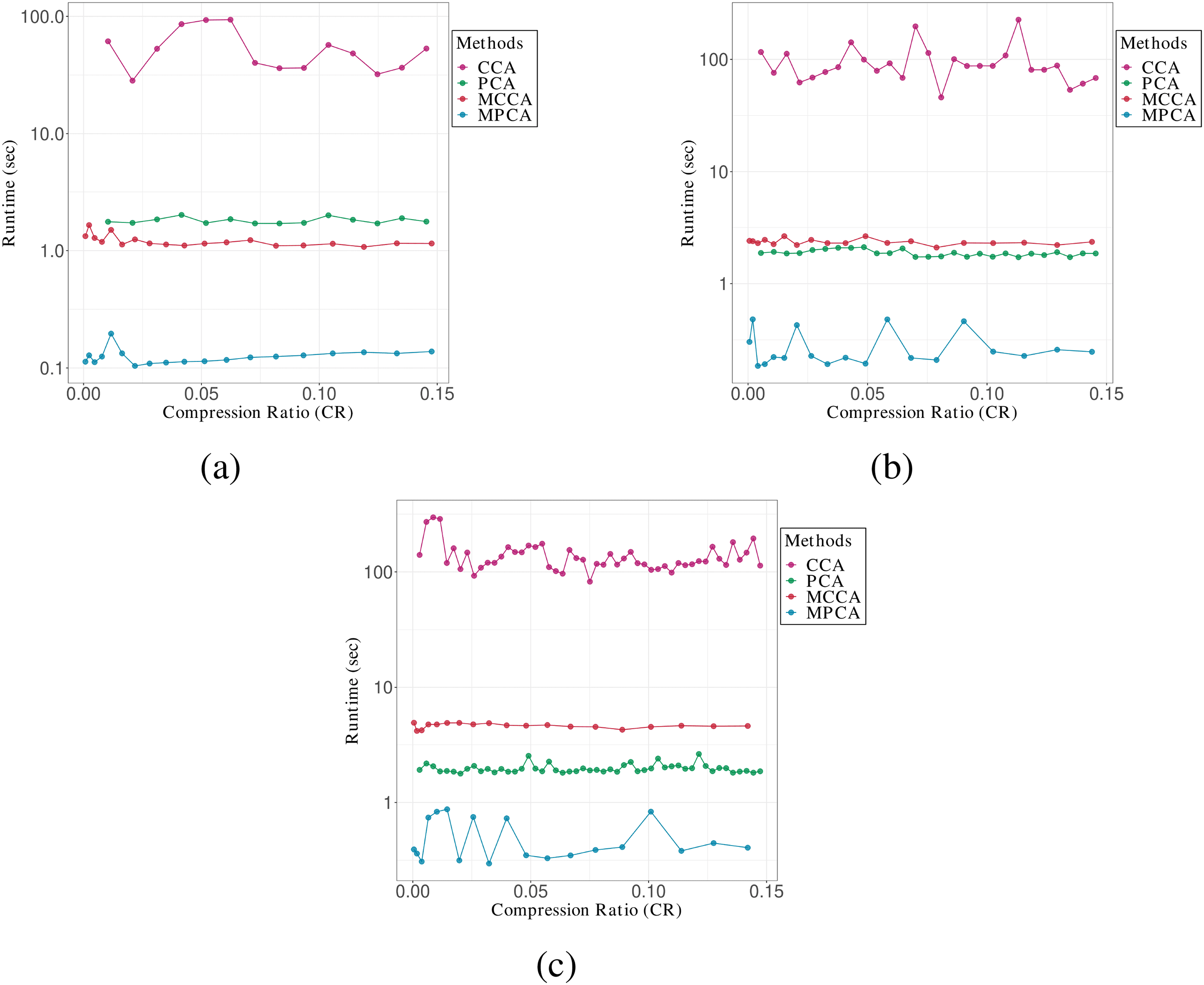
Chiffre 2 shows the comparison of runtime for the AT&T(ORL) data set
with group sizes of small, moyen, and large. Although Table 1 gives the
superiority of the computational complexity for MCCA, Chiffre 2 shows
that MCCA is slower than MPCA for any size of data set. This probably
arises from the difference of implementation of MCCA and MPCA: MCCA
is implemented by our hand-built source code, while MPCA is done by
the package rTensor. But when we compare MCCA with CCA, MCCA is
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2867
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2: Plots of runtime versus CR for the AT&T(ORL) data set of various
group sizes: (un) petit, (b) moyen, et (c) grand.
superior to CCA in terms of both computational complexity and the run-
time comparisons.
Chiffre 3 plots the reconstructed images for the AT&T(ORL) data set with
group sizes of the medium. This figure can be obtained by performing four
= 5 and R = 2. By setting the number
methodologies when we set R1
of the ranks in this way, we can compare the images with almost the same
CR, APC, CCA, and MPCA can recover the average structure of face images,
but they cannot deal with changes in the angle of the face. MCCA can also
recover the detailed differences in each image.
= R2
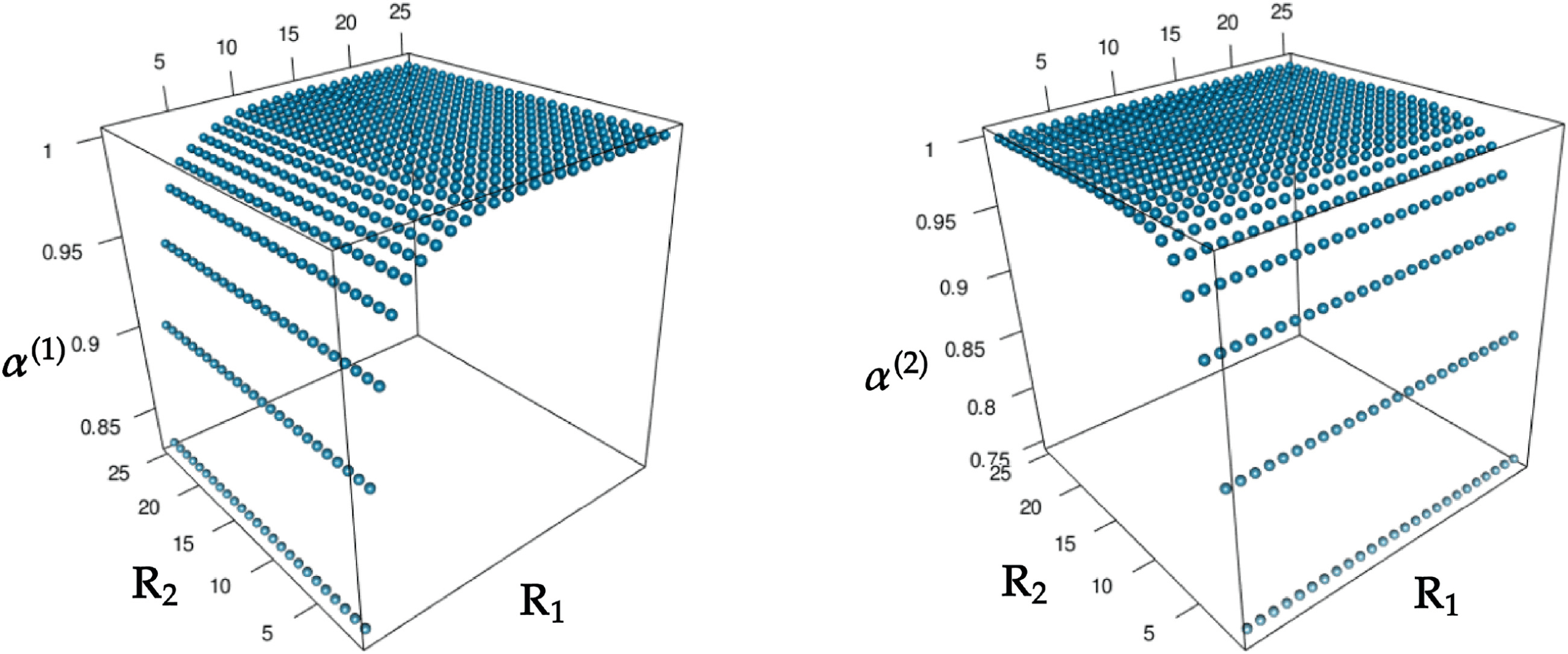
6.3 Behavior of Contraction Ratio. We examined the behavior of con-
traction ratio α(k). We performed MCCA on the AT&T(ORL) data set with
the medium group size and computed α(1) and α(2) with the various pairs
of reduced dimensions (R1
, R2) ∈ {1, 2, . . . , 25} × {1, 2, . . . , 25}.
Chiffre 4 shows the values of α(1) and α(2) for all pairs of R1 and R2. Comme
shown, un(1) and α(2) were invariant to variations in R2 and R1, respectivement.
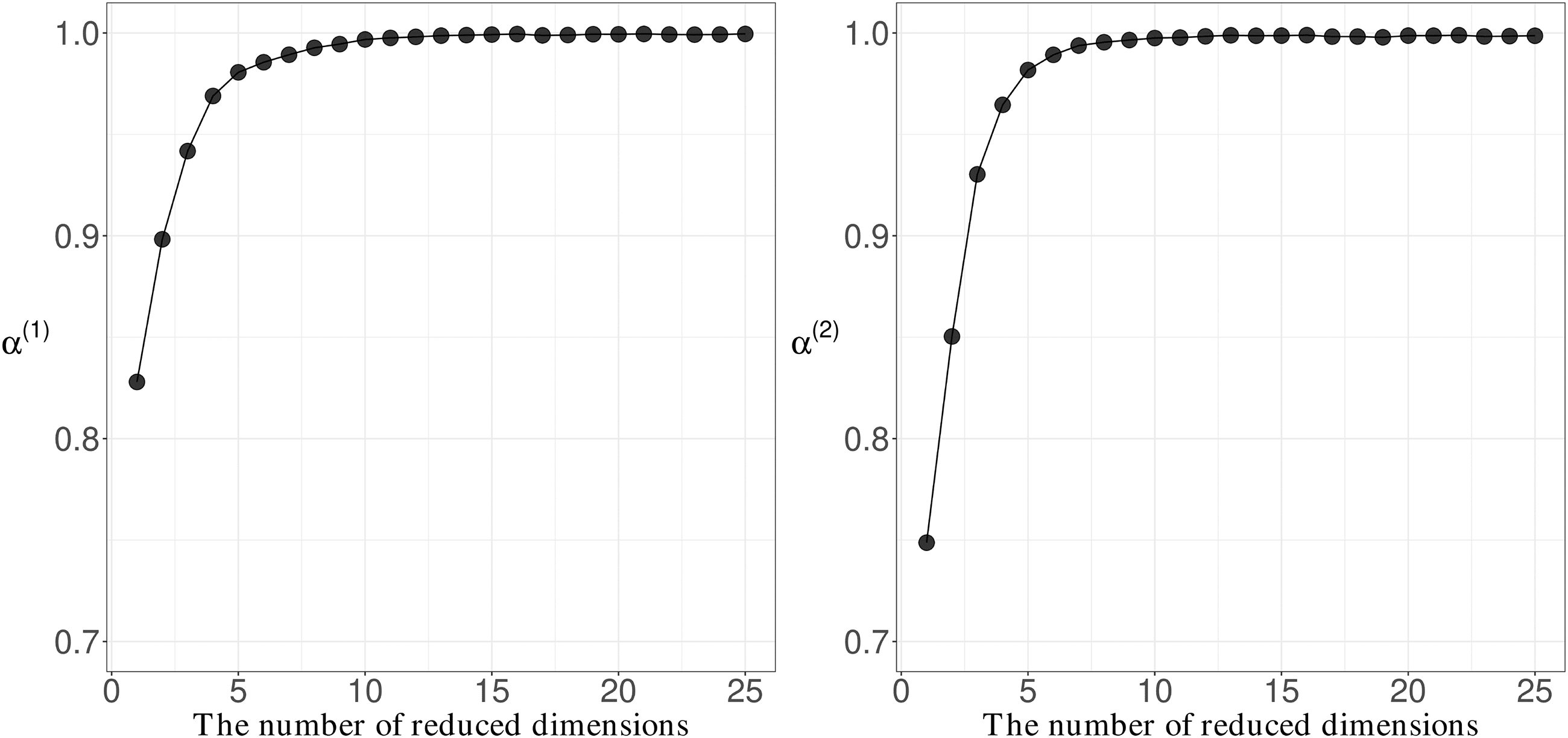
Donc, to facilitate visualization of changes in α(k), we draw Figure 5,
2868
K. Yoshikawa and S. Kawano
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
Chiffre 3: The reconstructed images for the AT&T(ORL) data set with the
medium group sizes under almost
the same CR. Image source: AT&T
Laboratories Cambridge.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4: un(1) and α(2) versus pairs of reduced dimensions (R1
, R2).
which represents α(1) and α(2) pour, respectivement, R2
= 1. Depuis
ces, we observe that when both R1 and R2 are greater than eight, les deux
un(1) and α(2) are close to one.
= 1 and R1
6.4 Efficacy of Solving the Quadratic Programming Problem. We in-
vestigated the usefulness of determining the initial value of w(k) by solv-
ing the quadratic programming problem 4.1. We applied MCCA to the
Multilinear Common Component Analysis
2869
Chiffre 5: un(1) and α(2) versus R1 and R2, respectivement.
AT&T(ORL) data set with the small, moyen, and large number of groups.
En outre, we used the smaller group size of three. For determining
the initial value of w(k), we consider three methods: solving the quadratic
programming problem 4.1 (MCCA:QP); setting all values of w(k) to one
(MCCA:FIX); and setting the values by random sampling according to the
uniform distribution U(0, 1) (MCCA:RANDOM). We computed the α(k)
= R2 (∈ {1, 2, . . . , 10}) for each of these
with the reduced dimensions R1
méthodes.
To evaluate the performance of these methods, we compared the val-
ues of α(k) and the number of iterations in the estimation. The number of
iterations in the estimation is the number of repetitions of lines 7 à 9 in al-
gorithm 1. For MCCA(RANDOM), we performed 50 trials and calculated
averages of each of these indices.
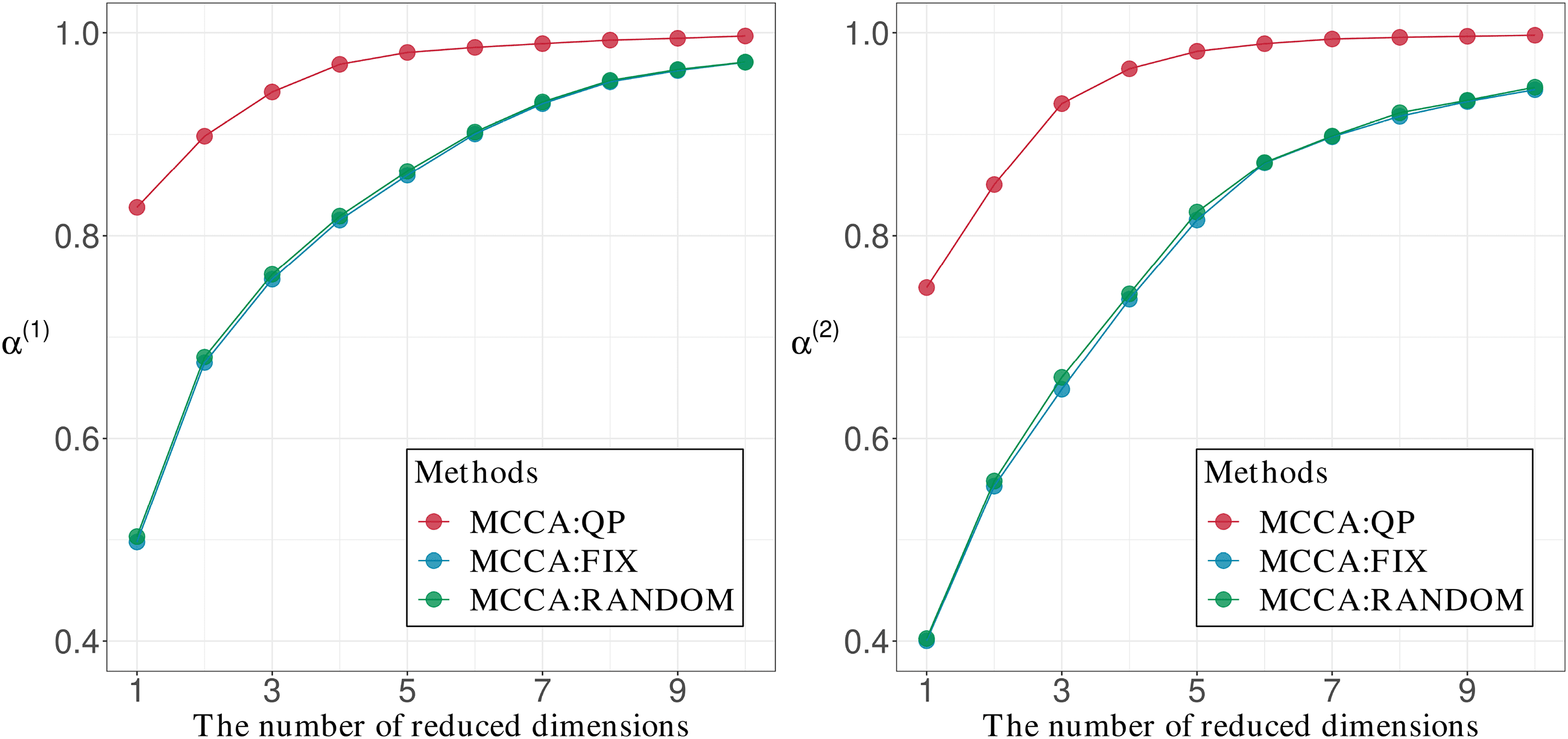
Chiffre 6 shows the comparisons of α(1) and α(2) when the initializa-
tion was performed by MCCA:QP, MCCA:FIX, and MCCA:RANDOM for
the AT&T(ORL) data set with a group size of three. It was confirmed that
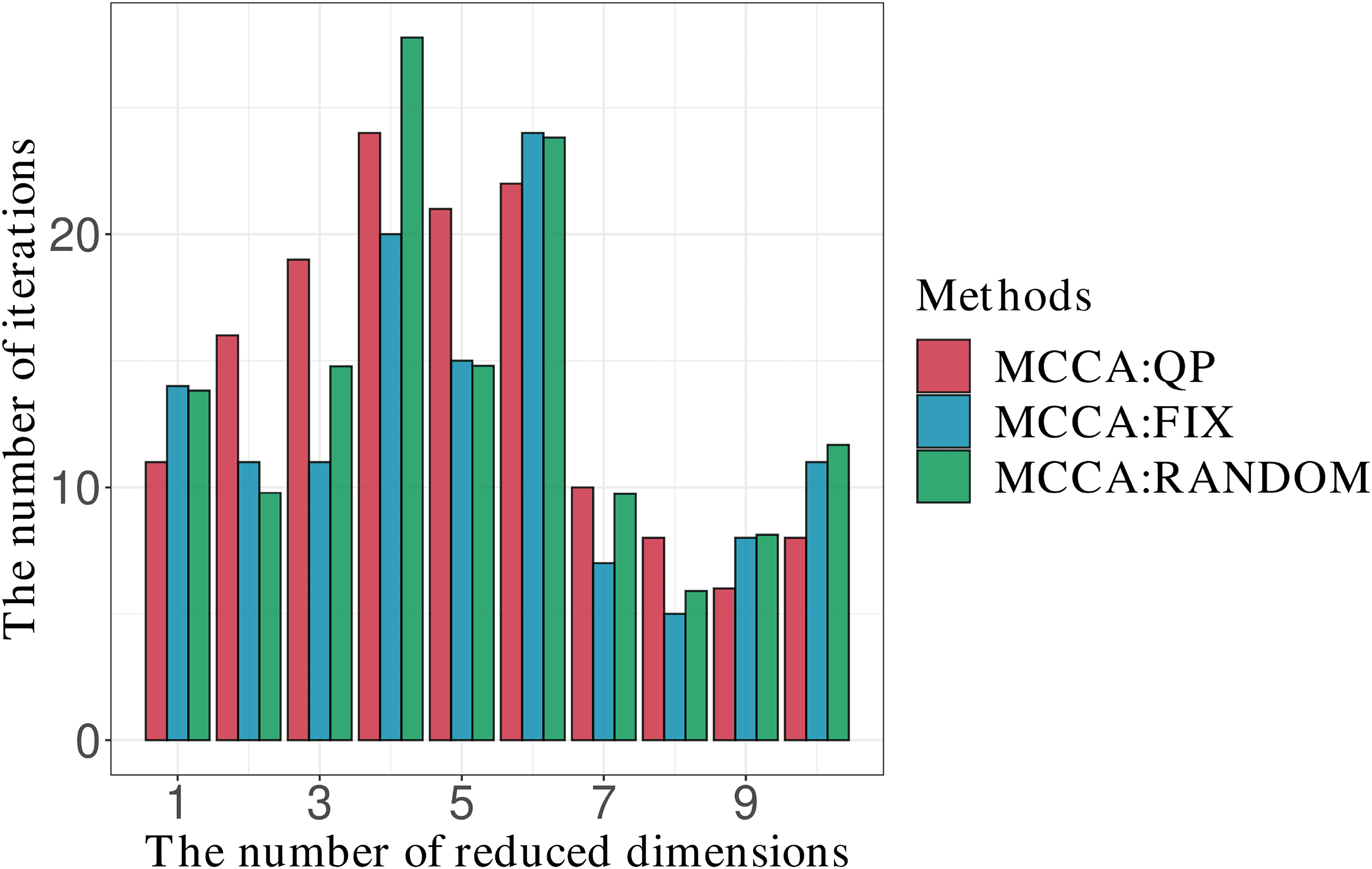
MCCA:QP provides the largest values of α(1) and α(2). Chiffre 7 shows the
number of iterations. MCCA:QP gives the smallest number of iterations
for almost all values of the reduced dimensions. This result indicates that
MCCA:QP converges to a solution faster than the other initialization meth-
ods. Cependant, when the reduced dimension is greater than or equal to eight,
the other methods are competitive with MCCA:QP. A lack of difference in
the number of iterations could result from the closeness of the initial values
and the global optimal solution. Note that when the R1 and R2 are greater
than or equal to eight, un(1) and α(2) are sufficiently close to one, based on
Chiffre 6. This indicates that the initial values are close to the global optimal
solution obtained from theorem 1. Ainsi, the result shows almost the same
number of iterations for the three methods.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2870
K. Yoshikawa and S. Kawano
Chiffre 6: Comparisons of α(1) and α(2) computed by using the initial values ob-
tained from the initializations MCCA:QP, MCCA:FIX, and MCCA:RANDOM
with the AT&T(ORL) data set for a group size of three.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
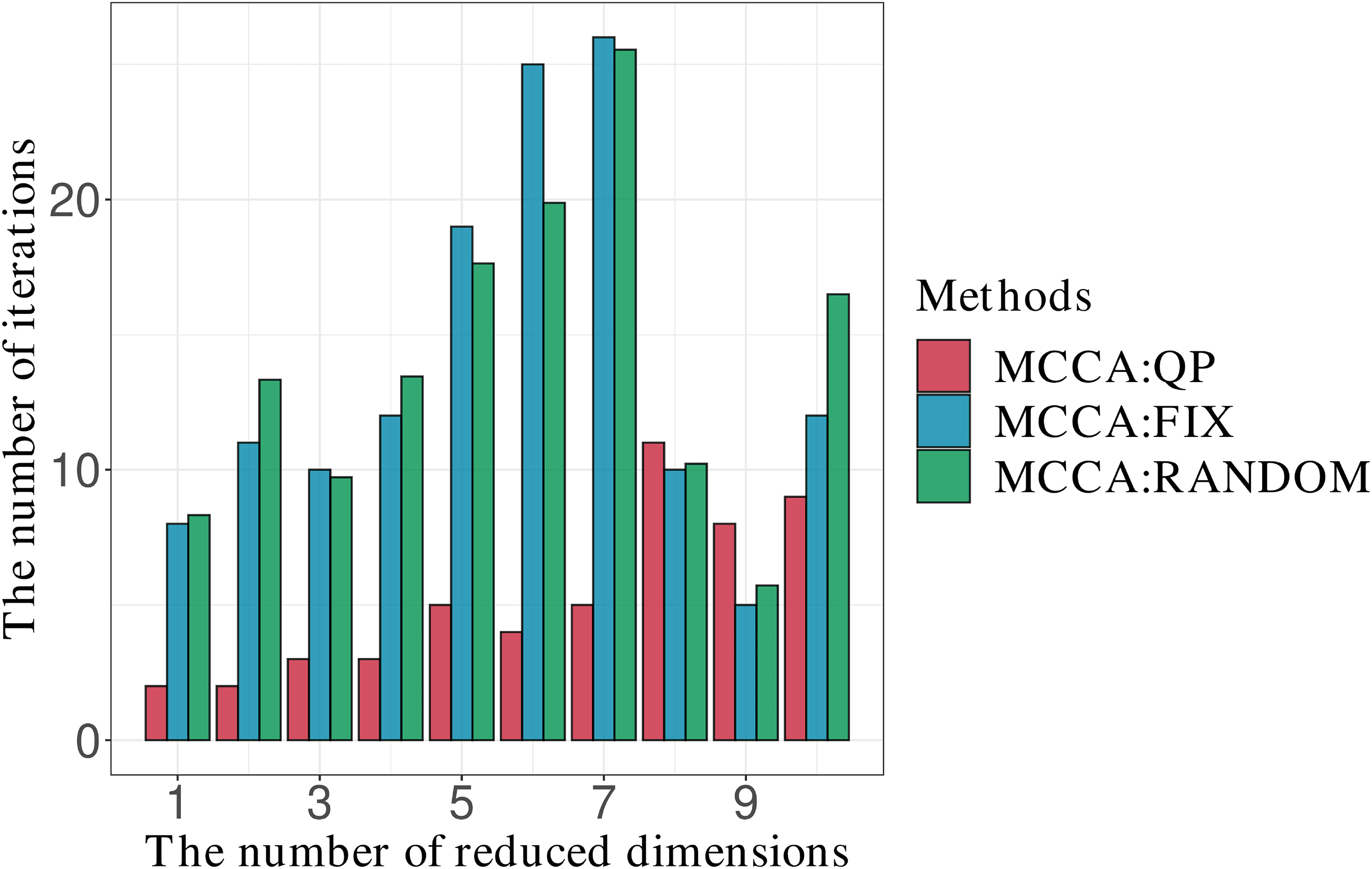
Chiffre 7: Comparison of the number of iterations when the initialization
was performed by MCCA:QP, MCCA:FIX, and MCCA:RANDOM with the
AT&T(ORL) data set for a group size of three.
Figures 8 et 9 show comparisons for the AT&T(ORL) data set with the
medium group size. Since the figures for the results of other group sizes are
similar to Figures 8 et 9, we show them in the supplementary materials
S2. Chiffre 8 shows results similar those in Figure 6, whereas Figure 9 shows
competitive performances for all reduced dimensions.
Multilinear Common Component Analysis
2871
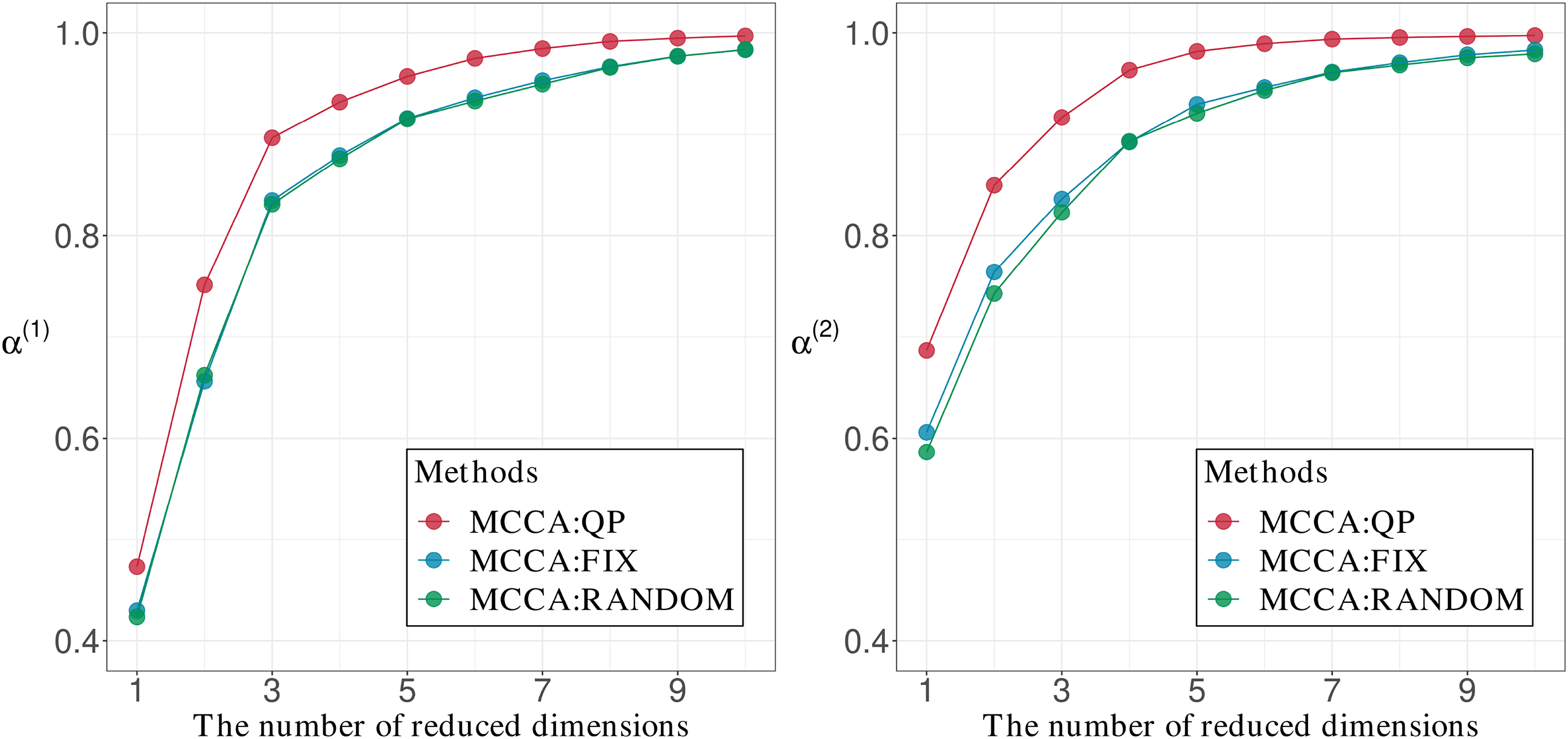
Chiffre 8: Comparisons of α(1) and α(2) computed using the initial values ob-
tained from the initialization of MCCA:QP, MCCA:FIX, and MCCA:RANDOM
with the AT&T(ORL) data set and the medium group size.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 9: Comparison of the number of iterations when the initialization
was perfomed by MCCA:QP, MCCA:FIX, and MCCA:RANDOM with the
AT&T(ORL) data set and the medium group size.
7 Conclusion
We have developed the multilinear common components analysis (MCCA)
by introducing a covariance structure based on the Kronecker product. À
efficiently solve the nonconvex optimization problem for MCCA, we have
2872
K. Yoshikawa and S. Kawano
proposed an iteratively updating algorithm that exhibits some superior the-
oretical convergence properties. Numerical experiments have shown the
usefulness of MCCA.
Spécifiquement, MCCA was shown to be competitive among the initializa-
tion methods in terms of the number of iterations. As the number of groups
increases, the overall number of samples increases. This may be the reason
why all methods required almost the same number of iterations for small,
moyen, and large groups. Note that in this study, we used the Kronecker
product representation to estimate the covariance matrix for tensor data
sets. Greenewald, Zhou, and Hero (2019) used the Kronecker sum repre-
sentation for estimating the covariance matrix, and it would be interesting
to extend the MCCA to this and other covariance representations.
Appendix A: Proof of Lemma 1
We provide two basic lemmas about Kronecker products before we prove
lemma 1.
Lemma 2. For matrices A, B, C, and D such that matrix products AC and BD
can be calculated, the following equation holds:
(A ⊗ B)(C ⊗ D) = AC ⊗ BD.
Lemma 3. For square matrices A and B, the following equation holds:
tr(A ⊗ B) = tr(UN)tr(B).
These lemmas are known as the mixed-product property and the spec-
trum property, respectivement. See Harville (1998) for detailed proofs.
Proof of Lemma 1. For the maximization problem 3.5, move the summa-
tion over index g out of the tr(·) and replace S∗
⊗
· · · ⊗ S(M.)
(g) and V∗
(g) and V(1) ⊗ V(2) ⊗ · · · ⊗ V(M.), respectivement. Alors
with S(1)
(g)
⊗ S(2)
(g)
G(cid:2)
g=1
maximum
V(k)
k=1,2,…,M.
(cid:15)
#(cid:15)
tr
V(1) ⊗ · · · ⊗ V(M.)
(cid:16)(cid:2) (cid:15)
S(1)
(g)
(cid:16) (cid:15)
(cid:16)
⊗ · · · ⊗ S(M.)
(g)
V(1) ⊗ · · · ⊗ V(M.)
V(1) ⊗ · · · ⊗ V(M.)
(cid:16)(cid:2) (cid:15)
S(1)
(g)
(cid:16) (cid:15)
(cid:16)$
⊗ · · · ⊗ S(M.)
(g)
V(1) ⊗ · · · ⊗ V(M.)
,
s.t. V(k)
(cid:2)
V(k) = IRk
.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2873
By lemmas 2 et 3, we have
G(cid:2)
(cid:20)(cid:15)
tr
V(1)
g=1
(cid:2)
S(1)
(g)V(1)V(1)
(cid:2)
S(1)
(g)V(1)
(cid:16)
maximum
(cid:2)
V(k)
V(k) =IRk
k=1,2,…,M.
(cid:15)
V(M.)
(cid:2)
· · ·
S(M.)
(g) V(M.)V(M.)
(cid:2)
(cid:16)(cid:21)
S(M.)
(g) V(M.)
(cid:21)
= max
V(k)
(cid:2)
V(k) =IRk
k=1,2,…,M.
(cid:20)
V(k)
(cid:2)
tr
S(k)
(g)V(k)V(k)
(cid:2)
G(cid:2)
M.(cid:19)
g=1
k=1
S(k)
(g)V(k)
.
This leads to the maximization problem in lemma 1.
(cid:2)(cid:2)
Appendix B: Proof of Theorem 1
Theorem 1 can be easily shown from the following lemma.
Lemma 4. Consider the maximization problem
maximum
V(k)
F
(cid:8)
k(V(k)) = max
V(k)
tr
⎧
⎨
⎩V(k)
⎛
(cid:2)
⎝
G(cid:2)
g=1
⎞
⎠ V(k)
⎫
⎬
⎭
.
(B.1)
w(−k)
(g) S(k)
(g)S(k)
(g)
Let M(k) = tr
(cid:20)(cid:5)
G
g=1
w(−k)
(g) S(k)
(g)S(k)
(g)
(cid:21)
. Alors
F (cid:8)
k(V(k))2
M.(k)
≤ fk(V(k)) ≤ f
(cid:8)
k(V(k)).
Proof of Lemma 4. D'abord, we prove fk(V(k)) ≤ f (cid:8)
onal matrix V(k) ∈ RPk
×(Pk
V(k)
V(k)
k(V(k)). For any orthog-
×Rk , we can always find an orthogonal matrix
(cid:2) +
⊥ = O. Then the equation V(k)V(k)
−Rk ) that satisfies V(k)(cid:2)V(k)
= IPk holds. By definition,
⊥ ∈ RPk
(cid:2)
⊥ V(k)
⊥
fk(V(k)) = tr
≤ tr
⎧
⎨
⎩V(k)
⎧
⎨
⎩V(k)
⎛
(cid:2)
G(cid:2)
⎝
g=1
⎛
(cid:2)
G(cid:2)
⎝
g=1
⎞
w(−k)
(g) S(k)
(g)V(k)V(k)
(cid:2)
S(k)
(g)
⎠ V(k)
⎫
⎬
⎭
w(−k)
(g) S(k)
(g)
(cid:15)
V(k)V(k)
(cid:2)
(cid:16)
(cid:2)
+ V(k)
⊥ V(k)
⊥
⎞
S(k)
(g)
⎠ V(k)
⎫
⎬
⎭
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2874
K. Yoshikawa and S. Kawano
⎞
⎠ V(k)
⎫
⎬
⎭
w(−k)
(g) S(k)
(g)S(k)
(g)
⎧
⎨
⎩V(k)
⎛
(cid:2)
G(cid:2)
⎝
g=1
= tr
= f
(cid:8)
k(V(k)).
Ainsi, we have obtained fk(V(k)) ≤ f (cid:8)
k(V(k)).
Suivant, we prove f (cid:8)
k (V(k) )2
M.(k)
matrices:
≤ fk(V(k)). We define the following block
)*
)*
A =
B =
w(−k)
(1) S(k)
(1)
1
2 V(k)V(k)
(cid:2)
S(k)
(1)
1
2 , . . . ,
*
+
w(−k)
(1) S(k)
(1)
, . . . ,
w(−k)
(G) S(k)
(G)
.
*
w(−k)
(G) S(k)
(G)
1
2 V(k)V(k)
(cid:2)
S(k)
(G)
+
1
2
,
Note that since S(k)
decomposed to S(k)
(g)
respectivement:
1
2 S(k)
(g)
(g) is a symmetric positive-definite matrix, S(k)
(g) can be
2 . We calculate the traces of AA, AB, and BB,
1
,
–
w(−k)
(g) tr
S(k)
(g)
1
2 V(k)V(k)
(cid:2)
S(k)
(g)
1
2 S(k)
(g)
1
2 V(k)V(k)
(cid:2)
1
2
S(k)
(g)
G(cid:2)
g=1
G(cid:2)
tr (AA) =
=
w(−k)
(g) tr
(cid:20)
(cid:2)
V(k)
S(k)
(g)V(k)V(k)
(cid:2)
S(k)
(g)V(k)
(cid:21)
g=1
⎧
⎨
⎩V(k)
= tr
⎛
(cid:2)
G(cid:2)
⎝
g=1
⎞
w(−k)
(g) S(k)
(g)V(k)V(k)
(cid:2)
S(k)
(g)
⎠ V(k)
⎫
⎬
⎭
= fk(V(k)),
tr (AB) =
=
=
G(cid:2)
g=1
G(cid:2)
g=1
G(cid:2)
g=1
S(k)
(g)
1
2 V(k)V(k)
(cid:2)
S(k)
(g)
1
2 S(k)
(g)
–
w(−k)
(g) tr
,
,
w(−k)
(g) tr
S(k)
(g)
1
2 V(k)V(k)
(cid:2)
S(k)
(g)
1
2 S(k)
(g)
1
2 S(k)
(g)
1
2
–
(cid:20)
w(−k)
(g) tr
(cid:2)
V(k)
(g)S(k)
S(k)
(g)V(k)
(cid:21)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2875
⎞
⎠ V(k)
⎫
⎬
⎭
w(−k)
(g) S(k)
(g)S(k)
(g)
⎧
⎨
⎩V(k)
⎛
(cid:2)
G(cid:2)
⎝
g=1
= tr
= f
(cid:8)
k(V(k)),
tr (BB) = tr
⎛
G(cid:2)
⎝
g=1
⎞
⎠ = M(k).
w(−k)
(g) S(k)
(g)S(k)
(g)
From the Cauchy–Schwarz inequality, we have
fk(V(k))M.(k) = tr (AA) tr (BB) ≥
(cid:28)
tr (AB)
(cid:29)
2 = f
(cid:8)
k(V(k))2.
By dividing both sides of the inequality by M(k), we obtain f
(cid:8)
k (V(k) )2
M.(k)
≤ fk(V(k)).
(cid:2)
Proof of Theorem 1. Let f (cid:8) maximum
F (cid:8)
V(k)
k(V(k)). From lemma 4 and the definition of α(k), we have
0
be the global maximum of f (cid:8)
k(V(k)) et
k
= arg max
V(k)
un(k) F
(cid:8) maximum
k
= f (cid:8)
0 )2
k(V(k)
M.(k)
≤ fk(V(k)
0 ).
Let f max
k
f max
. Ainsi,
k
be the global maximum of fk(V(k)). It then holds that fk(V(k)
0 ) ≤
un(k) F
(cid:8) maximum
k
≤ f max
k
.
Let V(k)
0∗ = arg max
V(k)
fk(V(k)). From lemma 4, we have
f max
k
= fk(V(k)
0∗ ) ≤ f
(cid:8)
k(V(k)
0∗ ).
Since f (cid:8)
k(V(k)
0∗ ) ≤ f (cid:8) maximum
k
, we have
f max
k
≤ f
(cid:8) maximum
k
.
Ainsi, we have obtained α(k) F (cid:8) maximum
k
≤ f max
k
≤ f (cid:8) maximum
k
.
(cid:2)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2876
K. Yoshikawa and S. Kawano
Appendix C: Proof of Theorem 2
Proof of Theorem 2. By definition
(cid:15)(cid:5)
(cid:2)
un(k) = f (cid:8) maximum
k
M.(k)
tr
=
(cid:20)
V(k)
0
G
g=1
G
g=1
w(−k)
(g) S(k)
w(−k)
(g) S(k)
(g)S(k)
(g)
(cid:21)
(g)S(k)
(g)
(cid:20)(cid:5)
tr
(cid:16)
(cid:21)
V(k)
0
.
(C.1)
By using the eigenvalue representation, we can rewrite the numerator of
un(k) comme
(cid:8) maximum
k
F
=
G(cid:2)
g=1
w(−k)
(g)
Rk(cid:2)
je = 1
.
λ(k)
(g)je
The denominator of α(k) can be represented as the sum of eigenvalues as
follows:
M.(k) =
G(cid:2)
g=1
w(−k)
(g)
Pk(cid:2)
je = 1
.
λ(k)
(g)je
Ainsi, we can transform α(k) as follows:
un(k) =
(cid:5)
(cid:5)
G
g=1
G
g=1
w(−k)
(g)
w(−k)
(g)
(cid:5)
(cid:5)
Rk
je = 1
Pk
je = 1
λ(k)
(g)je
λ(k)
(g)je
.
When we set
⎡
⎣
Pk(cid:2)
i=Rk
+1
,
λ(k)
(1)je
Pk(cid:2)
i=Rk
+1
, . . . ,
λ(k)
(2)je
(cid:26)
Pk(cid:2)
je = 1
(cid:17)
w(−k)
(1)
,
λ(k)
(1)je
Pk(cid:2)
je = 1
, . . . ,
λ(k)
(2)je
, w(−k)
(2)
, . . . , w(−k)
(G)
Pk(cid:2)
je = 1
(cid:18)(cid:2)
,
λ(k)
0
=
λ(k)
1
=
w(k) =
⎤
(cid:2)
⎦
λ(k)
(G)je
,
Pk(cid:2)
i=Rk
+1
(cid:27)(cid:2)
λ(k)
(G)je
,
we can reformulate α(k) comme
(cid:15)
(cid:16)(cid:2)
un(k) =
λ(k)
1
− λ(k)
0
(cid:2)
λ(k)
1
w(k)
w(k)
.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2877
Ainsi, we obtain the following maximization problem:
(cid:15)
λ(k)
1
maximum
w(k)
(cid:16)(cid:2)
w(k)
− λ(k)
0
(cid:2)
λ(k)
1
w(k)
,
s.t. w(k) > 0.
Note that the constraints can be obtained by the definition of w(k). In addi-
tion, this maximization problem can be reformulated as
(cid:15)
λ(k)
1
maximum
w(k)
(cid:16)(cid:2)
w(k)
− λ(k)
0
(cid:2)
λ(k)
1
w(k)
= max
w(k)
1 −
(cid:2)
(cid:2)
w(k)
w(k)
λ(k)
0
λ(k)
1
= min
w(k)
(cid:2)
(cid:2)
w(k)
w(k)
.
λ(k)
0
λ(k)
1
(cid:2)
(cid:2)
w(k)/λ(k)
1
Since λ(k)
w(k) is nonnegative, solving the optimization problem
0
for the squared function of the objective function maintains generality.
Ainsi, we can consider the following minimization problem:
min
w(k)
w(k)
w(k)
(cid:2)
(cid:2)
(cid:2)λ(k)
0
(cid:2)λ(k)
1
λ(k)
0
λ(k)
1
w(k)
w(k)
,
s.t. w(k) > 0.
En plus, from the invariance under multiplication of w(k) by a constant,
we obtain the following objective function of the quadratic programming
problem:
(cid:2)
w(k)
λ(k)
0
λ(k)
0
(cid:2)
w(k),
min
w(k)
s.t. w(k) > 0, w(k)
(cid:2)
(cid:2)
λ(k)
1
λ(k)
1
w(k) = 1.
(cid:2)
Appendix D: Proof of Theorem 3
Proof of Theorem 3. We define the following block matrices:
)*
As =
w(−k)
(1) S(k)
(1)
1
2 V(k)
s V(k)
s
(cid:2)
S(k)
(1)
1
2 , . . . ,
*
w(−k)
(G) S(k)
(G)
1
2 V(k)
s V(k)
s
+
1
2
.
(cid:2)
S(k)
(G)
Ici, we calculate the traces of AsAs, AsAs+1, and As+1As+1. The calcula-
tions of tr (AsAs) and tr (As+1As+1) are the same as that of tr (AA) by replac-
ing V(k) with V(k)
s+1, respectivement, in lemma 4. Ainsi, nous
obtain
s and V(k) with V(k)
tr (AsAs) = fk(V(k)
s ),
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2878
K. Yoshikawa and S. Kawano
tr (AsAs+1) =
=
G(cid:2)
g=1
G(cid:2)
,
w(−k)
(g) tr
S(k)
(g)
1
2 V(k)
s V(k)
s
(cid:2)
S(k)
(g)
1
2 S(k)
(g)
1
2 V(k)
s+1V(k)
s+1
–
(cid:2)
1
2
S(k)
(g)
w(−k)
(g) tr
(cid:20)
V(k)
s+1
(cid:2)
S(k)
(g)V(k)
s V(k)
s
(cid:2)
(cid:21)
(g)V(k)
S(k)
s+1
⎞
w(−k)
(g) S(k)
(g)V(k)
s V(k)
s
(cid:2)
S(k)
(g)
⎠ V(k)
s+1
⎫
⎬
⎭
,
g=1
⎧
⎨
⎩V(k)
s+1
= tr
⎛
(cid:2)
G(cid:2)
⎝
g=1
tr (As+1As+1) = fk(V(k)
s+1).
Since V(k)
s+1
= arg max
V(k)
tr
(cid:15)(cid:5)
(cid:2)
(cid:20)
V(k)
G
g=1
w(−k)
(g) S(k)
(g)V(k)
s V(k)
s
(cid:16)
(cid:21)
V(k)
, we have
(cid:2)
S(k)
(g)
fk(V(k)
s ) = tr
≤ tr
⎛
G(cid:2)
⎝
g=1
⎛
(cid:2)
s
⎧
⎨
⎩V(k)
⎧
⎨
⎩V(k)
s+1
w(−k)
(g) S(k)
(g)V(k)
s V(k)
s
⎞
(cid:2)
S(k)
(g)
⎠ V(k)
s
⎫
⎬
⎭
(cid:2)
G(cid:2)
⎝
g=1
w(−k)
(g) S(k)
(g)V(k)
s V(k)
s
⎞
(cid:2)
S(k)
(g)
⎠ V(k)
s+1
⎫
⎬
⎭
= tr (AsAs+1) .
From the positivity of both sides of the inequality, it holds that
fk(V(k)
s )2 ≤ [tr (AsAs+1)]2 .
En outre, from the Cauchy–Schwarz inequality, we have
fk(V(k)
s ) fk(V(k)
s+1) = tr (AsAs) tr (As+1As+1)
≥ [tr (AsAs+1)]2 .
Ainsi,
fk(V(k)
s ) fk(V(k)
s+1) ≥ [tr (AsAs+1)]2 ≥ fk(V(k)
s )2.
Alors, we have obtained fk(V(k)
sides of the inequality by fk(V(k)
fk(V(k)
s+1).
s ) fk(V(k)
s )2 ≤ fk(V(k)
s ), we obtain the inequality fk(V(k)
s+1). By dividing both
s ) ≤
(cid:2)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilinear Common Component Analysis
2879
Remerciements
We thank the reviewer for helpful comments and constructive suggestions.
S.K. was supported by JSPS KAKENHI grants JP19K11854 and JP20H02227,
and MEXT KAKENHI grants JP16H06429, JP16K21723, and JP16H06430.
Les références
Allen, G. (2012). Sparse higher-order principal components analysis. In Proceedings
of the Fifteenth International Conference on Artificial Intelligence and Statistics (pp.
27–36).
Badeau, R., & Boyer, R.. (2008). Fast multilinear singular value decomposition for
structured tensors. SIAM Journal on Matrix Analysis and Applications, 30(3), 1008–
1021.
Bensmail, H., & Celeux, G. (1996). Regularized gaussian discriminant analysis
through eigenvalue decomposition. Journal of the American Statistical Association,
91(436), 1743–1748.
Boik, R.. J.. (2002). Spectral models for covariance matrices. Biometrika, 89(1), 159–182.
Carroll, J.. D., & Chang, J.-J. (1970). Analysis of individual differences in multidi-
mensional scaling via an N-way generalization of “Eckart-Young” decomposi-
tion. Psychometrika, 35(3), 283–319.
Flury, B. N. (1984). Common principal components in K groups. Journal of the Amer-
ican Statistical Association, 79(388), 892–898.
Flury, B. N. (1986). Asymptotic theory for common principal component analysis.
Annals of Statistics, 14(2), 418–430.
Flury, B. N. (1988). Common principal components and related multivariate models. Nouveau
York: Wiley.
Flury, B. N., & Gautschi, W. (1986). An algorithm for simultaneous orthogonal trans-
formation of several positive definite symmetric matrices to nearly diagonal
formulaire. SIAM Journal on Scientific and Statistical Computing, 7(1), 169–184.
Greenewald, K., Zhou, S., & Hero III, UN. (2019). Tensor graphical Lasso (TeraLasso).
Journal of the Royal Statistical Society: Série B (Statistical Methodology), 81(5), 901–
931.
Harshman, R.. UN. (1970). Foundations of the PARAFAC procedure: Models and con-
ditions for an “explanatory” multimodal factor analysis. UCLA Working Papers in
Phonetics, 16(1), 84.
Harville, D. UN. (1998). Matrix algebra from a statistician’s perspective. New York:
Springer-Verlag.
Jolliffe, je. (2002). Analyse en composantes principales. New York: Springer-Verlag.
Kermoal, J.. P., Schumacher, L., Pedersen, K. JE., Mogensen, P.. E., & Frederiksen, F.
(2002). A stochastic MIMO radio channel model with experimental validation.
IEEE Journal on Selected Areas in Communications, 20(6), 1211–1226.
Kiers, H. UN. (2000). Towards a standardized notation and terminology in multiway
analyse. Journal of Chemometrics, 14(3), 105–122.
Kolda, T. G., & Bader, B. W. (2009). Tensor decompositions and applications. SIAM
Review, 51(3), 455–500.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
2880
K. Yoshikawa and S. Kawano
Lai, Z., Xu, Y., Chen, Q., Lequel, J., & Zhang, D. (2014). Multilinear sparse principal
component analysis. IEEE Transactions on Neural Networks and Learning Systems,
25(10), 1942–1950.
Lecun, Y., Bottou, L., Bengio, Y., & Haffner, P.. (1998). Gradient-based learning ap-
plied to document recognition. In Proceedings of the IEEE, 86(11), 2278–2324.
Lu, H., Plataniotis, K. N., & Venetsanopoulos, UN. N. (2008). MPCA: Multilinear prin-
cipal component analysis of tensor objects. IEEE Transactions on Neural Networks,
19(1), 18–39.
Manly, B. F. J., & Rayner, J.. C. W. (1987). The comparison of sample covariance ma-
trices using likelihood ratio tests. Biometrika, 74(4), 841–847.
Martinez, UN., & Benavente., R.. (1998). The AR face database (CVC Technical Report
24).
Martinez, UN. M., & Kak, UN. C. (2001). PCA versus LDA. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 23(2), 228–233.
Parc, H., & Konishi, S. (2020). Sparse common component analysis for multiple high-
dimensional datasets via noncentered principal component analysis. Statistical
Papers, 61, 2283–2311.
Pearson, K. (1901). LIII. On lines and planes of closest fit to systems of points in space.
Londres, Édimbourg, and Dublin Philosophical Magazine and Journal of Science, 2(11),
559–572.
Pourahmadi, M., Daniels, M.. J., & Parc, T. (2007). Simultaneous modelling of the
Cholesky decomposition of several covariance matrices. Journal of Multivariate
Analysis, 98(3), 568–587.
R Core Team (2019). R.: A language and environment for statistical computing. Vienne,
Autriche: R Foundation for Statistical Computing.
Wang, H., Banerjee, UN., & Boley, D. (2011). Common component analysis for multiple
covariance matrices. In Proceedings of the 17th ACM SIGKDD International Confer-
ence on Knowledge Discovery and Data Mining (pp. 956–964). New York: ACM.
Wang, S., Sun, M., Chen, Y., Pang, E., & Zhou, C. (2012). STPCA: Sparse tensor prin-
cipal component analysis for feature extraction. In Proceedings of the 21st Interna-
tional Conference on Pattern Recognition (pp. 2278–2281). Piscataway, New Jersey: IEEE.
Werner, K., Jansson, M., & Stoica, P.. (2008). On estimation of covariance matrices
with Kronecker product structure. IEEE Transactions on Signal Processing, 56(2),
478–491.
Yu, K., Bengtsson, M., Ottersten, B., McNamara, D., Karlsson, P., & Beach, M.. (2004).
Modeling of wide-band MIMO radio channels based on NLOS indoor measure-
ments. IEEE Transactions on Vehicular Technology, 53(3), 655–665.
Received November 20, 2020; accepted April 27, 2021.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
3
3
1
0
2
8
5
3
1
9
8
2
2
5
6
n
e
c
o
_
un
_
0
1
4
2
5
p
d
.
/
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3