Guido Kramann
Fachbereich Technik
Technische Hochschule Brandenburg
Magdeburger Strasse 50, 14770
Brandenburg an der Havel, Allemagne
kramann@th-brandenburg.de
Composing by Laypeople:
A Broader Perspective
Provided by Arithmetic
Operation Grammar
Abstrait: Many existing approaches to teaching laypeople to compose are based, to a certain extent, on simply hiding
the theoretical background. This is done, Par exemple, by offering ready-made musical events that can be combined
in any way to organize them in time. A different approach is taken in the work presented here. As an alternative to
classical music theory, with all its complications, the generative composition method Arithmetic Operation Grammar
(AOG) is used, which is much easier to learn. This approach has been taken in the conviction that the leaner theory
on which it is based, in combination with the compact symbolic representation of entire compositions, can make a
significant contribution to bringing forward the “everyday creativity” in the field of ubiquitous music. En outre, dans
the field of sonification, AOG offers the possibility of sonifying data that do not inherently include time as an ordering
parameter. To prove practical use of this approach, AOG is combined with a user interface that is more suitable for
adults as a target group and another one that is more appropriate for primary school children.
There will always be great masterworks and
great performances by individuals of exceptional
knowledge and skill. . . . But anyone who thinks
that such works should or will indefinitely
maintain an exclusive dominance over all other
musical forms and processes has not been
paying much attention to musical history or
ethnography, to what is going on musically in
this world right now, or to what else—besides
masterworks and virtuosi—people really do
love about music (Spiegel, 1998).
The magic of performing a classical concert lies
not least in the illusion of lightness and spontane-
ity with which a virtuoso on stage interacts with
the orchestra. This is all, cependant, painstakingly
worked out in years of musical study and even
longer intensive practice of the musical instrument.
Nowadays, impressive successes have been achieved
in giving amateurs and children the opportunity to
create real-time compositions themselves, Et ainsi
to have the exhilarating experience of becoming the
creator of a perfect musical moment, so to speak.
Current approaches typically focus on providing spe-
cial user interfaces (UIs) that allow users to organize
preproduced and preselected sound elements in time
(Jakobsen et al. 2016; Stolfi et al. 2018; Figueir ´o,
Soares, and Rohde 2019). This preselection ensures
Computer Music Journal, 44:1, pp. 17–34, Spring 2020
est ce que je:10.1162/COMJ a 00550
c(cid:2) 2021 Massachusetts Institute of Technology.
that the provided sound events can be combined
arbitrarily. Alternately, some approaches postpro-
cess the user interaction; nowadays more and more
through the use of artificial intelligence (Biles 2007;
Garcia-Valdez et al. 2013). The necessity to provide
a theoretical background is thereby avoided. But the
disadvantage of this procedure is also obvious: Once
the given tonal material has been used extensively,
it does not open up any further perspectives. Au-delà
an initial experience of what composing is, un
remains, so to speak, caught in a hermetic world
of sound with only limited possibilities. To move
further beyond this point, the only option would
be to deal with the traditional theoretical materials
as supported, Par exemple, by Almeida, Cabral, et
Almeida (2019).
In the approach described here, a different path is
taken. A method of composing will be introduced
that also makes it possible to create compositions—
even quite complex ones—that satisfy laws similar
to those of the classical theory of harmony and
counterpoint, but without having to refer directly
to those laws or to any other music theory at
tous. The method presented here, called Arithmetic
Operation Grammar (AOG), opens up an approach to
composing for laypeople that does not require years
of study, but does not need to hide the complexity of
the mechanisms behind it, since these mechanisms
are much simpler than those of classical music
théorie. The price for this convenience, cependant, est
that it is not easy to emulate any existing musical
style using AOG. The results achieved with AOG
Kramann
17
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
have certain qualities that have to be accepted as
they stand.
Although AOG was presented for the first time in
2019 at the International Symposium on Computer
Music Multidisciplinary Research (Kramann 2019),
the focus will now be on the extent to which the
use of AOG in combination with suitable UIs can
simplify access to composing for laypeople. Mais
what is meant by the claim that it is easier for
amateurs to compose with AOG than on the basis
of classical music theory? In slightly simplified
termes, one can say that classical theory consists
of a collection of rules and prohibitions. Following
Noam Chomsky (1956, 1959), AOG represents a
generative grammar of Type 3 . This means that the
results are well-formed, which in turn means that
in this case, apart from the generative rules of how
music is generated from a symbolic representation,
no further rules are needed to analyze and correct
the result after its generation. Ainsi, AOG also takes
a special position among generative grammars in
relation to music: Typical representatives, tel que
Lindenmayer systems or cellular automata, produce
patterns using symbolic representations before
decisions have been made about how those patterns
might be used musically. This means that these
are extramusical procedures (Supper 2001), alors que
AOG directly provides a musical structure that
does not need further manipulation, beyond musical
interpretation (instrumentation, playing techniques,
dynamics, etc., which are still necessary). Ainsi
AOG goes beyond other categories of generative
grammar.
In an attempt to categorize AOG, it would also
be conceivable, bien sûr, to compare this technique
with other approaches that use mathematical meth-
ods in some way to perform musical composition.
These other approaches usually originate from stud-
ies of music theory in which mathematical models
are created to put some aspects of composition into
a more general context. Chord progressions are one
such aspect. These approaches, typically, create
topologies of all chord progressions that comply
with a certain musical style. Choosing and travers-
ing paths through these topologies can be seen as a
rudimentary form of composing that involves this
kind of modeling (voir, par exemple., Hu and Gerhard 2019).
The difference to this type of approach is that the
mathematics in AOG do not represent a model of
an existing type of music. Plutôt, special proper-
ties of a given mathematical object, namely, prime
factorization of natural numbers, are exploited to
create music. From the perspective of AOG the
sequence of natural numbers contains an infinite
number of intertwined melodies that are already
in rhythmic and harmonic relationships with each
other. These melodies are extracted by mathemat-
ical operations and made audible by a so-called
selective division (explained in detail in the section
“Arithmetic Operation Grammar”). By doing so,
not only is a partial aspect of composing imple-
mented, but also polyphonic compositions are gen-
erated in which melody, rhythm, and harmony are
inherent.
If one would like to relate the compositional
results achieved with AOG to any existing com-
positional styles, one is most likely to find corre-
spondences in those 21st-century compositional
directions that still essentially organize pitches in
time but allow a broader spectrum of possibilities
than is provided for in classical theory, such as the
“tintinnabuli” harmony of Arvo P ¨art, or in certain
forms of free jazz. Rhythmic correspondences can be
found above all in the repetitive elements of minimal
musique. But to get a first impression of the composi-
tions that can be generated on the basis of AOG, refer
to Section 1 of the thematically arranged selection
of examples at http://kramann.info/98 AOG.
Arithmetic Operation Grammar
As mentioned above, AOG uses as a base element
the natural numbers, considered as a time series.
More precisely, this basic element consists of the
nonnegative integers (including zero), in mathemat-
ical literature represented symbolically as N or N0,
or any continuous finite subset. To show something
like an inner musical organization of this sequence
of numbers, a method will be used in the following
to quantify the degree of dissonance of two integers.
This method goes back to Leonhard Euler, OMS
called it gradus suivitatis, written as g (Busch 1970).
18
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
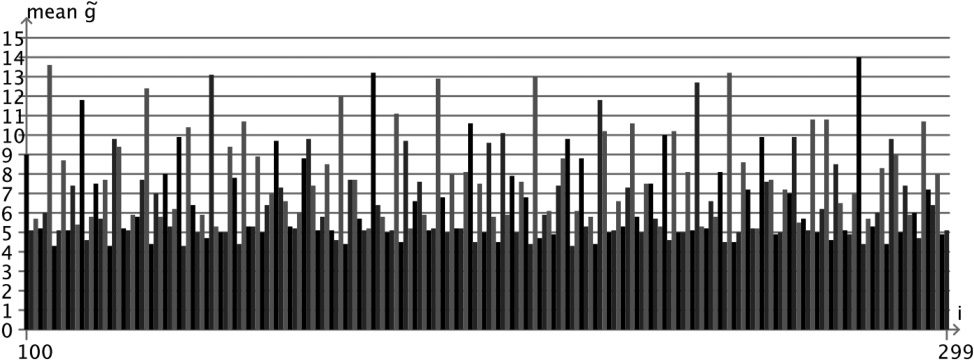
Chiffre 1. Mean value for ˜g
between a number and its
ten nearest neighbors (five
smaller and five larger) dans
the range of natural
numbers i from 100 à 299.
Larger values tend to occur
as individual peaks and
not in clusters.
To a certain degree, what is determined by this
measure also corresponds to our auditory perception
when the respective numbers are taken as oscilla-
tion periods or frequencies. The limitations of this
method in terms of its transferability to human
acoustic perception are deliberately accepted in this
work in favor of the simplicity of the method and
the fact that it works quite well over considerable
ranges. It should be mentioned, cependant, that the
two prime numbers 1,999 et 2,999, Par exemple,
provide a quite high value for g, but we would
hear them as a perfect fifth (ratio 2:3). For further
information see, Par exemple, papers by Schneider
and Frieler (2008) and by Kramann (2015). In the
following I will use the terms gradus suivitatis and
degree of dissonance, understood in the musical
sense, synonymously—aware that, from a musical
point of view, I am not taking a subtly differentiated
approche. But I am also not doing anything really
out of the ordinary.
Calculating gradus suivitatis
Now, if the gradus suivitatis is to be determined for
two integers a and b, one first factors out the greatest
common divisor of a and b, then for the remaining
prime factors pi, one considers their powers ki (le
number of times the prime number is multiplied in
the remaining factorization). According to Euler, le
gradus suivitatis is then:
g = 1 +
n(cid:2)
je = 1
ki · ( pi − 1).
Par exemple, for a = 16 = 4 · 22 and b = 20 = 4 · 51
(a major third), the result is
g(16, 20) = 1 + 2 · (2 − 1) + 1 · (5 − 1) = 7.
For a = 36 = 6 · 21 · 31 and b = 30 = 6 · 51 (a minor
troisième), the result is
g(36, 30) = 1 + 1 · (2 − 1) + 1 · (3 − 1) + 1 · (5 − 1) = 8.
If one now considers the gradus suivitatis between a
selected natural number and its closest neighbors, it
is clear that as the selected number increases, larger
and larger values of g will also tend to occur, depuis
the larger the selected number and its neighbors are,
the larger are their prime factors, on average.
If we use a modified gradus ˜g limited to the
first four primes (2, 3, 5, et 7), cependant, and if we
limit the exponents used with these prime factors,
a different picture emerges. The larger the value of
the modified averaged ˜gmean, the less often it occurs
for any number. En plus, it is typically the
case that large ˜gmean values are surrounded by small
ones. They tend to appear as single peaks and not in
clusters (voir la figure 1).
Kramann
19
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The modified function ˜g can be defined for two
natural numbers a and b as follows: If u is the
greatest common denominator of both numbers,
it follows that a = u · x and b = u · y. The prime
factors that are not common to both numbers are
then c = x · y = 2 p · 3q · 5r · 7s · REST, where REST
refers to the product of all the prime factors greater
que 7. To calculate ˜g, upper limits are defined for
p, q, r and s. These capped parameters are denoted
¯p,
¯q, ¯r , and ¯s. As upper limits for the exponents
we use ¯pmax = 3, ¯qmax = 2, ¯rmax = 1 and ¯smax = 1. Pour
example, if the value of q is 4, then only 2 may be
transferred to ¯q. For the modified gradus, we obtain
˜g(un, b) = 1 + ¯p· (2 − 1) + ¯q· (3 − 1) + ¯r · (5 − 1) + ¯s · (7 − 1).
Voir la figure 1, dans lequel, for every number in the
range 100 à 299, these limited gradus suivitatis
are calculated with the five left and five right
neighboring values, and the mean of all ten values is
shown as a bar.
Using the Modified gradus suivitatis
A preliminary motivation for this limited gradus
suivitatis is that in music (insofar as it is an orga-
nization of sound events of defined pitch in time),
rather small prime factors play a formative role,
concerning both the frequency ratios of musical
intervals and the rhythm. But if, with the help of
the limited gradus suivitatis, what could be called
this humanized perspective on the natural num-
bers, something remarkable occurs: The fact that
numbers that are more dissonant with the numbers
surrounding them tend to occur as individual peaks,
and not in clusters, corresponds quite well with
the common musical rules of traditional West-
ern composition. Par exemple, in classical choral
composition, roughly speaking, any number of con-
sonances may be strung together, but dissonances
should always alternate with consonances. Ce
means that they should occur less frequently and be
well distributed throughout the movement. (Recall
that AOG uses the natural numbers as a time series.)
To make this tendency even more visible, consider
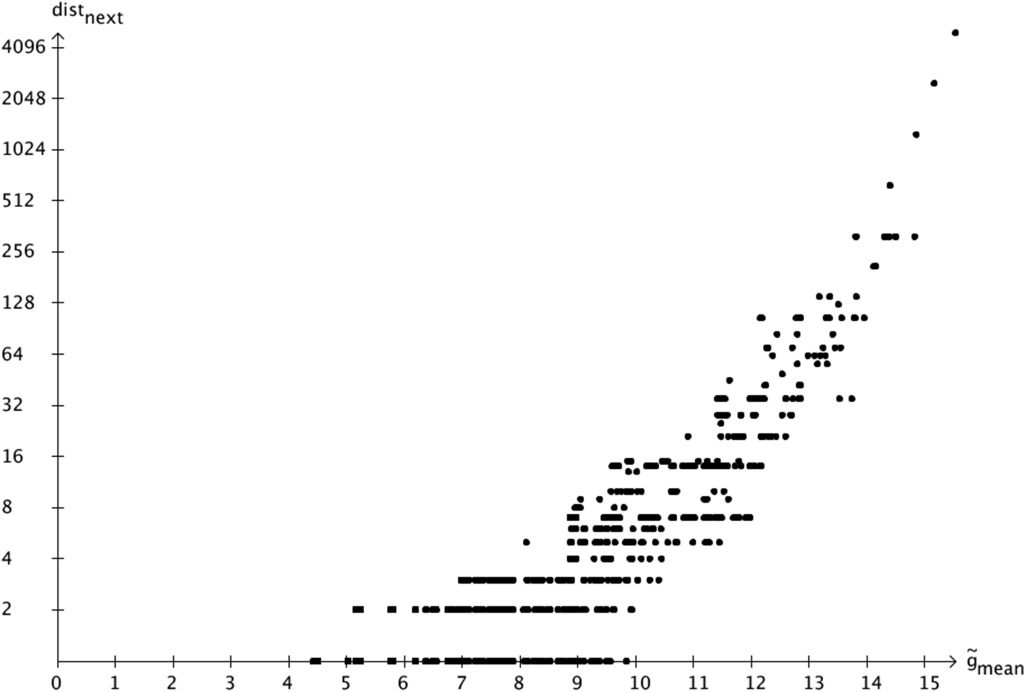
Chiffre 2. This time, the points entered in this
semilogarithmic graph represent all natural numbers
in the range between 100 et 5,100. The x-axis in
this graph corresponds to the mean value for ˜g
between the number in question and its 180 closest
neighbors (90 smaller and 90 larger). The y-axis is
a logarithmic representation of how far from the
current number the next number with the same
or greater value of ˜gmean is. This selection was
made as a relatively arbitrary example. It has been
shown, cependant, that the basic structure visible
here remains intact, even if changes are made to the
range of numbers shown, or the number of neighbors
considered. In the graph, one can see a band of points
lying diagonally with a positive gradient. This can
be interpreted to mean that as the value of ˜gmean
increases, the distance to a next value with at
least the same value of ˜gmean actually increases
exponentially. This corresponds to the previous
statement that the greater the corresponding ˜gmean,
the more isolated the values.
Or, seeing N as a time series and interpreted
musically: Tones that lie in a dissonant relationship
to other tones nearby in time occur sporadically and
increasingly rarely, the greater this dissonance value
is on average.
Composing with Natural Numbers
Here then, in the form of this inner structure of
natural numbers from the perspective of ˜g, nous
have the basic element mentioned above, lequel
already satisfies musical laws. Remarquablement, this is
an element that did not need to be invented but only
discovered, and which is infinitely large and diverse.
By exercising restraint in constructing or creatively
designing a basic element, one has been revealed
that is literally ubiquitous and so corresponds to the
ideal of ubiquitous music on an unexpected level.
The next step is to show how this basic element
can be represented audibly. The source code in
Chiffre 3 simply goes through the natural numbers
and filters the powers of the first four prime numbers
out of each number. As in ˜g, the respective exponents
that are still considered are also capped here. Ce
is done with a kind of selective division. For this
but, first the number B is calculated as the
20
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2. Correlation
between ˜gmean and the
distance to the next
number whose ˜gmean is at
least as large; see text for
further details.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
product of the maximum powers of the individual
prime numbers 2, 3, 5, et 7. In the example here,
B = 23 · 32 · 51 · 71 = 2,520. Each natural number
currently under consideration divides B only with
the prime factors 2, 3, 5, et 7, and this with
a maximum exponent of 3 for the number 2, un
maximum exponent of 2 pour 3, and a maximum
exponent of 1 for both 5 et 7. The symbol // will
be used for this selective division.
A few concrete examples for clarificatation:
B//12 = 2 · 3 · 5 · 7
B//35 = 2 · 2 · 2 · 3 · 3
B//13 = B
B//16 = 3 · 3 · 5 · 7.
In the last example, 16 = 24 exceeds the maxi-
mum power allowed for the prime 2, c'est à dire., 23 = 8,
so only 8 is used in selective division; in other
words, B//16 = B//8. The result of this selective
division is rendered as a note of that frequency and
is played if this frequency is inside the range of the
musical instrument (acoustic or electronic) être
used. The program was implemented in Processing/
Java, see the example “BASIC Sound of N” in the
contributed library “ComposingForEveryone” at
https://www.processing.org. In the interest of keep-
ing the examples brief, no effort was made to achieve
a particularly interesting sound. A more elaborate
realization of the same principle can be seen in the
YouTube video https://youtu.be/e81wd1b3FEE.
Other pieces of music are now created by changing
this basic element through the application of
Kramann
21
Chiffre 3. Simple sonification
of the natural numbers.
Chiffre 4. A short phrase
composed using AOG.
int BASENUMBER = 2*2*2*3*3*5*7;
/*t: finite section of the natural numbers as a time series*/
pour(int t=0;t<1000;t++)
{
int f = BASENUMBER;
/*Selective division: Extract prime factors 2,3,5,7 from t*/
/*and factor them out of the BASENUMBER (% is modulo):*/
while(t>=2 && t%2==0 && f>=2 && f%2==0) {t=t/2;f=f/2;}
alors que(t>=3 && t%3==0 && f>=3 && f%3==0) {t=t/3;f=f/3;}
alors que(t>=5 && t%5==0 && f>=5 && f%5==0) {t=t/5;f=f/5;}
alors que(t>=7 && t%7==0 && f>=7 && f%7==0) {t=t/7;f=f/7;}
/*Interpret the result as a frequency and play it:*/
si(f>=55 && F<=1760) play(f);
delay(200); /*time delay of e.g., 200 milliseconds*/
}
Figure 3
Figure 4
arithmetic operations, including modulo division,
and also using selective division for the resulting
sequence elements to obtain a temporal progression
of pitches. In AOG, “composing” means defining
formulas according to which the basic element id(N)
is modified. (The notation id(N) means “identity
of N,” a mathematical expression stating that
N is mapped to itself, i.e., it forms a series. In
an algorithmic terminology this corresponds to
the succession function.) At least for the basic
arithmetic operations, the resulting sequence also
satisfies the Peano axioms and so retains all the
properties of the natural numbers, including the
musical ones (Russell 1920, pp. 1–10). In other
words: the basic structure visualized in Figure 2
remains similar for these modifications of the basic
approach.
But for the operation of division, this is only the
case if one excludes all the division results that
have a remainder. Several formulas can be used
simultaneously to generate multiple voices. This
will be illustrated using a simple, concrete example.
The two formulas
f1 = B//((t + 16) mod 17)
f2 = B//(((t ∗ 34) mod 10) + 8)
with B = 2,520 and t = 9,000 . . . 9,022 provide the
two-part musical phrase shown in Figure 4.
22
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
a
_
0
0
5
5
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The generally occurring harmonic and contrapun-
tal interrelationships between two or more voices
that are generated by AOG and run polyphonically
have not yet been systematically investigated in
my work. One could argue that in AOG the same
sequence t, which is an extract of id(N) for all voices,
is the starting point for the following operations. In t
all divisors occur with a fixed period that is equal to
their value. For example, the divisor 3 has a period
of 3, as in the sequence 0 . . 3 . . 6 . . 9 . . , etc. Con-
sidering this fact, the preservation of a harmonically
meaningful relationship can now be shown, for at
least some special cases, to make the existence of
a general tendency for this at least plausible: When
applying multiplications by numbers consisting
only of prime factors greater than 7, the relevant
part of the factorization-structure of the resulting
sequence does not change with regard to the original
sequence before multiplication. Multiplications
with small prime factors, like 2 or 3, create a rather
consonant relation of elements of both sequences,
which are close in time.
For example,
t = {. . . 6, 7, 8, 9, 10, 11, 12, . . .};
f1 = 2520//t
= {. . . 420, 360, 315, 280, 252, 0, 210, . . .};
2t = {. . . 12, 14, 16, 18, 20, 22, 24, . . .};
f2 = 2520//(2t)
= {. . . 210, 180, 315, 140, 126, 1260, 105, . . .}
where 2,520 is the base number B. The values for f1
and f2 are frequencies in Hertz. The multiplication
here by two results, in most cases, in a transposition
by an octave downwards. One exception is the
interval of a unison for the frequency 315, because,
as noted earlier, B//16 = B//8. Another exception
is the next-to-last values in the two sequences,
f1 = 2520//11 and f2 = 2520//2. In the case of
f1 the selective division is not possible and the
resulting zero means that no note is played. In
contrast, selective division becomes possible at this
point in sequence f2, after the multiplication by
two, and yields 1,260 Hz.
Similarly, rather consonant relationships are
created by the addition of numbers that are rich in
the prime factors 2, 3, 5, and 7, because such shifts
are widely in phase with the rhythms in which
just these divisors appear. Following on from the
previous example,
t + 6 = {. . . 12, 13, 14, 15, 16, 17, 18, . . .};
f3 = 2520//(t + 6)
= {. . . 210, 0, 180, 168, 315, 0, 140 . . .}.
In f3 the 168 is “new,” but harmonizes well, since
252 = 168 · (3/2), a perfect fifth.
Composing for Everyone
Figure 5 supplies the MIDI pitches from the formu-
las that correspond to the notes shown in the score
of Figure 4. A musical phrase (melody, rhythm, and
harmony) is created from these few lines of code. Of
course, in program code intended for an application,
the formulas would not be hardcoded. Instead, they
could be constantly changed by the user with the
aid of an editor, as for example in a correspond-
ing Android app freely available on Google Play
(https://play.google.com/store/apps/details?id=info.
kramann.cfe, see Figure 6). For the sake of com-
pactness, this editor does not use parentheses, nor
does it display the selective division that is always
performed. The fact that the operations are applied
to t = id(N) is not displayed. This example could
be displayed in the app simply as “+16 ≡ 17” and
“·34 ≡ 10 + 8” (in the editor the symbol ≡ is used
for modulo division).
Having now introduced AOG by means of an
example, it will now be shown at which points
specifications were made that not only apply to
the specific example but can generally be varied to
change the characteristic of the generated music. We
will also look at the meaning of the operations from
a musical point of view. First, it should be noted
that, despite the effort made here to demonstrate
the relationship between AOG and traditional
compositional methods, the method itself is quite
simple. The example shown here could easily be
reproduced with paper and pencil, apart from the
Kramann
23
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
a
_
0
0
5
5
0
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Composing a
small phrase on the basis
of AOG. Transposition up
by a half step results as no
accidentals are necessary
for the representation of
the notes. This clarifies the
diatonic character of the
tone scale resulting from
B = 2,520.
int B = 2520; /*base number*/
for(int t=9000;t<=9022;t++) /*Extract from the natural numbers*/
{
int x = (t+16)%17; /*Formula 1*/
int y = ((t*34)%10)+8; /*Formula 2*/
int f1 = B;
/*Selective division 1:*/
while(f1>=2 && f1%2==0 && x>=2 && x%2==0) {f1=f1/2;x=x/2;}
alors que(f1>=3 && f1%3==0 && x>=3 && x%3==0) {f1=f1/3;x=x/3;}
alors que(f1>=5 && f1%5==0 && x>=5 && x%5==0) {f1=f1/5;x=x/5;}
alors que(f1>=7 && f1%7==0 && x>=7 && x%7==0) {f1=f1/7;x=x/7;}
int f2 = B;
/*Selective division 2:*/
alors que(f2>=2 && f2%2==0 && y>=2 && y%2==0) {f2=f2/2;y=y/2;}
alors que(f2>=3 && f2%3==0 && y>=3 && y%3==0) {f2=f2/3;y=y/3;}
alors que(f2>=5 && f2%5==0 && y>=5 && y%5==0) {f2=f2/5;y=y/5;}
alors que(f2>=7 && f2%7==0 && y>=7 && y%7==0) {f2=f2/7;y=y/7;}
/*Mapping the resulting frequencies to midi pitches:*/
float factor = pow(2.0, 69.0/12.0)/440.0;
int midi1 = (int)round(12.0*log((float)f1*factor)/log(2.0));
int midi2 = (int)round(12.0*log((float)f2*factor)/log(2.0));
/*midi==0 means no sound or continue previous tone.*/
/*Otherwise transpose a half tone upwards to avoid accidentals*/
si(midi1<52 || midi1>89) midi1=0; else midi1=midi1+1;
si(midi2<52 || midi2>89) midi2=0; else midi2=midi2+1;
/*Simple output of the results on the terminal for checking:*/
println(t+” “+midi1+” “+midi2);
}
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
quantization due to the tempered scale. This fact
is emphasized here, since the goal was to present
a substitute for classical music theory that would
be easier to learn. It should not be misunderstood,
cependant, that the reason why most people will
find it easy to learn and understand this method
is that they have already learned arithmetic in
their school years and have practiced the use of
equation systems. But even if one would have to
learn all this to use AOG, the gain would still be
the highly compact representation of a composition
using algebraic expressions and the possibility to
change the character of a composition in its entirety
just by changing a few symbols. The example given
here is brief. A piece described by AOG is, cependant,
potentially infinitely long and diverse, because the
time sequence of natural numbers forming the input
can be continued infinitely, supplying ever-new
variants of sequences of successive powers of prime
factors.
Composing with AOGdogma
To avoid the impression that all pieces created with
AOG have the minimalist style of the example in
Chiffre 4, at least one more piece should be presented
as a contrast, a piece that is much more demanding
in its musical conception, that uses more than a
pentatonic scale, and in which the instruments
are playing with many pitch classes. The latter is
achieved by the fact that the base number changes
during the course of the piece (voir la figure 7 et le
demonstration at https://youtu.be/BYzr9RpfFhc).
User-Specified Attributes of AOG
The character of compositions created using
AOG is determined by specifying the following
elements.
D'abord, the user can specify the number of sources
of t = id(N) to be used.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
24
Computer Music Journal
Chiffre 6. The Android app
CFE (Composing for
Everyone) is a direct
implementation of AOG
and can be obtained on
Google Play. An AOG
formula can be entered for
each of four addressable
musical instruments using
the on-screen keyboard.
The resulting piano roll is
displayed in the lower
portion of the screen to
provide direct feedback. Dans
addition to the basic
arithmetic operations and
modulo, expérimental
operations are available
that support direct
manipulation of the
powers of the prime factors
2, 3, 5, et 7. Each of the
upper four lines in the
editor controls one of four
musical instruments. With
the entries to be seen and
in the symbolic notation
introduced here, le
frequencies passed through
by these instruments are
then calculated as follows:
f1 = B//(t + 6),
f2 = B//(t + 12),
f3 = B//(t + 18), et
f4 = B//(t + 24).
that x, which is a result of applying arithmetic
operations to the sequence of natural numbers, pour
example x = t/7 + 3, appears in the denominator
in selective division. The base number is the
numerator. To limit the type and count of the prime
factors considered, it is possible to extract them
directly from x and interpret this result as frequency
instead of introducing selective division. This can
then be expressed symbolically as f = B ∗∗ x. En fait,
both operations are used in the somewhat more-
sophisticated composition “Elegie” (see Section 1 à
http://kramann.info/98 AOG). If f = B//x leads to
no playable result, but f = B ∗∗ x does, the latter is
used. An advantage of the former (selective division)
compared to the latter (pure selection) is that even
a very small x results in a playable frequency. Le
harmonic relations of two numbers do not change,
regardless if they are taken directly or as reciprocal
valeurs.
A sixth parameter is whether to directly use the
integer frequencies calculated, or to quantize these
frequencies to equal temperament. In the latter case,
the frequency range can be compressed or stretched
by a certain factor before this quantization, and after
that the entire composition can be transposed at
will, comme, Par exemple, in the example above by a half
step upwards (as in Figure 5). All three elements
ensemble, c'est, the base number, a stretch factor,
and a transposition, can be used to produce a
certain desired musical scale. This scale can also be
microtonal.
En plus, all of the above elements can be
changed over time—slowly, relative to the time
sequence t = id(N).
Enfin, in the postprocessing layer there should
be an algorithm for the musical interpretation of the
incoming notes to be played. Concretely, a mech-
anism has been implemented that uses the gravus
suivitatis between the current tone and the n imme-
diately preceding and all simultaneously sounding
tones to adjust its playing technique (staccato,
legato, etc.) and dynamics. What is more, commer-
cial physical modeling software was used for the
sound generation. All the pieces of music to which
reference was made at the beginning and some more
Kramann
25
Deuxième, the user can configure the operations to
be applied to each ti, and the order in which they are
appliqué.
Troisième, the user can specify how to treat operations
that are inapplicable or invalid in certain conditions.
Par exemple, a pending division by zero could either
result in not playing a note at all on the current
tick due to the formula in which the operation
occurs, or the operation could simply be skipped.
Instead of omitting decimal places after a division,
the operation could be skipped when the division
occurs, et ainsi de suite.
Fourth, in the chain of operations applied to
each integer in the series, the user can specify
at which operations a sound conversion can take
place through application of selective division. If
the result after each operation is used to produce
sounds, one obtains exactly as many voices as there
are operations. This can be used directly with poly-
phonic instruments, such as the piano, to control
their dynamics. If the same frequency appears as a
result of several operations simultaneously, ces
can overlap to form a louder tone. Alternativement, un
can proceed in such a way that, along a sequence of
opérations, only the last playable tone is heard. Dans
this case, the number of voices is identical to the
number of active formulas.
The fifth user-configurable parameter is the base
number. This value is mainly responsible for which
frequencies can be generated with the respective
AOG mechanism. At this point it bears repeating
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 7. Excerpt from the
score and its AOG
representation of the
composition AOGdogma#3,
which was generated using
the real-time composition
framework AOGdogma
(www.kramann.info/
90 AOGdogma). C'est un
composition for violin and
vibraphone lasting four
minutes. The sequence of
operations applied to the
parameter t for the violin
are represented by xg,
those for the vibraphone
by xv. Thus the frequencies
that are passed through on
both instruments are
calculated as fg = Bg//xg
and fv = Bv//xv. Le
following applies here:
Bg = Bv = 25 · 32 · 51 ·
71 · PP. The parameters
VC, PP, QQ, and FF
“drift," c'est, ils
provide a slow
metamorphosis of both the
two AOG formulas and
their base numbers. Le
parameter t is the extract
of the natural numbers
that are passed through
starting with 70,000 dans
steps of one with an
equidistant time interval
de 100 millisecondes; tm is
a counting process that
proceeds more slowly and
controls the drifting
parameters. By adding a
language element for the
description of drifting
parameters and the
possibility to use it at any
position of the AOG
formulas, and by providing
this together with an
editor for real-time
composition, AOGdogma
makes it possible to
compactly represent whole
compositions and to create
them interactively.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
are representatives of this approach (See Sections 1,
4, 5, et 7 at http://kramann.info/98 AOG).
AOG and Traditional Musical Forms
For the effect of the individual operations, direct
correspondences can, in some cases, be shown to
certain traditional musical forms:
1. Addition. This brings a sound event forward
in time. An addition of 3 maps the sequence
{0, 1, 2, 3, 4, 5} à {3, 4, 5, 6, 7, 8}. If
+3 is entered for one voice and +6 for the
other, this results in a kind of two-part
canon. After these operations, sélectif
division followed by a rendering of the
resulting number as a note of that frequency
est, bien sûr, always performed. In the
formula notation introduced, one then has
a melody in the simplest case, resulting
from fi = B//(ti + 3), and a second melody
resulting from ˜fi = B//(ti + 6), whereby the
latter is three ticks ahead of the former. Le
following points should be understood in the
same sense.
2. Divisions. Compared to the unchanged
voice, when for instance a division by two is
performed, the new voice is twice as slow.
This corresponds to the musical procedure
of canon by augmentation.
3. Modulo or Remainder-after-Division. Le
result of this operation is always the integer
26
Computer Music Journal
remainder of a division using the same
operand. Modulo 6, Par exemple, maps the
séquence {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} to the
séquence {0, 1, 2, 3, 4, 5, 0, 1, 2, 3}. Le
musical structures that arise are reminiscent
of the repetitive phrases typically found in
minimal music.
User Interfaces
As examples, two UIs are described below, both of
which are based on AOG. The first is a formula
editor, more suitable for adults. The second is
a system in which compositions are created by
decorating balls with colored tape, beads, pompoms,
and other items. The latter interface is intended for
use by primary school children.
The formula editor was tried by attendees of a
TEDx event (see Section 2 at http://kramann.info/
98 AOG). In groups of four attendees at a time,
people could enter AOG operations using four An-
droid tablets, with each tablet assigned to a voice.
The UI design is similar to that of the Android
app seen in Figure 6. The formulas entered were
converted into music according to the AOG method
by a personal computer connected to all tablets
over a wireless local area network. De même, tous
currently valid formulas were displayed to all those
present with the aid of a projector. The four formulas
were displayed in color-coded form and, based on
a previous introduction, the participants should
have been familiar with the link between a formula
and the musical instrument assigned to it, dont
individual sound was chosen to be distinct from
each of the other three instruments. Through this
feedback a certain exchange of information was
established among the participants after some time,
and a certain learning effect could be observed:
The participants started to copy other participants’
formulas if they liked the result and then exper-
imented again with variations of this basic form.
The functions of the editor and the basic effects
of the individual operations on the musical result
were explained to the audience in the previous
lecture. To what extent the lecture was consciously
referred to could not be determined within the 20
minutes in which the audience experiment took
place.
The observed casual collaboration by “copy and
variation” was possible with the system because
the symbolic representation of the resulting com-
position is so compact that it could be grasped at a
glance and quickly adopted.
The promotion of this type of cooperation by
copy and variation through an easy-to-capture form
of feedback is also a central feature of the second
UI presented here, called “The Flippin’ Pompoms”
(TFP). The role of the formulas, which are visible
to all in the formula editor, is played in TFP by
colorfully decorated balls, which are kept visible to
tous, with each ball representing a composition. Some
examples are shown in Figure 8. More examples,
including a video of the system in action, can be
found at Section 5 on http://kramann.info/98 AOG.
Due to the COVID-19 pandemic, cependant, le
practical experiences with TFP have so far been
limited to small example experiments with children.
En particulier, it had been planned to use this system
in a STEM project day at a primary school; this plan
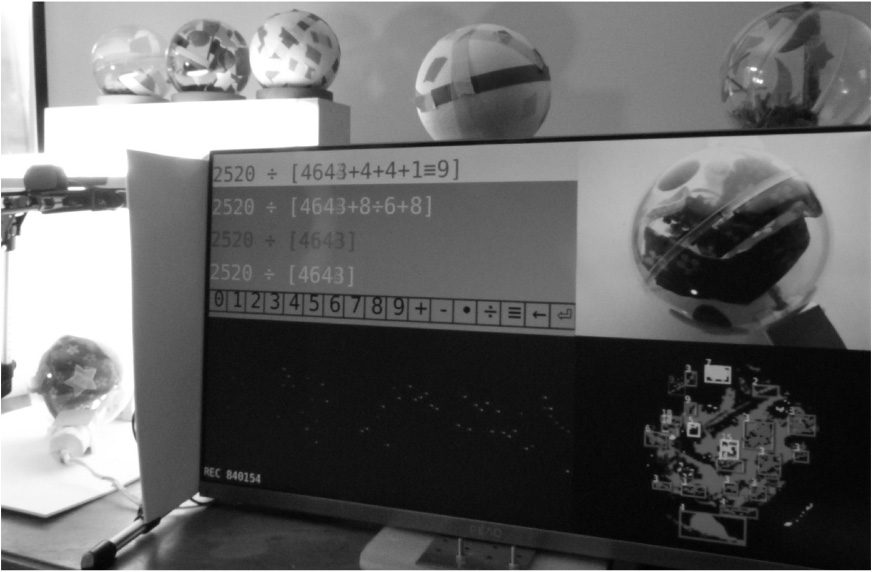
has had to be postponed indefinitely.
The balls can be designed according to composi-
tional considerations. Par exemple, there is a ball
in which a pompom is pasted with colored areas.
Whenever the pompom flips, a new variant of the
musical structure appears. The resulting balls are
placed on a motorized support that slowly rotates
the balls around two axes, while a webcam con-
tinuously records the changing view and passes it
on to the software as a pixel image. Because this
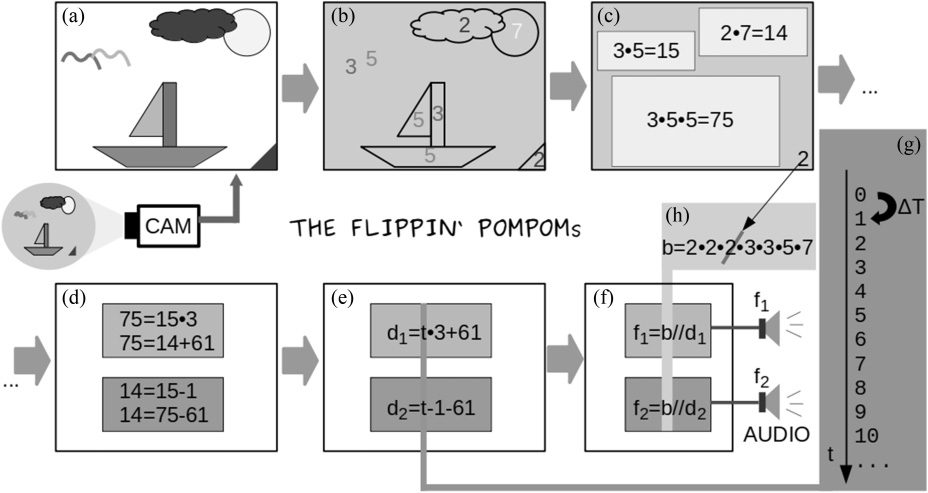
textual description may give an overview of the
functionality, despite not being possible to repro-
duce every detail exactly, the source code for TFP
was provided as an example within the contributed
Processing Library “ComposingForEveryone” (voir
Section 9 at http://kramann.info/98 AOG). Dans ce
software the image is filtered in such a way that
there is only a black background and colored shapes
in red, vert, blue, and yellow (Figure 9a). In the next
step, single-colored contiguous areas are segmented.
Several such areas can be connected again and form
a colorful contiguous area. Alternately, they may
exist separately without connection to other areas.
For areas that are composed of several colored areas,
Kramann
27
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 8. Setup for The
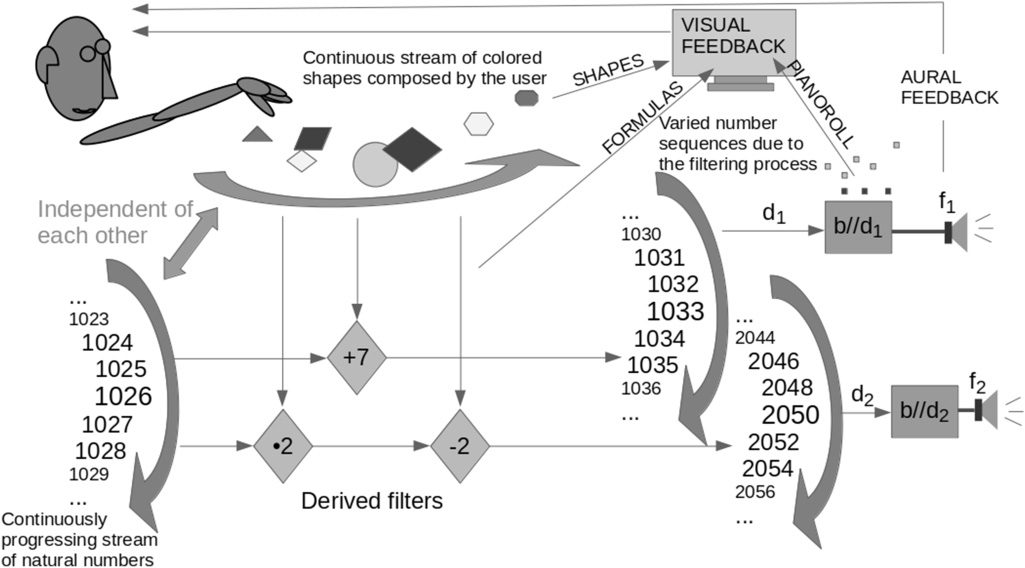
Flippin’ Pompoms.
Variations of spheres are
visible in the image. Sur
the bottom left, le
motorized device for
automatic rotation of a
ball is shown. On the top
right of the screen, le
image captured by the
camera of the ball
currently resting on the
rotating device is shown.
Below, also on the screen,
the segmented colored
areas of this sphere can be
seen. Enfin, the AOG
formulas resulting from
this segmentation can be
seen on the left side of the
screen. These can also be
edited directly.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
the number of areas in each color is counted. Using
a color coding in which blue represents 2 red 3
vert 5 and yellow 7 a multiplication of all the
prime numbers assigned to the areas with each
other is performed, and one obtains exactly one
number for each individual contiguous colored area
(Figures 9b, c).
Now the software determines which arithmetic
operation is best suited to get from one number
to another. The order in which the areas are
selected is determined on the basis of neighborhood
relations and the absolute sizes of the areas in
pixels. When selecting the “suitable” operations,
the system first looks to see whether a modulo
operation is possible in which the operand c lies
somewhere between the two values a and b. Le
relation between a, b, and c is then a mod c = b.
The idea behind this is that only if a > c > b can
b be a real remainder of the modulo operation
a mod c. Par exemple, 100 mod 30 = 10. If this
fails, the software checks whether multiplication
or division is possible. If this also fails, an addition
or subtraction is always possible to get from one
number to another (Figure 9d). Because the nearest
neighbor is always taken from the largest areas,
a path is created from a maximum of four largest
domaines, which encompasses different colored areas.
The different paths can also run over the same areas
to some extent. This has proven to be beneficial
for the quality of the music, probably because
the resulting voices have significant commonality
while still differing slightly. This has not yet been
examined in more detail. Each of the sequences
of operations found then represents a formula in
the sense of AOG. The further processing of these
formulas, up to the conversion into sounds, est
performed from this point on in the same way as
with the formula editor, c'est à dire., as described earlier in
the section “Arithmetic Operation Grammar” and
as visualized in Figures 9e–h.
En fait, the software for TFP is based directly
on that of the formula editor. This goes so far that
the latter is still displayed in TFP (as shown in
Chiffre 8) and changes to the formulas can also be
28
Computer Music Journal
Chiffre 9. Specific
processing scheme of The
Flippin’ Pompoms from
image capture to sound
generation (voir le texte).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
made there. Ainsi, a multimodal UI is available here,
which provides possibilities for influencing the
formulas on two possible levels, whereby the ball
design always represents the entire composition and
the currently visible formula typically represents
a phrase that varies slightly over the course of
temps. En particulier, cependant, TFP always keeps
the AOG-related perspective open and thus offers
users the opportunity to theoretically understand
the underlying compositional principle and to
emancipate themselves from the use of the given
tool.
Discussion
To open up access to composing with AOG, surtout-
cially for primary school children, without requiring
knowledge of school arithmetic, advantage is taken
of the fact that arithmetic operations ultimately
help to handle sets. The route back to this starting
point was taken by letting children arrange colorful
forms into groups. In terms of data sonification,
the children create a kind of data set. At first, je
noticed that, because the compositions are realized
with rotating spheres decorated with colored sur-
faces, the three-dimensionality in the 2-D camera
image results in different topologies of the colored
groupes, depending on the perspective from which
the webcam views the sphere. Although children
are not working directly with musical elements,
by applying this technique of recombining colored
surfaces, something emerges that has much in com-
mon with composing. Varying musical structures
in this way would be extremely difficult when
working directly in a score. The decoration of the
balls opens up a powerful and efficient metalevel
with which children can compose. This is probably
the deeper reason for the usefulness of the so-called
facade pattern used in software development. In the
search for descriptive possibilities to characterize
meaningful settings for ubiquitous music, conception
patterns were also considered (Keller, Lazzarini, et
Pimenta 2014, pp. xi–xxiii).
The attempt is now being made to transfer
something from the world of design patterns, dont
elements often characterize software components,
to the overall system presented here, which includes
not only the software but also the user and hardware.
The facade pattern represents a structure that seems
Kramann
29
Chiffre 10. Abstrait
processing scheme of The
Flippin’ Pompoms from
image capture to sound
generation (see text for
details).
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
to correspond to the previously described setting:
It simplifies the use of a subsystem consisting of
many components by allowing a client to ensure the
completion of common tasks via a single method
instead of making a multitude of method calls to
different elements of the subsystem to achieve the
same goal. The nonstandard client still retains the
ability to make calls at the subsystem level that
are not bundled in the facade (Gemma et al. 1995,
pp. 185–193). The role of the client is played here
by TFP users. The balls to be decorated represent
the facade, and the subsystem controlled by them
is all the rest, consisting of the formula level down
to the sound generation, as was seen in Figure 8.
It is possible to bypass the facade by directly
typing in AOG formulas and by getting feedback
directly from the subsystem in the form of the
perceptible musical event, its visualization as a
piano roll, and the viewing of the AOG formulas
(voir la figure 10). This means that at the beginning of
working with TFP, the facade completely hides the
subsystem: The children tinker with balls, lequel
they decorate with colored shapes. Little by little,
via the feedback channels, the user (the client) gains
a deeper knowledge of the connections behind the
facade (in this case, the ball). Little by little, certain
contexts are recognized, how certain configurations
of the balls can influence the sound, as follows.
While a transparent sphere is spinning smoothly,
and if the shape of the object inside is more cuboid
rather than spherical, it can happen that the inside
shape suddenly falls from one side to another. Tel
a change in the shape of an object leads to sudden
changes. For this type of twisting, areas can be
covered by others and new combinations of colored
areas can emerge. Moving elements within the ball
can gradually combine with other elements of the
ball surface through the ball’s rotation, Et ainsi
vary the sound event. The colors determine which
instrument dominates. Isolated, single-color areas
are used to influence the base number. There may
être, par exemple, areas with more- or less-complex
motifs; voir la figure 11. From the perspective of
a person who has just started with TFP, all this
30
Computer Music Journal
Chiffre 11. Decorating
transparent and opaque
spheres as a compositional
method.
happens at the beginning, either by chance or by
intentional reference to the visual form rather than
the sonic one. In the best case, cependant, au fil du temps
these relationships become increasingly clear and
can be taken advantage of by the user. On the level
of the facade design model, this would mean that
instead of an initial, simplified method of accessing
the functionality of the subsystem, methods of
greater sophistication would gradually emerge,
passing more parameters. Or these parameters have
always been passed, but gradually the user becomes
aware of them. The Flippin’ Pompoms can be used
to convey the meaning of what it is like to compose
and to make the experience of holding one’s own
composition (as a ball) in one’s hand and making it
heard whenever desired.
Conclusions and Further Work
In this article, we explained in detail what Arith-
metic Operation Grammar is and what potential it
has in combination with suitable UIs to give laypeo-
ple the opportunity to compose their own music.
But what contribution does this work make in the
field of ubiquitous music and sonification? Ce
should be made more explicit in this concluding
section.
From the perspective of sonification, the method
presented here differs from other sonification
methods in that time does not have to be present as
an order parameter in the input data, as would be the
case with a still image. A time parameter—as would
be present if the input were represented by a video—
is in any case a prerequisite for sonifications that
do not themselves have a temporal macrostructure
(voir, par exemple., Braund and Miranda 2013; Denjean et al.
2019). Nor does the microstructure—that is, le
actual sound—need to be obtained directly from
input data, as is done in sonification methods that
essentially compress or stretch the system time
of the source data to obtain an audible frequency
range (as by Holtzman et al. 2013). This temporal
independency makes the AOG approach ideal for
sonification of data that does not, in itself, contain
time as an ordering parameter, and none of the other
parameters need be interpreted as time. This does
pas, cependant, exclude the possibility of sonifying
data in which time does appear as a parameter.
Because of this independence, the AOG method also
allows a free choice in the design of the sound and,
thus, the possibility of using high-quality, software-
based musical instruments. Enfin, the resulting
Kramann
31
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
macrostructure meets higher musical demands than
might be met by many other common sonification
méthodes (see e.g., Matsubara, Morimoto, and Uchide
2019). Dans l'ensemble, it can be said that there could be
application niches for the procedure presented here
in the field of sonification.
Because as described above, AOG is an example
of a Chomskian third-order grammar, it is not neces-
sary to explicitly acquire a theoretical apparatus of
rules, even if at some point one emancipates oneself
from the provided software tool and goes one’s
own way on the basis of AOG. Unlike comparable
software tools, complexity is not hidden but the
underlying mechanism is per se simple and easy to
learn.
Par exemple, Gil Weinberg (2002) discusses
holding back the theoretical background. He justifies
this by asserting that laypeople study differently
than professionals, arguing that the underlying
theory would overwhelm the target group and
spoil the joy of composing. En outre, Weinberg
states that such initial experiences can motivate
the study of music theory at some later point. Mais
that claim is formulated more as a hope than as a
consequence of the use of the described composition
tool.
I believe that providing novices with the power
to create and phrase a melody by manipulating
its contour, regardless of its exact pitches
and intervals, offers them a unique creative
experience that is usually reserved for experts
and that can serve as an entry point for further
investigations into more advanced concepts
such as harmony and counterpoint (Weinberg
2002, p. 45).
It would, bien sûr, be possible at this point to
counter the arguments made against the teaching
of music theory to laypeople, such as the obvious
fact that many professionals no longer need to
study music theory at all and that laypeople are not
necessarily associated with a lack of comprehension.
On the other hand, one has to give credit to
the approach taken by Weinberg, and to related
approaches, for having successfully given novices
the ability to also record musical ideas. Ce
possibility is not available for users of AOG in its
current form. The dominant experimenting with
formulas and forms is not currently compatible
with AOG. Plutôt, the two UIs presented here each
provide a compact, easy-to-grasp representation
layer of the emerging composition. In the one case
it is the symbolic AOG formula, in the other it
is the colorfully decorated spheres representing
entire compositions. The audience experiment
discussed earlier has also shown that it is precisely
this compactness of the representation that greatly
promotes creative cooperation between the people
involved, because on this basis an exchange of ideas
between the participants is strongly promoted. Ce
shows a certain affinity to the tagging metaphor
(Keller, Lazzarini, and Pimenta 2014, p. XVIII).
In connection with this metaphor, Keller and
colleagues point out that creative activities take
place through interaction with material or mental
objects and that these are at best designed to form a
suitable channel for these interactions.
On the whole, one can simply say that different
approaches to helping laypeople to compose can
each be successful in their own way, in the sense
that “music is inclusive, and musics and their
techniques and forms are cumulative, not mutually
exclusive” (Spiegel 1998, p. 6).
But with respect to the work presented here, un
could object that, for all the universality of the set of
natural numbers N, the special operations introduced
and applied to it indirectly result in a preselection of
the sound material provided, et ça, furthermore,
the musical examples presented all have a certain
characteristic style that one may or may not like.
At this point it is up to me now to express my hopes
and convictions, lequel, cependant, with reference
to work that has already been continued but not
yet completed, can be presented in conclusion in a
well-founded manner:
The decision to use id(N) as the basic element
was taken mainly because it was possible to prove
properties described as musical. If one drops this
restriction and goes over to the use of other types
of potentially infinite series, completely different
perspectives arise with regard to the results that
can be achieved, as can be seen from the examples
in Section 10 at http://kramann.info/98 AOG. Comme
a preliminary justification for this step it may be
32
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
said that all these other series can be represented
as mathematical mappings of the basic sequence
id(N). Whether it will be possible to extend the
theory introduced here by such elements, alors que
simultaneously preserving the current compact
formulaire, remains to be seen.
In the meantime, more extensive research has
been conducted into the relationship between com-
positions generated with AOG and traditionally
composed music, in which sound events with
specific pitches are organized in time. A corre-
sponding experiment can be seen at Section 8
on http://kramann.info/98 AOG. By means of an
optimization algorithm, an attempt was made to
optimize a group of four AOG formulas, each con-
taining 16 opérations, in such a way that for the
length of four ticks at a certain starting value t0
they represent the familiar canon “Fr `ere Jacques,” if
all four voices have already begun there. This was
réussi, but in the ticks before, the musical set
obtained with AOG converges towards the desired
piece and immediately afterwards diverges away
from it. This is straightforward to follow in the
included sound conversion. As a preliminary result,
a solution of this inverse problem may be possible in
principle, but is by no means trivial. To achieve bet-
ter results, the next step would be to test alternative
opérations.
A criticism may also be raised that the UIs
presented in this article, which are more oriented
towards pictorial design, do not convey the satisfac-
tion of experiencing a direct sonic reaction resulting
from an action. Feedback mechanisms, cependant,
which have the goal of tracing such sound events
directly generated by the user back to AOG formulas
that could have generated them to obtain automatic
accompaniment, are currently also the subject of fur-
ther development of the possibilities that arise with
AOG (see Section 7 at http://kramann.info/98 AOG
for samples). The advantage of the offline ap-
proaches, where a composition is described but not
played, is that they provide the possibility of being
embraced, distributed, and handled cooperatively by
participants who are far away from each other, depuis
latencies do not play a major role. En particulier, au-
tomatic and parallel sound conversion can also take
place asynchronously at the respective locations.
This possibility is also mentioned by Lazzarini et al.
(2014) for the design of ubiquitous music systems.
Last but not least, AOG’s explicitly comprehen-
sible connection between music and mathematics
offers welcome starting points for the planned
STEM project day and all those who may follow
it, to turn it into a STEAM project day (with an
“A” for the arts) in the sense of John Maeda (2013),
thus breaking the ground for a way of thinking that
goes beyond the well-worn categories of isolated
disciplines and making a significant contribution to
bringing forward the “every day creativity” (Keller,
Lazzarini, and Pimenta 2014, pp. 5–7, 29–30) dans le
field of ubiquitous music.
Les références
Almeida, je. C., G. Cabral, and G. B. Almeida. 2019.
“AMIGO: An Assistive Musical Instrument to Engage,
Create and Learn Music.” In Proceedings of the
International Conference on New Interfaces for Musical
Expression, pp. 168–169.
Biles, J.. 2007. “Improvising with Genetic Algorithms:
GenJam.” In E. Miranda and J. Biles, éd.. Evolutionary
Computer Music. Berlin: Springer, pp. 137–169.
Braund, E., et R. Miranda. 2013. “Music with Un-
conventional Computing: A System for Physarum
Polycephalum Sound Synthesis.” In M. Aramaki et al.,
éd.. Sound, Music, and Motion. Berlin: Springer, pp.
161–174.
Busch, H. 1970. Leonhard Eulers Beitrag zur Musiktheorie.
Regensburg, Allemagne: Bosse.
Chomsky, N. 1956. “Three Models for Description of
Language.” IRE Transactions on Information Theory
2(3):113–124.
Chomsky, N. 1959. “On Certain Formal Properties
of Grammars.” Information and Control 2(3):137–
167.
Denjean, S., et autres. 2019. “Zero-Emission Vehicles Soni-
fication Strategy Based on Shepard-Risset Glissando.”
In Proceedings of the International Symposium on
Computer Music Multidisciplinary Research, pp.
966–976.
Figueir ´o, C., G. Soares, et B. Rohde. 2019. “ESMERIL:
An Interactive Audio Player and Composition System
for Collaborative Experimental Music Netlabels.” In
Proceedings of the International Conference on New
Interfaces for Musical Expression, pp. 170–173.
Kramann
33
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Garcia-Valdez, M., et autres. 2013. “EvoSpace-Interactive:
A Framework to Develop Distributed Collaborative-
Interactive Evolutionary Algorithms for Artistic De-
sign.” In P. Machado, J.. McDermott, et un. Carballal,
éd.. Evolutionary and Biologically Inspired Music,
Sound, Art, et conception. Berlin: Springer, pp. 121–132.
Gemma, E., et autres. 1995. Design Patterns. Boston, Mas-
sachusetts: Addison-Wesley.
Holtzman, B., et autres. 2013. “Seismic Sound Lab: Sights,
Sounds, and Perception of the Earth as an Acoustic
Space.” In M. Aramaki et al., éd.. Sound, Music, et
Motion. Berlin: Springer, pp. 161–174.
Hu, H., and D. Gerhard. 2019. “Modelling 4-Dimensional
Tonal Pitch Spaces.” In Proceedings of the International
Symposium on Computer Music Multidisciplinary
Research, pp. 38–50.
Jakobsen, K., et autres. 2016. “Hitmachine: Collective Musical
Expressivity for Novices.” In Proceedings of the
International Conference on New Interfaces for Musical
Expression, pp. 241–246.
Keller, D., V. Lazzarini, and M. Pimenta. 2014. Ubiquitous
Music. Berlin: Springer.
Kramann, G. 2015. “An Overtone-Based Algorithm
Unifying Counterpoint and Harmonics.” In Proceedings
of the International Symposium on Computer Music
Multidisciplinary Research, pp. 791–805.
Kramann, G. 2019. “Generative Grammar Based on
Arithmetic Operations for Realtime Composition.”
In Proceedings of the International Symposium on
Computer Music Multidisciplinary Research, pp.
346–360.
Lazzarini, V., et autres. 2014. “Prototyping of Ubiquitous
Music Ecosystems.” Cadernos de Inform ´atica 8(4):69–
80.
Maeda, J.. 2013. “STEM + Art = STEAM.” The STEAM
Journal 1(1):Art. 34.
Matsubara, M., Oui. Morimoto, and T. Uchide. 2019. “Audi-
tory Gestalt Formation for Exploring Dynamic Trigger-
ing Earthquakes.” In Proceedings of the International
Symposium on Computer Music Multidisciplinary
Research, pp. 983–987.
Russell, B. 1920. Introduction to Mathematical Philoso-
phy. New York: Macmillian. Réimprimé 1993. Mineola,
New York: Dover. Citations refer to the Dover edition.
Schneider, UN., and K. Frieler. 2008. “Perception of
Harmonic and Inharmonic Sounds: Results from
Ear Models.” In S. Ystad, R.. Kronland-Martinet,
and K. Jensen, éd.. Computer Music Modeling and
Retrieval. Berlin: Springer, pp. 18–44.
Spiegel, L. 1998. “Letter to the Editor: Should Music-
Making Be Reserved for an Elite?” Computer Music
Journal 22(1):6–7.
Stolfi, UN., et autres. 2018. “Playsound.space: Inclusive Free
Music Improvisations Using Audio Commons.” In
International Conference on New Interfaces for Musical
Expression, pp. 228–233.
Supper, M.. 2001. “A Few Remarks on Algorithmic
Composition.” Computer Music Journal 25(1):48–
53.
Weinberg, G. 2002. “Playpens, Fireflies and Squeezables:
New Musical Instruments for Bridging the Thoughtful
and the Joyful.” Leonardo Music Journal 12:43–51.
34
Computer Music Journal
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
c
o
m
j
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
4
4
1
1
7
2
0
0
5
2
8
7
/
c
o
m
_
un
_
0
0
5
5
0
p
d
.
j
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3