Communicated by Richard Lippmann
A Multiple-Map Model for Pattern Classification
Alan Rojer
Eric Schwartz
Computational Neuroscience Laboratory, New York University Medical Center,
Courant Institute of Mathematical Sciences, New York University,
New York, New York 1001 6, Etats-Unis
A characteristic feature of vertebrate sensory cortex (and midbrain) est
the existence of multiple two-dimensional map representations. Some
workers have considered single-map classification (e.g. Kohonen 1984)
but little work has focused on the use of multiple maps. We have
constructed a multiple-map classifier, which permits abstraction of the
computational properties of a multiple-map architecture. We identify
three problems which characterize a multiple-map classifier: classifica-
tion in two dimensions, mapping from high dimensions to two dimen-
sions, and combination of multiple maps. We demonstrate component
solutions to each of the problems, using Parzen-window density esti-
mation in two dimensions, a generalized Fisher discriminant function
for dimensionality reduction, and splivmerge methods to construct a
“tree of maps” for the multiple-map representation. The combination
of components is modular and each component could be improved
or replaced without affecting the other components. The classifier
training procedure requires time linear in the number of training ex-
amples; classification time is independent of the number of training
examples and requires constant space. Performance of this classifier
on Fisher’s iris data, Gaussian clusters on a five-dimensional simplex,
and digitized speech data is comparable to competing algorithms, tel
as nearest-neighbor, back-propagation and Gaussian classifiers. Ce
work provides an example of the computational utility of multiple-
map representations for classification. It is one step towards the goal
of understanding why brain areas such as visual cortex utilize multiple
map-like representations of the world.
1 Introduction
One of the most prominent features of the vertebrate sensory system is
the use of multiple two-dimensional maps to represent the world. Le
observational data base for cortical maps is excellent, and this area rep-
resents one of the better-understood aspects of large-scale brain archi-
tecture. Recently, through the use of a system for computer-aided neu-
Neural Computation 1,104-115 (1989) @ 1989 Massachusetts Institute of Technology
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Multiple-Map Model for Pattern Classification
105
roanatomy, we have been able to obtain high-precision reconstructions of
primary visual cortex map and column architectures, have constructed
accurate models of both columnar and topographic architecture of pri-
mary visual cortex, and have suggested several computational algorithms
which are contingent on the specific forms of column and map architec-
ture which occur in this first visual area of monkey cortex (Schwartz et
al. 1988). We expect to be able to extend these methods and ideas to
other cortical areas. There is thus good progress in the areas of measur-
ing, modeling, and computing with single-map representations. Comment-
jamais, the problem of how to make use of multiple maps has been little
explored.
Other workers have considered the application of single-map repre-
sentations to classification. Kohonen (1984) has developed an algorithm
for representing a feature space in a map; this algorithm constructs a
space-variant representation, in rough analogy to the space-variant na-
ture of primate visual cortex. Cependant, this work does not provide a
computational model for computing with multiple maps.
We believe that a classifier utilizing a multiple-map architecture must
incorporate the following modules:
An efficient algorithm for classification in two dimensions.
A projection of high dimensional data into a two-dimensional rep-
resentation.
An algorithm for combining multiple two-dimensional representa-
tion.
Our strategy in this work has been to use simple components to con-
struct our multiple-map classifier. In particular, we were seeking al-
gorithms which require one pass through the data and which are not
sensitive to convergence issues (e.g. local minima in an energy function).
We are interested in the overall properties of the classifier, and we are
trying to deemphasize the role of the individual components, which are
modular and hence subject to improvement or replacement.
2 Classification in Two Dimensions
We assume that the items, or instances, we wish to classify are represented
as vectors z E Rd, where each component of 2 is a feature measurement.
Each instance belongs to a class k . We also have a training set, a set
of instances of known class (training examples). We refer to the set of
training examples in class k as xk. Our problem is to construct a set of
discriminant functions fk : Rd + R., k = 1,. . . , c. An arbitrary instance x
is assigned to the class k for which f&)
is maximal.
Because the instances are represented as vectors, we can refer to the
distance between an instance and a training example as 115 – 2’11. Nous
compute discriminant functions
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
106
Alan Rojer and Eric Schwartz
where g ( r ) is some function which decreases as T increases. If we let
g be a probability density (c'est à dire. nonnegative and integrating to one over
its support) this is the Parzen-window estimate (Parzen 1962) for the a
posteriori density; c'est à dire. F&) = p(klz). Since this is the same term which is
maximized in the Bayes classifier, our classifier performance approaches
the Bayesian limit as the approximation above approaches the actual
probability density. This algorithm is related to the nearest-neighbor
classifier. Its principal novelty is to use maps to store fk(z). Alors, given
the training examples, we can compute fk(x> by convolution in one pass.
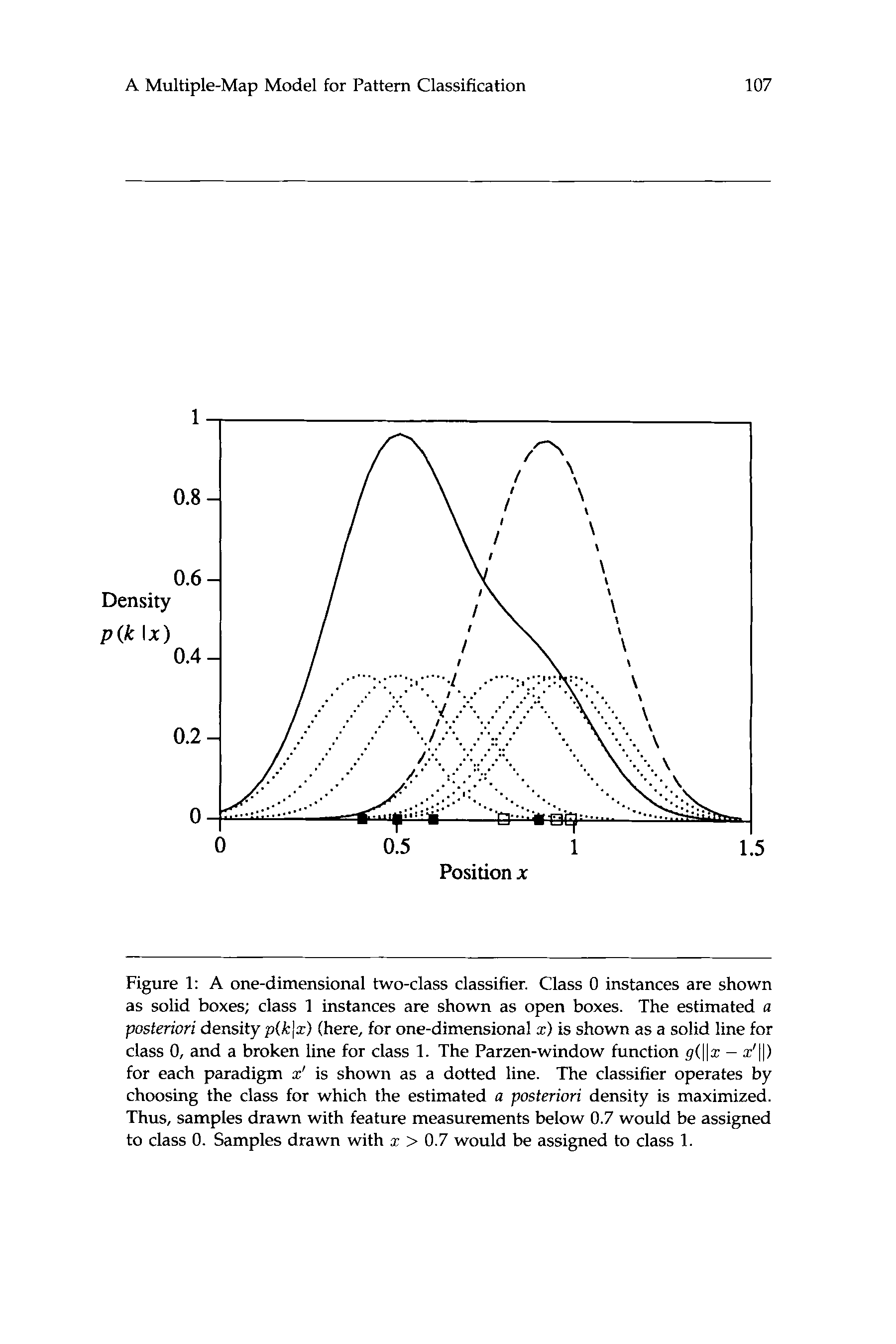
For illustration, see figure 1. We depict a two-class, one-dimensional
classifier. Le “map” is simply a segment of the real line. The training
examples are shown on the z-axis as boxes. The weighting function g(z)
is a Gaussian function. The individual convolutions g(X) * 6(z – z’) sont
shown as dotted lines. The class-specific density estimates, which are
also the discriminant functions, are shown as a solid and broken line,
respectivement.
We consider a two-dimensional, three-class problem in figure 2 et
chiffre 3. The weighting function is a circular two-dimensional Gaus-
sian function. The instances have been drawn from prespecified two-
dimensional multivariate normal distributions; this permits construction
of a Bayes classifier to determine minimal error rate. In figure 2, nous
show a comparison between the Parzen-window density estimates f k ( l c )
and the actual probability density functions for each class. In figure 3,
the classifier is compared to a Bayesian classifier. The visual compar-
ison indicates that the classifier is capturing much of the character of
the Bayesian classifier. When the classifier was trained on 400 samples
from each class, and tested on 300 (different) instances, its error rate was
16.0%, which may be compared to 14.4% for the Bayesian classifier.
One important issue in the application of this method is the choice
of the weighting function (or kernel). We have typically used Gaussian
kernels, in which case we need to choose the kernel variance CT* (or co-
variance matrix x,,, in higher dimensions). This is a difficult problem
in general; we have used heuristic algorithms. Par exemple, if we de-
sire an isotropic kernel, we might use CT = N-‘/”&, where X I is the
largest eigenvalue of the covariance matrix resulting from the projection
of the data into an rn-dimensional map. The factor N-‘/” arises from
the heuristic decision to give each training instance an equal amount of
map volume; since the kernel is m-dimensional, the volume scales as cP.
Plus généralement, we could use C, = h P C , where P is the projection into
the map (see below). In experimental studies, we have found that the
performance of the classifier is insensitive to small changes in the kernel
size or shape.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Multiple-Map Model for Pattern Classification
107
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
0
0.5
Position x
je
1.5
Chiffre 1: A one-dimensional two-class classifier. Class 0 instances are shown
as solid boxes; class 1 instances are shown as open boxes. The estimated a
posteriori density p ( k l z ) (ici, for one-dimensional z) is shown as a solid line for
class 0, and a broken line for class 1. The Parzen-window function g(11z – 2’11)
for each paradigm x’ is shown as a dotted line. The classifier operates by
choosing the class for which the estimated a posteriori density is maximized.
Ainsi, samples drawn with feature measurements below 0.7 would be assigned
to class 0. Samples drawn with z > 0.7 would be assigned to class 1.
108
Alan Rojer and Eric Schwartz
Binormal densities
Map estimates
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2: Comparison of actual binormal density against estimated density f&)
computed by our classifier. Here a higher density corresponds to a darker region
of the plot. The top row shows density plots for three binormal distributions
in R2. The bottom row shows the estimates fk(X) computed by the classifier
pour 400 samples drawn from each of these three distributions. The weighting
function used is a circular Gaussian with a variance approximately 1/60 le
width of the figure.
3 From d Dimensions to Two Dimensions
Dans la section précédente, we showed that the performance (as measured by
error rate) approaches that of the Bayesian classifier for two-dimensional
A Multiple-Map Model for Pattern Classification
109
Bayesian classifier
Map Classifier
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 3: Comparison of decision regions computed by our classifier against
decision regions of a hypothetical Bayes classifier which had complete knowl-
edge of the underlying class distributions. Regions in the Bayes classifier are
clipped due to round-off.
data drawn from Gaussian distributions. Actually there is nothing in our
derivation which restricts us to two dimensions; a d-dimensional classi-
fier is defined as above, except that the density estimate p k ( z ) will require
a d-dimensional map. In practice we limit ourselves to two dimensions
for three reasons. D'abord, our original motivation is to understand the
functional utility of laminar structures such as neocortex for pattern clas-
sification in the brain. Deuxième, two-dimensional maps can be processed
110
Alan Rojer and Eric Schwartz
by conventional image processing software and hardware, and the user of
the classifier gets the benefit of visual displays of the intermediate struc-
tures in the classifier (e.g. P k ( Z ) and the computed partition). Enfin,
the number of bins required to store the maps P k ( Z ) grows exponentially
with the dimensionality d, and thus favors small d.
Restriction to two dimensions introduces an interesting aspect to the
classification problem. Although our original data is in d dimensions, c'est à dire.
the data is composed of d measurements, we must somehow extract only
two measurements or combinations of measurements with which to con-
struct our classifier. The classification problem then spawns a problem of
feature derivation. We can formulate the dimensionality reduction prob-
lem as construction of a function P : Rd .+ R2 which maps d-dimensional
instances to two-dimensional map positions. The two dimensions of the
map constitute the two derived features. We need to specify what kind
of function P we will allow. To date, we have only considered linear
projections, but nonlinear functions could also be used (e.g. Kohonen’s
self-organizing feature map; Kohonen 1984).
We apply the generalized Fisher discriminant which was first intro-
duced for a projection to R (Pêcheur 1936) and later generalized to a domain
of arbitrary dimensionality (Bryan 1951). A discussion of the technique
may be found in (Duda and Hart 1973). The two vectors which com-
prise P turn out to be the eigenvectors associated with the two largest
eigenvalues in the generalized eigenvalue system
sbu = XSwu,
where S, is the “within-class” scatter matrix, given by
(3.1)
(3.2)
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
with c k the class mean and N k the number of training examples repre-
senting class k , and sb is the “between-class” scatter matrix, given by
(3.3)
Ici, z is the mean over all the training examples. In practice, we have
found that S, is nonsingular, so the system can be reduced to a standard
eigenvalue problem
S i ‘ s b U = Xu.
(3.4)
The extraction of the principal eigenvalue and its eigenvector are real-
izable using a typical Hebb synapse model with a fixed-length weight
vector (Oja 1982).
The performance of the discriminant can be observed with Fisher’s
classical iris data. This data describes a four-dimensional, three-class
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Multiple-Map Model for Pattern Classification
111
problem. Chiffre 4 depicts the classifier constructed from the projection
of the iris data into the two-dimensional subspace which maximizes the
ratio described above. The classes can be seen to be fairly well sep-
arated. The classifier was tested by splitting the 150 instances into a
100-instance training set and a 50-instance test set. After training on the
100 instances, the classifier achieved 98% correct classification on the 50
instances in the test set. By comparison, the nearest-neighbor classifier
operating on the same training and test sets achieved 98% correct clas-
sification, the Gaussian classifier achieved 94% correct classification, et
a multilayer perceptron trained using back-propagation’ achieved 96%
correct classification.
4 Using Multiple Maps: A Tree of Maps
The previous example showed that for a relatively easy four-dimensional
three-class problem, the generalized Fisher discriminant analysis was ad-
equate to obtain a map which permitted good classifier performance. Mais
in general, the discriminant analysis does not yield enough separation.
Par exemple, consider a regular five-dimensional simplex; this is a set of
six equidistant points on the unit sphere in R5. Locate a spherical multi-
variate normal distribution at each vertex of the simplex. This is a point
swarm whose density declines as exp(-r2), where T is the distance from
the vertex. We construct the classifier by utilizing discriminant analysis
to find a projection P : R5 + R2. With 600 training points and 300 test
points, the error rate is 36%.
Heureusement, we are not confined to one map. One method of using
multiple maps utilizes a split/merge technique to reduce one many-class
problem to several problems, each with fewer classes. We merge the
original base classes into superclasses, each of which is represented by the
union of training examples from its underlying base classes. We then
apply discriminant analysis to the newly formed superclasses. If we can
achieve an adequate separation, we proceed as above with a separate map
for each superclass. If necessary, we can again perform merges among
the elements of a superclass, until we have divided each superclass into
component base classes.
The consequence of this approach is to create a tree of maps. From the
root of the tree, we project instances into a superclass. If the superclass is
a base class, we assign that class to the instance. Otherwise, the instance
is assigned to a superclass, which has its own map. We project the
instance into that map, and continue as above, until the instance lands
in a region assigned to a base class. In the training phase, we construct
‘A multilayer perceptron with 4 hidden units was trained using back-propagation
(Rumelhart et al. 1986) avec 5000 iterations through the training set, with E = 0.02 et
a = 0.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
112
Alan Rojer and Eric Schwartz
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4: Iris classifier constructed from 100 training points drawn from the
iris data (shaded background). Projection of four-dimensional iris data points
into the two-dimensional subspace which maximizes the ratio of between-class
variance to within-class variance (foreground data points).
a classifier in R2 for each internal node in the tree to classify instances
into one of the superclasses for that node.
We can illustrate this algorithm with the simplex data. We partition
the classes so that three maps are used to classify. In the first map, nous
merge classes 2-5 into a superclass, letting classes 0 et 1 remain as base
classes. In the second map, we will resolve the superclass composed
of classes 2-5 into classes 2 et 3 and a superclass formed of 4 et 5.
Enfin, in the third map, we will resolve the superclass formed from 4
et 5 above into component base classes. The error rate of the three-map
classifier is found to be 4.7%, a dramatic improvement over the single-
map classifier (36% error rate). This may be compared to error rates
de 2%, 6% et 2.7% respectively for the Gaussian, nearest-neighbor and
A Multiple-Map Model for Pattern Classification
113
multilayer perceptron classifiem2 We have also applied our classifier to
real-world data which consisted of 22 cepstral parameters from digitized
~ p e e c h . ~ Each of 16 data sets represented one speaker; seven classes
(monosyllabic words) were present in each data set. Each set consisted of
70 training instances and 112 test instances. The results are summarized:
Nearest- Multilayer
Classifier: Multiple-map Gaussian4 neighbor perceptron5
Average
error
rate(% 1:
6.5
6.0
5.9
6.3
Range (%):
1.8-12.5
3.6-10.7
1.8-15.2
1.8-11.6
from which it may be seen that all four classifiers under consideration
had closely comparable performance.
5 Automatic Generation of the Map Tree
In the preceding examples of multiple map usage, we interactively chose
a map tree. In this section we explore a simple approach to automatic
generation of the map tree. This is a clustering problem; we want to
group classes into superclasses which in some way reflect the natural
similarity between classes.
We introduce the distance matrix A for the classes. For any interclass
distance measure dist(je,j), UN,, = A,, = dist(je, j ) . We use a very simple tree
generation algorithm. we treat A as a graph with each class represented
by a node, and each edge weighted according to interclass distance. Nous
then compute the minimal spanning tree. We form superclasses by re-
cursively removing the largest edge in the tree, yielding two subtrees,
each of which forms a superclass. We can use a variety of interclass
distance measures; we have experimented with distances between class
moyens, overlap of the one-dimensional Fisher discriminant projections,
and overlap of the two-dimensional Fisher discriminant projections.
2A multilayer perceptron with 7 hidden units was trained using back-propagation
(Rumelhart et al. 1986) avec 5000 iterations through the training set, with E = 0.02 et
N = 0.
3We are grateful to R. Lippmann of MIT Lincoln Laboratory for providing this data.
4Covariance matrix estimates were obtained by pooling data from all 16 speakers
for each class.
5Multilayer perceptrons for each speaker used 15 hidden units.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
114
6 Discussion
Alan Rojer and Eric Schwartz
Our classifier is inspired by the prevalence of maps in the vertebrate
brain. Its components are two-dimensional map units which implement
Parzen-window density estimation, a dimensionality reduction method-
ology, and a scheme for decomposing a problem so that it can be solved
by a system of maps. The training and running costs are favorably low. Il
admits an easy formal description. The intermediate results of classifier
construction, e.g. the density estimates p&) and the partition computed
by the classifier, are easily observed by a human user. This allows insight
into the structure of the data that is hard to gain from other algorithms.
Many of the operations can be implemented with conventional image
processing operations (and thus can take advantage of special-purpose
image processing hardware). The error rate is comparable to popular
parametric, nonparametric, and neural network classifiers.
Only a few other workers have considered the role of maps in pattern
classification. In particular, Kohonen (1984) has considered iterative al-
gorithms for “self-organizing feature maps.” We wish to distinguish his
work from ours. In our classifier, the map function comprises a linear
projection of a data instance to determine a position in the map followed
by a reference to that position. Kohonen maps an instance via a distance
computation at each node of his map, followed by a winner-take-all cycle
to obtain the nearest-neighbor to the instance among all the map nodes.
The projection we use is computed with one pass through the training
set to compute second-order statistics, which are diagonalized in a step
which has a cost related only to the dimensionality of the data, but not
the number of samples. Kohonen uses a very large number of iterations
through the training set. Most importantly, we emphasize the use of
multiple maps, which is not considered in (Kohonen 1984). We could
use a Kohonen-type feature map as a module in our classifier (replacing
the Fisher discriminant analysis) although we would then sacrifice these
advantages.
Tree classifiers have been considered at length in Breiman et al. (1984).
There are similarities between their classifiers and ours at classification
temps, although the training algorithms are quite distinct. The principal
difference in classifier operation is that we use two-dimensional density
estimation at each node, while they use one-dimensional linear discrim-
inants. Their discriminant is typically a threshold comparison of one
feature value, although they also describe an iterative technique for ob-
taining a discriminant from a linear combination of a subset of the feature
variables. There are much larger differences in the classifier training algo-
rithms; we present an example of a simple heuristic for generating map
trees (based on minimal spanning trees) whereas they examine a large set
of possible splits in the data to generate trees. We wish to emphasize that
our tree classifier is one possible technique for utilizing multiple maps;
examination of alternative approaches is an important research problem.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
A Multiple-Map Model for Pattern Classification
115
Perceptual (and probably cognitive) functions of the brain are medi-
ated by laminar cortical systems. Three carefully investigated systems
(monkey vision, bat echolocation, and auditory localization in the owl)
are committed to multiple two-dimensional spatial maps. The present pa-
per describes the first attempt to construct a pattern classification system
which has high performance and which is based on a multiple parallel
map-like representation of feature vectors. The algorithms described in
this paper allow us to begin to investigate the pattern classification and
perceptual performance of such map-based architectures.
Remerciements
Supported by AFOSR-88-0275.
Les références
Breiman, L., J.H. Freedman, R.A. Olshen, and C.J. Stone. 1984. Classification and
Regression Trees. Bellmont, Californie: Wadsworth.
Bryan, J.G. 1951. The Generalized Discriminant Function: Mathematical Foun-
dation and Computation Routine. Harvard Educ. Rev. 21, 90-95.
Duda, R.O. and P.E. Hart. 1973. Pattern Classification and Scene Analysis. Nouveau
York Wiiey.
Pêcheur, R.A. 1936. The Use of Multiple Discriminant Measurements in Taxo-
nomic Problems. Ann. Eugenics 7, 179-188.
Kohonen, T. 1984. Self-organization and Associative Memory. New York: Springer-
Verlag.
Oja, E. 1982. A Simplified Neuron Model as a Principal Component Analyzer.
J.. Math. Biol. 15, 267-273.
Parzen, E. 1962. On Estimation of a Probability Density Function and Mode.
Ann. Math. Stat 33, 1065-1076.
Rumelhart, D.E., G.E. Hinton, and R.J. Williams. 1986. Learning Representa-
tions by Back-propagating Errors. Nature 323, 533-536.
Schwartz, E.L., B. Merker, E. Wolfson, and A. Shaw. 1988. Informatique
Neurosciences: Applications of Computer Graphics and Image Processing
to Two and Three Dimensional Modeling of the Functional Architecture of
Visual Cortex. IEEE Computer Graphics and Applications ]uly 1988, 13-28.
Reçu 1 Octobre; accepted 18 Novembre 1988.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
toi
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
1
0
4
8
1
1
8
0
9
n
e
c
o
1
9
8
9
1
1
1
0
4
p
d
.
.
.
.
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3