Communicated by Carver Mead
Criteria for Robust Stability In A Class Of Lateral
Inhibition Networks Coupled Through Resistive
Grids
John L. Wyatt, Jr..
David L. Standley
Department of EJectrical Engineering and Computer Science,
Massachusetts Institute of TechnoJogy, Cambridge, MA 02139, Etats-Unis
In the analog VLSI implementation of neural systems, it is sometimes
convenient to build lateral inhibition networks by using a locally con-
nected on-chip resistive grid to interconnect active elements. A serious
problem of unwanted spontaneous oscillation often arises with these
circuits and renders them unusable in practice. This paper reports on
criteria that guarantee these and certain other systems will be stable,
even though the values of designed elements in the resistive grid may
be imprecise and the location and values of parasitic elements may be
unknown. The method is based on a rigorous, somewhat novel math-
ematical analysis using Tellegen’s theorem (Penfield et al. 1970) depuis
electrical circuits and the idea of a Popov multiplier (Vidyasagar 1978;
Desoer and Vidyasagar 1975) from control theory. The criteria are lo-
cal in that no overall analysis of the interconnected system is required
for their use, empirical in that they involve only measurable frequency
response data on the individual cells, and robust in that they are insen-
sitive to network topology and to unmodelled parasitic resistances and
capacitances in the interconnect network. Certain results are robust
in the additional sense that specified nonlinear elements in the grid do
not affect the stability criteria. The results are designed to be applica-
ble, with further development, to complex and incompletely modelled
living neural systems.
1 Introduction
In the VLSI implementation of lateral inhibition and certain other types
of networks, active cells are locally interconnected through an on-chip re-
sistive grid. Linear resistors fabricated in, e g , polysilicon, could yield a
very compact realization, and nonlinear resistive grids, made from MOS
transistors, have been found useful for image segmentation (Hutchinson
et autres. 1988). Networks of this type can be divided into two classes: feed-
back systems and feedforward-only systems. In the feedfonvard case
Neural Computation 1, 58457 (1989) 0 1989 Massachusetts Institute of Technology
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Robust Stability In A Class Of Lateral Inhibition Networks
59
one set of amplifiers imposes signal voltages or currents on the grid and
another set reads out the resulting response for subsequent processing,
while the same amplifiers both ”write to” the grid and ”read from” it in a
feedback arrangement. Feedforward networks of this type are inherently
stable, but feedback networks need not be.
A practical example is one of Mahowald and Mead’s retina chips
(Mead and Mahowald 1988; Mead 1988) that achieve edge enhancement
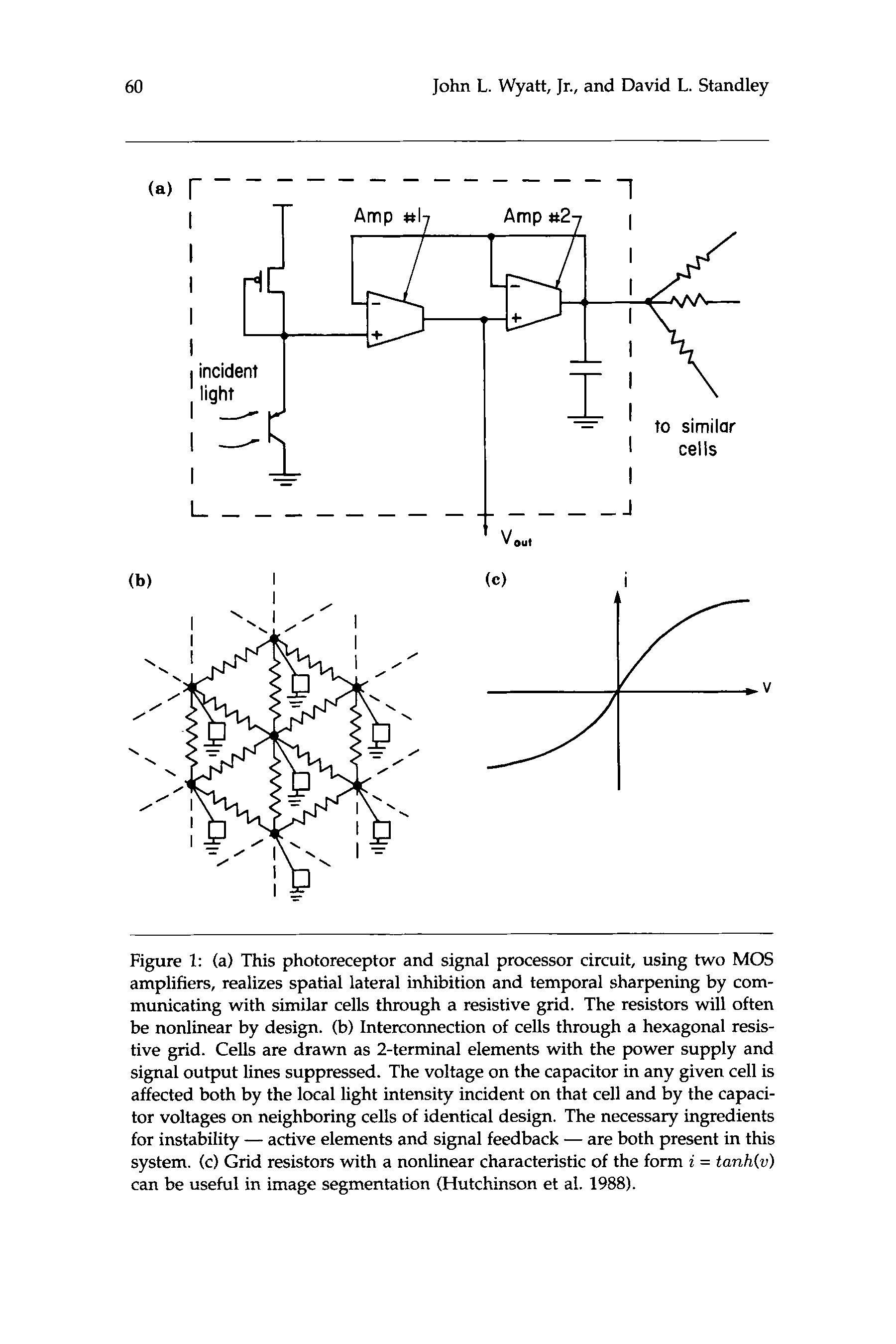
by means of lateral inhibition through a resistive grid. Figure l a shows
a single cell in an earlier version of this chip, and figure l b illustrates the
network of interconnected cells. Experiment has shown that the individ-
ual cells in this system are open-circuit stable and remain stable when
the output of amplifier #2 is connected to a voltage source through a
resistor, but the interconnected system oscillates so badly that the earlier
design is scarcely usable’ (Mahowald and Mead 1988). Such oscillations
can readily occur in most resistive grid circuits with active elements and
feedback, even when each individual cell is quite stable. Analysis of the
conditions of instability by conventional methods appears hopeless, depuis
the number of simultaneously active feedback loops is enormous.
This paper reports a practical design approach that rigorously guar-
antees such a system will be stable if the active cells meet certain criteria.
The work begins with the naiv6 observation that the system would be
stable if we could design each individual cell so that, although inter-
nally active, it acts like a passive system as seen from the resistive grid.
The design goal in that case would be that each cell’s output impedance
should be a positive-real (Vidyasagar 1978; Desoer and Vidyasagar 1975;
Anderson and Vongpanitlerd 1973) fonction. This is sometimes possible
in practice; we will show that the original network in figure la would
satisfy this condition in the absence of certain parasitic elements. Fourrure-
thermorer, it is a condition one can verify experimentally by frequency-
response measurements.
It is obvious that a collection of cells that appear passive at their
terminals will form a stable system when interconnected through a pas-
sive medium such as a resistive grid, and that the stability of such a
system is robust to perturbations by passive parasitic elements in the net-
travail. The work reported here goes beyond that observation to provide
(je) a demonstration that the passivity or positive-real condition is much
stronger than we actually need and that weaker conditions, more easily
achieved in practice, suffice to guarantee robust stability of the linear
active network model, et (ii) an extension of the analysis to the nonlin-
ear domain that furthermore rules out sustained large-signal oscillations
under certain conditions. A key feature of the integrated circuit environ-
ment that makes these results applicable is the almost total absence of
on-chip inductance. While the cells can appear inductive, as in figure 3c,
‘The later design reported in (Mead and Mahowald 1988) avoids stability problems
altogether, at a small cost in performance, by redesigning the circuits to passively sense
the grid voltage in a ”feedforward” style as described above.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
60
John L. Wyatt, Jr., and David L. Standley
je
je
je
I incident
light
je – r
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 1: (un) This photoreceptor and signal processor circuit, using two MOS
amplifiers, realizes spatial lateral inhibition and temporal sharpening by com-
municating with similar cells through a resistive grid. The resistors will often
be nonlinear by design. (b) Interconnection of cells through a hexagonal resis-
tive grid. Cells are drawn as 2-terminal elements with the power supply and
signal output lines suppressed. The voltage on the capacitor in any given cell is
affected both by the local light intensity incident on that cell and by the capaci-
tor voltages on neighboring cells of identical design. The necessary ingredients
for instability – active elements and signal feedback – are both present in this
système. (c) Grid resistors with a nonlinear characteristic of the form i = tanh(v)
can be useful in image segmentation (Hutchinson et al. 1988).
Robust Stability In A Class Of Lateral Inhibition Networks
61
the absence of inductance in our grid models makes these theorems pos-
sible.
Note that these results do not apply directly to networks created by
interconnecting neuron-like elements, as conventionally described in the
literature on artificial neural systems. The ”neurons” in, par exemple., a Hopfield
réseau (Hopfield 1984) are unilateral 2-port elements in which the input
and output are both voltage signals. The input voltage uniquely and
instantaneously determines the output voltage of such a neuron model,
but the output can only affect the input via the resistive grid. En revanche,
the cells in our system are I-port electrical elements (temporarily ignoring
the optical input channel) in which the port voltage and port current are
the two relevant signals, and each signal affects the other through the
cell’s internal dynamics (modeled as a Thevenin equivalent impedance)
as well as through the grid’s response.
It is apparent that uncontrolled spontaneous oscillation is a potential
problem in living neural systems, which typically also consist of active
elements arranged in feedback loops. Biological systems have surely
solved the same problem we attack in this paper. It is reasonable to believe
that stability has strongly constrained the set of network configurations
nature has produced. Whatever Nature’s solutions may be, we suspect
they have at least three features in common with the ones proposed here:
(1) robustness in the face of wide component variation and the presence
of parasitic network elements, (2) reliance on empirical data rather than
anything we would recognize as a theory or analytic method, (3) stabil-
ity strategies based on predominantly local information available to each
network element.
Several reports on this work have appeared and will appear in (Wyatt
and Standley 1988; Standley 1989; Standley and Wyatt 1989; 1988un; 198813)
during its development; a longer tutorial exposition will be given in the
second printing of (Mead 1988).
2 The Linear Theory
2.1 Terminology. The output impedance of a linear system is a mea-
sure of the voltage response due to a change in output current while the
input (light intensity in this case) is held constant. This standard elec-
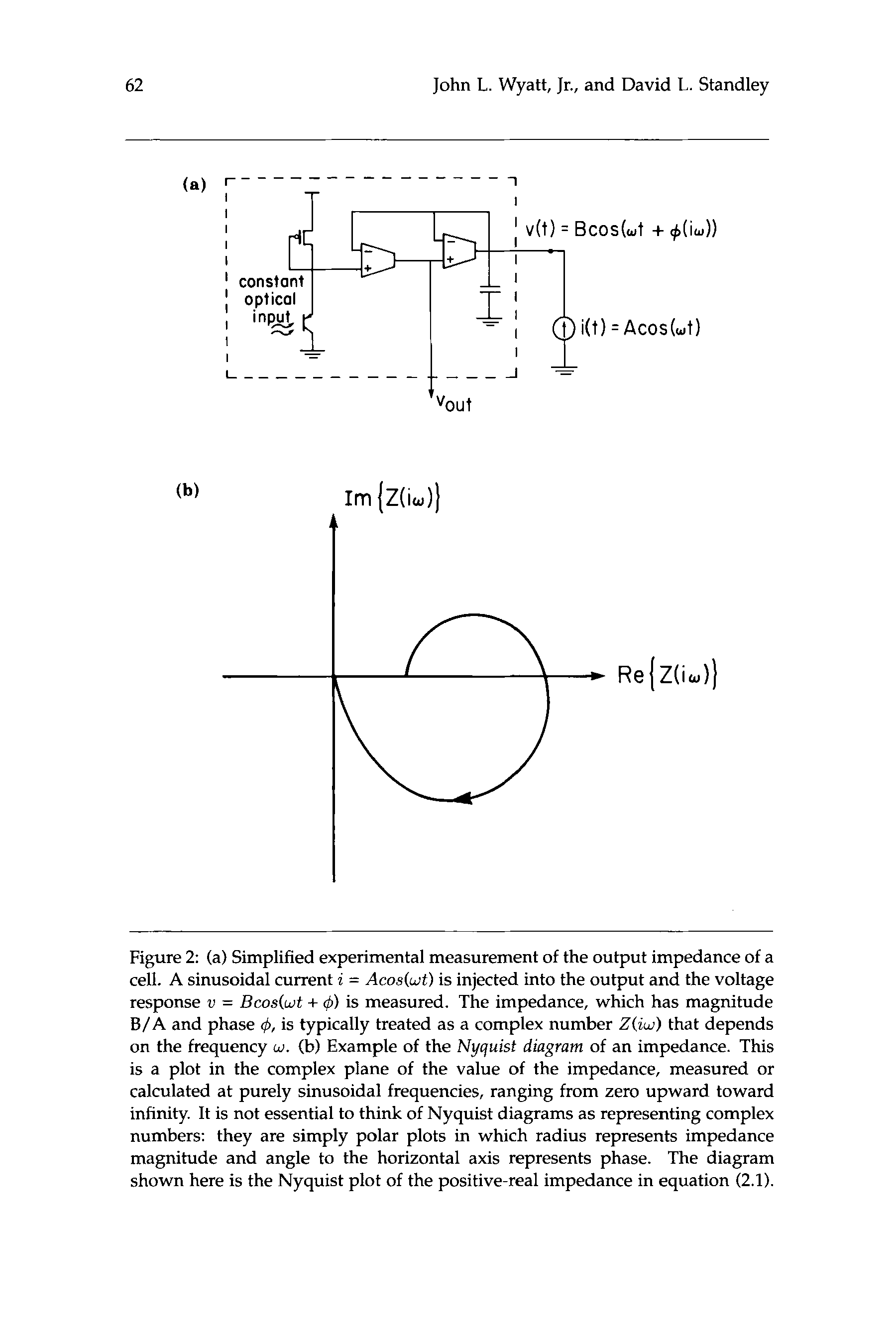
trical engineering concept will play a key role here. Figure 2a illustrates
one experimental method for measuring the output impedance, and fig-
ure 2b is a standard graphical representation of an impedance, known as
a Nyquist diagram. Similar plots have been used in experimental physi-
œnologie (Cole 1932).
In the context of this work, an impedance is said to be positive-real
(Vidyasagar 1978, Desoer and Vidyasagar 1975, Anderson and Vongpan-
itlerd 1973) if it is stable (c'est à dire., has no poles or zeroes in the right-half plane)
and its Nyquist diagram lies entirely in the right-half plane (c'est à dire., dans le
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
62
John L. Wyatt, Jr., and David L. Standley
(un) r – – – – – – – – – – – – – – –
1
je
T
je
je
Bcos (wt +
I =K I
cv
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 2: (un) Simplified experimental measurement of the output impedance of a
cell. A sinusoidal current i = Acos(wt) is injected into the output and the voltage
response u = Bcos(wt + 4) is measured. The impedance, which has magnitude
B/A and phase 4, is typically treated as a complex number Z(iw) that depends
on the frequency w. (b) Example of the Nyquist diagram of an impedance. Ce
is a plot in the complex plane of the value of the impedance, measured or
calculated at purely sinusoidal frequencies, ranging from zero upward toward
infinity. It is not essential to think of Nyquist diagrams as representing complex
numbers: they are simply polar plots in which radius represents impedance
magnitude and angle to the horizontal axis represents phase. The diagram
shown here is the Nyquist plot of the positive-real impedance in equation (2.1).
Robust Stability In A Class Of Lateral Inhibition Networks
63
(b) r—
je
je
je
je
je
je
1
je
je
je
je
je . – je –
je
je
– –
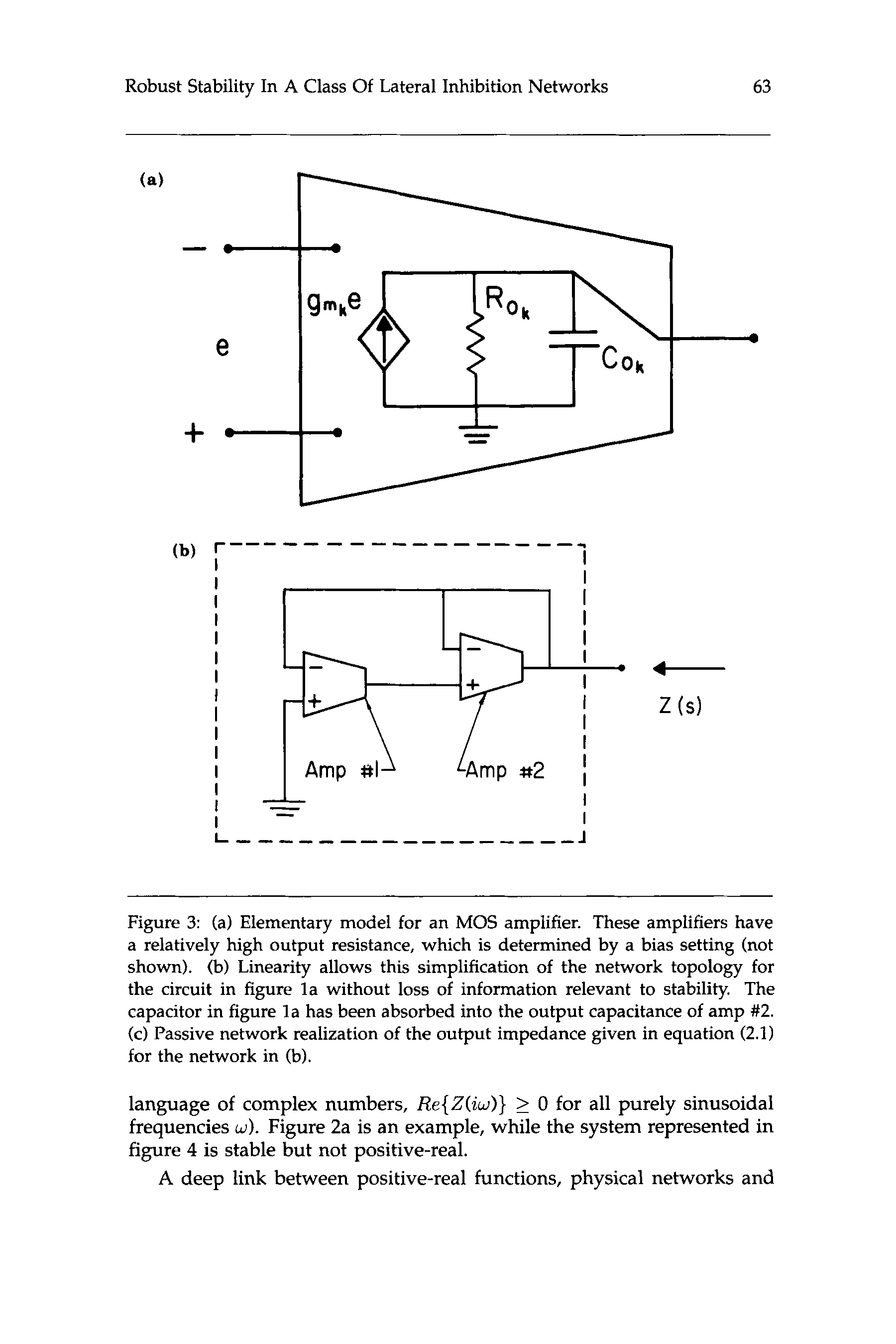
Chiffre 3: (un) Elementary model for an MOS amplifier. These amplifiers have
a relatively high output resistance, which is determined by a bias setting (pas
shown). (b) Linearity allows this simplification of the network topology for
the circuit in figure la without loss of information relevant to stability. Le
capacitor in figure l a has been absorbed into the output capacitance of amp #2.
(c) Passive network realization of the output impedance given in equation (2.1)
for the network in (b).
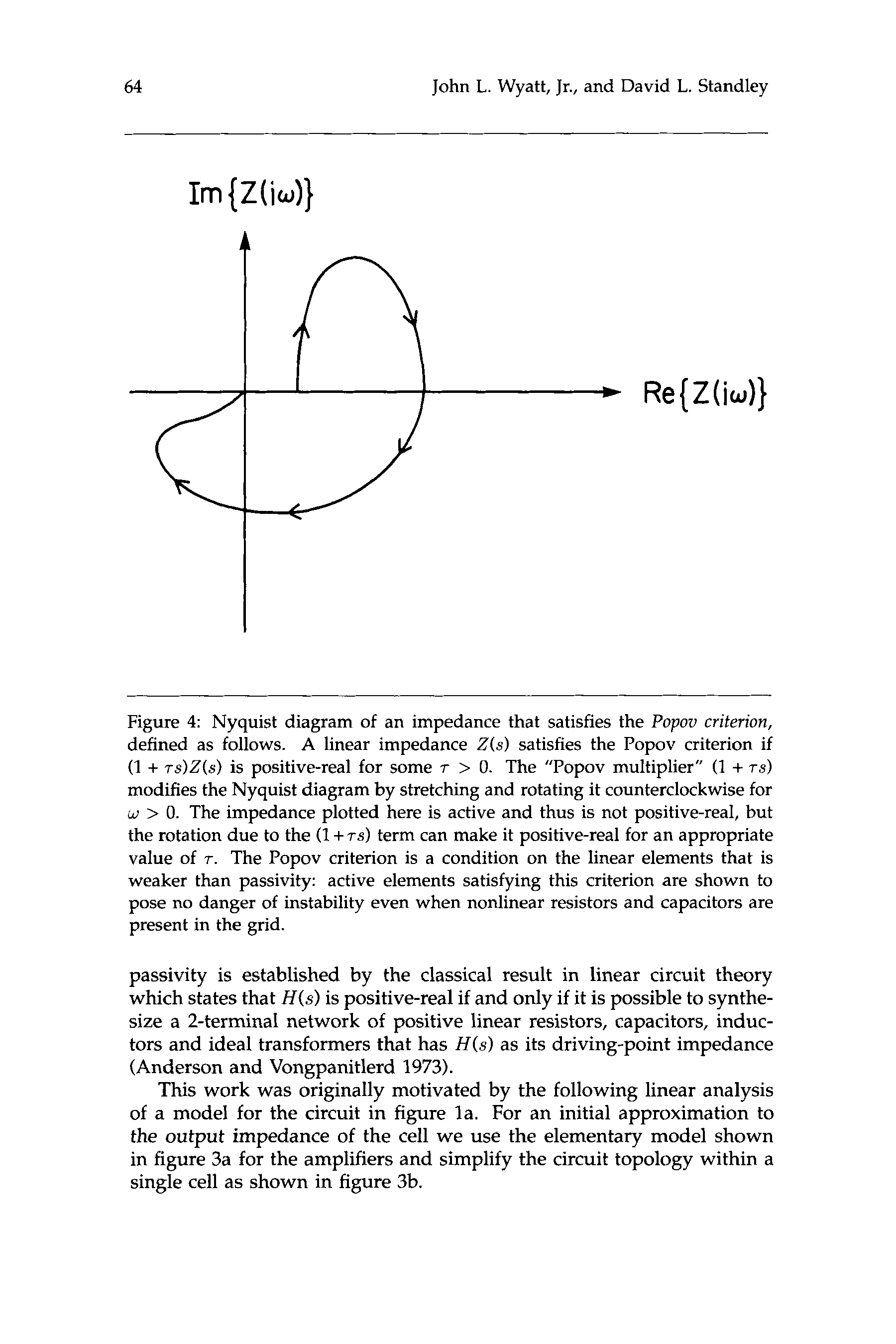
language of complex numbers, Re{Z(iw)} 2 0 for all purely sinusoidal
frequencies w). Figure 2a is an example, while the system represented in
chiffre 4 is stable but not positive-real.
A deep link between positive-real functions, physical networks and
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
64
John L. Wyatt, Jr., and David L. Standley
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 4: Nyquist diagram of an impedance that satisfies the Popov criterion,
defined as follows. A linear impedance Z(s) satisfies the Popov criterion if
(1 + TS)Z(S) is positive-real for some T > 0. The “Popov multiplier” (1 + T S )
modifies the Nyquist diagram by stretching and rotating it counterclockwise for
w > 0. The impedance plotted here is active and thus is not positive-real, mais
the rotation due to the (1 + T S ) term can make it positive-real for an appropriate
value of T . The Popov criterion is a condition on the linear elements that is
weaker than passivity: active elements satisfying this criterion are shown to
pose no danger of instability even when nonlinear resistors and capacitors are
present in the grid.
passivity is established by the classical result in linear circuit theory
which states that H ( s ) is positive-real if and only if it is possible to synthe-
size a 2-terminal network of positive linear resistors, capacitors, induc-
tors and ideal transformers that has H ( s ) as its driving-point impedance
(Anderson and Vongpanitlerd 1973).
This work was originally motivated by the following linear analysis
of a model for the circuit in figure l a . For an initial approximation to
the output impedance of the cell w e use the elementary model shown
in figure 3a for the amplifiers and simplify the circuit topology within a
single cell as shown in figure 3b.
Robust Stability In A Class Of Lateral Inhibition Networks
65
Straightforward calculations show that the output impedance is given
par
This is a positive-real impedance that could be realized by a passive
network of the form shown in figure 3c, où
Of course this model is oversimplified, since the circuit does oscillate.
Transistor parasitics and layout parasitics cause the output impedance
of the individual active cells to deviate from the form given in equa-
tion (2.1) et (2.21, and any very accurate model will necessarily be
quite high order. The following theorem shows how far one can relax
the positive-real condition and still guarantee that the entire network is
robustly stable. It obviously applies to a much wider range of linear
networks than has been discussed here.
A linear network is said to be stable if for any initial condition the
transient response converges asymptotically to a constant.
Theorem 1. Consider the class of linear networks of arbitrary topology, con-
sisting of any number of positive 2-terminal resistors and capacitors and
of N lumped linear impedances Z,(s), n = 1,2,. . . , N, that are open- et
short-circuit stable in isolation, c'est à dire.. that have no poles or zeroes in the
closed right-half plane. Everby such network is stable if at each frequency
w 2 0 there exists a phase angle O(w) such that 0 2 Ô(w) 2 -90″ et
ILZ,,(iw) – Ô(iw)je < 90",n = 1 , 2 , . . . , N.
An equivalent statement of this last condition is that the Nyquist
plot of each cell's output impedance for w 2 0 never intersects the 2nd
quadrant of the complex plane (figure 4 is an example), and that no two
cells' output impedance phase angles can ever differ by as much as 180".
If all the active cells are designed identically and fabricated on the same
chip, their phase angles should track fairly closely in practice, and thus
this second condition is a natural one.
The theorem is intuitively reasonable and serves as a practical design
goal. The assumptions guarantee that the cells cannot resonate with one
another at any purely sinusoidal frequency s = jw since their phase an-
gles can never differ by as much as 180", and they can never resonate
with the resistors and capacitors since they can never appear simultane-
ously active and inductive at any sinusoidal frequency. A more advanced
argument (Standley and Wyatt 1989) shows that exponentially growing
instabilities are also ruled out.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
66
John L. Wyatt, Jr., and David L. Standley
3 Stability Result for Networks with Nonlinear Resistors and
Capacitors
The previous results for linear networks can afford some limited insight
into the behavior of nonlinear networks. If a linearized model is stable,
then the equilibrium point of the original nonlinear network must be
locally stable. But the result in this section, in contrast, applies to the
full nonlinear circuit model and allows one to conclude that in certain
circumstances the network cannot oscillate or otherwise fail to converge
wen if the initial state is arbitrarily fur from the equilibrium point. Figure 4
introduces the Popov criterion, which is the basis of the following theorem.
This is the first nonlinear result of its type that requires no assumptions
on the network topology.
Theorem 2. Consider any network consisting of nonlinear resistors and ca-
pacitors and linear active cells with output impedances Zn(s), n = 1,2,. . . , N .
Suppose
(a) the nonlinear resistor and capacitor characteristics, ij = g3(vj) and
q k = hk(vk), respectively, are monotone increasing continuously differ-
entiable functions, and
(b) the impedances Z,(s> all satisfy the Popov criterion for some common
value of r > 0.
Then the network is stable in the sense that, for any initial condition
at t = 0,
(3.1)
Remerciements
We sincerely thank Professor Carver Mead of Cal Tech for encouraging
this work, which was supported by Defense Advanced Research Projects
Agency (DARPA) Contract No. N00014-87-K-0825 and National Science
Fondation (NSF) Contract No. MIP-8814612.
Les références
Anderson, B.D.O. et S. Vongpanitlerd. 1973. Network Analysis and Synthesis
– A Modern Systems Theory Approach, Englewood Cliffs, New Jersey: Prentice-Hall.
Cole, K.S. 1932. Electric Phase Angle of Cell Membranes. J.. General Physiology
156,64149.
Desoer, C. and M. Vidyasagar. 1975. Feedback Systems: Input-Output Properties.
New York Academic Press.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
.
Robust Stability In A Class Of Lateral Inhibition Networks
67
Hopfield, J.J. 1984. Neurons with Graded Response have Collective Computa-
tional Properties Like Those of Two-state Neurons. Proc. Nat’l. Acad. Sci.
81,3088-3092.
Hutchinson, J., C. Koch, J.. Luo, and C. Mead. 1988. Computing Motion Using
Analog and Binary Resistive Networks. Computer 21:3, 52-64.
Mahowald, M.A. and C.A. Mead. 1988. Personal communication.
Mead, C.A. 1988. Analog VLSI and Neural Systems. Addison-Wesley.
Mead, C.A. and M.A. Mahowald. 1988. A Silicon Model of Early Visual Pro-
cessation. Neural Networks 1:1, 91-97.
Penfield, P., Jr., R.. Spence, et S. Duinker. 1970. Tellegen’s Theorem and Electrical
Networks. Cambridge, MA: MIT Press.
Standley, D.L. 1989. Design Criteria Extensions for Stable Lateral Inhibition
Networks in the Presence of Circuit Parasitics. PYOC. 1989 I E E E Int. Symp. sur
Circuifs and Systems, Portland, OR.
Standley, D.L. and J.L. Wyatt, Jr.. 1989. Stability Criterion for Lateral Inhibition
Networks that is Robust in the Presence of Integrated Circuit Parasitics.
I E E E Trans. Circuits and Systems, to appear.
. 1988un. Stability Theorem for Lateral Inhibition Networks that is Robust
in the Presence of Circuit Parasitics. Proc. I E E E Int. Conf. on Neural Networks
je, San Diego, Californie, 27-36.
. 1988b. Circuit Design Criteria for Stability in a Class of Lateral Inhibi-
tion Neural Networks. Proc. I E E E Conf. on Decision and Control, Austin, TX,
328-333.
Vidyasagar, M.. 1978. Nonlinear Systems Analysis. Englewood Cliffs, New Jersey: Prentice-
Hall.
Wyatt, J.L., Jr.. and D.L. Standley. 1988. A Method for the Design of Stable Lat-
eral Inhibition Networks that is Robust in the Presence of Circuit Parasitics.
Dans: Neural Information Processing Systems, éd. D. Anderson, American In-
stitute of Physics, New York, 860-867.
Reçu 30 Septembre; accepted 13 Octobre 1988.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
/
e
d
u
n
e
c
o
un
r
t
je
c
e
–
p
d
/
je
F
/
/
/
/
/
1
1
5
8
8
1
1
8
2
1
n
e
c
o
1
9
8
9
1
1
5
8
p
d
.
.
.
.
.
F
b
oui
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3