Best-First Beam Search
Clara Meister(cid:2) Tim Vieira(cid:2) Ryan Cotterell∗, (cid:2)
(cid:2)ETH Z¨urich (cid:2)Johns Hopkins University ∗University of Cambridge
clara.meister@inf.ethz.ch tim.vieira@gmail.com
ryan.cotterell@inf.ethz.ch
Abstrait
Decoding for many NLP tasks requires an ef-
fective heuristic algorithm for approximating
exact search because the problem of searching
the full output space is often intractable, ou
impractical in many settings. The default algo-
rithm for this job is beam search—a pruned
version of breadth-first search. Quite surpris-
franchement, beam search often returns better results
than exact inference due to beneficial search
bias for NLP tasks. In this work, we show that
the standard implementation of beam search
can be made up to 10x faster in practice. Notre
method assumes that the scoring function is
monotonic in the sequence length, lequel
allows us to safely prune hypotheses that can-
not be in the final set of hypotheses early on.
We devise effective monotonic approxima-
tions to popular nonmonontic scoring functions,
including length normalization and mutual
information decoding. Dernièrement, we propose a
memory-reduced variant of best-first beam search,
which has a similar beneficial search bias in
terms of downstream performance, but runs in
a fraction of the time.
1
Introduction
Beam search is a common heuristic algorithm for
decoding structured predictors (par exemple., neural ma-
chine translation models and transition-based
parsers). Because of the widespread adoption of
recurrent neural networks and other non-Markov
models, traditional dynamic programming solu-
tion, such as the Viterbi algorithm (Viterbi,
1967), are prohibitively inefficient; this makes
beam search a common component of many state-
of-the-art NLP systems. Despite offering no
formal guarantee of finding the highest-scoring
hypothesis under the model, beam search yields
impressive performance on a variety of tasks—
795
unexpectedly providing a beneficial search bias
over exact search for many tasks (Stahlberg and
Byrne, 2019).
Within NLP, most research on beam search has
focused on altering the log-probability scoring
function to return improved results, Par exemple,
higher BLEU scores (Wu et al., 2016; Murray and
Chiang, 2018; Shu and Nakayama, 2018; Lequel
et coll., 2018) or a more diverse set of outputs
(Vijayakumar et al., 2016). Cependant, little work
has been done to speed up beam search itself.
Filling this gap, this paper focuses on reform-
ulating beam search in order to make it faster.
We propose best-first beam search, a priori-
tized version of traditional beam search that is up
to an order of magnitude faster in practice while
still returning the same set of results. We add-
itionally discuss an even faster heuristic version
of our algorithm that further limits the number of
candidate solutions, leading to a smaller memory
footprint while still finding good solutions.
Concretely, we offer a novel interpretation of
beam search as an agenda-based algorithm where
traditional beam search is recovered by utilizing
a length-based prioritization scheme. We prove
that a specific best-first prioritization scheme, comme
in classic A∗ search (Hart et al., 1968), allows
for the elimination of paths that will necessarily
fall off the beam; for many scoring functions,
including standard log-probability scoring, we can
still guarantee the same k hypotheses as traditional
beam search are returned. En effet, our algorithm
returns beam search’s top hypothesis the first time
it encounters a complete hypothesis, allowing the
program to stop early. Plus loin, we discuss the ap-
plication of best-first beam search to several
popular scoring functions in the literature (He et
al., 2016; Li et al., 2016); this demonstrates that we
have a general framework for adapting a variety
of rescoring methods and alternate objectives to
work with our algorithm.
Transactions of the Association for Computational Linguistics, vol. 8, pp. 795–809, 2020. https://doi.org/10.1162/tacl a 00346
Action Editor: Kristina Toutanova. Submission batch: 2/2020; Revision batch: 6/2020; Published 12/2020.
c(cid:3) 2020 Association for Computational Linguistics. Distributed under a CC-BY 4.0 Licence.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Empirically, we compare best-first beam search
to ordinary beam search on two NLP sequence-to-
sequence tasks: neural machine translation (NMT)
and abstractive summarization (AS). On NMT,
we find that our algorithm achieves roughly a
30% speed-up over traditional beam search with
increased gains for larger beams (par exemple., ≈ 10x
for a beam of 500). We find similar results
hold for AS. Enfin, we show that our memory-
reduced version, which limits the number of active
hypotheses, leads to additional speed-ups over
best-first beam search across beam sizes while
maintaining similar BLEU scores.
2 Sequence Transduction
A core operation in structured prediction models
is the determination of the highest-scoring output
for a given input under a learned scoring model.
oui(cid:2) def= arg max
y∈Y(X)
score(X, oui)
(1)
where x is an input and Y(X) is a set of well-
formed outputs for the input. An important ex-
ample of (1) is maximum a posteriori (MAP),
words, every valid sequence begins and ends with
distinguished tokens (BOS and EOS, respectivement).1
En outre, each sequence has at most length
nmax(X)—which is typically dependent on x—a
restriction we impose to ensure termination. Some
applications may require a stronger coupling
between Y(X) and x (par exemple., |X| = |oui|). We drop the
dependence of Y and nmax on x when it is clear
from context.
Scoring. We consider a general additively de-
composable scoring model of the form
score(X, oui) =
Ny(cid:2)
t=1
score(X, oui
6:
7:
8:
9:
10:
11:
12:
13:
14:
continue
POPS[|oui|] ← POPS[|oui|] + 1
if y.last() = EOS :
Q.push((cid:6)sh, y◦ EOS(cid:7))
else:
for y ∈ V :
s ← score(X, y ◦ y)
sh ← s+ h(X, y ◦ y)
Q.push((cid:6)sh, y ◦ y(cid:7))
15:
16: return Q.pop() if not Q.empty() else null
3.1 Choice Points of 2
Here we review the components of our meta
algorithme (the highlighted sections in Alg. 2) que
can be varied to recover different search strategies:
1 (cid:2) : y × y → {True, False}. A priority queue
Q maintains the set of active hypotheses.
Elements in this set are ordered according to
a generic comparator (cid:2). When its peek() (ou
pop()) methods are called, the first element
ordered by (cid:2) is returned (or returned and
removed).
2 stop(·) : Collection(cid:6)oui(cid:7) → {True, False}.
The algorithm terminates according to
configurable stopping criterion based on the
current set of elements in Q.
5If the last token of y(cid:12) is the end symbol (par exemple., EOS), then y(cid:12)
is not expanded any further. One can either regard y(cid:12) as any
other hypothesis albeit with y(cid:12) ◦ yt = y(cid:12) or keep appending
EOS (c'est à dire., oui(cid:12) ◦ yt = y(cid:12) ◦ EOS ) so that time step and length can
be regarded as synonymous. We adopt the latter standard for
comparability with subsequent algorithms.
797
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Beam Search
h, oui(cid:12)(cid:7) ⇐⇒ |oui| < |y|(cid:12)
(cid:6)sh, y(cid:7) (cid:2) (cid:6)s(cid:12)
h)
or (|y| = |y|(cid:12) and sh ≥ s(cid:12)
stop(Q) ⇐⇒
y.last() = EOS ∀y ∈ Q
k = beam size
0
(cid:6)sh, y(cid:7) (cid:2) (cid:6)s(cid:12)
h, y(cid:12)(cid:7) ⇐⇒ |y| < |y|(cid:12)
h)
or (|y| = |y|(cid:12) and sh ≥ s(cid:12)
stop(Q) ⇐⇒
y.last() = EOS ∀y ∈ Q
k = ∞
0
1
2
3
4
1
2
3
4
Best-First Beam Search
A∗ Beam Search
(cid:6)sh, y(cid:7) (cid:2) (cid:6)s(cid:12)
or (sh = s(cid:12)
h, y(cid:12)(cid:7) ⇐⇒ sh > s(cid:12)
h and |oui| < |y|(cid:12))
h
(cid:6)sh, y(cid:7) (cid:2) (cid:6)s(cid:12)
or (sh = s(cid:12)
h, y(cid:12)(cid:7) ⇐⇒ sh > s(cid:12)
h and |oui| < |y|(cid:12))
h
stop(Q) ⇐⇒
Q.peek().last() = EOS
k = beam size
0
stop(Q) ⇐⇒
Q.peek().last() = EOS
k = beam size
any admissible heuristic
A∗ Search
h, y(cid:12)(cid:7) ⇐⇒ sh > s(cid:12)
h and |oui| < |y|(cid:12))
h
(cid:6)sh, y(cid:7) (cid:2) (cid:6)s(cid:12)
or (sh = s(cid:12)
(cid:6)sh, y(cid:7) (cid:2) (cid:6)s(cid:12)
or (sh = s(cid:12)
h, y(cid:12)(cid:7) ⇐⇒ sh > s(cid:12)
h and |oui| < |y|(cid:12))
h
stop(Q) ⇐⇒
Q.peek().last() = EOS
k = ∞
0
stop(Q) ⇐⇒
Q.peek().last() = EOS
k = ∞
any admissible heuristic
Breadth-First Search
Best-First Search
Table 1: Values at choice points for various search algorithms. Note that any admissible heuristic may
be used for variants of A∗ search.
3 k ∈ N>0. Only k paths of a given length
are considered. If the algorithm has already
encountered k paths of a given length,
subsequent paths of that
length are not
evaluated. If we take k = ∞, we recover
unpruned search algorithms.
4 h(·, ·) : x × y → R. A heuristic function
h(X, oui) can be used during search to change
the priority in which paths are evaluated.
We note that with pruning, a heuristic may
change the value of the k-optimal hypothesis
(see § 4.1).
Recovering Beam Search. To recover beam
search from Algorithm 2, we use the choice
points from Table 1. Explicitly, the comparator
prioritizes hypotheses from earlier time steps
d'abord, but breaks ties with the hypotheses’ scores
under the model. We note that while the standard
algorithm for beam search does not prioritize by
score within a time step, variations of the algorithm
use this strategy so they can use early-stopping
strategies (Klein et al., 2017; Huang et al., 2017).
Beam search terminates once either all hypotheses
end in EOS or the queue is empty (c'est à dire., when the
k beams have been extended nmax time steps but
none end in EOS). In the second case, no complete
hypothesis is found. Enfin, choosing the heuris-
tic h(X, oui) = 0 makes the algorithm a case of
standard best-first search.
Note that, while standard beam search returns a
ensemble, Alg 2 only returns the k-optimal hypothesis.
This behavior is sufficient for the majority of
use cases for beam search. Cependant, if the full
set of k hypotheses is desired, the stopping crite-
rion can be changed to evaluate true only when
k hypotheses are complete. Under the other beam
search settings, this would probably return the
same set as beam search (see § 4.1).
Recovering A∗. To recover the traditional A∗
search algorithm, we use the comparator that
prioritizes hypotheses with a higher score first; liens
are broken by hypothesis length. The algorithm
terminates when the first item of Q contains an
EOS. If we take k = ∞, best-first beam search
recovers A∗. Any admissible heuristic may be
used for h(X, oui).
Definition 3.1. Admissible Heuristic. A heuristic
h is admissible if it never overestimates the future
cost—or underestimates the future reward—of
continuing down a path.
3.2 Best-First Beam Search
In its original form, A∗ search may traverse the
entire O(|V|nmax) graph, which as discussed ear-
lier, is intractable for many decoding problems.
While standard beam search addresses this prob-
lem by limiting the search space,
it still has
computational inefficiencies—namely, we must
analyze k hypotheses of a given length (c'est à dire., temps
step), regardless of how poor their scores may
already be, before considering longer hypotheses.
798
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Cependant, prioritization by length is not strictly
necessary for finding a k-optimal hypothesis. Comme
is done in A∗, we can use score as the prioritiza-
tion scheme and still guarantee optimality–or k-
optimality–of the paths returned by the algorithm.
We define A∗ beam search as the A∗ algorithm
where breadth is limited to size k. Plus loin, nous
define best-first beam search as the case of A∗
beam search when no heuristic is used (see Table 1
for algorithm settings). This formulation has two
large advantages over standard beam search: (1)
we gain the ability to remove paths from the
queue that are guaranteed to fall off the beam
et (2) we can terminate the algorithm the first
time a complete hypothesis is encountered. Nous
can therefore reduce the computation required for
decoding while still returning the same set of
résultats.
The mathematical property that makes this
short-circuiting of computation possible is the
monotonicity of the scoring function. Note that
not all scoring functions are monotonic, but many
important ones are, including log-probability (5).
We discuss effective approximations for popular
non-monotonic scoring functions in § 5.
Definition 3.2. Monotonicity. A scoring function
score(·, ·) is monotonic in t if for all x, oui
Lemma 4.2. The first hypothesis that best-first
beam search pops that ends in EOS is k-optimal.
Proof. Let y be the first hypothesis popped by
best-first beam search ending in EOS. By rules of
the priority queue, no other active hypothesis has a
higher score than y. En plus, by monotonicity
of the scoring function, no other hypothesis can
subsequently have score greater than y. Donc
y must be k-optimal.
Lemma 4.3. If best-first beam search pops a
hypothèse, then beam search necessarily pops
that same hypothesis.
Proof. We prove the lemma by induction on
hypothesis length. The base case holds trivially:
For hypotheses of length 0, both best-first beam
search and beam search must pop the (cid:6)BOS(cid:7) as it is
the only item in the queue after initialization.
By the inductive hypothesis, suppose Lemma 4.3
holds for hypotheses of length < t. Suppose best-
first beam search pops a hypothesis y = y
∀i ∈ 1, . . . , k. This implies that for beam search,
y≤t+j would not be in the top-k paths at
time step t + j since by Lemma 4.3, paths
{oui(1)
} would also be evaluated by
beam search. Therefore y cannot be in H
BS, lequel
is a contradiction.
≤t+j, . . . , oui(k)
≤t+j
Case 2: For no time step t + j (j ≥ 0) do we
pop k paths. This can only happen if the algorithm
stops early, namely, we have found k complete
hypotheses y(1), . . . , oui(k). If this is the case, alors
by rules of the priority queue, each y(1), . . . , oui(k)
must have score greater than score(X, oui
BS,
which is a contradiction.
Non-monotonic
Scoring Functions. Non-
monotonic scoring functions (Definition 3.2)
break the assumptions of § 4.1, in which case
best-first beam search is not guaranteed to return a
k-optimal hypothesis. Cependant, when the scoring
801
function is boundable from above, we can alter
the original stopping criterion ( 2 in Alg. 2) tel
that k-optimality is again guaranteed.
Given our assumed restriction on the search
space—namely, |oui(cid:2) ∈ Y(X)| ≤ nmax(X)—we can
upper-bound the maximal score of any hypothesis
under the scoring function in use. Officiellement, pour
any function score we have:
stop(Q) ⇐⇒
score(X, ˆy) ≥ score(X, oui(cid:12)) + U(X, oui(cid:12))
∀y(cid:12) ∈ Q
(6)
where ˆy is the best complete hypothesis found
so far and U(X, oui(cid:12)) is the score function-
dependent upper bound on how much the score
of y(cid:12) can increase as y(cid:12) is expanded further.7
In this situation, best-first beam search only
terminates once no other hypothesis in Q can
have a score greater
finished
hypothèse. We note that Huang et al. (2017) use a
similar scheme for optimal stopping with bounded
length normalization. We discuss examples of
non-monotonic scoring functions in § 5.
than the best
A Note on Heuristics. Our analysis shows the
equivalence of beam search and best-first beam
recherche, c'est, when h(X, oui) = 0. The analysis
does not hold for arbitrary admissible heuristics. UN
poor heuristic (par exemple., one that grossly overestimates
the future score of continuing down one path)
may cause other items to be pruned from best-first
beam search that otherwise would have remained
on the beam in standard beam search.
4.2 Runtime
Theorem 4.6. The runtime of best-first beam
search is O(nmaxk (|V| log(k) + log(nmax)))
Proof. We pop at most nmax · k items. Chaque
pop requires us to push |V| items. Each push
requires log(k) time when the priority queue is
implemented with a min–max heap (Atkinson
et coll., 1986) and incrementally pruned so that it
has no more than k items. After pushing those
|V| items, we have to perform a percolation in the
priority queue of priority queues, which requires
log(nmax) temps. This yields O(nmaxk (|V| log(k)+
log(nmax))) temps.
Theorem 4.7. The runtime of standard beam
search is O(nmax k |V| log(k)).
7For monotonic scoring functions, we have U (X, oui(cid:12)) = 0.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Proof. The proof is the same as Theorem 4.6,
but we can forgo the percolation step in the
queue of queues because standard beam search
proceeds in order of hypothesis length. This yields
Ô(nmaxk|V| log(k)).
Although the theoretical bound of best-first
beam search has an additional log factor compared
with standard beam search, we find this to be neg-
ligible in practice. Plutôt, we find number of calls
to score, the scoring function under our model
(par exemple., a neural network), is often the bottleneck
operation when decoding neural networks (see § 6
for empirical evidence). In terms of this metric,
the beam search algorithm makes O(knmax) calls
to score, as score is called once for each active
hypothesis in B and B may evolve for nmax rounds.
The worst-case number of calls to score will be
the same as for beam search, which follows from
Lemma 4.3.
5 Scoring Functions
Even before the findings of Stahlberg and Byrne
(2019), it was well known that the best-scoring
hypothesis with respect to the traditional likeli-
hood objective can be far from ideal in practice
(Wu et al., 2016; Murray and Chiang, 2018;
Yang et al., 2018). For language generation tasks
specifically, the results returned by neural models
using the standard scoring function are often short
and default to high-frequency words (Vinyals and
Le, 2015; Shen et al., 2016).
To alleviate such problems, methods that revise
hypothesis scores to incorporate preferences for
longer, less repetitive, or more diverse options
have been introduced and are often used in prac-
tice. While most such techniques change the
scoring function such that it is no longer mono-
tonic, we can still guarantee the k-optimality
of the returned hypothesis for (upper) bounded
scoring functions using the methods discussed
in § 4.1. In the remainder of this section, nous
present alternate scoring schemes adapted to work
with best-first beam search. En plus, nous
present several heuristics which, while breaking
the k-optimality guarantee, provide another set of
decoding strategies worth exploring.
Length Normalization. Length normalization
is a widely used hypothesis scoring method that
aims to counteract the propensity for shorter se-
quences to have higher scores under neural mod-
le;
this is done by normalizing scores by
hypothesis length (see Murray and Chiang [2018]
for more detail).
For early stopping in beam search with length
normalization, Huang et al. (2017) propose bound-
ing the additive length reward as the minimum of
a pre-determined optimal sequence length ratio r
and the final sequence length Ny:
scoreLN(X, oui) = score(X, oui)
+ β · min{r|X|, Ny}
(7)
where β is the scaling parameter for the reward.
We note, cependant, that the same can be done with
the maximum sequence length nmax such that the
traditional length reward used by He et al. (2016)
is recovered:
scoreLN(X, oui) = score(X, oui) + β min{nmax, Ny}
= score(X, oui) + βNy
(8)
We formally propose two methods for length
normalization. We use the scoring functions in (7)
ou (8) with either: (1) the following heuristic:
(cid:3)
h(X, oui) =
for y.last () = EOS
0
β max{b − |oui|, 0} for y.last () (cid:18)= EOS
(9)
where b can be r|X| or nmax;8 ou (2) stopping
criterion as in (6) albeit with scoring function
scoreLN and upper-bound function:
U(X, oui) = β max{0, b − |oui|}
(10)
Despite their similarities, these two methods are
not guaranteed to return the same results. Whereas
the second method will return the same k-optimal
hypotheses as beam search, using a heuristic
during pruned search means we can no longer
guarantee the k-optimality of the results with
respect to the scoring function as the heuristic
may push hypotheses off of the beam. We present
experimental results for both methods in § 6.
Mutual Information. Maximum mutual infor-
mation decoding (Li et al., 2016) aims to alleviate
the inherent preference of neural models for high-
frequency tokens when using the log-probability
8We enforce r|X| < nmax.
802
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
l
a
c
_
a
_
0
0
3
4
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
decoding objective. Rather than choosing the
hypothesis y to maximize conditional probability
with respect to the input x, we instead choose y to
maximize pointwise mutual information (PMI):
PMI(x; y) = log
p(x, y)
p(x)p(y)
(11)
Note that (11) is equivalent to log p(y|x)
p(y) , which can
be rewritten as log p(y | x) − log p(y), making
the objective additive and thus (11) can conform
to (4).
From this last form, we can see how mutual
information decoding penalizes high-frequency
and generic outputs; the negative p(y) term, as Li
et al. (2016) point out, acts as an ‘‘anti-language
model.’’ One unfortunate side effect of this
objective is that ungrammatical and nonsensical
outputs, which have probabilities close to 0 under a
language model like p(y), end up with high scores
because of the second term in the score function.
To address this problem, and to upper-bound
the scoring function, we propose lower-bounding
the language model term by a hyperparameter
1 ≥ ε > 0. We additionally use the strength
hyperparameter λ employed by Li et al. (2016):
scorePMI(X, oui) = log p(oui | X)
− λ log max{p(oui), ε} (12)
Similarly to our methods for length normali-
zation, we can use the scoring function in (12)
either with the heuristic:
(cid:3)
h(X, oui) =
0
−λ log ε(nmax−|oui|)
for y.last () = EOS
for y.last () (cid:18)= EOS
(13)
or with stopping criterion as in (6) albeit with
scorePMI and upper-bound function:
U(X, oui) = −λ log ε(nmax − |oui|)
(14)
Because −λ log ε is the best possible score at any
given time step, clearly we can bound the increase
in scorePMI by the above function. Cependant, as with
our length normalization strategy, we lose the k-
optimality guarantee with the heuristic method
for mutual
information decoding. We present
experimental results for both methods in § 6.
6 Experiments
We run our algorithm on several language-related
tasks that typically use beam search for decoding:
NMT and AS. Spécifiquement, experiments are per-
formed on IWSLT’14 De-En (Cettolo et al., 2012),
WMT’17 De-En (Bojar et al., 2017), MTTT Fr-En
(Duh, 2018), and CNN-DailyMail (Hermann et coll.,
2015) using both Transformers (Vaswani et al.,
2017) and Convolutional sequence-to-sequence
models (Gehring et al., 2017).
For reproducibility, we use the data pre-processing
scripts provided by fairseq (Ott et al., 2019) et
follow their methods for training sequence trans-
duction models. Hyperparameters are set in accor-
dance with previous works. Spécifiquement, sur
IWSLT’14 and MTTT tasks, we follow the rec-
ommended Transformer settings for IWSLT’14 in
fairseq,9 which are based on Vaswani et al. (2017)
and Gehring et al. (2017). Hyperparameters for
models trained on the WMT task are set following
version 3 of the Tensor2Tensor toolkit (Vaswani
et coll., 2018). We use byte-pair encoding (BPE;
Sennrich et al. 2016) for all languages. Vocabulary
sizes for WMT and IWSLT’14 are set from rec-
ommendations for the respective tasks in fairseq;
for the MTTT tasks, vocabulary sizes are tuned
on models trained with standard label-smoothing
regularization. De la même manière,
the CNN/DailyMail
dataset is pre-processed and uses BPE following
the same steps as (Lewis et al., 2019); model
hyperparameters are likewise copied. Details are
available on fairseq’s Web site.10
We use BLEU (Papineni et al., 2002) (evaluated
using SacreBLEU [Post, 2018]) for MT metrics
and ROUGE-L (Lin, 2004) for abstractive summar-
ization metrics. We build our decoding framework
in SGNMT.11
6.1 Running Time
In Table 2, we report values as the average number
of calls to the scoring function per input; nous
do not use wall-clock time as this is heavily
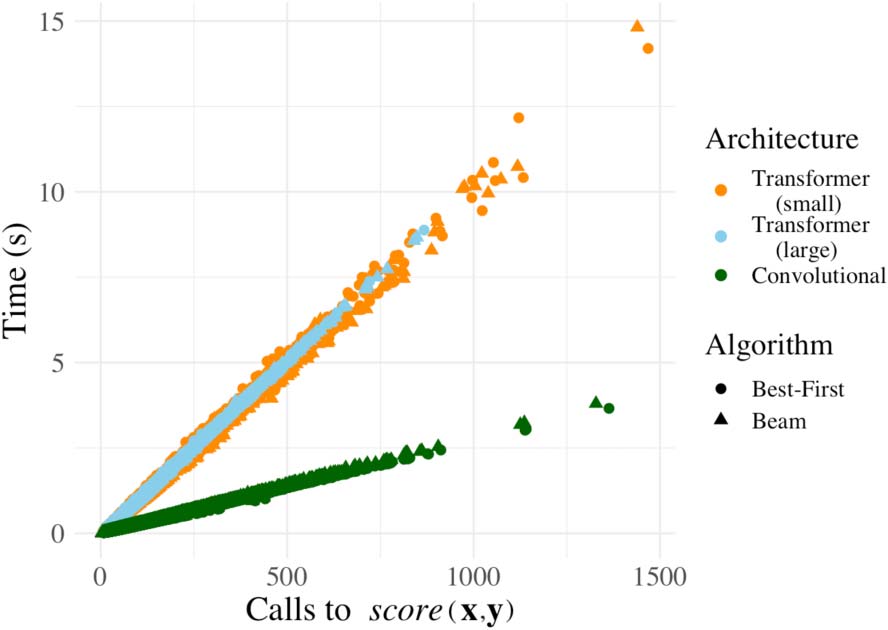
dependent on hardware. See Fig. 1 for empirical
justification of the correlation between calls to the
scoring function and runtime on the hardware our
9https://github.com/pytorch/fairseq/tree
/master/examples/translation.
10https://github.com/pytorch/fairseq/blob
/master/examples/bart/README.cnn.md.
11https://github.com/ucam-smt/sgnmt.
803
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
IWSLT’14 De-En
k = 5
(35.6)
k = 10
(35.4)
k = 100
(34.7)
k = 500
(7.9)
k = 10
(33.0)
MTTT Fr-En
k = 100
(9.9)
k = 500
(1.2)
CNN-DailyMail
k = 5
(31.5)
k = 10
(30.9)
k = 100
(29.1)
BF beam search
885 (836%) 200 (33%) 305 (43%) 2960 (92%)
Beam search (ES) 107 (7%) 210 (9%) 2047 (12%) 7685 (27%) 196 (9%) 1310 (58%) 4182 (98%) 224 (19%) 357 (22%) 3942 (59%)
Beam search
93 (24%) 169 (36%) 1275 (79%) 1168 (736%) 184 (16%)
867 (138%)
2286
2066
9770
5673
8281
115
229
266
214
435
Tableau 2: Average number of calls (rounded to nearest whole digit) to score, the sequence transduction
model, per generated sequence when using different decoding algorithms. Green percentages are
performance improvements over standard beam search. Beam search (ES) refers to the OpenNMT
early-stopping method (Klein et al., 2017). All methods provably return the same solution and thus,
evaluation metrics (in dark blue) for a given beam size are identical.
IWSLT’14 De-En
k
method
search error
BLEU
# calls
10
100
10
100
shrinking
early
BF BS
shrinking
early
BF BS
shrinking
early
BF BS
shrinking
early
BF BS
0%
0%
−
31.7%
31.7%
−
35.4
35.4
35.4
13.2
13.2
34.7
WMT’17 De-En
0%
0%
−
1.7%
1.7%
−
28.6
28.6
28.6
26.4
26.4
26.9
229 (0%)
225 (2%)
169 (36%)
2278 (0%)
1738 (31%)
1275 (79%)
260 (0%)
252 (3%)
230 (12%)
2587 (0%)
2402 (8%)
2046 (26%)
Tableau 3: BLEU, search error, and average number
of calls to score for different stopping criterion.
‘‘shrinking’’ refers to the shrinking beam method
of Bahdanau et al. (2015) and ‘‘early’’ refers
to the stopping criterion of Huang et al. (2017).
Note that neither method is guaranteed to return
the same result as standard beam search. Recherche
error and performance increases are with respect
to standard beam search.
in Table 4. We find that both methods,
que
est, changing the stopping criterion and using a
heuristic during search, provide improvements
over baseline BLEU scores albeit with different
hyperparameter settings; increases are similar to
improvements reported by Murray and Chiang
(2018). Notably, using a heuristic causes a large
percentage of search errors with respect to stand-
ard beam search using the same scoring function.
Cependant, the difference in results appears to be
beneficial in terms of BLEU.
Chiffre 1: Number of calls to scoring function score
vs. total sequence generation time. Each point is a
decoded sequence. Colors represent different model
architectures and shapes signify the decoding algorithm
used (beam sizes 3 et 10 are included for each). Là
is no notable difference in the overhead (time-wise) de
best-first beam search and beam search.
experiments were run on. For reference, in our
experiments, the scoring function took on average
> 99% of the total computation time, even with
larger beam sizes, when overhead of the search
algorithm is most significant.
We find that best-first (BF) beam search leads to
significant speed-ups over both traditional beam
search and beam search with early stopping, with a
performance increase12 of ≈ 8x for a beam size of
500. We likewise find that best-first beam search
offers speed-ups over early stopping methods that
are not guaranteed to return the same results as
standard beam search (see Table 3).
6.2 Length Normalization
We experiment with both forms of
length
normalization presented in § 5 and provide results
12Performance increase is defined as (old − new)/new.
804
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
IWSLT’14 De-En
β
# calls
b
k
search BLEU
error
Heuristic
Stopping Criterion
5 0.8 |X|
115 (0%)
10 1.2 |X|
229 (0%)
73 (58%) −
5 0.5 nmax
10 0.5 nmax 130 (76%) −
40.6% 33.9 +0.3
54.7% 33.8 +0.5
33.7 +0.1
33.7 +0.4
Baseline
Heuristic
Stopping Criterion
k
ε
β
# calls
search BLEU
error
−
−
5 −
33.2
.05 115
10 −
.05 229
33.0
.05 129 (0%) 42.7% 33.2
5 .02
.05 256 (0%) 42.7% 33.0
10 .02
5 3e–4 .05 114 (1%) 29.2% 33.2
10 5e–5 .05 224 (2%) 26.6% 33.0
Heuristic
Stopping Criterion
MTTT Fr-En
5 0.8 .7|X| 100 (8%)
10 1.0 .7|X| 196 (9%)
5 1.0 nmax
10 1.2 nmax
65 (66%) −
88 (143%) −
16.2% 33.5 +0.2
25.2% 33.6 +0.6
34.1 +0.8
34.1 +1.1
Tableau 4: BLEU search error, and average number
of calls to score for output obtained with length
normalization scoring function on the IWSLT’14
De-En and MTTT Fr-En test sets. Increase in BLEU
is over baseline with no length normalization.
Search error and performance increases are with
respect to standard beam search decoding using
the same scoring function.
6.3 Mutual Information
We train a language model on the IWSLT dataset
and use it to calculate p(oui) depuis (12) as margin-
alizing over y is intractable (see Li et al. [2016] pour
further justification). We run experiments using
both of the methods discussed in § 5 and present
results in Table 5. We find that both methods
provide results of equivalent BLEU score compared
with the baseline output, namely, results obtained
with the unbounded PMI objective and beam
recherche. Encore, despite the high search error rate
demonstrated by the heuristic method, evaluation
metrics are still comparable.
6.4 Memory Usage
We conduct a set of experiments where we limit
total queue capacity to k·γ for γ ∈ {1, . . . , nmax},
as described in § 3.3, and report the BLEU score of
the resulting set of hypotheses.
As shown in Table 6, we find that restricting
the queue capacity does not harm output quality
et, additionally, leads to even greater runtime
performance increase. Par exemple, runtime for
decoding of IWSLT’14 with a beam size of
10 can be improved by > 3x while returning
results with better evaluation metrics. We find
that improvements are even more pronounced
for larger beam sizes. Across beam widths and
tasks, we find that search error (with respect to
standard beam search) is quite low for γ = 5.
En plus, for smaller γ, the change in BLEU
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Tableau 5: BLEU scores with mutual
information
scoring function on IWSLT’14 De-En. Baseline
is PMI decoding with unbounded p(oui), c'est,
ε = 0. Search error is with respect to beam search
decoding of baseline with same β.
k
5
10
5
10
c
2
5
nmax
2
5
nmax
2
5
nmax
2
5
nmax
IWSLT’14 De-En
recherche
BLEU
error
# calls
22.7% 35.7 +0.1
4.4% 35.8 +0.2
−
35.6
43.8 (163%)
79.8 (44%)
93.0 (24%)
22.6% 35.7 +0.3
4.5% 35.6 +0.2
−
35.4
48.4 (374%)
126.9 (81%)
169.0 (36%)
WMT’17 De-En
29.0% 29.7 +0.2
1.2% 29.5 +0.0
−
29.5
77.5 (75%)
115.8 (12%)
118.8 (10%)
36.6% 29.5 +0.2
2.6% 29.3 +0.0
−
29.3
97.3 (165%)
230.0 (12%)
230.2 (12%)
Tableau 6: BLEU scores and the number of calls
to score on the IWSLT’14 De-En validation
set and WMT’17 De-En test set with queue
size restricted to nmax · k. Note that γ = nmax is
the standard best-first beam search algorithm.
Performance increases are over standard beam
recherche. Search error is with respect to beam
search with same beam width.
score demonstrates that search error in this context
does not necessarily hurt the quality of results.
7 Related Work
Our work is most similar to that of Zhou and
Hansen (2005), who propose beam stack search.
Cependant, they are focused on exact inference and
still evaluate hypotheses in breadth-first order.
805
En plus, their algorithm requires O(nmaxk)
mémoire; although best-first beam search has
the same requirements, we introduce effective
methods for reducing them, namely, mémoire-
reduced best-first beam search.
Huang et al. (2017) propose and prove the
optimality of an early-stopping criterion for beam
recherche. The authors find in practice though that
reduction in computation from their algorithm was
generally not significant. We build on this work
and introduce additional methods for avoiding
unnecessary computation. Our method leads to
better performance, as shown in Table 2.
Klein and Manning (2003) use A∗ for PCFG
parsing; cependant, they use the un-pruned version
for exact search, which is not applicable for
NMT or AS as the memory requirements of
the algorithm are far too large for these tasks.
Subsequently, Pauls and Klein (2009) provide a
method for pruning this search algorithm, albeit
using a threshold rather than explicitly limiting
the state space. Huang et al. (2012) also adapt A∗
for a k-best decoding algorithm. Although their
methods differ notably from ours, they likewise
use pruning techniques that allow for substantial
speedups.
Stahlberg and Byrne (2019) create an exact
inference algorithm for decoding and use it
to analyze the output of neural NMT models.
Whereas they likewise utilize the monotonicity
of the scoring function to make their method
tractable, they do not focus on speed or mimicking
the results of standard beam search.
8 Conclusion
pour
We propose best-first beam search, an algorithm
faster decoding while still
that allows
guaranteeing k-optimality. We provide results on
several sequence-to-sequence transduction tasks
that show the speed-ups that our algorithm
provides over standard beam search for decoding
neural models. We adapt several popular alternate
scoring functions to best-first beam search and
provide a framework that can be used to
adapt other scoring methods such as coverage
normalization (Wu et al., 2016) or diverse beam
recherche (Vijayakumar et al., 2016). We also provide
a memory-reduced version of our algorithm,
which returns competitive results in a fraction
of the time needed for standard beam search.
Les références
M.. D. Atkinson, J.. R.. Sack, N. Santoro, and T.
Strothotte, 1986. Min-max heaps and general-
ized priority queues. Communications of ACM:
29(10). EST CE QUE JE: https://doi.org/10.1145
/6617.6621
Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua
Bengio. 2015. Neural machine translation by
jointly learning to align and translate.
Dans
Proceedings of the International Conference
on Learning Representations.
Ondˇrej Bojar, Rajen Chatterjee, Christian
Federmann, Yvette Graham, Barry Haddow,
Shujian Huang, Matthias Huck, Philipp Koehn,
Qun Liu, Varvara Logacheva, Christof Monz,
Matteo Negri, Matt Post, Raphael Rubino,
Lucia Specia, and Marco Turchi. 2017.
Findings of the 2017 conference on machine
translation. In Proceedings of the Conference
on Machine Translation, Volume 2: Shared
Task Papers, Copenhagen, Denmark. EST CE QUE JE:
https://doi.org/10.18653/v1/W17-4717
Mauro Cettolo, Christian Girardi, and Marcello
Federico. 2012. Wit3: Web inventory of
transcribed and translated talks. In Proceedings
of the Conference of the European Association
for Machine Translation.
Edsger W. Dijkstra. 1959. A note on two problems
in connexion with graphs. Numerische Mathe-
matik 1(1). EST CE QUE JE: https://doi.org/10.1007
/BF01386390
Kevin Duh. 2018. The multitarget TED talks task.
http://www.cs.jhu.edu/∼kevinduh
/a/multitarget-tedtalks/
Sergey Edunov, Myle Ott, Michael Auli, et
David Grangier. 2018. Understanding back-
translation at scale. In Proceedings of the 2018
Conference on Empirical Methods in Natural
Language Processing. Brussels, Belgium, Comme-
sociation for Computational Linguistics. EST CE QUE JE:
https://doi.org/10.18653/v1/D18
-1045
Jonas Gehring, Michael Auli, David Grangier, et
Yann Dauphin. 2017. A convolutional encoder
model for neural machine translation. En Pro-
ceedings of
the 55th Annual Meeting of
the Association for Computational Linguistics
806
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(Volume 1: Long Papers). Vancouver, Canada.
Association for Computational Linguistics.
EST CE QUE JE: https://doi.org/10.18653/v1
/P17-1012, PMID: 28964987, PMCID:
PMC6754825
Peter E. Hart, Nils J. Nilsson, and Bertram
Raphael. 1968. A formal basis for the heuristic
determination of minimum cost paths. IEEE
Transactions on Systems Science and Cyber-
netics, 4(2). EST CE QUE JE: https://est ce que je.org/10
.1109/TSSC.1968.300136
Wei He, Zhongjun He, Hua Wu, and Haifeng
Wang. 2016. Improved neural machine transla-
tion with SMT features. In Proceedings of the
AAAI Conference on Artificial Intelligence.
Karl Moritz Hermann, Tomas Kocisky, Edward
Grefenstette, Lasse Espeholt, Will Kay,
Mustafa Suleyman, and Phil Blunsom. 2015.
Teaching machines to read and comprehend,
Advances in Neural Information Processing
Systems.
Liang Huang, Kai Zhao, and Mingbo Ma. 2017.
When to finish? Optimal beam search for neural
text generation (modulo beam size). In Proceed-
le 2017 Conference on Empirical
ings of
Methods in Natural Language Processing,
Copenhagen, Denmark. Association for Com-
putational Linguistics. EST CE QUE JE: https://est ce que je
.org/10.18653/v1/D17-1227, PMID:
28564569
Zhiheng Huang, Yi Chang, Bo Long, Jean-
Francois Crespo, Anlei Dong, Sathiya Keerthi,
and Su-Lin Wu. 2012. Iterative Viterbi A*
algorithm for k-best sequential decoding. Dans
Proceedings of the 50th Annual Meeting of
the Association for Computational Linguistics
(Volume 1: Long Papers), Jeju Island, Korea.
Association for Computational Linguistics.
Dan Klein and Christopher D. Manning. 2003.
A* parsing: Fast exact Viterbi parse selection.
In Proceedings of the 2003 Human Language
Technology Conference of the North American
Chapter of the Association for Computatio-
nal Linguistics. EST CE QUE JE: https://doi.org
/10.3115/1073445.1073461
OpenNMT: Open-source toolkit
for neural
machine translation. In Proceedings of ACL
2017, System Demonstrations, Vancouver,
Canada. Association for Computational Lin-
guistics. EST CE QUE JE: https://doi.org/10.18653
/v1/P17-4012
Philipp Koehn and Rebecca Knowles. 2017. Six
challenges for neural machine translation. Dans
Proceedings of the First Workshop on Neural
Machine Translation, Vancouver. Association
for Computational Linguistics. EST CE QUE JE: https://
/10.18653/v1/W17-3204
John D. Lafferty, Andrew McCallum, et
Fernando C. N. Pereira. 2001. Conditional ran-
dom fields: Probabilistic models for segment-
ing and labeling sequence data. In Proceedings
of the International Conference on Machine
Apprentissage, ICML ’01, San Francisco, Californie, Etats-Unis.
Mike Lewis, Yinhan Liu, Naman Goyal, Marjan
Ghazvininejad, Abdelrahman Mohamed, Omer
Levy, Veselin Stoyanov, and Luke Zettlemoyer.
2019. BART: Denoising sequence-to-sequence
pre-training for natural language generation,
translation, and comprehension. In arXiv:1910.
13461. EST CE QUE JE: https://doi.org/10.18653
/v1/2020.acl-main.703
Jiwei Li, Michel Galley, Chris Brockett, Jianfeng
Gao, and Bill Dolan. 2016. A diversity-
promoting objective function for neural con-
versation models. In Proceedings of the 2016
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies, San Diego,
California. Association for Computational
Linguistics.
Chin-Yew Lin. 2004. ROUGE: A package for
automatic evaluation of summaries. In Text Sum-
marization Branches Out, Barcelona, Espagne.
Association for Computational Linguistics.
Andrew McCallum, Dayne Freitag, and Fernando
C. N. Pereira. 2000. Maximum entropy Markov
models for information extraction and segmen-
tation. In Proceedings of
the International
Conference on Machine Learning, ICML 00.
San Francisco, Californie, Etats-Unis.
Guillaume Klein, Yoon Kim, Yuntian Deng,
Jean Senellart, and Alexander Rush. 2017.
Kenton Murray and David Chiang. 2018. Correct-
ing length bias in neural machine translation.
807
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
In Proceedings of the Third Conference on
Machine Translation: Research Papers, Belgium,
Brussels. Association for Computational Lin-
guistics. EST CE QUE JE: https://doi.org/10.18653
/v1/W18-6322
Joakim Nivre, Igor M. Boguslavsky, and Leonid L.
Iomdin. 2008. Parsing the SynTagRus treebank
of Russian. In Proceedings of the 22nd Interna-
tional Conference on Computational Linguis-
tics (Coling 2008), Manchester, ROYAUME-UNI. Coling
2008 Organizing Committee. EST CE QUE JE: https://
doi.org/10.3115/1599081.1599162
Myle Ott, Sergey Edunov, Alexei Baevski, Angela
Fan, Sam Gross, Nathan Ng, David Grangier,
and Michael Auli. 2019. fairseq: A fast, exten-
sible toolkit for sequence modeling. En Pro-
ceedings of NAACL-HLT: Demonstrations.
EST CE QUE JE: https://doi.org/10.18653/v1
/N19-4009
Kishore Papineni, Salim Roukos, Todd Ward, et
Wei-Jing Zhu. 2002. BLEU: A method for
automatic evaluation of machine translation.
In Proceedings of the Annual Meeting on Asso-
ciation for Computational Linguistics. EST CE QUE JE:
https://doi.org/10.3115/1073083
.1073135
Adam Pauls and Dan Klein. 2009. Hierarchical
search for parsing. In Proceedings of Human
Language Technologies: Le 2009 Annual Con-
ference of the North American Chapter of the
Association for Computational Linguistics,
Boulder, Colorado. Association for Computa-
tional Linguistics. EST CE QUE JE: https://doi.org
/10.3115/1620754.1620835
Matt Post. 2018. A call for clarity in reporting
BLEU scores. In Proceedings of the Confer-
ence on Machine Translation: Research Pa-
pers. EST CE QUE JE: https://doi.org/10.18653
/v1/W18-6319
Rico Sennrich, Barry Haddow, and Alexandra
Birch.2016. Neural machine translation of rare
words with subword units. In Proceedings of
the Annual Meeting of the Association for Com-
putational Linguistics. EST CE QUE JE: https://est ce que je
.org/10.18653/v1/P16-1162
Iulian Serban, Tim Klinger, Gerald Tesauro,
Kartik Talamadupula, Bowen Zhou, Yoshua
Bengio, and Aaron Courville. 2017. Multireso-
lution recurrent neural networks: An application
to dialogue response generation.
Shiqi Shen, Yong Cheng, Zhongjun He, Wei
Il, Hua Wu, Maosong Sun, and Yang Liu.
2016. Minimum risk training for neural machine
translation. In Proceedings of the 54th Annual
Meeting of the Association for Computational
Linguistics (Volume 1: Long Papers), Berlin,
Allemagne. Association for Computational Lin-
guistics. EST CE QUE JE: https://doi.org/10.18v653
/v1/P16-1159, PMID: 27069146
Raphael Shu and Hideki Nakayama. 2018. Im-
proving beam search by removing monotonic
constraint for neural machine translation. Dans
Proceedings of the 56th Annual Meeting of
the Association for Computational Linguis-
tics (Volume 2: Short Papers), Melbourne,
for Computational
Australia. Association
Linguistics.
Felix Stahlberg and Bill Byrne. 2019. On NMT
search errors and model errors: Cat got your
tongue? In Proceedings of the Conference on
Empirical Methods in Natural Language Pro-
cessing and the 9th International Joint Con-
ference on Natural Language Processing
(EMNLP-IJCNLP). Hong Kong, Chine. EST CE QUE JE:
https://doi.org/10.18653/v1/D19
-1331
Ilya Sutskever, Oriol Vinyals, and Quoc V. Le.
2014, Sequence to sequence learning with neu-
ral networks. In Advances in Neural Inform-
ation Processing Systems.
Ben Taskar, Carlos Guestrin, and Daphne Koller.
2004. Max-margin markov networks. In Ad-
Information Processing
vances
Systems.
in Neural
Ashish Vaswani, Samy Bengio, Eugene Brevdo,
Francois Chollet, Aidan N. Gomez, Stephan
Gouws, Llion Jones, Łukasz Kaiser, Nal
Kalchbrenner, Niki Parmar, Ryan Sepassi,
Noam Shazeer, and Jakob Uszkoreit. 2018.
Tensor2tensor for neural machine translation.
CoRR.
Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N. Gomez,
Łukasz Kaiser, and Illia Polosukhin. 2017.
808
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Attention is all you need. In Advances in Neural
Information Processing Systems.
Tim Vieira, Ryan Cotterell, and Jason Eisner.
2016. Speed-accuracy tradeoffs in tagging with
variable-order CRFs and structured sparsity.
In Proceedings of the Conference on Empiri-
cal Methods in Natural Language Processing.
EST CE QUE JE: https://doi.org/10.18653/v1
/D16-1206
Ashwin K. Vijayakumar, Michael Cogswell,
Ramprasaath R. Selvaraju, Qing Sun, Stefan
Lee, David J. Crandall, and Dhruv Batra.
2016. Diverse beam search: Decoding diverse
solutions from neural sequence models. CoRR,
abs/1610.02424.
Oriol Vinyals and Quoc V. Le. 2015. A neural
conversational model. EST CE QUE JE: https://est ce que je
.org/10.1109/TIT.1967.1054010
Andrew Viterbi. 1967. Error bounds for convolu-
tional codes and an asymptotically optimum
decoding algorithm. IEEE Transactions on
Information Theory, 13(2).
kaiser, Stephan Gouws, Yoshikiyo Kato, Taku
Kudo, Hideto Kazawa, Keith Stevens, George
Kurian, Nishant Patil, Wei Wang, Cliff Young,
Jason Smith, Jason Riesa, Alex Rudnick,
Oriol Vinyals, Gregory S. Corrado, Macduff
Hughes, and Jeffrey Dean. 2016. Google’s
neural machine translation system: Bridging the
gap between human and machine translation.
Yilin Yang, Liang Huang, and Mingbo Ma.
2018. Breaking the beam search curse: UN
study of (re-)scoring methods and stopping
criteria for neural machine translation. En Pro-
ceedings of the 2018 Conference on Empiri-
cal Methods in Natural Language Processing,
Brussels, Belgium. Association for Computa-
tional Linguistics. EST CE QUE JE: https://doi.org
/10.18653/v1/D18-1342
Zhilin Yang, Zihang Dai, Yiming Yang, Jaime
Carbonell, Russ R. Salakhutdinov, and Quoc V.
Le. 2019. XLNet: Generalized autoregressive
pretraining for
Dans
Advances in Neural Information Processing
Systems.
language understanding.
Yonghui Wu, Mike Schuster, Zhifeng Chen,
Quoc V. Le, Mohammad Norouzi, Wolfgang
Macherey, Maxim Krikun, Yuan Cao, Qin
Gao, Klaus Macherey, Jeff Klingner, Apurva
Shah, Melvin Johnson, Xiaobing Liu, Lukasz
Rong Zhou and Eric A. Hansen. 2005. Beam-
stack search: Integrating backtracking with beam
recherche. In Proceedings of the International Con-
ference on International Conference on Auto-
mated Planning and Scheduling, ICAPS05.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
/
t
un
c
je
/
je
un
r
t
je
c
e
–
p
d
F
/
d
o
je
/
.
1
0
1
1
6
2
/
t
je
un
c
_
un
_
0
0
3
4
6
1
9
2
3
7
9
0
/
/
t
je
un
c
_
un
_
0
0
3
4
6
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
809