An Enhanced Hypercube-Based
Encoding for Evolving the
Placement, Density, et
Connectivity of Neurons
Sebastian Risi*,**
University of Central Florida
Kenneth O. Stanley**
University of Central Florida
Intelligence in nature is the product of living brains,
Abstrait
which are themselves the product of natural evolution. Although
researchers in the field of neuroevolution (NE) attempt to recapitulate
this process, artificial neural networks (ANNs) so far evolved
through NE algorithms do not match the distinctive capabilities of
biological brains. The recently introduced hypercube-based neuroevolution
of augmenting topologies (HyperNEAT) approach narrowed this gap by
demonstrating that the pattern of weights across the connectivity
of an ANN can be generated as a function of its geometry, thereby
allowing large ANNs to be evolved for high-dimensional problems.
Yet the positions and number of the neurons connected through
this approach must be decided a priori by the user and, unlike in
living brains, cannot change during evolution. Evolvable-substrate
HyperNEAT (ES-HyperNEAT), introduced in this article, addresses
this limitation by automatically deducing the node geometry from
implicit information in the pattern of weights encoded by HyperNEAT,
thereby avoiding the need to evolve explicit placement. Cette approche
not only can evolve the location of every neuron in the network,
but also can represent regions of varying density, which means
resolution can increase holistically over evolution. ES-HyperNEAT
is demonstrated through multi-task, maze navigation, and modular
retina domains, revealing that the ANNs generated by this new
approach assume natural properties such as neural topography and
geometric regularity. Also importantly, ES-HyperNEATʼs compact
indirect encoding can be seeded to begin with a bias toward a desired
class of ANN topographies, which facilitates the evolutionary search.
The main conclusion is that ES-HyperNEAT significantly expands
the scope of neural structures that evolution can discover.
Mots clés
Compositional pattern-producing
réseaux, indirect encoding, HyperNEAT,
neuroevolution, artificial neural networks,
generative and developmental systems
A version of this paper with color figures is
available online at http://dx.doi.org/10.1162/
artl_a_00071. Subscription required.
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1 Introduction
An ambitious long-term goal for neuroevolution—that is, evolving artificial neural networks (ANNs)
through evolutionary algorithms—is to evolve brainlike neurocontrollers with billions of neurons and
* Contact author.
** Department of Electrical Engineering and Computer Science, University of Central Florida, Orlando, FL 32816-2362. E-mail: sebastian.risi@
gmail.com (S.R.); kstanley@cs.ucf.edu (K.O.S.)
© 2012 Massachusetts Institute of Technology
Artificial Life 18: 331–363 (2012)
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
trillions of connections. Yet while neuroevolution has produced successful results in a variety of
domains [17, 42, 54, 56, 66], the scale of natural brains remains far beyond reach. The 100-trillion-
connection human brain is fair to describe as the most complex system known to exist [28, 67].
Cependant, its functionality stems not only from the astronomically high number of neurons and
relations, but also from its organizational structure, with regularities and repeating motifs such as
cortical columns [51].
As evolutionary algorithms are asked to evolve increasingly large and complex structures, interest
has increased in recent years in indirect neural network encodings, wherein the description of the solu-
tion is compressed in such a way that information can be reused [2, 4–6, 14, 15, 19, 22, 26, 27, 30, 37,
39, 40, 52, 57, 66]. Such compression allows the final solution to contain more components than its
description. Nevertheless, neuroevolution has historically produced networks with orders of magnitude
fewer neurons and significantly less organization and regularity than natural brains [58, 66].
While past approaches to neuroevolution generally concentrated on deciding which node is con-
nected to which (c'est à dire., neural topology) [17, 58, 66], the recently introduced hypercube-based neuro-
evolution of augmenting topologies (HyperNEAT) method [11, 18, 55] provided a new perspective
on evolving ANNs by showing that the pattern of weights across the connectivity of an ANN
can be generated as a function of its geometry. HyperNEAT employs an indirect encoding called
compositional pattern-producing networks (CPPNs) [52], which can compactly encode patterns
with regularities such as symmetry, repetition, and repetition with variation. En effet, the CPPN
in HyperNEAT paints a pattern within a four-dimensional hypercube that is interpreted as the
isomorphic connectivity pattern.
HyperNEAT exposed the fact that neuroevolution benefits from neurons that exist at locations within
the space of the brain and that by placing neurons at locations, evolution can exploit topography (comme
opposed to just topology), which makes it possible to correlate the geometry of sensors with the
geometry of the brain. While lacking in many ANNs, such geometry is a critical facet of natural brains
that is responsible, Par exemple, for topographic maps and modular organization across space [51].
This insight allowed large ANNs with regularities in connectivity to evolve through HyperNEAT
for high-dimensional problems [9, 18, 19, 55]. Yet a significant limitation is that the positions of the
nodes connected through this approach must be decided a priori by the user. Autrement dit, dans le
original HyperNEAT, the user must explicitly place nodes at locations within a two-dimensional or
three-dimensional space called the substrate.
This requirement does not merely create a new task for the user. A more subtle consequence is that
if the user dictates that hidden node n must exist at position (un, b) as in the original Hyper-NEAT, it
creates the unintentional constraint that any pattern of weights encoded by the CPPN must inter-
sect position (un, b) precisely with the correct weights. C'est, the pattern generated by the CPPN in
HyperNEAT must perfectly align the correct weights through all points (un, b, x2, y2) et (x1, y1, un, b). Encore
why should such an arbitrary a priori constraint on the locations of weights be imposed? It might be
easier for the CPPN to represent the correct pattern at a slightly different location, yet that would fail
under the user-imposed convention.
The key insight in this article is that a representation that encodes the pattern of connectivity across
a network (such as in HyperNEAT) automatically contains implicit clues on where the nodes should
be placed to best capture the information stored in the connectivity pattern. C'est, areas of uniform
weight ultimately encode very little information and hence little of functional value. Thus connections
(and hence the node locations that they connect) can be chosen to be expressed according to the
variance within their region of the CPPN-encoded function in the hypercube from which weights
are chosen. Autrement dit, to evolve the locations of nodes, there is no need for any new information
or any new representational structure beyond the very same CPPN that already encodes network
connectivity in HyperNEAT. Thus this article offers a comprehensive introduction to evolvable-substrate
HyperNEAT (ES-HyperNEAT), which was first described in conference papers by Risi et al. [44],
where it was introduced, and Risi and Stanley [46], where it was further refined.
The ES-HyperNEAT approach is able to fully determine the internal geometry of node placement
and density, based only on implicit information in an infinite-resolution pattern of weights. Thus the
332
Artificial Life Volume 18, Nombre 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
evolved ANNs exhibit natural properties such as topography and regularity without any need to evolve
explicit hidden-node placement. Because the placement of hidden nodes is entirely determined by the
algorithme, it circumvents the drawback of the original HyperNEAT that a pattern of weights encoded
by the CPPN must intersect specific positions with precisely the correct weights. Also importantly, ce
enhanced approach has the potential to create networks from several dozen nodes up to several million,
which will be necessary in the future to evolve more intelligent systems.
The main conclusion is that ES-HyperNEAT takes a step toward more biologically plausible
ANNs and significantly expands the scope of neural structures that evolution can discover, as demon-
strated by a series of experiments in this article. The first experiment, in a multi-task domain, explores
ES-HyperNEATʼs ability to evolve networks with multimodal input. The second experiment, in a decep-
tive maze navigation domain, shows that ES-HyperNEAT is able to elaborate on an existing structure
by holistically increasing the number of synapses and neurons in the ANN during evolution. The third
experiment, called the modular left & right retina problem [8, 29], indicates that ES-HyperNEAT can more
easily evolve modular ANNs than the original HyperNEAT, because it has the capability to start the
evolutionary search with a bias toward locality and from certain canonical ANN topographies.
The idea of seeding with a bias toward certain types of structures is important because it provides
a mechanism for emulating key biases in the natural world that are implicitly provided by physics, et
it makes it possible to insert specific kinds of domain knowledge into the evolutionary search.
The article begins with a review of NEAT and HyperNEAT in the next section. ES-HyperNEAT
is then motivated in Section 3, together with a description of the primary insight. The approach is
then detailed in Sections 4 et 5. Suivant, Sections 6, 7, et 8 present and describe results in the dual
task, maze navigation, and retina domains. The article concludes with a discussion and ideas for
future work in Section 9.
2 Background
This section reviews NEAT and HyperNEAT, which are the foundation of the ES-HyperNEAT
approach introduced in this article.
2.1 Neuroevolution of Augmenting Topologies
The HyperNEAT method that enables learning from geometry is an extension of the original NEAT
algorithm that evolves ANNs through a direct encoding.
The NEAT method was originally developed to evolve ANNs to solve difficult control and
sequential decision tasks and has proven successful in a wide diversity of domains [1, 53, 54, 56, 60,
65]. Evolved ANNs control agents that select actions based on their sensory inputs. NEAT is unlike
many previous methods that evolved neural networks (c'est à dire., neuroevolution methods), which tradi-
tionally evolve either fixed-topology networks [20, 48] or arbitrary random-topology networks [3, 22,
66]. Plutôt, NEAT begins evolution with a population of small, simple networks and complexifies the
network topology into diverse species over generations, leading to increasingly sophisticated behavior.
A similar process of gradually adding new genes has been confirmed in natural evolution [36, 64] et
shown to improve adaptation in a few prior evolutionary [64] and neuroevolutionary [25] approaches.
Cependant, a key feature that distinguishes NEAT from prior work in complexification is its unique
approach to maintaining a healthy diversity of complexifying structures simultaneously, as this section
reviews. Complete descriptions of the NEAT method, including experiments confirming the contribu-
tions of its components, are available in Stanley and Miikkulainen [56, 58] and Stanley et al. [54].
The NEAT method is based on three key ideas. D'abord, to allow network structures to increase in
complexity over generations, a method is needed to keep track of which gene is which. Otherwise, it
is not clear in later generations which individual is compatible with which in a population of diverse
structures, or how their genes should be combined to produce offspring. NEAT solves this problem
by assigning a unique historical marking to every new piece of network structure that appears through
a structural mutation. The historical marking is a number assigned to each gene corresponding to its
Artificial Life Volume 18, Nombre 4
333
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
order of appearance over the course of evolution. The numbers are inherited during crossover
unchanged, and allow NEAT to perform crossover among diverse topologies without the need for
expensive topological analysis.
Deuxième, historical markings make it possible for the system to divide the population into species
based on how similar networks are topologically. That way, individuals compete primarily within their
own niches instead of with the population at large. Because adding new structure is often initially dis-
advantageous, this separation means that unique topological innovations are protected and therefore
have time to optimize their structure before competing with other niches in the population.
Troisième, many systems that evolve network topologies and weights begin evolution with a population
of random topologies [22, 66]. In contrast, NEAT begins with a uniform population of simple net-
works with no hidden nodes, differing only in their initial random weights. Because of speciation,
novel topologies gradually accumulate over evolution, thereby allowing diverse and complex phenotype
patterns to be represented. No limit is placed on the size to which topologies can grow. New structure
is introduced incrementally as structural mutations occur, and only those structures survive that
are found to be useful through fitness evaluations. En effet, alors, NEAT searches for a compact,
appropriate topology by incrementally increasing the complexity of existing structure.
The next section reviews generative and developmental systems (GDSs), focusing on compositional pattern-
producing networks (CPPNs) and the HyperNEAT approach, which will be extended in this article.
2.2 Generative and Developmental Systems
In direct encodings like NEAT, each part of the solutionʼs representation maps to a single piece of
structure in the final solution [17, 66]. The significant disadvantage of this approach is that even
when different parts of the solution are similar, they must be encoded and therefore discovered
separately. Thus this article employs an indirect encoding instead, which means that the description
of the solution is compressed in such a way that information can be reused, allowing the final solu-
tion to contain more components than the description itself. Indirect encodings, which are the focus
of the field of GDSs, are powerful because they allow solutions to be represented as a pattern of
parameters, rather than requiring each parameter to be represented individually [5, 6, 19, 24, 26,
38, 52, 57]. The next section reviews one such indirect encoding in more detail.
2.2.1 Compositional Pattern-Producing Networks
Recently, NEAT was extended to evolve a high-level developmental abstraction called compositional
pattern-producing networks (CPPNs) [52]. The idea behind CPPNs is that patterns in nature can be
described at a high level as compositions of functions, wherein each function represents a stage
in development. CPPNs are similar to ANNs, but they rely on more than one activation function
(each representing a common regularity). Fait intéressant, because CPPNs are also connected graphs,
they can be evolved by NEAT just like ANNs. Thus the CPPN encoding does not require a new
evolutionary algorithm to evolve.
The indirect CPPN encoding can compactly encode patterns with regularities such as symmetry,
repetition, and repetition with variation [49, 50, 52]. Par exemple, simply by including a Gaussian func-
tion, which is symmetric, the output pattern can become symmetric. A periodic function such as the
sine creates segmentation through repetition. Le plus important, repetition with variation (par exemple., in the fingers
of the human hand) is easily discovered by combining regular coordinate frames (par exemple., sine and Gaussian)
with irregular ones (par exemple., the asymmetric x axis). Par exemple, a function that takes as input the sum
of a symmetric function and an asymmetric function outputs a pattern with imperfect symmetry.
In this way, CPPNs produce regular patterns with subtle variations. The potential for CPPNs to repre-
sent patterns with motifs reminiscent of patterns in natural organisms has been demonstrated in several
études [49, 50, 52]. Spécifiquement, CPPNs produce a phenotype that is a function of n dimensions, where n
is the number of dimensions in physical space. For each coordinate in that space, its level of expression
is an output of the function that encodes the phenotype. Chiffre 1 shows how a two-dimensional
phenotype can be generated by a function of two parameters that is represented by a network of
334
Artificial Life Volume 18, Nombre 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
Chiffre 1. CPPN encoding. (un) The function f takes arguments x and y, which are coordinates in a two-dimensional space.
When all the coordinates are drawn with an intensity corresponding to the output of f, the result is a spatial pattern,
which can be viewed as a phenotype whose genotype is f. (b) The CPPN is a graph that determines which functions are con-
nected. The connections are weighted so that the output of a function is multiplied by the weight of its outgoing connection.
composed functions. Because CPPNs are a superset of traditional ANNs, which can approximate any
fonction [10], CPPNs are also universal function approximators. Thus a CPPN can encode any pattern
within its n-dimensional space. The next section reviews the HyperNEAT extension to NEAT, which is
itself extended in this article.
2.2.2 HyperNEAT
HyperNEAT, reviewed in this section, is an indirect encoding extension of NEAT that is proven in a
number of challenging domains that require discovering regularities [8, 12, 18, 19, 55, 61]. For a full
description of HyperNEAT see Stanley et al. [55] and Gauci and Stanley [19].
The main idea in HyperNEAT is to extend CPPNs, which encode spatial patterns, to also represent
connectivity patterns [7, 18, 19, 55]. That way, NEAT can evolve CPPNs that represent large-scale
ANNs with their own symmetries and regularities. The key insight is that 2n-dimensional spatial pat-
terns are isomorphic to connectivity patterns in n dimensions, c'est, patterns in which the coordinate
of each endpoint is specified by n parameters. Consider a CPPN that takes four inputs labeled x1,
y1, x2, and y2; this point in four-dimensional space also denotes the connection between the two-
dimensional points (x1, y1) et (x2, y2), and the output of the CPPN for that input thereby represents
the weight of that connection (Chiffre 2). By querying every possible connection among a set of
points in this manner, a CPPN can produce a neural network, wherein each queried point is a neuron
position. The space in which these neurons are positioned is called the substrate. Because the connections
are produced by a function of their endpoints, the final structure is produced with knowledge of
Chiffre 2. Interpretation of hypercube-based geometric connectivity pattern. A collection of nodes, called the substrate, est
assigned coordinates that range from −1 to 1 in all dimensions. (1) Every potential connection in the substrate is queried
to determine its presence and weight; the dark directed lines in the substrate depicted in the figure represent a sample
of connections that are queried. (2) Internally, the CPPN (which is evolved) is a graph that determines which activation
functions are connected. As in an ANN, the connections are weighted so that the output of a function is multiplied by
the weight of its outgoing connection. For each query, the CPPN takes as input the positions of the two endpoints and
(3) outputs the weight of the connection between them. Ainsi, CPPNs can produce regular patterns of connections in space.
Artificial Life Volume 18, Nombre 4
335
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
its geometry. En effet, the CPPN is painting a pattern on the inside of a four-dimensional hypercube
that is interpreted as an isomorphic connectivity pattern, which explains the origin of the name
Hypercube-based NEAT (HyperNEAT). Connectivity patterns produced by a CPPN in this way are
called substrates so that they can be verbally distinguished from the CPPN itself, which has its own
internal topology.
Each queried point in the substrate is a node in an ANN. In traditional implementations of
HyperNEAT the experimenter specifies both the location and role (c'est à dire., hidden, input, or output)
of each such node. As a rule of thumb, nodes are placed on the substrate to reflect the geometry of
the task [8, 12, 18, 55]. That way, the connectivity of the substrate is a function of the task structure.
Par exemple, the sensors of an autonomous robot can be placed from left to right on the substrate in
the same order as on the robot. Outputs for moving left or right can also be placed in the same order,
allowing HyperNEAT to understand from the outset the correlation of sensors to effectors. In this way,
knowledge about the problem geometry can be injected into the search, and HyperNEAT can exploit
the regularities (par exemple., adjacency, or symmetry) of a problem that are invisible to traditional encodings.
The conventional method for controlling connectivity in HyperNEAT is a threshold that limits
the range of values output by the CPPN that can be expressed as weights. The threshold is a param-
eter specified at initialization that is uniformly applied to all connections queried. When the magnitude
of the output of the CPPN is below this threshold, the connection is not expressed.
Cependant, Verbancsics and Stanley [62] introduced an alternative to the traditional uniform threshold,
called the link expression output (HyperNEAT-LEO), that allowed HyperNEAT to evolve the pattern of
weights independently from the pattern of connection expression. The LEO is represented as an additional
output to the CPPN that indicates whether a connection should be expressed or not. If the LEO output
is greater than zero, then the corresponding connection is created and its weight is set to the original
CPPN weight output value. Because HyperNEAT evolves such patterns as functions of geometry,
important general topographic principles for organizing connectivity can be seeded into the initial
population [62]. Par exemple, HyperNEAT can be seeded with a bias toward local connectivity
implemented through LEO, in which locality is expressed through a Gaussian function. Because the
Gaussian function peaks when its input is 0.0, inputting a difference between coordinates (par exemple., Dx)
achieves the highest value when the coordinates are the same. In this way, such seeds provide the
concept of locality, because the more local the connection (c'est à dire., as Dx approaches 0.0), the greater
the output of the Gaussian function.
Because there are now two different thresholding methods for HyperNEAT, the new approach
introduced in this article is compared with both. Cependant, regardless of the approach to thresholding,
a problem that has endured with HyperNEAT is that the experimenter is left to decide how many
hidden nodes there should be and where to place them too. C'est, although the CPPN determines
how to connect nodes in a geometric space, it does not specify where the nodes should be, which is especially
ambiguous for hidden nodes.
In answer to this challenge, the next section introduces an extension to HyperNEAT in which the
placement and density of the hidden nodes do not need to be set a priori and in fact are completely
determined by implicit information in the CPPN itself.
3 Choosing Connections to Express
The placement of nodes in original HyperNEAT is decided by the user. Yet whereas it is often
possible to determine how sensors and effectors relate to domain geometry, it is difficult for the
user to determine the best placement and number of necessary hidden nodes a priori. Par exemple,
the location of the hidden nodes in the substrate in Figure 2 had to be decided by the user.
HyperNEAT thus creates the strange situation that it can decide with what weight any two nodes
in space should be connected, but it cannot tell us anything about where the nodes should be. Is
there a representation that can evolve the placement and density of nodes and that can potentially
span the range between networks of several dozen nodes and several billion?
336
Artificial Life Volume 18, Nombre 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
3.1 Implicit Information in the Hypercube
The novel insight behind ES-HyperNEAT is that a representation that encodes the pattern of connec-
tivity across a network automatically contains implicit information that could be useful for deciding
where the nodes should be placed. In HyperNEAT the pattern of connectivity is described by the
CPPN, where every point in the four-dimensional space denotes a potential connection between
two two-dimensional points (recall that a point in the four-dimensional hypercube is actually a connec-
tion weight and not a node). Because the CPPN takes x1, y1, x2, and y2 as input, it is a function of the
infinite continuum of possible coordinates for these points. Autrement dit, the CPPN encodes a poten-
tially infinite number of connection weights within the hypercube of weights. Thus one interesting way
to think about the hypercube is as a theoretically infinite pattern of possible connections that might be
incorporated into a neural network substrate. If a connection is chosen to be included, then by necessity
the nodes that it connects must also be included in the substrate. Thus by asking which connections to
include from the infinite set, we are also asking which nodes (and hence their positions) to include.
By shifting the question of what to include in the substrate from nodes to connections, deux
important insights follow: D'abord, the more such connections are included, the more nodes would also
be added to the substrate. Thus the node density increases with the number of connections. Deuxième,
for any given infinite-resolution pattern, there is some sampling density above which increasing the
density further offers no advantage. Par exemple, if the hypercube is a uniform gradient of maximal
connection weights (c'est à dire., all weights are the same constant), then in effect it encodes a substrate that
computes the same function at every node. Thus adding more such connections and nodes adds no
new information. On the other hand, if there is a stripe of differing weights running through the
hypercube, but otherwise uniform maximal connections everywhere else, then that stripe contains
information that would contribute to a different function from its redundantly uniform neighbors.
The key insight is thus that it is not always a good idea to add more connections, because for
any given finite pattern, at some resolution there is no more information and adding more weights
at such high resolution would be redundant and unnecessary. This maximal useful resolution varies
for different regions of the hypercube, depending on the complexity of the underlying weight pattern
in those regions. Thus the answer to the question of which connections should be included in
ES-HyperNEAT is that connections should be included at high enough resolution to capture the detail
(c'est à dire., information) in the hypercube. Any more than that would be redundant. Donc, an algorithm
is needed that can choose many points to express in regions of high variance and fewer points to
express in regions of relative homogeneity. Each such point is a connection weight in the substrate,
whose respective nodes will be expressed as well. The main principle is simple: Density follows information.
In this way, the placement of nodes in the topographic layout of an ANN is ultimately a signification of
where information is stored within weights.
To perform the task of choosing points (c'est à dire., weights) to express, a data structure is needed that
allows space to be represented at variable levels of granularity. One such multi-resolution technique
is the quadtree [16], which traditionally describes two-dimensional regions. It has been applied success-
fully in fields ranging from pattern recognition to image encoding [47, 59] and is based on recursively
splitting a two-dimensional region into four subregions. That way, the decomposition of a region
into four new regions can be represented as a subtree whose parent is the original region with one
descendant for each decomposed region. The recursive splitting of regions can be repeated until the
desired resolution is reached or until no further subdivision is needed because additional resolution is
no longer uncovering any new information. The next sections describe the ES-HyperNEAT algorithm
in more detail. A pseudocode implementation can be found in Appendix 2.
4 Quadtree Information Extraction
Instead of searching directly in the four-dimensional hypercube space (recall that it takes four dimen-
sions to represent a two-dimensional connectivity pattern), ES-HyperNEAT iteratively discovers the
ANN connections starting from the inputs and outputs of the ANN (which are prespecified by the
Artificial Life Volume 18, Nombre 4
337
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
user ). This approach focuses the search within the hypercube on two-dimensional cross sections of
the hypercube.
The foundation of the ES-HyperNEAT algorithm is the quadtree information extraction procedure,
which receives a two-dimensional position as input and then analyzes either the outgoing connectivity
pattern from that single neuron (if it is an input), or the incoming connectivity pattern (if it is an output).
Par exemple, given an input neuron at (un, b), the quadtree connection-choosing algorithm is applied only
to the two-dimensional outgoing connectivity patterns described by the function CPPN (un, b, x2, y2),
where x2 and y2 range between −1 and 1. The algorithm works in two main phases (Chiffre 3): In the
division and initialization phase (Chiffre 3 top) the quadtree is created by recursively subdividing the initial
square (lines 8–11 of Algorithm 1 in Appendix 2), which spans the space from (−1, −1) à (1, 1), jusqu'à
a desired initial resolution r is reached (par exemple., 4 × 4, which corresponds to a quadtree depth of 3).
For every quadtree square with center (X, oui), the CPPN is queried with arguments (un, b, X, oui) et le
resulting connection weight value w is stored (line 14 of Algorithm 1).
Given the values (w1, w2,… , wk) of the k leaf nodes in a subtree of quadtree node p and mean
kðw̄ − wiÞ2. Ce
weight w ̄, the variance of node p in the quadtree can be calculated as jp
1
variance is a heuristic indicator of the heterogeneity (c'est à dire., presence of information) of a region. If
the variance of the parent of a quadtree leaf is still higher than a given division threshold dt (line 20
of Algorithm 1), then the division phase can be reapplied for the corresponding leafʼs square, allow-
ing increasingly high densities. Just as the initialization resolution ensures that some minimum level
of sampling is enforced (so that the basic shape of the encoded pattern is likely to be discovered),
a maximum resolution level rm can also be set to place an upper bound on the number of possible
neurons if desired. Cependant, it is theoretically interesting that in principle this algorithm can yield
arbitrarily high density, which means that very large ANNs can be represented.
2 ¼ 1
k
P.
The quadtree representation created in the initialization phase serves as a heuristic variance
indicator to decide on the connections (and therefore placement and density of neurons) to express.
Because more connections should be expressed in regions of higher variance, a pruning and extraction
phase (Algorithm 2 in Appendix 2) is next executed (Chiffre 3 bottom), in which the quadtree is
traversed depth-first until the current nodeʼs variance is smaller than the variance threshold jt
2
Chiffre 3. Quadtree information extraction example. Given an input neuron at (un, b), the algorithm works in two main
étapes. (1) In the division and initialization phase the quadtree is created by recursively splitting each square into four new
squares until the desired resolution is reached (1un), while the values (1b) for each square with center (X, oui) are determined
by CPPN(un, b, X, oui) and the variance values of each higher node are calculated (1c). Gray nodes in the figure have a variance
greater than zero. Alors, in the pruning and extraction phase (2), the quadtree is traversed depth-first until the nodeʼs variance
is smaller than a given threshold (2un). A connection (un, b, X, oui) is created for each qualifying node with center (X, oui) (2b).
That way, the density of neurons in different regions will correspond to the amount of information in that region.
338
Artificial Life Volume 18, Nombre 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
Chiffre 4. Example connection selection. Chosen connections (depicted only by their target locations) originating from
(0, −1) are shown in (un) after the pruning stage but without band pruning. Points that still remain after band pruning
(par exemple., point P, whose neighbors at the same resolution have different CPPN activation levels) are shown in (b). Le
resulting point distribution reflects the information inherent in the pattern.
(line 4 of Algorithm 2) or until the node has no children (which means that the variance is zero).
Subsequently, a connection (un, b, X, oui) is created for each qualifying node with center (X, oui) (line 22 de
Algorithm 2; the band threshold in Algorithm 2 is explained shortly). The result is higher resolution
in areas of more variation.
Figure 4a shows an example of the outgoing connections from the source neuron (0, −1) (depicted
only by their target locations for clarity) chosen at this stage of the algorithm. The variance is high at
the borders of the circles, which results in a high density of expressed points near those locations.
Cependant, for the purpose of identifying connections to include in a neural topography, the raw pattern
output by the quadtree algorithm can be improved further. If we think of the pattern output by the
CPPN as a kind of language for specifying the locations of expressed connections, then it makes sense
additionally to prune the points around borders so that it is easy for the CPPN to encode points
definitively within one region or another.
Thus a more parsimonious language for describing density patterns would ignore the edges and
focus on the inner region of bands, which are points that are enclosed by at least two neighbors on
opposite sides (par exemple., left and right) with different CPPN activation levels (Figure 4b). En outre,
narrower bands can be interpreted as requests for more point density, giving the CPPN an explicit
mechanism for affecting density. Ainsi, to facilitate banding, a pruning stage is added that removes
points that are not in a band. Membership in a band for a square with center (X, oui) and width N is
determined by the band level
h ¼ maxðminðdtop; dbottomÞ; minðdleft; drightÞÞ;
where dleft is the difference in CPPN activation levels between the connection (un, b, X, oui) and its left
neighbor at (un, b, x − N, oui) (line 9 of Algorithm 2). The other values, dright, dbottom, and dtop, are calculated
similarly. If the band level h is below a given threshold ht, then the corresponding connection is not
expressed (line 19 of Algorithm 2). Figure 4b shows the resulting point selections with band pruning.
This approach also naturally enables the CPPN to increase the density of points chosen, by creat-
ing more bands or making them thinner. Thus no new information and no new representational
structure beyond the CPPN already employed in HyperNEAT is needed to encode node placement
and connectivity, as concluded in the next section.
5 ES-HyperNEAT Algorithm
The complete ES-HyperNEAT algorithm (Algorithm 3 in Appendix 2) is depicted in Figure 5. The con-
nections originating from an input at (0, −1) (Figure 5a; line 7 in Algorithm 3) are chosen with the approach
Artificial Life Volume 18, Nombre 4
339
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
described in the previous section. The corresponding hidden nodes are created if not already existent
(lines 9–10 in Algorithm 3). The approach can be iteratively applied to the discovered hidden nodes until
a user-defined maximum iteration level is reached (line 15 in Algorithm 3) or no more information is dis-
covered in the hypercube (Figure 5b). To tie the network into the outputs, the approach then chooses
connections based on each outputʼs incoming connectivity patterns (Figure 5c; line 27 in Algorithm 3).
Once all hidden neurons are discovered, only those are kept that have a path to an input and an
output neuron (Figure 5d; line 34 in Algorithm 3). This iterated approach helps to reduce computa-
tional costs by focusing the search on a sequence of two-dimensional cross sections of the hyper-
cube instead of searching for information directly in the full four-dimensional hyperspace.
ES-HyperNEAT ultimately unifies a set of algorithmic advances stretching back to NEAT, chaque
abstracted from an important facet of natural evolution that contributes to its ability to evolve com-
plexity. The first is that evolving complexity requires a mechanism to increase the information con-
tent in the genome over generations [56, 58]. Deuxième, geometry plays an important role in natural
neural connectivity; in neuroevolution, endowing neurons with geometric coordinates means that
the genome can in effect project regularities in connectivity across the neural geometry, thereby
providing a kind of scaffolding for situating cognitive structures [18, 19, 55]. Troisième, the placement
and density of neurons throughout the geometry of the network should reflect the complexity of the
underlying functionality of its respective parts [46].
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Chiffre 5. The ES-HyperNEAT algorithm. The algorithm starts by iteratively discovering the placement of the hidden
neurons from the inputs (un) and then ties the network into the outputs (c). The two-dimensional motif in (un) represents
outgoing connectivity patterns from a single input node, whereas the motif in (c) represents incoming connectivity pat-
terns for a single output node. The target nodes discovered (through the quadtree algorithm) are those that reside
within bands in the hypercube. In this way regions of high variance are sought only in the two-dimensional cross section
of the hypercube containing the source or target node. The algorithm can be iteratively applied beyond the inputs to the
discovered hidden nodes (b). Only those nodes are kept at the end that have a path to an input and an output neuron (d).
That way, the search through the hypercube is restricted to functional ANN topologies.
340
Artificial Life Volume 18, Nombre 4
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
Because ES-HyperNEAT can automatically deduce node geometry and density from CPPNs in-
stead of requiring a priori placement (as in original HyperNEAT), it significantly expands the scope
of neural structures that evolution can discover. The approach not only evolves the location of every
neuron in the brain, but also can represent regions of varying density, which means resolution can
increase holistically over evolution. The main insight is that the connectivity and hidden-node place-
ment can be automatically determined by information already inherent in the pattern encoded by the
CPPN. In this way, the density of nodes is automatically determined and effectively unbounded.
Thus substrates of unbounded density can be evolved and determined without any additional repre-
sentation beyond the original CPPN in HyperNEAT.
5.1 Key Hypotheses
Automatically determining the placement and density of hidden neurons introduces several advan-
tages beyond just liberating the user from making such decisions. This subsection introduces the key
hypotheses in this article that elucidate these advantages, which the experiments in Sections 6, 7, et
8 aim to validate.
Hypothesis 1. ES-HyperNEAT facilitates evolving networks with targeted connectivity for
multimodal tasks.
Although it produces regular patterns of weights, the original HyperNEAT tends to produce fully
or near fully connected networks [8], which may create a disadvantage in domains where certain
neurons should only receive input from one modality while other neurons should receive inputs from
multiple modalities, thus allowing the sharing of information about the underlying task similarities
in the hidden layer. In contrast, because ES-HyperNEAT only creates connections where there is
high variance in the hypercube, it should be able to find greater variation in connectivity for different
neurons. To test Hypothesis 1, the first experiment explores how ES-HyperNEAT performs in a
multitask domain (Section 6), which requires the agent to react differently according to the type of
input (par exemple., rangefinder or radar) il reçoit.
Hypothesis 2. The fixed locations of hidden nodes in original HyperNEAT that are chosen by
the user make finding an effective pattern of weights more difficult than does allowing the algorithm
itself to determine their locations, as in ES-HyperNEAT.
The problem is that when node locations are fixed, the pattern in the hypercube that is encoded
by the CPPN must intersect those node coordinates at precisely the right locations. Even if such a
CPPN encodes a pattern of weights that expresses an effective network, a slight shift (c'est à dire., a small
translation) of the pattern would cause it to detach from the correct node locations. Thus the net-
work would receive a low fitness even though it actually would encode the right pattern if only the
nodes were slightly shifted. In contrast, ES-HyperNEAT in effect tracks shifts in the underlying
pattern, because the quadtree algorithm searches for the appropriate locations of nodes regardless
of exactly where the pattern is expressed. This increased flexibility means that the feasible area of the
search space will be larger and hence easier to hit. Analyzing the resulting ANNs will demonstrate
whether ES-HyperNEAT can express hidden nodes at slightly different locations when the pattern
of weights changes.
Hypothesis 3. ES-HyperNEAT is able to elaborate on existing structure by increasing the number
of synapses and neurons in the ANN during evolution, while regular HyperNEAT takes the entire
set of ANN connection weights to represent a partial solution.
The second experiment in a deceptive maze navigation domain (Section 7) will isolate this issue by
examining the effect of a task with several intermediate milestones on both variants.
Artificial Life Volume 18, Nombre 4
341
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
Hypothesis 4. ES-HyperNEAT can evolve modular ANNs more easily than the original fixed-
substrate HyperNEAT, in part because it facilitates evolving networks with limited connectivity and
because it has the capability to start the evolutionary search with a bias toward locality and toward
certain canonical ANN topographies.
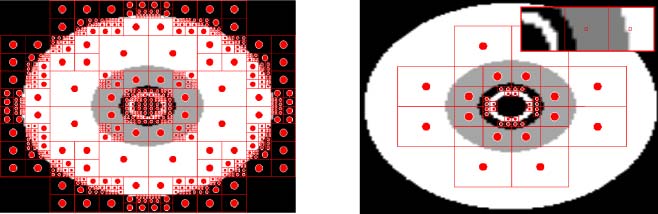
The third experiment, called the left & right retina problem [7, 29] (Section 8), will test the ability to
evolve modular structures, because the task benefits from separating different functional structures.
Whereas the original HyperNEAT was extended to allow seeding with a bias toward local connec-
tivity through HyperNEAT-LEO [62], ES-HyperNEAT can also be seeded with a CPPN that creates
certain ANN topographies (c'est à dire., geometry seeding ). This advance is enabled by ES-HyperNEATʼs ability
to place the hidden nodes according to the underlying information in the hypercube.
If these hypotheses are correct, then ES-HyperNEAT should not only match but outperform the
original HyperNEAT, as the experiments in the next sections will test.
6 Experiment 1: Dual Task
Organisms in nature have the ability to switch rapidly between different tasks, depending on the de-
mands of the environment. Par exemple, a rat should react differently when placed in a maze or in
an open environment with a visible food source. The dual task domain presented here (Chiffre 6) will
test the ability of ES-HyperNEAT and regular HyperNEAT to evolve such task differentiation for
a multimodal domain.
The dual task domain consists of two nondependent scenarios (c'est à dire., the performance in one
scenario does not directly influence the performance in the other scenario) that require the agent
to exhibit different behaviors and to react either to its rangefinders or to its pie-slice sensors. Be-
cause certain hidden neurons ideally would be responsible for information that should be treated
differently, while other hidden neurons should be able to share information where the tasks are
similar, this domain will likely benefit from ANNs that are not fully connected, which the original
HyperNEAT has struggled to produce in the past [7]. ES-HyperNEAT should facilitate the evolution
of networks with more targeted connectivity, as suggested by Hypothesis 1, because connections are
only included at a high enough resolution to capture the information in the hypercube.
The first scenario is a simple navigation task in which the agent has to navigate from a starting
point to an end point in a fixed amount of time, using only its rangefinder sensors to detect walls
= 1 − dg, where dg is the distance of the
(Figure 6a). The fitness in this scenario is calculated as fnav
robot to the goal point at the end of the evaluation, scaled into the range [0, 1]. The second scenario
is a food-gathering task in which a single piece of food is placed within a square room with an agent
that begins at the center (Figure 6b). The agent attempts to gather as much food as possible within a
time limit, using only its pie-slice sensors, which act as a compass toward the food item. Food only
appears at one location at a time and is placed at another random location once consumed by the
agent. The fitness for the food-gathering task is defined by ffood ¼ nþð1−dfÞ
, where n corresponds to
4
Chiffre 6. Dual task. In the dual task domain the agent has to exhibit either wall-following (un) or food-gathering behavior
(b), depending on the type of sensory input it receives.
342
Artificial Life Volume 18, Nombre 4
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
Chiffre 7. Substrate configuration and sensor layout. The controller substrate is shown at left. Whereas the number of
hidden nodes for the fixed-substrate approach is determined in advance, ES-HyperNEAT decides on the positions and
density of hidden nodes on its own. The sensor layout is shown on the right. The autonomous agent is equipped with
five distance and four pie-slice sensors. Each rangefinder sensor indicates the distance to the closest obstacle in that
direction. The pie-slice sensors act as a compass toward the goal (c'est à dire., food), activating when a line from the goal to
the center of the robot falls within the pie slice.
the number of collected food items (maximum four ), and df is the distance of the robot to the next
food item at the end of the evaluation.
The total fitness is calculated as the average of the fitness values in the two scenarios. The domain
is considered solved when the agent is able to navigate to the goal point in the first scenario and success-
fully collects all four food items in the second scenario, which corresponds to a fitness of 1.0.
6.1 Experimental Setup
Evolvable and fixed-substrate (original) HyperNEAT use the same placement of input and output
nodes on the substrate (Chiffre 7), which are designed to correlate senses and outputs geometrically
(par exemple., seeing something on the left and turning left). Thus the CPPN can exploit the geometry of the
agent. The agent is equipped with five rangefinder sensors that detect walls and four pie-slice sensors
that act as a compass toward the next food item. All rangefinder sensor values are scaled into the
range [0,1], where lower activation indicates closer proximity to a wall. A pie-slice sensor is set to 1.0
when a line from the next food item to the center of the robot falls within the pie slice, and is set to
0.0 otherwise. At each discrete moment of time, the number of units moved by the agent is 20F,
where F is the forward effector output. The agent also turns by (L − R) × 18°, where L is the left
effector output and R is the right effector output. A negative value is interpreted as a right turn.
To highlight the challenge of deciding the location and number of available hidden nodes,
ES-HyperNEAT is compared with four fixed-substrate variants (Chiffre 8). FS10x1 is the typical
setup with a single row of 10 hidden neurons in a horizontal line at y = 0 (Figure 8a). For the
FS1x10 variant 10 hidden neurons are arranged vertically at x = 0 (Figure 8b). FS5x5 has a substrate
containing 25 hidden nodes arranged in a 5 × 5 grid (Figure 8c). FS8x8 tests the effects on per-
formance of uniformly increasing the number of hidden nodes from 25 à 64 neurons (Figure 8d).
To generate such a controller for the original HyperNEAT, a four-dimensional CPPN with inputs x1,
y1, x2, and y2 queries the substrate shown in Figure 7 to determine the connection weights between
the input and hidden, the hidden and output, and the hidden and hidden nodes. In contrast,
ES-HyperNEAT decides the placement and density of nodes on its own.
Chiffre 8. Hidden-node layouts for the original HyperNEAT. This figure shows (un) a horizontal configuration of hidden
nodes, (b) a vertical arrangement, and two (c,d) grid configurations.
Artificial Life Volume 18, Nombre 4
343
je
D
o
w
n
o
un
d
e
d
F
r
o
m
h
t
t
p
:
/
/
d
je
r
e
c
t
.
m
je
t
.
e
d
toi
un
r
t
je
/
/
je
un
r
t
je
c
e
–
p
d
F
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
un
r
t
je
/
_
un
_
0
0
0
7
1
p
d
.
F
b
oui
g
toi
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. Ô. Stanley
An Enhanced Hypercube-Based Encoding
Experimental parameters for this experiment and all other experiments in this article are given in
Appendix 1.
6.2 Dual Task Results
All results are averaged over 20 runs. Chiffre 9 shows the training performance over generations for
the HyperNEAT variants on the dual task domain. ES-HyperNEAT solved the domain in all runs
and took on average 33 generations (j = 31), whereas the best-performing fixed-substrate variant,
FS5x5, found a solution in only 13 out of 20 runs. The difference in average final performance is
significant ( p < 0.001 according to the Studentʼs t-test).
The second HyperNEAT thresholding method, HyperNEAT-LEO, was seeded with global
locality [62], which should allow HyperNEAT to create more-sparsely connected networks. Indeed,
adding the LEO increases the average maximum fitness for all fixed-substrate HyperNEAT setups
significantly ( p < 0.001) (graphs not shown). The fixed-substrate approaches with LEO 10 × 1, 1 ×
10, 5 × 5, and 8 × 8 find a solution in 20, 18, 17, and 19 runs, respectively. The best fixed-substrate
approach with LEO (10 × 1) took 28 generations on average (j = 52), which is slightly, though
not significantly, faster than ES-HyperNEAT ( p = 0.68). However, the worst-performing fixed-
substrate approach with LEO (5 × 5) took 101 generations on average (j = 116) when successful,
which is significantly longer than ES-HyperNEAT ( p < 0.05). This result highlights that even
though HyperNEAT-LEO improves on the performance of regular HyperNEAT, the need to decide
the placement of nodes (which is removed with ES-HyperNEAT) remains a potential liability.
These results also suggest that a multimodal domain benefits from the ability of both ES-HyperNEAT
and HyperNEAT-LEO to generate more-sparsely connected ANNs than the original HyperNEAT
with uniform thresholding, which an analysis of the evolved ANNs confirms. An example of
three ANN solutions generated by ES-HyperNEAT and the CPPNs that encode them is shown
in Figure 10. While ES-HyperNEAT is able to find a greater variation in connectivity for different
neurons, the networks created by the original HyperNEAT are generally fully or near-fully connected.
Interestingly, the average CPPN complexity of solutions discovered by the best-performing setup
for regular HyperNEAT (5 × 5) is at 9.7 hidden nodes (j = 6.7), almost six times higher than CPPN
solutions by ES-HyperNEAT, which have 1.65 hidden nodes on average (j = 2.2). It is also three
times higher than CPPN solutions for the best-performing HyperNEAT-LEO setup (10 × 1), which
have 3.05 hidden nodes on average (j = 2.25). These results indicate that regular HyperNEAT
requires more effort to find solutions than either ES-HyperNEAT or HyperNEAT-LEO.
7 Experiment 2: Maze Navigation
To evolve controllers for more complicated tasks will require a neuroevolution method that benefits
from previously discovered partial solutions to find the final solution. While direct encodings like
Figure 9. Average performance. The average best fitness over generations is shown for the dual task domain for the
different HyperNEAT substrates, which are averaged over 20 runs. The main result is that ES-HyperNEAT significantly
outperforms the original HyperNEAT in a multimodal domain.
344
Artificial Life Volume 18, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Figure 10. ES-HyperNEAT ANN solutions and their underlying CPPNs. Three ANN solutions (bottom) and the CPPNs
(top) that encode them are shown together with the numbers of hidden neurons (n) and connections (c). ES-Hyper-
NEAT evolves a variety of different ANNs, showing varying degrees of symmetry and network connectivity. In the
electronic version, positive connections are dark (black), whereas negative connections are light (red). Line width
corresponds to connection strength. Hidden nodes with self-recurrent connections are denoted by a smaller concentric
circle. CPPN activation functions are denoted by G for Gaussian, S for sigmoid, and A for absolute value. The CPPNs
receive the length L of the queried connection as an additional input.
NEAT allow the network topology to complexify over generations, leading to increasingly sophisti-
cated behavior, they suffer from the problem of reinvention. That is, even if different parts of the
solution are similar, they must be encoded and therefore discovered separately.
HyperNEAT alleviated this problem by allowing the solution to be represented as a pattern of
parameters, rather than requiring each parameter to be represented individually. However, because
regular HyperNEAT tends to produce fully connected ANNs [7], it likely takes the entire set of
ANN connection weights to represent a partial task solution, while ES-HyperNEAT should be able
to elaborate on existing structure because it can increase the number of connections and nodes in
the substrate during evolution, as suggested by Hypothesis 3.
To test this third hypothesis on when ES-HyperNEAT provides an advantage, a task is needed in
which a solution is difficult to evolve without crossing several intermediate milestones. One such
task is the deceptive maze navigation domain introduced by Lehman and Stanley [32]. In this domain
(Figure 11), a robot controlled by an ANN must navigate in a maze from a starting point to an end
point in a fixed time. The robot has five rangefinders that indicate the distance to the nearest wall
within the maze, and four pie-slice radar sensors that fire when the goal is within the pie slice. The
experimental setup follows the one described in Section 6.1 with the same substrate configuration and
sensor layout (Figure 7). The agent thus sees walls with its rangefinders and the goal with its radars.
If fitness is rewarded proportionally to how close the robot is to the goal at the end, cul-de-sacs in
the maze that lead close to the goal but do not reach it are deceptive local optima [34]. Therefore, to
reduce the role of such deception in this article, the fitness function f rewards the agent explicitly for
discovering stepping stones toward the goal:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
(cid:2)
f ¼ 10
n þ ð1 − d Þ otherwise;
if the agent is able to reach the goal;
Artificial Life Volume 18, Number 4
345
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Figure 11. Maze navigation. The goal of the agent in the maze navigation domain is to reach goal point G. Because the task
is deceptive, the agent is rewarded for making incremental process toward the goal by following the waypoints.
where n is the number of passed waypoints (which are not visible to the agent) and d is the distance
of the robot to the next waypoint scaled into the range [0, 1] at the end of the evaluation. The idea is
that agents that can reach intermediate waypoints should make good stepping stones to those that
reach further waypoints. ES-HyperNEAT should be able to elaborate more efficiently on agents that
reach intermediate waypoints by gradually increasing their neural density.
7.1 Maze Navigation Results
ES-HyperNEAT performed significantly better than the other variants in the maze navigation do-
main ( p < 0.001) (Figure 12a) and finds a solution in 19 out of 20 runs in 238 generations on
average when successful (j = 262). The default setup for the original HyperNEAT, FS10x1, reaches
a significantly higher average maximum fitness than the vertically arrangement FS1x10 ( p < 0.001)
or the gridlike setup FS8x8 ( p < 0.05). The significantly lower performance of the vertical node
arrangement (FS1x10) highlights the challenge of deciding the best positions for the hidden nodes
and shows that certain substrate configurations make finding an effective pattern of weights more
difficult, as suggested by Hypothesis 2.
The differing performance of evolvable-and fixed-substrate HyperNEAT can also be appreciated
in how frequently they solve the problem perfectly (Figure 12b). ES-HyperNEAT significantly out-
performs all fixed-substrate variants and finds a solution in 95% of the 20 runs. FS10x1 solves the
domain in 45% of runs, whereas the vertical arrangement of the same number of nodes (FS1x10)
degrades performance significantly ( p < 0.001), also not finding a solution in any of the runs. FS5x5
finds a solution in 20% of all runs. Interestingly, uniformly increasing the number of hidden nodes
to 64 for FS8x8, which might be hypothesized to help, in fact degrades performance significantly
( p < 0.001), not finding a solution in any of the runs.
Extending the original HyperNEAT with the LEO and global locality seeding [62] increases its
average maximum fitness for all but the FS8x8 setup significantly ( p < 0.001) (graphs not shown).
The best-performing HyperNEAT-LEO setup (FS10x1) finds a solution in 17 out of 20 runs, in
Figure 12. Average performance and champion complexity. The average best fitness over generations is shown for
the maze navigation domain (a) for the different HyperNEAT variants, which are averaged over 20 runs. The fraction
of 20 runs that successfully solve the maze navigation domain is shown in (b) for each of the HyperNEAT variants after
1,000 generations. The average number of connections of the champion ANNs produced by ES-HyperNEAT and the
number of connections of the underlying CPPNs are shown in (c). Increasing CPPN complexity shows a positive (and
significant) correlation with an increase in ANN substrate complexity.
346
Artificial Life Volume 18, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
531 generations on average when successful (j = 262). While LEO improves HyperNEATʼs per-
formance, the best-performing fixed-substrate approach even with LEO still performs significantly
worse than ES-HyperNEAT ( p < 0.05). This result suggests that the maze navigation domain
depends not only on networks with limited connectivity (like the dual task domain in the previous
section), but also on a method that benefits from building on previously discovered partial solutions
to find the final solution.
In ES-HyperNEAT, there is a significant positive correlation (r = 0.95, p < 0.001 according to
Spearmanʼs rank correlation coefficient) between the number of connections in the CPPN and in the
resulting ANN (Figure 12c). This trend indicates that the substrate evolution algorithm may tend to
create increasingly complex indirectly encoded networks even though it is not explicitly designed to do so
(e.g., like regular NEAT). The complexity of ANN (substrate) solutions (242 connections on average)
is more than nine times greater than that of the underlying CPPNs (25 connections on average), which
suggests that ES-HyperNEAT can encode large ANNs from compact CPPN representations.
The conclusion is that evolving the substrate can significantly increase performance in tasks that
require incrementally building on stepping stones. The next two sections examine how this result
comes about.
7.2 Example Solution Lineage
To gain a better understanding of how an indirect encoding like ES-HyperNEAT elaborates a solu-
tion over generations, additional evolutionary runs in the maze navigation domain were performed
with sexual reproduction disabled (i.e., every CPPN has only one ancestor ). This change facilitates
analyzing the lineage of a single champion network. Disabling sexual reproduction did not result in a
significant performance difference.
An example of four milestone ANNs in the lineage of a solution and the CPPNs that encode
them is shown in Figure 13. All ANNs share common geometric features: Most prominent are the
symmetric network topology and denser regions of hidden neurons resembling the shape of an “H”
(except the second ANN). Between generations 24 and 237 the ANN evolves from not being able
to reach the first waypoint to solving the task.
The solution discovered at generation 237 shows a clear holistic resemblance to generation 106
despite some general differences. Both networks have strong positive connections to the three out-
put neurons that originate at slightly different hidden-node locations. This slight shift is due to a
movement of information within the hypercube for which ES-HyperNEAT can nevertheless com-
pensate, as suggested by Hypothesis 2. The number of connections gradually increases from 184 in
generation 24 to 356 in generation 237, indicating the incremental elaboration on existing ANN
structure, as suggested by Hypothesis 3. Interestingly, the final ANN solves the task without feed-
back from its pie-slice sensors.
Figure 13 also shows that ES-HyperNEAT can encode large ANNs from compact CPPN repre-
sentations. The solution ANN with 40 hidden neurons and 356 connections is encoded by a much
smaller CPPN with only five hidden neurons and 18 connections.
In contrast to direct encodings like NEAT [53, 55], genotypic CPPN mutations can have a more
global effect on the expressed ANN patterns. For example, changes in only four CPPN weights are
responsible for the change in topology from the second to the third ANN milestone. Other solution
lineages followed similar patterns, but single neuron or connection additions to the substrate do also
sometimes occur.
7.3 Initializing Regular HyperNEAT with a Solution ES-HyperNEAT Substrate
One might speculate that ES-HyperNEAT outperforms the original HyperNEAT only because it
finds a better substrate and not because it can compensate for movement of information within
the hypercube or because it can incrementally build on existing ANN structure. To test this hypoth-
esis, 20 additional runs were performed, in which HyperNEAT was given the solution substrate
generated by ES-HyperNEAT in Figure 13d.
Artificial Life Volume 18, Number 4
347
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Figure 13. ANN milestones and underlying CPPNs together with the agentʼs behavior from a single maze solution lineage.
Four ANN milestones (bottom) and the CPPNs (top) that encode them are shown together with the numbers of hidden
neurons (n) and connections (c). Fitness f is also shown. Positive connections are dark, whereas negative connections are
light. Line width corresponds to connection strength. Hidden nodes with self-recurrent connections are denoted by a
smaller concentric circle. CPPN activation functions are denoted by G for Gaussian, S for sigmoid, Si for sine, and A for absolute
value. The CPPNs receive the length L of the queried connection as an additional input. The gradual increase in substrate
connections indicates an increase of information in the hypercube, which in turn leads to an increase in performance.
HyperNEAT solved the task in 40% of all runs and reached an average maximum fitness of 7.30
(j = 2.33). It performed slightly worse than the FS10x1 setup, which solved the task in 45% of all
runs, and significantly worse than ES-HyperNEAT ( p < 0.001).
Thus the results confirm the hypothesis that ES-HyperNEATʼs better performance is not only
due to the topography of its generated substrates. The original HyperNEAT does not have the ability
to modify the locations of the hidden nodes, which, as suggested by Hypothesis 2, makes finding
an effective pattern of weights more difficult. Additionally, even with a substrate generated by
ES-HyperNEAT, HyperNEAT is not able to elaborate further on the existing structure, because it
takes the entire set of ANN connection weights to represent a partial solution.
7.4 Evolvability Analysis
Kirschner and Gerhart [31] define evolvability as “an organismʼs capacity to generate heritable pheno-
typic variation.” The highly evolvable representations found in biological systems have allowed natural
evolution to discover a great variety of diverse organisms. Thus facilitating a representationʼs effective
search (i.e., its evolvability) is an important research direction in evolutionary computation [43].
The dual task (Section 6) and the maze navigation domain (Section 7) suggest that the original
HyperNEAT fails to elaborate on existing ANN structure because it likely consumes the entire set
of connection weights to represent an intermediate solution. Furthermore, small mutations in the
CPPN can cause a shift in the location of information within the hypercube for which the original
HyperNEAT cannot compensate, making such evolved individuals fragile. However, ES-HyperNEAT
should be more robust, because it can compensate for shifts in the CPPN pattern by following
the movement of information within the hypercube (Hypothesis 2). This ability and the fact that
348
Artificial Life Volume 18, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
ES-HyperNEAT can elaborate on existing ANN structure (Hypothesis 3) should allow ES-HyperNEAT
to more easily generate individuals whose offspring exhibit diverse functional behaviors, and thus
more heritable phenotypic variation. To demonstrate this capability, the evolvability of the different
representations needs to be measured.
Kirschnerʼs definition reflects a growing consensus in biology that the ability to generate behav-
ioral variation is fundamental to evolvability [31, 41, 63]. Therefore, following Lehman and Stanley
[33], an individualʼs evolvability in this article is estimated by generating many children from it and
then measuring the degree of behavioral variation among those offspring. In effect, this measure
quantifies how well the underlying encoding enables behaviorally diverse mutations. To measure
variation, a behavioral distance measure is needed. Following Lehman and Stanley [33], behavioral
distance in the maze navigation domain is measured in this analysis by the Euclidean distance
between the ending positions of two individuals. Evolvability is measured every 50 generations,
when each individual in the population is forced to create 200 offspring by asexual reproduction.
A greedy algorithm calculates the evolvability by adding each individual to a list of behaviors if
its behavioral distance to all other individuals already in the list is higher than a given threshold.
Thus the number of added behaviors is an indicator of the individualʼs ability to generate behavioral
variation (i.e., its evolvability).
It is important to note that a random genetic mapping would likely not enable behaviorally diverse
mutations and therefore would have a low evolvability. Most of the networks produced would be
nonfunctional or display trivial behaviors (just going forward, spinning in circles, etc.), thus ending
in similar parts of the maze. The results in the previous section (Figure 12a) showed that evolv-
ing a successful maze navigator is a challenging task, which supports the hypothesis that generating
nontrivial behaviors through a random mapping is unlikely.
Figure 14 shows the average evolvability of the best-performing fixed-substrate variant FS10x1
compared with ES-HyperNEAT. The main result is that ES-HyperNEAT shows a significantly ( p <
0.001) higher evolvability across all generations, further explaining its better performance in the domains
presented in this article.
8 Experiment 3: Retina Problem
Modularity likely plays an important role in the evolvability of complex biological organisms [7, 13,
23, 29]. Lipson [35] defines functional modularity as the structural localization of function, which
allows parts of a solution to be optimized independently [29]. Because modularity enhances evolvability
and allows natural systems to scale to tasks of high complexity, it is an important ingredient in evolv-
ing complex networks, which is a major goal in the field of GDSs. ES-HyperNEAT should more easily
evolve modular ANNs than the original fixed-substrate HyperNEAT, because it has the capability to
start the evolutionary search with a bias toward locality and certain canonical ANN topographies, as
suggested by Hypothesis 4.
Figure 14. Comparing the evolvability of fixed-substrate and evolvable-substrate HyperNEAT. ES-HyperNEAT exhibits a
significantly higher evolvability throughout all generations. The results are averaged over 20 runs.
Artificial Life Volume 18, Number 4
349
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Figure 15. Retina problem. The artificial retina consists of 4 × 2 pixels that constitute the inputs to the ANN. Eight out of
16 possible patterns are considered left objects. The same is true for the right four pixels, though the eight valid patterns
are different. The picture is adapted from Kashtan and Alon [29].
Following Verbancsics and Stanley [62] and Clune et al. [7], the modular domain in this section is a
modified version of the retina problem, originally introduced by Kashtan and Alon [29]. The goal of the
ANN is to identify a set of valid 2 × 2 patterns on the left and right sides of a 4 × 2 artificial retina
(Figure 15). That is, the ANN must independently decide, for each pattern presented to the left and right
sides of the retina, if that pattern is a valid left or right pattern, respectively. Thus it is a good test of
the ability to evolve modular structures, because the left and right problem components are ideally
separated into different functional structures. The ANN setup is given below in Section 8.3.
While the original HyperNEAT approach and also the direct NEAT encoding perform poorly in
generating modular ANNs [7], HyperNEAT-LEO [62] showed that allowing HyperNEAT to evolve
the pattern of weights independently from the pattern of connection expression, while seeding
HyperNEAT with a bias toward local connectivity, allows modular structures to arise naturally.
Furthermore, the LEO achieved the best results in the retina left & right task by only seeding with
the concept of locality along the x axis [62]. That is, the seed CPPN starts with a Gaussian node G
− x2 as input and is connected to the LEO output. Therefore G peaks when the
that receives x1
two coordinates are the same, thereby seeding the CPPN with a concept of locality. This result
makes sense because the retina problem is distributed along the horizontal axis (Figure 15).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
8.1 Extending ES-HyperNEAT with the LEO
Because ES-HyperNEAT does not require any special changes to the traditional HyperNEAT
CPPN, enhancements like the LEO can in principle also be incorporated into ES-HyperNEAT.
Thus extending ES-HyperNEAT with an LEO is straightforward and should combine the advantages
of both methods: Evolving modular ANNs should be possible wherein the placement and density of
hidden nodes are determined solely from implicit information in the hypercube. In this combined
approach, once all connections are discovered by the weight-choosing approach (Section 5), only
those are kept whose LEO output is greater than zero. In fact, the idea that geometric concepts
such as locality can be imparted to the CPPN opens an intriguing opportunity to go further than
the LEO locality seed. That is, it is also possible to start the evolutionary search in ES-HyperNEAT
with a bias toward certain ANN topographies (which is not possible with HyperNEAT or
HyperNEAT-LEO), as explained in Section 8.2.
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
8.2 ES-HyperNEAT Geometry Seeding
Because the pattern output by the CPPN in ES-HyperNEAT is a kind of language for specifying
the locations of expressed connections and nodes, ES-HyperNEAT can be seeded to begin with a
bias toward certain ANN structures (e.g., ANNs with multiple hidden layers and connected inputs
and outputs) that should facilitate the evolutionary search. Especially in the initial generations,
ES-HyperNEAT runs the risk of being trapped in local optima where high fitness can be achieved
only by incorporating a subset of the available inputs. The new idea introduced in this article is to start
the evolutionary search with a bias toward certain ANN topographies, which provide a mechanism
for emulating key biases in the natural world that are provided ultimately by physics. For example,
350
Artificial Life Volume 18, Number 4
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
evolution could be seeded with an ANN topography that resembles the organization of the cortical
columns found in the human brain [51], potentially allowing higher cognitive tasks to be solved.
Providing such bias means escaping the black box of evolutionary optimization to provide a kind of
general domain knowledge. Even though ES-HyperNEAT could in principle discover the appropriate
ANN topography by itself, biasing the search with a good initial topography should thus make the search
less susceptible to local optima. While ES-HyperNEAT can modify and elaborate on such initial ANN
structure, the original HyperNEAT and HyperNEAT-LEO would likely not benefit from geometry
seeding, because they cannot compensate for movement of information within the hypercube, and
certain structures are a priori not representable if the nodes are not placed in the correct locations.
Figure 16 shows a CPPN that combines seeded locality and seeded geometry. In addition to the
Gaussian node G1 that specifies locality along the x axis [62], a second Gaussian node G2 is added
that receives y1 − y2 + b, where b is a bias, as input (Figure 16) and therefore creates horizontal
stripes of differing weights running through the hypercube along y1. Interestingly, changing the bias
input of G2 thus can immediately create ANNs with more or fewer hidden layers. In the experiments
reported here a bias weight of 0.33 was chosen, resulting in initial ANNs with two hidden layers,
which is similar to the setup of the fixed-substrate variant explained in the next section. It is
important to note that most connections will initially not be expressed, because of the locality seeding.
However, slight perturbations of the seed in the initial generation provide a variety of local connectivity
patterns and ANN topographies. That the organization of a locally connected two-hidden-layer
substrate can be entirely described by two new hidden nodes in the initial CPPN suggests the power
of the encoding and the expressiveness that is possible when seeding ES-HyperNEAT.
8.3 Retina Problem Setup
The substrate, which is based on setups of Verbancsics and Stanley [62] and Clune et al. [7], has eight input
nodes and two output nodes (Figure 17). Fixed-substrate HyperNEAT has two layers of hidden
nodes, with four hidden nodes each. Note that the substrate has three dimensions (x, y, z ). The ANN
substrate inputs receive either −3.0 or 3.0, depending on the state (e.g., off or on) for each retina input.
The left and right outputs specify the classification for the left and right retinas, respectively, where
values close to 1.0 indicate valid patterns. Values close to −1.0 indicate an invalid pattern. Six different
HyperNEAT approaches are compared to isolate the effects of the LEO and the hidden-layer seeding:
(cid:129) In the ES-HyperNEAT approach the placement and density of the hidden nodes and their
connections to the input and output nodes are determined entirely from the CPPN by the
algorithm in Section 3 without any seeding.
Figure 16. X-locality and geometry seeding. The CPPN is initialized with two Gaussian hidden nodes G1 and G2 that
take as input x1 − x2 and y1 − y2 + b, respectively. Whereas G1 is connected to the LEO with a bias of −1, G2 connects
to the weight output. G1 peaks when x1 and x2 are the same, thereby seeding the initial CPPNs with locality along the
x axis. G2 creates horizontal stripes of differing weights running through the hypercube, which induces the expression of
multiple hidden layers in the decoded ANN. Positive connections are dark, and negative connections are light.
Artificial Life Volume 18, Number 4
351
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Figure 17. Substrate configuration. The substrate consists of four layers with the inputs at y = 0.0, the first hidden layer
at y = 0.37, a second hidden layer at y = 0.61, and the outputs at y = 1.0. Note that this substrate has three dimensions.
The z coordinates are indicated by the different circle patterns. This substrate configuration is derived from the setups of
Verbancsics and Stanley [62] and Clune et al. [7], which established such a three-dimensional setup as standard for the
retina problem.
(cid:129) ES-HyperNEAT-LEO extends ES-HyperNEAT with LEO, which should facilitate the
evolution of modular ANNs.
(cid:129) ES-HyperNEAT with geometry seeding tests ES-HyperNEATʼs ability to take advantage of
initial geometric seeding through the CPPN. The seed, shown in Figure 16, creates ANNs
with two hidden layers with four neurons each, corresponding to the fixed-substrate retina
setup (Figure 17). Note that the functionality of the LEO is disabled in this setup.
(cid:129) ES-HyperNEAT-LEO with geometry seeding tests the hypothesis that both extensions,
LEO with locality seeding and geometric seeding (Figure 16), should be complementary
in increasing ES-HyperNEATʼs ability to generate modular networks for complicated
classification problems.
(cid:129) Following Verbancsics and Stanley [62], FS-HyperNEAT-LEO with x-locality seeding is the
original HyperNEAT approach with a fixed substrate and an additional LEO.
(cid:129) In the FS-HyperNEAT-LEO with geometry seeding approach the original Hyper-NEAT is also
seeded with x-locality and initial weight patterns (Figure 16) that intersect the positions of
the fixed hidden nodes (Figure 17). The hypothesis is that the additional geometric seeding
should not significantly increase fixed-substrate HyperNEATʼs performance, because small
variations in the initial seed will disrupt the alignment between the CPPN-expressed pattern
and hidden-node positions, for which the original HyperNEAT cannot compensate.
Note that the seed CPPN for all approaches lacks direct connections from the inputs to the weight
output in the CPPN. However, mutations on the seed to create the initial generation can connect
arbitrary inputs to arbitrary outputs. This setup has shown generally better performance than starting
with a fully connected CPPN. The fitness, which is computed the same way for all approaches,
is inversely proportional to the summed distance of the outputs from the correct values for all
256 possible patterns: F = 1000.0/(1.0 + E2), where E is the error. Other parameters are detailed
in Appendix 1.
8.4 Results
All results are averaged over 40 runs. Figure 18 shows the training performance over generations
for the different HyperNEAT variants and how frequently they solve the problem perfectly (i.e.,
correctly classify 100% of the patterns). Because FS-HyperNEAT-LEO succeds in almost every
352
Artificial Life Volume 18, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
run after 5,000 generations [62], to highlight the differences in the HyperNEAT variants, runs were
performed for a much shorter period of 2,000 generations (Figure 18b).
While ES-HyperNEAT solves the retina domain in only 30% of the runs, augmenting
ES-HyperNEAT with LEO and geometry seeding improves the chance of finding a solution to
57%. ES-HyperNEAT-LEO with geometry seeding reaches a significantly higher average best
fitness and finds a solution significantly faster than the other variants ( p < 0.05), confirming
Hypothesis 4 and the advantages of both ES-HyperNEAT extensions for the evolution of modular
ANNs. The performance of the original FS-HyperNEAT with LEO, on the other hand, decreases
from finding a solution in 30% of the runs to only finding the solution in 25% when seeded with
geometry, confirming that only ES-HyperNEAT can take advantage of such geometry seeding.
Surprisingly, just extending ES-HyperNEAT with an LEO alone does not increase performance but
instead decreases it slightly (though not significantly). Especially in the first 1,000 generations, there
is almost no increase in performance (Figure 18a), which suggests that pruning connections based on
the amount of information in the hypercube and additionally through the LEO without any geometry
seeding hinders the evolution of functional networks (i.e., ANNs with paths from the input to the
output neurons). Additionally, only seeding with geometry but not extending ES-HyperNEAT with
the LEO (i.e., ES-HyperNEAT with only geometry seeding) also decreases performance, which is
likely due to the increased crosstalk in the more fully connected ANNs.
A closer look at the structure of some final solutions gives insight into how ES-HyperNEAT-
LEO can elaborate on initial geometric seeding (Figure 19). ES-HyperNEAT-LEO can successfully
build on the initial structure, creating networks of varying complexity and resemblance to the initial
seed (Figure 16). Modularity is the prevailing pattern (Figure 19a,b,e), but non-modular ANNs also
emerge (Figure 19c). While most networks display a high degree of symmetry (Figure 19a–c),
reflecting the symmetry in the retina patterns (Figure 15), less symmetric ANNs are also discovered
(Figure 19d,e).
The main result is that it is the combination of LEO and geometry seeding that allows
ES-HyperNEAT more easily to evolve ANNs for the modular retina problem. The original
HyperNEAT approach, on the other hand, cannot take full advantage of those extensions and performs
significantly worse, even though it too benefits from the LEO.
9 Discussion and Future Work
The central insight in this article is that a representation that encodes the pattern of connectivity
across a network (such as in HyperNEAT) automatically contains implicit clues on where the nodes
should be placed to best capture the information stored in the connectivity pattern. Experimental
results show that ES-HyperNEAT significantly outperforms the original HyperNEAT while taking a
Figure 18. Average performance. The average best fitness over generations is shown for the retina domain (a) for the
different HyperNEAT variants, which are averaged over 40 runs. The fraction of 40 runs that successfully solve the domain
is shown in (b) for each of the HyperNEAT variants after 2,000 generations. The main result is that ES-HyperNEAT-LEO
with geometry seeding significantly outperforms all other approaches.
Artificial Life Volume 18, Number 4
353
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Figure 19. Example connectivity patterns from ES-HyperNEAT-LEO with geometry seeding in a modular domain. Modularity
is commonly found when ES-HyperNEAT-LEO is seeded with the geometry seed (a, b). Once modularity is found, the reg-
ularities needed to solve the task for each module can be discovered in the weight pattern. ES-HyperNEAT-LEO evolves
a variety of different ANNs with more or fewer hidden neurons and connections. Non-modular ANNs that solve the task
are also discovered (c), although with less frequency. Hidden nodes with recurrent connections are denoted by a smaller
concentric circle. In the electronic version, positive connections are dark (black), and negative connections are light (red).
step toward more biologically plausible ANNs and significantly expanding the scope of neural
structures that evolution can discover. This section explores the implications of this capability
and its underlying methodology.
9.1 Dictating Node Locations
The convention in HyperNEAT of the last several years that the user would simply decide a priori
where the nodes belong evaded the deeper mystery about how connectivity relates to node place-
ment. As suggested by Hypothesis 2, dictating the location of nodes makes it harder for the original
HyperNEAT to represent the correct pattern, which the reported results in a variety of domains
confirm. While ES-HyperNEAT can compensate for movement of information within the hyper-
cube by expressing the hidden nodes at slightly different locations (e.g., Figure 13c,d), representing the
correct pattern for the original HyperNEAT is more difficult. The significantly reduced performance of
the vertical node arrangement FS1x10 in the maze navigation domain (Figure 12a) indicates that the
more complex the domain, the more restrictive it is to have nodes at fixed locations.
One way to interpret the preceding argument is that the locations of useful information in the
hypercube are where the nodes need to be. That way, the size of the brain is roughly correlated with
its complexity. There is no need for a billion neurons to express a simple Braitenberg vehicle. Even if
a billion neurons were summoned for the task, many of their functions would end up redundant,
which geometrically means that large cross sections of the hypercube would be uniform, containing
no useful information. The ES-HyperNEAT approach in this article is a heuristic attempt to formalize
this notion and thereby correlate size with complexity. In this context, nodes become a kind of
harbinger of complexity, proliferating where it is present and receding where it is not. Thus the solu-
tion to the mystery of the relationship between nodes and connections is that nodes are sentinels of
complex connectivity; they are beacons of information in an infinite cloud of possible connections.
9.2 Incrementally Building on Stepping Stones
Previous work showed that ES-HyperNEAT and the original HyperNEAT exhibit similar performance
in a simple navigation domain [44]. However, in the more complicated navigation domain presented
354
Artificial Life Volume 18, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
here (Section 7), the best fixed-substrate HyperNEAT method (FS10x1) solves the domain in only
45% of runs. How can this poor performance be explained?
The problem is that the increased complexity of the domain requires incrementally building on
previously discovered stepping stones. While direct encodings like NEAT [56, 58] can complexify
ANNs over generations by adding new nodes and connections through mutation, the indirect
HyperNEAT encoding tends to start with already fully connected ANNs [8], which take the
entire set of ANN connection weights to represent a partial task solution. On the other hand,
ES-HyperNEAT is able to elaborate on existing structure in the substrate during evolution (Fig-
ure 13), confirming Hypothesis 3. This result is important because the more complicated the task,
the more likely that it will require a neuroevolution method that benefits from previously discovered
stepping stones.
These results also explain why uniformly increasing the number of hidden nodes in the substrate
does not necessarily increase HyperNEATʼs performance. In fact, FS8x8 performs significantly
worse than FS5x5, which is likely due to the increased crosstalk that each neuron experiences.
9.3 Network Complexity
An important question is whether the number of neurons created in ES-HyperNEAT networks
is too large. In fact, in some cases the approach may find solutions with several times more nodes
and connections than needed for the minimum solution. While the real test of this question will
emerge from further research, perhaps the singular focus within the field of NE on absolute minimal
structure is misplaced. When the products of evolution contain potentially billions of neurons as in
nature, it is almost certainly necessary that an encoding that can reach such levels has the ability to
solve particular problems with significant flexibility in the number of neurons in the solution. Of
course, if a particular level of intelligence can be achieved with only a million neurons, then a solu-
tion with a billion would be undesirable. However, too much restriction on variation in the number
of neurons is likely to be equally disruptive. In this situation, quibbling about a few dozen more
or fewer neurons may be missing the forest for the trees. In a larger context, all of the networks
reported in this work are small in a biological sense, as they should be.
It is important to keep in mind that the larger ES-HyperNEAT solutions are nevertheless optimized
more quickly than their fixed-substrate counterparts. An indirectly encoded neuroevolution algorithm
is not the same as a direct encoding like NEAT that complexifies by adding one node at a time to
find just the right number of nodes for a task. The promise of the indirect encoding is rather to evolve
very large networks that would be prohibitive to such direct encodings, with thousands or more nodes.
Figure 12c shows that the substrate evolution algorithm can actually create increasingly complex
indirectly encoded networks even though it is not explicitly designed to do so (e.g., like regular
NEAT) and that it can encode large ANNs from compact CPPN representations. One reason for this
capability is often to increase the impact of adding new nodes and connections to the CPPN increases
the complexity of the pattern it encodes. Because ES-HyperNEAT in effect attempts to match the
structures it discovers in the hypercube to the complexity of the pattern within it, it makes sense that
as the size of the CPPN increases, the complexity of the ANN substrate it encodes would generally
increase as well.
ES-HyperNEATʼs new capabilities and its higher evolvability (Figure 14) should enable more
complex tasks to be solved in the future that require placing a large and unknown number of nodes,
and the traversal of many stepping stones. The more complex the task, the more important it will
be to free the user from the burden of configuring the substrate by hand. Also importantly, the
approach has the potential to create networks from several dozen nodes up to several million or
more, which will be necessary in the future to create truly intelligent systems.
9.4 Geometry Seeding
Whereas the original HyperNEAT only allowed seeding with a bias toward local connectivity [62],
ES-HyperNEAT can also be seeded with a bias toward certain ANN topographies. The results in
Artificial Life Volume 18, Number 4
355
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
the retina problem confirm Hypothesis 4: The combination of LEO and geometry seeding allows
the approach more easily to evolve modular ANNs, yet the original HyperNEAT approach cannot
take full advantage of such a seed.
While the work of Verbancsics and Stanley [62] took a step in the direction of incorporating
important geometric principles (e.g., locality) that are helpful to create structures that resemble those
of nature, the geometry seeding presented here takes a step further. The idea of seeding with a bias
toward certain types of structures is important because it provides a mechanism for emulating key
biases in the natural world (such as the efficiency of modular separation) that are provided ultimately
by physics.
As noted by Verbancsics and Stanley [62], the better performance with an initial bias toward
locality suggests that the path to encoding locality is inherently deceptive with respect to the fitness
function in the retina task. Such deception may turn out to be common when geometric principles
such as locality that are conceptually orthogonal to the main objective are nevertheless essential to
achieving the goal. Thus seeding with the right geometric bias may prove an important tool to avert
deception in many domains.
Overall, ES-HyperNEAT thus advances the state of the art in neuroevolution beyond the original
HyperNEAT and has the potential to create large-scale ANNs for more complicated tasks, such as
robots driven by raw high-resolution vision, strategic game players, or robot assistants. For the field
of AI, the idea that we are beginning to be able to reproduce some of the phenomena produced
through natural evolution (e.g., compactly encoded regular and modular networks) at a high level of
abstraction is important because the evolution of brains ultimately produced the seat of intelligence
in nature.
Another interesting future research direction is to augment ES-HyperNEAT with the ability to
indirectly encode plastic ANNs as a pattern of local learning rules [45]. Plastic networks can adapt
and learn from past experience and, together with ES-HyperNEATʼs ability to create complex
ANNs, could allow the evolution of agents for more lifelike cognitive tasks.
10 Conclusions
This article has presented a novel approach to automatically deducing node geometry based on
implicit information in an infinite-resolution pattern of weights. Evolvable-substrate HyperNEAT
not only evolves the location of every neuron in the brain, but also can represent regions of varying
density, which means resolution can increase holistically over evolution. To demonstrate this
approach, ES-HyperNEAT evolved controllers for dual task, maze navigation, and modular retina
problems. Analysis of the results and the evolved ANNs showed that the improved performance
stems from ES-HyperNEATʼs ability to evolve ANNs with partial and targeted connectivity,
elaborate an existing ANN structure, and compensate for movement of information within the
underlying hypercube. Additionally, ES-HyperNEAT can more easily evolve modular ANNs when
biased toward locality and certain canonical ANN topographies. The main conclusion is thus that
ES-HyperNEAT is a promising new approach that can create complex, regular, and modular ANNs
as a function of neural geometry.
Acknowledgments
The authors would like to thank the Editor and anonymous reviewers for their valuable comments
and suggestions, which were helpful in improving the article. This material is based upon work sup-
ported by the US Army Research Office under Award No. W911NF-11-1-0489 and the DARPA
Computer Science Study Group (CSSG Phase 3) Grant No. N11AP20003. It does not necessarily
reflect the position or policy of the government, and no official endorsement should be inferred.
References
1. Aaltonen, T., et al. (2010). Measurement of the top quark mass with dilepton events selected using
neuroevolution at CDF. Physical Review D, 81, 030102.
356
Artificial Life Volume 18, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
2. Angeline, P. J. (1995). Morphogenic evolutionary computations: Introduction, issues and examples.
In J. R. McDonnell, R. G. Reynolds, & D. B. Fogel (Eds.), Evolutionary Programming IV: The Fourth
Annual Conference on Evolutionary Programming (pp. 387–401).
3. Angeline, P. J., Saunders, G. M., & Pollack, J. B. (1994). An evolutionary algorithm that constructs
recurrent neural networks. IEEE Transactions on Neural Networks, 5(1), 54–65.
4. Astor, J. S., & Adami, C. (2000). A developmental model for the evolution of artificial neural networks.
Artificial Life, 6(3), 189–218.
5. Bentley, P. J., & Kumar, S. (1999). The ways to grow designs: A comparison of embryogenies for
an evolutionary design problem. In Proceedings of the Genetic and Evolutionary Computation Conference
(GECCO-1999) (pp. 35–43).
6. Bongard, J. (2002). Evolving modular genetic regulatory networks. In Proceedings of the 2002 Congress
on Evolutionary Computation (CEC-2002), Vol. 2 (pp. 1872–1877).
7. Clune, J., Beckmann, B. E., McKinley, P., & Ofria, C. (2010). Investigating whether HyperNEAT
produces modular neural networks. In GECCO ʼ10: Proceedings of the Genetic and Evolutionary Computation
Conference (pp. 635–642).
8. Clune, J., Beckmann, B. E., Ofria, C., & Pennock, R. T. (2009). Evolving coordinated quadruped
gaits with the HyperNEAT generative encoding. In Proceedings of the IEEE Congress on Evolutionary
Computation (CEC-2009) Special Section on Evolutionary Robotics.
9. Clune, J., Stanley, K., Pennock, R., & Ofria, C. (2011). On the performance of indirect encoding across
the continuum of regularity. IEEE Transactions on Evolutionary Computation, 15(3), 346–367.
10. Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of Control,
Signals, and Systems, 2(4), 303–314.
11. DʼAmbrosio, D., & Stanley, K. O. (2007). A novel generative encoding for exploiting neural
network sensor and output geometry. In Proceedings of the Genetic and Evolutionary Computation Conference
(GECCO 2007).
12. Drchal, J., Koutnık, J., & Šnorek, M. (2009). HyperNEAT controlled robots learn to drive on roads
in simulated environment. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2009).
13. Dürr, P., Mattiussi, C., & Floreano, D. (2010). Genetic representation and evolvability of modular neural
controllers. IEEE Computational Intelligence Magazine, 5(3), 10–19.
14. Eggenberger, P. (1997). Creation of neural networks based on developmental and evolutionary principles.
In W. Gerstner, A. Germond, M. Hasler, & J.-D. Nicoud (Eds.), Seventh International Conference on Artificial
Neural Networks (ICANN-97) (pp. 337–342).
15. Eggenberger, P. (1997). Evolving morphologies of simulated 3D organisms based on differential
gene expression. In Fourth European Conference on Artificial Life (pp. 205–213).
16. Finkel, R., & Bentley, J. (1974). Quad trees: A data structure for retrieval on composite keys.
Acta Informatica, 4(1), 1–9.
17. Floreano, D., Dürr, P., & Mattiussi, C. (2008). Neuroevolution: From architectures to learning.
Evolutionary Intelligence, 1(1), 47–62.
18. Gauci, J., & Stanley, K. O. (2008). A case study on the critical role of geometric regularity in machine
learning. In Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence (AAAI-2008).
19. Gauci, J., & Stanley, K. O. (2010). Autonomous evolution of topographic regularities in artificial
neural networks. Neural Computation, 22, 1860–1898.
20. Gomez, F. J., & Miikkulainen, R. (1999). Solving non-Markovian control tasks with neuroevolution.
In Proceedings of the 16th International Joint Conference on Artificial Intelligence (pp. 1356–1361).
21. Green, C. (2003–2006). SharpNEAT homepage. http://sharpneat.sourceforge.net/.
22. Gruau, F., Whitley, D., & Pyeatt, L. (1996). A comparison between cellular encoding and direct
encoding for genetic neural networks. In Genetic Programming 1996: Proceedings of the First Annual
Conference (pp. 81–89).
23. Hansen, T. F. (2003). Is modularity necessary for evolvability? Remarks on the relationship between
pleiotropy and evolvability. Biosystems, 69(2–3), 83–94.
Artificial Life Volume 18, Number 4
357
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
24. Harding, S., Miller, J. F., & Banzhaf, W. (2010). Developments in Cartesian genetic programming:
Self-modifying CGP. Genetic Programming and Evolvable Machines, 11(3–4), 397–439.
25. Harvey, I. (1993). The artificial evolution of adaptive behavior. Ph.D. thesis, School of Cognitive and
Computing Sciences, University of Sussex, UK.
26. Hornby, G. S., & Pollack, J. B. (2002). Creating high-level components with a generative representation
for body-brain evolution. Artificial Life, 8(3), 223–246.
27. Jakobi, N. (1995). Harnessing morphogenesis. In Proceedings of Information Processing in Cells and Tissues
(pp. 29–41).
28. Kandel, E. R., Schwartz, J. H., & Jessell, T. M. (Eds.). (1991). Principles of neural science (3rd ed.).
Amsterdam: Elsevier.
29. Kashtan, N., & Alon, U. (2005). Spontaneous evolution of modularity and network motifs. Proceedings
of the National Academy of Sciences of the United States of America, 102(39), 13773.
30. Khan, G. M., Miller, J. F., & Halliday, D. M. (2011). Evolution of Cartesian genetic programs for
development of learning neural architecture. Evolutionary Computation, 19(3), 469–523.
31. Kirschner, M., & Gerhart, J. (1998). Evolvability. Proceedings of the National Academy of Sciences of the
United States of America, 95(15), 8420.
32. Lehman, J., & Stanley, K. O. (2008). Exploiting open-endedness to solve problems through the search
for novelty. In S. Bullock, J. Noble, R. Watson, & M. Bedau (Eds.), Proceedings of the Eleventh International
Conference on Artificial Life (Alife XI).
33. Lehman, J., & Stanley, K. O. (2011). Improving evolvability through novelty search and self-adaptation.
In Proceedings of the 2011 IEEE Congress on Evolutionary Computation (pp. 2693–2700).
34. Lehman, J., & Stanley, K. O. (2011). Abandoning objectives: Evolution through the search for novelty
alone. Evolutionary Computation, 19(2), 189–223.
35. Lipson, H. (2007). Principles of modularity, regularity, and hierarchy for scalable systems. Journal of
Biological Physics and Chemistry, 7(4), 125.
36. Martin, A. P. (1999). Increasing genomic complexity by gene duplication and the origin of vertebrates.
The American Naturalist, 154(2), 111–128.
37. Miller, J. F. (2004). Evolving a self-repairing, self-regulating, French flag organism. In Proceedings of the
Genetic and Evolutionary Computation Conference (GECCO-2004).
38. Miller, J. F., & Thomson, P. (2000). Cartesian genetic programming. In Proceedings of the Third European
Conference on Genetic Programming (pp. 121–132).
39. Mjolsness, E., Sharp, D. H., & Reinitz, J. (1991). A connectionist model of development. Journal of
Theoretical Biology, 152, 429–453.
40. Nolfi, S., & Parisi, D. (1992). Growing neural networks. In C. G. Langton (Ed.), Proceedings of the Workshop
on Artificial Life (ALIFE ʼ92).
41. Pigliucci, M. (2008). Is evolvability evolvable? Nature Reviews Genetics, 9(1), 75–82.
42. Reil, T., & Husbands, P. (2002). Evolution of central pattern generators for bipedal walking in a
real-time physics environment. IEEE Transactions on Evolutionary Computation, 6(2), 159–168.
43. Reisinger, J., Stanley, K. O., & Miikkulainen, R. (2005). Towards an empirical measure of evolvability.
In Genetic and Evolutionary Computation Conference (GECCO2005) workshop program (pp. 257–264).
44. Risi, S., Lehman, J., & Stanley, K. O. (2010). Evolving the placement and density of neurons in the
HyperNEAT substrate. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2010)
(pp. 563–570).
45. Risi, S., & Stanley, K. O. (2010). Indirectly encoding neural plasticity as a pattern of local rules.
In S. Doncieux, B. Girard, A. Guillot, J. Hallam, J.-A. Meyer, & J.-B. Mouret (Eds.), From Animals
to Animats 11, Proceedings of the 11th International Conference on Simulation of Adaptive Behavior (pp. 533–543).
Berlin: Springer.
46. Risi, S., & Stanley, K. O. (2011). Enhancing ES-HyperNEAT to evolve more complex regular
neural networks. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2011)
(pp. 1539–1546).
358
Artificial Life Volume 18, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
47. Rosenfeld, A. (1980). Quadtrees and pyramids for pattern recognition and image processing. In Proceedings
of the 5th International Conference on Pattern Recognition (pp. 802–809).
48. Saravanan, N., & Fogel, D. B. (1995). Evolving neural control systems. IEEE Expert: Intelligent Systems
and Their Applications, 10(3), 23–27.
49. Secretan, J., Beato, N., DʼAmbrosio, D. B., Rodriguez, A., Campbell, A., Folsom-Kovarik, J. T., &
Stanley, K. O. (2011). Picbreeder: A case study in collaborative evolutionary exploration of design space.
Evolutionary Computation, 19(3), 373–403.
50. Secretan, J., Beato, N., DʼAmbrosio, D. B., Rodriguez, A., Campbell, A., & Stanley, K. O. (2008).
Picbreeder: Evolving pictures collaboratively online. In CHI ʼ08: Proceedings of the Twenty-sixth Annual
SIGCHI Conference on Human Factors in Computing Systems (pp. 1759–1768).
51. Sporns, O. (2002). Network analysis, complexity, and brain function. Complexity, 8(1), 56–60.
52. Stanley, K. O. (2007). Compositional pattern producing networks: A novel abstraction of development.
Genetic Programming and Evolvable Machines, 8(2), 131–162.
53. Stanley, K. O., Bryant, B. D., & Miikkulainen, R. (2003). Evolving adaptive neural networks with
and without adaptive synapses. In Proceedings of the 2003 IEEE Congress on Evolutionary Computation
(CEC-2003).
54. Stanley, K. O., Bryant, B. D., & Miikkulainen, R. (2005). Real-time neuroevolution in the NERO
video game. IEEE Transactions on Evolutionary Computation, 9(6), 653–668.
55. Stanley, K. O., DʼAmbrosio, D. B., & Gauci, J. (2009). A hypercube-based indirect encoding for
evolving large-scale neural networks. Artificial Life, 15(2), 185–212.
56. Stanley, K. O., & Miikkulainen, R. (2002). Evolving neural networks through augmenting topologies.
Evolutionary Computation, 10, 99–127.
57. Stanley, K. O., & Miikkulainen, R. (2003). A taxonomy for artificial embryogeny. Artificial Life, 9(2),
93–130.
58. Stanley, K. O., & Miikkulainen, R. (2004). Competitive coevolution through evolutionary complexification.
Journal of Artificial Intelligence Research, 21, 63–100.
59. Strobach, P. (1991). Quadtree-structured recursive plane decomposition coding of images. Signal
Processing, 39, 1380–1397.
60. Taylor, M. E., Whiteson, S., & Stone, P. (2006). Comparing evolutionary and temporal difference
methods in a reinforcement learning domain. In GECCO 2006: Proceedings of the Genetic and Evolutionary
Computation Conference (pp. 1321–1328).
61. Verbancsics, P., & Stanley, K. O. (2010). Evolving static representations for task transfer. Journal of
Machine Learning Research, 99, 1737–1769.
62. Verbancsics, P., & Stanley, K. O. (2011). Constraining connectivity to encourage modularity in
HyperNEAT. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2011).
63. Wagner, G. P., & Altenberg, L. (1996). Perspective: Complex adaptations and the evolution of
evolvability. Evolution, 50(3), 967–976.
64. Watson, J. D., Hopkins, N. H., Roberts, J. W., Steitz, J. A., & Weiner, A. M. (1987). Molecular biology of
the gene (4th ed.). Menlo Park, CA: Benjamin Cummings.
65. Whiteson, S., & Stone, P. (2006). Evolutionary function approximation for reinforcement learning.
Journal of Machine Learning Research, 7, 877–917.
66. Yao, X. (1999). Evolving artificial neural networks. Proceedings of the IEEE, 87(9), 1423–1447.
67. Zigmond, M. J., Bloom, F. E., Landis, S. C., Roberts, J. L., & Squire, L. R. (Eds.). (1999). Fundamental
neuroscience. London: Academic Press.
Artificial Life Volume 18, Number 4
359
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Appendix 1: Experimental Parameters
All experiments were run with the HyperSharpNEAT Simulator and Experimental Platform v1.0,
which builds on a modified version of the public domain SharpNEAT package [21]. The simulator
and the ES-HyperNEAT source code can be found at http://eplex.cs.ucf.edu/ESHyperNEAT.
Because HyperNEAT differs from the original NEAT only in its set of activation functions, it uses
mainly the same parameters [56]. All experiments in this article used the same parameters except as
explained below. The size of each population was 300 with 10% elitism. Sexual offspring (50%) did
not undergo mutation. Asexual offspring (50%) had 0.94 probability of link weight mutation, 0.03
of link addition, and 0.02 of node addition. The NEAT coefficients for determining species similarity
were 1.0 for nodes and connections, and 0.1 for weights. Parameter settings are based on standard
SharpNEAT defaults and prior reported settings for NEAT [56, 58]. Through preliminary experimenta-
tion, they were found to be robust to moderate variation.
The available CPPN activation functions for the dual task and navigation domain were sigmoid,
Gaussian, absolute value, and sine. Following Verbancsics and Stanley [62], the activation functions for
the retina problem were absolute value, sigmoid, Gaussian, linear, sine, step, and ramp. As in previous
work [55], all CPPNs received the length of the queried connection as an additional input. The band-
pruning threshold for all ES-HyperNEAT experiments was set to 0.3. Iterated ES-HyperNEAT had an
initial and maximum resolution of 8 × 8 for the dual task and navigation experiment. The maximum
resolution for the retina problem was increased to 32 × 32 with a division threshold of 0.5, reflecting
the increased task complexity. The variance and division threshold were set to 0.03. Finally, the itera-
tion level was 1, which means that ES-HyperNEAT checks for hidden nodes one iteration beyond the
first hidden nodes discovered directly from the inputs.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
360
Artificial Life Volume 18, Number 4
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Appendix 2: ES-HyperNEAT Pseudocode
Algorithm 1: DivisionAndInitialization(a, b, outgoing)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Artificial Life Volume 18, Number 4
361
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Algorithm 2: PruningAndExtraction(a, b, connections, p, outgoing)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
362
Artificial Life Volume 18, Number 4
S. Risi and K. O. Stanley
An Enhanced Hypercube-Based Encoding
Algorithm 3: ES-HyperNEAT
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Artificial Life Volume 18, Number 4
363
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
8
4
3
3
1
1
6
6
3
1
2
1
a
r
t
l
/
_
a
_
0
0
0
7
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3