Jing Liu**
University of New South Wales
Hussein A. Abbass**
University of New South Wales
Weicai Zhong*,**
University of New South Wales
David G. Green†
Monash University
Keywords
Complex networks, community, scale-free
networks
Local-Global Interaction and the
Emergence of Scale-Free Networks
with Community Structures
Abstract Understanding complex networks in the real world is a
nontrivial task. In the study of community structures we normally
encounter several examples of these networks, which makes any
statistical inferencing a challenging endeavor. Researchers resort to
computer-generated networks that resemble networks encountered in
the real world as a means to generate many networks with different
sizes, while maintaining the real-world characteristics of interest. The
generation of networks that resemble the real world turns out in itself
to be a complex search problem. We present a new rewiring algorithm
for the generation of networks with unique characteristics that
combine the scale-free effects and community structures encountered
in the real world. The algorithm is inspired by social interactions in
the real world, whereby people tend to connect locally while
occasionally they connect globally. This local-global coupling turns
out to be a powerful characteristics that is required for our proposed
rewiring algorithm to generate networks with community structures,
power law distributions both in degree and in community size,
positive assortative mixing by degree, and the rich-club phenomenon.
1 Introduction
Complex networks describe a wide range of systems in nature and society. Commonly cited examples
include the Internet, e-mail interactions, gene regulatory networks, science collaboration networks,
sensor and communication networks, citation networks, food webs, metabolic networks, and many
more [2, 20, 29, 30, 39, 47, 52, 54]. Because of their significant contribution to our understanding of
complex systems, complex networks have been attracting much interest and their study has under-
gone a remarkable development over the last decade. Most of the work in this field has concentrated
on two aspects: properties found in real-world networks, and ways to find models to build under-
standing about the emergence of these properties and the self-organizing process in complex systems
[19, 51].
Two of the best-known properties exhibited by many real-world networks are the small-world
property [59] and the scale-free property [4]. The former suggests that a network has a high degree
* Contact author.
** School of Engineering and Information Technology, The University of New South Wales at the Australian Defence Force Academy,
Canberra, ACT 2600, Australia. E-mail: jing.liu@adfa.edu.au ( J.L.); h.abbass@adfa.edu.au (H.A.A.); w.zhong@adfa.edu.au (W.Z.)
† Centre for Research in Intelligent Systems, Monash University, Clayton, Victoria 3800, Australia. E-mail: david.green@monash.edu
© 2011 Massachusetts Institute of Technology
Artificial Life 17: 263–279 (2011)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
of clustering and a small average distance between any two nodes, while the latter entails a power-
law distribution of node degrees, P(k) ∼ k-g, where P(k) is the probability that a node in the net-
work has k connections to other nodes and g is a positive real number determined by the given
network. With the progress of our understanding about networks, another property appeared on the
stage and attracted considerable attention recently, namely, communities [21, 35, 41], which are groups
of nodes characterized by having more internal than external connections between them.
There is a long list of work contributing to the understanding of the emergence of the above
properties. The available network models are all based on one aspect of reality. Many scientists have
focused their attention on growing networks in which a new node is added to networks over time
[4]. However, as indicated by [31], growth models of this type are quite inappropriate as models of
the growth of social networks. One of the reasons is that, although new nodes are of course con-
tinually added to social networks, the time scale on which people make and break social connections
is much shorter than the time scale on which nodes join or leave the network. Thus, the addition and
removal of nodes will not be a major factor determining the instantaneous structure of social net-
works, and to a first approximation these networks can therefore be treated using a model with a
constant number of nodes but a varying number and arrangement of edges. Many models of this
type have been proposed [24, 31, 33, 55], in which the frequently used methods to tune the con-
nections are limited degree and random weights.
Further, there is also another important class of network model in which both the numbers of
nodes and edges are constant through the whole evolutionary process, namely, rewiring network
models. The classic example of Watts and Strogatz [59] for small-world networks is of this type,
and there is also some work dedicated to the scale-free case [9, 42, 46, 61]. Network rewiring is
related to some multiurn models [22, 23, 43, 44] and to the zero-range process [16, 17, 53]. Because
most systems in the real world cannot grow indefinitely, networks of constant size have many ap-
plications, such as pottery designs, dog breeds, and baby name popularity in the transmission of
cultural artifacts [5–7, 27, 28, 36], the distribution of family names in constant populations [62],
the diversity of genes [12, 32], the voter model [34, 56], and minority game strategies [3]. Exact
solutions are also given in [18] for the rewiring model of a bipartite graph, using a mixture of random
and preferential attachment. The full mean-field equations for the degree distribution and its gen-
erating function are given.
Grönlund and Holme [25] extended the original seceder model [13, 14, 57] to a social network
rewiring model by starting from an Erdős-Rényi (ER) random graph [15]. This model reproduces
the emergence of community structures, which is attributed to the effect of the agentsʼ personal
rationales as well as to the properties of high clustering and positive assortative mixing by degree.
However, the degree distribution in networks generated by this model is not a power law, but a peak
around the average degree that is exponentially decaying. Moreover, no analysis of the distribution of
community size is given.
In this article, we propose a rewiring network model based on social interactions. Although social
interactions can be formalized in many different ways, one of the frequently used classifications
being friendship [55], we use a more general and simpler way, namely, daily people-to-people inter-
actions without considering their friendship. Such interactions between people often exhibit two
distinct forms and occur at different times. In many scenarios, people normally interact with a small
group of individuals, such as their office colleagues or close family members, but at times will come
into contact with a wider group, as when they attend meetings or visit family members far away. We
refer to the former case as local interaction and to the latter as global interaction. Here, we use the edge
rewiring process in undirected graphs to depict such interactions.
Similar to the model in [25], in our model no weights are attached to edges and no limitation is
put on the degree of each node. Also, the evolution starts from an ER graph, and only rewiring is
conducted. However, on tuning the single parameter governing the ratio of the two types of inter-
actions, the resulting networks undergo a gradual structural transition from a community-free and
Gaussian degree distribution topology to one of scale-free degree distribution and community struc-
ture with both high quality and power law community size distribution.
264
Artificial Life Volume 17, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
In the rest of this article, the network model is first described in the next section. Sections 3 and 4
study the community structure and degree distribution of the generated networks, respectively. Sec-
tion 5 studies assortative mixing at both the network level and local level. After that, Section 6 com-
pares networks generated by our model with real-world Internet topology at the autonomous system
(AS) level—namely, the AS graph—and studies the rich-club phenomenon. Finally, we discuss the
experimental results and summarize the conclusions in Section 7.
2 Model
During the evolutionary process, a sequence of graphs {Gt} is produced. The set of nodes, V, of
each graph in this sequence is the same; it consists of N nodes, while the set of edges, Et , is time-
dependent but always has M edges. Here, the number of iterations of the algorithm determines the
simulation time t = 0, 1, 2, … , tmax. {G0} is the initial graph, which is constructed by the ER random
graph model: A graph with N nodes and M edges is constructed by starting from isolated nodes and
then iteratively introducing edges between node pairs chosen with uniform randomness and with the
restriction that no multiple edges or loops are allowed. However, since the original ER model does
not guarantee the connectivity of the generated networks, we revise it slightly: Edges are first created
to connect all nodes, and then more edges are created. After the initial graph is constructed, the
following rewiring procedures are repeated until tmax is reached.
(cid:129) Step 1: A node vi is selected with probability Pvi , which is proportional to viʼs degree kvi.
That is,
Pvi
¼ kviP
N
j¼1 kvj
Let Vvi be the set of nearest neighbors of vi (i.e., there is an edge connecting vi and each
>1 be the set of nearest neighbors of vi whose degrees are larger than 1 (i.e.,
2 be the set of
>1, vi is not the only nearest neighbor of that node), and Vvi
node in Vvi
for each node in Vvi
nearest neighbors of all nodes in Vvi.
), Vvi
(cid:129) Step 2: Randomly draw a real number from [0, 1], and if this number is smaller than Plocal, a
predefined parameter, go to step 3; otherwise, go to step 4.
(cid:129) Step 3 (local interactions):
>1 or Vvi
(i) If Vvi
(ii) Delete the edge between vi and vi
2/Vvi is empty, then go to step 1.
j, where vi
j denotes the j th element in Vv
>1 and
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
Vvi
kv j
∩ Vv j
− 1
i
i
ð1Þ
ð2Þ
is the smallest for j = 1, 2, … , |Vvi
>1|, where |· | denotes the cardinality of the set.
(iii) If the resulting network is not connected, recover the edge deleted in (ii), and then go
back to step 1.
(iv) Select a node in Vvi
go to step 1.
2 based on a probability proportional to its degree to connect to vi, and
Artificial Life Volume 17, Number 4
265
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
(cid:129) Step 4 (global interactions):
= N − 1, so that vi already connects to all other N − 1 nodes, go to step 1.
j based
(i) If kvi
(ii) Delete the edge between vi and one of its nearest neighbors vi
on a probability inversely proportional to its degree. That is,
j, and select vi
¼ 1−
Pv j
i
kv j
iPkvi
l ¼1 kv1
i
ð3Þ
(iii) If the resulting network is not connected, recover the edge deleted in (ii) and go to
step 1.
(iv) Select a node that is not in Vvi, based on a probability proportional to its degree, to
connect to vi, and go to step 1.
If Vvi
2/Vvi is empty, all viʼs neighborsʼ neighbors are also viʼs neighbors, and step 3(ii) is used to
evaluate the number of shared members between vi and its nearest neighbors. In general, the above
model evolves random networks using two kinds of interactions, in which the choice is governed by
the only parameter, Plocal. At each time step, only one edge is rewired. In local interactions, an edge is
rewired to one of one endʼs neighborsʼ neighbors, while in global interactions, an edge is rewired to
any node that is not one of the two endsʼ neighbors. However, in both interactions, the connectivity
of the whole network is always maintained.
In local interactions, we used the analogy that we often become a friendʼs friend, while in global
interactions, we used the idea of preferential attachments. Although each of these ideas has been
studied in depth previously, our work focuses on studying their combined effect, since our model is
completely characterized by the ratio of global to local interactions. In the following sections, we
simulate the above model and study various properties of the generated networks.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3 Community Structure
A large body of work has been devoted to identifying community structures in networks. Newman
and Girvan [41] introduced an elegant concept, the modularity Q, to measure the goodness of a
community partition. Suppose a network is divided into m disjoint communities. Then
Q ¼
(cid:4)
eii − a2
i
Xm
(cid:3)
i¼1
ð4Þ
where eii is the fraction of edges that fall within community i, and ai is the fraction of all ends of
edges that are attached to nodes in community i; that is, ai = ∑j eij .
Basically, Q measures the deviation between the chance for edges among communities to be
generated due to the community structure and the chance for the edges to be generated randomly.
Extensive experimental results have demonstrated that Q is an effective measure for community
quality, in that a maximal Q is a good indicator of the best community structure and therefore
the best community number m. In practice, a value of Q greater than 0.3 appears to indicate sig-
nificant community structure, and the value of Q for real-world networks typically falls in the range
from 0.3 to 0.7. Higher values are rare.
266
Artificial Life Volume 17, Number 4
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
In the following experiments, we use the method proposed in [40] to extract communities from
networks at certain time steps, and Q to evaluate the quality of the extracted communities. The
first part is devoted to studying the community quality, and the second part focuses on community
sizes.
3.1 Community Quality
Since Plocal is our sole parameter, we first study how Plocal affects community quality. We increase
Plocal from 0.5 to 1.0 in steps of 0.05. The number of nodes and the average degree are set to 1000
and 10, respectively. For each different Plocal value, 10 graph instances are evolved independently,
and to be sure that the structure of the random graph disappears, we run the model until t max = 5 ×
104. The obtained Q values for each parameter setting are shown in Figure 1.
Figure 1 clearly shows the trend of Q changing with Plocal. The larger the value of Plocal is, the
larger the value of Q is. When Plocal is smaller than 0.75, Q is always smaller than 0.3, which indicates
no community structure emerging, while when Plocal is larger than 0.75, Q is always larger than 0.3
and even increases to nearly 0.9 when Plocal reaches 1.00. That is to say, when 0.75 ≤ Plocal ≤ 1.00,
significant community structures emerge in the evolving networks.
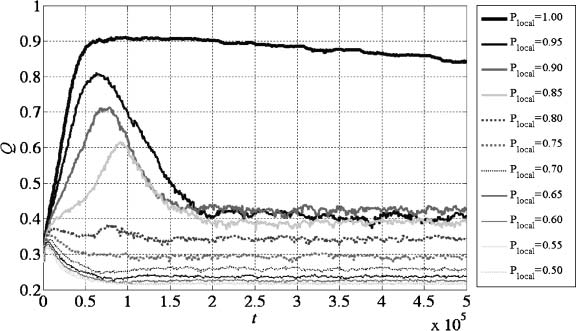
To get a further view on the dynamic of the evolutionary process of Q, Figure 2 shows how the
values of Q change with t for different Plocal values. The Q value is calculated every 1000 time steps
and averaged over the 10 instances at the same time step. As can be seen, on starting from random
networks, the evolution of Q follows different paths depending on Plocal. Since t ≥ 5 × 104, the value
of Q for Plocal such that Plocal ≤ 0.70 is always smaller than 0.3, while that for Plocal ≥ 0.80 is always
larger than 0.3. The Q for Plocal = 0.75 fluctuates around 0.3. That is to say, when Plocal > 0.75,
the model starts to have the ability to reproduce a community structure. When we further look
at the results in this parameter range, we find the evolution of Q is also different. When Plocal =
=
0.80, the evolution of Q is quite stable, and is always in the range of 0.3–0.4. The cases when Plocal
0.85, 0.90, and 0.95 are similar. The value of Q always first increases to a high value and then drops
to the range of 0.3–0.5. High-quality communities are formed at the early stage of evolution, and then
smaller communities merge to form larger communities, which results in a drop of Q. For Plocal =
1.00, the value of Q is always very high.
To show the scalability of the model, we increase the network size to 20,000 nodes. The evolu-
tionary process of Q is shown in Figure 3, and we can see that the results are similar. In addition,
Figure 1. How the value of Q changes with Plocal, where t max = 5 × 104, and gray circles represent the data for each of the
10 graph instances with lines connecting the means.
Artificial Life Volume 17, Number 4
267
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
Figure 2. The evolution of Q of networks with 1000 nodes.
we also calculated Q of networks with the same edge density generated by the Barabási-Albert
(BA) model [4], which are a typical type of scale-free networks. The results show that no matter
what the number of nodes is (1000 or 20,000), Q is always about 0.27; that is, no community
structure emerged.
Similar to [24, 25, 55], the above results show that the community structure emerges naturally in
our model, without the need of prelabeling a community for each node as in [58]. Clearly, the com-
munity formation in our model is based on the ratio of local to global interactions during the evolu-
tionary process. When that ratio is above a threshold (0.75, or more safely 0.80), community
structures emerge. Local interactions are responsible for the formation of community. However,
if only local interactions are used, namely Plocal = 1.00, the values of Q are too high, which is rarely
seen in real networks. Another indication of the above results is that as long as global interactions
exist, small communities will merge to larger ones as the network evolves. Then, the community
quality will be reduced, but still be above 0.3, which manifests a substantial community structure.
The above results accord with our knowledge about social interactions. Most of the time, people
live in their own communities and contact those friends and colleagues whom they often meet; just
Figure 3. The evolution of Q of networks with 20,000 nodes.
268
Artificial Life Volume 17, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
occasionally they attend meetings in other places. That is to say, the fraction of local interactions is
much higher than that of global interactions. Furthermore, although the fraction of global inter-
actions is low, it is an indispensable part of our life.
3.2 Community Size
We will check community size from two perspectives, namely the largest community size and the
community size distribution. The above experimental results showed that global interactions are an
indispensable part, since the community quality is too high to match the situation in real-world net-
works when only local interactions are used. Here, the following experiments will further show the
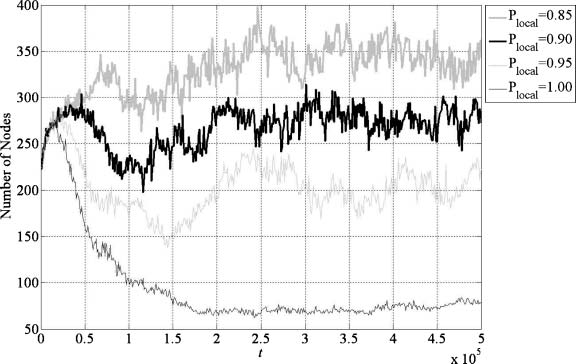
role of the global interactions in forming communities. The evolution of the largest community size
for different Plocal values is shown in Figure 4. The number of nodes is 1000, and the size is sampled
every 1000 time steps and averaged over the 10 instances at the same time step.
Although the largest community size fluctuates with time, the general trend is still clear. We can
= 1.00, when t >
see that the larger the value of Plocal is, the smaller the community size is. For Plocal
105, the community size is always smaller than 100. These results clearly show that global inter-
actions are useful in forming large communities, which once again confirms the above conclusion that
global interactions are indispensable.
Real networks are characterized by heterogeneous distributions of node degree. Likewise, it is not
correct to assume that all communities have the same size. In fact, the distribution of community
sizes of real networks is also broad, with a tail that can be fairly well approximated by a power law
[10, 11, 26, 45]. Figure 5 shows the community size distribution in networks with 20,000 nodes for
Plocal such that 0.85 ≤ Plocal
≤ 1.00 when t = 3 × 107.
As can be seen, when Plocal = 0.85, 0.90, and 0.95, the community size distributions can be ap-
proximated by power law distributions with exponents 3.49, 2.92, and 3.08, respectively; that is,
most communities are small in size, while only a few large communities exist, which matches
real-world situations. When Plocal = 1.00, the distribution can still be approximated by a power
law distribution without taking into account the leftmost data point.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
4 Degree Distribution
Figure 6 shows the degree distribution of networks with 20,000 nodes when Plocal
0.95, and 1.00, where t = 3 × 107. As can be seen, when Plocal
= 0.85, 0.90,
= 0.85, 0.90, and 0.95, the degree
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. The evolution of the largest community size in networks with 1000 nodes.
Artificial Life Volume 17, Number 4
269
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
Figure 5. The community size distribution of networks with 20,000 nodes when t = 3 × 107 for Plocal = (a) 0.85, (b) 0.90,
(c) 0.95, and (d) 1.00.
distribution can be approximated by power law distributions with exponents 1.94, 1.77, and 1.95,
respectively. But when Plocal = 1.00, the model fails to form an approximate power law distribution.
These results confirm the roles of global and local interactions we found in previous experiments.
Although local interactions are useful in creating the community structure, without global interac-
tions, local interactions cannot create a network with both community structure and power law degree
distribution.
5 Assortative Mixing
Another important network feature is the correlation between properties of adjacent network nodes,
which is known in the ecology and epidemiology literature as assortative mixing. Assortative mixing
can have a profound effect on the structural properties of a network. For example, assortative mix-
ing of a network by a discrete characteristic will tend to break the network up into separate com-
munities [38]. Newman [37] defines the assortativity coefficient r of an undirected network as the
Pearson correlation coefficient of the degrees at the ends of an edge:
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
P
P
M-1
P
N
i¼2
N
i¼2
P
i
j¼1
i
j¼1avi vj kvi kvj
(cid:3)
1
k2
2 avi vj
vi
þ k2
vj
−
(cid:5)
M-1
(cid:5)
(cid:4)
−
r ¼
M-1
270
P
P
N
i¼2
P
i
ðkvi
1
2 avi vj
j¼1
P
i
1
2 avi vj
j¼1
þ kvj
ðkvi
N
i¼2
M-1
þ kvj
(cid:6)
2
Þ
(cid:6)
2
Þ
ð5Þ
Artificial Life Volume 17, Number 4
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
The evolution of r in networks with 1000 nodes for Plocal such that 0.85 ≤ Plocal
where avi vj = 1 when the edge between vi and vj exists, and avi vj = 0 otherwise. r has a value in the range
[−1, 1], with positive assortativity indicating that nodes preferentially link to nodes with similar degrees.
≤ 1.00 is shown
in Figure 7, which is sampled every 1000 time steps and averaged over 10 instances at the same time
step. All values of r are always larger than 0 when t ≥ 5 × 104, which indicates that nodes are pref-
erentially linked to nodes with similar degree. Moreover, the relationship between local interactions
and the assortativity coefficient is clearly shown; namely, the larger the amount of local interactions
is, the higher the value of r is.
Recently, Piraveenan et al. [48] argued that the above network-level measure conveys insufficient
information about the local level structure and motifs present in networks. They introduced a mea-
sure of local assortativeness that quantifies the level of assortative mixing for individual nodes in the
context of the overall network, and used this measure to study the growth of the Internet [49]. Since
two networks with the same network assortativeness and similar degree distributions may have en-
tirely different local assortativeness distributions [48], next, we further study local assortativeness of
networks generated by our model.
Local assortativeness of a given node v is defined as follows [50]:
jð j þ 1Þ
(cid:4)
(cid:3)
k̄ − A
q
2Mj2
q
U
v
¼
ð6Þ
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. The degree distribution of networks with 20,000 nodes when t = 3 × 107 for Plocal = (a) 0.85, (b) 0.90, (c) 0.95,
and (d) 1.00.
Artificial Life Volume 17, Number 4
271
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
Figure 7. The evolution of the assortativity coefficient in networks with 1000 nodes.
where j is the nodeʼs excess degree, k̄ is the average excess degree of its neighbors, Aq is the
expectation of the excess degree distribution, jq is the standard deviation of this distribution, and
M is the number of edges in the network. In fact, in a network with N nodes, we have
r ¼
XN
i¼1
U
i
ð7Þ
Since local assortativeness is a property of a node, it is possible to construct local assortativeness
distributions for a given network, enabling us to plot local assortativeness values against degrees.
Figure 8 shows the local assortativeness distributions of networks with 20,000 nodes, where the
values are averaged over all nodes with the same degree.
As can be seen, in networks generated by our model, the local assortativeness increases with
degree in general. Moreover, the larger the value of Plocal is, the clearer this pattern is. We also show
the result of the BA model. Since the assortativity coefficient of the BA model is nearly 0, there is no
clear relationship between local assortativeness and degree. Furthermore, in Figure 8b, we zoom in
on the part corresponding to degrees from 0 to 200. We can see that although the assortativity
coefficient of the network generated by our model is positive, a large number of disassortative nodes
(U < 0) exists, no matter what the value of Plocal is, which confirms the observation in [48].
6 Internet Topology and the Rich-Club Phenomenon
In this section, networks generated by our model are compared with real-world Internet topology at
the autonomous system (AS) level, namely, the AS graph. In this graph, each node represents an
autonomous system present in the Internet, and the edges represent a commercial agreement be-
tween two Internet service providers (which own the two ASs). Such an agreement specifies
whether they agree to exchange data traffic and how to charge each other. Thus the AS graph is
the “control plane” of the Internet and presents very realistic opportunities to gain insight into the
evolution of complex networks. The growth of this network has been well documented, snapshots
272
Artificial Life Volume 17, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. The local assortativeness distributions of networks with 20,000 nodes when t = 3 × 107, where (b) is a mag-
nified part of (a).
of the network being available on a regular basis [1]. The AS graph used in the following studies is
the one used in [63], which has 11,461 nodes and 32,730 edges, and our model and the BA model
use the same numbers of nodes and edges.
First, Table 1 compares the community structure in the AS graph, the BA model, and our model.
The results show that the value of Q in the AS graph is equal to 0.5719, which is closer to the cases
when Plocal = 0.85 and 0.90 (0.6296 and 0.5339, respectively). When Plocal = 0.95 and 1.00, Q is
much higher than that in the AS graph, while Q in the BA model (0.3862) is much lower. Next,
Figure 9 compares the degree distributions in the AS graph, the BA model, and our model. As can
Artificial Life Volume 17, Number 4
273
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
Table 1. The community structure in the AS graph, our model (t = 11,461 × 80), and the BA model.
Network
AS graph
Our model:
BA model
Plocal = 0.85
0.90
0.95
1.00
Q
0.5719
0.6296
0.5339
0.8983
0.9786
0.3862
be seen, when Plocal = 0.85 and 0.90, the degree distribution in our model is closer to that in the
AS graph.
Another interesting property of the AS graph is the rich-club phenomenon; that is, the rich nodes,
which are a small number of nodes with large numbers of links, are very well connected to each other
[63]. The rich-club phenomenon is a simple qualitative way to differentiate between power law topol-
ogies and provides a criterion for new network models. Therefore, Figure 10 checks whether this
phenomenon exists in our model, where the rich-club connectivity is calculated according to [63].
That is to say, nodes in the network are sorted by decreasing number of links that each node contains.
The rich club is defined as nodes with rank less than rmax, the normalized position of a node on the
ordered list. The rich-club connectivity is defined as the ratio of the total actual number of links to the
maximum possible number of links between members of the rich club. As can be seen, our model
= 0.85, 0.90, and 0.95, the rich-
also reproduces the rich-club phenomenon. Moreover, when Plocal
club connectivity curves are much closer to that in the AS graph.
Finally, Table 2 further compares the properties of the AS graph with those of networks gener-
ated by different models, where the data of Inet-3.0 [60] and the fitness BA model [8] are cited
from [63], l(ri ≤ 5%, rj) is the number of links connecting with the top 5% rich nodes, and l(ri ≤
5%, rj ≤ 5%) is the number of links connecting between the top 5% rich nodes. The results
show that the values of l(ri ≤ 5%, rj) in the networks generated by our model with Plocal
= 0.85
and 0.90 are as close as that in Inet-3.0, which are closest to that in the AS graph, while the values
=
when Plocal
0.85, 0.90, and 0.95 are larger than 10,000, but are closer to the value of the AS graph (8910) than that
of Inet-3.0, which is only 3697. In terms of the maximum node degree, our model is outperformed
by Inet-3.0.
= 0.95 and 1.00 are much smaller. The values of l(ri ≤ 5%, rj ≤ 5%) when Plocal
To summarize, all the above comparisons between our model and the AS graph show that our
≤ 0.95 can generate networks that reproduce many properties observed
model with 0.85 ≤ Plocal
in AS graph, except the maximum node degree. This further confirms the roles of global and
local interactions.
7 Discussion and Conclusion
In this article, a network rewiring model is proposed, based on a simple view of social interactions.
Extensive simulation results show that by varying only the parameter Plocal, the model can evolve
from random networks to those with structural characteristics closely matching empirical social net-
works. The results show that when Plocal is larger than 0.85, significant community structure always
274
Artificial Life Volume 17, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. The degree distributions in the AS graph, the BA model, and our model (t = 11461 × 80). (a) Plocal = 0.85. (b)
Plocal = 0.90. (c) Plocal = 0.95. (d) Plocal = 1.00. (e) The BA model.
emerges, and as long as Plocal is smaller than 0.95, both the community size distribution and the
degree distribution can be approximated by a power law distribution. In the above range of Plocal,
the model also exhibits positive assortative mixing by degree and the rich-club phenomenon.
The results clearly show the different roles of local and global interactions. Local interactions are
responsible for the formation of the community structure, and have a positive correlation with assor-
tative mixing. Meanwhile, global interactions play an important role in forming large communities
Artificial Life Volume 17, Number 4
275
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
Figure 10. Rich-club connectivity against node rank.
Table 2. Comparison between properties of the AS graph and other models.
Network
AS Graph
M
l (ri ≤ 5%, rj )
l (ri ≤ 5%, rj ≤ 5%) Maximum node degree Average node degree
32,730
28,610
8,910
2,432
Our model: Plocal = 0.85
32,730
22,725
11,189
0.90
32,730
22,664
13,935
0.95
32,730
15,249
10,009
1.00
32,730
5,446
2,216
BA model
34,377
13,710
Inet-3.0
24,171
22,620
Fitness BA
34,366
20,929
1,498
3,697
1,426
198
267
112
20
227
2,010
1,793
5.7
5.7
5.7
5.7
5.7
6.0
4.2
6.0
and evolving the community size distribution and the degree distribution to a power law distribution.
In general, both local and global interactions are indispensable in evolving the model from random
networks to those matching various properties exhibited by the real-world networks, and the frac-
tion of local interactions should be much higher than that of global interactions. These results accord
with our experience in the real world. That is, we make local contacts, and just occasionally we
contact someone far away from us.
Acknowledgments
This work was partially funded by an Australian ARC Discovery Project Grant. The authors would
like to thank the reviewers for their helpful comments and valuable suggestions.
276
Artificial Life Volume 17, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
References
1. Caida data sets (2006). http://www.caida.org/data/.
2. Albert, E., & Barabási, A. L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics,
74, 47–97.
3. Anghel, M., Toroczkai, Z., Bassler, K. E., & Korniss, G. (2004). Competition-driven network
dynamics: Emergence of a scale-free leadership structure and collective efficiency. Physical Review Letters,
92, 058701.
4. Barabási, A. L., & Albert, R. (1999). Emergence of scaling in random networks. Science, 286, 509–512.
5. Bentley, R. A., Hahn, M. W., & Shennan, S. J. (2004). Random drift and culture change. Proceedings of the
Royal Society of London Series B, 271, 1443–1450.
6. Bentley, R. A., & Shennan, S. J. (2003). Cultural evolution and stochastic network growth. American
Antiquities, 68, 459–485.
7. Bentley, R. A., & Shennan, S. J. (2005). Random copying and cultural evolution. Science, 309, 877–879.
8. Bianconi, G., & Barabási, A. L. (2001). Competition and multiscaling in evolving networks. Europhysics
Letters, 54, 436.
9. Burda, Z., Correia, J. D., & Krzywicki, A. (2001). Statistical ensemble of scale-free random graphs. Physical
Review E, 64, 046118.
10. Caldarelli, G., & Vespignani, A. (Eds.). (2007). Large scale structure and dynamics of complex networks: From
information technology to finance and natural science. Singapore: World Scientific.
11. Clauset, A., Newman, M. E. J., & Moore, C. (2004). Finding community structure in very large networks.
Physical Review E, 70, 066111.
12. Crow, J. F., & Kimura, M. (1970). An introduction to population genetics theory. New York: Harper and Row.
13. Dittrich, P. (2000). The seceder effect in bounded space. InterJournal, MS 363.
14. Dittrich, P., Liljeros, F., Soulier, A., & Banzhaf, W. (2000). Spontaneous group formation in the seceder
model. Physical Review Letters, 84, 3205.
15. Erdős, P., & Rényi, A. (1959). On random graphs. Publicationes Mathematicae Debrecen, 6, 290–297.
16. Evans, M. R. (2000). Phase transitions in one-dimensional nonequilibrium systems. Brazilian Journal of
Physics, 30, 42.
17. Evans, M. R., & Hanney, T. (2005). Nonequilibrium statistical mechanics of the zero-range process and
related models. Journal of Physics A: Mathematical and Theoretical, 38, R195.
18. Evans, T. S., & Plato, A. D. K. (2007). Exact solution for the time evolution of network rewiring models.
Physical Review E, 75, 056101.
19. Gershenson, C. (2008). Towards self-organizing bureaucracies. International Journal of Public Information
Systems, 1, 1–24.
20. Ghoneim, A., Abbass, H. A., & Barlow, M. (2008). Characterizing game dynamics in two-player strategy
games using network motifs. IEEE Transactions on Systems, Man and Cybernetics B, 38, 682–690.
21. Girvan, M., & Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings
of the National Academy of Sciences of the U.S.A., 99, 7821.
22. Godrèche, C., Bouchaud, J. P., & Mézard, M. (1995). Entropy barriers and slow relaxation in some random
walk models. Journal of Physics A: Mathematical and Theoretical, 28, L603.
23. Godrèche, C., & Luck, J. M. (2002). Nonequilibrium critical dynamics of ferromagnetic spin systems.
Journal of Physics: Condensed Matter, 14, 1589.
24. González, M. C., Lind, P. G., & Herrmann, H. J. (2006). System of mobile agents to model social networks.
Physical Review Letters, 96, 088702.
25. Grönlund, A., & Holme, P. (2004). Networking the seceder model: Group formation in social and
economic systems. Physical Review E, 70, 036108.
26. Guimerà, R., Danon, L., Díaz-Guilera, A., Giralt, F., & Arenas, A. (2003). Self-similar community structure
in a network of human interactions. Physical Review E, 68, 065103(R).
Artificial Life Volume 17, Number 4
277
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
27. Hahn, M. W., & Bentley, R. A. (2003). Drift as a mechanism for cultural change: An example from baby
names. Proceedings of the Royal Society of London Series B, 270, S120–S123.
28. Herzog, H. A., Bentley, R. A., & Hahn, M. W. (2004). Random drift and large shifts in popularity of dog
breeds. Proceedings of the Royal Society of London Series B, 271, S353–S356.
29. Huberman, B. A. (2001). The laws of the web. Cambridge, MA: MIT Press.
30. Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N., & Barabási, A. L. (2000). The large-scale organization of
metabolic networks. Nature, 407, 651–654.
31. Jin, E. M., Girvan, M., & Newman, M. E. J. (2001). Structure of growing social networks. Physical Review E,
64, 046132.
32. Kimura, M., & Crow, J. F. (1964). The number of alleles that can be maintained in a finite population.
Genetics, 49, 725–738.
33. Kumpula, J. M., Onnela, J. P., Saramäki, J., Kaski, K., & Kertész, J. (2007). Emergence of communities in
weighted networks. Physical Review Letters, 99, 228701.
34. Liggett, T. M. (1985). Interacting particle systems. Berlin: Springer-Verlag.
35. Liu, J., Zhong, W., Abbass, H. A., & Green, D. (2010). Separated and overlapping community detection in
complex networks using multiobjective evolutionary algorithms. In Proceedings of IEEE 2010 Congress on
Evolutionary Computation (CEC).
36. Neiman, F. D. (1995). Stylistic variation in evolutionary perspective: Inferences from decorative
diversity and interassemblage distance in Illinois woodland ceramic assemblages. American Antiquities,
60, 7–36.
37. Newman, M. E. J. (2002). Assortative mixing in networks. Physical Review Letters, 89, 208701.
38. Newman, M. E. J. (2003). Mixing patterns in networks. Physical Review E, 67, 026126.
39. Newman, M. E. J. (2003). The structure and function of complex networks. SIAM Review, 45,
167–256.
40. Newman, M. E. J. (2004). Fast algorithm for detecting community structure in networks. Physical Review E,
69, 066133.
41. Newman, N. E. J., & Girvan, M. (2004). Finding and evaluating community structure in networks. Physical
Review E, 69, 026113.
42. Ohkubo, J., Tanaka, K., & Horiguchi, T. (2005). Generation of complex bipartite graphs by using a
preferential rewiring process. Physical Review E, 72, 036120.
43. Ohkubo, J., Yasuda, M., & Tanaka, K. (2005). Preferential urn model and nongrowing complex networks.
Physical Review E, 72, 065104(R).
44. Ohkubo, J., Yasuda, M., & Tanaka, K. (2006). Replica analysis of preferential urn model. Journal of the Physical
Society of Japan, 75, 074802.
45. Palla, G., Derényi, I., Farkas, I., & Vicsek, T. (2005). Uncovering the overlapping community structure of
complex networks in nature and society. Nature, 435, 814–818.
46. Park, K., Lai, Y. C., & Ye, N. (2005). Self-organized scale-free networks. Physical Review E, 72, 026131.
47. Pimm, S. L. (2002). Food webs. Chicago, IL: University of Chicago Press.
48. Piraveenan, M., Prokopenko, M., & Zomaya, A. Y. (2008). Local assortativeness in scale-free networks.
Europhysics Letters, 84, 28002.
49. Piraveenan, M., Prokopenko, M., & Zomaya, A. Y. (2009). Local assortativity and growth of internet. The
European Physical Journal B, 70, 275–285.
50. Piraveenan, M., Prokopenko, M., & Zomaya, A. Y. (2010). Local assortativeness in scale-free networks—
Addendum. Europhysics Letters, 89, 49901.
51. Prokopenko, M., Boschetti, F., & Ryan, A. (2009). An information-theoretic primer on complexity,
self-organisation and emergence. Complexity, 15, 11–28.
52. Prokopenko, M., Wang, P., Price, D. C., Valencia, P., Foreman, M., & Farmer, A. J. (2005). Self-organizing
hierarchies in sensor and communication networks. Artificial Life, 11(4), 407–426.
278
Artificial Life Volume 17, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
J. Liu et al.
Local-Global Interaction and the Emergence of Scale-Free Networks
53. Pulkkinen, O., & Merikoski, J. (2005). Phase transitions on Markovian bipartite graphs—An application
of the zero-range process. Journal of Statistical Physics, 119, 881.
54. Scott, J. (2000). Social network analysis: A handbook. Thousand Oaks, CA: Sage Publications.
55. Singer, H. M., Singer, I., & Herrmann, H. J. (2009). Agent-based model for friendship in social networks.
Physical Review E, 80, 026113.
56. Sood, V., & Redner, S. (2005). Voter model on heterogeneous graphs. Physical Review Letters, 94, 178701.
57. Soulier, A., & Halpin-Healy, T. (2003). The dynamics of multidimensional secession: Fixed points and
ideological condensation. Physical Review Letters, 90, 258103.
58. Watts, D. J., Dodds, P. S., & Newman, M. E. J. (2002). Identity and search in social networks. Science,
296, 1302–1305.
59. Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-world” networks. Nature, 393,
440–442.
60. Winick, J., & Jamin, S. (2002). Inet-3.0: Internet topology generator (Tech. report UM-CSE-TR-456-02).
Ann Arbor: University of Michigan.
61. Xie, Y. B., Zhou, T., & Wang, B. H. (2008). Scale-free networks without growth. Physica A: Statistical
Mechanics and Its Applications, 387, 1683–1688.
62. Zanette, D., & Manrubia, S. (2001). Vertical transmission of culture and the distribution of family names.
Physica A: Statistical Mechanics and Its Applications, 295, 1–8.
63. Zhou, S., & Mondragón, R. J. (2004). The rich-club phenomenon in the Internet topology. IEEE
Communications Letters, 8, 180–182.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Artificial Life Volume 17, Number 4
279
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
7
4
2
6
3
1
6
6
2
7
9
7
a
r
t
l
/
_
a
_
0
0
0
3
8
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3