Communicated by David Touretzky

Product Units: A Computationally Powerful and
Biologically Plausible Extension to Backpropagation
Networks

Richard Durbin
David E. Rumelhart
Department of Psycholoa, Stanford University, Stanford, CA 94305, USA

We introduce a new form of computational unit for feedfoxward learn-
ing networks of the backpropagation type. Instead of calculating a
weighted sum this unit calculates a weighted product, where each in-
put is raised to a power determined by a variable weight. Such a unit
can learn an arbitrary polynomial term, which would then feed into
higher level standard summing units. We show how learning operates
with product units, provide examples to show their efficiency for vari-
ous types of problems, and argue that they naturally extend the family
of theoretical feedforward net structures. There is a plausible neurobi-
ological interpretation for one interesting configuration of product and
summing units.

1 Introduction

The success of multilayer networks based on generalized linear threshold
units depends on the fact that many real-world problems can be well
modeled by discriminations based on linear combinations of the input
variables. What about problems for which this is not so? It is clear
that for some tasks higher order combinations of some of the inputs, or
ratios of inputs, may be appropriate to help form a good representation
for solving the problem (for example cross-correlation terms can give
translational invariance). This observation led to the proposal of ”sigma-
pi units” which apply a weight not only to each input, but also to all
second and possibly higher order products of inputs (Rumelhart, Hinton,
and McClelland; Maxwell et al. 1987). The weighted sum of all these
terms is then passed through a non-linear thresholding function. The
problem with sigma-pi units is that the number of terms, and therefore
weights, increases very rapidly with the number of inputs, and becomes
unacceptably large for use in many situations. Normally only one or a
few of the non-linear terms are relevant. We therefore propose a different
type of unit, which represents a single higher order term, but learns
which one to represent. The output of this unit, which we will call a
product unit, is

Neural Computation 1, 133-142 (1989) @ 1989 Massachusetts Institute of Technology

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

1
1
1
3
3
8
1
1
8
1
3
n
e
c
o
1
9
8
9
1
1
1
3
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

134

Richard Durbin and David E. Rumelhart

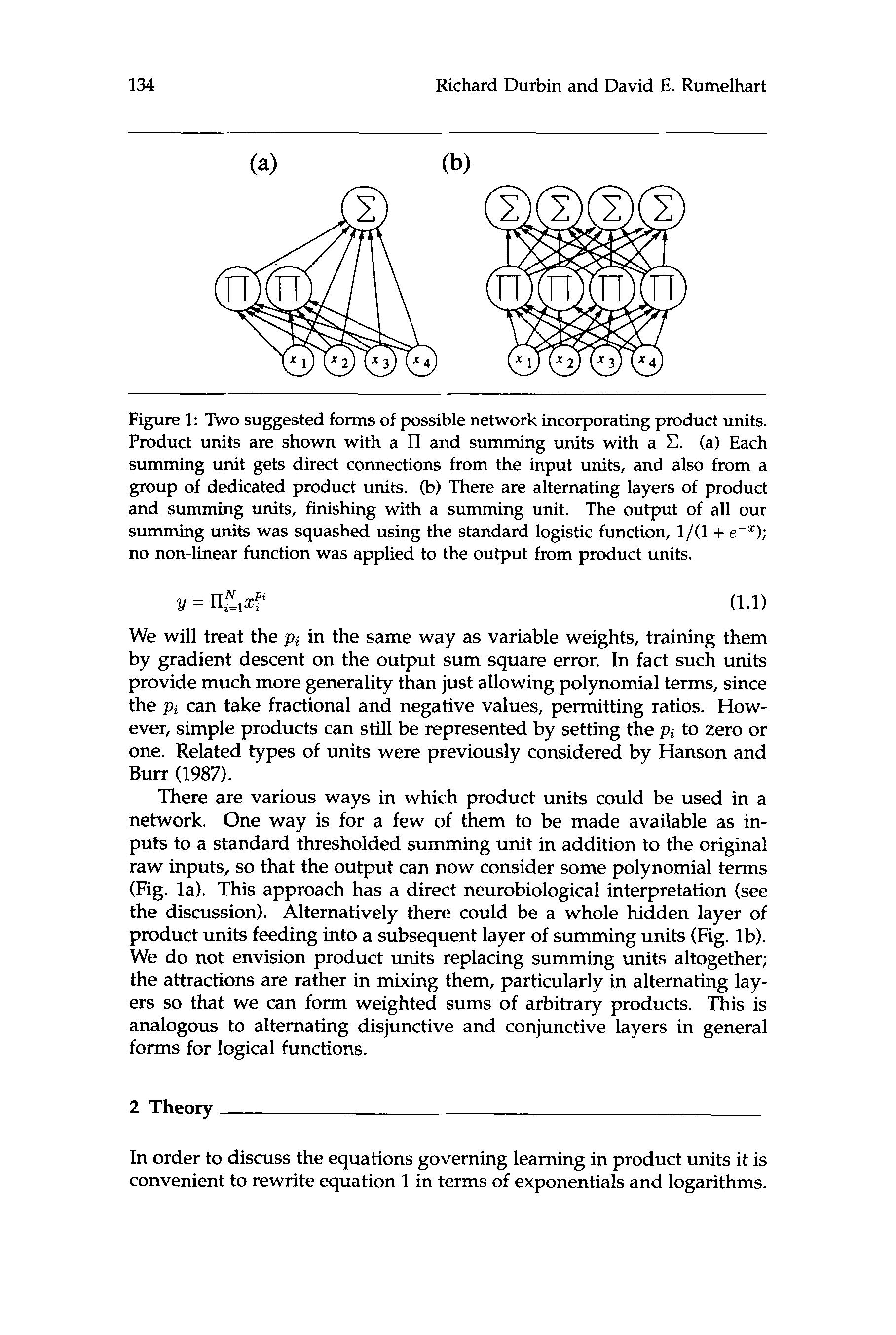
Figure 1: Two suggested forms of possible network incorporating product units.
Product units are shown with a II and summing units with a C. (a) Each
summing unit gets direct connections from the input units, and also from a
group of dedicated product units. (b) There are alternating layers of product
and summing units, finishing with a summing unit. The output of all our
summing units was squashed using the standard logistic function, 1/(1 + e-”);
no non-linear function was applied to the output from product units.

We will treat the pi in the same way as variable weights, training them
by gradient descent on the output sum square error. In fact such units
provide much more generality than just allowing polynomial terms, since
the pi can take fractional and negative values, permitting ratios. How-
ever, simple products can still be represented by setting the pi to zero or
one. Related types of units were previously considered by Hanson and
Burr (1987).

There are various ways in which product units could be used in a
network. One way is for a few of them to be made available as in-
puts to a standard thresholded summing unit in addition to the original
raw inputs, so that the output can now consider some polynomial terms
(Fig. la). This approach has a direct neurobiological interpretation (see
the discussion). Alternatively there could be a whole hidden layer of
product units feeding into a subsequent layer of summing units (Fig. lb).
We do not envision product units replacing summing units altogether;
the attractions are rather in mixing them, particularly in alternating lay-
ers so that we can form weighted sums of arbitrary products. This is
analogous to alternating disjunctive and conjunctive layers in general
forms for logical functions.

2 Theory

In order to discuss the equations governing learning in product units it is
convenient to rewrite equation 1 in terms of exponentials and logarithms.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

1
1
1
3
3
8
1
1
8
1
3
n
e
c
o
1
9
8
9
1
1
1
3
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Product Units for Backpropagation Networks

J 1

135

(2.1)

In this form we can see that a product unit acts like a summing unit
whose inputs are preprocessed by taking logarithms, and whose output
is passed through an exponential, rather than a squashing function. If
L , is negative then log, zz = log, 12, I + ZT, which is complex, and so equa-
tion (2.1) becomes

(2.2)

We want to be able to consider negative inputs because the non-linear
characteristics of product units, which we want to use computationally,
are centered on the origin. There are two main alternatives to dealing
with the resulting complex-valued expressions. One is to handle the
whole network in the complex domain, and at the end fit the real com-
ponent to the data (either ignoring the complex component or fitting it
to 0). The other is to keep the system in the real domain by ignoring the
imaginary component of the output from each product unit, restricting
us to real-valued weights. For most problems the latter seems preferable.
In the case where all the exponents pi are integral, as with a true polyno-
mial term, then the approximation of ignoring the imaginary component
is exact. Given this, it can be viewed that we are extending the space
of polynomial terms to fractional exponents in a well behaved fashion,
so as to permit smooth learning of the exponents. Additionally, in sim-
ulations we seem to gain nothing for the added complexity of working
in the complex domain (it doubles the number of equations and weight
variables). On the other hand, for some physical problems it may be
appropriate to consider complex-valued networks.

In order to train the weights by gradient descent we need to be able
to calculate two sets of derivatives for each unit. First we need the
derivative of the output y with respect to each weight pi so as to be able
to update the weights. Second we need the derivative with respect to
each input zi so as to be able to propagate the error back to previous
layers using the chain rule. Let us set I, equal to 1 if xi is negative,
otherwise 0, and define U , V by

Then the equations we need for the real-valued version are

y = eucosTv

(2.3)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

1
1
1
3
3
8
1
1
8
1
3
n
e
c
o
1
9
8
9
1
1
1
3
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

136

Richard Durbin and David E. Rumelhart

It is possible to add an extra constant input to a product unit, correspond-
ing to the bias for a summing unit. In this case the appropriate constant
is -1, since a positive value would simply multiply the output by a scalar,
which is irrelevant when there is a variable multiplicative weight from
the output to a higher level summing unit. Although this multiplicative
bias is often eventually redundant, we have found it to be important
during the learning process for some tasks, such as the symmetry task
(see below and Fig. 2).

One property that we have lost with product units is that they are vul-
nerable to translation and rotation of the input space, in the sense that
a learnable problem may no longer be learnable after translation. Sum-
ming units with a threshold are not vulnerable to such transformations.
If desired, we can regain translational invulnerability by introducing new
parameters pi to allow an explicit change of origin. This would replace
xi by (xi – pi) in all the above equations. We can once again learn the pi
by gradient descent. With the pi present a product unit can approximate
a linear threshold unit arbitrarily closely, by working on only a small
region of the exponential function. Alternatively, we can notice that ro-
tational and translational vulnerability of single product units is in part
compensated for if a number of them are being used in parallel, which
will often be the case. This is because a single product transforms to a
set of products in a rotated and translated space. In any case, there may
be some benefit to the asymmetry of a product unit’s capabilities under
affine transformation of the input space. For non-geometric sets of input
variables this type of extra computational power may well be useful.

3 Results

Many of the problems that are studied using networks use Boolean input.
For product units it is best to use Boolean values -1 and 1, in which case
the exponential terms in equations (3) disappear, and the units behave
like cosine summing units with 1 and 0 inputs. Examples of the use of
product units for learning Boolean functions are provided by networks
that learn the parity and symmetry functions. These functions are hard to
learn using summing units: the parity function requires as many hidden
units as inputs, while symmetry requires 2 hidden units, but often gets
stuck in a local minimum unless more are given. Both functions are
learned rapidly using a single product hidden unit (Fig. 2 a,b). A good
example of a problem that multilayer nets with product units find good
solutions for is the multiplexing task shown in figure 2c. Here two of the
inputs code which of the four remaining inputs to output. This task has
a biological interpretation as an attentional mechanism, and is therefore
relevant for computational models of sensory information processing.
Indeed, the neurobiological interpretation of just the type of hybrid net

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

1
1
1
3
3
8
1
1
8
1
3
n
e
c
o
1
9
8
9
1
1
1
3
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Product Units for Backpropagation Networks

137

(a) Q

– 1

-1

– 1

– I

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

1
1
– 1
– 1

1
-1
1
-I

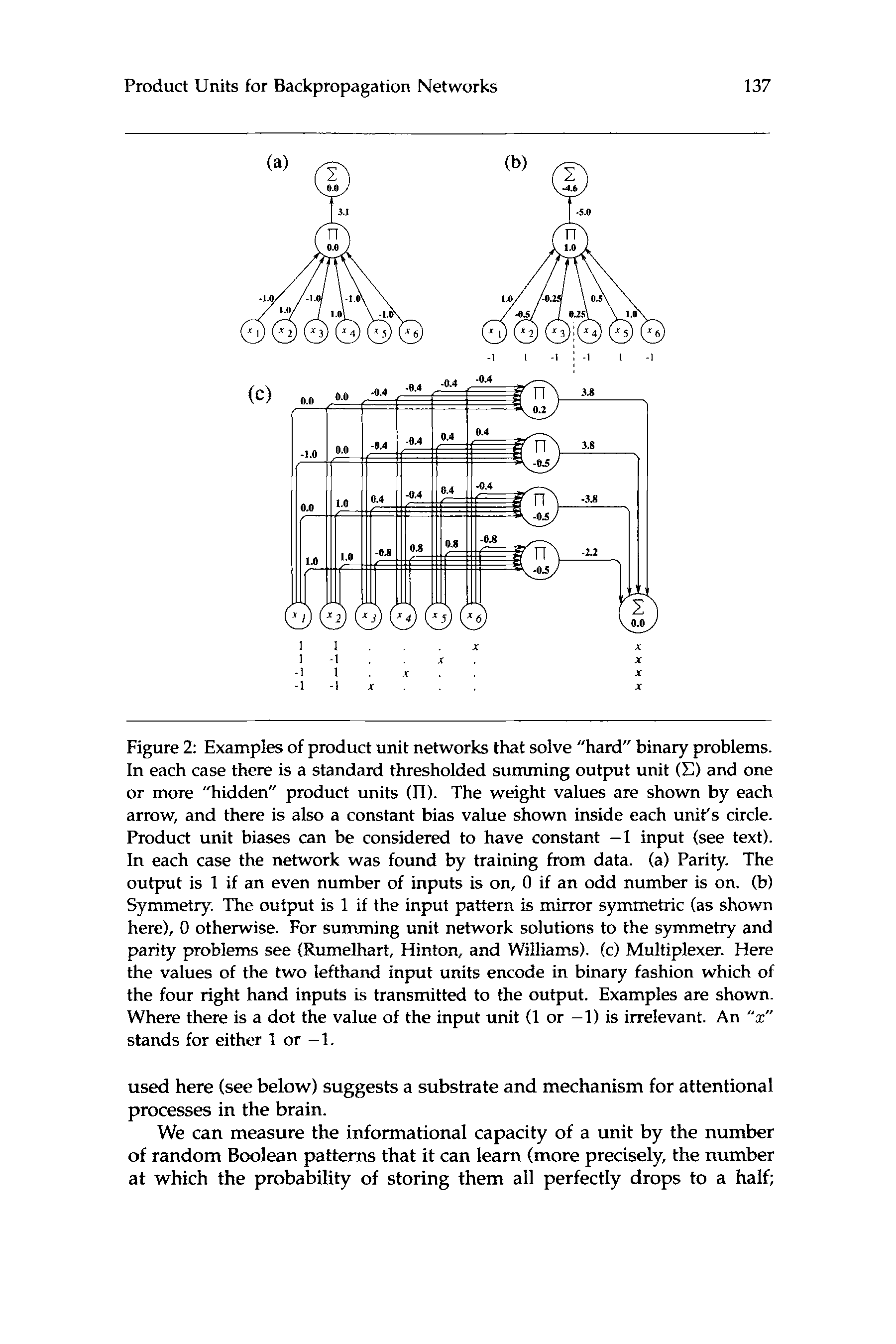
Figure 2: Examples of product unit networks that solve “hard” binary problems.
In each case there is a standard thresholded summing output unit (C) and one
or more “hidden” product units (II). The weight values are shown by each
arrow, and there is also a constant bias value shown inside each unit’s circle.
Product unit biases can be considered to have constant -1 input (see text).
In each case the network was found by training from data. (a) Parity. The
output is 1 if an even number of inputs is on, 0 if an odd number is on. (b)
Symmetry. The output is 1 if the input pattern is mirror symmetric (as shown
here), 0 otherwise. For summing unit network solutions to the symmetry and
parity problems see (Rumelhart, Hinton, and Williams). (c) Multiplexer. Here
the values of the two lefthand input units encode in binary fashion which of
the four right hand inputs is transmitted to the output. Examples are shown.
Where there is a dot the value of the input unit (1 or -1) is irrelevant. An “d’
stands for either 1 or -1.

used here (see below) suggests a substrate and mechanism for attentional
processes in the brain.

We can measure the informational capacity of a unit by the number
of random Boolean patterns that it can learn (more precisely, the number
a t which the probability of storing them all perfectly drops to a haIf;

1
1
1
3
3
8
1
1
8
1
3
n
e
c
o
1
9
8
9
1
1
1
3
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

138

Richard Durbin and David E. Rumelhart

Structure M

Product unit Summing unit
percentage

percentage

6 1

12 1

6 2 1

12
18
20

24
36
40

6 2 1
fixed
output

92
49
28

100
66
20

100
82
58

100
45
14

18
3
1

29
0
0

2
0
0

Table 1: Results on storage of random data. The number of successful storage
attempts in 100 trials is shown in the last two columns for various net structures
and numbers of vectors, M . Storage is termed successful if all input vectors
produce output on the correct side of 0.5. Input vectors were random, q = -1
or 1, and output values for each vector were random 0 or 1. The “6 1” and
”12 1” nets had a single learning unit with 6 or 12 inputs. For these compar-
isons the output of a product unit was passed through the standard summing
unit squashing function, e”/(l + e”). The single summing units do not attain
the M=2N theoretical limit (Cover 1965), presumably because the squashing
function output creates local minima not present for a simple perceptron. The
“6 2 1” nets had 2 hidden units (either product or summing) and one summing
output unit, which was trainable for the first set of results, and fixed with all
weights equal for the second set. These results indicate that storage capacity
for product units is at least 3 bits per weight, as opposed to no more than 2 bits
per weight for summing units, and that fixed output units do not drastically
reduce computational power in multilayer networks.

Mitchison and Durbin 1989). For a single summing unit with N inputs
the capacity can be shown theoretically to be 2N (Cover 1965). The
empirical capacity of a single product unit is significantly higher than
this at around 3N (table 1). The relative improvement is maintained in a
comparison of multilayer networks with product hidden units compared
with ones consisting purely of summing units (table 11, indicating that
product units cooperate well with summing units.

We can also consider the performance of product units when the in-
are real valued. An example is the ability of a network with two

puts

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

1
1
1
3
3
8
1
1
8
1
3
n
e
c
o
1
9
8
9
1
1
1
3
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Product Units for Backpropagation Networks

(a> & -20.0

2.0

0.0

2.0

-3.0

-12.3

2.3 gq

139

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

1
1
1
3
3
8
1
1
8
1
3
n
e
c
o
1
9
8
9
1
1
1
3
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

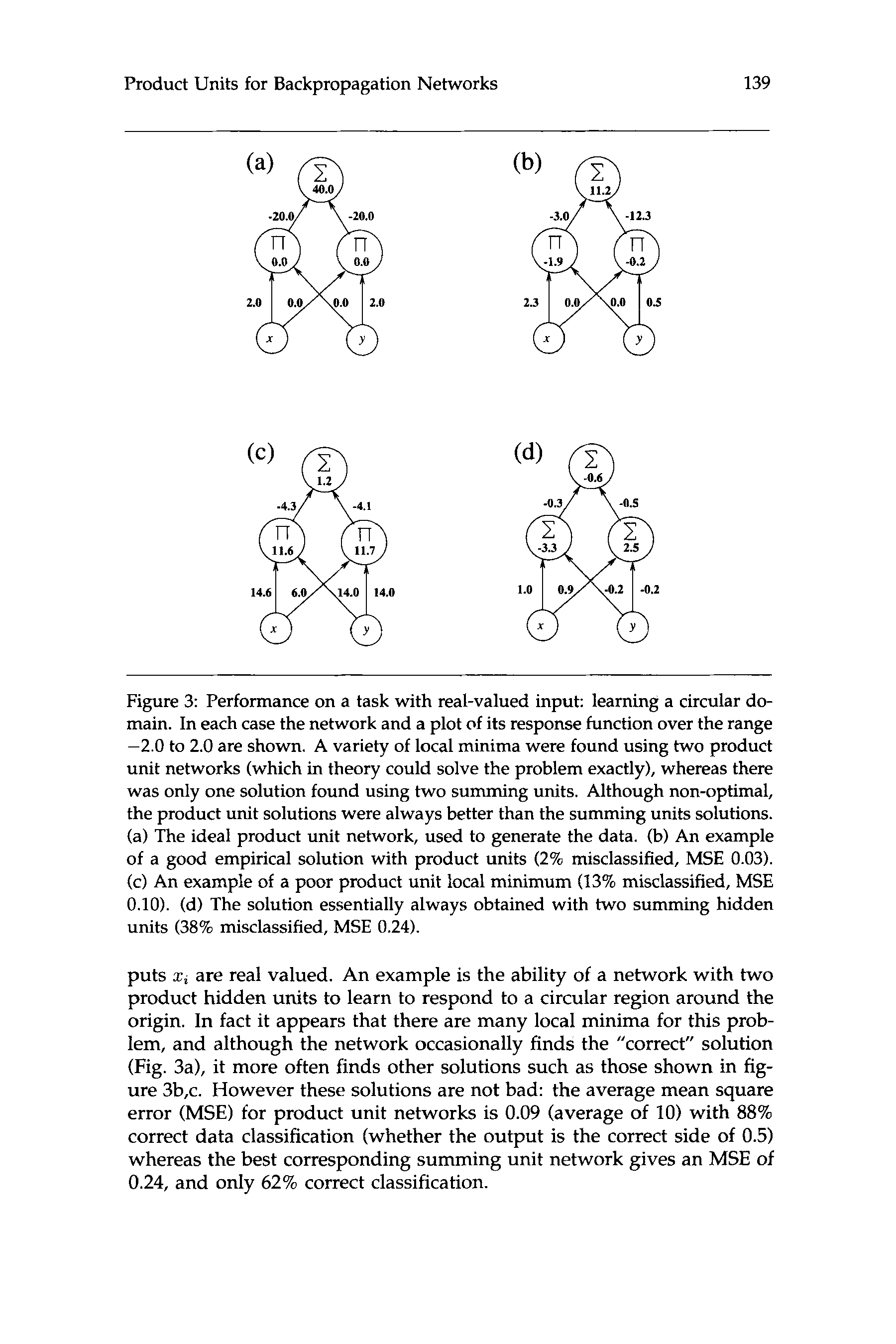
Figure 3: Performance on a task with real-valued input: learning a circular do-
main. In each case the network and a plot of its response function over the range
-2.0 to 2.0 are shown. A variety of local minima were found using two product
unit networks (which in theory could solve the problem exactly), whereas there
was only one solution found using two summing units. Although non-optimal,
the product unit solutions were always better than the summing units solutions.
(a) The ideal product unit network, used to generate the data. (b) An example
of a good empirical solution with product units (2% misclassified, MSE 0.03).
(c) An example of a poor product unit local minimum (13% misclassified, MSE
0.10). (d) The solution essentially always obtained with two summing hidden
units (38% misclassified, MSE 0.24).

puts 2 , are real valued. An example is the ability of a network with two
product hidden units to learn to respond to a circular region around the
origin. In fact it appears that there are many local minima for this prob-
lem, and although the network occasionally finds the “correct” solution
(Fig. 3a), it more often finds other solutions such as those shown in fig-
ure 3b,c. However these solutions are not bad: the average mean square
error (MSE) for product unit networks is 0.09 (average of 10) with 88%
correct data classification (whether the output is the correct side of 0.5)
whereas the best corresponding summing unit network gives an MSE of
0.24, and only 62% correct classification.

140

Richard Durbin and David E. Rumelhart

4 Discussion

We have proposed a new type of computational unit to be used in layered
networks along with standard thresholded summing units. The underly-
ing idea behind this unit is that it can learn to represent any generalized
polynomial term in the inputs. It can therefore help to form a better
representation of the data in cases where higher order combinations of
the inputs are significant. Unlike sigma-pi units, which to some extent
perform the same task, product units do not increase the number of free
parameters, since there is only one weight per input, as with summing
units. Although we have been unable to prove that product units are
guaranteed to learn a learnable task, as can be shown for a single simpli-
fied summing unit (Rosenblatt 1962), we have shown that product units
can be trained efficiently using gradient descent, and allow much simpler
solutions of various standard learning problems. In addition, as isolated
units they have a higher empirical learning capacity than summing units,
and they act efficiently to create a hidden layer representation for an out-
put summing unit (table 1).

There is a natural neurobiological interpretation for this type of com-
bination of product and summing units in terms of a single neuron. Local
regions of dendritic arbor could act as product units whose outputs are
summed at the soma. Equation (2.1) shows that a product unit acts like
a summing unit with an exponential output function, whose inputs are
preprocessed by passing them through a log function. Both these trans-
fer functions are realistic. When there are voltage sensitive dendritic
channels, such as NMDA receptors, the post-synaptic voltage response
is qualitatively exponential around a critical voltage level (Collingridge
and Bliss 1987); an effect that will be influenced by other local input
apart from the specific input at the synapse. Presynaptically, there are
saturation effects giving an approximately logarithmic form to the voltage
dependency of transmitter release. In fact just these features have been
presented as problems with the standard thresholded summing model
of neurons. Standard summing inputs could still be made using neuro-
transmitters that do not stimulate voltage sensitive channels. As far as
learning in the biological model is concerned, it is acceptable that the sec-
ond layer summing weights, corresponding to the degree of influence of
dendritic regions at the soma, are not very variable. Systems with fixed
summing output layers are nearly as computationally powerful as fully
variable ones, both in theory (Mitchison and Durbin 19891, and simula-
tions (table 1). Learning at the input synapses is still essentially Hebbian
(equation 2.2b), with an additional term when the input 2, is negative.
Although the periodic form of this term appears unbiological, some type
of additional term is not unreasonable for inhibitory input, which may
well have different learning characteristics. Alternatively, it might be that
the learning model only applies to excitatory input. Further considera-
tion of this neurobiological model is required, but it seems likely that this

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

1
1
1
3
3
8
1
1
8
1
3
n
e
c
o
1
9
8
9
1
1
1
3
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

Product Units for Backpropagation Networks

141

approach will lead to a plausible new computational model of a neuron
that is potentially much more powerful than the standard McCulloch-
Pitts model.

One possible criticism of introducing a new type of unit is that it
is trivially going to improve the representational capabilities of the net-
works: one can always improve a fit to data by making a model more
complex, and this is rarely worth the price of throwing away elegance.
The defence to this must be that the extension is in some sense natural,
which we believe that it is. Product units provide the continuous analogy
to general Boolean conjunctions in the same way that summing units are
continuous analogs of Boolean disjunctions (although both continuous
forms are much more powerful, sufficiently so that either can represent
any arbitrary disjunction or conjunction on Boolean input). In fact many
of the proofs of capabilities of networks to perform general tasks rely
on the “abuse” of thresholded summing units to perform multiplicative
or conjunctive tasks, often in alternating layers with units being used
in an additive or disjunctive fashion. Such proofs will be much simpler
for networks with both product and summing units, indicating that such
networks are more appropriate for finding simple models of general data.
It might be argued that in opening up such generality the special prop-
erties of learning networks will be lost, because they no longer provide
strong constraints on the type of model that is created. We feel that this
misses the point. The real justification for layered network models ap-
pears when a number of different output functions are fit to some set of
data. By using a layered model the fit of each function influences and
constrains the fit of all the others. If there is some underlying natural
representation this will be modeled by the intermediate layers, since it
will be appropriate for all the output functions. This cross-constraining
of learning is not easily available in many other systems, which therefore
miss out on a vast amount of data that is relevant, although indirectly so.
Product units provide a natural extension of the use of summing units
in this framework.

Acknowledgments

R.M.D is a Lucille P. Markey Visiting Fellow at Stanford University. We
thank T.J. Sejnowski for pointing out the neurobiological interpretation.

References

Collingridge, G.L. and T.V.P. Bliss. 1987. NMDA receptors – their role in

long-term potentiation. Trends Neurosci. 10, 288-293.

Cover, T. 1965. Geometrical and Statistical Properties of Systems of Linear
Inequalities with Applications in Pattern Recognition. IEEE Trans. Elect.
Cornp. 14,326-334.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d

f
/

1
1
1
3
3
8
1
1
8
1
3
n
e
c
o
1
9
8
9
1
1
1
3
3
p
d

b
y
g
u
e
s
t

o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3

142

Richard Durbin and David E. Rumelhart

Hanson, S.J. and D.J. Burr. 1987. Knowfedge Representation in Connectionist Nef-
works. Technical Report Bell Communication Research, Morristown, NJ.
Maxwell, T., C.G. Giles, and Y.C. Lee. 1987. Generalization in Neural Networks,
the Contiguity Problem. In: Proceedings IEEE First International Conference
on Neural Networks 2 , 4 1 4 5 .

Mitchison, G.J. and R.M. Durbin. 1988. Bounds on the Learning Capacity of

Some Multilayer Networks. Biofogical Cybernetics, in press.
Rosenblatt, F. 1962. Principles of Neurodynamics. New York Spartan.
Rumelhart, D.E., G.E. Hinton, and J.L. McClelland. 1986. A General Framework
for Parallel Distributed Processing. In: Parallel Distributed Processing 1,45-
76. Cambridge, MA, and London: MIT Press.

Rumelhart, D.E., G.E. Hinton, and R.J. Williams. 1986. Learning Internal Rep-
resentations by Errtjr Propagation. In: Parallel Distributed Processing 1,
318-362. Cambridge, MA, and London: MIT Press.

Received 11 November; accepted 17 December 1988.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d