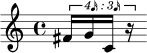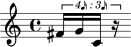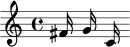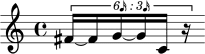Brian Bemman and David Meredith
Department of Architecture, Design,
and Media Technology
Aalborg University
Rendsburggade 14, 9000 Aalborg,
Denmark
{bb, dave}@create.aau.dk
Generating New Musical
Works in the Style of
Milton Babbitt
Abstract: Milton Babbitt is noted for composing twelve-tone and serial music that is both complex and highly
constrained. He has written extensively on a variety of topics in music and his writings have had a profound and lasting
impact on musical composition. In this article, we first review in detail his compositional process and the techniques
he developed, focusing in particular on the all-partition array, time-point system, and equal-note-value strings used
in his later works. Next, we describe our proposed procedure for automating his compositional process using these
techniques. We conclude by using our procedure to automatically generate an entirely new musical work that we argue
is in the style of Babbitt.
Introduction
Milton Babbitt (1916–2011) was a composer of
twelve-tone and serial music whose works and the-
oretical writings had a profound impact on modern
musical composition. Beginning in the 1950s and
over the course of the next two decades, Babbitt
formalized the twelve-tone system and established
techniques such as the time-point system and the
all-partition array (Babbitt 1955, 1960, 1961, 1962,
1973). Many of these techniques remain of interest
to composition and music research today (Tanaka,
Bemman, and Meredith 2016b; Bernstein 2017;
Bemman and Meredith, forthcoming). Indeed, music
theorists and computer scientists alike have writ-
ten at length on these techniques and the highly
constrained and often complex structures in Bab-
bitt’s music that result (Mead 1987, 1994; Bemman
and Meredith 2015, 2016; Tanaka, Bemman, and
Meredith 2016a; Bernstein 2017). In recent years,
the sketches for many of his works have been made
publicly available by the Library of Congress in
Washington, DC (http://lccn.loc.gov/2014565648).
Researchers are now able to examine Babbitt’s
compositional process in much greater detail than
before.
In this article we describe the process Babbitt
devised in composing his later works (from approxi-
mately 1980 to 2011), focusing in particular on the
notions of the all-partition array, the time-point
system, and the equal-note-value string. The con-
straints under which he composed his music at this
Computer Music Journal, 42:1, pp. 60–79, Spring 2018
doi:10.1162/COMJ a 00451
c(cid:2) 2018 Massachusetts Institute of Technology.
time are strict, and his application of these tech-
niques follows an often well-defined procedure. For
this reason, we suggest that Babbitt’s compositional
process is inherently algorithmic in nature and that,
therefore, many of these techniques can be modeled
by machine. This line of reasoning follows years
of research in the field of computational music
analysis and generation, with similar efforts having
been made, for example, to harmonize chorales in
the style of Bach (Ebcio˘glu 1987) and, more recently,
to generate the structures found in Babbitt’s own
music (Bemman and Meredith 2016; Tanaka, Bem-
man, and Meredith 2016a,b). The primary purpose
of this article, however, is simply to provide further
insight into the nature of Babbitt’s compositional
process, notably through the creation of an algorith-
mic model. We should note that this model is not
necessarily intended to be a tool for computer-aided
algorithmic composition nor an explanation for
how other twelve-tone composers (e.g., Webern,
Schoenberg, Carter) might have composed their
music, although such uses would be welcomed.
In the remainder of this article, we present
our proposed procedure for automating Babbitt’s
compositional process in his later works. First, we
introduce a method for generating the pitches and
time points of a piece from its all-partition array.
Then we show how this same method can be used
to generate pitch repetitions (i.e., a single pitch that
occurs at more than one point in time), which occur
frequently in Babbitt’s music. Next we describe a
method for determining the rhythms in a piece as
well as the placement of rests and ties. We conclude
by using this procedure to automatically generate
a novel musical work that we believe to be in the
style of Babbitt.
60
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 1. Excerpt
containing three ordered
mosaics from the
all-partition array found in
Babbitt’s None but the
Lonely Flute. Each ordered
mosaic is a partitioning of
the aggregate that has
been ordered from top to
bottom into sets of pitch
classes each ordered from
left to right.
All-Partition Array
Both the pitch and the rhythmic content in Babbitt’s
later works are organized according to a structure
known as the all-partition array (Mead 1994; Bem-
man and Meredith 2016). In an all-partition array,
Babbitt constructed aggregates (i.e., collections of
the twelve musical pitch classes) so that each was a
distinct set of partitioned pitch-class segments called
an ordered mosaic (Bemman and Meredith 2016).
For example, (cid:2)(cid:2)2, 0, 1, 3(cid:3), (cid:2)5, 4, 6, 7(cid:3), (cid:2)8, 9, 11, 10(cid:3)(cid:3) is
one ordered mosaic made up of three pitch-class
segments of length 4. We denote ordered sets using
angle brackets, (cid:2)·(cid:3), and unordered sets with braces,
{·}. As is standard in musical set theory, we use num-
bers to denote pitch classes of the equal-tempered
chromatic scale independent of octave register,
where C = 0, C(cid:2) = 1, D = 2, . . . , B = 11. A second
ordered mosaic might contain three pitch-class
segments in which two are of length 5 and one is
of length 2, e.g., (cid:2)(cid:2)6, 1, 11, 4, 2(cid:3), (cid:2)5, 7(cid:3), (cid:2)0, 9, 8, 3, 10(cid:3)(cid:3).
Each pitch-class segment in an ordered mosaic is
then assigned to a “voice” on the musical surface,
forming what is known as a lyne (Mead 1994).
Collectively, these pitch-class segments in each
lyne for all ordered mosaics form a concatenation
of twelve-tone rows that may or may not contain
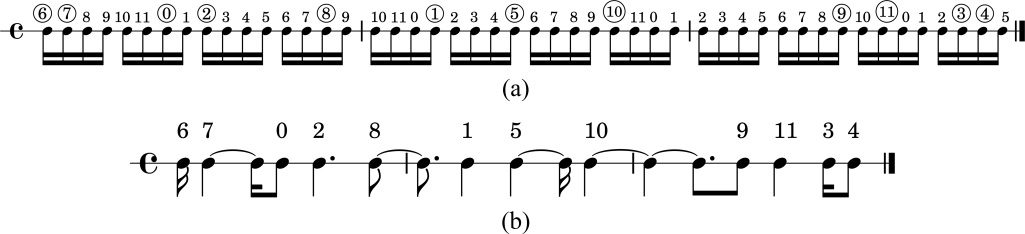
repetitions. Figure 1 shows an excerpt from the
all-partition array in Babbitt’s None but the Lonely
Flute with six such lynes and the first three of its
ordered mosaics.
Note, in Figure 1, that the pitch-class segments in
the first ordered mosaic are distributed across each
of the six possible lynes but that in the third ordered
mosaic, these pitch-class segments appear in only
three lynes—1, 2, and 5. In the third ordered mosaic,
the first pitch class in each segment is a repetition
from the previous ordered mosaics: pitch classes 2
and 6 from the first ordered mosaic and pitch class
4 from the second ordered mosaic. An all-partition
array must contain a number of ordered mosaics
equal to the number of distinct ways in which
twelve can be partitioned into k parts (i.e., lynes) or
fewer, with each of these partitions represented by
a distinct ordered mosaic. Babbitt used four-, six-,
and twelve-part all-partition arrays containing 34,
58, and 77 ordered mosaics, respectively. In earlier
publications we provide a more detailed look at the
mathematical construction of an all-partition array
and the difficulty associated with generating one
(cf. Bemman and Meredith 2016 and Tanaka et al.
2016a,b).
Time-Point System
Babbitt himself laid the foundations for his time-
point system and outlined general principles for
applying it to composition (Babbitt 1962). With
the time-point system, Babbitt sought to derive a
correspondence between the twelve-tone row and
time. By replacing the interval of a half-step in a
twelve-tone row with a fixed period of time called a
unit, the time-point intervals (analogous to directed
pitch-class intervals) between adjacent members
become lengths of time measured in units rather
than pitch intervals measured in semitones. In his
later works, Babbitt typically used a sixteenth note
as the unit (Bernstein 2017). Figure 2 shows a left-
to-right linear ordering of twelve time points from
the opening of Babbitt’s None but the Lonely Flute
using a sixteenth note as the unit and one possible
rhythmic representation (not used by Babbitt in this
piece).
Note, in Figure 2, how time points denote onsets
in time corresponding to new rhythmic events. In
Figure 2b, these rhythmic events have a duration
equal to the interonset intervals of each time
point. Babbitt often sought less straightforward
rhythmic interpretations of his time points than
that shown in Figure 2b, however, and in the
following sections we will see in greater detail how
his use of additional techniques gave his later works
their characteristically varied and often complex
rhythms.
Bemman and Meredith
61
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. A linear ordering
of twelve time points set
against a grid of
sixteenth-note units (a)
and one possible rhythmic
interpretation of this
ordering (b), in which
duration is equal to
interonset interval,
meaning there are no rests
or overlapping notes.
Figure 3. Pitch-class
ordered mosaic (PcOM)
distinguished by register
(a) and time-point class
ordered mosaic (TpcOM)
distinguished by dynamic
level (b).
Babbitt’s Compositional Process in Later Works
In this section, we describe in detail Babbitt’s
compositional process as found in his later works.
Many of the techniques he used in this process have
been described elsewhere (Mead 1994; Bernstein
2017), yet a thorough understanding of how exactly
this process comes to form the musical surface of
his works is essential in explaining how we have
automated this process.
Figure 3
Linear Orderings from Ordered Mosaics
In many of Babbitt’s later works based on the
all-partition array, the available linear orderings of
pitch classes and time-point classes are the same
because they are both constructed from the same
ordered mosaics. We introduced the term linear
ordering in an earlier publication (Bemman and
Meredith, forthcoming), and it is equivalent to what
Babbitt variously called a secondary-set (Babbitt
1961, p. 86) or linear aggregate (Babbitt 1973),
and what Leong and McNutt (2005) refer to as an
aggregate realization. A linear ordering differs from
a twelve-tone row both in the way it is constructed
(i.e., from an ordered mosaic and not from the four
transformations of transposition, inversion, retro-
grade, and retrograde inversion) and the number of
elements it can contain (i.e., more than twelve). Typ-
ically, Babbitt used register to distinguish pitch-class
segments, and dynamic level to distinguish time-
point class segments (Mead 1994). Figure 3a shows
a pitch-class ordered mosaic (hereafter abbreviated
“PcOM”), and Figure 3b displays a time-point class
ordered mosaic (hereafter abbreviated “TpcOM”),
both taken from the same all-partition array.
An ordered mosaic places constraints on the
possible orderings that can be constructed from it.
Each segment in a mosaic is ordered, meaning that
elements, when “linearized” to form an ordering
(e.g., as in Figure 2b), must remain in the left-to-
right order in which they occur in their segment. For
example, in Figure 3, possible orderings from both
mosaics may begin with (cid:2)7, 2, . . .(cid:3) but not (cid:2)2, 7, . . .(cid:3).
Similarly, elements from other segments may
intervene, so long as their left-to-right order is not
violated. For example, (cid:2)7, 8, 2, 3 . . .(cid:3) is allowed but
not (cid:2)7, 3, 2, 8 . . .(cid:3). Figure 4a shows a possible ordering
of pitch classes. Figure 4b indicates a possible
ordering of time-point classes taken from the
ordered mosaics in Figures 3a and 3b, respectively.
Note, in Figure 4a, how segments of pitch classes
are distinguished from each other by pitch-register
and, in Figure 4b, how the changes in dynamic
level mark the arrival of a time point belonging to
a different segment. Perceptually, these new time
points act as both temporal boundaries of local
62
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
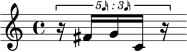
Figure 4. Opening
orderings of pitch classes
(a) and time-point classes
(b) from Babbitt’s None
but the Lonely Flute. The
musical notations on the
right are taken from the
respective ordered mosaics
on the left. Note that in in
the pitch-class ordering no
time information is
specified, nor is any pitch
information specified in
the time-point ordering.
Figure 5. Opening of
Babbitt’s None but the
Lonely Flute corresponding
to the linear orderings of
pitch classes and
time-point classes shown
in Figure 4. Note that the
vertical dashed line in
measure 5 marks the
boundary between the first
and second linear
orderings of pitch classes.
Figure 4
Figure 5
events and reminders of a global stream of temporal
events unfolding in each time-point class segment,
made clear by differing dynamic levels.
The musical surface of Babbitt’s later works is
formed by uniting the pitch information specified
by a linear ordering constructed from a PcOM with
the timing information specified by some rhythmic
interpretation of a linear ordering constructed from
a TpcOM. Figure 5 shows the opening of Babbitt’s
None but the Lonely Flute and how the ordering of
Bemman and Meredith
63
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Four
equal-note-value strings
(one for each time-point
interval) in an excerpt
from the opening of
Babbitt’s None but the
Lonely Flute shown in
Figure 5.
points is equal to a sixteenth note, this time-point
interval of 6 is equal to a dotted quarter note. This
interval has then been equally divided by each of its
equal-note-value string’s four pitch classes into four
durations, each equal to a dotted sixteenth note.
In fact, each time-point interval in the example
shown in Figure 6 contains an equal-note-value
string. For example, there is an equal-note-value
string of length 1 between time points 0 and 2
(pitch-class 7) and between time points 7 and 0 (a
tied note pitch-class 0). Between time points 6 and
7 there is an equal-note-value string of length 2 in
which the first member is a rest. We will see in the
following sections, in our discussion of automating
Babbitt’s compositional process, how exactly Babbitt
determined the rests, ties, and repetitions of pitches
that appear frequently in his music.
Generating Orderings from Ordered Mosaics
In this section, we begin the discussion of our
proposed procedure for modeling Babbitt’s compo-
sitional process described previously. In computer
science, a stack is an abstract data type that stores
a collection of elements using a “last-in-first-out”
protocol (for a more detailed introduction, see, e.g.,
Cormen et al. 2009, pp. 232–236). A stack has two
associated operations, pop and push, that remove its
top element and insert an element at the top of the
stack, respectively. By representing each segment of
an ordered mosaic as a stack, such that the leftmost
element lies on the top of each stack, we can account
for the left-to-right order in which time-point classes
or pitch classes must be taken from each segment
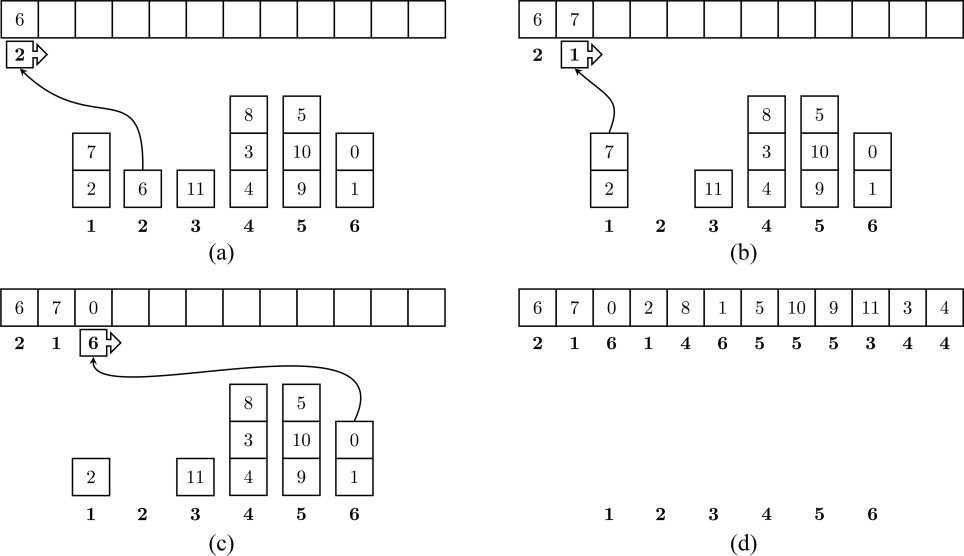
when constructing an ordering. Figure 7 shows how
an ordering of time-point classes or pitch classes can
be generated from an ordered mosaic represented as
a sequence of stacks.
Note, in Figure 7a–c, that at each step the top
element of each indicated stack is popped and stored
from left-to-right to form the sequence of elements
above. As this process unfolds, the stack number
is simultaneously stored below its corresponding
element. In Figure 7d, this process concludes with
the completed ordering of time-point classes from
Figure 4b and an empty sequence of stacks.
pitch-classes shown in Figure 4a and the ordering
of time-point classes shown in Figure 4b have been
united to form the musical surface.
In Figure 5, note that on the musical surface,
depending on the chosen rhythmic interpretation,
pitches generally proceed faster than the time points
(Mead 1994). For example, at time point 2 there
are four corresponding pitch classes: 8, 6, 2, and
1. Nevertheless, Babbitt is often careful to ensure
that time points are allowed to “catch up” as, for
example, at time points 8, 1, and 5, where there is
only a single pitch class, 1. Indeed, Mead has noted
that Babbitt has had a “longtime predilection for
manifesting similar sorts of distributions of events
in different domains over different spans of time”
(Mead 1994, p. 49). It is clear then that the chosen
rhythmic interpretation of time points, as shown, for
example, in Figure 4b, is crucial to maintaining such
a uniform distribution of pitch and time events.
Equal-Note-Value Strings and Rhythm
A rhythmic interpretation of an ordering of time
points, as shown for example in Figure 4b, is
determined by Babbitt’s choice of equal-note-value
strings taken from a PcOM to form an ordering
of pitch classes. An equal-note-value string is a
string of n pitch classes that subdivide a time-point
interval into n equal durations (i.e., note values)
(Mead 1994; Bernstein 2017). Figure 6 provides an
example of Babbitt’s use of equal-note-value strings
from the opening of None but the Lonely Flute.
As shown by the dotted line in Figure 6, an
equal-note-value string containing the pitch classes
8, 6, 2 and 1 equally subdivides the time-point
interval of 6, occurring between time points 2
and 8. Because the unit in this ordering of time
64
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. The process of
selecting elements from
stacks, numbered 1–6, in
an ordered mosaic to
generate a linear ordering
of pitch-classes or
time-point classes. This
example begins with
taking the top element
from stack 2 (a), with the
element then removed
from the stack. This is
followed by taking the top
element from stack 1 (b),
then by an element from
stack 6 (c). The process
continues until eventually
all stacks are empty (d).
Note that the generated
ordering corresponds to the
time-point class ordering
shown in Figure 4b.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Because only the top element of each stack is
a possible next choice after every chosen element,
the sequence of stack numbers shown in Figure 7,
(cid:2)2, 1, 6, 1, 4, 6, 5, 5, 5, 3, 4, 4(cid:3), uniquely encodes its
corresponding ordering above (given the ordered
mosaic). Computing all distinct permutations of
such a sequence of stack numbers then corresponds
to all possible orderings that can be generated from
a given ordered mosaic. The ordered mosaic shown
in Figure 7, for example, produces 3,324,000 distinct
possible permutations. In a parallel publication
we show how this number is computed using the
formula for the multinomial coefficient (Bemman
and Meredith, forthcoming).
Pitch-Class Repetitions in Equal-Note-Value Strings
That there are pitch repetitions in Babbitt’s music
distinguishes it from the works of several other
twelve-tone composers. In looking at Babbitt’s later
works, we find two sorts of repetition, those in
which a pitch is immediately repeated (as used by
other twelve-tone composers), e.g., (cid:2)6, 6(cid:3), and those
in which the most recently chosen pitch from a
stack is repeated (largely unique to Babbitt), e.g.,
(cid:2)6, 7, 6(cid:3) in the ordered mosaics shown in Figure 3.
When and where these repetitions occur in an
ordering of pitch classes are determined, in part,
by the equal-note-value strings used to construct
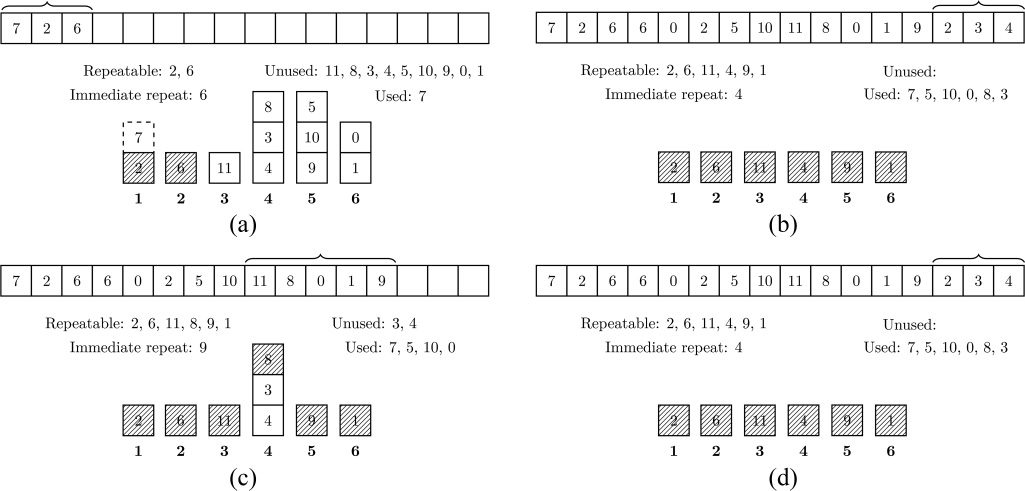
the linear ordering. Figure 8 shows the process of
constructing a linear ordering of pitch classes with
repetitions, this time, by grouping pitch classes from
its PcOM into equal-note-value strings.
Note, in Figure 8, that pitch classes in a PcOM
can be in any one of three states in the process
of constructing a pitch-class ordering: (1) unused
(indicated by the white boxes), (2) repeatable (indi-
cated by the shaded boxes), or (3) used (indicated
by their removal from a stack). In Figure 8a, after
the first equal-note-value string is generated, the
repeatable pitch classes are 6 and 2, but not 7, as 2
and 7 belong to the same segment (i.e., stack) and 7
is not the most recent pitch class to be taken from
this segment. In Figure 8b, this equal-note-value
string contains two repeatable pitch classes, 6 and 2,
Bemman and Meredith
65
Figure 8. Process of
generating a pitch-class
ordering of
equal-note-value strings
containing repetitions
from stacks, numbered
1–6, in a PcOM. In each
step, one equal-note-value
string (indicated by a
brace above the ordering
at top) is constructed for a
given time-point class.
Shaded boxes below the
ordering indicate pitch
classes that are repeatable
and white boxes indicate
unused pitch classes.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
where 6 is an immediate repetition (from Figure 8a).
In Figure 8c, this equal-note-value string contains
only a single repeatable pitch class, 0, that is not
immediate. In Figure 8d, we have a completed linear
ordering of twelve distinct pitch classes contain-
ing four equal-note-value strings for a total of 16
elements due to its four repetitions.
When and Where Pitch Repetitions Occur
The problem of determining where exactly pitch
repetitions may occur in Babbitt’s music is addressed
by Babbitt himself, who states that “pitch repetition
is not a pitch procedure, but a temporal procedure,
independent of the considerations of the pitch
system, and, if a time-point system is assumed, the
temporal placements of such pitch repetitions are
determined by the time-point structure, not by pitch
considerations” (Babbitt 1962, p. 65). It is likely that
Babbitt used repetitions to articulate any number
of temporal or nontemporal events, including beat,
meter, and syncopation, among others. In our
model, however, immediate repetitions are those
that occur predominantly on the beat, whereas all
other repeatable pitches primarily occur off the
beat.
Let us suppose in a piece we have a sequence
of time points P = (cid:2) p1, p2, . . . , pn(cid:3). The time-point
intervals of n time points form the sequence
T = (cid:2)t1, t2, . . . , tn−1(cid:3), where ti = pi+1 − pi (mod 12).
Whether or not a time point pi falls on the beat in
an implied meter is determined by the prefix sum
of time-point interval ti−1 modulo the number of
time-point units u between consecutive beats. (The
prefix sum of a sequence of numbers is equivalent to
the cumulative sum or additive sum of its elements.)
We therefore define an on-the-beat indicator oi to be
1 if and only if pi falls on a beat, as follows:
⎧
⎪⎪⎨
oi =
i−1(cid:6)
1,
if
tj ≡ 0 (mod u); and
⎪⎪⎩
j=1
0, otherwise.
(1)
In Equation 1, when oi = 1, the equal-note-value
string at time point pi for time-point interval ti−1
falls on the beat. For example, in a common-time
meter with four sixteenth-note units to the beat and
where a time-point interval ti−1 has a prefix sum
i−1
j=1 tj = 4, the modulo u = 4 operation
equal to
(cid:7)
66
Computer Music Journal
Table 1. Probabilities of Pitch-Class Events
Immediate
Repetition
Other
Repetition
New Pitch
Class
oi =
1
0
50%
0%
25%
25%
25%
75%
Probabilities in our model of different classes of
events occurring either on the beat, oi = 1, or off the
beat, oi = 0.
would result in 0, and thus the time-point pi falls
on the beat.
As shown in Figure 8, possible pitch-class events
in an equal note-value string are (1) an immediate
repetition, (2) some other repetition, and (3) a new
pitch class, respectively denoted ir, or, and np. To
promote a variety of musically interesting events
in the music generated by our model, we assign
varying probabilities to these possible events at
each given time-point interval. We have chosen
these probabilities based on observations of the
approximate number of times these musical events
occur in Babbitt’s music. We should note, however,
that no systematic corpus analysis was used in
determining this number, as very few encodings of
Babbitt’s works exist. Therefore, the actual number
of occurrences of various events in Babbitt’s music
remains unknown. Nonetheless, the probabilities
we arrived at are summarized in Table 1.
In the case that the chosen pitch-class event is
either some other repetition or a new pitch class
and there is more than one pitch class available in
an ordered mosaic, we ensure that each available
pitch class has an equal probability of being chosen.
This occurs, for example, in Figure 8b with three
other repetitions (2, 6, 0) and six unused pitch
classes (11, 8, 3, 4, 9, 1). Naturally, there is only ever
one available repetition that can be immediate. In
Babbitt’s later works, all the pitch classes in a given
equal-note-value string must be distinct, implying
that only the first pitch class in such a string can be
an immediate repeat. The remaining pitch classes in
such a string can be either other repeats or new pitch
classes. In general, however, the equal-note-value
strings Babbitt constructed contain in their entirety
only two repetitions. We suspect this ensured for
Babbitt that the lengths of pitch-class orderings on
the musical surface do not grow exceedingly long
with repetitions. Accordingly, the equal-note-value
strings generated by our model are constrained to
contain only two repetitions.
Maximum Length of an Equal-Note-Value String
As illustrated by the opening of Babbitt’s None but
the Lonely Flute, shown in Figure 5, the juxtapo-
sition of different length equal-note-value strings
and time-point intervals contributes to a musically
interesting result in which the distributions of time
points and pitch classes can remain approximately
uniform. It seems, however, that Babbitt did not
consider all combinations of string length and time-
point intervals to be musically meaningful and,
indeed, avoided certain combinations altogether.
Consider, for example, how difficult it might be
for a human to perform a twelve-note tuplet in the
time of a sixteenth note at even a moderate tempo.
To avoid such problems, for any given time-point
interval we constrain the maximum length of its
corresponding equal-note-value string.
The maximum allowable length for a given equal-
note-value string can neither exceed the number
of unused pitch classes in its PcOM at any given
point in constructing a pitch-class ordering (i.e.,
the white boxes shown in the process described in
Figure 8) nor can it result in subdivisions with a
duration smaller than some fixed note value. The
maximum length of an equal-note-value string si for
a time-point interval ti is given by
|si|max = min(r , tid),
(2)
where d is the length of the time-point unit in
thirty-second notes and r is the number of unused
pitch classes in the PcOM before constructing si.
For example, when the unit in an ordering of time
points is equal to a sixteenth note (i.e., d = 2), and
the current time-point interval is 3, then an equal-
note-value string of length 3 · 2 = 6 is acceptable
in a PcOM with six or more unused pitch classes.
Each of the durations in this equal-note-value string
would then be equal to a thirty-second note.
Bemman and Meredith
67
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. An equal-note-
value string, (cid:2)6, 11(cid:3),
constructed from two
segments in the first PcOM
that references a single
segment, (cid:2)6, 11, 10, 0(cid:3),
belonging to the third
PcOM.
Generating Rests and Ties in Equal-Note-Value
Strings
As illustrated in Figure 1, pitch classes in a lyne and,
by extension, their corresponding segments from all
PcOMs in an all-partition array are ordered as a result
of the twelve-tone rows to which they belong. In
Figure 8, however, we saw how an equal-note-value
string generated from a PcOM can contain pitch
classes not necessarily belonging to a single segment
or lyne. It is therefore possible that such strings may
contain an ordering of pitch classes not found in
any of the twelve-tone rows in the lynes of an all-
partition array. Generally speaking, Babbitt found
this undesirable because it violates an essential
principle of twelve-tone composition—namely, that
pitch classes from a twelve-tone row appear in their
given order. In Babbitt’s later works, he ensured
that the ordering of pitch classes in an equal-note-
value string corresponded to the orderings found
in these twelve-tone rows by checking that either
the string in its entirety or its substrings belong to
one or more segments from other PcOMs in its all-
partition array. In this way, Babbitt was able to use
equal-note-value strings to create a dense network
of motivic ideas across a piece by linking different
ordered mosaics in an all-partition array (Mead
1994; Bernstein 2017). This process of constructing
equal-note-value strings that can also be constructed
from other PcOMs has been called referenced array
segments (Bernstein 2017).
The array segments of an all-partition array are all
the pitch-class segments found in any of the PcOMs
in an all-partition array. For example, the excerpt
from Figure 1 contains one pitch-class segment of
length 6, one segment of length 4, six segments
of length 3, three segments of length 2, and two
segments of length 1. A complete all-partition array,
containing 34, 58, or 77 ordered mosaics, will have
many more segments. An equal-note-value string s
is said to reference an array segment a (typically in
another PcOM) if a substring of s is a substring of a.
For example, Figure 9 shows the excerpt from the
all-partition array shown in Figure 1 with an equal-
note-value string constructed from two segments in
its first PcOM that references a segment in its third
PcOM.
Note that in Figure 9, how the referenced array
segment (cid:2)6, 11, 10, 0(cid:3) in the third PcOM contains a
substring equal to the equal-note-value string (cid:2)6, 11(cid:3),
constructed from the first PcOM. Moreover, in both
PcOMs, the process of selecting elements (shown in
Figure 7) to form this substring is not violated.
When constructing an equal-note-value string in
this way, we argue that Babbitt sought to minimize
the number of referenced array segments required to
account for all its pitch classes. More formally, we
propose that Babbitt desired a minimum cardinality
set C of substrings from an equal-note-value string
s (1) that covers s and (2) whose members ci are
substrings of array segments other than those used
to construct s. If we return again to Figure 9, the
6 in our equal-note-value string (cid:2)6, 11(cid:3) could have
referred to the segment (cid:2)6, 11, 10, 0(cid:3) in the third
PcOM and the 11 could have referred to the segment
(cid:2)11, 3, 4(cid:3), in the second. This would require a set
C = (cid:2)(cid:2)6(cid:3), (cid:2)11(cid:3)(cid:3) having a cardinality of 2, however,
which would be considered less optimal than our
original reference to (cid:2)6, 11, 10, 0(cid:3).
Rests and Ties
It is possible that many equal-note-value strings
might not have a minimum cardinality set. It
is also possible that a referenced array segment
might contain more pitch classes than its equal-
note-value string (as shown in Figure 9), whether
it has a minimum cardinality set or not. It is in
these cases that rests and ties arise. As Bernstein
(2017) has noted, Babbitt indicated in his sketches
the ordinal positions of a string’s pitch classes
in their referenced array segments. Because each
reference must be a substring, numbers belonging
to the same array segment must be sequential in
68
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
ascending order. For example, an equal-note-value
string (cid:2)6, 11, 7(cid:3) would have the ordinal positions 1, 2,
3 in a reference to a single array segment (cid:2)(cid:2)6, 11, 7(cid:3)(cid:3)
or 1, 2, 1 in a reference to two array segments, e.g.,
(cid:2)(cid:2)6, 11(cid:3), (cid:2)7, 9, 2, 10(cid:3)(cid:3). Babbitt indicated the lengths
of each referenced array segment by noting their
final ordinal positions with either an underscore
or parentheses. In the example using two array
segments just provided, these lengths could be
indicated by the following: 1,2,(1).
As Bernstein continues, an underscore indicates
that this final pitch class of an array segment should
“sound” on the musical surface and parentheses
indicate that this pitch class should not. We take
this to mean that parentheses indicate rests and
that underscores, in general, indicate ties. We have
observed that Babbitt does not typically embed rests
in the middle of an equal-note-value string in his
later works, opting instead to append or prepend
them to a string. On the other hand, although ties
do appear at the ends of equal-note-value strings,
we only permit them to appear inside a string in
our model. We have chosen to do this because it
was not always possible to ensure that the pitch
required to complete a tied note from the final
position of one equal-note-value string was available
in the first position of the next equal-note-value
string. This could be due to, for example, being
in a new PcOM where the required pitch does
not appear as the first element in the appropriate
segment or falling on an off-beat where immediate
repetitions are not allowed according to Table 1.
An equal-note-value string, (cid:2)6, 11(cid:3), in our model,
for example, that references the array segment,
(cid:2)6, 11, 2(cid:3), would contain a rest in its final position.
This then transforms the original string of length 2
into one of length 3, (cid:2)6, 11, rest(cid:3). On the other hand,
a tie in our model can only occur from a referenced
array segment containing more pitch classes than
the substring from its equal-note-value string. This
is because, for there to be a tie or “underscore,” there
must be a right-most pitch class in the referenced
array segment that does not belong to the substring
of the equal-note-value string. For example, an
equal-note-value string (cid:2)6, 11(cid:3) that references the
two array segments, (cid:2)6, 7(cid:3), (cid:2)11(cid:3) would contain a tie
in its second position, (cid:2)6, tie, 11(cid:3). Table 2 shows
various referenced array segments and the musical
output for a given input of a string (cid:2)6, 7, 0(cid:3) and a
time-point interval equal to three sixteenth notes.
Note, in Table 2, how the minimum cardinality
set (cid:2)(cid:2)6, 7, 0(cid:3)(cid:3) for the referenced array segment (cid:2)6, 7, 0(cid:3)
in the first row is optimal and so its corresponding
musical output contains no rests or ties. In the
second row, its referenced array segment, although
forming a minimum cardinality set, nonetheless
contains more pitch classes than its equal-note-
value string. As such, the corresponding output
contains a single rest at the end and we consider
this slightly less optimal. In the sixth row, note
how the presence of pitch-class 4 in the referenced
array segment causes a tie to appear in the output.
We believe this is least optimal. Finally, note that
the reference in the eighth row is not possible, as
it does not contain substrings that belong to this
equal-note-value string (i.e., 6 and 7 are out of order).
In our model, the covers (cid:2)(cid:2)6, 7(cid:3), (cid:2)0(cid:3)(cid:3) and (cid:2)(cid:2)6(cid:3), (cid:2)7, 0(cid:3)(cid:3)
would be considered equally good.
It is important to note that equal-note-value
strings in our model differ slightly from those
in Babbitt’s practice. In Babbitt’s later works, he
ensured that the referenced array segments in a
piece form an exhaustive cover of all array segments
found in its all-partition array, with every pitch class
in any one segment referenced at least once. Finding
such a cover of an all-partition array by equal-note-
value strings is a difficult problem. Presently, we
do not have a method for solving this problem. For
this reason, we have adopted a “greedy” approach
in which equal-note-value strings are constructed
according to the first possible reference (searching
from shortest-length segments first) and where a
single array segment may be referenced more than
once without having all array segments referenced.
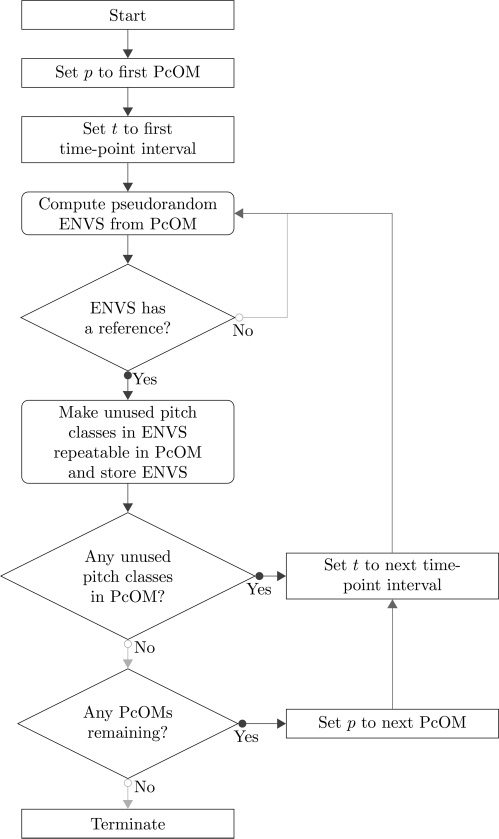
Automating the Compositional Process Found
in Babbitt’s Later Works
We begin with an all-partition array as input,
generated using either of the methods described
by Bemman and Meredith (2016) or by Tanaka,
Bemman, and Meredith (2016a). For each of the n
ordered mosaics in this array, we first generate a
Bemman and Meredith
69
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Table 2. Possible Output from One Equal-Note-Value String
Set of Substrings Referenced Array Segments
Output
(cid:2)(cid:2)6, 7, 0(cid:3)(cid:3)
(cid:2)(cid:2)6, 7, 0(cid:3)(cid:3)
(cid:2)6, 7, 0(cid:3)
(cid:2)6, 7, 0, 9(cid:3)
(cid:2)(cid:2)6, 7(cid:3), (cid:2)0(cid:3)(cid:3)
(cid:2)6, 7(cid:3) and (cid:2)0(cid:3)
(cid:2)(cid:2)6, 7(cid:3), (cid:2)0(cid:3)(cid:3)
(cid:2)6, 7(cid:3) and (cid:2)0, 9(cid:3)
(cid:2)(cid:2)6, 7(cid:3), (cid:2)0(cid:3)(cid:3)
(cid:2)2, 6, 7(cid:3) and (cid:2)0, 9(cid:3)
(cid:2)(cid:2)6, 7(cid:3), (cid:2)0(cid:3)(cid:3)
(cid:2)6, 7, 4(cid:3) and (cid:2)0, 9(cid:3)
(cid:2)(cid:2)6(cid:3), (cid:2)7(cid:3), (cid:2)0(cid:3)(cid:3)
(cid:2)6, 8(cid:3) and (cid:2)7, 4(cid:3) and (cid:2)0, 9(cid:3)
(cid:2)(cid:2)6, 7, 0(cid:3)(cid:3)
(cid:2)4, 9, 7, 6, 0(cid:3)
N/A
Various referenced array segments and the musical output for a given input
equal-note-value string s = (cid:2)6, 7, 0(cid:3) and time-point interval equal to 3 (unit equal to a
sixteenth note). Note that an optimal cover is the minimum cardinality set of substrings
that covers s). The final referenced array segment, (cid:2)4, 9, 7, 6, 0(cid:3), does not contain a
substring equal to its corresponding set of substrings of s (shown at left) and so it does not
have any output (indicated by “N/A”).
time-point ordering of twelve distinct time points,
resulting in a one-dimensional string of n × 12 time
points. We select suitable time-point orderings
based on how well they induce a beat, according to
a heuristic we developed (Bemman and Meredith,
forthcoming). This string of n × 12 time points
serves as the foundation on which the pitch content
is generated through equal-note-value strings
using the steps outlined in this article. Figure 10
shows our proposed procedure for automating the
compositional process seen in Babbitt’s later works.
For each of the (n × 12) − 1 time-point intervals,
we compute, from its corresponding PcOM, a pseu-
dorandom equal-note-value string according to the
probabilities of immediate repeats, other repeats,
and new pitch classes (described in Table 1) and
ensuring its maximum length is not exceeded (as de-
scribed in Equation 2). If this equal-note-value string
has any referenced array segments, we adopt a greedy
approach in which we select the one that produces
a minimum cardinality set cover (or as optimal a
cover as possible, as shown in Table 2), retaining
the appropriate rests and ties. On the other hand, if
this particular equal-note-value string does not have
any reference, we generate a new string containing
the same number of pitch classes and try again to
find a reference. Because references can be difficult
to find for larger lengths, attempting this process
more than once ensures that smaller lengths are
not favored and that a variety of string lengths will
occur in the music. If still no reference is found after
five attempts, we choose a new length and a new
string of pitch classes, repeating this entire process
of attempting to find a referenced array segment.
70
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 10. Proposed
procedure for modeling the
compositional process of
Babbitt’s late-practice
pieces based on the
all-partition array,
time-point system, and
equal-note-value strings
(ENVSs).
Generated Piece
In this section, we present a novel piece automat-
ically generated using the procedure proposed in
this article. This piece, shown in Appendix A, is
a work for flute and string quartet in which each
instrument contains an all-partition array of 34
ordered mosaics in four lynes. In the flute part,
its all-partition array has four lynes or “voices”
distributed across two registers from C4–B5. In the
quartet, each instrument similarly contains four
lynes distributed across two registers with the cello
from C2 to B3, the viola from C3 to B4, violin II from
G3 to F(cid:2)5, and violin I from C4 to B5. Both the flute
and quartet use the same sequence of time points so
that each change in dynamic level aligns for every
instrument. This piece makes use of only the first
17 of its all-partition array’s 34 PcOMs. Ordinarily
in Babbitt’s music, the pitch material exhausts all
PcOMS in the underlying all-partition array, result-
ing in a characteristically long piece of music. The
completion of pitch material in these works typi-
cally signals the end of the piece, often without the
time points having used all the TpcOMs (Bernstein
2017). Similarly, our piece ends with the completion
of its 17 PcOMs by the flute, without all TpcOMs
being used. At about its midpoint (the ninth PcOM),
the piece changes the value of d (shown in Equa-
tion 2) from a sixteenth to a thirty-second note. This
change allows for equal-note-value strings to now
contain shorter durations and when combined with
the manually indicated return to tempo marking
in measure 22, creates a feeling of quickness in the
second half of the piece.
It is important to note that pitch, onset, duration,
voice, dynamic level, and meter have all been
automatically generated in our piece. Meters have
been chosen by dividing the prefix sum of time-point
intervals by the number of units to a beat, from left
to right until this value lies between two and six
beats, inclusive. The fractional meters that result are
more common in Babbitt’s earlier practice, although
they do appear at times in his later works. To ensure
that not all instruments play together at all times,
we have randomly chosen for a given time-point
interval whether or not an equal-note-value string
will occur for each instrument. Similarly, we have
randomly chosen whether or not simultaneities will
occur in an equal-note-value string of the stringed
instruments. Such simultaneities are constrained to
not exceed two and must belong to either segments
1 and 2 or 3 and 4 in their PcOM. This ensures pitch
distance between simultaneities is not exceedingly
large and impossible to perform on the instruments.
Finally, the spelling of pitches (whether a flat
or sharp) has been arbitrarily fixed to avoid flat
symbols, favoring sharps throughout.
Bemman and Meredith
71
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Conclusion
In this article, we have proposed a procedure for
automating the compositional process used in Bab-
bitt’s later works. This process includes his use of
techniques such as the all-partition array, time-
point system, and equal-note-value strings. As our
generated piece has demonstrated, these techniques
alone are sufficient for generating a number of mu-
sical parameters that appear on the musical surface,
including pitch, onset, duration, voice, and dynamic
level. Additional parameters, such as articulation,
phrase markings, tempo indication, and form, have
not been included in our procedure. We would not be
surprised, however, if further analysis of his sketches
were to reveal similar algorithmic techniques for
determining these additional parameters.
Acknowledgments
We would like to thank Laura Piras (flute), Clifton
Harrison (violin I), Abigail Dance (violin II), Chris
Brody (viola), and Anna Tam (cello) for their per-
formance in the premiere of the piece presented in
this article, which was held 28 September 2016 at
the Vortex Jazz Club in London. The work reported
here was carried out as part of the project “Learn-
ing to Create” (Lrn2Cre8), and we acknowledge
the financial support of the Future and Emerging
Technologies (FET) program within the seventh
framework program for research of the European
Commission, under FET grant number 610859.
References
Babbitt, M. 1955. “Some Aspects of Twelve-Tone Compo-
sition.” The Score and IMA Magazine 12:53–61.
Babbitt, M. 1960. “Twelve-Tone Invariants as Composi-
tional Determinants.” Musical Quarterly 46(2):246–
259.
Babbitt, M. 1961. “Set Structure as a Compositional
Determinant.” Journal of Music Theory 5(1):72–94.
Babbitt, M. 1962. “Twelve-Tone Rhythmic Structure and
the Electronic Medium.” Perspectives of New Music
1(1):49–79.
Babbitt, M. 1973. “Since Schoenberg.” Perspectives of
New Music 12(1/2):3–28.
Bemman, B., and D. Meredith. 2015. “Exact Cover
Problem in Milton Babbitt’s All-Partition Array.” In
T. Collins, D. Meredith, and A. Volk, eds. Mathematics
and Computation in Music, Lecture Notes in Artificial
Intelligence, volume 9110. Berlin: Springer, pp. 237–242.
Bemman, B., and D. Meredith. 2016. “Generating Milton
Babbitt’s All-Partition Arrays.” Journal of New Music
Research 45(2):184–204.
Bemman, B., and D. Meredith. forthcoming. “Predicting
Babbitt’s Orderings of Time-Point Classes from Array
Aggregate Partitions in None but the Lonely Flute and
Around the Horn.” Journal of Mathematics and Music.
Bernstein, Z. 2017. “The Problem of Completeness in
Milton Babbitt’s Music and Thought.” Music Theory
Spectrum 38(2):241–264.
Cormen, T. H., et al. 2009. Introduction to Algorithms.
Cambridge, Massachusetts: MIT Press, 3rd edition.
Ebcio˘glu, K. 1987. “Report on the CHORAL Project: An
Expert System for Harmonizing Four-Part Chorales.”
Technical Report RC12628. IBM T. J. Watson Research
Center. Available online at global-supercomputing
.com/people/kemal.ebcioglu/pdf/RC12628.pdf. Ac-
cessed 7 November 2017.
Leong, D., and E. McNutt. 2005. “Virtuosity in Babbitt’s
Lonely Flute.” Music Theory Online 11(1):Article 4.
Mead, A. 1987. “About About Time’s Time: A Sur-
vey of Milton Babbitt’s Recent Rhythmic Practice.”
Perspectives of New Music 25(1–2):182–235.
Mead, A. 1994. An Introduction to the Music of Milton
Babbitt. Princeton, New Jersey: Princeton University
Press.
Tanaka, T., B. Bemman, and D. Meredith. 2016a. “Con-
straint Programming Approach to the Problem of
Generating Milton Babbitt’s All-Partition Arrays.” In
M. Rueher, ed. Principles and Practice of Constraint
Programming. Berlin: Springer, pp. 802–810.
Tanaka, T., B. Bemman, and D. Meredith. 2016b. “Integer
Programming Formulation of the Problem of Generating
Milton Babbitt’s All-Partition Arrays.” In Proceedings
of the International Conference on Music Information
Retrieval, pp. 171–177.
Appendix
On the following pages we present the complete
score of a composition for flute and string quartet
automatically generated in the style of Babbitt using
the procedure proposed in this article.
72
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Bemman and Meredith
73
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
74
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Bemman and Meredith
75
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
76
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Bemman and Meredith
77
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
78
Computer Music Journal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
c
o
m
j
/
l
a
r
t
i
c
e
–
p
d
f
/
/
/
/
4
2
1
6
0
2
0
0
5
5
4
2
/
c
o
m
_
a
_
0
0
4
5
1
p
d
.
j
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Bemman and Meredith
79