ARTICLE
Communicated by Hrushikesh Mhaskar
On PDE Characterization of Smooth Hierarchical
Functions Computed by Neural Networks
Khashayar Filom
filom@umich.edu
Department of Mathematics, University of Michigan, Ann Arbor,
MI 48109, U.S.A.
Roozbeh Farhoodi
roozbeh@seas.upenn.edu
Konrad Paul Kording
kording@upenn.edu
Departments of Bioengineering and Department of Neuroscience,
University of Pennsylvania, Philadelphia, PA 1910, U.S.A.
Neural networks are versatile tools for computation, having the ability
to approximate a broad range of functions. An important problem in
the theory of deep neural networks is expressivity; that is, we want to
understand the functions that are computable by a given network. We
study real, infinitely differentiable (smooth) hierarchical functions im-
plemented by feedforward neural networks via composing simpler func-
tions in two cases: (1) each constituent function of the composition has
fewer inputs than the resulting function and (2) constituent functions are
in the more specific yet prevalent form of a nonlinear univariate function
(e.g., tanh) applied to a linear multivariate function. We establish that
in each of these regimes, there exist nontrivial algebraic partial differen-
tial equations (PDEs) that are satisfied by the computed functions. These
PDEs are purely in terms of the partial derivatives and are dependent
only on the topology of the network. Conversely, we conjecture that such
PDE constraints, once accompanied by appropriate nonsingularity condi-
tions and perhaps certain inequalities involving partial derivatives, guar-
antee that the smooth function under consideration can be represented by
the network. The conjecture is verified in numerous examples, including
the case of tree architectures, which are of neuroscientific interest. Our
approach is a step toward formulating an algebraic description of func-
tional spaces associated with specific neural networks, and may provide
useful new tools for constructing neural networks.
Neural Computation 33, 3204–3263 (2021) © 2021 Massachusetts Institute of Technology
https://doi.org/10.1162/neco_a_01441
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3205
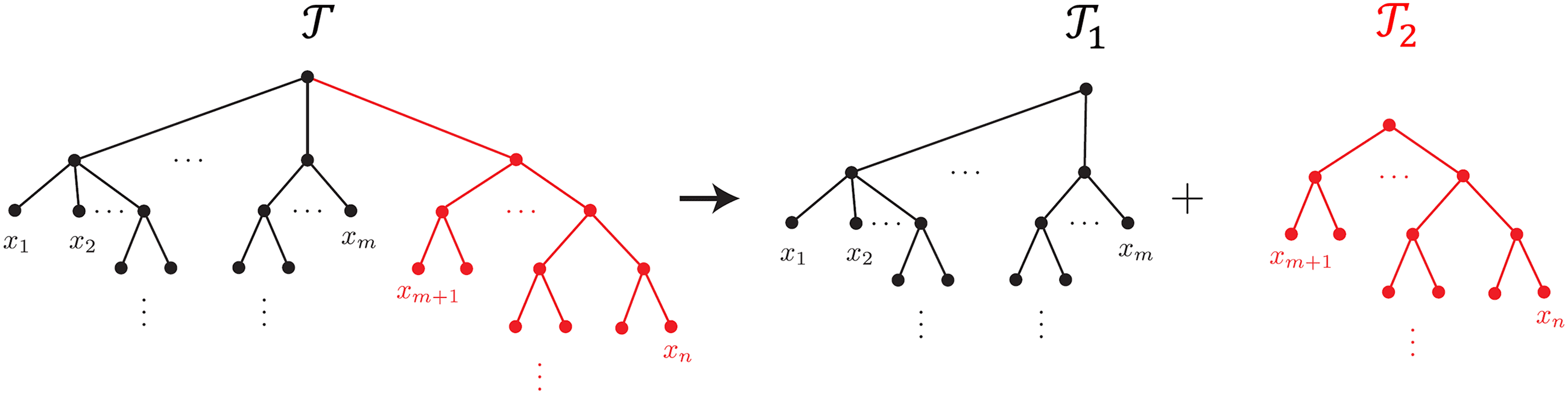
1 Introduction
1.1 Motivation. A central problem in the theory of deep neural net-
works is to understand the functions that can be computed by a partic-
ular architecture (Raghu, Poole, Kleinberg, Ganguli, & Dickstein, 2017;
Poggio, Banburski, & Liao, 2019). Such functions are typically superposi-
tions of simpler functions, that is, compositions of functions of fewer vari-
ables. This article aims to study superpositions of real smooth (i.e., infinitely
differentiable or C∞
) functions that are constructed hierarchically (see Fig-
ure 3). Our core thesis is that such functions (also referred to as hierarchical
or compositional interchangeably) are constrained in the sense that they sat-
isfy certain partial differential equations (PDEs). These PDEs are dependent
only on the topology of the network and could be employed to characterize
smooth functions computable by a given network.
1.1.1 Example 1. One of the simplest examples of a superposition is when
a trivariate function is obtained from composing two bivariate functions; for
instance, let us consider the composition
F(x, y, z) = g ( f (x, y), z)
(1.1)
of functions f = f (x, y) and g = g(u, z) that can be computed by the network
in Figure 1. Assuming that all functions appearing here are twice continu-
ously differentiable (or C2), the chain rule yields
Fx = gu fx,
Fy = gu fy.
If either Fx or Fy – say the former – is nonzero, the equations above imply
that the ratio between Fx and Fy is independent of z:
Fy
Fx
= fy
fx
.
Therefore, its derivative with respect to z must be identically zero:
(cid:3)
(cid:2)
Fy
Fx
= FyzFx − FxzFy
(Fx)2
z
= 0.
This amounts to
FyzFx = FxzFy,
(1.2)
(1.3)
(1.4)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3206
K. Filom, R. Farhoodi, and K. Kording
Figure 1: The architecture on the left (studied in example 1) can compute func-
tions of the form g( f (x, y), z) as in the middle. They involve the smaller class of
functions of the form g(w
4z + b2) on the right.
2y + b1) + w
1x + w
3 f (w
an equation that always holds for functions of form 1.1. Notice that one may
readily exhibit functions that do not satisfy the necessary PDE constraint
FxzFy = FyzFx and so cannot be brought into form 1.1, for example,
xyz + x + y + z.
(1.5)
Conversely, if the constraint FyzFx = FxzFy is satisfied and Fx (or Fy) is
nonzero, we can reverse this processes to obtain a local expression of the
form 1.1 for F(x, y, z). By interpreting the constraint as the independence of
of z, one can devise a function f = f (x, y) whose ratio of partial deriva-
Fx
Fy
tives coincides with Fx
(this is a calculus fact; see theorem 5). Now that equa-
Fy
tion 1.2 is satisfied, the gradient of F may be written as
∇F =
⎤
⎥
⎦ = Fx
fx
⎡
⎢
⎣
Fx
Fy
Fz
⎡
⎢
⎣
fx
fy
0
⎤
⎥
⎦ + Fz
⎤
⎥
⎦ ,
⎡
⎢
⎣
0
0
1
that is, as a linear combination of gradients of f (x, y) and z. This guaran-
tees that F(x, y, z) is (at least locally) a function of the latter two (see the
discussion at the beginning of section 3). So there exists a bivariate function
g defined on a suitable domain with F(x, y, z) = g( f (x, y), z). Later in the ar-
ticle, we generalize this toy example to a characterization of superpositions
computed by tree architectures (see theorem 3).
Functions appearing in the context of neural networks are more spe-
cific than a general superposition such as equation 1.1; they are predomi-
nantly constructed by composing univariate nonlinear activation functions
and multivariate linear functions defined by weights and biases. In the
case of a trivariate function F(x, y, z), we should replace the representation
g( f (x, y), z) studied so far with
F(x, y, z) = g(w
3 f (w
1x + w
2y + b1) + w
4z + b2).
(1.6)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3207
Figure 2: Implementations of superpositions of the form F(x, y, z) = g( f (x, y),
h(x, z)) (studied in examples 2 and 7) by three-layer neural networks.
Assuming that activation functions f and g are differentiable, now new con-
straints of the form 1.3 are imposed. The ratio
, hence it is
not only independent of z as equation 1.3 suggests, but indeed a constant
function. So we arrive at
is equal to
w
2
w
1
Fy
Fx
(cid:2)
Fy
Fx
(cid:3)
(cid:2)
=
x
(cid:3)
(cid:2)
=
y
(cid:3)
z
Fy
Fx
Fy
Fx
= 0,
or, equivalently,
FxyFx = FxxFy,
FyyFx = FxyFy,
FyzFx = FxzFy.
Again, these equations characterize differentiable functions of the form 1.6;
this is a special case of theorem 7 below.
1.1.2 Example 2. The preceding example dealt with compositions of func-
tions with disjoint sets of variables and this facilitated our calculations. But
this is not the case for compositions constructed by most neural networks,
for example, networks may be fully connected or may have repeated inputs.
For instance, let us consider a superposition of the form
F(x, y, z) = g( f (x, y), h(x, z))
(1.7)
of functions f (x, y), h(x, z), and g(u, v ) as implemented in Figure 2. Apply-
ing the chain rule tends to be more complicated than the case of equation
1.1 and results in identities
Fx = gu fx + gv hx,
Fy = gu fy,
Fz = gv hz.
(1.8)
Nevertheless, it is not hard to see that there are again (perhaps cumber-
some) nontrivial PDE constraints imposed on the hierarchical function F, a
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3208
K. Filom, R. Farhoodi, and K. Kording
fact that will be established generally in theorem 1. To elaborate, notice that
identities in equation 1.8 together imply
Fx = A(x, y)Fy + B(x, z)Fz,
(1.9)
and B := hx
hz
where A := fx
are independent of z and y, respectively. Repeat-
fy
edly differentiating this identity (if possible) with respect to y, z results in
linear dependence relations between partial derivatives of F (and hence
PDEs) since the number of partial derivatives of Fx of order at most n with
respect to y, z grows quadratically with n, while on the right-hand side,
the number of possibilities for coefficients (partial derivatives of A and B
with respect to y and z, respectively) grows only linearly. Such dependen-
cies could be encoded by the vanishing of determinants of suitable matrices
formed by partial derivatives of F. In example 7, by pursuing the strategy
just mentioned, we complete this treatment of superpositions 1.7 by deriv-
ing the corresponding characteristic PDEs that are necessary and (in a sense)
sufficient conditions on F that it be in the form of equation 1.7. Moreover,
in order to be able to differentiate several times, we shall assume that all
functions are smooth (or C∞
) hereafter.
1.2 Statements of Main Results. Fixing a neural network hierarchy for
composing functions, we shall prove that once the constituent functions
of corresponding superpositions have fewer inputs (lower arity), there ex-
ist universal algebraic partial differential equations (algebraic PDEs) that
have these superpositions as their solutions. A conjecture, which we ver-
ify in several cases, states that such PDE constraints characterize a generic
smooth superposition computable by the network. Here, genericity means
a nonvanishing condition imposed on an algebraic expression of partial
derivatives. Such a condition has already occurred in example 1 where in
the proof of the sufficiency of equation 1.4 for the existence of a represen-
tation of the form 1.1 for a function F(x, y, z), we assumed either Fx or Fy
is nonzero. Before proceeding with the statements of main results, we for-
mally define some of the terms that have appeared so far.
Terminology
• We take all neural networks to be feedforward. A feedforward neural
network is an acyclic hierarchical layer to layer scheme of computa-
tion. We also include residual networks (ResNets) in this category: an
identity function in a layer could be interpreted as a jump in layers.
Tree architectures are recurring examples of this kind. We shall al-
ways assume that in the first layer, the inputs are labeled by (not nec-
, . . . , xn,
essarily distinct) labels chosen from coordinate functions x1
and there is only one node in the output layer. Assigning functions to
nodes in layers above the input layer implements a real scalar-valued
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3209
Figure 3: The neural network on the left can compute the hierarchical function
(cid:11)(cid:11)
(cid:10)
(cid:10)
(cid:10)
, x2
, x3) = f (3)
, x3), f (1)
, x2), f (1)
F(x1
3
once appropriate functions are assigned to its nodes as on the right.
, x3)
f (1)
2
f (2)
1
f (1)
1
(x2
(x1
(x2
2
1
(x3
, x1)
(cid:11)
, f (2)
2
function F = F(x1
ing at nodes (see Figure 3).
, . . . , xn) as the superposition of functions appear-
• In our setting, an algebraic PDE is a nontrivial polynomial relation
such as
(cid:10)
Fx1
(cid:2)
, . . . , Fxn
, Fx2
1
, Fx1x2
, . . . , Fxα , . . .
= 0
(1.10)
(cid:11)
among the partial derivatives (up to a certain order) of a smooth
function F = F(x1
, . . . , αn) of non-
, . . . , xn). Here, for a tuple α := (α
1
(which is of order
negative integers, the partial derivative
+ · · · + αn) is denoted by Fxα . For instance, asking for a poly-
|α| := α
1
nomial expression of partial derivatives of F to be constant amounts
to n algebraic PDEs given by setting the first-order partial derivatives
of that expression with respect to x1
, . . . , xn to be zero.
+···+αn F
∂ α
1
α
αn
…∂x
∂x
1
n
1
• A nonvanishing condition imposed on smooth functions F =
, . . . , xn) is asking for these functions not to satisfy a particular
F(x1
algebraic PDE, namely,
(cid:10)
(cid:11)
(cid:5)
Fx1
, . . . , Fxn
, Fx2
1
, Fx1x2
, . . . , Fxα , . . .
(cid:4)= 0,
(1.11)
for a nonconstant polynomial (cid:5). Such a condition could be deemed
pointwise since if it holds at a point p ∈ Rn, it persists throughout a
small enough neighborhood. Moreover, equation 1.11 determines an
open dense subset of the functional space; so, it is satisfied generically.
Theorem 1. Let N be a feedforward neural network in which the number of in-
puts to each node is less than the total number of distinct inputs to the network.
Superpositions of smooth functions computed by this network satisfy nontrivial
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3210
K. Filom, R. Farhoodi, and K. Kording
constraints in the form of certain algebraic PDEs that are dependent only on the
topology of N .
In the context of deep learning, the functions applied at each node are in
the form of
y (cid:6)→ σ ((cid:8)w, y(cid:9)) ;
(1.12)
that is, they are obtained by applying an activation function σ to a linear
functional y (cid:6)→ (cid:8)w, y(cid:9). Here, as usual, the bias term is absorbed into the
weight vector. The bias term could also be excluded via composing σ with
a translation since throughout our discussion, the only requirement for a
function σ to be the activation function of a node is smoothness, and acti-
vation functions are allowed to vary from a node to another. In our setting,
σ in equation 1.12 could be a polynomial or a sigmoidal function such as
hyperbolic tangent or logistic functions, but not ReLU or maxout activa-
tion functions. We shall study functions computable by neural networks as
either superpositions of arbitrary smooth functions or as superpositions of
functions of the form 1.12, which is a more limited regime. Indeed, the ques-
tion of how well arbitrary compositional functions, which are the subject of
theorem 1, may be approximated by a deep network has been studied in
the literature (Mhaskar, Liao, & Poggio, 2017; Poggio, Mhaskar, Rosasco,
Miranda, & Liao, 2017).
In order to guarantee the existence of PDE constraints for superpositions,
theorem 1 assumes a condition on the topology of the network. However,
theorem 2 states that by restricting the functions that can appear in the su-
perposition, one can still obtain PDE constraints even for a fully connected
multilayer perceptron:
Theorem 2. Let N be an arbitrary feedforward neural network with at least two
distinct inputs, with smooth functions of the form 1.12 applied at its nodes. Any
function computed by this network satisfies nontrivial constraints in the form of
certain algebraic PDEs that are dependent only on the topology of N .
1.2.1 Example 3. As the simplest example of PDE constraints imposed on
compositions of functions of the form 1.12, recall that d’Alembert’s solution
to the wave equation,
utt = c2uxx,
(1.13)
is famously given by superpositions of the form f (x + ct) + g(x − ct). This
function can be implemented by a network with two inputs x, t and with
one hidden layer in which the activation functions f, g are applied (see Fig-
ure 4). Since we wish for a PDE that works for this architecture universally,
= c2; that is
we should get rid of c. The PDE 1.13 may be written as utt
uxx
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3211
Figure 4: The neural network on the left can compute the function F(x, t) =
σ (a(cid:10)(cid:10) f (ax + bt) + b(cid:10)(cid:10)g(a(cid:10)x + b(cid:10)t)) once, as on the right, the activation functions
σ, f, g and appropriate weights are assigned to the nodes. Such functions are
the subject of examples 3 and 11.
the ratio utt
uxx
should be written as
must be constant. Hence, for our purposes, the wave equation
(cid:11)
(cid:11)
(cid:10)
(cid:10)
utt
uxx
=
x
utt
uxx
t
= 0, or equivalently,
uxttuxx − uttuxxx = 0,
utttuxx − uttuxxt = 0.
A crucial point to notice is that the constant c2 is nonnegative; thus an in-
≥ 0 or uxxutt ≥ 0 is imposed as well. In example 11,
equality of the form uxx
utt
we visit this network again and study functions of the form
F(x, t) = σ (a
(cid:10)(cid:10)
(cid:10)(cid:10)
f (ax + bt) + b
g(a
(cid:10)
(cid:10)
x + b
t))
(1.14)
via a number of equalities and inequalities involving partial derivatives
of F.
The preceding example suggests that smooth functions implemented by
a neural network may be required to obey a nontrivial algebraic partial
differential inequality (algebraic PDI). So it is convenient to have the fol-
lowing setup of terminology.
Terminology
• An algebraic PDI is an inequality of the form
(cid:10)
(cid:11)
(cid:7)
Fx1
, . . . , Fxn
, Fx2
1
, Fx1x2
, . . . , Fxα , . . .
> 0
(1.15)
involving partial derivatives (up to a certain order) where (cid:7) is a real
polynomial.
Remark 1. Without any loss of generality, we assume that the PDIs are strict
since a nonstrict one such as (cid:7) ≥ 0 could be written as the union of (cid:7) > 0
and the algebraic PDE (cid:7) = 0.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3212
K. Filom, R. Farhoodi, and K. Kording
Theorem 1 and example 1 deal with superpositions of arbitrary smooth
functions while theorem 2 and example 3 are concerned with superposi-
tions of a specific class of smooth functions, functions of the form 1.12.
In view of the necessary PDE constraints in both situations, the following
question then arises: Are there sufficient conditions in the form of algebraic
PDEs and PDIs that guarantee a smooth function can be represented, at least
locally, by the neural network in question?
Conjecture 1. Let N be a feedforward neural network whose inputs are labeled by
, . . . , xn. Suppose we are working in the setting of one
the coordinate functions x1
of theorems 1 or 2. Then there exist
• finitely many nonvanishing conditions
• finitely many algebraic PDEs
(cid:12)
• finitely many algebraic PDIs
(cid:12)
(cid:2)
j
(cid:13)
(cid:13)
(cid:7)
k
(Fxα )|α|≤r
(cid:14)
(Fxα )|α|≤r
(cid:15)
(Fxα )|α|≤r
(cid:14)
= 0
(cid:15)
> 0
j
k
(cid:13)
(cid:12)
(cid:5)
i
(cid:14)
(cid:4)= 0
(cid:15)
i
with the following property: For any arbitrary point p ∈ Rn, the space of smooth
functions F = F(x1
(cid:4)= 0 at p and
are computable by N (in the sense of the regime under consideration) is nonvacuous
and is characterized by PDEs (cid:2)
= 0 and PDIs (cid:7)
k
, . . . , xn) defined in a vicinity1 of p that satisfy (cid:5)
> 0.
j
i
To motivate the conjecture, notice that it claims the existence of
functionals
(cid:12)
F (cid:6)→ (cid:5)
i
(cid:13)
(Fxα )|α|≤r
(cid:14)(cid:15)
i
(cid:12)
F (cid:6)→ (cid:2)
j
(cid:13)
,
(Fxα )|α|≤r
(cid:14)(cid:15)
,
j
(cid:12)
F (cid:6)→ (cid:7)
k
(cid:13)
(Fxα )|α|≤r
(cid:14)(cid:15)
k
,
(cid:15)
(cid:12)
(cid:2)
(cid:16)
which are polynomial expressions of partial derivatives, and hence con-
tinuous in the Cr-norm,2 such that in the space of functions computable
by N , the open dense3 subset given by {(cid:5)
i can be described in
terms of finitely many equations and inequalities as the locally closed sub-
. (Also see corollary 1.) The usage of Cr-norm
set
here is novel. For instance, with respect to Lp-norms, the space of func-
tions computable by N lacks such a description and often has unde-
sirable properties like nonclosedness (Petersen, Raslan, & Voigtlaender,
2020). Besides, describing the functional space associated with a neural
> 0}
k
(cid:4)= 0}
{(cid:7)
k
= 0
j
j
i
1
2
3
To be mathematically precise, the open neighborhood of p on which F admits a com-
positional representation in the desired form may be dependent on F and p. So conjecture
1 is local in nature and must be understood as a statement about function germs.
Convergence in the Cr-norm is defined as the uniform convergence of the function
and its partial derivatives up to order r.
In conjecture 1, the subset cut off by equations (cid:5)
i
= 0 is meager: It is a closed and
(due to the term nonvacuous appearing in the conjecture) proper subset of the space of
functions computable by N , and a function implemented by N at which a (cid:5)
i vanishes
could be perturbed to another computable function at which all of (cid:5)
i’s are nonzero.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3213
network N with finitely many equations and inequalities also has an alge-
braic motivation: it is reminiscent of the notion of a semialgebraic set from
real algebraic geometry. To elaborate, take the activation functions to be
polynomials. Such neural networks have been studied in the literature (Du
& Lee, 2018; Soltanolkotabi, Javanmard, & Lee, 2018; Venturi, Bandeira, &
Bruna, 2018; Kileel, Trager, & Bruna, 2019). By bounding the degrees of
constituent functions of superpositions computed by a polynomial neural
network, the functional space formed by these superpositions sits inside a
finite-dimensional ambient space of real polynomials and is hence finite-
dimensional and amenable to techniques of algebraic geometry. One can,
for instance, in each degree associate a functional variety to a neural net-
work N whose dimension could be interpreted as a measure of expressive
power (Kileel et al., 2019). Our approach to describing real functions com-
putable by neural networks via PDEs and PDIs has ramifications to the
study of polynomial neural networks as well. Indeed, if F = F(x1
, . . . , xn)
is a polynomial, an algebraic PDE of the form 1.10 translates to a polyno-
mial equation of the coefficients of F, and the condition that an algebraic
PDI such as equation 1.15 is valid throughout Rn can again be described
via equations and inequalities involving the coefficients of F (see examples
12 and 13). A notable feature here is the claim of the existence of a universal
characterization dependent only on the architecture from which a descrip-
tion as a semialgebraic set could be read off in any degree.
Conjecture 1 is settled in (Farhoodi, Filom, Jones, and Körding, 2019) for
trees (a particular type of architectures) with distinct inputs, a situation in
which no PDI is required, and the inequalities should be taken to be trivial.
Throughout the article, the conjecture above will be established for a num-
ber of architectures; in particular, we shall characterize tree functions (cf.
theorems 3 and 4 below).
1.3 Related Work. There is an extensive literature on the expressive
power of neural networks. Although shallow networks with sigmoidal ac-
tivation functions can approximate any continuous function on compact
sets (Cybenko, 1989; Hornik, Stinchcombe, & White, 1989; Hornik, 1991;
Mhaskar, 1996), this cannot be achieved without the hidden layer getting
exponentially large (Eldan & Shamir, 2016; Telgarsky, 2016; Mhaskar et al.,
2017; Poggio et al., 2017). Many articles thus try to demonstrate how the
expressive power is affected by depth. This line of research draws on a
number of different scientific fields including algebraic topology (Bian-
chini & Scarselli, 2014), algebraic geometry (Kileel et al., 2019), dynam-
ical systems (Chatziafratis, Nagarajan, Panageas, & Wang, 2019), tensor
analysis (Cohen, Sharir, & Shashua, 2016), Vapnik–Chervonenkis theory
(Bartlett, Maiorov, & Meir, 1999), and statistical physics (Lin, Tegmark, &
Rolnick, 2017). One approach is to argue that deeper networks are able
to approximate or represent functions of higher complexity after defining
a “complexity measure” (Bianchini & Scarselli, 2014; Montufar, Pascanu,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3214
K. Filom, R. Farhoodi, and K. Kording
Cho, & Bengio, 2014; Poole, Lahiri, Raghu, Sohl-Dickstein, & Ganguli, 2016;
Telgarsky, 2016; Raghu et al., 2017). Another approach more in line with this
article is to use the “size” of an associated functional space as a measure of
representation power. This point of view is adapted in Farhoodi et al. (2019)
by enumerating Boolean functions, and in Kileel et al. (2019) by regarding
dimensions of functional varieties as such a measure.
A central result in the mathematical study of superpositions of func-
tions is the celebrated Kolmogorov-Arnold representation theorem (Kol-
mogorov, 1957), which resolves (in the context of continuous functions)
the thirteenth problem on Hilbert’s famous list of 23 major mathematical
problems (Hilbert, 1902). The theorem states that every continuous func-
tion F(x1
, . . . , xn) on the closed unit cube may be written as
F(x1
, . . . , xn) =
2n+1(cid:17)
⎛
n(cid:17)
⎝
fi
i=1
j=1
⎞
φ
⎠
i, j(x j )
(1.16)
j
φ
i with λ
j’s and φ
i, j are be taken to be in the form of λ
for suitable continuous univariate functions fi, φ
i, j defined on the unit in-
terval. (See Vituškin and Henkin, 1967, chap. 1, or Vituškin, 2004, for a his-
torical account.) In more refined versions of this theorem (Sprecher, 1965;
Lorentz, 1966), the outer functions fi are arranged to be the same, and the
inner ones φ
i’s
independent of F. Based on the existence of such an improved represen-
tation, Hecht-Nielsen argued that any continuous function F can be im-
plemented by a three-layer neural network whose weights and activation
functions are determined by the representation (Hecht-Nielsen, 1987). On
the other hand, it is well known that even when F is smooth, one cannot
arrange for functions appearing in representation 1.16 to be smooth (Vi-
tuškin, 1964). As a matter of fact, there exist continuously differentiable
functions of three variables that cannot be represented as sums of super-
positions of the form g ( f (x, y), z) with f and g being continuously differ-
entiable as well (Vituškin, 1954) whereas in the continuous category, one
can write any trivariate continuous functions as a sum of nine superpo-
sitions of the form g ( f (x, y), z) (Arnold, 2009b). Due to this emergence of
nondifferentiable functions, it has been argued that Kolmogorov-Arnold’s
theorem is not useful for obtaining exact representations of functions via
networks (Girosi & Poggio, 1989), although it may be used for approxima-
tion (K ˚urková, 1991, 1992). More on algorithmic aspects of the theorem and
its applications to the network theory can be found in Brattka (2007).
Focusing on a superposition
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
F = f (L)
1
(cid:10)
(cid:10)
f (L−1)
1
f (L−1)
NL−1
f (L−2)
a1
(cid:10)
f (L−2)
aNL−1
(cid:11)
(. . .), . . .
(cid:10)
, . . . , f (L−1)
(cid:11) (cid:11)
j
f (L−2)
a j
(. . .), . . .
(cid:11)
, . . . ,
(. . .), . . .
(1.17)
PDE Characterization of Functions Computed by Neural Networks
3215
of smooth functions (which can be computed by a neural network as in
Figure 3), the chain rule provides descriptions for partial derivatives of F
in terms of partial derivatives of functions f (i)
that constitute the super-
j
position. The key insight behind the proof of theorem 1 is that when the
former functions have fewer variables compared to F, one may eliminate
the derivatives of f (i)
’s to obtain relations among partial derivatives of F.
j
This idea of elimination has been utilized in Buck (1981b) and Rubel (1981)
to prove the existence of universal algebraic differential equations whose
C∞ solutions are dense in the space of continuous functions. The fact that
there will be constraints imposed on derivatives of a function F that is writ-
ten as a superposition of differentiable functions was employed by Hilbert
himself to argue that certain analytic functions of three variables are not
superpositions of analytic functions of two variables (Arnold, 2009a, p. 28),
and by Ostrowski to exhibit an analytic bivariate function that cannot be
represented as a superposition of univariate smooth functions and multi-
variate algebraic functions due to the fact that it does not satisfy any non-
trivial algebraic PDE (Vituškin, 2004, p. 14; Ostrowski, 1920). The novelty
of our approach is to adapt this point of view to demonstrate theoretical
limitations of smooth functions that neural networks compute either as a
superposition as in theorem 1 or as compositions of functions of the form
1.12 as in theorem 2, and to try to characterize these functions via calculat-
ing PDE constraints that are sufficient too (cf. conjecture 1). Furthermore,
necessary PDE constraints enable us to easily exhibit functions that cannot
be computed by a particular architecture; see example 1. This is reminiscent
of the famous Minsky XOR Theorem (Minsky & Papert, 2017). An interest-
ing nonexample from the literature is F(x, y, z) = xy + yz + zx which cannot
be written as a superposition of the form 1.7 even in the continuous cate-
gory (Pólya & Szegö, 1945; Buck, 1979, 1981a; von Golitschek, 1980; Arnold,
2009a).
To the best of our knowledge, the closest mentions of a characterization
of a class of superpositions by necessary and sufficient PDE constraints in
the literature are papers (Buck, 1979, 1981a) by R. C. Buck. The first one
(along with its earlier version, Buck, 1976) characterizes superpositions of
the form g( f (x, y), z) in a similar fashion as example 1. Also in those pa-
pers, superpositions such as g( f (x, y), h(x, z)) (which appeared in example
2) are discussed although only the existence of necessary PDE constraints
is shown; see (Buck, 1979, lemma 7), and (Buck, 1981a, p. 141). We exhibit
a PDE characterization for superpositions of this form in example 7. These
papers also characterize sufficiently differentiable nomographic functions of
the form σ ( f (x) + g(y)) and σ ( f (x) + g(y) + h(z)).
A special class of neural network architectures is provided by rooted
trees where any output of a layer is passed to exactly one node from one of
the layers above (see Figure 8). Investigating functions computable by trees
is of neuroscientific interest because the morphology of the dendrites of a
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3216
K. Filom, R. Farhoodi, and K. Kording
Figure 5: Theorems 3 and 4 impose constraints 1.18 and 1.19 for any three leaves
xi, x j, and xk. In the former theorem, the constraint should hold whenever (as
on the left) there exists a rooted full subtree separating xi and x j from xk, while
in the latter theorem, the constraint is imposed for certain other triples as well
(as on the right).
neuron processes information through a tree that is often binary (Kollins
& Davenport, 2005; Gillette & Ascoli, 2015). Assuming that the inputs to
a tree are distinct, in our previous work (Farhoodi et al., 2019), we have
completely characterized the corresponding superpositions through for-
mulating necessary and sufficient PDE constraints; a result that answers
conjecture 1 in positive for such architectures.
Remark 2. The characterization suggested by the theorem below is a gen-
eralization of example 1 which was concerned with smooth superpositions
of the form 1.1. The characterization of such superpositions as solutions of
PDE 1.4 has also appeared in a paper (Buck, 1979) that we were not aware
of while writing (Farhoodi et al., 2019).
Theorem 3 (Farhoodi et al., 2019). Let T be a rooted tree with n leaves that are
, . . . , xn) be a smooth
labeled by the coordinate functions x1
function implemented on this tree. Then for any three leaves of T corresponding to
, xk of F with the property that there is a (rooted full) subtree of T
, x j
variables xi
, x j while missing the leaf xk (see Figure 5), F must satisfy
containing the leaves xi
, . . . , xn. Let F = F(x1
Fxixk Fx j
= Fx jxk Fxi
.
(1.18)
Conversely, a smooth function F defined in a neighborhood of a point p ∈ Rn can
be implemented by the tree T provided that equation 1.18 holds for any triple
, xk) of its variables with the above property; and moreover, the non-vanishing
(xi
conditions below are satisfied:
, x j
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
• For any leaf xi with siblings either Fxi (p) (cid:4)= 0 or there is a sibling leaf xi(cid:10) with
(cid:10) (p) (cid:4)= 0.
Fxi
This theorem was formulated in Farhoodi et al. (2019) for binary trees
and in the context of analytic functions (and also that of Boolean functions).
Nevertheless, the proof carries over to the more general setting above. Be-
low, we formulate the analogous characterization of functions that trees
PDE Characterization of Functions Computed by Neural Networks
3217
Figure 6: Theorem 4 imposes constraint 1.20 for any four leaves xi
that belong to two different rooted full subtrees emanating from a node.
, xi(cid:10) and x j
, x j(cid:10)
compute via composing functions of the form 1.12. Proofs of theorems 3
and 4 are presented in section 4.
Theorem 4. Let T be a rooted tree admitting n leaves that are labeled by the co-
, . . . , xn. We formulate the following constraints on smooth
ordinate functions x1
functions F = F(x1
, . . . , xn):
• For any two leaves xi and x j of T , we have
Fxixk Fx j
= Fx jxk Fxi
(1.19)
for any other leaf xk of T that is not a leaf of a (rooted full) subtree that has
exactly one of xi or x j (see Figure 5). In particular, equation 1.19 holds for
any xk if the leaves xi and x j are siblings, and for any xi and x j if the leaf xk
is adjacent to the root of T .
• For any two (rooted full) subtrees T
1 and T
2 that emanate from a node of T
(see Figure 6), we have
(cid:22)
Fxixi
Fxi Fx j
(cid:13)
Fxixi
=
(cid:10) Fx j
(cid:10) x j
+ Fxixi
(cid:10) − Fxix j
(cid:10) Fx jxi
(cid:10) − Fxi Fx jxi
(cid:11)
(cid:10) x j
(cid:23)
(cid:10)
(cid:10) Fx jx j
(cid:14) (cid:10)
(cid:10) Fx j
− Fxi Fx jxi
(cid:10)
Fxix j
(cid:10) Fx j
+ Fxi Fx jx j
(cid:10)
(1.20)
if xi, xi(cid:10) are leaves of T
1 and x j, x j(cid:10) are leaves of T
2.
, . . . , xn) is a superposition of functions of
These constraints are satisfied if F(x1
the form y (cid:6)→ σ ((cid:8)w, y(cid:9)) according to the hierarchy provided by T . Conversely, a
smooth function F defined on an open box-like region4 B ⊆ Rn can be written as
such a superposition on B provided that the constraints 1.19 and 1.20 formulated
above hold and, moreover, the nonvanishing conditions below are satisfied through-
out B:
4
An open box-like region in Rn is a product I1
× · · · × In of open intervals.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3218
K. Filom, R. Farhoodi, and K. Kording
• For any leaf xi with siblings either Fxi
(cid:4)= 0 or there is a sibling leaf xi(cid:10) with
Fxi
(cid:10)
(cid:4)= 0;
• For any leaf xi without siblings Fxi
(cid:4)= 0.
The constraints that appeared in theorems 3 and 4 may seem tedious, but
they can be rewritten more conveniently once the intuition behind them is
explained. Assuming that partial derivatives do not vanish (a nonvanish-
ing condition) so that division is allowed, equations 1.18 and 1.19 may be
written as
(cid:24)
(cid:25)
Fxi
Fx j
xk
= 0 ⇔
(cid:2)
Fxi
Fxk
(cid:3)
(cid:2)
=
x j
(cid:3)
,
xi
Fx j
Fxk
while equation 1.20 is
⎛
(cid:2)
(cid:3)
⎜
⎜
⎜
⎝
Fxi
Fx j
Fxi
Fx j
⎞
⎟
⎟
⎟
⎠
xi
(cid:10)
(cid:10)
x j
= 0.
(1.21)
(1.22)
Fxi
Fx j
Equation 1.21 simply states that the ratio
is independent of xk. Notice that
=
in comparison with theorem 3, theorem 7, requires the equation Fxixk Fx j
, xk) of leaves
Fx jxk Fxi to hold in a greater generality and for more triples (xi
(see Figure 5).5 The second simplified equation 1.22, holds once the function
Fxi
Fx j
, . . . , xn) may be split into a product such as
of (x1
, x j
q1(. . . , xi
, . . . , xi(cid:10) , . . .) q2(. . . , x j
, . . . , x j(cid:10) , . . .).
Lemma 4 discusses the necessity and sufficiency of these equations for the
existence of such a splitting.
Remark 3. A significant feature of theorem 7 is that once the appropriate
conditions are satisfied on a box-like domain, the smooth function under
consideration may be written as a superposition of the desired form on the
entirety of that domain. On the contrary, theorem 3 is local in nature.
Aside from neuroscientific interest, studying tree architectures is impor-
tant also because any neural network can be expanded into a tree network
5
A piece of terminology introduced in Farhoodi et al. (2019) may be illuminating here.
, xk ) of (not necessarily distinct) leaves of T is called the out-
A member of a triple (xi
sider of the triple if there is a (rooted full) subtree of T that misses it but has the other
= Fx j xk Fxi whenever xk is the outsider, while
two members. Theorem 3 imposes Fxixk Fx j
theorem 4 imposes the constraint whenever xi and x j are not outsiders.
, x j
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3219
Figure 7: A multilayer neural network can be expanded to a tree. The figure is
adapted from Farhoodi et al. (2019).
with repeated inputs through a procedure called TENN (the Tree
Expansion of the Neural Network; see Figure 7). Tree architectures with
repeated inputs are relevant in the context of neuroscience too because the
inputs to neurons may be repeated (Schneider-Mizell et al., 2016; Gerhard,
Andrade, Fetter, Cardona, & Schneider-Mizell, 2017). We have already seen
an example of a network along with its TENN in Figure 2. Both networks
implement functions of the form F(x, y, z) = g( f (x, y), h(x, z)). Even for this
simplest example of a tree architecture with repeated inputs, the derivation
of characteristic PDEs is computationally involved and will be done in ex-
ample 7. This verifies conjecture 1 for the tree that appeared in Figure 2.
1.4 Outline of the Article. Theorems 1 and 2 are proven in section 2
where it is established that in each setting, there are necessary PDE condi-
tions for expressibility of smooth functions by a neural network. In section
3 we verify conjecture 1 in several examples by characterizing computable
functions via PDE constraints that are necessary and (given certain nonva-
nishing conditions) sufficient. This starts by studying tree architectures in
section 3.1. In example 7, we finish our treatment of a tree function with
repeated inputs initiated in example 2; and, moreover, we present a num-
ber of examples to exhibit the key ideas of the proofs of theorems 3 and
4, which are concerned with tree functions with distinct inputs. The sec-
tion then proceeds with switching from trees to other neural networks in
section 3.2 where, building on example 3, example 11 demonstrates why
the characterization claimed by conjecture 1 involves inequalities. We end
section 3 with a brief subsection on PDE constraints for polynomial neural
networks. Examples in section 3.1 are generalized in the next section to a
number of results establishing conjecture 1 for certain families of tree ar-
chitectures: Proofs of theorems 3 and 4 are presented in section 4. The last
section is devoted to few concluding remarks. There are two appendices
discussing technical proofs of propositions and lemmas (appendix A), and
the basic mathematical background on differential forms (appendix B).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3220
K. Filom, R. Farhoodi, and K. Kording
2 Existence of PDE Constraints
The goal of the section is to prove theorems 1 and 2. Lemma 1 below is our
main tool for establishing the existence of constraints:
, . . . , tm) of polynomials on m
, . . . , tm), . . . , pl (t1
Lemma 1. Any collection p1(t1
indeterminates are algebraically dependent provided that l > m. In other words, if
l > m, there exists a nonconstant polynomial (cid:2) = (cid:2)(s1
, . . . , sl ) dependent only
on the coefficients of pi’s for which
(cid:2) (p1(t1
, . . . , tm), . . . , pl (t1
, . . . , tm)) ≡ 0.
(cid:13)
(cid:14)
a+l
l
(cid:13)
. . . pal
, . . . , deg pl
monomials such
+ · · · + al not greater than a. But
, . . . , tm of total degree at most ad where
(cid:14)
(cid:14)
ad+m
m
Proof. For a positive integer a, there are precisely
as pa1
l with their total degree a1
1
each of them is a polynomial of t1
d := max{deg p1
}. For a large enough,
because the degree of the former as a polynomial of a is l, while the de-
, . . . , pal
gree of the latter is m. For such an a, the number of monomials pa1
1
l
, . . . , tm of to-
is larger than the dimension of the space of polynomials of t1
tal degree at most ad. Therefore, there exists a linear dependency among
these monomials that amounts to a nontrivial polynomial relation among
(cid:2)
p1
, . . . , xn) be a superposition of smooth
Proof of Theorem 1. Let F = F(x1
functions
is greater than
, . . . , pl.
a+l
l
(cid:13)
f (1)
1
, . . . , f (1)
N1
; . . . ; f (i)
1
, . . . , f (i)
Ni
; . . . ; f (L)
1
(2.1)
, . . . , f (i)
Ni
according to the hierarchy provided by N where f (i)
are the func-
1
tions appearing at the neurons of the ith layer above the input layer (in
f (L)
the last layer,
NL=1 appears at the output neuron). The total number of
these functions is N := N1
+ · · · + NL, namely, the number of the neurons
of the network. By the chain rule, any partial derivative Fxα of the super-
position may be described as a polynomial of partial derivatives of order
not greater than |α| of functions that appeared in equation 2.1. These poly-
nomials are determined solely by how neurons in consecutive layers are
connected to each other, that is, the architecture. The function F of n vari-
− 1 partial derivatives (excluding the function itself) of
ables admits
order at most r, whereas the same number for any of the functions listed in
− 1 because by the hypothesis, each of them is
equation 2.1 is at most
dependent on less than n variables. Denote the partial derivatives of order
at most r of functions f (i)
(evaluated at appropriate points as required by the
j
, . . . , tm. Following the previous discussion,
chain rule) by indeterminates t1
(cid:10)(cid:13)
one has m ≤ N
. Hence, the chain rule describes the partial
(cid:14)
r+n
n
r+n−1
n−1
− 1
(cid:11)
(cid:13)
(cid:14)
(cid:13)
(cid:14)
r+n−1
n−1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3221
derivatives of order not greater than r of F as polynomials (dependent only
on the architecture of N ) of t1
, . . . , tm. Invoking lemma 1, the partial deriva-
tives of F are algebraically dependent once
(cid:3)
(cid:2)
r + n
n
− 1 > N
(cid:2)(cid:2)
(cid:3)
(cid:3)
− 1
.
r + n − 1
n − 1
(2.2)
Indeed, the inequality holds for r large enough since the left-hand side is a
polynomial of degree n of r, while the similar degree for the right-hand side
(cid:2)
is n − 1.
Proof of Theorem 2. In this case F = F(x1
functions of the form
, . . . , xn) is a superposition of
(cid:14)
, .(cid:9)
(cid:13)
σ (1)
1
(cid:8)w(1)
1
(cid:13)
. . . ; σ (L)
1
(cid:8)w(L)
1
, . . . , σ (1)
N1
(cid:14)
, .(cid:9)
(cid:13)
(cid:8)w(1)
N1
(cid:14)
, .(cid:9)
; . . . ; σ (i)
1
(cid:13)
(cid:8)w(i)
1
(cid:14)
, .(cid:9)
, . . . , σ (i)
Ni
(cid:13)
(cid:8)w(i)
Ni
(cid:14)
, .(cid:9)
;
(2.3)
(cid:14)
, .(cid:9)
(cid:13)
(cid:8)w(i)
j
is applied to the inner product
appearing at neurons. The jth neuron of the ith layer above the input layer
(1 ≤ i ≤ N, 1 ≤ j ≤ Ni) corresponds to the function σ (i)
where a
j
univariate smooth activation function σ (i)
j
of the weight vector w(i)
j with the vector formed by the outputs of neurons
in the previous layer which are connected to the neuron of the ith layer. We
proceed as in the proof of theorem 1. The chain rule describes each partial
derivative Fxα as a polynomial, dependent only on the architecture, of com-
ponents of vectors w(i)
j up to order
at most |α| (each evaluated at an appropriate point). The total number of
components of all weight vectors coincides with the total number of con-
nections (edges of the underlying graph), and the number of the derivatives
of activation functions is the number of neurons times |α|. We denote the to-
tal number of connections and neurons by C and N, respectively. There are
(cid:13)
r+n
− 1 partial derivatives Fxα of order at most r (i.e., |α| ≤ r) of F and, by
n
the previous discussion, each of them may be written as a polynomial of
C + Nr quantities given by components of weight vectors and derivatives
of activation functions. Lemma 1 implies that these partial derivatives of F
are algebraically dependent provided that
j along with derivatives of functions σ (i)
(cid:14)
(cid:3)
(cid:2)
r + n
n
− 1 > Nr + C,
(2.4)
an inequality that holds for sufficiently large r as the degree of the left-hand
(cid:2)
side with respect to r is n > 1.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3222
K. Filom, R. Farhoodi, and K. Kording
Corollary 1. Let N be a feedforward neural network whose inputs are labeled by
, . . . , xn and satisfies the hypothesis of either of theorems
the coordinate functions x1
1 or 2. Define the positive integer r as
• r = n (#neurons − 1) in the case of theorem 1
(cid:14)
• r = max
n−1 (cid:17), #connections
(cid:16)n (#neurons)
(cid:13)
1
+ 2 in the case of theorem 2,
where #connections and #neurons are, respectively, the number of edges of the un-
derlying graph of N and the number of its vertices above the input layer. Then the
smooth functions F = F(x1
, . . . , xn) computable by N satisfy nontrivial algebraic
partial differential equations of order r. In particular, the subspace formed by these
functions lies in a subset of positive codimension, which is closed with respect to
the Cr-norm.
Proof. One only needs to verify that for the values of r provided by the
corollary the inequalities 2.2 and 2.4 are valid. The former holds if
(cid:13)
(cid:14)
(cid:13)
r+n
n
r+n−1
n−1
(cid:14) = r + n
n
is not smaller than N, that is, if r ≥ n(N − 1). As for equation 2.4, notice that
(cid:2)
(cid:3)
r + n
n
− 1 − Nr ≥ rn
n!
(cid:10)
− Nr = r
(cid:2)
rn−1
n!
(cid:3)
− N
;
(cid:11)
hence, it suffices to have r
1. The latter inequality is valid once r ≥ n.N
(cid:25)
(cid:24)
rn−1
n!
− N
> C. This holds if r > C and rn−1
n−1 + 2, since then:
n!
1
rn−1
n!
=
r
1
n−1
(n!)
≥ N + 2(n − 1)
n
n−1
(cid:10)
(cid:11)
n−1
≥
r
n
(cid:2)
≥
N
1
n−1 + 2
n
(cid:3)
n−1
.N
n−2
n−1 ≥ N + 1.
− N ≥
(cid:2)
Remark 4. It indeed follows from the arguments above that there is a mul-
titude of algebraically independent PDE constraints. By a simple dimension
(cid:10)(cid:13)
(cid:13)(cid:13)
(cid:11)
(cid:14)
(cid:14)
(cid:14)
in the first case of corol-
count, this number is
(cid:14)
(cid:13)(cid:13)
− 1
lary 1 and
(cid:14)
r+n
n
− 1
r+n
n
− N
− Nr in the second case.
r+n−1
n−1
− 1
Remark 5. The approach here merely establishes the existence of nontrivial
algebraic PDEs satisfied by the superpositions. These are not the simplest
PDEs of this kind and hence are not the best candidates for the purpose of
characterizing superpositions. For instance, for superpositions 1.7, which
networks in Figure 2 implement, one has n = 3 and #neurons = 3. Corollary
1 thus guarantees that these superpositions satisfy a sixth-order PDE. But in
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3223
example 7, we shall characterize them via two fourth-order PDEs (compare
with Buck, 1979, lemma 7).
1+e−x or tangent hyperbolic ex−e
Remark 6. Prevalent smooth activation functions such as the logistic func-
−x
tion 1
ex+e−x satisfy certain autonomous algebraic
ODEs. Corollary 1 could be improved in such a setting. If each activation
function σ = σ (x) appearing in equation 2.3 satisfies a differential equation
of the form
dkσ
dxk
= p
(cid:2)
σ, dσ
dx
, . . . , dk−1σ
dxk−1
(cid:3)
+
where p is a polynomial, one can change equation 2.4 to
C where kmax is the maximum order of ODEs that activation functions in
equation 2.3 satisfy.
− 1 > Nkmax
(cid:13)
(cid:14)
r+n
n
3 Toy Examples
, . . . , xn) is written as g(ξ
1
This section examines several elementary examples demonstrating how
one can derive a set of necessary or sufficient PDE constraints for an ar-
chitecture. The desired PDEs should be universal, that is, purely in terms
of the derivatives of the function F that is to be implemented and not de-
pendent on any weight vector, activation function, or a function of lower
dimensionality that has appeared at a node. In this process, it is often nec-
essary to express a smooth function in terms of other functions. If k < n
, . . . , ξ
and f (x1
k) throughout an open neighbor-
hood of a point p ∈ Rn where each ξ
, . . . , xn) is a smooth func-
= ξ
i
tion, the gradient of f must be a linear combination of those of ξ
, . . . , ξ
1
k
due to the chain rule. Conversely, if ∇ f ∈ Span{∇ξ
} near p, by
1
the inverse function theorem, one can extend (ξ
, . . . , ξ
k) to a coordinate
1
system (ξ
, . . . , ξn) on a small enough neighborhood of p pro-
1
vided that ∇ξ
k(p) are linearly independent; a coordinate system
i vanishes for k < i ≤ n; the fact that im-
in which the partial derivative fξ
plies f can be expressed in terms of ξ
k near p. Subtle mathematical
1
issues arise if one wants to write f as g(ξ
k) on a larger domain con-
1
taining p:
; ξ
1(p), . . . , ∇ξ
, . . . , ∇ξ
k
, . . . , ξ
, . . . , ξ
, . . . , ξ
i(x1
k+1
k
• A k-tuple (ξ
1
, . . . , ξ
k) of smooth functions defined on an open sub-
set U of Rn whose gradient vector fields are linearly independent
at all points cannot necessarily be extended to a coordinate system
(ξ
, . . . , ξn) for the whole U. As an example, consider
1
x2 + y2 whose gradient is nonzero at any point of R2 − {(0, 0)},
r =
but there is no smooth function h : R2 − {(0, 0)} → R with ∇h (cid:4) (cid:18) ∇r
throughout R2 − {(0, 0)}. The level set r = 1 is compact, and so the
, . . . , ξ
(cid:28)
k+1
; ξ
k
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3224
K. Filom, R. Farhoodi, and K. Kording
restriction of h to it achieves its absolute extrema, and at such points
∇h = λ∇ f (λ is the Lagrange multiplier).
• Even if one has a coordinate system (ξ
1
, . . . , ξn) on
a connected open subset U of Rn, a smooth function f : U → R
≡ 0 cannot necessarily be written globally as f =
with fξ
g(ξ
, . . . , fξn
k). One example is the function
k+1
, . . . , ξ
, . . . , ξ
k+1
; ξ
1
k
f (x, y) :=
⎧
⎪⎪⎨
⎪⎪⎩
0
−1
x
e
−e
−1
x
if x ≤ 0
if x > 0, y > 0
if x > 0, y < 0
defined on the open subset R2 − [0, ∞) ⊂ R2 for which fy ≡ 0. It may
only locally be written as f (x, y) = g(x); there is no function g : R → R
with f (x, y) = g(x) for all (x, y) ∈ R2 − [0, ∞). Defining g(x0) as the
value of f on the intersection of its domain with the vertical line
x = x0 does not work because, due to the shape of the domain, such
intersections may be disconnected. Finally, notice that f , although
smooth, is not analytic (Cω); indeed, examples of this kind do not exist
in the analytic category.
, . . . , ξ
This difficulty of needing a representation f = g(ξ
k) that remains
1
valid not just near a point but over a larger domain comes up only in the
proof of theorem 4 (see remark 3); the representations we work with in the
rest of this section are all local. The assumption about the shape of the do-
main and the special form of functions 1.12 allows us to circumvent the
difficulties just mentioned in the proof of theorem 4. Below we have two
related lemmas that we use later.
Lemma 2. Let B and T be a box-like region in Rn and a rooted tree with the coor-
, . . . , xn labeling its leaves as in theorem 7. Suppose a smooth
dinate functions x1
function F = F(x1
, . . . , xn) on B is implemented on T via assigning activation
functions and weights to the nodes of T . If F satisfies the nonvanishing conditions
described at the end of theorem 7, then the level sets of F are connected and F can
be extended to a coordinate system (F, F2
, . . . , Fn) for B.
+ · · · + anxn) sat-
, . . . , xn) of the form σ (a1x1
Lemma 3. A smooth function F(x1
= Fx jxk Fxi for any 1 ≤ i, j, k ≤ n. Conversely, if F has a first-order
isfies Fxixk Fx j
partial derivative Fx j which is nonzero throughout an open box-like region B in
= 0; that is,
its domain, each identity Fxixk Fx j
Fxi
for any 1 ≤ i ≤ n, the ratio
Fx j
guarantee that F admits a representation of the form σ (a1x1
= Fx jxk Fxi could be written as
should be constant on B, and such requirements
+ · · · + anxn) on B.
Fxi
Fx j
xk
(cid:13)
(cid:14)
In view of the discussion so far, it is important to know when a smooth
vector field,
V(x1
, . . . , xn) = [V1(x1
, . . . , xn) . . . Vn(x1
, . . . , xn)]T,
(3.1)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3225
on an open subset U ⊂ Rn is locally given by a gradient. Clearly, a necessary
condition is to have
(Vi)x j
= (Vj )xi
∀ i, j ∈ {1, . . . , n}.
(3.2)
It is well known that if U is simply connected, this condition is sufficient too
and guarantees the existence of a smooth potential function ξ on U satisfy-
ing ∇ξ = V (Pugh, 2002). A succinct way of writing equation 3.2 is dω = 0
where ω is defined as the differential form:
ω := V1 dx1
+ · · · + Vn dxn.
(3.3)
Here is a more subtle question also pertinent to our discussion: When may
V be rescaled to a gradient vector field? As the reader may recall from the
elementary theory of differential equations, for a planer vector field, such
a rescaling amounts to finding an integration factor for the corresponding
first order ODE (Boyce & DiPrima, 2012). It turns out that the answer could
again be encoded in terms of differential forms:
Theorem 5. A smooth vector field V is parallel to a gradient vector field near
each point only if the corresponding differential 1-form ω satisfies ω ∧ dω = 0.
Conversely, if V is nonzero at a point p ∈ Rn in the vicinity of which ω ∧ dω = 0
holds, there exists a smooth function ξ defined on a suitable open neighborhood of
p that satisfies V (cid:18) ∇ξ (cid:4)= 0. In particular, in dimension 2, a nowhere vanishing
vector field V is locally parallel to a nowhere vanishing gradient vector field, while
in dimension 3, that is the case if and only if V . curlV = 0.
A proof and background on differential forms are provided in ap-
pendix B.
3.1 Trees with Four Inputs. We begin with officially defining the terms
related to tree architectures (see Figure 8).
Terminology
A tree is a connected acyclic graph. Singling out a vertex as its root turns
it into a directed acyclic graph in which each vertex has a unique pre-
decessor/parent. We take all trees to be rooted. The following notions
come up frequently:
• Leaf: a vertex with no successor/child.
• Node: a vertex that is not a leaf, that is, has children.
• Sibling leaves: leaves with the same parent.
• Subtree: all descendants of a vertex along with the vertex itself.
Hence in our convention, all subtrees are full and rooted.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3226
K. Filom, R. Farhoodi, and K. Kording
Figure 8: A tree architecture and the relevant terminology.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9: Two tree architectures with four distinct inputs. Examples 4, 5, and 6
characterize functions computable by them.
To implement a function, the leaves pass the inputs to the functions
assigned to the nodes. The final output is received from the root.
The first example of the section elucidates theorem 3.
3.1.1 Example 4. Let us characterize superpositions
F(x, y, z, w) = g( f (x, y), z, w)
of smooth functions f, g, which correspond to the first tree architecture in
Figure 9. Necessary PDE constraints are more convenient to write for certain
ratios. So to derive them, we assume for a moment that first-order partial
derivatives of F are nonzero, although by a simple continuity argument, the
constraints will hold regardless. Computing the numerator and the denom-
inator of Fx
and
Fy
is, hence, independent of z, w. One thus obtains
via the chain rule indicates that this ratio coincides with fx
fy
PDE Characterization of Functions Computed by Neural Networks
3227
(cid:2)
(cid:3)
z
Fy
Fx
= 0,
(cid:3)
(cid:2)
Fy
Fx
= 0,
w
or, equivalently,
FyzFx = FxzFy,
FywFx = FxwFy.
Assuming Fx (cid:4)= 0, the preceding constraints are sufficient. The gradient ∇F
is parallel with
⎤
⎥
⎥
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎢
⎢
⎣
1
Fy
Fx
Fz
Fx
Fw
Fx
Fy
Fx
= fy
fx
where the second entry
Fy
Fx
is dependent only on x and y and thus may be
for an appropriate bivariate function f = f (x, y) defined
written as
throughout a small enough neighborhood of the point under consideration
(at which Fx is assumed to be nonzero). Such a function exists due to theo-
rem 5. Now we have
∇F (cid:18)
⎡
⎢
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎥
⎦
1
fy
fx
0
0
⎡
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
0
0
1
0
+ Fw
Fx
⎤
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎣
0
0
0
1
+ Fz
Fx
∈ Span
(cid:12)
∇ f, ∇z, ∇w
(cid:15)
,
which guarantees that F(x, y, z, w) may be written as a function of
f (x, y), z, w.
The next two examples serve as an invitation to the proof of theorem 4
in section 4 and are concerned with trees illustrated in Figure 9.
3.1.2 Example 5. Let us study the example above in the regime of
activation functions. The goal is to characterize functions of the form
F(x, y, z, w) = σ (τ (ax + by) + cz + dw). The ratios
, Fz
Fw must be constant
Fw are dependent merely on x, y as they are equal to
while Fx
Fz
τ (cid:10)
(ax + by), respectively. Equating the corresponding par-
a
c
tial derivatives with zero, we obtain the following PDEs:
and Fx
(ax + by) and a
d
Fy
Fx
τ (cid:10)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3228
K. Filom, R. Farhoodi, and K. Kording
FxyFx = FxxFy,
FxzFw = FxwFz,
FxzFz = FzzFx,
FyyFx = FxyFy,
FyzFw = FywFz,
FxwFz = FzwFx;
FyzFx = FxzFy,
FzzFw = FzwFz,
FxzFw = FzwFx,
FywFx = FxwFy;
FzwFw = FwwFz;
FxwFw = FwwFx.
One can easily verify that they always hold for functions of the form above.
We claim that under the assumptions of Fx (cid:4)= 0 and Fw (cid:4)= 0, these conditions
guarantee the existence of a local representation of the form σ (τ (ax + by) +
cz + dw) of F. Denoting Fx
and Fz
Fw
by c1 and c2, respectively, we have
Fw by β(x, y) and the constant functions
Fy
Fx
∇F =
⎤
⎥
⎥
⎥
⎦
!
!
⎡
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎣
Fx
Fy
Fz
Fw
Fx
Fw
Fy
Fw
Fz
Fw
1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎣
=
⎤
⎥
⎥
⎥
⎦
β(x, y)
β(x, y)
c1
c2
1
!
! ∇( f (x, y) + c2z + w),
#
. Such a potential function f for
"
β(x, y)
β(x, y)
c1
#
=
"
β(x, y)
β(x, y)
c1
where ∇ f =
⎤
⎡
⎣
Fx
Fw
Fy
Fw
⎦ exists since
(cid:2)
Fx
Fw
(cid:3)
(cid:2)
=
y
Fy
Fw
(cid:3)
(cid:2)
⇔
x
Fy
Fx
(cid:3)
= 0,
w
= c1 is constant (see lemma
and it must be in the form of τ (ax + by) as
3). Thus, F is a function of τ (ax + by) + c2z + w because the gradients are
parallel.
fy
fx
The next example is concerned with the symmetric tree in Figure 9. We
shall need the following lemma:
Lemma 4. Suppose a smooth function q = q
written as a product
(cid:10)
y(1)
1
, . . . , y(1)
n1
, . . . , y(2)
n2
(cid:10)
y(2)
1
q2
q1
(cid:11)
(cid:11)
(cid:10)
(cid:11)
y(1)
1
, . . . , y(1)
n1
; y(2)
1
, . . . , y(2)
n2
is
(3.4)
, q2. Then q qy(1)
for any 1 ≤ a ≤ n1 and 1 ≤
of smooth functions q1
b ≤ n2. Conversely, for a smooth function q defined on an open box-like region
⊆ Rn1 × Rn2 , once q is nonzero, these identities guarantee the existence of
B1
such a product representation on B1
= qy(1)
× B2.
× B2
qy(2)
a y(2)
b
b
a
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3229
1(ax + by) + τ
3.1.3 Example 6. We aim for characterizing smooth functions of four vari-
2(cz + dw)). Assuming for
, Fz
Fw
ables of the form F(x, y, z, w) = σ (τ
a moment that all first-order partial derivatives are nonzero, the ratios
Fw is equal to aτ (cid:10)
1(ax+by)
must be constant while Fx
2 (cz+dw) and hence (along with its
dτ (cid:10)
, Fy
constant multiples Fx
Fw ) splits into a product of bivariate functions of
Fz
x, y and z, w, a requirement that by lemma 4 is equivalent to the following
identities:
, Fy
Fz
Fy
Fx
(cid:2)
(cid:3)
(cid:2)
(cid:3)
(cid:2)
(cid:3)
(cid:2)
(cid:3)
(cid:2)
(cid:3)
(cid:2)
(cid:3)
Fx
Fw
Fx
Fw
(cid:2)
Fx
Fw
Fx
Fw
=
=
(cid:2)
xz
(cid:3)
yz
Fx
Fw
Fx
Fw
Fx
Fw
Fx
Fw
,
,
z
(cid:3)
z
x
(cid:3)
(cid:2)
y
Fx
Fw
Fx
Fw
(cid:2)
Fx
Fw
Fx
Fw
=
=
(cid:2)
xw
(cid:3)
yw
Fx
Fw
Fx
Fw
x
(cid:3)
(cid:2)
y
Fx
Fw
Fx
Fw
,
.
w
(cid:3)
w
After expanding and cross-multiplying, the identities above result in PDEs
of the form 1.20 imposed on F that hold for any smooth function of the
form F(x, y, z, w) = σ (τ
2(cz + dw)). Conversely, we claim that
if Fx (cid:4)= 0 and Fw (cid:4)= 0, then the constraints we have noted guarantee that F
Fy
and
locally admits a representation of this form. Denoting the constants
Fx
β(x,y)
Fw by c1 and c2, respectively, and writing Fx
Fz
γ (z,w) , we
obtain
(cid:4)= 0 in the split form
1(ax + by) + τ
Fw
∇F =
⎤
⎥
⎥
⎥
⎦
!
!
⎡
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎣
Fx
Fy
Fz
Fw
⎡
⎢
⎢
⎢
⎢
⎢
⎣
=
⎤
⎥
⎥
⎥
⎥
⎥
⎦
Fx
Fw
Fy
Fw
Fz
Fw
1
β(x,y)
γ (z,w)
β(x,y)
γ (z,w)
c1
c2
1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎣
!
!
⎤
⎥
⎥
⎥
⎦
.
β(x, y)
β(x, y)
c1
γ (z, w)
c2
γ (z, w)
We desire functions f = f (x, y) and g = g(z, w) with ∇ f =
"
β(x, y)
β(x, y)
c1
#
and
"
∇g =
#
γ (z, w)
c2
γ (z, w)
, because then, ∇F (cid:18) ∇( f (x, y) + g(z, w)) and hence F =
σ ( f (x, y) + g(z, w)) for an appropriate σ . Notice that f (x, y) and g(z, w) are
= c1
1(ax + by) and τ
automatically in the forms of τ
and fz
= c2 are constants (see lemma 3). To establish the existence of f and
fw
γw = γz.
g, one should verify the integrability conditions βy = c1
βx and c2
Fy
= c1 is
We only verify the first one; the second one is similar. Notice that
Fx
while βy = β ( Fx
Fw )y
γ (z,w) implies that βx = β ( Fx
Fw )x
Fx
Fx
Fw
Fw
2(cz + dw) because
constant, and Fx
Fw
= β(x,y)
. So the
fy
fx
question is whether
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3230
K. Filom, R. Farhoodi, and K. Kording
(cid:2)
Fx
Fw
Fy
Fx
(cid:3)
(cid:2)
=
x
Fy
Fx
Fx
Fw
(cid:3)
(cid:2)
=
x
(cid:3)
x
Fy
Fw
(cid:10)
(cid:11)
and
(cid:10)
as
Fx
Fw
(cid:11)
Fy
Fx
w
coincide, which is the case since
y
= 0.
(cid:10)
(cid:11)
(cid:10)
(cid:11)
Fy
Fw
=
x
Fx
Fw
y
can be rewritten
Fw
Fy
Fx
a and Fz
Remark 7. Examples 5 and 6 demonstrate an interesting phenomenon: one
can deduce nontrivial facts about the weights once a formula for the im-
plemented function is available. In example 5, for a function F(x, y, z, w) =
≡ c
≡ b
σ (τ (ax + by) + cz + dw), we have
d . The same identities are
valid for functions of the form F(x, y, z, w) = σ (τ
2(cz + dw))
1(ax + by) + τ
in example 6.6 This seems to be a direction worthy of study. In fact, there
are papers discussing how a neural network may be “reverse-engineered”
in the sense that the architecture of the network is determined from the
knowledge of its outputs, or the weights and biases are recovered without
the ordinary training process involving gradient descent algorithms (Fef-
ferman & Markel, 1994; Dehmamy, Rohani, & Katsaggelos, 2019; Rolnick &
Kording, 2019). In our approach, the weights appearing in a composition of
functions of the form y (cid:6)→ σ ((cid:8)w, y(cid:9)) could be described (up to scaling) in
terms of partial derivatives of the resulting superposition.
3.1.4 Example 7. Let us go back to example 2. In (Farhoodi et al., 2019,
c, 7.2), a PDE constraint on functions of the form 1.7 is obtained via differ-
entiating equation 1.9 several times and forming a matrix equation, which
implies that a certain determinant of partial derivatives must vanish. The
paper then raises the question of existence of PDE constraints that are both
necessary and sufficient. The goal of this example is to derive such a char-
acterization. Applying differentiation operators ∂y, ∂z, and ∂yz to equation
1.9 results in
⎡
⎢
⎢
⎢
⎣
0
Fz
Fyz
Fzz
Fy
Fyy
0
Fyz
Fz
Fyyz Fyzz Fyz Fyz
0
Fy
0
⎤
⎡
⎥
⎥
⎥
⎦
⎢
⎢
⎢
⎣
⎤
⎥
⎥
⎥
⎦
A
B
Ay
Bz
=
⎤
⎥
⎥
⎥
⎦
.
⎡
⎢
⎢
⎢
⎣
Fx
Fxy
Fxz
Fxyz
6
Notice that this is the best one can hope to recover because through scaling the
weights and inversely scaling the inputs of activation functions, the function F could also
be written as σ ( ˜τ (λax + λby) + cz + dw) or σ ( ˜τ
2(cz + dw)) where ˜τ (y) :=
(cid:14)
y
τ
. Thus, the other ratios a
λ
1(λax + λby) + τ
c and b
d are completely arbitrary.
1(y) := τ
1
and ˜τ
y
λ
(cid:13)
(cid:13)
(cid:14)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3231
If this matrix is nonsingular, a nonvanishing condition, Cramer’s rule pro-
vides descriptions of A, B in terms of partial derivatives of F, and then
Az = By = 0 yield PDE constraints. Reversing this procedure, we show that
these conditions are sufficient too. Let us assume that
(cid:5) :=
$ $ $ $ $ $ $ $ $ $
Fy
Fyy
Fyz
Fz
Fyz
Fzz
0
Fy
0
0
0
Fz
Fyyz Fyzz Fyz Fyz
$ $ $ $ $ $ $ $ $ $
= (Fy)2FzFyzz − (Fy)2FyzFzz − Fy(Fz)2Fyyz + (Fz)2FyzFyy (cid:4)= 0.
(3.5)
Notice that this condition is nonvacuous for functions F(x, y, z) of the form
1.7 since they include all functions of the form g(y, z). Then the linear
system
⎤
⎥
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎢
⎣
Fx
Fxy
Fxz
Fxyz
⎡
⎢
⎢
⎢
⎢
⎣
Fy
Fyy
Fyz
=
Fz
Fyz
Fzz
0
Fy
0
⎤
⎡
⎥
⎥
⎥
⎥
⎦
⎢
⎢
⎢
⎢
⎣
0
0
Fz
Fyyz Fyzz Fyz Fyz
⎤
⎥
⎥
⎥
⎥
⎦
A
B
C
D
may be solved as
(3.6)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
$ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $
A =
Fx
Fxy
Fxz
Fz
Fyz
Fzz
0
Fy
0
0
0
Fz
Fxyz Fyzz Fyz Fyz
Fy
0
Fz
0
Fyy
Fyz
Fyz
Fzz
Fy
0
0
Fz
Fyyz Fyzz Fyz Fyz
$ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
= 1
(cid:5) [−Fy(Fz)2Fxyz + FyFzFxzFyz + FxFyFzFyzz
− FxFyFyzFzz + (Fz)2FxyFyz − FxFz(Fyz)2]
(3.7)
3232
and
$ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $
B =
0
0
Fy
0
Fx
Fxy
Fxz
Fy
Fyy
0
Fyz
Fz
Fyyz Fxyz Fyz Fyz
Fy
0
Fyy
0
Fyz
Fz
Fyyz Fyzz Fyz Fyz
Fz
Fyz
Fzz
0
Fy
0
K. Filom, R. Farhoodi, and K. Kording
$ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $
= 1
(cid:5) [(Fy)2FzFxyz − (Fy)2FxzFyz − FyFzFxyFyz
− FxFyFzFyyz + FxFy(Fyz)2 + FxFzFyyFyz].
(3.8)
Denote the numerators of 3.7 and 3.8 by (cid:5)
1 and (cid:5)
2, respectively:
(cid:5)
1
= −Fy(Fz)2Fxyz + FyFzFxzFyz + FxFyFzFyzz
− FxFyFyzFzz + (Fz)2FxyFyz − FxFz(Fyz)2,
(cid:5)
2
= (Fy)2FzFxyz − (Fy)2FxzFyz − FyFzFxyFyz
− FxFyFzFyyz + FxFy(Fyz)2 + FxFzFyyFyz.
(3.9)
Requiring A = (cid:5)
amounts to
(cid:5) and B = (cid:5)
1
2
(cid:5) to be independent of z and y, respectively,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
(cid:2)
1 := ((cid:5)
1)z(cid:5) − (cid:5)
1
(cid:5)z = 0, (cid:2)
2 := ((cid:5)
2)y(cid:5) − (cid:5)
2
(cid:5)y = 0.
(3.10)
2
= 0 and
A simple continuity argument demonstrates that the constraints (cid:2)
1
(cid:2)
= 0 above are necessary even if the determinant 3.5 vanishes: if (cid:5) is
identically zero on a neighborhood of a point p ∈ R3, the identities 3.10
obviously hold throughout that neighborhood. Another possibility is that
(cid:5)(p) = 0, but there is a sequence {pn}n of nearby points with pn → p and
(cid:5)(pn) (cid:4)= 0. Then the polynomial expressions (cid:2)
2 of partial derivatives
vanish at any pn and hence at p by continuity.
1, (cid:2)
To finish the verification of conjecture 1 for superpositions of the form
1.7, one should establish that PDEs (cid:2)
= 0 from equation 3.10 are
1
sufficient for the existence of such a representation provided that the nonva-
nishing condition (cid:5) (cid:4)= 0 from equation 3.5 holds. In that case, the functions
A and B from equations 3.7 and 3.8 satisfy equation 1.9. According to theo-
rem 5, there exist smooth locally defined f (x, y) and h(x, z) with fx
= A(x, y)
fy
= 0, (cid:2)
2
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3233
Figure 10: An asymmetric tree architecture that computes the superpositions
of the form F(x, y, z) = g(x, f (h(x, y), z)). These are characterized in example 8.
and hx
hz
= B(x, z). We have:
⎡
⎢
⎣
∇F =
A(x, y)Fy + B(x, z)Fz
Fy
Fz
⎡
⎤
⎡
⎤
⎤
⎥
⎦ = Fy
⎡
⎢
⎣
A(x, y)
1
⎤
⎥
⎦ + Fz
⎡
⎢
⎣
B(x, z)
0
⎤
⎥
⎦
0
1
⎢
⎣
= Fy
fy
fx
fy
0
⎥
⎦ + Fz
hz
⎢
⎣
hx
0
hz
⎥
⎦ ∈ Span{∇ f, ∇h};
hence, F can be written as a function g( f (x, y), h(x, z)) of f and h for an
appropriate g.
3.1.5 Example 8. We now turn to the asymmetric tree with four repeated
inputs in Figure 10 with the corresponding superpositions,
F(x, y, z) = g(x, f (h(x, y), z)).
(3.11)
In our treatment here, the steps are reversible, and we hence derive PDE
constraints that are simultaneously necessary and sufficient. The existence
of a representation of the form 3.11 for F(x, y, z) is equivalent to the existence
of a locally defined coordinate system,
(ξ := x, ζ , η),
with respect to which Fη = 0; moreover, ζ = ζ (x, y, z) must be in the form of
f (h(x, y), z), which, according to example 1, is the case if and only if
=
0. Here, we assume that ζx, ζy (cid:4)= 0 so that
is well defined and ∇ξ , ∇ζ
are linearly independent. We denote the preceding ratio by β = β(x, y) (cid:4)= 0.
Conversely, theorem 5 guarantees that there exists ζ with
= β for any
ζy
ζx
ζy
ζx
(cid:10)
(cid:11)
z
ζy
ζx
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3234
K. Filom, R. Farhoodi, and K. Kording
smooth β(x, y). The function F could be locally written as a function of ξ = x
and ζ if and only if
∇F =
⎤
⎥
⎦ ∈ Span
⎧
⎪⎨
⎪⎩
⎡
⎢
⎣
Fx
Fy
Fz
∇x, ∇ζ =
⎡
⎢
⎣
ζx
ζy = β(x, y)ζx
ζz
⎤
⎥
⎦
⎫
⎪⎬
⎪⎭
.
Clearly, this occurs if and only if Fz
coincides with
Fy
needs to arrange for β(x, y) so that the vector field
ζz
ζy
. Therefore, one only
∇ζ =
1
ζx
⎡
⎢
⎢
⎣
1
ζy
ζx
ζz
ζx
⎤
⎥
⎥
⎦ =
⎡
⎢
⎢
⎣
⎤
⎥
⎥
⎦
1
β(x, y)
β(x, y) Fz
Fy
is parallel to a gradient vector field ∇ζ . That is, we want the vector field to
be perpendicular to its curl (see theorem 5). We have:
(cid:2)
∂
∂x
= βy
+ β(x, y)
(cid:2)
∂
+ β(x, y)
∂y
(cid:2)
(cid:3)
∂
Fz
∂z
Fy
(cid:3)
+ β
Fz
Fy
Fz
Fy
− β 2
y
Fz
Fy
.
x
(cid:3)
(cid:2)
. curl
∂
∂x
+ β(x, y)
∂
∂y
+ β(x, y)
(cid:3)
Fz
Fy
∂
∂z
The vanishing of the expression above results in a description of
the linear combination
(cid:3)
(cid:2)
Fz
Fy
=
x
βy
β 2
Fz
Fy
+ 1
β
(cid:2)
(cid:3)
y
Fz
Fy
(cid:10)
(cid:11)
whose coefficients
βy
β2
= −
1
β
y
and 1
β are independent of z. Thus, we are
in a situation similar to that of examples 2 and 7, where we encountered
identity 1.9. The same idea used there could be applied again to obtain PDE
constraints: Differentiating equation 3.12 with respect to z results in a linear
system:
⎡
⎢
⎣
Fz
Fy
(cid:11)
(cid:10)
Fz
Fy
z
(cid:10)
(cid:11)
(cid:10)
Fz
Fy
Fz
Fy
y
(cid:11)
yz
⎤
⎥
⎦
⎡
⎣
−
(cid:10)
(cid:11)
⎤
⎡
(cid:10)
(cid:11)
⎤
y
⎦ =
⎢
⎣
(cid:10)
1
β
1
β
Fz
Fy
Fz
Fy
⎥
⎦ .
x
(cid:11)
xz
(cid:10)
(cid:11)
Fz
Fy
as
x
(3.12)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3235
(cid:11)
(cid:10)
(cid:10)
(cid:11)
Fz
Fy
Assuming the matrix above is nonsingular, Cramer’s rule implies
$ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $
1
β
1
β
(cid:11)
xz
Fz
Fy
Fz
Fy
Fz
Fy
Fz
Fy
Fz
Fy
Fz
Fy
Fz
Fy
Fz
Fy
Fz
Fy
Fz
Fy
Fz
Fy
=
=
−
(cid:3)
(cid:2)
(cid:10)
(cid:10)
(cid:10)
(cid:11)
(cid:10)
(cid:11)
(cid:10)
(cid:11)
(cid:10)
(cid:10)
(cid:10)
(cid:11)
(cid:11)
(cid:11)
(cid:10)
(cid:11)
(cid:10)
(cid:10)
(cid:11)
(cid:11)
(cid:11)
yz
xz
,
.
y
y
y
y
x
x
z
Fz
Fy
z
Fz
Fy
yz
Fz
Fy
z
Fz
Fy
yz
(3.13)
We now arrive at the desired PDE characterization of superpositions 3.11.
In each of the ratios of determinants appearing in equation 3.13, the numer-
ator and denominator are in the form of polynomials of partial derivatives
divided by (Fy)4. So we introduce the following polynomial expressions:
$ $ $ $ $ $ $ $ $ $ $ $ $ , , (cid:5) 1 = (Fy)4 (cid:5) 2 = (Fy)4 (cid:5) 3 = (Fy)4 $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ $ (cid:10) (cid:11) (cid:11) y yz (cid:11) (cid:11) x Fz Fy (cid:11) (cid:10) Fz Fy z Fz Fy (cid:11) (cid:10) Fz Fy (cid:10) z (cid:11) (cid:10) Fz Fy Fz Fy (cid:10) (cid:10) Fz Fy Fz Fy (cid:10) (cid:10) Fz Fy Fz Fy (cid:11) x (cid:10) xz Fz Fy Fz Fy xz (cid:11) (cid:11) y yz $ $ $ $ $ $ $
.
Then in view of equation 3.13,
(cid:3)
(cid:2)
(cid:5)
(cid:5)
2
1
= 1
β
,
(cid:5)
(cid:5)
= −
3
1
1
β
.
y
(3.14)
(3.15)
Hence
(cid:10)
(cid:11)
y
(cid:5)
(cid:5)
2
1
+ (cid:5)
(cid:5)
3
1
= 0; furthermore,
(cid:10)
(cid:11)
z
(cid:5)
(cid:5)
2
1
= 0 since β is independent of z:
(cid:2)
1 := (cid:5)
1((cid:5)
2)y − ((cid:5)
1)y(cid:5)
2
+ (cid:5)
(cid:5)
3
1
= 0, (cid:2)
2 := (cid:5)
1((cid:5)
2)z − ((cid:5)
1)z(cid:5)
2
= 0.
(3.16)
Again as in example 7, a continuity argument implies that the algebraic
PDEs above are necessary even when the denominator in equation 3.13 (i.e.,
(cid:5)
1) is zero. As for the nonvanishing conditions, in view of equations 3.14
2 (recall that β (cid:4)= 0):
and 3.15, we require Fy to be nonzero as well as (cid:5)
1 and (cid:5)
(cid:5)
1
(cid:4)= 0, (cid:5)
2
(cid:4)= 0, Fy (cid:4)= 0.
(3.17)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3236
K. Filom, R. Farhoodi, and K. Kording
Figure 11: The space of functions computed by the neural network on the left
is strictly smaller than that of its TENN on the right. See example 9.
It is easy to see that these conditions are not vacuous for functions of the
form 3.11. If F(x, y, z) = (xy)2z + z3, neither Fy nor the expression (cid:5)
1 or (cid:5)
is identically zero.
2
In summary, a special case of conjecture 1 has been verified in this exam-
ple. A function F = F(x, y, z) of the form 3.11 satisfies the constraints 3.16;
conversely, a smooth function satisfying them along with the nonvanishing
conditions 3.17 admits a local representation of that form.
3.2 Examples of Functions Computed by Neural Networks. We now
switch from trees to examples of PDE constraints for neural networks. The
first two examples are concerned with the network illustrated on the left of
Figure 11; this is a ResNet with two hidden layers that has x, y, z, w as its
inputs. The functions it implements are in the form of
F(x, y, z, w) = g(h1( f (x, y), z), h2( f (x, y), w)),
(3.18)
where f and h1
, h2 are the functions appearing in the hidden layers.
3.2.1 Example 9. On the right of Figure 11, the tree architecture corre-
sponding to the neural network discussed above is illustrated. The func-
tions implemented by this tree are in the form of
F(x, y, z, w) = g(h1( f1(x, y), z), h2( f2(x, y), w)),
(3.19)
which is a form more general than the form 3.18 of functions computable
by the network. In fact, there are PDEs satisfied by the latter class that
functions in the former class, equation 3.19, do not necessarily satisfy. To
see this, observe that for a function F(x, y, z, w) of the form 3.18, the ra-
and is thus independent of z and w—hence the
tio
PDEs FxzFy = FyzFx and FxwFy = FywFx. Neither of them holds for the function
F(x, y, z, w) = xyz + (x + y)w, which is of the form 3.19. We deduce that the
coincides with
Fy
Fx
fy
fx
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3237
set of PDE constraints for a network may be strictly larger than that of the
corresponding TENN.
3.2.2 Example 10. Here we briefly argue that conjecture 1 holds for
the network in Figure 11 (which has two hidden layers). The goal is to
obtain PDEs that, given suitable nonvacuous, nonvanishing conditions,
characterize smooth functions F(x, y, z, w) of the form 3.18. We seek a
description of the form g(F1(x, y, z), F2(x, y, w)) of F(x, y, z, w) where the
trivariate functions F1(x, y, z) and F2(x, y, w) are superpositions h1( f (x, y), z)
and h2( f (x, y), w) with the same bivariate function f appearing in both of
them. Invoking the logic that has been used repeatedly in section 3.1, ∇F
must be a linear combination of ∇F1 and ∇F2. Following example 1, the only
restriction on the latter two gradients is
⎡
⎢
⎢
⎢
⎢
⎢
⎣
!
!
∇F1
⎤
⎥
⎥
⎥
⎥
⎥
⎦
1
(F1 )y
(F1 )x
= fy
fx
α(x, y, z) := (F1 )z
(F1 )x
0
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
!
!
, ∇F2
1
(F2 )y
(F2 )x
= fy
fx
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
;
β(x, y, w) := (F2 )w
(F2 )x
and as observed in example 9, the ratio
. Thus, the exis-
tence of a representation of the form 3.18 is equivalent to the existence of a
linear relation such as
coincides with
Fy
Fx
fy
fx
⎤
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎣
Fx
Fy
Fz
Fw
⎡
⎢
⎢
⎢
⎢
⎢
⎣
1
Fy
Fx
α(x, y, z)
⎤
⎥
⎥
⎥
⎥
⎥
⎦
+ Fw
β
⎡
⎢
⎢
⎢
⎢
⎢
⎣
= Fz
α
0
⎤
⎥
⎥
⎥
⎥
⎥
⎦
.
1
Fy
Fx
0
β(x, y, w)
This amounts to the equation
(cid:3)
(cid:2)
1
α
Fz
+ Fw
(cid:3)
(cid:2)
1
β
= Fx.
(cid:13)
(cid:14)
1
α
= 0, ap-
Now the idea of examples 2 and 7 applies. As
plying the operators ∂z, ∂w, and ∂zw to the last equation results in a linear
system with four equations and four unknowns: 1
. If
nonsingular (a nonvanishing condition), the system may be solved to ob-
tain expressions purely in terms of partial derivatives of F for the aforemen-
= 0, along with the equations
tioned unknowns. Now
= 0 and
= 0 and
z, and
α , 1
β ,
(cid:11)
(cid:10)
(cid:11)
(cid:10)
1
α
1
β
1
β
(cid:13)
(cid:14)
(cid:13)
(cid:14)
w
w
z
1
α
w
1
β
z
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(cid:10)
(cid:11)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
3238
K. Filom, R. Farhoodi, and K. Kording
FxzFy = FyzFx, FxwFy = FywFx from example 9, yield four algebraic PDEs char-
acterizing superpositions 3.18.
The final example of this section finishes example 3 from the section 1.
3.2.3 Example 11. We go back to example 3 to study PDEs and PDIs sat-
into inner functions,
isfied by functions of the form 1.14. Absorbing a(cid:10)(cid:10), b(cid:10)(cid:10)
we can focus on the simpler form:
(cid:10)
F(x, t) = σ ( f (ax + bt) + g(a
(cid:10)
x + b
t)).
(3.20)
Let us for the time being forget about the outer activation function σ . Con-
sider functions such as
(cid:10)
G(x, t) = f (ax + bt) + g(a
(cid:10)
x + b
t).
Smooth functions of this form constitute solutions of a second-order linear
homogeneous PDE with constant coefficients
UGxx + VGxt + WGtt = 0,
where (a, b) and (a(cid:10), b(cid:10)
) satisfy
UA2 + VAB + WB2 = 0.
(3.21)
(3.22)
The reason is that when (a, b) and (a(cid:10), b(cid:10)
tial operator U∂xx + V∂xt + W∂tt can be factorized as
) satisfy equation 3.22, the differen-
(b∂x − a∂t )(b
(cid:10)∂x − a
(cid:10)∂t )
to a composition of operators that annihilate the linear forms ax + bt and
a(cid:10)x + b(cid:10)t. If (a, b) and (a(cid:10), b(cid:10)
) are not multiples of each other, they constitute a
new coordinate system (ax + bt, a(cid:10)x + b(cid:10)t) in which the mixed partial deriva-
tives of F all vanish; so, at least locally, F must be a sum of univariate func-
tions of ax + bt and a(cid:10)x + b(cid:10)t.7 We conclude that assuming V 2 − 4UW > 0,
functions of the form G(x, t) = f (ax + bt) + g(a(cid:10)x + b(cid:10)t) may be identified
with solutions of PDEs of the form 3.21. As in example 1, we desire alge-
braic PDEs purely in terms of F and without constants U, V, and W. One
way to do so is to differentiate equation 3.21 further, for instance:
UGxxx + VGxxt + WGxtt = 0.
(3.23)
7
Compare with the proof of lemma 4 in appendix A.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3239
Notice that equations 3.21 and 3.23 could be interpreted as (U, V, W ) be-
ing perpendicular to (Gxx, Gxt, Gtt ) and (Gxxx, Gxxt, Gxtt ). Thus, the cross-
product
(GxtGxtt − GttGxxt, GttGxxx − GxxGxtt, GxxGxxt − GxtGxxx)
of the latter two vectors must be parallel to a constant vector. Under the
nonvanishing condition that one of the entries of the cross-product, say
the last one, is nonzero, the constancy may be thought of as ratios of
the other two components to the last one being constants. The result is
a characterization (in the vein of conjecture 1) of functions G of the form
f (ax + bt) + g(a(cid:10)x + b(cid:10)t), which are subjected to GxxGxxt − GxtGxxx (cid:4)= 0 and
GxtGxtt − GttGxxt
GttGxxx − GxxGxtt
GxxGxxt − GxtGxxx
GxxGxxt − GxtGxxx
(GttGxxx − GxxGxtt )2 > 4(GxtGxtt − GttGxxt )(GxxGxxt − GxtGxxx).
are constants,
and
(3.24)
Notice that the PDI is not redundant here. For a solution G = G(x, t) of
Laplace’s equation, the fractions from the first line of equation 3.24 are con-
stants, while on the second line, the left-hand side of the inequality is zero
but its right-hand side is 4(GxtGxtt − GttGxxt )2 ≥ 0.
Composing G with σ makes the derivation of PDEs and PDIs imposed
on functions of the form 3.20 even more cumbersome. We provide only a
sketch. Under the assumption that the gradient of F = σ ◦ G is nonzero, the
univariate function σ admits a local inverse τ . Applying the chain rule to
G = τ ◦ F yields
Gxx = τ (cid:10)(cid:10)
Gxt = τ (cid:10)(cid:10)
Gtt = τ (cid:10)(cid:10)
(F)(Fx)2 + τ (cid:10)
(F)FxFt + τ (cid:10)
(F)(Ft )2 + τ (cid:10)
(F)Fxx,
(F)Fxt,
(F)Ftt.
Plugging them in the PDE 3.21 that G satisfies results in
τ (cid:10)(cid:10)
(F)
(cid:13)
U(Fx)2 + VFxFt + W (Ft )2
(cid:14)
+ τ (cid:10)
(F) (UFxx + VFxt + WFtt ) = 0,
or, equivalently,
UFxx + VFxt + WFtt
U(Fx)2 + VFxFt + W (Ft )2
= −
τ (cid:10)(cid:10)
(F)
τ (cid:10)(F)
(cid:3)
(cid:2)
τ (cid:10)(cid:10)
τ (cid:10)
(F).
= −
(3.25)
It suffices for the ratio
since then τ may be recovered as τ =
the beginning of section 3, this is equivalent to
UFxx+VFxt +WFtt
U(Fx )2+VFxFt +W (Ft )2 to be a function of F such as ν(F)
. Following the discussion at
e
(
−
ν
(
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3240
K. Filom, R. Farhoodi, and K. Kording
(cid:2)
∇
UFxx + VFxt + WFtt
U(Fx)2 + VFxFt + W (Ft )2
(cid:3)
!
! ∇F.
This amounts to an identity of the form
(cid:2)
1(F)U 2 + (cid:2)
2(F)V 2 + (cid:2)
3(F)W 2 + (cid:2)
4(F)UV + (cid:2)
5(F)VW + (cid:2)
6(F)UW = 0,
where (cid:2)
i(F)’s are complicated nonconstant polynomial expressions of par-
tial derivatives of F. In the same way that the parameters U, V, and W in
PDE 3.21 were eliminated to arrive at equation 3.24, one may solve the ho-
mogeneous linear system consisting of the identity above and its deriva-
tives in order to derive a six-dimensional vector,
(cid:13)
(cid:18)
1(F), (cid:18)
2(F), (cid:18)
3(F), (cid:18)
4(F), (cid:18)
5(F), (cid:18)
(cid:14)
6(F)
(3.26)
of rational expressions of partial derivatives of F parallel to the constant
vector
(U 2, V 2, W 2, UV, VW, UW ).
(3.27)
4(F)2, and the ratios
2(F) =
The parallelism amounts to a number of PDEs, for example, (cid:18)
(cid:18)
i(F)
j (F) must be constant because they coincide with
the ratios of components of equation 3.27. Moreover, V 2 − 4UW > 0 implies
(cid:10)
≥ 0. Replacing with the corresponding ratios of components
1(F) (cid:18)
− 4
(cid:18)
(cid:18)
(cid:11)
V 2
UW
V 2
UW
of equation 3.26, we obtain the PDI
(cid:13)
(cid:18)
2(F) − 4 (cid:18)
(cid:14)
6(F)
(cid:18)
2(F) (cid:18)
6(F) ≥ 0,
which must be satisfied by any function of the form 3.20.
3.3 Examples of Polynomial Neural Networks. The superpositions we
study in this section are constructed out of polynomials. Again, there are
two different regimes to discuss: composing general polynomial functions
of low dimensionality or composing polynomials of arbitrary dimension-
ality but in the simpler form of y (cid:6)→ σ ((cid:8)w, y(cid:9)) where the activation func-
tion σ is a polynomial of a single variable. The latter regime deals with
polynomial neural networks. Different aspects of such networks have been
studied in the literature (Du & Lee, 2018; Soltanolkotabi et al., 2018; Venturi
et al., 2018; Kileel et al., 2019). In the spirit of this article, we are interested in
the spaces formed by such polynomial superpositions. Bounding the total
degree of polynomials from the above, these functional spaces are subsets
of an ambient polynomial space, say, the space Polyd,n of real polynomials
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3241
, . . . , xn) of total degree at most d, which is an affine space of dimension
P(x1
(cid:13)
(cid:14)
d+n
. By writing a polynomial P(x1
n
, . . . , xn) of degree d as
P(x1
, x2
, . . . , xn) =
(cid:17)
ca1
,a2
,…,an xa1
1 xa2
2
. . . xan
n
,
(3.28)
,a2
a1
+a2
,…,an ≥0
+···+an ≤d
a1
,a2
,…,an provide a natural coordinate system on Polyd,n. As-
the coefficients ca1
sociated with a neural network N that receives x1
, . . . , xn as its inputs, there
are polynomial functional spaces for any degree d that lie in the ambient
space Polyd,n:
1. The subset Fd(N ) of Polyd,n consisting of polynomials P(x1
, . . . , xn)
of total degree at most d that can be computed by N via assigning
real polynomial functions to its neurons
2. The smaller subset Fact
d (N ) of Polyd,n consisting of polynomials
, . . . , xn) of total degree at most d that can be computed by N via
P(x1
assigning real polynomials of the form y (cid:6)→ σ ((cid:8)w, y(cid:9)) to the neurons
where σ is a polynomial activation function
In general, subsets Fd(N ) and Fact
d (N ) of Polyd,n are not closed in the al-
gebraic sense (see remark 8). Therefore, one may consider their Zariski clo-
sures Vd(N ) and Vact
d (N ), that is, the smallest subsets defined as zero loci of
d (N )
polynomial equations that contain them. We shall call Vd(N ) and Vact
the functional varieties associated with N . Each of the subsets Vd(N ) and
d (N ) of Polyd,n could be described with finitely many polynomial equa-
Vact
tions in terms of ca1
,…,an ’s. The PDE constraints from section 2 provide non-
trivial examples of equations satisfied on the functional varieties: In any de-
gree d, substituting equation 3.28 in an algebraic PDE that smooth functions
computed by N must obey results in equations in terms of the coefficients
that are satisfied at any point of Fd(N ) or Fact
d (N ) and hence at the points of
d (N ). This will be demonstrated in example 12 and results in
Vd(N ) or Vact
the following corollary to theorems 1 and 2.
,a2
Corollary 2. Let N be a neural network whose inputs are labeled by the coordi-
, . . . , xn. Then there exist nontrivial polynomials on affine spaces
nate functions x1
Polyd,n that are dependent only on the topology of N and become zero on func-
d (N ) ⊂ Polyd,n. The same holds for functional varieties Vd(N )
tional varieties Vact
provided that the number of inputs to each neuron of N is less than n.
Proof. The proof immediately follows from theorem 2 (in the case of
d (N )) and from theorem 1 (in the case of Vd(N )). Substituting a poly-
Vact
nomial P(x1
, . . . , xn) in a PDE constraint
(cid:10)
Px1
(cid:2)
, . . . , Pxn
, Px2
1
, Px1x2
, . . . , Pxα , . . .
= 0
(cid:11)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3242
K. Filom, R. Farhoodi, and K. Kording
that these theorems suggest for N and equating the coefficient of a mono-
mial xa1
n with zero results in a polynomial equation in ambient
polynomial spaces that must be satisfied on the associated functional
(cid:2)
varieties.
. . . xan
1 xa2
2
3.3.1 Example 12. Let N be a rooted tree T with distinct inputs x1
, . . . , xn.
= Fx jxk Fxi are not only necessary conditions
Constraints of the form Fxixk Fx j
for a smooth function F = F(x1
, . . . , xn) to be computable by T ; but by
the virtue of theorem 3, they are also sufficient for the existence of a lo-
cal representation of F on T if suitable nonvanishing conditions are sat-
isfied. An interesting feature of this setting is that when F is a polynomial
P = P(x1
, . . . , xn), one can relax the nonvanishing conditions; and P actually
admits a global representation as a composition of polynomials if it satisfies
the characteristic PDEs (Farhoodi et al., 2019, proposition 4). The basic idea
is that if P is locally written as a superposition of smooth functions accord-
ing to the hierarchy provided by T , then comparing the Taylor series shows
that the constituent parts of the superposition could be chosen to be poly-
nomials as well. Now P and such a polynomial superposition must be the
same since they agree on a nonempty open set. Consequently, each Fd(N )
coincides with its closure Vd(N ) and can be described by equations of the
= Px jxk Pxi in the polynomial space. Substituting an expression
form Pxixk Px j
of the form
P(x1
, . . . , xn) =
(cid:17)
a1
,…,an≥0
ca1
,…,an xa1
1
. . . xan
n
in Pxixk Px j
with zero yields
− Px jxk Pxi
(cid:17)
(cid:10)
a
i
(cid:10)(cid:10)
+a
i
(cid:10)
+1, a
=ai
j
(cid:10)(cid:10)
(cid:10)
+a
a
s
s
(cid:10)(cid:10)
+a
j
(cid:10)(cid:10)
+a
k
=as ∀s∈{1,…,n}−{i, j,k}
(cid:10)
+1, a
k
=a j
=ak
= 0 and equating the coefficient of a monomial xa1
1
. . . xan
n
(cid:13)
(cid:10)
k
a
(cid:10)
ia
(cid:10)(cid:10)
j
a
− a
(cid:10)
ja
(cid:10)(cid:10)
i
(cid:14)
ca(cid:10)
1
+1
,…,a(cid:10)
n ca(cid:10)(cid:10)
1
,…,a(cid:10)(cid:10)
n
= 0.
(3.29)
, . . . , an ≥ 0 and for triples
We deduce that equations 3.29 written for a1
(i, j, k) with the property that xk is separated from xi and x j by a subtree
of T (as in theorem 3) describe the functional varieties associated with T .
In a given degree d, to obtain equations describing T in Polyd,n, one should
+ · · · + bn > d to be zero in equation 3.29. No such a
set any cb1
coefficient occurs if d ≥ a1
+ · · · + an + 3, and thus for d large enough, equa-
tion 3.29 defines an equation in Polyd,n as is.
d (N ) =
Similarly, theorem 7 can be used to write equations for Fact
d (N ). In that situation, a new family of equations corresponding to equa-
Vact
tion 1.20 emerges that are expected to be extremely complicated.
,…,bn with b1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3243
3.3.2 Example 13. Let N be the neural network appearing in Figure 4. The
d (N ) is formed by polynomials P(x, t) of total degree at
functional space Fact
most d that are in the form of σ ( f (ax + bt) + g(a(cid:10)x + b(cid:10)t)). By examining the
Taylor expansions, it is not hard to see that if P(x, t) is written in this form
for univariate smooth functions σ , f , and g, then these functions could be
chosen to be polynomials. Therefore, in any degree d, our characterization
of superpositions of this form in example 11 in terms of PDEs and PDIs re-
sults in polynomial equations and inequalities that describe a Zariski open
d (N ) which is the complement of the locus where the nonva-
subset of Fact
nishing conditions fail. The inequalities disappear after taking the closure,
so Vact
d (N ) is strictly larger than Fact
d (N ) here.
Remark 8. The emergence of inequalities in describing the functional
spaces, as observed in example 13, is not surprising due to the Tarski–
Seidenberg theorem (see Coste, 2000), which implies that the image of a
polynomial map between real varieties (i.e., a map whose components are
polynomials) is semialgebraic; that is, it could be described as a union of
finitely many sets defined by polynomial equations and inequalities. To
elaborate, fix a neural network architecture N . Composing polynomials of
bounded degrees according to the hierarchy provided by N yields polyno-
mial superpositions lying in FD(N ) for D sufficiently large. The composition
thus amounts to a map
Polyd1
,n1
× · · · × PolydN,nN
→ PolyD,n
,
where, on the left-hand side, the polynomials assigned to the neurons of N
appear, and D (cid:23) d1
, . . . , dn. The image, a subset of FD(N ), is semialgebraic
and thus admits a description in terms of finitely many polynomial equa-
tions and inequalities. The same logic applies to the regime of activation
functions too; the map just mentioned must be replaced with
RC × Polyd1
,1
× · · · × PolydN,1
→ PolyD,n
D (N ), and its domain is the Cartesian product of
whose image lies in Fact
spaces of polynomial activation functions assigned to the neurons by the
space RC of weights assigned to the connections of the network.
4 PDE Characterization of Tree Functions
Building on the examples of the previous section, we prove theorems 3 and
4. This will establish conjecture 1 for tree architectures with distinct inputs.
Proof of Theorem 3. The necessity of the constraints from equation 1.18 fol-
lows from example 1. As demonstrated in Figure 12, picking three of vari-
= z where the former two are separated from the
ables xi
= y, and xk
= x, x j
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3244
K. Filom, R. Farhoodi, and K. Kording
Figure 12: The necessity of constraint 1.18 in theorem 3 follows from the case of
trivariate tree functions discussed in example 1. Choosing three of the variables
(red leaves) and fixing the rest (gray leaves) results in a superposition of the
form g( f (x, y), z) that must obey constraint 1.4.
latter by a subtree and taking the rest of variables to be constant, we obtain
a superposition of the form F(x, y, z) = g( f (x, y), z) studied in example 1; it
should satisfy FxzFy = FyzFx or, equivalently, equation 1.18.
We induct on the number of variables, which coincides with the number
of leaves, to prove the sufficiency of constraint 1.18 and the nonvanishing
conditions in theorem 3 for the existence of a local implementation, in the
form of a superposition of functions of lower arity, on the tree architecture
in hand. Consider a rooted tree T with n leaves labeled by the coordinate
, . . . , xn. The inductive step is illustrated in Figure 13. Remov-
functions x1
ing the root results in a number of smaller trees T
l and a number
of single vertices8 corresponding to the leaves adjacent to the root of T . By
renumbering x1
, . . . , xn one may write the leaves as
, . . . , T
1
x1
, . . . , xm1
xm1
+···+ml
+1
, . . . , xm1
; xm1
+1
; . . . ; xn,
+m2
; . . . ; xm1
+···+ml−1
+1
, . . . , xm1
+···+ml
;
(4.1)
where xm1
+···+ms−1
tree Ts while xm1
The goal is to write F(x1
+1
+···+ml
, . . . , xn) as
, . . . , xm1
+ms (1 ≤ s ≤ l) are the leaves of the sub-
+1 through xn are the leaves adjacent to the root of T .
+···+ms−1
g(G1(x1
, . . . , xm1 ), . . . , Gl (xm1
+···+ml−1
+1
, . . . , xm1
+···+ml ), xm1
+···+ml
+1
, . . . , xn),
(4.2)
where each smooth function,
Gs(xm1
+···+ms−1
+1
, . . . , xm1
+···+ms−1
+ms ),
8
A single vertex is not considered to be a rooted tree in our convention.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3245
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 13: The inductive step in the proof of theorem 3. The removal of the root
of T results in a number of smaller rooted trees along with single vertices that
were the leaves adjacent to the root of T (if any).
satisfies the constraints coming from Ts and thus, by invoking the induction
hypothesis, is computable by the tree Ts. Following the discussion before
theorem 5, it suffices to express ∇F as a linear combination of the gradients
∇G1
, . . . , ∇xn. The nonvanishing conditions in theo-
rem 3 require the first-order partial derivative with respect to at least one of
the leaves of each Ts to be nonzero; we may assume Fxm1
(cid:4)= 0 without
any loss of generality. We should have
, . . . , ∇Gl
, ∇xm1
+···+ml
+···+ms−1
+1
+1
(cid:22)
Fx1
∇F =
. . . Fxm1
⎡
=
l(cid:17)
s=1
Fxm1
+···+ms−1
⎢
⎣
+1
+···+ms−1
m1
) *+ ,
0 · · · 0
. . . Fxm1
+···+ml−1
+1
. . . Fxm1
+···+ml
Fxm1
+···+ml
+1
. . . Fxn
(cid:23)
T
1
Fxm1
Fxm1
+···+ms−1
+2
· · ·
+···+ms−1
+1
Fxm1
Fxm1
+···+ms−1
+···+ms−1
+1
+ms
n−(m1
+···+ms )
) *+ ,
0 · · · 0
⎤
T
⎥
⎦
+ Fxm1
∂
+···+ml
+1
∂xm1
+···+ml
+1
+ · · · + Fxn
∂
∂xn
3246
K. Filom, R. Farhoodi, and K. Kording
.
T
∈ Span {∇G1(x1
∇xm1
+···+ml
+1
, . . . , xm1 ), . . . , ∇Gl (xm1
, . . . , ∇xn}.
+···+ml−1
+1
, . . . , xm1
+···+ml ),
–
the vector
In the expressions above,
+···+ms−1
+···+ms−1
only on the variables
(which is
+···+ms , which are the leaves of Ts: any other leaf
xm1
+1
+···+ms−1
xk is separated from them by the subtree Ts of T , and, hence, for any leaf
= 0
+ · · · + ms, we have
of
, . . . , xm1
+ · · · + ms−1
is dependent
+···+ms−1
+···+ms−1
< i ≤ m1
xi with m1
size ms)
+ms
(cid:3)
(cid:2)
1
+1
+2
+1
· · · Fxm1
Fxm1
Fxm1
Fxm1
Fxi
+···+ms−1
+1
Fxm1
xk
due to the simplified form 1.21 of equation 1.18. To finish the proof, one
should establish the existence of functions Gs(xm1
+···+ms )
+1
-
should
appearing in equation 4.2; that is,
1
be shown to be parallel to a gradient vector field ∇Gs. Notice that the in-
duction hypothesis would be applicable to Gs since any ratio
of partial
+1
+1
Fxm1
Fxm1
+···+ms−1
+···+ms−1
+2
, . . . , xm1
.
T
+ms
+···+ms−1
· · · Fxm1
Fxm1
+···+ms−1
+···+ms−1
(Gs )xi
(Gs )x j
derivatives is the same as the corresponding ratio of partial derivatives of
F. Invoking theorem 5, to prove the existence of Gs, we should verify that
the 1-form
ωs :=
m1
+···+ms−1
+ms(cid:17)
Fxi
i=m1
+···+ms−1
+1
Fxm1
+···+ms−1
+1
dxi
(1 ≤ s ≤ l)
satisfies ωs ∧ dω
s = 1; other cases are completely similar. We have
= 0. We finish the proof by showing this in the case of
s
ω
1
∧ dω
1
=
=
=
=
⎞
⎠
∧ dx j
(cid:3)
(cid:2)
Fx j
Fx1
(cid:24)
m1(cid:17)
i=1
(cid:24)
m1(cid:17)
i=1
Fxi
Fx1
Fxi
Fx1
(cid:17)
(cid:25)
dxi
∧
⎛
m1(cid:17)
⎝
j=1
⎛
d
(cid:24)
(cid:25)
m1(cid:17)
⎝
∧
(cid:2)
m1(cid:17)
j=1
k=1
dxi
-
Fx j
Fx1
(cid:25)
dxk
∧ dx j
⎞
⎠
(cid:3)
xk
.
dxi
∧ dxk
∧ dx j
Fxi Fx j Fx1xk
(Fx1 )3
Fxi Fx jxk
(Fx1 )2
(cid:25)
−
⎛
(cid:17)
Fx jxk dxk
∧ dx j
⎞
⎠
i, j,k∈{1,...,m1
(cid:24)
}
m1(cid:17)
Fxi
(Fx1 )2 dxi
⎝
∧
i=1
⎛
⎝
+
j,k∈{1,...,m1
}
⎞
(cid:17)
Fxi Fx j dxi
∧ dx j
⎠ ∧
i, j∈{1,...,m1
}
(cid:24)
m1(cid:17)
k=1
(cid:25)
.
Fx1xk
(Fx1 )3 dxk
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3247
The last two terms are zero because, in the parentheses, the 2-forms
(cid:17)
Fx jxk dx j
∧ dxk
,
(cid:17)
j,k∈{1,...,m1
}
i, j∈{1,...,m1
}
Fxi Fx j dxi
∧ dx j
,
are zero since interchanging j and k or i and j in the summations results in
(cid:2)
the opposite of the original differential form.
Remark 9. The formulation of theorem 3 in Farhoodi et al. (2019) is con-
cerned with analytic functions and binary trees. The proof presented above
follows the same inductive procedure but utilizes theorem 5 instead of Tay-
lor expansions. Of course, theorem 5 remains valid in the analytic category,
so the tree representation of F constructed in the proof here consists of ana-
lytic functions if F is analytic. An advantage of working with analytic func-
tions is that in certain cases, the nonvanishing conditions may be relaxed.
For instance, if in example 1 the function F(x, y, z) satisfying equation 1.4 is
analytic, it admits a local representation of the form 1.1, while if F is only
smooth, at least one of the conditions Fx (cid:4)= 0 of Fy (cid:4)= 0 is required. (See Far-
hoodi et al., 2019, sec. 5.1 and 5.3, for details.)
Proof of Theorem 4. Establishing the necessity of constraints 1.19 and
1.20 is straightforward. An implementation of a smooth function F =
F(x1
, . . . , xn) on the tree T is in a form such as
(cid:24)
(cid:24)
σ
· · ·
˜w. ˜σ
w
.τ
1
1
· · ·
. ˜τ
1(cxi
1
+ · · ·) + ˜˜w
. ˜˜τ
(cid:10)
1(c
1
xi(cid:10) + · · ·) + · · ·
(cid:2)
(cid:10)
(cid:10)
˜w
+ w
.τ
2
2
(cid:10)
(cid:10)
(cid:10)
˜w
2
· · ·
(cid:11)
. ˜τ
2(dx j
(cid:3)
+ · · ·) + ˜˜w
(cid:25)
(cid:25)
+ w
.τ
3
3
· · ·
+ · · ·
+ · · ·
· · ·
(cid:10)
. ˜˜τ
2
2(d
x j(cid:10) + · · ·) + · · ·
(cid:11)
(cid:11)
· · ·
(cid:11)
(cid:11)
· · ·
(4.3)
for appropriate activation functions and weights. In the expression above,
variables xs appearing in
(cid:2)
(cid:10)
˜σ
w
.τ
1
1
· · ·
+ w
.τ
2
2
(cid:10)
(cid:10)
1
(cid:10)
˜w
(cid:10)
˜w
(cid:11)
· · ·
+ · · ·) + ˜˜w
. ˜˜τ
(cid:10)
1(c
1
xi(cid:10) + · · ·) + · · ·
(cid:11)
(cid:11)
· · ·
. ˜τ
1(cxi
+ · · ·) + ˜˜w
. ˜˜τ
2
2(d
(cid:10)
x j(cid:10) + · · ·) + · · ·
(cid:11)
(cid:11)
· · ·
2
. ˜τ
2(dx j
(cid:3)
+ w
.τ
3
3
· · ·
+ · · ·
are the leaves of the smallest (full) subtree of T in which both xi and x j
/T , the activation function applied
appear as leaves. Denoting this subtree by
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3248
K. Filom, R. Farhoodi, and K. Kording
at the root of
we write as
/T
1 and
/T is ˜σ , and the subtrees emanating from the root of
/T
, /T
, τ
3
2
1
/T , which
, . . . assigned to their roots. Here,
/T
2 contain xi and x j, respectively, and are the largest (full) subtrees
is
that have exactly one of xi and x j. To verify equation 1.19, notice that
, . . ., have τ
1
, /T
3
, τ
2
Fxi
Fx j
proportional to
(cid:10)
(cid:10)
τ (cid:10)
1
(cid:10)
τ (cid:10)
2
· · ·
(cid:10)
˜w
· · ·
˜w
. ˜τ
1(cxi
1
+ · · ·) + ˜˜w
. ˜˜τ
1(c(cid:10)xi(cid:10) + · · ·) + · · ·
1
. ˜τ
2(dx j
2
+ · · ·) + ˜˜w
. ˜˜τ
2(d(cid:10)x j(cid:10) + · · ·) + · · ·
2
· · ·
(cid:11)
(cid:11)
· · ·
(cid:11)
(cid:11)
. . . ˜τ (cid:10)
1(cxi
+ · · ·)
. . . ˜τ (cid:10)
2(dx j
+ · · ·)
(4.4)
with the constant of proportionality being a quotient of two products of
certain weights of the network. The ratio 4.4 is dependent only on those
/T
variables that appear as leaves of
1 and
/T
2, so
(cid:24)
(cid:25)
Fxi
Fx j
xk
= 0 ⇔ Fxixk Fx j
= Fx jxk Fxi
unless there is a subtree of T containing the leaf xk and exactly one of xi or x j
/T
/T
2). Before switching to constraint
1 or
(which forcibly will be a subtree of
1.20, we point out that the description of F in equation 4.3 assumes that the
leaves xi and x j are not siblings. If they are, F may be written as
(cid:10)
σ
· · ·
(cid:10)
˜w. ˜σ
(cid:13)
w.τ (cxi
+ dx j
+ · · ·) + · · ·
(cid:14)
(cid:11)
+ · · ·
· · ·
(cid:11)
,
= c
Fxi
Fx j
in which case,
d is a constant and hence equation 1.21 holds for all
1 ≤ k ≤ n. To finish the proof of necessity of the constraints introduced in
theorem 7, consider the fraction from equation 4.4, which is a multiple of
Fxi
, xi(cid:10) , . . . (leaves of
Fx j
/T
1) by a function of x j
. This has a description as a product of a function of xi
, x j(cid:10) , . . . (leaves of
/T
2). Lemma 4 now implies that for
any leaf xi(cid:10) of
/T
1 and any leaf x j(cid:10) of
/T
2,
⎛
(cid:2)
(cid:3)
⎜
⎜
⎜
⎝
Fxi
Fx j
Fxi
Fx j
⎞
⎟
⎟
⎟
⎠
xi
(cid:10)
(cid:10)
x j
= 0;
hence, the simplified form, equation 1.22 of 1.20.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3249
Figure 14: The first case of the inductive step in the proof of theorem 4. The
removal of the leaves directly connected to the root of T results in a smaller
rooted tree.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 15: The second case of the inductive step in the proof of theorem 4. There
is no leaf directly connected to the root of T . Separating one of the rooted sub-
trees adjacent to the root results in two smaller rooted trees.
We induct on the number of leaves to prove the sufficiency of constraints
1.19 and 1.20 (accompanied by suitable nonvanishing conditions) for the
existence of a tree implementation of a smooth function F = F(x1
, . . . , xn)
as a composition of functions of the form 1.12. Given a rooted tree T with n
, . . . , xn, the inductive step has two cases demonstrated
leaves labeled by x1
in Figures 14 and 15:
• There are leaves, say, xm+1
their removal results in a smaller tree T (cid:10)
Figure 14). The goal is to write F(x1
, . . . , xn) as
, . . . , xn, directly adjacent to the root of T ;
, . . . , xm (see
with leaves x1
σ (G(x1
, . . . , xm) + cm+1xm+1
+ · · · + cnxn),
(4.5)
with G satisfying appropriate constraints that, invoking the induction
hypothesis, guarantee that G is computable by T (cid:10)
.
• There is no leaf adjacent to the root of T , but there are smaller sub-
, . . . , xn.
1 with leaves
trees. Denote one of them with T
Removing this subtree results in a smaller tree T
2 and show its leaves by xm+1
3250
K. Filom, R. Farhoodi, and K. Kording
x1
, . . . , xm (see Figure 15). The goal is to write F(x1
, . . . , xn) as
σ (G1(x1
, . . . , xm) + G2(xm+1
, . . . , xn)),
(4.6)
with G1 and G2 satisfying constraints corresponding to T
2, and
hence may be implemented on these trees by invoking the induction
hypothesis.
1 and T
Following the discussion at the beginning of section 3, F may be locally writ-
ten as a function of another function with nonzero gradient if the gradients
are parallel. This idea has been frequently used so far, but there is a twist
here: we want such a description of F to persist on the box-like region B that
is the domain of F. Lemma 2 resolves this issue. The tree function in the ar-
gument of σ in either of equation 4.5 or 4.6, which here we denote by ˜F, shall
be constructed below by invoking the induction hypothesis, so ˜F is defined
at every point of B. Besides, our description of ∇ ˜F below (cf. equations 4.7
and 4.9) readily indicates that just like F, it satisfies the nonvanishing con-
(cid:15)
(cid:12)
x ∈ B | ˜F(x) = c
ditions of theorem 7. Applying lemma 2 to ˜F, any level set
is connected, and ˜F can be extended to a coordinate system ( ˜F, F2
, . . . , Fn)
for B. Thus, F, whose partial derivatives with respect to other coordinate
functions vanish, realizes precisely one value on any coordinate hypersur-
(cid:15)
. Setting σ (c) to be the aforementioned value of F de-
x ∈ B | ˜F(x) = c
face
fines a function σ with F = σ ( ˜F). After this discussion on the domain of
definition of the desired representation of F, we proceed with constructing
˜F = ˜F(x1
+ · · · + cnxn in the case
, . . . , xn) in the case of equation
of equation 4.5 or as G(x1
4.6.
, . . . , xn) as either G(x1
, . . . , xm) + cm+1xm+1
, . . . , xm) + G2(xm+1
(cid:12)
In the case of equation 4.5, assuming that, as theorem 7 requires, one
, . . . , Fxn , example Fxn , is nonzero, we should
of the partial derivatives Fxm+1
have
0
0
∇F =
Fx1
. . . Fxm Fxm+1
. . . Fxn−1 Fxn
1
T
=
Gx1
= ∇(G(x1
· · · Gxm cm+1
· · · cn−1 1
, . . . , xm) + cm+1xm+1
1
-
!
!
T
Fx1
Fxn
· · · Fxm
Fxn
Fxm+1
Fxn
· · · Fxn−1
Fxn
.
T
1
+ · · · + cn−1xn−1
+ xn).
(4.7)
Fx j
Fxn
where m < j ≤ n must be a constant, which we show by
Here, each ratio
c j, due to the simplified form equation 1.21 of equation 1.19: the only (full)
subtree of T containing either x j or xn is the whole tree since these leaves
· · · Fxm
are adjacent to the root of T . On the other hand,
appearing
Fxn
, . . . , xm) again
in equation 4.7 is a gradient vector field of the form ∇G(x1
where 1 ≤ i ≤ m is
as a by-product of equations 1.19 and 1.21: each ratio
Fx1
Fxn
(cid:23)
T
(cid:22)
Fxi
Fxn
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3251
independent of xm+1
function of (x1
, . . . , xn by the same reasoning as above; and this vector
, . . . , xm) is integrable because for any 1 ≤ i, i(cid:10) ≤ m,
(cid:2)
Fxi
Fxn
(cid:3)
(cid:2)
=
xi
(cid:10)
(cid:3)
xi
(cid:10)
Fxi
Fxn
⇔ Fxixn Fxi
(cid:10) = Fxi
(cid:10) xn Fxi
.
Hence, such a G(x1
inductions hypothesis since any ratio
, . . . , xm) exists; moreover, it satisfies constraints from the
coincides with the corresponding
Gx j
Gx j
(cid:10)
ratio of partial derivatives of F, a function assumed to satisfy equations 1.21
and 1.22.
Next, in the second case of the inductive step, let us turn to equation
4.6. The nonvanishing conditions of theorem 7 require a partial derivative
, . . . , Fxn to be
among Fx1
(cid:4)= 0. We
nonzero. Without any loss of generality, we assume Fx1
want to apply lemma 4 to split the ratio
, . . . , Fxm and also a partial derivative among Fxm+1
(cid:4)= 0 and Fxn
(cid:4)= 0 as
Fx1
Fxn
Fx1
Fxn
= β(x1
, . . . , xm)
1
γ (xm+1
, . . . , xn) =
β(x1
γ (xm+1
, . . . , xm)
, . . . , xn)
.
(4.8)
To do so, it needs to be checked that
⎛
(cid:10)
⎜
⎝
(cid:11)
xi
Fx1
Fxn
Fx1
Fxn
⎞
⎟
⎠
x j
= 0
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
for any two indices 1 ≤ i ≤ m and m < j ≤ n. This is the content of equation
1.20, or its simplified form, equation 1.22, when xi belongs to the same max-
imal subtree of T adjacent to the root that has x1 and holds for other choices
, . . . , xm} too since in that situation, by the simplified form equa-
of xi
(cid:10)
must be zero because x1,
tion 1.21, of equation 1.19, the derivative
xi, and xn belong to different maximal subtrees of T . Next, the gradient of
F could be written as
∈ {x1
Fx1
Fxn
(cid:11)
xi
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
∇F =
0
Fx1 Fx2
-
!
!
Fx1
Fxn
. . . Fxm Fxm+1
. . . Fxn−1 Fxn
1
T
Fx2
Fxn
· · · Fxm
Fxn
Fxm+1
Fxn
· · · Fxn−1
Fxn
.
T
1
-
=
Fx1
Fxn
Fx2
Fx1
. Fx1
Fxn
· · · Fxm
Fx1
. Fx1
Fxn
Fxm+1
Fxn
· · · Fxn−1
Fxn
.
T
1
3252
K. Filom, R. Farhoodi, and K. Kording
⎡
⎣1
= Fx1
Fxn
Fx2
Fx1
· · · Fxm
Fx1
⎤
⎦
n−m
) *+ ,
0 · · · 0
⎡
T
⎣
+
m) *+ ,
0 · · · 0
⎤
T
⎦
.
1
Fxm+1
Fxn
· · · Fxn−1
Fxn
Combining with equation 4.8:
⎡
!
!
∇F
⎣β(x1
, . . . , xm) β(x1
, . . . , xm). Fx2
Fx1
· · · β(x1
, . . . , xm). Fxm
Fx1
⎤
T
⎦
n−m
) *+ ,
0 · · · 0
"
+
m) *+ ,
0 · · · 0 γ (xm+1
, . . . , xn). Fxm+1
Fxn
#T
· · · γ (xm+1
, . . . , xn)
. Fxn−1
Fxn
γ (xm+1
, . . . , xn)
.
(4.9)
, . . . , xm) and G2(xm+1
To establish equation 4.6, it suffices to argue that the vectors on the
right-hand side are in the form of ∇G1 and ∇G2 for suitable functions
, . . . , xn), to which the induction hypothesis can
G1(x1
be applied by the same logic as before. Notice that the first one is dependent
, . . . , xn,
, . . . , xm, while the second one is dependent only on xm+1
only on x1
again by equations 1.19 and 1.21. For any 1 ≤ i ≤ m and m < j ≤ n, we have
(cid:10)
(cid:11)
= 0) since there is no subtree of T that has
= 0 (respectively,
(cid:10)
(cid:11)
Fx j
Fxn
xi
Fxi
Fx1
x j
only one of x1 and xi (resp. only one of xn and x j) and also x j (resp. also xi).
We finish the proof by verifying the corresponding integrability conditions,
(cid:2)
β Fxi
Fx1
(cid:3)
(cid:2)
=
xi
(cid:10)
(cid:10)
β Fxi
Fx1
(cid:3)
(cid:2)
,
xi
γ
Fx j
Fxn
(cid:3)
(cid:2)
=
γ
(cid:10)
x j
(cid:3)
,
x j
(cid:10)
Fx j
Fxn
for any 1 ≤ i, i(cid:10) ≤ m and m < j, j(cid:10) ≤ n. In view of equation 4.8, one can
change β and γ above to
, respectively, and write the desired iden-
tities as the new ones,
(cid:24)
or Fxn
Fx1
Fx1
Fxn
(cid:24)
(cid:25)
(cid:25)
(cid:2)
(cid:3)
(cid:2)
(cid:3)
(cid:2)(cid:2)Fx1
Fxn
Fxi
(cid:2)(cid:2)Fx1
=
xi
(cid:10)
(cid:2)(cid:2)Fx1
Fxn
(cid:10)
Fxi
(cid:2)(cid:2)Fx1
,
xi
which hold due to equation 1.21.
(cid:3)(cid:3)Fxn
Fx1
Fx j
(cid:3)(cid:3)Fxn
=
(cid:10)
x j
(cid:3)(cid:3)Fxn
Fx1
(cid:10)
Fx j
(cid:3)(cid:3)Fxn
,
x j
(cid:2)
Remark 10. As mentioned in remark 3, working with functions of the form
1.12 in theorem 7 rather than general smooth functions has the advantage of
enabling us to determine a domain on which a superposition representation
exists. In contrast, the sufficiency part of theorem 3 is a local statement since
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3253
it relies on the implicit function theorem. It is possible to say something
nontrivial about the domains when functions are furthermore analytic. This
is because the implicit function theorem holds in the analytic category as
well (Krantz & Parks, 2002, sec. 6.1) where lower bounds on the domain of
validity of the theorem exist in the literature (Chang, He, & Prabhu, 2003).
5 Conclusion
In this article, we proposed a systematic method for studying smooth real-
valued functions constructed as compositions of other smooth functions
that are either of lower arity or in the form of a univariate activation func-
tion applied to a linear combination of inputs. We established that any such
smooth superposition must satisfy nontrivial constraints in the form of al-
gebraic PDEs, which are dependent only on the hierarchy of composition
or, equivalently, only on the topology of the neural network that produces
superpositions of this type. We conjectured that there always exist charac-
teristic PDEs that also provide sufficient conditions for a generic smooth
function to be expressible by the feedforward neural network in question.
The genericity is to avoid singular cases and is captured by nonvanishing
conditions that require certain polynomial functions of partial derivatives
to be nonzero. We observed that there are also situations where nontriv-
ial algebraic inequalities involving partial derivatives (PDIs) are imposed
on the hierarchical functions. In summary, the conjecture aims to describe
generic smooth functions computable by a neural network with finitely
many universal conditions of the form (cid:2) (cid:4)= 0, (cid:5) = 0, and (cid:7) > 0, where (cid:2),
(cid:5), and (cid:7) are polynomial expressions of the partial derivatives and are de-
pendent only on the architecture of the network, not on any tunable pa-
rameter or any activation function used in the network. This is reminiscent
of the notion of a semialgebraic set from real algebraic geometry. Indeed,
in the case of compositions of polynomial functions or functions computed
by polynomial neural networks, the PDE constraints yield equations for the
corresponding functional variety in an ambient space of polynomials of a
prescribed degree.
The conjecture was verified in several cases, most importantly, for tree
architectures with distinct inputs where, in each regime, we explicitly ex-
hibited a PDE characterization of functions computable by a tree network.
Examples of tree architectures with repeated inputs were addressed as well.
The proofs were mathematical in nature and relied on classical results of
multivariable analysis.
The article moreover highlights the differences between the two regimes
mentioned at the beginning: the hierarchical functions constructed out
of composing functions of lower dimensionality and the hierarchical
functions that are compositions of functions of the form y (cid:6)→ σ ((cid:8)w, y(cid:9)).
The former functions appear more often in the mathematical literature
on the Kolmogorov-Arnold representation theorem, while the latter are
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3254
K. Filom, R. Farhoodi, and K. Kording
ubiquitous in deep learning. The special form of functions y (cid:6)→ σ ((cid:8)w, y(cid:9))
requires more PDE constraints to be imposed on their compositions,
whereas their mild nonlinearity is beneficial in terms of ascertaining the
domain on which a claimed compositional representation exists.
Our approach for describing the functional spaces associated with feed-
forward neural networks is of natural interest in the study of expressivity
of neural networks and could lead to new complexity measures. We be-
lieve that the point of view adapted here is novel and might shed light on
a number of practical problems such as comparison of architectures and
reverse-engineering deep networks.
Appendix A: Technical Proofs
Proof of Lemma 2. We first prove that F can be extended to a coordinate
system on the entirety of the box-like region B, which we shall write as
, . . . , xn
I1
according to the maximal subtrees of T in which they appear:
× · · · × In. As in the proof of theorem 3, we group the variables x1
x1
, . . . , xm1
xm1
+···+ml
+1
; xm1
+1
; . . . ; xn,
, . . . , xm1
+m2
; . . . ; xm1
+···+ml−1
+1
, . . . , xm1
+···+ml
;
1
+1
+1
+···+ml
, . . . , T
+···+ms−1
where, denoting the subtrees emanating from the root of T by T
l, for
any 1 ≤ s ≤ l the leaves of Ts are labeled by xm1
, . . . , xm1
+ms ;
, . . . , xn represent the leaves that are directly connected to the
and xm1
root (if any); see Figure 13. Among the variables labeling the leaves of T
1,
there should exist one with respect to which the first-order partial derivative
(cid:4)= 0
of F is not zero. Without any loss of generality, we may assume that Fx1
at any point of B. Hence, the Jacobian of the map (F, x2
, . . . , xn) : B → Rn
is always invertible. To prove that the map provides a coordinate system,
, . . . , xn constant and
we just need to show that it is injective. Keeping x2
varying x1, we obtain a univariate function of x1 on the interval I1 whose
derivative is always nonzero and is hence injective.
+···+ms−1
Next, to prove that the level sets of F : B → R are connected, notice that
F admits a representation
F(x1
, . . . , xn) = σ
(cid:13)
w
1G1
+ · · · + w
lGl
+ w(cid:10)
m1
+···+ml
+1xm1
+···+ml
+1
+ · · · + w(cid:10)
nxn
(cid:14)
(A.1)
+1
+···+ms−1
where Gs = Gs(xm1
, . . . , xm1
+ms ) is the tree function that
Ts computes by receiving xm1
+ms from its leaves;
+···+ms−1
σ is the activation function assigned to the root of T ; and w
, . . . , w
l,
1
w(cid:10)
n are the weights appearing at the root. A simple appli-
cation of the chain rule implies that G1, which is a function implemented
on the tree T
1, satisfies the nonvanishing hypotheses of theorem 7 on the
+···+ms−1
+1
, . . . , xm1
, . . . , w(cid:10)
+···+ms−1
+···+ml
+1
m1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3255
× · · · × Im1 ; moreover, the derivative of σ is nonzero at
box-like region I1
any point of its domain9 because otherwise there exists a point of p ∈ B at
which Fxi (p) = 0 for any leaf xi. By the same logic, the weight w
1 must be
nonzero because otherwise all first-order partial derivatives with respect
to the variables appearing in T
1 are identically zero. We now show that an
arbitrary level set Lc := {x ∈ B | F(x) = c} is connected. Given the represen-
tation (see equation A.1) of F, the level set is empty if σ does not attain the
value c. Otherwise, σ attains c at a unique point σ −1(c) of its domain. So one
, . . . , xn) = c as
may rewrite the equation F(x1
= −
G1
w
w
2
1
− · · · −
G2
w(cid:10)
m1
l
−
Gl
w
w
1
+1
+···+ml
w
1
xm1
+···+ml
+1
− · · · −
w(cid:10)
n
w
1
xn + 1
w
1
σ −1(c).
(A.2)
The left-hand side of equation A.2 is a function of x1
hand side, which we denote by ˜G, is a function of xm1
the level set Lc is the preimage of
, . . . , xm1 , while its right-
, . . . , xn. Therefore,
+1
(cid:12)
(y, ˜x) ∈ R × (Im1
+1
(cid:15)
× · · · × In) | y = ˜G(˜x)
(A.3)
under the map
2
π : B = (I1
, . . . , xm1
(x1
× · · · × Ims ) × (Im1
; ˜x) (cid:6)→ (G1(x1
, . . . , xm1 ), ˜x) .
× · · · × In) → R × (Im1
+1
× · · · × In)
+1
(A.4)
The following simple fact can now be invoked: Let π : X → Y be a continu-
ous map of topological spaces that takes open sets to open sets and has connected
level sets. Then the preimage of any connected subset of Y under π is connected.
Here, Lc is the preimage of the set from equation A.3, which is connected
since it is the graph of a continuous function, under the map π defined in
equation A.4, which is open because the scalar-valued function G1 is: its
gradient never vanishes. Therefore, the connectedness of the level sets of F
is implied by the connectedness of the level sets of π. A level set of the map,
equation A.4, could be identified with a level set of its first component G1.
Consequently, we have reduced to the similar problem for the function G1,
which is implemented on the smaller tree T
1. Therefore, an inductive argu-
ment yields the connectedness of the level sets of F. It only remains to check
the basic case of a tree whose leaves are directly connected to the root. In
9
As the vector (x1
, . . . , xn ) of inputs varies in the box-like region B, the inputs to each
node form an interval on which the corresponding activation function is defined.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3256
K. Filom, R. Farhoodi, and K. Kording
, . . . , xn) is in the form of σ (a1x1
+ · · · + anxn) (the family of
that setting, F(x1
functions that lemma 3 is concerned with). By repeating the argument used
before, the activation function σ is injective. Hence, a level set F(x) = c is the
+ · · · + anxn = σ −1(c) with the box-like
intersection of the hyperplane a1x1
(cid:2)
region B. Such an intersection is convex and thus connected.
= Fx jxk Fxi follows
Proof of Lemma 3. The necessity of conditions Fxixk Fx j
(cid:4)= 0
from a simple computation. For the other direction, suppose Fx j
Fxi
throughout an open box-like region B ⊆ Rn and any ratio
is constant on
Fx j
= 1. They form
, . . . , an with a j
B. Denoting it by ai, we obtain numbers a1
· · · an]T parallel to ∇F. Thus, F could have nonzero first-order
a vector [a1
partial derivative only with respect to the first member of the coordinate
system,
(a1x1
+ · · · + anxn, x1
, . . . , x j−1
, x j+1
, . . . , xn),
the
for B. The coordinate hypersurfaces are connected since they are intersec-
tions of hyperplanes in Rn with the convex region B. This fact enables us to
+ · · · + anxn globally. (cid:2)
deduce that F can be written as a function of a1x1
Proof of Lemma 4. For a function q = q1 q2 such as equation 3.4,
form q qy(1)
equalities of
hold since both sides
q =
coincide with q1 q2 (q1)y(1)
(q2)y(2)
(cid:10)
(cid:11)
, . . . , y(2)
y(1)
q
be a smooth function on an open box-like re-
n2
1
for any 1 ≤ a ≤ n1
gion B1
and 1 ≤ b ≤ n2, and never vanishes. So q is either always positive or always
negative. One may assume the former by replacing q with −q if necessary.
Hence, we can define a new function p := Ln(q) by taking the logarithm.
We have
; y(2)
1
⊆ Rn1 × Rn2 that satisfies q qy(1)
qy(2)
the other direction,
, . . . , y(1)
n1
× B2
a y(2)
b
. For
= qy(1)
= qy(1)
qy(2)
a y(2)
b
let
b
b
b
a
a
a
=
py(1)
a y(2)
b
(cid:3)
(cid:2)
qy(1)
a
q
y(2)
b
q qy(1)
a y(2)
b
=
qy(2)
b
− qy(1)
q2
a
= 0.
It suffices to show that this vanishing of mixed partial derivatives
+
; y(2)
1
, . . . , y(1)
n1
, . . . , y(1)
n1
, . . . , y(2)
n2
(cid:10)
y(1)
1
(cid:10)
y(1)
1
as p1
(cid:11)
(cid:11)
p2
respectively. The domain of p is a box-like region of the form
since then exponentiating yields q1 and q2 as ep1 and ep2 ,
allows us to write p
, . . . , y(2)
n2
(cid:10)
y(2)
1
(cid:11)
B1
× B2
=
(cid:25)
I(1)
a
×
(cid:24)
n13
a=1
(cid:25)
I(2)
b
.
(cid:24)
n23
b=1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
PDE Characterization of Functions Computed by Neural Networks
3257
Picking an arbitrary point z(1)
1
implies
∈ I(1)
1 , the fundamental theorem of calculus
(cid:10)
y(1)
1
, . . . , y(1)
n1
; y(2)
1
, . . . , y(2)
n2
(cid:11)
p
4
=
z(1)
1
+ p
y(1)
1
(cid:10)
s(1)
1
py(1)
1
, y(1)
2
, . . . , y(1)
n1
; y(2)
1
, . . . , y(2)
n2
ds(1)
1
(cid:11)
(cid:10)
z(1)
1
, y(1)
2
, . . . , y(1)
n1
; y(2)
1
, . . . , y(2)
n2
(cid:11)
.
On the right-hand side, the integral is dependent only on y(1)
n1 be-
1
, . . . , y(2)
cause the partial derivatives of the integrand with respect to y(2)
(cid:11)
n2
1
, . . . , y(2)
; y(2)
are all identically zero. The second term, p
,
n2
1
is a function on the smaller box-like region
, . . . , y(1)
n1
(cid:10)
z(1)
1
, . . . , y(1)
, y(1)
2
(cid:24)
n13
a=2
(cid:25)
(cid:24)
I(1)
a
×
(cid:25)
n23
b=1
I(2)
b
in Rn1
appropriate summation form.
−1 × Rn2 and thus, proceeding inductively, can be brought into the
(cid:2)
Appendix B: Differential Forms
Differential forms are ubiquitous objects in differential geometry and tensor
calculus. We only need the theory of differential forms on open domains in
Euclidean spaces. Theorem 5 (which has been used several times through-
out the, for example, in the proof of theorem 3) is formulated in terms of
differential forms. This appendix provides the necessary background for
understanding the theorem and its proof.
We begin with a very brief account of the local theory of differential
forms. (For a detailed treatment see Pugh, 2002, chap. 5.) Let U be an open
subset of Rn. A differential k-form ω on U assigns a scalar to any k-tuple of
tangent vectors at a point p of U. This assignment, denoted by ωp, must
be multilinear and alternating. We say ω is smooth (resp. analytic) if ωp
varies smoothly (resp. analytically) with p. In other words, feeding ω with
, . . . , Vk on U results in a func-
k smooth (resp. analytic) vector fields V1
tion ω(V1
, . . . , Vk) : U → R that is smooth (resp. analytic). We next exhibit
an expression for ω. Consider the standard basis
of vector
fields on U where
assigns ei to each point. The dual basis is denoted
, . . . , ∂
∂xn
∂
∂x1
(cid:11)
(cid:10)
∂
∂xi
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
–
p
d
/
l
f
/
/
/
/
3
3
1
2
3
2
0
4
1
9
7
4
3
3
4
n
e
c
o
_
a
_
0
1
4
4
1
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3258
K. Filom, R. Farhoodi, and K. Kording
, . . . , dxn), which at each point yields the dual of the standard basis
, . . . , dxn is a 1-form
by (dx1
(e1
on U, and any k-form ω can be written in terms of them:
, . . . , en) for Rn, that is, dxi
i j. Each of dx1
∂
∂x j
≡ δ
(cid:11)
(cid:10)
(cid:17)
ω =
1≤i1
<...