A Notion of Semantic Coherence for - Specialized Research AI at MIT

A Notion of Semantic Coherence for
Underspeciﬁed Semantic Representation

Mehdi Manshadi∗
University of Rochester

Daniel Gildea∗∗
University of Rochester

James F. Allen†
University of Rochester

The general problem of ﬁnding satisfying solutions to constraint-based underspeciﬁed represen-
tations of quantiﬁer scope is NP-complete. Existing frameworks, including Dominance Graphs,
Minimal Recursion Semantics, and Hole Semantics, have struggled to balance expressivity and
tractability in order to cover real natural language sentences with efﬁcient algorithms. We
address this trade-off with a general principle of coherence, which requires that every variable
introduced in the domain of discourse must contribute to the overall semantics of the sentence.
We show that every underspeciﬁed representation meeting this criterion can be efﬁciently pro-
cessed, and that our set of representations subsumes all previously identiﬁed tractable sets.

1. Introduction

Quantiﬁer scope ambiguity is a big challenge in deep language understanding systems.
Consider the following conversation:

Woman: I believe there is one true soulmate for every person.

Man: He must be very busy.1

Most people ﬁnd the man’s answer unusual (humorous, sarcastic, etc.). This is because
one of the two scopings of the woman’s sentence feels so obvious that the less likely

∗

∗∗

†

Department of Computer Science, University of Rochester, Rochester, NY 14627.
E-mail: mehdih@cs.rochester.edu.
Department of Computer Science, University of Rochester, Rochester, NY 14627.
E-mail: gildea@cs.rochester.edu.
Department of Computer Science, University of Rochester, Rochester, NY 14627.
E-mail: james@cs.rochester.edu.

1 dilbert.com/strip/2001-04-19.

Submission received: 2 June 2016; revised version received: 13 March 2017; accepted for publication:
1 August 2017.

doi:10.1162/COLI a 00307

© 2017 Association for Computational Linguistics
Published under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International
(CC BY-NC-ND 4.0) license

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

scoping is often missed at ﬁrst glance. In the most likely interpretation, where there are
many soulmates, the quantiﬁer every has wide scope, and, in the second interpretation,
where there is a unique soulmate, every has narrow scope. The following conversation
is of a similar nature:

Bob: How long have you and Opal been married now Earl?

Earl: I’ve lost track. But I can tell you this … I don’t regret one day of it.

Bob: Which day don’t you regret?2

The difference, however, is that, in this example, the scope ambiguity is not be-
tween two quantiﬁers, but between a quantiﬁer (one) and a scopal operator (negation).
Underspeciﬁcation, that is, generating an unscoped semantic representation, has been
the most common way of dealing with quantiﬁer scope ambiguity since the early days
of natural language processing. Underspeciﬁcation is not adopted only because quan-
tiﬁer scope disambiguation is difﬁcult, but also because, for most practical purposes,
an underspeciﬁed representation (UR)3 will do the job. Equations (1) and (2) show an
unscoped logical form (LF) for the sentences There is one soulmate for every person and
I do not regret one day, respectively.

One x Soulmate
(cid:105)

(cid:104)

Every y Person
(cid:105)

(cid:104)
Of(x, y)

(1)

One x Day
(cid:105)

(cid:104)
Not(Regret(I, x))

Equation (3) shows the two scopings of the unscoped LF in Equation (2):

One(x, Day(x), Not(Regret(I, x)))

Not(One(x, Day(x), Regret(I, x)))

(2)

(3)

When the number of quantiﬁers increases, the number of possible scopings will increase
exponentially. More recent underspeciﬁcation formalisms are constraint-based—that is,
they allow for constraints, restricting the order of quantiﬁers, to be added to ﬁlter out
unwanted scopings. The constraints can come from different sources, including deeper
processing steps, such as discourse or pragmatics. Several constraint-based underspec-
iﬁcation frameworks have been developed over the past couple of decades. Minimal
Recursion Semantics (MRS) (Copestake, Lascarides, and Flickinger 2001), Hole Seman-
tics (Bos 2002), and Dominance Constraints (Koller, Niehren, and Thater 2003) are
among those frameworks. Each framework is different in the type of constraints it
allows, and has its own advantages and disadvantages. A constraint-based UR deﬁnes

2 From Pickles (Brian Crane, 2005).
3 In the literature, UR is used to refer to underspeciﬁed representation within the context of Hole

Semantics. In this article, unless otherwise speciﬁed, we use UR as a blanket term for any
scope-underspeciﬁed representation.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

a computational problem that needs to be solved: Given a UR with a set of constraints,
one needs to check if these constraints are consistent, that is, whether there is a scoping
satisfying all the constraints. This is called the satisﬁability problem. The satisﬁability
problem for all these three frameworks, in their general form, is intractable (Althaus
et al. 2003). There has been some effort towards deﬁning a notion of well-formedness
within the context of these frameworks. The goal has been to deﬁne a subset of URs, the
so-called well-formed UR, for which the satisﬁability problem becomes tractable. For ex-
ample, Niehren and Thater (2003) deﬁned the notion of (weak) net to characterize such
a subset. Well-formedness was also intended to bridge the gap between these under-
speciﬁcation formalisms; the hope was that the differences between these formalisms
disappear and they become equivalent once restricted to well-formed structures.

As seen in Niehren and Thater (2003) and Fuchss et al. (2004), the problem with
those efforts on deﬁning a notion of well-formedness is that their satisfaction of both
properties was only empirically supported, and hence the correctness of those state-
ments has remained a conjecture. In better words, ﬁrst, there was no mathematical proof
to show that nets enforce the equivalence of qeq vs. dominance relations, the two dif-
ferent types of constraint used in MRS vs. Dominance Constraints/Hole Semantics, and
second, although they were proved to be tractable, there was no convincing linguistic
justiﬁcation as to why nets cover all URs corresponding to coherent sentences. In fact,
this claim was later falsiﬁed when Thater (2007) presented examples of coherent sen-
tences that were unaccounted for by nets (Section 7.1). In summary, it has remained an
open question whether there is a linguistically justiﬁed notion of well-formedness that
not only (provably) bridges the gap between the above formalisms, but also guarantees
tractability. In this article, we propose such a notion of semantic coherence that not
only answers both of these open questions but also solves several other unanswered
questions within the context of scope underspeciﬁcation. The contribution of this work
can be summarized as follows:

(cid:114)

We extend the previous tractable frameworks to cover those natural
language sentences that were known to be unaccounted for without
increasing the complexity of the algorithms.

We go beyond those known unaccounted examples and, once and
for all, prove that every semantically coherent natural language sentence
(based on a linguistically justiﬁed notion of semantic coherence) can be
solved in polynomial time, presenting a deﬁnitive answer to the open
question of whether solving unscoped representations of real-life natural
language sentences within the context of these formalisms is
tractable.

We prove that, under our notion of coherence, the two fundamentally
different types of constraint, dominance and qeq, become equivalent,
hence, the principal difference between these formalisms disappears.

We further bridge the gap between the constraint-based formalisms by
proving that binding constraints (constraints enforcing that quantiﬁed
variables be bound within the scope of their quantiﬁers), which are

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

label-to-label dominance relations in nature, can be represented by
hole-to-label dominance relations, as long as the URs are coherent.
This explains how a formalism such as Hole Semantics, which does
not incorporate label-to-label dominance relations, does not lack the
power to model binding constraints.

(cid:114)

Finally, given that quantiﬁer scoping has traditionally been treated as an
ordering problem (i.e., predicting a permutation of quantiﬁers), whereas in
the constraint-based formalisms it is deﬁned as predicting a tree structure,
our notion of coherence allows us to explain this discrepancy. We show
that, for coherent URs, quantiﬁer scoping is reduced from predicting a tree
structure to ﬁnding a permutation.

Whereas we focus on ﬁnding solutions to underspeciﬁed representations with hard
constraints, our results have implications for statistical systems based on soft con-
straints. Because weighted soft constraints generalize hard constraints, ﬁnding efﬁcient
algorithms for solving systems with hard constraints is a ﬁrst step toward ﬁnding
efﬁcient algorithms for ﬁnding the highest-scoring solution under weighted constraints.
We also show how our algorithm for ﬁnding solutions under hard constraints can be
used to guide search for the highest scoring solution given a combination of hard and
soft constraints.

Some of this article’s results (or a weaker version of them) have been proved in
our own previous work. In Manshadi, Allen, and Swift (2008b), we proved the equiv-
alence of qeq and dominance for canonical form MRS, which motivated the notion of
completeness. In Manshadi, Allen, and Swift (2009), we introduced the notion of heart-
connectedness, which, in the current work, forms the basis of coherence. In another line
of work (Manshadi and Allen 2012), we introduced a superset of nets, called supernets,
that covered the known examples unaccounted for by nets.

In this article, however, we combine completeness and heart-connectedness to
deﬁne a mathematically characterized notion of coherence. We show that this notion
directly follows from a linguistic property of semantically coherent sentences, as dis-
cussed by Frege (1923), among others. Under such a linguistically justiﬁed and math-
ematically characterized notion of coherence, we prove that (i) the given formalisms
become equivalent, (ii) coherence guarantees tractability, and (iii) quantiﬁer scoping is
reduced to an ordering problem. More importantly, to connect our work to the previous
work within the context of Dominance Graph, we deﬁne the notion of hypernet, the
largest tractable subset of Dominance Graph found so far. Hypernets, in particular,
contain downward-connected nets (Koller and Thater 2007) as well as all coherent URs.
In order to build a mathematical infrastructure to be able to rigorously prove these
properties, in particular, the equivalence of different formalisms within a newly deﬁned
notion of well-formedness (i.e., coherence), we deﬁne a framework, the underspeciﬁ-
cation graph, by simultaneously incorporating both qeq and dominance constraints.
This allows us to compare URs represented within each of the individual formalisms
under a universal framework (as shown schematically in Figure 1), and ultimately to
formally prove equivalence. The structure of this paper is as follows. In Section 2, we

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Underspeciﬁcation Graph
Section 2

Dominance Graph

MRS

Weakly Normal DG

Complete UG
Section 3

Normal DG

Hypernet
Section 5

CF-MRS

Hole Semantics’s UR
(satisﬁable and hyper-normally connected)
Section 7.3

Weak net
Section 7.1

Coherent UG
Section 4

Coherent MRS
(satisﬁable and heart-connected)
Section 7.2

Figure 1
Classes of underspeciﬁcation graph introduced in this article. We deﬁne hypernet, show that it is
computationally tractable, and further show that it covers all coherent sentences, and that it
subsumes previously identiﬁed tractable classes.

give a formal deﬁnition of our universal framework (i.e., underspeciﬁcation graph).
Section 3 deﬁnes a notion of completeness and proves that, under this notion, the
two fundamentally different types of constraint used in underspeciﬁcation formalisms
(qeq and dominance) become equivalent. Section 4 deﬁnes a notion of coherence for a
complete UR. Section 5 discusses the tractability issue. We propose a tractable subset
of URs and prove that it is the largest tractable subset found so far. We then show that
every coherent UR belongs to this set, and we discuss implications for systems of mixed
hard and soft constraints. Section 6 shows that scope disambiguation can be treated as
an ordering problem. Finally, Section 7 gives a detailed comparison of our framework
with previous work, and Section 8 concludes.

2. Underspeciﬁcation Graph

Consider the following example.

Every child of a politician runs.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

Early systems (Schubert and Pelletier 1982; Hobbs and Shieber 1987; Allen 1995) repre-
sented the semantics of such a sentence using an unscoped LF of the following general
form:

Every(x, Child(x, y),

), A(y, Politician(y),

), Run(x)

(cid:13)

(4)

To scope this LF, at each step, a quantiﬁer is picked and the main predication (i.e.,
Run(x)) or the partially scoped formula built so far is fused to its body hole:

Step 1. Every(x, Child(x, y), Run(x))

Step 2. A(y, Politician(y), Every(x, Child(x, y), Run(x)))

(5)

By picking quantiﬁers in different orders, different scopings are generated.

Next, the notion of constraints was introduced into the domain of scope underspeci-
ﬁed semantics. For example, Quasi Logical Form (Alshawi and Crouch 1992) allows for
constraints such as A > Every to be used to force one quantiﬁer to rest within the scope
of another. By inventing some machinery that allows for Discourse Representation
Theory (Kamp 1981) to support scope underspeciﬁcation, Underspeciﬁed Discourse
Representation Theory (or UDRT) (Reyle 1993) takes the notion of constraint-based
underspeciﬁcation to a new level. UDRT introduces a complex system of constraints,
that, among other things, can deﬁne a maximum and a minimum range for the scope of
a quantiﬁer relative to other scope bearing elements. It is fair to say that Reyle’s work
inspired the next two decades of research on constraint-based scope underspeciﬁcation,
resulting in several underspeciﬁcation formalisms such as Hole Semantics (HS; Bos
1996), MRS (Copestake, Lascarides, and Flickinger 2001), and Dominance Graph (DG;
Thater 2007). Unlike Quasi Logical Form or UDRT, the new formalisms treat underspec-
iﬁcation as an abstract algebraic framework which is independent of the target object
language, whether it is ﬁrst order predicate calculus, modal logic, Discourse Represen-
tation Theory, etc. A UR in these formalisms is a set of abstract labeled formulas with
holes that can be ﬁlled in with other labeled formulas. The formulas come with a set of
constraints between the labels and holes, and in order for a scoping to be considered
valid, the set of constraints ought to be respected. Despite all the similarities, as will be
seen shortly, HS/DG and MRS differ in how they interpret the constraints.

Figure 2 shows the graphical depiction of the UR of Example (1) as proposed by
MRS. Solid nodes represent labeled formulas, and are called label nodes. The holes
of the formulas are represented by nodes with hollow circles, called the hole nodes.
Scopings of such a structure are built by fusing label nodes to hole nodes as shown
in Figure 2(b). This UR leaves both the body and the restriction of the quantiﬁers
underspeciﬁed. This is to allow for scopings such as Figure 2(c), in which quantiﬁer A
lies between quantiﬁer Every and its restriction. The dotted line between the label node
Child(x,y), call it l, and the restriction hole of Every, call it h, is an example of a constraint.
This constraint (also represented as h =q l), requires that either h is directly ﬁlled by l or
h is ﬁlled by a quantiﬁer and the body hole of that quantiﬁer is ﬁlled by l (or by another
quantiﬁer and the body hole of the latter is ﬁlled by l, and so on so forth). This type of
constraint, ﬁrst introduced by the MRS framework, is called a qeq constraint. It is easy

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

(a) UR for Example 1

(b) Fusing labels to holes

(d) Explicit binding constraints

Figure 2
Using graphical notation to represent unscoped LF.

to see that qeq directly implements the idea of wrapping a quantiﬁer around a formula
as shown in Equation (5). It is easy to see that not every assignment of labels to holes
in the UR is a valid scoping, even if it satisﬁes both qeq constraints. This is because, in
addition to qeq constraints, the UR carries a group of implicit constraints, the so-called
binding constraints. The binding constraints force every variable (x, y, etc.) to be in the
scope of its quantiﬁer. Unlike qeq, binding constraints enforce a mere outscoping (a.k.a.
dominance) relation. That is, to satisfy a binding constraint from u to v, it is enough that
u outscopes (a.k.a. dominates) v.

To simplify things, let us make the binding constraints explicit by using unlabeled
dotted edges as shown in Figure 2(d). We call the resulting representation that incor-
porates both dominance and qeq constraints an underspeciﬁcation graph (UG).

Before moving to the formal deﬁnition of UG, it should be emphasized that what
is deﬁned here as UG is nothing but the integration of the three existing concepts:
MRS, HS, and DG. Deﬁning a framework that subsumes all three has proved very
useful in substantiating the results we have obtained and in providing rigorous proofs.
Otherwise, from a practical standpoint (as proved later), UG has little to no advantage
over DG. In addition, it serves us better to ﬁrst deﬁne the general framework, and then
introduce subsets of it, rather than the other way around.

2.1 The Formal Deﬁnition

Quantiﬁers and scopal and non-scopal predications are the building blocks of a UR. As
seen in Figure 2, in graphical notation, they are depicted as single solid nodes or trees
with solid edges. In DG terminology, these are called fragments. We alternatively use
the term elementary tree, emphasizing that these are analogous to the MRS’s elementary
predications (Section 7.2).

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Politician(y)A(y)Child(x,y)Every(x)Run(x)qqPolitician(y)A(y)Child(x,y)Every(x)Run(x)Every(x)A(y)Politician(y)Run(x)Child(x, y)

Computational Linguistics

Volume 44, Number 1

(a) General form of ET

(b) An example of UG

Figure 3
Elementary tree and underspeciﬁcation graph.

Deﬁnition 1 (Elementary Tree)
An elementary tree or ET (a.k.a. fragment) is an ordered4 tree of depth 0 or 1. The roots
of all ETs are represented by small solid circles and are referred to as label nodes or
simply labels. All the leaf nodes of the ETs of depth 1 are represented as big hollow
circles and are referred to as hole nodes or simply holes. ETs with holes are called
scopal ETs.5

Figure 3(a) shows the general form of an elementary tree for both cases of depth = 0

and depth = 1. When depth = 0, the elementary tree is a singleton.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Deﬁnition 2 (Underspeciﬁcation Graph)
The 8-tuple U =
Graph or in short UG, if it is a ﬁnite structure with the following properties:

LU, HU, EU, QU, DU, TU, Lq

U, PU(cid:105)

(cid:104)

is called a (scope) Underspeciﬁcation

(cid:114)

(cid:104)

LU, HU, EU, PU(cid:105)

is a forest of elementary trees, with LU being the set

FU =
of label nodes, HU the set of hole nodes, and EU the set of directed solid
edges, going from the root of ETs to their holes. The order of holes in each
ET is deﬁned by PU.6 In graphical notation, PU is not explicitly given, as it
is implicit in the left-to-right order by which the hole nodes of each ET are
depicted.

QU is a relation from HU to LU, that is, QU ⊂
notation, each (h, l)
∈
l marked with a label q, called a qeq constraint.

HU ×
QU is represented as a directed dotted edge from h to

LU. In graphical

4 Throughout this paper, unless otherwise speciﬁed, by tree we always mean a rooted ordered tree.
5 A mathematically precise deﬁnition requires ETs to be deﬁned as graphs over pairs (u, s), where u is a

(for label nodes) or

node and s is a symbol of the value
cumbersome and may become confusing, especially given that we later need to deﬁne two types of
edges, and even two types of dotted edges. Therefore, although we understand that the underlying
mathematical model is deﬁned in this precise way, we avoid adopting the notation. Instead, we use l, l1,
and so forth, to denote labels and h, h1, and so forth, to denote holes. The same applies to different types
of edges deﬁned later.

(for hole nodes). Such notation will be quite

6 Therefore, PU is a partial order over HU that deﬁnes, for each ET (cid:15), a total order over the set of holes of (cid:15).

llh1hnqql2l4l3l5h1h2h3h4ql0l1h0

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

(cid:114)

∈

LU. Each (u, v)

DU is called a dominance

DU is a relation over HU ∪
constraint and, in graphical notation, is represented as a directed
dotted edge from node u to node v. The dominance constraints can go
from any node to any node, except from holes to holes, therefore, DU ⊂
(LU ∪
default constraint type, therefore, the label d is dropped for the sake
of brevity.

HU. Dominance (as opposed to qeq) is the

(LU ∪

HU ×

HU )

−

LU, h0 ∈

HU, and e0 = (l0, h0)

l0}
˜LU is the set of ﬂoating scopal nodes. The ETs rooted at these nodes

TU is a dummy ET of depth 1, with l0 ∈
∈
being its root, its single hole, and its single edge. It is deﬁned to be the
designated root of every scoping, therefore, TU, l0, and h0 are called top
ET, top label, and top hole, respectively.7 The set of all labels except l0 is
denoted by ˜LU, that is, ˜LU =def LU − {
Lq
U ⊂
are called ﬂoating scopal ETs. Every scopal ET other than the ﬂoating
scopal ETs is called a ﬁxed-scopal ET. Floating scopal ETs are required to
have a hole as the right-most child of the root. This hole and its connecting
edge (sometimes distinguished with a label “b” for emphasis) are called
the body hole, and the body edge, respectively. In practice, ﬂoating scopal
ETs correspond to (generalized) quantiﬁers. Therefore, we use the terms
ﬂoating-scopal and (generalized) quantiﬁer interchangeably. Quite often,
we do not explicitly deﬁne Lq
recognized from the context. Because quantiﬁers have one restriction and
one body preposition, throughout this article we only consider ﬂoating
scopals with two holes.

U, because (generalized) quantiﬁers can be

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

Scopings of a UG are built by fusing labels to holes. We call this a fusion.8

Deﬁnition 3 (Fusion)
Given a UG U, a (total) fusion f is a total function from ˜LU to HU. A partial fusion f is a
partial function from ˜LU to HU.

Figure 4(a) demonstrates a fusion for the UG U in Figure 3(b). Given a fusion f ,
TU, f from U
˜LU, as illustrated in

the corresponding scoping is denoted by
by removing all the constraint edges and fusing l to f (l) for each l

TU, f . We construct the graph of

∈

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

7 Most underspeciﬁcation frameworks, such as MRS or Hole Semantics, implement such an ET, which does
not correspond to an actual predication of the sentence, but serves as the highest level predication of the
sentence, encompassing the overall semantics. For example, in a typed feature structure formalism like
MRS, this ET contains attribute-value pairs, encoding some global semantic properties of the sentence,
such as the speech act, which is not particular to any individual elementary predication.

8 We intentionally avoid using the existing term plugging from Hole Semantics, because plugging is deﬁned
as a function from holes to labels (Bos 1996), while, in order to be able to fuse multiple labels to a single
hole, we deﬁne fusion in the opposite direction. This gives UG the power to model MRS’s operation of
forming conjunctions by equating labels.

Computational Linguistics

Volume 44, Number 1

(a) Graphical depiction of a fusion function

(b) TU, f for fusion f on left

Figure 4
Building a solution for a UG.

Figure 4(b). Intuitively, we expect scopings to form a tree. Theorem 1 states the necessary
and sufﬁcient condition for

TU, f to be a tree.

Theorem 1
Given a UG U and a total fusion f of U,

TU, f is a rooted tree if and only if

TU, f is acyclic.
Proof. The “only if” direction is trivial. The “if” direction holds for the following reason.
Because f is a function, every label is fused into at most one hole, hence, has at most one
TU, f . If f is total, then every label except l0 is fused into exactly one hole, hence,
parent in
TU, f . Therefore, with U being ﬁnite, if we start at any arbitrary
has exactly one parent in
node and follow the sequence of parents, we have to end up at l0. This means
TU, f is a
(cid:50)
tree rooted at l0.
Although fusion is deﬁned as any function from ˜L to H, we are only interested in

fusions that result in valid readings, that is, satisfy the constraints.

Deﬁnition 4 (Constraint Satisfaction and Admissibility)
Fusion f (similarly

TU, f ) satisﬁes

(cid:114)

a qeq constraint q = (h, l), if h = f (l), or the directed path from h to l in
9 consists of only the body edges of quantiﬁer ETs (called a b-path);

TU, f
a dominance constraint d = (u, v), if u dominates v in

TU, f .

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Fusion f of U is admissible if

TU, f is acyclic and satisﬁes all the constraints in U.

So far we have informally used the term scoping to refer to a fully scope-

disambiguated UR. We now formally deﬁne this notion and call it a solution.

9 Note that each node u of a solution

(except the root) corresponds to exactly one hole hi and at least one

label ljof U with f (lj ) = hi. Hence, when we say node hi, node lj, or node (lj, hi ) of
we are referring to the same node u of
.

, in all three cases,

l2l0l4l3l5h1h2h0h3h4l1l0l3(),h1l5(),h3l1(),h4l4(),h2l2(),h0

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Deﬁnition 5 (Solution)

is called a solution of a UG U iff

TU, f for some admissible, total, and onto10 fusion
T
f of U. In informal contexts, solutions are sometimes referred to as readings. U is called
satisﬁable if U has at least one solution.

In this deﬁnition, admissibility ensures the satisfaction of all constraints, totality
ensures that every label (except the top) is fused into some hole, and onto-ness ensures
that no hole is left unfused. Following Lemma 1, Deﬁnition 5 guarantees that every
solution is a tree structure. The fusion in Figure 4(a) is admissible, total, and onto, and
hence, Figure 4(b) is a solution.

The following deﬁnition will later be used for the comparison of our framework

with other frameworks.

Deﬁnition 6 (Merging-Free Solutions)
The solution
called a merging solution.

TU, f is called a merging-free, if f is a one-to-one function. Otherwise, it is

The following lemma directly follows from the deﬁnition.

Lemma 1
Given a UG U and a solution

of U,

is merging-free if and only if

˜LU|

HU|

Corollary 1
Either all the solutions of a UG are merging-free or none are.

In practice, merging solutions only happen when the underspeciﬁed representation
is incomplete, that is, when there are ETs that are ﬂoating around and, in order to build
a solution, they must be ﬁxed up with other ETs to make conjunctions. In Section 3, we
prove that all solutions of a complete UG are merging-free.

2.2 Variations of UG

The deﬁnition of UG requires each ET to be of depth at most one and, when the depth
is exactly one, all the leaf nodes to be hole nodes. This deﬁnition perfectly imitates
the notion of elementary predications in MRS, but some frameworks, such as Hole
Semantics, use the concept of (labeled) formula, which does not precisely ﬁt into this
deﬁnition. Figure 5(a) shows a graph, roughly corresponding to the UR that Hole
Semantics assigns to the sentence Every child of a politician runs. As seen in this ﬁgure,
we have to deal with ETs with depth more than one and leaves that are not necessarily a
hole. Even in MRS, ETs can be stacked to form trees of depth more than one. Figure 5(b)

10 A function f is onto if its image is equal to its codomain.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

(a) Hole Semantics UR with stacked ET

(b) MRS structure for the sentence in Example (2)

Figure 5
Examples of stacked ETs.

shows the MRS structure of the following sentence in graphical notation, obtained from
English Resource Grammar.11

Every dog barks and chases a cat.

Finally, a partially scoped UG U, even if all the ETs of U are standard, will inevitably
have these non-standard tree structures. Therefore, for the sake of the robustness of our
deﬁnitions, we should be able to model these structures. Fortunately, we will be able to
do this without too much effort. This is because a stacked ET can be converted into a
standard ET without affecting the number of solutions of the UG. This conversion has
been demonstrated in Figure 6(a). We now formally express this intuition.

Deﬁnition 7 (Stacked ET)
A stacked ET is an ordered tree of arbitrary depth whose interior nodes are all label
nodes, and whose leaves can be holes and/or labels.

Deﬁnition 8 (UG.1: variation 1 of UG)
A UG.1 is a 9-tuple ˙U =
(L(cid:48)˙U is the only additional
is a forest
element with respect to standard UG), where
of stacked ETs with L(cid:48)˙U being the set of non-root label nodes. Everything else in
Deﬁnition 2 remains the same.12

L ˙U, L(cid:48)˙U, H ˙U, E ˙U, Q ˙U, D ˙U, T ˙U, Lq
˙U
F ˙U =

, P ˙U(cid:105)
L ˙U, L(cid:48)˙U, H ˙U, E ˙U, P ˙U(cid:105)
(cid:104)

(cid:104)

The deﬁnitions of fusion, admissibility, and solution for UG.1 will be exactly the
same as the deﬁnitions of those concepts for standard UG, as stated in Deﬁnitions 3,
4, and 5.

11 http://erg.delph-in.net/.
12 Note that stacked ﬂoating-scopal ETs, exactly the same as standard ones, are required to have a hole as

the right-most child of the root.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Every(x)Child(x)Run(x)A(y)Politician(y)Of(x, y)AndCat(y)A(y)Dog(x)Every(x)Chase(x, y)qqBark(x)And

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

(a) Converting stacked ET into standard ET

(b) Hole-to-hole into hole-to-label

Figure 6
Conversion to original UG.

Theorem 2
Every UG.1 can be converted into a UG, while the solutions remain in a one-to-one
correspondence.

Proof. Consider a UG.1 ˙U with its set of solutions
T2, . . . ˙
collapsing the set L(cid:48)˙U,
demonstrated in Figure 6(a). Similarly, we convert each tree ˙
nodes L(cid:48)˙U,
into l
E
set of solutions of U.

of non-root label nodes of each stacked ET
Tj into
. It is easy to see that

for each stacked ET

. We build the UG U by
into its root l
, as
E
Tj by collapsing the
is the
{T1,
(cid:50)

T2, . . . ,

T1, ˙
˙

TK}

{

In deﬁning UG, we ruled out dominance constraints that go from holes to holes.
This does not restrict the power of UG, because hole-to-hole dominance constraints can
be replaced with hole-to-label constraints, while the set of solutions remains the same,
as demonstrated in Figure 6(b). In the following, we will state this idea formally.

Deﬁnition 9 (UG.2: variation 2 of UG)
A UG.2 is a 8-tuple ¨U, in which the constraints in D ¨U can go from any node to any node.
Everything else in Deﬁnition 2 remains the same.

Theorem 3
Every UG.2 can be transformed into a UG, while the set of solutions remains the same.

Proof. Consider the UG.2 ¨U and a constraint ¨d = (h1, h2) in ¨U (Figure 6(b)), and let l2 be
the parent of h2. We build U by replacing ¨d in ¨U with d = (h1, l2), as demonstrated in
Figure 6(b). ¨U and U have the same set of solutions. This is because if
is a solution of
T
¨U, then h1 dominates h2 in
, h1 dominates l2
. Because l2 immediately dominates h2 in
T
satisﬁes d. The other direction is trivial. This procedure can be repeated
as well, hence,
(cid:50)
until all hole-to-hole constraints are transformed.

In the preceding sections, we deﬁned two variations of UG that relaxed some
restrictions of the original deﬁnition, but we showed that this did not increase their
power. In the following, we deﬁne some other variations, imposing some restrictions

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

qqqqqh1h2l2qh1h2l2

Computational Linguistics

Volume 44, Number 1

on UG. These restrictions, however, limit the power of UG. The main motivation behind
deﬁning these variations is to be able to compare UG with other frameworks (Section 7).

Deﬁnition 10 (Normality)
A UG is said to be normal iff all its dominance constraints go from holes to labels, that
is, DU ⊂

HU ×

LU.

Normality therefore rules out constraints emanating from a label node.

Deﬁnition 11 (Weak Normality)
A UG is said to be weakly normal, iff for every dominance constraint d = (u, v), v is a
label node.

Note that weak normality only rules out label-to-hole constraints.

3. Completeness

In this section, we deﬁne the notion of completeness. Intuitively, completeness means
that we have the minimum connectivity in terms of constraints that is required by the
syntax/semantic interface for a complete sentence. Here, we formally deﬁne the notion
of completeness and prove some properties.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Deﬁnition 12 (Canonical Form)
A UG is in canonical form (CF-UG) if

(cid:114)

The body hole of ﬂoating scopals is not involved in any qeq edge.
Every other hole has exactly one outgoing qeq edge.

Floating scopal nodes, as well as the top label, are not involved in any
qeq constraints. Every other label has exactly one incoming qeq edge.

Before we continue, let us deﬁne the notion of spanning sub/super-UG. Intuitively,
spanning sub/super-UG of G has the same ETs as the G, and only its set of constraints
differs. The motivation is to deﬁne a type of sub/super relation under which complete-
ness is closed (a super-UG of a complete UG is not necessarily complete, because it may
have one or more additional ETs that violate completeness conditions).

Deﬁnition 13 (Spanning Sub-UG)
QU. Every other element of the
U(cid:48) is a spanning sub-UG of U, if DU(cid:48)
tuple U(cid:48) is identical to the corresponding item in the tuple U. In particular, notice that
the set of ETs is the same in both U and U(cid:48), hence, the term spanning. U(cid:48) is a spanning
super-UG of U, if U is a spanning sub-UG of U(cid:48). Uq is deﬁned as the spanning sub-UG
of U with no dominance edges, that is, DUq =

and QUq = QU.

DU and QU(cid:48)

⊂

∅

Theorem 4 shows that CF-UGs, ignoring dominance edges, are in the form of

Figure 7.

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Figure 7
Uq of a generic CF-UG U.

Theorem 4
If U is in canonical form, then Uq is a forest of exactly
RU =def Lq

are called the roots of U.

U ∪ {

l0}

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

Lq
U|

+ 1 trees, rooted at Lq

U ∪ {

l0}

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Proof. According to the second condition in Deﬁnition 12, the n quantiﬁer nodes and l0
are the only nodes with no incoming edge, therefore they form all and the only n + 1
roots of the graph of a CF-UG. Every other label or hole node must be dominated by
one of those n + 1 roots. According to the ﬁrst condition of Deﬁnition 12, the body holes
of quantiﬁers have no outgoing edge, therefore every other node must be either under
(cid:50)
the restriction of a quantiﬁer or under h0.

Because qeq constraints were introduced by MRS, in Section 7.2, we show that, in
practice, all MRS structures generated by MRS’s proposed syntax/semantic interface
are in canonical form. Canonical form deﬁnes the smallest complete UG over a set of
ETs.

Deﬁnition 14 (Completeness)
A UG is complete if it has a spanning sub-UG in canonical form.

The following set of deﬁnitions become handy throughout the rest of this

paper.

Deﬁnition 15 (Floating Scopal Trees/Restriction Trees/Heart Tree)
We refer to T1, T2, . . . , Tn, the trees in Uq rooted at Lq
U, as ﬂoating scopal trees
1, Tr
(a.k.a. quantiﬁer trees); Tr
n, the trees rooted at the restriction hole of the
ﬂoating scopals, as the restriction trees; and T0, the tree rooted at l0, as the heart
tree.

2, . . . , Tr

Computational Linguistics

Volume 44, Number 1

3.1 Equivalence of Qeq and Dominance Relations

In this section, we show that, for every complete UG, qeq and dominance relations
are equivalent. That is, as stated by Theorem 5, if qeq constraints are replaced with
dominance relations, the solutions of the UG remain the same. This fact explains why
frameworks such as Dominance Graph are able to model scope underspeciﬁcation
even though they only use dominance constraints, and helps to bridge the gap between
the two sets of formalisms. We ﬁrst prove this for the case when there is no quantiﬁer
in U.

Lemma 2
Let U be a complete UG with no quantiﬁer. Let
treating all qeq edges as dominance constraints, that is, D ˆU = DU ∪
Every solution of U is a solution of ˆU and vice versa.

ˆU be the UG obtained from U by
.

QU and Q ˆU =

∅

Proof. The ﬁrst direction is trivial because qeq is a special case of dominance. In order
to prove the other direction, consider the leaf label nodes of ˆU (Figure 8(a)). In any
solution of ˆU, these label nodes have to be fused to the hole from which they have re-
ceived a dominance constraint. Let us fuse these labels, and then, following Theorem 2,
collapse the EPs with the fused hole(s) into a single node. We can now apply the same
argument to the newly leaf nodes and repeat this until we reach the top (remember
that UGs are ﬁnite). This shows that every hole h of ˆU has to be fused with the label l
QU. Because h is fused directly with l, following the deﬁnition of qeq, the
where (h, l)
constraint between h and l is satisﬁed, even if it is treated as qeq. This means that ˆ
is
T
(cid:50)
also a solution of U.

∈

Theorem 5
Let U be a complete UG, and ˆU be the UG obtained from U by treating all qeq edges
. Every solution of ˆU is a
as dominance constraints, that is, D ˆU = DU ∪
solution of U and vice versa.

QU and Q ˆU =

∅

(a) A UG with no quantiﬁer

(b) Inductive proof

Figure 8
Proof of Lemma 2 and Theorem 5.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

lqnuvwˆTuwb⌧n⌧rn⌧bn⌧bnˆT0

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Proof. Because qeq always implies dominance, it is trivial that every solution of U is a
solution of ˆU. Using the lemma and induction on n, the number of quantiﬁers, we prove
the other direction, that is, if ˆ
T

is a solution of ˆU, then it is also a solution of U.

, according to Lemma 2, every hole h is

Let n = 0. Because there is no quantiﬁer in ˆ
T

∈

fused with l where (h, l)

QU, therefore, every qeq constraint is satisﬁed.

Now let n > 0 and U be an arbitrary UG with n quantiﬁers (see Figure 7), and ˆ
be
T
a solution of ˆU. Consider the quantiﬁer node lq with the longest distance from the root
of ˆ
(breaking ties arbitrarily), meaning that lq does not outscope any other quantiﬁer
T
node in ˆ
n, and ˆτb
n to refer
T
to the trees rooted at lq
, respectively, as shown
in Figure 8(b). According to Lemma 2:

. Without loss of generality, assume that lq = lq

n and the left and the right child of lq

n and use ˆτn, ˆτr

n in ˆ
T

(i)

All qeq constraints in the quantiﬁer tree Tr

n are satisﬁed in ˆ
T

Now let us remove the quantiﬁer tree rooted at lq
n from U and ˆU and call the resulting
UGs U(cid:48) and ˆU(cid:48), respectively. Accordingly, detach the tree ˆτn from ˆ
, replace it with ˆτb
n
T
(cid:48) is a solution of ˆU(cid:48), and hence
and call the new tree ˆ
T
(based on the induction assumption) is a solution of U(cid:48). Therefore, all qeq constraints in
U(cid:48) are satisﬁed in ˆ
T

(cid:48), as demonstrated in Figure 8(b). ˆ
T

(cid:48), which also proves:

(ii)

All qeq constraints in U(cid:48) are satisﬁed in ˆ
T

This is because if two nodes are connected with a b-path in ˆ
T
with a b-path (possibly including an additional b-edge (lq
n, w)) in ˆ
T

From (i) and (ii) every (h, l)

QU is satisﬁed in ˆ
T

, hence ˆ
T

∈

(cid:48), they are also connected

is a solution of U.

(cid:50)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

The next section introduces the heart of our framework, the concept of semantic

coherence.

4. Coherence

In this section, we introduce the notion of sentence-level semantic coherence based on
a simple principle: that every variable introduced in the domain of discourse must
contribute to the overall meaning of the sentence. We formally characterize this quality
as a property of a UG, and refer to sentences whose interpretation is a coherent UG as
coherent sentences. We posit as a general principle of language the requirement that
sentences should be coherent. This general principle goes back at least as far as Frege
(1923), and is widely accepted, although, because it is not a mathematical statement, it
cannot be proved. Our deﬁnition of coherent UG, on the other hand, is mathematically
precise, and can be used to prove that all coherent sentences are tractable, as we will see
in Section 5.

4.1 Mathematical Characterization of Semantic Coherence

A variable introduced in the domain of discourse is called relevant if it contributes
to the overall meaning of a sentence. This contribution may happen in two different

Computational Linguistics

Volume 44, Number 1

ways, either by directly participating in the main predication13 or by participating in
the deﬁnition of another relevant variable. If variable x participates in the deﬁnition of
y, we say that y is (semantically) dependent on x. To summarize, a variable x is relevant if
either the heart or another relevant variable depends on it. For example, in the sentence
Every child of a politician runs, the variable x, quantiﬁed by Every, is relevant, because it
is an argument of the main predication, and the variable y, quantiﬁed by A, is relevant,
because x depends on it. Following these intuitions and given that dependencies in a UG
are encoded in the binding (i.e., dominance) constraints, we formally deﬁne relevance
as follows.

Deﬁnition 16 (Dependence/Relevance)
Consider a complete U,14 with the top hole l0 and lq

i , lq

j ∈

Lq
U:

(cid:114)

(i)

(ii)

lq
j (l0, for j = 0) depends on lq
tree Tr
j .

i , if (lq

i , u)

lq
i is said to be relevant if
l0 depends on lq
j depends on lq
lq

i ; or
i , and lq

j is relevant.

DU for some u in a restriction

∈

Deﬁnition 17 (Coherence)
A complete UG U is called coherent if every lq

i in U is relevant.

Trivially, relevance is closed under the increment of constraint edges, resulting in

the following lemma.

Lemma 3
Coherence is closed under the increment of (dominance) constraint edges.

In Manshadi, Allen, and Swift (2009), we deﬁned the notion of semantic de-
pendency graph and a property of such graphs called heart-connectedness. Heart-
connectedness is nothing but a notational variant of coherence. In this article, we shall
use the notion of semantic dependency graph to compare our framework with Hole
Semantics (Section 7.3). Therefore, in the rest of this section, we formally deﬁne this
notion and prove that the two formulations of coherence are in fact equivalent.

Deﬁnition 18 (Semantic Dependency Graph)
Given a CF-UG U, we deﬁne semantic dependency graph or SDG of U as SDGU =
(V, E), where

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

(cid:114)

V =

(i, j)

0, 1, . . . , n
}

{

, where n =

E if and only if i

∈

Lq
.
U|
= j, i > 0, and (lq

i , u)

DU, where u is a node in Tr
j .

∈

13 Here, by participation, we mean ﬁlling an argument position.
14 Hence, dependence and relevance are deﬁned only if U is complete.

(cid:54)

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

(a) Every child of a politician runs

(b) If some dog in a room barks every cat runs

(d) SDG of the UG in (b)

Figure 9
Constructing semantic dependency graph.

Intuitively, SDGU is obtained by taking the CF-UG U and collapsing its heart and
quantiﬁer trees—that is, each of the trees T0, . . . , Tn—into a single node, resulting in
a directed graph G of n + 1 nodes. Figure 9 demonstrates this transformation for two
real-life CF-UGs. The dependencies in U are simply encoded in the edges of G. In other
words, if i is the node of G corresponding to Ti, an edge from i to j in G means that lq
j
(l0, if j = 0) depends on lq
i in U. From Deﬁnition 18, SDGs are simple graphs, that is, (i)
they have no self-loops, and (ii) for every i, j there is at most one (directed) edge from
i to j. Node 0, which corresponds to the heart of the CF-UG, hence called the heart of
SDG, has no outgoing edge, therefore the heart is always a sink node.

Deﬁnition 19 (Heart-Connectedness)
A SDG G is called heart-connected if every node in G reaches the heart by a directed
path. A CF-UG U is called heart-connected, if SDGU is heart-connected.

Theorem 6
A CF-UG U is coherent if and only if it is heart-connected.

The theorem directly follows from the following lemma.

Lemma 4
The node lq

i is relevant in a CF-UG U, if and only if i reaches the heart in SDGU.

Proof. Following Deﬁnition 16, the set R of all the relevant nodes in U can be constructed
as follows:

(cid:114)

R0 =

l0}

{

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Politician(y): A(y)Child(x,y): Every(x)Run(x)l q1l q2ql 0qqDog(x) & In(x, y): Some(x)Room(y): A(y)Cat(z): Every(z)Bark(x)If-thenRun(z)qqqqqql q2l q1l 0l q32 1 0 0 3 1 2

Computational Linguistics

Volume 44, Number 1

(a)

(b)

Figure 10
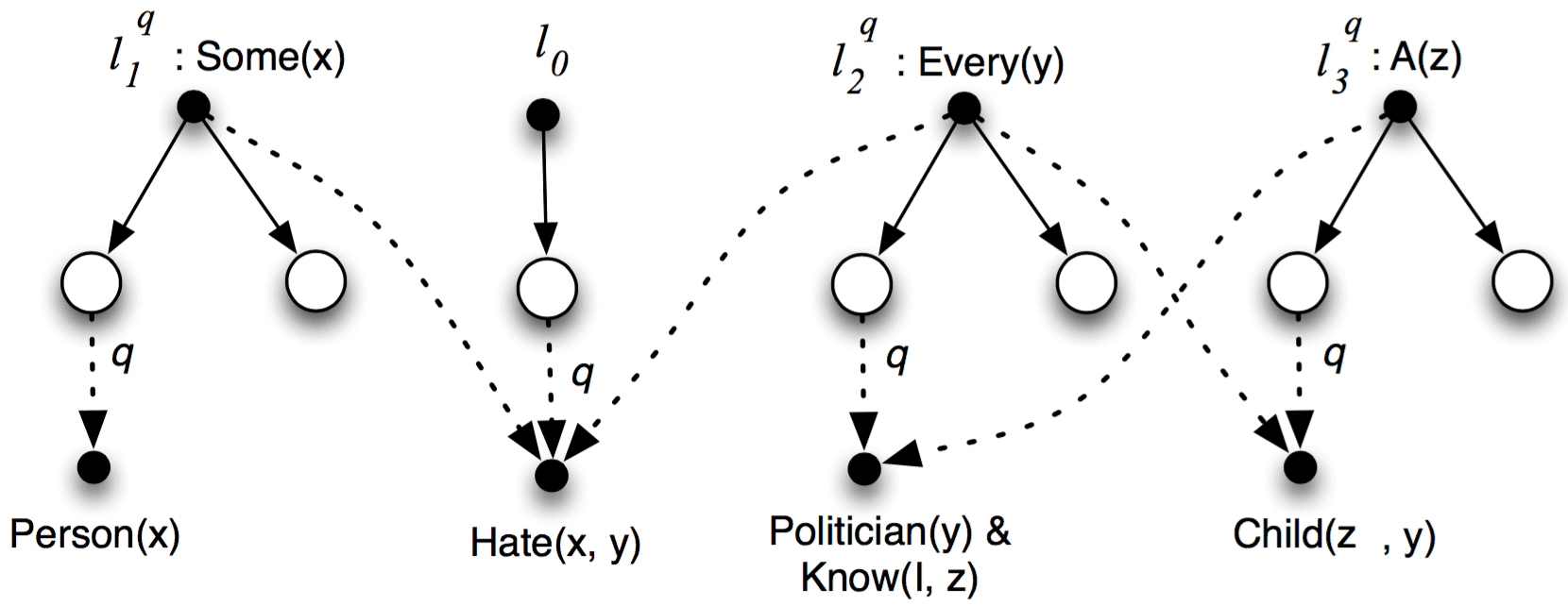
UG and SDG for Somebody hates every politician whom I know a child of.

(cid:114)

R = (cid:83)n
depends on.15

m=0 Rm, where Rm (m > 0) is the set of nodes that R(m

−

Using induction on m, it is easy to see that for every node lq
in SDGU using a directed path of length m.

i ∈

R, node i reaches the heart
(cid:50)

All examples of UG given so far are acyclic. This may suggest that the SDG of
every sentence is acyclic, but this is not the case. As a counterexample, consider the UG
in Figure 10, motivated by an example from Hobbs and Shieber (1987). This example
shows that coherent UGs form a very broad class of UGs, subsuming other previously
proposed classes, as we will see in Section 7. Notwithstanding their broad applicability,
coherent UGs can be tractably processed, as we will see in the next section.

5. Tractability

An algorithmic problem arising within the context of constraint-based underspeciﬁca-
tion frameworks is to determine whether a given UG has a solution or not. This is called
the satisﬁability problem, or, in short, SAT. This becomes important when new con-
straints are incrementally added at the deeper levels of language processing. Another
closely related problem commonly studied within the same context is to enumerate all
possible solutions, the enumeration problem, or, in short, ENUM. All the constraint-
based underspeciﬁcation frameworks that we have built UG upon (HS, MRS, and DG)
are intractable in their general form, meaning that their satisﬁability problem is NP-
complete. Over the last decade, there has been a series of work on ﬁnding a subset of
these frameworks that can be solved efﬁciently. The previously found tractable subset

15 We require that Rm ⊂

q
L
U −

(cid:83)(m

1)
j=0 Rj.
−

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

2 3 0 1

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

is inadequate in that it does not cover all natural language sentences (see Deﬁnition 29
in Section 7.1 for details), leaving open the question whether there is a tractable subset
with sufﬁcient expressivity. In this section, we answer this question by introducing the
largest tractable subset found so far and prove that every coherent sentence, under our
linguistically justiﬁed notion of semantic coherence, belongs to this subset.

5.1 Dominance Graph

In the previous sections, we showed that for coherent (in fact, complete) UGs, qeq and
dominance constraints are equivalent. A UG with only dominance constraints is called a
dominance graph, or, in short, DG, which is the core concept of the Dominance Graphs
framework. Most of the work on ﬁnding a tractable subset of URs has previously
been done within the realm of this framework. Because coherent UGs are a subset of
dominance graphs, our work is built on top of this work, hence, in this section we only
work within this framework.

Remember from Deﬁnition 2 that a UG is an 8-tuple

. With
no qeq constraints, a dominance graph has no Q component. As a result, there is no
need to distinguish ﬂoating scopal (i.e., quantiﬁer) ETs; and hence, there is also no
Lq component, which in turn means that there is no designated top ET in dominance
graphs. Therefore, all labels can potentially form the root of a solution. We now give a
formal deﬁnition of dominance graph.

L, H, E, Q, D, T, Lq, P
(cid:105)

(cid:104)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Deﬁnition 20 (Dominance Graph)
A Dominance Graph, or DG, is a 5-tuple G =
where all the compo-
nents are as deﬁned in Deﬁnition 2. Because there is no designated top node, analogous
to ˜LU, we deﬁne ˜Ll
G = LU − {
for every label node l. All the variations of UG deﬁned
l
in Section 2.2 are deﬁned correspondingly for DG.

LU, HU, EU, DU, PU(cid:105)

}

(cid:104)

It should be noted that in order to build a fusion, we have to ﬁrst pick an arbitrary

label l, and then construct f as a function from ˜Ll
TU, f
(the only root, if f is total). Following this deﬁnition, every UG can be converted into a
DG by dropping the top ET and treating all qeq constraints as dominance constraints.

G to H. The node l will be a root of

Deﬁnition 21 (DG Counterpart)
Given a UG U, GU,
is obtained by removing the
top ET from U and converting all qeq edges into dominance. More precisely, GU =
, DG =
where HG = HU − {
HG, LG, EG, DG, PG(cid:105)
h0}
(cid:104)
, PG = PU.
u, v
(u, v)
QU − {
DU ∪
∅}
| {

the DG counterpart of U,

, EG = EU − {

, LG = LU − {

=
l0, h0} (cid:54)

(l0, h0)
}

} ∩ {

l0}

The following lemma directly results from Theorem 5.

Lemma 5
There is a one-to-one relationship between the solutions of a complete UG U and those
of its DG counterpart GU.

In order to prove the tractability of coherent UG, we deﬁne a mathematically (more)
convenient notion, a subset of DG called hypernet. Hypernet includes all coherent UGs,

Computational Linguistics

Volume 44, Number 1

Figure 11
Recursive construction of solutions.

and we treat it as the mathematical characterization of coherence within the context of
DGs. The deﬁnition of hypernet is motivated by the deﬁnition of (weak) nets (Niehren
and Thater 2003), a previously found tractable subset of DG, and it translates our
semantically motivated concept of coherence into (a slightly more powerful version of)
the already popular structures of DG. Built on top of the fairly complex notion of nets
together with the incorporation of heart-connectedness (as the mathematical characteri-
zation of coherence), there should be no surprise that the deﬁnition of hypernet is quite
complex. For this reason, instead of presenting the complete deﬁnition at once, we step
by step justify our way through the full deﬁnition of hypernet.

Remember that our ultimate goal is to efﬁciently solve (a subset of) DGs. Here is a
recursive approach. Pick an ET for the root of the solution and remove it from the DG.
Recursively solve each of the remaining smaller DGs and plug the root of the resulting
trees into the holes of that ET. Figure 11 demonstrates this procedure and Table 1 lists
the steps. In order for this approach to work, each of the resulting subgraphs should be
a valid DG. Let us make this intuition formal.

Deﬁnition 22 (Sub-DG)
A sub-DG G(cid:48) of G is a DG whose set of ETs and constraints is a subset of ETs and
constraints in G, respectively. A spanning sub-DG of G is a sub-DG that includes all the
ETs in G. An induced sub-DG G(cid:48) of G (by a subset
of ETs in G) is a sub-DG of G in
and) a constraint of G is present in G(cid:48), if and only if both its
which (the set of ETs is

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

MumbleWhenYawnNotSpeakOrMumbleWhenYawnNotSpeakUOrU1U2MumbleWhenYawnNotSpeakOrT1T2(a)(b)MumbleWhenYawnNotSpeakOrT1T2(d)(c)T

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Table 1
Recursive procedure followed in Figure 11.

1: procedure SOLVE(DG G)
2:

satisfying all the conditions to be the root of a solution, otherwise,

If G contains a single (label) node, return that node as a single-node tree
Pick an ET
fail.
Let Gr, Gb be the two DGs resulting from the removal of
b =SOLVE(Gb)
Let
T
r into hr and
Build
T
return
T

r =SOLVE(Gr),
T
by plugging
T
.

b into hb.

(Figure 11(b)).

(a) DG G

(b) Solution

of G

(cid:48)

Figure 12
DG counterpart of the UG for Every child of a politician runs and a sub-DG of it.

ends are present in G(cid:48). Given a solution
induced by

(cid:48) is the sub-DG induced by the set of ETs of

of G and a subtree 16

(cid:48) of

, a sub-DG G(cid:48)

(cid:48).

Figure 12 gives an example of these concepts. The following property, which di-
rectly follows from the deﬁnition, will help in proving the completeness of the recursive
method (Section 5.3).

Lemma 6
Consider a DG G, a solution
induced by

(cid:48), then

(cid:48) is a solution of G(cid:48).

of G, and a subtree

(cid:48) of

. If G(cid:48) is the sub-DG of G

The notion of sub-DG helps in solving DGs recursively, as shown in Figure 12.
Depending on whether, at step 3, among all nodes satisfying the conditions, we pick a
node arbitrarily or iteratively determines whether the algorithm will be a SAT algorithm
(generating an arbitrary solution on success) or an iterative ENUM algorithm (every
branch of which builds one solution). Note that, whereas the total size of the output
for ENUM may be exponential, we are interested in bounding its running per solution
produced.

16 Throughout this article, by “subtree of a tree T,” we mean a node and all of its decedents in T.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Politician(y)Child(x,y)Every(x)Run(x)A(y)Every(x)A(y)Politician(y)Run(x)Child(x, y)T0Politician(y)Child(x,y)A(y)

Computational Linguistics

Volume 44, Number 1

In the rest of this section, we form this intuition into a detailed algorithm and deﬁne
hypernet as a subset of DG for which the algorithm is both sound and complete. Because
label-to-hole constraints add another level of complexity, we ﬁrst ignore those edges and
only consider weakly normal DGs. We then adopt the algorithm by Koller and Thater
(2007) to take care of label-to-hole constraints.

5.2 Hypernets

A look at the steps in Table 1 reveals that the heart of this procedure is to ﬁnd the roots
of the solutions. The rest is simply recursing on the smaller DGs.

Deﬁnition 23 (Freeness)
A label l is said to be free if it is the root of some solution
if its root is free.

of G. An ET

is called free

Subsequently, we use some graph theory terminology that we need to deﬁne.
Remember that two nodes of a digraph are weakly connected if there is an undirected
path between the two. Because weak connectedness is an equivalence relation, it par-
titions the graph into equivalence classes each of which is called a weakly connected
component or WCC.

Theorem 7 states some necessary conditions for freeness, but ﬁrst, we state a lemma

that is the key to the proof of this theorem.

Lemma 7
Given a weakly normal DG G and a solution
of G, if nodes u and v in G are weakly
connected using an undirected path p, there exists a node w on p such that w dominates
both u and v in

This lemma is analogous to Lemma 3 in Bodirsky et al. (2004). A detailed proof of

the lemma can be found there. We are now prepared to prove the theorem.

Theorem 7
Let G be a weakly normal DG and
free label, only if

be an ET with m holes rooted at label l. l can be a

T7a.

l has no incoming (constraint) edge; and

T7b.

Every distinct hole of

is in a distinct WCC in G

l; and

−

T7c.

−E

Proof. Let
T
containing h.

consists of at least m WCCs.

be a solution rooted at l, h a hole of

, and Gh the WCC of G

−

T7a.

This condition is trivial.

T7b.

Following Lemma 7, every node in Gh must be in the scope of h (because
for any arbitrary node u in Gh, there is a node w dominating both h and u

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

, but the only possible w is w = h). Because

is a tree, this proves that

in
every two holes of

belong to two distinct WCCs.

T7c.

This follows from T7b and the fact that no hole may be left unfused.

(cid:50)

We now look for a subset of DG, for which the conditions in T7a through T7c are
not only necessary, but also sufﬁcient. In deﬁning this subset, the following notion from
Althaus et al. (2003) plays an important role.

Deﬁnition 24 (Hyper-Normal Connectedness)
Given a DG G, a hyper-normal path is an undirected path with no two consecutive
constraint edges emanating from the same node. Node u is hyper-normally connected
to node v if there is at least one hyper-normal path between the two. G is called hyper-
normally connected if every pair of nodes in G are hyper-normally connected.

For example, in Figure 13, p2 is a hyper-normal path, but p1 is not. In spite of that,
the whole graph is hyper-normally connected, because even though p1 is not a hyper-
normal path, there is another hyper-normal path connecting the same two nodes. The
following notion from Thater (2007) will also come in handy.

Deﬁnition 25 (Openness)
A label or hole node u is called an open node if it has no outgoing constraint edge.

For example, l in Figure 14(a) is an open label node and h2 in Figure 14(b) is an open

hole.

Deﬁnition 26 (Hypernet)
A DG G is called a hypernet if it has a weakly normal spanning sub-DG G(cid:48) in which for
every elementary tree

rooted at l:

D26a.

D26b.

has at most one open node.

E
If l1 and l2 are two dominance children of a hole h of
hyper-normally connected in G(cid:48)

−

D26c.

has no open hole in G(cid:48):

Figure 13
Illustration of hyper-normal path.

, then l1 and l2 are

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

p1p2

Computational Linguistics

Volume 44, Number 1

Figure 14
Three types of elementary trees: (a) open-root (b) open-hole (c) closed.

(cid:114)

Each dominance child of l is hyper-normally connected to a hole of

in G(cid:48)

−
Otherwise (i.e., when

has an open hole):

All dominance children of l, not connected to a hole of
are hyper-normally connected together.

in G(cid:48)

−

Here, by dominance children of u, we mean nodes v where (u, v) is a dominance
edge. Notice that by enforcing conditions (D26a) through (D26c) on a spanning sub-DG
of G rather than G itself, we allow the hypernet to be closed under the increment of
constraint edges. This is in line with the deﬁnition of coherence, which imposes only
a minimum connectivity, hence, closed under the increment of dominance constraint
edges.17 Following condition (D26a), a weakly normal hypernet may have three types
of scopal ET, characterized in the following deﬁnition.

Deﬁnition 27
Given a DG G and an ET

is called

D27a. Open-root: iff only the root of

D27b. Open-hole: iff only a hole of

is open in G.

E
is open in G.

D27c. Closed: iff

has no open node in G.

Figures 14(a–c) show the three types of

following property.

, respectively. Deﬁnition 26 guarantees the

Theorem 8
Let G be a weakly normal hypernet and
E
l satisﬁes the conditions in Theorem 7, G
−E
is a (weakly normal) hypernet.

be an ET of G with m holes and rooted at l. If
consists of exactly m WCCs, each of which

17 Koller and Thater (2007) call this property “downward connectedness.”

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

lh1h2U1U2lh1h2U1U2(a)(b)lh1h2U1U2(c)

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

−E

). Based on condition (T7c), G

consists of at most m WCCs (since
Proof. Following conditions (D26b) and (D26c), G
are hyper-normally connected, they stay connected in
the children of each node of
G
has exactly
m WCCs. To prove that each of these WCCs is a hypernet, we show that, for any two
, if u and v are hyper-normally connected in G, they
nodes u and v not belonging to
are also hyper-normally connected in G
. We do so by proving that there is no hyper-
normal path between u and v in G that visits some node of

has at least m WCCs. Therefore, G

−E

Suppose that

is an open-hole ET rooted at l (Figure 14(b); a similar line of reason-
ing can be used for open-root and closed ETs). Assume to the contrary that there is a
hyper-normal path p between u and v that visits some node of
. Because an ET consists
of a single label node l with some number of holes as children, one of the following three
cases holds:

ii.

p visits exactly one node of

E
p visits (at least) two holes of

iii.

p visits l and exactly one hole of

All three cases result in a contradiction: Case (i) means that p is not hyper-normal;
violates condition (T7b); and case (iii) proves that G is not a
case (ii) shows that
(cid:50)
hypernet, because

E
violates condition (D26c).

The following corollary will be helpful in the subsequent subsections when stating

the relation between heart-connectedness and hyper-connectedness.

Corollary 2
Let G be a weakly normal hypernet and
the sub-DG of G induced by

be a solution of G. For any subtree

(cid:48) of

(cid:48) is a (weakly normal) hypernet.

We are now ready to prove the main result of this subsection.

Theorem 9
If G is a satisﬁable weakly normal hypernet, the necessary conditions of freeness
(Theorem 7) are also sufﬁcient.

rooted at l be an ET satisfying the freeness conditions in Theorem 7. Among
Proof. Let
in which the depth d of l is minimal. Using
all the solutions of G, we pick a solution
proof by contradiction, we show that d = 0, hence, l is the root of
. Assume to the
contrary that d > 0, meaning that there is some node l(cid:48) outscoping l (Figure 15(a)).
Without loss of generality assume that
has only exactly two holes (Left and Right).
We show that at least one of the trees in Figures 15(b,c) is a solution of G, which means
G has a solution in which the depth of l is smaller than d—a contradiction!

Figure 15(d) shows G with the two WCCs of G

T2 and
the nodes in
show subgraphs of G induced by
we assume that
there are some unsatisﬁed constraints in
that are satisﬁed in

l called GL and GR. Note that all
−
T3 have to be in GL and GR, respectively (in the ﬁgure, G2 and G3
Tb or
T3). In order to show that
Tc is a solution,
Tb is not a solution,
Tc is. Because
Tb. However, there are not many constraints
T1,

Tb (e.g., any constraints between the two nodes in

Tb is not a solution and prove that

T2 and

but not in

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

Figure 15
Proof of Theorem 9.

T2, or in

T3 are also satisﬁed in

in
Tb). In fact, an unsatisﬁed constraint can only be in the
form of (l(cid:48), l2) or (h(cid:48), l2) with h(cid:48) being the right hole of l(cid:48) (the hole to which l is fused in
Tb
T
either, but such a constraint does not exist as l is a free node). Because l2 is in GL and
there is a constraint between l(cid:48) or h(cid:48) and l2, l(cid:48) belongs to GL as well.

T2 (it is true that a constraint from l(cid:48) to l is not satisﬁed in

), and l2 being a label in

Similar to

Tb, in order for

Tc not to be a solution, there must be a constraint (l(cid:48), v3)
T3, and hence, in GR. But l(cid:48) and h(cid:48) are in GL, so
or (h(cid:48), v3) violated, where v3 is a node in
such constraints cannot exist. This means there cannot be any unsatisﬁed constraint in
(cid:50)
Tc. This proves that Tc is a solution in which l has a lower depth.

5.3 SAT and ENUM Algorithms

Following Theorems 8 and 9, Table 2 gives the algorithms for SAT and ENUM.

Theorem 10
ENUM and SAT are correct for all weakly normal hypernets.

Table 2
SAT and ENUM algorithms for weakly normal hypernets.
1: procedure SOLVE(Weakly normal hypernet G)
2:

If G contains a single (label) node, return the single-node tree
Pick an ET

).
satisfying the freeness conditions in Theorem 7, otherwise, fail.

{}

= (

{

}

(cid:46) For SAT, pick arbitrarily.
(cid:46) For ENUM, pick iteratively.

Let l be the root and m the number of holes of
Let G1, G2, . . . , Gm be WCCs of G
−E
Ti =SOLVE(Gi) for i = 1, . . . , m.
Let
Let hi be the hole of
E

connected to Gi in G

−
has an open hole hk, let Gk be the WCC not connected to any hole of
Ti into hi, for i = 1, . . . , m.
by plugging the root of
.

l, for i = 1, . . . , m.

If
E
Build
T
return
T

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Proof. Using Theorem 8 and induction on the depth of recursion, it is easy to see that if
is a solution of G. This proves that ENUM and SAT are
ENUM or SAT return a tree
sound.

An inductive proof is used to prove the completeness as well. By completeness,
we mean that any solution of G is arbitrarily/iteratively generated by SAT/ENUM. Let
Tn be the subtrees of
T
Tn must be the solutions to G1, . . . , Gn, the
has an open hole hk,
−
E
l). Based on the induction
is
(cid:50)

be an arbitrary solution of G rooted at the ET
T
under the holes h1, . . . , hn of
T
E
to be a solution of G, the subtrees
WCCs of G
Gk will be the WCC not connected to any hole of
assumption,
also arbitrarily/iteratively generated.

. Following Lemma 6 (Section 5.1), in order for
T1, . . . ,
connected to h1, . . . , hn in G

E
Tn are arbitrarily/iteratively generated by SOLVE(). Therefore,

−E
T1, . . . ,

l, respectively (if

T1, . . . ,

, and

in G

−

L
|

). At each call, it takes O(

The running time of the algorithms is proportional to the number of recursive calls
to SOLVE(), that is, O(
) to ﬁnd the set of free ETs (Bodirsky
+
=def |
L
et al. 2004) and also to compute G
|
G
L
D
) time, meaning
|
|
||
|
that the worst-case time-complexity of SAT (and each branch of ENUM) is quadratic in
the size of G.

G
|
−E
. Therefore, SAT (as well as each branch of ENUM) runs in O(

for some free ET

, where

E
|

and

This result is for weakly normal hypernets—that is, when there are no label-to-
hole constraints. Kallmeyer and Romero (2008) demonstrate cases where having such
constraints is meaningful. The function of label-to-hole constraints is quite counter-
(cid:48) rooted at l and l(cid:48) and containing holes h and h(cid:48),
intuitive. Consider the two ETs
respectively. A label-to-hole constraint (l(cid:48), h) results in two types of solutions: those in
which l(cid:48) dominates l, and those in which l(cid:48) is plugged into h. The algorithm presented
in Table 2 may be easily modiﬁed to solve any hypernet by taking care of label-to-hole
is picked. At step 3.1, every label-to-hole constraint (l, h(cid:48))
constraints after a free ET
may be replaced with (l, l(cid:48)). Every (l(cid:48), h) is taken care of by plugging l(cid:48) into h. This latter
step results in a stacked ET, but we know how to convert this into a standard ET without
affecting the set of solutions (Theorem 2). Note that, here, we have to recursively take
care of the incoming constraints to the holes of
(cid:48). Koller and Thater (2007) prove that
adding such a step to the algorithm increases the complexity from quadratic to cubic,
when label-to-hole constraints exist. Following this discussion, we have:

Lemma 8
Every hypernet can be solved in polynomial time.

5.3.1 Weighted Constraints. Although we focus on hard constraints on UG solutions in
this article, our ﬁndings also have implications for statistical disambiguation systems
based on soft, or weighted, constraints. Hard constraints are equivalent to soft con-
straints with inﬁnite weights, so NP-completeness results for hard constraints also
apply to systems with weighted constraints. By deﬁning a framework that is tractable
with hard constraints, we open the theoretical possibility of efﬁcient algorithms for
ﬁnding the highest scoring solution according to a set of weighted constraints. We now
brieﬂy discuss two possible approaches to this problem.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

Table 3
Viterbi algorithm for weakly normal hypernets. We use a function sig to determine the dynamic
programming signature of a solution, an array δ to maintain the best scores found for partial
solutions, and an array best to maintain the best partial solutions themselves. Arrays δ and best
are indexed by a subgraph G and a signature. We use best[G] to denote the set of all the best
solutions found for G, regardless of their signature.

1: procedure VITERBI(Weakly normal hypernet G)
2:

δ[G]
best[G]
if G contains a single (label) node then

← −∞
← ∅

(cid:46) Initialize for all signatures

)

{

= (
l
{}
}
T
δ[G, sig(
)]
T
best[G, sig(
return
for each ET

←
)]

score(

)

← T

satisfying the freeness conditions in Theorem 7 do

Let l be the root and m the number of holes of
Let G1, G2, . . . , Gm be WCCs of G
For i = 1, . . . , m
if not deﬁned best(Gi) then

−E

for (

VITERBI(Gi)
T1, . . . ,
Tm)
Let hi be the hole of
If

∈

best[G1]

best[Gm] do
× · · · ×
connected to Gi in G

l, for i = 1, . . . , m.

−

has an open hole hk, let Gk be the WCC not connected to any hole of

Build
if score(

by plugging the root of
)] then
)

) > δ[G, sig(

T
score(

δ[G, sig(
)]
best[G, sig(

←
)]

← T

Ti into hi, for i = 1, . . . , m.

10:

11:

12:

13:

14:

15:

16:

17:

18:

19:

20:

21:

The ﬁrst approach is simply to use the ENUM algorithm as the framework for
search in statistical scope disambiguation systems. We can use ENUM to list solutions
meeting the hard constraints and score each solution individually. This rescoring ap-
proach may take exponential time in the worst case, but may be an effective algorithm
when the hard constraints leave a tractable number of solutions in practice. This ap-
proach has the advantage that it can take advantage of arbitrary weighted constraints,
also known as features, in scoring candidate solutions.

The second approach is to use dynamic programming to score candidate UGs. In
this approach, we use the recursive ENUM algorithm as a framework for scoring partial
solutions to the input UG, as shown in the algorithm of Table 3. Dynamic programming
requires that the features used to score solutions must be local, that is, that they must be
functions of some local subgraph of the solution. We refer to this local subgraph as the
signature of a solution, and use it to index the dynamic programming chart.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

As an example of applying the ENUM together with dynamic programming, sup-
pose that the weighted features of the statistical system are restricted to consider only
an ET and the hole into which it is plugged. In this case, we can construct a dynamic
programming chart indexed by the subset of ETs covered by a partial solution, and the
identity of the ET at the root of the partial solution. The size of this chart is O(n2n) in the
number of ETs—still exponential in the worst case. However, as with the more general
features, the ENUM algorithm, memoizing recursive calls with the chart, can take ad-
vantage of the hard constraints of the UG to lower the time complexity in practice. More
generally, we can deﬁne a dynamic programming chart indexed by whatever features
of the partial solution are distinct to the statistical model, and memoize recursive calls
to ENUM according to this dynamic programming structure.

More efﬁcient algorithms for ﬁnding the highest scoring solution may be possible,
and are an important area for future work. Our polynomial-time SAT algorithm does
not translate directly into a Viterbi algorithm that is polynomial in the size of the input
UG. However, we emphasize that for any NP-hard problem with hard constraints, the
weighted generalization is also NP-hard. Therefore, identifying a subset of UGs that is
tractable with hard constraints makes it possible to attempt to ﬁnd efﬁcient algorithms
for weighted constraints.

5.4 Coherence and Tractability

In this section, we show that coherent UGs are a subset of hypernets. Remember that
the key notion for deﬁning hypernets is hyper-normal connectedness and for coher-
ence is heart-connectedness. Therefore, as the ﬁrst step, we demonstrate how heart-
connectedness relates to hyper-normal connectedness.

Theorem 11
Let U be a CF-UG. If i is connected to j through a directed path in SDGU, then lq
are hyper-normally connected in GU.

i and lq

i , u) in U for some node u of Tr

Proof. First assume that i is directly connected to j through the edge (i, j). This means
that there is a dominance constraint (lq
j . Being the root of
j reaches u by a directed, and hence hyper-normal, path p. The path pi,j between lq
Tj, lq
i
j , which is the concatenation of p and (lq
and lq
Now assume that i is connected to j through a directed path −→d . Following the
previous result, lq
j in GU through a path p, which is the concatenation
of hyper-normal paths corresponding to the edges of −→d . Because, at each point of
concatenation, one of the two edges is a solid edge (Figure 16(a)), the concatenation
(cid:50)
remains hyper-normal.

i , u), is therefore hyper-normal.

i is connected to lq

This theorem proves that heart-connectedness subsumes hyper-normal connected-
ness for the following reason. Given any two arbitrary nodes u and v belonging to
trees Ti and Tj, both i and j can reach the heart through some directed path in SDGU.
Therefore, lq
j are hyper-normally connected to the heart through hyper-normal
paths p1 and p2, as shown in Figure 16(b). Concatenating p1 and p2 while taking out the
common part, we can construct a hyper-normal path p connecting u and v.

i and lq

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

(a) Hyper-normal paths between lq

i , lq

j , and lq

(b) Constructing p from p1 and p2

Figure 16
The relation between heart-connectedness and hyper-normal connectedness.

Corollary 3
If U is a heart-connected CF-UG, GU is hyper-normally connected.
We now have the tools to prove our main theorem.

Theorem 12
For every coherent UG U, GU is a hypernet, and hence, tractable.

Proof. U is coherent, hence according to Theorem 6, U has a heart-connected canonical
form sub-UG U(cid:48). In the following proof, we show that U(cid:48) is a hypernet. Because hyper-
nets are closed under the increment of constraint edges, it follows that U is a hypernet.
Let

be an arbitrary ET in GU(cid:48) rooted at l.

T12a.

(Proof of condition D26a) We need to show that
hole.

has at most one open

(cid:114)

is of one of the following three types:

Floating scopal. Because U(cid:48) is complete, the only possibly open
hole of
E
also be closed.

is its body hole. Since U(cid:48) is coherent, the root of

Eq must

Fixed scopal. Because U(cid:48) is complete,
the only potentially open node is the root of

has no open hole, hence,

Non-scopal.
open node.

has a single label node, hence, its only potentially

(Proof of condition D26b) We need to prove the following statement.
If l1 and l2 are two dominance children of a hole h of
hyper-normally connected in G(cid:48)U −
because no hole of G(cid:48)U can have two or more dominance children, that is,
the antecedent never holds (this is because, in a CF-UG, the body hole of

E
h. This statement is vacuously true,

, l1 and l2 are

T12b.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

TiTjTkT0l0’liqljqlkquvheartwpp1p2

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

quantiﬁers have no outgoing constraint and every other hole has exactly
one).

T12c.

(Proof of condition D26c) First consider the case where
has no open hole.
Because U(cid:48) is a CF-UG,
must be either a ﬁxed scopal or a non-scopal ET.
In either case, l has no dominance children in G(cid:48)U, hence, the statement is
has an open hole. Because
vacuously true. Now consider the case where
E
must be a ﬂoating scopal ET. Therefore, l has no incoming
U(cid:48) is a CF-UG,
dominance edge. Let u, v be the dominance children of l not connected to a
. Following Theorem 3, u and v are connected together through a
hole of
hyper-normal path p. p cannot visit l, otherwise u or v are hyper-normally
connected to a hole of
go through a hole of
v in the ﬁrst place. This proves that p is a path in G
hyper-normally connected in G

(l has no incoming dominance edge, hence, p must
E
), which is in contradiction with how we chose u and

l, hence u and v are

−

(cid:50)

This theorem is the main result of our article. Given that coherence seems to be
a natural condition on the semantic interpretation of any sentence, this result implies
that it is tractable to resolve the quantiﬁer scope of any sentence. Formally proving that
a semantic interpretation system always yields coherent representations will depend
on the speciﬁcs of the syntax/semantics interface. In Section 7, we will show that the
syntax semantics interfaces speciﬁed by MRS and HS do in fact always yield a coherent
representation.

6. Quantiﬁer Scoping Is an Ordering Problem

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

Traditionally, scoping has been treated as an ordering problem. For example, all sta-
tistical scope disambiguation systems deﬁne scoping as learning to predict an order
(Higgins and Sadock 2003; Srinivasan and Yates 2009; Manshadi, Gildea, and Allen
2013). For this reason, n! has always been considered as the upper bound on the number
of readings of a sentence with n quantiﬁers. This is in contrast with the frameworks
discussed in this article, in which scoping means predicting a tree structure. A UG with
n quantiﬁers has 2n holes, hence (2n)! fusings can be built (assuming that the solutions
are merging-free). Some of these fusings can be ﬁltered out, if we take qeq relations into
account. For example, given the following deﬁnition of ﬁrst-order CF-UG, a ﬁrst-order
CF-UG with two quantiﬁers has four potential solutions, as shown in Figure 17.

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Deﬁnition 28 (First Order UG)
A UG U with no ﬁxed-scopal ETs is called a ﬁrst-order UG.

It is easy to calculate this number for n quantiﬁers.

Lemma 9
If U is a ﬁrst-order CF-UG with n quantiﬁers , then Uq has exactly 2n

1n! solutions.

−

The factor 2n

1 results from the fact that once Q1 is decided to be in the scope of
Q2, there are two possible conﬁgurations based on whether Q1 is in the scope of the

−

Computational Linguistics

Volume 44, Number 1

Figure 17
All potential solutions for ﬁrst-order CF-UG with two quantiﬁers.

restriction or the body of Q2. It seems that in the past it has been taken for granted
that every permutation of quantiﬁers uniquely imposes a tree structure. One idea is
to ﬁlter some of these trees by taking dominance constraints into account, although it
should be noted that, unlike qeq constraints, the distribution of dominance constraints
is not predeﬁned. The good news is that, using the machinery provided and the results
obtained in the last section, we can prove this conjecture. That is, although the exact
distribution of dominance constraints is not given, the minimum connectivity required
by hypernets guarantees this property. Next, we use the notion of tree order, which is the
order in which nodes of a tree are visited and depends on the traversal method (e.g.,
in pre-order traversal, ﬁrst the branches are visited, then the node itself, while the post
order is the opposite). For this theorem, it does not matter which order is picked, but
once picked, we should stick to it.

Theorem 13
Let G be a hypernet, and π be an arbitrary permutation of ETs. There exists at most one
solution

of G with π being a tree order of ETs in T.

Proof. We prove this using induction on e the number of ETs in G. For e = 1, this is
trivial. Assume that it holds for e = k (k > 0) and let G be a DG with k + 1 ETs. If G has
no solution, whose tree order of ETs is π, we are done. Otherwise,
(the head of π), is
has exactly m WCCs G1, . . . , Gm, where m is the
a free ET. Based on Theorem 7, G
. Based on the induction assumption, each sub-DG Gi has exactly
number of holes in
Ei whose tree order of ETs matches π. In addition, because G is a hypernet,
one solution
into
following the third condition of Deﬁnition 26 (D26c), there is a unique hole of
Ei can be plugged. Therefore, G has a unique solution whose tree
which the root of each
(cid:50)
order of ETs is π.

− E

This theorem proves that if the underspeciﬁed representation is coherent, then

quantiﬁer scoping is indeed an ordering problem.

7. Comparison with Other Formalisms

In this section, we compare our work with the three frameworks it was built upon.
We show that our deﬁnition of coherence extends the set of tractable representations

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

l 0l q1l q2l 0l q1l q2l 0l q2l q1l 0l q2l q1(a) (b) (c) (d)

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

previously identiﬁed by the Dominance Graph framework. We further show that
the semantic representations returned by the syntax/semantics interfaces speciﬁed by
Minimal Recursion Semantics and Hole Semantics are always coherent, and hence
tractable. Our strategy in this section will be to show subsumption relations among
classes of underspeciﬁcation graphs, as shown in Figure 1. We say that one class is
subsumed by another if it is a subset of the second class, or if there exists a (generally
very simple) syntactic transformation from elements of the ﬁrst class to elements of the
second class such that the set of solutions remains the same. In either case, any algorithm
for ﬁnding solutions for the second class can be applied to graphs from the ﬁrst class,
which is the property that we will use to establish tractability.

7.1 Dominance Graphs

Dominance Graphs18 and Underspeciﬁcation Graphs19 are in fact equivalent when the
underspeciﬁed representation is complete. The only difference between the two is that
UG incorporates qeq relations in addition to dominance constraints, but, as we have
shown before, the two constraints become equivalent for complete UGs. The main
reason for us to deﬁne UG has been to provide a foundation to prove this equivalence.20
There is also a subtle difference in the terminology between the two frameworks.
What we have deﬁned as solution in our framework corresponds to the notion of conﬁg-
uration in Dominance Graphs framework. Therefore, the satisﬁability (or enumeration)
algorithm presented in this article, in Dominance Graphs terminology, decides whether
a DG has a conﬁguration (or enumerates all possible conﬁgurations of a DG).

A major contribution of this paper was to extend the coverage of the previously
known tractable subset of DG, called weak net (Niehren and Thater 2003). We achieved
this goal by deﬁning the notion of hypernet, motivated by and built upon weak net. In
the following, we give the deﬁnition of weak net from Thater (2007), translated into our
own terminology.

Deﬁnition 29 (Weak Net)
A weakly normal UG U is a weak net if and only if for every elementary tree

D29a.

D29b.

has exactly one open node.

E
If l1, l2 are two dominance children of a node u of
hyper-normally connected in U

−

, then l1 and l2 are

18 Dominance Graphs were derived from Dominance Constraints. Dominance Constraints were originally
developed as a broad framework for representing arbitrary tree structures. Dominance Graphs is a
revision of Dominance Constraints, which is better suited for modeling scope underspeciﬁcation.
For details on how Dominance Graphs compare to Dominance Constraints, see Thater (2007).

19 When capitalized, the terms “Dominance Constraints,” “Dominance Graphs,” and “Underspeciﬁcation
Graphs” refer to the frameworks; otherwise, and when abbreviated, they refer to a notion within the
framework.

20 Another advantage could be the ability to model an incomplete underspeciﬁed representation, for

example, when dealing with fragments, broken parse trees, and so forth. The latter, however, is not the
subject of this article.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

(a)

(b)

Figure 18
A coherent UG which belongs to hypernet but is not a weak net, because the dominance children
of the quantiﬁer Every, labeled Run(x) and Child(x, y), are not hyper-normally connected, if the
quantiﬁer node is removed from the graph as in (b).

Comparing the deﬁnition of hypernet (Deﬁnition 26) with weak net, it is clear that
weak net is a subset of hypernet. By giving examples of natural language sentences
whose underspeciﬁed representation is a hypernet but not a weak net, we show that
weak net is a proper subset of hypernet. Consider GU in Figure 18(a), where U is the
CF-UG for the following sentence.

3. Every politician, whom I know a child of, probably runs.

Let

be the ET for the quantiﬁer Every and l be the root of

. The two dominance
l, as shown in Figure 18(b).
children of l are not (hyper-normally) connected in GU −
Therefore, GU is not a weak net. What makes this example special is that SDGU has a
loop. Weak net misses a whole class of sentences with similar structures. Because we
have proved that hypernet covers all coherent UGs, it should not be surprising that GU
is a hypernet, and hence, covered by our framework. This is because hypernet does
not require all the dominance children of the quantiﬁer node u to be hyper-normally
u, but only those that are not hyper-normally connected to a hole of u
connected in G
(Condition D26c). Therefore, for this UG, since the node labeled Child(x, y) is hyper-
u, it is not required to be hyper-normally
normally connected to a hole of u in G
u.
connected to the node labeled Run(x) in G

−

−
−

7.2 Minimal Recursion Semantics

As the ofﬁcial semantic language of the LinGo English Resource Grammar (Copestake
and Flickinger 2000), Minimal Recursion Semantics has been used relatively widely in
practice. As mentioned before, UG has been deﬁned in a way that it subsumes both
DG and MRS. Although MRS is not originally deﬁned in graph terms, a limited version
of UG can serve as the notational variant of MRS. The limitation is on the usage of
dominance constraints. MRS only implicitly uses dominance constraints, and that is to
satisfy binding constraints, hence, only realizes dominance constraints that go from a
quantiﬁer node to a non-quantiﬁer label node. By restricting UG to only allow those
dominance constraints, we can obtain a notational variant of MRS in graphical form.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

ProbablyPolitician(x) & Know(I,y)Every(x)Run(x)Child(y,x)A(y)ProbablyPolitician(x) & Know(I,y)Run(x)Child(y,x)A(y)

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

The heart of MRS is the notion of Elementary Predication or EP, a labeled predica-

tion over a set of ﬁrst order variables x, y, . . . and second order variables h1, h2, . . .

l : P(x, y, . . . , h1, h2, . . .)

(6)

We have deﬁned ET as the notational variant of EP. Similarly, the deﬁnitions of the
three types of ET—non scopal, ﬁxed scopal, and ﬂoating scopal—have been inspired
by their EP counterparts. MRS does not notation-wise distinguish between holes and
labels. They are both referred to as handle and are represented by the letter h, often
subscripted with a number. In deﬁning UG, we followed, for mathematical convenience,
the tradition of Hole Semantics and DG and distinguished between the two terms: A
handle that is the label of an EP is called a label, and the top handle (see below) and any
handle that is an argument of an EP is called a hole. The motivating example given at
the beginning of Section 2 was nothing but an MRS structure as a graph (Figure 2(d)).
Equation (7) represents the MRS of the same sentence in the original MRS language as
deﬁned by Copestake, Lascarides, and Flickinger (2001).

h0,

(cid:104)

h1 = Every(x, h2, h3), h4 = Child(x), h5 : A(y, h6, h7), h8 : Politician(y),
{

h9 : Of (x, y), h10 : Run(x)
}

{

h0 =q h10, h2 =q h4, h6 =q h8

}(cid:105)

(7)

The handle represented as h0 is called (global) top handle and plays the role of the top
ET in UG. It is equivalent to having a dummy EP l0 : h0 as the top but then removing the
, where
label node and leaving a ﬂoating hole. An MRS is deﬁned as the triple
GT is the top handle, R is the set of EPs, and C is the set of qeq constraints. As mentioned
before, the implicit binding constraints encoded in the ﬁrst order variables x, y of the
MRS are made explicit in UG through dominance constraints. Given an MRS, a scope-
resolved structure (equivalent to the notion of solution in UG) is built by equating
handles.

GT, R, C
(cid:105)

(cid:104)

h0 = h1, h2 = h5, h3 = h10, h6 = h8, h7 = h4, h9 = h4

(8)

∧

Note that h9 = h4 in Equation (8) equates the label of two EPs, resulting in the EP
Of (x, y). UG allows EP conjunctions in two different ways: (1)
conjunction Child(x)
by deﬁning fusion as a many-to-one mapping from labels to holes (e.g., fusing both h4
and h9 to h7); (2) Using stacked ETs. The second approach models the case where EP
conjunctions are built during the semantic composition and before any scope resolution
(something that can happen in MRS). Copestake et al. (2005) deﬁne a semantic compo-
sition process, presenting an algorithm on building MRS structures from constituency
trees. This algorithm has motivated our notion of canonical form. By following this
algorithm, Manshadi, Allen, and Swift (2008a) proved the following theorem.

Theorem 14
Every output of MRS’s semantic composition process (as spelled out by Copestake
et al. [2005]) is either in canonical form or trivially unsatisﬁable.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

The detailed proof of this theorem can be found in Manshadi, Allen, and Swift
(2008a). Given that the result of the MRS semantic composition process is in canonical
form, we can use the tools developed in Section 5 to show that it is also tractable.

Theorem 15
Every output M of the semantic composition algorithm on a coherent sentence is either
trivially unsatisﬁable or a coherent UG, and therefore tractable.

Proof. By Theorem 14, every output M of the semantic composition algorithm on a
coherent sentence is either trivially unsatisﬁable or in canonical form. By Deﬁnition 14,
a canonical form UG is complete. The interpretation of a coherent sentence must be
heart-connected, and by Theorem 6, a heart-connected, complete UG is a coherent UG.
By Theorem 12, a coherent UG is a hypernet, and, by Lemma 8, a hypernet is tractable.(cid:50)

7.3 Hole Semantics

Corresponding to the concept of UG in our framework, Hole Semantics deﬁnes the no-
tion of UR (Underspeciﬁed Representation). UR 21 is a subset of normal DGs, therefore
it allows for only one type of constraint, hole-to-label dominance constraints. Analogous
to the notion of coherence, which was motivated by the canonical form of the output
of MRS syntax/semantic interface, URs generated by the syntax/semantic interface,
as demonstrated by Koller, Niehren, and Thater (2003), conform to the following two
properties: (1) they are leaf-labeled (they call a DG with no open holes leaf-labeled); (2)
they are hyper-normally connected. Therefore, Hole Semantics UR equals the set of all
hyper-normally connected leaf-labeled normal DGs.

Now, we show that all satisﬁable URs are hypernets.

Lemma 10
Let a hyper-normally connected normal DG G, with a solution T be given. If T(cid:48) is a
subtree of T, then G(cid:48), the sub-DG of G induced by T(cid:48) is also hyper-normally connected.

Proof. Assume to the contrary that G(cid:48) is not hyper-normally connected. Consider the two
nodes of G(cid:48) that are not hyper-normally connected in G(cid:48), and let P be the hyper-normal
path that connects these two nodes in G. We prove that l, the root of T(cid:48), is dominated by
two mutually exclusive nodes, which is a contradiction.

Without loss of generality, we assume that both nodes are label nodes (l1 and l2) and

that P contains no other node in G(cid:48).22

Because G is normal, the two nodes immediately after l1 and l2 in P have to be hole
nodes h1 and h2 with outgoing constraint edges to l1 and l2, respectively (see Figure 19).
= h2, otherwise, P is not hyper-normal. The path between h1 and h2 cannot
Note that h1 (cid:54)
be a directed path, because no solid edge leaves a hole, and no constraint edge leaves
h1 or h2 either (otherwise, P would not be a hypernormal path). Therefore, there are

21 Throughout this subsection, by UR we mean Hole Semantics’s UR.
22 Among all pairs of node not hyper-normally connected in G(cid:48), consider the pair for which the length of P

is the shortest.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Figure 19
Proof of Lemma 10.

two back-to-back solid edges emanating from a node l3 on P, as shown in the ﬁgure on
the left.

We consider two options:

The segments of P between h3 and l1 and between h4 and l2 are both
directed, hence, l1 and l2 are under the scope of h3 and h4, respectively,
which means l is under the scope of both h3 and h4. Contradiction!

One of the two parts, say the segment of P between h4 and l2, is not
directed. Therefore, P has a segment like the one in the ﬁgure on the right.
Two possible cases may happen in T: h5 is in the scope of h6 or vice versa.
In either case l1 and l2, and hence l, are under the scope of two mutually
exclusive holes. Contradiction!

(cid:50)

Theorem 16
Every satisﬁable hyper-normally connected leaf-labeled normal DG is a hypernet.

Proof. Consider a normal DG G, an arbitrary ET
of G. We
have to prove that the three conditions in Deﬁnition 26 hold. Condition D26a directly
follows from leaf-labeledness, which guarantees that there is no open hole in a UR.23
To prove condition D26b, consider l1 and l2, the two dominance children of a hole h of
h.
rooted at l, and G(cid:48)

, and assume to the contrary that l1 and l2 are not hyper-normally connected in G

E
Because G is satisﬁable, let

rooted at l, and a solution

(cid:48) be the subtree of

be a solution of G,

−

23 In fact, since we are only considering satisﬁable URs, we do not need to presume leaf-labeledness,

because it follows from hyper-normal connectedness. Assume to the contrary that this is not the case,
and h is the open hole of
T
l(cid:48) is hyper-normally connected to l, and hence to some hole h(cid:48) of
induced by the subtree of
to Lemma 7, l(cid:48) must be dominated by h(cid:48) in
contradiction!

l, where Gl is the sub-DG of G
= h, because h is open, but h(cid:48) is not, hence, according

, meaning that l(cid:48) is dominated by two distinct holes of

. Let l(cid:48) be the label plugged into h in

rooted at l. Clearly, h(cid:48) (cid:54)

. Because G is hyper-normally connected,

in Gl

−

;

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

l1l2h1h2ll1l2h1h2lh3h4h5h6l6l4l5l3G′G′

Computational Linguistics

Volume 44, Number 1

−

be the sub-DG of G induced by
(cid:48). l1 and l2 are hyper-normally connected in G, and, by
Lemma 10, are hyper-normally connected in G(cid:48), but are not hyper-normally connected
h. This means that the hyper-normal path p connecting the two nodes passes
in G(cid:48)
h. Because l is the root of solution
(cid:48), it does not have an incoming dominance edge,
therefore any path that connects l1 and l2 and passes h must also pass another hole h(cid:48) of
. Let l1 be the node that connects to h(cid:48) by a path P without ﬁrst going through l. Then
E
according to Lemma 7, there is a node u on P such that all the nodes on P are dominated
by u in T(cid:48). The only nodes dominating h(cid:48) in T(cid:48) are h(cid:48) itself and l, but l is not on P, hence,
u = h(cid:48). This means that one of the nodes l1 or l2 must be in the scope of h(cid:48), but we
know that they both are also in the scope of h. This is a contradiction! Condition D26c
(cid:50)
is vacuously true because

has no open hole and l has no dominance children.

This theorem shows that, practically speaking, UR is a subset of hypernet. An
important question arising is, given that it does not allow for label-to-label constraints,
is Hole Semantics powerful enough to cover all coherent UGs? In other words, given
that some constraints, such as the binding constraints, are inherently label to label, how
does Hole Semantics get away without it? This question has remained unanswered
in the past. Once again, we use our notion of coherence to answer this question. We
show that, in coherent UGs, those label-to-label dominance constraints that implement
variable binding may be replaced with hole-to-label constraints without affecting the
set of solutions. First, we deﬁne some terminology.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Deﬁnition 30 (Ancestor/Disjoint)
Consider a complete UG U, SDGU = (V, E), and a node i

∈

(cid:114)

Anc(i) is the set of nodes that reaches i (through a directed path) in SDGU
(including i itself);

Dis(i) is the set of nodes that reaches the heart (through a directed path)
without going through i (including the heart itself).

For example, for the SDG in Figure 10, Anc(2) =

. If U is
}
coherent, SDGU is heart-connected, hence the following lemma directly follows from the
deﬁnition.

, Dis(2) =

0, 1

2, 3

{

}

Lemma 11
Given a coherent UG U and SDGU = (V, E), for every i, j in V:

ii.

Anc(i)

Dis(i) = V.

∪
Dis(j)

i /
∈

∈

⇒

Dis(i).

a solution of U, and consider the quantiﬁers Qi and Qj,

Theorem 17
Let U be a coherent UG, and
i outscopes lq
where lq
j in
(cid:114)
j is under the restriction of lq
Anc(i), lq
j is under the body of lq

Dis(i), lq

i in

if j

∈

(cid:114)

∈

i in

;

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Figure 20
Proof of Theorem 17 (lr

k represents an arbitrary node in Tr
k).

∈

i and τb

i be the subtrees of

Anc(i), and τr
Proof. Let j
body hole of lq
P
i respectively, as shown in Figure 20. We use induction on
|
|
of the path P from j to i in SDGU, to show that lq
j is in the restriction of lq
i . For
j immediately dominates i in SDGU, hence there is a dominance edge from lq
node lr
i ∈
the scope of lq
j in
P
Now let

rooted at the restriction and
, the length
= 1,
P
|
j to some
i must be in

i is the restriction tree of lq
i , lq

1) and k be the node immediately after j on P. Because j

i (Deﬁnition 13). Therefore, lr

j must also be in τr
i .

. Since lr
T
= n + 1 (n

i , where Tr
Tr

i is in τr

immediately dominates k in SDGU, there is a dominance edge from lq
k, which means lr
Tr
lq
k, and hence lr

k must be in the scope of lq

j must also be in τr
i .

i . Therefore, lq

i , is in τr

k ∈
j . According to the induction assumption,

j to some node lr

≥

A similar argument applies for the second part, that is, when j

Dis(i).

∈

(cid:50)

Corollary 4
Let U be a coherent UG, and Qi and Qj two quantiﬁers in U. If j
there exists no solution of U in which lq

i outscopes lq
j .
Now, we are ready to prove our main theorem.

Anc(i)

∩

∈

Dis(i), then

Theorem 18
In a coherent UG U, all label-to-label constraints emanating from quantiﬁer label nodes
to some node other than a quantiﬁer label node may be replaced with hole-to-label
constraints with the set of solutions remaining exactly the same.

Proof. Consider a coherent UG U, an arbitrary quantiﬁer Qi labelled at lq
i , and an
arbitrary dominance edge (lq
i , u) emanating from Qi. We need to show that either u is
always (i.e., in all solutions of U) under the body of Qi or always under its restriction.
Because U is coherent, it has a canonical form sub-UG (Figure 7 in Section 3); therefore,
u = lr
j belongs to the heart tree, hence
u is always under the body of Qi. Throughout the rest, we only consider the case where
j > 0, that is, u is a node in the restriction tree of Qj.

j is some node in the tree Tr

j . When j = 0, lr

j , where lr

First, notice that because of the dominance edge (lq

i , lr

j ), SDGU = (V, E) contains an

edge from i to j. This means:

Anc( j)

∈

(9)

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

l 0l qil ri⌧rib l r0⌧biijikj|P|=1|P|=n+1

Computational Linguistics

Volume 44, Number 1

Now consider Anc(i); depending on whether j
cases, and prove that the premise holds in both cases.

∈

Anc(i) or not, we consider two possible

Case i.

(a)

(b)

Anc(i)24

j
We further consider two situations depending on whether i

∈

Dis(j) or not.

Dis(j). Following Equation (9), i

∈
i
Dis( j), which means
∈
Qj does not dominate Qi in any solution of U (Corollary 4). Because
Qi dominates a node in the restriction tree of Qj, it cannot be
disjoint either, hence, Qi outscopes Qj in every solution of U. Since
j
Anc(i), following Theorem 17, Qj is under the restriction of Qi,
and so is u.

Anc( j)

∈

∩

Dis( j). Following Lemma 11: j

i /
∈
meaning that Qj outscopes Qi in every solution, from which and
Anc( j), Qi is under the restriction of Qj. This means
given that i
every node in the restriction tree of Qj, including u, is under the
body of Qi.25

Dis(i), hence j

Anc(i)

∩

∈

Dis(i),

Case ii.

Anc(i)

j /
∈

Unlike case i, here it is possible to simultaneously have both the solutions
where Qi outscopes Qj and those where Qj has the wide scope.
Interestingly (and again unlike case i), in both types of solution, u is
always under the body of lq
i . We show this for each type separately.

(a)

(b)

Qj dominates Qi in
Given that i
that every node in Tr
Qi.

∈

Anc( j), Qi is in the restriction of Qj in

, meaning

j , including u, is under the scope of the body of

Qi dominates Qj in
T
Because j /
Anc(i), j
∈
∈
is u.

Dis(i), hence, Qj is in the body of Qi, and so

Here we showed that, for a coherent UG, if Qi dominates some node u, it is impossible
to simultaneously have solutions where u is in the body of Qi and those where u is in
the restriction of Qj. This means that it is possible to build a UG U(cid:48) by replacing (lq
i , u)
(cid:50)
with either (hb

i , u) while the set of solutions of U and U(cid:48) is the same.

i , u) or (hr

Following this theorem, Hole Semantics is able to enforce variable binding using
hole-to-label dominance constraints. Figure 21 summarizes the expressive power of all

24 In this case, SDGU has a loop, which means, as discussed in the previous section (see Figure 18), U is not
a (weak) net. Therefore, as seen in the following, if it was not for the non-net cases, we could always
replace these label-to-label constraints with constraints emanating from the body hole of the quantiﬁers.

25 In the proof of the equivalence of qeq and dominance constraints in complete UGs (Section 3,

Theorem 5), we showed that given a solution
Tr
j have to be under the scope of the body hole of Qi.
Qj, all the nodes u

of a complete U, if Qi is plugged in the restriction hole of

∈

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Section 5.1

Section 7.2

Deﬁnitions 11, 20

Theorem 5

MRS

Weakly Normal DG

Section 5.4

Complete UG

Deﬁnition 12

Deﬁnitions 10, 20

Deﬁnition 26

Deﬁnition 14

Normal DG

Hypernet

Deﬁnition 17

CF-MRS

Section 7.3

Theorem 16

Deﬁnition 29

Theorem 12

Hole Semantics’s UR
(satisﬁable and hyper-normally connected)

Weak net

Coherent UG

Theorem 14

Theorem 18

Theorem 15

Coherent MRS
(satisﬁable and heart-connected)

Figure 21
Summary of subsumption relations shown in this article.

proposed subsets. The outcome of this theorem is demonstrated by the edge from Hole
Semantics’s UR to coherent MRS.

8. Conclusion

We have solved several open questions within the context of the prevalent constraint-
based scope underspeciﬁcation frameworks: Minimal Recursion Semantics, Hole
Semantics, and Dominance Constraints.

Although these frameworks are fundamentally different, there has been a conjecture
that they become equivalent once restricted to the well-formed structures correspond-
ing to actual URs of natural language sentences. Until now, the characterization of this
well-formedness has been an open question, and so has the proof of the conjecture.

Ever since their satisﬁability problem was proved to be intractable, there have been
efforts on ﬁnding a tractable subset of the frameworks that is expressive enough to cover
all well-formed structures. But even “(weak) net,” the largest tractable subset previously
found, leaves a group of natural language sentences uncovered.

Figure 21 summarizes this paper. At the top of this ﬁgure is UG, a framework we
have deﬁned in this paper to encompass all the rest of constraint-based frameworks
shown here. In the heart of this ﬁgure, there are two subsets: coherent UG and hypernet.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Computational Linguistics

Volume 44, Number 1

Coherent UG is the relevant part of UG. It is, in fact, our characterization of what
has been referred to in the past as well-formedness. We have linguistically justiﬁed
that the complete UGs of all coherent sentences belong to this subset. Analogous to
this linguistically motivated subset, we have the mathematically motivated notion of
hypernet, deﬁned to guarantee the mathematical and computational properties we have
been looking for, but to be large enough to cover coherent UG. It is based on the notion of
(weak) net from Dominance Graph but expanded to include all coherent UGs. Another
central notion in this ﬁgure is CF, or canonical form, whose importance lies in the fact
that, within this subset, qeq and normal dominance constraints become equivalent, and,
hence, the main difference between UG (read MRS) and DG disappears.

There are several other properties of URs that have been taken for granted in the
past. For example, although scoping in general is about predicting a tree structure, it has
been treated as an ordering problem. We prove that for hypernet, and hence all coherent
UGs, scoping is indeed an ordering problem. Finally, a framework like Hole Semantics
has taken for granted that binding constraints, which are label-to-label in nature, may
be modeled by hole-to-label constraints. Here, we have proved that for coherent UGs,
label-to-label binding constraints may in fact be replaced with hole-to-label constraints,
bridging another gap between MRS and Hole Semantics.

Acknowledgments
We are grateful to the anonymous reviewers
for many suggestions improving this article.

References
Allen, James. 1995. Natural Language
Understanding (2nd ed.). Benjamin-
Cummings Publishing Co., Inc.,
Redwood City, CA.

Alshawi, Hiyan and Richard Crouch. 1992.
Monotonic semantic interpretation. In
Proceedings of the 30th Annual Conference of
the Association for Computational Linguistics
(ACL-92), pages 32–39, Newark, DE.
Althaus, Ernst, Denys Duchier, Alexander

Koller, Kurt Mehlhorn, Joachim Niehren,
and Sven Thiel. 2003. An efﬁcient
graph algorithm for dominance
constraints. Journal of Algorithms, 48(1):
194–219.

Bodirsky, Manuel, Denys Duchier, Joachim

Niehren, and Sebastian Miele.
2004. A new algorithm for normal
dominance constraints. In ACM-SIAM
Symposium on Discrete Algorithms,
pages 59–67, Vancouver.

Bos, Johan. 1996. Predicate logic unplugged.

In Proceedings of the 10th Amsterdam
Colloquium, pages 133–143, Amsterdam.

Bos, Johan. 2002. Underspeciﬁcation and

Resolution in Discourse Semantics. Ph.D.
thesis. Saarland University.

Copestake, Ann and Dan Flickinger. 2000.
An open source grammar development
environment and broad-coverage English
grammar using HPSG. In Proceedings of
Language Resources and Evaluation
Conference (LREC-2000), pages 591–600,
Athens.

Copestake, Ann, Dan Flickinger, Carl

Pollard, and Ivan A. Sag. 2005. Minimal
recursion semantics—an introduction.
Research on Language and Computation,
3:281–332.

Copestake, Ann, Alex Lascarides, and Dan
Flickinger. 2001. An algebra for semantic
construction in constraint-based
grammars. In Proceedings of the 39th Annual
Conference of the Association for
Computational Linguistics (ACL-01),
pages 140–147, Toulouse.

Frege, Gottlob. 1923. “gedankengef ¨uge”
[“compound thought”]. Beitr¨age zur
Philosophie des Deutschen Idealismus,
III:36–51.

Fuchss, Ruth, Alexander Koller, Joachim

Niehren, and Stefan Thater. 2004. Minimal
recursion semantics as dominance
constraints: Translation, evaluation, and
analysis. In Proceedings of the 42nd Annual
Conference of the Association for

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/

4
4
1
3
9
1
8
0
8
9
0
9
/
c
o

l
i

_
a
_
0
0
3
0
7
p
d

b
y
g
u
e
s
t

o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3

Manshadi, Gildea, and Allen

Semantic Coherence for Underspeciﬁed Semantics

Computational Linguistics (ACL-04),
pages 247–254, Barcelona.

Higgins, Derrick and Jerrold M. Sadock.
2003. A machine learning approach to
modeling scope preferences. Computational
Linguistics, 29(1):73–96.

Hobbs, Jerry R. and Stuart M. Shieber. 1987.
An algorithm for generating quantiﬁer
scopings. Computational Linguistics,
13(1-2):47–63.

disambiguation. In Proceedings of the 51st
Annual Meeting of the Association for
Computational Linguistics (ACL-13),
pages 64–72, Soﬁa.

Manshadi, Mehdi H., James F. Allen, and
Mary Swift. 2008b. Toward a universal
underspeciﬁed semantic representation.
In Proceedings of the 13th Conference on
Formal Grammar (FG), pages 77–94,
Hamburg.

Kallmeyer, Laura and Maribel Romero. 2008.

Manshadi, Mehdi H., James F. Allen, and

Scope and situation binding in LTAG
using semantic uniﬁcation. Research on
Language and Computation, 6(1):3–52.
Kamp, Hans. 1981. A theory of truth and

semantic representation. In P. Portner and
B. H. Partee, editors, Formal Semantics—the
Essential Readings. Blackwell.
pages 189–222.

Koller, Alexander, Joachim Niehren, and
Stefan Thater. 2003. Bridging the gap
between underspeciﬁcation formalisms:
Hole semantics as dominance constraints.
In 10th Conference of the European Chapter
of the Association for Computational
Linguistics (EACL-03), pages 195–202,
Budapest.

Koller, Alexander and Stefan Thater. 2007.

Solving unrestricted dominance graphs. In
Proceedings of the 12th Conference on Formal
Grammar, pages 1–12, Dublin.

Manshadi, Mehdi and James Allen. 2012.

Expanding the range of tractable
scope-underspeciﬁed semantic
representations. In *SEM 2012: The First
Joint Conference on Lexical and Computational
Semantics, pages 142–150, Montr´eal.
Manshadi, Mehdi, James Allen, and Mary

Swift. 2008a. Towards a universal
underspeciﬁed semantic representation.
In Proceedings of the 13th International
Conference on Formal Grammar,
Hamburg.

Manshadi, Mehdi, Daniel Gildea, and

James F. Allen. 2013. Plurality, negation,
and quantiﬁcation: Towards
comprehensive quantiﬁer scope

Mary Swift. 2009. An efﬁcient enumeration
algorithm for canonical form
underspeciﬁed semantic representations.
In Proceedings of the 14th Conference on
Formal Grammar (FG), pages 85–101,
Bordeaux.

Niehren, Joachim and Stefan Thater. 2003.

Bridging the gap between
underspeciﬁcation formalisms:
Minimal recursion semantics as
dominance constraints. In Proceedings
of the 41th Annual Conference of the
Association for Computational Linguistics
(ACL-03), pages 367–374, Sapporo.

Reyle, Uwe. 1993. Dealing with ambiguities

by underspeciﬁcation: Construction,
representation and deduction. Journal of
Semantics, 10(2):123–179.

Schubert, Lenhart K. and Francis Jeffry
Pelletier. 1982. From English to logic:
Context-free computation of
“conventional” logical translation.
Computational Linguistics,
8(1):26–44.

Srinivasan, Prakash and Alexander Yates.
2009. Quantiﬁer scope disambiguation
using extracted pragmatic knowledge:
Preliminary results. In Conference on
Empirical Methods in Natural Language
Processing (EMNLP-09), pages 1465–1474,
Singapore.

Thater, Stefan. 2007. Bridging the Gap Between

Underspeciﬁcation Formalisms: Minimal
Recursion Semantics as Dominance
Constraints. Ph.D. thesis, Universit¨at des
Saarlandes.

D
o
w
n
o
a
d
e
d

f
r
o
m
h

t
t

:
/
/

d
i
r
e
c
t
.

i
t
.

e
d
u
/
c
o

l
i
/

a
r
t
i
c
e
–
p
d

f
/