Song, L., Ren, Y., Shuhan, X., Hou, Y. & Er, X. (2023). A hybrid spatio-temporal deep belief network and sparse
representation based framework reveals multi-level core functional components in decoding multi-task fMRI signals. Netzwerk
Neurowissenschaften, Advance publication. https://doi.org/10.1162/netn_a_00334.

1

2

3

4

5

6

7

A Hybrid Spatio-Temporal Deep Belief Network and Sparse Representation-Based

Framework Reveals Multi-Level Core Functional Components in Decoding Multi-Task

fMRI Signals

Limei Song1#, Yudan Ren1#*, Shuhan Xu1, Yuqing Hou1, Xiaowei He1

1 School of Information Science & Technologie, Northwest University, China;

# These authors contributed equally to this work and should be considered co-first authors.

* Corresponding authors.

8

Abstrakt

9

Decoding human brain activity on various task-based functional brain imaging data is of great

10

significance for uncovering the functioning mechanism of the human mind. Currently, most

11

feature extraction model-based methods for brain state decoding are shallow machine learning

12

Modelle, which may struggle to capture complex and precise spatio-temporal patterns of brain

13

activity from the highly noisy fMRI raw data. Darüber hinaus, although decoding models based on

14

deep learning methods benefit from their multi-layer structure that could extract spatio-

15

temporal features at multi-scale, the relatively large populations of fMRI datasets are

16

indispensable and the explainability of their results is elusive. To address the above problems,

17

we proposed a computational framework based on hybrid spatio-temporal deep belief network

18

and sparse representations to differentiate multi-task fMRI (tfMRI) Signale. Using a relatively

19

small cohort of tfMRI data as a testbed, our framework can achieve an average classification

20

accuracy of 97.86% and define the multi-level temporal and spatial patterns of multiple

21

cognitive tasks. Intriguingly, our model can characterize the key components for differentiating

1

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

.

/

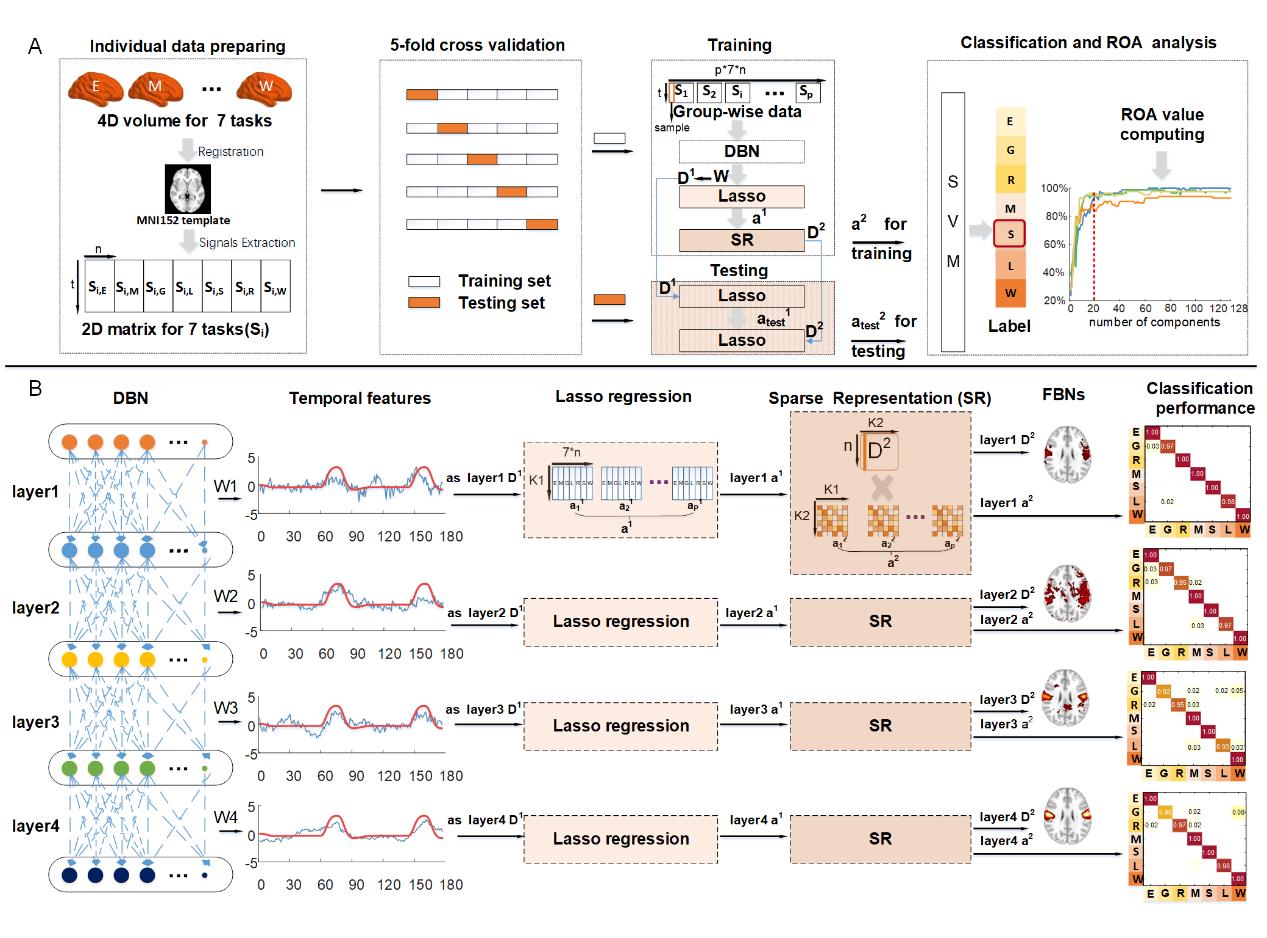
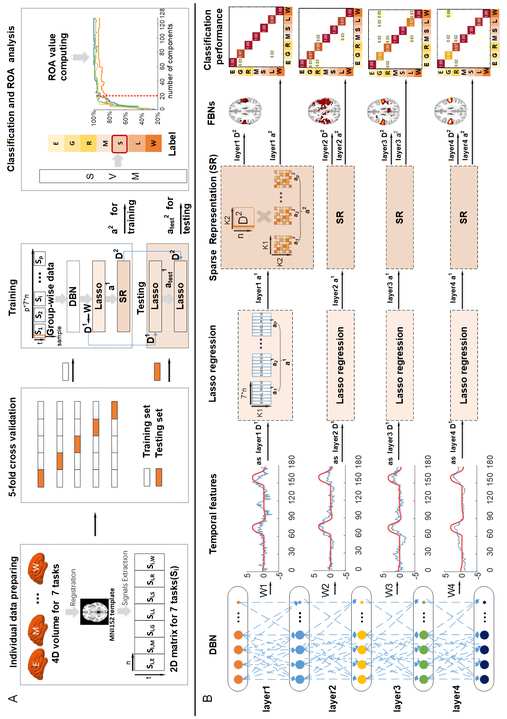
1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

22

the multi-task fMRI signals. Gesamt, the proposed framework can identify the interpretable

23

and discriminative fMRI composition patterns at multiple scales, offering an effective

24

methodology for basic neuroscience and clinical research with relatively small cohorts.

25

Schlüsselwörter: Multi-task classification, Task-based fMRI, Deep belief network, Sparse

26

representation, Functional brain network.

27

Einführung

28

For years, researchers have been attempting to decode the human brain states based on

29

functional magnetic resonance imaging (fMRT) Daten (Haynes & Rees, 2006; Jang, Plis, Calhoun,

30

& Lee, 2017; Rubin et al., 2017; Stanislas Dehaene, 1998), where distinguishing different

31

cognitive tasks from fMRI data and extracting discriminative fMRI composition patterns are

32

effective means to improve our understanding of the relationship among current cognitive tasks,

33

brain responses, and individual behavior (Friston, 2009; Logothetis, 2008). To decode

34

meaningful neurological patterns embedded in diverse task-based fMRI data, various

35

computational and statistical methods have been proposed in the last decades. The most widely

36

used brain state decoding strategy is multi-voxel pattern analysis (MVPA) (Davatzikos et al.,

37

2005; Jang et al., 2017; Kriegeskorte & Bandettini, 2007). Despite its popularity, its commonly-

38

used classification strategy support vector machine (SVM) usually struggles to perform well

39

on high-dimensional fMRI data and thus requires effective techniques for feature

40

selection/extraction (LeCun, Bengio, & Hinton, 2015; Vieira, Pinaya, & Mechelli, 2017).

41

Somit, the feasibility of feature selection/extraction has been investigated using various

42

machine learning methods (LeCun et al., 2015; Vieira et al., 2017; S. Zhang et al., 2016).

2

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

/

T

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

.

/

F

B
j
G
u
e
S
T

T

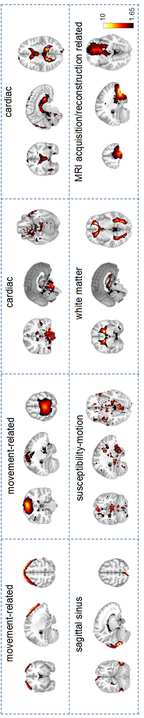
Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

43

Jedoch, most of these machine learning methods rely on shallow models, and their shallow

44

nature may hinder them from effectively capturing non-linear relationships in the highly noisy

45

fMRI raw data, resulting in difficulties in extracting complex and specific spatio-temporal

46

Merkmale (Qiang et al., 2020; Rashid, Singh, & Goyal, 2020; Varoquaux & Thirion, 2014).

47

Kürzlich, studies applying deep learning models such as deep neural network (DNN) Und

48

convolutional neural networks (CNN) to decode brain states based on task-based fMRI signals

49

have been reported (J. Hu et al., 2019; Liu, Er, Chen, & Gao, 2019; Sotetsu Koyamadaa, 2015;

50

Y. Zhang, Tetrel, Thirion, & Bellec, 2021). Such deep learning models take the advantage of

51

being a multi-layer architecture by stacking multiple building blocks with similar structure,

52

which has demonstrated the ability to significantly reduce noises in raw fMRI data and model

53

the non-linear relationships among neural activities of brain regions, allowing for the extraction

54

of multi-level spatio-temporal features (Bengio, Courville, & Vincent, 2012; Najafabadi et al.,

55

2015; Ren, Xu, Tao, Song, & Er, 2021). Trotzdem, there are still some limitations in current

56

brain state decoding strategies based on deep learning models. Erste, as large-size samples are

57

indispensable for the deep learning model, current decoding models are not suitable for small

58

datasets (Bo Liu, 2017; Litjens et al., 2017; Wang et al., 2020; Wen et al., 2018). Zum Beispiel,

59

Wang et al. (2020) proposed a DNN-based model for tfMRI signal classification, welche

60

requires 1034 Fächer, making it less practical for clinical populations. Zweite, most of the

61

decoding models based on deep learning are end-to-end learning and the explainability of such

62

models is elusive (J. Hu et al., 2019; LeCun et al., 2015; Wang et al., 2020). Kürzlich, manche

63

researchers have attempted to define the key components for decoding brain states using the

64

machine learning method. Zum Beispiel, our previous study based on sparse dictionary learning

3

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

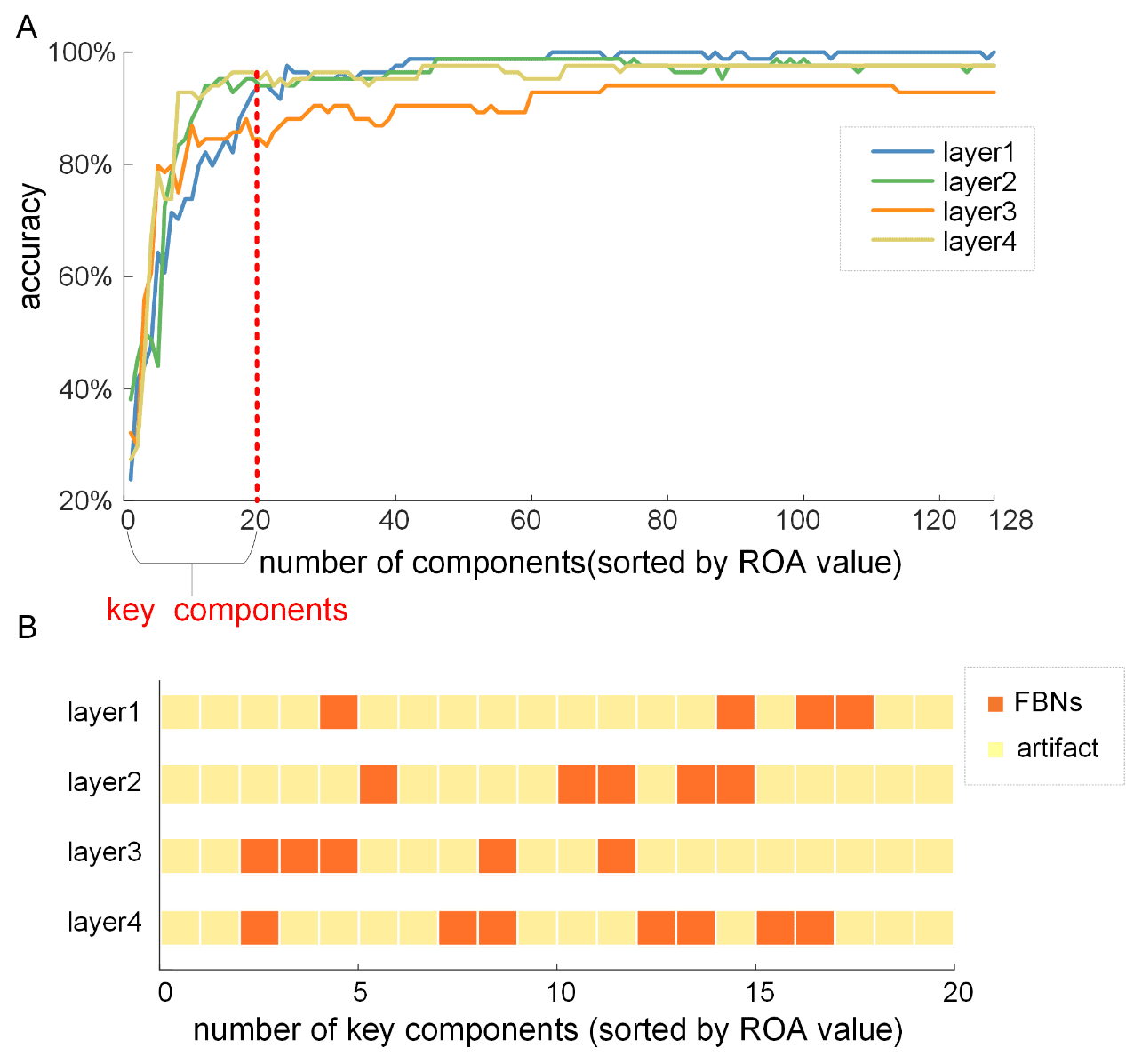
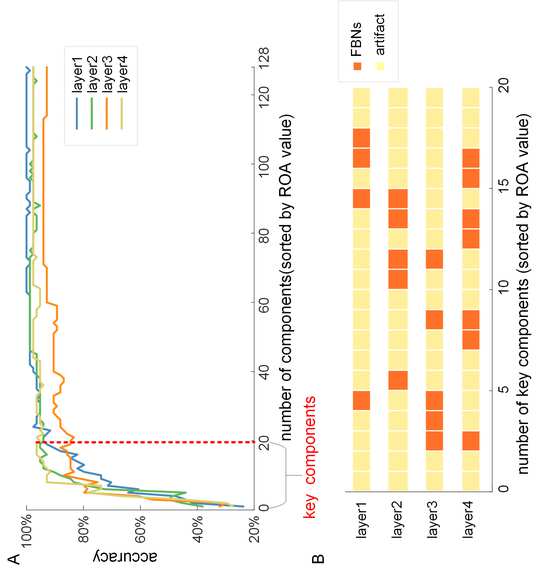
M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
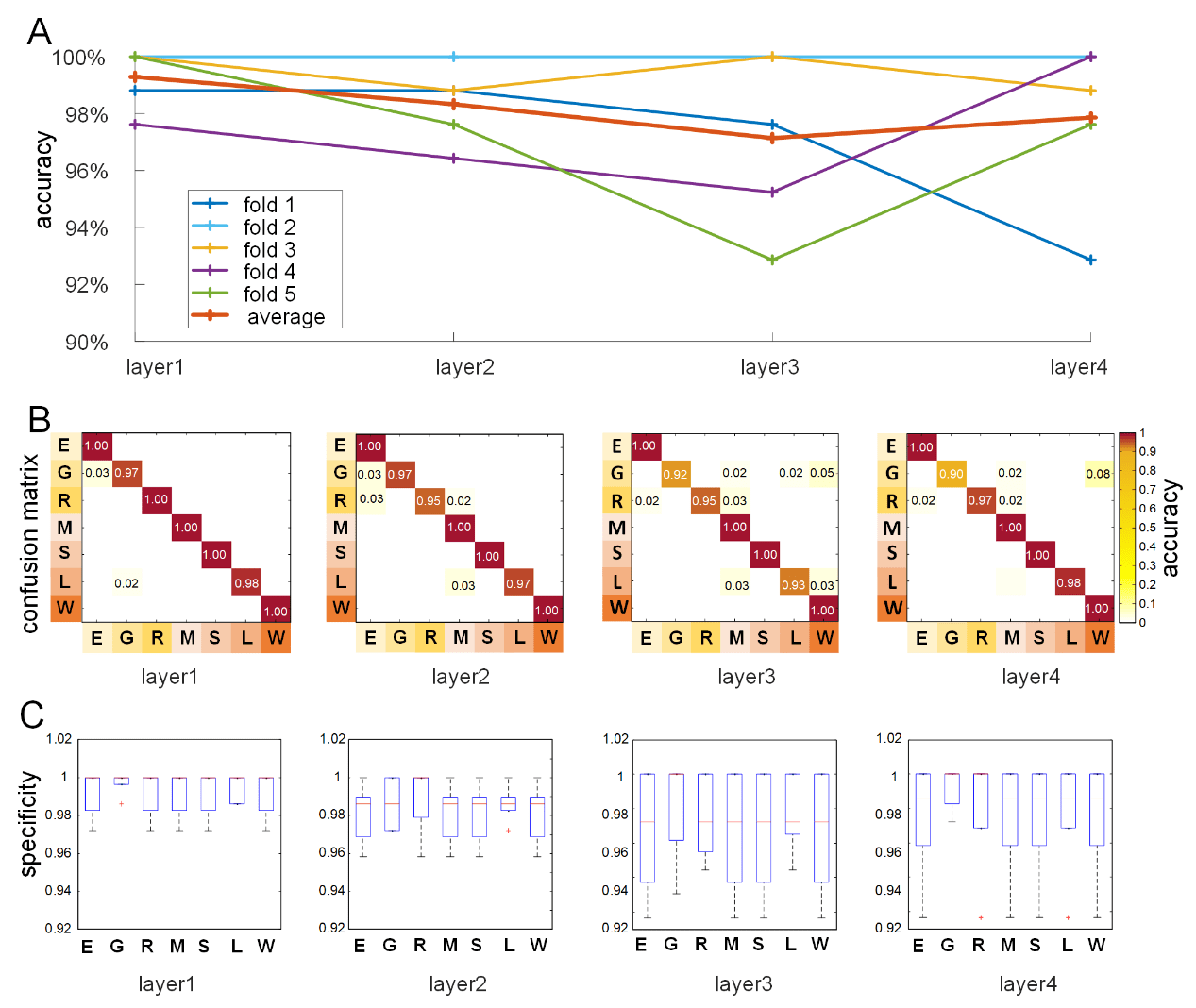
e
–
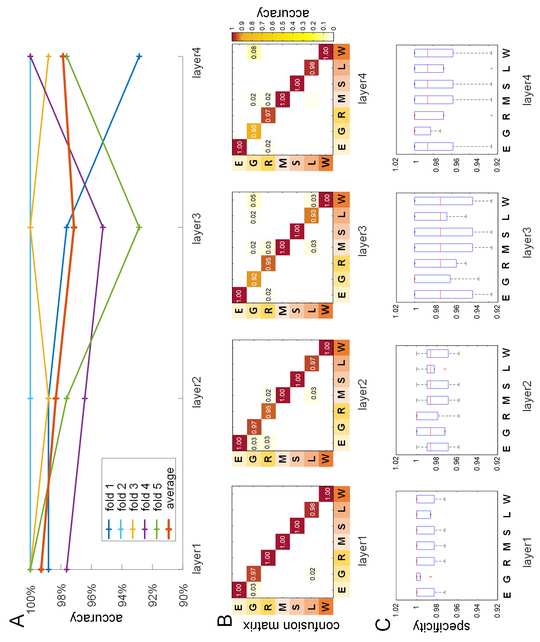
P
D

l

F
/

D
Ö

ich
/

.

/

/

T

1
0
1
1
6
2
N
e
N
_
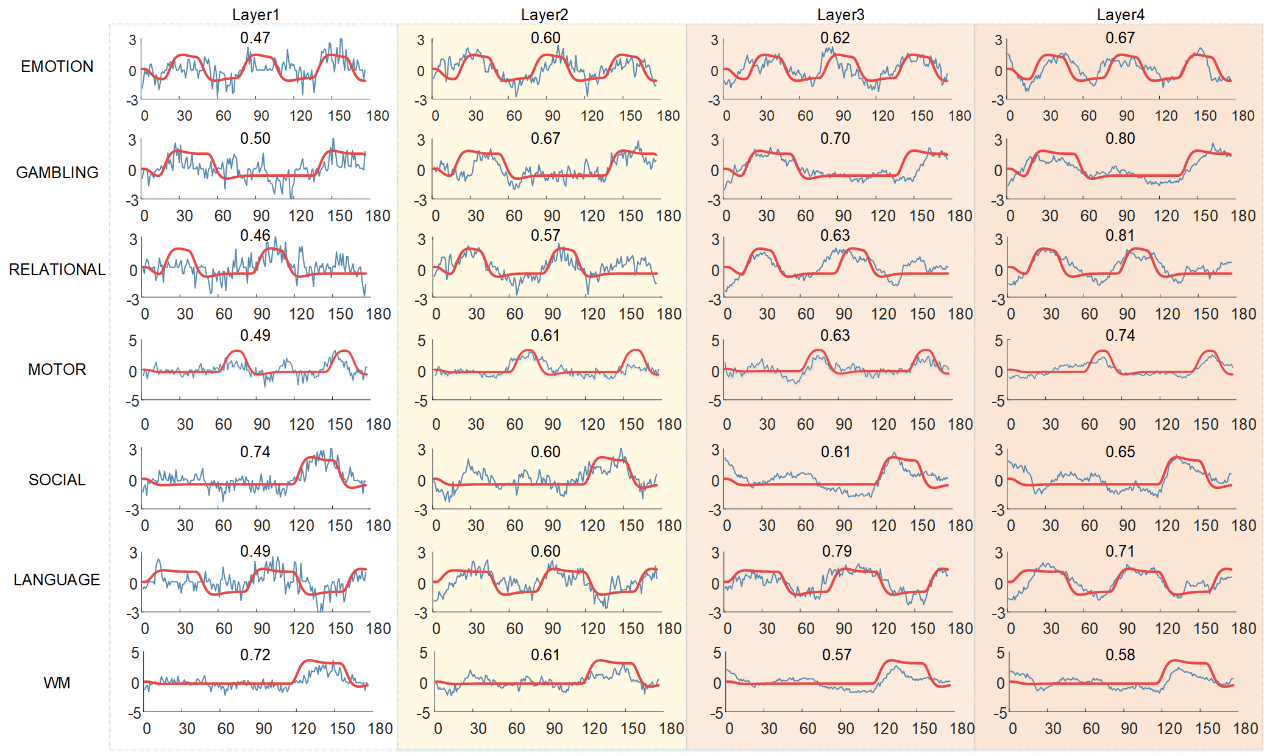
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
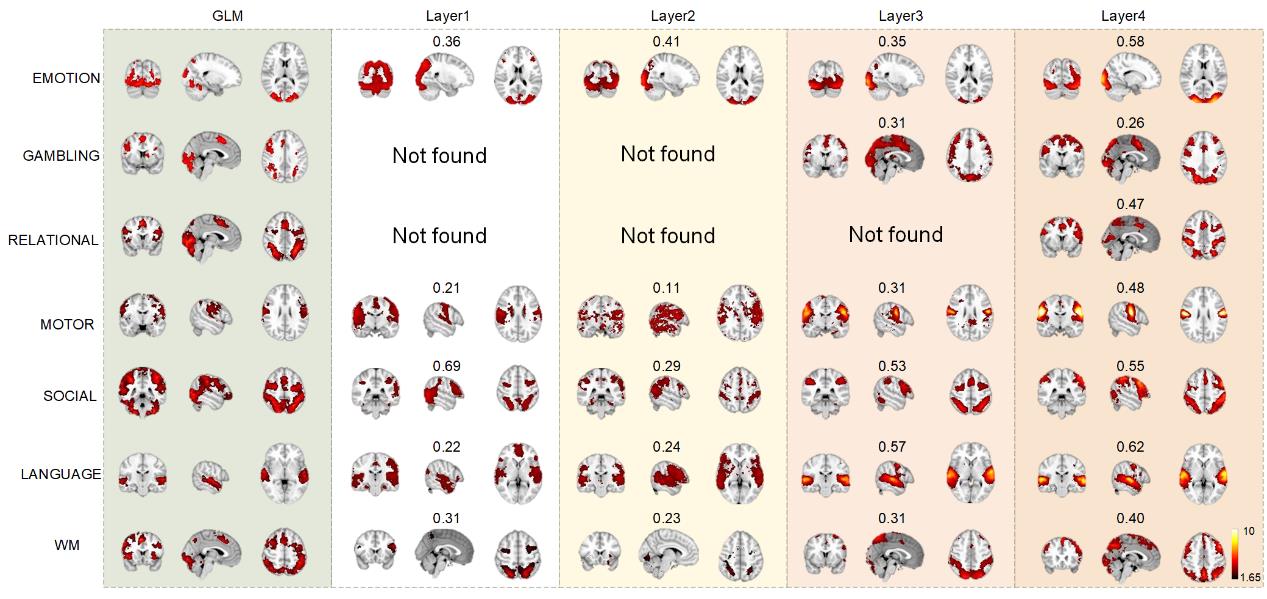
P
D

T

.

/

F

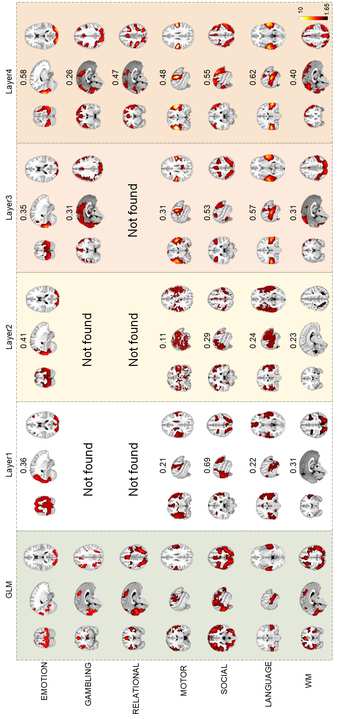
B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

65

has determined that the key components for multi-task classification tend to be functional brain

66

Netzwerke (FBNs) (Song, Ren, Hou, Er, & Liu, 2022). Another research has shown that artifact

67

components such as movement-related artifacts are significantly more informative with respect

68

to the classification accuracy of the multi-task electroencephalogram (EEG) Signale

69

(McDermott et al., 2021). Jedoch, uncovering the interpretable key features in decoding

70

tfMRI signals has received much less attention.

71

Due to the pitfalls in existing research, it is desirable to develop an appropriate framework

72

capable of identifying the interpretable and discriminative fMRI composition patterns

73

embedded in multi-task fMRI data. Daher, in this study, we aim to extract both multi-level

74

group-wise temporal features and spatial features from tfMRI signals, and define interpretable

75

classification features for multi-task fMRI data simultaneously. Recent studies have revealed

76

that the deep belief network (DBN) can effectively identify multi-layer spatial and temporal

77

features from fMRI signals (Dong, 2020; Ren et al., 2021), which is typically stacked by

78

multiple Boltzmann machine (RBM) (Geoffrey E Hinton & Sejnowski, 1986) and thus can

79

naturally act as a multi-level feature extractor. Außerdem, these prior studies have integrated

80

the least absolute shrinkage and selection operator (LASSO) regression with the DBN model,

81

indicating the efficacy of LASSO regression in extracting relevant spatial patterns. Daher, Wir

82

here proposed a novel two-stage feature extraction framework based on hybrid DBN and sparse

83

representations framework (DBN-SR) to decode multi-task fMRI signals with the capability of

84

extracting multi-scale deep features. Speziell, the DBN model was utilized to capture multi-

85

level group-wise temporal features, based on which the individual spatial features were

86

estimated by LASSO regression. Subsequently, a sparse representation method that combines

4

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

87

dictionary learning and LASSO regression was utilized to further characterize the group-wise

88

spatial features and individual spatio-temporal features for the purpose of classification. Based

89

on the correspondence between the individual classification features and the group-wise spatial

90

Merkmale, a relationship between the decoding capability of classification features and their

91

spatial patterns can be effectively established, which can facilitate the interpretation of neural

92

implications associated with the classification features. Endlich, due to its strong generalization

93

capabilities in small sample sizes, SVM was employed for the multi-class classification task.

94

Our results demonstrated that the proposed framework could successfully classify seven

95

task fMRI signals on a relatively small dataset. Darüber hinaus, by taking advantage of DBN in

96

extracting mid-level and high-level features and sparse coding in brain functional network

97

representation (Lv, Jiang, Li, Zhu, Chen, et al., 2015; Ren et al., 2021; Song et al., 2022), unser

98

framework could effectively characterize the multi-level spatiotemporal features embedded in

99

multi-task fMRI signals, which provides the bases to identify the interpretable key components

100

for well characterizing and differentiating multi-task signals. Gesamt, the proposed model can

101

disclose the underlying neural implications of key components with greater classification

102

Kapazität, offering an effective and interpretable methodology for decoding fMRI data.

103

Materials and methods

104

Overview

105

The framework of our proposed method is illustrated in Figure 1. The pipeline of the proposed

106

framework can divide into four stages: 1) individual data preparation; 2) data preparation for

5

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

T

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

107

five-fold cross-validation; 3) training and testing process; 4) SVM-based classification and

108

Ratio of activation (ROA) Analyse (Feige. 1A). In the data preparation stage, each individual’s

109

tfMRI data of seven different tasks were extracted and then spatially concatenated to one signal

110

Matrix (the first panel in Fig. 1A). In this work, five-fold cross-validation was performed for

111

model validation, thus the whole dataset was randomly divided into five folds (the second panel

112

in Fig. 1A). In training process, four folds were served as training set, and the tfMRI signal

113

matrices of all the subjects in training set were spatially concatenated to a multi-subject signal

114

Matrix. Dann, the DBN model was applied to training set to derive the weight matrix W, welche

115

served as group-wise temporal features 𝑫1. Dann, the LASSO regression aims to extract the

116

corresponding loading coefficient 𝜶1 based on the defined temporal dictionary 𝑫1 . In the

117

second stage of our model, the loading coefficient 𝜶1 was employed as input to sparse

118

Darstellungen (SR) Modell, where they were decomposed into group-wise dictionaries 𝑫2 and

119

loading coefficient 𝜶2. In testing process, the individual signal matrix in testing set and the

120

group-wise dictionary 𝑫1 obtained during the training phase was utilized as the inputs to the

121

LASSO regression. This yielded the loading coefficients 𝜶𝑡𝑒𝑠𝑡

1

. Subsequently, employing 𝜶𝑡𝑒𝑠𝑡

1

122

and the 𝑫2 obtained during the training phase, we performed a second LASSO regression to

123

obtain 𝜶𝑡𝑒𝑠𝑡

2

, which were then used as the classification features for the testing subjects (Die

124

third panel in Fig. 1A). Note that during the training phase, we utilized the independent training

125

data to learn and train regularization parameters employed for LASSO regression, sowie

126

the group-wise dictionaries 𝑫1 and 𝑫2 , without using any information from the test data.

127

Nachher, to further assess the multi-task fMRI data classification performance of proposed

128

Modell, the loading coefficient 𝜶2 derived from training set was used to train support vector

6

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

.

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

129

machine (SVM) for classification, where the loading coefficient 𝜶𝑡𝑒𝑠𝑡

2

derived from testing set

130

was then fed into this trained SVM model to identify the testing set labels (the last panel in Fig.

131

1A).

132

Our DBN-SR based framework can also identify the multi-level temporal features, spatial

133

Merkmale, and features for multi-task classification (Feige. 1B). Speziell, the DBN model took

134

fMRI time series from training data as input and produced a weight matrix W for each layer

135

jeweils, which represent the multi-layer temporal features of group-wise tfMRI signals

136

(the first two panels in Fig. 1B). These multi-layer temporal features W were served as the

137

temporal dictionary 𝑫1 and used as input to the LASSO algorithm to regress corresponding

138

loading coefficient 𝜶1, which represents individual-level spatial patterns (the third panel in Fig.

139

1B). Nächste, the loading coefficient 𝜶1 was used as the input of SR stage to derive the common

140

dictionary 𝑫2 and the loading coefficient 𝜶2, which represent group-wise spatial patterns and

141

features for multi-task classification for each layer, jeweils (the last three panels in Fig.

142

1B).

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

T

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

7

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

143

Figur 1. The overview of hybrid deep belief network and sparse representation framework

144

(DBN-SR). (A) The pipeline of multi-task fMRI data classification analysis via the proposed

145

Modell. The seven capital letters refer to seven different tasks respectively (E: emotion, G:

146

gambling, R: relational, M: motor, L: Sprache, S: sozial, and W: work memory). (B) Der

147

detailed illustration of using DBN and SR model to extract multi-level temporal features,

148

spatial features, and features for classification from multi-task fMRI signals. In the second

149

block, the blue line represents temporal features derived from the weights of DBN, während die

150

red line represents task design paradigms.

8

151

Data acquisition and preprocessing

152

We employed the seven task fMRI data from Q1 release of Human Connectome Project (HCP)

153

in this study (Barch et al., 2013). The details of tfMRI data acquisition and preprocessing

154

pipeline could be referred to our previous study (Song et al., 2022).

155

Speziell, the seven tasks are emotion, gambling, relational, motor, Sprache, sozial,

156

and working memory (WM). The number of time points for each task is shown in Table 1. Als

157

the tfMRI data consist of different time points, we truncated all tfMRI signals to the same time

158

Länge (176 frames). In this work, 60 subjects were used from the released dataset

159

Table1. Details of the condition and frames for seven tasks

TASK

EMOTION GAMBLING RELATIONAL MOTOR

LANGUAGE

SOCIAL WM

Condition

Frames

2

176

2

253

2

232

6

284

2

316

2

8

274

405

160

The truncation preprocessing, unavoidably, influences the integrity of task design. Für

161

Beispiel, four conditions are excluded from the WM task due to data truncation. dennoch,

162

in terms of other tasks, the truncated tfMRI data include not less than one block for all events

163

(sFig. 1).

164

Data preparation

165

Erste, we extracted the whole-brain fMRI signal for each subject using the standard MNI152

166

template as the mask, resulting in each 2-dimensional matrix. Then the signal matrices of the

167

168

seven tasks for each subject were spatially concatenated into a large matrix 𝑺𝑖

1 (𝑺𝑖

1= [𝑺𝑖,𝐸

1 ,
1 , 𝑺𝑖,𝐺

1 , 𝑺𝑖,𝑀
𝑺𝑖,𝑅

1 , 𝑺𝑖,𝐿

1 , 𝑺𝑖,𝑆

1 , 𝑺𝑖,𝑊

1 ] ∈𝑅t×(n×7), where 𝑺𝑖,𝐸

1 ∈𝑅t×n had 𝑡 time points and 𝑛 voxels. Der

169

seven capital letter subscripts refer to seven different tasks respectively (E: emotion, G:

9

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

.

/

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

170

gambling, R: relational, M: motor, L: Sprache, S: sozial, and W: work memory). TfMRI time

171

series for each voxel were normalized to derive zero mean and unit norm. In this work, five-

172

fold cross-validation scheme was chosen. Daher, 60 subjects were randomly divided into five

173

equal folds. In each iteration, one fold (12 Fächer) was taken for testing and the rest four (48

174

Fächer) for training. It is noteworthy that the training and testing sets for each iteration were

175

completely independent. Dann, the multi-task fMRI signal matrices of all the subjects in the

176

1 ,
training set were spatially concatenated to compose a multi-subject fMRI matrix 𝑺1 = [𝑺1

177

178

1,…, 𝑺𝑝
𝑺2

1] ∈𝑅t×(n×7×𝑝), where 𝑝 is the number of training subjects (𝑝 = 48 ) (Feige. 1A).

As whole-brain fMRI data generally contain enormous voxels, the group-wise tfMRI

179

signals consisting of multiple tasks and subjects exhibit relatively high dimensionality,

180

inevitably resulting in an overloaded computational burden and memory consumption. To

181

tackle these problems, we randomly selected only 10% of voxels’ whole-brain signals for each

182

subject in training stage (Huan Liu 2017; Song et al., 2022). To ensure the uniform distribution

183

of sampled voxels across different brain regions, we employed the Fisher-Yates shuffle

184

algorithm implemented by the “randperm” function in MATLAB, known for generating

185

random permutations with a uniform distribution (Fischer & Yates, 1938). The distribution of

186

the randomly selected 10% voxels across all subjects can be found in the Supplementary

187

Materials (sFig. 6-7).

188

Deep belief network model-based analysis

189

In this work, we chose DBN to extract group-wise temporal features based on previous research

190

demonstrating its ability to identify meaningful FBNs (Qiang et al., 2020; Ren et al., 2021). In

10

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

.

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

191

allgemein, DBN can be regarded as stacked blocks of Restricted Boltzmann Machines (RBM) (G.

192

E. Hinton, Osindero, & Teh, 2006), an energy-based probability generation model that

193

simulates the potential distribution of input data via interactions between visible and hidden

194

Variablen. While units between visible layer 𝑣 and hidden layer ℎ are connected by weights,

195

there is no connection within the layer. As a multiple stacked RBM model, the DBN model is

196

designed to learn and train weights for each layer. As described in Asja Fischer (2012) and X.

197

Hu et al. (2018), the energy function of the DBN model adopted to update the weights layer by

198

layer is defined as follows:

199

𝐸(𝑣, ℎ) = ∑ 𝑏𝑖𝑣𝑖 − ∑ 𝑏𝑗ℎ𝑗 − ∑ 𝑣𝑗ℎ𝑗𝑤𝑗

(1)

200

Where 𝑣𝑖 and ℎ𝑗 refer to the activation state of two layers; 𝑏𝑖 and 𝑏𝑗 represent their bias; 𝑤𝑗

201

indicate the weight between layer 𝑖 and layer 𝑗.

202

As introduced in the previous section, the tfMRI signals of randomly selected 10% voxels

203

in each individual’s whole brain of multi-task in training set were spatially concatenated to

204

generate a multi-subject fMRI matrix for model training, and thus the group-wise tfMRI time

205

Serie (176 time points) were taken as training samples for the DBN model. In our work, Die

206

neural architecture of DBN model was set as 4 layers and 128 neurons experimentally and

207

empirically (see Parameter Selection part). Speziell, the number of visible variables 𝑡 is the

208

same as the number of time points of fMRI signal (d.h., 176 in our study), und die Anzahl der

209

hidden variables 𝑘1 in each hidden layer represents the number of latent components expressed

210

in fMRI data (𝑘1=128). The DBN model was adopted to model group-wise tfMRI matrix 𝑺1

211

to obtain a weight matrix 𝑤𝑗 from each layer. The weight matrix of visible layer is represented

212

by 𝑤1𝜖𝑅𝑡×𝑘1, and the weight matrix of each hidden layer refers to 𝑤𝑗𝜖𝑅𝑘1×𝑘1 (𝑗 =2,3,4). Der

11

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

.

T

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

213

multi-layer temporal features 𝑊𝑗 in each layer of DBN model can be derived by successive

214

multiplication of the weight matrices on the adjacent layers ( 𝑊𝑗𝜖𝑅𝑡×𝑘1 ), that is,

215

𝑊4 = 𝑤4 ∗ 𝑤3 ∗ 𝑤2 ∗ 𝑤1 , 𝑊3 = 𝑤3 ∗ 𝑤2 ∗ 𝑤1 , 𝑊2 = 𝑤2 ∗ 𝑤1 , 𝑊1 = 𝑤1. Since each sample

216

input to the DBN model consists of all time points for each voxel, the weights 𝑤𝑗 (𝑗 =1,2,3,4)

217

across 4 layers represent the temporal features of the input fMRI data at different levels of

218

abstraction. Daher, the successive multiplication of weight matrix 𝑊𝑗 (𝑗 =1,2,3,4) obtained from

219

each layer of the DBN model represents multi-level temporal features embedded in fMRI

220

Signale.

221

Drawing inspiration from the successful application of LASSO regression for deriving

222

spatial features in previous studies (Haufe et al., 2014; Lee, Jeong, & Ye, 2013), we performed

223

the LASSO regression to derive individual spatial features. Speziell, the multi-layer

224

temporal features 𝑊𝑗 derived by the DBN model were normalized and then served as the

225

temporal dictionary 𝑫1𝜖𝑅𝑡×𝑘1 (Calhoun et al., 2001; Tibshirani, 2011). Hier, as the successive

226

multiplication of weight matrices leads to the larger scale of deeper dictionaries, A

227

normalization procedure ensures reasonable performance of LASSO regression at the same

228

scale. Subsequently, we employed the original individual signal matrix 𝑺𝑖 (𝑖 ∈1, 2, …, P),

229

along with the temporal dictionary 𝑫1 as input to the LASSO algorithm, which produce the

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

.

T

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

230

dazugehörigen

individual

loading coefficient 𝜶𝑖

1 (𝜶𝑖

1 ∈ 𝑅𝑘1×n, n=228453). Since 𝑫1

231

1
incorporates the group-wise temporal features, the resulting individual loading coefficients 𝜶𝑖

232

obtained through regression can be considered as spatial sparse representations of each

233

individual’s fMRI signals 𝑺𝑖 on the common temporal dictionary 𝑫1 . Folglich, Die

234

individual loading coefficients 𝜶𝑖

1 represent the individual spatial features. Hier, all the loading

12

235

236

237

coefficient matrix derived from LASSO regression refers to 𝜶1 (𝜶1=[𝜶1

1, 𝜶2

1, …, 𝜶𝑖

1, …, 𝜶𝑝
1 ]

∈𝑅 k1×(n×7×𝑝), 𝜶𝑖

1= [𝜶𝑖,𝐸

1 , 𝜶𝑖,𝐺

1 , 𝜶𝑖,𝑅

1 , 𝜶𝑖,𝑀

1 , 𝜶𝑖,𝐿

1 , 𝜶𝑖,𝑆

1 , 𝜶𝑖,𝑊

1 ]∈𝑅k1×(n×7).

Ähnlich, in order to derive the loading coefficient matrix 𝜶𝑡𝑒𝑠𝑡

1

for testing set of each

238

layer, the group-wise time-series dictionary matrix 𝑫1 derived from the training stage was

239

applied to model 𝑺𝑡𝑒𝑠𝑡

1

to obtain 𝜶𝑡𝑒𝑠𝑡

1

by resolving a typical l-1 regularized LASSO problem.

240

In this work, the regularization parameter 𝜆 1 of LASSO regression was set as 0.1

241

experimentally and empirically.

242

Sparse Representation model

243

Although we successfully obtained individual loading coefficient matrices 𝜶1 and 𝜶𝑡𝑒𝑠𝑡

1

244

through LASSO regression for the training and testing sets, jeweils, these features were

245

unsuitable for classification due to their high dimensionality (𝜶1 ∈ 𝑅𝑘1×n, 𝑘1=128, n=228453).

246

daher, our next goal was to extract the multi-level group-wise spatial patterns based on the

247

individual spatial patterns, and finally excavate multi-level features for multi-task classification

248

that could distinguish multi-task fMRI signals and reveal the distinctive organization patterns

249

of different task stimulations. Hier, we adopted a sparse representation based model, welche

250

has already been proven as an effective algorithm in previous research to identify the intrinsic

251

spatial functional patterns and features for multi-task classification from fMRI data (Song et

252

al., 2022; S. Zhang et al., 2016). Speziell, we first aggregated all the loading coefficient

253

matrices 𝜶𝑖

1 of all the subjects into one matrix 𝑺2 for each layer of the DBN model (𝑺2= [𝑺1
2,

254

255

2,…,𝑺𝑖
𝑺2

2,…, 𝑺𝑝

2] ∈𝑅k1×(n×7×p), where 𝑺𝑖

2= [(𝜶𝑖,𝐸

1 )T , (𝜶𝑖,𝐺

1 )T, (𝜶𝑖,𝑅

1 )T, (𝜶𝑖,𝑀

1 )T, (𝜶𝑖,𝐿

1 )T, (𝜶𝑖,𝑆

1 )T,

1 )T] ∈𝑅n×(7×k1). Dann, 𝑺2 would be served as the input for dictionary learning and sparse

(𝜶𝑖,𝑊

13

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

256

representation to derive a group-wise spatial dictionary 𝑫2∈𝑅n×k2 and the corresponding

257

loading coefficients 𝜶2 for each layer, jeweils. Note that 𝑘2 represents the number of

258

259

dictionary atoms, which was set as the same value as 𝑘1 (𝑘2 =128). Hier, 𝜶𝟐 =[𝜶1

2 , 𝜶2

2 , …,

𝜶𝑖

2 , …, 𝜶𝑝

2 ]∈𝑅k2 ×(k1 ×7×p) , where 𝜶𝑖

2 =[𝜶𝑖,𝐸

2 , 𝜶𝑖,𝐺

2 , 𝜶𝑖,𝑅

2 , 𝜶𝑖,𝑀

2 , 𝜶𝑖,𝐿

2 , 𝜶𝑖,𝑆

2 , 𝜶𝑖,𝑊

2 ]∈𝑅k2 ×k1 ×7 .

260

The loss function of sparse representation model yields a sparse resolution constraint on the

261

loading coefficient 𝜶 2 with an l1 regularization (Eq. (2)), where 𝜆 2 is a regularization

262

parameter that can balance the regression residual and sparsity level. 𝜆 2 was set as 0.05.

263

264

𝑀𝑖𝑛

1

2

‖𝑺2 − 𝑫2𝜶2‖𝐹

2 + λ2‖𝜶2‖1,1

(2)

To prevent 𝑫2 from arbitrarily large values that cause the trivial solution of the

265

optimization, the columns 𝑑 1, 𝑑 2, …, 𝑑 k are restricted by Equation (3).

266

267

𝐶 ≜ {𝑫2∈𝑅t×k2,𝑠 .𝑡 .∀𝑗 = 1,⋯,𝑘 2 , 𝑑𝑗

𝑇𝑑𝑗 ≤ 1}

(3)

As the dictionary 𝑫2 was obtained by a sparse representation of 𝜶𝟏, which comprise all

268

individual spatial features, the learned dictionary 𝑫2consequently represents the group-wise

269

spatial features. Correspondingly, 𝜶𝑖

2 was a sparse representation on the common spatial

270

dictionary 𝑫2 . Given the ability of a sparse representation model to effectively reduce the

271

dimensionality of raw fMRI data while retaining its essential information, the resulting intrinsic

272

Merkmale (𝜶𝑖

2) derived from the extraction of common temporal and spatial dictionaries can

273

effectively capture the variations in spatio-temporal patterns of functional brain activity across

274

different tasks. Infolge, these intrinsic features were suitable for multi-task classification.

275

To derive the 𝜶𝑡𝑒𝑠𝑡

2

of testing set for post-hoc classification analysis, we also leveraged

276

the LASSO regression algorithm for each layer. Speziell, the loading coefficient matrix

277

1
𝜶𝑡𝑒𝑠𝑡

was regarded as the input matrix 𝑺𝑡𝑒𝑠𝑡

2

, and the dictionary matrix 𝑫2 derived from the

14

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

.

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

/

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

278

training stage was employed to model 𝑺𝑡𝑒𝑠𝑡

2

to learn the loading coefficient 𝜶𝑡𝑒𝑠𝑡

2

. All the

279

parameters in testing stage were set the same as in the training stage.

280

Parameter Selection

281

The determination of hyperparameters, such as the number of cross-validation folds, Die

282

number of layers and neurons of the DBN model, and the regularization parameters of the

283

sparse representation model, was accomplished through a combination of referring to previous

284

studies and learning from the training set, the testing set was not involved in any parameter

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

285

selection process.

286

The choice of cross-validation folds is crucial as it offers a trade-off between precision

287

and computational cost for performance estimation (Hansen et al., 2013). Commonly used

288

cross-validation folds in current machine learning experiments often include 2-fold, 5-fold, 10-

289

fold, or the leave-one-out method. In theory, while some studies suggest the 10-fold or leave-

290

one-out method may provide a higher estimated accuracy (Kohavi, 1995), some reveals that 5-

291

fold or 10-fold is the optimal choice for balancing computational cost and accuracy (Hansen et

292

al., 2013). Jedoch, due to the need for our framework to combine all individuals within the

293

training set to extract group-wise temporal features during training phase, the computational

294

resource demands of the 10-fold or leave-one-out method are greater. daher, we opted for

295

the 5-fold approach. To further validate our selection, we conducted a comparative analysis

296

between the 2-fold and 5-fold to assess the decoding accuracy. The findings revealed that the

297

average decoding rate was slightly lower for the 2-fold compared to the 5-fold, providing

298

additional confirmation of our initial selection. (sTab. 1).

15

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

299

Our selection of a 4-layer, 128-neuron DBN structure was set based on our previous study

300

utilizing the neural architecture search technique (NAS) for recognizing spatio-temporal

301

features from fMRI data (Xu, Ren, Tao, Song, & Er, 2022),which effectively determined the

302

optimal structure for DBN model with 3 layers and 120-150 Neuronen. daher, in our study,

303

we defined the number of neurons as 128 and experimented with both 3-layer and 4-layer

304

configurations to extract meaningful task-related temporal features. Speziell, we compared

305

the group-wise temporal features derived from DBN model with 3-layer and 4-layer structures,

306

in terms of their Pearson correlation coefficient (PCC) with task paradigm curve, based on

307

training set (fold 5). The results revealed that the 4-layer DBN outperformed in capturing

308

temporal features, as indicated by the higher PCC values observed in 4-layer structure (Tab. 2).

309

In terms of selecting the number of neurons, we took into consideration computational

310

efficiency. We determined that selecting 128 Neuronen, a power of two within the desired range

311

von 120-150, would optimize computational speed. Somit, we concluded that the optimal

312

configuration for the DBN model with 128 neurons and 4 layers.

313

The regularization parameter (λ) plays a crucial role in sparse representation and LASSO

314

regression. Although no golden standard exists for determining the value of λ, previous studies

315

on FBN recognition have experimentally set λ within the range of 0.05 Zu 0.5 (Fangfei Ge,

316

2018; Lv, Jiang, Li, Zhu, Chen, et al., 2015; Shu Zhang 2017). In our previous work on task

317

fMRI data classification using a two-stage sparse representation approach, we conducted

318

parameter selection experiments within the range of λ from 0.05 Zu 0.5 and found that the

319

highest accuracy was achieved when λ1=0.1 and λ2=0.05 or 0.1 (Song et al., 2022). Hier, λ1

320

and λ2 represent the regularization parameters for the LASSO regression and sparse

16

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

.

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

321

representation, jeweils. daher, in this study, we determined the λ1 as 0.1, Und

322

systematically changed the setting of the regularization parameter in the sparse representation

323

λ2 (λ2=0.05, 0.1) while evaluating their impact on the obtained group-wise spatial features

324

derived from training set (fold 5). The results showed that when λ2 was set to 0.05, a greater

325

number of FBNs could be identified in the group-wise spatial features 𝑫2 by comparison with

326

the general linear model (GLM) -derived activation patterns (Tab. 3). Folglich, we set

327

λ1=0.1 and λ2=0.05 as regularization parameters for LASSO regression and sparse

328

representation stage, jeweils. To further validate this, we assessed the classification

329

accuracy on testing dataset using these two different λ2 values (0.05, 0.1) while keeping λ1=0.1

330

for all 5 folds. The results demonstrated that λ2=0.05 achieved higher accuracy, reconfirming

331

our choice (sTab. 2).

332

Tisch 2. Comparison of Pearson correlation coefficient (PCC) for 3-layer structure and

333

4-layer structure.

Structure
3-layer

4-layer

Layer1
0.48±0.12

0.55±0.00

Layer2
0.52±0.06

0.63±0.01

Layer3
0.50±0.06

0.66±0.03

Layer4

0.71±0.02

Mean±SD
0.50±0.08

0.64±0.02

334

Tisch 3. Comparison of the number of identified FBNs cross each layer for different λ2

335

Werte.

λ2
0.05

0.1

Layer1
15

12

Layer2
17

13

Layer3
22

18

Layer4
45

27

336

Identification of multi-level temporal patterns

337

As mentioned in the “Deep belief network model based analysis” section, 𝑊𝑗 of the 𝑗-th hidden

338

layer (𝑗 = 1,2,3,4) represents the temporal features of group-wise tfMRI for respective layer

17

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

/

T

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

/

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

339

(Feige. 1B). Here we used PCC as a metric to identify the task-related temporal features (Benesty,

340

Chen, Huang, & Cohen, 2009; Lv, Jiang, Li, Zhu, Chen, et al., 2015). Speziell, we first

341

calculated the task paradigm curves convolved with hemodynamic response function (HRF).

342

Nächste, we computed the PCC values between the convolved task paradigm curves and the atoms

343

in the group-wise temporal features 𝑫1 derived from the DBN model, following standard

344

procedures employed in previous studies (Kay, Rokem, Winawer, Dougherty, & Wandell, 2013;

345

O’Reilly, Woolrich, Behrens, Schmied, & Johansen-Berg, 2012). The PCC of the identified

346

temporal features and the task-based stimulus can be defined as Equation (4).

347

348

1
Pcorr, c =corr (𝑫𝑐

, TASK)

(4)

Hier, 𝑫𝑐

1 refers to the c-th component in temporal features 𝑫1 derived from DBN stage (c = 1,

349

⋯,𝑘 1). TASK represents the task paradigm curves convolved with HRF. Im Wesentlichen, Pcorr, C,

350

measures the temporal similarity between the temporal patterns of 𝑫𝑐

1 and the task stimulus.

351

The atoms with the highest PCC value in group-wise temporal features 𝑫1 were chosen to

352

represent the multi-layer temporal features.

353

Identification of multi-level spatial patterns

354

The multi-level spatial patterns can also be identified in the second stage of sparse

355

356

representation model. Speziell, the 𝑺𝑖,𝑡

1 can be factorized into 𝑫1 and the loading

coefficient 𝜶𝑖,𝑡

1 , which represent the group-wise temporal features and the individual spatial

357

Merkmale, jeweils. Hier, 𝑖 refers to 𝑖 -th subjects (i∈1, 2, …, P, and p=48 in this work), 𝑡

358

means 𝑡 kind of task, 𝑡∈ 𝚽 = {E, G, R, 𝑀 , L, 𝑆 , W}. To further derive the group-wise spatial

359

Merkmale, the transposition of 𝜶1 could be then decomposed into 𝑫2 and 𝜶2 as shown in

18

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

T

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

360

361

Gleichung (5). Since the transpose of 𝜶𝑖,𝑡

1 can be expressed as dictionary 𝑫2 multiplied by

loading coefficient 𝜶𝑖,𝑡

2 (Gleichung (5)), the relationship between 𝑺𝑖,𝑡

1 and 𝑫1 , 𝑫2 , 𝜶2 can be

362

deduced as Equation (6) shown, which also consistent with previous studies (Huan Liu 2017;

363

Song et al., 2022).

364

365

366

2 = (𝜶𝑖,𝑦
𝑺𝑖,𝑡

2
1 )𝑇= 𝑫2 × 𝜶𝑖,𝑡

1 = 𝑫1×𝜶𝑖,𝑡
𝑺𝑖,𝑡

1 = 𝑫1 × (𝑫2 ×𝜶𝑖,𝑡

2 )𝑇

(5)

(6)

Since all subjects share the same group-wise temporal dictionary 𝑫1 , the common

367

dictionary 𝑫2 contained group-wise spatial patterns, of which atoms could be used to define

368

the FBNs. Daher, the corresponding multi-layer spatial features were derived from the common

369

dictionary 𝑫2 for each layer of the proposed framework (the fourth and fifth panels in Fig. 1B).

370

We then identified the spatial correlation coefficient (SCC) to quantify the similarity

371

between spatial patterns obtained from the proposed framework and the GLM -derived

372

activation patterns. Speziell, the GLM-based analysis was performed individually, followed

373

by group-wisely analysis using FSL FEAT (http://www.fmrib.ox.ac.uk/fsl/feat5/index.html).

374

The group-level GLM-based results were employed for comparison. More details of GLM

375

analysis are available in previous literature (Lv, Jiang, Li, Zhu, Zhang, et al., 2015). The SCC

376

is defined in Equation (7) (Ben J. Harrison, 2008; Zuo et al., 2010):

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

/

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

377

𝐑 (𝑿 , 𝑻 ) =

𝑛 (𝑋𝑝−𝑋̅)(𝑇𝑝−𝑇̅)
𝛴𝑝=1
2

√𝛴𝑝=1

𝑛 (𝑋𝑝−𝑋̅)

𝑛 (𝑇𝑝−𝑇̅)

⋅𝛴𝑝=1

2

(7)

378

where 𝑿 is the spatial functional network derived by the proposed framework, 𝑻 represents

379

the GLM-derived activation template, and 𝑛 refers to the number of voxels of whole brain.

19

380

SVM-based classification method

381

To further classify multi-task fMRI signals, we performed five-fold cross-validation to evaluate

382

the classification performance of the proposed framework. As the linear SVM has optimization

383

and generalization capability in limited sample sizes, as well as its proven effectiveness in

384

multi-class classification (Chang & Lin, 2011B; Jang et al., 2017), we conducted multi-task

385

classification analysis based on linear SVM classifier, which was established by the LIBSVM

386

toolbox (Chang & Lin, 2011A). For each layer, as the loading coefficient 𝜶2 contains both

387

temporal and spatial features embedded in fMRI signals, we first trained the SVM classifier

388

using 𝜶2 derived from training set, and then evaluated the classification performance by

389

feeding the 𝜶𝑡𝑒𝑠𝑡

2

of testing set into the trained SVM model. Based on the true label of seven

390

tasks for each loading coefficient 𝜶𝑡𝑒𝑠𝑡

2

, the classification accuracy of each layer in each fold

391

was defined as the percentage of correctly predicted samples. The final classification accuracy

392

for each layer is the average of five folds for seven tasks. We then calculated the specificity of

393

each fold for each layer, and the final specificity for each layer is the average of the five folds.

394

ROA-based analysis

395

The further goal aimed at uncovering discriminative functional components for multi-task

396

classification. Inspired by the successful use of the Ratio of activation (ROA) in identifying

397

discriminative components for decoding resting state fMRI (rsfMRI) and tfMRI (S. Zhang et

398

al., 2016), we raised a novel ROA metric to identify the key components for seven-task

399

classification. The ROA of the 𝑗-th row in loading coefficients 𝜶2 could be defined as follows:

400

𝑁𝑡 = |𝜶2(𝑗, 𝑘)|0, 𝑘𝑡ℎ 𝑐𝑜𝑙𝑢𝑚𝑛 𝑏𝑒𝑙𝑜𝑛𝑔𝑠 𝑡𝑜 𝑡𝑎𝑠𝑘(𝑡)
20

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

T

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

/

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

401

402

403

ROA𝑗 = √1

𝑇

∑ (𝑁𝑡 − 𝑁𝑡̅̅̅)2

𝑇
𝑡=1

(8)

In Equation (8), 𝜶2 represent all the individual spatio-temporal features, 𝜶2= [𝜶1

2, 𝜶2

2, …,

𝜶𝑖

2, …, 𝜶𝑝

2]∈𝑅k2 ×(k1 ×7×p) (𝑘1= 𝑘2=128, p=48). 𝑖 refers to 𝑖 -th subject (𝑖 ∈1, 2, …, P). 𝑡

404

represents task index (t∈1, 2, …, 7), and 𝑇 represents the number of task paradigms (d.h., 7 In

405

unsere Arbeit). Task (𝑡) represents each of the seven different tasks. 𝑁𝑡 represents the activation

406

level for each task, and 𝑁𝑡̅̅̅ represents the average of 𝑁𝑡 (𝑡 = 1, ⋯,7). Hier, the activation level

407

𝑁𝑡 was defined by counting the number of non-zero entries marked as each task in the

408

corresponding each row vector of 𝜶2 (t∈1, 2, …, 7). As 𝜶2 is a sparse matrix, the task with a

409

higher count of nonzero elements in the row vectors of 𝜶2 is deemed to be more “active”.

410

daher, 𝑁𝑡 represents each task’s activation level in the row vectors of 𝜶2. The ROA was

411

calculated by counting the standard deviation of 𝑁𝑡 across the seven tasks. A larger ROA value

412

(d.h., larger standard deviation) indicates greater differences in activity levels across the seven

413

tfMRI signals, which were more discriminative for multi-task classification.

414

To validate that the components of higher ROA values capture greater capacity in

415

classifying the multi-task fMRI signals, an experiment was designed as illustrated below. Nach

416

sorting the ROA values for all components (d.h., rows in loading coefficients 𝜶2) from highest

417

to lowest, we iteratively adopted more rows sorted by their ROA values in 𝜶2 as feature inputs

418

for training the SVM classifier, das ist, the components with higher ROA values were used

419

preferentially for training. Afterwards, the corresponding components of 𝜶𝑡𝑒𝑠𝑡

2

from testing set

420

were entered into the trained SVM model to evaluate the classification accuracy. Speziell,

421

to define the key components with greater capacity for multi-task classification in each layer,

422

we have repeated this ROA analysis using 𝜶2 derived from each layer of proposed model. Hier

21

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

423

we applied the same classification scheme described in the previous section “SVM-based

424

classification method”.

425

After establishing the ROA metric for the classification features 𝜶2 , our subsequent

426

objective is to elucidate the neural implications of these classification features. Given that each

427

row of 𝜶2 corresponds to each column of 𝑫2 (d.h., each atom in 𝑫2), and these atoms can be

428

mapped back to brain space, we thus established a relationship between the brain activations

429

derived from the atoms in 𝑫2 and the ROA values of the row vectors of 𝜶2. This connection

430

allows us to interpret neural implications of classification features.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

431

Result

432

Classification performance of multi-task fMRI signals

433

By applying the proposed DBN-SR framework to multi-task fMRI data using five-fold cross-

434

validation strategy, our results reveal that the fMRI data of seven tasks can be accurately

435

classified. In detail, the classification accuracy for five-fold ranges from 92.86% Zu 100%, mit

436

an average accuracy of 97.86%±3.42% (Mean ± SD) in the layer 4 (Feige. 2A), welche

437

demonstrated the proposed framework can effectively uncover the inherent differences in

438

composition patterns of multi-task fMRI signals.

439

We also explored the classification performance based on features derived from each layer

440

of the proposed framework (Feige. 2). The trend of the classification accuracy curves for five

441

folds is relatively steady, with an average accuracy of 98.15%±0.90% (Mean±SD) (Feige. 2A).

442

Darüber hinaus, the average accuracies across five-fold from layer1 to layer4 are 99.29%, 98.33%,

22

443

97.14%, Und 97.86%, jeweils. We depicted confusion matrices for each layer to represent

444

the average classification accuracy of the seven tasks, as shown in Figure 2b. The results

445

indicate that all the average classification accuracies for seven tasks across five-fold are greater

446

als 95% in each layer, except for three major confusions, das ist, gambling task in layer 3 Und

447

layer 4, relational task in layer 2 and layer 3, and language task in layer 3 (Feige. 2B). Zusätzlich,

448

the specificity of classification results of the first two layers is slightly higher than that of the

449

deeper two layers (Feige. 2C). Gesamt, the classification performance of the shallower layers is

450

relatively better than that of the deeper layers.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

451

452

Figur 2. Classification performance. (A) The classification accuracy of five-fold in each layer.

453

(B) The average confusion matrices of five-fold cross-validation on the seven tasks. (C) Der

23

454

average specificity of five-fold cross-validation classification on the seven tasks.

455

Identified multi-level temporal and spatial patterns of multi-task fMRI signals

456

Multi-level temporal patterns

457

Our DBN-SR based framework can effectively identify the temporal patterns of multi-task

458

fMRI signals at multi-scale (Feige. 3). In each layer, we quantitatively compared the PCC of the

459

identified temporal features and each task-based stimulus. Those atoms with the highest PCC

460

value in temporal dictionary 𝑫1 were chosen to represent the task-related temporal patterns.

461

We randomly select one training fold as an example to show the representative temporal

462

patterns for each layer (fold 5) (Feige. 3). The average PCC values of seven tasks for all 5-fold

463

can be found in Supplemental Table 6.

464

The overall multi-level temporal patterns are relatively consistent with the task design

465

paradigms. Speziell, the average PCC of seven tasks from layer1 to layer4 is 0.55±0.12,

466

0.61±0.03, 0.65±0.07, and 0.71±0.08 (Mean ± SD), jeweils, where the highest correlation

467

is observed in layer4 (Feige. 3). Intriguingly, there exist gradient in the resolution of temporal

468

patterns derived from different layers. In the shallow layer, all the identified temporal patterns

469

are mixed with many random noises, resulting in a relatively poor correlation with task

470

paradigms. In comparison, in the deeper layer, the temporal patterns are smoother and more

471

consistent with the original task design curves, indicating that DBN-SR model can filter noises

472

in each layer while keeping useful information of brain activities, which agrees with the former

473

Forschung (H. Huang et al., 2018; Wei Zhang, 2020).

24

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

.

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

474

475

Figur 3. Comparison of group-wise temporal patterns for seven tasks across different layers,

476

including the identified temporal features (blue lines) and the task paradigms (red lines). Der

477

quantitative similarities (PCC) of identified temporal features with task paradigms are also

478

provided. The y-axis represents the stimulus response amplitude, while the x-axis represents

479

time point. The background colors represent different layers of our DBN-SR model. The lighter

480

colors represent shallower layers, while the darker colors represent deeper layers.

481

Multi-level spatial patterns

482

Our framework can also effectively identify the spatial patterns from different layers. Am meisten

483

predominant spatial patterns identified by the proposed framework are the task-evoked FBNs,

484

including emotion, gambling, relational, motor, sozial, Sprache, and working memory. In each

485

layer, we quantitatively compared the SCC of the identified spatial patterns and the GLM-

486

derived activation patterns. Those atoms with the highest SCC value in spatial dictionaries 𝑫2

487

were chosen to represent the spatial pattern. We randomly selected one training fold to illustrate

25

488

the representative FBNs for each layer (Feige. 4).

489

Gesamt, the spatial patterns are generally consistent with the GLM-derived activation

490

patterns, with increasingly precise resolution from shallow to deep layers. Quantitatively, Die

491

average SCC of seven tasks from layer1 to layer4 is 0.36±0.20, 0.26±0.11, 0.40±0.12, Und

492

0.48±0.12 (Mean ± SD), jeweils, where the highest SCC is observed in layer 4 (Feige. 4).

493

Intriguingly, there exist distinct differences among spatial patterns derived from different layers.

494

The spatial patterns across layers show a trend of increasing consistency with the GLM-derived

495

activation patterns, and are more compact in deeper layers for most tasks. In der Zwischenzeit, mehr

496

FBNs can be found in the deeper layers compared with shallow layer. Zum Beispiel, some FBNs

497

cannot be identified in the first three layers, such as FBNs related to gambling and relational

498

tasks (Feige. 4).

499

Figur

500

4.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

501

Comparison of group-wise spatial patterns for seven tasks across different layers. The spatial

502

correlation coefficient (SCC) between each identified spatial pattern and GLM-derived

503

activation pattern is labeled on top of each brain map.

504

505

Apart from FBNs, the proposed framework can also effectively detect various artifact-

related components. Speziell, the atoms in spatial dictionary 𝑫2 can represent the group-
26

506

wise spatial features and can be mapped back to the 3D brain volume. Subsequently, Wir

507

manually inspected whether spatial map matched the known types of artifacts based on

508

previous study (Salimi-Khorshidi et al., 2014). Through this process, we found several artifact-

509

related components, including movement-related, cardiac-related, sagittal sinus, susceptibility-

510

Bewegung, white-matter, and MRI acquisition/reconstruction related (Feige. 5).

511

512

Figur 5. Identified artifact components, including movement-related, cardiac-related, sagittal

513

sinus, susceptibility-motion, white-matter, and MRI acquisition/reconstruction related.

514

Gesamt, our effective DBN-SR model is capable of characterizing the multi-level

515

spatiotemporal features of brain function. The quantitative analysis further demonstrates that,

516

in deeper layer, the representative temporal features correspond well with task design curves,

517

and the spatial features are relatively more consistent with the GLM-derived activation. In

518

addition to task-evoked functional components, our framework could also effectively identify

519

artifact components from group-wise multi-task fMRI data, laying the groundwork for further

520

research into the functional role of these components in multi-task classification.

521

Identification of discriminative features by ROA analysis

522

As depicted in the “ROA-based analysis” section, we first computed the ROA index by sorting

523

the ROA values of all the components in loading coefficients 𝜶2 of the training set, Dann, In

524

order to evaluate the classification performance, the corresponding components in the loading

27

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

525

coefficient 𝜶𝑡𝑒𝑠𝑡

2

of testing set were fed sequentially into the trained SVM classifier according

526

to the ROA index. Hier, the classification results of each layer on one randomly selected testing

527

fold dataset (fold 5) using different number of components, sorted by their ROA values, Sind

528

illustrated in Fig. 6A. While the number of components increases from 1 Zu 20, the accuracy

529

curves of four layers grow monotonically, and the average accuracy of all curves rises to

530

91.96%. When more than twenty components are included for classification, the accuracy

531

curves of four layers exhibit a plateau with accuracies reaching close to 100%, indicating that

532

the additional components with lower ROA values contribute less to the successful

533

classification of multi-task signals. Daher, the top twenty components with higher ROA values

534

can be regarded as key components for the classification task to some extent. Generally, unser

535

method can effectively disclose the key components with great classification capacity. In

536

addition, the findings are consistent across different testing folds, hence the additional results

537

of the other four folds are included in the Supplementary Materials (sFig2-5).

538

To further investigate the neural implications of key components with greater

539

classification capacity, we inspected the spatial patterns of the top twenty key components

540

identified by ROA analysis in each layer. By further analyzing the composition of the twenty

541

key components in each layer, we found that these key atoms are either FBNs or artifact-related

542

components, which were identified by visually examining their spatial patterns with established

543

templates and further calculating their SCC with GLM-derived activation maps.

544

Intriguingly, our results show that the top twenty key components in the four layers are

545

largely composed of artifacts, while the proportion of FBNs in key components is small as a

546

ganz. Andererseits, the proportion of FBNs is relatively higher in deeper layers compared

28

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

.

/

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

547

to shallower layers (Feige. 6B). This conclusion aligns with the findings when using the top 40

548

components as key components (sFig. 8).

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

549

550

Figur 6. ROA classification results in each layer (fold 5). (A) Classification accuracy for

551

SVM-based classification of four layers using the different number of components sorted by

552

their ROA values. (B) The composition of twenty key components sorted by ROA value across

553

each layer.

554

Diskussion

555

In this study, we proposed a hybrid spatio-temporal deep belief network and sparse

556

representation framework to decode multi-task fMRI signals on a relatively small cohort

29

557

dataset. Our framework could classify fMRI signals of seven tasks with high accuracy and

558

detect multi-level temporal patterns and FBNs, suggesting the effectiveness of the proposed

559

method. Zusätzlich, our framework can reveal key components including artifact components

560

and functional brain networks in multi-task classification and uncover their underlying

561

neurological implication.

562

Our proposed framework is composed of several elements, including DBN model,

563

LASSO regression, sparse representation, and SVM classifier, resulting in a relatively complex

564

Struktur. Trotzdem, our framework achieved a relatively higher classification accuracy in

565

comparison to prior research that also conducted classification of 7 task states on the HCP

566

dataset (X. Huang, Xiao, & Wu, 2021; Wang et al., 2020), while also yielding interpretable

567

classification components. Speziell, Wang et al. (2020) reported two standard machine

568

learning algorithms, namely MVPA-SVM and DNN, and X. Huang et al. (2021) proposed a

569

novel framework (CRNN) incorporating multiple modules such as CNN, recurrent neural

570

Netzwerk (RNN), and attention mechanism. The average accuracy of our framework (98.15%)

571

is much higher than that of MVPA-SVM (69.2%) and comparable to the accuracies of DNN-

572

based model (93.7%) and CRNN-based model (94.31%) (X. Huang et al., 2021; Wang et al.,

573

2020). Zusätzlich, the neuroscientific implications of their results remain elusive. In

574

conclusion, our proposed model achieved higher decoding accuracy than these models, while

575

also providing a more comprehensive and interpretable methodology for decoding fMRI data.

576

Außerdem, our model unveils multi-level temporal and spatial patterns, demonstrating

577

a resolution gradient spanning from shallow to deep layers. Speziell, in the deeper layers,

578

the identified temporal features are better correlated to the original task paradigm curves.

30

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

T

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

579

In der Zwischenzeit, more diverse FBNs can be detected and the spatial features show more consistency

580

with the GLM-derived activation patterns, in deeper layers.

581

Intriguingly, although more higher-order FBNs can be detected in deeper layers, Die

582

classification accuracy using features for multi-task classification derived from deeper layers

583

is lower than that of shallower layers, indicating that these higher-order FBNs are not much

584

helpful for multi-task classification. To validate this observation, we specifically selected only

585

FBNs components from all available components across all five folds for multi-task

586

classification, resulting in an average accuracy of 97.08%±2.14% (Mean±SD), slightly lower

587

than the classification rate obtained using all components (98.15%±0.90%) (sTab. 3). Der

588

possible reason is that the FBNs evoked by different cognitive tasks may have co-activated

589

Gehirnregionen, thus the FBNs components alone may not fully reveal the potential fundamental

590

differences in functional composition patterns of multi-task fMRI data. On the other hand,

591

ROA-based analyses indicate that artifact components occupy higher proportion of key

592

components for multi-task classification in shallower layers than that in deeper layers, along

593

with higher classification accuracy and specificity in the shallower layers. These findings

594

suggest that the artifact components play an important role in multi-task fMRI signal

595

classification, which is also consistent with previous research, where the artifact components

596

of the EEG signal are significantly more informative than brain activity concerning

597

classification accuracy (McDermott et al., 2021).

598

While our study provides novel insight into the core functional components in decoding

599

multi-task fMRI signals, it is important to note that there are three limitations. The first

600

limitation is the manual setting of parameters for DBN and sparse representation framework,

31

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

/

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

601

mainly including the number of neuron nodes and layers in DBN and the sparsity penalty

602

parameter of SR. Daher, automatic optimization of model parameters is one of the future

603

research directions. The second limitation stems from our inability to detect FBNs related to

604

gambling and relational tasks within the first two to three layers of the DBN-SR framework.

605

This could be attributed to more noise present in the group-wise temporal features 𝑫1 extracted

606

at lower levels (Feige. 1). Zusätzlich, LASSO regression may not be well-suited for handling

607

noisy shallow features, thus making it challenging for LASSO regression to accurately capture

608

the underlying spatial patterns. To address this limitation, future studies could explore

609

alternative regression approaches that are better suited for handling noisy shallow features,

610

thereby improving the accurate acquisition of the underlying spatial patterns. The third

611

limitation is that our study employed a relatively small dataset, consisting of 60 individuals out

612

von 68 from HCP Q1 dataset. To assess the robustness of our model, we included the remaining

613

8 individuals from the same dataset as a hold-out dataset, 6 of which do not have complete data

614

for all 7 tasks (sTab. 4). Jedoch, this does not affect their suitability as an independent lock

615

box dataset to test the performance of our trained model. The results revealed that the average

616

decoding accuracy for these 8 individuals (96.43%) was comparable to the 5-fold cross-

617

validation accuracy of the 60 individuals (sTab. 5), suggesting the robustness of our model.

618

dennoch, we acknowledge that a larger dataset would lend further support to our findings.

619

In future work, we aim to apply our model to more extensive or multicenter datasets to evaluate

620

its generalizability and robustness.

621

Gesamt, with the superiority of interpretability and effectiveness of DBN-SR model on

622

small datasets, our framework could potentially be useful to differentiate abnormal brain

32

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

.

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

623

function in clinical research.

624

Danksagungen

625

This work was supported by the National Natural Science Foundation of China (Grant. NEIN.

626

62006187), the Youth Innovation Team Foundation of Education Department of Shaanxi

627

Province Government (Grant. NEIN. 21JP119), the China Postdoctoral Science Foundation

628

Funded Project (Grant No. 2021M702650), the National Natural Science Foundation of China

629

(Grant. NEIN. 61971350), the National Natural Science Foundation of China (Grant. NEIN.

630

12271434), Natural Science Basic Research Program of Shaanxi (Grant. NEIN. 2023-JC-JQ-57),

631

and the Key Research and Development Program Project of Shaanxi Province (Grant. NEIN.

632

2020SF-036). We thank the Human Connectome Project for providing Quarter 1 (Q1) Dataset

633

(https://www.humanconnectome.org/study/hcp-young-adult/document/q1-data-release).

634

Reference

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

.

T

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

.

/

T

635

636

637

638

639

640

641

Asja Fischer, C. ICH. (2012). An Introduction to Restricted Boltzmann Machines. Paper presented at the

Iberoamerican Congress on Pattern Recognition, Berlin.

Barch, D. M., Bürger, G. C., Harms, M. P., Petersen, S. E., Schlaggar, B. L., Corbetta, M., . . .

Konsortium, W. U.-M. H. (2013). Function in the human connectome: task-fMRI and individual

differences in behavior. Neurobild, 80, 169-189. doi:10.1016/j.neuroimage.2013.05.033

Ben J. Harrison, J. P., Marina Lo´ pez-Sola, Rosa Herna´ ndez-Ribas, Joan Deus, Hector Ortiz, Carles

Soriano-Mas, Murat Yu¨ cel, Christos Pantelis, and Narcı´s Cardoner. (2008). Consistency and

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

33

642

643

644

645

646

647

648

649

650

651

652

653

654

655

656

657

658

659

660

661

662

663

functional specialization in the default mode brain network. PNAS, 105, 9781–9786.

Benesty, J., Chen, J., Huang, Y., & Cohen, ICH. (2009). Pearson correlation coefficient. In Noise reduction

in speech processing (S. 1-4): Springer.

Bengio, Y., Courville, A. C., & Vincent, P. (2012). Unsupervised feature learning and deep learning: A

review and new perspectives. CoRR, abs/1206.5538, 1(2665), 2012.

Bo Liu, Y. W., Yu Zhang, Qiang Yang. (2017, August). Deep Neural Networks for High Dimension, Low

Sample Size Data. Paper presented at the IJCAI, Melbourne.

Calhoun, V. D., Adali, T., McGinty, V. B., Pekar, J. J., Watson, T. D., & Pearlson, G. D. (2001). fMRT

activation in a visual-perception task: network of areas detected using the general linear model

Und

independent

components

Analyse.

Neurobild,

14(5),

1080-1088.

doi:10.1006/nimg.2001.0921

Chang, C.-C., & Lin, C.-J. (2011A). Libsvm. ACM Transactions on Intelligent Systems and Technology,

2(3), 1-27. doi:10.1145/1961189.1961199

Chang, C.-C., & Lin, C.-J. (2011B). LIBSVM: a library for support vector machines. ACM transactions

on intelligent systems and technology (TIST), 2(3), 1-27.

Davatzikos, C., Ruparel, K., Fan, Y., Shen, D. G., Acharyya, M., Loughead, J. W., . . . Langleben, D. D.

(2005). Classifying spatial patterns of brain activity with machine learning methods: application

to lie detection. Neurobild, 28(3), 663-668. doi:10.1016/j.neuroimage.2005.08.009

Dong, Q. (2020). Modeling Hierarchical Brain Networks via Volumetric Sparse Deep Belief Network

(VSDBN). Computerized Medical Imaging and Graphics.

Fangfei Ge, J. L., Xintao Hu , Lei Guo , Junwei Han , Shijie Zhao, Tianming Liu (2018, April 4-7).

Exploring intrinsic networks and their interactions using group wise temporal sparse coding.

34

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

/

/

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

664

665

666

667

668

669

670

671

672

673

674

675

676

677

678

679

680

681

682

683

684

685

Paper presented at the International Symposium on Biomedical Imaging (ISBI 2018),

Washington, D.C., USA.

Fischer, R. A., & Yates, F. (1938). Statistical tables for biological, agricultural aad medical research.

Statistical tables for biological, agricultural aad medical research.

Friston, K. J. (2009). Modalities, Modes, and Models in Functional Neuroimaging. SCIENCE, 326, 399-

403.

Hansen, K., Montavon, G., Biegler, F., Fazli, S., Rupp, M., Scheffler, M., . . . Müller, K. R. (2013).

Assessment and Validation of Machine Learning Methods for Predicting Molecular Atomization

Energies. J Chem Theory Comput, 9(8), 3404-3419. doi:10.1021/ct400195d

Haufe, S., Meinecke, F., Görgen, K., Dähne, S., Haynes, J.-D., Blankertz, B., & Bießmann, F. (2014).

On the interpretation of weight vectors of linear models in multivariate neuroimaging.

Neurobild, 87, 96-110.

Haynes, J. D., & Rees, G. (2006). Decoding mental states from brain activity in humans. Nat Rev

Neurosci, 7(7), 523-534. doi:10.1038/nrn1931

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

/

.

Hinton, G. E., Osindero, S., & Teh, Y. W. (2006). A fast learning algorithm for deep belief nets. Neuronal

Comput, 18(7), 1527-1554. doi:10.1162/neco.2006.18.7.1527

Hinton, G. E., & Sejnowski, T. J. (1986). Learning and relearning in Boltzmann machines. Parallel

distributed processing: Explorations in the microstructure of cognition, 1(282-317), 2.

Hu, J., Kuang, Y., Liao, B., Cao, L., Dong, S., & Li, P. (2019). A Multichannel 2D Convolutional Neural

Network Model for Task-Evoked fMRI Data Classification. Comput Intell Neurosci, 2019,

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

5065214. doi:10.1155/2019/5065214

Hu, X., Huang, H., Peng, B., Han, J., Liu, N., Lv, J., . . . Liu, T. (2018). Latent source mining in FMRI

35

686

687

688

689

690

691

692

693

694

695

696

697

698

699

700

701

702

703

704

705

706

707

via restricted Boltzmann machine. Hum Brain Mapp, 39(6), 2368-2380. doi:10.1002/hbm.24005

Huan Liu , M. Z., Xintao Hu , Yudan Ren , Shu Zhang , Junwei Han , Lei Guo , Tianming Liu (2017).

Fmri data classification based on hybrid temporal and spatial sparse representation. Paper

presented at the IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017),

Melbourne, VIC, Australia.

Huang, H., Hu, X., Zhao, Y., Makkie, M., Dong, Q., Zhao, S., . . . Liu, T. (2018). Modeling Task fMRI

Data Via Deep Convolutional Autoencoder. IEEE Trans Med Imaging, 37(7), 1551-1561.

doi:10.1109/TMI.2017.2715285

Huang, X., Xiao, J., & Wu, C. (2021). Design of Deep Learning Model for Task-Evoked fMRI Data

Classification. Comput Intell Neurosci, 2021, 6660866. doi:10.1155/2021/6660866

Jang, H., Plis, S. M., Calhoun, V. D., & Lee, J. H. (2017). Task-specific feature extraction and

classification of fMRI volumes using a deep neural network initialized with a deep belief network:

Evaluation

verwenden

sensorimotor

tasks.

Neurobild,

145(Pt

B),

314-328.

doi:10.1016/j.neuroimage.2016.04.003

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

.

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
4
2
1
5
6
8
1
3
N
e
N
_
A
_
0
0
3
3
4
P
D

T

.

/

Kay, K., Rokem, A., Winawer, J., Dougherty, R., & Wandell, B. (2013). GLMdenoise: a fast, automated

technique for denoising task-based fMRI data. Frontiers in neuroscience, 247.

Kohavi, R. (1995). A study of cross-validation and bootstrap for accuracy estimation and model

F

B
j
G
u
e
S
T

T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Auswahl. Paper presented at the Ijcai.

Kriegeskorte, N., & Bandettini, P. (2007). Analyzing for information, not activation, to exploit high-

resolution fMRI. Neurobild, 38(4), 649-662.

LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Natur, 521(7553), 436-444.

doi:10.1038/nature14539

36

708

709

710

711

712

713

714

715

716

717

718

719

720

721

722

723

724

725

726

727

728

729

Lee, J., Jeong, Y., & Ye, J. C. (2013). Group sparse dictionary learning and inference for resting-state

fMRI analysis of Alzheimer’s disease. Paper presented at the 2013 IEEE 10th International

Symposium on Biomedical Imaging.

Litjens, G., Kooi, T., Bejnordi, B. E., Setio, A. A. A., Ciompi, F., Ghafoorian, M., . . . Sanchez, C. ICH.

(2017). A survey on deep learning in medical image analysis. Med Image Anal, 42, 60-88.