Restoration of fMRI Decodability Does Not Imply - Am MIT spezialisierte KI-Forschung

Restoration of fMRI Decodability Does Not Imply
Latent Working Memory States

Sebastian Schneegans and Paul M. Bays

Abstrakt

■ Recent imaging studies have challenged the prevailing
view that working memory is mediated by sustained neural
Aktivität. Using machine learning methods to reconstruct mem-
ory content, these studies found that previously diminished
representations can be restored by retrospective cueing or
other forms of stimulation. These findings have been inter-
preted as evidence for an activity-silent working memory state
that can be reactivated dependent on task demands. Hier, Wir
test the validity of this conclusion by formulating a neural pro-

cess model of working memory based on sustained activity
and using this model to emulate a spatial recall task with retro-
cueing. The simulation reproduces both behavioral and fMRI
results previously taken as evidence for latent states, in par-
ticular the restoration of spatial reconstruction quality follow-
ing an informative cue. Our results demonstrate that recovery
of the decodability of an imaging signal does not provide
compelling evidence for an activity-silent working memory
state. ■

EINFÜHRUNG

The dominant view of the neural mechanism underlying
working memory is that memory representations are
maintained in the sustained spiking activity of neurons
(Chaudhuri & Fiete, 2016; Bays, 2015; Eriksson, Vogel,
Lansner, Bergström, & Nyberg, 2015; Funahashi, Bruce,
& Goldman-Rakic, 1989; Fuster & Alexander, 1971). Das
sustained activity may arise from local self-excitation in
populations of neurons or reverberatory loops between
different cortical areas ( Wang, 2001). Working memory
representations can be modeled as attractor states in
the neural activation dynamics. For continuous features,
such as location, color, or orientation of visual stimuli,
population codes with homogeneous recurrent connec-
tivity form continuous attractors such that each possible
feature value can be maintained in working memory
(Johnson, Simmering, & Buss, 2014; Wei, Wang, & Wang,
2012; Compte, Brunel, Goldman-Rakic, & Wang, 2000).
Errors arise at encoding and when the attractors drift to
neighboring feature values or decay under the influence
of random noise ( Wimmer, Nykamp, Constantinidis, &
Compte, 2014; Burak & Fiete, 2012; Camperi & Wang,
1998).

Models of this type have successfully accounted for
memory-related neural activity at a high level of physio-
logical detail (Wimmer et al., 2014; Compte et al., 2000).
Zusätzlich, they have been used to explain a wide range
of behavioral findings, such as performance and capacity
limits in change detection tasks (Engel & Wang, 2011;

University of Cambridge

Johnson, Spencer, & Schöner, 2009), biases in visual
Arbeitsgedächtnis (Schneegans, Spencer, Schöner, Hwang,
& Hollingworth, 2014; Simmering, Spencer, & Schöner,
2006; Camperi & Wang, 1998), and developmental changes
in working memory performance (Schutte & Spencer,
2009; Edin, Macoveanu, Olesen, Tegnér, & Klingberg,
2007).

A strikingly different account of working memory pro-
poses that memory representations are maintained in
an activity-silent state (d.h., without sustained neural
firing) through biochemical or morphological changes
in neurons (Stokes, 2015; Barak & Tsodyks, 2014). A
prominent candidate mechanism is rapid synaptic plas-
ticity (Erickson, Maramara, & Lisman, 2010), which may
allow sensory stimulation to produce changes in neural
connection patterns over short timescales and create
assemblies of neurons that may later be reactivated by
nonspecific input (Mi, Katkov, & Tsodyks, 2017; Mongillo,
Barak, & Tsodyks, 2008). Proponents of such working
memory mechanisms suggest that persistent neural activ-
ity only reflects sustained attention to the currently task-
relevant item, whereas other items can be held in an
activity-silent state (Rose et al., 2016; LaRocque, Lewis-
Peacock, Drysdale, Oberauer, & Postle, 2013; Lewis-
Peacock, Drysdale, Oberauer, & Postle, 2012).

An important source of information about the neural
basis of working memory is provided by fMRI studies
that measure neural activity during the delay periods of
working memory tasks. Results of early studies were con-
sistent with the sustained firing account, finding elevated
BOLD signals in regions of prefrontal and parietal cortex
(Xu & Chun, 2006; Todd & Marois, 2004; Linden et al.,

© 2017 Massachusetts Institute of Technology. Published under a
Creative Commons Atrribution 3.0 Unportiert (CC BY 3.0) Lizenz.

Zeitschrift für kognitive Neurowissenschaften 29:12, S. 1977–1994
doi:10.1162/jocn_a_01180

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

T
T

F
/

ich
T
.

:
/
/

H
T
T
P
:
/
D
/
Ö
M
w
ich
N
T
Ö
P
A
R
D
C
e
.
D
S
F
ich
R
Ö
l
M
v
e
H
R
C
P
H
A
D
ich
ich
R
R
e
.
C
C
T
.
Ö
M
M
/
J
e
Ö
D
u
C
N
Ö
/
C
A
N
R
A
T
R
ich
T
ich
C
C
l
e
e
–
P
–
D
P
D
2
F
9
/
1
2
2
9
/
1
1
9
2
7
/
7
1
1
9
9
7
5
7
3
/
2
1
8
0
7
8
Ö
6
C
8
N
9
_
6
A
/
_
J
0
Ö
1
C
1
N
8
0
_
A
P
_
D
0
1
B
1
j
8
G
0
u
.
e
P
S
T
D
Ö
F
N
B
0
j
8
S
M
e
ICH
P
T
e
M
L
ich
B
B
e
R
R
A
2
R
0
2
ich
3
e
S

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

2003; Courtney, Ungerleider, Keil, & Haxby, 1997). Wie-
immer, the interpretation of these univariate fMRI results is
not necessarily straightforward. More recent studies have
applied multivariate pattern analysis and reconstruction
methods to BOLD signal data to characterize working
memory representation (Sprague, Ester, & Serences,
2014; Riggall & Postle, 2012; Harrison & Tong, 2009;
Serences, Ester, Vogel, & Awh, 2009). Such studies have
found a dissociation between cortical regions with ele-
vated BOLD signal and regions from which the features
of remembered items could be successfully decoded
(Emrich, Riggall, LaRocque, & Postle, 2013; Riggall &
Postle, 2012).

Kürzlich, such reconstruction methods have also been
used to investigate how working memory representa-
tions change when informative cues are provided during
the delay period. In the task used by Sprague, Ester, Und
Serences (2016), participants had to memorize the loca-
tions of two colored disks. In some trials, a color cue
given midway through the memory period indicated
which location would be tested at the end. The recon-
struction quality for the cued item’s location decreased
over the course of the delay period but showed a sig-
nificant restoration following this spatially nonspecific
retro-cue. This was interpreted as evidence for an activity-
silent component in location working memory, welche
cannot be decoded from the BOLD signal data but can
be reactivated (and thereby contribute to reconstruction
quality again) by the retro-cue.

Similar conclusions have been drawn from several
prominent studies applying reconstruction methods to
fMRI and EEG data. Rose et al. (2016) found that the cat-
egory of a currently task-relevant item could be success-
fully decoded from fMRI recordings, but not the category
of a second item concurrently held in working memory
(that became task relevant at a later stage). The authors
concluded that this second item is held in an activity-
silent state and is only restored into a sustained activity
representation when cued as immediately task relevant.
A restoration of decoding quality from EEG data has been
observed following TMS pulses (Rose et al., 2016) oder
presentation of salient, but uninformative, visuelle Reize
( Wolff, Jochim, Akyürek, & Stokes, 2017; Wolff, Ding,
Myers, & Stokes, 2015). This was interpreted as effect
of interactions between the unspecific stimulation and a
silent working memory representation, realized in a
changed neural connectivity pattern.

In this study, we critically examine the interpretation
that the restoration of reconstruction quality following
a cue is evidence for activity-silent working memory
Staaten. We implement a neural model of working memory
based on the principle of sustained activity through self-
excitation in neural populations and derive simulated
BOLD signal data from this model. We then apply the
same kind of reconstruction method as was previously
used for the analysis of experimental data. Focusing on
the study by Sprague et al. (2016), we demonstrate that

the neural model can reproduce both the behavioral and
fMRI reconstruction results, despite relying only on active
memory representations. Insbesondere, in a minimal neu-
ral model of the retro-cue task, a spatially nonspecific
color cue can selectively strengthen the reconstruction
of the cued item’s location. The neural model demon-
strates that the assumption of activity-silent WM states
is not necessary to explain these experimental results
and highlights the importance of considering the func-
tional neural architectures involved in the task when
interpreting imaging data.

METHODEN

Neural Model

We aim to provide a minimal neural model that can
perform the delayed estimation task with retro-cueing
(Figure 1A) and account for the behavioral and fMRI
results from the experimental study of Sprague et al.
(2016). We formulate this model within the framework
of dynamic neural fields, a form of recurrent neural net-
work that describes the continuous evolution of activity
distributions in neural populations through differential
Gleichungen (Schneegans & Schöner, 2008). Neural fields
are continuous in space: Rather than simulating the ac-
tivity of individual neurons, each point in a neural field
reflects the mean activity of neurons with the corre-
sponding spatial selectivity. Working memory is realized
in this framework through localized peaks of activation
that are sustained through self-excitation (balanced by
surround inhibition), forming attractor states in the neu-
ral dynamics. Neural field models generate continuous
time courses of neural activity patterns, making them well
suited for modeling fMRI data ( Wijeakumar, Ambrose,
Spencer, & Curtu, 2016).

We employ a single combined perceptual and working
memory representation to emulate neural activation in
the task (Figure 1B). Stimulus locations are represented
in a population code over 2-D visual space. Wichtig,
the model also needs to represent the item color asso-
ciated with each location to select the correct memo-
rized item for response following a color cue. Following
a recent model of feature binding in visual working
Erinnerung, we employ a conjunctive code for color–location
bindings (Schneegans & Bays, 2017; Schneegans,
Spencer, & Schöner, 2016). To keep the model simple,
we represent only the two stimulus colors used in the
original experiment (red and blue), yielding two neural
fields for these discrete colors over the same 2-D visual
Raum. These can be interpreted as slices from a full
population code for possible color–location conjunc-
tionen (compare Richter, Lins, Schneegans, & Schöner,
2014; Lipinski, Schneegans, Sandamirskaya, Spencer, &
Schöner, 2012).

The activation in these fields, which can be equated
with the mean membrane potential of neurons with the

1978

Zeitschrift für kognitive Neurowissenschaften

Volumen 29, Nummer 12

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

F
/

T
T

ich
T
.

:
/
/

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

interactions within the model, and ξ is a random noise
Begriff.

The lateral interactions are based on the current field
output, a continuous homologue of the neural firing rate,
which is computed from the activation a via a sigmoid
(logistic) function f:

f að Þ ¼

1
1 þ e−a

(2)

The output is close to zero for low (negative) Aktivierung
Werte, rises for activation values around zero, and satu-
rates at a value of one for higher activations. This pro-
duces the effect that only regions with high activation
contribute to interactions within the field.

Lateral interactions consist of three components: A
local excitatory component, described by a normalized
2-D Gaussian function ϕ(X; σexc) with mean zero and
width parameter σexc that is scaled with an excitatory
weight cexc; a uniform inhibitory component within each
color field with weight cinhc; and a global inhibitory com-
ponent over both fields with weight cinhg. The input from
lateral interactions for each field position is computed as

D
g l; X; T

Þ ¼

f a l; x0; T
D
D
Þ
dx0 − cinhg

Þ cexcϕ x − x0; σexc
D
X
f a l0; x0; T
D
Þ
D

Þ − cinhc
Þ dx0

(3)

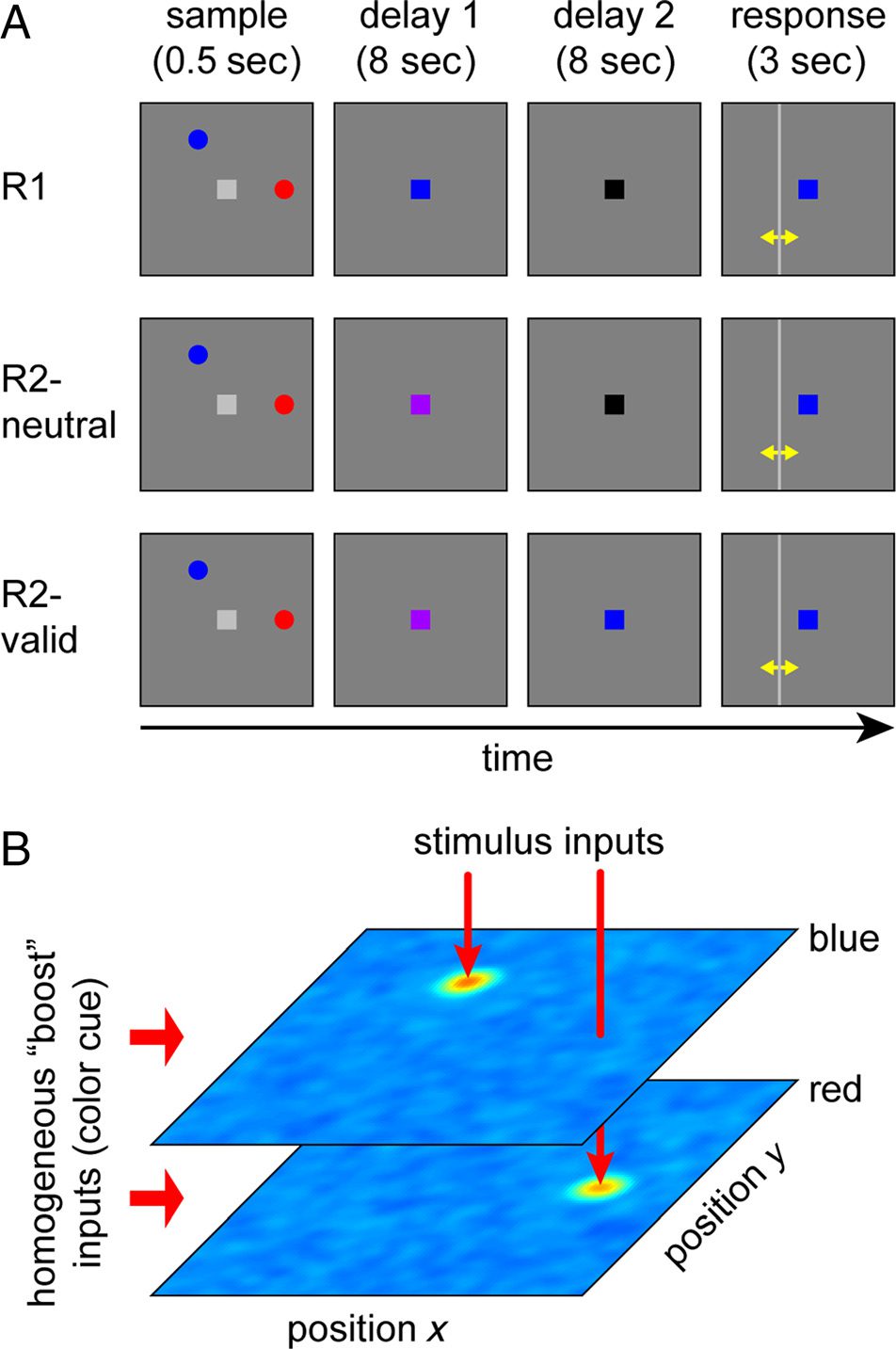
Figur 1. (A) Experimental task of Sprague et al. (2016). Teilnehmer
view a sample array of two colored discs and have to report the location
of one item (the target) by adjusting a vertical or horizontal bar (Gelb
arrows are not part of the experimental display). The color of the
fixation point can change at different times during the delay period
to indicate the target item. (B) Architecture of the neural model.
Two neural fields over retinal space, with selectivity matching the
two colors (blue and red) used in the task, are shown as color-coded
activation distributions. Each colored sample stimulus provides localized
input to the corresponding field, generating a peak of activity that
encodes the stimulus location. The informative color cue generates a
homogeneous input to the field of matching color, boosting activity
throughout the population.

corresponding selectivity (Amari, 1977), is governed by
the differential equation

τ _a l; X; T
D

D
Þ ¼ −a l; X; T
D
þ ξ l; X; T

Þ þ h þ s l; X; T
Þ

D
Þ þ g l; X; T

(1)

where a(l, X, T) is the activation for color l 2 {Rot, Blau},
spatial position x = (X, j), and time t. The notation _a
indicates the rate of change of activation over time, mit
a time constant τ. The scalar variable h is the global resting
level of activation that the field will relax to in the absence
of input and lateral interactions, s is the local external
input to each field location, g is the input from lateral

l0
The noise term ξ describes spatially correlated random
noise with amplitude cnoise, generated from white noise
by convolution with a Gaussian kernel (using the same
width parameter σexc as in the lateral interactions):

D
ξ l; X; T

Þ ¼ cnoise

v l; x0; T
D
D
v l; X; T

Þϕ x − x0; σexc
D
Þ
Þ ∼ N 0; 1D

Þdx0;

(4)

Model parameters were adjusted manually to produce a
close fit to the behavioral and fMRI reconstruction data
and are fixed across task conditions. All parameter values
are listed in Table 1. The model was simulated numerically
by sampling the visual space in the range [−6°, 6°] ×
[−6°, 6°] mit 100 × 100 sampling points and approxi-
mating the temporal evolution of activation using the
Euler method with a fixed time step of 10 ms.

Behavioral Task and Emulation in the Model

We use the neural model to emulate the delayed estima-
tion task used by Sprague et al. (2016), shown in
Figure 1A. Participants had to memorize the locations
of two colored discs (one red and one blue, diameter
0.15°) presented for 500 ms. The discs were located
on an invisible circle (radius 3.5°) around a central fixa-
tion point, offset from each other by ±60°, ±120°, oder
180°. An additional small trial-to-trial variation of relative
positions was introduced by adding a random value uni-
formly distributed in [−0.3°, 0.3°] independently to each
horizontal and vertical stimulus position. Participants had

Schneegans and Bays

1979

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

T
T

F
/

ich
T
.

:
/
/

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

Tisch 1. Parameter Values for Neural Model and Generation of
Simulated BOLD Signals

Parameter

Description

Wert

cexc
σexc

cinhc

cinhg

cnoise

cstim
σstim

ccue

cforget
σvox

cnvox

Time constant of neural dynamics

100 ms

Field resting level

Lateral excitatory weight

Width of lateral excitation

Inhibitory weight (within color field)

Inhibitory weight (global)

Noise amplitude

Stimulus amplitude

Stimulus width

Color cue amplitude

Deactivation amplitude after trial

Voxel range parameter

Voxel noise amplitude

−5

0.25°

2.6

0.52

2°

17.5

1.5

2.5

to remember stimulus locations over a delay interval of
16 sec in total, then report the location of one stimulus
cued by its color.

Memory load in this task was manipulated across three
Bedingungen: In the “remember one” condition (R1), Die
fixation point changed color to either red or blue imme-
diately after offset of the sample stimuli, indicating with
100% reliability which item was to be tested. The fixation
point then changed to a neutral color (black) nach 8 Sek.
In the “remember two” condition, the color of the fixa-
tion point changed to purple at the beginning of the
delay period, indicating that either item could be tested.
Nach 8 Sek, the fixation point’s color then either changed
to black (R2-neutral), or it changed to one of the item
colors, acting as a retro-cue that indicated the item to
be tested with 100% reliability (R2-valid). In all condi-
tionen, the fixation point took the color of the tested item
at the beginning of the response period (after the 16-sec
delay). The participant then had to adjust either a hori-
zontal or vertical line displayed on the screen to report
the horizontal or vertical location of the cued item.

In the neural model, memory sample stimuli are emu-
lated as (nonnormalized) Gaussian inputs (with ampli-
tude cstim and width parameter σstim), centered at the
stimulus location ml for a stimulus with color l. Der
input for each colored stimulus only drives activation
in the field for the matching color and remains active
for a 500-msec interval [Tonne, toff]:

D
s l; X; T

Þ ¼ cstim exp −

jjx − mljj2
2σ2

stim

for ton ≤ t ≤ toff

(5)

The informative color cue is modeled as a homogeneous
“boost” input with amplitude ccue to the field with match-
ing color lcue that is active for 500 msec after onset of the
cue (see Lipinski et al., 2012, for an analogous mecha-
nism at the perceptual level):

D
s lcue; X; T

Þ ¼ ccue for tcue ≤ t ≤ tcue þ 500 ms

(6)

Behavioral results in retro-cue experiments indicate that
processing of a retro-cue takes about 300–500 msec
(Souza & Oberauer, 2016; Souza, Rerko, & Oberauer,
2014; Tanoue & Berryhill, 2012), and we assume that
the cue has no further effect after this, even though it
remains visible. The uninformative cues (black or purple)
are not modeled explicitly.

For the generation of the spatial response in the model,
the response color cue input is presented for 500 ms
in the same fashion as described above and 500 msec after
the offset of the cue; the spatial center of mass (xresp,
yresp) of the field outputs (summed over colors) is deter-
mined as

xresp ¼

l
X

yresp ¼

l
X

D
x f a l; X; T

Þdx

D
f a l; X; T
D

Þdx

D
y f a l; X; T

Þdx

D
f a l; X; T
D

Þdx

(7)

Note that under normal conditions, there will be a peak
of activation in only one of the two fields after the pre-
sentation of the response cue (with low homogeneous
activity in the other field), so this method yields the
estimated location of the cued item. Response error is
determined as absolute deviation of the report location
from the location of the cued stimulus, either in the
horizontal or vertical direction (randomly selected) Zu
emulate the experimental response procedure. Nach
response generation, the activation levels of both fields
are transiently decreased by a value cforget for 500 ms
(beginnend 500 msec after response time) to extinguish any
existing activation peaks.

We numerically simulated 10 blocks of 216 Versuche (72 Versuche
per condition) of this task, with trials in each block fully
counterbalanced for possible stimulus positions, angular
distance between stimuli, and cued item color. Stimulus
parameters directly emulate the original study, und das
total number of trials approximates the number of trials
across participants in that study.

In the original fMRI study, an additional mapping task
was performed as basis for the reconstruction of spatial
representations from voxel BOLD signals. In this task,
participants memorized the location of a single stimulus,
then a flickering checkerboard disc (radius 1.083°) War
presented for 3000 ms, covering the location of the

1980

Zeitschrift für kognitive Neurowissenschaften

Volumen 29, Nummer 12

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

T
T

F
/

ich
T
.

:
/
/

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

memory stimulus. After this presentation, a probe stimulus
wurde gezeigt, and participants had to report whether the
memorized stimulus location was to the left or right (oder
above or below) the probe. The checkerboard stimulus
was shown in 36 locations on a hexagonal grid, welche
was again rotated in 12 different ways across sessions.

We emulate the checkerboard stimulus as a Gaussian
input with the same amplitude cstim and width σstim as
the stimuli in the main task that is applied to the same
location in the fields for both colors. We do not emulate
the working memory component of the mapping task,
because the simple model architecture does not allow
differentiation between perceptual and working memory
Artikel. This does not affect the reconstruction procedure,
because only the checkerboard stimulus locations were
taken into account for computing the reconstructions
in the original study. We performed four sets of this map-
ping task for each block of working memory trials, rotat-
ing the hexagonal stimulus grid by increments of 15°
across sets and by increments of 5° across blocks.

Generating Simulated BOLD Signals

The original study measured BOLD signals for individual
voxels and used an additional localizer task to assign
these voxels to different cortical areas of interest (inkl-
ing V1, V3A, IPS0, IPS2, and sPCS). We do not aim to cap-
ture this division into different cortical regions in the
model and only generate a single set of BOLD signals
to compare it to the combined results from the fMRI
Studie (which contains all of the key effects reported in
that study).

The interpretation of the original study’s fMRI results
as evidence for activity-silent working memory is based
on the assumption that the BOLD signal reflects neural
spiking activity. We follow this assumption here and de-
rive the simulated BOLD signal directly from the field
output in the neural model (the continuous homologue
of the firing rate). We note that this is most likely an
oversimplification, but we believe that it allows the most
direct test of the conclusions drawn from the original
Studie. We define a simulated voxel by selecting a ran-
dom sample of points from the two fields, {(l1, x1),…,
(ln, xn)}. Building on the assumption that the visual
areas under investigation are at least partly organized
retinotopically, spatial locations of sampling points are
drawn from a mixture of a Gaussian and a uniform
distribution,

D
p li; xi

D
Þ ∝ 0:5 þ 0:5ϕ x − xvox; σvox

(8)

The center xvox = (xvox, yvox) of the Gaussian distribu-
tion for each voxel is chosen uniformly from the space
[−6°, 6°] × [−6°, 6°] and applies to both color fields.
The color li for each sampling point is chosen with
equal probabilities from {Rot, Blau}.

from the neural model at these sampling points and
convolving this signal in time with the canonical hemo-
dynamic response function h:
Z ∞

D
b tscan

Þ ¼

D
f a li; xi; tscan − t

Þdt

h tð Þ 1
N
D

0
ich
þ cnvoxχ tscan

(9)

Hier, χ ∼ N (0,1) is random noise added to each voxel
to reflect neural activity not directly related to the task.
The hemodynamic response function, as defined by
Lindquist, Loh, Atlas, and Wager (2009), Ist

h tð Þ ¼ t α1−1

Þβα1 e −βt
D
Þ
Γ α1ð

− c

D
t α2−1

Þβα2 e −βt
D
Þ
Γ α2ð

(10)

with standard parameters α1 = 6, α2 = 16, β = 1, Und
c = 1/6.

Emulating the procedure in the original study, Wir
generated BOLD signals for 10 time points in each trial
of the working memory task, spaced in intervals of
2250 msec beginning at memory stimulus onset. Im
mapping task, a single set of BOLD signals was generated
for each trial. For each block of trials in the working
memory task (and the associated trials of the mapping
Aufgabe), a new mapping of voxels to points in the neural
fields was randomly generated. Wir verwendeten 1000 voxels with
1000 points per voxel. All simulated BOLD signals were
transformed into z scores before further analysis, inde-
pendently between blocks of trials and between mapping
task and working memory task.

Reconstruction and Analysis of
Spatial Representations

The reconstruction of neural representations from simu-
lated BOLD signals is performed in the same way as the
reconstruction from actual fMRI data in the original
Studie (see Sprague et al., 2016, for details). In brief, Die
z-transformed BOLD signal for each voxel is modeled as
a linear combination of 37 information channels (spatial
filters over 2-D visual space). The data from the spatial
mapping task is used to estimate a weight matrix that
maps expected filter responses (based on the known
stimulus locations in this task) onto the observed BOLD
Signale. This matrix is then inverted to compute channel
activations for each trial and time point in the working
memory task from measured BOLD signals.

For further analysis and visualization, reconstructed
activation distributions over visual space are generated
as superpositions of the spatial filters of each channel
weighted with the estimated channel activation. Target
positions in different trials can be aligned with each
other in the reconstructions by rotating, flipping, Und
shifting the pattern of spatial filters associated with each
channel.

D
Ö
w
N
l
Ö
A
D
e
D

F
R
Ö
M

/
J

T
T

F
/

ich
T
.

:
/
/

/
J

u
S
e
R

Ö
N

1
7

M
A
j

2
0
2
1

The simulated BOLD signal b for one voxel at time tscan
is then computed by averaging over the output signal

To visualize and compare spatial representations over
time in the different task conditions, trials are grouped by

Schneegans and Bays

1981

condition and absolute angular distance between memory
Reize (60°, 120°, and 180° ), and reconstructions are
generated, aligned with respect to the positions of the
two stimuli (ignoring the small random offset in stimulus
locations from trial to trial). For further analysis, Versuche
are grouped by condition only, and reconstructions are
generated, aligned by the exact location of the cued stim-
ulus (half of the trials with a stimulus separation of 180°
are omitted here to obtain equal numbers of stimulus
separations −120°, −60°, 60°, 120°, and 180°). Eins-
dimensional reconstructions over an angular space are
extracted from the obtained activation distributions
over visual space by interpolating and averaging acti-
vations within a ring of 2.9°–4.1° eccentricity around the
center.

We apply the same analyses on these reconstructions
as employed in the experimental study. A fidelity mea-
sure F of target representation in the 1-D reconstructions
R(θ) (aligned with the cued stimulus position always at
null) is defined as the mean product of the reconstruc-
tion with a cosine function,

F ¼ 1
2π

r θð Þ cos θð Þdθ

(11)

Activation profiles in the 1-D reconstructions are quan-
tified by fitting with a function

8
< (cid:2) f θð Þ ¼ b þ a 0:5 þ 0:5 cos : b; (cid:3) j 7 2π θ − μ j σfit ; if θ − μ j j < σfit otherwise (12) where b is baseline activation, a is amplitude of a Gaussian- like component, σfit is the width parameter for this com- ponent, and μ is an angular bias of the peak limited to a small range around zero. For analysis of the model be- havior, we also apply this function fitting directly to the field output in the neural model (averaged across trials, without generation of simulated BOLD signals and re- construction from them). To determine significance of fidelity and differences in fitting parameters, we used a bootstrapped sign test. Over 1000 iterations, we resampled with replacement from the 1-D single-trial reconstructions (with 720 trials per condi- tion) and computed fidelity and function fit for the aver- age over resampled reconstructions. For comparing fitting parameters between two conditions or time periods, we computed the proportion in which the difference between these variables was greater than zero and the proportion in which it was less than zero and doubled the smaller of these proportions to obtain the p value. For testing whether the fidelity measure was greater than zero, we performed a one-tailed sign test and report the proportion of re- sampling iterations with F < 0. RESULTS Model Mechanism and Behavioral Results We applied a neural model of working memory based on sustained activity in neural populations to emulate the retro-cue task used by Sprague et al. (2016). In this task (Figure 1A), participants were presented with two col- ored disks, which they memorized in three different conditions: On R1 trials, a colored cue at the start of the trial indicated one of the items whose location was to be remembered; on R2-neutral trials, both items had to be remembered to the end of the trial; and on the critical R2-valid trials, a retro-cue delivered midway through the trial indicated which item would be tested, allowing participants to forget the other item. The model (Figure 1B) describes activity of two spatial- and color-selective populations (neural “fields”) with color selectivity matching the two colors used in the task. 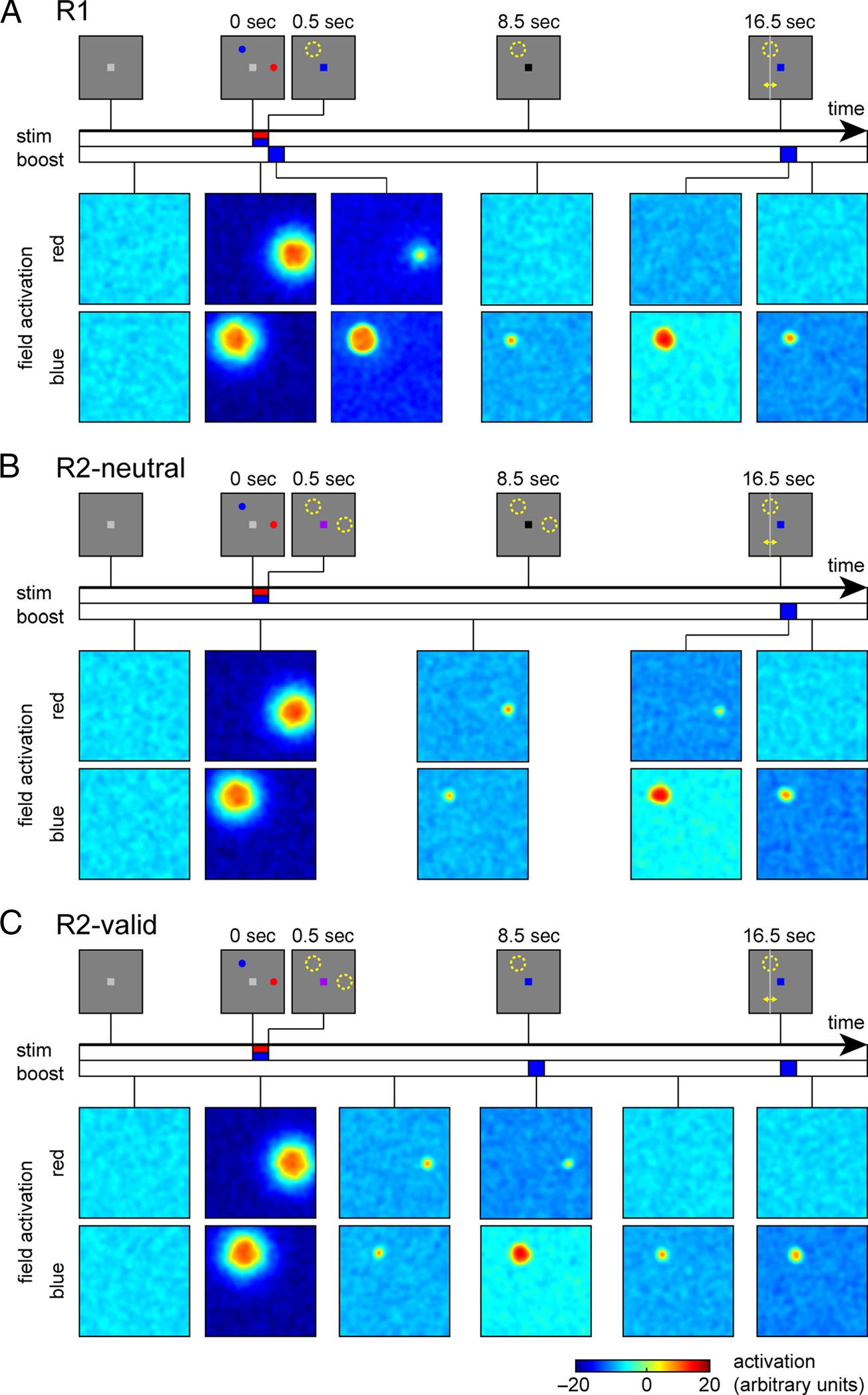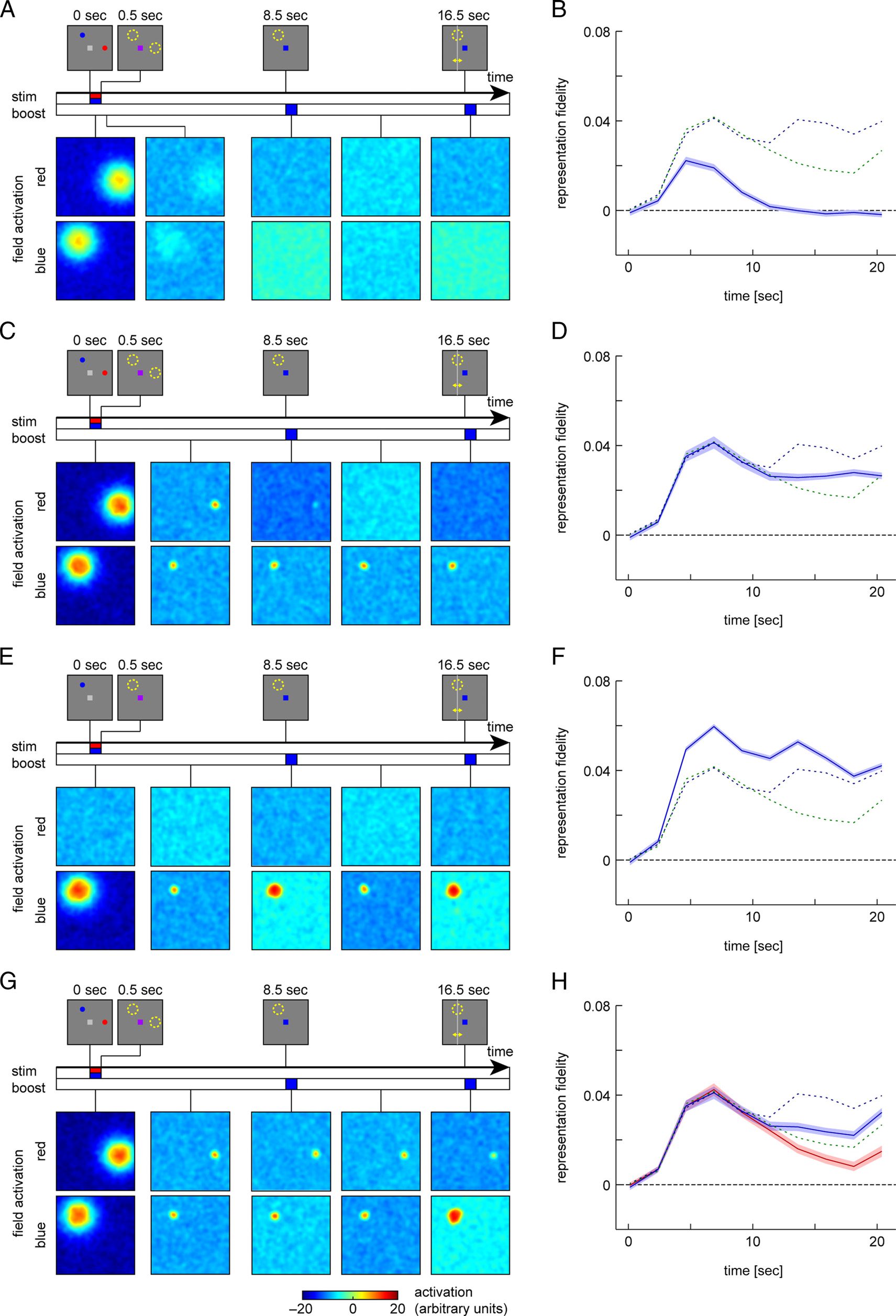There is localized lateral excitation within each field and global inhibition within and between fields. Figure 2 illustrates the activation time course in the model for a single trial in each task condition to demonstrate the basic mechanisms of the model. The figure shows the activa- tion distributions in both fields at different points in time (at this stage, without generation of simulated BOLD sig- nals or reconstructions from them). At the beginning of the R1 trial (Figure 2A), both fields show uniformly low activation, with small fluctuations due to random noise. Presentation of the memory sam- ple stimuli induces strong activation in both fields that is localized at the stimulus positions and specific for the color of each stimulus. Immediately following the sample stimuli, a blue color cue is presented in this trial, which homogeneously raises activation levels in the blue color field. Because of the effects of lateral interactions, this strengthens the existing peak of activation in this field, whereas activation in other parts of the field is held rela- tively low by the increased global inhibition arising from this peak. In addition, the global inhibitory effect acts on the activation levels in the red color field. It reduces the strength of the existing activation peak in that field such that it ceases to generate sufficient self-excitation and ultimately collapses. After the color cue input is turned off, the activation level in the blue field decreases, but a smaller localized peak of activation remains stable throughout the delay period, sustained by local self-excitation and surround inhibition within the field. During the response period, the color cue is activated again and strengthens the re- maining peak but does not qualitatively alter the activa- tion patterns in the model. After this second cue input has ceased, the response location is determined as the center of mass of the field output over visual space (summed over both fields). The R2-neutral trial begins in the same way as the R1 trial (Figure 2B), but here no informative color cue is given until the response period. Following the presentation of D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j / f . t u s e r o n 1 7 M a y 2 0 2 1 1982 Journal of Cognitive Neuroscience Volume 29, Number 12 Figure 2. Evolution of activation patterns in the neural model during a single trial in each condition. Stimulus displays during different phases of the task are shown at the top of each panel. Colored bars along the time axes indicate duration of stimulus and cue inputs in the model. Activation patterns in the two fields of the model (for colors red and blue) are shown color-coded below for different points during the course of each trial. D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f / . t u s e r o n 1 7 M a y 2 0 2 1 the sample array, the activation peaks in both fields settle at a lower activation level, but they both remain stable throughout the delay period. When the color cue is pre- sented at the end of the trial, it raises activation levels in the blue field, and the activation in the red field is sup- pressed through mutual inhibition. Only the activation peak for the blue item remains and forms the basis for the response generation as before. The model simulations of the R2-valid trials combine aspects from the two previous conditions (Figure 2C). Following the presentation of the sample stimuli, local- ized activation peaks form in both fields and remain sta- ble during the first half of the delay period, analogous to the R2-neutral trial. When the color retro-cue is then pre- sented, it strengthens activation in the blue field and, in turn, suppresses activation in the red field. The activation peak for the blue item then returns again to a lower activation level when the homogeneous input ceases, although it remains slightly stronger than during the first memory period because it no longer experiences inhibi- tion from a second activation peak. The response period then proceeds in the same way as in the R1 condition. 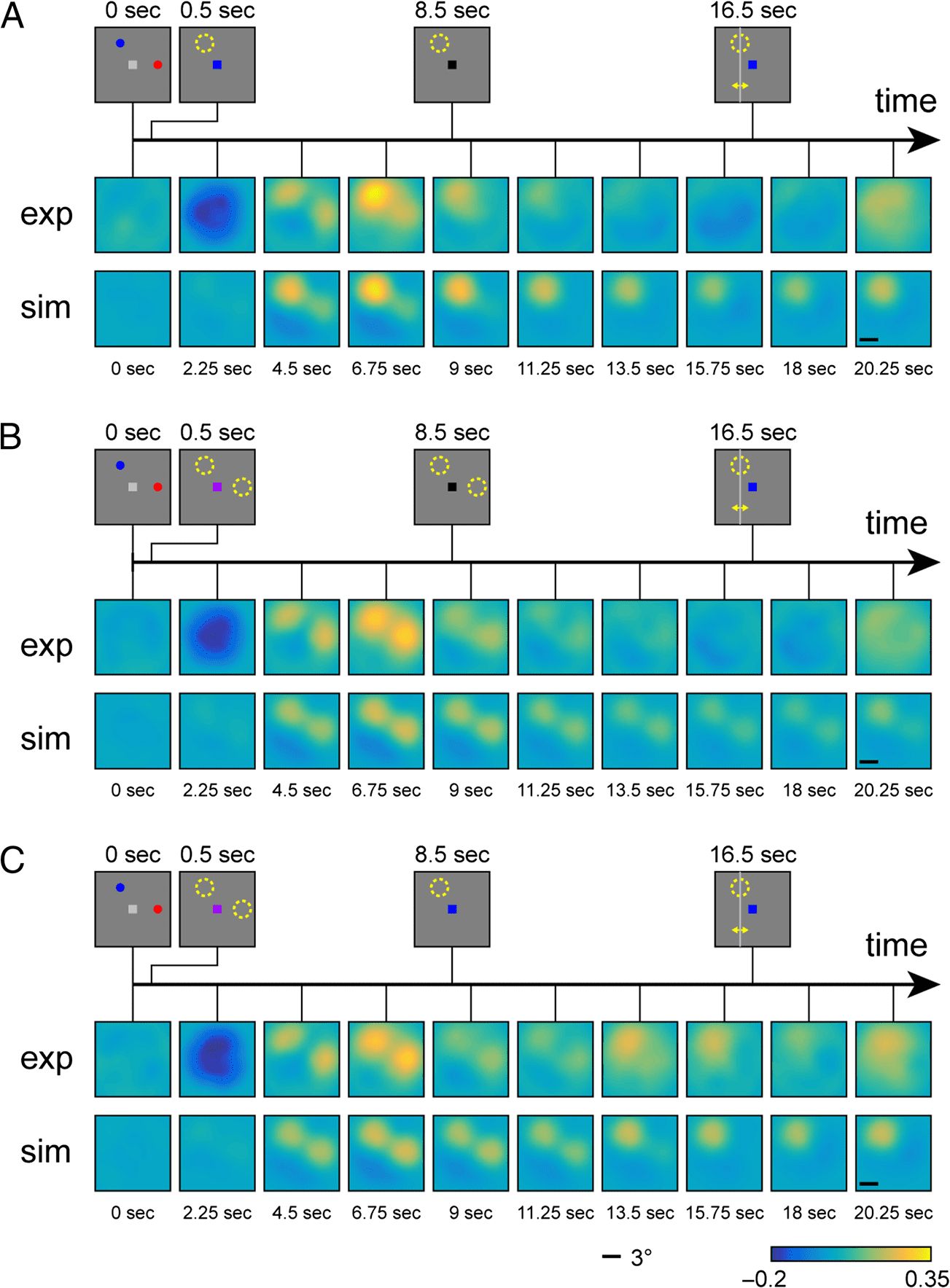Schneegans and Bays 1983 In the averaged and spatially aligned reconstructions over all trials for each condition (shown for one stimulus separation in Figure 4), the representations of stimulus locations are clearly discernible, and the reconstructions qualitatively match the activation patterns and changes over time from the fMRI study. In the R1 condition, the location of the cued and uncued stimulus can be seen with some delay after stimulus presentation (reconstruc- tion for time point 4.5 sec), but only the location of the cued item remains active in the subsequent time points, with activation slowly diminishing over time. It should be noted that this slow decrease in activation levels does not reflect the time course in the neural model itself (where the activation levels settle into a stable state within less than one second after stimulus offset) but is created by the low-pass filter properties of the hemodynamic re- sponse function. In the R2-neutral condition, both memory stimuli are equally represented in reconstructions throughout most of the trial, appearing with some delay after stimulus pre- sentation and slowly diminishing in activation until the response period. The activation time course in the R2- valid condition is indistinguishable from that in the R2- neutral condition during the first half of the trial, as would be expected. After the presentation of the infor- mative retro-cue, however, the activation increases for the location of the cued item and disappears for the location of the uncued item. This reproduces the key observation in the experimental study that a spatially un- informative retro-cue can lead to a selective strengthen- ing of the cued item’s spatial reconstruction in fMRI. Quantitative Analysis of Reconstructions Additional quantitative analyses are based on 1-D re- constructions of the spatial representations, which reflect activation distributions in an annulus around the fixation point. These reconstructions are aligned such that the position of the cued stimulus (the target) is always at zero and are averaged over all stimulus separations for each condition. The fidelity of target representations in these reconstructions is then determined from the con- centration of activation at the target location. 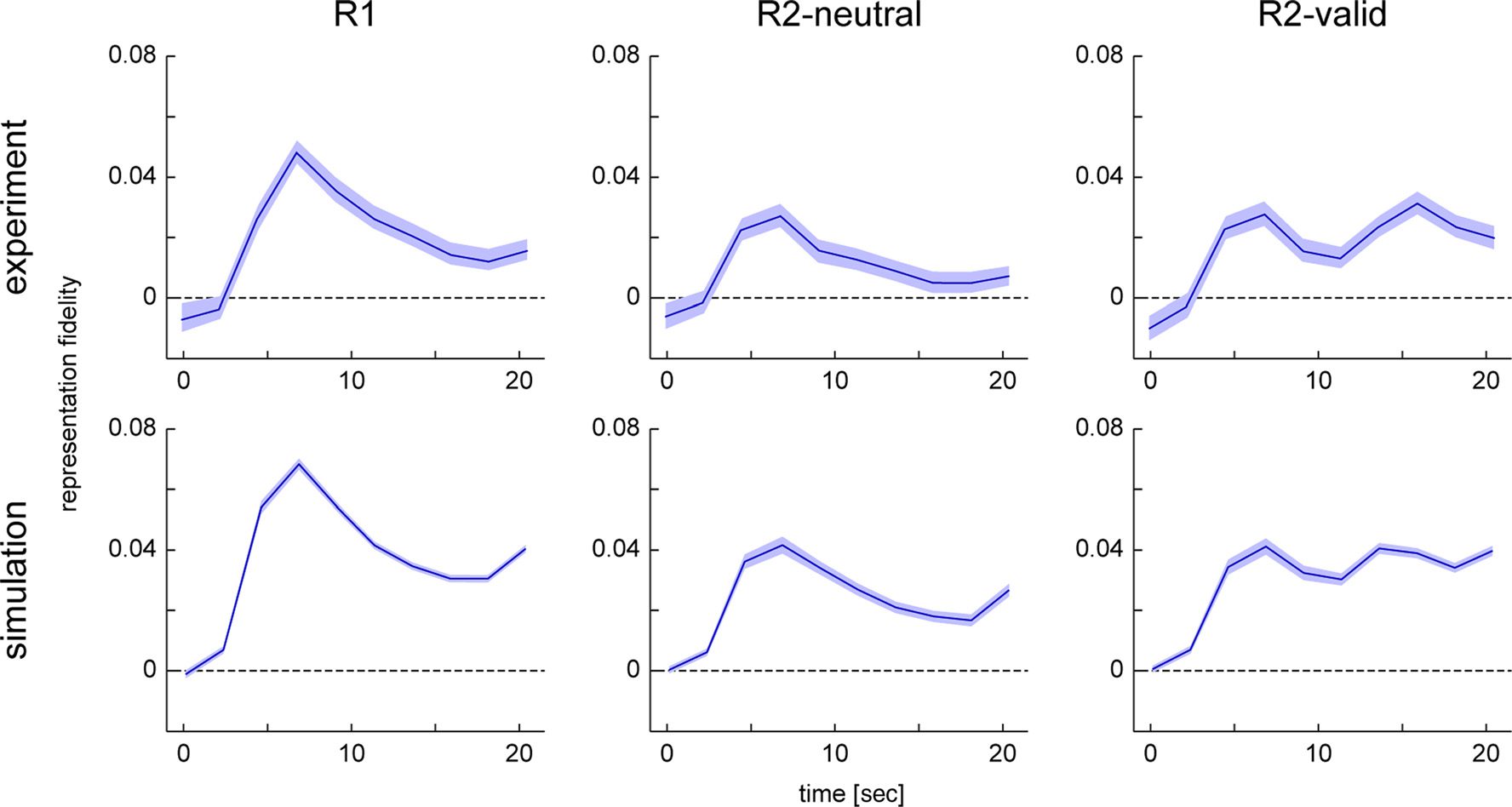The time course of target representation fidelity for the three task conditions is shown in Figure 5. Fidelity of target representation is significantly greater than zero in all conditions and for all time points starting 2.25 sec after stimulus presentation. This is to be expected given that the cued item was continuously represented as a sustained activation peak in the neural model in all trials (except for the small proportion of trials in which the peak collapsed). The fidelity time courses quantitatively repro- duce the results from the experimental study. Fidelity rises sharply following the presentation of the stimulus, then decreases over time in the R1 and R2-neutral conditions, with overall higher fidelity levels in the R1 than R2-neutral condition. 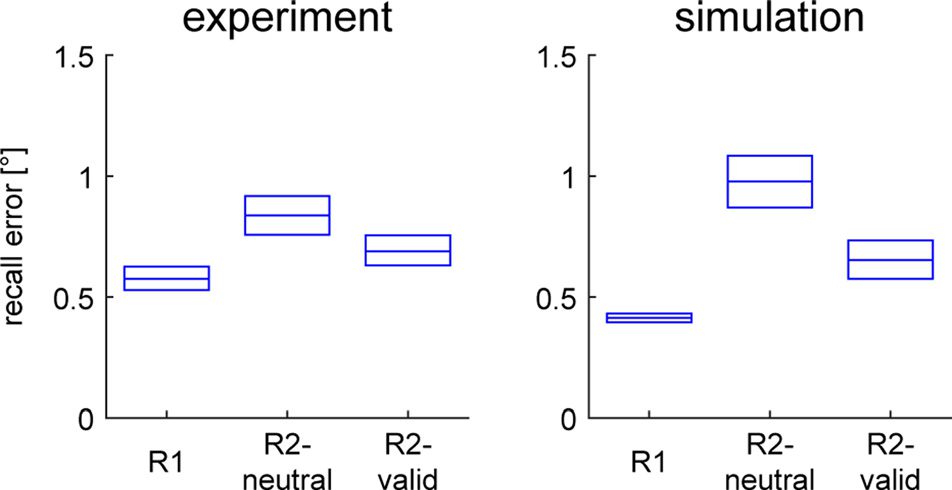Critically, in the R2-valid condition, fidelity rises Figure 3. Mean recall errors for different task conditions in experimental and simulation results. Boxes show 95% confidence interval based on resampling. Figure 3 shows the mean recall errors generated by the model. The model reproduces the pattern of mean response errors in the fMRI study, with lowest errors in the R1 condition, highest in the R2-neutral condition, and intermediate in the R2-valid condition (resampling pro- cedure producing significant difference for all pairwise comparisons, p < .001). Deviations of the response posi- tion from the position of the sample stimulus are gener- ally caused by random noise in the model. Noise causes deviations between an external input and the induced activation peak during encoding and random drift in the peak location over time (Camperi & Wang, 1998). If it transiently lowers the activation level in a region by a sufficient amount, it can also cause the collapse of a peak. This is much more likely to occur when two lo- cations are held in memory simultaneously such that the corresponding activation peaks inhibit each other. Consequently, the rate of peak collapse in the model is higher in the R2-neutral condition (21.7% of trials) than the R2-valid condition (11.6%) and the R1 condition (0%). In the case of a peak collapse, the homogeneous input for the color cue during the response phase typi- cally induces a new activation peak at a random location, producing higher mean response errors. Reconstruction of Spatial Representations To compare our simulation results with the results of the fMRI study, we first generated simulated voxel BOLD sig- nals from the output signals (homologue of neural firing rate) in the model and then performed the same recon- struction method on these simulated signals that was used for the experimental data. The generation of simu- lated BOLD signals and subsequent reconstructions intro- duces significant noise in the single trial data (compared with directly plotting the neural field activations for a trial as in Figure 2), spatial smoothing, and temporal fil- tering (due to the hemodynamic response function). Moreover, the purely spatial reconstruction collapses activation from the separate fields for the two colors into a single representation. 1984 Journal of Cognitive Neuroscience Volume 29, Number 12 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f t / . u s e r o n 1 7 M a y 2 0 2 1 Figure 4. Two-dimensional reconstructions of spatial activation patterns in the R1 condition (A), R2-neutral condition (B), and R2-valid condition (C). In each panel, the stimulus displays for different phases of the trial are shown at the top. The first row shows reconstructions from the fMRI study (Sprague et al., 2016); the second row shows reconstructions from neural model simulations. D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j / . t f u s e r o n 1 7 M a y 2 0 2 1 again following the presentation of the retro-cue, repro- ducing this key signature of the retro-cue effect in the experimental data. The fidelity of target representation in the simulation results also rises at the end of the trial. This is an effect of the response cue given at this time, which is realized in the same way as the retro-cue in the neural model. A rise in fidelity at the end of the trial can also be observed in the experimental results for the R1 and R2-neutral con- dition, although weaker than in the simulation. At least for the R2-neutral condition, we would expect that the color cue at the end of the trial should have a similar ef- fect as a cue presented earlier. However, it is possible that, in the experimental data, there is interference in the reconstruction from motor planning activity for re- sponse generation, which is not captured in the model. We analyze the simulation result that a color cue can in- crease fidelity even when only a single item is held in working memory below. We further note that variability of fidelity within each condition was lower in our simula- tions than in the experimental data. To fully capture the experimental results, the model would likely have to in- corporate additional sources of variability such as fluctu- ations in attention across trials. 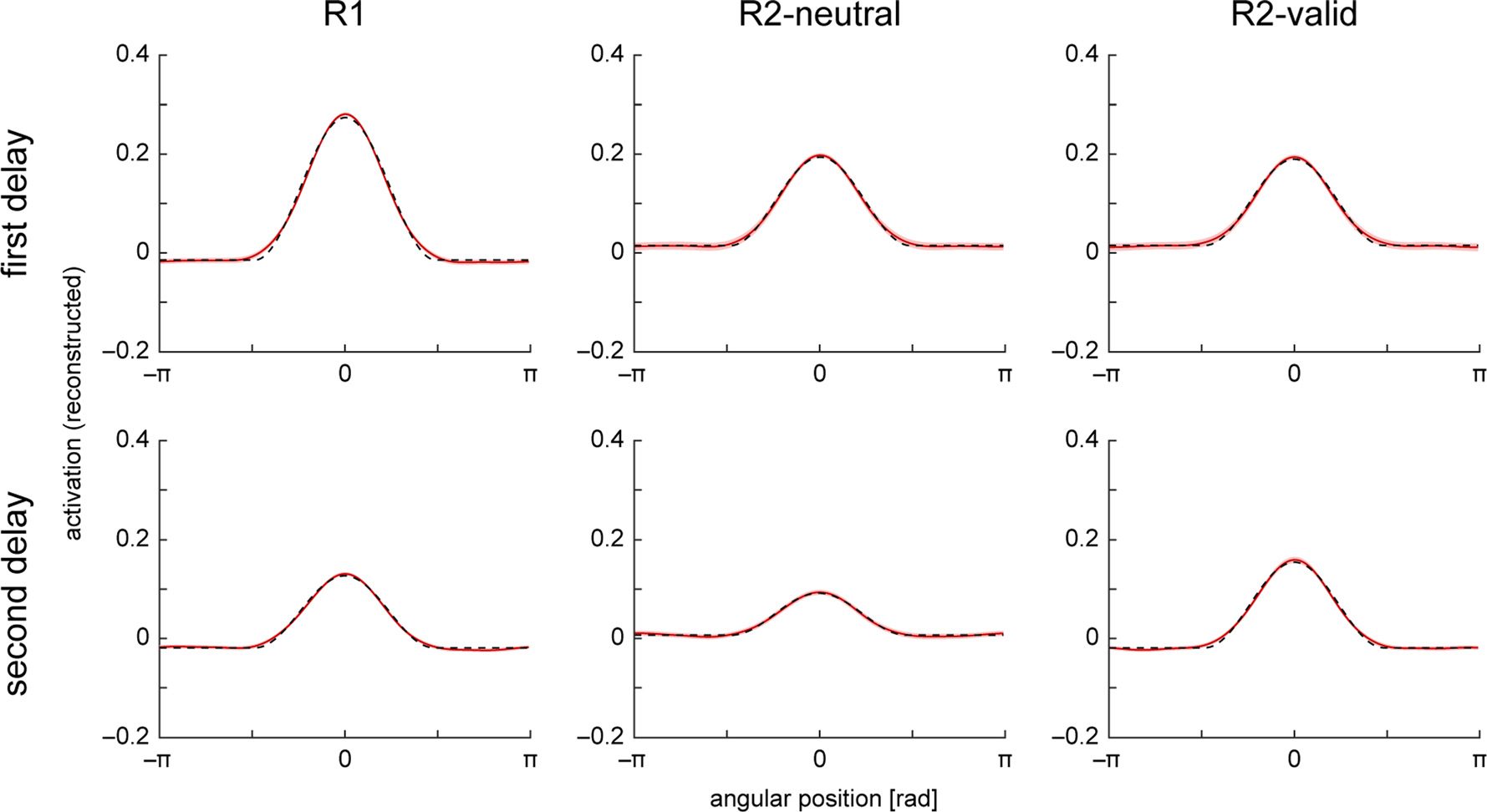Following the analysis in the fMRI study, we fit the ac- tivation profiles in all conditions with a Gaussian-like function with variable baseline, separately for the first (6.75 and 9 sec) and second memory period (15.75 and 18 sec). The mean activation profiles and function fits are shown in Figure 6. We used a resampling procedure to determine significance of differences in the fitted param- eters between conditions and delay periods. For the first memory period, we found a significantly higher ampli- tude of the central activation peak in the R1 condition compared with both R2-neutral and R2-valid conditions ( p < .001). Conversely, the baseline of the fit was higher Schneegans and Bays 1985 Figure 5. Time course of representational fidelity for target location in different task conditions for the experimental results (adapted from Sprague et al., 2016) and model simulations. Shaded areas indicate 95% confidence interval based on resampling. in the R2-neutral and R2-valid conditions than in the R1 condition ( p < .001). No other significant differences between the fitted parameters for different conditions were observed for the first memory period. These find- ings fully reproduce the observed effects of set size in the fMRI study. The findings can be explained from the evolution of activation in the neural model and the effects of the re- construction procedure. The target representation in the R1 condition is stronger due to the color cue that is pre- sented right after stimulus offset in this condition. This raises activation in the whole field for the cued color and, in particular, strengthens the existing activation peak in this field, yielding higher activation for the cued item’s location in the reconstruction (in which the fields for different colors are collapsed). In the neural model, D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f . t / u s e r o n 1 7 M a y 2 0 2 1 Figure 6. One-dimensional reconstructions over angular space for different task conditions in neural model simulations. Mean activation profiles across trials are shown separately for the first (top row) and second delay period (bottom row) of the task. Red line shows reconstructions, with shaded red area indicating 95% confidence interval based on resampling. Dashed black lines show fitted functions. 1986 Journal of Cognitive Neuroscience Volume 29, Number 12 the single sustained activation peak during the memory period in the R1 condition is also stronger than the cor- responding peaks in the R2 conditions due to lack of mutual inhibition between peaks. The inhibitory inter- actions implement a form of normalization of total work- ing memory activity in the model. This aspect is consistent with continuous resource models of working memory capacity (Bays, 2014; Bays & Husain, 2008), although we note that the neural field model also incorporates aspects of discrete representations linking them to slot models (Johnson et al., 2014). In the R2 conditions, the additional sustained peaks for the nontarget item in each trial are reflected in the acti- vation profiles. Nontarget positions are offset from the target position by ±60°, ±120°, or 180° (with some addi- tional random variations), so that the corresponding ac- tivation peaks are distributed evenly in orientation space when the reconstructions are aligned on the target posi- tion. They contribute therefore to a higher baseline acti- vation in the fitted function. Because the fit amplitude is determined as height of the central activation peak over this baseline, the increased baseline itself also contrib- utes to a reduced amplitude estimate in the reconstruc- tions for the R2 condition. These effects in the model were confirmed by directly applying the function fits to the field output (summed over both fields of the model), taken at the midpoint of the first delay period. As in the reconstructions, we found a significantly higher amplitude, but lower base- line, in the R1 condition compared with both R2-neutral and R2-valid conditions (all ps < .001). The higher base- line component in the R2 conditions was greatly dimin- ished when applying the fits only to the field containing the target item in each trial, confirming that it primarily reflects contributions from nontarget items. The higher amplitude for the R1 condition was still preserved in this case, showing that the activation for the target item is stronger in this condition. During the second memory period, the same set size effects in the reconstructions were observed when com- paring R1 and R2-neutral condition, with higher ampli- tude ( p < .001) and lower baseline ( p < .001) in the R1 condition. In the R2-valid condition, however, target representation amplitude following the informative retro- cue is higher than in both the R2-neutral ( p < .001) and R1 conditions ( p < .001). These results reproduce analogous findings in the fMRI study. One effect from that study that we did not observe in the simulation re- sults was an increased baseline activation in the R2-valid condition. In fact, we found baseline values in the R2- valid condition that were significantly lower than in the R2-neutral condition ( p < .001) and not significantly dif- ferent from the R1 condition ( p = .95). No further sig- nificant differences in parameters across conditions were observed for the second memory periods. In the neural model, the effects of the retro-cue on peak amplitude in the second memory period are ex- plained by the same mechanisms as the set size effects in the first memory period. The color cue input tran- siently strengthens the activation peak for the cued item and, by suppressing the sustained peak for the noncued item, removes inhibition from that peak for the second memory period. The color cue also globally raises the activation level (and, to some extent, the output signal derived from it) for the whole field of the matching color. This may, in principle, provide an explanation for the experimentally observed increase in fit baseline for the R2-valid condition compared with the R2-neutral condition. However, in the present model implementa- tion, this effect is outweighed by the decrease in baseline that is brought about by the disappearance of the sus- tained activation peak for the noncued item. We again tested these explanations by fitting the field output directly, now at the midpoint of the second delay period. We found the same effects as in the reconstruc- tions when comparing R1 and R2-neutral conditions (all ps < .001). For the R2-valid condition, both amplitude and baseline were intermediate between R1 and R2- neutral condition ( p < .001 for all comparisons). Fit amplitude in this condition did spike during the pre- sentation of the retro-cue but then quickly diminished again in the neural model. In the reconstruction, this transient spike is carried over to the second delay period due to the low-pass filter properties of the hemodynamic response function. Correlations between Reconstructions and Response Errors Having demonstrated that the neural model can repro- duce both behavioral and reconstruction results, we now analyze interactions between trial-to-trial report performance and reconstruction quality. We divided the trials of each block within each condition into two groups with recall error lower and higher than median recall error in that block, respectively. We then generated re- constructions and function fits for each group and each condition. We found a significantly higher amplitude of the target representation in the low-error group com- pared with the high-error group for the R2-neutral and R2-valid condition in the second delay period (R2-neutral: mean amplitude 0.058 vs. 0.033, p < .001; R2-valid: mean amplitude 0.095 vs. 0.076, p = .012). Similar findings were reported in the experimental study, although a sig- nificant effect of error rate on fit amplitude was observed only in the R2-valid condition for the second delay period and in the R2-neutral condition for the first memory period. These results were interpreted as evidence that the reconstruction quality reflects the quality of the working memory representations. In the neural simulations, these results can be ex- plained by the fact that the high-error group will most likely contain all trials in which the activation peak for the target item collapsed during the delay period as a Schneegans and Bays 1987 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j t . f / u s e r o n 1 7 M a y 2 0 2 1 result of random noise, as well as those trials in which there was significant drift in peak position. For trials in which the activation peak collapsed, the reconstruction will either show no peak or a peak at a new random location (which can form in response to the retro-cue). Both will contribute only to baseline activation in the aligned reconstructions. Trials with high drift of the acti- vation peak will contribute to a central peak in the recon- structions, but this peak will be smeared out when trials are aligned with respect to the stimulus position. Overall, peak amplitude in the aligned reconstructions will then be lower in high-error versus low-error trials. It should be noted here that the retro-cue in the neural model cannot retroactively restore memory precision. Although the cue does strengthen the sustained activa- tion peak for the cued item, any drift in peak position that occurred before the cue will still be reflected in peak position after the cue. Also, if the activation peak col- lapsed before the retro cue was given, the spatially un- informative cue can only induce a new peak at a random location. Thus, the interactions between report perfor- mance and reconstruction quality and the observed in- crease in reconstruction quality after the retro-cue do not provide any evidence that a retro-cue actually restores representational precision. The retro-cue may merely re- duce further loss of precision after the cue is presented. Components of the Retro-cue Effect Using the neural model, we can selectively assess the contribution of different components of the neural repre- sentation to the reconstruction quality and its restoration following the retro-cue. Although we cannot tell from simulation results alone whether the components iden- tified here also play a role in the biological neural system, we can make predictions regarding their signatures in reconstructions that could be tested with fMRI data. As a first component in the full reconstruction, we ana- lyze the effect of the stimulus presentation in the absence of any working memory processes. To this end, we set the weight cexc of excitatory interactions in the neural model to zero. With this modification, the neural popu- lation representation in the model still forms peaks of activation in response to external stimulation, but these peaks collapse as soon as the stimuli disappear (i.e., the model does not show any working memory capabilities; Figure 7A). The time course of reconstruction fidelity for this model in the R2-valid condition is shown in Figure 7B (the time courses for the R1 and R2-neutral conditions are virtually identical in this modified model). During the first half of the trial, the time course of fidelity is similar to those ob- served in the full model for the R2-valid and R2-neutral con- dition, but then fidelity decreases and even becomes negative during the second half of the trial. This reflects the shape of the canonical hemodynamic response func- tion, which likewise takes negative values about 12 sec after a pulse of activation. These results suggest that a large part of the early reconstructions are dominated by a sensory response (and possibly attention effects, which we do not capture as a separate component in the model), but it also shows that a working memory component is necessary to account for the positive reconstruction fidelity in the latter part of the trial. The simulation results also confirm that the spatially nonspecific color cue input, which is provided after the first half of the delay period, has no effect on reconstruction fidelity in the absence of sustained activity. In a second model variant, we assess how removing irrelevant items from working memory contributes to the increase of reconstruction fidelity following an infor- mative retro-cue. In the original model, the retro-cue is implemented as a positive homogeneous input to the neural field corresponding to the cue color, which in- creases activation levels in this field and leads to the ex- tinction of the activation peak for the uncued item through global inhibitory interactions. As an alternative, we now implement the retro-cue as an inhibitory input to the neural field corresponding to the uncued color (with amplitude cforget), which extinguishes any activa- tion peaks in this field without directly strengthening activation for the cued item (Figure 7C). Figure 7D shows the time course of reconstruction fidelity of this model variant in the R2-valid condition. Removal of the noncued item leads to an increased fidel- ity in the second half of the trial compared with the R2-neutral condition (compare to dashed green line). However, the rise in fidelity following the retro-cue is weaker and occurs with longer delay than in the original model. The removal of an irrelevant item thus contributes to the retro-cue effect in the model but does not fully account for it. To test the direct contribution of the cue input to re- construction quality in the model, we return to the orig- inal model variant but modify the task. Instead of presenting two colored stimuli in the beginning, we only present a single one, which is always the cued item and response target (Figure 7E). This means that the retro- cue does not provide any additional information for the task. Nonetheless, we find that the retro-cue signifi- cantly increases the reconstruction quality in the model (Figure 7F) in a manner very similar to the retro-cue effect in the original task (dashed blue line). Note that overall reconstruction quality is higher in this condition due to the absence of the nontarget item. This result can be explained by interaction effects in the neural model. The color cue is emulated as a homo- geneous positive input to the neural field. In the absence of any sustained activation, this input would simply raise activation equally over the whole field, which would not produce any change in the fidelity measure (as demon- strated in the model variant without working memory states; Figure 7B). When a sustained peak of activation is present, activation initially also rises homogeneously; 1988 Journal of Cognitive Neuroscience Volume 29, Number 12 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j . / f t u s e r o n 1 7 M a y 2 0 2 1 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f . / t u s e r o n 1 7 M a y 2 0 2 1 Figure 7. Evolution of activation patterns and fidelity time courses in model simulations for different model and task variants based on the original R2-valid condition. (A, B) Neural model without lateral excitatory interactions. (C, D) Model variant with color cue realized through inhibition of noncued items. (E, F) Task variant with only the target item presented in the sample array. (G, H) Model variant with weak (unreliable) retro-cue input. The field activations are shown for the case of a valid retro-cue; fidelity plots are shown for both valid (blue) and invalid (red) retro-cue. The dashed lines in the fidelity plots show the mean fidelity from the original R2-valid (blue) and R2-neutral condition (green) for comparison. Shaded areas in fidelity plots indicate 95% confidence interval based on resampling. Schneegans and Bays 1989 but as it does, the field output that drives lateral inter- actions (computed from the activation via a sigmoid function, Equation 2) increases most strongly at the edges of the existing peak. The peak expands further under the influence of local excitation and consequently suppresses activation in the remaining field (as well as the second, noncued field) through global inhibition (Figure 7E). Overall, the concentration of activation at the location of the existing peak is increased, leading to the increase in measured reconstruction fidelity. We note that, for this simulation, we assumed that the cue would have the same effect as in the original task de- spite being uninformative. Human observers would likely pay less attention to the cue or ignore it entirely under these conditions, leading to diminished effects on work- ing memory representations. We did not observe any benefit of the retro-cue on behavioral performance in the model (compared with simulations with a single tar- get stimulus without retro-cue; mean response error in both cases 0.41°, p = .91). This is due to the fact that behavioral cueing effects in the model are based on bias- ing the competition between different working memory items, which does not occur in the case of a single item. Generalization of the Model to Unreliable Retro-cues The experiment we emulated with the neural model (Sprague et al., 2016) exclusively uses retro-cues with 100% reliability, but many studies on retro-cues use lower reliabilities, such that participants have an incen- tive to retain uncued items in memory as well (Souza & Oberauer, 2016). Here, we test whether the neural model can be adapted to this scenario. We make a single change to the implementation, namely reducing the strength of the homogeneous boost input that emulates the color cue (amplitude 2.5 compared with 17.5 in the original model; the amplitude for the definitive response cue at the end of the trial is left unchanged). With this setting, the input transiently strengthens the sustained activation for the cued item but does not increase its activation levels to such a degree that the peak for the noncued item will be extinguished (Figure 7G). We tested the model in trials with either a valid (matching the target color) or invalid retro-cue (match- ing the nontarget color) provided after the first half of the delay period and an unambiguous response cue indi- cating the target at the end. The fidelity time course for these simulations is shown in Figure 7H. The valid retro- cue causes a small rise in fidelity, whereas the invalid retro-cue causes a faster drop in the representational fidel- ity of the target compared with the original R2-neutral condition (dashed green line). Nonetheless, even with an invalid retro-cue the fidelity remains above zero through- out the trial and recovers when the response cue is given, indicating that the uncued item is retained in working memory in a majority of trials. We found a significant effect of cue validity on re- sponse errors, with response error lower than in the original R2-neutral condition for valid retro-cues (mean error 0.74°) and higher for invalid retro-cues (1.46°; sig- nificantly different based on resampling procedure, p < .001). This qualitatively reproduces the most prominent effect of retro-cueing in the literature (see, e.g., Pertzov, Bays, Joseph, & Husain, 2013). The retro-cue effect on performance was driven by a lower rate of peak col- lapse in the valid than in the invalid retro-cue condition (14.0% vs. 43.5%). We did not find a significant differ- ence in precision for those trials where the peak was sustained (mean response error 0.41° for both condi- tions, p = .96), likely due to the fact that the separate fields for red and blue item do not allow any local inter- actions between the two activation peaks in the model. Behavioral studies on retro-cue effects have consistently shown a benefit for the probability of reporting the cor- rect item (rather than guessing or reporting the feature of nontarget item), with only some of the studies show- ing a precision benefit (see Souza & Oberauer, 2016, for a review). We note that our model does not produce any swap errors, which contribute significantly to non- target responses in behavioral studies. These might potentially be addressed by extending the model with an additional purely spatial memory representation that does not capture binding information (Matthey, Bays, & Dayan, 2015). DISCUSSION We have presented a neurodynamic model of retro-cue effects in visual working memory, and we have demon- strated that this model can reproduce behavioral and re- construction results from an fMRI study, which were interpreted as supporting a latent working memory state (Sprague et al., 2016). The study had found an increase in reconstruction quality after a retro-cue, as well as cor- relations between reconstruction quality and response error. The authors had argued that these findings provide evidence for a working memory state that is not detect- able in the fMRI signal but that can be reactivated by the retro-cue. They proposed that this was likely an activity- silent state, encoded, for example, in changes in synaptic connectivity or sustained subthreshold changes in mem- brane potential (Stokes, 2015). The neural model pre- sented here does not feature such a latent memory state, relying entirely on sustained neural activity for working memory representations (Wang, 2001). The fact that the model can nonetheless reproduce all key exper- imental findings refutes the argument for an activity- silent working memory state. Such a state may still exist, but it is not necessary to explain any of the experimental findings from the fMRI study. We aimed to keep the neural model as simple as pos- sible, making only minimal assumptions about the neural architecture beyond the basic mechanism of sustained 1990 Journal of Cognitive Neuroscience Volume 29, Number 12 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j . / t f u s e r o n 1 7 M a y 2 0 2 1 activity through self-excitation. In particular, we em- ployed a continuous approximation of the discrete spik- ing activity in biological neural systems. Previous models of sustained memory activity using continuous firing rates have produced results very similar to more detailed spiking models (Compte et al., 2000; Camperi & Wang, 1998), so we believe that this simplification does not qualitatively alter model behavior. As a further simplifica- tion, we did not separately model individual cortical areas or distinguish between sensory and working memory representations. The simulation results suggest that a large portion of the fMRI signal in the experimental study is driven directly by the visual stimuli (which may comprise both purely sensory activity and working memory encod- ing), but a sustained working memory component is still necessary to fully explain the signal. Spatial attention may also contribute to the fMRI signal and the observed retro- cue effect, given that previous behavioral studies have found that a color cue can enhance spatial attention for a memorized item location even if the location is not task relevant (Theeuwes, Kramer, & Irwin, 2011). However, neither the experimental study nor the model presented here investigates the role of attention in this task. One key assumption we did make in the model is that the working memory representation captures the bind- ing between colors and locations (Treisman, 1996). Bind- ing information is essential to solve the behavioral task (reporting the location of the cued item, rather than randomly reporting the location of either stimulus) but is not reflected in the reconstructions used by Sprague et al. (2016). Following previous neural field models of feature binding in visual working memory (Schneegans et al., 2016; Johnson, Spencer, & Schöner, 2008), we employ a population representation with conjunctive coding. This kind of representation has recently been shown to account for behavioral signatures of binding failures in working memory tasks (Schneegans & Bays, 2017; Matthey et al., 2015). Some of the previous imple- mentations have combined the conjunctive coding with separate feature-specific representation for more efficient representation of individual feature values (Schneegans et al., 2016; Matthey et al., 2015). We omitted such a mechanism here for the sake of simplicity, but we note that some of the neural representations for working memory and attention that contribute to the fMRI signal are likely to be purely spatial and only indirectly interact with representations of stimulus color. The proposed model constitutes to our knowledge the first neural process model of retro-cue effects. The neu- rodynamic mechanism employed here integrates several hypotheses about the mechanisms underlying retro-cue effects (Souza & Oberauer, 2016). The cue directly in- creases activation of the sustained activation peak that reflects the cued item, making use of the conjunctive coding to increase activation in the spatial representation in response to a color cue. This realizes a form of refresh- ing of the cued item (Rerko & Oberauer, 2013; Chun & Johnson, 2011). Increasing the activation of one working memory item reduces activation for other items by means of lateral inhibition in the model, consistent with resource models of working memory (Bays, 2014; van den Berg, Shin, Chou, George, & Ma, 2012; Bays, Catalao, & Husain, 2009; Bays & Husain, 2008). For fully reliable retro-cues, this leads to the complete extinction of other working memory items, consistent with the idea that retro- cues act through removal of irrelevant items (Souza et al., 2014; Kuo, Stokes, & Nobre, 2012). The model also qualita- tively captures effects of less reliable cues, which decrease the chance of forgetting the cued item (through noise- induced collapse of the sustained activation peak) at the cost of an increased chance of forgetting noncued items. All performance effects of the retro-cue in the present model are due to protection of the cued item from decay after the retro-cue. This is consistent with previous find- ings from delayed estimation tasks showing a continuous decrease of response precision with retention interval duration that can be alleviated by a valid retro-cue (Pertzov et al., 2013). This explanation has been questioned by Souza and Oberauer (2016) based on contradictory find- ings from Gressmann and Janczyk (2016), but these latter findings were based on a change detection task, which may not provide sufficient sensitivity to detect changes in memory precision. Souza and Oberauer (2016) also point to findings that retro-cues increase performance compared with no-cue trials with shorter delay period (matched to the time before the retro-cue; Makovski, Sussman, & Jiang, 2008). A possible cause for this effect is that the retro-cue triggers the retrieval of the cued item without the per- ceptual interference that may be created by elements of the response display (such as probe stimuli in change de- tection tasks or a color wheel in delayed estimation tasks; Souza, Rerko, & Oberauer, 2016; Makovski, Watson, Koutstaal, & Jiang, 2010). Accounting for such effects is beyond the scope of the present model. The retro-cue mechanism in the neural model accounts for the restoration of reconstruction quality for the target item’s location that was observed in the fMRI study. Sprague et al. (2016) interpreted this effect of the retro-cue as evi- dence for an activity-silent working memory state based on the following reasoning: By the time the retro-cue was given, the working memory representation of the memo- rized location as measured by fMRI reconstruction quality was already degraded to a certain degree; the retro-cue did not provide any spatial information, so it could not have improved the representation of the target’s location; thus, the improved reconstruction quality after the retro-cue must have been caused by the reactivation of an activity-silent working memory representation (realized, e.g., through changes in synaptic connectivity) that was not detectable in the fMRI data before the retro-cue. We argue that there are several problems with this line of reasoning. First, although the color cue does not provide any spatial information by itself, it does allow the selection of a single memorized location if the working memory Schneegans and Bays 1991 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j . / t f u s e r o n 1 7 M a y 2 0 2 1 representation provides information about the binding of colors to locations, as we have argued above. This allows, at the very least, the selective removal of uncued items from working memory. We have demonstrated in model simula- tions that the selective removal of uncued items produces an increase in reconstruction quality for the cued item using the fidelity measure proposed by Sprague et al. (2016). The reconstruction method does not attempt to estimate memorized color information and thereby loses part of the information that is necessary to explain the effect of the color cue on the spatial representation. Second, even an entirely uninformative cue can pro- duce an increase in reconstruction quality through the effects of neural interactions in conjunction with sus- tained activation states. We have shown in the simu- lations that, even when only a single item is held in working memory, a color cue for that item produces a rise in the fidelity of its reconstruction. The same color cue does not affect fidelity in the absence of sustained working memory activity. In this latter case, the cue only produces a homogeneous rise in activation. But in the presence of a sustained activation peak, the elementary connection pattern of local excitation and surround inhi- bition in the model transforms this homogeneous input into a specific increase of activation for the existing peak. In a more complex neural architecture with multiple inter- connected representations, the combination of a non- specific input with a sustained activation state may even have much more dramatic effects. Such effects have been employed to drive complex state transitions in neuro- dynamic models (Schneegans et al., 2016; Richter et al., 2014). The results of other reconstruction studies may still pose a challenge for the present model. In several exper- iments, decoding quality was found to fall to chance level for memorized items outside the focus of attention but could be restored at a later time following informative cues or unspecific stimulation ( Wolff et al., 2017; Rose et al., 2016). In the neural model, once sustained activity has ceased and the activation peak has collapsed, it can- not be restored by unspecific external stimulation. It is possible, however, that the experimental studies merely failed to detect the signatures of weak neural activity that was sustained throughout the memory period. This might occur because the relationship between firing rate and BOLD/EEG signal is less straightforward than the direct linear relationship assumed here (e.g., Logothetis, Pauls, Augath, Trinath, & Oeltermann, 2001). If this is the case, mechanisms similar to the ones described in this study may explain how weak sustained activity can be amplified and become detectable again in response to unspecific input to the neural system. Acknowledgments We thank Thomas C. Sprague, Edward F. Ester, and John T. Serences for making data and analysis code from their study avail- able online. This work was supported by the Wellcome Trust. Reprint requests should be sent to Sebastian Schneegans, Department of Psychology, University of Cambridge, Downing Street, Cambridge CB2 3EB, UK, or via e-mail: ss2361@cam.ac.uk. REFERENCES Amari, S. (1977). Dynamics of pattern formation in lateral- inhibition type neural fields. Biological Cybernetics, 27, 77–87. Barak, O., & Tsodyks, M. (2014). Working models of working memory. Current Opinion in Neurobiology, 25, 20–24. Bays, P. M. (2014). Noise in neural populations accounts for errors in working memory. Journal of Neuroscience, 34, 3632–3645. Bays, P. M. (2015). Spikes not slots: Noise in neural populations limits working memory. Trends in Cognitive Sciences, 19, 431–438. Bays, P. M., Catalao, R. F., & Husain, M. (2009). The precision of visual working memory is set by allocation of a shared resource. Journal of Vision, 9, 7.1–7.11. Bays, P. M., & Husain, M. (2008). Dynamic shifts of limited working memory resources in human vision. Science, 321, 851–854. Burak, Y., & Fiete, I. R. (2012). Fundamental limits on persistent activity in networks of noisy neurons. Proceedings of the National Academy of Sciences, U.S.A., 109, 17645–17650. Camperi, M., & Wang, X.-J. (1998). A model of visuospatial working memory in prefrontal cortex: Recurrent network and cellular bistability. Journal of Computational Neuroscience, 5, 383–405. Chaudhuri, R., & Fiete, I. (2016). Computational principles of memory. Nature Neuroscience, 19, 394–403. Chun, M. M., & Johnson, M. K. (2011). Memory: Enduring traces of perceptual and reflective attention. Neuron, 72, 520–535. Compte, A., Brunel, N., Goldman-Rakic, P. S., & Wang, X.-J. (2000). Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cerebral Cortex, 10, 910–923. Courtney, S. M., Ungerleider, L. G., Keil, K., & Haxby, J. V. (1997). Transient and sustained activity in a distributed neural system for human working memory. Nature, 386, 608–611. Edin, F., Macoveanu, J., Olesen, P., Tegnér, J., & Klingberg, T. (2007). Stronger synaptic connectivity as a mechanism behind development of working memory-related brain activity during childhood. Journal of Cognitive Neuroscience, 19, 750–760. Emrich, S. M., Riggall, A. C., LaRocque, J. J., & Postle, B. R. (2013). Distributed patterns of activity in sensory cortex reflect the precision of multiple items maintained in visual short-term memory. Journal of Neuroscience, 33, 6516–6523. Engel, T. A., & Wang, X.-J. (2011). Same or different? A neural circuit mechanism of similarity-based pattern match decision making. Journal of Neuroscience, 31, 6982–6996. Erickson, M. A., Maramara, L. A., & Lisman, J. (2010). A single brief burst induces glur1-dependent associative short-term potentiation: A potential mechanism for short-term memory. Journal of Cognitive Neuroscience, 22, 2530–2540. Eriksson, J., Vogel, E. K., Lansner, A., Bergström, F., & Nyberg, L. (2015). Neurocognitive architecture of working memory. Neuron, 88, 33–46. Funahashi, S., Bruce, C. J., & Goldman-Rakic, P. S. (1989). Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex. Journal of Neurophysiology, 61, 331–349. Fuster, J. M., & Alexander, G. E. (1971). Neuron activity related to short-term memory. Science, 173, 652–654. 1992 Journal of Cognitive Neuroscience Volume 29, Number 12 D o w n l o a d e d f r o m l l / / / / j f / t t i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j . / f t u s e r o n 1 7 M a y 2 0 2 1 Gressmann, M., & Janczyk, M. (2016). The (un)clear effects of invalid retro-cues. Frontiers in Psychology, 7, 244. Harrison, S. A., & Tong, F. (2009). Decoding reveals the contents of visual working memory in early visual areas. Nature, 458, 632–635. Johnson, J. S., Simmering, V. R., & Buss, A. T. (2014). Beyond slots and resources: Grounding cognitive concepts in neural dynamics. Attention, Perception, & Psychophysics, 76, 1630–1654. Johnson, J. S., Spencer, J. P., & Schöner, G. (2008). Moving to higher ground: The dynamic field theory and the dynamics of visual cognition. New Ideas in Psychology, 26, 227–251. Johnson, J. S., Spencer, J. P., & Schöner, G. (2009). A layered neural architecture for the consolidation, maintenance, and updating of representations in visual working memory. Brain Research, 1299, 17–32. Kuo, B.-C., Stokes, M. G., & Nobre, A. C. (2012). Attention modulates maintenance of representations in visual short-term memory. Journal of Cognitive Neuroscience, 24, 51–60. LaRocque, J. J., Lewis-Peacock, J. A., Drysdale, A. T., Oberauer, K., & Postle, B. R. (2013). Decoding attended information in short-term memory: An EEG study. Journal of Cognitive Neuroscience, 25, 127–142. Lewis-Peacock, J. A., Drysdale, A. T., Oberauer, K., & Postle, B. R. (2012). Neural evidence for a distinction between short-term memory and the focus of attention. Journal of Cognitive Neuroscience, 24, 61–79. Linden, D. E., Bittner, R. A., Muckli, L., Waltz, J. A., Kriegeskorte, N., Goebel, R., et al. (2003). Cortical capacity constraints for visual working memory: Dissociation of fMRI load effects in a fronto-parietal network. Neuroimage, 20, 1518–1530. Lindquist, M. A., Loh, J. M., Atlas, L. Y., & Wager, T. D. (2009). Modeling the hemodynamic response function in fMRI: Efficiency, bias and mis-modeling. Neuroimage, 45, S187–S198. Lipinski, J., Schneegans, S., Sandamirskaya, Y., Spencer, J. P., & Schöner, G. (2012). A neurobehavioral model of flexible spatial language behaviors. Journal of Experimental Psychology: Learning, Memory, and Cognition, 38, 1490. Logothetis, N. K., Pauls, J., Augath, M., Trinath, T., & Oeltermann, A. (2001). Neurophysiological investigation of the basis of the fMRI signal. Nature, 412, 150–157. Makovski, T., Sussman, R., & Jiang, Y. V. (2008). Orienting attention in visual working memory reduces interference from memory probes. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 369. Makovski, T., Watson, L. M., Koutstaal, W., & Jiang, Y. V. (2010). Method matters: Systematic effects of testing procedure on visual working memory sensitivity. Journal of Experimental Psychology: Learning, Memory, and Cognition, 36, 1466. Matthey, L., Bays, P. M., & Dayan, P. (2015). A probabilistic palimpsest model of visual short-term memory. PLoS Computational Biology, 11, e1004003. Mi, Y., Katkov, M., & Tsodyks, M. (2017). Synaptic correlates of working memory capacity. Neuron, 93, 323–330. Mongillo, G., Barak, O., & Tsodyks, M. (2008). Synaptic theory of working memory. Science, 319, 1543–1546. Pertzov, Y., Bays, P. M., Joseph, S., & Husain, M. (2013). Rapid forgetting prevented by retrospective attention cues. Journal of Experimental Psychology: Human Perception and Performance, 39, 1224. Rerko, L., & Oberauer, K. (2013). Focused, unfocused, and defocused information in working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39, 1075. Richter, M., Lins, J., Schneegans, S., & Schöner, G. (2014). A neural dynamic architecture resolves phrases about spatial relations in visual scenes. In S. Wermter, C. Weber, W. Duch, T. Honkela, O. Koprinkova-Hristova, S. Magg, G. Palm, & A. E. P. Villa (Eds.), International Conference on Artificial Neural Networks (pp. 201–208). Cham: Springer. Riggall, A. C., & Postle, B. R. (2012). The relationship between working memory storage and elevated activity as measured with functional magnetic resonance imaging. Journal of Neuroscience, 32, 12990–12998. Rose, N. S., LaRocque, J. J., Riggall, A. C., Gosseries, O., Starrett, M. J., Meyering, E. E., et al. (2016). Reactivation of latent working memories with transcranial magnetic stimulation. Science, 354, 1136–1139. Schneegans, S., & Bays, P. M. (2017). Neural architecture for feature binding in visual working memory. Journal of Neuroscience, 37, 3913–3925. Schneegans, S., & Schöner, G. (2008). Dynamic field theory as a framework for understanding embodied cognition. In P. Calvo & T. Gomila (Eds.), Handbook of cognitive science: An embodied approach (pp. 241–271). Amsterdam: Elsevier. Schneegans, S., Spencer, J. P., & Schöner, G. (2016). Integrating “what” and “where”: Visual working memory for objects in a scene. In G. Schöner & J. P. Spencer (Eds.), Dynamic thinking: A primer on dynamic field theory (pp. 197–226). New York: Oxford University Press. Schneegans, S., Spencer, J. P., Schöner, G., Hwang, S., & Hollingworth, A. (2014). Dynamic interactions between visual working memory and saccade target selection. Journal of Vision, 14, 1–23. Schutte, A. R., & Spencer, J. P. (2009). Tests of the dynamic field theory and the spatial precision hypothesis: Capturing a qualitative developmental transition in spatial working memory. Journal of Experimental Psychology: Human Perception and Performance, 35, 1698. Serences, J. T., Ester, E. F., Vogel, E. K., & Awh, E. (2009). Stimulus-specific delay activity in human primary visual cortex. Psychological Science, 20, 207–214. Simmering, V. R., Spencer, J. P., & Schöner, G. (2006). Reference-related inhibition produces enhanced position discrimination and fast repulsion near axes of symmetry. Attention, Perception, & Psychophysics, 68, 1027–1046. Souza, A. S., & Oberauer, K. (2016). In search of the focus of attention in working memory: 13 Years of the retro-cue effect. Attention, Perception, & Psychophysics, 78, 1839–1860. Souza, A. S., Rerko, L., & Oberauer, K. (2014). Unloading and reloading working memory: Attending to one item frees capacity. Journal of Experimental Psychology: Human Perception and Performance, 40, 1237. Souza, A. S., Rerko, L., & Oberauer, K. (2016). Getting more from visual working memory: Retro-cues enhance retrieval and protect from visual interference. Journal of Experimental Psychology: Human Perception and Performance, 42, 890. Sprague, T. C., Ester, E. F., & Serences, J. T. (2014). Reconstructions of information in visual spatial working memory degrade with memory load. Current Biology, 24, 2174–2180. Sprague, T. C., Ester, E. F., & Serences, J. T. (2016). Restoring latent visual working memory representations in human cortex. Neuron, 91, 694–707. Stokes, M. G. (2015). “Activity-silent” working memory in prefrontal cortex: A dynamic coding framework. Trends in Cognitive Sciences, 19, 394–405. Tanoue, R. T., & Berryhill, M. E. (2012). The mental wormhole: Internal attention shifts without regard for distance. Attention, Perception, & Psychophysics, 74, 1199–1215. Theeuwes, J., Kramer, A. F., & Irwin, D. E. (2011). Attention on our mind: The role of spatial attention in visual working memory. Acta Psychologica, 137, 248–251. Schneegans and Bays 1993 D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j f t / . u s e r o n 1 7 M a y 2 0 2 1 Todd, J. J., & Marois, R. (2004). Capacity limit of visual short- term memory in human posterior parietal cortex. Nature, 428, 751–754. neural fields: An integrative cognitive neuroscience approach. Journal of Mathematical Psychology, 76, 212–235. Treisman, A. (1996). The binding problem. Current Opinion in Neurobiology, 6, 171–178. van den Berg, R., Shin, H., Chou, W.-C., George, R., & Ma, W. J. (2012). Variability in encoding precision accounts for visual short-term memory limitations. Proceedings of the National Academy of Sciences, U.S.A., 109, 8780–8785. Wang, X.-J. (2001). Synaptic reverberation underlying mnemonic persistent activity. Trends in Neurosciences, 24, 455–463. Wei, Z., Wang, X.-J., & Wang, D.-H. (2012). From distributed resources to limited slots in multiple-item working memory: A spiking network model with normalization. Journal of Neuroscience, 32, 11228–11240. Wijeakumar, S., Ambrose, J. P., Spencer, J. P., & Curtu, R. (2016). Model-based functional neuroimaging using dynamic Wimmer, K., Nykamp, D. Q., Constantinidis, C., & Compte, A. (2014). Bump attractor dynamics in prefrontal cortex explains behavioral precision in spatial working memory. Nature Neuroscience, 17, 431–439. Wolff, M. J., Ding, J., Myers, N. E., & Stokes, M. G. (2015). Revealing hidden states in visual working memory using electroencephalography. Frontiers in Systems Neuroscience, 9, 123. Wolff, M. J., Jochim, J., Akyürek, E. G., & Stokes, M. G. (2017). Dynamic hidden states underlying working-memory-guided behavior. Nature Neuroscience, 20, 864–871. Xu, Y., & Chun, M. M. (2006). Dissociable neural mechanisms supporting visual short-term memory for objects. Nature, 440, 91–95. D o w n l o a d e d f r o m l l / / / / j t t f / i t . : / / h t t p : / D / o m w i n t o p a r d c e . d s f i r o l m v e h r c p h a d i i r r e . c c t . o m m / j e o d u c n o / c a n r a t r i t i c c l e e - p - d p d 2 f 9 / 1 2 2 9 / 1 1 9 2 7 / 7 1 1 9 9 7 5 7 3 / 2 1 8 0 7 8 o 6 c 8 n 9 _ 6 a / _ j 0 o 1 c 1 n 8 0 _ a p _ d 0 1 b 1 y 8 g 0 u . e p s t d o f n b 0 y 8 S M e I p T e m L i b b e r r a 2 r 0 2 i 3 e s / j . f / t u s e r o n 1 7 M a y 2 0 2 1 1994 Journal of Cognitive Neuroscience Volume 29, Number 12 Restoration of fMRI Decodability Does Not Imply image

PDF Herunterladen