Isomorphic Controllers and - Am MIT spezialisierte KI-Forschung

Isomorphic Controllers and
Dynamic Tuning: Invariant
Fingering over a Tuning
Kontinuum

Andrew Milne,* William Sethares,** and James
Plamondon†
*Department of Music
University of Jyväskylä
Finland
andymilne@tonalcentre.org
**Department of Electrical and
Computer Engineering
University of Wisconsin-Madison
Madison, WI 53706 USA
sethares@ece.wisc.edu
†Thumtronics Inc.
6911 Thistle Hill Way
Austin, TX 78754 USA
jim@thumtronics.com

In the Western musical tradition, two pitches are
generally considered the “same” if they have nearly
equal fundamental frequencies. Likewise, zwei
pitches are in the “same” pitch class if the frequency
of one is a power-of-two multiple of the other. Two
intervals are the “same” (in one sense, mindestens) Wenn
they are an equal number of cents wide, even if
their constituent pitches are different. Two melodies
are the “same” if their sequences of intervals, In
rhythm, are identical, even if they are in different
keys. Many other examples of this kind of “same-
ness” exist.

It can be useful to “gloss over” obvious differ-
ences if meaningful similarities can be found. Das
article introduces the idea of tuning invariance, von
which relationships among the intervals of a given
scale remain the “same” over a range of tunings.
This requires that the frequency differences be-
tween intervals that are considered the “same” are
“glossed over” to expose underlying similarities.
This article shows how tuning invariance can be a
musically useful property by enabling (among other
Dinge) dynamic tuning, das ist, real-time changes
to the tuning of all sounded notes as a tuning vari-
able changes along a smooth continuum. On a key-
board that is (1) tuning invariant and (2) equipped
with a device capable of controlling one or more
continuous parameters (such as a slider or joystick),
one can perform novel real-time polyphonic musi-
cal effects such as tuning bends and temperament
modulations—and even new chord progressions—

Computermusikjournal, 31:4, S. 15–32, Winter 2007
© 2007 Massachusetts Institute of Technology.

all within the time-honored framework of tonality.
Such novel musical effects are discussed brieﬂy in
the section on dynamic tuning, but the bulk of this
article deals with the mathematical and perceptual
abstractions that are their prerequisite.

How can one identify those note layouts that are
tuning invariant? What does it mean for a given in-
terval to be the “same” across a range of tunings?
How is such a “range of tunings” to be deﬁned for a
given temperament? The following sections answer
these questions in a concrete way by examining two
ways of organizing the perception of intervals (Die
rational and the ordinal), by deﬁning useful meth-
ods of mapping an underlying just intonation (JI)
template to a simple tuning system and scalic struc-
tur, and by describing the isomorphic mapping of
that tuning system to a keyboard layout so that the
resulting system is capable of both transpositional
and tuning invariance.

Hintergrund

On the standard piano-style keyboard, intervals and
chords often have different shapes in different keys.
Zum Beispiel, the geometric pattern of the major
third C–E is different from the geometric pattern of
the major third D–F-sharp. Ähnlich, the major
scale is ﬁngered differently in each of the twelve
keys. (In diesem Artikel, the term “ﬁngering” is used to
denote the geometric pattern, without regard to
which digits of the hand press which keys.) Other
playing surfaces, such as the keyboards of Bosan-
quet (1877) and Wicki (1896) have the property that

Milne et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

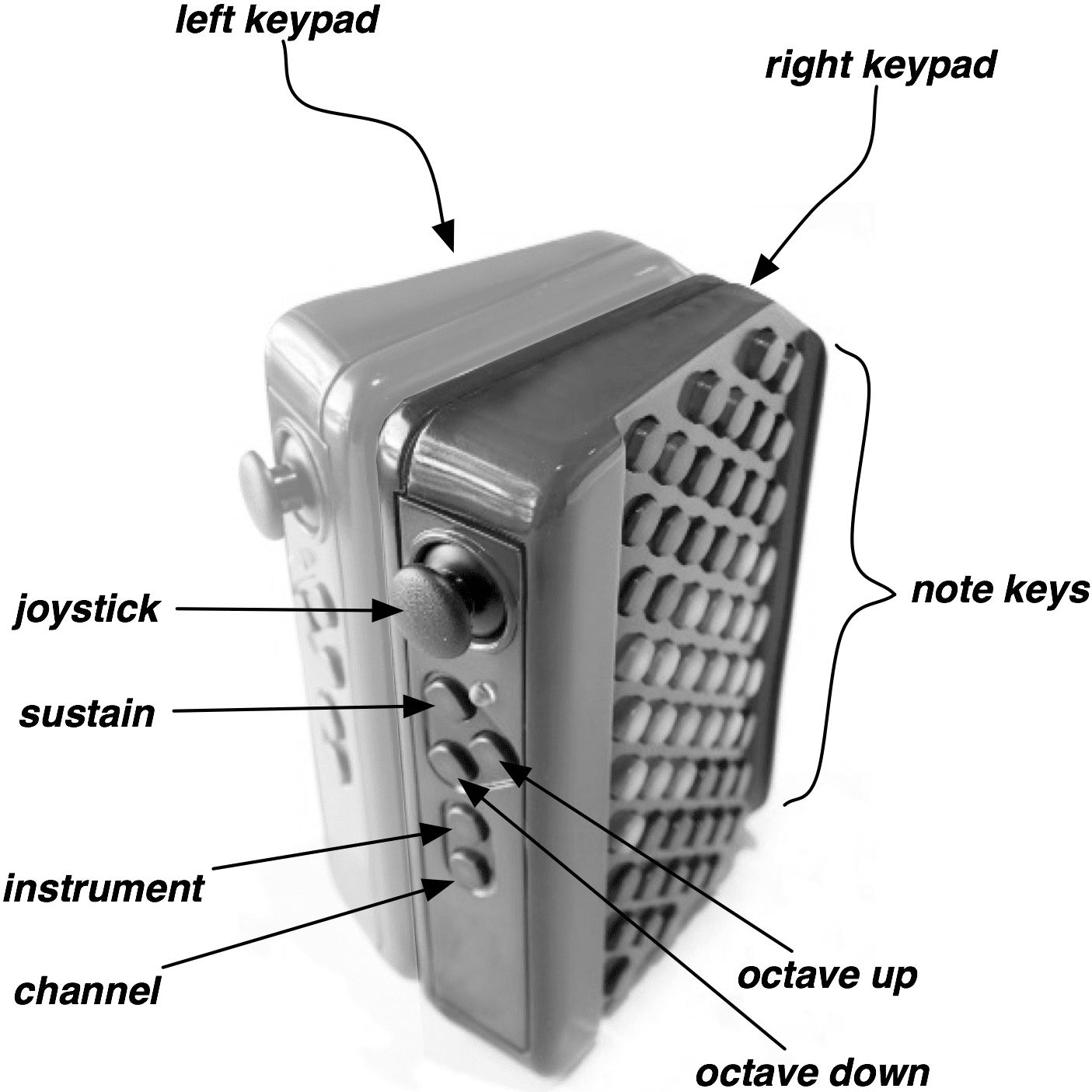
Figur 1. Thumtronics’
forthcoming USB-MIDI
controller, the Thummer,
contains two Wicki-layout
keyboards, each with 57
note-controlling buttons.
A variety of controllers in-

clude two thumb-operated
joysticks and optional in-
ternal motion sensors.
The Thummer can be held
like a concertina (A) oder
laid ﬂat, like most key-
board instruments (B).

(A)

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

other keyboard layouts such as those of Fokker
(1955) or Bosanquet could have been used instead.
The Wicki layout can be conveniently mapped to a
standard computer keyboard, facilitating the explo-
ration of the ideas presented in this article.
Thumtronics’ forthcoming Thummer music con-
troller (see www.thummer.com), shown in Figure 1,
uses the Wicki note layout by default.

There are several technical, musical, and percep-

tual questions that must be addressed to realize a
keyboard that is both transpositionally and tuning
invariant. Erste, there must be a range of tunings
over which pitch intervals—and therefore their ﬁn-
gerings—remain in some sense the “same.” This re-
quires that differently tuned intervals be identiﬁed
as serving the same role; zum Beispiel, the 12-TET
ﬁfth must be identiﬁed with the just ﬁfth and the
19-TET ﬁfth. Said differently, tuning invariance re-
quires that there be a number of distinguishable in-
tervals by which the invariance can be measured,
because to say that two numerically different inter-
vals are both “perfect ﬁfths,” it is necessary to iden-
tify a perfect ﬁfth as an interval distinguishable
from a major third, or a perfect fourth, or a dimin-
ished ﬁfth, und so weiter. This issue of the identity of

each interval, chord, and scale type have the same
geometric shape in every key. Such keyboards are
said to be transpositionally invariant (Keislar 1987).
There are many possible ways to tune musical in-
tervals and scales, and the introduction of computer
and software synthesizers makes it possible to real-
ize any sound in any tuning (Carlos 1987). Typi-
cally, Jedoch, keyboard controllers are designed
primarily for the familiar 12-tone equal tempera-
ment (12-TET), which divides the octave into twelve
logarithmically equal pieces. Is it possible to create
a keyboard surface that is capable of supporting
many possible tunings? Is it possible to do so in a
way that analogous musical intervals are ﬁngered
the same throughout the various tunings, so that
(Zum Beispiel) the 12-TET ﬁfth is ﬁngered the same
as the just ﬁfth and the 17-TET ﬁfth? (Just intervals
are those consisting of notes whose constituent fre-
quencies are related by ratios of small integers; für
Beispiel, the just ﬁfth is given by the ratio 3:2, Und
the just major third is 5:4.)

This article answers this question by presenting
examples of two related tuning continua (parameter-
ized families of tunings where each speciﬁc tuning
corresponds to a particular value of the parameter)
that exhibit tuning invariance (Wo, on an appro-
priate instrument, all intervals and chords within a
speciﬁed set have the same geometric shape in all of
the tunings of the continuum). A keyboard that is
transpositionally invariant, tuning-invariant, Und
has a continuous controller has three advantages.
Erste, having a single set of ﬁngerings within and
across all keys of any given tuning makes it easier
to visualize the underlying structure of the music.
Zweite, having this same single set of interval
shapes across the tuning continuum makes it easier
for musicians to explore the use of alternative tun-
ings such as the various meantones, Pythagorean,
17-TET, and beyond. Dritte, assigning the continu-
ous parameter to a control interface enables a
unique form of expression, Zum Beispiel, dynami-
cally tuning (or retuning) all sounded notes in real
Zeit, where the scalic function of the notes remains
the same, even as the tuning changes.

In diesem Artikel, the Wicki layout is used to con-
cretely demonstrate the formation of the pitches
and notes on a practical keyboard surface, obwohl

Computermusikjournal

Figure 1—continued

(B)

musical intervals is discussed in detail in the next
section (“Intervals”) by contrasting rational and or-
dinal modes of interval identiﬁcation. The rational
mode is determined by the correspondence of an in-
terval to a low-ratio JI interval, and the ordinal
mode is determined by the number of scale notes an
interval spans.

Zweite, there must be a tuning system that is itself
transpositionally invariant with regard to both forms
of identiﬁcation. This requires that each and every
note in the system has identical intervals above and
below, and that the presumed temperament-mapping
of JI to this tuning system is consistent. Such a tun-
ing system is called a regular tuning system, Und
the embodiment of a such a temperament-mapping
in a regular tuning system is called a regular tem-
perament. These are deﬁned more fully in the sec-
tion “Tuning Systems and Temperaments.”

Dritte, given such a tuning system, it is necessary

to deﬁne useful sets of scales. The section entitled
“Scales” focuses on those scales known as MOS or
well-formed, which have a number of musically
advantageous properties.

that are not) invariant in both transposition and
tuning. The tuning continuum pictured in Figure 2
provides the primary example of this article. It be-
gins at 7-TET, and by varying the size of the perfect
ﬁfth, it moves continuously through various mean-
tone tunings, 12-TET, Pythagorean, and many other
tunings, ending at 5-TET, while retaining ﬁngering
invariance throughout. Endlich, a musical example
illustrates static snapshots of the dynamic retuning
Verfahren.

Intervals

This section investigates how intervals are identi-
ﬁed and distinguished, and it discusses criteria by
which two numerically different intervals may be
said to play analogous roles in different tuning sys-
Systeme. Intervals may be identiﬁed—and therefore
discriminated—in at least two ways, here deﬁned as
the rational and the ordinal.

Vierte, it is necessary to layout-map the regular

Rational Identiﬁcation

temperament to a keyboard or button-ﬁeld in a
manner that maintains transpositional and tuning
invariance. The layout-mappings described in the
section “Button-Lattices and Layouts” translate
the generating intervals of the tuning to the key-
board surface. It is shown that transpositional
invariance is identical to linearity of the layout-
mapping. Successive sections then provide ex-
amples of keyboard layouts that are (and others

The rational mode of identiﬁcation is presumed to
occur primarily for harmonic intervals,nämlich, those
formed from simultaneously sounded notes. It pre-
sumes that just intervals that are perceived as con-
sonant act as perceptual and cognitive landmarks (A
Vorlage) against which sounded intervals can be
mentally compared and identiﬁed. This is reason-
ably uncontroversial for orchestral instruments

Milne et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

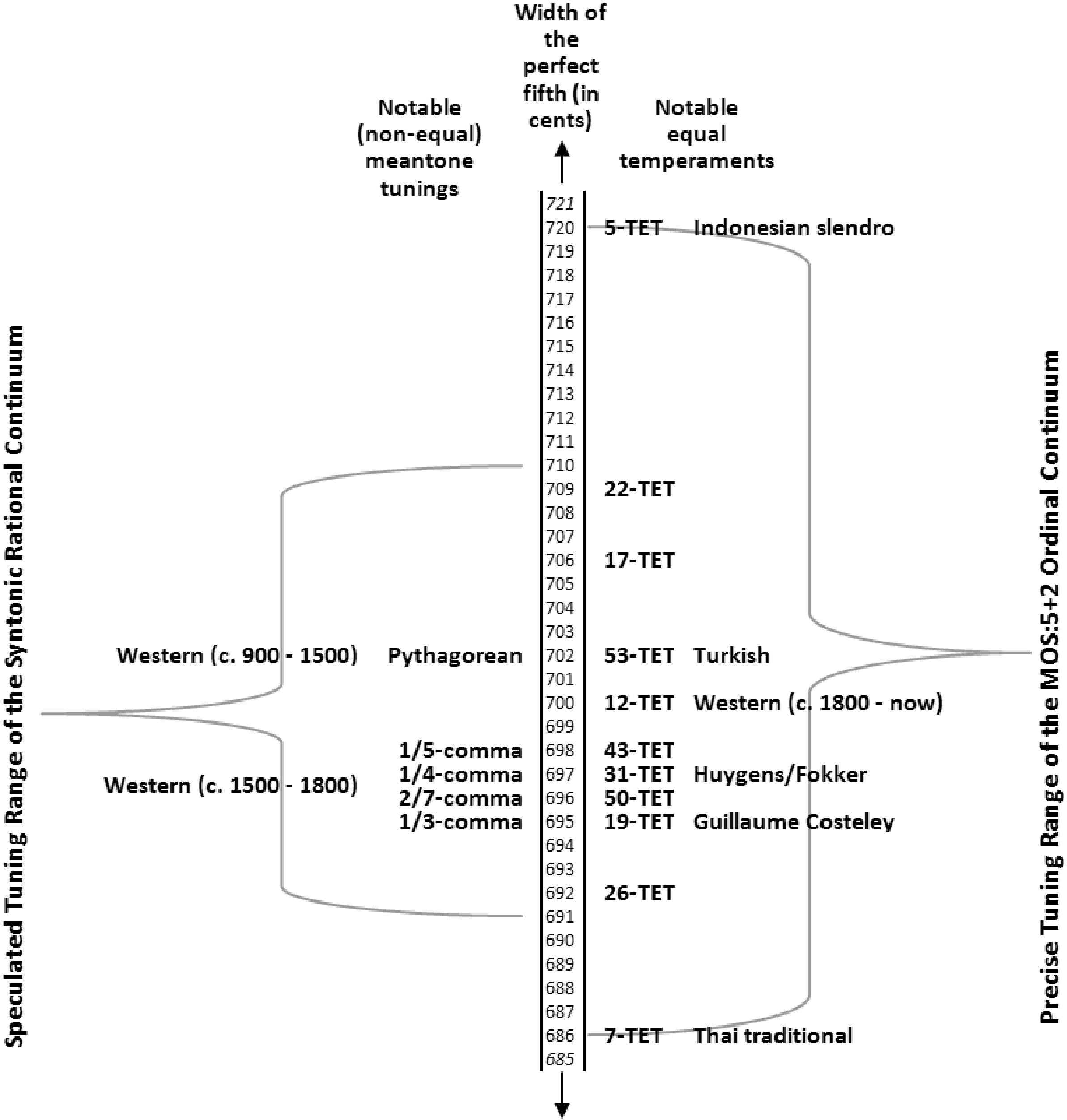
Figur 2. The syntonic ra-
tional continuum and
MOS:5+2 ordinal contin-
uum (both deﬁned later).
The ﬁgure also shows the
historical and ethnic us-
ages of many notable tun-
ings found within these

continua (compiled from
information in Barbour
1951, Lorentz 2001,
Sethares 2004, und das
Huygens-Fokker Founda-
tion Web site at
www.xs4all.nl/huygensf).

with harmonic spectra. For inharmonic, computer-
generated sounds, inharmonic bells, and non-
Western instruments such as the metallophones of
the Indonesian gamelan, these sensory consonances
may occur at different intervals (Sethares 2004), Und
so other templates may be more appropriate.

For sounds with harmonic spectra, when a sounded
interval is tuned close to a small-integer-ratio JI in-
terval (wie zum Beispiel 3:2 oder 5:4), it may be heard as a repre-
sentation of that ratio. Using semiotic terminology,
the sounded interval is an indexical signiﬁer of the
just ratio it approximates. Zum Beispiel, when an in-
terval is tuned to 702 cents (the closest integer
value to 3:2), it is likely to be heard as a representa-
tion of the 3:2 just ﬁfth. As the interval’s tuning is
moved away from 702 cents, it gradually moves to a
state where it is likely to be heard as an imperfect
representation of 3:2. (It will sound more or less
“out of tune.”) As the tuning is moved still further
aus 702 cents, the perceived interval will eventu-
ally no longer represent 3:2 (and not even an out-of-
tune 3:2). At this point, the just interval is no longer
signiﬁed by the sounded interval. When an interval

is not just, but is within its range of rational identi-
ﬁcation, it is called a tempered interval.

Ordinal Identiﬁcation

The ordinal mode of identiﬁcation is presumed to
occur primarily for melodic intervals (formed from
successively sounded notes). It presumes that when
an interval is played as part of an aesthetically con-
sistent or conventionalized scale, it is identiﬁed by
the number of scale notes (or steps) it spans. Zum Beispiel-
reichlich, Wilson (1975) writes that “our perception of
Fourth-ness is not just acoustic, d.h., 4/3-determined,
it is melodic and/or rhythmic-inﬂuenced to a high
degree” (P. 1). Like rational identiﬁcation, this is an
indexical signiﬁcation but one that requires the
presence of a scalic background (d.h., Kontext) to give
meaning to “second-ness,” “third-ness,” “fourth-
ness,” etc. For a scale to serve as a background, Es
must have intrinsic aesthetic consistency (d.h., Sei
perceived as somehow complete and “correct”)
and/or be conventionalized (d.h., made familiar
through repetitive use).

The diatonic scale can serve as a scalic back-
ground for common-practice music. Zum Beispiel,
against the background of a C-major (diatonic) scale,
the intervals C–D, D–E, E–F, F–G, und so weiter, Sind
heard as “seconds” because they each span two ad-
jacent scale notes; the intervals C–E, D–F, E–G, F–A,
und so weiter, are heard as “thirds” because they each
span three successive scale notes.

Dual Identiﬁcation

The two modes of identiﬁcation overlap: the ra-
tional mode plays a part in the identiﬁcation of
melodic intervals, the ordinal in the identiﬁcation
of harmonic intervals. Zum Beispiel, a melodic inter-
val of approximately 3:2 will usually be heard as “in
tune” or “out of tune” according to its proximity to
this just interval; similarly, a harmonic interval ap-
proximating 3:2 Wille, in a traditional diatonic con-
Text, be heard as spanning ﬁve notes of the scale.

Außerdem, in real-world music it is not always

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

possible to make a strict distinction between har-
monic intervals and melodic intervals. An arpeggio
is at least partially a harmonic structure. The bass
note of a “stride bass” pattern, which is sounded
only for the ﬁrst and third beats of a bar, cognitively
grounds the rest of the bar. Counterpoint, welches ist
the interweaving of many melodies into a coherent
harmonic structure, blurs the distinction between
melody and harmony.

Thus the rational and ordinal modes of identiﬁca-

tion are intertwined. In der Tat, in Western tonal mu-
sic, there is a consistent linkage between the number
of steps an interval contains and its harmonic ratio.
Zum Beispiel, the interval that spans three scale
notes (d.h., der dritte) is commonly an interval that is
close to 5:4 oder 6:5 (hence the names major third and
minor third). Ähnlich, the interval that spans four
scale notes (d.h., the fourth) is typically an interval
that is close to 4:3. Außerdem, where these links
differ, the interval often has a tonally dissonant
function that requires resolution to a more stable
interval. (Zum Beispiel, an augmented second com-
monly resolves to a perfect fourth; a diminished
ﬁfth commonly resolves to a major third.)

In conventionalized musical systems such as
Western tonal music, where particular step sizes
and harmonic ratios are consistently associated,
ordinality can (by association) symbolically signify
Verhältnis, and ratio can (by association) symbolically
signify ordinality. Das bedeutet, dass, within such a
conventionalized context, the tuning ratio over
which an interval can still signify a given just ratio
may be wider than expected if it were judged by
analyzing harmonies isolated from the musical con-
Text. In common practice, Zum Beispiel, the conven-
tional association of “5:4-ness” and “third-ness”
means that a melodic third can be tuned very wide
but still signify 5:4. Zum Beispiel, the ultra-sharp
supra-Pythagorean major thirds (greater than 408
cents) that are sometimes used by string players for
expressive intonation (Sundberg et al. 1989) may be
harmonically uncomfortable, but they still signify
the same musical interval as the just quarter-
comma meantone thirds of 386 cents. (Sie sind,
schließlich, different expressions of the same notated
interval.) Thus the tuning range over which a given

interval can be identiﬁed and therefore discrimi-
nated from other intervals has “fuzzy” boundaries
that are context-dependent.

Tuning Ranges of Invariant Identiﬁcation

The previous discussion suggests that it may be ad-
vantageous to deﬁne the tuning range over which an
interval preserves both its rational and ordinal iden-
tity as that interval’s tuning range of invariant
identiﬁcation. Because there are two modes by
which an interval can be identiﬁed, there are two
relevant tuning ranges to be considered that them-
selves depend on a listener’s innate abilities, expe-
riences, and training. Musical context is also
important; the tuning range of invariant rational
identity may also change based on the spectrum
and/or timbre of the sounds (Sethares 2004). Für
these reasons, the ﬁnal judgment as to the speciﬁc
tuning boundaries may best lie in the hands of the
artist and not the theorist.

dennoch, in the presence of a scalic back-
Boden, invariant ordinal identiﬁcation can be pre-
cisely bounded; Außerdem, given a scale in a
regular tuning system (as deﬁned subsequently), Die
size of every interval in the scale is determined by
the values of the generating intervals. This implies
that the range of generator tunings over which all of
that scale’s intervals can be retuned but still main-
tain their ordinal identity—that scale’s ordinal con-
tinuum—is limited by the points at which one or
more of that scale’s steps shrink in size to zero (oder
gleichwertig, the points at which two of the scale
steps “cross”).

In a regular temperament (as deﬁned in the next

section), the sizes of all the intervals that are ca-
pable of being rationally identiﬁed are controlled by
the values of its generating intervals. This implies
that the range over which all of that temperament’s
identiﬁable intervals can be retuned but still main-
tain their rational identity—that temperament’s
rational continuum—is delimited by context and
subject-dependent “fuzzy” boundaries.

Figur 2 shows the precisely bounded continuum

for the twelve-note chromatic scale generated by

Milne et al.

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

ﬁfths and octaves. Also shown on this chart is a
conjectured “fuzzy” boundary for the rational con-
tinuum of the regular temperament deﬁned by the
syntonic comma (which is explained in the next
section). This conjectured range has been estimated
by assuming that only the common practice conso-
nances are rationally identiﬁable, and that their ra-
tional identiﬁcation switches from one common
practice consonance to another at the tuning that is
midway between their just tunings. In common-
practice music, these two continua are convention-
ally associated, though the ordinal continuum is
wider than the rational.

Tuning Systems and Temperaments

A tuning system is deﬁned here to be a collection of
precisely tuned musical intervals. There are many
ways in which the intervals may be chosen: A “bou-
tique” tuning system might have all of its intervals
chosen arbitrarily, and another tuning system might
be generated by a predeﬁned mathematical proce-
dure (McLaren 1991). The regular tunings form one
class of tuning systems in which all of the intervals
are generated multiplicatively from a ﬁnite number
of generating intervals (or generators). Such tuning
systems ensure that every given note has the same
set of intervals above and below it as every other
note in the system; this means that regular tuning
systems are inherently transpositionally invariant.
An example regular tuning system is 3-limit JI (Auch
known as Pythagorean tuning), which has two gen-
erators G1 = 2 and G2 = 3, and consists of all prod-
j = 2i × 3j, where i and j are
ucts of the form G1
integers. Thus the intervals of 3-limit JI can all be
found in a series of stacked just perfect ﬁfths, erlauben-
ing for octave equivalence. Allgemein, a regular tun-
ing is characterized by n generators G1 to Gn and
consists of all intervals G1
i2, . . . , in are integer-valued exponents.

In, where the i1,

i2 . . . Gn

i1 G2

i G2

Altering the tuning of a generator affects the tun-
ing of the system in a predictable way. Zum Beispiel,
–1 G2 (d.h., 2–1 × 3). Wenn
the perfect ﬁfth in 3-limit JI is G1
A (non-JI) regular tuning is created by changing the
value of G2, the value of the ﬁfth, and all other in-
tervals, changes in a patterned way. Assigning the

magnitude of one or more of the generating inter-
vals to a control interface provides a convenient
means to “navigate” the tuning continuum. Partic-
ular values within this continuum may produce
some intervals that approximate JI intervals and so
are rationally identiﬁable; we might consider, Dort-
Vordergrund, that there has been a mapping of JI intervals to
that tuning system.

For such a temperament-mapping to be transposi-
tionally invariant, it must be linear, though it need
not be invertible (d.h., it need not be one-to-one).
The embodiment of such a temperament-mapping
in a suitable tuning system is called a regular tem-
perament, and it can be characterized by the small
JI intervals called commas that are tempered to
unison (Schmied 2006). This means that a regular
temperament is characterized by its temperament-
mapping, not its tuning, so any given temperament
has a range of suitable tunings. To be concrete, zwei
or more intervals a1, a2, . . . , an are said to be multi-
plicatively dependent if there are integers z1,
z2, . . . , zn, not all zero, such that a1
z2 . . . ein
zn = 1.
If there are no such zi, then the ai are said to be mul-
tiplicatively independent. The rank of a tuning sys-
tem is the number of multiplicatively independent
intervals needed to generate it. A regular tempera-
ment typically has lower rank than the JI system
that is temperament-mapped to it (d.h., the mapping
is non-invertible). When the temperament-mapping
loses rank, all intervals can no longer be just. Wie-
immer, as long as there is a range of generator values
over which the intervals are correctly rationally
identiﬁed, the regular temperament can be consid-
ered to be valid.

z1 a2

This is analogous to the way a projection of the

three-dimensional surface of a globe to a two-
dimensional map inevitably distorts distance, Bereich,
and angle. Jedoch, so long as the countries have
identiﬁable shapes, the projection can be considered
valid. Different map projections result in different
distortions, and some map projections are more or
less suitable to speciﬁc purposes. Some projections
(such as the Mercator Projection) have the virtue of
wide familiarity; so it is also with temperament-
mappings (such as those that lead to 12-TET).
Zum Beispiel, 3-limit JI can be temperament-
mapped to a one-dimensional system using an ap-

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

a G2

b = 1, where a and b are

propriate comma G1
integers. One notable tempering retains the octave
G1 = 2 and tempers G2 to 219/12 ≈ 3, which requires
that a = 19 and b = –12, resulting in the familiar 12-
TET. This comma can be interpreted musically by
saying that in this temperament, 19 octaves minus
twelve equal-tempered perfect twelfths equals a
unison. A second example is in 5-limit JI, welche
consists of all intervals of the form 2i 3j 5k, where i,
J, and k are integers. This can be reduced to a two-
dimensional regular temperament by choosing G1
(typically near 2), G2 (near 3), and G3 (near 5) so that

G G Ga
C
3

B
2

(1)

where a, B, and c are speciﬁed integers. Gleichung 1
deﬁnes a comma that is tempered to unison. Der
well known syntonic comma (which has an untem-
pered tuning of 81/80) is the special case where a =
–4, b = 4, and c = –1; tempering the generators so
that Equation 1 holds, produces various tunings of
the syntonic temperament (as illustrated in Figure 2).
The comma can be solved for one of its terms as
G3 = G1
–b/c, and a typical interval of the regular
temperament can be written in terms of two gener-
ating intervals α = G1
where GCD(N, M) is the greatest common divisor of
n and m. Thus G1 = α|C|/GCD(A,C), G2 = β|C|/GCD(B,C), G3 =
α–aSIGN(C)/|GCD(A,C)| β–b/SIGN(C)|GCD(B,C)|, and a typical inter-
val G1
α(ci–ak)/|GCD(A,C)| β(cj–bk)/|GCD(B,C)|. In matrix notation, Die
vector (ich, J, k)T is temperament-mapped by

k of the JI is temperament-mapped to

GCD(A,C)/|C| and β = G2

–a/c G2

GCD(B,C)/|C|

jG3

iG2

R =

GCD

a c
( , )

GCD

b c
( , )

− ⋅
A
GCD
− ⋅
B
GCD

C
( )
SIGN
a c
( , )
C
( )
SIGN
b c
( , )

i c

−

SIGN

C
( )

j c

−

SIGN

C
( )

a c
GCD( , )

b c
GCD( , )

where T is the transpose operator. Daher, Die
temperament-mapping is linear and (typically)
loses rank. For the syntonic comma,

R =

1
0

0
1

−
4
4

(3)

and any note (ich, J, k)T is mapped to (i – 4k, J + 4k)T.
Zum Beispiel, a just major third 5/4 = 2–2 30 51 Ist
represented by the vector (–2, 0, 1)T. Das ist
temperament-mapped by G to (–6, 4)T, which repre-
sents the tempered interval α–6β4. If α were tem-
pered to 2 (no change in the octave) and β were
tempered to 230/19 (the 19-TET twelfth), then α–6β4 =
2–62120/19 ≈ 1.24469 ≈ 5/4 is the 19-TET approxima-
tion to the just major third. Ähnlich, if α were tem-
pered to 2 and β were tempered to 3 × (81/80)–1/4 (Die
quarter-comma meantone ﬁfth), then α–6β4 = 5/4 Ist
the justly tuned major third found in the quarter-
comma meantone tuning.

Syntonic Rational Continuum

The rational continuum of a rank-r regular tem-
perament is here deﬁned as that (r-dimensional)
range of generator tunings within which the ra-
tional identity of all rationally identiﬁable intervals
is maintained. The rational continuum of the syn-
tonic temperament is therefore called the syntonic
rational continuum. As described previously, Die
tuning range of this continuum is context-
dependent and not easily speciﬁed a priori.

The syntonic rational continuum extends beyond

the narrower range implied by “meantone,” which
usually refers to the range of syntonic tunings pro-
viding reasonably pure-sounding tunings (for sounds
with harmonic spectra) and/or which have an estab-
lished historical use—a range of approximately 19-
TET to 12-TET. (Siehe Abbildung 2.)

A scale is here deﬁned to be a subset of a tuning sys-
tem used for a speciﬁc musical purpose. When using
a rank-2 tuning system with generators α and β, A
scale can be simply constructed by stacking integer
powers of β and then reducing (dividing or multiply-
ing by integer powers of α) so that every term lies
zwischen 1 and α. This is called an α-reduced β-chain,
and it produces a scale that repeats at intervals of α;
α = 2, representing repetition at the octave, ist der
most common value. Any arbitrary segment of an

Milne et al.

(2)

Scales

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

⎡
⎣
⎢
⎤
⎦
⎥

⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥

⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥

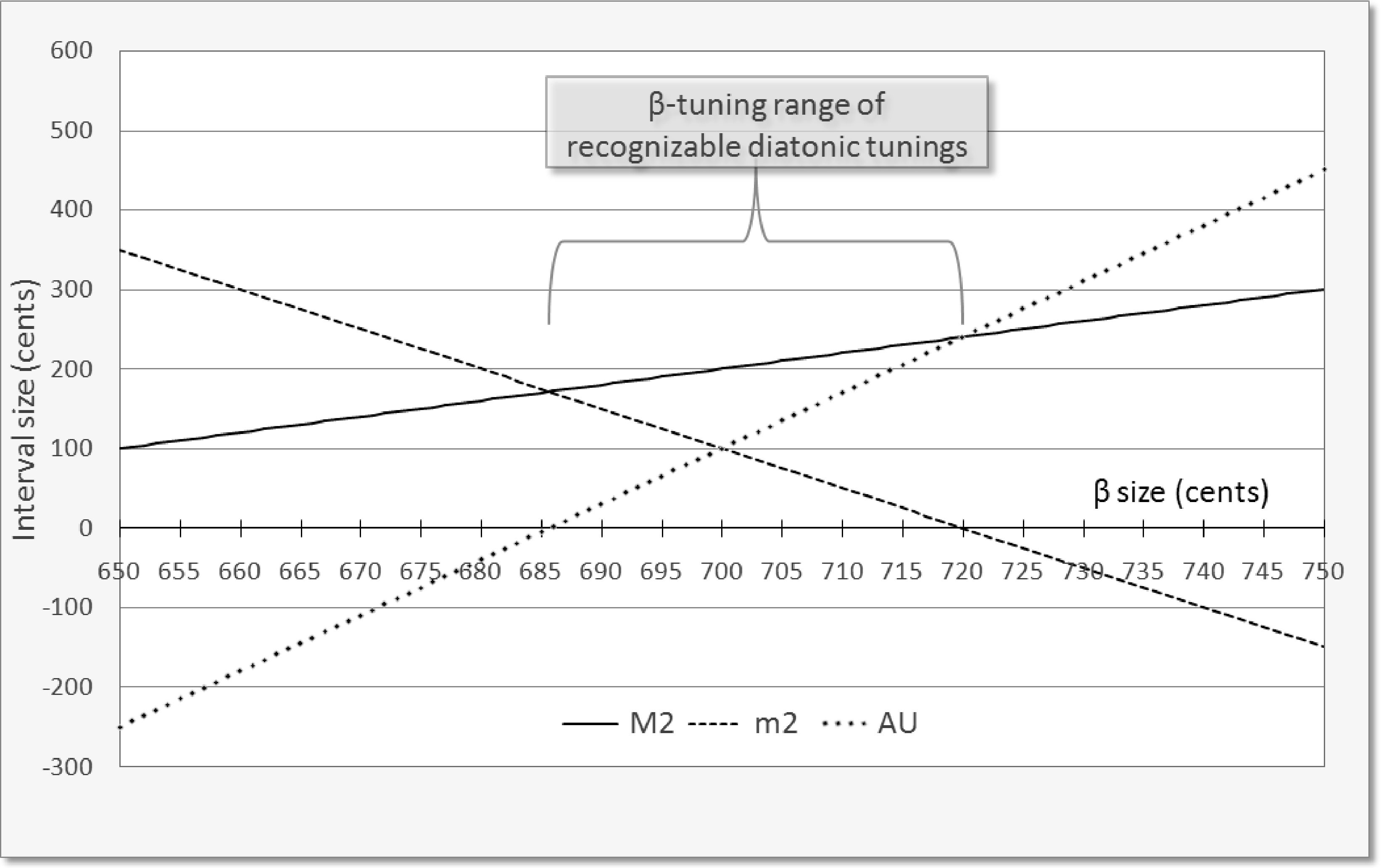
Figur 3. Sizes of the major
zweite (M2), minor second
(m2), and augmented uni-
Sohn (AU), over a range of
β generator tunings.

α-reduced β-chain can be used to form a scale, Und
the number of notes it contains is called its cardi-
nality. For a given tuning of α and β, α-reduced β-
chains with certain cardinalities are called moment
of symmetry (MOS) Waage (Wilson 1975; also known
as well-formed scales after Carey and Clampitt
1989). Such scales have a number of musically ad-
vantageous properties: they are distributionally
sogar, which means that the scale has two step sizes
that are distributed as evenly as possible (Clough et
al. 1999); they have constant structure, welche
means that every given interval always spans the
same number of notes (Grady 1999). Two familiar
MOS scales generated by α = 2 and β ≈ 3/2 are the
ﬁve-note pentatonic scale (z.B., D, E, G, A, C) Und
the seven-note diatonic scale (z.B., C, D, E, F, G, A,
B); other β-values generate MOS scales with quite
different intervallic structures. These provide fertile
resources for non-standard microtonal scales.

Every MOS scale with speciﬁed generators and
cardinality has a valid tuning range over which it
can exist; beyond this range, notes must be added to
or removed from the scale to regain distributional
evenness and constant structure. The boundaries of
this tuning range mark the tuning points at which
some of the scale’s steps shrink to unison, Und
therefore the tuning points at which the ordinal
identity of intervals in that scale changes. An MOS
scale generated by α and β with cardinality c has a
two-dimensional valid tuning range of αp/q < β < αr/s, where p/q and r/s are adjacent members of a Farey sequence of order c–1. (A Farey sequence of order n is the set of irreducible fractions between 0 and 1 with denominators less than n, arranged in increas- ing order.) For example, the 12-note MOS scale generated by α = 2 and β ≈ 3/2, which is the chromatic scale that provides the background for common practice mu- sic, has a valid tuning range of 24/7 < β < 23/5 (4/7 and 3/5 being adjacent members of the Farey sequence of order 11). Expressing this range in simpler terms, the “perfect ﬁfth” is between 1200 × 4/7 = 685.7 and 1200 × 3/5 = 720 cents in size. Consider the familiar seven-note diatonic scale as the tuning traverses this range: starting with a generating interval β tuned to the 12-TET ﬁfth 27/12, the scale consists of ﬁve large steps (whole tones) and two small steps (half tones). As β is increased, the whole tones grow larger and the half tones grow smaller. When β reaches 23/5, the semitones disappear completely; above 23/5, there is no seven-note MOS scale avail- able, because the seven-note scale contains three different step sizes. On the other hand, as β is de- creased below 27/12, the tones get smaller and the semitones get larger. When β reaches 24/7, the tones and semitones become the same size; below 24/7, the MOS scale’s internal structure changes so that it has ﬁve small intervals and two large intervals, a scale structure that is the inverse of the familiar di- atonic scale. These changing step sizes are illus- trated in Figure 3. This tuning range is equivalent to Blackwood’s “range of recognizable diatonic tun- ings” (1985). The valid tuning ranges for MOS scales are, therefore, a generalization of the concept of range of recognizability beyond the familiar dia- tonic/chromatic context. The MOS scale that is recognizably diatonic is called MOS:5+2 (i.e., it contains ﬁve large steps and two small steps). The valid tuning range of this MOS scale is 24/7 < β < 23/5 (see Figure 2) and it pre- serves, therefore, the ordinal identity of the diatonic and chromatic intervals used in common practice. When intervals are played as a part of a conven- tionalized or aesthetically consistent scale, they can be ordinally identiﬁed by the number of notes or in- tervals they span. Owing to their distributional evenness and constant structure, MOS scales are likely to be heard as intrinsically aesthetically con- sistent, so the valid tuning range of any given MOS scale is equivalent to the range within which all of 22 Computer Music Journal l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o m j / l a r t i c e - p d f / / / / 3 1 4 1 5 1 8 5 4 9 5 6 / c o m j . . 2 0 0 7 3 1 4 1 5 p d . . . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 its intervals are ordinally invariant. Furthermore, these ranges hold for many musically useful alter- ations of MOS scales such as the harmonic minor scale (A, B, C, D, E, F, G-sharp). generating intervals (1, 0) and (0, 1), and the layout- mapping L is the 2 × 2 matrix L = ψ ψ x y ω ω x y (4) MOS:5+2 Ordinal Continuum The ordinal continuum of an MOS:a+b scale, which has a large steps and b small steps, is here deﬁned as the (two-dimensional) range of generator tunings that gives this scale form. It is equivalent to αp/q < β < αr/s, where p/q and r/s are adjacent members of a Farey sequence of order 2a + b – 1. The ordinal continuum of MOS:5+2 is, therefore, called the MOS:5+2 ordinal continuum. Button Lattices and Layouts Instruments capable of playing a number of discrete pitches may use many buttons (or keys). For an in- strument to have transpositional invariance, it is necessary that the buttons are arranged in a regular and spatially repeating pattern; such a structure is called a lattice (Insall, Rowland, and Weisstein 2007). If the lattice has one dimension, it may be called a button row; if it has two dimensions, it may be called a button ﬁeld. A layout is here deﬁned as the physical embodiment of an invertible, but not necessarily linear, layout-mapping from a regular temperament to an integer-valued button lattice. In the same way that a regular temperament has a ﬁ- nite number of generating intervals (e.g., α and β) that generate all its intervals, a lattice can be repre- sented with a ﬁnite number of basis vectors that generate all its vectors. The logical means to layout- map from a temperament to a button lattice is to map the temperament’s generating intervals to the lattice’s basis vectors. Let L : Zn → Zn map from the n generating inter- vals of the temperament to the n-dimensional but- ton lattice. For example, with n = 2, the temperament contains two generating intervals α and β. Any in- terval of the temperament can be expressed as a two-vector (j, k) representing the interval αjβk. The standard basis for the temperament consists of the x, ω x, ψ y) which transforms the temperament’s generating in- tervals into the lattice’s basis vectors ψ = (ψ and ω = (ω y). The elements of L must be integers (or else some intervals will be layout-mapped to lo- cations without buttons), L must be invertible (that is, the determinant of L is nonzero, or else either some buttons would have no assigned note or some notes would have no corresponding button), and the determinant of L must be ±1 (or else the inverse will not be integer-valued). This mapping provides the mathematical setting for two results. First, if the layout-mapping L is linear, the layout is trans- positionally invariant (Theorem 1). Second, the converse holds as well: if the keyboard layout is transpositionally invariant, the layout-mapping L must be linear (Theorem 2). Theorem 2 justiﬁes the use of linear (matrix) no- tation for the layout-mapping. Proof of the theo- rems is given in Appendices A and B. The theorems presume an inﬁnitely sized button-lattice; physical keyboards will necessarily have ﬁnite size, and the linearity will be violated at the edges. The ﬁnite size also limits the number of octaves that can be realized. There are many possible layout matrices L, and several concrete examples are given in the next section. The choice of L impacts the ease with which particular scales and chords can be ﬁngered, as well as the balance between the number of octave- reduced intervals and overall octave range that can ﬁt on a keyboard of a given geometry. For some lay- outs, such as that of Fokker, the playability-related metrics vary greatly as the tuning is changed, whereas these metrics are more stable across a wide range of tunings on some other layouts, such as the Wicki. Identifying and quantifying such metrics is an important area for future investigation. Because a layout-mapping is invertible, by deﬁni- tion, it can be linear only if it does not lose rank. Linear and invertible mappings are called isomor- phic, and henceforth all layouts with this type of layout-mapping will be referred to as isomorphic layouts. The theorems show that given a regular Milne et al. 23 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o m j / l a r t i c e - p d f / / / / 3 1 4 1 5 1 8 5 4 9 5 6 / c o m j . . 2 0 0 7 3 1 4 1 5 p d . . . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ temperament, transpositional invariance requires an isomorphic layout; and given a regular tempera- ment and an MOS-scalic background, tuning invari- ance requires that the tunings of the generating intervals (as embodied in the layout) remain within that temperament’s and MOS scale’s tuning range for invariant identiﬁcation. This means that trans- positional invariance on a button-row is only pos- sible for a rank-one (i.e., equal) temperament. To get transpositional invariance across the tuning range of rank-two temperaments (like the non-equal meantone tunings), a button ﬁeld of at least two di- mensions is required. Because it is difﬁcult to con- ceive of a button lattice operating effectively in more than two dimensions, only rank-one and rank- two temperaments are considered in this article. The following examples illustrate these points by demonstrating concrete isomorphic layouts that are invariant in both transposition and tuning. Examples of Layout-Mappings The examples in this section use the syntonic tem- perament tuned to quarter-comma meantone, 12- TET, and 19-TET, and assume an MOS:5+2 scalic background—design choices that are compatible with common-practice tonal music. Two types of layouts are shown. One-dimensional button rows provide the simplest setting; drawings such as Fig- ures 4–6 should be interpreted as consisting of a single row of identical buttons. For two-dimensional button ﬁelds, there are several ways in which the buttons can be arranged: in a rectangular grid, in off- set rows (like brickwork), in a hexagonal grid, or as a tiling of parallelograms. The Wicki layout provides our primary two-dimensional example, though ob- viously other layouts could be used. Layout-Mapping from a Rank-One Temperament to a Button Row The familiar 12-TET has a single generating interval α of 21/12 (100 cents) and tempers out the syntonic comma (among other commas). An octave consists of twelve of these generating intervals, a perfect ﬁfth contains seven, and a major third contains four. The layout-mapping can be either L = 1 or L = –1. If the 12-TET generating interval is layout-mapped to +1, the notes progress sequentially higher in pitch from left to right, which corresponds to a linear key- board as shown in Figure 4. The tuning range of rational invariance for this temperament is small. Increasing the size of the generator by just two cents increases the size of the octave by 24 cents. Though the piano is frequently tuned with stretched octaves, this stretching is typi- cally less than about half a cent on the generating interval (about six cents per octave). The tuning range of ordinal invariance is unbounded, because no amount of retuning of the generator changes the order of the notes. For this case, the ordinal range is not a useful measure. Owing to the isomorphic layout-mapping, this layout has the property that any rationally identiﬁ- able interval or chord (such as the major triad) is ﬁn- gered the same for any position on the button-row. Starting on any note (for instance C), a major triad is played using the buttons four and seven steps to the right. The geometric shape of a major triad is, there- fore, always 0–4–7 for all transpositions. Similarly, a melody is ﬁngered the same wherever it is located on the button-row. Starting on any note (for in- stance C), the melody Re–Mi–Fa–Fi–Sol is played using a button, then a button two steps to the right, then one more step to the right, then one more step to the right, then one more step to the right. The geometric shape of this melody is, therefore, always 0–2–3–4–5 for all transpositions. A different rank-one temperament that also tem- pers out the syntonic comma (among others) is 19- TET, as shown in Figure 5. This temperament has a single generating interval α = 21/19 (approximately 63.2 cents), and the octave consists of 19 of these generating intervals. The perfect ﬁfth is eleven gen- erating intervals wide, and the major third is six generating intervals wide. Any isomorphic layout- mapping of 19-TET (e.g., L = 1) has, like the above 12-TET example, a small range of rational tuning invariance and a similar transpositional invariance. However, the ﬁngering of both the major triad 0–6– 11 and the Re–Mi–Fa–Fi–Sol melody 0–3–5–6–8 are 24 Computer Music Journal l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o m j / l a r t i c e - p d f / / / / 3 1 4 1 5 1 8 5 4 9 5 6 / c o m j . . 2 0 0 7 3 1 4 1 5 p d . . . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. The one- dimensional keyboard lay- out L = 1 in 12-TET. Figure 5. Note positions of 19-TET using L = 1. Figure 6. Nonlinear piano- style layout for a rank-2 temperament, such as quarter-comma meantone. Figure 4 Figure 5 Figure 6 different from the 12-TET design in Figure 4. This shows concretely how the linear one-dimensional design fails to be tuning invariant. Layout-Mapping from a Rank-Two Temperament to a Button Row A layout-mapping is invertible by deﬁnition, so a layout-mapping from a rank-two regular tempera- ment to a one-dimensional button-row must be nonlinear. As established previously, a nonlinear (non-isomorphic) layout-mapping “breaks” transpo- sitional invariance. A common example of a nonlin- ear layout-mapping is a piano-style layout, which takes a ﬁnite subset of the notes produced by a rank-two meantone (such as quarter-comma), and layout-maps them in pitch order to a twelve-note- per-octave keyboard, as illustrated in Figure 6. The physical/geometrical irregularity of the piano key- board, interpreted as a row of black keys inter- spersed with a row of white keys, is collapsed here to a single row for the sake of simplicity. Such layout-mappings (as applied to standard, geometrically irregular keyboards) were used in the 17th century (Barbour 1951), though sometimes A- ﬂat was used in place of G-sharp. In quarter-comma (or any other meantone tuning requiring two gener- ating intervals), major thirds (e.g., C–E) are tuned differently than diminished fourths (e.g., C-sharp– F). In the nonlinear layout of Figure 6, ascending four steps sometimes produces a major third and sometimes produces a diminished fourth, thus breaking transpositional invariance. For example, starting from C and proceeding four steps to E pro- duces a just major third of size 386 cents, which is clearly identiﬁable as 5:4. On the other hand, start- ing at C-sharp and ascending four steps to F pro- duces a diminished fourth of 427 cents. This is a so-called “wolf” interval that is unlikely, in this context (where there exist more closely tuned major thirds), to be rationally identiﬁed as 5:4. The only way to gain transpositional invariance for this layout is to tune the ﬁfths to 27/12, which is the only (octave-reduced) tuning that does not dif- ferentiate between major thirds and diminished fourths. This is consistent with the theorem be- cause when the ﬁfth is tuned to 27/12 and the octave is tuned to 2, the two generating intervals are no longer multiplicatively independent. In this case, the rank of the temperament has collapsed to one and the tuning has become 12-TET. A similar argu- ment shows that for a button-row with N notes per octave, any tuning that produces an n-TET where n = N will have transpositional invariance, but for this tuning only. To summarize: On a button-row with keys of ﬁxed size, the physical size of any given interval is different in 12-TET, 17-TET, 19-TET, quarter- Milne et al. 25 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o m j / l a r t i c e - p d f / / / / 3 1 4 1 5 1 8 5 4 9 5 6 / c o m j . . 2 0 0 7 3 1 4 1 5 p d . . . 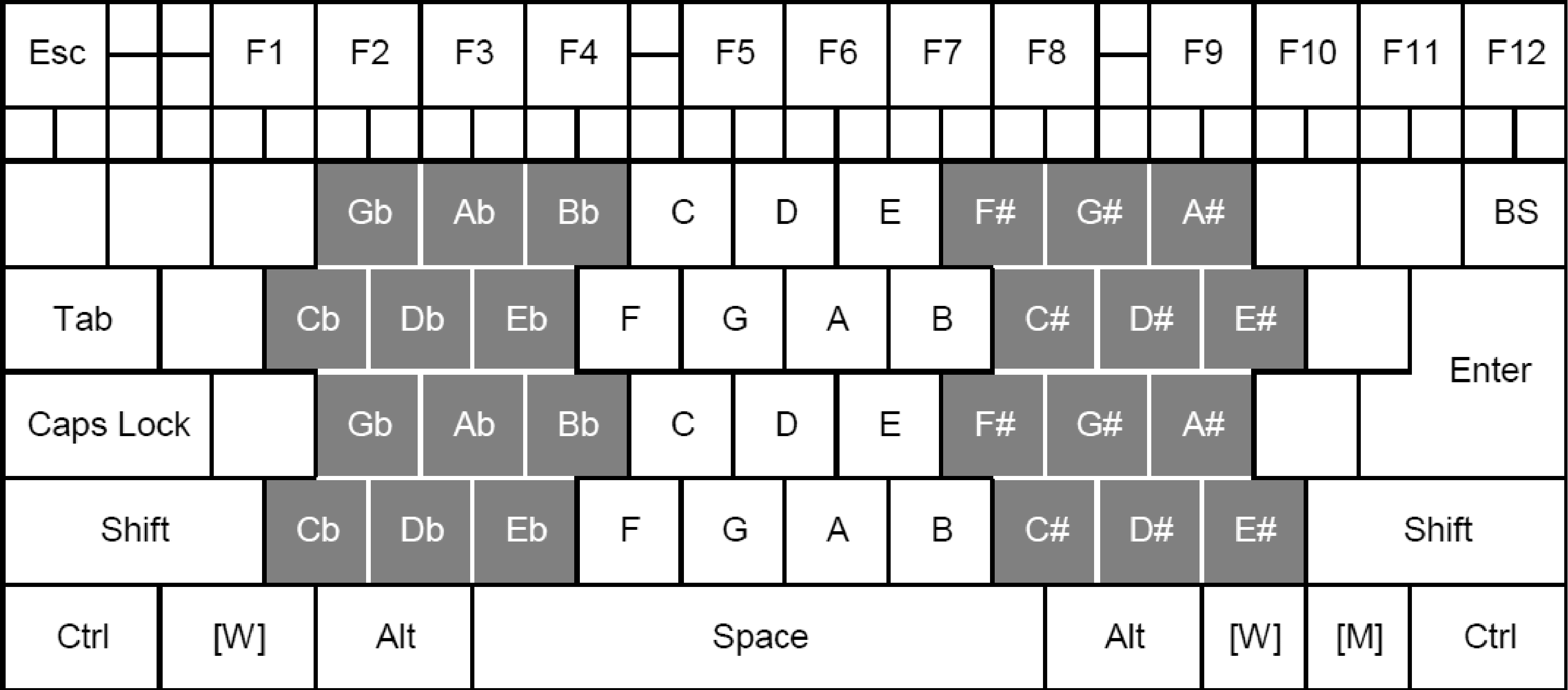f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 7. The position of notes using the Wicki layout on a Thummer keyboard. Figure 8. The position of notes using the Wicki layout on a QWERTY keyboard. comma, or any alternative tuning. In each tuning, the performer’s ﬁngers have to press different keys to produce intervals that are the same (within the deﬁnition of a given temperament). A keyboard that is tuning-invariant is preferable, so that the per- former’s ﬁngers press the same keys to produce the same intervals (within a given temperament), inde- pendent of the current tuning. Layout-Mapping from a Rank-Two Temperament to a Button Field One solution to these problems is to use a two- dimensional button-ﬁeld so that the layout- mapping from the rank-two syntonic temperament to the button-ﬁeld is isomorphic. The simplicity af- forded by the invariant ﬁngering of an isomorphic layout is illustrated in the following examples using the Wicki layout. To be concrete, Wicki is a layout-mapping to a hexagonal button-ﬁeld (which can be approximated by rotating an integer valued button-ﬁeld by 45°), such that the two generating intervals α and β are layout-mapped to the basis vectors ψ = (1, 1)T and ω = (1, 0)T, i.e., L = 1 1 1 0 as illustrated in Figure 7. This layout provides a good balance of octave- reduced intervals versus overall octave range for rel- atively small button ﬁelds (such as the QWERTY computer keyboard as illustrated in Figure 8) when using syntonic tunings (α ≈ 3/2), and it also func- tions well over many non-syntonic tuning continua (where β may take any value). Additionally, the Wicki layout allows a wide range of pitches to be played with a single hand, and all notes of any MOS scale are always clustered in a simple vertical band. (Proof of the latter property is beyond the scope of this article.) However, it has a less obvious relation- ship between pitch and button position than is found, for instance, in the design of Bosanquet. (For syntonic tunings, Bosanquet has an “easterly” pitch axis, like the standard keyboard, while the Wicki layout has a less obvious “north-northeasterly” pitch axis.) The basic principles illustrated in the following examples may also be applied to other regular temperaments, MOS scales, and layouts. 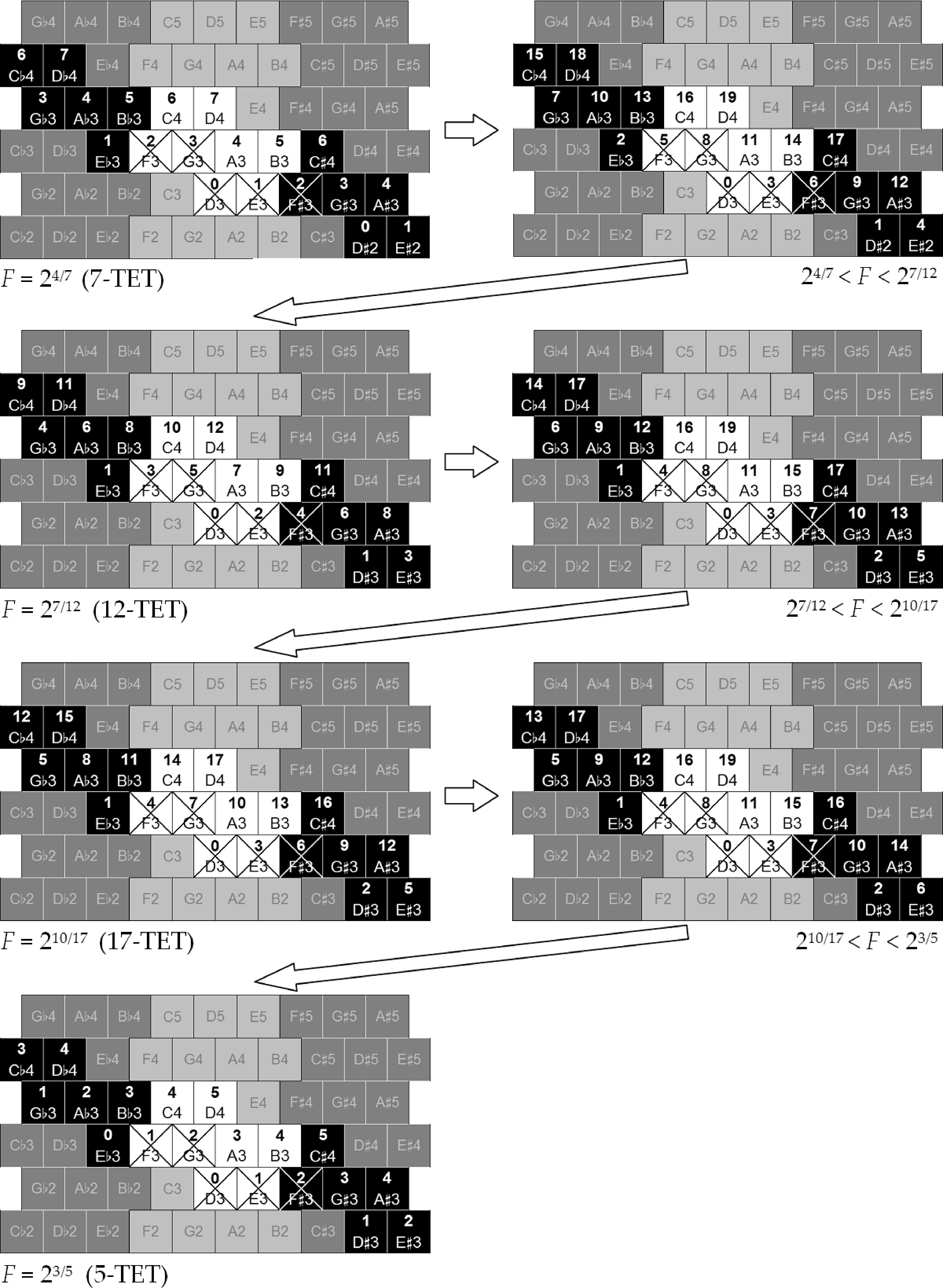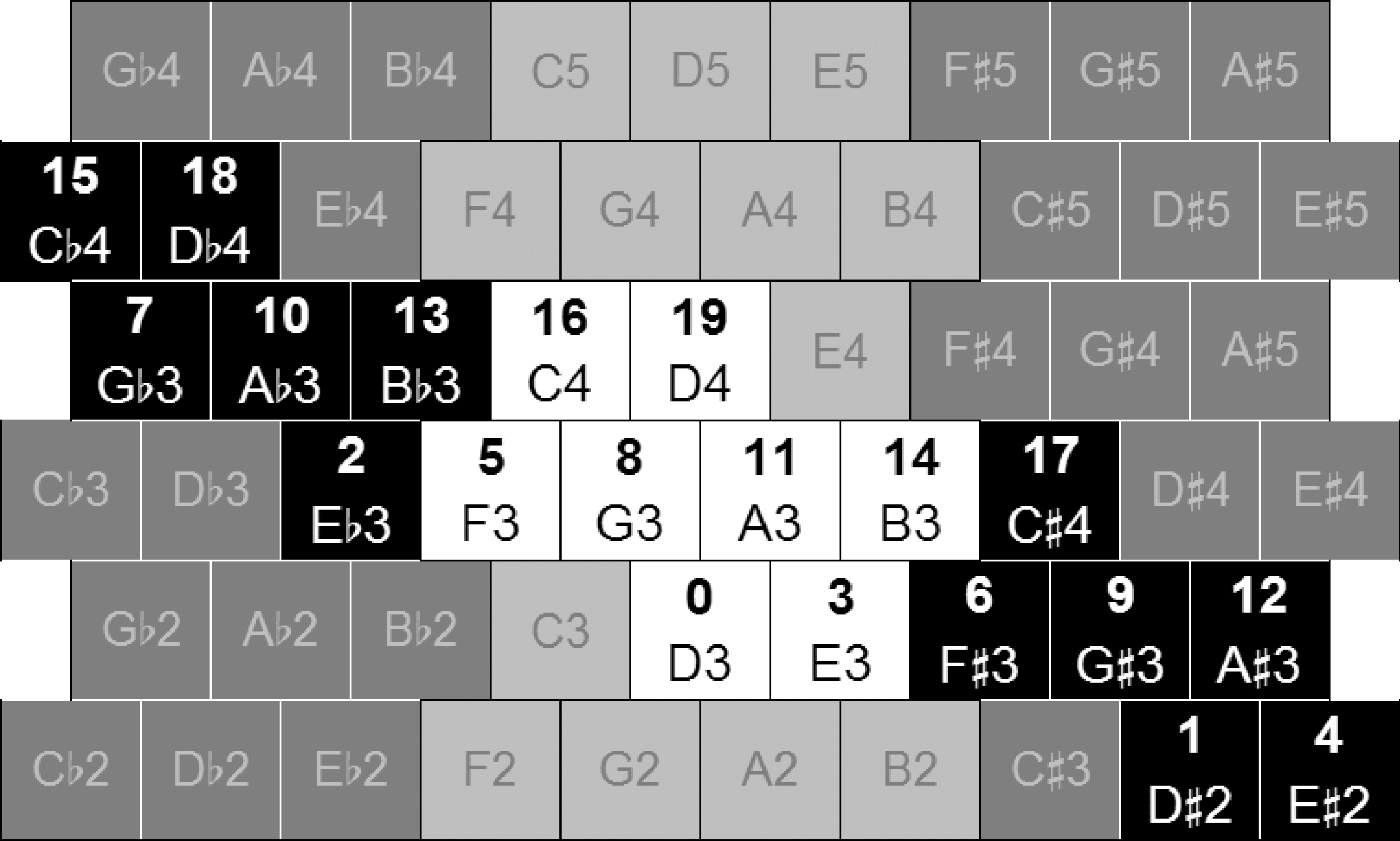Tuning Ranges of Invariance Assuming that the generating intervals are α = 2 (an octave), and β = F (an alterable tempered perfect ﬁfth), the pitch order of buttons on a Wicki layout that is ten buttons wide has seven different conﬁgu- rations as the tuning of F moves across the MOS:5+2 ordinal continuum of 24/7 < F < 23/5. Figure 9 shows the pitch order of the buttons, starting from D3 (num- bered 0) up to D4 (an octave above), as F traverses this range. Despite these different conﬁgurations, every melodic interval that is “legal” to common practice has its order preserved. (Intervals such as G-sharp–A-ﬂat, F-ﬂat–E-sharp, or C-ﬂat–B-sharp typically have no melodic function in common- practice music.) For example, observe that although the pitch order changes as the tuning is raised from 24/7 to 23/5, the diatonic notes (colored white in this ﬁgure) remain in the same order, and so do the “le- gal” chromatic intervals. The shape of the chromatic melody Re–Mi–Fa–Fi–Sol is indicated by crosses, 26 Computer Music Journal l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o m j / l a r t i c e - p d f / / / / 3 1 4 1 5 1 8 5 4 9 5 6 / c o m j . . 2 0 0 7 3 1 4 1 5 p d . . . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ Figure 9. Pitch order of notes across the MOS:5+2 ordinal continuum’s tun- ing range. The notes within the D3 to D4 octave have been highlighted. (a) F = 24/7 (7-TET); (b) 24/7 < F < 27/12; (c) F = 27/12 (12-TET); (d) 27/12 < F < 210/17; (e) F = 210/17 (17-TET); (f) 210/17 < F < 23/5; (g) F = 23/5 (5-TET). (a) (c) (e) (g) (b) (d) (f) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o m j / l a r t i c e - p d f / / / / 3 1 4 1 5 1 8 5 4 9 5 6 / c o m j . . 2 0 0 7 3 1 4 1 5 p d . . . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Milne et al. 27 Figure 10. The step posi- tions for a selection of meantone n-TETs. The notes within the D3 to D4 octave have been high- lighted. For n-TETs where n > 19, some of the notes
fall beyond the edges of

this button-ﬁeld. (A) Mean-
tone n-TET (19-TET); (B)
meantone n-TET (50-TET);
(C) meantone n-TET (31-
TET); (D) meantone n-TET
(43-TET); (e) meantone
n-TET (12-TET).

(A)

(C)

(e)

(B)

(D)

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

not easily speciﬁed a priori. Figur 2 zeigt die
MOS:5+2 ordinal tuning range, which corresponds
roughly with a reasonable (though inexact) syntonic
rational tuning range.

Using an isomorphic keyboard, a performer can
maintain the same ﬁngerings of chords and melodies
throughout the relevant range of this tuning contin-
uum. Note that Figure 2 indicates only the syntonic
temperament, but a given tuning can belong to
more than one regular temperament. Zum Beispiel,
it is likely that 53-TET tuning falls within the tun-
ing ranges of invariant rational identity for both the
syntonic and the schismatic temperament (welche
tempers the 5-limit generators of Equation 1 mit
a = –15, b = 8, and c = 1).

Dynamic Tuning

Keyboard designs that are invariant in both transpo-
sition and tuning offer several performance possibil-
ities to the computer-based musician and composer.
All the tunings of the syntonic (or MOS:5+2) con-
tinuum can be characterized by the width of their
tempered ﬁfth. The exact value of this ﬁfth can be

and the pitch order within this shape remains the
same, only breaking down when F ≤ 24/7 or F ≥ 23/5.
Another natural consequence of invariant ﬁnger-

ing is that the steps of the various n-TETs falling
within any given continuum automatically line up
to the correct button position. This is illustrated by
Figur 10, which shows a selection of meantone
n-TETs.

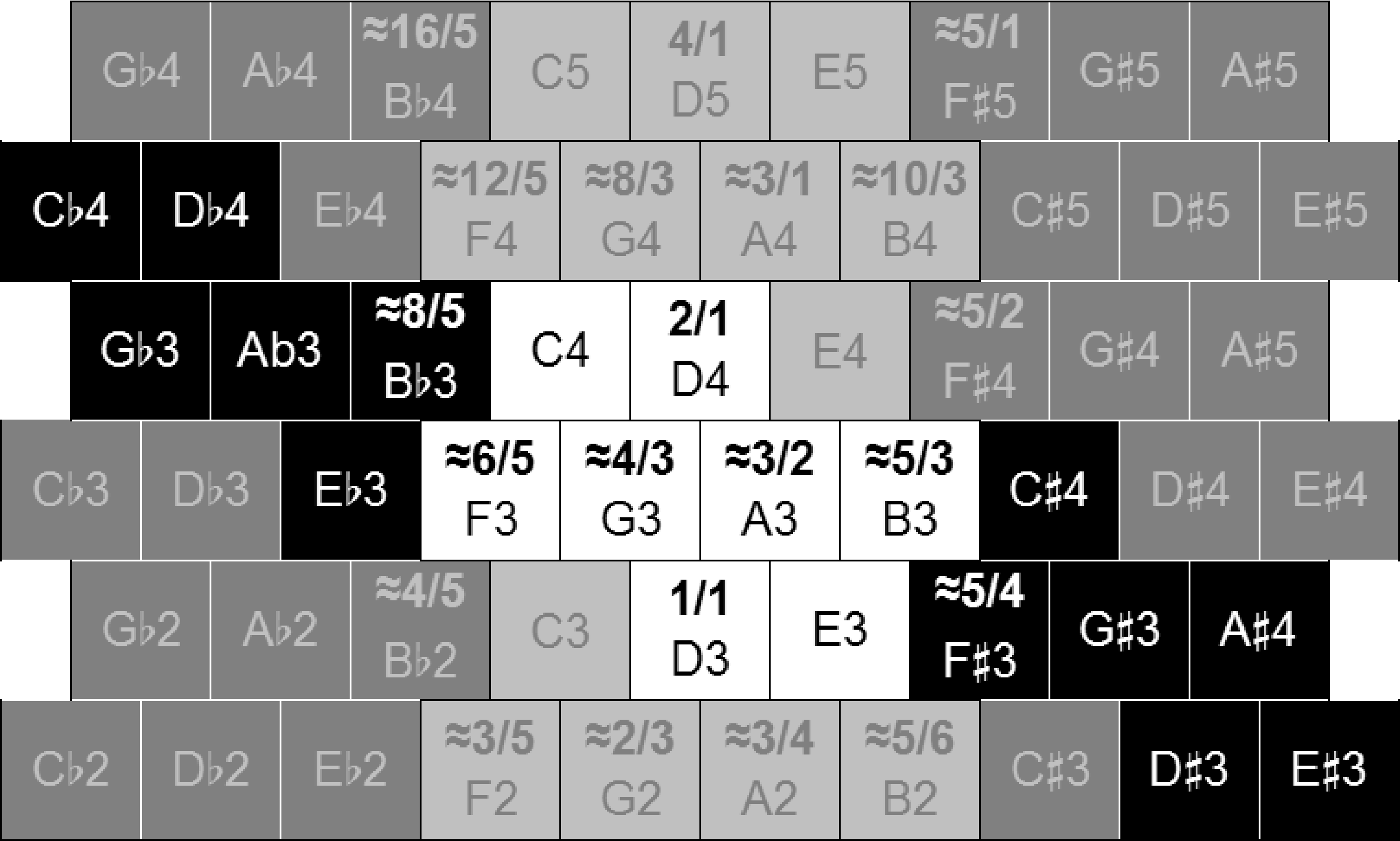
Figur 11 shows the positions on the Wicki layout
of the common practice harmonic consonances that
can be signiﬁed over a range of values of the ﬁfth F.
This example is again centered on the note D3 (ein
arbitrary choice).

As discussed previously, the limits for invariant
rational identiﬁcation are context-dependent and

Computermusikjournal

Figur 11. Position of the
signiﬁed common practice
harmonic consonances us-
ing the Wicki layout and
the syntonic temperament.

Figur 12. A simple chord
progression annotated
with the scale-step num-
bers in 31-TET, 12-TET,
and 17-TET. On an isomor-
phic keyboard, this chord

progression can be played
with identical fingerings
in all keys and all tunings
of the syntonic rational
continuum.

linked to a single slider, modulation wheel, joystick
axis, or other control device. As the performer
moves this control, thereby changing the width of
the tempered perfect ﬁfth, the pitches of all sounded
notes will change correspondingly to match the cur-
rent tuning. If the extremes of the control’s range
correspond to the extremes of the MOS:5+2 ordinal
continuum, then sliding that control from one end
to the other will result in the continuum of tunings
shown in Figures 2 Und 9.

Zum Beispiel, one might choose to perform a

simple I–IV–V–I pattern such as shown in Figure 12.
The three staves show the score as it would be writ-
ten in conventional notation; the numerical annota-
tions show the scale steps in each of three tunings
(31-TET, 12-TET, and 17-TET) as the parameter β
moves from 218/31 Zu 27/12 Zu 210/17. As shown in Fig-
ure 9, the ﬁngering remains the same throughout
the continuum. Daher, players of a tuning-invariant
keyboard may be able to transfer competence in one
tuning (such as 12-TET) to others; hard-won manual
dexterity can be transferred directly to other tun-
ings within the continuum. This is not possible on
the piano keyboard, guitar fretboard, or other com-
mon musical interfaces.

The tuning can also be changed dynamically dur-

ing performance. By analogy with pitch bend, Das
might be called “tuning bend,” where the exact tun-
ing of each note in each interval is changed in re-
sponse to the physical motion of the controller. Für
Beispiel, the performer might push up into a supra-
Pythagorean tuning (like 17-TET) to give melodies
more expressive power, drop down to 12-TET to
perform a smooth enharmonic modulation, Und
then drop down to a quasi-meantone tuning (wie
31-TET) for more pleasing triads. This may give

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

keyboard players greater ﬂexibility in mimicking
the kinds of expressive pitch deviations that string
(and aerophone) players reveal when altering their
intonation phrase by phrase (Sundberg et al. 1989).
Darüber hinaus, tuning bends are not limited to mono-
phonic implementations. Rocking the controller
back-and-forth describes a kind of (polyphonic) vi-
brato where each note might have a different
amount and direction of pitch deviation.

Diskussion

Music education, Leistung, and composition
can beneﬁt from the transpositional and tuning in-
variance provided by isomorphic button ﬁelds. Der
piano-style keyboard is incapable of achieving the
advantages of an isomorphic keyboard for three rea-
sons. Erste, it is essentially one-dimensional, Und

Milne et al.

one-dimensional layouts can only have transposi-
tional invariance for equal temperaments. Zweite,
its offset pattern of twelve keys per octave is only
well suited to tunings that use twelve (or fewer)
notes per octave. Dritte, the piano keyboard’s offset
white and black keys hide the consistent patterns of
12-TET—let alone any other tunings—forcing stu-
dents to learn each key’s scales, chords, and other
properties by rote.

Im Gegensatz, with an isomorphic button-ﬁeld, A
student need only learn the geometric shape of a
given interval once (within a given temperament),
and thereafter apply that knowledge to all occur-
rences of that interval, independent of its location
within a key, across keys, or across tunings. This re-
duces rote memorization considerably and engages
the student’s visual and tactile senses in discerning
the consistency of music’s patterns.

Außerdem, the MOS:5+2 ordinal continuum
includes the tunings of many cultures and eras.
At one of the continuum’s extremes, Zum Beispiel,
7-TET provides a close approximation to tradi-
tional Thai music (Morton 1980) and to tradition-
ally tuned African balafon music (Jessup 1983),
and at the other extreme, 5-TET is close to Indone-
sian slendro (Surjodiningrat, Sudarjana, and Susanto
1993). Between these two extremes can be found
many tunings that have been explored in European
Geschichte, such as quarter-comma meantone,
Pythagorean tuning, and today’s ubiquitous 12-TET.
A student, having mastered the use of an isomor-
phic button ﬁeld in any one of these tunings, can
apply the same motor skills and music theory to all
the rest, making multi-cultural music education
considerably easier.

Although this article has focused on the syntonic

temperament and diatonic and chromatic scales,
the beneﬁts of tuning invariance are gained by all
rank-two regular temperaments, such as schis-
matic, porcupine, magic, and hanson (Tonalsoft
2007), and their respective MOS scales. The differ-
ent geometries of different temperaments and MOS
scales on the same keyboard make it easier for stu-
dents to compare, Kontrast, and understand them,
experiencing those differences through sight and
touch in addition to hearing.

boards. Consider that accompanists are often asked
to transpose a piece at sight to accompany the range
of a particular vocalist. Being able to transpose on
the ﬂy may be the mark of a master musician today,
but with an isomorphic keyboard, the task becomes
signiﬁcantly easier. With an isomorphic keyboard
and dynamic tuning, performers can also execute
real-time polyphonic tuning bends, temperament
modulations, and other effects that are simply im-
possible on a piano keyboard or guitar fretboard.

Composers can also beneﬁt from the transposi-

tional and tuning invariance of isomorphic key-
boards. Just as Beethoven was the ﬁrst to exploit the
novel technology of the metronome to specify pre-
cise tempi (Stadlen 1967), composers writing for iso-
morphic keyboards can indicate appropriate tunings
for pieces that are meant to imply a baroque (quarter-
comma), medieval Ars Nova (Pythagorean), or mod-
ern atonal (12-TET) fühlen.

Natürlich, there are also disadvantages to such
isomorphic keyboards compared to that of the pi-
ano. The playing of diatonic intervals connected by
parallel motion is more complex than on the white
keys of the piano, and with some layouts, there is a
less obvious linear relationship between pitch
height and location on the keyboard. Although iso-
morphic keyboards have been proposed and built in
die Vergangenheit, they do not have a large installed user base
or a deep repertoire. This paper has shown that iso-
morphic keyboards can be coupled with appropriate
computer technology to provide the deeper beneﬁts
of tuning invariance and dynamic tuning.

Verweise

Barbour, J. M. 1951. Tuning and Temperament: A Histori-
cal Survey. East Lansing, Michigan: Michigan State
College Press. Reprint, New York: Da Capo Press, 1973.
Reprint, New York, Dover, 2004.

Blackwood, E. 1985. The Structure of Recognizable Dia-
tonic Tunings. Princeton, New Jersey: Princeton Uni-
versity Press.

Bosanquet, R. H. M. 1877. Elementary Treatise on Musi-
cal Intervals and Temperament. London: Macmillan.
Cited in Helmholtz (1877).

Carey, N., and D. Clampitt. 1989. “Aspects of Well-

Performers can also beneﬁt from isomorphic key-

Formed Scales.” Music Theory Spectrum 11:187–206.

Computermusikjournal

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Carlos, W. 1987. “Tuning: At the Crossroads.” Computer

Tonalsoft. 2007. “Equal Temperament.” Encyclopedia of

Musikjournal 11(1):29–43.

Clough, J., N. Engebretsen, and J. Kochavi. 1999. “Scales,
Sets, and Interval Cycles.” Music Theory Spectrum
10:19–42.

Fokker, A. D. 1955. “Equal Temperament and the Thirty-
One-Keyed Organ.” The Scientiﬁc Monthly 81(4):161–
166. Available online at www.xs4all.nl/~huygensf/doc/
fokkerorg.html. (Zugriff 26 Marsch 2007.)

Grady, K. 1999. “CS.” Message posted to Alternate Tun-
ings Mailing List. Available online at launch.groups
.yahoo.com/group/tuning/message/5244. (Zugriff 11
Oktober 2006.)

Helmholtz, H. L. F. 1877. On the Sensations of Tone.
Trans. A.J. Ellis. Reprint, New York: Dover, 1954.
Insall, M., T. Rowland, and E. Weisstein. 2007. “Point
Lattice.” MathWorld—A Wolfram Web Resource.
Available online at mathworld.wolfram.com/
PointLattice.html. (Zugriff 4 Juni 2007.)

Jessup, L. 1983. The Mandinka Balafon: An Introduction
with Notation for Teaching. La Mesa, Kalifornien: Xylo
Veröffentlichungen.

Keislar, D. 1987. “History and Principles of Microtonal
Keyboards.” Computer Music Journal, 11(1):18–28.
Published with corrections in 1988 as “History and
Principles of Microtonal Keyboard Design," Bericht
STAN-M-45, Universität in Stanford. Online verfügbar unter
ccrma.stanford.edu/STANM/stanms/stanm45. (Ac-
cessed 13 Juni 2007.)

Lorentz, R. 2001. “19-TET in a Renaissance Chanson by
Guillaume Costeley.” Paper presented at Microfest,
Claremont, Kalifornien, April 6.

McLaren, B. 1991. “General Methods for Generating Mu-

sical Scales.” Xenharmonikon 13:20–44.

Morton, D. 1980. “The Music of Thailand.” In E. Mai, Hrsg.
Music of Many Cultures. Berkeley, Kalifornien: Univer-
sity of California Press, pp.63–82.

Sethares, W. A. 2004. Tuning, Timbre, Spectrum, Scale,

2nd ed. London: Springer-Verlag.

Schmied, G.W. 2006. “Xenharmony.” Available online at

bahamas.eshockhost.com/xenharmo. (Accessed Octo-
ber 2006.)

Stadlen, P. 1967. “Beethoven and the Metronome.” Music

and Letters 48:330–349.

Sundberg, J., F. Anders, and L. Frydén. 1989. “Rules for
Automated Performance of Ensemble Music.” Con-
temporary Music Review 3(1):89–109.

Surjodiningrat, W., P. J. Sudarjana, and A. Susanto. 1993.

Tone Measurements of Outstanding Javanese Gamelan
in Yogyakarta and Surakarta. Yogyakarta, Indonesien:
Gadjah Mada University Press.

Microtonal Music Theory. Online verfügbar unter
tonalsoft.com/enc/e/equal-temperament.aspx.
(Zugriff 26 Marsch 2007.)

Wicki, K. 1896. “Tastatur für Musikinstrumente.” Swiss

patent 13329.

Wilson, E. 1975. “Letter to Chalmers Pertaining to Mo-
ments Of Symmetry/Tanabe Cycle.” Available online
at www.anaphoria.com/mos.PDF. (Zugriff 26 Marsch
2007.)

Appendix A: Proof of Theorem 1

Let f : Z2 → Z2 be an invertible mapping from the
two-dimensional generators of a rank-2 tempera-
ment to the two-dimensional button-lattice. Any
note N in the temperament can be represented in
terms of its generators α and β as N = αn βm, welche
can be written as the vector (N, M) for n, m ∈ Z. Der
note is located on the button-lattice at f(N) = f(N, M).
An interval I is a ratio of two notes

N
1
N

n m
1

(cid:2) (cid:3)
1
(cid:2) (cid:3)
2

n m

(A.1)

which can be written (J, k), where j = n1–n2 and k =
m1–m2. A layout is transpositionally invariant if
every ﬁxed interval I is ﬁngered in the same man-
ner, d.h., Wenn

f N
)
(
1

−

f N
(

)
2

f N
(

)
3

−

f N
(

)
4

(A.2)

whenever

N
1
N

N
N

ICH

(A.3)

Daher, transpositional invariance requires that the

difference in locations between notes on the key-
board depends only on the interval (the j and k) Und
not on the particular notes (the n1 and m1). Expand-
ing Equation A.2 yields

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u
/
C
Ö
M

J
/

A
R
T
ich
C
e
–
P
D

F
/

3
1
4
1
5
1
8
5
4
9
5
6
/
C
Ö
M

J
.

2
0
0
7
3
1
4
1
5
P
D

B
j
G
u
e
S
T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

⎟ −

N
1
M
1

+
N
J
1
+
m k

⎟ =

⎟ −

N
3
M
3

+
N
J
3
+
m k

(A.4)

where we used the equality of the intervals from
Equation A.3, d.h., that n2 = n1 + J, m2 = m1 + k, n4 =
n3 + J, and m4 = m3 + k. If the mapping f is linear,
then this can be rewritten

Milne et al.

⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎛
⎝
⎜
⎞
⎠
⎟

⎟ −

N
1
M
1

⎟ +

N
1
M
1

J
⎟ =
k

⎟ −

N
3
M
3

⎟ +

N
3
M
3

J
k

(A.5)

which collapses to an identity for any ni and mi.
This demonstrates that linear layout mappings are
transpositionally invariant. An analogous argument
works for any invertible rank-r mapping f : Zr → Zr.

Additivity

Because Equation B.1 holds for all x and y, it must
hold for x = j and y = 0. Substituting into Equation
B.1 shows f(J + ich) – f(J) = f(0 + ich) – f(0). Because f(0) = 0,
this can be rearranged to show f(ich + J) = f(ich) + F(J).

Appendix B: Proof of Theorem 2

Homogeneity

The converse of Theorem 1 is demonstrated by
showing that transpositional invariance implies lin-
earity of f. This will ﬁrst be shown in the scalar
Fall, where the deﬁning Equation (A.1) for transpo-
sitional invariance is that for all ﬁxed intervals i,

−

ich
)

f x
(

f x
( )

(B.1)
for every x, y ∈ Z. We also assume that f(0) = 0. Lin-
earity of f is shown by demonstrating additivity and
homogeneity.

f y
( )

f y
(

ich
)

Since Equation B.1 holds for all x and y, it must
hold for x = i and y = 0. Substituting into Equation
B.1 shows f(ich + ich) – f(ich) = f(0 + ich) – f(0). Because f(0) = 0,
this can be rearranged to show f(2ich) = 2f(ich). Induction
can be used to show the general case. Nehme an, dass
F((k – 1)ich) = (k – 1)F(ich). Let x = (k – 1)i and y = 0. Substi-
tuting into Equation B.1 shows f((k – 1)ich + ich) – f((k –
1)ich) = f(ich). Using the inductive hypothesis, this can
be rearranged to show f(ki) = (k – 1)F(ich) + F(ich) = kf(ich).
The generalization to two (or n) dimensions is
straightforward.