Distributed Neural Systems Support Flexible Attention - Am MIT spezialisierte KI-Forschung

Distributed Neural Systems Support Flexible Attention
Updating during Category Learning

Emily R. Weichart*, Daniel G. Evans*, Matthew Galdo,
Giwon Bahg, and Brandon M. Turner

Abstrakt

■ To accurately categorize items, humans learn to selectively
attend to the stimulus dimensions that are most relevant to
the task. Models of category learning describe how attention
changes across trials as labeled stimuli are progressively
observed. The Adaptive Attention Representation Model
(AARM), Zum Beispiel, provides an account in which categoriza-
tion decisions are based on the perceptual similarity of a new
stimulus to stored exemplars, and dimension-wise attention
is updated on every trial in the direction of a feedback-based
error gradient. Als solche, attention modulation as described by
AARM requires interactions among processes of orienting,
visual perception, memory retrieval, prediction error, und Ziel

maintenance to facilitate learning. The current study explored
the neural bases of attention mechanisms using quantitative
predictions from AARM to analyze behavioral and fMRI
data collected while participants learned novel categories.
Generalized linear model analyses revealed patterns of BOLD
activation in the parietal cortex (orienting), visual cortex
(perception), medial temporal lobe (memory retrieval), basal
ganglia (prediction error), and pFC (goal maintenance) Das
covaried with the magnitude of model-predicted attentional
tuning. Results are consistent with AARM’s specification of
attention modulation as a dynamic property of distributed cog-
nitive systems. ■

EINFÜHRUNG

When grouping items into categories, humans are extraor-
dinarily adept at identifying regularities across dimensions
and mapping features to category labels. As we get to
know a new person, Zum Beispiel, we may be able to cate-
gorize their mood as happy, sad, or angry based on specific
elements of their facial expression, tone of voice, or body
Sprache. In an effort to explain how humans can learn
new categories quickly even when they are multivariate,
probabilistic, or nonlinearly separable, rechnerisch
models of categorization aim to formalize the processing
stream that links memories of previous experiences to
representations of new items (Galdo, Weichart, Sloutsky,
& Turner, 2021; Liebe, Medin, & Gureckis, 2004; Kruschke,
1992; Nosofsky, 1986). Across contemporary models, Die
dynamic allocation of selective attention to goal-relevant
dimensions is often implicated as the critical mechanism
through which categorization accuracy improves across
Versuche.

Models differ considerably, Jedoch, in their descrip-
tions of how attention is distributed to facilitate categori-
zation accuracy. The influential Generalized Context

This article is part of a Special Focus entitled Integrating Theory
and Data: Using Computational Models to Understand Neuro-
imaging Data; deriving from a symposium at the 2020 Jährlich
Meeting of the Cognitive Neuroscience Society.
Ohio State University, Columbus
*These authors share first authorship.

Modell (GCM; Nosofsky, 1986), Zum Beispiel, describes
a static distribution of attention based on overall dimen-
sion diagnosticity across the items represented in
Erinnerung. Adaptive attention models, by contrast, vorschlagen
that attention is updated on every trial according to a
feedback-based error gradient, requiring dynamic moni-
toring of attention-outcome contingencies (Love et al.,
2004; Kruschke, 1992). Although previous fMRI work
has provided evidence of representational reorganization
in the hippocampus that is consistent with an adaptive
attention account (speziell, SUSTAIN; Mack, Liebe, &
Preston, 2016), questions about the nature of attention,
its component processes, and the neural systems that
are recruited during attention deployment still remain.
The aim of our study, daher, is to discuss the brain
functions that contribute to attentional updating in the
context of category learning, and to evaluate a theory of
dynamic, gradient-based attention through model-based
fMRI analyses.

The current study focuses specifically on the Adaptive
Attention Representation Model (AARM; Galdo et al.,
2021), an example of the class of adaptive attention
models described above. The conceptual basis of AARM
comes from context theory, which assumes previously
experienced items (d.h., exemplars) are stored in memory
as discrete episodic traces along with associated category
labels (Medin & Schaffer, 1978). As in GCM, AARM
describes how category representations are formed
according to the similarity between new stimuli and stored

Zeitschrift für kognitive Neurowissenschaften 34:10, S. 1761–1779
https://doi.org/10.1162/jocn_a_01882

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u

/
J

Ö
C
N
A
R
T
ich
C
e
–
P
D

F
/

3
4
1
0
1
7
6
1
2
0
4
1
8
2
5

/
J

Ö
C
N
_
A
_
0
1
8
8
2
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

exemplars. An attention vector weights the influence of
plausible feature-to-category mappings when the observer
makes a choice. AARM additionally includes mechanisms
for feedback-based attention updates, which are intended
to optimize future responses with respect to the goals of
the learner. AARM’s attention updating mechanisms there-
fore incorporates notions of prediction error in a manner
that is conceptually related to models of reinforcement
learning (RL). Whereas the equation that defines the pre-
diction error signal in standard RL models calculates a gra-
dient of reward as a function of time (Sutton & Barto,
2018), AARM computes the gradient as a function of atten-
tion during each individual trial.

Previous work provided support for AARM’s mecha-
nisms of attention allocation through fits to simultaneous
streams of choice and eye-tracking data that were col-
lected while participants learned novel categories (Galdo
et al., 2021). Across paradigms of varying complexity,
AARM accurately predicted increases in accuracy that coin-
cided with increased probability of selectively attending to
goal-relevant dimensions, as measured by trial-level gaze
fixations. Although these results provided support for
AARM by way of eye-tracking data as the terminal output
of human attention dynamics (Blair, Watson, Walshe, &
Maj, 2009; Rehder & Hoffman, 2005A, 2005B), the extent
to which AARM’s mechanisms reflect expected patterns
of neural activity remains to be determined. The current
study therefore investigates the neural plausibility of atten-
tion updating as described by AARM, given current knowl-
edge about the multifaceted neural loci of its theoretical
Teilprozesse. Insbesondere, we expect the trial-level mag-
nitude of model-predicted attention updates to covary
with BOLD activation in five relevant functional clusters
(für eine Rezension, see Seger & Müller, 2010): 1) parietal cor-
tex (orienting); 2) visual cortex (perceptual processing);
3) hippocampus and medial temporal lobe (MTL; epi-
sodic memory and recognition); 4) midbrain dopami-
nergic systems and basal ganglia (prediction error); Und
5) pFC (goal maintenance and representation).

For our purposes, we used behavioral and fMRI data that
were collected by Mack et al. (2016) and were made freely
available via the Open Science Foundation (OSF; https://
osf.io/5byhb/). In the task, participants were asked to cat-
egorize novel insects into two groups according to the fea-
tures contained in three dimensions: legs, antennae, Und
mouth. Corrective feedback was provided on every trial,
allowing participants to effectively map features to cate-
gory labels. Given the layers of complexity provided by
the task paradigm in the form of multidimensional stimuli,
trial-and-error learning, unidimensional and exclusive-OR
categorization rules, and rule-switches, we deemed the
data set to be ideal for the purpose of identifying the
functional components of adaptive attention.

The current article is organized as follows. We begin by
providing a conceptual overview of AARM and highlighting
the brain regions that we hypothesized to contribute to
dynamic attentional tuning. Zweite, we will summarize

the methods related to data collection (as described by
Mack et al., 2016), model-fitting, and model-based fMRI
Analysen. Endlich, we relate the attentional tuning mecha-
nism in AARM to BOLD activation in the ROIs identified
in our analysis, and discuss our results in terms of canon-
ical category learning findings.

AARM
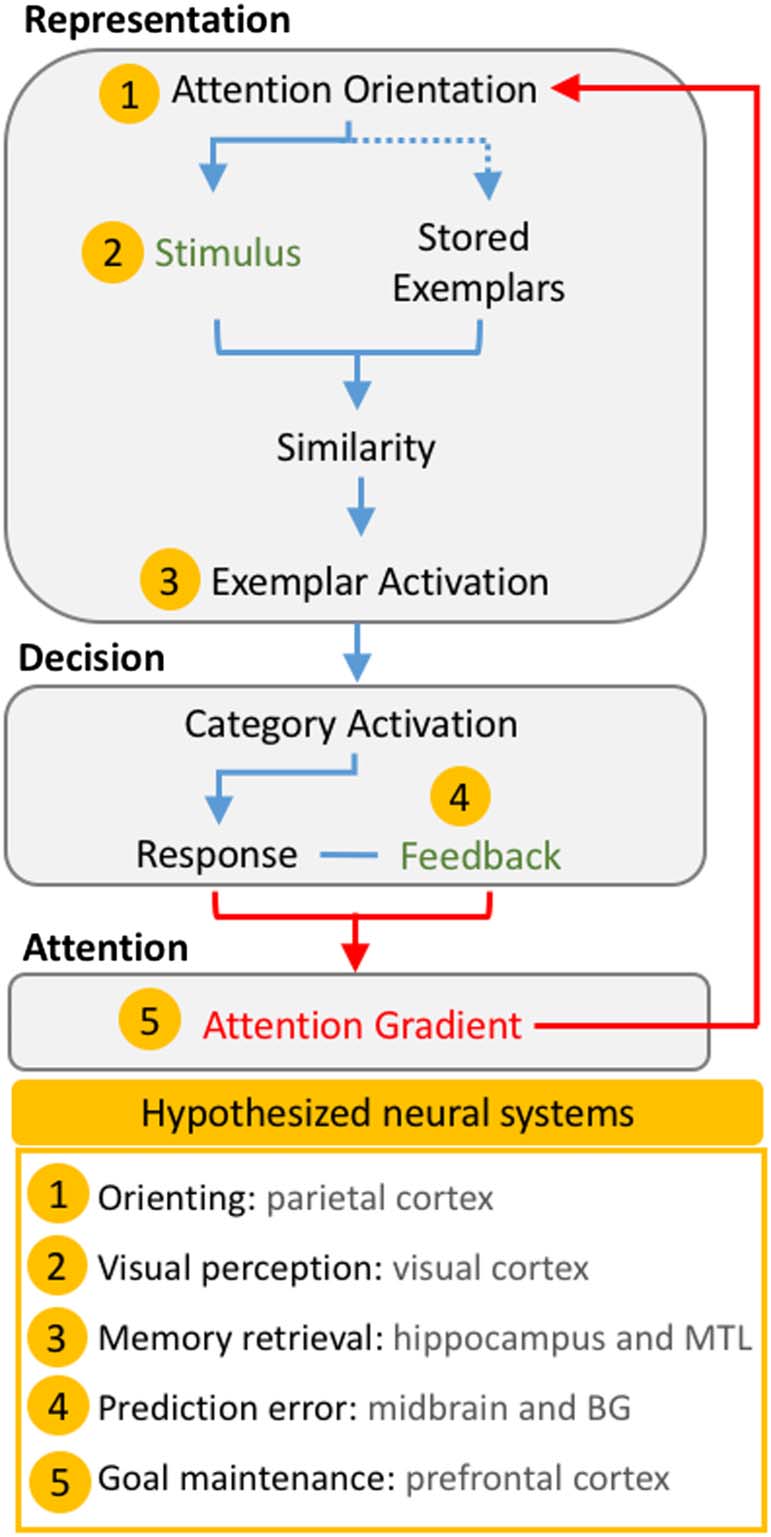
Figur 1 provides a conceptual overview of AARM’s com-
ponent mechanisms. Additional mathematical details will
be provided in the AARM Technical Specifications section
to follow. Allgemein, AARM defines the processes through
which new items are represented in psychological space

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u

/
J

Ö
C
N
A
R
T
ich
C
e
–
P
D

F
/

3
4
1
0
1
7
6
1
2
0
4
1
8
2
5

/
J

Ö
C
N
_
A
_
0
1
8
8
2
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figur 1. Conceptual overview of the Adaptive Attention Representation
Modell. Basic mechanisms that occur within each component during a
single trial are shown as a flowchart. Green text indicates information
that was provided to the observer during the trial, and all other
processes are considered to be latent. Red arrows indicate the direct
role of the attention gradient. Yellow markers indicate conceptually
associated neural functions. The dotted line indicates that attention
modulates the representation of stored exemplars despite not being
physically present at the time of stimulus processing. MTL = medial
zeitlich

lobe; BG = basal ganglia.

1762

Zeitschrift für kognitive Neurowissenschaften

Volumen 34, Nummer 10

and mapped to category labels. Learning (d.h., erhöht
categorization accuracy across trials) is conceptualized as
a natural consequence of storing experiences of stimuli
and associated feedback as they occur, and preferentially
allocating attention to the most relevant dimensions.
Hier, we will introduce the framework in terms of three
core components: representation, Entscheidung, and attention
(Weichart, Galdo, Sloutsky, & Turner, 2021; Turner, 2019).
The representation component of AARM specifies how
the low-level perceptual qualities of a new stimulus are
interpreted and contextualized by the observer’s goals
and experiences. At the beginning of a trial, attention
orients to spatial locations due to a combination of
salience and learned relevance. When a new stimulus is
introduced, the observer then samples information from
dimensions according to a learned trajectory of dimension
prioritization. This sampling process activates memories
of similar items with known category labels, which allow
the observer to form a representation of the stimulus that
is relevant to the task. Similarity is determined from the
feature-level comparison of the current stimulus to all stored
exemplars and is modulated by attention (Gleichung 1). Als
solch, an exemplar will be perceived to be more similar to
the current stimulus if its features match on highly
attended dimensions, or more dissimilar if its features
mismatch on highly attended dimensions.

The decision component describes how the observer
maps the representation of the current stimulus to a cate-
gory response. Because corrective feedback is typically
provided during category learning tasks, AARM presumes
that each stored exemplar carries an association to
a known category label. The observer therefore has
access to the necessary information for mapping the
similarity-based activation of each exemplar to its respec-
tive category. Als solche, the total activation across exemplars
that are associated with a common category label can be
interpreted as decision evidence in favor of the corre-
sponding response. When making a response, Die
observer is presumed to select a category in proportion
to the relative decision evidence among the available
options (Gleichung 3).

After the observer makes a decision and corrective feed-
back is observed, the stimulus and the category label are
stored in memory for future use. Within the attention
component, AARM subsequently updates attention in a
manner that is intended to optimize for the goals of the
observer on future trials (z.B., improve accuracy, reduce
sampling; Gleichung 4) and occurs in consideration of the
predicted response probability relative to the observed
Rückmeldung. If a highly attended dimension provides evi-
dence in favor of the incorrect category label, Zum Beispiel,
attention to that dimension will be reduced. The newly
updated attention vector is fed back into the representa-
tion component in preparation for the next trial.

It is critical to highlight that the specifications of the rep-
resentation and decision components of AARM were
based on GCM, a model of categorization that assumes

attention is calculated retrospectively after all stimuli have
been observed (Turner, 2019; Nosofsky, 1986). GCM can
generate accurate categorization predictions using a stable
attention vector that preferentially considers task-relevant
dimensions when making decisions. The GCM conceptu-
alization of attention, Jedoch, does not naturally extend
to questions of category learning. When in a novel task
environment with novel stimuli, the observer cannot pos-
sibly know which dimensions are going to be relevant and
which to attend unless explicitly instructed. This insight
can only come from experience.

AARM’s innovation relative to GCM, daher, lies in its
inclusion of a gradient-based mechanism for updating
attention according to feedback. Because attention is re-
distributed on every trial based only on what the observer
has experienced up until that point, AARM can account for
the gradual accrual of information that is required for iden-
tifying the task-relevant dimensions concurrent with learn-
ing (Galdo et al., 2021; Weichart et al., 2021).

Relative to other adaptive attention models like
ALCOVE (Kruschke, 1992) and SUSTAIN (Love et al.,
2004), AARM’s advancement is its specification of
gradient-based attention updating mechanisms that opti-
mize for the individual goals of the learner, rather than
error minimization alone. The gradient calculation allows
for the possibility that secondary computational goals bear
an impact on the representation of new items, wie zum Beispiel ein
implicit desire to maximize information sampling effi-
ciency. Given that it is often the case that multiple dimen-
sions provide similarly diagnostic information, the learner
could conceivably seek to reduce time or effort spent on
each individual trial by only attending to a subset of infor-
mative dimensions before making a response, with min-
imal detriment to overall accuracy. This idea has been
supported by our previous presentation of AARM. Wann
additional mechanisms were added to the model to opti-
mize for secondary computational goals, the expanded
variant outperformed a baseline unconstrained variant
when fit to behavioral and eye-tracking data (Galdo
et al., 2021). Although a strict error-reduction policy for
attention updating that is standard among contemporary
adaptive attention models was sufficient for predicting
accuracy across trials, accounting for individualized com-
putational goals in the gradient specification was neces-
sary for predicting trial-level
information sampling
behavior via eye-tracking. Related mechanisms for
dimension reduction have been implemented in RL
models as well and have proven necessary for predicting
human-like attention operations in naturalistic multi-
dimensional environments (Leong, Radulescu, DeWoskin,
& Niv, 2017; Niv et al., 2015).

Hypothesized Neural Systems

As an extension to our previous results, the current study
investigates the neural plausibility of AARM’s attention
updating mechanism. In order for this mechanism to be

Weichart et al.

1763

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u

/
J

Ö
C
N
A
R
T
ich
C
e
–
P
D

F
/

3
4
1
0
1
7
6
1
2
0
4
1
8
2
5

/
J

Ö
C
N
_
A
_
0
1
8
8
2
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

considered theoretically viable, it should, mindestens,
covary with neural activation in the distributed systems
that are hypothesized to contribute to continuous tuning
across trials. The neural systems that we expect to be
recruited during attentional tuning come directly from
the literature on the neural correlates of category and
RL. Insbesondere, we discuss five functional clusters for
category learning that were defined by Seger and Miller
(2010) in an independent review.

The parietal cortex is involved in orientation of spatial
attention ( Yin et al., 2012; Bisley & Goldberg, 2010), welche
is instantiated in AARM via the connection between the
attention gradient and the mechanism for sampling infor-
mation from new stimuli (Point 1 in Abbildung 1). The visual
cortex is known to be involved in the formation of low-
level perceptual representations (Folstein & Palmeri,
2013; Point 2 in Abbildung 1). The hippocampus and MTL
are involved in the maintenance and retrieval of past learn-
ing instances (Cutsuridis & Yoshida, 2017; Seger & Müller,
2010; O’Reilly & Munakata, 2000), as well as modulation of
object representations during category learning (Mack
et al., 2016). We therefore expect these regions to be
involved in attention modulation in AARM, given the
mechanism’s critical reliance on activation of past exem-
plars (Point 3 in Abbildung 1). The midbrain dopaminergic sys-
tems and basal ganglia have been implicated in behaviors
related to prediction error in RL (Averbeck & O’Doherty,
2022). Because category predictions and observed feed-
back are critical inputs to the attention updating mecha-
nisms in AARM, we expect attention to require the influence
of prediction error-based action selection functions in
these regions (Point 4 in Abbildung 1). The pFC is known to
be involved in goal-directed behaviors, particularly in
higher-level monitoring of rule-based performance
(Bogdanov, Timmermann, Glaescher, Hummel, & Schwabe,
2018), as would be expected for an update rule that opti-
mizes for the learner’s goals of reducing errors and main-
taining computational parsimony (Point 5 in Abbildung 1).

Although we do not make specific predictions about the
computations that are performed in each set of brain
Regionen, our study seeks to establish that attentional
tuning recruits the contributions of distributed systems
as described by AARM’s dynamic structure. Further review
of the candidate brain regions and how they relate to
category learning are provided in the Discussion.

EXPERIMENTAL METHODS

Data Set

The task paradigm from Mack et al. (2016) builds upon the
classic experiments of Shepard, Hovland, and Jenkins
(1961), which have become a benchmark test for models
of human category learning. The benchmark study used
stimuli that consisted of three binary dimensions to con-
struct six types of category delineations (referred to as
Types I–VI). The results, which have been replicated

several times (z.B., Crump, McDonnell, & Gureckis,
2013; Nosofsky, Gluck, Palmeri, McKinley, & Glauthier,
1994), showed a progression of learning difficulty from
Type I (one dimension was perfectly diagnostic of cate-
gory membership) to Type VI (all three dimensions
needed to be attended to produce a correct response).
The observed relative learning rates across category types
provide considerable empirical constraint that contem-
porary theories of category learning are expected to
account for to be regarded as viable (z.B., Galdo et al.,
2021; Guter Mann, Tenenbaum, Feldman, & Griffiths,
2008; Nosofsky et al., 1994; Kruschke, 1992).

The paradigm designed by Mack et al. (2016) vorgeführt
participants with three different categorization types within
the same task context, using a common set of stimulus
Merkmale. The paradigm therefore posed a unique challenge
to participants, such that they had to identify and adapt to
new categorization rules in order to maintain high accuracy.
In the original study, the inclusion of rule-switches allowed
the authors to investigate the hypothesis that learning in a
dynamic task environment is made possible by continuous
modulation of object representations. Model-based fMRI
analyses using SUSTAIN (Mack et al., 2016; Love et al.,
2004) supported their hypothesis and provided evidence
that shifting attention to rule-relevant dimensions impacted
object representations in the hippocampus.

Our study builds upon these results, taking a more gen-
eral approach to understanding the functional correlates of
attention. Insbesondere, we use a latent input approach to
analyze whole-brain fMRI data, which was described by
Turner, Forstmann, Liebe, Palmeri, and van Maanen (2017)
to be ideal for exploratory analysis. Given that the adaptive
attention mechanism specified by AARM requires dynamic
interactions among multiple cognitive systems, our study
tests for evidence of distributed system coactivation in the
brain during attentional tuning. Relevant details of the stim-
uli and procedures are provided in the following sections,
but the reader is directed to Mack et al. (2016) for more
Information.

Stimuli

Stimuli were eight images of insects, each of which was com-
posed of a body, legs, antennae, and a mouth. Although all
insects had an identical body shape, each of the other
dimensions contained one of two possible features: legs
could be thick or thin, antennae could be thick or thin,
and mouths could be shovel- or pincer-shaped. Teilnehmer
were instructed to learn how to classify the insects according
to their features, using the corrective feedback that would
be provided after every trial as a guide. Examples of stimuli
are shown in the top of Figure 2.

Task Paradigm

Participants completed three subtasks during the experi-
ment, each with a different type of categorization

1764

Zeitschrift für kognitive Neurowissenschaften

Volumen 34, Nummer 10

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u

/
J

Ö
C
N
A
R
T
ich
C
e
–
P
D

F
/

3
4
1
0
1
7
6
1
2
0
4
1
8
2
5

/
J

Ö
C
N
_
A
_
0
1
8
8
2
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u

/
J

Ö
C
N
A
R
T
ich
C
e
–
P
D

F
/

3
4
1
0
1
7
6
1
2
0
4
1
8
2
5

/
J

Ö
C
N
_
A
_
0
1
8
8
2
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

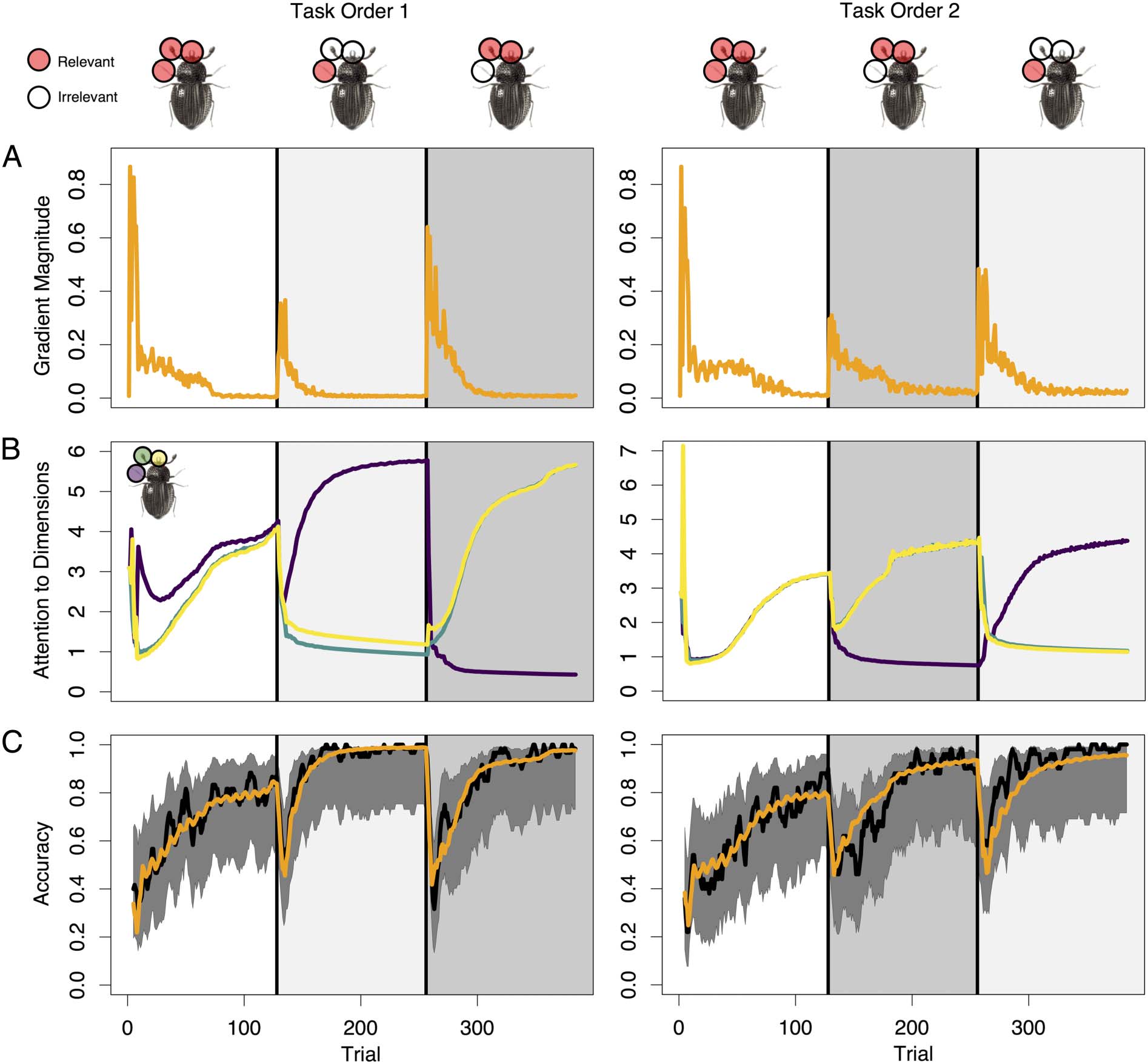
Figur 2. Attention to dimensions affects accuracy. Circles overlaying the insect stimuli indicate which dimensions were relevant in each subtask.
In all panels, vertical black lines indicate transitions between subtasks. (A) Orange lines show mean model-generated gradient magnitude values
across participant-level simulations. (B) Purple, Grün, and yellow lines correspond to mean model-generated attention (α) quantities allocated to
leg, antennae, and mouth dimensions, jeweils. (C) Lines show means of observed (black) and model-generated (orange) accuracy across
Teilnehmer. Shaded gray regions show the 95% Bayesian posterior credible intervals assuming a Beta (1, 1) prior on the probability of responding
correctly.

rule (Types I, II, and VI; Shepard et al., 1961). From the
participants’ perspective, subtasks were delineated by a
change in the instructions. Zum Beispiel, a participant
may have been asked to categorize insects according to
their temperature preference (warm or cool) during the
first subtask, and according to the hemisphere in which
they are typically found (eastern or western) during the
zweite. Beyond the change in instructions, Teilnehmer
were not informed of any potential change in rule
complexity.

In the Type I subtask, the category label of each stimulus
could be determined from the feature value of one dimen-
sion. Zum Beispiel, participants could learn to selectively
attend to the relevant “legs” dimension upon observing

that all insects with thick legs preferred warm tempera-
tures and all insects with thin legs preferred cool temper-
atures. The Type II subtask used an exclusive disjunction
(d.h., exclusive-OR) rule and required participants to
attend to two dimensions to categorize the insects cor-
rectly. Insects typically found in the eastern hemisphere,
Zum Beispiel, might have thick antennae with a pincer-
shaped mouth or thin antennae with a shovel-shaped
mouth, whereas insects found in the western hemisphere
might have thick antennae with a shovel-shaped mouth or
thin antennae with a pincer-shaped mouth. In this case,
the antennae and mouth dimensions were relevant and
the legs dimension was irrelevant. The Type VI subtask
extended the logic of Type II and required participants

Weichart et al.

1765

to learn the feature-category mappings and contingencies
among all three dimensions. Als solche, all three dimensions
were relevant for identifying category membership. Alle
participants completed the Type VI task first, and the sub-
sequent order of Types I and II was counterbalanced
between participants.

Participants completed the three subtasks in the MRI
scanner, and indicated category responses using a button
box. A subtask consisted of four functional runs, each with
32 Versuche. During a trial, the stimulus was presented for a
duration of 3.5 Sek, followed by a 0.5- to 4.5-sec jittered
fixation. Participants were then presented with a feedback
screen containing the stimulus, accuracy information,
and the correct category label for 2 Sek, followed by a
4- to 8-sec jittered fixation. Each functional run lasted
388 sec and included four repetitions of each unique
stimulus.

Data Description

The data set contains MRI and behavioral data from 23
right-handed participants (12 men, age 18–31 years) mit
normal or corrected-to-normal vision. One participant’s
data were corrupted and were therefore excluded from
all analyses presented here. Participants completed four
consecutive runs corresponding to each of the three cate-
gorization rules (Types I, II, and VI, as previously
described). Out of all data files that were made available
by Mack et al. (2016) via OSF, the following were used in
the current study: 1) magnetization prepared rapid gradi-
ent echo T1 anatomical images (Sichtfeld = 256 mm,
1-mm isotropic voxels); 2) 12 functional timeseries
acquired with a T2*-weighted multiband EPI sequence
(repetition time = 2 Sek, Echozeit = 31 ms, flip angle =
73°, Sichtfeld = 220 mm, 72 Scheiben, 1.7-mm isotropic
voxels); Und 3) behavioral data consisting of stimulus
and timing information, categorization responses, Und
correct category feedback.

Modeling Procedures

As a complement to the conceptual overview of AARM
that was provided previously, we now provide the math-
ematical details of the model as it was specifically used
in our current model-based fMRI analyses. AARM was
originally presented by Galdo et al. (2021) as a general
framework designed to account for attention “shortcuts”
that humans often take when completing a classification
Aufgabe. Zum Beispiel, if stimuli contain a large number of
dimensions, adult participants tend to consider only a
small subset of them when making decisions (Blanco,
Turner, & Sloutsky, Submitted). One interpretation of
this behavior is that in addition to the goal of achieving
high accuracy on a task, humans pursue secondary com-
putational goals like reducing the amount of time and
effort they spend on individual trials. The extent to

which these shortcuts impact behavior, Jedoch, varies
according to the demands of the task.

The full AARM framework contains various mecha-
nisms that instantiate biases for computational simplic-
ität. For our current purposes, we used the variant of
AARM that was identified in a switchboard analysis
conducted by Galdo et al. (2021) to provide the best fits
to five data sets, including Mack et al. (2016). Der
model description provided here therefore includes
mechanisms for regularization (tendency toward low-
dimensional representations) and competition (increas-
ing attention to one dimension results in a decrease in
attention to the others). For more information on
AARM’s mechanisms for attentional shortcuts, the inter-
ested reader is directed to Galdo et al. (2021) for a
thorough investigation in various contexts of task com-
plexity with quantified comparisons to traditional atten-
tion constraints.

AARM Technical Specifications

When introducing model notation, we will use unbolded
symbols to represent scalar values, bold lowercase sym-
bols to represent vectors, and bold uppercase symbols
to represent matrices.

(cid:1)

AARM describes how humans learn to categorize a
sequence of stimuli E ¼ e1; e2; …
(cid:2). Each D-dimensional
stimulus belongs to one of C categories and is represented
as row vector et , where t denotes the trial number. Der
model assumes that learning occurs via interactions
between two continuously updated processes: Erinnerung
acquisition and attention to task-relevant dimensions. To
acquire new memories, the model assumes that the stim-
ulus presented on Trial t, et, is stored as an episodic trace
T (d.h., an “exemplar”). Each exemplar
xi ¼ xi;1 xi;2…xi;D
is associated with a memory strength mt;i and a category
label fi 2 1; 2; …; C
g acquired by feedback. The feature
F
Werte, memory weights, and category labels associated
with the exemplars can be conceptualized as matrices that
are updated after each trial is completed. On Trial t, the full
history of exemplar feature values are contained within
Xt ¼ x1…xN
(cid:2), memory strengths are contained within
½
(cid:1)
Mt ¼ mt;1 mt;2…mt;N
, and the relevant category labels
are contained within Ft ¼ f1…fN

(cid:2).

(cid:3)

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u

/
J

Ö
C
N
A
R
T
ich
C
e
–
P
D

F
/

3
4
1
0
1
7
6
1
2
0
4
1
8
2
5

/
J

Ö
C
N
_
A
_
0
1
8
8
2
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

When a new stimulus is presented, it activates memo-
ries for stored exemplars on the basis of perceived
Ähnlichkeit. Similarity is computed by way of a factorizable
exponential similarity kernel (Shepard, 1987; Nosofsky,
1986), such that activation at, i of the i-th exemplar in
response to the stimulus et on Trial t is given by

(cid:5)

X
D

(cid:4)
(cid:4)

(cid:6)

(cid:4)
(cid:4)

bei;i ¼ exp −δ

αt;j et;j − xi;J

mt;ich

(1)

j¼1
where δ is the specificity of the similarity kernel function,
and αt, j is the attention applied to the j-th dimension on
Trial t. Attention to each dimension can be represented

1766

Zeitschrift für kognitive Neurowissenschaften

Volumen 34, Nummer 10

succinctly as a D-dimensional vector αt. The values of αt
modulate the observer’s perception of each exemplar’s
similarity to the current stimulus. Zum Beispiel, im
extreme case where αt, j is 0, the differences across dimen-
sion j has no impact on exemplar activation. Im Gegensatz, als
αt, j approaches infinity, an exemplar must have identical
values to the stimulus et along the j-th dimension to
maintain activation of the exemplar. We account for lag-
based memory strength using a modified temporal decay
function that allows for different temporal weighting struc-
tures depending on three parameters (Pooley, Lee, &
Shankle, 2011):

(cid:5)

mt;i ¼ 1 − 1 − (cid:2)ich
P

(cid:6)

ich

(cid:7)

1 − (cid:2)Nt−iþ1
R

(cid:8)

1 − η

Þ þ η

(2)

Wo (cid:2)p and (cid:2)R 2 [0,1] are primacy and recency weights,
η 2 [0,1] is a lower bound for memory weights, and Nt
is the number of exemplars stored on Trial t. Nach
computing each exemplar’s activation, a Luce choice
rule is used to compute categorization choice probability.
Speziell, the probability of making a Category c
response is

P ″c″jαt; et; Ft; Xt; Mt
D

Þ ¼

i¼1 at;iI fi ¼ c
D
P
N
i¼1 at;ich

(3)

here I fi ¼ c
D
the i-th exemplar xi is associated with Category c:

Þ is an indicator function that returns a one if

(cid:9)

I fi ¼ c
D

Þ ¼

1
0

fi ¼ c
ansonsten

daher, the probability of choosing c is the summed
similarity of the exemplars associated with the c-th cate-
gory, normalized by the total activation of all exemplars.
AARM assumes αt changes according to a competitive
stochastic gradient-based update rule in an effort to
minimize error and is subject to attentional constraints
of regularization and competition. Although the AARM
framework supports other variations of attention update
rules (Galdo et al., 2021), the specification that is relevant
to the current article is as follows:

(cid:2)

Þ − λ1

αtþ1 ¼ αt þ Γ ∇α log P ftjαt; et; Ft; Xt; Mt
D

(4)
where log(P( ft| αt, et, Ft,Xt, Mt)) is the log likelihood of
making a choice that is consistent with Feedback ft on
Trial t, Und 1 is a D-dimensional column vector whose
elements are all one. Hier, ∇α is a shorthand denoting a
“gradient operator” for computing the set of partial
derivatives of a function f(A) with respect to each element
of the vector α = [α1,⋯,αD]T:
(cid:10)

∂
∂α2
The positive parameter λ determines the strength of
L1-norm or LASSO regularization and is related to atten-
tional capacity constraints and bias toward low-
dimensional representations. Γ is a matrix whose diagonal

∇αf að Þ :¼

∂
∂αD

f að Þ ⋯

∂
∂α1

f að Þ

(cid:11)

elements contain the gradient step-size parameter γ0 and
off-diagonal elements are −β such that

6
6
6
6
4

Γ ¼

γ
0
−β
0
−β −β

−β −β …: −β
γ
−β …: −β
⋱ −β
γ
0
⋱
⋱
−β −β −β …:

⋮

⋮
γ
0

7
7
7
7
5

where β, γ0 2 (0,∞). β determines the strength of compe-
tition between dimensions during the attention update. In
other words, for objective function g(αt), β controls the
extent to which increasing attention to one dimension
results in a reciprocal decrease in attention to the other
dimensions.

To avoid negative values of attention, αt is constrained
to be positive. Jedoch, the attention update equation
may still propose negative values. To facilitate uncon-
strained optimization, attention is updated on the log
scale. Setting υt = log (αt) and using the change-of-
variable technique, we can rewrite the attention update
equation υt as

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u

/
J

Ö
C
N
A
R
T
ich
C
e
–
P
D

F
/

3
4
1
0
1
7
6
1
2
0
4
1
8
2
5

/
J

Ö
C
N
_
A
_
0
1
8
8
2
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

vtþ1 ¼ vt þ Γ½f∇α log P ftjαt; et; Ft; Xt; Mt
D
− λ1g (cid:3) exp vtð

Þ(cid:2)

(5)

Wo (cid:3) is the element-wise multiplication or Hadamard
product operator. Because the logarithm is a one-to-one
monotonic function, finding the optimal υt is equivalent
to finding the optimal αt. Derivations of the attention
gradient and a parameter recovery study are provided in
the work of Galdo et al. (2021).

Model Fitting

The fits to behavioral data from Mack et al. (2016) that are
used in the current study were originally presented by
Galdo et al. (2021). The model was fit to data from each
participant independently, with the general goal of identi-
fying the set of parameters that maximized the likelihood
function provided in Equation 3. In an effort to ensure
robust optimization, a three-step algorithmic approach
was used. Erste, a Differential Evolution procedure using
the DEoptimR package was implemented for 100 itera-
tions using 13 particles (2κ + 1, where κ is the number
of free parameters) to effectively sample the parameter
space and identify reasonable initial values (Brest, Greiner,
Boskovic, Mernik, & Zumer, 2006; Storn & Price, 1997).
Zweite, the initial values were used as input in R’s base
implementation of the Nelder–Mead optimization algo-
rithm (Nelder & Mead, 1965). Dritte, in the event of failure
to meet the base convergence criterion after 1000 itera-
tionen, R’s base implementation of simulated annealing
wurde verwendet für 5000 Iterationen ( Van Laarhoven & Aarts,
1987). The result of this procedure was a single set of
best-fitting parameters for each participant.

Weichart et al.

1767

A few constraints were imposed in an effort to maintain
parameter identifiability. The similarity kernel specificity
parameter was constrained to δ = 1 for all participants. Ini-
tialized values for the three-dimensional attention vector
α0 = [α0,1,α0,2,α0,3]T were constrained to be equivalent
such that α0;1 ¼ α0;2 ¼ α0;3 ¼ α(cid:4)
0, and a single parameter
α(cid:4)
0 was freely estimated. To initialize the representation,
two “background exemplars” per category were provided
with feature values of [0.5, 0.5, 0.5] (Turner, 2019;
Nosofsky, 1986). This setting assumes the observer begins
the task with equal evidence for each category response,
such that the initial state is uncertain rather than unin-
formed (Estes, 1994). The model contained a total of six
free parameters: learning rate (γ0), initial attention (α(cid:4)
0),
competition (β), regularization (λ), primacy ((cid:2)P), recency
((cid:2)R), and baseline memory strength (η).

To facilitate our model-based fMRI analyses, we input
each participant’s best-fitting parameters back into the
Modell, along with the corresponding participant’s unique
experience of trial-level stimuli and feedback. We were
therefore able to generate participant-level predictions
for changes in the attention gradient across trials in the
Mack et al. (2016) Experiment. Because we were inter-
ested in observing which brain areas contribute to
dynamic changes in attention during learning, we calcu-
lated a single “attention gradient magnitude” value for
each trial, which was the Euclidean norm of model-
ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
P
D
;
j¼1 u2
J

generated attention update values: uj

j ¼

u ¼ Γ ∇α log P ftjαt; et; Ft; Xt; Mt
D

Þ−λ1

G(cid:3) exp vtð

(cid:2)

is the attention update vector shown in Equation 5. Der
attention gradient magnitude was subsequently used as
a regressor in our fMRI analyses.

MRI Data Preprocessing and Analysis

Preprocessing and analysis of the fMRI data were per-
formed primarily using fMRI Expert Analysis Tool ( Version
6.0.5), a tool within FSL (FMRIB’s Software Library; https://
fsl.fmrib.ox.ac.uk/fsl/). Functional EPI data were cor-
rected for excessive motion using MCFLIRT ( Motion
Correction FMRIB’s Linear Image Registration Tool;
Jenkinson, Bannister, Brady, & Schmied, 2002), stripped
of nonbrain structures using BET (Brain Extraction Tool;
Schmied, 2002), spatially smoothed with a 3.4-mm FWHM
Gaussian kernel, and temporally filtered with a high-pass
filter cutoff of 100 Sek. Anatomical T1 images were regis-
tered to standard space using FNIRT (FMBRIB’s Non-linear
Image Registration Tool), which generated a transforma-
tion matrix for each participant. To align a participant’s
functional and anatomical images, the functional data
were first registered to the participant’s T1 image using
the brain-boundary-based registration method in FLIRT
(FMRIB’s Linear Image Registration Tool; Greve & Fischl,
2009; Jenkinson et al., 2002) and then transformed into a

standard space (MNI152 with 1-mm resolution) by apply-
ing the same transformation matrix generated from T1
registration. Zusätzlich, FAST (FMRIB’s Automated Seg-
mentation Tool; Zhang, Brady, & Schmied, 2001) was used
to segment the T1 image into three tissue types: gray mat-
ter, white matter, and cerebrospinal fluid (CSF). The CSF
mask from this segmentation was subsequently trans-
formed into the functional space to extract the timeseries
of mean CSF signal from each run.

After preprocessing, we used FSL’s FILM tool (FMRIB’s
Improved Linear Model; Woolrich, Ripley, Brady, & Schmied,
2001) to conduct a three-level whole-brain generalized
linear model (GLM) Analyse. The goal was to identify the
brain areas involved in attentional tuning, as predicted by
AARM. Trial-wise attention gradient magnitudes were gen-
erated by AARM, time-locked to the onset of each trial’s
feedback period, and then concatenated to create the
regressor of interest.

At the first level of the analysis, a GLM was fit to the time-
series of attention gradient magnitudes in each individual
run. The model included 32 trial-specific regressors, welche
were time-locked to the onset of each stimulus and lasted
the duration of the decision period during each trial.
These trial-specific regressors were included to ensure
that any signal attributed to the attention gradient magni-
tude was not confounded by the influence of cognitive
processes involved in the decision period. Zusätzlich, Zu
isolate the effects of attentional updating from the effects
of error processing, trial-level accuracy was included as a
regressor during the feedback periods (correct trials =
1, incorrect trials = 0). The attention gradient magnitude,
accuracy, and trial-specific regressors for each of 32 Versuche
were convolved with a standard double-gamma hemo-
dynamic response function, temporally filtered with a
high-pass filter cutoff of 100 Sek, and prewhitened.
The temporal derivatives of these 34 regressors were
also included in the GLM. Endlich, nuisance regressors
representing the standard six motion parameters (pitch,
yaw, roll, and x,j,z shifts) and mean CSF signal were added
to the model to control for signal, which does not originate
from the BOLD response. All columns of the design matrix
were demeaned before fitting the model. The effect of
attentional tuning on BOLD signal was calculated as a con-
trast of the gradient magnitude regressor versus no activity
(d.h., gradient magnitude signal greater than zero).

At the second level of analysis, a fixed-effects model was
used to calculate the effect of attentional tuning across all
runs within participant. Because the attentional tuning
mechanism in AARM is a general cognitive mechanism that
is not constrained by the changing categorization rules of
the task, we collapsed across all runs for each participant.
The third level of analysis considered group-level effects
of attentional tuning. Group effects were identified
through a mixed effects GLM, which was fit by FSL’s
FLAME 1 + 2 Algorithmus ( Woolrich, Behrens, Beckmann,
Jenkinson, & Schmied, 2004). The algorithm combines an
approximation of the Bayesian posterior distribution and

1768

Zeitschrift für kognitive Neurowissenschaften

Volumen 34, Nummer 10

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

:
/
/

D
ich
R
e
C
T
.

ich
T
.

e
D
u

/
J

Ö
C
N
A
R
T
ich
C
e
–
P
D

F
/

3
4
1
0
1
7
6
1
2
0
4
1
8
2
5

/
J

Ö
C
N
_
A
_
0
1
8
8
2
P
D

B
j
G
u
e
S
T

Ö
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Markov Chain Monte Carlo methods to estimate coeffi-
cients for each voxel, and was identified by Eklund,
Nichols, and Knutsson (2016) to produce minimal false
positives (< 5%) across a battery of fMRI analyses. The sample size of n = 22 from Mack et al. (2016) was deemed sufficient for our purposes on the basis of three factors: 1) Large-scale sensitivity and reliability examina- tions of group fMRI studies with GLM analyses have indi- cated that 20 or more participants should be included to achieve sufficient reliability (Zandbelt et al., 2008; Thirion et al., 2007); 2) several previous studies using model-based fMRI approaches have identified significant effects during category learning using similar sample sizes (n = 18–22; Mack, Preston, & Love, 2013; Davis, Love, & Preston, 2012; Nosofsky, Little, & James, 2012); and 3) recovery of AARM’s parameters for fits to individual participants was verified in previous work (Galdo et al., 2021), providing assurance of regressor stability within our core analysis. RESULTS We now present our results in two sections. First, we show the behavioral results from Mack et al. (2016) and the corresponding predictions from AARM, including the tra- jectory of latent attention across trials and rule-changes. Second, we show the results of a model-based fMRI anal- ysis that was designed to identify the brain regions that contribute to attentional tuning, as specified by AARM. Taken together, our results demonstrate that AARM can accurately predict learning in a complex category learning task via a gradient-based attentional tuning signal, and the same signal fluctuates across trials in a manner that is consistent with BOLD activation in regions with known relevance to category learning. Fits to Behavioral Data After fitting AARM to data, best-fitting parameters were used to generate a predicted progression of latent atten- tional tuning and associated responses across trials for each participant. Model-predicted category responses to the unique set of stimuli experienced by each participant were converted to “correct” or “incorrect” accuracy infor- mation via comparison to the true category labels. A qual- itative evaluation of model fits is shown in Figure 2C, where model-predicted accuracy was aggregated across participants and displayed as an orange line. Observed group-level mean accuracy is shown as a black line, with a 95% Bayesian credible interval (CI) shown as a gray shaded region. Model predictions fall well within the 95% CI range and closely follow the trajectory of the group-level mean across trials in both conditions of task order (left: Task Order 1, Types VI–I–II; right: Task Order 2, Types VI–II–I). Whereas only qualitative fits are shown here, quantitative comparisons conducted by Galdo et al. (2021) showed that the current model provided the best fits to behavioral data from a set of five studies (including Mack et al., 2016) compared with all alternative specifica- tions of AARM and a selection of competing models. Figure 2B provides insight into how AARM was able to predict learning across categorization rule types. By updat- ing dimension-wise attention on every trial in response to feedback, AARM gradually learns to prioritize information from the most relevant dimensions. Figure 2B shows an increase in attention that is allocated to the relevant dimensions, as indicated by the corresponding categoriza- tion rule type. For example, one group of participants experienced Task Order 1, where Type VI blocks (all three dimensions were relevant) were followed by Type I blocks (one dimension was relevant, two were irrelevant), which were followed by Type II blocks (two dimensions were rel- evant, one was irrelevant). This information is indicated by the stimuli pictured above Figure 2A, in which the relevant dimensions for each subtask are highlighted in red. Mapping the relevant dimensions to model-generated attention shown in Figure 2B, we observe that the progres- sion of attention mirrors the prescribed subtask order. Purple, green, and yellow lines reflecting attention to the legs, antennae, and mouth dimensions, respectively, all increase during the first subtask when all three dimensions were relevant for determining category membership. In the second subtask where only the legs dimension was relevant, the corresponding purple line quickly increases from the starting point, whereas the green and yellow lines drop off to indicate reduced attention to the antennae and mouth dimensions. In the third subtask, the antennae and mouth dimensions become relevant, and the legs dimen- sion becomes irrelevant. The green and yellow lines that correspond to the newly relevant dimensions show an increase in attention relative to the second subtask, and the purple line decreases. A conceptually similar pattern of predictions was observed for participants who experi- enced Task Order 2, where the lines representing dimension-wise attention in Figure 2B follow a trajectory that is consistent with dimension relevance in each subtask. Figure 2A shows the progression of latent attention gra- dient magnitude across trials. We observe that the magni- tude of between-trial attentional tuning is maximized when choice accuracy is low. As the observer learns the diagnosticity of each dimension, attention is optimally dis- tributed toward the relevant dimension(s) and, therefore, smaller changes of attention are required. Because there is less tuning needed, the gradient magnitude tends to diminish toward zero, but quickly rises again when the categorization rule changes. Neural Covariation of the Attention Gradient Trial-level attention gradient magnitude was used as the regressor of interest in our GLM analysis. Correct or incorrect accuracy information was included as an addi- tional regressor to isolate changes related to attention from changes related to error processing. As shown in Figure 2A, the largest magnitude of attentional change Weichart et al. 1769 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 tended to coincide with rule-switches. Because AARM uses a cross-entropy loss function to calculate the attention gradient that is highly sensitive to errors, it is well in line with expectation that moments of uncertainty about which dimensions were relevant (Figure 2B) would result in a high probability of predicted errors (orange line, Figure 2C) and correspondingly large adjustments in attention (Figure 2A). As such, our fMRI GLM analysis identified ROIs where BOLD activation reflected changes across trials that were consistent with learning and associ- ated changes in attention. Maps from the group-level GLM were converted to z scores and were thresholded at Z ≥ 3.1 within each voxel. Spatially contiguous voxel clusters were corrected for family-wise error at p < .001 ( Woo, Krishnan, & Wager, 2014) using FSL’s implementation of Gaussian Random Field Theory. Smoothness was estimated using FSL’s “smoothest” function on group-level residuals. 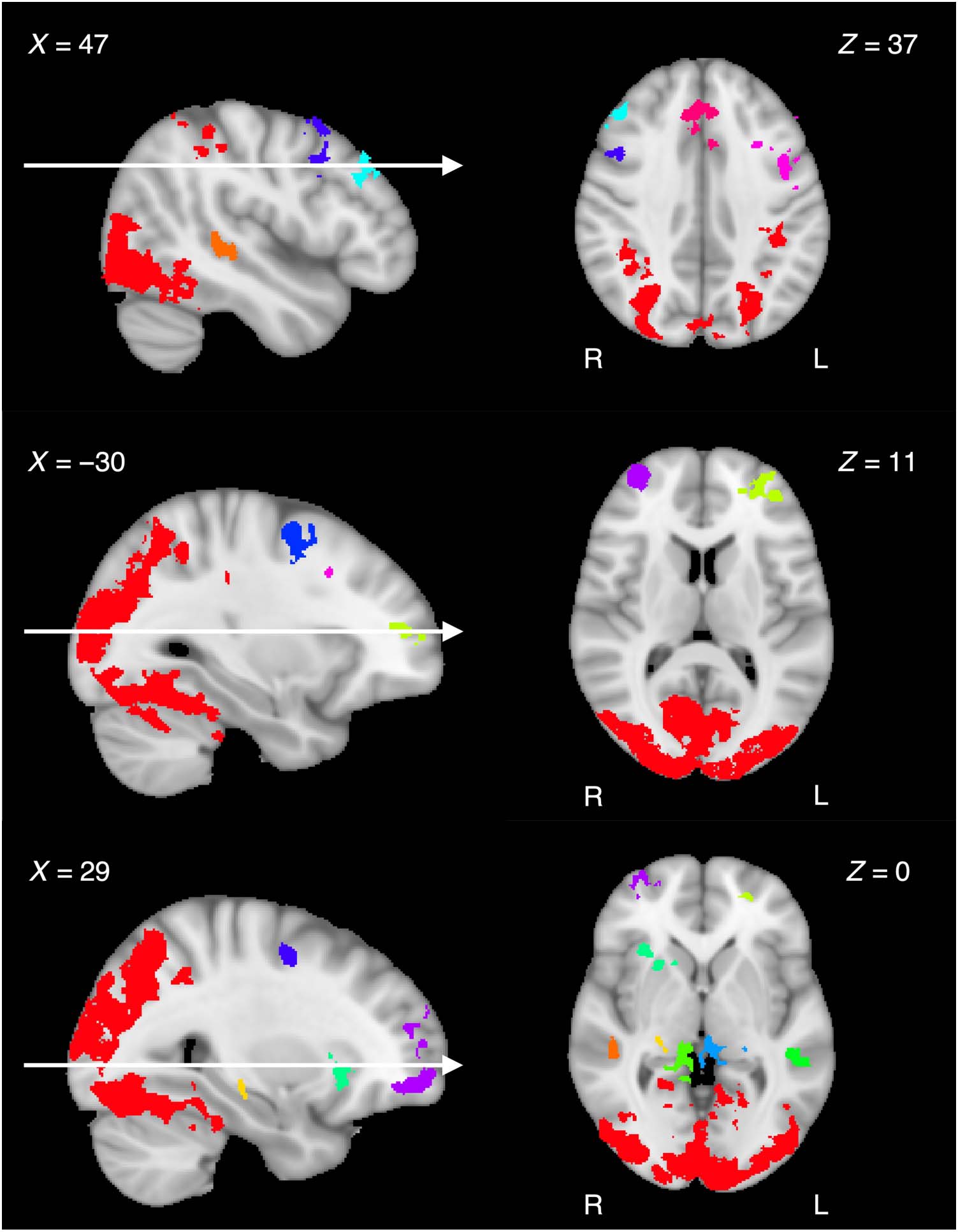This resulted in 14 unique clusters where model-generated attention gradient magnitude accounted for significant variability in BOLD signal across trials. Figure 3 shows the spatial location of each ROI in Montreal Neurological Insti- tute (MNI152) standard space. Because some ROIs appear to be noncontiguous when displayed as two-dimensional slices, each ROI was randomly assigned a unique color to properly visualize the spatial differentiation. Sagittal and axial slices in Figure 3 were selected in an effort to display all ROIs as parsimoniously as possible. Table 1 shows the l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 3. ROIs resulting from fMRI generalized linear model analysis. Each cluster is presented as a unique color rendered in MNI152 1-mm standard space. Arrows in the sagittal slices indicate the position of corresponding axial slices. 1770 Journal of Cognitive Neuroscience Volume 34, Number 10 Table 1. ROIs Resulting from fMRI Generalized Linear Model Analysis Region(s) 1. Bilateral visual pathways, superior parietal 2. Bilateral dorsal ACC, superior frontal gyrus 3. L middle frontal and precentral gyrus 4. R frontal pole 5. R superior middle frontal gyrus, premotor cortex 6. L superior middle frontal gyrus, premotor cortex 7. Thalamus, hippocampus, superior colliculus 8. R dorsolateral pFC 9. R insular cortex, putamen, caudate 10. L posterior middle temporal gyrus 11. R thalamus, parahippocampal gyrus 12. L frontal pole 13. hippocampus 14. R posterior middle temporal gyrus x 12 0 −48 38 28 −42 −7 43 21 −58 11 −28 21 47 y −101 25 8 53 −4 3 −33 32 15 −40 −44 54 −25 −28 z 1 45 53 −5 49 62 −3 34 0 4 −2 9 −8 −1 Cluster Size Max z Score 117004 11.00 6283 4142 3985 2556 1432 1249 1212 1124 1120 898 812 747 392 6.43 6.79 6.88 6.11 6.78 5.10 6.67 5.19 6.05 5.94 5.70 5.00 5.55 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Coordinates and clusters are in 1-mm MNI152 space. Spatially contiguous voxel clusters corrected for family-wise error at p < .001. ROIs are listed in descending order of cluster size. L = left; R = right; ACC = anterior cingulate cortex. corresponding MNI coordinates and the peak z value of each ROI, where ROIs are listed in descending order of cluster size. We observe a high degree of overlap between the ROIs identified here and the five functional clusters of interest as defined by Seger and Miller (2010). The largest ROI (ROI 1 in Table 1) is primarily reflective of the parietal cortex and visual cortex functional clusters, which are thought to be used for spatial orientation and low-level perceptual object representations during category learning, respectively. The hippocampus and MTL functional cluster consists of five ROIs (ROIs 7, 10, 11, 13, and 14 in Table 1) and is thought to form higher-level object representations in reference to previously encoded stimuli in an effort to orthogonalize experiences in memory. Two ROIs are consistent with the midbrain dopaminergic systems and basal ganglia func- tional cluster (ROIs 7 and 9 in Table 1), which is thought to be involved in prediction error and converting information inputs into actions. Seven ROIs overlap with the pFC func- tional cluster (ROIs 2, 3, 4, 5, 6, 8, and 12 in Table 1), which is involved in action policy updating in the presence of rule-switches and changing environments. In consider- ation of previous literature, these ROIs characterize a diverse set of neural systems that reflect dynamic adjusting of attentional weights upon observation of feedback, beyond what is accounted for by error processing alone. DISCUSSION In the current study, we investigated the hypothesis that adaptive attention mechanisms require the synchronized involvement of orienting, visual processing, memory retrieval, prediction error, and goal maintenance systems to effectively facilitate learning of novel categories. Our analytical approach focused specifically on the theoretical predictions of one category learning model, AARM. As illustrated in Figure 1, attention in AARM is influenced by the decision component of the observer’s experience on each trial and is then fed back into the representation com- ponent to modulate category activations on subsequent trials. As such, attention is conceptualized as the critical mechanism for learning, while also being an emergent property of the learning process itself. It therefore follows that attentional tuning should engage a diverse distribu- tion of neural systems during category learning that are involved in components of representation, decision, and attention (Figure 1). In previous work, we demonstrated that AARM can pre- dict human-like learning across several complex category learning paradigms using simultaneous streams of behav- ioral and eye-tracking data (Galdo et al., 2021). As origi- nally demonstrated by Rehder and Hoffman (2005a), humans gradually show a fixation preference for the most relevant dimensions over the course of learning tasks, and this fixation bias co-occurs with increasing accuracy. The authors argued that learning is not simply a process of pure stimulus-to-category association, but rather involves a gradual acquisition of information about dimension rel- evance that eventually allows the observer to categorize items as efficiently as a model like GCM (Nosofsky, 1986). By fitting AARM to eye-tracking data in previous work, we were able to show that AARM’s mechanisms of attention predict learning not only at the level of response accuracy but also at the level of information sampling Weichart et al. 1771 behaviors with increasing reliance on relevant dimensions as the task proceeds. Additional work showed that AARM extends to within-trial dynamics, such that it can accurately predict the order in which individuals will fixate to dimen- sions after gaining sufficient experience with the structure of the task ( Weichart et al., 2021). Because gaze fixations during goal-directed behaviors are often considered to be a terminal output of latent attention processes (Blair et al., 2009; Kuhn, Tatler, & Cole, 2009; Itti & Koch, 2000), dem- onstrating accurate fixation predictions provided support for AARM’s ability to capture how humans interact with new stimuli during learning. The current study took an alternative approach, investigating the dynamic processes that give rise to adaptive attention rather than the behav- iors that result from it. As shown in Figure 2C, AARM predicts changes in accuracy across task blocks that closely resemble the aggregate behavior of human participants: observed behavior and model predictions show a decrease in accu- racy after each rule-switch that soon re-approaches ceiling- level performance. Although the available feature values are consistent throughout the task, AARM is able to predict shifts in accuracy by way of feedback-informed attention weights to each dimension (Figure 2B), which naturally incur large update magnitudes immediately following a rule-switch (Figure 2A). Using attention gradient magni- tude as a regressor in a GLM, model-based fMRI analyses identified statistically significant covariation in 14 ROIs. Consistent with our hypothesis, our results provided evi- dence that latent attention mechanisms in AARM indeed covary with BOLD activation in neural systems canonically involved in orienting, visual perception, memory retrieval, prediction error, and goal maintenance aspects of cate- gory learning (Seger & Miller, 2010). We additionally con- sider our results to be consistent with findings from RL modeling work, in which attention mechanisms are inves- tigated as a vehicle for posterror changes in behavior and neural activation. Niv et al. (2015), for example, provided evidence that attentional tuning during an RL paradigm facilitated interactions between the intraparietal sulcus, precuneus, and dorsolateral PFC (dlPFC) to update the task representation and provoke action selection via the basal ganglia. Follow-up work by Leong et al. (2017) showed that attention served dual purposes of biasing value computations during the decision period and value-updating across learning, as reflected by activation in the ventromedial pFC and basal ganglia. Together with the results of the current work, these findings support the notion that attention and learning bear bidirectional influ- ences on one another, in a manner that recruits operations from widely distributed systems across the brain. Although the results presented here provide prelimi- nary neural support for AARM, our approach has several limitations. AARM comprises a set of dynamic mechanisms that are hypothesized to be involved in category learning, but the analyses presented here were not intended to make any claims about the computations that occur in the regions identified. Instead, the interpretations that we can draw from a GLM are limited to the notion that model-generated attention gradient magnitude accounts for significant variability in BOLD signal change in the regions specified. We additionally opted not to conduct similar analyses with attention signals generated by any alternative theoretical accounts. We therefore do not claim that our results could only be identified by AARM, as it is likely that other adaptive attention models would also recruit activation of similar brain regions. For our pur- poses, it was sufficient to demonstrate that adaptive atten- tion in AARM covaried with neural activation in a manner that a model with stable attention across trials would not be equipped to do. Finally, it is important to note that the current data set and analysis cannot suitably arbitrate between activation related to attention updating and acti- vation related to traditional notions of prediction error as described by RL accounts (Sutton & Barto, 2018). This is because 1) prediction error is implicit to AARM’s mecha- nisms for attention updating and 2) transitions between subtasks of the Mack et al. (2016) design naturally give rise to both a high probability of prediction error and the necessity to redistribute attention to newly relevant dimensions. Although we do not consider this distinction to be antithetical to the conclusions presented here, follow-up work will investigate AARM’s predictions in the context of task paradigms that were designed to dissociate between the respective roles of attention and error pro- cessing (e.g., Calderon et al., 2021). The relative simplicity of our analytical approach never- theless provided us with the opportunity to explore the potential reach of adaptive attention, without imposing constraints on the particular nature of the connection between the latent signal of interest and neural activation in each region. Now that we have established a set of ROIs that coactivate with attentional tuning, the findings pre- sented here will serve as an impetus for future joint modeling work using AARM as a tool to understand the dynamic neural computations involved in learning (Turner, Forstmann, & Steyvers, 2019; Turner et al., 2013, 2017). In the following sections, we discuss the ROIs shown in Figure 3 in terms of the functional clusters for category learning that were defined by Seger and Miller (2010). Parietal Cortex The largest ROI that was identified by our GLM analysis contained the superior parietal lobe (ROI 1 in Table 1), which is known to play a role in attention orienting and prioritization (Bisley & Goldberg, 2010). In the context of category learning, the process of tuning attention weights can be understood as a matter of orienting attention to the appropriate dimensions, similar to how attention must reorient following an invalid cue in an attentional cueing task (e.g., Posner cueing paradigm; Posner, 1980). When a spatial location (or object) is cued with an invalid cue, attention to the cued location must be 1772 Journal of Cognitive Neuroscience Volume 34, Number 10 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 diminished to facilitate detection of the target elsewhere, which leads to slower response times on invalid trials (i.e., the cueing effect). In this context, BOLD activation in the superior parietal lobe has been shown to track processing differences between validly and invalidly cued targets ( Vossel, Weidner, Thiel, & Fink, 2009), and individuals with parietal lesions demonstrate a disrupted ability to inhibit invalid cues (Sapir, Hayes, Henik, Danziger, & Rafal, 2004). Other work has suggested that the lateral intraparietal area is critically involved in integrating bottom–up (salience-based) and top–down (relevance- based) influences on overt attention (for a review, see Bisley & Goldberg, 2010). In particular, Bisley and Goldberg (2010) argued that the lateral intraparietal area serves as a “priority map,” whereby saccades occur in proportion to behavioral relevance with influences from rapid visual response. In connection to AARM’s mecha- nisms for attention, the parietal cortex serves a function that is conceptually consistent with allocation of atten- tion to spatial locations according to a combination of learned dimension relevance with potential influences from secondary computational goals. Visual Cortex Along with superior parietal lobe, the largest ROI that we identified also contained the bilateral visual pathways in the visual cortex (ROI 1 in Table 1), which has been shown to be involved in tasks that require visual processing of spatial locations or visual features (Maunsell & Treue, 2006; for reviews, see the works of Ungerleider & Kastner, 2000; Posner & Gilbert, 1999). Important insights on the role of visual cortex in attention, for example, came from early single-cell recordings from macaques (Chelazzi, Miller, Duncan, & Desimone, 2001; McAdams & Maunsell, 1999, 2000; Chelazzi, Duncan, Miller, & Desimone, 1998; Luck, Chelazzi, Hillyard, & Desimone, 1997), which broadly demonstrated neuronal firing preferences for search targets that closely matched a cue. Some studies have additionally shown that after sufficient training, neurons in the inferior temporal gyrus can selectively respond to targets that match a cue on the basis of a par- ticular, task-relevant feature despite mismatching on others (De Baene, Ons, Wagemans, & Vogels, 2008; Bichot, Rossi, & Desimone, 2005; Sigala & Logothetis, 2002) and similar correlates of learned discriminability have been observed via human fMRI (Braunlich & Love, 2019; Folstein & Palmeri, 2013; Reber, Gitelman, Parrish, & Mesulam, 2003; Saenz, Buracas, & Boynton, 2002). In general, the visual cortex is thought to represent objects at the basic perceptual level (e.g., contrast sensitiv- ity and spatial resolution) in a manner that connects to orientation and can be modulated by covert attention (Barbot & Carrasco, 2017; for a review, see Carrasco, 2011). It is therefore notable that model-generated atten- tion covaries with low-level sensory processing in the visual cortex. Hippocampus and MTL Five ROIs overlap with the hippocampus and MTL func- tional cluster described by Seger and Miller (2010; ROIs 7, 10, 11, 13, and 14 in Table 1). The MTL is thought to be responsible for functions related to the encoding and maintenance of individual learning instances (Cutsuridis & Yoshida, 2017; O’Reilly & Munakata, 2000). The CA3 field of the hippocampus is thought to be particularly relevant to category learning, given its role in forming autoassociative links between items. This mechanism is characterized by the representational reactivation of previ- ously observed items during encoding to properly orthog- onalize cues that overlap on a subset of dimensions (Becker & Wojtowicz, 2007; Gluck, Meeter, & Myers, 2003; O’Reilly & McClelland, 1994; Sutherland & Rudy, 1989). Learners therefore are able to quickly store activa- tion patterns of similar items with minimal interference (for a review, see Hunsaker & Kesner, 2013). As expected, several studies have demonstrated MTL recruitment during category learning tasks, both alongside human fMRI (Seger & Cincotta, 2006; Poldrack et al., 2001; Poldrack, Prabhakaran, Seger, & Gabrieli, 1999) and monkey neurophysiology methods (Hampson, Pons, Stanford, & Deadwyler, 2004). Other work, however, has suggested that the involvement of the MTL is contingent upon the mode of learning that is required to complete a particular task. Whereas rule-based categorization (i.e., categories are disso- ciable by a single dimension) tends to result in maximal differential activation in the hippocampus, information inte- gration (i.e., information from multiple dimensions is required to identify the category) and paradigms that contain unannounced rule-switches tend to additionally recruit the basal ganglia (Seger & Cincotta, 2005; Poldrack et al., 1999) and pFC (Nomura & Reber, 2008; Nomura et al., 2007). The MTL is nevertheless consistently recruited during initial training across paradigms (Poldrack et al., 1999, 2001). This suggests that the MTL is necessary for learning, but that familiarity-based activation may be insufficient for categorization in more complex tasks. Studies have shown that item representations in the hippocampus are reorga- nized in accordance with changing rule states when multi- ple training periods occur within a single experiment (Aly & Turk-Browne, 2016a, 2016b). Importantly, model-based fMRI work using SUSTAIN additionally showed that this reorganization is influenced by selective attention to dimensions with learned relevance to the current task state (Mack et al., 2016). In light of these results and the fact that attention updating in AARM critically relies on continuous comparisons of probes to stored exemplars, identifying ROIs in the MTL that covary with model- predicted attention was consistent with expectation. Midbrain Dopaminergic Systems and the Basal Ganglia Two ROIs overlap with the midbrain dopaminergic systems and basal ganglia functional cluster (ROIs 7 and Weichart et al. 1773 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 9 in Table 1). The basal ganglia are thought to serve as a hub for converting information inputs to actions, in the form of selecting both movements (Humphries, Stewart, & Gurney, 2006) and task strategies (Frank, 2005). As part of the midbrain dopaminergic system (Schultz & Romo, 1992), their role in action selection is critically influenced by reward-related influxes in dopamine (Seymour, Daw, Dayan, Singer, & Dolan, 2007; Schultz, Apicella, Ljungberg, Romo, & Scarnati, 1993). The superior colliculus, for example, has been shown to be involved in RL by way of biasing visual responses in a reward-seeking manner (Shires, Joshi, & Basso, 2010). Model-based RL accounts explain that this type of learn- ing can arise from the continuous calculation of prediction errors, which are the differences between expected and observed rewards following particular sequences of actions (Nasser, Calu, Schoenbaum, & Sharpe, 2017; Schultz, 2016; Frank & Badre, 2012a, 2012b). More generally, RL com- prises an iterative process of prediction, action selection, observation of outcome, and error-based policy (i.e., strat- egy) updating, such that observers use their experiences to guide future behaviors. Although seemingly straightfor- ward, RL implicitly raises the problem of balancing explo- ration and exploitation: Is it better to exploit an action that is already known to produce a reward, or to explore other actions in the hopes of acquiring a larger, less effortful, or more consistent reward? A compelling line of computa- tional and neurophysiology work (Humphries, Khamassi, & Gurney, 2012; Frank, Doll, Oas-Terpstra, & Moreno, 2009; Frank, Moustafa, Haughey, Curran, & Hutchinson, 2007; Frank, Seeberger, & O’Reilly, 2004) has suggested that the explore versus exploit tradeoff is directly modu- lated by striatal dopamine, such that increasing tonic stria- tal dopamine decreases the probability of explorative action selection output from the basal ganglia to the superior colliculus. fMRI studies have additionally shown that exploration tends to engage the frontal pole, whereas exploitation engages the ventromedial pFC (Daw, O’Doherty, Dayan, Seymour, & Dolan, 2006), suggesting dissociable downstream executive effects of action selec- tion via the basal ganglia (Averbeck & O’Doherty, 2022). In the context of category learning, the basal ganglia are involved in tasks that require learning by trial and error (Cincotta & Seger, 2007). Similar to action selection in RL, it has been suggested that the basal ganglia are involved in the selection of category representations and strategies for sampling information from various dimen- sions (Seger & Miller, 2010; Seger, 2008) with the goal of maximizing accuracy. Turner et al. (2021), for example, provided evidence that observers may “exploit” dimen- sions via fixations that are known to carry probabilistic category information, or they may “explore” other dimen- sions in the hopes of identifying the one that is most reli- ably diagnostic of category membership. ROI results are consistent with the expectation that model-generated attention covaries with activation related to prediction error and policy updating in these regions. pFC Seven ROIs overlap with the pFC functional cluster (ROIs 2, 3, 4, 5, 6, 8, and 12 in Table 1). pFC is broadly thought to be involved in goal-directed behavior (for a review, see Bogdanov et al., 2018). In category learning tasks where the goal is to efficiently discriminate between categories, goal-directed behaviors refer to the rapid identification and exploitation of the categorization rule. Evidence from monkey neurophysiology has shown robust learning- related differences in neuronal firing between categories, even when stimuli contain multiple overlapping irrelevant features (Freedman, Riesenhuber, Poggio, & Miller, 2001, 2002, 2003). Similarly, human fMRI work has shown that learned boundaries between categories as well as relevant feature conjunctions in information integration tasks are represented in pFC (Li, Mayhew, & Kourtzi, 2009; Jiang, Bradley, & Rini, 2007). pFC has been shown to be engaged during category learning ( Vogels, Sary, Dupont, & Orban, 2002; Reber, Stark, & Squire, 1998), and pFC activation is the earliest predictor of the choice after category distinctions have been acquired (Antzoulatos & Miller, 2011, 2014; Pasupathy & Miller, 2005; Djurfeldt, Eleberg, & Graybiel, 2001). pFC has additionally been shown to be involved in error monitoring and corrective behaviors, particularly in the anterior cingulate cortex (ACC) and dlPFC (Antzoulatos & Miller, 2014; Hadland, Rushworth, Gaffan, & Passingham, 2003; Carter et al., 1998). Whereas the basal ganglia appear to be involved in tun- ing the current stimulus-action policy from trial to trial, pFC is responsible for higher-level monitoring to identify rule-shifts and inhibit the newly ineffective policy as needed (Bissonette, Powell, & Roesch, 2013). Interactions between the ACC and dlPFC have therefore been fre- quently identified in tasks that involve set-shifting, like the Wisconsin Card Sorting Task (Monchi, Petrides, Petre, Worsley, & Dagher, 2001). Because AARM predicts attention updates in the direction of an error gradient, it is consistent with expectation that the increased error frequency that accompanied rule-shifts were associated with both substantial changes to the distribution of attention and increased activity in pFC. Conclusions AARM defines a mechanism of attentional tuning that arises as a consequence of the observer’s categorization decisions in relation to feedback and, in turn, directly impacts the psychological representations of future stim- uli. Therefore, attention is adaptive in that it adjusts to the experiences of the individual, and facilitates learning in a goal-directed manner. The current study demonstrated that with its unique specification of attentional tuning, AARM was able to accurately predict behavior in a complex task paradigm that required continuous monitoring of goals and representations. Importantly, the attentional 1774 Journal of Cognitive Neuroscience Volume 34, Number 10 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 tuning mechanisms that made it possible for AARM to predict human-like learning behaviors also covaried with activation in distributed neural systems that have been implicated in distinct aspects of category learning. Given that learning is known to require complex interactions among cognitive functions of orienting, visual perception, memory retrieval, prediction error, and goal maintenance, our results provide preliminary support for AARM as a neurally plausible theory for how these interactions occur, and are facilitated by continuous updates to attention. Acknowledgments This work was supported by a CAREER award from the National Science Foundation (B. M. T.). Reprint requests should be sent to Brandon M. Turner, Depart- ment of Psychology, Ohio State University, 1827 Neil Avenue, Columbus, Ohio 43210–1132, United States, or via e-mail: turner.826@gmail.com. Data Availability Statement Data were collected by Mack et al. (2016) and are freely available via the OSF (https://osf.io/5byhb/). Model code will be available upon publication at https://github.com /MbCN-Lab. Author Contributions Emily R. Weichart: Writing—Original draft; Writing— Review & editing. Daniel G. Evans: Formal analysis; Visual- ization; Writing—Original draft; Writing—Review & editing. Matthew Galdo: Formal analysis. Giwon Bahg: Validation; Writing—Review & editing. Brandon M. Turner: Conceptualization; Funding acquisition; Project administration; Supervision; Writing—Review & editing. Funding Information Brandon M. Turner, National Science Foundation (https:// dx.doi.org/10.13039/100000001), grant number: CAREER. Diversity in Citation Practices Retrospective analysis of the citations in every article pub- lished in this journal from 2010 to 2021 reveals a persistent pattern of gender imbalance: Although the proportions of authorship teams (categorized by estimated gender iden- tification of first author/ last author) publishing in the Journal of Cognitive Neuroscience ( JoCN ) during this period were M(an)/ M = .407, W(oman)/ M = .32, M/ W = .115, and W/ W = .159, the comparable propor- tions for the articles that these authorship teams cited were M/M = .549, W/M = .257, M/ W = .109, and W/ W = .085 (Postle and Fulvio, JoCN, 34:1, pp. 1–3). Conse- quently, JoCN encourages all authors to consider gender balance explicitly when selecting which articles to cite and gives them the opportunity to report their article’s gender citation balance. REFERENCES Aly, M., & Turk-Browne, N. (2016a). Attention promotes episodic encoding by stabilizing hippocampal representations. Proceedings of the National Academy of Sciences, U.S.A., 113, E420–E429. https://doi.org/10.1073/pnas.1518931113, PubMed: 26755611 Aly, M., & Turk-Browne, N. (2016b). Attention stabilizes representations in the human hippocampus. Cerebral Cortex, 26, 783–796. https://doi.org/10.1093/cercor/bhv041, PubMed: 25766839 Antzoulatos, E., & Miller, E. (2011). Differences between neural activity in prefrontal cortex and striatum during learning of novel abstract categories. Neuron, 71, 243–249. https://doi .org/10.1016/j.neuron.2011.05.040, PubMed: 21791284 Antzoulatos, E., & Miller, E. (2014). Increases in functional connectivity between prefrontal cortex and striatum during category learning. Neuron, 83, 216–225. https://doi.org/10 .1016/j.neuron.2014.05.005, PubMed: 24930701 Averbeck, B., & O’Doherty, J. (2022). Reinforcement-learning in fronto-striatal circuits. Neuropsychopharmacology, 47, 147–162. https://doi.org/10.1038/s41386-021-01108-0, PubMed: 34354249 Barbot, A., & Carrasco, M. (2017). Attention modifies spatial resolution according to task demands. Psychological Science, 28, 285–296. https://doi.org/10.1177/0956797616679634, PubMed: 28118103 Becker, S., & Wojtowicz, M. (2007). A model of hippocampal neurogenesis in memory and mood disorders. Trends in Cognitive Sciences, 11, 70–76. https://doi.org/10.1016/j.tics .2006.10.013, PubMed: 17174137 Bichot, N., Rossi, A., & Desimone, R. (2005). Parallel and serial neural mechanisms for visual search in macaque area V4. Science, 308, 529–534. https://doi.org/10.1126/science .1109676, PubMed: 15845848 Bisley, J., & Goldberg, M. (2010). Attention, inattention, and priority in the parietal lobe. Annual Review of Neuroscience, 33, 1–21. https://doi.org/10.1146/annurev-neuro-060909 -152823, PubMed: 20192813 Bissonette, G., Powell, E., & Roesch, M. (2013). Neural structures underlying set-shifting: Roles of medial prefrontal cortex and anterior cingulate cortex. Behavioral Brain Research, 250, 91–101. https://doi.org/10.1016/j.bbr.2013.04 .037, PubMed: 23664821 Blair, M., Watson, M., Walshe, R., & Maj, F. (2009). Extremely selective attention: Eye-tracking studies of the dynamic allocation of attention to stimulus features in categorization. Journal of Experimental Psychology: Learning, Memory, and Cognition, 35, 1196–1206. https://doi.org/10.1037 /a0016272, PubMed: 19686015 Blanco, N., Turner, B., & Sloutsky, V. (Submitted). The benefits of immature cognitive control: How distributed attention guards against learning traps. Bogdanov, M., Timmermann, J., Glaescher, J., Hummel, F., & Schwabe, L. (2018). Causal role of the inferolateral prefrontal cortex in balancing goal-directed and habitual control of behavior. Scientific Reports, 8, 1–11. https://doi.org/10.1038 /s41598-018-27678-6, PubMed: 29925889 Braunlich, K., & Love, B. (2019). Occipitotemporal representations reflect individual differences in conceptual knowledge. Journal of Experimental Psychology: General, 148, 1192. https://doi.org/10.1037/xge0000501, PubMed: 30382719 Weichart et al. 1775 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Brest, J., Greiner, S., Boskovic, B., Mernik, M., & Zumer, V. (2006). Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Transactions on Evolutionary Computation, 10, 646–657. https://doi.org/10.1109/TEVC.2006.872133 Calderon, C., De Loof, E., Ergo, E., Snoeck, A., Boehler, C., & Verguts, T. (2021). Signed reward prediction errors in the ventral striatum drive episodic memory. Journal of Neuroscience, 41, 1716–1726. https://doi.org/10.1523 /JNEUROSCI.1785-20.2020, PubMed: 33334870 Carrasco, M. (2011). Visual attention: The past 25 years. Vision Research, 51, 1484–1525. https://doi.org/10.1016/j.visres.2011 .04.012, PubMed: 21549742 Carter, C., Braver, T., Barch, D., Botvinick, M., Noll, D., & Cohen, J. (1998). Anterior cingulate cortex, error detection, and the online monitoring of performance. Science, 280, 747–749. https://doi.org/10.1126/science.280.5364.747, PubMed: 9563953 Chelazzi, L., Duncan, J., Miller, E., & Desimone, R. (1998). Responses of neurons in inferior temporal cortex during memory-guided visual search. Journal of Neurophysiology, 80, 2918–2940. https://doi.org/10.1152/jn.1998.80.6.2918, PubMed: 9862896 Chelazzi, L., Miller, E., Duncan, J., & Desimone, R. (2001). Responses of neurons in macaque area V4 during memory-guided visual search. Cerebral Cortex, 11, 761–772. https://doi.org/10.1093/cercor/11.8.761, PubMed: 11459766 Cincotta, C., & Seger, C. (2007). Dissociation between striatal regions while learning to categorize via feedback and via observation. Journal of Cognitive Neuroscience, 19, 249–265. https://doi.org/10.1162/jocn.2007.19.2.249, PubMed: 17280514 Crump, M., McDonnell, J., & Gureckis, T. (2013). Evaluating Amazon’s mechanical turk as a tool for experimental behavioral research. PLoS One, 8, e57410. https://doi.org/10 .1371/journal.pone.0057410, PubMed: 23516406 Cutsuridis, V., & Yoshida, M. (2017). Memory processes in medial temporal lobe: Experimental, theoretical and computational approaches. Frontiers in Systems Neuroscience, 11, 19. https://doi.org/10.3389/fnsys.2017.00019, PubMed: 28428747 Davis, T., Love, B., & Preston, A. (2012). Learning the exception to the rule: Model-based fMRI reveals specialized representations for surprising category members. Cerebral Cortex, 22, 260–273. https://doi.org/10.1093/cercor/bhr036, PubMed: 21666132 Daw, N., O’Doherty, J., Dayan, P., Seymour, B., & Dolan, R. (2006). Cortical substrates for exploratory decisions in humans. Nature, 441, 876–879. https://doi.org/10.1038 /nature04766, PubMed: 16778890 De Baene, W., Ons, B., Wagemans, J., & Vogels, R. (2008). Effects of category learning on the stimulus selectivity of macaque inferior temporal neurons. Learning & Memory, 15, 717–727. https://doi.org/10.1101/lm.1040508, PubMed: 18772261 Djurfeldt, M., Eleberg, O., & Graybiel, A. (2001). Cortex-basal ganglia interaction and attractor states. Neurocomputing, 38, 573–579. https://doi.org/10.1016/S0925-2312(01)00413-1 Eklund, A., Nichols, T., & Knutsson, H. (2016). Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rates. Proceedings of the National Academy of Sciences, U.S.A., 113, 7900–7905. https://doi.org/10.1073/pnas .1602413113, PubMed: 27357684 Estes, W. (1994). Classification and cognition. Oxford, UK: Oxford University Press. https://doi.org/10.1093/acprof:oso /9780195073355.001.0001 Folstein, J., & Palmeri, T. (2013). Category learning increases discriminability of relevant object dimensions in visual cortex. Cerebral Cortex, 23, 814–823. https://doi.org/10.1093/cercor /bhs067, PubMed: 22490547 Frank, M. (2005). Dynamic dopamine modulation in the basal ganglia: A neurocomputational account of cognitive deficits in medicated and nonmedicated parkinsonism. Journal of Cognitive Neuroscience, 17, 51–72. https://doi.org/10.1162 /0898929052880093, PubMed: 15701239 Frank, M., & Badre, B. (2012a). Mechanisms of hierarchical reinforcement learning in cortico-striatal circuits 1: Computational analysis. Cerebral Cortex, 22, 509–526. https://doi.org/10.1093/cercor/bhr114, PubMed: 21693490 Frank, M., & Badre, B. (2012b). Mechanisms of hierarchical reinforcement learning in cortico-striatal circuits 2: Evidence from fMRI. Cerebral Cortex, 22, 527–536. https://doi.org/10 .1093/cercor/bhr117, PubMed: 21693491 Frank, M., Doll, B., Oas-Terpstra, J., & Moreno, F. (2009). The neurogenetics of exploration and exploitation: Prefrontal and striatal dopaminergic components. Nature Neuroscience, 12, 1062. https://doi.org/10.1038/nn.2342, PubMed: 19620978 Frank, M., Moustafa, A., Haughey, H., Curran, T., & Hutchinson, K. (2007). Genetic triple dissociation reveals multiple roles for dopamine in reinforcement learning. Proceedings of the National Academy of Sciences, U.S.A., 104, 16311–16316. https://doi.org/10.1073/pnas.0706111104, PubMed: 17913879 Frank, M., Seeberger, L., & O’Reilly, R. (2004). By carrot or by stick: Cognitive reinforcement learning in parkinsonism. Science, 306, 1940–1943. https://doi.org/10.1126/science .1102941, PubMed: 15528409 Freedman, D., Riesenhuber, M., Poggio, T., & Miller, E. (2001). Categorical representation of visual stimuli in the primate prefrontal cortex. Science, 291, 312–316. https://doi.org/10.1126/science.291.5502.312, PubMed: 11209083 Freedman, D., Riesenbuber, M., Poggio, T., & Miller, E. (2002). Visual categorization and the primate prefrontal cortex: Neurophysiology and behavior. Journal of Neurophysiology, 88, 929–941. https://doi.org/10.1152/jn.2002.88.2.929, PubMed: 12163542 Freedman, D., Riesenbuber, M., Poggio, T., & Miller, E. (2003). A comparison of primate prefrontal and inferior temporal cortices during visual categorization. Journal of Neuroscience, 23, 5235–5246. https://doi.org/10.1523 /JNEUROSCI.23-12-05235.2003, PubMed: 12832548 Galdo, B., Weichart, E., Sloutsky, V., & Turner, B. (2021). The quest for simplicity in human learning: Identifying the constraints on attention. PsyArXiv. https://doi.org/10.31234 /osf.io/xgfmb Gluck, M., Meeter, M., & Myers, C. (2003). Computational models of the hippocampal region: Linking incremental learning and episodic memory. Trends in Cognitive Sciences, 7, 269–276. https://doi.org/10.1016/S1364-6613(03)00105-0, PubMed: 12804694 Goodman, N., Tenenbaum, J., Feldman, J., & Griffiths, T. (2008). A rational analysis of rule-based concept learning. Cognitive Science, 32, 108–154. https://doi.org/10.1080 /03640210701802071, PubMed: 21635333 Greve, D., & Fischl, B. (2009). Accurate and robust brain image alignment using boundary-based registration. Neuroimage, 48, 63–72. https://doi.org/10.1016/j.neuroimage.2009.06.060, PubMed: 19573611 Hadland, K., Rushworth, M., Gaffan, D., & Passingham, R. (2003). The anterior cingulate and reward-guided selection of actions. Journal of Neurophysiology, 89, 1161–1164. https:// doi.org/10.1152/jn.00634.2002, PubMed: 12574489 Hampson, R., Pons, T., Stanford, T., & Deadwyler, S. (2004). Categorization in the monkey hippocampus: A possible mechanism for encoding information into memory. 1776 Journal of Cognitive Neuroscience Volume 34, Number 10 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Proceedings of the National Academy of Sciences, U.S.A., 101, 3184–3189. https://doi.org/10.1073/pnas.0400162101, PubMed: 14978264 Humphries, M., Khamassi, M., & Gurney, K. (2012). Dopaminergic control of the exploration–exploitation trade-off via the basal ganglia. Frontiers in Neuroscience, 6, 9. https://doi.org/10.3389/fnins.2012.00009, PubMed: 22347155 Humphries, M., Stewart, R., & Gurney, K. (2006). A physiologically plausible model of action selection and oscillatory activity in the basal ganglia. Journal of Neuroscience, 26, 12921–12942. https://doi.org/10.3389/fnins .2012.00009, PubMed: 17167083 Hunsaker, M., & Kesner, R. (2013). The operation of pattern separation and pattern completion processes associated with different attributes or domains of memory. Neuroscience & Biobehavioral Reviews, 37, 36–58. https://doi.org/10.1016/j.neubiorev.2012.09.014, PubMed: 23043857 Itti, L., & Koch, C. (2000). A saliency-based search mechanism for overt and covert shifts of visual attention. Vision Research, 40, 1489–1506. https://doi.org/10.1016/S0042-6989 (99)00163-7, PubMed: 10788654 Jenkinson, M., Bannister, P., Brady, M., & Smith, S. (2002). Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage, 17, 825–841. https://doi.org/10.1006/nimg.2002 .1132, PubMed: 12377157 Jiang, X., Bradley, E., & Rini, R. (2007). Categorization training results in shape- and category-selective human neural plasticity. Neuron, 53, 891–903. https://doi.org/10.1016/j .neuron.2007.02.015, PubMed: 17359923 Kruschke, J. (1992). ALCOVE: An exemplar-based connectionist model of category learning. Psychological Review, 99, 22–44. https://doi.org/10.1037/0033-295X.99.1.22, PubMed: 1546117 Kuhn, G., Tatler, B., & Cole, G. (2009). You look where I look! Effect of gaze cues on overt and covert attention in misdirection. Visual Cognition, 17, 925–944. https://doi.org /10.1080/13506280902826775 Leong, Y., Radulescu, A., DeWoskin, V., & Niv, Y. (2017). Dynamic interaction between reinforcement learning and attention in multidimensional environments. Neuron, 93, 451–463. https://doi.org/10.1016/j.neuron.2016.12.040, PubMed: 28103483 Li, S., Mayhew, S., & Kourtzi, Z. (2009). Learning shapes the representation of behavioral choice in the human brain. Neuron, 62, 441–452. https://doi.org/10.1016/j.neuron.2009 .03.016, PubMed: 19447098 Love, B., Medin, D., & Gureckis, T. (2004). SUSTAIN: A network model of category learning. Psychological Review, 111, 309–332. https://doi.org/10.1037/0033-295X.111.2.309, PubMed: 15065912 Luck, S., Chelazzi, L., Hillyard, S., & Desimone, R. (1997). Neural mechanisms of spatial selective attention in areas V1, V2, and V4 of macaque visual cortex. Journal of Neurophysiology, 77, 24–42. https://doi.org/10.1152/jn.1997 .77.1.24, PubMed: 9120566 Mack, M., Love, B., & Preston, A. (2016). Dynamic updating of hippocampal object representations reflects new conceptual knowledge. Proceedings of the National Academy of Sciences, U.S.A., 113, 13203–13208. https://doi.org/10.1073/pnas.1614048113, PubMed: 27803320 Mack, M., Preston, A., & Love, B. (2013). Decoding the brain’s algorithm for categorization from its neural implementation. Current Biology, 23, 2023–2027. https://doi.org/10.1016/j.cub .2013.08.035, PubMed: 24094852 Maunsell, J., & Treue, S. (2006). Feature-based attention in visual cortex. Trends in Neuroscience, 29, 317–322. https:// doi.org/10.1016/j.tins.2006.04.001, PubMed: 16697058 McAdams, C., & Maunsell, J. (1999). Effects of attention on the reliability of individual neurons in monkey visual cortex. Neuron, 23, 765–773. https://doi.org/10.1016/S0896-6273(01) 80034-9, PubMed: 10482242 McAdams, C., & Maunsell, J. (2000). Attention to both space and feature modulates neuronal responses in macaque area V4. Journal of Neurophysiology, 83, 1751–1755. https://doi.org /10.1152/jn.2000.83.3.1751, PubMed: 10712494 Medin, D., & Schaffer, M. (1978). Context theory of classification learning. Psychological Review, 85, 207–238. https://doi.org/10.1037/0033-295X.85.3.207 Monchi, O., Petrides, M., Petre, V., Worsley, K., & Dagher, A. (2001). Wisconsin card sorting revisited: Distinct neural circuits participating in different stages of the task identified by event-related functional magnetic resonance imaging. Journal of Neuroscience, 21, 7733–7741. https://doi .org/10.1523/JNEUROSCI.21-19-07733.2001, PubMed: 11567063 Nasser, H., Calu, D., Schoenbaum, G., & Sharpe, M. (2017). The dopamine prediction error: Contributions to associative models of reward learning. Frontiers in Psychology, 8, 244. https://doi.org/10.3389/fpsyg.2017.00244, PubMed: 28275359 Nelder, J., & Mead, R. (1965). A simplex method for function minimization. Computer Journal, 7, 308–313. https://doi.org /10.1093/comjnl/7.4.308 Niv, Y., Daniel, R., Geana, A., Gershman, S., Leong, Y., Radulescu, A., et al. (2015). Reinforcement learning in multidimensional environments relies on attention mechanisms. Journal of Neuroscience, 35, 8145–8157. https://doi.org/10.1523/JNEUROSCI.2978-14.2015, PubMed: 26019331 Nomura, E., Maddox, W., Filoteo, J., Ing, A., Gitelman, D., Parrish, T., et al. (2007). Neural correlates of rule-based and information-integration visual category learning. Cerebral Cortex, 17, 37–43. https://doi.org/10.1093/cercor/bhj122, PubMed: 16436685 Nomura, E., & Reber, P. (2008). A review of medial temporal lobe and caudate contributions to visual category learning. Neuroscience & Biobehavioral Reviews, 32, 279–291. https:// doi.org/10.1016/j.neubiorev.2007.07.006, PubMed: 17868867 Nosofsky, R. (1986). Attention, similarity, and the identification–categorization relationship. Journal of Experimental Psychology: General, 115, 39–57. https://doi .org/10.1037/0096-3445.115.1.39, PubMed: 2937873 Nosofsky, R., Gluck, M., Palmeri, T., McKinley, S., & Glauthier, P. (1994). Comparing models of rule-based classification learning: A replication and extension of Shepard, Hovland, and Jenkins (1961). Memory & Cognition, 22, 352–369. https://doi.org/10.3758/BF03200862, PubMed: 8007837 Nosofsky, R., Little, D., & James, T. (2012). Activation in the neural network responsible for categorization and recognition reflects parameter changes. Proceedings of the National Academy of Sciences, U.S.A., 109, 333–338. https:// doi.org/10.1073/pnas.1111304109, PubMed: 22184233 O’Reilly, R., & McClelland, J. (1994). Hippocampal conjunctive encoding, storage, and recall: Avoiding a trade-off. Hippocampus, 4, 661–682. https://doi.org/10.1002/hipo .450040605, PubMed: 7704110 O’Reilly, R., & Munakata, Y. (2000). Computational explorations in cognitive neuroscience: Understanding the mind by simulating the brain. Cambridge, MA: MIT Press. https://doi.org/10.7551/mitpress/2014.001.0001 Pasupathy, A., & Miller, E. (2005). Different time courses of learning-related activity in the prefrontal cortex and striatum. Weichart et al. 1777 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Nature, 433, 873–876. https://doi.org/10.1038/nature03287, PubMed: 15729344 Poldrack, R., Clark, J., Pare-Blagoev, E., Shohamy, D., Creso, M., Myers, C., et al. (2001). Interactive memory systems in the human brain. Nature, 414, 546–550. https://doi.org/10.1038 /35107080, PubMed: 11734855 Poldrack, R., Prabhakaran, V., Seger, C., & Gabrieli, J. (1999). Striatal activation during acquisition of a cognitive skill. Neuropsychology, 13, 564–574. https://doi.org/10.1037/0894 -4105.13.4.564, PubMed: 10527065 Pooley, J., Lee, M., & Shankle, W. (2011). Understanding memory impairment with memory models and hierarchical Bayesian analysis. Journal of Mathematical Psychology, 55, 47–56. https://doi.org/10.1016/j.jmp.2010.08.003 Posner, M. (1980). Orienting of attention. Quarterly Journal of Experimental Psychology, 32, 3–25. https://doi.org/10.1080 /00335558008248231, PubMed: 7367577 Posner, M., & Gilbert, C. (1999). Attention and primary visual cortex. Proceedings of the National Academy of Sciences, U.S.A., 96, 2585–2587. https://doi.org/10.1073/pnas.96.6.2585, PubMed: 10077552 Reber, P., Gitelman, D., Parrish, T., & Mesulam, M. (2003). Dissociating explicit and implicit category knowledge with fMRI. Journal of Cognitive Neuroscience, 15, 574–583. https:// doi.org/10.1162/089892903321662958, PubMed: 12803968 Reber, P., Stark, C., & Squire, L. (1998). Cortical areas supporting category learning identified using functional MRI. Proceedings of the National Academy of Sciences, U.S.A., 95, 747–750. https://doi.org/10.1073/pnas.95.2.747, PubMed: 9435264 Rehder, B., & Hoffman, A. (2005a). Eyetracking and selective attention in category learning. Cognitive Psychology, 51, 1–41. https://doi.org/10.1016/j.cogpsych.2004.11.001, PubMed: 16039934 Rehder, B., & Hoffman, A. (2005b). Thirty–something categorization results explained: Selective attention, eyetracking, and models of category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 31, 811–829. https://doi.org/10.1037/0278-7393.31 .5.811, PubMed: 16248736 Saenz, M., Buracas, G., & Boynton, G. (2002). Global effects of feature-based attention in human visual cortex. Nature Neuroscience, 5, 631–632. https://doi.org/10.1038/nn876, PubMed: 12068304 Sapir, A., Hayes, A., Henik, A., Danziger, S., & Rafal, R. (2004). Parietal lobe lesions disrupt saccadic remapping of inhibitory location tagging. Journal of Cognitive Neuroscience, 16, 503–509. https://doi.org/10.1162/089892904323057245, PubMed: 15165343 Seger, C., & Cincotta, C. (2005). The roles of the caudate nucleus in human classification learning. Journal of Neuroscience, 25, 2941–2951. https://doi.org/10.1523 /JNEUROSCI.3401-04.2005, PubMed: 15772354 Seger, C., & Cincotta, C. (2006). Dynamics of frontal, striatal, and hippocampal systems during rule learning. Cerebral Cortex, 16, 1546–1555. https://doi.org/10.1093/cercor/bhj092, PubMed: 16373455 Seger, C., & Miller, E. (2010). Category learning in the brain. Annual Review of Neuroscience, 33, 203–219. https://doi.org /10.1146/annurev.neuro.051508.135546, PubMed: 20572771 Seymour, B., Daw, N., Dayan, P., Singer, T., & Dolan, R. (2007). Differential encoding of losses and gains in the human striatum. Journal of Neuroscience, 27, 4826–4831. https://doi .org/10.1523/JNEUROSCI.0400-07.2007, PubMed: 17475790 Shepard, R. (1987). Toward a universal law of generalization for psychological science. Science, 237, 1317–1323. https://doi .org/10.1126/science.3629243, PubMed: 3629243 Shepard, R., Hovland, C., & Jenkins, H. (1961). Learning and memorization of classifications. Psychological Monographs: General and Applied, 75, 1–42. https://doi.org/10.1037 /h0093825 Shires, J., Joshi, S., & Basso, M. (2010). Shedding new light on the role of the basal ganglia-superior colliculus pathway in eye movements. Current Opinion in Neurobiology, 20, 717–725. https://doi.org/10.1016/j.conb.2010.08.008, PubMed: 20829033 Sigala, N., & Logothetis, N. (2002). Visual categorization shapes feature selectivity in the primate temporal cortex. Nature, 415, 318–320. https://doi.org/10.1038/415318a, PubMed: 11797008 Smith, S. (2002). Fast robust automated brain extraction. Human Brain Mapping, 17, 143–155. https://doi.org/10.1002 /hbm.10062, PubMed: 12391568 Storn, R., & Price, K. (1997). Differential evolution: A simple and efficient hueristic for global optimization over continuous spaces. Journal of Global Optimization, 11, 341–359. https:// doi.org/10.1023/A:1008202821328 Sutherland, R., & Rudy, J. (1989). Configural association theory: The role of the hippocampal formation in learning, memory, and amnesia. Psychobiology, 17, 129–144. https://doi.org/10 .3758/BF03337828 Sutton, R., & Barto, A. (2018). Reinforcement learning: An introduction. Cambridge, MA: MIT Press. Thirion, B., Pinel, P., Meriaux, S., Roche, A., Dehaene, S., & Poline, J. (2007). Analysis of a large fMRI cohort: Statistical and methodological issues for group analyses. Neuroimage, 35, 105–120. https://doi.org/10.1016/j.neuroimage.2006.11 .054, PubMed: 17239619 Schultz, W. (2016). Dopamine reward prediction-error Turner, B. (2019). Toward a common representational signalling: A two-component response. Nature Reviews Neuroscience, 17, 183–1995. https://doi.org/10.1038/nrn .2015.26, PubMed: 26865020 Schultz, W., Apicella, P., Ljungberg, T., Romo, R., & Scarnati, E. (1993). Reward-related activity in the monkey striatum and substantia nigra. In A. Arbuthnott & P. Emson (Eds.), Chemical signalling in the basal ganglia (Vol. 99, pp. 227–235). Elsevier. https://doi.org/10.1016/S0079-6123 (08)61349-7 Schultz, W., & Romo, R. (1992). Role of primate basal ganglia and frontal cortex in the internal generation of movements. Experimental Brain Research, 91, 363–384. https://doi.org /10.1007/BF00227834, PubMed: 1483512 Seger, C. (2008). How do the basal ganglia contribute to categorization? Their roles in generalization, response selection, and learning via feedback. Neuroscience & Biobehavioral Reviews, 32, 265–278. https://doi.org/10.1016/j .neubiorev.2007.07.010, PubMed: 17919725 framework for adaptation. Psychological Review, 126, 660. https://doi.org/10.1037/rev0000148, PubMed: 30973248 Turner, B., Forstmann, B., Love, B., Palmeri, T., & van Maanen, L. (2017). Approaches to analysis in model-based cognitive neuroscience. Journal of Mathematical Psychology, 76, 65–79. https://doi.org/10.1016/j.jmp.2016.01.001, PubMed: 31745373 Turner, B., Forstmann, B., Wagenmakers, E., Brown, S., Sederberg, P., & Steyvers, M. (2013). A Bayesian framework for simultaneously modeling neural and behavioral data. Neuroimage, 72, 193–206. https://doi.org/10.1016/j .neuroimage.2013.01.048, PubMed: 23370060 Turner, B. M., Forstmann, B. U., & Steyvers, M. (2019). Joint models of neural and behavioral data. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-030 -03688-1 Turner, B., Kvam, P., Unger, L., Sloutsky, V., Ralston, R., & Blanco, N. (2021). Cognitive inertia: How loops among 1778 Journal of Cognitive Neuroscience Volume 34, Number 10 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 attention, representation, and decision making distort reality. PsyArXiv. https://doi.org/10.31234/osf.io/8zvey Ungerleider, S., & Kastner, S. (2000). Mechanisms of visual attention in the human cortex. Annual Review of Neuroscience, 23, 315–341. https://doi.org/10.1146/annurev .neuro.23.1.315, PubMed: 10845067 Van Laarhoven, E., & Aarts, E. (1987). Simulated annealing. In simulated annealing: Theory and applications (pp. 7–15). Dordrecht: Springer. https://doi.org/10.1007/978-94-015-7744-1_2 Vogels, R., Sary, G., Dupont, P., & Orban, G. (2002). Human brain regions involved in visual categorization. Neuroimage, 16, 401–414. https://doi.org/10.1006/nimg.2002.1109, PubMed: 12030825 Vossel, S., Weidner, R., Thiel, C., & Fink, G. (2009). What is “odd” in Posner’s location-cueing paradigm? Neural responses to unexpected location and feature changes compared. Journal of Cognitive Neuroscience, 21, 30–41. https://doi.org/10.1162/jocn.2009.21003, PubMed: 18476756 Weichart, E., Galdo, M., Sloutsky, V., & Turner, B. (2021). As within, so without; as above, so below: Common mechanisms can support between- and within-trial category learning dynamics. PsyArXiv. https://doi.org/10.31234/osf.io/94csh Woo, C., Krishnan, A., & Wager, T. (2014). Cluster-extent based thresholding in fMRI analyses: Pitfalls and recommendations. Neuroimage, 91, 412–419. https://doi.org/10.1016/j .neuroimage.2013.12.058, PubMed: 24412399 Woolrich, M., Behrens, T., Beckmann, C., Jenkinson, M., & Smith, S. (2004). Multilevel linear modelling for fMRI group analysis using Bayesian inference. Neuroimage, 21, 1732–1747. https://doi.org/10.1016/j.neuroimage.200.3.12 .023, PubMed: 15050594 Woolrich, M., Ripley, B., Brady, M., & Smith, S. (2001). Temporal autocorrelation in univariate linear modeling of fMRI data. Neuroimage, 14, 1370–1386. https://doi.org/10 .1006/nimg.2001.0931, PubMed: 11707093 Yin, X., Zhao, L., Xu, J., Evans, A., Fan, L., Ge, H., et al. (2012). Anatomical substrates of the alerting, orienting and executive control components of attention: Focus on the posterior parietal lobe. PLoS One, 7, e50590. https://doi.org/10.1371 /journal.pone.0050590, PubMed: 23226322 Zandbelt, B., Gladwin, T., Raemaekers, M., van Buuren, M., Neggers, S., Kahn, R., et al. (2008). Within-subject variation in BOLD-fMRI signal changes across repeated measurements: Quantification and implications for sample size. Neuroimage, 42, 196–206. https://doi.org/10.1016/j.neuroimage.2008.04 .183, PubMed: 18538585 Zhang, Y., Brady, M., & Smith, S. (2001). Segmentation of brain MR images through a hidden markov random field model and the expectation-maximization algorithm. IEEE Transactions on Medical Imaging, 20, 45–57. https:// doi.org/10.1016/j.neuroimage.2009.06.060, PubMed: 11293691 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / j / o c n a r t i c e - p d l f / / / 3 4 1 0 1 7 6 1 2 0 4 1 8 2 5 / / j o c n _ a _ 0 1 8 8 2 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Weichart et al. 1779 Distributed Neural Systems Support Flexible Attention image

PDF Herunterladen