Communicated by Dana Ballad
Part Segmentation for Object Recognition
Alex Pentland
Vision Sciences Group, The Media Lab, Massachusetts Institute of Technology,
Room E15-410, 20 Ames Street, Cambridge, M A 02139, USA
Visual object recognition is a difficult problem that has been solved
by biological visual systems. An approach to object recognition is
described in which the image is segmented into parts using two simple,
biologically-plausible mechanisms: a filtering operation to produce a
large set of potential object “Teile,” followed by a new type of network
that searches among these part hypotheses to produce the simplest,
most likely description of the image’s part structure.
1 Einführung
In order to recognize objects one must be able to compute a stable, canon-
ical representation that can be used to index into memory (Binford 1971;
Marr and Nishihara 1978; Hoffman and Richards 1985). The most widely
accepted theory on how people recognize objects seems to be that they
first segment the object into its component parts and then recognition
occurs by using this part description to classify the object, perhaps by
use of an associative network.
Despite the importance of object recognition, most vision research –
and especially neural network research -has been aimed at understand-
ing early visual processing. In part this focus on early vision is because
the uniform, parallel operations typical of early vision are easily mapped
onto neural networks, and are more easily understood than the nonho-
mogeneous, nonlinear processing required to segment an object into parts
and then recognize it. As a consequence, the process of object recognition
is little understood.
The goal of this research is to automatically recover accurate part
descriptions for object recognition. I have approached this objective by
developing a system that segments an imaged object into convex parts
using a neural network that is similar to that described by Hopfield and
Tank (Hopfield and Tank 19851, but which uses a temporally-decaying
feedback loop to achieve considerably better performance. For the sake
of efficiency and simplicity I have used silhouettes, obtained from grey-
scale images by intensity, Bewegung, and texture thresholding, rather than
operating on the grey-scale images directly.
Neural Computation 1, 82-91 (1989) @ 1989 Massachusetts Institute of Technology
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Part Segmentation for Object Recognition
83
2 A Computational Theory of Segmentation
Many machine vision systems employ matched filters to find particular
2-D shapes in an image, typically using a multiresolution approach that
allows efficient search over a wide range of scales. Daher, in machine
vision, a natural way to locate the parts of a silhouetted object is to make
filter patterns that cover the spectrum of possible 2-D part-shapes (as is
shown in figure l(A)), match these 2-D patterns against the silhouette,
and then pick the best matching filter. If the match is sufficiently good,
then we register the detection of a part whose shape is roughly that of
the best-matching filter.
A biological version of this approach might use many hypercolumns
each containing receptive fields with excitatory regions shaped as in fig-
ure 1. The cell with the best-matching excitatory field would be selected
by introducing strong lateral inhibition within the hypercolumn in or-
der to suppress all but the best-responding cells. This arrangement of
receptive fields and within-hypercolumn inhibition produces receptive
fields with oriented, center-surround spatial structure, such as is shown
in figure l(B).
The major problem with such a filtering/receptive field approach is
that all such techniques incorporate a noise threshold that balances the
number of false detections against the number of missed targets. Daher
we will either miss many of the object’s parts because they don’t quite
fit any of our 2-D patterns, or we will have a large number of false
detections.
This false-alarm versus miss problem occurs in almost every image
processing domain, and there are only two general approaches to over-
coming the problem. The first is to improve the discriminating power of
the filter so as to improve the false-alarm/miss tradeoff. The success of
this approach depends upon precise characterization of the target and so
is not applicable to this problem.
In the second approach, each non-zero response of a filter/receptive
field is considered as an hypothesis about the object’s part structure rather
than being considered as a detection. One therefore uses a very low
threshold to obtain a large number of hypotheses, and then searches
through them to find the “real” detections. This approach depends upon
having some method of measuring the likelihood of a set of hypotheses,
d.h., of measuring how good a particular segmentation into parts is as
an explanation of the image data. It is this second, “best explanation”
approach that I have adopted in this paper.
2.1 Global Optimization: The Likelihood Principle and Occam’s
Razor. The notion that vision problems can be solved by optimizing
some “goodness of fit” measure is perhaps the most powerful paradigm
found in current computational research (Hopfield and Tank 1985; BalIard
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
84
Alex Pentland
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 1: (A) Two-dimensional binary patterns used to segment silhouettes into
Teile. (B) Spatial structure of a receptive field corresponding to one of these
binary patterns.
et al. 1983; Hummel and Zucker 1983; Poggio et al. 1985). Obwohl
heuristic measures are sometimes employed, the most attractive schemes
have been based on the likelihood principle (the scientific principle that
the most likely hypothesis is the best one), d.h., they have posed the
problem in terms of an a priori model with unknown parameter values,
and then searched for the parameter settings that maximize the likelihood
of the model given the image data.
Recently it has been proven (Rissanen 1983) that one method of find-
ing this maximum likelihood estimate is by use of the formal, Information-
theoretic version of Occam’s Razor: the scientific principle that the sim-
plest hypothesis is the best one. In information theory the simplicity or
complexity of a description is measured by the number of bits (binary
digits) needed to encode both the description and remaining residual
noise. This new result tells us that both the likelihood principle and Oc-
cam’s Razor agree that the best description of image data is the one that
provides the bitwise shortest encoding.
This method of finding the maximum likelihood estimate is partic-
Part Segmentation for Object Recognition
85
ularly useful in vision problems because it gives us a simple way to
produce maximum likelihood estimates using image models that are too
complex for direct optimization (Leclerc 1988). Insbesondere, to find the
maximum likelihood estimate of an object’s part structure one needs only
to find the shortest description of the image data in terms of parts.
2.2 A Computational Procedure. How can the shortest/most likely
image description be computed? Let { H } be a set of n part hypotheses
H, produced by our filters/receptive fields, and let { H ‘ } be a subset of
{ H } containing m hypotheses. The particular elements which comprise
{ H * } can be indicated by a vector F consisting of n – m zeros and m
ones, with a one in slot L indicating that hypothesis h, is an element of
{H*}-
The presence of part hypothesis h, in the set {H} indicates that a
particular pattern from among those illustrated in figure l(A) has at least
a minimal correspondence to the image data at some particular image
location. Let us designate the number of image pixels at which h, Und
the image agree (have the same value) by a,,, and the number of image
pixels at which h, and the image disagree (have different values) von
e?,. Then h, provides an encoding of the image which saves S(H,) bits as
compared to simple pixel-by-pixel description of the image pixel values.
The amount of this savings, in bits, Ist:
S(H,) = klutz – k2ezz – k3
(2.1)
where kl is the average number of bits needed to specify a single image
pixel value, k2 is the average number of bits needed to specify that a par-
ticular pixel is erroneously encoded by h,, and k3 is the cost of specifying
H, selbst. The ratio between kl and kz is our a priori estimate of the signal
to noise ratio, including both image noise and noise from quantization of
the set of 2-D shape patterns. The parameter k3 is equal to the minus log
of the probability of a particular part hypothesis. By default we make k3
equal for all h,; Jedoch, we can easily incorporate a priori knowledge
about the likelihood of each h, by setting k3 to the minus log probability
associated with each h,.
Gleichung 2.1 allows us to find the single hypothesis which provides the
best image description by simply maximizing S(H,) over all the hypothe-
ses h,. To find the overall maximum-likelihood/simplest description,
Jedoch, we must search from among the power set of { H } to find that
subset { H * } which maximizes S(2). Thus we must be able to account for
interactions between the various h, In {If*}.
Let
be the number of image pixels at which h,, H,, and the image
all agree, and e,, be number of image pixels at which both h, and h,
disagree with the image. We then define a matrix A with values a,, An
the diagonal, and values -1/2u,, for z # 3 , and similarly a matrix E with
values e,, on the diagonal, and values -1/2eZJ for L + 1. Ignoring points
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
86
Alex Pentland
where three or more hi overlap, the savings generated by encoding the
image data using { H * } (as specified by the vector i?) is simply
S(2) = klZAZT – kzZEZT – k3ZZT.
(2.2)
Gleichung 2.2 can easily be extended to include overlaps between three
or more parts by adding in additional terms that express these higher-
order overlaps. Jedoch, these higher-order overlaps are expensive to
calculate. Darüber hinaus, such high-order overlaps seem to be infrequent
in real imagery. I have chosen, daher, to assume that in the final
solution that there are a negligible number of image points covered by
three or more hi. Note that we are not assuming that this is true of the
entire set { H } , where such high-order overlaps will be common. Der
important consequence of this assumption is that the maximum of the
savings function S ( 3 over all Z is also the maximum of equation 2.2.
The solution to equation 2.2 is straightforward when the matrix Q
Q = klA – kzE – k3I
(2.3)
is positive (or negative) definite. Bedauerlicherweise, this is not the case in this
Problem. As a consequence, relaxation techniques (Hummel and Zucker
1983) such as the Hopfield-Tank network (Hopfield and Tank 1985) give
a very poor solution.
I have therefore devised a new method of solution (and correspond-
ing network) which can provide a good solution to equation 2.2. Das
new technique is a type of continuation method: one first picks a problem
related to the original problem that can be solved, and then iteratively
solves a series of problems that are progressively closer to the original
Problem, each time using the last solution as the starting point for the
next iteration.
In the problem at hand, Q is easily solved when k3 is large enough,
as then Q is diagonally dominant and thus negative definite. daher,
I can obtain a globally good solution by first solving using a large k3, Und
Dann – using that answer as starting point – progressively resolve using
smaller and smaller values of k3 until the desired solution is obtained.
Because k j is the cost of adding a model to our description, the effect
of this continuation technique is to solve for the largest, most prominent
parts first, and then to progressively add in smaller and smaller parts
until the entire figure is accounted for.
The neural network interpretation of this solution method is a Hop-
field-Tank network placed in a feedback loop where the diagonal weights
are initially quite large and decay over time until they finally reach the
desired values. In each “time step” the Hopfield-Tank network stabilizes,
the diagonal weights are reduced, and the network outputs are fed back
into the inputs. When the diagonal weights reach their final values, Die
desired outputs are obtained.
It can be shown that for many well-behaved problems (Zum Beispiel,
when the largest eigenvalues are all of one sign, with opposite-signed
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Part Segmentation for Object Recognition
87
eigenvalues of much smaller magnitude) this feedback technique will
produce an answer that is on average substantially better than that ob-
tained by Hopfield-Tank or relaxation methods. As with relaxation tech-
niques (Hummel and Zucker 19831, this feedback method can be applied
to problems with asymmetric weights.
A biological equivalent of our solution method is to use a set of hyper-
columns (each containing cells with the excitatory subfields illustrated in
figure 1) that are tied together by a Hopfield-Tank network augmented by
a time-decaying feedback loop. The action of this network is to suppress
activity in all but a small subset of the hypercolumns. After this network
has stabilized, each of the remaining active cells correspond exactly to
one part of the imaged object. The characteristics of that cell’s excitatory
subfield correspond to the shape of the imaged part.
3 Segmentation Examples
This technique has been tested on over two hundred synthetic images,
with widely varying noise levels (Pentland 1988). In these tests the
number of visible parts was correctly determined 85-95% of the time
(depending on noise level), with largely obscured or very small parts
accounting for almost all of the errors. Estimates of part shape were sim-
ilarly accurate. The following three examples illustrate this segmentation
Leistung.
The first example uses synthetic range data with a dynamic range of
4 bits. In this example, nur 72 2-D shape patterns were employed in
order to illustrate the effects of coarse quantization in both orientation
and size. The intent of this example is to demonstrate that a high-quality
segmentation into parts can be achieved despite coarse quantization in
both orientation, Größe, and range values, and despite wide variation in
the weights. In the remaining examples, the 2-D shape patterns shown
in figure l(A) were employed.
Figur 2(A) shows an intensity image of a CAD model; synthetic range
data from this model is shown in figure 2(B). These range data were
histogrammed and automatically thresholded, producing the silhouette
shown in figure 2(C).
Figur 2(D) shows the operation of our new solution method. Der
parameter k3 is initially set to a large value, thus making equation 2.2
diagonally dominant. In this first step only the very largest parts are
recovered, as is shown in the first frame of figure 2(D). The parameter k3
is then progressively reduced and the equation resolved, allowing smaller
and smaller parts to be recovered. This is shown in the remaining frames
of figure 2(D). This solution method therefore constructs a scale hierarchy
of object parts, with the largest and most visible at the top of the hierarchy
and the smallest parts on the bottom. This scale hierarchy can be useful
in matching and recognition processes.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
88
Alex Pentland
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 2: (A) Intensity image of a CAD model. (B) Range image of this model.
(C) Silhouette of the range data. (D) This sequence of images illustrates how
our continuation method constructs a scale-space description of part structure,
first recovering only large, important parts and then recovering progressively
smaller part structure. (el Final segmentation into parts obtained using only
very coarsely quantized 2-D patterns; 3-D models corresponding to recovered
parts are used to illustrate the recovered structure. (F) Segmentations for a 5 : 1
ratio of the parameters ki, showing that the segmentation is stable.
The final segmentation for this figure is shown in figure 2(e); Hier
3-D volumetric models have been substituted for their Corresponding’ 2-
D shapes in order to better illustrate how the silhouette was segmented
into parts. The z dimension of these 3-D models is arbitrarily set equal
to the smaller of the 5 and y dimensions. It can be seen that, apart from
coarse quantization in orientation and size, the part segmentation is a
good one.
‘That is, for each 2-D pattern we substituted a 3-D CAD model whose outline cor-
responds exactly to the 2-D shape pattern.
Part Segmentation for Object Recognition
89
One important question is the stability of segmentation with respect
to the parameters k,. Figur 2(F) shows the results of varying the ratio
of parameters k , , k2, and kj over a range of 5 : 1. It can be seen that the
part segmentation is stable, although as the relative cost of each model
erhöht sich (the final value of k3 becomes large) small details (such as the
Füße) disappear.
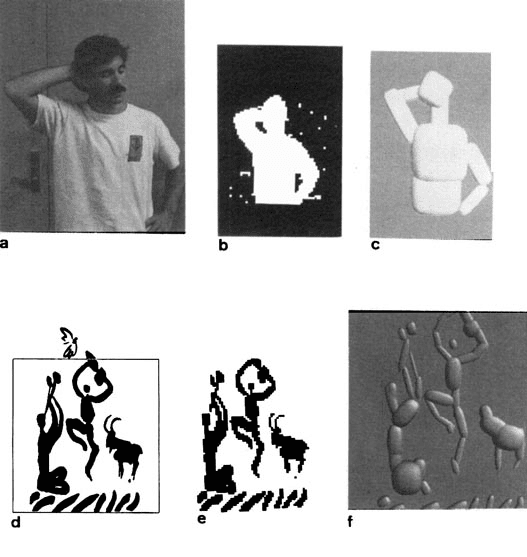
The second example of segmenting a silhouette into parts uses a real
image of a person, shown in figure 3(A). A silhouette was produced by
automatic thresholding of a fractal measure of texture smoothness; Das
silhouette is shown in figure 3(B). The resulting segmentation into parts
is shown in figure 3(C).
An example of segmenting a more complex silhouette into parts uses
the Rites of Spring, a drawing by Picasso, shown in figure 3(C). The area
within the box was digitized and the intensity thresholded to produce a
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figur 3: (A) Image of a person. (B) Silhouette produced by thresholding a
fractal texture measure. (C) Automatic segmentation into parts. (D) The Rites of
Frühling, by Picasso. (e) Digitized version. (F) The automatic segmentation into
Teile.
90
Alex Pentland
coarse silhouette, as shown in figure 3(D). The automatic segmentation
is shown in figure 3(e). It is surprising that such a good segmentation
can be produced from this hand-drawn, coarsely digitized image (Notiz
that very small details, z.B., the goat’s horns, were missed because they
were smaller than any of the 2-D patterns).
4 Summary
I have described a method for segmenting 2-D images into their com-
ponent parts, a critical stage of processing in many theories of object
recognition. This method uses two stages: a detection stage which uses
matched filters to extract hypotheses about part structure, and an opti-
mization stage, where all hypotheses about the object’s part structure are
combined into a globally optimum (d.h., simplest, most likely) explana-
tion of the image data. The first stage is implemented by local competi-
tion among the filters illustrated in figure l(A), and the second stage is
implemented by a new type of neural network that gives substantially
better answers than previously suggested optimization networks. Das
new network may be described as a relaxation or Hopfield-Tank network
augmented by time-decaying feedback. For additional details the reader
is referred to reference (Pentland 1988).
Danksagungen
This research was made possible in part by National Science Foundation,
Grant No. IRI-8719920. I wish to especially thank Yvan Leclerc for his
Kommentare, and for reviving my interest in minimal length encoding.
Verweise
Ballard, D.H., G.E. Hinton, and T.J. Sejnowski. 1983. Parallel Visual Computa-
tion. Natur 306, 21-26.
Binford, T.O. 1971. Visual Perception by Computer. Proceeding of the IEEE
Conference on Systems and Control, Miami.
Hoffman, D. and W. Richards. 1985. Parts of Recognition. In: From Pixels to
Predicates, Hrsg. A. Pentland. New Jersey: Ablex Publishing Co.
Hopfield, J.J. and D.W. Tank. 1985. Neural Computation of Decisions in Opti-
mization Problems. Biological Cybernetics 52, 141-152.
Hummel, R.A. and S.W. Zucker. 1983. On the Foundations of Relaxation Label-
ing Processes. IEEE Transactions on Pattern Analysis and Machine lntelligence
53,267-287.
Leclerc, Y. 1988. Construction Simple Stable Descriptions for Image Partitioning.
Proc. DARPA lmage Understanding Workshop, April 6-8, Boston, MA, 365-382.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Part Segmentation for Object Recognition
91
Man; D. and K. Nishihara. 1978. Representation and Recognition of the Spatial
Organization of Three-dimensional Shapes. Proceedings of the Royal Society-
London B 200, 269-94
Pentland, A. 1988. Automatic Recove y of Deformable Part Models. Massachusetts
Institute of Technology Media Lab Vision Sciences Technical Report 104.
Poggio, T., V. Torre, and C. Koch. 1985. Computational Vision and Regulariza-
tion Theory. Natur 317, 314-319.
Rissanen, J. 1983. Minimum-iength Description Principle. Encyclopedia of Slatis-
tical Sciences 5, 523-527. New York Wiley.
Erhalten 23 September; accepted 8 November 1988.
l
D
Ö
w
N
Ö
A
D
e
D
F
R
Ö
M
H
T
T
P
:
/
/
D
ich
R
e
C
T
.
M
ich
T
.
/
e
D
u
N
e
C
Ö
A
R
T
ich
C
e
–
P
D
/
l
F
/
/
/
/
/
1
1
8
2
8
1
1
8
3
1
N
e
C
Ö
1
9
8
9
1
1
8
2
P
D
.
.
.
.
.
F
B
j
G
u
e
S
T
T
Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3