Arbabyazd, L., Petkoski, S., Breakspear, M., Solodkin, A., Battaglia, D., & Jirsa, V. (2023). State switching and high-order
spatiotemporal organization of dynamic Functional Connectivity are disrupted by Alzheimer’s Disease. Netzwerkneurowissenschaften, Advance
Veröffentlichung. https://doi.org/10.1162/netn_a_00332.

State switching and high-order spatiotemporal

organization of dynamic Functional Connectivity are

disrupted by Alzheimer’s Disease

Lucas Arbabyazd1,* , Spase Petkoski1, Michael Breakspear2, Ana Solodkin3, Demian

Battaglia1,4+,@, Viktor Jirsa1,+,@

1

Université Aix-Marseille, INSERM UMR 1106, Institut de Neurosciences des Systèmes,

Marseille, Frankreich

2 University of Newcastle, Callaghan, NSW, Australia

3 Neurosciences, School of Behavioral and Brain Sciences. UT Dallas. Richardson, TX, USA

4 University of Strasbourg Institute for Advanced Studies, Strasbourg, Frankreich.

*first author; +shared last authors; @corresponding authors

Contacts: demian.battaglia@univ-amu.fr; viktor.jirsa@univ-amu.fr

Short title (< 70 characters) Spatiotemporal dFC organization in AD Keywords (up to six) Dynamic Functional Connectivity | High-Order Interactions | Resting State | fMRI | Alzheimer’s Disease | Mild Cognitive Impairment 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / t . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 Abstract (< 200 words) Spontaneous activity during the resting state, tracked by BOLD fMRI imaging, or shortly rsfMRI, gives rise to brain-wide dynamic patterns of inter-regional correlations, whose structured flexibility relates to cognitive performance. Here we analyze resting state dynamic Functional Connectivity (dFC) in a cohort of older adults, including amnesic Mild Cognitive Impairment (aMCI, N = 34) and Alzheimer’s Disease (AD, N = 13) patients, as well as normal control (NC, N = 16) and cognitively “super-normal” (SN, N = 10) subjects. Using complementary state-based and state-free approaches, we find that resting state fluctuations of different functional links are not independent but are constrained by high-order correlations between triplets or quadruplets of functionally connected regions. When contrasting patients with healthy subjects, we find that dFC between cingulate and other limbic regions is increasingly bursty and intermittent when ranking the four groups from SNC to NC, aMCI and AD. Furthermore, regions affected at early stages of AD pathology are less involved in higher- order interactions in patient than in control groups, while pairwise interactions are not significantly reduced. Our analyses thus suggest that the spatiotemporal complexity of dFC organization is precociously degraded in AD and provides a richer window into the underlying neurobiology than time-averaged FC connections. (199 words) l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / t / . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t Author Summary (< 125 words) Brain functions emerge from the coordinated dynamics of many brain regions. Dynamic Functional Connectivity (dFC) analyses are a key tool to describe such dynamic complexity and have been shown to be good predictors of cognitive performance. This is particularly true in the case of Alzheimer’s Disease (AD) in which an impoverished dFC could indicate compromised functional reserve due to the detrimental effects of neurodegeneration. Here we observe that in healthy ageing dFC is indeed spatiotemporally organized, as reflected by high- order correlations between multiple regions. However, in people with aMCI or AD, dFC becomes less “entangled”, more random-like, and intermittently bursty. We speculate that this degraded spatiotemporal coordination may reflect dysfunctional information processing, thus ultimately leading to worsening of cognitive deficits. (120 words) f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 Introduction Alzheimer’s Disease (AD) is the most common neurodegenerative illness with an estimated prevalence of 10-30% in people older than 65 years (Hou et al., 2019; Masters et al., 2015). Yet, despite substantial research, we are far from fully understanding the mechanisms that link pathophysiology to cognitive impairments. Neurodegeneration in AD has been traditionally associated with the extracellular accumulation of insoluble amyloid-β42 (Aβ) neuritic plaques (Glenner and Wong, 1984; Lemere et al., 1996) along with the intracellular accumulation of abnormally phosphorylated tau (pTau), that constitute the neurofibrillary tangles (Spires-Jones and Hyman, 2014). These processes yield to widespread neuronal death, synaptic loss, and atrophy (Bateman et al., 2012), with a progression of structural damages not occurring uniformly throughout the brain (Braak and Braak, 1991). However, the progression of neurodegenerative processes does not correlate linearly with the severity of cognitive impairment possibly due to a “cognitive reserve” accrued through education, cognitive training and a healthy lifestyle (Rentz et al., 2010; Snowdon, 2003). Furthermore, the severity of cognitive impairment symptoms in a patient can fluctuate substantially within the same day, faster than the time scales of neurodegeneration (Palop et al., 2006). Together, these findings suggest that AD involve alterations of neural dynamics and that these dynamical changes may be the mechanistic substrate leading to functional impairment or preservation. As molecular and structural changes alone do not fully account for cognitive impairment, alternative studies based on Functional Connectivity (FC) analyses have sought to fill the gap. In particular, resting state FC (Fox and Raichle, 2007) quantifies brain-wide correlations of BOLD signals, capturing interactions between regions. In this context it has been suggested that structural alterations in AD lead to FC changes (Dennis and Thompson, 2014), and that the early manifestation of Aβ toxicity preceding overt atrophy can be detected using resting state functional Magnetic Resonance Imaging (rsfMRI) (Hedden et al., 2009; Sheline et al., 2010a; Sheline et al., 2010b; Mormino et al., 2011). Changes in FC in AD include reduced connectivity within the default mode network (DMN, Greicius et al., 2004; Rombouts et al., 2005; Wang et al., 2006, 2007; Sorg et al., 2007; Fleisher et al., 2009; Zhang et al., 2009, 2010; Jones et al., 2011; Petrella et al., 2011), in a spatially non-uniform fashion (Damoiseaux et al., 2012). Besides Aβ, the deposition of pTau affects FC as well (Franzmeier et al., 2022). Furthermore, additional FC alterations have been reported, leading to functional disconnection between hemispheres (Shi et al., 2020; Wang et al., 2015) and a reduction of small-world l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 88 89 90 91 92 93 94 95 96 97 98 99 topology (Brier et al., 2014; Sanz-Arigita et al., 2010; Stam et al., 2009, 2007; Supekar et al., 2008). More recently, investigations of FC in AD have been extended to encompass time-varying, rather than time-averaged FC. Indeed, rsfMRI networks undergo a continuous reconfiguration of their weighed topology, and the statistical structure of spontaneous network reconfiguration carries information potentially useful to discriminate cohorts (Calhoun et al., 2014; Hutchison et al., 2013; Preti et al., 2017). The flexibility of dynamic Functional Connectivity (dFC) has been shown to correlate with cognitive performance (Bassett et al., 2011; Battaglia et al., 2020; Braun et al., 2015; Jia et al., 2014; Lombardo et al., 2020; Shine et al., 2016). In this view, ongoing variability of FC networks is not noise but rather, an actual resource subserving computation. The capacity to actively maintain a spatiotemporally organized yet variable dFC would confer the system resilience to cope with variable cognitive and environmental 100 conditions (Lombardo et al., 2020). Hence, the preservation of a “healthy” structured dFC 101 variability may provide a form of functional compensation and a likely neural substrate for 102 103 “cognitive reserve” (cf. also other studies linking mental training with enhanced dFC variability, e.g. Premi et al., 2020). Conversely, dynamic FC-based metrics thus promise to 104 better characterize the impact of AD pathology. 105 106 107 A number of studies have quantified dFC changes in healthy aging (Battaglia et al., 2020; Davison et al., 2016; Hutchison and Morton, 2015; Lavanga et al., 2022; Petkoski et al., 2023; Qin et al., 2015; Viviano et al., 2017) and in conditions such as schizophrenia (Damaraju et al., 108 2014; Sakoğlu et al., 2010), epilepsy (Liao et al., 2014; Liu et al., 2017) and Parkinson’s disease 109 (Fiorenzato et al., 2019; Kim et al., 2017). In AD, probabilities of temporal transitions between 110 alternative FC states have been shown to be altered (Jones et al., 2011; Fu et al., 2019; Gu et 111 112 al., 2020; Schumacher et al., 2019). Moreover, machine learning applications have achieved greater accuracy in differentiating between healthy control and aMCI or AD subjects when 113 trained with dFC-based rather than static FC metrics (Chen et al., 2017, 2016; de Vos et al., 114 2018; Wee et al., 2016). Although the contributions of these studies are promising, they are 115 largely descriptive and do not propose an explicit theory of why dFC changes lead to functional 116 117 consequences. Furthermore, the plethora of methods for dFC quantification (Hutchison et al., 2013; Preti et al., 2017) – from extracting discrete FC states (Allen et al., 2014; Thompson and 118 Fransson, 2016) to continuously time-resolved approaches (Battaglia et al., 2020; Lindquist et 119 al., 2014)– hinder the convergence of results. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / . / t / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 120 Here, we start from a theoretical tenet: efficient cognition requires spatiotemporally 121 organized FC variability, which is neither trivial, nor random, but complex. This assumption is 122 based on empirical evidence. Fluctuations in dFC are not a mere unstructured “Drunkard’s 123 walk”: More highly structured dFC trajectories are observed in individuals with higher 124 125 performance on general cognition domains (Battaglia et al., 2020; Lavanga et al., 2022). Further, individual FC links do not fluctuate independently but with network reconfigurations 126 governed by higher order coordination patterns, manifest by: non-trivial inter-link covariance 127 patterns (Davison et al., 2015; Faskowitz et al., 2020; Petkoski et al., 2023); “back-bones” 128 partially scaffolding dFC (Braun et al., 2015); and dFC flowing under the influence of 129 130 competing “meta-hubs (Lombardo et al., 2020). Reiterating, our hypothesis suggests that spatiotemporal structure of dFC between order and randomness allows for rich computation to 131 emerge from the systems’ collective activity (cf. Crutchfield, 2012). Correspondingly, we 132 predict that individuals with higher cognitive performance should display an enhanced 133 organization of dFC compared to those with impaired cognition (aMCI or AD) in which, 134 conversely, a loss of dFC spatiotemporal organization should be evident. 135 Here we analyze resting-state fMRI data acquired from individuals with better-than-normal 136 or normal cognitive performance –“supernormal” (SNC) and “normal controls (NC)– and those 137 clinically diagnosed with amnestic Mild Cognitive Impairment (aMCI) or Alzheimer’s Disease 138 139 (AD). We first characterized dFC across groups using two complementary methods. First, we use a state-based dFC analysis paradigm, in which we assume the existence of a small set of 140 possible discrete FC configurations and quantify dwell times in different states and the temporal 141 stability of different FC network links along state switching transitions (Thompson and 142 Fransson (2016)). Second, we use a state-free dFC analysis paradigm, where FC networks are 143 144 described as continually morphing in time. Through these complementary but convergent approaches, as described in the following, we find that the fluctuations of different links show 145 different degrees of mutual inter-dependence across the considered groups, shifting from a 146 “liquid-like” dFC (flexible but constrained) for SNC and NC toward a “gas-like” dFC 147 (uncorrelated and disordered) for patient groups. We also show that these changes in dFC 148 149 coordination cannot be fully accounted by changes occurring at the level of ordinary pairwise FC, but stem from the weakening of genuine higher-order interactions observed especially for 150 regions which are among the first to be physio-pathologically affected by AD. 151 152 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 153 Results 154 FC and dFC across a spectrum of cognitive performance 155 156 We considered an fMRI dataset including resting state sessions from subjects with varying degrees of cognitive skills. As our interest focusses not only on disease but also in healthy 157 cognition, healthy controls were subclassified in two groups (SNC and NC) based primarily on 158 composite memory Z scores to define the SNC and NC groups. That is, SNC had a higher 159 performance in the composite memory scores (Z > 1.5) and at least a Z > 0.7 in all other

160

161

cognitive domains (attention, Sprache, visuo-spatial and executive; see Materials and Methods

for more details). Healthy control subjects between NC and SNC or below NC were not

162

considered in the study. As shown in Fig. 1A, aus 73 Fächer, 10 were classified as

163

supernormal controls (SNC), 16 as normal controls (NC), 34 as amnesic mild cognitive

164

Beeinträchtigung (aMCI), Und 13 as Alzheimer’s disease (AD). Across the four clinical groups, Dort

165

were no significant differences in age and sex.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

166

Based on rsfMRI time-series from these cohorts, we then computed (and compared across

F
/

D
Ö

ich
/

.

T

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

/

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

167

groups) a variety of static and dynamic Functional Connectivity (FC and dFC) metrics,

168

extracted with complementary approaches, assuming or not the existence of discrete FC states

169

170

in time (Feige. 1B). Wichtig, as detailed below, we did not uniquely consider pairwise

interactions between two brain regions at a time, but also considered more complex

171

coordination patterns between larger groups of regions. Classic FC links express the existence

172

of a correlation between the BOLD fluctuations of two brain regions and are represented as a

173

link between two regional nodes: we refer hence to them as dimers, since they are computed

174

175

out of two parts. In classical FC analyses, dimers are static, as their strength is averaged over

the duration of complete resting state sessions. In dFC analyses, however dimer strengths

176

fluctuate in time. We can thus also compute correlations between different dimers. Estimating

177

these “correlations between correlations” requires jointly monitoring the BOLD fluctuations of

178

three (Feige. 1C, top) or four (Feige. 1C, bottom) Regionen, hence the names of trimers and tetramers

179

–collections of three or four parts, respectively– used in the following.

180

We chose to focus in this study on dFC within a network of limbic brain regions of particular

181

interest (Feige. 1D). The rationale was twofold: Erste, the regions included in the chosen limbic

182

subnetwork are highly interconnected brain regions that degenerate early in the disease process

183

(Arnold et al., 1991; Braak and Braak, 1991); zweite, previous modelling work confirmed their

184

185

central role in shaping the evolution of FC alterations comparing healthy controls to aMCI or

AD stages (J. Zimmermann et al., 2018).

l

D
Ö
w
N
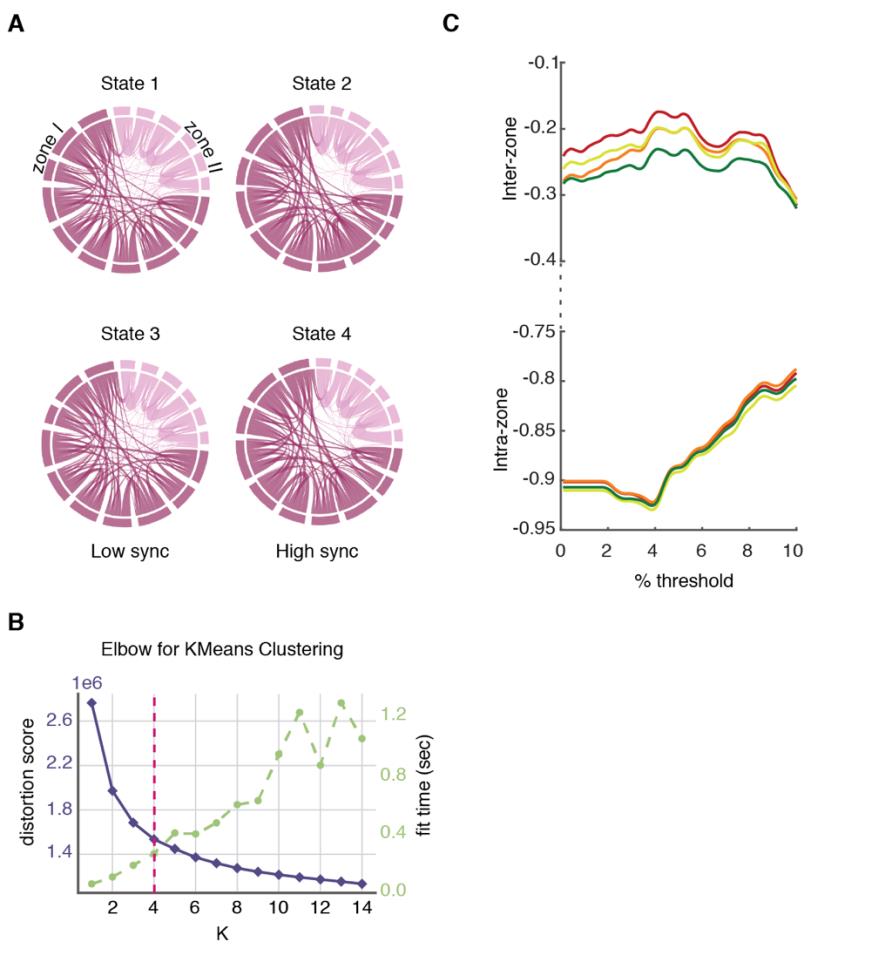
Ö
A
D
e
D

F
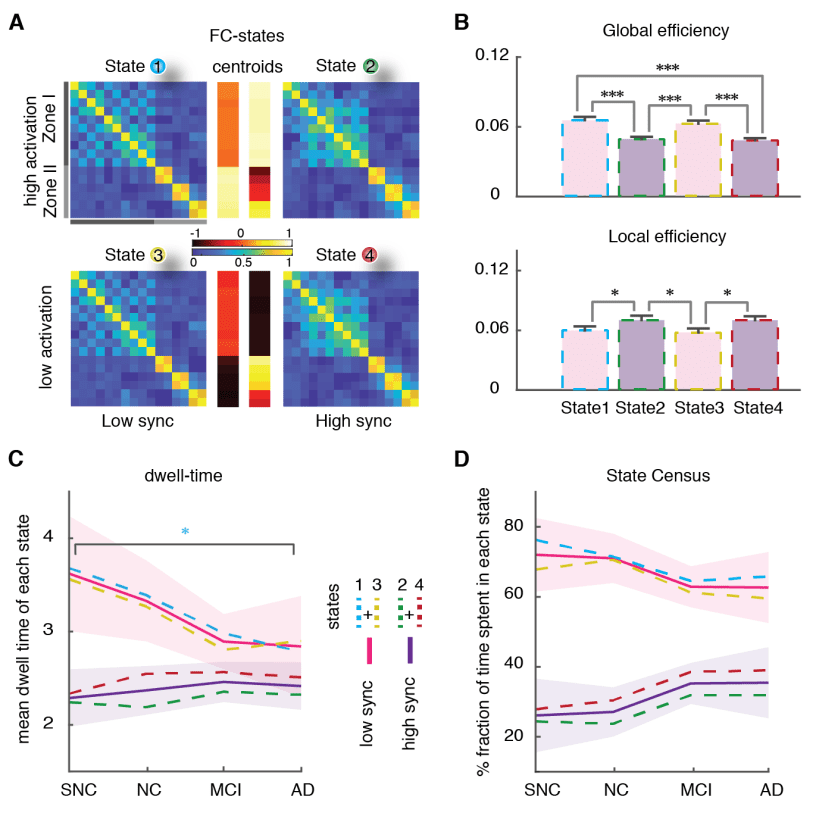
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

186
187

188

189

190

191

192

193

194

195

196

197

198

199

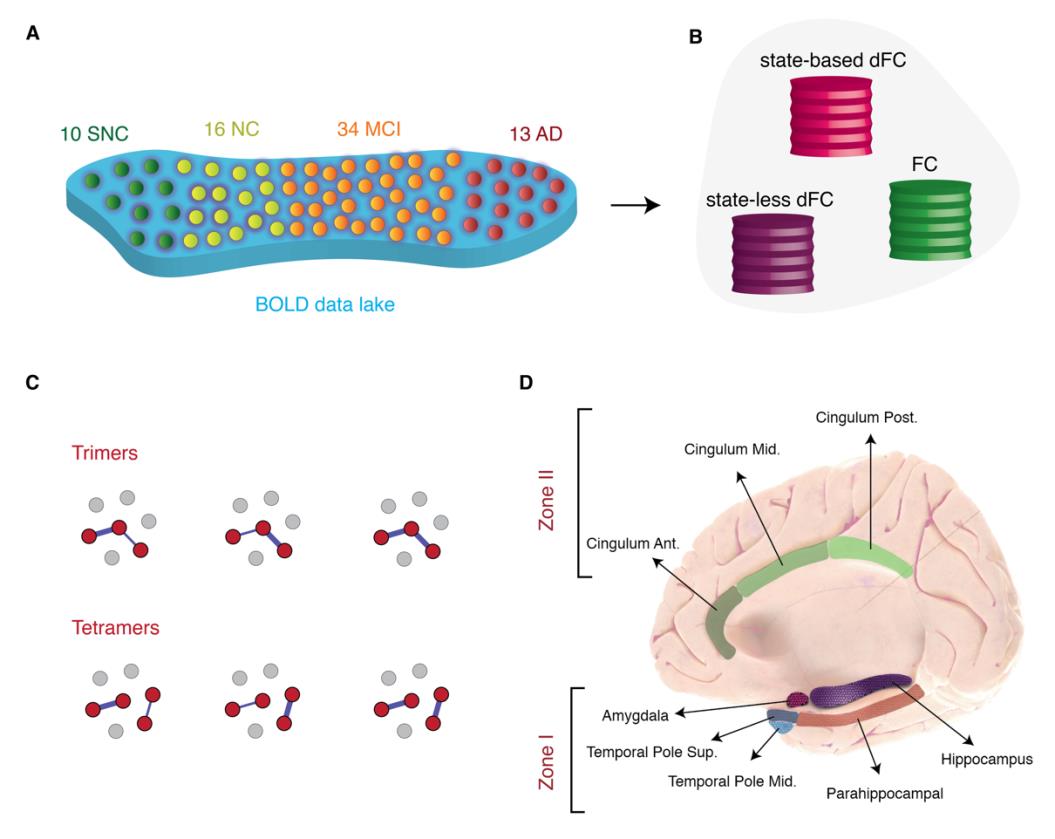
Feige. 1. Overview of approaches. (A) Subjects were stratified in 4 different clinical groups: Supernormal

Kontrollen (SNC), Normal controls (NC), amnesic MCI (aMCI) and Alzheimer’s disease (AD) (B) Wir

used two dynamic functional connectivity (dFC) methods to study the spatiotemporal properties of

resting-state fMRI signals: A state-based dFC called point-based method (PBM) and a state-free dFC

method called meta-connectivity (MC) Ansatz. Both approaches address the dynamics of pairwise

links of interactions, which we call here “dimers”. (C) The study of coordinated fluctuations of dimers

is at the core of the MC approach. Coordination can occur between dimers converging on a common

root (“trimers”) or between non-incident dimers (“tetramers”). (D) We focused on a limbic subnetwork

based on the AAL parcellation that was divided into two zones: a ventrally located “Zone I” that

included the temporal pole (superior and medial), parahippocampal gyrus, hippocampus proper and

amygdala; and a dorsally located Zone II included the anterior, medial and posterior cingulate cortices.

200

State-based dFC: two zones and four dFC states

201

In order to assess FC changes along time, we started with a state-based dFC approach, called

202

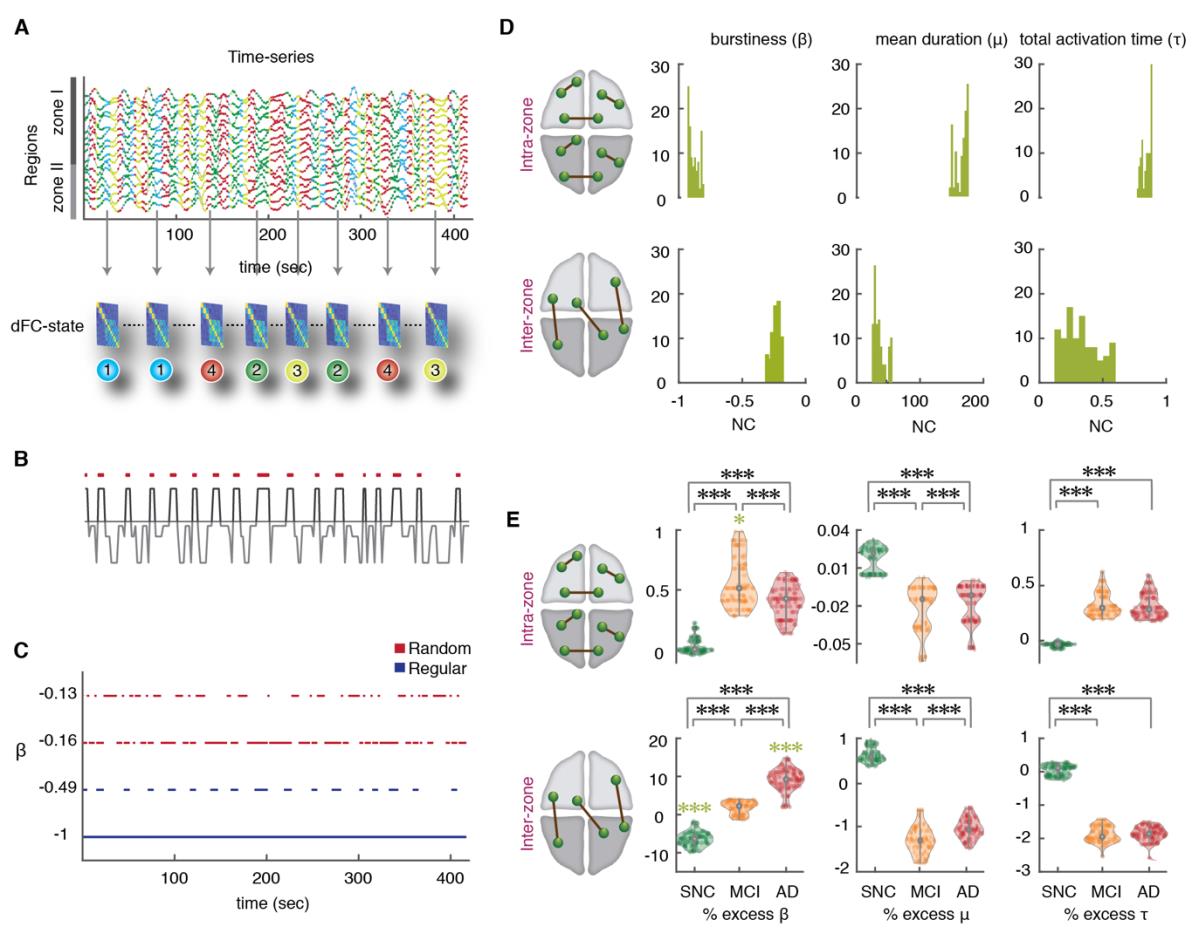
the point-based method (PBM) and first introduced by Thompson and Fransson (2016). In diesem

203

204

Rahmen, different instantaneous images of brain-wide BOLD activation are first clustered

via an unsupervised procedure into K states, and state-specific FC matrices FC(λ) are constructed

F
/

D
Ö

ich
/

/

.

/

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

/

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

205

by evaluating BOLD correlations limited to timeframes assigned to a given state cluster

206

(λ = 1…K, see Materials and Methods for details). Feige. 2A show the weighed adjacency

207

matrices FC(λ) (obtained as centroids of their respective cluster) for each of four different states

208

of dFC, called S-graphlets by Thompson and Fransson (2016). An alternative graph

209

210

representation of these templates is shown in Fig. S1A. The optimal number of K = 4 War

determined based on a statistical elbow criterion (Feige. S1B) and confirmed post-hoc by the

211

consistency of our results.

212

Based on these four dFC states, we obtained the spatial profile of neural activation across

213

Regionen (Feige. 2A). The spatial organization of the observed neural activation profiles naturally

214

215

schlägt vor, in this study, to group the regions in two subsets, characterized by having an activity

level transiently higher or lower than their average level. We defined “zone I” as the subset of

216

ventral limbic regions including amygdala, temporal pole (superior and medial), hippocampus,

217

and parahippocampal gyrus. “Zone II”, included the cingulate gyrus (anterior, medial, Und

218

hintere). In states 1 Und 2, zone II (dorsal regions) and zone I (ventral regions) war

219

220

221

respectively active above average level (high activation states). Im Gegensatz, in states 3 Und 4,

zone II and zone I regions were respectively active below average levels (low activation states).

Außerdem, these four states were noted based on the topology of their FC(λ) networks and

222

the level of internal synchronization within zone I. Quantitatively, connection weights between

223

224

regions within zone I tended to be stronger for states 2 Und 4 than for states 1 Und 3 (average

within zone I FC weights = 0.23 ± 0.16 for states 1 Und 3 vs = 0.29 ± 0.18 for states 2 Und 4).

225

Somit, Staaten 2 Und 4 displayed higher internal synchrony, in contrast to states 1 Und 3. Dann

226

we computed local and global efficiency metrics (Achard and Bullmore, 2007; Latora and

227

228

229

Marchiori, 2001) for the four FC(λ) Netzwerke. Global efficiency quantifies how well

communication pathways can be established between any two nodes in a weighed network.

Local efficiency quantifies the robustness of communication and the possibility to find

230

alternative routes if local connectivity is disrupted. We found that the high sync states 2 Und 4

231

have a lower global efficiency (Feige. 2B; Mann-Whitney U test, P < 0.001) but a greater local 232 efficiency (Fig. 2B, Mann-Whitney U test, p ~ 0.023), reflecting a denser within-zone but a 233 234 235 weakened between-zone connectivity (average between zone I and zone II FC weights = 0.026 ± 0.069 for states 1 and 3 vs = -0.013 ± 0.071 for states 2 and 4). Thus, in short, the overall four states that we find are obtained as combinations of two 236 qualitatively different network topologies an two possible levels of activation, so that each 237 topology can exist in a low and high activity versions. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / . t / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / / / t . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 Fig. 2. State-based dynamic Functional Connectivity (dFC) analyses: four dFC states. (A) BOLD time-series of all subjects were concatenated temporally and then z-scored and clustered based on BOLD activation to extract four states. The associated FC-state matrices (FC(λ), λ = 1…4) were constructed by evaluation BOLD fluctuation correlations limited to time-points within a given state (cf. also Fig. S1A). The centroids of activation of four states (middle) distinguished two subsets of regions (Zone I and Zone II) where their activity was transiently higher or lower than average. States 1 and 2 (or 3 and 4) showed above (or below) average level activation for zones II and I, respectively, therefore were labelled as high (or low) activation states. We referred to states 2 and 4 as high synchronization states because the FC connection weights within zone I tended to be stronger than states 1 and 3 (low synchronization; average within zone I FC weights = 0.23 ± 0.16 for states 1 and 3 vs = 0.29 ± 0.18 for states 2 and 4). (B) Global and Local efficiency as measure of robustness in the communication pathways can be established between regions and was applied on the FC-states. States 1 and 3 with low synchronization showed higher global and lower local efficiency compared to high synchronization states 2 and 4. (C) States with low synchronization showed decrease in mean dwell-time across clinical groups (~3.6 TR = 7.4 s, for SNC; ~2.8 TR = 5.7 s, for AD), where the decrease of state 1 was significant (blue; p-value ~ 0.032; Mann-Whitney U test). States 2 and 4 showed a slight increase from the control groups to the patient groups. A decrease in average dwell-time of states with relatively higher global efficiency indicates that they are less stable. (D) Analogously, the relative fraction of time spent in states with low synchronization was decreased in aMCI and AD compared to NC. Note the increase from SNC to AD groups for states with high synchronization. 260 261 Stability of globally efficient dFC states decreases along the clinical spectrum 262 We quantified the stability of dFC both by the longer or shorter duration of transient epochs 263 within a given state (average dwell time, Fig. 2C) and by the overall time fraction spent within 264 265 a state (average state census, Fig. 2D). As shown in Fig. 2C, group differences were identified in the mean dwell-time of low sync states, with longer dwell-time for the two control groups 266 (~3.6 TR = 7.4 s, for SNC at one extreme) and shorter for the MCI and AD groups 267 (~2.8 TR = 5.7 s, for AD at the other extreme). However, the mean dwell-time of high sync 268 states were not different. 269 270 Analogously, Fig. 2D shows that the relative fraction of time spent in low sync states decreased in aMCI and AD compared to healthy controls (ranging from 62% for AD to 72% 271 for SNC). 272 In summary, low-sync and globally efficient dFC states were less frequent and more 273 transient in aMCI and AD, suggesting a reduction of their overall stability. 274 275 Inter-zone dFC dimers are more intermittent in patient than in control groups 276 The next step, also following Thompson and Fransson (2016), was to map a state-based dFC 277 temporal network to each subject’s resting-state acquisition. To do so, we constructed a 278 279 sequence of network time-frames FC(t) set to be equal to the FC(λ) graph specific for the state λ visited at time t (Fig. 3A; see Materials and Methods for details). Thompson and Fransson 280 (2016) called such a temporal network a T-graphlet. 281 In this approach, each link can assume up to four possible strength values, corresponding to its 282 283 284 strengths in the FC(λ) associated to each of the four states. Hence, any variability of dFC dimers reflects exclusively state-switching dynamics. Figure 3B shows the time-course for a representative fluctuating dFC dimer. The temporal organization of link fluctuations (periodic 285 or bursty) can be highlighted by a binarization procedure, where a link is set to 1 if its 286 instantaneous strength is above the threshold θ, or to 0 otherwise (see Materials and Methods). 287 The result of this procedure is shown in Fig. 3C, for a few representative links and a specific 288 289 choice of threshold. A link whose strength remains steadily above (below) threshold will result as constantly –or tonically– “active” (“inactive”). In contrast, a link whose fluctuating strength 290 crosses the threshold through the different dFC-state frames will undergo several activation and 291 inactivation events at specific threshold crossing times. Yet, there can be various types of l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / t / . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 292 intermittency, with different temporal statistical properties. The durations of different link 293 activation and inactivation epochs could all be roughly similar, resulting in a more periodic 294 type of intermittency (blue color link activation rasters in Fig. 3C). Alternatively, they could be 295 more variable, stochastically alternating between shorter and longer activation epochs (red 296 297 color rasters in Fig. 3C). The degree of temporal regularity in link activation and deactivation dynamics can be evaluated, link-by-link, by the quantification of a burstiness coefficient (β). 298 We also define the mean duration of a link’s transient activation events as mean activation (μ) 299 and the total fraction of time in which a link is active relative to imaging session duration, total 300 active time fraction (τ). The burstiness coefficient is bounded in the range -1 ≤ β ≤ 1, with: 301 302 β < 0, corresponding to near-tonic or periodic link activation dynamics; β = 0, corresponding to Poisson (random-like) link activation dynamics; and β > 0, corresponding to time-clustered

303

(bursty) events of link activation. Mean activation times μ are bounded to the length of time-

304

Serie. Total active time fraction is also bounded, 0 ≤ τ ≤ 1.

305

306

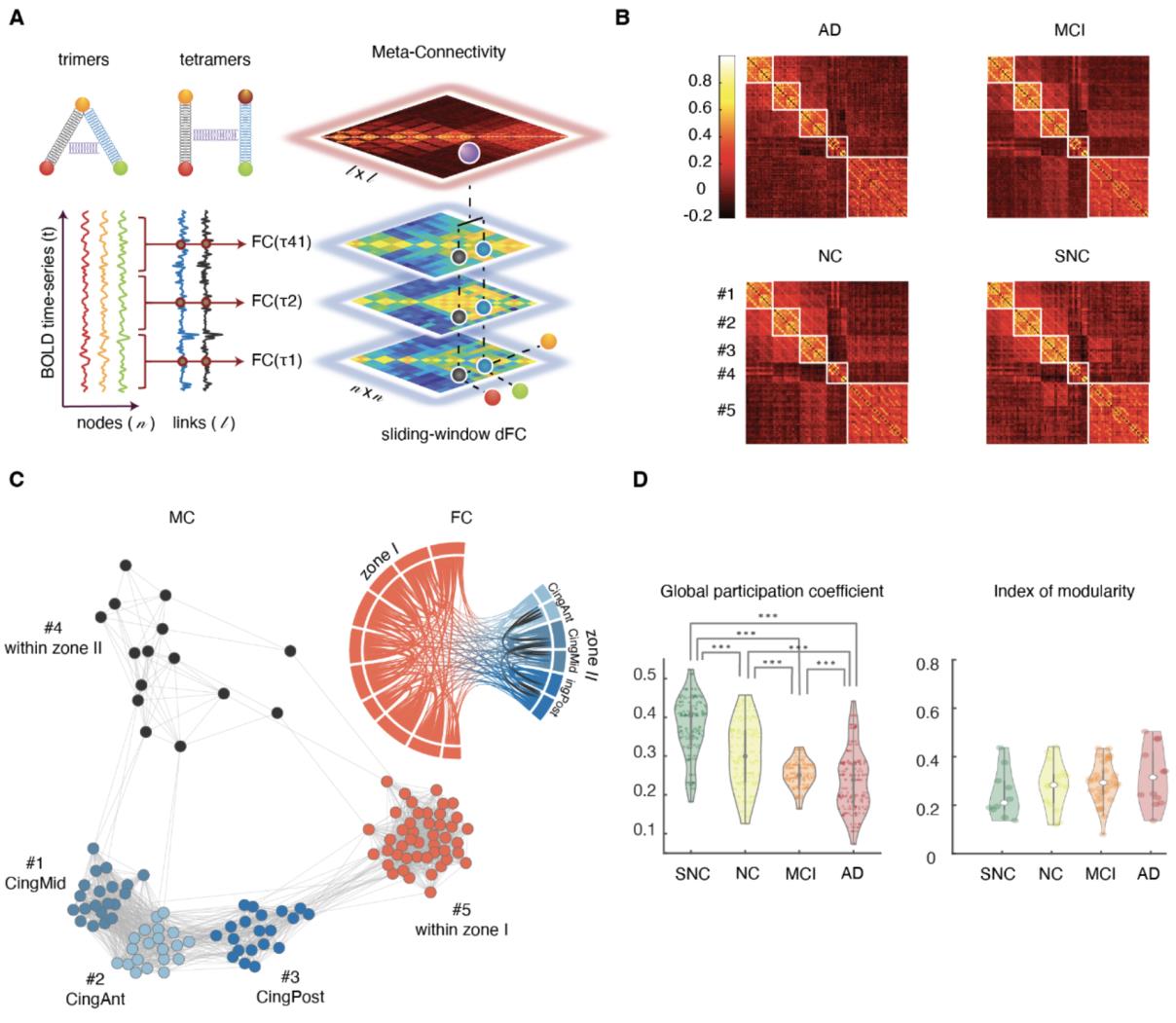
307

In this approach, three numbers β (burstiness coefficient), M (mean activation) and τ (total

active fraction) fully characterize the binarized dynamics of a link (for a given choice of the

308

strength threshold θ). These metrics were evaluated for the two categories of dFC dimers: intra-

309

zone (between two regions within either zone I or II) and inter-zone (between one region in

310

311

zone I and one region in zone II). Our results show that these two categories have distinct

distributions of β, μ and τ, first exemplified in NC subjects (Feige. 3D). Whereas Inter-zone dFC

312

dimers are closer to a Poisson-like intermittency (β = -0.229 ± 0.020, median ± m.a.d), intra-

313

zone dimers, present a tonic activation time-course (β = -0.890 ± 0.027, median ± m.a.d). In

314

addition, inter-zone dimers are also less active (τ = 0.312 ± 0.099 for inter-zone vs.

315

316

τ = 0.855 ± 0.027

für

intra-zone dimers) and activate

for shorter

transient

mal

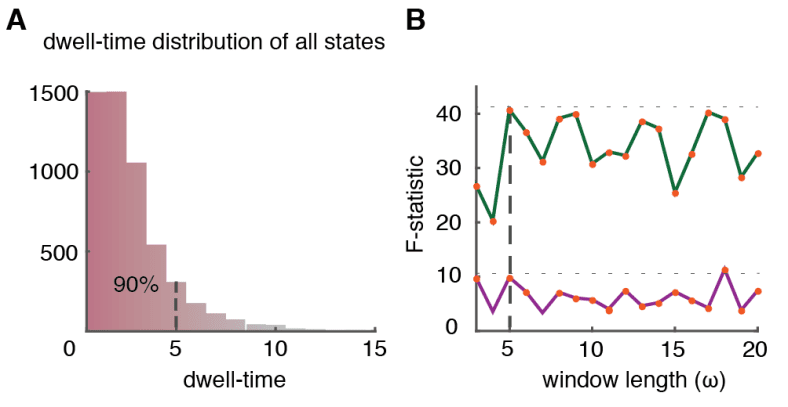
(μ = 34.926 ± 4.439 for inter-zone vs. μ = 178.995 ± 7.378 for intra-zone dimers). These results

317

suggest a smaller average strength of inter-zone time-averaged FC than for intra-zone FC.

318

Using NC subjects as reference group, we measure indeed an average FC(T) strength = 0.083 ±

319

0.135 for inter-zone and of 0.564 ± 0.155 for intra-zone dimers (average ± s.d.). Similar

320

321

differences were found for all groups (Table S1). The relative differences in β, μ and τ between

intra- and inter-zone dimers are maintained over the entire range of possible thresholds θ (Feige.

322

S1C for bustiness coefficient). Inter-zone dimers also displayed more burstiness, were more

323

transient and less active than intra-zone dimers in all groups.

324

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

/

T

/

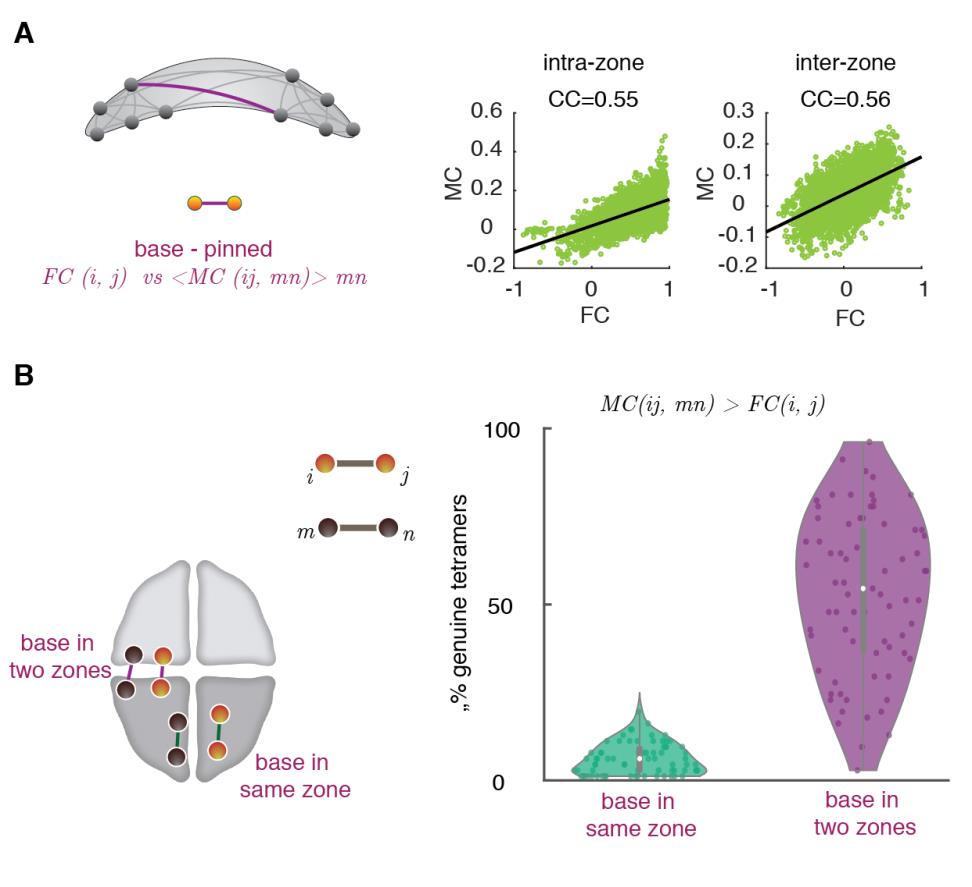
1
0
1
1
6
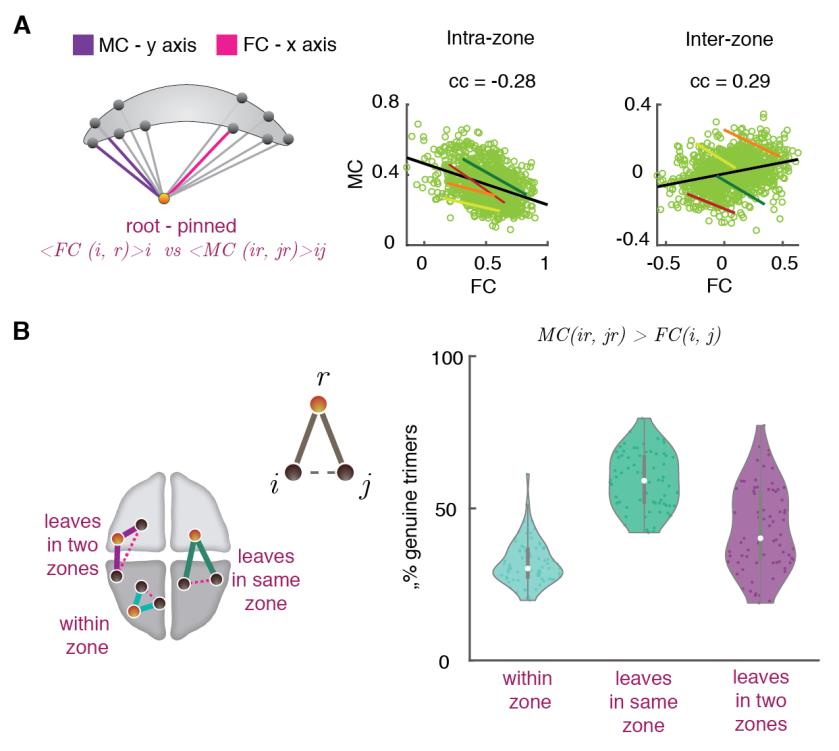
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
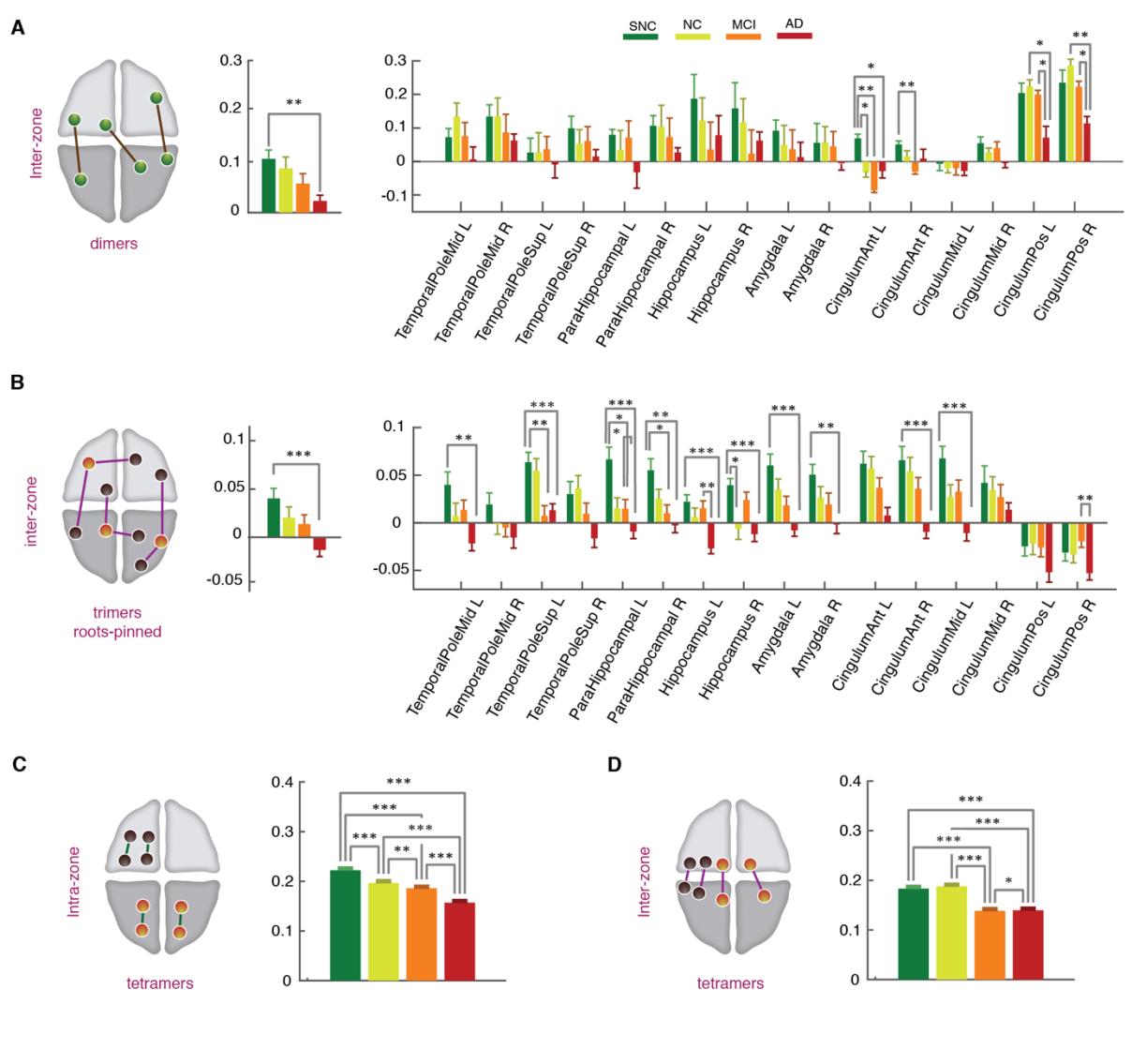
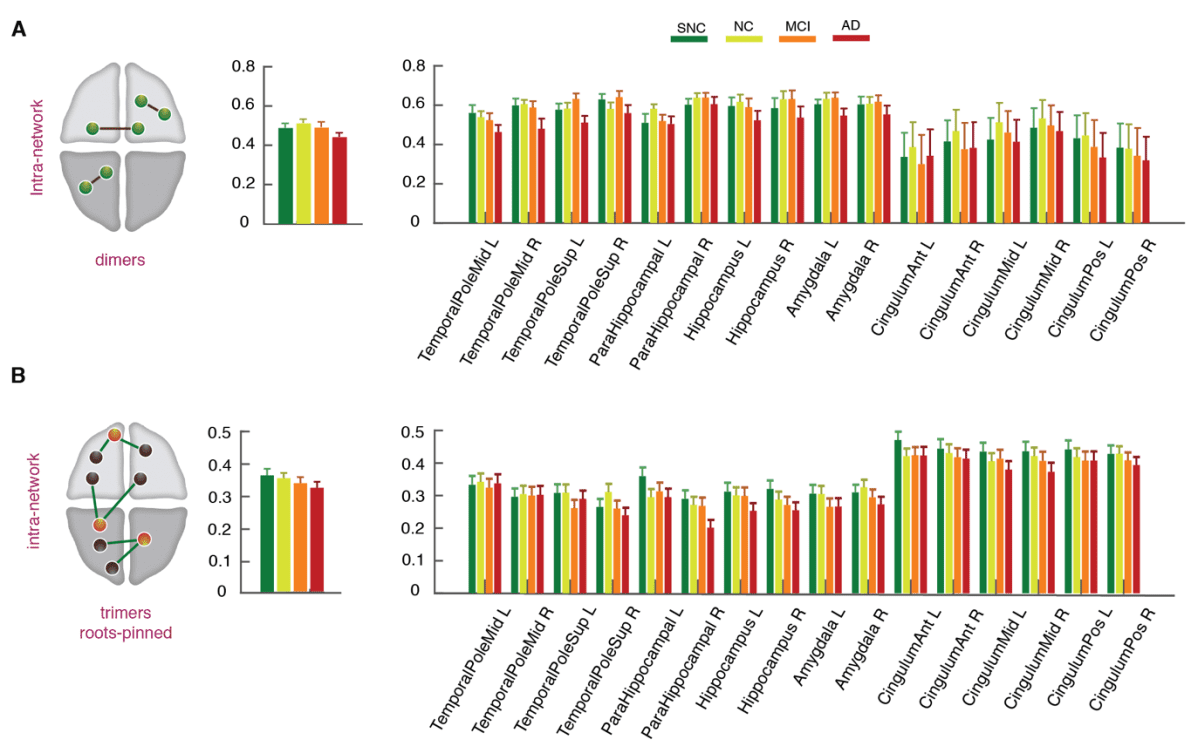
R
2
0
2
3

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

325
326

327

328

329

330

331

332

333

334

335

336

337

338

339

340

341

342

343

344

Feige. 3. State-based dFC analyses: increase of intermittency in inter-zone links. (A) To construct the

state-based dFC temporal network, a specific FC(λ) graph was assigned to each BOLD signal intensity

time-point (we show here 416 time-points = 20 minutes of rsfMRI acquisition, for two concatenated

Fächer). Folglich, there is a time-course for every FC links where they can assume up to four

possible different strength values (link dynamics due to state switching). (B) The temporal organization

of link fluctuations can be assessed by determining intervals of link activation and inactivation (via a

thresholding of dynamic strengths with a global threshold θ on all the links). The threshold θ ranges

aus 1 Zu 10 % of the maximum strength over the dataset. The figure shows binarization for a

representative dFC dimer. (C) The degree of temporal regularity in link activation/deactivation was

assessed by quantifying the burstiness coefficient β, the mean activation time μ and the total activation

time τ for every link and subject. The burstiness coefficient is bounded in the range -1 ≤ β ≤ 1 where it

approaches to -1 if the link is tonic/periodic (blue lines), or it can approach to 0 if it has Poissonian

(random-like) patterns of activation (red lines); β = +1 corresponds to links with bursty-like events of

Aktivierung. (D) Distributions of β, μ and τ for the NC group, later used as reference. Upper and lower

rows represent distributions over, jeweils, intra zone and inter zone links (for an intermediate

threshold, 0.0087 < θ < 0.0870). Left: Distribution of burstiness coefficients across different thresholds averaged over two subsets of intra- and inter-zone links. The β of intra-zone dimers approach to -1 and have more tonic/periodic patterns of activation (β = -0.890 ± 0.027, median ± m.a.d), while the β inter- 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 zone are closer to 0 and show more Poisson-like intermittency (β = -0.229 ± 0.020, median ± m.a.d). Middle: The mean duration μ which is bounded to the length of time-series for one subject (208 time- points), for the intra-zone links was longer than inter-zone links. Right: Analogously, the normalized total activation time (τ) of intra-zone links were longer than inter-zone links. (E) Mean values for the NC group were used as reference and percent relative variations were computed for the other SNC, aMCI and AD groups, combining relative values for different thresholds (see Materials and Methods). Upper and lower rows refer to intra- and inter-zone links. Left: Notice the large burstiness increase across groups for the inter-zone links (~1.8% for aMCI and ~9% for AD; green stars, p-value < 0.001; Mann-Whitney U-test) compared to a slight increase in the burstiness values of intra-zone links (~0.5%). In contrast, SNCs showed a significant decrease of ~ -6.5% relative to NC group in the inter-zone links. Comparisons between SNC, aMCI and AD for both intra- and inter-zone links were all significant (black stars). Middle: The mean activation durations of inter-zone links showed a relative negative decrease of roughly -1% for aMCI and AD subjects. Right: Total activation time τ was reduced to roughly -2% in aMCI and AD compared to NCs. Thus, temporal dynamics of dFC dimers are more tonic/periodic in SNCs than NCs and more intermittent in aMCI and AD subjects, particularly for inter-zone dimers. To achieve a robust and more precise comparison of β, μ and τ distributions between the cohorts (Fig. 3E), we computed percent changes of the three indicators in SNC, aMCI and AD 363 groups relatively to normal controls. The advantage of relative comparisons is that they can be 364 collated for different threshold values θ, resulting in a threshold-independent analysis. We 365 found that, moving from NC to aMCI and AD subjects, many dFC dimer links tended to have 366 367 larger burstiness values. In contrast, moving from NC to SNC subjects, dFC dimers tended to be more tonic. These trends of β were smaller yet significant for intra-zone FC dimers (Fig. 368 3E), compared to inter-zone dimers, reaching +1.869 ± 1.663 % for aMCI patients, +9.071 ± 369 3.001 % for AD patients and -6.404 ± 1.938 % for SNC subjects (Fig. 3E) that had larger values. 370 371 372 These results reinforce the notion of a significant reduction of inter-zone time-averaged FC along the clinical spectrum (cf. Table. S1). More importantly and beyond this reduction of average strength, our results point to a degradation of the temporal regularity of FC fluctuations. 373 While the total active time fraction τ of inter-zone dFC dimers decreased by less than -2% from 374 NC subjects to aMCI and AD patients (Fig. 3E; and even increased for intra-zone dimers), the 375 376 burstiness of inter-zone links increased over 10%, showing a real alteration in the temporal statistics of link activation, well beyond the trivial decrease necessarily induced by the observed 377 reduction of average strength. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / . / / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 378 We also observed a significant decrease of the mean activation time μ (Fig. 3E), for both 379 intra-zone and inter-zone dFC dimers (-1.275 ± 0.227 % for aMCI and AD subjects compared 380 to NCs). For SNC relative to NC, however inter-zone link burstiness decreased and their 381 activation time increased (+0.613 ± 0.161 % for SNCs). 382 383 Goh and Barabasi (2008) also defined another metric related to burstiness, the memory coefficient. This coefficient λ (see Methods for exact definition) becomes significantly positive 384 when autocorrelation exists in the duration of consecutive link activation events, i.e. when long- 385 (short-) lasting activation events tend to be followed by activation events which also are long 386 (short). Computing λ, we found a weak median autocorrelation in all four groups, for both intra- 387 388 and inter-zone links. Values (see Supplementary Table S2) were small but still significant given the large number of activation events. Furthermore, memory was decreasing across the four 389 groups from SNC to AD, providing yet another indication of increased disorder. 390 In summary, the temporal dynamics of dFC dimers between regions in different zones is 391 altered along the SNC-AD spectrum from tonic and periodic in SNC to more intermittent in 392 393 aMCI and AD subjects. Together with the finding of altered dwell times and transition dynamics between dFC states (Figs. 2C, D), our state-based dFC analyses based on the PBM 394 approach suggest that changes towards AD involve a degradation of global integration and an 395 increased disorderliness of dynamic functional interactions between zones. 396 397 State-free dFC: entangled dFC flows in continuous time 398 The PBM approach to dFC analyses reduces the description of FC network reconfiguration 399 to the tracking of discrete state switching events. Alternatively, sliding-window approaches 400 evaluate the evolution of FC links as a continuous reconfiguration along time. As shown in Fig. 401 402 4A, all dFC dimers FC(t1) can be evaluated in a time-resolved manner restricting their estimation to BOLD signal time-series within a window centered at time t1. The window is then 403 shifted at a slightly increased time t1 + δt, providing an updated set of values FC(t1 + δt). The 404 result is a collection of smoothly varying continuous time-series FC(t) for each possible dFC 405 dimer (Allen et al., 2014; Battaglia et al., 2020). 406 407 As in the case of node activity time-series, it is possible to study covariance between the temporal evolutions of different dimers. The case in which their fluctuations are not 408 independent –or, in other words, that the dimers are “entangled”– will be signaled by 409 significantly positive or negative correlations between dimers. These correlations can be l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 410 represented graphically by trimer and tetramer diagrams in which the two entangled dimers are 411 linked by a spring (Fig. 4A, top left; we will omit in the following to draw this spring, for the 412 sake of a clearer visualization). The stronger the correlation between the fluctuations of 413 different dFC dimers in a trimer or tetramer, the stronger will be their “entanglement” (i.e., 414 metaphorically, the stiffness of the spring). 415 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / d o i / / / t . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 416 417 418 419 420 421 422 423 424 425 Fig. 4. State-free dFC: Meta-Connectivity. (A) We slid a window of length 𝜔 = 5 TRs (10 s) with no overlap on the BOLD signals from the n considered regions. We then computed n x n FC matrices for each window using Pearson’s correlation between pair of regions. In this way each of the l possible pairwise links of FC becomes associated to a continuous time-series of varying FC strength. Correlations between these link time-series can be compiled in a l x l Meta-Connectivity (MC) matrix. We represent here trimer and tetramers with a spring between the involved dimers, as, in presence of meta- connectivity, pairwise links are not free to fluctuate independently. (B) Group average MC matrices for the four clinical groups. Louvain algorithm was applied on the MC matrices resulting in five modules. (C) A graph representation of the MC for the NC group, together with a chord-diagram of FC for the 426 427 428 429 430 431 432 433 434 same group. Each node in the MC graph corresponds to a link in the FC graph. The different MC graph modules correspond thus to different types of links: MC modules #1, #2 and #3 include inter-zone links incident, respectively, to medial, anterior and posterior cingulate cortices (edges within these modules are thus inter-zone trimers rooted in Zone II); MC module #4 and #5 include links, respectively, within zones II and I. (D) Modules are also connected between them. The relative amount of inter-module meta-links is captured by the global participation coefficient (averaged over the five modules) which showed a significant decrease across the clinical groups (Mann-Whitney U-test, p < 0.001). These strengths of entanglement between FC dimers can be compiled into a meta- connectivity matrix (MC; Fig. 4A). The notion of MC (Lombardo et al., 2020) is strongly related 435 to the edge-centric FC discussed by Faskowitz et al. (2020). The key difference is that MC is 436 obtained by using a short smoothing window in the estimation of the stream of FC(t) matrices, 437 while edge-centric connectivity captures coincidences between instantaneous fluctuations. The 438 439 denoising brought by the smoothing window allows an easier extraction of the modular structure of MC, with respect to edge-centric FC (cf. Lombardo et al., 2020), but the two 440 concepts are otherwise equivalent. The choice of window size (here 5 TRs, Materials and 441 Methods) was motivated by the fact that the state-based PBM method suggested that ~90% of 442 epochs within a coherent state lasted less than 5 TRs (Fig. S2A), indicating a fast intrinsic 443 444 timescale of link fluctuation. Furthermore, we can observe post-hoc that the use of larger (or smaller) windows would not improve the capability to separate our groups based on MC values 445 (Fig. S2B). 446 Group-averaged MC matrices are shown in Fig. 4B for the four groups. Their modular 447 structure is evident at simple visual inspection. A module in the MC matrix –also called dFC 448 449 module or meta-module (Lombardo et al. (2020))– corresponds to a set of co-fluctuating dynamic FC links, i.e. to FC subnetworks whose overall strength waxes and wanes transiently 450 along the resting state in an internally synchronous manner. The existence of non-uniform MC 451 matrices indicates that the flow of dFC reconfiguration is not mere noise but rather, it is 452 organized by specific arrangements of “springs between the links”. In other words, fluctuations of FC dimers are entangled in complex patterns reflecting higher-order correlations (non- vanishing trimers and tetramers) between the coordinated activation of multiple regions. 453 454 455 456 dFC flow in patients is less globally entangled 457 458 MC matrices can also be represented as graphs, in which MC-nodes correspond to different FC-links and MC-links appear due to the entanglement between the FC-links. An example l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / . / / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 459 graph embedding is shown in Fig. 4C for the MC matrix of the NC group. Graph vertices are 460 color-coded depending on the type of associated FC link (i.e. start and end zones of the links, 461 cf. FC diagram with matching colors at the top right of Fig. 4C). Notably, the different dFC 462 modules, visible as blocks in the MC matrices of Fig. 4B and as uniform-color node 463 464 communities in the graph of Fig. 4C, are composed of FC dimers with internally homogeneous start and ending zones. 465 A standard graph-theoretical notion useful when commenting about dimer arrangements into 466 trimers and tetramers is the one of incidence: a link is incident to a node (or a node incident to 467 a link), if the link is attached to the node (the notion of incidence complements the more familiar 468 469 one of adjacency, where two nodes are said to be adjacent if connected by a link). Equipped with this terminology, we call root the common region incident to both the dimers within a 470 trimer, while the other two regions form the leaves of the trimer. We can then describe the first 471 three dFC modules (#1, #2 and #3) of the MC matrix as including mutually entangled FC dimers 472 originating in either one of the Zone II cingulate regions and terminating in Zone I. The 473 474 entanglement of FC dimers gives thus rise to strong inter-zone trimers with “roots” in Zone II and “leaves” reaching out to Zone I regions. The two other dFC modules #4 and #5 include 475 dimers within Zone I and Zone II, respectively, forming strong within-zone trimers or tetramers. 476 Entanglement is thus particularly strong between dimers within a same zone and between inter- 477 zone dimers incident on a common root region (in Zone II). 478 Although the MC graph is highly modular, it is not split into disconnected components and 479 some entanglement exists also between dimers located in different dFC modules. Inter-module 480 connections in the MC graph can arise e.g. due to the existence of trimers with a root in zone I 481 (entangling dimers across dFC modules #1, #2 and #3) or inter-zone tetramers (entangling 482 483 dimers across dFC modules #4 and #5). In other words, MC reveals some degree of global, widespread entanglement between FC dimers, beyond modular entanglement. The strength of 484 such global entanglement is quantified by the so-called average participation coefficient of the 485 MC matrix, a graph-theoretical quantity measuring inter-module coupling (Guimerà & Amaral, 486 2005; see Materials and Methods). 487 488 The distribution of MC participation coefficients for each group are shown in Fig. 4D. We found that the participation coefficients decreased significantly (Fig. 4D, left; Mann-Whitney 489 U-test, p <0.001) from SNC to AD, while overall modularity did not vary significantly (Fig. 490 4D, right). These results suggest that, in patients, coordination structure between fluctuations l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / t . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 491 of FC dimers is impoverished: global entanglement is disrupted, making dimer fluctuations in 492 different modules more random and mutually independent. 493 494 Interlude: trimers and tetramers are genuine or “dimers are not enough”! 495 496 Before entering a more detailed and regional specific account of changes to dFC organization observed at the regional level along the SNC-to-AD spectrum, it is important to stress that 497 trimer and tetramer analyses are not redundant with the dimer-based analyses. Indeed, some 498 studies have suggested that correlation between edges (captured by higher-order trimer and 499 tetramer in a MC matrix) could just be an automatic byproduct of existing lower-order dimer 500 501 interactions (Novelli and Razi, 2022). This can be easily understood through some examples. Let consider for instance two strong dimers FCri and FCrj sharing a common root region r. If a 502 third strong dimer FCij also exists –closing the triangle of edges (ri), (rj), (ij), then it is not 503 surprising that a strong trimer MCri, rj is also detected: indeed, the fluctuations of the two leaf 504 regions i and j are coordinated through a transverse dimer interaction, i.e. the strength of the 505 506 trimer would be the byproduct of a triangular motif of dimers and would thus be a redundant consequence of them. Analogously, we may consider the case of a square motif of dimers FCij, 507 FCjk , FCkl and FCli which could also give rise to strong tetramers because of the presence of 508 one or more pairs of strong dimers. In other words, the detection of strong trimer and tetramer 509 510 entries within the MC (or other forms of edge-centric FC) is not a sufficient condition for the existence of genuine high-order interactions (Battiston et al., 2020) that cannot be explained as 511 stemming from motif arrangements of lower-order pairwise interactions. On the contrary, the 512 existence of genuinely high-order interactions could be established by detecting trimer or 513 tetramer couplings between the dimers in a motif, stronger than the dimers themselves involved 514 515 516 in the motif. The question that then arises is, what is the structure of MC that we observe in our data? To investigate the genuine or spurious nature of trimer and tetramer interactions, we 517 systematically studied the inter-relations between MC and FC entries. First, we define the dimer 518 strength FCr = Σi FCri of a region r as the sum of the strengths of all the dimers incident to it. 519 520 Analogously, we introduced the (root-pinned) trimer strength MCr = Σij MCri, rj of a region r as the sum of the strengths of all the trimers of which r is the root. Conceptually, whereas FCr 521 measures the average coordinating influence that the region r exerts on its adjacent nodes, MCr 522 can be understood as quantifying the coordinating influence that r exerts on its incident links. 523 As shown by Fig. 5A, the correlations between dimer and trimer strengths of a region are weak l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / t / . / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 524 and not significant, both at the global (black lines) and within each group (bundles of colored 525 lines) levels, and for both within-zone and inter-zone trimers and dimers strengths. Of note, the 526 average strength of between-zone trimers and dimers strengths had a larger variance across 527 groups, hence the positively slanted shape of the global point cloud when confounding all 528 529 groups, despite negative trends within each group. Although weak, within-subject correlations between FCr and MCr were negative, suggesting that some regions can be “meta-hubs” 530 (Lombardo et al., 2020) but not “hubs”, i.e. they can be the center of an entangled star subgraph 531 of incident dimers, even if these dimers are individually weak and unable to systematically 532 synchronize the fluctuations of adjacent nodes. Such meta-hubs could not have been identified through ordinary pairwise FC analyses only and manifest thus the existence of a real high-order multi-regional coordination. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Fig. 5. State-free dFC: Inter-relations between dFC trimers and FC dimers. We studied whether regions with a large FC strength (“FC hubs”, i.e. they are the center of a star of links strong on average) also have a large trimer strength (MC “meta-hubs”, i.e. they are the center of a star of links whose fluctuations are temporally correlated). (A) To do so we computed the correlation between dimer and FC strengths, for both within and between zones trimers and dimers. As shown by the scatter plots, these correlations were low, both at the global (light green cloud) and at the single clinical group (colored solid lines; green: SNC, yellow: NC, orange: aMCI, red: AD) levels. Within each group, they were furthermore moderately negative. Therefore, FC hubness and MC meta-hubness tend to be slightly anti- correlated. (B) Trimers were divided into three groups dependent on the location of their roots and 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 leaves. We considered genuine a trimer such that the MC between the two dimers composing the trimer is stronger than the FC between the trimer leaves. The violin plots at the right show fractions of genuine trimers (for all trimers and subjects) as a function of the trimer type. For all types, there were substantial fractions of genuine trimers (i.e. higher-order interactions not fully explained by the underlying dimer interactions arrangement). See Figure S3 for analogous analyses on tetramers. We then moved to consider how many trimers cannot be considered as a manifestation of underlying triangular motifs of dimers. We defined a trimer rooted in a region r to be genuine if MCri,rj > FCij , i.e. if the observed trimer strength cannot be fully explained by a strong

555

synchronization between the leaves. We then measured the observed fractions of genuine

556

trimers. As shown by Fig. 5B, substantial fractions of genuine trimers could be found for all

557

trimer types: genuine fractions amounted to 32 ± 7 % for within zone trimers (root and both

558

559

leaves in a same zone) and increased to 43 ± 13 % for inter-zone trimers with leaves in two

different zones, oder 58 ± 9 % for inter-zone trimers with the root in a different zone than the

560

leaves. Especially for inter-zone trimers, many trimers could not be trivially explained by the

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

561

existence of triangles of dimers.

F
/

D
Ö

ich
/

562

563

Considering tetramers, we found larger redundancy with dimers. We defined the tetramer

strength MCij = Σkl MCij, kl of a link (ij) as its total entanglement with other links. Figure S3A

564

shows that a significant positive correlation existed between the dimer strength FCij of a link

565

(ij) and its tetramer strength. That is, the stronger links were also the most entangled.

566

Interessant, several tetramers could still be considered genuine. We defined a tetramer

567

568

genuine when MCij,kl > FCij , i.e. when the two composing dimers were strongly correlated,

despite (at least one of) the dimers being individually weak. Under this definition, Figure S3B

569

shows that up to 55 ± 10 % of tetramers composed of interzone dimers were genuine.

570

We conclude that in general, the information conveyed by trimer and tetramer analyses is

571

not completely redundant with the one conveyed by dimers, as many trimer and tetramer

572

573

metrics cannot be explained solely in terms of dimers and thus express actual higher-order

correlations.

574

dFC trimers and tetramers are more impacted in aMCI and AD than FC dimers

575

After defining various metrics to quantify the involvement of specific regions and links into

576

pairwise and higher-order interactions, as previously described, we then studied how dimer,

577

trimer and tetramer strengths varied across the four cohorts in our study.

/

/

.

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

578

Erste, we found that for both dimer and trimer interactions, the stronger effects were found

579

considering inter-zone interactions. Figure 6A reports group differences for inter-zone dimers

580

and Figure 6B for inter-zone trimers (mixed-zone or same-zone leaves are not treated

581

separately). Results for within-zone dimers and trimers are shown in Figures S4A and S4B,

582

583

584

585

jeweils. In contrast to within-zone interactions, group-level comparisons for within-zone

dimer and trimer interactions were not significant.

Allgemein, when averaging over all brain regions (Figs. 6A and 6B, links), general averages

586

of dimer and trimer strengths progressively decreased from SNC, to NC, aMCI and AD groups.

587

588

This decrease, vor allem, was significant when comparing the two extreme SNC and AD groups.

The effect was particularly strong for inter-zone trimer strengths (p = 0.005, Mann-Whitney U-

589

test, Bonferroni correction, for trimers), whose average value for the AD group not only

590

decreased but changed its sign as it became negative. Im Gegensatz, within-zone trimer strengths

591

remained strongly positive (Feige. S4B). Das bedeutet, dass, in the AD group, several regions are

592

593

involved in a mixture of negative and positive trimer interactions. Positive interactions tend to

synchronize the fluctuations of FC links, unlike negative interactions that tend to push them in

594

an anti-phase interaction. Außerdem, the mixture of positive and negative couplings results

595

in a dynamic conflict scenario, known in the statistical mechanics as “frustration”

596

597

(Vannimenus and Toulouse, 1977) and has been associated to disordered organization and a

slowed-down relaxation to equilibrium (Mezard et al., 1988). The emergence of frustrated inter-

598

zone trimer interactions is a strong qualitative discriminative marker of the AD group (sehen

599

Discussion for possible interpretations of this finding).

600

601

602

The decrease of inter-zone trimer-strengths and their switch to negativity in the AD group is

confirmed also when focusing on individual brain regions, rather than the average (Figure 6B,

Rechts). Remarkably, strong decrease in trimer strengths were observed in regional subdivisions

603

of the Temporal Pole and of the Parahippocampal gyrus, along the Hippocampus proper and

604

Amygdala. Some of these regions (Entorhinal cortex in the Parahimpocampal gyrus and the

605

Hippocampus), are among the first to be affected by neurofibrillary accumulation in AD

606

607

pathology (Braak stages 1 Und 2). In these same regions, we found a similar trend at the level

of dimer strengths even when differences were not significant (Figure 6A, Rechts). Of interest,

608

the stronger effects at the level of dimer strengths were found in the Cingulate gyrus which are

609

affected by early beta amyloid depositions and later on with neurofibrillary accumulation.

610

Interessant, the regions exhibiting the strongest effects at the level of trimers were not the

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

T

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

611

ones with the strongest effects at the level of dimers (und umgekehrt; Feige. 6A right vs Fig. 6B

612

Rechts). The two analyses reveal thus complementary aspects of how pathology affects the

613

spatiotemporal organization of functional interactions.

614

615
616

617

618

619

620

621

622

623

624

625

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

/

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Feige. 6. State-free dFC: strengths of inter-zone FC dimers, trimers and tetramers across clinical

groups. (A) Average strength of inter-zone FC dimers decreased from SNC-to-AD both globally (links)

and locally at the level of individual regions (Rechts). At the global level, significant differences were

found between the SNC and AD groups (p-value = 0.005, Mann-Whitney U-test, Bonferroni correction).

Locally the decrease was significant in anterior and posterior cingulate gyrus, bilaterally (Mann-

Whitney U-test, Bonferroni correction). (B) Inter-zone trimer strengths, similarly to FC dimers, showed

a reduction trend across the groups, both globally (links) and locally (Rechts). At the regional-level the

reductions in dFC trimers were widespread among regions, including early-affected regions without

noticeable FC strength variations across clinical groups, with an interesting tendency toward negative

trimer strengths in the AD group, associated to developing “frustration” of higher-order interactions in

626

627

628

629

630

a statistical mechanics sense (Und, correspondingly, increased dynamical disorder and conflict; sehen

Diskussion). Endlich, (C-D) tetramers strength showed a significant drop from SNC to AD groups in

both brain-wide averaged intra-zone (C) and inter-zone (D) subsets. See Figure S4 for intra-zone dimer

and trimer strengths, not showing significant variations across groups.

zuletzt, we assessed differences on tetramer strengths across groups. In Abbildung 6 we show the

631

average tetramer strengths for intra-zone (Feige. 6C) and inter-zone (Feige. 6D) tetramers. In both

632

633

Fälle, we observed a significant reduction of tetramer interactions from the SNC, to the NC,

MCI and AD groups. In the case of inter-zone tetramers, the drop in strength was large in the

634

MCI group, with levels close to those in the AD group.

635

Zusammenfassend, AD was associated with extensive reductions of not only dimer strengths, Aber

636

more importantly, trimer and tetramer strengths. Außerdem, inter-group differences were

salient when considering higher-order trimer and tetramer compared to dimer interactions.

637

638

639

640

Diskussion

641

We have shown a large variety of changes associated with dFC across the cognitive spectrum

642

from cognitively over-performing SNC subjects to AD. The rich set of complementary analysis

643

approaches we deployed consistently converge toward a common message: AD is associated

644

with a disordering of the rich spatiotemporal fluctuations that characterize healthy dFC.

645

646

It is worth noting that while BOLD activity misses many fast neuronal processes due to its

slow sampling rate, what Functional Connectivity dynamics track are not neural level processes

647

but variations of global brain state that can occur on much slower time-scales. So dFC with a

648

long TR accounts for variations of the way in which the repertoire of internal states is sampled,

649

more than for variations of neural signals themselves. As a side note, these slow fluctuations

650

651

are also what mean-field connectome-based whole-brain models are fit to reproduce via the

stochastic sampling of their emergent repertoire of dynamic modes (Hansen et al., 2015, Fousek

652

et al., 2022).

653

Our results showed that a pertinent description of dFC organization and its changes across

654

groups can be formulated in terms of two anatomical zones segregating ventral from dorsal

655

656

Bereiche (Feige. 6D). We found that the system spends less time in states with fluid Zone I dynamics

and high global integration, visiting them more transiently, while it gets stuck on the contrary

657

in less integrated states exhibiting Zone I hypersynchronisation (Feige. 2). At the dimer level,

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

.

/

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

658

pairwise interactions between regions in different zones get more irregularly bursty (Feige. 3). Bei

659

the level of higher order trimers and tetramers, meta-connectivity analysis revealed a loss of

660

coordination between the fluctuations of different sets of links, as quantified by dropping

661

participation coefficients (Feige. 4D). Trimer interactions between Zone I and Zone II, sowie

662

663

tetramers, were weakened more distinctively than the inter-zone dimer interactions.

Remarkably, regions in our limbic subnetwork for which conventional dimer analyses were not

664

different between groups, showed a remarkably reduced involvement in trimer interactions

665

between zones (Feige. 6). Gesamt, these findings point together toward a “loss of structure” in

666

dFC in parallel to the cognitive gradient across groups. This is in agreement with previous

667

668

669

studies that showed a reduction of the complexity of spontaneous fluctuations of coordinated

Aktivität (Tait et al., 2020).

Trotzdem, even though being quite encouraging, a conclusive validation of our findings

670

would require using larger cohorts, which preferably contains information on cortical thinning

671

and PET scans of tau and Aβ depositions, to test whether their distributions correlate with the

672

673

local network dynamics alterations we observe (thus establishing them as potential

physiopathological causes of these changes) or not (advocating for alternative explanations, sehen

674

later discussion). Ähnlich, our choice of regions and parcellations was arbitrary, generally

675

based on the successful use of the same parcellation in previous modelling-based analyses of

676

677

the same cohort (Zimmermann et al., 2018B). A better resolution fMRI from further cohorts

would allow validating our results with finer and more extended parcelations, especially for the

678

subcortical regions (Tian et al., 2020) that constitute the core of the limbic network on which

679

we have focused.

680

681

682

Interessant, our qualitative description emerges from radically different approaches to dFC

parameterization: a state-based approach (the PBM method by Thompson and Fransson,

(2016)); and a state-less approach (the random walk descriptions of dFC by Battaglia et al.

683

(2020) and Lombardo et al. (2020)). The PBM method is firmly rooted in the developing field

684

of temporal network theory (Holme and Saramäki, 2012). Temporal networks allow describing

685

inter-regional communication as it unfolds in time, similarly to a call-center, where operators

686

687

can handle a multitude of brief first-contact calls at certain moments and dedicate extensive

time to select customers at other times (Kovanen et al., 2013). Or to a primary school, Wo

688

students interact in small groups during lectures and play in mixed larger groups in the

689

playground during school-breaks (Gemmetto et al., 2014). Eventually, even fluctuations

690

between segregated or integrated states in brain systems at different scales (Shine et al., 2016;

691

Pedreschi et al., 2020) give rise to network dynamics not dissimilar to these social systems.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

T

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

692

Note that our use of terms such as “burstiness” or “activation” (vgl. Feige. 3D and E) is also

693

mediated from the jargon of temporal networks theory and should not be mistaken with the

694

usual meaning of these terms in neuroscience, as they refer to FC link dynamics rather than to

695

neuronal firing rates (exactly as we use the adjective “temporal” in the sense of “time-

696

dependent” and not in association with “temporal lobe”).

697

The dFC random walk approach (Arbabyazd et al., 2020; Battaglia et al., 2020; Lombardo

698

et al., 2020; Petkoski et al., 2023) models rs dFC as a temporal network as well, but focuses on

699

the variation from one network frame to the next, more than on the geometry of individual

700

network frames. dFC is seen as a flow in network space and the non-randomness of network

701

702

reconfiguration was investigated via a time-to-time correlation approach known as Meta-

Konnektivität (Lombardo et al., 2020). In a dFC context in which the mode of coordination

703

between regions is not frozen in time but changes smoothly, meta-connectivity reveals how the

704

fluctuations of one or more regions modulate the degree of coordination between the

705

fluctuations of other regions. Mit anderen Worten, meta-connectivity is an indicator of “many-body

706

707

coordination”. In der Tat, the terminology of dFC “dimers, trimers, tetramers” is reminiscent of

perturbative diagrammatic expansions in Statistical Physics, such as the virial expansion

708

(Landau and Lifshitz, 1980), in which clusters of increasingly large size account for

709

progressively more elaborate and nonlinear patterns of many-body interactions. MC can thus

710

711

be considered yet another form of high-order functional connectivity, adding up to a list of other

approaches to track higher-order coupling (Torres et al., 2021; Santoro et al., 2023) als

712

hypergraph or homological methods (Battiston et al., 2020; Petri and Barrat, 2018; Sizemore et

713

al., 2018), which have already identified synergistic aspects of human brain functioning (Luppi

714

et al., 2022; Varley et al., 2023).

715

716

Bedauerlicherweise, both of the dFC methods implemented in this study provide results depending

on specific parameter choices. Zum Beispiel, concerning the state-less random walk approach,

717

the selection of a window-size remains ultimately arbitrary. The window-size selected was short

718

in contrast to other studies. Jedoch, our statistical analyses suggest that this window size

719

results in similar discriminatory power as longer windows (Feige. S2A). Außerdem, it is

720

721

necessary to use short windows because the PBM method suggests that dwell-times in

consistent FC state epochs are often short and thus dFC is intrinsically fast (Feige. S2B). The need

722

to track the covariance of fast FC fluctuations has inspired additional approaches analogous to

723

MC, as edge-centric Functional Connectivity (eFC; Faskowitz et al., 2020). In this approach,

724

covariance is estimated between individual events of instantaneous co-fluctuation, without

725

arbitrary windowing. Jedoch, we showed in Lombardo et al. (2020) Das, despite the

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

.

T

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

726

significant relation between MC and eFC, the use of a sliding-window in the MC approach

727

produces a smoothing effect that partially denoises the graph structure of inter-link meta-

728

connections, allowing a cleaner determination of modules and “meta-hub” nodes with large

729

trimer strengths.

730

731

An additional aspect of the state-based PBM approach, is that it involves partially arbitrary

steps as the choice of a number of states. The retrieved FC states depend on the extracting

732

algorithm that depends on the brain parcellation and choice of regions of interest utilized. Wir

733

found four states and increased dwell-times in states with hyper-connectivity within Zone I.

734

This finding of increased probability in AD of visiting hyper-connected states is in agreement

735

736

with some state-based dFC studies (Gu et al., 2020), but in contrast with others (Fu et al., 2019;

Schumacher et al., 2019), which instead find higher dwell-times in disconnected states. Solch

737

discrepancies may arise because in the PBM method clustering of states is performed on

738

activation patterns rather than on time-resolved functional networks. Our procedure has the

739

advantage of showing that network dynamics is partially dissociated from node dynamics, mit

740

741

the possibility of hyper-connected FC modules arising both in presence of higher or lower

activity of the nodes composing this module (Feige. 2A). It may reduce the chance, Jedoch, von

742

detecting extreme events along dFC or transient atypical network configurations that would be

743

naturally assigned to separate clusters when directly clustering networks. Endlich, the mentioned

744

745

studies used reference parcellations with a larger number of regions or focusing on more

distributed network components, while here we particularly emphasize selected regions of

746

interest, such as temporal and paralimbic cortices, known to develop epileptiform activity

747

(Bakker et al., 2012; Cretin et al., 2016; Vossel et al., 2013). Daher, within the probed sub-

748

system of interest, hypersynchrony may become particularly prominent and over-expressed

749

750

751

(somit, the enhanced dwell-time in hyper-connected FC states), a fact that has direct

pathophysiological relevance.

Despite the arbitrary steps involved, both approaches independently provide sets of results

752

with a high mutual consistency, making unlikely that our analyses reflect exclusively methods

753

artefacts. Both methods confirm indeed that a dFC description in terms of two zones is

754

755

pertinent, as the distinction between Zones I and II organizes the modular structure of both FC

states in the state-based PBM approach (Feige. 2A) and of the MC matrices in the state-free dFC

756

random walk approach (Feige. 5B and C). Außerdem, both methods confirm that the increased

757

severity of cognitive decline across the four groups correlates with a reduced inter-zone

758

coordination: more time spent in states with weaker integration (Figs. 2B-C) and reduced inter-

759

zone trimer strengths (Feige. 6B). Such semantic agreement is remarkable especially given the

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

/

T

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

760

limitations of our approaches. Meta-connectivity analyses could be improved by seeking,

761

beyond plain module detection, for a hierarchical community structure, that is often present in

762

large networks (Jeub et al., 2018; Peixoto, 2014). State-based analyses could profit of better

763

clustering approaches, as used by Rasero et al. (2018). Jedoch, while acknowledging these

764

765

766

Einschränkungen, we found our four states and MC communities to be already highly interpretable,

in term of the anatomical nature of the entangled links.

Particularly interesting is the fact that the weakening of inter-zone trimer interactions across

767

the four groups decreases to such extent that some of these trimer switch from a positive to a

768

negative value. As previously mentioned, the coexistence of negative and positive couplings in

769

770

a graph or a hypergraph of interacting units is referred to in statistical physics as “frustration”

(Toulouse, 1986), since it is associated with the emergence of conflicts preventing smooth

771

relaxation to an equilibrium. To put these results in context, let us imagine that a dynamic FC

772

link (a dimer FCij) is positively coupled to a second dimer FCkl and negatively coupled to a

773

third dimer FCmn, and that the second and the third dimer simultaneously increase in strength

774

775

(i.e. FCkl and FCmn get larger). Then the dynamics of FCij will “freeze” under the contrasting

influence of the positive bias applied by FCkl (pushing it to assumer stronger values), und das

776

negative bias applied by FCmn (pushing it to assume smaller values). Daher, the change of

777

positive to a negative inter-zone influence –as the one signaled by the negative inter-zone trimer

778

779

strengths of many limbic region within Zone I– gives rise to conflicts between the flows of

Zone I and Zone II regions in AD patients, in contrast to control subjects where the fluctuations

780

of the same regions are naturally synchronized.

781

In particular in the context of cognition, Zone II regions such as the posterior Cingulate

782

Kortex (pCC) have been postulated to play a regulatory role on the level of brain meta-stability,

783

784

balancing “free-wheeling” internal cognition and focused outward attention (Leech et al., 2012;

Leech and Sharp, 2014). In control groups, pCC has strong positive dimer coupling and

785

moderately negative trimer coupling with regions in Zone I (Feige. 6). This could allow the pCC

786

to quickly coordinate with individual Zone I regions (and share information with them via direct

787

positive FC dimers), while simultaneously “lowering the volume” of

intra-zone I

788

789

communication (via pCC-rooted negative trimers with Zone I leaves). In AD subjects, Das

subtle equilibrium is lost, resulting potentially in perturbed integration of information within

790

and between Zone I regions. Remarkably, pCC is also a key hub of the Default Mode Network

791

(Raichle et al., 2001), a system whose dFC had already been suggested as a biomarker in the

792

conversion to AD (Jones et al., 2012; Puttaert et al., 2020).

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

.

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

793

Interessant, our analyses on trimer strengths could detect inter-group differences within

794

Zone I regions, for which the dimer analyses did not found significant differences. A possible

795

explanation for the better sensitivity of trimer-based analyses could trivially be due to a larger

796

sample-size, as there were more possible trimers than dimers, resulting in similar average

797

798

strengths but with a lower variance. Jedoch, another possibility could be that higher-order

interactions are readily affected by the pathology process earlier or at a higher degree than

799

pairwise interactions. This fact is difficult to assess from our dataset, which is not longitudinal.

800

Noch, this possibility is supported by our results showing that higher-order trimers and tetramers

801

terms convey in many cases genuinely new information, not redundant with dimer analyses.

802

803

In der Tat, even if we agree with other reports (Novelli and Razi, 2022) that dimer terms can

sometimes explain trimer and tetramer term, we found in addition important trimer

804

entanglement among otherwise individually weak dimers (Feige. 5A) that lacked strong pairwise

805

interactions between their dangling leaves (Feige. 5B). Such genuine trimers cannot be explained

806

by dimer motifs and describe thus a qualitatively different phenomenology, invisible to

807

808

conventional FC analyses. Similar considerations apply to tetramers (Feige. S3), which although

generally weaker in strength than dimers and trimers, form an additional and pervasive

809

background “medium” which also actively steer coordinated FC dimer fluctuations, with an

810

overall influence degraded by the pathological process (Feige. 5C and D). In the future, for an

811

812

even better appreciation of pathology effects on higher-order interactions, one may use methods

that facilitates the generalization to arbitrarily high orders, even higher than the third or the

813

fourth one, such as maximum entropy fitting (Ezaki et al., 2018; Savin and Tkačik, 2017) oder

814

other information-theory approaches (Rosas et al., 2019).

815

816

817

Another question is what the mechanistic origin could be of the observed spatio-temporal

complexity of dFC (and of its alterations). Previous studies have shown that structured dFC

may emerge as an effect of global brain network dynamics to be tuned at a slightly subcritical

818

working point (Arbabyazd et al., 2020; Glomb et al., 2017; Hansen et al., 2015), or as a

819

consequence of cascades of neuronal activations (Rabuffo et al., 2021) that occur due to the

820

flow on the manifold created by the symmetry breaking of the connectome (Fousek et al., 2022).

821

822

Jedoch, these studies did not use very precise criteria when referring to their capacity to

render dFC. In the future, the statistical descriptors of dFC alterations that we introduce here,

823

such as regional spectra of trimer and tetramer strengths, may be used as more detailed fitting

824

targets for the tuning of mean-field models aiming at explaining the circuit mechanisms for the

825

emergence of higher-order interactions. Such models, once fitted, may also allow reverse-

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

826

engineering the physiological changes that are responsible for the degradation of spatiotemporal

827

dFC complexity along the SNC-to-AD spectrum.

828

It is likely that the dFC alterations we observe between groups are caused at least in part by

829

underlying biological causes of AD, as the aggregation of misfolded proteins that cause cell

830

831

death and atrophy (Soto & Pritzkow, 2018). Jedoch, not all the symptoms can be explained

by these mechanisms. Among them, the existence of symptom severity fluctuating across hours

832

in a way not accountable for sudden variations of amyloid load (Palop et al., 2006) oder, yet, Die

833

phenomenon of cognitive reserve where subjects with virtually identical or even higher amount

834

of amyloid load than others can maintain a very efficient cognition, (vgl. Snowdon (2005) für

835

836

the famous “Nun Study” or Rentz et al., (2010) for a review of other studies with similar

conclusions). These findings suggest that neurodegeneration may coexist with compensations

837

of unspecified nature that allow “cognitive software” to operate properly despite “hardware

838

damage” (see e.g. Petkoski et al. (2023) for examples of dynamic compensation in healthy

839

Altern, or Courtiol et al. (2020) for a similar phenomenon in epilepsy). Hier, we propose the

840

841

hypothesis that preserved dFC complexity may act as a possible form of cognitive reserve. Wir

stress once again that, to check the soundness of this hypothesis, future analysis should rely on

842

richer datasets that contain PET scans of tau and Aβ depositions, and possibly even a

843

mechanistic model (Stefanovski et al., 2019; 2021) for their impact to the neuronal activity.

844

845

Letzten Endes, the degradation of dFC organizational complexity that we here described may

not only correlate with cognitive decline but also, eventually, contribute to cause it. In der Tat, A

846

dFC with a complex organization could be the hallmark of brain dynamics implementing

847

“healthy” cognitive processing. Computation can emerge from collective dynamics as long as

848

this dynamics is sufficiently complex, i.e. neither too ordered nor too random (Crutchfield,

849

850

2012; Crutchfield and Mitchell, 1995). More fundamentally, the existence of alternative

information processing states –transient FC networks?– and of non-random transitions between

851

these states –structured and complex dFC switching?– are two necessary conditions for

852

whatever information processing system to perform computation (Turing, 1937). A speculative

853

hypothesis is thus that the complexity of neural dynamics –and, more specifically the

854

855

complexity of ongoing dFC which is a measurable shadow of hidden neural processes– is an

instrumental resource for cognitive information processing. Cognitive deficits in pathology

856

could arise just in virtue of this resource becoming scarcer, because of less structured and more

857

random dynamics. This phenomenon has been speculatively observed in hippocampal neuronal

858

assembly dynamics in epilepsy (Clawson et al, 2021). In this line of thinking, preserved dFC

859

complexity would act as a “dynamic reserve” allowing the implementation of elaborate neural

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

/

T

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

/

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

860

computations (or “software patches”) to compensate for progressing neurodegeneration.

861

Analogously, enhanced dynamic complexity could be the substrate for the superior cognitive

862

performance achieved by subjects in the SNC group with respect to NC subjects. A more direct

863

exploration of the link between dFC complexity and cognitive processing in the healthy and

864

pathological brain will be needed to inquire into this suggestive hypothesis.

865

866

867

Materials and methods

868

Teilnehmer

869

870

871

The study included 73 subjects between 70 Und 90 years of age from the fourth wave of the

Sydney Memory and Ageing study (Sachdev et al., 2010; Tsang et al., 2013). The use of the

database was approved by the Human Research Ethics Committee of the University Texas at

872

Dallas. For detailed descriptive summaries on neuropsychological assessments for AD and

873

amnesic aMCI, we refer the reader to Zimmermann et al. (2018).

874

875

A specificity of our approach is the stratification of healthy controls with an additional

“super normal” category putting our focus not only on mechanisms of disease but also on

876

mechanisms of “health” based on cognitive performance. Ergebnisse

aus

zwölf

877

neuropsychological

tests were combined

In

Die

following

cognitive domains:

878

attention/processing speed, Erinnerung, Sprache, visuospatial ability, and executive function. In

879

880

brief (Mapstone et al., 2017) we classified cognitive membership for each subject based on the

composite Z-scores as supernormal controls (SNC) or normal controls (NC). For this, Die

881

supernormal (SNC) group was defined as Zmem > 1.35 SD (~90th percentile) and Zcog > 0.7 SD.

882

The normal control participants are conservatively defined with Zmem ± 0.7 SD (~15th %ile–

883

85th %ile) of the cohort median. The classification of subjects as AD and aMCI described in

884

885

Zimmermann et al was done by consensus included the following: The amnesic MCI group

was described by a cognitive decline at least in the memory domain (Zmem and/or Zcog < 1.5 SD 886 below normative values), paired to subjective complaint of cognitive deficit and without deficits 887 in activities of daily living (ADL). The AD group in presence of a diagnosis of Alzheimer's 888 Disease according to DSM-IV criteria (American Psychiatric Association, 2000) assessed by a 889 890 clinical expert panel that included significant cognitive decline in several cognitive domains in addition to significant decrease in ADLs (American Psychiatric Association, 2000; J. 891 Zimmermann et al., 2018). 892 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / / . t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 893 fMRI acquisition and preprocessing 894 Details about resting state functional MRI acquisition and preprocessing can be found in 895 Zimmermann et al. (2018). We briefly mention, as relevant here that during the fMRI 896 acquisition, participants were instructed to lie quietly in the scanner with their eyes closed. The 897 898 TR used for the T2* weighted EPI sequence of time-resolved BOLD imaging was 2000 ms. The acquisition time was of ~7 minutes. Data from all MRI modalities was preprocessed using 899 FSL and QA followed Smith et al. (Smith et al., 2004). Subjects were removed if any of their 900 scan acquisitions contained excessive artifacts including slice dropouts on the diffusion-images 901 (defined by zebra-like blurring or complete dropout; Pannek et al., 2012), the presence of 902 903 orbitofrontal EPI signal dropout (Weiskopf et al., 2007), excessive motion on T1-images (i.e., ringing), or severe geometric warping. For details of additional fMRI preprocessing details 904 (slice-timing correction, realignment and co-registration, linear detrending, head motion 905 regression, probabilistic segmentation, spatial smoothing, etc.) please refer to Perry et al. 906 (2017). 907 908 Network parcellation 909 For structural and functional parcellation the AAL atlas was used focused on 16 limbic 910 regions (see Fig. 6D) associated with early degeneration in AD according to Braak and Braak 911 912 staging as we did before (Joelle Zimmermann et al., 2018). The regions of interest included: Cingulate cortices (anterior, medial and posterior), Parahippocampal gyrus (including 913 Entorhinal cortex), Hippocampus proper, amygdala, and temporal pole (superior and middle). 914 In this study, as pertinent given the spatial organization retrieved in many of the analysis results, 915 we categorize regions as belonging: either to “Zone I”, including ventral regions (superior and 916 917 medial portion of the temporal pole, parahippocampal gyrus, hippocampus proper and amygdala in both hemispheres); or to “Zone II”, which included the six cingulate cortical 918 regions (posterior, medial, and anterior) in both hemispheres; Fig. 6D). This subdivision in two 919 separate zones allowed us the categorization of network links from dimers to higher-order 920 arrangements (trimers, tetramers) determining “within zone” or “between zone” interactions 921 922 based on the relative zone membership of the different nodes involved. We remark that the delimitations of Zone I and Zone II are inspired from data-driven considerations (the spatial 923 organization of FC state centroids in Figs 2 and MC modules in Fig. 4) rather than from a-priori 924 subdivisions. 925 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / / / . t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 926 State-based dynamic Functional Connectivity 927 In this study, we applied two complementary dynamic functional connectivity (dFC) 928 approaches to investigate non-stationarity of BOLD signals and capture the recurring, time- 929 varying, functional patterns. The first one was the so called point-based method (PBM) 930 931 932 introduced by Thompson and Fransson (2016), referred here as state-based dFC. This method assumes the existence of a small set of possible discrete FC configurations. In this approach, BOLD signals of each subject were concatenated along the temporal 933 dimension and transformed to z-scores using Fisher’s z-transformation to stabilize variance 934 prior to further analysis. Following Thompson and Fransson (2016), we applied a k-means 935 936 clustering algorithm on the concatenated time-series (Lloyd, 1982), to determine states based on global activity patterns (best partition out of 100 repetitions, max iterations 100). The 937 optimal number of 4 clusters (k = 4) was validated based on detecting an elbow in the variation 938 of the distortion score as a function of changing number of clusters k (Fig. S1B). Based on the 939 collections of activity patterns at times assigned to each of the states, we computed Pearson 940 941 correlation matrices, yielding k state-specific FC matrix FC(λ) (λ =1…4). A state was hence characterized by the centroid activation pattern of time-frames within the state cluster and by 942 its state-specific FC matrix (see Fig. 2A and Fig. S1A). To characterize the spatial properties 943 of state-specific FC, we then used a graph-theoretical approach and measured global and local 944 945 946 efficiencies (Achard and Bullmore, 2007; Latora and Marchiori, 2001) of the four FC(λ) networks (Fig. 2B) using the Brain Connectivity Toolbox (Rubinov and Sporns, 2010). To study the properties of the sequence of the dynamical states and the resulting temporal 947 network dynamics, we followed Thompson and Fransson (2016) to construct a temporal 948 network by using as network frame at a time t the graph FC(λ) of the state λ observed at time t. 949 This procedure transformed each fMRI session with T timestamps into a temporal network with 950 T frames, each including 𝑙 = 𝑛(𝑛 − 1)/2 links between each undirected pair of nodes. These 951 temporal networks were binarized thresholding links as a function of an arbitrary common 952 953 threshold θ. We then computed various temporal metrics describing network dynamics. First, we calculated the mean dwell-time for each subject by averaging the number of consecutive 954 time-points belonging to a given state before changing to a different state (Fig. 2C). Second, 955 we computed the proportion of time spent in each state as measured by percentage relative time 956 (state census) (Fig. 2D). Third (for this step, binarization was necessary), we measured inter- 957 958 contact times (ICT) of different links. ICTs for each link was defined as the temporal distance between events of link activation (i.e. link strength going above threshold) and offset (link l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / / . / t 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 959 strength going below threshold). For each link and each value of threshold θ, we computed the 960 mean activation μ as a measure of mean duration of a link’s active intervals; the total active 961 time fraction τ which is the total fraction of time in which a link was active relative to the 962 duration of the imaging acquisition; and the burstiness coefficient (Goh and Barabási, 2008) 963 assessed by: 964 θ = 𝛽𝑙 𝜎𝜏 − 𝜇𝜏 𝜎𝜏 + 𝜇𝜏 965 where 𝜎𝜏 and 𝜇𝜏 are, respectively, standard deviation and the mean of the ICTs along the 966 considered temporal network instance. The burstiness coefficient is bounded in the range 967 −1 ≤ 𝛽 ≤ 1, such that 𝛽 = −1 indicates a periodic/tonic link activation time-course, 𝛽 = 0 a 968 sequence with Poisson-like activation, and 𝛽 = 1 corresponds to bursty (time-clustered) events 969 of link activation (Fig. 3C). We finally evaluated also the memory coefficient (see always Goh 970 and Barabási, 2008), which is the autocorrelation of the sequence of link activation times; i.e., 971 972 973 974 975 if E(l) s is the duration of the s-th individual activation of link l, then memory coefficient for link l is λ(l) = CC(E(l) s , E(l) s+1), where CC denotes normalized Pearson correlation. Analogously, the burstiness and memory coefficients were averaged across links (or link classes, such as between-zone or within-zone links). Unlike the mean dwell-time or state census, mean ICTs and the quantifications computed 976 from them, depend on the specific choice of threshold θ. In absence of clear criteria to choose 977 an optimum threshold value, we varied systematically θ in the range 1% 𝑀𝐴𝑋 < 𝜃 < 978 10% 𝑀𝐴𝑋 and MAX is the global maximum FC entry across the retained FC(λ) state. The 979 maximum value was equal to MAX = 0.87, therefore the range was 0.0087 < 𝜃 < 0.087. 980 Absolute values of μ, τ and 𝛽 varied with θ, however we pooled them together across different 981 threshold values by computing relative variations (at each fixed θ) with respect to reference 982 values (threshold-dependent), based on the NC group. For instance, for burstiness, we 983 computed the relative excess burstiness for SNC, aMCI, and AD groups with respect to NCs 984 (Fig. 2E) as: 985 %𝛽𝜑,𝑧 θ = θ θ − 𝛽𝑁𝐶,𝑧 𝛽𝜑,𝑧 θ abs(𝛽𝜑,𝑧 θ + 𝛽𝑁𝐶,𝑧 ) 986 where 𝜑 = SNC, aMCI, AD and 𝑧 refer to intra-zone, and subsets of inter-zone links. 987 Analogously, we evaluated excess deviations for the SNC, aMCI, and AD relative to the NCs, 988 across all possible thresholds, for μ and τ. 989 990 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / . t / 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 991 State-free dynamic Functional Connectivity 992 In a second approach, we assumed that FC networks are continually morphing in time, 993 without priors on the existence of discrete state switching events, following Battaglia et al. 994 (2020), that conceptualized the evolution of FC as a stochastic walk in the high-dimensional 995 996 space of possible network configurations. This stochastic walk however is not trivial, as different inter-regional links covary according to a specific higher-order correlation structure 997 called meta-connectivity (Lombardo et al., 2020). State-free and smoothly varying dFC 998 temporal networks were extracted using a sliding window approach, adopting the random- 999 walks and meta-connectivity approaches (Battaglia et al., 2020; Lombardo et al., 2020; Petkoski 1000 et al., 2023) released within the dFCwalk toolbox (Arbabyazd et al., 2020). 1001 A short window of size 𝜔 = 5 TRs (10 s) was stepped without overlap over the BOLD time- 1002 series acquired in each fMRI session and then functional connectivity matrices (FC) were 1003 computed as window-restricted Pearson’s correlation matrices between BOLD time-series 1004 segments. Each temporal frame provides hence 𝑙 = 𝑛(𝑛 − 1)/2 undirected time-resolved link 1005 estimates, which can be collected into a 𝑙 × 𝑇 dFC stream, where T is the total number of 1006 windows. Each row of this stream provides the time-series of smoothed “instantaneous” 1007 variation of each FC link and the covariance between these variations can be described by a 1008 l x l matrix called the meta-connectivity (MC, Fig. 3B, (Lombardo et al., 2020)). The general 1009 entry of MC is given by: 1010 MC𝑙𝑖𝑗𝑙𝑚𝑛 = 𝑐𝑜𝑟𝑟 [dFC𝑙𝑖𝑗, dFC𝑙𝑚𝑛] 1011 for every pair of links (𝑙𝑖𝑗 and 𝑙𝑚𝑛) formed respectively between the regions (ij) and (mn). Our 1012 choice of window length 𝜔 = 5 TRs was guided by: first, the observation from state-based dFC 1013 analyses that ~90% of epochs within a state lasted less than 5 TRs (Fig. S2A), so that fast dFC 1014 dynamics may be lost using much longer windows; second, one-way ANOVA analysis on MC 1015 for a range of windows (from 3 to 20 TRs) showed that the best discrimination between SNC, 1016 NC, MCI and AD groups was achieved for 𝜔 = 5 TRs, with high between-group standard 1017 deviation and low within-group standard deviation (Fig. S2B). These analyses together suggest 1018 a small window of size 𝜔 = 5 TRs is both needed and sufficient to describe ongoing fast dFC 1019 fluctuations. 1020 Following and based on the correlation matrix between “dimers” (dynamic FC links between 1021 two regions i and j), the entries MCij, kl of the MC matrix are either computed based on the 1022 dynamics of four regions involved in the links (ij) and (kl), or at least three regions, when the l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / d o i / / / t . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 1023 two considered dimers share a common vertex (e.g. i = k). MC can thus be seen as a collation 1024 of higher-order interactions within the system, involving more than “two parts” (tetramers or 1025 trimers). In the case of a trimer, the region on which the two dimers converge to a “root” region, 1026 and the other two regions are the “leaves” of the trimer. In the case of a tetramer, each of the 1027 two non-incident dimers are called a “base”. 1028 MC modularity 1029 We used a graph-theory approach to quantify the communities of MC matrices. MC for all 1030 subjects were constructed and then averaged for each of the four subject’s groups (Fig. 3B). To 1031 detect the modular structures of MC, we used the community Louvain algorithm (Rubinov and 1032 Sporns, 2011). We used a parameter Γ = 1.4, determined heuristically to yield a modular 1033 partition naturally interpretable in anatomical terms. To quantify the modularity changes across 1034 the groups, we computed the index of modularity (Q*) as measure of degree of intra-module 1035 connectivity. Since MC is a signed matrix, we applied disproportionate scaling to the positive 1036 and negative values of modularity indices to consider a lower contribution of negative meta- 1037 link weights to the index of modularity (Rubinov and Sporns, 2011). To quantify the degree of 1038 inter-modular connectivity of group averaged MCs, we computed the Participation coefficient 1039 of each dFC dimer node following (Guimera, Roger; Amaral et al., 2005). This metric can be 1040 computed exactly as for an ordinary graph keeping in mind that FC links and meta-links among 1041 them are, respectively nodes and links in the MC graph. The Participation coefficient is close 1042 to one when meta-links of a link are distributed uniformly, therefore, integrated across MC 1043 modules and it is zero when all the meta-links of a link are segregated within its own MC 1044 module. 1045 Meta-strengths 1046 MC describes largely delocalized interactions but, for enhanced interpretability, it is 1047 important to describe the overall contribution of individual regions to the different higher-order 1048 interactions. Hence, we defined various indices of meta-strength. 1049 Concerning trimer interaction, a natural definition of the trimer strength of a region j is given 1050 by: 1051 MC𝑗 3 = ∑ ∑ MC𝑖𝑗,𝑗𝑛 𝑛 𝑖 ; 𝑖, 𝑛 ≠ 𝑗 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / d o i / t / / . 1 0 1 1 6 2 n e n _ a _ 0 0 3 3 2 2 1 5 3 2 5 2 n e n _ a _ 0 0 3 3 2 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 1052 Here j is the root of the summed trimers, hence the name of “root-pinned” trimer strength (to 1053 contrast it with alternative definitions, not used in this study, where the pinned region may lie 1054 at a leaf). Analogously, we can define tetramer strengths of a link (ij): 1055 MC𝑖𝑗 4 = ∑ ∑ MC𝑖𝑗,𝑚𝑛 ; 𝑖𝑗 ≠ 𝑚𝑛 𝑛𝑚 1056 denoted as “base-pinned” as the frozen link is a dimer base of the tetramer. 1057 A trimer is defined between zones or within zones depending on the zones to which its leaves 1058 belong. If all leaves are in the same zone (independently from where the root is) then the trimer 1059 is considered within zone, otherwise it is considered between zones. For tetramers we 1060 distinguished tetramers with base within a zone (if both bases are within zone dimers) or base 1061 between zones (if both bases are between zones). There are more combinatorial cases for 1062 tetramers that were ignored in this study for simplicity. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . 1063 1064 Comparing MC and FC 1065 1066 We also computed more conventional FC strengths (dimer strengths) for each node as: FC𝑟 𝜆 = ∑ FC𝑖𝑟 𝑖 1067 where 𝜆 is an index referring to intra-zone if 𝑖 and 𝑟 are in the same zones (Fig. S4A), or inter- 1068 zone if they belong to different zones (Fig. 5A). To evaluate MC-FC redundancy on the single 1069 subject-level, we computed the Pearson’s correlation between roots-pinned trimers and FC 1070 node-degrees for all nodes and subject (Fig. 4A)., by the following formula: 1071 ∆𝑛𝑜𝑑𝑒−𝑙𝑒𝑣𝑒𝑙 = 𝑐𝑜𝑟𝑟[FC𝑟 𝜆, MC𝑟 3𝜆 ] 1072 For the tetramers case, the same MC-FC comparison was done for edges computing: 1073 ∆𝑒𝑑𝑔𝑒−𝑙𝑒𝑣𝑒𝑙 = 𝑐𝑜𝑟𝑟[FC𝑖𝑗 𝜆 , MC𝑖𝑗 4𝜆 ] 1074 on the subject-level and for two intra- and inter-zone subsets (Fig. S3A). 1075 We also introduced notions of genuine trimer and tetramers, to identify higher-order 1076 interactions that were not completely explained by existing motifs of dimer interactions. We 1077 separated trimers into three groups: 1) within zone, 2) leaves in same zone, and 3) leaves in two 1078 zones. For a given trimer with 𝑟 as root and 𝑖, 𝑗 as leave regions, we defined the following 1079 condition: 1080 𝑀𝐶𝑖𝑟,𝑗𝑟 > 𝐹𝐶𝑖𝑗

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

.

/

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1081

for a trimer to be considered “genuine”, meaning that the trimer interaction coupling 𝑖 and 𝑗 via

1082

𝑟 is not a mere byproduct of the dimer between 𝑖 and 𝑗 but it is actually stronger (another

1083

interpretation is that the interaction path between i and j is “shorter” when the interaction is

1084

mediated by r than when it is direct). Analogously, we separated tetramers into two groups: 1)

1085

base in two zones, Und 2) base in same zone. For a give tetramer with (𝑖, 𝑗) Und (𝑚, 𝑛) dimers,

1086

we the defined the following genuinity condition:

1087

1088

1089

Verweise

𝑀𝐶𝑖𝑗,𝑚𝑛 > 𝐹𝐶𝑖𝑗

1090

1091

1092

1093

1094

1095

1096

1097

1098

1099

1100

1101

1102

1103

1104

1105

1106

1107

1108

1109

1110

1111

1112

Achard, S., Bullmore, E., 2007. Efficiency and cost of economical brain functional networks. PLoS

Comput. Biol. https://doi.org/10.1371/journal.pcbi.0030017

Allen, E.A., Damaraju, E., Plis, S.M., Erhardt, E.B., Eichele, T., Calhoun, V.D., 2014. Tracking

whole-brain connectivity dynamics in the resting state. Cereb. Kortex 24, 663–676.

https://doi.org/10.1093/cercor/bhs352

American Psychiatric Association, 2000. Diagnostic and statistical manual of mental disorders (4th

Ed. text revised). Diagnostic Stat. Man. Ment. Disord. 4th Ed. TR.

Arbabyazd, L.M., Lombardo, D., Blin, O., Didic, M., Battaglia, D., Jirsa, V., 2020. Dynamic

Functional Connectivity as a complex random walk: Definitions and the dFCwalk toolbox.

MethodsX 7, 101168. https://doi.org/10.1016/j.mex.2020.101168

Arnold, S.E., Hyman, B.T., Flory, J., Damasio, A.R., Van Hoesen, G.W., 1991. The topographical and

neuroanatomical distribution of neurofibrillary tangles and neuritic plaques in the cerebral cortex

of patients with alzheimer’s disease. Cereb. Kortex 1. https://doi.org/10.1093/cercor/1.1.103

Bakker, A., Krauss, G.L., Albert, M.S., Speck, C.L., Jones, L.R., Stark, C.E., Yassa, M.A., Bassett,

S.S., Shelton, A.L., Gallagher, M., 2012. Reduction of Hippocampal Hyperactivity Improves

Cognition in Amnestic Mild Cognitive Impairment. Neuron.

https://doi.org/10.1016/j.neuron.2012.03.023

Bassett, D.S., Wymbs, N.F., Porter, M.A., Mucha, P.J., Carlson, J.M., Grafton, S.T., 2011. Dynamic

reconfiguration of human brain networks during learning. PNAS.

https://doi.org/10.1073/pnas.1018985108

Bateman, R.J., Xiong, C., Benzinger, T.L.S., Fagan, A.M., Goate, A., Fuchs, N.C., Marcus, D.S., Cairns,

N.J., Xie, X., Blazey, T.M., Holtzman, D.M., Santacruz, A., Buckles, V., Oliver, A., Moulder,

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

.

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1113

1114

1115

1116

1117

1118

1119

1120

1121

1122

1123

1124

1125

1126

1127

1128

1129

1130

1131

1132

1133

1134

1135

1136

1137

1138

1139

1140

1141

1142

1143

1144

1145

1146

K., Aisen, P.S., Ghetti, B., Klunk, W.E., McDade, E., Martins, R.N., Masters, C.L., Mayeux, R.,

Ringman, J.M., Rossor, M.N., Schofield, P.R., Sperling, R.A., Salloway, S., Morris, J.C., 2012.

Clinical and biomarker changes in dominantly inherited Alzheimer’s disease. N. Engl. J. Med.

https://doi.org/10.1056/NEJMoa1202753

Battaglia, D., Boudou, T., Hansen, E.C.A., Lombardo, D., Chettouf, S., Daffertshofer, A., McIntosh,

A.R., Zimmermann, J., Ritter, P., Jirsa, V., 2020. Dynamic Functional Connectivity between

order and randomness and its evolution across the human adult lifespan. Neurobild 222,

117156. https://doi.org/10.1016/j.neuroimage.2020.117156

Battiston, F., Cencetti, G., Iacopini, ICH., Latora, V., Lucas, M., Patania, A., Jung, J.G., Petri, G., 2020.

Networks beyond pairwise interactions: Structure and dynamics. Phys. Rep. 874, 1–92.

https://doi.org/10.1016/j.physrep.2020.05.004

Braak, H., Braak, E., 1991. Neuropathological stageing of Alzheimer-related changes. Acta

Neuropathol. https://doi.org/10.1007/BF00308809

Braun, U., Schäfer, A., Walter, H., Erk, S., Romanczuk-Seiferth, N., Haddad, L., Schweiger, J.I.,

Grimm, O., Heinz, A., Tost, H., Meyer-Lindenberg, A., Bassett, D.S., 2015. Dynamic

reconfiguration of frontal brain networks during executive cognition in humans. PNAS.

https://doi.org/10.1073/pnas.1422487112

Brier, HERR., Thomas, J.B., Fagan, A.M., Hassenstab, J., Holtzman, D.M., Benzinger, T.L., Morris,

J.C., Ances, B.M., 2014. Functional connectivity and graph theory in preclinical Alzheimer’s

Krankheit. Neurobiol. Altern. https://doi.org/10.1016/j.neurobiolaging.2013.10.081

Calhoun, V.D., Müller, R., Pearlson, G., Adali, T., 2014. The Chronnectome: Time-Varying

Connectivity Networks as the Next Frontier in fMRI Data Discovery. Neuron 84, 262–274.

https://doi.org/10.1016/j.neuron.2014.10.015

Chen, X., Zhang, H., Gao, Y., Wee, C.Y., Li, G., Shen, D., 2016. High-order resting-state functional

connectivity network for MCI classification. Hum. Brain Mapp.

https://doi.org/10.1002/hbm.23240

Chen, X., Zhang, H., Zhang, L., Shen, C., Lee, S.W., Shen, D., 2017. Extraction of dynamic functional

connectivity from brain grey matter and white matter for MCI classification. Hum. Brain Mapp.

https://doi.org/10.1002/hbm.23711

Courtiol, J., Guye, M., Bartolomei, F., Petkoski, S., Jirsa, V.K., 2020. Dynamical mechanisms of

interictal resting-state functional connectivity in epilepsy. J. Neurosci. 40, 5572–5588.

doi:10.1523/JNEUROSCI.0905-19.2020

Cretin, B., Sellal, F., Philippi, N., Bousiges, O., Di Bitonto, L., Martin-Hunyadi, C., Blanc, F., 2016.

Epileptic Prodromal Alzheimer’s Disease, a Retrospective Study of 13 New Cases: Expanding

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

T

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1147

1148

1149

1150

1151

1152

1153

1154

1155

1156

1157

1158

1159

1160

1161

1162

1163

1164

1165

1166

1167

1168

1169

1170

1171

1172

1173

1174

1175

1176

1177

1178

1179

1180

the Spectrum of Alzheimer’s Disease to an Epileptic Variant? J. Alzheimer’s Dis.

https://doi.org/10.3233/JAD-150096

Crutchfield, J.P., 2012. Between order and chaos. Nat. Phys. https://doi.org/10.1038/nphys2190

Crutchfield, J.P., Mitchell, M., 1995. The evolution of emergent computation. PNAS.

https://doi.org/10.1073/pnas.92.23.10742

Damaraju, E., Allen, E.A., Belger, A., Ford, J.M., McEwen, S., Mathalon, D.H., Mueller, B.A.,

Pearlson, G.D., Potkin, S.G., Preda, A., Turner, J.A., Vaidya, J.G., Van Erp, T.G., Calhoun,

V.D., 2014. Dynamic functional connectivity analysis reveals transient states of dysconnectivity

in schizophrenia. NeuroImage Clin. https://doi.org/10.1016/j.nicl.2014.07.003

Damoiseaux, J.S., Prater, K.E., Müller, B.L., Greicius, M.D., 2012. Functional connectivity tracks

clinical deterioration in Alzheimer’s disease. Neurobiol. Altern.

https://doi.org/10.1016/j.neurobiolaging.2011.06.024

Davison, E.N., Schlesinger, K.J., Bassett, D.S., Lynall, M.E., Müller, M.B., Grafton, S.T., Carlson,

J.M., 2015. Brain Network Adaptability across Task States. PLoS Comput. Biol.

https://doi.org/10.1371/journal.pcbi.1004029

Davison, E.N., Turner, B.O., Schlesinger, K.J., Müller, M.B., Grafton, S.T., Bassett, D.S., Carlson,

J.M., 2016. Individual Differences in Dynamic Functional Brain Connectivity across the Human

Lifespan. PLoS Comput. Biol. https://doi.org/10.1371/journal.pcbi.1005178

von dir, F., Koini, M., Schouten, T.M., Seiler, S., van der Grond, J., Lechner, A., Schmidt, R., von

Rooij, M., Rombouts, S.A.R.B., 2018. A comprehensive analysis of resting state fMRI measures

to classify individual patients with Alzheimer’s disease. Neurobild.

https://doi.org/10.1016/j.neuroimage.2017.11.025

Dennis, E.L., Thompson, P.M., 2014. Functional brain connectivity using fMRI in aging and

Alzheimer’s disease. Neuropsychol. Rev. https://doi.org/10.1007/s11065-014-9249-6

Ezaki, T., Sakaki, M., Watanabe, T., Masuda, N., 2018. Age-related changes in the ease of dynamical

transitions in human brain activity. Hum. Brain Mapp. https://doi.org/10.1002/hbm.24033

Faskowitz, J., Esfahlani, F.Z., Jo, Y., Spurns, O., Betzel, R.F., 2020. Edge-centric functional network

representations of human cerebral cortex reveal overlapping system-level architecture. Nat.

Neurosci. 23, 1644–1654. https://doi.org/10.1038/s41593-020-00719-y

Fiorenzato, E., Strafella, A.P., Kim, J., Schifano, R., Weis, L., Antonini, A., Biundo, R., 2019.

Dynamic functional connectivity changes associated with dementia in Parkinson’s disease.

Gehirn. https://doi.org/10.1093/brain/awz192

Fleisher, A.S., Sherzai, A., Taylor, C., Langbaum, J.B.S., Chen, K., Buxton, R.B., 2009. Resting-state

BOLD networks versus task-associated functional MRI for distinguishing Alzheimer’s disease

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

/

.

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1181

1182

1183

1184

1185

1186

1187

1188

1189

1190

1191

1192

1193

1194

1195

1196

1197

1198

1199

1200

1201

1202

1203

1204

1205

1206

1207

1208

1209

1210

1211

1212

1213

risk groups. Neurobild. https://doi.org/10.1016/j.neuroimage.2009.06.021

Fousek, J., Rabuffo, Gi., Gudibanda, K., Sheheitli, H., Jirsa, V., Petkoski, S., 2022. The structured

flow on the brain’s resting state manifold. eNeuro 8. doi:10.1523/ENEURO.0283-21.2021.

Fuchs, M.D., Rachel, M.E., 2007. Spontaneous fluctuations in brain activity observed with functional

magnetic resonance imaging. Nat Rev Neurosci 8, 700–711. https://doi.org/10.1038/nrn2201

Fu, Z., Caprihan, A., Chen, J., Von, Y., Adair, J.C., Sui, J., Rosenberg, G.A., Calhoun, V.D., 2019.

Altered static and dynamic functional network connectivity in Alzheimer’s disease and

subcortical ischemic vascular disease: shared and specific brain connectivity abnormalities.

Hum. Brain Mapp. https://doi.org/10.1002/hbm.24591

Gemmetto, V., Barrat, A., Cattuto, C., 2014. Mitigation of infectious disease at school: Targeted class

closure vs school closure. BMC Infect. Dis. https://doi.org/10.1186/s12879-014-0695-9

Glenner, G.G., Wong, C.W., 1984. Alzheimer’s disease: Initial report of the purification and

characterization of a novel cerebrovascular amyloid protein. Biochem. Biophys. Res. Commun.

https://doi.org/10.1016/S0006-291X(84)80190-4

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

Glomb, K., Ponce-Alvarez, A., Gilson, M., Ritter, P., Deco, G., 2017. Resting state networks in

F
/

D
Ö

ich
/

/

.

T

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

/

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

empirical and simulated dynamic functional connectivity. Neurobild.

https://doi.org/10.1016/j.neuroimage.2017.07.065

Goh, K.I., Barabási, A.L., 2008. Burstiness and memory in complex systems. EPL.

https://doi.org/10.1209/0295-5075/81/48002

Greicius, M.D., Srivastava, G., Reiss, A.L., Menon, V., 2004. Default-mode network activity

distinguishes Alzheimer’s disease from healthy aging: Evidence from functional MRI. PNAS.

https://doi.org/10.1073/pnas.0308627101

Gu, Y., Lin, Y., Huang, L., Ma, J., Zhang, J., Xiao, Y., Dai, Z., 2020. Abnormal dynamic functional

connectivity in Alzheimer’s disease. CNS Neurosci. Ther. https://doi.org/10.1111/cns.13387

Guimera, Roger; Amaral, L.N., NICO, Guimerà, R., Amaral, L.A.N., 2005. Functional cartography of

complex metabolic networks. Natur 433, 895–900. https://doi.org/10.1038/nature03286.1.

Guimerà, R., Amaral, L.A.N., 2005. Functional cartography of complex metabolic networks. Natur.

https://doi.org/10.1038/nature03288

Hansen, E.C.A., Battaglia, D., Spiegler, A., Deco, G., Jirsa, V.K., 2015. Funktionale Konnektivität

Dynamik: Modeling the switching behavior of the resting state. Neurobild 105, 525–535.

https://doi.org/10.1016/j.neuroimage.2014.11.001

Hedden, T., Van Dijk, K.R.A., Becker, J.A., Mehta, A., Sperling, R.A., Johnson, K.A., Buckner, R.L.,

2009. Disruption of functional connectivity in clinically normal older adults harboring amyloid

1214

1215

1216

1217

1218

1219

1220

1221

1222

1223

1224

1225

1226

1227

1228

1229

1230

1231

1232

1233

1234

1235

1236

1237

1238

1239

1240

1241

1242

1243

1244

1245

1246

1247

burden. J. Neurosci. https://doi.org/10.1523/JNEUROSCI.3189-09.2009

Holme, P., Saramäki, J., 2012. Temporal networks. Phys. Rep.

https://doi.org/10.1016/j.physrep.2012.03.001

Hou, Y., Und, X., Babbar, M., Wei, Y., Hasselbalch, S.G., Croteau, D.L., Bohr, V.A., 2019. Ageing as

a risk factor for neurodegenerative disease. Nat. Rev. Neurol. https://doi.org/10.1038/s41582-

019-0244-7

Hutchison, R.M., Morton, J.B., 2015. Tracking the brain’s functional coupling dynamics over

Entwicklung. J. Neurosci. https://doi.org/10.1523/JNEUROSCI.4638-14.2015

Hutchison, R.M., Womelsdorf, T., Allen, E.A., Bandettini, P.A., Calhoun, V.D., Corbetta, M., Della

Penna, S., Duyn, J.H., Glover, G.H., Gonzalez-Castillo, J., Handwerker, D.A., Keilholz, S.,

Kiviniemi, V., Leopold, D.A., de Pasquale, F., Spurns, O., Walter, M., Chang, C., 2013.

Dynamic functional connectivity: Promise, issues, and interpretations. Neurobild.

https://doi.org/10.1016/j.neuroimage.2013.05.079

Jeub, L.G.S., Spurns, O., Fortunato, S., 2018. Multiresolution Consensus Clustering in Networks. Sci.

Rep. 8. doi:10.1038/s41598-018-21352-7

Jia, H., Hu, X., Deshpande, G., 2014. Behavioral relevance of the dynamics of the functional brain

connectome. Brain Connect. https://doi.org/10.1089/brain.2014.0300

Jones, D.T., MacHulda, M.M., Vemuri, P., McDade, E.M., Zeng, G., Senjem, M.L., Gunter, J.L.,

Przybelski, S.A., Avula, R.T., Knopman, D.S., Boeve, B.F., Petersen, R.C., Jack, C.R., 2011.

Age-related changes in the default mode network are more advanced in Alzheimer disease.

Neurologie. https://doi.org/10.1212/WNL.0b013e318233b33d

Jones, D.T., Vemuri, P., Murphy, M.C., Gunter, J.L., Senjem, M.L., Machulda, M.M., Przybelski,

S.A., Gregg, B.E., Kantarci, K., Knopman, D.S., Boeve, B.F., Petersen, R.C., Jack, C.R., 2012.

Non-stationarity in the “resting brain’s” modular architecture. PLoS One.

https://doi.org/10.1371/journal.pone.0039731

Kim, J., Criaud, M., Cho, S.S., Díez-Cirarda, M., Mihaescu, A., Coakeley, S., Ghadery, C., Valli, M.,

Jacobs, M.F., Houle, S., Strafella, A.P., 2017. Abnormal intrinsic brain functional network

dynamics in Parkinson’s disease. Gehirn. https://doi.org/10.1093/brain/awx233

Kovanen, L., Kaski, K., Kertész, J., Saramäki, J., 2013. Temporal motifs reveal homophily, Geschlecht-

specific patterns, and group talk in call sequences. PNAS.

https://doi.org/10.1073/pnas.1307941110

LANDAU, L.D., LIFSHITZ, E.M., 1980. COURSE OF THEORETICAL PHYSICS Volume 5,

STATISTICAL PHYSICS Part 1. Stat. Phys.

Latora, V., Marchiori, M., 2001. Efficient behavior of small-world networks. Phys. Rev. Lett.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1248

1249

1250

1251

1252

1253

1254

1255

1256

1257

1258

1259

1260

1261

1262

1263

1264

1265

1266

1267

1268

1269

1270

1271

1272

1273

1274

1275

1276

1277

1278

1279

1280

1281

https://doi.org/10.1103/PhysRevLett.87.198701

Lavanga, M., Stumme, J., Yalcinkaya, B.H., Jockwitz, C., Sheheitli, H., Bittner, N., Hashemi, M.,

Petkoski, S., Caspers, S., Jirsa, V.K., 2022. The virtual aging brain : a model-driven explanation

for cognitive decline in older subjects. bioRxiv (preprint) 1–57.

Leech, R., Braga, R., Sharp, D.J., 2012. Echoes of the brain within the posterior cingulate cortex. J.

Neurosci. https://doi.org/10.1523/JNEUROSCI.3689-11.2012

Leech, R., Sharp, D.J., 2014. The role of the posterior cingulate cortex in cognition and disease. Gehirn.

https://doi.org/10.1093/brain/awt162

Lemere, C.A., Blusztajn, J.K., Yamaguchi, H., Wisniewski, T., Saido, T.C., Selkoe, D.J., 1996.

Sequence of deposition of heterogeneous amyloid β-peptides and APO E in down syndrome:

Implications for initial events in amyloid plaque formation. Neurobiol. Dis.

https://doi.org/10.1006/nbdi.1996.0003

Liao, W., Zhang, Z., Mantini, D., Xu, Q., Ji, G.J., Zhang, H., Wang, J., Wang, Z., Chen, G., Tian, L.,

Jiao, Q., Zang, Y.F., Lu, G., 2014. Dynamical intrinsic functional architecture of the brain during

absence seizures. Brain Struct. Funct. https://doi.org/10.1007/s00429-013-0619-2

Lindquist, M.A., Xu, Y., Nebel, M.B., Caffo, B.S., 2014. Evaluating dynamic bivariate correlations in

resting-state fMRI: A comparison study and a new approach. Neurobild.

https://doi.org/10.1016/j.neuroimage.2014.06.052

Liu, F., Wang, Y., Li, M., Wang, W., Li, R., Zhang, Z., Lu, G., Chen, H., 2017. Dynamic functional

network connectivity in idiopathic generalized epilepsy with generalized tonic–clonic seizure.

Hum. Brain Mapp. https://doi.org/10.1002/hbm.23430

Lloyd, S.P., 1982. Least Squares Quantization in PCM. IEEE Trans. Inf. Theory.

https://doi.org/10.1109/TIT.1982.1056489

Lombardo, D., Cassé-Perrot, C., Ranjeva, J.P., Le Troter, A., Guye, M., Wirsich, J., Payoux, P.,

Bartrés Faz, D., Bordet, R., Richardson, J.C., Felician, O., Jirsa, V., Blin, O., Didic, M.,

Battaglia, D., 2020. Modular slowing of resting-state dynamic functional connectivity as a

marker of cognitive dysfunction induced by sleep deprivation. Neurobild 222.

https://doi.org/10.1016/j.neuroimage.2020.117155

Luppi, A.I., Mediano, P.A.M., Rosas, F.E., Holland, N., Fryer, T.D., O’Brien, J.T., Rowe, J.B.,

Menon, D.K., Bor, D., Stamatakis, E.A., 2022. A synergistic core for human brain evolution and

Erkenntnis. Nat. Neurosci. 25. doi:10.1038/s41593-022-01070-0

Mapstone, M., Cheema, A.K., Zhong, X., Fiandaca, M.S., Federoff, H.J., 2017. Biomarker validation:

Methods and matrix matter. Alzheimer’s Dement. https://doi.org/10.1016/j.jalz.2016.11.004

Masters, C.L., Bateman, R., Blennow, K., Rowe, C.C., Sperling, R.A., Cummings, J.L., 2015.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

/

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1282

1283

1284

1285

1286

1287

1288

1289

1290

1291

1292

1293

1294

1295

1296

1297

1298

1299

1300

1301

1302

1303

1304

1305

1306

1307

1308

1309

1310

1311

1312

1313

1314

Alzheimer’s disease. Nat. Rev. Dis. Prim. https://doi.org/10.1038/nrdp.2015.56

Mezard, M., Parisi, G., Virasoro, M.A., Thouless, D.J., 1988. Spin Glass Theory and Beyond. Phys.

Heute 41. https://doi.org/10.1063/1.2811676

Mormino, E.C., Smiljic, A., Hayenga, A.O., H. Onami, S., Greicius, M.D., Rabinovici, G.D., Janabi,

M., Bäcker, S.L., V. Yen, ICH., Madison, C.M., Müller, B.L., Jagust, W.J., 2011. Relationships

between beta-amyloid and functional connectivity in different components of the default mode

network in aging. Cereb. Kortex. https://doi.org/10.1093/cercor/bhr025

Novelli, L., Razi, A., 2022. A mathematical perspective on edge-centric brain functional connectivity.

Nat. Commun. 13, 2693. https://doi.org/10.1038/s41467-022-29775-7

Palop, J.J., Chin, J., Mucke, L., 2006. A network dysfunction perspective on neurodegenerative

diseases. Natur 443, 768–773. https://doi.org/10.1038/nature05289

Pannek, K., Guzzetta, A., Colditz, P.B., Rose, S.E., 2012. Diffusion MRI of the neonate brain:

Acquisition, processing and analysis techniques. Pediatr. Radiol. https://doi.org/10.1007/s00247-

012-2427-X

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

Pedreschi, N., Bernard, C., Clawson, W., Quilichini, P., Barrat, A., Battaglia, D., 2020. Dynamic core-

F
/

D
Ö

ich
/

periphery structure of information sharing networks in entorhinal cortex and hippocampus. Netw

Neurosci 4, 946–975. https://doi.org/10.1162/netn_a_00142

Peixoto, T.P., 2014. Hierarchical block structures and high-resolution model selection in large

Netzwerke. Phys. Rev. X 4. doi:10.1103/PhysRevX.4.011047

Petkoski, S., Ritter, P., Jirsa, V.K., 2023. White-matter degradation and dynamical compensation

support age-related functional alterations in human brain. Cereb. Cortex bhac500, 1–16.

https://doi.org/doi.org/10.1093/cercor/bhac500

Petrella, J.R., Sheldon, F.C., Prince, S.E., Calhoun, V.D., Doraiswamy, P.M., 2011. Default mode

network connectivity in stable vs progressive mild cognitive impairment. Neurologie.

https://doi.org/10.1212/WNL.0b013e31820af94e

Petri, G., Barrat, A., 2018. Simplicial Activity Driven Model. Phys. Rev. Lett.

https://doi.org/10.1103/PhysRevLett.121.228301

Premi, E., Gazzina, S., Diano, M., Girelli, A., Calhoun, V.D., Iraji, A., Gong, Q., Li, K., Cauda, F.,

Gasparotti, R., Padovani, A., Borroni, B., Magoni, M., 2020. Enhanced dynamic functional

Konnektivität (whole-brain chronnectome) in chess experts. Sci. Rep.

https://doi.org/10.1038/s41598-020-63984-8

Preti, M.G., Bolton, T.A., Van De Ville, D., 2017. The dynamic functional connectome: State-of-the-

art and perspectives. Neurobild. https://doi.org/10.1016/j.neuroimage.2016.12.061

/

T

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1315

1316

1317

1318

1319

1320

1321

1322

1323

1324

1325

1326

1327

1328

1329

1330

1331

1332

1333

1334

1335

1336

1337

1338

1339

1340

1341

1342

1343

1344

1345

1346

1347

1348

Puttaert, D., Coquelet, N., Wens, V., Peigneux, P., Fery, P., Rovai, A., Trotta, N., Sadeghi, N., Coolen,

T., Bier, J.C., Goldman, S., De Tiège, X., 2020. Alterations in resting-state network dynamics

along the Alzheimer’s disease continuum. Sci. Rep. https://doi.org/10.1038/s41598-020-76201-3

Qin, J., Chen, S.G., Hu, D., Zeng, L.L., Fan, Y.M., Chen, X.P., Shen, H., 2015. Predicting individual

brain maturity using dynamic functional connectivity. Front. Hum. Neurosci.

https://doi.org/10.3389/fnhum.2015.00418

Rabuffo, G., Fousek, J., Bernard, C., Jirsa, V., 2021. Neuronal cascades shape whole-brain functional

dynamics at rest. eNeuro 8. https://doi.org/10.1523/ENEURO.0283-21.2021

Rachel, M.E., MacLeod, A.M., Snyder, A.Z., Powers, W.J., Gusnard, D.A., Shulman, G.L., 2001. A

default mode of brain function. PNAS. https://doi.org/10.1073/pnas.98.2.676

Rasero, J., Aerts, H., Cortes, J.M., Stramaglia, S., Marinazzo, D., Fisica, D., Aldo, S., Bari, M.,

Nazionale, ICH., Bari, S., 2018. Predicting functional networks from region connectivity profiles in

task-based versus resting-state fMRI data 1–15. doi:10.1101/259077

Rentz, D.M., Locascio, J.J., Becker, J.A., Moran, E.K., Ing, E., Buckner, R.L., Sperling, R.A.,

Johnson, K.A., 2010. Cognition, reserve, and amyloid deposition in normal aging. Ann. Neurol.

https://doi.org/10.1002/ana.21904

Rombouts, S.A.R.B., Barkhof, F., Goekoop, R., Stam, C.J., Scheltens, P., 2005. Altered resting state

networks in mild cognitive impairment and mild Alzheimer’s disease: Eine fMRT-Studie. Hum.

Brain Mapp. https://doi.org/10.1002/hbm.20160

Rosas, F.E., Mediano, P.A.M., Gastpar, M., Jensen, H.J., 2019. Quantifying high-order

interdependencies via multivariate extensions of the mutual information. Phys. Rev. E 100,

32305. https://doi.org/10.1103/PhysRevE.100.032305

Rousseeuw, P.J., 1987. Silhouettes: A graphical aid to the interpretation and validation of cluster

Analyse. J. Comput. Appl. Math. https://doi.org/10.1016/0377-0427(87)90125-7

Rubinow, M., Spurns, O., 2011. Weight-conserving characterization of complex functional brain

Netzwerke. Neurobild 56, 2068–2079. https://doi.org/10.1016/j.neuroimage.2011.03.069

Rubinow, M., Spurns, O., 2010. Complex network measures of brain connectivity: Uses and

interpretations. Neurobild 52, 1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003

Sachdev, P.S., Brodaty, H., Reppermund, S., Kochan, N.A., Trollor, J.N., Draper, B., Slavin, M.J.,

Crawford, J., Kang, K., Broe, G.A., Mather, K.A., Lux, O., 2010. The Sydney Memory and

Ageing Study (MAS): Methodology and baseline medical and neuropsychiatric characteristics of

an elderly epidemiological non-demented cohort of Australians aged 70-90 Jahre. Int.

Psychogeriatrics. https://doi.org/10.1017/S1041610210001067

Sakoğlu, Ü., Pearlson, G.D., Kiehl, K.A., Wang, Y.M., Michael, A.M., Calhoun, V.D., 2010. A

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

/

.

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

T

.

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1349

1350

1351

1352

1353

1354

1355

1356

1357

1358

1359

1360

1361

1362

1363

1364

1365

1366

1367

1368

1369

1370

1371

1372

1373

1374

1375

1376

1377

1378

1379

1380

1381

1382

method for evaluating dynamic functional network connectivity and task-modulation:

Application to schizophrenia. Magn. Reson. Mater. Physik, Biol. Med.

https://doi.org/10.1007/s10334-010-0197-8

Santoro, A., Battiston, F., Petri, G., & Amico, E. (2023). Higher-order organization of multivariate

time series. Nature Physics, 1-9.

Sanz-Arigita, E.J., Schoonheim, M.M., Damoiseaux, J.S., Rombouts, S.A.R.B., Maris, E., Barkhof, F.,

Scheltens, P., Stam, C.J., 2010. Loss of “Small-World” Networks in Alzheimer’s Disease: Graph

Analysis of fMRI Resting-State Functional Connectivity. PLoS One.

https://doi.org/10.1371/journal.pone.0013788

Savin, C., Tkačik, G., 2017. Maximum entropy models as a tool for building precise neural controls.

Curr. Opin. Neurobiol. https://doi.org/10.1016/j.conb.2017.08.001

Schumacher, J., Peraza, L.R., Firbank, M., Thomas, A.J., Kaiser, M., Gallagher, P., O’Brien, J.T.,

Blamire, A.M., Taylor, J.P., 2019. Dynamic functional connectivity changes in dementia with

Lewy bodies and Alzheimer’s disease. NeuroImage Clin.

https://doi.org/10.1016/j.nicl.2019.101812

Sheline, Y.I., Morris, J.C., Snyder, A.Z., Price, J.L., Yan, Z., D’Angelo, G., Liu, C., Dixit, S.,

Benzinger, T., Fagan, A., Goate, A., Mintun, M.A., 2010A. APOE4 allele disrupts resting state

fMRI connectivity in the absence of amyloid plaques or decreased CSF Aβ42. J. Neurosci.

https://doi.org/10.1523/JNEUROSCI.3987-10.2010

Sheline, Y.I., Rachel, M.E., Snyder, A.Z., Morris, J.C., Kopf, D., Wang, S., Mintun, M.A., 2010B.

Amyloid Plaques Disrupt Resting State Default Mode Network Connectivity in Cognitively

Normal Elderly. Biol. Psychiatrie. https://doi.org/10.1016/j.biopsych.2009.08.024

Shi, J.Y., Wang, P., Wang, B.H., Xu, Y., Chen, X., Li, H.J., 2020. Brain Homotopic Connectivity in

Mild Cognitive Impairment APOE-ε4 Carriers. Neurowissenschaften.

https://doi.org/10.1016/j.neuroscience.2020.04.011

Shine, J.M., Bissett, P.G., Glocke, P.T., Koyejo, O., Balsters, J.H., Gorgolewski, K.J., Moodie, C.A.,

Poldrack, R.A., 2016. The Dynamics of Functional Brain Networks: Integrated Network States

during Cognitive Task Performance. Neuron. https://doi.org/10.1016/j.neuron.2016.09.018

Sizemore, A.E., Giusti, C., Kahn, A., Vettel, J.M., Betzel, R.F., Bassett, D.S., 2018. Cliques and

cavities in the human connectome. J. Comput. Neurosci. https://doi.org/10.1007/s10827-017-

0672-6

Schmied, S.M., Jenkinson, M., Woolrich, M.W., Beckmann, C.F., Behrens, T.E.J., Johansen-Berg, H.,

Bannister, P.R., De Luca, M., Drobnjak, ICH., Flitney, D.E., Niazy, R.K., Saunders, J., Vickers, J.,

Zhang, Y., De Stefano, N., Brady, J.M., Matthews, P.M., 2004. Advances in functional and

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

T

.

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

/

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1383

1384

1385

1386

1387

1388

1389

1390

1391

1392

1393

1394

1395

1396

1397

1398

1399

1400

1401

1402

1403

1404

1405

1406

1407

1408

1409

1410

1411

1412

1413

1414

1415

1416

structural MR image analysis and implementation as FSL, In: NeuroImage.

https://doi.org/10.1016/j.neuroimage.2004.07.051

Snowdon, D.A., 2003. Healthy Aging and Dementia: Findings from the Nun Study, In: Annals of

Internal Medicine. https://doi.org/10.7326/0003-4819-139-5_part_2-200309021-00014

Sorg, C., Riedl, V., Mühlau, M., Calhoun, V.D., Eichele, T., Läer, L., Drzezga, A., Förstl, H., Kurz,

A., Zimmer, C., Wohlschläger, A.M., 2007. Selective changes of resting-state networks in

individuals at risk for Alzheimer’s disease. PNAS. https://doi.org/10.1073/pnas.0708803104

Soto, C., Pritzkow, S., 2018. Protein misfolding, aggregation, and conformational strains in

neurodegenerative diseases. Nat. Neurosci. doi:10.1038/s41593-018-0235-9

Spires-Jones, T.L., Hyman, B.T., 2014. The Intersection of Amyloid Beta and Tau at Synapses in

Alzheimer’s Disease. Neuron. https://doi.org/10.1016/j.neuron.2014.05.004

Stam, C.J., De Haan, W., Daffertshofer, A., Jones, B.F., Manshanden, ICH., Van Cappellen Van Walsum,

A.M., Montez, T., Verbunt, J.P.A., De Munck, J.C., Van Dijk, B.W., Berendse, H.W., Scheltens,

P., 2009. Graph theoretical analysis of magnetoencephalographic functional connectivity in

Alzheimer’s disease. Gehirn. https://doi.org/10.1093/brain/awn262

Stam, C.J., Jones, B.F., Nolte, G., Breakspear, M., Scheltens, P., 2007. Small-world networks and

functional connectivity in Alzheimer’s disease. Cereb. Kortex.

https://doi.org/10.1093/cercor/bhj127

Stefanovski, L., Triebkorn, P., Spiegler, A., Diaz-Cortes, M.-A., Solodkin, A., Jirsa, V., McIntosh,

A.R., Ritter, P., Initiative, A.D.N., 2019. Linking Molecular Pathways and Large-Scale

Computational Modeling to Assess Candidate Disease Mechanisms and Pharmacodynamics in

Alzheimer’s Disease. Front Comput Neurosc 13, 54. https://doi.org/10.3389/fncom.2019.00054

Stefanovski, L., Meier, J.M., Pai, R.K., Triebkorn, P., Lett, T., Martin, L., Bülau, K., Hofmann-

Apitius, M., Solodkin, A., McIntosh, A.R., Ritter, P., 2021. Bridging Scales in Alzheimer’s

Krankheit: Biological Framework for Brain Simulation With The Virtual Brain. Frontiers

Neuroinformatics 15, 630172. https://doi.org/10.3389/fninf.2021.630172

Supekar, K., Menon, V., Rubin, D., Musen, M., Greicius, M.D., 2008. Network analysis of intrinsic

functional brain connectivity in Alzheimer’s disease. PLoS Comput. Biol.

https://doi.org/10.1371/journal.pcbi.1000100

Tait, L., Tamagnini, F., Stothart, G., Barvas, E., Monaldini, C., Frusciante, R., Volpini, M., Guttmann,

S., Coulthard, E., Braun, J.T., Kazanina, N., Goodfellow, M., 2020. EEG microstate complexity

for aiding early diagnosis of Alzheimer’s disease. Sci. Rep. https://doi.org/10.1038/s41598-020-

74790-7

Thompson, W.H., Fransson, P., 2016. Bursty properties revealed in large-scale brain networks with a

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

/

T

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1417

1418

1419

1420

1421

1422

1423

1424

1425

1426

1427

1428

1429

1430

1431

1432

1433

1434

1435

1436

1437

1438

1439

1440

1441

1442

1443

1444

1445

1446

1447

1448

1449

1450

point-based method for dynamic functional connectivity. Sci. Rep.

https://doi.org/10.1038/srep39156

Tian, Y., Margulies, D.S., Breakspear, M., Zalesky, A., 2020. Topographic organization of the human

subcortex unveiled with functional connectivity gradients. Nat. Neurosci. 23.

doi:10.1038/s41593-020-00711-6

Torres, L., Blevins, A. S., Bassett, D., & Eliassi-Rad, T. (2021). The why, Wie, and when of

representations for complex systems. SIAM Review, 63(3), 435-485.

Toulouse, G., 1986. Theory of the frustration effect in spin glasses: ICH.

https://doi.org/10.1142/9789812799371_0009

Tsang, R.S.M., Sachdev, P.S., Reppermund, S., Kochan, N.A., Kang, K., Crawford, J., Wen, W.,

Draper, B., Trollor, J.N., Slavin, M.J., Mather, K.A., Assareh, A., Seeher, K.M., Brodaty, H.,

2013. Sydney Memory and Ageing Study: An epidemiological cohort study of brain ageing and

Demenz. Int. Rev. Psychiatrie. https://doi.org/10.3109/09540261.2013.860890

Turing, A.M., 1937. On computable numbers, with an application to the entscheidungsproblem. Proc.

London Math. Soc. https://doi.org/10.1112/plms/s2-42.1.230

Vannimenus, J., Toulouse, G., 1977. Theory of the frustration effect. II. Ising spins on a square lattice.

J. Phys. C Solid State Phys. 10. https://doi.org/10.1088/0022-3719/10/18/008

Varley, T.F., Pope, M., Faskowitz, J., Spurns, O., 2023. Multivariate Information Theory Uncovers

Synergistic Subsystems of the Human Cerebral Cortex. Commun. Biol. 6, 1–12.

doi:10.1038/s42003-023-04843-w

Viviano, R.P., Raz, N., Yuan, P., Damoiseaux, J.S., 2017. Associations between dynamic functional

connectivity and age, metabolic risk, and cognitive performance. Neurobiol. Altern.

https://doi.org/10.1016/j.neurobiolaging.2017.08.003

Vossel, K.A., Beagle, A.J., Rabinovici, G.D., Shu, H., Lee, S.E., Naasan, G., Hegde, M., Cornes, S.B.,

Henry, M.L., Nelson, A.B., Seeley, W.W., Geschwind, M.D., Gorno-Tempini, M.L., Shih, T.,

Kirsch, H.E., Garcia, P.A., Müller, B.L., Mucke, L., 2013. Seizures and epileptiform activity in

the early stages of Alzheimer disease. JAMA Neurol.

https://doi.org/10.1001/jamaneurol.2013.136

Wang, K., Liang, M., Wang, L., Tian, L., Zhang, X., Li, K., Jiang, T., 2007. Altered functional

connectivity in early Alzheimer’s disease: A resting-state fMRI study. Hum. Brain Mapp.

https://doi.org/10.1002/hbm.20324

Wang, L., Zang, Y., Er, Y., Liang, M., Zhang, X., Tian, L., Wu, T., Jiang, T., Li, K., 2006. Changes

in hippocampal connectivity in the early stages of Alzheimer’s disease: Evidence from resting

state fMRI. Neurobild. https://doi.org/10.1016/j.neuroimage.2005.12.033

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

/

.

T

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

T

/

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Wang, Z., Wang, J., Zhang, H., Mchugh, R., Sun, X., Li, K., Yang, Q.X., 2015. Interhemispheric

functional and structural disconnection in Alzheimer’s disease: A combined resting-state fMRI

and DTI study. PLoS One. https://doi.org/10.1371/journal.pone.0126310

Wee, C.Y., Yang, S., Yap, P.T., Shen, D., 2016. Sparse temporally dynamic resting-state functional

connectivity networks for early MCI identification. Brain Imaging Behav.

https://doi.org/10.1007/s11682-015-9408-2

Weiskopf, N., Hutton, C., Josephs, O., Turner, R., Deichmann, R., 2007. Optimized EPI for fMRI

studies of the orbitofrontal cortex: Compensation of susceptibility-induced gradients in the

readout direction. Magn. Reson. Mater. Physik, Biol. Med. https://doi.org/10.1007/s10334-006-

0067-6

Zhang, H.Y., Wang, S.J., Liu, B., Ma, Z.L., Yang, M., Zhang, Z.J., Teng, G.J., 2010. Resting brain

Konnektivität: Changes during the progress of Alzheimer disease. Radiology.

https://doi.org/10.1148/radiol.10091701

Zhang, H.Y., Wang, S.J., Xing, J., Liu, B., Ma, Z.L., Yang, M., Zhang, Z.J., Teng, G.J., 2009.

Detection of PCC functional connectivity characteristics in resting-state fMRI in mild

Alzheimer’s disease. Behav. Brain Res. https://doi.org/10.1016/j.bbr.2008.08.012

Zimmermann, Joelle, Griffiths, J.D., McIntosh, A.R., 2018. Unique mapping of structural and

functional connectivity on cognition. J. Neurosci. 38, 9658–9667.

https://doi.org/10.1523/JNEUROSCI.0900-18.2018

Zimmermann, J., Perry, A., Breakspear, M., Schirner, M., Sachdev, P., Wen, W., Kochan, N.A.,

Mapstone, M., Ritter, P., McIntosh, A.R., Solodkin, A., 2018. Differentiation of Alzheimer’s

disease based on local and global parameters in personalized Virtual Brain models. NeuroImage

Clin. 19, 240–251. https://doi.org/10.1016/j.nicl.2018.04.017

1451

1452

1453

1454

1455

1456

1457

1458

1459

1460

1461

1462

1463

1464

1465

1466

1467

1468

1469

1470

1471

1472

1473

1474

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

T

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

.

T

/

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

/

.

T

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1475

Supplementary tables

1476

1477

1478

1479

1480
1481
1482

1483

1484

1485
1486
1487

1488
1489
1490

1491

Table S1. Differential impact of pathology on FC dimers and MC trimers and tetramers.

Intra-zone

SNC

NC

aMCI

AD

FC

0.543±0.170

0.564±0.155

0.549±0.186

0.490±0.180

Trimers

0.359±0.139

0.348±0.126

0.333±0.146

0.318±0.144

Tetramers***

0.222±0.096

0.196±0.087

0.186±0.077

0.156±0.088

Inter-zone

FC**

0.101±0.114

0.083±0.135

0.054±0.126

0.021±0.088

Trimers**

0.039±0.078

0.019±0.083

0.013±0.072

-0.012±0.052

Tetramers***

0.183±0.134

0.187±0.117

0.138±0.137

0.139±0.120

Average strengths of dimer, trimer and tetramer interactions, by clinical group and relation to anatomical zones.

Values are means ± SD; * significantly inter-group variations with P < 0.05; ** with P < 0.01; *** with P < 0.001 (one-way ANOVA test). Table S2. Memory coefficients for dynamic links in the four groups 5% 50% 95% 5% 50% 95% SNC 0.1561 0.1653 0.1746 0.1407 0.1452 0.1498 Intra-zone Inter-zone aMCI 0.1168 0.1238 0.1307 0.1404 0.1443 0.1481 NC 0.1310 0.1383 0.1457 0.1391 0.1428 0.1465 AD 0.1037 0.1098 0.1158 0.0901 0.0928 0.0954 The memory coefficient, by clinical group and relation to anatomical zones. Values are means and the confidence intervals; Intra-zone: SNC >>> NC, aMCI >>> NC, AD >>> NC ; Inter-zone : aMCI >>> NC, AD >>> NC ;

Wo, >>> means p-value smaller than 0.001.

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

T

/

/

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D

l

F
/

D
Ö

ich
/

/

T

.

/

1
0
1
1
6
2
N
e
N
_
A
_
0
0
3
3
2
2
1
5
3
2
5
2
N
e
N
_
A
_
0
0
3
3
2
P
D

.

/

T

F

B
j
G
u
e
S
T

T

Ö
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Supplementary figures

1492

1493

l

D
Ö
w
N
Ö
A
D
e
D

F
R
Ö
M
H

T
T

P

:
/
/

D
ich
R
e
C
T
.

M

ich
T
.

/

/

T

e
D
u
N
e
N
A
R
T
ich
C
e
–
P
D