ARTÍCULO
Communicated by Igor Goychuk
Fast and Accurate Langevin Simulations of Stochastic
Hodgkin-Huxley Dynamics
Shusen Pu
sxp600@case.edu
Department of Mathematics, Applied Mathematics, and Statistics, Case Western
Reserve University, Cleveland, OH 44106, EE.UU.
Peter J. tomás
pjthomas@case.edu
Department of Mathematics, Applied Mathematics, and Statistics; Biología; Cognitivo
Ciencia; and Electrical, Computadora, and Systems Engineering: Case Western Reserve
Universidad, Cleveland, OH 44106, EE.UU.
Fox and Lu introduced a Langevin framework for discrete-time stochas-
tic models of randomly gated ion channels such as the Hodgkin-
Huxley (S.S) sistema. They derived a Fokker-Planck equation with
state-dependent diffusion tensor D and suggested a Langevin formula-
tion with noise coefficient matrix S such that SS(cid:2) = D. Después,
several authors introduced a variety of Langevin equations for the HH
sistema. En este artículo, we present a natural 14-dimensional dynamics for
the HH system in which each directed edge in the ion channel state tran-
sition graph acts as an independent noise source, leading to a 14 × 28
noise coefficient matrix S. Nosotros mostramos que (1) the corresponding 14D sys-
tem of ordinary differential equations is consistent with the classical 4D
representation of the HH system; (2) the 14D representation leads to a
noise coefficient matrix S that can be obtained cheaply on each time step,
without requiring a matrix decomposition; (3) sample trajectories of the
14D representation are pathwise equivalent to trajectories of Fox and Lu’s
sistema, as well as trajectories of several existing Langevin models; (4) nuestro
14D representation (and those equivalent to it) gives the most accurate in-
terspike interval distribution, not only with respect to moments but un-
der both the L1 and L∞ metric-space norms; y (5) the 14D representation
gives an approximation to exact Markov chain simulations that are as fast
and as efficient as all equivalent models. Our approach goes beyond ex-
isting models, in that it supports a stochastic shielding decomposition
that dramatically simplifies S with minimal loss of accuracy under both
voltage- and current-clamp conditions.
Computación neuronal 32, 1775–1835 (2020) © 2020 Instituto de Tecnología de Massachusetts
https://doi.org/10.1162/neco_a_01312
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1776
1 Introducción
S. Pu and P. tomás
Many natural phenomena exhibit stochastic fluctuations arising at the
molecular scale, the effects of which impact macroscopic quantities. Y-
derstanding when and how microscale fluctuations will significantly con-
tribute to macroscale behavior is a fundamental problem spanning the
ciencias. The impact of random ion channel fluctuations on the timing of ac-
tion potentials in nerve cells provides an important example. Channel noise
can have a significant effect on spike generation (Como & Sejniano, 1995;
Schneidman, Liberto, & Segev, 1998), propagation along axons (Faisal &
Risue, 2007), and spontaneous (ectopic) action potential generation in
the absence of stimulation (O'Donnell & Van Rossum, 2015). At the network
nivel, channel noise can drive the endogenous variability of vital rhythms
such as respiratory activity (Yu, Dhingra, Dick, & Galán, 2017).
Hodgkin and Huxley’s quantitative model for active sodium and potas-
sium currents producing action potential generation in the giant axon of
Loligo suggested an underlying system of gating variables consistent with
a multistate Markov process description (Colina & Chen, 1972). The dis-
crete nature of individual ion channel conductances was confirmed ex-
perimentally (Neher & Sakmann, 1976). Después, numerical studies
of high-dimensional discrete-state, continuous-time Markov chain models
produced insights into the effects of fluctuations in discrete ion channel
populations on action potentials (Skaugen & Walløe, 1979; Strassberg & De-
Felice, 1993), also known as channel noise (Blanco, Klink, alonso, & kay, 1998;
Blanco, Rubinstein, & kay, 2000).
In the standard molecular-level HH model, which we adopt here, el
K+
channel comprises four identical n gates that open and close indepen-
dently, giving a five-vertex channel-state diagram with eight directed edges;
the channel conducts a current only when in the rightmost state (ver figura-
channel comprises three identical m gates and a single
ura 1, arriba). The Na
h gate, all independent, giving an eight-vertex diagram with 20 directed
bordes, of which one is conducting (ver figura 1, abajo).
+
Discrete-state channel noise models are numerically intensive, si
implemented using discrete-time binomial approximations to the underly-
ing continuous-time Markov process (Skaugen & Walløe, 1979; Schmandt
& Galán, 2012) or continuous-time hybrid Markov models with exponen-
tially distributed state transitions and continuously varying membrane po-
tential. The latter were introduced by Clay and DeFelice (1983) and are in
principle exact (anderson, Ermentrout, & tomás, 2015). Under voltage-
clamp conditions, the hybrid conductance-based model reduces to a
time-homogeneous Markov chain (Colquhoun & Hawkes, 1981) that can
be simulated using standard methods such as Gillespie’s exact algorithm
(Duende, 1977, 2007). Even with this simplification, such Markov chain
(Mc) algorithms are numerically expensive to simulate with realistic
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1777
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 1: Molecular potassium (K+) and sodium (Na+) channel states for the
Hodgkin-Huxley model. Filled circles mark conducting states n4 and m31. Por
capita transition rates for each directed edge (a
h) are volt-
age dependent (cf. equations B.1 and B.6). Directed edges are numbered 1 a 8
(K+ channel) y 1 a 20 (Na+-channel), marked in small red numerals.
h and β
metro, a
metro, b
norte, a
norte, b
population sizes of thousands of channels or greater. Por lo tanto, there is an
ongoing need for efficient and accurate approximation methods.
Following Clay and DeFelice’s exposition of continuous time Markov
chain implementations, Fox and Lu (1994) introduced a Fokker-Planck
ecuación (FPE) framework that captured the first- and second-order statis-
tics of HH ion channel populations in a 14-dimensional representation. Tak-
ing into account conservation of probability, one needs four variables to
represent the population of K
, and one for volt-
edad, leading to a 12-dimensional state-space description. The resulting high-
dimensional partial differential equation is impractical to solve numerically.
Sin embargo, as Fox and Lu observed, “To every Fokker-Planck description,
there is associated a Langevin description” (Zorro & Lu, 1994). They there-
fore introduced a Langevin stochastic differential equation:
canales, seven for Na
+
+
C
dv
dt
dM
dt
dN
dt
= Iapp(t) − ¯gNaM8 (V − VNa) − ¯gKN5 (V − VK) − gleak(V − Vleak),
= ANaM + S1
ξ
1
,
= AKN + S2
ξ
2
,
(1.1)
(1.2)
(1.3)
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1778
S. Pu and P. tomás
+
+
and K
, and N5 the open channel fraction for K
where C is the capacitance, Iapp is the applied current, maximal conduc-
tances are denoted ¯gion, with Vion being the associated reversal potential,
and ohmic leak current gleak(V − Vleak). M ∈ R8 and N ∈ R5 are vectors for
channels in each state, with M8 representing the
the fractions of Na
+
open channel fraction for Na
(ver
Cifra 1). Vectors ξ
2(t) ∈ R5 are independent gaussian white
1(t) ∈ R8 and ξ
1(t)ξ (cid:2)
δ(t − t(cid:6)
noise processes with zero mean and unit variances (cid:5)ξ
)
y (cid:5)ξ
). The state-dependent rate matrices ANa and
AK are given in equations 2.10 y 2.11. In Fox and Lu’s formulation, S must
satisfy S =
D, where D is a symmetric, positive semidefinite k × k “diffu-
sion matrix” (see appendix D for the D matrices for the standard HH K
y
N / A
canales). We will refer to the 14-dimensional Langevin equations 1.1
a 1.3, with S =
D, as the Fox-Lu model.
2(t)ξ (cid:2)
2 (t(cid:6)
√
δ(t − t(cid:6)
)(cid:7) = I8
)(cid:7) = I5
1 (t(cid:6)
√
+
+
+
The original Fox-Lu model, later called the conductance noise model by
Goldwyn and Shea-Brown (2011), did not see widespread use until gains
in computing speed made the square root calculations more feasible. Seek-
ing a more efficient approximation, Fox and Lu (1994) also introduced a
four-dimensional Langevin version of the HH model. This model was sys-
tematically studied in Fox (1997), which can be written as
= Iapp(t) − ¯gNam3h (V − VNa) − ¯gKn4 (V − VK) − gleak(V − Vleak),
= αx(1 − x) − βxx + ξx(t), where x = m, h, o, norte,
where ξx(t) are gaussian processes with covariance function
mi[ξx(t), ξx(t
(cid:6)
)] =
αx(1 − x) + βxx
norte
δ(t − t
(cid:6)
).
(1.4)
(1.5)
(1.6)
C
dv
dt
dx
dt
+
+
Here N represents the total number of Na
canales (respectivamente, el total
canales), and δ(·) is the Dirac delta function. Este modelo, re-
number of K
ferred to as the “subunit noise model” by Goldwyn and Shea-Brown (2011),
has been widely used as an approximation to MC ion channel models (ver
the references in Bruce, 2009; Goldwyn & Marrón marrón, 2011). Por ejemplo,
Schmid et al. (2001) used this approximation to investigate stochastic reso-
nance and coherence resonance in forced and unforced versions of the HH
modelo (p.ej. in the excitable regime). Sin embargo, the numerical accuracy of
this method was criticized in several studies (Mino, Rubinstein, & Blanco,
2002; bruce, 2009), which found that its accuracy does not improve even
with increasing numbers of channels.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1779
Although more accurate approximations based on Gillespie’s algorithm
(using a piecewise constant propensity approximation: bruce, 2009; Mino
et al., 2002) and even based on exact simulations (Clay & DeFelice, 1983;
Newby, Bressloff, & Keener, 2013; Anderson et al., 2015) became avail-
capaz, they remained prohibitively expensive for large network simulations.
Mientras tanto, Goldwyn and Shea-Brown’s rediscovery of Fox and Lu’s ear-
lier conductance-based model (Goldwyn & Marrón marrón, 2011; Goldwyn,
Marrón marrón, & Rubinstein, 2010) launched a flurry of activity seeking the
best Langevin-type approximation. Goldwyn and Shea-Brown (2011) introducción-
duced a faster decomposition algorithm to simulate equations 1.1 a 1.3 y
showed that Fox and Lu’s (1994) method accurately captured the fractions
of open channels and the interspike interval (ISI) Estadísticas, in comparison
with Gillespie-type Monte Carlo (Mc) simulaciones. Sin embargo, a pesar de la
development of efficient singular value decomposition based algorithms
for solving S =
D, this step still causes a bottleneck in the algorithms
based on Fox and Lu (1994), Goldwyn and Shea-Brown (2011), y oro-
wyn, Imennov, Famulare, and Shea-Brown (2011).
√
Many variations on Fox and Lu’s (1994) Langevin model have been pro-
posed in recent years (Dangerfield, kay, & Burrage, 2010, 2012; Linaro,
Storace, & Giugliano, 2011; Orio & Soudry, 2012; Güler, 2013b; Huang, Rüdi-
ger, & Shuai, 2013, 2015; Pezo, Soudry, & Orio, 2014; Zorro, 2018), incluido
Goldwyn et al.’s work (Goldwyn & Marrón marrón, 2011; Goldwyn et al., 2011),
each with its own strengths and weaknesses. One class of methods imposes
projected boundary conditions (Dangerfield et al., 2010, 2012); as we will
show in section 5, this approach leads to inaccurate interspike interval dis-
tribution and is inconsistent with a natural multinomial invariant manifold
structure for the ion channels. Several methods implement correlated noise
at the subunit level, as in equations 1.5 y 1.6 (Zorro, 1997; Linaro et al.,
2011; Güler, 2013a, 2013b). Sin embargo, if one recognizes that at the molec-
ular level, the individual directed edges represent the independent noise
sources in ion channel dynamics, then the approach incorporating noise at
the subunit level obscures the biophysical origin of ion channel fluctuations.
Some methods introduce the noisy dynamics at the level of edges rather
than nodes but lump reciprocal edges together into pairs (Orio & Soudry,
2012; Dangerfield et al., 2012; Huang et al., 2013; Pezo et al., 2014). This ap-
proach implicitly assumes, en efecto, that the ion channel probability distri-
bution satisfies a detailed balance (or microscropic reversibility) condición.
Sin embargo, while detailed balance holds for the HH model under stationary
voltage clamp, this condition is violated during active spiking. Finalmente, el
stochastic shielding approximation (Schmandt & Galán, 2012; Schmidt &
tomás, 2014; Schmidt et al., 2018) does not have a natural formulation in
the representation associated with an n × n noise coefficient matrix S; en el
cases of rectangular S matrices used in Orio and Soudry (2012) and Danger-
field et al. (2012) stochastic shielding can only be applied to reciprocal pairs
of edges. We elaborate on these points in section 6.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1780
S. Pu and P. tomás
En este artículo, we introduce a new variation of Fox and Lu’s conductance-
noise model that avoids the limitations we have described. Nosotros mostramos que
preserving each directed edge in the channel transition graph (ver figura 1)
as an independent noise source leads to a natural, biophysically motivated
Langevin model that does not require any matrix decomposition step. Our
construction lends itself to direct application of stochastic shielding meth-
probabilidades, leading to faster simulations that retain the accuracy of Fox and Lu’s
método.
As an additional benefit, our method answers an open question in the lit-
erature, arising from the fact that the decomposition D = SS(cid:2)
is not unique.
As Fox (2018) recently pointed out, subblock determinants of the D matrices
play a major role in the structure of the S matrix elements. Fox conjectured
that “a universal form for S may exist.” In this article, we obtain the uni-
versal form for the noise coefficient matrix S. Además, we prove that our
model is equivalent to Fox and Lu’s 1994 model in the strong sense of path-
wise equivalence.
The remainder of the article is organized as follows. En la sección 2, eran-
view the canonical deterministic 14D version of the HH model. We prove
a series of lemmas that show (1) the multinomial submanifold M is an
invariant manifold within the 14D space and (2) the velocity on the 14D
space and the pushforward of the velocity on the 4D space are identical.
Además, mostramos (numerically) eso (3) the submanifold M is globally
attracting, even under current clamp conditions. Cifra 2 illustrates the
relationship between the 4D and 14D deterministic HH models. Sección
3 lays out our 14 × 28 Langevin HH model. Like Orio and Soudry (2012),
Dangerfield et al. (2012), and Pezo et al. (2014), we avoid matrix decompo-
sition by computing S directly. The key difference between our approach
and its closest relative (Pezo et al., 2014) is to use a rectangular n × k matrix
S for which each directed edge is treated as an independent noise source
rather than lumping reciprocal edges together in pairs. In the new Langevin
modelo, the form of our S matrix reflects the biophysical origins of the un-
derlying channel noise and allows us to apply the stochastic shielding ap-
proximation by neglecting the noise on selected individual directed edges.
As we prove in section 4, our model (without the stochastic shielding ap-
proximation) is pathwise equivalent to all those in a particular class of bio-
physically derived Langevin models, including those used in Fox and Lu
(1994), Goldwyn et al. (2011), Goldwyn and Shea-Brown (2011), Orio and
Soudry (2012), Pezo et al. (2014), and Fox (2018). In addition to 4D and 14D
deterministic trajectories, Cifra 2 shows a stochastic trajectory generated
by our Langevin model. Finalmente, we compare our Langevin model to sev-
eral alternative stochastic neural models in terms of accuracy (of the full ISI
distribución) and numerical efficiency in section 5.
Matlab code to generate the figures throughout the article is available
on github from https://github.com/shusenpu/Stochastic_shielding and
on ModelDB at accession number 266551.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1781
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
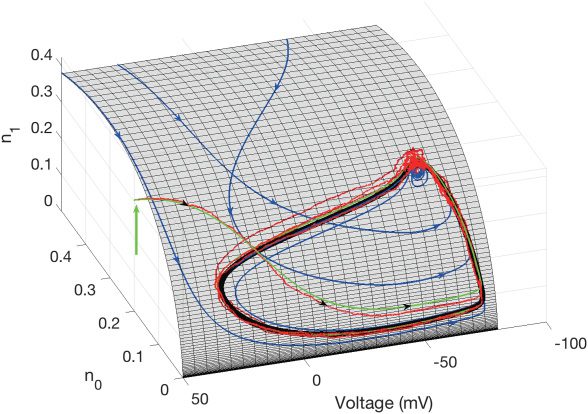
Cifra 2: 4D and 14D HH models. The meshed surface is a three-dimensional
projection of the 14D state space onto three axes representing the voltage, v, el
probability of all four potassium gates being in the closed state, n0, and the prob-
ability of exactly one potassium gate being in the open state, n1. Blue curves:
Trajectories of the deterministic 14D HH model with initial conditions located
on the 4D multinomial invariant submanifold, METRO. We prove that M is an in-
variant submanifold in section 2.3. Black curve: The deterministic limit cycle
solution for the 14D HH model, which forms a closed loop within M. Verde
curva: A trajectory of the deterministic 14D HH model with initial conditions
(vertical green arrow) off the multinomial submanifold. Red curve: A trajectory
of the stochastic 14D HH model (mira la sección 3) with the same initial conditions
as the green trajectory. The blue and black arrows mark the directions of the
trajectories. Note that trajectories starting away from M converge to M, and all
deterministic trajectories converge to the deterministic limit cycle. Parameters
of the simulation are given in Table 5.
2 The Deterministic 4D and 14D HH Models
En esta sección, we review the classical four-dimensional model of Hodgkin
and Huxley (1952) S.S), as well as its natural 14-dimensional version
(Dayán & Abbott, 2001, segundo. 5.7), with variables comprising membrane
voltage and the occupancies of five potassium channel states and eight
sodium channel states. The deterministic 14D model is the mean field of
the channel-based Langevin model proposed by Fox and Lu (1994); this ar-
ticle describes both the Langevin and the mean field versions of the 14D
Hodgkin-Huxley system. For completeness of exposition, we briefly review
1782
S. Pu and P. tomás
the 4D deterministic HH system and its 14D deterministic counterpart. En
sección 4, we prove that the sample paths of a class of Langevin stochas-
tic HH models are equivalent; in section 2.3, we review analogous results
relating trajectories of the 4D and 14D deterministic ODE systems.
En particular, we show that the deterministic 14D model and the origi-
nal 4D HH model are dynamically equivalent, in the sense that every flow
(solución) of the 4D model corresponds to a flow of the 14D model. El
consistency of trajectories between the 14D and 4D models is easy to ver-
ify for initial data on a 4D submanifold of the 14D space given by choos-
ing multinomial distributions for the gating variables (Dayán & Abbott,
2001; Goldwyn et al., 2011). Similarmente, Keener established results on multi-
nomial distributions as invariant submanifolds of Markov models with ion
channel kinetics under several circumstances (Keener, 2009, 2010; Earnshaw
& Keener, 2010a, 2010b), but without treating the general current-clamped
caso. Consistent with these results, we show that the set of all 4D flows maps
to an invariant submanifold of the state space of the 14D model. Además,
we show numerically that solutions of the 14D model with arbitrary ini-
tial conditions converge to this submanifold. Thus the original HH model
“lives inside” the 14D deterministic model in the sense that the former em-
beds naturally and consistently within the latter (ver figura 2).
In the stochastic case, the 14D model has a natural interpretation as a hy-
brid stochastic system with independent noise forcing along each edge of
the potassium (8 directed edges) and sodium (20 directed edges) channel
state transition graphs. The hybrid model leads naturally to a biophysically
grounded Langevin model that we describe in section 3. In contrast to the
ODE case, the stochastic versions of the 4D and 14D models are not equiv-
alente (Goldwyn & Marrón marrón, 2011).
2.1 The 4D Hodgkin-Huxley Model. The 4D voltage-gated ion channel
HH model is a set of four ordinary differential equations:
C
dv
dt
dm
dt
DH
dt
dn
dt
= − ¯gNam3h(v − VNa) − ¯gKn4(v − VK) − gL(v − VL) + Iapp
,
(2.1)
= αm(v )(1 − metro) − βm(v )metro,
= α
h(v )(1 − h) − β
h(v )h,
= αn(v )(1 − n) − βn(v )norte,
(2.2)
(2.3)
(2.4)
where v is the membrane potential, Iapp is the applied current, y 0 ≤
+
metro, norte, h ≤ 1 are dimensionless gating variables associated with Na
y
canales. The constant ¯gion is the maximal value of the conductance
k
for the sodium and potassium channel, respectivamente. Parameters Vion and C
+
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1783
are the ionic reversal potentials and capacitance, respectivamente. The quanti-
ties αx and βx, x ∈ {metro, norte, h} are the voltage-dependent per capita transition
tarifas, defined in appendix B.
This system is a C∞
vector field on a four-dimensional manifold
(with boundary) contained in R4: X = {−∞ < v < ∞, 0 ≤ m, h, n ≤ 1} =
R × [0, 1]3. The manifold is forward and backward invariant in time. If Iapp
is constant then X has an invariant subset given by X ∩ {v
},
max
where v
max are calculated in lemma 1.
min and v
≤ v ≤ v
min
As pointed Keener and Sneyd (1998) and Keener (2009) pointed out, for
voltage either fixed or given as a prescribed function of time, the equations
for m, h, and n can be interpreted as the parameterization of an invariant
manifold embedded in a higher-dimensional time-varying Markov system.
Several papers developed this idea for a variety of ion channel models and
related systems (Keener, 2009; Earnshaw & Keener, 2010b), but the theory
developed is restricted to the voltage-clamped case.
Under a fixed voltage clamp, the ion channels form a time-homogeneous
Markov process with a unique (voltage-dependent) stationary probability
distribution. Under a time-varying current clamp, the ion channels never-
theless form a Markov process, albeit no longer time homogeneous. Under
these conditions, the ion channel state converges rapidly to a multinomial
distribution indexed by a low-dimensional set of time-varying parameters
(m(t), h(t), n(t)) (Keener, 2010). In the current-clamped case, the ion chan-
nel process, considered alone, is neither stationary nor Markovian, making
the analysis of this case significantly more challenging from a mathematical
point of view.
2.2 The Deterministic 14D Hodgkin-Huxley Model. For the HH kinet-
ics given in Figure 1, we define the eight-component state vector M for the
Na+
gates, respec-
tively, as
gates and the five-component state vector N for the K
+
M = [m00
, m10
N = [n0
, n2
, n1
(cid:2)
(cid:2)
, m20
, n3
, m30
, n4]
, m11
, m01
(cid:2) ∈ [0, 1]5,
(cid:2)
= 1 and
4
i=0 ni
= m31 and is N5
3
i=0
1
j=0 mi j
where
Na+ channel is M8
istic 14D HH equations may be written (compare equations 2.1 to 2.4)
= 1. The open probability for the
= n4 for the K+ channel. The determin-
, m21
, m31]
(cid:2) ∈ [0, 1]8.
(2.5)
(2.6)
C
dV
dt
dM
dt
dN
dt
= − ¯gNaM8(V − VNa) − ¯gKN5(V − VK) − gL(V − VL) + Iapp
, (2.7)
= ANa(V )M,
= AK(V )N,
(2.8)
(2.9)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1784
S. Pu and P. Thomas
where the voltage-dependent drift matrices ANa and AK are given by
ANa(V ) =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0
α
h
0
0
0
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
AK(V ) =
0
βm
ANa(1)
0
3αm ANa(2) 2βm
0
0
2αm ANa(3) 3βm
0
β
h
0
0
0
β
h
0
αm ANa(4)
0
0
0
α
h
0
0
0
α
h
0
0
βm
ANa(5)
0
3αm ANa(6) 2βm
0
0
2αm ANa(7) 3βm
0
αm ANa(8)
0
0
α
h
0
0
0
0
β
h
0
0
0
0
β
h
0
AK(1) βn(V )
4αn(V ) AK(2) 2βn(V )
0
0
0
0
0
0
3αn(V ) AK(3) 3βn(V )
0
0
2αn(V ) AK(4) 4βn(V )
αn(V ) AK(5)
0
0
0
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
(2.10)
(2.11)
and the diagonal elements
Aion(i) = −
(cid:9)
j : j(cid:11)=i
Aion( j, i), for ion ∈ {Na, K}.
2.3 Relation Between the 14D and 4D Deterministic HH Models.
Earnshaw and Keener (2010b) suggest that it is reasonable to expect that the
global flow of the 14D system should converge to the 4D submanifold but
also that it is far from obvious that it must. Existing theory applies to the
voltage-clamped case (Keener, 2009; Earnshaw & Keener, 2010b). Here, we
consider instead the current-clamped case, in which the fluctuations of the
ion channel state influences the voltage evolution, and vice versa.
In the remainder of this section, we (1) define a multinomial submani-
fold M and show that it is an invariant manifold within the 14D space, and
(2) we show that the velocity on the 14D space and the pushforward of the
velocity on the 4D space are identical. In section 2.4, we (3) provide numer-
ical evidence that M is globally attracting within the higher-dimensional
space.
In order to compare the trajectories of the 14D HH equations with tra-
jectories of the standard 4D equations, we define lower-dimensional and
higher-dimensional domains X and Y, respectively, as
X = {−∞ < v < ∞, 0 ≤ m ≤ 1, 0 ≤ h ≤ 1, 0 ≤ n ≤ 1} = R × [0, 1]3 ⊂ R4,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1785
Table 1: R: Map from the 14D HH Model (m00
Model (m, h, n).
, . . . , m31
, n0
, . . . , n4) to the 4D HH
14D Model
(v, m00
v
1
3 (m11
m01
n1
+ m11
/4 + n2
, . . . , m31
, n0
, . . . , n4 )
+ m20 ) + m31
+ m10 ) + 2
+ m21
/2 + 3n3
3 (m21
+ m31
/4 + n4
4D Model
(v, m, h, n)
v
m
h
n‘
+ m30
Note: Note that both {m00
low multinomial distributions.
, . . . , m31
} and {n0
, . . . , n4
} fol-
Table 2: H: Map from the 4D HH Model (m, h, n) and the 14D HH Model
(m00
, . . . , n4).
, . . . , m31
, n0
4D Model
(v, m, h, n)
v
(1 − n)4
4(1 − n)3n
6(1 − n)2n2
4(1 − n)n3
n4
(1 − m)3(1 − h)
3(1 − m)2m(1 − h)
3(1 − m)m2(1 − h)
m3(1 − h)
(1 − m)3h
3(1 − m)2mh
3(1 − m)m2h
m3h
(v, m00
, . . . , n4 )
14D Model
, n0
, . . . , m31
v
n0
n1
n2
n3
n4
m00
m10
m20
m30
m01
m11
m21
m31
Y = {−∞ < v < ∞} ∩
⎧
⎨
⎩0 ≤ mi j
,
3(cid:9)
1(cid:9)
i=0
j=0
mi j
= 1
⎫
⎬
⎭
(cid:16)
∩
0 ≤ ni
,
(cid:17)
ni
= 1
4(cid:9)
i=0
= R × (cid:6)7 × (cid:6)4 ⊂ R14,
(2.12)
where (cid:6)k is the k-dimensional simplex in Rk+1 given by y1
=
1, yi
≥ 0. The 4D HH model dx
= F(x), equations 2.1 to 2.4, is defined for
dt
x ∈ X , and the 14D HH model dy
= G(y), equations 2.7 and 2.9, is defined
dt
for y ∈ Y. We introduce a dimension-reducing mapping R : Y → X as in
Table 1 and a mapping from lower to higher dimension, H : X → Y, as in
Table 2. We construct R and H in such a way that R ◦ H acts as the identity on
X , that is, for all x ∈ X , x = R(H(x)). The maps H and R are consistent with
+ . . . + yk+1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1786
S. Pu and P. Thomas
+
a multinomial structure for the ion channel state distribution, in the follow-
ing sense. The space Y covers all possible probability distributions on the
eight sodium channel states and the five potassium channel states. Those
distributions, which are products of one multinomial distribution on the
-channel,2
K
form a submanifold of (cid:6)7 × (cid:6)4. In this way we define a submanifold, de-
noted M = H(X ), the image of X under H.
+
-channel1and a second multinomial distribution on the Na
Before showing that the multinomial submanifold M is an invariant
manifold within the 14D space, we first show that the deterministic 14D
HH model is defined on a bounded domain. Having a bounded forward-
invariant manifold is a general property of conductance-based models,
which may be written in the form
dV
dt
= f (V, N
(cid:16)
open)
= 1
C
Iapp
− gleak(V − Vleak) −
(cid:17)
(cid:19)
open(V − Vi)
giNi
(cid:9)
(cid:18)
i∈I
dN
dt
= A(V )N and
N
open
= O[N ].
(2.13)
(2.14)
(2.15)
Here, C is the membrane capacitance, Iapp is an applied current with upper
and lower bounds I±, respectively, and gi is the conductance for the ith ion
channel. The index i runs over the set of distinct ion channel types in the
model, I. The gating vector N represents the fractions of each ion chan-
nel population in various ion channel states, and the operator O gives the
fraction of each ion channel population in the open (or conducting) channel
states. The following lemma establishes that any conductance-based model
(including the 4D or 14D HH model) is defined on a bounded domain.
Lemma 1. For a conductance-based model of the form 2.13 to 2.15 and for any
≤ I+, there exist upper and lower bounds Vmax
bounded applied current I− ≤ Iapp
and Vmin such that trajectories with initial voltage condition V ∈ [Vmin
, Vmax] re-
main within this interval for all times t > 0, regardless of the initial channel state.
} ∨ Vleak, where the index
Prueba. Let V1
i runs over I, the set of distinct ion channel types. Note that for all i, 0 ≤
} ∧ Vleak, and V2
= max
i∈I
= min
i∈I
{VI
{VI
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Eso es, distributions indexed by a single open probability n, with the five states hav-
1
2
ing probabilities
(cid:20)
(cid:21)
4
i
ni(1 − n)4−i for 0 ≤ i ≤ 4.
(cid:20)
Eso es, distributions indexed by two open probabilities m and h, with the eight states
having probabilities
mi(1 − metro)3−ih j (1 − h)1− j, para 0 ≤ yo ≤ 3, y 0 ≤ j ≤ 1.
(cid:21)
3
i
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1787
(2.16)
(2.17)
(2.18)
(2.19)
(2.20)
(2.21)
(2.22)
(2.23)
En
abierto
≤ 1, and gi
(cid:16)
> 0, gleak
> 0. Por lo tanto, when V ≤ V1,
dv
dt
= 1
C
Iapp
− gleak(V − Vleak) −
(cid:9)
(cid:18)
giNi
(cid:9)
i∈I
(cid:18)
giNi
(cid:17)
(cid:19)
abierto(V − Vi)
(cid:17)
(cid:19)
abierto(V − V1)
i∈I
(cid:9)
i∈I
(cid:17)
(cid:22)
soldado americano
(cid:23)
× 0 × (V − V1)
(cid:16)
≥ 1
C
≥ 1
C
= 1
C
Iapp
− gleak(V − V1) −
(cid:16)
Iapp
− gleak(V − V1) −
(cid:24)
Iapp
(cid:25)
− gleak(V − V1)
.
= min
i∈I
> 0 and Ni
abierto
{VI
} ∧ Vleak, and inequality 2.18
(cid:26)
≥ 0. Let Vmin := min
+
I−
gleak
> 0. Por lo tanto, V will not decrease beyond Vmin.
Inequality 2.17 follows because V1
follows because V − V1
(cid:27)
≤ 0, soldado americano
V1
. When V < Vmin, dV , V1 dt Similarly, when V ≥ V2, (cid:16) dV dt = 1 C Iapp − gleak(V − Vleak) − (cid:9) (cid:18) giNi (cid:9) i∈I (cid:18) giNi (cid:17) (cid:19) open(V − Vi) (cid:17) (cid:19) open(V − V2) i∈I (cid:9) i∈I (cid:17) (cid:22) gi (cid:23) × 0 × (V − V2) (cid:16) ≤ 1 C ≤ 1 C = 1 C Iapp − gleak(V − V2) − (cid:16) Iapp − gleak(V − V2) − (cid:24) Iapp (cid:25) − gleak(V − V2) . Inequality 2.21 holds because V2 = max i∈I {Vi } ∨ Vleak , and inequality 2.22 (cid:27) holds because V − V2 . When V > Vmax
, V2
We conclude that
V2
abierto
> 0 and Ni
≥ 0. Let Vmax
≥ 0, soldado americano
, dv
dt
Iapp
gleak
< 0. Therefore, V will not go beyond Vmax.
if V takes an initial condition in the interval
(cid:2)
+
[Vmin
, Vmax], then V (t) remains within this interval for all t ≥ 0.
(cid:26)
= max
Given that y ∈ Y has a bounded domain, lemma 2 follows directly
and establishes that the multinomial submanifold M is a forward-time–
invariant manifold within the 14D space. The proof of lemma 2 is in
appendix C.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1788
S. Pu and P. Thomas
Lemma 2. Let X and Y be the lower-dimensional and higher-dimensional
Hodgkin-Huxley manifolds given by equation 2.12, and let F and G be the vector
fields on X and Y defined by equations 2.1 to 2.4 and 2.7 to 2.9, respectively. Let
H : X → M ⊂ Y and R : Y → X be the mappings given in Tables 2 and 1, respec-
tively, and define the multinomial submanifold M = H(X ). Then M is forward-
time-invariant under the flow generated by G. Moreover, the vector field G, when
restricted to M, coincides with the vector field induced by F and the map H. That
is, for all y ∈ M, G(y) = DxH(R(y)) · F(R(y)).
Lemma 2 establishes that the 14D HH model given by equations 2.7 to
2.9 is dynamically consistent with the original 4D HH model given by equa-
tions 2.1 to 2.4.
In section 2.4 we provide numerical evidence that the flow induced by
G on Y converges to M exponentially fast. Thus, an initial probability dis-
tribution over the ion channel states that is not multinomial quickly ap-
proaches a multinomial distribution with dynamics induced by the 4D HH
equations. Similar results, restricted to the voltage-clamp setting, were es-
tablished by Keener and Earnshaw (Keener & Sneyd, 1998; Keener, 2009;
Earnshaw & Keener, 2010b).
2.4 Local Convergence Rate. Keener and Earnshaw (Keener & Sneyd,
1998; Keener, 2009; Earnshaw & Keener, 2010b) showed that for Markov
chains with constant (even time-varying) transition rates, (1) the multino-
mial probability distributions corresponding to mean-field models (such as
the HH sodium or potassium models) form invariant submanifolds within
the space of probability distributions over the channel states, and (2) ar-
bitrary initial probability distributions converged exponentially quickly to
the invariant manifold. For systems with prescribed time-varying transi-
tion rates, such as for an ion channel system under voltage clamp with a
prescribed voltage V (t) as a function of time, the distribution of channel
states had an invariant submanifold, again corresponding to the multino-
mial distributions, and the flow on that manifold induced by the evolution
equations was consistent with the flow of the full system.
In the preceding section, we established the dynamical consistency of
the 14D and 4D models with enough generality to cover both the voltage-
clamp and current-clamp systems; the latter is distinguished by not hav-
ing a prescribed voltage trace, but rather having the voltage coevolve along
with the (randomly fluctuating) ion channel states. Here, we give numerical
evidence for exponential convergence under current clamp similar to that
established under voltage clamp by Keener and Earnshaw.
Rather than providing a rigorous proof, we give numerical evidence for
the standard deterministic HH model that y → M under current clamp
(spontaneous firing conditions) in the following sense: if y(t) is a solution of
˙y = G(y) with arbitrary initial data y0
∈ Y, then ||y(t) − H(R(y(t)))|| → 0 as
t → ∞, exponentially quickly. Moreover, the convergence rate is bounded
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1789
Na
, λ
, λ
K), where λ
by λ = max(λ
ion is the least negative nontrivial eigen-
v
≤
value of the channel state transition matrix (over the voltage range Vmin
v ≤ Vmax) for a given ion, and −1/λ
v is the largest value taken by the mem-
≤ v ≤ Vmax). In practice, we find that the
brane time constant (for Vmin
membrane time constant does not determine the slowest timescale for con-
vergence to M. In fact it appears that the second-least-negative eigenvalues
(not the least-negative eigenvalues) of the ion channel matrices set the con-
vergence rate.
gates,
∂M
∂m and
gates, given by
, i ∈ {0, 1, 2, . . . , 7} be the eight eigenvalues of ANa and v
v
i
Note that y ∈ Y can be written as y = [V; M; N]. As shown in appendix
∂H
C, the Jacobian matrix
∂x consists of three block matrices: one for the volt-
∂M
∂V
∂h ; and
∂v ; one associated with the Na
age terms,
∂N
∂n . Fixing a particular voltage v, let
one corresponding to the K
λ
i be the associ-
i
ated eigenvectors, that is, ANa
i for the rate matrix in equations 2.8.
Similarly, let η
, i ∈ {0, 1, 2, . . . , 4} be the five eigenvalues and the asso-
i
i
w
ciated eigenvectors of AK, that is, AK
i, for the rate matrix in equa-
tions 2.9. If we rank the eigenvalues of either matrix in descending order,
the leading eigenvalue is always zero (because the sum of each column for
ANa and AK is zero for every V) and the remainder are real and negative.
Let λ
1 denote the largest (least negative) nontrivial eigenvalues of
ANa and AK, respectively, and let v
∈ R5 be the corresponding
eigenvectors.
∈ R8 and w
1 and η
= λ
i
= η
, w
w
v
+
+
1
1
i
i
The eigenvectors of the full 14D Jacobian are not simply related to the
eigenvectors of the component submatrices, because the first (voltage) row
and column contain nonzero off-diagonal elements. However, the eigenvec-
tors associated with the largest nonzero eigenvectors of ANa and AK (respec-
tively, v
2) are parallel to ∂M/∂h and ∂N/∂n, regardless of voltage. In
other words, the slowest decaying directions for each ion channel, v
1 and
w
1, transport the flow along the multinominal submanifold of Y. Therefore,
it is reasonable to make the hypothesis that if Y(t) is a solution of ˙y = G(y)
with arbitrary initial data y ∈ Y, then
2 and w
(cid:18)y(t) − H(R(y(t)))(cid:18)
(cid:18)y(0) − H(R(y(0)))(cid:18)
−λ
2t
(cid:3) e
(2.24)
2 being the second largest nonzero eigenvalue of AK and ANa over all v
for λ
in the range v
max. The convergence behavior is plotted numeri-
cally in Figure 3 and is consistent with the Ansatz equation 2.24. We calcu-
late the distance from a point y to M as
< v < v
min
ymax
= argmax
y∈Y
(cid:28)
(cid:28)
(cid:28)2 .
(cid:28)
y − H(R(y))
(2.25)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1790
S. Pu and P. Thomas
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
∈ Y,
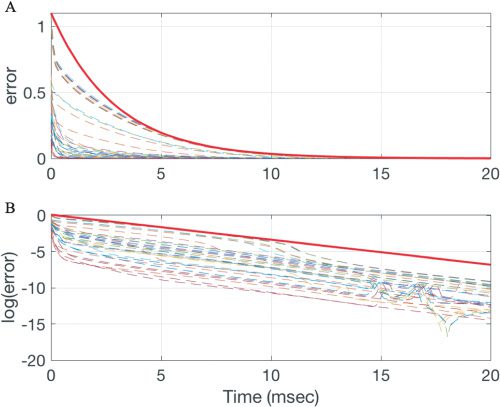
Figure 3: Convergence of trajectories y(t), for arbitrary initial conditions y0
to the multinomial submanifold M, for an ensemble of random initial con-
ditions. (A) Distance (see equation 2.25) between y(t) and M. (B) Logarithm
of the distance in panel A. The red solid line shows dmaxe−λ
2t in panel A and
log(dmax) − λ
2t in panel B.
In order to obtain an upper bound on the distance as a function of time, we
begin with the farthest point in the simplex from M by numerically finding
the solution to the argument 2.25, which is
ymax
= [v, 0.5, 0, 0, 0.5, 0, 0, 0, 0, 0.5, 0, 0, 0, 0.5].
This vector represents the furthest possible departure from the multinomial
distribution: all probability equally divided between the extreme states m00
and m03 for the sodium channel and the extremal states n0 and n4 for potas-
sium. The maximum distance from the multinomial submanifold M, dmax,
is calculated using this point. As shown in Figure 3, the function dmax e−λ
2t
provides a tight upper bound for the convergence rate from arbitrary initial
data y ∈ Y to the invariant submanifold M.
3 Stochastic 14D Hodgkin-Huxley Models
Finite populations of ion channels generate stochastic fluctuations (“chan-
nel noise”) in ionic currents that influence action potential initiation and
timing (White et al., 1998; Schneidman et al., 1998). At the molecular level,
fluctuations arise because transitions between individual ion channel states
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1791
are stochastic (Hill & Chen, 1972; Neher & Sakmann, 1976; Skaugen &
Walløe, 1979). Each directed edge in the ion channel state transition dia-
grams (see Figure 1) introduces an independent noise source. It is of inter-
est to be able to attribute variability of the interspike interval timing distri-
bution to specific molecular noise sources, specifically individual directed
edges in each channel state graph. In order to explore these contributions,
we develop a system of Langevin equations for the Hodgkin-Huxley equa-
tions, set in a 14-dimensional phase space.
Working with a higher-dimensional stochastic model may appear incon-
venient, but in fact has several advantages. First, any projection of an under-
lying 14D model onto a lower (e.g., 4D) stochastic model generally entails
loss of the Markov property. Second, the higher-dimensional representation
allows us to assess the contribution of individual molecular transitions to
the macroscopically observable variability of timing in the interspike inter-
val distribution. Third, by using a rectangular noise coefficient matrix con-
structed directly from the transitions in the ion channel graphs, we avoid
a matrix decomposition step. This approach leads to a fast algorithm that
is equivalent to the slower algorithm due to (Fox & Lu, 1994; Goldwyn &
Shea-Brown, 2011) in a strong sense (pathwise equivalence) that we detail
in section 4.
3.1 Exact Stochastic Simulation of HH Kinetics: The Random–
Time-Change Representation. An “exact” representation of the Hodgkin-
Huxley system with a population of Mtot sodium channels and Ntot
potassium channels treats each of the 20 directed edges in the sodium chan-
nel diagram, and each of the 8 directed edges in the potassium channel
diagram, as independent Poisson processes, with voltage-dependent per
capita intensities. As in the deterministic case, the sodium and potassium
(cid:2)
4
i=0 Ni.3
channel population vectors M and N satisfy
Thus, they are constrained, respectively, to a 7D simplex embedded in
R8 and a 4D simplex embedded in R5. In the random-time-change rep-
resentation (Anderson & Kurtz, 2015) the exact evolution equations are
written in terms of sums over the directed edges E for each ion channel,
E
= {1, . . . , 8}, (see Figure 1),
Na
(cid:29)
= {1, . . . , 20} and E
1
j=0 Mi j
≡ 1 ≡
3
i=0
(cid:2)
(cid:2)
(cid:31)
K
(cid:30)
M(t) = M(0) + 1
Mtot
(cid:9)
N(t) = N(0) + 1
Ntot
t
0
ζ Na
k YNa
k
Mtot
αNa
k
(V (s))Mi(k)(s) ds
,
(3.1)
k∈E
(cid:9)
Na
(cid:29)
ζ K
k YK
k
Ntot
k∈E
K
(cid:31)
αK
k (V (s))Ni(k)(s) ds
.
(3.2)
(cid:30)
t
0
3
We annotate the stochastic population vector M as either [M00
, . . . , M8], whichever is more convenient. In either notation M31
, M10
, . . . , M31] or as
≡ M8 is the conduct-
channel. For the K
channel, N4 denotes the conducting state.
+
[M1
ing state of the Na
+
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1792
S. Pu and P. Thomas
k
k
− eion
= eion
j(k)
i(k).4 Each Yion
Here ζ ion
is the stoichiometry vector for the kth directed edge. If we write
i(k) for the source node and j(k) for the destination node of edge k, then
ζ ion
(τ ) is an independent unit-rate Poisson pro-
k
cess, evaluated at “internal time” (or integrated intensity) τ , represent-
ing the independent channel noise arising from transitions along the kth
edge. The voltage-dependent per capita transition rate along the kth edge
is αion
(v ), and Mi(k)(s) (resp. Ni(k)(s)) is the fractional occupancy of the
k
source node for the kth transition at time s. Thus, for example, the quan-
(V (s))Mi(k)(s) gives the net intensity along the kth directed edge
tity Mtot
channel graph at time s.
in the Na
αNa
k
+
Remark 1. Under voltage-clamp conditions, with the voltage V held fixed,
equations 3.1 and 3.2 reduce to a time-invariant first-order transition pro-
cess on a directed graph (Schmidt & Thomas, 2014; Gadgil, Lee, & Othmer,
2005).
Under current-clamp conditions, the voltage evolves according to a con-
ditionally deterministic current balance equation of the form
dV
dt
{Iapp(t) − ¯gNaM31 (V − VNa) − ¯gKN4 (V − VK)
= 1
C
− gleak(V − Vleak)}.
(3.3)
Here, C (μF/cm2) is the capacitance, Iapp (nA/cm2) is the applied current, the
maximal conductance is ¯gchan (mS/cm2), Vchan (mV) is the associated reversal
potential, and the ohmic leak current is gleak(V − Vleak).
The random-time-change representation, equations 3.1 to 3.3, leads to an
exact stochastic simulation algorithm, given in Anderson and Kurtz (2015);
equivalent simulation algorithms have been used previously (Clay &
DeFelice, 1983; Newby et al., 2013). Many authors substitute a simpli-
fied Gillespie algorithm that imposes a piecewise-constant propensity ap-
proximation, ignoring the voltage dependence of the transition rates αion
between channel transition events (Goldwyn et al., 2011; Goldwyn & Shea-
Brown, 2011; Orio & Soudry, 2012; Pezo et al., 2014). The two methods
(cid:4) 40 (Anderson & Kurtz,
give similar moment statistics, provided Ntot
2015); their similarity regarding path-dependent properties (including in-
terspike interval distributions) has not been studied in detail. Moreover,
both Markov chain algorithms are prohibitively slow for modest numbers
(e.g., thousands) of channels; the exact algorithm may be even slower than
the approximate Gillespie algorithm. For consistency with previous studies,
in this article, we use the piecewise-constant propensity Gillespie algorithm
= 1800 K+ channels as our gold standard
with Mtot
Markov chain (MC) model, as in Goldwyn and Shea-Brown (2011).
= 6000 Na+ and Ntot
, Mtot
k
4
We write eNa
i
and eK
i for the ith standard unit vector in R8 or R5, respectively.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1793
In section 3.2 we develop a 14D conductance-based Langevin model with
28 independent noise sources – one for each directed edge – derived from
the random-time-change representation equations 3.1 to 3.3. In previous
work (Schmidt & Thomas, 2014), we established a quantitative measure
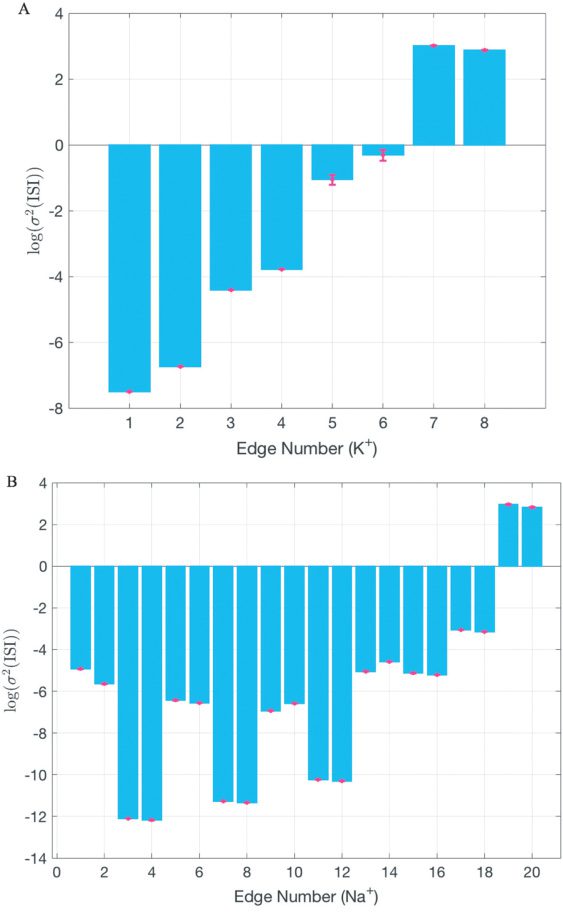
of edge importance, namely, the contribution of individual transitions (di-
rected edges) to the variance of channel state occupancy under steady-state
voltage-clamp conditions. Under voltage clamp, the edge importance was
identical for each reciprocal pair of directed edges in the graph, a conse-
quence of detailed balance. Some Langevin models lump the noise contri-
butions of each pair of edges (Dangerfield et al., 2010, 2012; Orio & Soudry,
2012; Pezo et al., 2014). Under conditions of detailed balance, this simpli-
fication is well justified. However, as we will show (see Figure 5), under
current-clamp conditions (e.g., for an actively spiking neuron) detailed bal-
ance is violated, the reciprocal edge symmetry is broken, and each pair of
directed edges makes a distinct contribution to ISI variability.
3.2 Langevin Equations of the 14D HH Model. For sufficiently large
number of channels, Schmidt and Thomas (2014) and Schmidt et al.
(2018) showed that under voltage clamp, equations 3.1 and 3.2 can be ap-
proximated by a multidimensional Ornstein-Uhlenbeck (OU) process (or
Langevin equation) in the form5
dM =
dN =
20(cid:9)
k=1
8(cid:9)
k=1
ζ Na
k
αNa
k
(V )Mi(k)dt +
(cid:12)NaαNa
k
(V )Mi(k) dW Na
k
,
!
"
!
ζ K
k
k (V )Ni(k)dt +
αK
(cid:12)KαK
k (V )Ni(k) dW K
k
"
.
(3.4)
(3.5)
k
, and αion
Here, M, N, ζ ion
k have the same meaning as in equations 3.1 and
3.2. The channel state increments in a short time interval dt are dM and
dN, respectively. The finite-time increment in the Poisson process Yion
is
now approximated by a gaussian process, namely, the increment dW ion
in
a Wiener (Brownian motion) process associated with each directed edge.
These independent noise terms are scaled by (cid:12)Na = 1/Mtot and (cid:12)K = 1/Ntot,
respectively.
k
k
Equations 3.3 to 3.5 comprise a system of Langevin equations for the
HH system (under current clamp) on a 14-dimensional phase space driven
by 28 independent white noise sources, one for each directed edge. These
equations may be written succinctly in the form
dX = f(X) dt +
√
(cid:12)G(X) dW(t)
(3.6)
5
The convergence of the discrete channel system to a Langevin system under voltage
clamp is a special case of Kurtz’s theorem (Kurtz, 1981).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1794
S. Pu and P. Thomas
where we define the 14-component vector X = (V; M; N), and W(t) is a
Wiener process with 28 independent components. The deterministic part
of the evolution equation f(X) =
dV
is the same as the mean
dt
field, equations 2.7 to 2.9. The state-dependent noise coefficient matrix G
is 14 × 28 and can be written as
; dM
dt
; dN
dt
(cid:23)
(cid:22)
√
(cid:12)G =
⎞
⎟
⎟
⎠ .
⎛
⎜
⎜
⎝
01×20 01×8
SNa 08×8
05×20 SK
The coefficient matrix SK is
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
SK
= 1√
Ntot
√
−
√
4αnn0
√
βnn1
√
βnn1
−
4αnn0
0
0
0
· · ·
0
0
0
0
0
2αnn2
2αnn2
√
−
√
0
3αnn1
√
−
√
3αnn1
0
0
)
2βnn2
)
2βnn2
0
−
· · ·
0
0
)
0
3βnn3
)
−
3βnn3
0
0
0
0
0
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
0
√
−
√
αnn3
)
4βnn4
)
0
0
αnn3
−
4βnn4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
and SNa is given in appendix D. Note that each of the 8 columns of SK cor-
responds to the flux vector along a single directed edge in the K
channel
transition graph. Similarly, each of the 20 columns of SNa corresponds to the
flux vector along a directed edge in the Na
graph (see appendix D).
+
+
Remark 2. Although the ion channel state trajectories generated by equa-
tion 3.6 are not strictly bounded to remain within the nonnegative simplex,
empirically, the voltage nevertheless remains within specified limits with
overwhelming probability.
To facilitate comparison of the model, equations 3.3 to 3.5, prior work
(Fox & Lu, 1994; Fox, 1997; Goldwyn & Shea-Brown, 2011), we may rewrite
the 14 × 28D Langevin description in the equivalent form:
C
dV
dt
= Iapp(t) − ¯gNaM8 (V − VNa) − ¯gKN5 (V − VK) − gleak(V − Vleak),
(3.7)
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
dM
dt
dN
dt
= ANaM + SNa
ξ
Na
,
= AKM + SK
ξ
K
.
1795
(3.8)
(3.9)
The drift matrices ANa and AK remain the same as in Fox and Lu (1994), and
are the same as in the 14D deterministic model, equations 2.10 and 2.11. SNa
and SK are constructed from direct transitions of the underlying kinetics
in Figure 1, and ξ
∈ R8 are vectors of independent gaussian
white noise processes with zero mean and unit variance.
∈ R20 and ξ
K
Na
Fox and Lu’s original approach (Fox & Lu, 1994) requires solving a ma-
trix square root equation SS(cid:2) = D to obtain a square (8 × 8 for Na+ or 5 × 5
for K+) noise coefficient matrix consistent with the state-dependent diffu-
sion matrix D. As an advantage, the ion channel representation equations
3.7 to 3.9, uses sparse, nonsquare noise coefficient matrices (8 × 20 for the
Na+ channel and 5 × 8 for the K+ channel), which exposes the independent
sources of noise for the system.
The new Langevin model in equations 3.7 to 3.9 does not require detailed
balance, which gives more insight into the underlying kinetics. Review pa-
pers (e.g., Goldwyn & Shea-Brown, 2011; Pezo et al., 2014; Huang et al.,
2015) did systematic comparison of various stochastic versions of the HH
model. In sections 4 and 5, we quantitatively analyze the connection be-
tween the new model and other existing models (Fox & Lu, 1994; Goldwyn
et al., 2011; Goldwyn & Shea-Brown, 2011; Dangerfield et al., 2010, 2012;
Orio & Soudry, 2012; Huang et al., 2013, 2015; Pezo et al., 2014; Fox, 2018).
Problems such as the boundary constraints are beyond the scope of this ar-
ticle; however, we would like to connect the new model to another type of
approximation to the MC model; the stochastic shielding approximation.
3.3 Stochastic Shielding for the 14D HH Model. The stochastic shield-
ing (SS) approximation was introduced by Schmandt and Galán (2012), in
order to approximate the Markov process using fluctuations from only a
subset of the transitions, namely, those corresponding to changes in the
observable states. In Schmidt and Thomas (2014), we showed that under
voltage clamp, each directed edge makes a distinct contribution to the
steady-state variance of the ion channel conductance, with the total vari-
ance being a sum of these contributions. We call the variance due to the kth
directed edge the edge importance; assuming detailed balance, it is given by
Rk
= Jk
n(cid:9)
n(cid:9)
(cid:29)
i=2
j=2
(cid:31)
−1
+ λ
j
λ
i
(cid:2)v
(c
i)
(cid:20)
w(cid:2)
i
ζ
k
(cid:21) (cid:20)
ζ (cid:2)
k
w
j
(cid:21) *
v (cid:2)
j c
+
.
(3.10)
Here, Jk is the steady-state probability flux along the kth directed edge;
λn < λn−1
< 0 are the eigenvalues of the drift matrix (ANa or AK,
≤ . . . ≤ λ
2
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
1796
S. Pu and P. Thomas
Figure 4: Stochastic shielding under voltage clamp. Redrawn (with permission)
from Figures 10 and 13 of Schmidt and Thomas (2014). Each curve shows the
edge importance Rk (see equation 3.10) as a function of voltage in the range
[−100, 100] mV for a different edge pair. For the K+ kinetics, R7
= R8 are the
largest Rk value in the voltage range above. For the Na+ kinetics, R11
= R12 have
the largest Rk values in the subthreshold voltage range (c. [−100, −25] mV),
= R20 have the largest Rk values in the suprathreshold voltage range
and R19
(c. [−25, 100] mV).
i (resp. w
respectively), and v
i) are the corresponding right (resp. left) eigen-
vectors of the drift matrix. Each edge’s stoichiometry vector ζ
k has compo-
nents summing to zero; consequently, the columns of ANa and AK all sum
to zero. Thus, each drift matrix has a leading trivial eigenvalue λ
≡ 0. The
1
vector c specifies the unitary conductance of each ion channel state; for the
8 or eK
HH model, it is proportional to eNa
5 , respectively.
and K
Figure 4 shows the edge importance for each pair of edges in the HH
+
Na
ion channel graph, as a function of voltage in the range
[−100, 100] mV. Note that reciprocal edges have identical Rk due to detailed
balance. Under voltage clamp, the largest value of Rk for the HH channels
always corresponds to directly observable transitions, that is, edges k such
that |c(cid:2)ζ
| > 0, although this condition need not hold in general (Schmidt,
k
Galán, & tomás, 2018).
+
To apply the stochastic shielding method under current clamp, we sim-
ulate the model with noise from only a selected subset E (cid:6) ⊂ E of directed
bordes, replacing equations 3.8 a 3.9 con
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
,
ξ
N / A
(cid:6)
N / A
= AKM + S
= ANaM + S
dM
dt
dN
dt
where S(cid:6)
N / A (resp. S(cid:6)
ficients from the most important edges E (cid:6)
edges with the largest edge-importance values Rk.
(cid:6)
k
ξ
k
,
k) is a reduced matrix containing only the noise coef-
. Eso es, mi (cid:6)
contains a subset of
(3.11)
(3.12)
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1797
Schmandt and Galán (2012) assumed that the edges with the largest
contribution to current fluctuations under voltage clamp would also make
the largest contributions to variability in voltage and timing under current
= {7, 8}) and edges
clamp and included edges 7 y 8 of the K
= {11, 12, 19, 20}), producir-
11 y 12 y 19 y 20 of the Na
ing an 8 × 4 matrix S(cid:6)
k. They demonstrated numer-
ically that restricting stochastic forcing to these edges gave a significantly
faster simulation with little appreciable change in statistical behavior: y-
der voltage clamp, the mean current remained the same, with a small (pero
noticeable) decrease in the current variance; mientras tanto, similar interspike
interval (ISI) statistics were observed.
Na and a 5 × 2 matrix S(cid:6)
+
channel (mi (cid:6)
N / A
channel (mi (cid:6)
k
+
Under current clamp, detailed balance is violated, and it is not clear from
mathematical principles whether the edges with the largest Rk under volt-
age clamp necessarily make the largest contribution under other circum-
posturas. In order to evaluate the contribution of the fluctuations driven by
each directed edge on ISI variability, we test the stochastic shielding method
by removing all but one column of Sion at a time. Eso es, we restrict to a sin-
gle noise source and observe the resulting ISI variance empirically. por ejemplo-
amplio, to calculate the importance of the kth direct edge in the Na
channel,
we suppress the noise from all other edges by setting S(cid:6)
k
+
= 05×1 and
ξ
k
(cid:6)
N / A
S
= [08×1
, · · · , SNa(:, k), · · · , 08×1] ,
eso es, we include only the kth column of SNa and set other columns to
be zeros. The ISI variance was calculated from an ensemble of 104 voltage
traces, each spanning about 500 ISIs.
Figure 5A plots the logarithm of the ISI variance for each edge in E
k.
Vertical bars (cian) show the ensemble mean of the ISI variance, con un
95% confidence interval superimposed (magenta). Several observations are
en orden. Primero, the ISI variance driven by the noise in each edge decreases
rapidly the farther the edge is from the observable transitions (bordes 7,8),
reflecting the underlying “stochastic shielding” phenomenon. Segundo, el
symmetry of the edge importance for reciprocal edge pairs—(1,2), (3,4),
(5,6), y (7,8)—that is observed under voltage clamp is broken under cur-
rent clamp. The contribution of individual directed edges to timing variabil-
ity under current clamp has another important difference compared with
the edge importance (current fluctuations) under voltage clamp. A simi-
lar breaking of symmetry for reciprocal edges is seen for the Na+
channel,
again reflecting the lack of detailed balance during active spiking.
Figure 5B shows the ISI variance when channel noise is included on in-
dividual edges of E
. Aquí, the difference between voltage and current
clamp is striking. Under voltage clamp, the four most important edges are
always those representing observable transitions, in the sense that the tran-
sition’s stoichiometry vector ζ is not orthogonal to the conductance vector c.
N / A
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1798
S. Pu and P. tomás
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 5: Logarithm of variance of ISI for stochastic shielding under current
clamp. The cyan bar is the mean of ISI, and the magenta plots the 95% estafa-
fidence interval of the mean ISI (see text for details). The applied current is
10 nA with other parameters specified in the appendixes. For the K+ kinetics,
the largest contribution edge is 7, y 8 is slightly smaller, ranking the second
largest. For the Na+ kinetics, the largest contribution pair is 19 y 20, con 20
slightly smaller than 19. Además, borde 17 y 18 is the second largest pair.
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1799
Eso es, the four most important pairs are always 11 y 12 y 19 y
20, regardless of voltage (ver figura 4). Under current clamp, the most im-
portant edges are 17, 18, 19, y 20. Although edges 11 y 12 are among
the four most important sources of channel population fluctuations under
voltage clamp, they are not even among the top 10 contributors to ISI vari-
ance when taken singly. Even though edges 17 y 18 are hidden, significado
they do not directly change the instantaneous channel conductance, estos
edges are nevertheless the second most important pair under current clamp.
Por lo tanto, when we implement the stochastic-shielding based approxima-
ción, we include the pairs 17 y 18 y 19 y 20 in equation 3.11. Nos referimos
to the approximate SS model driven by these six most important edges as
el 14 × 6D HH model.
Given the other parameters we use for the HH model (ver tabla 5 in ap-
= 10 nA is slightly beyond the region
pendix B), the input current of Iapp
of multistability associated with a subcritical Andronov-Hopf bifurcation.
In order to make sure the results are robust against increases in the applied
actual, we tried current injections ranging from 20 a 100 nA. While inject-
ing larger currents decreased the ISI variance, it did not change the rank
order of the contributions from the most important edges.
4 Pathwise Equivalence for a Class of Langevin Models
Fox and Lu’s method has been widely used since its appearance (see ref-
erences in Bruce, 2009; Goldwyn & Marrón marrón, 2011; Huang et al., 2015),
and the “best” approximation for the underlying Markov chain (Mc) modelo
has been a subject of ongoing discussion for decades. Several studies (Mino
et al., 2002; bruce, 2009; Sengupta, Risue, & Niven, 2010) attested to dis-
crepancies between Fox’s later approach (Zorro, 1997) and the discrete-state
MC model, raising the question of whether Langevin approximations could
ever accurately represent the underlying fluctuations seen in the gold stan-
dard MC models. An influential review paper (Goldwyn & Marrón marrón,
2011) found that these discrepancies were due to the way in which noise
is added to the stochastic differential equations, 1.1 a 1.3. Recent studies,
including Dangerfield et al. (2010, 2012); Linaro et al. (2011); Goldwyn and
Marrón marrón (2011); Goldwyn et al. (2011); Orio and Soudry (2012); Güler
(2013b); Huang et al. (2013, 2015); Pezo et al. (2014); and Fox (2018), dis-
cussed various ways of incorporating channel noise into HH kinetics based
on the original work by Fox and Lu (Zorro & Lu, 1994; Zorro, 1997), algunos de
which have the same SDEs but with different boundary conditions. Differ-
ent boundary conditions (BCs) are not expected to have much impact on
computational efficiency. En efecto, if BCs are neglected, the main difference
between channel-based (or conductance-based) models is the diffusion ma-
trix S in the Langevin euqations 1.2 y 1.3. As the discussion about where
and how to incorporate noise into the HH model framework goes on, Zorro
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1800
S. Pu and P. tomás
(2018) recently asked whether there is a way of relating different models
with different S matrices. We give a positive answer to this question below.
En la sección 4.1 we demonstrate the equivalence (neglecting the bound-
ary conditions) of a broad class of previously proposed channel-based
Langevin models (Zorro & Lu, 1994; Dangerfield et al., 2010, 2012; Goldwyn &
Marrón marrón, 2011; Orio & Soudry, 2012; Huang et al., 2013; Pezo et al., 2014;
Zorro, 2018) and the 14D Langevin HH model with 28 independent noise
sources (one for each directed edge in the channel state transition graph),
eso es, nuestro 14 × 28D Langevin model.
4.1 When Are Two Langevin Equations Equivalent? Two Langevin
models are pathwise equivalent if the sample paths (trajectories) of one
model can be made to be identical to the sample paths of the other under an
appropriate choice of gaussian white noise samples for each. To make this
notion precise, consider two channel-based Langevin models of the form
dX = f(X) dt + GRAMO(X) dW with the same mean dynamics f ∈ Rd and two dif-
ferent d × n matrices (possibly with different values of n1 and n2), G1 and
G2. Denote
F : Rd → Rd,
G1 : Rd → Rd×n1 ,
G2 : Rd → Rd×n2 .
(4.1)
(4.2)
(4.3)
(cid:2)
and X∗
1 (t), X∗
trajectories produced by the
(t) = [X∗
two models,
1 (t), W ∗
(cid:2)
2 (t), . . . , X∗
(cid:2)
Let X(t) = [X1(t), X2(t), . . . , Xd(t)]
d (t)]
and let W(t) =
ser
(cid:2)
2 (t), . . . , W ∗
and W∗
[W1(t), W2(t), . . . , Wn1 (t)]
n2 (t)]
be vec-
tors of Weiner processes. Eso es, Wi(t), i = 1, 2, . . . , n1 and W ∗
j (t), j = 1, 2,
δ(t − s)
. . . , n2 are independent Wiener processes with (cid:5)Wi(s)Wj(t)(cid:7) = re
yo j
y (cid:5)W ∗
δ(t − s). Note that n1 and n2 need not be equal. Como
defined in (allen, allen, Arciniega, & madera verde, 2008), the stochastic
differential equation (SDE) modelos
j (t)(cid:7) = re
(t) = [W ∗
i (s)W ∗
yo j
dX = f(t, X(t))dt + G1(t, X(t))dW(t)
y
dX
∗ = f(t, X
∗
∗
(t))dt + G2(t, X
∗
(t))dW
(t)
(4.4)
(4.5)
are pathwise equivalent if systems 4.4 y 4.5 possess the same probability
distribution and, además, a sample path solution of one equation is also a
sample solution to the other one. Allen et al. (2008) proved a theorem giving
general conditions under which the trajectories of two SDEs are equivalent.
We follow their construction closely below, adapting it to the case of two
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1801
different Langevin equations for the Hodgkin-Huxley system represented
in a 14-dimensional state space.
As in section 3, channel-based Langevin models for the stochastic dy-
namics of HH can be written as
dX = f(X) dt + S (X) dW(t),
(4.6)
(cid:23)
where the 14-component random vector X = (V; METRO; norte) yf(X) =
(cid:22)
; dM
; dN
dv
is the same as the mean-field, ecuaciones 2.7 a 2.9. Recuerda que
dt
dt
dt
(cid:2)
x = [v, metro, norte]
. Here we write
⎛
⎞
S (X) =
⎝
01×m
01×n
SNa(metro) 08×n
SK(norte)
05×m
⎠ , con
SNa : R8 → R8×m,
for the Na
+
channel and
SK : R5 → R5×n
(4.7)
(4.8)
+
channel. Aquí, m is the number of independent white noise forc-
for the K
ing terms affecting the sodium channel variables, while n is the number
of independent noise sources affecting the potassium gating variables. Nosotros
write
(cid:2)
W.(t) = [W1(t), W2(t), . . . , Wm+n(t)]
for a Wiener process incorporating both the sodium and potassium noise
forcing. Given two channel-based models with diffusion matrices,
SNa,1 : R8 → R8×m1 ,
SNa,2 : R8 → R8×m2 ,
for the Na+ channel, y
SK,1 : R5 → R5×n1 ,
SK,2 : R5 → R5×n2 ,
(4.9)
(4.10)
(4.11)
(4.12)
+
channel, we construct the diffusion matrix D = SS (cid:2)
for the K
. In order for
the two models to generate equivalent sample paths, it suffices that they
have the same diffusion matrix:
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1802
S. Pu and P. tomás
D = S
S (cid:2)
1
1
=
⎛
⎞
⎝
01×1 01×8 01×5
08×1 DNa 08×5
05×1 05×8 DK
⎠ = S
S (cid:2)
2
.
2
The SDEs corresponding to the two channel-based Langevin models are
dX = f(t, X(t))dt + S
∗
(t))dt + S
∗ = f(t, X
1(t, X(t))dW(t),
∗
∗
2(t, X
(t))dW
dX
(t).
(4.13)
(4.14)
The probability density function p(t, X) for random variable X in equa-
ción 4.13 satisfies the Fokker-Planck equation:
∂ p(t, X)
∂t
= 1
2
−
= 1
2
8(cid:9)
8(cid:9)
yo=1
j=1
8(cid:9)
yo=1
∂
∂xi
8(cid:9)
8(cid:9)
yo=1
j=1
(cid:18)
∂ 2
∂xix j
pag(t, X)
+n1(cid:9)
m1
L = 1
S (i,yo)
1
(t, X)S ( j,yo)
1
(cid:19)
(t, X)
(cid:18)
(cid:19)
FI(t, X)pag(t, X)
(cid:18)
(cid:19)
D(i, j)(t, X)pag(t, X)
−
∂ 2
∂xix j
(cid:18)
(cid:19)
,
FI(t, X)pag(t, X)
8(cid:9)
yo=1
∂
∂xi
where S (i, j)
ción 4.15 holds because
1
(t, X) es el (i, j)th entry of the diffusion matrix S
(4.15)
1(t, X). Equa-
D(i, j)(t, X) =
+n1(cid:9)
m1
L = 1
S (i,yo)
1
(t, X)S ( j,yo)
1
(t, X).
If z1, z2
∈ R14 and z1
(cid:5) z2, entonces
(cid:30)
z2,14
PAG(Z1
(cid:5) X(t) (cid:5) z2) =
(cid:30)
z2,13
(cid:30)
z2,1
· · ·
pag(t, X)dx1dx2
· · · dx8
.
z1,14
z1,13
z1,1
Note that equations 4.13 y 4.14 have the same expression equation 4.15,
for the Fokker-Planck equation; por lo tanto, X and X∗
possess the same prob-
ability density function. En otras palabras, the probability density function of
X in equation 4.6 is invariant for different choices of the diffusion matrix S.
4.2 Map Channel-based Langevin Models to Fox and Lu’s Model. Nosotros
now explicitly construct a mapping between Fox and Lu’s (1994) 14D model
and any channel-based model (given the same boundary conditions). Nosotros
begin with a channel-based Langevin description
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
dX = f(t, X(t))dt + S (t, X(t))dW(t),
and Fox and Lu’s (1994) modelo,
dX
∗ = f(t, X
∗
(t))dt + S
∗
0(t, X
∗
(t))dW
(t),
1803
(4.16)
(4.17)
where S is a d by m matrix satisfying SS (cid:2) = D (note that S is not necessarily
a square matrix), and S
D.
√
=
0
Let T be the total simulation time of the random process in equations 4.16
y 4.17. Para 0 (cid:5) t (cid:5) t, denote the singular value decomposition (SVD) de
S as
S (t) =P(t)(cid:13)(t)q(t),
where P(t) is a d × d orthogonal matrix (es decir., PAG(cid:2)P = PP(cid:2) = Id), q(t) is an
m × m orthogonal matrix, y (cid:13)(t) is a d × m matrix with rank((cid:13)) = r (cid:5) d
positive diagonal entries and d − r zero diagonal entries.
Primero, we prove that given a Wiener trajectory, W.(t), t ∈ [0, t] y el
(t) semejante
, is also a solution to equation 4.16. En
(t), tal que
solution to equation 4.16 X(t), there exists a Wiener trajectory W∗
that the solution to equation 4.17, X∗
otras palabras, for a Wiener process W(t), we can construct a W∗
X∗
(t) = X(t), para 0 ≤ t ≤ T.
Following Allen et al. (2008), we construct the vector W∗
(t) of d indepen-
dent Wiener processes as follows:
∗
(t) =
W.
(cid:30)
t
0
(cid:18)(cid:20)
PAG(s)
(cid:13)(s)(cid:13)(cid:2)
(cid:19)+
(cid:21) 1
(s)
2
(cid:13)(s)q(s)dW(s) +
(cid:30)
t
0
∗∗
PAG(s)dW
(s)
(4.18)
para 0 (cid:5) t (cid:5) t, where W∗∗(t) is a vector of length d with the first r entries
igual a 0 and the next d − r entries independent Wiener processes, y
(cid:18)(cid:20)
(cid:19)+
(cid:21) 1
(cid:21) 1
(s)
2
is the pseudoinverse of
(s)
2 . Consider that
(cid:20)
(cid:13)(s)(cid:13)(cid:2)
(cid:13)(s)(cid:13)(cid:2)
D(t) = S (t)S (cid:2)
(cid:18)
PAG(t)(cid:13)(t)q(t)
(t) =P(t)(cid:13)(t)q(t)
(cid:19)(cid:2)
=P(t)(cid:13)(t)(cid:13)(cid:2)
= [S
0(t)]2,
(t)PAG
(cid:2)
(t)
(4.19)
(4.20)
(4.21)
where S
*
(cid:13)(t)(cid:13)(cid:2)
0(t) =P(t)
+ 1
(t)
2
PAG(cid:2)
(t) is a square root of D, por construcción.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
(4.22)
(4.23)
1804
S. Pu and P. tomás
The diffusion term on the right side of equation 4.17 with X∗
(t) replaced
by X(t) satisfies
S
∗
0(t, X(t))dW
*
(t)
(cid:18)(cid:20)
= S
(t)
PAG(t)
0(t)
*
(cid:13)(t)(cid:13)(cid:2)
=P(t)
*
(cid:13)(t)(cid:13)(cid:2)
+ PAG(t)
(cid:25)
(cid:24)
PAG(t)(cid:13)(t)q(t)
=
(cid:19)+
(cid:21) 1
(t)
2
(cid:13)(t)(cid:13)(cid:2)
+ 1
(cid:13)(t)q(t)dW(t) + PAG(t)dW
(cid:18)(cid:20)
(cid:19)+
(cid:21) 1
∗∗
+
(t)
(cid:2)
2
PAG
(t)PAG(t)
(cid:13)(t)(cid:13)(cid:2)
(t)
2
(cid:13)(t)q(t)dW(t)
(t)PAG(t)dW
∗∗
(t)
+ 1
2
(t)
(cid:2)
PAG
dW(t).
From the SVD of S = P(cid:13)q, we conclude that
S
∗
0(t, X(t))dW
(t) = S (t, X(t))dW(t).
ción 4.17 X∗
processes as
(cid:30)
W.(t) =
0
Por eso, dX = f(t, X(t))dt + S
lution of equation 4.17.
0(t, X(t))dW
∗
t , eso es, X(t) is a sample path so-
Similarmente, given a Wiener trajectory W∗
(t) and the solution to equa-
(t), we can construct a vector W(t) of m independent Winner
t
(cid:2)
q
(s)(cid:13)+
(cid:22)
(s)
(cid:13)(s)(cid:13)(cid:2)
(cid:23)
(s)
1/2
(cid:2)
PAG
(s)dW
∗
(s) +
(cid:30)
t
0
(cid:2)
q
(s)dW
∗∗∗
(s)
(4.24)
para 0 (cid:5) t (cid:5) t, where W∗∗∗
(t) is a vector of length m with the first r entries
igual a 0 and the next m − r entries independent Wiener processes, y
(cid:13)+
(s) is the pseudoinverse of (cid:13)(s). Entonces, by an argument parallel to equa-
ción 4.22, we conclude that
∗
S (t, X
(t))dW (t) = S
∗
0(t, X
∗
(t))dW
(t).
(4.25)
∗ = f(t, X∗
(t))dt + S (t, X∗
Por eso, dX
(t) is also a solu-
tion to equation 4.16. Por lo tanto, we can conclude that the channel-based
Langevin model in equation 4.16 is pathwise equivalent to Fox and Lu’s
modelo.
(t))dW(t), eso es, X∗
To illustrate pathwise equivalence, Cifra 6 plots trajectories of the
14 × 28D stochastic HH model and Fox and Lu’s model using noise traces
dictated by the preceding construction. In panel A, we generated a sam-
ple path for equation 4.16 and plot three variables in X: the voltage V,
channel open probability N4.
N / A
The corresponding trajectory, X∗
, for Fox and Lu’s model was generated
channel open probability M31, and K
+
+
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1805
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
Cifra 6: Pathwise equivalency of 14D HH model and Fox and Lu’s model.
(A) Given a sample path of the 14 × 28D Langevin model in equation 4.16, we
construct the noise by equation 4.18 and generate the sample trajectory of Fox
and Lu’s model using equation 4.17. (B) Given a sample path of Fox and Lu’s
model in equation 4.17, we construct the noise by equation 4.24 and generate
the sample trajectory of the 14 × 28D Langevin model using equation 4.16. Para
ambos casos, we plot the voltage V, the open probability of the Na+ channel (M31),
and the open probability of the K+ channel (N4). We obtain excellent agreement
in both directions.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1806
S. Pu and P. tomás
+
+
31 and K
, N / A
4 in X∗
channel open probability M∗
from equation 4.17 and the corresponding Wiener trajectory was calculated
using equation 4.18. The top three subplots in panel A superposed the volt-
age V ∗
channel open proba-
bility N∗
against those in X. The bottom three subplots in panel A
plot the point-wise differences of each variable. Ecuaciones 4.16 y 4.17 son
numerically solved in Matlab using the Euler-Maruyama method with a
time step dt = 0.001 EM. The slight differences observed arise in part due
to numerical errors in calculating the singular value decomposition of S (en
ecuación 4.16); another source of error is the finite accuracy of the Euler-
Maruyama method.6 As shown in Figure 6, most differences occur near the
spiking region, where the system is numerically very stiff and the numerical
accuracy of the SDE solver accounts for most of the discrepancies (análisis
of which is beyond the scope of this article). To illustrate pathwise equiva-
lence, Cifra 6 shows superposed voltage trajectories for each simulation,
as well as the point-wise voltage differences of each. We can conclude from
the comparison in Figure 6 that the 14 × 28D Langevin model is pathwise
equivalent with Fox and Lu’s model. Similarmente, the same analogy applies
for other channel-based Langevin models such that with the same diffusion
matriz D(X).
We have shown that our 14 × 28D model, with a 14-dimensional state
space and 28 independent noise sources (one for each directed edge), es
pathwise equivalent to Fox and Lu’s original 1994 modelo, as well as other
channel-based models (under corresponding boundary conditions) incluir-
ing Goldwyn et al. (2011); Goldwyn and Shea-Brown (2011); Orio and
Soudry (2012); Pezo et al. (2014); Zorro (2018). As we shall see in section 5, el
pathwise equivalent models give statistically indistinguishable interspike
interval distributions under the same BCs. We emphasize the importance of
boundary conditions for pathwise equivalence. Two simulation algorithms
with the same Ai and Si matrices will generally have nonequivalent tra-
jectories if different boundary conditions are imposed. Por ejemplo, Y-
gerfield et al. (2012) employ the same dynamics as Orio and Soudry (2012)
away from the boundary, where ion channel state occupancy approaches
zero or one. But where the latter allow trajectories to move freely across this
boundary (which leads only to small, short-lived excursions into “nonphys-
ical” values), Dangerfield imposes reflecting boundary conditions through
a projection step at the boundary. As we will see ln section 5, this difference
in boundary conditions leads to a statistically significant difference in the
ISI distribution, as well as a loss of accuracy when compared with the gold
standard Markov chain simulation.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
6
The forward Euler method is first-order accurate for ordinary differential equations,
dt) accurate for stochastic differen-
√
but the forward Euler-Maruyama method is only O(
tial equations (Kloeden & Platen, 1999).
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1807
5 Model Comparison
En la sección 3, we studied the contribution of every directed edge to the ISI
variability and proposed how stochastic shielding could be applied under
current clamp. Además, in section 4, we proved that a family of Langevin
models is pathwise equivalent.
Here we compare the accuracy and computational efficiency of sev-
eral models,
including the “subunit model” (Zorro, 1997; Goldwyn &
Marrón marrón, 2011), Langevin models with different S matrices or bound-
ary conditions (Zorro & Lu, 1994; Goldwyn & Marrón marrón, 2011; Dangerfield
et al., 2012; Orio & Soudry, 2012; Pezo et al., 2014), the 14D HH model (pro-
posed in section 3.2), the 14D stochastic shielding model with six indepen-
dent noise sources (proposed in section 3.3), and the gold standard Markov
chain model (discussed in section 3.1). Where other studies have compared
moment statistics such as the mean firing frequency (under current clamp)
and stationary channel open probababilies (under voltage clamp), we base
our comparison on the entire interspike interval (ISI) distribuciones, bajo
current clamp with a common fixed driving current. We use two different
comparisons of ISI distributions, the first based on the L1 norm of the dif-
ference between two distributions (the Wasserstein distance; Wasserstein,
1969), in section 5.1 and the second based on the L∞ norm (the Kolmogorov-
Smirnov test; Agujero, 1933; Smirnov, 1948), in section 5.2. We find
similar results using both measures: como se esperaba, the models that produce
pathwise equivalent trajectories (Zorro & Lu, 1994; Orio & Soudry; and our
14 × 28D model) have indistinguishable ISI statistics, while the nonequiv-
alent models (Zorro, 1997; Dangerfield, 2010, 2012; Goldwyn & Marrón marrón,
2011; nuestro 14 × 6D stochastic-shielding model) have significantly different
ISI distributions. De estos, el 14 × 6D SS model is the closest to the models
en el 14 × 28D class and as fast as any other model considered.
5.1 L1 Norm Difference of ISIs. We first evaluate the accuracy of dif-
ferent stochastic simulation algorithms by comparing their ISI distributions
under current clamp to that produced by a reference algorithm, a saber, el
discrete-state Markov chain (Mc) algoritmo.
Let X1
, . . . , Xn be n independent samples of ISIs with a true cumu-
lative distribution function F. Let Fn(·) denote the corresponding empirical
cumulative distribution function (ECDF) definido por
, X2
Fn(X) = 1
norte
norte(cid:9)
yo=1
1{Xi
≤x},
x ∈ R,
(5.1)
where we write 1A to denote the indicator function for the set A. Let Q and
QM be the quantile functions of F and FM, respectivamente. The L1-Wasserstein
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1808
S. Pu and P. tomás
Mesa 3: Summary of the L1-Wasserstein Distances of ISI Distributions for
Langevin Type Hodgkin-Huxley Models Compared to the MC Model.
Modelo
Mc
Fox94
Fox97
Dangerfield
Goldwyn
Orio
14 × 28D
SS
Variables
V+M+N S Matrix
Noise Dimensions
Na+K
L1 Norm (msec.)
(Wasserstein Dist.)
Run Time
(sec.)
1+8+5
1+7+4
1+2+1
1+8+5
1+8+5
1+8+5
1+8+5
1+8+5
n / A
√
S =
D
n / A
SEF
√
S =
D
Spaired
Ssingle
Sss
20+8
7+4
3
10+4
8+5
10+4
20+8
4+2
2.27 e-4 ± 7.15 e-5
4.74 e-2 ± 1.93 e-4
8.01 e-1 ± 9.48 e-4
2.18 e-1 ± 2.14 e-4
1.83 e-1 ± 1.93 e-4
4.52 e-2 ± 2.08 e-4
4.93 e-2 ± 1.94 e-4
7.62 e-2 ± 7.57 e-5
3790
2436
67
655
2363
577
605
73
Notas: Modelo (see text for details): Mc: Markov chain. Fox94; From Fox and Lu (1994).
Fox97: Zorro (1997). Goldwyn: Goldwyn and Shea-Brown (2011). Dangerfield: Dangerfield
et al. (2010, 2012). 14 × 28D: model proposed in section 3.2. SS: stochastic-shielding model
(mira la sección 3.3). Variables: number of degrees of freedom in Langevin equation represent-
ing voltage, sodium gates, and potassium gates, respectivamente. S Matrix: Form of the noise
coefficient matrix in equations 1.1 a 1.3. Noise dimensions: number of independent gaus-
sian white noise sources represented for sodium and potassium, respectivamente. L1 Norm:
Empirically estimated L1-Wasserstein distance between the model’s ISI distribution and
the MC model’s ISI distribution. For MC versus MC, independent trials were compared.
a ± b: mean±standard deviation. Run time (in seconds): see text for details.
distance between two CDF’s FM and F can be written as (Shorack & Wellner,
2009)
ρ
1(F, FM) =
(cid:30) ∞
0
,
,
,
,
F(X) − FM(X)
dx =
(cid:30)
0
1
,
,
,
,
q(X) − QM(X)
dx.
(5.2)
Note that ρ
Mesa 3 have units of milliseconds.
1 has the same units as dx. De este modo, the L1 distances reported in
When two models have the same number of samples, norte, ecuación 5.2 poder
be estimated by
(cid:30)
0
1
,
,
,
,
q(X) − QM(X)
dx ≈ 1
norte
norte(cid:9)
yo=1
|Xi
− Yi
| := ρ
1(Fn, FM
norte ),
(5.3)
, · · · , Xn and Y1
where X1
cending order with CDF F and FM, respectivamente.
, · · · , Yn are n independent samples sorted in as-
We numerically calculate ρ
norte ) to compare several Langevin mod-
els against the MC model. We consider the following models: “Fox94” de-
notes the original model proposed by Fox and Lu (1994), which requires
1(Fn, FM
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1809
√
+
+
gates and 8 N / A
a square root decomposition (S =
D) for each step in the simulation (ver
ecuaciones 1.1 a 1.3). “Fox97” is the widely used “subunit model” of Fox
(1997); see equations 1.4 y 1.5). “Goldwyn” denotes the method taken
from Goldwyn and Shea-Brown (2011), where they restrict the 14D sys-
tema (V, 5 k
puertas) to the 4D multinomial submanifold
(V, metro, norte, yh; mira la sección 4.2), with gating variables truncated to [0,1].
We write “Orio” for the model proposed by Orio and Soudry (2012), dónde
they constructed a rectangular matrix S such that SS(cid:2) = D (referred to as
Spaired in Table 3) combining fluctuations driven by pairs of reciprocal edges,
thereby avoiding taking matrix square roots at each time step. The model
“Dangerfield” represents Dangerfield et al. (2012), which used the same S
matrix as in Orio and Soudry (2012) but added a reflecting (no-flux) atado-
ary condition via orthogonal projection (referred to as SEF in Table 3). fi-
finalmente, we include the 14 × 28D model we proposed in section 3.2, or “14D”
(referred to as Ssingle in Table 3); “SS” is the stochastic shielding model spec-
ified in section 3.3.
For each model, we ran 10,000 independent samples of the simulation,
= 10 nA), and initial condi-
holding channel number, injected current (Iapp
tions fixed. Throughout the article, we presume a fixed channel density of
60 channels/μm2 for sodium and 18 channels/μm2 for potassium in a mem-
brane patch of area 100 μm2, consistent with prior work such as Goldwyn
and Shea-Brown (2011) and Orio and Soudry (2012). The initial condition
is taken to be the point on the deterministic limit cycle at which the volt-
age crosses upward through −60 mV. An initial transient corresponding to
10 a 15 ISIs is discarded, to remove the effects of the initial condition. (Ver
Mesa 5 in appendix B for a complete specification of simulation parame-
ters.) We compared the efficiency and accuracy of each model through the
los siguientes pasos:
1. For each model, a single run simulates a total time of 84,000 millisec-
onds (EM) with time step 0.008 EM, recording at least 5000 ISIs.
2. For each model, repeat 10,000 runs in step 1.
3. Create a reference ISI distribution by aggregating all 10,000 runs of
the MC model, eso es, based on roughly 5 × 107 ISIs.
4. For each of 104 individual runs, align all ISI data into a single vector
and calculate the ECDF using equation 5.1.
5. Compare the ISI distribution of each model with the reference MC
distribution by calculating the L1-difference of the ECDFs using
ecuación 5.3.
6. To compare the computational efficiency, we take the average execu-
tion time of the MC model as the reference. The relative computa-
tional efficiency is the ratio of the average execution time of a model
with that of the MC model (acerca de 3790 segundo).
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1810
S. Pu and P. tomás
Mesa 3 gives the empiricially measured L1 difference in ISI distribution
between several pairs of models.7 The first row (“MC”) gives the average
L1 distance between individual MC simulations and the reference distri-
bution generated by aggregating all MC simulations, in order to give an
estimate of the intrinsic variability of the measure. Cifra 8 plots the L1-
Wasserstein differences versus the relative computational efficiency of sev-
eral models against the MC model. These results suggest that the Fox94,
Orio, y 14 × 28D models are statistically indistinguishable when com-
pared with the MC model using the L1-Wasserstein distance. This result
is expected in light of our results (mira la sección 4) showing that these three
models are pathwise-equivalent. (We will make pairwise statistical com-
parisons between the ISI distributions of each model in see section 5.2.)
Among these equivalent models, sin embargo, el 14 × 28D and Orio mod-
els are significantly faster than the original Fox94 model (and the Gold-
wyn model) because they avoid the matrix square root computation. El
Dangerfield model has speed similar to the 14 × 28D model, but the use
of reflecting boundary conditions introduces significant inaccuracy in the
ISI distribution. The imposition of truncating boundary conditions in the
Goldwyn model also appears to affect the ISI distribution. Of the models
consideró, the Fox97 subunit model is the fastest; sin embargo, it makes a par-
ticularly poor approximation to the ISI distribution of the MC model. Nota
that the maximum L1-Wasserstein distance between two distributions is 2.
The ISI distribution of the Fox97 subunit model to that of the MC model is
más que 0.8, cual es 10 times larger than the L1-Wasserstein distance of
the SS model, and almost half of the maximum distance. As shown in Fig-
ura 7, the Fox97 subunit model fails to achieve the spike firing threshold and
produces longer ISIs. Because of its inaccuracy, we do not include the sub-
unit model in our remaining comparisons. The stochastic shielding model,
por otro lado, has nearly the same speed as the Fox97 model, Pero es
encima 100 times more accurate (in the L1 sense). The SS model is an order
of magnitude faster than the 14 × 28D model and has less than twice the
L1 discrepancy versus the MC model (L1 norm 76.2 versus 49.3 microsec-
onds). While this difference in accuracy is statistically significant, it may
not be practically significant, depending on the application (mira la sección 6
for further discussion of this point).
5.2 Two-Sample Kolmogorov-Smirnov Test. In addition to using the
L1-Wasserstein distances to test the differences between two CDFs, podemos
also make a pairwise comparison between each model by applying the
Dvoretzky-Kiefer-Wolfowitz inequality (Dvoretzky, Kiefer, & Wolfowitz,
7
Run times in Table 3, rounded to the nearest integer number of seconds, were ob-
tained by averaging the run times on a distribution of heterogeneous compute nodes from
Case Western Reserve University’s high-performance computing cluster.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1811
Cifra 7: The probability density of interspike intervals (ISIs) for Fox97 (azul)
and the MC model (rojo). The probability densities were calculated over more
que 5.4 × 107 ISIs.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 8: The L1-Wasserstein distances and relative computational efficiency
versus the MC model. Fox94 (green circle), Goldwyn (black cross), Orio (cian
square), 14D (blue star), SS (magenta downward-pointing triangle), Dangerfield
(red upward-pointing triangle), and the MC (brown diamond) modelo. The L1 er-
ror for ISI distribution was computed using the L1-Wasserstein distance, equa-
ción 5.3, with discrete time Gillespie/Monte Carlo simulations as a reference.
The relative computational efficiency is the ratio of the recorded run time to
the mean recorded time of the MC mode (3790 artículos de segunda clase). The mean and 95%
confidence intervals were calculated using 100 repetitions of 10,000 runs each
(5 × 109 ISIs total).
1812
S. Pu and P. tomás
1956) and the two-sample Kolmogorov-Smirnov (KS) prueba (Agujero,
1933; Smirnov, 1948). While the Wasserstein distance is based on the L1
norm, the KS statistic is based on the L∞ (or supremum) norm.
The Dvoretzky-Kiefer-Wolfowitz inequality (Dvoretzky et al., 1956) es-
tablishes confidence bounds for the CDF. Específicamente, the interval that con-
tains the true CDF, F(·), with probability 1 − α, es dado por
|Fn(X) − F(X)| ≤ ε where ε =
–
ln 2
a
2norte
.
(5.4)
When comparing samples XM
n obtained from an approximate
1
model M against the gold standard, in section 5.1 we computed the L1 dif-
ference of the empirical density functions as an approximation for the L1 dif-
ference of the true distributions. En cambio, we work here with the L∞ norm:
, . . . , XM
, XM
2
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
ρ∞(Fn, FM
norte ) = lim
p→∞
= sup
0≤x<∞
(cid:29)(cid:30) ∞
,
,
,
,p
n (x) − Fn(x)
FM
(cid:31)
1/p
dx
0
(cid:20),
,
,
,
n (x) − Fn(x)
FM
(cid:21)
.
(5.5)
For each x ≥ 0, equation 5.4 bounds the discrepancy between the true
and empirical distribution differences as follows. By the triangle inequality
and independence of the Xi from the XM
i
, the inequality
|FM − F| = |FM − FM
n
≤ |FM − FM
n
≤ 2ε + |FM
n
+ Fn − F + FM
n
| + |Fn − F| + |FM
n
− Fn|
− Fn|
− Fn|
holds with probability (1 − α)2. Similarly,
|FM
n
− Fn| = |FM
− FM
n
n
≤ |FM − FM
n
≤ 2ε + |FM − F|
+ F − Fn + FM − F|
| + |Fn − F| + |FM − F|
(5.6)
(5.7)
holds with probability (1 − α)2. Together, equations 5.6 and 5.7 indicate that
the discrepancy between the difference of empirical distributions and the
difference of true distributions is bounded as
,
,
,|FM − F| − |FM
n
,
,
, ≤ 2ε
− Fn|
with probability (1 − α)2, for ε =
!
ln 2
α
2n .
(5.8)
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
n
e
c
o
_
a
_
0
1
3
1
2
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1813
We will use the pointwise difference of the ECDFs for a large sample as
an estimate for the pointwise difference between two true CDFs. The two-
sample Kolmogorov-Smirnov (KS) test (Kolmogorov, 1933; Smirnov, 1948)
offers a statistics to test whether two samples are from the same distribution.
The two-sample KS statistic is
Dn,m = sup
x
|F1,n(x) − F2,m(x)|,
(5.9)
where F1,n and F2,m are two ECDFs for two samples defined in equation
5.1 and the sup is the supremum function. The reference statistic, Rn,m(α),
depending on the significance level α, is defined as
Rn,m(α) =
.
− log(α/2)
2
.
n + m
nm
,
(5.10)
where n and m are the sample sizes. The null hypothesis that “the two sam-
ples come from the same distribution” is rejected at the significance level α
if
Dn,m > Rn,metro(a).
(5.11)
Cifra 9 plots the logarithm of ratio of the two-sample KS statistics,
Dn,metro
Rn,metro (0.01) , for Fox94 (Zorro & Lu, 1994), Goldwyn (Goldwyn & Marrón marrón,
2011), Dangerfiled (Dangerfield et al., 2012), Orio (Orio & Soudry, 2012), 14D
(el 14 × 28D model we proposed in section 3.2). Data of “self-comparison”
(p.ej. Fox94 versus Fox 94) was obtained by comparing two ISI ECDFs from
independent simulations. Como se muestra en la figura 9, models that we previously
proved were pathwise equivalent in section 4, a saber, the Fox94, Orio,
and 14D models, are not distinguishable at any confidence level justified
by our data. Note that those three models use the same boundary con-
ditions (free boundary condition as in Orio & Soudry, 2012) and the ra-
tio Dn,m/Rn,metro(a) of pairwise comparison is on the same magnitude of that
for the self-comparisons. The models of Fox and Lu and Orio and Soudry,
and our 14D model generate indistinguishable ISI distributions but are dis-
tinguishable from Dangerfield’s model and Fox’s 97 modelo. De este modo, como el
bottom panel of Figure 9 muestra, Fox94, Orio, y 14 × 28D form a block
of statistically indistinguishable samples. Sin embargo, as pointed out above,
these statistically equivalent simulation algorithms have different computa-
tional efficiencies (ver figura 8). Among these methods, Orio and Soundry’s
algoritmo (14-dimensional state space with 14 undirected edges as noise
sources) and our method (14-dimensional state space with 28 directed edges
as noise sources) have similar efficiencies, with Orio’s method being about
5% faster than our method. Our 14 × 28D method provides the additional
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1814
S. Pu and P. tomás
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
the ratio of Kolmogorov-Smirnov test statistic
Cifra 9: Logarithm of
/Rn,metro(a), ecuaciones 5.9 y 5.10, for samples from the ISI distribution for
Dn,metro
each pair of models. (Top) Box and whisker plots showing mean and 95% confi-
dence intervals based on 10,000 pairwise comparisons. The first five plots show
self-comparisons (green bars); the remainder compare distinct pairs (gray bars).
A: Fox94 (Zorro & Lu, 1994), B: Orio (Orio & Soudry, 2012), C: 14D (14 × 28D
modelo, sección 3.2), D: Dangerfield (Dangerfield et al., 2012), mi: Goldwyn (Oro-
wyn & Marrón marrón, 2011). (Bottom) Mean logarithms (as in top panel) for all
pairwise comparisons.
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1815
advantage that it facilitates further acceleration under the stochastic shield-
ing approximation (mira la sección 6).
In contrast to the statistically equivalent Orio, 14 × 28D, and Fox94
modelos, algorithms using different boundary conditions are not pathwise
equivalente, which is again verified in Figure 9. Algorithms with subunit ap-
proximation and truncated boundary condition (es decir., “Goldwyn”) y el
reflecting boundary condition (es decir., “Dangerfield”) are significantly differ-
ent in accuracy (y, En particular, they are less accurate) than models in the
14 × 28D class.
6 Discussion and Conclusions
6.1 Summary. The exact method for Markov chain (Mc) simula-
tion for an electrotonically compact (single compartment) conductance-
based stochastic model under current clamp is a hybrid discrete (channel
estado)/continuo (voltage) model of the sort used by Clay and DeFelice
(1983), Newby et al. (2013), and Anderson et al. (2015). While MC methods
are computationally expensive, simulations based on gaussian/Langevin
approximation can capture the effects of stochastic ion channel fluctua-
tions with reasonable accuracy and excellent computational efficiency. Desde
Goldwyn and Shea Brown’s work focusing the attention of the computa-
tional neuroscience community on Fox and Lu’s Langevin algorithm for the
Hodgkin-Huxley system (Zorro & Lu, 1994; Goldwyn & Marrón marrón, 2011),
several variants of this approach have appeared in the literature.
channel, and eight states of the Na
En este artículo, we advocate for a class of models combining the best fea-
tures of conductance-based Langevin models with the recently developed
stochastic shielding approximation (Schmandt & Galán, 2012; Schmidt &
tomás, 2014; Schmidt et al., 2018). We propose a Langevin model with
a 14-dimensional state space, representing the voltage, five states of the
K+
+
-channel; and a 28-dimensional rep-
resentation of the driving noise: one independent gaussian noise term for
each directed edge in the channel-state transition graph. We showed in sec-
ción 2 that the corresponding mean-field 14D ordinary differential equation
model is consistent with the classical HH equations in the sense that the
latter correspond to an invariant submanifold of the higher-dimensional
modelo, to which all trajectories converge exponentially quickly. Cifra 2
illustrated the relation between the deterministic 4D and 14D Hodgkin-
Huxley systems. Building on this framework, we introduced the 14 × 28D
modelo, with independent noise sources corresponding to each ion channel
transition (mira la sección 3). We proved in section 4 that given identical bound-
ary conditions, nuestro 14 × 28D model is pathwise equivalent to Fox and Lu’s
original Langevin model and to a 14-state model with 14 independent noise
sources due to Orio and Soudry (2012).
The original 4D HH model, the 14D deterministic HH model, y el
family of equivalent 14D Langevin models we consider here form a nested
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1816
S. Pu and P. tomás
familia, each contained within the next. Específicamente, the 14D ODE model is
the mean-field version of the 14D Langevin model, and the 4D ODE model
forms an attracting invariant submanifold within the 14D ODE model, como
we establish in our lemma 2. So in a very specific sense, the original HH
equations “live inside” the 14D Langevin equations. De este modo, these three mod-
els enjoy a special relationship. A diferencia de, the 4D Langevin equations stud-
ied in Fox (1997) do not bear an especially close relationship to the other
tres.
In addition to rigorous mathematical analysis, we also performed nu-
merical comparisons (mira la sección 5) mostrando que, como se esperaba, the pathwise
equivalent models produced statistically indistinguishable interspike inter-
vale (ISI) distribuciones. Además, the ISI distributions for our model (y
its equivalents) were closer to the ISI distribution of the gold standard MC
model under two different metric space measures. Our method (junto con
Orio and Soudry’s) proved computationally more efficient than Fox and
Lu’s original method and Dangerfield’s model (Dangerfield et al., 2012).
Además, our method lends itself naturally to model reduction (via the
stochastic shielding approximation) to a significantly faster 14 × 6D simu-
lation that preserves a surprisingly high level of accuracy.
6.2 Discrete Gillespie Markov Chain Algorithms. The discrete-state
MC algorithm due to Gillespie is often taken to be the gold standard simu-
lation for a single-compartment stochastic conductance-based model. Mayoría
former literature on Langevin HH models (Goldwyn & Marrón marrón, 2011;
Linaro et al., 2011; Orio & Soudry, 2012; Huang et al., 2013), when establish-
ing a reference MC model, consider a version of the discrete Gillespie algo-
rithm that assumes a piecewise-constant propensity approximation, eso es,
it does not take into account that the voltage changes between transitions,
which changes the transition rates. This approximation can lead to biophys-
ically unrealistic voltage traces for very small system sizes (ver figura 2 de
Kispersky & Blanco, 2008; top trace with N = 1 ion channel) aunque el
differences appear to be mitigated for N (cid:4) 40 canales (Anderson et al.,
2015). In this article our MC simulations are based on 6000 Na+ and 1800
K+ channels (as in Goldwyn & Marrón marrón, 2011), and we too use the ISI
distribution generated by a piecewise-constant propensity MC algorithm
as our reference distribution. Como se muestra en la tabla 3 y figura 8, el com-
putation time for MC is one order of magnitude larger than efficient meth-
ods such as Orio and Soudry (2012) and Dangerfield et al. (2012) y el
14 × 28D model. The computational cost of the MC model increases dra-
matically as the number of ion channels grows; por lo tanto, even the approx-
imate MC algorithm is inapplicable for a large number of channels.
6.3 Langevin Models. It is worth pointing out that the accuracy of Fox
and Lu’s original Langevin equations has not been fully appreciated. De hecho,
Fox and Lu’s model (Zorro & Lu, 1994) gives an approximation to the MC
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1817
model that is just as accurate as that of Orio and Soudry (2012) both in the
gating variable statistics (Goldwyn & Marrón marrón, 2011) and the ISI dis-
tribution sense (mira la sección 5), porque, as we have established, these mod-
els are pathwise equivalent! Sin embargo, the original implementation requires
taking a matrix square root in every time step in the numerical simulation,
which significantly reduces its computational efficiency.
Models based on modifications of Fox and Lu’s (1994) work can be di-
vided into three classes: the subunit model (Zorro, 1997), effective noise mod-
los (Linaro et al., 2011; Güler, 2013b), and channel-based Langevin models
(p.ej., Goldwyn & Marrón marrón, 2011; Dangerfield et al., 2012; Orio & Soudry,
2012; Pezo et al., 2014; Huang et al., 2013).
6.3.1 Subunit Model. The first modification of Fox and Lu’s model is the
subunit model (Zorro, 1997), which keeps the original form of the HH model,
and adds noise to the gating variables (metro, h, y N) (Zorro, 1997; Goldwyn
& Marrón marrón, 2011). The subunit approximation model was widely used
because of its fast computational speed. Sin embargo, as Bruce (2009) and oth-
ers pointed out, the inaccuracy of this model remains significant even for
large number of channels. Además, Goldwyn and Shea-Brown (2011) y
Huang et al. (2015) found that the subunit model fails to capture the statis-
tics of the HH Na+
puertas. En este artículo, we also observed that the
subunit model is more efficient than channel-based Langevin models but
tends to delay spike generation. Como se muestra en la figura 7, the subunit model
generates significantly longer ISIs than the MC model.
and K
+
6.3.2 Effective Noise Models. Another modification to Fox and Lu’s algo-
rithm is to add colored noise to the channel open fractions. Though colored
noise models such as those of Linaro et al. (2011) and Güler (2013b) no
included in our model comparison, Huang et al. (2015) found that both of
these effective noise models generate shorter ISIs than the MC model with
the same parameters. Though the comparison we provided in section 5 solo
include the Fox and Lu 94, Fox97, Goldwyn, Dangerfield, Orio, SS, y el
14 × 28D models, combining the results from Goldwyn and Shea-Brown
(2011) and Huang et al. (2015), el 14 × 28D model could be compared to a
variety of models (p.ej., Zorro & Lu, 1994; Zorro, 1997; Goldwyn & Marrón marrón,
2011; Linaro et al., 2011; Orio & Soudry, 2012; Dangerfield et al., 2012; Huang
et al., 2013; Güler, 2013b).
6.3.3 Channel-based Langevin Models. The main focus of this article is
the modification based on the original Fox and Lu’s matrix decomposi-
tion method, a saber, the channel-based (or conductance-based) Langevin
modelos. We proved in section 4 that under the same boundary conditions,
Fox and Lu’s original model, Orio’s model, and our 14 × 28D model are
pathwise equivalent, which was also verified from our numerical simula-
tions in sections 4 y 5. En la sección 4 we discussed channel-based Langevin
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1818
S. Pu and P. tomás
modelos (Zorro & Lu, 1994; Goldwyn & Marrón marrón, 2011; Dangerfield et al.,
2012; Orio & Soudry, 2012; Zorro, 2018). We excluded Fox’s more recent im-
complementación (Zorro, 2018) in section 5 for two reasons. Primero, the algorithm is
pathwise equivalent to others considered there. Además, the method is
vulnerable to numerical instability when the Cholesky decomposition is
performed. Específicamente, some of the elements in the S matrix from the
Cholesky decomposition in Fox (2018) involve square roots of differences of
several quantities, with no guarantee that the differences will result in non-
negative terms—even with strictly positive value of the gating variables.
Sin embargo, this model would be in the equivalence class and in any case
would not be more efficient than the Orio model because of the noise dimen-
sion and complicated operations (involving taking multiple square roots) en
each step.
6.4 Model Comparisons. If two random variables have similar distri-
butions, then they will have similar moments, but not vice versa. Por lo tanto,
comparison of the full interspike-interval distributions produced by dif-
ferent simulation algorithms gives a more rigorous test than comparison
of first and second moments of the ISI distribution. Most previous evalua-
tions of competing Langevin approximations were based on the accuracy
of low-order moments, Por ejemplo, the mean and variance of channel
state occupancy under voltage clamp, or the mean and variance of the
interspike interval distribution under current clamp (Goldwyn et al., 2011;
Goldwyn & Marrón marrón, 2011; Schmandt & Galán, 2012; Linaro et al., 2011;
Dangerfield et al., 2012; Orio & Soudry, 2012; Huang et al., 2013, 2015).
Aquí, we compare the accuracy of the different algorithms using the full ISI
distribution but using the L1 norm of the difference (Wasserstein metric)
and the L∞ norm (Kolmogorov-Smirnov test). madera verde, McDonnell,
and Ward (2015) previously compared the ISI distributions generated by
the Markov chain (Gillespie algorithm) to the distribution generated by
different types of Langevin approximations (LA), including the original
Langevin models (Zorro & Lu, 1994; Goldwyn & Marrón marrón, 2011), el
channel-based LA with colored noise (Linaro et al., 2011; Güler, 2013b),
and LA with a 14 × 14 variant of the diffusion coefficient matrix S (Orio &
Soudry, 2012). They concluded that Orio and Soudry’s method provided
the best match to the Markov chain model, específicamente, “Fox-Goldwyn, y
Orio-Kurtz8 methods both generate ISI histograms very close to those of
“Micro.”9 (Greenwood et al., 2015). We note that the comparison reported
in this article simply superimposed plots of the ISI distributions, allowing
a qualitative comparison, while our metric-space analysis is fully quan-
titative. En todo caso, their conclusions are consistent with our findings;
we showed in section 4 that the Fox-Goldwyn and the Orio-Kurtz model
8
9
We refer to this model as “Orio.”
This is the model we refer to as the Markov chain model.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1819
are pathwise equivalent (when implemented with the same boundary
condiciones), which accounts for the similarity in the ISI histograms they
generate. De hecho, because of pathwise equivalence, we can conclude that
the true distributions for these models are identical, and any differences
observed just reflect finite sampling.
6.5 Stochastic Shielding Method. The stochastic shielding (SS) ap-
proximation (Schmandt & Galán, 2012) provides an efficient and accurate
method for approximating the Markov process with only a subset of ob-
servable states. For conductance-based models, rather than aggregating
ion channel states, SS affects dimension reduction by selectively eliminat-
ing those independent noise sources that have the least impact on current
fluctuations. Recent work in (Pezo, Soudry, & Orio, 2014) compared pre-
vious methods (Duende, 1977; Orio & Soudry, 2012; Dangerfield et al.,
2012; Huang et al., 2013; Schmandt & Galán, 2012) in accuracy, applicabil-
idad, and simplicity, as well as computational efficiency. They concluded that
for mesoscopic numbers of channels, stochastic shielding methods com-
bined with diffusion approximation methods can be an optimal choice. Como
Orio and Soudry (2012), the stochastic shielding method proposed by Pezo
et al. (2014) also assumed a detailed balance of transitions between adjacent
states and used edges that are directly connected to the open gates of HH
Na+
. We calculated the edge importance in section 3.3 and found
that the 4 (fuera de 20) most important directed edges for the Na
gates are
no el 4 edges directly connected to the conducting state, as assumed in
previous application of the SS method (Schmandt & Galán, 2012).
and K
+
+
6.6 Which Model to Use? Among all modifications of Fox and Lu’s
method considered here, Orio and Soudry’s approach and our 14 × 28D
model provide the best approximation to the gold standard MC model, con
the greatest computational efficiency. Several earlier models were studied
in the review paper by Goldwyn and Shea-Brown (2011), where they re-
discovered that the original Langevin model proposed by Fox and Lu is
the best approximation to the MC model among those considered. Más tarde
trabajar (Huang et al., 2015) further surveyed a wide range of Langevin ap-
proximations for the HH system (Zorro & Lu, 1994; Zorro, 1997; Goldwyn &
Marrón marrón, 2011; Linaro et al., 2011; Güler, 2013b; Orio & Soudry, 2012;
Huang et al., 2013) and explored models with different boundary con-
ditions. Huang et al. (2015) concluded that the bounded and truncated-
restored Langevin model (Huang et al., 2013) and the unbounded model
(Orio & Soudry, 2012) provide the best approximation to the MC model.
As shown in sections 4 y 5, el 14 × 28D Langevin model naturally
derived from the channel structure is pathwise equivalent to the Fox94,
Fox18, and Orio-Soudry models under the same boundary conditions. El
14 × 28D model is more accurate than the reflecting boundary condition
method of Dangerfield et al. (2012) and also better than the approximation
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1820
S. Pu and P. tomás
method proposed by Goldwyn and Shea-Brown (2011) when the entire ISI
distribution is taken into account. We note that Huang et al. (2015) treated
Goldwyn’s method (Goldwyn & Marrón marrón, 2011) as the original Fox and
Lu model in their comparison; sin embargo, the simulation in Goldwyn and
Marrón marrón (2011) uses the 4D multinomial submanifold to update gating
variables. Our analysis and numerical simulations suggest that the original
Fox and Lu model is indeed as accurate as the Orio-Soudry model, a pesar de
the computational cost remains a major concern.
Aunque el 14 × 28D model has similar efficiency and accuracy as that
of Orio and Soudry (2012), it has several advantages. Primero, the rectangu-
lar S matrix (in equations 1.2 y 1.3) in Orio’s model merges the noise
contributions of reciprocal pairs of edges. Sin embargo, this dimension reduc-
tion assumes, en efecto, that detailed balance holds along reciprocal edges,
which our results show is not the case, under current clamp (ver figura 5).
Además, el 14 × 28D model arises naturally from the individual transi-
tions of the exact evolution equations (see equations 3.1 y 3.2) para el
underlying Markov chain model, which makes it conceptually easier to
understand. Además, our method for defining the 14 × 28D Langevin
model and finding the best SS model extends to channel-based models with
arbitrary channel gating schemes beyond the standard HH model. Dado
any channel state transition graph, the Langevin equations may be read off
from the transitions, and the edge importance under current clamp can be
evaluated by applying the stochastic shielding method to investigate the
contributions of noise from each individual directed edge. Finalmente, in ex-
change for a small reduction in accuracy, the stochastic shielding method
affords a significant gain in efficiency. El 14 × 28D model thus offers a
natural way to quantify the contributions of the microscopic transitions to
the macroscopic voltage fluctuations in the membrane through the use of
stochastic shielding. For general ion channel models, extending a biophys-
ically based Langevin model analogous to our 14 × 28D HH model, a-
gether with the stochastic shielding method, may provide the best available
tool for investigating how unobservable microscopic behaviors (such as ion
channel fluctuations) affect the macroscopic variability in many biological
sistemas.
6.7 Limitaciones. All Langevin models, including our proposed 14 ×
28D model, proceed from the assumption that the ion channel population
is large enough (and the ion channel state transitions frequent enough) eso
the gaussian approximations by which the white noise forcing terms are
derived are justified. De este modo, when the system size is too small, no Langevin
system will be appropriate. Fortunately the Langevin approximation ap-
pears quite accurate for realistic population sizes.
El 14 × 28D model uses more noise sources than other approaches.
Sin embargo, stochastic shielding allows us to jettison noise sources that do
not significantly affect the system dynamics (the voltage fluctuations and
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1821
ISI distribution). Además, in order to compare the ISI distribution in de-
tail among several variants of the Fox94’ model versus the Markov chain
estándar, we have considered a single value of the driving current, mientras
other studies have compared parameterized responses such as the firing
tasa, ISI variance, or other moments, as a function of applied current. Accu-
rate comparisons require large ensembles of independent trajectories, forc-
ing a trade-off between precision and breadth; we opted here for precise
comparisons at a representative level of the driving current.
From a conceptual point of view, a shortcoming of most Langevin mod-
els is the tendency for some channel state variables x to collide with the
domain boundaries x ∈ [0, 1] and to cross them during numerical simula-
tions with finite time steps. We adopted the approach advocated by Orio
and Soudry (2012) of using “free boundaries” in which gating variables
can make excursions into the (unphysical) range x < 0 or x > 1. Prácticamente,
these excursions are always short if the time step is reasonably small, como
they tend to be self-correcting.10 Another approach is to construct reflect-
ing boundary conditions; different implementations of this idea were used
in Dangerfield et al. (2010), Fox and Lu (1994), and Schmid, Goychuk, y
Hänggi (2001). Dangerfield’s method proved both slower and less accurate
than the free boundary method. As an alternative method, one uses a biased
rejection sampling approach, testing each gating variable of the 14D model
on each time step and repeating the noise sample for any time step violat-
ing the domain conditions (Zorro & Lu, 1994; Schmid et al., 2001). Encontramos
that this method had accuracy similar to that of Dangerfield’s method (L1-
Wasserstein difference ≈ 4.4e-1 msec; ver tabla 3) and run time similar to
that of the Fox94 implementation, about four times slower than our 14D
Langevin model.
Yet another approach that in principle can guarantee that the stochas-
tic process remains within proscribed bounds, rederives a “best diffusional
approximation” Fokker-Planck equation based on matching a master-
equation birth-and -death description of a (binomial) population of two-
state ion channels, leading to modified drift and diffusion terms (Goychuk,
2014). This method does not appear to extend readily to the 14D setting,
with underlying multinomial structure of the ion channel gates, so we do
not dwell on it further.
Mesa 3 gives the accuracies with which each model reproduces the
ISI distribution, compared to a standard reference distribution generated
through a large number of samples of the MC method. The mean L1 dif-
ference between a single sample and the reference sample is about 0.227
microseconds. For a nonnegative random variable T ≥ 0, the difference in
the mean under two probability distributions is bounded above by the L1
10
To avoid complex entries, Usamos |X| when calculating entries in the noise coefficient
matrix.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1822
S. Pu and P. tomás
difference in their cumulative distribution functions.11 Thus, the L1 norm
gives an idea of the temporal accuracy with which one can approximate
a given distribution by another. The mean difference between the ISI dis-
tribution generated by a single run of the full 14 × 28D model is about 49
μsec, and the discrepancy produced by the (significantly faster) SS model
is about 76 μsec. When would this level of accuracy matter for the func-
tion of a neuron within a network? The barn owl Tyto alba uses interau-
ral time difference to localize its prey to within 1 a 2 degrees, a feat that
requires encoding information in the precise timing of auditory system ac-
tion potentials at the scale of 5 a 20 microseconds (Moiseff & Konishi, 1981;
Gerstner, Kemper, Van Hemmen, & Wagner, 1996). For detailed studies of
the effects of channel noise in this system, the superior accuracy of the MC
model might be preferred. Por otro lado, the timescale of information
encoding in the human auditory nerve is thought to be in the millisecond
rango (Goldwyn, Marrón marrón, & Rubinstein, 2010), with precision in the
feline auditory system reported as low as 100 μs (Imennov & Rubinstein,
2009; see also Woo, Molinero, & Abbas, 2009). For these and other mammalian
sistemas, the stochastic shielding approximation should provide sufficient
exactitud.
6.8 Trabajo futuro. En la sección 3.3 we compared the ISI variance when
noise was included one edge at a time and found that the edges making the
greatest contribution to population fluctuations under voltage clamp were
not identical to the edges having the largest effect on ISI variance when
taken one at a time. Sin embargo, the ISI, considered as a random variable de-
termined through a first-passage time process, depends on the entire trajec-
conservador, not just on the occupancy of the conducting states. The HH dynamics
are strongly nonlinear, producing a limit cycle in the deterministic case, y
it is not immediately clear whether the effects of channel noise on ISI vari-
ability should be additive. In future work, we plan to address the question
of the additive contribution of individual/molecular noise sources on ISI
variabilidad.
A principal motivation for using the stochastic shielding algorithm is to
develop fast and accurate algorithms for ensemble simulations of forward
models for parameter estimation in a data assimilation framework. We ex-
pect that our method may prove useful for such studies based on current-
clamp electrophysiological data in the future.
11
For a nonnegative random variable T with cumulative distribution function F(t) =
/ ∞
PAG[T ≤ t], the mean satisfies E[t] =
0 (1 − F(t)) dt (Grimmett & Stirzaker, 2005). Allá-
delantero, the difference in mean under two distributions F1 and F2 satisfies |E1[t] − E2[t]| =
,
/ ∞
,
0 F1(t) - F2(t) dt
,
, ≤ ρ
, F2 ).
1(F1
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1823
Apéndice A: Table of Common Symbols and Notations
Mesa 4: Common Symbols and Notations in This Article.
Symbol
Significado
, VL
, VK
C
v
VNa
Iapp
metro, h, norte
αx, βx x ∈ {metro, norte, h}
X
m = [M1
, m10
[m00
, m11
m01
norte = [N1
, n2
, n1
[n0
Mtot, Ntot
X
Y
(cid:6)k
, M2
, m20
, m21
, N2
, n3
, · · · , M8]
,
, m30
(cid:2)
, m31]
, · · · , N5]
(cid:2)
, n4]
METRO
ANa, AK
D
S, S1, S2, SNa, SK
ξ
, X2
, W2
, . . . , Xd]
, . . . , Wn]
X = [X1
W = [W1
δ(·)
δ
yo j
Fn
+
+
, k
Membrane capacitance (μF/cm2)
Membrane potential (MV)
Ionic reversal potential for Na
Applied current to the membrane (nA/cm2)
Dimensionless gating variables for Na
Voltage-dependent rate constant (1/mseg)
Vector of state variables
Eight-component state vector for the Na
Components for the Na
puertas
+
+
+
puertas
and leak (MV)
and K
+
canales
+
+
+
puertas
puertas
+
Five-component state vector for the K
Components for the K
Total number of Na
and K
4-dimensional manifold domain for 4D HH model
14-dimensional manifold domain for 14D HH model
k-dimensional simplex in Rk+1 given by
= 1, yi
+ . . . + yk+1
canales
≥ 0
y1
Multinomial submanifold within the 14D space
State-dependent rate matrix
State diffusion matrix
Noise coefficient matrices
Vector of independent δ-correlated gaussian white noise with
zero mean and unit variance
A d-dimensional random variable for sample path
A Wiener trajectory with n components
The Dirac delta function
The Kronecker delta
Empirical cumulative distribution function with n
observaciones (in section 5, we use m, n as sample sizes)
Mesa 5: Parameters Used for Simulations in This Article.
Symbol
Significado
C
¯gNa
¯gK
gleak
VNa
Membrane capacitance
Maximal sodium conductance
Maximal potassium conductance
Conductancia de fuga
Sodium reversal potential for Na
+
Valor
1 μF/cm2
120 μS/cm2
36 μS/cm2
0.3 μS/cm2
50 MV
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1824
S. Pu and P. tomás
Mesa 5: Continuado.
Symbol
Significado
VK
Vleak
Iapp
A
Mtot
Ntot
+
Potassium reversal potential for K
Potencial de inversión de fugas
Applied current to the membrane
Membrane area
Total number of Na
+
Total number of K
canales
canales
+
Valor
−77 mV
−54.4 mV
10 nA/cm2
100 μm2
6,000
18,00
apéndice B: Parameters and Transition Matrices
Subunit kinetics for the Hodgkin and Huxley equations are given by
αm(v ) =
0.1(25 − v )
exp.(2.5 − 0.1v ) − 1
,
βm(v ) = 4 exp.(−v/18),
a
h(v ) = 0.07 exp.(−v/20),
h(v ) =
b
1
exp.(3 − 0.1v ) + 1
0.01(10 − v )
exp.(1 − 0.1v ) − 1
βn(v ) = 0.125 exp.(−v/80)
αn(v ) =
,
,
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
(B.1)
(B.2)
(B.3)
(B.4)
(B.5)
(B.6)
0
0
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
NS(1) βn(v )
4αn(v ) NS(2) 2βn(v )
0
0
0
3αn(v ) NS(3) 3βn(v )
0
2αn(v ) NS(4) 4βn(v )
αn(v ) NS(5)
0
0
0
βm
DNa(1)
0
3αm DNa(2) 2βm
0
0
2αm DNa(3) 3βm
0
αm DNa(4)
0
0
0
b
h
0
0
0
b
h
0
⎡
AK(v ) =
ANa
=
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0
0
0
a
h
0
0
0
0
a
h
0
0
0
a
h
0
0
0
a
h
0
0
βm
DNa(5)
0
3αm DNa(6) 2βm
0
0
2αm DNa(7) 3βm
0
αm DNa(8)
0
0
0
b
h
0
0
0
0
b
h
0
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1825
where the diagonal elements
Dión(i) = -
(cid:9)
j: j(cid:11)=i
Aion( j, i),
ion ∈ {N / A, k}.
Apéndice C: Proof of Lemma 2
For the reader’s convenience, we restate this lemma.
Lema 2. Let X and Y be the lower-dimensional and higher-dimensional
Hodgkin-Huxley manifolds given by equation 2.12, and let F and G be the vector
fields on X and Y defined by equations 2.1 a 2.4 y 2.7 a 2.9, respectivamente. Dejar
h : X → M ⊂ Y and R : Y → X be the mappings given in Tables 2 y 1, respetar-
activamente, and define the multinomial submanifold M = H(X ). Then M is forward-
time-invariant under the flow generated by G. Además, the vector field G, cuando
restricted to M, coincides with the vector field induced by F and the map H. Eso
es, for all y ∈ M, GRAMO(y) = DxH(R(y)) · F(R(y)).
The main idea of the proof is to show that for every y ∈ Y, GRAMO(y) es una estafa-
(cid:26)
∂H
∂xi
tained in the span of the four vectors
(R(y))
(cid:27)
.
4
yo=1
Prueba. The map from the 4D HH model to the 14D HH model is given in
Mesa 2 como {h : x → y | x ∈ X , y ∈ Y}, and the map from the 14D HH model
to the 4D HH model is given in Table 1 como {R : y → x | x ∈ X , y ∈ Y}. El
partial derivatives
∂H
∂x of the map H are given by
dm00
dm
dm10
dm
dm20
dm
dm30
dm
dm01
dm
= −3(1 − metro)2(1 − h)
= 3(1 − h)(3m2 − 4m + 1)
= 3(1 − h)(2m − 3m2)
= 3(1 − h)m2
= −3h(1 − metro)2
dm00
DH
dm10
DH
dm20
DH
dm30
DH
dm01
DH
= -(1 − metro)3
= −3(1 − metro)2metro
= −3(1 − metro)m2
= −m3
= (1 − metro)3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1826
S. Pu and P. tomás
dm11
dm
dm21
dm
dm31
dm
= 3h(3m2 − 4m + 1)
= 3h(2m − 3m2)
= 3hm2
dm11
DH
dm21
DH
dm31
DH
= 3(1 − metro)2metro
= 3(1 − metro)m2
= m3.
We can write ∂H/∂x in matrix form as:
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
∂H
∂x
=
0
−(1 − metro)3
1
0
−3(1 − metro)2(1 − h)
0
0
0 3(1 − h)(3m2 − 4m + 1) −3(1 − metro)2metro
−3(1 − metro)m2
0
−m3
(1 − metro)3
3(1 − metro)2metro
3(1 − metro)m2
m3
0
3(1 − h)(2m − 3m2)
3(1 − h)m2
−3h(1 − metro)2
3h(3m2 − 4m + 1)
3h(2m − 3m2)
3hm2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
0
0
0
0
0
0
0
0
0
−4(1 − n)3
4(1 − n)2(1 − 4n)
12norte(1 − n)(1 − 2n)
4n2(3 − 4n)
4n3
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
We write out the vector fields 2.8 y 2.9 component by component:
dM1
dt
dM2
dt
dM3
dt
= βmM2
+ b
hM5
− (3αm + a
h)M1
= −3(1 − metro)2(1 − h) [(1 − metro)αm − mβm]
+ (1 − metro)3 [hβ
h
− (1 − h)a
h] ,
= 3αmM1
+ 2βmM3
+ b
hM6
− (2αm + βm + a
h)M2
= 3(1 − h)(3m2 − 4m + 1) [(1 − metro)αm − mβm]
+ 3(1 − metro)2metro [hβ
h
− (1 − h)a
h] ,
= 2αmM2
+ 3βmM4
+ b
hM7
− (αm + 2βm + a
h)M3
,
= 3(1 − h)(2m − 3m2) [(1 − metro)αm − mβm]
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1827
+ 3(1 − metro)m2 [hβ
h
− (1 − h)a
h] ,
= αmM3
+ b
hM8
− (3βm + a
h)M4
,
= 3(1 − h)m2 [(1 − metro)αm − mβm] + m3 [hβ
h
− (1 − h)a
h] ,
= βmM6
+ a
hM1
− (3αm + b
h)M5
,
= −3h(1 − metro)2 [(1 − metro)αm − mβm]
+ (1 − metro)3 [hβ
h
− (1 − h)a
h] ,
= 3αmM5
+ 2βmM7
+ a
hM2
− (2αm + βm + b
h)M6
,
= 3h(3m2 − 4m + 1) [(1 − metro)αm − mβm]
− 3(1 − metro)2metro [hβ
h
− (1 − h)a
h] ,
= 2αmM6
+ 3βmM8
+ a
hM3
− (αm + 2βm + b
h)M7
,
= 3h(2m − 3m2) [(1 − metro)αm − mβm]
h] ,
− 3(1 − metro)m2 [hβ
h
− (1 − h)a
= αmM7
+ a
hM4
− (3βm + b
h)M8
,
= 3hm2 [(1 − metro)αm − mβm] − m3 [hβ
h
− (1 − h)a
h] ,
= βnN2
− 4αnN1
= −4(1 − n)3[αn(1 − n) − nβn],
= 4αnN1
+ 2βnN3
− (3αn + βn)N2
= 4(1 − n)2(1 − 4n)[αn(1 − n) − nβn],
= 3αnN2
+ 3βnN4
− (2αn + 2βn)N3
= 12n(1 − n)(1 − 2n)[αn(1 − n) − nβn],
= 2αnN3
+ 4βnN5
− (3αn + 3βn)N4
= 4n2(3 − 4n)[αn(1 − n) − nβn],
= αnN4
− 4βnN5
= 4n3[αn(1 − n) − nβn].
dM4
dt
dM5
dt
dM6
dt
dM7
dt
dM8
dt
dN1
dt
dN2
dt
dN3
dt
dN4
dt
dN5
dt
By extracting common factors from the previous expressions it is clear that
GRAMO(y) may be written, for all y ∈ Y, como
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1828
GRAMO(y) =
S. Pu and P. tomás
− ¯gNaM8(V − VNa) − ¯gKN5(V − VK ) − gL(V − VL) + Iapp
C
∂H
∂m
)αm − m
(cid:6)
(1 − metro
(cid:6)βm
»
(cid:23)
(cid:22)
+
(cid:22)
−
(cid:6)b
h
h
− (1 − h
(cid:6)
)a
h
(cid:23)
+ [αn(1 − n
(cid:6)
) − n
(cid:6)βn]
∂H
∂h
∂H
∂n
(R(y))
»
(R(y))
»
(R(y))
,
»
∂H
∂v (R(y))
(C.1)
+ M8 and n(cid:6) = N2
where m(cid:6) = (M2
+
/4 + N5. De este modo, GRAMO(y) is in the span of
M7
the column vectors ∂H/∂v, ∂H/∂m, ∂H/∂n, and ∂H/∂h, as was to be shown.
Por otro lado, the vector field for the 4D HH ODE, ecuaciones 2.1 a
+ M6)/3 + 2(M3
/4 + N3
+ M8), h(cid:6) = M5
+ M7)/3 + (M4
/2 + 3N4
+ M6
2.4, es dado por
⎡
⎢
⎢
⎢
⎣
(cid:20)
− ¯gNam3h(V − VNa) − ¯gKn4(V − VK ) − gL(V − VL) + Iapp
αm(V )(1 − metro) − βm(V )metro
a
h(V )(1 − h) − β
h(V )h
αn(V )(1 − n) − βn(V )norte
(cid:21)
/C
⎤
⎥
⎥
⎥
⎦
.
F =
Referring to equation C.1, we see that G(y) = DxH(R(y)) F(R(y)). Thus we
(cid:2)
complete the proof of lemma 2.
Apéndice D: Diffusion Matrix of the 14D Model
As defined in equations 2.5 y 2.6,
m = [m00
norte = [n0
, m10
, n2
, n1
, m20
, n3
, m30
, m01
(cid:2),
, n4]
, m11
, m21
, m31]
(cid:2),
(D.1)
(D.2)
the diffusion matrices DNa and DK are given by
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
=
NS
−4αnn0
0
0
0
NS(1, 1)
−4αnn0
− βnn1
− βnn1
NS(2, 2)
3αnn1
0
− 2βnn2
−3αnn1
− 2βnn2
0
0
NS(3, 3)
· · ·
−2αnn2
− 3βnn3
0
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1829
0
0
− 3βnn3
· · ·
−2αnn2
NS(4, 4)
−αnn3
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
0
0
0
− 4βnn4
DNa(1, 1)
−αnn3
−3αmm00
− 4βnn4
− βmm10
NS(5, 5)
− βmm10
DNa(2, 2)
−2αmm10
0
− 2βmm20
−3αmm00
0
0
− β
hm01
−α
hm00
0
0
0
0
−2αmm10
− 2βmm20
0
0
− β
hm11
−α
hm10
0
0
−α
hm00
− β
hm01
0
− 3βmm30
−αmm20
0
0
DNa(3, 3)
−αmm20
−α
hm20
− 3βmm30
0
0
− β
hm21
0
0
− β
hm11
−α
hm10
0
DNa(4, 4)
0
0
0
− β
hm31
−α
hm30
0
0
− β
hm21
−α
hm20
0
−2αmm11
0
− 2βmm21
−3αmm01
0
0
DNa(5, 5)
0
−3αmm01
− βmm11
− βmm11
DNa(6, 6)
0
0
0
0
− β
hm31
−α
hm30
0
0
− 3βmm31
−2αmm11
− 2βmm21
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
DNa(7, 7)
−αmm21
−αmm21
− 3βmm31
DNa(8, 8)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
D(1:3)
N / A
=
D(4:6)
N / A
=
D(7:8)
N / A
=
dónde
Dión(i, i) = -
(cid:9)
j : j(cid:11)=i
Dión( j, i), for ion ∈ {N / A, k}.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1830
S. Pu and P. tomás
The matrices SK and SNa for the 14 × 28D HH model are given by
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
S(1:5)
N / A
=
S(6:10)
N / A
=
S(11:15)
N / A
=
S(16:20)
N / A
=
√
−
a
hm00
0
0
√
a
√
−
0
hm00
b
hm11
0
0
√
√
0
b
hm11
2αmm10
0
√
b
hm01
0
0
√
−
0
b
hm01
0
0
0
√
)
−
−
0
2αmm10
2βmm20
0
√
−
0
b
hm11
0
0
0
0
0
0
0
0
√
−
√
0
αmm20
αmm20
0
)
0
3βmm30
)
3βmm30
0
−
0
0
0
0
0
0
0
0
0
0
0
0
−
−
√
0
3αmm01
√
βmm11
0
0
−
√
√
√
0
βmm11
2αmm11
2αmm11
0
√
−
√
3αmm00
3αmm00
0
√
−
βmm10
√
βmm10
0
0
0
0
0
0
0
0
√
a
0
hm20
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
√
−
0
a
hm10
0
0
0
√
−
0
b
hm21
0
⎤
0
0
0
√
b
hm21
0
0
0
0
0
√
a
0
hm20
0
√
−
0
b
hm21
0
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
√
0
0
0
b
hm31
00
0
√
−
0
b
hm31
0
0
0
0
√
3αmm01
0
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
)
−
0
2βmm20
√
a
hm20
0
0
0
0
0
0
0
0
a
√
−
hm30
0
0
√
0
hm30
a
0
0
0
0
0
0
0
0
0
0
0
0
0
0
√
−
√
0
αmm21
αmm21
)
0
3βmm31
)
3βmm31
−
)
0
2βmm21
)
2βmm21
0
−
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
,
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1831
where S(i: j)
Na is the ith − jth column of SNa, y
√
√
⎡
−
√
4αnn0
4αnn0
0
−
βnn1
√
βnn1
0
=
SK
⎢
⎢
⎢
⎢
⎢
⎢
⎣
√
−
√
0
3αnn1
3αnn1
0
)
0
2βnn2
)
2βnn2
0
−
· · ·
0
0
0
0
0
· · ·
√
0
0
2αnn2
0
0
0
)
−
0
3βnn3
0
0
√
αnn3
αnn3
−
√
0
0
)
0
4βnn4
)
4βnn4
−
⎤
⎥
⎥
⎥
⎥
⎦
.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Expresiones de gratitud
We thank David Friel (Case Western Reserve University) for illuminating
discussions of the impact of channel noise on neural dynamics and the
anonymous referees for many detailed and constructive comments.
This work was made possible in part by grants from the National Sci-
ence Foundation (DMS-1413770 and DEB-1654989) and the Simons Foun-
dación. P.T. thanks the Oberlin College Department of Mathematics for
research support. This research has been supported in part by the Math-
ematical Biosciences Institute and the National Science Foundation under
grant DMS-1440386. Large-scale simulations made use of the High Perfor-
mance Computing Resource in the Core Facility for Advanced Research
Computing at Case Western Reserve University.
Referencias
allen, mi. J., allen, l. J., Arciniega, A., & madera verde, PAG. mi. (2008). Construction of
equivalent stochastic differential equation models. Stochastic Analysis and Appli-
cationes, 26(2), 274–297.
anderson, D. F., Ermentrout, B., & tomás, PAG. j. (2015). Stochastic representations of
ion channel kinetics and exact stochastic simulation of neuronal dynamics. Hacer-
nal of Computational Neuroscience, 38(1), 67–82.
anderson, D. F., & Kurtz, t. GRAMO. (2015). Stochastic analysis of biochemical systems, volumen. 1.
Berlina: Saltador.
bruce, I. C. (2009). Evaluation of stochastic differential equation approximation of
ion channel gating models. Annals of Biomedical Engineering, 37(4), 824–838.
Clay, j. r., & DeFelice, l. j. (1983). Relationship between membrane excitability and
single channel open-close kinetics. Biophys. J., 42(2), 151–157.
1832
S. Pu and P. tomás
Colquhoun, D., & Hawkes, A. (1981). On the stochastic properties of single ion chan-
nels. Proc. R. Sociedad. Lond. B, 211(1183), 205–235.
Dangerfield, C., kay, D., & Burrage, k. (2010). Stochastic models and simulation of
ion channel dynamics. Procedia Computer Science, 1(1), 1587–1596.
Dangerfield, C. MI., kay, D., & Burrage, k. (2012). Modeling ion channel dynam-
ics through reflected stochastic differential equations. Revisión física e, 85(5),
051907.
Dayán, PAG., & Abbott, l. F. (2001). Theoretical neuroscience: Computational and mathemat-
ical modeling of neural systems. Cambridge, MAMÁ: CON prensa.
Dvoretzky, A., Kiefer, J., & Wolfowitz, j. (1956). Asymptotic minimax character of the
sample distribution function and of the classical multinomial estimator. Annals
of Mathematical Statistics, 27(3), 642–669.
Earnshaw, B., & Keener, j. (2010a). Global asymptotic stability of solutions of nonau-
tonomous master equations. SIAM Journal on Applied Dynamical Systems, 9(1),
220–237.
Earnshaw, B., & Keener, j. (2010b). Invariant manifolds of binomial-like nonau-
tonomous master equations. SIAM Journal on Applied Dynamical Systems, 9(2),
568–588.
Faisal, A. A., & Risue, S. B. (2007). Stochastic simulations on the reliability of
action potential propagation in thin axons. PLOS Biología computacional, 3, 5.
Zorro, R. F. (1997). Stochastic versions of the Hodgkin-Huxley equations. Biophysical
Diario, 72(5), 2068–2074.
Zorro, R. F. (2018). Critique of the Fox-Lu model for Hodgkin-Huxley fluctuations in neuron
ion channels. arXiv:1807.07632.
Zorro, r., & Lu, Y. (1994). Emergent collective behavior in large numbers of globally
coupled independently stochastic ion channels. Phys. Rdo. E Stat. Phys. Plasmas
Fluids Relat. Interdiscip. Topics, 49(4), 3421–3431.
Gadgil, C., Sotavento, C. h., & Othmer, h. GRAMO. (2005). A stochastic analysis of first-order
reaction networks. Bulletin of Mathematical Biology, 67, 901–946.
Gerstner, w., Kemper, r., Van Hemmen, j. l., & Wagner, h. (1996). A neuronal learn-
ing rule for sub-millisecond temporal coding. Naturaleza, 383(6595), 76–78.
Duende, D. t. (1977). Exact stochastic simulation of coupled chemical reactions. j.
Phys. Chem., 81, 2340–2361.
Duende, D. t. (2007). Stochastic simulation of chemical kinetics. Annu. Rdo. Phys.
Chem., 58, 35–55.
Goldwyn, j. h., Imennov, norte. S., Famulare, METRO., & Marrón marrón, mi. (2011). estocástico
differential equation models for ion channel noise in Hodgkin-Huxley neurons.
Revisión física e, 83(4), 041908.
Goldwyn, j. h., & Marrón marrón, mi. (2011). The what and where of adding channel
noise to the Hodgkin-Huxley equations. PLOS Comput. Biol., 7(11), e1002247.
Goldwyn, j. h., Marrón marrón, MI., & Rubinstein, j. t. (2010). Encoding and decoding
amplitude-modulated cochlear implant stimuli—a point process analysis. Diario
of Computational Neuroscience, 28(3), 405–424.
Goychuk, I. (2014). Stochastic modeling of excitable dynamics, improved Langevin
model for mesoscopic channel noise. In Proceedings of the International Con-
ference on Nonlinear Dynamics of Electronic Systems (páginas. 325–332). Berlina:
Saltador.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1833
madera verde, PAG. MI., McDonnell, METRO. D., & Pabellón, l. METRO. (2015). Dynamics of gamma
bursts in local field potentials. Computación neuronal, 27(1), 74–103.
Grimmett, GRAMO., & Stirzaker, D. (2005). Probability and random processes (3tercera ed.). Nuevo
york: prensa de la Universidad de Oxford.
Güler, METRO. (2013a). An investigation of the stochastic Hodgkin-Huxley models under
noisy rate functions. Computación neuronal, 25(9), 2355–2372.
Güler, METRO. (2013b). Stochastic Hodgkin-Huxley equations with colored noise terms
in the conductances. Computación neuronal, 25(1), 46–74.
Colina, t. l., & Chen, Y.-D. (1972). On the theory of ion transport across the nerve mem-
brane: IV. Noise from the open-close kinetics of K+ channels. Revista biofísica,
12(8), 948–959.
Hodgkin, A. l., & Huxley, A. F. (1952). A quantitative description of membrane cur-
rent and its application to conduction and excitation in nerve. j. Physiol., 117, 500–
544.
Huang, y., Rüdiger, S., & Shuai, j. (2013). Channel-based Langevin approach for the
stochastic Hodgkin-Huxley neuron. Revisión física e, 87(1), 012716.
Huang, y., Rüdiger, S., & Shuai, j. (2015). Accurate Langevin approaches to simulate
Markovian channel dynamics. Physical Biology, 12(6), 061001.
Imennov, norte. S., & Rubinstein, j. t. (2009). Stochastic population model for electri-
cal stimulation of the auditory nerve. IEEE Transactions on Biomedical Engineering,
56(10), 2493–2501.
Keener, j. PAG. (2009). Invariant manifold reductions for Markovian ion channel dy-
namics. j. Matemáticas. Biol., 58(3), 447–457.
Keener, j. PAG. (2010). Exact reductions of Markovian dynamics for ion channels with
a single permissive state. j. Matemáticas. Biol., 60(4), 473–479.
Keener, j. PAG., & Sneyd, j. (1998). Mathematical physiology, volumen. 1. Berlina: Saltador.
Kispersky, T., & Blanco, j. A. (2008). Stochastic models of ion channel gating. Scholar-
pedia, 3(1), 1327.
Kloeden, PAG. MI., & Platen, mi. (1999). Numerical solution of stochastic differential equations.
Berlina: Saltador.
Agujero, A. (1933). Sulla determinazione empirica di una lgge di distribuzione.
Inst. Ital. Attuari, Giorn., 4, 83–91.
Kurtz, t. GRAMO. (1981). Approximation of population processes. Filadelfia: SIAM.
Linaro, D., Storace, METRO., & Giugliano, METRO. (2011). Accurate and fast simulation of
channel noise in conductance-based model neurons by diffusion approximation.
PLOS Biología computacional, 7(3), e1001102.
Como, z. F., & Sejniano, t. j. (1995). Reliability of spike timing in neocortical neu-
ron. Ciencia, 268(5216), 1503–1506.
Mino, h., Rubinstein, j. T., & Blanco, j. A. (2002). Comparison of algorithms for the
simulation of action potentials with stochastic sodium channels. Ann. Biomed.
Eng., 30(4), 578–587.
Moiseff, A., & Konishi, METRO. (1981). The owl’s interaural pathway is not in-
volved in sound localization. Journal of Comparative Physiology, 144(3), 299–
304.
Neher, MI., & Sakmann, B. (1976). Single-channel currents recorded from membrane
of denervated frog muscle fibres. Naturaleza, 260(5554), 799.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1834
S. Pu and P. tomás
Newby, j. METRO., Bressloff, PAG. C., & Keener, j. PAG. (2013). Breakdown of fast-slow
analysis in an excitable system with channel noise. Phys. Rdo. Letón., 111(12),
128101.
O'Donnell, C., & Van Rossum, METRO. C. (2015). Spontaneous action potentials and neural
coding in unmyelinated axons. Computación neuronal, 27(4), 801–818.
Orio, PAG., & Soudry, D. (2012). Simple, fast and accurate implementation of the dif-
fusion approximation algorithm for stochastic ion channels with multiple states.
PLOS One, 7(5), e36670.
Pezo, D., Soudry, D., & Orio, PAG. (2014). Diffusion approximation-based simulation of
stochastic ion channels: Which method to use? Frontiers in Computational Neuro-
ciencia, 8, 139.
Schmandt, norte. T., & Galán, R. F. (2012). Stochastic-shielding approximation of Markov
chains and its application to efficiently simulate random ion-channel gating.
Physical Review Letters, 109(11), 118101.
Schmid, GRAMO., Goychuk, I., & Hänggi, PAG. (2001). Stochastic resonance as a collective
property of ion channel assemblies. Europhysics Letters, 56(1), 22.
Schmidt, D. r., Galán, R. F., & tomás, PAG. j. (2018). Stochastic shielding and edge
importance for Markov chains with timescale separation. PLOS Computational Bi-
ology, 14(6), e1006206.
Schmidt, D. r., & tomás, PAG. j. (2014). Measuring edge importance: A quantita-
tive analysis of the stochastic shielding approximation for random processes on
gráficos. Journal of Mathematical Neuroscience, 4(1), 6.
Schneidman, MI., Liberto, B., & Segev, I. (1998). Ion channel stochasticity may be
critical in determining the reliability and precision of spike timing. Comedia neural-
putación, 10(7), 1679–1703.
Sengupta, B., Risue, S., & Niven, j. (2010). Comparison of Langevin and Markov
channel noise models for neuronal signal generation. Revisión física e, 81(1),
011918.
Shorack, GRAMO. r., & Wellner, j. A. (2009). Empirical processes with applications to statistics.
Filadelfia: SIAM.
Skaugen, MI., & Walløe, l. (1979). Firing behaviour in a stochastic nerve membrane
model based upon the Hodgkin-Huxley equations. Acta Physiol. Scand., 107(4),
343–363.
Smirnov, norte. (1948). Table for estimating the goodness of fit of empirical distributions.
Annals of Mathematical Statistics, 19(2), 279–281.
Strassberg, A. F., & DeFelice, l. j. (1993). Limitations of the Hodgkin-Huxley for-
malism: Effects of single channel kinetics on transmembrane voltage dynamics.
Computación neuronal, 5(6), 843–855.
Wasserstein, l. norte. (1969). Markov processes over denumerable products of spaces
describing large systems of automata. Problems of Information Transmission, 5(3),
47–52.
Blanco, j. A., Klink, r., alonso, A., & kay, A. R. (1998). Noise from voltage-gated
ion channels may influence neuronal dynamics in the entorhinal cortex. Diario
de neurofisiología, 80(1), 262–269.
Blanco, j. A., Rubinstein, j. T., & kay, A. R. (2000). Channel noise in neurons. Trends
in Neurosciences, 23(3), 131–137.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Fast and Accurate Stochastic Hodgkin-Huxley Simulations
1835
Cortejar, J., Molinero, C. A., & Abbas, PAG. j. (2009). Simulation of the electrically stimulated
cochlear neuron: Modeling adaptation to trains of electric pulses. IEEE Transac-
tions on Biomedical Engineering, 56(5), 1348–1359.
Yu, h., Dhingra, R. r., Dick, t. MI., & Galán, R. F. (2017). Effects of ion channel noise on
neural circuits: An application to the respiratory pattern generator to investigate
breathing variability. Revista de neurofisiología, 117(1), 230–242.
Recibido febrero 20, 2020; accepted June 5, 2020.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
1
0
1
7
7
5
1
8
6
5
2
8
5
norte
mi
C
oh
_
a
_
0
1
3
1
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3