INVESTIGACIÓN
Parcels and particles: Markov blankets
in the brain
Karl J. Friston1, Erik D. Fagerholm2, Tahereh S. Zarghami3, Thomas Parr1,
Inês Hipólito4, Loïc Magrou5, and Adeel Razi1,6
1Wellcome Centre for Human Neuroimaging, University College London, Londres, Reino Unido
2Department of Neuroimaging, King’s College London, Londres, Reino Unido
3Bio-Electric Department, School of Electrical and Computer Engineering, University of Tehran, Amirabad, Tehran, Iran
4Berlin School of Mind and Brain, and Institut für Philosophie, Universidad Humboldt de Berlín, Berlina, Alemania
5Univ Lyon, Université Claude Bernard Lyon 1, Inserm, Stem Cell and Brain Research Institute U1208, Bron, Francia
6Turner Institute for Brain and Mental Health, Monash University, Clayton, Australia
un acceso abierto
diario
Palabras clave: Conectividad funcional, Effective connectivity, Markov blankets, Renormalization group,
Dynamic causal modeling, Intrinsic brain networks
ABSTRACTO
At the inception of human brain mapping, two principles of functional anatomy underwrote
most conceptions—and analyses—of distributed brain responses: a saber, functional
segregation and integration. There are currently two main approaches to characterizing
integración funcional. The first is a mechanistic modeling of connectomics in terms of
directed effective connectivity that mediates neuronal message passing and dynamics on
neuronal circuits. The second phenomenological approach usually characterizes undirected
conectividad funcional (es decir., measurable correlations), in terms of intrinsic brain networks,
self-organized criticality, dynamical instability, etcétera. This paper describes a treatment
of effective connectivity that speaks to the emergence of intrinsic brain networks and critical
dinámica. It is predicated on the notion of Markov blankets that play a fundamental role in
the self-organization of far from equilibrium systems. Using the apparatus of the
renormalization group, we show that much of the phenomenology found in network
neuroscience is an emergent property of a particular partition of neuronal states, encima
progressively coarser scales. Tal como, it offers a way of linking dynamics on directed graphs
to the phenomenology of intrinsic brain networks.
RESUMEN DEL AUTOR
This paper describes a treatment of effective connectivity that speaks to the emergence of
intrinsic brain networks and critical dynamics. It is predicated on the notion of Markov
blankets that play a fundamental role in the self-organization of far from equilibrium systems.
Using the apparatus of the renormalization group, we show that much of the phenomenology
found in network neuroscience is an emergent property of a particular partition of neuronal
estados, over progressively coarser scales. Tal como, it offers a way of linking dynamics on
directed graphs to the phenomenology of intrinsic brain networks.
INTRODUCCIÓN
A persistent theme in systems neuroscience, especially neuroimaging, is the search for princi-
ples that underlie the functional anatomy of distributed neuronal processes. Estos principios
are usually articulated in terms of functional segregation (or differentiation) and integration,
which inherit from centuries of neuroanatomical, neurophysiological, and neuropsychological
Citación: Friston, k. J., Fagerholm,
mi. D., Zarghami, t. S., Parr, T., Hipólito,
I., Magrou, l., & Razi, A. (2021). Parcels
and particles: Markov blankets in the
cerebro. Neurociencia en red, 5(1),
211–251. https://doi.org/10.1162
/netn_a_00175
DOI:
https://doi.org/10.1162/netn_a_00175
Supporting Information:
https://doi.org/10.1162/netn_a_00175
Recibió: 19 Julio 2020
Aceptado: 24 Noviembre 2020
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Razi Adeel
adeel.razi@monash.edu
Editor de manejo:
Randy McIntosh
Derechos de autor: © 2020
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
Conectividad funcional:
A (undirected) measure of the
statistical dependencies between
spatially remote neurophysiological
events.
Effective connectivity:
A measure of the directed (causal)
influence of one neural system over
another using a model of neuronal
interactions.
Dynamic causal modeling:
A Bayesian framework that is used to
infer causal interaction between
coupled or distributed neuronal
sistemas.
estudiar (Zeki & Shipp, 1988). In recent thinking about functional integration, people have turned
to formal accounts of (predictive) processing in the brain (p.ej., Bastos et al., 2012; Keller
& Mrsic-Flogel, 2018; Parr & Friston, 2018; Rao & Ballard, 1999; Spratling, 2008) to understand
la naturaleza de (neuronal) message passing on graphs, where edges correspond to connectivity
and nodes correspond to neuronal populations. Fundamentalmente, this characterization rests upon the
asymmetric and directed connectivity that defines cortical and subcortical hierarchies (p.ej.,
Bastos et al., 2012; Crick & Koch, 1998; Felleman & VanEssen, 1991; k. j. Friston, Parr, &
de Vries, 2017; Keller & Mrsic-Flogel, 2018; norte. Markov et al., 2013; norte. t. Markov et al.,
2014; Mesulam, 1998; Stachenfeld, Botvinick, & Gershman, 2017; Zeki & Shipp, 1988). Usu-
ally, these asymmetries are expressed in terms of things like laminar specificity that distin-
guish between forward and backward connections (Buffalo, Fries, Landman, Buschman, &
Desimone, 2011; Grossberg, 2007; Haeusler & Maass, 2007; Hilgetag, O’Neill, & Joven,
2000; Thomson & Bannister, 2003; Trojanowski & jacobson, 1977). More recently, asym-
metries in spectral content have become an emerging theme (Arnal & Giraud, 2012; Bastos
et al., 2015; Buffalo et al., 2011; Giraud & Poeppel, 2012; Hovsepyan, Olasagasti, & Giraud,
2018; Self, van Kerkoerle, Goebel, & Roelfsema, 2019; Cantante, Sejnowski, & Rakic, 2019;
van Kerkoerle et al., 2014).
A diferencia de, analyses of functional connectivity have focused on distributed patterns of co-
herent fluctuations in neuronal activity and phenomenological descriptions of the implicit dy-
namics (bassett & despreciar, 2017; Biswal, Van Kylen, & Hyde, 1997; bullmore & despreciar, 2009;
Gilson, Moreno-Bote, Ponce-Alvarez, Ritter, & decoración, 2016; Gu et al., 2018; Lynall et al., 2010;
van den heuvel & despreciar, 2013). This phenomenology ranges from intrinsic brain networks—
which are conserved over subjects in resting-state functional magnetic resonance imaging—
to the dependence of neuronal dynamics on cortical excitability (Freyer, Roberts, Ritter, &
romper la lanza, 2012; Roy et al., 2014). The principles that are brought to bear on this kind of
characterization could be seen as ascribing neuronal dynamics to various universality classes,
such as self-organized criticality (Bak, Espiga, & Wiesenfeld, 1988; romper la lanza, Heitmann, &
Daffertshofer, 2010; cocineros, Perdido, Brilla, & romper la lanza, 2017; decoración & Jirsa, 2012;
Haimovici, Tagliazucchi, Balenzuela, & Chialvo, 2013; Kitzbichler, Herrero, Christensen, &
bullmore, 2009; López, Litvak, Espinosa, Friston, & Barnes, 2014; espinilla & kim, 2006). (Nota:
Although we have subsumed criticality and dynamic instability under phenomenological ap-
se acerca, criticality can refer to the dynamics of neurons and neural assemblies—as opposed
to the statistical properties of data leveraged by functional connectivity. A simple example
of criticality is a branching process, an inherently directed process. Neurobiological models
of these kinds of processes have been derived from causal neural field models with directed
(corticothalamic) interactions [Freyer et al., 2011] and with coupled oscillators [decoración & Jirsa,
2012]. In this setting, criticality acquires a more mechanistic aspect, as we will see below.)
This dual-pronged approach to functional integration invites an obvious question: Is there a
way of linking the two?
Practically, the study of context-sensitive, directed coupling between the nodes of neuronal
networks calls for an estimate of effective connectivity, under some model of how measured
brain signals are generated. One then has to resolve the ill-posed problem of recovering the
underlying (conectividad) parameters of the model, usually using Bayesian inference. The best
example here is dynamic causal modeling (k. j. Friston, harrison, & Penny, 2003; k. j. Friston,
Kahan, Biswal, & Razi, 2014; Razi & Friston, 2016). The complementary approach—based
upon functional connectivity—borrows ideas from network science and graph theory. Este
entails specifying an adjacency matrix, usually formed by thresholding a functional connec-
tivity matrix summarizing dependencies among nodes, where the nodes are generally defined
in terms of some parcellation scheme (bassett & despreciar, 2017; bullmore & despreciar, 2009).
Neurociencia en red
212
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
Markov blanket:
A Markov blanket allows one to
distinguish a collection of states that
belong to a particle from states that
do not.
Jacobian:
A matrix that contains a first-order
partial derivative for a vector
función.
Lyapunov exponent:
It gives the rate of exponential
divergence from perturbed initial
condiciones.
In what follows, we will consider a particular parcellation scheme based upon effective
connectivity and ask whether it leads to the same phenomenology seen in network neuro-
ciencia. Al hacerlo, podemos, in principle, explain and quantify the emergence of large-scale
intrinsic brain networks and their characteristic dynamics. A crucial aspect of the particular
parcellation or partition—employed in this work—means that it can be applied recursively
in the spirit of the renormalization group (Schwabl, 2002). This means that there is a formal
way of quantifying the dynamics at various spatiotemporal scales. Our hypothesis was that
the spatiotemporal dynamics of coarser scales would evince both the functional anatomy of
intrinsic brain networks and the emergence of (self-organized) criticality—as assessed in terms
of dynamical instability.
Although this work is framed as addressing issues in network neuroscience (bassett & despreciar,
2017), it was originally conceived as a parcellation scheme for multiscale analyses of neuro-
imaging time series. En otras palabras, it was intended as a first principle approach to dimen-
sion reduction and decomposition, as a prelude for subsequent graph theoretic or dynamic
causal modeling (k. j. Friston, Kahan, et al., 2014; Razi, Kahan, rees, & Friston, 2015; Razi
et al. 2017; Zhou y cols., 2018). Sin embargo, the theoretical foundations—and uniqueness of the
partition—proved too involved to support a simple and practical procedure.
En cambio, qué
follows is offered as a case study of emergence in coupled dynamical systems, using the brain
as a paradigm example.
This paper comprises five sections. en el primero, we review the notion of Markov blankets and
how recursive applications of a partition or parcellation of states into Markov blankets allows
one to express dynamics at increasing scales. We will use the notion of the renormalization
grupo (RG) to motivate this recursive parcellation because there are some formal constructs (en
terms of RG scaling) that furnish an insight into how dynamics change as we move from one
scale to the next. The second section describes a simple (dynamic causal modeling) análisis
of directed effective connectivity at the finest spatial scale, as summarized with a Jacobian.
This plays the role of a directed adjacency matrix, which is all that is needed for successive
renormalization to higher scales. The renormalization group is illustrated with an exemplar
conjunto de datos, to show what the ensuing parcellation scheme looks like. This section concludes with
a brief consideration of sparse coupling at the finest scale, in terms of excitatory and inhibitory
connections. The subsequent sections consider dynamics at different scales of parcellation, en
terms of intrinsic (within parcel) and extrinsic (between parcel) conectividad. Our focus here
is on the progressive slowing of intrinsic dynamics as we move from one scale to the next—a
slowing that organizes the dynamics at coarser (más alto) scales towards critical regimes of in-
stability and slowly fluctuating dynamical modes. The third section illustrates the emergence
of autonomous dynamics, in terms of characteristic frequencies associated with intrinsic con-
conectividad, and in terms of positive Lyapunov exponents that speak to transcritical bifurcations
en, and only at, coarser scales. The fourth section focuses on extrinsic connectivity and the
coupling between (complex) modes or patterns of activity and how this relates to functional
connectivity and intrinsic brain networks (Fox et al., 2005). The final section reviews the dy-
namical phenomenology at hand from the point of view of statistical physics, with a special
focus on dissipative dynamics and detailed balance at nonequilibrium steady state. Nosotros estafamos-
clude with a brief discussion and qualification of this particular (sic) approach to functional
integración.
MARKOV BLANKETS AND THE RENORMALIZATION GROUP
The last section concluded with reference to a particular partition. The use of the word
“particular” has a double entendre here. It is predicated on a more fundamental (or perhaps
Neurociencia en red
213
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
foundational) analysis of coupled dynamical systems that consider the emergence of “parti-
cles.” Full details of this treatment can be found in K. Friston (2019). From the current per-
perspectiva, we just need to know how to define Markov blankets (clark, 2017; Kirchhoff, Parr,
Palacios, Friston, & Kiverstein, 2018; Pearl, 1988; Pellet & Elisseeff, 2008) and how Markov
blankets engender particles and particular partitions (k. Friston, 2019). For readers interested
in Markov blankets for dynamical systems, fairly comprehensive discussions can be found in
k. Friston, Da Costa, and Parr (2020) and Parr, Da Costa, and Friston (2020).
In brief, a Markov blank et allows one to distinguish a collection of vector states (lo sucesivo,
simply states) that belong to a particle from states that do not. This provides an operational
definition of a particle that, in the present setting, can be regarded as a region of interest or
parcel of brain states. This means that a particular partition becomes a parcellation scheme,
in terms of functional anatomy. The particular partition refers to a partition of a (potentially
grande) set of states into a smaller number of particles, where each particle is distinguished from
other particles, in virtue of possessing a Markov blanket. A Markov blanket is simply a set of
states that separate or insulate—in a statistical sense—states that are internal to the blanket
and states that are on the outside; a saber, external states. Technically, this means that internal
states are conditionally independent of external states, when conditioned upon their blanket
estados (Pearl, 2009).
In a particular partition, all external states are assigned to particles, to create an ensemble
of particles that are constituted by their blanket states and the internal states within or be-
neath the blanket. The crucial aspect of this partition is that we only need the blanket states
to understand coupling between particles. This follows from the conditional independence
between internal and external states, where the external states “that matter” are the blanket
states of other particles. En breve, the particular partition is a principled way of dividing states
into particles or parcels that is defined in terms of statistical dependencies or coupling among
estados. In more complete treatments, one can divide the blanket states into active states and
sensory states, according to the following rules: Sensory states are not influenced by internal
estados, while active states are not influenced by external states.
En efecto, it is the absence of
these influences that enables us to identify the Markov blanket of any given set of internal
estados. Please see the Supporting Information for a formal definition of Markov blankets in this
dynamical context.
As noted above, we are dealing with vector states (not scalar variables). So, what is a vector
estado? A vector state is the multidimensional state of a particle, Por ejemplo, the principal
eigenstates of its Markov blanket. Sin embargo, we have just said that a particle arises from a
partition of states—and now we are saying that a state is an eigenstate (es decir., a linear mixture) de
the blanket states of a particle. So, is a particle a collection of states or is a state the attribute
of a particle (es decir., its blanket states)? The answer is both, because we have particles at multiple
niveles.
This is where the renormalization group comes in, via a recursive application of the par-
ticular partition.
En otras palabras, if we start with some states at any level, we can partition
these states into a set of particles, based upon how the states are coupled to each other. Nosotros
can then take the principal eigenstates of each particle’s blanket states to form new states at
the scale above, and start again. This recursive application of a grouping or partition opera-
colina (GRAMO)—followed by a dimension reduction (R)—leads to the renormalization group based
upon two operators, R and G. In theoretical physics, the renormalization group (RG) refers to
a transformation that characterizes a system when measured at different scales (Cardy, 2015;
Schwabl, 2002). A working definition of renormalization rests on three things (lin, Tegmark,
& Rolnick, 2017): vectors of random variables, a coarse-graining operation, and a requirement
Neurociencia en red
214
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
that the operation does not change the functional form of the Lagrangian to within a multiplica-
tive constant. Por ejemplo, under a transformation of position and velocity variables x and ˙x
given by x → ax and ˙x → b ˙x, the corresponding Lagrangian λ transforms (if scale-invariant)
according to λ(X, ˙x) → λ(ax, b ˙x) = cλ(X, ˙x), where a, b, and c are constants (Landau &
Lifshitz, 1976). Equivalently, a scale-invariant system’s equation of motion must remain per-
fectly unchanged under the rescaling operation. This can readily be seen by applying the
Euler-Lagrange equation to the scaled Lagrangian:
∂(cλ)
∂ ˙x
d
dt
(cid:20)
(cid:21)
=
∂(cλ)
∂x
⇒ c
∂(λ)
∂ ˙x
d
dt
(cid:20)
(cid:21)
=c
∂(λ)
∂x
.
(1)
Aquí, the rescaling constant c cancels, leaving the original equation of motion.
En
what follows, instead of dealing with real positions and velocities, we will deal with complex
variables that have real and complex parts.)
(Nota:
In our case, the random variables are states; the coarse-graining operation corresponds to
the grouping into a particular partition (GRAMO) and a dimension reduction (R) inherent in retaining
the principal eigenstates of particular blanket states. The dimension-reduction operator (R) tiene
two parts. Primero, we can eliminate the internal states because they do not contribute to cou-
pling between particles. Segundo, we can eliminate the eigenstates that dissipate very quickly;
a saber, those with large negative eigenvalues. These are the fast or stable modes of a dynami-
cal system (Carr, 1981; Haken, 1983). This leaves us with the slow, unstable eigenstates picked
out by the dimension reduction, which we can now see as an adiabatic approximation. Please
note that in quantum mechanics, the adiabatic approximation refers to those solutions to the
Schrödinger equation that make use of a timescale separation between fast and slow degrees
of freedom.
Formalmente, we can express the coarse-graining or blocking transformation R ◦ G as a com-
position of a particular partition and adiabatic reduction applied to any random dynamical
sistema (at scale i) that can be characterized as coupled subsets of states. The n-th subset
(i)
n ⊂ x(i)constitutes the vector state of a particle, subject to random fluctuations, Vaya
X
(i)
norte :
˙x
(i)
n = ∑m λ
(i)
nmx
(i)
metro + Vaya
(i)
n ⇒ J(X
(i)
norte , X
(i)
metro ) , ∂ ˙x
∂x
(i)
norte
(i)
metro
= λ
(i)
nm.
(2)
These equations of motion for the states of the n-th particle comprise intrinsic and extrinsic
componentes, determined by the states of the particle in question and other particles, respetar-
(i)
nn ∈ C, deter-
activamente. In this form, the diagonal elements of the Jacobian or coupling matrix, λ
mine the frequency and decay of oscillatory responses to extrinsic perturbations and random
fluctuations. The grouping operator (GRAMO) groups states into particles, where particles comprise
(i)
j }. The blocking transformation (R) then reduces
blanket and internal states: Pi
the number of states, by eliminating internal states at the lower level and retaining slow eigen-
(i)
(i)
norte )) of the Jacobian of blanket states
n = eig(j(b
states using the principal eigenvectors ξ
(i)
norte . These eigenstates then become the vector states at the next scale:
b
(i)
j = {b
(i)
norte , b
(i)
j
, µ
(i)
norte
X
= R ◦ G ◦
(i−1)
norte
X
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Neurociencia en red
{λ
{b
(i)
norte }
(i)
nm}
{X
(i)
norte }
GRAMO
−→ {Pi
oh
norte
{λ
oh
(i)
nm} = β({λ
(i)
j
(i)−
norte
(i)
j = {b
} = {ξ
(i)
j }: Pi
(i+1)
norte
R
−→ {X
b
−→ {λ
(i+1)
nm } = {ξ
(i)−
norte
, µ
norte
(i−1)
nm })
(i)
j }
(i)
norte }: ξ
(i)
norte , b
j(b
b
(i)
n = eig(j(b
(i)
(i)
metro }.
metro )ξ
(i)
norte , b
(i)
norte ))
(3)
215
Markov blankets in the brain
(i)
nm, cuyo
Aquí, the parameters of the Lagrangian are taken to be the coupling parameters λ
changes are implemented by a beta function that is said to induce a renormalization group flow
(or RG flow). The key aspect of this flow rests upon the adiabatic reduction, which renders
the dynamics progressively slower at successive macroscopic scales. This follows because,
by construction, only slow eigenstates are retained, where the intrinsic coupling among these
eigenstates is a diagonal matrix of (negative) eigenvalues, which determine how quickly the
eigenstates decay:
mi[Re(λ
(i)
nn)] ≤ E[Re(λ
(i+1)
nn
)] · · · ≤ 0.
(4)
The RG flow speaks to a progressive move from dynamics with high amplitude, fast fluctua-
ciones (p.ej., mecánica cuántica) through to deterministic systems that are dominated by slow
(i)
dinámica (p.ej., classical mechanics). In deterministic systems, the real parts of λ
nn play the
role of Lyapunov exponents (cf. critical exponents), which quantify the rate of separation of in-
finitesimally close trajectories (Lyapunov & Batán, 1992; Pyragas, 1997). This suggests that as
we move from one scale to the next, there is a concomitant increase in the tendency to critical
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
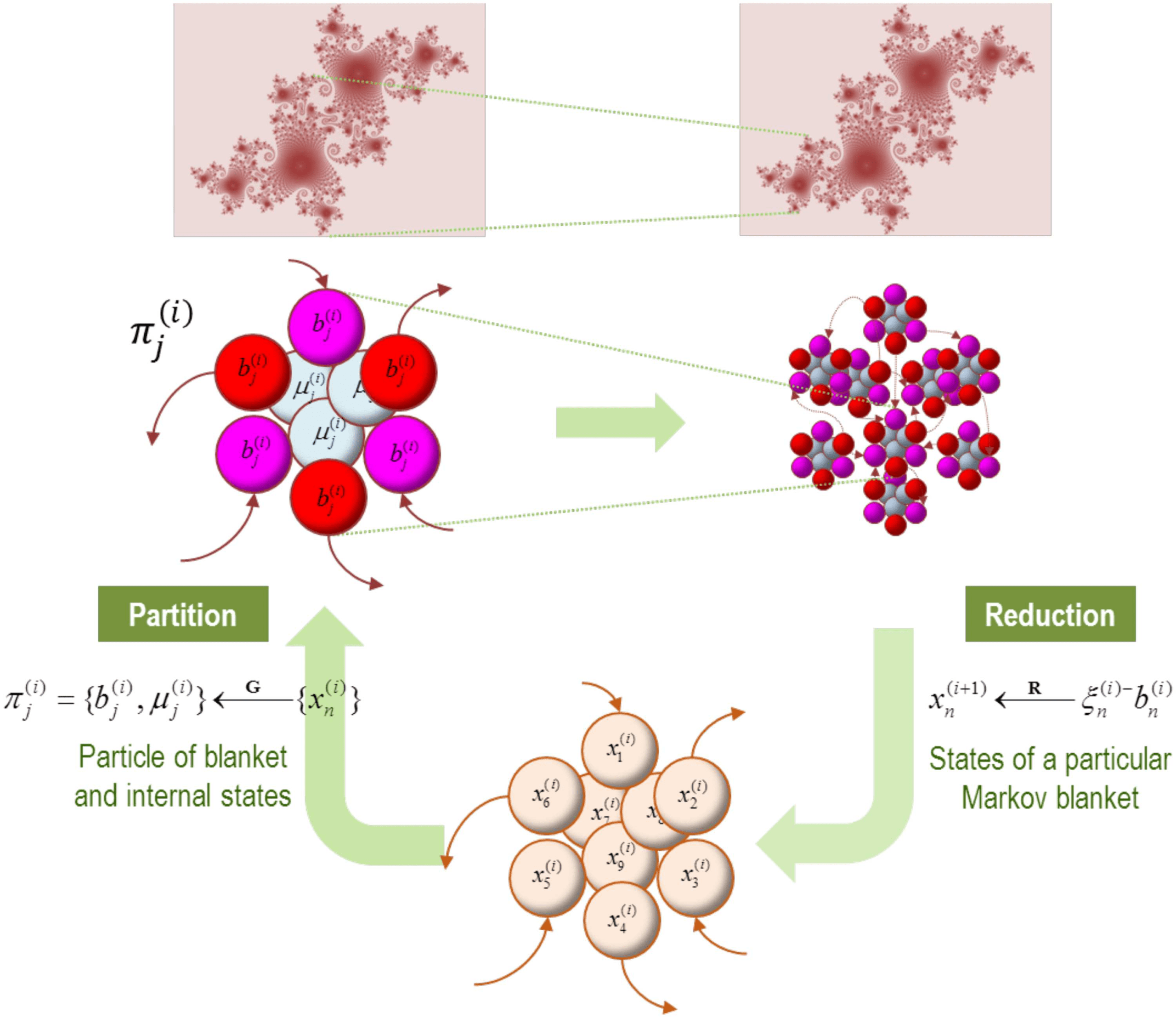
Cifra 1. Blankets of blankets. This schematic illustrates the recursive procedure by which suc-
cessively coarser scale (and slower) dynamics arise from subordinate levels. At the bottom of the
figura (lower panel), we start with an ensemble of vector states (here nine). The conditional de-
pendencies among these vector states (es decir., eigenstates) define a particular partition into particles
(upper panels). Fundamentalmente, this partition equips each particle with a bipartition into blanket and in-
ternal states, where blanket states comprise active (rojo) and sensory (magenta) estados. The behavior
of each particle can now be summarized in terms of (slow) eigenstates or mixtures of its blanket
states to produce states at the next level or scale. These constitute an ensemble of vector states and
the process starts again. Formalmente, one can understand this in terms of coarse-graining the dynam-
ics of a system via two operators. The first uses the particular partition to group subsets of states
(GRAMO), while the second uses the eigenstates of the resulting blanket states to reduce dimensionality
(R). The upper panels illustrate the bipartition for a single particle (left panel) and an ensemble of
particles, eso es, the particular partition per se (right panel). The insets on top illustrate the implicit
self-similarity of particular dependencies pictorially, in moving from one scale to the next. Please
see the main text for a definition of the variables used in this figure.
Neurociencia en red
216
Markov blankets in the brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
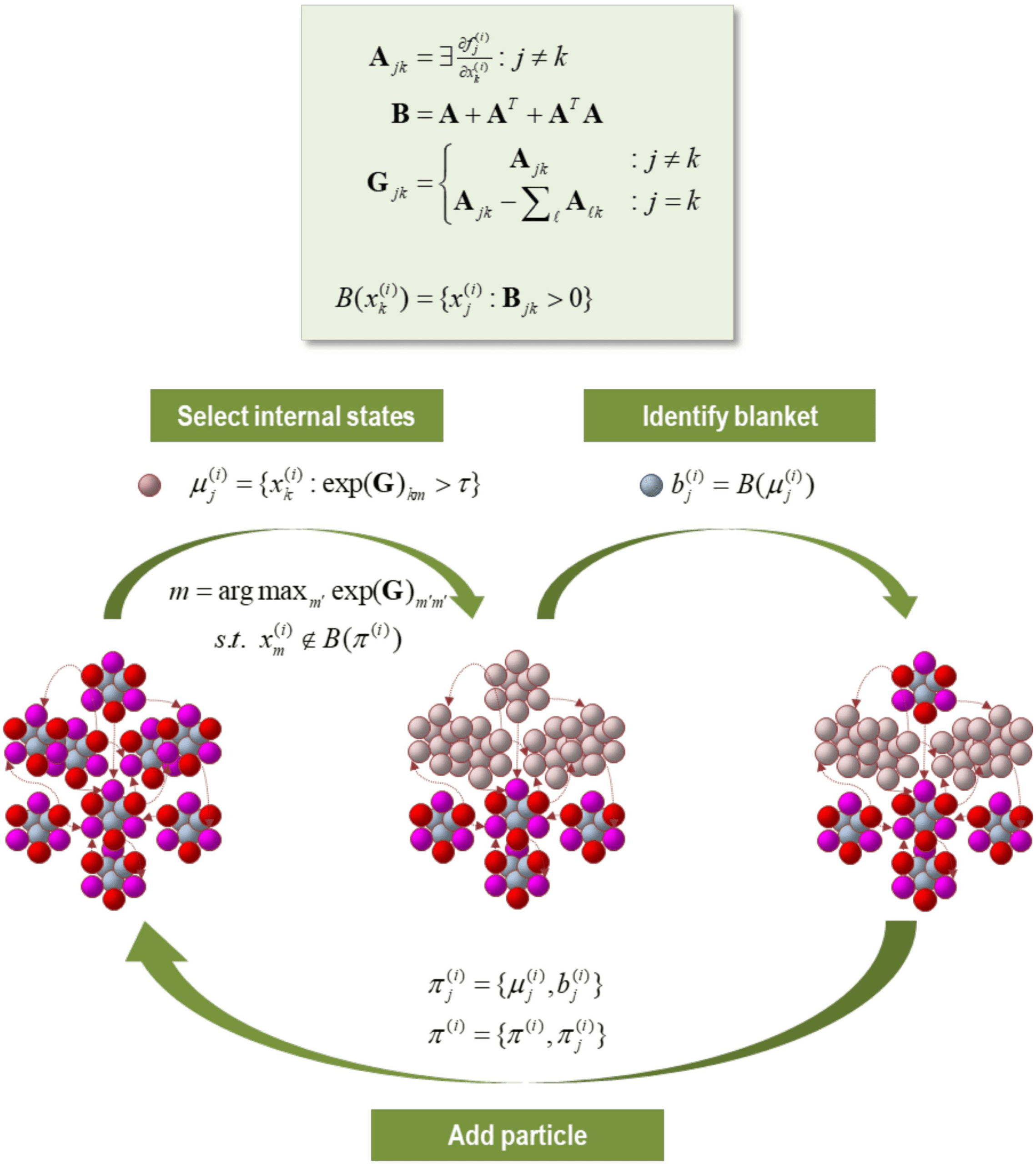
Cifra 2. The particular partition. This schematic illustrates a partition of eigenstates (small col-
ored balls) into particles (comprising nine vectors), where each particle has six blanket states (rojo
and magenta for active and sensory states, respectivamente) and three internal states (cyan). The upper
panel summarizes the operators used to create a particular partition. We start by forming an adja-
cency matrix that characterizes the coupling between different vectors’ states. This is based upon the
Jacobian and implicitly the flow of vector states. The resulting adjacency matrix defines a Markov
blanket–forming matrix (B), which identifies the children, padres, and parents of the children. El
same adjacency matrix is used to form a graph Laplacian (GRAMO) that is used to define neighboring (es decir.,
coupled) internal states. One first identifies a set of internal states using the graph Laplacian. Aquí,
the j-th subset of internal states at level i are chosen, based upon dense coupling with the vector
state with the largest graph Laplacian. Coupled internal states are then selected from the columns
of the graph Laplacian that exceed some threshold. En la práctica, the examples used later specify the
number of internal states desired for each level of the hierarchical decomposition. Having identified
a new set of internal states (that are not members of any particle that has been identified so far), es
Markov blanket is recovered using the Markov blanket–forming matrix. The internal and blanket
states then constitute a new particle, which is added to the list of particles identified. This proce-
dure is repeated until all vector states have been accounted for. Usually, towards the end of this
procedimiento, candidate internal states are exhausted because all remaining unassigned vector states
belong to the Markov blanket of the particles identified previously. In this instance, the next particle
can be an active or sensory state, depending upon whether there is a subset (of active states) eso
is not influenced by another. In the example here, we have already identified four particles and
the procedure adds a fifth (arriba) particle to the list of particles, thereby accounting for nine of the
remaining vector states.
slowing and dynamic itinerancy (Cessac, Blanchard, & Krüger, 2001; Pavlos, Karakatsanis, &
Xenakis, 2012).
En esto (RG) configuración, a relevant variable is said to describe the macroscopic behavior of
the system. From our perspective, the relevant variables in question correspond to the slow
Neurociencia en red
217
Markov blankets in the brain
eigenstates. En breve, we can reduce many states to a small number of eigenstates that summa-
rize the dynamics “that matter.” These eigenstates are the relevant variables that underwrite
critical slowing. Figures 1 y 2 provide a graphical illustration of this recursive partition-
ing and reduction based upon an adiabatic approximation (es decir., eliminating fast eigenstates
and approximating dynamics with the remaining slow eigenstates). This adiabatic reduction
is commonplace in physics, where it plays a central role in synergetics through the enslaving
principle (Haken, 1983) y, in a related form, in the center manifold theorem (Carr, 1981).
We now have at hand a principled procedure to repeatedly coarse-grain a system of loosely
coupled particles (p.ej., nonlinear neuronal oscillators) at successively coarser spatiotemporal
escamas. One can see that, by construction, as we ascend scales, things will get coarser and
slower. It is this progressive slowing towards criticality that is the primary focus of the examples
pursued below. Sin embargo, before we can apply the particular partition to some empirical
datos, we first need to quantify the coupling among particles at a suitably fine or small scale.
Having characterized this coupling in terms of some dynamical system or state space model,
we can then use the Jacobian to identify a particular partition, compute the Jacobian of the
blanket states, and then take the ensuing eigenstates to the next level, as described above.
This furnishes a description of dynamics in terms of the intrinsic (within particle) coupling (es decir.,
(i)
nm. Lo haremos
eigenvalues) of any particle λ
unpack the meaning of these terms later using numerical examples and analysis. Actualmente,
we will focus on estimating the coupling among a large number of particles at the smallest
escala.
(i)
nn and their extrinsic (between particle) coupling λ
STARTING FROM THE BOTTOM
To use the machinery of Markov blankets, in the setting of loosely coupled dynamical systems,
we need to specify the coupling among vector states (that we can associate with the eigenstates
of the smallest particles under consideration). Para hacer esto, one can use a simplified form of
dynamic causal modeling that can be applied to hundreds or thousands of neuronal states.
This is easier than it might sound, provided one commits to low (primero) order approximations
(p.ej., Frassle et al., 2017). Consider the state space model describing the coupling among a
large number of states, where the flow is subject to random fluctuations (dropping superscripts
for clarity):
˙x = f (X) + ωx
y = k ∗ x + ωx
(5)
Notice that we have introduced a convolution operator that converts latent (neuronal) estados
to some observable measurement (p.ej., hemodynamic signals from functional magnetic reso-
nance imaging). Aquí, y(t) is a linear convolution (with kernel k) of some states x(t) subject to
observation and system noise, respectivamente. We have also assumed that there is an observation
for each relevant state. Linearizing this state space model, where J = ∂x f (X) and † denotes
conjugate transpose, we have the following:
Dx = xJ† + ωx
y = Kx + ωy)
⇒
KDx = KxJ† + Kωx
(
Dy = KDx + Dωy)
⇒
Dy = yJ† + Vaya
ω = Kωx + Dωy − ωy J†
(
.
(6)
Aquí, the states have been arranged into a matrix, with one row for each point in time and
a column for each dimension. This means we can replace the derivative and convolution
operators in Equation 5 with the matrix operators in Equation 6 that commute, eso es, KD =
NS. (Nota: This is due to the linearity of the convolution operator and is true regardless of
whether the temporal derivative is in matrix form. Intuitivamente, a linear combination of velocities
Neurociencia en red
218
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
Bayesian model reduction:
A Bayesian inversion and
comparison of models that are
reduced (or sparsed) forms of a full
(or parent) modelo.
is equivalent to the rate of change of a linear combination of positions.) Sucesivamente, this means we
can approximate the system with a general linear model:
Dy = yJ† + Vaya
cov(Vaya) = γ1KK† + γ2DD† + γ3 I
(7)
This approximation assumes that J† J ∝ I. This assumption is licensed by the fact that the Jaco-
bian of relevant states will be dominated by large negative leading diagonals (that underwrite
the stability of each state). Ecuación 7 is a straightforward general linear model, with random
fluctuations that have distinct covariance components, that depends upon the form of the (p.ej.,
hemodynamic) convolution kernel and the amplitude of state and observation noise. If K is
specified in terms of the basis set of convolution kernels, then the covariance components of
the linearized system can be expressed as the following:
K = ∑k κkKk ⇒
KK† = ∑ij κiκjKiK†
j
,
(8)
such that κiκj replaces the hyperparameter γ1 above.
This linearized system can now be solved using standard (variational Laplace) schemes
for parametric empirical Bayesian (PEB) modelos, to provide (approximate) Gaussian poste-
riors over the unknown elements of the Jacobian—and the unknown covariance parame-
ters encoding the amplitude of various random effects (k. Friston, Mattout, Trujillo-Barreto,
Ashburner, & Penny, 2007). This Bayesian model inversion requires priors on the parameters
and hyperparameters (es decir., covariance component parameters), specified as Gaussian shrink-
age priors. For nonnegative hyperparameters, Gaussian shrinkage priors are generally applied
to log-transformed hyperparameters (es decir., a lognormal prior over nonnegative scale parameters).
el
Equipped with posterior densities over the coupling parameters—or elements of
Jacobian—we can now use Bayesian model reduction to eliminate redundant parameters
(k. j. Friston et al., 2016); a saber, parameters whose shrinkage to zero increases model evi-
dence by removing redundancy or complexity. As described elsewhere (k. Friston & Penny,
2011), this can be done very efficiently, because we know the form of the posteriors, antes
and after reducing the model. Además, we can apply other prior constraints to eliminate
redundant coupling parameters.
In the examples below, we performed Bayesian model reduction to enforce reciprocal cou-
pling among states, given that extrinsic connections in the brain are almost universally re-
current (Felleman & VanEssen, 1991; norte. Markov et al., 2013; norte. t. Markov et al., 2014).
This was implemented by combining the changes in variational free energy—or log model
evidence—when removing connections between two states in both directions. If model evi-
dence increased by three natural units (es decir., a log odds ratio of exp(3):1 o 20:1), both connec-
tions were removed but not otherwise. Además, we precluded long-range coupling (más allá de
32 mm) and used Bayesian model reduction to identify the most likely upper bound on the
spatial reach of coupling between nonhomologous particles (es decir., particles that did not occupy
homologous positions in each hemisphere). These empirical connectivity priors were based
upon a body of empirical work, suggesting that the density of axonal projections—from one
area to another—declines exponentially as a function of anatomical separation (Ercsey-Ravasz
et al., 2013; Finlay, 2016; Horvát et al., 2016; Wang & Kennedy, 2016). We will later exam-
ine the evidence for this kind of distance rule, based upon coupling among particles at the
finest scale.
Neurociencia en red
219
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
En resumen, Ecuación 7 is used to evaluate the effective connectivity of a dynamic causal
model based upon the Jacobian of a stochastic differential equation under some simplifying
suposiciones. In brief, we start with a linear state space model, in which the response variable y
(the multivariate BOLD time series) is a linear convolution (k) of some hidden states x subject
to observation and system noise ωy and ωx, respectivamente (cf. Ecuación 5). We can linearize this
state space model (cf. Ecuación 6) such that it can be written in matrix form as a general linear
modelo (cf. Ecuación 7). This linearized system is then solved using standard variational Laplace
for parametric empirical Bayes (PEB) that provides the (Gaussian) posterior estimates for the
system parameters (elements of the Jacobian) and hyperparameters (the unknown covariance
of the observation and system noise). Since this scheme uses PEB for model inversion, es
automatically protected against becoming trapped in local minima. PEB uses the formal appa-
ratus of variational Laplace, which optimizes a free energy lower bound, which optimizes the
trade-off between model complexity and accuracy. Given the posterior distributions over the
system parameters (and hyperparameters) and the model evidence, one can then use Bayesian
model reduction procedures to prune away any redundant couplings. This constitutes a com-
putationally efficient inversion scheme that can invert very large systems within minutes on a
standard laptop. At the finest scale, the Jacobian had 1,024 por 1,024 elements taking about
45 min to infer the model parameters.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
FUNCTIONAL PARCELLATION
Computationally, the benefit of linearizing the system in this way means that one can evaluate
the posterior coupling parameters or elements of the Jacobian region by region (cf. Frassle
et al., 2017). This means that, provided one is prepared to wait long enough, one can invert
large systems with thousands of regions or parcels. On a personal computer, it takes about an
hour to evaluate the Jacobian for coupling among 1,024 estados. To illustrate the renormaliza-
tion group procedure practically, we applied it to the fMRI time series from a single subject.
These time series are the same data used to illustrate previous developments in dynamic causal
modelado. Time series data were acquired from a normal subject at 2 Tesla using a Magnetom
VISION (Siemens, Erlangen) whole-body MRI system. Contiguous multislice images were ac-
quired with a gradient echo-planar sequence (TE = 40 EM; TR = 3.22 s; matrix size = 64 ×
64 × 32, voxel size 3 × 3 × 3 mm). Four consecutive 100-scan sessions were acquired, com-
prising a sequence of 10-scan blocks under five conditions. The first was a dummy condition
In the second, Fixation, the subject viewed a fixa-
to allow for magnetic saturation effects.
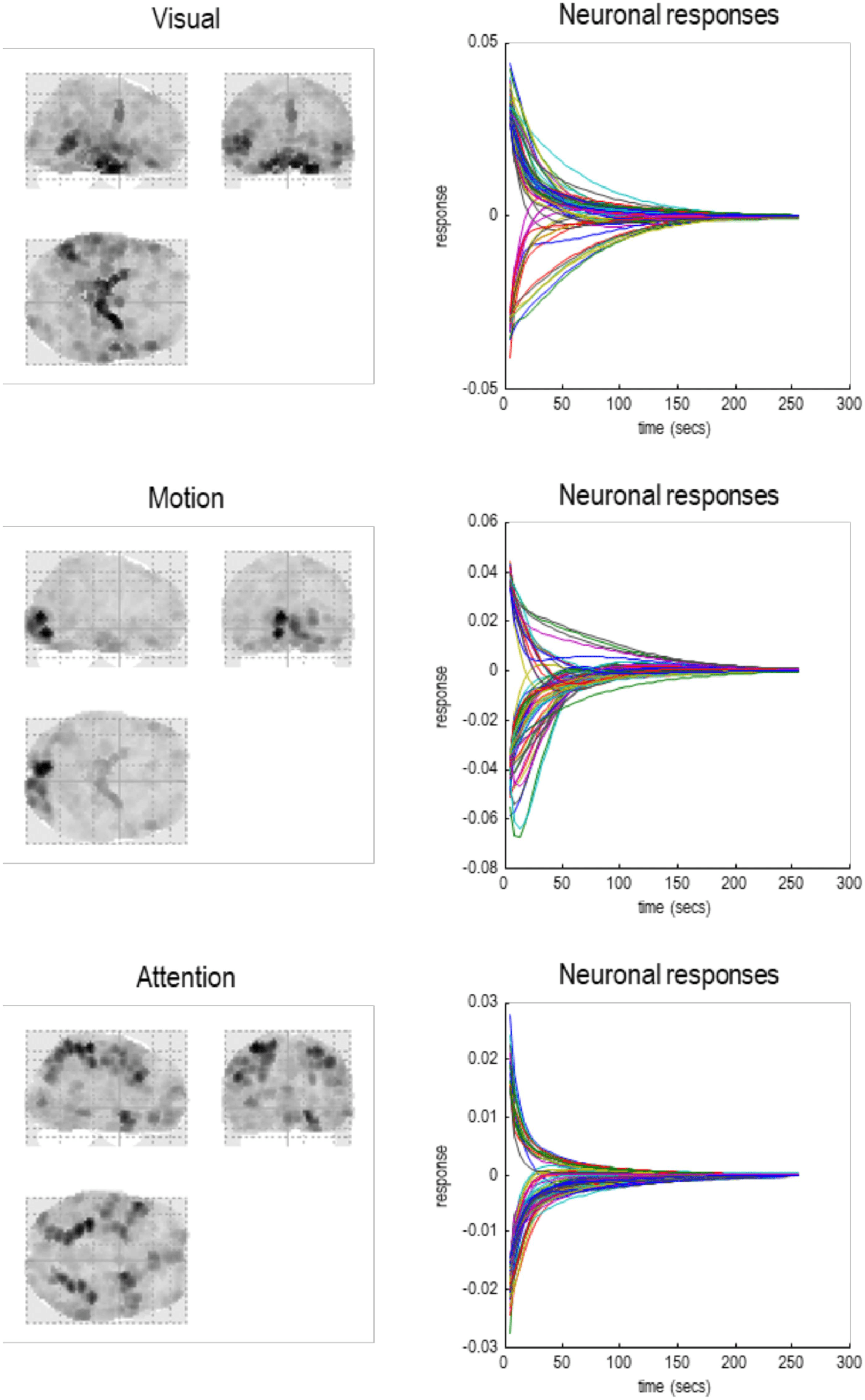
tion point at the center of the screen. In an Attention condition, the subject viewed 250 dots
moving radially from the center at 4.7 degrees per second and was asked to detect changes in
radial velocity. In No attention, the subject was asked to look at the moving dots. In the last
condición, subject viewed stationary dots. The order of the conditions alternated between Fix-
ation and photic stimulation. The subject fixated on the center of the screen in all conditions.
No overt response was required in any condition, and there were no actual speed changes.
In contradistinction to normal procedures in functional connectivity fMRI analyses, el tiempo
series were not smoothed (other than adjusting for ultraslow scanner drifts). This is because
the random fluctuations at all timescales play a material role in the decomposition at hand.
Informed consent from the subject was obtained and the study was approved by the Human
Ethics Review Committee of University College London.
In the exemplar analyses below, we started at a scale where each particle can be plausi-
bly summarized with a single state. This single state was the principal eigenstate following a
principal components analysis of voxels that lay within about 4 mm of each other. This can
be thought of as reducing the dynamics to a single mode of the Markov blanket of this small
Neurociencia en red
220
Markov blankets in the brain
collection of voxels. Practically, this simply involved taking all voxels within a fixed radius
of the voxel showing the largest variance, performing a singular value decomposition, y
recording the first eigenvariate. These voxels were then removed, and the procedure repeated
until the entire multivariate time series was reduced to 1,024 eigenstates, where each eigen-
state corresponds to a simple particle. See Figure 3. Claramente, we could have summarized the
dynamics of each collection of voxels with two or more eigenstates; sin embargo, por simplicidad
we will assume that the eigenstate with the greatest variance is a sufficient summary of the
slow, non-dissipative, dynamics of this smallest scale.
Curiosamente, this variance is propor-
tional to the characteristic time constant of systemic dynamics; a saber, the negative inverse of
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
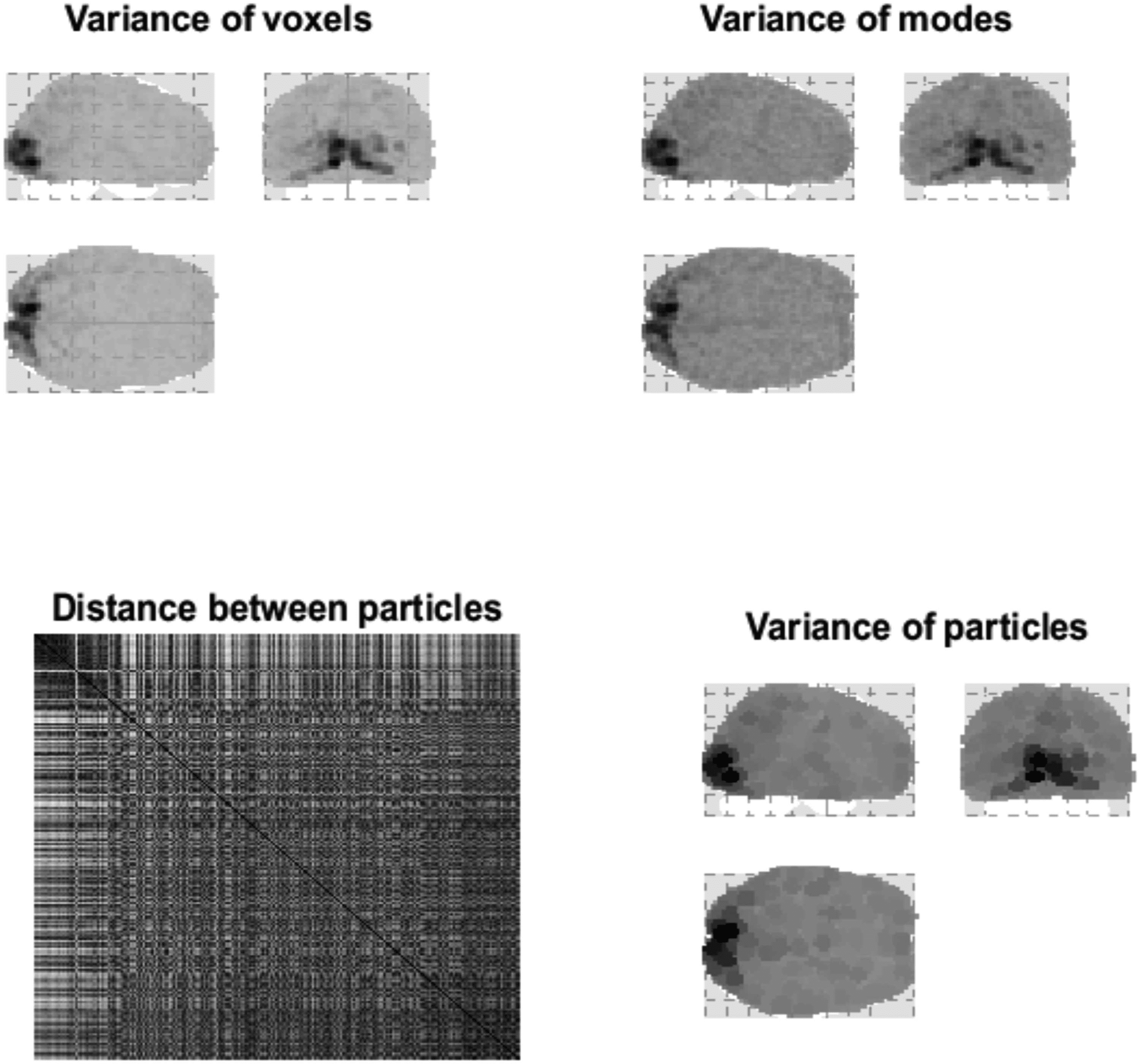
Cifra 3. Distributed variance. This figure illustrates the variance explained by particles at the first
nivel. The upper panel is a maximum intensity projection of the variance of the fMRI time series,
for a single subject over 360 scans (with a repetition time of 3.22 s) in voxel space. One can see
that visual (es decir., striate) and extrastriate regions have been preferentially engaged; sin embargo, hay
distributed activity throughout the brain. The upper right panel shows the corresponding variance
in terms of the eigenmodes of 1,024 particles. As in subsequent figures, these projections involve
weighting the absolute value of each eigenmode by the quantity in question; aquí, the variance.
This maximum intensity projection shows that the particles furnish a reasonably faithful summary
of voxel-specific variance. The lower right panel shows the same variance assigned to the spatial
support of each eigenmode, to illustrate the coarse-graining when assembling particles from voxels.
These characterizations of fluctuations over time have been framed in terms of variance. We will see
later that variance can be interpreted as a dissipative time constant. En otras palabras, in this example,
visual areas show the least dissipation, with dynamics that decay slowly. The lower left panel shows
the Euclidean distance between the centers of pairs of particles. The center of each particle was
defined as the expected anatomical location, where the probability density over location was taken
to be a softmax function of the absolute value of the eigenmode over voxels. In this and subsequent
figuras, Euclidean distances are evaluated after projecting centers across the sagittal plane, eso es,
superimposing homologous particles in the right and left hemispheres. We calculated the Euclidean
distance after projecting the particle centers across the sagittal plane so that each parcel will be in
close vicinity to the homologous particle in the opposite hemisphere. This reflects our prior beliefs
about interhemispheric coupling—which brings homologous regions close together—in terms of
path lengths.
Neurociencia en red
221
Markov blankets in the brain
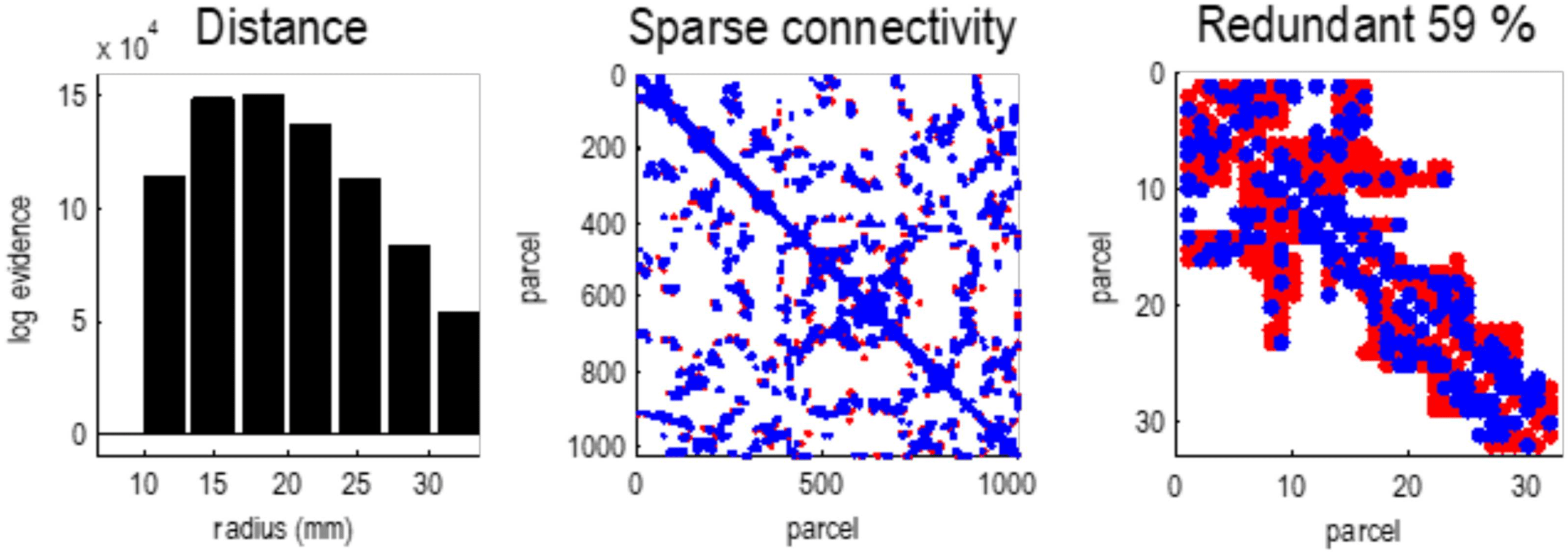
Cifra 4. Sparse connectivity. This figure illustrates the sparsity of effective connectivity using
Bayesian model reduction. The left panel shows the log evidence for a series of models that pre-
cluded connections beyond a certain distance or radius. This log evidence has been normalized
to the log evidence of the model with the least marginal likelihood (es decir., coupling over less than
10 mm). These results show that a model with local connectivity (acerca de 18 mm) has the greatest
evidencia. En otras palabras, effective connections beyond this distance are redundant, in the sense
that they add more complexity to log evidence that is licensed by an increase in accuracy. El
middle panel shows the ensuing sparse coupling (within the upper bound of 32 mm) as an adja-
cency matrix, where particles have been ordered using a nearest neighbor scheme in voxel space.
The blue dots indicate connections that have been removed by Bayesian model reduction. En esto
instancia, cerca de 60% of estimated connections were redundant. The right panel zooms in on the
primero 32 particles, to show some local connections that were retained (rojo) or removed (azul).
the eigenvalues of the underlying Jacobian (see the final section). En otras palabras, como el (nega-
tivo) principal eigenvalue of effective connectivity approaches zero from below, the principal
eigenvalue of functional connectivity (es decir., variance) aumenta; see Equation 9 in Lopez et al.
(2014).
Following Bayesian model reduction, we now have a sparse Jacobian or directed, weighted
adjacency matrix describing the dynamical coupling between univariate states of 1,024 par-
ticles (ver figura 4). This Jacobian can now be subject to a particular partition to identify the
most connected internal states and their Markov blanket, following the procedures summa-
rized in Figure 2. This grouping process (es decir., the G operator) was repeated until all 1,024
states are accounted for: in this example, grouping 1,024 states into 57 particles. For simplic-
idad, and for consistency with the first level, each particle was assigned a single internal state.
The ensuing partition was then subject to an adiabatic reduction (es decir., the R operator) by taking
the eigenvectors of the Jacobian describing the intrinsic dynamics of each particle’s blanket
estados.
The eight principal eigenstates were retained if their eigenvalues were less than 1. Esto es
the adiabatic approximation that dispenses with modes that dissipate quickly, aquí, Dentro de un
(i)
nn, corresponding to the
segundo. This reduces the intrinsic coupling to a diagonal matrix λ
(i)
nm contains complex
eigenvalues of the intrinsic Jacobian ∂xn f
elements that couple the eigenstates of one particle to the eigenstates of another. Lo haremos
return to how these Jacobians manifest in terms of connectivity later.
(i)
norte . The extrinsic coupling λ
En breve, we now have a summary of dynamics at the scale above in terms of the eigenstates
of a particle that, by construction, have been orthogonalized. These constitute the vector states
for the next application of the RG operator to produce a description of dynamics at subsequent
escamas. See Figure 5 through Figure 8. These examples show that by the fourth scale, tenemos
reduced the dynamics to a single particle, shown in a maximum intensity projection format in
Cifra 8. We can project particles onto anatomical space because each state that constitutes a
particle at any scale is a mixture of states that, al final, can be associated with a particular
Neurociencia en red
222
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
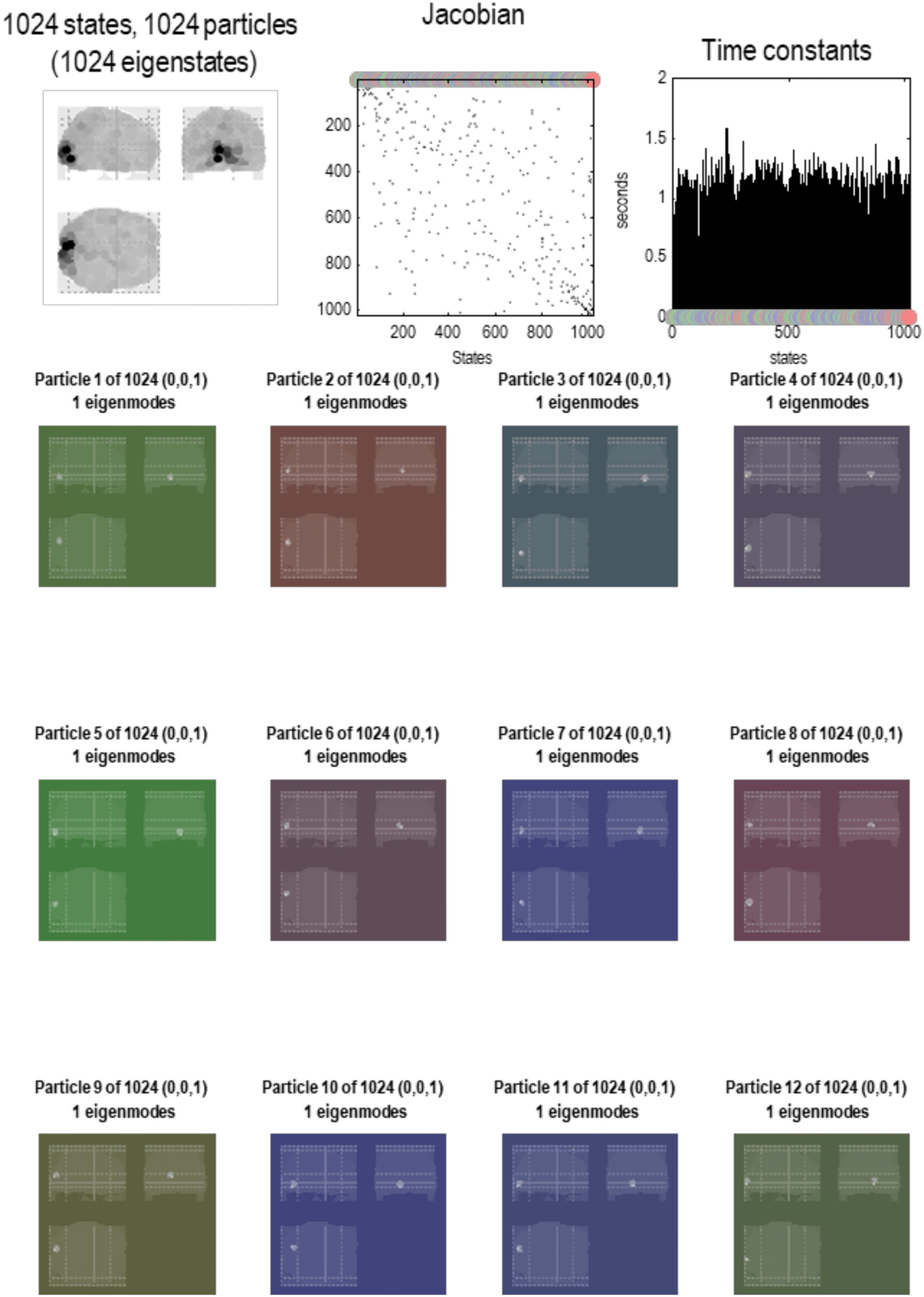
Cifra 5. Brain particles. This figure illustrates the partition of states at the first level. The format
of this figure is replicated in subsequent figures that detail a particular decomposition at increasing
escamas. The upper left panel shows all the constituent particles as a maximum intensity projection,
where the spatial support of each particle has been color-coded according to the variance explained
by its eigenmode. One can see that nearly the entire brain volume has been effectively tiled by 1,024
particles. The upper middle panel shows the corresponding adjacency matrix or coupling among
particles. The colored circles encode the identity of each particle. In this instance, the particles have
been arranged in order of descending dissipation (es decir., the real part of the eigenvalue of each par-
ticle’s Jacobian). The upper right panel shows these eigenvalues above the corresponding particle
(encoded by colored dots) in terms of rate constants (es decir., the negative inverse of the eigenvalues).
The remaining panels show the first 12 particles as maximum intensity projections. The color of
the background corresponds to the color that designates each particle. In this first level, each parti-
cle has a single eigenstate. The numbers in parentheses above each maximum intensity projection
correspond to the number of internal, active, and sensory states, respectivamente, where the active and
sensory states comprise blanket states. At this finest level, every eigenstate is a sensory state because
it can influence—and be influenced by—the eigenstates of other particles. At this scale, one can see
that the particles are small, with a standard deviation of about 3 mm (based on the softmax function
of the absolute value of each particle’s eigenmodes). Aquí, the characteristic time constants of these
particles are about 1 s. This should be compared with the equivalent distribution in the upper right
panel of the next figure.
Neurociencia en red
223
Markov blankets in the brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
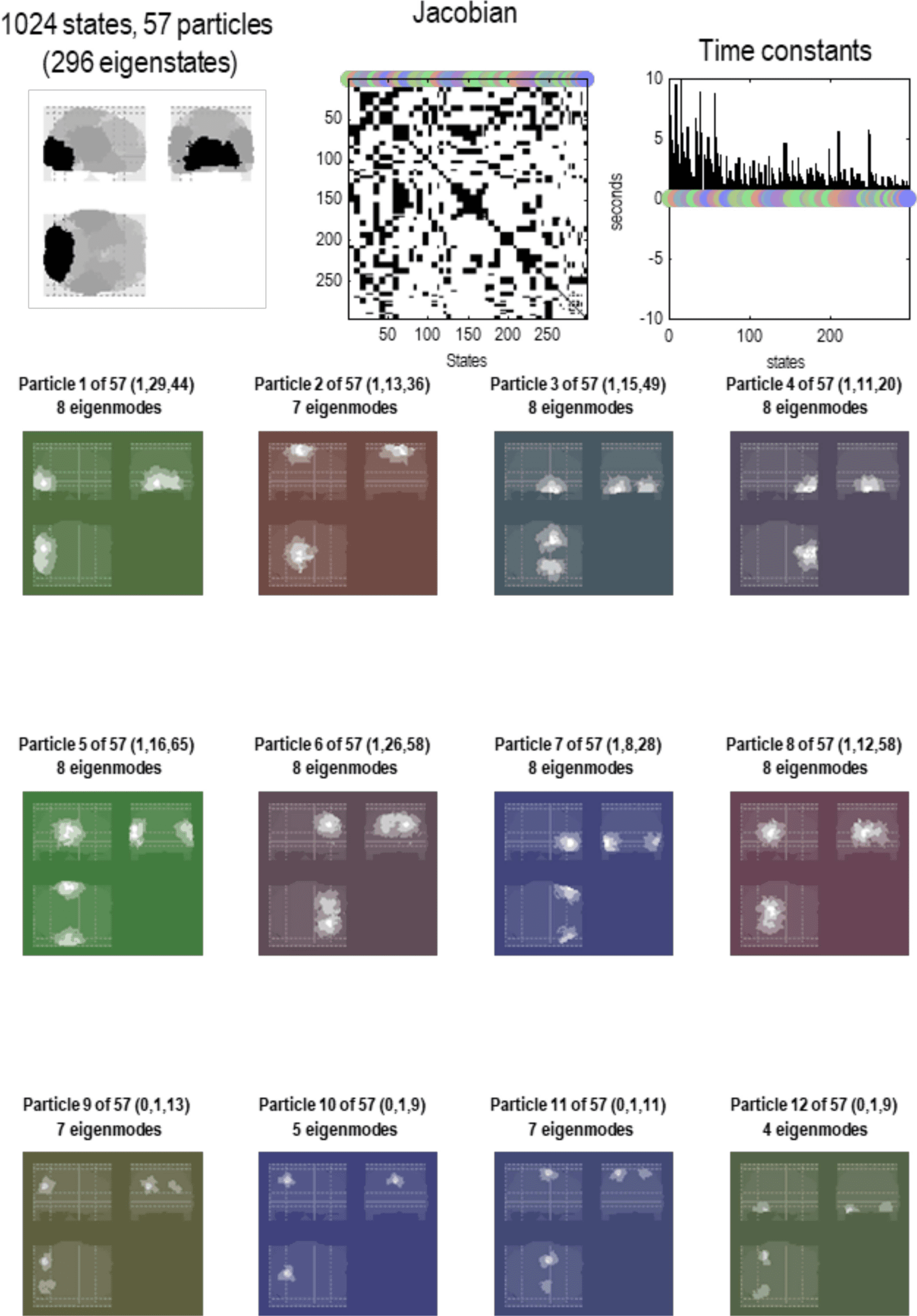
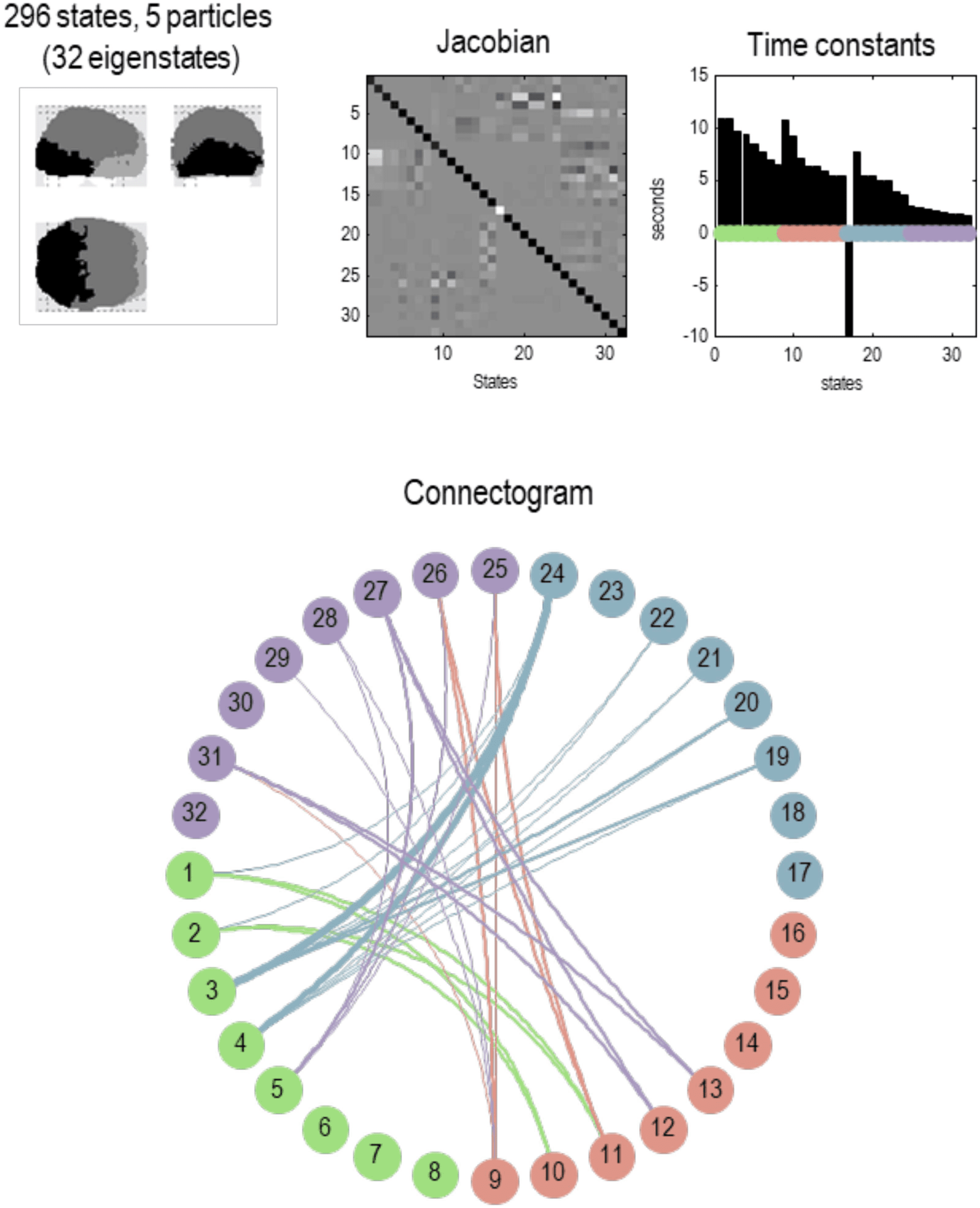
Cifra 6. Particular partition at the second scale. This figure uses the same format as the previous
figura; sin embargo, aquí, we are looking at particles at the next scale. En otras palabras, aggregates of
the eigenstates of the blankets of first-level particles. Aquí, Había 1,024 such eigenstates that
have been partitioned into 57 particles. Each particle has one or more eigenstates; aquí, a total
de 296. At this level, time constants have started to increase, including some particles that evince
slow dynamics of about 10 s. Note that the particles now have a greater spatial scale and have,
in most instances, a symmetric spatial deployment across hemispheres. This reflects the fact that
Jacobian includes transcallosal or interhemispheric coupling. Por ejemplo, the first particle has one
internal state (por diseño), 29 active states, y 44 sensory states. These different states are color-
coded with white, light gray, and dark gray, respectivamente, to illustrate the characteristic “fried egg”
arrangement in which internal states (white) are surrounded by blanket (es decir., active and sensory)
estados (in gray). The eigenmodes of this particle cover voxels in primary visual and extrastriate
corteza. The second particle sits across the bilateral superior parietal cortices, while the third particle
encompasses anterior (es decir., polar) temporal regions—and so on. The spatial scale of these particles
corresponds roughly to a cytoarchitectonic parcellation. The ensuing (57) particles collectively
comprise 296 eigenstates that are partitioned into five particles at the next level, correspondiente
roughly to lobar neuroanatomy.
Neurociencia en red
224
Markov blankets in the brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
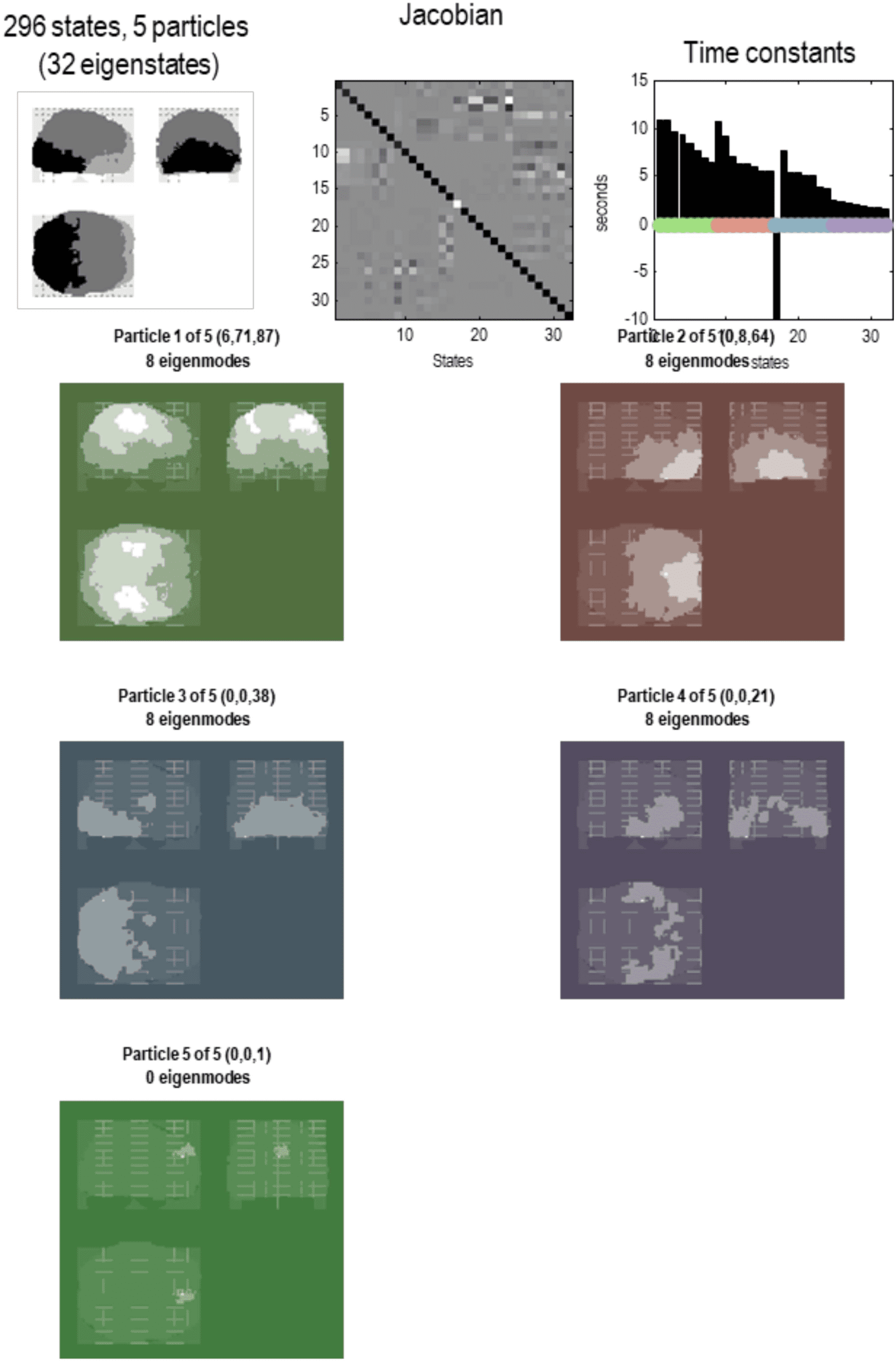
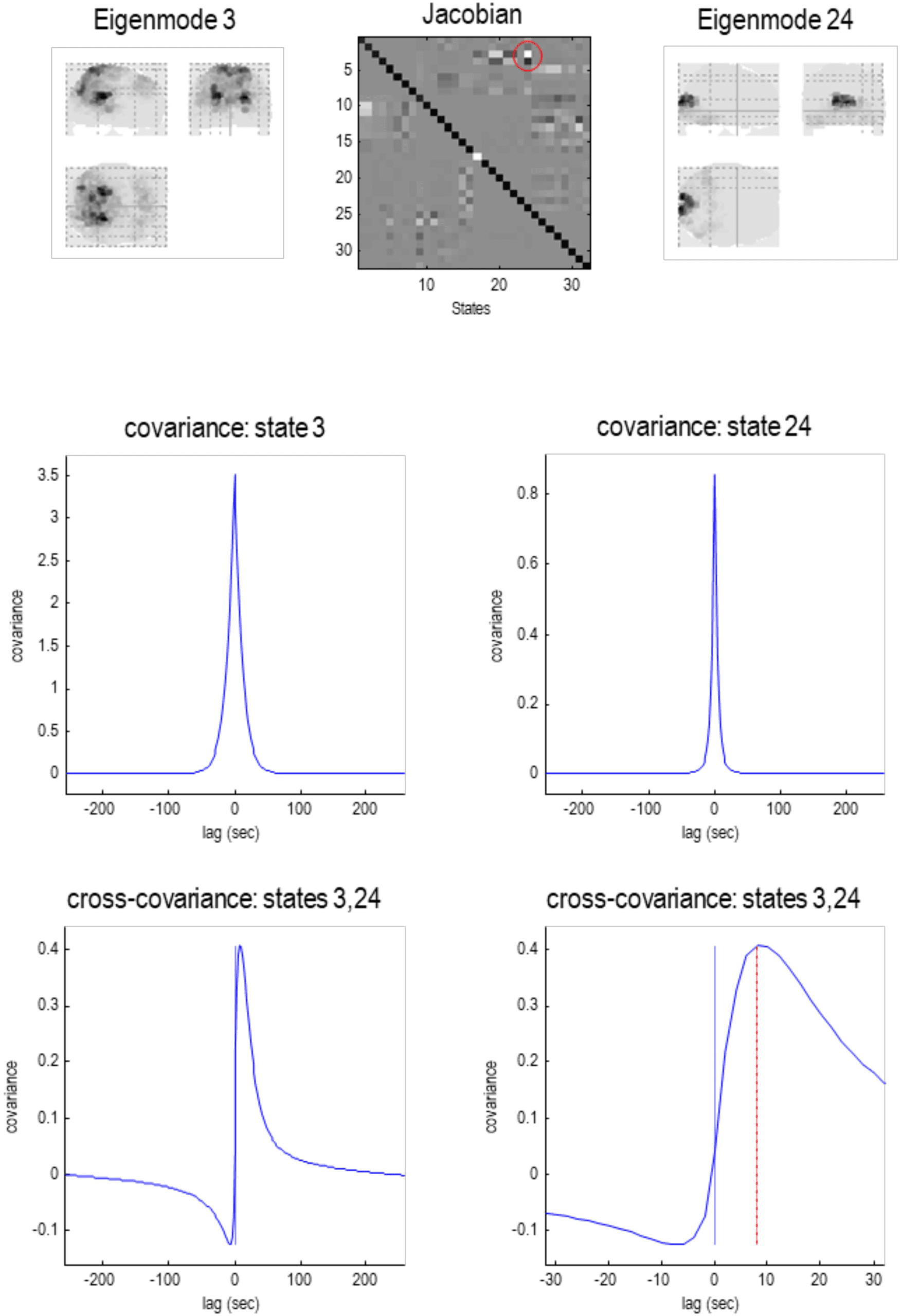
Cifra 7. Particular partition at the third level. This follows the same format as the previous figures.
Aquí, el 57 particles from the previous scale are now partitioned into five particles that, collectively,
possess 32 eigenstates. Aquí, the adjacency matrix is shown in image format, in terms of the real
part of each (complex) Jacobian. At this scale, dynamics of each particle are becoming increasingly
slow, with typical time constants between 5 y 10 s. The negative time constant reflects a positive
eigenvalue that denotes an exponential divergence of trajectories that underwrites stochastic chaos.
The five particles retain a degree of interhemispheric symmetry: the first particle has six internal
estados, 71 active states, y 87 sensory states. This particle covers a large dorsal portion of cortex,
including parietal cortex and frontal eye fields. En cambio, the second particle covers large regions
of frontal cortex, with the eight active states located in orbitofrontal regions. The third particle is
located in posterior visual and inferotemporal regions, while the fourth particle subsumes anterior
temporal and ventral regions. Curiosamente, there is one small particle (with a single sensory state)
in the anterior medial prefrontal cortex. These five lobe-like particles (con 32 eigenstates) now
contribute to a single particle at the final (fourth) nivel.
Neurociencia en red
225
Markov blankets in the brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
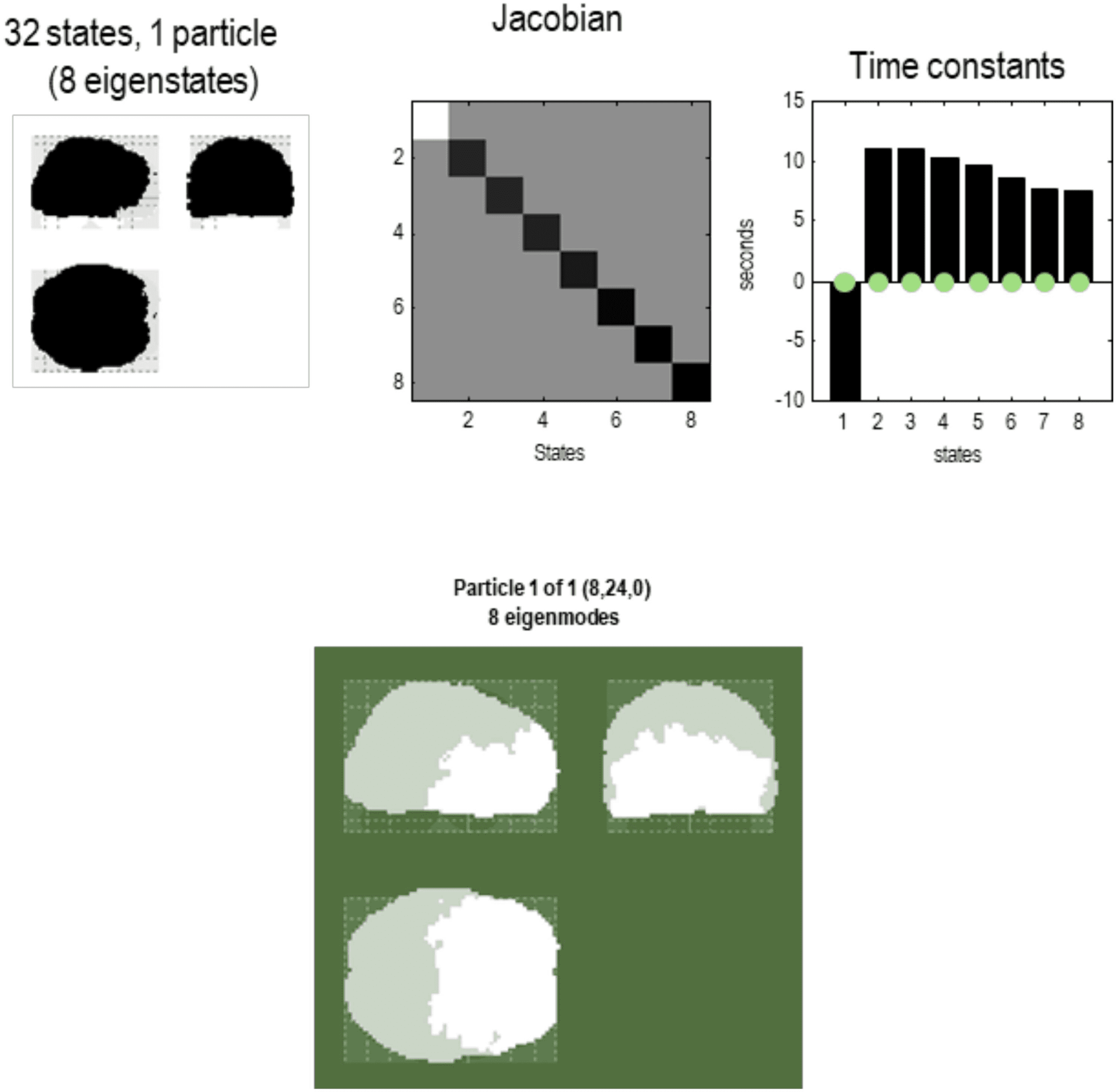
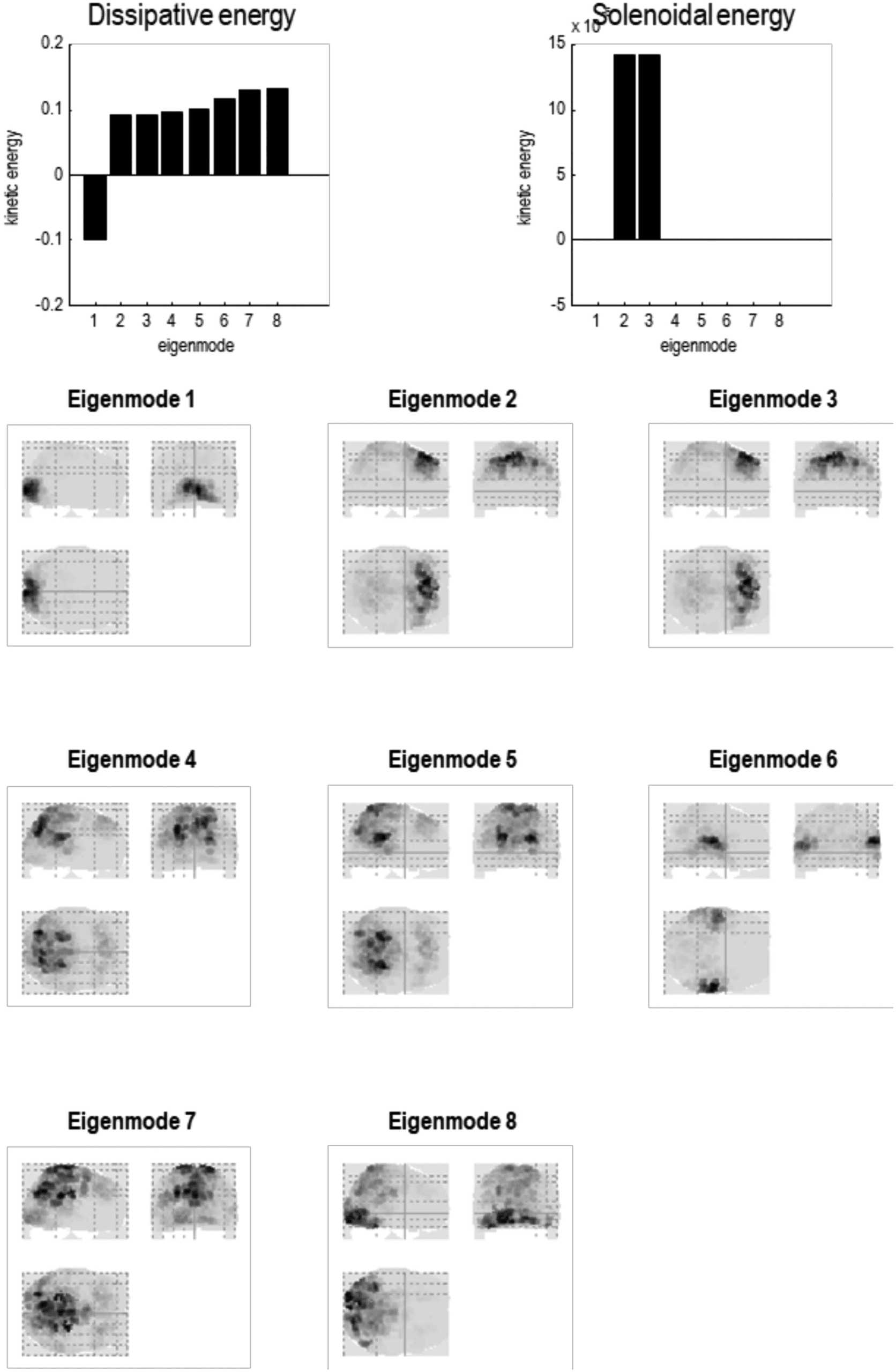
Cifra 8. Particular partition at the fourth scale. The five particles of the previous level have now
been partitioned into a single particle with eight internal states (in rostral regions) y 24 sensorial
estados (in caudal regions), in white and light gray, respectivamente. This particle possesses eight eigen-
estados, the first of which has a positive eigenvalue—or negative time constant (denoting stochastic
caos). At this scale, all of the eigenstates have protracted dynamics, with time constants in the
order of 10 s. Note that there is no coupling among the eigenstates in the Jacobian. This means the
dynamics are completely characterized by the leading diagonal terms, eso es, the complex eigen-
values of the eight constituent eigenstates.
En otras palabras, particles inherit a spatial location from the scale
location in voxel space.
abajo, enabling one to visualize (and quantify) the spatial scale of particles at successively
higher scales. We will refer to this characterization of an eigenstate as an eigenmode; a saber,
a pattern in voxel space whose amplitude is determined by the corresponding eigenstate. Uno
can express the eigenmodes in terms of the eigenvectors at each scale as follows:
(i)
nj = ξ(1)ξ(2) . . . ξ
(i)
nj
υ
, ξ(i) =
. . .
(i)
1
ξ
.
ξ
(i)
norte
This gives the eigenmode of the j-th eigenstate of the n-th particle at the i-th scale.
(9)
226
Eigenmode:
A stable state (es decir., mode) de un
dynamical system in which all parts
of the system oscillate at the same
frequency.
Neurociencia en red
Markov blankets in the brain
Note that it would have been possible to reevaluate the Jacobian using another dynamic
causal model of the eigenstates at any particular level and then use Bayesian model reduction
to eliminate redundant coupling parameters. This is an interesting alternative to using the esti-
mates of the Jacobian based upon the first-order approximation at the smallest scale. Lo haremos
explore the impact of reevaluating the Jacobian in subsequent work. For the purposes of the
current illustration, we will retain the linear solutions at higher scales—based upon the finest
scale—to illustrate that one can still reproduce the emergent phenomena of interest described
abajo. These dynamical phenomena are therefore directly attributable to local linear cou-
pling with a particular sparsity structure that is sufficient to produce interesting self-organized
dynamics at higher scales. Before taking a closer look at dynamics over scales, this section
concludes with a brief characterization of coupling at the smallest scale.
SPARSE COUPLING
The Jacobian from the above analysis summarizes the effective connectivity at the smallest
escala, where each node particle has a reasonably precise anatomical designation. This means
that we can interpret the elements of the Jacobian in terms of directed (effective) conectividad.
We had anticipated that this would mirror the exponential distance rule established through
anatomical tracing studies (Finlay, 2016; Horvát et al., 2016; Wang & Kennedy, 2016). Cómo-
alguna vez, it did not. En cambio, este (linear) characterization of effective connectivity was better ex-
plained with a power law that, interestingly, was quantitatively distinct for inhibitory (es decir.,
negative) and excitatory (es decir., positivo) connections (es decir., elements of the Jacobian).
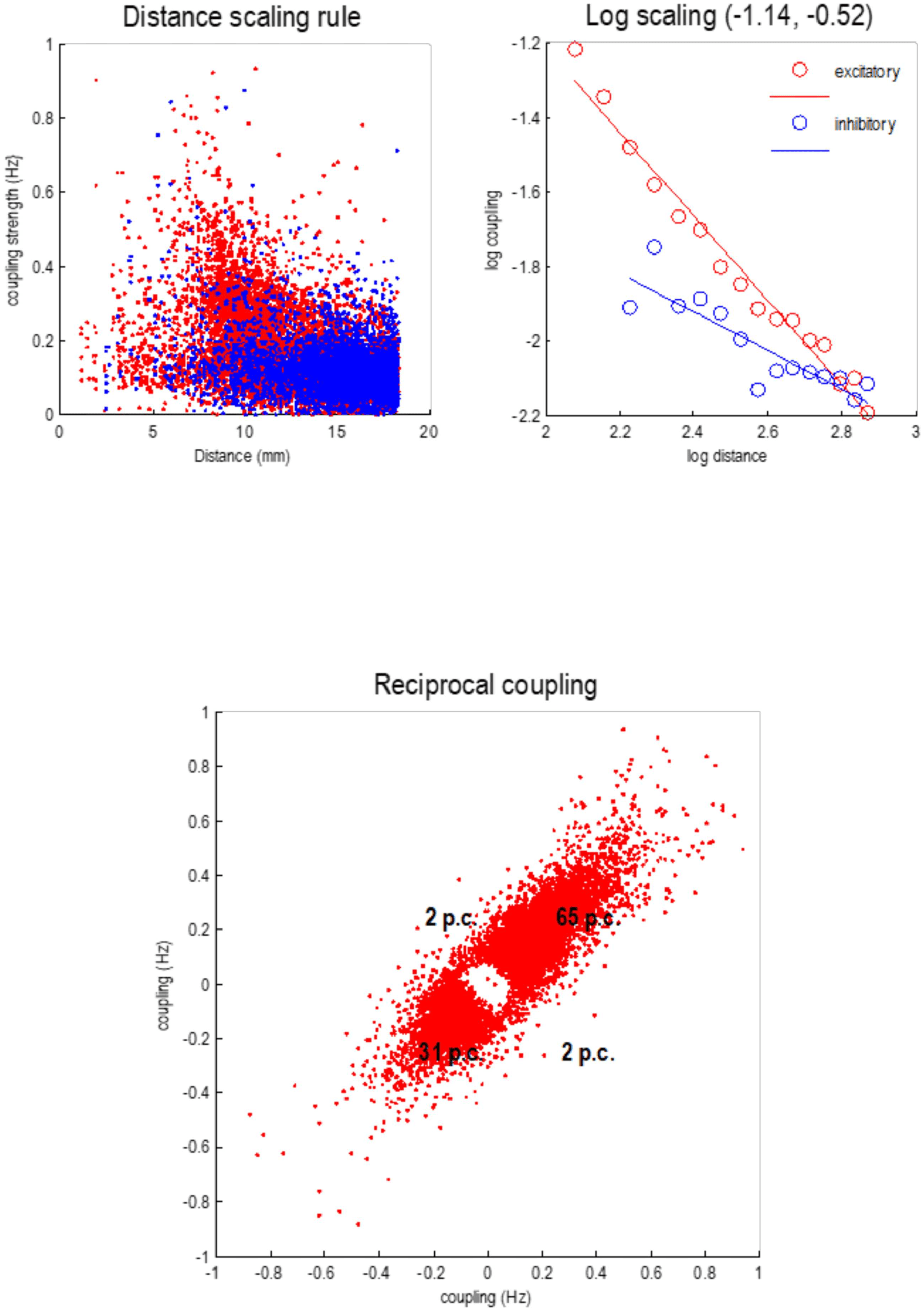
Cifra 9 summarizes the statistical characteristics of coupling among particles at the first
nivel. The upper left panel shows each connection in terms of the real part of the correspond-
ing Jacobian in hertz, against the distance spanned by the connection (es decir., Euclidean distance
between the centers of the two particles). Two things are evident from this scatterplot: primero,
positivo (excitatory, red dots) connections dominate in the short range (alrededor 8 mm), mientras
negative (inhibitory, blue dots) dominate around 16 mm. Although there is variability, the de-
pendency of the coupling strength on distance shows some lawful behavior that is disclosed
by plotting the log-coupling (real part) against log-distance (upper right panel). The circles are
the averages in bins (discrete ranges) of the dots in the upper left panel. A linear regression
suggests a scaling exponent of −1.14 for excitatory coupling and a smaller scaling exponent of
−0.52 for inhibitory coupling. This dissociation is consistent with a Mexican hat–like coupling
kernel, with short-range excitation and an inhibitory penumbra. This kind of architecture pre-
dominates in neural field models of cortical and subcortical coupling (p.ej., Coombes, 2005;
Itskov, Curto, Pastalkova, & Buzsaki, 2011; Moran, Pinotsis, & Friston, 2013).
The lower panel plots the strength of reciprocal connections against each other, to illustrate
the relative proportions of recurrent excitatory and inhibitory coupling, aquí 65% y 31%,
respectivamente. There are only about 4% of connections that show an antisymmetry, eso es,
excitatory in one direction and inhibitory in the other. The rarefied region in the center of this
scatterplot reflects the fact that connections with small coupling strengths have been eliminated
during Bayesian model reduction (ver figura 4). In the next section, we will see how this sparse
local coupling engenders progressively more structured and itinerant dynamics at increasing
spatial and temporal scales.
INTRINSIC DYNAMICS
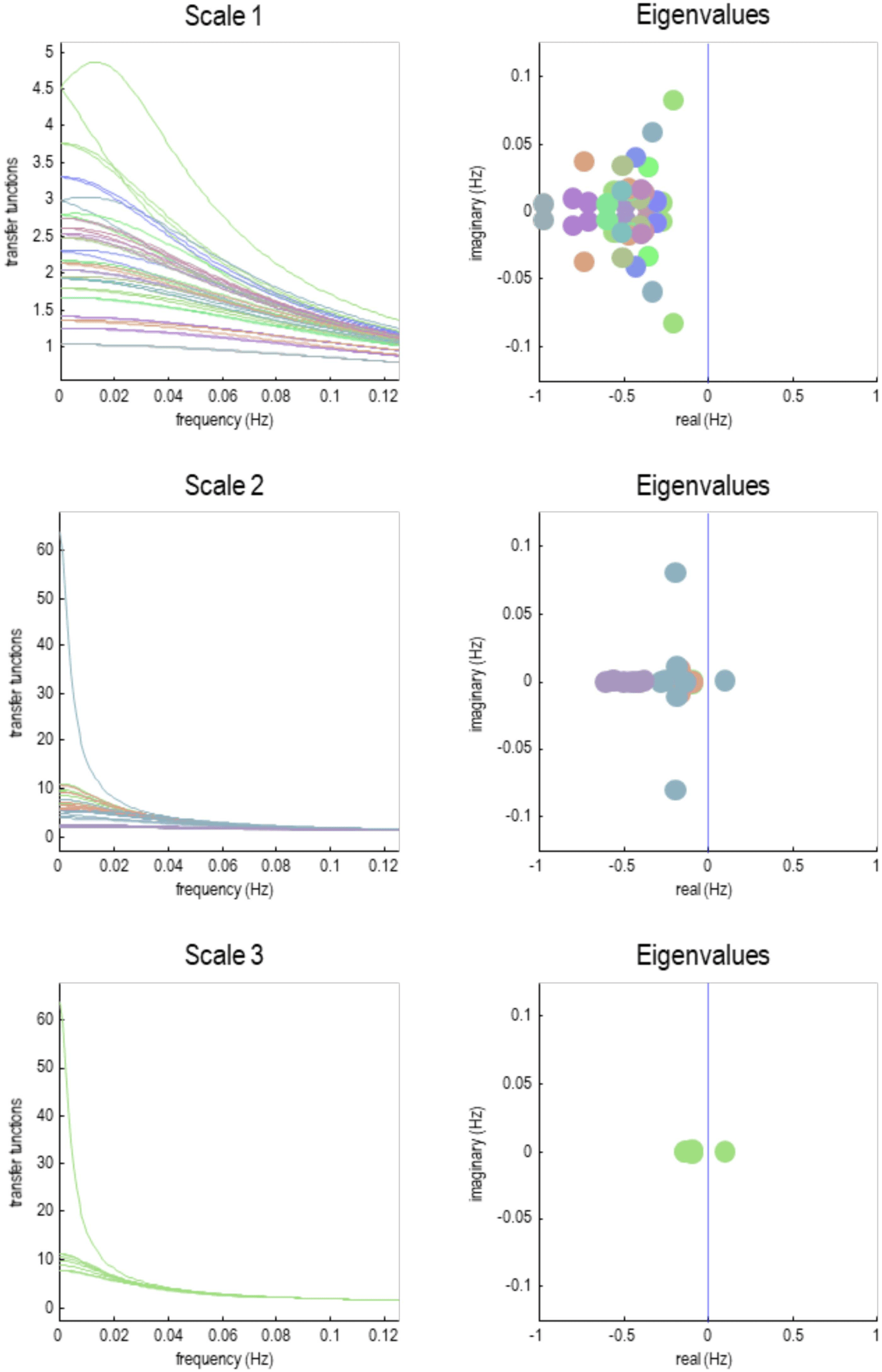
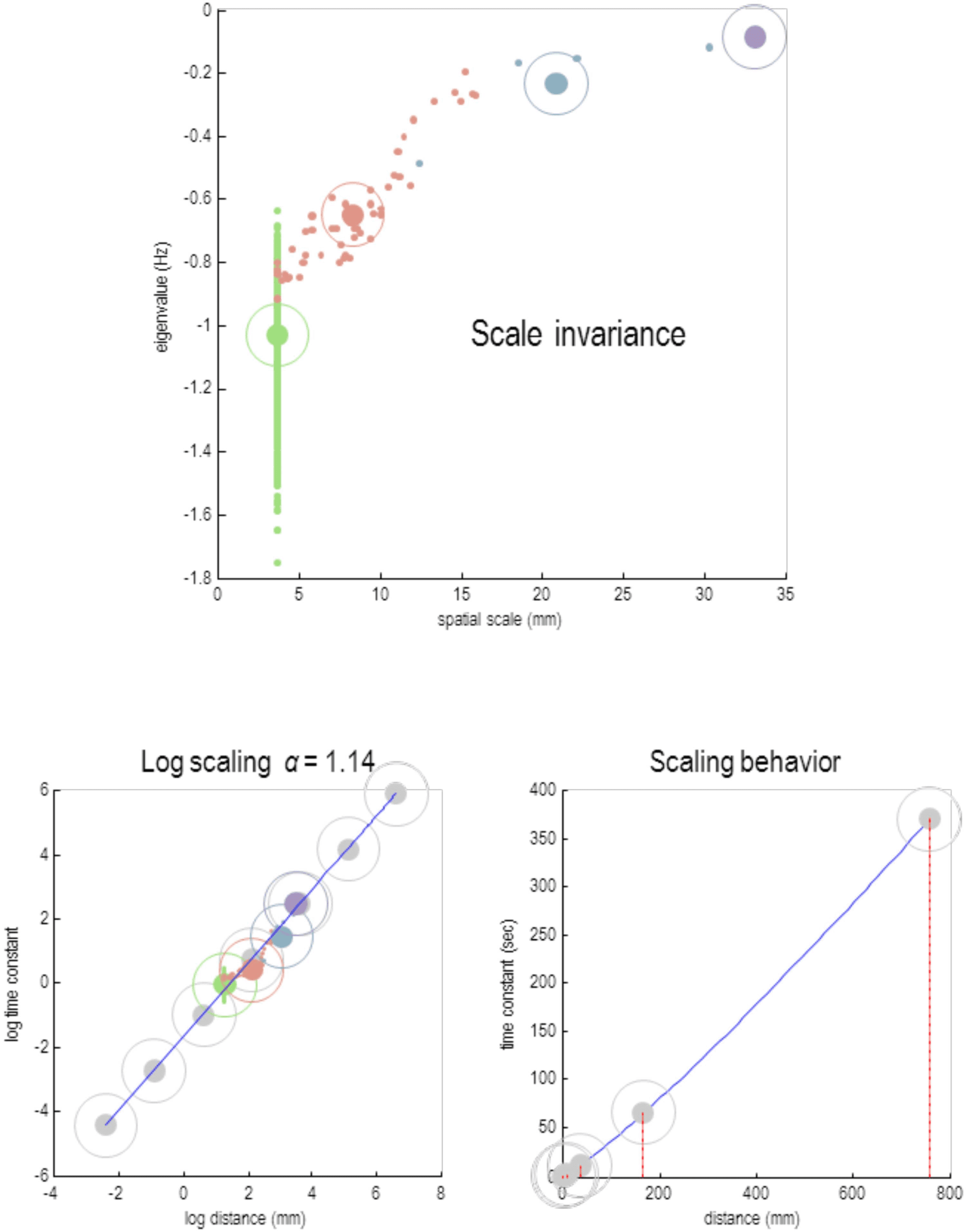
This section focuses on the intrinsic dynamics of each particle at different scales by asso-
ciating the Jacobian of each particle with Lyapunov exponents. For people not familiar with
Neurociencia en red
227
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 9. Local connectivity. This figure reports some of the statistics of dynamical coupling
among particles at the first level. The upper left panel plots each connection in terms of the real part
of the Jacobian in hertz, against the distance spanned by the connection. Two things are evident
from this scatterplot: primero, positivo (excitatory, red dots) connections dominate in the short range
(alrededor 8 mm), while negative (inhibitory, blue dots) dominate around 16 mm. The upper right
panel plots the log-coupling (real part) against log-distance, where circles report the averages in
bins (discrete ranges) of the dots in the left panel. A linear regression gives a scaling exponent of
−1.14 for excitatory coupling and a scaling exponent of the −0.52, for inhibitory coupling. El
lower panel plots the strength of reciprocal connections against each other, to illustrate the relative
proportions of recurrent excitatory and inhibitory coupling; aquí 65% y 31%, respectivamente.
dynamical systems theory, the Lyapunov exponents score the average exponential rate of diver-
gence or convergence of
trajectories in state space (Lyapunov & Batán, 1992; Pavlos
et al., 2012; Yuan, Mamá, Yuan, & Ao, 2011). Because we are dealing with a linearized system,
the Lyapunov exponents are the same as the eigenvalues of the Jacobian describing intrinsic
coupling. Por construcción, this is a leading diagonal matrix containing intrinsic eigenvalues
whose real values are close to zero. In terms of a linear stability analysis, the real part of these
eigenvalues (es decir., self-induced decay) corresponds to the rate of decay. This means that as
the eigenvalue approaches zero from below, the pattern of activity encoded by this eigenstate
decays more and more slowly. This is the essence of critical slowing and means that, de
the point of view of dynamical stability, this eigenstate has become unstable (Haken, 1983;
Jirsa, Friedrich, Haken, & Kelso, 1994; Mantegna & Stanley, 1995; Pavlos et al., 2012). El
Neurociencia en red
228
Markov blankets in the brain
complement of critical instability is a stable fast eigenstate that decays very quickly, eso es, un
eigenstate whose eigenvalue has a large negative real part.
The imaginary part of the eigenvalue describes the characteristic frequency at which this
decay is manifest. If the imaginary part is zero, the system decays monotonically. Sin embargo,
complex values mean that the intrinsic dynamics acquire a sinusoidal aspect. Because each
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 10. Transfer functions. This figure characterizes the dynamics at successive scales in terms
of transfer functions, as quantified by the complex eigenvalues (cf. a pole-zero map). The left
column shows the transfer functions of frequency for all particles with a complex eigenvalue (en
successive scales). These eigenvalues are shown in the right column in the complex number plane.
As we ascend from one scale to the next, the real part of the eigenvalue approaches zero from the
left—and the number of eigenvalues (es decir., number of particles) falls with the coarse-graining. El
complex part of an eigenvalue corresponds to the peak frequency of the associated transfer function,
while the dispersion around this peak decreases as the real part approaches zero. The emergence
of spectral peaks in the transfer functions inherit from the complex part of the eigenvalues, cual
emerge under asymmetric coupling with solenoidal flow. The next figure addresses the following
pregunta: Do these solenoidal dynamics vary in a systematic way over the brain?
Neurociencia en red
229
Markov blankets in the brain
particle has a number of eigenstates, an ensemble of particles can be construed as loosely
coupled phase oscillators (romper la lanza & estampar, 2005; De Monte, d’Ovidio, & Mosekilde, 2003;
Kaluza & Meyer-Ortmanns, 2010; Kayser & Ermentrout, 2010), featuring multiple frequencies.
The associated dynamics of a single particle can be visualized by plotting its eigenvalues in the
complex number plane. The closer the eigenvalue to the vertical axis, the slower the dynamics,
such that as the real eigenvalue approaches zero (es decir., from the left), the particle approaches a
transcritical bifurcation (at zero) and displays a simple form of critical slowing.
This characterization of intrinsic dynamics—at different scales—is illustrated in the right
panels of Figure 10. Note that the complex values are symmetrically paired (dots of the same
color). The key thing to observe here is that when we look at the eigenvalues of particles at
higher scales, there are some eigenstates that approach criticality and start to show intrinsic
oscillatory behavior. This is one of the key observations from the current renormalization
scheme; a saber, there is a necessary slowing as one progresses from one scale to the scale
arriba. Además, at higher scales intrinsic dynamics start to appear with progressively
slower frequencies.
Another way of characterizing temporal dynamics is to use linear systems theory to map the
eigenvalues to the spectral density of the time series that would be measured empirically. Este
rests upon standard transforms and the convolution theorem that enables us to express the sys-
tems’ first-order kernels as a function of the Jacobian (Lopez et al., 2014). In frequency space,
these kernels correspond to transfer functions and describe the spectral power that is transferred
from the random fluctuations to the macroscopic dynamics of each eigenstate. The left panels
of Figure 10 show the transfer functions of the eigenstates of each particle at different scales.
At the finest scale, power is spread over a large range of frequencies. At progressively higher
escamas, the power becomes more concentrated in the lower frequencies with a transfer func-
tion that has a characteristic Lorentzian form. Fundamentalmente, the frequencies at the highest scale
correspond to the characteristic ultraslow frequencies studied in resting-state fMRI; a saber,
< 0.01 Hz. This is an interesting observation, which suggests that one can explain ultraslow
fluctuations in resting-state fMRI purely in terms of local directed coupling among small par-
ticles of brain tissue. Note that this explanation does not involve any hemodynamics because
the Jacobian that gives rise to these slow oscillations pertains to the neuronal states (prior to
hemodynamic convolution). In other words, this is not an artefact of removing fast frequencies
from the measured fMRI signals.
One might ask whether there is any systematic variation of these ultraslow frequencies
across the brain. Figure 11 reports the implicit intrinsic timescales at intermediate scales (sec-
ond scale, upper rows; third scale, lower rows). The left column shows the eigenmodes in
terms of their principal frequency, that is, the largest complex eigenvalue (divided by 2π). The
right column shows the corresponding eigenmodes in terms of their principal time constants,
that is, the reciprocal of the largest negative real part. These two characterizations—principal
frequency and time constant—speak to different aspects of intrinsic timescales, both of which
contribute to the shape of an eigenstate’s transfer function. The first quantifies the frequency of
solenoidal flow, while the second reflects the rate of decay associated with the dissipative flow.
We will unpack solenoidal and dissipative flows in the last section, in terms of density dynam-
ics. In brief, the flows of a random dynamical system, at nonequilibrium steady state, can be
decomposed into two orthogonal components. The first (dissipative) component is a gradient
flow, in the direction of increasing density. This flow counters the dispersive effect of random
fluctuations. The solenoidal (non-dissipative) component circulates on the isoprobability con-
tours, thereby having no effect on the nonequilibrium steady-state density. Heuristically, if
Network Neuroscience
230
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
Intrinsic timescales in the brain. This figure reports intrinsic timescales at intermediate
Figure 11.
scales (second scale, upper rows; third scale, lower rows). The left column shows the eigenmodes
in terms of their principal frequency, that is, the largest complex eigenvalue (divided by 2π). The
right column shows the corresponding eigenmodes in terms of their principal time constants, that
is, the reciprocal of the largest negative real part.
one imagines water flowing down a plughole, the dissipative part is the flow out of the basin,
while the solenoidal part accounts for the circular motion of water. Generally speaking, when
the random fluctuations are small, the gradient flows disappear (at steady state), leaving the
solenoidal flow, that is, the classical mechanics that would apply to heavenly bodies. How-
ever, when random fluctuations are in play, both solenoidal and dissipative flows characterize
the dynamics at steady state.
It is clear from these results that caudal (i.e., posterior) regions have faster intrinsic frequen-
cies, relative to rostral (i.e., anterior) regions. Interestingly, in this example, the inferotemporal
and ventral eigenmodes also show a relatively high frequency. At the third scale, this caudal-
rostral gradient is more evident, suggesting that faster solenoidal dynamics dominate in poste-
rior parts of the brain. This is consistent with both theoretical and empirical findings suggestive
of a gradient of timescales—as one moves from the back to the front of the brain and, implicitly,
from hierarchically lower areas to higher areas (Cocchi et al., 2016; Hasson, Yang, Vallines,
Heeger, & Rubin, 2008; Kiebel, Daunizeau, & Friston, 2008; Liegeois et al., 2019; Murray
et al., 2014; Wang & Kennedy, 2016). Note that the frequencies in question here are very slow;
namely, about 0.01 Hz or below. These are the ultraslow frequencies typically characterized
in resting-state fMRI (Liegeois et al., 2019). In the present setting, these ultraslow frequencies
are an emergent property of scale-invariant behavior, when one moves from spatial temporal
scales suitable for describing lobar dynamics or large intrinsic brain networks.
The eigenvalues in Figure 10 take positive real values at higher (second and third) scales.
This means that they have crossed the zero threshold to engender a transcritical bifurcation.
Strictly speaking, these produce solutions that cannot be realized because of an exponen-
tial divergence of trajectories. This reflects the first-order approximation that we are using
to summarize the dynamics. Although this linear approximation precludes stochastic chaos,
Network Neuroscience
231
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
positive real values speak to the notion that some particles at higher scales become excitable
for short periods of time. This means that we are moving away from a loosely coupled oscilla-
tor model—that has a fixed point or limit cycle attractor—towards what physicists call active
or excitable matter (Keber et al., 2014; Ramaswamy, 2010). This is a nice metaphor for the
brain and means that if the particles that constitute active (gray) matter are considered in iso-
lation, they can show autonomous dynamics that can be characterized as stochastic chaos or
itinerancy.
At this point we can return to the renormalization group and RG scaling behavior. This
scaling behavior depends upon the link between various parameters of the systems Lagrangian
(or equivalent characterization of dynamics) between successively higher levels. Consider the
following RG flow or beta function as an instance of Equation 4:
(i+1)
σ
τ
(i)
= eβτ σ
τ
(i)
τ = E[−Re(λ
σ
(i)
nnj)]
This says as we move from one scale to the next, the timescale increases by eβτ ≥ 1. Invoking
the same beta function for spatial scale induces a relationship between temporal and spatial
scales in the form of a power law with a scaling exponent α. This exponent corresponds to the
ratio of the time and spatial exponents of the beta functions:
(i+1)
σ
τ
(i+1)
σ
ℓ
(i)
= eβτ σ
τ
(i)
= eβℓ σ
ℓ )
⇒
(0)
(i)
τ = eiβτ σ
σ
τ
(0)
(i)
ℓ = eiβℓ σ
σ
ℓ )
(
(i)
⇒ ln σ
τ
(0)
σ
τ
(i)
=α ln σ
ℓ
(0)
σ
ℓ
⇒
(i)
ℓ )α
(i)
τ =γ(σ
σ
σ = βτ
βℓ
, λ = σ
(0)
(0)
τ (σ
ℓ
(10)
)−α
The last quality in the first line follows by eliminating the scale i from the pair of beta functions.
Intuitively, this scaling behavior means that as we move from one scale to the next, things get
slower and bigger—but at different geometric rates. This difference gives rise to a scaling
exponent that links the increases in spatial scale to increases in temporal scale. We evaluated
the characteristic time and spatial constants for each scale by taking the mean of the real
eigenvalues and the spatial dispersion of the corresponding eigenmodes associated with all
particles at each scale:
(i)
τ = E[−Re(λ
σ
(i)
(i)
nj |1/3]
ℓ = E[|ν
σ
(i)
nnj)]
(11)
Plotting the logarithms of these values against each other allows one to estimate the scaling
exponent using linear regression. Figure 12 shows the results of this analysis across all scales.
The scaling exponent here was 1.14. This is not dissimilar to the value of 1.47 obtained with
a similar analysis of murine calcium imaging data (Fagerholm et al., 2019), where coarse-
graining was implemented by averaging over spatial blocks. To put this value into perspective,
the scaling exponent for Kepler’s laws of motion is 1.5. This scaling exponent reflects the
disparity in spatial and temporal constants, where the temporal constant increases by a factor
of 2.37 from one scale the next, while the spatial support increases by 2.13.
This scale-free behavior means that we can evaluate the time constants at scales that we
have not characterized empirically. Table 1 lists these extrapolated or projected timescales
right down to the nanoscale and up to higher scales that would be appropriate to talk about
networks of brains or social communities or institutions. Note that the extrapolation of scaling
Network Neuroscience
232
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 12. Scale invariance. This figure illustrates scaling behavior across the scales of the partic-
ular decomposition. The upper panel plots the real part of the eigenvalues of each particle against
its spatial scale; namely the caliper width of each particle’s eigenmode. This is replicated for each
of the four scales, denoted by the different colors (green, pink, cyan, and puce, respectively). The
expected values are shown as encircled large dots. The lower left panel plots the logarithms of these
temporal and spatial expectations against each other. The resulting regression slope corresponds to
the scaling exponent; here, 1.14. The light gray circles correspond to what would have been seen
at higher and lower scales. The lower right plot shows the same regression in terms of the implicit
time constant, as a function of spatial scale expressed in millimeters. The red lines correspond to the
coarse scales (of i = 6 and i = 8) depicted in the left panel—suggesting characteristic time constants
in the order of 60 and 360 s. This scaling behavior suggests that as we increase the spatial scale or
coarse-graining, dynamics become slower, as the real parts of particular eigenvalues approach zero
from below.
to conferences (Table 1) should not be taken too seriously. There would be good reason to
estimate the scaling exponent from a larger database, since small errors in the estimation of
scaling exponents can amplify quickly in extrapolation.
It may help to distinguish between scalable and scale-free systems. A scalable system is one
in which performing a scale transformation to a system’s state gives a new state, but crucially,
one that is also a solution of the governing equation of motion. This is what Landau refers to as
“mechanical similarity” in the context of Lagrangian mechanics. For example, orbital trajec-
tories are scalable, seeing as increasing the scale of the system gives new (larger) orbits with
different (slower) periods. Crucially however, these new orbits also follow Newton’s second
Network Neuroscience
233
Markov blankets in the brain
Table 1. Spatiotemporal scales and examples
Scale
−8
Spatial scale
4.38 µm
Timescale
380 µs
−4
89.3 µm
11.9 ms
0
4
8
12
16
1.82 mm
374 ms
37.2 mm
11.8 s
6.15 min
758 mm
15.5 m
0.31 km
Example
Dendritic spines occur at a density of up to 5 spines per µm of
dendrite. Spines contain fast voltage-gated ion channels with time
constants in the order of 1 ms.
A cortical minicolumn: A minicolumn measures of the order of
40–50 µm in transverse diameter 80 µm spacing (Peters & Yilmaz,
1993). The membrane time constant of a typical cat layer III pyra-
midal cell is about 20 ms.
A cortical hypercolumn (e.g., a 1-mm expense of V1 containing
ocular dominance and orientation columns for a particular region
in visual space; Mountcastle, 1997). Typical duration of evoked
responses in the order of 1 to 300 ms (cf. the cognitive moment).
The cerebellum is about 50 mm in diameter, corresponding to the
size of cortical lobes. Sympathetic unit activity associated with
Mayer waves within frequency of 0.1 Hz (wavelength of 10 s).
A dyadic interaction (e.g., a visit to your doctor).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
3.22 hr
A dinner party for six guests, lasting for several hours.
4.21 days An international scientific conference (pre-coronavirus).
law regardless of size—hence qualifying as “scalable.” On the other hand, a scale-free sys-
tem has no characteristic-length scale and images taken at different resolutions are statistically
unchanging.
This completes our discussion of scale invariance and associated dynamics, where we have
taken a special interest in the temporal scaling behavior that emerges from local connectivity
at smaller scales of analysis. In the next section, we turn to the coupling between particles and
see what this has to say in terms of how intrinsic brain networks influence each other.
EXTRINSIC DYNAMICS
In this section, we consider the off-diagonal elements of the Jacobian at the successive scales
afforded by the renormalization group. By construction, these terms couple different particles.
The ij-th element of the nm-th block of the Jacobian couples the j-th eigenstate of the m-th
particle to the i-th eigenstate of the n-th particle.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(i)
11
λ
...
λ
(i)
n1
· · · λ
. . .
· · · λ
(i)
1n
...
(i)
nn
=
J =
λ
(i)
1111
...
0
λ
(i)
n111
...
λ
(i)
n1j1
· · ·
. . .
· · · λ
...
· · · λ
. . .
· · · λ
0
...
(i)
11jj
(i)
n11j
...
(i)
n1jj
λ
(i)
1n11
...
λ
(i)
1nj1
(i)
nn11
λ
...
0
· · ·
. . .
· · ·
· · · λ
. . .
· · · λ
...
· · ·
. . .
· · · λ
(i)
1n1j
...
(i)
1njj
0
...
(i)
nnjj
.
(12)
This directed coupling is generally complex. The complex part can be thought of as inducing
a phase shift or delay in the influence of one eigenstate on another. The real part is of more
Network Neuroscience
234
Markov blankets in the brain
interest here and corresponds to a rate constant, much like the real part of the Lyapunov ex-
ponents of the intrinsic coupling describe the rate of decay. However, here, we are talking
about the rate at which an eigenstate of one particle responds to the eigenstate of another. This
means that large positive or negative real extrinsic coupling becomes interesting (previously,
we have been discarding eigenstates with large negative intrinsic eigenvalues because they
dissipate almost immediately). Figure 13 illustrates this extrinsic (between particle) coupling
at the penultimate scale (scale three) in the form of a connectogram.
The implications of complex extrinsic coupling can be understood in terms of cross-covariance
functions of time that characterize delayed or lagged dependencies. Please note that the cross-
covariance functions can be evaluated in a straightforward manner from the complex transfer
functions, shown in Figure 10. In other words, they can be derived directly from the Jacobian,
under first-order assumptions. For example, Figure 14 characterizes these dependencies be-
tween the two eigenstates with the strongest coupling at this (third) scale. The implicit coupling
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 13. Extrinsic connectivity. This figure illustrates asymmetric extrinsic (between particle)
coupling at the penultimate scale (scale three). The upper panels reproduce the results in Figure 7,
while the lower panel is a connectogram illustrating the coupling among the (32) eigenstates that
constitute the five particles at this scale. The width of each connector reflects the strength of the
coupling, after dividing the strength into five bins and eliminating the lowest bin. The color of the
dots corresponds to the color of the particle in the upper right panel. The color of the connectors
corresponds to the source of the strongest (reciprocal) connection.
In this example, the largest
afferent connection is from eigenstate 24 to eigenstate 3. This corresponds to an influence of the
first eigenstate of the fourth (cyan) particle on the third eigenstate of the first (green) particle. The
coupling strength corresponds to the real part of the Jacobian, in hertz. The fact that coupling is
mediated by complex coupling coefficients means that the influence of one eigenstate on another
can show profound asymmetries in time. This is illustrated in the next figure, which examines the
largest connection above in more detail.
Network Neuroscience
235
Markov blankets in the brain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 14. Dynamic coupling. This figure characterizes the coupling between the two eigenstates
of the previous figure with the strongest coupling at the third scale. This coupling is mediated by
the corresponding element of the (complex) Jacobian, circled in red in the upper middle panel.
The flanking panels on the left and right show the corresponding eigenmodes in voxel space. The
middle row shows the autocovariance functions of the two eigenstates, illustrating serial correlations
that can last for many seconds. The lower two panels report the cross-covariance function between
the two eigenstates, over 256 s (lower left panel) and 32 s (lower right panel). The red line indicates
the peak cross covariance at about 8-s lag.
is mediated by the corresponding element of the (complex) Jacobian—circled in red in the up-
per middle panel. The flanking panels on the left and right show the associated eigenmodes
in voxel space. The middle row shows the autocovariance functions of the two eigenstates,
illustrating serial correlations that can last for many seconds. The interesting part of this figure
is in the lower panels: These report the cross-covariance function between the two eigenstates,
over 256 s (lower left panel) and 32 s (lower right panel), respectively. The key thing to ob-
serve here is that the peak cross-covariance emerges at an 8-s lag from the 24th to the third
eigenstate. This asymmetrical cross-covariance (and implicitly cross-correlation) function re-
flects the solenoidal coupling and implicit breaking of detailed balance accommodated by the
particular decomposition (see the next section). Note that the (zero lag) correlation is almost
zero. This speaks to the potential importance of using cross-covariance functions (or complex
cross spectral in frequency space), when characterizing functional connectivity in distributed
brain responses (K. J. Friston, Bastos, et al., 2014; Mohanty, Sethares, Nair, & Prabhakaran,
2020). This brief treatment of extrinsic coupling has made much of the complex nature of
Network Neuroscience
236
Markov blankets in the brain
dynamical coupling and how it manifests in terms of functional connectivity. In the final sec-
tion, we revisit this kind of coupling in terms of nonequilibrium steady states.
DYNAMICS AND STATISTICAL PHYSICS
Above, we have referred to solenoidal and dissipative flows, in relation to the complex and real
parts of intrinsic eigenvalues—and how they manifest in terms of intrinsic brain networks. This
section unpacks this relationship by applying the statistical physics of nonequilibrium steady
states to neuronal fluctuations. Our focus will be on the relationship between conventional
characterizations of functional connectivity and the more general formulation afforded by a
particular decomposition. Specifically, we will see that conventional formulations assume a
special case that discounts solenoidal flow—and implicitly assumes neuronal dynamics attain
steady state at statistical equilibrium.
In the previous section, we examined extrinsic coupling among particles in terms of their co-
variance. Here, we return to coupling and dynamics that are intrinsic to a particle; namely, the
final particle at the last level. In this example, the particle has eight eigenstates, whose complex
eigenvalues imply a loss of detailed balance and implicit steady state that is far from equilib-
rium. To understand the link between detailed balance and equilibria versus nonequilibrium
steady states, it is useful to consider the eigen-decomposition of the final particle in relation to
standard analyses of functional connectivity (e.g., singular value decomposition or principal
component analysis of covariance matrices). In what follows, we first rehearse the relationship
between flow and steady-state distributions over states afforded by the Helmholtz decompo-
sition. We then look at what this implies under the assumption of symmetric coupling—and
how this leads to equilibrium mechanics and a simple relationship between the Jacobian and
covariances among their respective eigenstates. We then revisit these relationships but replac-
ing solenoidal flow, to clarify the differences between summarizing dynamics in terms of the
eigenvectors of the Jacobian and the eigenvectors of the functional connectivity matrix.
In general, one can express the flow at steady state in terms of a Helmholtz decomposition
of the solution to density dynamics (as described by the Fokker-Planck equation). This is an im-
portant expression that underwrites much of physics and related treatments of self-organization
in the biological sciences. (Note: It is also known known as the fundamental theorem of vec-
tor calculus. This decomposition is at the heart of most formulations of nonequilibrium steady
state in nonlinear systems, ranging from molecular interactions to evolution. See Ao, 2004,
2005; Qian & Beard, 2005; Zhang, Xu, Zhang, Wang, & Wang, 2012. For a concise deriva-
tion of Equation 13, under simplifying assumptions, please see Lemma D.1 in K. Friston & Ao,
2012.) Starting with a Langevin formulation of neuronal dynamics, we can express the flow of
states in Equation 2 as follows:
˙x = f (x) + ω
f (x) = (Q − Γ)∇ℑ(x)
(13)
Here, ℑ(x) = −ln p (x) is a potential energy that quantifies the surprise at finding the brain
in any state. The positive definite matrix Γ ∝ I plays the role of a diffusion tensor describing
the amplitude of random fluctuations, ω (assumed to be a Wiener process), while the anti-
symmetric matrix Q = −Q†mediates solenoidal flow. Equation 13 says that the expected flow
at any point in state space has two components: a dissipative gradient flow, −Γ∇ℑ, on the
logarithm of the steady-state density, and a solenoidal flow, Q∇ℑ, that circulates on the iso-
contours of this density. In brief, the gradient flow counters the dispersive effects of random
fluctuations, thereby rendering the probability density stationary. Please note here that we
Network Neuroscience
237
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
Network Neuroscience
have omitted (correction) terms that generalize this (Helmholtz) decomposition, because we
are assuming that the amplitude of random fluctuations and the solenoidal terms change slowly
over state space. We have also dropped the scale superscripts for clarity. On differentiating
the Helmholtz decomposition, with respect to systemic states we have, ∀x:
f (x) = (Q − Γ)∇ℑ(x) ⇒ J(x) = (Q − Γ)Π(x).
(14)
Here, the Jacobian J = ∇ f (x) and Hessian Π(x) = ∇2ℑ(x) are functions of states. Because
the Hessian matrix is symmetrical, there are linear constraints on the solenoidal coupling (Qian
& Beard, 2005):
(Q − Γ)−1 J(x) = Π(x) = Π(x)T = J(x)T(Q − Γ)−T
⇒
QJ(x)T + J(x)Q = Γ J(x)T − J(x)Γ.
These constraints mean that in the absence of solenoidal coupling—when random fluctuations
have the same amplitude everywhere—the Jacobian has to be symmetric Q = 0 ⇒ Γ J(x)T =
J(x)Γ. In other words, symmetric coupling guarantees detailed balance (i.e., an absence of
solenoidal flow).
DETAILED BALANCE AND HEISENBERG’S UNCERTAINTY PRINCIPLE
So how does this help us connect conventional analyses of functional connectivity to the eigen-
vectors of the Jacobian? First, if we make the simplifying assumption that effective connectivity
is symmetric, we can ignore solenoidal flow. If we make the further assumption that the steady
state is Gaussian, the Hessian can be interpreted as a precision matrix (i.e., inverse covariance
or functional connectivity matrix). Note that this Gaussian assumption is usually motivated in
terms of a first-order approximation to the flow (in terms of the Jacobian) around the maxima
of the steady-state density. To the extent that the steady-state density approximates a Gaussian,
then this local linear approximation becomes global. Under these simplifying assumptions,
the Jacobian becomes a scaled version of the precision: setting Q = 0 in Equation 14 gives
the following:
J(x) = −ΓΠ(x).
(15)
This means that the eigenvalues of the Jacobian, which reflect the rate of dissipation of each
mode, are inversely related to the eigenvalues of the precision matrix. In other words, if we
were to perform a principal component analysis of the covariance matrix Σ = Π−1, the prin-
cipal eigenvalues would be interpreted as explaining the most variance in the eigenstates.
However, this is exactly the same as identifying the eigenstates whose flow has the smallest
rate constant. In other words, the principal components are just the slow, unstable modes that
do not dissipate quickly.
ξ− Jξ = λ
ξ−Σξ = −Γλ−1
(16)
One can quantify the dissipative aspect of the eigenmodes in terms of the expected dispersion
of the flow:
E[ f × f ] = JΣJT = ΓΠΓ ⇒ E[ f × f ]E[x × x] = Γ2
Σ = E[x × x] = Π−1
f = Jx
(17)
238
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
This expression shows that the uncertainty about the flow—over state space at steady state—is
inversely proportional to the corresponding uncertainty about the state (i.e., variance). This is
Heisenberg’s uncertainty principle. The connection to the uncertainty principle can be made
explicit by associating the amplitude of random fluctuations with inverse mass (K. Friston,
2019), where the constant of proportionality is Planck’s constant. Equation 17 can then be
expressed as the following:
E[m f × m f ]E[x × x] =
2
¯h
2
(cid:16)
(cid:17)
2Γ = ¯h
m
ℑ(x) = 1
2 x · Π · x
f (x) = − ¯h
Π = ∇2ℑ
2m ∇ℑ = − ¯h
2m ∇2ℑ · x
(18)
This can be interpreted as follows: If we are fairly certain about the state of a system, we
will be very unsure about its flow – and vice versa. This follows from the fact that, at steady
state, systems with predictable, slow flows become dispersed over state space, in virtue of the
random fluctuations. Conversely, if a system can “gather it states up” and locate them in a
small regime of state space, the requisite flows must be fast and varied.
In summary, if we assume detailed balance (i.e., discount solenoidal flow), we are assuming
an equilibrium steady state of the sort studied in quantum and statistical mechanics. In this
special case, there is a direct relationship between the (eigenvectors of) the Jacobian and the
Hessian matrix (i.e., precision, or inverse functional connectivity) matrix. Furthermore, there
is also a direct relationship between the Jacobian and the variance of the expected flow or
dynamics. The assumption of detailed balance is licensed in many situations; in particular, if
we are dealing with ensembles of states or particles that are exchangeable (e.g., an idealized
gas). This renders the Jacobian symmetrical and ensures detailed balance. The Jacobian is
symmetrical because the influence of one particle on a second is the same as the influence
of the second on the first. However, this symmetry cannot be assumed in biological systems
that break detailed balance, especially the brain. We now rehearse the above analysis by
retaining the symmetry breaking, solenoidal flow that underwrites nonequilibrium steady-state
dynamics.
NONEQUILIBRIUM STEADY STATES AND SOLENOIDAL FLOW
In the presence of solenoidal flow, the eigenvectors of the Jacobian and Hessian are no longer
the same. So, which is the best summary of dynamics? Clearly, there is no definitive answer to
this question; however, if we are interested in relevant quantities “that matter,” we are specifi-
cally interested in non-dissipative, slow, unstable dynamics. By construction, this is what the
particular decomposition “picks out,” by discarding fast fluctuations at each successive scale.
This means that the eigenstates of the final particle should have identified slow, unstable, or
critical dynamics. In contrast, had we just taken the principal components of the covariance
matrix of the data (i.e., functional connectivity), we may not have identified the slow modes.
This begs the question, to what extent do solenoidal dynamics contribute to the intrinsic
dynamics of the final particle? One can evaluate the relative contribution of dissipative gradient
Network Neuroscience
239
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
flows and non-dissipative solenoidal flow in terms of their expected dispersion:
E[ f × f ] = JΣJT = (Q − Γ)Π(Q − Γ)T
= ΓΠΓ + QΠQT − ΓΠQT − QΠΓ
.
(19)
non-dissipative
|
{z
}
Clearly, to do this, we need estimates of the amplitude of intrinsic fluctuations and the solenoidal
term. However, under local linear (i.e., Gaussian) assumptions, these two quantities must sat-
isfy JQ + QJT = JT Γ − Γ J, or in terms of eigenstates, λQ + Qλ† = λ†Γ − Γλ. We can use this
constraint to decompose the kinetic energy of the flow in terms of, and only of, the eigenvalues
of the Jacobian, where κ = −Re(λ):
dissipative
non-disspative
m
¯h E[ f × f †] =
Re(λ)2 +
z }| {
−2Re(λ)
Im(λ)2
z }| {
=
λ†λ
2κ
kinetic energy
λ = ξ− Jξ
|
Γ = ξ−Γξ =
Im(λ)
Re(λ)
Q = −i
}
{z
¯h
2m
Γ ⇒ λQ + Qλ† = λ†Γ − Γλ
(20)
Π = 1
Γ Re(λ) ⇒ λ = (Q − Γ)Π
The first equality follows from substituting the subsequent equalities in Equation 19. The use of
kinetic energy here appeals to Equation 18, in which the amplitude of random fluctuations is
associated with inverse mass. This equality says that the dissipative part of flow is determined
by the real part of an eigenstate’s eigenvalue, while the solenoidal contribution is the imaginary
part squared, divided by the real part. Intuitively, this would be like decomposing the kinetic
energy of the Earth into a solenoidal component corresponding to its orbital velocity—and a
dissipative component, as it is drawn towards the sun. This speaks to an increase in kinetic
energy with the frequency of (e.g., neuronal) oscillations, which is not unrelated to the Plank-
Einstein and de Broglie relations in physics.
Note that when working with eigenstates, the solenoidal terms are encoded by Q, which
is a leading diagonal matrix of imaginary values. Similarly, the dissipative terms are encoded
by Γ, which is a leading diagonal matrix of real values. In other words, nonequilibrium steady
state—as defined by the prevalence of solenoidal flow—manifests as the imaginary parts of the
Helmholtz decomposition, when the system is projected onto the eigenvectors of the Jacobian.
Figure 15 shows the dissipative and solenoidal (kinetic) energy of the eigenstates at the
final scale. (Note: Kinetic energy is normally positive because it involves a squared quantity—
momentum—usually assumed to be purely real; see Equation 20. However, when we relax
this assumption and allow complex momenta-like quantities, squaring no longer guarantees
positivity. Hence kinetic energy can take negative values [see Figure 15, top left panel] in this
complex state space.) The corresponding eigenmodes are shown in the subsequent panels as
maximum intensity projections (of their absolute values). In terms of dissipative dynamics, the
first eigenmode has the smallest dissipative energy. In other words, it features the slowest, most
unstable mode macroscopic (intrinsic) dynamics. Eigenmodes 2 and 3 are a conjugate pair,
with complex parts—and, implicitly, a solenoidal contribution to their (kinetic) energy. These
nodes are most pronounced in dorsal mid-prefrontal regions. Note that the kinetic energy
Network Neuroscience
240
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 15. Dissipative and solenoidal dynamics. This figure unpacks the intrinsic coupling at the
final (fourth, single particle) level. At this level, there can be no coupling between particles and—by
construction—the dynamics are completely characterized in terms of the eigenstates that comprise
the particle. In turn, these are completely characterized by their complex eigenvalues; namely, the
intrinsic complex coupling. The upper panels show the dissipative and solenoidal (kinetic) energy
of the eight eigenstates that comprise the particle. The corresponding eigenmodes are shown in
the subsequent panels as maximum intensity projections (of their absolute values).
In terms of
dissipative dynamics, the first eigenmode has the smallest dissipative energy. In other words, it is
the slowest, most unstable mode of this particle. Eigenmodes 2 and 3 are a conjugate pair, with
complex parts—and, implicitly, a solenoidal contribution to their (kinetic) energy. These nodes
are most pronounced in dorsal mid-prefrontal regions, with some expression in posterior parietal
regions. The dissipative energy is, effectively, driven by intrinsic fluctuations that, at the finest level,
include the fluctuations in active states, which play the role of experimental or sensory inputs.
of the first eigenstate is negative. This may seem counterintuitive; however, it is a simple
reflection of the fact that the principal eigenvalue has a real part that is greater than zero.
Clearly, the implicit exponential divergence of trajectories cannot persist globally. In a more
complete analysis, the (stochastic) trajectory would quickly enter regimes of dissipation, such
that the average real part (cf. Lyapunov exponent) was less than zero. One might ask where the
dissipative energy comes from. It is effectively driven by intrinsic fluctuations that, at the finest
level, include the fluctuations in active states, which play the role of experimental or sensory
inputs. This raises an interesting question: At what scale do experimental inputs manifest?
Network Neuroscience
241
Markov blankets in the brain
DISSIPATIVE BRAIN RESPONSES
An intuitive way of thinking about the distinction between dissipative and solenoidal dynam-
ics is in terms of the fluctuations in bath water when perturbed (e.g., when the tap or faucet
is running), as opposed to the ripples and waves that persist after the perturbation is removed
In one case, the water is trying to find its free
(e.g., when the tap or faucet is turned off).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Induced responses. This figure illustrates the expression of experimental or condition-
Figure 16.
specific effects at different scales of the particular decomposition. The top panel is an unusual form
of statistical parametric map; namely, an image of the F statistic, testing for the significance of an
effect of any of the three exogenous inputs (i.e., visual, motion, and attention). Each row of the
F-statistic map corresponds to a scale—and comprises the F statistic for each successive particle
at that scale. This map shows that the effect of (some linear mixture of) exogenous inputs can be
detected at all scales, as evidenced by the dark bars in all four rows. For example, at the third
scale, eigenmode 17 shows an extremely significant effect of inputs with an F statistic of over 150
and an exceedingly small p value of less than 0.0001. This eigenmode is shown on the lower
left in voxel space. Its expression over time—in terms of its real value—is depicted in the middle
panel (blue line), with the best fitting prediction based upon exogenous input (green line). This
prediction is a contrast (i.e., linear mixture) of the input functions shown in the design matrix on the
lower right. The coefficients of this contrast are shown below the design matrix, demonstrating that
the largest contribution is from the second (motion) input. The last column of the design matrix is
simply a column of ones. The associated eigenmode picks out primary visual cortex and extrastriate
areas, encroaching upon motion-sensitive regions in its lateral extremity. The next figure provides a
complementary perspective on the effects of inputs, in terms of their first-order kernels or impulse
response functions throughout the brain, and over extended periods of time.
Network Neuroscience
242
Markov blankets in the brain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 17.
Induced responses over space and time. This figure characterizes induced responses
in terms of first-order Volterra kernels—that is, impulse response functions—of particles at the first
(finest) scale of coarse-graining. Each row corresponds to the three inputs considered (i.e., visual,
motion, and attention effects). The left column shows the expression of these inputs over parti-
cles (weighted by the absolute value of their eigenmodes). This effect is the variance attributable
to each input (i.e., square of the corresponding kernel, summed over time), shown in the left row.
These kernels are shown for the 32 particles with the greatest (absolute) magnitude. The key thing
to take from these results is that motion influences the dynamics of visual and extrastriate (presum-
ably, motion-sensitive regions), while attention has protracted influences on parietal, prefrontal,
and medial temporal regions, including the frontal eye fields and intraparietal sulcus. Interestingly,
visual input per se seems to be expressed preferentially in subcortical systems, including the lateral
geniculate but also other subcortical and medial temporal regions. In addition, visual input appears
to selectively engage posterior superior temporal regions in the left hemisphere—often associated
with biological motion processing. The more telling aspect of this characterization is the protracted
nature of the kernels, which decay to small values after 100 s or so. Notice that these dynamics are
supposedly neuronal in nature because we have accommodated hemodynamic convolution at the
point of estimating the Jacobian.
energy minimum, while in the second case solenoidal, divergence free flow is more like the
complicated swinging of a frictionless pendulum that neither consumes nor creates energy. In
this view, it becomes interesting to characterize the response of the system to perturbation—
here, the exogenous inputs provided by the experimental design. Conceptually, we can regard
Network Neuroscience
243
Markov blankets in the brain
experimental inputs (such as visual afferents to the lateral geniculate) as (active states of) exter-
nal particles that influence (but are not influenced by) the sensory states of particles at the finest
level. Practically, these experimental inputs were included in the estimation of the coupling
parameters that subtend the Jacobian at the finest scale.
Figure 16 characterizes the influence of exogenous, condition-specific effects at different
scales in terms of correlations between fluctuations in the eigenstates that can be explained by
any of the three experimental inputs (i.e., visual, motion, and attention). This analysis suggests
that the effect of exogenous inputs can be detected at all scales. For example, at the third
scale, eigenmode 17 shows an extremely significant effect of sensory perturbation, dominated
by visual motion. The associated eigenmode picks out primary visual cortex and extrastriate
areas, encroaching upon motion-sensitive regions. Note that eigenmode 17 has a negative time
constant, and hence the real part of its eigenvalue is positive. This suggests that during part of
its orbit, it becomes transiently unstable, while following the temporal structure of exogenous
fluctuations.
Figure 17 provides a complementary and revealing perspective on the effects of sensory per-
turbation. This figure characterizes induced responses in terms of first-order Volterra kernels—
that is, impulse response functions—of particles at the first (finest) scale of coarse-graining.
These kernels are based upon the Jacobian and quantify the effects of changing an input on
each eigenmode over time (based on the parameters mediating the influence of experimental
inputs on motion of states at the first scale). The maximum intensity projections on the left
report the variance attributable to each input, based upon the sum of squared kernels over
time (i.e., the autocovariance function at zero lag under each input). Note that this is a fun-
damentally different characterization of brain “activation” because it is modeling the variance
induced by an input that is distributed in space and time through recurrent coupling among
brain regions.
In this example, motion induces responses in visual and extrastriate—presumably, motion-
sensitive eigenmodes—while attention has protracted influences on parietal, prefrontal, and
medial temporal regions, including the frontal eye fields and intraparietal sulcus. Visual in-
put per se seems to be expressed preferentially in subcortical systems, including the lateral
geniculate but also other subcortical and medial temporal regions. In addition, it appears to
selectively engage posterior superior temporal regions in the left hemisphere, often associated
with biological motion processing. The interesting aspect of this characterization is the pro-
tracted nature of the kernels, which decay to small values after 100 s or so. In effect, this means
that although induced responses may be expressed in a regionally specific way almost instan-
taneously, there are enduring effects that can last for a minute or so, following any exogenous
perturbation. Clearly, these effects will be overwritten by ongoing sensory input; however,
this suggests that brain systems—and accompanying distributed neuronal responses—have a
greater memory than might have been anticipated. Heuristically, this means that I should be
able to tell you whether you have “seen something” in the past minute or so by examining
your brain activity at this moment in time.
CONCLUSION
In summary, we have introduced a particular partition that plays the role of a functional par-
cellation scheme for a system of loosely coupled nonlinear oscillators, such as neuronal pop-
ulations in the brain. The key aspect of this parcellation scheme is that it can be applied
recursively in the spirit of the renormalization group. This enables one to examine the scale-
invariant behavior of the ensuing spatiotemporal dynamics in a principled way. The numerical
Network Neuroscience
244
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
Graph Laplacian:
A matrix representation of graph that
combines node adjacency and node
degree in mathematical formulation
and belongs to spectral graph theory.
analyses above confirm the analytic intuitions that as we move from one scale to the next,
there is a progressive slowing and loss of stability of eigenstates associated with each parcel
or particle. This manifests as a form of self-organized criticality, in the sense that slow un-
stable (non-dissipative) eigenmodes supervene on lower scales. Quantitatively speaking, the
spatial scale of a particle, its characteristic frequencies and Lyapunov exponents, all fit nicely
with empirical observations of (dynamic) functional connectivity within and among large-scale
intrinsic brain networks (Liegeois et al., 2019; Northoff, Wainio-Theberge, & Evers, 2019).
The use of an eigen-decomposition of this sort is particularly interesting in relation to recent
eigenmode-decompositions of structural connectivity (Atasoy, Donnelly, & Pearson, 2016),
cortical geometry (Tokariev et al., 2019), and spatially embedded neural fields (Robinson
et al., 2016). These related applications are slightly simpler than the current analysis because
they can assume symmetric coupling—of one sort or another—and therefore need only deal
with real variables and symmetric modes. For a complementary approach to coarse-graining
fMRI data, and then plotting cross-scale covariance functions (including time-asymmetric de-
compositions), please see Breakspear, Bullmore, Aquino, Das, and Williams (2006), espe-
It is also worth noting that our use of the graph Laplacian (G) to
cially Figures 10 and 11.
define neighboring (i.e., coupled) internal states bears a similarity to the graph signal process-
ing (GSP) scheme (Huang et al., 2018). GSP is used to analyze and integrate structural and
functional connectomes, where the (functional) brain activity at the graph nodes is studied on
the underlying graph’s (anatomical) structure. In the GSP framework, the eigen-decomposition
of graph Laplacian (constructed from structural connectome) is used to identify eigenmodes of
low and high frequency (together they define graph Fourier transform).
Because this paper is a technical (foundational) description of the procedures entailed by the
existence of Markov blankets, we have focused on the simplest implementation. This means
that we started off with linearization assumptions, and propagated this approximation to higher
levels. Clearly, it would be nice to revisit the particular partition using higher order approx-
imations that retain nonlinearity in the equations of motion; for example, Equation 14. This
would require a more careful analysis of the Lyapunov exponents, which would involve inte-
grating the system and averaging the eigenvalues over the ensuing state-dependent Jacobian:
The Jacobian becomes a function of states when one includes nonlinearities in the equations
of motion. This raises the interesting issue of how to identify the adjacency matrix used to de-
fine the Markov blankets. In other words, we need to establish the conditional independences
in terms of a zero entry in the Jacobian. However, if the Jacobian is fluctuating over time,
over an orbit in state space, then there may be times when the Jacobian element is zero (i.e.,
zero coupling) and nonzero at other times. Related numerical analyses of nonlinear systems
(K. Friston, 2013) usually require that the Jacobian is zero over a suitably long period of time,
when forming the adjacency matrix in Figure 2. Clearly, this would involve evaluating the
Jacobian over all the solutions to the trajectory in state space. This may be a time-consuming
but otherwise interesting exercise.
We have already mentioned some limitations and extensions. These include starting off with
multivariate characterizations of intrinsic dynamics at the finest level. As noted above, this is
easy to implement by using the first few principal eigenstates, following a singular decompo-
sition of the smallest particles. Another extension is repeating the dynamic causal modeling at
each scale, to reevaluate the Jacobian with suitable high-order (i.e., nonlinear) approximations
to the equations of motion.
The nonuniqueness of the particular partition is a key practical issue. There is no pretense
that there is any unique particular partition. There are a vast number of particular partitions for
Network Neuroscience
245
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
Generative model:
A model for randomly generating
observable data values, typically
given some hidden parameters.
any given coupled dynamical system. In other words, by simply starting with different internal
states —or indeed the number of internal states per particle—we would get a different particu-
lar partition. Furthermore, the thresholds used in the elimination of fast dissipative eigenmodes
will also change the nature of the partition, leading to more or less inclusive dynamics at the
scales above. This latter aspect is probably more defensible in terms of summarizing multi-
scale behavior, in the sense that we can easily motivate the adiabatic approximation in terms
of the relative stability of eigenmodes at a particular level. However, the number of internal
states to consider—and how to pick them—introduces a more severe form of nonuniqueness.
In this paper, we used the state that was maximally coupled to other states as the internal state
of the next particle. This was based upon the graph Laplacian of the adjacency matrix at the
appropriate scale. This is a sensible but somewhat arbitrary definition of an internal state and
speaks to the point that there are a multitude of particular partitions—and implicit Markov
blankets—that could be used. There are two ways that one could handle this nonuniqueness.
(Note: As noted by one of our reviewers, it might be useful to fix the [initial] centroids of the
particles to the centroids of brain atlases [for example, Glasser et al., 2016; Schaefer et al.,
2018]. This might ease the interpretation of the findings, as well as comparisons between the
current and complementary brain network studies.) One would be to embrace it and focus
on the statistics of characterizations over different particular partitions and look for scaling be-
haviors that are conserved over partitions. The alternative is to think about a unique particular
partition and how this would be identified. This as an outstanding issue; namely, what is the
“best” particular partition and, indeed, is the notion of the best partition appropriate?
Another important caveat is the fact that we have predicated the illustrative analyses in
this paper on a single-subject dataset acquired under an experimental activation paradigm.
We chose this dataset because it has been used to illustrate previous developments of dy-
namic causal modeling. Conceptually, this means that the particular partition is specific to
this subject and the subject’s responses to the attentional paradigm (summarized in Figure 17).
Because this paradigm introduced context-sensitive or condition-specific changes in effective
connectivity, it was designed to change the Jacobian over different periods of stimulation (e.g.,
attentional modulation of coupling between visual motion areas and early visual cortex). We
did not attempt to model these effects here; this would require the nonlinear modeling men-
tioned above.
If this modeling was to second order, we would end up with a bilinear form
for Equation 2, which is the basis of most DCM analyses of fMRI data. This speaks to the fact
that the parcellation scheme may not produce the same results when applied to a different
paradigm. In turn, this means that there is further work to be done in terms of finding a par-
ticular partition that accommodates variability in functional anatomy.
In theory, this would
probably be best addressed using a generative model; in other words, assuming one under-
lying sparse Jacobian at any given scale and then adding random effects, so that it could be
used to explain multiple paradigms or subjects. Having said this, the current analyses can be
taken as proof of principle that this sort of multiscale decomposition can be applied to empir-
ical neuroimaging time series and leads to the same phenomenology reported in functional
connectivity literature.
SOFTWARE NOTE
The software producing the figures in this figure are available as part of the academic software
SPM. They can be accessed by invoking DEM graphical user interface and selecting the DCM
and blankets button (DEMO_DCM_MB.m). Please see https://www.fil.ion.ucl.ac.uk/spm/.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00175.
Network Neuroscience
246
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
n
e
n
_
a
_
0
0
1
7
5
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Markov blankets in the brain
AUTHOR CONTRIBUTIONS
Karl J. Friston: Conceptualization; Methodology; Visualization; Writing – original draft. Erik D.
Fagerholm: Methodology; Writing – review & editing. Tahereh S. Zarghami: Writing – review
& editing. Thomas Parr: Methodology; Writing – review & editing. Inês Hipólito: Writing –
review & editing. Loïc Magrou: Writing – review & editing. Adeel Razi: Conceptualization;
Methodology; Writing – review & editing.
FUNDING INFORMATION
Karl J. Friston, Wellcome Trust (http://dx.doi.org/10.13039/100004440), Award ID: 088130/Z/
09/Z. Erik D. Fagerholm, King’s College London Prize Fellowship. Tahereh S. Zarghami, Cog-
nitive Sciences and Technologies Council of Iran international research visit. Adeel Razi, Aus-
tralian Research Council, Award ID: DE170100128. Adeel Razi, Australian Research Council,
Award ID: DP200100757. Adeel Razi, National Health and Medical Research Council, Award
ID: 1194910.
REFERENCES
Ao, P. (2004). Potential in stochastic differential equations: Novel
Journal of Physics A: Mathematical and General,
construction.
37(3), L25–L30. DOI: https://doi.org/10.1088/0305-4470/37/3/l01
(2005). Laws in Darwinian evolutionary theory. Physics
of Life Reviews, 2(2), 117–156. DOI: https://doi.org/10.1016/j
.plrev.2005.03.002
Ao, P.
Arnal, L. H., & Giraud, A. L. (2012). Cortical oscillations and sen-
sory predictions. Trends in Cognitive Sciences, 16(7), 390–398.
DOI:
PMID:
https://doi.org/10.1016/j.tics.2012.05.003
22682813
Atasoy, S., Donnelly, I., & Pearson, J.
(2016). Human brain net-
works function in connectome-specific harmonic waves. Na-
ture Communications, 7, 10340. DOI: https://doi.org/10.1038
/ncomms10340, PMID: 26792267, PMCID: PMC4735826
Bak, P., Tang, C., & Wiesenfeld, K. (1988). Self-organized critical-
ity. Physical Review A: General Physics, 38(1), 364–374. DOI:
https://doi.org/10.1103/PhysRevA.38.364, PMID: 9900174
Bassett, D. S., & Sporns, O.
(2017). Network neuroscience.
Nature Neuroscience, 20(3), 353–364. DOI: https://doi.org/10
.1038/nn.4502, PMID: 28230844, PMCID: PMC5485642
Bastos, A. M., Usrey, W. M., Adams, R. A., Mangun, G. R., Fries,
P., & Friston, K. J. (2012). Canonical microcircuits for predictive
coding. Neuron, 76(4), 695–711. DOI: https://doi.org/10.1016/j
.neuron.2012.10.038, PMID: 23177956, PMCID: PMC3777738
J. M.,
Oostenveld, R., Dowdall, J. R., . . . Fries, P.
(2015). Visual
areas exert feedforward and feedback influences through dis-
tinct frequency channels. Neuron, 85(2), 390–401. DOI: https://
doi.org/10.1016/j.neuron.2014.12.018, PMID: 25556836
J., Bosman, C. A., Schoffelen,
Bastos, A. M., Vezoli,
Biswal, B. B., Van Kylen, J., & Hyde, J. S.
(1997). Simultaneous
assessment of flow and BOLD signals in resting-state functional
connectivity maps. NMR in Biomedicine, 10(4–5), 165–170. DOI:
https://doi.org/10.1002/(SICI)1099-1492(199706/08)10:4/5<165
::AID-NBM454>3.0.CO;2-7
romper la lanza, METRO., bullmore, mi. T., Aquino, K., El, PAG., & williams,
l. METRO. (2006). The multiscale character of evoked cortical activity.
NeuroImagen, 30(4), 1230–1242. DOI: https://doi.org/10.1016
/j.neuroimage.2005.10.041, PMID: 16403656
romper la lanza, METRO., Heitmann, S., & Daffertshofer, A.
(2010). generación-
erative models of cortical oscillations: Neurobiological implica-
tions of the Kuramoto model. Frontiers in Human Neuroscience,
4(190). DOI: https://doi.org/10.3389/fnhum.2010.00190, PMID:
21151358, PMCID: PMC2995481
romper la lanza, METRO., & estampar, C. j.
(2005). Dynamics of a neural sys-
tem with a multiscale architecture. Philosophical Transactions of
the Royal Society of London B: Ciencias Biologicas, 360(1457),
1051–1074. DOI: https://doi.org/10.1098/rstb.2005.1643, PMID:
16087448, PMCID: PMC1854927
Buffalo, mi. A., Fries, PAG., Landman, r., Buschman, t. J., & Desimone,
R. (2011). Laminar differences in gamma and alpha coherence
in the ventral stream. Actas de la Academia Nacional de
Ciencias, 108(27), 11262–11267. DOI: https://doi.org/10.1073
/pnas.1011284108, PMID: 21690410, PMCID: PMC3131344
bullmore, MI., & despreciar, oh. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Naturaleza
Reseñas Neurociencia, 10(3), 186–198. DOI: https://doi.org/10
.1038/nrn2575, PMID: 19190637
Cardy, j. l. (2015). Scaling and renormalization in statistical physics.
Carr, j. (1981). Applications of centre manifold theory. Berlina, Ger-
muchos: Editorial Springer. DOI: https://doi.org/10.1007/978-1-4612
-5929-9
Cessac, B., Blanchard, PAG., & Krüger, t. (2001). Lyapunov exponents
and transport in the Zhang model of self-organized criticality.
Physical Review E: Statistical, Nonlinear, and Soft Matter Physics,
64(1 punto. 2), 016133. DOI: https://doi.org/10.1103/PhysRevE.64
.016133, PMID: 11461357
clark, A.
(2017). How to knit Your own Markov blanket. In T. k.
Metzinger & W.. Wiese (Editores.), Philosophy and Predictive Process-
En g. Frankfurt am Main, Alemania: MIND Group.
cocineros, l., Perdido, l. l., Brilla, A., & romper la lanza, METRO.
(2017).
Criticality in the brain: A synthesis of neurobiology, modificación-
els and cognition. Progress in Neurobiology, 158, 132–152.
Neurociencia en red
247
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
DOI: https://doi.org/10.1016/j.pneurobio.2017.07.002, PMID:
28734836
cocineros, l., Sale, METRO. v., Perdido, l. l., Campana, PAG. T., Nguyen, V. T.,
(2016). A hierarchy of time-
Brilla, A., . . . Mattingley, j. B.
scales explains distinct effects of local inhibition of primary visual
cortex and frontal eye fields. eVida, 5. DOI: https://doi.org/10.7554
/eLife.15252, PMID: 27596931, PMCID: PMC5012863
Coombes, S.
(2005). Waves, bumps, and patterns in neural field
teorías. Cibernética biológica, 93(2), 91–108. DOI: https://doi
.org/10.1007/s00422-005-0574-y, PMID: 16059785
Crick, F., & Koch, C. (1998). Constraints on cortical and thalamic
projections: The no-strong-loops hypothesis. Naturaleza, 391(6664),
245–250. DOI: https://doi.org/10.1038/34584, PMID: 9440687
De Monte, S., d’Ovidio, F., & Mosekilde, mi. (2003). Coherent re-
gimes of globally coupled dynamical systems. Physical Review
Letras, 90(5), 054102. DOI: https://doi.org/10.1103/PhysRevLett
.90.054102, PMID: 12633359
decoración, GRAMO., & Jirsa, V. k.
(2012). Ongoing cortical activity at rest:
Journal of Neu-
Criticality, multistability, and ghost attractors.
roscience, 32(10), 3366–3375. DOI: https://doi.org/10.1523
/JNEUROSCI.2523-11.2012,
PMCID:
PMC6621046
22399758,
PMID:
Ercsey-Ravasz, METRO., Markov, norte. T., lamy, C., VanEssen, D. C.,
Knoblauch, K., Toroczkai, Z., & Kennedy, h. (2013). A predictive
network model of cerebral cortical connectivity based on a dis-
tance rule. Neurona, 80(1), 184–197. DOI: https://doi.org/10.1016
/j.neuron.2013.07.036, PMID: 24094111, PMCID: PMC3954498
Fagerholm, mi. D., Foulkes, W.. METRO. C., Gallero-Salas, y., Helmchen,
F., Friston, k. J., Sanguijuela, r., & Moran, R. j. (2019). Network con-
straints in scale free dynamical systems. arXiv:1908.06678.
Felleman, D., & VanEssen, D. C. (1991). Distributed hierarchical
processing in the primate cerebral cortex. Corteza cerebral, 1, 1–47.
DOI: https://doi.org/10.1093/cercor/1.1.1, PMID: 1822724
Finlay, B. l.
(2016). Principles of network architecture emerging
from comparisons of the cerebral cortex in large and small brains.
Biología PLoS, 14(9), e1002556. DOI: https://doi.org/10.1371
/journal.pbio.1002556, PMID: 27631433, PMCID: PMC5025234
Fox, METRO. D., Snyder, A. Z., Vincent, j. l., Corbetta, METRO., VanEssen,
D. C., & Raichle, METRO. mi. (2005). The human brain is intrinsically
organized into dynamic, anticorrelated functional networks.
procedimientos de la Academia Nacional de Ciencias, 102(27),
9673–9678. DOI: https://doi.org/10.1073/pnas.0504136102,
PMID: 15976020, PMCID: PMC1157105
Frassle, S., Lomakina, mi. I., Razi, A., Friston, k. J., Buhmann, j. METRO.,
& Esteban, k. mi. (2017). Regression DCM for fMRI. NeuroImagen,
155, 406–421. DOI: https://doi.org/10.1016/j.neuroimage.2017
.02.090, PMID: 28259780
Freyer, F., Roberts, j. A., Becker, r., robinson, PAG. A., Ritter, PAG.,
& romper la lanza, METRO. (2011). Biophysical mechanisms of multistabil-
Revista de neurociencia,
ity in resting-state cortical rhythms.
31(17), 6353–6361. DOI: https://doi.org/10.1523/JNEUROSCI
.6693-10.2011, PMID: 21525275, PMCID: PMC6622680
Freyer, F., Roberts,
j. A., Ritter, PAG., & romper la lanza, METRO.
(2012).
A canonical model of multistability and scale-invariance in bio-
logical systems. Biología Computacional PLoS, 8(8), e1002634.
DOI: https://doi.org/10.1371/journal.pcbi.1002634, PMID:
22912567, PMCID: PMC3415415
Friston, k. (2013). Life as we know it. Journal of the Royal Society
Interface, 10(86), 20130475. DOI: https://doi.org/10.1098/rsif
.2013.0475, PMID: 23825119, PMCID: PMC3730701
Friston, k. (2019). A free energy principle for a particular physics.
arXiv:1906.10184. Retrieved from https://ui.adsabs.harvard.edu
/abs/2019arXiv190610184F
Friston, K., & Ao, PAG. (2012). Free energy, valor, and attractors. Com-
putational and Mathematical Methods in Medicine, 2012, 937860.
DOI: https://doi.org/10.1155/2012/937860, PMID: 22229042,
PMCID: PMC3249597
Friston, K., Da Costa, l., & Parr, t. (2020). Some interesting obser-
vations on the free energy principle. arXiv:2002.04501.
Friston, K., Mattout,
J., Trujillo-Barreto, NORTE., Ashburner,
J., &
Penny, W..
(2007). Variational free energy and the Laplace ap-
proximation. NeuroImagen, 34(1), 220–234. DOI: https://doi.org
/10.1016/j.neuroimage.2006.08.035, PMID: 17055746
Friston, K., & Penny, W.. (2011). Post hoc Bayesian model selection.
NeuroImagen, 56(4), 2089–2099. DOI: https://doi.org/10.1016
/j.neuroimage.2011.03.062,
PMCID:
PMC3112494
21459150,
PMID:
Friston, k. J., Bastos, A. METRO., Oswal, A., del barrio, B., Richter, C.,
(2014). Granger causality revisited. NeuroImagen,
& Litvak, V.
101, 796–808. DOI: https://doi.org/10.1016/j.neuroimage.2014
.06.062, PMID: 25003817, PMCID: PMC4176655
Friston, k. J., harrison, l., & Penny, W..
(2003). Dynamic causal
modelling. NeuroImagen, 19, 1273–1302. DOI: https://doi.org/10
.1016/S1053-8119(03)00202-7
Friston, k. J., Kahan, J., Biswal, B., & Razi, A. (2014). A DCM for
resting state fMRI. NeuroImagen, 94, 396–407. DOI: https://
doi.org/10.1016/j.neuroimage.2013.12.009, PMID: 24345387,
PMCID: PMC4073651
Friston, k. J., Litvak, v., Oswal, A., Razi, A., Esteban, k. MI.,
del barrio, B. C. METRO., . . . Zeidman, PAG.
(2016). Bayesian model
reduction and empirical Bayes for group (DCM) estudios. Neuro-
Image, 128, 413–431. DOI: https://doi.org/10.1016/j.neuroimage
.2015.11.015, PMID: 26569570, PMCID: PMC4767224
Friston, k. J., Parr, T., & de Vries, B.
(2017). The graphical brain:
Belief propagation and active inference. Neurociencia en red,
1(4), 381–414. DOI: https://doi.org/10.1162/NETN_a_00018,
PMID: 29417960, PMCID: PMC5798592
Gilson, METRO., Moreno-Bote, r., Ponce-Alvarez, A., Ritter, PAG.,
& decoración, GRAMO. (2016). Estimation of directed effective connectivity
from fMRI functional connectivity hints at asymmetries of corti-
cal connectome. Biología Computacional PLoS, 12(3), e1004762.
PMID:
https://doi.org/10.1371/journal.pcbi.1004762,
DOI:
26982185, PMCID: PMC4794215
Giraud, A. l., & Poeppel, D.
(2012). Cortical oscillations and
speech processing: Emerging computational principles and op-
erations. Neurociencia de la naturaleza, 15(4), 511–517. DOI: https://doi
.org/10.1038/nn.3063, PMID: 22426255, PMCID: PMC4461038
vidrio, METRO. F., carbonero, t. S., robinson, mi. C., hacker, C. D.,
Harwell, J., Yacoub, MI., . . . VanEssen, D. C.
(2016). A multi-
modal parcellation of human cerebral cortex. Naturaleza, 536(7615),
171–178. DOI: https://doi.org/10.1038/nature18933, PMID:
27437579, PMCID: PMC4990127
Neurociencia en red
248
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
Grossberg, S. (2007). Towards a unified theory of neocortex: Lami-
nar cortical circuits for vision and cognition. Progress in Brain
Investigación, 165, 79–104. DOI: https://doi.org/10.1016/S0079
-6123(06)65006-1
Gu, S., Cieslak, METRO., Baird, B., Muldoon, S. F., Grafton, S. T.,
Pasqualetti, F., & bassett, D. S.
(2018). The energy landscape
of neurophysiological activity implicit in brain network struc-
tura. Scientific Reports, 8(1), 2507. DOI: https://doi.org/10.1038
/s41598-018-20123-8, PMID: 29410486, PMCID: PMC5802783
A statistical analysis
of information-processing properties of lamina-specific cortical
microcircuit models. Corteza cerebral, 17(1), 149–162. DOI:
https://doi.org/10.1093/cercor/bhj132, PMID: 16481565
Haeusler, S., & Maass, W..
(2007).
Haimovici, A., Tagliazucchi, MI., Balenzuela, PAG., & Chialvo, D. R.
(2013). Brain organization into resting state networks emerges
at criticality on a model of the human connectome. Físico
Review Letters, 110(17), 178101. DOI: https://doi.org/10.1103
/PhysRevLett.110.178101, PMID: 23679783
Haken, h. (1983). Synergetics: An introduction. Non-equilibrium
phase transition and self-selforganisation in physics, chemistry
y biología. Berlina, Alemania: Springer Verlag.
Hasson, Ud., Cual, MI., Vallines,
I., Heeger, D. J., & Frotar, norte.
(2008). A hierarchy of temporal receptive windows in human cor-
tex. Revista de neurociencia, 28(10), 2539–2550. DOI: https://
doi.org/10.1523/JNEUROSCI.5487-07.2008, PMID: 18322098,
PMCID: PMC2556707
Hilgetag, C. C., O’Neill, METRO. A., & Joven, METRO. PAG.
(2000). Hierar-
chical organization of macaque and cat cortical sensory systems
explored with a novel network processor. Philosophical Trans-
actions of the Royal Society B: Ciencias Biologicas, 355(1393),
71–89. DOI: https://doi.org/10.1098/rstb.2000.0550, PMID:
10703045, PMCID: PMC1692720
Horvát, S., G˘am˘anu¸t, r., Ercsey-Ravasz, METRO., Magrou, l., G˘am˘anu¸t,
B., VanEssen, D. C., . . . Kennedy, h.
(2016). Spatial em-
bedding and wiring cost constrain the functional layout of the
cortical network of rodents and primates. Biología PLoS, 14(7),
e1002512. DOI: https://doi.org/10.1371/journal.pbio.1002512,
PMID: 27441598, PMCID: PMC4956175
Hovsepyan, S., Olasagasti, I., & Giraud, A.-L. (2018). Combining
predictive coding with neural oscillations optimizes on-line
bioRxiv:477588. DOI: https://doi.org/10
speech processing.
.1101/477588
Huang, W.. y., Bolton, t. A. w., Medalla, j. D., bassett, D. S.,
Ribeiro, A., & Van De Ville, D. (2018). A graph signal processing
perspective on functional brain imaging. Actas del IEEE,
106(5), 868–885. DOI: https://doi.org/10.1109/JPROC.2018
.2798928
Itskov, v., Curto, C., Pastalkova, MI., & Buzsaki, GRAMO.
(2011). Cell
assembly sequences arising from spike threshold adaptation
keep track of time in the hippocampus. Revista de neurociencia,
31(8), 2828–2834. DOI: https://doi.org/10.1523/JNEUROSCI
.3773-10.2011, PMID: 21414904, PMCID: PMC3097063
Jirsa, V. K., Friedrich, r., Haken, h., & Kelso, j. A.
(1994). A
theoretical model of phase transitions in the human brain. Bio-
logical Cybernetics, 71(1), 27–35. DOI: https://doi.org/10.1007
/BF00198909, PMID: 8054384
Kaluza, PAG., & Meyer-Ortmanns, h. (2010). On the role of frustration
in excitable systems. Chaos, 20(4), 043111. DOI: https://doi.org
/10.1063/1.3491342, PMID: 21198081
Kayser, C., & Ermentrout, B. (2010). Complex times for earthquakes,
stocks, and the brain’s activity. Neurona, 66(3), 329–331. DOI:
https://doi.org/10.1016/j.neuron.2010.04.039, PMID: 20471345
Keber, F. C., Loiseau, MI., Sanchez, T., DeCamp, S. J., Giomi, l.,
Bowick, METRO. J., . . . Bausch, A. R. (2014). Topology and dynam-
ics of active nematic vesicles. Ciencia, 345(6201), 1135–1139.
DOI: https://doi.org/10.1126/science.1254784, PMID: 25190790,
PMCID: PMC4401068
Keller, GRAMO. B., & Mrsic-Flogel, t. D. (2018). Predictive processing:
A canonical cortical computation. Neurona, 100(2), 424–435.
DOI:
PMID:
https://doi.org/10.1016/j.neuron.2018.10.003,
30359606, PMCID: PMC6400266
Kiebel, S. J., Daunizeau, J., & Friston, k.
(2008). A hierarchy
of time-scales and the brain. Biología Computacional PLoS, 4,
e1000209. DOI: https://doi.org/10.1371/journal.pcbi.1000209,
PMID: 19008936, PMCID: PMC2568860
Kirchhoff, METRO., Parr, T., Palacios, MI., Friston, K., & Kiverstein, j.
(2018). The Markov blankets of life: Autonomy, active infer-
ence and the free energy principle. Journal of the Royal Society
Interface, 15(138). DOI: https://doi.org/10.1098/rsif.2017.0792,
PMID: 29343629, PMCID: PMC5805980
Kitzbichler, METRO. GRAMO., Herrero, METRO. l., Christensen, S. r., & bullmore,
(2009). Broadband criticality of human brain network syn-
mi.
chronization. Biología Computacional PLoS, 5(3), e1000314. DOI:
https://doi.org/10.1371/journal.pcbi.1000314, PMID: 19300473,
PMCID: PMC2647739
Landau, l. D., & Lifshitz, mi. METRO.
(1976). Mechanics (3tercera ed.).
volumen. 1 of Course of Theoretical Physics. Oxford, United
Kingdom: Prensa de Pérgamo.
Liegeois, r., li,
J., kong, r., Orban, C., Van De Ville, D.,
Ge, T., . . . yo, B. t. t.
(2019). Resting brain dynamics at
different timescales capture distinct aspects of human behavior.
Comunicaciones de la naturaleza, 10(1), 2317. DOI: https://doi.org/10
.1038/s41467-019-10317-7,
PMCID:
PMC6534566
31127095,
PMID:
lin, h. w., Tegmark, METRO., & Rolnick, D. (2017). Why does deep and
cheap learning work so well? Journal of Statistical Physics, 168,
1223–1247. DOI: https://doi.org/10.1007/s10955-017-1836-5
López, j. D., Litvak, v., Espinosa, j. J., Friston, K., & Barnes, GRAMO. R.
(2014). Algorithmic procedures for Bayesian MEG/EEG source
reconstruction in SPM. NeuroImagen, 84, 476–487. DOI: https://
doi.org/10.1016/j.neuroimage.2013.09.002, PMID: 24041874,
PMCID: PMC3913905
Lyapunov, A. METRO., & Batán, A. t. (1992). The general problem of the
stability of motion. Londres, Reino Unido: taylor & Francisco.
Lynall, METRO. MI., bassett, D. S., Kerwin, r., McKenna, PAG. J., Kitzbichler,
METRO., Muller, Ud., & bullmore, mi. (2010). Conectividad funcional
and brain networks in schizophrenia. Revista de neurociencia,
30(28), 9477–9487. DOI: https://doi.org/10.1523/JNEUROSCI
.0333-10.2010, PMID: 20631176, PMCID: PMC2914251
Mantegna, R. NORTE., & Stanley, h. mi. (1995). Scaling behavior in the dy-
namics of an economic index. Naturaleza, 376(6535), 46–49. DOI:
https://doi.org/10.1038/376046a0
Neurociencia en red
249
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
Markov, NORTE., Ercsey-Ravasz, METRO., VanEssen, D., Knoblauch, K.,
Toroczkai, Z., & Kennedy, h. (2013). Cortical high-density coun-
Ciencia, 342(6158), 1238406. DOI:
terstream architectures.
https://doi.org/10.1126/science.1238406, PMID: 24179228,
PMCID: PMC3905047
Markov, norte. T., Vezoli, J., Chameau, PAG., Falchier, A., Quilodran, r.,
Huissoud, C., . . . Kennedy, h.
(2014). Anatomy of hierarchy:
Feedforward and feedback pathways in macaque visual cor-
tex. Journal of Comparative Neurology, 522(1), 225–259. DOI:
https://doi.org/10.1002/cne.23458, PMID: 23983048, PMCID:
PMC4255240
Mesulam, METRO. METRO. (1998). From sensation to cognition. Cerebro, 121,
1013–1052. DOI: https://doi.org/10.1093/brain/121.6.1013,
PMID: 9648540
Mohanty, r., Sethares, W.. A., Nair, V. A., & Prabhakaran, V.
(2020). Rethinking measures of functional connectivity via fea-
ture extraction. Scientific Reports, 10(1), 1298. DOI: https://doi
.org/10.1038/s41598-020-57915-w, PMID: 31992762, PMCID:
PMC6987226
Moran, r., Pinotsis, D. A., & Friston, k. (2013). Neural masses and
fields in dynamic causal modeling. Frontiers in Computational
Neurociencia, 7, 57. DOI: https://doi.org/10.3389/fncom.2013
.00057, PMID: 23755005, PMCID: PMC3664834
Mountcastle, V. B. (1997). The columnar organization of the neo-
corteza. Cerebro, 120(punto. 4), 701–722. DOI: https://doi.org/10.1093
/brain/120.4.701, PMID: 9153131
Murray, j. D., Bernacchia, A., Freedman, D. J., Romo, r., Wallis,
j. D., Cai, X., . . . Wang, X. j.
(2014). A hierarchy of intrin-
sic timescales across primate cortex. Neurociencia de la naturaleza,
17(12), 1661–1663. DOI: https://doi.org/10.1038/nn.3862,
PMID: 25383900, PMCID: PMC4241138
Northoff, GRAMO., Wainio-Theberge, S., & Evers, k. (2019). Is temporo-
spatial dynamics the “common currency” of brain and mind?
In quest of “spatiotemporal neuroscience.” Physics of Life Re-
puntos de vista. DOI: https://doi.org/10.1016/j.plrev.2019.05.002, PMID:
31221604
Parr, T., Da Costa, l., & Friston, k. (2020). Markov blankets,
information geometry and stochastic thermodynamics. Philo-
sophical Transactions of the Royal Society A: Matemático,
Físico, and Engineering Sciences, 378(2164), 20190159.
DOI: https://doi.org/10.1098/rsta.2019.0159, PMID: 31865883,
PMCID: PMC6939234
Parr, T., & Friston, k. j.
(2018). The anatomy of inference: generación-
erative models and brain structure. Frontiers in Computational
Neurociencia, 12(90). DOI: https://doi.org/10.3389/fncom.2018
.00090, PMID: 30483088, PMCID: PMC6243103
Pavlos, GRAMO. PAG., Karakatsanis, l. PAG., & Xenakis, METRO. norte. (2012). Tsallis
non-extensive statistics, intermittent turbulence, SOC and chaos
in the solar plasma, Part one: Sunspot dynamics. Physica A:
Statistical Mechanics and Its Applications, 391(24), 6287–6319.
DOI: https://doi.org/10.1016/j.physa.2012.07.066
Pearl, j. (1988). Probabilistic reasoning in intelligent systems: Net-
works of plausible inference. San Fransisco, California: Morgan Kaufmann.
DOI: https://doi.org/10.1016/B978-0-08-051489-5.50015-1
Pearl, j. (2009). Causality. Cambridge, Reino Unido: Cambridge
Prensa universitaria. DOI: https://doi.org/10.1017/CBO978051180
3161
Pellet, j. PAG., & Elisseeff, A.
(2008). Using Markov blankets for
causal structure learning. Journal of Machine Learning Research,
9, 1295–1342.
Peters, A., & Yilmaz, mi. (1993). Neuronal organization in area 17 de
cat visual cortex. Corteza cerebral, 3(1), 49–68. DOI: https://doi
.org/10.1093/cercor/3.1.49, PMID: 7679939
Pyragas, k. (1997). Conditional Lyapunov exponents from time se-
ries. Physical Review E, 56(5), 5183–5187. DOI: https://doi.org
/10.1103/PhysRevE.56.5183
Qian, h., & Beard, D. A. (2005). Thermodynamics of stoichiometric
biochemical networks in living systems far from equilibrium.
Biophysical Chemistry, 114(2–3), 213–220. DOI: https://doi.org
/10.1016/j.bpc.2004.12.001, PMID: 15829355
Ramaswamy, S. (2010). The mechanics and statistics of active mat-
ter. Annual Review of Condensed Matter Physics, 1, 323–345.
DOI: https://doi.org/10.1146/annurev-conmatphys-070909-10
4101
Rao, R. PAG., & Ballard, D. h.
(1999). Predictive coding in the vi-
sual cortex: A functional interpretation of some extra-classical
receptive-field effects. Neurociencia de la naturaleza, 2(1), 79–87. DOI:
https://doi.org/10.1038/4580, PMID: 10195184
Razi, A., & Friston, k. j.
(2016). The connected brain: Causality,
IEEE Signal Processing Mag-
modelos, and intrinsic dynamics.
azine, 33(3), 14–35. DOI: https://doi.org/10.1109/MSP.2015
.2482121
Razi, A., Kahan, J., rees, GRAMO., & Friston, k. j. (2015). Construct vali-
dation of a DCM for resting state fMRI. NeuroImagen, 106(1–4),
222–241. DOI: https://doi.org/10.1016/j.neuroimage.2014.11
.027, PMID: 25463471, PMCID: PMC4295921
Razi, A., Seghier, METRO. l., zhou, y., McColgan, PAG., Zeidman, PAG.,
Parque, h. J., . . . Friston, k. j.
(2017). Large-scale DCMs for
resting-state fMRI. Neurociencia en red, 1(3), 222–241. DOI:
https://doi.org/10.1162/NETN_a_00015,
29400357,
PMCID: PMC5796644
PMID:
robinson, PAG. A., zhao, X., Aquino, k. METRO., Griffiths, j. D., Sarkar, S.,
& Mehta-Pandejee, GRAMO.
(2016). Eigenmodes of brain activity:
Neural field theory predictions and comparison with experi-
mento. NeuroImagen, 142, 79–98. DOI: https://doi.org/10.1016/j
.neuroimage.2016.04.050, PMID: 27157788
roy, D., Un cerdo, r., romper la lanza, METRO., McIntosh, A. r., Jirsa, V. K.,
decoración, GRAMO., & Ritter, PAG. (2014). Using the virtual brain to re-
veal the role of oscillations and plasticity in shaping brain’s dy-
namical landscape. Brain Connectivity, 4(10), 791–811. DOI:
https://doi.org/10.1089/brain.2014.0252, PMID: 25131838
Schaefer, A., kong, r., gordon, mi. METRO., Laumann, t. o., Zuo,
X. NORTE., holmes, A. J., . . . yo, B. t. t.
(2018). Local-global
parcellation of the human cerebral cortex from intrinsic func-
tional connectivity MRI. Corteza cerebral, 28(9), 3095–3114.
DOI: https://doi.org/10.1093/cercor/bhx179, PMID: 28981612,
PMCID: PMC6095216
Schwabl, F. (2002). Phase transitions, scale invariance, renormal-
In Statistical mechanics
ization group theory, and percolation.
(páginas. 327–404). Berlina, Alemania: Saltador. DOI: https://doi.org
/10.1007/978-3-662-04702-6_7
Self, METRO. w., van Kerkoerle, T., Goebel, r., & Roelfsema, PAG. R.
(2019). Benchmarking laminar fMRI: Neuronal spiking and
Neurociencia en red
250
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Markov blankets in the brain
synaptic activity during top-down and bottom-up processing
in the different layers of cortex. NeuroImagen, 197, 806–817.
DOI: https://doi.org/10.1016/j.neuroimage.2017.06.045, PMID:
28648888
espinilla, C. w., & kim, S. (2006). Self-organized criticality and scale-
free properties in emergent functional neural networks. Phys-
ical Review E: Statistical, Nonlinear, and Soft Matter Physics,
74(4 punto. 2), 45101. DOI: https://doi.org/10.1103/PhysRevE.74
.045101, PMID: 17155118
Cantante, w., Sejnowski, t. J., & Rakic, PAG.
The neo-
corteza. Retrieved from http://mitpress.mit.edu/9780262043243.
DOI: https://doi.org/10.7551/mitpress/12593.001.0001
(2019).
Spratling, METRO. W.. (2008). Predictive-coding as a model of biased
competition in visual attention. Vision Research, 48, 1391–1408.
DOI: https://doi.org/10.1016/j.visres.2008.03.009, PMID:
18442841
Stachenfeld, k. l., Botvinick, METRO. METRO., & Gershman, S. j. (2017). El
hippocampus as a predictive map. Neurociencia de la naturaleza, 20(11),
1643–1653. DOI: https://doi.org/10.1038/nn.4650, PMID:
28967910
Thomson, A. METRO., & Bannister, A. PAG.
Interlaminar con-
nections in the neocortex. Corteza cerebral, 13(1), 5–14. DOI:
https://doi.org/10.1093/cercor/13.1.5, PMID: 12466210
(2003).
Tokariev, A., Roberts,
j. A., Brilla, A., zhao, X., Vanhatalo,
S., romper la lanza, METRO., & cocineros, l. (2019). Large-scale brain modes
reorganize between infant sleep states and carry prognostic infor-
mation for preterms. Comunicaciones de la naturaleza, 10(1), 2619. DOI:
https://doi.org/10.1038/s41467-019-10467-8, PMID: 31197175,
PMCID: PMC6565810
Trojanowski, J., & jacobson, S. (1977). The morphology and laminar
distribution of cortico-pulvinar neurons in the rhesus monkey.
Experimental Brain Research, 28, 51–62. DOI: https://doi.org/10
.1007/BF00237085, PMID: 407094
van den heuvel, METRO. PAG., & despreciar, oh. (2013). Network hubs in the hu-
man brain. Tendencias en Ciencias Cognitivas, 17(12), 683–696. DOI:
https://doi.org/10.1016/j.tics.2013.09.012, PMID: 24231140
van Kerkoerle, T., Self, METRO. w., Dagnino, B., Gariel-Mathis, METRO. A.,
Poort, J., van der Togt, C., & Roelfsema, PAG. R.
(2014). Alpha
and gamma oscillations characterize feedback and feedforward
processing in monkey visual cortex. Actas del Nacional
Academia de Ciencias, 111(40), 14332–14341. DOI: https://doi
.org/10.1073/pnas.1402773111, PMID: 25205811, PMCID:
PMC4210002
Wang, X.-J., & Kennedy, h. (2016). Brain structure and dynamics
across scales: In search of rules. Current Opinion in Neurobi-
ology, 37, 92–98. DOI: https://doi.org/10.1016/j.conb.2015.12
.010, PMID: 26868043, PMCID: PMC5029120
Yuan, r., Mamá, y., Yuan, B., & Ao, PAG.
(2011). Potential function
in dynamical systems and the relation with Lyapunov function.
Paper presented at the Proceedings of the 30th Chinese Control
Conferencia.
Zeki, S., & Shipp, S. (1988). The functional logic of cortical con-
nections. Naturaleza, 335, 311–317. DOI: https://doi.org/10.1038
/335311a0, PMID: 3047584
zhang, F., Xu, l., zhang, K., Wang, MI., & Wang, j.
(2012). El
Diario de
potential and flux landscape theory of evolution.
Chemical Physics, 137(6), 065102. DOI: https://doi.org/10.1063
/1.4734305, PMID: 22897313
zhou, y., Friston, k. J., Zeidman, PAG., Chen, J., li, S., & Razi, A.
(2018). The hierarchical organization of the default, dorsal atten-
tion and salience networks in adolescents and young adults.
Corteza cerebral, 28(2), 726–737. DOI: https://doi.org/10.1093
/cercor/bhx307, PMID: 29161362, PMCID: PMC5929108
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
5
1
2
1
1
1
8
8
9
7
8
5
norte
mi
norte
_
a
_
0
0
1
7
5
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Neurociencia en red
251