ARTÍCULO
Communicated by Tilo Schwalger
Inference of a Mesoscopic Population Model
from Population Spike Trains
Alexandre René
arene010@uottawa.ca
Department of Physics, University of Ottawa, Ottawa K1N 6N5, Canada; máx.
Planck Research Group Neural Systems Analysis, Center of Advanced European
Studies and Research (caesar), Bonn 53175, Alemania; and Institute of Neuroscience
y medicina (INM-6) and Institute for Advanced Simulation (IAS-6) y
JARA-Institute Brain Structure-Function Relationships (INM-10), Jülich Research
Centre, Jülich 52425, Alemania
André Longtin
alongtin@uottawa.ca
Department of Physics, University of Ottawa, Ottawa K1N 6N5, Canada, and Brain
and Mind Research Institute, University of Ottawa, Ottawa K1H 8M5, Canada
Jakob H. Macke
macke@tum.de
Max Planck Research Group Neural Systems Analysis, Center of Advanced European
Studies and Research (caesar), Bonn 53175, Alemania, and Computational
Neuroengineering, Department of Electrical and Computer Engineering, Técnico
University of Munich, Munich 80333, Alemania
Understanding how rich dynamics emerge in neural populations re-
quires models exhibiting a wide range of behaviors while remaining
interpretable in terms of connectivity and single-neuron dynamics. Cómo-
alguna vez, it has been challenging to fit such mechanistic spiking networks at
the single-neuron scale to empirical population data. To close this gap,
we propose to fit such data at a mesoscale, using a mechanistic but low-
dimensional and, por eso, statistically tractable model. The mesoscopic
representation is obtained by approximating a population of neurons
as multiple homogeneous pools of neurons and modeling the dynamics
of the aggregate population activity within each pool. We derive the
likelihood of both single-neuron and connectivity parameters given this
actividad, which can then be used to optimize parameters by gradient as-
cent on the log likelihood or perform Bayesian inference using Markov
chain Monte Carlo (MCMC) muestreo. We illustrate this approach
using a model of generalized integrate-and-fire neurons for which
mesoscopic dynamics have been previously derived and show that both
single-neuron and connectivity parameters can be recovered from
Computación neuronal 32, 1448–1498 (2020) © 2020 Instituto de Tecnología de Massachusetts
https://doi.org/10.1162/neco_a_01292
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
8
1
4
4
8
1
8
6
5
0
4
3
norte
mi
C
oh
_
a
_
0
1
2
9
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Inference of a Mesoscopic Population Model
1449
simulated data. En particular, our inference method extracts posterior
correlations between model parameters, which define parameter subsets
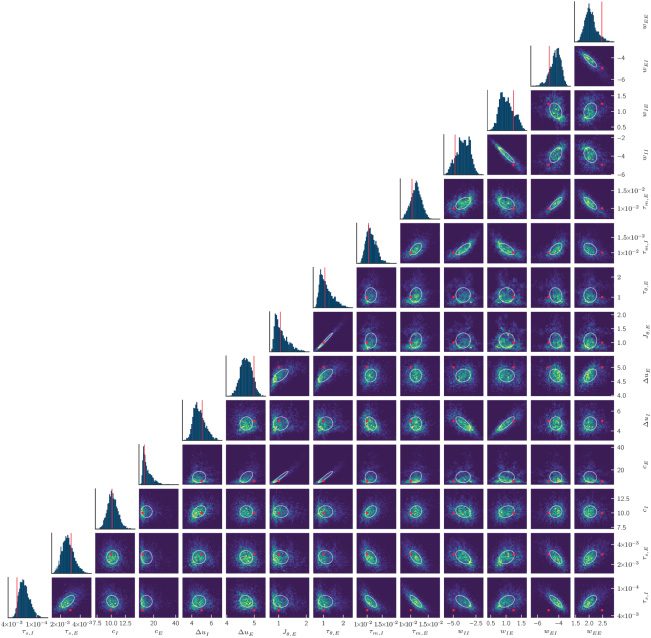
able to reproduce the data. We compute the Bayesian posterior for com-
binations of parameters using MCMC sampling and investigate how the
approximations inherent in a mesoscopic population model affect the
accuracy of the inferred single-neuron parameters.
1 Introducción
Neuron populations produce a wide array of complex collective dynam-
circuitos integrados. Explaining how these emerge requires a mathematical model that not
only embodies the network interactions but is also parameterized in terms
of interpretable neuron properties. Just as crucial, in order to draw data-
supported conclusions, we also need to be able to infer those parameters
from empirical observations. These requirements tend to involve a trade-
off between model expressiveness and tractability. Low-dimensional state-
space models (Macke et al., 2011; Pandarinath et al., 2018; Pillow et al., 2008;
zhao & Parque, 2016) are simple enough to allow for inference but achieve
that simplicity by focusing on phenomenology: any mechanistic link to the
individual neurons is ignored. En cambio, microscopic mechanistic mod-
els with thousands of simulated neurons do provide that link between pa-
rameters and output (Hawrylycz et al., 2016; Potjans & Diesmann, 2014);
sin embargo, this complexity makes the analysis difficult and is limited to net-
works with highly simplified architectures (Doiron, Litwin-kmar, rosa-
baum, ocre, & Josic, 2016; Martí, Brunel, & Ostojic, 2018). Since methods to
fit these models to experimental data are limited to single neurons (Mensi
et al., 2012), it is also unclear how to set their parameters such that they
capture the dynamics of large, heterogeneous neural populations.
To reduce the problem to a manageable size and scale, one can con-
sider models that provide a mesoscopic dynamical description founded
on microscopic single-neuron dynamics (Dumont, Payeur, & Longtin, 2017;
Nykamp & Tranchina, 2000; Wallace, Benayoun, van Drongelen, & Cowan,
2011). Específicamente, we will focus on the model described in Schwalger,
Deger, and Gerstner (2017), where neurons are grouped into putative ex-
citatorio (mi) e inhibitorio (I) populations in a cortical column. The key ap-
proximation is to replace each population with another of equal size but
composed of identical neurons, resulting in an effective mesoscopic model
of homogeneous populations. In contrast with previous work on popula-
tion rate dynamics (Gerstner, 2000; Nykamp & Tranchina, 2000; wilson &
Cowan, 1972), Schwalger et al. (2017) correct their mean-field approxima-
tions for the finite size of populations. They are thus able to provide stochas-
tic equations for the firing rate of each population with explicit dependence
on the population sizes, neuron parameters, and connectivities between
poblaciones (ver Figura 1A, arriba). We use these equations to fit the model
to traces of population activity.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
8
1
4
4
8
1
8
6
5
0
4
3
norte
mi
C
oh
_
a
_
0
1
2
9
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1450
A. René, A. Longtin, y j. Macke
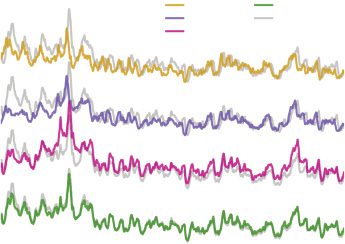
Cifra 1: (A) General procedure to infer parameters of a mesoscopic popula-
tion model from microscopic data. A microscopic model of GIF neurons is used
to generate spike trains, which are averaged to obtain traces of population ac-
actividad; these traces constitute our data. A mesoscopic model of either two or four
populations is then fit to these traces. Simulating the mesoscopic model with the
inferred parameters allows us to evaluate how well it reproduces the true dy-
namics. (B) For heterogeneous systems, average parameters might not predict
mean activity. Mean activity (línea) and its standard deviation (shaded area) para
a heterogeneous microscopic model (izquierda) and mesoscopic models attempting to
approximate it (medio, bien). A mesoscopic model constructed by averaging
parameters across the microscopic population overestimates the population’s
variabilidad (medio). Inferred parameters in this case deviate from these aver-
ages and provide a better representation of the true activity (bien). Models are
como en la figura 5; traces are for the inhibitory population. Means and standard de-
viations are computed from 50 realizations and averaged over disjoint bins of
10 EM.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
8
1
4
4
8
1
8
6
5
0
4
3
norte
mi
C
oh
_
a
_
0
1
2
9
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Directly inferring mesoscopic model parameters has a number of ad-
vantages compared to extrapolating from those obtained by fitting a mi-
croscopic model. For one, it allows the use of data that do not have single-
neuron resolution. Además, since neuron parameters in a mesoscopic
model represent a whole population, there may not be a clear way to re-
late micro- and mesoscopic parameters if the former are heterogeneous. Por
inferring population parameters from population recordings, we target the
values that best compensate for the mismatch between the data and the ide-
alized mesoscopic model (ver Figura 1B).
The method we present assumes that the model to be inferred can be
expressed as a set of stochastic equations and that we have access to time
series for both the observed (and possibly aggregated) neural activities and
external input. It is thus not limited to mesoscale models and could also be
applied to, decir, Hodgkin Huxley-type neurons in isolation or networks.
Sin embargo, in this article, the underlying microscopic model does make
the inferred parameters more readily interpretable and provides a good
idea of what values an inference algorithm should find for the parameters.
Inference of a Mesoscopic Population Model
1451
Methods have recently been developed for inferring models where
stochastic equations are treated as a black box simulator (Greenberg, No-
nenmacher, & Macke, 2019; Lueckmann et al., 2017; Papamakarios & Mur-
ray, 2016; Papamakarios, Sterratt, & Murray, 2018). In such a case, one does
not have access to the internal variables of the model and thus cannot com-
pute the likelihood of its parameters; en cambio, these methods make use of
repeated simulations to find suitable parameters. While this makes them
applicable to a wide range of models, the repeated simulations can make
them computationally expensive and best suited to optimizing a set of sta-
tistical features rather than full-time traces. Además, for the models of
interest here, the likelihood can be derived from the stochastic evolution
ecuaciones.
We show in this work that the likelihood can indeed be used to
infer model parameters using non-convex optimization. La resultante
optimization problem shares many similarities with training recurrent
redes neuronales (RNNs) popular in machine learning (Goodfellow, bengio,
& Courville, 2016; Waibel, Hanazawa, Hinton, Shikano, & Lang, 1989) y
allows us to leverage optimization tools from that field. Sin embargo, RNNs in
machine learning are typically based on generic, nonmechanistic models,
which implies that interpretation of the resulting network can be challeng-
En g (but see work on RNN visualization by Barak et al. (Barak, 2017; Haviv,
Rivkind, & Barak, 2019; Susillo & Barak, 2012). De este modo, our approach can be
regarded as complementary to RNN approaches, as we directly fit a mech-
anistically interpretable model.
This article is organized as follows. In sections 2.1 y 2.2, we estab-
lish that maximum likelihood inference for our chosen mesoscopic model
is sound, y en la sección 2.3 we provide empirical estimates for the amount
of data this procedure requires. Using the example of heterogeneous popu-
laciones, sección 2.4 then shows how inference can find effective parameters,
which compensate for the mismatch between data and model. En la sección
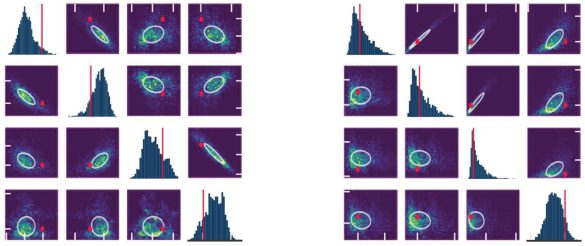
2.5 we identify codependence between multiple model parameters by re-
covering the full Bayesian posterior. Finalmente, sección 2.6 demuestra que
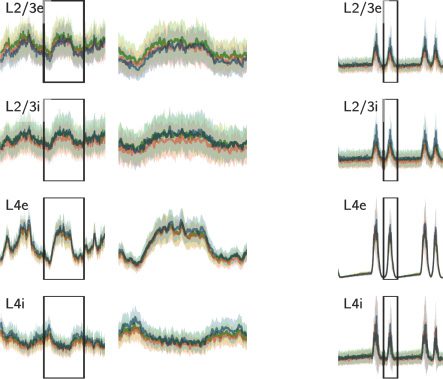
the approach scales well by considering a more challenging four-population
model with 36 free parameters. Sección 3 discusses our results, with an em-
phasis on circumscribing the class of models amenable to our approach.
Method details are provided in section 4, along with technical insights
gained as we adapted likelihood inference to a detailed dynamical model.
Additional details, including a full specification of parameter values used
throughout the article, are given in appendixes A to I.
2 Resultados
2.1 Model Summary. We studied the pair of microscopic and meso-
scopic models presented in Schwalger et al. (2017), which is designed to
represent excitatory (mi) e inhibitorio (I) populations of a putative cortical
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
8
1
4
4
8
1
8
6
5
0
4
3
norte
mi
C
oh
_
a
_
0
1
2
9
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
1452
A. René, A. Longtin, y j. Macke
column of four neural layers (Potjans & Diesmann, 2014). Para este estudio,
we considered only layers 2/3 y 4 and made minor parameter adjust-
ments to maintain realistic firing rates (see appendix A). We also reduced
all population sizes by a factor of 50 to ease the simulation of the micro-
scopic model. This increases the variance of population activities and so
does not artificially simplify the task of inferring mesoscopic parameters.
The microscopic model is composed of either two or four populations of
generalized integrate-and-fire (GIF) neuronas. Neurons are randomly con-
nected, with connectivity probabilities depending on the populations. El
combination of excitatory and inhibitory input, along with internal adap-
tation dynamics, produces for each neuron i a time-dependent firing rate
l
i(t|Ht ); this rate is conditioned on the spike history up to t, denoted Ht (para
ecuaciones, mira la sección 4.1). Whether that neuron spikes within a time win-
dow [t, t + (cid:3)t) is then determined by sampling a Bernoulli random variable
(Schwalger et al., 2017),
si(t|Ht ) ∼ Bernoulli(l
i(t|Ht )(cid:3)t),
(2.1)
i(t|Ht )(cid:3)t (cid:3) 1 is always true; we later refer
dónde (cid:3)t is chosen such that λ
to this stochastic process as escape noise. If all parameters are shared across
all neurons within each population, we call this a homogeneous microscopic
modelo. En cambio, we call a model heterogeneous if at least one parameter is
unique to each neuron. We denote Iα the set of indices for neurons belong-
ing to a population α.
The expected activity aα of a population α is the normalized expected num-
ber of spikes,
aα (t|Ht ) = 1
Nα
(cid:2)
i∈Iα
i(t|Ht ),
l
(2.2)
which is a deterministic variable once we know the history up to t. en contra-
contraste, the activity Aα of that population is a random variable corresponding
to the number of spikes actually observed:
Aα (t|Ht ) := 1
Nα
(cid:2)
i∈Iα
si(t|Ht ).
(2.3)
These variable definitions are summarized in Table 1.
En la práctica, data are discretized into discrete time steps {tk
}l
K = 1, que nosotros
assume to have uniform lengths (cid:3)t and to be short enough for spike events
of different neurons to be independent within one time step (this condition
is always fulfilled when the time step is less than the synaptic transmission
demora). Under these assumptions, ecuación 2.3 can be approximated by a
binomial distribution (Schwalger et al., 2017),
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
3
2
8
1
4
4
8
1
8
6
5
0
4
3
norte
mi
C
oh
_
a
_
0
1
2
9
2
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Inference of a Mesoscopic Population Model
1453
Mesa 1: Key Variable Definitions.
Variable Definition
Nα
METRO
l
(cid:3)t
Iα
si(t)
Aα (t)
aα (t)
Number of neurons in population α
Number of populations, un = 1, . . . , METRO
Number of time steps used to compute the likelihood
Time step
Set of indices of neurons belonging to population α
1 if neuron i spiked within time window [t, t + (cid:3)t), 0 de lo contrario
Activity in population α averaged over time window [t, t + (cid:3)t)
Expectation of A(t) conditioned on {A(t
)}
(cid:5)
t(cid:5)