ALIVIO: Un enfoque multivariado estructurado para la eliminación de latentes
enterrar- scanner effects
Rongqian Zhanga, Lindsay D. Oliverb, Aristotle N. Voineskosb,C, Jun Young Parka,d
aDepartment of Statistical Sciences, universidad de toronto, toronto, Canada
bCentre for Addiction and Mental Health, toronto, Canada
cDepartment of Psychiatry, universidad de toronto, toronto, Canada
dDepartment of Psychology, universidad de toronto, toronto, Canada
Autor correspondiente: Jun Young Park (junjy.park@utoronto.ca)
ABSTRACTO
Combining data collected from multiple study sites is becoming common and is advantageous to researchers to
increase the generalizability and replicability of scientific discoveries. Sin embargo, at the same time, unwanted inter-
scanner biases are commonly observed across neuroimaging data collected from multiple study sites or scanners,
rendering difficulties in integrating such data to obtain reliable findings. While several methods for handling such
unwanted variations have been proposed, most of them use univariate approaches that could be too simple to cap-
ture all sources of scanner- specific variations. Para abordar estos desafíos, we propose a novel multivariate harmo-
nization method called RELIEF (REmoval of Latent Inter- scanner Effects through Factorization) for estimating and
removing both explicit and latent scanner effects. Our method is the first approach to introduce the simultaneous
dimension reduction and factorization of interlinked matrices to a data harmonization context, which provides a new
direction in methodological research for correcting inter- scanner biases. Analyzing diffusion tensor imaging (DTI) datos
from the Social Processes Initiative in Neurobiology of the Schizophrenia (SPINS) study and conducting extensive
simulation studies, we show that RELIEF outperforms existing harmonization methods in mitigating inter- scanner
biases and retaining biological associations of interest to increase statistical power. RELIEF is publicly available as an
RAPACIO R.
Palabras clave: batch effects, covariance heterogeneity, dimension reduction, inter-scanner biases, neuroimaging, ALIVIO
1.
INTRODUCCIÓN
It is increasingly common in neuroimaging and genom-
ics to combine data collected from multiple study sites
to increase the power and the reproducibility of scien-
tific discoveries. Sin embargo, combining such data comes
with unwanted non- biological variations that need to be
removed for successful data integration. In neuroimag-
En g, this is often characterized by inter- scanner biases
(scanner effects) when subject data are obtained by using
different magnetic resonance imaging (resonancia magnética) scanners
with different optimization protocols. These inter- scanner
biases have been shown to be present in most neuroim-
aging data types, including diffusion ( Vollmar et al., 2010;
Zhu et al., 2011), structural ( Han et al., 2006; Takao,
Hayashi, & Ohtomo, 2014), and functional ( Dansereau
et al., 2017) resonancia magnética. These terms are analogous to batch
effects in genomic studies that are observed with
genome- wide microarray or RNA sequencing data with
different sample preparation and sequencing methods.
There have been numerous efforts in statistics, semejante
as ComBat, to capture and remove these unwanted vari-
ations and increase the signal- a- noise ratio ( J.- PAG. Fortin
Recibió: 27 Junio 2023 Aceptado: 2 Agosto 2023 Available Online: 11 Agosto 2023
Neurociencia de la imagen, Volumen 1, 2023
https://doi.org/10.1162/imag_a_00011
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
© 2023 Instituto de Tecnología de Massachusetts. Publicado bajo una atribución Creative Commons 4.0 Internacional (CC POR 4.0) licencia. Research ArticleR. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
et al., 2017, 2018; Johnson, li, & Rabinovic, 2007; METRO. Yu
et al., 2018; Y. zhang, Parmigiani, & Johnson, 2020).
ComBat ( Johnson et al., 2007) is a popular regression-
based batch correction approach first motivated from
microarray data, and has been promising in removing
enterrar- scanner biases in many neuroimaging data types,
including fractional anisotropy and mean diffusivity ( J.- PAG.
Fortin et al., 2017), cortical thickness ( J.- PAG. Fortin et al.,
2018), and functional connectivity ( METRO. Yu et al., 2018). En
ComBat, scanner effects are characterized by an additive
scanner effect (ubicación) and a multiplicative scanner
efecto (escala) for each feature. While a regression model is
used in each feature, ComBat uses empirical Bayes to
stabilize estimates across features and provides robust-
ness in the case of small within- scanner sample sizes
( Johnson et al., 2007). In addition to showing its utility in
various neuroimaging data types, ComBat has been
extended to harmonize imaging data collected in a longi-
tudinal manner ( Beer et al., 2020), to preserve non- lineal
age trajectories of cortical thickness data in mega-
analysis in cross- sectional studies ( Pomponio et al.,
2020). It is also a versatile method that allows for harmo-
nization even without the need to share original data from
a study site with other sites, which relaxes concerns
about data privacy ( Chen, luo, et al., 2022).
The ComBat’s location- scale model is simple and inter-
pretable, pero, from the statistical perspective, it is insuffi-
cient to capture all sources of scanner effects. El
heterogeneity in covariances across different sites or scan-
ners has been overlooked in the neuroimaging literature,
and such heterogeneity might also lead to decreased sta-
tistical power. ComBat is oversimplified by the assumption
that additive scanner effects can be explained by only an
intercept for each scanner and feature. Recientemente, a new
harmonization method called CovBat ( Chen, Beer, et al.,
2022) was proposed to address covariance heterogeneity
in multi- site, multi- scanner studies by extending ComBat.
It applies ComBat twice: first to the original data, then to
the principal component scores from the residual matrix.
CovBat is an important development that expanded the
scope of statistical harmonization to address heteroge-
neous covariances, and it has been shown to be more effi-
cient than ComBat, como se esperaba ( Chen, Beer, et al., 2022;
Chen, Srinivasan, et al., 2022). Sin embargo, CovBat implicitly
assumes that the covariance scanner effect is contained
within the eigenspace of the residual matrix only, in the
form of a location- scale model. As Chen, Beer, et al. (2022)
noted, this assumption may limit the ability of CovBat to
characterize all sources of covariance heterogeneity,
which we also show in this paper.
The method for harmonizing covariances across
sca nners can be understood using the latent variable
formulation ( Chen, Beer, et al., 2022). Singular value
decomposition (SVD) and principal component analysis
(PCA) are commonly used techniques for removing or
adjusting for non- biological variations not explicitly
specified by scanner information. SVA (Surrogate Vari-
able Analysis) is a method that was originally developed
for genomic studies ( Leek & Storey, 2007) and then
adapted to neuroimaging studies ( J.- PAG. Fortin et al.,
2016). SVA includes latent factors of unwanted variation
as surrogate variables, which are not associated with
the biological covariates of interest. Instead of using
explicit variables to denote scanner effects, SVA identi-
fies and estimates scanner or other non- biological arti-
facts through permutation testing, then removes them as
surrogate variables. RAVEL ( J.- PAG. Fortin et al., 2016) es un
statistical method for correcting technical variability in
neuroimaging data. RAVEL applies SVD to obtain latent
factors of unwanted variations in the control regions and
then removes the latent factors and corresponding
effects in the test regions ( J.- PAG. Fortin et al., 2016, 2017).
These approaches that apply low- rank factorization
methods to all study subjects’ imaging features are fun-
damentally limited to addressing scanner- specific latent
efectos. Al mismo tiempo, efforts to identify low- rank fac-
tors for study subjects from the same scanner may over-
kill biological variations.
en este documento, we propose a novel harmonization
method called RELIEF (REmoval of Latent Inter- scanner
Effects through Factorization) to distinguish loadings
shared across scanners (which should be preserved)
from loadings specific to scanners (which should be
removed), which enhances the current understanding of
enterrar- scanner biases. We formulate latent scanner effects
from the perspective of linked matrix factorization by
extending the recent work of Park and Lock (2020) en el
harmonization context. It aligns with growing method-
ological developments on simultaneous dimension
reduction and factorization of multi- modal data (p.ej.,
Gaynanova & li, 2019; Lock, Hoadley, Marron, & Nobel,
2013; Lock, Parque, & Hoadley, 2022), which has also been
shown to be promising in neuroimaging data ( q. Yu, Riesgo,
zhang, & Marron, 2017). Through extensive data analy-
ses and simulations, we show our proposed method has
superior performance in identifying and removing latent
unwanted variations specific to each scanner, thus lead-
ing to covariance homogeneity across scanners and
increasing statistical power compared to existing meth-
probabilidades. También, our estimation procedure is scalable and takes
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
2
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
only a few seconds to implement, which supports its
practical utility.
The rest of the paper is organized as follows. Sección 2
describes our proposed method, ALIVIO, and compares
it to existing harmonization methods. In Section 3, nosotros
apply our method to the fractional anisotropy (FA) y
mean diffusivity (Maryland) data from the Social Processes Ini-
tiative in the Neurobiology of the Schizophrenia(s) (SPINS)
estudiar, where study subjects were collected from multiple
sites and scanners. We compare RELIEF to other harmo-
nization methods using a comprehensive evaluation
estructura. Sección 4 conducts extensive simulations to
evaluate performances in terms of Type 1 error rate and
statistical power. We conclude with some points of dis-
cussion in Section 5.
2. MÉTODOS
2.1. Notation and setup
METRO
yo=1
We let i = 1,…,M denote the index for each scanner
(lote), j = 1,…ni denote the subject index in ith scanner
∑ ni = n), and v = 1,…,V denote the index for imaging
(
características. We let x ij be the q- dimensional covariate vector
for jth subject in ith scanner (p.ej., age and sex). yijv is the
vth imaging feature of the jth subject of the ith scanner.
By stacking all observations of x ij, we let X be a n × q
matrix of q covariates observed for n study subjects. Sim-
ilarly, let Y be a V × n data matrix of V features. Entonces, a
group the subjects from the same scanner together, nosotros estafamos-
sider {Hacer : V × ni | i = 1,…, METRO} a partition of Y. The matrices
can be concatenated to form a matrix Y = [Y1;Y2;…;Y m].
We will use this notation for a general V × n matrix through-
out this paper.
2.2. Existing harmonization methods
2.2.1. Adjusted residuals (AdjRes)
The simplest approach to model inter- scanner bias is to
use a regression- based approach to characterize addi-
tive scanner- specific deviations for each feature. AdjRes
considers the following specifications,
yijv = αv + ′xij ββv + γ iv + εijv,
(1)
dónde, for the vth feature, αv is the intercept, ββv is the reg-
ression coefficients for x ij, and εijv is a Gaussian noise. El
parameters αv, ββv, γ iv can be estimated by the least
squares method. The scanner- specific means, γ iv, necesidades
to be removed and the harmonized data are constructed
by y ijv
AdjRes = ˆαv + x ij′
ˆββv + ˆε ijv.
2.2.2. ComBat
ComBat seeks to remove the additive and multiplicative
scanner effects ( Johnson et al., 2007). For the vth fea-
tura, ComBat characterizes the additive and multiplica-
tive scanner effects by
y ijv = αv + x ij′ ββv + γ iv + φivεijv.
(2)
In Equation (2), the scanner effects are characterized by
γ iv (the additive scanner effect) and φiv (the multiplicative
scanner effect). After obtaining ˆαv, ˆββv via least squares,
! )
ComBat estimates scanner effects in locations (es decir., γ iv
! ) via empirical Bayes for each feature
and scales (es decir., φiv
por separado, providing stable and robust estimations of
these parameters in the case of small within- scanner sam-
ple sizes ( Johnson et al., 2007). The ComBat- harmonized
data is defined by y ijv
ComBat = ˆαv + x ij′ ˆββv + ˆεijv
ComBat, dónde
ComBat =
ˆεijv
y ijv − ˆαv − x ij′
»
φiv
ˆββv − γ iv
»
.
(3)
2.2.3. CovBat
In addition to ComBat’s model in Equation (2), CovBat
assumes that the error terms εij = (εij1,εij2,…,εijV ′) ~
MVN (0, ∑∑ i ), where ∑∑ i is the covariance for the i th scan-
ner. CovBat further assumes the underlying pooled cova-
riance is homogeneous across scanners. Inspired by
how ComBat mitigates the difference between the vari-
ance within each scanner and the pooled variance,
CovBat shifts the within- scanner covariance to the
pooled covariance by using principal component (PC)
and PC scores. CovBat’s harmonization procedure is
summarized as follows. Primero, ComBat is applied to full
imaging data, yielding ComBat- residuals as in Equation
(3) with homogeneous variances across scanners. Aquellos-
Bat then conducts the eigendecomposition on the
sample covariance of Combat- residuals and applies
ComBat again to principal component scores to remove
heterogeneous means and variances, which yields
CovBat- residuals with an additional source of scanner
effect removed. The final CovBat- harmonized data is
CovBat = ˆαv + x ij′ ˆββv + ˆεijv
CovBat. CovBat assumes that the
y ijv
covariance scanner effects can be captured by the
ubicación- scale adjustments to the principal compo-
nents of the residuals. Despite its efficiency, we point
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
3
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
out that CovBat’s assumption might not be sufficient to
characterize all sources of covariance heterogeneity.
The RELIEF model assumes that εijv in Equation (1) es
decomposed into three additive variations. Específicamente:
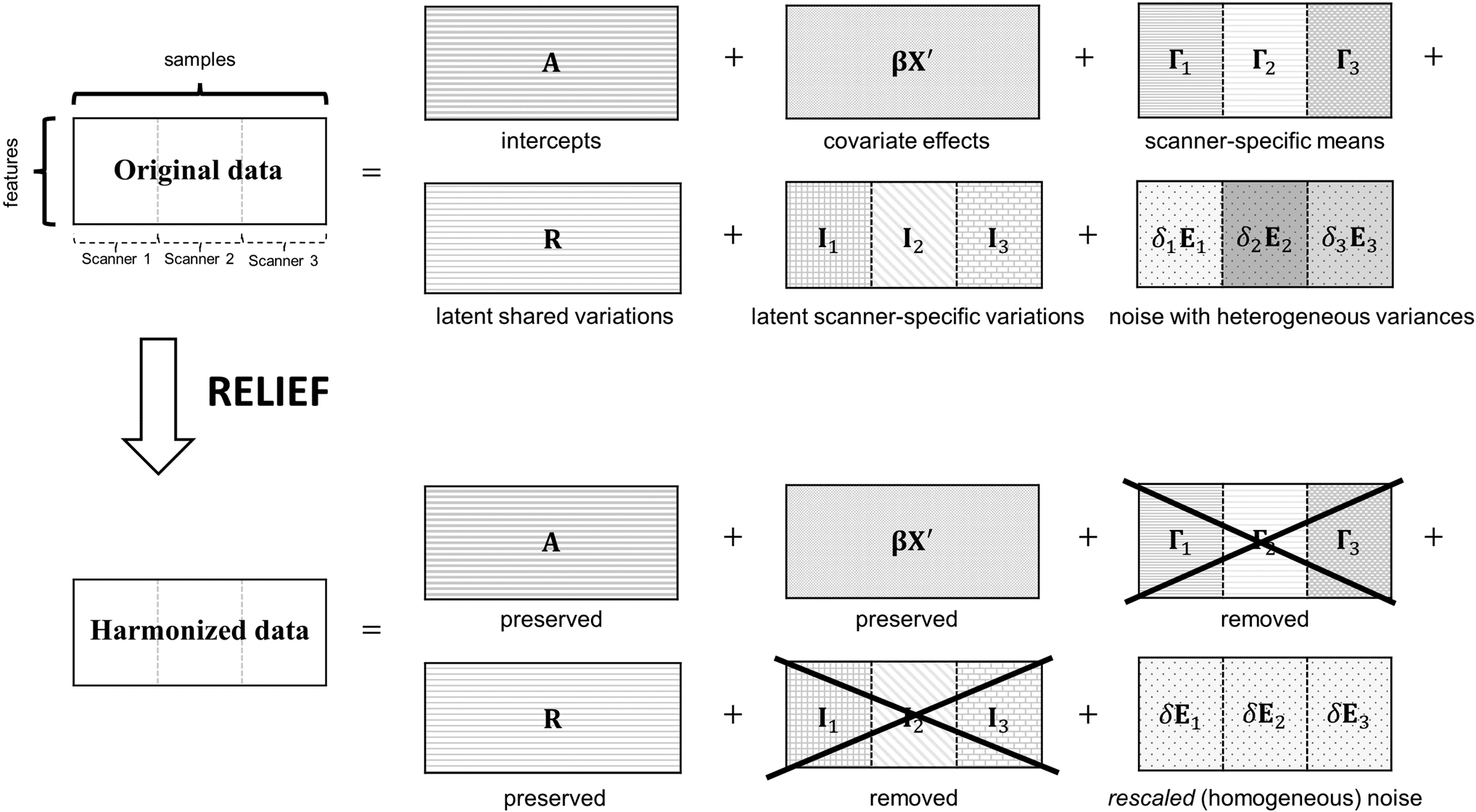
2.3. New method: ALIVIO (REemoval of Latent Inter- scanner
Effects through Factorization)
We first characterize three sources of scanner effects
(additive mean (ubicación), additive latent, and multiplica-
tive scanner effects (escala)) via an additive multivariate
model illustrated in Figure 1. We assume that the data
matrix Y consists of
Y = A + ββ ′X + ΓΓ1;…; ΓΓM +R +
⎡⎣
]
[I1;…;SOY +] [ δ1E1;…;δMEM
⎤⎦,
(4)
where A is the intercept matrix (rank of 1), ββ is a V × q
matrix of regression coefficients (rank of min(V, q)), y
[ΓΓ1;…;ΓΓM ] is a matrix of additive scanner effects (locati-
cajón) for each feature (rank of M), where elements of each
row of Γi take the same value. Note that A + ββ ′X + [ ΓΓ1;…; ΓΓM ]
in Equation
the collection of
αv + ′x ij ββv + γ iv in Equation (1) across all imaging features.
(4) corresponds
a
• R is a V × n matrix of the latent structure explaining
shared variations across all scanners but not
explained by covariate effects. It includes (i) no-
linear covariate effects from X or (II) any additional
variations due to unobserved covariates. Desde
viewpoint of scanner- effect correction, this should
be preserved after harmonization.
• Ii is a V × ni matrix of latent variations explaining latent
scanner effects in the ith scanner beyond scanner-
specific means ΓΓi (ubicación). This might include any
no- linear scanner effects ( Cetin- Karayumak et al.,
2020). It should be removed after harmonization.
• δ iEi is a V × ni noise matrix, and each element of Ei
is assumed have a unit variance. δ i characterizes
the variance heterogeneity as specified in ComBat,
which has shown to be promising in neuroimaging.
From the viewpoint of scanner- effect correction, δ is
should be standardized to have a common variance
across scanners.
Higo. 1. Overview of RELIEF using data consisting of three scanners for illustrations. It decomposes original data as (i)
covariate effects, (II) scanner- specific means (ubicación), (III) latent shared variations, (IV) latent scanner- specific variations,
y (v) noise with heterogeneous variances (escamas). For harmonization purposes, RELIEF removes (II) y (IV) specific to
scanners and homogenizes (v).
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
4
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
Throughout this paper, we assume R as well as each of
I1,…,IM to be low rank, and estimate their ranks using a
modelo- based approach.
Our approach is summarized by (i) removing scanner,
feature- specific means and obtaining covariate effects
primero, (II) standardizing the data matrix to have homoge-
neous variance, (III) decomposing it into scanner- specific
and scanner- independent factors, y (IV) reconstructing
harmonized data.
Steps (i) y (II) are achieved through the preprocess-
ing step. We obtain ˆA, ˆββ and [ ˆΓΓ1;…; ˆΓΓM ] by using the two-
step regression. Específicamente, we first fit GLM using the
intercept and covariates (A and β) and obtain residuals
(Y − ˆA − ˆββ ′X ). Entonces, using the residuals from the first step,
we remove scanner- specific means for each feature (Γ) a
obtain the second- step residuals [ Y1 − ˆA1 − ˆββ ′X1 − ˆΓΓ1;…;
YM − ˆA M − ˆββ ′X M − ˆΓΓM] to be used in subsequent steps.
When the variability of the second- step residuals differs
across features, we can easily scale each residual by its
residual standard deviation, apply steps (III) y (IV), y
scale back each feature.
Step (III) is achieved by simultaneous dimension reduc-
tion and factorization methods proposed by Park and
Lock (2020) and Lock et al. (2022). We first scale each
residual matrix from the last step by ˆδ i in order to make
the residual variances homogeneous across i = 1,…,METRO:
ΔΔ ≡ [(Y1 − ˆA1 − ˆββX′1 − ˆΓΓ1) / ˆδ1;…;(YM − ˆA M − ˆββX′M − ˆΓΓM ) / ˆδM].
Following Park and Lock (2020) and Lock et al. (2022), nosotros
estimate ˆδ i by the median of the singular values of resid-
ual matrices for each scanner divided by the square root
of the median of the Marcenko– Pastur distribution
( Gavish & Donoho, 2017). Provided that ˆδ i ≈ δ i, we first
note that Δ is represented by
ΔΔ = R!+ I! + mi,
(5)
where R! = [R1 / ˆδ1,…,RM / ˆδM ] is a variation shared
! ] = [I1 / ˆδ1;…;SOY / ˆδM ] son
across all scanners, I! = [I1
!;…;SOY
individual variations shared only in each scanner.
From model (5), ˆR! and ˆI ! are obtained by
{ ˆR!, ˆI ! } = arg min
}
{
R! ,I!
{
|| ΔΔ – R!− I! || F
2 + l || R! ||* +
METRO
∑ λ i || Ii
yo=1
! ||*
},
(6)
2 y || ⋅ ||* are the squared Frobenious norm
dónde || ⋅ ||F
(sum of squared elements) and the nuclear norm (sum of
singular values), respectivamente. The nuclear norm penalties
en la ecuación (6) ensure that the resulting estimates ˆR!, ˆI !
are low- rank ( Hastie, Mazumder, Sotavento, & Zadeh, 2015).
Although tuning λ and λ is may be tricky, we use the rec-
ommended values from Park and Lock (2020) by setting
λ = p + n and λ i = p + ni , which was shown to per-
form well with independent Gaussian noise. With λ and
λ is specified, an iterative algorithm can be applied to
estimate R! and Ii
!s.
ˆRi
ˆR1
! … ˆδM
In Step (IV), we scale ˆR! back to ˆR! ( ˆδ i
!) to make sure
ˆR = ˆδ1
is in the original scale. To keep the
⎡
⎣
noise variance homogeneous, we scale ˆE to ˆδ ˆE, dónde
(
ˆδ2 =
is the weighted mean of
scanner- specified noise variance. Por lo tanto, the final har-
monized data is given by
ˆRM
(
) /
METRO
∑ ni
yo=1
METRO
∑ ni
yo=1
)
ˆδ i
⎤
⎦
2
!
Y RELIEF =
ˆA
!
intercepts
+
ˆββ ′X
!
covariate effects
+
[ ˆδ1
ˆR1
! «##
!;…; ˆδM
original−scale shared variations
ˆRM
! ]
$##
+
ˆδ ˆE
!
rescaled noise
.
(7)
2.4. Using covariates in RELIEF
When a primary interest is to test for an association with
a covariate of interest, including the covariate in RELIEF
may lead to an inflated false positive rate. Intuitivamente, es
because our objective function (6) does not enforce
scores of ˆI to be independent of the covariate of interest.
Por lo tanto, we suggest not including covariates of interest
when applying RELIEF. In practice, we found that not
including any covariates in RELIEF does not result in a
noticeable difference because the covariate effects are
actually low- rank (with the rank equal to the number of
covariables) and are captured by R (in a high signal- a-
noise ratio (SNR)) or by E (in a low SNR), provided that
covariates are independent to scanners. En la sección 4, nosotros
show that RELIEF still achieves higher power than other
harmonization method even when the covariate of inter-
est is not specified as an input in RELEF.
2.5. Preventing distorted covariate effects in RELIEF
Many existing harmonization methods, including Adj
Res, ComBat, CovBat, and RELIEF, account for explicit
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
5
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
covariate effects in the form of regression, but there
might be hidden covariate effects from unobserved
covariables. For downstream analyses, it is critical to pre-
serve these effects in the original scale. In RELIEF, semejante
effects correspond to the R term, and therefore, we scale
! back to ˆδ i in Equation (7) although δ i were used to
ˆRi
characterize variance heterogeneity.
We point out that ComBat (and CovBat that uses
ComBat in the first step) models observed covariate
effects only and all unobserved covariate effects are
attributed to the residuals. Since residuals are eventually
scaled differently for each scanner/site in the harmoniza-
tion steps, ComBat and CovBat could be prone to dis-
torted covariate effects for unobserved covariates after
harmonization, especially when variance heterogeneity
across scanners is evident.
3. DATA ANALYSIS
3.1. Data preparation and preprocessing
We used diffusion tensor imaging (DTI) data from Social
Processes Initiative in the Neurobiology of the Schizo-
phrenia(s) (SPINS) study to empirically evaluate RELIEF’s
actuación. The study subjects consisted of 256 indi-
viduals with schizophrenia spectrum disorders (SSDs)
y 175 controls. Subjects were 18– 55 years old, y
268 of the participants were males (163 hembras). Partic-
ipants with SSDs met DSM- 5 diagnostic criteria for
schizophrenia, schizoaffective disorder, schizophreni-
form disorder, delusional disorder, or psychotic disorder
not otherwise specified, assessed using the Structured
Clinical Interview for DSM (SCID- IV- TR), and had no
change in antipsychotic medication or decrement in
functioning/support level in the 30 days prior to enroll-
mento. Controls did not have a current or past Axis I psy-
chiatric disorder, except adjustment disorder, phobic
disorder, and past major depressive disorder (encima
2 years prior; presently unmedicated), or a first- grado
relative with a history of psychotic mental disorder. adi-
tional exclusion criteria included a history of head trauma
resulting in unconsciousness, a substance use disorder
(confirmed by urine toxicology screening), intellectual
disability, debilitating or unstable medical illness, or other
neurological diseases. Participants also had normal or
corregido- a- normal vision. All participants signed an
informed consent agreement, and the protocol was
approved by the respective research ethics and institu-
tional review boards. All research was conducted in
accordance with the Declaration of Helsinki.
The scans were acquired at three different imaging
sites, including the Centre for Addiction and Mental Health
(CAMH), Maryland Psychiatric Research Center (MPRC),
and Zucker Hillside Hospital (ZHH). General Electric 3T
MRI scanners were used at CAMH and ZHH (750w Dis-
covery and Signa, respectivamente), and the Siemens Tim Trio
3T MRI scanner at MPRC. Sin embargo, during the middle of
el estudio, all study sites switched to Siemens Prisma 3T
scanners for data collection. A high- angular resolution
axial EPI dual spin echo sequence diffusion scan was
acquired on all scanners. Within the limits of scanner hard-
mercancía, parameters were prospectively harmonized as fol-
mínimo: 60 gradient directions, b = 1,000, 5 b = 0 imágenes,
TR = 8,800 EM (one scanner TR = 17,000 EM), TE = 85 EM,
FOV = 256 mm; en- plane matrix 128×128, y 2.0 mm iso-
tropic voxels. All images were preprocessed using the
same pipeline across sites. Skull- stripping was performed
via a two- step process combining FSL (BET) and AFNI to
optimize brain extraction, after which MRtrix3 (dwi2mask)
was used for brain masking. FSL eddy was used for eddy
actual- induced distortion and motion correction, incluir-
ing volume- a- volume and within- volume movement
( Tournier et al., 2019). Eddy models the effects of partici-
pant movement and diffusion eddy currents simultane-
iosamente, predicting undistorted data using a Gaussian
Process. Eddy also outputs quality control metrics, incluir-
ing average absolute motion (mm) for each participant as
one measure of volume- a- volume movement. Fieldmap-
free susceptibility distortion correction was performed
using BrainSuite (BDP; Bhushan et al., 2015). Outputs
were visually inspected after each preprocessing step to
ensure data quality.
Participants’ white matter tracts were reconstructed
using deterministic unscented Kalman Filter (UKF) tractog-
rafy ( Malcolm, Shenton, & Rathi, 2010) in 3D Slicer
(https://girub . com / SlicerDMRI). The ORG
(O'Donnell
Research Group) white matter atlas ( F. Zhang et al., 2018)
was used to parcellate fibers into anatomical tracts. Este
atlas has been validated across different scanners and
protocols (p.ej., number of gradient directions, spatial res-
olutions, b- valores; F. Zhang et al., 2019). Metrics were
included from 56 deep white matter fiber tracts from the
asociación, cerebellar, commissural, and projection tracts
(the cortico- ponto- cerebellar tract was excluded due to
parcellation issues), y 16 superficial tract categories
according to the brain lobes they connect, resulting in
V = 72 características. Mean FA values and mean diffusivity (Maryland)
values were calculated along each tract. FA measures the
degree to which diffusion of water molecules is restricted
by microstructural elements such as cell bodies, axones,
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
6
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
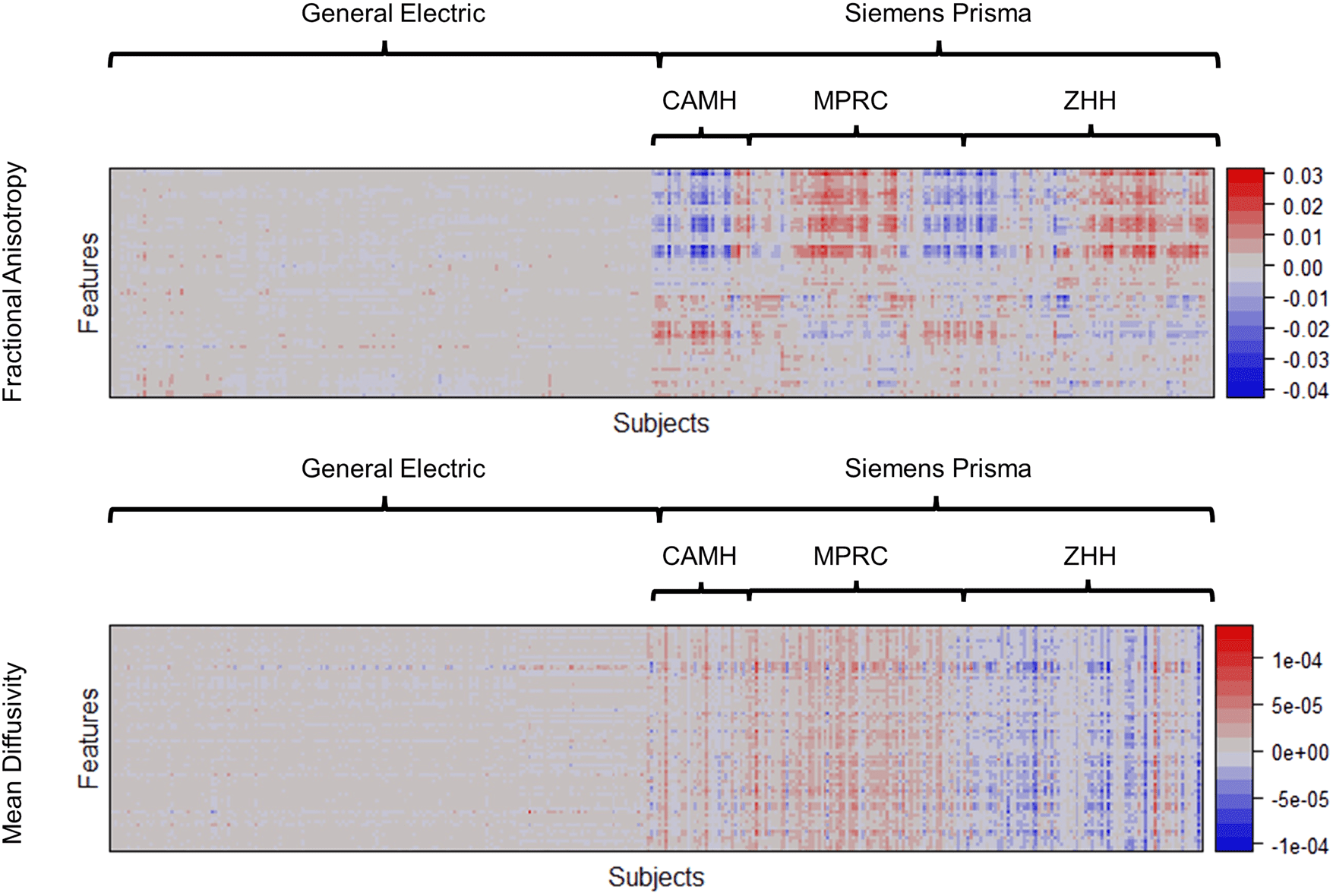
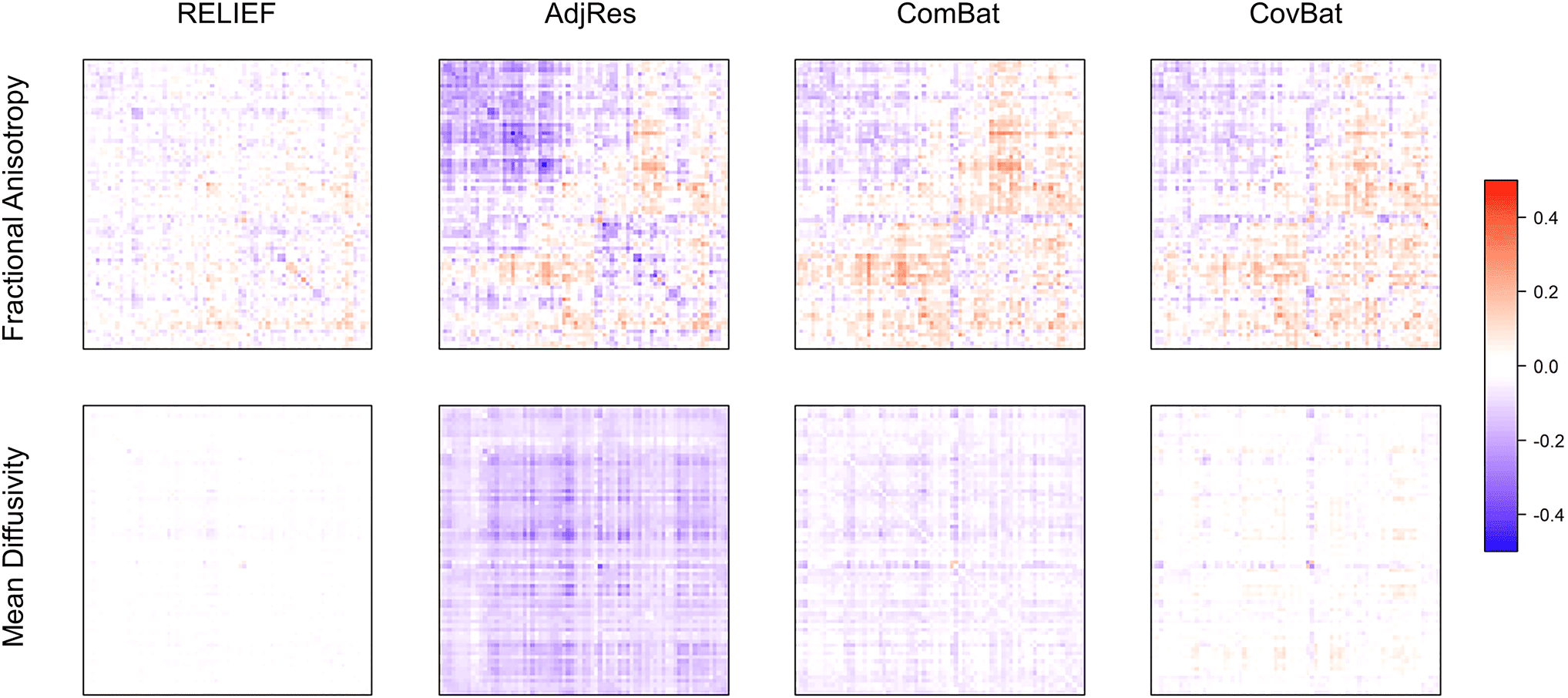
Higo. 2. Heatmaps of the estimated latent scanner- specific variations (ˆI) of the FA and MD from the SPINS study. Para
visualizations, imaging features were reordered by applying hierarchical clustering; subjects scanned by General Electric
3T were reordered separately, and subjects scanned by Siemens Prisma 3T were reordered within each site subgroup
(CAMH, MPRC, and ZHH). Feature indices were also reordered by applying hierarchical clustering to concatenated I for FA
and MD. RELIEF identified substantial variations present mostly on Siemens Prisma but not on General Electric, y el
variations are highly associated with sites.
mielina, and other constituents of cytoskeleton ( Beaulieu,
2002). MD is a measure of the magnitude of water diffu-
sión, independent of direction ( O'Donnell & Westin, 2011).
Visual quality control was performed after initial tractogra-
phy, registration to the ORG atlas, and tract creation. Datos
from seven participants were excluded on the basis of
missing or poor tractography for >15 tracts across the
whole brain.
Since the number of samples from Siemens Tim Trio is
pequeño, we used images from two scanner types (GE and
SP) in our analysis. Participants without DTI data were also
excluded from the study. The final sample consists of 351
subjects across 2 scanner types, con 172 subjects imaged
on scanners manufactured by GE (67 hembras, 111
pacientes, edad 18- 55), 179 on Prisma scanners manufac-
tured by Siemens (71 hembras, 98 pacientes, edad 18- 55).
3.2. Resultados
We harmonized data by using RELIEF, ComBat, CovBat,
and AdjRes. We used age, age2, género, diagnosis, un
interaction between age and gender (age × gender), y
an interaction between age and diagnosis (age × diagno-
hermana) to model covariate effects in harmonization.
Cifra 2 shows the heatmap of the estimated latent
scanner effects ˆI of RELIEF for the FA and MD data from
the SPINS study. As RELIEF’s crucial components, el
latent scanner effects are identified and removed to reduce
the inter- scanner variations directly. En figura 2, the most
scanner- specific variations were attributed to Siemens
Prisma for both FA and MD. To investigate the potential
sources of latent Siemens Prisma- specific variations in
relation to existing non- biological information, we applied
hierarchical clustering to the site subgroups of ˆISP in
Cifra 2 and reordered subjects within Siemens Prisma so
that ˆISP within the same site were arranged together. Nosotros
observed the latent scanner effects within each site tended
to share similar patterns, which suggests that the varia-
tions in ˆISP are highly associated with sites.
We performed statistical analysis to quantify the rela-
tionship between existing non- biological information,
including site information and motion parameters. En
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
7
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
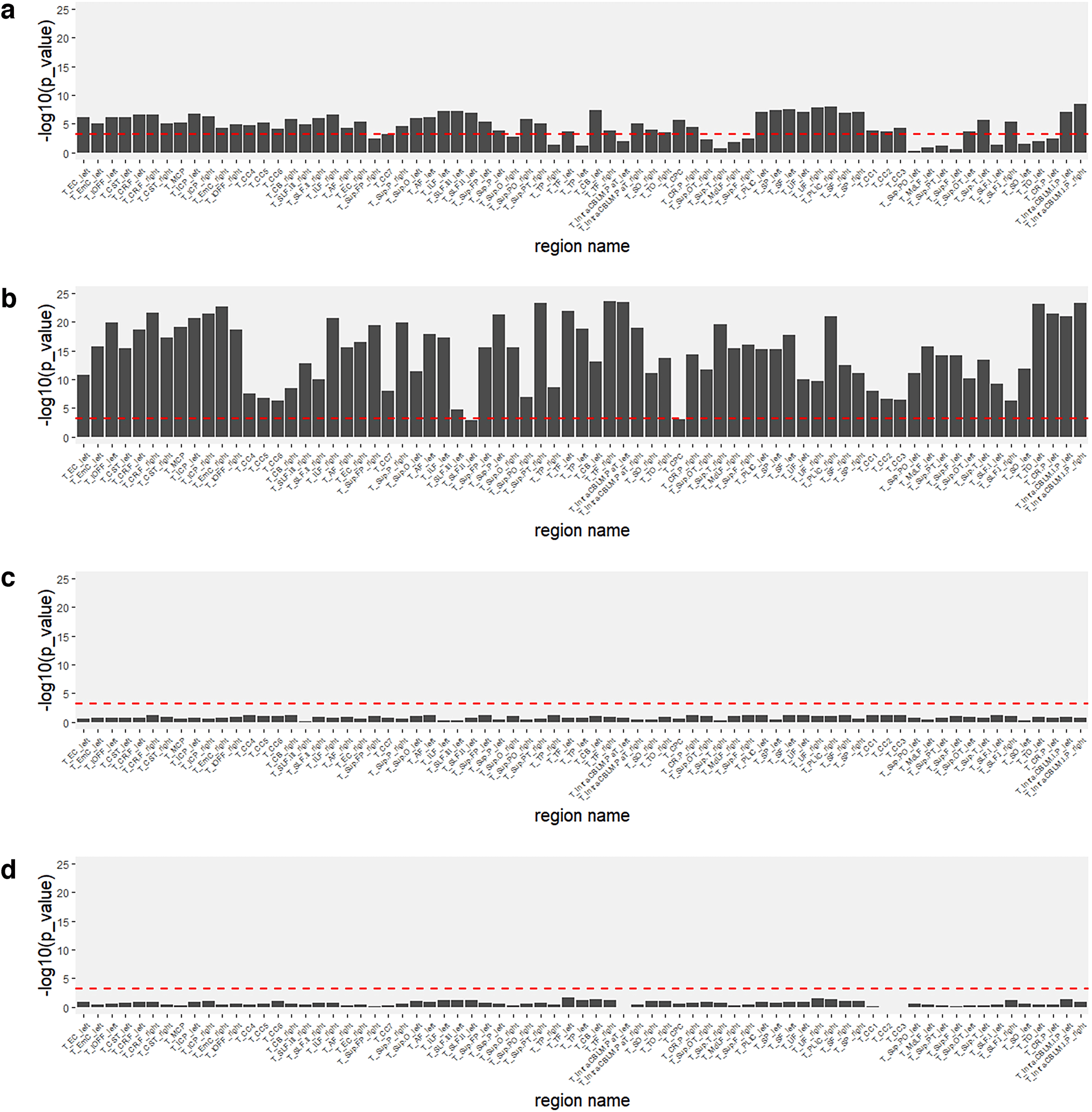
Investigating the potential sources of latent Siemens Prisma- specific variations in relation to existing non-
Higo. 3.
biological information (site information and a motion parameter). (a) y (b) show one- way ANOVA p values of (a) FA and
(b) MD in relation to three study sites. (C) y (d) show p values for the correlation between latent factors and the average
absolute motion from the reference volume (in mm) para (C) FA and (d) Maryland. All p values were negative log- transformado (con
base 10) for visualizations. The red dashed horizontal line is Bonferroni- corrected threshold (0.05 / 72 ≈ 6.9 × 10−4). El
region names agree with the order in Figure 2.
Cifra 3 (a) y (b), we performed one- way ANOVA to
compare different latent scanner effects of the Siemens
Prisma across sites for FA and MD data, respectivamente. Nosotros
found that the latent factors of most features specific to
Simens Prisma were highly associated with the sites,
particularly for MD data. En figura 3 (C) y (d), nosotros por-
formed correlation tests between the latent scanner
effects in the Siemens Prisma scanner and the motion
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
8
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
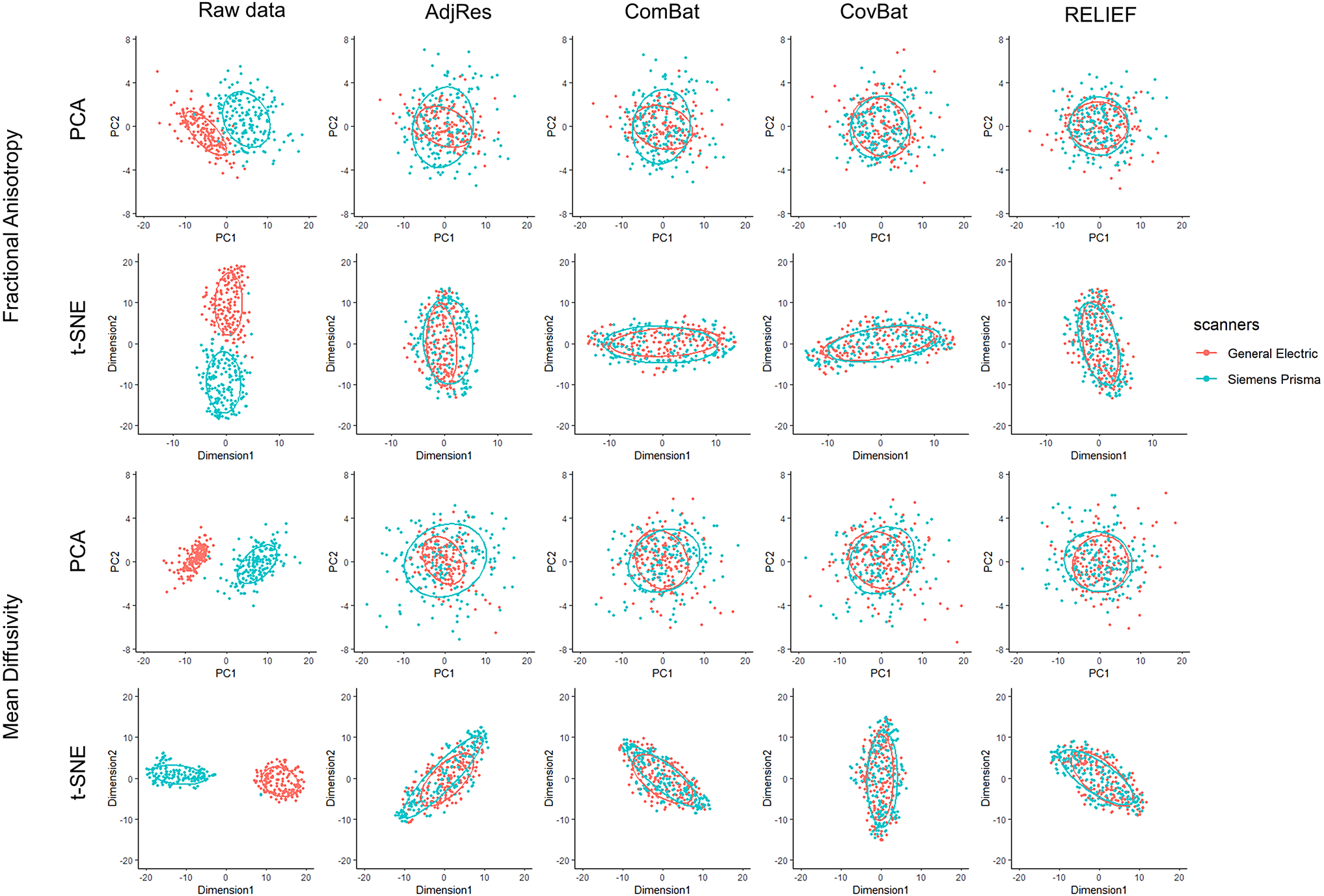
Higo. 4. Scatterplots of principal component scores and t- SNE scores before and after applying harmonization to the
SPINS DTI data.
parameter for FA and MD data, respectivamente. We calcu-
lated the average absolute motion from the reference vol-
ume (in mm) to represent subject motion during the scan
and averaged it for the six motion parameters (tres
translations and three rotations). Our findings revealed
that the latent factors showed no significant associations
with the motion parameter. En general, our analyses pro-
vided insights into how existing non- biological informa-
tion can impact the interpretation of latent scanner- specific
variaciones.
To visualize whether most variations in the data are
still associated with scanners after harmonization, nosotros
applied two unsupervised data reduction techniques:
principal component analysis (PCA) and t- distributed
stochastic neighbor embedding (t- SNE) to the original
and harmonized FA and MD data from diffusion tensor
imagen (DTI). As a nonlinear technique, t- SNE empha-
sizes preserving the variations in the local structure of
los datos, while PCA focuses more on preserving varia-
tions in the overall data set. The data projected into the
first two PCs/dimensions are presented in Figure 4. Para
raw data, we observed that most variations are clearly
explained by the scanner information (General Electric
vs. Siemens Prisma). For AdjRes and ComBat, a pesar de
evidences of higher data quality, there is heteroscedas-
ticity of ellipses across scanners, which indicates that
there are still unremoved latent scanner effects. Para
CovBat and RELIEF, both PC scores and t- SNE scores
appear to be distributed similarly across scanners,
which suggests the variations associated with scanners
are substantially removed.
To evaluate if scanner- specific latent patterns are well-
removed, we computed the empirical covariances by
scanners as well as the difference between two scanner-
specific covariances. Cifra 5 shows that the covariance
differences remain notable in AdjRes harmonized data.
ComBat and CovBat performed slightly better than
AdjRes in mitigating covariance scanner effects. Notablemente,
sin embargo, these covariance differences are considerably
reduced with RELIEF. We also quantified these differences
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
9
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
Higo. 5. The difference of scanner- specific covariance matrices for harmonized SPINS data (GE– SP). The order of the
features agrees with Figures 2 y 3. The x- axis and y- axis indicate regions of interest, which are explicitly illustrated
in the x- axis of Figure 3. The color bar shows the range of values of the differences in covariances. RELIEF reveals the
lowest difference between two covariances.
in covariances by the Frobenius norm of the scanner-
specific covariance matrices. For FA, the norm for RELIEF
was the lowest (3.70) followed by CovBat (5.77), ComBat
(6.19), and AdjRes (8.10). For MD, the norm for RELIEF
was also the lowest (1.45) followed by CovBat (2.29),
ComBat (4.15), and AdjRes (8.74). These results suggest
the superior performance of RELIEF in constructing
homogeneous covariances.
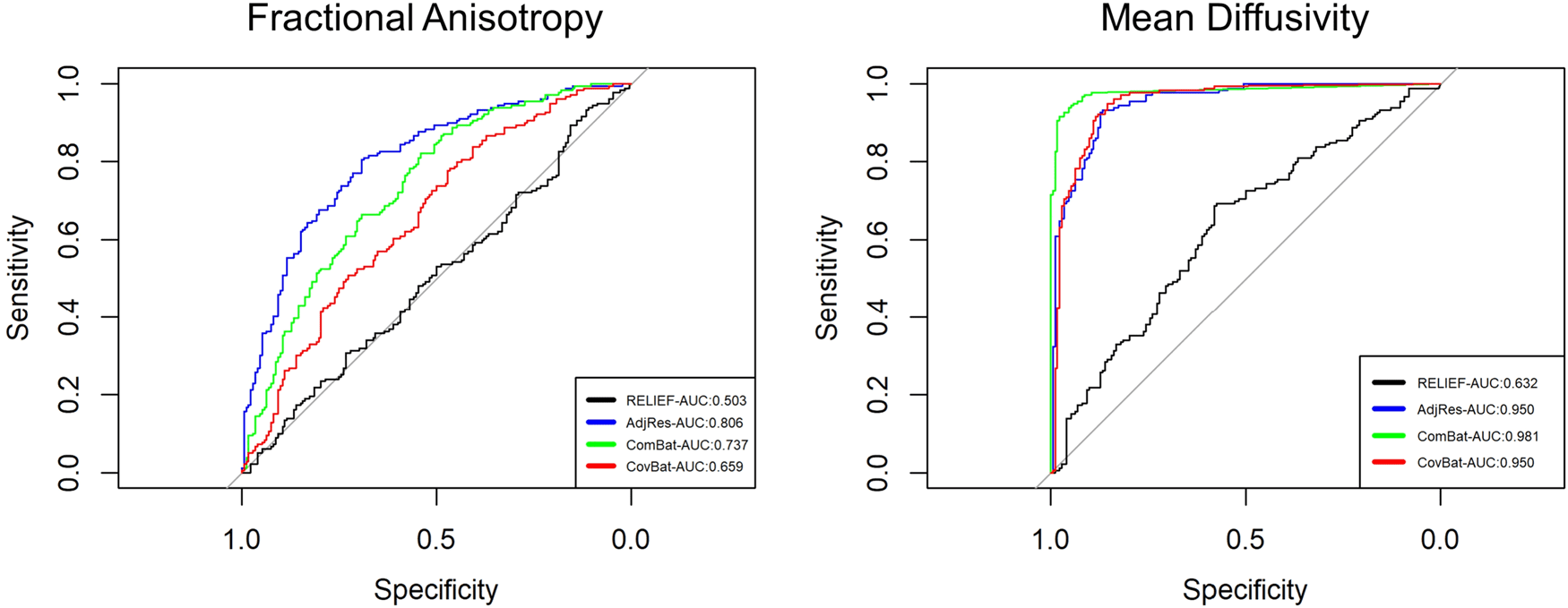
We also used Quadratic Discriminant Analysis (QDA)
to evaluate how data harmonized using each approach
predicts scanners. A harmonization method that per-
forms better in removing scanner effects would result in
worse predictive performance. Using machine- aprendiendo
methods to predict scanners from harmonized data has
been adopted in previous work in evaluating the perfor-
mance of different harmonization methods ( Chen, Beer,
et al., 2022; J.- PAG. Fortin et al., 2018). We chose QDA
because the classifier is constructed based on the mean
vectors and covariance matrices only, where differences
in predictive performances are attributed to the harmoni-
zation of scanner- specific means and covariances. Usando
leave- uno- out cross- validación, we computed the aver-
age accuracy, ROC curve, and its area under the curve
(AUC) for each harmonized data after regressing out
covariate effects. For FA, the RELIEF method achieved
the lowest prediction accuracy (49.6%) close to a ran-
dom prediction, followed by CovBat (59.3%), ComBat
(66.1%), and AdjRes (70.1%). For MD, RELIEF also
achieved the lowest prediction accuracy (61.0%) fol-
lowed by CovBat (82.6%), ComBat (83.2%), and AdjRes
(87.5%) The results of the AUC, como se muestra en la figura 6, eran
similar to the prediction accuracy, suggesting the lowest
AUC for RELIEF.
Por último, we investigated whether RELIEF preserves
the biological variability in the data. This step is neces-
sary because the multivariate harmonization methods
could be prone to potentially overkilling too much varia-
ción, including biological variations. Aquí, we evaluated
whether the different harmonization methods maintain
the biological associations of interest through multiple
linear regression. For each FA/MD feature in each har-
monized data, we built a regression for each feature by
using the same set of covariates (edad, age2, género,
diagnosis, age × gender, and age × diagnosis) as the
harmonization step. We then computed t statistics of
the estimated coefficients across all covariates and fea-
turas. The boxplots of t statistics are shown in Figure 7.
We observed that, for FA data, the magnitude of t statis-
tics of all harmonized data appeared to be similar, cual
confirms that RELIEF did not lose biological information
compared with other methods. Sin embargo, for MD data,
RELIEF clearly showed more significant associations
with diagnosis and age × diagnosis than other methods,
which suggests that RELIEF not only provided a thor-
ough removal of scanner effects but also maintained
biological associations well.
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
10
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
Higo. 6. The ROC curves for predicting scanners by using SPINS data harmonized by different methods. We used QDA as
a classifier and leave- uno- out cross- validación (LOOCV) to obtain individualized predictions. The ROC curve of the RELIEF
was closest to the diagonal line, suggesting that it successfully harmonized latent inter- scanner biases.
Higo. 7. The boxplots for t statistics for each biological covariate used in our analysis.
4. SIMULATION STUDIES
4.1. Simulation designs
of false positives and power, we used two models to
generate heterogeneous covariances across scanners.
En esta sección, we performed extensive simulation studies
to evaluate the performance of RELIEF and to compare it
to other methods in controlled settings. We included Com-
Bat, CovBat, and AdjRes as our competitors and evalu-
ated how well- harmonized data preserve biological
variations through power analysis. To evaluate the control
4.1.1. Simulation 1: RELIEF model
We generated data using the sum of low- rank features
following Equation (4). We simulated 1,000 null data sets
with n1 = n2 = 50 (so that n = 100), and V = 100 características.
Our data- generating model is summarized by
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
11
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
Y
!
rank 100
= A
!
rank1
+ ββX′
!
rank4
+ ΓΓ
! + R
rank 3
rank2
! + c ⋅I
!
rank 6
+ δ1E1,…,δMEM
⎡⎣
⎤⎦.
We used four nuisance covariates for the covariate
efectos, where each element of ββ and each row of A were
generated from N ( 0,12 ). The covariate vector for each
subject was generated from the multivariate normal dis-
tribution with zero means, and we used AR(1) for the
covariance matrix with the autocorrelation parameter 0.2.
Segundo, we generated R by first generating a V × n matrix
whose entries are drawn from N (0,12 ), then taking the
first three principal components. Similarmente, we generated
each Ii by generating a V × ni matrix using N (0,12 ) entonces
taking the top 3 principal components. Por último, we also
generated the additive scanner effect (ubicación) γ iv by
fixing it to be the same for all i and from N (0, 1.52 ), y
multiplicative scanner effect (escala) δ i from Uniform
(1, 1.5). Finalmente, the elements of E were generated from
norte (0,12 ) .
The constant c was chosen between 0, 1, 2, 3 to eval-
uate the impact of scanner- specific latent patterns on
statistical power. Note that we also considered c = 0 a
investigate whether it has comparable performance when
los datos- generating model does not include latent scan-
ner effects.
4.1.2. Simulation 2: CovBat model
We generated data by modifying the simulation design
introduced by Chen, Beer, et al. (2022). To address poten-
tial covariance scanner effects, CovBat model uses prin-
cipal component (PC) scores to shift each within- scanner
covariance to the pooled covariance structure. Por lo tanto,
the design aimed to evaluate whether harmonization
methods can approximate the underlying covariance
structure when covariance scanner effects are captured
by its PC shifts.
We simulated 1,000 null data sets based on SPINS data
so that n1 = 172,n2 = 179 (so that n = 351) and V = 72 fea-
turas. The data y ijv was generated by y ijv = αv + γ iv + δ ivεijv,
where αα = (α1,…,αV )′ is the sample mean vector of Scan-
ner General Electric observations in the SPINS data. El
additive scanner effects γγ i = (γ i1,…, γ iV )′’s are vectors
drawn from N (0,0.12 ). For multiplicative scanner effects,
we used δ1v ~ IG(46, 50) and δ2v ~ IG ( 51, 50) siguiente
Chen, Beer, et al. (2022). From the sample correlation matrix
of DTI- FA observations in the SPINS data (termed S)
decomposition
con
∑ ˆλ l ˆψ l ˆ ′ψ l, we generated εij = (εij1,…,εijV )′ that con-
S =
correspondiente
eigen
es
72
L = 1
tained scanner- specific shifts. The design was to investi-
gate how the rank of the covariance effect influences
harmonization results, and we generated error terms
∑ ˆλ l ˆψ l ˆ ′ψ l
by εij ~ MVN 0,S + ci
), where c1 = −
y
3
4
L = 1
(
l
. We considered different L including
L = 0,10,20,30.
c2 =
3
4
In both simulation designs, we generated our covari-
ate of interest, Zk (k = 1,…,norte), randomly from 0 o 1, para
evaluation of power. We randomly chose 20% (for Sim-
ulación 1) y 50% (for Simulation 2) of features and
added τv ⋅ Zk to the null data, where τv ≥ 0 is the effect
size for the vth feature, which controls whether the simu-
lated data follow the null hypothesis H0 : τ1 = … = τV = 0
or the alternative hypothesis H1 : at least one of τv ≠ 0
(v = 1,…,V ). We used permutation to control family- inteligente
error rate (FWER) en 5%.
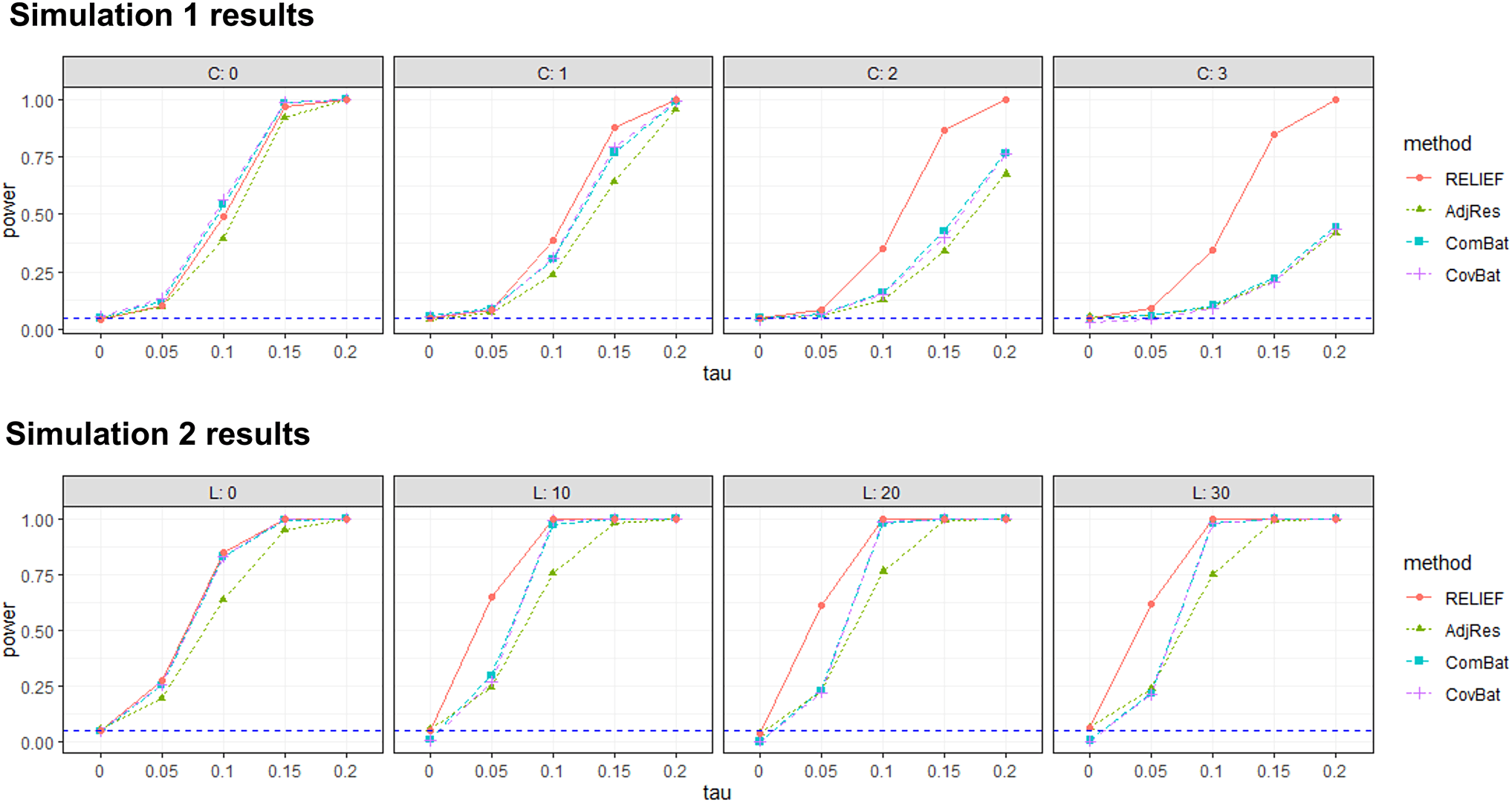
4.2. Resultados de la simulación
The results for Simulation 1 are summarized in the first
row of Figure 8. RELIEF controlled family- wise error prop-
erly, with empirical FWER of 0.044, 0.047, 0.048, y
0.052 regardless of the choice of c. In our simulations,
while other methods controlled FWER appropriately in
most scenarios, CovBat was conservative in controlling
false positives when the proportion of individual latent
patterns increased. In terms of power, RELIEF’s perfor-
mance was nearly the same as ComBat or CovBat even
when there are no latent scanner effects (es decir., c = 0),
which supports the robustness of the proposed method.
También, as the degree of latent scanner effects (C) aumentó,
RELIEF showed substantial power gain compared to oth-
ers, partially because it correctly identified and removed
the scanner- specific latent patterns in the data. The lower
power of ComBat and AdjRes is expected as they do not
consider these latent patterns in their model, y el
lower power of CovBat is also expected because
RELIEF’s data- generating model is different from Cov-
Bat’s assumption on PC shifts.
The results for Simulation 2 are summarized in the
second row of Figure 8. RELIEF’s empirical FWERs are
0.05, 0.051, 0.038, y 0.052 for L = 0, 10, 20, 30, mientras
ComBat, CovBat are conservative in controlling false
positives when covariance scanner effects exist. Para
fuerza, we note that when covariance scanner effects do
not exist (L = 0), all harmonization methods increased
statistical power and performed similarly, except for
AdjRes whose power was lower. When L was large,
RELIEF still showed superior performance to other meth-
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
12
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
Higo. 8. Summary of power for four harmonization methods. From the first row, the plots from left to right are with the
increased proportion of individual latent patterns. From the second row, the plots from left to right are with the increased
rank of the covariance effect. The blue dashed horizontal line is FWER = 0.05. RELIEF controls for false positives
accurately and shows superior power to competitors in both settings.
probabilidades, which supports the robustness of RELIEF even
when the data- generating model did not follow the
assumption of RELIEF. Además, when SNR was low
(es decir., τ = 0.05), RELIEF gained higher power than compet-
itors, which supports its ability to denoise scanner effects
and preserve true biological associations.
4.3. Additional simulations
To address Section 2.4 empíricamente, we repeated Simula-
ción 1 to evaluate FWER when the covariate of interest
was specified in RELEF. In this simulation, we obtained
empirical FWER values of 0.058 (95% CI: (0.052, 0.064))
when c = 0 y 0.159 (95% CI: (0.152, 0.166)) when c = 1,
indicating that RELIEF, when covariates of interest were
specified in the model, had inflated false positives.
5. DISCUSIÓN
We proposed a novel harmonization method, called RELIEF,
that estimates and removes both explicit (additive and mul-
tiplicative) and latent scanner effects. RELIEF aligns with
ongoing efforts to integrate neuroimaging data collected
from different scanners or sites. En particular, Nuestros métodos
address covariance heterogeneity across different scan-
ners, which has been a promising direction in mitigating
enterrar- scanner biases. Our approach provides an interpreta-
ble way to harmonize heterogeneous covariances by mod-
eling scanner- specific latent patterns under the low- rank
assumption. We characterized inter- scanner bias with (i)
scanner- specific means (ubicación), (II) scanner- specific
variances (escamas), y (III) scanner- specific latent patterns.
We showed that identification of (III), which has been over-
looked in previous methods, is critical in homogenizing
data from multi- site, multi- scanner neuroimaging studies.
RELIEF is a general multivariate approach that does
not impose data- specific assumptions. It also does not
require traveling subjects or matched controls that are
often needed in supervised harmonization methods,
which are infeasible in many imaging studies. También, como nosotros
extend a regression- based approach, preserving clinical
covariate effects is straightforward. Además, it also pre-
serves shared variations from unobserved covariates
or non- linear covariate effects using a low- dimensional
representation of such variations, in which existing
regresión- based harmonization methods are limited.
In the analysis of the fractional anisotropy (FA) y
mean diffusivity (Maryland) data from the SPINS study, dónde
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
13
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
study samples were scanned using General Electric or
Siemens Prisma scanners, we showed that there are sub-
stantial variations specific to Siemens Prisma. Notablemente, nuestro
data analysis reveals that these latent scanner effects for
Siemens Prisma are heterogeneous across features
(Higo. 2). This result aligns with previous studies showing
that inter- site variability in fractional anisotropy is specific
to tissues or regions ( J.- PAG. Fortin et al., 2017; Vollmar et al.,
2010). ALIVIO, which removed these variations in addition
to the scanner- specific means and variance, successfully
impaired the detection of scanners with a machine-
learning method, resulting in a more homogeneous covari-
ance as expected. A correlation analysis with existing
no- biological information helped us understand the
mechanism that induces these latent scanner effects.
RELIEF is not without limitations. Primero, our current
approach is evaluated with a moderate number of samples.
RELIEF assumes that the original data matrix consists of
bajo- rank signals (including latent scanner effects) plus full-
rank noises to scale data and choose tuning parameters.
To detect these low- rank variations well, it requires a mod-
erate number of samples to ensure the objective function of
RELIEF performs more promisingly than simplified meth-
probabilidades (p.ej., ComBat) with fewer assumptions. Segundo,
although low- rank decomposition is a useful way to cap-
ture arbitrary covariance structures, it might not always be
the case when there is structured covariance in imaging
datos. Por ejemplo, vertex- level cortical thickness data has
at most 160,000 features in each brain hemisphere in
FreeSurfer and reveals a high degree of spatial autocorrela-
ción. In such a case, the low- rank assumption made in
RELIEF should be evaluated carefully ( Karayumak et al.,
2019; Mirzaalian et al., 2016). También, although RELIEF does
not require intense cross- validation to choose tuning
parameters or ranks, it requires applying singular value
decomposition (SVD) iteratively, and the computational
cost increases non- linearly with increased sample size (norte)
or features (V ). Por lo tanto, it takes more time than existing
métodos (p.ej., ComBat), whose computation time increase
linearly with V . Sin embargo, the computation time for RELIEF
is still moderate in most downstream neuroimaging data
analyses with, a lo sumo, up to hundreds of features. Más
en tono rimbombante, we believe the powerful performance of RELIEF
outweighs the cost of some additional computation time.
También, there were recent investigations showing how
pre- processing can affect the performance of ComBat
harmonization, which could also be the case in RELIEF.
Cetin- Karayumak et al. (2020) evaluated the effect of
minor differences in pre- processing on ComBat’s perfor-
mance for harmonization of fractional anisotropy (FA)
data across sites and showed that minor differences in
the preprocessing steps resulted in non- linear changes in
the input data. Because the SPINS study performed con-
sistent preprocessing pipelines across sites, we expect
its impact on our analysis to be marginal. Aún, evaluating
the robustness of RELIEF with respect to different pre-
processing pipelines would be an interesting area of
investigación, which we leave as future work.
RELIEF is the first approach that adopted the struc-
tured factorization of interlinked matrices into the data
harmonization context, which used the concept of latent
variables to characterize scanner effects. In the past
decade, there have been a number of methodological
developments in linked matrix factorization ( feng, Jiang,
Hannig, & Marron, 2018; Gaynanova & li, 2019; Lock
et al., 2013), which provided novel insights into under-
standing multimodal data ( q. Yu et al., 2017), enfermedad
subtypes, or clustering. We believe more methodological
research on data harmonization from the viewpoint of the
linked matrix factorization would lead to further improve-
ments in the harmonization quality.
To summarize, we proposed a new harmonization
método, ALIVIO, that contributes to ongoing efforts on
integrating heterogeneous multi- site, multi- scanner stud-
ies in neuroimaging. Our novel contribution is the develop-
ment of a multivariate harmonization method that captures
scanner- specific latent factors, which have not been
addressed in existing methods. With the three- fuente
characterization of inter- scanner biases (ubicación, escala,
latent), RELIEF shows promising results in harmonizing all
de ellos, eventually resulting in higher power in association
studies than existing harmonization methods.
6. SOFTWARE
RELIEF is made publicly available as an R package on
GitHub: https://girub . com / junjypark / ALIVIO. It requires
the same input as neuroComBat (https://github.com/
Jfortin1/ComBatHarmonization) (imaging data matrix,
covariables, and scanner information), producing harmo-
nized imaging data in the same format. Our harmoniza-
tion took approximately 4 seconds on a Macbook Pro
2018 to harmonize data with 72 imaging features from
351 sujetos, which supports the computational effi-
ciency of the proposed method.
DATA AND CODE AVAILABILITY
The R package for implementing RELIEF is publicly avail-
able at https://girub . com / junjypark / ALIVIO.
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
14
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
CONTRIBUCIONES DE AUTOR
Rongqian Zhang: Metodología, Software, Formal analy-
hermana, Validación, Visualización, and Writing— original draft.
Lindsay D. Oliver: Data curation, Supervisión, y
Writing— review & edición. Aristotle N. Voineskos: Super-
visión, Funding acquisition, and Writing— review & edit-
En g. Jun Young Park: Conceptualización, Metodología,
Validación, Supervisión, Software, Writing— review & edit-
En g, and Funding acquisition.
DECLARATION OF COMPETING INTEREST
None.
EXPRESIONES DE GRATITUD
The authors would like to thank the reviewers for their
helpful comments. The authors would like to thank all
participants for their contribution to this work, y el
research staff who performed data collection and man-
agencia. The SPINS study was supported by the
National Institute of Mental Health (1/3R01MH102324- 01,
2/3R01MH102313- 01, 3/3R01MH102318- 01). L.D.O.
was supported by the Brain & Behavior Research Foun-
dación. A.N.V. was supported by the National Institute of
Mental Health (1/3R01MH102324 & 1/5R01MH114970),
Canadian Institutes of Health Research, Canada Founda-
tion for Innovation, CAMH Foundation, and University of
toronto. J.Y.P. was supported by Natural Sciences and
Engineering Research Council of Canada (NSERC)
(RGPIN- 2022- 04831) and the University of Toronto’s Data
Ciencia
(Catalyst Grant). The computing
resources were enabled in part by support provided by
the University of Toronto and the Digital Research Alli-
ance of Canada (alliancecan.ca).
Instituto
REFERENCIAS
Beaulieu, C. (2002). The basis of anisotropic water diffusion
115, 269–280. https://doi . organizar / 10 . 1016 / j . neuroimage . 2015
. 03 . 050
Cetin- Karayumak, S., Stegmayer, K., Walther, S., Szeszko,
PAG. r., Crow, T., Jaime, A., … Rathi, Y. (2020). Exploring
the limits of ComBat method for multi- site diffusion MRI
harmonization. bioRxiv, 2020– 2011. https://doi . organizar / 10
. 1101 / 2020 . 11 . 20 . 390120
Chen, A. A., Beer, j. C., Tustison, norte. J., Cocinar, PAG. A.,
Shinohara R. T., shou, h., & Initiative, A. D. norte. (2022).
Mitigating site effects in covariance for machine learning
in neuroimaging data. Mapeo del cerebro humano, 43(4),
1179–1195. https://doi . organizar / 10 . 1002 / hbm . 25688
Chen, A. A., luo, C., Chen, y., Shinohara, R. T., shou, h.,
Initiative, A. D. NORTE., et al. (2022). Privacy- preserving
harmonization via distributed ComBat. NeuroImagen,
248, 118822. https://doi . organizar / 10 . 1016 / j . neuroimage . 2021
. 118822
Chen, A. A., Srinivasan, D., Pomponio, r., Admirador, y., Nasrallah,
I. METRO., Resnick, S. METRO., … Shou, h. (2022). Harmonizing
functional connectivity reduces scanner effects in
community detection. NeuroImagen, 256, 119198. https://
doi . organizar / 10 . 1016 / j . neuroimage . 2022 . 119198
Dansereau, C., Benhajali, y., Risterucci, C., Pich, mi. METRO.,
Orban, PAG., arnold, D., & Bellec, PAG. (2017). Statistical
power and prediction accuracy in multisite resting- estado
fMRI connectivity. Neuroimagen, 149, 220–232. https://doi
. organizar / 10 . 1016 / j . neuroimage . 2017 . 01 . 072
feng, P., Jiang, METRO., Hannig, J., & Marron, j. (2018). Angle-
based joint and individual variation explained. Diario de
Multivariate Analysis, 166, 241–265. https://doi . organizar / 10
. 1016 / j . jmva . 2018 . 03 . 008
Fortin, J.- PAG., Cullen, NORTE., Sheline, Y. I., taylor, W.. D.,
Aselcioglu, I., Cocinar, PAG. A., … Shinohara, R. t. (2018).
Harmonization of cortical thickness measurements
across scanners and sites. NeuroImagen, 167, 104–120.
https://doi . organizar / 10 . 1016 / j . neuroimage . 2017 . 11 . 024
Fortin, J.- PAG., parker, D., Tunç, B., Watanabe, T., eliot,
METRO. A., Ruparel, K., … Shinohara, R. t. (2017).
Harmonization of multi- site diffusion tensor imaging data.
NeuroImagen, 161, 149–170. https://doi . organizar / 10 . 1016 / j
. neuroimage . 2017 . 08 . 047
Fortin, J.- PAG., Sweeney, mi. METRO., Muschelli, J., Crainiceanu,
C. METRO., Shinohara, R. T., Initiative, A. D. NORTE., et al. (2016).
Removing inter- subject technical variability in magnetic
resonance imaging studies. NeuroImagen, 132, 198–212.
https://doi . organizar / 10 . 1016 / j . neuroimage . 2016 . 02 . 036
Gavish, METRO., & Donoho, D. l. (2017). Optimal shrinkage of
singular values. Transacciones IEEE sobre teoría de la información,
63(4), 2137–2152. https://doi . organizar / 10 . 1109 / TIT . 2017
. 2653801
in the nervous system— A technical review. NMR in
Biomedicine: An International Journal Devoted to the
Development and Application of Magnetic Resonance In
Vivo, 15(7– 8), 435–455. https://doi . organizar / 10 . 1002 / nbm . 782
Gaynanova, I., & li, GRAMO. (2019). Structural learning and
integrative decomposition of multi- view data. Biometrics,
75(4), 1121–1132. https://doi . organizar / 10 . 1111 / biom . 13108
Él, X., Jovicich, J., Salat, D., van der Kouwe, A., quinn,
Beer, j. C., Tustison, norte. J., Cocinar, PAG. A., Davatzikos, C.,
Sheline, Y. I., Shinohara, R. T., … Initiative, A. D. norte.
(2020). Longitudinal ComBat: A method for harmonizing
longitudinal multi- scanner imaging data. NeuroImagen,
220, 117129. https://doi . organizar / 10 . 1016 / j . neuroimage . 2020
. 117129
Bhushan, C., Haldar, j. PAG., Choi, S., Joshi, A. A., shattuck,
D. w., & Leahy, R. METRO. (2015). Co- registration and
distortion correction of diffusion and anatomical images
based on inverse contrast normalization. Neuroimagen,
B., Czanner, S., … Fischl, B. (2006). Reliability of
resonancia magnética- derived measurements of human cerebral cortical
thickness: The effects of field strength, scanner upgrade
and manufacturer. Neuroimagen, 32(1), 180–194. https://
doi . organizar / 10 . 1016 / j . neuroimage . 2006 . 02 . 051
Hastie, T., Mazumder, r., Sotavento, j. D., & Zadeh, R. (2015).
Matrix completion and low- rank SVD via fast alternating
mínimos cuadrados. The Journal of Machine Learning
Investigación, 16(1), 3367–3402. https://www . ncbi . nlm . nih
. gobierno / pmc / artículos / PMC6530939/
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
15
R. zhang, L.D. Oliver, A.N. Voineskos et al.
Neurociencia de la imagen, Volumen 1, 2023
Johnson, W.. MI., li, C., & Rabinovic, A. (2007). Adjusting
batch effects in microarray expression data using
empirical Bayes methods. Biostatistics, 8(1), 118–127.
https://doi . organizar / 10 . 1093 / biostatistics / kxj037
Karayumak, S. C., Bouix, S., Y, l., Jaime, A., Crow, T.,
Shenton, METRO., … Rathi, Y. (2019). Retrospective
harmonization of multi- site diffusion MRI data acquired
with different acquisition parameters. Neuroimagen, 184,
180–200. https://doi . organizar / 10 . 1016 / j . neuroimage . 2018 . 08
. 073
Leek, j. T., & Storey, j. D. (2007). Capturing heterogeneity
in gene expression studies by surrogate variable
análisis. PLoS Genetics, 3(9), e161. https://doi . organizar / 10
. 1371 / journal . pgen . 0030161
estudios. Neuroimagen, 84, 133–140. https://doi . organizar / 10
. 1016 / j . neuroimage . 2013 . 08 . 046
Tournier, J.- D., Herrero, r., Raffelt, D., Tabbara, r.,
Dhollander, T., Pietsch, METRO., … Connelly, A. (2019).
Mrtrix3: A fast, flexible and open software framework
for medical image processing and visualisation.
Neuroimagen, 202, 116137. https://doi . organizar / 10 . 1016 / j
. neuroimage . 2019 . 116137
Vollmar, C., O’Muircheartaigh, J., Pregonero, GRAMO. J., Symms,
METRO. r., Thompson, PAG., Kumari, v., … Koepp, METRO. j. (2010).
Identical, but not the same: Intra- site and inter- site
reproducibility of fractional anisotropy measures on two
3.0 T scanners. Neuroimagen, 51(4), 1384–1394. https://
doi . organizar / 10 . 1016 / j . neuroimage . 2010 . 03 . 046
Lock, mi. F., Hoadley, k. A., Marron, j. S., & Nobel, A. B.
Yu, METRO., Linn, k. A., Cocinar, PAG. A., Phillips, METRO. l., McInnis,
(2013). Joint and individual variation explained (JIVE) para
integrated analysis of multiple data types. The Annals of
Applied Statistics, 7(1), 523. https://doi . organizar / 10 . 1214 / 12
– aoas597
Lock, mi. F., Parque, j. y., & Hoadley, k. A. (2022).
Bidimensional linked matrix factorization for pan- omics
cacerola- cancer analysis. The Annals of Applied Statistics,
16(1), 193. https://doi . organizar / 10 . 1214 / 21 – AOAS1495
Malcolm, j. GRAMO., Shenton, METRO. MI., & Rathi, Y. (2010). Filtered
multitensor tractography. IEEE Transactions on Medical
Imaging, 29(9), 1664–1675. https://doi . organizar / 10 . 1109 / TMI
. 2010 . 2048121
Mirzaalian, h., Y, l., Savadjiev, PAG., Pasternak, o.,
Bouix, S., Michailovich, o., … Rathi, Y. (2016). Enterrar- site
e inter- scanner diffusion MRI data harmonization.
NeuroImagen, 135, 311–323. https://doi . organizar / 10 . 1016 / j
. neuroimage . 2016 . 04 . 041
O'Donnell, l. J., & Westin, C.- F. (2011). An introduction to
diffusion tensor image analysis. Neurosurgery Clinics, 22(2),
185–196. https://doi . organizar / 10 . 1016%2Fj . nec . 2010 . 12 . 004
Parque, j. y., & Lock, mi. F. (2020). Integrative factorization of
bidimensionally linked matrices. Biometrics, 76(1), 61–74.
https://doi . organizar / 10 . 1111 / biom . 13141
Pomponio, r., Erus, GRAMO., Habes, METRO., Doshi, J., Srinivasan, D.,
Mamourian, MI., … Davatzikos, C. (2020). Harmonization
of large MRI datasets for the analysis of brain imaging
patterns throughout the lifespan. NeuroImagen, 208,
116450. https://doi . organizar / 10 . 1016 / j . neuroimage . 2019 . 116450
Takao, h., Hayashi, NORTE., & Ohtomo, k. (2014). Efectos de
study design in multi- scanner voxel- based morphometry
METRO., Fava, METRO., … Sheline, Y. I. (2018). Statistical
harmonization corrects site effects in functional
connectivity measurements from multi- site fMRI data.
Mapeo del cerebro humano, 39(11), 4213–4227. https://doi
. organizar / 10 . 1002 / hbm . 24241
Yu, P., Riesgo, B. B., zhang, K., & Marron, j. (2017). JIVE
integration of imaging and behavioral data. NeuroImagen,
152, 38–49. https://doi . organizar / 10 . 1016 / j . neuroimage . 2017
. 02 . 072
zhang, F., Wu, y., norton, I., Rathi, y., Golby, A. J., &
O'Donnell, l. j. (2019). Test– retest reproducibility of
white matter parcellation using diffusion mri tractography
fiber clustering. Mapeo del cerebro humano, 40(10), 3041–
3057. https://doi . organizar / 10 . 1002 / hbm . 24579
zhang, F., Wu, y., norton, I., Rigolo, l., Rathi, y., Makris, NORTE.,
& O'Donnell, l. j. (2018). An anatomically curated fiber
clustering white matter atlas for consistent white matter
tract parcellation across the lifespan. NeuroImagen, 179,
429–447. https://doi . organizar / 10 . 1016 / j . neuroimage . 2018 . 06
. 027
zhang, y., Parmigiani, GRAMO., & Johnson, W.. mi. (2020).
ComBat- seq: Batch effect adjustment for RNA- seq count
datos. NAR Genomics and Bioinformatics, 2(3), lqaa078.
https://doi . organizar / 10 . 1093 / nargab / lqaa078
Zhu, T., Hu, r., Qiu, X., taylor, METRO., Tso, y., Yiannoutsos,
C., … Zhong, j. (2011). Quantification of accuracy and
precision of multi- center DTI measurements: A diffusion
phantom and human brain study. Neuroimagen, 56(3),
1398–1411. https://doi . organizar / 10 . 1016 / j . neuroimage . 2011
. 02 . 010
Descargado de http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00011/2156061/imag_a_00011.pdf by guest on 07 Septiembre 2023
16