TRADE AND UNCERTAINTY
Dennis Novy and Alan M. Taylor*
Abstract—We offer a new explanation as to why international trade is so
volatile in response to economic shocks. Our approach combines the idea of
uncertainty shocks with international trade. Firms order inputs from home
and foreign suppliers. In response to an uncertainty shock firms dispro-
portionately cut orders of foreign inputs due to higher fixed costs. 在里面
aggregate, this leads to a bigger contraction in international trade flows
than in domestic activity, a magnification effect. We confront the model
with newly compiled US import and industrial production data. Our results
help to explain the Great Trade Collapse of 2008–2009.
我.
介绍
THE recent global economic crisis saw an unusually large
and rapid decline in output across the world. Yet even
more striking, the accompanying decline in international
trade volumes was sharper still and almost twice as big.
全球范围, industrial production fell 12% and trade volumes
跌倒了 20% in the twelve months from April 2008, shocks
of a magnitude not witnessed since the Great Depression
(Eichengreen & O’Rourke, 2010). Just as the causes of the
trade collapse in the 1930s are hotly disputed to this day,
so too, we think, the recent reprise will be an object of de-
bate by economists for years to come. 为什么? Already one
clear reason stands out: standard models of international
trade and macroeconomics fail to account for the severity
of the events in 2008–2009 now known as the Great Trade
Collapse.
As we explain in the next section, it is quite easy for these
models—based on standard first-moment shocks, 我们
do not deny are clearly in operation—to explain why trade
falls in proportion to output, or demand. But without the
addition of auxiliary arguments based on the composition
Received for publication June 16, 2016. Revision accepted for publication
可能 1, 2019. Editor: Amit K. Khandelwal.
∗Novy: University of Warwick and CEPR; 泰勒: University of Califor-
尼亚, 戴维斯; NBER and CEPR.
We thank the Souder Family Professorship at the University of Virginia,
the Center for the Evolution of the Global Economy at the University of
加利福尼亚州, 戴维斯, the Economic and Social Research Council (ESRC grant
ES/P00766X/1) and the Centre for Competitive Advantage in the Global
Economy (CAGE, ESRC grant ES/L011719/1) at the University of Warwick
for financial support. Travis Berge and Jorge F. Chavez provided valuable
research assistance. We thank Ian Dew-Becker and Robert Feenstra for shar-
ing data with us. We thank the editor and three anonymous referees for con-
structive comments. We thank Nicholas Bloom for helpful conversations.
We are also grateful for comments by Nuno Limão, Giordano Mion, Veron-
ica Rappoport, and John Van Reenen, as well as seminar participants at the
2011 Econometric Society Asian Meeting, 这 2011 Econometric Society
North American Summer Meeting, 这 2011 LACEA-LAMES Meetings,
这 2012 CAGE/CEP Workshop on Trade Policy in a Globalised World,
这 2013 Economic Geography and International Trade Research Meeting,
the NBER ITI Spring Meeting 2013, 这 2013 CESifo Global Economy
会议, 这 2013 Stanford Institute for Theoretical Economics Sum-
mer Workshop on the Macroeconomics of Uncertainty and Volatility, 这
Monash-Warwick Workshop on Development Economics, Boston College,
伦敦政治经济学院, Nottingham, 牛津, Penn State, the University of Hong Kong and
Warwick. All errors are ours.
A supplemental appendix is available online at http://www.mitpress
journals.org/doi/suppl/10.1162/rest_a_00885.
of trade—plus a theory as to why some components fall
disproportionately—such models cannot easily explain why
trade typically falls roughly twice as much as GDP in mas-
sive downturn episodes like the post-2008 years or the early
1930s.
在本文中, we examine why international trade is so
much more volatile in response to economic shocks. 和
rather than assuming composition effects, we provide a the-
ory as to why some components of trade are more volatile than
其他的. On the theoretical side, we combine the uncertainty
shock concept due to Bloom (2009) with a model of interna-
tional trade. This real options approach is motivated by high-
profile events that trigger an increase in uncertainty about
the future path of the economy, 例如, 这 9/11 terror-
ist attacks or the collapse of Lehman Brothers. In the wake
of such events, firms adopt a wait-and-see approach, slowing
their hiring and investment activities. Bloom shows that bouts
of heightened uncertainty can be modeled as second-moment
shocks to demand or productivity and that these events typi-
cally lead to sharp recessions. Once the degree of uncertainty
subsides, firms revert to their normal hiring and investment
patterns and the economy recovers.
We bring the uncertainty shock approach into an open
经济. Unlike the previous closed-economy setup, ours
is a theoretical framework in which firms import nondurable
(材料) and durable (首都) inputs from foreign and do-
mestic suppliers. This structure is motivated by the observa-
tion that a large fraction of international trade now consists of
goods such as industrial machinery or capital goods, a feature
of the global production system that has taken on increas-
ing importance in recent decades.1 In the model we develop,
due to fixed costs of ordering associated with transportation,
firms hold an inventory of inputs, but the ordering costs are
larger for foreign inputs. Following Hassler’s (1996) inven-
tory model with time-varying uncertainty, we show that in
response to a large uncertainty shock in business conditions,
whether to productivity or the demand for final products,
firms optimally execute their inventory policy by cutting or-
ders of foreign inputs much more than for domestic inputs.
因此, 在聚集, this differential response leads to
a bigger contraction and subsequently a stronger recovery
in international trade than in domestic trade—that is, 贸易
exhibits more volatility. In a nutshell, uncertainty shocks
1看, 例如, Campa and Goldberg (1997), Feenstra and Hanson
(1999), Eaton and Kortum (2001), and Engel and Wang (2011). The World
Bank WITS database reports that in 2014, capital goods made up 31% 的
global trade, 相比 33% for consumer goods, 21% for intermediate
商品, 和 11% for raw materials. Levchenko, Lewis, and Tesar (2010)
stress that sectors with goods used as intermediate inputs experienced sub-
stantially bigger drops in international trade during the Great Recession.
同样地, Bems, 约翰逊, and Yi (2011) confirm the important role of
trade in intermediate goods.
The Review of Economics and Statistics, 十月 2020, 102(4): 749–765
© 2019 由哈佛大学和麻省理工学院的校长和研究员撰写. 根据知识共享署名发布 4.0
国际的 (抄送 4.0) 执照.
https://doi.org/10.1162/rest_a_00885
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
r
e
s
t
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
A
_
0
0
8
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
750
THE REVIEW OF ECONOMICS AND STATISTICS
magnify the response of international trade, given the dif-
ferential cost structure.
of the unusually large decline in trade in 2008–2009 was in
response to this spike in uncertainty.2
This is a new prediction that has never been tested be-
fore, or even proposed, but we show that it is matched by
数据. On the empirical side, we confront the model with
high-frequency monthly US import and industrial production
数据, some new and hand-collected, going back to 1962. 我们的
results suggest a tight link between uncertainty shocks and
the cyclical behavior of international trade when we employ
an identical VAR empirical framework to the one pioneered
by Bloom (2009) but applied here to trade as well as output
数据. Specifically, we find that imports respond negatively,
and in a statistically significant way, and more than output,
when there is a shock to a standard uncertainty measure: 这
VXO stock market option-implied volatility index.
We can further show that our proposed model generates
a wider array of additional and original testable predictions,
which we also take to the data and test in this paper. The mag-
nification effect should be muted for industries characterized
by high depreciation rates. Nondurable goods are a case in
观点. The fact that such goods have to be ordered frequently
means that importers have little choice but to keep ordering
them even if uncertainty rises. 反过来, durable goods can
be seen as representing the opposite case of very low depre-
ciation rates. Our model predicts that for those goods, 我们
should expect the largest degree of magnification in response
to uncertainty shocks. 直观地, the option value of waiting
is most easily realized by delaying orders for durable goods.
We find strong evidence of this pattern in the data when we
examine the cross-industry response of imports to uncertainty
shocks using US disaggregated monthly trade data, also a first
result of its kind.
We stress that the magnification effect is in operation
within industries by varying extent as predicted by the model.
Using disaggregated data, we find that the effect is strongest
in the durable and capital goods sectors and weak to nonex-
istent in other sectors. Our results are therefore not driven by
composition effects—that is, they arise not merely from the
fact that international trade is heavier in durable goods.
To wrap up, we show how our proposed mechanism helps
to quantitatively explain a part of the Great Trade Collapse
of 2008–2009. We use the VAR model in a simulation exer-
cise and impose shocks that reproduce the exceptional rise in
uncertainty in 2008 (from the subprime crisis to the collapse
of Lehman Brothers). Using standard Cholesky ordering to
ensure identification of the response in the trade equation
to an uncertainty shock while simultaneously controlling for
first-moment shocks to business conditions proxied by em-
ployment, we show empirically that second-moment shocks
have a sizable and independent effect on trade. The result
holds also for just the exogenous shocks (terror/war/oil) 那
Bloom (2009) identified. 至关重要的是, using disaggregated data,
we can show that these uncertainty effects are concentrated in
exactly the traded sectors needed to match the compositional
variation seen in the trade collapse. The results suggest that if
we place a lot of emphasis on uncertainty shocks, up to half
因此, the recent downturn is qualitatively quite comparable
to previous postwar contractions in international trade and
can be modeled similarly. 实际上, we think that our approach
may advance our understanding of trade contractions and
volatility over the long run, not only during the Great Trade
Collapse.
The paper is organized as follows. In section II, we re-
view the literature. In sections III, IV, 和V, we outline our
theoretical model, do comparative statics, and present simu-
lation results. Section VI presents our empirical evidence. 在
section VII we ask to what extent uncertainty shocks can em-
pirically account for the recent Great Trade Collapse. 部分
VIII concludes. We also provide a detailed online appendix.
二. The Literature on the Great Trade Collapse
Departing from conventional static trade models, 例如
those based on the gravity equation, our paper focuses on
the dynamic response of international trade. The novelty is
that shocks to the volatility of idiosyncratic disturbances (IE。,
second-moment shocks) can be the driver of very different
changes in imported and domestic inputs. Previous theoret-
ical and empirical work has almost exclusively focused on
first-moment shocks, such as to productivity, exchange rates,
or trade costs. Our approach is relevant for researchers and
policymakers alike who seek to understand the crash and re-
covery process in response to the Great Recession, and it may
also be relevant for understanding historical events like the
Great Depression. It could also help account for the response
of international trade in future economic crises.
We are not the first authors to consider uncertainty and
real option values in the context of international trade, 但
so far the literature has not focused on uncertainty shocks.
例如, Baldwin and Krugman (1989) adopt a real op-
tions approach to explain the hysteresis of trade in the face
of large exchange rate swings, but their model features only
standard first-moment shocks. 最近, the role of un-
certainty has attracted new interest in the context of trade pol-
icy and trade agreements (Handley, 2014; Handley & Limão,
2015; Limão & Maggi, 2015). Closer to our approach, in in-
dependent and contemporaneous work, Taglioni and Zavacka
(2012) empirically investigate the relationship between un-
certainty and trade for a panel of countries using quarterly as
opposed to monthly data. But they do not provide a theoretical
mechanism and do not speak to variation across industries.3
2相似地, Bloom, Bond, and Van Reenen (2007) provide empirical ev-
idence that fluctuations in uncertainty can lead to quantitatively large ad-
justments of firms’ investment behavior.
3While Bloom (2009) considers US domestic data, Carrière-Swallow and
Céspedes (2013) consider domestic data on investment and consumption
across forty countries and their response to uncertainty shocks. Gourio,
Siemer, and Verdelhan (2013) examine the performance of G7 countries in
response to heightened volatility. None of these papers consider interna-
tional trade flows.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
r
e
s
t
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
A
_
0
0
8
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
TRADE AND UNCERTAINTY
751
The Great Trade Collapse of 2008–2009 has been docu-
mented by many authors (see Baldwin, 2009, for a collection
of approaches, and Bems, 约翰逊, & Yi, 2013, for a survey).
Eaton et al. (2016) develop a structural model of interna-
tional trade where the decline in trade is attributed to various
combined first-moment shocks, in particular a decline in the
efficiency of investment in durable manufactures, a collapse
in the demand for tradable goods, and an increase in trade
frictions.4 They find that the first explains the majority of de-
clining trade. Our approach is different in that the collapse in
demand is generated by a second-moment uncertainty shock,
and we can endogenize the differential response across sec-
托尔斯. Firms react to the uncertainty by adopting a wait-and-see
方法, and we do not require first-moment shocks or an
increase in trade frictions to account for the excess volatility
of trade.
Our approach is consistent with the view that trade fric-
tions did not materially change in the recent crisis. Evenett
(2010) and Bown (2011) find that protectionism was con-
tained during the Great Recession. This view is underlined
by Bems et al. (2013). 更具体地说, Kee, Neagu, 和
Nicita (2013) find that less than 2% of the Great Trade Col-
lapse can be explained by a rise in tariffs and antidumping
duties. Bown and Crowley (2013) find that compared to pre-
vious downturns, during the Great Recession governments
notably refrained from imposing temporary trade barriers
against partners that experienced economic difficulties.
Amiti and Weinstein (2011) and Chor and Manova (2012)
highlight the role of financial frictions and the drying up of
trade credit. 然而, based on evidence from Italian manu-
facturing firms, Guiso and Parigi (1999) show that the nega-
tive effect of uncertainty on investment cannot be explained
by liquidity constraints. We do not incorporate credit fric-
tions here, but such mechanisms may be complementary
to our approach, and we do not rule out a role for other
mechanisms.
As Engel and Wang (2011) point out, 的组成
international trade is tilted toward durable goods. 建筑
a two-sector model in which only durable goods are traded,
they can replicate the higher volatility of trade relative to
general economic activity. 相比之下, we relate the excess
volatility of trade to inventory adjustment in response to un-
certainty shocks. As this mechanism applies within an in-
工业化的, compositional effects do not drive the volatility of
international trade in our model.
Our paper is also related to Alessandria, Kaboski, 和
Midrigan (2010A, 2011) who rationalize the decline in inter-
national trade by changes in firms’ inventory behavior driven
by a first-moment supply shock and procyclical inventory in-
vestment (Ramey & 西方, 1999). 相比之下, we focus on the
role of increased uncertainty when second-moment shocks
are the driver of firms’ inventory adjustments. In our US data,
heightened uncertainty stands out as a defining feature of the
Great Recession, and we employ an observable measure of it.
然而, as we show, there is little evidence in the US data
of a major first-moment TFP shock coincident with the onset
of the crisis.
最后, Alessandria et al. (2015) model second-moment
shocks, but their framework does not have inventory. As far
as we are aware, ours is the first paper to jointly model inven-
tory holdings and uncertainty shocks in one framework. 和-
like in our paper, a second-moment shock in Alessandria et al.
(2015) is a shock to the variance of the heterogeneous pro-
ductivity distribution. They find that trade rises in response to
a second-moment shock. This result is driven by the differen-
tial impact of the rising productivity dispersion on exporters
versus nonexporters. 直观地, exporters tend to be at the
upper tail of the productivity distribution. Increases in the
dispersion of productivity shocks thus confer an even greater
advantage to exporters compared to nonexporters.5 This is
different from our setting, where the probability of getting
hit by a shock changes symmetrically for all firms, and trade
falls in response to a second-moment shock.
三、. A Model of Trade with Uncertainty Shocks
We adopt Hassler’s (1996) setting of investment under un-
certainty and embed it into a model of trade in capital inputs.
We then introduce second-moment uncertainty shocks.
Hassler’s (1996) model starts from the well-established
premise that uncertainty has an adverse effect on investment.
In our setup, we model investment as firms’ investing in in-
ventory of capital inputs required for production. Due to fixed
costs of ordering, firms build up an inventory that they run
down over time and replenish at regular intervals. Some in-
puts are ordered domestically, and others are imported from
国外. 因此, we turn the model into an open economy.
此外, firms will face uncertainty over “business con-
ditions” (using Bloom’s terminology), which means they
experience unexpected fluctuations in productivity or de-
要求, 或两者. What’s more, the degree of uncertainty varies
随着时间的推移. Firms might therefore enjoy periods of calm
when business conditions are relatively stable, or they might
have to weather uncertainty shocks that lead to a volatile
business environment characterized by large fluctuations.
全面的, this formulation allows us to model the link between
生产, international trade, and shifting degrees of uncer-
污点. Hassler’s (1996) key innovation is to formally model
how changes in uncertainty influence investment. His model
therefore serves as a natural starting point for our analysis of
uncertainty shocks.
4Leibovici and Waugh (2019) show that the increase in implied trade
frictions can be rationalized by a model with time-to-ship frictions such
that agents need to finance future imports upfront (similar to a cash-in-
advance technology) and become less willing to import in the face of a
negative income shock.
5As Alessandria et al. (2015) recognize, they uncover “a puzzle for the
standard business cycle model used to understand micro-level trade dynam-
集成电路: Increases in firm-level dispersion lead to large increases in trade rather
than the steep declines typically observed during recessions.”
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
r
e
s
t
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
A
_
0
0
8
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
752
THE REVIEW OF ECONOMICS AND STATISTICS
A. Production and Demand
Each firm has a Cobb-Douglas production function,
F (A, KD, KF ) = AK α
DK 1−α
F
,
(1)
where A is productivity, KD is a capital input sourced domes-
抽搐地, and KF is a capital input sourced from foreign sup-
pliers. We assume that KD and KF are differentiated through
the Armington assumption so that firms need to import both
类型. These capital inputs depreciate at rate δ (so “durable”
would map to low δ, “nondurable” to high δ). Each firm faces
isoelastic demand Q for its output, with elasticity σ, so that
Q = BP−σ,
(2)
where B is a demand shifter. As we focus on the firm’s short-
run behavior, we assume that the firm takes the prices of the
production factors as given and serves the demand for its
product.6 We thus adopt a partial equilibrium approach to
keep the model tractable.
乙.
Inventory and Trade
The factors KD and KF are capital inputs—say, special-
ized machinery from domestic and foreign suppliers. 之后
在, in our empirical trade and production data at the four-
digit industry level, examples include electrical equipment;
engines, turbines, and power transmission equipment; com-
munications equipment; and railroad rolling stock. 我们可以
consider the firm described in our model as ordering a mix
of such products.7
Since the inputs depreciate, the firm has to reorder them
once in a while. Because the firm has to pay a fixed cost
of ordering per shipment, it stores the inputs as inventory
and follows an s, S inventory policy. Scarf (1959) shows that
in the presence of such fixed costs of ordering, an s, S pol-
icy is an optimal solution to the dynamic inventory problem.
Ordering inputs leads to domestic trade flows and imports,
分别. We assume that ordering foreign inputs is asso-
ciated with higher fixed costs compared to domestic inputs,
0 < fD < fF . This assumption is consistent with evidence by
Kropf and Sauré (2014), who show that fixed costs per ship-
ment are strongly correlated with shipping distance, and they
are substantially higher between countries speaking different
6We do not model monetary effects and prices. This modeling strategy is
supported by the empirical regularity documented by Gopinath, Itskhoki,
and Neiman (2012) showing that prices of differentiated manufactured
goods (both durables and nondurables) barely changed during the Great
Trade Collapse of 2008–2009. They conclude that the sharp decline in the
value of international trade in differentiated goods was “almost entirely a
quantity phenomenon.” In contrast, prices of nondifferentiated manufac-
tures decreased considerably. In the empirical part of the paper we most
heavily rely on differentiated products. For a sample that also includes non-
US countries, Haddad, Harrison, and Hausman (2010) find some evidence
of rising manufacturing import prices, consistent with the hypothesis of
supply-side frictions such as credit constraints.
7This setup is related to a situation where inventories are seen as a factor
of production (Ramey, 1989).
languages and not sharing a free trade agreement. Otherwise,
we treat the two types of fixed costs in the same way.8
Given the input prices, the Cobb-Douglas production func-
tion, equation (1), implies that the firm’s use of KD and KF
is proportional to output Q regardless of productivity and de-
mand fluctuations. Similar to Hassler (1996), we assume that
the firm has target levels of inputs to be held as inventory,
denoted by M∗
F , which are proportional to both Q, as
well as KD and KF , respectively. Thus, we can write
D and M∗
m∗
D
= cD + q,
(3)
≡ ln(M∗
where cD is a constant, m∗
D) denotes the log inven-
D
tory target, and q ≡ ln(Q) denotes log output. Grossman and
Laroque (1990) show that such a target level can be rational-
ized as the optimal solution to a consumption problem in the
presence of adjustment costs.9 In our context, the target level
can be similarly motivated if it is costly for the firm to adjust
its level of production up or down. An analogous equation
holds for m∗
F , but, for simpler notation, we drop the D and F
subscripts from now on.
We follow Hassler (1996) in modeling the dynamic inven-
tory problem. In particular, we assume a quadratic loss func-
tion that penalizes deviations z from the target m∗ as 1
2 z2 with
z ≡ m − m∗. Note that the loss function is specified in loga-
rithms such that when expressed in levels, negative deviations
from the target are relatively more costly. Losses associated
with negative deviations could be seen as the firm’s desire to
avoid a stockout. Losses associated with positive deviations
could be seen as a desire to avoid excessive storage costs. We
refer to the theory appendix where we discuss stockout avoid-
ance in more detail and introduce an asymmetric loss function
based on Elliott, Komunjer, and Timmermann (2005).
Clearly, in the absence of ordering costs, the firm would
choose to continuously set m equal to the target m∗, with 0
deviation. However, since we assume positive ordering costs
( f > 0), the firm faces a trade-off: balancing the fixed costs,
一方面, and the costs of deviating from the target, 在
另一个. Changes in inventory are brought about whenever
the firm pays the fixed costs f to adjust m.10
We solve for the optimal solution to this inventory problem
subject to a stochastic process for output q. The optimal con-
trol solution can be characterized in the following way: 什么时候
the deviation of inventory z reaches a lower trigger point s,
8Guided by the empirical evidence on the importance of adjustment
through the intensive margin (贝伦斯, Corcos, & Mion, 2013; Bricon-
gne et al., 2012), we do not model firms’ switching from a foreign to a
domestic supplier, or vice versa. As we discuss in section V, this would
arguably reinforce the negative impact of uncertainty shocks on imports.
9In their model, consumers have to decide how much of a durable good
they should hold given that they face fluctuations in their wealth. Adjustment
is costly due to transaction costs. Under the assumption of the consumers’
utility exhibiting constant relative risk aversion, the optimal amount of the
durable good turns out to be proportional to their wealth.
10As an alternative interpretation, we could also regard the firm’s problem
as a capital investment problem. The firm faces a fixed adjustment cost due
to the ordering costs and a quadratic penalty for deviating in investment
from the target. This interpretation is more closely in line with Engel and
王 (2011).
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
/
r
e
s
t
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
A
_
0
0
8
8
5
p
d
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
TRADE AND UNCERTAINTY
753
the firm orders the amount φ so that the inventory rises to a
return point of deviation S = s + φ. 11 正式地, we can state
the problem as follows:
(西德:4)
(西德:5)
(西德:6)
(西德:2)
(西德:3) ∞
e−rt
1
2
z2
t
+ It f
dt
,
(4)
min
{它 ,zt }∞
0
E0
0
subject to
z0 = z;
(西德:7)
zt+dt =
(西德:7)
自由的
zt − δdt − dq otherwise;
if mt is adjusted,
It dt =
1 if mt is adjusted,
0 否则.
It is a dummy variable that takes the value 1 whenever the
firm adjusts mt by paying f , r > 0 is a constant discount
速度, and δ > 0 is the depreciation rate for the input so that
dKt /K = δdt. Note that the input depreciates only if used in
生产, not if it is merely in storage as inventory.
C. Business Conditions with Time-Varying Uncertainty
Due to market clearing, output can move due to shifts in
productivity A in equation (1) or demand B in equation (2).
We refer to the combination of supply and demand shifters
as business conditions. Specifically, we assume that output q
follows a stochastic marked point process that is known to
the firm. With an instantaneous probability λ/2 per unit of
time and λ > 0, q shifts up or down by the amount ε:
⎧
⎪⎨
⎪⎩
qt+dt =
qt + ε with probability (λ/2)dt,
with probability 1 − λdt,
qt
qt − ε with probability (λ/2)dt.
(5)
The shock ε can be interpreted as a sudden change in business
状况. Through the proportionality between output and
the target level of inventory embedded in equation (3), a shift
in q leads to an updated target inventory level m∗. 下列的
Hassler (1996), we assume that ε is sufficiently large such
that it becomes optimal for the firm to adjust m.12 That is,
a positive shock to output increases m∗ sufficiently to lead
to a negative deviation z that reaches below the lower trigger
11那是, in full notation, we have sD, 标清, φD for domestic inputs and sF ,
SF , φF for foreign inputs.
12Hassler (1996, 秒. 4) reports that relaxing the large shock assumption,
while rendering the model more difficult to solve, appears to yield no qual-
itatively different results. Choosing different values for ε does not affect
our simulation results in section V as long as ε is sufficiently large to trig-
ger adjustment. The reason is that in the aggregate across many firms, 这
idiosyncratic shocks wash out to 0. We note that the shock is permanent,
but the frequency with which the firm gets hit by the shock is subject to a
stochastic transition process as given in expression (6). We are not aware
of evidence in this context as to whether firms get predominantly hit by
transitory or permanent shocks.
point s. 因此, the firm restocks m . Vice versa, a negative
shock reduces m∗ sufficiently such that z reaches above the
upper trigger point and the firm destocks m.13 Thus, to keep
our model tractable, we allow the firm to both restock and
destock depending on the direction of the shock.
The process of equation (5) has a first moment equal to 0
and constant, independent of ε. 下文中, we hold ε
fixed. 因此, the arrival rate of shocks λ is the main measure
of uncertainty and will be our key parameter of interest. It de-
termines the second moment of shocks. We interpret changes
in λ as changes in the degree of uncertainty. Note that λ
determines the frequency of shocks, not their size. Higher
uncertainty here does not mean an increased probability of
larger shocks.
Specifically, as the simplest possible setup, we follow Has-
sler (1996) by allowing an indexed level of uncertainty λω to
switch stochastically between two states ω ∈ {0, 1}: a state
of low uncertainty λ0 and a state of high uncertainty λ1 with
λ0 < λ1. The transition of the uncertainty states follows a
Markov process,
(cid:7)
ωt+dt =
ωt with probability 1 − γωdt,
ωt with probability γωdt,
(6)
where ωt = 1 if ωt = 0, and vice versa. The probability of
switching the uncertainty state in the next instant dt is there-
fore γωdt, with the expected duration until the next switch
given by γ−1
ω .
Below, when we calibrate the model, we will choose pa-
rameter values for λ0, λ1, γ0, and γ1 that are consistent
with uncertainty fluctuations as observed over the past few
decades.14 We assume the firm knows the parameters of the
stochastic process described by equations (5) and (6) and
takes them into account when solving its optimization prob-
lem (4).
The theory appendix shows how the Bellman equation for
the inventory problem can be set up and how the system can
be solved. We have to use numerical methods to obtain values
for the four main endogenous variables of interest: the bounds
s0 and S0 for the state of low uncertainty λ0 and the bounds
s1 and S1 for the state of high uncertainty λ1.
IV. Time-Varying Uncertainty and Firm
Inventory Behavior
The main purpose of this section is to explore how the
firm endogenously changes its s, S bounds in response to
13To keep the exposition concise, we do not explicitly describe the upper
trigger point, and focus on the lower trigger point s and the return point S.
But it is straightforward to characterize the upper trigger point.
14Overall, the stochastic process for uncertainty is consistent with Bloom
(2009). In his setting, uncertainty also switches between two states (low
and high uncertainty) with given transition probabilities. But he models
uncertainty as the time variation of the volatility of a geometric random
walk.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
754
THE REVIEW OF ECONOMICS AND STATISTICS
increased uncertainty. Our key result is that the firm lowers
the bounds in response to increased uncertainty. In addition,
we are interested in comparative statics for the depreciation
rate δ and the fixed cost of ordering f . As just explained,
the model cannot be solved analytically, so we use numerical
methods.
A. Parameterizing the Model
We choose the same parameter values for the interest
rate and rate of depreciation as Bloom (2009): r = 0.065
and δ = 0.1 per year. The interest rate value corresponds
to the long-run average for the US firm-level discount rate.
Based on data for the US manufacturing sector from 1960 to
1988, Nadiri and Prucha (1996) estimate depreciation rates
of 0.059 for physical capital and 0.12 for R&D capital. As
reported in their paper, those are somewhat lower than esti-
mates by other authors. We therefore take δ = 0.1 as a rea-
sonable baseline, although NIPA-based estimates are usually
lower.
For the stochastic uncertainty process described by equa-
tions (5) and (6), we choose parameter values that are con-
sistent with Bloom’s (2009) data on stock market volatility.
In his table II, he reports that an uncertainty shock has an
average half-life of two months. This information can be ex-
pressed in terms of the transition probabilities in equation (6)
with the help of a standard process of exponential decay for
a quantity Dt :
Dt = D0 exp(−gt ).
12 years yields a rate of decay g = 4.1588
Setting t equal to 2
for Dt to halve. The decaying quantity Dt in that process
can be thought of as the number of discrete elements in a
certain set. We can then compute the average length of time
that an element remains in the set. This is the mean lifetime
of the decaying quantity, and it is simply given by g−1. It
corresponds to the expected duration of the high-uncertainty
state, γ−1
1 , which is then given by 4.1588−1 = 0.2404 years
(88 days) with γ1 = g = 4.1588.
Bloom (2009) furthermore reports a frequency of sev-
enteen uncertainty shocks in 46 years. Hence, an uncer-
= 2.7059 years.
tainty shock arrives on average every 46
17
Given the duration of high-uncertainty periods from above,
in our model this would imply an average duration of low-
uncertainty periods of 2.7059 − 0.2404 = 2.4655 years. It
follows from this that γ0 = 2.4655−1 = 0.4056.
The uncertainty term λdt in the marked point process,
equation (5), indicates the probability that output is hit in
the next instant by a supply or demand shock that is suffi-
ciently large to shift the target level of inventory. Thus, the
expected length of time until the next shock is λ−1. It is diffi-
cult to come up with an empirical counterpart of the frequency
of such shocks since they are unobserved. For the baseline
level of uncertainty, we set λ0 = 1, which implies that the
target level of inventory is adjusted on average once a year.
This value can therefore be interpreted as an annual review
of inventory policy.
However, we point out here that our results are not partic-
ularly sensitive to the λ0 value. In our baseline specification,
we follow Bloom (2009, table II) by doubling the standard
deviation of business conditions in the high-uncertainty state.
This corresponds to λ1 = 4.15 In the comparative statics be-
low, we also experiment with other values for λ1. An uncer-
tainty shock is defined as a sudden shift from λ0 to λ1, with
the persistence of the high-uncertainty state implied by γ1.
Finally, we need to find an appropriate value for the fixed
costs of ordering, fF and fD. Based on data for a US steel
manufacturer, Alessandria, Kaboski, and Midrigan (2010b)
report that “domestic goods are purchased every 85 days,
while foreign goods are purchased every 150 days.” To match
the behavior of foreign import flows, we set fF to ensure
that the interval between orders is on average 150 days in
the low-uncertainty state.16 This implies fF = 0.00005846
as our baseline value. Matching the interval of 85 days for
domestic flows would imply fD = 0.00001057. These fixed
costs differ by a large amount (by a factor of about 5.5), and
that difference might seem implausibly large. However, in
the theory appendix, we show that quantitatively, we can still
obtain large declines in trade flows in response to uncertainty
shocks even with values for fF that are not so high as in this
baseline specification. That is, we are able to obtain a large
decline in trade flows for a ratio of fF / fD that is lower than
implied by the above values and might be considered more
realistic.
B. A Rise in Uncertainty
Given the above parameter values, we solve the model
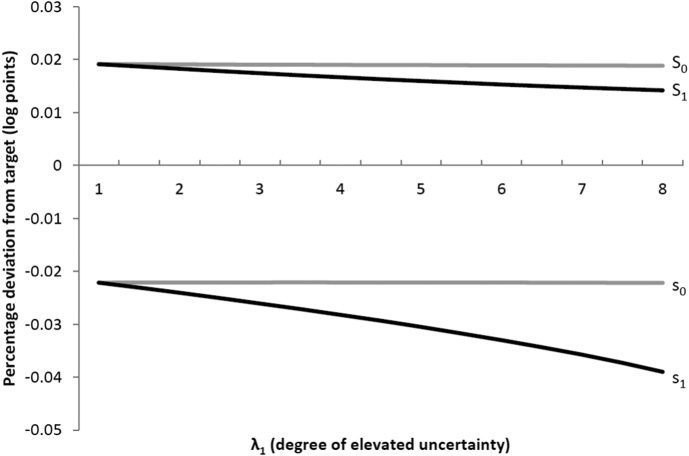
numerically. Figure 1 illustrates the change in s, S bounds in
response to rising uncertainty. The vertical scale indicates the
percentage deviation from the target m∗. Note that there are
two sets of s, S bounds: one set for the low-uncertainty state
0 and the other for the high-uncertainty state 1. The level
of low uncertainty is fixed at λ0 = 1, but the level of high
uncertainty λ1 varies on the horizontal axis (as our baseline
value, we will use λ1 = 4 in later sections). At λ0 = λ1 = 1,
the bounds for the two states coincide, by construction. As
the s, S bounds are endogenous, all of them in principle shift
15For a given λ, the conditional variance of process (5) is proportional
to λ so that the standard deviation is proportional to the square root of
λ. Thus, we have to quadruple λ0 to double the standard deviation. This
parameterization is also consistent with Bloom et al. (2018, table V). They
roughly double the standard deviation in the high-uncertainty state at the
aggregate level. They more than triple it based on an idiosyncratic shock
process and microlevel data. But since there are no idiosyncratic shocks in
our model, we prefer to side with the more conservative rise.
16In the model, the interval between orders corresponds to the normalized
bandwidth, (S0 − s0 )/δ. In the case of fF , we set it equal to 150 days,
or 150/365 years. Hornok and Koren (2015) report that the average time
for importing across 179 countries, excluding the actual shipping time, is
around one month. Longer shipping times are associated with less frequent
shipments. Also see Kropf and Sauré (2014) for estimates of substantial
fixed shipment costs based on transaction-level data.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
TRADE AND UNCERTAINTY
755
FIGURE 1.—CHANGE IN s, S BOUNDS (TRIGGER POINT, RETURN POINT) DUE TO HIGHER UNCERTAINTY. THE LOW-UNCERTAINTY
STATE IS IN GRAY, THE HIGH-UNCERTAINTY STATE IN BLACK.
FIGURE 2.—SUMMARY: HOW UNCERTAINTY PUSHES DOWN THE s, S BOUNDS AND INCREASES THE BANDWIDTH
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
in response to an increase λ1. But clearly the bounds for the
low-uncertainty state are essentially not affected by a rising
λ1.
Two observations stand out. First, the lower trigger point
always deviates farther from the target than the return point.
This is true for both states of uncertainty (i.e., |s0| > S0 and
|s1| > S1). As we show in the theory appendix, in the pres-
ence of uncertainty, a symmetric band around the target (IE。,
|sω| = S0) would not be optimal. The reason is that with un-
肯定, there is a positive probability of the firm’s output
getting hit by a shock, leading the firm to adjust its inventory
to the return point. 因此, the higher the shock probability,
the more frequently the firm would adjust its inventory above
目标. To counteract this tendency, it is optimal for the firm
to set the return point relatively closer to the target.
第二, the bounds for the high-uncertainty state decrease
with the extent of uncertainty, 那是, ∂S1/∂λ1 < 0 and
∂s1/∂λ1 < 0. The intuition for the drop in the return point
S1 is the same as above: increasing uncertainty means more
frequent adjustment so that S1 needs to be lowered to avoid
excessive inventory holdings. The intuition for the drop in
the lower trigger point s1 reflects the rising option value of
waiting. Suppose the firm is facing a low level of inventory
and decides to pay the fixed costs of ordering f to stock up. If
the firm gets hit by a shock in the next instant, it would have
to pay f again. The firm could have saved one round of fixed
costs by waiting. Waiting longer corresponds to a lower value
of s1. This logic follows immediately from the literature on
uncertainty and the option value of waiting (McDonald &
Siegel, 1986; Dixit, 1989; Pindyck, 1991).
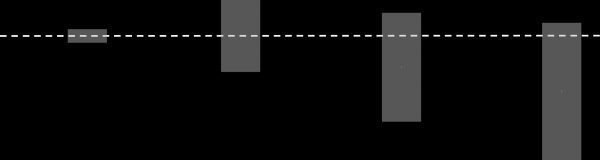
Figure 2 summarizes the main qualitative results in a com-
pact way. Case 1 depicts the (hypothetical) situation where
both fixed costs f and uncertainty λ are negligible. Due to
the very low fixed costs the bandwidth (i.e., the height of the
box) is tiny, and due to the lack of uncertainty, the s1 and S1
bounds are essentially symmetric around the target level m∗.
756
THE REVIEW OF ECONOMICS AND STATISTICS
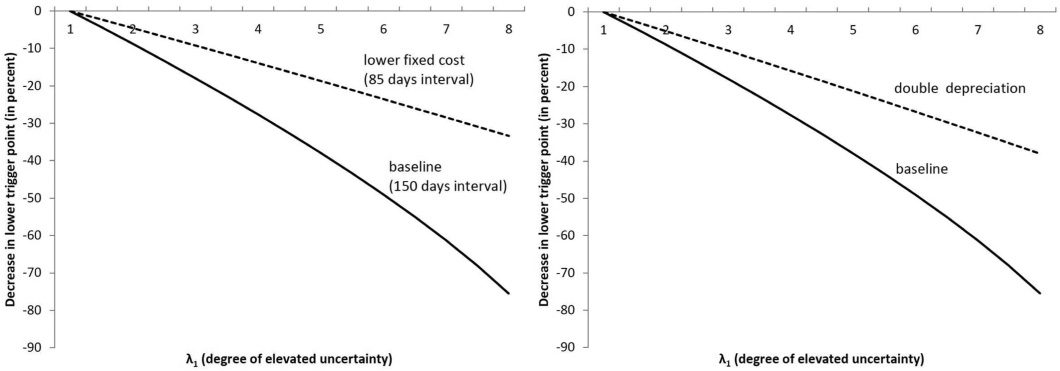
FIGURE 3.—THE EFFECT OF LOWER FIXED COSTS (LEFT) AND A HIGHER DEPRECIATION RATE (RIGHT) ON THE DECREASE IN THE LOWER TRIGGER POINT
In case 2, the fixed costs become larger, which pushes both
s1 and S1 farther away from the target but in a symmetric
way. Cases 3a and 3b correspond to the situation we con-
sider in this paper with nonnegligible degrees of uncertainty.
The uncertainty in case 3a induces two effects compared to
case 2. First, both s1 and S1 shift down so that they are no
longer symmetric around the target. Second, the bandwidth
increases further. A shift to even more uncertainty (case 3b)
reinforces these two effects.
C. Comparative Statics
We have assumed fixed costs of ordering to be lower when
the input is ordered domestically: fD < fF . The left panel of
figure 3 shows the effect of using the value fD from above
that corresponds to an average interval of 85 days between
domestic orders compared to the baseline value fF that cor-
responds to 150 days. Lower fixed costs imply more frequent
ordering and therefore allow the firm to keep its inventory
closer to the target level. This means that for any given level
of uncertainty, the optimal lower trigger point with low fixed
costs does not deviate as far from the target compared to the
high fixed cost scenario.
Some types of imports observed in the data are inher-
ently difficult to store as inventory—for instance, nondurable
goods. We model such a difference in storability with a higher
rate of depreciation of δ = 0.2 compared to the baseline value
of δ = 0.1. In general, the larger the depreciation rate, the
smaller the decreases in the lower trigger point and the return
point in response to heightened uncertainty. Intuitively, with
a larger depreciation rate the firm orders more frequently. The
value of waiting is therefore diminished. The right panel of
figure 3 graphs the percentage decline in the lower trigger
point s1 relative to s0 for both the baseline depreciation rate
and the higher value. We provide more comparative statics
results for changes in f and δ in the theory appendix.
V.
Simulating Uncertainty Shocks
So far we have described the behavior of a single firm. We
now simulate an economy of 50,000 firms in partial equilib-
rium where each individual firm receives shocks according
to the stochastic uncertainty process in equations (5) and (6).
These shocks are idiosyncratic for each firm but drawn from
the same distribution. The firms are identical in all other re-
spects. We use the same parameter values as in section IVA,
and we focus on the foreign-sourced input KF and the asso-
ciated fixed costs fF .
We simulate an uncertainty shock by permanently shifting
the economy from low uncertainty λ0 to high uncertainty λ1.
A key result from section IVB is that firms lower their s, S
bounds in response to increased uncertainty. This shift leads
to a strong downward adjustment of input inventories and
thus a strong decline in imports.
In figure 4 we plot simulated imports, normalized to 1 for
the average value, in continuous time (focus on the solid line;
we will explain the dashed and dotted lines below). Given our
parameterization, imports decrease by up to 25% at an instant
in response to the shock. The decrease happens quickly within
one month, followed by a quick recovery and, in fact, an
overshoot (we comment on the overshoot below). This pattern
of sharp contraction and recovery is typical for uncertainty
shocks. In the theory appendix, as a comparison, we express
the same simulated data in discrete time at monthly frequency.
There, we also allow for a temporary shock where uncertainty
shifts back to its low level.
In our model, the reaction of aggregate imports can be
more clearly thought of in terms of two effects, depicted in
figure 4. The dashed line (at the bottom) represents a “pure”
uncertainty effect, and the dotted line (at the top) is a volatility
effect. The volatility effect is responsible for the overshoot,
and we comment on it in more detail in the theory appendix.
While the trade collapse and recovery happen quickly in
the simulation, this process takes longer in the data. For
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
FIGURE 4.—SIMULATING AND DECOMPOSING THE RESPONSE OF AGGREGATE IMPORTS TO AN UNCERTAINTY SHOCK: THE TOTAL EFFECT (BASELINE), THE “PURE”
UNCERTAINTY EFFECT, AND THE VOLATILITY EFFECT
TRADE AND UNCERTAINTY
757
instance, during the Great Recession, German imports peaked
in the second quarter of 2008, rapidly declined by 32%,
and returned to their previous level only by the third quar-
ter of 2011.17 Greater persistence could be introduced into
our simulation by staggering firms’ responses. Currently,
all firms perceive uncertainty in exactly the same way and
thus synchronize their reactions. It might be more realis-
tic to introduce some degree of heterogeneity by allowing
firms to react at slightly different times. In particular, firms
might have different assessments as to the time when un-
certainty has faded and business conditions have normalized
(see Bernanke, 1983). This would stretch out the recovery of
trade, and it would also diminish the amplitude of the impact.
Moreover, delivery lags could be introduced that vary across
industries. We abstracted from such extensions here in order
to keep the model tractable.
Apart from being heterogeneous in terms of when they re-
act to a shock, firms could also differ in more fundamental
ways. Consistent with the literature on heterogeneous firms
and trade, aggregate imports tend to be dominated by the
most productive firms in an economy. Only those firms are
able to cover the higher fixed costs of sourcing inputs from
abroad. In the current model, we do not model an exten-
sive margin response, that is, firms do not switch from a for-
eign to a domestic supplier over the simulation period, or
vice versa.18 Allowing for extensive margin responses would
be an important avenue for future research. We conjecture
17Most high-income countries experienced similar patterns. US and
Japanese imports declined by 38% and 40% over that period, respectively
(source: IMF, Direction of Trade Statistics).
18This approach is motivated by empirical evidence based on micro-
data. Examining Belgian firm-level data during the 2008–2009 recession,
Behrens et al. (2013) find that most of the changes in international trade
across trading partners and products occurred at the intensive margin, while
that the extensive margin would amplify uncertainty shocks.
Firms would likely switch to domestic suppliers in the face
of higher uncertainty, thus reinforcing the effects of higher
uncertainty. But since changing suppliers entails switching
costs, an extensive margin response might also make the ef-
fect of an uncertainty shock more persistent in the aggregate.
Firms will not switch to domestic suppliers immediately but
rather wait a while such that the overall effect on international
trade flows is more drawn out. Moreover, once the uncer-
tainty shock has subsided, firms might be slow in switching
back to foreign suppliers, delaying the recovery. Of course,
to trace this mechanism, we would need firm-level data on
foreign and domestic input orders, both at a reasonably high
frequency. Alternatively, and trivially, persistence might arise
by having multiple persistent uncertainty shocks arrive one
after the other. This may well match the reality of 2008 and
is an approach we explore in section VII.
In the theory appendix, we provide further simulation re-
sults involving comparative statics (changes in fixed costs
and the depreciation rate). We also explore the role of first-
moment shocks.
VI. Empirical Evidence
We now turn to the task of providing more formal empirical
evidence for the new theoretical channels linking uncertainty
shocks to domestic activity and foreign trade that we have
proposed. Specifically, we set out to explore the dynamic re-
lationship of uncertainty, production, and international trade
trade fell most for consumer durables and capital goods. Bricongne et al.
(2012) confirm the overarching importance of the intensive margin for
French firm-level export data. Haddad et al. (2010) present similar evidence
for US imports, which we consider in our empirical analysis.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
758
THE REVIEW OF ECONOMICS AND STATISTICS
by estimating vector autoregressions (VARs) with US data.
Here, for comparability, we deliberately follow current state
of the art, and we follow the canonical framework established
by Bloom (2009) in running a VAR to generate an impulse
response function (IRF) relating the reactions of key model
quantities—in this case, not only industrial production but
also imports—to the underlying impulses that take the form
of shocks to uncertainty.
We contend that as with the application to production, the
payoffs to an uncertainty-based approach can be substantial
in the new setting we propose for modeling trade volatility.
Why? Recall that in the view of Bloom (2009, p. 627):
More generally, the framework in this paper
also provides one response to the “where are
the negative productivity shocks?” critique of
real business cycle theories. In particular, since
second-moment shocks generate large falls in
output, employment, and productivity growth,
it provides an alternative mechanism to first-
moment shocks for generating recessions.
The same might then be said of theories of the trade col-
lapse that rely on negative productivity shocks.19 Moreover,
by the same token, the framework in our paper provides one
response to the “where are the increases in trade frictions?”
objection that is often cited when standard static models are
unable to otherwise explain the amplified nature of trade col-
lapses in recessions, relative to declines in output.
The model above, and evidence below, can thus be
seamlessly integrated with the closed-economy view of
uncertainty-driven recessions, while matching a separate and
distinct aggregate phenomenon that has long vexed interna-
tional economists. Our new approach tackles an enduring
puzzle, a crucial and recurrent feature of international eco-
nomic experience: the highly magnified volatility of trade,
which has been a focus of inquiry since at least the 1930s and
since the onset of the Great Recession has flared again as an
object of curiosity and worry to scholars and policymakers
alike.
A. Testable Hypotheses
To sum up the bottom line, our empirical results expose
new and important stylized facts that are consistent with our
theoretical framework.
First, trade volumes do respond to uncertainty shocks, and
the impacts are quantitatively and statistically significant. In
addition, trade volume responds much more to uncertainty
shocks than does the volume of industrial production; this
magnification shows that there is something fundamentally
different about the dynamics of traded goods supplied via
19Of course, first-moment demand shocks are less controversial in the
context of the Great Trade Collapse.
the import channel, as compared to supply originating from
domestic industrial production.
Second, we will confirm that these findings are true not just
at the aggregate level, but also at the disaggregated level, indi-
cating that the amplified dynamic response of traded goods is
not just a sectoral composition effect. In addition, we find that
the impact and magnification are greatest in durable goods
sectors as compared to nondurable goods sectors, consistent
with the theoretical model where a decrease in the depreci-
ation parameter (interpreted as a decrease in perishability)
leads to a larger response.
The subsequent parts of this section are structured as fol-
lows. The first section briefly spells out the empirical VAR
methods we employ. The second section spells out the data
we have at our disposal, some newly collected, to examine
the differences between trade and industrial production in this
framework. The subsequent sections discuss our findings.
B. Computing the Responses to an Uncertainty Shock
In typical business cycle empirical work, researchers are
often interested in the response of key variables, most of all
output, to various shocks, most often a shock to the level of
technology or productivity. The analysis of such first-moment
shocks has long been a centerpiece of the macroeconomic
VAR literature. Bloom’s (2009) innovation was to construct,
simulate, and empirically estimate a model where the key
shock of interest is a second-moment shock, which is con-
ceived of as an uncertainty shock of a specific form. In his
setup, this shock amounts to an increase in the variance, but
not the mean, of a composite business conditions disturbance
in the model, which can be flexibly interpreted as a demand
or supply shock.
For empirical purposes, when the model is estimated us-
ing data on the postwar United States, changes in the VXO
US stock market volatility index are used as a proxy for the
uncertainty shock. The VXO, and its newer cousin, VIX, pro-
vided by the Chicago Board Options Exchange, have formed
the basis of the most widely traded options-implied volatility
contracts, and they reference the daily standard deviation of
the S&P 500 index over a thirty-day forward horizon. With an
implicit nod to rational expectations, realized volatility was
used to backfill a proxy for VXO in historical periods before
1986 back to 1962 when the VXO is not available. A plot
of this series, scaled to an annualized form and extended to
2012 for use here is shown in figure 5.20
20As Bloom (2009, figure 1) notes, “Pre-1986 the VXO index is unavail-
able, so actual monthly returns volatilities are calculated as the monthly
standard deviation of the daily S&P500 index normalized to the same mean
and variance as the VXO index when they overlap from 1986 onward. Ac-
tual and VXO are correlated at 0.874 over this period. The asterisks indicate
that for scaling purposes the monthly VXO was capped at 50. Uncapped
values for the Black Monday peak are 58.2 and for the credit crunch peak
are 64.4. LTCM is Long Term Capital Management.” For comparability,
we follow exactly the same definitions here and thank Nicholas Bloom for
providing us with an updated series extended to 2012.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
TRADE AND UNCERTAINTY
759
FIGURE 5.—THE UNCERTAINTY INDEX: MONTHLY US STOCK MARKET VOLATILITY, 1962–2012
VXO index and proxies. Capped at 50 (*). From Bloom (2009) and updates. See the appendix.
log(S&P500 stock market
We evaluate the impact of uncertainty shocks using VARs
on monthly data from 1962 (the same as in Bloom) to
February 2012 (going beyond Bloom’s end date of June
2008). The full set of variables, in VAR estimation Cholesky
ordering, are as follows:
in-
dex), stock market volatility indicator, Federal Funds rate,
log(average hourly earnings), log(consumer price index),
hours, log(employment), and log(industrial production). We
do not find our results are sensitive to the Cholesky order-
ing.21 For simplicity, the baseline results we present are esti-
mated using a more basic quadvariate VAR (log stock market
levels, the volatility indicator, log employment, and the log
industrial production or trade indicator).
C. Data
Many of our key variables are exactly as in Bloom (2009):
log industrial production in manufacturing (Federal Reserve
Board of Governors, seasonally adjusted), employment in
manufacturing (BLS, seasonally adjusted), a monthly stock
market volatility indicator as above, and the log of the S&P
500 stock market index. All variables are HP detrended, with
parameter λ = 129,600. Full details are provided in the data
appendix. Collection of these data was updated to February
2012.
However, in some key respects, our data requirements are
much larger. For starters, we are interested in assessing the
21We follow Bloom (2009) exactly for comparability. As he notes, “This
ordering is based on the assumptions that shocks instantaneously influence
the stock market (levels and volatility), then prices (wages, the consumer
price index (CPI), and interest rates), and finally quantities (hours, employ-
ment, and output). Including the stock-market levels as the first variable in
the VAR ensures the impact of stock-market levels is already controlled for
when looking at the impact of volatility shocks.”
response of trade, so we needed to collect monthly import
volume data. In addition, we are interested in computing dis-
aggregated responses of trade and industrial production (IP)
in different sectors, in the aftermath of uncertainty shocks, to
gauge whether some of the key predictions of our theory are
sustained. Thus, we needed to assemble new monthly trade
data (aggregate and disaggregate) as well as new disaggre-
gated monthly IP data.
We briefly explain the provenance of these newly collected
data, all of which are also HP filtered for use in the VARs, as
above. More details of sources and construction are given in
the data appendix.
• US aggregated monthly real import volume. These data
run from 1962:1 to 2012:2. After 1989, total imports
for general consumption were obtained from the USITC
dataweb. From 1968 to 1988, data were collected by hand
from FT900 reports, where imports are only available
from 1968 as F.A.S. (free alongside ship) at foreign port
of export, general imports, seasonally unadjusted; the se-
ries change to C.I.F. (cost, insurance, and freight) in 1974,
and the definition changes to customs value in 1982. Prior
to 1968, we use NBER series 07028, a series that is called
“total imports, free and dutiable” or else “imports for con-
sumption and other”; for the 1962 to 1967 window, this
NBER series is a good match, as it is sourced from the
same FT900 reports as our hand-compiled series. The en-
tire series was then deflated by the monthly CPI.
• US disaggregated monthly real imports. These data run
only from 1989:1 to 2012:2. In each month, total imports
for general consumption disaggregated at the four-digit
NAICS level were obtained from the USITC dataweb.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
760
THE REVIEW OF ECONOMICS AND STATISTICS
All series were then deflated by the monthly CPI. In this
way, 108 sector-level monthly real import series were
compiled.
• US disaggregated monthly industrial production. These
data run only from 1972:1 to 2012:2 at a useful level of
granularity. Although aggregate IP data are provided by
the Fed going back to 1919, the sectorally disaggregated
IP data start only in 1939 for 7 large sectors, with ever finer
data becoming available in 1947 (24 sectors), 1954 (39
sectors), and 1967 (58 sectors). However, it is in 1972 that
IP data are available using the four-digit NAICS classifi-
cation, which permits sector-by-sector compatibility with
the import data above. From 1972, we used Fed G.17 re-
ports to compile sector-level IP indices, yielding data on
98 sectors at the start, expanding to 99 in 1986.
D.
IRFs at Aggregate Level for Trade and IP
The world witnessed an unusually steep decline in inter-
national trade in 2008–2009, the most dramatic since the
Great Depression. International trade plummeted by 30% or
more in many cases. Some countries suffered particularly
badly. For example, Japanese imports declined by about 40%
from September 2008 to February 2009. In addition, the de-
cline was remarkably synchronized across countries. Bald-
win (2009) notes that “all 104 nations on which the WTO
reports data experienced a drop in both imports and exports
during the second half of 2008 and the first half of 2009.”
This synchronization hints at a common cause (Imbs, 2010).
The first evidence we present on the importance of uncer-
tainty shocks for trade uses aggregate data on US real imports
and industrial production (IP). We estimate a vector autore-
gression (VAR) with monthly data from 1962 through 2012,
following the main specification in Bloom (2009) exactly, as
explained above and more fully in the appendix.
Figure 6 presents our baseline quadvariate VAR results
for the aggregate US data, for both log real imports and log
IP, as well as their ratio, all in a row. The impulse response
functions (IRFs) from the VAR are based on a one-period
uncertainty shock where the uncertainty measure increases
by one unit (the measure is an equity market option implied-
volatility index, VXO, all data are HP filtered). In figure 6a,
the upper panel, we employ Bloom’s standard uncertainty
shock series. In figure 6b, the lower panel, to support the idea
of causality, we rely on his “exogenous” uncertainty shock
series that only uses events associated with terrorist attacks,
war, and oil shocks.
The bottom line is very clear from this figure. Look first
at figure 6a. The uncertainty shock is associated with a de-
cline in both industrial production and imports. However, the
response of imports is clearly many times stronger—about
five to ten times as strong on average in the period of peak
impact during year 1. The response of imports is also highly
statistically significant. At its peak, the IRF is 3 or 4 standard
errors below 0, whereas the IRF for IP is only just about 2
standard errors below 0, and only just surmounts the 95%
confidence threshold. To confirm that the response of im-
ports is more negative than the response of IP, the third chart
in row 1 shows the IRF computed when using the log ratio of
real imports to IP: clearly this ratio falls after an uncertainty
shock, and the 95% confidence interval lies below 0.
To provide further evidence and a robustness check, con-
sider figure 6b, where now only the exogenous “clean” un-
certainty shocks indicator from Bloom (2009) is used, scaled
by observed volatility, to purge endogenous uncertainty dy-
namics from the estimations.22 As this figure shows, even if
we restrict attention to these events, which arguably provide
a stricter approach to identification at the cost of a smaller
sample of candidate shocks, we get the same basic finding: a
sharp, negative shock to trade after an uncertainty shock and
a response that is much larger than that seen for industrial
production. We also refer to the appendix where we provide
additional IRF results based on the uncertainty measures by
Baker, Bloom, and Davis (2016) and Berger, Dew-Becker,
and Giglio (2020).
E.
IRFs Disaggregated by Durables and Nondurables for
Trade and IP
Having established empirically that trade reacts more neg-
atively than IP to an uncertainty shock, we next look at the
same responses at a disaggregated level. Specifically, we look
at a key prediction of our model that these differences should
be magnified in the case of more durable goods, as captured
in the theoretical model by the depreciation parameter.
For this we move to the three- or four-digit NAICS level,
sourcing data from USITC dataweb and the Fed G.17 releases
at a monthly frequency starting in 1989. The overlap between
these two sources allows us to work with 51 individual sec-
tors. (A list of NAICS codes at this level of disaggregation,
with accompanying descriptors, is provided in the appendix.)
We reestimate every IRF at this disaggregated level, using the
exact same specification as before and repeating the exercise
for each NAICS sector with imports and IP.
To offer a presentation of the results in a way that cor-
responds to the durable-nondurable distinction, we then ag-
gregate up the IRFs into two bins, corresponding to durable
and nondurable manufacturing sectors, according the NAICS
classification of sectors by the BLS.23 The resulting weighted
average IRFs for months 1 to 12 are presented as sum-
mary statistics in figure 7. The correspondence between the
22Virtually identical results, available on request, are produced when the
unscaled shock is used. Specifically, Bloom (2009) identifies seventeen
high-volatility episodes since the 1960s, such as the assassination of JFK,
the 1970s oil shocks, the Black Monday market crash of October 1987, the
1998 bailout of Long-Term Capital Management, 9/11, and the collapse
of Lehman Brothers in September 2008. These high-volatility episodes are
strongly correlated with alternative indicators of uncertainty.
23See https://www.bls.gov/jlt/jltnaics.htm.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
TRADE AND UNCERTAINTY
761
FIGURE 6.—IRFS AT AGGREGATE LEVEL FOR UNCERTAINTY SHOCKS, PROXIED BY VXO SHOCKS
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Sample is 1962:1–2012:2. The quadvariate VAR Cholesky ordering as in Bloom (2009) is stock market, volatility measure, log employment, followed by either log real imports or log IP. In the top panel, the volatility
measure we use is actual VXO shocks; in the bottom panel, we use Bloom’s exogenous VXO-scaled shocks. No rescaling of shocks. 95% confidence intervals shown. See text and appendix.
theoretical model’s predictions and the estimated cumulative
responses over the one-year horizon is notable. In nondurable
goods sectors, the response to uncertainty shocks is small. In
durable goods sectors, the response to uncertainty shocks is
larger (two times). In both cases, the responses in real imports
are larger than in IP (two times), and that is confirmed when
we look at the response of the ratio of real imports to IP:
the durable response is large and statistically significant; the
nondurable response is neither. Thus, on a key dimension, the
disaggregated responses for durable and nondurable manu-
facturing sectors also accord with the theoretical mechanism
we propose.24 However, since the confidence intervals of the
IRFs largely overlap for the durable-nondurable bins, our pre-
ferred interpretation is to emphasize the qualitative result of
a significant response for durables. We urge more caution
about the precise point estimates.
Finally, we refer to the appendix where we provide addi-
tional robustness checks exploiting the granting of Permanent
Normal Trade Relations (PNTR) status to China (see Pierce
& Schott, 2016; Handley & Limão, 2017). There we employ
US import data from China and the European Union at the
four-digit level.
F.
IRFs Disaggregated by Source Country Fixed Costs
24In the appendix, we offer further results by classifying industries ac-
cording to End Use categories.
Next, we look at another key prediction of our model:
that differences in responses to uncertainty shocks should be
762
THE REVIEW OF ECONOMICS AND STATISTICS
FIGURE 7.—AVERAGE REAL IMPORT AND IP IRFS COMPARED IN MONTHS 1–12 FOR MANUFACTURING INDUSTRIES, BY BLS DURABLE-NONDURABLE BINS, WITH
UNDERLYING IRF ESTIMATION AT THE THREE- OR FOUR-DIGIT NAICS LEVEL
Cumulative IRF for months 1–12. Flow data at the three- or four-digit NAICS level, aggregated up to BLS durable-nondurable bins for manufacturing industries using output weights from the Fed’s US 2002 makeuse
table. Sample is 1989:1–2012:2. Imports from USITC dataweb, deflated by CPI; IP from Fed G.17; all other data as in Bloom (2009), updated. Uncertainty shocks for quadvariate VARs. Ordering is stock market,
volatility, log employment, followed by either log real imports or log IP. Data updated through February 2012. No rescaling of shocks. See text and appendix.
magnified when fixed costs of importing are higher, as cap-
tured in the theoretical model by the fF parameter.
To test this, we divide monthly US imports into two bins,
for source countries that are in the lowest and highest quartiles
of the World Bank’s Ease of Doing Business (EODB) index.25
We think this is a reasonable proxy for variations in country-
specific fixed (rather than variable) costs of doing business
that would affect firms trying to export from that source to
the United States.
Figure 8 contains the results of this exercise, conducted on
the sample period 1989:1 to 2012:12. The left panel shows
that US imports from countries with high fixed costs (low
EODB) have large-amplitude responses to our measure of un-
certainty shocks, but the right panel shows that countries with
low fixed costs (high EODB) have relatively small-amplitude
responses in comparison. Thus, our results seem consistent
with the model’s prediction, although the confidence intervals
in the two panels overlap quantitatively.
VII. Can the Great Trade Collapse of 2008–2009
Be Explained?
We have shown that empirical evidence over recent
decades suggests a tight link between uncertainty shocks and
trade contractions, especially for durable goods, in a way that
is qualitatively consistent with our theoretical framework.
Now we wrap up by asking a rather more demanding ques-
tion: To what extent can this approach, which takes second-
moment uncertainty shocks seriously as a main driver, pro-
25See http://www.doingbusiness.org/rankings.
vide a quantitatively plausible account of the Great Trade
Collapse of 2008–2009?
We thus conclude by presenting a simulation exercise, us-
ing our baseline aggregate VAR from section VI, to argue
that this mechanism could indeed have been an important
contributing factor, even if other forces were in play. To do
this, we need to construct a set of plausible exogenous shocks
to the uncertainty variable that match its observed outcomes
in the crisis and then feed them into the VAR model to obtain
predicted paths for imports and IP that can be compared to
actual post-2008 outcomes.
As is well known, the four months following the collapse
of Lehman Brothers were characterized by strong increases
in uncertainty as measured by the volatility index VXO from
September to December 2008, with elevated volatility persist-
ing into the first quarter of 2009. To simulate this shock, we
choose to feed into the model a series of exogenous volatility
shocks that generate a path of volatility similar to that ob-
served. That is, we assume that the dynamics are driven pri-
marily by an exogenous shock to the system from the volatil-
ity index and the subsequent endogenous responses of the
variables in the system.
We found in the baseline VAR that the own-response of
volatility to itself in the orthogonalized impulse response
(not shown here) is about 3, with significant short-term per-
sistence. In mid-2008, the real-world data showed a VXO
level of 20, which we take as a starting value for our sim-
ulation and which in the VAR we then subject to a se-
ries monthly shocks of +20,+5,+5,+5,+5,+5,+5 starting in
September 2008. Through endogenous VAR dynamics, these
shocks take simulated VXO up to just over 80 at peak (via
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
TRADE AND UNCERTAINTY
763
FIGURE 8.—IRFS AT AGGREGATE LEVEL FOR HIGH- AND LOW-FIXED COST SOURCE COUNTRIES (LOW AND HIGH EODB, RESPECTIVELY)
Sample is 1989:1–2012:12. The quadvariate VAR Cholesky ordering as in Bloom (2009) is stock market, volatility measure, log employment, followed by either log real imports or log IP. As the volatility measure,
we use actual VXO shocks. No rescaling of shocks. 95% confidence intervals shown. See text and appendix.
FIGURE 9.—ACTUAL AND SIMULATED VXO, REAL IMPORTS, AND IP DURING AND AFTER THE 2008 LEHMAN UNCERTAINTY SHOCK
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
cumulation/persistence), and the additional shocks keep the
simulated VXO very elevated for several months before the
decay commences. In actuality, the real-world VXO rose
from its precrisis mean of about 20 to almost 90 in the last
quarter of 2008, a shift of +70, and thus the simulated im-
pulses we impose create a close match to the actual path of
VXO quite well, as shown in figure 9, in the left panel. Could
such shocks generate a large trade collapse with a magnifi-
cation effect present?
Yes, to some extent. Given these “Lehman shocks” im-
posed to the VXO process starting from its starting level
of 20, the model-implied and the actual observed responses
of IP and real imports are shown in figure 9, in the right
panel, relative to a September 2008 reference level. As can
be seen, the model is capable of explaining a large frac-
tion of the actual observed IP response, especially up to
six months out. It is also capable of explaining a decent
fraction of the real import response over a similar horizon.
Overall, these simulations show that if we push hard on
these very specific shocks, our model can explain perhaps
around half of the import collapse out to the twelve-month
horizon.
764
THE REVIEW OF ECONOMICS AND STATISTICS
All that said, we want to be cautious and not claim too
much: we can see that, especially in early to mid-2009, some
additional factors must have been at work that are not cap-
tured by the uncertainty shock. This suggests our approach
should be viewed as a partial attempt and complementary to
other explanations put forward in the literature on the Great
Trade Collapse, such as trade credit shocks, especially in the
acute phase of the crisis (see section II).
In their survey of that literature, Bems et al. (2013) note
that no study has so far integrated the various competing ex-
planations into a unified framework. Nevertheless, based on
estimates from various independent papers but excluding the
role of second-moment shocks, they loosely suggest that 65%
to 80% of the trade collapse could be attributed to composi-
tional effects associated with changes in final expenditure and
trade-intensive durable goods in particular. A further 15% to
20% are due to credit supply shocks. Inventory adjustments as
an amplification mechanism may account for around 20%.26
Our work suggests that the latter share may be larger be-
cause of second-moment shocks, not least since inventories
are relevant for both intermediate and final goods. But a pre-
cise decomposition is yet to be carried out and remains as
an important topic for future work. Finally, we believe that
uncertainty shocks may also provide a better handle on the
recovery dynamics as shown in figure 9, capturing both the
decline and the resurgence of trade.
VIII. Conclusion
We argue that trade can be modeled as reacting to uncer-
tainty shocks in theory and in practice. We introduce second-
moment uncertainty shocks into a dynamic, open-economy
model. Firms import inputs and due to fixed costs of ordering
follow an optimal s, S inventory policy. We show that elevated
uncertainty leads firms to shift down their s, S bounds, which
induces a sharp contraction of international trade flows fol-
lowed by a swift recovery. In contrast, output remains unaf-
fected, assuming other shocks are absent. Uncertainty shocks
can therefore explain why trade is more volatile than domes-
tic economic activity.
Qualitatively, our empirical evidence suggests a tight link
between uncertainty shocks and trade contractions, and we
can also show substantial heterogeneity in responses at the
sectoral level, for both imports and industrial production, in
a way consistent with our proposed model.
Quantitatively, our simulation results offer a partial ex-
planation for the Great Trade Collapse of 2008–2009, and
potentially for previous trade slowdowns, in a way that dif-
fers from the conventional static trade models or dynamic
inventory models seen before. The introduction of second-
moment shocks may be useful as a driver since the required
first-moment shocks are either absent on the impulse side or
26These estimates do not necessarily sum up to 100% since they are ob-
tained from independent papers.
insufficient on the propagation side (for plausible parameters)
to fully explain the events witnessed.
REFERENCES
Alessandria, G., H. Choi, J. Kaboski, and V. Midrigan, “Microeconomic Un-
certainty, International Trade, and Aggregate Fluctuations,” Journal
of Monetary Economics 69 (2015), 20–38.
Alessandria, G., J. Kaboski, and V. Midrigan, “The Great Trade Collapse
of 2008–09: An Inventory Adjustment?” IMF Economic Review 58
(2010a), 254–294.
——— “Inventories, Lumpy Trade, and Large Devaluations,” American
Economic Review 100 (2010b), 2304–2339.
——— “US Trade and Inventory Dynamics,” American Economic Review
101 (2011), 303–307.
Amiti, M., and D. Weinstein, “Exports and Financial Shocks,” Quarterly
Journal of Economics 126 (2011), 1841–1877.
Baker, S., N. Bloom, and S. Davis, “Measuring Economic Policy Uncer-
tainty,” Quarterly Journal of Economics 131 (2016), 1593–1636.
Baldwin, R., ed., The Great Trade Collapse: Causes, Consequences and
Prospects (London: Centre for Economic Policy Research, 2009).
Baldwin, R., and P. Krugman, “Persistent Trade Effects of Large Exchange
Rate Shocks,” Quarterly Journal of Economics 104 (1989), 635–
654.
Behrens, K., G. Corcos, and G. Mion, “Trade Crisis? What Trade Crisis?”
this REVIEW 95 (2013), 702–709.
Bems, R., R. Johnson, and K.-M. Yi, “Vertical Linkages and the Collapse of
Global Trade,” American Economic Review 101 (2011), 308–312.
——— “The Great Trade Collapse,” Annual Review of Economics 5 (2013),
375–400.
Berger, D., I. Dew-Becker, and S. Giglio, “Uncertainty Shocks as Second-
Moment News Shocks,” Review of Economic Studies 87 (2020),
40–76.
Bernanke, B., “Irreversibility, Uncertainty, and Cyclical Investment,” Quar-
terly Journal of Economics 98 (1983), 85–106.
Bloom, N., “The Impact of Uncertainty Shocks,” Econometrica 77 (2009),
623–685.
Bloom, N., S. Bond, and J. Van Reenen, “Uncertainty and Investment Dy-
namics,” Review of Economic Studies 74 (2007), 391–415.
Bloom, N., M. Floetotto, N. Jaimovich, I. Saporta-Eksten, and S. Terry, “Re-
ally Uncertain Business Cycles,” Econometrica 86 (2018), 1031–
1065.
Bown, C., ed., The Great Recession and Import Protection: The Role of
Temporary Trade Barriers (London: Centre for Economic Policy
Research and World Bank, 2011).
Bown, C., and M. Crowley, “Import Protection, Business Cycles, and Ex-
change Rates: Evidence from the Great Recession,” Journal of In-
ternational Economics 90 (2013), 50–64.
Bricongne, J., L. Fontagné, G. Gaulier, D. Taglioni, and V. Vicard, “Firms
and the Global Crisis: French Exports in the Turmoil,” Journal of
International Economics 87 (2012), 134–146.
Campa, J., and L. Goldberg, “The Evolving External Orientation of Manu-
facturing Industries: Evidence from Four Countries,” NBER work-
ing paper 5919 (1997).
Carrière-Swallow, Y., and L. Céspedes, “The Impact of Uncertainty Shocks
in Emerging Economies,” Journal of International Economics 90
(2013), 316–325.
Chor, D., and K. Manova, “Off the Cliff and Back? Credit Conditions and
International Trade during the Global Financial Crisis,” Journal of
International Economics 87 (2012), 117–133.
Dixit, A., “Entry and Exit Decisions under Uncertainty,” Journal of Political
Economy 97 (1989), 620–638.
Eaton, J., and S. Kortum, “Trade in Capital Goods,” European Economic
Review 45 (2001), 1195–1235.
Eaton, J., S. Kortum, B. Neiman, and J. Romalis, “Trade and the Global
Recession,” American Economic Review 106 (2016), 3401–3438.
Eichengreen, B., and K. H. O’Rourke, “A Tale of Two Depressions,”
VoxEU.org (2010).
Elliott, G., I. Komunjer, and A. Timmermann, “Estimation and Testing
of Forecast Rationality under Flexible Loss,” Review of Economic
Studies 72 (2005), 1107–1125.
Engel, C., and J. Wang, “International Trade in Durable Goods: Understand-
ing Volatility, Cyclicality, and Elasticities,” Journal of International
Economics 83 (2011), 37–52.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
TRADE AND UNCERTAINTY
765
Evenett, S., ed., Tensions Contained … For Now: The 8th GTA Report (Lon-
don: Centre for Economic Policy Research, 2010).
Feenstra, R. C., and G. H. Hanson, “Productivity Measurement and the Im-
pact of Trade and Technology on Wages: Estimates for the U.S.,
1972–1990,” Quarterly Journal of Economics 114 (1999), 907–
940.
Gopinath, G., O. Itskhoki, and B. Neiman, “Trade Prices and the Global
Trade Collapse of 2008–2009,” IMF Economic Review 60 (2012),
303–328.
Gourio, F., M. Siemer, and A. Verdelhan, “International Risk Cycles,” Jour-
nal of International Economics 89 (2013), 471–484.
Grossman, S., and G. Laroque, “Asset Pricing and Optimal Portfolio Choice
in the Presence of Illiquid Durable Consumption Goods,” Economet-
rica 58 (1990), 25–51.
Guiso, L., and G. Parigi, “Investment and Demand Uncertainty,” Quarterly
Journal of Economics 114 (1999), 185–227.
Haddad, M., A. Harrison, and C. Hausman, “Decomposing the Great Trade
Collapse: Products, Prices, and Quantities in the 2008–2009 Crisis,”
NBER working paper 16253 (2010).
Handley, K., “Exporting under Trade Policy Uncertainty: Theory and Evi-
dence,” Journal of International Economics 94 (2014), 50–66.
Handley K., and N. Limão, “Trade and Investment under Policy Uncer-
tainty: Theory and Firm Evidence,” American Economic Journal:
Policy 7 (2015), 189–222.
——— “Policy Uncertainty Trade, and Welfare: Theory and Evidence
for China and the United States,” American Economic Review 107
(2017), 2731–2783.
Hassler, J., “Variations in Risk and Fluctuations in Demand: A Theoretical
Model,” Journal of Economic Dynamics and Control 20 (1996),
1115–1143.
Hornok, C., and M. Koren, “Per-Shipment Costs and the Lumpiness of
International Trade,” this REVIEW 97 (2015), 525–530.
Imbs, J., “The First Global Recession in Decades,” IMF Economic Review
58 (2010), 327–354.
Kee, H., C. Neagu, and A. Nicita, “Is Protectionism on the Rise? Assessing
National Trade Policies during the Crisis of 2008,” this REVIEW 95
(2013), 342–346.
Kropf, A., and P Sauré, “Fixed Costs Per Shipment,” Journal of Interna-
tional Economics 92 (2014), 166–184.
Leibovici, F., and M. Waugh, “International Trade and Intertemporal Sub-
stitution,” Journal of International Economics 117 (2019), 158–174.
Levchenko, A., L. Lewis, and L. Tesar, “The Collapse of International Trade
during the 2008–2009 Crisis: In Search of the Smoking Gun,” IMF
Economic Review 58 (2010), 214–253.
Limão, N., and G. Maggi, “Uncertainty and Trade Agreements,” American
Economic Journal: Microeconomics 7 (2015), 1-42.
McDonald, R., and D. Siegel, “The Value of Waiting to Invest,” Quarterly
Journal of Economics 101 (1986), 707–727.
Nadiri, M., and I. Prucha, “Estimation of the Depreciation Rate of Physical
and R&D Capital in the U.S. Total Manufacturing Sector,” Economic
Inquiry 34 (1996), 43–56.
Pierce, J., and P. Schott, “The Surprisingly Swift Decline of US Manu-
facturing Employment,” American Economic Review 106 (2016),
1632–1662.
Pindyck, R., “Irreversibility, Uncertainty, and Investment,” Journal of Eco-
nomic Literature 29 (1991), 1110–1148.
Ramey, V., “Inventories as Factors of Production and Economic Fluctua-
tions,” American Economic Review 79 (1989), 338–354.
Ramey, V., and K. West, “Inventories” (pp. 863–923), in J. Taylor and M.
Woodford, eds., Handbook of Macroeconomics (Amsterdam: Else-
vier, 1999).
Scarf, H., “The Optimality of (S,s) Policies in the Dynamic Inventory Prob-
lem” (pp. 196–202), in K. Arrow, S. Karlin, and P. Suppes, eds.,
Mathematical Methods in the Social Sciences (Palo Alto, CA: Stan-
ford University Press, 1959).
Taglioni, D., and V. Zavacka, “Innocent Bystanders: How Foreign Uncer-
tainty Shocks Harm Exporters,” European Bank for Reconstruction
and Development working paper 149 (2012).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
r
e
s
t
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
0
2
4
7
4
9
1
8
8
1
3
4
6
/
r
e
s
t
_
a
_
0
0
8
8
5
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3