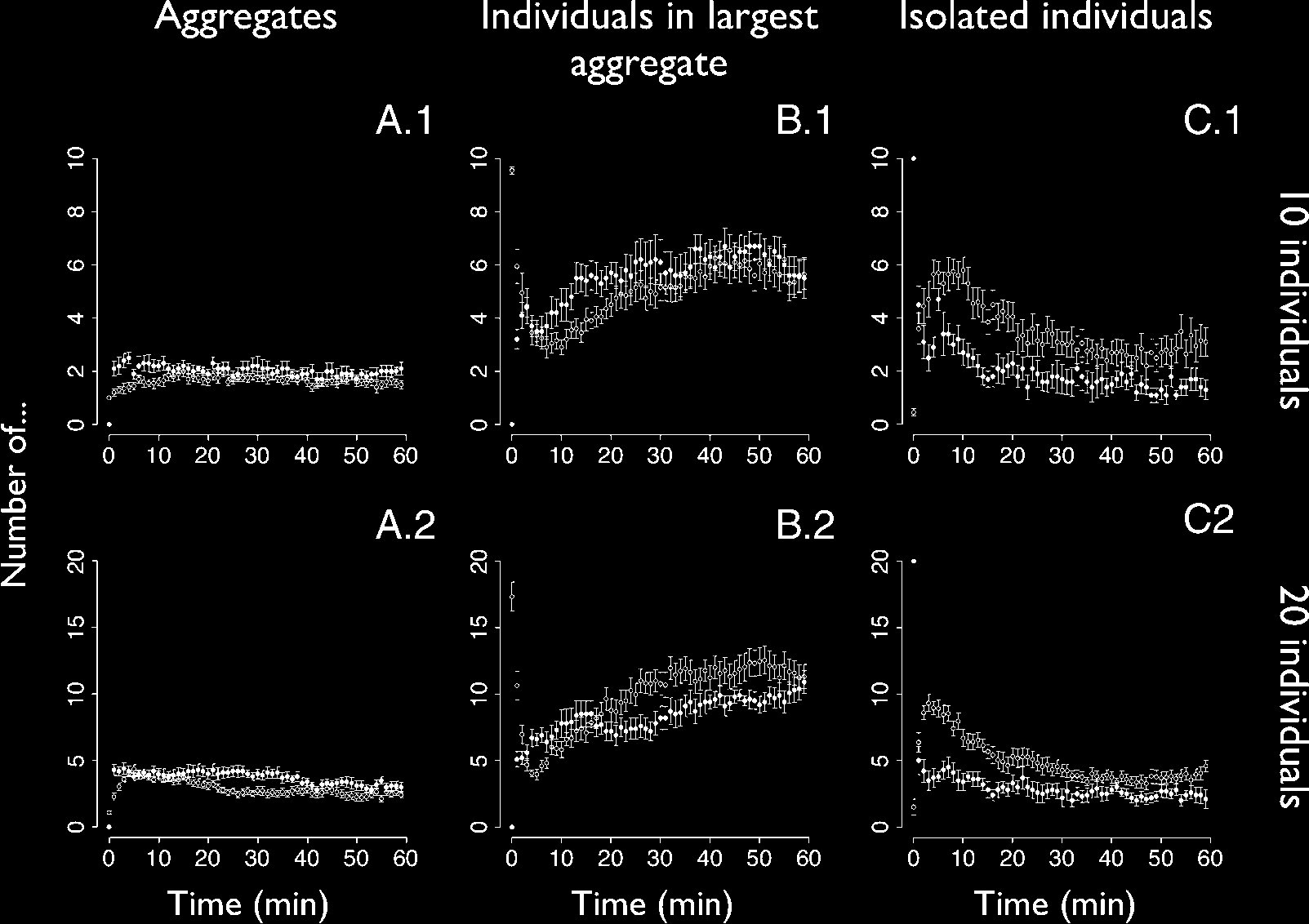The Embodiment of Cockroach
Aggregation Behavior in a
Group of Micro-robots
Simon Garnier*,**
Universite´ Paul Sabatier
Christian Jost**
Universite´ Paul Sabatier
Abstract We report the faithful reproduction of the self-organized
aggregation behavior of the German cockroach Blattella germanica with
a group of robots. We describe the implementation of the biological
model provided by Jeanson et al. in Alice robots, and we compare the
behaviors of the cockroaches and the robots using the same
experimental and analytical methodology. We show that the
aggregation behavior of the German cockroach was successfully
transferred to the Alice robot despite strong differences between
robots and animals at the perceptual, actuatorial, and computational
级别. This article highlights some of the major constraints one may
encounter during such a work and proposes general principles to
ensure that the behavioral model is accurately transferred to the
artificial agents.
Jacques Gautrais**
National Center for Scientific Research
Masoud Asadpoury,z
University of Tehran
Gilles Caprari§,z
ETH Zu¨rich
Raphae¨l Jeanson**
National Center for Scientific Research
Anne Grimal**
National Center for Scientific Research
Guy Theraulaz**
National Center for Scientific Research
关键词
Swarm robotics, autonomous robots,
self-organization, biomimetic robotics,
aggregation
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
A
r
t
我
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
1 介绍
Collective behaviors in social animals can be very impressive. They range from the coordinated
displacement of thousands of individuals [25, 52] to the building of complex structures [31, 44] 和
to the proper allocation of tasks among the members of a group [8, 18, 36]. During the last forty
年, a growing body of studies has been interested in understanding the mechanisms underlying
* Contact author.
** Centre de Recherches sur la Cognition Animale, UMR 5169, Baˆt 4R3, Universite´ Paul Sabatier – 法国国家科学研究中心, 118 Route de Narbonne,
F-31062 Toulouse cedex 4, 法国. 电子邮件: simon.garnier@cict.fr (S.G.); jost@cict.fr (C.J.); gautrais@cict.fr ( J.G.); jeanson@cict.fr (R.J.);
grimal@cict.fr (A.G.); theraula@cict.fr (G.T.)
y Robotics and AI Lab, ECE Dept, University of Tehran, 伊朗. 电子邮件: masoud.asadpour@epfl.ch
z This work was carried out while the author was at the Autonomous Systems Lab at EPFL, now moved to ETH Zu¨rich.
§ Autonomous Systems Lab, ETH Zu¨rich, ETH Zentrum CLA E31, Tannenstrasse 3, CH-8092 Zu¨rich, 瑞士. 电子邮件: g.caprari@
ieee.org
n 2008 麻省理工学院
人工生命 14: 387 – 408 (2008)
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
these biological systems. We now know that most of these collective behaviors can be seen as due to
decentralized systems made of autonomous units that are distributed in the environment and that
can be described as following simple probabilistic stimulus-response behaviors [9]. This peculiar
mode of organization, often based on self-organized processes, combines efficiency with flexibility,
robustness, and distributedness [7].
For about 20 年, such features have attracted people who are working on research topics
far from the study of animal behavior [9]. Probably the best-known example is the development
during the 1990s, by Dorigo and his colleagues [22, 23], of the so-called ant algorithms for routing
优化. But other research fields are now tightly linked with the study of collective behaviors
in social animals, collective robotics being one of them [2]. Aiming at controlling the behaviors of
groups of robots, swarm robotics was often inspired by the collective abilities demonstrated by social
动物, and particularly by social insects [56]. 的确, social animals represent promising models
for the decentralized organization and coordination of many autonomous robots [7]. 为了 15 年,
several studies have used bio-inspired robot controllers to deal with collective behaviors as manifold
as aggregation [46], 觅食 [57], task allocation [40], stick pulling [35], and site selection [28].
尽管如此, robotics also offers interesting tools for the study of animal behavior [62]. 最近
review by Webb [63] lists several works that studied animal behavior through robotic embodiments
and argues that a robotic implementation of a biological mechanism provides a strong ‘‘proof in
principle’’ (stronger than any computer simulation) that this mechanism really works as suggested.
Most of these works were concerned with motor and sensorimotor control, 导航, or learn-
ing in animals. Only a few of them dealt with biological self-organized behaviors or addressed ques-
tions about collective behaviors in animals. 例如, Beckers et al. [4], Holland and Melhuish
[34], and Melhuish et al. [48] led a series of studies about ant-inspired object clustering and sorting by
groups of robots. Their main goal was to design robot controllers, but they also discuss their results
in the context of biological stigmergic processes (stigmergy is a coordination process in which the
result of the previously accomplished work guides the animal’s next tasks [30, 58]). The work by
Kube and Bonabeau [41] on cooperative transport of objects by a group of robots can certainly be
considered as more biology-oriented. Though their results did not display very effective collective
运输, their robotic embodiment nevertheless was intended to display the first formalized model
of cooperative transport of prey by ants. 最后, whatever the main purpose of a robotic em-
bodiment of an animal collective behavior is, it remains an interesting means to test and to explore its
特性, since it shares with the animal the physics, constraints, and opportunities of the real world
[62, 63].
In the context of collective behaviors a robotics embodiment may fulfill an additional function.
Embodied agents could be used to ‘‘infiltrate’’ groups of animals and influence their individual and
collective behaviors [17]. Some recent works point in that direction. 例如, Michelsen et al.
[49] designed a mechanical model of a dancing bee to investigate the role of various components of
the waggle dance in the transfer of information to follower bees. Bo¨ehlen [6] performed a co-
habitation experiment between a robot and three chickens and identified cues that can be used to
increase the acceptance of the robot by the birds. As another example, Vaughan et al. [61] proposed
a behavioral algorithm for a robot that is able to control the displacement of a group of ducks inside
a closed arena. Fernandez-Juricic et al. [27] used birdlike robots to manipulate the behavior of
individuals and study the responses of flock members under different ecological and social con-
版本. As a last example, the recent LEURRE project1 has proposed to provide a general meth-
odology for the design and control of mixed societies made up of real animals and autonomous
artificial agents [11].
Getting a robot to become accepted by an animal as its conspecific does not necessarily require a
perfect matching between the artificial and the biological agents. An artificial decoy mimicking some
particular stimuli is often sufficient to induce a specific behavior in the animal [17]. 然而, 在里面
case of a mixed society that relies on self-organized behaviors, it can be necessary to accurately
1 http://leurre.ulb.ac.be
388
人工生命量 14, 数字 4
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
A
r
t
我
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
imitate with robots the relevant individual and collective animal behaviors in a qualitative as well as in
a quantitative sense. 的确,
in a recent theoretical study, Gautrais et al. [29] showed that it is
sufficient to modify the quantitative behavior of five individuals within a group of twenty cock-
roaches in order to change profoundly their self-organized aggregation pattern. This result empha-
sizes the need for precise compatibility between animal’s and artificial agent’s individual behaviors.
在本文中, we thus address the problem of accurately reproducing a self-organized biological
behavior with a group of small autonomous robots. We choose to study a grouping behavior, 哪个
is probably the most common collective behavior among living organisms. Grouping occurs in a
wide range of taxa, including bacteria, arthropods, fish, birds, and mammals [19, 50, 51]. More pre-
cisely, we report here a detailed description of the quantitative reproduction of the self-enhanced
aggregation behavior of the German cockroach Blattella germanica with groups of 10 和 20 robots.
The behavioral model we used to perform this embodiment was described by Jeanson et al. [37,
38]. They characterized the individual and collective behaviors of B. germanica within a descriptive
framework that considers almost all behaviors as probabilistic. This descriptive methodology is
common in studies of self-organized behaviors in biology [9] and offers a great advantage for our
工作: Because it describes the behavioral output of animals, it is independent of the perceptual
and cognitive process underlying such output. It therefore becomes possible to implement a self-
organized behavior in an artificial system with perceptual and cognitive abilities that can be very dif-
ferent from the biological model, provided that the artificial system has access to the information
required for the behavioral model to work.
在本文中, we will first summarize the biological model of aggregation we used and then explain
in detail how this model was implemented in Alice mini-robots (部分 2). We will also emphasize the
difficulties encountered during the embodiment process and the solutions applied to solve these
问题. In a second part, we will report the experimental validation of this implementation (秒-
的 3). In particular we will compare the measurements of individual and collective behaviors of
robots with the same measurements made by Jeanson et al. [37, 38] on cockroaches. We will precisely
describe the analytical tools used to quantify behaviors in both insects and robots. 最后, 我们将
discuss the general problems we encountered when porting the animal behavior to the robots.
2 Materials and Methods
在这个部分, we summarily describe the biological and artificial systems used in our work, followed
by an overview of our experimental setup and a detailed description of the behavioral model of ag-
gregation and its implementation in the robots.
2.1 The Biological System: First-Instar Larvae of Blattella germanica
The German cockroach, 乙. germanica, is a worldwide urban pest, which lives in close association with
人类 [55]. It is commonly found in kitchens, restaurants, and supermarkets. This species presents
a rudimentary type of social organization and thus could be qualified as presocial. 乙. germanica
commonly forages at night. During the day, this insect rests hidden (under kitchen appliances, sinks,
behind baseboards, ETC。), forming mixed and dense aggregates of individuals of both sexes and all
developmental stages, especially at low external humidity [16, 43].
The behavioral model was developed from experiments conducted with first-instar larvae of B.
germanica (24 h old). At this developmental stage, the body is about 3 mm long (excluding the an-
tennae) 和 2 mm wide, and the antenna length is 3 毫米. The individuals do not present any poly-
morphism (IE。, the existence of two or more forms of individuals within the same animal species) 或者
any sexual attraction. 看 [37, 38] for more details about the origin and the breeding of the animals.
2.2 The Artificial System: Alice Micro-robots
The Alice micro-robots were designed at the EPFL (洛桑, 瑞士) [12]. They are very
small robots (22 (西德:3) 21 (西德:3) 20 毫米) with a maximum speed of 40 mm s-1. They are equipped with two
人工生命量 14, 数字 4
389
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
A
r
t
我
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
watch motors with wheels and tires. Four infrared sensors and transmitters are used for obstacle
detection and local communication among Alices. Energy is provided by a nickel metal hydride
rechargeable battery allowing an autonomy of about 6 h in the configuration used during this study.
The Alice robots have a microcontroller PIC16LF877 with 8 Kb of flash EPROM memory,
368 bytes of RAM, and no built-in float operations. The implementation of the behavioral model
should thus be as parsimonious as possible, rely on integer operations, and avoid floating point
运营. Programming is done with the integrated development environment of the CCS-C compiler,
and the compiled programs are downloaded in the Alice memory with the PIC-downloader software.2
2.3 实验装置
The behavioral model was built from experiments performed in a uniform environment to avoid any
spatial heterogeneities that might bias the behavior of the cockroaches. The experimental setup used
with cockroaches consisted of a circular arena with diameter 11 cm and height 3 毫米, covered by a
glass plate (看 [37, 38] for further details).
Experiments with robots were conducted in the same kind of experimental setup. At this point
we have to consider the scale difference between a cockroach larva and the robot. A cockroach larva
是关于 3 mm long, while the Alice robot is 22 mm long. 还, cockroaches move at approximately
10 mm s-1, while the Alice robot has a maximal speed of 40 mm s-1. We choose to scale up from the
experimental system used with cockroaches by a factor of four: the Alice moves at maximal speed,
the arena has a diameter of 50 厘米, and all parameters with length units will be multiplied by four.
Note that on this scale the Alice robots are still double the size of a cockroach.
2.4 The Behavioral Model
This section summarizes the individual behavioral model reported in Jeanson et al. [37, 38]. 为了
further details, refer to the cited articles.
The radial distribution of cockroaches during the experiments showed that the larvae (哪些是
dropped in the center of the arena) tended to reach the periphery of the arena and stay in an external
ring (0.5 cm wide) for more than 50% of their time (见图 1). This is an example of thigmotactic
行为, 那是, a tendency to decelerate upon contact with the arena wall and remain in antennal
contact with it. We can thus subdivide the arena into a central zone and a peripheral zone. 这
analysis in Jeanson et al. [37] showed that cockroaches move at approximately constant speed in the
central zone. Their movement in that zone is a correlated random walk characterized by a constant
rate per unit time of changing direction and a forward-oriented turning-angle distribution. 在里面
peripheral zone, cockroaches follow the arena wall at approximately constant speed with a constant
rate of leaving and reentering the central zone. 此外, cockroaches can stop at any moment,
stay motionless for some time, and then move again.
Most of these processes are memoryless, 那是, the cockroaches have a constant probability per
unit time of changing state (from moving straight to turning, from moving to stopping, or leaving
the periphery): 换句话说, the probability of changing from state a to state b between time t and
time t + dt is constant and independent of the time already spent in state a. 因此, the time to remain
in a given state is exponentially distributed, and the rate of change can be estimated by survival curve
分析 [32]. A survival curve analysis consists of plotting on a log-linear scale the proportion of
individuals that remain in a given state as a function of the time (or distance) elapsed since the
beginning of this state. On this log-linear scale (provided that the process is truly memoryless), 这
decay of the proportion will follow a straight line (见图 2):
f ðtÞ ¼ log e-kt
(西德:1)
(西德:2) ¼ (西德:7)kt:
2 http://www.ehl.cz/pic/
390
人工生命量 14, 数字 4
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
A
r
t
我
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
数字 1. Radial distribution of Alice robots (black line) and cockroaches (gray polygon) in the arena during 60 min of free
步行.
The slope k of this straight line will give us the rate of changing state, and its reciprocal 1
k will give
us the mean time (or distance) to remain in the given state.
In contrast to the simple exponential distributions mentioned above, the stop times (要么在
center or in the periphery) followed a distribution that can be described as the sum of two expo-
nential distributions (we call such a distribution a biexponential distribution). On a log-linear scale the
decay of the proportion of individuals that remain stopped is described by (见图 3)
f ðtÞ ¼ log pe-k1t þ ð1 (西德:7) pÞe-k2t
(西德:1)
(西德:2)
This distribution can be explained by the cockroach’s being in either one of two stop states: A
short one (with mean stop time 1/k1, the animal shows some activity) and a long one (与平均值
stop time 1/k2, the animal does not show any activity), with probability p of being in the short state
[37, 38].
Interactions between individuals were studied by Jeanson et al. [38]. The stopping behavior of a
cockroach was obtained by analyzing the fraction of moving cockroaches that stopped when en-
countering a group of N stopped cockroaches (1 V N V 3). Note that the moving cockroach only
perceives its conspecifics in its immediate neighborhood. The fraction of stops increased with the
number of stopped cockroaches in the neighborhood. The spontaneous rate of starting to move for
a cockroach stopped in a cluster was deduced from the survival curves of aggregate lifetimes. 这些
lifetimes also followed a biexponential distribution (again interpreted as two stop states), 和
rates of leaving an aggregate (k1 and k2), as well as the probability of being in a short stop state ( p),
decreased with increasing number of neighbors.
The model (见图 4 for a schematic description of the behavioral model and Tables 1 和
2 for parameter values) was first implemented in computer simulations. Details about the simula-
tion can be found in [37] for the individual movement, 并在 [38] for the collective implementation.
简而言之, a spatially explicit individual-based model was designed to explore model predictions
by Monte Carlo simulations. In order to assess the model validity, a comparison between model
predictions and real experiments was performed. Collective behaviors were studied by putting 10 或者
人工生命量 14, 数字 4
391
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
A
r
t
我
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
数字 2. Survival curve of the Alice wall-following times, with the fitted regression line (solid) and the original cockroach
regression line (dashed).
20 cockroaches into an experimental arena. A camera placed above the arena was coupled with a
电脑, and image-processing software computed the position of each individual every 10 s
期间 60 min. Two cockroaches were assumed to belong to the same aggregate if their
interindividual distance was less than or equal to 1 厘米. The experimental data and the simulation
data were then processed to obtain the size of the largest aggregate every 10 s. The comparison
between experimental results and simulation results showed good agreement between the model and
the biological system on the individual level as well as on the collective level [37, 38].
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
A
r
t
我
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
数字 3. Survival curve of the Alice stop times, with the fitted regression line (solid) and the original cockroach regression
线 (dashed). These stop times are for a single Alice robot (without neighbors).
392
人工生命量 14, 数字 4
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
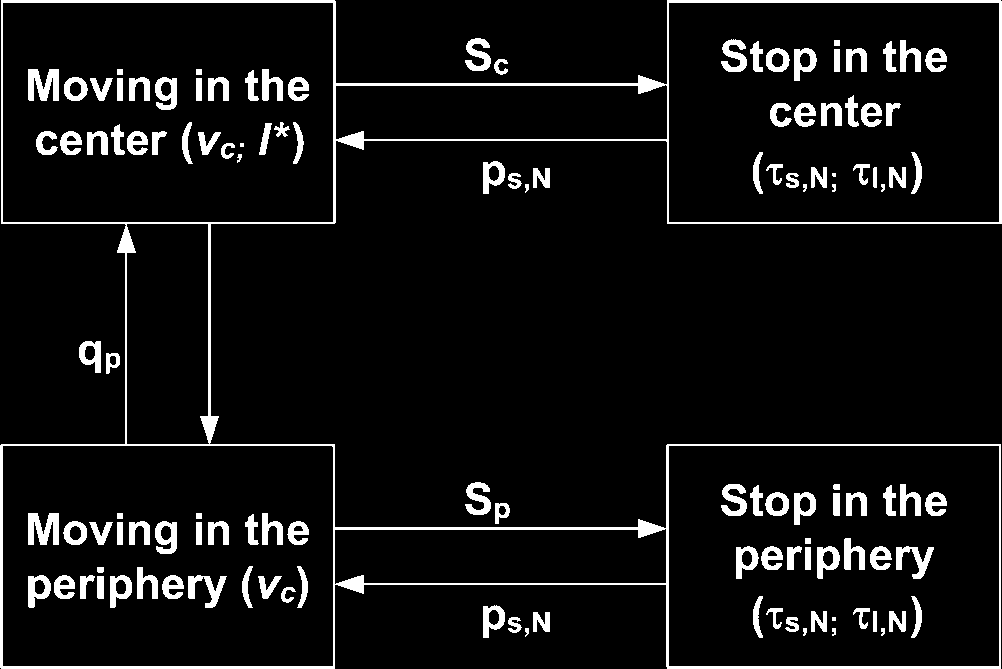
数字 4. The behavioral model of cockroach displacement. Parameters are: speed in the center, vc; speed in the
周边, vp; mean free transport path l*; rate to quit the periphery, qp; rate of stopping in the center (sc) or periphery
(sp); probability of being in the short stop state, ps,氮, with mean short stopping time Hs,N and mean long stopping time Hl,氮
(as a function of the number N of stopped neighbors). The probability of transition from moving in the center to moving
in the periphery is not directly encoded in the model, since it is a direct consequence of the random walk in the center.
The parameter values for the cockroaches [37, 38] are listed in Tables 1 和 2.
2.5 Implementation in the Alice Robots
The implementation of the behavioral model described above may be broken down into two parts:
displacement and stopping behavior. In the displacement part, we describe the behaviors involved in
the dispersal of the robots inside the arena; the stopping behavior part contains a description of the
core of the self-organized aggregation process.
桌子 1. Individual displacement parameters of the cockroaches [37] and their estimation from the analysis of the Alice’s
paths (mean F s.e.m.). 这里 * indicates that the standard error was estimated from a nonparametric bootstrap (200
迭代); y indicates that the standard error was computed from the measured fraction and the sample size with the
formula given by Zar [64].
范围
vc (cm s(西德:7)1 )
vp (cm s(西德:7)1 )
sc (s(西德:7)1 )
sp (s(西德:7)1 )
l* (厘米)
ps,0
Hs,0 (s)
Hl,0 (s)
Hexit (s)
Value
Cockroach
1.1 F 0.12*
Alice
3.97 F 0.01*
1.06 F 0.09*
3.68 F 0.01*
0.033 F 0.002y
0.026 F 0.001*
0.084 F 0.003y
0.074 F 0.004*
2.32
11.35
0.93 F 0.018*
0.943 F 0.010*
5.87 F 0.16*
7.52 F 0.28*
700 F 233*
626 F 103*
0.130 F 0.003y
0.108 F 0.006*
人工生命量 14, 数字 4
393
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
A
r
t
我
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
桌子 2. Interaction parameters among cockroaches [38] and their estimation from the analysis of the Alice robot’s
互动 (mean F s.e.m.). Each parameter is given for the three tested group sizes (2, 3, 和 4). 这里 * 表明
the standard error was estimated from a nonparametric bootstrap (200 迭代); z indicates that the standard error
was computed from the a-trimmed (a = 0.05) 价值观. The meaning of the parentheses is discussed in Section 3.2.2.
范围
Cockroach
Value
0.42
0.50
0.51
Alice
0.41 F 0.03
0.54 F 0.05
(0.72)
FStop,1
FStop,2
FStop,3
Hs,1 (s)
Hl,1 (s)
ps,1
Hs,2 (s)
Hl,2 (s)
ps,2
Hs,3 (s)
Hl,3 (s)
ps,3
16 F 2.9*
11.39 F 1.75*
1248 F 712* z
733 F 150*
0.66 F 0.3*
18.5 F 2.5*
0.62 F 0.07*
9.98 F 9.90*
1062 F 354* z
713 F 94*
0.34 F 0.04*
34.1 F 10.2*
1719 F 956* z
0.24 F 0.06*
0.27 F 0.12*
(6.64)
(910)
(0.09)
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
e
d
你
A
r
t
我
/
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
A
r
t
我
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
F
乙
y
G
你
e
s
t
t
哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3
2.5.1 移位
The correlated random walk used to describe the cockroach displacements [37] is characterized by a
series of straight moves (also called free paths) and turns. The lengths of straight moves are expo-
nentially distributed with a mean free path of length l. The distribution of turning angles was found
to be bell-shaped. One could implement this random walk in the Alice robot by repeatedly drawing a
random free path from an exponential distribution of mean l, with a random turning angle from a
fitted bell-shaped curve.
然而, since the final goal will be experiments with several robots at the same time, 有一个
simpler solution. 实际上, when averaged over many individuals and after a few diffusive events, A
random walk as described above is equivalent to one where the turning angles are distributed uni-
formly in [(西德:7)180; 180] deg (isotropic distribution) and the straight moves are exponentially dis-
tributed with mean l (西德:9) [13]. Here l (西德:9) corresponds to the transport mean free path and is computed
from l and the asymmetry parameter g a ((西德:7)1, 1) by the equation l(西德:9) ¼ l
1(西德:7)G. It represents the distance
beyond which the random walk becomes uncorrelated. g corresponds to the mean of the cosine of
the turning angle. It characterizes the tendency of the individual to continue in the same general di-
反应 (majority of turning angles in [0; +90[ 和 ](西德:7)90; 0] deg, 1 z g > 0) or to make U-turns
(majority of turning angles in ]+90; +180] 和 [(西德:7)180; (西德:7)90[ deg, (西德:7)1 V g < 0). See [37] for a more
detailed description. Given the limited computing capacities of the Alice robots, we choose to im-
plement this simplified random walk.
Uniform random numbers were generated with a Quick & Dirty algorithm ( Press et al. [53]).
Exponential random numbers with mean l * were created from a uniform random number r a (0, 1)
394
Artificial Life Volume 14, Number 4
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
transformed to (cid:7)(log r)l * with an algorithm using only integers (see Ahrens and Dieter [1] for the
algorithm). Letting the robot move or turn at maximum speed, we computed from these random
numbers the time (in milliseconds, the unit of the internal clock in the Alice robot ) that it should
move straight forward or turn. This random walk is continued until the robot detects an arena wall
with its infrared sensors.
When the robot detects a wall, it switches into wall-following behavior (provided with the pre-
programmed sensory-motor behaviors of Alice robots; see Caprari [10]). The time an Alice robot
follows the wall is also exponentially distributed with mean HExit [37] and was computed as described
above. Upon completion of this wall-following path the robot returns to the central zone with a random
angle drawn uniformly between 17 and 78 deg (as an approximation to the log-normal angle distri-
bution measured in [37]).
2.5.2 Stopping Behavior
The rate of stopping is constant per unit time (memoryless process); the above displacement is thus
interrupted every 500 ms, and a random number uniformly distributed between 0 and 100 is drawn
to decide whether or not the robot should stop. This probability is different when the robot is in the
center (sc) than when it is in the periphery (sp). It also varies with the number N of neighbors that an
Alice robot detects through its local infrared communication (sN, 0 V N V 3). Each robot broadcasts
with its infrared emitters two robot-specific identification numbers: an odd one if it is moving
(movement number) and an even one if it is stopped (stop number). This emission can be read by
other robots up to a distance of c4 cm. Each robot can thus detect the number of stopped robots
in its immediate neighborhood. In agreement with the behavioral model, the maximum number of
stopped robots that an Alice could detect at the same time was limited to three [38].
The stop duration has a biexponential distribution that varies according to the number N of
neighbors an Alice robot can detect (1 V N V 3; see above). This biexponential distribution is
generated by the superposition of two exponential distributions, one for short stops and one for long
stops. The robot thus first draws a random number uniformly distributed between 0 and 100 to
decide whether it will be a short stop (probability ps,N) or a long stop, and then draws an exponential
stop time that is either short (mean Hs,N) or long (mean Hl,N).
If the number of stopped neighbors changes during a robot’s stop, the robot has to modify the
duration of its halt according to the new number of neighbors. Because we deal with a memoryless
process, the time the robot has to remain stopped is independent of the time it has already spent in
this state. Consequently, when the number of stopped neighbors changes, the robot only draws a
new stop time from the appropriate exponential distribution. Note that the robot retains whether the
stop state is short or long.
Once the stop time has elapsed, the robot continues its displacement with either a random walk
(center) or a wall-following behavior (periphery).
3 Analysis and Comparison with Cockroach Behavior
In order to validate the implementation of the cockroach aggregation behavior in an Alice robot, we
performed the analysis of robot behaviors in conditions similar to those used for the characterization
of cockroach behaviors. This analysis is broken down into three different parts. The first (behavior
of an isolated robot ) and second (local interactions) parts validate the implementation at the in-
dividual level; the third part focuses on the collective output of the system. In each of these parts, the
data collected with robots are compared with the data collected with cockroaches in [37, 38].
3.1 Path Analysis for an Individual Robot
Individual displacements of robots were studied by letting a single individual move during 60 min
in the experimental arena. This experiment was repeated 10 times with 10 different robots.
Artificial Life Volume 14, Number 4
395
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
Displacements were recorded with a high-definition camera (Sony CDR-VX 2000 E), and the paths
were digitized with automatic tracking software (EthovisionR, version 1.90, Noldus Information
Technology, 1 pixel = 0.278 (cid:3) 0.219 cm). The sampling rate was chosen according to Tourtellot
et al.
[59]: The time interval between two successive points should let an individual move
approximately its own body length. Thus, the sampling rate was set to one point every 0.48 s for
the robots. The analysis of the different paths followed the procedures explained in [37]. These
procedures were implemented in the open-source software R [54] (scripts can be obtained from
the authors upon request ). The paths over a whole hour were divided into the pieces in the central
zone and the pieces in the peripheral zone (all coordinates less than 2.75 cm from arena walls).
Then these pieces were again subdivided into subpieces where the Alice robot moved and where it
was at a stop (defined as less than 7-mm distance between two successive coordinates for at least
0.96 s [14]). Standard errors for all parameters were estimated by a nonparametric bootstrap method
[26].
3.1.1 Central Zone
The speed in the center was computed as the total length of a path subpiece divided by the total time it
took the robot to pass through it. The mean (vc) of these velocities gave 3.97 F 0.01 cm s(cid:7)1 (mean F
s.e.m.).
To assess the random walk of the robots in the central zone, we computed the transport mean
free path l (cid:9). One could compute this value by means of the equation l(cid:9) ¼ l
1(cid:7)g given in Section 2.5.1.
But to compute l and g, one would need an unbiased criterion to compute the distribution of turning
angles, that is, to establish accurately at which moment the individual significantly changed the
direction of its path [59, 60]. To compute the value of l (cid:9) we rather used the same method as in
Jeanson et al. [37], which does not require the characterization of the distribution of turning angles.
The net squared displacement of a moving individual is given by [39]
(cid:3)
R2
n
(cid:4)cnmþl
0
l 2pðl Þ dl
where p(l ) dl is the probability that the length of each path has a value between l and l + dl. Thus
2i corresponds to the square of the straight line distance between the beginning of a path and the
hRn
position of the individual after n consecutive steps. In the case of a diffusive random walk, assume an
exponential distribution of the path lengths with a characteristic length l (cid:9):
pðl Þ ¼
1
l (cid:9) el =l (cid:9)
Then
(cid:3)
R2
n
(cid:4)cnmþl
0
l 2 1
l (cid:9) el =l (cid:9)
dl c2nðl (cid:9)Þ2
Assuming that the velocity v is constant, at time t we have
n ¼
tv
l (cid:9)
396
ð1Þ
ð2Þ
Artificial Life Volume 14, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
and substituting Equation 1 in Equation 2, we finally get
(cid:3)
R2
n
(cid:4)c2vcl (cid:9)t Z l (cid:9)c
(cid:4)
(cid:3)
R2
n
2vct
ð3Þ
For each path and each time step, we calculated the square of the distance Rn between the be-
ginning of the path (x0, y0) and the position (xn, yn) of the robot after n steps:
(cid:3)
R2
n
(cid:4) ¼ ðxn (cid:7) x0Þ2 þ ð yn (cid:7) y0Þ2
2i as a function of time for all paths recorded in the
Figure 5 shows the average squared distance hRn
central zone of the arena. During the diffusive regime, the mean squared net displacement increases
linearly with time and then reaches a plateau due to the finite space provided by the arena, which
prevents robots from diffusing further away. Fitting the initial linear part of the curve to get the
slope, we obtained (Figure 5)
(cid:3)
R2
n
(cid:4) ¼ 90:14t (cid:7) 150:24;
r ¼ 0:998
ð4Þ
With vc = 3.97 cm s(cid:7)1, Equations 3 and 4 predict a transport mean free path l (cid:9) c 11.35 cm,
which is of the same order as the expected value 9.28 cm corresponding to the transport mean free
path of cockroaches, 2.32 cm, scaled by a factor 4 (see Section 2.3).
To assess the probability of a robot to stop spontaneously (that is, without any interactions with
another robot ) in the central zone, we used only the paths of the robots that started in the peripheral
zone of the arena and that either stopped spontaneously in the central zone or returned to the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Mean net squared displacement hRn
dashed line represents the linear regression based on the linear part of the curve (hRn
2i of robots as a function of time. Each dot represents the mean F s.e.m. The
2i = 90.14t (cid:7) 150.24, r2 = 0.998).
Artificial Life Volume 14, Number 4
397
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
periphery. We computed the fraction FStop,c of paths that ended in a spontaneous stop in the central
zone. Assuming that the speed vc in the center of the arena is constant, knowing the diameter d of the
central zone, and using a recent result from Blanco and Fournier [5], the probability for a robot to
spontaneously stop in the central zone can be computed from the following equation (see [37] for
the detailed mathematics):
sc ¼
4vcðFStop;cÞ
pd
In the central zone of the arena, the fraction FStop,c was 22.7% (n = 616) for the robots. Thus, the
probability per unit time of spontaneously stopping in the central zone of the arena is sc = 0.026 F
0.001 s-1 for the robots.
3.1.2 Peripheral Zone
The speed in the periphery was computed as detailed above, giving a mean speed vp = 3.68 F
0.01 cm s-1. The rates to stop spontaneously in or to quit the periphery were estimated together by
first drawing the survival curve of all the times during which a robot followed the arena wall before
either spontaneously stopping or quitting it (see Figure 2). Given the proportion of these wall-
following path pieces that ended in a spontaneous stop in the periphery, one can decompose the
slope of this survival curve into the rate of quitting the periphery ( qp = 1/HExit ) and the rate of
spontaneously stopping (sp = 1/HStop) in it (see Jeanson et al. [37] for the details). This procedure
gave a quitting rate of 0.102 F 0.006 s-1 and a spontaneous stopping rate of 0.074 F 0.004 s-1.
3.1.3 Spontaneous Stopping Times
Spontaneous stopping times were also analyzed with a survival curve, and they showed, like the
cockroach data, a biexponential distribution (see Figure 3). We estimated the probability ps,0 for a
spontaneous stop to be of the short type and the mean duration of short (Hs,0) and long (Hl,0) stops
by fitting the following equation to the fraction of robots, F(t ), still motionless at time t (using the
least squares method):
FðtÞ ¼ ps;N e-t=Hs;N þ ð1 (cid:7) ps;N Þe-t=Hl ;N ;
N ¼ 0
ð5Þ
The best fit was obtained with ps,0 = 0.94 F 0.01, Hs,0 = 7.52 F 0.28 s, and Hl,0 = 626 F 103 s.
3.2 Interactions among Robots
In order to quantify interactions among robots we must determine when one individual detects
another. This was done by estimating the detection area of a single robot. A robot A was pro-
grammed to report the presence of neighbors in its vicinity. Another robot B was drawn near to A
from several different directions and orientations: parallel to the incoming direction with the front
toward A, parallel to the incoming direction with the back toward A, and perpendicular to the in-
coming direction (Figure 6). For each of these directions and orientations we then measured the
maximal distance from which A detected the approaching robot B. This gave us an estimate of the
neighbor detection area of A for each orientation of B (Figure 6). We finally defined the maximal
detection area of A as the superposition of the previous detection areas. In the rest of the analysis we
considered that a stopped robot was a neighbor of another one, and hence belonged to the same
aggregate, if its body crossed the maximal detection area of the other one, whatever its incoming
orientation.
398
Artificial Life Volume 14, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
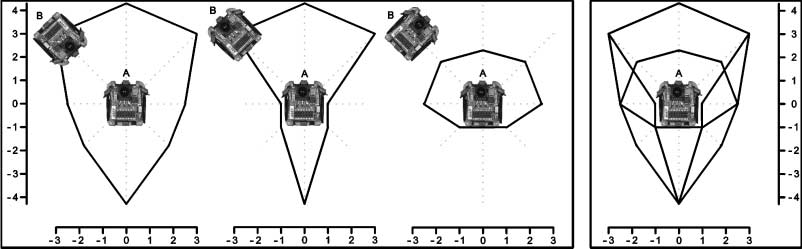
Figure 6. Left box: Estimated neighbor detection areas (scales are in centimeters) of a single robot A for different
orientations of the neighbor B. From the left to the right: neighbor front, neighbor back, and neighbor side aim at the
robot A. Right box: The estimated maximum neighbor detection area is the superposition of the three previous estimated
neighbor detection areas.
3.2.1 Probabilities of Joining and Leaving an Aggregate
To analyze the interactions among individuals, that is, to determine the behavioral rules based on local
information, we introduced several aggregates of N stopped robots in the arena (1 V N V 3), and then
we let a single robot move between them. Forty experiments lasting 60 min were performed.
The probability of stopping in an aggregate is defined in [38] as follows:
PStop;N ¼
v logð1 (cid:7) FStop;N Þ
d
with v the speed of the cockroach (either vc or vp, depending on the position of the animal in the
arena), d the maximum distance at which a moving cockroach could perceive a stopped one, and
FStop,N the fraction of cockroaches that stopped when encountering N (1 V N V 3) stopped
neighbors. d strongly depends on the size and shape of the maximal detection area of the cockroach,
which was defined as a disk of diameter 6 mm centered on the head of the animal. This disk cor-
responds to the area around the head of the cockroaches within which an antennal contact with
another cockroach can happen (antennae are 3 mm long). Because the maximal detection area
measured for robots does not match the size and shape of the one for cockroaches, we did not
compute PStop,N in robots, but we rather chose FStop,N to compare robots’ stopping behavior with
cockroaches’ stopping behavior. We thus recorded the number of encounters a moving robot made
with N stopped robots within its maximal detection area and the number of these encounters that
ended in a stop of the moving robot.
Once a robot was stopped near N robots, we computed the duration of that stop. We then drew
log-linear plots of the stop-time survival curve for each group size (2 to 4, counting the observed
robot ). As with the cockroaches, all the survival curves showed a bilinear pattern (biexponential on a
normal scale). Since in our setup only one robot could leave the aggregate, we could estimate the
stopping parameters for each group size [probability of being in the short stopping state ( ps,N), mean
duration of short stops (Hs,N), and mean duration of long stops (Hl,N)] by directly fitting Equation 5.
3.2.2 Calibration of Interaction Parameters
Interactions among robots and neighbor detection are based on local communication through
infrared transmitters and sensors. However, the quality of this local communication is somewhat
restricted, particularly in the case of bad alignment or multiple robots emitting at the same time in
the same place [10]. In our experiments, a robot could obtain the following false identification
numbers: a stop number from a moving robot, a movement number from a stopped robot, or two
different numbers from the same robot (identification numbers are sent every 50 ms and stored in
Artificial Life Volume 14, Number 4
399
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
memory for at most 1 s). This noisy perception of the number of stopped neighbors had to be taken
into account during the implementation of the behavioral model.
At the behavioral level, the major consequence was a discrepancy between the stopping pro-
bability (estimated by FStop,N) and time (estimated by ps,N, Hs,N, and Hl,N) measured in experiments
and those coded in a robot’s controller. Thus, the hardware constraints have altered the behavioral
output of the robot in comparison with the programmed behavioral algorithm. To correct for this
hardware problem, we decided to calibrate the interaction parameters programmed in the robots by a
modified bisection method. More precisely, we ran a first set of 40 experiments to assess the initial
discrepancy between implemented and observed interaction values. If this discrepancy was negative
(implemented < observed), the implemented value was excessively increased; if it was positive, the
implemented value was excessively decreased. Another set of 40 experiments gave us a new as-
sessment of the discrepancy with an opposite sign: positive if it was formerly negative, and negative if
it was formerly positive. This gave us a first interval that contained the set of implementation
parameters that would result in the correct behavioral values (those of the cockroaches). We then
reduced this interval by a dichotomous process. For each parameter we computed the mean of the
upper and lower bounds of the interval and implemented it in the robots’ controller. We then ran a
new set of 40 experiments, and we checked whether the correct behavioral values were below or
above this mean. If the correct values were below the mean, it became the upper bound of the
interval. Otherwise, it became the lower bound. This process was repeated until no statistical dif-
ference was observed between robots’ and cockroaches’ interaction behaviors.
After the last set of 40 experiments, we obtained interaction parameter values with robots in
agreement with those found in cockroaches, except for N = 3: Stop events in these experiments with
at least three robots inside the maximal detection area were too scarce to confidently estimate the
interaction values. Thus, the values of the different interaction parameters for more than two neigh-
bors are given without any confidence interval and are displayed in parentheses in Table 2.
FStop,N, the fraction of cockroaches that stopped when encountering N (1 V N V 3) stopped
neighbors, increased with the number of stopped neighbors (Table 2). Thus, the probability for a
robot to join an aggregate increased with the number of neighbors, as in cockroaches. Regarding
ps,N, Hs,N, and Hl,N, the results (see Figure 7 and Tables 1 and 2) indicated that the stop times, either
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Survival curves of robot stop times near 0 (circles), 1 (plus signs), or 2 (triangles) neighbors, with their fitted
regression lines.
400
Artificial Life Volume 14, Number 4
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
short (Hs,N) or long (Hl,N), remained inside the confidence interval of cockroach values. The prob-
ability of belonging to short stop durations ( ps,N) decreased as the number of neighbors increased
and remained in the confidence interval of cockroach values.
3.3 Collective Behaviors
For the final validation of our implementation of the cockroach aggregation behavior in Alice robots,
we compared the collective structures that resulted from this self-organized clustering process be-
tween robots and cockroaches. The movement of 10 robots (10 replications) or 20 robots (10 rep-
lications) was recorded over 60 min with a high-definition camera (Sony CDR-VX 2000 E). Every
minute, we computed three collective behavioral measures: the number of aggregates, the size of the
largest one, and the number of isolated robots. An example experiment can be seen in Figure 8.
The results of the collective experiments with the robots were compared with the results of the
same experiments made with 10 (20 replications) or 20 (22 replications) cockroaches by Jeanson et al.
[38]. This comparison is shown in Figure 9. Note that the cockroaches are introduced at the center
of the experimental arena under CO2 narcosis [37, 38]. After recovery from this narcosis, cock-
roaches first ran around in an excited way. Furthermore, all the cockroaches in a group introduced
into the arena did not wake up simultaneously. Therefore, to compare the dynamics of aggregation,
one should not take into account the first 5 min of the experiments with cockroaches.
Qualitatively, the curves of robots and cockroaches display a similar shape whatever the observed
measure. All the curves have reached a stationary state after 40 min. We then computed for each
experiment and each behavioral measurement the mean over the last 20 min and compared, using an
exact Wilcoxon rank sum test for nonpaired data, the set of robot experiments with the set of cock-
roach experiments.
Regarding the number of aggregates, experiments with 10 agents resulted in 1.905 F 0.174 robot
aggregates versus 1.590 F 0.109 cockroach aggregates (NS, W = 134.5, p = 0.13). Experiments
with 20 agents resulted in 3.160 F 0.210 robot aggregates versus 2.502 F 0.250 cockroach ag-
gregates (NS, W = 158, p = 0.051).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
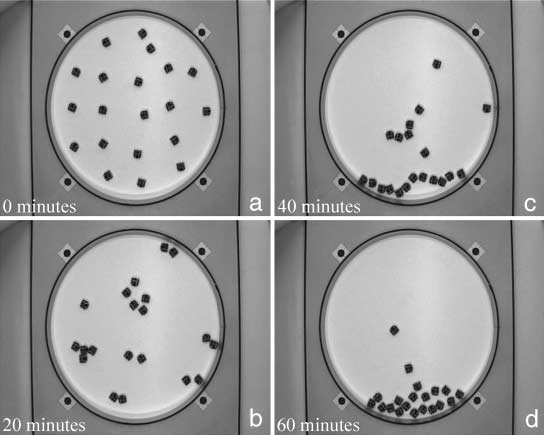
Figure 8. An example of a collective experiment with 20 robots that ends with a single large aggregate. Snapshots were
done (a) at the beginning of the experiment, (b) after 20 min, (c) after 40 min, and (d) at the end of the experiment.
Artificial Life Volume 14, Number 4
401
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
Figure 9. Dynamics of aggregation in robots (black dots) and cockroaches (white dots; data from [38]). Data points
represent the mean F s.e.m. Row 1 represents experiments with 10 individuals (10 replications with robots, 20
replications with cockroaches). Row 2 represents experiments with 20 individuals (10 replications with robots, 22
replications with cockroaches). Column A represents the mean number of aggregates as a function of time. Column B
represents the mean size of the largest aggregate as a function of time. Column C represents the mean number of
isolated individuals as a function of time.
In experiments with 10 agents, the size of the largest cluster was 6.200 F 0.489 in robots and 5.895 F
0.480 in cockroaches (NS, W = 109, p = 0.71). In experiments with 20 agents, the size of the largest
cluster was 9.740 F 0.538 in robots and 11.818 F 0.900 in cockroaches (NS, W = 74, p = 0.15).
At the end, the number of isolated individuals in experiments with 10 agents was 1.455 F 0.143
in robots and 2.7675 F 0.447 in cockroaches (NS, W = 60, p = 0.08). The number of isolated
individuals in experiments with 20 agents was 2.430 F 0.232 in robots and 3.723 F 0.342 in cock-
roaches (significant difference, W = 53, p = 0.02).
Quantitatively, experiments with 10 robots showed very good agreement with the biological
system all along the experiment. Experiments with 20 robots also showed good agreement with the
cockroaches, except for the number of isolated individuals, which is significantly higher in cock-
roaches than in robots.
4 Discussion
To build a realistic representation of an animal behavior with robots raises several problems. The
very first of them is to determine which level of description is required to capture the main ex-
planatory mechanisms underlying a given behavior. Should we study the group level, the individual
level, the cognitive level, the physiological level? Actually, this problem is not specific to a robotics
model of animal behaviors. It is rather a general concern for all people involved in modeling animal
behavior, whatever their analytical and modeling tools are. Yet, it can have major implications for the
design of the robot architecture and controller. This level of description conditions what part of the
402
Artificial Life Volume 14, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
biological model has to be faithfully reproduced and what part permits a less accurate implemen-
tation because it is only weakly linked with the studied behavior.
For instance, Lambrinos et al. [42] have tested their hypothesis about the navigation behavior of
the Saharan ant Cataglyphis with a mobile robot called Sahabot. Their main purpose was to gain
insight about the way this insect uses the polarized-light pattern of the sky to find its way back home
after a foraging trip. Thus, they concentrated their efforts on the robotic embodiment of the de-
tection and the treatment of the polarized light as made by this ant. On the contrary, the other parts
of the robot were designed without caring about biological realism: The robot was much larger than
the ants, it had wheels instead of legs, it moved on a soft synthetic material in Zu¨rich rather than on
sand in the middle of the Sahara desert. However, their Sahabot correctly reproduced the charac-
teristic homing trajectories of the ant Cataglyphis and thus strengthened the hypothesis about the
major role of the polarized-light pattern of the sky in the navigation abilities of this desert ant.
In the case of a self-organized behavior the level of description focuses on the interactions be-
tween the agents and between them and their environment. More precisely, the behavioral hy-
potheses mainly concentrate on the two following questions:
1. How does an agent’s activity evolve in space and/or time in a homogeneous environment and in
the absence of other agents?
2. How is this evolution modified by the presence of environmental discontinuities? How is it
modified by the activities or the result of the activities of the other agents?
In most cases it is possible to answer these two questions without making any hypothesis about
the physiology of the agents, but rather by performing a statistical description (i.e., in terms of mean,
confidence interval, and/or probability) of the observable output of the agent, that is, its behavior.
For instance, question 1 applied to the aggregation behavior studied in this article is answered by
simply tracking the successive positions of the animal in order to obtain characteristic measurements
of its displacement: length of free paths, distribution of turning angles, and duration of spontaneous
stops. These three measurements are sufficient to reproduce with any moving agent the dispersal of
cockroaches in space and time. No additional information is required, for example, about walking
mechanisms. Question 2 can be answered as well by simply measuring the modification of the stop
duration if the animal is in the presence of a given number of conspecifics. Here again, no additional
hypotheses are needed about the way the animal estimates the neighbor density. One can thus
reproduce the cockroach aggregation behavior with any agent able to estimate this density. This is in
fact what we did with Alice robots, and one could do it again with any kind of robot able to move,
to stop, and to detect its conspecifics in a rather limited range. Of course these actions have to be
performed with space and time scales properly adapted to the size and speed of the robots, so that
the dynamics of the self-organized behavior remain the same.
More generally the models of self-organized animal behaviors can often be considered as in-
dependent of the animal’s physiology. Their implementation in artificial agents only requires that
the agents be able to accomplish the actions stated in the model with corresponding space and time
scales. However, if the model is independent of the animal’s physiology, its implementation remains
conditioned by the artificial agent’s ‘‘physiology,’’ that is, everything that is involved in the agent’s
functioning: hardware, firmware, operating system, and so on. The problem of the unstable de-
tection of neighbors met in Section 3.2.2 well illustrates that point.
The infrared local communication between robots was noisy and introduced undesired fluctua-
tions in the neighbor count. Noise of course exists in nature, and its creative role in self-organized
biological systems has already been emphasized in many studies (see for instance [9, 20, 21, 33]). But
in our case, the variability of cockroach behavior was already considered in the model. Indeed, the
description of the animal behavior in terms of probabilities or in terms of means and confidence in-
tervals accommodated the biological noise. Therefore, the noisy infrared communication added an
artificial fluctuation over the fluctuations already included in the biological model. This additional
fluctuation could have deeply modified the collective output of the model and thus could have
Artificial Life Volume 14, Number 4
403
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
jeopardized our main objective, which was to quantitatively reproduce the self-organized aggregation
of cockroaches with a group of robots. Indeed we already knew that the self-organized aggregation
process implemented in this article can produce a wide variety of aggregation patterns depending
on the balance between the tendencies to join and to leave an aggregate [29].
Thus, the ‘‘physiology’’ of the robots can have an important influence on the realistic imple-
mentation of a biological model. To achieve this implementation, it is necessary to control the effects
of the robot’s ‘‘physiology’’ on the output of the biological model. First, the differences between the
biological model and its robotic implementation must be evaluated. This has to be done with exactly
the same protocol as the one applied to study the animal behavior and to build the biological model.
The study of the robot behavior must be done with an experimental environment, an observation
methodology, and a procedure of analysis identical to the one used with the animal model. This
ensures the realism of the implementation and facilitates the detection of discrepancies. All through
the work presented in this article, we observed this principle, which allowed us to detect the im-
plementation flaw introduced by the communication channel of the Alice robots.
After the difference between the model and the robot behavior has been established, it has to be
reduced as far as possible. However, this problem has to be handled on a case-by-case basis, since it
strongly depends on the hardware part of the robot that is used: Two different kinds of robots with
different hardware (or ‘‘physiology’’) but endowed with the same model can display different be-
havioral output. As regards our work, the effect of the noisy infrared communication on the stop
and restart behavior was counterbalanced thanks to a dichotomous calibration of stop and restart
probabilities implemented in the robot controller. Although this method looks rather rough and
time-consuming, it turned out to be efficient in finding a good set of stop and restart parameters.
Moreover, it saved us an exhaustive analysis of infrared communication noise, which could have
eventually cost more time.
Once all the mechanisms that constitute the biological model have been correctly reproduced, the
last step of the work is to verify that the final output of the implementation acts as the animal does.
This final stage is of great importance, since it validates that the model is compatible with the real
phenomenon and that its implementation does not suffer a flaw. In the case of self-organized be-
havior, the final output corresponds to the collective behavior of the agents. In our work, this col-
lective behavior resulted in an aggregation of the robots which was defined through three dynamic
measures: number of robots remaining alone, number of clusters formed, and number of robots in
the largest cluster. Here again, these measurements were obtained in the same experimental con-
ditions as for cockroaches and allowed a direct comparison between the collective behavior of
animals and robots. The results displayed in Section 3.3 show good qualitative agreement between
cockroaches and Alice robots for the three measurements. Quantitatively, this agreement remains
good, except for an increased tendency of the cockroaches to remain isolated.
Thus, robots seem to slightly overaggregate. This could be consistent with the results in Jeanson
et al. [38] that show a higher aggregation intensity in simulated cockroaches than in real ones.
However, the discrepancy observed between the simulations and the cockroaches is much more
significant than the small discrepancy observed between the cockroaches and the robots. The
simulations in [38] did not implement a physical occlusion between the simulated cockroaches. As a
consequence a simulated cockroach passing near a given cluster could perceive not only the cock-
roaches at the periphery of the cluster, but also those inside. Therefore, the resulting aggregation was
faster and more stable. Experiments with robots, on the contrary, naturally took the physical
occlusion into account. This explains why the collective behavior of the robots was closer to the
collective behavior of the cockroaches. It also emphasizes the effect of physical constraints on the
regulation of aggregation in cockroaches, and more generally their role in self-organized behavior as
a potential source of negative feedback.
Another reason for the slight over-aggregation of robots could be the difference between the
maximal perception area of robots and cockroaches. The perception area of cockroaches was es-
timated by Jeanson et al. [38] as a 6-mm-diameter disk around the head of the cockroach. Scaled by
four to match the robot size, this area corresponds to 4.5 cm2. The perception area of the robots as
404
Artificial Life Volume 14, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
described in Figure 6 corresponds to 30.7 cm2. As stated by Martinoli et al. [45], the probability for
a moving agent to encounter a conspecific inside a closed arena grows with its perception area.
Moreover, with a macroscopic implementation (difference equations) of the aggregation model used
in this article, Correll and Martinoli [15] showed that the number of agents in clusters grows with the
encounter probability. Together, this could easily explain why robots in our experiments had a ten-
dency to remain more clustered than cockroaches. This also highlights the potential effect of small
physiological differences in agents on the dynamics of self-organized behaviors.
5 Conclusion
We report in this article the implementation of self-organized aggregation behavior in a group of
small autonomous robots. The main originality of this work lies in the nature of this implementation.
Most of the works about self-organized behaviors in collective robotics focus on the design of
controllers that solve or that optimize the solving of multi-robot coordination problems (see Mataric´
[47] for a general discussion; see Baldassarre et al. [3] and Dorigo et al. [24] for examples of self-
organized aggregation of robots). On the contrary, our purpose was to realistically reproduce with a
group of Alice mini-robots the self-organized aggregation behavior of a social animal, namely the
German cockroach B. germanica. Thus, this work comes close to other biology-oriented studies like
those reviewed by Webb [62, 63], even if these studies are mostly dedicated to the understanding of
individual animal behaviors.
To reach our goal, we have used a behavioral model of this biological phenomenon previously
studied in Jeanson et al. [37, 38] that described the individual behaviors of the animals in a stochastic
framework. Such a description makes the model independent of the animal’s physiology and thus
allows its implementation in a wide variety of artificial agents. However, at least if the artificial agent
is a robot, it should be noted that its ‘‘physiology’’ can have some undesired effects on its individual
behaviors that may strongly modify the collective behavior of the group. If these effects cannot
be eliminated with a hardware or firmware solution, they can be reduced thanks to a careful imple-
mentation of the model driven by an experimental assessment of the behavioral differences.
Finally, the present work provides a basic framework for further thinking and experimental
studies about the realistic implementation of biological models in collective robotics:
1. because it highlights the main constraints that one may encounter during the realistic
implementation of self-organized behaviors in groups of robots;
2. because it proposes general principles to ensure that the behavioral model is accurately and
faithfully transferred to the artificial agents.
It can thus be considered as an important step in the process linking the study of self-organized
animal behaviors to their control by groups of biomimetic robots as proposed in Caprari et al. [11].
Acknowledgments
We thank Jean-Louis Deneubourg, Nikolaus Correll, and three anonymous reviewers for helpful
advice. This work was partly supported by a European Community grant given to the LEURRE
project under the ‘‘Information Society Technologies’’ Programme (1998 –2002), contract FET-
OPEN-IST-2001-35506 of the Future and Emerging Technologies arm, and by the Programme
Cognitique from the French Ministry of Scientific Research. Simon Garnier is supported by a
research grant from the French Ministry of Education, Research and Technology.
References
1. Ahrens, J. H., & Dieter, U. (1972). Computer methods for sampling from the exponential and normal
distributions. Communication of the ACM, 15(10), 873 – 882.
2. Arnaud, P. (2000). Des moutons et des robots. Presses Polytechniques et Universitaires Romandes.
Artificial Life Volume 14, Number 4
405
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
3. Baldassarre, G., Nolfi, S., & Parisi, D. (2003). Evolving mobile robots able to display collective behaviors.
Artificial Life, 9(3), 255 – 267.
4. Beckers, R., Holland, O. E., & Deneubourg, J.-L. (1994). From local actions to global tasks: Stigmergy and
collective robotics. In R. Brooks & P. Maes (Eds.), Proceedings of the Fourth Workshop on Artificial Life
(pp. 181 – 189). Cambridge, MA: MIT Press.
5. Blanco, S., & Fournier, R. (2003). An invariance property of diffusive random walks. Europhysics Letters,
61(2), 168 – 173.
6. Bo¨ehlen, M. (1999). A robot in a cage. In Proceedings of the IEEE International Symposium on Computational
Intelligence in Robotics and Automation.
7. Bonabeau, E., Dorigo, M., & Theraulaz, G. (1999). Swarm intelligence: From natural to artificial systems.
New York: Oxford University Press.
8. Bonabeau, E., & Theraulaz, G. (1999). Role and variability of response thresholds in the regulation of
division of labor in insect societies. In C. Detrain, J.-L. Deneubourg, & J. M. Pasteels (Eds.), Information
processing in social insects (pp. 141 – 163). Basel: Birkha¨user Verlag.
9. Camazine, S., Deneubourg, J.-L., Franks, N. R., Sneyd, J., Theraulaz, G., & Bonabeau, E. (2001).
Self-organization in biological systems. Princeton, NJ: Princeton University Press.
10. Caprari, G. (2003). Autonomous micro-robots: Applications and limitations. Ph.D. thesis, E´ cole Polytechnique
Fe´de´rale, Lausanne, Switzerland.
11. Caprari, G., Colot, A., Siegwart, R., Halloy, J., & Deneubourg, J.-L. (2005). Animal and robot mixed
societies: Building cooperation between microrobots and cockroaches. IEEE Robotics & Automation
Magazine, 12(2), 58 – 65.
12. Caprari, G., & Siegwart, R. (2005). Mobile micro-robots ready to use: Alice. In Proceedings of the 2005
IEEE/RSJ International Conference on Intelligent Robots and Systems (pp. 3295 – 3300).
13. Case, K., & Zweifel, P. (1967). Linear transport theory. New York: Addison-Wesley.
14. Collins, R. D., Tourtellot, M. K., & Bell, W. J. (1995). Defining stops in search pathways. Journal of
Neurosciences Methods, 60(1 – 2), 95 – 98.
15. Correll, N., & Martinoli, A. (2007). Modeling self-organized aggregation in a swarm of miniature robots. In
Proceedings of the IEEE 2007 International Conference on Robotics and Automation Workshop on Collective Behaviors
Inspired by Biological and Biochemical Systems.
16. Dambach, M., & Goehlen, B. (1999). Aggregation density and longevity correlate with humidity in first
instar nymphs of the cockroach (Blattella germanica L., Dictyoptera). Journal of Insect Physiology, 45, 423 – 429.
17. De Schutter, G., Theraulaz, G., & Deneubourg, J.-L. (2001). Animal-robots collective intelligence. Annals of
Mathematics and Artificial Intelligence, 31(1 – 4), 223 – 238.
18. Deneubourg, J.-L., Goss, S., Pasteels, J. M., Fresneau, D., & Lachaud, J.-P. (1987). Self-organization
mechanisms in ant societies (ii): Learning in foraging and division of labor. In J. M. Pasteels & J.-L.
Deneubourg (Eds.), From individual characteristics to collective organisation: The example of social insects
(pp. 177 – 196). Basel, Switzerland: Birkha¨user.
19. Deneubourg, J.-L., Lioni, A., & Detrain, C. (2002). Dynamics of aggregation and emergence of cooperation.
Biological Bulletin, 202(3), 262 – 267.
20. Deneubourg, J.-L., Pasteels, J. M., & Verhaeghe, J. C. (1983). Probabilistic behaviour in ants: A strategy of
errors? Journal of Theoretical Biology, 105, 259 – 271.
21. Detrain, C., & Deneubourg, J.-L. (2006). Self-organized structures in a superorganism: Do ants ‘‘behave’’
like molecules? Physics of Life Reviews, 3(3), 162 – 187.
22. Dorigo, M., Bonabeau, E., & Theraulaz, G. (2000). Ant algorithms and stigmergy. Future Generation Computer
Systems, 16(8), 851 – 871.
23. Dorigo, M., & Gambardella, L. M. (1997). Ant colonies for the travelling salesman problem. Biosystems,
43(2), 73 – 81.
24. Dorigo, M., Trianni, V., Sahin, E., Gross, R., Labella, T. H., Baldassarre, G., Nolfi, S., Deneubourg, J.-L.,
Mondada, F., Floreano, D., & Gambardella, L. M. (2004). Evolving self-organizing behaviors for a
swarm-bot. Autonomous Robots, 17(2 – 3), 223 – 245.
25. Dussutour, A., Fourcassie´, V., Helbing, D., & Deneubourg, J.-L. (2004). Optimal traffic organization in ants
under crowded conditions. Nature, 428(6978), 70 – 73.
406
Artificial Life Volume 14, Number 4
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
26. Efron, B., & Tibshirani, R. J. (1993). An introduction to the bootstrap. London: Chapman and Hall.
27. Fernandez-Juricic, E., Gilak, N., McDonald, J. C., Pithia, P., & Valcarcel, A. (2006). A dynamic method to study
the transmission of social foraging information in flocks using robots. Animal Behaviour, 71(4), 901– 911.
28. Garnier, S., Jost, C., Jeanson, R., Gautrais, J., Asadpour, M., Caprari, G., & Theraulaz, G. (2005).
Aggregation behaviour as a source of collective decision in a group of cockroach-like robots. In
M. Capcarrere (Ed.), Advances in Artificial Life, Proceedings of the 8th European Conference on Artificial
Life (vol. 3630 of Lecture Notes in Artificial Intelligence) (pp. 169 – 178). Berlin: Springer-Verlag.
29. Gautrais, J., Jost, C., Jeanson, R., & Theraulaz, G. (2004). How individual interactions control aggregation
patterns in gregarious arthropods. Interaction Studies, 5(2), 245 – 269.
30. Grasse´, P.-P. (1959). La reconstruction du nid et les coordinations interindividuelles chez Bellicositermes
natalensis et Cubitermes sp. La the´orie de la stigmergie: Essai d’interpre´tation du comportement des termites
constructeurs. Insectes Sociaux, 6, 41 – 81.
31. Grasse´, P.-P. (1984). Termitologia, tome II. Fondation des socie´te´s. Construction. Paris: Masson.
32. Haccou, P., & Meelis, E. (1992). Statistical analysis of behavioural data: An approach based on time structured models.
Oxford, UK: Oxford University Press.
33. Helbing, D., Farkas, I. J., & Vicsek, T. (2000). Freezing by heating in a driven mesoscopic system. Physical
Review Letters, 84(6), 1240 – 1243.
34. Holland, O. E., & Melhuish, C. (1999). Stigmergy, self-organization, and sorting in collective robotics.
Artificial Life, 5, 173 – 202.
35. Ijspeert, A., Martinoli, A., Billard, A., & Gambardella, L. (2001). Collaboration through the exploitation of
local interactions in autonomous collective robotics: The stick pulling experiment. Autonomous Robots,
V11(2), 149 – 171.
36. Jeanne, R. L. (1996). Regulation of nest construction behaviour in Polybia occidentalis. Animal Behaviour, 52(3),
473 – 488.
37. Jeanson, R., Blanco, S., Fournier, R., Deneubourg, J.-L., Fourcassie´, V., & Theraulaz, G. (2003). A model of
animal movements in a bounded space. Journal of Theoretical Biology, 225(4), 443 – 451.
38. Jeanson, R., Rivault, C., Deneubourg, J.-L., Blanco, S., Fournier, R., Jost, C., & Theraulaz, G. (2005).
Self-organized aggregation in cockroaches. Animal Behaviour, 69(1), 169 – 180.
39. Kareiva, P., & Shigesada, N. (1983). Analyzing insect movement as a correlated random walk. Oecologica, 56,
234 – 238.
40. Krieger, M. J. B., Billeter, J.-B., & Keller, L. (2000). Ant-like task allocation and recruitment in cooperative
robots. Nature, 406(6799), 992 – 995.
41. Kube, C. R., & Bonabeau, E. (2000). Cooperative transport by ants and robots. Robotics and Autonomous
Systems, 30, 85 – 101.
42. Lambrinos, D., Moller, R., Labhart, T., Pfeifer, R., & Wehner, R. (2000). A mobile robot employing insect
strategies for navigation. Robotics and Autonomous Systems, 30(1), 39 – 64.
43. Ledoux, A. (1945). Etude expe´rimentale du gre´garisme et de l’interattraction sociale chez les blattide´s.
Annales des Sciences Naturelles Zoologie et Biologie Animale, 7, 76 – 103.
44. Lu¨scher, M. (1961). Air-conditioned termite nests. Scientific American, 205, 138 – 145.
45. Martinoli, A., Easton, K., & Agassounon, W. (2004). Modeling swarm robotic systems: A case study in
collaborative distributed manipulation. The International Journal of Robotics Research, 23(4 – 5), 415 – 436.
46. Martinoli, A., Jispeert, A. J., & Mondada, F. (1999). Understanding collective aggregation mechanisms:
From probabilistic modelling to experiments with real robots. Robotics and Autonomous Systems, 29, 51 – 63.
47. Mataric´, M. J. (1995). Issues and approaches in the design of collective autonomous agents. Robotics and
Autonomous Systems, 16, 321 – 331.
48. Melhuish, C., Wilson, M., & Sendova-Franks, A. (2001). Patch sorting: Multiobject clustering using
minimalist robots. In ECAL ’01: Proceedings of the 6th European Conference on Advances in Artificial Life
(pp. 543 – 552). Berlin: Springer-Verlag.
49. Michelsen, A., Andersen, B. B., Storm, J., Kirchner, W. H., & Lindauer, M. (1992). How honeybees perceive
communication dances, studied by means of a mechanical model. Behavioral Ecology and Sociobiology, 30(3),
143 – 150.
Artificial Life Volume 14, Number 4
407
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
S. Garnier et al.
The Embodiment of Cockroach Aggregation Behavior
50. Parrish, J. K., & Edelstein-Keshet, L. (1999). Complexity, pattern, and evolutionary trade-offs in animal
aggregation. Science, 284(5411), 99 – 101.
51. Parrish, J. K., & Hamner, W. M. (1997). Animal groups in three dimensions. Cambridge, UK: Cambridge
University Press.
52. Partridge, B. (1982). The structure and function of fish schools. Scientific American, 246(6), 114 – 123.
53. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. (1992). Numerical recipes in C: The art of
scientific computing (2nd ed.). Cambridge, UK: Cambridge University Press.
54. R Development Core Team (2006). R: A language and environment for statistical computing. Vienna: R Foundation
for Statistical Computing.
55. Rust, M. K., Owens, J. M., & Reierson, D. A. (1995). Understanding and controlling the German cockroach.
Oxford, UK: Oxford University Press.
56. Sahin, E. (2005). Swarm robotics: From sources of inspiration to domains of application. In E. Sahin &
W. M. Spears (Eds.), Swarm Robotics, Proceedings of the SAB 2004 International Workshop (vol. 3342 of Lecture
Notes in Computer Science) (pp. 10 – 20). Berlin: Springer.
57. Sugawara, K., & Sano, M. (1997). Cooperative acceleration of task performance: Foraging behavior of
interacting multi-robots system. Physica D: Nonlinear Phenomena, 100(3 – 4), 343 – 354.
58. Theraulaz, G., & Bonabeau, E. (1999). A brief history of stigmergy. Artificial Life, 5(2), 97 – 116.
59. Tourtellot, M. K., Collins, R. D., & Bell, W. J. (1991). The problem of movelength and turn definition in
analysis of orientation data. Journal of Theoretical Biology, 150(3), 287 – 297.
60. Turchin, P. (1998). Quantitative analysis of movement. Sunderland, MA: Sinauer Associates.
61. Vaughan, R., Stumpter, N., Henderson, J., Frost, A., & Cameron, S. (2000). Experiments in automatic flock
control. Robotics and Autonomous Systems, 31, 109 – 117.
62. Webb, B. (2000). What does robotics offer animal behaviour? Animal Behaviour, 60(5), 545 – 558.
63. Webb, B. (2001). Can robots make good models of biological behaviour? Behavioral and Brain Sciences, 24(6),
1033 – 1094.
64. Zar, J. H. (1999). Biostatistical analysis. Englewood Cliffs, NJ: Prentice Hall.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
4
4
3
8
7
1
6
6
2
5
2
6
a
r
t
l
.
/
.
.
2
0
0
8
1
4
4
1
4
4
0
0
p
d
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
408
Artificial Life Volume 14, Number 4