声音合成 - 麻省理工学院人工智能研究专业

声音合成
听觉失真
产品

加里·S. 肯德尔,克里斯托弗·霍沃斯,†
和罗德里戈·F. C'阿迪兹**
＊炮兵连 40
114 45 斯德哥尔摩, 瑞典
garyskendall@me.com
†音乐学院
牛津大学
英石. 阿尔达特的,
牛津, 氧化酶1 1 数据库, 英国
christopher.p.haworth@gmail.com
***音频技术研究中心,
音乐学院
智利天主教天主教大学
的. 海梅·古兹曼·E. 3300
普罗维登斯, 圣地亚哥, 智利 7511261
rcadiz@uc.cl

抽象的: 本文介绍了基于听觉失真产物的声音合成方法, 经常被称为
组合音调. 在 1856, 亥姆霍兹是第一个将和音和差音确定为听觉产物的人
失真. 如今，这种现象在耳声发射的背景下得到了深入研究, 而“扭曲”是
被理解为所谓的耳蜗放大器的产品. 这些音调在音乐中有着丰富的历史
即兴创作者和无人机艺术家. 到目前为止, 失真音调在科技音乐中的使用很大程度上已经被
为了让观众听到失真产物，它是基本的并且依赖于非常高的振幅.
这里讨论的是使这些音调更容易听到并赋予它们动态特性的合成方法
传统声学声音, 从而使听觉失真成为声音合成的实用领域. 改编
单边带合成对于实时捕获音频输入的动态特性特别有效.
还提供了用于匹配目标频谱的多达四个谐波的分析解决方案. 最有趣的是, 这
这些技术产生的空间图像非常独特, 和通过扬声器的正常假设
空间听觉不适用. 提供音频示例来说明讨论.

本文介绍了声音合成的方法
基于听觉失真产品, 经常被称为
组合音调——创造受控音调的方法
对非声源的听觉错觉
存在于到达 lis 的物理信号中-
特纳的耳朵. 这些幻觉是, 实际上, 产品
听者听觉的神经力学
当系统受到特定属性的刺激时
物理声音. 许多作曲家都曾使用过
他们工作中的听觉失真产物, 和
这些失真产物的影响——经常被描述
嗡嗡作响, 靠近头部的幽灵般的音调——
很多演唱会观众都经历过.
历史上, 产生听觉的技术
音乐环境中的失真音调相当
初级的, 最初受限制-
模拟设备系统蒸发散总是要求高
大多数人听起来不舒服的声音水平-
呃. 在本文中, 我们描述声音的方法
两者都利用数字精度的合成

电脑音乐杂志, 38:4, PP. 5–23, 冬天 2014
土井:10.1162/COMJ一 00265
C(西德:2) 2014 麻省理工学院.

信号处理并且只需要中等声音
产生受控听觉错觉的水平. 我们的
目标是开拓声音合成领域
听觉失真产品显着
作曲探索.

听觉失真产品

关于什么的研究有着悠久的历史
通常被称为组合音 (CT).
大多数组合音调的研究都使用了两种
纯音 (IE。, 正弦曲线) 作为刺激和螺柱-
听者对第三声的感知, 不是
存在于原始刺激中, 但清晰可闻
给听者. 在 1856 赫尔曼·冯·亥姆霍兹
是第一个识别和音与差音的人
(冯·亥姆霍兹 1954). 对于两个正弦信号-
nals with frequencies f1 and f2 such that f2 >
f1, 和音与差音有 fre-
昆西 f1 + 分别为 f2 和 f2 – f1. 之后,
丰满 (1965) 确定了许多额外的组合-
频率为 f1 的民族音 + 氮( f2 - f1)
起初, 人们认为 CT 仅发生在

肯德尔等人.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
/
C
哦
米

j
/

我

A
r
t
我
C
e
–
p
d

F
/

3
8
4
5
1
9
7
1
6
7
5
/
C
哦
米
_
A
_
0
0
2
6
5
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

高强度水平，然后推动了本质上
物理听觉系统的线性力学
进入非线性区域. 最初的理论是
机械非线性位于中间
耳朵或基底膜.

戈德斯坦 (1967) 提供了特别彻底的

两种纯音产生的 CT 的研究.
频率, 振幅, 和dis的阶段-
扭音是使用以下方法确定的
声学消除, 茨维克首先提出
(1955). 重要的, 戈德斯坦证明了
即使在低刺激水平下也存在 CT
因此不可能是机械非线性的产物-
其最初构想的方式是真实的.

机械非线性理论

认识到部分内容后移位
内耳, 具体来说, 外毛细胞
基底膜, 充当有源放大器
系统. 所以, 而不是一个被动的系统
具有非线性, 耳朵是一个活跃的耳朵, 和
这些非线性可以最好地解释为
耳蜗放大器的工作原理 (金子 1948;
肯普 1978). 从这个角度来看, CT 可以
最好理解为主观声音
由物理声学信号引起并生成
由耳蜗的活性成分. 康比-
国音与耳声完全一样
排放量, 或者, 更具体地说, 畸变产物
耳声发射. 顺便, 畸变产品-
uct 耳声发射传播回
中耳，可在耳内测量
运河. 它们是健康听力系统的典型特征
他们的测试已成为一种常见的诊断方法
识别听力障碍的工具 (肯普 1978;
约翰森和埃尔伯林 1983). 要完全清楚,
然而, 当遇到失真产物时
一个倾听者, 这是对基底肌的直接刺激
产生声音感知的膜,
不是耳道内的声发射. 这是
为什么我们使用术语“失真产品”来指代
贯穿本文的一般现象.
在众多失真产品中, 两种类型是
对于音乐和声音合成特别有用
由于听众可以轻松地听到和记录-
认识他们: 二次差音 ( f2 – f1),
量子DT, 服从平方律畸变和
立方差音 (2 f1 – f2), CDT, 它服从

三次定律畸变. 尽管有共同点
他们的起源, 有相当大的差异
两者之间. CDT是最激烈的
畸变产物，可直接观察到
听者即使在声刺激相对处于
低强度水平. 然而, 因为语气的
频率 (2 f1 – f2) 一般都比较近
到 f1, mu里很少有人评论-
特定的语境 (一个重要的例外是让
西贝柳斯第一交响曲, 比照. 坎贝尔和格莱特
1994). CDT 的水平高度依赖于
纯音频率之比, f2 / f1,
最低水平产生最高水平
比率，然后迅速下降 (戈德斯坦
1967). 有超过的损失 20 之间的分贝
的比率 1.1 和 1.3.

量子DT ( f2 – f1) 需要更高的刺激-
紧张到可以听到, 但因为由此产生的音调
频率通常远低于刺激频率-
频率，因此可以更容易识别,
自诞生以来一直是音乐话题
塔蒂尼的发现 1754. QDT 显示很少
依赖于频率的比率
纯音; 水平再次最高，最低
比率，并且大致有一个 10 比率之间的 dB 损失
的 1.1 和 1.8 (戈德斯坦 1967). 即使是简单的性格-
CDT 和 CDT 之间的差异
QDT 存在争议, 我们的理解是
经常通过研究更新.

音乐音调研究

在一项与音乐音调很容易相关的研究中, 普雷斯尼策尔
和帕特森 (2001) 专注于贡献
CT 投球, 尤其是对于缺失的基本面.
他们使用了和声复合体来代替
通常的一对纯音. 在他们的第一次
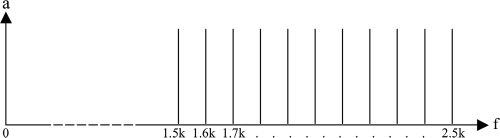
实验, 他们使用了一系列同相纯
之间的音调 1.5 千赫兹和 2.5 kHz，带间隔
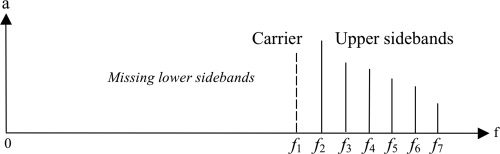
的 100 赫兹, 如图 1. 使用相同的
Goldstein 的取消技术, 他们测量了
得到的第一个的幅度和相位
四个同时失真产物 100 赫兹,
200 赫兹, 300 赫兹, 和 400 赫兹.

使用复合体的后果之一

纯音的每对相邻的

电脑音乐杂志

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
/
C
哦
米

j
/

我

A
r
t
我
C
e
–
p
d

F
/

3
8
4
5
1
9
7
1
6
7
5
/
C
哦
米
_
A
_
0
0
2
6
5
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

数字 1. 代表
和声
复杂使用
由普雷斯尼策尔和
帕特森 (2001) 在他们的
实验 1 测量

畸变产物. 这
信号由 11
纯音由
频率内部结构 100
赫兹之间 1.5 千赫兹和
2.5 千赫.

正弦曲线有助于产生的增益
基本的 (这在他们的子系统中得到了验证-
大量的实验). 他们报告说“谐波
复杂的语气 . . . 可以产生相当大的DS [迪斯-
扭转谱], 即使在中等到低的声音下
水平”。他们继续确定的水平
基本原理本质上是“向量和
二次失真音调 . . . 所有人都生产的
可能的初选对。” (这是一个好的第一
CDT 的影响为 ig 的近似值-
诺德。) 另一个后果是由此产生的
失真产物包含多重谐波-
基本原理 (1,700 – 1,500 = 200 赫兹;
1,800 – 1,500 = 300 赫兹; ETC。). 这些也是 ap-
对应对的近似向量和
纯音的. 和, 显著地, 阶段有一个临界
对这些载体产品的影响是因为-
相位纯音对产生异相失真
可以抵消同相产品的产品
当加在一起时. 所以, 创建dis-
增益最高的扭转产品, 全声学
组件应彼此同相.

此外, Pressnitzer 和 Patterson 证实

受试者间差异相对较小.
QDT 和畸变光谱的可预测性
为合成提供了实践基础
更复杂的音调和动态声源
听者听到的却完全是
声音中不存在. 实际上, 从
听众的视角, QDT 也可能是
外部产生的声音, 尽管有声音
一些虚幻的知觉属性.

缺失的基本面与
组合音调

(另请参阅音频示例 1 和 2a-b 中
附录 1.)

“缺失的基本面”是一种感性现象-
表面上与 CT 相关的名词. 在里面
心理声学文献, 缺失的基本面
最常被称为“残余沥青,”
其中“残差”指的是感知到的音调
调和复数对应于基波
即使基波分量的频率
声音信号中缺失. 最简单的
说明这一现象的方法是想象一个
100-Hz 周期脉冲串通过
高通滤波器. 未过滤, 声音会清晰
具有与 100 Hz 相对应的感知音高
基波以及整数倍谐波-
三频. 但设置高通滤波器
截止，以便消除 100 Hz 分量
不会导致音高消失; 有什么变化,
相当, 是感知到的音色. 什么时候
进一步提高截止频率, 球场
一直持续到除了一小部分中频之外的所有中频
谐波残留 (里兹玛 1962). 现在, 有关
回到普莱斯尼策和帕特森的实验
具有 100 Hz 基波的谐波, 我们
可能会问是否残留沥青和组合
音调本质上是同一现象.

确实，缺失的基本和
组合音调有着相互交织的历史.
早期研究人员 (谢弗和亚伯拉罕 1904;
弗莱彻 1924) 假设残余沥青为
本身就是一种非线性失真, 重新引入
当基音被移除时通过耳朵
(斯穆伦堡 1970). 舒腾 (1940) 反驳了
这, 然而, 通过证明残留物不是
被额外的声音信号掩盖. 这是
音频示例 1a–d 中进行了说明 (附录 1)
残留物未被噪声掩盖的地方, 然而
组合音是. 这是一个非常重要的
作曲家的要点, 因为 CT 很容易
被听者感知到的, 其他声音不得
掩盖失真频谱.

重要的, 豪斯玛和戈德斯坦 (1972)
确定残余物沥青不相关
基底上的组件相互作用
膜. 但请记住，戈德斯坦 (1967) 作为
以及普莱斯尼策和帕特森 (2001) 测量的
通过取消组合音调的属性
它们带有原声音调. 组合音调
需要基底上的组件相互作用

肯德尔等人.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
/
C
哦
米

j
/

我

A
r
t
我
C
e
–
p
d

F
/

3
8
4
5
1
9
7
1
6
7
5
/
C
哦
米
_
A
_
0
0
2
6
5
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

膜，而残余沥青则为
更高的听觉“模式识别”机制
(豪斯玛和戈德斯坦 1972).

说明了同样引人注目的差异
在音频示例 2a 和 2b 中, 其中每组
原声音调产生组合音调
相同的主观音调. 在音频示例 2a 中
声学音调是所感知的高次谐波
基本的, f1= 10 F . 在音频示例 2b 中
原声音调与基音不和谐,
f1= 10.7 F , 同时仍保持频率
基频分离, F . 这
组合音的主观印象是
本质上是一样的. 这说明 CT 确实
不依赖于谐波比. 总共, 虽然
CT 和缺失的基本面可能看起来是
有关的, 他们的潜在神经机制
一定是完全不同的.

音乐应用

尽管听觉科学家已经扩展了我们的
CT知识, 首先是一位音乐家
发现了他们, 以及许多作曲家和艺术家-
前辈们在他们的工作中利用了这些现象
作品继承了朱塞佩·塔蒂尼 (Giuseppe Tartini) 早期的魅力
他称之为 terzo suono [第三声].
正如我们将看到的, 电脑音乐家是techno-
逻辑上更好地利用这些现象,
鉴于人们可以对所有人施加严格的控制
声学方面. 由于历史原因,
然而, 这往往是即兴创作
提供了听觉方面的创造性实验
失真. 许多仪器都反映了这一点-
即兴创作者——例如, 和田耀志, 马特
英格尔斯, 约翰·布彻, 宝琳·奥利维洛斯, 和托尼
康拉德——描述现象的作用
在他们的实践中. 康拉德描述了他的剧院
与 La Monte 合作的《永恒音乐》即兴创作
杨和其他人作为“继续”工作的实践
来自声音“内部”的声音 (康拉德 2002,
p. 20), 他的性格间接说明了
为什么听觉失真在这种情况下盛行.
可以接受事故和人工制品的地方或
被拒绝, 或立即增强或减弱,
主观聆听“音乐”的机会

待开发层数最大; 最伟大的, 那是,
当表演者没有乐谱时. 埃文·帕克的
麒麟座 (1978) 是一个很好的例子
在这个传统中. 从麦克风录制
使用“直接切割”直接到黑胶母带
技术, 这张专辑由四位女高音独唱组成
萨克斯管即兴创作探索了一系列
包括循环呼吸在内的表演技巧-
过度吹捧. 这些使他能够实现
乐器的复调类型, 与三个
或同时探索更多寄存器. 当李斯-
倾向于足够高的音量, 快速级联
萨克斯管的高音区的音符
在听众耳中产生颤动的失真音调.
这首曲子纯粹的旋律密度, 然而,
使失真产物具有转瞬即逝的品质:
不知道听他们说话的听众可以
很容易错过他们. 这或许象征着
听觉失真产品的总体状况
在音乐史上——“幸福的意外”比
直接控制的音乐素材.

乔纳森·柯克 (2010) 和克里斯托弗·霍沃斯

(2011) 都描述了几个例子
20世纪音乐却并非如此, 和
听觉失真产物被视为
本身就是一种音乐材料. 像玛丽安这样的艺术家
阿马赫和雅各布·克尔凯郭尔通过以下方法实现了这一目标
计算机的帮助, 并为了准确控制
畸变产物, 纯音发生器的使用,
至少, 是必不可少的. 菲尔·尼布洛克是
在这方面特别值得注意, 一位艺术家
其接近正好落在耳朵之间-
帕克等人的指导工具工作
像阿马赫这样的人的严格方法. 他的
作品由致密的电子层组成
经过处理的仪器无人机. 他运用微色调
音调变化和频谱变化，以便
提高可听性和优势
自然出现的组合音调, 以及
介绍新的. 沃尔克·斯特雷贝尔 (2008), 在他的
Niblock作品分析, 数了多达
21 不同频率的CT 3 到 7 – 196 为了
大提琴和磁带 (镍块 1974).

Niblock 的无人机音乐说明了一个重要的问题
关于组合音调和感知的要点
显着性. 形式上静态, 明显静止的
构图可以揭示声学的多样性

电脑音乐杂志

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
/
C
哦
米

j
/

我

A
r
t
我
C
e
–
p
d

F
/

3
8
4
5
1
9
7
1
6
7
5
/
C
哦
米
_
A
_
0
0
2
6
5
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

专心聆听时的细节, 和听觉失真-
在这种情况下可能经常会注意到. 自由地
移动头部, 人们可以很容易地认识到这是如何
运动改变了强度和定位
由此产生的失真产物. 是音乐剧吗
形式迅速变化和发展, 这种
比较是不可能的, 所以在许多
听觉失真的情况可能根本无法被识别-
尼泽德. 因此，Niblock 的方法放大了
听觉障碍的辨别条件-
声学扭转. 期间设计的
编辑过程, 听觉的偶然品质
音乐表演中的失真是, 所以, 巧妙地
被抹去.

与大多数创造听觉的技术一样
失真, Niblock的方法可以被认为是
是“由内而外”,“ 那是, 他从声学开始
声音并操纵它直到失真
产品发出声音. 无论是一个 (喜欢
塔丁斯) 拉小提琴, 或者 (像尼布洛克) 数字地
将部分部分推至接近的比率内, 事实
仍然是作为音乐剧的失真产物
这里的材料基本上是难以捉摸的, 可控的
仅就其音调和响度而言. 为了
实现细粒度控制, 需要减少
声学变量只限于那些必要的.
电子音乐家很快就看到了
不断发展的概念的音乐可能性
听觉非线性. 例如, 英国人
广播电台作曲家达芙妮·奥拉姆
用了两章来考虑总和
以及她书中的不同音调, 个人笔记
(奥拉姆 1972). 几年后，这些想法诞生了
已故玛丽安·阿马赫 (Maryanne Amacher) 的成果, WHO
使听觉失真的诱使成为一种
艺术形式本身. 她的声音装置
现场表演因其
利用短正弦音的联锁模式
以非常高的音量再现旋律, 哪个
在耳朵中引起明显的失真音
听众. 内衬中对声音角色的注释
(第三只耳朵的制作), 阿马赫生动地讲述了
描述这些人的主观经历
音调:

当以正确的音量播放时, 这是
相当高且令人兴奋, 音乐中的音调

会让你的耳朵发挥神经语音功能
发出声音的乐器似乎
直接从你的头脑中发出 . . .
[我的观众] 发现他们正在生产
相互作用的音乐的音调维度
有旋律地, 有节奏地, 并在空间上与
房间里的音调. 音调“跳舞”
他们身体的直接空间, 他们周围
就像声波包裹一样, 耳内级联, 和出来
到他们眼前的空间 . . . 不要
惊慌! 您的耳朵表现得并不奇怪或
被损坏! . . . 这些虚拟音调是
听觉的自然且非常真实的物理方面
洞察力, 类似于两个图像的融合
产生第三个三维图像
双眼感知 . . . 我想发布这个
由听众创作的音乐 . . .
(阿马赫 1999, 班轮注释).

阿马赫用来产生这些效果的音调

使用 Triadex Muse 生成, 一个数字
爱德华·弗雷德金 (Edward Fredkin) 制造的音序器仪器
和麻省理工学院的马文·明斯基. 阿马切尔是第一个
声音作品引发真正独立的音乐流
从听觉失真, 主观的“第三
层,”她有时将其称为
“第三只耳朵” (阿马赫 2004). 这种客观化
这些之前被忽略的, 潜意识的声音非常
阿马赫的工作取得了成功, 重点是
我们在这项研究中取得了进展.

实际观察

为了使听觉失真产品
具有音乐意义的, 听者必须能够
将它们与声学声音区分开来; 否则,
为什么不简单地使用普通的声音信号? 作为
已经说明了, 纯声学的固定组合
音调将产生持续的失真音调
固定频率. 在这种情况下, 听者的
头部和身体的运动会产生重要的
用于分离两个声源的流提示
(请参阅空间图像部分, 随后).
出于音乐目的, 然而, 我们可能想要
创建纯音复合体序列, 从而
产生改变的失真音调模式

肯德尔等人.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
/
C
哦
米

j
/

我

A
r
t
我
C
e
–
p
d

F
/

3
8
4
5
1
9
7
1
6
7
5
/
C
哦
米
_
A
_
0
0
2
6
5
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

时间. 从音乐上来说, 音调序列是
更引人注目, 正如阿马赫 (Amacher) 所阐释的
1999 作品“头部节奏/玩具”。这件作品
具有重复的粗制序列, 纯音
引起迷失方向的叽叽喳喳声, 微妙地转变
不同失真音调的节奏模式
频率; 很容易从音调中辨别出来
用于生成它们. 但在音乐剧中
尚未合成的特性
系统方式是音调的动态特性
比如颤音, 颤音, 动态光谱, 空间的
地点, ETC. 计算机合成使
以一种方式探索这些可能性
早期从业者无法获得, 并且还没有
之前曾在音乐合成中被利用.

二次畸变的幅度, C ≈ 130 分贝
(法斯特和茨威克 2007). 实验数据在
取消音用于确定
QDT的振幅表现出相当规则的
行为. 听觉 QDT 被很好地建模为
二次畸变. 随着 L1 或 L2 的增加
取消水平几乎与预测一致
这种情况是否会发生
声信号的频率大或小.
例如, 对于 L1 = L2 = 90 分贝, 的水平
取消音大约是 50 分贝. (有
接受此观察的听众所占的百分比
崩溃了, 参见法斯特尔和茨威克 2007, PP. 280–
281.) 为了我们的目的, 有效的差异
幅度的影响相对较小
感知音色, 特别是动态的.

将听觉失真建模为
非线性系统

物理声学之间的确切关系
刺激和由此产生的听觉失真产物-
ucts相当复杂, 但在制定系统化的
合成方法, 一个好的第一个近似是
将失真产物的产生建模为
一般非线性系统. 我们从经典开始
幂级数表示 (冯·亥姆霍兹 1954):

y − a0 + a1x + 一个2x2 + ··· + 一个x2

(1)

其中 x 是系统的输入，y 是系统的输出.
an 是常数. 输出的非线性
随着输入电平增益的增加而增加, X, 增加.

二次差音

二次分量, 一个2x2, 贡献了
差音, f2 – f1, 以及组件
2 f1, f1 + f2, 和 2 f2, 虽然主观程度较低
级别. 二次失真音调的水平 (作为
通过声学抵消法测量) 是
给出的

L( f2−f1) - L1 + L2-c

(2)

其中 L1 和 L2 代表声学级别
信号的分贝数和 C 取决于相对

QDT 作为畸变产物

将 QDT 建模为非线性产品是相当困难的
直截了当. 如果我们考虑以下情况
其中有两个简单的正弦输入
二次方程:

y − x2,

(3)

我们发现:

y(t) = (A1的(ω1t) + A2罪(ω2t))2
2 罪恶2(ω2t)
1 罪恶2(ω1t) + A1

=A2

+ 2A1 A2 罪恶(ω1t) 罪(ω2t)

(4)

其中 ω1 和 ω2 是正弦频率，
A1和A2各自的幅度. 在拓展中
方程 4, 我们发现前两项产生
直流电 (直流) 成分, 和第三项
提供重要的组合音调:

y(t) =

A2
1
2

因斯(2ω1t) +

A2
A2
2
1
2
2
+ A1 A2 因斯((ω1 - ω2)t) − A1 A2 cos((奥1 + 氧气)t),

因斯(2ωt)

A2
2
2

在哪里 (奥1 + 氧气)和 (ω1 - ω2) 是总和和
差频. 差异的增益
频率为A1 A2 (以分贝为单位: L1 + L2). 此外

(5)

电脑音乐杂志

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
/
C
哦
米

j
/

我

A
r
t
我
C
e
–
p
d

F
/

3
8
4
5
1
9
7
1
6
7
5
/
C
哦
米
_
A
_
0
0
2
6
5
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

桌子 1. 两种纯音和 CDT 引发的和弦

f2/f1

1.25
1.2
1.166
1.1428
1.125
1.111

f1: f2

4:5
5:6
6:7
7:8
8:9
9:10

间隔

2f1-f2: f1: f2

结果和弦

大三度
小三度
～小三度
～大二度
大二
大二

3:4:5
4:5:6
5:6:7
6:7:8
7:8:9
8:9:10

大三和弦
大三和弦
～减三联征
非三元组
∼全音簇
全音簇

频率 f1 和 f2 产生第三音调, CDT, 频率为 2f1 − f2, 提供三音符中的最低音符
弦. 该表给出了前两个音之间的音程以及产生的和弦类型. 音程和和弦标记为
波形符 (～) 有点不协调.

总频率和差频率, 完整的
平方器的输出信号包含DC和COM-
两倍输入频率的分量, 成分
那些听不见的.

三次差音

立方分量, 一个3x3, 贡献立方
差音, 2 f1 – f2 以及 2 f2 – f1, 3 f1, ETC.
实验测试数据不太符合
将预测规则立方变形.
例如, CDT的水平很强
取决于之间的频率间隔
纯音, f2 – f1 (法斯特和茨威克 2007). 这
意味着听觉 CDT 没有很好地建模为
规则的三次变形. 其特点下
不同的情况更加特殊
比QDT. 尤其, 级别的依赖关系
关于频率间隔和频率范围
是 CDT 难以使用的另一个原因
以受控方式进行合成, 虽然
理想情况下 CDT 的水平为
明显高于QDT.

CDT比率

当比率达到以下时，CDT 的声音最为清晰：
声音信号的, f2/f1, 位于之间 1.1 和
1.25. 该范围内的比率与音乐一致
大二度和大三度之间的音程.
和, 正如我们所期望的音程, 比率
以下 1.14 产生听觉粗糙感 (或者那个-

从音乐的角度看南斯). 此外,
CDT 本身非常接近 f1 和 f2，以至于什么
人们通常认为是一种三音聚合.
以西贝柳斯第一交响曲为例
说明 (坎贝尔和格莱特 1994), 如果比率,
f2 / f1, 形成音程, CDT将成立
产生三音符和弦的另一个音程.
这些关系总结在表中 1
使用简单的整数比率进行说明.

合成技术

用于声音合成的目的, 直接的
二次和三次差音的生成
来自一对纯音遭受重要的限制-
迭代. 如前所述, CDT 相对而言
比 QDT 更响亮, 但距离很近
CDT 对声刺激的频率限制了
听者很容易辨别的情况-
从声调中消除它. 为了创造
QDT 处于听众可以识别的水平, 这
原声纯音必须在一定程度上呈现
这让大多数听众感到不舒服, 尤其
在任何延长的时间内.

Haworth 协同解决了 QDT 问题

通过利用正弦复合体进行设置
恒定差频, 类似于刺激
Pressnitzer 和 Patterson 之前讨论过. 在
作曲《相关性一号》 (2010),
每对相邻的正弦曲线都会产生相同的-
校准 QDT 频率, 线性增加其总增益
和, 从而, 增加失真程度

肯德尔等人.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
/
C
哦
米

j
/

我

A
r
t
我
C
e
–
p
d

F
/

3
8
4
5
1
9
7
1
6
7
5
/
C
哦
米
_
A
_
0
0
2
6
5
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

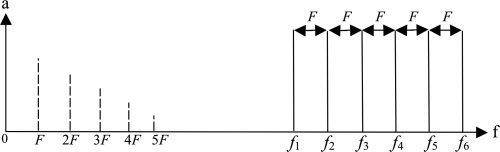
数字 2. 二次
差音 (量子DT)
光谱 (虚线)
由纯音产生
(实线) 与一个
恒定频率
F的区间.

语气 (霍沃斯 2011). 不仅是组合
声学正弦波增加增益, 但它也
产生的组件是谐波
初级QDT. 重要的, 增加数量
声学音调 (并因此传播它们
在更宽的频率范围内) 允许主观
要降低的声调级别, 因此
大大减少听众疲劳的问题.
清楚地, 听觉的音乐语境

失真产品的使用决定了大
效果的成功程度. 我们有
指出听众必须能够区分
音调的失真产物,
为了做到这一点，必须仔细注意
支付给频谱. 一般来说,
研究人员重点关注以下 QDT 1 千赫
之间有纯音 1 和 5 千赫. 这给出了
对最实用频率的一些指导
没有竞争声音时使用的范围.
识别听觉失真的存在
产品要求它们在听觉上与
通过音高或其他方式发出的声音. 这
对合成的选择有重要影响
方法. 其他高频声信号
重叠声波的频率范围
刺激听觉失真音调的信号
会产生意想不到的副作用并削弱
畸变产物的影响. 还, 存在
与该范围重叠的其他声音信号
失真产物本身可以掩盖
并破坏它们的效果. 可能很明显地说,
但听觉失真产物, 像许多其他人一样
综合方面, 都得到了最好的调整和优化
凭耳朵. 可以实现很多富有想象力的效果
通过创造性地运用合成. 我们总结一下
最重要的合成方法在这里.

直接加成合成

(另请参阅音频示例组 2 在附录中 1.)
普莱斯尼策和帕特森 (2001) 证明了
多个纯音按顺序合成
基波的高次谐波, F , 产生一个
具有基波 F 的谐波 QDT 谱 .
各个谐波分量的增益
该频谱是 QDT 的总和

每对纯音产生的贡献.
例如, 他们证明了谐波
15 到 25 100Hz 基频, 每个在 54 分贝
声压级, 产生谐波 QDT 谱
基波仅比增益低 10–15 dB
音调.

但要产生 QDT 谐波频谱, 这
原声纯音 ( f1, f2, f3, ETC。) 不需要
QDT 基波的谐波, 他们只需要
以恒定的频率间隔分开
F (F = f2 – f1 = f3 – f2, ETC。). 这会产生一个
基波为 F 的 QDT 谱，如图所示
数字 2. 产生的失真的确切质量
音调体验取决于 f1 和
声学数量, 正弦分量.

就其本身而言, 该技术可以产生 QDT 光谱

在典型的扬声器中清晰可闻
以中等声级再现. 并从
这个起点, 很多经典的时域
合成过程可以通过简单的引入
舒适, 例如, 调幅 (是).
AM 有两种可能性，每种都会产生
结果略有不同，具体取决于数量
声音信号正在产生效果. 调制
所有纯音一起产生一个单一的, 振幅-
调制声音. 调制所有纯音，除了
对于最低的, f1, 增强持续的效果
纯音加上调幅失真
产品. 后一种情况提供了更好的主观性
原声音调之间的音色分离
失真音调, 而在前一种情况下
两个倾向于融合. 改变调制率有
可预测的结果. 产生令人愉悦的颤音效果
最多大约 15 赫兹, 然后是“粗糙度”
之间 20 赫兹和 30 赫兹. 增加调制
速率进一步引入了边带
可能干扰预期目的的声音信号
畸变谱.

电脑音乐杂志

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
/
C
哦
米

j
/

我

A
r
t
我
C
e
–
p
d

F
/

3
8
4
5
1
9
7
1
6
7
5
/
C
哦
米
_
A
_
0
0
2
6
5
p
d

乙
y
G
你
e
s
t

哦
n
0
8
S
e
p
e
米
乙
e
r
2
0
2
3

对频率应用相同的原理
声波信号产生频率调制
QDT 光谱. 在最简单的情况下, f1
频率最好保持静态, 和调制
应用于之间的频率间隔
其他组件 ( f2–f1, f3–f2, ETC。). 在这个
方式, 基频的频率调制,
F , 很容易听到, 同时调制
声学成分不太明显，因为
它们的节距偏差要小得多
比原声音调.

AM 和 FM 的速率都需要微妙的
调整, 否则造成的粗糙度
声波频率的跳动会干扰
QDT 光谱的分离. 调频
速率参数, 尤其, 提供一些额外的
可能性. 如果设置足够高, 即使在
音调的频率偏差相对较小
失真音调的感觉将会消失. 在
本身, 这给出了相当沉闷的, 静态声音, 相当
像窄带噪声. 但如果一个人应用重复
声音流的短时间窗口序列,
类似于同步颗粒合成, 那么
结果变得更有趣. 如果我们选择慢速
调频速率 (<12 Hz) and a repeating envelope with sharp attack sloping decay, then, due to the closeness of distortion tone and its unresolved pitch, one perceives fluttery, wind-like sound that appears bristle against the ear. The techniques described here are employed in Haworth’s compositions “Correlation Number One” (2011) “Vertizontal Hearing (Up & Down, I then II)” (2012). Dynamic Sinusoidal Synthesis (Refer also Audio Example Group 3 in Appendix 1.) The basic processes this article can be applied situations which the fundamental frequency overall amplitude are dynamically changing. Most importantly, the pitch amplitude QDT spectrum can be made follow characteristics model signal, including recorded or real-time performance. 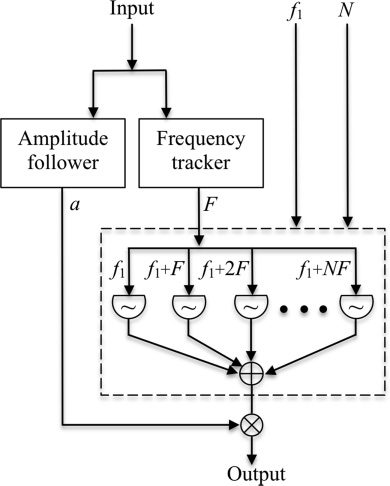Again, order for tone heard clearly by listener, synthesis must again rely Figure 3. Dynamic sinusoidal a QDT based on an audio signal input. The frequency lowest acoustic component is f1, and N number of additional sinusoids synthesized. on multiple pure tones constant frequency offset. Consider algorithm illustrated Figure 3. Here input fed frequency tracker an follower dynamically extract fundamental, F , amplitude, a. Then, sinusoidal oscillator bank along with two values set user: f1, frequency of lowest sinusoid, N, sinusoids synthesize. will determine the strength spectrum’s fundamental and possible harmonics. Typically one f1 remains constant, while additional oscillators follow the value at integral offsets from f1, + 2F . NF sum sinu- soids produced multiplied by output follower, a, recre- ate original envelope. result synthesis will like shown 2, only dynamic. In way, mimic the dynamic character live prerecorded sound. Of course, success depends on nature of the material degree there is fundamental extract. Then too, the same oscillator-bank technique used Kendall et al. 13 l D o w n o a d e d f r o m h t t p : > 6.
阿贝尔不可能性定理指出, 一般来说,
四次以上的多项式方程为
无法用有限的代数解
添加数量, 减法, 乘法,
部门, 和在公司上进行的根提取-
高效的 (切尼和金凯德 2009, PP. 705). 这
并不意味着高次多项式不是
可解的, 因为代数的基础理论
保证至少存在一个复杂的解决方案.
这真正意味着解决方案不能
总是用部首表示.

所以, 寻找代数表达式
对于任何 N 都是不切实际的; 如果我们想指定 s(t)
超过四个谐波通过计算
x 的系数(t), 这样做的唯一方法是
数值方法，例如 Newton-Rhapson,
拉盖尔, 或 Lin-Bairstrow 算法 (罗斯洛内茨
2008, PP. 29–47). 这就是为什么一个
数值解而不是代数解是
当高时解决此问题的正确方法
目标信号中的谐波数量是所需的.

我

D
哦
w
n
哦
A
d
e
d

F
r
哦
米
H

t
t

:
/
/

d
我
r
e
C
t
.

米

我
t
.

e
d
你
/
C
哦
米

j
/

我

A
r
t
我
C
e
–
p
d