So Good It Has to Be True: Wishful Thinking
in Theory of Mind
Daniel Hawthorne-Madell
1
and Noah D. 古德曼
1
1心理学系, 斯坦福大学
关键词: 妄想, computational social cognition, 心理理论, desirability bias
抽象的
In standard decision theory, rational agents are objective, keeping their beliefs independent
from their desires. Such agents are the basis for current computational models of Theory of
头脑 (ToM), but the accuracy of these models are unknown. Do people really think that
others do not let their desires color their beliefs? In two experiments we test whether people
think that others engage in wishful thinking. We find that participants do think others believe
that desirable events are more likely to happen, and that undesirable ones are less likely to
发生. 然而, these beliefs are not well calibrated as people do not let their desires
influence their beliefs in the task. Whether accurate or not, thinking that others wishfully
think has consequences for reasoning about them. We find one such consequence—people
learn more from an informant who thinks an event will happen despite wishing it was
否则. People’s ToM therefore appears to be more nuanced than the current rational
accounts in that it allows other’s desires to directly affect their subjective probability of
an event.
Whether thinking “I can change him/her” about a rocky relationship or the more benign “those
clouds will blow over” when at a picnic, people’s desires seem to color their beliefs. 然而,
such an explanation presupposes a direct link between his desires and beliefs, a link that is
currently absent in normative behavioral models and current Theory of Mind (ToM) 型号.
Does a causal link between desires and beliefs actually exist?1 The evidence is mixed.
There are a number of compelling studies that find “wishful thinking,” or a “desirability bias”
in both carefully controlled laboratory studies (Mayraz, 2011) and real-world settings, 这样的
as the behavior of sport fans (Babad, 1987; Babad & Katz, 1991), expert investors (Olsen,
1997), and voters (Redlawsk, 2002). 然而, other researchers have failed to observe the
effect—for example, Bar-Hillel and Budescu’s “The Elusive Wishful Thinking Effect” (1995)
has provided alternative accounts of previous experiments (Hahn & 哈里斯, 2014), 并且有
argued that there is insufficient evidence for a systematic wishful thinking bias (Hahn & 哈里斯,
2014; Krizan & Windschitl, 2007).
Whether or not there actually is a direct effect of desires on beliefs, people might think
that there is and use this fact when reasoning about other people. That is to say, 人民的
ToM might incorporate the wishful thinking link seen in Figure 1b. The direct influence of
desires on beliefs is a departure from classic belief–desire “folk” psychology in which beliefs
1 While the causal link between desires and beliefs may, 实际上, be bidirectional, we will focus on the evidence
for the a priori effect of desires on beliefs.
开放访问
杂志
引文: Hawthorne-Madell, D ., &
古德曼, D. 氮. (2017). So Good It Has
to Be True: Wishful Thinking in Theory
of Mind. 开放的心态: Discoveries in
认知科学, 1(2), 101–110.
https://doi.org/10.1162/opmi_a_00011
DOI:
https://doi.org/10.1162/opmi_a_00011
补充材料:
https://doi.org/10.1162/opmi_a_00011
已收到: 07 行进 2017
公认: 23 六月 2017
利益争夺: 作者有
no significant competing financial,
专业的, or personal interests that
might have influenced the execution or
presentation of the work described in
this manuscript.
通讯作者:
Daniel Hawthorne-Madell
d.j.hawthorne@alumni.stanford.edu
版权: © 2017
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
哦
p
米
我
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
1
2
1
0
1
1
8
6
8
2
7
1
哦
p
米
_
A
_
0
0
0
1
1
p
d
.
我
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
So Good It Has to Be True Hawthorne-Madell, 古德曼
数字 1. Competing models of Theory of Mind (ToM). Causal models of (A) rational ToM based
upon classic belief-desire psychology and (乙) optimistic ToM that includes a direct “wishful thinking”
link between desires and beliefs.
and desires are independent and jointly cause action (图1a). Previous models of ToM
formalize belief–desire psychology into probabilistic models of action and belief formation.
They show that inferring others’ beliefs (贝克, Saxe, & Tenenbaum, 2011), 优先 ( Jern,
Lucas, & 肯普, 2011), 和欲望 (贝克, Saxe, & Tenenbaum, 2009) can be understood as
Bayesian reasoning over these generative models. A fundamental assumption of these models
is that beliefs are formed on the basis of evidence, and a priori independent of desire. 我们
will call models that make this assumption rational theories of mind (rToM). We can contrast
this rationally motivated theory with one that incorporates the rose-colored lenses of a desire–
belief link, an optimistic ToM (oToM).2 We use their qualitative predictions to motivate two
experiments into the presence (and calibration) of wishful thinking in ToM and its impact on
social reasoning.
In Experiment 1 we explore wishful thinking in both ToM and behavior.
In the third-
person point-of-view (3-PoV) 状况, we test whether people use an rToM or an oToM when
reasoning about how others play a simple game—will manipulating an agent’s desire for an
outcome affect people’s judgments about the agent’s belief in that outcome? In the first person
point of view (1-PoV) condition we test whether people actually exhibit wishful thinking when
playing the game themselves. We carefully match the (3-PoV) 和 (1-PoV) conditions and run
them concurrently to have a clear test of whether people’s ToM assumptions lead them to make
appropriate inferences about people’s behavior in the game.3 Regardless of its appropriateness,
people’s ToM should have consequences for both how they reason about others’ actions and
how they learn from them. If people do attribute wishful thinking to others, it would have a
dramatic impact on their interpretation of others’ behavior. In Experiment 2 we therefore test
for a social learning pattern that only reasoners using an oToM would exhibit, highlighting the
impact ToM assumptions have on social reasoning.
EXPERIMENT 1: WISHFUL THINKING IN ToM (3-PoV) AND ONLINE BEHAVIOR
(1-PoV)
3-PoV Condition
To test for the presence of wishful thinking in people’s mental models of others we introduced
Josh, a person playing a game with a transparent causal structure. The causal structure of the
game was conveyed via the physical intuitions of the Galton board pictured in Figure 2b (在
which a simulated ball bounces off pegs to land in one of two bins). The outcome of the game
2 We formally describe Bayesian models of both rToM and oToM in the Supplemental Materials (Hawthorne-
Madell & 古德曼, 2017).
3 实验 1 is a slightly modified replication of the two conditions previously run as separate experiments
(see Supplemental Materials [Hawthorne-Madell & 古德曼, 2017]).
开放的心态: 认知科学的发现
102
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
哦
p
米
我
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
1
2
1
0
1
1
8
6
8
2
7
1
哦
p
米
_
A
_
0
0
0
1
1
p
d
.
我
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
So Good It Has to Be True Hawthorne-Madell, 古德曼
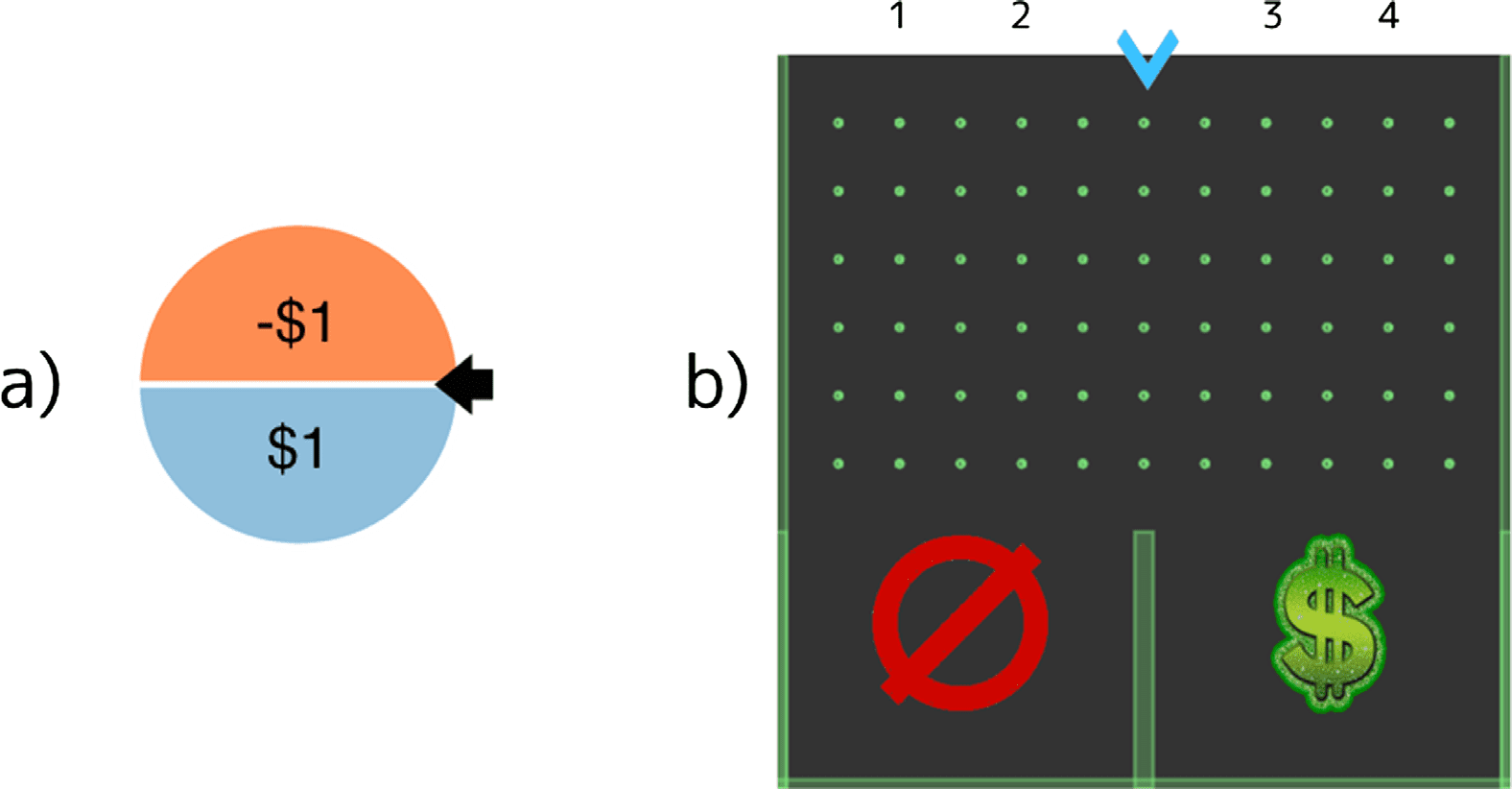
数字 2. Stimuli used in Experiment 1.
(A) The wheel used to determine the payout for the
next outcome and (乙) the Galton board used to decide the outcome. The blue arrow at the top
indicates where the marble will be dropped. The numbers indicate the four drop positions used in
the experiment.
is binary (there are two bins) with different values associated with each outcome (money won
or lost). We call the value of an outcome (IE。, the amount that Josh stands to win or lose) 这
utility of that outcome, U(outcome). Participants were asked what they think about Josh’s belief
(outcome). By manipulating outcome values we are able to
in the likelihood of the outcome pj
test for wishful thinking. If people incorporate wishful thinking into their ToM, we should find
that increasing an outcome’s utility results in higher estimates of Josh’s belief in the outcome’s
occurrence, pj
(outcome).
We first measured pj
(outcome|证据) without manipulating the desirability of the out-
come in the “baseline” block of trials. Then in the “utility” block of trials we assigned values
to outcomes, manipulating Josh’s U(outcome).4 In the utility block of trials we used a spin-
ning wheel (Figure 2a) to determine what Josh stood to win or lose based on the outcome of
the marble drop. By comparing these two blocks of trials we test for the presence of wishful
thinking in people’s ToM.
1-PoV Condition
To test whether people’s desires directly influence their beliefs in the Galton board game, 我们
simply had the participant directly play the game (replacing Josh) and asked them about their
belief in the likelihood of the outcome [their “self” belief ps(outcome)].
方法
参加者
Eighty participants (24 女性, μage = 32.93, σage = 9.68) were randomly assigned to either
the 3-PoV or the 1-PoV condition such that there were 40 in each.
4 至关重要的是, Josh’s U(outcome) should not be chosen by him, 例如, “I bet $5 that it lands in the right bin,” as such an action would render U(outcome) 和 p(outcome) conditionally dependent and both rToM and oToM would predict influence of desire on belief judgments. To test pure wishful thinking, Josh’s U(outcome) has to be assigned to him by a process independent of p(outcome)—in our case, a spinner. 开放的心态: 认知科学的发现 103 l 从http下载 : / / 直接的 . 米特 . / e d u o p m i / 拉蒂斯 – df / / / / / 1 2 1 0 1 1 8 6 8 2 7 1 o p m _ a _ 0 0 0 1 1 压力 . i f b y g u e s t t o n 0 7 九月 2 0 2 3 So Good It Has to Be True Hawthorne-Madell, Goodman Design and Procedure Participants were first introduced to Josh, who was playing a marble-drop 3-PoV Condition game with a Galton board (as seen in Figure 2b). Josh was personified as a stick figure and appeared on every screen. We then presented the causal structure (IE。, 物理) of the game by dropping a marble from the center of the board two times, with one landing in the orange bin (Figure 2b left bin) and one landing in the purple bin (Figure 2b right bin). After observing the two marble drops, participants began the baseline block of trials. In the four baseline trials, the marble’s drop position varied and participants were asked, “What do you think Josh thinks is the chance that the marble lands in the bin with the purple/orange box?” Participants’ responses were recorded on a continuous slider with endpoints labeled “Certainly Will” and “Certainly Won’t.” Color placement was randomized on each trial, and the color of the box in question varied between participants. The marble drop position was indicated with a blue arrow at the top of the Galton board, and there were four drop positions used (marblex; top of Figure 2b) that varied in how likely they were to deliver the marble into the bin in question. In the baseline and subsequent trials, participants did not observe the marble drop and outcome; they only observed the position the marble would be dropped from. After the baseline trials, participants were introduced to the utility trials, which included a spinning wheel that determined “how much Josh can win or lose” labeled with $1 and −$1. At the beginning of each trial the wheel was spun and the selected payout was displayed, 例如, “Josh has a chance of winning $1,” along with the Galton board. The bins were
labeled with a $ 和 (西德:0) symbol.5 If the marble landed in the $ bin then Josh won/lost the
钱. The location of the $ bin was randomized on each trial. After seeing the Galton board with marblex indicated with a blue arrow, participants were asked two questions sequentially. First they were asked, “What do you think Josh believes is the chance that the marble will land on the {$/−$} and he’ll {win/lose} $1?” with the response recorded on the same slider as
the baseline trials with endpoints labeled “Certainly Will” and “Certainly Won’t.” They were
then asked “How much does Josh care about the outcome?” with the response on a slider with
endpoints labeled from “Not at All” to “To a Great Extent.” Participants saw every combination
of the two outcomes ($1, −$1) and the four drop positions (see Figure 2b) for a total of eight
utility trials.
The procedure mirrored the 3-PoV condition with the participant taking the
1-PoV Condition
place of Josh. All questions were therefore reframed to ask the participant’s beliefs about the
outcome. The participants were given a $1 bonus initially and instructed that one trial at random would be selected to augment their current bonus, 那是, they could gain or lose $1.
结果
3-PoV Condition
In a rational theory of mind, beliefs and desires are a priori independent. Manipulating Josh’s
desires therefore shouldn’t have an effect on his beliefs, and we would predict that the util-
ity trials look like the baseline trials. 然而, as seen in Figure 3a, the utility trials varied
systematically from the baseline trials and, 所以, the predictions of an rToM. To quantify
(outcome) responses. 这
this deviation we fit a logistic mixed-effects model to participants’ pj
model used marblex and the categorically coded value of the outcome (negative, 基线, 和
5 $ when the payout was positive and −$ when it was negative, 和 (西德:0) representing no payout.
开放的心态: 认知科学的发现
104
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
哦
p
米
我
/
我
A
r
t
我
C
e
–
p
d
F
/
/
/
/
/
1
2
1
0
1
1
8
6
8
2
7
1
哦
p
米
_
A
_
0
0
0
1
1
p
d
.
我
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
So Good It Has to Be True Hawthorne-Madell, 古德曼
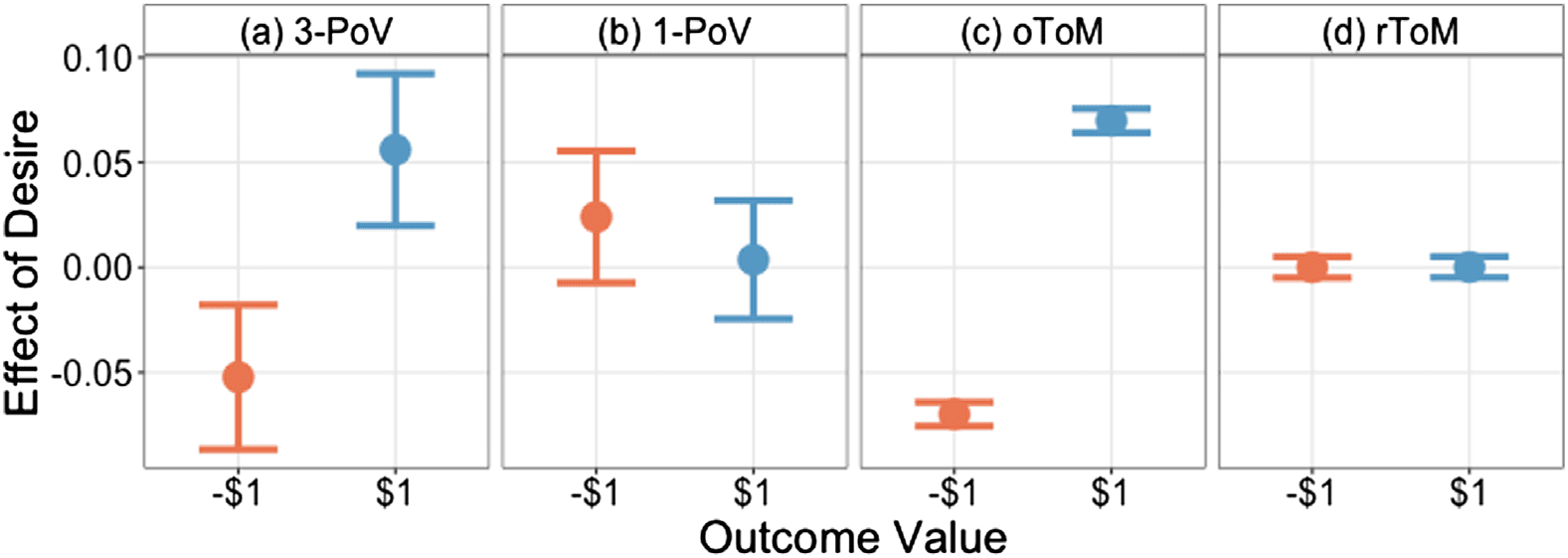
数字 3. 实验 1 数据. The effect of an agent’s desire for an outcome on the mean subjective
(outcome) attributed to the agent (和 95% CIs). For each participant, the mean effect of the
pj
positive utility ($1) and the negative utility (−$1) was determined by taking the difference between
(outcome) in each utility trial and the corresponding baseline trial. The effect is shown for the
the pj
(A) 3-PoV (point-of-view) 和 (乙) 1-PoV condition [where ps(outcome) is displayed]. These data are
compared with the posterior predictives of the (C) optimistic and (d) rational Theory of Mind (ToM)
型号 (see Supplemental Materials [Hawthorne-Madell & 古德曼, 2017]).
积极的) as fixed effects and included the random effect of marblex and intercept for each par-
ticipant. The resulting model indicated that if an outcome was associated with a utility for Josh,
participants thought that it would impact his beliefs about the probability of that outcome.
Participants thought that Josh would believe that an outcome that lost him money was
less likely than the corresponding baseline trial ( β = −0.70, z = −2.10, p = .036).6 他们还
thought that Josh would believe an outcome that would net him money was more likely than
the corresponding baseline trial ( β = 0.96, z = 2.87, p = .004).7 最后, marblex, 直接的
证据, had a significant influence ( β = 10.37, z = 11.78, p < .001). There was no evidence
that the effect of the outcome value was affected by marblex (the interactive model did not
provide a superior fit [ χ2(2) = 0.68, p = .736].
1-PoV Condition
Unlike in the 3-PoV condition, as seen in Figure 3b, there was no effect of utility on partici-
pants’ ps(outcome) responses compared with their baseline responses. Using the same logistic
mixed-model employed in the 3-PoV condition, neither outcomes that would lose the partic-
ipant money ( β = 0.09, z = 0.30, p = .760), nor outcomes that would win them money
( β = −0.09, z = 0.30, p = .760) influenced participants’ ps(outcome) responses. Similar to
the 3-PoV condition, a strong effect of the marble’s position was observed ( β = 8.88, z =
11.95, p < .001).
Comparing Conditions
To formalize the discrepancy of the effect of utility across conditions, we analyzed them to-
gether with a logistic mixed-model. We used the same model described previously except
we continuously coded the effect of utility and added an interaction between this utility and
6 All p values reported for Experiment 1 are based on the asymptotic Wald test.
7 There was no evidence of loss aversion in the relative magnitude of the wishful thinking effect for positive
In fact, the magnitude of the wishful thinking effect was slightly stronger for positive
and negative utilities.
utilities.
OPEN MIND: Discoveries in Cognitive Science
105
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
/
1
2
1
0
1
1
8
6
8
2
7
1
o
p
m
_
a
_
0
0
0
1
1
p
d
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
So Good It Has to Be True Hawthorne-Madell, Goodman
condition. The resulting model had a significant interaction between PoV (condition) and the
(outcome) responses (β = 0.43, z = 3.83, p < .001). This
effect of utility on participants’ pj/s
interactive model provided a better fit than the additive model [χ2(1) = 15.11, p < .001].
DISCUSSION
The results from the 3-PoV condition indicate that people’s ToM includes a direct “wishful
thinking” link. This is consistent with the qualitative predictions of the oToM model (see the
Supplemental Materials [Hawthorne-Madell & Goodman, 2017]; Equation 2), unlike rToM
models where beliefs and desires are a priori independent.8 However, the 1-PoV condition
did not find evidence that people are biased by their desires in the Galton board game. This dis-
connect suggests that people’s attribution of wishful thinking in this situation is miscalibrated.
That is to say that Experiment 1 represents a situation where wishful thinking is present in ToM
reasoning but absent in actual behavior—people think others will behave wishfully when,
in fact, they do not.
This miscalibration is consistent with an over attribution of wishful thinking. However,
the present study does not provide insights into why there is this miscalibration. Any number of
incorrect assumptions could lead to the results. Perhaps people think that everyone wishfully
thinks, but only they are clever enough to correct for it. Alternatively, they could think that
$1 or $5 is much more desirable for others than it is for themselves. There are a number of
actor–observer asymmetries and self-enhancement biases that could plausibly underpin the
observed inconsistency ( Jones & Nisbett, 1971; Kunda, 1999). Further study is necessary to
determine the cause of the over attribution.
Regardless of whether people actually engage in wishful thinking, if people assume
others do, then it should affect how they interpret others’ actions and learn from them.
In
Experiment 2 we therefore expand our sights to social learning situations where oToM (but,
crucially, not rToM) predicts that desires affect a social source’s influence.
EXPERIMENT 2: LEARNING FROM OTHERS WITH AN oToM
Do people consider a social source’s desires when learning from them? It would be important
to do so if they think that his desires have a direct influence on his beliefs. Consider a learner
using an oToM to reason about her uncle, a Chicago Cubs fan, who proudly proclaims that
this is the year the Cubs will win it all. Though her uncle knows a lot about baseball, the
oToM learner is unmoved from her (understandably) skeptical stance. However, if her aunt,
a lifelong Chicago White Sox fan (hometown rival to the Cubs), agrees that the Cubs do look
better than the Sox this year, then an oToM learner considers this a much stronger teaching
signal. In fact, a learner with an oToM would consider her aunt’s testimony as more persuasive
than an impartial source (see Figure 4b). A learner reasoning with an rToM wouldn’t distinguish
between these three social sources,9 as seen in Figure 4c.
We investigated which ToM best describes learning from social sources in a controlled
version of this biased opinion scenario. Participants were asked how likely a team (x) was
8 Interestingly, there was consistency in the magnitude of this effect when Josh stood to gain $1 (as in the present experiment) or $5 in Experiment 1b (see the Supplemental Materials [Hawthorne-Madell & Goodman,
2017]). The extent to which people attributed wishful thinking to Josh was therefore not sensitive to the magni-
tude of Josh’s potential payout for this range (where payout is our operationalization of his desire).
9 Assuming that the three sources are equally knowledgeable and their statements have no causal influence
on the game, for example, if the uncle is an umpire, his desires may matter through more objective routes.
OPEN MIND: Discoveries in Cognitive Science
106
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
/
1
2
1
0
1
1
8
6
8
2
7
1
o
p
m
_
a
_
0
0
0
1
1
p
d
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
So Good It Has to Be True Hawthorne-Madell, Goodman
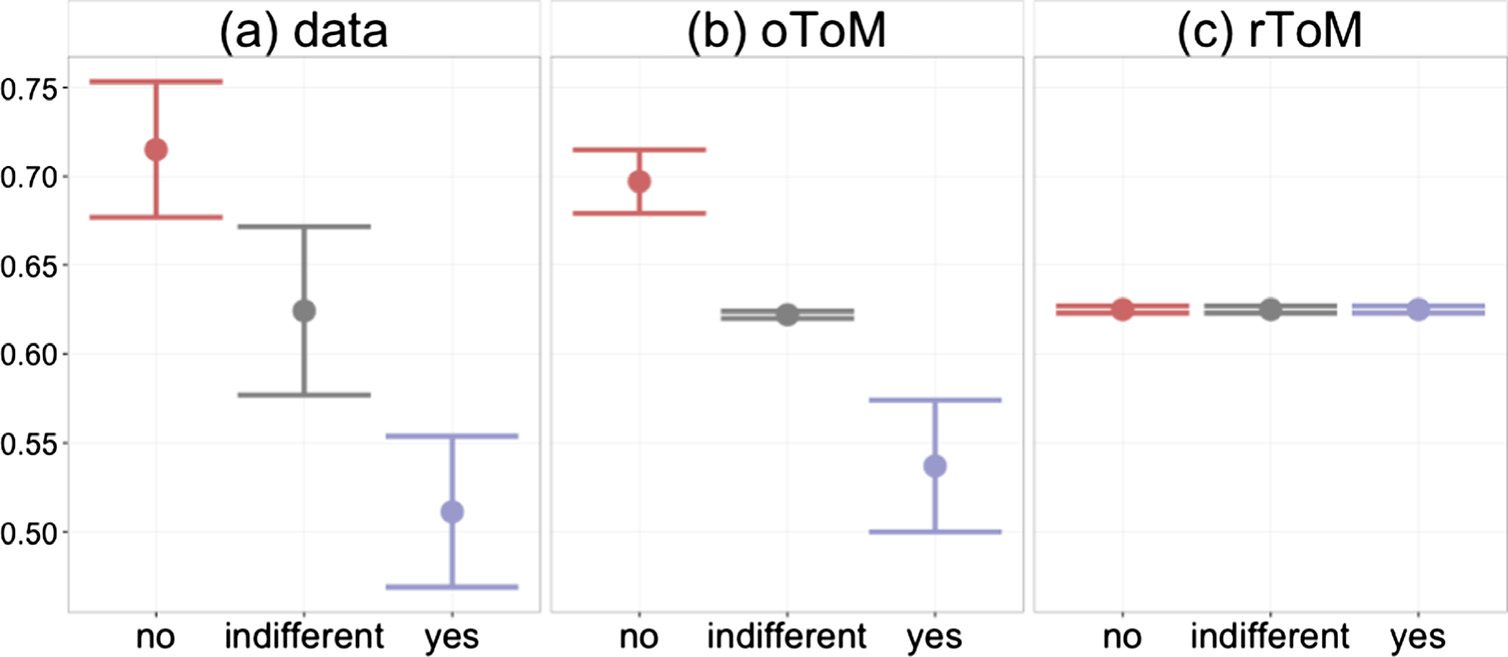
Figure 4. Experiment 2 data. Effect of a social sources’ desire on how others learn from them for
(a) data with 95% CIs, which we compare to the posterior predictives of (b) an optimistic Theory of
Mind (ToM) and (c) a rational ToM. Points represent the mean p(teamx) response after hearing
equally knowledgeable sources place a bet on teamx that is either consistent, unrelated, or
inconsistent with their desires.
to win an upcoming match, p(teamx), in a fictional college soccer tournament after seeing
a knowledgeable student bet on the team. The student was either a fan of one of the teams
facing off, or indifferent to the outcome. Participants therefore saw three trials—the consistent
trial where the student bet on the team he wanted to win, the inconsistent trial where he bet
on the team wished would lose, and the impartial trial where he didn’t care which team won
before he bet.
METHODS
Participants
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
/
1
2
1
0
1
1
8
6
8
2
7
1
o
p
m
_
a
_
0
0
0
1
1
p
d
.
i
One hundred twenty participants were randomly assigned into the consistent, inconsistent, or
impartial conditions.
Design and Procedure
Participants were first introduced to a (fictional) annual British collegiate soccer tournament
and told that they would see bets on these matches from a student who “Unbeknownst to his
friends makes a £100 bet online on which team he thinks will win this year’s game.”10 The stu-
dent would either be a fan of one of the teams (attending that college) or neither of the teams (at-
tending a different college). The students were equally knowledgeable across conditions, being
described as seeing the outcome of the last 10 matches these teams played against each other.
After the introduction, participants were given a test trial appropriate for their (randomly
assigned) condition in which the student bet consistently with his school, bet against his school,
or was impartial (not a fan of either school). After observing the student’s bet and allegiance
participants were asked “What do you think is the chance that teamx wins the match this year?”
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
10 See the Supplemental Materials [Hawthorne-Madell & Goodman, 2017] for complete experimental
materials.
OPEN MIND: Discoveries in Cognitive Science
107
So Good It Has to Be True Hawthorne-Madell, Goodman
RESULTS
As seen in Figure 4a, participants’ responses were sensitive to the student’s a priori desires,
consistent with learners who reason with an oToM (but not an rToM). Participants who saw an
impartial student bet on teamx thought the team was more likely to win than when they saw a
fan of teamx place an identical bet (d = 0.80, 95% CI [0.33 1.27], z = 3.35, p < .00111). This
is consistent with the learner thinking that the fan’s desire to see his team win made him think
it was objectively more likely. Additionally, participants who saw a fan of the other team bet
on teamx were more influenced than the same bet from the impartial student (d = 0.67, 95%
CI [0.21 1.14], z = 2.87, p = .004). As predicted by the model of the oToM learner, someone
who bets against their desires is more diagnostic of teamx being dominant than the indepen-
dent source. The oToM learner thinks that teamx had to be clearly dominant to overcome the
wishful thinking of a fan rooting against them.
DISCUSSION
Assuming that fans engage in wishful thinking allows oToM learners to make stronger infer-
ences about the strength of the fans’ evidence in some cases. For an rToM learner, the fan
would have to have seen teamx win a majority of the 10 observed matches in order to bet
on them, regardless of their predilections, resulting in the flat predictions seen in Figure 4c.
Meanwhile, the oToM learner thinks that a fan of teamx could bet on them even if the fan
only observed them win a few times.12 If, however, the fan bets against their team, the oToM
learner assumes that the fan must have seen their team trounced in the 10 observed matches.
Using these insights, an oToM learner using Bayesian inference to learn from the fan will ex-
hibit the qualitative pattern seen in Figure 4b, which is consistent with participants’ behavior
(as seen in Figure 4a). The pattern of results is consistent with the predictions of a learner
using an oToM, (but see the discussion of limitations and additional potential explanations in
the Supplemental Materials [Hawthorne-Madell & Goodman, 2017]).
GENERAL DISCUSSION
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
/
1
2
1
0
1
1
8
6
8
2
7
1
o
p
m
_
a
_
0
0
0
1
1
p
d
.
i
Current computational models of theory of mind are built upon the assumption that beliefs are
a priori independent of desires. Whether social reasoners use such a rational ToM (rToM) is
an empirical question. In two experiments we tested the independence of beliefs and desires
in ToM and found that people behave as if they think that others are wishful thinkers whose
beliefs are colored by their desires.
In the 3-PoV condition of Experiment 1, we found that people believe that others inflate
the probability of desirable outcomes and underestimate the probability of undesirable ones, as
they would if they have an optimistic ToM (oToM) with a direct link between desires and beliefs
(Figure 3). If people broadly attribute wishful thinking to others (as Experiment 1 suggests), it
should be reflected in their social reasoning. For example, social learners using an oToM
to make sense of an agent’s beliefs would be sensitive to that agent’s relevant desires. This
is exactly what we found in Experiment 2 (Figure 4)—how much people learned from an
agent’s beliefs depended on his desires. Agents whose beliefs ran against their desires were
more influential than impartial agents, who, in turn, were more influential than agents with
consistent beliefs and desires.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
11 Calculated with Fisher-Pitman permutation test.
12 In fact, if the oToM learner thinks that the fan is a completely wishful thinker, then his bet is no longer
diagnostic of his evidence (he could have seen anything!).
OPEN MIND: Discoveries in Cognitive Science
108
So Good It Has to Be True Hawthorne-Madell, Goodman
The observed presence of wishful thinking in ToM has no necessary relation to its ex-
istence in people’s “online” belief formation. Indeed, the 1-PoV conditions of Experiment 1
indicate that people’s model of others’ wishful thinking is not perfectly calibrated. They over
attribute wishful thinking to others in situations where they would actually form their beliefs
independently of their desires. Charting the situations where wishful thinking is over applied
in this way may be a fruitful avenue for further research. At the extreme, we could imagine
finding that everyone thinks one another wishfully thinks, but in fact everyone forms their be-
liefs independent of their desires! This radical thesis is surely too strong,13 but oToM may well
overestimate the strength of wishful thinking and over generalize it—amplifying a small online
effect into a larger social cognition effect. Attention to whether a task engages (potentially am-
plified) oToM representations could provide insight into the considerable heterogeneity of the
wishful thinking effect as it has been studied. Specifically, it could help explain why first-person
wishful thinking is reliably found in some paradigms and not others.
The paradigms in which wishful thinking is reliably found involve participants reasoning
about themselves or others, such as the 3-PoV condition of Experiment 1 where participants
reasoned about Josh’s beliefs (for a review of many tasks that may engage social reasoning,
see, e.g., Shepperd, Klein, Waters, & Weinstein, 2013, and Weinstein, 1980, but see Harris
& Hahn, 2011, and Hahn & Harris, 2014, for an alternative explanation). Whereas asocial
paradigms involving direct estimation of probabilities usually do not find the effect, like the
1-PoV condition of Experiment 1 where participants directly estimated the chance that the ball
would fall into a particular bin (for other examples of wishful thinking paradigms that do not
involve social reasoning, see Study 1 of Bar-Hillel & Budescu, 1995, and for a more general
review of asocial bias experiments, see the “bookbags” and “pokerchips” paradigms cited in
Hahn & Harris, 2014, but see Francis Irwin’s series of experiments for an example of asocial
paradigms that do find a wishful thinking effect—starting with Irwin, 1953).
Where people’s predictions of others’ behaviors (1-PoV, Experiment 1) and their actual
behavior (3-PoV, Experiment 1) diverge is also important to map because these disconnects
inject a systematic bias into social reasoning. Taking the social learning of Experiment 2 as
an example, oToM learners ignored the belief of the agent whose bet was consistent with his
desires. However, if this agent actually formed his beliefs without bias, then the learner would
be missing a valuable learning opportunity. Asserting that others let their desires cloud their
beliefs allows people to “explain away” those beliefs without seriously considering the possible
evidence on which they are based. Future work should explore the details of these effects. For
example, does a learner attribute bias equally to those who share his desires and those who
hold competing ones?
The experiments presented here suggest that people think that others are wishful thinkers;
this has broad consequences for social reasoning ranging from our inferences about heated sci-
entific debates to pundit-posturing. Our findings highlight the importance of further research
into the true structure of theory of mind. Do people think that others exhibit loss aversion
or overweight low probabilities? Is the connection between beliefs and desires bidirectional?
Rigorous examination of questions like these may buttress new, empirically motivated compu-
tational models of ToM that capture the nuance of human social cognition—an idea so good
it has to be true.
13 As seen in well-controlled examples of desires influencing online belief formation (e.g., Mayraz, 2011).
OPEN MIND: Discoveries in Cognitive Science
109
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
/
1
2
1
0
1
1
8
6
8
2
7
1
o
p
m
_
a
_
0
0
0
1
1
p
d
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
So Good It Has to Be True Hawthorne-Madell, Goodman
ACKNOWLEDGMENTS
This work was supported by ONR Grants N000141310788 and N000141310341, and a James
S. McDonnell Foundation Scholar Award. We would also like to thank Joshua Hawthorne-
Madell, Gregory Scontras, and Andreas Stuhlmüller for their careful reading and thoughtful
comments on the manuscript.
AUTHOR CONTRIBUTIONS
All authors developed the study concept and design. Testing, data collection, and analy-
sis were performed by DHM under supervision of NDG. DHM drafted the manuscript and
NDG provided critical revisions. All authors approved the final version of the manuscript for
submission.
REFERENCES
Babad, E.
(1987). Wishful thinking and objectivity among sports
fans. Social Behaviour, 2, 231–240.
Babad, E., & Katz, Y.
(1991). Wishful thinking—Against all odds.
Journal of Applied Social Psychology, 21, 1921–1938.
Baker, C. L., Saxe, R., & Tenenbaum, J. B.
(2009). Action under-
standing as inverse planning. Cognition, 113, 329–349.
Baker, C. L., Saxe, R., & Tenenbaum, J. B. (2011). Bayesian theory
of mind: Modeling joint belief-desire attribution.
In L. Carlson
(Ed.), Proceedings of the Thirty-Third Annual Conference of
the Cognitive Science Society (pp. 2469–2474). Austin, TX:
Cognitive Science Society.
Bar-Hillel, M., & Budescu, D. (1995). The elusive wishful thinking
effect. Thinking and Reasoning, 1, 71–104.
Hahn, U., & Harris, A. J. L. (2014). What does it mean to be biased:
Motivated reasoning and rationality. Psychology of Learning and
Motivation, 61, 41–102.
Harris, A. J., & Hahn, U. (2011, January). Unrealistic optimism about
future life events: A cautionary note. Psychological Review, 118,
135–154.
Hawthorne-Madell, D., & Goodman, N. D. (2017). Supplemental
material for “So good it has to be true: Wishful thinking in
theory of mind.” Open Mind: Discoveries in Cognitive Science,
1(2), 101–110. doi:10.1162/opmi_a_00011
Irwin, F. W.
(1953). Stated expectations as functions of proba-
Journal of Personality, 21,
bility and desirability of outcomes.
329–335. doi:10.1111/j.1467-6494.1953.tb01775.x
Taylor, R. S. Zemel, P. L. Bartlett, F. Pereira, & K. Q. Weinberger
(Eds.), Advances in neural information processing systems (Vol. 24,
pp. 2276–2284). Red Hook, NY: Curran Associates.
Jones, E. E., & Nisbett, R. E.
(1971). The actor and the observer:
Divergent perceptions of the causes of behavior. New York, NY:
General Learning Press.
Krizan, Z., & Windschitl, P. D.
(2007). The influence of outcome
desirability on optimism. Psychological Bulletin, 133, 95–121.
Kunda, Z.
(1999). Social cognition: Making sense of people.
Cambridge, MA: MIT Press.
Mayraz, G. (2011). Wishful thinking. CEP Discussion Paper. London,
England: Centre for Economic Performance, London School of
Economics.
Olsen, R. A. (1997). Desirability bias among professional investment
Journal of Behavioral
managers: Some evidence from experts.
Decision Making, 10, 65–72.
Redlawsk, D. P. (2002, November). Hot cognition or cool consid-
eration? Testing the effects of motivated reasoning on political
decision making. The Journal of Politics, 64, 1021–1044.
Shepperd, J. A., Klein, W. M. P., Waters, E. A., & Weinstein, N. D.
(2013). Taking stock of unrealistic optimism. Perspectives on
Psychological Science, 8, 395–411.
Weinstein, N. D.
(1980). Unrealistic optimism about future life
Journal of Personality and Social Psychology, 39, 806–
events.
820. doi:10.1037/0022-3514.39.5.806
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
/
1
2
1
0
1
1
8
6
8
2
7
1
o
p
m
_
a
_
0
0
0
1
1
p
d
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Jern, A., Lucas, C. G., & Kemp, C.
decision-making approach to preference learning.
(2011). Evaluating the inverse
In J. Shawe-
OPEN MIND: Discoveries in Cognitive Science
110