SCHOOL CHOICE IN AMSTERDAM: WHICH
SCHOOLS ARE CHOSEN WHEN SCHOOL
CHOICE IS FREE?
抽象的
Using discrete choice models, this paper investigates the deter-
minants of secondary school choice in the city of Amsterdam.
In this city, there are many schools to choose from and school
choice is virtually unrestricted (no catchment areas, low or no tu-
ition fees, short distances). We find that school choice is related
to exam grades and the quality of incoming students, but not to
progression in lower grades, no delay in higher grades, and a com-
posite measure of quality published by a national newspaper. 毛皮-
瑟莫雷, students appear to prefer schools that are close to their
home and schools that many of their former classmates in pri-
mary school attend.
Nienke Ruijs
(corresponding author)
Dutch Inspectorate of
教育
3544 AC Utrecht
荷兰人
n.m.ruijs@owinsp.nl
Hessel Oosterbeek
Amsterdam School of
经济学
University of Amsterdam
1018 WB Amsterdam
荷兰人
h.oosterbeek@uva.nl
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
F
/
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
F
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1
https://doi.org/10.1162/edfp_a_00237
© 2019 Association for Education Finance and Policy
School Choice in Amsterdam
I N T RO D U C T I O N
1 .
This paper uses conditional and mixed logit models to analyze the determinants of sec-
ondary school choice in the city of Amsterdam. Students in this city can choose any
school that offers education at their academic level, tuition fees are low, and schools
are easy to reach because of relatively short distances. These features create an ideal
environment to examine whether school choices are affected by different measures of
school quality. We do so using data of individual school choices for the school years
开始于 2007, 2008, 2009, 和 2010. Analyzing individual school choices (反而
of aggregate school enrollment data) allows us to compare the importance of school
quality for school choices to the importance of other factors, including traveling dis-
坦斯, whether the school was oversubscribed in the previous year, and the number of
classmates from primary school who attend the secondary school.
Analyzing the importance of school quality for school choices is important from
the perspective of the debate on school choice and competition. The main arguments
in favor of these policies are that by having more choice students can find a school
that better matches their specific needs and exposure to competition gives schools an
incentive to improve education quality.1 The direct evidence of the impact of school
competition on school quality and student achievement is mixed (Hoxby 2000a, 2007;
Cullen, 雅各布, and Levitt 2006; Hsieh and Urquiola 2006; Rothstein 2007; Böhlmark
and Lindahl 2015).2 A prerequisite for such an impact to emerge is that school choices
are at least partially driven by school quality. If this is not the case, improvement of
school quality does not raise student inflow and it is then not sensible for schools to
compete on this dimension.
In a recent study, Koning and Van der Wiel (2013) examine whether published in-
formation on school quality affects secondary school enrollment in the Netherlands.
They find higher quality scores are associated with a small but significant increase in
enrollment. 有, 然而, reasons to reexamine the findings of this study. 第一的,
Koning and Van der Wiel analyze data from the whole country, thereby also including
more remote areas where most schools are in fact local monopolists. By analyzing data
from a city where the supply of schools at any academic level is abundant, we focus on
a situation where students have more scope to respond to variation in quality.
第二, because of data limitations, Koning and Van der Wiel use enrollment in
the third year of secondary school as a proxy for applications in the first year. Since on
average 3.9 percent of Dutch secondary school students repeat a grade in a given year in
the first three years of secondary school (CBS 2012), this implies that in the third year,
7.8 percent of the enrollees have been replaced by 11.7 percent repeaters from previous
1. We will often phrase as if students are the decision makers. We acknowledge that in reality their parents have
2.
an important say in this.
In a famous study, Hoxby (2000A) finds that more school competition (measured as the number of school
districts in a metropolitan area) boosts student achievement in the United States. Identification is based on
variation in the number of school districts caused by the numbers of streams (河流). Rothstein (2007) 有
shown that Hoxby’s results are sensitive to the way in which streams are counted (see also Hoxby 2007). Hsieh
and Urquiola (2006) find no evidence that choice, triggered by the provision of vouchers, improved student
achievement in Chile. Using a comparable reform in Sweden, 然而, Böhlmark and Lindahl (2015) find a
positive effect of choice on student achievement. Using data from admission lotteries from the Chicago public
school system, Cullen, 雅各布, and Levitt (2006) find that students who lost the lottery—and therefore have a
restricted choice set—are not harmed in their achievement.
2
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
F
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
队列. These repeaters from previous cohorts have based their school choices on pub-
lished information on school quality from earlier years. 此外, a non-negligible
的分数 23 percent of secondary school students are transferred to a higher or lower
academic track by the time they reach the third year or have moved to another school
(Onderwijsinspectie 2007). 而且, because the most popular schools are oversub-
scribed and cannot admit all applicants, school choice in response to school quality is
better measured by applications rather than enrollment. Our data on school choice in
the city of Amsterdam contain information on first-year applications.
第三, the analysis of Koning and Van der Wiel does not include students in the
lowest levels of prevocational education, and thereby omits 25 percent of Dutch sec-
ondary school students. Our analysis covers all academic levels. Koning and Van der
Wiel (2013) focus on a single composite measure of school quality that is published
each year in a national newspaper in the Netherlands. In our main analysis, we report
results based on the same measure. 此外, we inquire about the importance of
the underlying components and we investigate whether the quality of the incoming
students influences school choices.3
Related to our paper are also the studies of Hastings, Kane, and Staiger (2009),
Burgess et al. (2015) and Glazerman and Dotter (2016). Hastings, Kane, and Staiger
(2009) use data from primary and middle school choices from a school district in the
美国. In that district, a school choice program was introduced where parents
could list their top three schools. Using exploded mixed logit models, the authors find
that the weight parents place on school characteristics is heterogeneous. 父母, 埃斯佩-
cially those of high socioeconomic status, tend to prefer schools with high test scores.
Parents also tend to prefer schools in which the majority of the students are of the same
race as their children. These results imply that minority parents face a trade-off be-
tween high performance and ethnic composition. 更远, the distance to schools and
the availability of transportation are relevant determinants of school choice. 伯吉斯
等人. (2015) combine survey and administrative data to estimate conditional logit mod-
els and find that most families strongly prefer the academic performance of schools.
Socioeconomic composition and distance are also important drivers of school choice.
More advantaged parents have stronger preferences for academic performance. Glaz-
erman and Dotter (2016) use information from rank-ordered lists to estimate school
preferences of 22,000 applicants to 200 schools in Washington, 直流. They find that
distance, school demographics, and academic indicators play important roles in school
选择. There is also heterogeneity of preferences.4
3.
In another recent study using Dutch data, Borghans, Golsteyn, and Zölitz (2015) investigate the determinants of
school choice of the parents of primary school students in the southern part of the southern province Limburg.
They find that parents tend to avoid the roughly 5 percent of the schools the Dutch Education Inspectorate
assesses to be weak. Primary schools with higher average scores on the national exit exam attract more students.
4. Other related studies analyzing revealed preferences include Weiher and Tedin (2002) who analyze data from
1,000 charter households in Texas and find that race is a good predictor of their revealed (and stated) 更喜欢-
恩塞斯; Harris and Larsen (2015) use application data from students in New Orleans to examine how school
choices differ before and after Hurricane Katrina; and Nathanson, Corcoran, and Baker-Smith (2013) analyze
application and admission data of five cohorts of high school students in New York City and focus on the
differences in choices and placement between low-achieving students and others. Nathanson, Corcoran, 和
Baker-Smith find that low-achieving students are matched more often to lower-performing schools than other
学生. This is mainly because of differential choices, not to differential rates of being placed in their top
choices. Studies that analyze stated preferences obtained through surveys include Collins and Snell (2000),
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
F
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
F
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
3
School Choice in Amsterdam
In the years in our study that we analyze, the secondary schools in Amsterdam
used a version of the adaptive Boston mechanism to assign students to schools. 更多的
具体来说, each student applied to one school that offers the academic track advised
to the student.5 If the number of applicants for a school (and track) does not exceed the
number of available seats, all applicants are placed. If a school is oversubscribed, it or-
ganizes a lottery. Students who lose the lottery can subsequently only choose from the
schools that then still have vacant seats. This matching algorithm potentially gives rise
to strategic behavior where students do not report their truly preferred school (Abdulka-
diro˘glu and Sönmez 2003; Calsamiglia and Guell 2014). In section 2 we discuss this
in more detail and explain why we think the parameters estimated by the logit models
will closely reflect students’ true preferences for school characteristics.
In addition to measures of school quality and oversubscription in the previous year,
we also consider the impact on school choice of the number of classmates from primary
school who attend a specific secondary school. Peer effects are intrinsically difficult to
identify. De Giorgi, Pellizzari, and Redaelli (2010) find that peer groups do not fully
overlap to identify peer effects in the choice of college majors. Lacking such a source of
variation and in the absence of random assignment of peers (as in Sacerdote 2001), 我们
restrict ourselves to testing the null-hypothesis of no peer effects in school choice.6
The main results of this paper are threefold. 第一的, school choices are related to mea-
sures of quality. 尤其, students prefer schools with higher exam grades and with
a better quality of incoming students. This is especially true for students in the higher
academic tracks. Choices are not driven by other dimensions of school quality (亲-
gression in lower grades and no delay in higher grades) that are included in the com-
posite quality-measure published by a national newspaper. 因此, the composite
measure is not a consistent predictor of school choice in Amsterdam. 第二, we find
some evidence that when a school conducts an admission lottery in the previous year,
students are deterred from choosing that school, suggesting that strategic behavior oc-
curs. 第三, our results reject the null-hypothesis of no peer effects in school choice.
When a larger share of a student’s primary school peers chooses a certain secondary
学校, the student is more likely to pick that school as well. This is even true when we
correct for the systematic component in the popularity of the specific secondary school
among the students in the student’s primary school.7 Although this result does not
prove the importance of peer effects in school choices, it is consistent with it.
This paper proceeds as follows. The next section describes the context of secondary
school choice in Amsterdam. 部分 3 describes the data. 部分 4 provides details of
the empirical strategy that we utilize. 部分 5 presents and discusses the empirical
findings. 部分 6 summarizes and concludes.
who look at 101 parents who sent their children to one of two neighboring schools in the United Kingdom;
Denessen, Driessen, and Sleegers (2005), using data from 10,000 parents in the Netherlands who were asked
which factors are driving the choice of primary school for their children; and Jochim et al. (2014), who surveyed
4,000 public school parents in eight “high-choice” cities in the United States and find that parents do exercise
their choice but want better options.
5. 部分 2 provides details about the tracking system in Dutch secondary education.
6. Angrist (2014) gives a critical assessment of the peer effects literature.
7. Further details are provided in section 4.
4
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
F
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
2 . C O N T E X T
This section begins by describing the key features of school choice in the Netherlands.
Next it explains the structure of secondary education in the Netherlands. The final sub-
section gives information about some specificities of secondary school choice in the
city of Amsterdam.
School Choice in the Netherlands
The Netherlands has a long history of free school choice. The constitution of 1848 guar-
antees the freedom to provide education. 在 1917, this freedom was extended with the
amendment that all schools receive state funding. In current practice, this means that
privately run schools (either with a religious background or subscribing to specific ped-
agogical approaches such as Montessori or Dalton) are publicly funded at the same level
as publicly run schools. 作为回报, schools have to adhere to certain rules. 尤其,
they are subject to quality inspections by the Dutch Education Inspectorate.
For students, these regulations imply that they are free to choose the school they
想; they are not restricted by measures such as catchment areas.8 Dutch students
make extensive use of this option: 70 percent of students in primary education and 75
percent of students in secondary education are enrolled in a publicly funded, privately
run school (CBS 2009). Privately funded schools are virtually nonexistent—in 2009,
仅有的 0.3 percent of students in secondary education attended a privately funded school
(Onderwijsinspectie 2010).
The government funding of schools is to a large extent dependent on student num-
bers, in which the money follows the student. There are additional funding schemes for
disadvantaged students. In primary education there is the system of weighted student
资金. For disadvantaged students, in terms of low parental education, schools can
get additional funding up to 1.2 times the regular per-student funding. In this paper we
use the weighted student funding to identify disadvantaged students.
Secondary Education in the Netherlands
Dutch secondary education starts around age 12 years and lasts four to six years. 这
length of secondary education depends on the school track (the Netherlands has a
tracked secondary school system). The lowest track (pre-vocational secondary educa-
的) lasts four years and gives access to vocational education programs. Within the
pre-vocational track, there are four different levels, each giving access to different levels
of vocational education programs. 在本文中, they are indicated with the numbers I
to IV, with IV being the highest level.9 The intermediate track (senior general secondary
教育) takes five years, and gives access to professional colleges. The highest track
(pre-university education) takes six years, and gives access to university education.
Which school track a student should take is mainly decided at the end of primary
教育. It is partly determined by standardized tests (in most cases the nationwide
exit test, called the “citotoets” [citotest]), and partly determined by the assessment of the
8. A small number of municipalities have put restrictions on primary school choice to foster desegregation (Ladd,
Fiske, and Ruijs 2011). In those projects, preferences are important in placement decisions as well.
9. Pre-vocational III will not be taken into account in the analyses, because only 2 percent of students receive a
pre-vocational III advice.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
F
/
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
F
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
5
School Choice in Amsterdam
primary school teacher. Not all secondary schools offer all school tracks, so the track ad-
vice is an important factor in secondary school choice. When offering more than one
school track, schools are allowed to teach children of different tracks together. Depend-
ing on student achievement and school policies, students may change tracks during
secondary education. 还, they may enroll in a higher track after finishing a lower
track.
Subject to some conditions, students may choose which courses they want to take
during their last years in secondary school. Secondary schools have to follow national
curriculum guidelines. Students take centrally determined national exams at the end
of secondary school. The national exams count for 50 percent of students’ final grades,
and the other 50 percent is determined by school-specific exams taken in the last two
or three years of secondary education.
Secondary School Choice in Amsterdam
Amsterdam is the capital of the Netherlands and is its largest city with 750,000 因哈比-
短裤. Each year, 5,500 到 6,000 students transfer from primary education to secondary
教育. In the city of Amsterdam, there are about fifty-four secondary schools, 前任-
cluding schools for students with special educational needs. 不出所料, 一些
schools are more popular than others. Each year some schools are oversubscribed and
conduct lotteries to allocate the available places.
In the years that we analyze, the secondary schools in Amsterdam use a version of
the adaptive Boston mechanism to assign students to schools. 更具体地说, each
student applies to one school that offers the academic track that was advised to the stu-
凹痕. There are no default schools—primary schools ensure that every student submits
an application form. If the number of applicants for a school (and track) does not exceed
the number of available seats, all applicants are placed. Students who perform on the
standardized test in line with the primary school teachers’ advice cannot be rejected by
the secondary school, which effectively means that it is hard for schools in Amsterdam
to select students.10
If a school is oversubscribed, it organizes a lottery. Some schools have oversubscrip-
tion for some school tracks but not for others. In that case, the lottery is conducted for
each school track separately. Schools are allowed to use a limited number of priority
规则, 那是, they can grant priority to siblings of current students, children of staff
members, and students from a primary school with similar special programs (对于前任-
充足, Montessori secondary schools can grant priority to children from a Montessori
primary school). These priority rules need to be announced before the application date,
so they are known to parents. In the years that we study, 大约 5 percent of the stu-
dents could not be placed in the school where they applied in the first round because
they lost the lottery.
10. The definitions for corresponding test scores are strictly prescribed. When a student has a lower score than
can be expected from the teacher’s advice, the secondary school should discuss the student with the primary
school and/or conduct an extra standardized test. In these cases, the secondary school has some discretion
in rejecting the student, which happens in about 5 percent of the cases. For most school tracks, 大多数
of the students (52 百分) have a test score in line with the primary school advice. An exception to this are
the vocational levels with additional support. 这里, all students are placed after discussions with the primary
学校.
6
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
F
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
Students who lose the lottery can subsequently only choose from the schools that
then still have vacant seats. This matching algorithm potentially gives rise to strategic
behavior where students do not report their truly preferred school (Abdulkadiro˘glu and
Sönmez 2003; Calsamiglia and Guell 2014). This implies that parameters estimated by
the logit models may deviate from the parameters of the utility function. We have rea-
son to believe, 然而, that such deviations are small. 最近几年, the secondary
schools in the city of Amsterdam switched from the adaptive Boston mechanism to the
truth-telling Deferred Acceptance mechanism. A study that compares school choices
under the two mechanisms in Amsterdam estimates that only 8 percent of the stu-
dents do not apply to their most-preferred school under the Boston mechanism (看
De Haan et al. 2016). 而且, the students who choose strategically do not choose
schools that are very different from the schools they rank first. This implies that 92
percent of the students choose the school they prefer most, whereas the other 8 每-
cent choose a school that is similar to their most preferred school.11 This concurs with
results reported by Burgess et al. (2015). These authors use data from England in which
roughly two-thirds of their observations are exposed to a truth-telling mechanism and
about one-third to a strategic mechanism. When they restrict their sample to the parents
exposed to the truth-telling mechanism, their results are robust. To further accommo-
date concerns about strategic choices, we include as covariate an indicator that equals
one if the school/track organized a lottery in the previous year.
3 . 数据
This section describes the data sources used in this paper. It first describes the data
about students, then the data about schools.
Student Information
Data come from the centralized application and placement system of the city of Am-
斯特丹. This database has information on 21,117 Amsterdam students choosing a
secondary school in Amsterdam in the four years from 2007 到 2010. The database
provides information on student background characteristics, such as sex and ethnicity
(but not income), and on primary school achievement, such as school track advice, 分数
on the standardized test (“citoscore”) at the end of primary school, and grade repetition
in primary school.
For each student, we know at which school he or she applied in the first round and
whether the student was enrolled at that school. For students who are not placed at the
school where they apply in the first round, subsequent choices are also registered. 这
信息, 然而, is not used here because the choice sets after the first round are
not sufficiently clear. 而且, because not many students lose a lottery in the first
round, this only involves a small number of observations.
Using information on students’ school track advice and information on the school
tracks offered by each secondary school, we can create the choice set for each student.
11. Switching schools during secondary school is not forbidden but relatively infrequent. Dependent on the school
track, 71 百分比到 84 percent of the secondary school students in Amsterdam are at the same school as where
they started in the fourth year of education (Gemeente Amsterdam 2013). Note that these numbers include
students who switch schools because they change school tracks or prefer pre-vocational courses that are not
offered at their school.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
F
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
7
School Choice in Amsterdam
桌子 1. Student Characteristics
Pre-university
Senior general/pre-university
Senior general
Pre-vocational IV/senior general
Pre-vocational IV
Pre-vocational II
Pre-vocational I/II
Pre-vocational I
全部的
Both Parents
Born in the
荷兰
Belonging to
Disadvantaged
团体
Citoscore
是的
(3)
0.60
0.45
0.39
0.28
0.22
0.16
0.14
0.14
0.34
Missing
(4)
0.04
0.05
0.05
0.06
0.05
0.06
0.05
0.07
0.05
是的
(5)
0.14
0.27
0.34
0.47
0.54
0.67
0.65
0.64
0.42
Missing
意思是
(6)
0.12
0.11
0.12
0.10
0.10
0.09
0.15
0.19
0.12
(7)
544.1
540.5
537.7
534.4
531.5
526.7
524.7
520.4
535.7
标清
(8)
7.4
6.1
6.4
6.2
6.7
8.1
9.0
10.6
10.1
Missing
(9)
0.01
0.01
0.02
0.02
0.03
0.19
0.33
0.58
0.12
氮
Students
Share
of Boys
(1)
4,374
2,819
3,133
2,028
2,881
2,130
1,039
2,713
21,117
(2)
0.50
0.49
0.50
0.49
0.50
0.49
0.48
0.47
0.49
Notes: Columns 2 到 6 report shares. The “No” category is omitted.
Although schools outside of Amsterdam can also be chosen, we limit the choice set to
schools in the city of Amsterdam. Schools outside of Amsterdam do not follow the same
enrollment rules and their students are not registered in the Amsterdam enrollment
系统. 相似地, children outside of Amsterdam can choose schools in Amsterdam.
Because their data are not consistently registered, these children are omitted from the
analysis as well. Because the enrollment procedures are different for special educa-
tional needs schools, we drop those schools from the sample. 而且, we drop some
students who have missing values on key variables.12
桌子 1 reports descriptive statistics on student characteristics. The first col-
umn shows that the pre-university track attracts around 21 percent of students. 一个-
其他 28 percent of students enter secondary school at the combined senior general
secondary/pre-university track or the senior general secondary track. The remaining 51
percent of students start secondary education at the pre-vocational tracks. 第二
column shows that the share of boys is fairly constant across the different secondary
school tracks. They are only somewhat underrepresented at the two lowest tracks.
12. 全面的, 7,432 students are dropped out of the initial sample of 28,549. We drop 3,913 of them because they
are living outside of Amsterdam or going to primary schools outside of Amsterdam. These students prefer
schools in Amsterdam over schools in their own municipalities. We drop these students because we only
have information about students applying to schools in Amsterdam, so we cannot compare characteristics
and choice preferences of students who decide to travel to Amsterdam with students choosing schools in
these other municipalities. Vice versa, we do not have information on students living in Amsterdam choosing
schools outside of Amsterdam. This group, 然而, is very small: 0.8 percent of the pre-university students
choose a school outside of Amsterdam (De Haan et al. 2016). We drop 1,488 students because they attend
special education needs schools; 1,123 students are dropped because their primary school advice (例如, 实际的
教育, pre-vocational III) is not taken into account; 103 students are dropped because their primary school
is unknown; 和 236 students are dropped because their address is not registered. We drop 416 学生
because they chose schools that should not be in their choice set given their primary school advice. This group
is distributed over all primary school advice. Within school advice, small groups of students go to the same
secondary school that offers either tracks just above or just below their primary school advice. Their citoscores
are generally either relatively low or relatively high. Given that we do not know the exact choice set of these
学生, they are dropped from the sample. 最后, 153 students are dropped because they go to a few very
small secondary schools that do not have enough observations to take into account in this study (these are
mainly religious schools, such as Jewish or Islamic schools).
8
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
F
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
桌子 2. Descriptive Information on Students’ Choice Set
Distance (in kilometers)
Actual
Share of Peers
Predicted
Share of Peers
Chosen
学校
Schools M (标清)
氮
Nearest
学校
中号 (标清)
全部
学校
中号 (标清)
Share of
Schools with
Lotteries
Chosen
学校
中号 (标清)
全部
学校
中号 (标清)
Chosen
学校
中号 (标清)
全部
学校
中号 (标清)
(1)
27
21
23
18
23
22
21
22
(2)
(3)
(4)
3.09
(2.13)
3.17
(2.15)
3.08
(2.16)
3.01
(2.10)
2.85
(2.08)
2.98
(2.29)
2.85
(2.23)
2.82
(2.12)
1.04
(0.71)
1.20
(0.78)
1.14
(0.73)
1.24
(0.71)
1.14
(0.72)
0.96
(0.59)
1.00
(0.66)
1.05
(0.69)
5.00
(2.90)
5.60
(3.08)
5.57
(3.04)
6.03
(3.28)
6.03
(3.20)
6.28
(3.40)
5.82
(3.16)
6.00
(3.15)
(5)
0.08
0.10
0.10
0.11
0.16
0.05
0.06
0.06
(6)
(7)
(8)
(9)
0.12
(0.12)
0.14
(0.14)
0.14
(0.14)
0.17
(0.16)
0.18
(0.17)
0.13
(0.15)
0.12
(0.15)
0.12
(0.13)
0.03
(0.06)
0.03
(0.07)
0.03
(0.07)
0.03
(0.07)
0.03
(0.07)
0.02
(0.06)
0.02
(0.06)
0.02
(0.07)
0.11
(0.11)
0.13
(0.12)
0.14
(0.13)
0.16
(0.14)
0.17
(0.15)
0.12
(0.12)
0.11
(0.12)
0.11
(0.11)
0.03
(0.06)
0.03
(0.06)
0.03
(0.06)
0.03
(0.07)
0.03
(0.07)
0.02
(0.06)
0.02
(0.05)
0.02
(0.06)
Pre-university
Senior general/pre-university
Senior general
Pre-vocational IV/senior general
Pre-vocational IV
Pre-vocational II
Pre-vocational I/II
Pre-vocational I
Notes: Column 3 reports the distances to the nearest school within a students’ choice set, 柱子 4 reports the average distance to all schools
within a students’ choice set. Column 6 describes the average share of peers from primary school that also chose the chosen secondary school.
The predicted share of peers is a linear prediction of the actual share of peers in a primary school that chooses for a certain secondary school
over the four years of the study.
Column 3 demonstrates the segregation of secondary school tracks in Amsterdam along
the lines of migrant status. Although the share of students in the population with both
parents born in the Netherlands is only around one-third, their share in the highest
track is 0.6, and this decreases monotonically to 0.14 in the lowest track. This carries
over to column 5, which shows the share of students with a disadvantaged background
by school track. Column 7 shows the monotonic relationship between students’ scores
on the exit exam in primary school and their track in secondary school (the scale for
this variable runs from 500 到 550).
School Information
桌子 2 reports descriptive information on the choice set and the chosen school for the
different school tracks. The first column reports the numbers of schools at each track
from which students can choose. Many schools appear multiple times in this column
because they offer more than one secondary school track.
Using information on students’ home addresses, we calculated the distances from
their house to Amsterdam schools in their choice set. These distances are calculated in
a straight line based on GPS coordinates.13 Columns 2 到 4 provide means and standard
deviations of the distances that students have to travel to the school they choose (柱子
2), to the school offering their advised track nearest to where they live (柱子 3) 和
the average over all schools at their advised track (柱子 4). The mean distance to
13. For a random sample of one hundred students, we calculated the road distance as well. The road distance
turned out to be very closely related to the distance in a straight line (r = 0.99).
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
F
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
9
School Choice in Amsterdam
the nearest school is close to one kilometer and this is very similar for the different
school tracks. The mean distance to the school that is actually chosen is about three
kilometers at all school tracks, whereas the mean of the average distance to all schools
at a given track is five to six kilometers, again with little variation across school tracks.
We constructed an indicator that equals one for tracks in schools that had a lottery in
the year prior to the year of application.14 Column 5 of table 2 shows the share of schools
that conducted a lottery, averaged over the four years of observations.
To study the relationship between a student’s own school choice and that of his
or her classmates, columns 6 到 9 provide information about the actual and predicted
shares of peers in primary school who go to the same secondary school, and the shares
of classmates who would go to the same school if students chose their secondary schools
randomly. For each student, we calculated the actual share of classmates in primary
school who apply to each of the secondary schools.15 Because some secondary schools
may always be more popular among students from a specific primary school (because of
distance or pedagogy), we also construct predictions to investigate classmates’ choices
for secondary schools in deviation from primary-school-specific trends. For these pre-
dictions we use the actual share of peers in the different years to estimate a linear trend
over the four years of our study, and the predicted values of those regressions as a
measure of predicted popularity. This is akin to the population variation used by, 为了
例子, Hoxby (2000乙). These shares show that classmates from the same primary
school tend to choose the same secondary school (the actual share of peers in chosen
schools exceeds the actual share of peers in all schools) even when corrected for the
usual popularity of secondary schools among students from a given primary school
(the actual share of peers in chosen schools exceeds the predicted share of peers in
chosen schools).
As described in section 2, Dutch schools are subject to quality inspections by the
Dutch Education Inspectorate. Their quality information is based on several aspects,
such as exam results and school visits. 自20世纪90年代以来, the Inspectorate’s quality as-
sessment of schools is public information, published on a yearly basis. A national news-
paper called Trouw makes the quantitative part of the information accessible to the
broader public, by publishing exam grades and other characteristics, and by computing
an overall quality score measured on a 5-point scale (“- -,” “-,” “0,” “+,” “++”).16 这
inputs for the newspaper’s quality scores are: final exam grades in the school track, 这
percentage of students getting a degree without grade repetition in the higher classes,
and the performance of the school in the lower years. For this last number, changes in
school track play a role: students enrolled in a lower track than their initial advice re-
duce the score, students enrolled in a higher track increase it. The overall quality score
14. The information we use for the lottery indicator is from a booklet published annually by the municipality of
阿姆斯特丹. This booklet includes one page of information on each secondary school, together with infor-
mation on the general enrollment procedure. It is handed out to all students in the last year of Amsterdam
primary schools. From our contacts with schools, we noticed that the booklets have a few errors on the lotteries.
Because students will visit the school before subscribing, and they will receive the correct information there,
we decided to adjust these cases to match the information from the schools.
15. Because we do not have information on classes within primary schools, we define classmates as all other
16.
students in the final grade of a students’ primary school.
在 2001, a news magazine called Elsevier also started publishing school quality information based on the In-
spectorate information. We choose to use the Trouw data because they were the first to publish this information
and because it has a wider circulation than Elsevier.
10
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
F
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
笔记: This figure shows the occurrence of different Trouw quality scores for Amsterdam schools published in December 2006 到
十二月 2009.
数字 1. Variation in Trouw Quality Scores
is calculated and published for each school track separately, so within a school, 那里
may be different quality scores. Very small schools or schools that miss values on the
underlying scores (例如, because a school is new) do not get an overall quality
分数.
The quality information we use for each student is the quality information pub-
lished in December before the student’s school choice in April. In 2009—the last pub-
lication relevant in our data—the 5-point scale was abolished and only the underlying
numbers were published. Since the 5-point scale was computed in the same way ev-
ery year, we are able to reconstruct the scores. We will study the 2009 quality scores
separately in the analyses.
Because only Amsterdam schools are included in this study, there are not enough
schools with the extreme quality scores “- -” and “++” in the sample. 所以, 我们
transformed the 5-point scale into a 3-point scale. As can be seen in figure 1, 那里
is substantial variation in the quality scores of the Amsterdam schools.17 The qual-
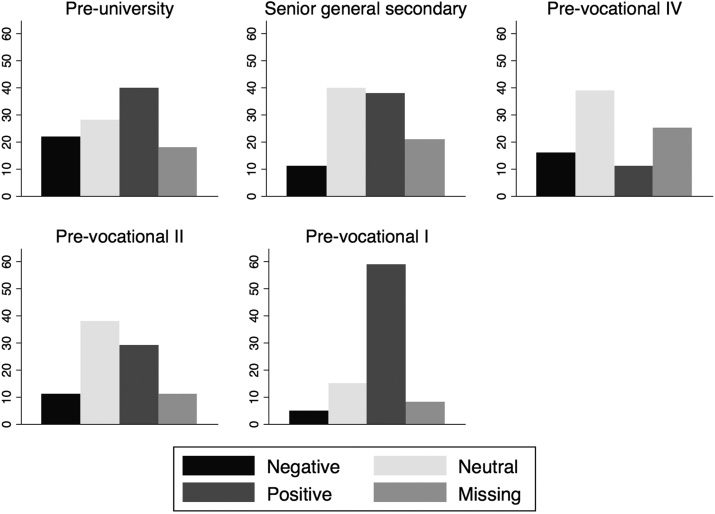
ity scores are not stable over time. 桌子 3 shows the variation of the quality scores
within schools in the four-year period of the study. 例如, only ten out of the
17. Four schools (with seven overlapping school tracks) are registered formally as two separate schools. These two
pairs of schools cooperate very closely, and only receive one quality score for the pair. 所以, we used this
quality score for both schools.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
F
/
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
11
School Choice in Amsterdam
桌子 3. Changes in School Quality Scores over Time
学校
Track
Pre-university
Senior general/pre-university
Senior general/pre-university
Senior general
Pre-vocational IV/senior general
Pre-vocational IV/senior general
Pre-vocational IV
Pre-vocational II
Pre-vocational I/II
Pre-vocational I/II
Pre-vocational I
氮
学校
氮
Stable
学校
Quality Scores
in Current
年
Pre-university
Quality Scores in Previous Year
Missing
Negative
Neutral
Positive
27
21
21
23
18
18
23
22
21
21
22
10
6
Missing
Negative
Neutral
Positive
全部的
Senior General Secondary
7
9
7
4
5
5
5
11
11
Missing
Negative
Neutral
Positive
全部的
Pre-vocational IV
Missing
Negative
Neutral
Positive
全部的
Pre-vocational II
Missing
Negative
Neutral
Positive
全部的
Pre-vocational I
Missing
Negative
Neutral
Positive
全部的
9
4
2
0
15
13
1
0
1
15
14
0
4
1
19
3
0
2
2
7
3
0
1
1
5
0
11
8
1
20
0
0
6
4
10
0
3
8
1
12
0
4
5
1
10
0
3
1
0
4
0
2
8
9
19
0
3
21
5
29
1
6
16
6
29
3
2
17
5
27
0
0
6
7
13
0
0
2
24
26
0
1
4
22
27
1
2
2
2
7
1
0
8
13
22
3
0
4
36
43
Notes: In this table, we include all relevant schools that have a quality score for a certain school track. We do not take into
account the fact that some schools are not in the choice set for combined tracks (a student with combined senior general
secondary/pre-university advice cannot go to a school that only offers pre-university education). The number of stable schools
indicates the number of schools that have the same quality score over the four included years.
twenty-seven schools that offer the pre-university track keep the same quality score for
four consecutive years.
4 . E M P I R I C A L S T R AT E G Y
The description of the empirical approach is divided into two parts. It begins with a
description of conditional and mixed logit models that we use for the main analysis.
下一个, it provides details about the approach we use to say something about the influence
that peers have on school choices.
12
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
F
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
Main Analysis
To study the determinants of secondary school choice we use discrete choice models.
Specifically, we will estimate conditional and mixed logit models. These models follow
from a random utility framework in which a student is assumed to choose the school
that maximizes her utility. The utility that student i choosing in year t derives from sec-
ondary school s is defined as Uits = Vits + εits, where Vits is the observed portion of utility
and εits is the unobserved portion of utility. εits is assumed to be an independently, iden-
tically distributed extreme value, in which the independence means the unobserved
utility for one alternative is unrelated to the unobserved utility for another alternative
(Train 2009). We will use different specifications of Vits, thereby imposing different as-
sumptions on the model. In all cases, we investigate school choice separately for each
group of students with the same school track advice because the students’ choice sets
differ by advised school track.
它是
β + w(西德:2)
ts
第一的, we analyze whether school choice can be predicted by student and school
特征, in which Vits = x(西德:2)
δ + z(西德:2)
γs. Here xits are characteristics that are
它
specific for a student–school combination. In the main analysis this will only be the
distance from home to school. In additional analyses it will also include the share
and the predicted share of a students’ primary school peers going to that secondary
学校. wts are secondary school–specific factors: the school quality characteristics and
whether the school had a lottery for that school track in the previous year. zit are student-
specific factors, included such that the coefficients of the variables of interest are con-
ditional on these variables. The included student specific factors are gender, 种族,
test score, student weight, and indicators for missing values on these characteristics.
The probability (pits) that student i in year t chooses for secondary school s is given
经过:
(西德:2)
(西德:3)
pits =
(西德:4)
X(西德:2)
β + w(西德:2)
经验值
(西德:2)
ts
它是
β + w(西德:2)
X(西德:2)
米
l exp
tl
itl
δ + z(西德:2)
γs
它
δ + z(西德:2)
它
(西德:3) ,
γl
(1)
The parameters β, δ, and γ are estimated using maximum likelihood estimation, 在
which the log likelihood function is given by LL(β, γs, δ) =
i yits ln pits, 在哪里
yits is a binary indicator equal to one if student i in year t chooses school s, and zero
否则.
S
s=1
(西德:4)
(西德:4)
In specification 1, we do not take into account differences between secondary
学校, apart from school quality and having a lottery in the previous year. It is likely,
然而, that unobserved characteristics (in our database) of the secondary school, 这样的
as the quality of the building and the availability of extracurricular activities, are impor-
tant in secondary school choice. In specification 2, we therefore add secondary school
fixed effects, ds j, as a secondary school dummy, which has ds j = 1 if s = j and ds j = 0
if s (西德:3)= j. Adding secondary school dummies changes the interpretation of the quality
scores—we no longer use the absolute scores of a secondary school but study how
school choices change when school quality scores change.
pits =
(西德:4)
(西德:5)
经验值
米
l exp
X(西德:2)
它是
(西德:5)
X(西德:2)
itl
β + w(西德:2)
ts
γs +
δ + z(西德:2)
它
δ + z(西德:2)
它
γl +
J
s j
j=2 d(西德:2)
(西德:4)
α j
j=2 d(西德:2)
l j
J
β + w(西德:2)
tl
(西德:4)
(西德:6)
(西德:6) ,
α j
(2)
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
F
/
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
13
School Choice in Amsterdam
楷模 1 和 2 are conditional logit models, which assume that the errors εits are inde-
pendent of each other, such that the unobserved portion of utility for one alternative is
unrelated to the unobserved portion of utility for another alternative. This lack of cor-
relation gives rise to the property of independence of irrelevant alternatives (IIA). IIA
means that for any two alternatives j and k, the relative odds of choosing j over k are the
相同的, such that the ratio is not dependent of the presence or attributes of other alterna-
特维斯 (Train 2009). 在实践中, this means that two schools (of the same track) will be
equally affected by the opening of a new competing school. This is not very likely—the
school that is more closely related in terms of distance or school policy will probably be
affected more. Mixed logit models do not have the IIA property. 所以, we have also
estimated mixed logit models for secondary school choice. As can be seen in equation
3, we estimated random coefficients for the student–school-specific characteristics and
the school-specific characteristics (质量, lottery in the previous year, and distance).
φ(β, δ|乙, d, 瓦 ) indicates the mixing distribution, in this case the normal density with
means b and d and covariance W .18
⎛
(西德:7)
pits =
⎝
(西德:4)
(西德:5)
X(西德:2)
它是
(西德:5)
X(西德:2)
itl
经验值
β + w(西德:2)
ts
米
l exp
β + w(西德:2)
tl
(西德:4)
γs +
δ + z(西德:2)
它
δ + z(西德:2)
它
γl +
J
s j
j=2 d(西德:2)
(西德:4)
J
α j
j=2 d(西德:2)
l j
(西德:6)
⎞
(西德:6)
⎠ φ (β, δ|乙, d, 瓦 ) dβ.
(3)
α j
Another advantage of the mixed logit model is that it allows for variation in pref-
erences for school characteristics. It might be that some students put a high weight
on the published quality scores, whereas others do not. Or some risk-averse students
may avoid a school that had a lottery in the previous year, whereas others do not care so
much. In the mixed logit model, we do not only estimate the means of the preferences
for school characteristics but also their standard deviations, which allows us to see to
what extent the preferences for secondary school characteristics vary across students.
Peer Effects in School Choices
The school choice literature typically assumes that students make their choices indi-
vidually and ignores possible influences of peers. Casual observation suggests this is
unrealistic. Students who go from a primary school to a secondary school seem to be
influenced by the choices of their classmates in primary school. They may coordinate
their school choices, or some students may follow the choices of others. There may, 在
也就是说, be peer effects in school choices.
Peer effects are intrinsically difficult to analyze (Manski 1993; Angrist 2014). 这
following identification problems are present. The first is the reflection or simultaneity
问题. In the presence of peer effects, it is not always clear how the causality runs—
do peers affect the respondent, or does the respondent affect peers? The second is the
self-selection problem. Group membership is endogenous—peers select themselves
on the basis of similar characteristics. 更远, in the presence of peer effects, 它不是
always clear whether effects are driven by behavior, or by unobserved characteristics
18. Rather than a normal density, Hastings, Kane, and Staiger (2009) assume a negative lognormal distribution
for distance, which imposes that all students dislike commuting. Without explicitly imposing this restriction,
we consistently find that students have a negative preference for distance.
14
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
F
/
/
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
F
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
that are correlated with it. 最后, there is the errors-in-variables problem—it is not
always clear how to define the relevant peer group.
The economics of education literature has so far been unsuccessful in addressing
all these problems in a satisfactory way. We follow Sacerdote (2001) and include the
fractions of primary school classmates choosing for each secondary school in the logit
model of students’ secondary school choice. The results are subject to the reflection
problem and the correlated errors problem, and can therefore not be given a causal
解释. The results are, 然而, informative about the degree of correlation in
the choices of classmates in primary school.
To address the correlated errors problem, we include two variables capturing peer
优先. We include the predicted share of peers in which we account for the (趋势
在里面) general popularity of a secondary school within a primary school. This captures
systematic feeder patterns related to factors, such as pedagogy and distance. 第二
variable, the actual share of peers, captures whether the choices of students’ primary
school classmates deviate from the choices of students from other cohorts in that pri-
mary school. If inclusion of the first component solves the correlated errors problem,
the estimate of the effect of the idiosyncratic component in classmates’ choices is only
biased due to the reflection problem. According to Sacerdote (2001), this allows us to
test the null hypothesis of no peer effects, which predicts no relationship between a
student’s own school choice and the idiosyncratic school choices of her classmates in
primary school.
5 . R E S U LT S
The empirical results are presented in four subsections. The first subsection presents
the main findings from the conditional logit models with and without school fixed ef-
fects. The next subsection explores the sensitivity for the inclusion of other measures of
school quality than the composite measure published by the national newspaper Trouw.
We then present the results from the mixed logit model that allows for heterogeneous
preferences across students. The final subsection covers the findings with respect to
the influence of peers.
Main Findings
桌子 4 presents estimates from the conditional logit model without school fixed ef-
fects separately for each secondary school track. The top part of the table reports the
estimates of the impact of school quality scores on students’ choices. For students with
a mixed advice (例如, senior general secondary/pre-university) the quality scores of both
tracks matter and estimates of the impact of two quality scores are reported, 哪里的
first estimate pertains to the highest of the two tracks.19 Neutral quality scores are the
reference category. As described before, the quality scores of 2009 are reported sep-
arately because only the underlying scores were published by Trouw in that year. 这
estimated coefficients for the quality scores provide no support for the hypothesis that
19. 考虑, 例如, the estimates for a negative quality score for students with a mixed senior general
secondary/pre-university advice. The estimate of –0.380 is the effect of a negative quality score of the pre-
university track in a school, and the estimate of 0.304 is the effect of a negative quality score of the senior
general secondary track in a school.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
F
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
15
School Choice in Amsterdam
桌子 4. Estimates from Conditional Logit Models without School Fixed Effects
Negative quality
Positive quality
Missing quality scores
Negative quality 2009
Positive quality 2009
Missing quality scores 2009
Distance
Lottery
N students
N schools
Log likelihood
Pseudo R2
Negative quality
Positive quality
Missing quality scores
Negative quality 2009
Positive quality 2009
Pre-university
0.371***
(0.111)
0.477***
(0.093)
−0.414***
(0.136)
−0.011
(0.229)
−0.293**
(0.119)
−0.118
(0.270)
−0.535***
(0.020)
0.335***
(0.067)
4,374
27
10,375.3
0.15
Senior General/
Pre-university
Senior General
Pre-vocational IV/
Senior General
−0.380***
(0.127)
0.304***
(0.108)
0.474***
(0.105)
0.046
(0.114)
−0.377**
(0.181)
−0.705**
(0.298)
0.696**
(0.268)
−0.503
(0.420)
0.062
(0.188)
−0.100
(0.162)
0.549
(0.590)
−0.768
(0.484)
−0.552***
(0.020)
−0.078
(0.064)
2,819
21
−5,991.1
0.24
0.106
(0.084)
0.122
(0.077)
−0.775***
(0.169)
−0.058
(0.383)
−0.274**
(0.107)
−0.006
(0.173)
−0.520***
(0.021)
0.035
(0.067)
3,133
23
−7,068.0
0.24
0.001
(0.101)
−0.307***
(0.109)
−0.055
(0.124)
−0.321**
(0.143)
−0.602
(0.413)
0.363
(0.393)
0.108
(0.459)
0.384
(0.289)
0.182
(0.159)
0.181
(0.208)
−0.222
(0.263)
−0.553***
(0.024)
0.462***
(0.137)
2,028
18
−3,703.4
0.31
Pre-vocational IV
Pre-vocational II
Pre-vocational I/II
Pre-vocational I
−0.222***
(0.085)
−0.189*
(0.098)
−0.260**
(0.129)
0.354**
(0.169)
−0.393**
(0.159)
0.080
(0.123)
0.034
(0.089)
0.160
(0.145)
−0.605
(0.482)
−0.317*
(0.170)
−0.115
(0.212)
−1.037
(0.735)
0.171
(0.131)
0.190
(0.169)
−0.382
(0.556)
0.380
(0.587)
−0.763
(0.578)
−0.657**
(0.259)
0.039
(0.293)
−0.538
(0.650)
−0.257
(0.777)
−0.355
(0.555)
0.069
(0.105)
0.058
(0.139)
0.385
(0.404)
0.238
(0.218)
−0.375
(0.377)
Missing quality scores 2009
−0.567***
(0.191)
−0.568**
(0.258)
16
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
F
e
d
你
e
d
p
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
A
_
0
0
2
3
7
p
d
.
F
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
桌子 4. Continued.
Pre-vocational IV
Pre-vocational II
Pre-vocational I/II
Pre-vocational I
Distance
Lottery
N students
N schools
Log likelihood
Pseudo R2
−0.546***
(0.022)
0.633***
(0.134)
2,881
23
−5,446.1
0.32
−0.482***
(0.017)
0.113
(0.338)
2,130
22
−4,365.7
0.29
−0.531***
(0.023)
0.219
(0.334)
1,039
21
−2,059.1
0.31
−0.582***
(0.017)
0.049
(0.183)
2,713
22
−5,400.9
0.33
Notes: Standard errors are clustered at the primary school level and reported in parentheses. Included
student level controls are gender, Dutch, missing ethnicity, test score, missing test score, student
重量, and missing student weight.
***p < 0.01; **p < 0.05; *p < 0.10.
school choice is systematically influenced by published quality scores. Two coefficients
for a positive quality score are significantly positive and three coefficients for a negative
quality score are significantly negative. At the same time, two coefficients for a positive
quality score are significantly negative, and two coefficients for a negative quality score
are significantly positive. Just focusing on the sign of the coefficients, it turns out that
fourteen of twenty-two coefficients have a sign that is consistent with the hypothesis
that a positive (negative) quality score makes it more (less) likely that a school is cho-
sen. We cannot reject that this number of correct signs is generated by chance (p =
0.86). By and large we can therefore not reject the hypothesis that published quality
scores have no systematic impact on students’ school choices.
Distance turns out to be a consistent and strong predictor of school choice. This is
in accordance with results from other studies (e.g., Hastings, Kane, and Staiger 2009;
Koning and Van der Wiel 2013). One way to interpret the size of the coefficients is in
terms of odds ratios. The logit coefficient for distance to pre-university schools in table
4 can be expressed as an odds ratio by taking the exponent: exp(–0.535) = 0.59. This
coefficient indicates that students with a pre-university advice are 41 percent less likely
to choose a school that is one kilometer farther away, as compared to an identical school
one kilometer closer. The odds ratios for the other school tracks indicate that students
are 38 percent to 44 percent less likely to choose a school one kilometer more distant.
Alternative specifications for distance also consistently indicate that students prefer
schools closer to their home.20
The coefficients for the lottery dummy are positive and significant in three of eight
cases, but they have the “wrong” sign in the sense that they suggest that students are
more likely to choose a school that had a lottery in the previous year. This result is
20. Specifically, we have estimated models using the log of distance, adding a quadratic term, using bins, distance
rank, and a closest school indicator. Compared with the lowest bin and closest school, all distance bins and
ranks have a negative and significant coefficient. The closest school indicator is positive and significant when
not including distance, but becomes negative and significant in three (lower) tracks when including distance,
implying that after taking into account distance, students do not prefer the school closest to their house. When
adding a quadratic term, the linear term remains negative and significant. Squared distance is always positive
and significant in four out of eight school tracks, implying that the negative value put on distance is nonlinear
and shaped like a parabola that opens upward.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
17
School Choice in Amsterdam
robust for different specifications of the lottery and for using different samples—we
obtain similar results when (1) we use the percentage of students losing the lottery in
the previous year instead of the binary indicator; (2) we account for the school mak-
ing an extra class in the year of school choice; and (3) we drop students who have
priority for admittance to their school of first choice. Results are reported in table
A.1 in Appendix A, which is available in a separate online appendix that can be ac-
cessed on Education Finance and Policy’s Web site at https://www.mitpressjournals.org
/doi/suppl/10.1162/edfp_a_00237.
Table 5 presents estimates from the conditional logit model, including secondary
school fixed effects. This alters the interpretation of the quality scores—we no longer
use the absolute scores of a secondary school but study how school choices respond to
changes in school quality scores. The estimation results are rather similar to those in
the previous table without school fixed effects. For the quality scores, fewer coefficients
are significant and some coefficients have changed their sign. As before, however, we
cannot reject the hypothesis that quality scores have no systematic impact on students’
school choices. The estimated effects for distance are also very similar to those in the
previous table. The inclusion of school fixed effects does, however, change the esti-
mates of the coefficients of the lottery indicator. Now, five of eight coefficients have the
expected negative sign, with two coefficients being significant at the 10 percent level
and one coefficient being significant at the 5 percent level. In the models with school
fixed effects, schools are compared with themselves in years in which there is no lot-
tery. Therefore, these results are more likely to capture a pure lottery effect. There is
thus some evidence that students avoid schools that conducted a lottery in the previous
year. This finding carries over to different specifications of the lottery (see table A.1 in
online Appendix A). The odds ratios for the significant coefficients range from 0.51 to
0.89, implying that students are 11 percent to 49 percent less likely to choose a school
when it conducted an admission lottery in the previous year. Another way to interpret
these coefficients is in terms of willingness to travel: Wtt = βlottery/βdistance. The results
imply that students are willing to travel 0.22 to 1.41 kilometers to avoid a school that
conducted an admission lottery in the previous year.
We have also investigated whether preferences differ over time. For instance, as the
centralized system started in 2005, it could be that students responded differently to lot-
teries in 2006 than to lotteries in 2009. We have therefore interacted the lottery dummy
and quality indicators with year dummies. The results are reported in table B.1 in on-
line Appendix B. For the quality variables in the specifications without fixed effects, the
results show no consistent pattern of increasing or decreasing preferences for school
quality scores. For the lottery, the results in the models without fixed effects slightly
shift over the years. For 2006, four coefficients are negative and insignificant, two are
positive and insignificant, and two are positive and significant. For 2009, only one coef-
ficient is negative and significant, three are positive and insignificant, and four are pos-
itive and significant. Thus, there is some evidence that parental preference for schools
that conducted school admission lotteries in the previous year increases over time.21
21. For some track/year combinations the lottery indicator cannot be estimated because no single school in that
track conducted a lottery in that year. For senior general/pre-university there were no schools conducting
18
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
Table 5. Estimates from Conditional Logit Models with School Fixed Effects
Negative quality
Positive quality
Missing quality scores
Negative quality 2009
Positive quality 2009
Missing quality scores 2009
Distance
Lottery
N students
N schools
Log likelihood
Pseudo R2
Pre-university
0.288**
(0.123)
0.397***
(0.102)
−0.252
(0.156)
0.321
(0.248)
−0.350***
(0.125)
0.442
(0.378)
−0.588***
(0.023)
0.066
(0.064)
4,374
27
−10,112.1
0.17
Senior General/
Pre-university
−0.097
(0.146)
0.174*
(0.105)
0.284***
(0.108)
0.065
(0.114)
−0.092
(0.189)
−0.225
(0.332)
0.236
(0.280)
0.439
(0.492)
−0.032
(0.191)
−0.069
(0.166)
0.349
(0.630)
−0.419
(0.473)
−0.609***
(0.023)
−0.103
(0.069)
2,819
21
−5,891.0
0.25
Senior
General
0.071
(0.088)
0.006
(0.076)
−0.069
(0.236)
0.634
(0.466)
−0.210*
(0.113)
0.132
(0.182)
−0.555***
(0.021)
−0.113*
(0.065)
3,133
23
−6,916.4
0.25
Pre-vocational IV/
Senior General
0.022
(0.101)
−0.079
(0.116)
0.014
(0.129)
−0.321**
(0.153)
−0.151
(0.433)
0.168
(0.409)
−0.265
(0.493)
0.523*
(0.308)
0.100
(0.171)
−0.119
(0.248)
−0.334
(0.274)
−0.576***
(0.024)
0.003
(0.131)
2,028
18
−3,557.8
0.34
Pre-vocational IV
Pre-vocational II
Pre-vocational I/II
Pre-vocational I
Negative quality
−0.153*
(0.091)
0.195
(0.121)
Positive quality
−0.174*
(0.102)
−0.082
(0.094)
Missing quality scores
0.022
(0.163)
−0.028
(0.161)
Negative quality 2009
Positive quality 2009
0.578***
(0.189)
−0.528***
(0.172)
0.165
(0.520)
−0.296*
(0.163)
Missing quality scores 2009
−0.563***
(0.196)
−0.329
(0.264)
1.698***
(0.646)
0.052
(0.111)
0.027
(0.145)
0.419
(0.408)
0.217
(0.220)
−0.438
(0.387)
0.082
(0.212)
−0.651
(0.976)
0.014
(0.141)
0.167
(0.195)
−0.367
(0.555)
0.109
(0.612)
−0.861
(0.598)
−0.360
(0.283)
−0.215
(0.338)
−0.085
(0.676)
−0.874
(0.832)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
19
School Choice in Amsterdam
Table 5. Continued.
Pre-vocational IV
Pre-vocational II
Pre-vocational I/II
Pre-vocational I
Distance
Lottery
N students
N schools
Log likelihood
Pseudo R2
−0.557***
(0.022)
−0.291*
(0.175)
2,881
23
−5,272.8
0.34
−0.495***
(0.018)
−0.678**
(0.287)
2,130
22
−4,240.6
0.31
−0.552***
(0.024)
−0.151
(0.320)
1,039
21
−2,003.0
0.33
−0.588***
(0.017)
0.026
(0.187)
2,713
22
−5,344.0
0.33
Notes: Standard errors are clustered at the primary school level and reported in parentheses. Included
student level controls are gender, Dutch, missing ethnicity, test score, missing test score, student
weight, and missing student weight.
***p < 0.01; **p < 0.05; *p < 0.10.
For the models with fixed effects (results not shown) most coefficients are insignificant
and the signs are inconsistent.22
Alternative Measures of Secondary School Quality
In the previous subsection, we concluded that school quality scores do not clearly pre-
dict school choice. A potential explanation is that parents value the underlying quality
measures described in section 3 over the composite quality measure. Therefore, in spec-
ification 1 in table 6, the underlying quality measures are added to the models in table
4. Descriptive statistics about these underlying quality measures are reported in table
C.1 in online Appendix C. It turns out that exam grades are positively related to school
choice: nine of eleven coefficients are positive, of which five are significant (at the 10
percent level). The significant coefficients are mainly at the higher school tracks. The
willingness-to-travel ratios imply that students (ceteris paribus) are willing to travel up
to 1.41 kilometers more to attend a school with a one-point higher average exam grade
(or 0.48 kilometers more to attend a school with a 1 standard deviation (SD) higher exam
grade). The percentage of students getting a degree without delay in the higher classes
seems to be negatively related to school choice: five of eleven coefficients are negative,
of which four are significant. Willingness to travel ratios indicate that students are will-
ing to travel up to 0.39 kilometers to attend a school with a 1 SD lower percentage of
students getting a degree without delay in the higher classes. This could be because
more delay in the higher grades is related to better exam grades. Grade progression
in the lower grades does not predict school choice. When adding school fixed effects to
lotteries in 2008. For the lowest three tracks, there was only one school conducting a lottery, which was also
the only school that missed quality scores for these tracks in 2008.
22. As a falsification test, we have also used future (changes in) quality and lottery indicators on current year deci-
sions. For the quality variables, the majority of coefficients is insignificant, although the number of coefficients
with an unexpected and significant sign decreases, whereas the number of coefficients with an expected and
significant sign slightly increases. For the future lottery indicators, the coefficients for the models without fixed
effects are positive and significant for seven of eight school tracks. For the models with fixed effects, the coef-
ficients are also more often positive, but generally insignificant. However, as the future lottery indicator is an
indicator for having a lottery in the year of school choice (instead of a lottery in the previous year), and schools
only have a lottery when they are oversubscribed for that school track, it makes sense that this lottery indicator
is positively related to number of applicants for a school.
20
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
Table 6. Models Including Underlying School Characteristics (without school fixed effects)
(1) Index grade progression in
lower grades
Exam grades
Degrees without delay
N students
(2) Index grade progression in
lower grades
Exam grades
Degrees without delay
Primary school test scores
of inflow
N students
Pre-university
0.008*
(0.004)
0.761***
(0.157)
0.005
(0.004)
4,374
0.004
(0.005)
0.612***
(0.155)
0.005
(0.004)
0.060***
(0.015)
4,374
Senior general/
Pre-university
Senior general
Pre-vocational IV/
Senior General
0.000
(0.005)
0.069
(0.214)
0.490**
(0.200)
0.004
(0.004)
−0.012**
(0.005)
2,819
0.000
(0.005)
0.074
(0.213)
0.407**
(0.208)
0.004
(0.004)
−0.012**
(0.005)
0.032
(0.022)
2,819
−0.002
(0.004)
0.322**
(0.159)
−0.010**
(0.004)
3,133
−0.001
(0.004)
0.244
(0.166)
−0.010**
(0.004)
0.045***
(0.017)
3,133
−0.004
(0.004)
0.168
(0.196)
0.516*
(0.299)
−0.003
(0.006)
0.003
(0.006)
2,028
−0.005
(0.004)
−0.112
(0.209)
0.705**
(0.314)
−0.004
(0.006)
0.013**
(0.006)
0.049**
(0.023)
2,028
Pre-vocational IV
Pre-vocational II
Pre-vocational I/II
Pre-vocational I
(1) Index grade progression in
lower grades
Exam grades
−0.006*
(0.003)
−0.063
(0.196)
0.002
(0.006)
0.367*
(0.191)
Degrees without delay
0.003
(0.005)
−0.010*
(0.005)
N students
(2) Index grade progression in
lower grades
Exam grades
2,881
−0.005
(0.003)
0.040
(0.200)
2,130
0.005
(0.006)
0.461**
(0.178)
Degrees without delay
0.010**
(0.005)
−0.008
(0.005)
Primary school test scores
of inflow
N students
0.031**
(0.014)
2,881
0.027
(0.018)
2,126
−0.005
(0.010)
−0.107
(0.316)
0.310
(0.271)
−0.017**
(0.007)
0.001
(0.011)
1,039
−0.005
(0.009)
−0.234
(0.317)
0.300
(0.271)
−0.013**
(0.007)
−0.006
(0.011)
−0.009
(0.016)
1,022
0.002
(0.004)
0.105
(0.160)
0.003
(0.006)
2,713
0.003
(0.004)
0.007
(0.163)
0.007
(0.006)
−0.005
(0.012)
2,643
Notes: Standard errors are clustered at the primary school level and reported in parentheses. Models also include
indicators for school quality, distance, and a lottery indicator as in table 4. Included student level controls are gender,
Dutch, missing ethnicity, test score, missing test score, student weight, and missing student weight.
***p < 0.01; **p < 0.05; *p < 0.10.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
21
School Choice in Amsterdam
specification 1 in table 6 (results not shown) the coefficients become nonsignificant and
inconsistent in sign, indicating that parents and students do not respond to changes in
the underlying quality measures.23
The models in table 6 also include the composite quality measures,24 distance, and
the lottery indicator. The results for distance and the lottery indicator do not change
when including the underlying quality measures. For the composite quality measures,
the pattern of inconsistent signs remains and fewer coefficients are significant. Out of
the three significant coefficients for positive quality scores, two have a positive sign and
one a negative sign. For negative quality scores, there are two significant coefficients
with a positive sign and two with a negative sign. For the models with school fixed
effects, the composite quality measures remain insignificant.
To investigate whether the positive preference for schools with higher exam grades
is driven by a preference for a higher-achieving student population, specification 2 in
table 6 adds information about the (demeaned) average primary school test scores of
the current inflow to the models in specification 1. We computed the average citoscore
of the current inflow for each specific school track advice in a school in a certain year.25
We only compute models without school fixed effects, because a model with school
fixed effects would assume that parents respond to (small) changes in average primary
school test scores in the year in which the student applies. This information is not
available to parents.
The results indicate that students and parents also prefer schools with higher av-
erage primary school test scores in the advised school track. Six of eight coefficients
are positive, of which four are significant. The two negative (n.s.) coefficients are at
the lowest tracks. Willingness-to-travel ratios imply that students are willing to travel
up to 0.54 kilometers to attend a school with a 1 SD higher average of primary school
test scores. When including the primary school test scores of the current inflow, exam
grades remain a positive predictor of school choice: nine of eleven coefficients are pos-
itive of which four are significant. Degree without delay in the higher grades becomes
less consistent: six coefficients are negative, of which three are statistically significant,
and five coefficients are positive, of which two are statistically significant. Grade pro-
gression in the lower grades remains unrelated to school choice. The conclusions for
distance, the lottery indicator, and the composite quality measures do not change.
Heterogeneous Preferences
Table 7 presents estimation results of mixed logit models. In addition to the mean of the
preference weights for school characteristics, the mixed logit model also produces esti-
mates of their standard deviation. This allows us to see to what extent the preferences
for secondary school characteristics vary across students. Again, the estimates indicate
23.
Including different specifications of enrollment (log of enrollment, enrollment, lagged enrollment, log of
lagged enrollment), indicates that (lagged) enrollment is positively and significantly related to school choice. On
average, students and parents seem to prefer larger schools. When adding school fixed effects, the coefficients
are generally insignificant and inconsistent in sign.
24. Removing the composite measures of school quality yields similar results.
25. Almost 14 percent of all students miss information on their citoscore. In computing the average citoscores, we
do not take these students into account. This leads to losing some observations, as twenty-three school–year–
track combinations only have missing citoscores. The combinations that have no citoscores are mainly lower
tracks and early years.
22
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
Table 7. Estimates from Mixed Logit Models
Pre-university
Senior General/
Pre-university
Negative quality
Mean
−0.105
(0.184)
1.445***
(0.301)
SD
Mean
SD
Positive quality
0.458***
(0.118)
0.889**
(0.348)
Missing quality scores
−1.122*
(0.617)
1.851**
(0.726)
Negative quality 2009
0.314
(0.349)
0.553
(0.480)
Positive quality 2009
−0.192
(0.199)
1.164**
(0.585)
Missing quality scores 2009
−1.695
(1.170)
2.599**
(1.053)
Distance
Lottery
N students
N schools
Log likelihood
Pseudo R2
Negative quality
Positive quality
Missing quality scores
Negative quality 2009
Positive quality 2009
0.163**
(0.071)
0.450
(0.399)
−0.660***
(0.031)
0.028
(0.086)
4,374
27
10,197.6
0.16
Pre-vocational IV/
Senior General
Mean
SD
0.037
(0.109)
−0.128
(0.127)
−0.095
(0.178)
−0.351**
(0.163)
−0.133
(0.473)
−0.356
(0.565)
−0.628
(0.585)
0.643*
(0.358)
0.134
(0.247)
−0.165
(0.303)
0.027
(0.176)
0.020
(0.200)
0.899**
(0.413)
0.156
(0.182)
0.550
(0.443)
1.520***
(0.552)
1.253***
(0.404)
0.215
(0.352)
0.464
(1.359)
0.893
(0.684)
0.603
(0.450)
1.025**
(0.517)
0.854**
(0.352)
0.769**
(0.343)
2.486***
(0.523)
5.077**
(1.970)
1.656***
(0.517)
0.898
(0.554)
0.371
(0.933)
0.495
(0.621)
0.500
(0.599)
4.680***
(1.679)
0.174***
(0.059)
0.287
(0.246)
−0.196
(0.193)
−0.003
(0.241)
0.299***
(0.116)
0.090
(0.134)
−1.275**
(0.513)
−5.073*
(2.635)
0.023
(0.395)
0.453
(0.648)
0.087
(0.249)
−0.076
(0.195)
1.739*
(0.925)
−4.547**
(1.995)
−0.738***
(0.035)
−0.115
(0.073)
2,819
21
−5,936.0
0.25
Senior General
Mean
−0.006
(0.225)
SD
0.660
(0.753)
0.026
(0.081)
0.418
(0.328)
−2.431**
(0.976)
3.102***
(0.777)
0.139
(0.747)
1.973***
(0.575)
−0.218*
(0.121)
0.394
(0.365)
0.484
(0.331)
0.313
(0.899)
0.251***
(0.042)
0.035
(0.126)
−0.649***
(0.031)
−0.107
(0.068)
3,133
23
−7,007.5
0.24
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
.
f
Pre-vocational IV
Pre-vocational II
Mean
−0.176
(0.109)
SD
0.387
(0.307)
Mean
0.181
(0.126)
SD
0.086
(0.242)
−0.184*
(0.106)
0.004
(0.113)
−0.272*
(0.144)
1.002***
(0.351)
−0.122
(0.277)
0.786
(0.496)
0.005
(0.180)
0.266
(0.195)
0.214
(0.434)
1.645**
(0.694)
−2.138
(4.150)
2.512
(2.481)
−0.718*
(0.379)
1.075
(0.928)
−0.706
(0.520)
1.808
(1.247)
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
23
School Choice in Amsterdam
Table 7. Continued.
Pre-vocational IV/
Senior General
Pre-vocational IV
Pre-vocational II
Missing quality scores 2009
Mean
−0.873
(0.828)
SD
1.364
(1.222)
Mean
−1.077
(0.738)
SD
1.259
(1.168)
Mean
−0.497
(0.318)
SD
0.349
(0.539)
Distance
Lottery
N students
N schools
Log Likelihood
Pseudo R2
Negative quality
Positive quality
Missing quality scores
Negative quality 2009
Positive quality 2009
Missing quality scores 2009
Distance
Lottery
N students
N schools
Log likelihood
Pseudo R2
−0.671***
(0.036)
−0.021
(0.146)
2,028
18
−3,649.4
0.32
0.232***
(0.032)
0.282
(0.289)
−0.634***
(0.025)
−0.393
(0.285)
2,881
23
−5,358.8
0.33
0.192***
(0.033)
0.968
(0.589)
−0.558***
(0.026)
−1.804***
(0.666)
2,130
22
−4,227.0
0.31
Pre-vocational I/II
Pre-vocational I
0.152***
(0.035)
1.958***
(0.522)
Mean
SD
0.690
(0.945)
3.570
(3.042)
0.777
(0.690)
0.334**
(0.142)
0.232
(0.611)
1.410**
(0.580)
2.810*
(1.674)
1.138*
(0.658)
0.240
(0.319)
0.599
(0.414)
0.995
(0.737)
0.178***
(0.055)
1.946***
(0.668)
0.011
(0.336)
−3.989
(4.330)
−0.089
(0.218)
0.160
(0.206)
−0.364
(0.612)
−0.506
(0.826)
−3.000
(2.028)
−0.575
(0.431)
−0.232
(0.380)
−0.593
(0.754)
−0.862
(1.000)
−0.653***
(0.044)
−0.852
(0.690)
1,039
21
−1,984.8
0.34
Mean
−0.272
(1.387)
SD
2.955***
(0.615)
0.050
(0.113)
0.078
(0.241)
0.012
(0.155)
0.087
(0.506)
0.244
(0.664)
0.212
(0.234)
1.333**
(0.676)
2.017***
(0.712)
−1.373*
(0.778)
0.158
(0.487)
0.054
(0.035)
0.258
(0.677)
−0.615***
(0.018)
−0.017
(0.202)
2,713
22
−5,324.8
0.33
Notes: Standard errors are clustered at the primary school level and reported in parentheses. Included student level controls
are gender, Dutch, missing ethnicity, test score, missing test score, student weight, and missing student weight for pre-vocational
I, I/II, and II. For the pre-vocational IV to pre-university tracks, the missing indicators could not be included for computational
reasons. When using Wald tests to compare the coefficients for the variables in this table in conditional logit models with and
without the missing indicators, it turns out that the null hypothesis of equal coefficients cannot be rejected for the pre-vocational
IV to pre-university tracks.
***p < 0.01; **p < 0.05; *p < 0.10.
24
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
that students have a lower preference for schools that are farther from their home ad-
dress. At the same time, however, we see the aversion for distance varies significantly
across students. Regarding school quality, we again see inconsistent coefficients over
the different school tracks; we still cannot reject the hypothesis that composite quality
scores have no systematic impact on school choice. Some of the standard deviations
for the quality scores come out significantly, indicating that the preferences for certain
quality scores vary across students. Regarding the lottery indicator, it can be seen that
only the mean coefficient for pre-vocational II comes out significantly. For the other
school tracks, the coefficients are mainly negative but not significantly different from
zero.
The standard deviations in the mixed logit models only describe whether secondary
school preferences vary across families. They do not provide information on which char-
acteristics are valued by different types of families. Therefore, we have also interacted
the quality, distance, and lottery variables with the disadvantaged student indicator us-
ing conditional logit models. The results in table D.1 in online Appendix D show some
interesting patterns. As before, distance is negatively valued. The interaction of distance
and student weight is also negative and significant, implying that the negative prefer-
ence for distance is stronger for disadvantaged students. The interaction coefficient of
lottery and weight, on the other hand, is mainly negative and significant in five school
tracks, implying that parents of disadvantaged students do not have a positive prefer-
ence for schools that conducted school admission lotteries in the previous year. For the
quality variables, the main coefficients remain very similar. Ten of the thirty-three in-
teractions of the quality and weight variables are significant. All significant coefficients
have the opposite sign of the corresponding main effect, which implies that for disad-
vantaged students, the preferences for positive or negative quality indicators are close
to zero.
For similar models with school fixed effects (reported in table D.2 in online Ap-
pendix D) home-to-school distance and distance interacted with weight again have neg-
ative and significant coefficients, implying that disadvantaged students put a signifi-
cantly stronger negative value on the distance to school. For the admission lotteries,
nearly all coefficients and the interactions with weight are insignificant. For the qual-
ity indicators, the pattern that changes in quality scores are not consistently related to
choice remains, and none of the interactions with student weight is significant.26
Peer Effects
Figure 2 depicts for one single primary school from year-to-year how the students
spread out across the available secondary schools. It shows that some secondary schools
(such as schools 7, 12, 32, and 57) are in general more popular than other schools for
students in this primary school. But we also see some strong fluctuations. For example,
school 58 is not a popular destination in 2006–07 and 2007–08, is the most popular
destination in 2008–09, and is back to its original level in 2009–10. The same is true
26. We have also inquired whether students are more likely to apply to a school that offers multiple tracks. This
analysis is limited to students who have schools with single and multiple tracks in their choice set. The results
reveal that students at the pre-university level have a preference for single-track schools and this preference
is stronger for students with higher citoscores. Students at the pre-vocational (II and IV) level instead prefer
multiple-track schools.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
25
School Choice in Amsterdam
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Note: Frequency in the number of students choosing each school is depicted on the vertical axis, the horizontal axis shows secondary
schools.
Figure 2. Secondary School Choice in One Primary School
for school 66. Similar graphs for other primary schools reveal comparable patterns:
Students who leave the same primary school in the same year tend to choose the same
secondary schools. To some extent this can be attributed to a general popularity of a
specific secondary school among the students from certain primary schools. But there
is also idiosyncratic clustering at—apparently random—destination schools.
Table 8 reports results from conditional and mixed logit models of school choice that
also include the shares of classmates and predicted shares of classmates who choose
each secondary school as variables in xits. The table only reports the coefficients of these
two variables. Consistent with the pattern we observed in figure 2, all coefficients are
significantly positive. Not surprisingly, we see a positive and significant coefficient for
the predicted share of peers in the primary school. This coefficient captures the general
popularity of secondary schools in the primary school. On top of the predicted share
of peers, however, we see that the actual share of peers has a positive and significant
coefficient as well. This indicates that when a higher share of the primary school peers
26
Nienke Ruijs and Hessel Oosterbeek
Table 8. Estimates of Peer Coefficients: Various Logit Models
Pre-
university
Senior General/
Pre-university
Senior
General
Pre-vocational IV/
Senior General
Pre-
Pre-
Pre-
Pre-
vocational IV vocational II vocational I/II vocational I
Conditional Logit Without School Fixed Effects
Predicted share
of peers
Share of peers
3.706***
(0.586)
3.464***
(0.485)
3.063***
(0.684)
4.259***
(0.539)
4.643***
(0.595)
3.013***
(0.465)
3.062***
(0.653)
5.127***
(0.566)
3.625***
(0.625)
3.669***
(0.509)
2.025***
(0.723)
4.554***
(0.663)
5.573***
(1.192)
2.743***
(0.988)
3.642***
(0.642)
3.131***
(0.535)
Conditional Logit With School Fixed Effects
Predicted share
of peers
Share of peers
4.135***
(0.564)
3.336***
(0.477)
3.537***
(0.681)
4.282***
(0.530)
4.797***
(0.593)
2.916***
(0.460)
2.659***
(0.640)
5.131***
(0.568)
3.382***
(0.621)
3.635***
(0.500)
1.618**
(0.707)
4.506***
(0.650)
5.108***
(1.233)
2.741***
(1.000)
3.530***
(0.635)
3.135***
(0.535)
Predicted share
of peers
Share of peers
SD (predicted
share of peers
SD (share of
peers)
N students
N schools
4.513***
(0.644)
3.720***
(0.564)
1.526
(1.699)
−1.489
(1.174)
4,374
27
4.022***
(0.785)
5.721***
(0.649)
−0.012
(3.647)
3.965***
(0.750)
2,819
21
5.957***
(0.699)
3.586***
(0.564)
2.897
(2.954)
−3.399
(2.294)
3,133
23
Mixed Logit
4.417***
(0.862)
6.117***
(0.742)
−5.846***
(0.965)
−1.657
(2.134)
2,028
18
4.970***
(0.760)
4.318***
(0.594)
2.063
(2.792)
−3.886**
(1.717)
2,881
23
2.786***
(0.838)
5.654***
(0.831)
3.545***
(1.122)
4.977***
(0.779)
2,130
22
7.191***
(1.705)
4.529***
(1.305)
3.918***
(0.783)
3.808***
(0.718)
−0.820
(2.728)
1.033
(5.083)
7.189*** −3.925***
(1.730)
(0.810)
1,039
21
2,713
22
Notes: Standard errors are clustered at the primary school level and reported in parentheses. All models also include indicators for school
quality, lottery, and distance as in table 4. Included student level controls are gender, Dutch, missing ethnicity, test score, missing test score,
student weight, and missing student weight. For the pre-vocational IV to pre-university tracks, the missing indicators could not be included in
the mixed logit specification for computational reasons. When using Wald tests to compare the coefficients for the peer characteristics and
the indicators for quality, lottery, and distance in conditional logit models with and without the missing indicators, it turns out that the null
hypothesis of equal coefficients cannot be rejected for these levels.
***p < 0.01; **p < 0.05.
chooses for a certain secondary school, the student himself is more likely to pick this
school as well. We find this result for all specifications and also when we correct for
secondary school times year fixed effects, which makes it unlikely that this result is
driven by sudden changes in the attractiveness of secondary schools. The school times
year fixed effects results are reported in online Appendix E.
Because of the reflection problem and correlated unobservables, these coefficients
cannot be interpreted as causal effects of the school choices of classmates. The coef-
ficients do not inform us about the social multiplier. Does the choice of one student
influence all others, or is everyone affected by everyone? The coefficients also do not
exclude that the correlated school choices are caused by a third unobserved factor, such
as active recruitment by a specific secondary school in certain primary schools in a
particular year. The results in table 8 are therefore no proof of the importance of peer
effects—they are, however, consistent with it.
To get an idea on the magnitude of the peer coefficients, we can compute willingness
to travel coefficients if we interpret the peer coefficients as the actual preference to at-
tend the same secondary school as primary school classmates do: Wtt = βpeers/βdistance.
For pre-university schools, we get a willingness to travel of 3.464/−0.371 = −9.334,
indicating that students are willing to travel 9.3 kilometers for a 100 percent increase
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
27
School Choice in Amsterdam
in the percentage of peers, or 943 meters for a 10 percent increase in the percentage
of peers. Given that the average class size in primary schools is about twenty-five, a 10
percent increase in the percentage of peers means an increase of two or three class-
mates. For the other school tracks, the willingness to travel for a 10 percent increase in
the percentage of peers varies from 674 to 1,429 meters.
6 . C O N C L U S I O N S
We investigate which secondary schools students choose when school choice is not
restricted by catchment areas, high tuition fees, or large distances. This provides a good
opportunity to examine whether school choices depend on school quality, which is a key
assumption of advocates of school choice and competition. Our findings lend some
support for this assumption. Students prefer schools where graduating students have
higher exam grades and schools that attract incoming students with higher scores on
the exit test of primary education. This is especially true for students who are advised
into the higher academic tracks. The result of this is that good students cluster together
in good schools, leaving the not-so-good students behind in the not-so-good schools.
Our results reject the null-hypothesis of no peer effects in school choice. When a
larger share of a student’s primary school peers chooses for a certain secondary school,
the student is more likely to pick that school as well. This is even true when we correct
for the systematic component in the popularity of the specific secondary school among
the students in the student’s primary school.27 Although this result does not prove the
importance of peer effects in school choices, it is consistent with it. If students prefer to
enroll in the same secondary school as their primary school classmates, school assign-
ment mechanisms may facilitate this by permitting students to opt for combined lottery
numbers. This may be particularly useful when the deferred acceptance mechanism is
in place, especially with multiple-tie breaking when substantial shares of students will
not be assigned to their most-preferred school.
ACKNOWLEDGMENTS
We gratefully acknowledge valuable comments from two anonymous referees. We also thank
Adam Booij, Monique de Haan, Inge de Wolf, Pierre Koning, Geert Ridder, Jesse Rothstein,
Adriaan Soetevent, Karen van der Wiel, and seminar participants at various places for useful
comments and suggestions. We thank Herman Ozinga and Kees Waijenberg from the Amster-
dam municipal office for supplying the data.
REFERENCES
Abdulkadiro˘glu, Atila, and Tayfun Sönmez. 2003. School choice: A mechanism design approach.
American Economic Review 93(3): 729–747. doi:10.1257/000282803322157061.
Angrist, Joshua D. 2014. The perils of peer effects. Labour Economics 30: 98–108. doi:10.1016/j
.labeco.2014.05.008.
Böhlmark, Anders, and Mikael Lindahl. 2015. Independent schools and long-run educational
outcomes: Evidence from Sweden’s large scale voucher reform. Economica 82(327): 508–551.
doi:10.1111/ecca.12130.
27. Details are provided in section 3.
28
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
f
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Nienke Ruijs and Hessel Oosterbeek
Borghans, Lex, Bart H. H. Golsteyn, and Ulf Zölitz. 2015. Parental preferences for primary
school characteristics. B.E. Journal of Economic Analysis & Policy 15(1): 85–118. doi:10.1515/bejeap
-2014-0032.
Burgess, Simon, Ellen Greaves, Anna Vignoles, and Deborah Wilson. 2015. What parents want:
School preferences and school choice. Economic Journal (Oxford) 125(587): 1262–1289. doi:10.1111
/ecoj.12153.
Calsamiglia, Caterina, and Maia Guell. 2014. The illusion of school choice: Empirical evidence
from Barcelona. IZA Discussion Papers No. 8202.
Centraal Bureau voor de Statistiek (CBS). 2009. Jaarboek Onderwijs in Cijfers [Education in Num-
bers Yearbook]. The Hague: Centraal Bureau voor de Statistiek.
Centraal Bureau voor de Statistiek (CBS). 2012. Voortgezet onderwijs; vertraging opgesplitst naar op-
en afstroom [Secondary education: Delay split up to going to higher or lower school tracks]. Available
https://opendata.cbs.nl/statline/#/CBS/nl/dataset/71170ned/table?ts=1525345452844. Accessed
9 May 2018.
Collins, Alan, and Martin C. Snell. 2000. Parental preferences and choice of school. Applied
Economics 32(7): 803–813. doi:10.1080/000368400322147.
Cullen, Julie B., Brian A. Jacob, and Steven Levitt. 2006. The effect of school choice on partici-
pants: Evidence from randomized lotteries. Econometrica 74(5): 1191–1230. doi:10.1111/j.1468-0262
.2006.00702.x.
De Giorgi, Giacomo, Michele Pellizzari, and Silvia Redaelli. 2010. Identification of social interac-
tions through partially overlapping peer groups. American Economic Journal. Applied Economics
2(2): 241–275. doi:10.1257/app.2.2.241.
De Haan, Monique, Pieter A. Gautier, Hessel Oosterbeek, and Bas van der Klaauw. 2016. The
performance of school assignment mechanisms in practice. Working paper, University of Oslo.
Denessen, Eddie, Geert Driessen, and Peter Sleegers. 2005. Segregation by choice? A study of
group-specific reasons for school choice. Journal of Education Policy 20(3): 347–368. doi:10.1080
/02680930500108981.
Gemeente Amsterdam. 2013. Schoolloopbanen. Deel drie: resultaten per school. [School careers. Part
3: Results per school] Amsterdam: Gemeente Amsterdam.
Glazerman, Steven, and Dallas Dotter. 2016. Market signals: Evidence on the determinants
and consequences of school choice from a citywide lottery. Working paper, Mathematica Policy
Research.
Harris, Douglas N., and Matthew F. Larsen. 2015. What school do families want (and why)? New
Orleans families and their school choices before and after Katrina. New Orleans, LA: Policy brief,
Education Research Alliance for New Orleans.
Hastings, Justine S., Thomas J. Kane, and Douglas O. Staiger. 2009. Heterogeneous preferences
and the efficacy of public school choice. Working paper, Yale University.
Hoxby, Caroline M. 2000a. Does competition among public schools benefit students and taxpay-
ers? American Economic Review 90(5): 1209–1238. doi:10.1257/aer.90.5.1209.
Hoxby, Caroline M. 2000b. The effects of class size on student achievement: New evi-
dence from population variation. Quarterly Journal of Economics 115(4): 1239–1285. doi:10.1162
/003355300555060.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
f
/
/
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
.
f
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
29
School Choice in Amsterdam
Hoxby, Caroline M. 2007. Does competition among public schools benefit students and taxpay-
ers? [Reply]. American Economic Review 97(5): 2038–2055. doi:10.1257/aer.97.5.2038.
Hsieh, Chang-Tai, and Miguel Urquiola. 2006. The effects of generalized school choice on
achievement and stratification: Evidence from Chile’s voucher program. Journal of Public Eco-
nomics 90(8): 1477–1503. doi:10.1016/j.jpubeco.2005.11.002.
Jochim, Ashley, Michael DeArmond, Betheny Gross, and Robin Lake. 2014. How parents experi-
ence public school choice. Making school choice work series. Seattle, WA: Center on Reinventing
Public Education, University of Washington.
Koning, Pierre, and Karen Van der Wiel. 2013. Ranking the schools: How school-quality informa-
tion affects school choice in the Netherlands. Journal of the European Economic Association 11(2):
466–493. doi:10.1111/jeea.12005.
Ladd, Helen F., Edward B. Fiske, and Nienke M. Ruijs. 2011. Does parental choice foster segre-
gated schools? Insights from the Netherlands. In School choice and school improvement, edited by
Mark Berends, Marisa Cannata, and Ellen B. Goldring, pp. 233–253. Cambridge, MA: Harvard
Education Press.
Manski, Charles F. 1993. Identification of endogenous social effects: The reflection problem.
Review of Economic Studies 60(3): 531–542. doi:10.2307/2298123.
Nathanson, Lori, Sean P. Corcoran, and Christine Baker-Smith. 2013. High school choice in New
York City: A report on the school choices and placements of low-achieving students. New York
University Report, Research Alliance for New York City Schools.
Onderwijsinspectie. 2007. Aansluiting voortgezet onderwijs op het basisonderwijs [Connection be-
tween primary and secondary education]. Utrecht: Onderwijsinspectie.
Onderwijsinspectie. 2010. De staat van het onderwijs: Onderwijsverslag 2008/2009 [The state of
education: Education report 2008/2009]. Utrecht: Onderwijsinspectie.
Rothstein, Jesse. 2007. Does competition among public schools benefit students and taxpayers?
[Comment]. American Economic Review 97(5): 2026–2037. doi:10.1257/aer.97.5.2026.
Sacerdote, Bruce. 2001. Peer effects with random assignment: Results for Dartmouth room-
mates. Quarterly Journal of Economics 116(2): 681–704. doi:10.1162/00335530151144131.
Train, Kenneth E. 2009. Discrete choice methods with simulation, 2nd ed. New York: Cambridge
University Press. doi:10.1017/CBO9780511805271.
Weiher, Gregory R., and Kent L. Tedin. 2002. Does choice lead to racially distinctive schools?
Charter schools and household preferences. Journal of Policy Analysis and Management 21(1): 79–
92. doi:10.1002/pam.1041.
30
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
f
e
d
u
e
d
p
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
4
1
1
1
6
9
2
7
4
8
e
d
p
_
a
_
0
0
2
3
7
p
d
f
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3