REVIEW
Brain network similarity: 方法
and applications
Ahmad Mheich, Fabrice Wendling, and Mahmoud Hassan
Laboratoire Traitement du Signal et de l’Image, Institut National de la Santé et de la
Recherche Médicale, 雷恩, 法国
关键词: Brain networks, Network similarity, Graph matching, Graph comparison
抽象的
Graph theoretical approach has proved an effective tool to understand, characterize, 和
quantify the complex brain network. 然而, much less attention has been paid to methods
that quantitatively compare two graphs, a crucial issue in the context of brain networks.
Comparing brain networks is indeed mandatory in several network neuroscience
applications. 这里, we discuss the current state of the art, 挑战, and a collection of
analysis tools that have been developed in recent years to compare brain networks. We first
introduce the graph similarity problem in brain network application. We then describe the
methodological background of the available metrics and algorithms of comparing graphs,
their strengths, and limitations. We also report results obtained in concrete applications from
normal brain networks. 更确切地说, we show the potential use of brain network similarity
to build a “network of networks” that may give new insights into the object categorization in
the human brain. 此外, we discuss future directions in terms of network similarity
methods and applications.
介绍
The human brain is a complex network that operates at multiple time and space scales. 在
the macroscale, the brain can be represented as a graph where nodes denote the brain
regions and edges denote the connections (structural or functional) between these regions
(布莫尔 & 斯波恩斯, 2009). The emerging field of network neuroscience has significantly improved
our understanding about the structure and the function of the human brain (Bassett & 斯波恩斯,
2017). Graph theory, a branch of mathematics focusing on understanding systems of inter-
acting elements, has been shown to be a very powerful tool to understand, characterize, 和
quantify the complex brain network (瓦. Huang et al., 2018; Yu et al., 2018). Applying graph
theoretical measures to brain networks have revealed several nontrivial features such as small-
worldness (Bassett & 布莫尔, 2017), 模块化 (斯波恩斯 & 贝策尔, 2016), and scale-free
(van den Heuvel, 斯塔姆, Boersma, & Pol, 2008) behaviors. The usefulness of applying graph
theory and network science to brain network analysis has been widely reviewed in the last
decade from methodological (da Costa, Rodrigues, Travieso, & Villas Boas, 2007; X. F. 王
& 陈, 2003) and applicative (乙. 布莫尔 & 斯波恩斯, 2009; Christmas, Kittler, & Petrou, 1995;
Cordella, Foggia, Sansone, & Vento, 2004; Hassan & Wendling, 2018; Luo & Hancock, 2001)
viewpoints.
出奇, much less attention has been paid to methods that quantitatively compare
two graphs, a crucial issue in the context of brain networks. Comparing brain networks is
indeed mandatory in several network neuroscience applications, including but not limited
开放访问
杂志
引文: Mheich, A。, Wendling, F。, &
Hassan, 中号. (2020). Brain network
相似: methods and applications.
网络神经科学, 4(3), 507–527.
https://doi.org/10.1162/netn_a_00133
DOI:
https://doi.org/10.1162/netn_a_00133
已收到: 25 八月 2019
公认: 26 二月 2020
利益争夺: 作者有
声明不存在竞争利益
存在.
通讯作者:
Ahmad Mheich
mheich.ahmad@gmail.com
处理编辑器:
Alex Fornito
版权: © 2020
麻省理工学院
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
A
_
0
0
1
3
3
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Brain network similarity
图形:
A mathematical description of a
network comprising a set of nodes
and a set of edges representing the
pairwise relations between nodes.
到 (我) the estimation of similarity between structural and functional brain networks, (二) 这
tracking of the temporal similarity of dynamic brain networks, 和 (三、) and the computation of
这 (迪斯)similarity between normal and pathological brain networks or between two conditions
during a cognitive task (Avena-Koenigsberger, Misic, & 斯波恩斯, 2018; Liao, Vasilakos, & 他,
2017; Paban, Modolo, Mheich, & Hassan, 2019; Rizkallah et al., 2019; 斯波恩斯, 2014).
Graph theory:
A branch of mathematics that studies
the structural organization of graphs.
Functional brain networks:
A statistical relation between time
series of physiological activity of
neural assemblies (例如, 脑
地区).
Distance-based graph
comparison algorithms:
Methods that produce a distance or a
similarity score in order to compare
图表.
Graphs isomorphism:
Graphs that have the same number of
nodes and that are connected in the
same way.
Graph edit distance:
A graph similarity method defined as
the minimum cost of edit operations
to transform one graph to another.
Quantifying similarity between networks is, 然而, difficult because of the fact that complex
网络, such as the brain, are composed of multiscale (in time and space) systems whose
structure and dynamics are difficult to encapsulate in a single score. The existing graph distance
measures vary depending on the features used to compute the score: 节点, 边缘, 空间的
locations, and spectrum (Christmas et al., 1995; Luo & Hancock, 2001; Mheich et al., 2018;
Shimada, Hirata, Ikeguchi, & Aihara, 2016; Wilson & 朱, 2008). 最近, several algorithms
have been proposed to combine multiple features of networks when comparing two graphs
(Mheich et al., 2018; Schieber et al., 2017; Shimada et al., 2016).
In this review, we will discuss the current state of the art, challenges and a collection of
analysis tools that have been developed in recent years to compare brain networks. We first
introduce the graph similarity problem in brain network application. We then describe the
methodological background of the available metrics and algorithms of comparing graphs, 他们的
strengths and limitations. From technical viewpoint, we describe two main families of meth-
消耗臭氧层物质: (我) graph theoretical approach which consists of comparing the topological characteristics
of two graphs at global, nodal, or edge-wise, mainly at group level (乙. 布莫尔 & 斯波恩斯, 2009;
扎莱斯基, 假如, & 布莫尔, 2010); 和 (二) distance-based graph comparison algorithms
including graphs and subgraphs isomorphism (Cordella et al., 2004), graph edit distance
(高, Xiao, Tao, & 李, 2010), kernel approach (Shervashidze, Vishwanathan, Petri, Mehlhorn,
& Borgwardt, 2009), and other approaches (曹, 李, & Yin, 2013; Schieber et al., 2017;
Shimada et al., 2016).
From an applicative viewpoint, we present new results using a recently developed algorithm
called SimiNet (Mheich et al., 2018), which takes into account the physical locations of nodes
when computing similarity between two brain graphs. We show the potential use of network
similarity in building a “semantic map” of the brain (a network of networks).
The paper is organized as follows: we first introduce the graph similarity problem in the
context of network neuroscience. 第二, we introduce the graph theoretical analysis and the
methods and strategies used to compute distance between networks. 第三, we present new
results of the application for graph similarity methods in cognitive neuroscience. 最后, 我们
discuss certain methodological challenges and some possible future directions.
COMPARISON BETWEEN BRAIN NETWORKS
In several domains, to understand and characterize complex systems, network construction
and inference from data is crucial (Brugere, 加拉格尔, & Berger-Wolf, 2018; X. 刘, 孔, &
Ragin, 2017; Safavi, Sripada, & Koutra, 2017). In network neuroscience, the brain graph model
is an abstract mathematical representation of the interactions between brain elements (神经元,
neural assemblies, or brain regions). Nodes in this graph represent neuronal assemblies or
brain regions obtained from certain parcellation techniques. Edges represent either functional
(statistical dependence or level of synchronization between activity patterns of brain regions) 或者
structural links (direct anatomical connections) between neural elements (乙. 时间. 布莫尔 & Bassett,
2011; 假如, 扎莱斯基, & Breakspear, 2013; 假如, 扎莱斯基, & 布莫尔, 2016; 斯波恩斯, 2010).
Once the brain network is built, the comparison with other brain networks can be mandatory
(depending on the application).
网络神经科学
508
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
A
_
0
0
1
3
3
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Brain network similarity
Spectral analysis:
A branch of graph theory that studies
the spectrum of eigenvalues and
eigenvectors of the adjacency matrix
of the network.
Comparison techniques between brain networks have many applications because of the
current widespread use of network neuroscience. These applications include, but are not lim-
ited to, (我) the statistical comparisons between brain networks for different groups of subjects, 或者
for the same subject before and after treatment or stimulation; (二) the discrimination between
neurological disorders by quantifying functional and topological similarities (Calderone et al.,
2016); (三、) the quantification of the evolution of temporal brain networks at different timescales
(Hassan et al., 2015; Mheich, Hassan, Khalil, Berrou, & Wendling, 2015; O’Neill et al., 2018);
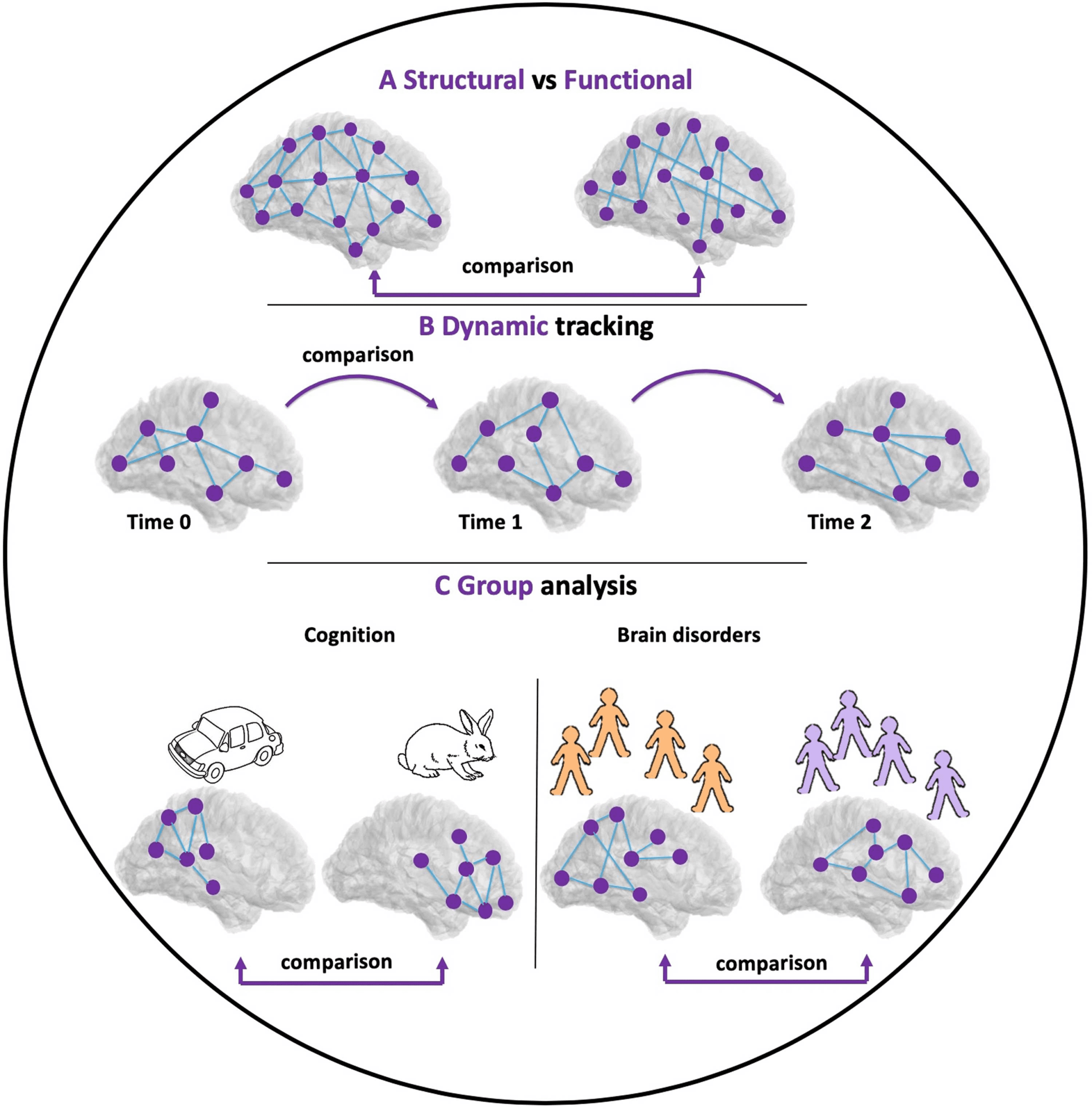
(4) the comparison between real brain networks and generative network models (数字 1); 和
(5) the comparison of the topological layout of nervous systems across species (van den Heuvel,
布莫尔, & 斯波恩斯, 2016).
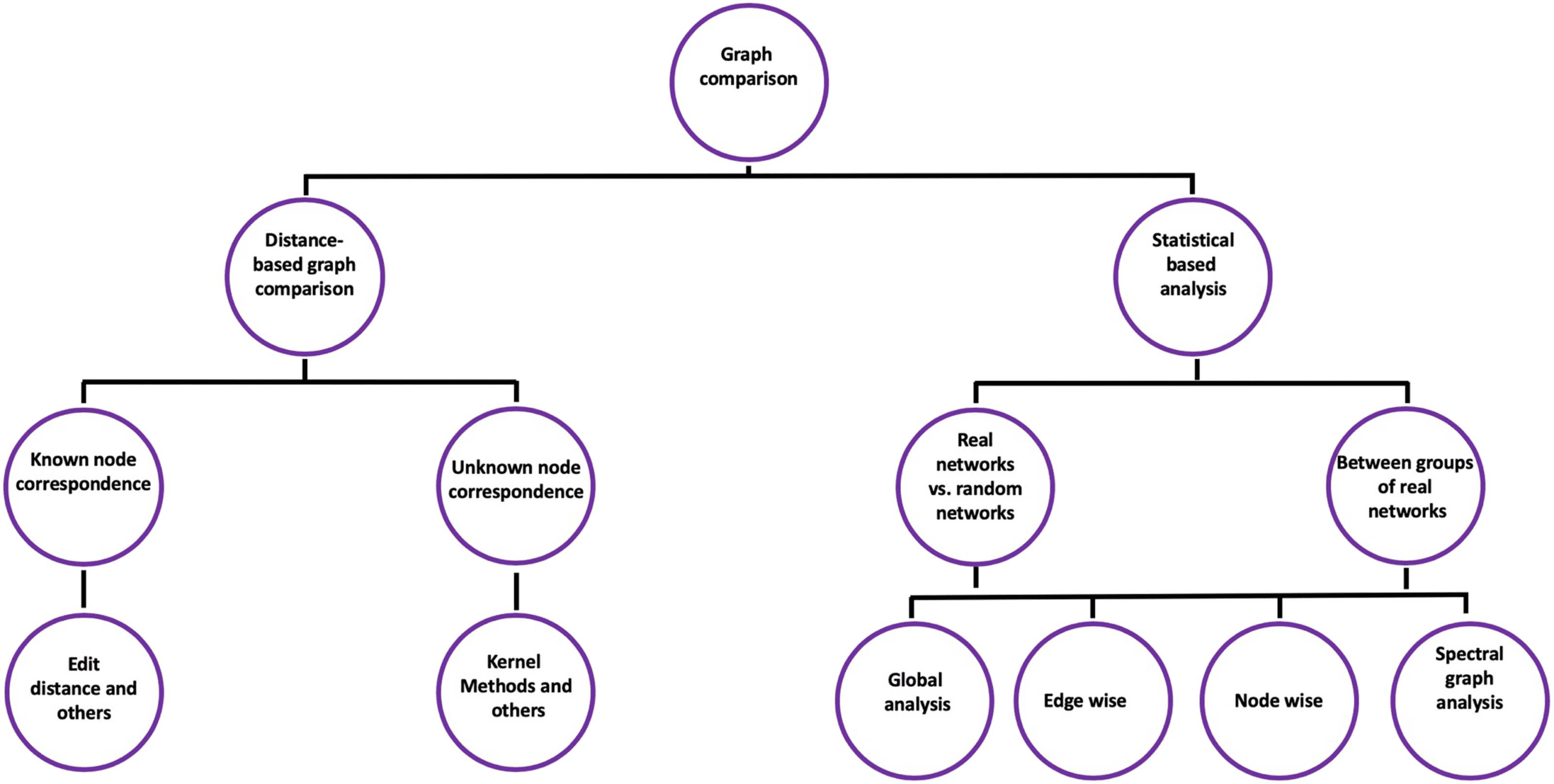
Methods and strategies used to compare brain networks can be classified into two main
类: the first one is the statistical comparison, where various graph theoretical metrics can
be applied to characterize the topological architecture of the brain networks. The defined
quantities and notations (related to graphs) used in this paper are listed in Table 1.
There are metrics of global network organization and others that can also be estimated at
node or edge level of the compared networks. These metrics are then quantitatively compared
between two groups of networks by using statistical tests. This class also includes spectral
在
分析, which witnesses an increase in its application in this field of brain networks.
后者, the comparison is based on the eigenvalues of adjacency/Laplacian matrices of the
compared graphs.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
A
_
0
0
1
3
3
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 1. Applications of graph comparison in network neuroscience. (A) Comparison between
structural and functional brain networks. (乙) Tracking the dynamic of brain networks during time.
(C) Comparison between two groups of brain networks for two different conditions.
网络神经科学
509
Brain network similarity
桌子 1. Notation and description.
符号
氮, n
乙, 米
G
λ
C
L
S
BC
d
dHamming(G
′, G
dGED(G
A
Λ
′ , G
)
′′
′′
D
ki
描述
Set of nodes, number of nodes
Set of edges, number of edges
图形
Eigenvalue
Clustering coefficient
Shortest path length
Synchronizability
Betweenness centrality
Density
′
′′
and G
′
and G
) Hamming distance between G
Graph edit distance between G
Adjacency matrix
Laplacian matrix
Degree matrix
Degree of node i
′′
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
The second class is the distance-based graph comparison algorithms, where the main pur-
pose is to quantify a distance (similarity score) between two networks by studying some char-
acteristics that are considered important from an application viewpoint. Although most of
the proposed algorithms are developed in specific domains, they represent promising tools to
quantify similarity between brain networks (数字 2).
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
A
_
0
0
1
3
3
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 2. Graph comparison methods.
网络神经科学
510
Brain network similarity
STATISTICAL COMPARISON
Statistical comparison between brain networks can be classified into two types. First is the
comparison of real brain networks to random networks, where the main purpose is to validate
if some characteristics of the brain networks are significantly different than chance. For a given
网络, a large number of random graphs can be generated, and graph theory metrics can be
extracted from these random graphs, as a point of reference, to test the randomness of the same
metrics measured in the real brain networks. The characteristics of these null models depend
mainly on the tested hypothesis. 例如, in many network neuroscience applications,
null model with same degree/strength distribution as the original network are widely used (看
鲁比诺夫 & 斯波恩斯, 2010). For a thorough review about null models and associated parameters,
we recommend Barabási (2016) and Fornito et al. (2016).
第二, the network statistical comparison can be used to compare brain networks of two
groups of subjects, such as healthy control and patients. We can classify metrics measured
for comparing brain networks into four categories: global-level, node-wise, edge-wise, 和
spectral graph analysis (for more details about the metrics, see Bullmore & 斯波恩斯, 2009;
Zalesky et al., 2010). In this review, we will present some of the metrics that can be used to
compare two networks. 然而, many other metrics (or new versions of mentioned metrics)
are currently available, and the reader can refer to specialized reviews about this topic. 对于一个
exhaustive review about the graph metrics, their limitations, and their applications in network
神经科学, we recommend Fornito et al. (2016). In the next section, we show a brief de-
scription of some selected metrics and their recent applications in brain network comparisons.
Our purpose here is to highlight some of these metrics in respect to the main characteristics
(hubness, segregation, and integration) of any given network.
Global-Level Analysis
在这种情况下, the graph metrics are computed over the entire network, and one value can be
derived per network. Statistical tests are then applied to compare the two groups (例如
healthy vs. 患者).
Small-worldness of a network was originally introduced by Newman and Watts
Small-worldness.
(1999). Other metrics associated with small-worldness, including the small-world coeffi-
cient (汉弗莱斯 & Gurney, 2008), small-world metric (Telesford, Joyce, Hayasaka, Burdette,
& Laurienti, 2011), small-world propensity (Muldoon, Bridgeford, & Bassett, 2016), 和
small-world index (Neal, 2017), were also proposed. It is characterized by a low average short-
est path length (L) and by a high clustering coefficient (CC). 简单地说, the averaged path length L
is defined as the average minimum number of edges that have to be traversed to pass from one
node to another in the network. The CC of a node is defined as the number of existing con-
nections between the neighbors of the node divided by all the possible connections between
他们. The CC quantifies the extent of local cliquishness or local efficiency of information
transfer of a network.
It has been also reported that functional brain networks derived from Alzheimer’s disease
patients have the characteristics of random networks with characteristic path lengths signifi-
cantly longer than the healthy subjects (Stam et al., 2008). Other studies showed the presence
of the small-world characteristics in the brain connectivity of healthy subjects, whereas these
characteristics were disrupted in schizophrenia patients (是. 刘等人。, 2008; Lynall et al., 2010;
Micheloyannis et al., 2006).
网络神经科学
511
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
A
_
0
0
1
3
3
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Brain network similarity
The modularity consists of partitioning a network into a number of nonoverlap-
模块化.
ping groups or modules, also called communities (鲁比诺夫 & 斯波恩斯, 2010). Network mod-
ules are defined by a subset of nodes in the graph that are densely intraconnected and weakly
connected to other nodes (Girvan & 纽曼, 2002; 斯波恩斯 & 贝策尔, 2016). Several meth-
ods have been proposed to resolve the community structure of complex networks in several
applications (Blondel, Guillaume, 兰比奥特, & Lefebvre, 2008; Lancichinetti & Fortunato,
2009; 纽曼, 2006). For brain networks applications, the modularity maximization method
(纽曼 & Girvan, 2004) is the most applied in the detection of brain networks modules. 这
main idea of this method is to split the nodes of a network into K nonoverlapping communities
in order to maximize the modularity quality function Q. A minimum value of Q near to 0
indicates that the network considered is close to a random one, whereas a maximum value of
Q near to 1 indicates a strong community structure.
A number of studies have found significant differences between the brain networks of two
groups by comparing their modules. 莫尼耶, 兰比奥特, and Bullmore (2010) investigated the
modular structure of the human brain networks derived from fMRI measurements for two
groups of younger and older adults by using a modularity maximization algorithm. The results
showed that the brain becomes less modular with age, a finding also reported by others
(Baum et al., 2017). In brain diseases applications, Alexander-Bloch et al. (2010) 表明
modularity decreases for schizophrenia patients compared with healthy subjects.
反过来,
Peraza, 泰勒, and Kaiser (2015) revealed an increase in modularity for patients with Lewy body
疾病. Other techniques like the allegiance matrix (Mattar, Cole, Thompson-Schill, & Bassett,
2015) and scaled inclusivity (Moussa, Steen, Laurienti, & Hayasaka, 2012; Steen, Hayasaka,
Joyce, & Laurienti, 2011) were also proposed to explore the consistency of community struc-
ture in brain networks.
The network efficiency quantifies the exchange of information across the whole
Efficiency.
It is defined as the inverse of the average path length (Achard & 布莫尔, 2007;
网络.
Latora & Marchiori, 2001). Global efficiency was used to compare functional brain networks
between two groups of healthy old and healthy young subjects (Achard & 布莫尔, 2007)
where authors showed a reduction in the efficiency for older people.
此外, several
studies showed that patients with schizophrenia, Alzheimer’s and Parkinson’s diseases had
a noticeable reduction in global efficiency compared with healthy controls (Berlot, Metzler-
Baddeley, Ikram, 琼斯, & O’Sullivan, 2016; Reijmer et al., 2013; Skidmore et al., 2011).
Node-Wise Analysis
在这种情况下, the graph metrics are calculated for each node, and then the node’s metric values
are compared between the two graphs. The main advantages of such an approach are (我) 这
possibility to explore more features in the graph, (二) the presence of more data (number of
节点) to compare between conditions, 和 (三、) this comparison will not only show if there is
a difference between two conditions but will also indicate where the difference is located (在
which brain regions). 然而, it can produce false positive results as the activities of the nodes
are not fully independent. This type of analysis required correction for multiple comparisons,
as comparison was done n (number of nodes) 次, using methods such as Bonferroni (米,
1989) or false discovery rate (FDR) (Genovese, Lazar, & Nichols, 2002). Several metrics can
be computed at the level of network’s nodes. For detailed and comprehensive review, 我们
recommend Rubinov and Sporns (2010). Globally speaking, these metrics reflect mainly three
behaviors in the network: segregation, 一体化, and hubness.
网络神经科学
512
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
A
_
0
0
1
3
3
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Brain network similarity
Segregation is the ability of the network to do specialized processing in a densely
Segregation.
interconnected group of nodes. This includes measures such as (我) clustering coefficient,
which is defined by the fraction of the nodes’ neighbors that are also neighbors of each other
(Watts & Strogatz, 1998); (二) local efficiency, which is a measure of the efficiency of infor-
mation transfer limited to neighboring nodes—it is calculated as the average nodal efficiency
among the neighboring nodes of node i, excluding node i itself; 和 (三、) intramodule degree,
which denotes how well connected is a node compared with other nodes of the same com-
社区. Chan et al.
found a decrease in segregation of brain network when age increases
(Chan, 公园, Savalia, 彼得森, & 假发, 2014). The network segregation was shown to be
improved in Alzheimer’s and schizophrenia patients (他, 陈, & 埃文斯, 2008; Kabbara et al.,
2018; Yao et al., 2010; 是. 张等人。, 2012) and reduced for epilepsy patients (Z. 张等人。,
2011).
Integration is the ability of the network to combine information from distant
Integration.
节点. This includes measures such things as (我) participation coefficient, which quantifies the
balance between the intramodule versus intermodule connectivity for a given node, 和 (二)
characteristic path length, which is defined as the average shortest path length between all pairs
of nodes in a network (Watts & Strogatz, 1998). Several studies were performed to compare
brain networks of healthy subjects and Alzheimer’s patients (斯塔姆, 琼斯, 诺尔特, Breakspear,
& Scheltens, 2006; Supekar, Menon, 鲁宾, Musen, & Greicius, 2008), and results showed an
increase of characteristic path length in patients.
This include measures such qualities as (我) strength, which describes the connec-
Hubness.
tion strength of node to all other nodes, 和 (二) betweenness centrality, defined as the fraction
of all shortest paths in the network that pass through a given node. Many studies showed that
brain disorders, such as Alzheimer’s disease, coma, and schizophrenia, are associated with
alterations in hubs, (Achard et al., 2012; Bassett et al., 2008; Crossley et al., 2014; He et al.,
2008; Lynall et al., 2010; van den Heuvel, Mandl, 斯塔姆, Kahn, & Pol, 2010). C. Yan et al. (2010)
used betweenness centrality to investigate the effects of sex on the topological organization
of human cortical anatomical network.
In clinical application, betweenness centrality was
used to compare brain networks of healthy subjects and patients with schizophrenia, depres-
锡安, and Alzheimer’s disease (Becerril, Repovs, & Barch, 2011; van den Heuvel et al., 2010;
Yao et al., 2010).
Other studies have compared brain networks of healthy subjects and patients diagnosed
with schizophrenia by using the degree of nodes (Bassett et al., 2008; Lynall et al., 2010).
The results showed a reduced degree in several brain nodes of schizophrenia patients. 其他
studies showed also that Parkinson’s disease patients have a significant decrease in the degree
of several brain regions in their functional network, such as left dorsal lateral prefrontal cortex
(Wu et al., 2009).
Edge-Wise Analysis
Edge-wise analysis consists of calculating a statistical test (such as Student’s t test) on each edge
in the graph. If the number of nodes in a graph are equal to n, then the maximum number
of edges (in the case of undirected network) is equal to (n × (n - 1) / 2). The statistical test
is calculated (n × (n - 1) / 2) 次. This method also requires correction for multiple com-
parisons by using methods such as Bonferroni or FDR. Other approaches have also been pro-
posed to deal with the family-wise error rate, such as the network-based statistic (NBS) 方法
(Zalesky et al., 2010). The main idea of this method (based on permutation analysis) is to find a
network “pattern” (a set of nodes connected by edges) instead of a single link that differentiates
网络神经科学
513
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
t
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
A
_
0
0
1
3
3
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Brain network similarity
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
/
t
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
A
_
0
0
1
3
3
p
d
.
t
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
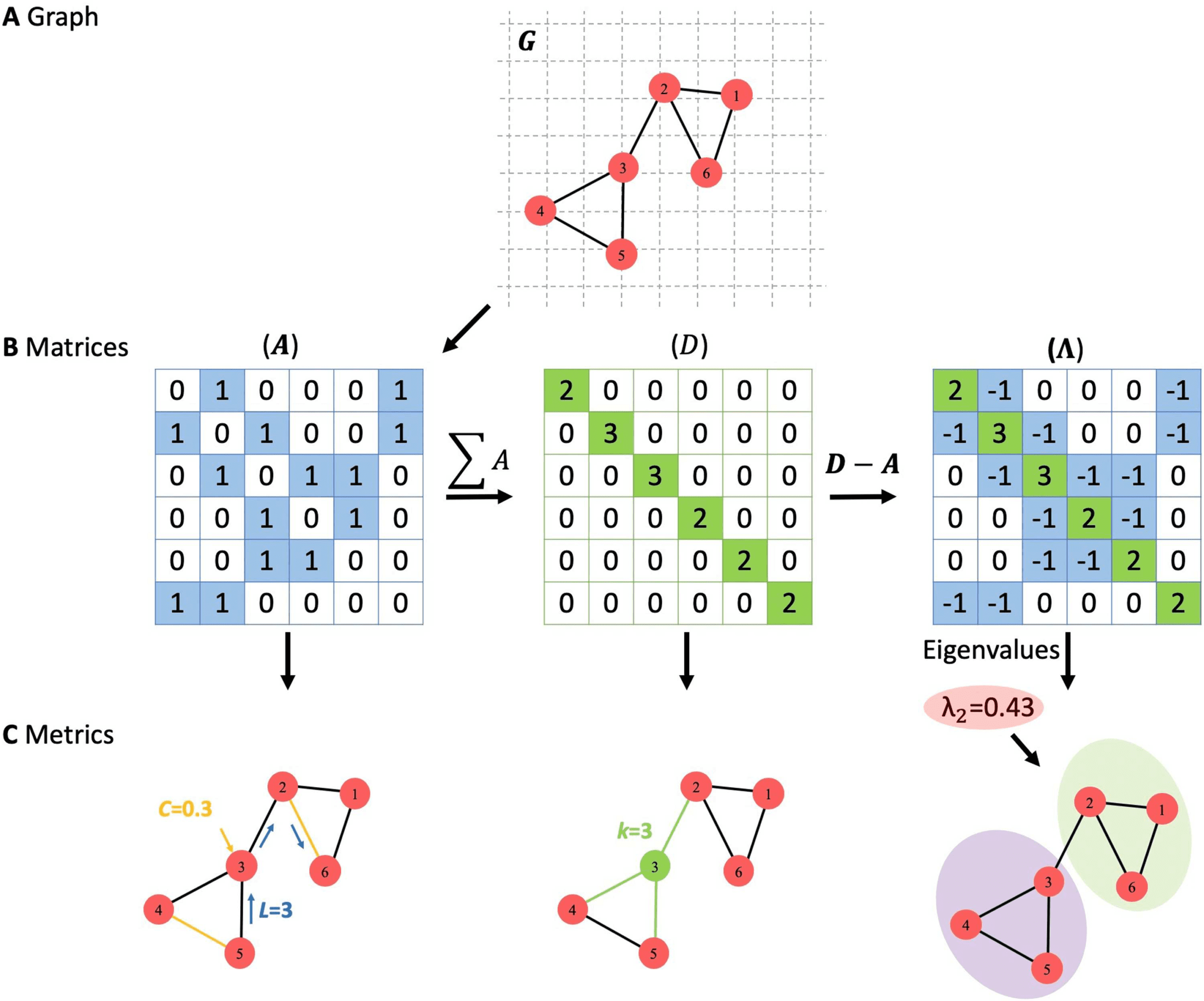
(A) A graph with six nodes and seven edges. (乙) Adjacency matrix (A), degree matrix
数字 3.
(D), and Laplacian matrix (∧).
(C) Some of graph metrics extracted from each matrix, where C
represents the clustering coefficient of node 3, L is the shortest path length between node 5 和
node 6, k represents the degree of node 3, and λ2 is the second eigenvalue of the graph G.
the two conditions. NBS has been widely used to identify alterations in brain networks asso-
ciated with psychiatric disorders such as schizophrenia and depression (Zalesky et al., 2011),
and to identify cognitive phenotypes in Parkinson’s disease patients (Hassan et al., 2017).
Spectral Graph Analysis
Spectral graph theory is a branch of graph theory which has been widely used to characterize
the properties of a graph and extract information about its structure. For a graph G(氮, 乙) 的
n nodes with adjacency matrix An×n and degree matrix Dn×n, the Laplacian matrix Λn×n is
computed using the following formula (数字 3):
Λ(我, j) =
Di f or i = j
−A(我, j) f or i 6= j
(
where i, j ∈ N
Once the Laplacian matrix is constructed, the eigenvalue of G can be computed (l1, λ2 . . . λn).
Spectral graph analysis is well known in many domains for its powerful characterization of net-
work properties (Banerjee, 2012; Farkas et al., 2002). It provides important information on rel-
evant network properties, such as connectivity levels, resilience to damage, and the spread of
information throughout the network (de Haan et al., 2012). Comparing brain networks by us-
ing spectral graph theory was recently performed in several studies, including the comparison
of network’s eigenvalue distributions over the structural brain networks of different species,
such as caenorhabditis elegans, macaque, and cat (de Lange, de Reus, & van Den Heuvel,
It was also used to detect network alterations in patients with Alzheimer’s disease
2014).
(de Haan et al., 2012).
Synchronizability (S) quantifies the robustness of the network with respect
Synchronizability.
to edge removals. It is computed as the report between the second smallest eigenvalue and
Adjacency matrix:
A matrix that describes the absence
or presence of a connection between
all pairs of nodes in a graph.
Laplacian matrix:
A matrix that carries important
properties about a graph, 许多
relating to its spectrum.
网络神经科学
514
Brain network similarity
数字 4. Graph G and G
′
.
桌子 2. Depiction of graph metrics.
Graphs Density
G1
′
G
1
笔记. BC = betweenness centrality; S = synchronizability.
BC Degree Global Efficiency
2
2
0.6
0.6
0.8
0.8
3
3
S
0.5
0.4
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
t
/
/
e
d
你
n
e
n
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
A
_
0
0
1
3
3
p
d
t
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
the highest eigenvalue of the Laplacian matrix of the network.
S =
λ2
λn
A network with low value of S is more vulnerable to disconnection. 作为回报, a high S value
means less vulnerable to disconnection. Several studies showed that many graph properties
such as clustering coefficient, average distance, average degree, and degree distribution failed
to characterize the synchronizability of networks. 作为回报, the spectral analysis can detect
this synchronizability for the same network (Atay, Bıyıko˘glu, & Jost, 2006).
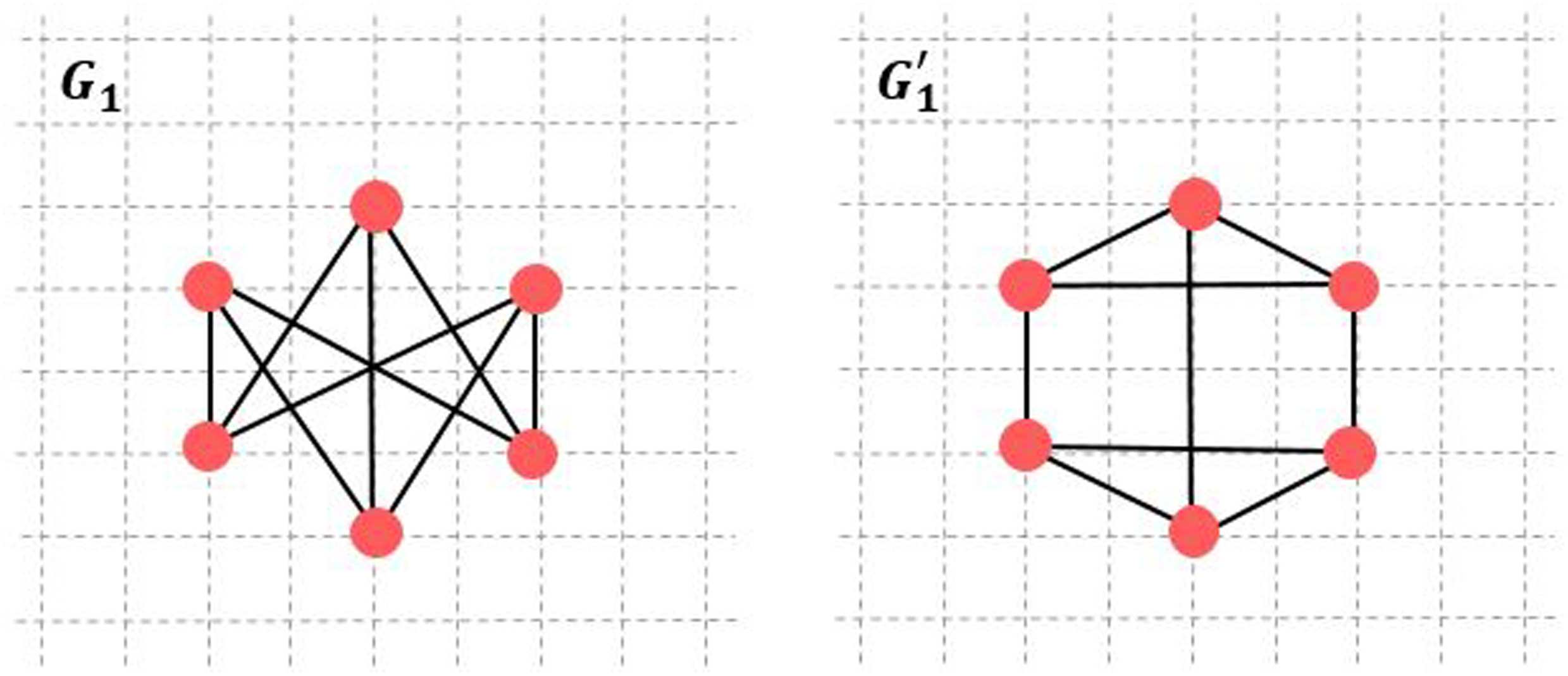
例如, two graphs G1 and G
1 have the same number of nodes (n = 6) and edges
(m = 9), shown in Figure 4. These two graphs share common statistical network metrics such
作为: density, betweenness centrality, average degree, and global efficiency (桌子 2), 但他们
′
are different in their S: λ2 (G1) = 3 and λ2(G
1) = 2, then S(G1) = 3/6 和S(G
′
1) = 2/5.
′
De Haan et al. (de Haan et al., 2012) used graph spectral analysis to study synchronizability
between healthy subjects and patients with Alzheimer’s disease. Results showed a decrease
in synchronizability and loss of network connectivity in all frequency bands for Alzheimer
disease patients.
DISTANCE-BASED GRAPH COMPARISON
The main idea of distance-based graph comparison methods consists of comparing two graphs
and providing a “similarity” score. This similarity value (if normalized) ranges from 0 (不
similarity at all) 到 1 (fully similar/same network). Distance-based graph comparison includes
two families of methods:
1. Known node correspondence. This includes methods based on edit distances that focus
on common and uncommon elements (nodes and edges), such as graph edit distance
(GED) and hamming distance (Gao et al., 2010). They also include more elaborate
techniques such as DeltaCon (Koutra, Vogelstein, & Faloutsos, 2013) and SimiNet
(Mheich et al., 2018).
网络神经科学
515
Brain network similarity
2. Unknown node correspondence. This includes, 例如, kernel methods (Borgwardt
& Kriegel, 2005; Shervashidze, Schweitzer, Leeuwen, Mehlhorn, & Borgwardt, 2011)
that focus on the structure of the networks by comparing their Laplacian matrices and
methods that use nodeinvariant graph statistics to compare graphs (数字 2).
Algorithms Based on Edit Distance
Quantifying the similarity/distance between two brain networks by using edit distance algo-
rithms allows one to find the common/uncommon nodes (brain regions) and edges (functional/
结构性的) between two brain networks.
The hamming distance is the most direct way to compare two networks
The hamming distance.
(Deza & Deza, 2013). It is defined as the sum of difference between the adjacency matrices
of two networks G
and G
:
′′
′
dHamming
′′
′
G
, G
where i and j are two nodes, 和一个
分别.
(西德:16)
′
(西德:17)
′′
和一个
′
ij 6= A
′′
ij
A
= ∑
i6=j
are the adjacency matrices of G
′
and G
′′
,
Graph edit distance. GED is another popular distance between two networks (Gao et al.,
2010), widely applied in several applications (X. 王, Ding, Tung, Ying, & Jin, 2012; 曾,
Tung,王, 冯, & 周, 2009). It is defined as the minimum-weight sequence of edit oper-
ations required to transform one graph into another (edit operations on a graph are insertion,
′
deletion, or substitution applied on both nodes and edges). The GED between two graphs G
and G
is defined as:
′′
dGED
′′
′
G
, G
(西德:16)
(西德:17)
= min ∑
u∈U
C(欧洲联盟)
′
′′
where c(欧洲联盟) is the cost of an edit operation from G
, and U is the total number of edit op-
erations. A difficult step in this approach is to define the cost function for different operations.
to G
An important characteristic, not integrated in the previous approaches, 是
SimiNet algorithm.
the spatial location of nodes, which denotes the 3D coordinates of the brain regions. The phys-
ical location of nodes can add additional key information when measuring similarity between
brain networks. 例如, two networks with identical properties but interconnecting dis-
tant brain regions can have low similarity. 反过来, two networks with dissimilar properties
but interconnecting spatially close brain regions can be very similar. 在此背景下, SimiNet
explores both the nodes and the edges when computing the similarity index. Concerning the
节点, the algorithm is based on four main steps: (我) detection of common nodes between
the two compared graphs, (二) substitution between two nodes where the cost of substitution
is equal to the distance between the substituted nodes, (三、) insertion for new nodes where
the cost of insertion is equal to a constant value, 和 (四号) deletion of nodes where the cost of
suppression is equal to the cost of insertion. 这 (成本 (substitution) < cost (insertion) + cost
(deletion)) is always preserved. The second step is to calculate the edges distance. It consists of
calculating the sum of the weight difference between two edges of two compared graphs. The
algorithm provides a normalized similarity index (SI): 0 for no similarity and 1 for two identical
networks (same properties and topology). The algorithm is detailed and compared with other
′′
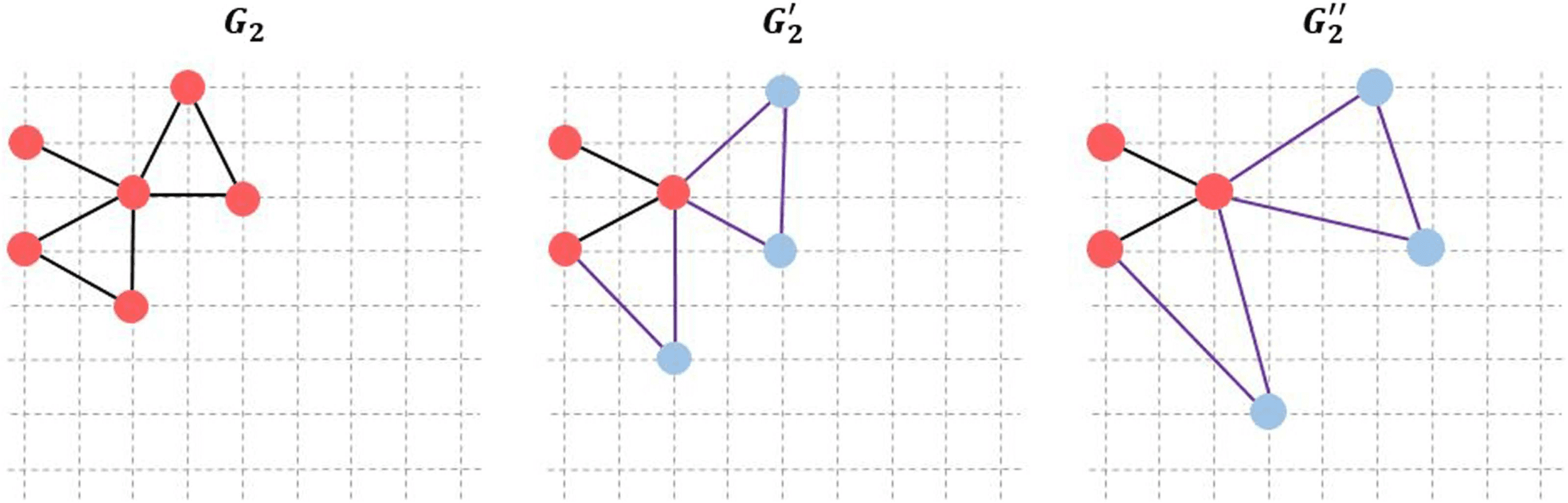
methodologies in Mheich et al. (2018). Figure 5 displays three graphs, G2 , G
2 , with
the same number of nodes (n = 6) and edges (m = 7); these graphs are located on a grid
′′
(8 × 8). Graphs G
2 are obtained by shifting three nodes of G2 randomly. The similarity
′
2, and G
′
2 and G
Network Neuroscience
516
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Brain network similarity
Figure 5. Three networks with the same number of nodes (6) and edges (7) located into a grid
(8 × 8).
score is then calculated between the three graphs by using the SimiNet, hamming, and GED
algorithms (Table 3). As can be seen in this example, Hamming and GED do not capture the
spatial shifting of nodes, which is the case with SimiNet.
Algorithms Based on Structure Distance
Computing the similarity/distance between two brain networks by using algorithms that prior-
itize network structures allow us to spot and to quantify structural topology differences such
as the presence or absence of important edges, nodes, cliques, or subgraphs that have influ-
ence on the information flow through the network. Several algorithms have been proposed to
compute the network similarity based on structure distance. Some of these approaches and
algorithms are briefly described hereafter.
The DeltaCon algorithm assesses the similarity for same-size networks
DeltaCon algorithm.
(two networks with same number of nodes) (Koutra et al., 2013). The idea of this method is
to compute the matrix of pairwise node affinities in the first network and to compare them
with the one in the second network, where node affinities is the influence of each node on the
other network’s nodes. The difference between the matrices is then computed to produce an
affinity score measuring the similarity between the compared networks. Readers may refer to
Koutra et al. (2013) for more details about the DeltaCon algorithm steps and implementation.
This algorithm also provides a normalized similarity value ranging from 0 (dissimilar graphs)
to 1 (identical graphs). DeltaCon satisfies some important network properties: (i) Edge im-
portance, where edges that connect two components are of higher cost than other edges; (ii)
Weight awareness for weighted networks, where changes on edges with high weight values
have more impact on the final similarity score; and (iii) Edge submodularity, where a specific
change on a network with few edges is more important than that in a denser network.
Recently, Schieber et al. (2017) proposed a new algorithm to quantify graph
D-measure.
dissimilarities. The dissimilarity score is bordered between 0 and 1, where a larger score
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Table 3. Depiction of similarity scores between the three networks (G2, G
SimiNet, Hamming distance, and graph edit distance (GED) algorithms
′
′′
2, and G
2) by using
Graphs
′
(G2, G
2)
(G2, G
2 )
′
2 )
2, G
(G
′′
′′
SimiNet Hamming GED
0.55
0.55
0.55
0.38
0.38
0.38
0.8
0.6
0.7
Network Neuroscience
517
Brain network similarity
Graph kernel methods:
A set of functions measuring the
similarity between graphs based on
the inner product.
corresponds to more dissimilar graphs, and a lower score to more similar graphs. The score
produced by the algorithm is based on a combination of three components: (i) dissimilarity in
average node connectivity; (ii) dissimilarity in a node dispersion metric, where node dispersion
for a graph measures the distribution of distances between nodes in this graph and allows to
make comparison with node dispersion in the second graph; and (iii) dissimilarity in node
α-centrality (measure of nodes centrality within a graph). The main advantage of this algorithm
is the ability to detect structural differences such as critical edges (connect two components)
that have an influence on the information through the graph. D-measure was applied to brain
networks in order to compare two groups of subjects (39 control and 68 alcoholic samples)
(Schieber et al., 2017). The algorithm was able to find the brain networks that discriminate
control and alcoholic participants.
Kernel methods. Graph kernel methods are based on first mapping the graphs into a higher
dimensional feature space, and then searching for the common features among the mapping
′
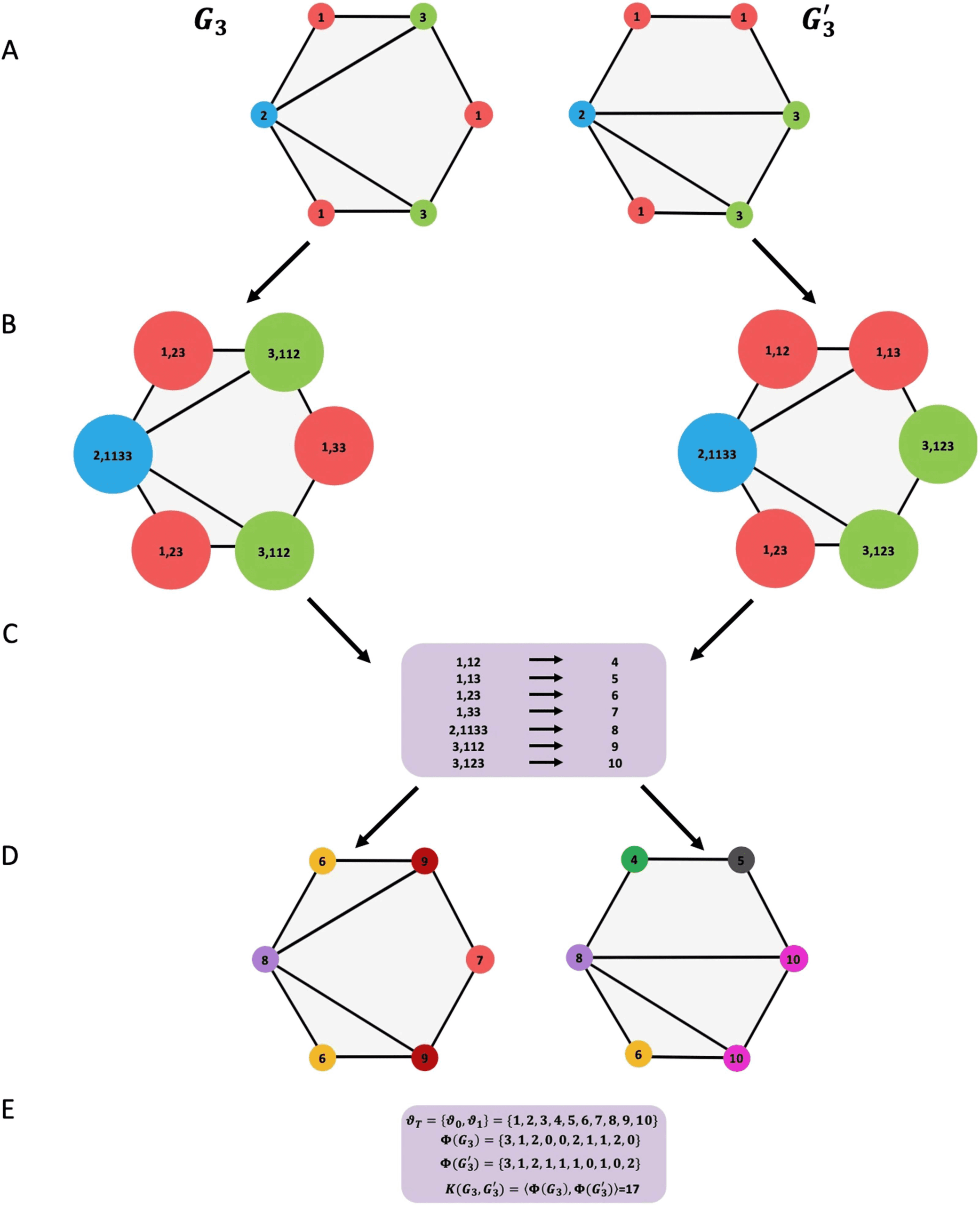
3, the basic idea behind graph kernel is to construct a
graphs. Given two graphs G3 and G
′
′
φ(G3) , φ(G
3 value
kernel ξ
3
′
corresponds to the scalar product between the two vectors φ(G3) and φ(G
3) in a Hilbert space.
Several graph kernels–based algorithms have been proposed to measure networks similarity
such as random walks, shortest paths, and Weisfeiler–Lehman.
where the similarity score between G3 and G
G3, G
3,
=
E
D
(cid:17)
(cid:16)
′
A random walk kernel counts the number of matching labeled random walks (Vishwanathan,
Schraudolph, Kondor, & Borgwardt, 2010). The matching between two nodes is determined
by comparing their attribute values. The measure of similarity between two random walks is
then defined as the product of the kernel values corresponding to the nodes encountered along
the walk.
Shortest path kernel computes the shortest path kernel for a set of graphs by exact matching
of shortest path lengths (Borgwardt & Kriegel, 2005). The Floyd–Warshall algorithm (Floyd,
′
1962) is usually used to calculate all the pairs shortest paths in G3 and G
3. The shortest path
kernel is then defined by comparing all the pairs of the shortest path lengths among nodes in G3
and G
′
3.
Weisfeiler–Lehman (Shervashidze et al., 2011) computes h-step Weisfeiler–Lehman kernel
for a set of graphs. The main idea of this algorithm is to increase the node labels by the sorted
set of node labels of neighboring nodes and compress these increased labels into new shorted
′
3 differ or the number of
labels. These steps are repeated until the node label sets of G3 and G
iterations reaches a maximum h. A detailed example is presented in Figure 6.
Other Graph Comparison Approaches
Some other approaches are indirectly related to graph similarity and may help to tackle some of
the graph similarity challenges. One of these approaches is “graph classification” in which the
main idea is to classify individual graphs into two or more categories based on graph features
comparison (Heimann, Safavi, & Koutra, 2019). A number of deep-learning algorithms have
been introduced also to classify graphs in different fields, such as artificial intelligence, image
analysis, and neuroscience (S. Wang et al., 2017; Y. Yan et al., 2019; M. Zhang, Cui, Neumann,
& Chen, 2018). Recently, based on latent graph feature/embedding comparison, Heimann et al.
(2019) proposed a randomized grid mapping that captures the distribution of a graph’s node
embeddings at multiple levels of resolution. The difference between similarity approaches and
these classification methods is that the latter does not necessarily produce a similarity score
as an output, but they can directly separate networks into classes, and thus can be very useful
Network Neuroscience
518
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Brain network similarity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Illustration of the construction process of the Weisfeiler–Lehman subtree kernel with
Figure 6.
′
h = 1 for two graphs G3 and G
3. (B) Augmented label
′
on graph G3 and G
3. (C) Label compression. (D) Relabeled graph. (E) Computation of the kernel
′
on graph G3 and G
3, where ϑ0 is the set of original node labels and ϑ1 the set of compressed node
labels; φ(G3) and φ(G
′
3. (A) The initial labeled graph G3 and G
3) are the count of node labels.
′
for some neuroscience applications. In network neuroscience, several machine/deep-learning
approaches were developed to learn latent features or extract meaningful information em-
bedded in networks (Hinton & Salakhutdinov, 2006; A. Huang, 2008; Kamiya et al., 2015;
Oh Song, Xiang, Jegelka, & Savarese, 2016). For instance, Kawahara et al. (2017) proposed
a new framework called BrainNetCNN that allows one to make predictions from brain net-
works such as the prediction of brain network development (H. Li, Satterthwaite, & Fan, 2018;
X. Li, Li, & Li, 2017.
NETWORK OF NETWORKS
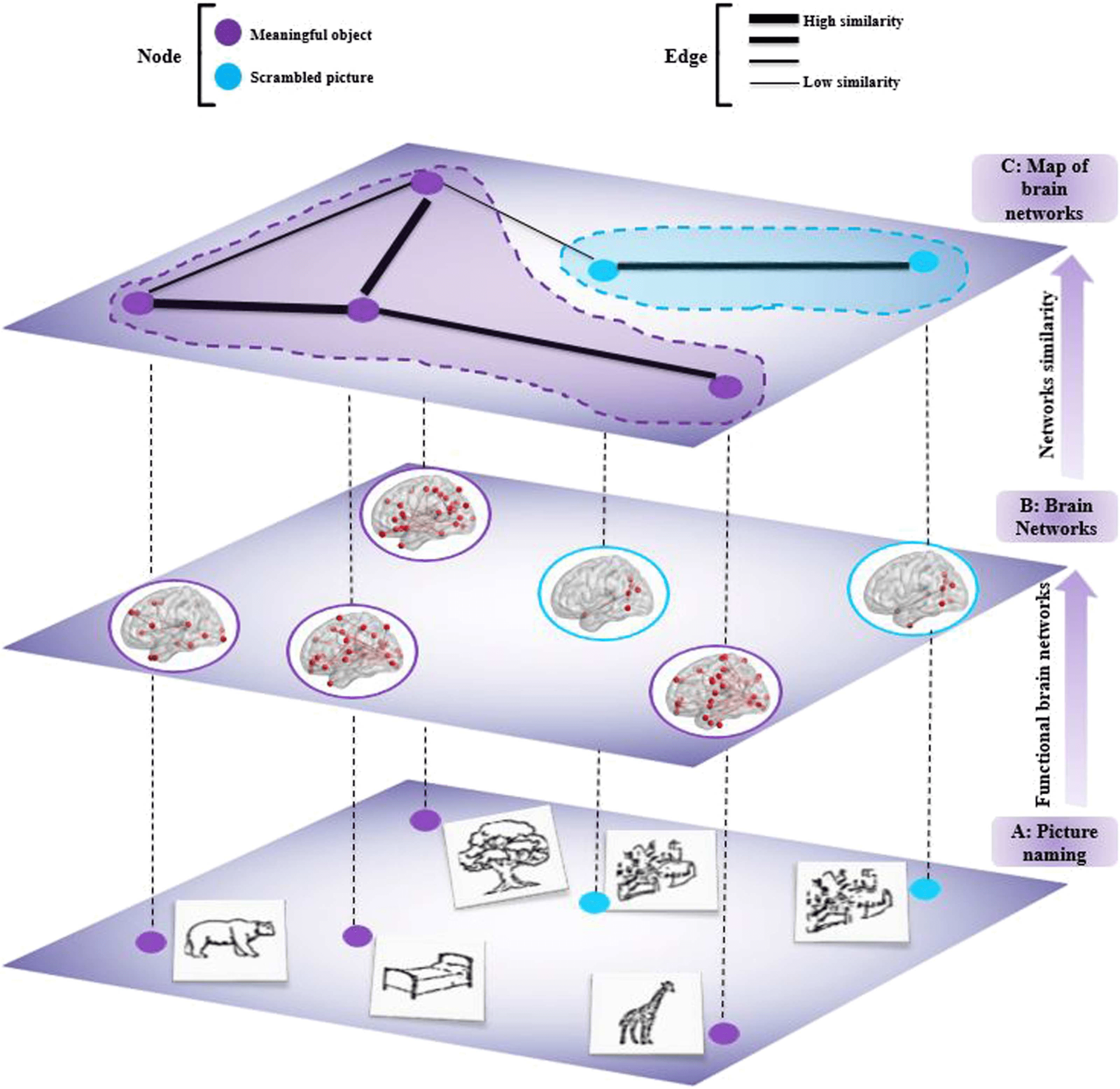
Analyzing similarity between brain networks can be useful for several applications in cogni-
tive and clinical neuroscience. Here, we show an example of its application to functional
networks estimated during visual object recognition task. To do so, we used dense electroen-
cephalography (256 electrodes) data from 20 subjects who were asked to name two cate-
gories of pictures (39 meaningful and 39 scrambled). Then, we construct a map based on
the similarity scores between brain functional networks (Figure 7). This data is described in
Network Neuroscience
519
Brain network similarity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. A schematic representation of the proposed method. (A) Signal recording during mean-
ingful and scrambled pictures naming task.
(B) Estimating the functional brain network for each
picture. (C) Measurement of the similarity between brain networks using SimiNet and classify them
into meaningful and scrambled pictures.
Mheich et al. (2018) and approved by the National Ethics Committee for the Protection of
Persons, Braingraph study, agreement number (2014-A01461-46), and promoter, Rennes Uni-
versity Hospital.
Functional brain network for each object (picture) was constructed at the cortical level by
using the EEG–source connectivity method (Hassan & Wendling, 2018). The similarity scores
between all the object-related functional networks were quantified using the SimiN et algo-
rithm, which produce a 78 × 78 similarity matrix. The similarity matrix was transformed into
a graph where nodes represent brain networks and edges represent the highest similarity score
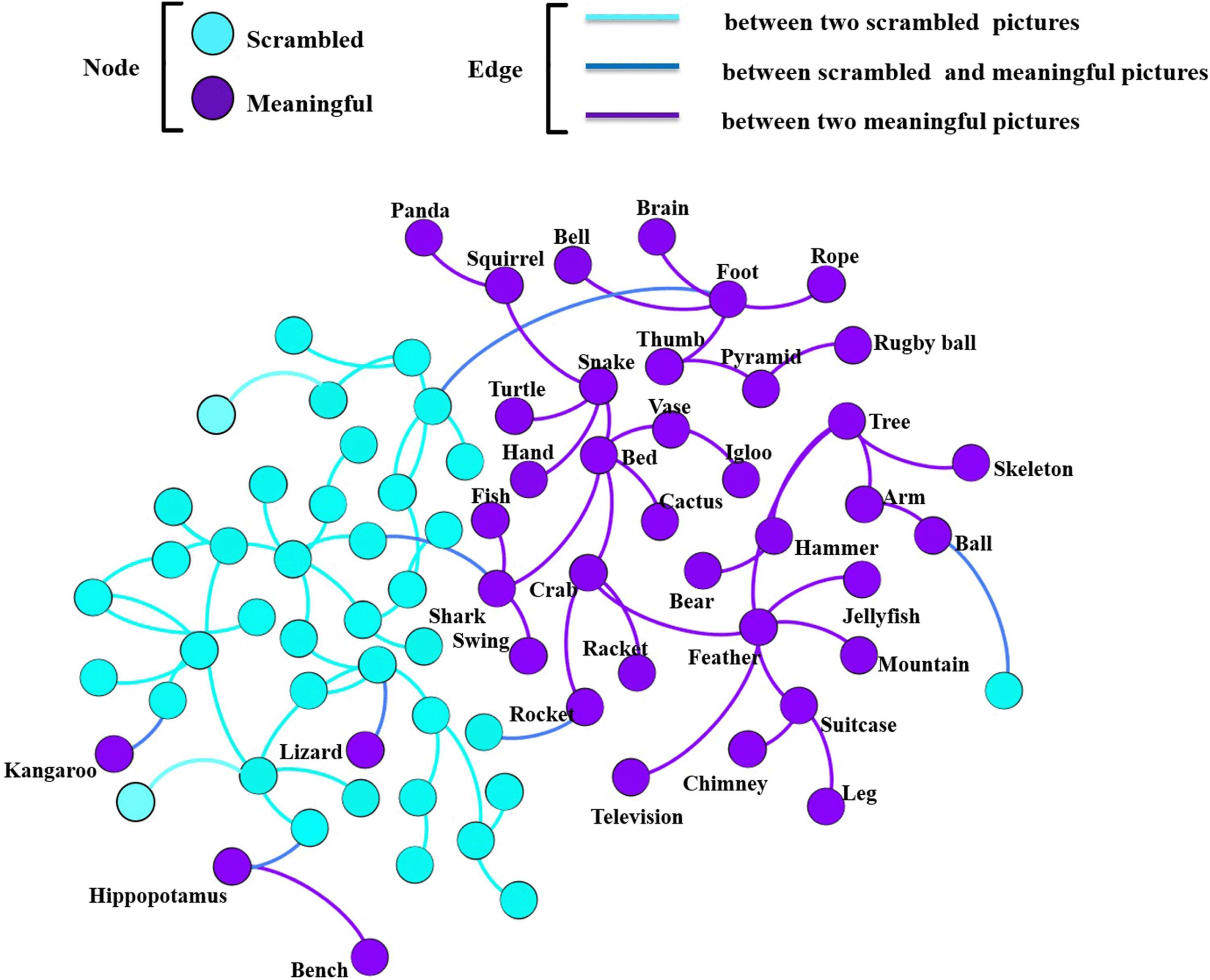
between the brain networks. This graph is illustrated in Figure 8. The visual inspection of this
graph (blue nodes for meaningful and purple nodes for scrambled) shows that the connections
between objects of the same category (N = 72) is clearly higher than connections between ob-
jects from different categories (N = 7). Constructing this network of networks can be seen as
a first attempt to evaluate categorization of visual objects in the human brain with a functional
network similarity-based approach.
DISCUSSION AND CONCLUSIONS
As long as there are functional/structural brain networks, there will be people looking for
comparisons between them. Here, we have presented the main methods and algorithms that
can be used to compare brain networks.
Which method then? The answer depends on the application itself. If the objective is to
reveal statistical difference between two groups (healthy subjects vs. patients, for instance)
Network Neuroscience
520
Brain network similarity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Network of brain networks. The purple nodes represent meaningful objects, and the blue
nodes represent scrambled objects. The purple edges represent a high similarity value between two
functional brain networks of meaningful category. The blue edges represent a high similarity value
between two functional brain networks of scrambled category, and the dark blue edges represent a
high similarity value between two brain networks of meaningful and scrambled objects.
then the methods based on the graph theoretical approach (node-wide or edge-wise) can be
good candidates provided that physiological hypothesis are well set and statistical parameters
are carefully chosen (correction for multiple comparisons, for instance).
However, if the objective is to produce a similarity score (usually normalized between 0
and 1), then the distance-based graph comparison methods are more appropriate. Validation
of algorithms, like the comparative analysis of Mheich et al. (2018), can allow us to identify a
set of methods that perform well on simulated networks. However, we do not know how well
real networks are described by currently used simulations.
Therefore, there is no guarantee that methods performing well on benchmarks also give
reliable results on real brain networks (advantages and limitations of some of these algorithms
are presented in Table 4).
From an application viewpoint, the network similarity is crucial in the identification of
what we called here “network of networks.” This can be used to build a “semantic map”
where nodes can represent the estimated networks of visual/auditory objects and edges can
denote the similarity between these networks (preliminary results are presented in this review).
This will undoubtedly require a very large number of stimuli and also the repetition of each
stimuli several times. When these conditions are respected, these semantic maps can give
new insights into the object categorization process in the human brain, from a network-based
perspective.
In clinical neuroscience, a potential application of network distance measures is the map-
ping of a “disease network” where the nodes may represent each brain disease and the edges
Network Neuroscience
521
B
r
a
i
n
n
e
t
w
o
r
k
s
i
m
i
l
a
r
i
t
y
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Table 4. Advantages and limitations of some selected graphs distance measures.
Computational cost
Structural difference
Available Code
Characteristics
Methods
SimiNet (Mheich et al., 2018)
D-measure (Schieber et al., 2017)
Spatial
location
+
_
Different
size
_
_
++
+(not for sparse graph)
DeltaCon (Koutra et al., 2013)
Kernel methods (Borgwardt et al., 2005;
Shervashidze et al., 2011)
_
_
_
+
+
_ _
_
+
+
+
https://github.com/amheich/SimiNet
https://github.com/tischieber/Quantifying-Network-
Structural-Dissimilarities
https://web.eecs.umich.edu/∼dkoutra/CODE/deltacon.zip
https://github.com/BorgwardtLab/GraphKernels
Note. Note that “–” indicates a characteristic that is not integrated in the similarity score of the method; “+” a characteristic that is integrated in the methods;
“– –” for worst computational time; and “++” for very good computational time. Spatial location = physical location of nodes; Different size = graphs with
different number of nodes; Computational cost = algorithm running time; Structural difference = detection of difference between node’s links in two graphs.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
N
e
t
w
o
r
k
N
e
u
r
o
s
c
e
n
c
e
i
5
2
2
Brain network similarity
can represent the similarity between the different networks associated to each disease (such
as Parkinson’s, Alzheimer’s, epilepsy, and so on). This application could help to further under-
stand the possible common altered network patterns in brain disease. A very recent review
by van den Heuvel and Sporns (2019a) showed indeed the importance of investigating such
cross-disorder connectivity patterns.
Another potential application of the network of networks approach is to construct a simi-
larity network across species connectomes (van den Heuvel et al., 2016), in which nodes can
denote species and edges the similarity between them. The major difficulty of this application
is to have access to connectome data from a range of species (human, drozophila, C. elegans,
cat, macaque, pigeon, mouse, rat, etc.). This may help to better understand cross-species com-
munalities and differences in term of brain structure and function. Moreover, a combination of
hypothesis-based selection of graph metrics (specific hubs, modules, etc.) with the similarity
algorithms may also improve the categorization and the classifications of these subnetworks.
Some Challenges in Brain Network Similarity
First, in the statistical comparison (graph theoretical–based approach), the major difficulty
arises from the fact that graph measures depend on the number of nodes and edges. To com-
pare two different brain networks, choosing equal size and density has become more popular
so that differences in graph measures appear solely through structural changes (van Wijk, Stam,
& Daffertshofer, 2010). However, this can be only achieved by taking a fixed number of nodes
and imposing a desired average degree by adjusting the binary threshold (van Wijk et al.,
2010).
Second, knowing the graph metrics that enable one to detect the difference between
brain networks is not obvious. The choice of this graph metric is often empirical. For a more
appropriate approach, these graph metrics should be driven by the physiopathology of the
analyzed neuroscience question or by adopting methods based on Network Representation
Learning (NRL). Indeed, these NRL approaches avoid the necessity for thorough feature en-
gineering and have led to very important results in network-based tasks, such as node clas-
sification, node clustering, and prediction (D. Zhang, Yin, Zhu, & Zhang, 2018). We believe
that NRL could be very useful to the network neuroscience community for the adaption of
representation learning techniques to specific applications that are of interest in the field. In
addition, a key challenge is to encapsulate several graph metrics in one similarity score that
can describe the difference between two graphs without missing any characteristics.
Third, the distance-based graph algorithms developed in different fields are indeed very
useful for detecting uncaptured characteristics by graph metrics. However, these algorithms
are still limited to undirected graphs. More efforts are needed to expand these algorithms to
deal with directed (causal) brain networks.
Possible Future Directions
From a methodological viewpoint, more efforts are needed to develop and optimize similarity
algorithms that combine several graph characteristics into one similarity score. These algo-
rithms should be first analyzed/validated using simulated data (where ground truth can be, to
some extent, obtained) before applying them to real brain networks. Another methodological
approach is to use similarity methods in brain dynamic algorithms in order to decipher how
brain networks change over time. In most dynamic analysis algorithms, a similarity/correlation
step is always needed to compare adjacent networks. This is usually done by using the classical
Network Neuroscience
523
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Brain network similarity
correlation coefficient (O’Neill et al., 2018). Adding a network-based similarity index into
brain dynamic algorithms can dramatically improve their performance.
From an application viewpoint, an interesting future clinical application is the construction of
a “network of brain diseases,” where nodes can represent brain diseases and edges represent
the similarity score between them. This map may help to characterize and visualize the common
landscapes between brain disorders, an issue recently reviewed by van den Heuvel and Sporns
(2019b).
We hope that the survey will motivate more researchers to contribute with other ideas than
those described above in the brain network similarity field, from a methodological and/or an
applicative perspective.
AUTHOR CONTRIBUTIONS
Ahmad Mheich: Conceptualization; Writing - Original Draft; Writing - Review & Editing.
Fabrice Wendling: Supervision. Mahmoud Hassan: Conceptualization; Supervision; Writing -
Review & Editing.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
REFERENCES
Achard, S., & Bullmore, E.
(2007). Efficiency and cost of econo-
mical brain functional networks. PLoS Computational Biology,
3(2), e17.
Achard, S., Delon-Martin, C., Vértes, P. E., Renard, F., Schenck,
M., Schneider, F., . . . Bullmore, E. T. (2012). Hubs of brain func-
tional networks are radically reorganized in comatose patients.
Proceedings of the National Academy of Sciences, 109(50),
20608–20613.
Alexander-Bloch, A. F., Gogtay, N., Meunier, D., Birn, R., Clasen,
L., Lalonde, F., . . . Bullmore, E. T. (2010). Disrupted modularity
and local connectivity of brain functional networks in childhood-
onset schizophrenia. Frontiers in Systems Neuroscience, 4, 147.
Atay, F. M., Bıyıko˘glu, T., & Jost, J. (2006). Network synchroniza-
tion: Spectral versus statistical properties. Physica D: Nonlinear
Phenomena, 224(1–2), 35–41.
Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Commu-
nication dynamics in complex brain networks. Nature Reviews
Neuroscience, 19(1), 17.
Banerjee, A. (2012). Structural distance and evolutionary relation-
ship of networks. Biosystems, 107(3), 186–196.
Barabási, A.-L. (2016). Network Science: Cambridge University Press.
Bassett, D. S., & Bullmore, E. T. (2017). Small-world brain networks
revisited. The Neuroscientist, 23(5), 499–516.
Bassett, D. S., Bullmore, E., Verchinski, B. A., Mattay, V. S.,
Weinberger, D. R., & Meyer-Lindenberg, A.
(2008). Hierar-
chical organization of human cortical networks in health and
schizophrenia. Journal of Neuroscience, 28(37), 9239–9248.
Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353.
Baum, G. L., Ciric, R., Roalf, D. R., Betzel, R. F., Moore, T. M.,
Shinohara, R. T., . . . Quarmley, M. (2017). Modular segregation
of structural brain networks supports the development of exec-
utive function in youth. Current Biology, 27(11), 1561–1572.
e1568.
Becerril, K. E., Repovs, G., & Barch, D. M.
(2011). Error pro-
cessing network dynamics in schizophrenia. Neuroimage, 54(2),
1495–1505.
Berlot, R., Metzler-Baddeley, C., Ikram, M. A., Jones, D. K., &
O’Sullivan, M. J. (2016). Global efficiency of structural networks
mediates cognitive control in mild cognitive impairment. Fron-
tiers in Aging Neuroscience, 8, 292.
Blondel, V. D., Guillaume, J.-L., Lambiotte, R., & Lefebvre, E.
(2008). Fast unfolding of communities in large networks. Journal
of Statistical Mechanics: Theory and Experiment, 2008(10),
P10008.
Borgwardt, K. M., & Kriegel, H.-P. (2005). Shortest-path kernels on
graphs. Paper presented at the Fifth IEEE International Conference
on Data Mining.
Brugere, I., Gallagher, B., & Berger-Wolf, T. Y.
(2018). Network
structure inference, a survey: Motivations, methods, and appli-
cations. ACM Computing Surveys (CSUR), 51(2), 24.
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186.
Bullmore, E. T., & Bassett, D. S.
(2011). Brain graphs: Graphical
models of the human brain connectome. Annual Review of Clin-
ical Psychology, 7, 113–140.
Calderone, A., Formenti, M., Aprea, F., Papa, M., Alberghina, L.,
Colangelo, A. M., & Bertolazzi, P. (2016). Comparing Alzheimer’s
and Parkinson’s diseases networks using graph communities
structure. BMC Systems Biology, 10(1), 25.
Cao, B., Li, Y., & Yin, J. (2013). Measuring similarity between graphs
based on the levenshtein distance. Applied Mathematics & Infor-
mation Sciences, 7(1L), 169–175.
Chan, M. Y., Park, D. C., Savalia, N. K., Petersen, S. E., & Wig,
G. S. (2014). Decreased segregation of brain systems across the
healthy adult lifespan. Proceedings of the National Academy of
Sciences, 111(46), E4997–E5006.
Network Neuroscience
524
Brain network similarity
Christmas, W. J., Kittler,
Structural
J., & Petrou, M.
matching in computer vision using probabilistic relaxation. IEEE
Transactions on Pattern Analysis and Machine Intelligence, 17(8),
749–764.
(1995).
Cordella, L. P., Foggia, P., Sansone, C., & Vento, M. (2004). A (sub)
IEEE
graph isomorphism algorithm for matching large graphs.
Transactions on Pattern Analysis and Machine Intelligence,
26(10), 1367–1372.
Crossley, N. A., Mechelli, A. S. J., Carletti, F., Fox, P. T., McGuire, P.,
& Bullmore, E. T. (2014). The hubs of the human connectome
are generally implicated in the anatomy of brain disorders. Brain,
137(8), 2382–2395.
da Costa, L. da F., Rodrigues, F. A., Travieso, G., & Villas Boas, P. R.
(2007). Characterization of complex networks: A survey of mea-
surements. Advances in Physics, 56(1), 167–242.
de Haan, W., van der Flier, W. M., Wang, H., van Mieghem,
P. F. A., Scheltens, P., & Stam, C. J. (2012). Disruption of func-
tional brain networks in Alzheimer’s disease: What can we learn
from graph spectral analysis of resting-state magnetoencephalog-
raphy? Brain Connectivity, 2(2), 45–55.
de Lange, S., de Reus, M., & van Den Heuvel, M.
(2014). The
Laplacian spectrum of neural networks. Frontiers in Computa-
tional Neuroscience, 7, 189.
Deza, M. M., & Deza, E. (2013). Voronoi diagram distances. En-
cyclopedia of Distances, (pp. 339—347). Springer.
Farkas, I., Derényi, I. J., Hawoong, Neda, Z., Oltvai, Z. N., Ravasz,
(2002). Networks in life: Scaling properties
E., . . . Vicsek, T.
and eigenvalue spectra. Physica A: Statistical Mechanics and Its
Applications, 314(1–4), 25–34.
Floyd, R. W. (1962). Algorithm 97: shortest path. Communications
of the ACM, 5(6), 345.
Fornito, A., Zalesky, A., & Breakspear, M..
(2013). Graph anal-
ysis of the human connectome: Promise, progress, and pitfalls.
Neuroimage, 80, 426–444.
Fornito, A., Zalesky, A., & Bullmore, E.
(2016). Fundamentals of
brain network analysis. Cambridge, MA: Academic Press.
Gao, X., Xiao, B., Tao, D., & Li, X. (2010). A survey of graph edit
distance. Pattern Analysis and Applications, 13(1), 113–129.
Genovese, C. R., Lazar, N. A., & Nichols, T.
(2002). Threshold-
ing of statistical maps in functional neuroimaging using the false
discovery rate. Neuroimage, 15(4), 870–878.
Girvan, M., & Newman, M. E. J.
(2002). Community structure
in social and biological networks. Proceedings of the National
Academy of Sciences, 99(12), 7821–7826.
Hassan, M., Benquet, P., Biraben, A., Berrou, C., Dufor, O., &
Wendling, F. (2015). Dynamic reorganization of functional brain
networks during picture naming. Cortex, 73, 276–288.
Hassan, M., Chaton, L., Benquet, P., Delval, A., Leroy, C.,
(2017). Func-
Plomhause, L., . . . van Kranen-Mastenbroek, V.
tional connectivity disruptions correlate with cognitive pheno-
types in Parkinson’s disease. NeuroImage: Clinical, 14, 591–601.
Hassan, M., & Wendling, F. (2018). Electroencephalography source
connectivity: Aiming for high resolution of brain networks in time
and space. IEEE Signal Processing Magazine, 35(3), 81–96.
He, Y., Chen, Z., & Evans, A.
(2008). Structural insights into
aberrant topological patterns of large-scale cortical networks in
Alzheimer’s disease. Journal of Neuroscience, 28(18), 4756–4766.
Heimann, M., Safavi, T., & Koutra, D. (2019). Distribution of node
embeddings as multiresolution features for graphs. IEEE Interna-
tional Conference on Data Mining.
Hinton, G. E., & Salakhutdinov, R. R.
(2006). Reducing the di-
mensionality of data with neural networks. Science, 313(5786),
504–507.
Huang, A. (2008). Similarity measures for text document clustering
Paper presented at the Proceedings of the Sixth New Zealand Com-
puter Science Research Student Conference (NZCSRSC2008).
Christchurch, New Zealand.
Huang, W., Bolton, T. A. W., Medaglia, J. D., Bassett, D. S., Ribeiro, A.,
& van De Ville, D. (2018). A graph signal processing perspective
on functional brain imaging. Proceedings of the IEEE, 106(5).
Humphries, M. D., & Gurney, K.
(2008). Network ‘small-world-
ness’: A quantitative method for determining canonical network
equivalence. PloS One, 3(4), e0002051.
Kabbara, A., Eid, H., El Falou, W., Khalil, M., Wendling, F., &
Hassan, M. (2018). Reduced integration and improved segrega-
tion of functional brain networks in Alzheimer’s disease. Journal
of Neural Engineering, 15(2), 026023.
Kamiya, K., Amemiya, S., Suzuki, Y., Kunii, N., Kawai, K., Mori,
H., . . . Ohtomo, K. (2015). Machine learning of DTI structural
brain connectomes for lateralization of temporal lobe epilepsy.
Magnetic Resonance in Medical Sciences, 15(1), 121–129.
Kawahara, J., Brown, C. J., Miller, S. P., Booth, B. G., Chau, V.,
Grunau, R. E., . . . Hamarneh, G. (2017). BrainnetCNN: Convo-
lutional neural networks for brain networks; towards predicting
neurodevelopment. NeuroImage, 146, 1038–1049.
Koutra, D., Vogelstein, J. T., & Faloutsos, C.
(2013). Deltacon: A
principled massive-graph similarity function. Paper presented at
the Proceedings of the 2013 SIAM International Conference on
Data Mining.
Lancichinetti, A., & Fortunato, S.
(2009). Community detection
algorithms: A comparative analysis. Physical Review E, 80(5),
056117.
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world
networks. Physical Review Letters, 87(19), 198701.
Li, H., Satterthwaite, T. D., & Fan, Y.
(2018). Brain age predic-
tion based on resting-state functional connectivity patterns us-
ing convolutional neural networks. Paper presented at the 2018
IEEE 15th International Symposium on Biomedical Imaging (ISBI
2018).
Li, X., Li, Y., & Li, X.
(2017). Predicting clinical outcomes of
Alzheimer’s disease from complex brain networks. Paper pre-
sented at the International Conference on Advanced Data Mining
and Applications.
Liao, X., Vasilakos, A. V., & He, Y.
(2017). Small-world human
brain networks: perspectives and challenges. Neuroscience &
Biobehavioral Reviews, 77, 286–300.
Liu, X., Kong, X., & Ragin, A. B.
(2017). Unified and contrasting
graphical lasso for brain network discovery. Paper presented at
the Proceedings of the 2017 SIAM International Conference on
Data Mining.
Liu, Y., Liang, M., Zhou, Y., He, Y., Hao, Y., Song, M., . . . Jiang, T.
(2008). Disrupted small-world networks in schizophrenia. Brain,
131(4), 945–961.
Luo, B., & Hancock, E. R.
(2001). Structural graph matching
using the EM algorithm and singular value decomposition. IEEE
Network Neuroscience
525
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Brain network similarity
Transactions on Pattern Analysis and Machine Intelligence,
23(10), 1120–1136.
cognitive impairment in Alzheimer disease. Neurology, 80(15),
1370–1377.
Lynall, M.-E., Bassett, D. S., Kerwin, R., McKenna, P. J., Kitzbichler,
M., Muller, U., & Bullmore, E. (2010). Functional connectivity
and brain networks in schizophrenia. Journal of Neuroscience,
30(28), 9477–9487.
Mattar, M. G., Cole, M. W., Thompson-Schill, S. L., & Bassett, D. S.
(2015). A functional cartography of cognitive systems. PLoS Com-
putational Biology, 11(12), e1004533.
Meunier, D., Lambiotte, R., & Bullmore, E. T. (2010). Modular and
hierarchically modular organization of brain networks. Frontiers
in Neuroscience, 4, 200.
Mheich, A., Hassan, M., Khalil, M., Berrou, C., & Wendling, F.
(2015). A new algorithm for spatiotemporal analysis of brain
functional connectivity. Journal of Neuroscience Methods, 242,
77–81.
Mheich, A., Hassan, M., Khalil, M., Gripon, V., Dufor, O., &
(2018). SimiNet: A novel method for quantifying
IEEE Transactions on Pattern Analysis
Wendling, F.
brain network similarity.
and Machine Intelligence, 40(9), 2238–2249.
Micheloyannis, S., Pachou, E., Stam, Cornelis J., Breakspear, M.,
(2006). Small-world
Bitsios, P., Vourkas, M., . . . Zervakis, M.
networks and disturbed functional connectivity in schizophrenia.
Schizophrenia Research, 87(1–3), 60–66.
Moussa, M. N., Steen, M. R., Laurienti, P. J., & Hayasaka, S. (2012).
Consistency of network modules in resting-state FMRI connec-
tome data. PloS One, 7(8), e44428.
Muldoon, S. F., Bridgeford, E. W., & Bassett, D. S. (2016). Small-
world propensity and weighted brain networks. Scientific Re-
ports, 6, 22057.
Neal, Z. P.
(2017). How small is it? Comparing indices of small
worldliness. Network Science, 5(1), 30–44.
Newman, M. E. J.
(2006). Modularity and community structure
in networks. Proceedings of the National Academy of Sciences,
103(23), 8577–8582.
Newman, M. E. J., & Girvan, M.
(2004). Finding and evaluat-
ing community structure in networks. Physical Review E, 69(2),
026113.
Newman, M. E. J., & Watts, D. J.
(1999). Renormalization group
analysis of the small-world network model. Physics Letters A,
263(4–6), 341–346.
O’Neill, G. C., Tewarie, P., Vidaurre, D., Liuzzi, L., Woolrich,
M. W., & Brookes, M. J. (2018). Dynamics of large-scale electro-
physiological networks: A technical review. Neuroimage, 180,
559–576.
Oh, S., Hyun, X., Yu, Jegelka, S., & Savarese, S. (2016). Deep metric
learning via lifted structured feature embedding. Paper presented
at the Proceedings of the IEEE Conference on Computer Vision
and Pattern Recognition.
Paban, V., Modolo, J., Mheich, A., & Hassan, M. (2019). Psycho-
logical resilience correlates with EEG source-space brain network
flexibility. Network Neuroscience, 3(2), 539–550.
Peraza, L. R., Taylor, J.-P., & Kaiser, M.
(2015). Divergent brain
functional network alterations in dementia with Lewy bodies and
Alzheimer’s disease. Neurobiology of aging, 36(9), 2458–2467.
Reijmer, Y. D., Leemans, A., Caeyenberghs, K., Heringa, S. M.,
Koek, H. L., Biessels, G. J., & Group, Utrecht Vascular Cognitive
Impairment Study. (2013). Disruption of cerebral networks and
Rice, W. R. (1989). The sequential Bonferroni test. Evolution, 43,
223–225.
Rizkallah, J., Annen, J., Modolo, J., Gosseries, O., Benquet, P.,
Mortaheb, S., . . . Thibaut, A. (2019). Decreased integration of
EEG source-space networks in disorders of consciousness. Neu-
roImage: Clinical, 23, 101841.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. Neuroimage, 52(3),
1059–1069.
Safavi, T., Sripada, C., & Koutra, D. (2017). Scalable hashing-based
network discovery. Paper presented at the 2017 IEEE Interna-
tional Conference on Data Mining (ICDM).
Schieber, T. A., Carpi, L., Díaz-Guilera, A., Pardalos, P. M.,
Masoller, C., & Ravetti, M. G. (2017). Quantification of network
structural dissimilarities. Nature Communications, 8, 13928.
Shervashidze, N., Schweitzer, P., van Leeuwen, E. J., Mehlhorn, K.,
(2011). Weisfeiler-lehman graph kernels.
& Borgwardt, K. M.
Journal of Machine Learning Research, 12(Sep), 2539–2561.
Shervashidze, N., Vishwanathan, S. V. N., Petri, T., Mehlhorn, K.,
& Borgwardt, K. (2009). Efficient graphlet kernels for large graph
comparison. Paper presented at the Artificial Intelligence and
Statistics.
Shimada, Y., Hirata, Y., Ikeguchi, T., & Aihara, K.
(2016). Graph
distance for complex networks. Scientific Reports, 6, 34944.
Skidmore, F., Korenkevych, D., Liu, Y., He, G., Bullmore, E., &
Pardalos, P. M.
(2011). Connectivity brain networks based
on wavelet correlation analysis in Parkinson fMRI data. Neuro-
science Letters, 499(1), 47–51.
Sporns, O.
Press.
(2010). Networks of the brain. Cambridge: MA: MIT
Sporns, O. (2014). Contributions and challenges for network mod-
els in cognitive neuroscience. Nature Neuroscience, 17(5), 652.
Sporns, O., & Betzel, R. F. (2016). Modular brain networks. Annual
Review of Psychology, 67, 613–640.
Stam, C. J., De Haan, W., Daffertshofer, A. B. F. J., Jones, B. F.,
van Manshanden, I., van Cappellen W. A.-M., . . . van Dijk,
B. W. (2008). Graph theoretical analysis of magnetoencephalo-
graphic functional connectivity in Alzheimer’s disease. Brain,
132(1), 213–224.
Stam, C. J., Jones, B. F., Nolte, G., Breakspear, M., & Scheltens,
P. (2006). Small-world networks and functional connectivity in
Alzheimer’s disease. Cerebral Cortex, 17(1), 92–99.
Steen, M., Hayasaka, S., Joyce, K., & Laurienti, P. (2011). Assess-
ing the consistency of community structure in complex networks.
Physical Review E, 84(1), 016111.
Supekar, K., Menon, V., Rubin, D., Musen, M., & Greicius, M. D.
(2008). Network analysis of intrinsic functional brain connec-
tivity in Alzheimer’s disease. PLoS Computational Biology, 4(6),
e1000100.
Telesford, Q. K., Joyce, K. E., Hayasaka, S., Burdette, J. H., &
(2011). The ubiquity of small-world networks.
Laurienti, P. J.
Brain Connectivity, 1(5), 367–375.
van den Heuvel, M. P., Bullmore, E. T., & Sporns, O.
(2016).
Comparative connectomics. Trends in Cognitive Sciences, 20(5),
345–361.
Network Neuroscience
526
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Brain network similarity
van den Heuvel, M. P., Mandl, R. C. W., Stam, C. J., Kahn, R. S.,
& Pol, H. E.
(2010). Aberrant frontal and temporal complex
network structure in schizophrenia: A graph theoretical analysis.
Journal of Neuroscience, 30(47), 15915–15926.
Yan, C., Gong, G., Wang, J., Wang, D., Liu, D., Zhu, C., . . . He, Y.
(2010). Sex-and brain size–related small-world structural corti-
cal networks in young adults: A DTI tractography study. Cerebral
Cortex, 21(2), 449–458.
van den Heuvel, M. P., & Sporns, O.
(2019a). A cross-disorder
connectome landscape of brain dysconnectivity. Nature Reviews
Neuroscience, 1.
Yan, Y., Zhu, J., Duda, M., Solarz, E., Sripada, C., & Koutra, D.
(2019). GroupINN: Grouping-based Interpretable Neural Net-
work for Classification of Limited, Noisy Brain Data.
van den Heuvel, M. P., & Sporns, O.
(2019b). A cross-disorder
connectome landscape of brain dysconnectivity. Nature Reviews
Neuroscience, 20(7), 435–446.
van den Heuvel, M. P., Stam, C. J., Boersma, M., & Pol, H. E. H.
(2008). Small-world and scale-free organization of voxel-based
resting-state functional connectivity in the human brain. Neu-
roimage, 43(3), 528–539.
Van W., Bernadette C. M., Stam, C. J., & Daffertshofer, A. (2010).
Comparing brain networks of different size and connectivity den-
sity using graph theory. PloS One, 5(10), e13701.
Vishwanathan, S. V. N., Schraudolph, N. N., Kondor, R., &
Journal of Machine
(2010). Graph kernels.
Borgwardt, K. M.
Learning Research, 11, 1201–1242.
Wang, S., He, L., Cao, B., Lu, C.-T., Yu, P. S., & Ragin, A. B. (2017).
Structural deep brain network mining. Paper presented at the
Proceedings of the 23rd ACM SIGKDD International Conference
on Knowledge Discovery and Data Mining.
Wang, X. F., & Chen, G. (2003). Complex networks: Small-world,
scale-free and beyond. IEEE Circuits And Systems Magazine, 3(1),
6–20.
Wang, X., Ding, X., Tung, A. K. H., Ying, S., & Jin, H. (2012). An
efficient graph indexing method. Paper presented at the Data En-
gineering (ICDE), 2012 IEEE 28th International Conference on.
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-
world’networks. Nature, 393(6684), 440.
Wu, T., Wang, L., Chen, Y., Zhao, C., Li, K., & Chan, P.
Wilson, R. C., & Zhu, P. (2008). A study of graph spectra for com-
paring graphs and trees. Pattern Recognition, 41(9), 2833–2841.
(2009).
Changes of functional connectivity of the motor network in the
resting state in Parkinson’s disease. Neuroscience Letters, 460(1),
6–10.
Yao, Z., Zhang, Y., Lin, L., Zhou, Y., Xu, C., Jiang, T., & Initiative,
Alzheimers Disease Neuroimaging.
(2010). Abnormal cortical
networks in mild cognitive impairment and Alzheimer’s disease.
PLoS Computational Biology, 6(11), e1001006.
Yu, Q., Du, Y., Chen, J., Sui, J., Adal¯e, T., Pearlson, G. D., &
(2018). Application of graph theory to assess
Calhoun, V. D.
static and dynamic brain connectivity: approaches for building
brain graphs. Proceedings of the IEEE, 106(5), 886–906.
Zalesky, A., Fornito, A., & Bullmore, E. T. (2010). Network-based
statistic: Identifying differences in brain networks. Neuroimage,
53(4), 1197–1207.
Zalesky, A., Fornito, A., Seal, M. L., Cocchi, L., Westin, C.-F.,
Bullmore, E. T., . . . Pantelis, C. (2011). Disrupted axonal fiber
connectivity in schizophrenia. Biological Psychiatry, 69(1), 80–89.
Zeng, Z., Tung, A. K. H., Wang, J., Feng, J., & Zhou, L. (2009). Com-
paring stars: On approximating graph edit distance. Proceedings
of the VLDB Endowment, 2(1), 25–36.
Zhang, D., Yin, J., Zhu, X., & Zhang, C. (2018). Network represen-
tation learning: a survey. IEEE Transactions on Big Data.
Zhang, M., Cui, Z., Neumann, M., & Chen, Y.
(2018). An end-
to-end deep learning architecture for graph classification. Pa-
per presented at the Thirty-Second AAAI Conference on Artificial
Intelligence.
Zhang, Y., Lin, L., Lin, C.-P., Zhou, Y., Chou, K.-H., Lo, C.-Y., . . .
Jiang, T.
(2012). Abnormal topological organization of struc-
tural brain networks in schizophrenia. Schizophrenia Research,
141(2–3), 109–118.
Zhang, Z., Liao, W., Chen, H., Mantini, D., Ding, J.-R., Xu, Q., . . .
Jiao, Q. (2011). Altered functional–structural coupling of large-
scale brain networks in idiopathic generalized epilepsy. Brain,
134(10), 2912–2928.
Network Neuroscience
527
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
3
5
0
7
1
8
6
7
2
9
1
n
e
n
_
a
_
0
0
1
3
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3