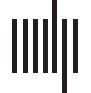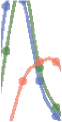RESEARCH ARTICLE
See further upon the giants: Quantifying
intellectual lineage in science
Woo Seong Jo1,2,3
, Lu Liu1,2,3,4
, and Dashun Wang1,2,3,5
1Center for Science of Science & 创新, Northwestern University, Evanston, 伊尔, 美国
2Northwestern Institute on Complex Systems, Northwestern University, Evanston, 伊尔, 美国
3Kellogg School of Management, Northwestern University, Evanston, 伊尔, 美国
4College of Information Sciences and Technology, Pennsylvania State University, 大学园, PA, 美国
5McCormick School of Engineering, Northwestern University, Evanston, 伊尔, 美国
关键词: citation network, cocitation, science of science, scientific impact
抽象的
Newton’s centuries-old wisdom of standing on the shoulders of giants raises a crucial yet
underexplored question: Out of all the prior works cited by a discovery, which one is its giant?
这里, we develop a discipline-independent method to identify the giant for any individual
纸, allowing us to better understand the role and characteristics of giants in science. 我们
find that across disciplines, 关于 95% of papers appear to stand on the shoulders of giants, 然而
the weight of scientific progress rests on relatively few shoulders. Defining a new measure of
giant index, we find that, while papers with high citations are more likely to be giants, 为了
papers with the same citations, their giant index sharply predicts a paper’s future impact and
prize-winning probabilities. Giants tend to originate from both small and large teams, 存在
either highly disruptive or highly developmental. Papers that did not have a giant tend to do
poorly on average, yet interestingly, if such papers later became a giant for other papers, 他们
tend to be home-run papers that are highly disruptive to science. Given the crucial importance
of citation-based measures in science, the developed concept of giants may offer a useful
dimension in assessing scientific impact that goes beyond sheer citation counts.
介绍
1.
“If I have seen further, it is by standing on the shoulders of giants.” Isaac Newton’s famous
1675 letter to Robert Hooke highlights a fundamental feature of science: its cumulative nature.
的确, new insights and discoveries rarely emerge in isolation; 反而, they build on prior
scientific work. Because scientists throughout the ages and across disciplines all acknowledge
ideas that inspired their research, we have an opportunity to explore citation relationships to
better understand how new research makes use of influential work (Clauset, Larremore, &
Sinatra, 2017; Fortunato, Bergstrom et al., 2018; Garfield, 2006; Price, 1965; Radicchi,
Fortunato, & Castellano, 2008; Redner, 2005; Waltman, 2016; 王 & 巴拉巴斯, 2021; 王,
歌曲, & 巴拉巴斯, 2013). 这里, we hone in on a specific, underexplored question: Is there a
way to estimate, given any paper, which reference is the “giant” whose shoulders the new
research stands upon?
Here we take advantage of the citation relationships between papers and develop a
network-based method that aims to estimate the relative intellectual significance of each ref-
erence to a paper, allowing us to estimate the potential giant for a paper. Our leading
开放访问
杂志
引文: Jo, 瓦. S。, 刘, L。, & 王, D.
(2022). See further upon the giants:
Quantifying intellectual lineage in
科学. Quantitative Science Studies,
3(2), 319–330. https://doi.org/10.1162
/qss_a_00186
DOI:
https://doi.org/10.1162/qss_a_00186
Peer Review:
https://publons.com/publon/10.1162
/qss_a_00186
支持信息:
https://doi.org/10.1162/qss_a_00186
已收到: 21 四月 2021
公认: 7 二月 2022
Corresponding Authors:
Lu Liu
luliu2131@gmail.com
Dashun Wang
dashun.wang@northwestern.edu
处理编辑器:
Staša Milojević
版权: © 2022 Woo Seong Jo, 鲁
刘, and Dashun Wang. 已发表
under a Creative Commons Attribution
4.0 国际的 (抄送 4.0) 执照.
麻省理工学院出版社
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantifying intellectual lineage in science
hypothesis is that, while each paper has many references, their importance to the paper can be
uneven, and the relationships among the listed references, revealed through the overall cita-
tion network, may help us understand the intellectual significance of each reference in the
context of the overall scientific discourse.
Citations are essential to scientific communication, allowing scientists to condense knowl-
边缘, bolster the strength of their evidence, attribute prior ideas to appropriate sources, 和更多
(王 & 巴拉巴斯, 2021). Partly because canonical papers tend to inspire follow-up research
which builds on them, citation relationships have been widely used to quantify scientific impact
(伯格斯特罗姆, 西方, & Wiseman, 2008; Cole & Cole, 1974; Garfield, 2006; Hirsch, 2005; 国王,
2004; 刘, 王等人。, 2018; Radicchi et al., 2008; Sinatra, 王等人。, 2016; Uzzi, Mukherjee
等人。, 2013; Waltman, 2016; 王等人。, 2013; 方式, Morgan et al., 2019; 吴, 王, & 埃文斯,
2019; Wuchty, 琼斯, & Uzzi, 2007). 同时, citations can be affected by myriad
因素: Publication venue, 年, and field of study are among many other reasons why authors
cite a given paper (Aksnes, 2006; Moravcsik & Murugesan, 1975; Radicchi, 2012; Simkin &
Roychowdhury, 2002), contributing to noise in evaluating and comparing their relative
重要性.
The need to quantify scientific impact by considering citations of different importance has
inspired various methods to identify the key references. Some examined the citation context by
analyzing the number of mentions and the sections and relative positions that a reference
appears (Bornmann & Daniel, 2008; Boyack, van Eck et al., 2018; Ding, 刘等人。, 2013; Ding,
张等人。, 2014; 胡, 陈, & 刘, 2013; 琼斯 & Hanney, 2016). Some combined features
from the full text, citation counts, and abstract similarity, and trained a classifier to predict
important references (Hassan, Akram, & Haddawy, 2017; 朱, Turney et al., 2015). 一些
developed a local diffusion method on the citation network and ranked references by their
diffusion score (Cui, Zeng et al., 2020). Other researchers conducted surveys for authors
and asked them to identify references that shaped the research idea and influenced the
研究 (Tahamtan & Bornmann, 2018; Zhu et al., 2015). These studies have also contributed
to the development of new metrics, such as weighting citations by the number of mentions and
the diffusion score on the citation network.
Here we study 33 million papers indexed by the Web of Science ( WoS) 之间 1955 和
2014, 和 962 million citations among them (Supplementary Material, Figure S1). To quantify
the intellectual significance of each reference to a given paper, we first use cocitation relation-
ships to establish a measure of proximity between references, which measures how many
times two papers are cited together by other papers. Cocitation has been used for a variety
of purposes from quantifying the topical relevance among papers (陈, 2006; 刘 & 陈,
2012; 小的, 1973) to author credit allocation within a paper (沉 & 巴拉巴斯, 2014) to eval-
uating impacts of authors (Ding, Yan et al., 2009) and suggesting relevant references (Sarol,
刘, & 施耐德, 2018). To identify the “giant” for a given paper, we first take all the papers
ever published up to the publication year of the focal paper, and identify all cocitation rela-
tionships (Figure 1A), with link weight indicating the number of times two papers are cocited.
This cocitation network can act as a proxy for the overall knowledge space at the time
(Figure 1B). 下一个, for the focal paper, we locate all its references to obtain the reference sub-
network embedded in the overall cocitation network, approximating the intellectual context in
which the paper is placed (Figure 1C). Here we focus on papers that contain at least five ref-
erences to ensure we have enough nodes for each reference subnetwork, 导致 25 米尔-
lion papers in total.
To identify local significance of a reference within the subnetwork while taking into
account its overall influence in the global network (Lü, 陈等人。, 2016; Lü & 周,
Quantitative Science Studies
320
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantifying intellectual lineage in science
Identifying the giant paper. (A) For a given reference (蓝色的), we find all other papers that are cocited with this reference (cocited
数字 1.
papers in grey) with link weight indicating the number of cocitations. (乙) We can follow the procedure in (A) to construct the entire cocitation
network for all papers published up to a certain year, representing the overall knowledge space at the time. (C) To identify the giant for a given
纸, we use the cocitation network in its publication year, and locate all its references (blue nodes) to pinpoint the reference subnetwork
from the overall cocitation network. (D) We give each reference the same number of “votes” to link to their most relevant paper in the global
cocitation network (both solid and dashed lines), but keep only the links formed within the reference subnetwork (solid line). We begin by
adding one connection (a vote) for each reference, and monitor the connectivity within the subnetwork. (乙) We increase the number of con-
nections iteratively, and stop when the average degree of the reference subnetwork is greater than 1: the minimum requirement to have a
cluster. We then pick the node with the largest degree as the giant paper (highlighted in purple). (F) 如果, 然而, the reference subnetwork
remains completely isolated at n = 1, we stop our algorithm without identifying giants for such cases.
2011), we develop a new method by borrowing concepts from democratic voting and perco-
lation theory. Our key insight is to give each reference the same number of “votes” to link to
their most relevant paper in the global cocitation network, but keep only the links formed
within the reference subnetwork (only counting the votes within the specific context). 我们
hypothesize that the giant of a paper should appear in its reference list and have high topical
relevance to the body of work, prompting us to focus on the votes in the reference subnetwork.
同时, the giant paper may also be captured by collective recognition within a
scientific community. 为此, our method recognizes the collective nature of the intellec-
tual lineage by exploring rich information embedded in the global cocitation network.
具体来说, we begin by adding one connection (a vote) for each reference, and monitor
the connectivity within the subnetwork (Figure 1D). We increase the number of connections
iteratively, and stop when the reference subnetwork starts to coalesce into a cluster, suggesting
plausible knowledge structures beginning to emerge within this subnetwork. Resorting to per-
colation theory, we stop at the minimal n votes needed for the subnetwork to cross the per-
colation threshold for the corresponding random network (纽曼, 2010, IE。, hkn > 1i,
where references within the subnetwork have at least one connection on average (Figure 1E).
We then select the node with the largest degree (k) as the giant paper (Supplementary Material,
Figure S2). The idea is to approximate the local importance of a reference by counting the
“votes” it received from other references. And the one with the most “votes” suggests its impor-
tance among other references. 同时, the idea of a percolation threshold also
affords us the possibility of not always identifying a giant for a paper. 的确, 如果, 然而,
the reference subnetwork remains completely isolated at n = 1 (Figure 1F), suggesting that
the paper’s references all belong to distinctive parts of the overall knowledge space, we stop
our algorithm at n = 1 without identifying giants for such cases.
One advantage of our method is to overcome mixed signals introduced by the skewed cita-
tion distribution (巴拉巴斯 & 阿尔伯特, 1999; Cui et al., 2020; Price, 1965; Radicchi et al., 2008).
的确, because highly cited papers tend to dominate the subnetwork of references, 直接地
Quantitative Science Studies
321
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantifying intellectual lineage in science
applying existing network-based methods to the cocitation network tends to favor papers with
overall high citation counts, which may or may not be the specific giant to a paper. 一个可以
somewhat mitigate this issue by keeping, 例如, the most essential links using network
sparsification methods such as backbone extraction (Radicchi, Ramasco, & Fortunato, 2011;
Serrano, Boguná, & Vespignani, 2009), yet it appears insufficient to overcome the dominance
of highly cited papers. This highlights one of the many challenges of this task: To identify the
giant for a specific paper, we need to balance between a reference’s local importance to the
specific context and its overall scientific impact. 同时, prior work reveals that cre-
ative works may not necessarily build from existing literature (Tahamtan & Bornmann, 2018),
and our method allows us to identify papers without giants, which is difficult to achieve using
citation count or the backbone algorithm. 全面的, we recognize that high-citation papers are
important and often instrumental in the development of the field, but it does not guarantee that
they are the most relevant for a specific paper in a field. This prompts us to take into account
both the local relevance of a paper within the reference list and its global impact in the overall
citation network, which may offer a complementary dimension of a paper’s impact to its cita-
tion count. We also note that each of the steps in the method can be further refined with dif-
ferent stopping criteria and a different number of giants to pick for a paper. Here we choose
this specification of the method for its simplicity and leave for future work to systematically
study the different variants of the method, which we shall discuss in more detail in the discus-
sion and limitation section of the paper.
2. 结果
We apply our method to millions of papers published over the past 60 年, allowing us to
study the giants we identify and examine patterns of intellectual lineage in science. 第一的, 我们
find that about 95% of papers have a giant associated with them (图2A). This overwhelm-
ing proportion of papers with identifiable giants offers quantitative evidence for the cumulative
nature of science. We further find that, despite the exponential growth of science and rise of
interdisciplinary research and collaborations, this prevalence of giants has held true over the
数字 2. Prevalence of giants in science. (A) Out of the 25 million papers we studied, 95% of them have a giant (绿色的). 相比之下, 仅有的
12% of papers later become giants for other papers (蓝色的). (乙) The fraction of papers that have an associated giant increases over the years. (C)
Breaking down the fraction of papers with giants by 12 different fields. (D) Breaking down the fraction of papers that later become a giant by 12
different fields. Papers in multidisciplinary sciences have the highest likelihood to become a giant. (乙) We calculate the fraction of papers
whose giant is not the most cited paper within its reference list, and show this fraction over time.
Quantitative Science Studies
322
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantifying intellectual lineage in science
ages but has risen gradually over time (图2B), growing from 91.6% 在 1955 到 95.8% 在
2014, which implies that research today is increasingly conducted on the shoulders of
giants. Yet at the same time, the papers that serve as giants are remarkably concentrated, 作为
仅有的 12% of the papers we analyzed fell into this category (图2A), consistent with what
the literature suggests (Bornmann, de Moya Anegón, & 莱德斯多夫, 2010; Cole & Cole, 1972).
We further find that these results are remarkably consistent across the disciplines we studied
(Figures 2C–D). 因此, despite the inherent differences in norm and culture across disciplines,
the shoulders of giants appear universally appreciated. 有趣的是, 的 12 不同的
scientific fields, multidisciplinary science has the highest fraction of giant papers (15.4%,
Figure 2D), suggesting a premium in bringing together diverse approaches. 全面的, 这些
results suggest that while the vast majority of papers stand on the shoulders of giants, 这
weight of scientific progress rests on only a few shoulders.
Is the identified giant for a given paper the most cited within its references? For each paper
that has a giant, we calculate the citation counts of all its references when the paper was pub-
列出. We find that the vast majority of giant papers are not the most cited within the reference
列表 (72.5%, dashed line in Figure 2E), and this fraction has mostly been trending upward over
the past 60 年 (Figure 2E). 例如, 在 1955, 44% of giants were also the most cited
参考, but that number decreased to only 26% 在 2014. These results suggest being the
most cited paper does not guarantee being the giant, implying that our measures of giant may
capture complementary dimensions of impact to citation counts, which prompt us to further
examine the overall characteristics of a giant paper.
To understand what kinds of papers tend to become a giant, we introduce a new index: 这
giant index (G), which calculates the number of times a paper is a giant for other papers. 我们
then compare a paper’s G with its citation count (C ). We first find that the likelihood of being a
giant posts a highly nonlinear relationship with its citation counts. 的确, among papers with
exceptional impact (C > 1,000), virtually all of them have a positive giant index. The proba-
bility for a paper to be a giant P(G > 0) increases with citation counts but undergoes a sharp
crossover for papers with respectable but more moderate citations (Figure 3A). To ensure that
the observed trend is not affected by self-citations, we remove self-citations and repeat our
分析, arriving at the same conclusion (Supplementary Material, Figure S3). These results
suggest that not all papers can be a giant, and a paper’s potential to become a giant may
be related to its citation impact, prompting us to further examine the correlation between a
paper’s giant index and its citations (Figure 3B). We find that for papers with dozens to hun-
dreds of citations, their giant index and citations follow a superlinear relationship, suggesting
that an increase in a paper’s citations is associated with an increasing return in the rate at
which a paper becomes a giant. Yet for papers on the right-hand tail of citation impacts, 他们的
giant index roughly follows a linear relationship with their citations, consistent with the trend
shown in Figure 3A, suggesting that papers with exceptional impact are disproportionately
more likely to be the shoulders that carry scientific progress in their field.
同时, the overall correlation between the giant index and citations (Figure 3B)
also masks heterogeneous relationships between the two. 的确, as both P(G) 和P(C ) follow
a fat-tailed distribution (Supplementary Material, Figure S4) and by design G ≤ C, we calculate
the conditional probability P (G|C ) (Figure 3C). We find that, as C increases, the distribution
systematically shifts to the right, consistent with the correlations observed in Figures 3A–B. 然而,
for papers with the same level of citations, their giant indexes are still characterized by a high
degree of heterogeneity, suggesting that a high citation count does not necessarily guarantee a
high giant index. 下一个, we show that this discrepancy between the giant index and citation
counts offers signals for a paper’s future impact.
Quantitative Science Studies
323
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantifying intellectual lineage in science
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
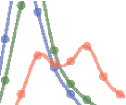
数字 3. The giant index. (A) The fraction of papers with a nonzero giant index as a function of citations. (乙) The giant index G as a function
of C. The two quantities follow a superlinear relationship when C < 1,000 but exhibit a linear relationship for high C regime (C > 1,000). (C)
Conditional distribution P(G|C ) shows that papers are characterized by a heterogeneous giant index even though they have the same level of
citation impacts. (D) We pick papers published in PRL between 1990 和 2000 that have between 100 和 200 citations in 5 年 (100 ≤
C5 ≤ 200). Depending on their giant index at year 5, G5, these papers exhibit different levels of future impacts. (乙) The same analysis as (D) 但
for a group of papers published in PNAS (100 ≤ C5 ≤ 200).
We select papers published in Physical Review Letters (PRL) 之间 1990 和 2000 但
which have a similar level of citation impact after 5 years of publication (within the range of
100 ≤ C5 ≤ 200 by Year 5) (Figure 3D). We divide these papers into three groups based on
their giant index at year 5 (G5): high G group (顶部 10% in giant score G5, hG5i ≈ 31.3), low G
团体 (底部 10% in G5, hG5i ≈ 1.0), and nongiant group (G5 = 0). We then trace the cita-
tions of these papers over the next 10 年. We find that at year 5, the three groups follow a
similar citation distribution, by construction. Yet with time, the high G group clearly stood out
from the pack, collecting citations at a much faster rate than the other two groups. Interest-
英利, there is a statistically significant difference between the G ≈ 1 and G = 0 groups by year
15, suggesting that papers with a small giant index are likely to have higher future impact. 我们
repeat the same analysis for a multidisciplinary journal, selecting papers published in Proceed-
ings of the National Academy of Sciences (PNAS ) (100 ≤ C5 ≤ 200, Figure 3E), finding again
the same patterns. 合在一起, 数字 3 shows that while a paper’s giant index and citation
counts are overall correlated, papers with the same citations can have vastly different giant
indexes and that a difference in giant index appears to substantially reveal a paper’s potential
for future impact. These results suggest that the giant index offers additional information on a
paper’s role in science that goes beyond its citation counts. 一起, they reflect the idea that
not all citations are the same, and those that frequently lend their shoulders to others tend to
distinguish themselves from those that do not.
To understand potential forces that might facilitate the production of giants, we further
examine the organization of scientific activity, probing the role of teams in shouldering
Quantitative Science Studies
324
Quantifying intellectual lineage in science
scientific progress. 的确, research shows that small and large teams are differentially posi-
tioned for innovation (Wu et al., 2019): Large teams tend to excel at furthering existing ideas
和设计, whereas small teams tend to disrupt current ways of thinking with new ideas and
机会. This distinction prompts us to measure whether the likelihood of producing
giants varies by team size. To control the effect of field and time, we normalize citations
and giant indexes with the average value for papers published in the same field and year
(Radicchi et al., 2008), computing the normalized citation C/hC if,y and normalized giant
index G/hGif,y. We first find that, across different fields, the normalized citation increases with
team size M (Figure 4A), confirming previous studies showing the citation premium conferred
upon large teams (Wu et al., 2019; Wuchty et al., 2007). We then repeat this analysis for giant
文件 (G > 0), finding that the normalized giant index posts a U-shaped curve (Figure 4B), 和
this nonlinear relationship holds the same across different fields (shaded curves in Figure 4B).
These results suggest that while works by large teams tend to garner higher citations, giants
that frequently lend their shoulders tend to originate from both small and large teams.
The relationship between team size and research outcomes prompted us to ask if the
observed nonlinear relationship between giant index and team size is related to the character
of work that teams of different size produce. 这里, we measure the relationship between a
paper’s giant index and its disruption percentile DP. We calculate the disruption score
following prior work (Funk & Owen-Smith, 2017; Wu et al., 2019). For each paper, 我们
calculate the number of subsequent papers citing the paper but not its references (ni), 这
number of subsequent papers citing both the paper and its references (nj), and the number
of subsequent papers citing the references but not the paper (nk). The raw disruption score
(D) is defined as D ¼ ni −nj
. We further normalized the raw score to its percentile, 这
ni þnj þnk
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
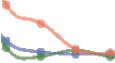
数字 4. Teams, disruption, and giant index. (A) We normalize citation by field and year C/hCif,y and plot it as a function of team size M. (乙)
We normalize the giant index by field and year, finding that it follows a U-shaped curve with team size. (C) The normalized giant index as a
function of disruption percentile DP, showing that either highly developmental (DP ≤ 20) or highly disruptive (DP ≥ 80) papers tend to a high
giant index. (D) Distributions of citations for papers with or without a giant. (乙) We categorize papers without giants into two groups based on
their giant index: G = 0 与. G > 0. The two groups show clearly different relationships with the citation impacts of these papers. (F) 这
distribution of disruption percentile DP for papers with (red circle) or without (yellow squares) a giant, showing that papers without a giant
are disproportionately more likely to be a highly disruptive paper. (Inset) The fraction of papers without a giant as a function of team size,
showing that such papers are more likely to be produced by small teams.
Quantitative Science Studies
325
Quantifying intellectual lineage in science
disruption percentile (DP ). DP measures the relative ranking among all papers published in the
same year, 和 100 indicating the most disruptive and 0 as the most developmental. We find
that giant index sharply increases for both highly developmental (DP < 20) and highly disrup-
tive (DP > 80) 工作 (Figure 4C). These results illustrate the divergent characters of giants in
科学, being either highly disruptive or highly developmental. Both types of giants shoulder
scientific progress, but they move science forward in different ways.
One advantage of our method is to allow the flexibility of not identifying a giant for a paper.
的确, as discussed in Figure 1, if all the references of a paper are initially isolated in the
reference subnetwork, it suggests that the paper draws upon disparate rather than established
knowledge clusters, and for these papers our method proceeds without assigning a giant (IE。,
papers without giants). 的 25 million papers we studied, 5.2% of them fall into this cate-
gory. Figure 4D plots the citation distributions for papers with and without a giant, 分别.
We find that papers without a giant tend to have overall fewer citations than those that stand
upon a giant’s shoulder, further suggesting the importance of giants in the production of
知识. Yet at the same time, Figure 4D also reveals an intriguing observation: 甚至
among papers without a giant, their citations are characterized by a high degree of heteroge-
neity, indicating that some papers do eventually garner high impacts, albeit uncommonly.
的确, we find that, among the papers without giants, 10% of them go on to become giants
for others. We separate the papers without giants into two groups, calculating the relative prob-
ability of observing a G > 0 与. G = 0 paper as a function of citations, and find that the two
groups follow clearly divergent patterns (Figure 4E): If a paper neither became a giant for others
(G = 0) nor stood on one’s shoulder when published, its impact is mostly concentrated within
the low-citation region, and the probability for such papers to garner higher citations dimin-
ishes rather rapidly. 相比之下, those that did not have a specific shoulder to rely upon but
later became a giant for others are systematically overrepresented in the high-citation region,
as their relative abundance rises precipitously with citations. These results paint a highly polar-
ized view for papers without a giant. 一方面, such papers have a rather limited
impact on average, suggesting that skipping the shoulders substantially limits a paper’s ability
to “see further.” Yet on the other hand, perhaps counterintuitively, papers without a giant may
also become home-run papers with right-tail citation impact. One conjecture is that papers
that emerge from a seeming vacuum that lies between knowledge clusters may reorient the
existing knowledge in a way that offers new ideas and opportunities. To test this conjecture,
we measure the disruption percentile DP, and find that papers without giants are sharply over-
represented in the highly disruptive region (Figure 4F), and much more likely to be produced
by small teams (Figure 4F inset).
最后的, as a further validation, we show that the giant index offers a simple yet additional
early signal for the Noble prize-winning papers. As the most prestigious prize in science,
the Nobel Prize recognizes some of the most crucial scientific breakthroughs. There have been
constant attempts to identify Nobel-Prize-winning discoveries based on citation counts
(Garfield & Malin, 1968; Revesz, 2015; Zakhlebin & Horvát, 2017). Despite their occasional
成功, citations appear to be a noisy signal for the Nobel, for a simple reason: While Nobel-
Prize-winning papers all tend to be highly cited, having high citations does not guarantee a
Nobel. This raises an intriguing question: Could the giant index offer additional information in
differentiating the prize-winning papers beyond citation counts? To answer this question, 我们
identified 370 Nobel-Prize-winning papers for physics, 化学, and medicine awarded
之间 1955 和 2014, and compared their giant index with papers published in the same
year and field with similar citations (the comparison group). We find that, by construction, 这
citation distribution P(C ) is largely indistinguishable between the two groups of papers
Quantitative Science Studies
326
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantifying intellectual lineage in science
数字 5. Giant index and Nobel-Prize-winning papers. (A) For each Nobel-Prize-winning paper,
we construct a comparison set of papers that are published in the same year and field and have a
similar number of citations (inset). We then compare the distributions of giant index for these two
groups of papers, calculating the relative probability P(G)/PC (G) as a function of the giant index,
where P(G) is the distribution of giant index for Nobel Prize papers and PC (G) is the distribution of
giant index for their nonprize-winning counterparts. (乙) We compare the giant index between the
prize-winning papers and their nonprize-winning counterparts in the comparison set. Red dots indi-
cate prize-winning papers that have a higher G than those in the comparison group. (C) The median
giant index for the Nobel-Prize-winning papers is 58 in physics, 51 in chemistry, 和 59.5 in med-
icine, 分别. 相比之下, the median giant index for papers in the comparison group with a
similar level of citations is 20 in physics, 22 in chemistry, 和 24 in medicine, 分别.
(Figure 5A, inset), yet the prevalence of Nobel-Prize-winning papers systematically increases
with their giant index (Figure 5A). 的确, if we just compare the giant index of prize-winning
papers with that of their nonprize-winning counterparts, we find a majority of prize-winning
papers have a higher G (67%) (Figure 5B). 因此, even though the two groups have the same
citations, simply comparing their giant index offers a stronger signal to distinguish them.
的确, we further compared the median giant index between the two samples, finding that
across physics, 化学, and medicine, the median giant index for prize-winning papers is
more than twice of that of the control group (Figure 5C). Note that the exercise shown in
数字 5 illustrates a relatively simple approach, suggesting that the utility of the giant index
can be further improved with additional features and more sophisticated models. 一起,
数字 5 not only offers further evidence that incorporating the giant index may offer an addi-
tional signal to identify influential work than citation count alone; it also suggests distinctions
between getting cited and being the reliable shoulder for ensuing science.
3. 讨论
总之, here we present a quantitative framework to test Newton’s canonical insight on
standing on the shoulders of giants. Several past efforts have attempted to identify a paper’s
influential references. While these attempts are mostly limited to small samples and require
domain knowledge or manual processes for classification, our method offers an alternative
way to quantitatively identify crucial references within a paper, which has several advantages
that are worth noting. 第一的, the method is discipline or journal independent, easily applicable
Quantitative Science Studies
327
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantifying intellectual lineage in science
to any paper corpus where citation information is available. 第二, it does not require ex-
post information, meaning that the giant paper can be identified at the time of publication,
which increases the practical utility of the method. 第三, as a framework, the method can
be further extended to allow for more flexibilities. 例如, although the proposed method
places an implicit assumption that each paper has just one giant, it can be easily extended to
incorporate multiple giants by picking the top k references of a paper or references whose
weight in the cociting network is above a threshold. 的确, it is reasonable to assume that
a paper may build upon multiple giants. Understanding papers with multiple giants is an
important direction for future work. It would be interesting to analyze these cases and compare
with the results obtained by picking one giant, which could be especially insightful when it
comes to multidisciplinary work and could further illuminate the roles of giants in the devel-
opment of new ideas.
The overall intuition behind the proposed measure is to recognize the uneven intellectual
influence of the references to a specific paper by quantifying the relationships among the ref-
erences cited in the paper through cocitation networks. 像这样, the method offers one way to
balance between a reference’s local importance to the specific context and its overall scientific
impact, helping us better understand the intellectual significance of each reference in the con-
text of the overall scientific discourse. 尽管如此, as an initial attempt to understand the role
and characteristics of giants in science, there are several important limitations of our work,
each suggesting important directions for future work. First and foremost is the validation of
the proposed framework. 在本文中, we calculated the giant score for Nobel-Prize-winning
文件. Future work may compare the giant identified by our method to existing metrics, 这样的
as the number of mentions and the appearance in difference sections of papers through full
text analysis. One could also assess the validity of the giant index through surveys, by asking,
例如, the lead authors of a paper to identify the most important reference for their work,
as well as asking whether there was any giant at all. This direction is especially important
given the algorithmic nature of our method, which may represent a crude approximation
for a paper’s intellectual lineage that inherently depends on a range of social and institutional
因素. 第二, while we propose one way to quantify the intellectual lineage among papers,
there could potentially be several other ways to quantify the shoulders of giants in science,
representing fruitful directions for future work, which may lead to more robust methods and
further insights. It is also important for future work to compare the performance and validity
of different methods in identifying giants. 第三, it is important to keep in mind that, as with
many citation-based indicators, the giant index does not account for the many individual and
institutional factors influencing a paper’s future impact. 更远, citation-based measures may
also have inherent biases against recent work, as it takes time for citations to accumulate,
suggesting that it may be more difficult to identify the giant(s) if a paper builds on a more recent
body of work. 最后的, the prediction task in the paper offers correlational evidence supporting the
relevance of the giant index. Future work with causal design may help improve the causative
interpretation of the idea of standing on the shoulders of giants.
全面的, given the crucial importance of citations in science decision-making, 包括
hiring, promotion, granting, and rewards, the developed concept of giant and its associated
giant index may offer a useful dimension in our quantitative understanding of science by
allowing us to appreciate those who shoulder scientific progress. 像这样, this measure is
not limited to individual discoveries but offers a complementary dimension to the growing
literature of the science of science (Fortunato et al., 2018; 王 & 巴拉巴斯, 2021), 和
can be fruitfully applied to assess the role of giants in careers, 团队, 机构, 和更多,
pointing to promising future directions.
Quantitative Science Studies
328
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantifying intellectual lineage in science
致谢
The authors thank all members of the Center for Science of Science and Innovation (CSSI) 为了
invaluable comments.
作者贡献
Woo Seong Jo: 数据管理, 形式分析, 调查, 方法, 可视化,
Writing—original draft, Writing—review & 编辑. Lu Liu: 形式分析, 调查,
方法, 可视化, Writing—original draft, Writing—review & 编辑. Dashun
王: 概念化, 资金获取, 调查, 方法, Project adminis-
翻译, 监督, Writing—original draft, Writing—review & 编辑.
COMPETING INTERESTS
The authors have no competing interests.
资金信息
This work is supported by Air Force Office of Scientific Research under award nos. FA9550-15-
1-0162, FA9550-17-1-0089, and FA9550-19-1-0354.
DATA AVAILABILITY
WoS data are available via Clarivate Analytics. The Nobel Prize data are from https://万维网
.nature.com/articles/s41597-019-0033-6.
参考
Aksnes, D. 瓦. (2006). Citation rates and perceptions of scientific
contribution. Journal of the American Society for Information
Science and Technology, 57(2), 169–185. https://doi.org/10
.1002/asi.20262
巴拉巴斯, A.-L., & 阿尔伯特, 右. (1999). Emergence of scaling in
random networks. 科学, 286(5439), 509–512. https://doi.org
/10.1126/science.286.5439.509, 考研: 10521342
伯格斯特罗姆, C. T。, 西方, J. D ., & Wiseman, 中号. A. (2008). 这
Eigenfactor (TM值) 指标. 神经科学杂志, 28(45),
11433–11434. https://doi.org/10.1523/jneurosci.0003-08.2008,
考研: 18987179
Bornmann, L。, & Daniel, H.-D. (2008). Functional use of frequently
and infrequently cited articles in citing publications. A content
analysis of citations to articles with low and high citation counts.
European Science Editing, 34(2), 35–38.
Bornmann, L。, de Moya Anegón, F。, & 莱德斯多夫, L. (2010). 做
scientific advancements lean on the shoulders of giants? A
bibliometric investigation of the Ortega hypothesis. PLOS ONE,
5(10), e13327. https://doi.org/10.1371/journal.pone.0013327,
考研: 20967252
Boyack, K. W., van Eck, 氮. J。, Colavizza, G。, & Waltman, L. (2018).
Characterizing in-text citations in scientific articles: 一个大规模的
分析. Journal of Informetrics, 12(1), 59–73. https://doi.org/10
.1016/j.joi.2017.11.005
陈, C. (2006). CiteSpace II: Detecting and visualizing emerging
trends and transient patterns in scientific literature. Journal of the
American Society for Information Science and Technology, 57(3),
359–377. https://doi.org/10.1002/asi.20317
Clauset, A。, Larremore, D. B., & Sinatra, 右. (2017). Data-driven pre-
dictions in the science of science. 科学, 355(6324), 477–480.
https://doi.org/10.1126/science.aal4217, 考研: 28154048
Cole, J. R。, & Cole, S. (1972). The Ortega hypothesis: Citation anal-
ysis suggests that only a few scientists contribute to scientific
进步. 科学, 178(4059), 368–375. https://doi.org/10.1126
/science.178.4059.368, 考研: 17815351
Cole, J. R。, & Cole, S. (1974). Social stratification in science.
Chicago and London: 芝加哥大学出版社. https://土井
.org/10.1119/1.1987897
Cui, H。, 曾, A。, Fan, Y。, & 从, Z. (2020). Identifying the key
reference of a scientific publication. Journal of Systems Science
and Systems Engineering, 29(4), 429–439. https://doi.org/10
.1007/s11518-020-5455-3
Ding, Y。, 刘, X。, Guo, C。, & 克朗的, 乙. (2013). The distribution of
references across texts: Some implications for citation analysis.
Journal of Informetrics, 7(3), 583–592. https://doi.org/10.1016/j
.joi.2013.03.003
Ding, Y。, 严, E., Frazho, A。, & Caverlee, J. (2009). PageRank for
ranking authors in co-citation networks. Journal of the American
Society for Information Science and Technology, 60(11),
2229–2243. https://doi.org/10.1002/asi.21171
Ding, Y。, 张, G。, Chambers, T。, 歌曲, M。, 王, X。, & Zhai, C.
(2014). Content-based citation analysis: The next generation of cita-
tion analysis. Journal of the Association for Information Science and
技术, 65(9), 1820–1833. https://doi.org/10.1002/asi.23256
Fortunato, S。, 伯格斯特罗姆, C. T。, Börner, K., 埃文斯, J. A。, Helbing, D ., ……
Uzzi, 乙. (2018). Science of science. 科学, 359(6379). https://
doi.org/10.1126/science.aao0185, 考研: 29496846
Funk, 右. J。, & Owen-Smith, J. (2017). A dynamic network measure
of technological change. Management Science, 63(3), 791–817.
https://doi.org/10.1287/mnsc.2015.2366
Garfield, 乙. (2006). Citation indexes for science. A new dimension
in documentation through association of ideas. 国际的
Quantitative Science Studies
329
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantifying intellectual lineage in science
Journal of Epidemiology, 35(5), 1123–1127. https://doi.org/10
.1093/ije/dyl189, 考研: 16987841
Garfield, E., & Malin, 中号. V. (1968). Can Nobel Prize winners be
预测的? 135th Annual Meeting of the American Association
for the Advancement of Science, 达拉斯, TX.
Hassan, S.-U., Akram, A。, & Haddawy, 磷. (2017). Identifying impor-
tant citations using contextual information from full text. 2017
ACM/IEEE Joint Conference on Digital Libraries ( JCDL). https://
doi.org/10.1109/JCDL.2017.7991558
Hirsch, J. 乙. (2005). An index to quantify an individual’s scientific
research output. 美国国家科学院院刊
科学, 102(46), 16569–16572. https://doi.org/10.1073/pnas
.0507655102, 考研: 16275915
胡, Z。, 陈, C。, & 刘, Z. (2013). Where are citations located in
the body of scientific articles? A study of the distributions of cita-
tion locations. Journal of Informetrics, 7(4), 887–896. https://土井
.org/10.1016/j.joi.2013.08.005
琼斯, 时间. H。, & Hanney, S. (2016). Tracing the indirect societal
impacts of biomedical research: Development and piloting of a
technique based on citations. Scientometrics, 107(3), 975–1003.
https://doi.org/10.1007/s11192-016-1895-4, 考研: 27340306
国王, D. A. (2004). The scientific impact of nations. 自然, 430(6997),
311–316. https://doi.org/10.1038/430311a, 考研: 15254529
刘, L。, 王, Y。, Sinatra, R。, 贾尔斯, C. L。, 歌曲, C。, & 王, D.
(2018). Hot streaks in artistic, 文化, and scientific careers.
自然, 559(7714), 396. https://doi.org/10.1038/s41586-018
-0315-8, 考研: 29995850
刘, S。, & 陈, C. (2012). The proximity of co-citation. Scientometrics,
91(2), 495–511. https://doi.org/10.1007/s11192-011-0575-7
Lü, L。, 陈, D ., Ren, X.-L。, 张, Q.-M., 张, Y.-C., & 周, 时间.
(2016). Vital nodes identification in complex networks. Physics
报告, 650, 1–63. https://doi.org/10.1016/j.physrep.2016.06.007
Lü, L。, & 周, 时间. (2011). Link prediction in complex networks:
一项调查. Physica A: Statistical Mechanics and its Applications,
390(6), 1150–1170. https://doi.org/10.1016/j.physa.2010.11.027
Moravcsik, 中号. J。, & Murugesan, 磷. (1975). Some results on the
function and quality of citations. Social Studies of Science, 5(1),
86–92. https://doi.org/10.1177/030631277500500106
纽曼, 中号. (2010). 网络: An introduction. 纽约:
牛津大学出版社. https://doi.org/10.1093/acprof:oso
/9780199206650.001.0001
Price, D. J. D. S. (1965). Networks of scientific papers. 科学,
149(3683), 510–515. https://doi.org/10.1126/science.149.3683
.510, 考研: 14325149
Radicchi, F. (2012). In science “there is no bad publicity”: 文件
criticized in comments have high scientific impact. Scientific
报告, 2(1), 1–5. https://doi.org/10.1038/srep00815, 考研:
23139864
Radicchi, F。, Fortunato, S。, & Castellano, C. (2008). Universality of
citation distributions: Toward an objective measure of scientific
impact. 美国国家科学院院刊,
1 0 5 ( 45 ) , 1 7 2 68 –1 7 2 72 . h t t p s : / / d o i . o rg / 1 0. 1 0 7 3/ p n a s
.0806977105, 考研: 18978030
Radicchi, F。, Ramasco, J. J。, & Fortunato, S. (2011). 信息
filtering in complex weighted networks. Physical Review E,
83(4), 046101. https://doi.org/10.1103/ PhysRevE.83.046101,
考研: 21599234
Redner, S. (2005). Citation statistics from 110 years of Physical
审查. Physics Today, 58(physics/0506056), 49. https://doi.org
/10.1063/1.1996475
Revesz, 磷. Z. (2015). Data mining citation databases: A new index
measure that predicts Nobel Prizewinners. 诉讼程序
19th International Database Engineering & Applications Sympo-
sium. https://doi.org/10.1145/2790755.2790763
Sarol, 中号. J。, 刘, L。, & 施耐德, J. (2018). Testing a citation and
text-based framework for retrieving publications for literature
reviews. CEUR Workshop Proceedings, 2080, 22–33.
Serrano, 中号. Á., Boguná, M。, & Vespignani, A. (2009). Extracting the
multiscale backbone of complex weighted networks. 会议记录
of the National Academy of Sciences, 106(16), 6483–6488. https://
doi.org/10.1073/pnas.0808904106, 考研: 19357301
沉, H.-W., & 巴拉巴斯, A.-L. (2014). Collective credit allocation
in science. 美国国家科学院院刊,
111(34), 12325–12330. https://doi.org/10.1073/pnas.1401992111,
考研: 25114238
Simkin, 中号. 五、, & Roychowdhury, V. 磷. (2002). Read before you cite!
arXiv preprint cond-mat/0212043.
Sinatra, R。, 王, D ., Deville, P。, 歌曲, C。, & 巴拉巴斯, A.-L. (2016).
Quantifying the evolution of individual scientific impact. Sci-
恩斯, 354(6312), aaf5239. https://doi.org/10.1126/science
.aaf5239, 考研: 27811240
小的, H. (1973). Co-citation in the scientific literature: A new mea-
sure of the relationship between two documents. Journal of the
American Society for Information Science, 24(4), 265–269.
https://doi.org/10.1002/asi.4630240406
Tahamtan, 我。, & Bornmann, L. (2018). Creativity in science and the
link to cited references: Is the creative potential of papers
reflected in their cited references? Journal of Informetrics, 12(3),
906–930. https://doi.org/10.1016/j.joi.2018.07.005
Uzzi, B., Mukherjee, S。, Stringer, M。, & 琼斯, 乙. (2013). Atypical
combinations and scientific impact. 科学, 342(6157),
468–472. https://doi.org/10.1126/science.1240474, 考研:
24159044
Waltman, L. (2016). A review of the literature on citation impact
指标. Journal of Informetrics, 10(2), 365–391. https://土井
.org/10.1016/j.joi.2016.02.007
王, D ., & 巴拉巴斯, A.-L. (2021). The science of science. 凸轮-
桥, 嘛: 剑桥大学出版社. https://doi.org/10.1017
/9781108610834
王, D ., 歌曲, C。, & 巴拉巴斯, A.-L. (2013). Quantifying
long-term scientific impact. 科学, 342(6154), 127–132.
https://doi.org/10.1126/science.1237825, 考研: 24092745
方式, S. F。, 摩根, A. C。, Larremore, D. B., & Clauset, A. (2019).
生产率, 突出, and the effects of academic environ-
蒙特. 美国国家科学院院刊, 116(22),
10729–10733. https://doi.org/10.1073/pnas.1817431116,
考研: 31036658
吴, L。, 王, D ., & 埃文斯, J. A. (2019). Large teams develop and small
teams disrupt science and technology. 自然, 566(7744), 378–382.
https://doi.org/10.1038/s41586-019-0941-9, 考研: 30760923
Wuchty, S。, 琼斯, 乙. F。, & Uzzi, 乙. (2007). The increasing dominance
of teams in production of knowledge. 科学, 316(5827),
1036–1039. https://doi.org/10.1126/science.1136099, 考研:
17431139
Zakhlebin, 我。, & Horvát, E.-Á. (2017). Network signatures of
成功: Emulating expert and crowd assessment in science,
艺术, 和技术. 在: C. Cherifi, H. Cherifi, 中号. Karsai, & 中号.
Musolesi (编辑。), Complex Networks & Their Applications VI.
COMPLEX NETWORKS 2017. 施普林格, 占婆. https://doi.org
/10.1007/978-3-319-72150-7_36
朱, X。, 特尼, P。, Lemire, D ., & Vellino, A. (2015). 测量
academic influence: Not all citations are equal. Journal of the
Association for Information Science and Technology, 66(2),
408–427. https://doi.org/10.1002/asi.23179
Quantitative Science Studies
330
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
3
2
3
1
9
2
0
3
1
9
0
0
q
s
s
_
A
_
0
0
1
8
6
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3