RESEARCH ARTICLE
How cumulative is technological knowledge?
Peter Persoon
, Rudi Bekkers
, and Floor Alkemade
School of Innovation Sciences, Eindhoven University of Technology
关键词: cumulativeness, 知识, 技术, patents, 网络
开放访问
杂志
抽象的
引文: Persoon, P。, Bekkers, R。, &
Alkemade, F. (2021). How cumulative is
technological knowledge? Quantitative
Science Studies, 2(3), 1092–1118.
https://doi.org/10.1162/qss_a_00140
DOI:
https://doi.org/10.1162/qss_a_00140
Peer Review:
https://publons.com/publon/10.1162
/qss_a_00140
支持信息:
https://doi.org/10.1162/qss_a_00140
已收到: 18 十一月 2020
公认: 10 行进 2021
通讯作者:
Peter Persoon
p.g.j.persoon@tue.nl
处理编辑器:
Ludo Waltman
版权: © 2021 Peter Persoon, Rudi
Bekkers, and Floor Alkemade.
在知识共享下发布
归因 4.0 国际的
(抄送 4.0) 执照.
麻省理工学院出版社
Technological cumulativeness is considered one of the main mechanisms for technological
进步, yet its exact meaning and dynamics often remain unclear. To develop a better
understanding of this mechanism, we approach a technology as a body of knowledge consisting
of interlinked inventions. Technological cumulativeness can then be understood as the extent
to which inventions build on other inventions within that same body of knowledge. 这
cumulativeness of a technology is therefore characterized by the structure of its knowledge base,
which is different from, but closely related to, the size of its knowledge base. We analytically
derive equations describing the relation between the cumulativeness and the size of the
knowledge base. 此外, we empirically test our ideas for a number of selected technologies,
using patent data. Our results suggest that cumulativeness increases proportionally with the size
of the knowledge base, at a rate that varies considerably across technologies. 此外, this rate
is inversely related to the rate of invention over time. This suggests that cumulativeness increases
relatively slowly in rapidly growing technologies. 总共, the presented approach allows for an
in-depth, systematic analysis of cumulativeness variations across technologies and the knowledge
dynamics underlying technology development.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
1.
介绍
Technology progresses when engineers adapt their designs based on learning about previous
designs. 最后, a key element of theories of technological change is the cumulative
nature of knowledge and invention: the idea that new results build on – or recombine – previous
结果 (Basalla, 1989; 弗里曼 & Soete, 1997; 纳尔逊 & 冬天, 1982; Trajtenberg, Henderson,
& Jaffe, 1997). 的确, many of today’s technologies have rich histories of development, 一些
going back all the way to antiquity. Although the size of the knowledge base of these technol-
ogies is substantial, this does not necessarily imply that the underlying knowledge structure is
cumulative: A pile of stones is different from a stone wall, and some walls are higher than others.
Cumulativeness (or sometimes “cumulativity”) may therefore vary per technology and over
时间. A better understanding of the underlying mechanisms of technological cumulativeness is
important for a number of reasons. From an economics perspective, the extent to which a tech-
nology develops in a cumulative manner has implications for how easy it is to enter or diversify
into that technology. Entry is considered more difficult in complex technologies that require
extensive and in-depth knowledge about the underlying principles (Breschi, 2000; Breschi,
How cumulative is technological knowledge?
Malerba, & Orsenigo, 2000; 冬天, 1984). Recent contributions from the geography of inno-
vation describe how regions are more likely to diversify into technologies that are related to
their existing knowledge base (Balland, 2016; Balland & Rigby, 2017; Boschma, Balland, &
Kogler, 2015). An understanding of the cumulative nature of technological development is thus
pivotal for ongoing efforts of smart specialization (Foray, 2014), where regions seek out attrac-
tive technologies for future specialization. From a philosophical perspective, a better under-
standing of cumulativeness and its role in the evolution of technological knowledge (Arthur,
2009) may help to clarify the relation between knowledge accumulation and the complexity
of that knowledge, which is an ongoing discussion in the “cumulative culture” literature (院长,
Vale et al., 2014; Tennie, Call, & Tomasello, 2009; Vaesen & Houkes, 2017). Developing this
understanding starts from a clear definition and measure of cumulativity.
出奇, despite the recognized importance of cumulativity, the exact meaning of the
concept often remains unclear. Characterizations vary from the incremental change in artifacts
(Basalla, 1989; 管家, 2014; Gilfillan, 1935乙; Ogburn, 1922), to the persistence of innovative
活动 (Cefis, 2003; Malerba & Orsenigo, 1993; Suárez, 2014), to the building of technolo-
gical knowledge on earlier findings (Enquist, Ghirlanda, & Eriksson, 2011; Merges & 纳尔逊,
1994; Scotchmer, 1991; Trajtenberg et al., 1997).
In this contribution we aim to develop a better understanding of technological cumulative-
ness by taking the following steps: 在部分 2 we present a comprehensive review of the various
perspectives on cumulativeness and identify their common grounds. 在部分 3 we use this
analysis to formulate two indicators that measure cumulativeness: the internal dependence
and internal path length. 在部分 4 we then discuss how the values of these indicators are
expected to change as a technology develops. 在部分 5 we test these expectations empiri-
cally for a number of technologies, using patent data as a proxy for inventions. 最后, we dis-
cuss some deeper implications of our contribution to the understanding of technological
cumulativeness in Section 6 and summarize our main conclusions in Section 7.
2. THEORETICAL PERSPECTIVES ON TECHNOLOGICAL CUMULATIVENESS
Where in most texts cumulative simply means “summed up,” in the innovation literature, 这
term has come to represent a type of technological development. Perspectives on cumulative
technological development however vary across contributions.
The earliest ideas about technological cumulativeness arise in studies of the gradual change
in pre-20th century artifacts (管家, 2014; Gilfillan, 1935A; Pitt-Rivers, 2018), which are remi-
niscent of fossil records of gradually evolving species. Inspired by evolutionary theory, 这些
theories understand technological change as a process in which antecedent artifacts are repli-
cated with incremental modifications, thereby creating descendant artifacts (Gilfillan, 1935乙;
Ogburn, 1922). In this first perspective, artifacts are literally the sum of many incremental
modifications, justifying the term cumulative.
Although the cumulative aspect of technology arises naturally in this perspective, 目前还不清楚
when a development is not cumulative: As in genetic lineage, each descendant is supposed to have
an antecedent. Some authors have argued that in reality, technological developments occasionally
“jump”; when a radical finding breaks fundamentally with past engineering practices and ideas
(Schoenmakers & Duysters, 2010; Verhoeven, Bakker, & Veugelers, 2016) it may initiate a new
model of solutions to selected technological problems (IE。, a new technological paradigm (Dosi,
1982)). In this second perspective, cumulative development is the opposite of radical development,
and interpreted as the incremental change happening within a technological paradigm.
Quantitative Science Studies
1093
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
然而, to base cumulative change solely on the notion of incremental change raises two diffi-
culties. 第一的, there is a certain arbitrariness to when a change is incremental or not. Depending
on context and knowledge of the subject, different people may characterize incrementality dif-
ferently. 第二, even if the change from an antecedent to descendant is radical, the antecedent
may still be of crucial importance to the formation of the descendant (Basalla, 1989).
These difficulties are sidestepped in a third perspective, where a development is cumulative
if a later result depends or builds on an earlier result (Breschi et al., 2000; Enquist et al., 2011;
Merges & 纳尔逊, 1994; Trajtenberg et al., 1997). “Dependence” or “dependency” is here
interpreted in the context of technology as a body of knowledge, where new technological
ideas or inventions (the “results”) draw on earlier insights, and are themselves used in later
ideas and inventions. Note that in this perspective, cumulativeness is a property of the devel-
选项 (not of one of the results). If we are interested in the cumulativeness of a technology,
we therefore consider all developments within that technology (IE。, all dependencies between
results that are part of that technology). 或者, authors have studied the cumulativeness
of the union of multiple (or all) 技术 (Acemoglu, Akcigit, & Kerr, 2016; Clancy, 2018;
Napolitano, Evangelou et al., 2018), thereby focusing on intertechnology developments or
dependencies. Both approaches are relevant to better understand the advancement of tech-
nology and knowledge production. 在这项工作中, 然而, we focus on the former approach,
as we are mainly interested in the question of to what extent cumulativeness is an intrinsic
property of a technology, and how this property varies for different technologies.
The relevance of cumulativeness as an intrinsic property of a technology is reflected by its
role as a defining element of a technological regime (纳尔逊 & 冬天, 1982), which defines the
relevant circumstances under which innovating firms or organizations compete, thrive, or fail.
Within a technological regime, higher cumulativeness is associated with greater appropriability
of innovation and greater (geographical) concentration of innovative activity (Breschi et al.,
2000; Malerba & Orsenigo, 1996; 冬天, 1984). The framework of technological regimes gave
rise to a number of contributions which use yet another perspective of cumulativeness, 在哪里
the emphasis is not so much on the dependence of later generations of a technology on earlier
那些, but more on the continuation of those generations (Apa, De Noni et al., 2018; Breschi,
2000; Cefis, 2003; Frenz & Prevezer, 2012; Hölzl & Janger, 2014; Malerba, Orsenigo, &
Peretto, 1997). Cumulativeness is then characterized by the persistence of inventive and inno-
vative activity in a technology: The longer a development continues (without significant inter-
破裂), the greater the cumulativeness. Where previous perspectives focus more on
cumulativeness as an intrinsic property of technology, this fourth perspective also attributes a
role to the creators of the technology (and their persistence to continue along a given path).
总之, we identify from these four different perspectives the key notions of technolo-
gical cumulativeness: (A) as replication with incremental modifications, (乙) as within-paradigm
(opposite to radical) 发展, (C) as dependence or building on earlier technology and (d) 作为
persistence of inventive or innovative activity. The first two perspectives approach cumulative-
ness as “incremental change”; the latter two perspectives approach cumulativeness as “contin-
uous dependence” of technology on earlier generations of technology. Though apparently very
不同的, there are similarities between incremental change and continuous dependence.
Incremental change supposes a series of modifications to what is, in some sense, a single object
(often pictured as an artifact). 相似地, continuous dependence supposes a series of
dependencies between objects which are, in some sense, 不同的 (often pictured as a set
of inventions). 本质上, 所以, the discrepancy is about the object(s) to which a series of
changes is applied, yet both advocate the relevance of a series of developmental steps. 更远,
for both incremental change and continuous dependence, cumulativeness appears in two
Quantitative Science Studies
1094
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
方面: (A) the size of each developmental step: If the modification is small (dependence is
great), the cumulativity is large; 和 (乙) the number of steps in the process: If there are many small
modifications (a long chain of dependency links) the cumulativity is large. 虽然 (A) 和 (乙)
both relate to cumulativity, they are theoretically very different, and we shall henceforth refer to
them as the transversal and longitudinal dimensions of cumulativity respectively. Although both
dimensions can be meaningfully interpreted in all four cumulativeness perspectives, 它出现
that the first two perspectives focus more on the transversal dimension and the latter two per-
spectives more on the longitudinal dimension. In the next section we will propose a separate
indicator for each dimension. We emphasize that both are measured within a certain technolo-
gical field or technology. Although the interaction between multiple fields or technologies is
interesting and worth studying, the focus of this work is on understanding these cumulativeness
dimensions within a single technology.
最后, we discuss the relation between technological cumulativeness and complexity. 在
this contribution, we will not enter the discussion about the exact meaning of technological
复杂 (for a good overview see Vaesen & Houkes, 2017), but instead work with the gen-
eral description of a complex system consisting of many, nontrivially interacting subsystems
(西蒙, 1962). One way to interpret this in the context of technology, is to consider an inven-
tion to be a system consisting of subsystems, 哪个是 (parts of ) other inventions or borrowed
ideas. The complex character of an invention is therefore in an abstract sense captured by the
transversal dimension of cumulativeness, which focuses on these direct dependencies.
直观地, the more subsystems and dependencies, the greater the complexity (although this
strongly depends on the chosen measure for complexity). 然而, this is not the entire story.
A relevant criterion for increasing complexity in the context of evolutionary systems is that a
representative sample of lineages of descent increases in complexity (McShea, 1991; Vaesen
& Houkes, 2017). Not only therefore should “more complex” systems appear in time, but these
should also fit into the lines connecting antecedents and descendants. In the context of tech-
nological knowledge, the lines of descent appear rather literally in the mentioned first perspec-
tive of cumulativeness, and correspond to the longitudinal dimension of cumulativeness. 在
articular, the joint consideration of the transversal and longitudinal dimensions of cumulative-
ness therefore allows us to study the dynamics of technological complexity.
3. MEASURING CUMULATIVENESS
In most contributions mentioning cumulative technological development, cumulativeness
remains an abstract property without explicit measure. There are a number of exceptions, 如何-
曾经, in particular the contributions adhering to the earlier mentioned “persistence perspective”
of cumulativeness. These contributions base their measures of cumulativeness on a variety of
来源: survey data (Breschi et al., 2000; Frenz & Prevezer, 2012; Hölzl & Janger, 2014),
licensing data (李, 公园, & Bae, 2017), and statistical properties of patent count time series
(Breschi, 2000; Cefis, 2003; Malerba et al., 1997). Although all of these highlight interesting
aspects of cumulative processes, none of them seem to directly proxy the key property of
knowledge building on knowledge. Survey data may offer detailed information on usage of
particular knowledge, yet it is challenging to quantify and generalize this information to com-
pare different technologies. Approaches based on counting backward citations (Apa et al.,
2018) arguably do measure the extent to which knowledge builds on earlier knowledge, 然而
without specifying which technologies are cited, only partially capture the underlying knowl-
edge structure of technologies. 然而, as was argued in the previous section, 去理解
technological cumulativeness along both the transversal and longitudinal dimensions, studying
the underlying knowledge structure is pivotal. In this contribution our starting point is to
Quantitative Science Studies
1095
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
interpret this structure as a network of interconnected elements of knowledge. Each node then
represents a single invention, and each link represents a knowledge flow. A link thus naturally
corresponds to a dependence, or knowledge building on other knowledge. This approach has
been successfully applied to the analysis of breakthrough innovation (Dahlin & 贝伦斯, 2005;
Fleming, 2001; Verhoeven et al., 2016), main paths (Hummon & Dereian, 1989; Verspagen,
2007), emerging technologies (Érdi, Makovi et al., 2013; Shibata, Kajikawa et al., 2009), 和
technological network evolution (Valverde, Solé et al., 2007). We denote the knowledge flows
to an invention (IE。, the links that indicate on which knowledge the invention builds) 作为
“backward links” and the knowledge flows from an invention as “forward links.”
更远, we assume that there is a technology classification that allows us to assign each inven-
tion to at least one class, hence allowing us to distinguish between internal links (link to an invention
in the same class) and external links (link to an invention of another class)1. In the previous section
we introduced the transversal and longitudinal dimensions of cumulativeness. By exploiting useful
network structures, we will in the next two subsections introduce two indicators measuring the
cumulativeness along these dimensions. For the transversal dimensions we introduce the internal
dependence and for the longitudinal dimension we introduce the internal path length.
3.1. The Transversal Dimension: Internal Dependence
The transversal dimension of cumulativeness reflects the extent to which findings in a given
technology depend on other findings within that technology. In a network of inventions, each
directed link can rather literally be interpreted as a relation of dependence. 理想情况下, we would go
into the content of each knowledge link to distinguish a degree of dependence. Yet this approach
would be difficult to automate when the number of links and inventions becomes large (这是
the case for most technologies). Most network approaches to technology therefore count each
knowledge link equal, so the number of internal links becomes a measure for the dependence.
Each invention that is added to the technology introduces a number of backward internal links:
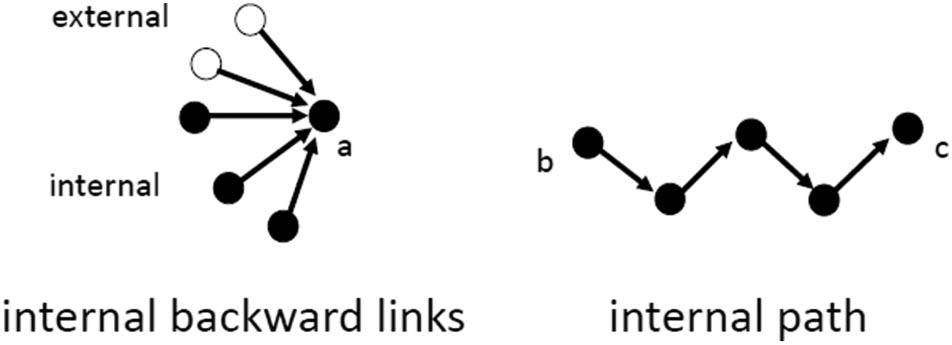
见图 1 (left panel) for a network illustration. The more internal backward links it introduces,
the more the technology builds on itself. As a measure for the transversal dimension, we there-
fore define the internal dependence (id ) of a technology as the average number of backward
internal links per invention. A high id signals high cumulativity in the transversal dimension.
3.2. The Longitudinal Dimension: Internal Path Length
The longitudinal dimension of cumulativity reflects the number of steps in a series of technolo-
gical developments. Approaching technology as a network of inventions, we can translate this
rather literally to a chain of internal inventions connected by links, which translates to the notion
of a “path” in the terminology of network analysis; 见图 1 (right panel) for a network illus-
翻译. The longer the internal paths, the longer a series of developments within a technology is
continued. As multiple knowledge aspects of a technology may develop in parallel, we gener-
ally deal with several, intertwined paths. As a measure for the longitudinal dimension, we there-
fore define the internal path length (ipl ) of a technology as the average length of all paths within
that technology. A high ipl signals high cumulativity in the longitudinal dimension2.
1 Inevitably, there is some room for interpretation here as there can be various grounds on which technologies
are classified. 在部分 6 we discuss a number of alternative approaches to making the external–internal
distinction.
2 Similar ideas are presented in Frenken, Izquierdo, & Zeppini (2012), where innovations attain “higher
quality” with longer path lengths. The study of Frenken et al., which is based on numerical simulations,
thereby focuses on the (关于)combination principle in relation to diffusion.
Quantitative Science Studies
1096
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
数字 1. Useful network structures. 左边: The number of internal backward links of node a is 3.
正确的: the length of the internal path between node b and c is 4. For a precise definition of path and
path length we refer to Section 4.3.
4. MODELING THE KNOWLEDGE DYNAMICS
In this section we discuss how the values of the internal dependence (id) and internal path
length (ipl) are expected to change as a technology develops (IE。, when the size of its knowl-
edge base increases). 进一步来说, we analyze (A) how the id and ipl change as the num-
ber of inventions increases and (乙) how the id and ipl are interrelated. We thereby describe
both general and technology-specific elements.
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
4.1.
Invention as Search Process
In this section we sketch a highly simplified model of the invention process in a certain tech-
科学, which consists of an inventor performing a series of searches. 本质上, the inventor
searches until he or she succeeds in completing an invention, where a knowledge flow (equiva-
lent to a backward internal link) is picked up along with each search. The relevant quantity in
this process is the probability ρ of completing an invention before performing another search,
which may depend on the size of the knowledge base of a technology, as measured by the
number of inventions n. For each n, the probability of inventing is therefore ρ(n), 概率
for performing a search is 1 − ρ(n). We have two main assumptions in this model:
1. The probability ρ(n) decreases proportionally with the number of inventions n. This reflects
the intuition that it becomes harder, as a technology develops, to produce an invention
without using any prior knowledge developed in that technology. 换句话说, 这
inventor needs to consider some knowledge in a certain field before delivering a contri-
bution to that field, and the larger the field, the more the inventor needs to consider.
2. The probability of success is independent of the number of searches: In the invention
过程, there is no guarantee that a certain amount of effort will lead to success.
1
Given these assumptions, we may write down for the probability ρ(n) =
qnþm1, introducing
the technology specific constants q > 0 and m1 > 1. 这里, the parameter m1 describes the need
to have knowledge of the technology to invent at the initial stage of this technology, and q
describes how fast this need increases as the technology develops. As a consequence of the
two assumptions, the probability for a node to have m backward internal links (IE。, 问题-
ability that m searches take place before invention) is given by Pn(米) = (1 − ρ(n))mρ(n) (IE。, 这
number of backward internal links per node is distributed geometrically)3. This distribution is
characterized by a highly skewed shape towards lower values of m, yet as n increases, 它
slowly becomes less skewed.
3 We then assume that the number of backward links per node stays well below n, which appears to be
reasonable if we consider technologies with large n.
Quantitative Science Studies
1097
How cumulative is technological knowledge?
The rate q is related to the type of technological knowledge and we therefore assume it is a
technology-specific quantity. Yet we hypothesize that it is also related to the rate of invention
随着时间的推移. Our reasoning is as follows. If the rate of invention over time is high, this means that
more people work on the same technology at the same time. If multiple researchers work on
the same technology, they tend to specialize, focusing only on a particular subfield or subpart
of the technology. As an effect, multiple aspects of the technology develop in parallel, 也许
more so than if a smaller group of people had worked on it. As a result the development of the
technology is more fragmented into subfields, which causes inventors active in these subfields
to focus on the relevant findings within their subfield. We may therefore suppose that there is
structurally less need for these inventors to master the entire knowledge base, which leads to
lower values of q. In reverse, it is possible that a low need for prior knowledge of a technology
accelerates innovative activities in a technology, as it may then be more easily accessible, 因此
inviting more people to contribute. Deriving a more precise form and causal direction of the
inverse relation between q and rate of inventing over time, 然而, is beyond the scope of
this work. For a more elaborate discussion of the causality, we refer to Section 6.
4.2.
Internal Dependence Dynamics
磷
Using the distribution of the number of backward internal links, we can calculate hmi =
n
m¼0
mPn(米), the expected value of the number of backward internal links per invention (IE。, 这
internal dependence (id)). Assuming that n is large, we can approximate this sum by choosing
infinity for the upper limit and using the expression Pn(米) = (1 − ρ(n))mρ(n), obtaining
mh
i ¼
1
ρ nð Þ
−1 ¼ qn þ m1 − 1 ¼ qn þ m0;
(1)
- 1 for convenience. We therefore conclude that the id is expected to
introducing m0 = m1
increase proportionally with the number of inventions (IE。, with the size of the knowledge base),
where the rate can by approximated by q for a large number of inventions. This technology-
specific coefficient q describes how fast the need to have specialized knowledge increases to
produce an invention in that technology.
4.3.
Internal Path Length Dynamics
Next we will discuss how we expect the internal path length (ipl) to depend on the number of
inventions. Although these results can be generalized by including external links, we focus in this
contribution for simplicity on the role of internal links. A new invention creates at least one new
path with each of its internal backward links. The internal dependence, besides measuring a com-
plementary dimension of cumulativity, therefore also plays a key role in the ipl dynamics. 让我们
again consider a technology with n inventions, where the nth invention has on average hmi inter-
nal backward links. Some inventions, 然而, will have no backward links, which we will refer
to as initial inventions. As a first assumption, we take that the number of initial inventions n0 is a
fixed fraction r of n (IE。, n0 = rn)4. We use the initial inventions to define a path and path length:
(西德:129) A path is a sequence of inventions i0, i1, ……, ik in which for any k ≥ 0 and x > 0, ix has a
backward link to invention ix−1 and i0 is an initial invention.
(西德:129) The path length of path i0, i1, ……, ik is k.
4 As we explain in more detail in the supplementary material this assumption is compatible with the found
backward link distribution if q is small compared to m0; we then have that r (西德:2) 1/(m0 + 1).
Quantitative Science Studies
1098
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
We denote the number of paths of length k by fk(n). From the first assumption5, 我们有
那, f0(n) = rn. As a second assumption, each invention is equally likely to be used as prior
knowledge with probability 1
n. Let us consider what happens to fk(n) for k > 0 when we
introduce the (n + 1)th invention. If that invention builds on a prior invention i that has li,k−1
paths of length k − 1, each of these paths will increase by 1, hence fk(n) increases by li,k−1.
i li,k−1 = fk−1(n) paths of length k − 1. 为了
This holds for all inventions, which in total have
Δnfk(n) (IE。, the expected increase in fk(n) from n to n + 1), we therefore have Δnfk(n) / fk−1(n),
and for k > 1 我们有
磷
Δnfk nð Þ ¼ mh
i fk−1 nð Þ
n
:
(2)
In the previous section we established that hmi (西德:2) qn + m0. When n gets large, hmi/n → q, 更远
reducing Eq. 2 到
Δnfk nð Þ ¼ qfk−1 nð Þ:
(3)
As there are no paths for n = 0, we take that fk(0) = 0 for all k. Using this initial condition and the
expression for f0(n), the solution to Eq. 3 is derived to be
(西德:3)
(西德:2)
fk nð Þ ¼ rqk
n
k þ 1
;
(4)
(西德:2) (西德:3)
X
y
在哪里
is the binomial coefficient. The steps leading to this solution and later ones are
explained in more mathematical detail in the supplementary material. Summing over all k we
k¼0 fk (n) = r(1 + q)n/q − r/q. The total number of paths is
obtain the total number of paths
therefore expected to increase exponentially in n. For the normalized path length distribution
e
f k(n), describing the probability to have a path of length k, we subsequently obtain
(西德:2)
磷
(西德:3)
n
e
f k nð Þ ¼
n
k þ 1
qkþ1
ð
1 þ q
Þn − 1
;
(5)
which is a distribution closely related to the binomial distribution. This indicates that as n
增加, the path length distribution will shift from a skewed shape towards a more
symmetric, parabolic shape (on a log scale) and its maximum, the most frequent path length,
will continuously shift to higher values. 随后, we can calculate the expected path
length hki =
磷
n
k¼0 k
e
f k(n) (IE。, the ipl), which reduces for large n to
kh i (西德:2) q
q þ 1 n þ k0;
(6)
where k0 is some constant value. As we focus on large n behavior, we are less interested in this
持续的. What is more important is the expectation that the ipl increases proportionally with the
number of inventions, by a rate p = q/(q + 1). This rate p is a number between 0 和 1: For large q
it is close to 1 and for small q, it is close to q. We end this section by mentioning two extensions
of the model which improve its explanatory power.
(西德:129) In this derivation, we assumed that hmi/n (西德:2) q, even though we know that it in fact only
approaches q for large n. This approximation can be significantly improved by instead
calculating the average hmi/n for n inventions. We can determine this quantity in two
5 If we also consider external inventions, we can choose a more general definition, where a path can also start
at an external invention. 注意, ignoring the links to external inventions, the inventions which only link to
external inventions become initial inventions.
Quantitative Science Studies
1099
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
方法: (A) by directly using the data of the number of backward links for each invention
磷
(IE。, by calculating q0
n
i mi /i where mi is the number of backward links of
a = 1/n
invention i); 和 (乙) by using estimates for parameters in the relation hmi = m0 + nq
磷
(IE。, calculating q0
n
i q + m0 /i = q + m0H(n)/n, where H(n) is the nth harmonic
b = 1/n
数字). Analogous to Eq. 6, we then have q0
乙. p0
a is likely
to be more accurate as it is more directly based on the backward link data, yet p0
b is less
sensitive to outliers in this data. Both predictions should, 然而, be close to one
其他. Note that this correction depends proportionally on m0.
a and similar for p0
a/(1 + q0
A) = p0
(西德:129) 方程 2 implies that as we add the nth invention to the system, the number of paths of
length n increases from 0 to some positive value. 实际上, this equation therefore establishes a
“maximum speed” v of one path length per invention, faster than which the path lengths
cannot increase. This maximum speed is rather lenient: Technologies with paths increasing
with one length per invention (IE。, forming perfect chains) would be highly unrealistic.
Although Eq. 2 is accurate for the more frequent path lengths (IE。, the lengths close to the
意思是), it may therefore be less accurate for the less frequent path lengths (IE。, the shortest
and longest lengths). A more realistic estimate of the maximum speed v may therefore
help establish a better description of the overall distribution of path lengths. Let us suppose
that we at once add δn inventions to the system which do not connect among themselves,
and of which the total added number of backward links is M(n). Eq. 2 then becomes
ð
fkþ1 n þ δn
Þ − fkþ1 nð Þ ¼ M nð Þ fk nð Þ
n
(7)
If we choose δn such that M(n) (西德:2) n, then each of the n inventions in the system approxi-
mately obtains one forward link. This implies that all paths in the system increase on
average by 1, including the longest path(s). δn therefore defines a typical interval for
the longest path to increase by 1, and 1/δn therefore presents a more reasonable estimate
for the maximum speed v. We will use this idea to derive a new expression for the path
length distribution. Note that Eq. 7 then becomes
0
If we introduce the variable n
relation as f 0
+ 1) − f 0
using the condition that f 0
0
kþ1(n
0
k(n
0
kþ1(n
ð
fkþ1 n þ δn
Þ − fkþ1 nð Þ ¼ fk nð Þ:
= n/δn and the function f 0
) = f 0
0
k(n
), which is solved by f 0
0
k(n
(西德:2)
) = fk(n), we may write this
n0
k þ 1
0
) = r
k(n
(this time
(西德:3)
0
) = 0 for k < n
= nv). This leads to the normalized distribution
(cid:2)
(cid:3)
0
e
0ð
f
k n
Þ ¼
1
2n0 − 1
n0
k þ 1
and expected path length (i.e., the ipl)
kh i0 (cid:2) n0
2
þ k
0
0;
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
a
_
0
0
1
4
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
(8)
(9)
(10)
where k0
0 is again a constant we are less interested in. Rewriting this expression in terms of
n gives the coefficient 1
2, describing how fast the ipl increases with n. Assuming that
the earlier analysis with a greater maximum speed is accurate for the mean path length
values, this should coincide with the earlier established coefficient p. We can therefore
approximate the maximum speed as v (cid:2) 2p6. This implies that the paths with maximum
2δn or v
6 This is consistent with the earlier assertion that M(n) (cid:2) n. To see this, note that the total number of links is
nhmi (as hmi is an average), hence between n and n + δn we add δn(m0 + q(δn + 2n)) links. For this to equal n
in the limit where n becomes large, we require δn → 1
2q. In the same limit, p → q/(q + 1), which is approxi-
mately q for small q. This is therefore consistent with 1
δn = v (cid:2) 2p.
Quantitative Science Studies
1100
How cumulative is technological knowledge?
length grow about twice as fast as paths with mean length (i.e., the distribution becomes
0
more symmetric as n increases). Noting that n
as the maximum path
length after n inventions, which can be used to evaluate Eq. 9. Alternatively, we use the
expression for v = 2p to rewrite this expression in terms of n and p,
0
= nv, we identify n
e
f k nð Þ ¼
1
4pn − 1
(cid:2)
(cid:3)
2pn
k þ 1
:
(11)
5. EMPIRICAL ANALYSIS
In this section we empirically test the models developed in Section 4 using patent and patent
citation data. First, we discuss our type of data and a number of limitations of these data.
Subsequently, we perform the analysis on three different levels: First we consider the develop-
ment and distributions of both cumulativeness indicators for four focus technologies in detail.
Second, we consider the relation between the two indicators and the consistency of the indica-
tors, using a larger set of technologies. Third, we choose a more aggregated level of technology
classification to obtain a more general overview of the cumulativeness variation across different
technological fields, which also allows us to compare our findings to earlier results from the
literature and to some extent validate the indicators.
5.1. Data Description
To study the knowledge dynamics empirically, we need some codification of that knowledge.
Patents are an important codification of technological knowledge, as each patent is a detailed
description of a new, nontrivial technological development. Furthermore, patent systems have
two elements that allow us to study technological content without necessarily having to consider
the detailed meaning of each individual patent. The first element is that of patent citations, which
identify one-to-one directional content relations between patents. This enables us to study the
flow of knowledge ( Jaffe, 1989; Jaffe, Trajtenberg, & Henderson, 1993). The second element is
that of the patent classifications, which hierarchically groups patents on the basis of their
content. This enables us to focus specifically on the development of a particular technology,
distinguishing between internal and external knowledge. A basic assumption of our work is that
cumulativeness is an intrinsic property of technology, which is independent of the way the
technology is patented. It is therefore important to keep in mind the limitations of representing
technological knowledge by patent data, which we will henceforth discuss. For each limitation
we mention how we attempt to account for it.
1. Not all technology is or can be patented (Jaffe & de Rassenfosse, 2017), and the “quality”
of patents (evaluated against the patentability requirements) varies (de Rassenfosse,
Griffiths et al., 2016; Jaffe & Lerner, 2004). In particular, when the number of patents
involved is small, without a detailed examination of the content we risk misrepresenting
a technology. In this analysis we therefore choose technologies for which the number of
patents is relatively large. Also, we only consider granted patents, which have withstood
the critical assessment of patent examiners.
2. Citations may not always represent actual knowledge flows (Criscuolo & Verspagen,
2008). Citations may be provided by inventors but may also be added by examiners,
and although the first may be more indicative of knowledge flow, the distinction was
not always documented by all patent offices (Azagra-Caro & Tur, 2018). We therefore
include an additional analysis in the supplementary material of the effect of both types
of citations (examiner or inventor added) to the knowledge dynamics.
Quantitative Science Studies
1101
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
q
s
s
/
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
a
_
0
0
1
4
0
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
How cumulative is technological knowledge?
3. There are institutional differences between patent offices around the globe, which may
affect the way inventions and linkages to prior art are documented (Bacchiocchi &
Montobbio, 2010). An important difference, for example, is the greater tendency to cite
in the United States patent system than in the European patent system (Criscuolo &
Verspagen, 2008), which may impact the value of our indicators. To account for these
differences we therefore do this analysis for patents from two different patent systems,
choosing the US system (organized by the US patent office USPTO) and European sys-
tem (organized by the European Patent Office EPO).
To aggregate patents of which the technological content is the same, we choose a patent
family as a basic unit or node, creating a US data set selecting families with at least one
USPTO member and a European data set selecting families with at least one EPO member7.
In the US data set each unique reference (backward citation) of a US member of each family to
any member of another family in our data set represents a unique link (hence we do not limit
our selection to US–US citations only)8. Our European data set is created analogously.
Henceforth by “US patent” we actually refer to a patent family containing a US member that
is granted, and similarly for “European patent” or “EP patent.”
To select and demarcate technologies, we used the Cooperative Patent Classification (CPC)
(CPC, 2018). In this analysis we consider technologies on two levels of classification: the CPC
group/subgroup level and a more aggregated level of classification. For the group/subgroup
analysiswe choose a set of 24 arbitrary technologies, yet making sure that (a) the set is diverse
(including technologies from each main CPC section and from mostly different subclasses) and
(b) each technology contains a reasonably large number of patents (for US >700 and EP >200).
桌子 1 and a more complete overview in the supplementary material indicate the CPC codes
and number of patents of these technologies. 桌子 1 singles out four “focus technologies,”
which we will analyze in more detail. The subselection of the focus technologies was made
by choosing considerable variation in (A) knowledge base size (where nuclear fission has
3,608 US patents, photovoltaics has over 9,000), (乙) 年龄 (where nuclear fission started devel-
oping in the 1960s, the main development of wind turbines starts from the 1990s), 和 (C) 这
在职的 (theoretical) principles behind the technologies (varying from nuclear physics to aero-
dynamics). From Table 1 it is clear there are generally more US than European patents, 甚至
taking into account that the EP patents do not go back further than 1978. As the column with
the number of patents in the same family indicates, most European patents (大约 75 每
分) have a US equivalent as well.
For the more aggregated level of classification we grouped together patent classes analo-
gous to the approach by Malerba and Orsenigo (1996). 然而, given that their publication
now dates more than 20 years back, and the patent classification system is subject to constant
改变, some differences between their grouping of classes and ours is inevitable9. In the sup-
plementary material we present an overview of our grouping; note that we take the union of
CPC classes (hence counting each patent once). The data in this research comes from the
Patstat 2019 spring edition. Time is not adopted as an explicit variable in our models, 然而
7 准确地说, we choose the DOCDB type of patent family, where all family members have exactly the
same priorities.
8 Note that if we had selected any family citation we effectively take the union of all citations, hence failing to
distinguish between the citing tendencies of different patent systems.
9 事实上, the CPC did not yet exist at the time of the Malerba and Orsenigo paper, yet the closely
related International Patent Classification (IPC) 做过.
Quantitative Science Studies
1102
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
桌子 1. Description of the four focus technologies. The selected patents have an earliest filing year <2009
Technology short name
Nuclear fission
CPC code
Y02E 30>100,000), we limit
this analysis to determining the id of these technological fields. We plot the id for the number
of patents for these fields for the US patents in Figure 9, where we also include a legend. 笔记
that the different icon colors correspond to the different CPC main sections. 数字 10 显示了一个
similar plot for the European patents.
For a deeper understanding of a technology’s cumulativeness, we again stress the need to
additionally consider the cumulativeness relative to the size of the knowledge base. 对于前-
充足, 图中 9, although the knowledge base size is similar for the field Packing &
Transporting and the field Optics & 摄影, the latter has reached a far greater level
of cumulativeness. 相似地, Nucleonics reaches the same cumulativeness level as Packing
& Transporting, although the knowledge base is about 15 times larger in the latter. The cumu-
lativeness therefore appears to increase faster with each patent for Nucleonics and Optics &
Photography than for Packing & Transporting. The expected increase in cumulativeness for the
knowledge base size is indicated by the fits (dashed line) in Figures 9 和 10 and may depend
on the level of classification. For this level of classification we can use these fits to distinguish
relatively high cumulativeness (above the line) from relatively low cumulativeness (below the
线). Using this distinction we see that for the US patents the fields belonging to CPC sections
Physics (red icons), Electricity (yellow icons), and Chemistry (purple icons) show relatively
high levels of cumulativeness. Fields belonging to the sections Human Necessities (棕色的
icons) and Performing operations & Transporting (blue icons) show relatively low levels of
cumulativeness. The larger fields in the sections Textiles (pink icons) and Fixed
Constructions (black icons) also show relatively low levels of cumulativeness.
The study by Malerba and Orsenigo (中号&氧) distinguishes a number of highly aggregated
technologies as Schumpeter Mark I (associated with low cumulativeness) and Schumpeter
Mark II (associated with high cumulativeness). Our observations are in overall agreement with
the general conclusion of M&O that
Schumpeter Mark I technological classes are to be found especially in the “traditional”
部门, in the mechanical technologies, in instruments as well as in the white electric
行业. 反过来, most of the chemical and electronic technologies are characterized
by the Schumpeter Mark II model12.
To make a more detailed comparison, we individually consider 23 technological fields that
occur in both M&O and our own set of fields and which M&O classify as either Schumpeter I
11 The contribution by Breschi is largely consistent with the one by Marlerba and Orsenigo. As the latter con-
siders more detailed technological classes and a wider geographical range of patents, we will focus on the
后者.
12 We interpret M&O’s “traditional” sectors to correspond to the early industrial and craft-like sectors, 例如
纺织品, Domestic Articles, and Wearables.
Quantitative Science Studies
1110
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
数字 9. Cumulativeness versus size of knowledge base for US patents. We plot the cumulativeness (measured by the internal dependence)
for the knowledge base size (measured by the number of patents) 为了 40 technological fields based on USPTO data. Fields in the same CPC
section are colored similarly. Note both axes are logarithmic; hence the fitted regression line is a power law. The cumulativeness of technol-
ogies appearing substantially above (以下) the fitted line can be identified as relatively high (低的).
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
数字 10. Cumulativeness versus size of knowledge base for European patents. Same as Figure 9, but for European patents. A legend for the
icons is included in Figure 9.
Quantitative Science Studies
1111
How cumulative is technological knowledge?
or II. For the purpose of this comparison, we associate a technological field below the fitted line
with low cumulativeness (which should correspond to M&O’s Schumpeter Mark I) 和
technologies on or above with high cumulativeness (corresponding to M&O’s Schumpeter
Mark II). 从 23 thus considered technologies, 18 are identified correctly: seven as low
cumulativeness ( Wearables, Domestic Articles, 农业, Shaping of Materials, Railways &
Ships, 建筑, Mechanical Engineering) 和 11 as high cumulativeness (Aviation; Petroleum,
Gas, & Coke; Macromolecules; Biochemistry; Engines, & Pumps; 武器; 摄影, &
Optics; Nucleonics; Telecommunications; 计算, & Controlling; Electronic Components
& Circuitry Q3). Five technological fields do not correspond to M&O’s labeling: Inorganic
Chemistry (Mark II), Printing & Decoration (Mark II), Lighting (Mark I), Measurement &
Testing (Mark I) and Health and Wellbeing (Mark II). Note the first four are rather close to the
线, 然而. The cumulativeness of Health and Wellbeing is exceptionally high in our
分析, 尽管. The reason for these deviations is not directly clear. We emphasize that
中号&O’s Schumpeter Mark I or II labels are based on various aspects of the organization of
创新, and are therefore only an indirect indication of cumulativeness. 还, there might
be some variation between the grouping of patent classes by M&O and ours. 最后, 一些
technologies may have developed substantially between the M&O study (1996) and the final
year we consider (2009).
The variations found across technological fields using the European patents in Figure 10 是
largely similar to those we observed for the US patents. Notable differences are that for the
European patents, the chemistry fields show relatively high cumulativeness and the physics
and electricity fields show relatively low cumulativeness (as compared to the US patents).
In general the variations across technological fields are less for the European patents than
for the US patents, which is likely related to the fact that the number of patents is substantially
lower for the former. Although there are some differences with the US patents, the European
patents too show overall agreement with the results of M&氧 (的 23 fields, 18 are identified
correctly). The agreement between the M&O approach to cumulativeness and our results pro-
vides a validation for the use of the id to measure the cumulativeness of a technology, 和
indirectly for the ipl, given the earlier established close relation between both indicators.
6. 讨论
In this paper we have established an approach to interpret, 模型, and measure the cumula-
tive nature of technological knowledge development. We can identify an number of deeper
implications and possible extensions of the theoretical model developed in this contribution.
A main point in the search model is the increasing difficulty of inventing without any prior
knowledge of the field, which leads to a geometric distribution for the number of backward links.
In a number of other approaches, invention is perceived as a process of (关于)combining existing
pieces of knowledge (Arthur, 2009; Fleming, 2001; Fleming & Sorenson, 2001). If we were to focus
on the number of combinations allowed by the number of existing inventions, a reasonable sug-
gestion for the distribution of backward links would be a binomial type of distribution. This option
may seem attractive, as assigning equal probability to each combination would lead the expected
value of the number of backward links per invention to increase proportionally with the number of
inventions, in agreement with observation. 然而, for the id, we fail to observe the character-
istics of a binomial type of distribution. The fact that we obtain stronger evidence in the supple-
mentary material for a geometric distribution suggests therefore that the mechanism of
combination plays a lesser role than we might expect, or at least that we are dealing with a special
type of combination, 在哪里, 例如, only a small subset of the combinations is allowed.
Quantitative Science Studies
1112
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
Although linear relations are common in descriptions of social phenomena, we emphasize
that the linearity of the id and ipl in the number of inventions is neither an obvious nor an
expected result. In a number of network approaches to knowledge dynamics, it is instead sup-
posed that the number of backward links per node is on average constant as the number of
nodes increase (阿尔伯特 & 巴拉巴斯, 2002; Price, 1976; 王, 歌曲, & 巴拉巴斯, 2013). It can
be demonstrated this would imply a constant id and a logarithmically increasing or even con-
stant ipl. These mechanisms would thus predict a stagnating cumulativeness, even though the
number of inventions keeps increasing. One may raise the objection that the external nodes
are not included in our analysis, and that the id linearity may disappear once these are included.
Additional checks on the four focus technologies in Table 1, 然而, reveal that the external
dependence (IE。, the average number of external nodes each node builds on) equally well
shows a linear increase. Although considering only four technologies gives no guarantee, 这是
an indication that the linearity is a more general phenomenon. In this contribution we ex-
plored some possible mechanisms driving the increase of id and ipl. At the same time we
acknowledge that there may be other societal factors driving the increase, such as increased
computerization or other factors improving the availability of search results. Accounting for
the effect of these factors is, 然而, 具有挑战性的, as it would require us to compare similar
technological developments over different time periods.
Our approach suggests that the cumulativeness of technologies develops largely in sync
with the size of the respective knowledge base, which suggests that these knowledge dy-
namics are to some extent time independent (IE。, less impacted by historical events).
同样地, the description was formulated independent of spatial (geographical) 因素 (和
appeared consistent between the United States and Europe). This appears to contradict a com-
monly held notion that technology development is highly path-dependent (IE。, that history
and local circumstances crucially matter). 然而, the time and space independence here
only applies to the relation between cumulativeness and the size of the knowledge base;
hence the crucial choices determining particular technological content may still largely de-
pend on historical or local events. 此外, we observed that the rate of invention of this
technology over time is inversely related to the rate of proportionality between the cumula-
tiveness and size of the knowledge base. If there is causation from former to latter, then tech-
nological cumulativeness may in the end be less determined by intrinsic knowledge properties
than generally understood. If there is causation from latter to former, then the cumulativeness
rate of a technology can be interpreted as a key determinant and predictor of its rate of inven-
的. 或者, a simultaneous effect of both causalities may also be the case. Regardless of
a possible causality direction, it would for later work be interesting to compare the deviations
from linearity in Figure 2 with different phases in the technology life cycles (Abernathy &
Utterback, 1978; 安德森 & Tushman, 1990). The development of combustion engines
and nuclear fission indeed show hints of typical life cycle S-shapes in Figure 3, the points
of acceleration and deceleration corresponding to the deviations in Figure 2. 虽然
present model does not account for these deviations, we note that, at least for the technologies
considered here, the deviations are minor, and linearity remains the dominant pattern.
In this contribution we focused on the cumulativity of technological knowledge. It would be
interesting to compare this to cumulativity in other fields of knowledge such as science or art.
The indicators and models discussed in this contribution can reasonably well be generalized
to these areas. 还, it would be interesting to look at science-technology or art-technology
dependencies, which then allow us to consider the cumulativity of technology as a whole
(IE。, consider all technology as internal and the influence of science and/or art as “external”).
These questions are, 然而, beyond the scope of this work.
Quantitative Science Studies
1113
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
最后, we mention two limitations to our approach. 第一的, our results critically depend on a
particular choice for a demarcation/classification of different technologies, in our case the CPC.
Even though this is a validated classification, innovation researchers should keep in mind that
the CPC is in the first place designed to aid patent examiners in their search for prior art, 哪个
may not always align with the technology definitions and level of detail researchers require.
此外, as new technologies develop, the CPC is continuously restructured, causing
possible misalignment with the researchers’ time perspective of a developing technology. 到
allow for a more detailed classification or a more sophisticated internal-external distinction
researchers may consider alternatives based on textual analysis of patents (凯莉, Papanikolaou
等人。, 2018), technological relatedness (Castaldi, Frenken, & Los, 2015) or distance measures
(Gilsing, Nooteboom et al., 2008; Jaffe, 1989). Although we acknowledge these points, we note
that the main focus of this work was on developing a methodology to determine a technology’s
cumulativeness, which is generally applicable once the internal-external distinction is in place. 在
一般的, we emphasize that a better understanding of the applicability of our analysis requires us to
research a greater number of technologies. This would also help us understand if more closely
related technologies also differ less in cumulativeness (hints of which we observe in Figures 9
和 10). 第二, we kept the models in this contribution as simple as possible, thereby excluding
a number of arguably relevant factors, 除其他外: (A) the average time lag between the appear-
ance of knowledge and the usage of that knowledge; (乙) more advanced mechanisms in patent
networks such as preferential attachment effect (阿尔伯特 & 巴拉巴斯, 2000; Érdi et al., 2013;
Valverde et al., 2007); 和 (C) linkage to external inventions, which allows paths to start directly
from external nodes. Though we can think of possible extensions of the model including these
因素, we preferred a simple version for clarity.
7. 结论
This paper presents both a theoretical and an empirical investigation of technological cumula-
主动性. Theoretical perspectives agree that technological cumulativeness involves a series of
developmental steps within a technology, where the cumulativeness is higher (A) 当。。。的时候
dependence between subsequent steps is larger, 和 (乙) when the total number of subsequent-
steps is higher. We capture these transversal (A) and longitudinal (乙) dimensions of cumula-
tiveness through our indicators internal dependence (id) and internal path length (ipl).
We then analytically derive how the id and ipl interrelate, and how they change as the size
of the knowledge base of a technology increases (as measured by the total number of inven-
系统蒸发散). 为此, we model the invention process as a series of searches. A relevant para-
meter in this process is the technology-specific rate q at which it becomes harder to invent
without using the existing knowledge in the field. We expect q to be inversely related to
the rate of invention over time, as there tends to be more specialization (and henceless need
for complete knowledge) at greater rates of invention. From this model we deduce that the id
and ipl, while following different distributions, are both expected to increase linearly with the
size of the knowledge base. The coefficients of these linear relations are predicted to approx-
imate q as the knowledge base becomes larger.
Empirical tests on several technologies, using patent and citation data from both the USPTO
and the EPO as proxies for invention and knowledge flow, provide empirical support for these
expectations and show that the id and ipl can be used consistently for both patent systems.
更远, the variations in cumulativeness across technological fields are found to be largely
consistent with earlier contributions, which used different approaches to technological cumu-
lativeness: Chemistry, physics and to some extent electronics are generally characterized by
Quantitative Science Studies
1114
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
relatively high cumulativeness, and the craft-like and mechanical engineering fields show re-
latively low cumulativeness.
Our study leads to a number of new insights about technological cumulativity and its rela-
tion to technological knowledge:
1. The cumulativeness of a technology develops proportionally with the size of its knowl-
edge base, with a technology-specific cumulativeness rate. A thorough understanding
of a technology’s cumulativeness therefore considers the cumulativeness in absolute
terms as well as relative to the size of its knowledge base.
2. The measurements of cumulativity along the transversal dimension and the longitudinal
dimension are found to be consistent for various technologies. It appears, 所以, 那
both provide an equivalent description of a technology’s cumulativeness. Measuring the
transversal dimension by means of the internal dependence is (computationally) 简单的,
and therefore provides a relatively fast and reliable indication of a technology’s
cumulativeness.
3. The time development of the cumulativeness indicators is largely synchronized with the
time development of the knowledge base size. This suggests that short-term immediate
effects have a limited influence on the relation between cumulativeness and knowledge
base size (meaning that the cumulativeness rate remains constant). 然而, across
technologies we observe an inverse relation between the cumulativeness rate and the
rate of invention over time. This suggests that effects acting over longer periods of time,
such as the gradual acceleration or deceleration of inventive efforts, may therefore affect
the cumulativeness rate.
4. Technological cumulativeness is understood to be a mechanism for the emergence of
technological complexity. For a comprehensive understanding of the dynamics of tech-
nological complexity, it is important to take into account both the transversal and long-
itudinal dimensions of cumulativeness. Our study shows that cumulativeness increases
along both these dimensions (for the considered technologies), which suggests an over-
all increase of technological complexity as well, yet this partially depends on the cho-
sen measure of complexity.
These insights lead to a number of implications for innovation policies, which benefit from
a detailed understanding of the cumulativeness of technologies, such as smart specialization.
In their consideration of various technologies, these policies are advised to choose a compre-
hensive approach, including both the absolute cumulativeness and the cumulativeness rela-
tive to the size of the knowledge base. Where the first is indicative of the overall difficulty of
entry in a technology, the second is indicative of the relative difficulty of entry as compared to
technologies with similar sized knowledge bases. 此外, given that near-future inven-
tive activity (and with that knowledge output) allows for some estimation or planning, 这些
policies are advised to additionally take into account the expected development of the cumu-
lativeness of these technologies. Although these developments are sometimes considered a
black box, we have demonstrated that the cumulativeness in fact develops rather predictably
with the size of the knowledge base. In the longer run, policymakers should be aware that the
rate of invention over time of a technology, usually a direct or indirect subject of policy inter-
公约, is inversely related to the cumulativeness rates. Although the possible causality in
this relation is as yet unclear, the consequences are considerable either way. In the most
extreme cases, it either implies a certain “counter effect”—that a substantial acceleration of
inventive activities indirectly slows down the cumulativeness rate of a technology—or it
Quantitative Science Studies
1115
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
implies that, despite efforts of acceleration or deceleration, the inventive rate is largely condi-
tioned by the cumulativeness rate alone.
致谢
We would like to thank Anton Pichler, Thomas Schaper and three anonymous reviewers for
helpful comments on the manuscript. The icons in Figures 9 和 10 are made by Freepik,
Eucalyp, fjstudio, Those Icons, Pixel perfect, Kiranshastry, Becris, Smashicons, Prosymbols,
and Good Ware from www.flaticon.com.
COMPETING INTERESTS
The authors have no competing interests.
资金信息
This work was supportedby NWO (Dutch Research Council) grant nr. 452-13-010.
DATA AVAILABILITY
The data used in this contribution originate from the Patstat patent database, which is available
for licensing by the EPO (European Patent Office). In the supplementary material we include
the code that allows for the replication of our results using Patstat data.
参考
Abernathy, 瓦. J。, & Utterback, J. 中号. (1978). Patterns of industrial
创新. Technology Review, 80(7), 40–47.
Acemoglu, D ., Akcigit, U。, & Kerr, 瓦. 右. (2016). Innovation network.
美国国家科学院院刊, 113(41),
11483–11488. https://doi.org/10.1073/pnas.1613559113,
考研: 27681628
阿尔伯特, R。, & 巴拉巴斯, A.-L. (2000). Topology of evolving networks:
Local events and universality. 物理评论快报, 85(24),
5234–5237. https://doi.org/10.1103/ PhysRevLett.85.5234,
考研: 11102229
阿尔伯特, R。, & 巴拉巴斯, A.-L. (2002). Statistical mechanics of com-
plex networks. Reviews of Modern Physics, 74(1), 47–97. https://
doi.org/10.1103/RevModPhys.74.47
安德森, P。, & Tushman, 中号. L. (1990). Technological discontinu-
ities and dominant designs: A cyclical model of technological
改变. Administrative Science Quarterly, 35(4), 604–633.
https://doi.org/10.2307/2393511
A pa , 右 . , D e No n i ,
我 . , O rs i , L . , & S ed i t a , S . 右 .
( 2 0 18 ) .
Knowledgespace oddity: How to increase the intensity and rele-
vance of the technologicalprogress of European regions.
Research Policy, 47(9), 1700–1712. https://doi.org/10.1016/j
.respol.2018.06.002
Arthur, 瓦. (2009). The nature of technology. Free Press.
Azagra-Caro, J. M。, & Tur, 乙. 中号. (2018). Examiner trust in applicants
t o the European Pat ent Office: Count ry specifi cities.
Scientometrics, 117(3), 1319–1348. https://doi.org/10.1007
/s11192-018-2894-4, 考研: 30546168
Bacchiocchi, E., & Montobbio, F. (2010). International knowledge
diffusion and home-bias effect: Do USPTO and EPO patent
citations tell the same story? Scandinavian Journal of Economics,
112(3), 441–470. Retrieved November 5, 2019, 来自 https://万维网
.jstor.org/stable/40783300. https://doi.org/10.1111/j.1467-9442
.2010.01614.X
Balland, P.-A. (2016). Relatedness and the geography of innova-
的. 在R中. Shearmu, C. Carrincazeaux, & D. Doloreux (编辑。),
Handbook on the Geographies of Innovation (PP. 127–141).
Edward Elgar Publishing. Retrieved June 23, 2020, 来自 https://
ideas.repec.org/ h/elg/eechap/16055_6.html. https://doi.org/10
.4337/9781784710774.00016
Balland, P.-A., & Rigby, D. (2017). The geography of complex
知识. Economic Geography, 93(1), 1–23. https://doi.org
/10.1080/00130095.2016.1205947
Basalla, G. (1989). The evolution of technology. 剑桥
大学出版社. https://doi.org/10.1017/CBO9781107049864
Boschma, R。, Balland, P.-A., & Kogler, D. F. (2015). Relatedness
and technological change in cities: The rise and fall of technolo-
gical knowledge in US metropolitan areas from 1981 到 2010.
Industrial and Corporate Change, 24(1), 223–250. https://土井
.org/10.1093/icc/dtu012
Breschi, S. (2000). The geography of innovation: A cross-sector
分析. Regional Studies, 34(3), 213–229. https://doi.org/10
.1080/00343400050015069
Breschi, S。, Malerba, F。, & Orsenigo, L. (2000). Technological
regimes and Schumpeterian patterns of innovation. 经济的
杂志, 110(463), 388–410. 四月检索 9, 2020, 从
https://www.jstor.org/stable/2566240. https://doi.org/10.1111
/1468-0297.00530
管家, S. (2014). The notebooks of Samuel Butler. The Floating
按.
Castaldi, C。, Frenken, K., & Los, 乙. (2015). Related variety, unrelated
variety and technological breakthroughs: An analysis of US state-
level patenting. Regional Studies, 49(5), 767–781. https://doi.org
/10.1080/00343404.2014.940305
Cefis, 乙. (2003). Is there persistence in innovative activities?
International Journal of Industrial Organization, 21(4), 489–515.
https://doi.org/10.1016/S0167-7187(02)00090-5
Quantitative Science Studies
1116
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
Clancy, 中号. S. (2018). Combinationsof technology in US patents,
1926–2009: A weakening base for future innovation?
Economics of Innovation and New Technology, 27(8), 770–785.
https://doi.org/10.1080/10438599.2017.1410007
CPC. (2018). Cooperative Patent Classification—Table. Retrieved
七月 20, 2018, 来自 https://www.cooperativepatentclassification
.组织/
Criscuolo, P。, & Verspagen, 乙. (2008). Does it matter where patent
citations come from? Inventor vs. examiner citations in European
patents. Research Policy, 37(10), 1892–1908. https://doi.org/10
.1016/j.respol.2008.07.011
Dahlin, K. B., & 贝伦斯, D. 中号. (2005). When is an invention really
radical? Research Policy, 34(5), 717–737. https://doi.org/10.1016
/j.respol.2005.03.009
院长, L. G。, Vale, G. L。, 拉朗德, K. N。, Flynn, E., & Kendal, 右. L.
(2014). Human cumulative culture: A comparative perspective.
Biological Reviews, 89(2), 284–301. https://doi.org/10.1111/brv
.12053, 考研: 24033987
de Rassenfosse, G。, Griffiths, W.E., Jaffe, A.B., & 韦伯斯特, 乙. (2016).
Low-quality patents in the eye of the beholder: 证据来自
multiple examiners ( Working Paper No. 22244). 国家的
经济研究局. https://doi.org/10.3386/w22244
Dosi, G. (1982). Technological paradigms and technological trajec-
保守党: A suggested interpretation of the determinants and direc-
tions of technical change. Research Policy, 11(3), 147–162.
https://doi.org/10.1016/0048-7333(82)90016-6
Enquist, M。, Ghirlanda, S。, & Eriksson, K. (2011). Modelling the
evolution and diversity of cumulative culture. 哲学
Transactions of the Royal Society of London. Series B,
Biological Sciences, 366(1563), 412–423. https://doi.org/10
.1098/rstb.2010.0132, 考研: 21199845
Érdi, P。, Makovi, K., Somogyvári, Z。, Strandburg, K., Tobochnik, J。,
… Zalányi, L. (2013). Prediction of emerging technologies based
on analysis of the U.S. patent citation network. Scientometrics,
95(1), 225–242. https://doi.org/10.1007/s11192-012-0796-4
Fleming, L. (2001). Recombinant uncertainty in technological
搜索. Management Science, 47(1), 117–132. https://doi.org
/10.1287/mnsc.47.1.117.10671
Fleming, L。, & Sorenson, 氧. (2001). Technology asa complex adap-
tivesystem: Evidence from patent data. Research Policy, 30(7),
1019–1039. https://doi.org/10.1016/S0048-7333(00)00135-9
Foray, D. (2014). Smart specialisation: Opportunities and chal-
lenges for regional innovation policy. 泰勒 & Francis. https://
books.google.nl/books?id=Qj9HBAAAQBAJ. https://doi.org/10
.4324/9781315773063
弗里曼, C。, & Soete, L. (1997). The economics of industrial inno-
休假. Pinter. https://books.google.nl/books?id=jAwaOpEELhcC
Frenken, K., Izquierdo, L. R。, & Zeppini, 磷. (2012). Branching
创新, recombinant innovation, and endogenous techno-
Innovation and Societal
logicaltransitions. Environmental
Transitions, 4, 25–35. https://doi.org/10.1016/j.eist.2012.06.001
Frenz, M。, & Prevezer, 中号. (2012). What can CIS data tell us about
technological regimes and persistence of innovation? Industry and
创新, 19(4), 285–306. https://doi.org/10.1080/13662716
.2012.694676
Gilfillan, S. (1935A). Inventing the ship: A study of the inventions
made in her history between floating log and rotorship; a self-
contained but companion volume to the author’s “Sociology of
invention”; 和 80 插图, bibliographies, notes and index.
Follett Publishing Company. https:// books.google.nl/ books?id
=JsI0AAAAIAAJ
Gilfillan, S. (1935乙). The sociology of invention: An essay in the
social causes of technic invention and some of its social results;
especially as demonstrated in the history of the ship. A companion
volume to the same author’s inventing the ship. Follett Publishing
公司. https://books.google.nl/books?id=imlGAAAAYAAJ
Gilsing, 五、, Nooteboom, B., Vanhaverbeke, W., Duysters, G。, & van
den Oord, A. (2008). Network embeddednessand the exploration
of novel technologies: Technological distance, betweenness
centrality and density. Research Policy, 37(10), 1717–1731.
https://doi.org/10.1016/j.respol.2008.08.010
Hölzl, W., & Janger, J. (2014). Distance to the frontier and the
perception of innovation barriers across European countries.
Research Policy, 43(4), 707–725. https://doi.org/10.1016/j
.respol.2013.10.001
Hummon, 氮. P。, & Dereian, 磷. (1989). Connectivity in a citation
网络: The development of DNA theory. Social Networks,
11(1), 39–63. https://doi.org/10.1016/0378-8733(89)90017-8
Jaffe, A. (1989). Characterizing the ‘technological position’ of firms,
with application to quantifying technological opportunity and re-
search spillovers. Research Policy, 18(2), 87–97. https://doi.org
/10.1016/0048-7333(89)90007-3
Jaffe, A。, Trajtenberg, M。, & Henderson, 右. (1993). Geographic
localization of knowledge spilloversas evidencedby patent cita-
系统蒸发散. Quarterly Journal of Economics, 108(3), 577–598. https://
doi.org/10.2307/2118401
Jaffe, A. B., & Lerner, J. (2004). Innovation and its discontents.
普林斯顿大学出版社.
Jaffe A. B., & de Rassenfosse, G. (2017). Patentcitation data in
social science research: Overviewand best practices. 杂志
the Association for Information Science and Technology, 68(6),
1360–1374. https://doi.org/10.1002/asi.23731
凯莉, B., Papanikolaou, D ., Seru, A。, & Taddy, 中号. (2018).
Measuring technological innovation over the long run (科技.
Rep. 不. 25266). 国家经济研究局, Inc.
Retrieved January 25, 2021, 来自 https://ideas.repec.org/p/nbr
/nberwo/25266.html. https://doi.org/10.3386/w25266
李, J.-S., 公园, J.-H., & Bae, Z.-T. (2017). The effects of licensing-in
on innovative performance in different technologicalregimes.
Research Policy, 46(2), 485–496. https://doi.org/10.1016/j
.respol.2016.12.002
Malerba, F。, & Orsenigo, L. (1993). Technological regimes and firm
行为. Industrial and Corporate Change, 2(1), 45–71. https://
doi.org/10.1093/icc/2.1.45
Malerba, F。, & Orsenigo, L. (1996). Schumpeterian patterns of
innovation are technology-specific. Research Policy, 25(3),
451–478. https://doi.org/10.1016/0048-7333(95)00840-3
Malerba, F。, Orsenigo, L。, & Peretto, 磷. (1997). Persistence of inno-
vative activities, sectoral patterns of innovation and international
technological specialization. International Journal of Industrial
组织, 15(6), 801–826. https://doi.org/10.1016/S0167
-7187(97)00012-X
McShea, D. 瓦. (1991). Complexity and evolution: What everybody
knows. Biology and Philosophy, 6(3), 303–324. https://doi.org/10
.1007/BF00132234
Merges, 右. P。, & 纳尔逊, 右. 右. (1994). On limiting or encouraging
rivalry in technical progress: The effect of patent scope decisions.
Journal of Economic Behavior & 组织, 25(1), 1–24.
https://doi.org/10.1016/0167-2681(94)90083-3
Napolitano, L。, Evangelou, E., Pugliese, E., Zeppini, P。, & Room, G.
(2018). Technology networks: The autocatalytic origins of inno-
休假. Royal Society Open Science, 5(6), 172445. https://doi.org
/10.1098/rsos.172445, 考研: 30110482
纳尔逊, R。, & 冬天, S. (1982). Evolutionary theory of economic
改变. 哈佛大学出版社. https:// books.google.nl
/图书?id=5iAPkAEACAAJ
Quantitative Science Studies
1117
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
/
.
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
How cumulative is technological knowledge?
Ogburn, 瓦. (1922). Social change with respect to culture and ori-
ginal nature. 乙. 瓦. Huebsch, Incorporated. https://books.google
.nl/books?id=tTlFAAAAIAAJ
Pitt-Rivers, A. (2018). The evolution of culture: And other essays
(Classic Reprint). Fb&c Limited. https://books.google.nl/ books
?id=2LVbswEACAAJ
Price, D. d. S. (1976). A general theory of bibliometric and other
cumulative advantage processes. Journal of the American
Society for Information Science (pre-1986); 纽约, 27(5),
292–306. Retrieved May 18, 2020, 来自 https://search.proquest
.com/docview/216627603/abstract/5D59167716B74D8APQ/1.
https://doi.org/10.1002/asi.4630270505
Schoenmakers, W., & Duysters, G. (2010). The technological ori-
gins of radical inventions. Research Policy, 39(8), 1051–1059.
https://doi.org/10.1016/j.respol.2010.05.013
Scotchmer, S. (1991). Standing on the shoulders of giants:
Cumulative research and the patent law. Journal of Economic
Perspectives, 5(1), 29–41. https://doi.org/10.1257/jep.5.1.29
Shibata, N。, Kajikawa, Y。, Takeda, Y。, & Matsushima, K. (2009).
Comparative study on methods of detecting research fronts using
different types of citation. Journal of the American Society for
Information Science and Technology, 60(3), 571–580. https://
doi.org/10.1002/asi.20994
西蒙, H. A. (1962). The architecture of complexity. 会议记录
of the American Philosophical Society, 106(6), 467–482.
Retrieved September 14, 2020, 来自 https://www.jstor.org
/stable/985254
Suárez, D. (2014). Persistence of innovation in unstable environ-
评论: Continuity and change in the firm’s innovative behavior.
Research Policy, 43(4), 726–736. https://doi.org/10.1016/j.respol
.2013.10.002
Tennie, C。, Call, J。, & Tomasello, 中号. (2009). Ratcheting up the
ratchet: On the evolution of cumulative culture. 哲学
Transactions of the Royal Society B: Biological Sciences, 364(1528),
2405–2415. https://doi.org/10.1098/rstb.2009.0052, 考研:
19620111
Trajtenberg, M。, Henderson, R。, & Jaffe, A. (1997). University versus
corporate patents: A window on the basicness of invention.
Economics of Innovation and New Technology, 5(1), 19–50.
https://doi.org/10.1080/10438599700000006
Vaesen, K., & Houkes, 瓦. (2017). Complexity and technological
evolution: What everybody knows? 生物学 & Philosophy, 32(6),
1245–1268. https://doi.org/10.1007/s10539-017-9603-1,
考研: 29563656
Valverde, S。, 唯一, 右. 五、, 巴杜, 中号. A。, & 帕卡德, 氮. (2007).
Topology and evolution of technology innovation networks.
Physical Review E, 76(5). https://doi.org/10.1103/PhysRevE.76
.056118, 考研: 18233729
Verhoeven, D ., Bakker, J。, & Veugelers, 右. (2016). Measuring tech-
nological novelty with patent-based indicators. Research Policy,
45(3), 707–723. https://doi.org/10.1016/j.respol.2015.11.010
Verspagen, 乙. (2007). Mapping technologicaltrajectories aspatent-
citation networks: A study on the history of fuel cell research.
Advances in Complex Systems, 10(1), 93–115. https://doi.org
/10.1142/S0219525907000945
王, D ., 歌曲, C。, & 巴拉巴斯, A.-L. (2013). Quantifying long-
term scientific impact. 科学, 342(6154), 127–132. https://土井
.org/10.1126/science.1237825, 考研: 24092745
冬天, S. G. (1984). Schumpeterian competition in alternative
technological regimes. Journal of Economic Behavior &
组织, 5(3), 287–320. https://doi.org/10.1016/0167
-2681(84)90004-0
我
D
哦
w
n
哦
A
d
e
d
F
r
哦
米
H
t
t
p
:
/
/
d
我
r
e
C
t
.
米
我
t
.
/
e
d
你
q
s
s
/
A
r
t
我
C
e
–
p
d
我
F
/
/
/
/
2
3
1
0
9
2
1
9
7
0
7
9
0
q
s
s
_
A
_
0
0
1
4
0
p
d
.
/
F
乙
y
G
你
e
s
t
t
哦
n
0
7
S
e
p
e
米
乙
e
r
2
0
2
3
Quantitative Science Studies
1118